अवकल ज्यामिति
| ज्यामिति |
|---|
| File:Stereographic projection in 3D.svg |
| जियोमेटर्स |
विभेदक ज्यामिति एक गणित अनुशासन है जो चिकनी आकृतियों और चिकनी जगहों की ज्यामिति का अध्ययन करता है, अन्यथा चिकनी कई गुना के रूप में जाना जाता है। इसमें अवकलन कलन, समाकलन कलन, रेखीय बीजगणित और बहुरेखीय बीजगणित की तकनीकों का उपयोग किया जाता है। प्राचीन काल इस क्षेत्र की उत्पत्ति गोलाकार ज्यामिति के अध्ययन में हुई है। यह खगोल विज्ञान, पृथ्वी के भूगणित और बाद में लोबचेव्स्की द्वारा अतिशयोक्तिपूर्ण ज्यामिति के अध्ययन से भी संबंधित है। चिकने स्थानों के सबसे सरल उदाहरण वक्रों की विभेदक ज्यामिति और त्रि-आयामी यूक्लिडियन अंतरिक्ष में सतहों की विभेदक ज्यामिति हैं, और इन आकृतियों के अध्ययन ने 18वीं और 19वीं शताब्दियों के दौरान आधुनिक विभेदक ज्यामिति के विकास का आधार बनाया।
19वीं सदी के उत्तरार्ध के बाद से, विभेदक ज्यामिति अलग-अलग कई गुना पर ज्यामितीय संरचनाओं के साथ अधिक सामान्यतः संबंधित क्षेत्र में विकसित हो गई है। एक ज्यामितीय संरचना वह है जो आकार, दूरी, आयतन या अन्य कठोर संरचना की कुछ धारणा को परिभाषित करती है। उदाहरण के लिए, रीमानियन ज्यामिति में दूरी और कोण निर्दिष्ट किए गए हैं, सहानुभूति ज्यामिति में मात्रा की गणना की जा सकती है, अनुरूप ज्यामिति में केवल कोण निर्दिष्ट किए जाते हैं, और गेज सिद्धांत (गणित) में कुछ क्षेत्र अंतरिक्ष पर दिए जाते हैं। विभेदक ज्यामिति निकट से संबंधित है, और कभी-कभी अंतर सांस्थिति को सम्मालितकरने के लिए लिया जाता है, जो अलग-अलग कई गुना के गुणों से संबंधित होता है जो किसी भी अतिरिक्त ज्यामितीय संरचना पर भरोसा नहीं करते हैं (दो विषयों के बीच अंतर पर अधिक चर्चा के लिए लेख देखें)। विभेदक ज्यामिति भी अंतर समीकरण के सिद्धांत के ज्यामितीय पहलुओं से संबंधित है, अन्यथा ज्यामितीय विश्लेषण के रूप में जाना जाता है।
विभेदक ज्यामिति गणित और प्राकृतिक विज्ञान में अनुप्रयोगों को खोजती है। सबसे प्रमुख रूप से विभेदक ज्यामिति की भाषा का उपयोग अल्बर्ट आइंस्टीन ने अपने सामान्य सापेक्षता के सिद्धांत में और बाद में भौतिकविदों द्वारा क्वांटम क्षेत्र सिद्धांत और कण भौतिकी के मानक नमूना के विकास में किया था। भौतिकी के बाहर, विभेदक ज्यामिति का उपयोग रसायन विज्ञान , धरती शास्त्र, अभियांत्रिकी , नियंत्रण सिद्धांत , कंप्यूटर ग्राफिक्स और कंप्यूटर दृष्टी और हाल ही में मशीन लर्निंग में किया गया है।
इतिहास और विकास
एक विषय के रूप में विभेदक ज्यामिति का इतिहास और विकास कम से कम पारस्पारिक पुरातनता के रूप में प्रारंभ होता है। यह अंतरिक्ष और आकार की धारणा, और सांस्थिति, विशेष रूप से विविध के अध्ययन से अधिक सामान्यतःज्यामिति के विकास से जुड़ा हुआ है। इस खंड में हम मुख्य रूप से ज्यामिति के लिए अतिसूक्ष्म तरीकों के अनुप्रयोग के इतिहास पर और बाद में स्पर्शरेखा रिक्त स्थान के विचारों पर ध्यान केंद्रित करते हैं, और अंततः टेंसर और टेंसर क्षेत्रों के संदर्भ में विषय की आधुनिक औपचारिकता के विकास पर ध्यान केंद्रित करते हैं।
पुनर्जागरण तक पारस्पारिक पुरातनता (300 ई.पू – 1600 ई.)
विभेदक ज्यामिति का अध्ययन, या कम से कम चिकनी आकृतियों की ज्यामिति का अध्ययन, कम से कम पारस्पारिक पुरातनता का पता लगाया जा सकता है। विशेष रूप से, प्राचीन यूनानी गणितज्ञों के समय में, पृथ्वी की ज्यामिति, एक गोलाकार ज्यामिति के बारे में बहुत कुछ जाना जाता था। उत्कृष्ट रूप से, एराटोस्थनीज ने लगभग 200 ईसा पूर्व के नजदीक पृथ्वी की परिधि की गणना की थी, और लगभग 150 ईस्वी में टॉलेमी ने अपने भूगोल में पृथ्वी के आकार के आकृतिण के उद्देश्यों के लिए त्रिविम प्रक्षेपण की प्रारंभ की।[1] स्पष्ट रूप से इस पूरे समय के सिद्धांत जो विभेदक ज्यामिति और कलन की नींव बनाते हैं, का उपयोग भूगणित में किया जाता था, चूँकि बहुत सरल रूप में अर्थात्, यूक्लिड के तत्वों के रूप में यह समझा गया था कि एक सीधी रेखा को दो बिंदुओं के बीच सबसे छोटी दूरी प्रदान करने की अपनी संपत्ति से परिभाषित किया जा सकता है, और इसी सिद्धांत को पृथ्वी की सतह पर लागू करने से यह निष्कर्ष निकलता है कि बड़े वृत्त, जो केवल स्थानीय रूप से एक समतल तल में सीधी रेखाओं के समान होते हैं, पृथ्वी की सतह पर दो बिंदुओं के बीच सबसे छोटा रास्ता प्रदान करते हैं। वास्तव में एराटोस्थनीज और अन्य लोगों द्वारा इस तरह के geodesic पथों के साथ दूरी के मापन को वक्रों की चाप की लम्बाई का प्राथमिक माप माना जा सकता है, एक ऐसी अवधारणा जिसे 1600 के दशक तक कलन के संदर्भ में एक कठोर परिभाषा नहीं दिखाई देती थी।
इस समय के नजदीक ज्यामिति के अध्ययन के लिए इनफिनिटिमल्स के सिद्धांत के केवल न्यूनतम प्रत्यक्ष अनुप्रयोग थे, जो विषय के आधुनिक कलन-आधारित अध्ययन का अग्रदूत था। यूक्लिड के यूक्लिड के तत्वों में एक वृत्त के लिए एक रेखा की स्पर्शरेखा की धारणा पर चर्चा की जाती है, और आर्किमिडीज ने वृत्त जैसे चिकने आकार के क्षेत्रों की गणना करने के लिए थकावट की विधि लागू की, और गोले, शंकु, और बेलन जैसे चिकने त्रि-आयामी ठोस के आयतन की गणना की।[1]
पुरातनता और पुनर्जागरण की प्रारंभ के बीच अंतर ज्यामिति के सिद्धांत में बहुत कम विकास हुआ था। आइजैक न्यूटन और लाइबनिट्स द्वारा कलन के विकास से पहले, अंतर ज्यामिति की समझ में सबसे महत्वपूर्ण विकास जेरार्ड मर्केटर के मर्केटर प्रोजेक्शन के विकास से पृथ्वी के आकृतिण के तरीके के रूप में हुआ। मर्केटर को अपने आकृति आकृति के फायदे और नुकसान की समझ थी, और विशेष रूप से उनके प्रक्षेपण के अनुरूप आकृति प्रक्षेपण प्रकृति के साथ-साथ ही प्राग पृथ्वी पर सबसे छोटी दूरी की रेखाएं,और दिशा के के बीच अंतर, उसके आकृति पर सीधी रेखा पथ बारे में पता था। मर्केटर ने उल्लेख किया कि इस प्रक्षेपण में प्राग तिरछी वक्रता थी।[1] यह तथ्य एक समतल तल पर पृथ्वी की सतह के एक आइसोमेट्री | अव्व्याहो-संरक्षण आकृति की कमी को दर्शाता है, जो गॉस के बाद के प्रमेय एग्रेगियम का परिणाम है।
कलन के बाद (1600-1800)
गणना से इनफिनिटिमल्स के सिद्धांत और धारणाओं का उपयोग करते हुए ज्यामिति का पहला व्यवस्थित या कठोर उपचार 1600 के दशक के नजदीक प्रारंभ हुआ जब कलन को पहली बार गॉटफ्रीड लीबनिज और आइजैक न्यूटन द्वारा विकसित किया गया था। इस समय, रेने डेसकार्टेस के हालिया काम ने ज्यामिति के लिए विश्लेषणात्मक ज्यामिति की प्रारंभ की, जिससे बढ़ती जटिलता के ज्यामितीय आकृतियों को सख्ती से वर्णित किया जा सके। विशेष रूप से इस समय के नजदीक पियरे डी फ़र्माटा , न्यूटन और लाइबनिज़ ने समतल वक्र अवधारणाओं की जांच की अध्ययन प्रारंभ की जैसे कि विभक्ति बिंदु और दोलन वृत्त के वृत्त, जो वक्रता के मापन में सहायता करते हैं। वास्तव में पहले से ही अपने सबसे बड़े और सबसे छोटे के लिए एक नई विधि में कलन की नींव पर, लाइबनिज ने नोट किया कि असीम स्थिति एक मोड़ बिंदु के अस्तित्व को दर्शाता है। इस समय के कुछ समय बाद ही बर्नौली भाई , जैकब बर्नौली और जोहान बर्नौली ने ज्यामिति का अध्ययन करने के लिए इनफिनिटिमल्स के उपयोग में महत्वपूर्ण प्रारंभिक योगदान दिया। उस समय जोहान बर्नौली के व्याख्यानों में, बाद में बाद में ल'हॉपिटल द्वारा विभेदक कलन पर पहली पाठ्यपुस्तक में संकलित किया गया | एल'हॉपिटल द्वारा एनालिसिस डेस इन्फिनिमेंट पेटिट्स पोर एल'इंटेलिजेंस डेस लिग्नेस कॉर्ब्स द्वारा संकलित, विभिन्न प्रकार के समतल वक्रों की स्पर्शरेखाओं , की स्थिति का उपयोग करके गणना की जाती है। और इसी तरह विभक्ति के बिंदुओं की गणना की जाती है।[1]इसी समय एक समतल वक्र के दोलन वृत्तों और स्पर्शरेखा दिशाओं के बीच ओर्थोगोनालिटी का एहसास होता है, और एक मिलान वृत्त की त्रिज्या के लिए पहला विश्लेषणात्मक सूत्र, अनिवार्य रूप से वक्रता की धारणा के लिए पहला विश्लेषणात्मक सूत्र, नीचे लिखा गया है।
विश्लेषणात्मक ज्यामिति और समतल वक्रों के विकास के मद्देनजर, एलेक्सिस क्लेयरौट ने सिर्फ 16 साल की उम्र में अंतरिक्ष वक्रों का अध्ययन प्रारंभ किया कर दिया था।[2][1]अपनी पुस्तक क्लेराट में अंतरिक्ष वक्रों के लिए स्पर्शरेखा और उपस्पर्श दिशाओं की धारणा को उन दिशाओं के संबंध में पेश किया जो उस सतह के साथ होती हैं जिस पर अंतरिक्ष वक्र स्थित होता है। इस प्रकार क्लेराट ने सतह के स्पर्शरेखा स्थान की एक अंतर्निहित समझ का प्रदर्शन किया और पहली बार कलन का उपयोग करके इस विचार का अध्ययन किया। महत्वपूर्ण रूप से क्लेराउट ने वक्रता और दोहरी वक्रता की शब्दावली पेश की, अनिवार्य रूप से मुख्य वक्रता की धारणा बाद में गॉस और अन्य लोगों द्वारा अध्ययन की गई।
इसी समय के नजदीक, मूल रूप से जोहान बर्नौली के एक छात्र, लियोनहार्ड यूलर ने न केवल ज्यामिति के विकास के लिए, बल्कि गणित के लिए और अधिक व्यापक रूप से कई महत्वपूर्ण योगदान दिए।[3] विभेदक ज्यामिति के संबंध में, यूलर ने पहले विश्लेषणात्मक जियोडेसिक समीकरण को प्राप्त करने वाली सतह पर एक जियोडेसिक की धारणा का अध्ययन किया, और बाद में आंतरिक ज्यामिति के सिद्धांत की प्रारंभ करते हुए एक सतह पर आंतरिक समन्वय प्रणाली का पहला समूह पेश किया, जिस पर आधुनिक ज्यामितीय विचार आधारित हैं।[1] लगभग इसी समय मैकेनिक में यांत्रिकी के यूलर के अध्ययन से यह अहसास हुआ कि किसी सतह के साथ यात्रा करने वाला द्रव्यमान किसी भी बल के प्रभाव में नहीं आएगा, जो आइंस्टीन के सामान्य सापेक्षता के महत्वपूर्ण मूलभूत विचारों के प्रारंभिक अग्रदूत, और भी यूलर-लग्रेंज समीकरण और विविधताओं के कलन का पहला सिद्धांत, जो आधुनिक विभेदक ज्यामिति में सहानुभूतिपूर्ण ज्यामिति और ज्यामितीय विश्लेषण में कई तकनीकों को रेखांकित करता है। यूलर-लैग्रेंज समीकरण के संदर्भ में एक न्यूनतम सतह का वर्णन करने वाले पहले अंतर समीकरण को प्राप्त करने के लिए, इस सिद्धांत का उपयोग विविधताओं के कलन के सह-विकासकर्ता लैग्रेंज द्वारा किया गया था। 1760 में यूलर ने एक प्रमेय सिद्ध किया जो एक सतह पर एक अंतरिक्ष वक्र की वक्रता को मुख्य वक्रता के संदर्भ में व्यक्त करता है, जिसे यूलर के प्रमेय_(अंतर_ज्यामिति) के रूप में जाना जाता है।
बाद में 1700 के दशक में, गैसपार्ड मोंगे के नेतृत्व में नए फ्रांसीसी विद्यालय ने विभेदक ज्यामिति में योगदान देना प्रारंभ किया। मोंज ने समतल वक्रों, सतहों के सिद्धांत में महत्वपूर्ण योगदान दिया, और समतल वक्रों और अंतरिक्ष वक्रों के क्रांति और आवरण (गणित) की सतहों का अध्ययन किया। मोंज के कई छात्रों ने इसी सिद्धांत में योगदान दिया, और उदाहरण के लिए चार्ल्स डुपिन ने सिद्धांत वक्रता के संदर्भ में यूलर के प्रमेय की एक नई व्याख्या प्रदान की, जो समीकरण का आधुनिक रूप है।[1]
आंतरिक ज्यामिति और गैर-यूक्लिडियन ज्यामिति (1800-1900)
1800 के दशक में, मुख्य रूप से कार्ल फ्रेडरिक गॉस और बर्नहार्ड रीमैन के आधारभूत कार्य के माध्यम से, और महत्वपूर्ण योगदानों में, विभेदक ज्यामिति का क्षेत्र अपने आप में अध्ययन का एक क्षेत्र बन गया, जो विश्लेषणात्मक ज्यामिति के अधिक व्यापक विचार से अलग था। अतिशयोक्तिपूर्ण ज्यामिति और गैर-यूक्लिडियन ज्यामिति पर निकोलाई लोबचेव्स्की और इसी अवधि के दौरान प्रक्षेपी ज्यामिति का विकास भी हुआ।
विभेदक ज्यामिति के इतिहास में एकल सबसे महत्वपूर्ण काम करार दिया,[4] 1827 में गॉस ने घुमावदार सतहों के सामान्य सिद्धांत का विवरण देते हुए वाले सतहों के चारों ओर सामान्यीकरण का निर्माण किया।[5][4][6] इस काम में और सतहों के सिद्धांत पर उनके बाद के कागजात और अप्रकाशित नोट्स में, गॉस को गैर-यूक्लिडियन ज्यामिति का आविष्कारक और आंतरिक अंतर ज्यामिति का आविष्कारक करार दिया गया है।[6] अपने मौलिक पेपर में गॉस ने गॉस आकृति , गॉसियन वक्रता , पहला मौलिक रूप और दूसरा मौलिक रूप पेश किया, गॉसियन वक्रता की आंतरिक प्रकृति को दर्शाने वाले प्रमेय एग्रेगियम को सिद्ध किया, और सतहों पर विभिन्न गैर-यूक्लिडियन ज्यामिति में एक भूगणित त्रिभुज के क्षेत्र की गणना करते हुए, भूगर्भ विज्ञान का अध्ययन किया।
इस समय गॉस का पहले से ही यह विचार था कि यूक्लिडियन ज्यामिति के मानक प्रतिमान को त्याग दिया जाना चाहिए, जिसने भूगणित त्रिकोणों के उनके अध्ययन की जानकारी दी वह गैर-यूक्लिडियन ज्यामिति पर निजी पांडुलिपियों के अधिकार में था, ।[6][7] लगभग इसी समय जानोस बोल्याई और लोबचेव्स्की ने स्वतंत्र रूप से अतिशयोक्तिपूर्ण ज्यामिति की खोज की और इस प्रकार यूक्लिड के प्रतिमान के बाहर सुसंगत ज्यामिति के अस्तित्व का प्रदर्शन किया। 1860 के दशक में बाद में यूजेनियो बेल्ट्रामी द्वारा अतिपरवलिक ज्यामिति के ठोस नमूना तैयार किए गए, और फेलिक्स क्लेन ने 1871 में गैर-यूक्लिडियन ज्यामिति शब्द गढ़ा, और एर्लांगेन कार्यक्रम के माध्यम से यूक्लिडियन और गैर-यूक्लिडियन ज्यामिति को एक ही पायदान पर रखा।[8] स्पष्ट रूप से, पृथ्वी की गोलाकार ज्यामिति जिसका प्राचीन काल से ही अध्ययन किया गया था, एक गैर-यूक्लिडियन ज्यामिति, एक अण्डाकार ज्यामिति थी।
गॉस की भाषा में आंतरिक अंतर ज्यामिति का विकास उनके छात्र, बर्नहार्ड रीमैन ने अपनी आवास थीसिस में, उन परिकल्पनाओं पर किया था जो ज्यामिति की नींव पर स्थित हैं।[9] इस काम में रीमैन ने पहली बार एक रीमैनियन मीट्रिक और रीमैनियन वक्रता टेंसर की धारणा पेश की, और उच्च आयामों में विभेदक ज्यामिति का व्यवस्थित अध्ययन प्रारंभ किया। रिमेंनियन मीट्रिक के संदर्भ में यह आंतरिक दृष्टिकोण,रीमैन द्वारा निरूपित द्वारा, रैखिक तत्व के एक सतह बारे में गॉस के एक विचार का विकास था । इस समय रीमैन ने इस विषय में रेखीय बीजगणित और बहुरेखीय बीजगणित के व्यवस्थित उपयोग का परिचय देना प्रारंभ किया, मेट्रिक्स और वक्रता की अपनी जांच में द्विघात रूप के सिद्धांत का बहुत उपयोग किया। इस समय रीमैन ने अभी तक कई गुना आधुनिक धारणा विकसित नहीं की थी, क्योंकि एक संस्थानिक स्पेस की धारणा का भी सामना नहीं किया गया था, लेकिन उन्होंने प्रस्ताव दिया था कि स्पेससमय के मीट्रिक के गुणों की जांच या माप करना संभव हो सकता है अंतरिक्ष-समय के भीतर द्रव्यमान का विश्लेषण, यूलर के पहले के अवलोकन के साथ जोड़ना कि कोई भी बल के प्रभाव में द्रव्यमान सतहों पर जियोडेसिक्स के साथ यात्रा नहीं करेगा, और वैज्ञानिक साहित्य में प्रकट होने से पूरे 60 साल पहले आइंस्टीन के तुल्यता सिद्धांत के मौलिक अवलोकन की भविष्यवाणी करना।[6][4]
रीमैन के नए विवरण के मद्देनजर, अलग-अलग ज्यामिति का अध्ययन करने के लिए उपयोग की जाने वाली तकनीकों का ध्यान वक्र और सतहों के अध्ययन के तदर्थ और बाहरी तरीकों से टेन्सर कलन और क्लेन के एर्लांगेन कार्यक्रम के संदर्भ में अधिक व्यवस्थित दृष्टिकोण में स्थानांतरित हो गया,। परिवर्तनों के समूहों की धारणा सोफस ली और जीन गैस्टन डारबौक्स द्वारा विकसित की गई थी, जिससे झूठ समूहों और सहानुभूतिपूर्ण ज्यामिति के सिद्धांत में महत्वपूर्ण परिणाम सामने आए। घुमावदार स्थानों पर विभेदक कलन की धारणा का अध्ययन एल्विन क्रिस्टोफर द्वारा किया गया था, जिन्होंने 1868 में सहपरिवर्ती व्युत्पत्ति का वर्णन करने वाले क्रिस्टोफ़ेल प्रतीकों का परिचय दिया था, और यूजेनियो बेल्ट्रामी सहित अन्य लोगों द्वारा जिन्होंने कई गुना पर कई विश्लेषणात्मक प्रश्नों का अध्ययन किया था।[10] 1899 में लुइगी बियांची ने विभेदक ज्यामिति पर अपने लेक्चर्स का निर्माण किया, जिसमें रीमैन के नजरिए से विभेदक ज्यामिति का अध्ययन किया गया था, और एक साल बाद टुल्लियो लेवी-सिविटा और ग्रेगोरियो रिक्की-कर्बस्त्रो ने अपनी पाठ्यपुस्तक को व्यवस्थित रूप से निरपेक्ष अवकल कलन और टेंसर कलन के सिद्धांत को विकसित करते हुए तैयार किया।[11][4]यह इस भाषा में था कि आइंस्टीन द्वारा सामान्य सापेक्षता और छद्म-रिमैनियन ज्यामिति के विकास में अंतर ज्यामिति का उपयोग किया गया था।
आधुनिक अवकल ज्यामिति (1900-2000)
आधुनिक विभेदक ज्यामिति का विषय सांस्थिति की नींव पर हेनरी पॉइनकेयर के महत्वपूर्ण विश्लेषण साइटस (पेपर) सहित कई गणितज्ञों के मूलभूत योगदान के जवाब में 1900 के दशक की प्रारंभ में उभरा।[12] 1900 के दशक की प्रारंभ में गणित के भीतर एक प्रमुख आंदोलन था, जो कि हिल्बर्ट के कार्यक्रम के रूप में जाना जाने वाला कठोरता और सटीकता के संकट से बचने के लिए विषय के मूलभूत पहलुओं को औपचारिक रूप देने के लिए था। इस व्यापक आंदोलन के हिस्से के रूप में, 1914 में फ़ेलिक्स हॉसडॉर्फ़ द्वारा एक सांस्थिति स्पेस की धारणा को आसुत किया गया था, और 1942 तक एक मिश्रित और अवकल-ज्यामितीय प्रकृति के कई अलग-अलग विचार थे।[12]
इस विषय में रुचि आइंस्टीन के सामान्य सापेक्षता के सिद्धांत के उद्भव और आइंस्टीन समीकरणों क्षेत्र के महत्व से भी केंद्रित थी। आइंस्टीन के सिद्धांत ने रिक्की और लेवी-सिविटा के टेंसर कलन को लोकप्रिय बनाया और संकेतन की प्रारंभ की रीमैनियन मीट्रिक के लिए , और क्रिस्टोफेल प्रतीकों के लिए , दोनों गुरुत्वाकर्षण में G से आ रहे हैं। एली कार्टन ने बाहरी कलन और चलती फ्रेम के सिद्धांत के संदर्भ में चिकनी कई गुना के अंतर ज्यामिति की नींव को फिर से बनाने में सहायता की, जिससे भौतिकी की दुनिया में आइंस्टीन-कार्टन सिद्धांत का नेतृत्व किया।[13][4]
इस प्रारंभिक विकास के बाद, कई गणितज्ञों ने आधुनिक सिद्धांत के विकास में योगदान दिया, जिसमें जीन-लुई शर्ट्स सम्मालितहैं, जिन्होंने सम्बन्ध (वेक्टर बंडल) पेश किया, शिंग-शेन चेर्नो जिन्होंने विषय के लिए विशिष्ट वर्गों की प्रारंभ की और जटिल मैनिफोल्ड का अध्ययन प्रारंभ किया, डब्ल्यू.वी.डी. हॉज और गेर्गेस डी रहम जिन्होंने विभेदक रूप की समझ का विस्तार किया, चार्ल्स एहरसमैन जिन्होंने सिद्धांत फाइबर बंडलों और एह्रेसमैन सम्बन्ध , और अन्य को पेश किया।[13][4] विशेष महत्व का हरमन वेयलो था जिसने सामान्य सापेक्षता की नींव में महत्वपूर्ण योगदान दिया, वेइल टेंसर को अनुरूप ज्यामिति में अंतर्दृष्टि प्रदान की, और पहले गेज (गणित) की धारणा को परिभाषित किया जिससे भौतिकी और गेज सिद्धांत में गेज सिद्धांत के विकास की ओर अग्रसर हुआ। (अंक शास्त्र)।
मध्य और 20वीं सदी के अंत में एक विषय के रूप में विभेदक ज्यामिति का दायरा विस्तृत हुआ और गणित और भौतिकी के अन्य क्षेत्रों के साथ संबंध विकसित हुए। भौतिकी में गेज सिद्धांत और यांग-मिल्स सिद्धांत के विकास ने बंडलों और सम्बन्ध को केंद्र में लाया, जिससे गेज सिद्धांत (गणित) में विकास हुआ। अतिया-गायक सूचकांक प्रमेय के प्रमाण सहित कई विश्लेषणात्मक परिणामों की जांच की गई। जटिल ज्यामिति का विकास बीजगणितीय ज्यामिति में समानांतर परिणामों से प्रेरित था, और ज्यामिति और जटिल मैनिफोल्ड के वैश्विक विश्लेषण के परिणाम शिंग-तुंग याउ और अन्य द्वारा सिद्ध किए गए थे। 20 वीं शताब्दी के उत्तरार्ध में रिक्की प्रवाह जैसे वक्रता प्रवाह के संबंध में नई विश्लेषणात्मक तकनीकों का विकास किया गया, जिसकी परिणति त्वरित पेरेलमैन के पॉइन्केयर अनुमान के प्रमाण में हुई। इसी अवधि के दौरान मुख्य रूप से माइकल अतियाहो के प्रभाव के कारण, सैद्धांतिक भौतिकी और अंतर ज्यामिति के बीच नए संबंध बने। यांग-मिल्स समीकरणों और गेज सिद्धांत के तकनीकों का उपयोग गणितज्ञों द्वारा चिकने कई गुना के नए आविष्कारों को विकसित करने के लिए अध्ययन किया गया था। भौतिकविदों जैसे एडवर्ड विटन , एकमात्र भौतिक विज्ञानी जिन्हें फील्ड मेडल से सम्मानित किया गया है , इन्होने भविष्यवाणियां करने और नए कठोर गणित के लिए रूपरेखा प्रदान करने के लिए संस्थानिक क्वांटम फील्ड थ्योरी और स्ट्रिंग थ्योरी का उपयोग करके गणित में नए प्रभाव डाले, जिसके परिणामस्वरूप उदाहरण के लिए अनुमानित दर्पण समरूपता और सीबर्ग-विटन में अपरिवर्तनीय हुआ है।
शाखाएं
रिमानियन ज्यामिति
रीमैनियन ज्यामिति रीमैनियन मैनिफोल्ड का अध्ययन करती है, रीमैनियन सममित स्थान साथ चिकना कई गुना है । यह प्रत्येक बिंदु पर स्पर्शरेखा स्थान पर परिभाषित एक चिकना कार्य सकारात्मक निश्चित बिलिनियर रूप सममित बिलिनियर रूप के माध्यम से व्यक्त की गई दूरी की एक अवधारणा है। रीमैनियन ज्यामिति यूक्लिडियन ज्यामिति को उन स्थानों पर सामान्यीकृत करती है जो आवश्यक रूप से समतल नहीं होते हैं, चूँकिवे अभी भी प्रत्येक बिंदु पर यूक्लिडियन स्थान के समान होते हैं, अर्थात सन्निकटन के पहले क्रम में। लंबाई के आधार पर विभिन्न अवधारणाएं, जैसे वक्रों की चाप की लंबाई, समतल क्षेत्र ों का क्षेत्रफल, और ठोस पदार्थों का आयतन सभी में रीमैनियन ज्यामिति में प्राकृतिक अनुरूपता होती है। बहुचरीय कलन से किसी फ़ंक्शन के दिशात्मक व्युत्पन्न की धारणा को एक टेंसर के सहसंयोजक व्युत्पन्न की धारणा तक बढ़ाया गया है। विश्लेषण और अंतर समीकरणों की कई अवधारणाओं को रीमैनियन मैनिफोल्ड की स्थापना के लिए सामान्यीकृत किया गया है।
रीमैनियन कई गुना के बीच एक दूरी-संरक्षण अंतर को एक आइसोमेट्री कहा जाता है। इस धारणा को स्थानीय रूप से भी परिभाषित किया जा सकता है, अर्थात बिंदुओं के छोटे पड़ोस के लिए। कोई भी दो नियमित वक्र स्थानीय रूप से सममितीय होते हैं। चूँकि, कार्ल फ्रेडरिक गॉस के प्रमेय एग्रेगियम ने दिखाया कि सतहों के लिए, एक स्थानीय आइसोमेट्री का अस्तित्व लागू करता है कि संबंधित बिंदुओं पर गाऊसी वक्रता समान होनी चाहिए। उच्च आयामों में, रिमेंन वक्रता टेंसर एक रिमेंनियन मैनिफोल्ड से जुड़ा एक महत्वपूर्ण बिंदुवार अपरिवर्तनीय है जो मापता है कि यह फ्लैट होने के कितना करीब है। रीमैनियन मैनिफोल्ड का एक महत्वपूर्ण वर्ग रीमैनियन सममित रिक्त स्थान है, जिसकी वक्रता आवश्यक रूप से स्थिर नहीं है। ये यूक्लिडियन और गैर-यूक्लिडियन ज्यामिति में माने जाने वाले साधारण विमान और स्थान के निकटतम अनुरूप हैं।
छद्म-रीमैनियन ज्यामिति
छद्म रीमैनियन मैनिफोल्ड | आभासी -रीमैनियन ज्योमेट्री रीमैनियन ज्यामिति को उस स्थितियों में सामान्यीकृत करती है जिसमें मीट्रिक टेंसर को निश्चित निश्चित द्विरेखीय रूप |सकारात्मक-निश्चित होने की आवश्यकता नहीं है।
इसका एक विशेष स्थितिया लोरेंट्ज़ियन कई गुना है, जो आइंस्टीन की सामान्य सापेक्षता का गणितीय आधार है।
फिन्सलर ज्योमेट्री
फिन्सलर ज्यामिति में फिन्सलर कई गुना अध्ययन की मुख्य वस्तु के रूप में है। यह एक फिन्सलर मीट्रिक के साथ कई गुना अंतर है, जो कि प्रत्येक स्पर्शरेखा स्थान पर परिभाषित एक बैनाच मानदंड है। रीमैनियन कई गुना अधिक सामान्य फिन्सलर कई गुना के विशेष स्थितियों हैं। कई गुना M पर एक फिन्सलर संरचना एक फलन F : TM → [0, ∞) है जैसे कि:
- F(x, my) = m F(x, y) TM में सभी (x, y) के लिए और सभी m ≥ 0,
- F, TM ∖ {0}, में अपरिमित रूप से अवकलनीय है,
- F2का उर्ध्वाधर हेसियन सकारात्मक निश्चित है।
सहानुभूति ज्यामिति
सहानुभूति ज्योमेट्री सहानुभूति कई गुना का अध्ययन है। एक लगभग सहानुभूति कई गुना एक अवकल कई गुना है जो प्रत्येक स्पर्शरेखा स्थान पर सुचारू रूप से भिन्न गैर-पतित तिरछा-सममित द्विरेखीय रूप से सुसज्जित है | प्रत्येक स्पर्शरेखा स्थान पर तिरछा-सममित द्विरेखीय रूप , यानी एक गैर पतित 2-विभेदक रूप जिसे सहानुभूति रूप कहा जाता है। एक सहानुभूति कई गुना लगभग सहानुभूतिपूर्ण कई गुना है जिसके लिए सहानुभूति रूप ω बंद है: dω = 0.
दो सहानुभूति कई गुना के बीच एक भिन्नता जो सहानुभूति रूप को संरक्षित करती है, उसे सहानुभूतिपूर्ण कहा जाता है। गैर-पतित तिरछा-सममित द्विरेखीय रूप केवल सम-विम सदिश स्थानों पर ही सम्मालित हो सकते हैं, इसलिए सहानुभूतिपूर्ण मैनिफोल्ड में आवश्यक रूप से समान आयाम भी होते हैं। आयाम 2 में, एक सिम्पलेक्टिक मैनिफोल्ड सिर्फ एक सतह है जो एक क्षेत्र रूप से संपन्न है और एक सहानुभूतिपूर्ण एक क्षेत्र-संरक्षण भिन्नता है। एक यांत्रिक प्रणाली का चरण स्थान एक सहानुभूतिपूर्ण कई गुना है और उन्होंने पहले से ही विश्लेषणात्मक यांत्रिकी पर जोसेफ लुई लैग्रेंज के काम में और बाद में कार्ल गुस्ताव जैकोबिक और विलियम रोवन हैमिल्टन के हैमिल्टनियन यांत्रिकी में एक अंतर्निहित उपस्थिति बनायी।
रीमैनियन ज्योमेट्री के विपरीत, जहां वक्रता रीमैनियन कई गुना का एक स्थानीय अपरिवर्तनीय प्रदान करती है, डार्बौक्स के प्रमेय में कहा गया है कि सभी सहानुभूति कई गुना स्थानीय रूप से आइसोमोर्फिक हैं। सहानुभूति कई गुना के एकमात्र आविष्कार प्रकृति में वैश्विक हैं और सांस्थितिक पहलू सहानुभूति ज्यामिति में एक प्रमुख भूमिका निभाते हैं। सहानुभूति सांस्थिति में पहला परिणाम संभवतः पॉइनकेयर-बिरखॉफ प्रमेय है, जो हेनरी पॉइनकेयर द्वारा अनुमान लगाया गया था और फिर 1912 में जी.डी. बिरखॉफ द्वारा सिद्ध किया गया। यह दावा करता है कि यदि एक वलय(गणित) के आकृति को संरक्षित करने वाला क्षेत्र प्रत्येक सीमा घटक को विपरीत दिशाओं में घुमाता है, तब आकृति में कम से कम दो निश्चित बिंदु होते हैं।[14]
संपर्क ज्यामिति
संपर्क ज्यामिति विषम आयाम के कुछ कई गुना से संबंधित है। यह सहानुभूतिपूर्ण ज्यामिति के करीब है और बाद की तरह, यह पारस्पारिक यांत्रिकी के प्रश्नों में उत्पन्न हुआ। एक (2n + 1)-आयामी कईगुना M पर एक स्पर्शरेखा बंडल में एक चिकने हाइपरप्लेन फील्ड H द्वारा दिया जाता है जो एम पर एक अलग-अलग फलन के स्तर समूह से जुड़ा होने से जितना संभव है (तकनीकी शब्द पूरी तरह से अविभाज्य स्पर्शरेखा हाइपरप्लेन वितरण है)। प्रत्येक बिंदु p के पास, एक हाइपरप्लेन वितरण कहीं नहीं लुप्त होने वाले विभेदक रूप | 1-रूप द्वारा निर्धारित किया जाता है , जो कहीं न कहीं गायब होने वाले फलन द्वारा गुणा करने के लिए अद्वितीय है:
M पर एक स्थानीय 1-फॉर्म एक संपर्क फ़ॉर्म है यदि H के बाहरी व्युत्पन्न का प्रतिबंध एक गैर-पतित दो-रूप है और इस प्रकार Hp प्रत्येक बिंदु पर पर एक सहानुभूति संरचना को प्रेरित करता है। यदि वितरण H को वैश्विक एक-रूप द्वारा परिभाषित किया जा सकता है तो यह प्रपत्र संपर्क है यदि और केवल यदि शीर्ष-आयामी रूप
M पर एक आयतन रूप है, अर्थात् कहीं लुप्त नहीं होता। डार्बौक्स प्रमेय का एक संपर्क अनुरूप धारण करता है: विषम-आयामी कईगुना पर सभी संपर्क संरचनाएं स्थानीय रूप से समरूपी हैं और समन्वय प्रणाली के उपयुक्त विकल्प द्वारा एक निश्चित स्थानीय सामान्य रूप में लाया जा सकता है।
जटिल और काहलर ज्यामिति
जटिल विभेदक ज्यामिति जटिल कई गुना का अध्ययन है।
एक लगभग जटिल कईगुना एक वास्तविक कईगुना है,जो प्रकार (1, 1) के एक टेंसर के साथ संपन्न है , यानी एक वेक्टर बंडल (जिसे लगभग जटिल संरचना कहा जाता है)
- , ऐसा है कि
यह इस परिभाषा से अनुसरण करता है कि लगभग जटिल कई गुना सम-विमीय है।
यदि , जहा से संबंधित प्रकार (2, 1) का एक टेंसर है, तो एक लगभग जटिल कईगुना को जटिल कहा जाता है जिसे निजेनहुइस टेंसर (या कभी-कभी मरोड़) कहा जाता है।
एक लगभग जटिल कईगुना जटिल है यदि और केवल यह एक होलोमॉर्फिक फ़ंक्शन एटलस (सांस्थिति) को स्वीकार करता है।
एक हर्मिटियन मैनिफोल्ड एक लगभग जटिल संरचना जे द्वारा दिया जाता है, साथ ही रिमेंनियन मीट्रिक जी के साथ, अनुकूलता की स्थिति को संतुष्ट करता है
एक लगभग हर्मिटियन संरचना स्वाभाविक रूप से एक विभेदक रूप को विभेदक दो-रूप परिभाषित करती है।
निम्नलिखित दो शर्तें समतुल्य हैं:
जहा का लेवी-सिविटा सम्बन्ध है. इस स्थितियोंमें, काहलर मैनिफोल्ड कहा जाता है | काहलर संरचना, और एक काहलर मैनिफोल्ड एक काहलर संरचना के साथ कई गुना संपन्न है। विशेष रूप से, एक काहलर मैनिफोल्ड एक जटिल और एक सहानभूति मैनिफोल्ड दोनों है। काहलर कई गुना (हॉज कई गुना का वर्ग) का एक बड़ा वर्ग सभी चिकने बीजगणितीय ज्यामिति द्वारा दिया गया है।
सीआर ज्यामिति
सीआर संरचना जटिल मैनिफोल्ड में डोमेन की सीमाओं की आंतरिक ज्यामिति का अध्ययन है।
अनुरूप ज्यामिति
अनुरूप ज्यामिति अंतरिक्ष पर कोण-संरक्षण (अनुरूप) परिवर्तनों के समूह का अध्ययन है।
विभेदक सांस्थिति
विभेदक सांस्थिति एक मीट्रिक या सहानुभूतिपूर्ण रूप के बिना वैश्विक ज्यामितीय आक्रमणकारियों का अध्ययन है।
अवकल सांस्थिति प्राकृतिक संचालन से प्रारंभ होती है जैसे कि प्राकृतिक वेक्टर बंडलों झूठ व्युत्पन्न और अवकल अवस्था का एक्सटीरियर डेरिवेटिव। झूठ अलजेब्रॉइड्स के अलावा, कूरेंट बीजगणित भी अधिक महत्वपूर्ण भूमिका निभाने लगते हैं।
झूठ समूह
एक झूठ समूह चिकनी मैनिफोल्ड की श्रेणी में एक समूह (गणित) है। बीजगणितीय गुणों के अलावा यह विभेदक ज्यामितीय गुणों का भी आनंद लेता है। सबसे स्पष्ट निर्माण एक झूठ बीजगणित का है जो बाएं-अपरिवर्तनीय वेक्टर क्षेत्रों के बीच झूठ ब्रैकेट के साथ संपन्न इकाई में स्पर्शरेखा स्थान है। संरचना सिद्धांत के अलावा एक झूठ समूह के प्रतिनिधित्व का व्यापक क्षेत्र भी है।
ज्यामितीय विश्लेषण
ज्यामितीय विश्लेषण एक गणितीय अनुशासन है जहां अंतर समीकरणों से उपकरण, विशेष रूप से अंडाकार आंशिक अंतर समीकरणों का उपयोग अंतर ज्यामिति और अंतर सांस्थिति में नए परिणाम स्थापित करने के लिए किया जाता है।
गेज सिद्धांत
गेज सिद्धांत वेक्टर बंडलों और प्रमुख बंडलों पर सम्बन्ध का अध्ययन है, और गणितीय भौतिकी और भौतिक गेज सिद्धांत में समस्याओं से उत्पन्न होता है जो कण भौतिकी के मानक वस्तु को रेखांकित करता है। गेज सिद्धांत बंडलों पर सम्बन्ध के लिए अंतर समीकरणों के अध्ययन से संबंधित है, और इन समीकरणों के समाधान के परिणामी ज्यामितीय मॉड्यूल रिक्त स्थान के साथ-साथ उनसे प्राप्त होने वाले अपरिवर्तनीय भी हैं। ये समीकरण अधिकांशतः यूलर-लैग्रेंज समीकरण के रूप में उत्पन्न होते हैं जो क्वांटम क्षेत्र सिद्धांत में कुछ भौतिक प्रणालियों की गति के समीकरणों का वर्णन करते हैं, और इसलिए उनका अध्ययन भौतिकी में काफी रुचि रखता है।
बंडल और सम्बन्ध
बंडलों पर वेक्टर बंडलों, प्रमुख बंडलों और सम्बन्ध (गणित) का उपकरण आधुनिक अंतर ज्यामिति में असाधारण रूप से महत्वपूर्ण भूमिका निभाता है। एक चिकने मैनिफोल्ड में हमेशा एक प्राकृतिक वेक्टर बंडल, स्पर्शरेखा बंडल होता है। संक्षेप में, यह संरचना अपने आप में केवल कई गुना विश्लेषण विकसित करने के लिए पर्याप्त है, जबकि ज्यामिति करने के लिए, इसके अलावा, विभिन्न बिंदुओं पर स्पर्शरेखा रिक्त स्थान को जोड़ने के लिए किसी तरह की आवश्यकता होती है, यानी समानांतर परिवहन की धारणा। एक महत्वपूर्ण उदाहरण एफ़िन सम्बन्ध द्वारा प्रदान किया जाता है। R . में एक सतह के लिए3, विभिन्न बिंदुओं पर स्पर्शरेखा विमानों की पहचान परिवेशी यूक्लिडियन अंतरिक्ष द्वारा प्रेरित एक प्राकृतिक पथ-वार समानता का उपयोग करके की जा सकती है, जिसमें मीट्रिक और समानांतरवाद की एक प्रसिद्ध मानक परिभाषा है। रीमैनियन ज्यामिति में, लेवी-सिविता सम्बन्ध एक समान उद्देश्य प्रदान करता है। सामान्यतः , अवकल जियोमीटर एक सदिश बंडल के साथ रिक्त स्थान और एक मनमाना संबंध संबंध पर विचार करते हैं जो एक मीट्रिक के संदर्भ में परिभाषित नहीं है। भौतिकी में, मैनिफोल्ड स्पेससमय हो सकता है और बंडल और सम्बन्ध विभिन्न भौतिक क्षेत्रों से संबंधित हैं।
आंतरिक बनाम बाहरी
19वीं शताब्दी के आरंभ से और मध्य तक, बाहरी दृष्टिकोण से अंतर ज्यामिति का अध्ययन किया गया था: घटता और सतहों को उच्च आयाम के यूक्लिडियन स्थान में स्थित माना जाता था (उदाहरण के लिए तीन आयामों के परिवेश स्थान में एक सतह) . वक्रों की विभेदक ज्यामिति और सतहों की विभेदक ज्यामिति में सबसे सरल परिणाम हैं। बर्नहार्ड रीमैन के काम से प्रारंभ करते हुए, आंतरिक दृष्टिकोण विकसित किया गया था, जिसमें कोई ज्यामितीय वस्तु के बाहर जाने की बात नहीं कर सकता क्योंकि इसे मुक्त रूप से दिया जाना माना जाता है। यहां मौलिक परिणाम गॉस की प्रमेय एग्रेगियम है, इस प्रभाव के लिए कि गॉसियन वक्रता एक आंतरिक अपरिवर्तनीय है।
आंतरिक दृष्टिकोण अधिक लचीला है। उदाहरण के लिए, यह सापेक्षता में उपयोगी है जहां अंतरिक्ष-समय को स्वाभाविक रूप से बाहरी रूप में नहीं लिया जा सकता है। चूँकि, तकनीकी जटिलता में भुगतान करने के लिए एक कीमत है: वक्रता और सम्बन्ध (गणित) की आंतरिक परिभाषाएं दृष्टिगत रूप से बहुत कम सहज ज्ञान युक्त हो जाती हैं।
इन दो दृष्टिकोणों को समेटा जा सकता है, अर्थात बाह्य ज्यामिति को आंतरिक के अतिरिक्त एक संरचना के रूप में माना जा सकता है। (नैश एम्बेडिंग प्रमेय देखें।) ज्यामितीय कलन की औपचारिकता में कई गुना के बाह्य और आंतरिक ज्यामिति दोनों को एक द्विभाजक-मूल्यवान एक-रूप द्वारा चित्रित किया जा सकता है जिसे आकार संचालिका कहा जाता है।[15]
अनुप्रयोग
| Part of a series on |
| Spacetime |
|---|
 |
नीचे कुछ उदाहरण दिए गए हैं कि विभेदक ज्यामिति विज्ञान और गणित के अन्य क्षेत्रों में कैसे लागू होती है।
- भौतिकी में, अवकल ज्यामिति के कई अनुप्रयोग हैं, जिनमें सम्मालित हैं:
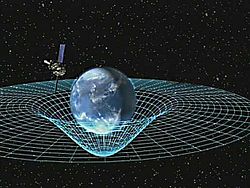
- विभेदक ज्यामिति वह भाषा है जिसमें अल्बर्ट आइंस्टीन के सापेक्षता के सामान्य सिद्धांत को व्यक्त किया गया है। सिद्धांत के अनुसार, ब्रह्मांड एक स्मूथ मैनिफोल्ड है जो छद्म-रीमैनियन मीट्रिक से सुसज्जित है, जो स्पेसटाइम की वक्रता का वर्णन करता है। पृथ्वी के चारों ओर कक्षा में उपग्रहों की स्थिति के लिए इस वक्रता को समझना आवश्यक है। गुरुत्वाकर्षण लेंसिंग और ब्लैक होल्स के अध्ययन में विभेदक ज्यामिति भी अपरिहार्य है।
- विद्युत चुंबकत्व के अध्ययन में विभेदक रूपों का उपयोग किया जाता है।
- विभेदक ज्यामिति मेंलाग्रंगियन यांत्रिकी और हैमिल्टनियन यांत्रिकी दोनों के लिए अनुप्रयोग हैं। विशेष रूप से सिम्पलेक्टिक मैनिफोल्ड का उपयोग हैमिल्टनियन प्रणाली का अध्ययन करने के लिए किया जा सकता है।
- रिमेंनियन ज्यामिति और संपर्क ज्यामिति का उपयोग जियोमेट्रोथर्मोडायनामिक्स की औपचारिकता के निर्माण के लिए किया गया है, जिसे पारस्पारिक संतुलन थर्मोडायनामिक्स में अनुप्रयोग मिला है।
- रसायन विज्ञान और जैवभौतिकी में जब अलग-अलग दबाव में कोशिका झिल्ली संरचना की मॉडलिंग की जाती है।
- अर्थशास्त्र में, विभेदक ज्यामिति का अर्थमिति के क्षेत्र में अनुप्रयोग है।[16]
- ज्यामितीय मॉडलिंग (कंप्यूटर ग्राफिक्स सहित) और कंप्यूटर कंप्यूटर एडेड ज्यामितीय डिजाइन विभेदक ज्यामिति के विचारों पर आधारित हैं।
- इंजीनियरिंग में, अंकीय संकेत प्रक्रिया में समस्याओं को हल करने के लिए विभेदक ज्यामिति को लागू किया जा सकता है।[17]
- नियंत्रण सिद्धांत में, अंतर ज्यामिति का उपयोग गैर-रेखीय नियंत्रकों, विशेष रूप से ज्यामितीय नियंत्रण का विश्लेषण करने के लिए किया जा सकता है[18]
- संभाव्यता, सांख्यिकी और सूचना सिद्धांत में, कोई विभिन्न संरचनाओं को रीमैनियन मैनिफोल्ड के रूप में व्याख्या कर सकता है, जो विशेष रूप से फिशर सूचना मीट्रिक के माध्यम से सूचना ज्यामिति के क्षेत्र को उत्पन्न करता है।
- संरचनात्मक भूविज्ञान में, भूगर्भीय संरचनाओं का विश्लेषण और वर्णन करने के लिए विभेदक ज्यामिति का उपयोग किया जाता है।
- कंप्यूटर विज़न में, आकृतियों का विश्लेषण करने के लिए विभेदक ज्यामिति का उपयोग किया जाता है।[19]
- मूर्ति प्रोद्योगिकी में, गैर सतहों पर जानकारी को प्रक्रिया और विश्लेषण करने के लिए विभेदक ज्यामिति का उपयोग किया जाता है।[20]
- रिक्की फ्लो की तकनीकों का उपयोग करते हुए पोंकारे अनुमान के ग्रिगोरी पेरेलमैन के प्रमाण ने सांस्थिति में प्रश्नों के लिए अंतर-ज्यामितीय दृष्टिकोण की शक्ति का प्रदर्शन किया और इसके विश्लेषणात्मक तरीकों द्वारा निभाई गई महत्वपूर्ण भूमिका पर प्रकाश ड
- बेतार संचार में, ग्रासमानियन कईगुना का उपयोग बहु ऐन्टेना प्रणालियों में MIMO सिस्टम में beamforming तकनीकों के लिए किया जाता है।[21]
यह भी देखें
- सार अंतर ज्यामिति
- Affine अंतर ज्यामिति
- फ्रैक्टल्स पर विश्लेषण
- घुमावदार स्पेसटाइम के गणित का मूल परिचय
- असतत अंतर ज्यामिति
- गॉस
- डिफरेंशियल ज्योमेट्री और टोपोलॉजी की शब्दावली
- गणित में प्रकाशनों की सूची#विभेदक ज्यामिति
- गणित में प्रकाशनों की सूची#विभेदक टोपोलॉजी
- अभिन्न ज्यामिति
- अंतर ज्यामिति विषयों की सूची
- गैर अनुमेय ज्यामिति
- प्रक्षेपी अंतर ज्यामिति
- सिंथेटिक अंतर ज्यामिति
- सिस्टोलिक ज्यामिति
- गेज सिद्धांत (गणित)
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Struik, D. J. “Outline of a History of Differential Geometry: I.” Isis, vol. 19, no. 1, 1933, pp. 92–120. JSTOR, www.jstor.org/stable/225188.
- ↑ Clairaut, A.C., 1731. Recherches sur les courbes à double courbure. Nyon.
- ↑ O'Connor, John J.; Robertson, Edmund F., "Leonhard Euler", MacTutor History of Mathematics archive, University of St Andrews
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 Spivak, M., 1975. A comprehensive introduction to differential geometry (Vol. 2). Publish or Perish, Incorporated.
- ↑ Gauss, C.F., 1828. Disquisitiones generales circa superficies curvas (Vol. 1). Typis Dieterichianis.
- ↑ 6.0 6.1 6.2 6.3 Struik, D.J. “Outline of a History of Differential Geometry (II).” Isis, vol. 20, no. 1, 1933, pp. 161–191. JSTOR, www.jstor.org/stable/224886
- ↑ O'Connor, John J.; Robertson, Edmund F., "Non-Euclidean Geometry", MacTutor History of Mathematics archive, University of St Andrews
- ↑ Milnor, John W., (1982) Hyperbolic geometry: The first 150 years, Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9–24.
- ↑ 1868 On the hypotheses which lie at the foundation of geometry, translated by W.K.Clifford, Nature 8 1873 183 – reprinted in Clifford's Collected Mathematical Papers, London 1882 (MacMillan); New York 1968 (Chelsea) http://www.emis.de/classics/Riemann/. Also in Ewald, William B., ed., 1996 “From Kant to Hilbert: A Source Book in the Foundations of Mathematics”, 2 vols. Oxford Uni. Press: 652–61.
- ↑ Christoffel, E.B. (1869). "दूसरी डिग्री के सजातीय विभेदक भावों के परिवर्तन के बारे में". Journal für die Reine und Angewandte Mathematik. 70.
- ↑ Ricci, Gregorio; Levi-Civita, Tullio (March 1900). "एब्सोल्यूट डिफरेंशियल कैलकुलस की विधियाँ और उनके अनुप्रयोग" [Methods of the absolute differential calculus and their applications]. Mathematische Annalen (in français). Springer. 54 (1–2): 125–201. doi:10.1007/BF01454201. S2CID 120009332.
- ↑ 12.0 12.1 Dieudonné, J., 2009. A history of algebraic and differential topology, 1900-1960. Springer Science & Business Media.
- ↑ 13.0 13.1 Fré, P.G., 2018. A Conceptual History of Space and Symmetry. Springer, Cham.
- ↑ The area preserving condition (or the twisting condition) cannot be removed. If one tries to extend such a theorem to higher dimensions, one would probably guess that a volume preserving map of a certain type must have fixed points. This is false in dimensions greater than 3.
- ↑ Hestenes, David (2011). "The Shape of Differential Geometry in Geometric Calculus" (PDF). In Dorst, L.; Lasenby, J. (eds.). अभ्यास में ज्यामितीय बीजगणित की मार्गदर्शिका. Springer Verlag. pp. 393–410. There is also a pdf[permanent dead link] available of a scientific talk on the subject
- ↑ Marriott, Paul; Salmon, Mark, eds. (2000). इकॉनोमेट्रिक्स के लिए डिफरेंशियल ज्योमेट्री के अनुप्रयोग. Cambridge University Press. ISBN 978-0-521-65116-5.
- ↑ Manton, Jonathan H. (2005). "On the role of differential geometry in signal processing". कार्यवाही। (आईसीएएसएसपी '05)। ध्वनिकी, भाषण और सिग्नल प्रोसेसिंग पर IEEE अंतर्राष्ट्रीय सम्मेलन, 2005. Vol. 5. pp. 1021–1024. doi:10.1109/ICASSP.2005.1416480. ISBN 978-0-7803-8874-1. S2CID 12265584.
- ↑ Bullo, Francesco; Lewis, Andrew (2010). यांत्रिक प्रणालियों का ज्यामितीय नियंत्रण: सरल यांत्रिक नियंत्रण प्रणालियों के लिए मॉडलिंग, विश्लेषण और डिजाइन. Springer-Verlag. ISBN 978-1-4419-1968-7.
- ↑ Micheli, Mario (May 2008). लैंडमार्क शेप मैनिफोल्ड्स की डिफरेंशियल ज्योमेट्री: मेट्रिक्स, जियोडेसिक्स और कर्वेचर (PDF) (Ph.D.). Archived from the original (PDF) on June 4, 2011.
- ↑ Joshi, Anand A. (August 2008). छवि प्रसंस्करण और सिग्नल विश्लेषण के लिए ज्यामितीय तरीके (PDF) (Ph.D.).
- ↑ Love, David J.; Heath, Robert W. Jr. (October 2003). "मल्टीपल-इनपुट मल्टीपल-आउटपुट वायरलेस सिस्टम के लिए ग्रासमैनियन बीमफॉर्मिंग" (PDF). IEEE Transactions on Information Theory. 49 (10): 2735–2747. CiteSeerX 10.1.1.106.4187. doi:10.1109/TIT.2003.817466. Archived from the original (PDF) on 2008-10-02.
अग्रिम पठन
- Ethan D. Bloch (27 June 2011). A First Course in Geometric Topology and Differential Geometry. Boston: Springer Science & Business Media. ISBN 978-0-8176-8122-7. OCLC 811474509.
- Burke, William L. (1997). Applied differential geometry. Cambridge University Press. ISBN 0-521-26929-6. OCLC 53249854.
- do Carmo, Manfredo Perdigão (1976). Differential geometry of curves and surfaces. Englewood Cliffs, N.J.: Prentice-Hall. ISBN 978-0-13-212589-5. OCLC 1529515.
- Frankel, Theodore (2004). The geometry of physics : an introduction (2nd ed.). New York: Cambridge University Press. ISBN 978-0-521-53927-2. OCLC 51855212.
- Elsa Abbena; Simon Salamon; Alfred Gray (2017). Modern Differential Geometry of Curves and Surfaces with Mathematica (3rd ed.). Boca Raton: Chapman and Hall/CRC. ISBN 978-1-351-99220-6. OCLC 1048919510.
- Kreyszig, Erwin (1991). Differential Geometry. New York: Dover Publications. ISBN 978-0-486-66721-8. OCLC 23384584.
- Kühnel, Wolfgang (2002). Differential Geometry: Curves – Surfaces – Manifolds (2nd ed.). Providence, R.I.: American Mathematical Society. ISBN 978-0-8218-3988-1. OCLC 61500086.
- McCleary, John (1994). Geometry from a differentiable viewpoint. Cambridge University Press. ISBN 0-521-13311-4. OCLC 915912917.
- Spivak, Michael (1999). A Comprehensive Introduction to Differential Geometry (5 Volumes) (3rd ed.). Publish or Perish. ISBN 0-914098-72-1. OCLC 179192286.
- ter Haar Romeny, Bart M. (2003). Front-end vision and multi-scale image analysis : multi-scale computer vision theory and applications, written in Mathematica. Dordrecht: Kluwer Academic. ISBN 978-1-4020-1507-6. OCLC 52806205.
इस पृष्ठ में अनुपलब्ध आंतरिक कड़ियों की सूची
- अतिशयोक्तिपूर्ण परवलयिक
- भूमंडल नापने का शास्र
- रीमैनियन ज्यामिति
- अलग करने योग्य कई गुना
- क्लासिकल एंटिक्विटी
- समाकलन गणित
- बहु रेखीय बीजगणित
- अंतर कलन
- लीनियर अलजेब्रा
- अतिपरवलयिक ज्यामिति
- अर्थशास्त्र
- बहुत छोता
- एरेटोस्थेनेज
- घेरा
- वक्राकार लंबाई
- थकावट की विधि
- महान घेरे
- पुनर्जागरण काल
- संक्रमण का बिन्दु
- ओस्क्यूलेटिंग सर्कल
- बरनौली परिवार
- प्रमुख वक्रता
- विविधताओं की गणना
- लिफाफा (गणित)
- प्रक्षेप्य ज्यामिति
- भूगणित त्रिभुज
- समानता सिद्धांत
- क्रिस्टोफर प्रतीक
- सहपरिवर्ती व्युत्पन्न
- झूठ बोलने वाले समूह
- पूर्ण अंतर गणना
- छद्म-रीमैनियन ज्यामिति
- साइट विश्लेषण (कागज)
- बाहरी आवरण
- विशेषता वर्ग
- दर्पण समरूपता (स्ट्रिंग सिद्धांत)
- सन्निकटन का पहला क्रम
- डिफियोमोर्फिज्म
- रीमैन वक्रता टेन्सर
- वक्राकार लंबाई
- सकारात्मक निश्चित द्विरेखीय रूप
- बनच मानदंड
- एनलस (गणित)
- ज्यामिति से संपर्क करें
- लगभग जटिल कई गुना
- लेट बीजगणित
- एक झूठ समूह का प्रतिनिधित्व
- मोडुली स्पेस
- मुख्य बंडल
- ज्यामितीय गणना
- सापेक्षता का सामान्य सिद्धांत
- भौतिक विज्ञान
- लग्रांगियन यांत्रिकी
- जीव पदाथ-विद्य
- संभावना
- भग्न पर विश्लेषण
- विभेदक ज्यामिति विषयों की सूची
बाहरी संबंध
- "Differential geometry", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- B. Conrad. Differential Geometry handouts, Stanford University
- Michael Murray's online differential geometry course, 1996 Archived 2013-08-01 at the Wayback Machine
- A Modern Course on Curves and Surfaces, Richard S Palais, 2003 Archived 2019-04-09 at the Wayback Machine
- Richard Palais's 3DXM Surfaces Gallery Archived 2019-04-09 at the Wayback Machine
- Balázs Csikós's Notes on Differential Geometry
- N. J. Hicks, Notes on Differential Geometry, Van Nostrand.
- MIT OpenCourseWare: Differential Geometry, Fall 2008
{{Navbox
| name =गणित के क्षेत्र
|state = autocollapse
| title =अंक शास्त्र
| bodyclass = hlist
|above =
| group1 = नींव
| list1 =* श्रेणी सिद्धांत
| group2 =बीजगणित | list2 =* सार
| group3 = विश्लेषण | list3 =* पथरी
- वास्तविक विश्लेषण
- जटिल विश्लेषण
- हाइपरकम्प्लेक्स विश्लेषण
- अंतर समीकरण
- कार्यात्मक विश्लेषण
- हार्मोनिक विश्लेषण
- माप सिद्धांत
| group4 = असतत | list4 =* कॉम्बीनेटरिक्स
| group5 =ज्यामिति | list5 =* बीजगणितीय
| group6 =संख्या सिद्धांत | list6 =* अंकगणित
| group7 =टोपोलॉजी | list7 =* सामान्य
| group8 = लागू | list8 =* इंजीनियरिंग गणित
- गणितीय जीव विज्ञान
- गणितीय रसायन विज्ञान
- गणितीय अर्थशास्त्र
- गणितीय वित्त
- गणितीय भौतिकी
- गणितीय मनोविज्ञान
- गणितीय समाजशास्त्र
- गणितीय सांख्यिकी
- संभावना
- सांख्यिकी
- सिस्टम साइंस
| group9 = कम्प्यूटेशनल | list9 =* कंप्यूटर विज्ञान
| group10 = संबंधित विषय | list10 =* अनौपचारिक गणित
| below =* '
 ' श्रेणी' '
' श्रेणी' '- Commons page ' कॉमन्स'
- WikiProject [[gikewikipedia: wikiproject matics | wikiproject]
}}