प्राकृतिक लघुगणक

"आधार e" redirects here. For नंबरिंग सिस्टम जो "e" को अपने आधार के रूप में उपयोग करता है, see संख्यांकन का गैर-पूर्णांक आधार § आधार e.

प्राकृतिक लघुगणक
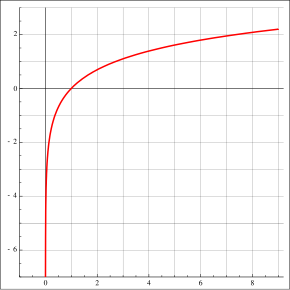प्राकृतिक लघुगणक फ़ंक्शन के भाग का ग्राफ़। जैसे-जैसे x बढ़ता है, फलन धीरे-धीरे धनात्मक अनन्तता की ओर बढ़ता है, और जैसे-जैसे x 0 की ओर बढ़ता है (x के किसी भी शक्ति नियम की तुलना में "धीरे") धीरे-धीरे ऋणात्मक अनन्तता की ओर बढ़ता है।
General information
सामान्य परिभाषा	$\ln x=\log _{e}x$
आविष्कार की प्रेरणा	विश्लेषणात्मक प्रमाण
आवेदन के क्षेत्र	शुद्ध और अनुप्रयुक्त गणित
Domain, Codomain and Image
डोमेन	$\mathbb {R} _{>0}$
कोडोमेन	$\mathbb {R}$
इमेज	$\mathbb {R}$
Specific values
+∞ पर मान	+∞
Value at e	1
Specific features
असिम्पटोट	$x=0$
रूट	1
उलटा	$\exp x$
व्युत्पन्न	$\ln 'x=1/x,x>0$
एंटीडेरिवेटिव	$\int \ln x\,dx=x\left(\ln x-1\right)+C$

किसी संख्या का प्राकृतिक लघुगणक गणितीय स्थिरांक e के आधार पर उसका लघुगणक हैं, जो एक अपरिमेय और पारलौकिक संख्या हैं, जो लगभग 2.718281828459 के बराबर हैं। x का प्राकृतिक लघुगणक समान्यतः ln x, log_e x, के रूप में लिखा जाता है और यदि आधार e अंतनिर्हित है, तो x को log x के रूप में लिखा जाता हैं। कोष्ठक कभी-कभी स्पष्टता देने के लिए जोड़े जाते हैं जैसे: ln(x), log_e(x), या log(x). यह विशेष रूप से तब किया जाता है जब अस्पष्टता को रोकने के लिए लघुगणक का तर्क एक प्रतीक नहीं है।

x का प्राकृतिक लघुगणक वह घातांक है जिससे e को x के बराबरी पर लाना होगा। उदाहरण के लिए, ln 7.5 2.0149... है क्योकि e^2.0149... = 7.5. e का प्राकृतिक लघुगणक अपने आप, ln e, 1 है, क्योकि e¹ = e, जबकि 1 का प्राकृतिक लघुगणक 0 हैं, क्योकि e⁰ = 1 है।

प्राकृतिक लघुगणक को अभिन्न क्षेत्र के रूप में किसी भी सकारात्मक वास्तविक संख्या a के लिए परिभाषित किया जा सकता है। y = 1/x से 1 प्रति a (क्षेत्र नकारात्मक होने के साथ जब 0 < a < 1)। इस परिभाषा की सादगी, जो प्राकृतिक लघुगणक से जुड़े कई अन्य सूत्रों से मेल खाती है, वह हमें "प्राकृतिक" शब्द की ओर ले जाती है। प्राकृतिक लघुगणक की परिभाषा को ऋणात्मक संख्याओं और सभी गैर-शून्य जटिल संख्याओं के लिए लघुगणक मान देने के लिए बढ़ाया जा सकता है, हालांकि यह एक बहु-मूल्यवान फलन की ओर जाता है: अधिक के लिए जटिल लघुगणक देखें।

प्राकृतिक लघुगणक प्रकार्य यदि एक सकारात्मक वास्तविक चर के वास्तविक-मूल्य प्रकार्य के रूप में माना जाता है, तो यह घातांक प्रकार्य का व्युत्क्रम प्रकार्य है, जो पहचान के लिए अग्रणी होता है:

${\begin{aligned}e^{\ln x}&=x\qquad {\text{ if }}x{\text{ is strictly positive,}}\\\ln e^{x}&=x\qquad {\text{ if }}x{\text{ is any real number.}}\end{aligned}}$

सभी लघुगणक की तरह, प्राकृतिक लघुगणक सकारात्मक संख्याओं के गुणन को योग में जोड़ता है:

$\ln(x\cdot y)=\ln x+\ln y~.$

लघुगणक को 1 के अलावा किसी भी सकारात्मक आधार के लिए परिभाषित किया जा सकता है, केवल e के लिए ही नही। हालाँकि, अन्य आधारों में लघुगणक केवल प्राकृतिक लघुगणक से एक स्थिर गुणक द्वारा भिन्न होते हैं, और बाद के संदर्भ में परिभाषित किए जा सकते हैं, $\log _{b}x=\ln x/\ln b=\ln x\cdot \log _{b}e$.

लघुगणक उन समीकरणों को हल करने के लिए उपयोगी होते हैं जो अज्ञात किसी अन्य मात्रा के घातांक के रूप में प्रकट होता है। उदाहरण के लिए, लघुगणक का उपयोग अर्ध-जीवन, क्षय स्थिरांक, या अज्ञात समय के लिए घातीय क्षय समस्याओं को हल करने के लिए किया जाता है। वे गणित और वैज्ञानिक विषयों की कई शाखाओं में महत्वपूर्ण हैं, और उनका उपयोग चक्रवृद्धि ब्याज से संबंधित समस्याओं को हल करने के लिए किया जाता है।

इतिहास

Main article: प्राकृतिक लघुगणक का इतिहास

प्राकृतिक लघुगणक की अवधारणा को 1649 से पहले ग्रेगोइरे डी सेंट विंसेंट और अल्फोन्स एंटोनियो डी सरसा द्वारा तैयार किया गया था। उनके काम में अतिपरवलिक चतुर्भुज के साथ समीकरण xy = 1, समिलित हैं। उनके समाधान ने अपेक्षित अतिपरवलिक लघुगणक फलन उत्पन्न किया, जिसमें अब प्राकृतिक लघुगणक से जुड़े गुण भी हैं।

प्राकृतिक लघुगणक का प्रारंभिक उल्लेख निकोलस मर्केटर ने 1668 में प्रकाशित अपनी कृति लॉगरिथमोटेक्निया में किया था। हालांकि गणित के शिक्षक जॉन स्पीडेल ने पहले ही 1619 में प्रभावी रूप से प्राकृतिक लघुगणक की एक तालिका तैयार कर ली थी। यह कहा गया है कि स्पीडेल के लघुगणक आधार e, के लिए थे, लेकिन पूर्णांकों के रूप में व्यक्त किए जाने वाले मानों के साथ जटिलताओं के कारण यह पूरी तरह से सत्य नहीं है।

नोटेशनल कन्वेंशन

ln x तथा log_e x दोनों संकेत स्पष्ट रूप से प्राकृतिक लघुगणक x को संदर्भित करते है, और बिना किसी स्पष्ट आधार के log x भी प्राकृतिक लघुगणक का उल्लेख कर सकता हैं। यह प्रयोग गणित के साथ-साथ कुछ वैज्ञानिक संदर्भों और कई प्रोग्रामिंग भाषाओं में आम है। कुछ अन्य संदर्भों में, जैसे कि रसायन विज्ञान, मे log x का उपयोग सामान्य लघुगणक (आधार 10) को निरूपित करने के लिए इस्तेमाल किया जा सकता है। यह कंप्यूटर विज्ञान के संदर्भ में बाइनरी लघुगणक (बेस 2) का भी उल्लेख कर सकता है, विशेष रूप से समय जटिलता के संदर्भ में।

परिभाषाएँ

प्राकृतिक लघुगणक को कई समान तरीकों से परिभाषित किया जा सकता है।

एक्सपोनेंशियल का व्युत्क्रम

सबसे सामान्य परिभाषा के व्युत्क्रम फलन के रूप में है $e^{x}$, ताकि $e^{\ln(x)}=x$. क्योकि $e^{x}$ किसी भी वास्तविक इनपुट $x$ के लिए सकारात्मक और उल्टा है। $\ln(x)$ की यह परिभाषा किसी भी सकारात्मक x के लिए अच्छी तरह परिभाषित है। जटिल लघुगणक के लिए, $e^{z}$ उल्टा नहीं है, इसलिए $\ln(z)$ एक बहुविकल्पीय कार्य है। $\ln(z)$ को एक उचित, एकल-आउटपुट फलन , बनाने के लिए हमें इसे एक विशेष प्रमुख शाखा तक सीमित करने की आवश्यकता है, जिसे अक्सर $\operatorname {Ln} (z)$ से निरूपित किया जाता है। जैसे कि $e^{z}$, के व्युत्क्रम कार्य को $\ln(z)$ की सामान्य परिभाषा को उलट कर परिभाषित किया जा सकता है

$e^{z}=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}$

ऐसा करने से फल मिलता है:

$\ln(z)=\lim _{n\to \infty }n\cdot ({\sqrt[{n}]{z}}-1)$

इसलिए यह परिभाषा nवें मूल की प्रधान शाखा से अपनी स्वयं की मुख्य शाखा प्राप्त करती है।

अभिन्न परिभाषा

ln a वक्र के नीचे छायांकित क्षेत्र के रूप में f(x) = 1/x से 1 प्रति a. यदि a से कम होता है 1, नकारात्मक होने के लिए लिया गया क्षेत्र।

The area under the hyperbola satisfies the logarithm rule. Here A(s,t) denotes the area under the hyperbola between s and t.

एक सकारात्मक, वास्तविक संख्या a के प्राकृतिक लघुगणक को समीकरण y = 1/x के बीच x = 1 तथा x = a के साथ अतिपरवलय के ग्राफ़ के अंतर्गत क्षेत्र के रूप में परिभाषित किया जा सकता है। यह अभिन्न है:$\ln a=\int _{1}^{a}{\frac {1}{x}}\,dx.$

यदि a, 1 से कम होता हैं, तो इस क्षेत्र को नकारात्मक माना जाता है।

यह फलन एक लघुगणक है क्योंकि यह एक लघुगणक के मौलिक गुणात्मक गुणों को संतुष्ट करता है:

$\ln(ab)=\ln a+\ln b.$

यह अभिन्न को विभाजित करके प्रदर्शित किया जा सकता है जो ln ab को दो भागों में परिभाषित करता है, और फिर प्रतिस्थापन द्वारा एकीकरण करता हैं x = at (इसलिए dx = a dt) को दूसरे भाग मे निम्नअनुसार बनाता हैं:

${\begin{aligned}\ln ab=\int _{1}^{ab}{\frac {1}{x}}\,dx&=\int _{1}^{a}{\frac {1}{x}}\,dx+\int _{a}^{ab}{\frac {1}{x}}\,dx\\[5pt]&=\int _{1}^{a}{\frac {1}{x}}\,dx+\int _{1}^{b}{\frac {1}{at}}a\,dt\\[5pt]&=\int _{1}^{a}{\frac {1}{x}}\,dx+\int _{1}^{b}{\frac {1}{t}}\,dt\\[5pt]&=\ln a+\ln b.\end{aligned}}$

प्राथमिक शब्दों में, यह केवल क्षैतिज दिशा में 1/a और ऊर्ध्वाधर दिशा में a द्वारा प्रवर्धन हैं। इस परिवर्तन के तहत क्षेत्र नहीं बदलता है, लेकिन a तथा ab के बीच का क्षेत्र पुन: समनुरूप किया गया है। क्योंकि फलन a/(ax) फलन 1/x के बराबर हैं, परिणामी क्षेत्र निश्चित रूप से ln b हैं।

संख्या e को अद्वितीय वास्तविक संख्या a के रूप में परिभाषित किया जा सकता है, जैसे कि ln a = 1.

प्राकृतिक लघुगणक का एक अनुचित अभिन्न प्रतिनिधित्व भी है, जिसे फ़ुबिनी के प्रमेय से निम्नानुसार प्राप्त किया जा सकता है:

$\ln \left(x\right)=\int _{1}^{x}{\frac {1}{u}}du=\int _{1}^{x}\int _{0}^{\infty }e^{-tu}\ dt\ du=\int _{0}^{\infty }\int _{1}^{x}e^{-tu}\ du\ dt=\int _{0}^{\infty }{\frac {e^{-t}-e^{-tx}}{t}}dt$

गुण

• $\ln 1=0$
• $\ln e=1$
• $\ln(xy)=\ln x+\ln y\quad {\text{for }}\;x>0\;{\text{and }}\;y>0$
• $\ln(x/y)=\ln x-\ln y$
• $\ln(x^{y})=y\ln x\quad {\text{for }}\;x>0$
• $\ln x<\ln y\quad {\text{for }}\;0<x<y$
• $\lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1$
• $\lim _{\alpha \to 0}{\frac {x^{\alpha }-1}{\alpha }}=\ln x\quad {\text{for }}\;x>0$<
• ${\frac {x-1}{x}}\leq \ln x\leq x-1\quad {\text{for}}\quad x>0$
• $\ln {(1+x^{\alpha })}\leq \alpha x\quad {\text{for}}\quad x\geq 0\;{\text{and }}\;\alpha \geq 1$

style="background: #F0F2F5; font-size:87%; padding:0.2em 0.3em; text-align:left; " | Proof

$x=0$, के लिए कथन सत्य है और अब हम उसे दिखाते हैं ${\frac {d}{dx}}\ln {(1+x^{\alpha })}\leq {\frac {d}{dx}}(\alpha x)$ सभी $x$, के लिए। जो कलन #प्रथम भाग के मौलिक प्रमेय द्वारा प्रमाण को पूरा करता है। इसलिए हम यह दिखाना चाहते हैं ${\frac {d}{dx}}\ln {(1+x^{\alpha })}={\frac {\alpha x^{\alpha -1}}{1+x^{\alpha }}}\leq \alpha ={\frac {d}{dx}}(\alpha x)$ (ध्यान दें कि हमने अभी तक यह सिद्ध नहीं किया है कि यह कथन सत्य है।) यदि यह सत्य है, तो मध्य कथन को धनात्मक मात्रा से गुणा करके $(1+x^{\alpha })/\alpha$ और $x^{\alpha }$ को घटाकर हम प्राप्त करेंगे $x^{\alpha -1}\leq x^{\alpha }+1$ $x^{\alpha -1}(1-x)\leq 1$ $x\geq 1$ के लिए यह कथन नगण्य सत्य है चूँकि बायीं ओर का भाग ऋणात्मक या शून्य होता है। $0\leq x<1$ के लिये यह अभी भी सत्य है क्योंकि बाईं ओर दोनों कारक 1 से कम हैं (याद रखें $\alpha \geq 1$). इस प्रकार यह अंतिम कथन सत्य है और अपने कदमों को उल्टे क्रम में दोहराने से हम पाते हैं कि ${\frac {d}{dx}}\ln {(1+x^{\alpha })}\leq {\frac {d}{dx}}(\alpha x)$ सभी $x$ के लिए यह प्रमाण को पूरा करता है। एक वैकल्पिक प्रमाण यह है कि $(1+x^{\alpha })\leq (1+x)^{\alpha }$ दी गई शर्तों के तहत यह सिद्ध किया जा सकता है, उदाहरण के लिए, आदर्श असमानताओं द्वारा। लघुगणक $\ln(1+x)\leq x$ लेना और प्रयोग करना, प्रमाण पूरा करता है।

व्युत्पन्न

धनात्मक वास्तविकताओं पर वास्तविक-मूल्यवान फलन के रूप में प्राकृतिक लघुगणक का व्युत्पन्न ${\frac {d}{dx}}\ln x={\frac {1}{x}}.$द्वारा दिया जाता है।

प्राकृतिक लघुगणक के इस व्युत्पन्न को कैसे स्थापित किया जाए, यह इस बात पर निर्भर करता है कि इसे पहले कैसे परिभाषित किया गया है। यदि प्राकृतिक लघुगणक को अभिन्न के रूप में परिभाषित किया गया है:

$\ln x=\int _{1}^{x}{\frac {1}{t}}\,dt,$

तो व्युत्पन्न तुरंत कलन के मौलिक प्रमेय के पहले भाग से अनुसरण करता हैं।

दूसरी ओर, यदि प्राकृतिक लघुगणक को घातीय फलन के व्युत्क्रम के रूप में परिभाषित किया जाता है, तो व्युत्पन्न (x > 0 के लिए) लघुगणक के गुणों और घातीय फलन की परिभाषा का उपयोग करके पाया जा सकता है। संख्या की परिभाषा $e=\lim _{u\to 0}(1+u)^{1/u},$ से घातीय फलन को इस प्रकार परिभाषित किया जा सकता है $e^{x}=\lim _{u\to 0}(1+u)^{x/u}=\lim _{h\to 0}(1+hx)^{1/h}$, जहां पर $u=hx,h=u/x.$ यह व्युत्पन्न तब पहले सिद्धांतों से पाया जा सकता है।

${\begin{aligned}{\frac {d}{dx}}\ln x&=\lim _{h\to 0}{\frac {\ln(x+h)-\ln x}{h}}\\&=\lim _{h\to 0}\left[{\frac {1}{h}}\ln \left({\frac {x+h}{x}}\right)\right]\\&=\lim _{h\to 0}\left[\ln \left(\left(1+{\frac {h}{x}}\right)^{\frac {1}{h}}\right)\right]\quad &&{\text{all above for logarithmic properties}}\\&=\ln \left[\lim _{h\to 0}\left(1+{\frac {h}{x}}\right)^{\frac {1}{h}}\right]\quad &&{\text{for continuity of the logarithm}}\\&=\ln e^{1/x}\quad &&{\text{for the definition of }}e^{x}=\lim _{h\to 0}(1+hx)^{1/h}\\&={\frac {1}{x}}\quad &&{\text{for the definition of the ln as inverse function.}}\end{aligned}}$

इसके अलावा, हमारे पास है:

${\frac {d}{dx}}\ln ax={\frac {d}{dx}}(\ln a+\ln x)={\frac {d}{dx}}\ln a+{\frac {d}{dx}}\ln x={\frac {1}{x}}.$

इसलिए, इसके व्युत्क्रम कार्य $e^{ax}$के विपरीत, फलन में एक स्थिरांक अंतर को नहीं बदलता है।

श्रृंखला

ln(1 + x) के लिए टेलर बहुपद केवल -1 < x ≤ 1 की सीमा में सटीक सन्निकटन प्रदान करते हैं। कुछ x > 1 से परे, उच्च स्तर के टेलर बहुपद तेजी से बदतर सन्निकटन हैं।

प्राकृतिक लघुगणक 0 पर अपरिभाषित है चूंकि , $\ln(x)$ में कई अन्य प्राथमिक कार्यों के विपरीत, स्वयं मैक्लॉरिन श्रृंखला नहीं है। इसके बजाय, अन्य बिंदुओं के आसपास टेलर के विस्तार की तलाश की जाती है। उदाहरण के लिए, अगर $\vert x-1\vert \leq 1{\text{ and }}x\neq 0,$ फिर

${\begin{aligned}\ln x&=\int _{1}^{x}{\frac {1}{t}}\,dt=\int _{0}^{x-1}{\frac {1}{1+u}}\,du\\&=\int _{0}^{x-1}(1-u+u^{2}-u^{3}+\cdots )\,du\\&=(x-1)-{\frac {(x-1)^{2}}{2}}+{\frac {(x-1)^{3}}{3}}-{\frac {(x-1)^{4}}{4}}+\cdots \\&=\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}(x-1)^{k}}{k}}.\end{aligned}}$

यह लगभग 1 के ln x के लिए टेलर श्रृंखला है। चरों के परिवर्तन से मर्केटर श्रृंखला प्राप्त होती है:

$\ln(1+x)=\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}}{k}}x^{k}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots ,$

|x| के लिए वैध ≤ 1 और x ≠ -1.

लियोनहार्ड यूलर, ने $x\neq -1$, की अवहेलना करते हुए, फिर भी इस श्रृंखला को x = −1 पर लागू किया, यह दिखाने के लिए कि हार्मोनिक श्रृंखला 1/(1 − 1) के (प्राकृतिक) लघुगणक के बराबर है, जो कि अनंत का लघुगणक है। आजकल, अधिक औपचारिक रूप से, कोई यह साबित कर सकता है कि जब N बड़ा है, तो हार्मोनिक श्रृंखला N के लघुगणक के करीब है। यूलर-मसचेरोनि स्थिरांक में अंतर के साथ अभिसरण होता है।

दाईं ओर ln(1 + x) की एक तस्वीर है इसके कुछ टेलर बहुपद 0 के आस-पास हैं। ये सन्निकटन केवल क्षेत्र −1 < x ≤ 1 में बाहर उच्च डिग्री टेलर बहुपद समारोह के लिए बदतर अनुमानों के लिए विकसित होते हैं।

सकारात्मक पूर्णांक n के लिए एक उपयोगी विशेष मामला, लेना $x={\tfrac {1}{n}}$, है:

$\ln \left({\frac {n+1}{n}}\right)=\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}}{kn^{k}}}={\frac {1}{n}}-{\frac {1}{2n^{2}}}+{\frac {1}{3n^{3}}}-{\frac {1}{4n^{4}}}+\cdots$

यदि $\operatorname {Re} (x)\geq 1/2,$ फिर

${\begin{aligned}\ln(x)&=-\ln \left({\frac {1}{x}}\right)=-\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}({\frac {1}{x}}-1)^{k}}{k}}=\sum _{k=1}^{\infty }{\frac {(x-1)^{k}}{kx^{k}}}\\&={\frac {x-1}{x}}+{\frac {(x-1)^{2}}{2x^{2}}}+{\frac {(x-1)^{3}}{3x^{3}}}+{\frac {(x-1)^{4}}{4x^{4}}}+\cdots \end{aligned}}$

अब, सकारात्मक पूर्णांक n के लिए $x={\tfrac {n+1}{n}}$ लेकर, हम प्राप्त करते हैं:

$\ln \left({\frac {n+1}{n}}\right)=\sum _{k=1}^{\infty }{\frac {1}{k(n+1)^{k}}}={\frac {1}{n+1}}+{\frac {1}{2(n+1)^{2}}}+{\frac {1}{3(n+1)^{3}}}+{\frac {1}{4(n+1)^{4}}}+\cdots$

यदि $\operatorname {Re} (x)\geq 0{\text{ और }}x\neq 0,$ फिर

$\ln(x)=\ln \left({\frac {2x}{2}}\right)=\ln \left({\frac {1+{\frac {x-1}{x+1}}}{1-{\frac {x-1}{x+1}}}}\right)=\ln \left(1+{\frac {x-1}{x+1}}\right)-\ln \left(1-{\frac {x-1}{x+1}}\right).$

तब से

${\begin{aligned}\ln(1+y)-\ln(1-y)&=\sum _{i=1}^{\infty }{\frac {1}{i}}\left((-1)^{i-1}y^{i}-(-1)^{i-1}(-y)^{i}\right)=\sum _{i=1}^{\infty }{\frac {y^{i}}{i}}\left((-1)^{i-1}+1\right)\\&=y\sum _{i=1}^{\infty }{\frac {y^{i-1}}{i}}\left((-1)^{i-1}+1\right){\overset {i-1\to 2k}{=}}\;2y\sum _{k=0}^{\infty }{\frac {y^{2k}}{2k+1}},\end{aligned}}$

हम पहुंचे

${\begin{aligned}\ln(x)&={\frac {2(x-1)}{x+1}}\sum _{k=0}^{\infty }{\frac {1}{2k+1}}{\left({\frac {(x-1)^{2}}{(x+1)^{2}}}\right)}^{k}\\&={\frac {2(x-1)}{x+1}}\left({\frac {1}{1}}+{\frac {1}{3}}{\frac {(x-1)^{2}}{(x+1)^{2}}}+{\frac {1}{5}}{\left({\frac {(x-1)^{2}}{(x+1)^{2}}}\right)}^{2}+\cdots \right).\end{aligned}}$

धनात्मक पूर्णांक n के लिए प्रतिस्थापन $x={\tfrac {n+1}{n}}$ का पुनः प्रयोग करके, हम प्राप्त करते हैं:

${\begin{aligned}\ln \left({\frac {n+1}{n}}\right)&={\frac {2}{2n+1}}\sum _{k=0}^{\infty }{\frac {1}{(2k+1)((2n+1)^{2})^{k}}}\\&=2\left({\frac {1}{2n+1}}+{\frac {1}{3(2n+1)^{3}}}+{\frac {1}{5(2n+1)^{5}}}+\cdots \right).\end{aligned}}$

यह वर्णित श्रृंखला का अब तक का सबसे तेज़ अभिसरण है।

प्राकृतिक लघुगणक को अनंत उत्पाद के रूप में भी व्यक्त किया जा सकता है:

$\ln(x)=(x-1)\prod _{k=1}^{\infty }\left({\frac {2}{1+{\sqrt[{2^{k}}]{x}}}}\right)$

दो उदाहरण हो सकते हैं:

$\ln(2)=\left({\frac {2}{1+{\sqrt {2}}}}\right)\left({\frac {2}{1+{\sqrt[{4}]{2}}}}\right)\left({\frac {2}{1+{\sqrt[{8}]{2}}}}\right)\left({\frac {2}{1+{\sqrt[{16}]{2}}}}\right)...$

$\pi =(2i+2)\left({\frac {2}{1+{\sqrt {i}}}}\right)\left({\frac {2}{1+{\sqrt[{4}]{i}}}}\right)\left({\frac {2}{1+{\sqrt[{8}]{i}}}}\right)\left({\frac {2}{1+{\sqrt[{16}]{i}}}}\right)...$

इस पहचान से, हम इसे आसानी से प्राप्त कर सकते हैं:

${\frac {1}{\ln(x)}}={\frac {x}{x-1}}-\sum _{k=1}^{\infty }{\frac {2^{-k}x^{2^{-k}}}{1+x^{2^{-k}}}}$

उदाहरण के लिए:

${\frac {1}{\ln(2)}}=2-{\frac {\sqrt {2}}{2+2{\sqrt {2}}}}-{\frac {\sqrt[{4}]{2}}{4+4{\sqrt[{4}]{2}}}}-{\frac {\sqrt[{8}]{2}}{8+8{\sqrt[{8}]{2}}}}\cdots$

एकीकरण में प्राकृतिक लघुगणक

प्राकृतिक लघुगणक g(x) = f '(x)/f(x) के कार्यों के सरल समाकलन की अनुमति देता है: g(x) का एक प्रति-अवकलन ln(|f(x)|) द्वारा दिया जाता है। श्रृंखला नियम और निम्नलिखित तथ्य के कारण ऐसा होता है:

${\frac {d}{dx}}\ln \left|x\right|={\frac {1}{x}}.$

दूसरे शब्दों में, अगर $x$ के साथ एक वास्तविक संख्या $x\not =0$, है फिर

$\int {\frac {1}{x}}\,dx=\ln |x|+C$

तथा

$\int {{\frac {f'(x)}{f(x)}}\,dx}=\ln |f(x)|+C.$

यहाँ g(x) = tan(x) के मामले में एक उदाहरण दिया गया है:

${\begin{aligned}&\int \tan x\,dx=\int {\frac {\sin x}{\cos x}}\,dx\\[6pt]&\int \tan x\,dx=\int {\frac {-{\frac {d}{dx}}\cos x}{\cos x}}\,dx.\end{aligned}}$

माना f(x) = cos(x):

$\int \tan x\,dx=-\ln \left|\cos x\right|+C$

$\int \tan x\,dx=\ln \left|\sec x\right|+C$

जहाँ C एकीकरण का एक मनमाना स्थिरांक है।

भागों द्वारा एकीकरण का उपयोग करके प्राकृतिक लघुगणक को एकीकृत किया जा सकता है:

$\int \ln x\,dx=x\ln x-x+C.$

माना :

$u=\ln x\Rightarrow du={\frac {dx}{x}}$

$dv=dx\Rightarrow v=x$

फिर:

${\begin{aligned}\int \ln x\,dx&=x\ln x-\int {\frac {x}{x}}\,dx\\&=x\ln x-\int 1\,dx\\&=x\ln x-x+C\end{aligned}}$

कुशल गणना

ln(x) के लिए जहां x > 1, x का मान 1 के जितना करीब होता है, उतनी ही तेज़ी से इसकी टेलर श्रृंखला की अभिसरण की दर 1 पर केंद्रित होती है। इसका फायदा उठाने के लिए लघुगणक से जुड़ी पहचानों का लाभ उठाया जा सकता है:

${\begin{aligned}\ln 123.456&=\ln(1.23456\cdot 10^{2})\\&=\ln 1.23456+\ln(10^{2})\\&=\ln 1.23456+2\ln 10\\&\approx \ln 1.23456+2\cdot 2.3025851.\end{aligned}}$

इस तरह की तकनीकों का उपयोग कैलकुलेटर से पहले किया जाता था, संख्यात्मक तालिकाओं का हवाला देकर और उपरोक्त जैसे जोड़-तोड़ करके।

10 का प्राकृतिक लघुगणक

10 का प्राकृतिक लघुगणक, जिसका दशमलव विस्तार 2.30258509... है, उदाहरण के लिए वैज्ञानिक संकेतन में प्रस्तुत संख्याओं के प्राकृतिक लघुगणक की गणना में एक भूमिका निभाता है, जैसे कि 10 की शक्ति से मंटिसा गुणा किया जाता है:

$\ln(a\cdot 10^{n})=\ln a+n\ln 10.$

इसका मतलब यह है कि कोई भी [1, 10) सीमा में दशमलव के अपेक्षाकृत छोटे सेट के लघुगणक का उपयोग करके बहुत बड़े या बहुत छोटे परिमाण वाली संख्याओं के लघुगणक की प्रभावी ढंग से गणना कर सकता है।

उच्च परिशुद्धता

परिशुद्धता के कई अंकों के साथ प्राकृतिक लघुगणक की गणना करने के लिए, टेलर श्रृंखला दृष्टिकोण कुशल नहीं है क्योंकि अभिसरण धीमा है। विशेष रूप से यदि x 1 के पास है, एक अच्छा विकल्प हैली की विधि या न्यूटन की विधि का उपयोग करके घातांक फलन को उल्टा करना है, क्योंकि घातीय फलन की श्रृंखला अधिक तेज़ी से अभिसरित होती है। y का मान ज्ञात करने के लिए exp(y) − x = 0 करना, या समकक्ष देना exp(y/2) − x exp(−y/2) = 0 हैली या न्यूटन की विधि का उपयोग करके, पुनरावृत्ति सरल हो जाती है।

$y_{n+1}=y_{n}+2\cdot {\frac {x-\exp(y_{n})}{x+\exp(y_{n})}}$

जिसका घन अभिसरण ln(x) हैं।

अत्यंत उच्च परिशुद्धता गणना के लिए एक अन्य विकल्प सूत्र है

$\ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2,$

जहां पे M 1और 4/s, के अंकगणितीय-ज्यामितीय माध्य को दर्शाता है, तथा

$s=x2^{m}>2^{p/2},$

m इसीलिए चुना गया हैं ताकि सटीकता से p के सूक्ष्मता प्राप्त की जा सके। (अधिकांश प्रयोजनों के लिए, m के लिए 8 का मान पर्याप्त है।) वास्तव में, यदि इस विधि का उपयोग किया जाता है, तो प्राकृतिक लघुगणक के न्यूटन व्युत्क्रमण का उपयोग एक्सपोनेंशियल फलन की कुशलता से गणना करने के लिए किया जा सकता है। (स्थिरांक ln 2 और π को कई ज्ञात त्वरित रूप से अभिसारी श्रृंखलाओं में से किसी का उपयोग करके वांछित सटीकता के लिए पूर्व-गणना की जा सकती है।) या, निम्न सूत्र का उपयोग किया जा सकता है:

$\ln x={\frac {\pi }{M\left(\theta _{2}^{2}(1/x),\theta _{3}^{2}(1/x)\right)}},\quad x\in (1,\infty )$

जहां पे

$\theta _{2}(x)=\sum _{n\in \mathbb {Z} }x^{(n+1/2)^{2}},\quad \theta _{3}(x)=\sum _{n\in \mathbb {Z} }x^{n^{2}}$

जकौबी थीटा फलन सहायक फलन हैं।

विलियम कहन के एक प्रस्ताव के आधार पर और पहली बार 1979 में कार्यान्वितहोने पर Hewlett-Packard HP-41C कैलकुलेटर में लागू किया गया (केवल डिस्प्ले में LN1 के तहत संदर्भित), कुछ कैलकुलेटर, ऑपरेटिंग सिस्टम (उदाहरण के लिए बर्कले UNIX 4.3BSD), कंप्यूटर बीजगणित प्रणाली और प्रोग्रामिंग भाषाएं (उदाहरण के लिए C99) एक विशेष प्राकृतिक लघुगणक प्लस 1 फलन प्रदान करती हैं, जिसे वैकल्पिक रूप से LNP1 या log1p नाम दिया गया है, ताकि फलन log1p(x) के किए शून्य के करीब लघुगणक के लिए अधिक सटीक परिणाम मिल सके। जो ln(y)। को वापस करने वाले फलन को 1 के क़रीब मान y पास करने के बजाय मान ln(1+x) लौटाता है। फलन log1p अस्थिर स्पर्शबिंदु अंकगणित में टेलर के विस्तार से दूसरे कार्यकाल के साथ पूर्ण शब्द 1 को रद्द करने से बचाता है। यह तर्क, परिणाम और मध्यवर्ती चरणों को शून्य के करीब रखता है जहां उन्हें अस्थिर-स्पर्शबिंदु नंबरों के रूप में सबसे सटीक रूप से प्रदर्शित किया जा सकता है

$\mathrm {log1p} (x)=\log(1+x)=2~\mathrm {artanh} \left({\frac {x}{2+x}}\right)\,,$

आधार e के अलावा IEEE 754-2008 मानक बाइनेरी और दशमलव लघुगणक के लिए 1 के पास समान लघुगनकीय कार्यों को परिभाषित करता है: log₂(1 + x) and log₁₀(1 + x). "expm1", "expm" or "exp1m" नाम के समान फलन भी मौजूद हैं, सभी का अर्थ expm1(x) = exp(x) − 1 हैं। जो व्युत्क्रम अतिपरवलयिक स्पर्शरेखा के संदर्भ में एक पहचान हैं,

${\displaystyle \mathrm {log1p} (x)=\log(1+x)=2~\mathrm {artanh} \left({\frac {x}{2+x}}\right)\,,}$

सिस्टम पर x के छोटे मानों के लिए एक उच्च परिशुद्धता मान देता है जो log1p(x) को लागू नहीं करता है।

कम्प्यूटेशनल जटिलता

Main article: गणितीय कार्यों की कम्प्यूटेशनल जटिलता

अंकगणित-ज्यामितीय माध्य (उपर्युक्त दोनों विधियों के लिए) का उपयोग करके प्राकृतिक लघुगणक की गणना की कम्प्यूटेशनल जटिलता सिद्धांत O(M(n) ln n) है। यहाँ n परिशुद्धता के अंकों की संख्या है जिस पर प्राकृतिक लघुगणक का मूल्यांकन किया जाना है और M(n) दो n-अंकीय संख्याओं को गुणा करने की कम्प्यूटेशनल जटिलता है।

निरंतर अंश

जब कोई सरल निरंतर अंश उपलब्ध नहीं होते हैं, तब कई सामान्यीकृत निरंतर भिन्न हैं, जिनमें समिलित हैं:

${\begin{aligned}\ln(1+x)&={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\cdots \\[5pt]&={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}\end{aligned}}$

${\begin{aligned}\ln \left(1+{\frac {x}{y}}\right)&={\cfrac {x}{y+{\cfrac {1x}{2+{\cfrac {1x}{3y+{\cfrac {2x}{2+{\cfrac {2x}{5y+{\cfrac {3x}{2+\ddots }}}}}}}}}}}}\\[5pt]&={\cfrac {2x}{2y+x-{\cfrac {(1x)^{2}}{3(2y+x)-{\cfrac {(2x)^{2}}{5(2y+x)-{\cfrac {(3x)^{2}}{7(2y+x)-\ddots }}}}}}}}\end{aligned}}$

ये निरंतर अंश विशेष रूप से अंतिम अंश 1 के करीब के मानों के लिए तेजी से अभिसरण करते हैं। हालांकि, छोटी संख्याओं को बार-बार जोड़कर और इसी तरह तेजी से अभिसरण करने से बहुत बड़ी संख्याओं के प्राकृतिक लघुगणकों की गणना आसानी से सकती है,

उदाहरण के लिए, चूंकि 2 = 1.25³ × 1.024, 2 के प्राकृतिक लघुगणक की गणना इस प्रकार की जा सकती है:

${\begin{aligned}\ln 2&=3\ln \left(1+{\frac {1}{4}}\right)+\ln \left(1+{\frac {3}{125}}\right)\\[8pt]&={\cfrac {6}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {6}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\end{aligned}}$

इसके अलावा, चूंकि 10 = 1.25¹⁰ × 1.024³, यहां तक ​​कि 10 के प्राकृतिक लघुगणक की भी इसी तरह गणना की जा सकती है:

${\begin{aligned}\ln 10&=10\ln \left(1+{\frac {1}{4}}\right)+3\ln \left(1+{\frac {3}{125}}\right)\\[10pt]&={\cfrac {20}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {18}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\end{aligned}}$

प्राकृतिक लघुगणक का व्युत्क्रम इस प्रकार भी लिखा जा सकता है:

${\frac {1}{\ln(x)}}={\frac {2x}{x^{2}-1}}{\sqrt {{\frac {1}{2}}+{\frac {x^{2}+1}{4x}}}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {x^{2}+1}{4x}}}}}}\ldots$

उदाहरण के लिए:

${\frac {1}{\ln(2)}}={\frac {4}{3}}{\sqrt {{\frac {1}{2}}+{\frac {5}{8}}}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {5}{8}}}}}}\ldots$

जटिल लघुगणक

Main article: जटिल लघुगणक

एक्सपोनेंशियल फलन को एक ऐसे फलन तक बढ़ाया जा सकता है जो एक जटिल संख्या देता है e^z किसी भी मनमाना जटिल संख्या के लिए z; बस के साथ अनंत श्रृंखला का प्रयोग करें x= जेड कॉम्प्लेक्स। इस घातीय फलन को एक जटिल लघुगणक बनाने के लिए उल्टा किया जा सकता है जो साधारण लघुगणक के अधिकांश गुणों को प्रदर्शित करता है। इसमें दो कठिनाइयाँ समिलित हैं: x e^x = 0; नही हैं और इससे यह पता चला है e^2iπ = 1 = e⁰. चूंकि गुणात्मक संपत्ति अभी भी जटिल घातीय कार्य के लिए काम करती है, सभी जटिल के लिए z और पूर्णांक k. के लिए। e^z = e^z+2kiπ

इसलिए लघुगणक को पूरे जटिल तल के लिए परिभाषित नहीं किया जा सकता है, और फिर भी यह बहु-मूल्यवान है- किसी भी जटिल लघुगणक 2iπ को किसी भी पूर्णांक गुणक को जोड़कर समतुल्य लघुगणक में बदला जा सकता है। काटे गए तल पर जटिल लघुगणक केवल एकल-मूल्यवान हो सकता है। उदाहरण के लिए,

ln i = iπ/2 या 5iπ/2 या -3iπ/2, आदि।; और हालांकि i⁴ = 1, 4 ln i के रूप में परिभाषित किया जा सकता है 2iπ, या 10iπ या −6iπ, और इसी तरह परिभाषित किया जा सकता है।

<गैलरी मोड = पैक्ड कैप्शन = जटिल तल (प्रमुख शाखा) पर प्राकृतिक लघुगणक समारोह के भूखंड Image:NaturalLogarithmRe.png|z = Re(ln(x + yi))

Image:NaturalLogarithmImAbs.png|z = |(Im(ln(x + yi)))|

Image:NaturalLogarithmAbs.png|z = |(ln(x + yi))|

Image:NaturalLogarithmAll.png| पिछले तीन रेखांकन का सुपरपोजिशन </गैलरी>

यह भी देखें

• मानसिक गणना#nat-exp|अनुमानित प्राकृतिक घातांक (लॉग बेस e)
• पुनरावृत्त लघुगणक
• नेपियरियन लघुगणक
• लघुगणकीय पहचान की सूची
• एक मैट्रिक्स का लघुगणक
• लॉगरिदमिक भेदभाव
• लॉगरिदमिक इंटीग्रल फलन
• निकोलस मर्केटर - प्राकृतिक लघुगणक शब्द का प्रयोग करने वाले पहले व्यक्ति
• बहुलघुगणक
• वॉन मैंगोल्ड समारोह