जियोडेसिक: Difference between revisions
mNo edit summary |
No edit summary |
||
| (41 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Straight path on a curved surface or a Riemannian manifold}} | {{Short description|Straight path on a curved surface or a Riemannian manifold}} | ||
{{About| | {{About|सामान्य तौर पर जियोडेसिक्स|सामान्य सापेक्षता में जियोडेसिक्स|जियोडेसिक(सामान्य सापेक्षता)|पृथ्वी के आकार का अध्ययन|भूमंडल नापने का शास्र|पृथ्वी पर आवेदन|पृथ्वी जियोडेसिक|अन्य उपयोग}} | ||
{{Citation style|date=April 2021}} | {{Citation style|date=April 2021}} | ||
[[ज्यामिति]] में, '''जियोडेसिक''' ({{IPAc-en|ˌ|dʒ|iː|.|ə|ˈ|d|ɛ|s|ɪ|k|,_|-|oʊ|-|,_|-|ˈ|d|iː|s|ɪ|k|,_|-|z|ɪ|k}}){{refn|{{Cite dictionary |url=http://www.lexico.com/definition/geodesic |archive-url=https://web.archive.org/web/20200316193343/https://www.lexico.com/definition/geodesic |url-status=dead |archive-date=2020-03-16 |title=geodesic |dictionary=[[Lexico]] UK English Dictionary |publisher=[[Oxford University Press]]}} }}{{refn|{{cite Merriam-Webster|geodesic}}}} एक [[वक्र]] है जो किसी अर्थ में एक सतह | [[ज्यामिति]] में, '''जियोडेसिक'''({{IPAc-en|ˌ|dʒ|iː|.|ə|ˈ|d|ɛ|s|ɪ|k|,_|-|oʊ|-|,_|-|ˈ|d|iː|s|ɪ|k|,_|-|z|ɪ|k}}){{refn|{{Cite dictionary |url=http://www.lexico.com/definition/geodesic |archive-url=https://web.archive.org/web/20200316193343/https://www.lexico.com/definition/geodesic |url-status=dead |archive-date=2020-03-16 |title=geodesic |dictionary=[[Lexico]] UK English Dictionary |publisher=[[Oxford University Press]]}} }}{{refn|{{cite Merriam-Webster|geodesic}}}} एक [[वक्र]] है जो किसी अर्थ में एक सतह के दो बिंदुओं के बीच या समान्यतः एक [[रीमैनियन कई गुना|रीमैनियन मैनिफोल्ड]] में छोटे [[चाप (ज्यामिति)|चाप]] को दर्शाता है।{{efn|For a [[pseudo-Riemannian manifold]], e.g., a [[Lorentzian manifold]], the definition is more complicated.|name=pseudo}} इस शब्द का एक संयोजक के साथ किसी विभेदक बहुआयामी में भी अर्थ हैं। यह एक [[सीधी रेखा|"सीधी रेखा"]] की धारणा का सामान्यीकरण है। | ||
संज्ञा [[जियोडेसिक | संज्ञा [[जियोडेसिक]] और विशेषण [[जियोडेटिक]], [[जियोडेसी]] से आते हैं, जो पृथ्वी के आकार को मापने का विज्ञान हैं, हालांकि कई अंतर्निहित सिद्धांत किसी भी दीर्घवृत्ताकार ज्यामिति पर लागू किए जा सकते हैं। मूल अर्थ में, जियोडेसिक [[ग्रहों की सतह|पृथ्वी की सतह]] पर दो बिंदुओं के बीच सबसे छोटा मार्ग था। एक [[गोलाकार पृथ्वी]] के लिए, यह एक बड़े वृत्त का एक [[रेखा खंड]] है([[ग्रेट-सर्कल दूरी]] भी देखें)। तब से यह शब्द अधिक अमूर्त गणितीय स्थानों के लिए सामान्यीकृत किया गया है; उदाहरण के लिए, [[ग्राफ सिद्धांत]] में, एक ग्राफ़ के दो शीर्षों/नोड्स के बीच एक जियोडेसिक पर विचार किया जा सकता है। | ||
रिमेंनियन मैनिफोल्ड या सबमनीफोल्ड में, जियोडेसिक्स के लोप हो जाने वाले [[जियोडेसिक वक्रता]] के गुणों की विशेषता है। | रिमेंनियन मैनिफोल्ड या सबमनीफोल्ड में, जियोडेसिक्स के लोप हो जाने वाले [[जियोडेसिक वक्रता]] के गुणों की विशेषता है। समान्यतः एक [[affine कनेक्शन|एफ़िन संबंध]] की उपस्थिति में, एक जियोडेसिक को एक वक्र के रूप में परिभाषित किया जाता है, जिसके [[स्पर्शरेखा स्थान|स्पर्शरेखा सदिश]] समानांतर रहते हैं यदि वे इसके साथ [[समानांतर परिवहन]] होते हैं। [[रिमेंनियन मीट्रिक]] के [[लेवी-Civita कनेक्शन|लेवी-किविटा संबंध]] पर इसे लागू करने से पिछली धारणा ठीक हो जाती है। | ||
[[सामान्य सापेक्षता]] में जियोडेसिक्स का विशेष महत्व है। सामान्य सापेक्षता में टाइमलाइक जियोडेसिक्स मुक्त गिरने वाले [[परीक्षण कण|परीक्षण कणों]] की गति का वर्णन करता है। | [[सामान्य सापेक्षता]] में जियोडेसिक्स का विशेष महत्व है। सामान्य सापेक्षता में टाइमलाइक जियोडेसिक्स मुक्त गिरने वाले [[परीक्षण कण|परीक्षण कणों]] की गति का वर्णन करता है। | ||
== परिचय == | == परिचय == | ||
एक घुमावदार जगह में दो दिए गए बिंदुओं के, बीच एक स्थानीय रूप से सबसे छोटा रास्ता माना जाता है{{efn|name=pseudo}}। एक [[रिमेंनियन मैनिफोल्ड]] होने के लिए, एक [[वक्र]] की | एक घुमावदार जगह में दो दिए गए बिंदुओं के, बीच एक स्थानीय रूप से सबसे छोटा रास्ता माना जाता है{{efn|name=pseudo}}। एक [[रिमेंनियन मैनिफोल्ड]] होने के लिए, एक [[वक्र]] की [[लंबाई]] के लिए [[समीकरण]] का उपयोग करके इसे परिभाषित किया जा सकता है(R के एक खुले अंतराल से अंतरिक्ष तक एक फलन f) और फिर विविधताओं की कलन का उपयोग करके बिंदुओं के बीच इसकी लंबाई को कम करना। इसमें कुछ साधारण तकनीकी समस्याएं हैं क्योंकि सबसे छोटे पथ को मापदण्ड करने के विभिन्न तरीकों का अनंत-आयामी स्थान है। वक्र के सेट को उन तक सीमित करना आसान है जो स्थिर गति 1 के साथ मापदण्डयुक्त हैं, जिसका अर्थ है कि वक्र के साथ f(s) से f(t) तक की दूरी |s−t| के बराबर है। समान रूप से, एक अलग मात्रा का उपयोग किया जा सकता है, जिसे वक्र की ऊर्जा कहा जाता है; ऊर्जा को कम करने से जियोडेसिक के लिए समान समीकरण होते हैं(यह 'निरंतर वेग' का एक परिणाम है)। {{citation needed|date=May 2018}} सहज रूप से, इस दूसरे निरूपण को इस बात से समझा जा सकता है कि दो बिंदुओं के बीच फैला एक [[लोचदार बैंड]] इसकी चौड़ाई को कम करेगा, और ऐसा करने से इसकी ऊर्जा कम हो जाएगी। बैंड का परिणामी आकार जियोडेसिक है। | ||
यह संभव है कि दो बिंदुओं के बीच कई अलग-अलग वक्र दूरी को कम कर दें, जैसा कि गोले पर दो बिल्कुल विपरीत बिंदुओं के मामले में होता है। ऐसी स्थिति में, इनमें से कोई भी वक्र भूगणितीय होता | यह संभव है कि दो बिंदुओं के बीच कई अलग-अलग वक्र दूरी को कम कर दें, जैसा कि गोले पर दो बिल्कुल विपरीत बिंदुओं के मामले में होता है। ऐसी स्थिति में, इनमें से कोई भी वक्र भूगणितीय होता हैं। | ||
जियोडेसिक का एक सन्निहित खंड फिर से जियोडेसिक होता है। | जियोडेसिक का एक सन्निहित खंड फिर से जियोडेसिक होता है। | ||
सामान्य तौर पर, जियोडेसिक्स दो बिंदुओं के बीच सबसे "छोटे वक्र" के समान नहीं है, हालांकि दोनों अवधारणाएं | सामान्य तौर पर, जियोडेसिक्स दो बिंदुओं के बीच सबसे "छोटे वक्र" के समान नहीं है, हालांकि दोनों अवधारणाएं आपस में संबंधित हैं। अंतर यह है कि जिओडेसिक्स केवल स्थानीय रूप से बिंदुओं के बीच की सबसे छोटी दूरी है, और "निरंतर गति" के साथ पैरामीटरकृत हैं। एक गोले पर दो बिंदुओं के बीच एक बड़े वृत्त पर लंबा रास्ता तय करना एक जियोडेसिक है, लेकिन यह बिंदुओं के बीच का सबसे छोटा रास्ता नहीं है। नक्शा <math>t \to t^2</math> वास्तविक संख्या रेखा पर इकाई अंतराल से स्वयं को 0 और 1 के बीच सबसे छोटा रास्ता देता है, लेकिन यह एक जियोडेसिक नहीं है क्योंकि एक बिंदु की संगत गति का वेग स्थिर नहीं है। | ||
जियोडेसिक्स | जियोडेसिक्स सामान्यतः [[रीमैनियन ज्यामिति]] और अधिक सामान्यतः [[मीट्रिक ज्यामिति]] के अध्ययन में देखा जाता है। [[सामान्य सापेक्षता]] में, [[अंतरिक्ष-समय]] में भूगर्भ विज्ञान अकेले गुरुत्वाकर्षण के प्रभाव में [[बिंदु कण|बिंदु कणों]] की गति का वर्णन करता है। विशेष रूप से, एक गिरती हुई चट्टान द्वारा लिया गया मार्ग, एक परिक्रमा करने वाले [[उपग्रह]], या एक [[ग्रहीय कक्षा]] का आकार घूमावदार अंतरिक्ष समय में जियोडेसिक्स हैं{{efn|The path is a local maximum of the interval k rather than a local minimum.}}। समान्यतः, [[उप-रिमेंनियन ज्यामिति]] का विषय उन रास्तों से संबंधित है जो वस्तुओं को ले सकते हैं जब वे मुक्त नहीं होते हैं, और उनका आंदोलन विभिन्न तरीकों से बाधित होता है। | ||
यह आलेख [[रीमानियन मैनिफोल्ड्स]] के मामले में भूगर्भ विज्ञान के अस्तित्व को परिभाषित करने, खोजने और साबित करने में | यह आलेख [[रीमानियन मैनिफोल्ड्स]] के मामले में भूगर्भ विज्ञान के अस्तित्व को परिभाषित करने, खोजने और साबित करने में सम्मिलित गणितीय औपचारिकता को प्रस्तुत करता है। यह लेख [[लेवी-सिविता]] संबंध [[छद्म-रीमैनियन मैनिफोल्ड]] के अधिक सामान्य परिस्थिति में चर्चा करता है और [[जियोडेसिक (सामान्य सापेक्षता)|जियोडेसिक(सामान्य सापेक्षता)]] के विशेष परिस्थिति में अधिक विस्तार से चर्चा करता है। | ||
=== उदाहरण === | === उदाहरण === | ||
[[File:Transpolar geodesic on a triaxial ellipsoid case A.svg|thumb|right|200px|एक त्रिअक्षीय दीर्घवृत्त पर एक जियोडेसिक।]] | [[File:Transpolar geodesic on a triaxial ellipsoid case A.svg|thumb|right|200px|एक त्रिअक्षीय दीर्घवृत्त पर एक जियोडेसिक।]] | ||
[[File:Insect on a torus tracing out a non-trivial geodesic.gif|thumb|right|यदि एक कीट को एक सतह पर रखा जाता है और लगातार आगे बढ़ता है, तो परिभाषा के अनुसार यह एक जियोडेसिक का पता लगाएगा।]]सबसे परिचित उदाहरण [[यूक्लिडियन ज्यामिति]] में सीधी रेखाएँ हैं। एक गोले पर, भूभौतिकी के चित्र वृहत [[वृत्त]] होते हैं। एक गोले पर बिंदु A से बिंदु B तक का सबसे छोटा रास्ता A और B से गुजरने वाले बड़े वृत्त के छोटे चाप (ज्यामिति) द्वारा दिया जाता है। यदि A और B प्रतिध्रुवीय बिंदु हैं, तो उनके बीच अपरिमित रूप से कई लघुतम पथ हैं। एक दीर्घवृत्त पर जियोडेसिक्स एक गोले की तुलना में अधिक जटिल तरीके से व्यवहार करता है; विशेष रूप से, वे सामान्य रूप से बंद नहीं होते हैं (आंकड़ा देखें)। | [[File:Insect on a torus tracing out a non-trivial geodesic.gif|thumb|right|यदि एक कीट को एक सतह पर रखा जाता है और लगातार आगे बढ़ता है, तो परिभाषा के अनुसार यह एक जियोडेसिक का पता लगाएगा।]]सबसे परिचित उदाहरण [[यूक्लिडियन ज्यामिति]] में सीधी रेखाएँ हैं। एक गोले पर, भूभौतिकी के चित्र वृहत [[वृत्त]] होते हैं। एक गोले पर बिंदु A से बिंदु B तक का सबसे छोटा रास्ता A और B से गुजरने वाले बड़े वृत्त के छोटे चाप(ज्यामिति) द्वारा दिया जाता है। यदि A और B प्रतिध्रुवीय बिंदु हैं, तो उनके बीच अपरिमित रूप से कई लघुतम पथ हैं। एक दीर्घवृत्त पर जियोडेसिक्स एक गोले की तुलना में अधिक जटिल तरीके से व्यवहार करता है; विशेष रूप से, वे सामान्य रूप से बंद नहीं होते हैं(आंकड़ा देखें)। | ||
=== त्रिकोण{{anchor|Triangle}}=== | === त्रिकोण{{anchor|Triangle}}=== | ||
{{see also| | {{see also|गॉस-बोनट प्रमेय # त्रिकोण के लिए|टोपोनोगोव की प्रमेय}} | ||
[[File:Spherical triangle.svg|thumb|left|150px|{{Anchor|Triangle}}गोले पर एक जियोडेसिक त्रिकोण।]]किसी दिए गए सतह पर तीन बिंदुओं में से प्रत्येक जोड़ी को जोड़ने वाले जियोडेसिक्स द्वारा एक '''जियोडेसिक त्रिकोण''' का निर्माण किया जाता है। गोले पर, | [[File:Spherical triangle.svg|thumb|left|150px|{{Anchor|Triangle}}गोले पर एक जियोडेसिक त्रिकोण।]]किसी दिए गए सतह पर तीन बिंदुओं में से प्रत्येक जोड़ी को जोड़ने वाले जियोडेसिक्स द्वारा एक '''जियोडेसिक त्रिकोण''' का निर्माण किया जाता है। गोले पर, जियोडेसिक वृहत वृत्त चाप होते हैं, जो एक [[गोलाकार त्रिकोण]] बनाते हैं। | ||
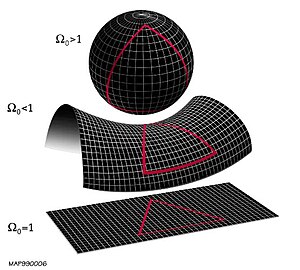
[[Image:End of universe.jpg|thumb|left|धनात्मक (शीर्ष), ऋणात्मक (मध्य) और शून्य (नीचे) वक्रता वाले स्थानों में जियोडेसिक त्रिभुज।]] | [[Image:End of universe.jpg|thumb|left|धनात्मक(शीर्ष), ऋणात्मक(मध्य) और शून्य(नीचे) वक्रता वाले स्थानों में जियोडेसिक त्रिभुज।]] | ||
== मीट्रिक ज्यामिति == | == मीट्रिक ज्यामिति == | ||
'''मीट्रिक ज्यामिति''' में, | '''मीट्रिक ज्यामिति''' में, जियोडेसिक एक वक्र होता है जो हर जगह [[स्थानीय रूप]] से एक [[दूरी]] न्यूनतमकर्ता होता है। अधिक सटीक रूप से, एक [[वक्र]] {{nowrap|''γ'' : ''I'' → ''M''}} एक अंतराल से लेकर [[मीट्रिक स्थान]] M तक एक '''जियोडेसिक''' है यदि कोई स्थिर {{nowrap|''v'' ≥ 0}} ऐसा हैं कि किसी भी {{nowrap|''t'' ∈ ''I''}} के लिए I में t का एक सन्निकट J है जैसे कि किसी के लिए {{nowrap|''t''<sub>1</sub>, ''t''<sub>2</sub> ∈ ''J''}} हमारे पास हैं | ||
:<math>d(\gamma(t_1),\gamma(t_2)) = v \left| t_1 - t_2 \right| .</math> | :<math>d(\gamma(t_1),\gamma(t_2)) = v \left| t_1 - t_2 \right| .</math> | ||
यह रिमेंनियन मैनिफोल्ड के लिए जियोडेसिक की धारणा को सामान्यीकृत करता है। हालांकि, मीट्रिक ज्यामिति में माना जाने वाला जियोडेसिक | यह रिमेंनियन मैनिफोल्ड के लिए जियोडेसिक की धारणा को सामान्यीकृत करता है। हालांकि, मीट्रिक ज्यामिति में माना जाने वाला जियोडेसिक प्रायः [[प्राकृतिक पैरामीटर|प्राकृतिक]] मापदण्ड से सुसज्जित होता है, अर्थात उपरोक्त पहचान में v = 1 और | ||
:<math>d(\gamma(t_1),\gamma(t_2)) = \left| t_1 - t_2 \right| .</math> | :<math>d(\gamma(t_1),\gamma(t_2)) = \left| t_1 - t_2 \right| .</math> | ||
यदि अंतिम समानता सभी के लिए संतुष्ट है {{nowrap|''t''<sub>1</sub>, ''t''<sub>2</sub> ∈ ''I''}}, जियोडेसिक को [[मिनिमाइज़िंग जियोडेसिक]] या सबसे [[छोटा रास्ता]] कहा जाता है। | यदि अंतिम समानता सभी के लिए संतुष्ट है {{nowrap|''t''<sub>1</sub>, ''t''<sub>2</sub> ∈ ''I''}}, जियोडेसिक को [[मिनिमाइज़िंग जियोडेसिक]] या सबसे [[छोटा रास्ता]] कहा जाता है। | ||
सामान्य तौर पर, स्थिर वक्रों को छोड़कर, मीट्रिक स्थान में कोई भूगर्भ विज्ञान नहीं हो सकता है। दूसरे चरम पर, लंबाई के मीट्रिक स्थान में कोई भी दो बिंदु [[सुधार योग्य पथ|सुधार योग्य पथों]] के एक न्यूनतम अनुक्रम से जुड़ जाते हैं, हालांकि इस न्यूनतम अनुक्रम को जियोडेसिक में अभिसरण करने की आवश्यकता नहीं है। | सामान्य तौर पर, स्थिर वक्रों को छोड़कर, मीट्रिक स्थान में कोई भूगर्भ विज्ञान नहीं हो सकता है। दूसरे चरम पर, लंबाई के मीट्रिक स्थान में कोई भी दो बिंदु [[सुधार योग्य पथ|सुधार योग्य पथों]] के एक न्यूनतम अनुक्रम से जुड़ जाते हैं, हालांकि इस न्यूनतम अनुक्रम को जियोडेसिक में अभिसरण करने की आवश्यकता नहीं है। | ||
== रीमानियन ज्यामिति == | == रीमानियन ज्यामिति == | ||
[[मीट्रिक टेंसर]] | [[मीट्रिक टेंसर]] G के साथ एक रिमेंनियन मैनिफोल्ड M में, एक निरंतर भिन्न वक्र की लंबाई L γ : [a,b] → M द्वारा परिभाषित किया गया है। | ||
:<math>L(\gamma)=\int_a^b \sqrt{ g_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t)) }\,dt.</math> | :<math>L(\gamma)=\int_a^b \sqrt{ g_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t)) }\,dt.</math> | ||
M के दो बिंदुओं p और q के बीच की दूरी d(p, q) | M के दो बिंदुओं p और q के बीच की दूरी d(p, q) समग्र ली गयी लंबाई के न्यूनतम के रूप में परिभाषित किया गया है [a, b]→M ऐसा है कि γ(a) = p और γ(b) = q. रिमेंनियन ज्यामिति में, सभी भूगणित स्थानीय रूप से दूरी को कम करने वाले पथ हैं, लेकिन इसका विलोम सत्य नहीं है। वास्तव में, केवल वे पथ जो स्थानीय रूप से दूरी को कम करने वाले और चाप-लंबाई के अनुपात में परिमाणित करने वाले हैं, वे भूगणित हैं। एक रिमेंनियन मैनिफोल्ड पर जियोडेसिक्स को परिभाषित करने का एक अन्य समकक्ष तरीका, उन्हें निम्न [[क्रिया (भौतिकी)|क्रिया या कार्यात्मक ऊर्जा]] के न्यूनतम के रूप मे [[ऊर्जा कार्यात्मक|परिभाषित]] करना है। | ||
:<math>E(\gamma)=\frac{1}{2}\int_a^b g_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t))\,dt.</math> | :<math>E(\gamma)=\frac{1}{2}\int_a^b g_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t))\,dt.</math> | ||
E के सभी न्यूनतम L के भी न्यूनतम हैं, लेकिन L एक बड़ा सेट है क्योंकि L के न्यूनतम पथ मनमाने ढंग से | E के सभी न्यूनतम L के भी न्यूनतम हैं, लेकिन L एक बड़ा सेट है क्योंकि L के न्यूनतम पथ मनमाने ढंग से दुबारा मापदण्ड किए जा सकते हैं(उनकी लंबाई को बदले बिना), जबकि E का न्यूनतम नहीं हो सकता। एक टुकड़े के लिए <math>C^1</math> वक्र(अधिक सामान्यतः, <math>W^{1,2}</math> वक्र), कॉची-श्वार्ज असमानता देता है | ||
:<math>L(\gamma)^2 \le 2(b-a)E(\gamma)</math> | :<math>L(\gamma)^2 \le 2(b-a)E(\gamma)</math> | ||
समानता के साथ यदि और केवल <math>g(\gamma',\gamma')</math> एक स्थिर a.e के बराबर है; पथ को निरंतर गति से यात्रा की जानी चाहिए। ऐसा होता है कि मिनिमाइज़र <math>E(\gamma)</math> भी कम करें <math>L(\gamma)</math>, क्योंकि वे परिबद्ध रूप से परिचालित हो जाते हैं, और असमानता एक समानता है। इस दृष्टिकोण की उपयोगिता यह है कि E के मिनिमाइज़र खोजने की समस्या एक अधिक मजबूत परिवर्तनशील समस्या है। वास्तव में, E का एक "उत्तल कार्य" है <math>\gamma</math>, ताकि उचित कार्यों के प्रत्येक समस्थानिक वर्ग के भीतर, किसी को अस्तित्व, विशिष्टता और मिनिमाइज़र की नियमितता की अपेक्षा करनी चाहिए। इसके विपरीत, कार्यात्मक के न्यूनतमकर्ता <math>L(\gamma)</math> प्रायः बहुत नियमित नहीं होते हैं, क्योंकि मनमाना पुनर्मूल्यांकन की अनुमति है। | समानता के साथ यदि और केवल <math>g(\gamma',\gamma')</math> एक स्थिर a.e के बराबर है; पथ को निरंतर गति से यात्रा की जानी चाहिए। ऐसा होता है कि मिनिमाइज़र <math>E(\gamma)</math> भी कम करें <math>L(\gamma)</math>, क्योंकि वे परिबद्ध रूप से परिचालित हो जाते हैं, और असमानता एक समानता है। इस दृष्टिकोण की उपयोगिता यह है कि E के मिनिमाइज़र खोजने की समस्या एक अधिक मजबूत परिवर्तनशील समस्या है। वास्तव में, E का एक "उत्तल कार्य" है <math>\gamma</math>, ताकि उचित कार्यों के प्रत्येक समस्थानिक वर्ग के भीतर, किसी को अस्तित्व, विशिष्टता और मिनिमाइज़र की नियमितता की अपेक्षा करनी चाहिए। इसके विपरीत, कार्यात्मक के न्यूनतमकर्ता <math>L(\gamma)</math> प्रायः बहुत नियमित नहीं होते हैं, क्योंकि मनमाना पुनर्मूल्यांकन की अनुमति है। | ||
क्रियात्मक E के लिए गति के [[Euler-Lagrange]] समीकरणों को इसके द्वारा स्थानीय निर्देशांकों में दिया जाता है | क्रियात्मक E के लिए गति के [[Euler-Lagrange|यूलर-लैग्रेंज]] समीकरणों को इसके द्वारा स्थानीय निर्देशांकों में दिया जाता है | ||
:<math>\frac{d^2x^\lambda }{dt^2} + \Gamma^{\lambda}_{\mu \nu }\frac{dx^\mu }{dt}\frac{dx^\nu }{dt} = 0,</math> | :<math>\frac{d^2x^\lambda }{dt^2} + \Gamma^{\lambda}_{\mu \nu }\frac{dx^\mu }{dt}\frac{dx^\nu }{dt} = 0,</math> | ||
जहाँ पर <math>\Gamma^\lambda_{\mu\nu}</math> मीट्रिक के क्रिस्टोफेल प्रतीक हैं। यह '''जियोडेसिक समीकरण''' है, जिसकी चर्चा नीचे की गई है। | जहाँ पर <math>\Gamma^\lambda_{\mu\nu}</math> मीट्रिक के क्रिस्टोफेल प्रतीक हैं। यह '''जियोडेसिक समीकरण''' है, जिसकी चर्चा नीचे की गई है। | ||
| Line 61: | Line 61: | ||
:<math>\delta E(\gamma)(\varphi) = \left.\frac{\partial}{\partial t}\right|_{t=0} E(\gamma + t\varphi).</math> | :<math>\delta E(\gamma)(\varphi) = \left.\frac{\partial}{\partial t}\right|_{t=0} E(\gamma + t\varphi).</math> | ||
पहली भिन्नता का [[महत्वपूर्ण बिंदु (गणित)|महत्वपूर्ण बिंदु]] ठीक भूगर्भ विज्ञान है। दूसरी भिन्नता | पहली भिन्नता का [[महत्वपूर्ण बिंदु (गणित)|महत्वपूर्ण बिंदु]] ठीक भूगर्भ विज्ञान है। दूसरी भिन्नता को इस प्रकार परिभाषित किया गया है | ||
:<math>\delta^2 E(\gamma)(\varphi,\psi) = \left.\frac{\partial^2}{\partial s \, \partial t} \right|_{s=t=0} E(\gamma + t\varphi + s\psi).</math> | :<math>\delta^2 E(\gamma)(\varphi,\psi) = \left.\frac{\partial^2}{\partial s \, \partial t} \right|_{s=t=0} E(\gamma + t\varphi + s\psi).</math> | ||
एक उपयुक्त अर्थ में, जियोडेसिक γ के साथ दूसरी भिन्नता के शून्य जैकोबी क्षेत्रों के साथ उत्पन्न होते हैं। जैकोबी क्षेत्रों को इस प्रकार जियोडेसिक्स के माध्यम से विविधता के रूप में माना जाता है। | एक उपयुक्त अर्थ में, जियोडेसिक γ के साथ दूसरी भिन्नता के शून्य जैकोबी क्षेत्रों के साथ उत्पन्न होते हैं। जैकोबी क्षेत्रों को इस प्रकार जियोडेसिक्स के माध्यम से विविधता के रूप में माना जाता है। | ||
[[शास्त्रीय यांत्रिकी]] से विविधतापूर्ण तकनीकों को लागू करके, भूगर्भ विज्ञान को हैमिल्टनियन प्रवाह के रूप में भी माना जा सकता है। वे संबंधित [[हैमिल्टन समीकरण]] के समाधान हैं, जिसमें (छद्म-) रीमैनियन मीट्रिक को [[हैमिल्टनियन यांत्रिकी]] के रूप में लिया गया है। | [[शास्त्रीय यांत्रिकी]] से विविधतापूर्ण तकनीकों को लागू करके, भूगर्भ विज्ञान को हैमिल्टनियन प्रवाह के रूप में भी माना जा सकता है। वे संबंधित [[हैमिल्टन समीकरण]] के समाधान हैं, जिसमें(छद्म-) रीमैनियन मीट्रिक को [[हैमिल्टनियन यांत्रिकी]] के रूप में लिया गया है। | ||
== एफ़िन जियोडेसिक्स == | == एफ़िन जियोडेसिक्स == | ||
{{See also| | {{See also|सामान्य सापेक्षता में जियोडेसिक्स}} | ||
एफ़िन | |||
एफ़िन संबंध ∇ के साथ एक चिकने मैनिफोल्ड ''M'' पर एक जियोडेसिक को वक्र γ(''t'') के रूप में परिभाषित किया गया है, जैसे कि वक्र के समानांतर परिवहन स्पर्शरेखा सदिश को वक्र में संरक्षित करता है, इसलिए | |||
{{NumBlk|:|<math> \nabla_{\dot\gamma} \dot\gamma= 0</math>|{{EquationRef|1}}}} | {{NumBlk|:|<math> \nabla_{\dot\gamma} \dot\gamma= 0</math>|{{EquationRef|1}}}} | ||
वक्र के साथ प्रत्येक बिंदु पर, जहाँ <math>\dot\gamma</math> के संबंध में डेरिवेटिव हैं <math>t</math>. अधिक सटीक रूप से, सहपरिवर्ती व्युत्पन्न को परिभाषित करने के लिए पहले <math>\dot\gamma</math> को बढ़ाना जरूरी है। <math>\dot\gamma</math> को एक खुले सेट में निरंतर भिन्न होने वाले [[वेक्टर क्षेत्र|सदिश क्षेत्र]] में विस्तारित किया जाए। हालाँकि, ({{EquationNote|1}}) का परिणामी मूल्य विस्तार की पसंद से स्वतंत्र है। | वक्र के साथ प्रत्येक बिंदु पर, जहाँ <math>\dot\gamma</math> के संबंध में डेरिवेटिव हैं <math>t</math>. अधिक सटीक रूप से, सहपरिवर्ती व्युत्पन्न को परिभाषित करने के लिए पहले <math>\dot\gamma</math> को बढ़ाना जरूरी है। <math>\dot\gamma</math> को एक खुले सेट में निरंतर भिन्न होने वाले [[वेक्टर क्षेत्र|सदिश क्षेत्र]] में विस्तारित किया जाए। हालाँकि,({{EquationNote|1}}) का परिणामी मूल्य विस्तार की पसंद से स्वतंत्र है। | ||
M पर [[स्थानीय निर्देशांक]] का उपयोग करके, हम 'जियोडेसिक समीकरण' (संकलन सम्मेलन का उपयोग करके) लिख सकते हैं। | M पर [[स्थानीय निर्देशांक]] का उपयोग करके, हम 'जियोडेसिक समीकरण'(संकलन सम्मेलन का उपयोग करके) लिख सकते हैं। | ||
:<math>\frac{d^2\gamma^\lambda }{dt^2} + \Gamma^{\lambda}_{\mu \nu }\frac{d\gamma^\mu }{dt}\frac{d\gamma^\nu }{dt} = 0\ ,</math> | :<math>\frac{d^2\gamma^\lambda }{dt^2} + \Gamma^{\lambda}_{\mu \nu }\frac{d\gamma^\mu }{dt}\frac{d\gamma^\nu }{dt} = 0\ ,</math> | ||
जहाँ पर <math>\gamma^\mu = x^\mu \circ \gamma (t)</math> वक्र γ(t) के निर्देशांक हैं और <math>\Gamma^{\lambda }_{\mu \nu }</math> | जहाँ पर <math>\gamma^\mu = x^\mu \circ \gamma (t)</math> वक्र γ(t) के निर्देशांक हैं और <math>\Gamma^{\lambda }_{\mu \nu }</math> संबंध ∇ के क्रिस्टोफेल प्रतीक हैं। यह निर्देशांकों के लिए एक साधारण अवकल समीकरण है। प्रारंभिक स्थिति और प्रारंभिक वेग दिए जाने पर इसका एक अनूठा समाधान है। इसलिए, शास्त्रीय यांत्रिकी के दृष्टिकोण से, भूगर्भ विज्ञान को कई गुना [[मुक्त कण|मुक्त कणों]] के प्रक्षेपवक्र के रूप में माना जा सकता है। दरअसल, समीकरण <math> \nabla_{\dot\gamma} \dot\gamma= 0</math> इसका मतलब है कि वक्र के [[त्वरण (अंतर ज्यामिति)|त्वरण सदिश]] का सतह की दिशा में कोई घटक नहीं है(और इसलिए यह वक्र के प्रत्येक बिंदु पर सतह के स्पर्शरेखा तल के लंबवत है)। तो, गति पूरी तरह से सतह के झुकने से निर्धारित होती है। यह सामान्य सापेक्षता का भी विचार है जहां कण भूगर्भ विज्ञान पर चलते हैं और झुकना गुरुत्वाकर्षण के कारण होता है। | ||
=== अस्तित्व और विशिष्टता === | === अस्तित्व और विशिष्टता === | ||
जियोडेसिक्स के लिए स्थानीय अस्तित्व और अद्वितीयता प्रमेय बताता है कि एफाइन | जियोडेसिक्स के लिए स्थानीय अस्तित्व और अद्वितीयता प्रमेय बताता है कि एफाइन संबंध के साथ एक चिकनी मैनिफोल्ड पर जियोडेसिक्स उपलब्ध हैं, और अद्वितीय हैं। अधिक सटीक रूप से | ||
: M में किसी भी बिंदु P के लिए और | : M में किसी भी बिंदु P के लिए और ''T<sub>p</sub>M'' में किसी भी सदिश V के लिए(P पर M के लिए स्पर्शरेखा स्थान) एक अद्वितीय जियोडेसिक उपलब्ध है <math>\gamma \,</math> : I → M ऐसा कि | ||
::<math>\gamma(0) = p \,</math> तथा | ::<math>\gamma(0) = p \,</math> तथा | ||
::<math>\dot\gamma(0) = V,</math> | ::<math>\dot\gamma(0) = V,</math> | ||
| Line 88: | Line 89: | ||
इस प्रमेय का प्रमाण साधारण अंतर समीकरणों के सिद्धांत से मिलता है, यह देखते हुए कि जियोडेसिक समीकरण एक दूसरे क्रम का ODE है। इसके बाद निर्धारित प्रारंभिक स्थितियों के साथ ODE के समाधान के लिए [[पिकार्ड-लिंडेलोफ प्रमेय]] से अस्तित्व और विशिष्टता का पालन होता है। γ P और V दोनों पर सुचारू कार्य निर्भर करता है। | इस प्रमेय का प्रमाण साधारण अंतर समीकरणों के सिद्धांत से मिलता है, यह देखते हुए कि जियोडेसिक समीकरण एक दूसरे क्रम का ODE है। इसके बाद निर्धारित प्रारंभिक स्थितियों के साथ ODE के समाधान के लिए [[पिकार्ड-लिंडेलोफ प्रमेय]] से अस्तित्व और विशिष्टता का पालन होता है। γ P और V दोनों पर सुचारू कार्य निर्भर करता है। | ||
सामान्य तौर पर, हो सकता है कि ''I'' पूरी तरह से 'R' न हो, उदाहरण के लिए 'R' में खुली डिस्क के | सामान्य तौर पर, हो सकता है कि ''I'' पूरी तरह से 'R' न हो, उदाहरण के लिए 'R' में खुली डिस्क के लिए कोई भी <sup>{{mvar|γ}} सभी {{mvar|ℝ}} तक विस्तारित होता है यदि और केवल अगर {{mvar|M}} [[भौगोलिक रूप]] से पूर्ण हो। | ||
=== जियोडेसिक प्रवाह{{anchor|Flow}}=== | === जियोडेसिक प्रवाह{{anchor|Flow}}=== | ||
'''जियोडेसिक''' प्रवाह एक स्थानीय '''R'''-ग्रुप एक्शन है जो निम्नलिखित तरीके से परिभाषित | '''जियोडेसिक''' प्रवाह एक स्थानीय '''R'''-ग्रुप एक्शन है जो निम्नलिखित तरीके से परिभाषित ''M'' के [[स्पर्शरेखा बंडल]] ''TM'' पर है। | ||
:<math>G^t(V)=\gamma_V(t)</math> | :<math>G^t(V)=\gamma_V(t)</math> | ||
जहां T ∈ ''''R'''<nowiki/>', V ∈ TM और <math>\gamma_V</math> प्रारंभिक डेटा के साथ जियोडेसिक को दर्शाता है <math>\dot\gamma_V(0)=V</math>। इस प्रकार, <math>G^t</math>(V) = exp(tV) | जहां T ∈ ''''R'''<nowiki/>', V ∈ TM और <math>\gamma_V</math> प्रारंभिक डेटा के साथ जियोडेसिक को दर्शाता है <math>\dot\gamma_V(0)=V</math>। इस प्रकार, <math>G^t</math>(V) = exp(tV) सदिश tV का चरघातांकी मानचित्र है। जियोडेसिक प्रवाह की बंद कक्षा M पर [[बंद जियोडेसिक]] से मेल खाती है। | ||
एक (छद्म-) रिमेंनियन मैनिफोल्ड पर, जियोडेसिक प्रवाह की पहचान कॉटेन्जेंट बंडल पर [[हैमिल्टनियन प्रवाह]] के साथ की जाती है। हेमिल्टनियन यांत्रिकी तब (छद्म-) रीमैनियन मीट्रिक के व्युत्क्रम द्वारा दी जाती है, जिसका मूल्यांकन [[विहित एक रूप]] के विरुद्ध किया जाता है। विशेष रूप से प्रवाह (छद्म-) रीमैनियन मीट्रिक को संरक्षित करता है <math>g</math>, अर्थात। | एक(छद्म-) रिमेंनियन मैनिफोल्ड पर, जियोडेसिक प्रवाह की पहचान कॉटेन्जेंट बंडल पर [[हैमिल्टनियन प्रवाह]] के साथ की जाती है। हेमिल्टनियन यांत्रिकी तब(छद्म-) रीमैनियन मीट्रिक के व्युत्क्रम द्वारा दी जाती है, जिसका मूल्यांकन [[विहित एक रूप]] के विरुद्ध किया जाता है। विशेष रूप से प्रवाह(छद्म-) रीमैनियन मीट्रिक को संरक्षित करता है <math>g</math>, अर्थात। | ||
: <math>g(G^t(V),G^t(V))=g(V,V). \, </math> | : <math>g(G^t(V),G^t(V))=g(V,V). \, </math> | ||
विशेष रूप से, जब V एक इकाई | विशेष रूप से, जब V एक इकाई सदिश है, <math>\gamma_V</math> पूरे समय इकाई गति बनी रहती है, इसलिए जियोडेसिक प्रवाह [[इकाई स्पर्शरेखा बंडल]] के लिए स्पर्शरेखा है। लिउविल की प्रमेय का अर्थ स्पर्शरेखा बंडल पर गतिज माप का व्युत्क्रम हैं। | ||
=== जियोडेसिक स्प्रे === | === जियोडेसिक स्प्रे === | ||
{{further| | {{further|स्प्रे(गणित) जियोडेसिक}} | ||
जियोडेसिक प्रवाह स्पर्शरेखा बंडल में वक्रों के एक परिवार को परिभाषित करता है। इन वक्रों के व्युत्पन्न स्पर्शरेखा बंडल के [[कुल स्थान]] पर एक [[वेक्टर क्षेत्र]] को परिभाषित करते हैं, जिसे '''जियोडेसिक''' [[स्प्रे (गणित)|स्प्रे]] के रूप में जाना जाता है। | जियोडेसिक प्रवाह स्पर्शरेखा बंडल में वक्रों के एक परिवार को परिभाषित करता है। इन वक्रों के व्युत्पन्न स्पर्शरेखा बंडल के [[कुल स्थान]] पर एक [[वेक्टर क्षेत्र|सदिश क्षेत्र]] को परिभाषित करते हैं, जिसे '''जियोडेसिक''' [[स्प्रे (गणित)|स्प्रे]] के रूप में जाना जाता है। | ||
अधिक सटीक रूप से, एक एफ़िन | अधिक सटीक रूप से, एक एफ़िन संबंध [[क्षैतिज बंडल]] और [[लंबवत बंडल|लंबवत बंडलो]] में [[डबल स्पर्शरेखा बंडल]] TT''M'' के विभाजन को जन्म देता है: | ||
:<math>TTM = H\oplus V.</math> | :<math>TTM = H\oplus V.</math> | ||
जियोडेसिक स्प्रे अद्वितीय क्षैतिज | जियोडेसिक स्प्रे अद्वितीय क्षैतिज सदिश क्षेत्र W सन्तोषजनक हैं | ||
:<math>\pi_* W_v = v\,</math> | :<math>\pi_* W_v = v\,</math> | ||
प्रत्येक बिंदु पर V ∈ TM; यहाँ π<sub>∗</sub>: TTM → TM स्पर्शरेखा बंडल से जुड़े प्रक्षेपण π : TM → M के साथ [[पुशफ़ॉरवर्ड (अंतर)]] को दर्शाता है। | प्रत्येक बिंदु पर V ∈ TM; यहाँ π<sub>∗</sub>: TTM → TM स्पर्शरेखा बंडल से जुड़े प्रक्षेपण π : TM → M के साथ [[पुशफ़ॉरवर्ड (अंतर)|जारी रखने वाले(अंतर)]] को दर्शाता है। | ||
प्रायः | प्रायः वही निर्माण स्पर्शरेखा बंडल पर किसी भी [[एह्रेसमैन कनेक्शन|एह्रेसमैन संबंध]] के लिए सदिश फ़ील्ड बनाने की अनुमति देता है। परिणामी सदिश फ़ील्ड के लिए एक स्प्रे(हटाए गए स्पर्शरेखा बंडल TM \ {0} पर) होने के लिए यह पर्याप्त है कि संबंध सकारात्मक पुनर्विक्रय के तहत समान हो, इसे रैखिक होने की आवश्यकता नहीं है। अर्थात्,([[एह्रेसमैन कनेक्शन|cf. एह्रेसमैन संबंध#सदिश बंडल और सहपरिवर्ती डेरिवेटिव)]] यह पर्याप्त है कि क्षैतिज वितरण संतुष्ट करता है। | ||
:<math>H_{\lambda X} = d(S_\lambda)_X H_X\,</math> | :<math>H_{\lambda X} = d(S_\lambda)_X H_X\,</math> | ||
प्रत्येक X ∈ TM \ {0} और λ > 0 के लिए। यहाँ d(S<sub>λ</sub>) | प्रत्येक X ∈ TM \ {0} और λ > 0 के लिए। यहाँ d(S<sub>λ</sub>) अदिश समरूपता के साथ जारी रखना हैं । <math>S_\lambda: X\mapsto \lambda X.</math> इस तरह से उत्पन्न होने वाले गैर-रैखिक संबंध का एक विशेष मामला [[फिन्सलर कई गुना|फिन्सलर मनिफॉल्ड]] से जुड़ा हुआ है। | ||
=== | === एफ़िन और प्रोजेक्टिव जियोडेसिक्स === | ||
समीकरण ({{EquationNote|1}}) | समीकरण({{EquationNote|1}}) एफ़िन पैरामीटराइजेशन के तहत अपरिवर्तनीय है; वह है, फॉर्म का पैरामीटराइजेशन | ||
:<math>t\mapsto at+b</math> | :<math>t\mapsto at+b</math> | ||
जहाँ a और b अचर वास्तविक संख्याएँ हैं। इस प्रकार सन्निहित वक्रों के एक निश्चित वर्ग को निर्दिष्ट करने के अलावा, जियोडेसिक समीकरण प्रत्येक वक्र पर मानकीकरणों के एक पसंदीदा वर्ग को भी निर्धारित करता है। तदनुसार, | जहाँ a और b अचर वास्तविक संख्याएँ हैं। इस प्रकार सन्निहित वक्रों के एक निश्चित वर्ग को निर्दिष्ट करने के अलावा, जियोडेसिक समीकरण प्रत्येक वक्र पर मानकीकरणों के एक पसंदीदा वर्ग को भी निर्धारित करता है। तदनुसार, समाधान({{EquationNote|1}}) को [[एफाइन पैरामीटर|एफाइन]] मापदण्ड के साथ जियोडेसिक्स कहा जाता है। | ||
एक | एक संबंध ''द्वारा निर्धारित'' होता है, की बंधुत्वपूर्ण पैरामिट्रीकृत जिओडेसिक्स के परिवार का होता है, [[मरोड़ टेंसर]] तक {{harv|स्पिवक 1999, अध्याय 6, परिशिष्ट।||loc=}}मरोड़ वास्तव में, जियोडेसिक्स के परिवार को प्रभावित नहीं करता है, क्योंकि जियोडेसिक समीकरण केवल संबंध के सममित भाग पर निर्भर करता है। अधिक सटीक रूप से, अगर <math>\nabla, \bar{\nabla}</math> दो संबंध ऐसे हैं कि अंतर टेंसर | ||
:<math>D(X,Y) = \nabla_XY-\bar{\nabla}_XY</math> | :<math>D(X,Y) = \nabla_XY-\bar{\nabla}_XY</math> | ||
[[तिरछा-सममित मैट्रिक्स]] है | तिरछा-सममित, तब <math>\nabla</math> तथा <math>\bar{\nabla}</math> एक ही जियोडेसिक्स है, एक ही | [[तिरछा-सममित मैट्रिक्स]] है | तिरछा-सममित, तब <math>\nabla</math> तथा <math>\bar{\nabla}</math> एक ही जियोडेसिक्स है, एक ही एफ़िन पैरामीटराइजेशन के साथ। इसके अलावा, एक ही जियोडेसिक्स के रूप में एक अनूठा संबंध है <math>\nabla</math>, लेकिन गायब होने वाले मरोड़ के साथ। | ||
एक विशेष | एक विशेष मापदण्ड के बिना जिओडेसिक्स को [[प्रक्षेपण कनेक्शन|प्रक्षेपण संबंध]] द्वारा वर्णित किया गया है। | ||
== कम्प्यूटेशनल तरीके == | == कम्प्यूटेशनल तरीके == | ||
| Line 141: | Line 141: | ||
| caption2 = The curved line drawn using the ribbon test is a straight line on a flat surface. This is because a cone can be made into a 2-d circular sector. | | caption2 = The curved line drawn using the ribbon test is a straight line on a flat surface. This is because a cone can be made into a 2-d circular sector. | ||
}} | }} | ||
'''रिबन टेस्ट''' एक भौतिक सतह पर जियोडेसिक खोजने का एक तरीका है।<ref>[[Michael Stevens (educator)|Michael Stevens]] (Nov 2, 2017), ''[https://www.youtube.com/watch?v=Xc4xYacTu-E]''.</ref> यह विचार एक सीधी रेखा(एक रिबन) के चारों ओर थोड़ा सा कागज एक घुमावदार सतह पर फिट करने के लिए है, जितना संभव हो सके रिबन को खींचे या निचोड़े बिना(इसकी आंतरिक ज्यामिति को बदले बिना)। | |||
उदाहरण के लिए, जब एक रिबन को एक शंकु के चारों ओर एक रिंग के रूप में लपेटा जाता है, तो रिबन शंकु की सतह पर नहीं रहेगा बल्कि बाहर चिपक जाएगा, ताकि शंकु पर वृत्त जियोडेसिक न हो। यदि रिबन को इस तरह समायोजित किया जाता है कि इसके सभी भाग शंकु की सतह को छूते हैं, तो यह एक जियोडेसिक को एक सन्निकटन देगा। | उदाहरण के लिए, जब एक रिबन को एक शंकु के चारों ओर एक रिंग के रूप में लपेटा जाता है, तो रिबन शंकु की सतह पर नहीं रहेगा बल्कि बाहर चिपक जाएगा, ताकि शंकु पर वृत्त जियोडेसिक न हो। यदि रिबन को इस तरह समायोजित किया जाता है कि इसके सभी भाग शंकु की सतह को छूते हैं, तो यह एक जियोडेसिक को एक सन्निकटन देगा। | ||
गणितीय रूप से रिबन टेस्ट को मैपिंग खोजने के रूप में तैयार किया जा सकता है <math>f: N(l) \to S</math> एक | गणितीय रूप से रिबन टेस्ट को मैपिंग खोजने के रूप में तैयार किया जा सकता है <math>f: N(l) \to S</math> के एक सन्निकट का <math>N</math> एक पंक्ति के <math>l</math> सतह में <math>S</math> विमान हैं ताकि मैपिंग हो सके, <math>f</math> आस-पास की दूरियों को ज्यादा नहीं बदलेगा <math>l</math> बहुत ज्यादा; अर्थात् दूरी पर <math>\varepsilon</math> से <math>l</math> अपने पास<math>g_N-f^*(g_S)=O(\varepsilon^2)</math> जहाँ पर <math>g_N</math> तथा <math>g_S</math> में <math>N</math> तथा <math>S</math> मेट्रिक्स हैं। | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
| Line 154: | Line 154: | ||
* पृथ्वी पर या उसके निकट क्षैतिज दूरी; [[पृथ्वी भूभौतिकी]] देखें | * पृथ्वी पर या उसके निकट क्षैतिज दूरी; [[पृथ्वी भूभौतिकी]] देखें | ||
* रेंडरिंग के लिए सतहों पर इमेज मैप करना; [[यूवी मैपिंग]] देखें | * रेंडरिंग के लिए सतहों पर इमेज मैप करना; [[यूवी मैपिंग]] देखें | ||
* आणविक गतिशीलता में कण गति | आणविक गतिशीलता (एमडी) कंप्यूटर सिमुलेशन<ref>{{Cite journal|last1=Ingebrigtsen|first1=Trond S.|last2=Toxvaerd|first2=Søren|last3=Heilmann|first3=Ole J.|last4=Schrøder|first4=Thomas B.|last5=Dyre|first5=Jeppe C.|date=2011|title=एनवीयू गतिकी। I. निरंतर-संभावित-ऊर्जा हाइपरसफेस पर जियोडेसिक गति|url=https://aip.scitation.org/doi/10.1063/1.3623585|journal=The Journal of Chemical Physics|volume=135|issue=10|pages=104101|doi=10.1063/1.3623585|pmid=21932870|arxiv=1012.3447|bibcode=2011JChPh.135j4101I|s2cid=16554305|issn=0021-9606}}</ref> | * आणविक गतिशीलता में कण गति | आणविक गतिशीलता(एमडी) कंप्यूटर सिमुलेशन<ref>{{Cite journal|last1=Ingebrigtsen|first1=Trond S.|last2=Toxvaerd|first2=Søren|last3=Heilmann|first3=Ole J.|last4=Schrøder|first4=Thomas B.|last5=Dyre|first5=Jeppe C.|date=2011|title=एनवीयू गतिकी। I. निरंतर-संभावित-ऊर्जा हाइपरसफेस पर जियोडेसिक गति|url=https://aip.scitation.org/doi/10.1063/1.3623585|journal=The Journal of Chemical Physics|volume=135|issue=10|pages=104101|doi=10.1063/1.3623585|pmid=21932870|arxiv=1012.3447|bibcode=2011JChPh.135j4101I|s2cid=16554305|issn=0021-9606}}</ref> | ||
* रोबोट [[गति योजना]] (जैसे, कार के पुर्जों को पेंट करते समय); [[सबसे छोटा पथ समस्या]] देखें | * रोबोट [[गति योजना]](जैसे, कार के पुर्जों को पेंट करते समय); [[सबसे छोटा पथ समस्या]] देखें | ||
== यह भी देखें == | == यह भी देखें == | ||
{{div col}} | {{div col}} | ||
* {{annotated link| | * {{annotated link|सामान्य सापेक्षता के गणित का परिचय}} | ||
* {{annotated link| | * {{annotated link|क्लैरॉट सम्बन्ध}} | ||
* {{annotated link| | * {{annotated link|अवकलनीय वक्र}} | ||
* सतहों की विभेदक ज्यामिति | * सतहों की विभेदक ज्यामिति | ||
* [[जियोडेसिक सर्कल]] | * [[जियोडेसिक सर्कल]] | ||
* {{annotated link| | * {{annotated link|हॉफ; रिनो प्रमेय}} | ||
* {{annotated link| | * {{annotated link|आंतरिक मीट्रिक}} | ||
* {{annotated link| | * {{annotated link|समदैशिक रेखा}} | ||
* {{annotated link| | * {{annotated link|जैकोबी फील्ड}} | ||
* {{annotated link| | * {{annotated link|मोर्स सिद्धांत}} | ||
* {{annotated link| | * {{annotated link|ज़ोल सतह}} | ||
* {{annotated link| | * {{annotated link|स्पाइडर और फ्लाई की समस्या}} | ||
{{div col end}} | {{div col end}} | ||
| Line 202: | Line 202: | ||
*सामान्य सापेक्षता में जियोडेसिक्स | *सामान्य सापेक्षता में जियोडेसिक्स | ||
*अलग करने योग्य कई गुना | *अलग करने योग्य कई गुना | ||
*दूरी (ग्राफ सिद्धांत) | *दूरी(ग्राफ सिद्धांत) | ||
*निर्बाध गिरावट | *निर्बाध गिरावट | ||
*ग्राफ (असतत गणित) | *ग्राफ(असतत गणित) | ||
*सतहों की अंतर ज्यामिति | *सतहों की अंतर ज्यामिति | ||
*खुला अंतराल | *खुला अंतराल | ||
| Line 230: | Line 230: | ||
*क्रिस्टोफर प्रतीक | *क्रिस्टोफर प्रतीक | ||
*चिकना समारोह | *चिकना समारोह | ||
*समूह क्रिया (गणित) | *समूह क्रिया(गणित) | ||
*प्रवाह (गणित) | *प्रवाह(गणित) | ||
*घातीय नक्शा (रीमैनियन ज्यामिति) | *घातीय नक्शा(रीमैनियन ज्यामिति) | ||
*धक्का आगे (अंतर) | *धक्का आगे(अंतर) | ||
*आर्थिक समीकरण | *आर्थिक समीकरण | ||
*आणविक गतिकी | *आणविक गतिकी | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
{{wikiquote}} | {{wikiquote}} | ||
* [http://www.cmsim.eu/papers_pdf/january_2012_papers/25_CMSIM_2012_Pokorny_1_281-298.pdf Geodesics Revisited] — Introduction to geodesics including two ways of derivation of the equation of geodesic with applications in geometry (geodesic on a sphere and on a [[torus]]), mechanics ([[brachistochrone]]) and optics (light beam in inhomogeneous medium). | * [http://www.cmsim.eu/papers_pdf/january_2012_papers/25_CMSIM_2012_Pokorny_1_281-298.pdf Geodesics Revisited] — Introduction to geodesics including two ways of derivation of the equation of geodesic with applications in geometry(geodesic on a sphere and on a [[torus]]), mechanics([[brachistochrone]]) and optics(light beam in inhomogeneous medium). | ||
* [http://www.map.mpim-bonn.mpg.de/Totally_geodesic_submanifold Totally geodesic submanifold] at the Manifold Atlas | * [http://www.map.mpim-bonn.mpg.de/Totally_geodesic_submanifold Totally geodesic submanifold] at the Manifold Atlas | ||
| Line 245: | Line 245: | ||
{{Tensors}} | {{Tensors}} | ||
{{Authority control}} | {{Authority control}} | ||
[[Category: | [[Category:All articles lacking in-text citations]] | ||
[[Category:All articles to be expanded]] | |||
[[Category:All articles with unsourced statements]] | |||
[[Category:Articles lacking in-text citations from July 2014]] | |||
[[Category:Articles to be expanded from June 2014]] | |||
[[Category:Articles using small message boxes]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:Articles with short description]] | |||
[[Category:Articles with unsourced statements from May 2018]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:CS1 maint]] | |||
[[Category:CS1 Ελληνικά-language sources (el)]] | |||
[[Category:Citation Style 1 templates|W]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 25/11/2022]] | [[Category:Created On 25/11/2022]] | ||
[[Category:Exclude in print]] | |||
[[Category:Interwiki category linking templates]] | |||
[[Category:Interwiki link templates]] | |||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite web]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Wikimedia Commons templates]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:जियोडेसिक (गणित)| ]] | |||
[[Category:विभेदक ज्यामिति]] | |||
Latest revision as of 10:09, 14 December 2022
This article has an unclear citation style. (April 2021) (Learn how and when to remove this template message) |
ज्यामिति में, जियोडेसिक(/ˌdʒiː.əˈdɛsɪk, -oʊ-, -ˈdiːsɪk, -zɪk/)[1][2] एक वक्र है जो किसी अर्थ में एक सतह के दो बिंदुओं के बीच या समान्यतः एक रीमैनियन मैनिफोल्ड में छोटे चाप को दर्शाता है।[lower-alpha 1] इस शब्द का एक संयोजक के साथ किसी विभेदक बहुआयामी में भी अर्थ हैं। यह एक "सीधी रेखा" की धारणा का सामान्यीकरण है।
संज्ञा जियोडेसिक और विशेषण जियोडेटिक, जियोडेसी से आते हैं, जो पृथ्वी के आकार को मापने का विज्ञान हैं, हालांकि कई अंतर्निहित सिद्धांत किसी भी दीर्घवृत्ताकार ज्यामिति पर लागू किए जा सकते हैं। मूल अर्थ में, जियोडेसिक पृथ्वी की सतह पर दो बिंदुओं के बीच सबसे छोटा मार्ग था। एक गोलाकार पृथ्वी के लिए, यह एक बड़े वृत्त का एक रेखा खंड है(ग्रेट-सर्कल दूरी भी देखें)। तब से यह शब्द अधिक अमूर्त गणितीय स्थानों के लिए सामान्यीकृत किया गया है; उदाहरण के लिए, ग्राफ सिद्धांत में, एक ग्राफ़ के दो शीर्षों/नोड्स के बीच एक जियोडेसिक पर विचार किया जा सकता है।
रिमेंनियन मैनिफोल्ड या सबमनीफोल्ड में, जियोडेसिक्स के लोप हो जाने वाले जियोडेसिक वक्रता के गुणों की विशेषता है। समान्यतः एक एफ़िन संबंध की उपस्थिति में, एक जियोडेसिक को एक वक्र के रूप में परिभाषित किया जाता है, जिसके स्पर्शरेखा सदिश समानांतर रहते हैं यदि वे इसके साथ समानांतर परिवहन होते हैं। रिमेंनियन मीट्रिक के लेवी-किविटा संबंध पर इसे लागू करने से पिछली धारणा ठीक हो जाती है।
सामान्य सापेक्षता में जियोडेसिक्स का विशेष महत्व है। सामान्य सापेक्षता में टाइमलाइक जियोडेसिक्स मुक्त गिरने वाले परीक्षण कणों की गति का वर्णन करता है।
परिचय
एक घुमावदार जगह में दो दिए गए बिंदुओं के, बीच एक स्थानीय रूप से सबसे छोटा रास्ता माना जाता है[lower-alpha 1]। एक रिमेंनियन मैनिफोल्ड होने के लिए, एक वक्र की लंबाई के लिए समीकरण का उपयोग करके इसे परिभाषित किया जा सकता है(R के एक खुले अंतराल से अंतरिक्ष तक एक फलन f) और फिर विविधताओं की कलन का उपयोग करके बिंदुओं के बीच इसकी लंबाई को कम करना। इसमें कुछ साधारण तकनीकी समस्याएं हैं क्योंकि सबसे छोटे पथ को मापदण्ड करने के विभिन्न तरीकों का अनंत-आयामी स्थान है। वक्र के सेट को उन तक सीमित करना आसान है जो स्थिर गति 1 के साथ मापदण्डयुक्त हैं, जिसका अर्थ है कि वक्र के साथ f(s) से f(t) तक की दूरी |s−t| के बराबर है। समान रूप से, एक अलग मात्रा का उपयोग किया जा सकता है, जिसे वक्र की ऊर्जा कहा जाता है; ऊर्जा को कम करने से जियोडेसिक के लिए समान समीकरण होते हैं(यह 'निरंतर वेग' का एक परिणाम है)।[citation needed] सहज रूप से, इस दूसरे निरूपण को इस बात से समझा जा सकता है कि दो बिंदुओं के बीच फैला एक लोचदार बैंड इसकी चौड़ाई को कम करेगा, और ऐसा करने से इसकी ऊर्जा कम हो जाएगी। बैंड का परिणामी आकार जियोडेसिक है।
यह संभव है कि दो बिंदुओं के बीच कई अलग-अलग वक्र दूरी को कम कर दें, जैसा कि गोले पर दो बिल्कुल विपरीत बिंदुओं के मामले में होता है। ऐसी स्थिति में, इनमें से कोई भी वक्र भूगणितीय होता हैं।
जियोडेसिक का एक सन्निहित खंड फिर से जियोडेसिक होता है।
सामान्य तौर पर, जियोडेसिक्स दो बिंदुओं के बीच सबसे "छोटे वक्र" के समान नहीं है, हालांकि दोनों अवधारणाएं आपस में संबंधित हैं। अंतर यह है कि जिओडेसिक्स केवल स्थानीय रूप से बिंदुओं के बीच की सबसे छोटी दूरी है, और "निरंतर गति" के साथ पैरामीटरकृत हैं। एक गोले पर दो बिंदुओं के बीच एक बड़े वृत्त पर लंबा रास्ता तय करना एक जियोडेसिक है, लेकिन यह बिंदुओं के बीच का सबसे छोटा रास्ता नहीं है। नक्शा वास्तविक संख्या रेखा पर इकाई अंतराल से स्वयं को 0 और 1 के बीच सबसे छोटा रास्ता देता है, लेकिन यह एक जियोडेसिक नहीं है क्योंकि एक बिंदु की संगत गति का वेग स्थिर नहीं है।
जियोडेसिक्स सामान्यतः रीमैनियन ज्यामिति और अधिक सामान्यतः मीट्रिक ज्यामिति के अध्ययन में देखा जाता है। सामान्य सापेक्षता में, अंतरिक्ष-समय में भूगर्भ विज्ञान अकेले गुरुत्वाकर्षण के प्रभाव में बिंदु कणों की गति का वर्णन करता है। विशेष रूप से, एक गिरती हुई चट्टान द्वारा लिया गया मार्ग, एक परिक्रमा करने वाले उपग्रह, या एक ग्रहीय कक्षा का आकार घूमावदार अंतरिक्ष समय में जियोडेसिक्स हैं[lower-alpha 2]। समान्यतः, उप-रिमेंनियन ज्यामिति का विषय उन रास्तों से संबंधित है जो वस्तुओं को ले सकते हैं जब वे मुक्त नहीं होते हैं, और उनका आंदोलन विभिन्न तरीकों से बाधित होता है।
यह आलेख रीमानियन मैनिफोल्ड्स के मामले में भूगर्भ विज्ञान के अस्तित्व को परिभाषित करने, खोजने और साबित करने में सम्मिलित गणितीय औपचारिकता को प्रस्तुत करता है। यह लेख लेवी-सिविता संबंध छद्म-रीमैनियन मैनिफोल्ड के अधिक सामान्य परिस्थिति में चर्चा करता है और जियोडेसिक(सामान्य सापेक्षता) के विशेष परिस्थिति में अधिक विस्तार से चर्चा करता है।
उदाहरण
सबसे परिचित उदाहरण यूक्लिडियन ज्यामिति में सीधी रेखाएँ हैं। एक गोले पर, भूभौतिकी के चित्र वृहत वृत्त होते हैं। एक गोले पर बिंदु A से बिंदु B तक का सबसे छोटा रास्ता A और B से गुजरने वाले बड़े वृत्त के छोटे चाप(ज्यामिति) द्वारा दिया जाता है। यदि A और B प्रतिध्रुवीय बिंदु हैं, तो उनके बीच अपरिमित रूप से कई लघुतम पथ हैं। एक दीर्घवृत्त पर जियोडेसिक्स एक गोले की तुलना में अधिक जटिल तरीके से व्यवहार करता है; विशेष रूप से, वे सामान्य रूप से बंद नहीं होते हैं(आंकड़ा देखें)।
त्रिकोण
किसी दिए गए सतह पर तीन बिंदुओं में से प्रत्येक जोड़ी को जोड़ने वाले जियोडेसिक्स द्वारा एक जियोडेसिक त्रिकोण का निर्माण किया जाता है। गोले पर, जियोडेसिक वृहत वृत्त चाप होते हैं, जो एक गोलाकार त्रिकोण बनाते हैं।
मीट्रिक ज्यामिति
मीट्रिक ज्यामिति में, जियोडेसिक एक वक्र होता है जो हर जगह स्थानीय रूप से एक दूरी न्यूनतमकर्ता होता है। अधिक सटीक रूप से, एक वक्र γ : I → M एक अंतराल से लेकर मीट्रिक स्थान M तक एक जियोडेसिक है यदि कोई स्थिर v ≥ 0 ऐसा हैं कि किसी भी t ∈ I के लिए I में t का एक सन्निकट J है जैसे कि किसी के लिए t1, t2 ∈ J हमारे पास हैं
यह रिमेंनियन मैनिफोल्ड के लिए जियोडेसिक की धारणा को सामान्यीकृत करता है। हालांकि, मीट्रिक ज्यामिति में माना जाने वाला जियोडेसिक प्रायः प्राकृतिक मापदण्ड से सुसज्जित होता है, अर्थात उपरोक्त पहचान में v = 1 और
यदि अंतिम समानता सभी के लिए संतुष्ट है t1, t2 ∈ I, जियोडेसिक को मिनिमाइज़िंग जियोडेसिक या सबसे छोटा रास्ता कहा जाता है।
सामान्य तौर पर, स्थिर वक्रों को छोड़कर, मीट्रिक स्थान में कोई भूगर्भ विज्ञान नहीं हो सकता है। दूसरे चरम पर, लंबाई के मीट्रिक स्थान में कोई भी दो बिंदु सुधार योग्य पथों के एक न्यूनतम अनुक्रम से जुड़ जाते हैं, हालांकि इस न्यूनतम अनुक्रम को जियोडेसिक में अभिसरण करने की आवश्यकता नहीं है।
रीमानियन ज्यामिति
मीट्रिक टेंसर G के साथ एक रिमेंनियन मैनिफोल्ड M में, एक निरंतर भिन्न वक्र की लंबाई L γ : [a,b] → M द्वारा परिभाषित किया गया है।
M के दो बिंदुओं p और q के बीच की दूरी d(p, q) समग्र ली गयी लंबाई के न्यूनतम के रूप में परिभाषित किया गया है [a, b]→M ऐसा है कि γ(a) = p और γ(b) = q. रिमेंनियन ज्यामिति में, सभी भूगणित स्थानीय रूप से दूरी को कम करने वाले पथ हैं, लेकिन इसका विलोम सत्य नहीं है। वास्तव में, केवल वे पथ जो स्थानीय रूप से दूरी को कम करने वाले और चाप-लंबाई के अनुपात में परिमाणित करने वाले हैं, वे भूगणित हैं। एक रिमेंनियन मैनिफोल्ड पर जियोडेसिक्स को परिभाषित करने का एक अन्य समकक्ष तरीका, उन्हें निम्न क्रिया या कार्यात्मक ऊर्जा के न्यूनतम के रूप मे परिभाषित करना है।
E के सभी न्यूनतम L के भी न्यूनतम हैं, लेकिन L एक बड़ा सेट है क्योंकि L के न्यूनतम पथ मनमाने ढंग से दुबारा मापदण्ड किए जा सकते हैं(उनकी लंबाई को बदले बिना), जबकि E का न्यूनतम नहीं हो सकता। एक टुकड़े के लिए वक्र(अधिक सामान्यतः, वक्र), कॉची-श्वार्ज असमानता देता है
समानता के साथ यदि और केवल एक स्थिर a.e के बराबर है; पथ को निरंतर गति से यात्रा की जानी चाहिए। ऐसा होता है कि मिनिमाइज़र भी कम करें , क्योंकि वे परिबद्ध रूप से परिचालित हो जाते हैं, और असमानता एक समानता है। इस दृष्टिकोण की उपयोगिता यह है कि E के मिनिमाइज़र खोजने की समस्या एक अधिक मजबूत परिवर्तनशील समस्या है। वास्तव में, E का एक "उत्तल कार्य" है , ताकि उचित कार्यों के प्रत्येक समस्थानिक वर्ग के भीतर, किसी को अस्तित्व, विशिष्टता और मिनिमाइज़र की नियमितता की अपेक्षा करनी चाहिए। इसके विपरीत, कार्यात्मक के न्यूनतमकर्ता प्रायः बहुत नियमित नहीं होते हैं, क्योंकि मनमाना पुनर्मूल्यांकन की अनुमति है।
क्रियात्मक E के लिए गति के यूलर-लैग्रेंज समीकरणों को इसके द्वारा स्थानीय निर्देशांकों में दिया जाता है
जहाँ पर मीट्रिक के क्रिस्टोफेल प्रतीक हैं। यह जियोडेसिक समीकरण है, जिसकी चर्चा नीचे की गई है।
विविधताओं की गणना
ऊर्जा कार्यात्मक E की जांच करने के लिए विविधताओं की शास्त्रीय गणना की तकनीकों को लागू किया जा सकता है। ऊर्जा की पहली भिन्नता को स्थानीय निर्देशांक में परिभाषित किया गया है
पहली भिन्नता का महत्वपूर्ण बिंदु ठीक भूगर्भ विज्ञान है। दूसरी भिन्नता को इस प्रकार परिभाषित किया गया है
एक उपयुक्त अर्थ में, जियोडेसिक γ के साथ दूसरी भिन्नता के शून्य जैकोबी क्षेत्रों के साथ उत्पन्न होते हैं। जैकोबी क्षेत्रों को इस प्रकार जियोडेसिक्स के माध्यम से विविधता के रूप में माना जाता है।
शास्त्रीय यांत्रिकी से विविधतापूर्ण तकनीकों को लागू करके, भूगर्भ विज्ञान को हैमिल्टनियन प्रवाह के रूप में भी माना जा सकता है। वे संबंधित हैमिल्टन समीकरण के समाधान हैं, जिसमें(छद्म-) रीमैनियन मीट्रिक को हैमिल्टनियन यांत्रिकी के रूप में लिया गया है।
एफ़िन जियोडेसिक्स
एफ़िन संबंध ∇ के साथ एक चिकने मैनिफोल्ड M पर एक जियोडेसिक को वक्र γ(t) के रूप में परिभाषित किया गया है, जैसे कि वक्र के समानांतर परिवहन स्पर्शरेखा सदिश को वक्र में संरक्षित करता है, इसलिए
-
(1)
वक्र के साथ प्रत्येक बिंदु पर, जहाँ के संबंध में डेरिवेटिव हैं . अधिक सटीक रूप से, सहपरिवर्ती व्युत्पन्न को परिभाषित करने के लिए पहले को बढ़ाना जरूरी है। को एक खुले सेट में निरंतर भिन्न होने वाले सदिश क्षेत्र में विस्तारित किया जाए। हालाँकि,(1) का परिणामी मूल्य विस्तार की पसंद से स्वतंत्र है।
M पर स्थानीय निर्देशांक का उपयोग करके, हम 'जियोडेसिक समीकरण'(संकलन सम्मेलन का उपयोग करके) लिख सकते हैं।
जहाँ पर वक्र γ(t) के निर्देशांक हैं और संबंध ∇ के क्रिस्टोफेल प्रतीक हैं। यह निर्देशांकों के लिए एक साधारण अवकल समीकरण है। प्रारंभिक स्थिति और प्रारंभिक वेग दिए जाने पर इसका एक अनूठा समाधान है। इसलिए, शास्त्रीय यांत्रिकी के दृष्टिकोण से, भूगर्भ विज्ञान को कई गुना मुक्त कणों के प्रक्षेपवक्र के रूप में माना जा सकता है। दरअसल, समीकरण इसका मतलब है कि वक्र के त्वरण सदिश का सतह की दिशा में कोई घटक नहीं है(और इसलिए यह वक्र के प्रत्येक बिंदु पर सतह के स्पर्शरेखा तल के लंबवत है)। तो, गति पूरी तरह से सतह के झुकने से निर्धारित होती है। यह सामान्य सापेक्षता का भी विचार है जहां कण भूगर्भ विज्ञान पर चलते हैं और झुकना गुरुत्वाकर्षण के कारण होता है।
अस्तित्व और विशिष्टता
जियोडेसिक्स के लिए स्थानीय अस्तित्व और अद्वितीयता प्रमेय बताता है कि एफाइन संबंध के साथ एक चिकनी मैनिफोल्ड पर जियोडेसिक्स उपलब्ध हैं, और अद्वितीय हैं। अधिक सटीक रूप से
- M में किसी भी बिंदु P के लिए और TpM में किसी भी सदिश V के लिए(P पर M के लिए स्पर्शरेखा स्थान) एक अद्वितीय जियोडेसिक उपलब्ध है : I → M ऐसा कि
- तथा
- जहां I 'R' में अधिकतम खुला अंतराल है जिसमें 0 है।
इस प्रमेय का प्रमाण साधारण अंतर समीकरणों के सिद्धांत से मिलता है, यह देखते हुए कि जियोडेसिक समीकरण एक दूसरे क्रम का ODE है। इसके बाद निर्धारित प्रारंभिक स्थितियों के साथ ODE के समाधान के लिए पिकार्ड-लिंडेलोफ प्रमेय से अस्तित्व और विशिष्टता का पालन होता है। γ P और V दोनों पर सुचारू कार्य निर्भर करता है।
सामान्य तौर पर, हो सकता है कि I पूरी तरह से 'R' न हो, उदाहरण के लिए 'R' में खुली डिस्क के लिए कोई भी γ सभी ℝ तक विस्तारित होता है यदि और केवल अगर M भौगोलिक रूप से पूर्ण हो।
जियोडेसिक प्रवाह
जियोडेसिक प्रवाह एक स्थानीय R-ग्रुप एक्शन है जो निम्नलिखित तरीके से परिभाषित M के स्पर्शरेखा बंडल TM पर है।
जहां T ∈ 'R', V ∈ TM और प्रारंभिक डेटा के साथ जियोडेसिक को दर्शाता है । इस प्रकार, (V) = exp(tV) सदिश tV का चरघातांकी मानचित्र है। जियोडेसिक प्रवाह की बंद कक्षा M पर बंद जियोडेसिक से मेल खाती है।
एक(छद्म-) रिमेंनियन मैनिफोल्ड पर, जियोडेसिक प्रवाह की पहचान कॉटेन्जेंट बंडल पर हैमिल्टनियन प्रवाह के साथ की जाती है। हेमिल्टनियन यांत्रिकी तब(छद्म-) रीमैनियन मीट्रिक के व्युत्क्रम द्वारा दी जाती है, जिसका मूल्यांकन विहित एक रूप के विरुद्ध किया जाता है। विशेष रूप से प्रवाह(छद्म-) रीमैनियन मीट्रिक को संरक्षित करता है , अर्थात।
विशेष रूप से, जब V एक इकाई सदिश है, पूरे समय इकाई गति बनी रहती है, इसलिए जियोडेसिक प्रवाह इकाई स्पर्शरेखा बंडल के लिए स्पर्शरेखा है। लिउविल की प्रमेय का अर्थ स्पर्शरेखा बंडल पर गतिज माप का व्युत्क्रम हैं।
जियोडेसिक स्प्रे
जियोडेसिक प्रवाह स्पर्शरेखा बंडल में वक्रों के एक परिवार को परिभाषित करता है। इन वक्रों के व्युत्पन्न स्पर्शरेखा बंडल के कुल स्थान पर एक सदिश क्षेत्र को परिभाषित करते हैं, जिसे जियोडेसिक स्प्रे के रूप में जाना जाता है।
अधिक सटीक रूप से, एक एफ़िन संबंध क्षैतिज बंडल और लंबवत बंडलो में डबल स्पर्शरेखा बंडल TTM के विभाजन को जन्म देता है:
जियोडेसिक स्प्रे अद्वितीय क्षैतिज सदिश क्षेत्र W सन्तोषजनक हैं
प्रत्येक बिंदु पर V ∈ TM; यहाँ π∗: TTM → TM स्पर्शरेखा बंडल से जुड़े प्रक्षेपण π : TM → M के साथ जारी रखने वाले(अंतर) को दर्शाता है।
प्रायः वही निर्माण स्पर्शरेखा बंडल पर किसी भी एह्रेसमैन संबंध के लिए सदिश फ़ील्ड बनाने की अनुमति देता है। परिणामी सदिश फ़ील्ड के लिए एक स्प्रे(हटाए गए स्पर्शरेखा बंडल TM \ {0} पर) होने के लिए यह पर्याप्त है कि संबंध सकारात्मक पुनर्विक्रय के तहत समान हो, इसे रैखिक होने की आवश्यकता नहीं है। अर्थात्,(cf. एह्रेसमैन संबंध#सदिश बंडल और सहपरिवर्ती डेरिवेटिव) यह पर्याप्त है कि क्षैतिज वितरण संतुष्ट करता है।
प्रत्येक X ∈ TM \ {0} और λ > 0 के लिए। यहाँ d(Sλ) अदिश समरूपता के साथ जारी रखना हैं । इस तरह से उत्पन्न होने वाले गैर-रैखिक संबंध का एक विशेष मामला फिन्सलर मनिफॉल्ड से जुड़ा हुआ है।
एफ़िन और प्रोजेक्टिव जियोडेसिक्स
समीकरण(1) एफ़िन पैरामीटराइजेशन के तहत अपरिवर्तनीय है; वह है, फॉर्म का पैरामीटराइजेशन
जहाँ a और b अचर वास्तविक संख्याएँ हैं। इस प्रकार सन्निहित वक्रों के एक निश्चित वर्ग को निर्दिष्ट करने के अलावा, जियोडेसिक समीकरण प्रत्येक वक्र पर मानकीकरणों के एक पसंदीदा वर्ग को भी निर्धारित करता है। तदनुसार, समाधान(1) को एफाइन मापदण्ड के साथ जियोडेसिक्स कहा जाता है।
एक संबंध द्वारा निर्धारित होता है, की बंधुत्वपूर्ण पैरामिट्रीकृत जिओडेसिक्स के परिवार का होता है, मरोड़ टेंसर तक (स्पिवक 1999, अध्याय 6, परिशिष्ट।)मरोड़ वास्तव में, जियोडेसिक्स के परिवार को प्रभावित नहीं करता है, क्योंकि जियोडेसिक समीकरण केवल संबंध के सममित भाग पर निर्भर करता है। अधिक सटीक रूप से, अगर दो संबंध ऐसे हैं कि अंतर टेंसर
तिरछा-सममित मैट्रिक्स है | तिरछा-सममित, तब तथा एक ही जियोडेसिक्स है, एक ही एफ़िन पैरामीटराइजेशन के साथ। इसके अलावा, एक ही जियोडेसिक्स के रूप में एक अनूठा संबंध है , लेकिन गायब होने वाले मरोड़ के साथ।
एक विशेष मापदण्ड के बिना जिओडेसिक्स को प्रक्षेपण संबंध द्वारा वर्णित किया गया है।
कम्प्यूटेशनल तरीके
किमेल और अन्य लोगों द्वारा इकोनल समीकरणों के रूप में पेश की गई सतहों पर न्यूनतम जियोडेसिक समस्या के लिए कुशल समाधानकर्ता प्रस्तावित किए गए हैं।[3][4]
रिबन टेस्ट
रिबन टेस्ट एक भौतिक सतह पर जियोडेसिक खोजने का एक तरीका है।[5] यह विचार एक सीधी रेखा(एक रिबन) के चारों ओर थोड़ा सा कागज एक घुमावदार सतह पर फिट करने के लिए है, जितना संभव हो सके रिबन को खींचे या निचोड़े बिना(इसकी आंतरिक ज्यामिति को बदले बिना)।
उदाहरण के लिए, जब एक रिबन को एक शंकु के चारों ओर एक रिंग के रूप में लपेटा जाता है, तो रिबन शंकु की सतह पर नहीं रहेगा बल्कि बाहर चिपक जाएगा, ताकि शंकु पर वृत्त जियोडेसिक न हो। यदि रिबन को इस तरह समायोजित किया जाता है कि इसके सभी भाग शंकु की सतह को छूते हैं, तो यह एक जियोडेसिक को एक सन्निकटन देगा।
गणितीय रूप से रिबन टेस्ट को मैपिंग खोजने के रूप में तैयार किया जा सकता है के एक सन्निकट का एक पंक्ति के सतह में विमान हैं ताकि मैपिंग हो सके, आस-पास की दूरियों को ज्यादा नहीं बदलेगा बहुत ज्यादा; अर्थात् दूरी पर से अपने पास जहाँ पर तथा में तथा मेट्रिक्स हैं।
अनुप्रयोग
This section needs expansion. You can help by adding to it. (June 2014) |
जियोडेसिक्स गणना के आधार के रूप में कार्य करता है:
- जियोडेसिक एयरफ्रेम; जियोडेसिक एयरफ्रेम या जियोडेटिक एयरफ्रेम देखें
- जियोडेसिक संरचनाएं - उदाहरण के लिए जियोडेसिक गुंबद
- पृथ्वी पर या उसके निकट क्षैतिज दूरी; पृथ्वी भूभौतिकी देखें
- रेंडरिंग के लिए सतहों पर इमेज मैप करना; यूवी मैपिंग देखें
- आणविक गतिशीलता में कण गति | आणविक गतिशीलता(एमडी) कंप्यूटर सिमुलेशन[6]
- रोबोट गति योजना(जैसे, कार के पुर्जों को पेंट करते समय); सबसे छोटा पथ समस्या देखें
यह भी देखें
टिप्पणियाँ
- ↑ 1.0 1.1 For a pseudo-Riemannian manifold, e.g., a Lorentzian manifold, the definition is more complicated.
- ↑ The path is a local maximum of the interval k rather than a local minimum.
संदर्भ
- ↑ "geodesic". Lexico UK English Dictionary. Oxford University Press. Archived from the original on 2020-03-16.
- ↑ "geodesic". Merriam-Webster Dictionary.
- ↑ Kimmel, R.; Amir, A.; Bruckstein, A. M. (1995). "स्तर सेट प्रसार का उपयोग करके सतहों पर सबसे छोटा रास्ता खोजना". IEEE Transactions on Pattern Analysis and Machine Intelligence. 17 (6): 635–640. doi:10.1109/34.387512.
- ↑ Kimmel, R.; Sethian, J. A. (1998). "मैनिफोल्ड्स पर जियोडेसिक पथों की गणना" (PDF). Proceedings of the National Academy of Sciences. 95 (15): 8431–8435. Bibcode:1998PNAS...95.8431K. doi:10.1073/pnas.95.15.8431. PMC 21092. PMID 9671694. Archived (PDF) from the original on 2022-10-09.
- ↑ Michael Stevens (Nov 2, 2017), [1].
- ↑ Ingebrigtsen, Trond S.; Toxvaerd, Søren; Heilmann, Ole J.; Schrøder, Thomas B.; Dyre, Jeppe C. (2011). "एनवीयू गतिकी। I. निरंतर-संभावित-ऊर्जा हाइपरसफेस पर जियोडेसिक गति". The Journal of Chemical Physics. 135 (10): 104101. arXiv:1012.3447. Bibcode:2011JChPh.135j4101I. doi:10.1063/1.3623585. ISSN 0021-9606. PMID 21932870. S2CID 16554305.
- Spivak, Michael (1999), A Comprehensive introduction to differential geometry (Volume 2), Houston, TX: Publish or Perish, ISBN 978-0-914098-71-3
अग्रिम पठन
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (July 2014) (Learn how and when to remove this template message) |
- Adler, Ronald; Bazin, Maurice; Schiffer, Menahem (1975), Introduction to General Relativity (2nd ed.), New York: McGraw-Hill, ISBN 978-0-07-000423-8. See chapter 2.
- Abraham, Ralph H.; Marsden, Jerrold E. (1978), Foundations of mechanics, London: Benjamin-Cummings, ISBN 978-0-8053-0102-1. See section 2.7.
- Jost, Jürgen (2002), Riemannian Geometry and Geometric Analysis, Berlin, New York: Springer-Verlag, ISBN 978-3-540-42627-1. See section 1.4.
- Kobayashi, Shoshichi; Nomizu, Katsumi (1996), Foundations of Differential Geometry, vol. 1 (New ed.), Wiley-Interscience, ISBN 0-471-15733-3.
- Landau, L. D.; Lifshitz, E. M. (1975), Classical Theory of Fields, Oxford: Pergamon, ISBN 978-0-08-018176-9. See section 87.
- Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0
- Ortín, Tomás (2004), Gravity and strings, Cambridge University Press, ISBN 978-0-521-82475-0. Note especially pages 7 and 10.
- Volkov, Yu.A. (2001) [1994], "Geodesic line", Encyclopedia of Mathematics, EMS Press.
- Weinberg, Steven (1972), Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, New York: John Wiley & Sons, ISBN 978-0-471-92567-5. See chapter 3.
इस पेज में लापता आंतरिक लिंक की सूची
- सामान्य सापेक्षता में जियोडेसिक्स
- अलग करने योग्य कई गुना
- दूरी(ग्राफ सिद्धांत)
- निर्बाध गिरावट
- ग्राफ(असतत गणित)
- सतहों की अंतर ज्यामिति
- खुला अंतराल
- वक्राकार लंबाई
- विविधताओं की गणना
- रबर बैण्ड
- अंतरिक्ष समय
- रिमानियन ज्यामिति
- ग्रहों की कक्षा
- उप-रिमानियन ज्यामिति
- स्यूडो-रीमैनियन मैनिफोल्ड
- त्रिअक्षीय दीर्घवृत्ताभ पर भूभौतिकी
- एंटीपोडल बिंदु
- एक दीर्घवृत्त पर जिओडेसिक्स
- गोलाकार त्रिभुज
- स्थानीय स्तर पर
- लंबाई मीट्रिक स्थान
- सबसे कम
- क्रिस्टोफर प्रतीक
- दूसरा रूपांतर
- हैमिल्टनियन प्रवाह के रूप में जियोडेसिक्स
- जैकोबी मैदान
- खुला सेट
- साधारण अंतर समीकरण
- क्रिस्टोफर प्रतीक
- चिकना समारोह
- समूह क्रिया(गणित)
- प्रवाह(गणित)
- घातीय नक्शा(रीमैनियन ज्यामिति)
- धक्का आगे(अंतर)
- आर्थिक समीकरण
- आणविक गतिकी
बाहरी संबंध
- Geodesics Revisited — Introduction to geodesics including two ways of derivation of the equation of geodesic with applications in geometry(geodesic on a sphere and on a torus), mechanics(brachistochrone) and optics(light beam in inhomogeneous medium).
- Totally geodesic submanifold at the Manifold Atlas