श्यानता
| Viscosity | |
|---|---|
 A simulation of liquids with different viscosities. The liquid on the left has lower viscosity than the liquid on the right. | |
सामान्य प्रतीक | η, μ |
अन्य मात्राओं से व्युत्पत्तियां | μ = G·t |
| Part of a series on |
| सातत्यक यांत्रिकी |
|---|
किसी तरल पदार्थ की तनुता किसी दिए गए दर पर विरूपण के लिए उसके ड्रैग का उचित उपाय है। इस प्रकार तरल पदार्थों के लिए, यह मोटाई की अनौपचारिक अवधारणा से मेल खाता है: उदाहरण के लिए, सिरप में पानी की तुलना में अधिक तनुता होती है।[1] यह तनुता सापेक्ष गति में तरल पदार्थ की आसन्न परतों के बीच आंतरिक घर्षण की मात्रा निर्धारित करती है। उदाहरण के लिए, जब किसी तनुता युक्त द्रव को किसी ट्यूब के माध्यम से रखा जाता है, तो यह ट्यूब की धुरी के पास इसकी दीवारों की तुलना में अधिक तेज़ी से प्रवाहित होने लगता है। प्रयोगों से पता चलता है कि प्रवाह को बनाए रखने के लिए कुछ तनाव (भौतिकी) (जैसे ट्यूब के दो सिरों के बीच दबाव अंतर) की आवश्यकता होती है। ऐसा इसलिए है क्योंकि सापेक्ष गति में तरल की परतों के बीच घर्षण को दूर करने के लिए एक बल की आवश्यकता होती है। प्रवाह की निरंतर दर वाली ट्यूब के लिए, क्षतिपूर्ति बल की ताकत द्रव की तनुता के समानुपाती होती है।
सामान्यतः, तनु द्रव की स्थिति पर निर्भर करता है, जैसे कि इसका तापमान, दबाव और विरूपण की दर को निरूपित करती हैं। चूंकि, इनमें से कुछ गुणों पर निर्भरता कुछ स्थितियों में नगण्य है। उदाहरण के लिए, न्यूटोनियन द्रव की तनुता विरूपण की दर के साथ महत्वपूर्ण रूप से भिन्न नहीं होती है। शून्य विस्कोसिटी (सेंसर तनाव का कोई प्रतिरोध नहीं) केवल अति तरल में क्रायोजेनिक्स में देखा जाता है; अन्यथा, ऊष्मप्रवैगिकी के दूसरे नियम में सभी तरल पदार्थों की धनात्मक तनुता की आवश्यकता होती है।[2][3] एक द्रव जिसमें शून्य तनुता होती है, आदर्श या इनविसिड कहलाता है।
व्युत्पत्ति
तनुता शब्द लैटिन से लिया गया है। विस्कम को मिस्टलेटो बेरीज से प्राप्त तनुता पूर्ण गोंद भी कहा जाता है।[4]
परिभाषा
गतिशील तनुता
सामग्री विज्ञान और अभियांत्रिकी में, अधिकांशतः सामग्री के विरूपण (यांत्रिकी) में सम्मिलित बलों या तनाव (यांत्रिकी) को समझने में रुचि होती है। उदाहरण के लिए, यदि सामग्री एक साधारण वसंत थी, तो इसका उत्तर हुक के नियम द्वारा दिया जाएगा, जो कहता है कि इसके द्वारा अनुभव किया गया बल संतुलन से विस्थापित दूरी के समानुपाती होता है। तनाव जो कुछ अवस्थाओं से सामग्री के विरूपण के लिए उत्तरदायी ठहराया जा सकता है, लोच (भौतिकी) तनाव कहा जाता है। अन्य सामग्रियों में, तनाव उपस्थित होते हैं जिन्हें समय के साथ तनाव दर के लिए उत्तरदायी ठहराया जा सकता है। इन्हें तनुता युक्त तनाव कहा जाता है। उदाहरण के लिए, पानी जैसे तरल पदार्थ में तरल पदार्थ को कतरने से उत्पन्न होने वाले तनाव तरल पदार्थ की दूरी पर निर्भर नहीं होते हैं; बल्कि, वे इस बात पर निर्भर करते हैं कि बाल काटना कितनी जल्दी होता है।
तनुता भौतिक गुण है जो किसी पदार्थ में विस्कस स्ट्रेस को विरूपण के परिवर्तन की दर (तनाव दर) से संबंधित करता है। यद्यपि यह सामान्य प्रवाह पर लागू होता है, लेकिन एक सरल कर्तन प्रवाह में कल्पना करना और परिभाषित करना सरल है, जैसे कि प्लानर कौएट प्रवाह इत्यादि।
कोउट्टे प्रवाह में किसी द्रव को दो विभिन्न रूप से बड़ी प्लेटों के बीच फंस जाता है, एक निश्चित और एक स्थिर गति से समानांतर गति में (दाईं ओर चित्रण देखें)। यदि शीर्ष प्लेट की गति अत्यधिक कम है (अशांति से बचने के लिए), तो स्थिर अवस्था में द्रव के कण इसके समानांतर चलते हैं, और उनकी गति से भिन्न होती है तल पर करने के लिए शीर्ष पर उपस्थित रहती हैं।[5] इस प्रकार द्रव की प्रत्येक परत अपने ठीक नीचे वाली परत की तुलना में तेजी से चलती है, और उनके बीच घर्षण उनके सापेक्ष गति का विरोध करने वाले बल (भौतिकी) को जन्म देता है। विशेष रूप से यह द्रव शीर्ष प्लेट पर अपनी गति के विपरीत दिशा में एक बल लगाता है, और नीचे की प्लेट पर एक समान लेकिन विपरीत बल लगाता है। इसलिए शीर्ष प्लेट को स्थिर गति से गतिमान रखने के लिए एक बाहरी बल की आवश्यकता होती है।
कई तरल पदार्थों में, शीर्ष पर प्रवाह वेग शून्य से नीचे तक रैखिक रूप से भिन्न होता है। इसके अतिरिक्त, बल का परिमाण, , शीर्ष प्लेट पर कार्य करना गति के समानुपाती पाया जाता है और क्षेत्र प्रत्येक प्लेट की, और उनके पृथक्करण के व्युत्क्रमानुपाती होता हैं:
- आनुपातिकता कारक द्रव की गतिशील तनुता है, जिसे अधिकांशतः तनुता के रूप में संदर्भित किया जाता है। इसे म्यू (अक्षर) द्वारा दर्शाया गया है (μ). गतिशील तनुता में आयामी विश्लेषण होता है , इसलिए इकाइयों की अंतर्राष्ट्रीय प्रणाली और एसआई व्युत्पन्न इकाई के परिणामस्वरूप:
- दबाव समय से गुणा।
उपरोक्त अनुपात सेंसर विरूपण या सेंसर वेग की दर कहा जाता है, और प्लेटों के सामान्य वेक्टर के लंबवत दिशा में द्रव की गति का व्युत्पन्न है (दाईं ओर चित्र देखें)। यदि वेग के साथ रैखिक रूप से भिन्न नहीं होता है , तो उपयुक्त सामान्यीकरण है:
जहाँ , और स्थानीय सेंसर वेग है। इस अभिव्यक्ति को न्यूटन के तनुता के नियम के रूप में जाना जाता है। प्लेनर समरूपता के साथ अपरूपण प्रवाह में, यह वही है जो को परिभाषित करता है . यह तनुता की सामान्य परिभाषा (नीचे देखें) का एक विशेष स्थिति है, जिसे समन्वय-मुक्त रूप में व्यक्त किया जा सकता है।
म्यू (पत्र) का उपयोग () गतिशील तनुता के लिए (कभी-कभी निरपेक्ष तनुता भी कहा जाता है) यांत्रिक अभियांत्रइकी और रासायनिक अभियांत्रिकी के साथ-साथ गणितज्ञों और भौतिकविदों के बीच सरल है।[6][7][8] चूंकि, एटा () का उपयोग रसायनज्ञों, भौतिकविदों और IUPAC द्वारा भी किया जाता है।[9] तनु कभी-कभी सेंसर तनुता भी कहा जाता है। चूंकि, कम से कम एक लेखक इस शब्दावली के उपयोग को हतोत्साहित करता है, यह देखते हुए कर्तन प्रवाह के अतिरिक्त गैर-सेंसर प्रवाह में प्रकट हो सकते हैं।[10]
किनेमेटिक तनु
द्रव गतिकी में, गतिज तनुता (कभी-कभी संवेग विसरण भी कहा जाता है) के संदर्भ में काम करना कभी-कभी अधिक उपयुक्त होता है, जिसे गतिज तनुता के अनुपात के रूप में परिभाषित किया जाता है जिसमें विभिन्न प्रतीक (μ) द्रव के घनत्व से अधिक (ρ) जिसे सामान्यतः (ν) (अक्षर) द्वारा दर्शाया जाता है :
और आयामी विश्लेषण ह ै इसलिए इकाइयों की अंतर्राष्ट्रीय प्रणाली और एसआई व्युत्पन्न इकाई के परिणामस्वरूप:
- विशिष्ट ऊर्जा को समय से गुणा किया जाता है।
सामान्य परिभाषा
बहुत सामान्य शब्दों में, तरल पदार्थ में तनु तनाव को विभिन्न द्रव कणों के सापेक्ष वेग से उत्पन्न होने के रूप में परिभाषित किया जाता है। जैसे, तनु तनाव प्रवाह वेग के स्थानिक प्रवणता पर निर्भर होना चाहिए। यदि वेग प्रवणता कम हैं, तो पहले सन्निकटन के लिए तनु तनाव केवल वेग के पहले डेरिवेटिव पर निर्भर करता है।[11] (न्यूटोनियन तरल पदार्थों के लिए, यह एक रैखिक निर्भरता भी है।) कार्तीय निर्देशांक में, सामान्य संबंध को तब इस रूप में लिखा जा सकता है
जहाँ एक तनु तनाव है जो वेग प्रवणता तनाव को मैप करता है तनु तनाव तनाव पर .[12] चूंकि इस अभिव्यक्ति में सूचकांक 1 से 3 तक भिन्न हो सकते हैं, जहाँ तनुता गुणांक कुल मिलाकर 81 हैं। चूंकि, यह मानते हुए कि विस्कोसिटी रैंक-4 तनाव समदैशिक है, इन 81 गुणांकों को तीन स्वतंत्र पैरामीटरों , , :में कम कर देता है
और इसके अतिरिक्त, यह माना जाता है कि जब द्रव सरल कठोर-पिंड के घूर्णन से गुजर रहा हो तो कोई तनु बल उत्पन्न नहीं हो सकता है , केवल दो स्वतंत्र पैरामीटर छोड़कर।[11] सबसे सामान्य अपघटन मानक (स्केलर) तनुता के रूप में होता है और थोक तनुता के रूप में होता हैं इसका मान इस प्रकार हैं कि और सदिश संकेतन में यह इस प्रकार प्रकट होता है:
जहाँ यूनिट टेन्सर है, और डैगर स्थानान्तरण को दर्शाता है।[10][13] इस समीकरण को न्यूटन के तनुता के नियम का सामान्यीकृत रूप माना जा सकता है।
बल्क विस्कोसिटी (जिसे वॉल्यूम विस्कोसिटी भी कहा जाता है) एक प्रकार के आंतरिक घर्षण को व्यक्त करता है जो किसी द्रव के अपरूपण संपीड़न या विस्तार का विरोध करता है। इस प्रकार यह मान के लिए द्रव गतिकी समस्याओं में अधिकांशतः आवश्यक नहीं रखता है। उदाहरण के लिए, एक असंपीड्य द्रव संतुष्ट करता है और इसलिए युक्त शब्द बाहर निकल जाता है। इसके अतिरिक्त, अधिकांशतः गैसों के लिए नगण्य माना जाता है क्योंकि यह है एकपरमाणुक आदर्श गैस में[10] एक स्थिति जिसमें स्टोक्स के नियम (ध्वनि क्षीणन) या स्टोक्स के ध्वनि क्षीणन के नियम द्वारा वर्णित ध्वनि और शॉक तरंगों में ऊर्जा हानि की गणना महत्वपूर्ण हो सकती है, क्योंकि इन घटनाओं में तेजी से विस्तार और संपीड़न सम्मिलित हैं।
तनुता के लिए परिभाषित समीकरण प्रकृति के मूलभूत नियम नहीं हैं, इसलिए उनकी उपयोगिता, साथ ही तनुता को मापने या गणना करने के तरीकों को अलग-अलग साधनों का उपयोग करके स्थापित किया जाना चाहिए। इसका एक संभावित विवाद यह है कि तनु, सिद्धांत रूप में, तरल पदार्थ की पूर्ण सूक्ष्म अवस्था पर निर्भर करता है, जिसमें सिस्टम में प्रत्येक कण की स्थिति और संवेग सम्मिलित होते हैं।[14] ऐसी अत्यधिक विस्तृत जानकारी सामान्यतः यथार्थवादी प्रणालियों में उपलब्ध नहीं होती है। चूंकि, कुछ शर्तों के अनुसार इनमें से अधिकांश जानकारी को नगण्य दिखाया जा सकता है। विशेष रूप से, न्यूटोनियन तरल पदार्थों के लिए संतुलन के पास और सीमाओं से दूर, तनु स्थानीय संतुलन को परिभाषित करने वाले स्थान और समय-निर्भर मैक्रोस्कोपिक क्षेत्रों (जैसे तापमान और घनत्व) पर निर्भर करता है।[14][15]
फिर भी, तनुता अभी भी तापमान, दबाव, और किसी बाहरी बल के आयाम और आवृत्ति जैसे कई सिस्टम गुणों पर एक गैर-नगण्य निर्भरता ले सकती है। इसलिए, तनुता के सटीक माप केवल परिभाषित होते हैं, इस प्रकार एक विशिष्ट द्रव अवस्था के संबंध में उपयोग किए जाते हैं।[16] प्रयोगों और सैद्धांतिक प्रारूप के बीच तुलना को मानकीकृत करने के लिए, तनुता डेटा को कभी-कभी आदर्श सीमित स्थितियों, जैसे कि शून्य सेंसर सीमा, या (गैसों के लिए) शून्य घनत्व सीमा के लिए एक्सट्रपलेशन किया जाता है।
मोमेंटम ट्रांसपोर्ट
परिवहन सिद्धांत संवेग परिवहन के संदर्भ में तनुता की एक वैकल्पिक व्याख्या प्रदान करता है: तनुता भौतिक संपत्ति है जो एक तरल के भीतर संवेग परिवहन की विशेषता है, ठीक वैसे गर्मी जैसे तापीय चालकता ऊष्मा परिवहन की विशेषता है, और (द्रव्यमान) द्रव्यमान विसरणता बड़े पैमाने पर परिवहन की विशेषता है।[17] यह परिप्रेक्ष्य न्यूटन के तनुता के नियम में निहित है, क्योंकि सेंसर तनाव एक संवेग प्रवाह के समतुल्य इकाइयाँ हैं, अर्थात प्रति इकाई समय प्रति इकाई क्षेत्र में गति का प्रकार हैं। इस प्रकार, में गति के प्रवाह को निर्दिष्ट करने के रूप में व्याख्या की जा सकती है जहाँ पर द्रव परत से दूसरी परत की दिशा को प्रदर्शित करता हैं। न्यूटन के तनुता के नियम के अनुसार, यह संवेग प्रवाह एक वेग प्रवणता में होता है, और संगत संवेग प्रवाह का परिमाण तनुता द्वारा निर्धारित किया जाता है।
ऊष्मा और द्रव्यमान स्थानांतरण की सादृश्यता को स्पष्ट किया जा सकता है। जिस प्रकार ऊष्मा उच्च तापमान से निम्न तापमान की ओर प्रवाहित होती है और द्रव्यमान उच्च घनत्व से निम्न घनत्व की ओर प्रवाहित होता है, उसी प्रकार संवेग उच्च वेग से निम्न वेग की ओर प्रवाहित होता है। इन सभी व्यवहारों को संघटित भावों द्वारा वर्णित किया गया है, जिन्हें संवैधानिक संबंध कहा जाता है, जिनके एक-आयामी रूप यहां दिए गए हैं:
जहाँ घनत्व है, और द्रव्यमान और ऊष्मा प्रवाह हैं, और और द्रव्यमान प्रसार और तापीय चालकता हैं।[18] तथ्य यह है कि निरंतर यांत्रिकी में द्रव्यमान, गति और ऊर्जा (गर्मी) परिवहन सबसे प्रासंगिक प्रक्रियाओं में से एक संयोग नहीं है: ये उन कुछ भौतिक मात्राओं में से हैं जो इंटरपार्टिकल संघट्टों में सूक्ष्म स्तर पर संरक्षित हैं। इस प्रकार, तेजी से और जटिल सूक्ष्म अंतःक्रियात्मक समय-सीमा द्वारा तय किए जाने के अतिरिक्त, उनकी गतिशीलता मैक्रोस्कोपिक समय-सीमा पर होती है, जैसा कि परिवहन सिद्धांत और हाइड्रोडायनामिक्स के विभिन्न समीकरणों द्वारा वर्णित है।
न्यूटोनियन और गैर-न्यूटोनियन तरल पदार्थ
न्यूटन का तनुता का नियम प्रकृति का एक मूलभूत नियम नहीं है, बल्कि एक संवैधानिक समीकरण है (जैसे हुक का नियम, फ़िक का नियम और ओम का नियम) जो तनुता क ो परिभाषित करने का काम करता है . इसका रूप प्रयोगों से प्रेरित है जो दिखाते हैं कि तरल पदार्थों की एक विस्तृत श्रृंखला के लिए, तनाव दर से स्वतंत्र है। ऐसे द्रवों को न्यूटोनियन द्रव कहते हैं। गैसों, पानी और कई सामान्य तरल पदार्थों को सामान्य परिस्थितियों और संदर्भों में न्यूटोनियन माना जा सकता है। चूंकि, कई गैर-न्यूटोनियन तरल पदार्थ हैं जो इस व्यवहार से महत्वपूर्ण रूप से विचलित होते हैं। उदाहरण के लिए:
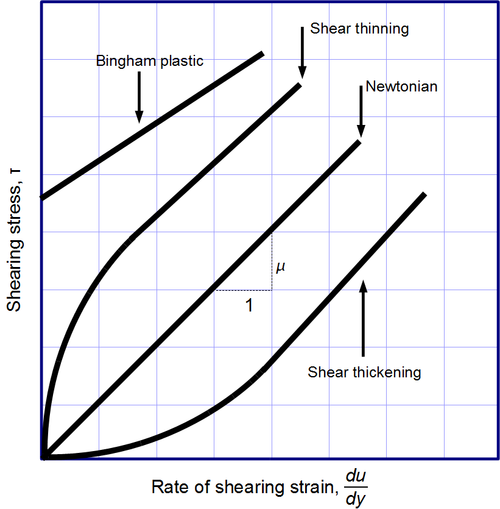
- अपरूपण सेंसर मोटा होना या सेंसर-गाढ़ा (पतला) तरल पदार्थ, जिसकी तनुता सेंसर तनाव की दर से बढ़ जाती है।
- शिअर थिनिंग या शेयर-थिनिंग तरल पदार्थ, जिनकी तनुता सेंसर तनाव की दर के साथ घट जाती है।
- थिक्सोट्रोपिक तरल पदार्थ, जो समय के साथ कम तनु हो जाता है जब हिलाया जाता है, उत्तेजित होता है, या अन्यथा जोर दिया जाता है।
- रियोपेक्टिक तरल पदार्थ, जो समय के साथ हिलने, उत्तेजित होने, या अन्यथा तनावग्रस्त होने पर अधिक तनु हो जाता है।
- बिंघम प्लास्टिक जो कम तनाव पर ठोस के रूप में व्यवहार करता है लेकिन उच्च तनाव पर तनु तरल पदार्थ के रूप में बहता है।
फ्रेडरिक थॉमस ट्राउटन का अनुपात विस्तारित तनुता का सेंसर तनुता का अनुपात है। न्यूटोनियन द्रव के लिए, ट्राउटन अनुपात 3 है।[19][20] सेंसर-पतली तरल पदार्थ बहुत आम हैं, लेकिन भ्रामक रूप से थिक्सोट्रॉपिक के रूप में वर्णित हैं।[21]
न्यूटोनियन तरल पदार्थ के लिए भी, तनु सामान्यतः इसकी संरचना और तापमान पर निर्भर करता है। गैसों और अन्य संकुचित तरल पदार्थों के लिए, यह तापमान पर निर्भर करता है और दबाव के साथ बहुत धीरे-धीरे परिवर्तित कर देता है। कुछ तरल पदार्थों की तनुता अन्य कारकों पर निर्भर हो सकती है। उदाहरण के लिए, चुंबकीय क्षेत्र के संपर्क में आने पर एक मैग्नेटोरियोलॉजिकल तरल पदार्थ गाढ़ा हो जाता है, संभवतः यही ठोस के समान व्यवहार करने के बिंदु पर रहती हैं।
ठोस पदार्थों में
द्रव प्रवाह के समय उत्पन्न होने वाली तनुता युक्त यह शक्ति लोच (भौतिकी) बलों से अलग होती हैं जो सेंसर, संपीड़न या विस्तार तनाव के जवाब में ठोस में होती हैं। जबकि उत्तरार्द्ध में तनाव सेंसर विरूपण की मात्रा के समानुपाती होता है, द्रव में यह समय के साथ विरूपण की दर के समानुपाती होता है। इस कारण से, जेम्स क्लर्क मैक्सवेल ने तरल पदार्थ की तनुता के लिए भगोड़ा लोच शब्द का प्रयोग किया गया था।
चूंकि, कई तरल पदार्थ (पानी सहित) अचानक तनाव के अधीन होने पर तनुता युक्त ठोस की तरह संक्षेप में प्रतिक्रिया करेंगे। इसके विपरीत, कई ठोस (यहां तक कि ग्रेनाइट भी) तरल पदार्थ की तरह बहेंगे, भले ही बहुत धीरे-धीरे, मनमाने ढंग से छोटे तनाव के अनुसार भी हैं।[22] ऐसी सामग्रियों को सबसे अच्छी तरह से तनु के रूप में वर्णित किया जाता है- अर्थात, दोनों लोच (विरूपण की प्रतिक्रिया) और तनु (विरूपण की दर पर प्रतिक्रिया) रखने के लिए उपयोग की जाती हैं।
Viscoelastic ठोस सेंसर तनुता और थोक तनुता दोनों प्रदर्शित कर सकते हैं। विस्तारित तनु सेंसर और थोक तनुता का एक रैखिक संयोजन है जो एक ठोस तनुता युक्त सामग्री की बढ़ाव की प्रतिक्रिया का वर्णन करता है। यह व्यापक रूप से पॉलिमर के लक्षण वर्णन के लिए उपयोग किया जाता है।
भूविज्ञान में, पृथ्वी सामग्री जो अपने तनुता युक्त विरूपण से अधिक परिमाण के कम से कम तीन ऑर्डर तनु विरूपण प्रदर्शित करती है, उन्हें कभी-कभी रिड्स कहा जाता है।[23]
नाप
तनुता को विभिन्न प्रकार के विस्कोमीटर और रियोमीटर से मापा जाता है। रियोमीटर का उपयोग उन तरल पदार्थों के लिए किया जाता है जिन्हें तनुता के एकल मान द्वारा परिभाषित नहीं किया जा सकता है और इसलिए विस्कोमीटर की तुलना में अधिक मापदंडों को सेट करने और मापने की आवश्यकता होती है। सटीक माप प्राप्त करने के लिए द्रव का बंद तापमान नियंत्रण आवश्यक है, विशेष रूप से स्नेहक जैसी सामग्री में, जिसकी तनुता केवल 5 डिग्री सेल्सियस के परिवर्तन के साथ दोगुनी हो सकती है।[24] कुछ तरल पदार्थों के लिए, सेंसर दरों (न्यूटोनियन तरल पदार्थ) की एक विस्तृत श्रृंखला पर तनुता स्थिर होती है। निरंतर तनुता (गैर-न्यूटोनियन तरल पदार्थ) के बिना तरल पदार्थ को एक संख्या द्वारा वर्णित नहीं किया जा सकता है। गैर-न्यूटोनियन तरल पदार्थ सेंसर तनाव और सेंसर दर के बीच विभिन्न प्रकार के विभिन्न सहसंबंध प्रदर्शित करते हैं।
कीनेमेटिक तनुता को मापने के लिए सबसे आम उपकरणों में से एक ग्लास केशिका विस्कोमीटर है।
परत उद्योगों में, तनुता को एक कप से मापा जा सकता है जिसमें प्रवाह का समय मापा जाता है। कई प्रकार के कप हैं - जैसे कि ज़हान कप और फोर्ड तनु कप - प्रत्येक प्रकार के उपयोग के साथ मुख्य रूप से उद्योग के अनुसार भिन्न होते हैं।
कोटिंग्स में भी उपयोग किया जाता है, एक स्टॉर्मर विस्कोमीटर तनुता निर्धारित करने के लिए लोड-आधारित रोटेशन को नियोजित करता है। क्रेब्स इकाइयों (केयू) में विस्कोसिटी की सूचना दी जाती है, जो स्टॉर्मर विस्कोमीटर के लिए अद्वितीय हैं।
वाइब्रेटिंग विस्कोमीटर का उपयोग विस्कोसिटी को मापने के लिए भी किया जा सकता है। दोलित्र या कंपन विस्कोमीटर तरल के भीतर सेंसर तरंगें बनाकर काम करते हैं। इस विधि में, संवेदक द्रव में डूबा होता है और एक विशिष्ट आवृत्ति पर प्रतिध्वनित होता है। जैसे ही सेंसर की सतह तरल के माध्यम से कतरती है, इसकी तनुता के कारण ऊर्जा खो जाती है। यह छितरी हुई ऊर्जा तब मापी जाती है और तनु पढ़ने में परिवर्तित हो जाती है। एक उच्च तनु ऊर्जा की अधिक हानि का कारण बनता है।
विस्तारित तनुता को विभिन्न रियोमीटर से मापा जा सकता है जो विस्तारित तनाव लागू करते हैं।
वॉल्यूम तनुता को एक ध्वनिक रियोमीटर से मापा जा सकता है।
स्पष्ट तनुता एक गणना है जो तेल या गैस कुओं के विकास में उपयोग किए जाने वाले ड्रिलिंग द्रव पर किए गए परीक्षणों से प्राप्त होती है। ये गणना और परीक्षण इंजीनियरों को आवश्यक विनिर्देशों के लिए खोदने वाला द्रव पदार्थ के गुणों को विकसित करने और बनाए रखने में सहायता करते हैं।
नैनोविस्कोसिटी (नैनोप्रोब द्वारा तनुता महसूस) को प्रतिदीप्ति सहसंबंध स्पेक्ट्रोस्कोपी द्वारा मापा जा सकता है।[25]
इकाइयां
इकाइयों की अंतर्राष्ट्रीय प्रणाली गतिशील तनुता की इकाई न्यूटन (इकाई)-सेकंड प्रति वर्ग मीटर (N·s/m) है2), अधिकांशतः पास्कल (यूनिट) -दूसरा (Pa·s), किलोग्राम प्रति मीटर प्रति सेकंड (किग्रा·मी)−1·से-1 के समतुल्य रूपों में भी व्यक्त किया जाता है) और पॉइज़्यूइल (पीएल)। सीजीएस प्रणाली यूनिट पोइज़ (यूनिट) (पी, या जी·सेमी−1·से−1 = 0.1 Pa·s),[26] जीन लियोनार्ड मैरी पॉइज़ुइल के नाम पर। यह सामान्यतः, विशेष रूप से एएसटीएम मानकों में, सेंटीपोइज़ (सीपी) के रूप में व्यक्त किया जाता है। सेंटीपोईस सुविधाजनक है क्योंकि 20 °C पर पानी की तनुता लगभग 1 cP होती है, और एक सेंटीपोईस SI मिलीपास्कल सेकंड (mPa·s) के बराबर होता है।
गतिज तनुता की SI इकाई वर्ग मीटर प्रति सेकंड (m2/s), जबकि काइनेमैटिक तनुता के लिए सीजीएस इकाई स्टोक्स (St, या cm) है।2·एस−1 = 0.0001 मी2·एस-1), सर जॉर्ज गेब्रियल स्टोक्स के नाम पर।[27] अमेरिकी उपयोग में, स्टोक को कभी-कभी एकवचन रूप में प्रयोग किया जाता है। सब मल्टीपल सेंटीस्टोक (cSt) का उपयोग अधिकांशतः इसके अतिरिक्त किया जाता है, 1 cSt = 1 मिमी2·एस−1 = 10−6 मि2·एस-1. 20 °C पर पानी की गतिज तनुता लगभग 1 cSt है।
इम्पीरियल और यूएस प्रथागत माप प्रणालियों की सबसे अधिक उपयोग की जाने वाली प्रणालियाँ हैं। यूएस प्रथागत, या इंपीरियल, इकाइयाँ फुट-पाउंड-सेकंड सिस्टम (बीजी) और अंग्रेजी इंजीनियरिंग इकाइयाँ (ईई) हैं। बीजी प्रणाली में, गतिशील तनुता में पाउंड (बल) की इकाइयां होती हैं - सेकंड प्रति वर्ग फुट (lb·s/ft)2), और ईई प्रणाली में इसकी इकाइयां पाउंड (बल)|पाउंड-बल-सेकंड प्रति वर्ग फुट (lbf·s/ft2). पौंड और पौंड-बल बराबर हैं; दो प्रणालियाँ केवल इस बात में भिन्न हैं कि बल और द्रव्यमान को कैसे परिभाषित किया जाता है। बीजी प्रणाली में पाउंड एक मूल इकाई है जिसमें से द्रव्यमान की इकाई (स्लग (इकाई)) को न्यूटन के द्वितीय नियम द्वारा परिभाषित किया गया है, जबकि ईई प्रणाली में बल और द्रव्यमान की इकाइयाँ (पाउंड-बल और पाउंड (द्रव्यमान) )या पाउंड-द्रव्यमान क्रमशः) जीसी (इंजीनियरिंग) या आनुपातिकता निरंतर Gc का उपयोग करके दूसरे नियम के माध्यम से स्वतंत्र रूप से परिभाषित किए गए हैं.
काइनेमैटिक विस्कोसिटी में वर्ग फुट प्रति सेकंड (फीट2/s) बीजी और ईई दोनों प्रणालियों में।
गैर-मानक इकाइयों में गतिशील तनुता की एक ब्रिटिश इकाई बारिश सम्मिलित है। मोटर वाहन उद्योग में तापमान के साथ तनुता के परिवर्तन का वर्णन करने के लिए तनु सूचकांक का उपयोग किया जाता है।
तनुता का गुणात्मक व्युत्क्रम तरलता है, जिसे सामान्यतः दर्शाया जाता है या , उपयोग किए गए सम्मेलन के आधार पर, पारस्परिक शिष्टता में मापा जाता है (पी-1, या सेंटीमीटर·सेकंड·चना-1), जिसे कभी-कभी री कहा जाता है। इंजीनियरिंग अभ्यास में तरलता का उपयोग शायद ही कभी किया जाता है।
एक समय में पेट्रोलियम उद्योग सैबोल्ट विस्कोमीटर के माध्यम से कीनेमेटिक तनुता को मापने और सैबोल्ट यूनिवर्सल सेकेंड (एसयूएस) की इकाइयों में कीनेमेटिक तनुता को व्यक्त करने पर निर्भर था।[28]अन्य संक्षिप्ताक्षर जैसे एसएसयू (सायबोल्ट सेकेंड यूनिवर्सल) या एसयूवी (सायबोल्ट यूनिवर्सल विस्कोसिटी) कभी-कभी उपयोग किए जाते हैं। एएसटीएम डी 2161 में प्रदान की गई अंकगणित और संदर्भ तालिका के अनुसार सेंटीस्टोक्स में कीनेमेटिक तनुता को एसयूएस से परिवर्तित किया जा सकता है।
आणविक उत्पत्ति
गैसों में संवेग परिवहन असतत आणविक संघट्टों द्वारा और तरल पदार्थों में आकर्षक बलों द्वारा मध्यस्थ होता है जो अणुओं को एक साथ बांधते हैं।[17] इस वजह से, तरल पदार्थों की गतिशील तनुता सामान्यतः गैसों की तुलना में बहुत अधिक होती है। इसके अतिरिक्त, तनुता गैसों में तापमान के साथ बढ़ती है और तरल पदार्थों में तापमान के साथ घट जाती है।
द्रवित-गैस महत्वपूर्ण बिंदु (ऊष्मागतिकी) के ऊपर, द्रवित और गैस फेज को एकल उप-तरल पदार्थ से परिवर्तित दिया जाता है। इस प्रभाव में, संवेग परिवहन के तंत्र तरल-जैसे और गैस-जैसे व्यवहार के बीच प्रक्षेपित होते हैं। उदाहरण के लिए, एक सुपरक्रिटिकल आइसोबैरिक प्रक्रिया (निरंतर-दबाव सतह) के साथ, कीनेमेटिक तनुता कम तापमान पर घट जाती है और उच्च तापमान पर बीच में न्यूनतम मान के साथ बढ़ जाती है।[29][30] इस प्रकार उक्त मान के लिए यह अनुमान कम से कम इस प्रकार रहता है-
जहाँ प्लैंक स्थिरांक है, इलेक्ट्रॉन द्रव्यमान है, और आणविक द्रव्यमान है।[30] सामान्यतः, एक प्रणाली की तनुता इस बात पर निर्भर करती है कि सिस्टम बनाने वाले अणु कैसे बातचीत करते हैं, और इसके लिए कोई सरल लेकिन सही सूत्र नहीं हैं। सबसे सरल सटीक अभिव्यक्तियाँ रेखीय सेंसर तनुता के लिए ग्रीन-कुबो संबंध हैं या 1988 में इवांस और मॉरिस द्वारा प्राप्त क्षणिक समय सहसंबंध फलन अभिव्यक्तियाँ हैं।[31] यद्यपि ये अभिव्यक्तियाँ प्रत्येक सटीक हैं, इन संबंधों का उपयोग करके घने द्रव की तनुता की गणना करने के लिए वर्तमान में आणविक गतिकी कंप्यूटर सिमुलेशन के उपयोग की आवश्यकता है। तनु गैस के लिए कुछ और प्रगति की जा सकती है, क्योंकि गैस के अणु कैसे चलते हैं और परस्पर क्रिया करते हैं, इसके बारे में प्रारंभिक धारणा तनुता की आणविक उत्पत्ति की मौलिक समझ को जन्म देती है। गैस अणुओं की गति के समीकरणों को व्यवस्थित रूप से मोटा-मोटा करके अधिक परिष्कृत उपचारों का निर्माण किया जा सकता है। इस प्रकार के उपचार का एक उदाहरण चैपमैन-एनस्कॉग सिद्धांत है, जो बोल्ट्जमैन समीकरण से तनु गैस की तनुता के लिए अभिव्यक्ति प्राप्त करता है।[15]
शुद्ध गैसें
एक तनु गैस के लिए तनुता की प्रारंभिक गणना Consider a dilute gas moving parallel to the -axis with velocity that depends only on the coordinate. To simplify the discussion, the gas is assumed to have uniform temperature and density.
Under these assumptions, the velocity of a molecule passing through is equal to whatever velocity that molecule had when its mean free path began. Because is typically small compared with macroscopic scales, the average velocity of such a molecule has the form
where is a numerical constant on the order of . (Some authors estimate ;[17][32] on the other hand, a more careful calculation for rigid elastic spheres gives .) Next, because half the molecules on either side are moving towards , and doing so on average with half the average molecular speed , the momentum flux from either side is
The net momentum flux at is the difference of the two:
According to the definition of viscosity, this momentum flux should be equal to , which leads to
गैसों में तनुता मुख्य रूप से आणविक प्रसार से उत्पन्न होती है जो प्रवाह की परतों के बीच संवेग का परिवहन करती है। तापमान पर तनु गैस के लिए एक प्राथमिक गणना और घनत्व देता है
जहाँ बोल्ट्जमैन स्थिरांक है, आणविक द्रव्यमान, और के क्रम पर एक संख्यात्मक स्थिरांक . मात्रा , औसत मुक्त पथ, टक्करों के बीच एक अणु द्वारा तय की गई औसत दूरी को मापता है। इस प्रकार बिना पूर्व जानकारी के भी , इस अभिव्यक्ति के गैर-तुच्छ प्रभाव हैं। विशेष रूप से इसके बाद से सामान्यतः घनत्व के व्युत्क्रमानुपाती होता है और तापमान के साथ बढ़ता है, स्वयं तापमान के साथ बढ़ना चाहिए और निश्चित तापमान पर घनत्व से स्वतंत्र होना चाहिए। इस प्रकार वास्तव में, ये दोनों भविष्यवाणियां अधिक परिष्कृत उपचारों में बनी रहती हैं, और इस प्रकार प्रायोगिक टिप्पणियों का सटीक वर्णन करती हैं। इसके विपरीत, तरल तनुता सामान्यतः तापमान के साथ घट जाती है।[17][32] इस प्रकार इस व्यास के कठोर तनुता युक्त क्षेत्रों के लिए , दे कर गणना की जा सकती है
इस स्थिति में तापमान से स्वतंत्र है, इसलिए . चूंकि, अधिक जटिल आणविक प्रारूप के लिए, गैर-तुच्छ तरीके से तापमान पर निर्भर करता है, और यहाँ उपयोग किए जाने वाले सरल गतिज तर्क अपर्याप्त हैं। अधिक मौलिक रूप से, एक परिमित सीमा पर बातचीत करने वाले कणों के लिए एक औसत मुक्त पथ की धारणा अनिश्चित हो जाती है, जो इस प्रकार वास्तविक दुनिया गैसों का वर्णन करने के लिए अवधारणा की उपयोगिता को सीमित करती है।[33]
चैपमैन-एन्सकॉग सिद्धांत
1900 की प्रारंभ में सिडनी चैपमैन (गणितज्ञ) और डेविड एनस्की द्वारा विकसित एक तकनीक अधिक परिष्कृत गणना की अनुमति देती है .[15] यह बोल्ट्ज़मैन समीकरण पर आधारित है, जो अंतर-आणविक अंतःक्रियाओं के संदर्भ में एक तनु गैस का सांख्यिकीय विवरण प्रदान करता है।[34] इस प्रकार इस तकनीक की सटीक गणना की अनुमति देता है आणविक प्रारूप के लिए जो कठोर तनुता युक्त क्षेत्रों की तुलना में अधिक यथार्थवादी हैं, जैसे कि इंटरमॉलिक्युलर आकर्षण को सम्मिलित करना हैं। इस प्रकार ऐसा करना सही तापमान निर्भरता को पुन: उत्पन्न करने के लिए आवश्यक है , जो प्रयोग दिखाते हैं की तुलना में अधिक तेजी से बढ़ता है कठोर तनुता युक्त क्षेत्रों के लिए प्रवृत्ति की भविष्यवाणी की थी।[17] इस प्रकार मुख्य रूप से चैपमैन-एनस्कॉग विश्लेषण से पता चलता है कि विभिन्न आणविक प्रारूप में मापदंडों को अलग-अलग करके अनुमानित तापमान निर्भरता को ट्यून किया जा सकता है। एक साधारण उदाहरण सदरलैंड प्रारूप है,[lower-alpha 1] जो कमजोर पारस्परिक आकर्षण वाले कठोर तनुता युक्त क्षेत्रों का वर्णन करता है। ऐसे स्थिति में, आकर्षक बल को क्षोभ सिद्धांत माना जा सकता है, जिसके लिए एक सरल अभिव्यक्ति होती है :
जहाँ तापमान से स्वतंत्र है, केवल इंटरमॉलिक्युलर आकर्षण के मापदंडों द्वारा निर्धारित किया जा रहा है। प्रयोग से जुड़ने के लिए, इसे फिर से लिखना सुविधाजनक है
जहाँ तापमान पर तनुता है .[35] यदि के प्रयोगों से जाना जाता है और फिर कम से कम एक और तापमान गणना की जा सकती है। के लिए यह मान इस प्रकार से प्राप्त कई सरल गैसों के लिए गुणात्मक रूप से सटीक हैं। थोड़ा अधिक परिष्कृत प्रारूप, जैसे लेनार्ड-जोन्स क्षमता, प्रयोगों के साथ बेहतर समझौता प्रदान कर सकते हैं, लेकिन केवल तापमान पर अधिक अपारदर्शी निर्भरता की कीमत पर। कुछ प्रणालियों में, गोलाकार समरूपता की धारणा को भी छोड़ दिया जाना चाहिए, जैसा कि पानी के गुणों जैसे अत्यधिक ध्रुवीय अणुओं वाले वाष्पों के स्थिति में होता है।2O. इन स्थितियों में, चैपमैन-एनस्कॉग विश्लेषण उल्लेखनीय रूप से अधिक जटिल है।[36][37]
थोक तनुता
काइनेटिक-आणविक चित्र में, गैसों में एक गैर-शून्य थोक तनुता उत्पन्न होती है जब अणुओं की ट्रांसलेशनल ऊर्जा और उनकी आंतरिक ऊर्जा के बीच ऊर्जा के आदान-प्रदान को नियंत्रित करने वाले गैर-नगण्य विश्राम समय होते हैं, उदा। घूर्णी ऊर्जा और कंपन। जैसे, थोक तनु है एकपरमाणुक आदर्श गैस के लिए, जिसमें अणुओं की आंतरिक ऊर्जा नगण्य होती है, लेकिन कार्बन डाइआक्साइड जैसी गैस के लिए शून्येतर होती है, जिसके अणुओं में घूर्णी और कंपन दोनों ऊर्जा होती है।[38][39]
शुद्ध तरल पदार्थ
गैसों के विपरीत, तरल पदार्थों में तनुता की आणविक उत्पत्ति के लिए कोई सरल लेकिन सटीक तस्वीर नहीं है।
विवरण के सरलतम स्तर पर, एक तरल में आसन्न परतों की सापेक्ष गति का मुख्य रूप से आकर्षक आणविक बलों द्वारा विरोध किया जाता है परत सीमा के पार कार्य करना आवश्यक हैं। इस प्रकार इस तस्वीर में, एक सही ढंग से बढ़ते तापमान के साथ तनुता कम होने की उम्मीद करता है। यह है क्योंकि बढ़ते तापमान से अणुओं की यादृच्छिक ऊष्मीय गति बढ़ जाती है, जिससे इस प्रकार उनके लिए अपनी आकर्षक अंतःक्रियाओं को पार करना सरल हो जाता है।[40] इस विज़ुअलाइज़ेशन पर निर्माण, एक ठोस की असतत संरचना के साथ सादृश्य में एक सरल सिद्धांत का निर्माण किया जा सकता है: एक तरल में अणुओं के समूह के रूप में कल्पना की जाती है जो एकल अणुओं को घेरते और घेरते हैं।[41] इस प्रकार इन केज में इन्हें बंद कर लिया जाता है या खाली किया जा सकता है, और शक्तिशाली आणविक आकर्षण मजबूत पिंजरों से मेल खाता है। इस प्रकार इस यादृच्छिक ऊष्मीय गति के कारण, एक अणु पिंजरों के बीच एक दर से उछलता है जो इस प्रकार आणविक आकर्षण की ताकत के साथ व्युत्क्रमानुपाती होता है। इस प्रकार ऊष्मागतिकी के संतुलन में ये हॉप्स किसी भी दिशा में पक्षपाती नहीं होते हैं। इस प्रकार दूसरी ओर, दो आसन्न परतों को एक दूसरे के सापेक्ष स्थानांतरित करने के लिए, हॉप्स को दिशा में पक्षपाती होना चाहिए जिसके सापेक्ष गति का इस निर्देशित गति को बनाए रखने के लिए आवश्यक बल का अनुमान किसी दिए गए सेंसर दर के लिए लगाया जा सकता है
अवोगाद्रो नियतांक है, प्लैंक स्थिरांक है, द्रव के एक मोल (इकाई) का आयतन है, और सामान्य क्वथनांक है। इस परिणाम का वही रूप है जो प्रसिद्ध अनुभवजन्य संबंध के रूप में है
-
(2)
जहाँ और डेटा से स्थिरांक फिट होते हैं।[41][42] दूसरी ओर, कई लेखक इस प्रारूप के संबंध में सावधानी व्यक्त करते हैं। समीकरण (1), फिटिंग समीकरण की तुलना में (2) प्रयोगात्मक डेटा के लिए।[41] अधिक मौलिक रूप से, भौतिक धारणा अंतर्निहित समीकरण (1) की आलोचना की गई है।[43] यह भी तर्क दिया गया है कि समीकरण में चरघातांकी निर्भरता (1) सरल, गैर-घातीय अभिव्यक्तियों की तुलना में प्रयोगात्मक अवलोकनों का अधिक सटीक वर्णन नहीं करता है।[44][45] इस प्रकार इन कमियों में कम तदर्थ प्रारूप का विकास व्यावहारिक रुचि का विषय है। परिशुद्धता के पक्ष में सरलता को छोड़कर, अणुओं के लिए गति के मौलिक समीकरणों से प्रारंभ होने वाली तनुता के लिए कठोर अभिव्यक्तियां लिखना संभव है। एक उत्कृष्ट उदाहरण इस दृष्टिकोण का इरविंग-किर्कवुड सिद्धांत है।[46] दूसरी ओर, ऐसे भाव मल्टीपार्टिकल सहसंबंध फलन (सांख्यिकीय यांत्रिकी) पर औसत के रूप में दिए गए हैं और इसलिए व्यवहार में लागू करना कठिन है।
सामान्यतः, आनुभविक रूप से व्युत्पन्न भाव (उपस्थिता श्यातना माप के आधार पर) तरल पदार्थों में तनुता की गणना करने का एकमात्र निरंतर विश्वसनीय साधन प्रतीत होता है।[47]
मिश्रण और मिश्रण
गैसीय मिश्रण
एकल घटक गैस की समान आणविक-गतिज तस्वीर को गैसीय मिश्रण पर भी लागू किया जा सकता है। उदाहरण के लिए, चैपमैन-एनस्कॉग दृष्टिकोण में तनुता गैसों के द्विअंगी मिश्रण की मात्रा को अलग-अलग घटक तनुता के रूप में लिखा जा सकता है , उनके संबंधित आयतन अंश और अंतर-आणविक अन्योन्यक्रिया।[15] एकल-घटक गैस के संबंध में, की निर्भरता इंटरमॉलिक्युलर इंटरैक्शन के मापदंडों पर विभिन्न टकराव वाले इंटीग्रल के माध्यम से प्रवेश करता है जो प्राथमिक कार्यों के संदर्भ में व्यक्त नहीं किया जा सकता है। के लिए प्रयोग करने योग्य भाव प्राप्त करने के लिए जो यथोचित रूप से प्रयोगात्मक डेटा से मेल खाते हैं, सामान्यतः विश्लेषणात्मक गणना और अनुभवजन्य फिटिंग के कुछ संयोजन का उपयोग करके समसामयिक अभिन्न का मूल्यांकन किया जाना चाहिए। इस तरह की प्रक्रिया का एक उदाहरण ऊपर चर्चा की गई एकल-घटक गैस के लिए सदरलैंड दृष्टिकोण है।
तरल पदार्थों का मिश्रण
शुद्ध तरल पदार्थों के लिए, आणविक सिद्धांतों से तरल पदार्थों के मिश्रण की तनुता की भविष्यवाणी करना कठिन है। शुद्ध तरल के लिए ऊपर प्रस्तुत आणविक पिंजरे सिद्धांत का विस्तार करना एक तरीका है। यह परिष्कार के विभिन्न स्तरों के साथ किया जा सकता है। इस तरह के विश्लेषण से उत्पन्न एक अभिव्यक्ति बाइनरी मिश्रण के लिए लेडरर-रोएगियर्स समीकरण है:
जहाँ एक अनुभवजन्य पैरामीटर है, और और घटक तरल पदार्थों के संबंधित तिल अंश और तनुता हैं।[48] चूंकि तनुता और तेल उद्योगों में सम्मिश्रण एक महत्वपूर्ण प्रक्रिया है, मिश्रण की तनुता की भविष्यवाणी करने के लिए विभिन्न प्रकार के अनुभवजन्य और औचित्य समीकरण उपस्थित हैं।[48]
समाधान और निलंबन
जलीय घोल
विलेय और सांद्रता की सीमा के आधार पर, एक जलीय इलेक्ट्रोलाइट घोल में समान तापमान और दबाव पर शुद्ध पानी की तुलना में अधिक या कम तनु हो सकता है। उदाहरण के लिए, 20% खारा (सोडियम क्लोराइड) घोल में शुद्ध पानी की तुलना में 1.5 गुना अधिक तनु होता है, जबकि 20% पोटेशियम आयोडाइड घोल में शुद्ध पानी की तुलना में लगभग 0.91 गुना तनु होता है।
पतला इलेक्ट्रोलाइटिक समाधानों का एक आदर्श प्रारूप तनुता के लिए निम्नलिखित समीकरण की ओर जाता है, इस प्रकार के मान को हम इस प्रकार प्राप्त कर सकते हैं:[49]
जहाँ विलायक की तनुता है, एकाग्रता है, और एक धनात्मक स्थिरांक है जो विलायक और विलेय दोनों गुणों पर निर्भर करता है। चूंकि, यह अभिव्यक्ति केवल बहुत पतला समाधान होने के लिए मान्य है 0.1 mol/L से कम।[50] उच्च सांद्रता के लिए, अतिरिक्त शर्तें आवश्यक हैं जो उच्च-क्रम आणविक सहसंबंधों के लिए उत्तरदायी हैं:
जहाँ और डेटा से फिट हैं। विशेष रूप से, का एक ऋणात्मक मूल्य कुछ समाधानों में देखी गई तनुता में कमी के लिए उत्तरदायी है। 25 °C (mol = मोल (यूनिट), L = लीटर) तापमान पर सोडियम क्लोराइड और पोटेशियम आयोडाइड के लिए इन स्थिरांकों के अनुमानित मान नीचे दिखाए गए हैं।[49]
| घुला हुआ पदार्थ | (mol−1/2 L1/2) | (mol−1 L) | (mol−2 L2) |
|---|---|---|---|
| सोडियम क्लोराइड (NaCl) | 0.0062 | 0.0793 | 0.0080 |
| पौटेशियम आयोडाइड (KI) | 0.0047 | −0.0755 | 0.0000 |
निलंबन
ठोस कणों के निलंबन में (जैसे माइक्रोन-आकार के गोले तेल में निलंबित), एक प्रभावी तनुता तनाव और तनाव घटकों के संदर्भ में परिभाषित किया जा सकता है जो निलंबित कणों के बीच की दूरी की तुलना में बड़ी मात्रा में औसत होते हैं, लेकिन मैक्रोस्कोपिक आयामों के संबंध में छोटे होते हैं।[51] ऐसे निलंबन सामान्यतः गैर-न्यूटोनियन व्यवहार प्रदर्शित करते हैं। चूंकि, स्थिर प्रवाह में तनु प्रणालियों के लिए, व्यवहार न्यूटोनियन है और अभिव्यक्ति के लिए सीधे कण गतिकी से प्राप्त किया जा सकता है। एक बहुत तनु प्रणाली में, मात्रा अंश के साथ , निलंबित कणों के बीच की बातचीत को नजरअंदाज किया जा सकता है। ऐसे स्थिति में कोई स्वतंत्र रूप से प्रत्येक कण के आसपास प्रवाह क्षेत्र की स्पष्ट रूप से गणना कर सकता है, और परिणाम प्राप्त करने के लिए संयोजन कर सकता है . गोले के लिए, इसका परिणाम आइंस्टीन समीकरण में होता है:
जहाँ निलंबित तरल की तनुता है। पर रैखिक निर्भरता इंटरपार्टिकल इंटरैक्शन की उपेक्षा का परिणाम है। सामान्यतः तनु प्रणालियों के लिए, कोई अपेक्षा करता है रूप लेने के लिए
जहां गुणांक कण आकार (जैसे गोले, छड़, डिस्क) पर निर्भर हो सकता है।[52] इसके सटीक मूल्य का प्रायोगिक निर्धारण चूंकि कठिन है: भविष्यवाणी भी क्षेत्रों के लिए निर्णायक रूप से मान्य नहीं किया गया है, विभिन्न प्रयोगों के साथ सीमा में मान खोज रहे हैं . प्रायोगिक स्थितियों को नियंत्रित करने में कठिनाई के कारण इस कमी को उत्तरदायी ठहराया गया है।[53]
सघन निलंबन में, पर एक अरैखिक निर्भरता प्राप्त करता है, इस प्रकार जो इंटरपार्टिकल इंटरैक्शन के महत्व को इंगित करता है। इस प्रभाव को पकड़ने के लिए विभिन्न विश्लेषणात्मक और अर्ध-अनुभवजन्य योजनाएँ उपस्थित हैं। सबसे मौलिक स्तर पर, एक शब्द द्विघात में जोड़ा जाता है :
और गुणांक प्रयोगात्मक डेटा से फिट है या सूक्ष्म सिद्धांत से अनुमानित है। चूंकि इस प्रकार कुछ लेखक इस तरह के सरल सूत्रों को लागू करने में सावधानी रखने की चेतावनी देते हैं क्योंकि गैर-न्यूटोनियन व्यवहार सघन निलंबन में प्रकट होता है ( गोले के लिए),[53] या लंबे या लचीले कणों के निलंबन में किया गया हैं।[51] इस प्रकार ऊपर वर्णित ठोस कणों के निलंबन और पायस के बीच अंतर है। उत्तरार्द्ध छोटी बूंदों का निलंबन है, जो स्वयं आंतरिक संचलन प्रदर्शित कर सकते हैं। आंतरिक संचलन की उपस्थिति प्रभावी तनुता को कम कर सकती है, और विभिन्न सैद्धांतिक या अर्ध-अनुभवजन्य प्रारूप का उपयोग किया जाना चाहिए।[54]
अनाकार सामग्री
उच्च और निम्न तापमान सीमा में, अक्रिस्टलीय ठोस में तनु प्रवाह (जैसे गिलास और पिघल में)[56][57][58] अरहेनियस समीकरण है:
जहाँ Q एक प्रासंगिक सक्रियण ऊर्जा है, जो आणविक मापदंडों के संदर्भ में दी गई है; T तापमान है; R दाढ़ गैस स्थिरांक है; और A लगभग स्थिर है। सक्रियण ऊर्जा Q उच्च या निम्न तापमान सीमा पर विचार किया जा रहा है या नहीं, इसके आधार पर एक अलग मूल्य लेता है: इस प्रकार यह उच्च मूल्य से बदलता है QH कम तापमान पर (कांचयुक्त अवस्था में) कम मूल्य पर QL उच्च तापमान पर (तरल अवस्था में) हैं।
मध्यवर्ती तापमान के लिए, तापमान के साथ गैर-तुच्छ रूप से भिन्न होता है और सरल अरहेनियस रूप विफल हो जाता है। दूसरी ओर, दो-घातीय समीकरण
जहाँ , , , सभी स्थिरांक हैं, तापमान की पूरी श्रृंखला पर प्रयोगात्मक डेटा के लिए एक अच्छा फिट प्रदान करता है, जबकि एक ही समय में कम और उच्च तापमान सीमा में सही अरहेनियस फॉर्म को कम करता है। यह अभिव्यक्ति परमाणु स्तर पर अनाकार सामग्री के विभिन्न सैद्धांतिक प्रारूप से प्रेरित हो सकती है।[57] तनुता के लिए एक दो-घातीय समीकरण को सुपरकूल्ड तरल पदार्थ के डायरे शोविंग प्रारूप के भीतर प्राप्त किया जा सकता है, जहां अरहेनियस ऊर्जा अवरोध की पहचान उच्च-आवृत्ति सेंसर मापांक से की जाती है, जो एक विशिष्ट शॉविंग वॉल्यूम है।[59][60] ऊष्मीय विस्तार के माध्यम से सेंसर मापांक की तापमान निर्भरता को निर्दिष्ट करने पर और अंतर-आणविक क्षमता के प्रतिकारक भाग के माध्यम से, एक और दो-घातीय समीकरण प्राप्त किया जाता है:[61]
जहाँ कांच संक्रमण तापमान के बराबर तापमान पर मूल्यांकन की गई सामग्री के उच्च आवृत्ति सेंसर मापांक को दर्शाता है , तथाकथित धक्का देने वाली मात्रा है, अर्ताथ यह धक्का देने वाली घटना में सम्मिलित परमाणुओं के समूह की विशेषता मात्रा है, जिसके द्वारा एक परमाणु/अणु निकटतम-पड़ोसियों के पिंजरे से निकल जाता है, इस प्रकार सामान्यतः इस मात्रा के क्रम में कुछ परमाणुओं द्वारा अधिकार कर लिया जाता है . आगे, सामग्री का ऊष्मीय विस्तार गुणांक है, एक पैरामीटर है जो रेडियल वितरण फलन के पहले शिखर के आरोही फ्लैंक के पावर-लॉ उदय की स्थिरता को मापता है, और मात्रात्मक रूप से अंतर-परमाणु क्षमता के प्रतिकारक भाग से संबंधित है।[61] अतंतः बोल्ट्जमैन स्थिरांक को दर्शाता है।
भंवर तनु
तरल पदार्थों में अशांति के अध्ययन में, सामान्य व्यावहारिक रणनीति गति में छोटे पैमाने के भंवर (या एडी (द्रव गतिकी)) को अनदेखा करना और एक प्रभावी तनुता के साथ बड़े पैमाने पर गति की गणना करना है, जिसे एड़ी तनु कहा जाता है, जो छोटे पैमाने के प्रवाह में ऊर्जा के परिवहन और अपव्यय की विशेषता है (बड़े एड़ी सिमुलेशन देखें)।[62][63] तरल पदार्थ की तनुता के विपरीत, जो ऊष्मप्रवैगिकी के दूसरे नियम द्वारा धनात्मक होना चाहिए, एड़ी तनुता ऋणात्मक हो सकती है।[64][65]
भविष्यवाणी
क्योंकि तनुता निरंतर तापमान और दबाव पर निर्भर करती है, इसे एक परिमित संख्या द्वारा पूरी तरह से प्रयोगात्मक माप के लिए चित्रित नहीं किया जा सकता है, इस प्रकार यदि प्रायोगिक मूल्य उपलब्ध नहीं हैं तो पूर्वानुमान सूत्र आवश्यक हो जाते हैं, तापमान और ब्याज के दबावों पर। थर्मोफिजिकल सिमुलेशन के लिए यह क्षमता महत्वपूर्ण है, जिसमें किसी तरल पदार्थ का तापमान और दबाव स्थान और समय के साथ निरंतर भिन्न हो सकता है। ऐसी ही स्थिति सामने आती है, शुद्ध तरल पदार्थों के मिश्रण के लिए, जहां तनु घटक तरल पदार्थों के एकाग्रता अनुपात पर निरंतर निर्भर करता है
सरलतम तरल पदार्थों के लिए, जैसे तनु एकपरमाण्विक गैसों और उनके मिश्रणों के लिए, अब से ही क्वांटम यांत्रिकी अभिकलन शब्दों में तनुता का सटीक अनुमान लगा सकते हैं। मौलिक परमाणु स्थिरांक, अर्ताथ उपस्थिता तनुता माप के संदर्भ के बिना किया जाता हैं।[66] इस प्रकार पतले हीलियम के विशेष स्थिति के लिए, प्रारंभिक गणना में तनुता की माप अनिश्चितता प्रयोगात्मक मूल्यों में अनिश्चितताओं की तुलना में छोटे परिमाण के दो क्रम हैं।[67] इस प्रकार अधिकांश तरल पदार्थों के लिए, ऐसी उच्च-सटीकता, प्रथम-सिद्धांत संगणना संभव नहीं है। बल्कि, सैद्धांतिक या अनुभवजन्य अभिव्यक्तियाँ इसमें उपस्थिता तनुता माप के लिए फिट होना चाहिए। यदि ऐसी अभिव्यक्ति तापमान की एक बड़ी श्रृंखला पर उच्च-निष्ठा डेटा के लिए उपयुक्त है, और इस प्रकार दबाव, तो इसे उस द्रव के लिए संदर्भ सहसंबंध कहा जाता है। इसके लिए संदर्भ सहसंबंध प्रकाशित किए गए हैं कई शुद्ध तरल पदार्थ; कुछ उदाहरण पानी, कार्बन डाइऑक्साइड, अमोनिया, बेंजीन और क्सीनन हैं।[68][69][70][71][72] इनमें से कई कवर तापमान और दबाव रेंज हैं जो गैस, तरल और सुपरक्रिटिकल द्रव चरणों को सम्मिलित करते हैं।
थर्मोफिजिकल प्रारूपिंग सॉफ्टवेयर अधिकांशतः उपयोगकर्ता द्वारा निर्दिष्ट तापमान और दबाव पर तनुता की भविष्यवाणी करने के लिए संदर्भ सहसंबंधों पर निर्भर करता है। इस प्रकार ये सहसंबंध मालिकाना सॉफ्टवेयर हो सकते हैं। उदाहरण संदर्भ प्रस्ताव[73] और कूलप्रॉप[74] (खुला स्त्रोत) हैं।
विस्कोसिटी की गणना फ़ार्मुलों का उपयोग करके भी की जा सकती है जो इसे व्यक्तिगत कण के आँकड़ों के रूप प्रक्षेपवक्र में व्यक्त करते हैं । इन फ़ार्मुलों में रैखिक अपरूपण तनुता के लिए ग्रीन-कुबो संबंध और क्षणिक समय सहसंबंध फलन सम्मिलित हैं, 1988 में इवांस और मॉरिस द्वारा व्युत्पन्न भाव प्रकट करती हैं।[75][31] इस प्रकार इन अभिव्यक्तियों का लाभ यह है कि वे सामान्य प्रणालियों के लिए औपचारिक रूप से सटीक और मान्य हैं। इससे होने वाली हानि यह है कि उन्हें विस्तृत की आवश्यकता होती है, इस प्रकार कण प्रक्षेपवक्र का ज्ञान, केवल आणविक गतिकी जैसे कम्प्यूटरीकृत रूप से महंगे सिमुलेशन में उपलब्ध है। इंटरपार्टिकल इंटरैक्शन के लिए एक सटीक प्रारूप की भी आवश्यकता होती है, जिसे जटिल अणुओं के लिए प्राप्त करना कठिन हो सकता है।[76]
चयनित पदार्थ
विस्कोसिटी के देखे गए मान परिमाण के कई क्रमों में भिन्न होते हैं, यहां तक कि सामान्य पदार्थों के लिए भी (नीचे परिमाण तालिका का क्रम देखें)। उदाहरण के लिए, एक 70% सुक्रोज (चीनी) के घोल में पानी की तुलना में 400 गुना और हवा की तुलना में 26000 गुना अधिक तनुता होती है।[78] अधिक नाटकीय रूप से, पिच में पानी की तुलना में 230 अरब गुना तनु होने का अनुमान लगाया गया है।[77]
पानी
गतिशील तनुता कमरे के तापमान (25 डिग्री सेल्सियस) पर पानी लगभग 0.89 mPa·s होता है। केल्विन में तापमान के कार्य के रूप में, अर्ध-अनुभवजन्य वोगेल-फुलचर-टैमन समीकरण का उपयोग करके तनुता का अनुमान लगाया जा सकता है:
जहां A = 0.02939 mPa·s, B = 507.88 K, और C = 149.3 K.[79] तनुता के प्रायोगिक रूप से निर्धारित मान भी नीचे दी गई तालिका में दिए गए हैं। 20 °C पर मान एक उपयोगी संदर्भ हैं: वहाँ, गतिशील तनुता लगभग 1 cP है और गतिज तनुता लगभग 1 cSt है।
| तापमान (°C) | तनुता (mPa·s or cP) |
|---|---|
| 10 | 1.3059 |
| 20 | 1.0016 |
| 30 | 0.79722 |
| 50 | 0.54652 |
| 70 | 0.40355 |
| 90 | 0.31417 |
वायु
मानक वायुमंडलीय स्थितियों (25 डिग्री सेल्सियस और 1 बार के दबाव) के अनुसार, हवा की गतिशील तनुता 18.5 μPa·s होती है, जो समान तापमान पर पानी की तनुता से लगभग 50 गुना कम होती है। अति उच्च दाब को छोड़कर वायु की तनुता अधिकतर तापमान पर निर्भर करती है। तापमान निर्भरता के लिए कई संभावित अनुमानित सूत्रों में से एक है:[80]
जो -20 डिग्री सेल्सियस से 400 डिग्री सेल्सियस की सीमा में सटीक है। इस सूत्र के मान्य होने के लिए, केल्विन में तापमान दिया जाना चाहिए; फिर Pa·s में तनुता के अनुरूप होता है।

अन्य सामान्य पदार्थ
| पदार्थ | विस्कोसिटी (mPa·s) | तापमान (°C) | रिफर |
|---|---|---|---|
| बेंजीन | 0.604 | 25 | [78] |
| जल | 1.0016 | 20 | |
| मरकरी | 1.526 | 25 | |
| दूध | 2.12 | 20 | [81] |
| सघन बियर | 2.53 | 20 | |
| ओलिव का तेल | 56.2 | 26 | [81] |
| शहद | 2000–10000 | 20 | [82] |
| केचप[lower-alpha 2] | 5000–20000 | 25 | [83] |
| पीनट बटर[lower-alpha 2] | 104–106 | [84] | |
| पिच | 2.3×1011 | 10–30 (चर) | [77] |
परिमाण अनुमानों का क्रम
निम्न तालिका सामान्य पदार्थों में पाए जाने वाले तनुता मानों की श्रेणी को दर्शाती है। जब तक अन्यथा ध्यान न दिया जाए, तापमान 25 डिग्री सेल्सियस और 1 वायुमंडल का दबाव माना जाता है।
सूचीबद्ध मूल्य केवल प्रतिनिधि अनुमान हैं, क्योंकि वे माप अनिश्चितताओं, भौतिक परिभाषाओं में परिवर्तनशीलता, या गैर-न्यूटोनियन व्यवहार के लिए उत्तरदायी नहीं हैं।
| फैक्टर (Pa·s) | विवरण | उदाहरण | मान (Pa·s) | रिफर |
|---|---|---|---|---|
| 10−6 | गैसीय तनुता की निचली सीमा | ब्यूटेन | 7.49 × 10−6 | [85] |
| हाइड्रोजन | 8.8 × 10−6 | [86] | ||
| 10−5 | गैसीय तनुता की ऊपरी सीमा | क्रिप्टन | 2.538 × 10−5 | [87] |
| नियाॅन | 3.175 × 10−5 | |||
| 10−4 | तरल तनुता की निचली सीमा | पेंटेन | 2.24 × 10−4 | [78] |
| गैसोलीन | 6 × 10−4 | |||
| जल | 8.90 × 10−4 | [78] | ||
| 10−3 | छोटे-अणु के लिए विशिष्ट श्रेणी
न्यूटोनियन तरल पदार्थ |
एथेनाॅल | 1.074 × 10−3 | |
| मर्करी | 1.526 × 10−3 | |||
| दूध(20 °C) | 2.12 × 10−3 | [81] | ||
| रक्त | 3 × 10−3 to 6 × 10−3 | [88] | ||
| द्रवित स्टील(1550 °C) | 6 × 10−3 | [89] | ||
| 10−2 – 100 | तेल और लंबी श्रृंखला वाले हाइड्रोकार्बन | लाइनसीड तेल | 0.028 | |
| ओलेइक तेल | 0.036 | [90] | ||
| ओलिव तेल | 0.084 | [81] | ||
| SAE 10 मोटर तेल | 0.085 to 0.14 | |||
| कैस्टोर तेल | 0.1 | |||
| SAE 20 मोटर तेल | 0.14 to 0.42 | |||
| SAE 30 मोटर तेल | 0.42 to 0.65 | |||
| SAE 40 मोटर तेल | 0.65 to 0.90 | |||
| ग्लिसरीन | 1.5 | |||
| पैनकेक सीरप | 2.5 | |||
| 101 – 103 | पेस्ट, जैल और अन्य अर्धठोस
(आम तौर पर गैर-न्यूटोनियन) |
केचप | ≈ 101 | [83] |
| मस्टर्ड | ||||
| सोर क्रीम | ≈ 102 | |||
| पीनट बटर | [84] | |||
| लार्ड | ≈ 103 | |||
| ≈108 | विस्कोलेस्टिक पॉलिमर | पिच | 2.3×108 | [77] |
| ≈1021 | एक विस्को इलास्टिक के अनुसार कुछ ठोस
विवरण |
मैंटल | ≈ 1019 to 1024 | [91] |
यह भी देखें
- डैशपॉट
- दबोरा संख्या
- रूचीपूर्ण
- हर्शल-बल्कली द्रव
- उच्च चिपचिपापन मिक्सर
- हाइपरविस्कोसिटी सिंड्रोम
- अंतर्भूत लसीलापन
- इनविसिड फ्लो
- जॉबैक विधि (आण्विक संरचना से तरल चिपचिपाहट का अनुमान)
- काये प्रभाव
- माइक्रोविस्कोसिटी
- मॉर्टन नंबर
- तेल का दबाव
- अर्ध-ठोस
- रियोलॉजी
- स्टोक्स फ्लो
- सुपरफ्लुइड हीलियम-4
- विस्कोप्लास्टिसिटी
- मिश्रण के लिए चिपचिपापन मॉडल
- जहान कप
संदर्भ
फुटनोट्स
- ↑ The discussion which follows draws from Chapman & Cowling 1970, pp. 232–237
- ↑ 2.0 2.1 These materials are highly non-Newtonian.
उद्धरण
- ↑ Symon 1971.
- ↑ Balescu 1975, pp. 428–429.
- ↑ Landau & Lifshitz 1987.
- ↑ Harper, Douglas (n.d.). "viscous (adj.)". Online Etymology Dictionary. Archived from the original on 1 May 2019. Retrieved 19 September 2019.
- ↑ Mewis & Wagner 2012, p. 19.
- ↑ Streeter, Wylie & Bedford 1998.
- ↑ Holman 2002.
- ↑ Incropera et al. 2007.
- ↑ Nič et al. 1997.
- ↑ 10.0 10.1 10.2 Bird, Stewart & Lightfoot 2007, p. 19.
- ↑ 11.0 11.1 Landau & Lifshitz 1987, pp. 44–45.
- ↑ Bird, Stewart & Lightfoot 2007, p. 18: This source uses an alternative sign convention, which has been reversed here.
- ↑ Landau & Lifshitz 1987, p. 45.
- ↑ 14.0 14.1 Balescu 1975.
- ↑ 15.0 15.1 15.2 15.3 Chapman & Cowling 1970.
- ↑ Millat 1996.
- ↑ 17.0 17.1 17.2 17.3 17.4 Bird, Stewart & Lightfoot 2007.
- ↑ Schroeder 1999.
- ↑ Różańska et al. 2014, pp. 47–55.
- ↑ Trouton 1906, pp. 426–440.
- ↑ Mewis & Wagner 2012, pp. 228–230.
- ↑ Kumagai, Sasajima & Ito 1978, pp. 157–161.
- ↑ Scherer, Pardenek & Swiatek 1988, p. 14.
- ↑ Hannan 2007.
- ↑ Kwapiszewska et al. 2020.
- ↑ McNaught & Wilkinson 1997, poise.
- ↑ Gyllenbok 2018, p. 213.
- ↑ ASTM D2161 : Standard Practice for Conversion of Kinematic Viscosity to Saybolt Universal Viscosity or to Saybolt Furol Viscosity, ASTM, 2005, p. 1
- ↑ Trachenko & Brazhkin 2020.
- ↑ 30.0 30.1 Trachenko & Brazhkin 2021.
- ↑ 31.0 31.1 Evans & Morriss 1988.
- ↑ 32.0 32.1 Bellac, Mortessagne & Batrouni 2004.
- ↑ Chapman & Cowling 1970, p. 103.
- ↑ Cercignani 1975.
- ↑ Sutherland 1893, pp. 507–531.
- ↑ Bird, Stewart & Lightfoot 2007, pp. 25–27.
- ↑ Chapman & Cowling 1970, pp. 235–237.
- ↑ Chapman & Cowling 1970, pp. 197, 214–216.
- ↑ Cramer 2012, p. 066102-2.
- ↑ Reid & Sherwood 1958, p. 202.
- ↑ 41.0 41.1 41.2 Bird, Stewart & Lightfoot 2007, pp. 29–31.
- ↑ Reid & Sherwood 1958, pp. 203–204.
- ↑ Hildebrand 1977.
- ↑ Hildebrand 1977, p. 37.
- ↑ Egelstaff 1992, p. 264.
- ↑ Irving & Kirkwood 1949, pp. 817–829.
- ↑ Reid & Sherwood 1958, pp. 206–209.
- ↑ 48.0 48.1 Zhmud 2014, p. 22.
- ↑ 49.0 49.1 Viswanath et al. 2007.
- ↑ Abdulagatov, Zeinalova & Azizov 2006, pp. 75–88.
- ↑ 51.0 51.1 Bird, Stewart & Lightfoot 2007, pp. 31–33.
- ↑ Bird, Stewart & Lightfoot 2007, p. 32.
- ↑ 53.0 53.1 Mueller, Llewellin & Mader 2009, pp. 1201–1228.
- ↑ Bird, Stewart & Lightfoot 2007, p. 33.
- ↑ Fluegel 2007.
- ↑ Doremus 2002, pp. 7619–7629.
- ↑ 57.0 57.1 Ojovan, Travis & Hand 2007, p. 415107.
- ↑ Ojovan & Lee 2004, pp. 3803–3810.
- ↑ Dyre, Olsen & Christensen 1996, p. 2171.
- ↑ Hecksher & Dyre 2015.
- ↑ 61.0 61.1 Krausser, Samwer & Zaccone 2015, p. 13762.
- ↑ Bird, Stewart & Lightfoot 2007, p. 163.
- ↑ Lesieur 2012, pp. 2–.
- ↑ Sivashinsky & Yakhot 1985, p. 1040.
- ↑ Xie & Levchenko 2019, p. 045434.
- ↑ Sharipov & Benites 2020.
- ↑ Rowland, Al Ghafri & May 2020.
- ↑ Huber et al. 2009.
- ↑ Laesecke & Muzny 2017.
- ↑ Monogenidou, Assael & Huber 2018.
- ↑ Avgeri et al. 2014.
- ↑ Velliadou et al. 2021.
- ↑ "रेफप्रॉप". Nist. Nist.gov. 18 April 2013. Archived from the original on 2022-02-09. Retrieved 2022-02-15.
- ↑ Bell et al. 2014.
- ↑ Evans & Morriss 2007.
- ↑ Maginn et al. 2019.
- ↑ 77.0 77.1 77.2 77.3 Edgeworth, Dalton & Parnell 1984, pp. 198–200.
- ↑ 78.0 78.1 78.2 78.3 Rumble 2018.
- ↑ Viswanath & Natarajan 1989, pp. 714–715.
- ↑ tec-science (2020-03-25). "तरल पदार्थ और गैसों की चिपचिपाहट". tec-science (in English). Archived from the original on 2020-04-19. Retrieved 2020-05-07.
- ↑ 81.0 81.1 81.2 81.3 Fellows 2009.
- ↑ Yanniotis, Skaltsi & Karaburnioti 2006, pp. 372–377.
- ↑ 83.0 83.1 Koocheki et al. 2009, pp. 596–602.
- ↑ 84.0 84.1 Citerne, Carreau & Moan 2001, pp. 86–96.
- ↑ Kestin, Khalifa & Wakeham 1977.
- ↑ Assael et al. 2018.
- ↑ Kestin, Ro & Wakeham 1972.
- ↑ Rosenson, McCormick & Uretz 1996.
- ↑ Zhao et al. 2021.
- ↑ Sagdeev et al. 2019.
- ↑ Walzer, Hendel & Baumgardner n.d.
स्रोत
- Abdulagatov, Ilmutdin M.; Zeinalova, Adelya B.; Azizov, Nazim D. (2006). "प्रायोगिक चिपचिपाहट बी-जलीय LiCl समाधानों के गुणांक". Journal of Molecular Liquids. 126 (1–3): 75–88. doi:10.1016/j.molliq.2005.10.006. ISSN 0167-7322.
- Assael, M. J.; et al. (2018). "तापीय चालकता और तरल पदार्थों की चिपचिपाहट के लिए संदर्भ मान और संदर्भ सहसंबंध". Journal of Physical and Chemical Reference Data. 47 (2): 021501. Bibcode:2018JPCRD..47b1501A. doi:10.1063/1.5036625. ISSN 0047-2689. PMC 6463310. PMID 30996494.
- Avgeri, S.; Assael, M. J.; Huber, M. L.; Perkins, R. A. (2014). "ट्रिपल प्वाइंट से 675 K और 300 MPa तक बेंजीन की चिपचिपाहट का संदर्भ सहसंबंध". Journal of Physical and Chemical Reference Data. AIP Publishing. 43 (3): 033103. Bibcode:2014JPCRD..43c3103A. doi:10.1063/1.4892935. ISSN 0047-2689.
- Balescu, Radu (1975). संतुलन और गैर-संतुलन सांख्यिकीय यांत्रिकी. John Wiley & Sons. ISBN 978-0-471-04600-4. Archived from the original on 2020-03-16. Retrieved 2019-09-18.
- Bell, Ian H.; Wronski, Jorrit; Quoilin, Sylvain; Lemort, Vincent (2014-01-27). "शुद्ध और छद्म-शुद्ध द्रव थर्मोफिजिकल संपत्ति मूल्यांकन और ओपन-सोर्स थर्मोफिजिकल प्रॉपर्टी लाइब्रेरी कूलप्रॉप". Industrial & Engineering Chemistry Research. American Chemical Society (ACS). 53 (6): 2498–2508. doi:10.1021/ie4033999. ISSN 0888-5885. PMC 3944605. PMID 24623957.
- Bellac, Michael; Mortessagne, Fabrice; Batrouni, G. George (2004). Equilibrium and Non-Equilibrium Statistical Thermodynamics. Cambridge University Press. ISBN 978-0-521-82143-8.
- Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (2007). Transport Phenomena (2nd ed.). John Wiley & Sons, Inc. ISBN 978-0-470-11539-8. Archived from the original on 2020-03-02. Retrieved 2019-09-18.
- Bird, R. Bryon; Armstrong, Robert C.; Hassager, Ole (1987), Dynamics of Polymeric Liquids, Volume 1: Fluid Mechanics (2nd ed.), John Wiley & Sons
- Cercignani, Carlo (1975). Theory and Application of the Boltzmann Equation. Elsevier. ISBN 978-0-444-19450-3.
- Chapman, Sydney; Cowling, T.G. (1970). The Mathematical Theory of Non-Uniform Gases (3rd ed.). Cambridge University Press. ISBN 9780521075770.
- Citerne, Guillaume P.; Carreau, Pierre J.; Moan, Michel (2001). "Rheological properties of peanut butter". Rheologica Acta. 40 (1): 86–96. doi:10.1007/s003970000120. S2CID 94555820.
- Cramer, M.S. (2012). "Numerical estimates for the bulk viscosity of ideal gases". Physics of Fluids. 24 (6): 066102–066102–23. Bibcode:2012PhFl...24f6102C. doi:10.1063/1.4729611. hdl:10919/47646. Archived from the original on 2022-02-15. Retrieved 2020-09-19.
- Doremus, R.H. (2002). "सिलिका की चिपचिपाहट". J. Appl. Phys. 92 (12): 7619–7629. Bibcode:2002JAP....92.7619D. doi:10.1063/1.1515132.
- Dyre, J.C.; Olsen, N. B.; Christensen, T. (1996). "कांच बनाने वाले आणविक तरल पदार्थों की चिपचिपा-प्रवाह सक्रियण ऊर्जा के लिए स्थानीय लोचदार विस्तार मॉडल". Physical Review B. 53 (5): 2171–2174. Bibcode:1996PhRvB..53.2171D. doi:10.1103/PhysRevB.53.2171. PMID 9983702.
- Edgeworth, R.; Dalton, B.J.; Parnell, T. (1984). "पिच ड्रॉप प्रयोग". European Journal of Physics. 5 (4): 198–200. Bibcode:1984EJPh....5..198E. doi:10.1088/0143-0807/5/4/003. S2CID 250769509. Archived from the original on 2013-03-28. Retrieved 2009-03-31.
- Egelstaff, P. A. (1992). An Introduction to the Liquid State (2nd ed.). Oxford University Press. ISBN 978-0-19-851012-3.
- Evans, Denis J.; Morriss, Gary P. (2007). नोनक्विलिब्रियम तरल पदार्थ के सांख्यिकीय यांत्रिकी. ANU Press. ISBN 9781921313226. JSTOR j.ctt24h99q. Archived from the original on 2022-01-10. Retrieved 2022-01-10.
- Evans, Denis J.; Morriss, Gary P. (October 15, 1988). "क्षणिक-समय-सहसंबंध कार्य और तरल पदार्थों का रियोलॉजी". Physical Review A. 38 (8): 4142–4148. Bibcode:1988PhRvA..38.4142E. doi:10.1103/PhysRevA.38.4142. PMID 9900865.
- Fellows, P. J. (2009). Food Processing Technology: Principles and Practice (3rd ed.). Woodhead. ISBN 978-1845692162.
- Fluegel, Alexander (2007). "चश्मे की चिपचिपाहट की गणना". Glassproperties.com. Archived from the original on 2010-11-27. Retrieved 2010-09-14.
- Gibbs, Philip (January 1997). "कांच तरल है या ठोस?". math.ucr.edu. Archived from the original on 29 March 2007. Retrieved 19 September 2019.
- Gyllenbok, Jan (2018). "एनसाइक्लोपीडिया ऑफ हिस्टोरिकल मेट्रोलॉजी, वेट एंड मेजर्स: वॉल्यूम 1". Encyclopaedia of Historical Metrology, Weights, and Measures. Vol. 1. Birkhäuser. ISBN 9783319575988.
- Hannan, Henry (2007). औद्योगिक और घरेलू सफाई उत्पादों के लिए तकनीशियन की सूत्रीकरण पुस्तिका. Waukesha, Wisconsin: Kyral LLC. p. 7. ISBN 978-0-6151-5601-9.
- Hecksher, Tina; Dyre, Jeppe C. (2015-01-01). "शोविंग मॉडल का परीक्षण करने वाले प्रयोगों की समीक्षा". Journal of Non-Crystalline Solids. 7th IDMRCS: Relaxation in Complex Systems (in English). 407: 14–22. Bibcode:2015JNCS..407...14H. doi:10.1016/j.jnoncrysol.2014.08.056. ISSN 0022-3093. Archived from the original on 2022-02-15. Retrieved 2021-10-17.
- Hildebrand, Joel Henry (1977). Viscosity and Diffusivity: A Predictive Treatment. John Wiley & Sons. ISBN 978-0-471-03072-0.
- Holman, Jack Philip (2002). गर्मी का हस्तांतरण. McGraw-Hill. ISBN 978-0-07-112230-6. Archived from the original on 2020-03-15. Retrieved 2019-09-18.
- Huber, M. L.; Perkins, R. A.; Laesecke, A.; Friend, D. G.; Sengers, J. V.; Assael, M. J.; Metaxa, I. N.; Vogel, E.; Mareš, R.; Miyagawa, K. (2009). "H2O की चिपचिपाहट के लिए नया अंतर्राष्ट्रीय सूत्रीकरण". Journal of Physical and Chemical Reference Data. AIP Publishing. 38 (2): 101–125. Bibcode:2009JPCRD..38..101H. doi:10.1063/1.3088050. ISSN 0047-2689.
- Incropera, Frank P.; et al. (2007). ऊष्मा और द्रव्यमान स्थानांतरण के मूल तत्व. Wiley. ISBN 978-0-471-45728-2. Archived from the original on 2020-03-11. Retrieved 2019-09-18.
- Irving, J.H.; Kirkwood, John G. (1949). "The Statistical Mechanical Theory of Transport Processes. IV. The Equations of Hydrodynamics". J. Chem. Phys. 18 (6): 817–829. doi:10.1063/1.1747782.
- Kestin, J.; Ro, S. T.; Wakeham, W. A. (1972). "नोबल गैसों की श्यानता 25-700°C तापमान रेंज में". The Journal of Chemical Physics. 56 (8): 4119–4124. Bibcode:1972JChPh..56.4119K. doi:10.1063/1.1677824. ISSN 0021-9606.
- Kestin, J.; Khalifa, H.E.; Wakeham, W.A. (1977). "पांच गैसीय हाइड्रोकार्बन की चिपचिपाहट". The Journal of Chemical Physics. 66 (3): 1132. Bibcode:1977JChPh..66.1132K. doi:10.1063/1.434048.
- Koocheki, Arash; et al. (2009). "केचप के रियोलॉजिकल गुण विभिन्न हाइड्रोक्लोइड्स और तापमान के एक समारोह के रूप में". International Journal of Food Science & Technology. 44 (3): 596–602. doi:10.1111/j.1365-2621.2008.01868.x.
- Krausser, J.; Samwer, K.; Zaccone, A. (2015). "अंतरपरमाण्विक प्रतिकर्षण कोमलता सीधे सुपरकूल्ड मेटैलिक मेल्ट्स की नाजुकता को नियंत्रित करती है". Proceedings of the National Academy of Sciences of the USA. 112 (45): 13762–13767. arXiv:1510.08117. Bibcode:2015PNAS..11213762K. doi:10.1073/pnas.1503741112. PMC 4653154. PMID 26504208.
- Kumagai, Naoichi; Sasajima, Sadao; Ito, Hidebumi (15 February 1978). "चट्टानों का दीर्घकालिक रेंगना: लगभग 20 वर्षों में प्राप्त बड़े नमूनों के परिणाम और लगभग 3 वर्षों में छोटे नमूनों वाले परिणाम". Journal of the Society of Materials Science (Japan). 27 (293): 157–161. NAID 110002299397. Archived from the original on 2011-05-21. Retrieved 2008-06-16.
- Kwapiszewska, Karina; Szczepański, Krzysztof; Kalwarczyk, Tomasz; Michalska, Bernadeta; Patalas-Krawczyk, Paulina; Szymański, Jędrzej; Andryszewski, Tomasz; Iwan, Michalina; Duszyński, Jerzy; Hołyst, Robert (2020). "साइटोप्लाज्म की नैनोस्केल विस्कोसिटी मानव कोशिका रेखाओं में संरक्षित है". The Journal of Physical Chemistry Letters. 11 (16): 6914–6920. doi:10.1021/acs.jpclett.0c01748. PMC 7450658. PMID 32787203.
- Laesecke, Arno; Muzny, Chris D. (2017). "कार्बन डाइऑक्साइड की चिपचिपाहट के लिए संदर्भ सहसंबंध". Journal of Physical and Chemical Reference Data. AIP Publishing. 46 (1): 013107. Bibcode:2017JPCRD..46a3107L. doi:10.1063/1.4977429. ISSN 0047-2689. PMC 5514612. PMID 28736460.
- Landau, L. D.; Lifshitz, E.M. (1987). तरल यांत्रिकी (2nd ed.). Elsevier. ISBN 978-0-08-057073-0. Archived from the original on 2020-03-21. Retrieved 2019-09-18.
- Maginn, Edward J.; Messerly, Richard A.; Carlson, Daniel J.; Roe, Daniel R.; Elliott, J. Richard (2019). "कंप्यूटिंग ट्रांसपोर्ट प्रॉपर्टीज के लिए सर्वोत्तम अभ्यास". Living Journal of Computational Molecular Science. University of Colorado at Boulder. 1 (1). doi:10.33011/livecoms.1.1.6324. ISSN 2575-6524. S2CID 104357320.
- Monogenidou, S. A.; Assael, M. J.; Huber, M. L. (2018). "ट्रिपल प्वाइंट से 725 के और 50 एमपीए तक अमोनिया की चिपचिपाहट के लिए संदर्भ सहसंबंध". Journal of Physical and Chemical Reference Data. AIP Publishing. 47 (2): 023102. Bibcode:2018JPCRD..47b3102M. doi:10.1063/1.5036724. ISSN 0047-2689. PMC 6512859. PMID 31092958.
- Lesieur, Marcel (2012). तरल पदार्थ में अशांति: स्टोचैस्टिक और न्यूमेरिकल मॉडलिंग. Springer. ISBN 978-94-009-0533-7. Archived from the original on 2020-03-14. Retrieved 2018-11-30.
- Mewis, Jan; Wagner, Norman J. (2012). कोलाइडल सस्पेंशन रिओलॉजी. Cambridge University Press. ISBN 978-0-521-51599-3. Archived from the original on 2020-03-14. Retrieved 2018-12-10.
- McNaught, A. D.; Wilkinson, A. (1997). "poise". आईयूपीएसी। रासायनिक शब्दावली का संग्रह ("गोल्ड बुक"). S. J. Chalk (2nd ed.). Oxford: Blackwell Scientific. doi:10.1351/goldbook. ISBN 0-9678550-9-8.
- Millat, Jorgen (1996). तरल पदार्थों के परिवहन गुण: उनका सहसंबंध, भविष्यवाणी और अनुमान. Cambridge: Cambridge University Press. ISBN 978-0-521-02290-3. OCLC 668204060.
- Mueller, S.; Llewellin, E. W.; Mader, H. M. (2009). "ठोस कणों के निलंबन की रियोलॉजी". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 466 (2116): 1201–1228. doi:10.1098/rspa.2009.0445. ISSN 1364-5021.
- Nič, Miloslav; et al., eds. (1997). "dynamic viscosity, η". रासायनिक शब्दावली का IUPAC संग्रह. Oxford: Blackwell Scientific Publications. doi:10.1351/goldbook. ISBN 978-0-9678550-9-7.
- Ojovan, M.I.; Lee, W.E. (2004). "डोरेमस दृष्टिकोण के भीतर नेटवर्क तरल पदार्थों की चिपचिपाहट". J. Appl. Phys. 95 (7): 3803–3810. Bibcode:2004JAP....95.3803O. doi:10.1063/1.1647260.
- Ojovan, M.I.; Travis, K. P.; Hand, R.J. (2007). "चिपचिपाहट-तापमान संबंधों से कांच की सामग्री में बांड के थर्मोडायनामिक पैरामीटर" (PDF). J. Phys.: Condens. Matter. 19 (41): 415107. Bibcode:2007JPCM...19O5107O. doi:10.1088/0953-8984/19/41/415107. PMID 28192319. S2CID 24724512. Archived (PDF) from the original on 2018-07-25. Retrieved 2019-09-27.
- Plumb, Robert C. (1989). "प्राचीन खिड़की के शीशे और सुपरकूल्ड तरल पदार्थों का प्रवाह". Journal of Chemical Education. 66 (12): 994. Bibcode:1989JChEd..66..994P. doi:10.1021/ed066p994. Archived from the original on 2005-08-26. Retrieved 2013-12-25.
- Rapaport, D.C. (2004). आणविक गतिशीलता सिमुलेशन की कला (2nd ed.). Cambridge University Press. ISBN 9780521825689. Archived from the original on 2018-06-25. Retrieved 2022-01-10.
- Reid, Robert C.; Sherwood, Thomas K. (1958). गैसों और तरल पदार्थों के गुण. McGraw-Hill.
- Reif, F. (1965), Fundamentals of Statistical and Thermal Physics, McGraw-Hill. एक उन्नत उपचार।
- Rosenson, R S; McCormick, A; Uretz, E F (1996-08-01). "स्वस्थ वयस्कों में रक्त चिपचिपापन मूल्यों और जैव रासायनिक सहसंबंधों का वितरण". Clinical Chemistry. Oxford University Press (OUP). 42 (8): 1189–1195. doi:10.1093/clinchem/42.8.1189. ISSN 0009-9147. PMID 8697575.
- Rowland, Darren; Al Ghafri, Saif Z. S.; May, Eric F. (2020-03-01). "एब इनिटियो गणना और चिपचिपाहट अनुपात माप के आधार पर तनु गैस परिवहन गुण के लिए व्यापक संदर्भ सहसंबंध". Journal of Physical and Chemical Reference Data. AIP Publishing. 49 (1): 013101. Bibcode:2020JPCRD..49a3101X. doi:10.1063/1.5125100. ISSN 0047-2689. S2CID 213794612.
- Różańska, S.; Różański, J.; Ochowiak, M.; Mitkowski, P. T. (2014). "विरोधी नोजल डिवाइस के उपयोग के साथ केंद्रित इमल्शन के विस्तारित चिपचिपापन माप" (PDF). Brazilian Journal of Chemical Engineering. 31 (1): 47–55. doi:10.1590/S0104-66322014000100006. ISSN 0104-6632. Archived (PDF) from the original on 2020-05-08. Retrieved 2019-09-19.
- Rumble, John R., ed. (2018). केमेस्ट्री और फ़ीजिक्स के लिए सीआरसी हैंडबुक (99th ed.). Boca Raton, FL: CRC Press. ISBN 978-1138561632.
- Sagdeev, Damir; Gabitov, Il'giz; Isyanov, Chingiz; Khairutdinov, Vener; Farakhov, Mansur; Zaripov, Zufar; Abdulagatov, Ilmutdin (2019-04-22). "वायुमंडलीय दबाव में ओलिक एसिड की घनत्व और चिपचिपाहट". Journal of the American Oil Chemists' Society. Wiley. 96 (6): 647–662. doi:10.1002/aocs.12217. ISSN 0003-021X. S2CID 150156106.
- Scherer, George W.; Pardenek, Sandra A.; Swiatek, Rose M. (1988). "सिलिका जेल में चिपचिपापन". Journal of Non-Crystalline Solids. 107 (1): 14. Bibcode:1988JNCS..107...14S. doi:10.1016/0022-3093(88)90086-5.
- Schroeder, Daniel V. (1999). थर्मल भौतिकी का एक परिचय. Addison Wesley. ISBN 978-0-201-38027-9. Archived from the original on 2020-03-10. Retrieved 2018-11-30.
- Sharipov, Felix; Benites, Victor J. (2020-07-01). "प्रारंभिक क्षमता के आधार पर महान गैसों के बहु-घटक मिश्रण के परिवहन गुणांक: चिपचिपाहट और तापीय चालकता". Physics of Fluids. AIP Publishing. 32 (7): 077104. arXiv:2006.08687. Bibcode:2020PhFl...32g7104S. doi:10.1063/5.0016261. ISSN 1070-6631. S2CID 219708359.
- Sivashinsky, V.; Yakhot, G. (1985). "बड़े पैमाने पर प्रवाह में नकारात्मक चिपचिपापन प्रभाव". The Physics of Fluids. 28 (4): 1040. Bibcode:1985PhFl...28.1040S. doi:10.1063/1.865025.
- Streeter, Victor Lyle; Wylie, E. Benjamin; Bedford, Keith W. (1998). तरल यांत्रिकी. WCB/McGraw Hill. ISBN 978-0-07-062537-2. Archived from the original on 2020-03-16. Retrieved 2019-09-18.
- Sutherland, William (1893). "एलआईआई। गैसों की चिपचिपाहट और आणविक बल" (PDF). The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 36 (223): 507–531. doi:10.1080/14786449308620508. ISSN 1941-5982. Archived (PDF) from the original on 2019-07-20. Retrieved 2019-09-18.
- Symon, Keith R. (1971). यांत्रिकी (3rd ed.). Addison-Wesley. ISBN 978-0-201-07392-8. Archived from the original on 2020-03-11. Retrieved 2019-09-18.
- Trachenko, K.; Brazhkin, V. V. (2020-04-22). "मौलिक भौतिक स्थिरांक से न्यूनतम क्वांटम चिपचिपाहट". Science Advances. American Association for the Advancement of Science (AAAS). 6 (17): eaba3747. arXiv:1912.06711. Bibcode:2020SciA....6.3747T. doi:10.1126/sciadv.aba3747. ISSN 2375-2548. PMC 7182420. PMID 32426470.
- Trachenko, Kostya; Brazhkin, Vadim V. (2021-12-01). "चिपचिपाहट का क्वांटम यांत्रिकी" (PDF). Physics Today. AIP Publishing. 74 (12): 66–67. Bibcode:2021PhT....74l..66T. doi:10.1063/pt.3.4908. ISSN 0031-9228. S2CID 244831744. Archived (PDF) from the original on 2022-01-10. Retrieved 2022-01-10.
- Trouton, Fred. T. (1906). "विस्कोस ट्रैक्शन के गुणांक और चिपचिपाहट के संबंध पर". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 77 (519): 426–440. Bibcode:1906RSPSA..77..426T. doi:10.1098/rspa.1906.0038. ISSN 1364-5021.
- Velliadou, Danai; Tasidou, Katerina A.; Antoniadis, Konstantinos D.; Assael, Marc J.; Perkins, Richard A.; Huber, Marcia L. (2021-03-25). "ट्रिपल प्वाइंट से 750 K और 86 MPa तक क्सीनन की चिपचिपाहट के लिए संदर्भ सहसंबंध". International Journal of Thermophysics. Springer Science and Business Media LLC. 42 (5): 74. Bibcode:2021IJT....42...74V. doi:10.1007/s10765-021-02818-9. ISSN 0195-928X. PMC 8356199. PMID 34393314.
- Viswanath, D.S.; Natarajan, G. (1989). तरल पदार्थ की चिपचिपाहट पर डेटा बुक. Hemisphere Publishing Corporation. ISBN 0-89116-778-1.
- Viswanath, Dabir S.; et al. (2007). तरल पदार्थों की चिपचिपाहट: सिद्धांत, अनुमान, प्रयोग और डेटा. Springer. ISBN 978-1-4020-5481-5.
- Walzer, Uwe; Hendel, Roland; Baumgardner, John (n.d.), Mantle Viscosity and the Thickness of the Convective Downwellings, archived from the original on 2007-06-11
- Xie, Hong-Yi; Levchenko, Alex (23 January 2019). "ग्राफीन में असंतुलित इलेक्ट्रॉन-छेद तरल का नकारात्मक चिपचिपापन और एड़ी प्रवाह". Phys. Rev. B. 99 (4): 045434. arXiv:1807.04770. Bibcode:2019PhRvB..99d5434X. doi:10.1103/PhysRevB.99.045434. S2CID 51792702.
- Yanniotis, S.; Skaltsi, S.; Karaburnioti, S. (February 2006). "विभिन्न तापमानों पर शहद की चिपचिपाहट पर नमी की मात्रा का प्रभाव". Journal of Food Engineering. 72 (4): 372–377. doi:10.1016/j.jfoodeng.2004.12.017.
- Zhao, Mengjing; Wang, Yong; Yang, Shufeng; Li, Jingshe; Liu, Wei; Song, Zhaoqi (2021). "प्लाज्मा द्वारा गर्म किए गए टू-स्ट्रैंड टुंडिश में पिघले हुए स्टील का प्रवाह व्यवहार और ताप हस्तांतरण". Journal of Materials Research and Technology. Elsevier BV. 13: 561–572. doi:10.1016/j.jmrt.2021.04.069. ISSN 2238-7854. S2CID 236277034.
- Zhmud, Boris (2014). "Viscosity Blending Equations" (PDF). Lube-Tech:93. Lube. No. 121. pp. 22–27. Archived (PDF) from the original on 2018-12-01. Retrieved 2018-11-30.
- "NIST संदर्भ द्रव थर्मोडायनामिक और ट्रांसपोर्ट गुण डेटाबेस (REFPROP): संस्करण 10". Nist. 2018-01-01. Archived from the original on 2021-12-16. Retrieved 2021-12-23.
- tec-science (2020-03-25). "तरल पदार्थ और गैसों की चिपचिपाहट". tec-science (in English). Archived from the original on 2020-04-19. Retrieved 2020-05-07.
बाहरी कड़ियाँ
- Fluid properties – high accuracy calculation of viscosity for frequently encountered pure liquids and gases
- Gas viscosity calculator as function of temperature
- Air viscosity calculator as function of temperature and pressure
- Fluid Characteristics Chart – a table of viscosities and vapor pressures for various fluids
- Gas Dynamics Toolbox – calculate coefficient of viscosity for mixtures of gases
- Glass Viscosity Measurement – viscosity measurement, viscosity units and fixpoints, glass viscosity calculation
- Kinematic Viscosity – conversion between kinematic and dynamic viscosity
- Physical Characteristics of Water – a table of water viscosity as a function of temperature
- Vogel–Tammann–Fulcher Equation Parameters
- Calculation of temperature-dependent dynamic viscosities for some common components
- "Test Procedures for Testing Highway and Nonroad Engines and Omnibus Technical Amendments" – United States Environmental Protection Agency
- Artificial viscosity
- Viscosity of Air, Dynamic and Kinematic, Engineers Edge