अतिपरवलयकार ज्यामिति: Difference between revisions
(Created page with "{{Short description|Non-Euclidean geometry}} {{Other uses|Hyperbolic (disambiguation)}} File:Hyperbolic.svg|frame|right|किसी दिए गए बिंदु P स...") |
|||
| Line 439: | Line 439: | ||
* | |||
* | |||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [http://cs.unm.edu/~joel/NonEuclid/NonEuclid.html Javascript freeware for creating sketches in the Poincaré Disk Model of Hyperbolic Geometry] University of New Mexico | * [http://cs.unm.edu/~joel/NonEuclid/NonEuclid.html Javascript freeware for creating sketches in the Poincaré Disk Model of Hyperbolic Geometry] University of New Mexico | ||
Revision as of 13:03, 13 February 2023
| ज्यामिति |
|---|
 |
| जियोमेटर्स |
गणित में, अतिपरवलयिक ज्यामिति (जिसे लोबचेवस्कियन ज्यामिति या जानोस बोल्याई-निकोलाई लोबचेव्स्की ज्यामिति भी कहा जाता है) एक [[गैर-[[यूक्लिडियन ज्यामिति]]]] है। यूक्लिडियन ज्यामिति के समानांतर सिद्धांत को इसके साथ बदल दिया गया है:
- किसी भी दी गई रेखा 'आर' और बिंदु 'पी' के लिए 'आर' पर नहीं, दोनों रेखा 'आर' और बिंदु 'पी' वाले विमान में कम से कम दो अलग-अलग रेखाएं हैं पी के माध्यम से जो आर को नहीं काटते हैं।
(उपरोक्त की तुलना Playfair की स्वयंसिद्ध से करें, जो यूक्लिड की समानांतर अभिधारणा का आधुनिक संस्करण है।)
अतिशयोक्तिपूर्ण समतल ज्यामिति भी छद्ममंडल की ज्यामिति है, एक निरंतर नकारात्मक गॉसियन वक्रता वाली सतहें। सैडल सतहों में कम से कम कुछ क्षेत्रों में नकारात्मक गॉसियन वक्रता होती है, जहां वे स्थानीय संपत्ति अतिशयोक्तिपूर्ण विमान के समान होती हैं।
अतिशयोक्तिपूर्ण ज्यामिति का एक आधुनिक उपयोग विशेष सापेक्षता के सिद्धांत में है, विशेष रूप से मिन्कोव्स्की मॉडल में।
जब जियोमीटर को पहली बार एहसास हुआ कि वे मानक यूक्लिडियन ज्यामिति के अलावा किसी अन्य चीज़ के साथ काम कर रहे हैं, तो उन्होंने अपनी ज्यामिति को कई अलग-अलग नामों से वर्णित किया; फेलिक्स क्लेन ने अंततः इस विषय को अतिपरवलयिक ज्यामिति नाम दिया ताकि इसे अब शायद ही कभी इस्तेमाल किए जाने वाले अनुक्रम अण्डाकार ज्यामिति (गोलाकार ज्यामिति), परवलयिक ज्यामिति (यूक्लिडियन ज्यामिति), और अतिशयोक्तिपूर्ण ज्यामिति में शामिल किया जा सके। सोवियत के बाद के राज्यों में, इसे आमतौर पर लोबाचेवस्कियन ज्यामिति कहा जाता है, जिसका नाम इसके खोजकर्ताओं में से एक के नाम पर रखा गया है, रूसी भूगर्भशास्त्री निकोलाई लोबचेव्स्की।
यह पृष्ठ मुख्य रूप से द्वि-आयामी (तलीय) अतिपरवलयिक ज्यामिति और यूक्लिडियन और अतिपरवलयिक ज्यामिति के बीच अंतर और समानता के बारे में है। हाइपरबोलिक ज्यामिति के बारे में अधिक जानकारी के लिए अतिशयोक्तिपूर्ण स्थान को तीन या अधिक आयामों तक विस्तारित देखें।
गुण
यूक्लिडियन ज्यामिति से संबंध
हाइपरबोलिक ज्यामिति यूक्लिडियन ज्यामिति से अधिक निकटता से संबंधित है जितना लगता है: केवल स्वयंसिद्ध अंतर समानांतर अभिधारणा है। जब यूक्लिडियन ज्यामिति से समानांतर अभिधारणा को हटा दिया जाता है तो परिणामी ज्यामिति पूर्ण ज्यामिति होती है। पूर्ण ज्यामिति दो प्रकार की होती है, यूक्लिडियन और हाइपरबोलिक। यूक्लिड के तत्वों में से एक पुस्तक के पहले 28 प्रस्तावों सहित पूर्ण ज्यामिति के सभी प्रमेय|यूक्लिड के तत्व, यूक्लिडियन और हाइपरबोलिक ज्यामिति में मान्य हैं। यूक्लिड के तत्वों की पुस्तक एक के प्रस्ताव 27 और 28 समानांतर/गैर-प्रतिच्छेदी रेखाओं के अस्तित्व को साबित करते हैं।
इस अंतर के भी कई परिणाम हैं: अवधारणाएं जो यूक्लिडियन ज्यामिति में समतुल्य हैं, अतिशयोक्तिपूर्ण ज्यामिति में समतुल्य नहीं हैं; नई अवधारणाओं को पेश करने की जरूरत है। इसके अलावा, समांतरता के कोण के कारण, अतिशयोक्तिपूर्ण ज्यामिति का एक निरपेक्ष पैमाना होता है, दूरी और कोण माप के बीच एक संबंध।
रेखाएँ
अतिपरवलयिक ज्यामिति में एकल रेखाओं के ठीक वही गुण होते हैं जो यूक्लिडियन ज्यामिति में एकल सीधी रेखाओं के होते हैं। उदाहरण के लिए, दो बिंदु विशिष्ट रूप से एक रेखा को परिभाषित करते हैं, और रेखा खंडों को असीम रूप से बढ़ाया जा सकता है।
यूक्लिडियन ज्यामिति में दो अन्तर्विभाजक रेखाओं के समान गुण होते हैं। उदाहरण के लिए, दो अलग-अलग रेखाएँ एक बिंदु से अधिक नहीं में प्रतिच्छेद कर सकती हैं, प्रतिच्छेद करने वाली रेखाएँ समान विपरीत कोण बनाती हैं, और प्रतिच्छेदी रेखाओं के आसन्न कोण पूरक कोण होते हैं।
जब एक तीसरी रेखा पेश की जाती है, तब प्रतिच्छेदी रेखाओं के गुण हो सकते हैं जो यूक्लिडियन ज्यामिति में प्रतिच्छेदी रेखाओं से भिन्न होते हैं। उदाहरण के लिए, दी हुई दो प्रतिच्छेदी रेखाएँ ऐसी अपरिमित रूप से अनेक रेखाएँ हैं जो दी गई किसी भी रेखा को नहीं काटती हैं।
ये गुण उपयोग किए गए अतिशयोक्तिपूर्ण तल के #मॉडल से स्वतंत्र हैं, भले ही रेखाएँ मौलिक रूप से भिन्न दिखें।
गैर-प्रतिच्छेदी/समानांतर रेखाएँ
अतिशयोक्तिपूर्ण ज्यामिति में गैर-अंतर्विभाजक रेखाओं में ऐसे गुण भी होते हैं जो यूक्लिडियन ज्यामिति में गैर-प्रतिच्छेदी रेखाओं से भिन्न होते हैं:
- किसी भी रेखा R और किसी भी बिंदु P के लिए, जो R पर स्थित नहीं है, रेखा R और बिंदु P वाले समतल में, P से होकर जाने वाली कम से कम दो अलग-अलग रेखाएँ हैं जो R को नहीं काटती हैं।
इसका तात्पर्य यह है कि P से होकर अनंत संख्या में समतलीय रेखाएँ हैं जो R को नहीं काटती हैं।
इन गैर-प्रतिच्छेदी रेखाओं को दो वर्गों में बांटा गया है:
- दो रेखाएँ (आरेख में x और y) सीमांत समानांतर हैं (कभी-कभी गंभीर रूप से समानांतर, होरोपैरेलल या सिर्फ समानांतर कहा जाता है): R के सिरों पर प्रत्येक आदर्श बिंदु की दिशा में एक है, स्पर्शोन्मुख रूप से R के निकट, हमेशा आर के करीब आ रहा है, लेकिन कभी नहीं मिल रहा है।
- अन्य सभी गैर-प्रतिच्छेदी रेखाओं में न्यूनतम दूरी का एक बिंदु होता है और उस बिंदु के दोनों ओर से विचलन होता है, और इसे अल्ट्रापैरेलल, डायवर्जिंग समानांतर या कभी-कभी गैर-प्रतिच्छेदन कहा जाता है।
कुछ जियोमीटर केवल समानांतर रेखाओं को सीमित करने के लिए वाक्यांश समानांतर रेखाओं का उपयोग करते हैं, साथ ही अल्ट्रापैरेलल लाइनों का अर्थ केवल गैर-अन्तर्विभाजक होता है।
ये सीमांत समांतर PB के साथ θ कोण बनाते हैं; यह कोण केवल समतल की गॉसियन वक्रता और दूरी PB पर निर्भर करता है और इसे समांतरता का कोण कहा जाता है।
अल्ट्रापैरेलल लाइनों के लिए, अल्ट्रापैरेलल प्रमेय बताता है कि हाइपरबोलिक प्लेन में एक अनूठी रेखा होती है जो अल्ट्रापैरेलल लाइनों के प्रत्येक जोड़े के लिए लंबवत होती है।
मंडलियां और डिस्क
अतिशयोक्तिपूर्ण ज्यामिति में, त्रिज्या r के एक वृत्त की परिधि से अधिक होती है .
होने देना , कहाँ पे विमान की गॉसियन वक्रता है। अतिशयोक्तिपूर्ण ज्यामिति में, ऋणात्मक है, इसलिए वर्गमूल धनात्मक संख्या का है।
फिर त्रिज्या r के एक वृत्त की परिधि इसके बराबर है:
और संलग्न डिस्क का क्षेत्रफल है:
इसलिए, अतिपरवलयिक ज्यामिति में किसी वृत्त की परिधि का उसकी त्रिज्या से अनुपात हमेशा कड़ाई से अधिक होता है , हालांकि इसे एक छोटे पर्याप्त वृत्त का चयन करके मनमाने ढंग से बंद किया जा सकता है।
यदि समतल की गॉसियन वक्रता -1 है तो त्रिज्या r के एक वृत्त की भूगणितीय वक्रता है: [1]
हाइपरसाइकिल और हॉरोसाइकल

अतिशयोक्तिपूर्ण ज्यामिति में, ऐसी कोई रेखा नहीं होती जिसके सभी बिंदु दूसरी रेखा से समदूरस्थ हों। इसके बजाय, वे बिंदु जिनके पास दी गई रेखा से समान ऑर्थोगोनल दूरी होती है, एक हाइपरसाइकल (हाइपरबोलिक ज्योमेट्री) नामक वक्र पर स्थित होते हैं।
एक अन्य विशेष वक्र चक्रचक्र है, एक वक्र जिसकी सामान्य (ज्यामिति) त्रिज्या (लम्बवत् रेखाएँ) सभी एक दूसरे के समानांतर सीमित होती हैं (सभी असम्बद्ध रूप से एक ही आदर्श बिंदु, कुंडली के केंद्र में एक दिशा में अभिसरित होती हैं)।
प्रत्येक जोड़ी बिंदुओं के माध्यम से दो कुंडली होती है। कुंडली के केंद्र उनके बीच रेखा-खंड के लंबवत द्विभाजक के आदर्श बिंदु हैं।
किसी भी तीन अलग-अलग बिंदुओं को देखते हुए, वे सभी या तो एक रेखा, हाइपरसाइकल (हाइपरबोलिक ज्योमेट्री), होरोसाइकल या सर्कल पर स्थित होते हैं।
रेखाखंड की लंबाई दो बिंदुओं के बीच की सबसे छोटी लंबाई है। दो बिंदुओं को जोड़ने वाले हाइपरचक्र की चाप-लंबाई रेखा खंड की तुलना में लंबी होती है और समान दो बिंदुओं को जोड़ने वाली कुंडली की तुलना में छोटी होती है। दो बिंदुओं को जोड़ने वाली दोनों कुंडली की चाप की लम्बाई बराबर होती है। दो बिंदुओं के बीच एक वृत्त की चाप-लंबाई दो बिंदुओं को जोड़ने वाली कुंडली की चाप-लंबाई से बड़ी होती है।
यदि समतल की गॉसियन वक्रता -1 है तो कुंडली की भूगणितीय वक्रता 1 होती है और अतिचक्र की वक्रता 0 और 1 के बीच होती है।[1]
त्रिकोण
यूक्लिडियन त्रिभुजों के विपरीत, जहां कोण हमेशा π कांति (180°, एक सीधा कोण) तक जुड़ते हैं, अतिपरवलयिक ज्यामिति में अतिपरवलयिक त्रिभुज के कोणों का योग हमेशा π रेडियन (180°, एक सीधा कोण) से कम होता है। अंतर को कोणीय दोष कहा जाता है।
अतिशयोक्तिपूर्ण त्रिभुज का क्षेत्रफल रेडियन में इसके दोष को R से गुणा करके दिया जाता है2</उप>। परिणामस्वरूप, सभी अतिपरवलयिक त्रिभुजों का क्षेत्रफल R से कम या बराबर होता है2π. एक अतिशयोक्तिपूर्ण आदर्श त्रिभुज का क्षेत्रफल जिसमें तीनों कोण 0° हैं, इस अधिकतम के बराबर है।
जैसा कि यूक्लिडियन ज्यामिति में होता है, प्रत्येक अतिपरवलयिक त्रिभुज में एक अंतःवृत्त होता है। अतिपरवलयिक ज्यामिति में, यदि इसके सभी तीन कोने एक कुंडली या हाइपरचक्र (अतिपरवलयिक ज्यामिति) पर स्थित होते हैं, तो त्रिभुज में कोई परिबद्ध वृत्त नहीं होता है।
गोलाकार ज्यामिति और अण्डाकार ज्यामिति की तरह, अतिपरवलयिक ज्यामिति में यदि दो त्रिभुज समान हैं, तो उन्हें सर्वांगसम होना चाहिए।
नियमित एपिरोगोन
अतिशयोक्तिपूर्ण ज्यामिति में एक विशेष बहुभुज नियमित एपिरोगोन है, एक समान बहुभुज जिसमें अनंत संख्या में भुजाएँ होती हैं।
यूक्लिडियन ज्यामिति में, इस तरह के बहुभुज के निर्माण का एकमात्र तरीका यह है कि भुजाओं की लंबाई शून्य हो जाए और एपिरोगोन एक वृत्त से अप्रभेद्य हो, या आंतरिक कोणों को 180 डिग्री तक बढ़ा दिया जाए और एपिरोगोन एक सीधी रेखा तक पहुंच जाए।
हालांकि, अतिशयोक्तिपूर्ण ज्यामिति में, एक नियमित एपिरोगोन में किसी भी लम्बाई के पक्ष होते हैं (यानी, यह एक बहुभुज बना रहता है)।
भुजा और कोण का द्विभाजन, भुजा की लंबाई और भुजाओं के बीच के कोण के आधार पर, समानांतर को सीमित या अलग करना होगा (देखें # रेखाएँ)। यदि समद्विभाजक समानांतर को सीमित कर रहे हैं तो एपिरोगोन को संकेंद्रित होरोसाइकल द्वारा अंकित और परिचालित किया जा सकता है।
यदि समद्विभाजक समानांतर विचलन कर रहे हैं तो एक स्यूडोगोन (एपिरोगोन से स्पष्ट रूप से भिन्न) को हाइपरसायकल (ज्यामिति) में अंकित किया जा सकता है (सभी कोने एक रेखा की समान दूरी हैं, अक्ष, साथ ही पार्श्व खंडों के मध्य बिंदु सभी समान दूरी पर हैं) एक ही धुरी।)
टेसेलेशन्स

यूक्लिडियन विमान की तरह चेहरे (ज्यामिति) के रूप में नियमित बहुभुजों के साथ हाइपरबोलिक विमान को टेसलेट करना भी संभव है।
श्वार्ज़ त्रिभुजों (p q r) पर आधारित अनंत संख्या में एकसमान टाइलें हैं जहाँ 1/p + 1/q + 1/r <1, जहाँ p,-q,-r मौलिक डोमेन के तीन बिंदुओं पर परावर्तन सममिति के प्रत्येक क्रम हैं। त्रिकोण, समरूपता समूह एक अतिशयोक्तिपूर्ण त्रिभुज समूह है। असीम रूप से कई समान झुकाव भी हैं जो श्वार्ज़ त्रिकोणों से उत्पन्न नहीं हो सकते हैं, उदाहरण के लिए कुछ चतुर्भुजों को मौलिक डोमेन के रूप में आवश्यक है।[2]
मानकीकृत गाऊसी वक्रता
हालांकि अतिशयोक्तिपूर्ण ज्यामिति किसी भी सतह के लिए एक निरंतर नकारात्मक गॉसियन वक्रता के साथ लागू होती है, यह आमतौर पर एक पैमाने पर मान लिया जाता है जिसमें वक्रता K -1 है।
इससे कुछ सूत्र सरल हो जाते हैं। कुछ उदाहरण निम्न हैं:
- किसी त्रिभुज का क्षेत्रफल रेडियन में उसके कोण दोष के बराबर होता है।
- किसी चक्रीय त्रिज्यखंड का क्षेत्रफल उसके चक्रीय चाप की लंबाई के बराबर होता है।
- कुंडली का एक चाप ताकि एक रेखा जो एक अंत बिंदु पर स्पर्शरेखा है, दूसरे समापन बिंदु के माध्यम से त्रिज्या के समानांतर सीमित है, की लंबाई 1 है।[3]
- दो संकेंद्रित कुंडलियों की दो त्रिज्याओं के बीच चाप की लंबाई का अनुपात जहां कुंडली एक दूसरे से 1 दूरी पर हैं, e (गणितीय स्थिरांक) है : 1.[3]
कार्टेशियन-जैसी समन्वय प्रणाली
हाइपरबोलिक ज्यामिति में, चतुर्भुज के कोणों का योग हमेशा 360 डिग्री से कम होता है, और हाइपरबोलिक आयतें यूक्लिडियन आयतों से बहुत भिन्न होती हैं क्योंकि कोई समदूरस्थ रेखाएँ नहीं होती हैं, इसलिए एक उचित यूक्लिडियन आयत को दो रेखाओं और दो हाइपरचक्रों से घिरा होना चाहिए। . ये सभी जटिल समन्वय प्रणाली हैं।
हालांकि अतिशयोक्तिपूर्ण समतल ज्यामिति के लिए अलग-अलग समन्वय प्रणालियाँ हैं। सभी एक चुनी हुई निर्देशित रेखा (एक्स-अक्ष) पर एक बिंदु (मूल) चुनने पर आधारित हैं और उसके बाद कई विकल्प मौजूद हैं।
लोबाचेव्स्की निर्देशांक x और y को x-अक्ष पर लंब गिराकर पाया जाता है। x लंब के पाद का लेबल होगा। y उसके पैर से दिए गए बिंदु के लंब के साथ दूरी होगी (एक तरफ सकारात्मक और दूसरी तरफ नकारात्मक)।
एक अन्य समन्वय प्रणाली बिंदु से कुंडली तक की दूरी को चारों ओर केंद्रित मूल के माध्यम से मापती है और इस कुंडली के साथ लंबाई।[4] अन्य समन्वय प्रणालियाँ नीचे वर्णित क्लेन मॉडल या पॉइंकेयर डिस्क मॉडल का उपयोग करती हैं, और यूक्लिडियन निर्देशांक को अतिशयोक्तिपूर्ण के रूप में लेती हैं।
दूरी
कार्टेशियन जैसा[citation needed] समन्वय प्रणाली (x, y) उन्मुख अतिपरवलयिक तल पर निम्नानुसार निर्मित है। इस रेखा पर एक ओरिएंटेशन और मूल ओ के साथ हाइपरबॉलिक विमान में एक रेखा चुनें। फिर:
- किसी बिंदु का x-निर्देशांक रेखा पर उसके प्रक्षेपण की हस्ताक्षरित दूरी है (उस बिंदु से रेखा के लंबवत खंड का पाद) मूल तक;
- वाई-निर्देशांक बिंदु से रेखा तक बिंदु से रेखा तक हस्ताक्षरित दूरी है, संकेत के अनुसार बिंदु उन्मुख रेखा के सकारात्मक या नकारात्मक पक्ष पर है या नहीं।
इस समन्वय प्रणाली में (x_i, y_i), i=1,2 द्वारा दर्शाए गए दो बिंदुओं के बीच की दूरी है[citation needed]
संबंधित मीट्रिक टेंसर फ़ील्ड है: .
इस समन्वय प्रणाली में, सीधी रेखाएँ इनमें से एक रूप लेती हैं ((x, y) रेखा पर एक बिंदु है; x0, वाई0, ए, और α पैरामीटर हैं):
एक्स-अक्ष के समानांतर
विषम रूप से नकारात्मक पक्ष पर समानांतर
विषम रूप से सकारात्मक पक्ष पर समानांतर
लंबवत रूप से प्रतिच्छेद करना
एक कोण α पर प्रतिच्छेद करना
आम तौर पर, ये समीकरण केवल एक बंधे हुए डोमेन (x मानों के) में ही होंगे। उस डोमेन के किनारे पर, y का मान ± अनंत तक बढ़ता है। अतिशयोक्तिपूर्ण समतल#ध्रुवीय निर्देशांक प्रणाली के लिए निर्देशांक प्रणालियाँ भी देखें।
इतिहास
यूक्लिड के तत्वों के लगभग 300 ईसा पूर्व के प्रकाशन के बाद से, कई ज्यामिति ने समानांतर अवधारणा को साबित करने का प्रयास किया। कुछ ने इसे विरोधाभास द्वारा उपपत्ति द्वारा सिद्ध करने का प्रयास किया। इनमें सबसे प्रमुख थे बंद किया हुआ, इब्न अल-हेथम (अलहसेन), उमर खय्याम,[5] नासिर अल-दीन अल-तुसी, विटेलो, गर्सोनाइडेस, बर्गोस का अब्नेर, और बाद में जियोवन्नी गेरोलामो साचेरी, जॉन वालिस, जोहान हेनरिक लैम्बर्ट और एड्रियन मैरी लीजेंड्रे[6] उनके प्रयास विफल होने के लिए अभिशप्त थे (जैसा कि अब हम जानते हैं, समानांतर अभिधारणा अन्य अभिधारणाओं से सिद्ध करने योग्य नहीं है), लेकिन उनके प्रयासों से अतिशयोक्तिपूर्ण ज्यामिति की खोज हुई।
इब्न अल-हयथम-लैंबर्ट चतुर्भुज और खय्याम-सचेरी चतुर्भुज सहित चतुष्कोणों पर अल्हसेन, खय्याम और अल-तुसी के प्रमेय, अतिशयोक्तिपूर्ण ज्यामिति पर पहले प्रमेय थे। अतिशयोक्तिपूर्ण ज्यामिति पर उनके कार्यों का इसके विकास पर बाद के यूरोपीय ज्यामितियों में काफी प्रभाव पड़ा, जिनमें विटेलो, गेर्सोनाइड्स, अल्फोंसो, जॉन वालिस और सैचेरी शामिल हैं।[7] 18वीं शताब्दी में, जोहान हेनरिक लैम्बर्ट ने अतिशयोक्तिपूर्ण कार्यों की शुरुआत की[8] और अतिशयोक्तिपूर्ण त्रिभुज के क्षेत्रफल की गणना की।[9]
उन्नीसवीं सदी के विकास
19वीं सदी में, निकोलाई इवानोविच लोबाचेव्स्की, जानोस बोल्याई, कार्ल फ्रेडरिक गॉस और फ्रांज टॉरिनस द्वारा अतिशयोक्तिपूर्ण ज्यामिति का बड़े पैमाने पर पता लगाया गया था। अपने पूर्ववर्तियों के विपरीत, जो केवल यूक्लिडियन ज्यामिति के स्वयंसिद्धों से समानांतर सिद्धांत को खत्म करना चाहते थे, इन लेखकों ने महसूस किया कि उन्होंने एक नई ज्यामिति की खोज की है।[10][11] गॉस ने फ्रांज टॉरिनस को 1824 के एक पत्र में लिखा था कि उन्होंने इसका निर्माण किया था, लेकिन गॉस ने अपने काम को प्रकाशित नहीं किया। गॉस ने इसे गैर-यूक्लिडियन ज्यामिति कहा[12] कई आधुनिक लेखकों को गैर-यूक्लिडियन ज्यामिति और अतिशयोक्तिपूर्ण ज्यामिति को पर्यायवाची मानने के लिए जारी रखने के कारण। टॉरिनस ने 1826 में अतिशयोक्तिपूर्ण त्रिकोणमिति पर परिणाम प्रकाशित किए, तर्क दिया कि अतिशयोक्तिपूर्ण ज्यामिति स्व-संगत है, लेकिन अभी भी यूक्लिडियन ज्यामिति की विशेष भूमिका में विश्वास किया जाता है। अतिशयोक्तिपूर्ण ज्यामिति की पूरी प्रणाली 1829/1830 में लोबचेव्स्की द्वारा प्रकाशित की गई थी, जबकि बोल्याई ने इसे स्वतंत्र रूप से खोजा और 1832 में प्रकाशित किया।
1868 में, यूजेनियो बेल्ट्रामी ने हाइपरबोलिक ज्यामिति के हाइपरबोलिक प्लेन|मॉडल (नीचे देखें) के #मॉडल प्रदान किए, और इसका उपयोग यह साबित करने के लिए किया कि हाइपरबोलिक ज्यामिति सुसंगत थी यदि और केवल यदि यूक्लिडियन ज्यामिति थी।
1871 में फेलिक्स क्लेन द्वारा हाइपरबॉलिक ज्यामिति शब्द पेश किया गया था।[13] क्लेन ने आइसोमेट्री का उत्पादन करने के लिए प्रोजेक्टिव ज्यामिति के परिवर्तनों का उपयोग करने के लिए आर्थर केली की एक पहल का पालन किया। विचार ने एक क्षेत्र को परिभाषित करने के लिए एक शंकु खंड या द्विघात का उपयोग किया, और एक मीट्रिक (गणित) को परिभाषित करने के लिए क्रॉस अनुपात का उपयोग किया। प्रक्षेप्य परिवर्तन जो शंकु खंड या चतुर्भुज अपरिवर्तनीय (गणित) # अपरिवर्तनीय सेट छोड़ते हैं, आइसोमेट्री हैं। क्लेन ने दिखाया कि यदि केली निरपेक्ष एक वास्तविक वक्र है, तो इसके इंटीरियर में प्रक्षेपी विमान का हिस्सा अतिशयोक्तिपूर्ण विमान के लिए आइसोमेट्रिक है ...[14] अधिक इतिहास के लिए, गैर-यूक्लिडियन ज्यामिति पर लेख और संदर्भ कॉक्सेटर देखें[15] और मिलनोर[16]
दार्शनिक परिणाम
अतिशयोक्तिपूर्ण ज्यामिति की खोज के महत्वपूर्ण दर्शन परिणाम थे। इसकी खोज से पहले कई दार्शनिकों (उदाहरण के लिए होब्स और स्पिनोजा) ने ज्यामितीय पद्धति के संदर्भ में दार्शनिक कठोरता को देखा, यूक्लिड के तत्वों में प्रयुक्त तर्क की विधि का जिक्र किया।
शुद्ध कारण # अंतरिक्ष और समय की आलोचना में कांत इस निष्कर्ष पर पहुंचे कि अंतरिक्ष (यूक्लिडियन ज्यामिति में) और समय मनुष्यों द्वारा दुनिया की वस्तुगत विशेषताओं के रूप में नहीं खोजा गया है, लेकिन हमारे अनुभवों को व्यवस्थित करने के लिए एक अपरिहार्य व्यवस्थित ढांचे का हिस्सा हैं।[17] ऐसा कहा जाता है कि गॉस ने अतिशयोक्तिपूर्ण ज्यामिति के बारे में कुछ भी प्रकाशित नहीं किया क्योंकि बोईओटिया#पीजोरेटिव शब्द के हंगामे के डर से, जो प्रिंसेप्स मैथेमेटिकोरम (लैटिन, गणितज्ञों के राजकुमार) के रूप में उनकी स्थिति को बर्बाद कर देगा।[18] Boeotians का हंगामा आया और चला गया, और गणितीय कठोरता, विश्लेषणात्मक दर्शन और तर्क में महान सुधारों को प्रोत्साहन दिया। अतिपरवलयिक ज्यामिति अंतत: सुसंगत सिद्ध हुई और इसलिए यह एक अन्य वैध ज्यामिति है।
ब्रह्मांड की ज्यामिति (केवल स्थानिक आयाम)
क्योंकि यूक्लिडियन, हाइपरबोलिक और दीर्घवृत्तीय ज्यामिति सभी सुसंगत हैं, प्रश्न उठता है: अंतरिक्ष की वास्तविक ज्यामिति कौन सी है, और यदि यह अतिशयोक्तिपूर्ण या अण्डाकार है, तो इसकी वक्रता क्या है?
लोबचेव्स्की ने पहले ही सीरियस के लंबन को मापकर और सीरियस को समांतरता के कोण के आदर्श बिंदु के रूप में मानकर ब्रह्मांड की वक्रता को मापने की कोशिश की थी। उन्होंने महसूस किया कि एक निश्चित उत्तर देने के लिए उनकी माप त्रुटि का मार्जिन थी, लेकिन वह इस निष्कर्ष पर पहुंचे कि यदि ब्रह्मांड की ज्यामिति अतिशयोक्तिपूर्ण है, तो #मानकीकृत गॉसियन वक्रता पृथ्वी की कक्षा के व्यास का कम से कम दस लाख गुना है (2000000 AU, 10 पारसेक)।[19] कुछ लोगों का तर्क है कि उनके माप पद्धतिगत रूप से त्रुटिपूर्ण थे।[20] हेनरी पोंकारे, अपने क्षेत्र-विश्व विचार प्रयोग के साथ, इस निष्कर्ष पर पहुंचे कि दैनिक अनुभव आवश्यक रूप से अन्य ज्यामिति को बाहर नहीं करता है।
ज्यामितिकरण अनुमान हमारे अंतरिक्ष की मौलिक ज्यामिति के लिए आठ संभावनाओं की पूरी सूची देता है। कौन सा लागू होता है यह निर्धारित करने में समस्या यह है कि, एक निश्चित उत्तर तक पहुंचने के लिए, हमें बहुत बड़ी आकृतियों को देखने में सक्षम होना चाहिए - पृथ्वी पर या शायद हमारी आकाशगंगा में भी किसी भी चीज़ से बहुत बड़ा।[21]
ब्रह्मांड की ज्यामिति (विशेष सापेक्षता)
विशेष सापेक्षता अंतरिक्ष और समय को समान स्तर पर रखती है, ताकि व्यक्ति अंतरिक्ष और समय पर अलग-अलग विचार करने के बजाय एक एकीकृत दिक्-काल की ज्यामिति पर विचार करे।[22][23] मिन्कोव्स्की अंतरिक्ष गैलिलियन ज्यामिति की जगह लेता है (जो गैलीलियन सापेक्षता के समय के साथ त्रि-आयामी यूक्लिडियन अंतरिक्ष है)।[24] सापेक्षता में, यूक्लिडियन, अण्डाकार और अतिपरवलयिक ज्यामिति पर विचार करने के बजाय, उपयुक्त ज्यामिति पर विचार करने के लिए मिंकोवस्की अंतरिक्ष, डी सिटर अंतरिक्ष और एंटी-डी सिटर स्थान हैं,[25][26] क्रमशः शून्य, सकारात्मक और नकारात्मक वक्रता के अनुरूप।
अतिपरवलयिक ज्यामिति विशेष आपेक्षिकता में तेज़ी के माध्यम से प्रवेश करती है, जो वेग के लिए खड़ा होता है, और एक अतिशयोक्तिपूर्ण कोण द्वारा व्यक्त किया जाता है। इस वेग ज्यामिति के अध्ययन को गैर-यूक्लिडियन ज्यामिति#किनेमेटिक ज्यामिति कहा गया है। सापेक्षतावादी वेगों के स्थान में एक त्रि-आयामी अतिशयोक्तिपूर्ण ज्यामिति है, जहाँ दूरी का कार्य निकट बिंदुओं (वेग) के सापेक्ष वेगों से निर्धारित होता है।[27]
अतिशयोक्तिपूर्ण तल की भौतिक प्रतीति

हाइपरबोलिक प्लेन एक ऐसा प्लेन है जहाँ हर बिंदु एक काठी बिंदु है। यूक्लिडियन अंतरिक्ष में विभिन्न छद्ममंडल मौजूद हैं जिनमें निरंतर नकारात्मक गॉसियन वक्रता का परिमित क्षेत्र है।
हिल्बर्ट के प्रमेय (विभेदक ज्यामिति) | हिल्बर्ट के प्रमेय द्वारा, एक त्रि-आयामी यूक्लिडियन अंतरिक्ष में एक पूर्ण हाइपरबॉलिक विमान (निरंतर नकारात्मक गॉसियन वक्रता की एक पूर्ण नियमित सतह) को सममित रूप से विसर्जन (गणित) करना संभव नहीं है।
हाइपरबोलिक ज्योमेट्री के हाइपरबोलिक प्लेन के अन्य उपयोगी #मॉडल यूक्लिडियन स्पेस में मौजूद हैं, जिसमें मेट्रिक संरक्षित नहीं है। स्यूडोस्फीयर पर आधारित एक विशेष रूप से प्रसिद्ध पेपर मॉडल विलियम थर्स्टन के कारण है।
क्रोशिए की कला का उपयोग किया गया है (देखें Mathematics and fiber arts § Knitting and crochet) हाइपरबोलिक विमानों को प्रदर्शित करने के लिए, इस तरह का पहला प्रदर्शन Daina Taimiņa द्वारा किया गया है।[28] 2000 में, कीथ हेंडरसन ने अतिशयोक्तिपूर्ण सॉकरबॉल (अधिक सटीक रूप से, एक छोटा क्रम -7 त्रिकोणीय टाइलिंग) नामक एक त्वरित-टू-बनाने वाले पेपर मॉडल का प्रदर्शन किया।[29][30] हिलामन फर्ग्यूसन द्वारा डिज़ाइन की गई हाइपरबोलिक रजाई बनाने के निर्देश,[31] जेफरी वीक्स (गणितज्ञ) द्वारा उपलब्ध कराया गया है।[32]
अतिशयोक्तिपूर्ण तल के मॉडल
विभिन्न छद्ममंडल - निरंतर नकारात्मक गॉसियन वक्रता वाली सतहें - मानक यूक्लिडियन मीट्रिक के तहत 3-आयामी अंतरिक्ष में एम्बेड की जा सकती हैं, और इसलिए इसे मूर्त भौतिक मॉडल में बनाया जा सकता है। इनमें से स्यूडोस्फीयर#ट्रैक्ट्रॉइड (अक्सर स्यूडोस्फीयर कहा जाता है) सबसे प्रसिद्ध है; हाइपरबोलिक तल के मॉडल के रूप में ट्रैक्टॉइड का उपयोग यूक्लिडियन तल के मॉडल के रूप में शंकु या बेलन का उपयोग करने के समान है। हालांकि, पूरे अतिशयोक्तिपूर्ण विमान को यूक्लिडियन अंतरिक्ष में इस तरह से एम्बेड नहीं किया जा सकता है, और हाइपरबोलिक ज्यामिति की अमूर्त खोज के लिए कई अन्य मॉडल अधिक सुविधाजनक हैं।
आमतौर पर हाइपरबॉलिक ज्यामिति के लिए उपयोग किए जाने वाले चार गणितीय मॉडल हैं: छोटा मॉडल, पॉइंकेयर डिस्क मॉडल, पॉइंकेयर हाफ-प्लेन मॉडल और लोरेंत्ज़ या हाइपरबोलाइड मॉडल ये मॉडल एक अतिपरवलयिक तल को परिभाषित करते हैं जो एक अतिशयोक्तिपूर्ण ज्यामिति के स्वयंसिद्धों को संतुष्ट करता है। उनके नामों के बावजूद, ऊपर बताए गए पहले तीन को यूजेनियो बेल्ट्रामी द्वारा हाइपरबॉलिक स्पेस के मॉडल के रूप में पेश किया गया था, न कि हेनरी पॉइनकेयर | पॉइनकेयर या फ़ेलिक्स क्लेन द्वारा। ये सभी मॉडल अधिक आयामों के लिए विस्तार योग्य हैं।
बेल्ट्रामी-क्लेन मॉडल
बेल्ट्रामी-क्लेन मॉडल, जिसे प्रोजेक्टिव डिस्क मॉडल, क्लेन डिस्क मॉडल और क्लेन मॉडल के रूप में भी जाना जाता है, का नाम यूजेनियो बेल्ट्रामी और फेलिक्स क्लेन के नाम पर रखा गया है।
दो आयामों के लिए यह मॉडल पूर्ण अतिपरवलयिक तल (गणित) के लिए इकाई वृत्त के आंतरिक भाग का उपयोग करता है, और इस वृत्त की जीवा (ज्यामिति) अतिशयोक्तिपूर्ण रेखाएँ हैं।
उच्च आयामों के लिए यह मॉडल यूनिट बॉल के आंतरिक भाग का उपयोग करता है, और इस एन-बॉल की कॉर्ड (ज्यामिति) अतिशयोक्तिपूर्ण रेखाएँ हैं।
- इस मॉडल का लाभ यह है कि रेखाएँ सीधी होती हैं, लेकिन नुकसान यह है कि कोण विकृत होते हैं (मानचित्रण अनुरूप मानचित्र नहीं है), और वृत्तों को भी वृत्तों के रूप में नहीं दर्शाया जाता है।
- इस मॉडल में दूरी क्रॉस-अनुपात का आधा लघुगणक है, जिसे आर्थर केली ने प्रक्षेपी ज्यामिति में पेश किया था।
पोंकारे डिस्क मॉडल

पॉइंकेयर डिस्क मॉडल, जिसे कंफर्मल डिस्क मॉडल के रूप में भी जाना जाता है, यूनिट सर्कल के इंटीरियर को भी नियोजित करता है, लेकिन लाइनों को सर्कल के आर्क्स द्वारा दर्शाया जाता है जो सीमा सर्कल के लिए ओर्थोगोनल हैं, साथ ही सीमा सर्कल के व्यास भी हैं।
- यह मॉडल कोणों को संरक्षित करता है, और इस प्रकार अनुरूप मानचित्र है। इस मॉडल के भीतर सभी आइसोमेट्री इसलिए मोबियस ट्रांसफॉर्मेशन हैं।
- डिस्क के भीतर पूरी तरह से मंडल मंडल बने रहते हैं, हालांकि सर्कल का यूक्लिडियन केंद्र सर्कल के अतिशयोक्तिपूर्ण केंद्र की तुलना में डिस्क के केंद्र के करीब है।
- होरोसाइकल डिस्क के भीतर के वृत्त होते हैं जो सीमा वृत्त के स्पर्शरेखा होते हैं, संपर्क बिंदु को घटाते हैं।
- हाइपरसाइकल (हाइपरबोलिक ज्योमेट्री) डिस्क के भीतर ओपन-एंडेड कॉर्ड्स और सर्कुलर आर्क्स हैं जो गैर-ऑर्थोगोनल कोणों पर सीमा चक्र पर समाप्त होते हैं।
पॉइंकेयर हाफ-प्लेन मॉडल
पॉइंकेयर हाफ-प्लेन मॉडल यूक्लिडियन प्लेन का आधा हिस्सा लेता है, जो प्लेन की एक लाइन बी से घिरा होता है, जो हाइपरबोलिक प्लेन का मॉडल होता है। लाइन बी मॉडल में शामिल नहीं है।
यूक्लिडियन तल को कार्तीय निर्देशांक प्रणाली वाला एक तल माना जा सकता है और x-अक्ष को रेखा B के रूप में लिया जाता है और आधा तल इस तल का ऊपरी आधा (y > 0) है।
- अतिपरवलयिक रेखाएँ तब या तो B के लिए अर्ध-वृत्त ऑर्थोगोनल होती हैं या किरणें B के लंबवत होती हैं।
- किरण पर एक अंतराल की लंबाई लॉगरिदमिक माप द्वारा दी जाती है, इसलिए यह एक समरूप परिवर्तन के तहत अपरिवर्तनीय है
- पॉइनकेयर डिस्क मॉडल की तरह, यह मॉडल कोणों को संरक्षित करता है, और इस प्रकार अनुरूप मानचित्र है। इसलिए इस मॉडल के भीतर सभी आइसोमेट्रीज़ विमान के मोबियस परिवर्तन हैं।
- हाफ-प्लेन मॉडल पॉइंकेयर डिस्क मॉडल की सीमा है जिसकी सीमा एक ही बिंदु पर B से स्पर्शरेखा है जबकि डिस्क मॉडल की त्रिज्या अनंत तक जाती है।
हाइपरबोलाइड मॉडल
hyperboloid मॉडल या लोरेंत्ज़ मॉडल 3-आयामी मिंकोव्स्की अंतरिक्ष में एम्बेडेड क्रांति के 2-आयामी हाइपरबोलॉइड (दो शीट्स का, लेकिन एक का उपयोग करके) को नियोजित करता है। इस मॉडल का श्रेय आम तौर पर पोंकारे को दिया जाता है, लेकिन रेनॉल्ड्स को[33] कहते हैं कि विल्हेम हत्या ने 1885 में इस मॉडल का इस्तेमाल किया था
- इस मॉडल का विशेष सापेक्षता पर सीधा अनुप्रयोग है, क्योंकि मिंकोव्स्की 3-स्पेस स्पेसटाइम के लिए एक मॉडल है, जो एक स्थानिक आयाम को दबाता है। घटनाओं (अंतरिक्ष-समय में स्थितियों) का प्रतिनिधित्व करने के लिए हाइपरबोलॉइड ले सकते हैं, जो एक सामान्य घटना से शुरू होने वाले संदर्भ पर्यवेक्षकों के विभिन्न जड़त्वीय फ्रेम, एक निश्चित उचित समय में पहुंचेंगे।
- हाइपरबोलॉइड पर दो बिंदुओं के बीच की हाइपरबोलिक दूरी को तब दो संबंधित पर्यवेक्षकों के बीच सापेक्ष तेज़ी से पहचाना जा सकता है।
- मॉडल सीधे एक अतिरिक्त आयाम के लिए सामान्यीकरण करता है: एक अतिशयोक्तिपूर्ण 3-स्थान त्रि-आयामी अतिपरवलयिक ज्यामिति Minkowski 4-अंतरिक्ष से संबंधित है।
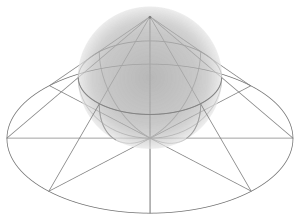
गोलार्द्ध मॉडल
Sphere#Hemisphere मॉडल को अक्सर अपने आप मॉडल के रूप में उपयोग नहीं किया जाता है, लेकिन यह अन्य मॉडलों के बीच परिवर्तनों को देखने के लिए एक उपयोगी उपकरण के रूप में कार्य करता है।
गोलार्द्ध मॉडल इकाई क्षेत्र के ऊपरी आधे हिस्से का उपयोग करता है: अतिशयोक्तिपूर्ण रेखाएँ गोलार्ध की सीमा के लिए अर्ध-वृत्त ओर्थोगोनल हैं।
गोलार्द्ध मॉडल एक रीमैन क्षेत्र का हिस्सा है, और विभिन्न अनुमान अतिशयोक्तिपूर्ण विमान के विभिन्न मॉडल देते हैं:
- से त्रिविम प्रक्षेपण विमान पर Poincare डिस्क मॉडल पर संबंधित बिंदुओं को प्रोजेक्ट करता है
- से त्रिविम प्रक्षेपण सतह पर हाइपरबोलॉइड मॉडल पर संबंधित बिंदुओं को प्रोजेक्ट करता है
- से त्रिविम प्रक्षेपण विमान पर Poincare हाफ-प्लेन मॉडल पर संबंधित बिंदुओं को प्रोजेक्ट करता है
- एक विमान पर लिखने का प्रक्षेपण बेल्ट्रामी-क्लेन मॉडल पर संबंधित बिंदुओं को प्रोजेक्ट करता है।
- गोले के केंद्र से विमान पर केंद्रीय प्रक्षेपण गन्स मॉडल पर संबंधित बिंदुओं को प्रोजेक्ट करता है
आगे देखें: #मॉडलों के बीच संबंध|मॉडलों के बीच संबंध (नीचे)
गन्स मॉडल
1966 में डेविड गन्स ने अमेरिकी गणितीय मासिक जर्नल में चपटा हाइपरबोलाइड मॉडल प्रस्तावित किया।[34] यह एक्स-प्लेन पर हाइपरबोलॉइड मॉडल का एक ऑर्थोग्राफ़िक प्रक्षेपण है। यह मॉडल अन्य मॉडलों की तरह व्यापक रूप से उपयोग नहीं किया जाता है, लेकिन फिर भी अतिशयोक्तिपूर्ण ज्यामिति की समझ में काफी उपयोगी है।
- क्लेन या पॉइनकेयर मॉडल के विपरीत, यह मॉडल पूरे यूक्लिडियन विमान का उपयोग करता है।
- इस मॉडल में रेखाओं को एक अतिपरवलय की शाखाओं के रूप में दर्शाया गया है।[35]
बैंड मॉडल
बैंड मॉडल यूक्लिडियन विमान के एक हिस्से को दो समानांतर रेखाओं के बीच नियोजित करता है।[36] बैंड के मध्य से होकर एक रेखा के साथ दूरी बनाए रखी जाती है। मान लें कि बैंड किसके द्वारा दिया गया है , मीट्रिक द्वारा दिया गया है .
मॉडलों के बीच संबंध
सभी मॉडल अनिवार्य रूप से एक ही संरचना का वर्णन करते हैं। उनके बीच का अंतर यह है कि वे एक ही मीट्रिक स्थान पर रखे गए विभिन्न एटलस (टोपोलॉजी) का प्रतिनिधित्व करते हैं, अर्थात् अतिपरवलयिक तल।
अतिपरवलयिक तल की विशेषता यह है कि इसमें एक निरंतर नकारात्मक गाऊसी वक्रता है, जो उपयोग किए गए समन्वय चार्ट के प्रति उदासीन है। geodesic्स समान रूप से अपरिवर्तनीय हैं: अर्थात, जियोडेसिक्स समन्वय परिवर्तन के तहत जियोडेसिक्स के लिए मैप करता है। अतिपरवलयिक ज्यामिति को आम तौर पर अतिपरवलयिक तल पर भूगर्भ विज्ञान और उनके चौराहों के संदर्भ में पेश किया जाता है।[37] एक बार जब हम एक समन्वय चार्ट (मॉडल में से एक) चुनते हैं, तो हम इसे हमेशा समान आयाम के यूक्लिडियन स्थान में विसर्जित (गणित) कर सकते हैं, लेकिन एम्बेडिंग स्पष्ट रूप से आइसोमेट्रिक नहीं है (चूंकि यूक्लिडियन अंतरिक्ष की वक्रता 0 है)। अतिशयोक्तिपूर्ण स्थान को असीम रूप से कई अलग-अलग चार्टों द्वारा दर्शाया जा सकता है; लेकिन इन चार विशिष्ट चार्टों के कारण यूक्लिडियन अंतरिक्ष में एम्बेडिंग कुछ दिलचस्प विशेषताएं दिखाती हैं।
चूंकि चार मॉडल एक ही मीट्रिक स्थान का वर्णन करते हैं, प्रत्येक को दूसरे में रूपांतरित किया जा सकता है।
उदाहरण के लिए देखें:
- बेल्ट्रामी-क्लेन मॉडल#हाइपरबोलॉइड मॉडल से संबंध|बेल्ट्रामी-क्लेन मॉडल का हाइपरबोलॉइड मॉडल से संबंध,
- Beltrami-Klein मॉडल#Poincare डिस्क मॉडल से संबंध| Beltrami-Klein मॉडल का Poincare डिस्क मॉडल से संबंध,
- और पॉइंकेयर डिस्क मॉडल#रिलेशन टू हाइपरबोलॉइड मॉडल|पॉइनकेयर डिस्क मॉडल का हाइपरबोलॉइड मॉडल से संबंध।
हाइपरबोलिक प्लेन की आइसोमेट्री
अतिशयोक्तिपूर्ण समतल के प्रत्येक आइसोमेट्री (ज्यामितीय परिवर्तन या गति (ज्यामिति)) को अधिकतम तीन परावर्तन (गणित) की संरचना के रूप में महसूस किया जा सकता है। एन-डायमेंशनल हाइपरबॉलिक स्पेस में, n+1 प्रतिबिंब तक की आवश्यकता हो सकती है। (ये यूक्लिडियन और गोलाकार ज्यामिति के लिए भी सही हैं, लेकिन नीचे दिया गया वर्गीकरण अलग है।)
अतिशयोक्तिपूर्ण तल के सभी समस्थानिकों को इन वर्गों में वर्गीकृत किया जा सकता है:
- अभिविन्यास संरक्षण
- पहचान कार्य - कुछ भी नहीं चलता; शून्य प्रतिबिंब; स्वतंत्रता की शून्य डिग्री।
- बिंदु प्रतिबिंब|एक बिंदु के माध्यम से उलटा (आधा मोड़) - दिए गए बिंदु से गुजरने वाली परस्पर लंबवत रेखाओं के माध्यम से दो प्रतिबिंब, यानी बिंदु के चारों ओर 180 डिग्री का घुमाव; स्वतंत्रता की दो डिग्री।
- एक सामान्य बिंदु के चारों ओर प्रतिबिंब (गणित) - दिए गए बिंदु से गुजरने वाली रेखाओं के माध्यम से दो प्रतिबिंब (एक विशेष मामले के रूप में उलटा शामिल है); बिंदु केंद्र के चारों ओर मंडलियों पर चलते हैं; स्वतंत्रता की तीन डिग्री।
- एक आदर्श बिंदु के चारों ओर घूमना (होरोलेशन) - आदर्श बिंदु की ओर जाने वाली रेखाओं के माध्यम से दो प्रतिबिंब; बिंदु आदर्श बिंदु पर केंद्रित होरोसाइकल के साथ चलते हैं; स्वतंत्रता की दो डिग्री।
- एक सीधी रेखा के साथ अनुवाद - दी गई रेखा के लंबवत रेखाओं के माध्यम से दो प्रतिबिंब; हाइपरसाइकल के साथ दी गई रेखा से दूर जाने वाले बिंदु; स्वतंत्रता की तीन डिग्री।
- अभिविन्यास उलटा
- एक रेखा के माध्यम से प्रतिबिंब - एक प्रतिबिंब; स्वतंत्रता की दो डिग्री।
- एक पंक्ति के माध्यम से संयुक्त प्रतिबिंब और एक ही पंक्ति के साथ अनुवाद - प्रतिबिंब और अनुवाद यात्रा; तीन प्रतिबिंब आवश्यक; स्वतंत्रता की तीन डिग्री।[citation needed]
कला में अतिशयोक्तिपूर्ण ज्यामिति
एम. सी. एस्चेर के प्रसिद्ध प्रिंट सर्कल लिमिट III और सर्कल लिमिट IV अनुरूप डिस्क मॉडल (Poincare डिस्क मॉडल) को अच्छी तरह से समझाएं। III में सफेद रेखाएं पूरी तरह से जियोडेसिक नहीं हैं (वे हाइपरसाइकल (हाइपरबोलिक ज्योमेट्री) हैं), लेकिन उनके करीब हैं। त्रिकोणों और वर्गों में कोणों के योग पर इसके प्रभाव के माध्यम से अतिशयोक्तिपूर्ण तल की नकारात्मक वक्रता को स्पष्ट रूप से देखना भी संभव है।
उदाहरण के लिए, वृत्त सीमा III में प्रत्येक शीर्ष तीन त्रिभुजों और तीन वर्गों से संबंधित है। यूक्लिडियन तल में, उनके कोणों का योग 450° होगा; यानी, एक सर्कल और एक चौथाई। इससे, हम देखते हैं कि अतिपरवलयिक तल में त्रिभुज के कोणों का योग 180° से छोटा होना चाहिए। एक और दृश्यमान संपत्ति घातीय वृद्धि है। सर्कल लिमिट III में, उदाहरण के लिए, कोई देख सकता है कि केंद्र से n की दूरी के भीतर मछलियों की संख्या तेजी से बढ़ती है। मछलियों का एक समान अतिशयोक्तिपूर्ण क्षेत्र होता है, इसलिए त्रिज्या n की एक गेंद का क्षेत्रफल n में तेजी से बढ़ना चाहिए।
क्रॉचेट की कला में गणित और फाइबर कलाएं हैं # बुनाई और क्रॉचेट हाइपरबॉलिक विमानों (ऊपर चित्रित) को प्रदर्शित करने के लिए पहली बार दैना तैमिना द्वारा बनाई गई हैं,[28]जिनकी किताब अतिशयोक्तिपूर्ण विमानों के साथ क्रॉचिंग एडवेंचर्स ने 2009 बुकसेलर/डायग्राम प्राइज फॉर ऑडेस्ट टाइटल ऑफ द ईयर जीता।[38] HyperRogue अतिशयोक्तिपूर्ण विमान के विभिन्न झुकावों पर सेट एक रॉगुलाइक गेम है।
उच्च आयाम
अतिशयोक्तिपूर्ण ज्यामिति 2 आयामों तक सीमित नहीं है; प्रत्येक उच्च संख्या के आयामों के लिए एक अतिपरवलयिक ज्यामिति मौजूद है।
सजातीय संरचना
आयाम n का हाइपरबोलिक स्थान गैर-कॉम्पैक्ट प्रकार के रिमेंनियन सममित स्थान का एक विशेष मामला है, क्योंकि यह भागफल के लिए समरूप है
ऑर्थोगोनल समूह O(1, n) मिन्कोव्स्की अंतरिक्ष आर पर मानक-संरक्षण परिवर्तनों द्वारा समूह क्रिया (गणित)।1,n, और यह समूह क्रिया (गणित)#मानदंड 1 सदिशों के दो-शीट हाइपरबोलाइड पर क्रियाओं के प्रकार कार्य करता है। टाइमलाइक लाइनें (यानी, सकारात्मक-मानक स्पर्शरेखा वाले) मूल के माध्यम से हाइपरबोलॉइड में एंटीपोडल बिंदुओं से गुजरती हैं, इसलिए ऐसी रेखाओं का स्थान हाइपरबॉलिक एन-स्पेस का एक मॉडल उत्पन्न करता है। किसी विशेष रेखा का स्टेबलाइज़र उपसमूह ऑर्थोगोनल समूहों O(n) और O(1) के समूहों के प्रत्यक्ष उत्पाद के लिए समरूप है, जहाँ O(n) हाइपरबोलाइड में एक बिंदु के स्पर्शरेखा स्थान पर कार्य करता है, और O(1) ) मूल बिंदु के माध्यम से रेखा को दर्शाता है। अतिशयोक्तिपूर्ण ज्यामिति में कई प्रारंभिक अवधारणाओं को रैखिक बीजगणितीय शब्दों में वर्णित किया जा सकता है: जियोडेसिक पथों को उत्पत्ति के माध्यम से विमानों के साथ चौराहों द्वारा वर्णित किया जाता है, हाइपरप्लेन के बीच डायहेड्रल कोणों को सामान्य वैक्टर के आंतरिक उत्पादों द्वारा वर्णित किया जा सकता है, और अतिशयोक्तिपूर्ण प्रतिबिंब समूहों को स्पष्ट रूप से दिया जा सकता है मैट्रिक्स अहसास।
छोटे आयामों में, लाइ समूहों के असाधारण समरूपताएं हैं जो अतिपरवलयिक रिक्त स्थान के समरूपता पर विचार करने के लिए अतिरिक्त तरीके उत्पन्न करते हैं। उदाहरण के लिए, आयाम 2 में, समरूपता SO+(1, 2) ≅ PSL(2, R) ≅ PSU(1, 1) भागफल के रूप में ऊपरी आधे समतल मॉडल की व्याख्या करने की अनुमति दें SL(2, R)/SO(2) और भागफल के रूप में पोंकारे डिस्क मॉडल SU(1, 1)/U(1). दोनों ही मामलों में, समरूपता समूह आंशिक रैखिक परिवर्तनों द्वारा कार्य करते हैं, क्योंकि दोनों समूह अभिविन्यास-संरक्षण स्टेबलाइजर्स हैं PGL(2, C) रीमैन क्षेत्र के संबंधित उप-स्थानों की। केली परिवर्तन न केवल अतिशयोक्तिपूर्ण तल के एक मॉडल को दूसरे तक ले जाता है, बल्कि एक बड़े समूह में संयुग्मन के रूप में समरूपता समूहों के समरूपता का एहसास करता है। आयाम 3 में, की आंशिक रैखिक क्रिया PGL(2, C) रीमैन क्षेत्र पर आइसोमोर्फिज्म द्वारा प्रेरित हाइपरबोलिक 3-स्पेस की अनुरूप सीमा पर कार्रवाई के साथ पहचाना जाता है O+(1, 3) ≅ PGL(2, C). यह प्रतिनिधि जटिल मैट्रिसेस के वर्णक्रमीय गुणों पर विचार करके हाइपरबोलिक 3-स्पेस के आइसोमेट्री का अध्ययन करने की अनुमति देता है। उदाहरण के लिए, परवलयिक परिवर्तन ऊपरी आधे-अंतरिक्ष मॉडल में कठोर अनुवादों के साथ संयुग्मित होते हैं, और वे वास्तव में वे परिवर्तन हैं जिन्हें एकतरफा त्रिकोणीय मैट्रिक्स मैट्रिसेस द्वारा दर्शाया जा सकता है।
यह भी देखें
- बैंड मॉडल
- अतिशयोक्तिपूर्ण ज्यामिति में निर्माण
- जेल्मस्लेव परिवर्तन
- अतिशयोक्तिपूर्ण 3-कई गुना
- अतिशयोक्तिपूर्ण कई गुना
- अतिशयोक्तिपूर्ण सेट
- अतिशयोक्तिपूर्ण पेड़
- क्लेनियन समूह
- लैम्बर्ट चतुर्भुज
- खुला ब्रह्मांड
- पॉइनकेयर मीट्रिक
- सैचेरी चतुर्भुज
- सिस्टोलिक ज्यामिति
- हाइपरबोलिक प्लेन में समान टाइलिंग
- δ-हाइपरबॉलिक स्पेस
टिप्पणियाँ
- ↑ 1.0 1.1 "हाइपरबोलिक तल पर वक्रों की वक्रता". math stackexchange. Retrieved 24 September 2017.
- ↑ Hyde, S.T.; Ramsden, S. (2003). "कुछ उपन्यास त्रि-आयामी यूक्लिडियन क्रिस्टलीय नेटवर्क द्वि-आयामी अतिशयोक्तिपूर्ण झुकाव से प्राप्त हुए". The European Physical Journal B. 31 (2): 273–284. Bibcode:2003EPJB...31..273H. CiteSeerX 10.1.1.720.5527. doi:10.1140/epjb/e2003-00032-8. S2CID 41146796.
- ↑ 3.0 3.1 Sommerville, D.M.Y. (2005). गैर-यूक्लिडियन ज्यामिति के तत्व (Unabr. and unaltered republ. ed.). Mineola, N.Y.: Dover Publications. p. 58. ISBN 0-486-44222-5.
- ↑ Ramsay, Arlan; Richtmyer, Robert D. (1995). हाइपरबोलिक ज्यामिति का परिचय. New York: Springer-Verlag. pp. 97–103. ISBN 0387943390.
- ↑ See for instance, "Omar Khayyam 1048–1131". Archived from the original on 2007-09-28. Retrieved 2008-01-05.
- ↑ "गैर-यूक्लिडियन ज्यामिति संगोष्ठी". Math.columbia.edu. Retrieved 21 January 2018.
- ↑ Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, p. 447–494 [470], Routledge, London and New York:
"Three scientists, Ibn al-Haytham, Khayyam and al-Tūsī, had made the most considerable contribution to this branch of geometry whose importance came to be completely recognized only in the 19th century. In essence their propositions concerning the properties of quadrangles which they considered assuming that some of the angles of these figures were acute of obtuse, embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between this postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investigations of their European counterparts. The first European attempt to prove the postulate on parallel lines – made by Witelo, the Polish scientists of the 13th century, while revising Ibn al-Haytham's Book of Optics (Kitab al-Manazir) – was undoubtedly prompted by Arabic sources. The proofs put forward in the 14th century by the Jewish scholar Levi ben Gerson, who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that Pseudo-Tusi's Exposition of Euclid had stimulated both J. Wallis's and G. Saccheri's studies of the theory of parallel lines."
- ↑ Eves, Howard (2012), Foundations and Fundamental Concepts of Mathematics, Courier Dover Publications, p. 59, ISBN 9780486132204,
We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions.
- ↑ Ratcliffe, John (2006), Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics, vol. 149, Springer, p. 99, ISBN 9780387331973,
That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
- ↑ Bonola, R. (1912). गैर-यूक्लिडियन ज्यामिति: इसके विकास का एक महत्वपूर्ण और ऐतिहासिक अध्ययन. Chicago: Open Court.
- ↑ Greenberg, Marvin Jay (2003). यूक्लिडियन और गैर-यूक्लिडियन ज्यामिति: विकास और इतिहास (3rd ed.). New York: Freeman. p. 177. ISBN 0716724464.
शून्य से मैंने एक अजीब नया ब्रह्मांड बनाया है। जैनोस बोल्याई
- ↑ Felix Klein, Elementary Mathematics from an Advanced Standpoint: Geometry, Dover, 1948 (reprint of English translation of 3rd Edition, 1940. First edition in German, 1908) pg. 176
- ↑ F. Klein. "Über die sogenannte Nicht-Euklidische Geometrie". Math. Ann. 4, 573–625 (also in Gesammelte Mathematische Abhandlungen 1, 244–350).
- ↑ Rosenfeld, B.A. (1988) A History of Non-Euclidean Geometry, page 236, Springer-Verlag ISBN 0-387-96458-4
- ↑ Coxeter, H. S. M., (1942) Non-Euclidean geometry, University of Toronto Press, Toronto.
- ↑ Milnor, John W., (1982) Hyperbolic geometry: The first 150 years, Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9–24.
- ↑ Lucas, John Randolph (1984). अंतरिक्ष, समय और करणीय. p. 149. ISBN 0-19-875057-9.
- ↑ Torretti, Roberto (1978). रीमैन से पॉइनकेयर तक ज्यामिति का दर्शन. Dordrecht Holland: Reidel. p. 255.
- ↑ Bonola, Roberto (1955). गैर-यूक्लिडियन ज्यामिति: इसके विकास का एक महत्वपूर्ण और ऐतिहासिक अध्ययन (Unabridged and unaltered republ. of the 1. English translation 1912. ed.). New York, NY: Dover. p. 95. ISBN 0486600270.
- ↑ Richtmyer, Arlan Ramsay, Robert D. (1995). हाइपरबोलिक ज्यामिति का परिचय. New York: Springer-Verlag. pp. 118–120. ISBN 0387943390.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ "प्रबुद्ध गणित - इकाई 8 - 8.8 ज्यामितीय अनुमान". Learner.org. Retrieved 21 January 2018.
- ↑ L. D. Landau; E. M. Lifshitz (1973). खेतों का शास्त्रीय सिद्धांत. Course of Theoretical Physics. Vol. 2 (4th ed.). Butterworth Heinemann. pp. 1–4. ISBN 978-0-7506-2768-9.
- ↑ R. P. Feynman; R. B. Leighton; M. Sands (1963). भौतिकी पर फेनमैन व्याख्यान. Vol. 1. Addison Wesley. p. (17-1)–(17-3). ISBN 0-201-02116-1.
- ↑ J. R. Forshaw; A. G. Smith (2008). गतिशीलता और सापेक्षता. Manchester physics series. Wiley. pp. 246–248. ISBN 978-0-470-01460-8.
- ↑ Misner; Thorne; Wheeler (1973). आकर्षण-शक्ति. pp. 21, 758.
- ↑ John K. Beem; Paul Ehrlich; Kevin Easley (1996). वैश्विक लोरेंट्ज़ियन ज्यामिति (Second ed.).
- ↑ L. D. Landau; E. M. Lifshitz (1973). खेतों का शास्त्रीय सिद्धांत. Course of Theoretical Physics. Vol. 2 (4th ed.). Butterworth Heinemann. p. 38. ISBN 978-0-7506-2768-9.
- ↑ 28.0 28.1 "हाइपरबोलिक स्पेस". The Institute for Figuring. December 21, 2006. Retrieved January 15, 2007.
- ↑ "अपनी खुद की हाइपरबोलिक सॉकर बॉल कैसे बनाएं" (PDF). Theiff.org. Retrieved 21 January 2018.
- ↑ "अतिशयोक्तिपूर्ण फुटबॉल". Math.tamu.edu. Retrieved 21 January 2018.
- ↑ "हेलमैन फर्ग्यूसन, अतिशयोक्तिपूर्ण रजाई". Archived from the original on 2011-07-11.
- ↑ "कैसे एक अतिशयोक्तिपूर्ण कंबल सीना". Geometrygames.org. Retrieved 21 January 2018.
- ↑ Reynolds, William F., (1993) Hyperbolic Geometry on a Hyperboloid, American Mathematical Monthly 100:442–455.
- ↑ Gans David (March 1966). "हाइपरबोलिक प्लेन का एक नया मॉडल". American Mathematical Monthly. 73 (3): 291–295. doi:10.2307/2315350. JSTOR 2315350.
- ↑ vcoit (8 May 2015). "कंप्यूटर विज्ञान विभाग" (PDF).
- ↑ "2" (PDF). टेकमुलर थ्योरी एंड एप्लीकेशंस टू ज्योमेट्री, टोपोलॉजी एंड डायनेमिक्स. Hubbard, John Hamal. Ithaca, NY: Matrix Editions. 2006–2016. p. 25. ISBN 9780971576629. OCLC 57965863.
{{cite book}}: CS1 maint: others (link) - ↑ Arlan Ramsay, Robert D. Richtmyer, Introduction to Hyperbolic Geometry, Springer; 1 edition (December 16, 1995)
- ↑ Bloxham, Andy (March 26, 2010). "हाइपरबोलिक प्लेन्स के साथ क्रॉचिंग एडवेंचर्स ने सबसे अजीब पुस्तक शीर्षक पुरस्कार जीता". The Telegraph.
संदर्भ
- A'Campo, Norbert and Papadopoulos, Athanase, (2012) Notes on hyperbolic geometry, in: Strasbourg Master class on Geometry, pp. 1–182, IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18, Zürich: European Mathematical Society (EMS), 461 pages, SBN ISBN 978-3-03719-105-7, DOI 10.4171–105.
- Coxeter, H. S. M., (1942) Non-Euclidean geometry, University of Toronto Press, Toronto
- Fenchel, Werner (1989). Elementary geometry in hyperbolic space. De Gruyter Studies in mathematics. Vol. 11. Berlin-New York: Walter de Gruyter & Co.
- Fenchel, Werner; Nielsen, Jakob (2003). Asmus L. Schmidt (ed.). Discontinuous groups of isometries in the hyperbolic plane. De Gruyter Studies in mathematics. Vol. 29. Berlin: Walter de Gruyter & Co.
- Lobachevsky, Nikolai I., (2010) Pangeometry, Edited and translated by Athanase Papadopoulos, Heritage of European Mathematics, Vol. 4. Zürich: European Mathematical Society (EMS). xii, 310~p, ISBN 978-3-03719-087-6/hbk
- Milnor, John W., (1982) Hyperbolic geometry: The first 150 years, Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9–24.
- Reynolds, William F., (1993) Hyperbolic Geometry on a Hyperboloid, American Mathematical Monthly 100:442–455.
- Stillwell, John (1996). Sources of hyperbolic geometry. History of Mathematics. Vol. 10. Providence, R.I.: American Mathematical Society. ISBN 978-0-8218-0529-9. MR 1402697.
- Samuels, David, (March 2006) Knit Theory Discover Magazine, volume 27, Number 3.
- James W. Anderson, Hyperbolic Geometry, Springer 2005, ISBN 1-85233-934-9
- James W. Cannon, William J. Floyd, Richard Kenyon, and Walter R. Parry (1997) Hyperbolic Geometry, MSRI Publications, volume 31.
बाहरी संबंध
- Javascript freeware for creating sketches in the Poincaré Disk Model of Hyperbolic Geometry University of New Mexico
- "The Hyperbolic Geometry Song" A short music video about the basics of Hyperbolic Geometry available at YouTube.
- "Lobachevskii geometry", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Gauss–Bolyai–Lobachevsky Space". MathWorld.
- Weisstein, Eric W. "Hyperbolic Geometry". MathWorld.
- More on hyperbolic geometry, including movies and equations for conversion between the different models University of Illinois at Urbana-Champaign
- Hyperbolic Voronoi diagrams made easy, Frank Nielsen
- Stothers, Wilson (2000). "Hyperbolic geometry". University of Glasgow.
{{cite journal}}: Cite journal requires|journal=(help), interactive instructional website. - Hyperbolic Planar Tesselations
- Models of the Hyperbolic Plane





