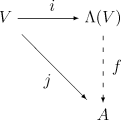बाह्य बीजगणित: Difference between revisions
No edit summary |
No edit summary |
||
| (11 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Algebra of exterior/ wedge products}} | {{short description|Algebra of exterior/ wedge products}} | ||
{{redirect| | {{redirect|वेज गुणनफल|टोपोलॉजिकल समष्टि पर संक्रिया|वेज राशि}} | ||
{{multiple image | {{multiple image | ||
| | |बाएं | footer = {{nowrap|1=''n'' = 0}} (सांकेतिक बिंदु), 1 (निर्देशित रेखा खंड, या सदिश), 2 (उन्मुख समतल घटक), 3 (उन्मुख आयतन) के लिए वास्तविक बाह्य बीजगणित में ग्रेड ''n'' तत्वों की ज्यामितीय व्याख्या। ''n'' सदिश के बाह्य गुणनफल को किसी भी ''n''-विमीय आकार के रूप में देखा जा सकता है (उदाहरण के लिए ''n''-[[पैरालेलेपिप्ड#पैरालेलोटोप|पैरालेलोटोप]], ''n''-[[दीर्घवृत्ताभ]]); परिमाण ([[हाइपरवॉल्यूम]]) के साथ, और [[दिग्विन्यास (सदिश समष्टि)|दिग्विन्यास]] इसकी {{nowrap|(''n'' − 1)}}-विमीय सीमा द्वारा परिभाषित किया गया है और जिस ओर आंतरिक भाग है।<ref name=Penrose07>{{cite book |first=R. |last=Penrose| title=[[The Road to Reality]]| publisher= Vintage books| year=2007 | isbn=978-0-679-77631-4}}</ref><ref>{{harvnb|Wheeler|Misner |Thorne|1973|p=83}}</ref> | ||
| width1 = 220 | | width1 = 220 | ||
| image1 = N vector positive.svg | | image1 = N vector positive.svg | ||
| caption1 = | | caption1 = दिग्विन्यास सदिश के एक क्रमित समुच्चय द्वारा परिभाषित किया गया है। | ||
| width2 = 220 | | width2 = 220 | ||
| image2 = N vector negative.svg | | image2 = N vector negative.svg | ||
| caption2 = | | caption2 = व्युत्क्रमित दिग्विन्यास बाह्य गुणनफल को अस्वीकार करने के अनुरूप है। | ||
}} | }} | ||
गणित में, '''बाह्य बीजगणित''', या '''ग्रासमैन बीजगणित''', जिसका नाम [[ हरमन ग्रासमैन |हरमन ग्रासमैन]] के नाम पर रखा गया है,<ref>{{harvcoltxt|Grassmann|1844}} introduced these as ''extended'' algebras (cf. {{harvnb|Clifford|1878}}). He used the word ''äußere'' (literally translated as ''outer'', or ''exterior'') only to indicate the ''produkt'' he defined, which is nowadays conventionally called ''exterior product'', probably to distinguish it from the ''[[outer product]]'' as defined in modern [[linear algebra]].</ref> '''बाह्य गुणनफल''' या '''वेज गुणनफल''' को इसके गुणन के रूप में उपयोग करने वाली एक प्रकार की बीजगणित है। गणित में, सदिशों का '''बाह्य गुणनफल''' या '''वेज गुणनफल''' एक बीजगणितीय संरचना है जिसका उपयोग [[ ज्यामिति |ज्यामिति]] में [[ क्षेत्र |क्षेत्रफलों]], आयतनों और उनके उच्च-विमीय अनुरूपों का अध्ययन करने के लिए किया जाता है। दो सदिशों <math> u </math> और <math> v </math> के बाह्य गुणनफल को <math> u \wedge v </math> से निरूपित किया जाता है जिसे [[ bivector |द्विसदिश (बाइवेक्टर)]] कहा जाता है और समष्टि में रहता है जिसे ''बाह्य वर्ग'' कहा जाता है, [[ सदिश स्थल |सदिश समष्टि]] जो सदिश के मूल समष्टि से भिन्न होता है। <math> u \wedge v </math> के [[ परिमाण (गणित) |परिमाण]]<ref>Strictly speaking, the magnitude depends on some additional structure, namely that the vectors be in a [[Euclidean space]]. We do not generally assume that this structure is available, except where it is helpful to develop intuition on the subject.</ref> की व्याख्या <math> u </math> और <math> v </math> भुजाओं वाले समांतर चतुर्भुज के क्षेत्रफल के रूप में की जा सकती है, जिसकी गणना दो सदिशों के सदिश गुणनफल का उपयोग करके तीन विमाओं में भी की जा सकती है। अत्यधिक सामान्य रूप से, एक ही [[ अभिविन्यास |दिग्विन्यास (ओरिएंटेशन)]] और क्षेत्र के साथ सभी समांतर समतल सतहों में उनके उन्मुख क्षेत्र के माप के रूप में एक ही द्विसदिश होता है। सदिश गुणनफल की तरह, बाह्य गुणनफल [[ विरोधाभास |प्रति-क्रमविनिमेय (एंटीकोम्यूटिव)]] है, जिसका अर्थ है कि <math> u \wedge v = -(v \wedge u) </math> सभी सदिश <math> u </math> और <math> v </math> के लिए है, लेकिन सदिश गुणनफल के विपरीत, बाह्य गुणनफल साहचर्य होता है। | |||
जब इस प्रकार माना जाता है, तो दो सदिशों के बाहरी गुणनफल को 2-[[ ब्लेड (ज्यामिति) |ब्लेड]] कहा जाता है। अत्यधिक सामान्य रूप से, सदिश के किसी भी संख्या ''k'' बाह्य गुणनफल को परिभाषित किया जा सकता है और कभी-कभी इसे ''k''-ब्लेड कहा जाता है। यह ''k''वीं बाह्य घातांक के रूप में ज्ञात समष्टि में रहता है। परिणामी ''k''-ब्लेड का परिमाण ''k''-विमीय समांतरोटोप (पैरलैलोटोपे) का उन्मुख हाइपरवोल्यूम (अति-आयतन) है जिसके किनारे दिए गए सदिश हैं, ठीक उसी प्रकार जैसे तीन विमाओं में सदिश के [[ स्केलर ट्रिपल उत्पाद |अदिश त्रिक गुणनफल]] का परिमाण उन सदिश द्वारा उत्पन्न समानांतर चतुर्भुज का आयतन प्रदान करता है। | |||
बाह्य बीजगणित एक बीजगणितीय विन्यास प्रदान करती है जिसमें ज्यामितीय प्रश्नों का उत्तर दिया जाता है। उदाहरण के लिए, ब्लेड की एक ठोस ज्यामितीय व्याख्या होती है, और बाह्य बीजगणित में वस्तुओं को स्पष्ट नियमों के एक समुच्चय के अनुसार प्रकलित किया जा सकता है। बाह्य बीजगणित में ऐसी वस्तुएँ होती हैं जो न केवल ''k''-ब्लेड होती हैं, बल्कि ''k''-ब्लेड का योग होती हैं; ऐसी राशि को ''k''-सदिश कहा जाता है।<ref>The term ''k-vector'' is not equivalent to and should not be confused with similar terms such as ''[[4-vector]]'', which in a different context could mean an element of a 4-dimensional vector space. A minority of authors use the term ''k''-multivector instead of ''k''-vector, which avoids this confusion.</ref> ''k''-ब्लेड, क्योंकि वे सदिशों के सरल गुणनफल होते हैं, बीजगणित के सरल घटक कहलाते हैं। किसी भी ''k''-सदिश की ''रैंक'' को उन सरल घटकों की सबसे छोटी संख्या के रूप में परिभाषित किया जाता है, जिनका यह योग है। बाह्य गुणनफल पूर्ण बाह्य बीजगणित तक विस्तारित है, जिससे बीजगणित के किसी भी दो घटकों का गुणा करना अर्थपूर्ण हो जाए। इस गुणनफल के साथ सुसज्जित, बाह्य बीजगणित साहचर्य बीजगणित होती है, जिसका अर्थ है कि किसी भी घटक <math> \alpha, \beta, \gamma </math> के लिए <math> \alpha \wedge (\beta \wedge \gamma) = (\alpha \wedge \beta) \wedge \gamma </math>। ''k''-सदिश की कोटि ''k'' होती है, जिसका अर्थ है कि वे ''k'' सदिश के गुणनफलों का योग हैं। जब भिन्न-भिन्न कोटि के घटकों को गुणा किया जाता है, तो कोटियां [[ बहुपद |बहुपदों]] के गुणन की तरह जुड़ जाती हैं। इसका अर्थ यह है कि बाह्य बीजगणित एक श्रेणीबद्ध बीजगणित है। | |||
बाह्य बीजगणित की परिभाषा समष्टियों के लिए अर्थपूर्ण है न कि केवल ज्यामितीय सदिशों की, बल्कि अन्य सदिश-जैसी वस्तुओं जैसे [[ वेक्टर क्षेत्र |सदिश फ़ील्ड]] या फलन (फ़ंक्शंस) के लिए। पूर्ण सामान्यता में, बाह्य बीजगणित को किसी [[ कम्यूटेटिव रिंग |कम्यूटेटिव रिंग]] पर [[ मॉड्यूल (गणित) |मॉड्यूल]] के लिए और [[ अमूर्त बीजगणित |अमूर्त बीजगणित]] में रुचि के अन्य संरचनाओं के लिए परिभाषित किया जा सकता है। यह इन अधिक सामान्य संरचनाओं में से एक है जहां बाह्य बीजगणित अपने सबसे महत्वपूर्ण अनुप्रयोगों में से एक प्राप्त होता है, जहां यह अवकल रूपों के बीजगणित के रूप में प्रकट होता है जो कि उन क्षेत्रों में मौलिक होते है जो अवकल ज्यामिति का उपयोग करते हैं। बाह्य बीजगणित में कई बीजगणितीय गुण भी होते हैं जो इसे बीजगणित में ही एक सुविधाजनक साधन बनाते हैं। सदिश समष्टि के लिए बाह्य बीजगणित का साहचर्य सदिश समष्टियों पर एक प्रकार का [[ फंक्टर |फंक्टर]] होता है, जिसका अर्थ है कि यह एक निश्चित तरीके से सदिश समष्टियों के [[ रैखिक परिवर्तन |रैखिक रूपांतरणों]] के साथ संगत है। बाह्य बीजगणित बायलजेब्रा का एक उदाहरण है, जिसका अर्थ है कि इसकी द्वैत समष्टि में भी एक गुणनफल है, और यह द्वैत गुणनफल बाह्य गुणनफल के साथ संगत है। यह द्वैत बीजगणित वैकल्पिक रूप से बहु-रेखीय रूपों का बीजगणित है, और बाह्य बीजगणित और इसके द्वैत के बीच का युग्म [[ आंतरिक उत्पाद |आंतरिक गुणनफल]] द्वारा दी गई है। | |||
=== | == प्रेरणात्मक उदाहरण == | ||
[[Image:Area parallellogram as determinant.svg|thumb|right|इसके दो | पहले दो उदाहरण एक [[ मीट्रिक टेंसर |मीट्रिक टेंसर]] फ़ील्ड और एक दिग्विन्यास मानते हैं; तीसरा उदाहरण या तो नहीं मानता। | ||
=== समतल क्षेत्र === | |||
[[Image:Area parallellogram as determinant.svg|thumb|right|इसके दो शीर्षों के निर्देशांक के आव्यूह के निर्धारक के संदर्भ में एक समांतर चतुर्भुज का क्षेत्रफल।]][[ कार्टेशियन विमान |कार्तीय तल]] <math> \mathbb R^2 </math> एक [[ वास्तविक संख्या |वास्तविक]] सदिश समष्टि है जो [[ इकाई वेक्टर |इकाई सदिशों]] के एक युग्म से युक्त बेसिस से सुसज्जित है | |||
:<math> | :<math> | ||
{\mathbf e}_1 = \begin{bmatrix}1\\0\end{bmatrix},\quad {\mathbf e}_2 | {\mathbf e}_1 = \begin{bmatrix}1\\0\end{bmatrix},\quad {\mathbf e}_2 | ||
= \begin{bmatrix}0\\1\end{bmatrix}, | = \begin{bmatrix}0\\1\end{bmatrix}, | ||
</math> | </math> दिग्विन्यास के साथ <math> \mathbf e_1 \times \mathbf e_2 </math> और मीट्रिक के साथ <math>\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix} </math>। | ||
मान लीजिए | |||
:<math>\mathbf{v} = \begin{bmatrix}a\\b\end{bmatrix} | :<math>\mathbf{v} = \begin{bmatrix}a\\b\end{bmatrix} | ||
| Line 37: | Line 36: | ||
= c \mathbf{e}_1 + d \mathbf{e}_2 | = c \mathbf{e}_1 + d \mathbf{e}_2 | ||
</math> | </math> | ||
में | घटकों में लिखे, <math>\R^2</math> में दिए गए सदिशों का एक युग्म है। दो भुजाएँ '''v''' और '''w''' वाला एक विशिष्ट समांतर चतुर्भुज हैं। इस समांतर चतुर्भुज का ''क्षेत्रफल'' मानक निर्धारक सूत्र द्वारा दिया गया है: | ||
:<math> | :<math> | ||
| Line 45: | Line 44: | ||
= \left| ad - bc \right| . | = \left| ad - bc \right| . | ||
</math> | </math> | ||
अब v और w के | अब '''v''' और '''w''' के बाह्य गुणनफल पर विचार करें: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 53: | Line 52: | ||
&= \left( ad - bc \right)\mathbf{e}_1 \wedge \mathbf{e}_2 | &= \left( ad - bc \right)\mathbf{e}_1 \wedge \mathbf{e}_2 | ||
\end{align}</math> | \end{align}</math> | ||
जहां पहला चरण | जहां पहला चरण बाह्य गुणनफल के लिए वितरण नियम का उपयोग करता है, और अंतिम चरण इस तथ्य का उपयोग करता है कि बाह्य गुणनफल वैकल्पिक है, और विशेष रूप से <math>\mathbf{e}_2 \wedge \mathbf{e}_1 = -(\mathbf{e}_1 \wedge \mathbf{e}_2)</math> होता है। (तथ्य यह है कि बाह्य गुणनफल वैकल्पिक रूप से भी <math> \mathbf{e}_1 \wedge \mathbf{e}_1 = \mathbf{e}_2 \wedge \mathbf{e}_2 = 0</math> को बल देता है) ध्यान दें कि इस अंतिम अभिव्यक्ति में गुणांक वास्तव में आव्यूह {{nowrap|1=['''v''' '''w''']}} का निर्धारक है। तथ्य यह है कि यह धनात्मक या ऋणात्मक हो सकता है इसका सहज अर्थ है कि '''v''' और '''w''' वामावर्त या दक्षिणावर्त अर्थ में उन्मुख हो सकते हैं क्योंकि वे समानांतर चतुर्भुज के कोने को परिभाषित करते हैं। इस तरह के क्षेत्र को समांतर चतुर्भुज का सांकेतिक क्षेत्रफल कहा जाता है: ''सांकेतिक क्षेत्रफल'' का निरपेक्ष मान साधारण क्षेत्रफल है, और चिन्ह इसके दिग्विन्यास को निर्धारित करता है। | ||
=== | तथ्य यह है कि यह गुणांक सांकेतिक क्षेत्रफल है, कोई घटना नहीं है। वास्तव में, यह देखना अपेक्षाकृत सरल है कि बाह्य गुणनफल को सांकेतिक क्षेत्रफल से संबंधित होना चाहिए यदि कोई इस क्षेत्र को बीजगणितीय संरचना के रूप में स्वयंसिद्ध करने की प्रयास करता है। विस्तार से, यदि {{nowrap|1=A('''v''', '''w''')}} समांतर चतुर्भुज के सांकेतिक क्षेत्रफल को दर्शाता है जिसमें सदिश '''v''' और '''w''' का युग्म दो आसन्न भुजाएँ बनाती है, तो A को निम्नलिखित गुणों को पूरा करना चाहिए: | ||
एक | # {{nowrap|1=A(''r'''''v''', ''s'''''w''') = ''rs''A('''v''', '''w''')}} किसी भी वास्तविक संख्या ''r'' और ''s'' के लिए, चूंकि दोनों भुजाओं में से किसी एक को पुनः स्केल करने से क्षेत्रफल को उसी राशि से पुनः स्केल किया जाता है (और भुजाओं में से किसी एक की दिशा को उत्क्रमित करने से समांतर चतुर्भुज का दिग्विन्यास उत्क्रमित हो जाता है)। | ||
# {{nowrap|1=A('''v''', '''v''') = 0}}, चूंकि '''v''' (अर्थात, [[ रेखा खंड |रेखा खंड]]) द्वारा निर्धारित पतित समांतर चतुर्भुज का क्षेत्रफल शून्य है। | |||
#{{nowrap|1=A('''w''', '''v''') = −A('''v''', '''w''')}}, '''v''' और '''w''' की भूमिकाओं को परस्पर क्रिया करने के पश्चात से समांतर चतुर्भुज के दिग्विन्यास को उत्क्रमित कर देता है। | |||
# किसी भी वास्तविक संख्या r के लिए {{nowrap|1=A('''v''' + ''r'''''w''', '''w''') = A('''v''', '''w''')}}, चूँकि '''v''' में '''w''' का एक गुणक जोड़ने से समांतर चतुर्भुज का न तो आधार और न ही ऊँचाई प्रभावित होती है और इसके परिणामस्वरूप इसका क्षेत्रफल संरक्षित रहता है। | |||
# {{nowrap|1=A('''e'''<sub>1</sub>, '''e'''<sub>2</sub>) = 1}}, चूंकि इकाई वर्ग का क्षेत्रफल एक है। | |||
[[Image:Exterior calc cross product.svg|upright=1.2|thumb|बाह्य गुणनफल (हल्का नीला समांतर चतुर्भुज) के संबंध में सदिश गुणनफल (नीला सदिश)। सदिश गुणनफल की लंबाई समांतर इकाई सदिश (<span style = color:#cc0000;>लाल</span>) की लंबाई है क्योंकि बाहरी उत्पाद का आकार संदर्भ समांतरोग्राम (हल्का लाल) के आकार के आकार का है।]]पिछले गुणधर्म के अपवाद के साथ, दो सदिशों का बाह्य गुणनफल क्षेत्र के समान गुणों को पूरा करता है। निश्चित अर्थ में, बाह्य गुणनफल एक समांतर चतुर्भुज के क्षेत्रफल की तुलना समानांतर समतल में किसी भी चयनित समांतर चतुर्भुज के क्षेत्र की अनुमति देकर अंतिम गुणधर्म को सामान्य करता है (यहाँ, भुजाओं वाला e1 और e2)। दूसरे शब्दों में, बाह्य गुणनफल क्षेत्र का ''बेसिस-स्वतंत्र'' सूत्रीकरण प्रदान करता है।<ref>This axiomatization of areas is due to [[Leopold Kronecker]] and [[Karl Weierstrass]]; see {{harvtxt|Bourbaki|1989b|loc=Historical Note}}. For a modern treatment, see {{harvtxt|Mac Lane|Birkhoff|1999|loc=Theorem IX.2.2}}. For an elementary treatment, see {{harvtxt|Strang|1993|loc=Chapter 5}}.</ref> | |||
=== सदिश और त्रिक गुणनफल === | |||
किसी बाईलीनियर अदिश गुणनफल के साथ 3-विमीय उन्मुख सदिश समष्टि में सदिश के लिए, बाह्य बीजगणित सदिश गुणनफल और त्रिक गुणनफल से निकटता से संबंधित है। [[ मानक आधार |मानक बेसिस]] {{nowrap|('''e'''<sub>1</sub>, '''e'''<sub>2</sub>, '''e'''<sub>3</sub>)}} का उपयोग करके, सदिशों के एक युग्म का बाह्य गुणनफल | |||
:<math> | :<math> | ||
| Line 83: | Line 80: | ||
+ (u_3 v_1 - u_1 v_3) (\mathbf{e}_3 \wedge \mathbf{e}_1) , | + (u_3 v_1 - u_1 v_3) (\mathbf{e}_3 \wedge \mathbf{e}_1) , | ||
</math> | </math> | ||
जहां {{nowrap|('''e'''<sub>1</sub> ∧ '''e'''<sub>2</sub>, '''e'''<sub>2</sub> ∧ '''e'''<sub>3</sub>, '''e'''<sub>3</sub> ∧ '''e'''<sub>1</sub>)}} त्रि-विमीय समष्टि <math display="inline"> \bigwedge\nolimits^2\left(\mathbb R^3\right) </math> के लिए बेसिस है। उपरोक्त गुणांक वही हैं जो किसी दिए गए दिग्विन्यास के साथ तीन विमाओं में सदिशों के सदिश गुणनफल की सामान्य परिभाषा में हैं, केवल अंतर यह है कि बाह्य गुणनफल एक सामान्य सदिश नहीं है, बल्कि इसके बजाय [[ 2 वेक्टर |2-सदिश]] है, और यह कि बाह्य गुणनफल दिग्विन्यास के विकल्प पर निर्भर नहीं करता है{{clarify|date=November 2022}}। | |||
एक तीसरे | एक अन्य तीसरे सदिश को उपयोग में लाने पर | ||
:<math> | :<math> | ||
\mathbf{w} = w_1 \mathbf{e}_1 + w_2 \mathbf{e}_2 + w_3 \mathbf{e}_3, | \mathbf{w} = w_1 \mathbf{e}_1 + w_2 \mathbf{e}_2 + w_3 \mathbf{e}_3, | ||
</math> | </math> | ||
तीन | तीन सदिशों का बाह्य गुणनफल है | ||
:<math> | :<math> | ||
| Line 97: | Line 94: | ||
(\mathbf{e}_1 \wedge \mathbf{e}_2 \wedge \mathbf{e}_3) | (\mathbf{e}_1 \wedge \mathbf{e}_2 \wedge \mathbf{e}_3) | ||
</math> | </math> | ||
जहाँ {{nowrap|'''e'''<sub>1</sub> ∧ '''e'''<sub>2</sub> ∧ '''e'''<sub>3</sub>}} एक-विमीय समष्टि <math display="inline"> \bigwedge\nolimits^3\left(\mathbb R^3\right) </math> के लिए आधार सदिश है। अदिश गुणांक तीन सदिशों का त्रिगुणात्मक गुणनफल है। | |||
तीन विमीय यूक्लिडियन सदिश समष्टि में सदिश गुणनफल और त्रिक गुणनफल [[ हॉज स्टार ऑपरेटर |हॉज स्टार द्वंद्व]] के माध्यम से ज्यामितीय और बीजगणितीय दोनों व्याख्याओं को स्वीकार करते हैं। सदिश गुणनफल {{nowrap|'''u''' × '''v'''}} को एक सदिश के रूप में व्याख्या किया जा सकता है जो '''u''' और '''v''' दोनों के लिए लंबवत है और जिसका परिमाण दो सदिशों द्वारा निर्धारित समांतरोग्राम के क्षेत्र के बराबर है। इसे सदिश के रूप में भी व्याख्या किया जा सकता है जिसमें कॉलम '''u''' और '''v''' के साथ आव्यूह के [[ मामूली (गणित) |उपसारणिक]] सम्मिलित हैं। '''u''', '''v''', और '''w''' के त्रिक गुणनफल एक ज्यामितीय उन्मुख मात्रा का प्रतिनिधित्व करने वाला एक सांकेतिक अदिश है। बीजगणितीय रूप से, यह कॉलम '''u''', '''v''', और '''w''' के साथ आव्यूह का निर्धारक है। तीन विमाओं में बाह्य गुणनफल समान व्याख्याओं की अनुमति देता है: यह भी, उन्मुख रेखाओं, क्षेत्रफलों, आयतनों, आदि के साथ पहचाना जा सकता है, जो एक, दो या अधिक सदिशों द्वारा फैलाए जाते हैं। बाह्य गुणनफल इन ज्यामितीय धारणाओं को सभी सदिश रिक्त समष्टि और किसी भी विमा के लिए सामान्य करता है, यहां तक कि अदिश गुणनफल की अनुपस्थिति में भी। | |||
=== विद्युत चुम्बकीय क्षेत्र === | |||
आइंस्टीन के सापेक्षता के सिद्धांतों में, [[ विद्युत चुम्बकीय |विद्युत चुम्बकीय क्षेत्र]] को सामान्यतः [[ 4-स्थान |4-समष्टि]] में अवकल 2-रूप <math> F = dA </math> के रूप में या समकक्ष [[ एंटीसिममेट्रिक टेंसर |वैकल्पिक टेंसर]] क्षेत्र <math> F_{ij} = A_{[i,j]} = A_{[i;j]}, </math> [[ विद्युत चुम्बकीय टेंसर |विद्युत चुम्बकीय टेंसर]] के रूप में दिया जाता है। फिर <math> dF = ddA = 0 </math> या समतुल्य बियांची पहचान <math> F_{[ij,k]} = F_{[ij;k]} = 0 </math>। इसमें से किसी को भी मीट्रिक की आवश्यकता नहीं है। | |||
लोरेन्ट्ज़ मीट्रिक और दिग्विन्यास जोड़ने से हॉज स्टार संकारक <math> \star </math> मिलता है और इस प्रकार <math> J = {\star}d{\star}F </math> या समकक्ष टेन्सर [[ विचलन |डाइवर्जेंस]] <math> J^i = F^{ij}_{,j} = F^{ij}_{;j} </math> को परिभाषित करना संभव हो जाता है जहाँ <math> F^{ij} = g^{ik}g^{jl}F_{kl} </math>। | |||
== औपचारिक परिभाषाएँ और बीजगणितीय गुण == | == औपचारिक परिभाषाएँ और बीजगणितीय गुण == | ||
फील्ड {{math|''K''}} पर सदिश समष्टि {{math|''V''}} का बाह्य बीजगणित <math display="inline"> \bigwedge(V) </math> को [[ टेंसर बीजगणित |टेंसर बीजगणित]] {{math|''T''(''V'')}} के कोशिएंट बीजगणित के रूप में परिभाषित किया गया है, जो दो तरफा अभीष्ट {{math|''I''}} द्वारा उत्पन्न {{math|1=''x'' ⊗ ''x''}} के लिए {{math|1=''x'' ∈ ''V''}} (अर्थात सभी टेंसर जिन्हें {{math|''V''}} में सदिश के टेन्सर गुणनफल के रूप में व्यक्त किया जा सकता है) के सभी घटकों द्वारा उत्पन्न होता है।<ref>{{harvtxt|Mac Lane|Birkhoff|1999}}</ref> अभीष्ट ''I'' में <math> x \otimes y + y \otimes x = (x + y) \otimes (x + y) - x \otimes x - y \otimes y </math> रूप के घटकों द्वारा उत्पन्न अभीष्ट ''J'' सम्मिलित है और यदि <math> \operatorname{char}(K) \ne 2 </math> (यदि <math> \operatorname{char}(K) = 2, </math> ये अभीष्ट [[ शून्य वेक्टर स्थान |शून्य सदिश समष्टि]] को छोड़कर भिन्न हैं) तो ये अभीष्ट के समान होता हैं। | |||
इसलिए, | इसलिए, | ||
:<math> {\textstyle\bigwedge}(V) = T(V)/I </math> | :<math> {\textstyle\bigwedge}(V) = T(V)/I </math> | ||
साहचर्य बीजगणित है। इसके गुणन को ''बाह्य गुणनफल'' कहा जाता है, और इसे {{math|∧}} से दर्शाया जाता है। इसका अर्थ यह है कि <math display="inline"> \bigwedge(V) </math> का गुणनफल {{math|''T''(''V'')}} के टेन्सर गुणनफल {{math|⊗}} से प्रेरित है। | |||
इसके गुणन को | |||
{{math|1=''T''<sup>0</sup> = ''K''}}, {{math|1=''T''<sup>1</sup> = ''V''}}, और <math> \left(T^0(V) \oplus T^1(V)\right) \cap I = \{ 0 \}, </math> के रूप में, {{math|''T''(''V'')}} में {{math|''K''}} और {{math|''V''}} का समावेश {{math|''K''}} और {{math|''V''}} के अंतःक्षेप को <math display="inline"> \bigwedge(V) </math> में प्रेरित करता है। इन अंतःक्षेपण को सामान्यतः समावेशन के रूप में माना जाता है, और इन्हें ''प्राकृतिक अंतःस्थापन'', ''प्राकृतिक अंतःक्षेप'' या ''प्राकृतिक समावेशन'' कहा जाता है। ''प्राकृतिक'' के समष्टि पर सामान्यतः ''विहित'' शब्द का भी प्रयोग किया जाता है। | |||
=== वैकल्पिक | === वैकल्पिक गुणनफल === | ||
बाह्य गुणनफल <math> V, </math> के घटकों पर ''वैकल्पिक'' से संरचना द्वारा है, जिसका अर्थ है कि उपरोक्त संरचना द्वारा सभी <math display="inline"> x \wedge x = 0 </math> के लिए <math> x \in V </math>। यह इस प्रकार है कि यह गुणनफल <math> V, </math> के घटकों पर भी [[ विरोधी |अप्रतिवर्तक (एंटीकम्यूटेटिव)]] है, यह मानने के लिए कि <math> x, y \in V, </math> | |||
:<math> | :<math> | ||
0 = (x + y) \wedge (x + y) | 0 = (x + y) \wedge (x + y) | ||
| Line 129: | Line 122: | ||
:<math> x \wedge y = -(y \wedge x). </math> | :<math> x \wedge y = -(y \wedge x). </math> | ||
अधिक | अधिक व्यापक रूप से, यदि ''σ'' पूर्णांक {{nowrap|[1, ..., ''k'']}}, और ''x''<sub>1</sub>, ''x''<sub>2</sub>, ..., ''x<sub>k</sub>'', ''V'' के अवयव हैं, का एक क्रमचय है, तो यह अनुसरण करता है कि | ||
:<math> | :<math> | ||
| Line 135: | Line 128: | ||
= \operatorname{sgn}(\sigma)x_1 \wedge x_2 \wedge \cdots \wedge x_k, | = \operatorname{sgn}(\sigma)x_1 \wedge x_2 \wedge \cdots \wedge x_k, | ||
</math> | </math> | ||
जहां | जहां sgn(''σ'') [[ एक क्रमपरिवर्तन का हस्ताक्षर |क्रमचय]] ''σ'' का संकेत है।<ref>A proof of this can be found in more generality in {{harvtxt|Bourbaki|1989}}.</ref> | ||
विशेष रूप से, यदि | |||
विशेष रूप से, यदि ''x<sub>i</sub>'' = ''x<sub>j</sub>'' कुछ ''i'' ≠ ''j'' के लिए, तो वैकल्पिक गुणधर्म का निम्नलिखित सामान्यीकरण भी मान्य है: | |||
:<math> x_{1} \wedge x_{2} \wedge \cdots \wedge x_{k} = 0. </math> | :<math> x_{1} \wedge x_{2} \wedge \cdots \wedge x_{k} = 0. </math> | ||
बाह्य गुणनफल की वितरणात्मक गुणधर्म के साथ, एक अन्य सामान्यीकरण यह है कि यदि और केवल यदि <math> \{ x_{1}, x_{2}, \cdots, x_{k} \} </math> सदिशों का रैखिक रूप से निर्भर समुच्चय है, तो | |||
:<math> x_{1} \wedge x_{2} \wedge \cdots \wedge x_{k} = 0. </math> | :<math> x_{1} \wedge x_{2} \wedge \cdots \wedge x_{k} = 0. </math> | ||
=== बाह्य घातांक === | |||
V के kवीं बाह्य घातांक, <math display="inline"> \bigwedge\nolimits^k(V) </math> को निरूपित करते है, <math display="inline"> \bigwedge(V) </math> की [[ वेक्टर उप -स्थान |सदिश उप-समष्टि]] है जो निम्नलिखित रूप में विस्तारित है | |||
V | |||
:<math> | :<math> | ||
x_1 \wedge x_2 \wedge \cdots \wedge x_k,\quad x_i \in V, i=1,2,\ldots, k. | x_1 \wedge x_2 \wedge \cdots \wedge x_k,\quad x_i \in V, i=1,2,\ldots, k. | ||
</math> | </math> | ||
यदि <math display=inline> \alpha \in \bigwedge\nolimits^k(V), </math> | यदि <math display="inline"> \alpha \in \bigwedge\nolimits^k(V), </math> है, तो α को ''k''-सदिश कहा जाता है। यदि, इसके अतिरिक्त, α को V के k घटकों के बाह्य गुणनफल के रूप में व्यक्त किया जा सकता है, तो α को '''वियोजनीय''' '''(डीकंपोज़ेबल)''' कहा जाता है। हालांकि वियोजनीय ''k''-सदिश <math display="inline"> \bigwedge\nolimits^k(V), </math> तक विस्तारित हैं, लेकिन <math display="inline"> \bigwedge\nolimits^k(V) </math> का प्रत्येक घटक वियोजनीय नहीं है। उदाहरण के लिए, <math> \mathbb R^4, </math> में निम्नलिखित 2-सदिश वियोजनीय नहीं है: | ||
:<math> \alpha = e_1 \wedge e_2 + e_3 \wedge e_4. </math> | :<math> \alpha = e_1 \wedge e_2 + e_3 \wedge e_4. </math> | ||
(यह | (यह साधारण रूप है, चूँकि {{nowrap|''α'' ∧ ''α'' ≠ 0}} है।<ref>See {{harvtxt|Sternberg|1964|loc=§III.6}}.</ref>) | ||
==== | ==== बेसिस और विमा ==== | ||
यदि [[ आयाम (रैखिक बीजगणित) ]] {{mvar| | यदि {{mvar|V}} की [[ आयाम (रैखिक बीजगणित) |विमा]] {{mvar|n}} है और {{math| { ''e''<sub>1</sub>, …, ''e''<sub>''n''</sub> <nowiki>}</nowiki>}} {{mvar|V}} का [[ आधार (रैखिक बीजगणित) |बेसिस]] है, तो समुच्चय | ||
:<math> | :<math> | ||
| Line 163: | Line 155: | ||
\big| ~~ 1 \le i_1 < i_2 < \cdots < i_k \le n \,\} | \big| ~~ 1 \le i_1 < i_2 < \cdots < i_k \le n \,\} | ||
</math> | </math> | ||
<math display="inline"> \bigwedge\nolimits^k(V) </math> के लिए बेसिस है। कारण निम्न है: किसी भी बाह्य गुणनफल को निम्नलिखित रूप से प्रदर्शित किया गया है | |||
:<math> v_1 \wedge \cdots \wedge v_k , </math> | :<math> v_1 \wedge \cdots \wedge v_k , </math> | ||
प्रत्येक सदिश {{mvar|v<sub>j</sub>}} को बेसिस सदिशों {{mvar|e<sub>i</sub>}} के एक [[ रैखिक संयोजन |रैखिक संयोजन]] के रूप में लिखा जा सकता है; बाह्य गुणनफल की बाईलीनियरिटी का उपयोग करके, इसे उन बेसिस सदिशों के बाह्य गुणनफलों के रैखिक संयोजन तक विस्तारित किया जा सकता है। कोई भी बाह्य गुणनफल जिसमें एक ही बेसिस सदिश एक से अधिक बार प्रकट होता है, शून्य होता है; कोई भी बाह्य गुणनफल जिसमें बेसिस सदिश उचित क्रम में प्रकट नहीं होते हैं, को पुनः व्यवस्थित किया जा सकता है, जब भी दो बेसिस सदिश समष्टि बदलते हैं, तो चिन्ह बदल सकते हैं। सामान्य तौर पर, बेसिस {{mvar|k}}-सदिश के परिणामी गुणांक की गणना [[ मैट्रिक्स (गणित) |आव्यूह]] के [[ नाबालिग (रैखिक बीजगणित) |अवयस्क]] के रूप में की जा सकती है जो बेसिस {{mvar|e<sub>i</sub>}} के संदर्भ में सदिश {{mvar|v<sub>j</sub>}} का वर्णन करता है। | |||
बेसिस घटकों की गणना करके, <math display="inline"> \bigwedge\nolimits^k(V) </math> का विमा एक [[ द्विपद गुणांक |द्विपद गुणांक]] के बराबर है: | |||
:<math> \dim {\textstyle\bigwedge}^k(V) = \binom{n}{k}\,. </math> | :<math> \dim {\textstyle\bigwedge}^k(V) = \binom{n}{k}\,. </math> | ||
जहां {{mvar|n}} सदिशों का विमा है और {{mvar|k}} गुणनफल में ''सदिशों'' की संख्या है। असाधारण स्थितियों के लिए भी द्विपद गुणांक सही परिणाम उत्पन्न करता है; विशेष रूप से, {{math| ''k'' > ''n''}} के लिए <math display="inline"> \bigwedge\nolimits^k(V) = \{ 0 \} </math>। | |||
बाह्य बीजगणित के किसी भी घटक को k-सदिशों के योग के रूप में लिखा जा सकता है। इसलिए, सदिश समष्टि के रूप में बाह्य बीजगणित प्रत्यक्ष संकलन है | |||
:<math> | :<math> | ||
| Line 182: | Line 174: | ||
\oplus \cdots \oplus {\textstyle\bigwedge}^n(V) | \oplus \cdots \oplus {\textstyle\bigwedge}^n(V) | ||
</math> | </math> | ||
(जहां | (जहां परिपाटी <math display="inline"> \bigwedge\nolimits^0(V) = K, </math> {{mvar|V}}, और <math display="inline"> \bigwedge\nolimits^1(V) = V </math> के नीचे की फील्ड), और इसलिए इसका विमा द्विपद गुणांक के योग के बराबर है, जो कि 2<sup>n</sup> है। | ||
==== | ==== ''k''-सदिश की रैंक ==== | ||
यदि <math display=inline> \alpha \in \bigwedge\nolimits^k(V) | यदि <math display="inline"> \alpha \in \bigwedge\nolimits^k(V) </math> है, तो ''α'' को ''k''-सदिश वियोजनीय का संयोजन के रैखिक संयोजन के रूप में व्यक्त करना संभव है: | ||
:<math> \alpha = \alpha^{(1)} + \alpha^{(2)} + \cdots + \alpha^{(s)} </math> | :<math> \alpha = \alpha^{(1)} + \alpha^{(2)} + \cdots + \alpha^{(s)} </math> | ||
जहां प्रत्येक α<sup>(i) </sup> | जहां प्रत्येक ''α<sup>(i)</sup>'' विघटित होता है, माना | ||
:<math> | :<math> | ||
| Line 196: | Line 188: | ||
= 1,2,\ldots, s. | = 1,2,\ldots, s. | ||
</math> | </math> | ||
'' K ''- | ''K''-सदिश ''α'' का '''रैंक''' ''α'' के इस तरह के विस्तार में ''k''-सदिश वियोजनीय की न्यूनतम संख्या है। यह [[ टेंसर रैंक |टेंसर रैंक]] की धारणा के समान ही है। | ||
2- | 2-सदिशों के अध्ययन में रैंक विशेष रूप से महत्वपूर्ण है {{harv|स्टर्नबर्ग|1964|loc=§III.6}} {{harv|ब्रायंट|Chern|Gardner|Goldschmidt|1991}}। 2-सदिश ''α'' की रैंक को बेसिस में ''α'' के गुणांकों के आव्यूह के आधे रैंक के साथ पहचाना जा सकता है। इस प्रकार यदि ''e<sub>i</sub>'' के लिए बेसिस है, तो ''α'' को अभीष्ट रूप से व्यक्त किया जा सकता है | ||
:<math> \alpha = \sum_{i,j}a_{ij}e_i \wedge e_j </math> | :<math> \alpha = \sum_{i,j}a_{ij}e_i \wedge e_j </math> | ||
जहाँ {{nowrap|1=''a''<sub>''ij''</sub> = −''a''<sub>''ji''</sub>}} (गुणांकों का आव्यूह विषम सममित है)। इसलिए आव्यूह ''a<sub>ij</sub>'' की कोटि सम है, और α के रूप की कोटि से दोगुनी है। | |||
विशेषता 0 में, 2- | विशेषता 0 में, 2-सदिश α का रैंक p है यदि और केवल यदि | ||
:<math> | :<math> | ||
| Line 210: | Line 202: | ||
\ \underset{p+1}{\underbrace{\alpha \wedge \cdots \wedge \alpha}} = 0. | \ \underset{p+1}{\underbrace{\alpha \wedge \cdots \wedge \alpha}} = 0. | ||
</math> | </math> | ||
=== श्रेणीबद्ध (ग्रेडेड) संरचना === | |||
''p''-सदिश के साथ ''k''-सदिश का बाह्य गुणनफल (''k'' + ''p'') -सदिश है, जो एक बार फिर बाईलीनियरिटी का आह्वान करता है। परिणाम के रूप में, पिछले अनुभाग का प्रत्यक्ष योग अपघटन | |||
=== ग्रेडेड संरचना === | |||
:<math> | :<math> | ||
{\textstyle\bigwedge}(V) = {\textstyle\bigwedge}^{\!0}(V) \oplus {\textstyle\bigwedge}^{\!1}(V) \oplus {\textstyle\bigwedge}^{\!2}(V) \oplus \cdots \oplus {\textstyle\bigwedge}^{\!n}(V) | {\textstyle\bigwedge}(V) = {\textstyle\bigwedge}^{\!0}(V) \oplus {\textstyle\bigwedge}^{\!1}(V) \oplus {\textstyle\bigwedge}^{\!2}(V) \oplus \cdots \oplus {\textstyle\bigwedge}^{\!n}(V) | ||
</math> | </math> | ||
बाह्य बीजगणित को एक वर्गीकृत बीजगणित की अतिरिक्त संरचना प्रदान करता है, अर्थात | |||
:<math> | :<math> | ||
| Line 225: | Line 215: | ||
\sub {\textstyle\bigwedge}^{k+p}(V). | \sub {\textstyle\bigwedge}^{k+p}(V). | ||
</math> | </math> | ||
इसके | इसके अतिरिक्त, यदि {{math|''K''}} आधार क्षेत्र है, अतः हमें निम्नलिखित प्राप्त होता है | ||
:<math> | :<math> | ||
| Line 232: | Line 222: | ||
{\textstyle\bigwedge}^{\!1}(V) = V. | {\textstyle\bigwedge}^{\!1}(V) = V. | ||
</math> | </math> | ||
बाह्य गुणनफल को एंटीकोम्यूटेटिव श्रेणीबद्ध किया गया है, जिसका अर्थ है कि यदि <math display="inline"> \alpha \in \bigwedge\nolimits^k(V) </math> और <math display="inline"> \beta \in \bigwedge\nolimits^p(V), </math> हैं, तो | |||
:<math> \alpha \wedge \beta = (-1)^{kp}\beta \wedge \alpha. </math> | :<math> \alpha \wedge \beta = (-1)^{kp}\beta \wedge \alpha. </math> | ||
बाह्य बीजगणित पर श्रेणीबद्ध संरचना का अध्ययन करने के अतिरिक्त, {{harvtxt|बोरबाकी|1989}} बाह्य बीजगणित पर अतिरिक्त वर्गीकृत संरचनाओं का अध्ययन करता है, जैसे कि [[ वर्गीकृत मॉड्यूल |वर्गीकृत मॉड्यूल]] के बाह्य बीजगणित पर (मॉड्यूल जो पहले से ही अपने स्वयं के उन्नयन को वहन करता है)। | |||
=== सार्वभौमिक | === सार्वभौमिक गुणधर्म === | ||
मान लीजिए {{math|''V''}} क्षेत्र {{math|''K''}} पर एक सदिश समष्टि है। अनौपचारिक रूप से, <math display="inline"> \bigwedge(V) </math> में गुणा प्रतीकों में प्रकलन करके और वितरण नियम, साहचर्य नियम लागू करके और {{math|''v'' ∈ ''V''}} के लिए पहचान <math> v \wedge v = 0 </math> का उपयोग करके किया जाता है। औपचारिक रूप से, <math display="inline"> \bigwedge(V) </math> "सबसे सामान्य" बीजगणित है जिसमें ये नियम गुणन के लिए धारण करते हैं, इस अर्थ में कि {{math|''V''}} पर वैकल्पिक गुणन के साथ {{math|''V''}} वाले किसी भी एकात्मक साहचर्य {{math|''K''}}-बीजगणित में <math display="inline"> \bigwedge(V) </math> की समरूप छवि होनी चाहिए। दूसरे शब्दों में, बाह्य बीजगणित में निम्नलिखित [[ सार्वभौमिक संपत्ति |सार्वभौमिक गुण]] होते हैं:<ref>See {{harvtxt|Bourbaki|1989|loc=§III.7.1}}, and {{harvtxt|Mac Lane|Birkhoff|1999|loc=Theorem XVI.6.8}}. More detail on universal properties in general can be found in {{harvtxt|Mac Lane|Birkhoff|1999|loc=Chapter VI}}, and throughout the works of Bourbaki.</ref> | |||
<div style = मार्जिन-लेफ्ट: 2EM;मार्जिन-सही: 2EM> | <div style = मार्जिन-लेफ्ट: 2EM;मार्जिन-सही: 2EM> | ||
किसी भी यूनिटल साहचर्य | किसी भी यूनिटल साहचर्य ''{{math|''K''}}''-बीजगणित {{math|''A''}} और किसी भी {{math|''K''}}-[[ रेखीय मानचित्र |रेखीय मैप]] <math> j : V \to A </math> को देखते हुए {{math|''V''}} में प्रत्येक {{math|''v''}} के लिए <math> j(v)j(v) = 0 </math>, तो ''शुद्ध रूप से'' इकाई बीजगणित समाकारिता <math display="inline"> f : \bigwedge(V)\to A </math> विद्यमान है जैसे कि {{math|1=''j''(''v'') = ''f''(''i''(''v''))}} {{math|''V''}} में सभी {{math|''v''}} के लिए (यहाँ {{math|''i''}} <math display="inline"> \bigwedge(V), </math> में {{math|''V''}} का स्वाभाविक समावेश है, ऊपर देखें)। | ||
</div> | </div> | ||
[[Image:ExteriorAlgebra-01.png|center| | [[Image:ExteriorAlgebra-01.png|center|बाह्य बीजगणित की सार्वभौमिक गुणधर्म]]सबसे सामान्य बीजगणित का संरचना करने के लिए जिसमें {{math|''V''}} सम्मिलित है और जिसका गुणन {{math|''V''}} पर वैकल्पिक है, सबसे सामान्य साहचर्य बीजगणित के साथ शुरू करना स्वाभाविक है जिसमें {{math|''V''}}, टेंसर बीजगणित {{math|''T''(''V'')}} सम्मिलित है, और फिर एक उपयुक्त कोशिएंट लेकर वैकल्पिक गुणधर्म को लागू करें। इस प्रकार हम {{math|''V''}} में {{math|''v''}} के लिए {{math|''v'' ⊗ ''v''}} के रूप के सभी घटकों द्वारा उत्पन्न {{math|''T''(''V'')}} में दो-तरफा अभीष्ट {{math|''I''}} लेते हैं, और <math display="inline"> \bigwedge(V) </math> को कोशिएंट के रूप में परिभाषित करते हैं। | ||
:<math> {\textstyle\bigwedge}(V) = T(V)/I\ </math> | :<math> {\textstyle\bigwedge}(V) = T(V)/I\ </math> | ||
(और | (और {{math|∧}} को <math display="inline"> \bigwedge(V) </math> में गुणन के प्रतीक के रूप में उपयोग करें)। इसके पश्चात यह दिखाना प्रत्यक्ष है कि <math display="inline"> \bigwedge(V) </math> में {{math|''V''}} है और उपरोक्त सार्वभौमिक गुणधर्म को संतुष्ट करता है। | ||
इस | इस संरचना के परिणामस्वरूप, सदिश समष्टि {{math|''V''}} को इसके बाह्य बीजगणित <math display="inline"> \bigwedge(V) </math> को नियुक्त करने का संचालन सदिश रिक्त समष्टि की [[ श्रेणी (गणित) |श्रेणी]] से बीजगणित की श्रेणी का फ़ंक्टर होता है। | ||
पहले <math display="inline"> \bigwedge(V) </math> को परिभाषित करने और फिर बाह्य घातांक <math display="inline"> \bigwedge\nolimits^k(V) </math> को कुछ उप-समष्टियों के रूप में पहचानने के बजाय, वैकल्पिक रूप से पहले रिक्त समष्टि <math display="inline"> \bigwedge\nolimits^k(V) </math> को परिभाषित किया जा सकता है और फिर बीजगणित <math display="inline"> \bigwedge(V) </math> बनाने के लिए उन्हें जोड़ा जा सकता है। इस दृष्टिकोण का उपयोग प्रायः अवकल ज्यामिति में किया जाता है और अगले भाग में वर्णित किया जाता है। | |||
=== सामान्यीकरण === | === सामान्यीकरण === | ||
क्रमविनिमेय रिंग ''R'' और ''R''-मॉड्यूल M को देखते हुए, हम बाह्य बीजगणित <math display="inline"> \bigwedge(M) </math> को उपरोक्त प्रकार से परिभाषित कर सकते हैं, जैसा कि टेन्सर बीजगणित '''T'''(''M'') के उपयुक्त कोशिएंट के रूप में है। यह समान सार्वभौमिक गुणधर्म को संतुष्ट करेगा। <math display="inline"> \bigwedge(M) </math> के कई गुणों के लिए यह भी आवश्यक है कि ''M'' एक [[ प्रोजेक्टिव मॉड्यूल |प्रोजेक्टिव मॉड्यूल]] हो। जहां परिमित विमीयता का उपयोग किया जाता है, गुणों के लिए आगे की आवश्यकता होती है कि ''M'' सूक्ष्म रूप से उत्पन्न और प्रक्षेपी हो। सबसे आम स्थितियों के लिए सामान्यीकरण {{harvtxt|बोरबाकी|1989}} में पाया जा सकता है। | |||
[[ वेक्टर बंडल ]] | ज्यामिति और टोपोलॉजी में [[ वेक्टर बंडल |सदिश बंडलों]] के बाह्य बीजगणित पर प्रायः विचार किया जाता है। सेरे-स्वान प्रमेय द्वारा परिमित-विमीय सदिश बंडलों के बाह्य बीजगणित के बीजगणितीय गुणों और सूक्ष्म रूप से उत्पन्न प्रोजेक्टिव मॉड्यूल के बाह्य बीजगणित के बीच कोई आवश्यक अंतर नहीं हैं। अधिक सामान्य बाह्य बीजगणित को मॉड्यूल के ढेरों के लिए परिभाषित किया जा सकता है। | ||
== | == वैकल्पिक टेन्सर बीजगणित == | ||
यदि | यदि ''K'' विशेषता 0 का एक क्षेत्र है,<ref>See {{harvtxt|Bourbaki|1989|loc=§III.7.5}} for generalizations.</ref> तो ''K'' पर सदिश समष्टि ''V'' के बाह्य बीजगणित को प्रतिसममित (एंटीसिमेट्रिक) टेंसरों से युक्त T(''V'') के सदिश उपसमष्टि के साथ कैनोनिक रूप से पहचाना जा सकता है। याद रखें कि बाह्य बीजगणित, {{nowrap|''x'' ⊗ ''x''}} के रूप के घटकों द्वारा उत्पन्न अभीष्ट ''I'' द्वारा T(''V'') का कोशिएंट है। | ||
मान लीजिए T<sup>''r''</sup>(''V'') डिग्री r के सजातीय टेन्सरों का समष्टि है। यह वियोजनीय टेंसरों द्वारा विस्तारित है | |||
:<math> v_1 \otimes \cdots \otimes v_r,\quad v_i \in V. </math> | :<math> v_1 \otimes \cdots \otimes v_r,\quad v_i \in V. </math> | ||
वियोजनीय टेन्सर के '''प्रतिसममितीकरण''' (या कभी-कभी '''विषम-सममितीकरण''') द्वारा परिभाषित किया गया है | |||
:<math> | :<math> | ||
| Line 270: | Line 260: | ||
= \frac{1}{r!}\sum_{\sigma \in \mathfrak{S}_r} \operatorname{sgn}(\sigma) v_{\sigma(1)} \otimes \cdots \otimes v_{\sigma(r)} | = \frac{1}{r!}\sum_{\sigma \in \mathfrak{S}_r} \operatorname{sgn}(\sigma) v_{\sigma(1)} \otimes \cdots \otimes v_{\sigma(r)} | ||
</math> | </math> | ||
जहां | जहां प्रतीक {1, ..., ''r''} पर क्रमपरिवर्तन के [[ सममित समूह |सममित समूह]] पर योग लिया जाता है। यह पूर्ण टेन्सर बीजगणित T(''V'') पर रैखिकता और एकरूपता द्वारा एक ऑपरेशन तक विस्तारित है, जिसे Alt द्वारा भी निरूपित किया जाता है। छवि Alt(T(''V'')) '''वैकल्पिक टेन्सर बीजगणित''' है, जिसे A(''V'') के रूप में दर्शाया गया है। यह T(''V'') की सदिश उपसमष्टि है, और यह T(''V'') से श्रेणीबद्ध सदिश समष्टि की संरचना को इनहेरिट करती है। यह साहचर्य श्रेणीबद्ध गुणनफल <math> \widehat{\otimes} </math> द्वारा परिभाषित किया गया है | ||
:<math> t~\widehat{\otimes}~s = \operatorname{Alt}(t \otimes s). </math> | :<math> t~\widehat{\otimes}~s = \operatorname{Alt}(t \otimes s). </math> | ||
यद्यपि यह | यद्यपि यह गुणनफल टेंसर गुणनफल से भिन्न है, ''Alt'' का कर्नेल शुद्ध रूप से अभीष्ट ''I'' है (पुनः, यह मानते हुए कि ''K'' में विशेषता 0 है), और कैनोनिकल समरूपता है | ||
:<math> A(V)\cong {\textstyle\bigwedge}(V). </math> | :<math> A(V)\cong {\textstyle\bigwedge}(V). </math> | ||
=== इंडेक्स संकेतन === | |||
मान लीजिए कि ''V'' का परिमित विमा ''n'' है, और ''V'' का बेसिस {{nowrap|'''e'''<sub>1</sub>, ..., '''e'''<sub>''n''</sub>}} दिया गया है। तब किसी भी वैकल्पिक टेन्सर {{nowrap|''t'' ∈ A<sup>''r''</sup>(''V'') ⊂ ''T''<sup>''r''</sup>(''V'')}} को इंडेक्स संकेतन में इस प्रकार लिखा जा सकता है | |||
=== | |||
मान लीजिए कि | |||
:<math> | :<math> | ||
t = t^{i_1i_2\cdots i_r}\, {\mathbf e}_{i_1} \otimes {\mathbf e}_{i_2} \otimes \cdots \otimes {\mathbf e}_{i_r}, | t = t^{i_1i_2\cdots i_r}\, {\mathbf e}_{i_1} \otimes {\mathbf e}_{i_2} \otimes \cdots \otimes {\mathbf e}_{i_r}, | ||
</math> | </math> | ||
जहां | जहां ti1⋅⋅⋅ir अपने सूचकांकों में पूरी तरह से अप्रतिवर्तक सममित होती है। | ||
रैंक | रैंक ''r'' और ''p'' के दो वैकल्पिक टेंसरों ''t'' और ''s'' का बाह्य गुणनफल द्वारा दिया गया है | ||
:<math> | :<math> | ||
| Line 292: | Line 280: | ||
= \frac{1}{(r+p)!}\sum_{\sigma \in {\mathfrak S}_{r+p}}\operatorname{sgn}(\sigma)t^{i_{\sigma(1)} \cdots i_{\sigma(r)}} s^{i_{\sigma(r+1)} \cdots i_{\sigma(r+p)}} {\mathbf e}_{i_1} \otimes {\mathbf e}_{i_2} \otimes \cdots \otimes {\mathbf e}_{i_{r+p}}. | = \frac{1}{(r+p)!}\sum_{\sigma \in {\mathfrak S}_{r+p}}\operatorname{sgn}(\sigma)t^{i_{\sigma(1)} \cdots i_{\sigma(r)}} s^{i_{\sigma(r+1)} \cdots i_{\sigma(r+p)}} {\mathbf e}_{i_1} \otimes {\mathbf e}_{i_2} \otimes \cdots \otimes {\mathbf e}_{i_{r+p}}. | ||
</math> | </math> | ||
इस | इस टेन्सर के घटक टेन्सर गुणनफल {{nowrap|''s'' ⊗ ''t''}} के घटकों के शुद्ध रूप से विषम भाग हैं, जो सूचकांकों पर वर्ग कोष्ठक द्वारा निरूपित हैं: | ||
:<math> | :<math> | ||
| Line 298: | Line 286: | ||
= t^{[i_1\cdots i_r}s^{i_{r+1}\cdots i_{r+p}]}. | = t^{[i_1\cdots i_r}s^{i_{r+1}\cdots i_{r+p}]}. | ||
</math> | </math> | ||
आंतरिक गुणनफल को इंडेक्स नोटेशन में भी इस तरह से वर्णित किया जा सकता है। मान लीजिए कि <math> t = t^{i_0i_1\cdots i_{r-1}} </math>कोटि ''r'' का एक असममित टेंसर है। फिर, {{nowrap|''α'' ∈ ''V''<sup>∗</sup>}} के लिए, ''i<sub>α</sub>t'' रैंक {{nowrap|''r'' − 1}} का एक वैकल्पिक टेन्सर है, जो निम्नलिखित द्वारा दिया गया है: | |||
आंतरिक | |||
:<math> | :<math> | ||
| Line 306: | Line 292: | ||
= r\sum_{j=0}^n\alpha_j t^{ji_1\cdots i_{r-1}}. | = r\sum_{j=0}^n\alpha_j t^{ji_1\cdots i_{r-1}}. | ||
</math> | </math> | ||
जहाँ ''n'', ''V'' का विमा है। | |||
== | == द्वैतता (द्वैधिटी) == | ||
=== | === वैकल्पिक संकारक === | ||
दो | दो सदिश रिक्त समष्टि ''V'' और ''X'' और एक प्राकृतिक संख्या के को देखते हुए, ''V<sup>k</sup>'' से ''X'' तक '''वैकल्पिक संकारक''' बहु-रैखिक मैप है | ||
:<math> f\colon V^k \to X </math> | :<math> f\colon V^k \to X </math> | ||
जब भी v<sub>1</sub>, ..., | इस प्रकार कि जब भी ''v''<sub>1</sub>, ..., ''v<sub>k</sub>'' ''V'' में एकघाततः परतंत्र सदिश हों, तब | ||
:<math> f(v_1,\ldots, v_k) = 0. </math> | :<math> f(v_1,\ldots, v_k) = 0. </math> | ||
मैप | |||
:<math> w\colon V^k \to {\textstyle\bigwedge}^{\!k}(V) </math> | :<math> w\colon V^k \to {\textstyle\bigwedge}^{\!k}(V) </math> | ||
जो | जो <math> V </math> से <math> k </math> सदिशों से जुड़ा है, उनका बाह्य गुणनफल, अर्थात उनका संबंधित <math> k </math>-सदिश भी वैकल्पिक है। वास्तव में, यह मैप <math> V^k </math> पर परिभाषित "सबसे सामान्य" वैकल्पिक संचालिका है; किसी भी अन्य वैकल्पिक संकारक <math> f : V^k \rightarrow X, </math> को देखते हुए, <math> f = \phi \circ w </math> के साथ एक अद्वितीय रैखिक मैप <math> \phi : \wedge^{k}(V) \rightarrow X </math> विद्यमान है। यह सार्वभौमिक गुणधर्म समष्टि <math> \wedge^{k}(V) </math> की विशेषता है और इसकी परिभाषा के रूप में काम कर सकती है। | ||
=== | === वैकल्पिक बहुरेखीय रूप === | ||
{{See also|वैकल्पिक बहुरेखीय रूप}} | |||
{{See also| | |||
[[File:N-form.svg|thumb|upright=0.6|'' N '' 1-रूपों (η, η, ω) के | [[File:N-form.svg|thumb|upright=0.6|'' N '' 1-रूपों (η, η, ω) के बाह्य गुणनफल के लिए ज्यामितीय व्याख्या एक '' n ''-रूप प्राप्त करने के लिए-[[ समन्वय सतह ]]ों का जाल, यहाँ समतलों),<ref name=Penrose07/>के लिए {{nowrap|1=''n'' = 1, 2, 3}}।परिसंचरण दिग्विन्यास (सदिश समष्टि) दिखाते हैं।<ref>''Note'': The orientations shown here are not correct; the diagram simply gives a sense that an orientation is defined for every ''k''-form.</ref><ref>{{cite book|title=Gravitation |first1=J.A. |last1=Wheeler |first2=C. |last2=Misner |first3=K.S. |last3=Thorne |publisher=W.H. Freeman & Co|year=1973|pages=58–60, 83, 100–9, 115–9|isbn=0-7167-0344-0}}</ref>]]उपरोक्त चर्चा स्थिति के लिए विशेषज्ञ है जब {{nowrap|1=''X'' = ''K''}}, आधार फील्ड। इस स्थिति में वैकल्पिक बहुरेखीय फलन | ||
:<math> f : V^k \to K\ </math> | :<math> f : V^k \to K\ </math> | ||
'''वैकल्पिक बहुरेखीय रूप''' कहा जाता है। सभी वैकल्पिक [[ बहुपक्षीय रूप |बहुरेखीय रूपों]] का समुच्चय [[ दोहरी वेक्टर स्थान |सदिश समष्टि]] होता है, क्योंकि ऐसे दो मैपों का योग, या एक अदिश के साथ ऐसे मैप का गुणनफल, पुनः वैकल्पिक होता है। बाह्य घातांक की सार्वभौमिक गुणधर्म द्वारा, ''V'' पर डिग्री ''k'' के वैकल्पिक रूपों का समष्टि स्वाभाविक रूप से द्वैत सदिश समष्टि <math display="inline"> \bigl(\bigwedge\nolimits^k(V)\bigr)^* </math> के साथ समाकृतिक (आइसोमोर्फिक) है। यदि ''V'' परिमित-विमीय है, तो पश्चात वाला स्वाभाविक रूप से आइसोमॉर्फिक है{{Clarify|date=December 2021|reason=By what isomorphism? See, for example, https://mathoverflow.net/q/68004|text=}} <math display="inline"> \bigwedge\nolimits^k\left(V^*\right) </math> तक। विशेष रूप से, यदि '''v''' ''n''-विमीय है, तो ''V<sup>k</sup>'' से ''K'' तक वैकल्पिक मैपों के समष्टि का विमा द्विपद गुणांक <math display="inline"> \binom{n}{k} </math> है। | |||
इस तरह की पहचान के अधीन, बाह्य गुणनफल प्रभावशाली रूप लेता है: यह दो दिए गए घटको से एक नया अप्रतिवर्तक सममित मैप तैयार करता है। मान लीजिए {{nowrap|''ω'' : ''V''<sup>''k''</sup> → ''K''}} और {{nowrap|''η'' : ''V''<sup>''m''</sup> → ''K''}} दो अप्रतिवर्तक सममित मैप हैं। बहुरेखीय मैप के [[ टेंसर उत्पाद |टेंसर गुणनफलों]] की तरह, उनके बाह्य गुणनफल के चरों की संख्या उनके चरों की संख्याओं का योग होती है। बहुरेखीय रूपों के साथ बाह्य घातांक के घटकों की पहचान के विकल्प के आधार पर, बाह्य गुणनफल को इस रूप में परिभाषित किया गया है | |||
:<math> \omega \wedge \eta = \operatorname{Alt}(\omega \otimes \eta) </math> | :<math> \omega \wedge \eta = \operatorname{Alt}(\omega \otimes \eta) </math> | ||
या के रूप में | या के रूप में | ||
| Line 340: | Line 325: | ||
= \frac{(k+m)!}{k!\,m!}\operatorname{Alt}(\omega \otimes \eta), | = \frac{(k+m)!}{k!\,m!}\operatorname{Alt}(\omega \otimes \eta), | ||
</math> | </math> | ||
जहां, यदि आधार फ़ील्ड K की विशेषता 0 है, तो | जहां, यदि आधार फ़ील्ड ''K'' की विशेषता ''0'' है, तो बहु-मैप के वैकल्पिक Alt को इसके चर के सभी क्रमों पर संकेत-समायोजित मूल्यों के औसत के रूप में परिभाषित किया गया है: | ||
:<math> | :<math> | ||
| Line 346: | Line 331: | ||
= \frac{1}{k!}\sum_{\sigma \in S_k}\operatorname{sgn}(\sigma)\, \omega(x_{\sigma(1)}, \ldots, x_{\sigma(k)}). | = \frac{1}{k!}\sum_{\sigma \in S_k}\operatorname{sgn}(\sigma)\, \omega(x_{\sigma(1)}, \ldots, x_{\sigma(k)}). | ||
</math> | </math> | ||
जब | जब फ़ील्ड ''K'' में [[ एक क्षेत्र की विशेषता |सीमित अभिलक्षण]] होती है, अतः किसी भी फैक्टरियल्स या किसी भी स्थिरांक के बिना दूसरी व्यंजक का एक समान संस्करण अच्छी तरह से परिभाषित होता है: | ||
:<math> | :<math> | ||
| Line 352: | Line 337: | ||
= \sum_{\sigma \in \mathrm{Sh}_{k,m}} \operatorname{sgn}(\sigma)\, \omega(x_{\sigma(1)}, \ldots, x_{\sigma(k)})\, \eta(x_{\sigma(k+1)}, \ldots, x_{\sigma(k+m)}), | = \sum_{\sigma \in \mathrm{Sh}_{k,m}} \operatorname{sgn}(\sigma)\, \omega(x_{\sigma(1)}, \ldots, x_{\sigma(k)})\, \eta(x_{\sigma(k+1)}, \ldots, x_{\sigma(k+m)}), | ||
</math> | </math> | ||
यहां | जहाँ यहां {{nowrap|Sh<sub>''k'',''m''</sub> ⊂ ''S''<sub>''k''+''m''</sub>}} (''k,m'') समवकुलन (शफल) का उपसमुच्चय है: समुच्चय {{nowrap|{1, 2, ..., ''k'' + ''m''}{{void}}}} का क्रमचय ''σ'' ऐसा है कि {{nowrap|''σ''(1) < ''σ''(2) < ⋯ < ''σ''(''k'')}}, और {{nowrap|''σ''(''k'' + 1) < ''σ''(''k'' + 2) < ⋯ < ''σ''(''k'' + ''m'')}}। | ||
=== आंतरिक | === आंतरिक गुणनफल === | ||
{{See also| | {{See also|आंतरिक गुणनफल}} | ||
मान लीजिए कि v परिमित | मान लीजिए कि '''v''' परिमित-विमीय है। यदि ''V''<sup>∗</sup> सदिश समष्टि ''V'' के लिए द्वैत समष्टि को दर्शाता है, तो प्रत्येक {{nowrap|''α'' ∈ ''V''<sup>∗</sup>}} के लिए, बीजगणित <math display="inline"> \bigwedge(V) </math> पर [[ व्युत्पत्ति (अमूर्त बीजगणित) |प्रतिपक्षी]] को परिभाषित करना संभव है, | ||
:<math> | :<math> | ||
i_\alpha:{\textstyle\bigwedge}^k V | i_\alpha:{\textstyle\bigwedge}^k V | ||
\rightarrow {\textstyle\bigwedge}^{k-1}V. | \rightarrow {\textstyle\bigwedge}^{k-1}V. | ||
</math> | </math> | ||
इस व्युत्पत्ति को '' α '', या कभी -कभी | इस व्युत्पत्ति को ''α'' के साथ '''आंतरिक गुणनफल''', या कभी-कभी '''अंतर्न्यास संकारक''', या ''α'' द्वारा '''संक्षेपण''' कहा जाता है। | ||
मान लीजिए कि <math display="inline"> w \in \bigwedge\nolimits^k V </math>। फिर '''w''', ''V''<sup>∗</sup> से ''K'' की बहुरेखीय मैपिंग है, इसलिए इसे ''k''-गुना कार्तीय गुणनफल {{nowrap|''V''<sup>∗</sup> × ''V''<sup>∗</sup> × ... × ''V''<sup>∗</sup>}} पर इसके मानों द्वारा परिभाषित किया गया है। यदि ''u''<sub>1</sub>, ''u''<sub>2</sub>, ..., ''u<sub>k</sub>''<sub>−1</sub>, V* के {{nowrap|''k'' − 1}} अवयव हैं, अतः परिभाषित करें | |||
:<math> | :<math> | ||
| Line 369: | Line 354: | ||
= {\mathbf w}(\alpha,u_1,u_2,\ldots, u_{k-1}). | = {\mathbf w}(\alpha,u_1,u_2,\ldots, u_{k-1}). | ||
</math> | </math> | ||
इसके अतिरिक्त, | इसके अतिरिक्त, मान लीजिए {{nowrap|1=''i''<sub>''α''</sub>''f'' = 0}} जब भी ''f'' शुद्ध अदिश है (अर्थात, <math display="inline"> \bigwedge\nolimits^0 V </math> से संबंधित)। | ||
==== स्वयंसिद्ध लक्षण वर्णन और गुण ==== | ==== स्वयंसिद्ध (एक्सिओमाटिक) लक्षण वर्णन और गुण ==== | ||
आंतरिक | आंतरिक गुणनफल निम्नलिखित गुणों को संतुष्ट करता है: | ||
# प्रत्येक k और प्रत्येक | # प्रत्येक ''k'' और प्रत्येक {{nowrap|''α'' ∈ ''V''<sup>∗</sup>}} के लिए,<math display=block> | ||
i_\alpha:{\textstyle\bigwedge}^k V\rightarrow {\textstyle\bigwedge}^{k-1}V. | i_\alpha:{\textstyle\bigwedge}^k V\rightarrow {\textstyle\bigwedge}^{k-1}V. | ||
</math> ( | </math> (अधिवेशन द्वारा, <math display="inline"> \bigwedge\nolimits^{-1}V=\{0\} </math>) | ||
# यदि v | # यदि ''v V'' (<math display="inline"> = \bigwedge\nolimits^1 V </math>) का एक घटक है, तो {{nowrap|1=''i''<sub>''α''</sub>''v'' = ''α''(''v'')}} ''V'' के घटकों और ''V''<sup>∗</sup> के घटकों के बीच द्वैत युग्म होते है। | ||
# प्रत्येक | # प्रत्येक {{nowrap|''α'' ∈ ''V''<sup>∗</sup>}} के लिए, ''i<sub>α</sub>'' डिग्री −1 की श्रेणीबद्ध व्युत्पत्ति है:<math display="block"> | ||
i_\alpha (a \wedge b) | i_\alpha (a \wedge b) | ||
= (i_\alpha a) \wedge b + (-1)^{\deg a}a \wedge (i_\alpha b). | = (i_\alpha a) \wedge b + (-1)^{\deg a}a \wedge (i_\alpha b). | ||
</math> | </math> | ||
ये तीन गुण आंतरिक | ये तीन गुण आंतरिक गुणनफल को चित्रित करने के साथ-साथ इसे सामान्य अनंत-विमीय स्थिति में परिभाषित करने के लिए पर्याप्त हैं। | ||
आंतरिक | आंतरिक गुणनफल के आगे के गुणों में सम्मिलित हैं: | ||
* <math> i_\alpha\circ i_\alpha = 0. </math> | * <math> i_\alpha\circ i_\alpha = 0. </math> | ||
* <math> i_\alpha\circ i_\beta = -i_\beta\circ i_\alpha. </math> | * <math> i_\alpha\circ i_\beta = -i_\beta\circ i_\alpha. </math> | ||
=== हॉज द्वैत === | |||
{{main article|हॉज स्टार संकारक}} | |||
मान लीजिए कि ''V'' का परिमित विमा ''n'' है। तब आंतरिक गुणनफल सदिश रिक्त समष्टि के कैनोनिकल कैनोनिकल समरूपता (आइसोमोर्फिज्म) को प्रेरित करता है | |||
मान लीजिए कि | |||
:<math> | :<math> | ||
| Line 397: | Line 381: | ||
\to {\textstyle\bigwedge}^{n-k}(V) | \to {\textstyle\bigwedge}^{n-k}(V) | ||
</math> | </math> | ||
प्रतिवर्तन (रिकर्सिव) परिभाषा द्वारा | |||
:<math> i_{\alpha \wedge \beta} = i_\beta \circ i_\alpha. </math> | :<math> i_{\alpha \wedge \beta} = i_\beta \circ i_\alpha. </math> | ||
ज्यामितीय | ज्यामितीय विन्यास में, शीर्ष बाह्य घातांक <math display="inline"> \bigwedge\nolimits^n(V) </math> (जो एक विमीय सदिश समष्टि है) का एक गैर-शून्य घटक को कभी-कभी [[ खंड रूप |'''आयतन रूप''']] (या '''दिग्विन्यास रूप''' कहा जाता है, हालांकि यह शब्द कभी-कभी अस्पष्टता का कारण बन सकता है)। नाम दिग्विन्यास रूप इस तथ्य से आता है कि विकल्प शीर्ष घटक का विकल्प पूरे बाह्य बीजगणित का दिग्विन्यास निर्धारित करता है, क्योंकि यह सदिश समष्टि के ऑर्डर किए गए आधार को ठीक करने के लिए समान है। अधिमानित आयतन रूप σ के सापेक्ष, समरूपता स्पष्ट रूप से निम्नलिखित द्वारा दी गई है | ||
:<math> | :<math> | ||
| Line 406: | Line 390: | ||
: \alpha \mapsto i_\alpha\sigma . | : \alpha \mapsto i_\alpha\sigma . | ||
</math> | </math> | ||
यदि, | यदि, आयतन रूप के अतिरिक्त, सदिश समष्टि V V के साथ V की पहचान करने वाले आंतरिक गुणनफल से सुसज्जित है, तो परिणामी समरूपता को '''हॉज स्टार संकारक''' कहा जाता है, जो अपने '''हॉज द्वैत''' के लिए एक घटक को मैप करता है: | ||
:<math> | :<math> | ||
| Line 412: | Line 396: | ||
\rightarrow {\textstyle\bigwedge}^{n-k}(V) . | \rightarrow {\textstyle\bigwedge}^{n-k}(V) . | ||
</math> | </math> | ||
<math> \star </math> का संघटन स्वयं {{nowrap|<math display=inline> \bigwedge\nolimits^k(V) </math> → <math display=inline> \bigwedge\nolimits^k(V) </math>}} मैपों के साथ है और हमेशा पहचान मैप का एक अदिश गुणक होता है। अधिकांश अनुप्रयोगों में, आयतन रूप आंतरिक गुणनफल के साथ इस अर्थ में संगत होता है कि यह V के ऑर्थोनॉर्मल आधार का एक बाह्य गुणनफल है। इस स्थिति में, | |||
:<math> \star \circ \star : {\textstyle\bigwedge}^k(V) \to {\textstyle\bigwedge}^k(V) = (-1)^{k(n-k) + q}\mathrm{id} </math> | :<math> \star \circ \star : {\textstyle\bigwedge}^k(V) \to {\textstyle\bigwedge}^k(V) = (-1)^{k(n-k) + q}\mathrm{id} </math> | ||
जहां आईडी | जहां आईडी तत्समक मैपिंग है, और आंतरिक गुणनफल में [[ मीट्रिक हस्ताक्षर |मीट्रिक संकेत]] {{nowrap|(''p'', ''q'')}}— ''p'' प्लसस और ''q'' माइनस हैं। | ||
=== आंतरिक | === आंतरिक गुणनफल === | ||
V के लिए एक परिमित- | ''V'' के लिए एक परिमित-विमीय समष्टि, V पर आंतरिक गुणनफल (या एक [[ छद्म-यूक्लिडियन स्थान |छद्म-यूक्लिडियन]] आंतरिक गुणनफल) ''V'' के साथ ''V'' के एक समरूपता को परिभाषित करता है, और इसलिए <math display="inline"> \bigwedge\nolimits^k V </math> के साथ <math display="inline"> \bigl(\bigwedge\nolimits^k V\bigr)^* </math> का एक समरूपता भी है। इन दो समष्टियों के बीच का युग्म भी आंतरिक गुणनफल का रूप ले लेती है। वियोजनीय ''k''-सदिश पर, | ||
:<math> | :<math> | ||
| Line 423: | Line 407: | ||
= \det\bigl(\langle v_i,w_j\rangle\bigr), | = \det\bigl(\langle v_i,w_j\rangle\bigr), | ||
</math> | </math> | ||
आंतरिक | आंतरिक गुणनफलों के आव्यूह का निर्धारक। विशेष स्थिति में {{nowrap|1=''v''<sub>''i''</sub> = ''w''<sub>''i''</sub>}}, आंतरिक गुणनफल k-सदिश का वर्ग मानदंड है, जिसे [[ ग्रामियन मैट्रिक्स |ग्रामियन आव्यूह]] {{nowrap|({{langle}}''v''<sub>''i''</sub>, ''v''<sub>''j''</sub>{{rangle}})}} के निर्धारक द्वारा दिया गया है। इसके पश्चात <math display="inline"> \bigwedge\nolimits^k V </math> पर गैर-पतित आंतरिक गुणनफल के लिए बाईलीनियरली (या जटिल स्थिति में सेस्क्विलिनियरली) विस्तारित किया जाता है। यदि ''e<sub>i</sub>'', {{nowrap|1=''i'' = 1, 2, ..., ''n''}}, ''V'' का ऑर्थोनॉर्मल बेसिस बनाते हैं, तो रूप के सदिश | ||
:<math> e_{i_1} \wedge \cdots \wedge e_{i_k},\quad i_1 < \cdots < i_k, </math> | :<math> e_{i_1} \wedge \cdots \wedge e_{i_k},\quad i_1 < \cdots < i_k, </math> | ||
<math display="inline"> \bigwedge\nolimits^k(V) </math> के लिए ऑर्थोनॉर्मल बेसिस बनता है, कॉची-बिनेट सूत्र के समतुल्य एक कथन। | |||
आंतरिक | आंतरिक गुणनफल के संबंध में, बाह्य गुणा और आंतरिक गुणनफल पारस्परिक रूप से जुड़े हुए हैं। विशेष रूप से, <math display="inline"> v \in \bigwedge\nolimits^{k-1}(V), </math> <math display="inline"> w \in \bigwedge\nolimits^{k}(V) </math> और <math display="inline"> x \in V, </math> के लिए, | ||
:<math> | :<math> | ||
\langle x \wedge \mathbf{v}, \mathbf{w}\rangle | \langle x \wedge \mathbf{v}, \mathbf{w}\rangle | ||
= \langle \mathbf{v}, i_{x^\flat}\mathbf{w}\rangle | = \langle \mathbf{v}, i_{x^\flat}\mathbf{w}\rangle | ||
</math> | </math> | ||
जहाँ {{nowrap|''x''<sup>♭</sup> ∈ ''V''<sup>∗</sup>}} संगीतमय समाकृतिकता है, जिसके द्वारा परिभाषित रेखीय प्रकार्यात्मक है | |||
:<math> x^\flat(y) = \langle x, y\rangle </math> | :<math> x^\flat(y) = \langle x, y\rangle </math> | ||
सभी {{nowrap|''y'' ∈ ''V''}} के लिए। यह गुणधर्म बाह्य बीजगणित पर आंतरिक गुणनफल को पूरी तरह से चित्रित करती है। | |||
वास्तव में, अत्यधिक सामान्य रूप से <math display="inline"> v \in \bigwedge\nolimits^{k-l}(V), </math> <math display="inline"> w \in \bigwedge\nolimits^{k}(V), </math> और <math display="inline"> x \in \bigwedge\nolimits^{l}(V) </math> के लिए, उपरोक्त आसन्न गुणों का पुनरावृति देता है | |||
:<math> | :<math> | ||
\langle \mathbf{x} \wedge \mathbf{v}, \mathbf{w}\rangle | \langle \mathbf{x} \wedge \mathbf{v}, \mathbf{w}\rangle | ||
= \langle \mathbf{v}, i_{\mathbf{x}^\flat}\mathbf{w}\rangle | = \langle \mathbf{v}, i_{\mathbf{x}^\flat}\mathbf{w}\rangle | ||
</math> | </math> | ||
जहां अब <math display="inline"> x^\flat \in \bigwedge\nolimits^l\left(V^*\right) \simeq \bigl(\bigwedge\nolimits^l(V)\bigr)^* </math> द्वैत एल-सदिश द्वारा परिभाषित किया गया है | |||
:<math> | :<math> | ||
\mathbf{x}^\flat(\mathbf{y}) = \langle \mathbf{x}, \mathbf{y}\rangle | \mathbf{x}^\flat(\mathbf{y}) = \langle \mathbf{x}, \mathbf{y}\rangle | ||
</math> | </math> | ||
सबके लिए <math display=inline> y \in \bigwedge\nolimits^l(V) | सबके लिए <math display="inline"> y \in \bigwedge\nolimits^l(V) </math>। | ||
=== बायलजेब्रा संरचना === | |||
श्रेणीबद्ध बीजगणित <math display="inline"> \bigwedge(V) </math> के श्रेणीबद्ध द्वैध और '''v''' पर बहुरेखीय रूपों के बीच समतुल्यता है। बाह्य बीजगणित (साथ ही सममित बीजगणित) बायलजेब्रा संरचना प्राप्त करता है, और, वास्तव में, टेन्सर बीजगणित से हॉफ बीजगणित संरचना। विषय के विस्तृत उपचार के लिए टेंसर बीजगणित पर लेख देखें। | |||
=== | |||
ऊपर परिभाषित मल्टीलाइनर रूपों का बाह्य गुणनफल <math display="inline"> \bigwedge(V), </math> पर परिभाषित एक [[ नक़ली |सह-गुणनफल]] के लिए दोहरा है, जो [[ कोयला |सह-बीजगणित (कोलजेब्रा)]] की संरचना देता है। सह-गुणनफल एक रैखिक फलन {{nowrap|Δ : <math display=inline> \bigwedge(V) </math> → <math display=inline> \bigwedge(V) </math> ⊗ <math display=inline> \bigwedge(V) </math>}} है, जो इसके द्वारा दिया गया है | |||
:<math> \Delta(v) = 1 \otimes v + v \otimes 1 </math> | :<math> \Delta(v) = 1 \otimes v + v \otimes 1 </math> | ||
घटकों पर ''v''∈''V''। प्रतीक 1 फील्ड ''K'' के इकाई तत्व को दर्शाता है। याद रखें कि {{nowrap|''K'' ⊂ <math display=inline> \bigwedge(V) </math>,}} ताकि उपरोक्त वास्तव में {{nowrap|<math display=inline> \bigwedge(V) </math> ⊗ <math display=inline> \bigwedge(V) </math>}} में निहित हो। सहगुणनफल की यह परिभाषा पूर्ण समष्टि <math display="inline"> \bigwedge(V) </math> तक (रैखिक) समरूपता द्वारा उठाई जाती है। इस समरूपता का सही रूप वह नहीं है जिसे कोई भोलेपन से लिख सकता है, बल्कि कोलजेब्रा लेख में सावधानी से परिभाषित किया जाना चाहिए। इस स्थिति में, एक प्राप्त करता है | |||
इस समरूपता का सही रूप वह नहीं है | |||
:<math> | :<math> | ||
\Delta(v \wedge w) = 1 \otimes (v \wedge w) + v \otimes w - w \otimes v + (v \wedge w) \otimes 1. | \Delta(v \wedge w) = 1 \otimes (v \wedge w) + v \otimes w - w \otimes v + (v \wedge w) \otimes 1. | ||
</math> | </math> | ||
विस्तार से | इसे विस्तार से विस्तारित करते हुए, निम्नलिखित अभिव्यक्ति को विघटित घटकों पर प्राप्त किया जाता है: | ||
:<math> | :<math> | ||
| Line 469: | Line 448: | ||
= \sum_{p=0}^k \; \sum_{\sigma \in Sh(p+1,k-p)} \; \operatorname{sgn}(\sigma) (x_{\sigma(0)} \wedge \cdots \wedge x_{\sigma(p)}) \otimes (x_{\sigma(p+1)} \wedge \cdots \wedge x_{\sigma(k)}). | = \sum_{p=0}^k \; \sum_{\sigma \in Sh(p+1,k-p)} \; \operatorname{sgn}(\sigma) (x_{\sigma(0)} \wedge \cdots \wedge x_{\sigma(p)}) \otimes (x_{\sigma(p+1)} \wedge \cdots \wedge x_{\sigma(k)}). | ||
</math> | </math> | ||
जहां | जहां सभी {{nowrap|(''p''+1, ''k''−''p'')}}-समवकुलन पर दूसरा योग लिया जाता है। फ़ील्ड एलिमेंट 1 का ट्रैक रखने के लिए उपरोक्त को नोटेशनल ट्रिक के साथ लिखा गया है: ट्रिक <math> x_0 = 1, </math> लिखने के लिए है और योग के विस्तार के दौरान इसे विभिन्न समष्टियों में समवकुलन किया जाता है। समवकुलन सह-बीजगणित के पहले स्वयंसिद्ध से सीधे अनुसरण करता है: घटकों का सापेक्ष क्रम <math> x_k </math> राइफल समवकुलन में संरक्षित है: राइफल शफल केवल आदेशित अनुक्रम को दो क्रमित अनुक्रमों में विभाजित करता है, एक बाईं ओर और एक दाईं ओर। | ||
निरीक्षण करें कि | निरीक्षण करें कि सह-गुणनफल बीजगणित की ग्रेडिंग को संरक्षित रखता है। पूर्ण समष्टि <math display="inline"> \bigwedge(V), </math> तक विस्तारित, एक के पास है | ||
:<math> | :<math> | ||
| Line 477: | Line 456: | ||
\to \bigoplus_{p=0}^k {\textstyle\bigwedge}^p(V) \otimes {\textstyle\bigwedge}^{k-p}(V) | \to \bigoplus_{p=0}^k {\textstyle\bigwedge}^p(V) \otimes {\textstyle\bigwedge}^{k-p}(V) | ||
</math> | </math> | ||
इस खंड में | इस खंड में प्रयुक्त टेन्सर प्रतीक ⊗ को कुछ सावधानी के साथ समझा जाना चाहिए: यह वही टेन्सर प्रतीक नहीं है जैसा कि वैकल्पिक गुणनफल की परिभाषा में उपयोग किया जा रहा है। सहज रूप से, इसे सिर्फ एक और, लेकिन भिन्न, टेन्सर गुणनफल के रूप में सोचना सबसे सरल है: यह अभी भी (द्वि-) रैखिक है, जैसा कि टेन्सर गुणनफलों को होना चाहिए, लेकिन यह गुणनफल है जो एक बायलजेब्रा की परिभाषा के लिए उपयुक्त है, अर्थात वस्तु {{nowrap|<math display=inline> \bigwedge(V) </math> ⊗ <math display=inline> \bigwedge(V) </math>}} बनाने के लिए। समानता {{nowrap|1=(1 ⊗ ''v'') ∧ (1 ⊗ ''w'') = 1 ⊗ (''v'' ∧ ''w'')}} और {{nowrap|1=(''v'' ⊗ 1) ∧ (1 ⊗ ''w'') = ''v'' ⊗ ''w''}} पर विचार करके किसी भी लंबे समय तक संदेह को हिलाया जा सकता है, जो कोलजेब्रा की परिभाषा से अनुसरण करता है, जैसा कि टेंसर और वेज प्रतीकों से जुड़े भोले-भाले जोड़तोड़ के विपरीत है। टेंसर बीजगणित पर लेख में इस अंतर को अधिक विस्तार से विकसित किया गया है। यहाँ, एक समस्या बहुत कम है, जिसमें वैकल्पिक गुणनफल ∧ स्पष्ट रूप से बायलजेब्रा में गुणन के अनुरूप है, जिससे प्रतीक ⊗ बाइलजेब्रा की परिभाषा में उपयोग के लिए मुक्त हो जाता है। व्यवहार में, यह कोई विशेष समस्या प्रस्तुत नहीं करता है, जब तक कि कोई एक अपवाद के साथ, वेज प्रतीक द्वारा ⊗ के वैकल्पिक योगों को बदलने के घातक जाल से बचता है। कोई भी ⊗ से एक वैकल्पिक गुणनफल बना सकता है, इस समझ के साथ कि यह एक भिन्न समष्टि में काम करता है। ठीक नीचे, एक उदाहरण दिया गया है: द्वैत समष्टि के लिए वैकल्पिक गुणनफल को प्रतिगुणनफल के संदर्भ में दिया जा सकता है। बाह्य बीजगणित के लिए वैकल्पिक संकेतों को सही ढंग से ट्रैक करने की आवश्यकता को छोड़कर, यहां बायलजेब्रा का संरचना टेंसर बीजगणित लेख में संरचना को लगभग समान बनाता है। | ||
सह-गुणनफल के संदर्भ में, द्वैत समष्टि पर बाह्य गुणनफल, सह-गुणनफल का केवल दो श्रेणीबद्ध है: | |||
:<math> | :<math> | ||
| Line 485: | Line 464: | ||
= (\alpha \otimes \beta)\left(\Delta(x_1 \wedge \cdots \wedge x_k)\right) | = (\alpha \otimes \beta)\left(\Delta(x_1 \wedge \cdots \wedge x_k)\right) | ||
</math> | </math> | ||
जहां | जहां दाईं ओर टेंसर गुणनफल बहुरेखीय रैखिक मैपों का है (असंगत सजातीय डिग्री के घटकों पर शून्य द्वारा बढ़ाया गया है: अधिक यथार्थ रूप से, {{nowrap|1=''α'' ∧ ''β'' = ''ε'' ∘ (''α'' ⊗ ''β'') ∘ Δ}}, जहां ε कॉउंट है, जैसा कि वर्तमान में परिभाषित किया गया है)। | ||
' | '''कॉउनिट''' समरूपता {{nowrap|1=''ε'' : <math display=inline> \bigwedge(V) </math> → ''K''}} है जो अपने तर्क के 0-श्रेणी वाले घटक को वापस करता है। बाह्य गुणनफल के साथ-साथ सह-गुणनफल और देश, बाह्य बीजगणित पर एक बायल्जेब्रा की संरचना को परिभाषित करते हैं। | ||
सजातीय घटकों पर <math> S(x) = (-1)^{\binom{\text{deg}\, x\, + 1}{2}}x, </math> द्वारा परिभाषित '''एंटीपोड''' के साथ बाह्य बीजगणित भी एक हॉप बीजगणित है।<ref>Indeed, the exterior algebra of ''V'' is the [[Universal enveloping algebra|enveloping algebra]] of the abelian [[Lie superalgebra]] structure on ''V''.</ref> | |||
== | == फुन्क्टरिअलिटी == | ||
मान लीजिए कि | मान लीजिए कि ''V'' और ''W'' सदिश समष्टियों का एक युग्म हैं और {{nowrap|''f'' : ''V'' → ''W''}} रैखिक मैप है। फिर, सार्वभौमिक गुणधर्म के द्वारा, वर्गीकृत बीजगणित का एक अद्वितीय समाकारिता विद्यमान है | ||
:<math> | :<math> | ||
| Line 506: | Line 483: | ||
= f : V={\textstyle\bigwedge}^1(V)\rightarrow W={\textstyle\bigwedge}^1(W). | = f : V={\textstyle\bigwedge}^1(V)\rightarrow W={\textstyle\bigwedge}^1(W). | ||
</math> | </math> | ||
विशेष रूप से, <math display=inline> \bigwedge\left(f\right) </math> सजातीय डिग्री को संरक्षित करता | विशेष रूप से, <math display="inline"> \bigwedge\left(f\right) </math> सजातीय डिग्री को संरक्षित करता है। <math display="inline"> \bigwedge\left(f\right) </math> के ''k''-श्रेणी वाले घटकों को वियोजनीय घटकों द्वारा दिया गया है | ||
:<math> | :<math> | ||
| Line 512: | Line 489: | ||
= f(x_1) \wedge \cdots \wedge f(x_k). | = f(x_1) \wedge \cdots \wedge f(x_k). | ||
</math> | </math> | ||
माना | |||
:<math> | :<math> | ||
| Line 519: | Line 496: | ||
: {\textstyle\bigwedge}^k(V) \rightarrow {\textstyle\bigwedge}^k(W). | : {\textstyle\bigwedge}^k(V) \rightarrow {\textstyle\bigwedge}^k(W). | ||
</math> | </math> | ||
''V'' और ''W'' के आधार पर रूपांतरण <math display="inline"> \bigwedge\nolimits^k\left(f\right) </math> के घटक, ''f'' के {{nowrap|''k'' × ''k''}} अवयस्क का आव्यूह है। विशेष रूप से, यदि {{nowrap|1=''V'' = ''W''}} और ''V'' परिमित विमा ''n'' का है, तो <math display="inline"> \bigwedge\nolimits^n\left(f\right) </math> स्वयं के लिए एक विमीय सदिश समष्टि <math display="inline"> \bigwedge\nolimits^n(V) </math> का मैपिंग है, और इसलिए इसे अदिश द्वारा दिया जाता है: ''f'' का निर्धारक। | |||
=== | === यथार्थता === | ||
यदि <math> 0 \to U \to V \to W \to 0 </math> | यदि <math> 0 \to U \to V \to W \to 0 </math> सदिश समष्टियों का लघु यथार्थ अनुक्रम है, तब | ||
:<math> | :<math> | ||
| Line 528: | Line 505: | ||
\to {\textstyle\bigwedge}(V) \to {\textstyle\bigwedge}(W) \to 0 | \to {\textstyle\bigwedge}(V) \to {\textstyle\bigwedge}(W) \to 0 | ||
</math> | </math> | ||
श्रेणीबद्ध सदिश समष्टि का यथार्थ अनुक्रम है,<ref>This part of the statement also holds in greater generality if ''V'' and ''W'' are modules over a commutative ring: That <math display="inline"> \bigwedge </math> converts epimorphisms to epimorphisms. See {{harvtxt|Bourbaki|1989|loc=Proposition 3, §III.7.2}}.</ref> जैसा है | |||
:<math display=inline> | :<math display=inline> | ||
0 \to \bigwedge(U) \to \bigwedge(V). | 0 \to \bigwedge(U) \to \bigwedge(V). | ||
</math><ref>This statement generalizes only to the case where ''V'' and ''W'' are projective modules over a commutative ring. Otherwise, it is generally not the case that <math display=inline> \bigwedge </math> converts monomorphisms to monomorphisms. See {{harvtxt|Bourbaki|1989|loc=Corollary to Proposition 12, §III.7.9}}.</ref> | </math><ref>This statement generalizes only to the case where ''V'' and ''W'' are projective modules over a commutative ring. Otherwise, it is generally not the case that <math display="inline"> \bigwedge </math> converts monomorphisms to monomorphisms. See {{harvtxt|Bourbaki|1989|loc=Corollary to Proposition 12, §III.7.9}}.</ref> | ||
=== प्रत्यक्ष संकलन === | |||
विशेष रूप से, प्रत्यक्ष संकलन का बाह्य बीजगणित बाह्य बीजगणित के टेन्सर गुणनफल के लिए समरूप है: | |||
=== प्रत्यक्ष | |||
विशेष रूप से, | |||
:<math> | :<math> | ||
| Line 542: | Line 517: | ||
\cong {\textstyle\bigwedge}(V) \otimes {\textstyle\bigwedge}(W). | \cong {\textstyle\bigwedge}(V) \otimes {\textstyle\bigwedge}(W). | ||
</math> | </math> | ||
यह | यह वर्गीकृत समरूपता है; अर्थात।, | ||
:<math> | :<math> | ||
| Line 548: | Line 523: | ||
\cong \bigoplus_{p+q=k} {\textstyle\bigwedge}^p(V) \otimes {\textstyle\bigwedge}^q(W). | \cong \bigoplus_{p+q=k} {\textstyle\bigwedge}^p(V) \otimes {\textstyle\bigwedge}^q(W). | ||
</math> | </math> | ||
अधिक | अधिक व्यापकता में, सदिश रिक्त समष्टि <math display="inline"> 0 \to U \mathrel{\overset{f}\to} V \mathrel{\overset{g}\to} W \to 0, </math> के एक छोटे से यथार्थ अनुक्रम के लिए एक प्राकृतिक निस्पंदन होता है | ||
:<math> | :<math> | ||
| Line 554: | Line 529: | ||
= {\textstyle\bigwedge}^k(V) | = {\textstyle\bigwedge}^k(V) | ||
</math> | </math> | ||
जहां <math> p \geq 1 </math> के लिए <math> F^p </math> को <math> u_i \in U </math> और <math> v_i \in V </math> के लिए <math> u_1 \wedge \ldots \wedge u_{k + 1-p} \wedge v_1 \wedge \ldots v_{p - 1} </math> के घटकों द्वारा फैलाया गया है। संबंधित उद्धरण एक प्राकृतिक समरूपता को स्वीकार करते हैं | |||
:<math> | :<math> | ||
| Line 561: | Line 535: | ||
</math> के द्वारा दिया गया <math> | </math> के द्वारा दिया गया <math> | ||
u_1 \wedge \ldots \wedge u_{k + 1 -p} \wedge v_1 \wedge \ldots \wedge v_{p - 1} | u_1 \wedge \ldots \wedge u_{k + 1 -p} \wedge v_1 \wedge \ldots \wedge v_{p - 1} | ||
\mapsto u_1 \wedge \ldots \wedge u_{k+1-p} \otimes g(v_1) \wedge \ldots \wedge g(v_{p - 1}) | \mapsto u_1 \wedge \ldots \wedge u_{k+1-p} \otimes g(v_1) \wedge \ldots \wedge g(v_{p - 1}) | ||
</math> | </math>। | ||
विशेष रूप से, यदि | विशेष रूप से, यदि ''U'' 1-विमीय है तो | ||
:<math> | :<math> | ||
| Line 570: | Line 544: | ||
\to {\textstyle\bigwedge}^k(W) \to 0 | \to {\textstyle\bigwedge}^k(W) \to 0 | ||
</math> | </math> | ||
यथार्थ है, और यदि ''W'' 1-विम है तो | |||
:<math> | :<math> | ||
| Line 577: | Line 551: | ||
\to {\textstyle\bigwedge}^{k-1}(U) \otimes W \to 0 | \to {\textstyle\bigwedge}^{k-1}(U) \otimes W \to 0 | ||
</math> | </math> | ||
यथार्थ है।<ref>Such a filtration also holds for [[vector bundle]]s, and projective modules over a commutative ring. This is thus more general than the result quoted above for direct sums, since not every short exact sequence splits in other [[abelian category|abelian categories]].</ref> | |||
== अनुप्रयोग == | == अनुप्रयोग == | ||
=== रैखिक बीजगणित === | === रैखिक बीजगणित === | ||
रैखिक बीजगणित के अनुप्रयोगों में, | रैखिक बीजगणित के अनुप्रयोगों में, बाह्य गुणनफल एक आव्यूह के निर्धारक और उपसारणिकों का वर्णन करने के लिए अमूर्त बीजगणितीय तरीका प्रदान करता है। उदाहरण के लिए, यह सर्वविदित है कि एक वर्ग आव्यूह का निर्धारक समांतरोटोप के आयतन के बराबर होता है, जिसके किनारे आव्यूह के स्तंभ होते हैं (दिग्विन्यास को ट्रैक करने के लिए चिह्न के साथ)। इससे पता चलता है कि निर्धारक को कॉलम सदिश के बाह्य गुणनफल के संदर्भ में परिभाषित किया जा सकता है। इसी तरह, आव्यूह के {{nowrap|''k'' × ''k''}} अवयस्क को एक समय में चयनित k कॉलम सदिश के बाह्य गुणनफलों को देखकर परिभाषित किया जा सकता है। इन विचारों को न केवल मैट्रिसेस तक बढ़ाया जा सकता है, बल्कि रैखिक परिवर्तनों के लिए भी: एक रैखिक परिवर्तन का निर्धारक वह कारक है जिसके द्वारा यह किसी भी दिए गए संदर्भ समांतरोटोप के उन्मुख मात्रा को मापता है। तो एक रैखिक परिवर्तन के निर्धारक को इस रूप में परिभाषित किया जा सकता है कि परिवर्तन शीर्ष बाह्य घातांक को क्या करता है। कम बाह्य घातांकयों पर एक रूपांतरण की क्रिया परिवर्तन के उपसारणिकों के बारे में बात करने का बेसिस-स्वतंत्र विधि प्रदान करती है। | ||
==== तकनीकी विवरण: परिभाषाएँ ==== | ==== तकनीकी विवरण: परिभाषाएँ ==== | ||
माना<ref>{{harvnb|Winitzki|2010}}</ref> <math> V </math> बेसिस <math> \{e_1, \ldots, e_n\} </math> के साथ फील्ड <math> K </math> पर ''n''-विमीय सदिश समष्टि बनें। | |||
* | * <math> A \in \operatorname{End}(V), </math> के लिए <math display="inline"> \bigwedge^k A \in \operatorname{End}\bigl(\bigwedge^k V\bigr) </math> को साधारण टेन्सर द्वारा परिभाषित करें<math display="block"> | ||
{\textstyle\bigwedge}^k A(v_1 \wedge \cdots \wedge v_k) = Av_1 \wedge \cdots \wedge Av_k | {\textstyle\bigwedge}^k A(v_1 \wedge \cdots \wedge v_k) = Av_1 \wedge \cdots \wedge Av_k | ||
</math> और सभी टेंसरों के लिए रैखिक रूप से | </math>और सभी टेंसरों के लिए परिभाषा को रैखिक रूप से विस्तारित करें। अत्यधिक सामान्य रूप से, हम <math display="inline"> \bigwedge^p A^k \in \operatorname{End}\bigl(\bigwedge^p V\bigr), (p \geq k) </math> को सरल टेंसरों पर परिभाषित कर सकते हैं <math display="block">\begin{align} | ||
&\left({\textstyle\bigwedge}^p A^k \right)(v_1 \wedge \cdots \wedge v_p) \\[10mu] | &\left({\textstyle\bigwedge}^p A^k \right)(v_1 \wedge \cdots \wedge v_p) \\[10mu] | ||
&\qquad= \sum_{0 \leq i_1 < \cdots < i_k \leq p} v_1 \wedge \cdots \wedge Av_{i_1} \wedge \cdots \wedge Av_{i_k} \wedge \cdots \wedge v_p | &\qquad= \sum_{0 \leq i_1 < \cdots < i_k \leq p} v_1 \wedge \cdots \wedge Av_{i_1} \wedge \cdots \wedge Av_{i_k} \wedge \cdots \wedge v_p | ||
\end{align}</math> | \end{align}</math>अर्थात k घटकों का चयन करें जिन पर A कार्य करेगा, फिर विभिन्न विकल्पों से प्राप्त सभी परिणामों का योग करें। यदि <math> p < k, </math> <math display="inline"> \bigwedge^p A^k = 0 </math> को परिभाषित करता है। चूंकि <math display="inline"> \bigwedge^n V </math> बेसिस <math> e_1 \wedge \cdots \wedge e_n, </math> के साथ 1-विमीय है, हम अद्वितीय संख्या <math> \kappa \in K </math> संतोषजनक के साथ <math display="inline"> \bigwedge^n A^k </math> की पहचान कर सकते हैं<math display="block"> | ||
{\textstyle\bigwedge}^n A^k (e_1 \wedge \cdots \wedge e_n) | {\textstyle\bigwedge}^n A^k (e_1 \wedge \cdots \wedge e_n) | ||
= \kappa (e_1 \wedge \cdots \wedge e_n) . | = \kappa (e_1 \wedge \cdots \wedge e_n) . | ||
</math> | </math> | ||
* | * <math> \varphi \in \operatorname{End}\bigl({\textstyle\bigwedge}^p V\bigr), </math> के लिए, किसी भी <math display="inline"> \omega_p \in {\textstyle\bigwedge}^p V</math> और <math display="inline"> \omega_{n-p} \in {\textstyle\bigwedge}^{n-p}V </math> के लिए <math display="inline"> (\varphi^\mathrm{T}\omega_{n-p}) \wedge \omega_p = \omega_{n-p} \wedge (\varphi \omega_p) </math> को संतुष्ट करने वाला अद्वितीय संकारक होने के लिए '''बाह्य परिवर्त''' <math display="inline"> \varphi^\mathrm{T} \in \operatorname{End}\bigl(\bigwedge^{n-p} V\bigr) </math> को परिभाषित करें। | ||
* | *<math> A \in \operatorname{End}(V), </math> के लिए <math display="inline"> \det A = \bigwedge^n A^n,</math> <math display="inline"> \operatorname{Tr}(A) = \bigwedge^n A^1, </math> <math display="inline"> \operatorname{adj} A = \bigl(\bigwedge^{n-1} A^{n-1}\bigr)^\mathrm{T} </math> को परिभाषित करें ये पिछली परिभाषाओं के बराबर हैं। | ||
==== मूल गुण ==== | ==== मूल गुण ==== | ||
निर्धारक, ट्रेस और आसन्न की अन्य परिभाषाओं से प्राप्त सभी परिणाम इस परिभाषा से प्राप्त किए जा सकते हैं ( | निर्धारक, ट्रेस और आसन्न की अन्य परिभाषाओं से प्राप्त सभी परिणाम इस परिभाषा से प्राप्त किए जा सकते हैं (चूंकि ये परिभाषाएं समकक्ष हैं)। यहाँ इन नई परिभाषाओं से संबंधित कुछ बुनियादी विशेषताएँ दी गई हैं: | ||
* <math> (\cdot)^\mathrm{T} </math> है <math> K </math>- | * <math> (\cdot)^\mathrm{T} </math> है <math> K </math>-रैखिक। | ||
* <math> (AB)^\mathrm{T} = B^\mathrm{T} A^\mathrm{T} | * <math> (AB)^\mathrm{T} = B^\mathrm{T} A^\mathrm{T} </math>। | ||
* | * हमे कैनोनिकल समरूपता (आइसोमोर्फिज्म) प्राप्त है<math display=block>\begin{cases} | ||
\psi:\operatorname{End}\bigl({\textstyle\bigwedge}^k V\bigr) | \psi:\operatorname{End}\bigl({\textstyle\bigwedge}^k V\bigr) | ||
\cong \operatorname{End}\bigl({\textstyle\bigwedge}^{n-k} V\bigr) \\ | \cong \operatorname{End}\bigl({\textstyle\bigwedge}^{n-k} V\bigr) \\ | ||
A \mapsto A^\mathrm{T} | A \mapsto A^\mathrm{T} | ||
\end{cases}</math> हालांकि, | \end{cases}</math>हालांकि, <math display="inline"> \bigwedge^k V </math> और <math display="inline"> \bigwedge^{n-k} V </math> के बीच कोई विहित समरूपता नहीं है। | ||
* <math display=inline> \operatorname{Tr} \bigl(\bigwedge^k A \bigr) = \bigwedge^n A^k. </math> की | * <math display=inline> \operatorname{Tr} \bigl(\bigwedge^k A \bigr) = \bigwedge^n A^k. </math> की परिवर्त आव्यूह की प्रविष्टियाँ <math display=inline> \bigwedge^k A </math> हैं <math> k \times k </math>-मिनर्स <math> A </math>। | ||
* | * प्रत्येक के लिए <math> | ||
k \leq n-1, p \leq k, A \in \operatorname{End}(V), | k \leq n-1, p \leq k, A \in \operatorname{End}(V), | ||
</math> <math display=block> | </math> <math display=block> | ||
| Line 628: | Line 600: | ||
= \sum_{q=0}^p \bigl({\textstyle\bigwedge}^n A^{p-q} \bigr)(-A)^q | = \sum_{q=0}^p \bigl({\textstyle\bigwedge}^n A^{p-q} \bigr)(-A)^q | ||
= \sum_{q=0}^p \operatorname{Tr} \bigl({\textstyle\bigwedge}^{p-q} A \bigr)(-A)^q. | = \sum_{q=0}^p \operatorname{Tr} \bigl({\textstyle\bigwedge}^{p-q} A \bigr)(-A)^q. | ||
</math> | </math>विशेष रूप से, <math display=block> | ||
\operatorname{adj} A | \operatorname{adj} A | ||
= \sum_{q=0}^{n-1} \bigl({\textstyle\bigwedge}^n A^{n-q-1} \bigr)(-A)^q. | = \sum_{q=0}^{n-1} \bigl({\textstyle\bigwedge}^n A^{n-q-1} \bigr)(-A)^q. | ||
| Line 652: | Line 624: | ||
= \sum_{k=0}^n (\det A)^{k-1} \left({\textstyle\bigwedge}^n A^{n-k} \right)(-t)^{n-k} | = \sum_{k=0}^n (\det A)^{k-1} \left({\textstyle\bigwedge}^n A^{n-k} \right)(-t)^{n-k} | ||
</math> | </math> | ||
==== लीवरियर का एल्गोरिथ्म ==== | |||
{{See also|फ़ड्डिव-लेवेरियर एल्गोरिथम}} | |||
<math display="inline"> \bigwedge^n A^k </math> अभिलाक्षणिक बहुपद में <math> (-t)^{n-k} </math> पदों के गुणांक हैं। वे <math display="inline"> \bigl(\bigwedge^{n-1} A^p\bigr)^\mathrm{T} </math> और <math display="inline"> \bigwedge^n (\operatorname{adj} A)^k </math> के व्यंजकों में भी दिखाई देते हैं। लेवेरियर का एल्गोरिद्म<ref>{{cite web |first=W. |last=Kahan |year=2000 |title=Jordan's normal form |work=Math. H110 |url=https://www.cs.berkeley.edu/~wkahan/MathH110/jordan.pdf}}</ref> <math display="inline"> \bigwedge^n A^k </math> और <math display="inline"> \bigwedge^{n-1} A^k \colon</math> की गणना करने का आर्थिक तरीका है | |||
:समुच्चय <math display=inline> \bigwedge^{n-1} A^0 = 1; </math> | |||
<math display=inline> \bigwedge^n A^k </math> | |||
: | |||
:के लिए <math> k = n-1, n-2, \ldots, 1, 0, </math> | :के लिए <math> k = n-1, n-2, \ldots, 1, 0, </math> | ||
::<math> | ::<math> | ||
| Line 668: | Line 639: | ||
- A \circ {\textstyle\bigwedge}^{n-1} A^{n-k-1}. | - A \circ {\textstyle\bigwedge}^{n-1} A^{n-k-1}. | ||
</math> | </math> | ||
=== भौतिकी === | |||
{{main|विद्युत चुम्बकीय टेंसर}} | |||
भौतिकी में, कई मात्राएँ स्वाभाविक रूप से वैकल्पिक संकारकों द्वारा प्रदर्शित की जाती हैं। उदाहरण के लिए, यदि किसी आवेशित कण की गति को चार-विमीय समष्टिटाइम में वेग और त्वरण सदिश द्वारा वर्णित किया जाता है, तो वेग सदिश के सामान्यीकरण के लिए आवश्यक है कि विद्युत चुम्बकीय बल वेग पर एक वैकल्पिक संकारक होना चाहिए। इसकी छह स्वतंत्रता की डिग्री विद्युत और चुंबकीय क्षेत्र से पहचानी जाती है। | |||
भौतिकी में, कई | |||
=== रैखिक ज्यामिति === | === रैखिक ज्यामिति === | ||
वियोजनीय ''k''-सदिश की ज्यामितीय व्याख्याएं हैं: द्विसदिश {{math|''u'' ∧ ''v''}} सदिश द्वारा फैलाए गए समतल का प्रतिनिधित्व करता है, "भारित" एक संख्या के साथ, ओरिएंटेड समांतर चतुर्भुज के क्षेत्र द्वारा यू और '''v''' के साथ दिया जाता है। अनुरूप रूप से, 3-सदिश {{math|''u'' ∧ ''v'' ∧ ''w''}} किनारों '''u''', '''v''', और '''w''' के साथ उन्मुख समांतर चतुर्भुज के आयतन द्वारा भारित विस्तारित हुए 3-समष्टि का प्रतिनिधित्व करता है। | |||
=== प्रोजेक्टिव ज्यामिति === | === प्रोजेक्टिव ज्यामिति === | ||
<math display="inline"> \bigwedge\nolimits^k V </math> में वियोजनीय ''k''-सदिश V के भारित के-विमीय रैखिक उप-समष्टियों के अनुरूप हैं। विशेष रूप से, V के के-विमीय उप-समष्टियों के [[ ग्रासमैनियन |ग्रासमैनियन]], जीआरके (वी) को निरूपित किया जाता है, जिसे स्वाभाविक रूप से [[ प्रोजेक्टिव स्पेस |प्रोजेक्टिव समष्टि]] <math display="inline"> P\bigl(\bigwedge\nolimits^k V\bigr) </math> की बीजगणितीय उप-विविधता के साथ पहचाना जा सकता है। इसे प्लकर एंबेडिंग कहा जाता है। | |||
=== | === अवकल ज्यामिति === | ||
बाह्य बीजगणित में अवकल ज्यामिति में उल्लेखनीय अनुप्रयोग हैं, जहाँ इसका उपयोग विभेदक रूपों को परिभाषित करने के लिए किया जाता है।<ref>{{cite book |first=A.T. |last=James |chapter=On the Wedge Product |title=Studies in Econometrics, Time Series, and Multivariate Statistics |editor-first=Samuel |editor-last=Karlin |editor2-first=Takeshi |editor2-last=Amemiya |editor3-first=Leo A. |editor3-last=Goodman |publisher=Academic Press |year=1983 |isbn=0-12-398750-4 |pages=455–464 |chapter-url=https://www.google.com/books/edition/_/-hDjBQAAQBAJ?hl=en&gbpv=1&pg=PA455 }}</ref> विभेदक रूप गणितीय वस्तुएं हैं जो सदिश की लंबाई, समांतर चतुर्भुज के क्षेत्रों और उच्च-विमीय निकायों के संस्करणों का मूल्यांकन करती हैं, इसलिए उन्हें वक्र, सतहों और उच्च विमीय मैनिफोल्ड पर इस तरह से एकीकृत किया जा सकता है जो पथरी से लाइन समाकल और सतह [[ अभिन्न |समाकल]] को सामान्य करता है। भिन्न-भिन्न मैनिफोल्ड के एक बिंदु पर एक विभेदक रूप बिंदु पर स्पर्शरेखा समष्टि पर एक वैकल्पिक मल्टीलाइनियर रूप है। समान रूप से, डिग्री k का एक विभेदक रूप [[ स्पर्शरेखा स्थान |स्पर्शरेखा समष्टि]] की ''k''-वें बाह्य घातांक पर एक [[ रैखिक कार्यात्मक |रैखिक कार्यात्मक]] है। नतीजतन, बहु-रेखीय रूपों का बाह्य गुणनफल अवकल रूपों के लिए प्राकृतिक बाह्य गुणनफल को परिभाषित करता है। अवकल रूप अवकल ज्यामिति के विविध क्षेत्रों में प्रमुख भूमिका निभाते हैं। | |||
एक | एक वैकल्पिक दृष्टिकोण कार्यों के [[ रोगाणु (गणित) |जर्म]] के संदर्भ में विभेदक रूपों को परिभाषित करता है। | ||
विशेष रूप से, [[ बाहरी व्युत्पन्न ]] | विशेष रूप से, [[ बाहरी व्युत्पन्न |बाह्य व्युत्पन्न]] अवकल ग्रेड बीजगणित की संरचना को मैनिफोल्ड भिन्न-भिन्न रूपों का बाह्य बीजगणित देता है। [[ विविध |मैनिफोल्ड]] के बीच चिकनी मैपिंग के साथ पुलबैक के साथ बाह्य व्युत्पन्न यात्रा करता है, और इसलिए यह एक प्राकृतिक अवकल संकारक है। अवकल रूप का बाह्य बीजगणित, बाह्य अवकलज से लैस, [[ कोचेन कॉम्प्लेक्स |कोचेन कॉम्प्लेक्स]] है, जिसके कोहोलॉजी को अंतर्निहित मैनिफोल्ड का [[ एक शॉवर के रूप में डी रहीम |डी रम कोहोलॉजी]] कहा जाता है और अवकल मैनिफोल्ड के बीजगणितीय टोपोलॉजी में महत्वपूर्ण भूमिका निभाता है। | ||
=== | === प्रतिनिधित्व सिद्धांत === | ||
प्रतिनिधित्व सिद्धांत में, | [[ प्रतिनिधित्व सिद्धांत |प्रतिनिधित्व सिद्धांत]] में, बाह्य बीजगणित सदिश रिक्त समष्टि की श्रेणी पर दो मूलभूत [[ शूर फंक्टर |शूर फ़ैक्टरों]] में से एक है, दूसरा सममित बीजगणित है। साथ में, इन संरचनाओं का उपयोग [[ सामान्य रैखिक समूह |सामान्य रैखिक समूह]] के अलघुकरणीय निरूपण उत्पन्न करने के लिए किया जाता है; [[ मौलिक प्रतिनिधित्व |मौलिक प्रतिनिधित्व]] देखें। | ||
=== | === अतिसमष्टि === | ||
जटिल संख्याओं पर | जटिल संख्याओं पर बाह्य बीजगणित एक [[ सुपरराल्जबरा |सुपरलेजेब्रा]] का मूल उदाहरण है, जो कि [[ फर्मियन |फर्मियन]] और [[ अध्याय |अतिसममिति]] से संबंधित भौतिक सिद्धांतों में एक मौलिक भूमिका निभाता है। बाह्य बीजगणित के एक घटक को '''सुपरनंबर'''<ref>{{cite book |author-link=Bryce DeWitt |first=Bryce |last=DeWitt |title=Supermanifolds |year=1984 |publisher=Cambridge University Press |isbn=0-521-42377-5 |chapter=Chapter 1 |page=1}}</ref> या [[ ग्रासमैन नंबर |ग्रासमैन नंबर]] कहा जाता है। बाह्य बीजगणित स्वयं तब केवल एक विमीय [[ अधीन करना |अतिसमष्टि]] है: यह बाह्य बीजगणित के सभी बिंदुओं का समुच्चय है। इस समष्टि पर [[ कमजोर टोपोलॉजी |टोपोलॉजी]] अनिवार्य रूप से कमजोर टोपोलॉजी है, [[ खुले सेट |खुले समुच्चय]] [[ सिलेंडर सेट |सिलेंडर समुच्चय]] होते हैं। एक {{math|''n''}}-विमीय अतिसमष्टि बाह्य बीजगणित का सिर्फ {{math|''n''}}-गुना गुणनफल है। | ||
=== | === लाई बीजगणित होमोलॉजी === | ||
''L'' को क्षेत्र ''k'' पर लाई बीजगणित होने दें, फिर एल के बाह्य बीजगणित पर श्रृंखला परिसर की संरचना को परिभाषित करना संभव है। यह एक ''k''-रैखिक मैपिंग है | |||
:<math> | :<math> | ||
\partial : {\textstyle\bigwedge}^{p+1}L \to {\textstyle\bigwedge}^p L | \partial : {\textstyle\bigwedge}^{p+1}L \to {\textstyle\bigwedge}^p L | ||
</math> | </math> | ||
द्वारा विघटित | द्वारा विघटित घटकों पर परिभाषित किया गया | ||
:<math> | :<math> | ||
| Line 705: | Line 675: | ||
= \frac{1}{p+1}\sum_{j<\ell}(-1)^{j+\ell+1}[x_j,x_\ell] \wedge x_1 \wedge \cdots \wedge \hat{x}_j \wedge \cdots \wedge \hat{x}_\ell \wedge \cdots \wedge x_{p+1}. | = \frac{1}{p+1}\sum_{j<\ell}(-1)^{j+\ell+1}[x_j,x_\ell] \wedge x_1 \wedge \cdots \wedge \hat{x}_j \wedge \cdots \wedge \hat{x}_\ell \wedge \cdots \wedge x_{p+1}. | ||
</math> | </math> | ||
जैकोबी पहचान है | जैकोबी पहचान रखती है यदि और केवल यदि {{nowrap|1=∂∂ = 0}}, और इसलिए यह एक आवश्यक और पर्याप्त स्थिति है जो एक एंटीकोम्यूटेटिव गैर-साहचर्य बीजगणित ''L'' के लिए एक लाई बीजगणित है। इसके अतिरिक्त, उस स्थिति में <math display="inline"> \bigwedge L </math> सीमा संकारक ∂ के साथ एक चेन कॉम्प्लेक्स है। इस कॉम्प्लेक्स से जुड़ी होमोलॉजी [[ झूठ बीजगणित होमोलॉजी |लाइ बीजगणित होमोलॉजी]] है। | ||
=== होमोलॉजिकल बीजगणित === | === होमोलॉजिकल बीजगणित === | ||
बाह्य बीजगणित, [[ जटिल शर्ट |कोज़ुल कॉम्प्लेक्स]] के संरचना में मुख्य घटक है, जो होमोलॉजिकल बीजगणित में एक मूलभूत वस्तु है। | |||
== इतिहास == | == इतिहास == | ||
बाह्य बीजगणित पहली बार 1844 में हरमन ग्रासमैन द्वारा ''ऑस्देहनुंगस्लेह्रे'', या ''विस्तार के सिद्धांत'' के कंबल शब्द के तहत प्रस्तुत किया गया था।<ref>{{harvcoltxt|Kannenberg|2000}} published a translation of Grassmann's work in English; he translated ''Ausdehnungslehre'' as ''Extension Theory''.</ref> यह सामान्यतः विस्तारित मात्राओं के एक बीजगणितीय (या स्वयंसिद्ध) सिद्धांत को संदर्भित करता है और एक सदिश समष्टि की आधुनिक धारणा के प्रारंभिक अग्रदूतों में से एक था। सेंट-वेनेंट ने भी बाह्य कैलकुलस के समान विचारों को प्रकाशित किया जिसके लिए उन्होंने ग्रासमैन पर प्राथमिकता का दावा किया।<ref>J Itard, Biography in Dictionary of Scientific Biography (New York 1970–1990).</ref> | |||
यह | |||
बीजगणित स्वयं नियमों, या स्वयंसिद्धों के एक | बीजगणित स्वयं नियमों, या स्वयंसिद्धों के एक समुच्चय से बनाया गया था, जो केली और सिल्वेस्टर के बहुसंकेतकों के सिद्धांत के औपचारिक पहलुओं को कैप्चर करता है। ज्यामितीय दृष्टि से औपचारिक तर्क के कार्य पर विशेष रूप से ध्यान केंद्रित करने के अतिरिक्त, यह इस प्रकार एक ''कैलकुलस'' था, जो प्रस्तावात्मक कैलकुलस की तरह था।<ref>Authors have in the past referred to this calculus variously as the ''calculus of extension'' ({{harvnb|Whitehead|1898}}; {{harvnb|Forder|1941}}), or ''extensive algebra'' {{harv|Clifford|1878}}, and recently as ''extended vector algebra'' {{harv|Browne|2007}}.</ref> विशेष रूप से, इस नए विकास ने विमा के एक ''स्वयंसिद्ध'' लक्षण वर्णन की अनुमति दी, एक गुणधर्म जिसे पहले केवल समन्वय बिंदु से जांचा गया था। | ||
विशेष रूप से, इस नए विकास ने | |||
सदिश और [[ बहुवक्षीय |बहुसदिश]] के इस नए सिद्धांत का आयात 19वीं शताब्दी के मध्य के गणितज्ञों द्वारा खो दिया गया था,<ref>{{harvnb|Bourbaki|1989|p=661}}.</ref> जब तक कि 1888 में ग्यूसेप पीनो द्वारा इसकी पूरी तरह से जांच नहीं की गई। सदी के अंत तक पियानो का काम भी कुछ हद तक अस्पष्ट रहा, जब इस विषय को फ्रेंच ज्यामिति स्कूल (विशेष रूप से हेनरी पॉइनकेयर, एली कार्टन, और [[ गैस्टन डारबॉक्स |गैस्टन डारबॉक्स]]) के सदस्यों द्वारा एकीकृत किया गया था, जिन्होंने ग्रासमैन के विचारों को विभेदक रूपों की गणना के लिए लागू किया था। | |||
1888 में | |||
कुछ देर पश्चात, [[ अल्फ्रेड नॉर्थ व्हाइटहेड |अल्फ्रेड नॉर्थ व्हाइटहेड]] ने पियानो और ग्रासमैन के विचारों से उधार लेते हुए, अपने सार्वभौमिक बीजगणित की शुरुआत की। इसके पश्चात बीजगणितीय प्रणाली की स्वयंसिद्ध धारणा को दृढ़ तार्किक आधार पर रखकर सार बीजगणित के 20वीं शताब्दी के विकास का मार्ग प्रशस्त किया। | |||
== यह भी देखें == | == यह भी देखें == | ||
*[[ बारी -बारी से बीजगणित ]] | *[[ बारी -बारी से बीजगणित |वैकल्पिक बीजगणित]] | ||
*[[ बाहरी कैलकुलस पहचान ]] | *[[ बाहरी कैलकुलस पहचान |बाह्य कैलकुलस पहचान]] | ||
*[[ क्लिफोर्ड बीजगणित ]], एक नॉनज़ेरो [[ द्विघात रूप ]] का उपयोग करके | *[[ क्लिफोर्ड बीजगणित |क्लिफोर्ड बीजगणित]], एक नॉनज़ेरो [[ द्विघात रूप ]] का उपयोग करके बाह्य बीजगणित का एक सामान्यीकरण | ||
*ज्यामितीय बीजगणित | *ज्यामितीय बीजगणित | ||
*कोसज़ुल कॉम्प्लेक्स | *कोसज़ुल कॉम्प्लेक्स | ||
| Line 731: | Line 699: | ||
*सममित बीजगणित, सममित एनालॉग | *सममित बीजगणित, सममित एनालॉग | ||
*टेंसर बीजगणित | *टेंसर बीजगणित | ||
*वेइल बीजगणित, एक सहानुभूतिपूर्ण रूप से सममित बीजगणित का एक [[ क्वांटम समूह ]] | *वेइल बीजगणित, एक सहानुभूतिपूर्ण रूप से सममित बीजगणित का एक [[ क्वांटम समूह |क्वांटम समूह]] | ||
== टिप्पणियाँ == | == टिप्पणियाँ == | ||
{{reflist|30em}} | {{reflist|30em}} | ||
== संदर्भ == | == संदर्भ == | ||
=== गणितीय संदर्भ === | === गणितीय संदर्भ === | ||
* {{citation |last1=Bishop |first1=R. |author1-link=Richard L. Bishop |last2=Goldberg |first2=S.I. |year=1980 |title=Tensor analysis on manifolds |publisher=Dover |isbn=0-486-64039-6 |url-access=registration |url=https://archive.org/details/tensoranalysison00bish }} | * {{citation |last1=Bishop |first1=R. |author1-link=Richard L. Bishop |last2=Goldberg |first2=S.I. |year=1980 |title=Tensor analysis on manifolds |publisher=Dover |isbn=0-486-64039-6 |url-access=registration |url=https://archive.org/details/tensoranalysison00bish }} | ||
*: | *: वैकल्पिक टेंसर्स और वैकल्पिक रूपों का उपचार, साथ ही इस लेख में अपनाए गए परिप्रेक्ष्य से हॉज द्वैत की विस्तृत चर्चा सम्मिलित है। | ||
* {{citation |last=Bourbaki |first=Nicolas |author-link=Nicolas Bourbaki |year=1989 |title=Elements of mathematics, Algebra I |publisher=Springer-Verlag |isbn=3-540-64243-9}} | * {{citation |last=Bourbaki |first=Nicolas |author-link=Nicolas Bourbaki |year=1989 |title=Elements of mathematics, Algebra I |publisher=Springer-Verlag |isbn=3-540-64243-9}} | ||
*: यह लेख के लिए मुख्य गणितीय संदर्भ है।यह एक कम्यूटेटिव रिंग पर एक मॉड्यूल के | *: यह लेख के लिए मुख्य गणितीय संदर्भ है।यह एक कम्यूटेटिव रिंग पर एक मॉड्यूल के बाह्य बीजगणित का परिचय देता है (हालांकि यह लेख मुख्य रूप से उस स्थिति में माहिर है जब रिंग एक क्षेत्र है), जिसमें सार्वभौमिक गुणधर्म, फुन्क्टरिअलिटी, द्वैत और बायलजबरा संरचना की चर्चा सम्मिलित है।§Iii.7 और §iii.11 देखें। | ||
* {{citation |last1=Bryant |first1=R.L. |author1-link=Robert Bryant (mathematician) |last2=Chern |first2=S.S. |author-link2=Shiing-Shen Chern |last3=Gardner |first3=R.B. |last4=Goldschmidt |first4=H.L. |last5=Griffiths |first5=P.A. |author-link5=Philip A. Griffiths |year=1991 |title=Exterior differential systems |publisher=Springer-Verlag}} | * {{citation |last1=Bryant |first1=R.L. |author1-link=Robert Bryant (mathematician) |last2=Chern |first2=S.S. |author-link2=Shiing-Shen Chern |last3=Gardner |first3=R.B. |last4=Goldschmidt |first4=H.L. |last5=Griffiths |first5=P.A. |author-link5=Philip A. Griffiths |year=1991 |title=Exterior differential systems |publisher=Springer-Verlag}} | ||
*: इस पुस्तक में [[ आंशिक अंतर समीकरण ]]ों में समस्याओं के लिए | *: इस पुस्तक में [[ आंशिक अंतर समीकरण ]]ों में समस्याओं के लिए बाह्य बीजगणित के अनुप्रयोग सम्मिलित हैं।रैंक और संबंधित अवधारणाएं प्रारंभिक अध्यायों में विकसित की जाती हैं। | ||
* {{citation |last1=Mac Lane |first1=S. |author-link1=Saunders Mac Lane |last2=Birkhoff |first2=G. |author-link2=Garrett Birkhoff |year=1999 |title=Algebra |publisher=AMS Chelsea |isbn=0-8218-1646-2}} | * {{citation |last1=Mac Lane |first1=S. |author-link1=Saunders Mac Lane |last2=Birkhoff |first2=G. |author-link2=Garrett Birkhoff |year=1999 |title=Algebra |publisher=AMS Chelsea |isbn=0-8218-1646-2}} | ||
*: अध्याय XVI सेक्शन 6-10 | *: अध्याय XVI सेक्शन 6-10 बाह्य बीजगणित का अधिक प्राथमिक खाता देते हैं, जिसमें द्वंद्व, निर्धारक और उपसारणिकों और वैकल्पिक रूप सम्मिलित हैं। | ||
* {{citation |last=Sternberg |first=Shlomo |author-link=Shlomo Sternberg |year=1964 |title=Lectures on Differential Geometry |publisher=Prentice Hall}} | * {{citation |last=Sternberg |first=Shlomo |author-link=Shlomo Sternberg |year=1964 |title=Lectures on Differential Geometry |publisher=Prentice Hall}} | ||
*: | *: बाह्य बीजगणित का एक शास्त्रीय उपचार वैकल्पिक टेनर्स के रूप में होता है, और अंतर ज्यामिति के लिए अनुप्रयोग। | ||
=== ऐतिहासिक संदर्भ === | === ऐतिहासिक संदर्भ === | ||
| Line 762: | Line 724: | ||
* {{citation |last=Peano |first=Giuseppe |author-link=Giuseppe Peano |year=1888 |title=Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva}}; {{citation |last=Kannenberg |first=Lloyd |year=1999 |title=Geometric calculus: According to the Ausdehnungslehre of H. Grassmann |publisher=Birkhäuser |isbn=978-0-8176-4126-9 |url-access=registration |url=https://archive.org/details/geometriccalculu0000pean }}। | * {{citation |last=Peano |first=Giuseppe |author-link=Giuseppe Peano |year=1888 |title=Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva}}; {{citation |last=Kannenberg |first=Lloyd |year=1999 |title=Geometric calculus: According to the Ausdehnungslehre of H. Grassmann |publisher=Birkhäuser |isbn=978-0-8176-4126-9 |url-access=registration |url=https://archive.org/details/geometriccalculu0000pean }}। | ||
* {{citation |last=Whitehead |first=Alfred North |author-link=Alfred North Whitehead |year=1898 |title=A Treatise on Universal Algebra, with Applications |publisher=Cambridge |url=http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=01950001&seq=5}} | * {{citation |last=Whitehead |first=Alfred North |author-link=Alfred North Whitehead |year=1898 |title=A Treatise on Universal Algebra, with Applications |publisher=Cambridge |url=http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=01950001&seq=5}} | ||
=== अन्य संदर्भ और आगे पढ़ना === | === अन्य संदर्भ और आगे पढ़ना === | ||
* {{citation |last=Browne |first=J.M. |year=2007 |title=Grassmann algebra – Exploring applications of Extended Vector Algebra with Mathematica |url=http://www.grassmannalgebra.info/grassmannalgebra/book/index.htm}} | * {{citation |last=Browne |first=J.M. |year=2007 |title=Grassmann algebra – Exploring applications of Extended Vector Algebra with Mathematica |url=http://www.grassmannalgebra.info/grassmannalgebra/book/index.htm}} | ||
*: | *: बाह्य बीजगणित, और ज्यामितीय बीजगणित का एक परिचय, अनुप्रयोगों पर ध्यान देने के साथ।एक इतिहास अनुभाग और ग्रंथ सूची भी सम्मिलित है। | ||
* {{citation |last=Spivak |first=Michael |author-link=Michael Spivak |year=1965 |title=Calculus on manifolds |publisher=Addison-Wesley |isbn=978-0-8053-9021-6}} | * {{citation |last=Spivak |first=Michael |author-link=Michael Spivak |year=1965 |title=Calculus on manifolds |publisher=Addison-Wesley |isbn=978-0-8053-9021-6}} | ||
*: | *: बाह्य बीजगणित के अनुप्रयोगों को अंतर रूपों में सम्मिलित किया गया है, विशेष रूप से अभिन्न और स्टोक्स के प्रमेय पर केंद्रित है।अंकन <math display=inline> \bigwedge\nolimits^k V </math> इस पाठ में '''v''' पर के-फॉर्म्स को वैकल्पिक करने के समष्टि का उपयोग करने के लिए उपयोग किया जाता है;अर्थात, स्पिवक के लिए <math display="inline"> \bigwedge\nolimits^k V </math> यह लेख क्या होगा <math display="inline"> \bigwedge\nolimits^k V^*. </math> स्पिवक ने एडेंडम 4 में इस पर चर्चा की। | ||
* {{citation |last=Strang |first=G. |author-link=Gilbert Strang |year=1993 |title=Introduction to linear algebra |publisher=Wellesley-Cambridge Press |isbn=978-0-9614088-5-5}} | * {{citation |last=Strang |first=G. |author-link=Gilbert Strang |year=1993 |title=Introduction to linear algebra |publisher=Wellesley-Cambridge Press |isbn=978-0-9614088-5-5}} | ||
*: | *: सांकेतिक क्षेत्रों, संस्करणों और उच्च-विमीय संस्करणों के रूप में निर्धारकों के स्वयंसिद्धता का एक प्राथमिक उपचार सम्मिलित है। | ||
* {{springer|id=E/e037080|title=Exterior algebra|author=Onishchik, A.L.}} | * {{springer|id=E/e037080|title=Exterior algebra|author=Onishchik, A.L.}} | ||
* {{citation |first=Fleming |last=Wendell |chapter=7. Exterior algebra and differential calculus |chapter-url={{GBurl|v-QlBQAAQBAJ|p=275}} |title=Functions of Several Variables |publisher=Springer |edition=2nd |orig-year=1977 |date=2012 |isbn=978-1-4684-9461-7 |pages=275–320 |url=}} | * {{citation |first=Fleming |last=Wendell |chapter=7. Exterior algebra and differential calculus |chapter-url={{GBurl|v-QlBQAAQBAJ|p=275}} |title=Functions of Several Variables |publisher=Springer |edition=2nd |orig-year=1977 |date=2012 |isbn=978-1-4684-9461-7 |pages=275–320 |url=}} | ||
*: [[ बहुभिन्नरूपी पथरी ]] में यह पाठ्यपुस्तक कॉलेजों के लिए कैलकुलस अनुक्रम में अंतर रूपों के | *: [[ बहुभिन्नरूपी पथरी ]] में यह पाठ्यपुस्तक कॉलेजों के लिए कैलकुलस अनुक्रम में अंतर रूपों के बाह्य बीजगणित का परिचय देती है। | ||
* {{citation |last=Winitzki |first=S. |year=2010 |title=Linear Algebra via Exterior Products |url=http://sites.google.com/site/winitzki/linalg}} | * {{citation |last=Winitzki |first=S. |year=2010 |title=Linear Algebra via Exterior Products |url=http://sites.google.com/site/winitzki/linalg}} | ||
*: | *: बाह्य गुणनफलों का उपयोग करके बुनियादी परिमित-विमीय रैखिक बीजगणित में समन्वय-मुक्त दृष्टिकोण का परिचय। | ||
* {{cite book | last1 = Shafarevich | first1 = I.R. | author-link1 = Igor Shafarevich | last2=Remizov |first2=A.O. | year = 2012 | title = रेखीय बीजगणित और ज्यामिति| publisher = [[Springer Science+Business Media|Springer]] | isbn = 978-3-642-30993-9 | url = https://www.springer.com/mathematics/algebra/book/978-3-642-30993-9}} | * {{cite book | last1 = Shafarevich | first1 = I.R. | author-link1 = Igor Shafarevich | last2=Remizov |first2=A.O. | year = 2012 | title = रेखीय बीजगणित और ज्यामिति| publisher = [[Springer Science+Business Media|Springer]] | isbn = 978-3-642-30993-9 | url = https://www.springer.com/mathematics/algebra/book/978-3-642-30993-9}} | ||
*: अध्याय 10: | *: अध्याय 10: बाह्य गुणनफल और बाह्य बीजगणित | ||
* [http://neo-classical-physics.info/uploads/3/0/6/5/3065888/burali-forti_-_grassman_and_proj._geom..pdfबाहरी बीजगणित के आवेदन पर सेसरे ब्यूरली-फ़ॉर्टी द्वारा प्रोजेक्टिव ज्यामिति के लिए नोट्स | * [[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/burali-forti_-_grassman_and_proj._geom..pdfबाहरी http://neo-classical-physics.info/uploads/3/0/6/5/3065888/burali-forti_-_grassman_and_proj._geom..pdfबाह्य] बीजगणित के आवेदन पर सेसरे ब्यूरली-फ़ॉर्टी द्वारा प्रोजेक्टिव ज्यामिति के लिए नोट्स | ||
* [http://neo-classical-physics.info/uploads/3/0/6/5/3065888/burali-forti_-_diff._geom._following_grassmann.pdf C. Burali-forti, | * [http://neo-classical-physics.info/uploads/3/0/6/5/3065888/burali-forti_-_diff._geom._following_grassmann.pdf C. Burali-forti, अवकल ज्यामिति के पश्चात परिचय,एच। ग्रासमैन की विधि] बाह्य बीजगणित के ज्यामितीय अनुप्रयोगों पर एक प्रारंभिक पुस्तक का एक अंग्रेजी अनुवाद | ||
* [http://neo-classical-physics.info/uploads/3/0/6/5/3065888/grassmann_-_mechanics_and_extensions.pdf यांत्रिकी, विस्तार के सिद्धांत के सिद्धांतों के अनुसार] एक ग्रासमैन के कागजों के एक अंग्रेजी | * [http://neo-classical-physics.info/uploads/3/0/6/5/3065888/grassmann_-_mechanics_and_extensions.pdf यांत्रिकी, विस्तार के सिद्धांत के सिद्धांतों के अनुसार] एक ग्रासमैन के कागजों के एक अंग्रेजी अनुवादबाह्य बीजगणित के अनुप्रयोगों पर | ||
{{Linear algebra}} | {{Linear algebra}} | ||
{{tensors}} | {{tensors}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:CS1 Deutsch-language sources (de)]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 05/01/2023]] | [[Category:Created On 05/01/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Missing redirects]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia articles needing clarification from December 2021]] | |||
[[Category:Wikipedia articles needing clarification from November 2022]] | |||
[[Category:Wikipedia metatemplates]] | |||
Latest revision as of 11:39, 24 January 2023
गणित में, बाह्य बीजगणित, या ग्रासमैन बीजगणित, जिसका नाम हरमन ग्रासमैन के नाम पर रखा गया है,[3] बाह्य गुणनफल या वेज गुणनफल को इसके गुणन के रूप में उपयोग करने वाली एक प्रकार की बीजगणित है। गणित में, सदिशों का बाह्य गुणनफल या वेज गुणनफल एक बीजगणितीय संरचना है जिसका उपयोग ज्यामिति में क्षेत्रफलों, आयतनों और उनके उच्च-विमीय अनुरूपों का अध्ययन करने के लिए किया जाता है। दो सदिशों और के बाह्य गुणनफल को से निरूपित किया जाता है जिसे द्विसदिश (बाइवेक्टर) कहा जाता है और समष्टि में रहता है जिसे बाह्य वर्ग कहा जाता है, सदिश समष्टि जो सदिश के मूल समष्टि से भिन्न होता है। के परिमाण[4] की व्याख्या और भुजाओं वाले समांतर चतुर्भुज के क्षेत्रफल के रूप में की जा सकती है, जिसकी गणना दो सदिशों के सदिश गुणनफल का उपयोग करके तीन विमाओं में भी की जा सकती है। अत्यधिक सामान्य रूप से, एक ही दिग्विन्यास (ओरिएंटेशन) और क्षेत्र के साथ सभी समांतर समतल सतहों में उनके उन्मुख क्षेत्र के माप के रूप में एक ही द्विसदिश होता है। सदिश गुणनफल की तरह, बाह्य गुणनफल प्रति-क्रमविनिमेय (एंटीकोम्यूटिव) है, जिसका अर्थ है कि सभी सदिश और के लिए है, लेकिन सदिश गुणनफल के विपरीत, बाह्य गुणनफल साहचर्य होता है।
जब इस प्रकार माना जाता है, तो दो सदिशों के बाहरी गुणनफल को 2-ब्लेड कहा जाता है। अत्यधिक सामान्य रूप से, सदिश के किसी भी संख्या k बाह्य गुणनफल को परिभाषित किया जा सकता है और कभी-कभी इसे k-ब्लेड कहा जाता है। यह kवीं बाह्य घातांक के रूप में ज्ञात समष्टि में रहता है। परिणामी k-ब्लेड का परिमाण k-विमीय समांतरोटोप (पैरलैलोटोपे) का उन्मुख हाइपरवोल्यूम (अति-आयतन) है जिसके किनारे दिए गए सदिश हैं, ठीक उसी प्रकार जैसे तीन विमाओं में सदिश के अदिश त्रिक गुणनफल का परिमाण उन सदिश द्वारा उत्पन्न समानांतर चतुर्भुज का आयतन प्रदान करता है।
बाह्य बीजगणित एक बीजगणितीय विन्यास प्रदान करती है जिसमें ज्यामितीय प्रश्नों का उत्तर दिया जाता है। उदाहरण के लिए, ब्लेड की एक ठोस ज्यामितीय व्याख्या होती है, और बाह्य बीजगणित में वस्तुओं को स्पष्ट नियमों के एक समुच्चय के अनुसार प्रकलित किया जा सकता है। बाह्य बीजगणित में ऐसी वस्तुएँ होती हैं जो न केवल k-ब्लेड होती हैं, बल्कि k-ब्लेड का योग होती हैं; ऐसी राशि को k-सदिश कहा जाता है।[5] k-ब्लेड, क्योंकि वे सदिशों के सरल गुणनफल होते हैं, बीजगणित के सरल घटक कहलाते हैं। किसी भी k-सदिश की रैंक को उन सरल घटकों की सबसे छोटी संख्या के रूप में परिभाषित किया जाता है, जिनका यह योग है। बाह्य गुणनफल पूर्ण बाह्य बीजगणित तक विस्तारित है, जिससे बीजगणित के किसी भी दो घटकों का गुणा करना अर्थपूर्ण हो जाए। इस गुणनफल के साथ सुसज्जित, बाह्य बीजगणित साहचर्य बीजगणित होती है, जिसका अर्थ है कि किसी भी घटक के लिए । k-सदिश की कोटि k होती है, जिसका अर्थ है कि वे k सदिश के गुणनफलों का योग हैं। जब भिन्न-भिन्न कोटि के घटकों को गुणा किया जाता है, तो कोटियां बहुपदों के गुणन की तरह जुड़ जाती हैं। इसका अर्थ यह है कि बाह्य बीजगणित एक श्रेणीबद्ध बीजगणित है।
बाह्य बीजगणित की परिभाषा समष्टियों के लिए अर्थपूर्ण है न कि केवल ज्यामितीय सदिशों की, बल्कि अन्य सदिश-जैसी वस्तुओं जैसे सदिश फ़ील्ड या फलन (फ़ंक्शंस) के लिए। पूर्ण सामान्यता में, बाह्य बीजगणित को किसी कम्यूटेटिव रिंग पर मॉड्यूल के लिए और अमूर्त बीजगणित में रुचि के अन्य संरचनाओं के लिए परिभाषित किया जा सकता है। यह इन अधिक सामान्य संरचनाओं में से एक है जहां बाह्य बीजगणित अपने सबसे महत्वपूर्ण अनुप्रयोगों में से एक प्राप्त होता है, जहां यह अवकल रूपों के बीजगणित के रूप में प्रकट होता है जो कि उन क्षेत्रों में मौलिक होते है जो अवकल ज्यामिति का उपयोग करते हैं। बाह्य बीजगणित में कई बीजगणितीय गुण भी होते हैं जो इसे बीजगणित में ही एक सुविधाजनक साधन बनाते हैं। सदिश समष्टि के लिए बाह्य बीजगणित का साहचर्य सदिश समष्टियों पर एक प्रकार का फंक्टर होता है, जिसका अर्थ है कि यह एक निश्चित तरीके से सदिश समष्टियों के रैखिक रूपांतरणों के साथ संगत है। बाह्य बीजगणित बायलजेब्रा का एक उदाहरण है, जिसका अर्थ है कि इसकी द्वैत समष्टि में भी एक गुणनफल है, और यह द्वैत गुणनफल बाह्य गुणनफल के साथ संगत है। यह द्वैत बीजगणित वैकल्पिक रूप से बहु-रेखीय रूपों का बीजगणित है, और बाह्य बीजगणित और इसके द्वैत के बीच का युग्म आंतरिक गुणनफल द्वारा दी गई है।
प्रेरणात्मक उदाहरण
पहले दो उदाहरण एक मीट्रिक टेंसर फ़ील्ड और एक दिग्विन्यास मानते हैं; तीसरा उदाहरण या तो नहीं मानता।
समतल क्षेत्र
कार्तीय तल एक वास्तविक सदिश समष्टि है जो इकाई सदिशों के एक युग्म से युक्त बेसिस से सुसज्जित है
- दिग्विन्यास के साथ और मीट्रिक के साथ ।
मान लीजिए
घटकों में लिखे, में दिए गए सदिशों का एक युग्म है। दो भुजाएँ v और w वाला एक विशिष्ट समांतर चतुर्भुज हैं। इस समांतर चतुर्भुज का क्षेत्रफल मानक निर्धारक सूत्र द्वारा दिया गया है:
अब v और w के बाह्य गुणनफल पर विचार करें:
जहां पहला चरण बाह्य गुणनफल के लिए वितरण नियम का उपयोग करता है, और अंतिम चरण इस तथ्य का उपयोग करता है कि बाह्य गुणनफल वैकल्पिक है, और विशेष रूप से होता है। (तथ्य यह है कि बाह्य गुणनफल वैकल्पिक रूप से भी को बल देता है) ध्यान दें कि इस अंतिम अभिव्यक्ति में गुणांक वास्तव में आव्यूह [v w] का निर्धारक है। तथ्य यह है कि यह धनात्मक या ऋणात्मक हो सकता है इसका सहज अर्थ है कि v और w वामावर्त या दक्षिणावर्त अर्थ में उन्मुख हो सकते हैं क्योंकि वे समानांतर चतुर्भुज के कोने को परिभाषित करते हैं। इस तरह के क्षेत्र को समांतर चतुर्भुज का सांकेतिक क्षेत्रफल कहा जाता है: सांकेतिक क्षेत्रफल का निरपेक्ष मान साधारण क्षेत्रफल है, और चिन्ह इसके दिग्विन्यास को निर्धारित करता है।
तथ्य यह है कि यह गुणांक सांकेतिक क्षेत्रफल है, कोई घटना नहीं है। वास्तव में, यह देखना अपेक्षाकृत सरल है कि बाह्य गुणनफल को सांकेतिक क्षेत्रफल से संबंधित होना चाहिए यदि कोई इस क्षेत्र को बीजगणितीय संरचना के रूप में स्वयंसिद्ध करने की प्रयास करता है। विस्तार से, यदि A(v, w) समांतर चतुर्भुज के सांकेतिक क्षेत्रफल को दर्शाता है जिसमें सदिश v और w का युग्म दो आसन्न भुजाएँ बनाती है, तो A को निम्नलिखित गुणों को पूरा करना चाहिए:
- A(rv, sw) = rsA(v, w) किसी भी वास्तविक संख्या r और s के लिए, चूंकि दोनों भुजाओं में से किसी एक को पुनः स्केल करने से क्षेत्रफल को उसी राशि से पुनः स्केल किया जाता है (और भुजाओं में से किसी एक की दिशा को उत्क्रमित करने से समांतर चतुर्भुज का दिग्विन्यास उत्क्रमित हो जाता है)।
- A(v, v) = 0, चूंकि v (अर्थात, रेखा खंड) द्वारा निर्धारित पतित समांतर चतुर्भुज का क्षेत्रफल शून्य है।
- A(w, v) = −A(v, w), v और w की भूमिकाओं को परस्पर क्रिया करने के पश्चात से समांतर चतुर्भुज के दिग्विन्यास को उत्क्रमित कर देता है।
- किसी भी वास्तविक संख्या r के लिए A(v + rw, w) = A(v, w), चूँकि v में w का एक गुणक जोड़ने से समांतर चतुर्भुज का न तो आधार और न ही ऊँचाई प्रभावित होती है और इसके परिणामस्वरूप इसका क्षेत्रफल संरक्षित रहता है।
- A(e1, e2) = 1, चूंकि इकाई वर्ग का क्षेत्रफल एक है।
पिछले गुणधर्म के अपवाद के साथ, दो सदिशों का बाह्य गुणनफल क्षेत्र के समान गुणों को पूरा करता है। निश्चित अर्थ में, बाह्य गुणनफल एक समांतर चतुर्भुज के क्षेत्रफल की तुलना समानांतर समतल में किसी भी चयनित समांतर चतुर्भुज के क्षेत्र की अनुमति देकर अंतिम गुणधर्म को सामान्य करता है (यहाँ, भुजाओं वाला e1 और e2)। दूसरे शब्दों में, बाह्य गुणनफल क्षेत्र का बेसिस-स्वतंत्र सूत्रीकरण प्रदान करता है।[6]
सदिश और त्रिक गुणनफल
किसी बाईलीनियर अदिश गुणनफल के साथ 3-विमीय उन्मुख सदिश समष्टि में सदिश के लिए, बाह्य बीजगणित सदिश गुणनफल और त्रिक गुणनफल से निकटता से संबंधित है। मानक बेसिस (e1, e2, e3) का उपयोग करके, सदिशों के एक युग्म का बाह्य गुणनफल
और
है
जहां (e1 ∧ e2, e2 ∧ e3, e3 ∧ e1) त्रि-विमीय समष्टि के लिए बेसिस है। उपरोक्त गुणांक वही हैं जो किसी दिए गए दिग्विन्यास के साथ तीन विमाओं में सदिशों के सदिश गुणनफल की सामान्य परिभाषा में हैं, केवल अंतर यह है कि बाह्य गुणनफल एक सामान्य सदिश नहीं है, बल्कि इसके बजाय 2-सदिश है, और यह कि बाह्य गुणनफल दिग्विन्यास के विकल्प पर निर्भर नहीं करता है[clarification needed]।
एक अन्य तीसरे सदिश को उपयोग में लाने पर
तीन सदिशों का बाह्य गुणनफल है
जहाँ e1 ∧ e2 ∧ e3 एक-विमीय समष्टि के लिए आधार सदिश है। अदिश गुणांक तीन सदिशों का त्रिगुणात्मक गुणनफल है।
तीन विमीय यूक्लिडियन सदिश समष्टि में सदिश गुणनफल और त्रिक गुणनफल हॉज स्टार द्वंद्व के माध्यम से ज्यामितीय और बीजगणितीय दोनों व्याख्याओं को स्वीकार करते हैं। सदिश गुणनफल u × v को एक सदिश के रूप में व्याख्या किया जा सकता है जो u और v दोनों के लिए लंबवत है और जिसका परिमाण दो सदिशों द्वारा निर्धारित समांतरोग्राम के क्षेत्र के बराबर है। इसे सदिश के रूप में भी व्याख्या किया जा सकता है जिसमें कॉलम u और v के साथ आव्यूह के उपसारणिक सम्मिलित हैं। u, v, और w के त्रिक गुणनफल एक ज्यामितीय उन्मुख मात्रा का प्रतिनिधित्व करने वाला एक सांकेतिक अदिश है। बीजगणितीय रूप से, यह कॉलम u, v, और w के साथ आव्यूह का निर्धारक है। तीन विमाओं में बाह्य गुणनफल समान व्याख्याओं की अनुमति देता है: यह भी, उन्मुख रेखाओं, क्षेत्रफलों, आयतनों, आदि के साथ पहचाना जा सकता है, जो एक, दो या अधिक सदिशों द्वारा फैलाए जाते हैं। बाह्य गुणनफल इन ज्यामितीय धारणाओं को सभी सदिश रिक्त समष्टि और किसी भी विमा के लिए सामान्य करता है, यहां तक कि अदिश गुणनफल की अनुपस्थिति में भी।
विद्युत चुम्बकीय क्षेत्र
आइंस्टीन के सापेक्षता के सिद्धांतों में, विद्युत चुम्बकीय क्षेत्र को सामान्यतः 4-समष्टि में अवकल 2-रूप के रूप में या समकक्ष वैकल्पिक टेंसर क्षेत्र विद्युत चुम्बकीय टेंसर के रूप में दिया जाता है। फिर या समतुल्य बियांची पहचान । इसमें से किसी को भी मीट्रिक की आवश्यकता नहीं है।
लोरेन्ट्ज़ मीट्रिक और दिग्विन्यास जोड़ने से हॉज स्टार संकारक मिलता है और इस प्रकार या समकक्ष टेन्सर डाइवर्जेंस को परिभाषित करना संभव हो जाता है जहाँ ।
औपचारिक परिभाषाएँ और बीजगणितीय गुण
फील्ड K पर सदिश समष्टि V का बाह्य बीजगणित को टेंसर बीजगणित T(V) के कोशिएंट बीजगणित के रूप में परिभाषित किया गया है, जो दो तरफा अभीष्ट I द्वारा उत्पन्न x ⊗ x के लिए x ∈ V (अर्थात सभी टेंसर जिन्हें V में सदिश के टेन्सर गुणनफल के रूप में व्यक्त किया जा सकता है) के सभी घटकों द्वारा उत्पन्न होता है।[7] अभीष्ट I में रूप के घटकों द्वारा उत्पन्न अभीष्ट J सम्मिलित है और यदि (यदि ये अभीष्ट शून्य सदिश समष्टि को छोड़कर भिन्न हैं) तो ये अभीष्ट के समान होता हैं।
इसलिए,
साहचर्य बीजगणित है। इसके गुणन को बाह्य गुणनफल कहा जाता है, और इसे ∧ से दर्शाया जाता है। इसका अर्थ यह है कि का गुणनफल T(V) के टेन्सर गुणनफल ⊗ से प्रेरित है।
T0 = K, T1 = V, और के रूप में, T(V) में K और V का समावेश K और V के अंतःक्षेप को में प्रेरित करता है। इन अंतःक्षेपण को सामान्यतः समावेशन के रूप में माना जाता है, और इन्हें प्राकृतिक अंतःस्थापन, प्राकृतिक अंतःक्षेप या प्राकृतिक समावेशन कहा जाता है। प्राकृतिक के समष्टि पर सामान्यतः विहित शब्द का भी प्रयोग किया जाता है।
वैकल्पिक गुणनफल
बाह्य गुणनफल के घटकों पर वैकल्पिक से संरचना द्वारा है, जिसका अर्थ है कि उपरोक्त संरचना द्वारा सभी के लिए । यह इस प्रकार है कि यह गुणनफल के घटकों पर भी अप्रतिवर्तक (एंटीकम्यूटेटिव) है, यह मानने के लिए कि
इसलिए
अधिक व्यापक रूप से, यदि σ पूर्णांक [1, ..., k], और x1, x2, ..., xk, V के अवयव हैं, का एक क्रमचय है, तो यह अनुसरण करता है कि
जहां sgn(σ) क्रमचय σ का संकेत है।[8]
विशेष रूप से, यदि xi = xj कुछ i ≠ j के लिए, तो वैकल्पिक गुणधर्म का निम्नलिखित सामान्यीकरण भी मान्य है:
बाह्य गुणनफल की वितरणात्मक गुणधर्म के साथ, एक अन्य सामान्यीकरण यह है कि यदि और केवल यदि सदिशों का रैखिक रूप से निर्भर समुच्चय है, तो
बाह्य घातांक
V के kवीं बाह्य घातांक, को निरूपित करते है, की सदिश उप-समष्टि है जो निम्नलिखित रूप में विस्तारित है
यदि है, तो α को k-सदिश कहा जाता है। यदि, इसके अतिरिक्त, α को V के k घटकों के बाह्य गुणनफल के रूप में व्यक्त किया जा सकता है, तो α को वियोजनीय (डीकंपोज़ेबल) कहा जाता है। हालांकि वियोजनीय k-सदिश तक विस्तारित हैं, लेकिन का प्रत्येक घटक वियोजनीय नहीं है। उदाहरण के लिए, में निम्नलिखित 2-सदिश वियोजनीय नहीं है:
(यह साधारण रूप है, चूँकि α ∧ α ≠ 0 है।[9])
बेसिस और विमा
यदि V की विमा n है और { e1, …, en } V का बेसिस है, तो समुच्चय
के लिए बेसिस है। कारण निम्न है: किसी भी बाह्य गुणनफल को निम्नलिखित रूप से प्रदर्शित किया गया है
प्रत्येक सदिश vj को बेसिस सदिशों ei के एक रैखिक संयोजन के रूप में लिखा जा सकता है; बाह्य गुणनफल की बाईलीनियरिटी का उपयोग करके, इसे उन बेसिस सदिशों के बाह्य गुणनफलों के रैखिक संयोजन तक विस्तारित किया जा सकता है। कोई भी बाह्य गुणनफल जिसमें एक ही बेसिस सदिश एक से अधिक बार प्रकट होता है, शून्य होता है; कोई भी बाह्य गुणनफल जिसमें बेसिस सदिश उचित क्रम में प्रकट नहीं होते हैं, को पुनः व्यवस्थित किया जा सकता है, जब भी दो बेसिस सदिश समष्टि बदलते हैं, तो चिन्ह बदल सकते हैं। सामान्य तौर पर, बेसिस k-सदिश के परिणामी गुणांक की गणना आव्यूह के अवयस्क के रूप में की जा सकती है जो बेसिस ei के संदर्भ में सदिश vj का वर्णन करता है।
बेसिस घटकों की गणना करके, का विमा एक द्विपद गुणांक के बराबर है:
जहां n सदिशों का विमा है और k गुणनफल में सदिशों की संख्या है। असाधारण स्थितियों के लिए भी द्विपद गुणांक सही परिणाम उत्पन्न करता है; विशेष रूप से, k > n के लिए ।
बाह्य बीजगणित के किसी भी घटक को k-सदिशों के योग के रूप में लिखा जा सकता है। इसलिए, सदिश समष्टि के रूप में बाह्य बीजगणित प्रत्यक्ष संकलन है
(जहां परिपाटी V, और के नीचे की फील्ड), और इसलिए इसका विमा द्विपद गुणांक के योग के बराबर है, जो कि 2n है।
k-सदिश की रैंक
यदि है, तो α को k-सदिश वियोजनीय का संयोजन के रैखिक संयोजन के रूप में व्यक्त करना संभव है:
जहां प्रत्येक α(i) विघटित होता है, माना
K-सदिश α का रैंक α के इस तरह के विस्तार में k-सदिश वियोजनीय की न्यूनतम संख्या है। यह टेंसर रैंक की धारणा के समान ही है।
2-सदिशों के अध्ययन में रैंक विशेष रूप से महत्वपूर्ण है (स्टर्नबर्ग 1964, §III.6) (ब्रायंट et al. 1991)। 2-सदिश α की रैंक को बेसिस में α के गुणांकों के आव्यूह के आधे रैंक के साथ पहचाना जा सकता है। इस प्रकार यदि ei के लिए बेसिस है, तो α को अभीष्ट रूप से व्यक्त किया जा सकता है
जहाँ aij = −aji (गुणांकों का आव्यूह विषम सममित है)। इसलिए आव्यूह aij की कोटि सम है, और α के रूप की कोटि से दोगुनी है।
विशेषता 0 में, 2-सदिश α का रैंक p है यदि और केवल यदि
- और
श्रेणीबद्ध (ग्रेडेड) संरचना
p-सदिश के साथ k-सदिश का बाह्य गुणनफल (k + p) -सदिश है, जो एक बार फिर बाईलीनियरिटी का आह्वान करता है। परिणाम के रूप में, पिछले अनुभाग का प्रत्यक्ष योग अपघटन
बाह्य बीजगणित को एक वर्गीकृत बीजगणित की अतिरिक्त संरचना प्रदान करता है, अर्थात
इसके अतिरिक्त, यदि K आधार क्षेत्र है, अतः हमें निम्नलिखित प्राप्त होता है
- और
बाह्य गुणनफल को एंटीकोम्यूटेटिव श्रेणीबद्ध किया गया है, जिसका अर्थ है कि यदि और हैं, तो
बाह्य बीजगणित पर श्रेणीबद्ध संरचना का अध्ययन करने के अतिरिक्त, बोरबाकी (1989) बाह्य बीजगणित पर अतिरिक्त वर्गीकृत संरचनाओं का अध्ययन करता है, जैसे कि वर्गीकृत मॉड्यूल के बाह्य बीजगणित पर (मॉड्यूल जो पहले से ही अपने स्वयं के उन्नयन को वहन करता है)।
सार्वभौमिक गुणधर्म
मान लीजिए V क्षेत्र K पर एक सदिश समष्टि है। अनौपचारिक रूप से, में गुणा प्रतीकों में प्रकलन करके और वितरण नियम, साहचर्य नियम लागू करके और v ∈ V के लिए पहचान का उपयोग करके किया जाता है। औपचारिक रूप से, "सबसे सामान्य" बीजगणित है जिसमें ये नियम गुणन के लिए धारण करते हैं, इस अर्थ में कि V पर वैकल्पिक गुणन के साथ V वाले किसी भी एकात्मक साहचर्य K-बीजगणित में की समरूप छवि होनी चाहिए। दूसरे शब्दों में, बाह्य बीजगणित में निम्नलिखित सार्वभौमिक गुण होते हैं:[10]
किसी भी यूनिटल साहचर्य K-बीजगणित A और किसी भी K-रेखीय मैप को देखते हुए V में प्रत्येक v के लिए , तो शुद्ध रूप से इकाई बीजगणित समाकारिता विद्यमान है जैसे कि j(v) = f(i(v)) V में सभी v के लिए (यहाँ i में V का स्वाभाविक समावेश है, ऊपर देखें)।
सबसे सामान्य बीजगणित का संरचना करने के लिए जिसमें V सम्मिलित है और जिसका गुणन V पर वैकल्पिक है, सबसे सामान्य साहचर्य बीजगणित के साथ शुरू करना स्वाभाविक है जिसमें V, टेंसर बीजगणित T(V) सम्मिलित है, और फिर एक उपयुक्त कोशिएंट लेकर वैकल्पिक गुणधर्म को लागू करें। इस प्रकार हम V में v के लिए v ⊗ v के रूप के सभी घटकों द्वारा उत्पन्न T(V) में दो-तरफा अभीष्ट I लेते हैं, और को कोशिएंट के रूप में परिभाषित करते हैं।
(और ∧ को में गुणन के प्रतीक के रूप में उपयोग करें)। इसके पश्चात यह दिखाना प्रत्यक्ष है कि में V है और उपरोक्त सार्वभौमिक गुणधर्म को संतुष्ट करता है।
इस संरचना के परिणामस्वरूप, सदिश समष्टि V को इसके बाह्य बीजगणित को नियुक्त करने का संचालन सदिश रिक्त समष्टि की श्रेणी से बीजगणित की श्रेणी का फ़ंक्टर होता है।
पहले को परिभाषित करने और फिर बाह्य घातांक को कुछ उप-समष्टियों के रूप में पहचानने के बजाय, वैकल्पिक रूप से पहले रिक्त समष्टि को परिभाषित किया जा सकता है और फिर बीजगणित बनाने के लिए उन्हें जोड़ा जा सकता है। इस दृष्टिकोण का उपयोग प्रायः अवकल ज्यामिति में किया जाता है और अगले भाग में वर्णित किया जाता है।
सामान्यीकरण
क्रमविनिमेय रिंग R और R-मॉड्यूल M को देखते हुए, हम बाह्य बीजगणित को उपरोक्त प्रकार से परिभाषित कर सकते हैं, जैसा कि टेन्सर बीजगणित T(M) के उपयुक्त कोशिएंट के रूप में है। यह समान सार्वभौमिक गुणधर्म को संतुष्ट करेगा। के कई गुणों के लिए यह भी आवश्यक है कि M एक प्रोजेक्टिव मॉड्यूल हो। जहां परिमित विमीयता का उपयोग किया जाता है, गुणों के लिए आगे की आवश्यकता होती है कि M सूक्ष्म रूप से उत्पन्न और प्रक्षेपी हो। सबसे आम स्थितियों के लिए सामान्यीकरण बोरबाकी (1989) में पाया जा सकता है।
ज्यामिति और टोपोलॉजी में सदिश बंडलों के बाह्य बीजगणित पर प्रायः विचार किया जाता है। सेरे-स्वान प्रमेय द्वारा परिमित-विमीय सदिश बंडलों के बाह्य बीजगणित के बीजगणितीय गुणों और सूक्ष्म रूप से उत्पन्न प्रोजेक्टिव मॉड्यूल के बाह्य बीजगणित के बीच कोई आवश्यक अंतर नहीं हैं। अधिक सामान्य बाह्य बीजगणित को मॉड्यूल के ढेरों के लिए परिभाषित किया जा सकता है।
वैकल्पिक टेन्सर बीजगणित
यदि K विशेषता 0 का एक क्षेत्र है,[11] तो K पर सदिश समष्टि V के बाह्य बीजगणित को प्रतिसममित (एंटीसिमेट्रिक) टेंसरों से युक्त T(V) के सदिश उपसमष्टि के साथ कैनोनिक रूप से पहचाना जा सकता है। याद रखें कि बाह्य बीजगणित, x ⊗ x के रूप के घटकों द्वारा उत्पन्न अभीष्ट I द्वारा T(V) का कोशिएंट है।
मान लीजिए Tr(V) डिग्री r के सजातीय टेन्सरों का समष्टि है। यह वियोजनीय टेंसरों द्वारा विस्तारित है
वियोजनीय टेन्सर के प्रतिसममितीकरण (या कभी-कभी विषम-सममितीकरण) द्वारा परिभाषित किया गया है
जहां प्रतीक {1, ..., r} पर क्रमपरिवर्तन के सममित समूह पर योग लिया जाता है। यह पूर्ण टेन्सर बीजगणित T(V) पर रैखिकता और एकरूपता द्वारा एक ऑपरेशन तक विस्तारित है, जिसे Alt द्वारा भी निरूपित किया जाता है। छवि Alt(T(V)) वैकल्पिक टेन्सर बीजगणित है, जिसे A(V) के रूप में दर्शाया गया है। यह T(V) की सदिश उपसमष्टि है, और यह T(V) से श्रेणीबद्ध सदिश समष्टि की संरचना को इनहेरिट करती है। यह साहचर्य श्रेणीबद्ध गुणनफल द्वारा परिभाषित किया गया है
यद्यपि यह गुणनफल टेंसर गुणनफल से भिन्न है, Alt का कर्नेल शुद्ध रूप से अभीष्ट I है (पुनः, यह मानते हुए कि K में विशेषता 0 है), और कैनोनिकल समरूपता है
इंडेक्स संकेतन
मान लीजिए कि V का परिमित विमा n है, और V का बेसिस e1, ..., en दिया गया है। तब किसी भी वैकल्पिक टेन्सर t ∈ Ar(V) ⊂ Tr(V) को इंडेक्स संकेतन में इस प्रकार लिखा जा सकता है
जहां ti1⋅⋅⋅ir अपने सूचकांकों में पूरी तरह से अप्रतिवर्तक सममित होती है।
रैंक r और p के दो वैकल्पिक टेंसरों t और s का बाह्य गुणनफल द्वारा दिया गया है
इस टेन्सर के घटक टेन्सर गुणनफल s ⊗ t के घटकों के शुद्ध रूप से विषम भाग हैं, जो सूचकांकों पर वर्ग कोष्ठक द्वारा निरूपित हैं:
आंतरिक गुणनफल को इंडेक्स नोटेशन में भी इस तरह से वर्णित किया जा सकता है। मान लीजिए कि कोटि r का एक असममित टेंसर है। फिर, α ∈ V∗ के लिए, iαt रैंक r − 1 का एक वैकल्पिक टेन्सर है, जो निम्नलिखित द्वारा दिया गया है:
जहाँ n, V का विमा है।
द्वैतता (द्वैधिटी)
वैकल्पिक संकारक
दो सदिश रिक्त समष्टि V और X और एक प्राकृतिक संख्या के को देखते हुए, Vk से X तक वैकल्पिक संकारक बहु-रैखिक मैप है
इस प्रकार कि जब भी v1, ..., vk V में एकघाततः परतंत्र सदिश हों, तब
मैप
जो से सदिशों से जुड़ा है, उनका बाह्य गुणनफल, अर्थात उनका संबंधित -सदिश भी वैकल्पिक है। वास्तव में, यह मैप पर परिभाषित "सबसे सामान्य" वैकल्पिक संचालिका है; किसी भी अन्य वैकल्पिक संकारक को देखते हुए, के साथ एक अद्वितीय रैखिक मैप विद्यमान है। यह सार्वभौमिक गुणधर्म समष्टि की विशेषता है और इसकी परिभाषा के रूप में काम कर सकती है।
वैकल्पिक बहुरेखीय रूप

उपरोक्त चर्चा स्थिति के लिए विशेषज्ञ है जब X = K, आधार फील्ड। इस स्थिति में वैकल्पिक बहुरेखीय फलन
वैकल्पिक बहुरेखीय रूप कहा जाता है। सभी वैकल्पिक बहुरेखीय रूपों का समुच्चय सदिश समष्टि होता है, क्योंकि ऐसे दो मैपों का योग, या एक अदिश के साथ ऐसे मैप का गुणनफल, पुनः वैकल्पिक होता है। बाह्य घातांक की सार्वभौमिक गुणधर्म द्वारा, V पर डिग्री k के वैकल्पिक रूपों का समष्टि स्वाभाविक रूप से द्वैत सदिश समष्टि के साथ समाकृतिक (आइसोमोर्फिक) है। यदि V परिमित-विमीय है, तो पश्चात वाला स्वाभाविक रूप से आइसोमॉर्फिक है[clarification needed] तक। विशेष रूप से, यदि v n-विमीय है, तो Vk से K तक वैकल्पिक मैपों के समष्टि का विमा द्विपद गुणांक है।
इस तरह की पहचान के अधीन, बाह्य गुणनफल प्रभावशाली रूप लेता है: यह दो दिए गए घटको से एक नया अप्रतिवर्तक सममित मैप तैयार करता है। मान लीजिए ω : Vk → K और η : Vm → K दो अप्रतिवर्तक सममित मैप हैं। बहुरेखीय मैप के टेंसर गुणनफलों की तरह, उनके बाह्य गुणनफल के चरों की संख्या उनके चरों की संख्याओं का योग होती है। बहुरेखीय रूपों के साथ बाह्य घातांक के घटकों की पहचान के विकल्प के आधार पर, बाह्य गुणनफल को इस रूप में परिभाषित किया गया है
या के रूप में
जहां, यदि आधार फ़ील्ड K की विशेषता 0 है, तो बहु-मैप के वैकल्पिक Alt को इसके चर के सभी क्रमों पर संकेत-समायोजित मूल्यों के औसत के रूप में परिभाषित किया गया है:
जब फ़ील्ड K में सीमित अभिलक्षण होती है, अतः किसी भी फैक्टरियल्स या किसी भी स्थिरांक के बिना दूसरी व्यंजक का एक समान संस्करण अच्छी तरह से परिभाषित होता है:
जहाँ यहां Shk,m ⊂ Sk+m (k,m) समवकुलन (शफल) का उपसमुच्चय है: समुच्चय {1, 2, ..., k + m} का क्रमचय σ ऐसा है कि σ(1) < σ(2) < ⋯ < σ(k), और σ(k + 1) < σ(k + 2) < ⋯ < σ(k + m)।
आंतरिक गुणनफल
मान लीजिए कि v परिमित-विमीय है। यदि V∗ सदिश समष्टि V के लिए द्वैत समष्टि को दर्शाता है, तो प्रत्येक α ∈ V∗ के लिए, बीजगणित पर प्रतिपक्षी को परिभाषित करना संभव है,
इस व्युत्पत्ति को α के साथ आंतरिक गुणनफल, या कभी-कभी अंतर्न्यास संकारक, या α द्वारा संक्षेपण कहा जाता है।
मान लीजिए कि । फिर w, V∗ से K की बहुरेखीय मैपिंग है, इसलिए इसे k-गुना कार्तीय गुणनफल V∗ × V∗ × ... × V∗ पर इसके मानों द्वारा परिभाषित किया गया है। यदि u1, u2, ..., uk−1, V* के k − 1 अवयव हैं, अतः परिभाषित करें
इसके अतिरिक्त, मान लीजिए iαf = 0 जब भी f शुद्ध अदिश है (अर्थात, से संबंधित)।
स्वयंसिद्ध (एक्सिओमाटिक) लक्षण वर्णन और गुण
आंतरिक गुणनफल निम्नलिखित गुणों को संतुष्ट करता है:
- प्रत्येक k और प्रत्येक α ∈ V∗ के लिए,(अधिवेशन द्वारा, )
- यदि v V () का एक घटक है, तो iαv = α(v) V के घटकों और V∗ के घटकों के बीच द्वैत युग्म होते है।
- प्रत्येक α ∈ V∗ के लिए, iα डिग्री −1 की श्रेणीबद्ध व्युत्पत्ति है:
ये तीन गुण आंतरिक गुणनफल को चित्रित करने के साथ-साथ इसे सामान्य अनंत-विमीय स्थिति में परिभाषित करने के लिए पर्याप्त हैं।
आंतरिक गुणनफल के आगे के गुणों में सम्मिलित हैं:
हॉज द्वैत
मान लीजिए कि V का परिमित विमा n है। तब आंतरिक गुणनफल सदिश रिक्त समष्टि के कैनोनिकल कैनोनिकल समरूपता (आइसोमोर्फिज्म) को प्रेरित करता है
प्रतिवर्तन (रिकर्सिव) परिभाषा द्वारा
ज्यामितीय विन्यास में, शीर्ष बाह्य घातांक (जो एक विमीय सदिश समष्टि है) का एक गैर-शून्य घटक को कभी-कभी आयतन रूप (या दिग्विन्यास रूप कहा जाता है, हालांकि यह शब्द कभी-कभी अस्पष्टता का कारण बन सकता है)। नाम दिग्विन्यास रूप इस तथ्य से आता है कि विकल्प शीर्ष घटक का विकल्प पूरे बाह्य बीजगणित का दिग्विन्यास निर्धारित करता है, क्योंकि यह सदिश समष्टि के ऑर्डर किए गए आधार को ठीक करने के लिए समान है। अधिमानित आयतन रूप σ के सापेक्ष, समरूपता स्पष्ट रूप से निम्नलिखित द्वारा दी गई है
यदि, आयतन रूप के अतिरिक्त, सदिश समष्टि V V के साथ V की पहचान करने वाले आंतरिक गुणनफल से सुसज्जित है, तो परिणामी समरूपता को हॉज स्टार संकारक कहा जाता है, जो अपने हॉज द्वैत के लिए एक घटक को मैप करता है:
का संघटन स्वयं → मैपों के साथ है और हमेशा पहचान मैप का एक अदिश गुणक होता है। अधिकांश अनुप्रयोगों में, आयतन रूप आंतरिक गुणनफल के साथ इस अर्थ में संगत होता है कि यह V के ऑर्थोनॉर्मल आधार का एक बाह्य गुणनफल है। इस स्थिति में,
जहां आईडी तत्समक मैपिंग है, और आंतरिक गुणनफल में मीट्रिक संकेत (p, q)— p प्लसस और q माइनस हैं।
आंतरिक गुणनफल
V के लिए एक परिमित-विमीय समष्टि, V पर आंतरिक गुणनफल (या एक छद्म-यूक्लिडियन आंतरिक गुणनफल) V के साथ V के एक समरूपता को परिभाषित करता है, और इसलिए के साथ का एक समरूपता भी है। इन दो समष्टियों के बीच का युग्म भी आंतरिक गुणनफल का रूप ले लेती है। वियोजनीय k-सदिश पर,
आंतरिक गुणनफलों के आव्यूह का निर्धारक। विशेष स्थिति में vi = wi, आंतरिक गुणनफल k-सदिश का वर्ग मानदंड है, जिसे ग्रामियन आव्यूह (⟨vi, vj⟩) के निर्धारक द्वारा दिया गया है। इसके पश्चात पर गैर-पतित आंतरिक गुणनफल के लिए बाईलीनियरली (या जटिल स्थिति में सेस्क्विलिनियरली) विस्तारित किया जाता है। यदि ei, i = 1, 2, ..., n, V का ऑर्थोनॉर्मल बेसिस बनाते हैं, तो रूप के सदिश
के लिए ऑर्थोनॉर्मल बेसिस बनता है, कॉची-बिनेट सूत्र के समतुल्य एक कथन।
आंतरिक गुणनफल के संबंध में, बाह्य गुणा और आंतरिक गुणनफल पारस्परिक रूप से जुड़े हुए हैं। विशेष रूप से, और के लिए,
जहाँ x♭ ∈ V∗ संगीतमय समाकृतिकता है, जिसके द्वारा परिभाषित रेखीय प्रकार्यात्मक है
सभी y ∈ V के लिए। यह गुणधर्म बाह्य बीजगणित पर आंतरिक गुणनफल को पूरी तरह से चित्रित करती है।
वास्तव में, अत्यधिक सामान्य रूप से और के लिए, उपरोक्त आसन्न गुणों का पुनरावृति देता है
जहां अब द्वैत एल-सदिश द्वारा परिभाषित किया गया है
सबके लिए ।
बायलजेब्रा संरचना
श्रेणीबद्ध बीजगणित के श्रेणीबद्ध द्वैध और v पर बहुरेखीय रूपों के बीच समतुल्यता है। बाह्य बीजगणित (साथ ही सममित बीजगणित) बायलजेब्रा संरचना प्राप्त करता है, और, वास्तव में, टेन्सर बीजगणित से हॉफ बीजगणित संरचना। विषय के विस्तृत उपचार के लिए टेंसर बीजगणित पर लेख देखें।
ऊपर परिभाषित मल्टीलाइनर रूपों का बाह्य गुणनफल पर परिभाषित एक सह-गुणनफल के लिए दोहरा है, जो सह-बीजगणित (कोलजेब्रा) की संरचना देता है। सह-गुणनफल एक रैखिक फलन Δ : → ⊗ है, जो इसके द्वारा दिया गया है
घटकों पर v∈V। प्रतीक 1 फील्ड K के इकाई तत्व को दर्शाता है। याद रखें कि K ⊂ , ताकि उपरोक्त वास्तव में ⊗ में निहित हो। सहगुणनफल की यह परिभाषा पूर्ण समष्टि तक (रैखिक) समरूपता द्वारा उठाई जाती है। इस समरूपता का सही रूप वह नहीं है जिसे कोई भोलेपन से लिख सकता है, बल्कि कोलजेब्रा लेख में सावधानी से परिभाषित किया जाना चाहिए। इस स्थिति में, एक प्राप्त करता है
इसे विस्तार से विस्तारित करते हुए, निम्नलिखित अभिव्यक्ति को विघटित घटकों पर प्राप्त किया जाता है:
जहां सभी (p+1, k−p)-समवकुलन पर दूसरा योग लिया जाता है। फ़ील्ड एलिमेंट 1 का ट्रैक रखने के लिए उपरोक्त को नोटेशनल ट्रिक के साथ लिखा गया है: ट्रिक लिखने के लिए है और योग के विस्तार के दौरान इसे विभिन्न समष्टियों में समवकुलन किया जाता है। समवकुलन सह-बीजगणित के पहले स्वयंसिद्ध से सीधे अनुसरण करता है: घटकों का सापेक्ष क्रम राइफल समवकुलन में संरक्षित है: राइफल शफल केवल आदेशित अनुक्रम को दो क्रमित अनुक्रमों में विभाजित करता है, एक बाईं ओर और एक दाईं ओर।
निरीक्षण करें कि सह-गुणनफल बीजगणित की ग्रेडिंग को संरक्षित रखता है। पूर्ण समष्टि तक विस्तारित, एक के पास है
इस खंड में प्रयुक्त टेन्सर प्रतीक ⊗ को कुछ सावधानी के साथ समझा जाना चाहिए: यह वही टेन्सर प्रतीक नहीं है जैसा कि वैकल्पिक गुणनफल की परिभाषा में उपयोग किया जा रहा है। सहज रूप से, इसे सिर्फ एक और, लेकिन भिन्न, टेन्सर गुणनफल के रूप में सोचना सबसे सरल है: यह अभी भी (द्वि-) रैखिक है, जैसा कि टेन्सर गुणनफलों को होना चाहिए, लेकिन यह गुणनफल है जो एक बायलजेब्रा की परिभाषा के लिए उपयुक्त है, अर्थात वस्तु ⊗ बनाने के लिए। समानता (1 ⊗ v) ∧ (1 ⊗ w) = 1 ⊗ (v ∧ w) और (v ⊗ 1) ∧ (1 ⊗ w) = v ⊗ w पर विचार करके किसी भी लंबे समय तक संदेह को हिलाया जा सकता है, जो कोलजेब्रा की परिभाषा से अनुसरण करता है, जैसा कि टेंसर और वेज प्रतीकों से जुड़े भोले-भाले जोड़तोड़ के विपरीत है। टेंसर बीजगणित पर लेख में इस अंतर को अधिक विस्तार से विकसित किया गया है। यहाँ, एक समस्या बहुत कम है, जिसमें वैकल्पिक गुणनफल ∧ स्पष्ट रूप से बायलजेब्रा में गुणन के अनुरूप है, जिससे प्रतीक ⊗ बाइलजेब्रा की परिभाषा में उपयोग के लिए मुक्त हो जाता है। व्यवहार में, यह कोई विशेष समस्या प्रस्तुत नहीं करता है, जब तक कि कोई एक अपवाद के साथ, वेज प्रतीक द्वारा ⊗ के वैकल्पिक योगों को बदलने के घातक जाल से बचता है। कोई भी ⊗ से एक वैकल्पिक गुणनफल बना सकता है, इस समझ के साथ कि यह एक भिन्न समष्टि में काम करता है। ठीक नीचे, एक उदाहरण दिया गया है: द्वैत समष्टि के लिए वैकल्पिक गुणनफल को प्रतिगुणनफल के संदर्भ में दिया जा सकता है। बाह्य बीजगणित के लिए वैकल्पिक संकेतों को सही ढंग से ट्रैक करने की आवश्यकता को छोड़कर, यहां बायलजेब्रा का संरचना टेंसर बीजगणित लेख में संरचना को लगभग समान बनाता है।
सह-गुणनफल के संदर्भ में, द्वैत समष्टि पर बाह्य गुणनफल, सह-गुणनफल का केवल दो श्रेणीबद्ध है:
जहां दाईं ओर टेंसर गुणनफल बहुरेखीय रैखिक मैपों का है (असंगत सजातीय डिग्री के घटकों पर शून्य द्वारा बढ़ाया गया है: अधिक यथार्थ रूप से, α ∧ β = ε ∘ (α ⊗ β) ∘ Δ, जहां ε कॉउंट है, जैसा कि वर्तमान में परिभाषित किया गया है)।
कॉउनिट समरूपता ε : → K है जो अपने तर्क के 0-श्रेणी वाले घटक को वापस करता है। बाह्य गुणनफल के साथ-साथ सह-गुणनफल और देश, बाह्य बीजगणित पर एक बायल्जेब्रा की संरचना को परिभाषित करते हैं।
सजातीय घटकों पर द्वारा परिभाषित एंटीपोड के साथ बाह्य बीजगणित भी एक हॉप बीजगणित है।[14]
फुन्क्टरिअलिटी
मान लीजिए कि V और W सदिश समष्टियों का एक युग्म हैं और f : V → W रैखिक मैप है। फिर, सार्वभौमिक गुणधर्म के द्वारा, वर्गीकृत बीजगणित का एक अद्वितीय समाकारिता विद्यमान है
ऐसा है कि
विशेष रूप से, सजातीय डिग्री को संरक्षित करता है। के k-श्रेणी वाले घटकों को वियोजनीय घटकों द्वारा दिया गया है
माना
V और W के आधार पर रूपांतरण के घटक, f के k × k अवयस्क का आव्यूह है। विशेष रूप से, यदि V = W और V परिमित विमा n का है, तो स्वयं के लिए एक विमीय सदिश समष्टि का मैपिंग है, और इसलिए इसे अदिश द्वारा दिया जाता है: f का निर्धारक।
यथार्थता
यदि सदिश समष्टियों का लघु यथार्थ अनुक्रम है, तब
श्रेणीबद्ध सदिश समष्टि का यथार्थ अनुक्रम है,[15] जैसा है
प्रत्यक्ष संकलन
विशेष रूप से, प्रत्यक्ष संकलन का बाह्य बीजगणित बाह्य बीजगणित के टेन्सर गुणनफल के लिए समरूप है:
यह वर्गीकृत समरूपता है; अर्थात।,
अधिक व्यापकता में, सदिश रिक्त समष्टि के एक छोटे से यथार्थ अनुक्रम के लिए एक प्राकृतिक निस्पंदन होता है
जहां के लिए को और के लिए के घटकों द्वारा फैलाया गया है। संबंधित उद्धरण एक प्राकृतिक समरूपता को स्वीकार करते हैं
- के द्वारा दिया गया ।
विशेष रूप से, यदि U 1-विमीय है तो
यथार्थ है, और यदि W 1-विम है तो
यथार्थ है।[17]
अनुप्रयोग
रैखिक बीजगणित
रैखिक बीजगणित के अनुप्रयोगों में, बाह्य गुणनफल एक आव्यूह के निर्धारक और उपसारणिकों का वर्णन करने के लिए अमूर्त बीजगणितीय तरीका प्रदान करता है। उदाहरण के लिए, यह सर्वविदित है कि एक वर्ग आव्यूह का निर्धारक समांतरोटोप के आयतन के बराबर होता है, जिसके किनारे आव्यूह के स्तंभ होते हैं (दिग्विन्यास को ट्रैक करने के लिए चिह्न के साथ)। इससे पता चलता है कि निर्धारक को कॉलम सदिश के बाह्य गुणनफल के संदर्भ में परिभाषित किया जा सकता है। इसी तरह, आव्यूह के k × k अवयस्क को एक समय में चयनित k कॉलम सदिश के बाह्य गुणनफलों को देखकर परिभाषित किया जा सकता है। इन विचारों को न केवल मैट्रिसेस तक बढ़ाया जा सकता है, बल्कि रैखिक परिवर्तनों के लिए भी: एक रैखिक परिवर्तन का निर्धारक वह कारक है जिसके द्वारा यह किसी भी दिए गए संदर्भ समांतरोटोप के उन्मुख मात्रा को मापता है। तो एक रैखिक परिवर्तन के निर्धारक को इस रूप में परिभाषित किया जा सकता है कि परिवर्तन शीर्ष बाह्य घातांक को क्या करता है। कम बाह्य घातांकयों पर एक रूपांतरण की क्रिया परिवर्तन के उपसारणिकों के बारे में बात करने का बेसिस-स्वतंत्र विधि प्रदान करती है।
तकनीकी विवरण: परिभाषाएँ
माना[18] बेसिस के साथ फील्ड पर n-विमीय सदिश समष्टि बनें।
- के लिए को साधारण टेन्सर द्वारा परिभाषित करेंऔर सभी टेंसरों के लिए परिभाषा को रैखिक रूप से विस्तारित करें। अत्यधिक सामान्य रूप से, हम को सरल टेंसरों पर परिभाषित कर सकते हैंअर्थात k घटकों का चयन करें जिन पर A कार्य करेगा, फिर विभिन्न विकल्पों से प्राप्त सभी परिणामों का योग करें। यदि को परिभाषित करता है। चूंकि बेसिस के साथ 1-विमीय है, हम अद्वितीय संख्या संतोषजनक के साथ की पहचान कर सकते हैं
- के लिए, किसी भी और के लिए को संतुष्ट करने वाला अद्वितीय संकारक होने के लिए बाह्य परिवर्त को परिभाषित करें।
- के लिए को परिभाषित करें ये पिछली परिभाषाओं के बराबर हैं।
मूल गुण
निर्धारक, ट्रेस और आसन्न की अन्य परिभाषाओं से प्राप्त सभी परिणाम इस परिभाषा से प्राप्त किए जा सकते हैं (चूंकि ये परिभाषाएं समकक्ष हैं)। यहाँ इन नई परिभाषाओं से संबंधित कुछ बुनियादी विशेषताएँ दी गई हैं:
- है -रैखिक।
- ।
- हमे कैनोनिकल समरूपता (आइसोमोर्फिज्म) प्राप्त हैहालांकि, और के बीच कोई विहित समरूपता नहीं है।
- की परिवर्त आव्यूह की प्रविष्टियाँ हैं -मिनर्स ।
- प्रत्येक के लिए विशेष रूप से,और इसलिए
- विशेष रूप से,
- विशेषता बहुपद का द्वारा दिया जा सकता है इसी तरह,
लीवरियर का एल्गोरिथ्म
अभिलाक्षणिक बहुपद में पदों के गुणांक हैं। वे और के व्यंजकों में भी दिखाई देते हैं। लेवेरियर का एल्गोरिद्म[19] और की गणना करने का आर्थिक तरीका है
- समुच्चय
- के लिए
भौतिकी
भौतिकी में, कई मात्राएँ स्वाभाविक रूप से वैकल्पिक संकारकों द्वारा प्रदर्शित की जाती हैं। उदाहरण के लिए, यदि किसी आवेशित कण की गति को चार-विमीय समष्टिटाइम में वेग और त्वरण सदिश द्वारा वर्णित किया जाता है, तो वेग सदिश के सामान्यीकरण के लिए आवश्यक है कि विद्युत चुम्बकीय बल वेग पर एक वैकल्पिक संकारक होना चाहिए। इसकी छह स्वतंत्रता की डिग्री विद्युत और चुंबकीय क्षेत्र से पहचानी जाती है।
रैखिक ज्यामिति
वियोजनीय k-सदिश की ज्यामितीय व्याख्याएं हैं: द्विसदिश u ∧ v सदिश द्वारा फैलाए गए समतल का प्रतिनिधित्व करता है, "भारित" एक संख्या के साथ, ओरिएंटेड समांतर चतुर्भुज के क्षेत्र द्वारा यू और v के साथ दिया जाता है। अनुरूप रूप से, 3-सदिश u ∧ v ∧ w किनारों u, v, और w के साथ उन्मुख समांतर चतुर्भुज के आयतन द्वारा भारित विस्तारित हुए 3-समष्टि का प्रतिनिधित्व करता है।
प्रोजेक्टिव ज्यामिति
में वियोजनीय k-सदिश V के भारित के-विमीय रैखिक उप-समष्टियों के अनुरूप हैं। विशेष रूप से, V के के-विमीय उप-समष्टियों के ग्रासमैनियन, जीआरके (वी) को निरूपित किया जाता है, जिसे स्वाभाविक रूप से प्रोजेक्टिव समष्टि की बीजगणितीय उप-विविधता के साथ पहचाना जा सकता है। इसे प्लकर एंबेडिंग कहा जाता है।
अवकल ज्यामिति
बाह्य बीजगणित में अवकल ज्यामिति में उल्लेखनीय अनुप्रयोग हैं, जहाँ इसका उपयोग विभेदक रूपों को परिभाषित करने के लिए किया जाता है।[20] विभेदक रूप गणितीय वस्तुएं हैं जो सदिश की लंबाई, समांतर चतुर्भुज के क्षेत्रों और उच्च-विमीय निकायों के संस्करणों का मूल्यांकन करती हैं, इसलिए उन्हें वक्र, सतहों और उच्च विमीय मैनिफोल्ड पर इस तरह से एकीकृत किया जा सकता है जो पथरी से लाइन समाकल और सतह समाकल को सामान्य करता है। भिन्न-भिन्न मैनिफोल्ड के एक बिंदु पर एक विभेदक रूप बिंदु पर स्पर्शरेखा समष्टि पर एक वैकल्पिक मल्टीलाइनियर रूप है। समान रूप से, डिग्री k का एक विभेदक रूप स्पर्शरेखा समष्टि की k-वें बाह्य घातांक पर एक रैखिक कार्यात्मक है। नतीजतन, बहु-रेखीय रूपों का बाह्य गुणनफल अवकल रूपों के लिए प्राकृतिक बाह्य गुणनफल को परिभाषित करता है। अवकल रूप अवकल ज्यामिति के विविध क्षेत्रों में प्रमुख भूमिका निभाते हैं।
एक वैकल्पिक दृष्टिकोण कार्यों के जर्म के संदर्भ में विभेदक रूपों को परिभाषित करता है।
विशेष रूप से, बाह्य व्युत्पन्न अवकल ग्रेड बीजगणित की संरचना को मैनिफोल्ड भिन्न-भिन्न रूपों का बाह्य बीजगणित देता है। मैनिफोल्ड के बीच चिकनी मैपिंग के साथ पुलबैक के साथ बाह्य व्युत्पन्न यात्रा करता है, और इसलिए यह एक प्राकृतिक अवकल संकारक है। अवकल रूप का बाह्य बीजगणित, बाह्य अवकलज से लैस, कोचेन कॉम्प्लेक्स है, जिसके कोहोलॉजी को अंतर्निहित मैनिफोल्ड का डी रम कोहोलॉजी कहा जाता है और अवकल मैनिफोल्ड के बीजगणितीय टोपोलॉजी में महत्वपूर्ण भूमिका निभाता है।
प्रतिनिधित्व सिद्धांत
प्रतिनिधित्व सिद्धांत में, बाह्य बीजगणित सदिश रिक्त समष्टि की श्रेणी पर दो मूलभूत शूर फ़ैक्टरों में से एक है, दूसरा सममित बीजगणित है। साथ में, इन संरचनाओं का उपयोग सामान्य रैखिक समूह के अलघुकरणीय निरूपण उत्पन्न करने के लिए किया जाता है; मौलिक प्रतिनिधित्व देखें।
अतिसमष्टि
जटिल संख्याओं पर बाह्य बीजगणित एक सुपरलेजेब्रा का मूल उदाहरण है, जो कि फर्मियन और अतिसममिति से संबंधित भौतिक सिद्धांतों में एक मौलिक भूमिका निभाता है। बाह्य बीजगणित के एक घटक को सुपरनंबर[21] या ग्रासमैन नंबर कहा जाता है। बाह्य बीजगणित स्वयं तब केवल एक विमीय अतिसमष्टि है: यह बाह्य बीजगणित के सभी बिंदुओं का समुच्चय है। इस समष्टि पर टोपोलॉजी अनिवार्य रूप से कमजोर टोपोलॉजी है, खुले समुच्चय सिलेंडर समुच्चय होते हैं। एक n-विमीय अतिसमष्टि बाह्य बीजगणित का सिर्फ n-गुना गुणनफल है।
लाई बीजगणित होमोलॉजी
L को क्षेत्र k पर लाई बीजगणित होने दें, फिर एल के बाह्य बीजगणित पर श्रृंखला परिसर की संरचना को परिभाषित करना संभव है। यह एक k-रैखिक मैपिंग है
द्वारा विघटित घटकों पर परिभाषित किया गया
जैकोबी पहचान रखती है यदि और केवल यदि ∂∂ = 0, और इसलिए यह एक आवश्यक और पर्याप्त स्थिति है जो एक एंटीकोम्यूटेटिव गैर-साहचर्य बीजगणित L के लिए एक लाई बीजगणित है। इसके अतिरिक्त, उस स्थिति में सीमा संकारक ∂ के साथ एक चेन कॉम्प्लेक्स है। इस कॉम्प्लेक्स से जुड़ी होमोलॉजी लाइ बीजगणित होमोलॉजी है।
होमोलॉजिकल बीजगणित
बाह्य बीजगणित, कोज़ुल कॉम्प्लेक्स के संरचना में मुख्य घटक है, जो होमोलॉजिकल बीजगणित में एक मूलभूत वस्तु है।
इतिहास
बाह्य बीजगणित पहली बार 1844 में हरमन ग्रासमैन द्वारा ऑस्देहनुंगस्लेह्रे, या विस्तार के सिद्धांत के कंबल शब्द के तहत प्रस्तुत किया गया था।[22] यह सामान्यतः विस्तारित मात्राओं के एक बीजगणितीय (या स्वयंसिद्ध) सिद्धांत को संदर्भित करता है और एक सदिश समष्टि की आधुनिक धारणा के प्रारंभिक अग्रदूतों में से एक था। सेंट-वेनेंट ने भी बाह्य कैलकुलस के समान विचारों को प्रकाशित किया जिसके लिए उन्होंने ग्रासमैन पर प्राथमिकता का दावा किया।[23]
बीजगणित स्वयं नियमों, या स्वयंसिद्धों के एक समुच्चय से बनाया गया था, जो केली और सिल्वेस्टर के बहुसंकेतकों के सिद्धांत के औपचारिक पहलुओं को कैप्चर करता है। ज्यामितीय दृष्टि से औपचारिक तर्क के कार्य पर विशेष रूप से ध्यान केंद्रित करने के अतिरिक्त, यह इस प्रकार एक कैलकुलस था, जो प्रस्तावात्मक कैलकुलस की तरह था।[24] विशेष रूप से, इस नए विकास ने विमा के एक स्वयंसिद्ध लक्षण वर्णन की अनुमति दी, एक गुणधर्म जिसे पहले केवल समन्वय बिंदु से जांचा गया था।
सदिश और बहुसदिश के इस नए सिद्धांत का आयात 19वीं शताब्दी के मध्य के गणितज्ञों द्वारा खो दिया गया था,[25] जब तक कि 1888 में ग्यूसेप पीनो द्वारा इसकी पूरी तरह से जांच नहीं की गई। सदी के अंत तक पियानो का काम भी कुछ हद तक अस्पष्ट रहा, जब इस विषय को फ्रेंच ज्यामिति स्कूल (विशेष रूप से हेनरी पॉइनकेयर, एली कार्टन, और गैस्टन डारबॉक्स) के सदस्यों द्वारा एकीकृत किया गया था, जिन्होंने ग्रासमैन के विचारों को विभेदक रूपों की गणना के लिए लागू किया था।
कुछ देर पश्चात, अल्फ्रेड नॉर्थ व्हाइटहेड ने पियानो और ग्रासमैन के विचारों से उधार लेते हुए, अपने सार्वभौमिक बीजगणित की शुरुआत की। इसके पश्चात बीजगणितीय प्रणाली की स्वयंसिद्ध धारणा को दृढ़ तार्किक आधार पर रखकर सार बीजगणित के 20वीं शताब्दी के विकास का मार्ग प्रशस्त किया।
यह भी देखें
- वैकल्पिक बीजगणित
- बाह्य कैलकुलस पहचान
- क्लिफोर्ड बीजगणित, एक नॉनज़ेरो द्विघात रूप का उपयोग करके बाह्य बीजगणित का एक सामान्यीकरण
- ज्यामितीय बीजगणित
- कोसज़ुल कॉम्प्लेक्स
- बहुस्तरीय बीजगणित
- सममित बीजगणित, सममित एनालॉग
- टेंसर बीजगणित
- वेइल बीजगणित, एक सहानुभूतिपूर्ण रूप से सममित बीजगणित का एक क्वांटम समूह
टिप्पणियाँ
- ↑ 1.0 1.1 Penrose, R. (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- ↑ Wheeler, Misner & Thorne 1973, p. 83
- ↑ Grassmann (1844) introduced these as extended algebras (cf. Clifford 1878). He used the word äußere (literally translated as outer, or exterior) only to indicate the produkt he defined, which is nowadays conventionally called exterior product, probably to distinguish it from the outer product as defined in modern linear algebra.
- ↑ Strictly speaking, the magnitude depends on some additional structure, namely that the vectors be in a Euclidean space. We do not generally assume that this structure is available, except where it is helpful to develop intuition on the subject.
- ↑ The term k-vector is not equivalent to and should not be confused with similar terms such as 4-vector, which in a different context could mean an element of a 4-dimensional vector space. A minority of authors use the term k-multivector instead of k-vector, which avoids this confusion.
- ↑ This axiomatization of areas is due to Leopold Kronecker and Karl Weierstrass; see Bourbaki (1989b, Historical Note). For a modern treatment, see Mac Lane & Birkhoff (1999, Theorem IX.2.2). For an elementary treatment, see Strang (1993, Chapter 5).
- ↑ Mac Lane & Birkhoff (1999)
- ↑ A proof of this can be found in more generality in Bourbaki (1989).
- ↑ See Sternberg (1964, §III.6).
- ↑ See Bourbaki (1989, §III.7.1), and Mac Lane & Birkhoff (1999, Theorem XVI.6.8). More detail on universal properties in general can be found in Mac Lane & Birkhoff (1999, Chapter VI), and throughout the works of Bourbaki.
- ↑ See Bourbaki (1989, §III.7.5) for generalizations.
- ↑ Note: The orientations shown here are not correct; the diagram simply gives a sense that an orientation is defined for every k-form.
- ↑ Wheeler, J.A.; Misner, C.; Thorne, K.S. (1973). Gravitation. W.H. Freeman & Co. pp. 58–60, 83, 100–9, 115–9. ISBN 0-7167-0344-0.
- ↑ Indeed, the exterior algebra of V is the enveloping algebra of the abelian Lie superalgebra structure on V.
- ↑ This part of the statement also holds in greater generality if V and W are modules over a commutative ring: That converts epimorphisms to epimorphisms. See Bourbaki (1989, Proposition 3, §III.7.2).
- ↑ This statement generalizes only to the case where V and W are projective modules over a commutative ring. Otherwise, it is generally not the case that converts monomorphisms to monomorphisms. See Bourbaki (1989, Corollary to Proposition 12, §III.7.9).
- ↑ Such a filtration also holds for vector bundles, and projective modules over a commutative ring. This is thus more general than the result quoted above for direct sums, since not every short exact sequence splits in other abelian categories.
- ↑ Winitzki 2010
- ↑ Kahan, W. (2000). "Jordan's normal form" (PDF). Math. H110.
- ↑ James, A.T. (1983). "On the Wedge Product". In Karlin, Samuel; Amemiya, Takeshi; Goodman, Leo A. (eds.). Studies in Econometrics, Time Series, and Multivariate Statistics. Academic Press. pp. 455–464. ISBN 0-12-398750-4.
- ↑ DeWitt, Bryce (1984). "Chapter 1". Supermanifolds. Cambridge University Press. p. 1. ISBN 0-521-42377-5.
- ↑ Kannenberg (2000) published a translation of Grassmann's work in English; he translated Ausdehnungslehre as Extension Theory.
- ↑ J Itard, Biography in Dictionary of Scientific Biography (New York 1970–1990).
- ↑ Authors have in the past referred to this calculus variously as the calculus of extension (Whitehead 1898; Forder 1941), or extensive algebra (Clifford 1878), and recently as extended vector algebra (Browne 2007).
- ↑ Bourbaki 1989, p. 661.
संदर्भ
गणितीय संदर्भ
- Bishop, R.; Goldberg, S.I. (1980), Tensor analysis on manifolds, Dover, ISBN 0-486-64039-6
- वैकल्पिक टेंसर्स और वैकल्पिक रूपों का उपचार, साथ ही इस लेख में अपनाए गए परिप्रेक्ष्य से हॉज द्वैत की विस्तृत चर्चा सम्मिलित है।
- Bourbaki, Nicolas (1989), Elements of mathematics, Algebra I, Springer-Verlag, ISBN 3-540-64243-9
- यह लेख के लिए मुख्य गणितीय संदर्भ है।यह एक कम्यूटेटिव रिंग पर एक मॉड्यूल के बाह्य बीजगणित का परिचय देता है (हालांकि यह लेख मुख्य रूप से उस स्थिति में माहिर है जब रिंग एक क्षेत्र है), जिसमें सार्वभौमिक गुणधर्म, फुन्क्टरिअलिटी, द्वैत और बायलजबरा संरचना की चर्चा सम्मिलित है।§Iii.7 और §iii.11 देखें।
- Bryant, R.L.; Chern, S.S.; Gardner, R.B.; Goldschmidt, H.L.; Griffiths, P.A. (1991), Exterior differential systems, Springer-Verlag
- इस पुस्तक में आंशिक अंतर समीकरण ों में समस्याओं के लिए बाह्य बीजगणित के अनुप्रयोग सम्मिलित हैं।रैंक और संबंधित अवधारणाएं प्रारंभिक अध्यायों में विकसित की जाती हैं।
- Mac Lane, S.; Birkhoff, G. (1999), Algebra, AMS Chelsea, ISBN 0-8218-1646-2
- अध्याय XVI सेक्शन 6-10 बाह्य बीजगणित का अधिक प्राथमिक खाता देते हैं, जिसमें द्वंद्व, निर्धारक और उपसारणिकों और वैकल्पिक रूप सम्मिलित हैं।
- Sternberg, Shlomo (1964), Lectures on Differential Geometry, Prentice Hall
- बाह्य बीजगणित का एक शास्त्रीय उपचार वैकल्पिक टेनर्स के रूप में होता है, और अंतर ज्यामिति के लिए अनुप्रयोग।
ऐतिहासिक संदर्भ
- Bourbaki (1989, Historical note on chapters II and III)
- Clifford, W. (1878), "Applications of Grassmann's Extensive Algebra", American Journal of Mathematics, The Johns Hopkins University Press, 1 (4): 350–358, doi:10.2307/2369379, JSTOR 2369379
- Forder, H.G. (1941), The Calculus of Extension, Internet Archive
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre – Ein neuer Zweig der Mathematik (in Deutsch) (रैखिक एक्सटेंशन थ्योरी-गणित की एक नई शाखा) वैकल्पिक संदर्भ
- Kannenberg, Lloyd (2000), Extension Theory (translation of Grassmann's Ausdehnungslehre), American Mathematical Society, ISBN 0-8218-2031-1
- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva; Kannenberg, Lloyd (1999), Geometric calculus: According to the Ausdehnungslehre of H. Grassmann, Birkhäuser, ISBN 978-0-8176-4126-9।
- Whitehead, Alfred North (1898), A Treatise on Universal Algebra, with Applications, Cambridge
अन्य संदर्भ और आगे पढ़ना
- Browne, J.M. (2007), Grassmann algebra – Exploring applications of Extended Vector Algebra with Mathematica
- बाह्य बीजगणित, और ज्यामितीय बीजगणित का एक परिचय, अनुप्रयोगों पर ध्यान देने के साथ।एक इतिहास अनुभाग और ग्रंथ सूची भी सम्मिलित है।
- Spivak, Michael (1965), Calculus on manifolds, Addison-Wesley, ISBN 978-0-8053-9021-6
- बाह्य बीजगणित के अनुप्रयोगों को अंतर रूपों में सम्मिलित किया गया है, विशेष रूप से अभिन्न और स्टोक्स के प्रमेय पर केंद्रित है।अंकन इस पाठ में v पर के-फॉर्म्स को वैकल्पिक करने के समष्टि का उपयोग करने के लिए उपयोग किया जाता है;अर्थात, स्पिवक के लिए यह लेख क्या होगा स्पिवक ने एडेंडम 4 में इस पर चर्चा की।
- Strang, G. (1993), Introduction to linear algebra, Wellesley-Cambridge Press, ISBN 978-0-9614088-5-5
- सांकेतिक क्षेत्रों, संस्करणों और उच्च-विमीय संस्करणों के रूप में निर्धारकों के स्वयंसिद्धता का एक प्राथमिक उपचार सम्मिलित है।
- Onishchik, A.L. (2001) [1994], "Exterior algebra", Encyclopedia of Mathematics, EMS Press
- Wendell, Fleming (2012) [1977], "7. Exterior algebra and differential calculus", Functions of Several Variables (2nd ed.), Springer, pp. 275–320, ISBN 978-1-4684-9461-7
- बहुभिन्नरूपी पथरी में यह पाठ्यपुस्तक कॉलेजों के लिए कैलकुलस अनुक्रम में अंतर रूपों के बाह्य बीजगणित का परिचय देती है।
- Winitzki, S. (2010), Linear Algebra via Exterior Products
- बाह्य गुणनफलों का उपयोग करके बुनियादी परिमित-विमीय रैखिक बीजगणित में समन्वय-मुक्त दृष्टिकोण का परिचय।
- Shafarevich, I.R.; Remizov, A.O. (2012). रेखीय बीजगणित और ज्यामिति. Springer. ISBN 978-3-642-30993-9.
- अध्याय 10: बाह्य गुणनफल और बाह्य बीजगणित
- [http://neo-classical-physics.info/uploads/3/0/6/5/3065888/burali-forti_-_grassman_and_proj._geom..pdfबाह्य बीजगणित के आवेदन पर सेसरे ब्यूरली-फ़ॉर्टी द्वारा प्रोजेक्टिव ज्यामिति के लिए नोट्स
- C. Burali-forti, अवकल ज्यामिति के पश्चात परिचय,एच। ग्रासमैन की विधि बाह्य बीजगणित के ज्यामितीय अनुप्रयोगों पर एक प्रारंभिक पुस्तक का एक अंग्रेजी अनुवाद
- यांत्रिकी, विस्तार के सिद्धांत के सिद्धांतों के अनुसार एक ग्रासमैन के कागजों के एक अंग्रेजी अनुवादबाह्य बीजगणित के अनुप्रयोगों पर