सामान्य वितरण

"बेल वक्र" redirects here. For other uses, see बेल वक्र (disambiguation).

Normal distribution

Probability density function 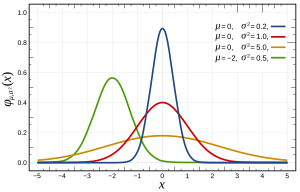The red curve is the standard normal distribution
Cumulative distribution function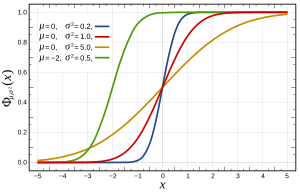
Notation	${\mathcal {N}}(\mu ,\sigma ^{2})$
Parameters	$\mu \in \mathbb {R}$ = mean (location) $\sigma ^{2}\in \mathbb {R} _{>0}$ = variance (squared scale)
Support	$x\in \mathbb {R}$
PDF	Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "ई" found.in 1:44"): {\displaystyle \frac{1}{\sigma\sqrt{2\pi}} ई^{-\frac{1}{2}\बाएं(\frac{x - \mu}{\sigma}\right)^2}}

स्टटिस्टिक्स में, एक सामान्य वितरण या गॉसियन डिस्ट्रीब्यूशन एक वास्तविक-मूल्यवान रैंडम चर के लिए निरंतर प्रायिकता वितरण का एक प्रकार है और जबकि वास्तविक-मूल्यवान रैंडम चर इसके प्रायिकता घनत्व फलन का सामान्य प्रकार है

$f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$

पैरामीटर $\mu$ वितरण का औसत माध्य अपेक्षित मूल्य है और इसकी माध्यिका और मोड सांख्यिकी पद्धति है, जबकि पैरामीटर $\sigma$ इसका मानक विचलन है और इस प्रकार वितरण का विचरण $\sigma ^{2}$ के रूप में है, गाऊसी वितरण के साथ एक रैंडम चर को सामान्य वितरण कहा जाता है और इसे सामान्य विचलन भी कहा जाता है।

सामान्य वितरण आंकड़ों में महत्वपूर्ण होते हैं और अधिकांशतः प्राकृतिक विज्ञान और सामाजिक विज्ञान में वास्तविक-मूल्य वाले रैंडम चर का प्रतिनिधित्व करने के लिए उपयोग किए जाते हैं जिनके वितरण ज्ञात नहीं होते हैं। और इस प्रकार उनका महत्व आंशिक रूप से केंद्रीय सीमा प्रमेय के कारण होता है। इसमें कहा गया है कि, कुछ शर्तों के अनुसार परिमित माध्य और विचरण के साथ एक रैंडम चर के कई नमूनों टिप्पणियों का औसत स्वयं एक रैंडम चर है, जिसका वितरण अभिसरण नमूने की संख्या बढ़ने पर सामान्य वितरण में होता है। इसलिए, भौतिक मात्राएँ जो कई स्वतंत्र प्रक्रियाओं का योग होने की आशंका की जाती हैं, जैसे माप त्रुटियां, अधिकांशतः ऐसे वितरण होते हैं जो लगभग सामान्य रूप में होते है।

इसके अतिरिक्त, गॉसियन वितरण में कुछ अद्वितीय गुण हैं जो विश्लेषणात्मक अध्ययनों में मूल्यवान हैं। उदाहरण के लिए, सामान्य विचलन के निश्चित संग्रह का कोई भी रैखिक संयोजन एक सामान्य विचलन है। इस प्रकार कई परिणाम और विधियाँ, जैसे कि अनिश्चितता का प्रसार और कम से कम वर्ग पैरामीटर फिटिंग विश्लेषणात्मक रूप से स्पष्ट रूप से प्राप्त की जा सकती हैं जब प्रासंगिक चर सामान्य रूप से वितरित किए जाते हैं।

एक सामान्य वितरण को कभी-कभी अनौपचारिक रूप से बेल कर्व कहा जाता है। चूंकि, कई अन्य डिस्ट्रीब्यूशन बेल के आकार के होते हैं, जैसे कॉची छात्र का t-डिस्ट्रीब्यूशन और लॉजिस्टिक वितरण इत्यादि के रूप में होते है। अन्य नामों के लिए नेमिंग देखते हैं।

मल्टवेरीेंएट सामान्य वितरण में सदिश के लिए और आव्यूह सामान्य वितरण में मेट्रिसेस के लिए यूनीवेरिएट प्रायिकता वितरण सामान्यीकृत किया जाता है।

परिभाषाएँ

मानक सामान्य डिस्ट्रीब्यूशन

सामान्य वितरण का सबसे सरल स्थिति मानक सामान्य वितरण या इकाई सामान्य वितरण के रूप में जाना जाता है। यह एक विशेष स्थिति है जब u = 0 और $\sigma =1$ और इसे इस प्रायिकता घनत्व फ़ंक्शन (या घनत्व) द्वारा वर्णित किया गया है

$\varphi (z)={\frac {e^{-z^{2}/2}}{\sqrt {2\pi }}}$

चर z का माध्य 0 है और विचरण और मानक विचलन घनत्व 1 है $\varphi (z)$ इसका शीर्ष $1/{\sqrt {2\pi }}$ पर $z=0$ है और मोड़ बिंदु $z=+1$ और $z=-1$.के रूप में है

यद्यपि उपरोक्त घनत्व को सामान्यतः सामान्य मानक के रूप में जाना जाता है, कुछ लेखकों ने उस शब्द का उपयोग सामान्य वितरण के अन्य संस्करणों का वर्णन करने के लिए किया है। उदाहरण के लिए, कार्ल फ्रेडरिक गॉस ने एक बार मानक को सामान्य के रूप में परिभाषित किया था

$\varphi (z)={\frac {e^{-z^{2}}}{\sqrt {\pi }}}$

जिसमें 1/2 का विचरण होता है और स्टीफन स्टिगलर एक बार मानक सामान्य के रूप में परिभाषित किया गया है

$\varphi (z)=e^{-\pi z^{2}}$

जिसका एक सरल कार्यात्मक रूप और $\sigma ^{2}=1/(2\pi )$ एक विचरण है

सामान्य सामान्य डिस्ट्रीब्यूशन

प्रत्येक सामान्य वितरण मानक सामान्य वितरण का एक संस्करण है, जिसका डोमेन एक कारक $\sigma$ मानक विचलन द्वारा बढ़ाया गया है और फिर $\mu$ द्वारा औसत मूल्य का अनुवाद किया गया है:

$f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sigma }}\varphi \left({\frac {x-\mu }{\sigma }}\right)$

प्रायिकता घनत्व $1/\sigma$ द्वारा स्केल किया जाना चाहिए जिससे की समाकलन 1 के रूप में होता है।

यदि $Z$ एक मानक सामान्य विचलन के रूप में है, तो $X=\sigma Z+\mu$ अपेक्षित मूल्य के साथ एक सामान्य वितरण होता है $\mu$ और मानक विचलन $\sigma$. के बराबर है और मानक सामान्य वितरण $Z$ के एक कारक द्वारा विस्तारित किया जा सकता है और इस प्रकार $\sigma$ द्वारा स्थानांतरित किया जाता है, एक भिन्न सामान्य वितरण प्राप्त करने के लिए $\mu$ द्वारा स्थानांतरित किया जा सकता है, जिसे $X$ कहा जाता है. इसके विपरीत यदि $X$ मापदंडों के साथ एक सामान्य विचलन $\mu$ और $\sigma ^{2}$ के रूप में है फिर यह $X$ वितरण को फिर से बढ़ाया जा सकता है और सूत्र के माध्यम से स्थानांतरित किया जा सकता है $Z=(X-\mu )/\sigma$ इसे मानक सामान्य वितरण में बदलने के लिए इस चर को $X$ का मानकीकृत रूप भी कहा जाता है.

अंकन

मानक गाऊसी बंटन का प्रायिकता घनत्व (मानक सामान्य डिस्ट्रीब्यूशन , शून्य माध्य और इकाई प्रसरण के साथ) को अधिकांशतः ग्रीक अक्षर से निरूपित किया जाता है $\phi$ (फाई (पत्र))। ग्रीक अक्षर फी का वैकल्पिक रूप, $\varphi$, भी अधिकांशतः प्रयोग किया जाता है।

सामान्य वितरण को अधिकांशतः कहा जाता है $N(\mu ,\sigma ^{2})$ या ${\mathcal {N}}(\mu ,\sigma ^{2})$. इस प्रकार जब एक रैंडम चर $X$ सामान्य रूप से माध्य के साथ वितरित किया जाता है $\mu$ और मानक विचलन $\sigma$, कोई लिख सकता है

$X\sim {\mathcal {N}}(\mu ,\sigma ^{2}).$

वैकल्पिक मानकीकरण

कुछ लेखक परिशुद्धता (सांख्यिकी) का उपयोग करने की वकालत करते हैं $\tau$ विचलन के बजाय वितरण की चौड़ाई को परिभाषित करने वाले पैरामीटर के रूप में $\sigma$ या भिन्नता $\sigma ^{2}$. परिशुद्धता को सामान्यतः विचरण के व्युत्क्रम के रूप में परिभाषित किया जाता है, $1/\sigma ^{2}$. वितरण का सूत्र तब बन जाता है

$f(x)={\sqrt {\frac {\tau }{2\pi }}}e^{-\tau (x-\mu )^{2}/2}.$

इस विकल्प का संख्यात्मक संगणना में लाभ होने का दावा किया जाता है $\sigma$ शून्य के बहुत करीब है, और कुछ संदर्भों में सूत्रों को सरल करता है, जैसे मल्टवेरीेंएट सामान्य वितरण वाले चर के बायेसियन आंकड़ों में।

वैकल्पिक रूप से, मानक विचलन का व्युत्क्रम $\tau ^{\prime }=1/\sigma$ परिशुद्धता के रूप में परिभाषित किया जा सकता है, जिस स्थिति में सामान्य वितरण की अभिव्यक्ति बन जाती है

$f(x)={\frac {\tau ^{\prime }}{\sqrt {2\pi }}}e^{-(\tau ^{\prime })^{2}(x-\mu )^{2}/2}.$

स्टिग्लर के अनुसार, यह सूत्रीकरण बहुत सरल और याद रखने में आसान सूत्र और वितरण की मात्राओं के लिए सरल अनुमानित सूत्रों के कारण लाभप्रद है।

सामान्य बंटन प्राकृतिक प्राचलों के साथ एक चरघातांकी परिवार बनाते हैं $\textstyle \theta _{1}={\frac {\mu }{\sigma ^{2}}}$ और $\textstyle \theta _{2}={\frac {-1}{2\sigma ^{2}}}$, और प्राकृतिक आँकड़े x और x^{2</उप>। सामान्य वितरण के लिए दोहरी अपेक्षा पैरामीटर हैं η₁ = μ और η₂ = μ2 + σ2.}

संचयी वितरण कार्य

मानक सामान्य बंटन का संचयी बंटन फलन (CDF), सामान्यतः बड़े ग्रीक अक्षर से दर्शाया जाता है $\Phi$ (फाई (अक्षर)), अभिन्न है

$\Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt$

संबंधित त्रुटि समारोह $\operatorname {erf} (x)$ एक रैंडम चर की संभावना देता है, माध्य 0 के सामान्य वितरण के साथ और भिन्नता 1/2 सीमा में गिरती है $[-x,x]$. वह है:

$\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt$

इन समाकलों को प्रारंभिक कार्यों के संदर्भ में व्यक्त नहीं किया जा सकता है, और अधिकांशतः इन्हें विशेष कार्य कहा जाता है। चूंकि , कई संख्यात्मक सन्निकटन ज्ञात हैं; अधिक के लिए सामान्य सीडीएफ और सामान्य क्वांटाइल फ़ंक्शन के लिए #Numerical सन्निकटन देखें।

दो कार्य बारीकी से संबंधित हैं, अर्थात्

$\Phi (x)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]$

घनत्व के साथ सामान्य सामान्य वितरण के लिए $f$, अर्थ $\mu$ और विचलन $\sigma$, संचयी बंटन फलन है

$F(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$

मानक सामान्य सीडीएफ का पूरक, $Q(x)=1-\Phi (x)$, अधिकांशतः क्यू समारोह कहा जाता है, खासकर इंजीनियरिंग ग्रंथों में। यह प्रायिकता देता है कि एक मानक सामान्य रैंडम चर का मान $X$ अधिक हो जाएगा $x$: $P(X>x)$. की अन्य परिभाषाएँ $Q$-फ़ंक्शन, जिनमें से सभी सरल रूपांतरण हैं $\Phi$, का भी कभी-कभी उपयोग किया जाता है। मानक सामान्य सीडीएफ के एक समारोह का ग्राफ $\Phi$ बिंदु (0,1/2) के चारों ओर 2 गुना घूर्णी समरूपता है; वह है, $\Phi (-x)=1-\Phi (x)$. इसका प्रतिपक्षी (अनिश्चितकालीन अभिन्न) निम्नानुसार व्यक्त किया जा सकता है:

$\int \Phi (x)\,dx=x\Phi (x)+\varphi (x)+C.$

मानक सामान्य वितरण के सीडीएफ को एक श्रृंखला में भागों द्वारा एकीकरण द्वारा विस्तारित किया जा सकता है:

$\Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+\cdots +{\frac {x^{2n+1}}{(2n+1)!!}}+\cdots \right]$

कहाँ $!!$ डबल फैक्टोरियल को दर्शाता है।

बड़े एक्स के लिए सीडीएफ का एक स्पर्शोन्मुख विस्तार भी भागों द्वारा एकीकरण का उपयोग करके प्राप्त किया जा सकता है। अधिक जानकारी के लिए, एरर फंक्शन#एसिम्प्टोटिक विस्तार देखें। टेलर श्रृंखला सन्निकटन का उपयोग करके मानक सामान्य वितरण सीडीएफ के लिए एक त्वरित सन्निकटन पाया जा सकता है:

$\Phi (x)\approx {\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\sum _{k=0}^{n}{\frac {\left(-1\right)^{k}x^{\left(2k+1\right)}}{2^{k}k!\left(2k+1\right)}}$

मानक विचलन और कवरेज

Further information: Interval estimation and Coverage probability

सामान्य वितरण के लिए, सेट के 68.27% के लिए औसत खाते से दूर एक मानक विचलन से कम मान; जबकि औसत खाते से दो मानक विचलन 95.45% हैं; और तीन मानक विचलन 99.73% हैं।

एक सामान्य वितरण से निकाले गए लगभग 68% मान एक मानक विचलन σ माध्य से दूर होते हैं; लगभग 95% मूल्य दो मानक विचलन के भीतर हैं; और लगभग 99.7% तीन मानक विचलन के भीतर हैं।इस तथ्य को 68–95–99.7 नियम|68-95-99.7 (अनुभवजन्य) नियम या 3-सिग्मा नियम के रूप में जाना जाता है।

अधिक सटीक रूप से, एक सामान्य विचलन के बीच की सीमा में होने की संभावना $\mu -n\sigma$ और $\mu +n\sigma$ द्वारा दिया गया है

$F(\mu +n\sigma )-F(\mu -n\sigma )=\Phi (n)-\Phi (-n)=\operatorname {erf} \left({\frac {n}{\sqrt {2}}}\right).$

12 महत्वपूर्ण अंकों के लिए, मान के लिए $n=1,2,\ldots ,6$ हैं:

$n$	$p=F(\mu +n\sigma )-F(\mu -n\sigma )$	${\text{i.e. }}1-p$	${\text{or }}1{\text{ in }}p$	OEIS
1	0.682689492137	0.317310507863	3 .15148718753	OEIS: A178647
2	0.954499736104	0.045500263896	21 .9778945080	OEIS: A110894
3	0.997300203937	0.002699796063	370 .398347345	OEIS: A270712
4	0.999936657516	0.000063342484	15787 .1927673
5	0.999999426697	0.000000573303	1744277 .89362
6	0.999999998027	0.000000001973	506797345 .897

बड़े के लिए $n$, कोई सन्निकटन का उपयोग कर सकता है $1-p\approx {\frac {e^{-n^{2}/2}}{n{\sqrt {\pi /2}}}}$.

क्वांटाइल फंक्शन

Further information: Quantile function § Normal distribution

किसी वितरण का मात्रात्मक फलन संचयी बंटन फलन का व्युत्क्रम होता है। मानक सामान्य वितरण के मात्रात्मक समारोह को प्रोबिट फ़ंक्शन कहा जाता है, और इसे व्युत्क्रम त्रुटि फ़ंक्शन के संदर्भ में व्यक्त किया जा सकता है:

$\Phi ^{-1}(p)={\sqrt {2}}\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

औसत के साथ एक सामान्य रैंडम चर के लिए $\mu$ और विचरण $\sigma ^{2}$, क्वांटाइल फ़ंक्शन है

$F^{-1}(p)=\mu +\sigma \Phi ^{-1}(p)=\mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

क्वांटाइल $\Phi ^{-1}(p)$ मानक सामान्य वितरण का सामान्य रूप से निरूपित किया जाता है $z_{p}$. इन मूल्यों का उपयोग परिकल्पना परीक्षण, विश्वास अंतराल के निर्माण और क्यू-क्यू भूखंडों में किया जाता है। एक सामान्य रैंडम चर $X$ अधिक हो जाएगा $\mu +z_{p}\sigma$ संभावना के साथ $1-p$, और अंतराल के बाहर होता है $\mu \pm z_{p}\sigma$ संभावना के साथ $2(1-p)$. विशेष रूप से, मात्रा $z_{0.975}$ 1.96 है; इसलिए एक सामान्य रैंडम चर अंतराल के बाहर होता है $\mu \pm 1.96\sigma$ केवल 5% स्थितियो में।

निम्न तालिका मात्रा देता है $z_{p}$ ऐसा है कि $X$ के दायरे में रहेगा $\mu \pm z_{p}\sigma$ एक निर्दिष्ट संभावना के साथ $p$. ये मान नमूना माध्य और नमूना सहप्रसरण # नमूना माध्य और सामान्य (या विषम रूप से सामान्य) वितरण वाले अन्य सांख्यिकीय अनुमानकों के लिए सहिष्णुता अंतराल निर्धारित करने के लिए उपयोगी हैं। ध्यान दें कि निम्न तालिका दिखाती है ${\sqrt {2}}\operatorname {erf} ^{-1}(p)=\Phi ^{-1}\left({\frac {p+1}{2}}\right)$, नहीं $\Phi ^{-1}(p)$ जैसा कि ऊपर परिभाषित किया गया है।

$p$	$z_{p}$		$p$	$z_{p}$
0.80	1.281551565545		0.999	3.290526731492
0.90	1.644853626951		0.9999	3.890591886413
0.95	1.959963984540		0.99999	4.417173413469
0.98	2.326347874041		0.999999	4.891638475699
0.99	2.575829303549		0.9999999	5.326723886384
0.995	2.807033768344		0.99999999	5.730728868236
0.998	3.090232306168		0.999999999	6.109410204869

छोटे के लिए $p$, क्वांटाइल फ़ंक्शन में उपयोगी स्पर्शोन्मुख विस्तार है

$\Phi ^{-1}(p)=-{\sqrt {\ln {\frac {1}{p^{2}}}-\ln \ln {\frac {1}{p^{2}}}-\ln(2\pi )}}+{\mathcal {o}}(1).$

गुण

सामान्य बंटन ही एकमात्र ऐसा बंटन है जिसके पहले दो से परे (अर्थात् माध्य और प्रसरण के अतिरिक्त ) संचयी शून्य होते हैं। यह निर्दिष्ट माध्य और विचरण के लिए अधिकतम एन्ट्रापी प्रायिकता वितरण के साथ निरंतर वितरण भी है। गीरी ने दिखाया है, यह मानते हुए कि माध्य और विचरण परिमित हैं, कि सामान्य वितरण ही एकमात्र वितरण है जहां स्वतंत्र ड्रा के सेट से गणना की गई माध्य और विचरण एक दूसरे से स्वतंत्र हैं। सामान्य वितरण अण्डाकार वितरण का एक उपवर्ग है। सामान्य वितरण अपने माध्य के बारे में सममित वितरण है, और संपूर्ण वास्तविक रेखा पर गैर-शून्य है। जैसे कि यह उन चरों के लिए उपयुक्त मॉडल नहीं हो सकता है जो स्वाभाविक रूप से सकारात्मक या दृढ़ता से विषम हैं, जैसे किसी व्यक्ति का वजन या शेयर (वित्त) की कीमत। ऐसे चरों को अन्य डिस्ट्रीब्यूशन ों द्वारा बेहतर वर्णित किया जा सकता है, जैसे लॉग-सामान्य वितरण या पारेटो डिस्ट्रीब्यूशन ।

सामान्य वितरण का मान व्यावहारिक रूप से शून्य होता है जब मान $x$ माध्य से कुछ मानक विचलनों से अधिक दूर स्थित है (उदाहरण के लिए, तीन मानक विचलनों का प्रसार कुल वितरण के 0.27% को छोड़कर सभी को कवर करता है)। इसलिए, यह एक उपयुक्त मॉडल नहीं हो सकता है जब कोई ग़ैर के एक महत्वपूर्ण अंश की अपेक्षा करता है - मान जो कई मानक विचलन को माध्य से दूर करते हैं - और कम से कम वर्ग और अन्य सांख्यिकीय अनुमान विधियां जो सामान्य रूप से वितरित चर के लिए इष्टतम हैं, लागू होने पर अधिकांशतः अत्यधिक अविश्वसनीय हो जाती हैं। ऐसे डेटा के लिए। उन स्थितियो में, एक अधिक भारी-पूंछ वाले वितरण को माना जाना चाहिए और उचित मजबूत सांख्यिकी विधियों को लागू किया जाना चाहिए।

गॉसियन वितरण स्थिर वितरण के परिवार से संबंधित है जो स्वतंत्र और समान रूप से वितरित रैंडम चर के योगों के आकर्षण हैं | स्वतंत्र, समान रूप से वितरित वितरण चाहे माध्य या विचरण परिमित हो या नहीं। गॉसियन को छोड़कर जो एक सीमित स्थिति है, सभी स्थिर डिस्ट्रीब्यूशन ों में भारी पूंछ और अनंत विचरण होता है। यह उन कुछ डिस्ट्रीब्यूशन ों में से एक है जो स्थिर हैं और जिनमें प्रायिकता घनत्व कार्य हैं जिन्हें विश्लेषणात्मक रूप से व्यक्त किया जा सकता है, अन्य कॉची वितरण और लेवी वितरण हैं।

समरूपता और डेरिवेटिव

घनत्व के साथ सामान्य वितरण $f(x)$ (अर्थ $\mu$ और मानक विचलन $\sigma >0$) के निम्नलिखित गुण हैं:

• यह बिंदु के चारों ओर सममित है $x=\mu ,$ जो एक ही समय में बहुलक (सांख्यिकी), माध्यिका और वितरण का माध्य है।
• यह अनिमॉडल है: इसका पहला यौगिक के लिए सकारात्मक है $x<\mu ,$ के लिए नकारात्मक $x>\mu ,$ और शून्य केवल पर $x=\mu .$
• वक्र और द से घिरा क्षेत्र $x$-अक्ष एकता है (अर्थात एक के बराबर)।
• इसकी पहली व्युत्पत्ति है $f^{\prime }(x)=-{\frac {x-\mu }{\sigma ^{2}}}f(x).$
• इसके घनत्व में दो विभक्ति बिंदु होते हैं (जहाँ दूसरा व्युत्पन्न होता है $f$ शून्य है और चिह्न बदलता है), मतलब से एक मानक विचलन दूर स्थित है, अर्थात् पर $x=\mu -\sigma$ और $x=\mu +\sigma .$* इसका घनत्व लघुगणकीय रूप से अवतल कार्य है | लॉग-अवतल।* इसका घनत्व असीम रूप से भिन्न कार्य है, वास्तव में ऑर्डर 2 का सुपरस्मूथ है।

इसके अतिरिक्त , घनत्व $\varphi$ मानक सामान्य वितरण का (अर्थात $\mu =0$ और $\sigma =1$) में निम्नलिखित गुण भी हैं:

• इसकी पहली व्युत्पत्ति है $\varphi ^{\prime }(x)=-x\varphi (x).$
• इसका दूसरा व्युत्पन्न है $\varphi ^{\prime \prime }(x)=(x^{2}-1)\varphi (x)$
• अधिक सामान्यतः, इसकी nवें व्युत्पन्न है $\varphi ^{(n)}(x)=(-1)^{n}\operatorname {He} _{n}(x)\varphi (x),$ कहाँ $\operatorname {He} _{n}(x)$ है n(संभाव्य) हर्मिट बहुपद।
• संभावना है कि एक सामान्य रूप से वितरित चर $X$ ज्ञात के साथ $\mu$ और $\sigma$ एक विशेष सेट में है, इस तथ्य का उपयोग करके गणना की जा सकती है कि भिन्न $Z=(X-\mu )/\sigma$ एक मानक सामान्य वितरण है।

क्षण

See also: List of integrals of Gaussian functions

एक चर का सादा और निरपेक्ष क्षण (गणित)। $X$ के अपेक्षित मूल्य हैं $X^{p}$ और $|X|^{p}$, क्रमश। यदि अपेक्षित मूल्य $\mu$ का $X$ शून्य है, इन मापदंडों को केंद्रीय क्षण कहा जाता है; अन्यथा, इन मापदंडों को गैर-केंद्रीय क्षण कहा जाता है। सामान्यतः हम केवल पूर्णांक क्रम वाले क्षणों में रुचि रखते हैं $\ p$.

यदि $X$ एक सामान्य वितरण है, गैर-केंद्रीय क्षण मौजूद हैं और किसी के लिए परिमित हैं $p$ जिसका वास्तविक भाग −1 से बड़ा है। किसी भी गैर-ऋणात्मक पूर्णांक के लिए $p$, सादे केंद्रीय क्षण हैं:

$\operatorname {E} \left[(X-\mu )^{p}\right]={\begin{cases}0&{\text{if }}p{\text{ is odd,}}\\\sigma ^{p}(p-1)!!&{\text{if }}p{\text{ is even.}}\end{cases}}$

यहाँ $n!!$ दोहरे क्रमगुणन को दर्शाता है, अर्थात सभी संख्याओं का गुणनफल $n$ से 1 तक जिसमें समान समानता है $n.$ केंद्रीय निरपेक्ष क्षण सभी समान आदेशों के लिए सादे क्षणों के साथ मेल खाते हैं, लेकिन विषम आदेशों के लिए अशून्य हैं। किसी भी गैर-ऋणात्मक पूर्णांक के लिए $p,$

${\begin{aligned}\operatorname {E} \left[|X-\mu |^{p}\right]&=\sigma ^{p}(p-1)!!\cdot {\begin{cases}{\sqrt {\frac {2}{\pi }}}&{\text{if }}p{\text{ is odd}}\\1&{\text{if }}p{\text{ is even}}\end{cases}}\\&=\sigma ^{p}\cdot {\frac {2^{p/2}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}.\end{aligned}}$

अंतिम सूत्र किसी भी गैर-पूर्णांक के लिए भी मान्य है $p>-1.$ जब मतलब $\mu \neq 0,$ सादे और निरपेक्ष क्षणों को संगम हाइपरज्यामितीय कार्यों के संदर्भ में व्यक्त किया जा सकता है ${}_{1}F_{1}$ और $U.$

${\begin{aligned}\operatorname {E} \left[X^{p}\right]&=\sigma ^{p}\cdot (-i{\sqrt {2}})^{p}U\left(-{\frac {p}{2}},{\frac {1}{2}},-{\frac {1}{2}}\left({\frac {\mu }{\sigma }}\right)^{2}\right),\\\operatorname {E} \left[|X|^{p}\right]&=\sigma ^{p}\cdot 2^{p/2}{\frac {\Gamma \left({\frac {1+p}{2}}\right)}{\sqrt {\pi }}}{}_{1}F_{1}\left(-{\frac {p}{2}},{\frac {1}{2}},-{\frac {1}{2}}\left({\frac {\mu }{\sigma }}\right)^{2}\right).\end{aligned}}$

ये भाव मान्य रहते हैं भले ही $p$ पूर्णांक नहीं है। हर्मिट बहुपद# ऋणात्मक प्रसरण भी देखें।

Order	Non-central moment	Central moment
1	$\mu$	$0$
2	$\mu ^{2}+\sigma ^{2}$	$\sigma ^{2}$
3	$\mu ^{3}+3\mu \sigma ^{2}$	$0$
4	$\mu ^{4}+6\mu ^{2}\sigma ^{2}+3\sigma ^{4}$	$3\sigma ^{4}$
5	$\mu ^{5}+10\mu ^{3}\sigma ^{2}+15\mu \sigma ^{4}$	$0$
6	$\mu ^{6}+15\mu ^{4}\sigma ^{2}+45\mu ^{2}\sigma ^{4}+15\sigma ^{6}$	$15\sigma ^{6}$
7	$\mu ^{7}+21\mu ^{5}\sigma ^{2}+105\mu ^{3}\sigma ^{4}+105\mu \sigma ^{6}$	$0$
8	$\mu ^{8}+28\mu ^{6}\sigma ^{2}+210\mu ^{4}\sigma ^{4}+420\mu ^{2}\sigma ^{6}+105\sigma ^{8}$	$105\sigma ^{8}$

की अपेक्षा $X$ इस घटना पर सशर्त $X$ अन्तराल में होता है $[a,b]$ द्वारा दिया गया है

$\operatorname {E} \left[X\mid a<X<b\right]=\mu -\sigma ^{2}{\frac {f(b)-f(a)}{F(b)-F(a)}}$

कहाँ $f$ और $F$ क्रमशः घनत्व और संचयी वितरण समारोह हैं $X$. के लिए $b=\infty$ इसे व्युत्क्रम मिल्स अनुपात के रूप में जाना जाता है। ध्यान दें कि ऊपर, घनत्व $f$ का $X$ व्युत्क्रम मिल्स अनुपात में मानक सामान्य घनत्व के बजाय प्रयोग किया जाता है, इसलिए यहां हमारे पास है $\sigma ^{2}$ के बजाय $\sigma$.

फूरियर रूपांतरण और विशिष्ट कार्य

एक सामान्य घनत्व का फूरियर रूपांतरण $f$ मतलब के साथ $\mu$ और मानक विचलन $\sigma$ है

${\hat {f}}(t)=\int _{-\infty }^{\infty }f(x)e^{-itx}\,dx=e^{-i\mu t}e^{-{\frac {1}{2}}(\sigma t)^{2}}$

कहाँ $i$ काल्पनिक इकाई है। यदि माध्य $\mu =0$, पहला कारक 1 है, और फूरियर ट्रांसफॉर्म एक स्थिर कारक के अतिरिक्त आवृत्ति डोमेन पर एक सामान्य घनत्व है, मतलब 0 और मानक विचलन के साथ $1/\sigma$. विशेष रूप से, मानक सामान्य वितरण $\varphi$ एक फूरियर रूपांतरण है#फूरियर रूपांतरण के ईजेनफंक्शंस।

प्रायिकता सिद्धांत में, एक वास्तविक-मूल्यवान रैंडम चर के प्रायिकता वितरण का फूरियर रूपांतरण $X$ विशेषता कार्य (संभावना सिद्धांत) से निकटता से जुड़ा हुआ है $\varphi _{X}(t)$ उस चर का, जिसे के अपेक्षित मूल्य के रूप में परिभाषित किया गया है $e^{itX}$, वास्तविक चर के एक समारोह के रूप में $t$ (फूरियर रूपांतरण की आवृत्ति पैरामीटर)। इस परिभाषा को विश्लेषणात्मक रूप से एक जटिल-मूल्य चर तक बढ़ाया जा सकता है $t$. दोनों के बीच संबंध है:

$\varphi _{X}(t)={\hat {f}}(-t)$

पल और संचयी जनरेटिंग फ़ंक्शन

एक वास्तविक रैंडम चर का क्षण उत्पन्न करने वाला कार्य $X$ का अपेक्षित मूल्य है $e^{tX}$, वास्तविक पैरामीटर के एक समारोह के रूप में $t$. घनत्व के साथ सामान्य वितरण के लिए $f$, अर्थ $\mu$ और विचलन $\sigma$, क्षण उत्पन्न करने वाला कार्य मौजूद है और इसके बराबर है

$M(t)=\operatorname {E} [e^{tX}]={\hat {f}}(it)=e^{\mu t}e^{{\tfrac {1}{2}}\sigma ^{2}t^{2}}$

संचयी उत्पादन समारोह पल जनरेटिंग फ़ंक्शन का लघुगणक है, अर्थात्

$g(t)=\ln M(t)=\mu t+{\tfrac {1}{2}}\sigma ^{2}t^{2}$

चूँकि यह एक द्विघात बहुपद है $t$, केवल पहले दो संचयी अशून्य हैं, अर्थात् माध्य$\mu$ और भिन्नता$\sigma ^{2}$.

स्टीन ऑपरेटर और वर्ग

स्टीन की विधि के भीतर स्टीन ऑपरेटर और एक रैंडम चर का वर्ग $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ हैं ${\mathcal {A}}f(x)=\sigma ^{2}f'(x)-(x-\mu )f(x)$ और ${\mathcal {F}}$ सभी बिल्कुल निरंतर कार्यों का वर्ग $f:\mathbb {R} \to \mathbb {R} {\mbox{ such that }}\mathbb {E} [|f'(X)|]<\infty$.

शून्य-विचरण सीमा

सीमा में (गणित) जब $\sigma$ शून्य हो जाता है, प्रायिकता घनत्व $f(x)$ अंततः शून्य हो जाता है $x\neq \mu$, लेकिन यदि बिना सीमा के बढ़ता है $x=\mu$, जबकि इसका समाकल 1 के बराबर रहता है। इसलिए, सामान्य बंटन को साधारण फलन (गणित) के रूप में परिभाषित नहीं किया जा सकता जब $\sigma =0$.

चूंकि , सामान्य वितरण को एक सामान्यीकृत फ़ंक्शन के रूप में शून्य विचरण के साथ परिभाषित किया जा सकता है; विशेष रूप से, Dirac delta function|Dirac's delta function के रूप में $\delta$ माध्यम से अनुवादित $\mu$, वह है $f(x)=\delta (x-\mu ).$ इसका सीडीएफ तब अर्थ द्वारा अनुवादित हैवीसाइड स्टेप फंक्शन है $\mu$, अर्थात्

$F(x)={\begin{cases}0&{\text{if }}x<\mu \\1&{\text{if }}x\geq \mu \end{cases}}$

अधिकतम एन्ट्रापी

एक निर्दिष्ट माध्य के साथ वास्तविक पर सभी प्रायिकता डिस्ट्रीब्यूशन ों में से $\mu$ और विचरण$\sigma ^{2}$, सामान्य वितरण $N(\mu ,\sigma ^{2})$ अधिकतम एंट्रॉपी प्रायिकता वितरण वाला एक है। यदि $X$ प्रायिकता घनत्व समारोह के साथ एक सतत रैंडम चर है $f(x)$, फिर की एन्ट्रापी $X$ परिभाषित किया जाता है

$H(X)=-\int _{-\infty }^{\infty }f(x)\log f(x)\,dx$

कहाँ $f(x)\log f(x)$ कभी भी शून्य समझा जाता है $f(x)=0$. इस कार्यात्मकता को अधिकतम किया जा सकता है, इस बाधा के अधीन कि वितरण उचित रूप से सामान्य है और भिन्नता कैलकुस का उपयोग करके एक निर्दिष्ट भिन्नता है। दो लग्रेंज गुणक वाले एक समारोह को परिभाषित किया गया है:

$L=\int _{-\infty }^{\infty }f(x)\ln(f(x))\,dx-\lambda _{0}\left(1-\int _{-\infty }^{\infty }f(x)\,dx\right)-\lambda \left(\sigma ^{2}-\int _{-\infty }^{\infty }f(x)(x-\mu )^{2}\,dx\right)$

कहाँ $f(x)$ अभी के लिए, माध्य के साथ कुछ घनत्व फलन के रूप में माना जाता है $\mu$ और मानक विचलन $\sigma$.

अधिकतम एन्ट्रापी पर, एक छोटा बदलाव $\delta f(x)$ के बारे में $f(x)$ भिन्नता उत्पन्न करेगा $\delta L$ के बारे में $L$ जो 0 के बराबर है:

$0=\delta L=\int _{-\infty }^{\infty }\delta f(x)\left(\ln(f(x))+1+\lambda _{0}+\lambda (x-\mu )^{2}\right)\,dx$

चूंकि यह किसी भी छोटे के लिए होना चाहिए $\delta f(x)$, कोष्ठक में शब्द शून्य होना चाहिए और के लिए हल करना चाहिए $f(x)$ पैदावार:

$f(x)=e^{-\lambda _{0}-1-\lambda (x-\mu )^{2}}$

हल करने के लिए विवश समीकरणों का उपयोग करना $\lambda _{0}$ और $\lambda$ सामान्य वितरण का घनत्व देता है:

$f(x,\mu ,\sigma )={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$

एक सामान्य वितरण की एन्ट्रॉपी बराबर होती है

$H(X)={\tfrac {1}{2}}(1+\log(2\sigma ^{2}\pi ))$

अन्य गुण

1. If the characteristic function $\phi _{X}$ of some random variable $X$ is of the form $\phi _{X}(t)=\exp ^{Q(t)}$, where $Q(t)$ is a polynomial, then the Marcinkiewicz theorem (named after Józef Marcinkiewicz) asserts that $Q$ can be at most a quadratic polynomial, and therefore $X$ is a normal random variable. The consequence of this result is that the normal distribution is the only distribution with a finite number (two) of non-zero cumulants.
2. If $X$ and $Y$ are jointly normal and uncorrelated, then they are independent. The requirement that $X$ and $Y$ should be jointly normal is essential; without it the property does not hold.^[proof] For non-normal random variables uncorrelatedness does not imply independence.
3. The Kullback–Leibler divergence of one normal distribution $X_{1}\sim N(\mu _{1},\sigma _{1}^{2})$ from another $X_{2}\sim N(\mu _{2},\sigma _{2}^{2})$ is given by:
   $$D_{\mathrm {KL} }(X_{1}\,\|\,X_{2})={\frac {(\mu _{1}-\mu _{2})^{2}}{2\sigma _{2}^{2}}}+{\frac {1}{2}}\left({\frac {\sigma _{1}^{2}}{\sigma _{2}^{2}}}-1-\ln {\frac {\sigma _{1}^{2}}{\sigma _{2}^{2}}}\right)$$

   The Hellinger distance between the same distributions is equal to Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "ई" found.in 3:1"): {\displaystyle H^2(X_1,X_2) = 1 - \sqrt{\frac{2\sigma_1\sigma_2}{\sigma_1^2+\sigma_2^2}} ई^{-\frac{1}{4}\frac{(\mu_1-\mu_2)^2}{\sigma_1^2+\sigma_2^2}} </ गणित> |4= एक सामान्य वितरण के लिए [[फिशर सूचना मैट्रिक्स]] w.r.t. गणित> \ mu</ गणित> और गणित>\sigma^2} विकर्ण है और रूप लेता है गणित प्रदर्शन = ब्लॉक>

      \mathcal I (\mu, \sigma^2) = \begin{pmatrix} \frac{1}{\sigma^2} & 0 \\ 0 & \frac{1}{2\sigma^4} \end{ pmatrix}
   

   </ गणित>
4. एक सामान्य बंटन के माध्य से पहले का संयुग्मी एक अन्य सामान्य बंटन है। विशेष रूप से, अगर $x_{1},\ldots ,x_{n}$ आईआईडी हैं $\sim N(\mu ,\sigma ^{2})$ और पूर्व है $\mu \sim N(\mu _{0},\sigma _{0}^{2})$, फिर के अनुमानक के लिए पश्च वितरण $\mu$ होगा
   $$\mu \mid x_{1},\ldots ,x_{n}\sim {\mathcal {N}}\left({\frac {{\frac {\sigma ^{2}}{n}}\mu _{0}+\sigma _{0}^{2}{\bar {x}}}{{\frac {\sigma ^{2}}{n}}+\sigma _{0}^{2}}},\left({\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}\right)^{-1}\right)$$
5. सामान्य वितरण का परिवार न केवल एक घातीय परिवार (ईएफ) बनाता है, बल्कि वास्तव में द्विघात विचरण समारोह (NEF-QVF) के साथ एक प्राकृतिक घातीय परिवार (एनईएफ) बनाता है। सामान्य वितरण के कई गुण एनईएफ-क्यूवीएफ वितरण, एनईएफ वितरण, या ईएफ वितरण के गुणों को आम तौर पर सामान्यीकृत करते हैं। एनईएफ-क्यूवीएफ वितरण में 6 परिवार शामिल हैं, जिनमें पोइसन, गामा, द्विपद और नकारात्मक द्विपद वितरण शामिल हैं, जबकि संभाव्यता और आंकड़ों में अध्ययन किए गए कई आम परिवार एनईएफ या ईएफ हैं।
6. सूचना ज्यामिति में, सामान्य वितरण का परिवार निरंतर वक्रता के साथ एक सांख्यिकीय कई गुना बनाता है $-1$. (±1)-कनेक्शन के संबंध में एक ही परिवार कई गुना फ्लैट है $\nabla ^{(e)}$ और $\nabla ^{(m)}$.

संबंधित डिस्ट्रीब्यूशन

केंद्रीय सीमा प्रमेय

जैसे-जैसे असतत घटनाओं की संख्या बढ़ती है, फ़ंक्शन एक सामान्य वितरण जैसा दिखने लगता है

प्रायिकता घनत्व कार्यों की तुलना, $p(k)$ के योग के लिए $n$ वृद्धि के साथ एक सामान्य वितरण के लिए उनके अभिसरण को दिखाने के लिए निष्पक्ष 6-पक्षीय पासा $na$, केंद्रीय सीमा प्रमेय के अनुसार। नीचे-दाएं ग्राफ़ में, पिछले ग्राफ़ के स्मूथ प्रोफाइल को सामान्य वितरण (ब्लैक कर्व) के साथ पुन: व्यवस्थित, आरोपित और तुलना की जाती है।

Main article: Central limit theorem

केंद्रीय सीमा प्रमेय कहता है कि कुछ (काफी सामान्य) स्थितियों के अनुसार , कई रैंडम चरों के योग का लगभग सामान्य वितरण होता है । अधिक विशेष रूप से, कहाँ $X_{1},\ldots ,X_{n}$ स्वतंत्र और समान रूप से समान डिस्ट्रीब्यूशन , शून्य माध्य और विचरण के साथ समान रूप से वितरित रैंडम चर हैं $\sigma ^{2}$ और $Z$ उनकी है मतलब द्वारा बढ़ाया गया ${\sqrt {n}}$

$Z={\sqrt {n}}\left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)$

फिर ऐसे $n$ बढ़ जाती है, की संभावना वितरण $Z$ शून्य माध्य और विचरण के साथ सामान्य वितरण की ओर प्रवृत्त होता है $\sigma ^{2}$.

प्रमेय को चरों तक बढ़ाया जा सकता है $(X_{i})$ जो स्वतंत्र नहीं हैं और/या समान रूप से वितरित नहीं हैं यदि कुछ बाधाओं को निर्भरता की डिग्री और वितरण के क्षणों पर रखा जाता है।

कई परीक्षण आँकड़े, स्कोर (सांख्यिकी), और अनुमानक अभ्यास में सामना करते हैं, उनमें कुछ रैंडम चर के योग होते हैं, और इससे भी अधिक अनुमानकों को प्रभाव समारोह (सांख्यिकी) के उपयोग के माध्यम से रैंडम चर के योग के रूप में दर्शाया जा सकता है। केंद्रीय सीमा प्रमेय का अर्थ है कि उन सांख्यिकीय मापदंडों में असमान रूप से सामान्य वितरण होंगे।

केंद्रीय सीमा प्रमेय का अर्थ यह भी है कि कुछ डिस्ट्रीब्यूशन ों को सामान्य वितरण द्वारा अनुमानित किया जा सकता है, उदाहरण के लिए:

• द्विपद वितरण $B(n,p)$ माध्य के साथ डी मोइवर-लाप्लास प्रमेय है $np$ और विचरण $np(1-p)$ बड़े के लिए $n$ और के लिए $p$ 0 या 1 के बहुत करीब नहीं।
• पैरामीटर के साथ प्वासों वितरण $\lambda$ औसत के साथ लगभग सामान्य है $\lambda$ और विचरण $\lambda$, के बड़े मूल्यों के लिए $\lambda$.
• ची-वर्ग वितरण $\chi ^{2}(k)$ औसत के साथ लगभग सामान्य है $k$ और विचरण $2k$, बड़े के लिए $k$.
• छात्र का टी-वितरण $t(\nu )$ माध्य 0 और प्रसरण 1 के साथ लगभग सामान्य है जब $\nu$ बड़ी है।

क्या ये सन्निकटन पर्याप्त रूप से सटीक हैं, यह उस उद्देश्य पर निर्भर करता है जिसके लिए उनकी आवश्यकता है, और सामान्य वितरण के अभिसरण की दर। सामान्यतः ऐसा होता है कि इस तरह के अनुमान वितरण के अंत में कम सटीक होते हैं।

केंद्रीय सीमा प्रमेय में सन्निकटन त्रुटि के लिए एक सामान्य ऊपरी सीमा बेरी-एसेन प्रमेय द्वारा दी गई है, सन्निकटन में सुधार एडगेवर्थ विस्तार द्वारा दिया गया है।

इस प्रमेय का उपयोग गॉसियन शोर के रूप में कई समान शोर स्रोतों के योग को सही ठहराने के लिए भी किया जा सकता है। एडब्ल्यूजीएन देखें।

सामान्य चर के संचालन और कार्य

a: किसी फ़ंक्शन का प्रायिकता घनत्व $\cos x^{2}$ एक सामान्य चर का $x$ साथ $\mu =-2$ और $\sigma =3$. बी: एक समारोह की संभावना घनत्व $x^{y}$ दो सामान्य चर के $x$ और $y$, कहाँ $\mu _{x}=1$, $\mu _{y}=2$, $\sigma _{x}=0.1$, $\sigma _{y}=0.2$, और $\rho _{xy}=0.8$. सी: दो सहसंबद्ध सामान्य चर के दो कार्यों की संयुक्त संभावना घनत्व का हीट मैप $x$ और $y$, कहाँ $\mu _{x}=-2$, $\mu _{y}=5$, $\sigma _{x}^{2}=10$, $\sigma _{y}^{2}=20$, और $\rho _{xy}=0.495$. डी: एक समारोह की संभावना घनत्व ${\textstyle \sum _{i=1}^{4}\vert x_{i}\vert }$ 4 iid मानक सामान्य चर के। इनकी गणना रे-ट्रेसिंग की संख्यात्मक विधि द्वारा की जाती है।

प्रायिकता घनत्व समारोह, संचयी वितरण समारोह, और एक या एक से अधिक स्वतंत्र या सहसंबद्ध सामान्य चर के किसी भी समारोह के व्युत्क्रम संचयी वितरण समारोह की गणना रे-ट्रेसिंग की संख्यात्मक विधि से की जा सकती है। (मैटलैब कोड)। निम्नलिखित अनुभागों में हम कुछ विशेष स्थितियो को देखते हैं।

एकल सामान्य चर पर संचालन

यदि $X$ माध्य के साथ सामान्य रूप से वितरित किया जाता है $\mu$ और विचरण $\sigma ^{2}$, तब

• $aX+b$, किसी भी वास्तविक संख्या के लिए $a$ और $b$, भी सामान्य रूप से माध्य के साथ वितरित किया जाता है $a\mu +b$ और मानक विचलन $|a|\sigma$. अर्थात्, रैखिक परिवर्तनों के अनुसार सामान्य वितरण का परिवार बंद है।
• का घातांक $X$ वितरित किया जाता है लॉग-सामान्य वितरण | लॉग-सामान्य रूप से: e^X ~ ln(N (μ, σ²)).
• का पूर्ण मूल्य $X$ सामान्य वितरण को मोड़ दिया है: |X| ~ N_f (μ, σ²). यदि $\mu =0$ इसे अर्ध-सामान्य वितरण के रूप में जाना जाता है।
• सामान्यीकृत अवशिष्टों का निरपेक्ष मान, |X - μ|/σ, में स्वतंत्रता की एक डिग्री के साथ ची वितरण है: $|X-\mu |/\sigma \sim \chi _{1}$.
• X/σ के वर्ग में स्वतंत्रता की एक डिग्री के साथ गैर-केन्द्रीय ची-वर्ग वितरण है: ${\textstyle X^{2}/\sigma ^{2}\sim \chi _{1}^{2}(\mu ^{2}/\sigma ^{2})}$. यदि $\mu =0$, बंटन को केवल काई-वर्ग बंटन|ची-वर्ग कहा जाता है।
• एक सामान्य चर की लॉग संभावना $x$ बस इसकी प्रायिकता घनत्व समारोह का लघुगणक है:
  $$\ln p(x)=-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}-\ln \left(\sigma {\sqrt {2\pi }}\right)=-{\frac {1}{2}}z^{2}-\ln \left(\sigma {\sqrt {2\pi }}\right).$$
  चूंकि यह एक मानक सामान्य चर का एक स्केल्ड और स्थानांतरित वर्ग है, इसे स्केल्ड और शिफ्ट किए गए ची-स्क्वायर वितरण | ची-स्क्वेर्ड चर के रूप में वितरित किया जाता है।
• वेरिएबल एक्स का वितरण एक अंतराल [ए, बी] तक सीमित है जिसे छोटा सामान्य वितरण कहा जाता है।
• (एक्स - μ)⁻² का लेवी वितरण स्थान 0 और स्केल σ के साथ है^{-2</सुप>.}

दो स्वतंत्र सामान्य चर पर संचालन

• यदि $X_{1}$ और $X_{2}$ साधन के साथ दो स्वतंत्रता ( प्रायिकता सिद्धांत) सामान्य रैंडम चर हैं $\mu _{1}$, $\mu _{2}$ और मानक विचलन $\sigma _{1}$, $\sigma _{2}$, फिर उनका योग $X_{1}+X_{2}$ भी सामान्य रूप से वितरित किया जाएगा,^{सामान्य रूप से वितरित रैंडम चर का योग|[सबूत]} माध्य के साथ $\mu _{1}+\mu _{2}$ और विचरण $\sigma _{1}^{2}+\sigma _{2}^{2}$.
• विशेष रूप से, यदि $X$ और $Y$ शून्य माध्य और विचरण के साथ स्वतंत्र सामान्य विचलन हैं $\sigma ^{2}$, तब $X+Y$ और $X-Y$ शून्य माध्य और विचरण के साथ स्वतंत्र और सामान्य रूप से वितरित भी हैं $2\sigma ^{2}$. यह ध्रुवीकरण की पहचान का एक विशेष स्थिति है।
• यदि $X_{1}$, $X_{2}$ माध्य के साथ दो स्वतंत्र सामान्य विचलन हैं $\mu$ और विचलन $\sigma$, और $a$, $b$ मनमाना वास्तविक संख्याएं हैं, फिर चर
  $$X_{3}={\frac {aX_{1}+bX_{2}-(a+b)\mu }{\sqrt {a^{2}+b^{2}}}}+\mu$$
  भी सामान्य रूप से माध्य के साथ वितरित किया जाता है $\mu$ और विचलन $\sigma$. यह इस प्रकार है कि सामान्य वितरण स्थिर वितरण है (घातांक के साथ $\alpha =2$).

दो स्वतंत्र मानक सामान्य चर पर संचालन

यदि $X_{1}$ और $X_{2}$ माध्य 0 और प्रसरण 1 के साथ दो स्वतंत्र मानक सामान्य रैंडम चर हैं

• उनका योग और अंतर सामान्य रूप से माध्य शून्य और विचरण दो के साथ वितरित किया जाता है: $X_{1}\pm X_{2}\sim N(0,2)$.
• उनका उत्पाद $Z=X_{1}X_{2}$ उत्पाद वितरण # स्वतंत्र केंद्रीय-सामान्य वितरण का अनुसरण करता है घनत्व समारोह के साथ $f_{Z}(z)=\pi ^{-1}K_{0}(|z|)$ कहाँ $K_{0}$ मैकडोनाल्ड समारोह है। यह वितरण शून्य के आसपास सममित है, पर असीम है $z=0$, और विशेषता कार्य (संभावना सिद्धांत) है $\phi _{Z}(t)=(1+t^{2})^{-1/2}$.
• उनका अनुपात मानक कॉची वितरण का अनुसरण करता है: $X_{1}/X_{2}\sim \operatorname {Cauchy} (0,1)$.
• उनका यूक्लिडियन मानदंड ${\sqrt {X_{1}^{2}+X_{2}^{2}}}$ रेले वितरण है।

कई स्वतंत्र सामान्य चर पर संचालन

• स्वतंत्र सामान्य विचलन का कोई भी रैखिक संयोजन एक सामान्य विचलन है।
• यदि $X_{1},X_{2},\ldots ,X_{n}$ स्वतंत्र मानक सामान्य रैंडम चर हैं, तो उनके वर्गों के योग में ची-वर्ग वितरण है $n$ स्वतंत्रता की कोटियां
  $$X_{1}^{2}+\cdots +X_{n}^{2}\sim \chi _{n}^{2}.$$
• यदि $X_{1},X_{2},\ldots ,X_{n}$ साधन के साथ सामान्य रूप से वितरित रैंडम चर स्वतंत्र हैं $\mu$ और प्रसरण $\sigma ^{2}$, तो उनका नमूना माध्य नमूना मानक विचलन से स्वतंत्र है, जिसे बसु के प्रमेय या कोचरन के प्रमेय का उपयोग करके प्रदर्शित किया जा सकता है। इन दो मात्राओं के अनुपात में छात्र का टी-वितरण होता है $n-1$ स्वतंत्रता की कोटियां:
  $$t={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}={\frac {{\frac {1}{n}}(X_{1}+\cdots +X_{n})-\mu }{\sqrt {{\frac {1}{n(n-1)}}\left[(X_{1}-{\overline {X}})^{2}+\cdots +(X_{n}-{\overline {X}})^{2}\right]}}}\sim t_{n-1}.$$
• यदि $X_{1},X_{2},\ldots ,X_{n}$, $Y_{1},Y_{2},\ldots ,Y_{m}$ स्वतंत्र मानक सामान्य रैंडम चर हैं, तो वर्गों के सामान्यीकृत योगों का अनुपात होता है F-distribution साथ (n, m) स्वतंत्रता की कोटियां:
  $$F={\frac {\left(X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^{2}\right)/n}{\left(Y_{1}^{2}+Y_{2}^{2}+\cdots +Y_{m}^{2}\right)/m}}\sim F_{n,m}.$$

एकाधिक सहसंबद्ध सामान्य चर पर संचालन

• सामान्य सदिश का द्विघात रूप, यानी द्विघात फलन ${\textstyle q=\sum x_{i}^{2}+\sum x_{j}+c}$ एकाधिक स्वतंत्र या सहसंबद्ध सामान्य चर का, एक सामान्यीकृत ची-स्क्वायर वितरण है। सामान्यीकृत ची-स्क्वायर चर।

घनत्व समारोह पर संचालन

विभाजित सामान्य वितरण को विभिन्न सामान्य डिस्ट्रीब्यूशन ों के घनत्व कार्यों के स्केल किए गए वर्गों में शामिल होने और एक में एकीकृत करने के लिए घनत्व को कम करने के संदर्भ में सबसे सीधे परिभाषित किया गया है। छोटा किया गया सामान्य वितरण एकल घनत्व फ़ंक्शन के एक खंड को फिर से स्केल करने का परिणाम है।

अनंत विभाज्यता और क्रैमर की प्रमेय

किसी भी सकारात्मक पूर्णांक के लिए ${\text{n}}$, माध्य के साथ कोई भी सामान्य वितरण $\mu$ और विचरण $\sigma ^{2}$ के योग का वितरण है ${\text{n}}$ स्वतंत्र सामान्य विचलन, प्रत्येक माध्य के साथ ${\frac {\mu }{n}}$ और विचरण ${\frac {\sigma ^{2}}{n}}$. इस संपत्ति को अनंत विभाज्यता ( प्रायिकता ) कहा जाता है। इसके विपरीत यदि $X_{1}$ और $X_{2}$ स्वतंत्र रैंडम चर और उनकी राशि हैं $X_{1}+X_{2}$ एक सामान्य वितरण है, फिर दोनों $X_{1}$ और $X_{2}$ सामान्य विचलन होना चाहिए। इस परिणाम को क्रैमर के अपघटन प्रमेय के रूप में जाना जाता है, और यह कहने के बराबर है कि दो डिस्ट्रीब्यूशन ों का कनवल्शन सामान्य है यदि और केवल यदि दोनों सामान्य हैं। क्रैमर के प्रमेय का तात्पर्य है कि स्वतंत्र गैर-गाऊसी चरों के एक रैखिक संयोजन का कभी भी बिल्कुल सामान्य वितरण नहीं होता है , चूंकि यह मनमाने ढंग से निकटता से संपर्क कर सकता है।

बर्नस्टीन की प्रमेय

बर्नस्टीन के प्रमेय में कहा गया है कि यदि $X$ और $Y$ स्वतंत्र हैं और $X+Y$ और $X-Y$ स्वतंत्र भी हैं, तो X और Y दोनों का सामान्य बंटन अनिवार्य रूप से होना चाहिए। अधिक सामान्यतः, यदि $X_{1},\ldots ,X_{n}$ स्वतंत्र रैंडम चर हैं, फिर दो भिन्न रैखिक संयोजन ${\textstyle \sum {a_{k}X_{k}}}$ और ${\textstyle \sum {b_{k}X_{k}}}$स्वतंत्र होता है यदि और केवल यदि सभी $X_{k}$ सामान्य हैं और ${\textstyle \sum {a_{k}b_{k}\sigma _{k}^{2}=0}}$, कहाँ $\sigma _{k}^{2}$ के विचरण को दर्शाता है $X_{k}$.

एक्सटेंशन

सामान्य वितरण की धारणा, प्रायिकता सिद्धांत में सबसे महत्वपूर्ण डिस्ट्रीब्यूशन ों में से एक होने के नाते, यूनीवेरिएट (जो कि एक आयामी है) स्थितियो े (केस 1) के मानक ढांचे से बहुत आगे तक बढ़ा दी गई है। इन सभी विस्तारों को सामान्य या गाऊसी कानून भी कहा जाता है, इसलिए नामों में एक निश्चित अस्पष्टता मौजूद है।

• मल्टवेरीेंएट सामान्य वितरण के-आयामी यूक्लिडियन अंतरिक्ष में गॉसियन कानून का वर्णन करता है। एक सदिश X ∈ R^k बहुभिन्नरूपी-सामान्य रूप से वितरित है यदि इसके घटकों का कोई रैखिक संयोजन है Σ^k
  _j=1a_j X_j एक (अविभाजित) सामान्य वितरण है। X का प्रसरण एक k×k सममित सकारात्मक-निश्चित आव्यूह V है। मल्टवेरीेंएट सामान्य वितरण अण्डाकार वितरण का एक विशेष स्थिति है। जैसे, k = 2 स्थितियो े में इसका आइसो-घनत्व लोकी दीर्घवृत्त हैं और मनमाने k के स्थितियो े में दीर्घवृत्त हैं।
• संशोधित गाऊसी वितरण सामान्य वितरण का एक संशोधित संस्करण है जिसमें सभी नकारात्मक तत्व 0 पर रीसेट हो जाते हैं
• जटिल सामान्य वितरण जटिल सामान्य सदिश से संबंधित है। एक जटिल वेक्टर X ∈ C^k सामान्य कहा जाता है यदि इसके वास्तविक और काल्पनिक दोनों घटक संयुक्त रूप से 2k-आयामी मल्टवेरीेंएट सामान्य वितरण रखते हैं। X की प्रसरण-सहप्रसरण संरचना को दो आव्यूहों द्वारा वर्णित किया गया है: प्रसरण आव्यूह Γ, और संबंध आव्यूह C।
• आव्यूह सामान्य वितरण सामान्य रूप से वितरित आव्यूह के स्थितियो े का वर्णन करता है।
• गॉसियन प्रक्रियाएं सामान्य रूप से वितरित स्टोकेस्टिक प्रक्रियाएं हैं। इन्हें कुछ अनंत-आयामी हिल्बर्ट अंतरिक्ष H के तत्वों के रूप में देखा जा सकता है, और इस प्रकार स्थितियो े के लिए मल्टवेरीेंएट सामान्य सदिश के अनुरूप हैं k = ∞. एक रैंडम तत्व h ∈ H किसी भी स्थिरांक के लिए सामान्य कहा जाता है a ∈ H स्केलर उत्पाद (a, h) एक (अविभाजित) सामान्य वितरण है। ऐसे गॉसियन रैंडम तत्व की विचरण संरचना को रैखिक सहप्रसरण के संदर्भ में वर्णित किया जा सकता है operator K: H → H. कई गाऊसी प्रक्रियाएँ अपने स्वयं के नाम रखने के लिए काफी लोकप्रिय हुईं:
  • वीनर प्रक्रिया,
  • ब्राउनियन पुल,
  • ऑर्स्टीन-उहलेनबेक प्रक्रिया।
• गॉसियन क्यू-वितरण एक सार गणितीय निर्माण है जो सामान्य वितरण के क्यू-एनालॉग का प्रतिनिधित्व करता है।
• क्ष-गाऊसी गॉसियन वितरण का एक एनालॉग है, इस अर्थ में कि यह सॉलिस एंट्रॉपी को अधिकतम करता है, और एक प्रकार का सॉलिस वितरण है। ध्यान दें कि यह वितरण उपरोक्त गॉसियन q-वितरण से भिन्न है।
• कनियादकिस गॉसियन वितरण | कनियादकिस κ-गाऊसी वितरण गॉसियन वितरण का एक सामान्यीकरण है जो कनियादकिस डिस्ट्रीब्यूशन ों में से एक होने के नाते, कनियादकिस आंकड़ों से उत्पन्न होता है।

एक रैंडम चर X में एक वितरण होने पर दो-टुकड़ा सामान्य वितरण होता है

$f_{X}(x)=N(\mu ,\sigma _{1}^{2}){\text{ if }}x\leq \mu$

$f_{X}(x)=N(\mu ,\sigma _{2}^{2}){\text{ if }}x\geq \mu$

जहां μ माध्य है और σ₁ और पी₂ क्रमशः माध्य के बाएँ और दाएँ वितरण के मानक विचलन हैं।

इस वितरण का माध्य, विचरण और तीसरा केंद्रीय क्षण निर्धारित किया गया है

$\operatorname {E} (X)=\mu +{\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})$

$\operatorname {V} (X)=\left(1-{\frac {2}{\pi }}\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}$

$\operatorname {T} (X)={\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})\left[\left({\frac {4}{\pi }}-1\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}\right]$

जहाँ E(X), V(X) और T(X) क्रमशः माध्य, विचरण और तीसरा केंद्रीय क्षण हैं।

गॉसियन कानून के मुख्य व्यावहारिक उपयोगों में से एक व्यवहार में आने वाले कई अलग-भिन्न रैंडम चरों के अनुभवजन्य डिस्ट्रीब्यूशन ों को मॉडल करना है। ऐसे स्थितियो े में एक संभावित विस्तार वितरण का एक समृद्ध परिवार होता है , जिसमें दो से अधिक पैरामीटर होंगे और इसलिए अनुभवजन्य वितरण को अधिक सटीक रूप से फिट करने में सक्षम होंगे। ऐसे एक्सटेंशन के उदाहरण हैं:

• पियर्सन बंटन — प्रायिकता बंटन का एक चार-पैरामीटर परिवार जो विभिन्न तिरछापन और कर्टोसिस मूल्यों को शामिल करने के लिए सामान्य कानून का विस्तार करता है।
• सामान्यीकृत सामान्य डिस्ट्रीब्यूशन , जिसे घातीय शक्ति वितरण के रूप में भी जाना जाता है, मोटे या पतले स्पर्शोन्मुख व्यवहार के साथ वितरण पूंछ की अनुमति देता है।

सांख्यिकीय निष्कर्ष

मापदंडों का अनुमान

See also: Maximum likelihood § Continuous distribution, continuous parameter space; and Gaussian function § Estimation of parameters

अधिकांशतः ऐसा होता है कि हम सामान्य वितरण के मापदंडों को नहीं जानते हैं, बल्कि इसके बजाय उन्हें अनुमान सिद्धांत करना चाहते हैं। यानी सैंपल लेना $(x_{1},\ldots ,x_{n})$ एक सामान्य से $N(\mu ,\sigma ^{2})$ जनसंख्या हम मापदंडों के अनुमानित मूल्यों को सीखना चाहेंगे $\mu$ और $\sigma ^{2}$. इस समस्या का मानक दृष्टिकोण अधिकतम संभावना विधि है, जिसके लिए लॉग-लाइबिलिटी फ़ंक्शन को अधिकतम करने की आवश्यकता होती है:

$\ln {\mathcal {L}}(\mu ,\sigma ^{2})=\sum _{i=1}^{n}\ln f(x_{i}\mid \mu ,\sigma ^{2})=-{\frac {n}{2}}\ln(2\pi )-{\frac {n}{2}}\ln \sigma ^{2}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}.$

के संबंध में डेरिवेटिव लेना $\mu$ और $\sigma ^{2}$ और पहले क्रम की स्थिति के परिणामी सिस्टम को हल करने से अधिकतम संभावना अनुमान प्राप्त होता है:

${\hat {\mu }}={\overline {x}}\equiv {\frac {1}{n}}\sum _{i=1}^{n}x_{i},\qquad {\hat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}.$

नमूना मतलब

See also: Standard error of the mean

अनुमानक <गणित शैली= लंबवत-संरेखण:-.3em >\textstyle\hat\mu</math> को नमूना माध्य कहा जाता है, क्योंकि यह सभी अवलोकनों का अंकगणितीय माध्य है। आँकड़ा <गणित शैली = लंबवत-संरेखण: 0 >\textstyle\overline{x}</math> पूर्ण आँकड़ा है और इसके लिए पर्याप्त आँकड़ा है गणित>\mu</math>, और इसलिए लेहमन-शेफ़े प्रमेय द्वारा, <गणित शैली= लंबवत-संरेखण:-.3em>\textstyle\hat\mu</math> समान रूप से न्यूनतम प्रसरण निष्पक्ष (UMVU) अनुमानक है . परिमित नमूनों में यह सामान्य रूप से वितरित किया जाता है:

${\hat {\mu }}\sim {\mathcal {N}}(\mu ,\sigma ^{2}/n).$

इस अनुमानक का प्रसरण व्युत्क्रम फिशर सूचना आव्यूह <गणित शैली = लंबवत-संरेखण: 0>\textstyle\mathcal{I}^{-1}</math> के μμ-तत्व के बराबर है। इसका तात्पर्य है कि अनुमानक कुशल अनुमानक | परिमित-नमूना कुशल है। व्यावहारिक महत्व का तथ्य यह है कि <गणित शैली= लंबवत-संरेखण:-.3em >\textstyle\hat\mu</math> की मानक त्रुटि (सांख्यिकी) <गणित शैली= लंबवत-संरेखण:-.3em के समानुपातिक है >\textstyle1/\sqrt{n}</math>, यानी, यदि कोई मानक त्रुटि को 10 के गुणक से घटाना चाहता है, तो उसे नमूने में अंकों की संख्या 100 के गुणक से बढ़ानी होगी। यह तथ्य है जनमत सर्वेक्षणों के लिए नमूना आकार और मोंटे कार्लो सिमुलेशन में परीक्षणों की संख्या निर्धारित करने में व्यापक रूप से उपयोग किया जाता है।

स्पर्शोन्मुख सिद्धांत (सांख्यिकी) के दृष्टिकोण से, <गणित शैली = लंबवत-संरेखण: - 3em>\textstyle\hat\mu</math> सुसंगत अनुमानक है, अर्थात, यह प्रायिकता में अभिसरण है $\mu$ जैसा $n\rightarrow \infty$. अनुमानक भी स्पर्शोन्मुख सामान्यता है, जो इस तथ्य का एक सरल परिणाम है कि यह परिमित नमूनों में सामान्य है:

${\sqrt {n}}({\hat {\mu }}-\mu )\,\xrightarrow {d} \,{\mathcal {N}}(0,\sigma ^{2}).$

नमूना विचरण

See also: Standard deviation § Estimation, and Variance § Estimation

अनुमानक <गणित शैली= लंबवत-संरेखण:0 >\textstyle\hat\sigma^2</math> को नमूना प्रसरण कहा जाता है, क्योंकि यह नमूने का प्रसरण है ( गणित>(x_1, \ldots, x_n)</गणित>)। व्यवहार में, <गणित शैली = लंबवत-संरेखण: 0>\textstyle\hat\sigma^2</math> के बजाय अधिकांशतः एक अन्य अनुमानक का उपयोग किया जाता है। यह अन्य अनुमानक निरूपित है $s^{2}$, और इसे नमूना विचरण भी कहा जाता है, जो शब्दावली में एक निश्चित अस्पष्टता का प्रतिनिधित्व करता है; इसका वर्गमूल $s$ नमूना मानक विचलन कहा जाता है। अनुमानक $s^{2}$ <गणित शैली= लंबवत-संरेखण:0 >\textstyle\hat\sigma^2</math> से भिन्न है (n − 1) भाजक में n के बजाय (तथाकथित बेसेल का सुधार):

$s^{2}={\frac {n}{n-1}}{\hat {\sigma }}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}.$

बीच में अंतर $s^{2}$ और <गणित शैली= लंबवत-संरेखण:0 >\textstyle\hat\sigma^2</math> बड़े n के लिए नगण्य रूप से छोटा हो जाता है'एस। चूंकि परिमित नमूनों में, के उपयोग के पीछे की प्रेरणा $s^{2}$ यह है कि यह अंतर्निहित पैरामीटर का निष्पक्ष अनुमानक है $\sigma ^{2}$, जबकि <गणित शैली= लंबवत-संरेखण:0 >\textstyle\hat\sigma^2</math> पक्षपातपूर्ण है। इसके अतिरिक्त , लेहमन-शेफ़े प्रमेय द्वारा अनुमानक गणित> एस ^ 2 </ गणित> समान रूप से न्यूनतम भिन्नता निष्पक्ष है (न्यूनतम-भिन्नता निष्पक्ष अनुमानक),जो इसे सभी निष्पक्ष लोगों के बीच सबसे अच्छा अनुमानक बनाता है। चूंकि यह दिखाया जा सकता है कि पक्षपाती अनुमानक <गणित शैली = लंबवत-संरेखण: 0>\textstyle\hat\sigma^2</math> से बेहतर है गणित> एस ^ 2 </ गणित> औसत चुकता त्रुटि (एमएसई) मानदंड के संदर्भ में। परिमित नमूनों में दोनों गणित>s^2</math> और <गणित शैली= लंबवत-संरेखण:0 >\textstyle\hat\sigma^2</math> के साथ स्केल किया हुआ ची-वर्ग वितरण है (n − 1) स्वतंत्रता की कोटियां:

$s^{2}\sim {\frac {\sigma ^{2}}{n-1}}\cdot \chi _{n-1}^{2},\qquad {\hat {\sigma }}^{2}\sim {\frac {\sigma ^{2}}{n}}\cdot \chi _{n-1}^{2}.$

इन भावों में से पहला दर्शाता है कि का विचरण $s^{2}$ के बराबर है $2\sigma ^{4}/(n-1)$, जो उलटा फ़िशर सूचना आव्यूह <गणित शैली = लंबवत-संरेखण: 0>\textstyle\mathcal{I}^{-1}</math> के σσ-तत्व से थोड़ा अधिक है। इस प्रकार, $s^{2}$ के लिए एक कुशल आकलनकर्ता नहीं है $\sigma ^{2}$, और इसके अतिरिक्त , चूंकि $s^{2}$ UMVU है, हम यह निष्कर्ष निकाल सकते हैं कि परिमित-नमूना कुशल अनुमानक के लिए $\sigma ^{2}$ मौजूद नहीं होना।

स्पर्शोन्मुख सिद्धांत को लागू करना, दोनों अनुमानक $s^{2}$ और <गणित शैली= लंबवत-संरेखण:0 >\textstyle\hat\sigma^2</math> संगत हैं, अर्थात वे प्रायिकता में अभिसरण करते हैं गणित>\sigma^2</math> नमूना आकार के रूप में गणित>n\rightarrow\infty</math>. दो अनुमानक भी दोनों स्पर्शोन्मुख रूप से सामान्य हैं:

${\sqrt {n}}({\hat {\sigma }}^{2}-\sigma ^{2})\simeq {\sqrt {n}}(s^{2}-\sigma ^{2})\,\xrightarrow {d} \,{\mathcal {N}}(0,2\sigma ^{4}).$

विशेष रूप से, दोनों अनुमानक विषम रूप से कुशल हैं $\sigma ^{2}$.

विश्वास अंतराल

See also: Studentization and 3-sigma rule

कोचरन के प्रमेय के अनुसार, सामान्य बंटन के लिए नमूने का मतलब <गणित शैली= लंबवत-संरेखण:-.3em >\textstyle\hat\mu</math> और नमूना प्रसरण s² स्वतंत्रता ( प्रायिकता सिद्धांत) हैं, जिसका अर्थ है कि उनके संयुक्त वितरण पर विचार करने से कोई लाभ नहीं हो सकता है। एक विलोम प्रमेय भी है: यदि एक नमूने में नमूना माध्य और नमूना विचरण स्वतंत्र हैं, तो नमूना सामान्य वितरण से आया होता है । तथाकथित टी-सांख्यिकी के निर्माण के लिए <गणित शैली = ऊर्ध्वाधर-संरेखण: -3em>\textstyle\hat\mu</math> और s के बीच की स्वतंत्रता को नियोजित किया जा सकता है:

गणित>

   t = \frac{\hat\mu-\mu}{s/\sqrt{n}} = \frac{\overline{x}-\mu}{\sqrt{\frac{1}{n(n-1) )}\sum(x_i-\overline{x})^2}} \sim t_{n-1}
 </ गणित>

इस मात्रा t में छात्र का t-बंटन है (n − 1) स्वतंत्रता की डिग्री, और यह एक सहायक आँकड़ा है (मापदंडों के मूल्य से स्वतंत्र)। इस t-सांख्यिकी के वितरण को बदलने से हमें μ के लिए विश्वास अंतराल का निर्माण करने की अनुमति मिलेगी; इसी तरह, χ को उल्टा करना² आँकड़ों का डिस्ट्रीब्यूशन ² हमें σ के लिए कॉन्फ़िडेंस इंटरवल देगा²:

$\mu \in \left[{\hat {\mu }}-t_{n-1,1-\alpha /2}{\frac {1}{\sqrt {n}}}s,{\hat {\mu }}+t_{n-1,1-\alpha /2}{\frac {1}{\sqrt {n}}}s\right],$

$\sigma ^{2}\in \left[{\frac {(n-1)s^{2}}{\chi _{n-1,1-\alpha /2}^{2}}},{\frac {(n-1)s^{2}}{\chi _{n-1,\alpha /2}^{2}}}\right],$

जहां टी_k,pऔर χ 2
k,p  t- और χ के pth मात्राएँ हैं²-वितरण क्रमशः। ये कॉन्फिडेंस इंटरवल आत्मविश्वास स्तर के होते हैं 1 − α, जिसका अर्थ है कि सच्चे मान μ और σ² प्रायिकता (या सार्थकता स्तर) α के साथ इन अंतरालों के बाहर आते हैं। व्यवहार में लोग सामान्यतः लेते हैं α = 5%, जिसके परिणामस्वरूप 95% विश्वास अंतराल होता है।

अनुमानित सूत्र $\textstyle {\hat {\mu }}$ और s के असिम्प्टोटिक वितरण से प्राप्त किए जा सकते हैं।²:

$\mu \in \left[{\hat {\mu }}-|z_{\alpha /2}|{\frac {1}{\sqrt {n}}}s,{\hat {\mu }}+|z_{\alpha /2}|{\frac {1}{\sqrt {n}}}s\right],$

$\sigma ^{2}\in \left[s^{2}-|z_{\alpha /2}|{\frac {\sqrt {2}}{\sqrt {n}}}s^{2},s^{2}+|z_{\alpha /2}|{\frac {\sqrt {2}}{\sqrt {n}}}s^{2}\right],$

अनुमानित सूत्र n के बड़े मानों के लिए मान्य हो जाते हैं, और मानक सामान्य क्वांटाइल्स z के बाद से मैन्युअल गणना के लिए अधिक सुविधाजनक होते हैं_α/2 एन पर निर्भर न हों। विशेष रूप से, का सबसे लोकप्रिय मूल्य α = 5%, का परिणाम |z_0.025| = 1.96.

सामान्यता परीक्षण

Main article: Normality tests

सामान्यता परीक्षण इस संभावना का आकलन करते हैं कि दिए गए डेटा सेट {x₁, ..., एक्स_n} सामान्य वितरण से आता है। आम तौर पर अशक्त परिकल्पना एच₀ यह है कि प्रेक्षण सामान्य रूप से अनिर्दिष्ट माध्य μ और विचरण σ के साथ वितरित किए जाते हैं², बनाम वैकल्पिक H_aकि वितरण मनमाना है। इस समस्या के लिए कई परीक्षण (40 से अधिक) तैयार किए गए हैं। उनमें से अधिक प्रमुख नीचे उल्लिखित हैं:

'नैदानिक ​​प्लॉट' अधिक सहज रूप से आकर्षक लेकिन एक ही समय में व्यक्तिपरक होते हैं, क्योंकि वे अशक्त परिकल्पना को स्वीकार या अस्वीकार करने के लिए अनौपचारिक मानवीय निर्णय पर भरोसा करते हैं।

• क्यू-क्यू प्लॉट, जिसे सामान्य प्रायिकता प्लॉट या रैंकिट प्लॉट के रूप में भी जाना जाता है - मानक सामान्य वितरण से संबंधित मात्राओं के अपेक्षित मूल्यों के विरुद्ध डेटा सेट से क्रमबद्ध मूल्यों का एक प्लॉट है। यही है, यह फॉर्म के बिंदु का एक प्लॉट है (Φ^-1(पृ_k), एक्स_(k)), जहां प्लॉटिंग पॉइंट पी_kपी के बराबर हैं_k= (k − α)/(n + 1 − 2α) और α एक समायोजन स्थिरांक है, जो 0 और 1 के बीच कुछ भी हो सकता है। यदि शून्य परिकल्पना सत्य है, तो प्लॉट किए गए बिंदुओं को लगभग एक सीधी रेखा पर स्थित होना चाहिए।
• पी-पी प्लॉट - क्यू-क्यू प्लॉट के समान, लेकिन बहुत कम बार उपयोग किया जाता है। इस पद्धति में बिंदुओं की साजिश रचने के होते हैं (Φ(z_(k)), पी_k), कहाँ $\textstyle z_{(k)}=(x_{(k)}-{\hat {\mu }})/{\hat {\sigma }}$. सामान्य रूप से वितरित डेटा के लिए यह प्लॉट (0, 0) और (1, 1) के बीच 45° रेखा पर स्थित होना चाहिए।

अच्छाई के योग्य परीक्षण:

क्षण-आधारित परीक्षण:

• डी'ऑगस्टिनो का के-स्क्वेर्ड परीक्षण
• जर्क-बेरा परीक्षण
• शापिरो-विल्क परीक्षण: यह इस तथ्य पर आधारित है कि क्यू-क्यू प्लॉट में रेखा का ढलान σ है। परीक्षण नमूना विचरण के मान के साथ उस ढलान के कम से कम वर्गों के अनुमान की तुलना करता है, और यदि ये दो मात्राएँ महत्वपूर्ण रूप से भिन्न हैं, तो अशक्त परिकल्पना को अस्वीकार कर देता है।

अनुभवजन्य वितरण समारोह के आधार पर परीक्षण:

• एंडरसन-डार्लिंग परीक्षण
• लिलिफ़ोर्स परीक्षण (कोल्मोगोरोव-स्मिर्नोव परीक्षण का एक रूपांतर)

सामान्य वितरण का बायेसियन विश्लेषण

सामान्य रूप से वितरित डेटा का बायेसियन विश्लेषण कई अलग-भिन्न संभावनाओं से जटिल है जिन पर विचार किया जा सकता है:

• या तो माध्य, या प्रसरण, या दोनों में से किसी को भी निश्चित मात्रा नहीं माना जा सकता है।
• जब भिन्नता अज्ञात होती है, तो विश्लेषण सीधे भिन्नता के संदर्भ में, या परिशुद्धता (सांख्यिकी), भिन्नता के पारस्परिक के संदर्भ में किया जा सकता है। सूत्रों को सटीकता के रूप में व्यक्त करने का कारण यह है कि अधिकांश स्थितियो का विश्लेषण सरल है।
• दोनों अविभाज्य और मल्टवेरीेंएट सामान्य वितरण स्थितियो पर विचार करने की आवश्यकता है।
• अज्ञात चर पर या तो संयुग्म पूर्व या अनुचित पूर्व वितरण रखा जा सकता है।
• बायेसियन रैखिक प्रतिगमन में स्थितियो का एक अतिरिक्त सेट होता है, जहां मूल मॉडल में डेटा को सामान्य रूप से वितरित माना जाता है, और सामान्य पुजारियों को प्रतिगमन गुणांक पर रखा जाता है। परिणामी विश्लेषण स्वतंत्र रूप से वितरित डेटा के मूल स्थितियो के समान है।

गैर-रैखिक-प्रतिगमन स्थितियो के सूत्रों को संयुग्मित पूर्व लेख में संक्षेपित किया गया है।

दो द्विघातों का योग

अदिश रूप

निम्नलिखित सहायक सूत्र पश्च वितरण अद्यतन समीकरणों को सरल बनाने के लिए उपयोगी है, जो अन्यथा काफी कठिन हो जाते हैं।

$a(x-y)^{2}+b(x-z)^{2}=(a+b)\left(x-{\frac {ay+bz}{a+b}}\right)^{2}+{\frac {ab}{a+b}}(y-z)^{2}$

यह समीकरण वर्गों का विस्तार करके, x में पदों को समूहित करके, और वर्ग को पूरा करके x में दो द्विघातों के योग को फिर से लिखता है। कुछ शर्तों से जुड़े जटिल निरंतर कारकों के बारे में निम्नलिखित पर ध्यान दें:

1. कारण ${\frac {ay+bz}{a+b}}$ y और z के भारित औसत का रूप है।
2. ${\frac {ab}{a+b}}={\frac {1}{{\frac {1}{a}}+{\frac {1}{b}}}}=(a^{-1}+b^{-1})^{-1}.$ इससे पता चलता है कि इस कारक को एक ऐसी स्थिति के परिणामस्वरूप माना जा सकता है जहां मात्राओं के गुणक व्युत्क्रम a और b सीधे जुड़ते हैं, इसलिए a और b को संयोजित करने के लिए, परिणाम को फिर से प्राप्त करना, जोड़ना और पुनः प्राप्त करना आवश्यक है। मूल इकाइयाँ। यह ठीक उसी तरह का ऑपरेशन है जो अनुकूल माध्य द्वारा किया जाता है, इसलिए यह आश्चर्यजनक नहीं है ${\frac {ab}{a+b}}$ a और b का आधा हार्मोनिक माध्य है।

सदिश रूप

दो वेक्टर चतुष्कोणों के योग के लिए एक समान सूत्र लिखा जा सकता है: यदि x, y, z लंबाई k के सदिश हैं, और A और B सममित आव्यूह हैं, आकार के व्युत्क्रमणीय आव्यूह $k\times k$, तब

${\begin{aligned}&(\mathbf {y} -\mathbf {x} )'\mathbf {A} (\mathbf {y} -\mathbf {x} )+(\mathbf {x} -\mathbf {z} )'\mathbf {B} (\mathbf {x} -\mathbf {z} )\\={}&(\mathbf {x} -\mathbf {c} )'(\mathbf {A} +\mathbf {B} )(\mathbf {x} -\mathbf {c} )+(\mathbf {y} -\mathbf {z} )'(\mathbf {A} ^{-1}+\mathbf {B} ^{-1})^{-1}(\mathbf {y} -\mathbf {z} )\end{aligned}}$

कहाँ

$\mathbf {c} =(\mathbf {A} +\mathbf {B} )^{-1}(\mathbf {A} \mathbf {y} +\mathbf {B} \mathbf {z} )$

ध्यान दें कि रूप x′ A x को द्विघात रूप कहा जाता है और यह एक अदिश (गणित) है:

$\mathbf {x} '\mathbf {A} \mathbf {x} =\sum _{i,j}a_{ij}x_{i}x_{j}$

दूसरे शब्दों में, यह x से तत्वों के जोड़े के उत्पादों के सभी संभावित संयोजनों को जोड़ता है, प्रत्येक के लिए एक भिन्न गुणांक के साथ। इसके अतिरिक्त , चूंकि $x_{i}x_{j}=x_{j}x_{i}$, केवल योग $a_{ij}+a_{ji}$ ए के किसी भी ऑफ-डायगोनल तत्वों के लिए मायने रखता है, और यह मानने में व्यापकता का कोई नुकसान नहीं है कि ए सममित आव्यूह है। इसके अतिरिक्त , यदि ए सममित है, तो फॉर्म $\mathbf {x} '\mathbf {A} \mathbf {y} =\mathbf {y} '\mathbf {A} \mathbf {x} .$

माध्य से भिन्नताओं का योग

एक अन्य उपयोगी सूत्र इस प्रकार है:

$$\sum _{i=1}^{n}(x_{i}-\mu )^{2}=\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}$$

कहाँ ${\textstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}.}$

ज्ञात विचरण के साथ

i.i.d के एक सेट के लिए सामान्य रूप से वितरित डेटा बिंदु X का आकार n है जहां प्रत्येक व्यक्तिगत बिंदु x अनुसरण करता है $x\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ ज्ञात विचरण σ के साथ², संयुग्म पूर्व वितरण भी सामान्य रूप से वितरित किया जाता है।

प्रसरण को परिशुद्धता (सांख्यिकी) के रूप में फिर से लिखकर, अर्थात τ = 1/σ का उपयोग करके इसे अधिक आसानी से दिखाया जा सकता है^{2</उप>। तो यदि $x\sim {\mathcal {N}}(\mu ,1/\tau )$ और $\mu \sim {\mathcal {N}}(\mu _{0},1/\tau _{0}),$ हम निम्नानुसार आगे बढ़ते हैं।}

सबसे पहले, संभावना कार्य है (उपरोक्त सूत्र का उपयोग माध्य से मतभेदों के योग के लिए):

${\begin{aligned}p(\mathbf {X} \mid \mu ,\tau )&=\prod _{i=1}^{n}{\sqrt {\frac {\tau }{2\pi }}}\exp \left(-{\frac {1}{2}}\tau (x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left(-{\frac {1}{2}}\tau \sum _{i=1}^{n}(x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right].\end{aligned}}$

फिर, हम निम्नानुसार आगे बढ़ते हैं:

${\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}$