3डी रोटेशन समूह

शास्त्रीय यांत्रिकी और ज्यामिति में, 3डी रोटेशन समूह, जिसे अधिकांशतः विशेष ऑर्थोगोनल समूह (3) से दर्शाया जाता है, त्रि-आयामी समिष्ट की उत्पत्ति (गणित) के बारे में सभी घुमावों का समूह (गणित) है। त्रि-आयामी समिष्ट $\mathbb {R} ^{3}$ फलन संरचना के संचालन के तहत आता है।

परिभाषा के अनुसार, मूल के बारे में घूर्णन परिवर्तन है जो मूल, यूक्लिडियन दूरी (इसलिए यह आइसोमेट्री है), और अभिविन्यास (अर्थात्, स्थान के हाथ के मुड़ को) को संरक्षित करता है। दो घूर्णनों को संयोजित करने से एक और घूर्णन होता है, प्रत्येक घूर्णन में अद्वितीय व्युत्क्रम फलन घूर्णन होता है, और पहचान मानचित्र घूर्णन की परिभाषा को संतुष्ट करता है। उपरोक्त गुणों (मिश्रित घुमावों की साहचर्य संपत्ति के साथ) के कारण, सभी घुमावों का समूह संरचना के तहत समूह (गणित) है।

प्रत्येक गैर-तुच्छ घूर्णन उसके घूर्णन अक्ष (मूल बिंदु से होकर जाने वाली रेखा) और उसके घूर्णन कोण द्वारा निर्धारित होता है। घूर्णन क्रमविनिमेय नहीं होते हैं (उदाहरण के लिए, x-y समतल में R 90° को यात्रा करने के बाद y-z समतल में S 90° को यात्रा करना R को यात्रा करने के समान नहीं है), जिससे 3डी घूर्णन समूह गैर-एबेलियन समूह बन जाता है। इसके अतिरिक्त, रोटेशन समूह में प्राकृतिक संरचना होती है जिसके लिए समूह संचालन सुचारू कार्य होता है, इसलिए यह वास्तव में झूठ समूह है। यह सघन समिष्ट है और इसका आयाम 3 है।

घूर्णन रैखिक परिवर्तन $\mathbb {R} ^{3}$ हैं और इसलिए इसे सदिश समष्टि के आधार पर बार आव्युह (गणित) द्वारा दर्शाया जा सकता है $\mathbb {R} ^{3}$ चुना गया है। विशेष रूप से, यदि हम लम्बवत आधार चुनते हैं $\mathbb {R} ^{3}$, प्रत्येक रोटेशन को ऑर्थोगोनल आव्युह द्वारा वर्णित किया गया है । ऑर्थोगोनल 3 × 3 आव्युह (यानी, वास्तविक प्रविष्टियों के साथ 3 × 3 मैट्रिक्स, जो इसके स्थानान्तरण से गुणा होने पर, पहचान आव्युह में परिणत होता है) निर्धारक 1 के साथ। समूह SO(3) इसलिए आव्युह गुणन के तहत इन आव्युह के समूह के साथ पहचाना जा सकता है। इन आव्यूहों को विशेष ऑर्थोगोनल आव्यूह के रूप में जाना जाता है, जो संकेतन SO(3) की व्याख्या करते हैं।

समूह SO(3) का उपयोग किसी वस्तु की संभावित घूर्णी समरूपता, साथ ही समिष्ट में किसी वस्तु के संभावित अभिविन्यास का वर्णन करने के लिए किया जाता है। इसके समूह निरूपण भौतिकी में महत्वपूर्ण हैं, जहां वे पूर्णांक स्पिन (भौतिकी) के प्राथमिक कणों का उत्पन्न होता है।

लंबाई और कोण

मात्र लंबाई को संरक्षित करने के अतिरिक्त, घूर्णन सदिशों के बीच के कोणों को भी संरक्षित करता है। यह इस तथ्य से पता चलता है कि दो सदिश यू और वी के बीच मानक डॉट उत्पाद हो सकता है जो केवल लंबाई के पूर्ण रूप में लिखा जा सकता है।

$$\mathbf {u} \cdot \mathbf {v} ={\frac {1}{2}}\left(\|\mathbf {u} +\mathbf {v} \|^{2}-\|\mathbf {u} \|^{2}-\|\mathbf {v} \|^{2}\right).$$

इसका परिणाम है कि $\mathbb {R} ^{3}$ में हर लंबाई संरक्षित रूपी रैखिक परिवर्तन डॉट उत्पन्न करता है, और इसलिए सदिश के बीच के कोण को भी संरक्षित करता है। घुमावों को अधिकांशतः रैखिक परिवर्तनों के रूप में परिभाषित किया जाता है जो $\mathbb {R} ^{3}$ पर आंतरिक गुणन को संरक्षित रखने के रूप में, जो उन्हें लंबाई को संरक्षित रखने की आवश्यकता के समान है।इस अधिक सामान्य दृष्टिकोण के उपचार के लिए "शास्त्रीय समूह" देखें, जहाँ SO(3) विशेष स्थितियों के रूप में प्रकट होता है।

ऑर्थोगोनल और रोटेशन मैट्रिक्स

Main articles: ऑर्थोगोनल आव्युह and रोटेशन आव्युह

प्रत्येक घूर्णन $\mathbb {R} ^{3}$ लंबात्मक आधार का मानचित्रण करता है। किसी अन्य दैहिक आधार पर। परिमित-आयामी सदिश स्थानों के किसी भी रैखिक परिवर्तन की तरह, रोटेशन को हमेशा आव्युह (गणित) द्वारा दर्शाया जा सकता है। होने देना R दिया गया घुमाव हो। मानक आधार के संबंध में e₁, e₂, e₃ का $\mathbb {R} ^{3}$ के कॉलम R द्वारा दिए गए हैं (Re₁, Re₂, Re₃). चूँकि मानक आधार लम्बवत् है, और तब से R कोणों और लंबाई, स्तंभों को सुरक्षित रखता है R और लंबात्मक आधार बनाएं। इस रूढ़िबद्धता की स्थिति को इस रूप में व्यक्त किया जा सकता है

$R^{\mathsf {T}}R=RR^{\mathsf {T}}=I,$

कहाँ R^T के स्थानान्तरण को दर्शाता है R और I है 3 × 3 शिनाख्त सांचा। वे आव्युह जिनके लिए यह गुण धारण करता है, ऑर्थोगोनल आव्युह कहलाते हैं। सबका समूह 3 × 3 ऑर्थोगोनल आव्युह को दर्शाया गया है O(3), और इसमें सभी उचित और अनुचित घुमाव शामिल हैं।

लंबाई को संरक्षित करने के अतिरिक्त, उचित घुमाव को अभिविन्यास को भी संरक्षित करना रखना आवश्यक है। आव्युह का निर्धारक सकारात्मक है या नकारात्मक, इसके अनुसार आव्युह अभिविन्यास को संरक्षित या उलट देगा। ऑर्थोगोनल आव्युह के लिए R, ध्यान दें कि det R^T = det R तात्पर्य (det R)² = 1, ताकि det R = ±1. निर्धारक के साथ ऑर्थोगोनल आव्युह का उपसमूह +1 को विशेष ऑर्थोगोनल समूह कहा जाता है, जिसे दर्शाया गया है SO(3).

इस प्रकार प्रत्येक घुमाव को इकाई निर्धारक के साथ ऑर्थोगोनल आव्युह द्वारा विशिष्ट रूप से दर्शाया जा सकता है। इसके अतिरिक्त, चूंकि घूर्णन की संरचना आव्युह गुणन से मेल खाती है, इसलिए घूर्णन समूह विशेष ऑर्थोगोनल समूह SO(3) के समरूपी है।

अनुचित घुमाव निर्धारक −1 के साथ ऑर्थोगोनल आव्युह के अनुरूप होते हैं, और वे समूह नहीं बनाते क्योंकि दो अनुचित घुमावों का गुणनफल उचित घुमाव होता है।

समूह संरचना

रोटेशन समूह फलन संरचना (या समकक्ष आव्युह उत्पाद) के अंतर्गत समूह (गणित) है। यह सामान्य रैखिक समूह का उपसमूह है जिसमें वास्तविक समन्वय समिष्ट के सभी उलटा आव्युह रैखिक परिवर्तन शामिल हैं । वास्तविक 3-समिष्ट $\mathbb {R} ^{3}$. इसके अतिरिक्त, घूर्णन समूह नॉनबेलियन समूह है। अर्थात्, घुमावों की रचना के क्रम से फर्क पड़ता है। उदाहरण के लिए, सकारात्मक x-अक्ष के चारों ओर चौथाई चक्कर और उसके बाद सकारात्मक y-अक्ष के चारों ओर चौथाई चक्कर, पहले y और फिर x के चारों ओर घूमने से प्राप्त घुमाव से भिन्न घूर्णन है।

ऑर्थोगोनल समूह, जिसमें सभी उचित और अनुचित घुमाव शामिल हैं, प्रतिबिंबों द्वारा उत्पन्न होता है। प्रत्येक उचित घुमाव दो प्रतिबिंबों की संरचना है, जो कार्टन-ड्युडोने प्रमेय का विशेष स्थितियों है।

परिमित उपसमूहों का पूर्ण वर्गीकरण

के परिमित उपसमूह $\mathrm {SO} (3)$ पूर्णतः वर्गीकरण प्रमेय हैं। प्रत्येक परिमित उपसमूह समतल सममिति के दो गणनीय अनंत परिवारों में से किसी के तत्व के लिए समरूपी होता है: चक्रीय समूह $C_{n}$ या डायहेड्रल समूह $D_{2n}$, या तीन अन्य समूहों में से एकचतुष्फलकीय समूह समूह $\cong A_{4}$, अष्टफलकीय समूह $\cong S_{4}$, या इकोसाहेड्रल समूह $\cong A_{5}$.

घूर्णन अक्ष

Main article: Axis–angle representation

3 आयामों में प्रत्येक गैर-तुच्छ उचित घुमाव अद्वितीय 1-आयामी रैखिक उप-समिष्ट को ठीक करता है $\mathbb {R} ^{3}$ जिसे घूर्णन अक्ष कहा जाता है (यह यूलर का घूर्णन प्रमेय है)। ऐसा प्रत्येक घुमाव इस अक्ष के ओर्थोगोनल समतल में सामान्य 2-आयामी घुमाव के रूप में कार्य करता है। चूँकि प्रत्येक 2-आयामी घुमाव को कोण φ द्वारा दर्शाया जा सकता है, मनमाना 3-आयामी घुमाव को इस अक्ष के चारों ओर घूमने के कोण के साथ-साथ घूर्णन की धुरी द्वारा निर्दिष्ट किया जा सकता है। (तकनीकी तौर पर, किसी को अक्ष के लिए अभिविन्यास निर्दिष्ट करने की आवश्यकता होती है और क्या इस अभिविन्यास के संबंध में रोटेशन को [[दक्षिणावर्त और वामावर्त]] या वामावर्त माना जाता है)।

उदाहरण के लिए, कोण φ द्वारा सकारात्मक z-अक्ष के बारे में वामावर्त घूर्णन द्वारा दिया जाता है

$R_{z}(\phi )={\begin{bmatrix}\cos \phi &-\sin \phi &0\\\sin \phi &\cos \phi &0\\0&0&1\end{bmatrix}}.$

इकाई सदिश n दिया गया है $\mathbb {R} ^{3}$ और कोण φ, मान लीजिए R(φ, 'n') 'n' के माध्यम से अक्ष के बारे में वामावर्त घुमाव का प्रतिनिधित्व करता है ('n' द्वारा निर्धारित अभिविन्यास के साथ)। तब

• R(0, 'n') किसी भी 'n' के लिए पहचान परिवर्तन है
• R(φ, 'n') = R(−φ, −'n')
• आर(π + φ, 'n') = R(π − φ, −'n').

इन गुणों का उपयोग करके कोई यह दिखा सकता है कि किसी भी घूर्णन को 0 ≤ φ ≤ की सीमा में अद्वितीय कोण φ द्वारा दर्शाया जा सकता है। π और यूनिट सदिश n ऐसा है

• n मनमाना है यदि φ = 0
• n अद्वितीय है यदि 0 < φ < π
• n चिन्ह (गणित) तक अद्वितीय है यदि φ = π (अर्थात्, घूर्णन R(π, ±n) समान हैं)।

अगले अनुभाग में, घुमावों के इस प्रतिनिधित्व का उपयोग त्रि-आयामी वास्तविक प्रक्षेप्य समिष्ट के साथ स्थलीय रूप से SO(3) की पहचान करने के लिए किया जाता है।

टोपोलॉजी

Main article: Hypersphere of rotations

लाई समूह SO(3) वास्तविक प्रक्षेप्य समिष्ट से भिन्नता है $\mathbb {P} ^{3}(\mathbb {R} ).$ ठोस गेंद पर विचार करें $\mathbb {R} ^{3}$ त्रिज्या का π (अर्थात, के सभी बिंदु $\mathbb {R} ^{3}$ दूरी का π या मूल से कम)। उपरोक्त को देखते हुए, इस गेंद में प्रत्येक बिंदु के लिए घूर्णन होता है, जिसमें अक्ष बिंदु और मूल बिंदु से होकर गुजरती है, और घूर्णन कोण मूल से बिंदु की दूरी के समान होता है। पहचान घुमाव गेंद के केंद्र पर बिंदु से मेल खाता है। 0 और - के बीच के कोणों से घूमनाπ मूल बिंदु से समान अक्ष और दूरी पर लेकिन मूल के विपरीत दिशा में स्थित बिंदु के अनुरूप। शेष मुद्दा यह है कि दो घूर्णन होते हैं π और इसके माध्यम से −π समान हैं। तो हम गेंद की सतह पर एंटीपोडल बिंदुओं को कोटिएंट समिष्ट (टोपोलॉजी) (या साथ गोंद) करते हैं। इस पहचान के बाद, हम रोटेशन समूह के लिए टोपोलॉजिकल समिष्ट होम्योमॉर्फिक पर पहुंचते हैं।

दरअसल, पहचाने गए एंटीपोडल सतह बिंदुओं वाली गेंद चिकनी मैनिफोल्ड है, और चिकनी कई गुना रोटेशन समूह के लिए भिन्नता है। यह वास्तविक प्रक्षेप्य स्थान।वास्तविक 3-आयामी प्रक्षेप्य समिष्ट से भिन्न भी है $\mathbb {P} ^{3}(\mathbb {R} ),$ इसलिए उत्तरार्द्ध रोटेशन समूह के लिए टोपोलॉजिकल मॉडल के रूप में भी काम कर सकता है।

ये पहचान दर्शाती हैं कि SO(3) जुड़ा हुआ समिष्ट है लेकिन केवल कनेक्टेड नहीं है। उत्तरार्द्ध के संबंध में, पहचाने गए एंटीपोडल सतह बिंदुओं वाली गेंद में, उत्तरी ध्रुव से सीधे आंतरिक भाग से होते हुए दक्षिणी ध्रुव तक चलने वाले पथ पर विचार करें। यह बंद लूप है, क्योंकि उत्तरी ध्रुव और दक्षिणी ध्रुव की पहचान की जाती है। इस लूप को बिंदु तक छोटा नहीं किया जा सकता है, क्योंकि इससे कोई फर्क नहीं पड़ता कि आप लूप को कैसे विकृत करते हैं, प्रारंभ और अंत बिंदु को एंटीपोडल रहना होगा, अन्यथा लूप टूट कर खुल जाएगा। घूर्णन के संदर्भ में, यह लूप z-अक्ष के बारे में घूर्णन के निरंतर अनुक्रम का प्रतिनिधित्व करता है (उदाहरण के लिए) पहचान (गेंद के केंद्र) पर शुरू होता है, दक्षिणी ध्रुव के माध्यम से, उत्तरी ध्रुव पर कूदता है और फिर से पहचान रोटेशन पर समाप्त होता है (यानी, ए) कोण φ के माध्यम से घूर्णन की श्रृंखला जहां φ 0 से मोड़ (ज्यामिति)।2 तक चलता हैπ).

आश्चर्य की बात है, यदि आप पथ पर दो बार दौड़ते हैं, यानी, उत्तरी ध्रुव से नीचे दक्षिणी ध्रुव तक दौड़ते हैं, उत्तरी ध्रुव पर वापस कूदते हैं (इस तथ्य का उपयोग करते हुए कि उत्तरी और दक्षिणी ध्रुव पहचाने जाते हैं), और फिर उत्तरी ध्रुव से नीचे दक्षिण की ओर दौड़ते हैं ध्रुव, ताकि φ 0 से 4 तक चलेπ, आपको बंद लूप मिलता है जिसे बिंदु तक छोटा किया जा सकता है: पहले पथों को लगातार गेंद की सतह पर ले जाएं, फिर भी उत्तरी ध्रुव को दक्षिणी ध्रुव से दो बार कनेक्ट करें। फिर दूसरे पथ को पथ को बिल्कुल भी बदले बिना एंटीपोडल पक्ष पर प्रतिबिंबित किया जा सकता है। अब हमारे पास गेंद की सतह पर साधारण बंद लूप है, जो उत्तरी ध्रुव को बड़े वृत्त के साथ जोड़ता है। इस वृत्त को बिना किसी समस्या के उत्तरी ध्रुव तक छोटा किया जा सकता है। प्लेट चाल और इसी तरह की ट्रिक्स इसे व्यावहारिक रूप से प्रदर्शित करती हैं।

समान तर्क सामान्य रूप से किया जा सकता है, और यह दर्शाता है कि SO(3) का मूल समूह क्रम 2 का चक्रीय समूह है (दो तत्वों वाला मूल समूह)। भौतिकी अनुप्रयोगों में, मौलिक समूह की गैर-तुच्छता ( से अधिक तत्व) स्पिनर्स के रूप में ज्ञात वस्तुओं के अस्तित्व की अनुमति देती है, और स्पिन-सांख्यिकी प्रमेय के विकास में महत्वपूर्ण उपकरण है।

SO(3) का सार्वभौमिक आवरण स्पिन(3) नामक झूठ समूह है। समूह स्पिन(3) विशेष एकात्मक समूह एसयू(2) का समरूपी है; यह इकाई 3-गोले एस से भिन्न भी है³और इसे छंदों के समूह (पूर्ण मान 1 के साथ चतुर्भुज) के रूप में समझा जा सकता है। चतुर्भुज और घूर्णन के बीच संबंध, जो आमतौर पर कंप्यूटर चित्रलेख में उपयोग किया जाता है, चतुर्भुज और स्थानिक घुमावों में समझाया गया है। एस से नक्शा³SO(3) पर जो S के एंटीपोडल बिंदुओं की पहचान करता है³ कर्नेल (बीजगणित) {±1} के साथ, लाई समूहों का विशेषण समरूपता है। स्थलाकृतिक दृष्टि से, यह मानचित्र दो-से- कवर करने वाला मानचित्र है। (प्लेट ट्रिक देखें।)

SO(3) और SU(2) के बीच संबंध

इस अनुभाग में, हम SO(3) पर SU(2) की दो-से- और विशेषण समरूपता की दो अलग-अलग संरचनाएँ देते हैं।

इकाई मानदंड के चतुर्भुज का उपयोग करना

Main article: Quaternions and spatial rotation

समूह SU(2) द्वारा दिए गए मानचित्र के माध्यम से इकाई मानदंड के चतुष्कोणों के लिए समूह समरूपता है

$$q=a\mathbf {1} +b\mathbf {i} +c\mathbf {j} +d\mathbf {k} =\alpha +\beta \mathbf {j} \leftrightarrow {\begin{bmatrix}\alpha &-{\overline {\beta }}\\\beta &{\overline {\alpha }}\end{bmatrix}}=U$$

तक सीमित ${\textstyle a^{2}+b^{2}+c^{2}+d^{2}=|\alpha |^{2}+|\beta |^{2}=1}$ कहाँ ${\textstyle q\in \mathbb {H} }$, ${\textstyle a,b,c,d\in \mathbb {R} }$, ${\textstyle U\in \operatorname {SU} (2)}$, और $\alpha =a+bi\in \mathbb {C}$, $\beta =c+di\in \mathbb {C}$.

आइये अब पहचानते हैं $\mathbb {R} ^{3}$ के विस्तार के साथ $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$. इसके बाद कोई इसे सत्यापित कर सकता है $v$ में है $\mathbb {R} ^{3}$ और $q$ तो फिर, इकाई चतुर्भुज है

$$qvq^{-1}\in \mathbb {R} ^{3}.$$

इसके अतिरिक्त, मानचित्र $v\mapsto qvq^{-1}$ का चक्र है $\mathbb {R} ^{3}.$ इसके अतिरिक्त, $(-q)v(-q)^{-1}$ वैसा ही है जैसा कि $qvq^{-1}$. इसका मतलब यह है कि वहाँ है 2:1 इकाई मानदंड के चतुर्भुज से 3डी रोटेशन समूह तक समरूपता SO(3).

कोई इस समरूपता को स्पष्ट रूप से कार्यान्वित कर सकता है: इकाई चतुर्भुज, q, साथ

$${\begin{aligned}q&=w+x\mathbf {i} +y\mathbf {j} +z\mathbf {k} ,\\1&=w^{2}+x^{2}+y^{2}+z^{2},\end{aligned}}$$

रोटेशन आव्युह में मैप किया गया है

$$Q={\begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{bmatrix}}.$$

यह सदिश के चारों ओर घूर्णन है (x, y, z) कोण से 2θ, कहाँ cos θ = w और |sin θ| = ||(x, y, z)||. के लिए उचित संकेत sin θ निहित है, बार अक्ष घटकों के संकेत तय हो गए हैं। वह 2:1-nature दोनों से स्पष्ट है q और −q उसी के लिए मानचित्र Q.

मोबियस परिवर्तनों का उपयोग करना

त्रिज्या के गोले से त्रिविम प्रक्षेपण 1/2उत्तरी ध्रुव से (x, y, z) = (0, 0, 1/2) विमान पर M द्वारा दिए गए z = −1/2 द्वारा समन्वित किया गया (ξ, η), यहां क्रॉस सेक्शन में दिखाया गया है।

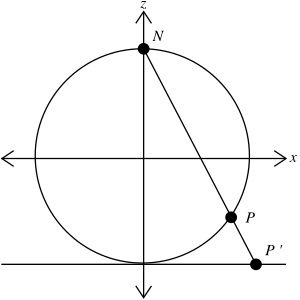
इस अनुभाग के लिए सामान्य संदर्भ है Gelfand, Minlos & Shapiro (1963). बिन्दु P गोले पर

$\mathbf {S} =\left\{(x,y,z)\in \mathbb {R} ^{3}:x^{2}+y^{2}+z^{2}={\frac {1}{4}}\right\}$

उत्तरी ध्रुव को छोड़कर, कर सकते हैं N, अंकों के साथ एक-से- आक्षेप में रखा जाए S(P) = P' विमान पर M द्वारा परिभाषित z = −1/2, रेखा - चित्र देखें। वो नक्शा Sत्रिविम प्रक्षेपण कहलाता है।

निर्देशांक चालू रखें M होना (ξ, η). रेखा L के माध्यम से गुजरते हुए N और P को इस प्रकार पैरामीट्रिज्ड किया जा सकता है

$L(t)=N+t(N-P)=\left(0,0,{\frac {1}{2}}\right)+t\left(\left(0,0,{\frac {1}{2}}\right)-(x,y,z)\right),\quad t\in \mathbb {R} .$

मांग कर रहे हैं कि z-coordinate का $L(t_{0})$ के समान होती है −1/2, कोई पाता है

$t_{0}={\frac {1}{z-{\frac {1}{2}}}}.$

हमारे पास है $L(t_{0})=(\xi ,\eta ,-1/2).$ इसलिए मानचित्र

${\begin{cases}S:\mathbf {S} \to M\\P=(x,y,z)\longmapsto P'=(\xi ,\eta )=\left({\frac {x}{{\frac {1}{2}}-z}},{\frac {y}{{\frac {1}{2}}-z}}\right)\equiv \zeta =\xi +i\eta \end{cases}}$

जहां, बाद की सुविधा के लिए, विमान M की पहचान जटिल तल से की जाती है $\mathbb {C} .$ व्युत्क्रम के लिए लिखिए L जैसा

$L=N+s(P'-N)=\left(0,0,{\frac {1}{2}}\right)+s\left(\left(\xi ,\eta ,-{\frac {1}{2}}\right)-\left(0,0,{\frac {1}{2}}\right)\right),$

और मांग x² + y² + z² = 1/4 ढूँढ़ने के लिए s = 1/1 + ξ² + η² और इस तरह

${\begin{cases}S^{-1}:M\to \mathbf {S} \\P'=(\xi ,\eta )\longmapsto P=(x,y,z)=\left({\frac {\xi }{1+\xi ^{2}+\eta ^{2}}},{\frac {\eta }{1+\xi ^{2}+\eta ^{2}}},{\frac {-1+\xi ^{2}+\eta ^{2}}{2+2\xi ^{2}+2\eta ^{2}}}\right)\end{cases}}$

अगर g ∈ SO(3) रोटेशन है, तो इस पर अंक लगेंगे S बिंदुओं पर S अपनी मानक क्रिया द्वारा Π_s(g)एम्बेडिंग समिष्ट पर $\mathbb {R} ^{3}.$ इस क्रिया को साथ बनाकर S व्यक्ति परिवर्तन प्राप्त करता है S ∘ Π_s(g) ∘ S⁻¹ का M,

$\zeta =P'\longmapsto P\longmapsto \Pi _{s}(g)P=gP\longmapsto S(gP)\equiv \Pi _{u}(g)\zeta =\zeta '.$

इस प्रकार Π_u(g) का रूपांतरण है $\mathbb {C}$ परिवर्तन से सम्बंधित है Π_s(g) का $\mathbb {R} ^{3}$.

यह पता चला है कि g ∈ SO(3) द्वारा इस प्रकार दर्शाया गया है Π_u(g) को आव्युह के रूप में व्यक्त किया जा सकता है Π_u(g) ∈ SU(2) (जहां आव्युह के परिवर्तन के लिए उसी नाम का उपयोग करने के लिए नोटेशन को पुनर्नवीनीकरण किया जाता है $\mathbb {C}$ यह प्रस्तुत करता है)। इस आव्युह की पहचान करने के लिए, पहले रोटेशन पर विचार करें g_φ के बारे में z-axis कोण के माध्यम से φ,

${\begin{aligned}x'&=x\cos \phi -y\sin \phi ,\\y'&=x\sin \phi +y\cos \phi ,\\z'&=z.\end{aligned}}$

इस तरह

$\zeta '={\frac {x'+iy'}{{\frac {1}{2}}-z'}}={\frac {e^{i\phi }(x+iy)}{{\frac {1}{2}}-z}}=e^{i\phi }\zeta ={\frac {e^{\frac {i\phi }{2}}\zeta +0}{0\zeta +e^{-{\frac {i\phi }{2}}}}},$

जो, आश्चर्यजनक रूप से, जटिल तल में घूर्णन है। इसी प्रकार, यदि g_θ के बारे में घूर्णन है x-axis कोण के माध्यम से θ, तब

$w'=e^{i\theta }w,\quad w={\frac {y+iz}{{\frac {1}{2}}-x}},$

जो, थोड़ा बीजगणित के बाद, बन जाता है

$\zeta '={\frac {\cos {\frac {\theta }{2}}\zeta +i\sin {\frac {\theta }{2}}}{i\sin {\frac {\theta }{2}}\zeta +\cos {\frac {\theta }{2}}}}.$

ये दो घुमाव, $g_{\phi },g_{\theta },$ इस प्रकार के द्विरेखीय परिवर्तनों के अनुरूप है R² ≃ C ≃ M, अर्थात्, वे मोबियस परिवर्तनों के उदाहरण हैं।

सामान्य मोबियस परिवर्तन द्वारा दिया गया है

$\zeta '={\frac {\alpha \zeta +\beta }{\gamma \zeta +\delta }},\quad \alpha \delta -\beta \gamma \neq 0.$

घूर्णन, $g_{\phi },g_{\theta }$ सभी उत्पन्न करें SO(3) और मोबियस परिवर्तनों के रचना नियम दर्शाते हैं कि कोई भी रचना $g_{\phi },g_{\theta }$ मोबियस परिवर्तनों की संगत संरचना का अनुवाद करता है। मोबियस परिवर्तनों को आव्युह द्वारा दर्शाया जा सकता है

${\begin{pmatrix}\alpha &\beta \\\gamma &\delta \end{pmatrix}},\qquad \alpha \delta -\beta \gamma =1,$

के सामान्य कारक के बाद से α, β, γ, δ रद्द करता है.

इसी कारण से, गुणा के बाद से आव्युह को विशिष्ट रूप से परिभाषित नहीं किया गया है −I का निर्धारक या मोबियस परिवर्तन पर कोई प्रभाव नहीं पड़ता है। मोबियस परिवर्तनों का रचना नियम संबंधित आव्यूहों का अनुसरण करता है। निष्कर्ष यह है कि प्रत्येक मोबियस परिवर्तन दो आव्युह से मेल खाता है g, −g ∈ SL(2, C).

इस पत्राचार का उपयोग करके कोई भी लिख सकता है

${\begin{aligned}\Pi _{u}(g_{\phi })&=\Pi _{u}\left[{\begin{pmatrix}\cos \phi &-\sin \phi &0\\\sin \phi &\cos \phi &0\\0&0&1\end{pmatrix}}\right]=\pm {\begin{pmatrix}e^{i{\frac {\phi }{2}}}&0\\0&e^{-i{\frac {\phi }{2}}}\end{pmatrix}},\\\Pi _{u}(g_{\theta })&=\Pi _{u}\left[{\begin{pmatrix}1&0&0\\0&\cos \theta &-\sin \theta \\0&\sin \theta &\cos \theta \end{pmatrix}}\right]=\pm {\begin{pmatrix}\cos {\frac {\theta }{2}}&i\sin {\frac {\theta }{2}}\\i\sin {\frac {\theta }{2}}&\cos {\frac {\theta }{2}}\end{pmatrix}}.\end{aligned}}$

ये आव्युह एकात्मक हैं और इस प्रकार Π_u(SO(3)) ⊂ SU(2) ⊂ SL(2, C). यूलर कोण के संदर्भ में कोई सामान्य घुमाव ढूंढता है

${\begin{aligned}g(\phi ,\theta ,\psi )=g_{\phi }g_{\theta }g_{\psi }&={\begin{pmatrix}\cos \phi &-\sin \phi &0\\\sin \phi &\cos \phi &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0\\0&\cos \theta &-\sin \theta \\0&\sin \theta &\cos \theta \end{pmatrix}}{\begin{pmatrix}\cos \psi &-\sin \psi &0\\\sin \psi &\cos \psi &0\\0&0&1\end{pmatrix}}\\&={\begin{pmatrix}\cos \phi \cos \psi -\cos \theta \sin \phi \sin \psi &-\cos \phi \sin \psi -\cos \theta \sin \phi \cos \psi &\sin \phi \sin \theta \\\sin \phi \cos \psi +\cos \theta \cos \phi \sin \psi &-\sin \phi \sin \psi +\cos \theta \cos \phi \cos \psi &-\cos \phi \sin \theta \\\sin \psi \sin \theta &\cos \psi \sin \theta &\cos \theta \end{pmatrix}},\end{aligned}}$

(1)

किसी के पास

${\begin{aligned}\Pi _{u}(g(\phi ,\theta ,\psi ))&=\pm {\begin{pmatrix}e^{i{\frac {\phi }{2}}}&0\\0&e^{-i{\frac {\phi }{2}}}\end{pmatrix}}{\begin{pmatrix}\cos {\frac {\theta }{2}}&i\sin {\frac {\theta }{2}}\\i\sin {\frac {\theta }{2}}&\cos {\frac {\theta }{2}}\end{pmatrix}}{\begin{pmatrix}e^{i{\frac {\psi }{2}}}&0\\0&e^{-i{\frac {\psi }{2}}}\end{pmatrix}}\\&=\pm {\begin{pmatrix}\cos {\frac {\theta }{2}}e^{i{\frac {\phi +\psi }{2}}}&i\sin {\frac {\theta }{2}}e^{i{\frac {\phi -\psi }{2}}}\\i\sin {\frac {\theta }{2}}e^{-i{\frac {\phi -\psi }{2}}}&\cos {\frac {\theta }{2}}e^{-i{\frac {\phi +\psi }{2}}}\end{pmatrix}}.\end{aligned}}$

(2)

इसके विपरीत, सामान्य आव्युह पर विचार करें

$\pm \Pi _{u}(g_{\alpha ,\beta })=\pm {\begin{pmatrix}\alpha &\beta \\-{\overline {\beta }}&{\overline {\alpha }}\end{pmatrix}}\in \operatorname {SU} (2).$

प्रतिस्थापन करें

${\begin{aligned}\cos {\frac {\theta }{2}}&=|\alpha |,&\sin {\frac {\theta }{2}}&=|\beta |,&(0\leq \theta \leq \pi ),\\{\frac {\phi +\psi }{2}}&=\arg \alpha ,&{\frac {\psi -\phi }{2}}&=\arg \beta .&\end{aligned}}$

प्रतिस्थापन के साथ, Π(g_{α, β}) (के दाहिने हाथ की ओर) का रूप धारण करता है2), जो नीचे मेल खाता है Π_u के आरएचएस के रूप में आव्युह के लिए (1) उसी के साथ φ, θ, ψ. जटिल मापदंडों के संदर्भ में α, β,

$g_{\alpha ,\beta }={\begin{pmatrix}{\frac {1}{2}}\left(\alpha ^{2}-\beta ^{2}+{\overline {\alpha ^{2}}}-{\overline {\beta ^{2}}}\right)&{\frac {i}{2}}\left(-\alpha ^{2}-\beta ^{2}+{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&-\alpha \beta -{\overline {\alpha }}{\overline {\beta }}\\{\frac {i}{2}}\left(\alpha ^{2}-\beta ^{2}-{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&{\frac {1}{2}}\left(\alpha ^{2}+\beta ^{2}+{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&-i\left(+\alpha \beta -{\overline {\alpha }}{\overline {\beta }}\right)\\\alpha {\overline {\beta }}+{\overline {\alpha }}\beta &i\left(-\alpha {\overline {\beta }}+{\overline {\alpha }}\beta \right)&\alpha {\overline {\alpha }}-\beta {\overline {\beta }}\end{pmatrix}}.$

इसे सत्यापित करने के लिए, प्रतिस्थापित करें α. β के आरएचएस पर आव्युह के तत्व (2). कुछ हेरफेर के बाद, आव्युह आरएचएस का रूप धारण कर लेता है (1).

यूलर कोणों के संदर्भ में स्पष्ट रूप से यह स्पष्ट है कि मानचित्र

${\begin{cases}p:\operatorname {SU} (2)\to \operatorname {SO} (3)\\\Pi _{u}(\pm g_{\alpha \beta })\mapsto g_{\alpha \beta }\end{cases}}$

अभी वर्णित सहज है, 2:1 और विशेषण समूह समरूपता। इसलिए यह सार्वभौमिक आवरण समिष्ट का स्पष्ट विवरण है SO(3) यूनिवर्सल कवरिंग ग्रुप से SU(2).

ली अलजेब्रा

प्रत्येक लाई समूह के साथ उसका लाई बीजगणित जुड़ा होता है, लाई समूह के समान आयाम का रैखिक स्थान, जो लेट ब्रैकेट नामक द्विरेखीय वैकल्पिक उत्पाद के तहत बंद होता है। का ली अलजेब्रा SO(3) द्वारा दर्शाया जाता है ${\mathfrak {so}}(3)$ और इसमें सभी तिरछा-सममित मैट्रिक्स।तिरछा-सममित शामिल हैं 3 × 3 मैट्रिक्स. इसे ऑर्थोगोनल आव्युह को अलग करके देखा जा सकता है, A^TA = I, A ∈ SO(3). के दो तत्वों का झूठ ब्रैकेट ${\mathfrak {so}}(3)$ आव्युह कम्यूटेटर द्वारा दिए गए प्रत्येक आव्युह समूह के बीजगणित के लिए, [A₁, A₂] = A₁A₂ − A₂A₁, जो फिर से तिरछा-सममित आव्युह है। लाई बीजगणित ब्रैकेट बेकर-कैंपबेल-हॉसडॉर्फ सूत्र द्वारा सटीक किए गए अर्थ में लाई समूह उत्पाद के सार को पकड़ता है।

के तत्व ${\mathfrak {so}}(3)$ घूर्णन के अनंत लघु जनक हैं, यानी, वे पहचान तत्व पर मैनिफोल्ड SO(3) के स्पर्शरेखा समिष्ट के तत्व हैं। अगर $R(\phi ,{\boldsymbol {n}})$ यूनिट सदिश द्वारा निर्दिष्ट अक्ष के बारे में कोण φ के साथ वामावर्त घुमाव को दर्शाता है ${\boldsymbol {n}},$ तब

$\forall {\boldsymbol {u}}\in \mathbb {R} ^{3}:\qquad \left.{\frac {\operatorname {d} }{\operatorname {d} \phi }}\right|_{\phi =0}R(\phi ,{\boldsymbol {n}}){\boldsymbol {u}}={\boldsymbol {n}}\times {\boldsymbol {u}}.$

इसका उपयोग यह दिखाने के लिए किया जा सकता है कि ली अलजेब्रा ${\mathfrak {so}}(3)$ (कम्यूटेटर के साथ) लाई बीजगणित के समरूपी है $\mathbb {R} ^{3}$ (क्रॉस उत्पाद के साथ)। इस समरूपता के तहत, अक्ष-कोण प्रतिनिधित्व#रोटेशन सदिश ${\boldsymbol {\omega }}\in \mathbb {R} ^{3}$ रेखीय मानचित्र से मेल खाता है ${\widetilde {\boldsymbol {\omega }}}$ द्वारा परिभाषित ${\widetilde {\boldsymbol {\omega }}}({\boldsymbol {u}})={\boldsymbol {\omega }}\times {\boldsymbol {u}}.$ अधिक विस्तार से, अधिकांशतः के लिए उपयुक्त आधार ${\mathfrak {so}}(3)$ के तौर पर 3-dimensional सदिश समिष्ट है

${\boldsymbol {L}}_{x}={\begin{bmatrix}0&0&0\\0&0&-1\\0&1&0\end{bmatrix}},\quad {\boldsymbol {L}}_{y}={\begin{bmatrix}0&0&1\\0&0&0\\-1&0&0\end{bmatrix}},\quad {\boldsymbol {L}}_{z}={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&0\end{bmatrix}}.$

इन आधार तत्वों के रूपान्तरण संबंध हैं,

$[{\boldsymbol {L}}_{x},{\boldsymbol {L}}_{y}]={\boldsymbol {L}}_{z},\quad [{\boldsymbol {L}}_{z},{\boldsymbol {L}}_{x}]={\boldsymbol {L}}_{y},\quad [{\boldsymbol {L}}_{y},{\boldsymbol {L}}_{z}]={\boldsymbol {L}}_{x}$

जो कि तीन मानक आधारों के संबंधों से सहमत हैं $\mathbb {R} ^{3}$ क्रॉस उत्पाद के अंतर्गत.

जैसा कि ऊपर बताया गया है, कोई भी इस लाई बीजगणित में यूलर सदिश के साथ किसी भी आव्युह की पहचान कर सकता है ${\boldsymbol {\omega }}=(x,y,z)\in \mathbb {R} ^{3},$

${\widehat {\boldsymbol {\omega }}}={\boldsymbol {\omega }}\cdot {\boldsymbol {L}}=x{\boldsymbol {L}}_{x}+y{\boldsymbol {L}}_{y}+z{\boldsymbol {L}}_{z}={\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}\in {\mathfrak {so}}(3).$

इस पहचान को कभी-कभी हैट-मैप भी कहा जाता है। इस पहचान के तहत, ${\mathfrak {so}}(3)$ ब्रैकेट में मेल खाता है $\mathbb {R} ^{3}$ क्रॉस उत्पाद के लिए,

$\left[{\widehat {\boldsymbol {u}}},{\widehat {\boldsymbol {v}}}\right]={\widehat {{\boldsymbol {u}}\times {\boldsymbol {v}}}}.$

आव्युह की पहचान सदिश से की गई ${\boldsymbol {u}}$ उसके पास वह संपत्ति है

${\widehat {\boldsymbol {u}}}{\boldsymbol {v}}={\boldsymbol {u}}\times {\boldsymbol {v}},$

जहां बाईं ओर हमारे पास साधारण आव्युह गुणन है। यह संकेत करता है ${\boldsymbol {u}}$ तिरछा-सममित आव्युह के शून्य समिष्ट में है जिसके साथ इसकी पहचान की जाती है, क्योंकि ${\boldsymbol {u}}\times {\boldsymbol {u}}={\boldsymbol {0}}.$

ली अलजेब्रा पर नोट

Main article: Angular momentum operator

See also: Representation theory of SU(2) and Jordan map

बीजगणित अभ्यावेदन में, समूह SO(3) रैंक 1 का कॉम्पैक्ट और सरल है, और इसलिए इसमें एकल स्वतंत्र कासिमिर तत्व है, जो तीन जनरेटर का द्विघात अपरिवर्तनीय कार्य है जो उन सभी के साथ संचार करता है। रोटेशन समूह के लिए किलिंग फॉर्म सिर्फ क्रोनकर डेल्टा है, और इसलिए यह कासिमिर अपरिवर्तनीय केवल जेनरेटर के वर्गों का योग है, ${\boldsymbol {J}}_{x},{\boldsymbol {J}}_{y},{\boldsymbol {J}}_{z},$ बीजगणित का

$[{\boldsymbol {J}}_{x},{\boldsymbol {J}}_{y}]={\boldsymbol {J}}_{z},\quad [{\boldsymbol {J}}_{z},{\boldsymbol {J}}_{x}]={\boldsymbol {J}}_{y},\quad [{\boldsymbol {J}}_{y},{\boldsymbol {J}}_{z}]={\boldsymbol {J}}_{x}.$

अर्थात्, कासिमिर अपरिवर्तनीय द्वारा दिया गया है

${\boldsymbol {J}}^{2}\equiv {\boldsymbol {J}}\cdot {\boldsymbol {J}}={\boldsymbol {J}}_{x}^{2}+{\boldsymbol {J}}_{y}^{2}+{\boldsymbol {J}}_{z}^{2}\propto {\boldsymbol {I}}.$

एकात्मक अघुलनशील ली अलजेब्रा प्रतिनिधित्व के लिए D^j, इस अपरिवर्तनीय के eigenvalues ​​​​वास्तविक और असतत हैं, और प्रत्येक प्रतिनिधित्व की विशेषता रखते हैं, जो कि आयामीता का परिमित आयामी है $2j+1$. यानी इस कासिमिर ऑपरेटर के eigenvalues ​​हैं

${\boldsymbol {J}}^{2}=-j(j+1){\boldsymbol {I}}_{2j+1},$

कहाँ j पूर्णांक या अर्ध-पूर्णांक है, और इसे स्पिन (भौतिकी) या कोणीय गति के रूप में जाना जाता है।

तो, ऊपर प्रदर्शित 3 × 3 जनरेटर एल ट्रिपलेट (स्पिन 1) प्रतिनिधित्व पर कार्य करते हैं, जबकि नीचे 2 × 2 जनरेटर, टी, स्पिनर (स्पिन-1/2) प्रतिनिधित्व पर कार्य करते हैं। . के क्रोनकर उत्पाद लेकर D^1/2 स्वयं के साथ बार-बार, कोई भी सभी उच्चतर अघुलनशील अभ्यावेदन का निर्माण कर सकता है D^j. अर्थात्, मनमाने ढंग से बड़े के लिए, तीन स्थानिक आयामों में उच्च स्पिन सिस्टम के लिए परिणामी जनरेटर j, इन स्पिन ऑपरेटरों और सीढ़ी ऑपरेटरों का उपयोग करके गणना की जा सकती है।

प्रत्येक एकात्मक अघुलनशील अभ्यावेदन के लिए D^j समतुल्य है, D^−j−1. सभी अनंत-आयामी इरेड्यूसबल निरूपण गैर-एकात्मक होना चाहिए, क्योंकि समूह कॉम्पैक्ट है।

क्वांटम यांत्रिकी में, कासिमिर अपरिवर्तनीय कोणीय-संवेग-वर्ग ऑपरेटर है; स्पिन के पूर्णांक मान j बोसॉन को चिह्नित करता है, जबकि अर्ध-पूर्णांक फरमिओन्स को महत्व देता है। ऊपर उपयोग किए गए स्क्यू-हर्मिटियन आव्युह आव्युह को स्पिन ऑपरेटरों के रूप में उपयोग किया जाता है, उन्हें गुणा करने के बाद i, इसलिए वे अब हर्मिटियन आव्युह हैं (पॉली आव्युह की तरह)। इस प्रकार, इस भाषा में,

$[{\boldsymbol {J}}_{x},{\boldsymbol {J}}_{y}]=i{\boldsymbol {J}}_{z},\quad [{\boldsymbol {J}}_{z},{\boldsymbol {J}}_{x}]=i{\boldsymbol {J}}_{y},\quad [{\boldsymbol {J}}_{y},{\boldsymbol {J}}_{z}]=i{\boldsymbol {J}}_{x}.$

और इसलिए

${\boldsymbol {J}}^{2}=j(j+1){\boldsymbol {I}}_{2j+1}.$

इनके लिए स्पष्ट अभिव्यक्तियाँ D^j हैं,

${\begin{aligned}\left({\boldsymbol {J}}_{z}^{(j)}\right)_{ba}&=(j+1-a)\delta _{b,a}\\\left({\boldsymbol {J}}_{x}^{(j)}\right)_{ba}&={\frac {1}{2}}\left(\delta _{b,a+1}+\delta _{b+1,a}\right){\sqrt {(j+1)(a+b-1)-ab}}\\\left({\boldsymbol {J}}_{y}^{(j)}\right)_{ba}&={\frac {1}{2i}}\left(\delta _{b,a+1}-\delta _{b+1,a}\right){\sqrt {(j+1)(a+b-1)-ab}}\\\end{aligned}}$

कहाँ j मनमाना है और $1\leq a,b\leq 2j+1$.

उदाहरण के लिए, स्पिन 1 के लिए परिणामी स्पिन मैट्रिसेस ($j=1$) हैं

${\begin{aligned}{\boldsymbol {J}}_{x}&={\frac {1}{\sqrt {2}}}{\begin{pmatrix}0&1&0\\1&0&1\\0&1&0\end{pmatrix}}\\{\boldsymbol {J}}_{y}&={\frac {1}{\sqrt {2}}}{\begin{pmatrix}0&-i&0\\i&0&-i\\0&i&0\end{pmatrix}}\\{\boldsymbol {J}}_{z}&={\begin{pmatrix}1&0&0\\0&0&0\\0&0&-1\end{pmatrix}}\end{aligned}}$

ध्यान दें, चूँकि, ये उपरोक्त की तुलना में समतुल्य, लेकिन भिन्न आधार, गोलाकार आधार#आधार आव्युह में परिवर्तन कैसे हैं iएल कार्टेशियन आधार पर। उच्च स्पिन के लिए, जैसे कि स्पिन 3/2 ($j={\tfrac {3}{2}}$):

${\begin{aligned}{\boldsymbol {J}}_{x}&={\frac {1}{2}}{\begin{pmatrix}0&{\sqrt {3}}&0&0\\{\sqrt {3}}&0&2&0\\0&2&0&{\sqrt {3}}\\0&0&{\sqrt {3}}&0\end{pmatrix}}\\{\boldsymbol {J}}_{y}&={\frac {1}{2}}{\begin{pmatrix}0&-i{\sqrt {3}}&0&0\\i{\sqrt {3}}&0&-2i&0\\0&2i&0&-i{\sqrt {3}}\\0&0&i{\sqrt {3}}&0\end{pmatrix}}\\{\boldsymbol {J}}_{z}&={\frac {1}{2}}{\begin{pmatrix}3&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&-3\end{pmatrix}}.\end{aligned}}$

स्पिन के लिए 5/2 ($j={\tfrac {5}{2}}$),

Main article: Spin (physics) § Higher spins

=== समरूपता 𝖘𝖚(2) === के साथ ली अलजेब्रा ${\mathfrak {so}}(3)$ और ${\mathfrak {su}}(2)$ समरूपी हैं। के लिए आधार ${\mathfrak {su}}(2)$ द्वारा दिया गया है

${\boldsymbol {t}}_{1}={\frac {1}{2}}{\begin{bmatrix}0&-i\\-i&0\end{bmatrix}},\quad {\boldsymbol {t}}_{2}={\frac {1}{2}}{\begin{bmatrix}0&-1\\1&0\end{bmatrix}},\quad {\boldsymbol {t}}_{3}={\frac {1}{2}}{\begin{bmatrix}-i&0\\0&i\end{bmatrix}}.$

ये पाउली आव्युह से संबंधित हैं

${\boldsymbol {t}}_{i}\longleftrightarrow {\frac {1}{2i}}\sigma _{i}.$

पाउली मैट्रिसेस लाई बीजगणित के लिए भौतिकविदों के सम्मेलन का पालन करते हैं। उस सम्मेलन में, बीजगणित तत्वों को गुणा किया जाता है i, घातीय मानचित्र (नीचे) को अतिरिक्त कारक के साथ परिभाषित किया गया है i घातांक और संरचना में स्थिरांक समान रहते हैं, लेकिन उनकी परिभाषा का कारक प्राप्त होता है i. इसी तरह, कम्यूटेशन संबंध का कारक प्राप्त होता है i. के लिए रूपान्तरण संबंध ${\boldsymbol {t}}_{i}$ हैं

$[{\boldsymbol {t}}_{i},{\boldsymbol {t}}_{j}]=\varepsilon _{ijk}{\boldsymbol {t}}_{k},$

कहाँ ε_ijk पूरी तरह से विरोधी-सममित प्रतीक है ε₁₂₃ = 1. के बीच समरूपता ${\mathfrak {so}}(3)$ और ${\mathfrak {su}}(2)$ कई तरीकों से स्थापित किया जा सकता है. बाद की सुविधा के लिए, ${\mathfrak {so}}(3)$ और ${\mathfrak {su}}(2)$ मैपिंग द्वारा पहचान की जाती है

${\boldsymbol {L}}_{x}\longleftrightarrow {\boldsymbol {t}}_{1},\quad {\boldsymbol {L}}_{y}\longleftrightarrow {\boldsymbol {t}}_{2},\quad {\boldsymbol {L}}_{z}\longleftrightarrow {\boldsymbol {t}}_{3},$

और रैखिकता द्वारा विस्तार।

घातांकीय मानचित्र

के लिए घातीय मानचित्र SO(3), है, चूँकि SO(3) आव्युह झूठ समूह है, जिसे मानक आव्युह घातीय श्रृंखला का उपयोग करके परिभाषित किया गया है,

${\begin{cases}\exp :{\mathfrak {so}}(3)\to \operatorname {SO} (3)\\A\mapsto e^{A}=\sum _{k=0}^{\infty }{\frac {1}{k!}}A^{k}=I+A+{\tfrac {1}{2}}A^{2}+\cdots .\end{cases}}$

किसी भी तिरछा-सममित आव्युह के लिए A ∈ 𝖘𝖔(3), e^A हमेशा अंदर है SO(3). प्रमाण आव्युह घातांक के प्रारंभिक गुणों का उपयोग करता है

$\left(e^{A}\right)^{\textsf {T}}e^{A}=e^{A^{\textsf {T}}}e^{A}=e^{A^{\textsf {T}}+A}=e^{-A+A}=e^{A-A}=e^{A}\left(e^{A}\right)^{\textsf {T}}=e^{0}=I.$

आव्युह के बाद से A और A^T कम्यूट, इसे तिरछा-सममित आव्युह स्थिति के साथ आसानी से सिद्ध किया जा सकता है। ये दिखाने के लिए ये काफी नहीं है 𝖘𝖔(3) के लिए संगत ली अलजेब्रा है SO(3), और अलग से सिद्ध किया जाएगा.

प्रमाण की कठिनाई का स्तर इस बात पर निर्भर करता है कि आव्युह समूह लाई बीजगणित को कैसे परिभाषित किया जाता है। Hall (2003) लाई बीजगणित को आव्यूहों के समुच्चय के रूप में परिभाषित करता है

$\left\{A\in \operatorname {M} (n,\mathbb {R} )\left|e^{tA}\in \operatorname {SO} (3)\forall t\right.\right\},$

किस स्थितियों में यह तुच्छ है. Rossmann (2002) परिभाषा के लिए चिकनी वक्र खंडों के डेरिवेटिव का उपयोग करता है SO(3)पहचान पर ली गई पहचान के माध्यम से, जिस स्थिति में यह कठिन है। निश्चित के लिए A ≠ 0, e^tA, −∞ < t < ∞ जियोडेसिक के साथ एक-पैरामीटर उपसमूह है SO(3). यह एक-पैरामीटर उपसमूह देता है जो घातीय मानचित्र के गुणों से सीधे अनुसरण करता है। घातीय मानचित्र मूल के पड़ोस के बीच भिन्नता प्रदान करता है 𝖘𝖔(3) और पहचान का पड़ोस SO(3). प्रमाण के लिए, बंद उपसमूह प्रमेय देखें।

घातांकीय मानचित्र विशेषणात्मक होता है। यह इस तथ्य से पता चलता है कि प्रत्येक R ∈ SO(3), चूँकि प्रत्येक घूर्णन अक्ष निश्चित छोड़ता है (यूलर का घूर्णन प्रमेय), और प्रपत्र के ब्लॉक विकर्ण आव्युह से संयुग्मित होता है

$D={\begin{pmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{pmatrix}}=e^{\theta L_{z}},$

ऐसा है कि A = BDB⁻¹, ओर वो

$Be^{\theta L_{z}}B^{-1}=e^{B\theta L_{z}B^{-1}},$

इस तथ्य के साथ कि 𝖘𝖔(3) के संयुक्त प्रतिनिधित्व के तहत बंद है SO(3), मतलब है कि BθL_zB⁻¹ ∈ 𝖘𝖔(3).

इस प्रकार, उदाहरण के लिए, लोकप्रिय पहचान की जांच करना आसान है

$e^{-\pi L_{x}/2}e^{\theta L_{z}}e^{\pi L_{x}/2}=e^{\theta L_{y}}.$

जैसा कि ऊपर दिखाया गया है, प्रत्येक तत्व A ∈ 𝖘𝖔(3) सदिश से जुड़ा है ω = θ u, कहाँ u = (x,y,z) इकाई परिमाण सदिश है। तब से u के शून्य समिष्ट में है A, यदि कोई अब किसी अन्य ऑर्थोगोनल आव्युह के माध्यम से नए आधार पर घूमता है O, साथ u के रूप में z अक्ष, नए आधार में रोटेशन आव्युह का अंतिम स्तंभ और पंक्ति शून्य होगी।

इस प्रकार, हम घातांक के सूत्र से पहले से जानते हैं exp(OAO^T) चले जाना चाहिए u तय। किसी फलन जैसे आधार के लिए सीधा सूत्र प्रदान करना गणितीय रूप से असंभव है u, क्योंकि इसका अस्तित्व बालों वाली गेंद प्रमेय का उल्लंघन करेगा; लेकिन प्रत्यक्ष घातांक संभव है, और अक्ष-कोण प्रतिनिधित्व#घातांक मानचित्र 𝖘𝖔(3) से SO(3) तक

${\begin{aligned}\exp({\tilde {\boldsymbol {\omega }}})&=\exp(\theta ({\boldsymbol {u\cdot L}}))=\exp \left(\theta {\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}\right)\\[4pt]&={\boldsymbol {I}}+2cs({\boldsymbol {u\cdot L}})+2s^{2}({\boldsymbol {u\cdot L}})^{2}\\[4pt]&={\begin{bmatrix}2\left(x^{2}-1\right)s^{2}+1&2xys^{2}-2zcs&2xzs^{2}+2ycs\\2xys^{2}+2zcs&2\left(y^{2}-1\right)s^{2}+1&2yzs^{2}-2xcs\\2xzs^{2}-2ycs&2yzs^{2}+2xcs&2\left(z^{2}-1\right)s^{2}+1\end{bmatrix}},\end{aligned}}$

कहाँ ${\textstyle c=\cos {\frac {\theta }{2}}}$ और ${\textstyle s=\sin {\frac {\theta }{2}}}$. इसे अक्ष के चारों ओर घूमने के लिए आव्युह के रूप में पहचाना जाता है u कोण से θ: सीएफ. रोड्रिग्स का घूर्णन सूत्र.

लघुगणक मानचित्र

दिया गया R ∈ SO(3), होने देना $A={\tfrac {1}{2}}\left(R-R^{\mathrm {T} }\right)$ एंटीसिमेट्रिक भाग को निरूपित करें और जाने दें ${\textstyle \|A\|={\sqrt {-{\frac {1}{2}}\operatorname {Tr} \left(A^{2}\right)}}.}$ फिर, का लघुगणक R द्वारा दिया गया है

$\log R={\frac {\sin ^{-1}\|A\|}{\|A\|}}A.$

यह रोड्रिग्स सूत्र के मिश्रित समरूपता रूप के निरीक्षण से प्रकट होता है,

$e^{X}=I+{\frac {\sin \theta }{\theta }}X+2{\frac {\sin ^{2}{\frac {\theta }{2}}}{\theta ^{2}}}X^{2},\quad \theta =\|X\|,$

जहां दाहिनी ओर पहला और अंतिम पद सममित है।

एकसमान यादृच्छिक नमूनाकरण

$SO(3)$ इकाई चतुर्भुजों के समूह द्वारा दोगुना आच्छादित है, जो 3-गोले के समरूपी है। चूंकि इकाई चतुर्भुज पर हार माप 4 आयामों में केवल 3-क्षेत्र माप है, इसलिए हार माप पर $SO(3)$ यह 3-क्षेत्रीय माप को आगे बढ़ाने वाला मात्र है।

परिणामस्वरूप, समान रूप से यादृच्छिक घूर्णन उत्पन्न होता है $\mathbb {R} ^{3}$ 3-गोले पर समान रूप से यादृच्छिक बिंदु उत्पन्न करने के समान है। इसे निम्नलिखित द्वारा पूरा किया जा सकता है

$$({\sqrt {1-u_{1}}}\sin(2\pi u_{2}),{\sqrt {1-u_{1}}}\cos(2\pi u_{2}),{\sqrt {u_{1}}}\sin(2\pi u_{3}),{\sqrt {u_{1}}}\cos(2\pi u_{3}))$$

जहाँ $u_{1},u_{2},u_{3}$ के समान रूप से यादृच्छिक प्रतिरूप हैं $[0,1]$.

बेकर-कैंपबेल-हॉसडॉर्फ सूत्र

Main article: बेकर-कैंपबेल-हॉसडॉर्फ फॉर्मूला

X और Y लाई बीजगणित में दिया गया है। उनके घातांक, exp(X) और exp(Y), रोटेशन आव्युह हैं, जिन्हें गुणा किया जा सकता है। चूँकि घातीय मानचित्र अनुमान है ली अलजेब्रा में कुछ Z के लिए, exp(Z) = exp(X) exp(Y), और कोई अस्थायी रूप से लिख सकता है

$Z=C(X,Y),$

C के लिए कुछ अभिव्यक्ति X और Y में दी गई है। जब exp(X) और exp(Y) घूमते हैं, तो Z = X + Y होता है, जटिल घातांक के व्यवहार की अनुकरण करता है।

सामान्य स्थितियों अधिक विस्तृत बीसीएच सूत्र द्वारा दिया गया है, जो नेस्टेड लाई ब्रैकेट्स का श्रृंखला विस्तार है। आव्युह के लिए, लाई ब्रैकेट कम्यूटेटर के समान प्रक्रिया है, जो गुणन में कम्यूटेटिविटी की कमी की निगरानी करता है। यह सामान्य विस्तार इस प्रकार सामने आता है,

$Z=C(X,Y)=X+Y+{\frac {1}{2}}[X,Y]+{\tfrac {1}{12}}[X,[X,Y]]-{\frac {1}{12}}[Y,[X,Y]]+\cdots .$

वह SO(3) के लिए BCH सूत्र में अनंत विस्तार को सघन रूप में कम कर देता है,

$Z=\alpha X+\beta Y+\gamma [X,Y],$

उपयुक्त त्रिकोणमितीय फलन गुणांक के लिए (α, β, γ)।

त्रिकोणमितीय गुणांक

वह (α, β, γ) द्वारा दिए गए हैं

$\alpha =\phi \cot \left({\frac {\phi }{2}}\right)\gamma ,\qquad \beta =\theta \cot \left({\frac {\theta }{2}}\right)\gamma ,\qquad \gamma ={\frac {\sin ^{-1}d}{d}}{\frac {c}{\theta \phi }},$

कहाँ

${\begin{aligned}c&={\frac {1}{2}}\sin \theta \sin \phi -2\sin ^{2}{\frac {\theta }{2}}\sin ^{2}{\frac {\phi }{2}}\cos(\angle (u,v)),\quad a=c\cot \left({\frac {\phi }{2}}\right),\quad b=c\cot \left({\frac {\theta }{2}}\right),\\d&={\sqrt {a^{2}+b^{2}+2ab\cos(\angle (u,v))+c^{2}\sin ^{2}(\angle (u,v))}},\end{aligned}}$

के लिए

$\theta ={\frac {1}{\sqrt {2}}}\|X\|,\quad \phi ={\frac {1}{\sqrt {2}}}\|Y\|,\quad \angle (u,v)=\cos ^{-1}{\frac {\langle X,Y\rangle }{\|X\|\|Y\|}}.$

आंतरिक उत्पाद हिल्बर्ट-श्मिट आंतरिक उत्पाद है और मानदंड संबद्ध मानदंड है। टोपी-समरूपता के तहत,

$\langle u,v\rangle ={\frac {1}{2}}\operatorname {Tr} X^{\mathrm {T} }Y,$

जो इसके कारकों की व्याख्या करता है θ और φ. यह कोण के व्यंजक में समाप्त हो जाता है।

See also: तीन आयामों में घूर्णन औपचारिकताएं § रोड्रिग्स पैरामीटर और गिब्स प्रतिनिधित्व

इस मिश्रित घूर्णन जनरेटर को इस प्रकार लिखना सार्थक है

$\alpha X+\beta Y+\gamma [X,Y]{\underset {{\mathfrak {so}}(3)}{=}}X+Y+{\frac {1}{2}}[X,Y]+{\frac {1}{12}}[X,[X,Y]]-{\frac {1}{12}}[Y,[X,Y]]+\cdots ,$

इस बात पर जोर देने के लिए कि यह ली अलजेब्रा पहचान है।

ऊपर का यह समीकरण 𝖘𝖔(3) के सभी वफादार प्रतिष्ठानों के लिए सही है। ली अलजेब्रा समरूपता का कर्नेल (बीजगणित) आदर्श (ली अलजेब्रा) है, लेकिन 𝖘𝖔(3), सरल (अमूर्त बीजगणित) होने के कारण, इसका कोई गैर-तुच्छ आदर्श नहीं है और इसलिए सभी गैर-तुच्छ निरूपण वफादार हैं। यह विशेष रूप से दोहरे या स्पिनर प्रतिनिधित्व में निहित है। इस प्रकार वही स्पष्ट सूत्र पाउली मैट्रिसेस, सीएफ के माध्यम से सरल तरीके से अनुसरण करता है। SU(2) के लिए 2×2 व्युत्पत्ति।

एसयू(2) स्थितियों

समान BCH सूत्र के पाउली वेक्टर का पाउली मैट्रिसेस#एक्सपोनेंशियल, SU(2) का कुछ हद तक सरल समूह संरचना नियम है,

$e^{ia'\left({\hat {u}}\cdot {\vec {\sigma }}\right)}e^{ib'\left({\hat {v}}\cdot {\vec {\sigma }}\right)}=\exp \left({\frac {c'}{\sin c'}}\sin a'\sin b'\left(\left(i\cot b'{\hat {u}}+i\cot a'{\hat {v}}\right)\cdot {\vec {\sigma }}+{\frac {1}{2}}\left[i{\hat {u}}\cdot {\vec {\sigma }},i{\hat {v}}\cdot {\vec {\sigma }}\right]\right)\right),$

कहाँ

$\cos c'=\cos a'\cos b'-{\hat {u}}\cdot {\hat {v}}\sin a'\sin b',$

कोज्या का गोलाकार नियम. (टिप्पणी a', b', c' कोण हैं, नहीं a, b, c ऊपर।)

यह स्पष्ट रूप से ऊपर बताए गए प्रारूप जैसा ही है,

$Z=\alpha 'X+\beta 'Y+\gamma '[X,Y],$

साथ

$X=ia'{\hat {u}}\cdot \mathbf {\sigma } ,\quad Y=ib'{\hat {v}}\cdot \mathbf {\sigma } \in {\mathfrak {su}}(2),$

ताकि

${\begin{aligned}\alpha '&={\frac {c'}{\sin c'}}{\frac {\sin a'}{a'}}\cos b'\\\beta '&={\frac {c'}{\sin c'}}{\frac {\sin b'}{b'}}\cos a'\\\gamma '&={\frac {1}{2}}{\frac {c'}{\sin c'}}{\frac {\sin a'}{a'}}{\frac {\sin b'}{b'}}.\end{aligned}}$

शामिल लाई बीजगणित में जनरेटर के एक समान सामान्यीकरण के लिए, पाउली मैट्रिक्स को के संदर्भ में व्यक्त करें t-मैट्रिसेस, σ → 2i t, जिससे

$a'\mapsto -{\frac {\theta }{2}},\quad b'\mapsto -{\frac {\phi }{2}}.$

यह सत्यापित करने के लिए कि ये ऊपर दिए गए समान गुणांक हैं, गुणांकों के अनुपात की गणना करें,

${\begin{aligned}{\frac {\alpha '}{\gamma '}}&=\theta \cot {\frac {\theta }{2}}&={\frac {\alpha }{\gamma }}\\{\frac {\beta '}{\gamma '}}&=\phi \cot {\frac {\phi }{2}}&={\frac {\beta }{\gamma }}.\end{aligned}}$

अंत में, γ = γ' पहचान दी d = sin 2c'.

सामान्य के लिए n × n स्थितियों में, कोई Ref का उपयोग कर सकता है।

The quaternion case

दो घूर्णन आर की संरचना का चतुर्भुज सूत्रीकरण_B और आर_A यह सीधे घूर्णन की धुरी और समग्र घूर्णन के कोण R को भी प्राप्त करता है_C = आर_BR_A.

मान लीजिए कि स्थानिक घूर्णन R से संबद्ध चतुर्भुज का निर्माण इसके घूर्णन के अक्ष S और इस अक्ष के घूर्णन कोण φ से होता है। संबंधित चतुर्भुज द्वारा दिया गया है,

$S=\cos {\frac {\phi }{2}}+\sin {\frac {\phi }{2}}\mathbf {S} .$

फिर घूर्णन की संरचना आर_R आर के साथ_A घूर्णन R है_C = आर_BR_A चतुष्कोणों के गुणनफल द्वारा परिभाषित घूर्णन अक्ष और कोण के साथ

$A=\cos {\frac {\alpha }{2}}+\sin {\frac {\alpha }{2}}\mathbf {A} \quad {\text{ and }}\quad B=\cos {\frac {\beta }{2}}+\sin {\frac {\beta }{2}}\mathbf {B} ,$

वह है

$C=\cos {\frac {\gamma }{2}}+\sin {\frac {\gamma }{2}}\mathbf {C} =\left(\cos {\frac {\beta }{2}}+\sin {\frac {\beta }{2}}\mathbf {B} \right)\left(\cos {\frac {\alpha }{2}}+\sin {\frac {\alpha }{2}}\mathbf {A} \right).$

प्राप्त करने के लिए इस उत्पाद का विस्तार करें

$\cos {\frac {\gamma }{2}}+\sin {\frac {\gamma }{2}}\mathbf {C} =\left(\cos {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}-\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} \right)+\left(\sin {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}\mathbf {B} +\sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\mathbf {A} +\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \times \mathbf {A} \right).$

इस समीकरण के दोनों पक्षों को पहचान से विभाजित करें, जो कोसाइन का गोलाकार नियम है,

$\cos {\frac {\gamma }{2}}=\cos {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}-\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} ,$

और गणना करें

$\tan {\frac {\gamma }{2}}\mathbf {C} ={\frac {\tan {\frac {\beta }{2}}\mathbf {B} +\tan {\frac {\alpha }{2}}\mathbf {A} +\tan {\frac {\beta }{2}}\tan {\frac {\alpha }{2}}\mathbf {B} \times \mathbf {A} }{1-\tan {\frac {\beta }{2}}\tan {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} }}.$

यह दो घूर्णनों की अक्षों के संदर्भ में परिभाषित मिश्रित घूर्णन की धुरी के लिए रोड्रिग्स का सूत्र है। उन्होंने यह सूत्र 1840 में निकाला (देखें पृष्ठ 408)। तीन घूर्णन अक्ष A, B, और C एक गोलाकार त्रिभुज बनाते हैं और इस त्रिभुज की भुजाओं द्वारा निर्मित तलों के बीच के विकर्ण कोणों को घूर्णन कोणों द्वारा परिभाषित किया जाता है।

घूर्णन का एहसास

Main article: तीन आयामों में घूर्णन औपचारिकताएँ

See also: SO(3) पर चार्ट

हमने देखा है कि घूर्णनों को प्रतिष्ठित करने के कई विधि हैं:

• निर्धारक 1 के साथ ऑर्थोगोनल आव्युह के रूप में,
• अक्ष और घूर्णन कोण द्वारा
• चतुर्धातुक बीजगणित में छंद और मानचित्र 3-गोले S³ → SO(3) के साथ (चतुर्भुज और स्थानिक घुमाव देखें)
• ज्यामितीय बीजगणित में रोटर के रूप में (गणित)
• तीन निश्चित अक्षों के बारे में तीन घुमावों के अनुक्रम के रूप में; यूलर कोण देखें.

गोलाकार हार्मोनिक्स

Main article: गोलाकार हार्मोनिक्स

See also: SO(3) का प्रतिनिधित्व

त्रि-आयामी यूक्लिडियन घुमावों के समूह SO(3) का हिल्बर्ट अंतरिक्ष पर अनंत-आयामी प्रतिनिधित्व है

$L^{2}\left(\mathbf {S} ^{2}\right)=\operatorname {span} \left\{Y_{m}^{\ell },\ell \in \mathbb {N} ^{+},-\ell \leq m\leq \ell \right\},$

यहाँ $Y_{m}^{\ell }$ गोलाकार हार्मोनिक्स हैं। इसके तत्व वर्गाकार पूर्णांक जटिल-मूल्यवान फलन हैं जो की स्फेरे पर हैं। इस स्थान पर आंतर गुणन से प्रदान किया जाता है।

$\langle f,g\rangle =\int _{\mathbf {S} ^{2}}{\overline {f}}g\,d\Omega =\int _{0}^{2\pi }\int _{0}^{\pi }{\overline {f}}g\sin \theta \,d\theta \,d\phi .$

(H1)

यदि f इकाई क्षेत्र S² पर परिभाषित मनमाना वर्ग पूर्णांक फलन है, तो इसे इस प्रकार व्यक्त किया जा सकता है

$|f\rangle =\sum _{\ell =1}^{\infty }\sum _{m=-\ell }^{m=\ell }\left|Y_{m}^{\ell }\right\rangle \left\langle Y_{m}^{\ell }|f\right\rangle ,\qquad f(\theta ,\phi )=\sum _{\ell =1}^{\infty }\sum _{m=-\ell }^{m=\ell }f_{\ell m}Y_{m}^{\ell }(\theta ,\phi ),$

(H2)

जहां विस्तार गुणांक दिए गए हैं

$f_{\ell m}=\left\langle Y_{m}^{\ell },f\right\rangle =\int _{\mathbf {S} ^{2}}{\overline {Y_{m}^{\ell }}}f\,d\Omega =\int _{0}^{2\pi }\int _{0}^{\pi }{\overline {Y_{m}^{\ell }}}(\theta ,\phi )f(\theta ,\phi )\sin \theta \,d\theta \,d\phi .$

(H3)

लोरेंत्ज़ समूह क्रिया SO(3) की प्रतिबंधित होती है और इसे निम्नलिखित रूप में व्यक्त किया जा सकता है:

$(\Pi (R)f)(\theta (x),\phi (x))=\sum _{\ell =1}^{\infty }\sum _{m=-\ell }^{m=\ell }\sum _{m'=-\ell }^{m'=\ell }D_{mm'}^{(\ell )}(R)f_{\ell m'}Y_{m}^{\ell }\left(\theta \left(R^{-1}x\right),\phi \left(R^{-1}x\right)\right),\qquad R\in \operatorname {SO} (3),\quad x\in \mathbf {S} ^{2}.$

(H4)

यह क्रिया एकात्मक अर्थात् एकात्मक है

$\langle \Pi (R)f,\Pi (R)g\rangle =\langle f,g\rangle \qquad \forall f,g\in \mathbf {S} ^{2},\quad \forall R\in \operatorname {SO} (3).$

(H5)

D^(ℓ) को ऊपर दिए गए D^(m, n) का क्लेबश-गॉर्डन गुणांकका उपयोग करके प्राप्त किया जा सकता है, लेकिन उन्हें विषम-आयामी su(2) प्रतिष्ठान के एक विस्तृत (यहां, 3-आयामी सही है 𝖘𝖔(3)) के एक प्रतिष्ठान के विस्तार के रूप में भी सीधे व्यक्त किया जा सकता है। इस स्थितियों में समिष्ट L²(S²) अघुलनशील विषम परिमित-आयामी निरूपणों के अनंत प्रत्यक्ष योग में बड़े करीने से विघटित हो जाता है V_{2i + 1}, i = 0, 1, ... के अनुसार

$L^{2}\left(\mathbf {S} ^{2}\right)=\sum _{i=0}^{\infty }V_{2i+1}\equiv \bigoplus _{i=0}^{\infty }\operatorname {span} \left\{Y_{m}^{2i+1}\right\}.$

(H6)

यह SO(3) की अनन्त-आयामी इकाई प्रतिष्ठानों की विशेषता है। यदि Π वियोज्य हिल्बर्ट समिष्ट पर अनंत-आयामी एकात्मक प्रतिनिधित्व है, तो यह सीधे योग के रूप में सीमित-आयामी इकाई प्रतिष्ठानों के सीधे योग में विभाजित होता है।इस प्रकार ऐसा प्रतिनिधित्व कभी भी अप्रासंगिक नहीं होता है। सभी अपरिवर्तनीय परिमित-आयामी निरूपण (Π, V)आंतरिक उत्पाद के उचित चयन द्वारा एकात्मक बनाया जा सकता है,

$\langle f,g\rangle _{U}\equiv \int _{\operatorname {SO} (3)}\langle \Pi (R)f,\Pi (R)g\rangle \,dg={\frac {1}{8\pi ^{2}}}\int _{0}^{2\pi }\int _{0}^{\pi }\int _{0}^{2\pi }\langle \Pi (R)f,\Pi (R)g\rangle \sin \theta \,d\phi \,d\theta \,d\psi ,\quad f,g\in V,$

जहां अभिन्न SO(3) अद्वितीय अपरिवर्तनीय अभिन्न है, जिसे 1 पर सामान्यीकृत किया गया है, यहां यूलर कोण पैरामीट्रिजेशन का उपयोग करके व्यक्त किया गया है। इंटीग्रल के अंदर का आंतरिक उत्पाद V किसी भी आंतरिक उत्पाद पर होता है।

सामान्यीकरण

घूर्णन समूह बहुत स्वाभाविक रूप से एन-आयामी यूक्लिडियन समिष्ट, $\mathbb {R} ^{n}$को बहुमुखी यूक्लिड संरचना के साथ सामान्यीकृत करता है। n आयामों में सभी उचित और अनुचित घुमावों के समूह को "ऑर्थोगोनल समूह" O(n) कहा जाता है, और उचित घुमावों के उपसमूह को विशेष ऑर्थोगोनल समूह SO(n) कहा जाता है, जो n(n − 1)/2 आयाम का ली समूह है।

विशेष सापेक्षता में, कोई 4-आयामी सदिश समिष्ट में काम करता है, जिसे 3-आयामी यूक्लिडियन समिष्ट के अतिरिक्त मिन्कोव्स्की समिष्ट के रूप में जाना जाता है। यूक्लिडियन समिष्ट के विपरीत, मिन्कोवस्की समिष्ट में अनिश्चित हस्ताक्षर वाला आंतरिक उत्पाद होता है। चूँकि, कोई अभी भी सामान्यीकृत घुमावों को परिभाषित कर सकता है जो इस आंतरिक उत्पाद को संरक्षित करते हैं। ऐसे सामान्यीकृत घुमावों को लोरेंत्ज़ परिवर्तन के रूप में जाना जाता है और ऐसे सभी परिवर्तनों के समूह को लोरेंत्ज़ समूह कहा जाता है।

घूर्णन समूह SO(3) को E⁺(3) के उपसमूह के रूप में वर्णित किया जा सकता है, जो यूक्लिडियन के प्रत्यक्ष आइसोमेट्री का यूक्लिडियन समूह है। इनमें से प्रत्येक मनमाना अक्ष के चारों ओर घूमने और अनुवाद का संयोजन है, या अलग विधि से कहें तो SO(3) के तत्व और मनमाना अनुवाद का संयोजन है।

सामान्यत:, किसी वस्तु का घूर्णन समूह प्रत्यक्ष आइसोमेट्रीज़ के समूह के भीतर समरूपता समूह होता है; अन्य कथन से, पूर्ण समरूपता समूह और प्रत्यक्ष आइसोमेट्री के समूह का प्रतिच्छेदन। चिरैलिटी (गणित) वस्तुओं के लिए यह पूर्ण समरूपता समूह के समान है।

यह भी देखें

• ओर्थोगोनल समूह
• कोनेदार गति
• समन्वय रोटेशन
• SO(3) पर चार्ट
• झूठ समूह का प्रतिनिधित्व#एक उदाहरण: रोटेशन समूह SO(3)|SO(3) का प्रतिनिधित्व
• यूलर कोण
• रॉड्रिग्स का घूर्णन सूत्र
• अतिसूक्ष्म घूर्णन
• पिन समूह
• चतुर्भुज और स्थानिक घुमाव
• सख्त शरीर
• गोलाकार हार्मोनिक्स
• घूर्णन का तल
• झूठ समूह
• पॉली मैट्रिक्स
• प्लेट ट्रिक
• त्रि-आयामी रोटेशन ऑपरेटर

ग्रन्थसूची

• Boas, Mary L. (2006), Mathematical Methods in the Physical Sciences (3rd ed.), John Wiley & sons, pp. 120, 127, 129, 155ff and 535, ISBN 978-0471198260
• Curtright, T. L.; Fairlie, D. B.; Zachos, C. K. (2014), "A compact formula for rotations as spin matrix polynomials", SIGMA, 10: 084, arXiv:1402.3541, Bibcode:2014SIGMA..10..084C, doi:10.3842/SIGMA.2014.084, S2CID 18776942
• Engø, Kenth (2001), "On the BCH-formula in 𝖘𝖔(3)", BIT Numerical Mathematics, 41 (3): 629–632, doi:10.1023/A:1021979515229, ISSN 0006-3835, S2CID 126053191 [1]
• Gelfand, I.M.; Minlos, R.A.; Shapiro, Z.Ya. (1963), Representations of the Rotation and Lorentz Groups and their Applications, New York: Pergamon Press
• Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2002), Classical Mechanics (third ed.), Addison Wesley, ISBN 978-0-201-65702-9
• Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3319134666
• Hall, Brian C. (2003). Lie groups, Lie algebras, and representations : an elementary introduction. Graduate Texts in Mathematics. Vol. 222. New York: Springer. ISBN 0-387-40122-9.
• Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover Publications, ISBN 978-0-486-47189-1
• Joshi, A. W. (2007), Elements of Group Theory for Physicists, New Age International, pp. 111ff, ISBN 978-81-224-0975-8
• Rossmann, Wulf (2002), Lie Groups – An Introduction Through Linear Groups, Oxford Graduate Texts in Mathematics, Oxford Science Publications, ISBN 0-19-859683-9
• van der Waerden, B. L. (1952), Group Theory and Quantum Mechanics, Springer Publishing, ISBN 978-3642658624 (translation of the original 1932 edition, Die Gruppentheoretische Methode in Der Quantenmechanik).
• Varadarajan, V. S. (1984). Lie groups, Lie algebras, and their representations. New York: Springer-Verlag. ISBN 978-0-387-90969-1.
• Veltman, M.; 't Hooft, G.; de Wit, B. (2007). "Lie Groups in Physics (online lecture)" (PDF). Retrieved 2016-10-24..