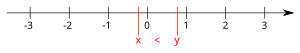रेखा (ज्यामिति)

For other uses, see रेखा.

द्वि-आयामी कार्टेशियन समन्वय प्रणाली पर उत्पत्ति (गणित) के पास लाल रेखा

ज्यामिति में, रेखा अनंत रूप से लंबी वस्तु होती है, जिसमें कोई चौड़ाई, गहराई या वक्रता नहीं होती है। इस प्रकार, रेखाएं एक-आयामी वस्तुएँ हैं- चूँकि वे दो, त्रि-आयामी, या उच्च आयाम वाले स्थानों में सन्निहित हो सकती हैं। शब्द रेखा का अर्थ या गणित में रेखा खंड को दो बिंदुओं के मध्य की रेखा के खंड के रूप में भी संदर्भित किया जा सकता है, जिसके सिरों को दर्शाने के लिए दो बिंदु हैं। इसमें रेखाओं को दो बिंदुओं द्वारा परिभाषित किया जा सकता है जो उस पर स्थित हैं (जैसे, ${\textstyle {\overleftrightarrow {AB}}}$) या अक्षर (उदा., $\ell$), जो उक्त खंड बनाते हैं।

यूक्लिड ने रेखा को चौड़ाई रहित लंबाई के रूप में वर्णित किया जो स्वयं पर बिंदुओं के संबंध में समान रूप से स्थित है; उन्होंने मूलभूत अप्राप्य गुणधर्मों के रूप में अनेक अभिधारणाओं को प्रस्तुत किया, जिनसे उन्होंने सभी ज्यामिति का निर्माण किया, यूक्लिडियन रेखा और यूक्लिडियन ज्यामिति19 दशक के अंत में प्रारम्भ की गई हैं सामान्यीकरणों, जैसे कि गैर-यूक्लिडियन, प्रक्षेपी और एफाइन ज्यामिति के साथ भ्रम से बचने के लिए प्रारम्भ किए गए शब्द हैं।

आधुनिक गणित में, प्रस्तावित ज्यामिति की भीड़ को देखते हुए (इस विचार के आधार पर कि कोई भी 3D वस्तु सतह यूक्लिडियन के समवर्ती नई ज्यामिति बनाती है, या निश्चित गति में कई आयामी स्थान भी गैर यूक्लिडियन हैं, किन्तु इसके अतिरिक्त गैर यूक्लिडियन स्थान वह स्थान है जो नहीं है गति में या अंतरिक्ष-समय में तय किया गया था, जितना कि यूक्लिड को ऐसी ज्यामितीय गणनाओं में कोई रूचि नहीं थी), आगे यह माना या प्रस्तावित किया जाता है कि इन काल्पनिक ज्यामिति में रेखा की अवधारणा काल्पनिक ज्यामिति का वर्णन करने के तरीके से निकटता से जुड़ी हुई है।

विश्लेषणात्मक ज्यामिति में, समतल में रेखा को प्रायः उन बिंदुओं के समूह के रूप में परिभाषित किया जाता है जिनके निर्देशांक किसी दिए गए रैखिक समीकरण को संतुष्ट करते हैं, किन्तु अधिक सार सेटिंग में, जैसे कोलोमोगोरोव के संयोजन ज्यामिति के उपक्षेत्र और अंतर ज्यामिति संयोजनीय घटना ज्यामिति का निरीक्षण करते हैं।

जब ज्यामिति का वर्णन स्वयंसिद्ध ों के समूह द्वारा किया जाता है, तो प्राथमिक शिक्षा में रेखा की धारणा को प्रायः अपरिभाषित ( तथाकथित आदिम धारणा वस्तु) छोड़ दिया जाता है। रेखाओं के गुण तब उन अभिगृहीतों द्वारा निर्धारित किए जाते हैं जो उन्हें संदर्भित करते हैं। इस दृष्टिकोण का फायदा यह है कि यह छात्रों, शिक्षार्थियों और ज्यामिति के सिद्धांतों को लागू करने वालों को लचीलापन देता है। इस प्रकार तुलनात्मक ज्यामिति और विभेदक ज्यामिति में, रेखा अन्य गणितीय वस्तुओं के साथ-साथ गणना का विषय होती है।

अनुप्रयुक्त गणित, वास्तुकला और भूगणित में, रेखा को भूगणित के रूप में व्याख्यायित किया जा सकता है ( फुट (इकाई) में मापे गए बिंदुओं के मध्य सबसे छोटा पथ, जो कि भूगणित में लागू सैन्य विज्ञान है)।

कुछ प्रक्षेपी ज्यामिति में, रेखा द्वि-आयामी सदिश दिशा होती है और सभी रेखाएँ और दो स्वतंत्र सदिशों का उनका रैखिक संयोजन उनके मध्य का स्थान होता है।

रेखा का लचीलापन यूक्लिडियन ज्यामिति से भिन्न का हिस्सा है, जहां अंतरिक्ष-समय में निश्चित गति को हटा दिया जाता है, कुछ भविष्यवादी प्रावधानवादियों के लिए यह गणित से भी आगे बढ़ता है।

भौतिकी और प्रकाशिकी (सैन्य विज्ञान सहित) में, भौतिक विज्ञान ी भी सामान्यतः प्रकाश किरण के मार्ग को रेखा मानते हैं, चूँकि अन्य प्रकाश संरचनाएं उनके सदिश गुणों, रेखाओं के अलावा अन्य संरचनाओं आदि के साथ उपस्थित होती हैं। ऐसा कहा जाता है कि रेखा हो सकती है स्वतंत्र वस्तु, उन बिंदुओं के समूह से भिन्न जो उस पर केवल तभी स्थित होते हैं जब दूसरी रेखा उस पर पड़ती है (जिसे भौतिकी में सिद्ध किया जा सकता है)।

किसी भी खींची गई गणितीय रैखिक वस्तु के रूप में भी रेखा जो फ़ंक्शन का प्रतिनिधित्व कर सकती है (सीधी रेखाओं के लिए y=x, y=x+n/x-n और बहुपद जैसे अन्य अधिक जटिल कार्य) या गोलाकार रेखाएं, या कोई अन्य गैर-सीधी सतह रेखाएं जो संभवतः विशेषता भी हो सकती हैं सतह, गणितीय वस्तु), यहाँ समतल या सतह में कार्य ज्यामितीय रूप से विशेषता रेखा के विपरीत है (चूँकि कुछ GCL की गणना कार्यों के रूप में की जा सकती है)।

गुण

जब तत्वों में यूक्लिड द्वारा ज्यामिति को प्रथम बार औपचारिक रूप दिया गया था, तो उन्होंने सामान्य रेखा (जिसे अब वक्र कहा जाता है) को चौड़ाई रहित लंबाई के रूप में परिभाषित किया, जिसमें सीधी रेखा ऐसी रेखा होती है जो स्वयं पर बिंदुओं के साथ समान रूप से स्थित होती है। ये परिभाषाएँ अधिक अल्प उद्देश्य की पूर्ति करती हैं, क्योंकि वे ऐसे शब्दों का उपयोग करती हैं जो स्वयं परिभाषित नहीं हैं। वास्तव में, यूक्लिड ने स्वयं इस कार्य में इन परिभाषाओं का उपयोग नहीं किया था, और संभवतः उन्हें केवल पाठक को यह स्पष्ट करने के लिए सम्मिलित किया था कि क्या उल्लेख किया जा रहा है। आधुनिक ज्यामिति में, रेखा को केवल अपरिभाषित वस्तु के रूप में लिया जाता है जिसमें स्वयंसिद्धों द्वारा दिए गए गुण होते हैं, किन्तु कभी-कभी रैखिक संबंध का पालन करने वाले बिंदुओं के समूह के रूप में परिभाषित किया जाता है जब कुछ अन्य मौलिक अवधारणा को अपरिभाषित त्याग दिया जाता है।

यूक्लिडियन ज्यामिति के स्वयंसिद्ध सूत्रीकरण में, जैसे कि हिल्बर्ट (यूक्लिड के मूल सिद्धांतों में विभिन्न दोष थे जिन्हें आधुनिक गणितज्ञों द्वारा ठीक किया गया है), रेखा को कुछ गुणों के लिए कहा जाता है जो इसे अन्य रेखाओं और बिंदुओं से संबंधित करता हैं। उदाहरण के लिए, किन्हीं दो भिन्न-भिन्न बिंदुओं के लिए, उनमें से अद्वितीय रेखा होती है, और कोई भी दो भिन्न-भिन्न रेखाएं अधिकतम बिंदु पर प्रतिच्छेद करती हैं। दो आयामों में (अर्थात, यूक्लिडियन विमान), दो रेखाएँ जो प्रतिच्छेद नहीं करती हैं, समानांतर कहलाती हैं। उच्च आयामों में, दो रेखाएँ जो प्रतिच्छेद नहीं करती हैं, यदि वे समतल में समाहित हैं, या तिरछी रेखाएँ नहीं हैं तो वे समानांतर होती हैं।

यूक्लिडियन तल पर, रेखा को दो क्षेत्रों के मध्य की सीमा के रूप में दर्शाया जा सकता है। सूक्ष्म रूप से विभिन्न रेखाओं का कोई भी संग्रह समतल को उत्तल बहुभुजों में विभाजित करता है (संभवतः असीमित); इस विभाजन को रेखाओं की व्यवस्था के रूप में जाना जाता है।

उच्च आयामों में

त्रि-आयामी अंतरिक्ष में, चर x, y, और z में प्रथम डिग्री समीकरण समतल को परिभाषित करता है, इसलिए दो ऐसे समीकरण, वे जिन विमानों को उत्पन्न करते हैं वे समानांतर नहीं हैं, रेखा को परिभाषित करें जो विमानों का प्रतिच्छेदन है। सामान्यतः, n-आयामी स्थान में n-1 प्रथम-डिग्री समीकरण n कार्टेशियन समन्वय प्रणाली चर में उपयुक्त परिस्थितियों में रेखा को परिभाषित करते हैं।

अधिक सामान्य यूक्लिडियन अंतरिक्ष में, 'R'ⁿ (और समान रूप से प्रत्येक दूसरे एफ़िन स्थान में), दो भिन्न-भिन्न बिंदुओं a और b से निकलने वाली रेखा L उपसमुच्चय है:

$$L=\left\{(1-t)\,a+tb\mid t\in \mathbb {R} \right\}$$

रेखा की दिशा a (t = 0) से b (t = 1) तक है, या दूसरे शब्दों में, सदिश b − a की दिशा में होती है। a और b के विभिन्न विकल्पों से रेखा प्राप्त हो सकती है।

समरेख बिंदु

Main article: समरैखिकता

तीन बिंदु एक ही रेखा पर स्थित होने पर संरेखी कहलाते हैं। तीन बिंदु सामान्यतः समतल का निर्धारण करते हैं, किन्तु तीन समरेख बिंदुओं की स्थिति में ऐसा नहीं होता है।

एफ़िन निर्देशांक में, n-आयामी स्थान में बिंदु X = (x₁, x₂, ..., x_n), Y = (y₁, y₂, ..., y_n), और Z = (z₁, z₂, ..., z_n) संरेख हैं यदि आव्यूह (गणित)

$${\begin{bmatrix}1&x_{1}&x_{2}&\cdots &x_{n}\\1&y_{1}&y_{2}&\cdots &y_{n}\\1&z_{1}&z_{2}&\cdots &z_{n}\end{bmatrix}}$$

श्रेणी 3 से अल्प है। विशेष रूप से, समतल (n = 2) में तीन बिंदुओं के लिए, उपरोक्त आव्यूह वर्गाकार है और बिंदु संरेख हैं यदि केवल इसका सारणिक शून्य है।

समान रूप से समतल में तीन बिंदुओं के लिए, अंक समरेखीय होते हैं यदि और केवल यदि जोड़ी बिंदुओं के मध्य ढलान किसी अन्य जोड़ी बिंदुओं के मध्य ढलान के बराबर होता है (जिस स्थिति में शेष जोड़ी बिंदुओं के मध्य ढलान अन्य ढलानों के बराबर होगा) . विस्तार से, तल में k बिंदु संरेख होते हैं यदि और केवल यदि कोई (k-1) बिंदुओं के जोड़े में समान जोड़ीदार ढलान हों।

यूक्लिडियन ज्यामिति में, दो बिंदुओं a और b के मध्य की यूक्लिडियन दूरी d(a,b) का उपयोग तीन बिंदुओं के मध्य संरेखता को व्यक्त करने के लिए किया जा सकता है:

बिंदु a, b और c संरेख हैं यदि और केवल यदि d(x,a) = d(c,a) और d(x,b) = d(c,b) का अर्थ x = c है।

हालाँकि, दूरी की अन्य धारणाएँ हैं (जैसे मैनहट्टन दूरी ) जिसके लिए यह गुण सत्य नहीं है।

ज्यामिति में जहां रेखा की अवधारणा आदिम धारणा है, जैसा कि कुछ सिंथेटिक ज्यामिति में हो सकता है, संरेखता निर्धारित करने के अन्य तरीकों की आवश्यकता होती है।

प्रकार

वक्र की स्पर्शरेखा। लाल रेखा लाल बिंदु द्वारा चिह्नित बिंदु पर वक्र के लिए स्पर्शरेखा है।

अर्थ में, यूक्लिडियन ज्यामिति में सभी रेखाएं समान होती हैं, इसमें निर्देशांक के बिना कोई उन्हें दूसरे से अलग नहीं बता सकता है। हालाँकि, रेखाएँ ज्यामिति में अन्य वस्तुओं के संबंध में विशेष भूमिका निभा सकती हैं और उस संबंध के अनुसार प्रकारों में विभाजित की जा सकती हैं। उदाहरण के लिए, शंकु खंड ( वृत्त, दीर्घवृत्त, परवलय , या अतिपरवलय) के संबंध में, रेखाएँ हो सकती हैं:

• स्पर्शरेखा रेखाएँ, जो बिंदु पर शंकु को स्पर्श करती हैं;
• छेदक रेखा एं, जो शंकु को दो बिंदुओं पर काटती हैं और इसके आंतरिक भाग से होकर गुजरती हैं;
• बाहरी रेखाएं, जो यूक्लिडियन तल के किसी भी बिंदु पर शंकु से नहीं मिलती हैं; या
• शंकु खंड का निर्देश, जिसकी बिंदु से दूरी यह स्थापित करने में मदद करती है कि बिंदु शंकु पर है या नहीं।

यूक्लिडियन ज्यामिति में समानांतर (ज्यामिति) निर्धारित करने के संदर्भ में, अनुप्रस्थ (ज्यामिति) ऐसी रेखा है जो दो अन्य रेखाओं को काटती है जो दूसरे के समानांतर हो भी सकती हैं और नहीं भी।

अधिक सामान्य बीजीय वक्र ों के लिए, रेखाएँ भी हो सकती हैं:

• i-secant रेखाएं, बिना बहुलता के गिने गए i बिंदुओं में वक्र को पूरा करना, या
• स्पर्शोन्मुख, जो वक्र बिना छुए मनमाने ढंग से निकट आता है।

यूक्लिडियन त्रिभुज के संबंध में हमारे पास है:

• यूलर लाइन ,
• सिमसन लाइन ्स, और
• केंद्रीय रेखा (ज्यामिति) ।

उत्तल बहुभुज चतुर्भुज के लिए जिसमें अधिकतम दो समानांतर भुजाएँ हों, न्यूटन रेखा वह रेखा है जो दो विकर्ण ों के मध्य बिंदुओं को जोड़ती है। षट्भुज के लिए जो शंकु पर स्थित है, हमारे पास पास्कल रेखा है और विशेष मामले में जहां शंकु रेखाओं की जोड़ी है, हमारे पास पप्पस का षट्भुज प्रमेय है।

समानांतर (ज्यामिति) ही तल में रेखाएँ हैं जो कभी भी पार नहीं करती हैं। लाइन-लाइन चौराहा समान बिंदु साझा करता है। संयोग रेखाएं आपस में संपाती होती हैं - प्रत्येक बिंदु जो उनमें से किसी पर होता है वह दूसरे पर भी होता है।

लम्बवत रेखाएँ वे रेखाएँ होती हैं जो समकोण पर प्रतिच्छेद करती हैं। त्रि-आयामी अंतरिक्ष में, तिरछी रेखाएँ वे रेखाएँ होती हैं जो ही तल में नहीं होती हैं और इस प्रकार दूसरे को नहीं काटती हैं।

स्वयंसिद्ध प्रणालियों में

रेखा की अवधारणा को प्रायः ज्यामिति में स्वयंसिद्ध प्रणाली में आदिम धारणा के रूप में माना जाता है, अर्थ यह अन्य अवधारणाओं द्वारा परिभाषित नहीं किया जा रहा है। उन स्थितियों में जहां रेखा परिभाषित अवधारणा है, जैसे समन्वय ज्यामिति में, कुछ अन्य मौलिक विचारों को आदिम के रूप में लिया जाता है। जब रेखा अवधारणा आदिम होती है, तो रेखाओं का व्यवहार और गुण उन स्वयंसिद्धों द्वारा निर्धारित होते हैं जिन्हें उन्हें संतुष्ट करना चाहिए। ज्यामिति के गैर-स्वयंसिद्ध या सरलीकृत स्वयंसिद्ध उपचार में, आदिम धारणा की अवधारणा से निपटने के लिए बहुत सारगर्भित हो सकता है। इस परिस्थिति में, आदिम धारणा का विवरण या मानसिक छवि प्रदान करना संभव है, उस धारणा को बनाने के लिए नींव देना जिस पर औपचारिक रूप से (अकथित) स्वयंसिद्धों पर आधारित होगा। इस प्रकार के विवरण, कुछ लेखकों द्वारा, प्रस्तुति की इस अनौपचारिक शैली में परिभाषा के रूप में संदर्भित किए जा सकते हैं। ये सही परिभाषाएं नहीं हैं, और इन्हें बयानों के औपचारिक प्रमाण में इस्तेमाल नहीं किया जा सकता है। यूक्लिड के तत्वों में रेखा की परिभाषा इस श्रेणी में आती है। यहां तक ​​​​कि उस मामले में जहां विशिष्ट ज्यामिति पर विचार किया जा रहा है (उदाहरण के लिए, यूक्लिडियन ज्यामिति), लेखकों के मध्य सामान्यतः स्वीकृत सहमति नहीं है कि जब विषय का औपचारिक रूप से इलाज नहीं किया जा रहा हो तो पंक्ति का अनौपचारिक विवरण क्या होना चाहिए।

परिभाषा

Main article: रेखा निर्देशांक

रैखिक समीकरण

Main article: रेखीय समीकरण

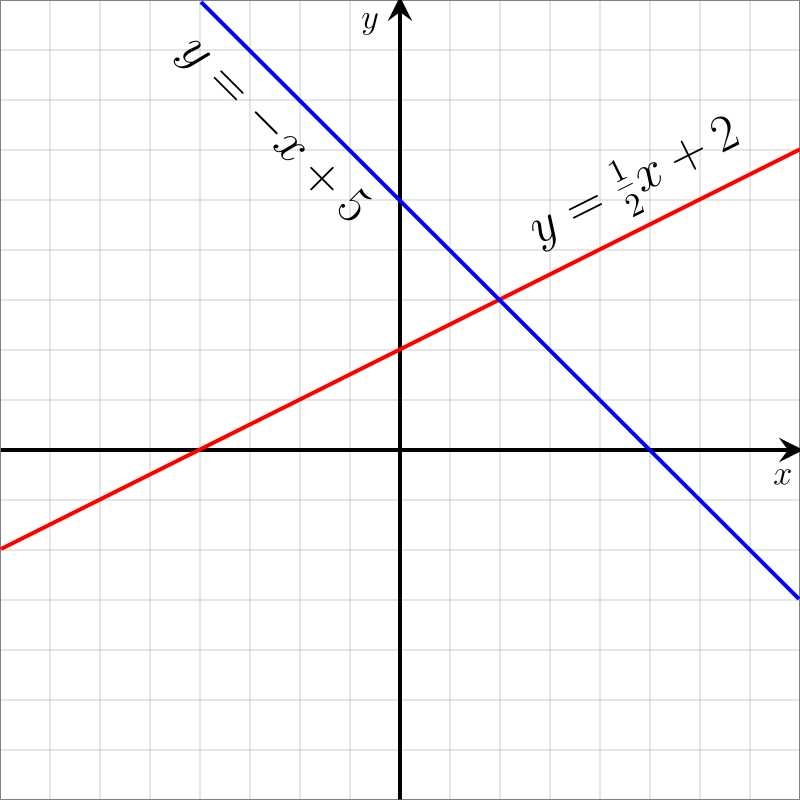कार्तीय तल में रेखाएं या, अधिक सामान्यतः, एफ़िन निर्देशांक में, रैखिक समीकरणों की विशेषता होती है। अधिक सटीक रूप से, प्रत्येक पंक्ति $L$ (ऊर्ध्वाधर रेखाओं सहित) उन सभी बिंदुओं का समुच्चय है जिनके कार्तीय निर्देशांक (x, y) रैखिक समीकरण को संतुष्ट करते हैं; वह है,

$$L=\{(x,y)\mid ax+by=c\},$$

जहाँ a, b और c स्थिर वास्तविक संख्या एँ (गुणांक कहलाती हैं) इस प्रकार हैं कि a और b दोनों शून्य नहीं हैं। इस रूप का उपयोग करते हुए, लंबवत रेखाएं b = 0 वाले समीकरणों के अनुरूप होती हैं।

कोई और भी मान सकता है c = 1 या c = 0, सब कुछ विभाजित करके c अगर यह शून्य नहीं है।

रेखा के समीकरण को लिखने के कई भिन्न तरीके हैं जिन्हें बीजगणितीय हेरफेर द्वारा से दूसरे में परिवर्तित किया जा सकता है। उपरोक्त प्रपत्र को कभी-कभी मानक रूप कहा जाता है। यदि अचर पद को बाईं ओर रखा जाए, तो समीकरण बन जाता है

$$ax+by-c=0,$$

और इसे कभी-कभी समीकरण का सामान्य रूप कहा जाता है। चूँकि , इस शब्दावली को सार्वभौमिक रूप से स्वीकार नहीं किया गया है, और कई लेखक इन दो रूपों में अंतर नहीं करते हैं।

इन रूपों को सामान्यतः उस लाइन के बारे में जानकारी (डेटा) के प्रकार से नामित किया जाता है जो फॉर्म को लिखने के लिए आवश्यक होती है। किसी रेखा के कुछ महत्वपूर्ण डेटा उसकी ढलान, फ़ंक्शन की जड़ | x-अवरोधन, रेखा पर ज्ञात बिंदु और y-अवरोधन हैं।

दो भिन्न-भिन्न बिंदुओं से गुजरने वाली रेखा का समीकरण $P_{0}(x_{0},y_{0})$ तथा $P_{1}(x_{1},y_{1})$ के रूप में लिखा जा सकता है

$$(y-y_{0})(x_{1}-x_{0})=(y_{1}-y_{0})(x-x_{0}).$$

यदि x₀ ≠ x₁, इस समीकरण को फिर से लिखा जा सकता है

$$y=(x-x_{0})\,{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}+y_{0}$$

या

$$y=x\,{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}+{\frac {x_{1}y_{0}-x_{0}y_{1}}{x_{1}-x_{0}}}\,.$$

द्वि-आयामी अंतरिक्ष में, गैर-ऊर्ध्वाधर रेखाओं के लिए समीकरण प्रायः ढलान-अवरोधन रूप में दिया जाता है:

$$y=mx+b$$

कहाँ पे:

• मी रेखा का ढाल या ढाल है।
• b रेखा का y-अवरोधन है।
• x फलन का स्वतंत्र चर है y = f(x).

बिंदुओं से होकर जाने वाली रेखा का ढलान $A(x_{a},y_{a})$ तथा $B(x_{b},y_{b})$, जब $x_{a}\neq x_{b}$, द्वारा दिया गया है $m=(y_{b}-y_{a})/(x_{b}-x_{a})$ और इस रेखा का समीकरण लिखा जा सकता है $y=m(x-x_{a})+y_{a}$.

पैरामीट्रिक समीकरण

Further information: पैरामीट्रिक समीकरण

पैरामीट्रिक समीकरणों का उपयोग रेखाओं को निर्दिष्ट करने के लिए भी किया जाता है, विशेष रूप से त्रि-आयामी अंतरिक्ष या अधिक में क्योंकि दो से अधिक आयामों में रेखाओं को एकल रैखिक समीकरण द्वारा वर्णित नहीं किया जा सकता है।

त्रिविमीय रेखाओं में प्रायः पैरामीट्रिक समीकरणों द्वारा वर्णित किया जाता है:

$${\begin{aligned}x&=x_{0}+at\\y&=y_{0}+bt\\z&=z_{0}+ct\end{aligned}}$$

कहाँ पे:

• x, y, और z सभी स्वतंत्र चर t के फलन हैं जो वास्तविक संख्याओं के ऊपर होते हैं।
• (एक्स₀, यू₀, साथ₀) रेखा पर कोई बिंदु है।
• ए, बी, और सी रेखा के ढलान से संबंधित हैं, जैसे कि दिशा सदिश (ज्यामितीय) (ए, बी, सी) रेखा के समानांतर है।

उच्च आयामों वाली रेखाओं के लिए पैरामीट्रिक समीकरण इस मायने में समान होते हैं कि वे रेखा पर बिंदु और दिशा सदिश के विनिर्देश पर आधारित होते हैं।

नोट के रूप में, तीन आयामों वाली रेखाओं को दो रैखिक समीकरणों के युगपत हल के रूप में भी वर्णित किया जा सकता है

$$a_{1}x+b_{1}y+c_{1}z-d_{1}=0$$

$$a_{2}x+b_{2}y+c_{2}z-d_{2}=0$$

ऐसा है कि $(a_{1},b_{1},c_{1})$ तथा $(a_{2},b_{2},c_{2})$ आनुपातिक नहीं हैं (रिश्ते $a_{1}=ta_{2},b_{1}=tb_{2},c_{1}=tc_{2}$ तात्पर्य $t=0$) यह इस प्रकार है क्योंकि तीन आयामों में एकल रैखिक समीकरण सामान्यतः समतल (ज्यामिति) का वर्णन करता है और रेखा वह है जो दो भिन्न-भिन्न प्रतिच्छेदन विमानों के लिए सामान्य है।

हेस्से सामान्य रूप

Main article: हेस्से सामान्य रूप

मूल O से रेखा E की दूरी की गणना हेस्से के सामान्य रूप से की जाती है। लाल रंग में सामान्य सदिश , हरे रंग में रेखा, बिंदु O नीले रंग में दिखाया गया है।

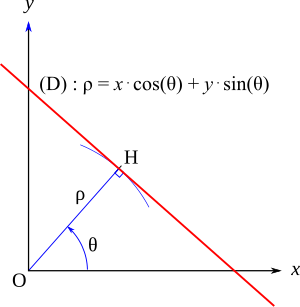
सामान्य रूप (जिसे हेस्से सामान्य रूप भी कहा जाता है, जर्मन गणितज्ञ ओटो हेस्से के बाद), किसी दी गई रेखा के लिए सामान्य (ज्यामिति) खंड पर आधारित है, जिसे मूल (गणित) से रेखा के लंबवत रेखा खंड के रूप में परिभाषित किया गया है। यह खंड मूल को मूल रेखा पर निकटतम बिंदु से जोड़ता है। समतल पर सीधी रेखा के समीकरण का सामान्य रूप निम्न द्वारा दिया गया है:

$$x\cos \varphi +y\sin \varphi -p=0,$$

कहाँ पे $\varphi$ सामान्य खंड के झुकाव का कोण है ( . के इकाई सदिश से उन्मुख कोण) x-इस खंड के लिए अक्ष), और p सामान्य खंड की (सकारात्मक) लंबाई है। सामान्य रूप को मानक रूप से प्राप्त किया जा सकता है $ax+by=c$ सभी गुणांकों को से विभाजित करके

$${\frac {c}{|c|}}{\sqrt {a^{2}+b^{2}}}.$$

ढलान-अवरोधन और अवरोधन रूपों के विपरीत, यह रूप किसी भी रेखा का प्रतिनिधित्व कर सकता है, किन्तु इसके लिए केवल दो परिमित मापदंडों की आवश्यकता होती है, $\varphi$ तथा p, निर्दिष्ट किया जाएगा। यदि p > 0, फिर $\varphi$ विशिष्ट रूप से परिभाषित मोडुलो . है 2π. दूसरी ओर, यदि रेखा मूल बिन्दु से होकर जाती है (c = p = 0), बूँदें c/|c| गणना करने के लिए शब्द $\sin \varphi$ तथा $\cos \varphi$, और यह इस प्रकार है $\varphi$ केवल परिभाषित मॉड्यूल है π.

अन्य अभ्यावेदन

सदिश

बिंदु A और B से होकर जाने वाली रेखा का सदिश समीकरण इस प्रकार दिया गया है: $\mathbf {r} =\mathbf {OA} +\lambda \,\mathbf {AB}$ (जहाँ λ अदिश राशि है)।

यदि a सदिश OA है और b सदिश OB है, तो रेखा का समीकरण लिखा जा सकता है: $\mathbf {r} =\mathbf {a} +\lambda (\mathbf {b} -\mathbf {a} )$

बिंदु A से प्रारंभ होने वाली किरण को सीमित करके वर्णित किया जाता है। किरण प्राप्त होती है यदि λ ≥ 0, और विपरीत किरण λ ≤ 0 से आती है।

ध्रुवीय निर्देशांक

ध्रुवीय निर्देशांक पर रेखा मूल से गुजरे बिना, ऊपर लिखे सामान्य पैरामीट्रिक समीकरण के साथ

कार्तीय तल में, ध्रुवीय निर्देशांक (r, θ) पैरामीट्रिक समीकरणों द्वारा कार्टेशियन निर्देशांकों से संबंधित हैं:

$$x=r\cos \theta ,\quad y=r\sin \theta .$$

ध्रुवीय निर्देशांक में, मूल (गणित) से न निकलने वाली रेखा का समीकरण - निर्देशांक वाला बिंदु (0, 0)—लिखा जा सकता है:

$$r={\frac {p}{\cos(\theta -\varphi )}},$$

r > 0 तथा $\varphi -\pi /2<\theta <\varphi +\pi /2.$ यहां, p रेखा के लंबवत और मूल और रेखा द्वारा सीमांकित रेखाखंड की (धनात्मक) लंबाई है, और $\varphi$ से (उन्मुख) कोण है x-इस खंड के लिए अक्ष।

कोण के रूप में समीकरण को व्यक्त करना उपयोगी हो सकता है $\alpha =\varphi +\pi /2$ के मध्य x-अक्ष और रेखा। इस मामले में, समीकरण बन जाता है

$$r={\frac {p}{\sin(\theta -\alpha )}},$$

साथ r > 0 तथा $0<\theta <\alpha +\pi .$ इन समीकरणों को #रेखा समीकरण के सामान्य रूप से सेट करके प्राप्त किया जा सकता है $x=r\cos \theta ,$ तथा $y=r\sin \theta ,$ और फिर साइन या कोज्या के लिए कोण अंतर पहचान लागू करना।

इन समीकरणों को त्रिकोणमितीय कार्यों को लागू करके ज्यामिति को भी सिद्ध किया जा सकता है#साइन और कोसाइन की समकोण त्रिभुज परिभाषाएं सही त्रिभुज में होती हैं जिसमें रेखा का बिंदु और मूल बिंदु के रूप में होता है, और रेखा और इसके लंबवत मूल के माध्यम से पक्षों के रूप में।

पिछले रूप मूल से गुजरने वाली रेखा के लिए लागू नहीं होते हैं, किन्तु सरल सूत्र लिखा जा सकता है: ध्रुवीय निर्देशांक $(r,\theta )$ मूल बिंदु से गुजरने वाली और का कोण बनाने वाली रेखा के बिंदुओं का $\alpha$ साथ x-अक्ष, जोड़े हैं $(r,\theta )$ ऐसा है कि

$$r\geq 0,\qquad {\text{and}}\quad \theta =\alpha \quad {\text{or}}\quad \theta =\alpha +\pi .$$

प्रक्षेप्य ज्यामिति

Further information: जियोडेसिक

बड़ा वृत्त गोले को दो बराबर गोलार्द्धों में विभाजित करता है, जबकि बिना वक्रता गुण को भी संतुष्ट करता है।

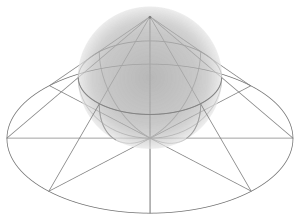
प्रक्षेपी ज्यामिति के विभिन्न प्रारूपों में, रेखा का प्रतिनिधित्व संभवतः ही कभी सीधी वक्र की धारणा के अनुरूप होता है जैसा कि यूक्लिडियन ज्यामिति में देखा जाता है। दीर्घवृत्तीय ज्यामिति में हम इसका विशिष्ट उदाहरण देखते हैं। दीर्घवृत्तीय ज्यामिति के गोलाकार निरूपण में, रेखाओं को गोले के बड़े वृत्तों द्वारा दर्शाया जाता है, जिसमें व्यास के विपरीत बिंदुओं की पहचान की जाती है। दीर्घवृत्तीय ज्यामिति के भिन्न प्रारूप में, मूल से निकलने वाले यूक्लिडियन विमानों द्वारा रेखाओं का प्रतिनिधित्व किया जाता है। भले ही ये निरूपण दृष्टिगत रूप से भिन्न हैं, वे सभी गुणों को संतुष्ट करते हैं (जैसे, अद्वितीय रेखा का निर्धारण करने वाले दो बिंदु) जो उन्हें इस ज्यामिति में रेखाओं के लिए उपयुक्त निरूपण बनाते हैं।

रेखा की संक्षिप्तता और सीधापन, संपत्ति के रूप में व्याख्या की जाती है कि किसी भी दो बिंदुओं के मध्य की रेखा के साथ की दूरी अल्प हो जाती है (त्रिकोण असमानता देखें), सामान्यीकृत किया जा सकता है और मापीय रिक्त स्थान में जियोडेसिक्स की अवधारणा की ओर जाता है।

एक्सटेंशन

रे

"रे (ज्यामिति)" redirects here. For गणित में अन्य उपयोग, see रे (बहुविकल्पी) विज्ञान और गणित.

रेखा और उस पर किसी बिंदु A को देखते हुए, हम A पर इस रेखा को दो भागों में विभाजित करने पर विचार कर सकते हैं।

ऐसे प्रत्येक भाग को 'किरण' कहा जाता है और बिंदु A को इसका प्रारंभिक बिंदु कहा जाता है। इसे अर्ध-रेखा, एक-आयामी अर्ध-स्थान के रूप में भी जाना जाता है। बिंदु A को किरण का सदस्य माना जाता है। सहज रूप से, किरण में A से निकलने वाली रेखा पर वे बिंदु होते हैं और अनिश्चित काल तक A से प्रारंभ होकर, केवल रेखा के साथ दिशा में आगे बढ़ते हैं। चूँकि, प्रमाण में किरण की इस अवधारणा का उपयोग करने के लिए अधिक त्रुटिहीन परिभाषा की आवश्यकता है।

भिन्न-भिन्न बिंदुओं A और B को देखते हुए, वे प्रारंभिक बिंदु A के साथ अद्वितीय किरण निर्धारित करते हैं। चूंकि दो बिंदु अद्वितीय रेखा को परिभाषित करते हैं, इस किरण में A और B (A और B सहित) के मध्य के सभी बिंदु और A और B के माध्यम से रेखा पर सभी बिंदु C होते हैं, जैसे कि B A और C के मध्य है। यह, कभी-कभी A और B द्वारा निर्धारित रेखा पर सभी बिंदुओं C के समुच्चय के रूप में भी व्यक्त किया जाता है, जिससे कि A, B और C के मध्य नहीं है। A और बी द्वारा निर्धारित रेखा पर बिंदु D, किन्तु B द्वारा निर्धारित प्रारंभिक बिंदु A के साथ किरण में नहीं, प्रारंभिक बिंदु A के साथ और किरण निर्धारित करता है। AB किरण के संबंध में, AD किरण विपरीत किरण कहलाती है।

इस प्रकार, हम कहेंगे कि दो भिन्न-भिन्न बिंदु, A और B, रेखा को परिभाषित करते हैं और इस रेखा का अपघटन मुक्त खंड (A, B) और दो किरणों, BC और AD के असंयुक्त संघ में होता है (बिंदु D आरेख में नहीं खींचा गया है, किन्तु रेखा AB पर A के बाईं ओर है)। ये विपरीत किरणें नहीं हैं क्योंकि इनके भिन्न-भिन्न प्रारंभिक बिंदु हैं।

यूक्लिडियन ज्यामिति में उभयनिष्ठ अंत बिंदु वाली दो किरणें कोण बनाती हैं।

किरण की परिभाषा रेखा पर बिंदुओं के मध्य की धारणा पर निर्भर करती है। यह इस प्रकार है कि किरणें केवल उन ज्यामितीयों के लिए उपस्थित हैं जिनके लिए यह धारणा उपस्थित है, सामान्यतः यूक्लिडियन ज्यामिति या आदेशित क्षेत्र पर एफ़िन ज्यामिति होती है। दूसरी ओर, किरणें प्रक्षेपी ज्यामिति में नहीं होती हैं और न ही किसी गैर-आदेशित क्षेत्र पर ज्यामिति में होती हैं, जैसे कि जटिल संख्याएँ या कोई परिमित क्षेत्र होता है।

रेखा खंड

Main article: रेखा खंड

रेखा a . पर रेखाखंड AB खींचना

रेखा खंड रेखा का ऐसा भाग होता है जो दो भिन्न-भिन्न अंत बिंदुओं से घिरा होता है और इसके अंत बिंदुओं के मध्य की रेखा पर प्रत्येक बिंदु होता है। रेखा खंड को कैसे परिभाषित किया जाता है, इस पर निर्भर करते हुए, दो अंतिम बिंदुओं में से कोई भी रेखा खंड का भाग हो भी सकता है और नहीं भी हो सकता है। दो या दो से अधिक रेखाखंडों में रेखाओं के समान संबंध हो सकते हैं, जैसे कि समानांतर, प्रतिच्छेदन, या तिरछा होना, किन्तु रेखाओं के विपरीत वे इनमें से कोई भी नहीं हो सकते हैं, यदि वे समतलीय हैं और या तो प्रतिच्छेद नहीं करते हैं या संरेख हैं।

संख्या रेखा

Main article: संख्या रेखा

संख्या रेखा, जिसमें चर x बाईं ओर और y दाईं ओर है। इसलिए, x, y से छोटा है।

संख्या रेखा पर बिंदु वास्तविक संख्या से युग्मित होता है। सामान्यतः, पूर्णांक समान रूप से रेखा पर स्थित होते हैं, जिसमें धनात्मक संख्याएँ दाईं ओर होती हैं, ऋणात्मक संख्याएँ बाईं ओर होती हैं। अवधारणा के विस्तार के रूप में, काल्पनिक संख्या का प्रतिनिधित्व करने वाली काल्पनिक रेखा को संख्या रेखा पर लंबवत खींचा जा सकता है। दो रेखाएँ सम्मिश्र तल बनाती हैं, जो सम्मिश्र संख्या के समुच्चय का ज्यामितीय प्रतिनिधित्व है।

ग्राफिक्स डिजाइन में

Main article: रेखा (ग्राफिक्स)

यह भी देखें

• एफ़िन परिवर्तन
• वक्र
• दो समानांतर रेखाओं के मध्य की दूरी
• बिंदु से रेखा की दूरी
• काल्पनिक रेखा (गणित)
• घटना (ज्यामिति)
• रेखा खंड
• लोकस (गणित)
• समतल ज्यामिति)
• पॉलीलाइन

इस पृष्ठ में अनुपलब्ध आंतरिक लिंक की सूची

• कार्तीय समन्वय प्रणाली
• द्वि-आयामी यूक्लिडियन अंतरिक्ष
• आयामी स्थान
• समतल ज्यामिति)
• अंतरिक्ष समय
• रेखीय समीकरण
• मांगना
• तिरछी रेखाएं
• समतल (गणित)
• लाइनों की व्यवस्था
• यूक्लिडियन स्पेस
• पहली डिग्री समीकरण
• एफाइन निर्देशांक
• सिद्ध
• अंडाकार
• घेरा
• अतिशयोक्ति
• शंकु खंड का निर्देश
• अनंतस्पर्शी
• चतुष्कोष
• न्यूटन लाइन
• यूक्लिडियन त्रिकोण
• लम्बवत रेखायें
• पास्कल लाइन
• निर्देशांक ज्यामिति
• गुणक
• समारोह की जड़
• ढलान अवरोधन प्रपत्र
• ढलान
• y- अंत
• धुवीय निर्देशांक
• कार्तीय विमान
• सही त्रिकोण
• मीट्रिक स्थान
• असमानित त्रिकोण
• महान चक्र
• अर्ध-अंतरिक्ष (ज्यामिति)
• समरैखिकता
• जटिल विमान

बाहरी संबंध

• "Line (curve)", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Equations of the Straight Line at Cut-the-Knot