बीटा वितरण: Difference between revisions
No edit summary |
No edit summary |
||
| (23 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Probability distribution}} | {{short description|Probability distribution}} | ||
{{Distinguish| | {{Distinguish|बीटा फलन}} | ||
{{Probability distribution | {{Probability distribution | ||
| name = Beta | | name = Beta | ||
| Line 37: | Line 37: | ||
}} | }} | ||
संभाव्यता सिद्धांत और सांख्यिकी में, बीटा वितरण दो | संभाव्यता सिद्धांत और सांख्यिकी में, '''बीटा वितरण''' के दो धनात्मक [[सांख्यिकीय पैरामीटर|सांख्यिकीय मापदंड]] होते है इसके संदर्भ में अंतराल [0,1] पर परिभाषित निरंतर संभाव्यता वितरण का परिवार है, जिसे 'अल्फा' (''α'') और बीटा (β) द्वारा दर्शाया गया है। जो वेरिएबल के घातांक और क्रमशः 1 के पूरक के रूप में दिखाई देते हैं, और वितरण के [[आकार पैरामीटर|आकार मापदंड]] को नियंत्रित करते हैं। | ||
विभिन्न प्रकार के विषयों में परिमित लंबाई के अंतराल तक सीमित [[यादृच्छिक चर]] | विभिन्न प्रकार के विषयों में परिमित लंबाई के अंतराल तक सीमित [[यादृच्छिक चर|यादृच्छिक वेरिएबल]] है जिन्हें उनके व्यवहार को मॉडल करने के लिए बीटा वितरण के रूप में प्रयुक्त किया गया है। बीटा वितरण प्रतिशत और अनुपात के यादृच्छिक व्यवहार के लिए उपयुक्त मॉडल है। | ||
बायेसियन अनुमान में, बीटा वितरण बर्नौली वितरण, [[द्विपद वितरण]], [[नकारात्मक द्विपद वितरण]] और [[ज्यामितीय वितरण]] वितरण के लिए [[संयुग्मित पूर्व वितरण]] है। | बायेसियन अनुमान में, बीटा वितरण बर्नौली वितरण, [[द्विपद वितरण]], [[नकारात्मक द्विपद वितरण|ऋणात्मक द्विपद वितरण]] और [[ज्यामितीय वितरण]] वितरण के लिए [[संयुग्मित पूर्व वितरण]] है। | ||
यहां चर्चा किए गए बीटा वितरण के सूत्रीकरण को पहली तरह के बीटा वितरण के रूप में भी जाना जाता है, जबकि | यहां चर्चा किए गए बीटा वितरण के सूत्रीकरण को पहली तरह के बीटा वितरण के रूप में भी जाना जाता है, जबकि दूसरी तरह का बीटा वितरण [[बीटा प्राइम वितरण]] का वैकल्पिक नाम है। अनेक वेरिएबलों के सामान्यीकरण को [[डिरिचलेट वितरण]] कहा जाता है। | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
=== संभाव्यता घनत्व | === संभाव्यता घनत्व फलन === | ||
[[File:PDF of the Beta distribution.gif|thumb|इसके मापदंडों के विभिन्न मूल्यों के लिए बीटा वितरण का एनीमेशन।]]प्रायिकता घनत्व | [[File:PDF of the Beta distribution.gif|thumb|इसके मापदंडों के विभिन्न मूल्यों के लिए बीटा वितरण का एनीमेशन।]]प्रायिकता घनत्व फलन (पीडीएफ) बीटा वितरण के लिए {{nowrap|0 ≤ ''x'' ≤ 1}}, और आकार मापदंड α, β > 0, वेरिएबल x और उसके प्रतिबिंब सूत्र का {{nowrap|(1 − ''x'')}} शक्ति कार्य है निम्नलिखित नुसार: | ||
: <math> | : <math> | ||
| Line 58: | Line 58: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहां Γ(z) गामा फलन है। [[बीटा समारोह]], <math>\Beta</math>, यह सुनिश्चित करने के लिए [[सामान्यीकरण स्थिरांक]] है कि कुल संभाव्यता 1 है। उपरोक्त समीकरणों में x यादृच्छिक | जहां Γ(z) गामा फलन है। [[बीटा समारोह|बीटा फलन]] , <math>\Beta</math>, यह सुनिश्चित करने के लिए [[सामान्यीकरण स्थिरांक]] है कि कुल संभाव्यता 1 है। उपरोक्त समीकरणों में x यादृच्छिक वेरिएबल X का अहसास (संभावना) है—एक प्रेक्षित मान जो वास्तव में हुआ है। | ||
इस परिभाषा में दोनों छोर | इस परिभाषा में दोनों छोर सम्मिलित हैं {{nowrap|1=''x'' = 0}} और {{nowrap|1=''x'' = 1}}, जो संभाव्यता वितरण की अन्य सूची के लिए परिभाषाओं के अनुरूप है, जो बीटा वितरण के विशेष स्तिथियाँ हैं, उदाहरण के लिए [[आर्क्सिन वितरण]], और अनेक लेखकों के साथ संगत है, जैसे '''|'''एन। एल. जॉनसन और एस. कोटज़।<ref name=JKB /><ref name=Keeping>{{cite book|last=Keeping|first=E. S.|title=सांख्यिकीय निष्कर्ष का परिचय|url=https://archive.org/details/introductiontost0000keep|url-access=registration|year=2010|publisher=Dover Publications|isbn=978-0486685021}}</ref><ref name=Wadsworth /><ref name="Hahn and Shapiro">{{cite book|last1=Hahn|first1=Gerald J.|last2=Shapiro|first2=S.|title=इंजीनियरिंग में सांख्यिकीय मॉडल (विली क्लासिक्स लाइब्रेरी)|year=1994|publisher=Wiley-Interscience|isbn=978-0471040651}}</ref> चूंकि, {{nowrap|1=''x'' = 0}} और {{nowrap|1=''x'' = 1}} का समावेश {{nowrap|''α'', ''β'' < 1}} के लिए काम नहीं करता है ; तदनुसार, विलियम फेलर सहित अनेक अन्य लेखक | डब्ल्यू। ,<ref name=Feller>{{cite book|last=Feller|first=William|title=An Introduction to Probability Theory and Its Applications, Vol. 2|year=1971|publisher=Wiley|isbn=978-0471257097|url=https://archive.org/details/introductiontopr00fell}}</ref><ref name="Handbook of Beta Distribution" /><ref name=Panik /> {{nowrap|1=''x'' = 0}} और {{nowrap|1=''x'' = 1}}, फलेर सिरों को बाहर करना चुनें (जिससे दो छोर वास्तव में घनत्व फलन के डोमेन का भाग न हों) और इसके अतिरिक्त {{nowrap|0 < ''x'' < 1}} पर विचार करें . | ||
नॉर्मन लॉयड जॉनसन सहित | नॉर्मन लॉयड जॉनसन सहित अनेक लेखक एन. एल. जॉनसन और सैमुअल कोट्ज़ (एस. कोटज़),<ref name=JKB /> बीटा वितरण के आकार मापदंडों के लिए प्रतीकों p और q (α और β के अतिरिक्त) का उपयोग करें,तथा यह पारंपरिक रूप से बर्नौली वितरण के मापदंडों के लिए उपयोग किए जाने वाले प्रतीकों की याद दिलाते हैं, क्योंकि बीटा वितरण सीमा में बर्नौली वितरण तक पहुंचता है जब दोनों आकार मापदंड α और β शून्य के मान तक पहुंचते हैं। | ||
निम्नलिखित में, | निम्नलिखित में, मापदंड α और β के साथ यादृच्छिक वेरिएबल X बीटा-वितरित द्वारा निरूपित किया जाएगा:<ref name="Mathematical Statistics with MATHEMATICA"/><ref name="Kruschke2011">{{cite book|last=Kruschke|first=John K.|author-link=John K. Kruschke|title=Doing Bayesian data analysis: A tutorial with R and BUGS|year=2011|publisher=Academic Press / Elsevier|location=p. 83|isbn=978-0123814852}}</ref> | ||
:<math>X \sim \operatorname{Beta}(\alpha, \beta)</math> | :<math>X \sim \operatorname{Beta}(\alpha, \beta)</math> | ||
सांख्यिकीय साहित्य में प्रयुक्त बीटा-वितरित यादृच्छिक | सांख्यिकीय साहित्य में प्रयुक्त बीटा-वितरित यादृच्छिक वेरिएबल के लिए अन्य अंकन <math>X \sim \mathcal{B}e(\alpha, \beta)</math><ref name=BergerDecisionTheory>{{cite book |last=Berger |first=James O. |title=सांख्यिकीय निर्णय सिद्धांत और बायेसियन विश्लेषण|edition=2nd |year=2010 |publisher=Springer |isbn=978-1441930743}}</ref> और <math>X \sim \beta_{\alpha, \beta}</math> हैं.<ref name=Feller /> | ||
=== संचयी वितरण फलन === | |||
संचयी वितरण फलन है | |||
:<math>F(x;\alpha,\beta) = \frac{\Beta{}(x;\alpha,\beta)}{\Beta{}(\alpha,\beta)} = I_x(\alpha,\beta) | |||
</math> | |||
जहाँ <math>\Beta(x;\alpha,\beta)</math> बीटा फलन है और <math>I_x(\alpha,\beta)</math> अधूरा बीटा फलन [[नियमित अधूरा बीटा फ़ंक्शन|नियमित अधूरा बीटा फलन]] है। | |||
=== वैकल्पिक | === वैकल्पिक मापदंडकरण === | ||
==== दो | ==== दो मापदंड ==== | ||
== माध्य और | == माध्य और प्रतिरूप आकार == | ||
बीटा वितरण को इसके औसत μ | बीटा वितरण को इसके औसत μ{{nowrap|1=(0 < ''μ'' < 1)}} और दो आकार के मापदंडों का योग {{nowrap|1= ''ν'' = ''α'' + ''β'' > 0}}( पी 83)<ref name="Kruschke2011" />. के संदर्भ में भी पुनर्मूल्यांकित किया जा सकता है α पोस्टीरियर और β पोस्टीरियर द्वारा पोस्टीरियर बीटा डिस्ट्रीब्यूशन के शेप मापदंड्स को अस्वीकार करना , जिसके परिणाम स्वरूप बेयस प्रमेय को द्विपदीय संभावना फलन और पूर्व संभावना पर प्रयुक्त किया जाता है, प्रतिरूप आकार होने के लिए दोनों आकार मापदंडों के जोड़ की व्याख्या = ν = α·पोस्टीरियर + β· हाल्डेन पूर्व संभाव्यता बीटा (0,0) के लिए केवल पश्च भाग ही सही है। विशेष रूप से, बेयस (यूनिफ़ॉर्म) पूर्व बीटा (1,1) के लिए सही व्याख्या प्रतिरूप आकार = α·पोस्टीरियर + β पोस्टीरियर - 2, या ν = (प्रतिरूप आकार) + 2 होगी। 2 से बहुत बड़े सैंपल आकार के लिए, इन दो पूर्वों के मध्य का अंतर नगण्य हो जाता है। (अधिक विवरण के लिए अनुभाग या बायेसियन अनुमान देखें।) ν = α + β को बीटा वितरण के प्रतिरूप आकार के रूप में संदर्भित किया जाता है, किन्तु किसी को यह याद रखना चाहिए कि यह सख्ती से बोलना,जरुरी है तथा द्विपदीय संभावना फलन का प्रतिरूप आकार केवल उपयोग करते समय बेज़ प्रमेय से पहले हाल्डेन बीटा (0,0) होता है । | ||
यह पैरामीट्रिजेशन बायेसियन | यह पैरामीट्रिजेशन बायेसियन मापदंड आकलन में उपयोगी हो सकता है। उदाहरण के लिए, कोई व्यक्ति अनेक व्यक्तियों को परीक्षण दे सकता है। यदि यह मान लिया जाए कि प्रत्येक व्यक्ति का स्कोर (0 ≤ θ ≤ 1) संख्या -स्तर बीटा वितरण से लिया गया है, तब महत्वपूर्ण आँकड़ा इस संख्या -स्तर वितरण का माध्य है। माध्य और प्रतिरूप आकार मापदंड आकार मापदंड α और β के माध्यम से संबंधित हैं<ref name=Kruschke2011/> | ||
: α = μν, β = (1 - μ)ν | : α = μν, β = (1 - μ)ν | ||
इस सांख्यिकीय | इस सांख्यिकीय मापदंड के अनुसार है , जिसको प्रतिरूप आकार के लिए धनात्मक वास्तविकताओं पर माध्य पर अनौपचारिक पूर्व संभावना, और अस्पष्ट पूर्व संभावना (जैसे घातीय या गामा वितरण) रख सकते हैं, यदि वे स्वतंत्र हैं, और पूर्व डेटा या विश्वासियें है तो इसे सही ठहराते हैं। | ||
=== मोड और एकाग्रता === | === मोड और एकाग्रता === | ||
अवतल कार्य बीटा वितरण | अवतल कार्य बीटा वितरण जिनके <math>\alpha,\beta>1</math> पास है मोड और एकाग्रता के संदर्भ में पैरामीट्रिज्ड किया जा सकता है। साधन, <math>\omega=\frac{\alpha-1}{\alpha+\beta-2}</math>, और एकाग्रता, <math>\kappa = \alpha + \beta</math>, का उपयोग सामान्य आकार के मापदंडों को निम्नानुसार परिभाषित करने के लिए किया जा सकता है:<ref name="Kruschke2015">{{cite book|last=Kruschke|first=John K.|author-link=John K. Kruschke|title=Doing Bayesian Data Analysis: A Tutorial with R, JAGS and Stan|year=2015|publisher=Academic Press / Elsevier|isbn=978-0-12-405888-0}}</ref> | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\alpha &= \omega (\kappa - 2) + 1\\ | \alpha &= \omega (\kappa - 2) + 1\\ | ||
\beta &= (1 - \omega)(\kappa - 2) + 1 | \beta &= (1 - \omega)(\kappa - 2) + 1 | ||
\end{align}</math> | \end{align}</math> | ||
मोड के लिए, <math>0<\omega<1</math>, अच्छी तरह से परिभाषित होने के लिए, हमें | मोड के लिए, <math>0<\omega<1</math>, अच्छी तरह से परिभाषित होने के लिए, हमें <math>\alpha,\beta>1</math>, या समकक्ष <math>\kappa>2</math>. की आवश्यकता है यदि इसके अतिरिक्त हम एकाग्रता को <math>c=\alpha+\beta-2</math> के रूप में परिभाषित करते हैं तो स्थिति <math>c>0</math> सरल हो जाती है और <math>\alpha=1+c\omega</math> और <math>\beta=1+c(1-\omega)</math> पर बीटा घनत्व पर इस प्रकार लिखा जा सकता है: | ||
:<math> | :<math> | ||
f(x;\omega,c) = \frac{x^{c\omega}(1-x)^{c(1-\omega)}}{\Beta\bigl(1+c\omega,1+c(1-\omega)\bigr)} | f(x;\omega,c) = \frac{x^{c\omega}(1-x)^{c(1-\omega)}}{\Beta\bigl(1+c\omega,1+c(1-\omega)\bigr)} | ||
</math> | </math> | ||
जहाँ <math>c</math> सीधे पर्याप्त आँकड़ों <math>\log(x)</math>और <math>\log(1-x)</math>. को मापता है, यह भी ध्यान दें कि सीमा में, <math>c\to0</math>, वितरण सपाट हो जाता है। | |||
=== माध्य और विचरण === | === माध्य और विचरण === | ||
उपरोक्त वर्गों में दिए गए (युग्मित) समीकरणों की प्रणाली को माध्य के समीकरणों के रूप में हल करना और मूल मापदंडों α और β के संदर्भ में बीटा वितरण का विचरण, माध्य के संदर्भ में α और β मापदंडों को व्यक्त कर सकता है ( μ) और विचरण (var): | उपरोक्त वर्गों में दिए गए (युग्मित) समीकरणों की प्रणाली को माध्य के समीकरणों के रूप में हल करना और मूल मापदंडों α और β के संदर्भ में बीटा वितरण का विचरण , माध्य के संदर्भ में α और β मापदंडों को व्यक्त कर सकता है ( μ) और विचरण (var): | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 112: | Line 110: | ||
\alpha&= \mu \nu =\mu \left(\frac{\mu(1-\mu)}{\text{var}}-1\right), \text{ if } \text{var}< \mu(1-\mu)\\ | \alpha&= \mu \nu =\mu \left(\frac{\mu(1-\mu)}{\text{var}}-1\right), \text{ if } \text{var}< \mu(1-\mu)\\ | ||
\beta &= (1 - \mu) \nu = (1 - \mu)\left(\frac{\mu(1-\mu)}{\text{var}}-1\right), \text{ if }\text{var}< \mu(1-\mu). | \beta &= (1 - \mu) \nu = (1 - \mu)\left(\frac{\mu(1-\mu)}{\text{var}}-1\right), \text{ if }\text{var}< \mu(1-\mu). | ||
\end{align}</math> | \end{align} | ||
बीटा वितरण का यह सांख्यिकीय | |||
</math> | |||
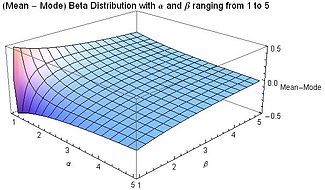
बीटा वितरण का यह सांख्यिकीय मापदंड मूल मापदंड α और β के आधार पर से अधिक सहज ज्ञान युक्त समझ उत्पन्न कर सकता है। उदाहरण के लिए, माध्य और विचरण के संदर्भ में मोड, विषमता, अतिरिक्त कुर्टोसिस और अंतर एन्ट्रापी को व्यक्त करके: | |||
[[File:Mode Beta Distribution for both alpha and beta greater than 1 - J. Rodal.jpg|325px]][[File:Mode Beta Distribution for both alpha and beta greater than 1 - another view - J. Rodal.jpg|325px]] | [[File:Mode Beta Distribution for both alpha and beta greater than 1 - J. Rodal.jpg|325px]][[File:Mode Beta Distribution for both alpha and beta greater than 1 - another view - J. Rodal.jpg|325px]] | ||
| Line 120: | Line 120: | ||
[[File:Differential Entropy Beta Distribution with mean from 0.2 to 0.8 and variance from 0.01 to 0.09 - J. Rodal.jpg|325px]][[File:Differential Entropy Beta Distribution with mean from 0.3 to 0.7 and variance from 0 to 0.2 - J. Rodal.jpg|325px]] | [[File:Differential Entropy Beta Distribution with mean from 0.2 to 0.8 and variance from 0.01 to 0.09 - J. Rodal.jpg|325px]][[File:Differential Entropy Beta Distribution with mean from 0.3 to 0.7 and variance from 0 to 0.2 - J. Rodal.jpg|325px]] | ||
====चार | ====चार मापदंड्स ==== | ||
दो आकार | दो आकार मापदंड α और β के साथ बीटा वितरण श्रेणी [0,1] या (0,1) पर समर्थित है। न्यूनतम, a, और अधिकतम c(c> a), वितरण के मूल्यों का प्रतिनिधित्व करने वाले दो और मापदंड प्रस्तुत करके वितरण के स्थान और पैमाने को बदलना संभव है,<ref name=JKB/> गैर-आयामी वेरिएबल को प्रतिस्थापित करने वाले रैखिक परिवर्तन द्वारा x नए वेरिएबल y के संदर्भ में (समर्थन [a, c] या (a, c) के साथ) और मापदंड a और c होंगे : | ||
:<math>y = x(c-a) + a, \text{ therefore }x = \frac{y-a}{c-a}.</math> | :<math>y = x(c-a) + a, \text{ therefore }x = \frac{y-a}{c-a}.</math> | ||
चार | चार मापदंड बीटा वितरण का प्रायिकता घनत्व फलन दो मापदंड वितरण के सामान्तर है, जिसे रेंज (c-a) द्वारा स्केल किया गया है, (जिससेघनत्व वक्र के अंतर्गत कुल क्षेत्रफल की संभावना के सामान्तर हो), और y वेरिएबल के साथ शिफ्ट हो गया और निम्नानुसार स्केल किया गया: | ||
::<math>f(y; \alpha, \beta, a, c) = \frac{f(x;\alpha,\beta)}{c-a} =\frac{\left(\frac{y-a}{c-a}\right)^{\alpha-1} \left (\frac{c-y}{c-a} \right)^{\beta-1} }{(c-a)B(\alpha, \beta)}=\frac{ (y-a)^{\alpha-1} (c-y)^{\beta-1} }{(c-a)^{\alpha+\beta-1}B(\alpha, \beta)}.</math> | ::<math>f(y; \alpha, \beta, a, c) = \frac{f(x;\alpha,\beta)}{c-a} =\frac{\left(\frac{y-a}{c-a}\right)^{\alpha-1} \left (\frac{c-y}{c-a} \right)^{\beta-1} }{(c-a)B(\alpha, \beta)}=\frac{ (y-a)^{\alpha-1} (c-y)^{\beta-1} }{(c-a)^{\alpha+\beta-1}B(\alpha, \beta)}. | ||
यह कि यादृच्छिक | |||
</math> | |||
यह कि यादृच्छिक वेरिएबल Y को चार मापदंड α, β, a, और c हैं बीटा-वितरित है जिसे निम्न द्वारा दर्शाया गया है | | |||
:<math>Y \sim \operatorname{Beta}(\alpha, \beta, a, c).</math> | :<math>Y \sim \operatorname{Beta}(\alpha, \beta, a, c).</math> | ||
| Line 139: | Line 141: | ||
नोट: ज्यामितीय माध्य और हार्मोनिक माध्य को रेखीय परिवर्तन द्वारा रूपांतरित नहीं किया जा सकता है, जिस तरह से माध्य, माध्यिका और मोड कर सकते हैं। | नोट: ज्यामितीय माध्य और हार्मोनिक माध्य को रेखीय परिवर्तन द्वारा रूपांतरित नहीं किया जा सकता है, जिस तरह से माध्य, माध्यिका और मोड कर सकते हैं। | ||
Y के आकार के मापदंडों को इसके माध्य और विचरण के रूप में लिखा जा सकता है | Y के आकार के मापदंडों को इसके माध्य और विचरण के रूप में लिखा जा सकता है | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 151: | Line 153: | ||
::<math>(\text{(mean deviation around mean)}(X))(c-a) =\frac{2 \alpha^{\alpha} \beta^{\beta}}{\Beta(\alpha,\beta)(\alpha + \beta)^{\alpha + \beta + 1}}(c-a)</math> | ::<math>(\text{(mean deviation around mean)}(X))(c-a) =\frac{2 \alpha^{\alpha} \beta^{\beta}}{\Beta(\alpha,\beta)(\alpha + \beta)^{\alpha + \beta + 1}}(c-a)</math> | ||
::<math> \text{var}(Y) =\text{var}(X)(c-a)^2 =\frac{\alpha\beta (c-a)^2}{(\alpha+\beta)^2(\alpha+\beta+1)}.</math> | ::<math> \text{var}(Y) =\text{var}(X)(c-a)^2 =\frac{\alpha\beta (c-a)^2}{(\alpha+\beta)^2(\alpha+\beta+1)}.</math> | ||
चूँकि [[तिरछापन]] और [[अतिरिक्त कर्टोसिस]] गैर-आयामी मात्राएँ हैं (जैसा कि क्षण (गणित) माध्य पर केंद्रित है और [[मानक विचलन]] द्वारा सामान्यीकृत है), वे | चूँकि [[तिरछापन|विषमता]] और [[अतिरिक्त कर्टोसिस]] गैर-आयामी मात्राएँ हैं (जैसा कि क्षण (गणित) माध्य पर केंद्रित है और [[मानक विचलन]] द्वारा सामान्यीकृत है), वे मापदंड a और c से स्वतंत्र हैं, और इसलिए ऊपर दिए गए भावों के सामान्तर हैं x (समर्थन के साथ [0,1] या (0,1)): | ||
::<math> \text{skewness}(Y) =\text{skewness}(X) = \frac{2 (\beta - \alpha) \sqrt{\alpha + \beta + 1} }{(\alpha + \beta + 2) \sqrt{\alpha \beta}}.</math> | ::<math> \text{skewness}(Y) =\text{skewness}(X) = \frac{2 (\beta - \alpha) \sqrt{\alpha + \beta + 1} }{(\alpha + \beta + 2) \sqrt{\alpha \beta}}.</math> | ||
::<math> \text{kurtosis excess}(Y) =\text{kurtosis excess}(X)=\frac{6[(\alpha - \beta)^2 (\alpha +\beta + 1) - \alpha \beta (\alpha + \beta + 2)]} | ::<math> \text{kurtosis excess}(Y) =\text{kurtosis excess}(X)=\frac{6[(\alpha - \beta)^2 (\alpha +\beta + 1) - \alpha \beta (\alpha + \beta + 2)]} | ||
{\alpha \beta (\alpha + \beta + 2) (\alpha + \beta + 3)} </math> | {\alpha \beta (\alpha + \beta + 2) (\alpha + \beta + 3)} </math> | ||
== गुण == | == गुण == | ||
| Line 165: | Line 165: | ||
α, β> 1 के साथ बीटा वितरित रैंडम वेरिएबल X का [[मोड (सांख्यिकी)]] वितरण का सबसे संभावित मान है (PDF में शिखर के अनुरूप), और निम्नलिखित अभिव्यक्ति द्वारा दिया गया है:<ref name=JKB>{{cite book|last1=Johnson|first1= Norman L. |first2= Samuel|last2= Kotz |first3= N. |last3= Balakrishnan| year=1995 |title=Continuous Univariate Distributions Vol. 2 |edition=2nd |publisher= Wiley |isbn= 978-0-471-58494-0 |chapter= Chapter 25:Beta Distributions}}</ref> | α, β> 1 के साथ बीटा वितरित रैंडम वेरिएबल X का [[मोड (सांख्यिकी)]] वितरण का सबसे संभावित मान है (PDF में शिखर के अनुरूप), और निम्नलिखित अभिव्यक्ति द्वारा दिया गया है:<ref name=JKB>{{cite book|last1=Johnson|first1= Norman L. |first2= Samuel|last2= Kotz |first3= N. |last3= Balakrishnan| year=1995 |title=Continuous Univariate Distributions Vol. 2 |edition=2nd |publisher= Wiley |isbn= 978-0-471-58494-0 |chapter= Chapter 25:Beta Distributions}}</ref> | ||
:<math>\frac{\alpha - 1} {\alpha + \beta - 2} .</math> | :<math>\frac{\alpha - 1} {\alpha + \beta - 2} .</math> | ||
जब दोनों | जब दोनों मापदंड (α, β <1) से कम होते हैं, तब यह एंटी-मोड होता है: प्रायिकता घनत्व वक्र का निम्नतम बिंदु।<ref name=Wadsworth>{{cite book|last=Wadsworth |first=George P. and Joseph Bryan |title=संभाव्यता और यादृच्छिक चर का परिचय|url=https://archive.org/details/introductiontopr0000wads |url-access=registration |year=1960|publisher=McGraw-Hill}}</ref> | ||
Α = β देने पर, मोड के लिए अभिव्यक्ति 1/2 तक सरल हो जाती है, यह दिखाते हुए कि α = β> 1 के लिए मोड (प्रतिक्रिया विरोधी मोड जब {{nowrap|''α'', ''β'' < 1}}), वितरण के केंद्र में है: यह उन | |||
[[File:Mode Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px|thumb|1 ≤ α ≤ 5 और 1 ≤ β ≤ 5 के लिए बीटा वितरण के लिए मोड]] | Α = β देने पर, मोड के लिए अभिव्यक्ति 1/2 तक सरल हो जाती है, यह दिखाते हुए कि α = β> 1 के लिए मोड (प्रतिक्रिया विरोधी मोड जब {{nowrap|''α'', ''β'' < 1}}), वितरण के केंद्र में है: यह उन स्थितियों में सममित है। α और β के इच्छानुसार मानों के लिए मोड स्थितियों की पूरी सूची के लिए इस आलेख में बीटा वितरण या आकार अनुभाग देखें, । इनमें से अनेक स्थितियों के लिए, घनत्व फलन का अधिकतम मान या दोनों सिरों पर होता है। कुछ स्थितियों में अंत में होने वाले घनत्व फलन का (अधिकतम) मान परिमित होता है। उदाहरण के लिए, α = 2, β = 1 (या α = 1, β = 2) के स्तिथियों में, घनत्व फलन त्रिकोणीय बंटन बन जाता है। समकोण-त्रिकोण वितरण जो दोनों सिरों पर परिमित है। अनेक अन्य स्थितियों में छोर पर [[गणितीय विलक्षणता]] होती है, जहां घनत्व फलन का मान अनंत तक पहुंचता है। उदाहरण के लिए, स्तिथियों में α = β = 1/2, बीटा वितरण आर्सेन वितरण बनने के लिए सरल हो जाता है। इनमें से कुछ स्थितियों को लेकर गणितज्ञों के मध्य बहस है और क्या छोरों (x = 0, और x = 1) को बहुलक कहा जा सकता है या नहीं।<ref name="Handbook of Beta Distribution" /><ref name="Mathematical Statistics with MATHEMATICA">{{cite book |last1=Rose |first1=Colin |last2=Smith |first2=Murray D. |title=गणित के साथ गणितीय सांख्यिकी|year=2002 |publisher=Springer |isbn=978-0387952345}}</ref> | ||
[[File:Mode Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px|thumb|1 ≤ α ≤ 5 और 1 ≤ β ≤ 5 के लिए बीटा वितरण के लिए मोड]]क्या सिरे घनत्व फलन के फलन के डोमेन का भाग हैं | |||
* क्या गणितीय विलक्षणता को कभी भी विधा कहा जा सकता है | * क्या गणितीय विलक्षणता को कभी भी विधा कहा जा सकता है | ||
* क्या दो मैक्सिमा वाले | * क्या दो मैक्सिमा वाले स्थितियों को बिमॉडल कहा जाना चाहिए | ||
==== मध्य ==== | ==== मध्य ==== | ||
[[File:Median Beta Distribution for alpha and beta from 0 to 5 - J. Rodal.jpg|325px|thumb|0 ≤ α ≤ 5 और 0 ≤ β ≤ 5 के लिए बीटा वितरण के लिए माध्यिका]] | [[File:Median Beta Distribution for alpha and beta from 0 to 5 - J. Rodal.jpg|325px|thumb|0 ≤ α ≤ 5 और 0 ≤ β ≤ 5 के लिए बीटा वितरण के लिए माध्यिका]] | ||
[[File:(Mean - Median) for Beta distribution versus alpha and beta from 0 to 2 - J. Rodal.jpg|thumb|(मीन-माध्यिका) बीटा वितरण बनाम 0 से 2 तक अल्फा और बीटा के लिए]]बीटा वितरण का माध्य अद्वितीय वास्तविक संख्या | [[File:(Mean - Median) for Beta distribution versus alpha and beta from 0 to 2 - J. Rodal.jpg|thumb|(मीन-माध्यिका) बीटा वितरण बनाम 0 से 2 तक अल्फा और बीटा के लिए]]इसमें बीटा वितरण का माध्य अद्वितीय वास्तविक संख्या <math>x = I_{\frac{1}{2}}^{[-1]}(\alpha,\beta)</math> है जिसके लिए नियमित अधूरा बीटा फलन <math>I_x(\alpha,\beta) = \tfrac{1}{2} </math>. α और β के इच्छानुसार मूल्यों के लिए बीटा वितरण के माध्यिका के लिए कोई सामान्य विवृत -रूप अभिव्यक्ति नहीं है। मापदंडों α और β के विशेष मूल्यों के लिए विवृत -रूप अभिव्यक्ति का पालन करें: | ||
* सममित | * सममित स्थितियों के लिए α = β, माध्यिका = 1/2। | ||
* α = 1 और β > 0 के लिए माध्यिका <math> =1-2^{-\frac{1}{\beta}}</math> (यह केस [[ दर्पण छवि ]] है | पावर | * α = 1 और β > 0 के लिए माध्यिका <math> =1-2^{-\frac{1}{\beta}}</math> (यह केस [[ दर्पण छवि ]] है | पावर फलन [0,1] डिस्ट्रीब्यूशन की मिरर-इमेज) | ||
* α > 0 और β = 1 के लिए माध्यिका = <math>2^{-\frac{1}{\alpha}}</math> (यह | * α > 0 और β = 1 के लिए माध्यिका = <math>2^{-\frac{1}{\alpha}}</math> (यह स्तिथि पावर फलन [0,1] वितरण है<ref name="Handbook of Beta Distribution" /> | ||
* α = 3 और β = 2 के लिए माध्यिका = 0.6142724318676105..., [[चतुर्थक समारोह]] 1 − 8x | * α = 3 और β = 2 के लिए माध्यिका = 0.6142724318676105..., [[चतुर्थक समारोह|चतुर्थक फलन]] 1 − 8x<sup>3</sup> + 6x<sup>4</sup> = 0 का वास्तविक समाधान , जो [0,1] में है। | ||
* α = 2 और β = 3 के लिए, माध्य = 0.38572756813238945... = 1−माध्यिका (बीटा (3, 2)) | * α = 2 और β = 3 के लिए, माध्य = 0.38572756813238945... = 1−माध्यिका (बीटा (3, 2)) | ||
एक | एक मापदंड परिमित (गैर-शून्य) के साथ निम्नलिखित सीमाएँ हैं और दूसरी इन सीमाओं तक पहुँच रही हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 187: | Line 188: | ||
\lim_{\alpha\to 0} \text{median}= \lim_{\beta \to \infty} \text{median} = 0. | \lim_{\alpha\to 0} \text{median}= \lim_{\beta \to \infty} \text{median} = 0. | ||
\end{align}</math> | \end{align}</math> | ||
α और β दोनों के लिए से अधिक या | α और β दोनों के लिए से अधिक या सामान्तर, बीटा वितरण के माध्यिका के मूल्य का उचित सन्निकटन सूत्र द्वारा दिया गया है<ref name=Kerman2011/> | ||
:<math>\text{median} \approx \frac{\alpha - \tfrac{1}{3}}{\alpha + \beta - \tfrac{2}{3}} \text{ for } \alpha, \beta \ge 1.</math> | :<math>\text{median} \approx \frac{\alpha - \tfrac{1}{3}}{\alpha + \beta - \tfrac{2}{3}} \text{ for } \alpha, \beta \ge 1.</math> | ||
जब α, β ≥ 1, इस सन्निकटन में सापेक्ष त्रुटि (माध्यिका द्वारा विभाजित [[सन्निकटन त्रुटि]]) 4% से कम है और α ≥ 2 और β ≥ 2 दोनों के लिए यह 1% से कम है। माध्य और मोड के | जब α, β ≥ 1, इस सन्निकटन में सापेक्ष त्रुटि (माध्यिका द्वारा विभाजित [[सन्निकटन त्रुटि]]) 4% से कम है और α ≥ 2 और β ≥ 2 दोनों के लिए यह 1% से कम है। माध्य और मोड के मध्य के अंतर से विभाजित सन्निकटन त्रुटि समान रूप से छोटी है: | ||
[[File:Relative Error for Approximation to Median of Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px|1 ≤ α ≤ 5 और 1 ≤ β ≤ 5 के लिए बीटा वितरण के लिए ABS [(माध्यिका-Appr.)/मध्यिका]]][[File:Error in Median Apprx. relative to Mean-Mode distance for Beta Distribution with alpha and beta from 1 to 5 - J. Rodal.jpg|325px|1≤α≤5 और 1≤β≤5 के लिए बीटा वितरण के लिए Abs[(माध्य-Appr.)/(मीन-मोड)]]] | [[File:Relative Error for Approximation to Median of Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px|1 ≤ α ≤ 5 और 1 ≤ β ≤ 5 के लिए बीटा वितरण के लिए ABS [(माध्यिका-Appr.)/मध्यिका]]][[File:Error in Median Apprx. relative to Mean-Mode distance for Beta Distribution with alpha and beta from 1 to 5 - J. Rodal.jpg|325px|1≤α≤5 और 1≤β≤5 के लिए बीटा वितरण के लिए Abs[(माध्य-Appr.)/(मीन-मोड)]]] | ||
मीन === | मीन === | ||
[[File:Mean Beta Distribution for alpha and beta from 0 to 5 - J. Rodal.jpg|325px|thumb|बीटा वितरण के लिए | [[File:Mean Beta Distribution for alpha and beta from 0 to 5 - J. Rodal.jpg|325px|thumb|बीटा वितरण के लिए कारण{{nowrap|0 ≤ ''α'' ≤ 5}} और {{nowrap|0 ≤ ''β'' ≤ 5}}]]दो मापदंड α और β के साथ बीटा वितरण यादृच्छिक वेरिएबल X का अपेक्षित मान (माध्य) (μ) इन मापदंडों के केवल β/α का फलन है:<ref name=JKB /> | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 204: | Line 205: | ||
&= \frac{1}{1 + \frac{\beta}{\alpha}} | &= \frac{1}{1 + \frac{\beta}{\alpha}} | ||
\end{align}</math> | \end{align}</math> | ||
उपरोक्त अभिव्यक्ति में {{nowrap|1=''α'' = ''β''}} देने पर {{nowrap|1=''μ'' = 1/2}} प्राप्त करता है {{nowrap|1=''α'' = ''β''}} माध्य वितरण के केंद्र में है: यह सममित है। साथ ही, उपरोक्त अभिव्यक्ति से निम्नलिखित सीमाएँ प्राप्त की जा सकती हैं: | |||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 210: | Line 211: | ||
\lim_{\frac{\beta}{\alpha} \to \infty} \mu = 0 | \lim_{\frac{\beta}{\alpha} \to \infty} \mu = 0 | ||
\end{align}</math> | \end{align}</math> | ||
इसलिए, β/α → 0 | इसलिए, β/α → 0 , या α/β → ∞ के लिए, माध्य दाहिने छोर पर स्थित है, {{nowrap|1=''x'' = 1}}. इन सीमा अनुपातबं के लिए, बीटा वितरण [[डिराक डेल्टा समारोह|डिराक डेल्टा फलन]] के साथ एक-बिंदु पतित वितरण बन जाता है, दाहिने छोर पर स्पाइक, {{nowrap|1=''x'' = 1}}, प्रायिकता 1 के साथ, और हर स्थान पर शून्य प्रायिकता पाई जाती है । 100% संभावना (पूर्ण निश्चितता) {{nowrap|1=''x'' = 1}} सही छोर पर केंद्रित है| . | ||
:<math> \begin{align} | <nowiki>:</nowiki><math> \begin{align} | ||
\lim_{\beta \to 0} \mu = \lim_{\alpha \to \infty} \mu = 1\\ | \lim_{\beta \to 0} \mu = \lim_{\alpha \to \infty} \mu = 1\\ | ||
\lim_{\alpha\to 0} \mu = \lim_{\beta \to \infty} \mu = 0 | \lim_{\alpha\to 0} \mu = \lim_{\beta \to \infty} \mu = 0 | ||
\end{align}</math> | \end{align}</math> | ||
जबकि ठेठ एकरूप वितरण के लिए (केंद्रीय रूप से स्थित मोड के साथ, मोड के दोनों किनारों पर नतिकरण बिंदु, और लंबी टेल ) (बीटा (α, β) के साथ जैसे कि {{nowrap|''α'', ''β'' > 2}}) यह ज्ञात है कि प्रतिरूप माध्य (स्थान के अनुमान के रूप में) प्रतिरूप माध्यिका के रूप में [[मजबूत आँकड़े|शक्तिशाली आँकड़े]] नहीं है, इसके विपरीत वर्दी या यू-आकार के बिमोडल वितरण (बीटा (α, β) के साथ) के स्तिथियों में है {{nowrap|''α'', ''β'' ≤ 1}}), वितरण के अंत में स्थित मोड के साथ। मोस्टेलर और टुकी टिप्पणी के रूप में (<ref name=MostellerTukey>{{cite book|last=Mosteller|first=Frederick and John Tukey|title=Data Analysis and Regression: A Second Course in Statistics|url=https://archive.org/details/dataanalysisregr0000most|url-access=registration|year=1977|publisher=Addison-Wesley Pub. Co.|isbn=978-0201048544|bibcode=1977dars.book.....M}}</ref> पी। 207) दो वेरिएबल म अवलोकनों का औसत सभी प्रतिरूप जानकारी का उपयोग करता है। यह दर्शाता है कि कैसे लघु-टेल वितरण के लिए, वेरिएबल म प्रेक्षणों को अधिक भार मिलना चाहिए। इसके विपरीत, यह वितरण के किनारे पर मोड के साथ यू-आकार के बिमोडल वितरण का माध्यिका है (बीटा (α, β) के साथ जैसे कि {{nowrap|''α'', ''β'' ≤ 1}}) शक्तिशाली नहीं है, क्योंकि प्रतिरूप माध्यिका अत्यधिक प्रतिरूप टिप्पणियों को विचार से हटा देती है। इसका व्यावहारिक अनुप्रयोग उदाहरण के लिए [[यादृच्छिक चाल]] के लिए होता है, क्योंकि रैंडम वॉक में मूल स्थान पर अंतिम विज़िट के समय की संभावना आर्क्सिन वितरण बीटा (1/2, 1/2) के रूप में वितरित की जाती है:<ref name=Feller/><ref name=WillyFeller1/>एक यादृच्छिक चलने की अनेक प्राप्ति (संभावना) का कारणऔसत से अधिक शक्तिशाली अनुमानक है (जो इस स्तिथियों में अनुचित प्रतिरूप माप अनुमान है)। | |||
==== ज्यामितीय माध्य ==== | |||
[[File:(Mean - GeometricMean) for Beta Distribution versus alpha and beta from 0 to 2 - J. Rodal.jpg|thumb|(मीन - जियोमेट्रिक मीन) बीटा वितरण बनाम α और 0 से 2 के लिए, ज्यामितीय माध्य के लिए α और β के मध्य विषमता दिखा रहा है]]यादृच्छिक वेरिएबल X के साथ वितरण का ज्यामितीय माध्य G<sub>X</sub> का लघुगणक ln(X) का अंकगणितीय माध्य है, या, समतुल्य, इसका अपेक्षित मान है | |||
:<math>\ln G_X = \operatorname{E}[\ln X]</math> | :<math>\ln G_X = \operatorname{E}[\ln X]</math> | ||
बीटा वितरण के लिए, अपेक्षित मान अभिन्न देता है: | बीटा वितरण के लिए, अपेक्षित मान अभिन्न देता है: | ||
| Line 239: | Line 235: | ||
&= \frac{\partial \ln \Gamma(\alpha)}{\partial \alpha} - \frac{\partial \ln \Gamma(\alpha + \beta)}{\partial \alpha} \\[4pt] | &= \frac{\partial \ln \Gamma(\alpha)}{\partial \alpha} - \frac{\partial \ln \Gamma(\alpha + \beta)}{\partial \alpha} \\[4pt] | ||
&= \psi(\alpha) - \psi(\alpha + \beta) | &= \psi(\alpha) - \psi(\alpha + \beta) | ||
\end{align}</math> | \end{align} </math> | ||
जहां ψ [[डिगामा समारोह]] है। | जहां ψ [[डिगामा समारोह|डिगामा फलन]] है। | ||
इसलिए, आकार | इसलिए, इसका आकार मापदंड α और β के साथ बीटा वितरण का ज्यामितीय माध्य α और β के डिगामा कार्यों का घातांक निम्नानुसार है: | ||
:<math>G_X =e^{\operatorname{E}[\ln X]}= e^{\psi(\alpha) - \psi(\alpha + \beta)}</math> | :<math>G_X =e^{\operatorname{E}[\ln X]}= e^{\psi(\alpha) - \psi(\alpha + \beta)}</math> | ||
जबकि समान आकार के | जबकि समान आकार के मापदंड α = β के साथ बीटा वितरण के लिए, यह इस प्रकार है कि विषमता = 0 और मोड = माध्य = औसत = 1/2, ज्यामितीय माध्य 1/2 से कम है: {{nowrap|0 < ''G''<sub>''X''</sub> < 1/2}}. इसका कारण यह है कि लॉगरिदमिक परिवर्तन X के मूल्यों को शून्य के समीप दृढ़ता से भारित करता है, क्योंकि ln(X) दृढ़ता से ऋणात्मक अनन्तता की ओर जाता है क्योंकि X शून्य तक पहुंचता है, जबकि ln(X) {{nowrap|''X'' → 1}} शून्य की ओर चपटा होता है . | ||
एक पंक्ति के साथ {{nowrap|1=''α'' = ''β''}}, निम्नलिखित सीमाएँ | एक पंक्ति के साथ {{nowrap|1=''α'' = ''β''}}, निम्नलिखित सीमाएँ प्रयुक्त होती हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 253: | Line 249: | ||
&\lim_{\alpha = \beta \to \infty} G_X =\tfrac{1}{2} | &\lim_{\alpha = \beta \to \infty} G_X =\tfrac{1}{2} | ||
\end{align}</math> | \end{align}</math> | ||
निम्नलिखित | निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 259: | Line 255: | ||
\lim_{\alpha\to 0} G_X = \lim_{\beta \to \infty} G_X = 0 | \lim_{\alpha\to 0} G_X = \lim_{\beta \to \infty} G_X = 0 | ||
\end{align}</math> | \end{align}</math> | ||
संलग्न आलेख शून्य से 2 तक आकृति | संलग्न आलेख शून्य से 2 तक आकृति मापदंड α और β उपयोग किये जाते है जिनके लिए माध्य और ज्यामितीय माध्य के मध्य अंतर दिखाता है। इस तथ्य के अतिरिक्त कि उनके मध्य का अंतर शून्य तक पहुंच जाता है क्योंकि α और β अनंत तक पहुंचते हैं और यह अंतर α के मानों के लिए बड़ा हो जाता है और β शून्य के समीप पहुंचने वाला होता है, आकार मापदंड α और β के संबंध में ज्यामितीय माध्य की स्पष्ट विषमता देखी जा सकती है। जब कि β और α के परिमाणों का आदान-प्रदान करने की तुलना में β के संबंध में α के छोटे मानों के लिए ज्यामितीय माध्य और माध्य के मध्य का अंतर बड़ा है। | ||
नॉर्मन लॉयड जॉनसन|एन. एल.जॉनसन और सैमुअल कोटज़ | नॉर्मन लॉयड जॉनसन|(एन. एल.जॉनसन) और सैमुअल कोटज़(एस. कोटज़)<ref name=JKB /> डिगामा फलन ψ(α) ≈ ln(α − 1/2) के लिए लघुगणक सन्निकटन का सुझाव देते है , जिसके परिणामस्वरूप ज्यामितीय माध्य के लिए निम्नलिखित सन्निकटन होता है: | ||
:<math>G_X \approx \frac{\alpha \, - \frac{1}{2}}{\alpha +\beta - \frac{1}{2}}\text{ if } \alpha, \beta > 1.</math> | :<math>G_X \approx \frac{\alpha \, - \frac{1}{2}}{\alpha +\beta - \frac{1}{2}}\text{ if } \alpha, \beta > 1. </math> | ||
इस सन्निकटन में सापेक्ष त्रुटि के लिए संख्यात्मक मान अनुसरण करते हैं: [{{nowrap|1=(''α'' = ''β'' = 1): 9.39%}}]; [{{nowrap|1=(''α'' = ''β'' = 2): 1.29%}}]; [{{nowrap|1=(''α'' = 2, ''β'' = 3): 1.51%}}]; [{{nowrap|1=(''α'' = 3, ''β'' = 2): 0.44%}}]; [{{nowrap|1=(''α'' = ''β'' = 3): 0.51%}}]; [{{nowrap|1=(''α'' = ''β'' = 4): 0.26%}}]; [{{nowrap|1=(''α'' = 3, ''β'' = 4): 0.55%}}]; [{{nowrap|1=(''α'' = 4, ''β'' = 3): 0.24%}}]। | इस सन्निकटन में सापेक्ष त्रुटि के लिए संख्यात्मक मान अनुसरण करते हैं: [{{nowrap|1=(''α'' = ''β'' = 1): 9.39%}}]; [{{nowrap|1=(''α'' = ''β'' = 2): 1.29%}}]; [{{nowrap|1=(''α'' = 2, ''β'' = 3): 1.51%}}]; [{{nowrap|1=(''α'' = 3, ''β'' = 2): 0.44%}}]; [{{nowrap|1=(''α'' = ''β'' = 3): 0.51%}}]; [{{nowrap|1=(''α'' = ''β'' = 4): 0.26%}}]; [{{nowrap|1=(''α'' = 3, ''β'' = 4): 0.55%}}]; [{{nowrap|1=(''α'' = 4, ''β'' = 3): 0.24%}}]। | ||
इसी तरह, ज्यामितीय माध्य के | इसी तरह, ज्यामितीय माध्य के सामान्तर 1/2 के लिए आवश्यक आकार मापदंडों के मान की गणना कर सकते हैं। मापदंड β के मान को देखते हुए, 1/2 के सामान्तर ज्यामितीय माध्य के लिए आवश्यक अन्य मापदंड α का मान क्या होगा?. उत्तर यह है कि (β > 1 के लिए), आवश्यक α का मान β → ∞ के रूप में β + 1/2 की ओर बढ़ता है। उदाहरण के लिए, इन सभी जोड़ों का 1/2 का समान ज्यामितीय माध्य है: [{{nowrap|1=''β'' = 1, ''α'' = 1.4427}}], [{{nowrap|1=''β'' = 2, ''α'' = 2.46958}}], [{{nowrap|1=''β'' = 3, ''α'' = 3.47943}}], [{{nowrap|1=''β'' = 4, ''α'' = 4.48449}}], [{{nowrap|1=''β'' = 5, ''α'' = 5.48756}}], [{{nowrap|1=''β'' = 10, ''α'' = 10.4938}}], [{{nowrap|1=''β'' = 100, ''α'' = 100.499}}]। | ||
ज्यामितीय माध्य का मौलिक गुण | ज्यामितीय माध्य का मौलिक गुण है जो किसी अन्य माध्य के लिए असत्य सिद्ध हो सकता है, | ||
:<math>G\left(\frac{X_i}{Y_i}\right) = \frac{G(X_i)}{G(Y_i)}</math> | :<math>G\left(\frac{X_i}{Y_i}\right) = \frac{G(X_i)}{G(Y_i)}</math> | ||
यह ज्यामितीय माध्य को एकमात्र सही माध्य बनाता है जब सामान्यीकृत परिणामों का औसत निकाला जाता है, अर्थात वे परिणाम जो संदर्भ मूल्यों के अनुपात के रूप में प्रस्तुत किए जाते हैं।<ref>Philip J. Fleming and John J. Wallace. ''How not to lie with statistics: the correct way to summarize benchmark results''. Communications of the ACM, 29(3):218–221, March 1986.</ref> यह प्रासंगिक है क्योंकि बीटा वितरण प्रतिशत के यादृच्छिक व्यवहार के लिए उपयुक्त मॉडल है और यह अनुपात के सांख्यिकीय मॉडलिंग के लिए विशेष रूप से उपयुक्त है। ज्यामितीय माध्य अधिकतम संभावना अनुमान में केंद्रीय भूमिका निभाता है, खंड | यह ज्यामितीय माध्य को एकमात्र सही माध्य बनाता है जब सामान्यीकृत परिणामों का औसत निकाला जाता है, अर्थात वे परिणाम जो संदर्भ मूल्यों के अनुपात के रूप में प्रस्तुत किए जाते हैं।<ref>Philip J. Fleming and John J. Wallace. ''How not to lie with statistics: the correct way to summarize benchmark results''. Communications of the ACM, 29(3):218–221, March 1986.</ref> यह प्रासंगिक है क्योंकि बीटा वितरण प्रतिशत के यादृच्छिक व्यवहार के लिए उपयुक्त मॉडल है और यह अनुपात के सांख्यिकीय मॉडलिंग के लिए विशेष रूप से उपयुक्त है। ज्यामितीय माध्य अधिकतम संभावना अनुमान में केंद्रीय भूमिका निभाता है,जिससे कि खंड मापदंड के अनुमान, तथा अधिकतम संभावना देखें जा सके। दरअसल, अधिकतम संभावना का अनुमान लगाते समय, यादृच्छिक वेरिएबल X के आधार पर ज्यामितीय माध्य G<sub>X</sub> के अतिरिक्त , और ज्यामितीय माध्य भी स्वाभाविक रूप से प्रकट होता है: रैखिक परिवर्तन के आधार पर ज्यामितीय माध्य--{{nowrap|(1 − ''X'')}}, X की दर्पण छवि, जिसे G<sub>(1−''X'')</sub> द्वारा निरूपित किया जाता है: | ||
: | |||
:<math>G_{(1-X)} = e^{\operatorname{E}[\ln(1-X)] } = e^{\psi(\beta) - \psi(\alpha + \beta)}</math> | :<math>G_{(1-X)} = e^{\operatorname{E}[\ln(1-X)] } = e^{\psi(\beta) - \psi(\alpha + \beta)}</math> | ||
एक पंक्ति के साथ {{nowrap|1=''α'' = ''β''}}, निम्नलिखित सीमाएँ | एक पंक्ति के साथ {{nowrap|1=''α'' = ''β''}}, निम्नलिखित सीमाएँ प्रयुक्त होती हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 280: | Line 277: | ||
&\lim_{\alpha = \beta \to \infty} G_{(1-X)} =\tfrac{1}{2} | &\lim_{\alpha = \beta \to \infty} G_{(1-X)} =\tfrac{1}{2} | ||
\end{align}</math> | \end{align}</math> | ||
निम्नलिखित | निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 288: | Line 285: | ||
इसका निम्नलिखित अनुमानित मूल्य है: | इसका निम्नलिखित अनुमानित मूल्य है: | ||
:<math>G_{(1-X)} \approx \frac{\beta - \frac{1}{2}}{\alpha+\beta-\frac{1}{2}}\text{ if } \alpha, \beta > 1.</math> | :<math>G_{(1-X)} \approx \frac{\beta - \frac{1}{2}}{\alpha+\beta-\frac{1}{2}}\text{ if } \alpha, \beta > 1. </math> | ||
चूंकि दोनों G<sub>''X''</sub> और G<sub>(1−''X'')</sub> असममित हैं, इस स्तिथियों में इनकी दोनों की आकार मापदंड समान {{nowrap|1=''α'' = ''β''}} हैं , ज्यामितीय साधन सामान्तर हैं: G<sub>''X''</sub> = G<sub>(1−''X'')</sub>. यह समानता दोनों ज्यामितीय साधनों के मध्य प्रदर्शित निम्नलिखित समरूपता से होती है: | |||
<nowiki>:</nowiki> | |||
:<math>G_X (\Beta(\alpha, \beta) )=G_{(1-X)}(\Beta(\beta, \alpha) ). </math> | :<math>G_X (\Beta(\alpha, \beta) )=G_{(1-X)}(\Beta(\beta, \alpha) ). </math> | ||
==== हार्मोनिक | ==== हार्मोनिक कारण ==== | ||
[[File:Harmonic mean for Beta distribution for alpha and beta ranging from 0 to 5 - J. Rodal.jpg|thumb|0 < α < 5 और 0 < β < 5 के लिए बीटा वितरण के लिए सुरीले माध्य]] | [[File:Harmonic mean for Beta distribution for alpha and beta ranging from 0 to 5 - J. Rodal.jpg|thumb|0 < α < 5 और 0 < β < 5 के लिए बीटा वितरण के लिए सुरीले माध्य]] | ||
[[File:(Mean - HarmonicMean) for Beta distribution versus alpha and beta from 0 to 2 - J. Rodal.jpg|thumb|0 से 2 तक बीटा वितरण बनाम α और β के लिए हार्मोनिक माध्य]] | [[File:(Mean - HarmonicMean) for Beta distribution versus alpha and beta from 0 to 2 - J. Rodal.jpg|thumb|0 से 2 तक बीटा वितरण बनाम α और β के लिए हार्मोनिक माध्य]]यादृच्छिक वेरिएबल X के साथ वितरण का हार्मोनिक माध्य H<sub>X</sub> का व्युत्क्रम 1/X का अंकगणितीय माध्य है या, समतुल्य, इसका अपेक्षित मान है। इसलिए, आकार मापदंड α और β के साथ बीटा वितरण का है: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
H_X &= \frac{1}{\operatorname{E}\left[\frac{1}{X}\right]} \\ | H_X &= \frac{1}{\operatorname{E}\left[\frac{1}{X}\right]} \\ | ||
| Line 306: | Line 301: | ||
&=\frac{1}{\int_0^1 \frac{x^{\alpha-1}(1-x)^{\beta-1}}{x \Beta(\alpha,\beta)}\,dx} \\ | &=\frac{1}{\int_0^1 \frac{x^{\alpha-1}(1-x)^{\beta-1}}{x \Beta(\alpha,\beta)}\,dx} \\ | ||
&= \frac{\alpha - 1}{\alpha + \beta - 1}\text{ if } \alpha > 1 \text{ and } \beta > 0 \\ | &= \frac{\alpha - 1}{\alpha + \beta - 1}\text{ if } \alpha > 1 \text{ and } \beta > 0 \\ | ||
\end{align}</math> | \end{align} </math> | ||
हार्मोनिक माध्य ( | α <1 के साथ बीटा वितरण का हार्मोनिक माध्य (H<sub>X</sub>) अपरिभाषित है, क्योंकि इसकी परिभाषित अभिव्यक्ति एकता से कम आकार मापदंड α के लिए [0, 1] में सीमित नहीं है। | ||
उपरोक्त व्यंजक में α = β देने से प्राप्त होता है | उपरोक्त व्यंजक में α = β देने से प्राप्त होता है | ||
| Line 314: | Line 310: | ||
दिखा रहा है कि α = β के लिए हार्मोनिक माध्य 0 से है, α = β = 1 के लिए, 1/2 के लिए, α = β → ∞ के लिए। | दिखा रहा है कि α = β के लिए हार्मोनिक माध्य 0 से है, α = β = 1 के लिए, 1/2 के लिए, α = β → ∞ के लिए। | ||
निम्नलिखित | निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 320: | Line 316: | ||
&\lim_{\alpha\to 1} H_X = \lim_{\beta \to \infty} H_X = 0 \\ | &\lim_{\alpha\to 1} H_X = \lim_{\beta \to \infty} H_X = 0 \\ | ||
&\lim_{\beta \to 0} H_X = \lim_{\alpha \to \infty} H_X = 1 | &\lim_{\beta \to 0} H_X = \lim_{\alpha \to \infty} H_X = 1 | ||
\end{align}</math> | \end{align} </math> | ||
ज्यामितीय माध्य के अतिरिक्त, हार्मोनिक माध्य चार | ज्यामितीय माध्य के अतिरिक्त, हार्मोनिक माध्य चार मापदंड स्तिथियों के लिए अधिकतम संभावना अनुमान में भूमिका निभाता है। दरअसल, हार्मोनिक माध्य H<sub>X</sub> के अतिरिक्त, चार मापदंड स्तिथियों के लिए अधिकतम संभावना अनुमान लगाते समययादृच्छिक वेरिएबल X के आधार पर, अन्य हार्मोनिक माध्य भी स्वाभाविक रूप से प्रकट होता है: रैखिक परिवर्तन (1 − X) पर आधारित हार्मोनिक माध्य, X की दर्पण-छवि, H द्वारा निरूपित<sub>1 − ''X''</sub>: | ||
:<math>H_{1-X} = \frac{1}{\operatorname{E} \left[\frac 1 {1-X}\right]} = \frac{\beta - 1}{\alpha + \beta-1} \text{ if } \beta > 1, \text{ and } \alpha> 0. </math> | :<math>H_{1-X} = \frac{1}{\operatorname{E} \left[\frac 1 {1-X}\right]} = \frac{\beta - 1}{\alpha + \beta-1} \text{ if } \beta > 1, \text{ and } \alpha> 0. | ||
हार्मोनिक माध्य (एच<sub>(1 − ''X'')</sub>β <1 के साथ बीटा वितरण अपरिभाषित है, क्योंकि इसकी परिभाषित अभिव्यक्ति [0, 1] में एकता से कम आकार | </math> | ||
हार्मोनिक माध्य (एच<sub>(1 − ''X'')</sub>β <1 के साथ बीटा वितरण अपरिभाषित है, क्योंकि इसकी परिभाषित अभिव्यक्ति [0, 1] में एकता से कम आकार मापदंड β के लिए बाध्य नहीं है। | |||
उपरोक्त व्यंजक में α = β देने से प्राप्त होता है | उपरोक्त व्यंजक में α = β देने से प्राप्त होता है | ||
| Line 331: | Line 328: | ||
दिखा रहा है कि α = β के लिए हार्मोनिक माध्य 0 से है, α = β = 1 के लिए, 1/2 के लिए, α = β → ∞ के लिए। | दिखा रहा है कि α = β के लिए हार्मोनिक माध्य 0 से है, α = β = 1 के लिए, 1/2 के लिए, α = β → ∞ के लिए। | ||
निम्नलिखित | निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 338: | Line 335: | ||
&\lim_{\alpha\to 0} H_{1-X} = \lim_{\beta\to \infty} H_{1-X} = 1 | &\lim_{\alpha\to 0} H_{1-X} = \lim_{\beta\to \infty} H_{1-X} = 1 | ||
\end{align}</math> | \end{align}</math> | ||
चूंकि दोनों H<sub>''X''</sub> और H<sub>1−''X''</sub> असममित हैं, इस स्तिथियों में α = β कि दोनों आकार मापदंड सामान्तर हैं, H<sub>''X''</sub> = H<sub>1−''X''</sub>. हार्मोनिक साधन सामान्तर हैं: यह समानता दोनों हार्मोनिक साधनों के मध्य प्रदर्शित निम्नलिखित समरूपता से होती है: | |||
:<math>H_X (\Beta(\alpha, \beta) )=H_{1-X}(\Beta(\beta, \alpha) ) \text{ if } \alpha, \beta> 1.</math> | :<math>H_X (\Beta(\alpha, \beta) )=H_{1-X}(\Beta(\beta, \alpha) ) \text{ if } \alpha, \beta> 1.</math> | ||
| Line 346: | Line 343: | ||
==== विचरण ==== | ==== विचरण ==== | ||
मापदंड α और β के साथ बीटा वितरण यादृच्छिक वेरिएबल X का विचरण (माध्य पर केंद्रित दूसरा क्षण) है:<ref name=JKB /><ref>{{cite web | url = http://www.itl.nist.gov/div898/handbook/eda/section3/eda366h.htm | title = NIST/SEMATECH e-Handbook of Statistical Methods 1.3.6.6.17. Beta Distribution | website = [[National Institute of Standards and Technology]] Information Technology Laboratory | access-date = May 31, 2016 |date = April 2012 }}</ref> | |||
:<math>\operatorname{var}(X) = \operatorname{E}[(X - \mu)^2] = \frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}</math> | :<math>\operatorname{var}(X) = \operatorname{E}[(X - \mu)^2] = \frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}</math> | ||
उपरोक्त व्यंजक में α = β देने से प्राप्त होता है | उपरोक्त व्यंजक में α = β देने से प्राप्त होता है | ||
:<math>\operatorname{var}(X) = \frac{1}{4(2\beta + 1)},</math> | :<math>\operatorname{var}(X) = \frac{1}{4(2\beta + 1)},</math> | ||
दिखा रहा है कि α = β के लिए | दिखा रहा है कि α = β के लिए जैसे जैसे {{nowrap|1=''α'' = ''β''}} बढ़ती है। वैसे वैसे विचरण नीरस रूप से घटता है समुच्चयिंग {{nowrap|1=''α'' = ''β'' = 0}} इस व्यंजक में, अधिकतम प्रसरण var(X) = 1/4 मिलता है<ref name=JKB />जो केवल {{nowrap|1=''α'' = ''β'' = 0}}. पर सीमा के निकट होता है, | ||
माध्य μ | बीटा वितरण को इसके माध्य μ (0 < μ < 1) और प्रतिरूप आकार ν = α + β (ν > 0) के संदर्भ में भी पैरामीट्रिज्ड किया जा सकता है (उपखंड माध्य और प्रतिरूप आकार देखें): | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 359: | Line 356: | ||
\beta &= (1 - \mu) \nu, \text{ where }\nu =(\alpha + \beta) >0. | \beta &= (1 - \mu) \nu, \text{ where }\nu =(\alpha + \beta) >0. | ||
\end{align}</math> | \end{align}</math> | ||
इस सांख्यिकीय | इस सांख्यिकीय मापदंड का उपयोग करते हुए, माध्य μ और प्रतिरूप आकार ν के संदर्भ में विचरण को निम्नानुसार व्यक्त किया जा सकता है: | ||
:<math>\operatorname{var}(X) = \frac{\mu (1-\mu)}{1 + \nu}</math> | :<math>\operatorname{var}(X) = \frac{\mu (1-\mu)}{1 + \nu}</math> | ||
| Line 367: | Line 364: | ||
:<math>\operatorname{var}(X) = \frac{1}{4 (1 + \nu)} \text{ if } \mu = \tfrac{1}{2}</math> | :<math>\operatorname{var}(X) = \frac{1}{4 (1 + \nu)} \text{ if } \mu = \tfrac{1}{2}</math> | ||
साथ ही, उपरोक्त भावों से निम्नलिखित सीमाएँ प्राप्त की जा सकती हैं (केवल विख्यात | साथ ही, उपरोक्त भावों से निम्नलिखित सीमाएँ प्राप्त की जा सकती हैं (केवल विख्यात वेरिएबल सीमा तक पहुँच रहे हैं): | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 376: | Line 373: | ||
[[File:Variance for Beta Distribution for alpha and beta ranging from 0 to 5 - J. Rodal.jpg|325px]] | [[File:Variance for Beta Distribution for alpha and beta ranging from 0 to 5 - J. Rodal.jpg|325px]] | ||
==== ज्यामितीय विचरण और सहप्रसरण ==== | ==== ज्यामितीय विचरण और सहप्रसरण ==== | ||
[[File:Beta distribution log geometric variances front view - J. Rodal.png|thumb|लॉग ज्यामितीय प्रसरण बनाम α और β]] | [[File:Beta distribution log geometric variances front view - J. Rodal.png|thumb|लॉग ज्यामितीय प्रसरण बनाम α और β]] | ||
[[File:Beta distribution log geometric variances back view - J. Rodal.png|thumb|लॉग ज्यामितीय प्रसरण बनाम α और β]]ज्यामितीय विचरण का लघुगणक, ln(var<sub>''GX''</sub>), यादृच्छिक | [[File:Beta distribution log geometric variances back view - J. Rodal.png|thumb|लॉग ज्यामितीय प्रसरण बनाम α और β]]ज्यामितीय विचरण का लघुगणक, ln(var<sub>''GX''</sub>), यादृच्छिक वेरिएबल X के साथ वितरण का X के लघुगणक का दूसरा क्षण X के ज्यामितीय माध्य ln(G<sub>X</sub>) पर केंद्रित है, | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 386: | Line 383: | ||
&= \operatorname{var}[\ln X] | &= \operatorname{var}[\ln X] | ||
\end{align}</math> | \end{align}</math> | ||
और इसलिए, ज्यामितीय विचरण है: | और इसलिए, ज्यामितीय विचरण है: | ||
:<math>\operatorname{var}_{GX} = e^{\operatorname{var}[\ln X]}</math> | :<math>\operatorname{var}_{GX} = e^{\operatorname{var}[\ln X]}</math> | ||
फिशर सूचना | फिशर सूचना आव्युह में, और लॉग संभावना फलन की वक्रता, प्रतिबिंब सूत्र वेरिएबल 1 − X के ज्यामितीय भिन्नता का लघुगणक और X और 1 − X के मध्य ज्यामितीय सहप्रसरण का लघुगणक प्रकट होता है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 405: | Line 402: | ||
& \\ | & \\ | ||
\operatorname{cov}_{G{X,(1-X)}} &= e^{\operatorname{cov}[\ln X, \ln(1-X)]} | \operatorname{cov}_{G{X,(1-X)}} &= e^{\operatorname{cov}[\ln X, \ln(1-X)]} | ||
\end{align}</math> | \end{align} </math> | ||
बीटा वितरण के लिए, दो गामा वितरणों के अनुपात के रूप में बीटा वितरण के प्रतिनिधित्व का उपयोग करके और अभिन्न के माध्यम से अंतर करके उच्च क्रम लॉगरिदमिक क्षण प्राप्त किए जा सकते हैं। उन्हें उच्च क्रम के पॉली-गामा कार्यों के संदर्भ में व्यक्त किया जा सकता है। अनुभाग देखें {{section link|| | बीटा वितरण के लिए, दो गामा वितरणों के अनुपात के रूप में बीटा वितरण के प्रतिनिधित्व का उपयोग करके और अभिन्न के माध्यम से अंतर करके उच्च क्रम लॉगरिदमिक क्षण प्राप्त किए जा सकते हैं। उन्हें उच्च क्रम के पॉली-गामा कार्यों के संदर्भ में व्यक्त किया जा सकता है। अनुभाग देखें {{section link||लघुगणकीय रूप से परिवर्तित यादृच्छिक चर के क्षण}}. लघुगणकीय वेरिएबल का प्रसरण और ln X और ln(1−X) का [[सहप्रसरण]] हैं: | ||
: <math>\operatorname{var}[\ln X]= \psi_1(\alpha) - \psi_1(\alpha + \beta)</math> | : <math>\operatorname{var}[\ln X]= \psi_1(\alpha) - \psi_1(\alpha + \beta)</math> | ||
: <math>\operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta)</math> | : <math>\operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta)</math> | ||
: <math>\operatorname{cov}[\ln X, \ln(1-X)] = -\psi_1(\alpha+\beta)</math> | : <math>\operatorname{cov}[\ln X, \ln(1-X)] = -\psi_1(\alpha+\beta)</math> | ||
जहाँ त्रिगामा फलन, ψ | जहाँ त्रिगामा फलन, ψ<sub>1</sub>(α) निरूपित करता है, तथा बहुग्राम कार्यों का दूसरा फलन है और इसे डिगामा फलन के व्युत्पन्न के रूप में परिभाषित किया गया है: | ||
:<math>\psi_1(\alpha) = \frac{d^2\ln\Gamma(\alpha)}{d\alpha^2}= \frac{d \, \psi(\alpha)}{d\alpha}.</math> | :<math>\psi_1(\alpha) = \frac{d^2\ln\Gamma(\alpha)}{d\alpha^2}= \frac{d \, \psi(\alpha)}{d\alpha}.</math> | ||
| Line 419: | Line 416: | ||
:<math> \ln \operatorname{var}_{G(1-X)} =\operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta)</math> | :<math> \ln \operatorname{var}_{G(1-X)} =\operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta)</math> | ||
:<math> \ln \operatorname{cov}_{GX,1-X} =\operatorname{cov}[\ln X, \ln(1-X)] = -\psi_1(\alpha+\beta)</math> | :<math> \ln \operatorname{cov}_{GX,1-X} =\operatorname{cov}[\ln X, \ln(1-X)] = -\psi_1(\alpha+\beta)</math> | ||
साथ वाले प्लॉट लॉग ज्यामितीय प्रसरण दिखाते हैं और ज्यामितीय सहप्रसरण बनाम आकृति | इसके साथ वाले प्लॉट लॉग ज्यामितीय प्रसरण दिखाते हैं और ज्यामितीय सहप्रसरण बनाम आकृति मापदंड α और β लॉग करते हैं। भूखंड दिखाते हैं कि लॉग ज्यामितीय संस्करण और लॉग ज्यामितीय सहप्रसरण आकार मापदंडों α और β 2 से अधिक के लिए शून्य के समीप हैं, और यह कि आकार मापदंड मान α और β एकता से कम के लिए लॉग ज्यामितीय संस्करण तेजी से मूल्य में वृद्धि करते हैं। आकार के मापदंडों के सभी मूल्यों के लिए लॉग ज्यामितीय संस्करण धनात्मक हैं। आकार के मापदंडों के सभी मूल्यों के लिए लॉग ज्यामितीय सहप्रसरण ऋणात्मक है, और यह एकता से कम α और β के लिए बड़े ऋणात्मक मूल्यों तक पहुंचता है। | ||
निम्नलिखित | निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 431: | Line 428: | ||
&\lim_{\beta\to 0} \ln \operatorname{cov}_{GX,(1-X)} = - \psi_1(\alpha) | &\lim_{\beta\to 0} \ln \operatorname{cov}_{GX,(1-X)} = - \psi_1(\alpha) | ||
\end{align}</math> | \end{align}</math> | ||
अलग-अलग दो | अलग-अलग दो मापदंड वाली सीमाएँ: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 438: | Line 435: | ||
&\lim_{\alpha\to 0} (\lim_{\beta \to 0} \ln \operatorname{cov}_{GX,(1-X)}) = \lim_{\beta\to 0} (\lim_{\alpha\to 0} \ln \operatorname{cov}_{GX,(1-X)}) = - \infty | &\lim_{\alpha\to 0} (\lim_{\beta \to 0} \ln \operatorname{cov}_{GX,(1-X)}) = \lim_{\beta\to 0} (\lim_{\alpha\to 0} \ln \operatorname{cov}_{GX,(1-X)}) = - \infty | ||
\end{align}</math> | \end{align}</math> | ||
चूंकि दोनों ln(varGX) और ln(varG(1 − X)) असममित हैं, जब आकार मापदंड सामान्तर होते हैं, तब α = β, में होता है: ln(var<sub>''GX''</sub>) = ln(varG(1 − X). यह समानता दोनों लॉग ज्यामितीय भिन्नताओं के मध्य प्रदर्शित निम्नलिखित समरूपता से होती है: | |||
:<math>\ln \operatorname{var}_{GX}(\Beta(\alpha, \beta))=\ln \operatorname{var}_{G(1-X)}(\Beta(\beta, \alpha)).</math> | :<math>\ln \operatorname{var}_{GX}(\Beta(\alpha, \beta))=\ln \operatorname{var}_{G(1-X)}(\Beta(\beta, \alpha)).</math> | ||
| Line 448: | Line 445: | ||
==== माध्य के आस-पास निरपेक्ष विचलन ==== | ==== माध्य के आस-पास निरपेक्ष विचलन ==== | ||
[[File:Ratio of Mean Abs. Dev. to Std.Dev. Beta distribution with alpha and beta from 0 to 5 - J. Rodal.jpg|thumb|मीन एब्स.देव का अनुपात। Std.Dev के लिए। α और β के साथ बीटा वितरण के लिए 0 से 5 तक]] | [[File:Ratio of Mean Abs. Dev. to Std.Dev. Beta distribution with alpha and beta from 0 to 5 - J. Rodal.jpg|thumb|मीन एब्स.देव का अनुपात। Std.Dev के लिए। α और β के साथ बीटा वितरण के लिए 0 से 5 तक]] | ||
[[File:Ratio of Mean Abs. Dev. to Std.Dev. Beta distribution vs. nu from 0 to 10 and vs. mean - J. Rodal.jpg|thumb|मीन एब्स.देव का अनुपात। Std.Dev के लिए। माध्य 0 ≤ μ ≤ 1 और | [[File:Ratio of Mean Abs. Dev. to Std.Dev. Beta distribution vs. nu from 0 to 10 and vs. mean - J. Rodal.jpg|thumb|मीन एब्स.देव का अनुपात। Std.Dev के लिए। माध्य 0 ≤ μ ≤ 1 और प्रतिरूप आकार 0 < ν ≤ 10 के साथ बीटा वितरण के लिए]]आकार मापदंडों α और β के साथ बीटा वितरण के लिए माध्य के आसपास औसत निरपेक्ष विचलन है:'''<ref name="Handbook of Beta Distribution" />''' | ||
:<math>\operatorname{E}[|X - E[X]|] = \frac{2 \alpha^{\alpha} \beta^{\beta}}{\Beta(\alpha,\beta)(\alpha + \beta)^{\alpha + \beta + 1}} </math> | :<math>\operatorname{E}[|X - E[X]|] = \frac{2 \alpha^{\alpha} \beta^{\beta}}{\Beta(\alpha,\beta)(\alpha + \beta)^{\alpha + \beta + 1}} </math> | ||
माध्य के चारों ओर औसत निरपेक्ष विचलन मोड के प्रत्येक पक्ष में | माध्य के चारों ओर औसत निरपेक्ष विचलन मोड के प्रत्येक पक्ष में टेल और विभक्ति बिंदुओं के साथ बीटा वितरण के लिए मानक विचलन की तुलना में [[सांख्यिकीय फैलाव]] का अधिक शक्तिशाली सांख्यिकी अनुमानक है, α,β > 2 के साथ बीटा(α, β) वितरण यह माध्य से वर्ग विचलन के अतिरिक्त रैखिक (पूर्ण) विचलन पर निर्भर करता है। इसलिए, माध्य से बहुत बड़े विचलन का प्रभाव उतना अधिक भारित नहीं होता है। | ||
गामा फलन के लिए स्टर्लिंग के सन्निकटन का उपयोग करते हुए, नॉर्मन लॉयड जॉनसन|एन.एल.जॉनसन और सैमुअल कोटज़|एस.कोट्ज़<ref name=JKB />एकता से अधिक आकार के मापदंडों के मूल्यों के लिए निम्नलिखित सन्निकटन प्राप्त किया (इस सन्निकटन के लिए सापेक्ष त्रुटि α = β = 1 के लिए केवल -3.5% है, और यह α → ∞, β → ∞ के रूप में शून्य हो जाती है): | गामा फलन के लिए स्टर्लिंग के सन्निकटन का उपयोग करते हुए, नॉर्मन लॉयड जॉनसन|(एन.एल.जॉनसन) और सैमुअल कोटज़|(एस.कोट्ज़)<ref name=JKB />एकता से अधिक आकार के मापदंडों के मूल्यों के लिए निम्नलिखित सन्निकटन प्राप्त किया (इस सन्निकटन के लिए सापेक्ष त्रुटि α = β = 1 के लिए केवल -3.5% है, और यह α → ∞, β → ∞ के रूप में शून्य हो जाती है): | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 459: | Line 456: | ||
&\approx \sqrt{\frac{2}{\pi}} \left(1+\frac{7}{12 (\alpha+\beta)}{}-\frac{1}{12 \alpha}-\frac{1}{12 \beta} \right), \text{ if } \alpha, \beta > 1. | &\approx \sqrt{\frac{2}{\pi}} \left(1+\frac{7}{12 (\alpha+\beta)}{}-\frac{1}{12 \alpha}-\frac{1}{12 \beta} \right), \text{ if } \alpha, \beta > 1. | ||
\end{align}</math> | \end{align}</math> | ||
सीमा α → ∞, β → ∞ पर, मानक विचलन (बीटा वितरण के लिए) के औसत पूर्ण विचलन का अनुपात सामान्य वितरण के लिए समान उपायों के अनुपात के | सीमा α → ∞, β → ∞ पर, मानक विचलन (बीटा वितरण के लिए) के औसत पूर्ण विचलन का अनुपात सामान्य वितरण के लिए समान उपायों के अनुपात के सामान्तर हो जाता है: <math>\sqrt{\frac{2}{\pi}}</math>. α = β = 1 के लिए यह अनुपात <math>\frac{\sqrt{3}}{2}</math> सामान्तर है , जिससे कि α = β = 1 से α, β → ∞ अनुपात 8.5% कम हो जाएगा। α = β = 0 के लिए मानक विचलन माध्य के चारों ओर [[पूर्ण विचलन]] के सामान्तर है। इसलिए, यह अनुपात α = β = 0 से α = β = 1 तक 15% कम हो जाता है, और α = β = 0 से α, β → ∞ तक 25% कम हो जाता है। चूंकि, विषम बीटा वितरण के लिए जैसे कि α → 0 या β → 0, मानक विचलन का औसत निरपेक्ष विचलन का अनुपात अनंत तक पहुंचता है (चूंकि उनमें से प्रत्येक, व्यक्तिगत रूप से, शून्य तक पहुंचता है) क्योंकि औसत निरपेक्ष विचलन शून्य की तुलना में तेजी से पहुंचता है मानक विचलन। | ||
माध्य μ और | माध्य μ और प्रतिरूप आकार ν = α + β > 0 के संदर्भ में सांख्यिकीय मापदंड का उपयोग करना: | ||
:α = μν, β = (1−μ)ν | :α = μν, β = (1−μ)ν | ||
माध्य μ और | माध्य μ और प्रतिरूप आकार ν के संदर्भ में माध्य के चारों ओर औसत निरपेक्ष विचलन को निम्नानुसार व्यक्त किया जा सकता है: | ||
:<math>\operatorname{E}[| X - E[X]|] = \frac{2 \mu^{\mu\nu} (1-\mu)^{(1-\mu)\nu}}{\nu \Beta(\mu \nu,(1-\mu)\nu)}</math> | :<math>\operatorname{E}[| X - E[X]|] = \frac{2 \mu^{\mu\nu} (1-\mu)^{(1-\mu)\nu}}{\nu \Beta(\mu \nu,(1-\mu)\nu)}</math> | ||
एक सममित वितरण के लिए, माध्य वितरण के मध्य में है | एक सममित वितरण के लिए, μ = 1/2, माध्य वितरण के मध्य में है,और इसलिए: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 475: | Line 472: | ||
\lim_{\nu \to \infty} \left (\lim_{\mu \to \frac{1}{2}} \operatorname{E}[| X - E[X]|] \right ) &= 0 | \lim_{\nu \to \infty} \left (\lim_{\mu \to \frac{1}{2}} \operatorname{E}[| X - E[X]|] \right ) &= 0 | ||
\end{align}</math> | \end{align}</math> | ||
साथ ही, उपरोक्त भावों से निम्नलिखित सीमाएँ प्राप्त की जा सकती हैं (केवल विख्यात | साथ ही, उपरोक्त भावों से निम्नलिखित सीमाएँ प्राप्त की जा सकती हैं (केवल विख्यात वेरिएबल सीमा तक पहुँच रहे हैं): | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 483: | Line 480: | ||
\lim_{\nu \to 0} \operatorname{E}[|X - E[X]|] &= \sqrt{\mu (1-\mu)} \\ | \lim_{\nu \to 0} \operatorname{E}[|X - E[X]|] &= \sqrt{\mu (1-\mu)} \\ | ||
\lim_{\nu \to \infty} \operatorname{E}[|X - E[X]|] &= 0 | \lim_{\nu \to \infty} \operatorname{E}[|X - E[X]|] &= 0 | ||
\end{align}</math> | \end{align} </math> | ||
==== [[मतलब पूर्ण अंतर]] ==== | ==== [[मतलब पूर्ण अंतर|कारणपूर्ण अंतर]] ==== | ||
बीटा वितरण के लिए औसत निरपेक्ष अंतर है: | बीटा वितरण के लिए औसत निरपेक्ष अंतर है: | ||
| Line 496: | Line 493: | ||
=== | === विषमता === | ||
[[File:Skewness for Beta Distribution as a function of the variance and the mean - J. Rodal.jpg|325px|thumb|विचरण और माध्य के कार्य के रूप में बीटा वितरण के लिए | [[File:Skewness for Beta Distribution as a function of the variance and the mean - J. Rodal.jpg|325px|thumb|विचरण और माध्य के कार्य के रूप में बीटा वितरण के लिए विषमता]]विषमता (बीटा वितरण का तीसरा क्षण माध्य पर केंद्रित, विचरण की 3/2 शक्ति द्वारा सामान्यीकृत) है<ref name=JKB /> | ||
:<math>\gamma_1 =\frac{\operatorname{E}[(X - \mu)^3]}{(\operatorname{var}(X))^{3/2}} = \frac{2(\beta - \alpha)\sqrt{\alpha + \beta + 1}}{(\alpha + \beta + 2) \sqrt{\alpha \beta}} .</math> | :<math>\gamma_1 =\frac{\operatorname{E}[(X - \mu)^3]}{(\operatorname{var}(X))^{3/2}} = \frac{2(\beta - \alpha)\sqrt{\alpha + \beta + 1}}{(\alpha + \beta + 2) \sqrt{\alpha \beta}} .</math> | ||
उपरोक्त अभिव्यक्ति में α = β देने से γ | उपरोक्त अभिव्यक्ति में α = β देने से γ<sub>1</sub> = 0 प्राप्त होता है ,तथा बार फिर दिखा रहा है कि α = β के लिए वितरण सममित है और इसलिए विषमता शून्य है। α < β के लिए धनात्मक विषम (दायां-टेल), α> β के लिए ऋणात्मक विषम (बायां-टेल)। | ||
औसत μ और | और औसत μ और प्रतिरूप आकार ν = α + β के संदर्भ में सांख्यिकीय मापदंड का उपयोग करना: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 508: | Line 505: | ||
\beta & {} = (1 - \mu) \nu , \text{ where }\nu =(\alpha + \beta) >0. | \beta & {} = (1 - \mu) \nu , \text{ where }\nu =(\alpha + \beta) >0. | ||
\end{align}</math> | \end{align}</math> | ||
माध्य μ और | माध्य μ और प्रतिरूप आकार ν के संदर्भ में विषमता व्यक्त किया जा सकता है: | ||
:<math>\gamma_1 =\frac{\operatorname{E}[(X - \mu)^3]}{(\operatorname{var}(X))^{3/2}} = \frac{2(1-2\mu)\sqrt{1+\nu}}{(2+\nu)\sqrt{\mu (1 - \mu)}}.</math> | :<math>\gamma_1 =\frac{\operatorname{E}[(X - \mu)^3]}{(\operatorname{var}(X))^{3/2}} = \frac{2(1-2\mu)\sqrt{1+\nu}}{(2+\nu)\sqrt{\mu (1 - \mu)}}.</math> | ||
विषमता केवल विचरण संस्करण और माध्य μ के रूप में निम्नानुसार व्यक्त किया जा सकता है: | |||
:<math>\gamma_1 =\frac{\operatorname{E}[(X - \mu)^3]}{(\operatorname{var}(X))^{3/2}} = \frac{2(1-2\mu)\sqrt{\text{ var }}}{ \mu(1-\mu) + \operatorname{var}}\text{ if } \operatorname{var} < \mu(1-\mu)</math> | :<math>\gamma_1 =\frac{\operatorname{E}[(X - \mu)^3]}{(\operatorname{var}(X))^{3/2}} = \frac{2(1-2\mu)\sqrt{\text{ var }}}{ \mu(1-\mu) + \operatorname{var}}\text{ if } \operatorname{var} < \mu(1-\mu)</math> | ||
विचरण और माध्य के कार्य के रूप में | विचरण और माध्य के कार्य के रूप में विषमता के साथ की साजिश से पता चलता है कि अधिकतम विचरण (1/4) शून्य विषमता और समरूपता की स्थिति (μ = 1/2) के साथ युग्मित है, और वह अधिकतम विषमता (धनात्मक या ऋणात्मक अनंत) तब होता है जब माध्य छोर या दूसरे छोर पर स्थित है, जिससे संभाव्यता वितरण का द्रव्यमान सिरों पर केंद्रित हो (न्यूनतम विचरण )। | ||
प्रतिरूप के आकार ν = α + β और विचरण संस्करण के संदर्भ में विषमता के वर्ग के लिए निम्नलिखित अभिव्यक्ति, चार मापदंडों के क्षणों के आकलन की विधि के लिए उपयोगी है: | |||
:<math>(\gamma_1)^2 =\frac{(\operatorname{E}[(X - \mu)^3])^2}{(\operatorname{var}(X))^3} = \frac{4}{(2+\nu)^2}\bigg(\frac{1}{\text{var}}-4(1+\nu)\bigg)</math> | :<math>(\gamma_1)^2 =\frac{(\operatorname{E}[(X - \mu)^3])^2}{(\operatorname{var}(X))^3} = \frac{4}{(2+\nu)^2}\bigg(\frac{1}{\text{var}}-4(1+\nu)\bigg)</math> | ||
यह अभिव्यक्ति सही ढंग से α = β के लिए शून्य का | यह अभिव्यक्ति सही ढंग से α = β के लिए शून्य का विषमता देती है, क्योंकि उस स्तिथियाँ में (देखें {{section link||वरिएंस }}): <math>\operatorname{var} = \frac{1}{4 (1 + \nu)}</math>. | ||
सममित | सममित स्तिथियाँ के लिए (α = β), विषमता = 0 पूरी सीमा पर, और निम्नलिखित सीमाएँ प्रयुक्त होती हैं: | ||
:<math>\lim_{\alpha = \beta \to 0} \gamma_1 = \lim_{\alpha = \beta \to \infty} \gamma_1 =\lim_{\nu \to 0} \gamma_1=\lim_{\nu \to \infty} \gamma_1=\lim_{\mu \to \frac{1}{2}} \gamma_1 = 0</math> | :<math>\lim_{\alpha = \beta \to 0} \gamma_1 = \lim_{\alpha = \beta \to \infty} \gamma_1 =\lim_{\nu \to 0} \gamma_1=\lim_{\nu \to \infty} \gamma_1=\lim_{\mu \to \frac{1}{2}} \gamma_1 = 0</math> | ||
असममित | असममित स्थितियों के लिए (α ≠ β) निम्नलिखित सीमाएँ (केवल विख्यात वेरिएबल सीमा के समीप पहुंचकर) उपरोक्त अभिव्यक्तियों से प्राप्त की जा सकती हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 536: | Line 533: | ||
[[File:Skewness Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px]][[File:Skewness Beta Distribution for alpha and beta from .1 to 5 - J. Rodal.jpg|325px]] | [[File:Skewness Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px]][[File:Skewness Beta Distribution for alpha and beta from .1 to 5 - J. Rodal.jpg|325px]] | ||
=== | === कुर्तबसिस === | ||
[[File:Excess Kurtosis for Beta Distribution as a function of variance and mean - J. Rodal.jpg|325px|thumb|विचरण और माध्य के कार्य के रूप में बीटा वितरण के लिए अतिरिक्त कर्टोसिस]]गियर के | [[File:Excess Kurtosis for Beta Distribution as a function of variance and mean - J. Rodal.jpg|325px|thumb|विचरण और माध्य के कार्य के रूप में बीटा वितरण के लिए अतिरिक्त कर्टोसिस]]गियर के हानि का आकलन करने के लिए ध्वनिक विश्लेषण में बीटा वितरण प्रयुक्त किया गया है, क्योंकि बीटा वितरण के कर्टोसिस को गियर की स्थिति का अच्छा संकेतक बताया गया है।<ref name=Oguamanam>{{cite journal |last1=Oguamanam |first1=D.C.D. |last2=Martin |first2=H. R. |last3=Huissoon |first3=J. P. |title=गियर क्षति विश्लेषण के लिए बीटा वितरण के अनुप्रयोग पर|journal=Applied Acoustics |year=1995 |volume=45 |issue=3 |pages=247–261 |doi=10.1016/0003-682X(95)00001-P}}</ref> कर्टोसिस का उपयोग किसी व्यक्ति के कदमों से उत्पन्न भूकंपीय संकेत को अन्य संकेत से अलग करने के लिए भी किया जाता है। जैसा कि जमीन पर चलने वाले व्यक्ति या अन्य लक्ष्य भूकंपीय तरंगों के रूप में निरंतर संकेत उत्पन्न करते हैं, उनके द्वारा उत्पन्न भूकंपीय तरंगों के आधार पर विभिन्न लक्ष्यों को अलग किया जा सकता है। कर्टोसिस आवेगी संकेतबं के प्रति संवेदनशील है, इसलिए यह वाहनों, हवाओं, ध्वनि आदि द्वारा उत्पन्न अन्य संकेत की तुलना में मानव पदचिन्हों द्वारा उत्पन्न संकेतबं के प्रति अधिक संवेदनशील है।<ref name=Liang>{{cite journal|author1=Zhiqiang Liang |author2=Jianming Wei |author3=Junyu Zhao |author4=Haitao Liu |author5=Baoqing Li |author6=Jie Shen |author7=Chunlei Zheng |title=कर्टोसिस का सांख्यिकीय अर्थ और भूकंपीय संकेतों के आधार पर व्यक्तियों की पहचान के लिए इसका नया अनुप्रयोग|journal=Sensors |date=27 August 2008 |volume=8 |issue=8 |pages=5106–5119 |doi=10.3390/s8085106|pmid=27873804 |pmc=3705491 |bibcode=2008Senso...8.5106L |doi-access=free }}</ref> दुर्भाग्य से, ककुदता के लिए अंकन मानकीकृत नहीं किया गया है। अतिरिक्त कर्टोसिस के लिए केनी और कीपिंग में प्रतीक γ<sub>2</sub> का प्रयोग करें <ref name="Abramowitz">{{cite book|last=Abramowitz|first=Milton and Irene A. Stegun|title=सूत्र, रेखांकन और गणितीय तालिकाओं के साथ गणितीय कार्यों की पुस्तिका|year=1965|publisher=Dover|isbn=978-0-486-61272-0|url=https://archive.org/details/handbookofmathe000abra}}</ref>, किन्तु [[अब्रामोवित्ज़ और स्टेगुन]] विभिन्न शब्दावली का प्रयोग करें।<ref name="Kenney and Keeping">{{cite book|last=Kenney|first=J. F., and E. S. Keeping|title=Mathematics of Statistics Part Two, 2nd edition|year=1951|publisher=D. Van Nostrand Company Inc.}}</ref> भ्रम को रोकने के लिए कर्टोसिस के मध्य (माध्य पर केंद्रित चौथा क्षण, विचरण के वर्ग द्वारा सामान्यीकृत)<ref name=Weisstein.Kurtosi>{{cite web|last=Weisstein.|first=Eric W.|title=कुकुदता|url=http://mathworld.wolfram.com/कुकुदता.html|publisher=MathWorld--A Wolfram Web Resource|access-date=13 August 2012}}</ref> और अतिरिक्त कर्टोसिस, प्रतीकों का उपयोग करते समय, उन्हें निम्नानुसार लिखा जाएगा:<ref name="Handbook of Beta Distribution">{{cite book|editor-last=Gupta|editor-first=Arjun K.|title=हैंडबुक ऑफ़ बीटा डिस्ट्रीब्यूशन एंड इट्स एप्लीकेशन्स|year=2004|publisher=CRC Press|isbn=978-0824753962}}</ref><ref name=Panik>{{cite book|last=Panik|first=Michael J|title=प्रारंभिक दृष्टिकोण से उन्नत सांख्यिकी|year=2005|publisher=Academic Press|isbn=978-0120884940}}</ref> | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\text{excess kurtosis} | \text{excess kurtosis} | ||
| Line 545: | Line 542: | ||
&=\frac{6[(\alpha - \beta)^2 (\alpha +\beta + 1) - \alpha \beta (\alpha + \beta + 2)]} | &=\frac{6[(\alpha - \beta)^2 (\alpha +\beta + 1) - \alpha \beta (\alpha + \beta + 2)]} | ||
{\alpha \beta (\alpha + \beta + 2) (\alpha + \beta + 3)} . | {\alpha \beta (\alpha + \beta + 2) (\alpha + \beta + 3)} . | ||
\end{align}</math> | \end{align} </math> | ||
उपरोक्त व्यंजक में α = β देने से प्राप्त होता है | उपरोक्त व्यंजक में α = β देने से प्राप्त होता है | ||
:<math>\text{excess kurtosis} =- \frac{6}{3+2\alpha} \text{ if }\alpha=\beta </math>. | :<math>\text{excess kurtosis} =- \frac{6}{3+2\alpha} \text{ if }\alpha=\beta </math>. | ||
इसलिए, सममित बीटा वितरण के लिए, अतिरिक्त कर्टोसिस | इसलिए, सममित बीटा वितरण के लिए, अतिरिक्त कर्टोसिस ऋणात्मक है, {α = β} → 0 के रूप में सीमा पर -2 के न्यूनतम मान से बढ़ रहा है, और शून्य के अधिकतम मान को {α = β} → ∞ के रूप में आ रहा है। तथा −2 का मान अतिरिक्त कर्टोसिस का न्यूनतम मूल्य है जिसे कोई भी वितरण (न केवल बीटा वितरण, किंतु किसी भी संभावित प्रकार का वितरण) कभी भी प्राप्त कर सकता है। यह न्यूनतम मूल्य तब प्राप्त होता है जब सभी प्रायिकता घनत्व पूरी तरह से प्रत्येक छोर x = 0 और x = 1 पर केंद्रित होते हैं, मध्य में कुछ भी नहीं होता है: प्रत्येक छोर पर समान संभावना 1/2 के साथ 2-बिंदु बर्नौली वितरण (एक सिक्का टॉस: देखें) आगे की चर्चा के लिए विषमता के वर्ग से घिरे कर्टोसिस के नीचे का खंड)। संभाव्यता वितरण के संभावित आउटलेयर (या संभावित दुर्लभ, वेरिएबल मान) के माप के रूप में [[ कुकुदता ]] का विवरण, बीटा वितरण सहित सभी वितरणों के लिए सही है। जब दुर्लभ, वेरिएबल म मान बीटा वितरण में हो सकते हैं, तब इसका कर्टोसिस जितना अधिक होगा; अन्यथा, कर्टोसिस कम होता है। α ≠ β, विषम बीटा वितरण के लिए, अतिरिक्त कर्टोसिस असीमित धनात्मक मूल्यों तक पहुंच सकता है (विशेष रूप से α → 0 के लिए परिमित β के लिए, या β → 0 के लिए परिमित α के लिए) क्योंकि मोड से दूर की ओर कभी-कभी चरम मान उत्पन्न होंगे। न्यूनतम कर्टोसिस तब होता है जब द्रव्यमान घनत्व प्रत्येक छोर पर समान रूप से केंद्रित होता है (और इसलिए माध्य केंद्र में होता है), और सिरों के मध्य द्रव्यमान घनत्व की कोई संभावना नहीं होती है। | ||
औसत μ और | औसत μ और प्रतिरूप आकार ν = α + β के संदर्भ में सांख्यिकीय मापदंड का उपयोग करना: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 558: | Line 555: | ||
\beta & {} = (1 - \mu) \nu , \text{ where }\nu =(\alpha + \beta) >0. | \beta & {} = (1 - \mu) \nu , \text{ where }\nu =(\alpha + \beta) >0. | ||
\end{align}</math> | \end{align}</math> | ||
माध्य μ और | माध्य μ और प्रतिरूप आकार ν के संदर्भ में अतिरिक्त कर्टोसिस को निम्नानुसार व्यक्त किया जा सकता है: | ||
:<math>\text{excess kurtosis} =\frac{6}{3 + \nu}\bigg (\frac{(1 - 2 \mu)^2 (1 + \nu)}{\mu (1 - \mu) (2 + \nu)} - 1 \bigg )</math> | :<math>\text{excess kurtosis} =\frac{6}{3 + \nu}\bigg (\frac{(1 - 2 \mu)^2 (1 + \nu)}{\mu (1 - \mu) (2 + \nu)} - 1 \bigg )</math> | ||
अतिरिक्त कर्टोसिस को केवल निम्नलिखित दो मापदंडों के संदर्भ में भी व्यक्त किया जा सकता है: विचरण संस्करण, और | अतिरिक्त कर्टोसिस को केवल निम्नलिखित दो मापदंडों के संदर्भ में भी व्यक्त किया जा सकता है: विचरण संस्करण, और प्रतिरूप आकार ν निम्नानुसार है: | ||
:<math>\text{excess kurtosis} =\frac{6}{(3 + \nu)(2 + \nu)}\left(\frac{1}{\text{ var }} - 6 - 5 \nu \right)\text{ if }\text{ var }< \mu(1-\mu)</math> | :<math>\text{excess kurtosis} =\frac{6}{(3 + \nu)(2 + \nu)}\left(\frac{1}{\text{ var }} - 6 - 5 \nu \right)\text{ if }\text{ var }< \mu(1-\mu)</math> | ||
| Line 567: | Line 564: | ||
:<math>\text{excess kurtosis} =\frac{6 \text{ var } (1 - \text{ var } - 5 \mu (1 - \mu) )}{(\text{var } + \mu (1 - \mu))(2\text{ var } + \mu (1 - \mu) )}\text{ if }\text{ var }< \mu(1-\mu)</math> | :<math>\text{excess kurtosis} =\frac{6 \text{ var } (1 - \text{ var } - 5 \mu (1 - \mu) )}{(\text{var } + \mu (1 - \mu))(2\text{ var } + \mu (1 - \mu) )}\text{ if }\text{ var }< \mu(1-\mu)</math> | ||
विचरण और माध्य के कार्य के रूप में अतिरिक्त कर्टोसिस की साजिश से पता चलता है कि अतिरिक्त | विचरण और माध्य के कार्य के रूप में अतिरिक्त कर्टोसिस की साजिश से पता चलता है कि अतिरिक्त कुर्तबसिस का न्यूनतम मूल्य (−2, जो किसी भी वितरण के लिए अतिरिक्त कर्टोसिस के लिए न्यूनतम संभव मूल्य है) अंतर के अधिकतम मूल्य के साथ घनिष्ठ रूप से जुड़ा हुआ है ( 1/4) और समरूपता की स्थिति: मध्य बिंदु पर होने वाली माध्य (μ = 1/2)। यह शून्य विषमता के साथ α = β = 0 के सममित स्तिथियाँ के लिए होता है। सीमा पर, यह 2 बिंदु बर्नौली वितरण है जिसमें समान संभावना 1/2 प्रत्येक डायराक डेल्टा फलन के अंत में x = 0 और x = 1 और हर स्थान शून्य संभावना है। (एक सिक्के का उछाल: सिक्के का फलक x = 0 और दूसरा फलक x = 1 है।) प्रसरण अधिकतम है क्योंकि वितरण के दो मोडल है और प्रत्येक छोर पर दो मोड (स्पाइक्स) के मध्य कुछ भी नहीं है। अतिरिक्त कर्टोसिस न्यूनतम है:क्योंकि संभाव्यता घनत्व द्रव्यमान माध्य पर शून्य है और यह प्रत्येक छोर पर दो चोटियों पर केंद्रित है। अतिरिक्त कर्टोसिस न्यूनतम संभव मान (किसी भी वितरण के लिए) तक पहुँच जाता है जब प्रायिकता घनत्व फलन के प्रत्येक छोर पर दो स्पाइक्स होते हैं: यह द्वि-शिखर होता है। और उनके मध्य में कुछ भी नहीं होता है | ||
दूसरी ओर, प्लॉट से पता चलता है कि अत्यधिक | दूसरी ओर, प्लॉट से पता चलता है कि अत्यधिक विषम स्थितियों के लिए, जहां माध्य या दूसरे छोर (μ = 0 या μ = 1) के पास स्थित है, विचरण शून्य के समीप है, और अतिरिक्त कर्टोसिस तेजी से अनंत तक पहुंचता है जब बंटन का माध्य या तब अंत की ओर पहुंचता है। | ||
वैकल्पिक रूप से, अतिरिक्त कर्टोसिस को केवल निम्नलिखित दो मापदंडों के संदर्भ में भी व्यक्त किया जा सकता है: | वैकल्पिक रूप से, अतिरिक्त कर्टोसिस को केवल निम्नलिखित दो मापदंडों के संदर्भ में भी व्यक्त किया जा सकता है: विषमता का वर्ग, और प्रतिरूप आकार ν निम्नानुसार है: | ||
:<math>\text{excess kurtosis} =\frac{6}{3 + \nu}\bigg(\frac{(2 + \nu)}{4} (\text{skewness})^2 - 1\bigg)\text{ if (skewness)}^2-2< \text{excess kurtosis}< \frac{3}{2} (\text{skewness})^2</math> | :<math>\text{excess kurtosis} =\frac{6}{3 + \nu}\bigg(\frac{(2 + \nu)}{4} (\text{skewness})^2 - 1\bigg)\text{ if (skewness)}^2-2< \text{excess kurtosis}< \frac{3}{2} (\text{skewness})^2</math> | ||
इस अंतिम अभिव्यक्ति से, [[कार्ल पियर्सन]] द्वारा अपने पेपर में व्यावहारिक रूप से सदी पहले प्रकाशित समान सीमाएँ प्राप्त कर सकते हैं,<ref name=Pearson />बीटा वितरण के लिए ( | इस अंतिम अभिव्यक्ति से, [[कार्ल पियर्सन]] द्वारा अपने पेपर में व्यावहारिक रूप से सदी पहले प्रकाशित समान सीमाएँ प्राप्त कर सकते हैं,<ref name=Pearson />बीटा वितरण के लिए (विषमता के वर्ग से घिरा कर्टोसिस शीर्षक वाला नीचे दिया गया अनुभाग देखें)। उपरोक्त व्यंजक में α + β= ν = 0 समुच्चय करने पर, पियर्सन की निचली सीमा प्राप्त होती है (सीमा के नीचे विषमता और अतिरिक्त कर्टोसिस के लिए मान (अतिरिक्त कर्टोसिस + 2 - विषमता<sup>2</sup> = 0) किसी भी वितरण के लिए नहीं हो सकता है, और इसलिए कार्ल पियर्सन ने उचित रूप से इस सीमा के नीचे के क्षेत्र को असंभव क्षेत्र कहा है)। α + β = ν → ∞ की सीमा पियर्सन की ऊपरी सीमा निर्धारित करती है। | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 583: | Line 580: | ||
:<math>(\text{skewness})^2-2< \text{excess kurtosis}< \tfrac{3}{2} (\text{skewness})^2</math> | :<math>(\text{skewness})^2-2< \text{excess kurtosis}< \tfrac{3}{2} (\text{skewness})^2</math> | ||
ν = α + β के मान जैसे कि ν शून्य से अनंत तक होता है, 0 < ν < ∞, बीटा वितरण के पूरे क्षेत्र को अतिरिक्त कर्टोसिस बनाम स्क्वायर | ν = α + β के मान जैसे कि ν शून्य से अनंत तक होता है, 0 < ν < ∞, बीटा वितरण के पूरे क्षेत्र को अतिरिक्त कर्टोसिस बनाम स्क्वायर विषमता के विमान में फैलाता है। | ||
सममित | सममित स्तिथियाँ (α = β) के लिए, निम्नलिखित सीमाएं प्रयुक्त होती हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 592: | Line 589: | ||
&\lim_{\mu \to \frac{1}{2}} \text{excess kurtosis} = - \frac{6}{3 + \nu} | &\lim_{\mu \to \frac{1}{2}} \text{excess kurtosis} = - \frac{6}{3 + \nu} | ||
\end{align}</math> | \end{align}</math> | ||
असममित | असममित स्थितियों के लिए (α ≠ β) निम्नलिखित सीमाएँ (केवल विख्यात वेरिएबल सीमा के समीप पहुंचकर) उपरोक्त अभिव्यक्तियों से प्राप्त की जा सकती हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 599: | Line 596: | ||
&\lim_{\beta \to \infty}\text{excess kurtosis} = \frac{6}{\alpha},\text{ } \lim_{\alpha \to 0}(\lim_{\beta \to \infty} \text{excess kurtosis}) = \infty,\text{ } \lim_{\alpha \to \infty}(\lim_{\beta \to \infty} \text{excess kurtosis}) = 0\\ | &\lim_{\beta \to \infty}\text{excess kurtosis} = \frac{6}{\alpha},\text{ } \lim_{\alpha \to 0}(\lim_{\beta \to \infty} \text{excess kurtosis}) = \infty,\text{ } \lim_{\alpha \to \infty}(\lim_{\beta \to \infty} \text{excess kurtosis}) = 0\\ | ||
&\lim_{\nu \to 0} \text{excess kurtosis} = - 6 + \frac{1}{\mu (1 - \mu)},\text{ } \lim_{\mu \to 0}(\lim_{\nu \to 0} \text{excess kurtosis}) = \infty,\text{ } \lim_{\mu \to 1}(\lim_{\nu \to 0} \text{excess kurtosis}) = \infty | &\lim_{\nu \to 0} \text{excess kurtosis} = - 6 + \frac{1}{\mu (1 - \mu)},\text{ } \lim_{\mu \to 0}(\lim_{\nu \to 0} \text{excess kurtosis}) = \infty,\text{ } \lim_{\mu \to 1}(\lim_{\nu \to 0} \text{excess kurtosis}) = \infty | ||
\end{align}</math> | \end{align} </math> | ||
[[File:Excess Kurtosis for Beta Distribution with alpha and beta ranging from 1 to 5 - J. Rodal.jpg|325px]][[File:Excess Kurtosis for Beta Distribution with alpha and beta ranging from 0.1 to 5 - J. Rodal.jpg|325px]] | [[File:Excess Kurtosis for Beta Distribution with alpha and beta ranging from 1 to 5 - J. Rodal.jpg|325px]][[File:Excess Kurtosis for Beta Distribution with alpha and beta ranging from 0.1 to 5 - J. Rodal.jpg|325px]] | ||
अभिलक्षणिक फलन (संभाव्यता सिद्धांत) प्रायिकता घनत्व फलन का [[फूरियर रूपांतरण]] है। बीटा डिस्ट्रीब्यूशन का विशिष्ट कार्य कंफ्लुएंट हाइपरजियोमेट्रिक | === विशेषता फलन === | ||
अभिलक्षणिक फलन (संभाव्यता सिद्धांत) प्रायिकता घनत्व फलन का [[फूरियर रूपांतरण]] है। बीटा डिस्ट्रीब्यूशन का विशिष्ट कार्य कंफ्लुएंट हाइपरजियोमेट्रिक फलन है। कुमेर का कंफ्लुएंट हाइपरजियोमेट्रिक फलन (पहली तरह का):<ref name="JKB" /><ref name="Abramowitz" /><ref name="Zwillinger_2014">{{cite book |author-first1=Izrail Solomonovich |author-last1=Gradshteyn |author-link1=Izrail Solomonovich Gradshteyn |author-first2=Iosif Moiseevich |author-last2=Ryzhik |author-link2=Iosif Moiseevich Ryzhik |author-first3=Yuri Veniaminovich |author-last3=Geronimus |author-link3=Yuri Veniaminovich Geronimus |author-first4=Michail Yulyevich |author-last4=Tseytlin |author-link4=Michail Yulyevich Tseytlin |author-first5=Alan |author-last5=Jeffrey |editor1-first=Daniel |editor1-last=Zwillinger |editor2-first=Victor Hugo |editor2-last=Moll |editor-link2=Victor Hugo Moll |translator=Scripta Technica, Inc. |title=इंटीग्रल्स, सीरीज़ और उत्पादों की तालिका|publisher=[[Academic Press, Inc.]] |date=2015 |orig-year=October 2014 |edition=8 |language=en |isbn=978-0-12-384933-5 |lccn=2014010276 <!-- |url=https://books.google.com/books?id=NjnLAwAAQBAJ |access-date=2016-02-21-->|title-link=Gradshteyn and Ryzhik}}</ref> | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\varphi_X(\alpha;\beta;t) | \varphi_X(\alpha;\beta;t) | ||
| Line 615: | Line 611: | ||
&= 1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r} \right) \frac{(it)^k}{k!} | &= 1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r} \right) \frac{(it)^k}{k!} | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ | |||
: <math>x^{(n)}=x(x+1)(x+2)\cdots(x+n-1)</math> | : <math>x^{(n)}=x(x+1)(x+2)\cdots(x+n-1)</math> | ||
| Line 622: | Line 618: | ||
:<math> \varphi_X(\alpha;\beta;0)={}_1F_1(\alpha; \alpha+\beta; 0) = 1 </math>. | :<math> \varphi_X(\alpha;\beta;0)={}_1F_1(\alpha; \alpha+\beta; 0) = 1 </math>. | ||
इसके | इसके अतिरिक्त, वेरिएबल टी की उत्पत्ति के संबंध में विशेषता फलन के वास्तविक और काल्पनिक भाग निम्नलिखित समरूपता का आनंद लेते हैं: | ||
:<math> \textrm{Re} \left [ {}_1F_1(\alpha; \alpha+\beta; it) \right ] = \textrm{Re} \left [ {}_1F_1(\alpha; \alpha+\beta; - it) \right ] </math> | :<math> \textrm{Re} \left [ {}_1F_1(\alpha; \alpha+\beta; it) \right ] = \textrm{Re} \left [ {}_1F_1(\alpha; \alpha+\beta; - it) \right ] </math> | ||
:<math> \textrm{Im} \left [ {}_1F_1(\alpha; \alpha+\beta; it) \right ] = - \textrm{Im} \left [ {}_1F_1(\alpha; \alpha+\beta; - it) \right ] </math> | :<math> \textrm{Im} \left [ {}_1F_1(\alpha; \alpha+\beta; it) \right ] = - \textrm{Im} \left [ {}_1F_1(\alpha; \alpha+\beta; - it) \right ] </math> | ||
सममित | सममित स्तिथि α = β [[बेसेल समारोह|बेसेल फलन]] के लिए बीटा वितरण के विशिष्ट कार्य को सरल करता है, क्योंकि विशेष स्तिथियों में α + β = 2α [[संगम हाइपरज्यामितीय समारोह|संगम हाइपरज्यामितीय फलन]] पहली तरह <math>I_{\alpha-\frac 1 2}</math> ) (पहली तरह का) बेसेल फलन (संशोधित बेसेल फलन) को कम करता है अर्नस्ट कुमेर | कुमेर के दूसरे परिवर्तन का उपयोग इस प्रकार है: | ||
बीमा रूपिंग अनुप्रयोगों के लिए सममित स्तिथियाँ α = β = n/2 का और उदाहरण चित्र 11 में पाया जा सकता है <ref>{{cite journal |url=https://www.researchgate.net/publication/347575735 |doi=10.13140/RG.2.2.16399.71848|year=2020 |last1=Buchanan |first1=Kris |last2=Wheeland |first2=Sara |last3=Flores |first3=Carlos |last4=Overturf |first4=Drew |last5=Adeyemi |first5=Timi |last6=Acevedo |first6=Vincent |last7=Huff |first7=Gregory |title=Analysis of Collaborative Beamforming for Circularly Bound Random Antenna Array Distributions }}</ref> | |||
:<math>\begin{align} {}_1F_1(\alpha;2\alpha; it) &= e^{\frac{it}{2}} {}_0F_1 \left(; \alpha+\tfrac{1}{2}; \frac{(it)^2}{16} \right) \\ | :<math>\begin{align} {}_1F_1(\alpha;2\alpha; it) &= e^{\frac{it}{2}} {}_0F_1 \left(; \alpha+\tfrac{1}{2}; \frac{(it)^2}{16} \right) \\ | ||
&= e^{\frac{it}{2}} \left(\frac{it}{4}\right)^{\frac{1}{2}-\alpha} \Gamma\left(\alpha+\tfrac{1}{2}\right) I_{\alpha-\frac 1 2}\left(\frac{it}{2}\right).\end{align}</math> | &= e^{\frac{it}{2}} \left(\frac{it}{4}\right)^{\frac{1}{2}-\alpha} \Gamma\left(\alpha+\tfrac{1}{2}\right) I_{\alpha-\frac 1 2}\left(\frac{it}{2}\right).\end{align}</math> | ||
साथ वाले भूखंडों में, सममित (α = β) और विषम (α ≠ β) | साथ वाले भूखंडों में, सममित (α = β) और विषम (α ≠ β) स्थितियों के लिए बीटा वितरण के विशेषता फलन (संभाव्यता सिद्धांत) की [[जटिल संख्या]] (Re) प्रदर्शित की जाती है। | ||
=== अन्य क्षण === | === अन्य क्षण === | ||
==== मोमेंट जनरेटिंग | ==== मोमेंट जनरेटिंग फलन ==== | ||
यह भी अनुसरण करता है<ref name=JKB /><ref name="Handbook of Beta Distribution" />वह [[क्षण उत्पन्न करने वाला कार्य]] है | यह भी अनुसरण करता है<ref name=JKB /><ref name="Handbook of Beta Distribution" /> वह [[क्षण उत्पन्न करने वाला कार्य]] है | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 645: | Line 641: | ||
&= \sum_{n=0}^\infty \frac {\alpha^{(n)}} {(\alpha+\beta)^{(n)}}\frac {t^n}{n!}\\[4pt] | &= \sum_{n=0}^\infty \frac {\alpha^{(n)}} {(\alpha+\beta)^{(n)}}\frac {t^n}{n!}\\[4pt] | ||
&= 1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r} \right) \frac{t^k}{k!} | &= 1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r} \right) \frac{t^k}{k!} | ||
\end{align}</math> | \end{align}</math> | ||
विशेष रूप से | विशेष रूप से ''M<sub>X</sub>''(''α''; ''β''; 0) = 1. | ||
==== उच्च क्षण ==== | ==== उच्च क्षण ==== | ||
मोमेंट जनरेटिंग | मोमेंट जनरेटिंग फलन का उपयोग करके, k-वें कारक [[कच्चा पल]] द्वारा दिया जाता है<ref name=JKB/> | ||
:<math>\prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r} </math> | :<math>\prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r} </math> | ||
(घातीय श्रृंखला) शब्द को गुणा करना <math>\left(\frac{t^k}{k!}\right)</math> पल | (घातीय श्रृंखला) शब्द को गुणा करना <math>\left(\frac{t^k}{k!}\right)</math> पल उत्पन्न करने वाले फलन की श्रृंखला में | ||
:<math>\operatorname{E}[X^k]= \frac{\alpha^{(k)}}{(\alpha + \beta)^{(k)}} = \prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r}</math> | :<math>\operatorname{E}[X^k]= \frac{\alpha^{(k)}}{(\alpha + \beta)^{(k)}} = \prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r}</math> | ||
जहाँ X<sup>k </sup> पोचहैमर प्रतीक है जो बढ़ती फैक्टोरियल का प्रतिनिधित्व करता है। इसे पुनरावर्ती रूप में भी लिखा जा सकता है | |||
:<math>\operatorname{E}[X^k] = \frac{\alpha + k - 1}{\alpha + \beta + k - 1}\operatorname{E}[X^{k - 1}].</math> | :<math>\operatorname{E}[X^k] = \frac{\alpha + k - 1}{\alpha + \beta + k - 1}\operatorname{E}[X^{k - 1}].</math> | ||
क्षण उत्पन्न करने के कार्य के | क्षण उत्पन्न करने के कार्य के पश्चात् से <math>M_X(\alpha; \beta; \cdot)</math> अभिसरण का धनात्मक सीमाहै, बीटा वितरण मोमेंट समस्या है।<ref>{{cite book|last1=Billingsley|first1=Patrick|title=संभाव्यता और माप|date=1995|publisher=Wiley-Interscience|isbn=978-0-471-00710-4|edition=3rd|chapter=30}}</ref> | ||
==== परिवर्तित यादृच्छिक | ==== परिवर्तित यादृच्छिक वेरिएबल के क्षण ==== | ||
=== रैखिक रूप से रूपांतरित, उत्पाद और उल्टे यादृच्छिक | === '''रैखिक रूप से रूपांतरित, उत्पाद और उल्टे यादृच्छिक वेरिएबल के''' क्षण === | ||
एक परिवर्तित यादृच्छिक | एक परिवर्तित यादृच्छिक वेरिएबल के लिए निम्नलिखित अपेक्षाएँ भी दिखा सकते हैं,<ref name=JKB/>जहां रैंडम वेरिएबल X को मापदंड α और β: X ~ बीटा (α, β) के साथ बीटा-वितरित किया गया है। वेरिएबल 1 − X का अपेक्षित मान X पर आधारित अपेक्षित मान का दर्पण-समरूपता है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 670: | Line 666: | ||
& \operatorname{E}[X (1-X)] =\operatorname{E}[(1-X)X ] =\frac{\alpha \beta}{(\alpha + \beta)(\alpha +\beta + 1) } | & \operatorname{E}[X (1-X)] =\operatorname{E}[(1-X)X ] =\frac{\alpha \beta}{(\alpha + \beta)(\alpha +\beta + 1) } | ||
\end{align}</math> | \end{align}</math> | ||
बीटा वितरण के प्रायिकता घनत्व | बीटा वितरण के प्रायिकता घनत्व फलन की दर्पण-समरूपता के कारण, वेरिएबल X और 1 − X पर आधारित प्रसरण समान हैं, और X(1 − X) पर सहप्रसरण प्रसरण का ऋणात्मक है: | ||
:<math>\operatorname{var}[(1-X)]=\operatorname{var}[X] = -\operatorname{cov}[X,(1-X)]= \frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}</math> | :<math>\operatorname{var}[(1-X)]=\operatorname{var}[X] = -\operatorname{cov}[X,(1-X)]= \frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}</math> | ||
इनवर्टेड वेरिएबल्स के लिए ये अपेक्षित मूल्य हैं, (ये हार्मोनिक साधनों से संबंधित हैं, देखें {{section link|| | इनवर्टेड वेरिएबल्स के लिए ये अपेक्षित मूल्य हैं, (ये हार्मोनिक साधनों से संबंधित हैं, देखें {{section link| |हार्मोनिक माध्य }}): | ||
:<math>\begin{align} | :<math>\begin{align} | ||
& \operatorname{E} \left [\frac{1}{X} \right ] = \frac{\alpha+\beta-1 }{\alpha -1 } \text{ if } \alpha > 1\\ | & \operatorname{E} \left [\frac{1}{X} \right ] = \frac{\alpha+\beta-1 }{\alpha -1 } \text{ if } \alpha > 1\\ | ||
& \operatorname{E}\left [\frac{1}{1-X} \right ] =\frac{\alpha+\beta-1 }{\beta-1 } \text{ if } \beta > 1 | & \operatorname{E}\left [\frac{1}{1-X} \right ] =\frac{\alpha+\beta-1 }{\beta-1 } \text{ if } \beta > 1 | ||
\end{align}</math> | \end{align}</math> | ||
निम्नलिखित परिवर्तन को | निम्नलिखित परिवर्तन को वेरिएबल X को उसकी दर्पण-छवि X/(1 − X) से विभाजित करके उल्टे बीटा वितरण या बीटा प्राइम वितरण (जिसे दूसरी तरह के बीटा वितरण या पियर्सन वितरण के रूप में भी जाना जाता है) के अपेक्षित मूल्य में परिणाम मिलता है। पियर्सन का प्रकार छठी):<ref name=JKB/> | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 685: | Line 681: | ||
& \operatorname{E}\left[\frac{1-X}{X}\right] =\frac{\beta}{\alpha- 1 }\text{ if }\alpha > 1 | & \operatorname{E}\left[\frac{1-X}{X}\right] =\frac{\beta}{\alpha- 1 }\text{ if }\alpha > 1 | ||
\end{align} </math> | \end{align} </math> | ||
इन रूपांतरित | इन रूपांतरित वेरिएबल के प्रसरणों को एकीकरण द्वारा प्राप्त किया जा सकता है, क्योंकि संबंधित वेरिएबल पर केंद्रित दूसरे क्षणों के अपेक्षित मान: | ||
:<math>\operatorname{var} \left[\frac{1}{X} \right] =\operatorname{E}\left[\left(\frac{1}{X} - \operatorname{E}\left[\frac{1}{X} \right ] \right )^2\right]=</math> | :<math>\operatorname{var} \left[\frac{1}{X} \right] =\operatorname{E}\left[\left(\frac{1}{X} - \operatorname{E}\left[\frac{1}{X} \right ] \right )^2\right]=</math> | ||
:<math>\operatorname{var}\left [\frac{1-X}{X} \right ] =\operatorname{E} \left [\left (\frac{1-X}{X} - \operatorname{E}\left [\frac{1-X}{X} \right ] \right )^2 \right ]= \frac{\beta (\alpha+\beta-1)}{(\alpha -2)(\alpha-1)^2 } \text{ if }\alpha > 2</math> | :<math>\operatorname{var}\left [\frac{1-X}{X} \right ] =\operatorname{E} \left [\left (\frac{1-X}{X} - \operatorname{E}\left [\frac{1-X}{X} \right ] \right )^2 \right ]= \frac{\beta (\alpha+\beta-1)}{(\alpha -2)(\alpha-1)^2 } \text{ if }\alpha > 2</math> | ||
इसके दर्पण-छवि (X/ | इसके दर्पण-छवि (X/1−X) द्वारा विभाजित वेरिएबल X का निम्नलिखित प्रसरण, उल्टे बीटा वितरण या बीटा प्राइम वितरण (जिसे दूसरी तरह के बीटा वितरण या पियर्सन वितरण के रूप में भी जाना जाता है) के विचरण में परिणाम देता है। पियर्सन का प्रकार छठी):<ref name=JKB/> | ||
:<math>\operatorname{var} \left [\frac{1}{1-X} \right ] =\operatorname{E} \left [\left(\frac{1}{1-X} - \operatorname{E} \left [\frac{1}{1-X} \right ] \right)^2 \right ]=\operatorname{var} \left [\frac{X}{1-X} \right ] =</math> | :<math>\operatorname{var} \left [\frac{1}{1-X} \right ] =\operatorname{E} \left [\left(\frac{1}{1-X} - \operatorname{E} \left [\frac{1}{1-X} \right ] \right)^2 \right ]=\operatorname{var} \left [\frac{X}{1-X} \right ] =</math> | ||
| Line 696: | Line 692: | ||
:<math>\operatorname{cov}\left [\frac{1}{X},\frac{1}{1-X} \right ] = \operatorname{cov}\left[\frac{1-X}{X},\frac{X}{1-X} \right] =\operatorname{cov}\left[\frac{1}{X},\frac{X}{1-X}\right ] = \operatorname{cov}\left[\frac{1-X}{X},\frac{1}{1-X} \right] =\frac{\alpha+\beta-1}{(\alpha-1)(\beta-1) } \text{ if } \alpha, \beta > 1</math> | :<math>\operatorname{cov}\left [\frac{1}{X},\frac{1}{1-X} \right ] = \operatorname{cov}\left[\frac{1-X}{X},\frac{X}{1-X} \right] =\operatorname{cov}\left[\frac{1}{X},\frac{X}{1-X}\right ] = \operatorname{cov}\left[\frac{1-X}{X},\frac{1}{1-X} \right] =\frac{\alpha+\beta-1}{(\alpha-1)(\beta-1) } \text{ if } \alpha, \beta > 1</math> | ||
ये अपेक्षाएँ और भिन्नताएँ चार- | ये अपेक्षाएँ और भिन्नताएँ चार-मापदंड फ़िशर सूचना आव्युह में दिखाई देती हैं ({{section link| |फिशर जानकारी}}.) | ||
=== लघुगणकीय रूप से परिवर्तित यादृच्छिक | === लघुगणकीय रूप से परिवर्तित यादृच्छिक वेरिएबल के क्षण === | ||
[[File:Logit.svg|thumbnail|right|350px|0 से 1 (क्षैतिज अक्ष) के डोमेन में लॉगिट (एक्स) = एलएन (एक्स / (1-एक्स)) (ऊर्ध्वाधर अक्ष) बनाम एक्स का प्लॉट। लॉगिट | [[File:Logit.svg|thumbnail|right|350px|0 से 1 (क्षैतिज अक्ष) के डोमेन में लॉगिट (एक्स) = एलएन (एक्स / (1-एक्स)) (ऊर्ध्वाधर अक्ष) बनाम एक्स का प्लॉट। लॉगिट ट्रांसरूपेशन रोचकहैं, क्योंकि वे सामान्यतः विभिन्न आकृतियों (जे-आकृतियों सहित) को (सामान्यतः विषम) घंटी के आकार के घनत्वों को लॉगिट वेरिएबल पर बदलते हैं, और वे मूल वेरिएबल पर अंतिम विलक्षणताओं को हटा सकते हैं।]][[लघुगणक परिवर्तन]] के लिए अपेक्षित मान (अधिकतम संभावना अनुमानों के लिए उपयोगी, देखें {{section link| |पैरामीटर अनुमान, अधिकतम संभावना }}) इस खंड में चर्चा कर रहे हैं। निम्नलिखित लघुगणक रैखिक परिवर्तन ज्यामितीय माध्य G<sub>X</sub> और G<sub>(1−''X'')</sub> से संबंधित हैं(देखना {{section link| |जियोमेट्रिक माध्य}}): | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 705: | Line 701: | ||
\operatorname{E}[\ln(1-X)] &=\psi(\beta) - \psi(\alpha + \beta)= - \operatorname{E} \left[\ln \left (\frac{1}{1-X} \right )\right]. | \operatorname{E}[\ln(1-X)] &=\psi(\beta) - \psi(\alpha + \beta)= - \operatorname{E} \left[\ln \left (\frac{1}{1-X} \right )\right]. | ||
\end{align}</math> | \end{align}</math> | ||
जहां डिगामा | जहां डिगामा फलन ψ(α) को गामा फलन के [[लघुगणक व्युत्पन्न]] के रूप में परिभाषित किया गया है:<ref name=Abramowitz/> | ||
:<math>\psi(\alpha) = \frac{d \ln\Gamma(\alpha)}{d\alpha}</math> | :<math>\psi(\alpha) = \frac{d \ln\Gamma(\alpha)}{d\alpha}</math> | ||
लॉग परिवर्तन | लॉग परिवर्तन रोचक हैं,<ref name=MacKay>{{cite book|last=MacKay|first=David|title=सूचना सिद्धांत, अनुमान और लर्निंग एल्गोरिदम|year=2003| publisher=Cambridge University Press; First Edition |isbn=978-0521642989|bibcode=2003itil.book.....M}}</ref> जैसा कि वे सामान्यतः विभिन्न आकारों (जे-आकृतियों सहित) को (सामान्यतः विषम) घंटी के आकार के घनत्वों को लॉजिट वेरिएबल पर बदलते हैं, और वे मूल वेरिएबल पर अंत विलक्षणताओं को हटा सकते हैं: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 714: | Line 710: | ||
\operatorname{E}\left [\ln \left (\frac{1-X}{X} \right ) \right ] &=\psi(\beta) - \psi(\alpha)= - \operatorname{E} \left[\ln \left (\frac{X}{1-X} \right) \right] . | \operatorname{E}\left [\ln \left (\frac{1-X}{X} \right ) \right ] &=\psi(\beta) - \psi(\alpha)= - \operatorname{E} \left[\ln \left (\frac{X}{1-X} \right) \right] . | ||
\end{align}</math> | \end{align}</math> | ||
जॉनसन<ref name=JohnsonLogInv>{{cite journal|last=Johnson|first=N.L.|title=अनुवाद के तरीकों द्वारा उत्पन्न आवृत्ति वक्रों की प्रणाली| journal=Biometrika|year=1949 |volume=36 |issue=1–2|pages=149–176|doi=10.1093/biomet/36.1-2.149|pmid=18132090|hdl=10338.dmlcz/135506|url=http://dml.cz/bitstream/handle/10338.dmlcz/135506/Kybernetika_39-2003-1_3.pdf}}</ref> लॉगिट-रूपांतरित | जॉनसन<ref name=JohnsonLogInv>{{cite journal|last=Johnson|first=N.L.|title=अनुवाद के तरीकों द्वारा उत्पन्न आवृत्ति वक्रों की प्रणाली| journal=Biometrika|year=1949 |volume=36 |issue=1–2|pages=149–176|doi=10.1093/biomet/36.1-2.149|pmid=18132090|hdl=10338.dmlcz/135506|url=http://dml.cz/bitstream/handle/10338.dmlcz/135506/Kybernetika_39-2003-1_3.pdf}}</ref> लॉगिट-रूपांतरित वेरिएबल ln(X/1−X) के वितरण पर विचार किया गया, जिसमें आकार मापदंड के बड़े मूल्यों के लिए इसके क्षण उत्पन्न करने वाले फलन और सन्निकटन सम्मिलित हैं। यह रूपांतरण वास्तविक रेखा (-∞, +∞) की दोनों दिशाओं में मूल वेरिएबल X के आधार पर परिमित समर्थन [0, 1] को अनंत समर्थन तक बढ़ाता है। | ||
दो गामा वितरणों के अनुपात के रूप में बीटा वितरण के प्रतिनिधित्व का उपयोग करके और अभिन्न के माध्यम से अंतर करके उच्च क्रम लॉगरिदमिक क्षण प्राप्त किए जा सकते हैं। उन्हें उच्च क्रम के पॉली-गामा कार्यों के रूप में निम्नानुसार व्यक्त किया जा सकता है: | दो गामा वितरणों के अनुपात के रूप में बीटा वितरण के प्रतिनिधित्व का उपयोग करके और अभिन्न के माध्यम से अंतर करके उच्च क्रम लॉगरिदमिक क्षण प्राप्त किए जा सकते हैं। उन्हें उच्च क्रम के पॉली-गामा कार्यों के रूप में निम्नानुसार व्यक्त किया जा सकता है: | ||
| Line 722: | Line 718: | ||
\operatorname{E} \left [\ln^2(1-X) \right ] &= (\psi(\beta) - \psi(\alpha + \beta))^2+\psi_1(\beta)-\psi_1(\alpha+\beta), \\ | \operatorname{E} \left [\ln^2(1-X) \right ] &= (\psi(\beta) - \psi(\alpha + \beta))^2+\psi_1(\beta)-\psi_1(\alpha+\beta), \\ | ||
\operatorname{E} \left [\ln (X)\ln(1-X) \right ] &=(\psi(\alpha) - \psi(\alpha + \beta))(\psi(\beta) - \psi(\alpha + \beta)) -\psi_1(\alpha+\beta). | \operatorname{E} \left [\ln (X)\ln(1-X) \right ] &=(\psi(\alpha) - \psi(\alpha + \beta))(\psi(\beta) - \psi(\alpha + \beta)) -\psi_1(\alpha+\beta). | ||
\end{align}</math> | \end{align} </math> | ||
इसलिए लघुगणकीय | इसलिए लघुगणकीय चरो का प्रसरण और ln(X) और ln(1−X) का सहप्रसरण हैं: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 735: | Line 731: | ||
&= \psi_1(\beta) - \psi_1(\alpha + \beta) \\ | &= \psi_1(\beta) - \psi_1(\alpha + \beta) \\ | ||
&= \psi_1(\beta) + \operatorname{cov}[\ln (X), \ln(1-X)] | &= \psi_1(\beta) + \operatorname{cov}[\ln (X), \ln(1-X)] | ||
\end{align}</math> | \end{align} </math> | ||
जहाँ त्रिगामा फलन, ψ | जहाँ त्रिगामा फलन, ψ<sub>1</sub>(α) निरूपित करता है बहुग्राम कार्यों का दूसरा है, और इसे डिगामा फलन के व्युत्पन्न के रूप में परिभाषित किया गया है: | ||
:<math>\psi_1(\alpha) = \frac{d^2\ln\Gamma(\alpha)}{d\alpha^2}= \frac{d \psi(\alpha)}{d\alpha}</math>. | :<math>\psi_1(\alpha) = \frac{d^2\ln\Gamma(\alpha)}{d\alpha^2}= \frac{d \psi(\alpha)}{d\alpha}</math>. | ||
लघुगणक रूप से रूपांतरित | लघुगणक रूप से रूपांतरित वेरिएबल X और (1−X) के प्रसरण और सहप्रसरण सामान्य रूप से भिन्न होते हैं, क्योंकि लघुगणक रूपांतरण मूल वेरिएबल X और (1−X) के दर्पण-समरूपता को नष्ट कर देता है, क्योंकि लघुगणक ऋणात्मक अनंतता तक पहुंचता है वेरिएबल शून्य के समीप पहुंच रहा है। | ||
ये लघुगणक प्रसरण और सहप्रसरण बीटा वितरण के लिए फिशर सूचना | ये लघुगणक प्रसरण और सहप्रसरण बीटा वितरण के लिए फिशर सूचना आव्युह के तत्व हैं। वे लॉग संभावना फलन की वक्रता का माप भी हैं (अधिकतम संभावना अनुमान पर अनुभाग देखें)। | ||
लॉग व्युत्क्रम | लॉग व्युत्क्रम वेरिएबल के प्रसरण लॉग वेरिएबल के प्रसरण के समान हैं: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\operatorname{var}\left[\ln \left (\frac{1}{X} \right ) \right] & =\operatorname{var}[\ln(X)] = \psi_1(\alpha) - \psi_1(\alpha + \beta), \\ | \operatorname{var}\left[\ln \left (\frac{1}{X} \right ) \right] & =\operatorname{var}[\ln(X)] = \psi_1(\alpha) - \psi_1(\alpha + \beta), \\ | ||
\operatorname{var}\left[\ln \left (\frac{1}{1-X} \right ) \right] &=\operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta), \\ | \operatorname{var}\left[\ln \left (\frac{1}{1-X} \right ) \right] &=\operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta), \\ | ||
\operatorname{cov}\left[\ln \left (\frac{1}{X} \right), \ln \left (\frac{1}{1-X}\right ) \right] &=\operatorname{cov}[\ln(X),\ln(1-X)]= -\psi_1(\alpha + \beta).\end{align}</math> | \operatorname{cov}\left[\ln \left (\frac{1}{X} \right), \ln \left (\frac{1}{1-X}\right ) \right] &=\operatorname{cov}[\ln(X),\ln(1-X)]= -\psi_1(\alpha + \beta).\end{align} </math> | ||
यह भी अनुसरण करता है कि लॉगिट रूपांतरित | यह भी अनुसरण करता है कि लॉगिट रूपांतरित वेरिएबल के संस्करण हैं: | ||
:<math>\operatorname{var}\left[\ln \left (\frac{X}{1-X} \right )\right]=\operatorname{var}\left[\ln \left (\frac{1-X}{X} \right ) \right]=-\operatorname{cov}\left [\ln \left (\frac{X}{1-X} \right ), \ln \left (\frac{1-X}{X} \right ) \right]= \psi_1(\alpha) + \psi_1(\beta)</math> | :<math>\operatorname{var}\left[\ln \left (\frac{X}{1-X} \right )\right]=\operatorname{var}\left[\ln \left (\frac{1-X}{X} \right ) \right]=-\operatorname{cov}\left [\ln \left (\frac{X}{1-X} \right ), \ln \left (\frac{1-X}{X} \right ) \right]= \psi_1(\alpha) + \psi_1(\beta)</math> | ||
| Line 756: | Line 752: | ||
=== जानकारी की मात्रा (एन्ट्रापी) === | === जानकारी की मात्रा (एन्ट्रापी) === | ||
एक बीटा वितरित यादृच्छिक | एक बीटा वितरित यादृच्छिक वेरिएबल , X ~ बीटा (α, β) को देखते हुए, X की [[सूचना एन्ट्रापी]] (नेट (यूनिट) में मापी गई है,<ref>{{cite journal |first1=A. C. G. |last1=Verdugo Lazo |first2=P. N. |last2=Rathie |title=निरंतर संभाव्यता वितरण की एन्ट्रापी पर|journal=IEEE Trans. Inf. Theory |volume=24 |issue=1 |pages=120–122 |year=1978 |doi=10.1109/TIT.1978.1055832 }}</ref> प्रायिकता घनत्व फलन के लघुगणक के ऋणात्मक का अपेक्षित मान: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 762: | Line 758: | ||
&=\int_0^1 -f(x;\alpha,\beta)\ln(f(x;\alpha,\beta)) \, dx \\[4pt] | &=\int_0^1 -f(x;\alpha,\beta)\ln(f(x;\alpha,\beta)) \, dx \\[4pt] | ||
&= \ln(\Beta(\alpha,\beta))-(\alpha-1)\psi(\alpha)-(\beta-1)\psi(\beta)+(\alpha+\beta-2) \psi(\alpha+\beta) | &= \ln(\Beta(\alpha,\beta))-(\alpha-1)\psi(\alpha)-(\beta-1)\psi(\beta)+(\alpha+\beta-2) \psi(\alpha+\beta) | ||
\end{align}</math> | \end{align} </math> | ||
जहाँ f(x; α, β) बीटा वितरण का प्रायिकता घनत्व फलन है: | जहाँ f(x; α, β) बीटा वितरण का प्रायिकता घनत्व फलन है: | ||
:<math>f(x;\alpha,\beta) = \frac{1}{\Beta(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1}</math> | :<math>f(x;\alpha,\beta) = \frac{1}{\Beta(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1}</math> | ||
डिगामा | डिगामा फलन ψ [[हार्मोनिक संख्या]]ओं के लिए यूलर के अभिन्न सूत्र के परिणाम के रूप में अंतर एंट्रॉपी के सूत्र में प्रकट होता है जो अभिन्न से अनुसरण करता है: | ||
:<math>\int_0^1 \frac {1-x^{\alpha-1}}{1-x} \, dx = \psi(\alpha)-\psi(1)</math> | :<math>\int_0^1 \frac {1-x^{\alpha-1}}{1-x} \, dx = \psi(\alpha)-\psi(1)</math> | ||
α = β = 1 (जिन मूल्यों के लिए बीटा वितरण एक[[समान वितरण (निरंतर)]] के समान है) को छोड़कर, शून्य से अधिक α और β के सभी मानों के लिए बीटा वितरण की सूचना एन्ट्रॉपी ऋणात्मक है, जहां सूचना एन्ट्रापी शून्य के अधिकतम और न्यूनतम मान तक पहुँच जाता है। यह उम्मीद की जानी चाहिए कि अधिकतम एन्ट्रापी तब होनी चाहिए जब बीटा वितरण समान वितरण के | जहाँ α = β = 1 है तो (जिन मूल्यों के लिए बीटा वितरण एक [[समान वितरण (निरंतर)]] के समान है) उनको को छोड़कर, शून्य से अधिक α और β के सभी मानों के लिए बीटा वितरण की सूचना एन्ट्रॉपी ऋणात्मक है, जहां सूचना एन्ट्रापी शून्य के अधिकतम और न्यूनतम मान तक पहुँच जाता है। यह उम्मीद की जानी चाहिए कि अधिकतम एन्ट्रापी तब होनी चाहिए जब बीटा वितरण समान वितरण के सामान्तर हो जाए, क्योंकि अनिश्चितता अधिकतम होती है जब सभी संभव घटनाएं परिवर्तनीय होती हैं। | ||
α या β शून्य के | जब α या β शून्य के समीप पहुंचने के लिए, सूचना एन्ट्रॉपी अपने मैक्सिमा और ऋणात्मक अनंतता के न्यूनतम मूल्य तक पहुंचती है। (या तब या दोनों) α या β शून्य के समीप पहुंचने के लिए, ऑर्डर की अधिकतम मात्रा होती है: सभी प्रायिकता घनत्व सिरों पर केंद्रित होते हैं, और सिरों के मध्य स्थित बिंदुओं पर शून्य प्रायिकता घनत्व होता है। इसी प्रकार (या तब या दोनों) α या β अनंत तक पहुंचने के लिए, अंतर एंट्रॉपी ऋणात्मक अनंतता के न्यूनतम मूल्य और ऑर्डर की अधिकतम मात्रा तक पहुंचता है। यदि या तब α या β अनंत तक पहुंचता है (और दूसरा परिमित है) सभी प्रायिकता घनत्व अंत में केंद्रित होते हैं, और प्रायिकता घनत्व हर स्थान शून्य होता है। यदि दोनों आकार मापदंड समान हैं (सममित स्तिथि ), α = β, और वे साथ अनंत तक पहुंचते हैं, तब प्रायिकता घनत्व मध्य x = 1/2 पर केंद्रित स्पाइक फलन (डायराक डेल्टा फलन) बन जाता है, और इसलिए 100% संभावना होती है मध्य में x = 1/2 और हर स्थान शून्य संभावना। | ||
[[File:Differential Entropy Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px]][[File:Differential Entropy Beta Distribution for alpha and beta from 0.1 to 5 - J. Rodal.jpg|325px]](निरंतर केस) सूचना एंट्रॉपी को शैनन ने अपने मूल पेपर में | [[File:Differential Entropy Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px]][[File:Differential Entropy Beta Distribution for alpha and beta from 0.1 to 5 - J. Rodal.jpg|325px]](निरंतर केस) सूचना एंट्रॉपी को शैनन ने अपने मूल पेपर में प्रस्तुत किया था (जहां उन्होंने इसे निरंतर वितरण की एंट्रॉपी नाम दिया था), उसी पेपर के समापन भाग के रूप में जहां उन्होंने सूचना एंट्रॉपी को परिभाषित किया था।<ref>{{cite journal |last=Shannon |first=Claude E. |title=संचार का एक गणितीय सिद्धांत|journal=Bell System Technical Journal |volume=27 |issue=4 |pages=623–656 |year=1948 |doi=10.1002/j.1538-7305.1948.tb01338.x }}</ref> तब से यह ज्ञात है कि अंतर एंट्रॉपी असतत एंट्रॉपी की असीमित सीमा से अनंत ऑफ समुच्चय से भिन्न हो सकती है, इसलिए अंतर एन्ट्रॉपी ऋणात्मक हो सकती है (जैसा कि यह बीटा वितरण के लिए है)। एंट्रॉपी के सापेक्ष मूल्य वास्तव में क्या मायने रखता है। | ||
दो बीटा वितरित यादृच्छिक | दो बीटा वितरित यादृच्छिक वेरिएबल दिए गए हैं, X<sub>1</sub> ~ बीटा (α', β') और X<sub>2</sub> ~ बीटा (α', β'), [[क्रॉस एन्ट्रापी]] है (नट्स में मापा जाता है)<ref name="Cover and Thomas">{{cite book|last=Cover|first=Thomas M. and Joy A. Thomas|title=Elements of Information Theory 2nd Edition (Wiley Series in Telecommunications and Signal Processing) |year=2006 |publisher=Wiley-Interscience; 2 edition |isbn=978-0471241959}}</ref> | ||
:<math>\begin{align} | :<math>\begin{align} | ||
H(X_1,X_2) &= \int_0^1 - f(x;\alpha,\beta) \ln (f(x;\alpha',\beta')) \,dx \\[4pt] | H(X_1,X_2) &= \int_0^1 - f(x;\alpha,\beta) \ln (f(x;\alpha',\beta')) \,dx \\[4pt] | ||
&= \ln \left(\Beta(\alpha',\beta')\right)-(\alpha'-1)\psi(\alpha)-(\beta'-1)\psi(\beta)+(\alpha'+\beta'-2)\psi(\alpha+\beta). | &= \ln \left(\Beta(\alpha',\beta')\right)-(\alpha'-1)\psi(\alpha)-(\beta'-1)\psi(\beta)+(\alpha'+\beta'-2)\psi(\alpha+\beta). | ||
\end{align}</math> | \end{align}</math> | ||
दो परिकल्पनाओं के | दो परिकल्पनाओं के मध्य की दूरी को मापने के लिए क्रॉस एन्ट्रॉपी का उपयोग त्रुटि मीट्रिक के रूप में किया गया है।<ref name=Plunkett>{{cite book|last=Plunkett|first=Kim, and Jeffrey Elman|title=Exercises in Rethinking Innateness: A Handbook for Connectionist Simulations (Neural Network Modeling and Connectionism)|year=1997|publisher=A Bradford Book|page=166|isbn=978-0262661058|url-access=registration|url=https://archive.org/details/exercisesinrethi0000plun}}</ref><ref name=Nallapati>{{cite thesis|last=Nallapati|first=Ramesh|title=The smoothed dirichlet distribution: understanding cross-entropy ranking in information retrieval|year=2006|publisher=Computer Science Dept., University of Massachusetts Amherst|url=http://maroo.cs.umass.edu/pub/web/getpdf.php?id=679}}</ref> इसका निरपेक्ष मान न्यूनतम होता है जब दो वितरण समान होते हैं। तथा यह लॉग अधिकतम संभावना से सबसे अधिक निकटता से संबंधित सूचना उपाय है <ref name="Cover and Thomas" />(मापदंड अनुमान पर अनुभाग देखें। अधिकतम संभावना अनुमान))। | ||
सापेक्ष एन्ट्रॉपी, या कुल्बैक-लीब्लर विचलन | सापेक्ष एन्ट्रॉपी, या कुल्बैक-लीब्लर विचलन D<sub>KL</sub>(X<sub>1</sub> || X<sub>2</sub>), यह मानने की अक्षमता का उपाय है कि वितरण X<sub>2</sub> है ~ बीटा (α', β') जब वितरण वास्तव में X<sub>1</sub> है ~ बीटा (α, β)। इसे निम्नानुसार परिभाषित किया गया है (नट्स में मापा गया)। | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 789: | Line 785: | ||
&= -h(X_1) + H(X_1,X_2)\\[4pt] | &= -h(X_1) + H(X_1,X_2)\\[4pt] | ||
&= \ln\left(\frac{\Beta(\alpha',\beta')}{\Beta(\alpha,\beta)}\right)+(\alpha-\alpha')\psi(\alpha)+(\beta-\beta')\psi(\beta)+(\alpha'-\alpha+\beta'-\beta)\psi (\alpha + \beta). | &= \ln\left(\frac{\Beta(\alpha',\beta')}{\Beta(\alpha,\beta)}\right)+(\alpha-\alpha')\psi(\alpha)+(\beta-\beta')\psi(\beta)+(\alpha'-\alpha+\beta'-\beta)\psi (\alpha + \beta). | ||
\end{align} </math> | \end{align} </math> | ||
सापेक्ष एन्ट्रापी, या कुल्बैक-लीब्लर विचलन, | सापेक्ष एन्ट्रापी, या कुल्बैक-लीब्लर विचलन, सदैव गैर-ऋणात्मक होता है। कुछ संख्यात्मक उदाहरण अनुसरण करते हैं: | ||
* | *''X''<sub>1</sub> ~ बीटा(1, 1) और ''X''<sub>2</sub> ~ बीटा(3, 3); ''D''<sub>KL</sub>(''X''<sub>1</sub> || ''X''<sub>2</sub>) = 0.598803; ''D''<sub>KL</sub>(''X''<sub>2</sub> || ''X''<sub>1</sub>) = 0.267864; ''h''(''X''<sub>1</sub>) = 0; ''h''(''X''<sub>2</sub>) = −0.2678 | ||
* | *''X''<sub>1</sub> ~ बीटा(3, 0.5) और ''X''<sub>2</sub> ~ बीटा (0.5, 3); ''D''<sub>KL</sub>(''X''<sub>1</sub> || ''X''<sub>2</sub>) = 7.21574; ''D''<sub>KL</sub>(''X''<sub>2</sub> || ''X''<sub>1</sub>) = 7.21574; ''h''(''X''<sub>1</sub>) = −1.10805; ''h''(''X''<sub>2</sub>) = −1.10805. | ||
कुल्बैक-लीब्लर विचलन सममित | कुल्बैक-लीब्लर विचलन सममित ''D<sub>KL</sub>(X<sub>1</sub> || X<sub>2</sub>) ≠ D<sub>KL</sub>(X<sub>2</sub> || X<sub>1</sub>)'' नहीं है उस स्तिथियों के लिए जिसमें व्यक्तिगत बीटा वितरण बीटा (1, 1) और बीटा (3, 3) सममित हैं, किन्तु अलग-अलग एंट्रॉपी ''h(x<sub>1</sub>) ≠ h(X<sub>2</sub>)'' हैं . कुलबैक डाइवर्जेंस का मान तय की गई दिशा पर निर्भर करता है: चाहे वह उच्च (डिफरेंशियल) एंट्रॉपी से लोअर (डिफरेंशियल) एंट्रॉपी में जा रहा हो या इसके विपरीत। उपरोक्त संख्यात्मक उदाहरण में, कुल्बैक विचलन यह मानने की अक्षमता को मापता है कि वितरण (घंटी के आकार का) बीटा (3, 3) है, बजाय (समान) बीटा (1, 1) के। बीटा (1, 1) की h एन्ट्रॉपी बीटा (3, 3) की h एन्ट्रॉपी से अधिक है क्योंकि समान वितरण बीटा (1, 1) में अधिकतम मात्रा में विकार है। कुलबैक डाइवर्जेंस दो गुना अधिक (0.267864 के अतिरिक्त 0.598803) से अधिक है, जब एंट्रॉपी घटने की दिशा में मापा जाता है: वह दिशा जो मानती है कि (समान) बीटा (1, 1) वितरण (घंटी के आकार का) बीटा (3,) है 3) इसके विपरीत नहीं। इस प्रतिबंधित अर्थ में, कुल्बैक विचलन ऊष्म प्रवैगिकी के दूसरे नियम के अनुरूप है। | ||
कुल्बैक-लीब्लर विचलन सममित | कुल्बैक-लीब्लर विचलन सममित ''D<sub>KL</sub>(X<sub>1</sub> || X<sub>2</sub>) = D<sub>KL</sub>(X<sub>2</sub> || X<sub>1</sub>)'' है विषम स्थितियों के लिए बीटा (3, 0.5) और बीटा (0.5, 3) जिसमें समान अंतर एंट्रॉपी h(X<sub>1</sub>) = h(X<sub>2</sub>).है | ||
समरूपता की स्थिति: | समरूपता की स्थिति: | ||
| Line 804: | Line 800: | ||
उपरोक्त परिभाषाओं से अनुसरण करता है और दर्पण-समरूपता f(x; α, β) = f(1−x; α, β) बीटा वितरण द्वारा आनंदित होता है। | उपरोक्त परिभाषाओं से अनुसरण करता है और दर्पण-समरूपता f(x; α, β) = f(1−x; α, β) बीटा वितरण द्वारा आनंदित होता है। | ||
=== सांख्यिकीय उपायों के | === सांख्यिकीय उपायों के मध्य संबंध === | ||
==== माध्य, विधा और मध्य संबंध ==== | ==== माध्य, विधा और मध्य संबंध ==== | ||
यदि 1 < α < β | यदि 1 < α < β तब बहुलक ≤ माध्यिका ≤ माध्य।<ref name=Kerman2011>Kerman J (2011) "A closed-form approximation for the median of the beta distribution". {{arxiv|1111.0433v1}}</ref> मोड को (केवल α, β > 1 के लिए) व्यक्त करना , और α और β के संदर्भ में माध्य: | ||
: <math> \frac{ \alpha - 1 }{ \alpha + \beta - 2 } \le \text{median} \le \frac{ \alpha }{ \alpha + \beta } ,</math> | : <math> \frac{ \alpha - 1 }{ \alpha + \beta - 2 } \le \text{median} \le \frac{ \alpha }{ \alpha + \beta } ,</math> | ||
यदि 1 < β < α | यदि 1 < β < α तब असमिकाओं का क्रम उल्टा हो जाता है। जहाँ α, β > 1 के लिए माध्य और माध्यिका के मध्य की पूर्ण दूरी x के अधिकतम और न्यूनतम मानों के मध्य की दूरी के 5% से कम है। दूसरी ओर, α = 1 और β = 1 के ([[पैथोलॉजिकल (गणित)]]) स्तिथियाँ के लिए, माध्य और मोड के मध्य की पूर्ण दूरी x के अधिकतम और न्यूनतम मानों के मध्य की दूरी के 50% तक पहुंच सकती है, जिसके लिए मान बीटा वितरण समान वितरण तक पहुंचता है और सूचना एन्ट्रापी अपने मैक्सिमा और मिनिमा मूल्य तक पहुंचता है, और इसलिए अधिकतम विकार। | ||
उदाहरण के लिए, α = 1.0001 और β = 1.00000001 के लिए: | उदाहरण के लिए, α = 1.0001 और β = 1.00000001 के लिए: | ||
| Line 819: | Line 815: | ||
* माध्य − माध्यिका = −9.65538 × 10<sup>−6</sup> | * माध्य − माध्यिका = −9.65538 × 10<sup>−6</sup> | ||
जहाँ | जहाँ पीडीएफ प्रायिकता घनत्व फलन के मान के लिए है। | ||
[[File:Mean Median Difference - Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px]] | [[File:Mean Median Difference - Beta Distribution for alpha and beta from 1 to 5 - J. Rodal.jpg|325px]] | ||
| Line 825: | Line 821: | ||
==== माध्य, ज्यामितीय माध्य और हार्मोनिक माध्य संबंध ==== | ==== माध्य, ज्यामितीय माध्य और हार्मोनिक माध्य संबंध ==== | ||
====कुर्टोसिस | [[अंकगणित और ज्यामितीय साधनों की असमानता]] से ज्ञात होता है कि ज्यामितीय माध्य माध्य से कम होता है। इसी तरह, हार्मोनिक माध्य ज्यामितीय माध्य से कम होता है। संलग्न प्लॉट से पता चलता है कि α = β के लिए, α = β के मान की परवाह किए बिना, माध्य और माध्यिका दोनों 1/2 के सामान्तर हैं, और α = β > 1 के लिए मोड भी 1/2 के सामान्तर है, चूँकि ज्यामितीय और हार्मोनिक साधन 1/2 से कम हैं और वे केवल α = β → ∞ के रूप में इस मान को स्पर्शोन्मुख रूप से प्राप्त करते हैं। | ||
[[File:(alpha and beta) Parameter estimates vs. excess Kurtosis and (squared) Skewness Beta distribution - J. Rodal.png|thumb|left|बीटा वितरण α और β | |||
====कुर्टोसिस विषमता के वर्ग से घिरा हुआ है ==== | |||
[[File:(alpha and beta) Parameter estimates vs. excess Kurtosis and (squared) Skewness Beta distribution - J. Rodal.png|thumb|left|बीटा वितरण α और β मापदंड बनाम अतिरिक्त कुर्तबसिस और वर्ग विषमता]]जैसा कि [[विलियम फेलर]] ने टिप्पणी की है,<ref name=Feller />[[पियर्सन वितरण]] में बीटा प्रायिकता घनत्व पियर्सन वितरण के रूप में प्रकट होता है (बीटा वितरण और पियर्सन के प्रकार I वितरण के मध्य कोई भी अंतर केवल सतही है और कुर्तबसिस और विषमता के मध्य संबंध के बारे में निम्नलिखित चर्चा के लिए कोई अंतर नहीं है)। कार्ल पियर्सन ने अपने पेपर के प्लेट 1 में दिखाया <ref name=Pearson>{{cite journal | |||
| last = Pearson | | last = Pearson | ||
| first = Karl | | first = Karl | ||
| Line 842: | Line 838: | ||
| doi = 10.1098/rsta.1916.0009 | | doi = 10.1098/rsta.1916.0009 | ||
| jstor=91092|bibcode = 1916RSPTA.216..429P | doi-access = free | | jstor=91092|bibcode = 1916RSPTA.216..429P | doi-access = free | ||
}}</ref> 1916 में प्रकाशित, ऊर्ध्वाधर अक्ष ([[तालमेल]]) के रूप में कर्टोसिस के साथ ग्राफ और क्षैतिज अक्ष ([[सूच्याकार आकृति का भुज]]) के रूप में | }}</ref> 1916 में प्रकाशित, ऊर्ध्वाधर अक्ष ([[तालमेल]]) के रूप में कर्टोसिस के साथ ग्राफ और क्षैतिज अक्ष ([[सूच्याकार आकृति का भुज]]) के रूप में विषमता का वर्ग, जिसमें अनेक वितरण प्रदर्शित किए गए थे।<ref name=Egon>{{cite journal|last=Pearson|first=Egon S.|title=फ़्रीक्वेंसी कर्व्स के उपयोग के विकास के माध्यम से कुछ ऐतिहासिक प्रतिबिंबों का पता लगाया गया|journal=THEMIS Statistical Analysis Research Program, Technical Report 38|date=July 1969|volume=Office of Naval Research, Contract N000014-68-A-0515|issue=Project NR 042–260|url=http://www.smu.edu/Dedman/Academics/Departments/Statistics/Research/TechnicalReports}}</ref> बीटा वितरण द्वारा कब्जा कर लिया गया क्षेत्र निम्नलिखित दो [[रेखा (ज्यामिति)]] से घिरा हुआ है (विषम<sup>2</sup>, कर्टोसिस) [[कार्तीय समन्वय प्रणाली]], या (विषमता<sup>2</sup>, अतिरिक्त कर्टोसिस) कार्तीय समन्वय प्रणाली: | ||
:<math>(\text{skewness})^2+1< \text{kurtosis}< \frac{3}{2} (\text{skewness})^2 + 3</math> | :<math>(\text{skewness})^2+1< \text{kurtosis}< \frac{3}{2} (\text{skewness})^2 + 3</math> | ||
या, समकक्ष, | या, समकक्ष, | ||
:<math>(\text{skewness})^2-2< \text{excess kurtosis}< \frac{3}{2} (\text{skewness})^2</math> | :<math>(\text{skewness})^2-2< \text{excess kurtosis}< \frac{3}{2} (\text{skewness})^2</math> | ||
ऐसे समय में जब शक्तिशाली डिजिटल कंप्यूटर नहीं थे, कार्ल पियर्सन ने | ऐसे समय में जब शक्तिशाली डिजिटल कंप्यूटर नहीं थे, तब कार्ल पियर्सन ने स्पष्ट रूप से आगे की सीमाओं की गणना की,<ref name="Hahn and Shapiro" /><ref name=Pearson />उदाहरण के लिए, U-आकार के वितरण को जे-आकार के वितरण से अलग करना। तथा निचली सीमा रेखा (अतिरिक्त कर्टोसिस + 2 - विषमता<sup>2</sup> = 0) टेढ़े U-आकार के बीटा वितरण द्वारा निर्मित होता है, जिसमें आकृति मापदंड α और β शून्य के समीप दोनों मान होते हैं। ऊपरी सीमा रेखा (अतिरिक्त कर्टोसिस - (3/2) विषमता<sup>2</sup> = 0) किसी मापदंड के बहुत बड़े मान और दूसरे मापदंड के बहुत छोटे मान के साथ अत्यधिक विषम वितरण द्वारा निर्मित होता है। जहाँ कार्ल पियर्सन ने दिखाया<ref name=Pearson/>कि यह ऊपरी सीमा रेखा (अतिरिक्त कर्टोसिस - (3/2) विषमता<sup>2</sup> = 0) पियर्सन के वितरण III के साथ प्रतिच्छेदन भी है, जिसका दिशा में (धनात्मक अनंत की ओर) असीमित समर्थन है, और घंटी के आकार का या J- आकार का हो सकता है। उनके बेटे, [[एगॉन पियर्सन]] ने दिखाया<ref name=Egon/>कि क्षेत्र (कर्टोसिस/स्क्वायर्ड-स्क्यूनेस प्लेन में) बीटा वितरण (समतुल्य रूप से, पियर्सन का वितरण) I द्वारा कब्जा कर लिया गया है क्योंकि यह इस सीमा तक पहुंचता है (अतिरिक्त कर्टोसिस - (3/2) विषमता<sup>2</sup> = 0) [[गैर-केंद्रीय ची-वर्ग वितरण]] के साथ साझा किया गया है। कार्ल पियर्सन<ref name=Pearson1895>{{cite journal | last = Pearson | first = Karl | author-link = Karl Pearson | year = 1895 | title = Contributions to the mathematical theory of evolution, II: Skew variation in homogeneous material | journal = Philosophical Transactions of the Royal Society | volume = 186 | pages = 343–414 | doi = 10.1098/rsta.1895.0010 | jstor=90649 | bibcode=1895RSPTA.186..343P| doi-access = free }}</ref> (पियर्सन 1895, पीपी. 357, 360, 373–376) ने यह भी दिखाया कि [[गामा वितरण]] पियर्सन प्रकार III वितरण है। इसलिए पियर्सन के प्रकार III वितरण के लिए यह सीमा रेखा गामा रेखा के रूप में जानी जाती है। (यह इस तथ्य से दिखाया जा सकता है कि गामा वितरण का अतिरिक्त कर्टोसिस 6/k है और विषमता का वर्ग 4/k है, इसलिए (अतिरिक्त कुर्तबसिस - (3/2) विषमता)<sup>2</sup> = 0) मापदंड k के मान की परवाह किए बिना गामा वितरण से समान रूप से संतुष्ट है)। पियर्सन ने पश्चात् में उल्लेख किया कि ची-स्क्वेर्ड वितरण पियर्सन के प्रकार III का विशेष स्तिथि है और इस सीमा रेखा को भी साझा करता है (जैसा कि इस तथ्य से स्पष्ट है कि ची-स्क्वेर्ड वितरण के लिए अतिरिक्त कर्टोसिस 12/के और वर्ग का वर्ग है। विषमता 8/k है, इसलिए (अतिरिक्त कर्टोसिस - (3/2) विषमता<sup>2</sup> = 0) मापदंड k के मान की परवाह किए बिना समान रूप से संतुष्ट है)। ची-स्क्वेर्ड वितरण X ~ χ के पश्चात् से इसकी उम्मीद की जानी चाहिए<sup>2</sup>(k) पैरामीट्रिजेशन X ~ Γ(k/2, 1/2) के साथ गामा वितरण का विशेष स्तिथि है, जहां k धनात्मक पूर्णांक है जो ची-वर्ग की स्वतंत्रता की डिग्री की संख्या को निर्दिष्ट करता वितरण है। | ||
ऊपरी सीमा के पास बीटा वितरण का उदाहरण (अतिरिक्त कर्टोसिस - (3/2) | ऊपरी सीमा के पास बीटा वितरण का उदाहरण (अतिरिक्त कर्टोसिस - (3/2) विषमता<sup>2</sup> = 0) α = 0.1, β = 1000 द्वारा दिया जाता है, जिसके लिए अनुपात (अतिरिक्त कुर्तबसिस)/(विषमता)<sup>2</sup>) = 1.49835 नीचे से 1.5 की ऊपरी सीमा तक पहुंचता है। निचली सीमा के पास बीटा वितरण का उदाहरण (अतिरिक्त कर्टोसिस + 2 - विषमता<sup>2</sup> = 0) α= 0.0001, β = 0.1 द्वारा दिया जाता है, जिसके लिए अभिव्यक्ति (अतिरिक्त कर्टोसिस + 2)/(विषमता)<sup>2</sup>) = 1.01621 ऊपर से 1 की निचली सीमा तक पहुंचता है। α और β दोनों के लिए अनंत सीमा में सममित रूप से शून्य पर पहुंचने पर, अतिरिक्त कर्टोसिस -2 पर अपने न्यूनतम मूल्य तक पहुंच जाता है। यह न्यूनतम मान उस बिंदु पर होता है जिस पर निचली सीमा रेखा ऊर्ध्वाधर अक्ष (समन्वय) को काटती है। (चूंकि, पियर्सन के मूल चार्ट में, अधिक कर्टोसिस के अतिरिक्त कोटि कर्टोसिस है, और यह ऊपर की बजाय नीचे की ओर बढ़ती है)। | ||
विषमता और निचली सीमा के नीचे अतिरिक्त कर्टोसिस के लिए मान (अतिरिक्त कुर्तबसिस + 2 - विषमता<sup>2</sup> = 0) किसी भी वितरण के लिए नहीं हो सकता है, और इसलिए कार्ल पियर्सन ने उचित रूप से इस सीमा के नीचे के क्षेत्र को असंभव क्षेत्र कहा जाता है। इस असंभव क्षेत्र के लिए सीमा (सममित या विषम) बिमोडल यू-आकार के वितरण द्वारा निर्धारित की जाती है जिसके लिए मापदंड α और β शून्य तक पहुंचते हैं और इसलिए सभी प्रायिकता घनत्व सिरों पर केंद्रित होते हैं: x = 0, 1 व्यावहारिक रूप से मध्य में कुछ भी नहीं उन्हें। चूंकि α ≈ β ≈ 0 के लिए प्रायिकता घनत्व दो सिरों x = 0 और x = 1 पर केंद्रित है, यह असंभव सीमा बर्नौली वितरण द्वारा निर्धारित की जाती है, जहां संबंधित संभावनाओं के साथ केवल दो संभावित परिणाम होते हैं p और q = के साथ होते है 1- p। समरूपता α = β, विषमता ≈ 0, अतिरिक्त कर्टोसिस ≈ −2 इस सीमा को सीमा तक पहुंचने वाले स्थितियों के लिए (यह किसी भी वितरण के लिए न्यूनतम अतिरिक्त कुर्तबसिस संभव है), और संभावनाएं p ≈ q ≈ 1/2 हैं। विषमता के साथ इस सीमा को सीमा तक पहुंचने वाले स्थितियों के लिए, अतिरिक्त कर्टोसिस ≈ −2 + विषमता<sup>2</sup>, और प्रायिकता घनत्व दूसरे छोर की तुलना में छोर पर अधिक केंद्रित है (व्यावहारिक रूप से मध्य में कुछ भी नहीं है), संभावनाओं के साथ <math>p = \tfrac{\beta}{\alpha + \beta}</math> बाएँ छोर पर x = 0 और <math>q = 1-p = \tfrac{\alpha}{\alpha + \beta}</math> दाएँ सिरे पर x = 1. | |||
=== [[समरूपता]] === | === [[समरूपता]] === | ||
सभी कथन α, β > 0 पर | सभी कथन α, β > 0 पर सनियम हैं | ||
* संभावना घनत्व | * संभावना घनत्व फलन समरूपता है | ||
::<math>f(x;\alpha,\beta) = f(1-x;\beta,\alpha)</math> | ::<math>f(x;\alpha,\beta) = f(1-x;\beta,\alpha)</math> | ||
* संचयी वितरण | * संचयी वितरण फलन होता है तथा समरूपता प्लस एकात्मक समरूपता है | ||
::<math>F(x;\alpha,\beta) = I_x(\alpha,\beta) = 1- F(1- x;\beta,\alpha) = 1 - I_{1-x}(\beta,\alpha)</math> | ::<math>F(x;\alpha,\beta) = I_x(\alpha,\beta) = 1- F(1- x;\beta,\alpha) = 1 - I_{1-x}(\beta,\alpha)</math> | ||
* मोड समरूपता प्लस एकात्मक समरूपता | * मोड समरूपता प्लस एकात्मक समरूपता है | ||
::<math>\operatorname{mode}(\Beta(\alpha, \beta))= 1-\operatorname{mode}(\Beta(\beta, \alpha)),\text{ if }\Beta(\beta, \alpha)\ne \Beta(1,1)</math> | ::<math>\operatorname{mode}(\Beta(\alpha, \beta))= 1-\operatorname{mode}(\Beta(\beta, \alpha)),\text{ if }\Beta(\beta, \alpha)\ne \Beta(1,1)</math> | ||
* मेडियन समरूपता प्लस एकात्मक समरूपता | * मेडियन समरूपता प्लस एकात्मक समरूपता है | ||
::<math>\operatorname{median} (\Beta(\alpha, \beta) )= 1 - \operatorname{median} (\Beta(\beta, \alpha))</math> | ::<math>\operatorname{median} (\Beta(\alpha, \beta) )= 1 - \operatorname{median} (\Beta(\beta, \alpha))</math> | ||
* मीन समरूपता प्लस एकात्मक समरूपता | * मीन समरूपता प्लस एकात्मक समरूपता है | ||
::<math>\mu (\Beta(\alpha, \beta) )= 1 - \mu (\Beta(\beta, \alpha) )</math> | ::<math>\mu (\Beta(\alpha, \beta) )= 1 - \mu (\Beta(\beta, \alpha) )</math> | ||
* ज्यामितीय | * ज्यामितीय कारण प्रत्येक व्यक्तिगत रूप से असममित है, और निम्नलिखित समरूपता 'X' के आधार पर ज्यामितीय माध्य और इसके प्रतिबिंब सूत्र (1-X) के आधार पर ज्यामितीय माध्य के मध्य प्रयुक्त होती है। | ||
::<math>G_X (\Beta(\alpha, \beta) )=G_{(1-X)}(\Beta(\beta, \alpha) ) </math> | ::<math>G_X (\Beta(\alpha, \beta) )=G_{(1-X)}(\Beta(\beta, \alpha) ) </math> | ||
* हार्मोनिक का अर्थ है कि प्रत्येक व्यक्तिगत रूप से असममित है, निम्नलिखित समरूपता ' | * हार्मोनिक का अर्थ है कि प्रत्येक व्यक्तिगत रूप से असममित है, निम्नलिखित समरूपता 'X' पर आधारित हार्मोनिक माध्य और इसके प्रतिबिंब सूत्र (1-X) के आधार पर हार्मोनिक माध्य के मध्य प्रयुक्त होती है। | ||
::<math>H_X (\Beta(\alpha, \beta) )=H_{(1-X)}(\Beta(\beta, \alpha) ) \text{ if } \alpha, \beta > 1 </math> . | ::<math>H_X (\Beta(\alpha, \beta) )=H_{(1-X)}(\Beta(\beta, \alpha) ) \text{ if } \alpha, \beta > 1 </math> . | ||
* भिन्नता समरूपता | * भिन्नता समरूपता | ||
::<math>\operatorname{var} (\Beta(\alpha, \beta) )=\operatorname{var} (\Beta(\beta, \alpha) )</math> | ::<math>\operatorname{var} (\Beta(\alpha, \beta) )=\operatorname{var} (\Beta(\beta, \alpha) )</math> | ||
* प्रत्येक ज्यामितीय भिन्नता व्यक्तिगत रूप से असममित है, निम्नलिखित समरूपता X पर आधारित लॉग ज्यामितीय भिन्नता और इसके प्रतिबिंब सूत्र (1-X) के आधार पर लॉग ज्यामितीय भिन्नता के | * प्रत्येक ज्यामितीय भिन्नता व्यक्तिगत रूप से असममित है, निम्नलिखित समरूपता X पर आधारित लॉग ज्यामितीय भिन्नता और इसके प्रतिबिंब सूत्र (1-X) के आधार पर लॉग ज्यामितीय भिन्नता के मध्य प्रयुक्त होती है। | ||
::<math>\ln(\operatorname{var_{GX}} (\Beta(\alpha, \beta))) = \ln(\operatorname{var_{G(1-X)}}(\Beta(\beta, \alpha))) </math> | ::<math>\ln(\operatorname{var_{GX}} (\Beta(\alpha, \beta))) = \ln(\operatorname{var_{G(1-X)}}(\Beta(\beta, \alpha))) </math> | ||
* ज्यामितीय सहप्रसरण समरूपता | * ज्यामितीय सहप्रसरण समरूपता है | ||
::<math>\ln \operatorname{cov_{GX,(1-X)}}(\Beta(\alpha, \beta))=\ln \operatorname{cov_{GX,(1-X)}}(\Beta(\beta, \alpha))</math> | ::<math>\ln \operatorname{cov_{GX,(1-X)}}(\Beta(\alpha, \beta))=\ln \operatorname{cov_{GX,(1-X)}}(\Beta(\beta, \alpha))</math> | ||
* माध्य समरूपता के चारों ओर पूर्ण विचलन | * माध्य समरूपता के चारों ओर पूर्ण विचलन है | ||
::<math>\operatorname{E}[|X - E[X]| ] (\Beta(\alpha, \beta))=\operatorname{E}[| X - E[X]|] (\Beta(\beta, \alpha))</math> | ::<math>\operatorname{E}[|X - E[X]| ] (\Beta(\alpha, \beta))=\operatorname{E}[| X - E[X]|] (\Beta(\beta, \alpha))</math> | ||
* | * विषमता [[समरूपता (गणित)]] | विषम-समरूपता | ||
::<math>\operatorname{skewness} (\Beta(\alpha, \beta) )= - \operatorname{ skewness} (\Beta(\beta, \alpha) )</math> | ::<math>\operatorname{skewness} (\Beta(\alpha, \beta) )= - \operatorname{ skewness} (\Beta(\beta, \alpha) )</math> | ||
* अतिरिक्त कर्टोसिस समरूपता | * अतिरिक्त कर्टोसिस समरूपता है | ||
::<math>\text{excess kurtosis} (\Beta(\alpha, \beta) )= \text{excess kurtosis} (\Beta(\beta, \alpha) )</math> | ::<math>\text{excess kurtosis} (\Beta(\alpha, \beta) )= \text{excess kurtosis} (\Beta(\beta, \alpha) )</math> | ||
* वास्तविक भाग की विशेषता | * वास्तविक भाग की विशेषता फलन (वेरिएबल टी की उत्पत्ति के संबंध में) समरूपता है | ||
::<math> \text{Re} [{}_1F_1(\alpha; \alpha+\beta; it) ] = \text{Re} [ {}_1F_1(\alpha; \alpha+\beta; - it)] </math> | ::<math> \text{Re} [{}_1F_1(\alpha; \alpha+\beta; it) ] = \text{Re} [ {}_1F_1(\alpha; \alpha+\beta; - it)] </math> | ||
* विशेषता | * विशेषता फलन समरूपता (गणित) है | [[काल्पनिक भाग]] (वेरिएबल टी की उत्पत्ति के संबंध ) की विषम-समरूपता है | ||
::<math> \text{Im} [{}_1F_1(\alpha; \alpha+\beta; it) ] = - \text{Im} [ {}_1F_1(\alpha; \alpha+\beta; - it) ] </math> | ::<math> \text{Im} [{}_1F_1(\alpha; \alpha+\beta; it) ] = - \text{Im} [ {}_1F_1(\alpha; \alpha+\beta; - it) ] </math> | ||
* [[निरपेक्ष मूल्य]] की विशेषता | * [[निरपेक्ष मूल्य]] की विशेषता फलन (वेरिएबल टी की उत्पत्ति के संबंध में) समरूपता है | ||
::<math> \text{Abs} [ {}_1F_1(\alpha; \alpha+\beta; it) ] = \text{Abs} [ {}_1F_1(\alpha; \alpha+\beta; - it) ] </math> | ::<math> \text{Abs} [ {}_1F_1(\alpha; \alpha+\beta; it) ] = \text{Abs} [ {}_1F_1(\alpha; \alpha+\beta; - it) ] </math> | ||
* विभेदक एन्ट्रापी समरूपता | * विभेदक एन्ट्रापी समरूपता | ||
::<math>h(\Beta(\alpha, \beta) )= h(\Beta(\beta, \alpha) )</math> | ::<math>h(\Beta(\alpha, \beta) )= h(\Beta(\beta, \alpha) )</math> | ||
* सापेक्ष एन्ट्रॉपी (जिसे कुल्बैक-लीब्लर डाइवर्जेंस भी कहा जाता है) समरूपता | * सापेक्ष एन्ट्रॉपी (जिसे कुल्बैक-लीब्लर डाइवर्जेंस भी कहा जाता है) समरूपता है | ||
::<math>D_{\mathrm{KL}}(X_1||X_2) = D_{\mathrm{KL}}(X_2||X_1), \text{ if }h(X_1) = h(X_2)\text{, for (skewed) }\alpha \neq \beta</math> | ::<math>D_{\mathrm{KL}}(X_1||X_2) = D_{\mathrm{KL}}(X_2||X_1), \text{ if }h(X_1) = h(X_2)\text{, for (skewed) }\alpha \neq \beta</math> | ||
* फिशर सूचना | * फिशर सूचना आव्युह समरूपता है | ||
::<math>{\mathcal{I}}_{i, j} = {\mathcal{I}}_{j, i}</math> | ::<math>{\mathcal{I}}_{i, j} = {\mathcal{I}}_{j, i}</math> | ||
| Line 900: | Line 899: | ||
=== प्रायिकता घनत्व फलन की ज्यामिति === | === प्रायिकता घनत्व फलन की ज्यामिति === | ||
==== विभक्ति बिंदु ==== | ==== विभक्ति बिंदु ==== | ||
[[File:Inflexion points Beta Distribution alpha and beta ranging from 0 to 5 large ptl view - J. Rodal.jpg|thumb|विभक्ति बिंदु स्थान बनाम α और β विभक्ति बिंदु वाले क्षेत्रों को दिखा रहा है]] | [[File:Inflexion points Beta Distribution alpha and beta ranging from 0 to 5 large ptl view - J. Rodal.jpg|thumb|विभक्ति बिंदु स्थान बनाम α और β विभक्ति बिंदु वाले क्षेत्रों को दिखा रहा है]] | ||
[[File:Inflexion points Beta Distribution alpha and beta ranging from 0 to 5 large ptr view - J. Rodal.jpg|thumb|विभक्ति बिंदु स्थान बनाम α और β दो विभक्ति बिंदुओं के साथ क्षेत्र दिखा रहा है]]आकार | [[File:Inflexion points Beta Distribution alpha and beta ranging from 0 to 5 large ptr view - J. Rodal.jpg|thumb|विभक्ति बिंदु स्थान बनाम α और β दो विभक्ति बिंदुओं के साथ क्षेत्र दिखा रहा है]]आकार मापदंड α और β के कुछ मूल्यों के लिए, संभाव्यता घनत्व फलन में विभक्ति बिंदु होते हैं, जिस पर [[वक्रता]] परिवर्तन चिन्ह होता है। इन [[मोड़ बिंदु]]ओं की स्थिति सांख्यिकीय फैलाव या वितरण के फैलाव के माप के रूप में उपयोगी हो सकती है। | ||
निम्नलिखित मात्रा को परिभाषित करना: | निम्नलिखित मात्रा को परिभाषित करना: | ||
:<math>\kappa =\frac{\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | :<math>\kappa =\frac{\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ||
विभक्ति के बिंदु होते हैं,<ref name=JKB /><ref name=Wadsworth /><ref name="Handbook of Beta Distribution" /><ref name=Panik />आकृति | विभक्ति के बिंदु होते हैं,<ref name=JKB /><ref name=Wadsworth /><ref name="Handbook of Beta Distribution" /><ref name=Panik />आकृति मापदंड α और β के मान के आधार पर निम्नानुसार है: | ||
*(α > 2, β > 2) वितरण घंटी के आकार का है (α = β के लिए सममित और अन्यथा | *(α > 2, β > 2) वितरण घंटी के आकार का है (α = β के लिए सममित और अन्यथा विषम), दो विभक्ति बिंदुओं के साथ, मोड से समान दूरी पर: | ||
::<math>x = \text{mode} \pm \kappa = \frac{\alpha -1 \pm \sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ::<math>x = \text{mode} \pm \kappa = \frac{\alpha -1 \pm \sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ||
* (α = 2, β > 2) वितरण असमान, | * (α = 2, β > 2) वितरण असमान, धनात्मक रूप से विषम, दाएं-टेल वाला, विभक्ति बिंदु के साथ, मोड के दाईं ओर स्थित है: | ||
::<math>x =\text{mode} + \kappa = \frac{2}{\beta}</math> | ::<math>x =\text{mode} + \kappa = \frac{2}{\beta} </math> | ||
* (α > 2, β = 2) वितरण असमान, | * (α > 2, β = 2) वितरण असमान, ऋणात्मक रूप से विषम, बायां-पुच्छ, विभक्ति बिंदु के साथ, मोड के बाईं ओर स्थित है: | ||
::<math>x = \text{mode} - \kappa = 1 - \frac{2}{\alpha}</math> | ::<math>x = \text{mode} - \kappa = 1 - \frac{2}{\alpha} </math> | ||
* (1 < α < 2, β > 2, α+β>2) वितरण असमान, | * (1 < α < 2, β > 2, α+β>2) वितरण असमान, धनात्मक रूप से विषम, दाएं-टेल वाला, विभक्ति बिंदु के साथ, मोड के दाईं ओर स्थित है: | ||
::<math>x =\text{mode} + \kappa = \frac{\alpha -1 +\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ::<math>x =\text{mode} + \kappa = \frac{\alpha -1 +\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2} | ||
*(0 < α < 1, 1 < β < 2) बंटन के बाएँ सिरे पर बहुलक x = 0 है और यह धनात्मक रूप से | </math> | ||
*(0 < α < 1, 1 < β < 2) बंटन के बाएँ सिरे पर बहुलक x = 0 है और यह धनात्मक रूप से विषम, दाएँ-टेल वाला है। मोड के दाईं ओर स्थित 'एक विभक्ति बिंदु' है: | |||
::<math>x = \frac{\alpha -1 +\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ::<math>x = \frac{\alpha -1 +\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ||
*(α > 2, 1 < β < 2) वितरण असमान | *(α > 2, 1 < β < 2) वितरण असमान ऋणात्मक रूप से विषम, बायां-टेल वाला, विभक्ति बिंदु के साथ, मोड के बाईं ओर स्थित है: | ||
::<math>x =\text{mode} - \kappa = \frac{\alpha -1 -\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ::<math>x =\text{mode} - \kappa = \frac{\alpha -1 -\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ||
*(1 < α < 2, 0 < β < 1) बंटन के दायें सिरे पर बहुलक | *(1 < α < 2, 0 < β < 1) बंटन के दायें सिरे पर बहुलक x=1 है और यह ऋणात्मक रूप से विषम, बायां-पुच्छ है। मोड के बाईं ओर स्थित 'एक विभक्ति बिंदु' है: | ||
::<math>x = \frac{\alpha -1 -\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ::<math>x = \frac{\alpha -1 -\sqrt{\frac{(\alpha-1)(\beta-1)}{\alpha+\beta-3}}}{\alpha+\beta-2}</math> | ||
शेष (सममित और | शेष (सममित और विषम) क्षेत्रों में कोई विभक्ति बिंदु नहीं हैं: U-आकार: (α, β <1) ऊपर-नीचे-U-आकार: (1 <α <2, 1 <β <2), रिवर्स- J- आकार (α < 1, β > 2) या J- आकार: (α > 2, β < 1) | ||
साथ वाले भूखंडों में विभक्ति बिंदु स्थान (0 से 1 तक लंबवत दिखाया गया है) बनाम α और β (क्षैतिज अक्ष 0 से 5 तक) दिखाते हैं। α = 1, β = 1, α = 2, और β = 2 को काटने वाली सतहों पर बड़े कट हैं क्योंकि इन मूल्यों पर बीटा वितरण 2 मोड से 1 मोड से नो मोड में बदल जाता है। | साथ वाले भूखंडों में विभक्ति बिंदु स्थान को (0 से 1 तक लंबवत दिखाया गया है) बनाम α और β (क्षैतिज अक्ष 0 से 5 तक) के रूप में दिखाते हैं। α = 1, β = 1, α = 2, और β = 2 को काटने वाली सतहों पर बड़े कट हैं क्योंकि इन मूल्यों पर बीटा वितरण 2 मोड से और 1 मोड से नो मोड में बदल जाता है। | ||
==== आकार ==== | ==== आकार ==== | ||
बीटा घनत्व | |||
बीटा घनत्व फलन दो मापदंड α और β के मानों के आधार पर विभिन्न प्रकार के विभिन्न आकार ले सकता है। आकार की इस महान विविधता को लेने के लिए बीटा वितरण की क्षमता (केवल दो मापदंडों का उपयोग करके) मॉडलिंग वास्तविक माप के लिए व्यापक आवेदन खोजने के लिए आंशिक रूप से जिम्मेदार है: | |||
=== सममित (α = β)== | === सममित (α = β)== | ||
* घनत्व | * घनत्व फलन समरूपता लगभग 1/2 (नीला और टील भूखंड) है। | ||
* माध्यिका = माध्य = 1/2। | * माध्यिका = माध्य = 1/2। | ||
* | * विषमता = 0। | ||
*विचरण = 1/(4(2α + 1)) | *विचरण = 1/(4(2α + 1)) | ||
*'α = β <1' | *'α = β <1' | ||
** | ** u-आकार (नीला प्लॉट)। | ||
** बाइमोडल: लेफ्ट मोड = 0, राइट मोड = 1, एंटी-मोड = 1/2 | ** बाइमोडल: लेफ्ट मोड = 0, राइट मोड = 1, एंटी-मोड = 1/2 | ||
**1/12 <वर ( | **1/12 <वर (X) <1/4<ref name=JKB/> | ||
**−2 <अतिरिक्त कर्टोसिस (X) <−6/5 | |||
** α = β = 1/2 आर्क्साइन वितरण है | ** α = β = 1/2 आर्क्साइन वितरण है | ||
*** वर ( | *** वर (X) = 1/8 | ||
*** अतिरिक्त कर्टोसिस ( | *** अतिरिक्त कर्टोसिस (X) = -3/2 | ||
*** | *** CF = रिंक (टी) <ref>{{Cite journal|last1=Buchanan|first1=K.|last2=Rockway|first2=J.|last3=Sternberg|first3=O.|last4=Mai|first4=N. N.|date=May 2016|title=सर्कुलर पतला यादृच्छिक सरणी का उपयोग कर रडार अनुप्रयोगों के लिए सम-अंतर बीमफॉर्मिंग|journal=2016 IEEE Radar Conference (RadarConf)|pages=1–5|doi=10.1109/RADAR.2016.7485289|isbn=978-1-5090-0863-6|s2cid=32525626|url=https://zenodo.org/record/1279364}}</ref> | ||
** α = β → 0 2-बिंदु बर्नौली वितरण है जिसमें प्रत्येक डायराक डेल्टा | ** α = β → 0 2-बिंदु बर्नौली वितरण है जिसमें प्रत्येक डायराक डेल्टा फलन अंत x = 0 और x = 1 पर समान संभावना 1/2 है और हर स्थान शून्य संभावना है। सिक्का टॉस: सिक्के का चेहरा x = 0 और दूसरा चेहरा x = 1 है। | ||
*** <math> \lim_{\alpha = \beta \to 0} \operatorname{var}(X) = \tfrac{1}{4} </math> | *** <math> \lim_{\alpha = \beta \to 0} \operatorname{var}(X) = \tfrac{1}{4} </math> | ||
*** <math> \lim_{\alpha = \beta \to 0} \operatorname{excess \ kurtosis}(X) = - 2</math> इससे कम मान किसी भी वितरण तक पहुंचना असंभव है। | *** <math> \lim_{\alpha = \beta \to 0} \operatorname{excess \ kurtosis}(X) = - 2</math> इससे कम मान किसी भी वितरण तक पहुंचना असंभव है। | ||
*** सूचना एन्ट्रापी मैक्सिमा और मिनिमा वैल्यू -∞ तक पहुंचती है | *** सूचना एन्ट्रापी मैक्सिमा और मिनिमा वैल्यू -∞ तक पहुंचती है | ||
* α = β = 1 | * α = β = 1 | ||
**समान वितरण (निरंतर)|समान [0, 1] वितरण | **समान वितरण (निरंतर)|समान [0, 1] वितरण | ||
** कोई मोड नहीं | ** कोई मोड नहीं | ||
**var(''X'') = 1/12 | **var(''X'') = 1/12 | ||
**अतिरिक्त कर्टोसिस(''X'') = -6/5 | **अतिरिक्त कर्टोसिस(''X'') = -6/5 | ||
** (कहीं भी | ** (कहीं भी ऋणात्मक ) सूचना एन्ट्रापी अपने अधिकतम और शून्य के न्यूनतम मान तक पहुँच जाती है | ||
** सीएफ = सिंक (टी) | ** सीएफ = सिंक (टी) | ||
*''α'' = ''β'' > 1 | *''α'' = ''β'' > 1 | ||
** सममित अनिमॉडल | ** सममित अनिमॉडल | ||
** मोड = 1/2। | ** मोड = 1/2। | ||
**0 <var(''X'') <1/12<ref name=JKB/>**−6/5 <अतिरिक्त कर्टोसिस ( | **0 <var(''X'') <1/12<ref name=JKB/> | ||
**−6/5 <अतिरिक्त कर्टोसिस (X) <0 | |||
**α = β = 3/2 अर्ध-अण्डाकार [0, 1] वितरण है, देखें: विग्नर अर्धवृत्त वितरण<ref>{{Cite journal|last1=Buchanan|first1=K.|last2=Flores|first2=C.|last3=Wheeland|first3=S.|last4=Jensen|first4=J.|last5=Grayson|first5=D.|last6=Huff|first6=G.|date=May 2017|title=राडार अनुप्रयोगों के लिए ट्रांसमिट बीमफॉर्मिंग गोलाकार टेपर्ड रैंडम ऐरे का उपयोग करते हुए|journal=2017 IEEE Radar Conference (RadarConf)|pages=0112–0117|doi=10.1109/RADAR.2017.7944181|isbn=978-1-4673-8823-8|s2cid=38429370}}</ref> | **α = β = 3/2 अर्ध-अण्डाकार [0, 1] वितरण है, देखें: विग्नर अर्धवृत्त वितरण<ref>{{Cite journal|last1=Buchanan|first1=K.|last2=Flores|first2=C.|last3=Wheeland|first3=S.|last4=Jensen|first4=J.|last5=Grayson|first5=D.|last6=Huff|first6=G.|date=May 2017|title=राडार अनुप्रयोगों के लिए ट्रांसमिट बीमफॉर्मिंग गोलाकार टेपर्ड रैंडम ऐरे का उपयोग करते हुए|journal=2017 IEEE Radar Conference (RadarConf)|pages=0112–0117|doi=10.1109/RADAR.2017.7944181|isbn=978-1-4673-8823-8|s2cid=38429370}}</ref> | ||
*** वार (एक्स) = 1/16। | *** वार (एक्स) = 1/16। | ||
*** अतिरिक्त कर्टोसिस ( | *** अतिरिक्त कर्टोसिस (X) = -1 | ||
*** सीएफ = 2 जिंक (टी) | *** सीएफ = 2 जिंक (टी) | ||
**α = β = 2 परवलयिक [0, 1] वितरण है | **α = β = 2 परवलयिक [0, 1] वितरण है | ||
*** वार ( | *** वार (X) = 1/20 | ||
*** अतिरिक्त कर्टोसिस ( | *** अतिरिक्त कर्टोसिस (X) = -6/7 | ||
*** सीएफ = 3 टिन (टी) <ref>{{Cite journal|last=Ryan|first=Buchanan, Kristopher|date=2014-05-29|title=एपेरियोडिक (यादृच्छिक) चरणबद्ध सारणियों का सिद्धांत और अनुप्रयोग|url=http://oaktrust.library.tamu.edu/handle/1969.1/157918|language=en}}</ref> | *** सीएफ = 3 टिन (टी) <ref>{{Cite journal|last=Ryan|first=Buchanan, Kristopher|date=2014-05-29|title=एपेरियोडिक (यादृच्छिक) चरणबद्ध सारणियों का सिद्धांत और अनुप्रयोग|url=http://oaktrust.library.tamu.edu/handle/1969.1/157918|language=en}}</ref> | ||
**α = β > 2 घंटी के आकार का है, मोड के दोनों ओर स्थित विभक्ति बिंदु के साथ | **α = β > 2 घंटी के आकार का है, मोड के दोनों ओर स्थित विभक्ति बिंदु के साथ | ||
***0 <वर (एक्स) <1/20 | ***0 <वर (एक्स) <1/20 | ||
***−6/7 <अतिरिक्त कर्टोसिस ( | ***−6/7 <अतिरिक्त कर्टोसिस (X) <0 | ||
**α = β → ∞ मिडपॉइंट x = 1/2 पर डायराक डेल्टा | **α = β → ∞ मिडपॉइंट x = 1/2 पर डायराक डेल्टा फलन स्पाइक के साथ 1-पॉइंट डिजनरेट डिस्ट्रीब्यूशन है, प्रायिकता 1 के साथ, और हर स्थान शून्य प्रायिकता। एकल बिंदु x = 1/2 पर केंद्रित 100% संभावना (पूर्ण निश्चितता) है। | ||
***<math> \lim_{\alpha = \beta \to \infty} \operatorname{var}(X) = 0 </math> | ***<math> \lim_{\alpha = \beta \to \infty} \operatorname{var}(X) = 0 </math> | ||
***<math> \lim_{\alpha = \beta \to \infty} \operatorname{excess \ kurtosis}(X) = 0</math> | ***<math> \lim_{\alpha = \beta \to \infty} \operatorname{excess \ kurtosis}(X) = 0</math> | ||
***सूचना एंट्रोपी −∞ के मैक्सिमा और मिनिमा वैल्यू तक पहुंचती है | ***सूचना एंट्रोपी −∞ के मैक्सिमा और मिनिमा वैल्यू तक पहुंचती है | ||
== | == विषम (α ≠ β) == | ||
घनत्व | घनत्व फलन विषमता है। मापदंड मानों का आदान-प्रदान प्रारंभिक वक्र की दर्पण छवि (विपरीत) उत्पन्न करता है, कुछ और विशिष्ट स्तिथियाँ : | ||
*'α <1, β <1' | *'α <1, β <1' | ||
** | ** U-आकार | ||
** α <β के लिए | ** α <β के लिए धनात्मक विषम, α> β के लिए ऋणात्मक विषम। | ||
** बाइमोडल: लेफ्ट मोड = 0, राइट मोड = 1, एंटी-मोड = <math>\tfrac{\alpha-1}{\alpha + \beta-2} </math> | ** बाइमोडल: लेफ्ट मोड = 0, राइट मोड = 1, एंटी-मोड = <math>\tfrac{\alpha-1}{\alpha + \beta-2} </math> | ||
** 0 <माध्यिका <1। | ** 0 <माध्यिका <1। | ||
** 0 <वर ( | ** 0 <वर (X) <1/4 | ||
*'ए> 1, बी> 1' | *'ए> 1, बी> 1' | ||
** यूनिमोडल (मैजेंटा और सियान प्लॉट), | ** यूनिमोडल (मैजेंटा और सियान प्लॉट), | ||
** α <β के लिए | ** α <β के लिए धनात्मक विषम, α> β के लिए ऋणात्मक विषम। | ||
**<math>\text{mode }= \tfrac{\alpha-1}{\alpha + \beta-2} </math> | **<math>\text{mode }= \tfrac{\alpha-1}{\alpha + \beta-2} </math> | ||
** 0 <माध्यिका <1 | ** 0 <माध्यिका <1 | ||
** 0 <वर ( | ** 0 <वर (X) <1/12 | ||
*'α <1, β ≥ 1' | *'α <1, β ≥ 1' | ||
**एक दाहिनी | **एक दाहिनी टेल के साथ रिवर्स j-आकार, | ||
** | **धनात्मक रूप से विषम, | ||
** कड़ाई से घटते हुए, उत्तल कार्य | ** कड़ाई से घटते हुए, उत्तल कार्य | ||
** मोड = 0 | ** मोड = 0 | ||
** 0 <माध्यिका <1/2। | ** 0 <माध्यिका <1/2। | ||
** <math>0 < \operatorname{var}(X) < \tfrac{-11+5 \sqrt{5}}{2}, </math> (अधिकतम विचरण के लिए होता है <math>\alpha=\tfrac{-1+\sqrt{5}}{2}, \beta=1</math>, या α = Φ गोल्डन अनुपात) | ** <math>0 < \operatorname{var}(X) < \tfrac{-11+5 \sqrt{5}}{2}, </math> (अधिकतम विचरण के लिए होता है <math>\alpha=\tfrac{-1+\sqrt{5}}{2}, \beta=1</math>, या α = Φ गोल्डन अनुपात) | ||
*α ≥ 1, β <1 | *α ≥ 1, β <1 | ||
** | ** J के आकार का बाईं टेल के साथ, | ||
** | ** ऋणात्मक विषम, | ||
** सख्ती से बढ़ रहा है, उत्तल कार्य | ** सख्ती से बढ़ रहा है, उत्तल कार्य | ||
** मोड = 1 | ** मोड = 1 | ||
** 1/2 <माध्यिका <1 | ** 1/2 <माध्यिका <1 | ||
** <math>0 < \operatorname{var}(X) < \tfrac{-11+5 \sqrt{5}}{2},</math> (अधिकतम विचरण के लिए होता है <math>\alpha=1, \beta=\tfrac{-1+\sqrt{5}}{2}</math>, या β = Φ गोल्डन अनुपात) | ** <math>0 < \operatorname{var}(X) < \tfrac{-11+5 \sqrt{5}}{2},</math> (अधिकतम विचरण के लिए होता है <math>\alpha=1, \beta=\tfrac{-1+\sqrt{5}}{2}</math>, या β = Φ गोल्डन अनुपात) | ||
* α = 1, β > 1 | * α = 1, β > 1 | ||
** | **धनात्मक रूप से विषम, | ||
** सख्ती से घट रहा है (लाल प्लॉट), | ** सख्ती से घट रहा है (लाल प्लॉट), | ||
**एक उलटा (मिरर-इमेज) पावर | **एक उलटा (मिरर-इमेज) पावर फलन [0,1] वितरण | ||
** माध्य = 1 / (β + 1) | ** माध्य = 1 / (β + 1) | ||
** माध्यिका = 1 - 1/2<sup>1/β</sup> | ** माध्यिका = 1 - 1/2<sup>1/β</sup> | ||
| Line 1,018: | Line 1,016: | ||
*** अवतल कार्य | *** अवतल कार्य | ||
*** <math>1-\tfrac{1}{\sqrt{2}}< \text{median} < \tfrac{1}{2}</math> | *** <math>1-\tfrac{1}{\sqrt{2}}< \text{median} < \tfrac{1}{2}</math> | ||
*** 1/18 <वर ( | *** 1/18 <वर (X) <1/12। | ||
**α = 1, β = 2 | **α = 1, β = 2 | ||
*** | *** स्लोप के साथ सीधी रेखा -2, दाएं-त्रिकोणीय वितरण बाएं छोर पर समकोण के साथ, x = 0 पर | ||
*** <math>\text{median}=1-\tfrac {1}{\sqrt{2}}</math> | *** <math>\text{median}=1-\tfrac {1}{\sqrt{2}}</math> | ||
*** वर ( | *** वर (X) = 1/18 | ||
**α = 1, β> 2 | **α = 1, β> 2 | ||
*** एक दाहिनी | *** एक दाहिनी टेल के साथ रिवर्स जे-आकार, | ||
*** उत्तल कार्य | *** उत्तल कार्य | ||
*** <math>0 < \text{median} < 1-\tfrac{1}{\sqrt{2}}</math> | *** <math>0 < \text{median} < 1-\tfrac{1}{\sqrt{2}}</math> | ||
*** 0 <वर ( | *** 0 <वर (X) <1/18 | ||
*'α > 1, β = 1' | *'α > 1, β = 1' | ||
** | ** ऋणात्मक विषम, | ||
** सख्ती से बढ़ रहा है (हरा प्लॉट), | ** सख्ती से बढ़ रहा है (हरा प्लॉट), | ||
** पावर | ** पावर फलन [0, 1] वितरण<ref name="Handbook of Beta Distribution" /> | ||
** माध्यिका = 1/2<sup>1/ | **माध्य = α / (α + 1) | ||
** माध्यिका = 1/2<sup>1/α </sup> | |||
** मोड = 1 | ** मोड = 1 | ||
**2> | **2> α> 1, बी = 1 | ||
*** अवतल कार्य | *** अवतल कार्य | ||
*** <math>\tfrac{1}{2} < \text{median} < \tfrac{1}{\sqrt{2}}</math> | *** <math>\tfrac{1}{2} < \text{median} < \tfrac{1}{\sqrt{2}}</math> | ||
*** 1/18 <वर ( | *** 1/18 <वर (X) <1/12 | ||
** α = 2, β = 1 | ** α = 2, β = 1 | ||
*** | *** स्लोप +2 के साथ सीधी रेखा, दाहिने सिरे पर समकोण के साथ समकोण-त्रिकोणीय वितरण, x = 1 पर होता है | ||
*** <math>\text{median}=\tfrac {1}{\sqrt{2}}</math> | *** <math>\text{median}=\tfrac {1}{\sqrt{2}}</math> | ||
*** वर ( | *** वर (X) = 1/18 | ||
**α> 2, β = 1 | **α> 2, β = 1 | ||
*** एक बाईं | *** एक बाईं टेल के साथ जम्मू के आकार का, उत्तल कार्य | ||
***<math>\tfrac{1}{\sqrt{2}} < \text{median} < 1</math> | ***<math>\tfrac{1}{\sqrt{2}} < \text{median} < 1</math> | ||
*** 0 <वर ( | *** 0 <वर (X) <1/18 | ||
== संबंधित वितरण == | == संबंधित वितरण == | ||
=== रूपांतरण === | === रूपांतरण === | ||
* यदि X ~ बीटा (α, β) | * यदि X ~ बीटा (α, β) तब 1 − X ~ बीटा (β, α) दर्पण छवि समरूपता है | | ||
* यदि | * यदि X ~ बीटा (α, β) तब <math>\tfrac{X}{1-X} \sim {\beta'}(\alpha,\beta)</math>. बीटा प्राइम डिस्ट्रीब्यूशन, जिसे दूसरी तरह का बीटा डिस्ट्रीब्यूशन भी कहा जाता है। | ||
* | * यदि <math>X\sim\text{Beta}(\alpha,\beta)</math>, तब <math>Y=\log\frac{X}{1-X}</math> घनत्व के साथ [[सामान्यीकृत रसद वितरण]] है <math>\frac{\sigma(y)^\alpha\sigma(-y)^\beta}{B(\alpha,\beta)}</math>, जहाँ <math>\sigma</math> [[लॉजिस्टिक सिग्मॉइड]] है। | ||
* यदि | * यदि X ~ बीटा (α, β) तब <math>\tfrac{1}{X} -1 \sim {\beta'}(\beta,\alpha)</math> होता है | ||
* यदि | * यदि X ~ बीटा (एन/2, एम/2) तब <math>\tfrac{mX}{n(1-X)} \sim F(n,m)</math> (एन > 0 और एम > 0 मानते हुए), एफ-वितरण | फिशर-स्नेडेकोर एफ वितरण। | ||
* | * यदि <math>X \sim \operatorname{Beta}\left(1+\lambda\tfrac{m-\min}{\max-\min}, 1 + \lambda\tfrac{\max-m}{\max-\min}\right)</math> फिर मिनट + X (अधिकतम - मिनट) ~ [[पीईआरटी]] (न्यूनतम, अधिकतम, एम, λ) जहां पीईआरटी पीईआरटी विश्लेषण में उपयोग किए जाने वाले [[पीईआरटी वितरण]] को दर्शाता है, और M = सबसे संभावित मूल्य होता है ।<ref name=NewPERT>Herrerías-Velasco, José Manuel and Herrerías-Pleguezuelo, Rafael and René van Dorp, Johan. (2011). Revisiting the PERT mean and Variance. European Journal of Operational Research (210), p. 448–451.</ref> पारंपरिक रूप से<ref name=Malcolm />PERT विश्लेषण में λ = 4 है । | ||
* यदि X ~ बीटा (1, β) | * यदि X ~ बीटा (1, β) तब X ~ [[कुमारस्वामी वितरण]] मापदंड (1, β) के साथ उपयोग किया जाता है | ||
* यदि | * यदि X ~ बीटा (α, 1) तब X ~ कुमारस्वामी वितरण मापदंड (α, 1) के साथ होता है | ||
* | * यदि X ~ बीटा (α, 1) तब −ln(X) ~ एक्सपोनेंशियल (α) है| | ||
=== विशेष और सीमित | === विशेष और सीमित स्तिथियाँ === | ||
[[File:Random Walk example.svg|thumb|0 से | [[File:Random Walk example.svg|thumb|0 से प्रारंभिक होने वाले आयाम में यादृच्छिक चलने के आठ अहसासों का उदाहरण: उत्पत्ति के अंतिम विज़िट के समय की संभावना बीटा (1/2, 1/2) के रूप में वितरित की जाती है]] | ||
[[File:Arcsin density.svg|thumb|बीटा (1/2, 1/2): [[हेरोल्ड जेफरीस]] द्वारा बर्नौली वितरण या बायेसियन अनुमान में द्विपद वितरण के लिए अनिश्चितता का प्रतिनिधित्व करने के लिए आर्सेन वितरण संभाव्यता घनत्व प्रस्तावित किया गया था, और अब इसे | [[File:Arcsin density.svg|thumb|बीटा (1/2, 1/2): [[हेरोल्ड जेफरीस]] द्वारा बर्नौली वितरण या बायेसियन अनुमान में द्विपद वितरण के लिए अनिश्चितता का प्रतिनिधित्व करने के लिए आर्सेन वितरण संभाव्यता घनत्व प्रस्तावित किया गया था, और अब इसे सामान्यतः [[जेफरीस पूर्व]] के रूप में संदर्भित किया जाता है: पी<sup>−1/2</sup>(1 − p)<sup>−1/2</sup>. यह वितरण अनेक रैंडम वॉक मूलभूत प्रमेयों में भी प्रकट होता है]]* बीटा(1, 1) ~ u(0, 1).समान वितरण (निरंतर) है | | ||
* बीटा ( | * बीटा (n, 1) ~ अधिकतम n स्वतंत्र आरवीएस। समान वितरण के साथ (सतत)| U(0, 1), कभी-कभी उस अंतराल पर घनत्व n x<sup>n-1</sup> के साथ a मानक पावर फलन वितरण कहा जाता है। | ||
* बीटा (1, | * बीटा (1, n) ~ न्यूनतम n स्वतंत्र आरवीएस। समान वितरण के साथ (निरंतर)| u(0, 1) | ||
* यदि X ~ बीटा(3/2, 3/2) और r > 0 | * यदि X ~ बीटा(3/2, 3/2) और r > 0 तब 2rX − r ~ विग्नेर अर्धवृत्त वितरण होता है । | ||
* बीटा(1/2, 1/2) आर्क्साइन वितरण के | * बीटा(1/2, 1/2) आर्क्साइन वितरण के सामान्तर है। यह बंटन बर्नौली बंटन और द्विपद बंटन के लिए जेफरी की पूर्व प्रायिकता भी है। तथा आर्क्सिन संभाव्यता घनत्व वितरण है जो अनेक रैंडम-वॉक मौलिक प्रमेयों में प्रकट होता है। उचित सिक्के में बेतरतीब ढंग से चलना, और मूल स्थान की अंतिम यात्रा के समय की संभावना को (यू-आकार) चाप वितरण के रूप में वितरित किया जाता है।<ref name=Feller/><ref name=WillyFeller1>{{cite book |last=Feller |first=William |title=प्रायिकता सिद्धांत और उसके आवेदन के लिए एक परिचय|volume=1 |edition=3rd |year=1968 |isbn=978-0471257080}}</ref> दो खिलाड़ियों के फेयर-कॉइन-टॉस गेम में, खिलाड़ी को लीड में रहने कहा जाता है यदि रैंडम वॉक (जो मूल पर प्रारंभिक हुआ) मूल से ऊपर है। तो लंबाई 2N के खेल में किसी दिए गए खिलाड़ी के नेतृत्व में होने की सबसे संभावित संख्या N नहीं है। इसके विपरीत, N कम से कम संभावना है कि खिलाड़ी लीड में होगा। जब कि लीड में सबसे संभावित संख्या 0 या 2N (आर्क्सिन वितरण के पश्चात्) है। | ||
* <math>\lim_{n \to \infty} n \operatorname{Beta}(1,n) = \operatorname{Exponential}(1)</math> घातीय वितरण। | * <math>\lim_{n \to \infty} n \operatorname{Beta}(1,n) = \operatorname{Exponential}(1)</math> घातीय वितरण। | ||
* <math>\lim_{n \to \infty} n \operatorname{Beta}(k,n) = \operatorname{Gamma}(k,1)</math> गामा वितरण। | * <math>\lim_{n \to \infty} n \operatorname{Beta}(k,n) = \operatorname{Gamma}(k,1)</math> गामा वितरण। | ||
* बड़े | * बड़े <math>n</math> के लिए , <math>\operatorname{Beta}(\alpha n,\beta n) \to \mathcal{N}\left(\frac{\alpha}{\alpha+\beta},\frac{\alpha\beta}{(\alpha+\beta)^3}\frac{1}{n}\right)</math> [[सामान्य वितरण]]। अधिक स्पष्ट, यदि <math>X_n \sim \operatorname{Beta}(\alpha n,\beta n)</math> है तब <math>\sqrt{n}\left(X_n -\tfrac{\alpha}{\alpha+\beta}\right)</math> माध्य 0 और विचरण के साथ वितरण में सामान्य वितरण में परिवर्तित हो जाता है जैसे n बढ़ता है। वैसे <math>\tfrac{\alpha\beta}{(\alpha+\beta)^3}</math> हो जाता है| | ||
=== अन्य वितरणों से प्राप्त === | === अन्य वितरणों से प्राप्त === | ||
* समान वितरण (निरंतर) से आकार n के | * समान वितरण (निरंतर) से आकार n के प्रतिरूप का kवां क्रम आँकड़ा बीटा यादृच्छिक वेरिएबल , U है<sub>(''k'')</sub> ~ बीटा (k, n+1−k)।<ref name=David1/> | ||
* | *यदि x~गामा(α, θ) और y~गामा(β, θ) स्वतंत्र हैं, तब <math>\tfrac{X}{X+Y} \sim \operatorname{Beta}(\alpha, \beta)\,</math>होगा . | ||
* यदि X ~ U(0, 1) और α > 0 | * यदि <math>X \sim \chi^2(\alpha)\,</math> और <math>Y \sim \chi^2(\beta)\,</math> स्वतंत्र हैं, तब <math>\tfrac{X}{X+Y} \sim \operatorname{Beta}(\tfrac{\alpha}{2}, \tfrac{\beta}{2}) </math> होगा . | ||
* | * यदि X ~ U(0, 1) और α > 0 तब X<sup>1/α</sup> ~ बीटा(α, 1). पावर फलन वितरण होता है | | ||
* यदि | * यदि <math> X \sim\operatorname{Binom}(k;n;p)</math> है तब <math>{X / (n+1)}\sim \operatorname{Beta}(\alpha, \beta)</math> n और k के असतत मानों के लिए होता है जहाँ <math>\alpha=k+1</math> और <math>\beta=n-k+1</math>होगा .<ref>{{Cite web|url=https://www.statlect.com/probability-distributions/beta-distribution|title=बीटा वितरण|website=www.statlect.com}}</ref> | ||
* यदि X ~ कॉची (0, 1) तब <math>\tfrac{1}{1+X^2} \sim \operatorname{Beta}\left(\tfrac12, \tfrac12\right)\, </math>होगा | |||
=== अन्य वितरणों के साथ संयोजन === | === अन्य वितरणों के साथ संयोजन === | ||
* | * X ~ बीटा (α, β) और Y ~ F (2β, 2α) फिर <math>\Pr(X \leq \tfrac \alpha {\alpha+\beta x}) = \Pr(Y \geq x)\,</math> सभी के लिए x> 0 होगा । | ||
=== अन्य वितरणों के साथ कंपाउंडिंग === | === अन्य वितरणों के साथ कंपाउंडिंग === | ||
* यदि | * यदि p~ बीटा (α, β) और X ~ बिन (k, p) तब X ~ [[बीटा-द्विपद वितरण]] होता है | ||
* यदि | *यदि p~ बीटा (α, β) और X ~ एनबी (r, p) तब X~ बीटा ऋणात्मक द्विपद वितरण होता है | ||
=== सामान्यीकरण === | === सामान्यीकरण === | ||
* | * अनेक वेरिएबल के लिए सामान्यीकरण, अर्थात डिरिचलेट वितरण, कहलाता है। डिरिचलेट वितरण के यूनीवेरिएट मार्जिनल में बीटा वितरण होता है। बीटा वितरण द्विपद और बर्नौली वितरण से ठीक उसी तरह संयुग्मित होता है जिस तरह डिरिचलेट वितरण [[बहुपद वितरण]] और [[श्रेणीबद्ध वितरण]] के लिए संयुग्मित होता है। | ||
* पियर्सन वितरण | * पियर्सन वितरण या पियर्सन प्रकार वितरण बीटा वितरण के समान है (मनमानी स्थानांतरण और पुन: स्केलिंग को छोड़कर जिसे बीटा वितरण के चार मापदंड पैरामीट्रिजेशन के साथ भी पूरा किया जा सकता है)। | ||
* बीटा वितरण [[गैर-केंद्रीय बीटा वितरण]] का विशेष | * बीटा वितरण [[गैर-केंद्रीय बीटा वितरण]] का विशेष स्तिथि है जहां <math>\lambda = 0</math>: <math>\operatorname{Beta}(\alpha, \beta) = \operatorname{NonCentralBeta}(\alpha,\beta,0)</math>.होता है | ||
* [[सामान्यीकृत बीटा वितरण]] पांच- | * [[सामान्यीकृत बीटा वितरण]] पांच-मापदंड वितरण परिवार है जिसमें विशेष स्तिथियों के रूप में बीटा वितरण होता है। | ||
* [[मैट्रिक्स चर बीटा वितरण]] धनात्मक-निश्चित आव्यूहों का वितरण है। | * [[मैट्रिक्स चर बीटा वितरण|आव्युह वेरिएबल बीटा वितरण]] धनात्मक-निश्चित आव्यूहों का वितरण है। | ||
== सांख्यिकीय निष्कर्ष == | == सांख्यिकीय निष्कर्ष == | ||
=== | === मापदंड अनुमान === | ||
====क्षणों की विधि==== | ====क्षणों की विधि==== | ||
=== दो अज्ञात | === दो अज्ञात मापदंड === | ||
दो अज्ञात | [0,1] अंतराल में समर्थित बीटा वितरण के दो अज्ञात मापदंड (<math> (\hat{\alpha}, \hat{\beta})</math> का अनुमान पहले दो क्षणों (प्रतिरूप माध्य और प्रतिरूप भिन्नता) के साथ क्षणों की विधि का उपयोग करके लगाया जा सकता है,जिसे निम्नानुसार किया जा सकता है। | ||
: <math>\text{sample mean(X)}=\bar{x} = \frac{1}{N}\sum_{i=1}^N X_i</math> | : <math>\text{sample mean(X)}=\bar{x} = \frac{1}{N}\sum_{i=1}^N X_i</math> | ||
प्रतिरूप औसत अनुमान हो और ये | |||
: <math>\text{sample variance(X)} =\bar{v} = \frac{1}{N-1}\sum_{i=1}^N (X_i - \bar{x})^2</math> | : <math>\text{sample variance(X)} =\bar{v} = \frac{1}{N-1}\sum_{i=1}^N (X_i - \bar{x})^2 </math> | ||
[[नमूना विचरण]] अनुमान हो। आघूर्णों की विधि (सांख्यिकी)| | [[नमूना विचरण|प्रतिरूप विचरण]] अनुमान हो। तथा आघूर्णों की विधि के (सांख्यिकी)| ,आघूर्ण प्राचलों के अनुमान हैं | ||
:<math>\hat{\alpha} = \bar{x} \left(\frac{\bar{x} (1 - \bar{x})}{\bar{v}} - 1 \right),</math> | :<math>\hat{\alpha} = \bar{x} \left(\frac{\bar{x} (1 - \bar{x})}{\bar{v}} - 1 \right),</math> यदि <math>\bar{v} <\bar{x}(1 - \bar{x}),</math> | ||
: <math>\hat{\beta} = (1-\bar{x}) \left(\frac{\bar{x} (1 - \bar{x})}{\bar{v}} - 1 \right),</math> | : <math>\hat{\beta} = (1-\bar{x}) \left(\frac{\bar{x} (1 - \bar{x})}{\bar{v}} - 1 \right),</math> यदि <math>\bar{v}<\bar{x}(1 - \bar{x}).</math> | ||
जब यादृच्छिक | जब यादृच्छिक वेरिएबल X के साथ [0, 1] के अतिरिक्त किसी ज्ञात अंतराल पर वितरण की आवश्यकता होती है, तब कहें [a, c] यादृच्छिक वेरिएबल Y के साथ, फिर प्रतिस्थापित करें <math>\bar{x}</math> साथ <math>\frac{\bar{y}-a}{c-a},</math> और <math>\bar{v}</math> साथ <math>\frac{\bar{v_Y}}{(c-a)^2}</math> आकार के मापदंडों के लिए उपरोक्त कुछ समीकरणों में (वैकल्पिक पैरामीट्रिजेशन देखें, नीचे चार मापदंड अनुभाग)।,<ref>{{Cite web|url=https://www.itl.nist.gov/div898/handbook/eda/section3/eda366h.htm|title=1.3.6.6.17. Beta Distribution|website=www.itl.nist.gov}}</ref> जहाँ : | ||
: <math>\text{sample mean(Y)}=\bar{y} = \frac{1}{N}\sum_{i=1}^N Y_i</math> | : <math>\text{sample mean(Y)}=\bar{y} = \frac{1}{N}\sum_{i=1}^N Y_i</math> | ||
| Line 1,117: | Line 1,117: | ||
=== चार अज्ञात | === चार अज्ञात मापदंड === | ||
[[File:(alpha and beta) Parameter estimates vs. excess Kurtosis and (squared) Skewness Beta distribution - J. Rodal.png|thumb| | [[File:(alpha and beta) Parameter estimates vs. excess Kurtosis and (squared) Skewness Beta distribution - J. Rodal.png|thumb|मापदंड अनुमान बनाम (प्रतिरूप ) अतिरिक्त कर्टोसिस और (प्रतिरूप ) वर्ग विषमता बीटा वितरण के लिए समाधान]]सभी चार मापदंड (<math>\hat{\alpha}, \hat{\beta}, \hat{a}, \hat{c}</math> [a, c] अंतराल में समर्थित बीटा वितरण का - खंड देखें तथा बीटा वितरण या चार मापदंड को दर्शाए | वैकल्पिक पैरामीट्रिजेशन, चार मापदंड -) का अनुमान लगाया जा सकता है, कार्ल पियर्सन द्वारा विकसित क्षणों की विधि का उपयोग करके, पहले चार केंद्रीय क्षणों (माध्य, विचरण , विषमता और अतिरिक्त कर्टोसिस) के प्रतिरूप और संख्या मूल्यों को समान करके।<ref name=JKB/><ref name=Elderton1906/><ref name="Elderton and Johnson">{{cite book|last=Elderton|first=William Palin and Norman Lloyd Johnson|title=फ़्रीक्वेंसी कर्व्स की प्रणाली|year=2009|publisher=Cambridge University Press|isbn=978-0521093361}}</ref> अतिरिक्त कर्टोसिस को विषमता के वर्ग के संदर्भ में व्यक्त किया गया था, और प्रतिरूप आकार ν = α + β, (पिछला अनुभाग बीटा वितरण देखें या कर्टोसिस | ) इस प्रकार है: | ||
:<math>\text{excess kurtosis} =\frac{6}{3 + \nu}\left(\frac{(2 + \nu)}{4} (\text{skewness})^2 - 1\right)\text{ if (skewness)}^2-2< \text{excess kurtosis}< \tfrac{3}{2} (\text{skewness})^2</math> | :<math>\text{excess kurtosis} =\frac{6}{3 + \nu}\left(\frac{(2 + \nu)}{4} (\text{skewness})^2 - 1\right)\text{ if (skewness)}^2-2< \text{excess kurtosis}< \tfrac{3}{2} (\text{skewness})^2 </math> | ||
इस समीकरण का उपयोग | इस समीकरण का उपयोग प्रतिरूप आकार ν = α + β को विषमता के वर्ग और अतिरिक्त कर्टोसिस के रूप में हल करने के लिए किया जा सकता है:<ref name=Elderton1906/> | ||
:<math>\hat{\nu} = \hat{\alpha} + \hat{\beta} = 3\frac{(\text{sample excess kurtosis}) - (\text{sample skewness})^2+2}{\frac{3}{2} (\text{sample skewness})^2 - \text{(sample excess kurtosis)}}</math> | :<math>\hat{\nu} = \hat{\alpha} + \hat{\beta} = 3\frac{(\text{sample excess kurtosis}) - (\text{sample skewness})^2+2}{\frac{3}{2} (\text{sample skewness})^2 - \text{(sample excess kurtosis)}}</math> | ||
:<math>\text{ if (sample skewness)}^2-2< \text{sample excess kurtosis}< \tfrac{3}{2} (\text{sample skewness})^2</math> | :<math>\text{ if (sample skewness)}^2-2< \text{sample excess kurtosis}< \tfrac{3}{2} (\text{sample skewness})^2</math> | ||
यह अंतरिक्ष में बीटा वितरण के लिए पहले से व्युत्पन्न सीमा सीमाओं के | यह अंतरिक्ष में बीटा वितरण के लिए पहले से व्युत्पन्न सीमा सीमाओं के मध्य अनुपात (3 के कारक से गुणा) है (जैसा कि मूल रूप से कार्ल पियर्सन द्वारा किया गया था)<ref name=Pearson /> अक्ष में विषमता के वर्ग के निर्देशांक और दूसरे अक्ष में अतिरिक्त कर्टोसिस के साथ परिभाषित किया गया है (देखें {{section link||कर्टोसिस विषमता के वर्ग से घिरा हुआ है}}): | ||
शून्य | शून्य विषमता का स्तिथि तुरंत हल किया जा सकता है क्योंकि शून्य विषमता के लिए, α = β और इसलिए ν = 2α = 2β, इसलिए α = β = ν/2 | ||
: <math>\hat{\alpha} = \hat{\beta} = \frac{\hat{\nu}}{2}= \frac{\frac{3}{2}(\text{sample excess kurtosis}) +3}{- \text{(sample excess kurtosis)}}</math> | : <math>\hat{\alpha} = \hat{\beta} = \frac{\hat{\nu}}{2}= \frac{\frac{3}{2}(\text{sample excess kurtosis}) +3}{- \text{(sample excess kurtosis)}}</math> | ||
: <math> \text{ if sample skewness}= 0 \text{ and } -2<\text{sample excess kurtosis}<0</math> | : <math> \text{ if sample skewness}= 0 \text{ and } -2<\text{sample excess kurtosis}<0</math> | ||
(अतिरिक्त कर्टोसिस बीटा वितरण के लिए शून्य | (अतिरिक्त कर्टोसिस बीटा वितरण के लिए शून्य विषमता के साथ ऋणात्मक है, -2 से 0 तक, जिससे <math>\hat{\nu}</math> -और इसलिए प्रतिरूप आकार मापदंड- धनात्मक है, शून्य से लेकर जब आकार मापदंड शून्य तक पहुंचते हैं और अतिरिक्त कर्टोसिस -2 तक पहुंचते हैं, अनंत तक जब आकार मापदंड अनंत तक पहुंचते हैं और अतिरिक्त कुर्तबसिस शून्य तक पहुंचते हैं)। | ||
गैर-शून्य | गैर-शून्य प्रतिरूप विषमता के लिए है जो कि जिसमे दो युग्मित समीकरणों की प्रणाली को हल करने की आवश्यकता होती है। चूंकि विषमता और अतिरिक्त कर्टोसिस मापदंडों से स्वतंत्र हैं तथा <math>\hat{a}, \hat{c}</math>, मापदंड <math>\hat{\alpha}, \hat{\beta}</math> दो ज्ञात वेरिएबल (प्रतिरूप विषमता और प्रतिरूप अतिरिक्त कर्टोसिस) और दो अज्ञात (आकार मापदंड) के साथ युग्मित समीकरणों को हल करके प्रतिरूप विषमता और प्रतिरूप अतिरिक्त कर्टोसिस से विशिष्ट रूप से निर्धारित किया जा सकता है: | ||
:<math>(\text{sample skewness})^2 = \frac{4(\hat{\beta}-\hat{\alpha})^2 (1 + \hat{\alpha} + \hat{\beta})}{\hat{\alpha} \hat{\beta} (2 + \hat{\alpha} + \hat{\beta})^2}</math> | :<math>(\text{sample skewness})^2 = \frac{4(\hat{\beta}-\hat{\alpha})^2 (1 + \hat{\alpha} + \hat{\beta})}{\hat{\alpha} \hat{\beta} (2 + \hat{\alpha} + \hat{\beta})^2}</math> | ||
| Line 1,140: | Line 1,140: | ||
जिसके परिणामस्वरूप निम्नलिखित समाधान होता है:<ref name=Elderton1906/> | जिसके परिणामस्वरूप निम्नलिखित समाधान होता है:<ref name=Elderton1906/> | ||
: <math>\hat{\alpha}, \hat{\beta} = \frac{\hat{\nu}}{2} \left (1 \pm \frac{1}{ \sqrt{1+ \frac{16 (\hat{\nu} + 1)}{(\hat{\nu} + 2)^2(\text{sample skewness})^2}}} \right )</math> | : <math>\hat{\alpha}, \hat{\beta} = \frac{\hat{\nu}}{2} \left (1 \pm \frac{1}{ \sqrt{1+ \frac{16 (\hat{\nu} + 1)}{(\hat{\nu} + 2)^2(\text{sample skewness})^2}}} \right ) </math> | ||
: <math>\text{ if sample skewness}\neq 0 \text{ and } (\text{sample skewness})^2-2< \text{sample excess kurtosis}< \tfrac{3}{2} (\text{sample skewness})^2</math> | : <math>\text{ if sample skewness}\neq 0 \text{ and } (\text{sample skewness})^2-2< \text{sample excess kurtosis}< \tfrac{3}{2} (\text{sample skewness})^2</math> | ||
जहां निम्न प्रकार से उपाय करना चाहिए: <math>\hat{\alpha}>\hat{\beta}</math> के लिए ( | जहां निम्न प्रकार से उपाय करना चाहिए:जहाँ <math>\hat{\alpha}>\hat{\beta}</math> के लिए (ऋणात्मक ) प्रतिरूप विषम <0, और <math>\hat{\alpha}<\hat{\beta}</math> (धनात्मक) प्रतिरूप विषमता > 0 के लिए उपयोग किया जाता है । | ||
संलग्न प्लॉट इन दो समाधानों को अंतरिक्ष में सतहों के रूप में क्षैतिज अक्षों (प्रतिरूप अतिरिक्त कर्टोसिस) और (प्रतिरूप वर्ग विषमता) और ऊर्ध्वाधर अक्ष के रूप में आकार मापदंडों के साथ दिखाता है। सतहों को इस नियम से विवश किया जाता है कि प्रतिरूप अतिरिक्त कर्टोसिस उपरोक्त समीकरण में निर्धारित प्रतिरूप वर्ग विषमता से घिरा होना चाहिए। दो सतहें शून्य विषमता द्वारा परिभाषित दाहिने किनारे पर मिलती हैं। इस दाहिने किनारे के साथ,दोनों मापदंड समान हैं और वितरण α = β <1 के लिए सममित U- आकार का है, α = β = 1 के लिए समान है, 1 < α = β <2 के लिए उल्टा-U-आकार का है और बेल- α = β> 2 के लिए आकार। सतहें असंभव सीमा रेखा (अतिरिक्त कर्टोसिस + 2 - विषमता<sup>2</sup>) द्वारा परिभाषित सामने (निचले) किनारे पर भी मिलती हैं = 0). इस मोर्चे (निचली) सीमा के साथ दोनों आकार मापदंड शून्य तक पहुंचते हैं, और संभाव्यता घनत्व दूसरे छोर की तुलना में छोर पर अधिक केंद्रित होता है (व्यावहारिक रूप मध्य में कुछ भी नहीं होता है ), | |||
संभावनाओं के साथ <math>p=\tfrac{\beta}{\alpha + \beta}</math> बाएँ छोर पर x = 0 और <math>q = 1-p = \tfrac{\alpha}{\alpha + \beta} </math> दाएँ सिरे पर x = 1। पीछे के किनारे की ओर दो सतहें और दूर हो जाती हैं। इस पिछले किनारे पर सतह के मापदंड दूसरे से अधिक अलग हैं। जैसा कि टिप्पणी की गई है, उदाहरण के लिए, बोमन और शेंटन द्वारा,<ref name="BowmanShenton">{{cite journal|last=Bowman|first=K. O.|author1-link=Kimiko O. Bowman|author2=Shenton, L. R.|title=बीटा वितरण, क्षण विधि, कार्ल पियर्सन और आर.ए. मछुआ|journal=Far East J. Theo. Stat.|year=2007|volume=23|issue=2|pages=133–164| url=http://www.csm.ornl.gov/~bowman/fjts232.pdf }}</ref> लाइन के निकटतम में प्रतिरूप करण (प्रतिरूप अतिरिक्त कुर्तबसिस - (3/2)(प्रतिरूप विषमता)<sup>2</sup> = 0) (पीछे के किनारे का जस्ट-जे-आकार का भाग जहां नीला बेज रंग से मिलता है), खतरनाक रूप से अराजकता के समीप है, क्योंकि उस रेखा पर अनुमान के लिए उपरोक्त अभिव्यक्ति का भाजक ν = α + β शून्य हो जाता है और इसलिए ν अनंत तक पहुंचता है क्योंकि उस रेखा तक पहुंच जाती है। बोमन और शेंटन <ref name="BowmanShenton" />लिखें कि उच्च क्षण के मापदंड (कर्टोसिस और विषमता) अत्यधिक नाजुक (उस रेखा के पास) हैं। चूंकि, माध्य और मानक विचलन अधिक विश्वसनीय हैं। इसलिए, समस्या बहुत विषम वितरणों के लिए चार मापदंड अनुमान के स्तिथियों के लिए है, जैसे कि अतिरिक्त कर्टोसिस विषमता के वर्ग (3/2) गुना तक पहुंचता है। यह सीमा रेखा मापदंड के बहुत बड़े मूल्यों और दूसरे मापदंड के बहुत छोटे मूल्यों के साथ अत्यंत विषम वितरणों द्वारा निर्मित होती है। देखना {{section link||कर्टोसिस विषमता के वर्ग से घिरा हुआ है}} संख्यात्मक उदाहरण के लिए और इस रियर एज सीमा रेखा के बारे में आगे की टिप्पणी (प्रतिरूप अतिरिक्त कर्टोसिस - (3/2) (प्रतिरूप विषमता)<sup>2</sup> = 0). जैसा कि स्वयं कार्ल पियर्सन ने टिप्पणी की है <ref name="Pearson1936" />यह उद्देश्य अधिक व्यावहारिक महत्व का नहीं हो सकता है क्योंकि यह समस्या केवल बहुत विषम जे-आकार (या दर्पण-छवि जे-आकार) वितरण के लिए उत्पन्न होती है, जो आकार के मापदंडों के बहुत अलग मूल्यों के साथ होती है जो व्यवहार में बहुत अधिक होने की संभावना नहीं है)। अभ्यास में होने वाले सामान्य विषम-बेल-आकार के वितरण में यह मापदंड अनुमान समस्या नहीं होती है। | |||
शेष दो | शेष दो मापदंड <math>\hat{a}, \hat{c}</math> विभिन्न समीकरणों का उपयोग करके प्रतिरूप माध्य और प्रतिरूप भिन्नता का उपयोग करके निर्धारित किया जा सकता है।<ref name="JKB" /><ref name="Elderton1906" /> विकल्प समर्थन अंतराल सीमा की गणना करना है <math>(\hat{c}-\hat{a})</math> प्रतिरूप विचरण और प्रतिरूप कर्टोसिस के आधार पर होता है। इस प्रयोजन के लिए कोई भी सीमा के संदर्भ में हल कर सकता है <math>(\hat{c}- \hat{a})</math>, प्रतिरूप विचरण और प्रतिरूप आकार ν के संदर्भ में अतिरिक्त कुर्तबसिस को व्यक्त करने वाला समीकरण (देखें {{section link||कर्टोसिस}} और {{section link||वैकल्पिक पैरामीट्रिज़ेशन, चार पैरामीटर}}): | ||
:<math>\text{sample excess kurtosis} =\frac{6}{(3 + \hat{\nu})(2 + \hat{\nu})}\bigg(\frac{(\hat{c}- \hat{a})^2}{\text{(sample variance)}} - 6 - 5 \hat{\nu} \bigg)</math> | :<math>\text{sample excess kurtosis} =\frac{6}{(3 + \hat{\nu})(2 + \hat{\nu})}\bigg(\frac{(\hat{c}- \hat{a})^2}{\text{(sample variance)}} - 6 - 5 \hat{\nu} \bigg)</math> | ||
| Line 1,152: | Line 1,154: | ||
:<math> (\hat{c}- \hat{a}) = \sqrt{\text{(sample variance)}}\sqrt{6+5\hat{\nu}+\frac{(2+\hat{\nu})(3+\hat{\nu})}{6}\text{(sample excess kurtosis)}}</math> | :<math> (\hat{c}- \hat{a}) = \sqrt{\text{(sample variance)}}\sqrt{6+5\hat{\nu}+\frac{(2+\hat{\nu})(3+\hat{\nu})}{6}\text{(sample excess kurtosis)}}</math> | ||
एक अन्य विकल्प समर्थन अंतराल सीमा | एक अन्य विकल्प समर्थन में अंतराल सीमा <math>(\hat{c}-\hat{a})</math> की गणना करना है और प्रतिरूप विचरण और प्रतिरूप विषमता के आधार पर उपयोग किया जाता है ।<ref name=Elderton1906/> इस प्रयोजन के लिए कोई भी इसको सीमा <math>(\hat{c}-\hat{a})</math> के संदर्भ में प्रतिरूप विचरण के संदर्भ में वर्ग विषमता व्यक्त करने वाला समीकरण और प्रतिरूप आकार ν हल कर सकता है (विषमता और वैकल्पिक पैरामीट्रिजेशन शीर्षक वाला अनुभाग देखें, चार मापदंड): | ||
:<math>(\text{sample skewness})^2 = \frac{4}{(2+\hat{\nu})^2}\bigg(\frac{(\hat{c}- \hat{a})^2}{ \text{(sample variance)}}-4(1+\hat{\nu})\bigg)</math> | :<math>(\text{sample skewness})^2 = \frac{4}{(2+\hat{\nu})^2}\bigg(\frac{(\hat{c}- \hat{a})^2}{ \text{(sample variance)}}-4(1+\hat{\nu})\bigg)</math> | ||
| Line 1,158: | Line 1,160: | ||
:<math> (\hat{c}- \hat{a}) = \frac{\sqrt{\text{(sample variance)}}}{2}\sqrt{(2+\hat{\nu})^2(\text{sample skewness})^2+16(1+\hat{\nu})}</math> | :<math> (\hat{c}- \hat{a}) = \frac{\sqrt{\text{(sample variance)}}}{2}\sqrt{(2+\hat{\nu})^2(\text{sample skewness})^2+16(1+\hat{\nu})}</math> | ||
शेष | शेष मापदंड प्रतिरूप माध्य और पहले प्राप्त मापदंड से निर्धारित किया जा सकता है: <math>(\hat{c}-\hat{a}), \hat{\alpha}, \hat{\nu} = \hat{\alpha}+\hat{\beta}</math>: | ||
:<math> \hat{a} = (\text{sample mean}) - \left(\frac{\hat{\alpha}}{\hat{\nu}}\right)(\hat{c}-\hat{a}) </math> | :<math> \hat{a} = (\text{sample mean}) - \left(\frac{\hat{\alpha}}{\hat{\nu}}\right)(\hat{c}-\hat{a}) </math> | ||
और अंत में, <math>\hat{c}= (\hat{c}- \hat{a}) + \hat{a} </math>. | और अंत में, <math>\hat{c}= (\hat{c}- \hat{a}) + \hat{a} </math>. | ||
उपरोक्त सूत्रों में, उदाहरण के लिए, | उपरोक्त सूत्रों में, उदाहरण के लिए, प्रतिरूप क्षणों के अनुमान के रूप में लिया जा सकता है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,170: | Line 1,172: | ||
\text{sample skewness} &= G_1 = \frac{N}{(N-1)(N-2)} \frac{\sum_{i=1}^N (Y_i-\overline{y})^3}{\overline{v}_Y^{\frac{3}{2}} } \\ | \text{sample skewness} &= G_1 = \frac{N}{(N-1)(N-2)} \frac{\sum_{i=1}^N (Y_i-\overline{y})^3}{\overline{v}_Y^{\frac{3}{2}} } \\ | ||
\text{sample excess kurtosis} &= G_2 = \frac{N(N+1)}{(N-1)(N-2)(N-3)} \frac{\sum_{i=1}^N (Y_i - \overline{y})^4}{\overline{v}_Y^2} - \frac{3(N-1)^2}{(N-2)(N-3)} | \text{sample excess kurtosis} &= G_2 = \frac{N(N+1)}{(N-1)(N-2)(N-3)} \frac{\sum_{i=1}^N (Y_i - \overline{y})^4}{\overline{v}_Y^2} - \frac{3(N-1)^2}{(N-2)(N-3)} | ||
\end{align}</math> | \end{align} </math> | ||
अनुमानक | अनुमानक G<sub>1</sub> विषमता और G<sub>2</sub> के लिए कर्टोसिस के लिए [[डीएपी (सॉफ्टवेयर)]]/[[एसएएस सिस्टम|एसएएस प्रणाली]] , [[पीएसपीपी]]/[[एसपीएसएस]] और [[Index.php?title=माइक्रोसॉफ्ट एक्सेल|माइक्रोसॉफ्ट एक्सेल]] द्वारा उपयोग किया जाता है। चूँकि, उनका उपयोग [[Index.php?title=बीएमडीपी|बीएमडीपी]] द्वारा नहीं किया जाता है और (के अनुसार <ref name="Joanes and Gill"/> वे 1998 में [[Index.php?title=मिनीटैब|मिनीटैब]] द्वारा उपयोग नहीं किए गए थे। दरअसल, जोनेस और गिल ने 1998 के अपने अध्ययन में<ref name="Joanes and Gill">{{cite journal|last=Joanes|first=D. N.|author2=C. A. Gill|title=नमूना तिरछापन और कर्टोसिस के उपायों की तुलना करना|journal=The Statistician|year=1998|volume=47|issue=Part 1|pages=183–189|doi=10.1111/1467-9884.00122}}</ref> निष्कर्ष निकाला कि [[Index.php?title=बीएमडीपी|बीएमडीपी]] और मिनीटैब (उस समय) में उपयोग किए जाने वाले विषमता और कर्टोसिस अनुमानक में सामान्य प्रतिरूपों में छोटा विचलन और माध्य-वर्ग त्रुटि थी, किन्तु DAP (सॉफ़्टवेयर)/SAS प्रणाली, PSPP/SPSS में उपयोग किए जाने वाले विषमता और कुर्तबसिस अनुमानक, अर्थात् G<sub>1</sub> और G<sub>2</sub>, बहुत ही विषम वितरण से प्रतिरूपों में छोटी माध्य-वर्गीय त्रुटि थी। यह इस कारण से है कि हमने उपरोक्त सूत्रों में प्रतिरूप विषमता आदि को स्पष्ट किया है, जिससेयह स्पष्ट हो सके कि उपयोगकर्ता को समस्या के अनुसार सबसे अच्छा अनुमानक चुनना चाहिए, क्योंकि विषमता और कर्टोसिस के लिए सबसे अच्छा अनुमानक निर्भर करता है और विषमता की मात्रा बताता है (जैसा कि जोनेस और गिल द्वारा दिखाया गया है<ref name="Joanes and Gill"/>). | ||
==== अधिकतम संभावना ==== | ==== अधिकतम संभावना ==== | ||
=== दो अज्ञात | === दो अज्ञात मापदंड === | ||
जैसा कि गामा वितरण के लिए अधिकतम संभावना अनुमानों के स्तिथियों में भी है, वैसे ही बीटा वितरण के लिए अधिकतम संभावना अनुमानों में आकृति मापदंडों के इच्छानुसार मूल्यों के लिए सामान्य विवृत रूप समाधान नहीं है। यदि स्वतंत्र यादृच्छिक वेरिएबल X<sub>1</sub>, ..., X<sub>N</sub> हैं जिनमें से प्रत्येक में बीटा वितरण है, N [[स्वतंत्र और समान रूप से वितरित यादृच्छिक चर|स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल]] अवलोकनों के लिए संयुक्त लॉग संभावना कार्य करता है: | |||
जैसा कि गामा वितरण के लिए अधिकतम संभावना अनुमानों के | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,186: | Line 1,185: | ||
&= \sum_{i=1}^N \ln \left (\frac{X_i^{\alpha-1}(1-X_i)^{\beta-1}}{\Beta(\alpha,\beta)} \right ) \\ | &= \sum_{i=1}^N \ln \left (\frac{X_i^{\alpha-1}(1-X_i)^{\beta-1}}{\Beta(\alpha,\beta)} \right ) \\ | ||
&= (\alpha - 1)\sum_{i=1}^N \ln (X_i) + (\beta- 1)\sum_{i=1}^N \ln (1-X_i) - N \ln \Beta(\alpha,\beta) | &= (\alpha - 1)\sum_{i=1}^N \ln (X_i) + (\beta- 1)\sum_{i=1}^N \ln (1-X_i) - N \ln \Beta(\alpha,\beta) | ||
\end{align}</math> | \end{align} </math> | ||
आकार | आकार मापदंड के संबंध में अधिकतम ढूँढना तथा आकार मापदंड के संबंध में आंशिक व्युत्पन्न लेना और अभिव्यक्ति मापदंड के अधिकतम संभावना अनुमानक को शून्य के सामान्तर अभिव्यक्ति समुच्चय करना सम्मिलित है: | ||
:<math>\frac{\partial \ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \alpha} = \sum_{i=1}^N \ln X_i -N\frac{\partial \ln \Beta(\alpha,\beta)}{\partial \alpha}=0</math> | :<math>\frac{\partial \ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \alpha} = \sum_{i=1}^N \ln X_i -N\frac{\partial \ln \Beta(\alpha,\beta)}{\partial \alpha}=0</math> | ||
:<math>\frac{\partial \ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \beta} = \sum_{i=1}^N \ln (1-X_i)- N\frac{\partial \ln \mathrm{B}(\alpha,\beta)}{\partial \beta}=0</math> | :<math>\frac{\partial \ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \beta} = \sum_{i=1}^N \ln (1-X_i)- N\frac{\partial \ln \mathrm{B}(\alpha,\beta)}{\partial \beta}=0</math> | ||
जहाँ : | |||
:<math>\frac{\partial \ln \Beta(\alpha,\beta)}{\partial \alpha} = -\frac{\partial \ln \Gamma(\alpha+\beta)}{\partial \alpha}+ \frac{\partial \ln \Gamma(\alpha)}{\partial \alpha}+ \frac{\partial \ln \Gamma(\beta)}{\partial \alpha}=-\psi(\alpha + \beta) + \psi(\alpha) + 0</math> | :<math>\frac{\partial \ln \Beta(\alpha,\beta)}{\partial \alpha} = -\frac{\partial \ln \Gamma(\alpha+\beta)}{\partial \alpha}+ \frac{\partial \ln \Gamma(\alpha)}{\partial \alpha}+ \frac{\partial \ln \Gamma(\beta)}{\partial \alpha}=-\psi(\alpha + \beta) + \psi(\alpha) + 0</math> | ||
:<math>\frac{\partial \ln \Beta(\alpha,\beta)}{\partial \beta}= - \frac{\partial \ln \Gamma(\alpha+\beta)}{\partial \beta}+ \frac{\partial \ln \Gamma(\alpha)}{\partial \beta} + \frac{\partial \ln \Gamma(\beta)}{\partial \beta}=-\psi(\alpha + \beta) + 0 + \psi(\beta)</math> | :<math>\frac{\partial \ln \Beta(\alpha,\beta)}{\partial \beta}= - \frac{\partial \ln \Gamma(\alpha+\beta)}{\partial \beta}+ \frac{\partial \ln \Gamma(\alpha)}{\partial \beta} + \frac{\partial \ln \Gamma(\beta)}{\partial \beta}=-\psi(\alpha + \beta) + 0 + \psi(\beta)</math> | ||
चूंकि डिगामा | चूंकि डिगामा फलन ने ψ(α) को निरूपित किया है, इसे गामा फलन के लॉगरिदमिक व्युत्पन्न के रूप में परिभाषित किया गया है:<ref name=Abramowitz/> | ||
:<math>\psi(\alpha) =\frac {\partial\ln \Gamma(\alpha)}{\partial \alpha}</math> | :<math>\psi(\alpha) =\frac {\partial\ln \Gamma(\alpha)}{\partial \alpha}</math> | ||
यह सुनिश्चित करने के लिए कि शून्य स्पर्शरेखा | यह सुनिश्चित करने के लिए कि शून्य स्पर्शरेखा स्लोप वाले मान वास्तव में अधिकतम हैं (एक सैडल-पॉइंट या न्यूनतम के अतिरिक्त) किसी को भी इस नियम को पूरा करना होगा कि वक्रता ऋणात्मक है। यह संतबषजनक है कि आकार के मापदंडों के संबंध में दूसरा आंशिक व्युत्पन्न ऋणात्मक है | ||
:<math>\frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \alpha^2}= -N\frac{\partial^2\ln \Beta(\alpha,\beta)}{\partial \alpha^2}<0</math> | :<math>\frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \alpha^2}= -N\frac{\partial^2\ln \Beta(\alpha,\beta)}{\partial \alpha^2}<0</math> | ||
: | |||
:<math>\frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \beta^2} = -N\frac{\partial^2\ln \Beta(\alpha,\beta)}{\partial \beta^2}<0</math> | :<math>\frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \beta^2} = -N\frac{\partial^2\ln \Beta(\alpha,\beta)}{\partial \beta^2}<0</math> | ||
पिछले समीकरणों का उपयोग करते हुए, यह इसके | पिछले समीकरणों का उपयोग करते हुए, यह इसके सामान्तर है: | ||
:<math>\frac{\partial^2\ln \Beta(\alpha,\beta)}{\partial \alpha^2} = \psi_1(\alpha)-\psi_1(\alpha + \beta) > 0</math> | :<math>\frac{\partial^2\ln \Beta(\alpha,\beta)}{\partial \alpha^2} = \psi_1(\alpha)-\psi_1(\alpha + \beta) > 0</math> | ||
: | |||
:<math>\frac{\partial^2\ln \Beta(\alpha,\beta)}{\partial \beta^2} = \psi_1(\beta) -\psi_1(\alpha + \beta) > 0</math> | :<math>\frac{\partial^2\ln \Beta(\alpha,\beta)}{\partial \beta^2} = \psi_1(\beta) -\psi_1(\alpha + \beta) > 0</math> | ||
जहां त्रिगामा | जहां त्रिगामा फलन, ''ψ<sub>1</sub>(α)'' को निरूपित करता है,तथा बहुग्राम कार्यों का दूसरा है, और इसे डिगामा फलन के व्युत्पन्न के रूप में परिभाषित किया गया है: | ||
:<math>\psi_1(\alpha) = \frac{\partial^2\ln\Gamma(\alpha)}{\partial \alpha^2}=\, \frac{\partial\, \psi(\alpha)}{\partial \alpha}.</math> | :<math>\psi_1(\alpha) = \frac{\partial^2\ln\Gamma(\alpha)}{\partial \alpha^2}=\, \frac{\partial\, \psi(\alpha)}{\partial \alpha}.</math> | ||
ये स्थितियाँ यह बताने के | ये स्थितियाँ यह बताने के सामान्तर हैं कि लघुगणक रूप से परिवर्तित वेरिएबल के प्रसरण धनात्मक हैं, क्योंकि: | ||
:<math>\operatorname{var}[\ln (X)] = \operatorname{E}[\ln^2 (X)] - (\operatorname{E}[\ln (X)])^2 = \psi_1(\alpha) - \psi_1(\alpha + \beta) </math> | :<math>\operatorname{var}[\ln (X)] = \operatorname{E}[\ln^2 (X)] - (\operatorname{E}[\ln (X)])^2 = \psi_1(\alpha) - \psi_1(\alpha + \beta) </math> | ||
: | |||
:<math>\operatorname{var}[\ln (1-X)] = \operatorname{E}[\ln^2 (1-X)] - (\operatorname{E}[\ln (1-X)])^2 = \psi_1(\beta) - \psi_1(\alpha + \beta) </math> | :<math>\operatorname{var}[\ln (1-X)] = \operatorname{E}[\ln^2 (1-X)] - (\operatorname{E}[\ln (1-X)])^2 = \psi_1(\beta) - \psi_1(\alpha + \beta) </math> | ||
इसलिए, अधिकतम ऋणात्मक वक्रता की स्थिति | इसलिए, अधिकतम ऋणात्मक वक्रता की स्थिति कथनों के सामान्तर है: | ||
: <math> \operatorname{var}[\ln (X)] > 0</math> | : <math> \operatorname{var}[\ln (X)] > 0</math> | ||
: <math> \operatorname{var}[\ln (1-X)] > 0</math> | : <math> \operatorname{var}[\ln (1-X)] > 0</math> | ||
वैकल्पिक रूप से, अधिकतम पर | वैकल्पिक रूप से, अधिकतम पर ऋणात्मक वक्रता की स्थिति भी यह बताने के सामान्तर है कि ज्यामितीय के निम्न लघुगणकीय डेरिवेटिव का अर्थ G<sub>X</sub> और G<sub>(1−X)</sub> धनात्मक हैं, क्योंकि: | ||
: <math>\psi_1(\alpha) - \psi_1(\alpha + \beta) = \frac{\partial \ln G_X}{\partial \alpha} > 0</math> | : <math>\psi_1(\alpha) - \psi_1(\alpha + \beta) = \frac{\partial \ln G_X}{\partial \alpha} > 0</math> | ||
: <math>\psi_1(\beta) - \psi_1(\alpha + \beta) = \frac{\partial \ln G_{(1-X)}}{\partial \beta} > 0</math> | : <math>\psi_1(\beta) - \psi_1(\alpha + \beta) = \frac{\partial \ln G_{(1-X)}}{\partial \beta} > 0</math> | ||
जबकि ये | जबकि ये स्लोप वास्तव में धनात्मक हैं, अन्य स्लोप ऋणात्मक हैं: | ||
:<math>\frac{\partial\, \ln G_X}{\partial \beta}, \frac{\partial \ln G_{(1-X)}}{\partial \alpha} < 0.</math> | :<math>\frac{\partial\, \ln G_X}{\partial \beta}, \frac{\partial \ln G_{(1-X)}}{\partial \alpha} < 0.</math> | ||
α और β के संबंध में माध्य और माध्यिका के | α और β के संबंध में माध्य और माध्यिका के स्लोप समान संकेत व्यवहार प्रदर्शित करते हैं। | ||
इस | इस नियम के अनुसार अधिकतम आकार मापदंड के संबंध में आंशिक व्युत्पन्न शून्य के सामान्तर है, तथा हम युग्मित [[अधिकतम संभावना अनुमान]] समीकरणों की निम्नलिखित प्रणाली प्राप्त करते हैं (औसत लॉग-संभावना के लिए) जिसे (अज्ञात) प्राप्त करने के लिए उलटा करने की आवश्यकता होती है। आकार मापदंड अनुमान X<sub>1</sub>, ..., X<sub>N</sub>: प्रतिरूप के लॉगरिदम के (ज्ञात) औसत के संदर्भ में <math>\hat{\alpha},\hat{\beta}</math> होते है <ref name=JKB /> | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,232: | Line 1,234: | ||
\hat{\operatorname{E}}[\ln(1-X)] &= \psi(\hat{\beta}) - \psi(\hat{\alpha} + \hat{\beta})=\frac{1}{N}\sum_{i=1}^N \ln (1-X_i)= \ln \hat{G}_{(1-X)} | \hat{\operatorname{E}}[\ln(1-X)] &= \psi(\hat{\beta}) - \psi(\hat{\alpha} + \hat{\beta})=\frac{1}{N}\sum_{i=1}^N \ln (1-X_i)= \ln \hat{G}_{(1-X)} | ||
\end{align}</math> | \end{align}</math> | ||
जहां हम | जहां हम प्रतिरूप ज्यामितीय माध्य के लघुगणक के रूप में <math>\log \hat{G}_X </math> को पहचानते हैं और <math>\log \hat{G}_{(1-X)}</math> (को लघुगणक के रूप में पहचानते है 1 − X), आधारित प्रतिरूप ज्यामितीय माध्य । के लिए X की दर्पण छवि पर <math>\hat{\alpha}=\hat{\beta}</math>,उपयोग किया जाता है यह इस प्रकार है कि <math>\hat{G}_X=\hat{G}_{(1-X)} </math>.होगा | ||
: | |||
:<math>\begin{align} | :<math>\begin{align} | ||
\hat{G}_X &= \prod_{i=1}^N (X_i)^{1/N} \\ | \hat{G}_X &= \prod_{i=1}^N (X_i)^{1/N} \\ | ||
\hat{G}_{(1-X)} &= \prod_{i=1}^N (1-X_i)^{1/N} | \hat{G}_{(1-X)} &= \prod_{i=1}^N (1-X_i)^{1/N} | ||
\end{align}</math> | \end{align}</math> | ||
आकार | : | ||
आकार मापदंड अनुमानों के डिगामा कार्यों वाले ये युग्मित समीकरण <math>\hat{\alpha},\hat{\beta}</math> संख्यात्मक विधियों द्वारा हल किया जाना चाहिए, उदाहरण के लिए, बेकमैन एट अल द्वारा।<ref>{{cite journal|last=Beckman|first=R. J.|author2=G. L. Tietjen|title=बीटा वितरण के लिए अधिकतम संभावना अनुमान|journal=Journal of Statistical Computation and Simulation|year=1978|volume=7|issue=3–4|pages=253–258|doi=10.1080/00949657808810232}}</ref> ज्ञानदेसिकन एट अल। कुछ स्थितियों के लिए संख्यात्मक समाधान दें।<ref>{{cite journal |last=Gnanadesikan |first=R.,Pinkham and Hughes|title=सबसे छोटे क्रम के आँकड़ों से बीटा वितरण के मापदंडों का अधिकतम संभावना अनुमान|journal=Technometrics |year=1967|volume=9|issue=4|pages=607–620 |doi=10.2307/1266199|jstor=1266199}}</ref> नॉर्मन लॉयड जॉनसन|एन.एल.जॉनसन और सैमुअल कोटज़|एस.कोट्ज़<ref name=JKB />सुझाव है कि बहुत छोटे आकार के मापदंड अनुमानों के लिए नहीं <math>\hat{\alpha},\hat{\beta}</math>, डिगामा फलन के लिए लॉगरिदमिक सन्निकटन <math>\psi(\hat{\alpha}) \approx \ln(\hat{\alpha}-\tfrac{1}{2})</math> पुनरावृत्त समाधान के लिए प्रारंभिक मान प्राप्त करने के लिए उपयोग किया जा सकता है, क्योंकि इस सन्निकटन से उत्पन्न समीकरणों को ठीक से हल किया जा सकता है: | |||
: | |||
:<math>\ln \frac{\hat{\alpha} - \frac{1}{2}}{\hat{\alpha} + \hat{\beta} - \frac{1}{2}} \approx \ln \hat{G}_X </math> | :<math>\ln \frac{\hat{\alpha} - \frac{1}{2}}{\hat{\alpha} + \hat{\beta} - \frac{1}{2}} \approx \ln \hat{G}_X </math> | ||
:<math>\ln \frac{\hat{\beta} - \frac{1}{2}}{\hat{\alpha} + \hat{\beta} - \frac{1}{2}}\approx \ln \hat{G}_{(1-X)} </math> | :<math>\ln \frac{\hat{\beta} - \frac{1}{2}}{\hat{\alpha} + \hat{\beta} - \frac{1}{2}}\approx \ln \hat{G}_{(1-X)} </math> | ||
जो पुनरावृत्त समाधान के लिए प्रारंभिक मानों ( | जो पुनरावृत्त समाधान के लिए प्रारंभिक मानों (प्रतिरूप ज्यामितीय साधनों के संदर्भ में अनुमान आकार मापदंडों के) के लिए निम्नलिखित समाधान की ओर ले जाता है: | ||
:<math>\hat{\alpha}\approx \tfrac{1}{2} + \frac{\hat{G}_{X}}{2(1-\hat{G}_X-\hat{G}_{(1-X)})} \text{ if } \hat{\alpha} >1</math> | :<math>\hat{\alpha}\approx \tfrac{1}{2} + \frac{\hat{G}_{X}}{2(1-\hat{G}_X-\hat{G}_{(1-X)})} \text{ if } \hat{\alpha} >1</math> | ||
| Line 1,248: | Line 1,253: | ||
वैकल्पिक रूप से, क्षणों की विधि द्वारा प्रदान किए गए अनुमानों को डिगम्मा कार्यों के संदर्भ में अधिकतम संभावना युग्मित समीकरणों के पुनरावृत्त समाधान के लिए प्रारंभिक मानों के रूप में उपयोग किया जा सकता है। | वैकल्पिक रूप से, क्षणों की विधि द्वारा प्रदान किए गए अनुमानों को डिगम्मा कार्यों के संदर्भ में अधिकतम संभावना युग्मित समीकरणों के पुनरावृत्त समाधान के लिए प्रारंभिक मानों के रूप में उपयोग किया जा सकता है। | ||
जब | जब किसी ज्ञात अंतराल पर वितरण की आवश्यकता होती है, [0, 1] यादृच्छिक वेरिएबल X के साथ के अतिरिक्त तब [a, c] को यादृच्छिक वेरिएबल Y के साथ कहें, फिर पहले समीकरण में ln(X<sub>i</sub>) को बदलें | | ||
:<math>\ln \frac{Y_i-a}{c-a},</math> | :<math>\ln \frac{Y_i-a}{c-a},</math> | ||
| Line 1,254: | Line 1,259: | ||
:<math>\ln \frac{c-Y_i}{c-a}</math> | :<math>\ln \frac{c-Y_i}{c-a}</math> | ||
(नीचे वैकल्पिक पैरामीट्रिजेशन, चार | (नीचे वैकल्पिक पैरामीट्रिजेशन, चार मापदंड अनुभाग देखें)। | ||
यदि आकार के मापदंडों में से ज्ञात है, | यदि आकार के मापदंडों में से ज्ञात है, तब समस्या अधिक सरल हो जाती है। निम्नलिखित लॉग परिवर्तन का उपयोग अज्ञात आकार मापदंड के लिए हल करने के लिए किया जा सकता है (विषम स्थितियों के लिए जैसे कि <math>\hat{\alpha}\neq\hat{\beta}</math>, अन्यथा, यदि सममित, दोनों-सामान्तर-मापदंड ज्ञात होने पर ज्ञात होते हैं): | ||
:<math>\hat{\operatorname{E}} \left[\ln \left(\frac{X}{1-X} \right) \right]=\psi(\hat{\alpha}) - \psi(\hat{\beta})=\frac{1}{N}\sum_{i=1}^N \ln\frac{X_i}{1-X_i} = \ln \hat{G}_X - \ln \left(\hat{G}_{(1-X)}\right) </math> | :<math>\hat{\operatorname{E}} \left[\ln \left(\frac{X}{1-X} \right) \right]=\psi(\hat{\alpha}) - \psi(\hat{\beta})=\frac{1}{N}\sum_{i=1}^N \ln\frac{X_i}{1-X_i} = \ln \hat{G}_X - \ln \left(\hat{G}_{(1-X)}\right) </math> | ||
यह लॉगिट | यह लॉगिट परिवर्तन का लघुगणक है जो वेरिएबल X को उसकी दर्पण-छवि (X/1 - X) से विभाजित करता है जिसके परिणाम स्वरूप उलटा बीटा वितरण या बीटा प्राइम वितरण होता है (जिसे दूसरी तरह के बीटा वितरण या पियर्सन के प्रकार VI के रूप में भी जाना जाता है) | समर्थन के साथ [0, +∞) जैसा कि पहले अनुभाग में लघुगणक रूप से परिवर्तित यादृच्छिक वेरिएबल के क्षण", की खण्ड में चर्चा की गई थी| जॉनसन द्वारा अध्ययन लघुगणक परिवर्तन <math>\ln\frac{X}{1-X}</math>, किया गया, के आधार पर परिमित समर्थन [0, 1] का विस्तार करता है।<ref name=JohnsonLogInv/> वास्तविक रेखा (−∞, +∞) की दोनों दिशाओं में अनंत समर्थन के लिए मूल वेरिएबल X होता है | | ||
यदि, उदाहरण के लिए, <math>\hat{\beta}</math> ज्ञात है, अज्ञात | यदि, उदाहरण के लिए, <math>\hat{\beta}</math> ज्ञात है, अज्ञात मापदंड <math>\hat{\alpha}</math> प्रतिलोम के रूप में प्राप्त किया जा सकता है<ref name=invpsi.m>{{cite web|last=Fackler |first=Paul|title=उलटा दिग्मा समारोह (मतलब)|url=http://hips.seas.harvard.edu/content/inverse-digamma-function-matlab|publisher=Harvard University School of Engineering and Applied Sciences|access-date=2012-08-18}}</ref> इस समीकरण के दाहिने हाथ की ओर का डिगम्मा कार्य: | ||
:<math>\psi(\hat{\alpha})=\frac{1}{N}\sum_{i=1}^N \ln\frac{X_i}{1-X_i} + \psi(\hat{\beta}) </math> | :<math>\psi(\hat{\alpha})=\frac{1}{N}\sum_{i=1}^N \ln\frac{X_i}{1-X_i} + \psi(\hat{\beta}) </math> | ||
: | |||
:<math>\hat{\alpha}=\psi^{-1}(\ln \hat{G}_X - \ln \hat{G}_{(1-X)} + \psi(\hat{\beta})) </math> | :<math>\hat{\alpha}=\psi^{-1}(\ln \hat{G}_X - \ln \hat{G}_{(1-X)} + \psi(\hat{\beta})) </math> | ||
विशेष रूप से, यदि आकार के मापदंडों में से में एकता का मान है, उदाहरण के लिए <math>\hat{\beta} = 1</math> (परिबद्ध समर्थन | विशेष रूप से, यदि आकार के मापदंडों में से में एकता का मान है, उदाहरण के लिए <math>\hat{\beta} = 1</math> (परिबद्ध समर्थन के साथ पावर फलन वितरण),[0,1] पहचान ψ(x + 1) का उपयोग करके = ψ(x) + 1/x समीकरण में <math>\psi(\hat{\alpha}) - \psi(\hat{\alpha} + \hat{\beta})= \ln \hat{G}_X</math>, अज्ञात मापदंड <math>\hat{\alpha}</math> के लिए अधिकतम संभावना अनुमानक है,<ref name=JKB />बिल्कुल: | ||
: | |||
:<math>\hat{\alpha}= - \frac{1}{\frac{1}{N}\sum_{i=1}^N \ln X_i}= - \frac{1}{ \ln \hat{G}_X} </math> | :<math>\hat{\alpha}= - \frac{1}{\frac{1}{N}\sum_{i=1}^N \ln X_i}= - \frac{1}{ \ln \hat{G}_X} </math> | ||
: | |||
अंत में, बीटा वितरण के आकार मापदंडों के अधिकतम संभावना अनुमान (सामान्य रूप से) | बीटा का समर्थन [0, 1] है इसलिए <math>\hat{G}_X < 1</math>, और इसलिए <math>(-\ln \hat{G}_X) >0</math>, और इसलिए <math>\hat{\alpha} >0.</math> | ||
अंत में, बीटा वितरण के आकार मापदंडों के अधिकतम संभावना अनुमान (सामान्य रूप से) प्रतिरूप ज्यामितीय माध्य का जटिल कार्य है, और प्रतिरूप ज्यामितीय माध्य (1−X), X की दर्पण-छवि पर आधारित है। कोई पूछ सकता है, यदि क्षणों की विधि के साथ दो आकृति मापदंडों का अनुमान लगाने के लिए विचरण (माध्य के अतिरिक्त) आवश्यक है, तब अधिकतम संभावना विधि के साथ दो आकार के मापदंडों का अनुमान लगाने के लिए (लघुगणक या ज्यामितीय) विचरण क्यों आवश्यक नहीं है? कौन सा केवल ज्यामितीय का कारणपर्याप्त है? उत्तर इसलिए है क्योंकि माध्य उतनी जानकारी प्रदान नहीं करता जितनी कि ज्यामितीय माध्य। समान आकार के मापदंडों α = β के साथ बीटा वितरण के लिए, आकृति मापदंडों के मान की परवाह किए बिना, और इसलिए सांख्यिकीय फैलाव (भिन्नता) के मूल्य की परवाह किए बिना, माध्य ठीक 1/2 है। दूसरी ओर, समान आकार के मापदंड α=β के साथ बीटा वितरण का ज्यामितीय माध्य आकार मापदंड के मान पर निर्भर करता है, और इसलिए इसमें अधिक जानकारी होती है। इसके अतिरिक्त, बीटा वितरण का ज्यामितीय माध्य माध्य द्वारा संतुष्ट सममिति नियम को संतुष्ट नहीं करता है, इसलिए, X पर आधारित ज्यामितीय माध्य और (1 − X) पर आधारित ज्यामितीय माध्य दोनों को नियोजित करके, अधिकतम संभावना विधि प्रदान करने में सक्षम है दोनों मापदंड α=β के लिए सर्वोत्तम अनुमान, भिन्नता को नियोजित किए बिना। | |||
कोई भी पर्याप्त आँकड़ों ( | कोई भी पर्याप्त आँकड़ों (प्रतिरूप ज्यामितीय साधनों) के संदर्भ में प्रति n स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल टिप्पणियों के संयुक्त लॉग संभावना को निम्नानुसार व्यक्त कर सकता है: | ||
:<math>\frac{\ln \mathcal{L} (\alpha, \beta\mid X)}{N} = (\alpha - 1)\ln \hat{G}_X + (\beta- 1)\ln \hat{G}_{(1-X)}- \ln \Beta(\alpha,\beta).</math> | :<math>\frac{\ln \mathcal{L} (\alpha, \beta\mid X)}{N} = (\alpha - 1)\ln \hat{G}_X + (\beta- 1)\ln \hat{G}_{(1-X)}- \ln \Beta(\alpha,\beta). </math> | ||
हम आकार | हम आकार मापदंड α और β के फलन के रूप में संभावना फलन के व्यवहार को देखने के लिए प्रतिरूप ज्यामितीय साधनों के निश्चित मूल्यों के लिए प्रति n अवलोकनों के संयुक्त लॉग संभावना को प्लॉट कर सकते हैं। ऐसी साजिश में, आकृति मापदंड अनुमानक <math>\hat{\alpha},\hat{\beta}</math> संभावना फलन की अधिकतमता के अनुरूप। संलग्न ग्राफ़ देखें जो दर्शाता है कि सभी संभावित कार्य α = β = 1 पर प्रतिच्छेद करते हैं, जो आकार के मापदंडों के मूल्यों से मेल खाता है जो अधिकतम एन्ट्रापी देता है (एकता के सामान्तर आकृति मापदंडों के लिए अधिकतम एन्ट्रापी होती है: समान वितरण)। प्लॉट से यह स्पष्ट है कि संभावना फलन शून्य के समीप आकार मापदंड अनुमानकों के मूल्यों के लिए तेज चोटियां देता है, किन्तु आकार मापदंड अनुमानकों के मूल्यों के लिए से अधिक होने पर, कम परिभाषित चोटियों के साथ संभावना फलन अधिक सपाट हो जाता है। किन्तु है, आकार मापदंड अनुमानकों के बड़े मूल्यों के लिए बीटा वितरण के लिए अधिकतम संभावना मापदंड अनुमान विधि कम स्वीकार्य हो जाती है, क्योंकि शिखर परिभाषा में अनिश्चितता आकार मापदंड अनुमानकों के मूल्य के साथ बढ़ जाती है। ही निष्कर्ष पर यह ध्यान देकर पहुंचा जा सकता है कि संभावना फलन की वक्रता के लिए अभिव्यक्ति ज्यामितीय भिन्नताओं के संदर्भ में है | ||
:<math>\frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \alpha^2}= -\operatorname{var}[\ln X]</math> | :<math>\frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \alpha^2}= -\operatorname{var}[\ln X]</math> | ||
:<math>\frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \beta^2} = -\operatorname{var}[\ln (1-X)]</math> | :<math>\frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{\partial \beta^2} = -\operatorname{var}[\ln (1-X)]</math> | ||
आकार | आकार मापदंड α और β के छोटे मानों के लिए ये भिन्नताएं (और इसलिए वक्रताएं) बहुत बड़ी हैं। चूँकि, आकार मापदंड मान α, β > 1 के लिए, प्रसरण (और इसलिए वक्रता) समतल हो जाते हैं। समतुल्य रूप से, यह परिणाम क्रैमर-राव बाउंड से आता है, क्योंकि बीटा वितरण के लिए फिशर सूचना आव्युह घटक ये लघुगणक प्रसरण हैं। क्रैमर-राव बाउंड बताता है कि किसी भी निष्पक्ष अनुमानक का प्रसरण <math>\hat{\alpha}</math> α का फिशर जानकारी के गुणक व्युत्क्रम से घिरा है: | ||
:<math>\mathrm{var}(\hat{\alpha})\geq\frac{1}{\operatorname{var}[\ln X]}\geq\frac{1}{\psi_1(\hat{\alpha}) - \psi_1(\hat{\alpha} + \hat{\beta})}</math> | :<math>\mathrm{var}(\hat{\alpha})\geq\frac{1}{\operatorname{var}[\ln X]}\geq\frac{1}{\psi_1(\hat{\alpha}) - \psi_1(\hat{\alpha} + \hat{\beta})}</math> | ||
| Line 1,284: | Line 1,293: | ||
इसलिए अनुमानकों का प्रसरण बढ़ते हुए α और β के साथ बढ़ता है, क्योंकि लघुगणक प्रसरण घटते हैं। | इसलिए अनुमानकों का प्रसरण बढ़ते हुए α और β के साथ बढ़ता है, क्योंकि लघुगणक प्रसरण घटते हैं। | ||
प्रतिरूप ज्यामितीय साधनों के लघुगणक के लिए डिगामा फलन एक्सप्रेशंस के संदर्भ में एन स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल टिप्पणियों के प्रति संयुक्त लॉग संभावना को भी व्यक्त कर सकते हैं: | |||
:<math>\frac{\ln\, \mathcal{L} (\alpha, \beta\mid X)}{N} = (\alpha - 1)(\psi(\hat{\alpha}) - \psi(\hat{\alpha} + \hat{\beta}))+(\beta- 1)(\psi(\hat{\beta}) - \psi(\hat{\alpha} + \hat{\beta}))- \ln \Beta(\alpha,\beta)</math> | :<math>\frac{\ln\, \mathcal{L} (\alpha, \beta\mid X)}{N} = (\alpha - 1)(\psi(\hat{\alpha}) - \psi(\hat{\alpha} + \hat{\beta}))+(\beta- 1)(\psi(\hat{\beta}) - \psi(\hat{\alpha} + \hat{\beta}))- \ln \Beta(\alpha,\beta)</math> | ||
यह अभिव्यक्ति क्रॉस-एन्ट्रॉपी के | यह अभिव्यक्ति क्रॉस-एन्ट्रॉपी के ऋणात्मक के समान है (जानकारी की मात्रा (एन्ट्रॉपी) पर अनुभाग देखें)। इसलिए, आकार मापदंडों के संयुक्त लॉग संभावना की अधिकतम खोज, प्रति N स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकन, बीटा वितरण के लिए न्यूनतम क्रॉस-एन्ट्रॉपी खोजने के समान है, आकार मापदंडों के फलन के रूप में। | ||
:<math>\frac{\ln\, \mathcal{L} (\alpha, \beta\mid X)}{N} = - H = -h - D_{\mathrm{KL}} = -\ln\Beta(\alpha,\beta)+(\alpha-1)\psi(\hat{\alpha})+(\beta-1)\psi(\hat{\beta})-(\alpha+\beta-2)\psi(\hat{\alpha}+\hat{\beta})</math> | :<math>\frac{\ln\, \mathcal{L} (\alpha, \beta\mid X)}{N} = - H = -h - D_{\mathrm{KL}} = -\ln\Beta(\alpha,\beta)+(\alpha-1)\psi(\hat{\alpha})+(\beta-1)\psi(\hat{\beta})-(\alpha+\beta-2)\psi(\hat{\alpha}+\hat{\beta})</math> | ||
| Line 1,295: | Line 1,304: | ||
=== चार अज्ञात | === चार अज्ञात मापदंड === | ||
प्रक्रिया दो अज्ञात | प्रक्रिया दो अज्ञात मापदंड स्तिथियों में अपनाई गई प्रक्रिया के समान है। यदि y<sub>1</sub>, ...,y<sub>N</sub> और स्वतंत्र यादृच्छिक वेरिएबल हैं जिनमें से प्रत्येक में चार मापदंडों के साथ बीटा वितरण है, N स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल टिप्पणियों के लिए संयुक्त लॉग संभावना कार्य है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,303: | Line 1,312: | ||
&= \sum_{i=1}^N \ln\,\frac{(Y_i-a)^{\alpha-1} (c-Y_i)^{\beta-1} }{(c-a)^{\alpha+\beta-1}\Beta(\alpha, \beta)}\\ | &= \sum_{i=1}^N \ln\,\frac{(Y_i-a)^{\alpha-1} (c-Y_i)^{\beta-1} }{(c-a)^{\alpha+\beta-1}\Beta(\alpha, \beta)}\\ | ||
&= (\alpha - 1)\sum_{i=1}^N \ln (Y_i - a) + (\beta- 1)\sum_{i=1}^N \ln (c - Y_i)- N \ln \Beta(\alpha,\beta) - N (\alpha+\beta - 1) \ln (c - a) | &= (\alpha - 1)\sum_{i=1}^N \ln (Y_i - a) + (\beta- 1)\sum_{i=1}^N \ln (c - Y_i)- N \ln \Beta(\alpha,\beta) - N (\alpha+\beta - 1) \ln (c - a) | ||
\end{align}</math> | \end{align} </math> | ||
आकार | आकार मापदंड के संबंध में अधिकतम ढूँढना तथा आकार मापदंड के संबंध में आंशिक व्युत्पन्न लेना और अभिव्यक्ति मापदंड के अधिकतम संभावना अनुमानक को शून्य के सामान्तर अभिव्यक्ति समुच्चय करना आदि सम्मिलित है: | ||
:<math>\frac{\partial \ln \mathcal{L} (\alpha, \beta, a, c\mid Y) }{\partial \alpha}= \sum_{i=1}^N \ln (Y_i - a) - N(-\psi(\alpha + \beta) + \psi(\alpha))- N \ln (c - a)= 0</math> | :<math>\frac{\partial \ln \mathcal{L} (\alpha, \beta, a, c\mid Y) }{\partial \alpha}= \sum_{i=1}^N \ln (Y_i - a) - N(-\psi(\alpha + \beta) + \psi(\alpha))- N \ln (c - a)= 0</math> | ||
: | |||
:<math>\frac{\partial \ln \mathcal{L} (\alpha, \beta, a, c\mid Y) }{\partial \beta} = \sum_{i=1}^N \ln (c - Y_i) - N(-\psi(\alpha + \beta) + \psi(\beta))- N \ln (c - a)= 0</math> | :<math>\frac{\partial \ln \mathcal{L} (\alpha, \beta, a, c\mid Y) }{\partial \beta} = \sum_{i=1}^N \ln (c - Y_i) - N(-\psi(\alpha + \beta) + \psi(\beta))- N \ln (c - a)= 0</math> | ||
: | |||
:<math>\frac{\partial \ln \mathcal{L} (\alpha, \beta, a, c\mid Y) }{\partial a} = -(\alpha - 1) \sum_{i=1}^N \frac{1}{Y_i - a} \,+ N (\alpha+\beta - 1)\frac{1}{c - a}= 0</math> | :<math>\frac{\partial \ln \mathcal{L} (\alpha, \beta, a, c\mid Y) }{\partial a} = -(\alpha - 1) \sum_{i=1}^N \frac{1}{Y_i - a} \,+ N (\alpha+\beta - 1)\frac{1}{c - a}= 0</math> | ||
: | |||
:<math>\frac{\partial \ln \mathcal{L} (\alpha, \beta, a, c\mid Y) }{\partial c} = (\beta- 1) \sum_{i=1}^N \frac{1}{c - Y_i} \,- N (\alpha+\beta - 1) \frac{1}{c - a} = 0</math> | :<math>\frac{\partial \ln \mathcal{L} (\alpha, \beta, a, c\mid Y) }{\partial c} = (\beta- 1) \sum_{i=1}^N \frac{1}{c - Y_i} \,- N (\alpha+\beta - 1) \frac{1}{c - a} = 0</math> | ||
इन समीकरणों को चार युग्मित समीकरणों की निम्नलिखित प्रणाली के रूप में फिर से व्यवस्थित किया जा सकता है (पहले दो समीकरण ज्यामितीय साधन हैं और दूसरे दो समीकरण हार्मोनिक साधन हैं | : | ||
इन समीकरणों को चार युग्मित समीकरणों की निम्नलिखित प्रणाली के रूप में फिर से व्यवस्थित किया जा सकता है (पहले दो समीकरण ज्यामितीय साधन हैं और दूसरे दो समीकरण हार्मोनिक साधन हैं चार मापदंडों के लिए अधिकतम संभावना अनुमानों के संदर्भ में <math>\hat{\alpha}, \hat{\beta}, \hat{a}, \hat{c}</math>: | |||
:<math>\frac{1}{N}\sum_{i=1}^N \ln \frac{Y_i - \hat{a}}{\hat{c}-\hat{a}} = \psi(\hat{\alpha})-\psi(\hat{\alpha} +\hat{\beta} )= \ln \hat{G}_X</math> | :<math>\frac{1}{N}\sum_{i=1}^N \ln \frac{Y_i - \hat{a}}{\hat{c}-\hat{a}} = \psi(\hat{\alpha})-\psi(\hat{\alpha} +\hat{\beta} )= \ln \hat{G}_X</math> | ||
| Line 1,316: | Line 1,329: | ||
:<math>\frac{1}{\frac{1}{N}\sum_{i=1}^N \frac{\hat{c} - \hat{a}}{Y_i - \hat{a}}} = \frac{\hat{\alpha} - 1}{\hat{\alpha}+\hat{\beta} - 1}= \hat{H}_X</math> | :<math>\frac{1}{\frac{1}{N}\sum_{i=1}^N \frac{\hat{c} - \hat{a}}{Y_i - \hat{a}}} = \frac{\hat{\alpha} - 1}{\hat{\alpha}+\hat{\beta} - 1}= \hat{H}_X</math> | ||
:<math>\frac{1}{\frac{1}{N}\sum_{i=1}^N \frac{\hat{c} - \hat{a}}{\hat{c} - Y_i}} = \frac{\hat{\beta}- 1}{\hat{\alpha}+\hat{\beta} - 1} = \hat{H}_{1-X}</math> | :<math>\frac{1}{\frac{1}{N}\sum_{i=1}^N \frac{\hat{c} - \hat{a}}{\hat{c} - Y_i}} = \frac{\hat{\beta}- 1}{\hat{\alpha}+\hat{\beta} - 1} = \hat{H}_{1-X}</math> | ||
प्रतिरूप ज्यामितीय साधनों के साथ: | |||
:<math>\hat{G}_X = \prod_{i=1}^{N} \left (\frac{Y_i - \hat{a}}{\hat{c}-\hat{a}} \right )^{\frac{1}{N}}</math> | :<math>\hat{G}_X = \prod_{i=1}^{N} \left (\frac{Y_i - \hat{a}}{\hat{c}-\hat{a}} \right )^{\frac{1}{N}}</math> | ||
:<math>\hat{G}_{(1-X)} = \prod_{i=1}^{N} \left (\frac{\hat{c} - Y_i}{\hat{c}-\hat{a}} \right )^{\frac{1}{N}}</math> | :<math>\hat{G}_{(1-X)} = \prod_{i=1}^{N} \left (\frac{\hat{c} - Y_i}{\hat{c}-\hat{a}} \right )^{\frac{1}{N}}</math> | ||
मापदंड <math>\hat{a}, \hat{c}</math> गैर-रैखिक तरीके से (शक्ति 1/n) में ज्यामितीय माध्य अभिव्यक्तियों के अंदर एम्बेडेड हैं। यह सामान्य रूप से, विवृत रूप समाधान को रोकता है, यहां तक कि पुनरावृति प्रयोजनों के लिए प्रारंभिक मूल्य सन्निकटन के लिए भी। विकल्प चार मापदंड स्तिथियों के लिए क्षणों के समाधान की विधि से प्राप्त मूल्यों को पुनरावृत्ति के लिए प्रारंभिक मानों के रूप में उपयोग करना है। इसके अतिरिक्त, हार्मोनिक साधनों के भाव केवल <math>\hat{\alpha}, \hat{\beta} > 1</math> के लिए अच्छी तरह से परिभाषित हैं , जो चार-मापदंड स्तिथियों में एकता से कम आकार के मापदंडों के लिए अधिकतम संभावना समाधान को रोकता है। चार मापदंड स्तिथियों के लिए फिशर की सूचना आव्युह [[सकारात्मक-निश्चित मैट्रिक्स|धनात्मक -निश्चित आव्युह]] है। धनात्मक -निश्चित केवल α, β> 2 के लिए (आगे की चर्चा के लिए, फिशर सूचना आव्युह पर अनुभाग देखें, चार मापदंड स्तिथि ), घंटी के आकार (सममित या असममित) बीटा वितरण, मोड के दोनों ओर स्थित विभक्ति बिंदुओं के साथ। निम्नलिखित फिशर सूचना घटकों (जो लॉग संभावना फलन की वक्रता की अपेक्षाओं का प्रतिनिधित्व करते हैं) में निम्नलिखित मानों पर गणितीय विलक्षणता है: | |||
:<math>\alpha = 2: \quad \operatorname{E} \left [- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial a^2} \right ]= {\mathcal{I}}_{a, a}</math> | :<math>\alpha = 2: \quad \operatorname{E} \left [- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial a^2} \right ]= {\mathcal{I}}_{a, a}</math> | ||
| Line 1,326: | Line 1,339: | ||
:<math>\alpha = 2: \quad \operatorname{E}\left [- \frac{1}{N}\frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha \partial a}\right ] = {\mathcal{I}}_{\alpha, a} </math> | :<math>\alpha = 2: \quad \operatorname{E}\left [- \frac{1}{N}\frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha \partial a}\right ] = {\mathcal{I}}_{\alpha, a} </math> | ||
:<math>\beta = 1: \quad \operatorname{E}\left [- \frac{1}{N}\frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta \partial c} \right ] = {\mathcal{I}}_{\beta, c} </math> | :<math>\beta = 1: \quad \operatorname{E}\left [- \frac{1}{N}\frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta \partial c} \right ] = {\mathcal{I}}_{\beta, c} </math> | ||
(आगे की चर्चा के लिए फिशर सूचना | (आगे की चर्चा के लिए फिशर सूचना आव्युह पर अनुभाग देखें)। इस प्रकार, चार-मापदंड बीटा वितरण परिवार से संबंधित कुछ प्रसिद्ध वितरणों जैसे [[निरंतर समान वितरण]] (बीटा (1, 1, a, c)), और आर्क्साइन वितरण के लिए अधिकतम संभावना अनुमान को सख्ती से प्रयुक्त करना संभव नहीं है, (बीटा (1/2, 1/2, a, c))। नॉर्मन लॉयड जॉनसन|(एन.एल.जॉनसन) और सैमुअल कोटज़|(एस.कोट्ज़)<ref name=JKB />हार्मोनिक साधनों के लिए समीकरणों को अनदेखा करें और इसके अतिरिक्त सुझाव दें कि यदि a और c अज्ञात हैं, और a, c, α और β के अधिकतम संभावना अनुमानक आवश्यक हैं, तब उपरोक्त प्रक्रिया (दो अज्ञात मापदंड स्तिथियों के लिए, X को X साथ = Y − a)/(c − a)) के रूप में रूपांतरित किया गया है उत्तराधिकार का उपयोग करके दोहराया जा सकता है a और c के परीक्षण मूल्यों के , जब तक कि जोड़ी (a, c) जिसके लिए अधिकतम संभावना (दिया गया a और c) जितना अधिक हो सके, है प्राप्त (जहाँ, स्पष्टता के प्रयोजन के लिए, मापदंडों के लिए उनके अंकन को वर्तमान अंकन में अनुवादित किया गया है)। | ||
====फिशर सूचना | ====फिशर सूचना आव्युह==== | ||
मान लें कि यादृच्छिक | मान लें कि यादृच्छिक वेरिएबल X का प्रायिकता घनत्व f(x;α) है। लॉग संभावना फलन के (अज्ञात, और अनुमानित) मापदंड α के संबंध में आंशिक व्युत्पन्न को [[स्कोर (सांख्यिकी)]] कहा जाता है। स्कोर के दूसरे क्षण को फिशर सूचना कहा जाता है: | ||
:<math>\mathcal{I}(\alpha)=\operatorname{E} \left [\left (\frac{\partial}{\partial\alpha} \ln \mathcal{L}(\alpha\mid X) \right )^2 \right],</math> | :<math>\mathcal{I}(\alpha)=\operatorname{E} \left [\left (\frac{\partial}{\partial\alpha} \ln \mathcal{L}(\alpha\mid X) \right )^2 \right],</math> | ||
स्कोर (सांख्यिकी) का अपेक्षित मूल्य शून्य है, इसलिए फिशर की जानकारी भी स्कोर के माध्य पर केंद्रित दूसरा क्षण है: स्कोर का | स्कोर (सांख्यिकी) का अपेक्षित मूल्य शून्य है, इसलिए फिशर की जानकारी भी स्कोर के माध्य पर केंद्रित दूसरा क्षण है: स्कोर का विचरण । | ||
यदि लॉग संभावना | यदि लॉग संभावना फलन मापदंड α के संबंध में दो बार भिन्न होता है, और कुछ नियमितता नियम के अनुसार ,<ref name=Silvey>{{cite book|last=Silvey|first=S.D.|title=सांख्यिकीय निष्कर्ष|year=1975|publisher=Chapman and Hal|page=40|isbn=978-0412138201}}</ref> तब फ़िशर जानकारी को निम्नानुसार भी लिखा जा सकता है (जो अधिकांशतः गणना उद्देश्यों के लिए अधिक सुविधाजनक रूप होता है): | ||
:<math>\mathcal{I}(\alpha) = - \operatorname{E} \left [\frac{\partial^2}{\partial\alpha^2} \ln (\mathcal{L}(\alpha\mid X)) \right].</math> | :<math>\mathcal{I}(\alpha) = - \operatorname{E} \left [\frac{\partial^2}{\partial\alpha^2} \ln (\mathcal{L}(\alpha\mid X)) \right].</math> | ||
इस प्रकार, फिशर की जानकारी लॉग संभावना | इस प्रकार, फिशर की जानकारी लॉग संभावना फलन के मापदंड α के संबंध में दूसरे व्युत्पन्न की अपेक्षा का ऋणात्मक है। इसलिए, फिशर की जानकारी α के लॉग संभावना फलन की वक्रता का उपाय है। कम वक्रता (और इसलिए वक्रता (गणित) की उच्च त्रिज्या), चापलूसी लॉग संभावना फलन वक्र में कम फ़िशर जानकारी होती है; जबकि बड़ी वक्रता (और इसलिए वक्रता की कम त्रिज्या (गणित)) के साथ लॉग संभावना फलन वक्र में उच्च फ़िशर जानकारी होती है। जब फिशर सूचना आव्युह की गणना मापदंडों के मूल्यांकन पर की जाती है (देखा गया फिशर सूचना आव्युह) यह टेलर की श्रृंखला सन्निकटन द्वारा सही लॉग संभावना सतह के प्रतिस्थापन के सामान्तर है, जहाँ तक द्विघात शब्दों को लिया गया है।<ref name=Edwardsसंभावना>{{cite book|last=Edwards|first=A. W. F.|title=संभावना|year=1992 |publisher=The Johns Hopkins University Press|isbn=978-0801844430}}</ref> शब्द सूचना, फिशर जानकारी के संदर्भ में, मापदंडों के बारे में जानकारी को संदर्भित करता है। जानकारी जैसे: अनुमान, पर्याप्तता और अनुमानकों के प्रसरण के गुण। क्रैमर-राव बाउंड बताता है कि फिशर सूचना का व्युत्क्रम मापदंड α के किसी भी अनुमानक के विचरण पर निचली सीमा है: | ||
:<math>\operatorname{var}[\hat\alpha] \geq \frac{1}{\mathcal{I}(\alpha)}.</math> | :<math>\operatorname{var}[\hat\alpha] \geq \frac{1}{\mathcal{I}(\alpha)}.</math> | ||
स्पष्टता जिसके लिए कोई मापदंड α के अनुमानक का अनुमान लगा सकता है, लॉग संभावना फलन के फ़िशर सूचना द्वारा सीमित है। फिशर जानकारी वितरण के मापदंड का अनुमान लगाने में सम्मिलित न्यूनतम त्रुटि का उपाय है और इसे मापदंड के दो वैकल्पिक परिकल्पनाओं के मध्य भेदभाव करने के लिए आवश्यक प्रयोग की संकल्प शक्ति के माप के रूप में देखा जा सकता है।<ref name=Jaynes>{{cite book|last=Jaynes|first=E.T.|title=संभाव्यता सिद्धांत, विज्ञान का तर्क|year=2003|publisher=Cambridge University Press|isbn=978-0521592710}}</ref> | |||
जब एन | |||
जब एन मापदंड होते हैं | |||
:<math> \begin{bmatrix} \theta_1 \\ \theta_{2} \\ \dots \\ \theta_{N} \end{bmatrix},</math> | :<math> \begin{bmatrix} \theta_1 \\ \theta_{2} \\ \dots \\ \theta_{N} \end{bmatrix},</math> | ||
तब फिशर जानकारी विशिष्ट तत्व के साथ | तब फिशर जानकारी विशिष्ट तत्व के साथ ''N× N'' धनात्मक अर्ध-निश्चित आव्युह [[सममित मैट्रिक्स|सममित आव्युह]], फिशर सूचना आव्युह का रूप लेती है: | ||
:<math>{(\mathcal{I}(\theta))}_{i, j}=\operatorname{E} \left [\left (\frac{\partial}{\partial\theta_i} \ln \mathcal{L} \right) \left(\frac{\partial}{\partial\theta_j} \ln \mathcal{L} \right) \right ].</math> | :<math>{(\mathcal{I}(\theta))}_{i, j}=\operatorname{E} \left [\left (\frac{\partial}{\partial\theta_i} \ln \mathcal{L} \right) \left(\frac{\partial}{\partial\theta_j} \ln \mathcal{L} \right) \right ].</math> | ||
कुछ नियमितता | कुछ नियमितता नियम के अनुसार ,<ref name="Silvey" />फिशर इंरूपेशन आव्युह को निम्नलिखित रूप में भी लिखा जा सकता है, जो अधिकांशतः गणना के लिए अधिक सुविधाजनक होता है: | ||
:<math>{(\mathcal{I}(\theta))}_{i, j} = - \operatorname{E} \left [\frac{\partial^2}{\partial\theta_i \, \partial\theta_j} \ln (\mathcal{L}) \right ]\,.</math> | :<math>{(\mathcal{I}(\theta))}_{i, j} = - \operatorname{E} \left [\frac{\partial^2}{\partial\theta_i \, \partial\theta_j} \ln (\mathcal{L}) \right ]\,.</math> | ||
X<sub>1</sub> ..., X<sub>N</sub> [[iid]] यादृच्छिक वेरिएबल के साथ , पक्षों N-आयामी बॉक्स का निर्माण X<sub>1</sub>, ..., X<sub>N</sub> के साथ किया जा सकता है कोस्टा और आवरण <ref name="CostaCover">{{cite book|last=Costa|first=Max, and Cover, Thomas|title=एंट्रॉपी पावर असमानता और ब्रून मिन्कोव्स्की असमानता की समानता पर|date=September 1983|publisher=Tech.Report 48, Dept. Statistics, Stanford University|url=https://isl.stanford.edu/people/cover/papers/transIT/0837cost.pdf}}</ref> दिखाएँ कि (शैनन) डिफरेंशियल एन्ट्रापी ''h(X)'' विशिष्ट समुच्चय की मात्रा से संबंधित है (प्रतिरूप एन्ट्रापी को सही एन्ट्रापी के समीप होने पर), जबकि फिशर की जानकारी इस विशिष्ट समुच्चय की सतह से संबंधित है। | |||
=== दो | === दो मापदंड === | ||
X<sub>1</sub> ..., X<sub>''N''</sub> स्वतंत्र यादृच्छिक वेरिएबल के लिए प्रत्येक में जो आकार मापदंडों α और β के साथ पैरामीट्रिज्ड होता है N स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकनों के लिए संयुक्त लॉग संभावना फलन है: | |||
:<math>\ln (\mathcal{L} (\alpha, \beta\mid X) )= (\alpha - 1)\sum_{i=1}^N \ln X_i + (\beta- 1)\sum_{i=1}^N \ln (1-X_i)- N \ln \Beta(\alpha,\beta) </math> | :<math>\ln (\mathcal{L} (\alpha, \beta\mid X) )= (\alpha - 1)\sum_{i=1}^N \ln X_i + (\beta- 1)\sum_{i=1}^N \ln (1-X_i)- N \ln \Beta(\alpha,\beta) </math> | ||
इसलिए संयुक्त लॉग संभावना कार्य प्रति | इसलिए संयुक्त लॉग संभावना कार्य प्रति n स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकन है: | ||
:<math>\frac{1}{N} \ln(\mathcal{L} (\alpha, \beta\mid X)) = (\alpha - 1)\frac{1}{N}\sum_{i=1}^N \ln X_i + (\beta- 1)\frac{1}{N}\sum_{i=1}^N \ln (1-X_i)-\, \ln \Beta(\alpha,\beta)</math> | :<math>\frac{1}{N} \ln(\mathcal{L} (\alpha, \beta\mid X)) = (\alpha - 1)\frac{1}{N}\sum_{i=1}^N \ln X_i + (\beta- 1)\frac{1}{N}\sum_{i=1}^N \ln (1-X_i)-\, \ln \Beta(\alpha,\beta)</math> | ||
दो | दो मापदंड स्तिथियों के लिए, फिशर जानकारी में 4 घटक होते हैं: 2 विकर्ण और 2 ऑफ-विकर्ण। चूंकि फिशर सूचना आव्युह सममित है, इनमें से विकर्ण घटक स्वतंत्र है। इसलिए, फिशर सूचना आव्युह में 3 स्वतंत्र घटक (2 विकर्ण और 1 विकर्ण) हैं। | ||
आर्यल और नादराजा<ref name=Aryal>{{cite journal|last=Aryal|first=Gokarna|author2=Saralees Nadarajah|title=बीटा वितरण के लिए सूचना मैट्रिक्स|journal=Serdica Mathematical Journal (Bulgarian Academy of Science)| year=2004| volume=30|pages=513–526|url=http://www.math.bas.bg/serdica/2004/2004-513-526.pdf}}</ref> चार- | आर्यल और नादराजा<ref name=Aryal>{{cite journal|last=Aryal|first=Gokarna|author2=Saralees Nadarajah|title=बीटा वितरण के लिए सूचना मैट्रिक्स|journal=Serdica Mathematical Journal (Bulgarian Academy of Science)| year=2004| volume=30|pages=513–526|url=http://www.math.bas.bg/serdica/2004/2004-513-526.pdf}}</ref> चार-मापदंड स्तिथियों के लिए फिशर की सूचना आव्युह की गणना की गई, जिससे दो मापदंड स्तिथियाँनिम्नानुसार प्राप्त किए जा सकते हैं: | ||
:<math>- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\partial \alpha^2}= \operatorname{var}[\ln (X)]= \psi_1(\alpha) - \psi_1(\alpha + \beta) ={\mathcal{I}}_{\alpha, \alpha}= \operatorname{E}\left [- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\partial \alpha^2} \right ] = \ln \operatorname{var}_{GX} </math> | :<math>- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\partial \alpha^2}= \operatorname{var}[\ln (X)]= \psi_1(\alpha) - \psi_1(\alpha + \beta) ={\mathcal{I}}_{\alpha, \alpha}= \operatorname{E}\left [- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\partial \alpha^2} \right ] = \ln \operatorname{var}_{GX} </math> | ||
:<math>- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\,\partial \beta^2} = \operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta) ={\mathcal{I}}_{\beta, \beta}= \operatorname{E}\left [- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\partial \beta^2} \right]= \ln \operatorname{var}_{G(1-X)} </math> | :<math>- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\,\partial \beta^2} = \operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta) ={\mathcal{I}}_{\beta, \beta}= \operatorname{E}\left [- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\partial \beta^2} \right]= \ln \operatorname{var}_{G(1-X)} </math> | ||
:<math>- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N \, \partial \alpha \, \partial \beta} = \operatorname{cov}[\ln X,\ln(1-X)] = -\psi_1(\alpha+\beta) ={\mathcal{I}}_{\alpha, \beta}= \operatorname{E}\left [- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\,\partial \alpha\,\partial \beta} \right] = \ln \operatorname{cov}_{G{X,(1-X)}}</math> | :<math>- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N \, \partial \alpha \, \partial \beta} = \operatorname{cov}[\ln X,\ln(1-X)] = -\psi_1(\alpha+\beta) ={\mathcal{I}}_{\alpha, \beta}= \operatorname{E}\left [- \frac{\partial^2\ln \mathcal{L}(\alpha,\beta\mid X)}{N\,\partial \alpha\,\partial \beta} \right] = \ln \operatorname{cov}_{G{X,(1-X)}} </math> | ||
चूंकि फिशर सूचना | चूंकि फिशर सूचना आव्युह सममित है | ||
:<math> \mathcal{I}_{\alpha, \beta}= \mathcal{I}_{\beta, \alpha}= \ln \operatorname{cov}_{G{X,(1-X)}}</math> | :<math> \mathcal{I}_{\alpha, \beta}= \mathcal{I}_{\beta, \alpha}= \ln \operatorname{cov}_{G{X,(1-X)}}</math> | ||
फिशर सूचना घटक लॉग ज्यामितीय प्रसरण और लॉग ज्यामितीय सहप्रसरण के | फिशर सूचना घटक लॉग ज्यामितीय प्रसरण और लॉग ज्यामितीय सहप्रसरण के सामान्तर हैं। इसलिए, उन्हें त्रिगामा कार्यों के रूप में व्यक्त किया जा सकता है, जिसे ψ<sub>1</sub>(α) निरूपित किया जाता है, बहुग्राम कार्यों का दूसरा, डिगामा फलन के व्युत्पन्न के रूप में परिभाषित किया गया है: | ||
: : : : : : : : : : : : : : : : : : : : : : : : :<math>\psi_1(\alpha) = \frac{d^2\ln\Gamma(\alpha)}{\partial\alpha^2}=\, \frac{\partial \psi(\alpha)}{\partial\alpha}. </math> | : : : : : : : : : : : : : : : : : : : : : : : : :<math>\psi_1(\alpha) = \frac{d^2\ln\Gamma(\alpha)}{\partial\alpha^2}=\, \frac{\partial \psi(\alpha)}{\partial\alpha}. </math> | ||
ये डेरिवेटिव भी में व्युत्पन्न हैं {{section link|| | ये डेरिवेटिव भी में व्युत्पन्न हैं {{section link||दो अज्ञात पैरामीटर }} और लॉग संभावना फलन के प्लॉट भी उस अनुभाग में दिखाए जाते हैं। {{section link||ज्यामितीय विचरण और सहप्रसरण }} में फिशर सूचना आव्युह घटकों के प्लॉट और आगे की चर्चा सम्मिलित है: लॉग ज्यामितीय प्रसरण और लॉग ज्यामितीय सहप्रसरण आकार मापदंड α और β के फलन के रूप में। {{section link||लघुगणकीय रूप से परिवर्तित यादृच्छिक चर के क्षण}} लघुगणक रूप से परिवर्तित यादृच्छिक वेरिएबल के क्षणों के लिए सूत्र सम्मिलित हैं। फिशर सूचना घटकों के लिए छवियां <math>\mathcal{I}_{\alpha, \alpha}, \mathcal{I}_{\beta, \beta}</math> और <math>\mathcal{I}_{\alpha, \beta}</math> में दर्शाए गए हैं {{section link||ज्यामितीय विचरण}}. | ||
फ़िशर के सूचना | फ़िशर के सूचना आव्युह का निर्धारक रुचि का है (उदाहरण के लिए जेफ़रीज़ पूर्व संभाव्यता की गणना के लिए)। फिशर सूचना आव्युह के अलग-अलग घटकों के भावों से, यह इस प्रकार है कि बीटा वितरण के लिए फिशर (सममित) सूचना आव्युह का निर्धारक है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,382: | Line 1,396: | ||
\lim_{\alpha\to 0} \det(\mathcal{I}(\alpha, \beta)) &=\lim_{\beta \to 0} \det(\mathcal{I}(\alpha, \beta)) = \infty\\[4pt] | \lim_{\alpha\to 0} \det(\mathcal{I}(\alpha, \beta)) &=\lim_{\beta \to 0} \det(\mathcal{I}(\alpha, \beta)) = \infty\\[4pt] | ||
\lim_{\alpha\to \infty} \det(\mathcal{I}(\alpha, \beta)) &=\lim_{\beta \to \infty} \det(\mathcal{I}(\alpha, \beta)) = 0 | \lim_{\alpha\to \infty} \det(\mathcal{I}(\alpha, \beta)) &=\lim_{\beta \to \infty} \det(\mathcal{I}(\alpha, \beta)) = 0 | ||
\end{align}</math> | \end{align} </math> | ||
सिल्वेस्टर की कसौटी से (यह जांचना कि क्या विकर्ण तत्व सभी | सिल्वेस्टर की कसौटी से (यह जांचना कि क्या विकर्ण तत्व सभी धनात्मक हैं), यह इस प्रकार है कि दो मापदंड केस के लिए फिशर सूचना आव्युह धनात्मक -निश्चित आव्युह है। धनात्मक -निश्चित (मानक स्थिति के अनुसार α > 0 और β > 0आकार मापदंड धनात्मक हैं ). | ||
=== चार | === चार मापदंड === | ||
यदि y<sub>1</sub>, ..., y<sub>N</sub>स्वतंत्र यादृच्छिक वेरिएबल हैं जिनमें से प्रत्येक में चार मापदंडों के साथ बीटा वितरण होता है: एक्सपोनेंट्स α और β, और a (वितरण सीमा का न्यूनतम), और c (वितरण सीमा का अधिकतम) (वैकल्पिक पैरामीट्रिजेशन शीर्षक वाला खंड, चार मापदंड) प्रायिकता घनत्व फलन के साथ: | |||
:<math>f(y; \alpha, \beta, a, c) = \frac{f(x;\alpha,\beta)}{c-a} =\frac{ \left (\frac{y-a}{c-a} \right )^{\alpha-1} \left (\frac{c-y}{c-a} \right)^{\beta-1} }{(c-a)B(\alpha, \beta)}=\frac{ (y-a)^{\alpha-1} (c-y)^{\beta-1} }{(c-a)^{\alpha+\beta-1}B(\alpha, \beta)}. </math> | |||
: | |||
संयुक्त लॉग संभावना फलन प्रति n स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकन है: | |||
:<math>\frac{1}{N} \ln(\mathcal{L} (\alpha, \beta, a, c\mid Y))= \frac{\alpha -1}{N}\sum_{i=1}^N \ln (Y_i - a) + \frac{\beta -1}{N}\sum_{i=1}^N \ln (c - Y_i)- \ln \Beta(\alpha,\beta) - (\alpha+\beta -1) \ln (c-a) </math> | :<math>\frac{1}{N} \ln(\mathcal{L} (\alpha, \beta, a, c\mid Y))= \frac{\alpha -1}{N}\sum_{i=1}^N \ln (Y_i - a) + \frac{\beta -1}{N}\sum_{i=1}^N \ln (c - Y_i)- \ln \Beta(\alpha,\beta) - (\alpha+\beta -1) \ln (c-a) </math> | ||
चार | चार मापदंड केस के लिए, फिशर जानकारी में 4*4=16 घटक होते हैं। इसमें 12 ऑफ-डायगोनल घटक = (4 × 4 कुल - 4 विकर्ण) हैं। चूंकि फिशर सूचना आव्युह सममित है, इनमें से आधे घटक (12/2 = 6) स्वतंत्र हैं। इसलिए, फिशर सूचना आव्युह में 6 स्वतंत्र ऑफ-विकर्ण + 4 विकर्ण = 10 स्वतंत्र घटक हैं। आर्यल और नादराजा<ref name=Aryal/>निम्नानुसार चार मापदंड स्तिथियों के लिए फिशर की सूचना आव्युह की गणना: | ||
:<math>- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha^2}= \operatorname{var}[\ln (X)]= \psi_1(\alpha) - \psi_1(\alpha + \beta) = \mathcal{I}_{\alpha, \alpha}= \operatorname{E}\left [- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha^2} \right ] = \ln (\operatorname{var_{GX}}) </math> | :<math>- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha^2}= \operatorname{var}[\ln (X)]= \psi_1(\alpha) - \psi_1(\alpha + \beta) = \mathcal{I}_{\alpha, \alpha}= \operatorname{E}\left [- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha^2} \right ] = \ln (\operatorname{var_{GX}}) </math> | ||
:<math>-\frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta^2} = \operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta) ={\mathcal{I}}_{\beta, \beta}= \operatorname{E} \left [- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta^2} \right ] = \ln(\operatorname{var_{G(1-X)}}) </math> | :<math>-\frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta^2} = \operatorname{var}[\ln (1-X)] = \psi_1(\beta) - \psi_1(\alpha + \beta) ={\mathcal{I}}_{\beta, \beta}= \operatorname{E} \left [- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta^2} \right ] = \ln(\operatorname{var_{G(1-X)}}) </math> | ||
:<math>-\frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha\,\partial \beta} = \operatorname{cov}[\ln X,(1-X)] = -\psi_1(\alpha+\beta) =\mathcal{I}_{\alpha, \beta}= \operatorname{E} \left [- \frac{1}{N}\frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha \, \partial \beta} \right ] = \ln(\operatorname{cov}_{G{X,(1-X)}})</math> | :<math>-\frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha\,\partial \beta} = \operatorname{cov}[\ln X,(1-X)] = -\psi_1(\alpha+\beta) =\mathcal{I}_{\alpha, \beta}= \operatorname{E} \left [- \frac{1}{N}\frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \alpha \, \partial \beta} \right ] = \ln(\operatorname{cov}_{G{X,(1-X)}})</math> | ||
उपरोक्त भावों में, भावों में Y के स्थान पर X का प्रयोग var[ln(X)] = ln(var<sub>''GX''</sub>) कोई त्रुटि नहीं है। लॉग ज्यामितीय प्रसरण और लॉग ज्यामितीय सहप्रसरण के संदर्भ में अभिव्यक्तियाँ दो | उपरोक्त भावों में, भावों में Y के स्थान पर X का प्रयोग var[ln(X)] = ln(var<sub>''GX''</sub>) कोई त्रुटि नहीं है। लॉग ज्यामितीय प्रसरण और लॉग ज्यामितीय सहप्रसरण के संदर्भ में अभिव्यक्तियाँ दो मापदंड X ~ बीटा (α, β) पैरामीट्रिजेशन के कार्यों के रूप में होती हैं क्योंकि चार मापदंड स्तिथियों में घातांक (α, β) के संबंध में आंशिक डेरिवेटिव लेते समय , दो मापदंड स्तिथियों के लिए समान अभिव्यक्ति प्राप्त करता है: चार मापदंड फिशर सूचना आव्युह की ये नियम ें वितरण की सीमा के न्यूनतम ए और अधिकतम सी से स्वतंत्र हैं। घातांक α और β के संबंध में लॉग संभावना फलन के दोहरे विभेदन पर एकमात्र गैर-शून्य शब्द बीटा फलन के लॉग का दूसरा व्युत्पन्न है: ln(B(α, β))। यह शब्द वितरण की सीमा के न्यूनतम a और अधिकतम c से स्वतंत्र है। इस पद के दोहरे विभेदन के परिणामस्वरूप त्रिगामा फलन उत्पन्न होते हैं। अधिकतम संभावना, दो अज्ञात मापदंड और चार अज्ञात मापदंड शीर्षक वाले खंड भी इस तथ्य को दर्शाते हैं। | ||
एन आई.डी. के लिए फिशर जानकारी | एन आई.डी. के लिए फिशर जानकारी प्रतिरूप व्यक्तिगत फिशर जानकारी का N गुना है (eq. 11.279, आवरण और थॉमस का पृष्ठ 394<ref name="Cover and Thomas"/>). (आर्यल और नादराजा<ref name=Aryal/>फिशर जानकारी के निम्नलिखित घटकों की गणना करने के लिए एकल अवलोकन, एन = 1 लें, जो प्रति एन अवलोकन लॉग संभावना के डेरिवेटिव पर विचार करने के समान परिणाम की ओर जाता है। इसके अतिरिक्त, के लिए गलत अभिव्यक्ति के नीचे <math>{\mathcal{I}}_{a, a}</math> आर्यल और नादराजाह में सुधार किया गया है।) | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,412: | Line 1,426: | ||
\operatorname{E}\left[- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta \,\partial a} \right ] &= {\mathcal{I}}_{\beta, a} = -\frac{1}{(c-a)} \\ | \operatorname{E}\left[- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta \,\partial a} \right ] &= {\mathcal{I}}_{\beta, a} = -\frac{1}{(c-a)} \\ | ||
\beta > 1: \quad \operatorname{E}\left[- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta \, \partial c} \right ] &= \mathcal{I}_{\beta, c} = -\frac{\alpha}{(\beta-1)(c-a)} | \beta > 1: \quad \operatorname{E}\left[- \frac{1}{N} \frac{\partial^2\ln \mathcal{L} (\alpha, \beta, a, c\mid Y)}{\partial \beta \, \partial c} \right ] &= \mathcal{I}_{\beta, c} = -\frac{\alpha}{(\beta-1)(c-a)} | ||
\end{align}</math> | \end{align} </math> | ||
फिशर सूचना | : | ||
फिशर सूचना आव्युह की निचली दो विकर्ण प्रविष्टियाँ, मापदंड a (वितरण की सीमा का न्यूनतम) के संबंध में: <math>\mathcal{I}_{a, a}</math>, और मापदंड c के संबंध में (वितरण की अधिकतम सीमा): <math>\mathcal{I}_{c, c}</math> क्रमशः घातांक α > 2 और β > 2 के लिए परिभाषित हैं। फिशर सूचना आव्युह घटक <math>\mathcal{I}_{a, a}</math> ऊपर से 2 तक पहुंचने वाले घातांक α के लिए न्यूनतम ए दृष्टिकोण अनंत और फिशर सूचना आव्युह घटक के लिए <math>\mathcal{I}_{c, c}</math> ऊपर से 2 की ओर आने वाले घातांक β के लिए अधिकतम c अनंत की ओर अग्रसर होता है। | |||
चार | चार मापदंड स्तिथियों के लिए फिशर सूचना आव्युह न्यूनतम a और अधिकतम c के व्यक्तिगत मूल्यों पर निर्भर नहीं करता है, किन्तु केवल कुल सीमा (c-a) पर निर्भर करता है। इसके अतिरिक्त, फिशर सूचना आव्युह के घटक जो रेंज (c-a) पर निर्भर करते हैं, केवल इसके व्युत्क्रम (या व्युत्क्रम के वर्ग) के माध्यम से निर्भर करते हैं, जैसे कि फिशर की जानकारी बढ़ती रेंज (c-a) के लिए घट जाती है। | ||
संलग्न छवियां फिशर सूचना घटकों को दिखाती हैं <math>\mathcal{I}_{a, a}</math> और <math>\mathcal{I}_{\alpha, a}</math>. फिशर सूचना घटकों के लिए छवियां <math>\mathcal{I}_{\alpha, \alpha}</math> और <math>\mathcal{I}_{\beta, \beta}</math> में दर्शाए गए हैं {{section link|| | संलग्न छवियां फिशर सूचना घटकों को दिखाती हैं <math>\mathcal{I}_{a, a}</math> और <math>\mathcal{I}_{\alpha, a}</math>. फिशर सूचना घटकों के लिए छवियां <math>\mathcal{I}_{\alpha, \alpha}</math> और <math>\mathcal{I}_{\beta, \beta}</math> में दर्शाए गए हैं {{section link||ज्यामितीय विचरण }}. ये सभी फिशर सूचना घटक बेसिन की तरह दिखते हैं, जिसमें बेसिन की दीवारें मापदंडों के कम मूल्यों पर स्थित होती हैं। | ||
निम्नलिखित चार- | निम्नलिखित चार-मापदंड-बीटा-वितरण फिशर जानकारी घटकों को दो-मापदंड के संदर्भ में व्यक्त किया जा सकता है: X ~ बीटा (α, β) रूपांतरित अनुपात ((1-X)/X) और इसकी दर्पण छवि की अपेक्षाएं (एक्स/(1-एक्स)), श्रेणी (c−a) द्वारा स्केल किया गया, जो व्याख्या के लिए सहायक हो सकता है: | ||
:<math>\mathcal{I}_{\alpha, a} =\frac{\operatorname{E} \left[\frac{1-X}{X} \right ]}{c-a}= \frac{\beta}{(\alpha-1)(c-a)} \text{ if }\alpha > 1</math> | :<math>\mathcal{I}_{\alpha, a} =\frac{\operatorname{E} \left[\frac{1-X}{X} \right ]}{c-a}= \frac{\beta}{(\alpha-1)(c-a)} \text{ if }\alpha > 1</math> | ||
:<math>\mathcal{I}_{\beta, c} = -\frac{\operatorname{E} \left [\frac{X}{1-X} \right ]}{c-a}=- \frac{\alpha}{(\beta-1)(c-a)}\text{ if }\beta> 1</math> | :<math>\mathcal{I}_{\beta, c} = -\frac{\operatorname{E} \left [\frac{X}{1-X} \right ]}{c-a}=- \frac{\alpha}{(\beta-1)(c-a)}\text{ if }\beta> 1</math> | ||
: | |||
ये इन्वर्टेड बीटा डिस्ट्रीब्यूशन या बीटा प्राइम डिस्ट्रीब्यूशन के अपेक्षित मूल्य भी हैं (जिसे दूसरी तरह के बीटा डिस्ट्रीब्यूशन या पियर्सन डिस्ट्रीब्यूशन के रूप में भी जाना जाता है। पियर्सन टाइप VI) <ref name=JKB/>और इसकी दर्पण छवि, श्रेणी (c − a) द्वारा स्केल की गई। | ये इन्वर्टेड बीटा डिस्ट्रीब्यूशन या बीटा प्राइम डिस्ट्रीब्यूशन के अपेक्षित मूल्य भी हैं (जिसे दूसरी तरह के बीटा डिस्ट्रीब्यूशन या पियर्सन डिस्ट्रीब्यूशन के रूप में भी जाना जाता है। पियर्सन टाइप VI) <ref name=JKB/>और इसकी दर्पण छवि, श्रेणी (c − a) द्वारा स्केल की गई। | ||
साथ ही, निम्न फ़िशर सूचना घटकों को हार्मोनिक (1/X) प्रसरणों या अनुपात रूपांतरित | साथ ही, निम्न फ़िशर सूचना घटकों को हार्मोनिक (1/X) प्रसरणों या अनुपात रूपांतरित चरो ((1-X)/X) के आधार पर प्रसरणों के रूप में निम्नानुसार व्यक्त किया जा सकता है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,432: | Line 1,448: | ||
\mathcal{I}_{a, c} &=\operatorname{cov} \left [\frac{1}{X},\frac{1}{1-X} \right ]\frac{(\alpha-1)(\beta-1)}{(c-a)^2} = \operatorname{cov} \left [\frac{1-X}{X},\frac{X}{1-X} \right ] \frac{(\alpha-1)(\beta-1)}{(c-a)^2} =\frac{(\alpha+\beta-1)}{(c-a)^2} | \mathcal{I}_{a, c} &=\operatorname{cov} \left [\frac{1}{X},\frac{1}{1-X} \right ]\frac{(\alpha-1)(\beta-1)}{(c-a)^2} = \operatorname{cov} \left [\frac{1-X}{X},\frac{X}{1-X} \right ] \frac{(\alpha-1)(\beta-1)}{(c-a)^2} =\frac{(\alpha+\beta-1)}{(c-a)^2} | ||
\end{align}</math> | \end{align}</math> | ||
इन अपेक्षाओं के लिए रैखिक रूप से रूपांतरित, उत्पाद और उल्टे यादृच्छिक | इन अपेक्षाओं के लिए रैखिक रूप से रूपांतरित, उत्पाद और उल्टे यादृच्छिक वेरिएबल के क्षण देखें। | ||
फ़िशर के सूचना | फ़िशर के सूचना आव्युह का निर्धारक रुचि का है (उदाहरण के लिए जेफ़रीज़ पूर्व संभाव्यता की गणना के लिए)। अलग-अलग घटकों के भावों से, यह अनुसरण करता है कि चार मापदंडों के साथ बीटा वितरण के लिए फिशर (सममित) सूचना आव्युह का निर्धारक है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,443: | Line 1,459: | ||
& {}-\mathcal{I}_{\alpha ,a} \mathcal{I}_{\alpha ,c} \mathcal{I}_{\beta ,a} \mathcal{I}_{\beta ,c}+\mathcal{I}_{a,c} \mathcal{I}_{\alpha ,\alpha } \mathcal{I}_{\beta ,a} \mathcal{I}_{\beta ,c}-\mathcal{I}_{c,c} \mathcal{I}_{\alpha ,a}^2 \mathcal{I}_{\beta ,\beta }\\ | & {}-\mathcal{I}_{\alpha ,a} \mathcal{I}_{\alpha ,c} \mathcal{I}_{\beta ,a} \mathcal{I}_{\beta ,c}+\mathcal{I}_{a,c} \mathcal{I}_{\alpha ,\alpha } \mathcal{I}_{\beta ,a} \mathcal{I}_{\beta ,c}-\mathcal{I}_{c,c} \mathcal{I}_{\alpha ,a}^2 \mathcal{I}_{\beta ,\beta }\\ | ||
& {}+2 \mathcal{I}_{a,c} \mathcal{I}_{\alpha ,a} \mathcal{I}_{\alpha, c} \mathcal{I}_{\beta ,\beta }-\mathcal{I}_{a,a} \mathcal{I}_{\alpha ,c}^2 \mathcal{I}_{\beta ,\beta }-\mathcal{I}_{a,c}^2 \mathcal{I}_{\alpha ,\alpha } \mathcal{I}_{\beta ,\beta }+\mathcal{I}_{a,a} \mathcal{I}_{c,c} \mathcal{I}_{\alpha ,\alpha } \mathcal{I}_{\beta ,\beta }\text{ if }\alpha, \beta> 2 | & {}+2 \mathcal{I}_{a,c} \mathcal{I}_{\alpha ,a} \mathcal{I}_{\alpha, c} \mathcal{I}_{\beta ,\beta }-\mathcal{I}_{a,a} \mathcal{I}_{\alpha ,c}^2 \mathcal{I}_{\beta ,\beta }-\mathcal{I}_{a,c}^2 \mathcal{I}_{\alpha ,\alpha } \mathcal{I}_{\beta ,\beta }+\mathcal{I}_{a,a} \mathcal{I}_{c,c} \mathcal{I}_{\alpha ,\alpha } \mathcal{I}_{\beta ,\beta }\text{ if }\alpha, \beta> 2 | ||
\end{align}</math> | \end{align} </math> | ||
सिल्वेस्टर की कसौटी का उपयोग करना (जांच करना कि क्या विकर्ण तत्व सभी | सिल्वेस्टर की कसौटी का उपयोग करना (जांच करना कि क्या विकर्ण तत्व सभी धनात्मक हैं), और विकर्ण घटकों के पश्चात् से <math>{\mathcal{I}}_{a, a}</math> और <math>{\mathcal{I}}_{c, c}</math> α=2 और β=2 पर गणितीय विलक्षणता है यह इस प्रकार है कि चार मापदंड स्तिथियों के लिए फिशर सूचना आव्युह धनात्मक -निश्चित आव्युह है। α>2 और β>2 के लिए धनात्मक -निश्चित है। चूंकि α > 2 और β > 2 के लिए बीटा वितरण (सममित या असममित) घंटी के आकार का है, यह अनुसरण करता है कि फिशर सूचना आव्युह केवल घंटी के आकार (सममित या असममित) बीटा वितरण के लिए धनात्मक -निश्चित है, जिसमें विभक्ति बिंदु स्थित हैं मोड के दोनों ओर। इस प्रकार, चार-मापदंड बीटा वितरण परिवार से संबंधित महत्वपूर्ण प्रसिद्ध वितरण, जैसे परवलयिक वितरण (बीटा (2,2, a, c)) और निरंतर समान वितरण (बीटा (1,1, a, c)) फिशर सूचना घटक (<math>\mathcal{I}_{a, a},\mathcal{I}_{c, c},\mathcal{I}_{\alpha, a},\mathcal{I}_{\beta, c}</math>) जो चार-मापदंड स्तिथियों में उड़ते हैं (अनंत तक पहुंचते हैं) (चूंकि उनके फिशर सूचना घटक सभी दो मापदंड स्तिथियों के लिए परिभाषित हैं)। चार-मापदंड विग्नर अर्धवृत्त वितरण (बीटा(3/2,3/2,a,c)) और आर्क्साइन वितरण (बीटा(1/2,1/2,a,c)) में चार के लिए ऋणात्मक फिशर सूचना निर्धारक हैं -मापदंड स्तिथि । | ||
=== बायेसियन अनुमान === | === बायेसियन अनुमान === | ||
{{Main| | {{Main|बायेसियन अनुमान}} | ||
[[File:Beta(1,1) Uniform distribution - J. Rodal.png|thumb|<math>Beta(1,1)</math>: बायेसियन अनुमान में पूर्व संभावनाओं की अज्ञानता का प्रतिनिधित्व करने के लिए [[थॉमस बेयस]] द्वारा समान वितरण (निरंतर) संभाव्यता घनत्व प्रस्तावित किया गया था।]]बायेसियन अनुमान में बीटा वितरण का उपयोग इस तथ्य के कारण है कि वे द्विपद वितरण (बर्नौली वितरण सहित) और ज्यामितीय वितरण के लिए संयुग्मित पूर्व वितरण का परिवार प्रदान करते हैं। बीटा वितरण के क्षेत्र को प्रायिकता के रूप में देखा जा सकता है, और वास्तव में बीटा वितरण का उपयोग प्रायिकता मान p के वितरण का वर्णन करने के लिए किया जाता है:<ref name=MacKay/> | [[File:Beta(1,1) Uniform distribution - J. Rodal.png|thumb|<math>Beta(1,1)</math>: बायेसियन अनुमान में पूर्व संभावनाओं की अज्ञानता का प्रतिनिधित्व करने के लिए [[थॉमस बेयस]] द्वारा समान वितरण (निरंतर) संभाव्यता घनत्व प्रस्तावित किया गया था।]]बायेसियन अनुमान में बीटा वितरण का उपयोग इस तथ्य के कारण है कि वे द्विपद वितरण (बर्नौली वितरण सहित) और ज्यामितीय वितरण के लिए संयुग्मित पूर्व वितरण का परिवार प्रदान करते हैं। बीटा वितरण के क्षेत्र को प्रायिकता के रूप में देखा जा सकता है, और वास्तव में बीटा वितरण का उपयोग प्रायिकता मान p के वितरण का वर्णन करने के लिए किया जाता है:<ref name=MacKay/> | ||
:<math>P(p;\alpha,\beta) = \frac{p^{\alpha-1}(1-p)^{\beta-1}}{\Beta(\alpha,\beta)}.</math> | :<math>P(p;\alpha,\beta) = \frac{p^{\alpha-1}(1-p)^{\beta-1}}{\Beta(\alpha,\beta)}.</math> | ||
बेयसियन अनुमान में पूर्व | बेयसियन अनुमान में पूर्व मापदंड मानों की अज्ञानता का प्रतिनिधित्व करने के लिए पूर्व संभावनाओं के रूप में उपयोग किए जाने वाले बीटा वितरण के उदाहरण बीटा (1,1), बीटा (0,0) और बीटा (1/2,1/2) हैं। | ||
==== उत्तराधिकार का नियम ==== | ==== उत्तराधिकार का नियम ==== | ||
{{Main| | {{Main|उत्तराधिकार का नियम}} | ||
बीटा वितरण का क्लासिक अनुप्रयोग [[उत्तराधिकार का नियम]] है, जिसे 18वीं शताब्दी में [[पियरे-साइमन लाप्लास]] द्वारा | बीटा वितरण का क्लासिक अनुप्रयोग [[उत्तराधिकार का नियम]] है, जिसे 18वीं शताब्दी में [[पियरे-साइमन लाप्लास]] द्वारा प्रस्तुत किया गया था।<ref name=Laplace>{{cite book|last=Laplace|first=Pierre Simon, marquis de|title=संभावनाओं पर एक दार्शनिक निबंध|year=1902|publisher=New York : J. Wiley ; London : Chapman & Hall|isbn=978-1-60206-328-0|url=https://archive.org/details/philosophicaless00lapliala}}</ref> [[सूर्योदय की समस्या]] के उपचार के दौरान। इसमें कहा गया है कि, n [[सशर्त स्वतंत्रता|सनियम स्वतंत्रता]] बर्नौली परीक्षणों में संभाव्यता p के साथ सफलताओं को देखते हुए, कि अगले परीक्षण में अपेक्षित मूल्य का अनुमान है <math>\frac{s+1}{n+2}</math>. यह अनुमान p, अर्थात् बीटा(s+1, n−s+1) पर पश्च वितरण का अपेक्षित मूल्य है, जो बेज़ के नियम द्वारा दिया जाता है यदि कोई p पर समान पूर्व संभावना मानता है (अर्थात, बीटा(1, 1)) और फिर देखता है कि p ने n परीक्षणों में सफलताएँ उत्पन्न की हैं। लाप्लास के उत्तराधिकार के नियम की प्रमुख वैज्ञानिकों ने आलोचना की है। R T कॉक्स ने लाप्लास के सूर्योदय समस्या के उत्तराधिकार के नियम के अनुप्रयोग का वर्णन किया जाता है (<ref name=CoxRT>{{cite book|last=Cox|first=Richard T.|title=संभावित अनुमान का बीजगणित|year=1961|publisher=The Johns Hopkins University Press|isbn=978-0801869822}}</ref> पी। 89) इस सिद्धांत के उचित उपयोग के उपहास के रूप में। कीन्स टिप्पणी (<ref name=KeynesTreatise>{{cite book|last=Keynes|first=John Maynard|title=A Treatise on Probability: The Connection Between Philosophy and the History of Science|orig-year=1921|year=2010|publisher=Wildside Press|isbn=978-1434406965}}</ref> Ch.XXX, पी. 382) वास्तव में यह इतना मूर्खतापूर्ण प्रमेय है कि इसका मनोरंजन करना निंदनीय है। कार्ल पियर्सन<ref name=PearsonRuleSuccession>{{cite journal|last=Pearson|first=Karl|title=भविष्य की अपेक्षाओं पर पिछले अनुभव के प्रभाव पर|journal=Philosophical Magazine|year=1907|volume=6|issue=13|pages=365–378}}</ref> n परीक्षणों में n सफलताओं के पश्चात् अगले (n + 1) परीक्षणों के सफल होने की संभावना केवल 50% है, जिसे जेफरीज़ जैसे वैज्ञानिकों द्वारा बहुत कम और प्रयोग की वैज्ञानिक प्रक्रिया के प्रतिनिधित्व के रूप में अस्वीकार्य माना गया है। प्रस्तावित वैज्ञानिक नियम का परीक्षण करने के लिए। जैसा कि जेफरीस ने बताया है (<ref name=Jeffreys/>पी। 128) (सी. डी. ब्रॉड का श्रेय<ref name=BroadMind>{{cite journal|last=Broad|first=C. D.|title=प्रेरण और संभाव्यता के बीच संबंध पर|journal=MIND, A Quarterly Review of Psychology and Philosophy|date=October 1918|volume=27 (New Series)|issue=108|pages=389–404|jstor=2249035|doi=10.1093/mind/XXVII.4.389}}</ref> ) लाप्लास के उत्तराधिकार का नियम अगले परीक्षण में सफलता की उच्च संभावना ((n+1)/(n+2)) स्थापित करता है, किन्तु केवल मध्यम संभावना (50%) कि और प्रतिरूप (n+1) आकार में तुलनीय है समान रूप से सफल होंगे। जैसा कि पर्क्स द्वारा बताया गया है,<ref name=Perks>{{cite journal|last=Perks|first=Wilfred|title=व्युत्क्रम संभाव्यता पर कुछ अवलोकन जिसमें एक नया उदासीनता नियम शामिल है|journal=Journal of the Institute of Actuaries|date=January 1947|volume=73|issue=2|pages=285–334|url=http://www.actuaries.org.uk/research-and-resources/documents/some-observations-inverse-probability-including-new-indifference-ru|doi=10.1017/S0020268100012270}}</ref> उत्तराधिकार के नियम को ही स्वीकार करना कठिन है। यह अगले परीक्षण के लिए संभावना प्रदान करता है जिसका अर्थ है कि देखा गया वास्तविक रन औसत रन है और हम सदैव औसत रन के अंत में होते हैं। यह सोचना होगा, यह मान लेना अधिक उचित होगा कि हम औसत रन के मध्य में थे। स्पष्ट रूप से दोनों संभावनाओं के लिए उच्च मूल्य आवश्यक है यदि वे उचित विश्वास के अनुरूप हों। लाप्लास के उत्तराधिकार के नियम के साथ इन समस्याओं ने हाल्डेन, पर्क्स, जेफरीज़ और अन्य को पूर्व संभाव्यता के अन्य रूपों की खोज करने के लिए प्रेरित किया (अगला देखें) {{section link||बायेसियन अनुमान }}). जेनेस के अनुसार,<ref name=Jaynes/>उत्तराधिकार के नियम के साथ मुख्य समस्या यह है कि यह मान्य नहीं है जब s=0 या s=n (इसकी वैधता के विश्लेषण के लिए उत्तराधिकार का नियम देखें)। | ||
====बेयस-लाप्लास पूर्व संभावना (बीटा(1,1))==== | ====बेयस-लाप्लास पूर्व संभावना (बीटा(1,1))==== | ||
बीटा वितरण बीटा (1,1) के लिए अधिकतम अंतर एंट्रॉपी प्राप्त करता है: [[समान घनत्व]] संभाव्यता घनत्व, जिसके लिए वितरण के डोमेन में सभी मूल्यों में समान घनत्व होता है। थॉमस बेयस द्वारा इस समान वितरण बीटा (1,1) का सुझाव दिया गया था (बहुत संदेह के साथ)।<ref name="ThomasBayes"/>पूर्व संभाव्यता वितरण के रूप में सही पूर्व वितरण के बारे में अज्ञानता व्यक्त करने के लिए। यह पूर्व वितरण अपनाया गया था ( | बीटा वितरण बीटा (1,1) के लिए अधिकतम अंतर एंट्रॉपी प्राप्त करता है: [[समान घनत्व]] संभाव्यता घनत्व, जिसके लिए वितरण के डोमेन में सभी मूल्यों में समान घनत्व होता है। थॉमस बेयस द्वारा इस समान वितरण बीटा (1,1) का सुझाव दिया गया था (बहुत संदेह के साथ)।<ref name="ThomasBayes"/>पूर्व संभाव्यता वितरण के रूप में सही पूर्व वितरण के बारे में अज्ञानता व्यक्त करने के लिए। यह पूर्व वितरण अपनाया गया था (किन्तुा तौर पर, उनके लेखन से, संदेह के छोटे संकेत के साथ<ref name=Laplace/> पियरे-साइमन लाप्लास द्वारा, और इसलिए इसे 20 वीं शताब्दी के पहले छमाही के प्रकाशनों में बेयस-लाप्लास नियम या व्युत्क्रम संभाव्यता के लाप्लास नियम के रूप में भी जाना जाता था। 19वीं सदी के उत्तरार्ध और 20वीं सदी के प्रारंभिक भाग में, वैज्ञानिकों ने अनुभूत किया कि एकसमान समान संभाव्यता घनत्व की धारणा वास्तविक कार्यों पर निर्भर करती है (उदाहरण के लिए क्या रैखिक या लघुगणकीय मापदंड सबसे उपयुक्त था) और प्रयुक्त पैरामीट्रिजेशन। विशेष रूप से, परिमित समर्थन के साथ वितरण के सिरों के पास व्यवहार (उदाहरण के लिए x = 0 के पास, x = 0 पर प्रारंभिक समर्थन वाले वितरण के लिए) विशेष ध्यान देने की आवश्यकता है। कीन्स (<ref name=KeynesTreatise/>Ch.XXX, पी. 381) ने बेयस की समान पूर्व संभाव्यता (बीटा (1,1)) के उपयोग की आलोचना की, जो कि शून्य और के मध्य के सभी मूल्यों को परिवर्तनीय है, इस प्रकार है: इस प्रकार अनुभव, यदि यह कुछ भी दिखाता है, तब यह दर्शाता है कि सांख्यिकीय अनुपातबं का बहुत ही स्पष्ट क्लस्टरिंग है शून्य और एकता के निकटतम में, धनात्मक सिद्धांतबं के लिए और शून्य के निकटतम में धनात्मक गुणों के मध्य संबंध के लिए, और ऋणात्मक सिद्धांतबं के लिए और एकता के निकटतम में ऋणात्मक गुणों के मध्य संबंध के लिए। | ||
===={{Anchor|Haldane prior}हल्डेन की पूर्व प्रायिकता (बीटा(0,0))= | ===={{Anchor|Haldane prior}हल्डेन की पूर्व प्रायिकता (बीटा(0,0))= | ||
[[File:Beta distribution for alpha and beta approaching zero - J. Rodal.png|thumb|<math>Beta(0,0)</math>: हाल्डेन पूर्व संभाव्यता पूर्व सूचना के बारे में पूरी अज्ञानता व्यक्त करती है, जहां हम यह भी निश्चित नहीं हैं कि किसी प्रयोग के लिए भौतिक रूप से संभव है या | [[File:Beta distribution for alpha and beta approaching zero - J. Rodal.png|thumb|<math>Beta(0,0)</math>: हाल्डेन पूर्व संभाव्यता पूर्व सूचना के बारे में पूरी अज्ञानता व्यक्त करती है, जहां हम यह भी निश्चित नहीं हैं कि किसी प्रयोग के लिए भौतिक रूप से संभव है या तब सफलता या विफलता। Α, β → 0 के रूप में, बीटा वितरण दो-बिंदु बर्नौली वितरण तक पहुंचता है, जिसमें प्रत्येक छोर पर 0 और 1 पर केंद्रित सभी प्रायिकता घनत्व होते हैं, और मध्य में कुछ भी नहीं होता है। सिक्का उछालना: सिक्के का फलक 0 पर और दूसरा फलक 1 पर होना।]]बीटा (0,0) वितरण J.B.S द्वारा प्रस्तावित किया गया था। हाल्डेन,<ref>{{cite journal|last=Haldane|first=J.B.S.|title=व्युत्क्रम संभाव्यता पर एक नोट|journal=Mathematical Proceedings of the Cambridge Philosophical Society|year=1932|volume=28|issue=1|pages=55–61|doi=10.1017/s0305004100010495|bibcode=1932PCPS...28...55H|s2cid=122773707 }}</ref> जिन्होंने सुझाव दिया कि पूर्ण अनिश्चितता का प्रतिनिधित्व करने वाली पूर्व संभाव्यता p<sup>−1</sup>(1−p)<sup>-1</sup> के समानुपाती होनी चाहिए और फलन p<sup>−1</sup>(1−p)<sup>−1</sup> को बीटा वितरण के अंश की सीमा के रूप में देखा जा सकता है क्योंकि दोनों आकार मापदंड शून्य तक पहुंचते हैं: α, β → 0. बीटा फलन (बीटा वितरण के हर में) दोनों मापदंड के लिए अनंत तक पहुंचता है अर्थात् यह शून्य की ओर अग्रसर, α, β → 0. इसलिए, p<sup>−1</sup>(1−p)<sup>−1</sup> को बीटा फलन द्वारा विभाजित करने पर 0 और 1 पर प्राप्त होता है तथा प्रत्येक सिरे पर 1/2 की समान प्रायिकता के साथ 2-बिंदु बर्नौली वितरण प्राप्त होता है, और मध्य में कुछ भी नहीं होता है, जैसा कि α, β → 0. सिक्का-टॉस: सिक्के का फलक 0 पर है और दूसरा फलक 1 पर है। हाल्डेन पूर्व संभाव्यता वितरण बीटा (0,0) [[अनुचित पूर्व]] है क्योंकि इसका एकीकरण (0 से 1 तक) प्रत्येक छोर पर विशिष्टता के कारण 1 में सख्ती से अभिसरण करने में विफल रहता है चूँकि, जब तक प्रतिरूप आकार बहुत छोटा न हो, तब तक पश्च संभावनाओं की गणना के लिए यह कोई समस्या नहीं है। इसके अतिरिक्त, ज़ेलनर<ref name=Zellner>{{cite book|last=Zellner |first=Arnold|title=अर्थमिति में बायेसियन अनुमान का परिचय|year=1971|publisher=Wiley-Interscience|isbn=978-0471169376}}</ref> बताते हैं कि [[लॉग-बाधाओं]] की स्केल पर, (लॉगिट ट्रांसफ़ॉर्मेशन ln(p/1−p)), हल्डेन पूर्व समान रूप से सपाट पूर्व है। तथ्य यह है कि लॉगिट रूपांतरित परिवर्तनीय ln(p/1−p) (डोमेन के साथ (-∞, ∞)) पर समान पूर्व संभावना, डोमेन [0, 1] से पहले हाल्डेन के सामान्तर है जिसे हेरोल्ड जेफरीस द्वारा इंगित किया गया था। उनकी पुस्तक थ्योरी ऑफ प्रॉबेबिलिटी के पहले संस्करण (1939) में (<ref name=Jeffreys/>पी। 123). जेफरीस लिखते हैं निश्चित रूप से यदि हम बेयस-लाप्लास नियम को वेरिएबल M सीमा तक ले जाते हैं तब हम ऐसे परिणामों की ओर अग्रसर होते हैं जो किसी के सोचने के तरीके के अनुरूप नहीं होते हैं। (हल्दाने) नियम dx/(x(1−x)) दूसरे तरीके से बहुत दूर जाता है। इससे यह निष्कर्ष निकलता है कि यदि किसी संपत्ति के संबंध में प्रतिरूप इस प्रकार का होता है तब संभावना 1 होती है जैसे कि पूरी संख्या उस प्रकार की ही है। तथ्य यह है कि वर्दी पैरामीट्रिजेशन पर निर्भर करती है, जेफ़रीज़ को पूर्व के रूप की तलाश करने के लिए प्रेरित करती है जो विभिन्न पैरामीट्रिज़ेशन के अनुसार अपरिवर्तनीय होगा। | ||
==== जेफरी की पूर्व संभावना (बीटा (1/2,1/2) बर्नौली के लिए या द्विपद वितरण के लिए) ==== | ==== जेफरी की पूर्व संभावना (बीटा (1/2,1/2) बर्नौली के लिए या द्विपद वितरण के लिए) ==== | ||
{{Main| | {{Main|जेफ़्रीज़ पूर्व}} | ||
[[File: | [[File:Jeffreys prior probability for the beta distribution - J. Rodal.png|thumb|बीटा वितरण के लिए जेफरी की पूर्व संभावना: फिशर की सूचना आव्युह के निर्धारक का वर्गमूल: <math>\scriptstyle\sqrt{\det(\mathcal{I}(\alpha, \beta))} = \sqrt{\psi_1(\alpha)\psi_1(\beta)-( \psi_1(\alpha)+\psi_1(\beta) )\psi_1(\alpha + \beta)}</math> त्रिगामा फलन ψ का फलन है<sub>1</sub> आकार के मापदंड ए, बी]] | ||
[[File:Beta distribution for 3 different prior probability functions | [[File:Beta distribution for 3 different prior probability functions - J. Rodal.png|thumb|सफलता वाले प्रतिरूपों के साथ पश्च बीटा घनत्व = s, विफलता = f of s/(s + f) = 1/2, और s + f = {3,10,50}, 3 अलग-अलग पूर्व संभाव्यता कार्यों के आधार पर: Haldane (बीटा) (0,0), जेफरीस (बीटा(1/2,1/2)) और बेयस (बीटा(1,1))। छवि से पता चलता है कि 50 के प्रतिरूप आकार के साथ पोस्टीरियर के लिए प्राथमिकताओं के मध्य थोड़ा अंतर है ( पी = 1/2 के पास अधिक स्पष्ट चोटी के साथ)। बहुत छोटे प्रतिरूप आकार के लिए महत्वपूर्ण अंतर दिखाई देते हैं (3 के प्रतिरूप आकार के लिए चापलूसी वितरण)]] | ||
हेरोल्ड जेफरीस<ref name=Jeffreys>{{cite book|last=Jeffreys|first=Harold|title=संभाव्यता का सिद्धांत|year=1998|publisher=Oxford University Press, 3rd edition|isbn=978-0198503682}}</ref><ref name=JeffreysPRIOR>{{cite journal|last=Jeffreys|first=Harold|title=अनुमान समस्याओं में पूर्व संभावना के लिए एक अपरिवर्तनीय प्रपत्र|journal=Proceedings of the Royal Society|date=September 1946|volume=186|series=A 24|issue=1007|pages=453–461|doi=10.1098/rspa.1946.0056|pmid=20998741|bibcode=1946RSPSA.186..453J|doi-access=free}}</ref> गैर-सूचनात्मक पूर्व संभाव्यता माप का उपयोग करने का प्रस्ताव है जो [[पैरामीट्रिजेशन इनवेरिएंस]] होना चाहिए: फिशर की सूचना | [[File:Beta distribution for 3 different prior probability functions, skewed case - J. Rodal.png|thumb|सफलता वाले प्रतिरूपों के साथ पश्च बीटा घनत्व = s, विफलता = f of s/(s + f) = 1/4, और s + f ∈ {3,10,50}, तीन अलग-अलग पूर्व संभाव्यता कार्यों के आधार पर: Haldane (बीटा (0,0), जेफरीस (बीटा(1/2,1/2)) और बेयस (बीटा(1,1))। छवि से पता चलता है कि 50 के प्रतिरूप आकार के साथ पोस्टीरियर के लिए प्राथमिकताओं के मध्य थोड़ा अंतर है ( पी = 1/4 के पास अधिक स्पष्ट चोटी के साथ)। बहुत छोटे प्रतिरूप आकार के लिए महत्वपूर्ण अंतर दिखाई देते हैं (प्रतिरूप आकार के पतित स्तिथियों के लिए बहुत विषम वितरण = 3, इस पतित और असंभावित स्तिथियों में हाल्डेन पूर्व परिणाम रिवर्स जे आकार में होता है p = 1/4 के अतिरिक्त p = 0 पर मोड के साथ। यदि पर्याप्त प्रतिरूप (आँकड़े) हैं, तब बेज़ (बीटा (1,1)), जेफ़रीज़ (बीटा (1/2,1/2)) के तीन पूर्व और हाल्डेन (बीटा (0,0)) को समान पश्च संभाव्यता घनत्व प्राप्त करना चाहिए।]]हेरोल्ड जेफरीस<ref name="Jeffreys">{{cite book|last=Jeffreys|first=Harold|title=संभाव्यता का सिद्धांत|year=1998|publisher=Oxford University Press, 3rd edition|isbn=978-0198503682}}</ref><ref name="JeffreysPRIOR">{{cite journal|last=Jeffreys|first=Harold|title=अनुमान समस्याओं में पूर्व संभावना के लिए एक अपरिवर्तनीय प्रपत्र|journal=Proceedings of the Royal Society|date=September 1946|volume=186|series=A 24|issue=1007|pages=453–461|doi=10.1098/rspa.1946.0056|pmid=20998741|bibcode=1946RSPSA.186..453J|doi-access=free}}</ref> गैर-सूचनात्मक पूर्व संभाव्यता माप का उपयोग करने का प्रस्ताव है जो [[पैरामीट्रिजेशन इनवेरिएंस]] होना चाहिए: फिशर की सूचना आव्युह के निर्धारक के वर्गमूल के समानुपाती। बर्नौली वितरण के लिए, इसे इस प्रकार दिखाया जा सकता है: एक सिक्के के लिए जो प्रायिकता p ∈ [0, 1] के साथ "हेड्स" है और दिए गए (H,T) ∈ { के लिए प्रायिकता 1 - p के साथ "टेल्स" है। (0,1), (1,0)} संभावना p<sup>H</sup>(1 − p)<sup>T</sup> है। चूँकि T = 1 - H, बर्नौली वितरण p<sup>H</sup>(1 - p)<sup>1 - H</sup> है। p को एकमात्र पैरामीटर मानते हुए, यह इस प्रकार है कि बर्नौली वितरण के लिए लॉग संभावना है | ||
:<math>\ln \mathcal{L} (p\mid H) = H \ln(p)+ (1-H) \ln(1-p).</math> | :<math>\ln \mathcal{L} (p\mid H) = H \ln(p)+ (1-H) \ln(1-p).</math> | ||
फिशर सूचना | फिशर सूचना आव्युह में केवल घटक है (यह अदिश राशि है, क्योंकि केवल मापदंड है: p), इसलिए: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,483: | Line 1,497: | ||
&= \sqrt{p^1 (1-p)^0 \left( \frac{1}{p} - \frac{0}{1-p}\right)^2 + p^0 (1-p)^1 \left(\frac{0}{p} - \frac{1}{1-p}\right)^2} \\ | &= \sqrt{p^1 (1-p)^0 \left( \frac{1}{p} - \frac{0}{1-p}\right)^2 + p^0 (1-p)^1 \left(\frac{0}{p} - \frac{1}{1-p}\right)^2} \\ | ||
&= \frac{1}{\sqrt{p(1-p)}}. | &= \frac{1}{\sqrt{p(1-p)}}. | ||
\end{align}</math> | \end{align} </math> | ||
इसी तरह, n | इसी तरह, n बर्नोली परीक्षणों के साथ द्विपद वितरण के लिए, यह दिखाया जा सकता है | ||
:<math>\sqrt{\mathcal{I}(p)}= \frac{\sqrt{n}}{\sqrt{p(1-p)}}.</math> | :<math>\sqrt{\mathcal{I}(p)}= \frac{\sqrt{n}}{\sqrt{p(1-p)}}.</math> | ||
इस प्रकार, | इस प्रकार, बर्नोली बंटन, और द्विपद बंटन के लिए, जेफ्रेय्स पूर्व के लिए आनुपातिक है <math>\scriptstyle \frac{1}{\sqrt{p(1-p)}}</math>, जो डोमेन वेरिएबल x = p, और आकार मापदंड α = β = 1/2, आर्क्साइन वितरण के साथ बीटा वितरण के समानुपाती होता है: | ||
:<math>Beta(\tfrac{1}{2}, \tfrac{1}{2}) = \frac{1}{\pi \sqrt{p(1-p)}}.</math> | :<math>Beta(\tfrac{1}{2}, \tfrac{1}{2}) = \frac{1}{\pi \sqrt{p(1-p)}}.</math> | ||
यह अगले खंड में दिखाया जाएगा कि जेफ़रीज़ प्रायर के लिए सामान्यीकरण स्थिरांक अंतिम परिणाम के लिए सारहीन है क्योंकि [[बेयस प्रमेय]] में पश्च संभाव्यता के लिए सामान्यीकरण निरंतर रद्द हो जाता है। इसलिए बीटा (1/2,1/2) का उपयोग बर्नौली और द्विपद वितरण दोनों के लिए पहले जेफरीज़ के रूप में किया जाता है। जैसा कि अगले भाग में दिखाया गया है, जब इस अभिव्यक्ति का उपयोग बेयस प्रमेय में संभावना के पूर्व संभाव्यता गुणा के रूप में किया जाता है, | यह अगले खंड में दिखाया जाएगा कि जेफ़रीज़ प्रायर के लिए सामान्यीकरण स्थिरांक अंतिम परिणाम के लिए सारहीन है क्योंकि [[बेयस प्रमेय]] में पश्च संभाव्यता के लिए सामान्यीकरण निरंतर रद्द हो जाता है। इसलिए बीटा (1/2,1/2) का उपयोग बर्नौली और द्विपद वितरण दोनों के लिए पहले जेफरीज़ के रूप में किया जाता है। जैसा कि अगले भाग में दिखाया गया है, जब इस अभिव्यक्ति का उपयोग बेयस प्रमेय में संभावना के पूर्व संभाव्यता गुणा के रूप में किया जाता है, तब पश्च संभाव्यता बीटा वितरण बन जाती है। चूंकि, यह अनुभूत करना महत्वपूर्ण है कि जेफ़रीज़ पूर्व के समानुपाती है <math>\scriptstyle \frac{1}{\sqrt{p(1-p)}}</math> बर्नोली और द्विपद वितरण के लिए होता है , किन्तु बीटा वितरण के लिए नहीं। बीटा वितरण के लिए जेफरीस पहले बीटा वितरण के लिए फिशर की जानकारी के निर्धारक द्वारा दिया गया है, जैसा कि दिखाया गया है {{section link||फिशर सूचना आव्युह}} त्रिगामा फलन ψ<sub>1</sub> का फलन है आकार के मापदंड α और β निम्नानुसार हैं: | ||
:<math> \begin{align} | :<math> \begin{align} | ||
| Line 1,496: | Line 1,510: | ||
\lim_{\alpha\to 0} \sqrt{\det(\mathcal{I}(\alpha, \beta))} &=\lim_{\beta \to 0} \sqrt{\det(\mathcal{I}(\alpha, \beta))} = \infty\\ | \lim_{\alpha\to 0} \sqrt{\det(\mathcal{I}(\alpha, \beta))} &=\lim_{\beta \to 0} \sqrt{\det(\mathcal{I}(\alpha, \beta))} = \infty\\ | ||
\lim_{\alpha\to \infty} \sqrt{\det(\mathcal{I}(\alpha, \beta))} &=\lim_{\beta \to \infty} \sqrt{\det(\mathcal{I}(\alpha, \beta))} = 0 | \lim_{\alpha\to \infty} \sqrt{\det(\mathcal{I}(\alpha, \beta))} &=\lim_{\beta \to \infty} \sqrt{\det(\mathcal{I}(\alpha, \beta))} = 0 | ||
\end{align}</math> | \end{align} </math> | ||
जैसा कि पहले चर्चा की गई थी, बर्नौली और द्विपद वितरण के लिए जेफरीस आर्क्सिन वितरण बीटा (1/2,1/2) के समानुपाती है, आयामी वक्र जो बर्नौली के | जैसा कि पहले चर्चा की गई थी, बर्नौली और द्विपद वितरण के लिए जेफरीस आर्क्सिन वितरण बीटा (1/2,1/2) के समानुपाती है, आयामी वक्र जो बर्नौली के मापदंड p के फलन के रूप में बेसिन की तरह दिखता है और द्विपद वितरण है। बेसिन की दीवारें p के सिरों p → 0 और p → 1 पर सिंग्युलेरिटी के समीप पहुंचने से बनती हैं, जहां बीटा (1/2,1/2) अनंत तक पहुंचता है। तथा बीटा वितरण से पहले जेफ़रीज़ 2-आयामी सतह (त्रि-आयामी अंतरिक्ष में एम्बेडेड) है जो बेसिन की तरह दिखती है जिसकी केवल दो दीवारें कोने α = β = 0 पर मिलती हैं (और अन्य दो दीवारों को गायब कर देती हैं) बीटा वितरण के आकार मापदंड α और β का कार्य है । इस 2-आयामी सतह की दो निकटवर्ती दीवारें α, β → 0 पर एकवचन (ट्राइगामा फलन के) के पास आकृति मापदंडों α और β द्वारा बनाई गई हैं। इसमें α, β → ∞ के लिए कोई दीवार नहीं है क्योंकि इस स्तिथियों में बीटा वितरण के लिए फिशर के सूचना आव्युह का निर्धारक शून्य तक पहुंचता है। | ||
यह अगले खंड में दिखाया जाएगा कि जेफरी की पूर्व संभाव्यता का परिणाम पश्च संभाव्यता में होता है (जब द्विपद संभावना | यह अगले खंड में दिखाया जाएगा कि जेफरी की पूर्व संभाव्यता का परिणाम पश्च संभाव्यता में होता है (जब द्विपद संभावना फलन द्वारा गुणा किया जाता है) जो हाल्डेन और बेयस पूर्व संभावनाओं के पश्च संभाव्यता परिणामों के मध्य मध्यवर्ती हैं। | ||
जेफरीज़ पहले विश्लेषणात्मक रूप से प्राप्त करना | जेफरीज़ पहले विश्लेषणात्मक रूप से प्राप्त करना जटिल हो सकता है, और कुछ स्थितियों के लिए यह उपस्थित नहीं है (असममित त्रिकोणीय वितरण जैसे सरल वितरण कार्यों के लिए भी)। बर्जर, बर्नार्डो और सन, 2009 के पेपर में<ref name="BergerBernardoSun">{{cite journal|last=Berger|first=James |author2=Bernardo, Jose |author3=Sun, Dongchu|title=संदर्भ पुरोहितों की औपचारिक परिभाषा|journal=The Annals of Statistics|year=2009|volume=37|issue=2|pages=905–938|doi=10.1214/07-AOS587|url= http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdfview_1&handle=euclid.aos/1236693154|arxiv=0904.0156|bibcode=2009arXiv0904.0156B |s2cid=3221355 }}</ref> संदर्भ पूर्व संभाव्यता वितरण परिभाषित किया गया है जो (जेफ्रीस पूर्व के विपरीत) असममित त्रिकोणीय वितरण के लिए उपस्थित है। वे अपने संदर्भ के लिए पूर्व में विवृत -रूप अभिव्यक्ति प्राप्त नहीं कर सकते हैं, किन्तु संख्यात्मक गणना यह दर्शाती है कि यह पूर्व (उचित) द्वारा लगभग पूरी तरह से फिट है। | ||
:<math> \operatorname{Beta}(\tfrac{1}{2}, \tfrac{1}{2}) \sim\frac{1}{\sqrt{\theta(1-\theta)}}</math> | :<math> \operatorname{Beta}(\tfrac{1}{2}, \tfrac{1}{2}) \sim\frac{1}{\sqrt{\theta(1-\theta)}}</math> | ||
जहां θ समर्थन के साथ असममित त्रिकोणीय वितरण के लिए | जहां θ समर्थन के साथ असममित त्रिकोणीय वितरण के लिए वेरिएबल है [0, 1] (त्रिकोणीय वितरण पर विकिपीडिया के आलेख में निम्नलिखित मापदंड मानों के अनुरूप: वर्टेक्स सी = θ, बाएं अंत = 0, और दायां अंत बी = 1 ). बर्जर एट अल। अनुमानी तर्क भी देते हैं कि बीटा (1/2,1/2) वास्तव में असममित त्रिकोणीय वितरण के लिए स्पष्ट बर्जर-बर्नार्डो-सन संदर्भ हो सकता है। इसलिए, बीटा (1/2,1/2) न केवल बर्नौली और द्विपद वितरण के लिए जेफ्रीस पूर्व है, किंतु असममित त्रिकोणीय वितरण के लिए बर्जर-बर्नार्डो-सूर्य संदर्भ भी प्रतीत होता है (जिसके लिए जेफ्रीस पूर्व नहीं करता है) उपस्थित है कि परियोजना प्रबंधन और परियोजना कार्यों की निवेश और अवधि का वर्णन करने के लिए पीईआरटी विश्लेषण में उपयोग किया जाने वाला वितरण। | ||
क्लार्क और बैरोन<ref>{{cite journal|last=Clarke|first=Bertrand S.|author2=Andrew R. Barron|title=जेफरीज़ का पूर्व एन्ट्रापी जोखिम के तहत विषम रूप से कम से कम अनुकूल है|journal=Journal of Statistical Planning and Inference|year=1994|volume=41|pages=37–60|url=http://www.stat.yale.edu/~arb4/publications_files/jeffery's%20prior.pdf|doi=10.1016/0378-3758(94)90153-8}}</ref> | क्लार्क और बैरोन<ref>{{cite journal|last=Clarke|first=Bertrand S.|author2=Andrew R. Barron|title=जेफरीज़ का पूर्व एन्ट्रापी जोखिम के तहत विषम रूप से कम से कम अनुकूल है|journal=Journal of Statistical Planning and Inference|year=1994|volume=41|pages=37–60|url=http://www.stat.yale.edu/~arb4/publications_files/jeffery's%20prior.pdf|doi=10.1016/0378-3758(94)90153-8}}</ref> सिद्ध करें कि, निरंतर धनात्मक पुजारियों के मध्य, जेफ़रीज़ पूर्व (जब यह उपस्थितहै) आकार n और मापदंड के प्रतिरूप के मध्य शैनन की पारस्परिक जानकारी को स्पर्शोन्मुख रूप से अधिकतम करता है, और इसलिए जेफ़्रीज़ पूर्व सबसे असंक्रामक पूर्व है (शैनन जानकारी के रूप में जानकारी को मापना)। प्रमाण iid यादृच्छिक वेरिएबल के लिए संभाव्यता घनत्व कार्यों के मध्य कुल्बैक-लीब्लर विचलन की परीक्षा पर टिकी हुई है। | ||
==== पश्च बीटा वितरण पर विभिन्न पूर्व संभाव्यता विकल्पों का प्रभाव ==== | ==== पश्च बीटा वितरण पर विभिन्न पूर्व संभाव्यता विकल्पों का प्रभाव ==== | ||
यदि यादृच्छिक | यदि यादृच्छिक वेरिएबल X की संख्या से प्रतिरूप लिए जाते हैं, जिसके परिणाम स्वरूप "n" बर्नौली में सफलताएँ और f विफलताएँ होती हैं तो परीक्षण n = s + f, फिर पैरामीटर s और f के लिए संभावना फलन x = p दिया गया है (नीचे दिए गए भावों में x = p संकेतन इस बात पर जोर देगा कि डोमेन x द्विपद वितरण में पैरामीटर p के मान को दर्शाता है), निम्नलिखित द्विपद वितरण है: | ||
:<math>\mathcal{L}(s,f\mid x=p) = {s+f \choose s} x^s(1-x)^f = {n \choose s} x^s(1-x)^{n - s}. </math> | :<math>\mathcal{L}(s,f\mid x=p) = {s+f \choose s} x^s(1-x)^f = {n \choose s} x^s(1-x)^{n - s}. </math> | ||
यदि पूर्व संभाव्यता जानकारी के बारे में मान्यताओं को | : | ||
यदि पूर्व संभाव्यता जानकारी के बारे में मान्यताओं को α प्रायर और β प्रायर मापदंडों के साथ बीटा वितरण द्वारा यथोचित रूप से अच्छी तरह से अनुमानित किया गया है, तो: | |||
:<math>{\operatorname{PriorProbability}}(x=p;\alpha \operatorname{Prior},\beta \operatorname{Prior}) = \frac{ x^{\alpha \operatorname{Prior}-1}(1-x)^{\beta \operatorname{Prior}-1}}{\Beta(\alpha \operatorname{Prior},\beta \operatorname{Prior})}</math> | :<math>{\operatorname{PriorProbability}}(x=p;\alpha \operatorname{Prior},\beta \operatorname{Prior}) = \frac{ x^{\alpha \operatorname{Prior}-1}(1-x)^{\beta \operatorname{Prior}-1}}{\Beta(\alpha \operatorname{Prior},\beta \operatorname{Prior})}</math> | ||
एक निरंतर घटना स्थान के लिए बेयस के प्रमेय के अनुसार, पश्च संभाव्यता पूर्व संभाव्यता और संभावना फलन के उत्पाद द्वारा दी जाती है (दिए गए साक्ष्य s और f = n n − s), सामान्यीकृत | : | ||
एक निरंतर घटना स्थान के लिए बेयस के प्रमेय के अनुसार, पश्च संभाव्यता पूर्व संभाव्यता और संभावना फलन के उत्पाद द्वारा दी जाती है (दिए गए साक्ष्य s और f = n n − s), सामान्यीकृत है जिससे वक्र के नीचे का क्षेत्र सामान्तर हो होता है , निम्नलिखित नुसार: | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 1,523: | Line 1,539: | ||
= {} & \frac{x^{s+\alpha \operatorname{Prior}-1}(1-x)^{n-s+\beta \operatorname{Prior}-1}}{\int_0^1 \left(x^{s+\alpha \operatorname{Prior}-1}(1-x)^{n-s+\beta \operatorname{Prior}-1}\right) dx} \\[6pt] | = {} & \frac{x^{s+\alpha \operatorname{Prior}-1}(1-x)^{n-s+\beta \operatorname{Prior}-1}}{\int_0^1 \left(x^{s+\alpha \operatorname{Prior}-1}(1-x)^{n-s+\beta \operatorname{Prior}-1}\right) dx} \\[6pt] | ||
= {} & \frac{x^{s+\alpha \operatorname{Prior}-1}(1-x)^{n-s+\beta \operatorname{Prior}-1}}{\Beta(s+\alpha \operatorname{Prior},n-s+\beta \operatorname{Prior})}. | = {} & \frac{x^{s+\alpha \operatorname{Prior}-1}(1-x)^{n-s+\beta \operatorname{Prior}-1}}{\Beta(s+\alpha \operatorname{Prior},n-s+\beta \operatorname{Prior})}. | ||
\end{align}</math> | \end{align} </math> | ||
: | |||
[[द्विपद गुणांक]] | [[द्विपद गुणांक]] | ||
:<math>{s+f \choose s}={n \choose s}=\frac{(s+f)!}{s! f!}=\frac{n!}{s!(n-s)!}</math> | :<math>{s+f \choose s}={n \choose s}=\frac{(s+f)!}{s! f!}=\frac{n!}{s!(n-s)!}</math> | ||
पश्च संभाव्यता के अंश और भाजक दोनों में प्रकट होता है, और यह एकीकरण | पश्च संभाव्यता के अंश और भाजक दोनों में प्रकट होता है, और यह एकीकरण वेरिएबल x पर निर्भर नहीं करता है, इसलिए यह रद्द हो जाता है, और यह अंतिम परिणाम के लिए अप्रासंगिक है। इसी तरह पूर्व संभाव्यता के लिए सामान्य कारक, बीटा फलन बी (α प्रायर, β प्रायर) रद्द हो जाता है और यह अंतिम परिणाम के लिए सारहीन है। यदि कोई पूर्व-सामान्यीकृत पूर्व का उपयोग करता है तब समान पश्च संभाव्यता परिणाम प्राप्त किया जा सकता है | ||
:<math>x^{\alpha \operatorname{Prior}-1}(1-x)^{\beta \operatorname{Prior}-1}</math> | :<math>x^{\alpha \operatorname{Prior}-1}(1-x)^{\beta \operatorname{Prior}-1}</math> | ||
क्योंकि सामान्य करने वाले कारक सभी रद्द हो जाते हैं। | : | ||
क्योंकि सामान्य करने वाले कारक सभी रद्द हो जाते हैं। अनेक लेखक (स्वयं जेफरीज़ सहित) इस प्रकार गैर-सामान्यीकृत पूर्व सूत्र का उपयोग करते हैं क्योंकि सामान्यीकरण निरंतर रद्द हो जाता है। पश्च संभाव्यता का अंश पूर्व संभाव्यता और संभावना कार्य के केवल (असामान्यीकृत) उत्पाद होने के कारण समाप्त होता है, और भाजक शून्य से तक इसका अभिन्न अंग है। भाजक में बीटा फलन B(s + α प्रायर, n − s + β प्रायर), यह सुनिश्चित करने के लिए सामान्यीकरण स्थिरांक के रूप में प्रकट होता है कि कुल पश्च संभाव्यता एकता में एकीकृत हो जाती है। | |||
परीक्षणों की कुल संख्या के लिए सफलताओं की संख्या का अनुपात द्विपद | परीक्षणों की कुल संख्या के लिए सफलताओं की संख्या का अनुपात द्विपद स्तिथियों में पर्याप्त आंकड़ा है, जो निम्नलिखित परिणामों के लिए प्रासंगिक है। | ||
'बेयस पूर्व संभाव्यता (बीटा (1,1)) के लिए, पश्च संभाव्यता है: | 'बेयस पूर्व संभाव्यता (बीटा (1,1)) के लिए, पश्च संभाव्यता है: | ||
| Line 1,543: | Line 1,561: | ||
:<math>\operatorname{posterior probability}(p=x\mid s,f) = \frac{x^{s-1}(1-x)^{n-s-1}}{\Beta(s,n-s)}, \text{ with mean} = \frac{s}{n},\text{ (and mode= }\frac{s-1}{n-2}\text{ if } 1 < s < n -1).</math> | :<math>\operatorname{posterior probability}(p=x\mid s,f) = \frac{x^{s-1}(1-x)^{n-s-1}}{\Beta(s,n-s)}, \text{ with mean} = \frac{s}{n},\text{ (and mode= }\frac{s-1}{n-2}\text{ if } 1 < s < n -1).</math> | ||
उपरोक्त भावों से यह पता चलता है कि s/n = 1/2 के लिए) उपरोक्त सभी तीन पूर्व संभावनाओं का परिणाम पश्च संभाव्यता माध्य = मोड = 1/2 के लिए समान स्थान पर होता है। s/n < 1/2 के लिए, निम्नलिखित प्राथमिकताओं का उपयोग करते हुए, | : | ||
उपरोक्त भावों से यह पता चलता है कि s/n = 1/2 के लिए) उपरोक्त सभी तीन पूर्व संभावनाओं का परिणाम पश्च संभाव्यता माध्य = मोड = 1/2 के लिए समान स्थान पर होता है। s/n < 1/2 के लिए, निम्नलिखित प्राथमिकताओं का उपयोग करते हुए,उपयोग किया जाता है इसके पश्चात् की संभावनाओं का कारण इस प्रकार है: बेयस पूर्व के लिए कारण जेफरीस पूर्व के लिए कारण हाल्डेन पूर्व के लिए कारण। s/n > 1/2 के लिए इन असमानताओं के क्रम को उलट दिया जाता है जैसे कि हाल्डेन पूर्व संभाव्यता का परिणाम सबसे बड़ा पश्च माध्य होता है। हाल्डेन पूर्व संभाव्यता बीटा (0,0) माध्य (अगले परीक्षण में सफलता की संभावना के लिए अपेक्षित मान) के साथ पश्च संभाव्यता घनत्व का परिणाम है, जो परीक्षणों की कुल संख्या के लिए सफलताओं की संख्या के अनुपात s/n के समान है। . इसलिए, हाल्डेन पूर्व परिणाम अगले परीक्षण में अपेक्षित मूल्य के साथ अधिकतम संभावना के सामान्तर पश्च संभाव्यता में परिणाम देता है। बेयस पूर्व संभाव्यता बीटा (1,1) अनुपात s/n (अधिकतम संभावना) के समान मोड के साथ पश्च संभाव्यता घनत्व में परिणाम देता है। | |||
इस | इस स्तिथियों में यह है कि 100% परीक्षण सफल रहे हैं s= n, बेयस पूर्व संभावना बीटा (1,1) के परिणामस्वरूप उत्तराधिकार के नियम (n + 1)/(n + 2) के सामान्तर पश्च प्रत्याशित मान होता है, जबकि हाल्डेन पूर्व बीटा (0,0) का परिणाम 1 के पश्चात् के अपेक्षित मूल्य (अगले परीक्षण में सफलता की पूर्ण निश्चितता) में होता है। जेफ़रीज़ पूर्व संभाव्यता के परिणामस्वरूप (n + 1/2)/(n + 1) के सामान्तर पश्च प्रत्याशित मान होता है। सुविधाएं<ref name=Perks/>(पृष्ठ 303) बताते हैं: यह उत्तराधिकार का नया नियम प्रदान करता है और लेने के लिए 'उचित' स्थिति को व्यक्त करता है, अर्थात्, एन सफलताओं के अटूट रन के पश्चात् हम अगले परीक्षण के लिए संभावना मानते हैं कि हम इस धारणा के सामान्तर हैं औसत रन के लगभग आधे रास्ते पर हैं, अर्थात हम (2n + 2) परीक्षणों में बार विफलता की उम्मीद करते हैं। बेयस-लाप्लास नियम का तात्पर्य है कि हम औसत रन के अंत के समीप हैं या हम (n + 2) परीक्षणों में बार विफलता की उम्मीद करते हैं। तुलना स्पष्ट रूप से 'तर्कसंगतता' के दृष्टिकोण से नए परिणाम (जिसे अब जेफ़रीज़ प्रायर कहा जाता है) का समर्थन करती है। | ||
इसके विपरीत, इस | इसके विपरीत, इस स्तिथियों में है कि 100% परीक्षणों के परिणाम स्वरूप विफलता (s = 0) हुई है, बेज़ पूर्व संभाव्यता बीटा (1,1) के परिणाम 1/(n + के सामान्तर अगले परीक्षण में सफलता के लिए अपेक्षित मान हैं। 2), जबकि हाल्डेन पूर्व बीटा (0,0) का परिणाम 0 के अगले परीक्षण में सफलता के पश्चात् के अपेक्षित मूल्य में होता है (अगले परीक्षण में विफलता की पूर्ण निश्चितता)। जेफ़्रीज़ की पूर्व संभाव्यता का परिणाम अगले परीक्षण में सफलता के लिए अपेक्षित पश्चगामी मान होता है, जो (1/2)/(n + 1) के सामान्तर होता है, जिसका फ़ायदा होता है<ref name=Perks/>(पृष्ठ 303) बताते हैं: बेयस-लाप्लास परिणाम 1/(एन + 2) की तुलना में कहीं अधिक उचित रूप से दूरस्थ परिणाम है। | ||
जेनेस<ref name=Jaynes/>प्रश्न (वर्दी पूर्व बीटा (1,1) के लिए) स्थितियों के लिए इन सूत्रों का उपयोग s = 0 या s = n होगा क्योंकि इंटीग्रल अभिसरण नहीं करते हैं (बीटा (1,1) s = 0 या के लिए अनुचित पूर्व है s = n) होगा । व्यवहार में, पूर्व बेज़ के लिए दोनों सिरों के मध्य मोड के उपस्थित होने के लिए आवश्यक 0<s<n नियममों में सामान्यतः पूरी होती हैं, और इसलिए बेज़ पूर्व (0 < s < n तक) का परिणाम दोनों के मध्य स्थित पश्च मोड में होता है डोमेन के अंत तक होता है । | |||
जैसा कि उत्तराधिकार के नियम पर अनुभाग में टिप्पणी की गई है, के. पियर्सन ने दिखाया कि n परीक्षणों में n सफलताओं के | जैसा कि उत्तराधिकार के नियम पर अनुभाग में टिप्पणी की गई है, के. पियर्सन ने दिखाया कि n परीक्षणों में n सफलताओं के पश्चात् पश्च संभाव्यता (पूर्व संभाव्यता के रूप में बेयस बीटा (1,1) वितरण के आधार पर) कि अगला (n + 1) परीक्षण सभी सफल होंगे,जो कि ठीक 1/2 है, चाहे n का मान कुछ भी हो। जिसके पूर्व संभाव्यता के रूप में हाल्डेन बीटा (0,0) वितरण के आधार पर होता है , यह पश्च संभाव्यता 1 है (पूर्ण निश्चितता है कि n परीक्षणों में n सफलताओं के पश्चात् अगला (n + 1) परीक्षण सभी सफल होंगे)। सुविधाएं<ref name=Perks/>(पृ. 303) दर्शाता है कि, जिसे अब जेफ़रीज़ प्रायर के नाम से जाना जाता है, उसके लिए यह प्रायिकता ((n + 1/2)/(n + 1))((n + 3/2)/(n + 2) है )...(2n + 1/2)/(2n + 1), जो n = 1, 2, 3 के लिए 15/24, 315/480, 9009/13440 देता है; तेजी से सीमित मूल्य के समीप पहुंच रहा है <math>1/\sqrt{2} = 0.70710678\ldots</math> n के रूप में अनंत की ओर जाता है। पर्क्स टिप्पणी करते हैं कि जिसे अब जेफ़रीज़ प्रायर के रूप में जाना जाता है: स्पष्ट रूप से या तब बेज़-लाप्लास परिणाम या जेफ़रीज़ द्वारा अस्वीकार किए गए (हाल्डेन) वैकल्पिक नियम के परिणाम की तुलना में अधिक 'उचित' है जो संभाव्यता के रूप में निश्चितता देता है। यह स्पष्ट रूप से प्रेरण की प्रक्रिया के साथ बहुत उत्तम पत्राचार प्रदान करता है। क्या यह उद्देश्य के लिए 'बिल्कुल' उचित है, अर्थात क्या यह अभी तक अधिक बड़ा है, एकता तक पहुंचने की बेतुकापन के बिना, यह तय करने का स्तिथि है। किन्तु यह अनुभूत किया जाना चाहिए कि परिणाम प्रतिरूप करण प्रयोग से पहले पूर्ण उदासीनता और ज्ञान की अनुपस्थिति की धारणा पर निर्भर करता है। | ||
इन तीन पूर्व संभाव्यता वितरणों के साथ प्राप्त पश्च वितरण के प्रसरण निम्नलिखित हैं: | इन तीन पूर्व संभाव्यता वितरणों के साथ प्राप्त पश्च वितरण के प्रसरण निम्नलिखित हैं: | ||
बेयस की पूर्व संभावना (बीटा (1,1)) के लिए, पश्च विचरण है: | बेयस की पूर्व संभावना (बीटा (1,1)) के लिए, पश्च विचरण है: | ||
:<math>\text{variance} = \frac{(n-s+1)(s+1)}{(3+n)(2+n)^2},\text{ which for } s=\frac{n}{2} \text{ results in variance} =\frac{1}{12+4n}</math> | :<math>\text{variance} = \frac{(n-s+1)(s+1)}{(3+n)(2+n)^2},\text{ which for } s=\frac{n}{2} \text{ results in variance} =\frac{1}{12+4n}</math> | ||
जेफरीज़ की पूर्व संभावना (बीटा (1/2,1/2)) के लिए, पश्च विचरण है: | : | ||
जेफरीज़ की पूर्व संभावना (बीटा (1/2,1/2)) के लिए, पश्च विचरण है: | |||
: <math>\text{variance} = \frac{(n-s+\frac{1}{2})(s+\frac{1}{2})}{(2+n)(1+n)^2} ,\text{ which for } s=\frac n 2 \text{ results in var} = \frac 1 {8 + 4n}</math> | : <math>\text{variance} = \frac{(n-s+\frac{1}{2})(s+\frac{1}{2})}{(2+n)(1+n)^2} ,\text{ which for } s=\frac n 2 \text{ results in var} = \frac 1 {8 + 4n}</math> | ||
और हाल्डेन पूर्व संभावना (बीटा (0,0)) के लिए, पश्च विचरण है: | : | ||
और हाल्डेन पूर्व संभावना (बीटा (0,0)) के लिए, पश्च विचरण है: | |||
:<math>\text{variance} = \frac{(n-s)s}{(1+n)n^2}, \text{ which for }s=\frac{n}{2}\text{ results in variance} =\frac{1}{4+4n}</math> | :<math>\text{variance} = \frac{(n-s)s}{(1+n)n^2}, \text{ which for }s=\frac{n}{2}\text{ results in variance} =\frac{1}{4+4n}</math> | ||
: | |||
तब, जैसा कि सिल्वे ने टिप्पणी की,<ref name=Silvey/>बड़े n के लिए, विचरण छोटा है और इसलिए पश्च वितरण अत्यधिक केंद्रित है, जबकि माना गया पूर्व वितरण बहुत फैला हुआ था। यह इस बात के अनुरूप है कि कोई क्या उम्मीद करेगा, क्योंकि अस्पष्ट पूर्व ज्ञान (बेयस प्रमेय के माध्यम से) सूचनात्मक प्रयोग द्वारा अधिक स्पष्ट पश्च ज्ञान में परिवर्तित हो जाता है। छोटे n के लिए हल्डेन बीटा (0,0) सबसे बड़े पश्च विचरण में पूर्व परिणाम जबकि बेयस बीटा (1,1) पूर्व परिणाम अधिक केंद्रित पश्च में। जेफ़्रीज़ पूर्व बीटा (1/2,1/2) के परिणाम स्वरूप अन्य दो के मध्य पश्च विचरण होता है। जैसे-जैसे n बढ़ता है, वैरियंस तेजी से घटता जाता है जिससे कि तीनों पूर्ववर्तियों के लिए पश्च विचरण लगभग समान मान में ही परिवर्तित हो जाता है (शून्य प्रसरण के रूप में n → ∞)। पिछले परिणाम को याद करते हुए कि हाल्डेन पूर्व संभाव्यता बीटा (0,0) का परिणाम माध्य के साथ पश्च संभाव्यता घनत्व (अगले परीक्षण में सफलता की संभावना के लिए अपेक्षित मूल्य) के समान सफलताओं की संख्या के अनुपात s/n के समान है। परीक्षणों की कुल संख्या, यह उपरोक्त अभिव्यक्ति से अनुसरण करता है कि हाल्डेन पूर्व बीटा (0,0) परिणाम भी अधिकतम के संदर्भ में व्यक्त भिन्नता के समान भिन्नता के साथ पश्च में होता है। संभावना अनुमान s/n और प्रतिरूप आकार (में {{section link||विचरण }}): | |||
:<math>\text{variance} = \frac{\mu(1-\mu)}{1 + \nu}= \frac{(n-s)s}{(1+n) n^2} </math> | :<math>\text{variance} = \frac{\mu(1-\mu)}{1 + \nu}= \frac{(n-s)s}{(1+n) n^2} </math> | ||
कारण μ=s/n और प्रतिरूप आकार ν=n के साथ। | |||
बायेसियन अनुमान में, द्विपद वितरण से पहले [[पूर्व वितरण]] बीटा ( | बायेसियन अनुमान में, द्विपद वितरण से पहले [[पूर्व वितरण]] बीटा (α प्रायर, β प्रायर) का उपयोग करना सफलता की वास्तविक संख्या में (α प्रायर − 1) छद्म-अवलोकन और (β प्रायर − 1) विफलता की छद्म-अवलोकन जोड़ने के सामान्तर है और विफलताओं का अवलोकन किया जाता है ,उसके बाद फिर वास्तविक और छद्म-अवलोकन दोनों पर सफलताओं के अनुपात द्वारा द्विपद वितरण के मापदंड p का अनुमान लगाया जाता है । समान पूर्व बीटा(1,1) किसी छद्म अवलोकन को नहीं जोड़ता (या घटाता) है क्योंकि बीटा(1,1) के लिए यह (α प्रायर − 1) = 0 और (β प्रायर − 1) =0 का अनुसरण करता है। बीटा (0,0) प्रत्येक से छद्म अवलोकन घटाता है और जेफरीस पूर्व बीटा (1/2,1/2) सफलता के 1/2 छद्म-अवलोकन और विफलता की समान संख्या घटाता है। इस घटाव का पश्च वितरण को सुचारू करने का प्रभाव है। यदि सफलताओं का अनुपात αप्रायर और βप्रायर के 50% (s/n ≠ 1/2) मान 1 से कम नहीं है (और इसलिए ऋणात्मक (α प्रायर − 1) और (β प्रायर − 1)) स्पार्सिटी का पक्ष लेते हैं, अर्थात वितरण जहां मापदंड p या तब 0 या 1 के समीप है। वास्तव में, 0 और 1 के मध्य αप्रायर और βप्रायर के मान, साथ संचालन करते समय, [[एकाग्रता पैरामीटर|एकाग्रता मापदंड]] के रूप में कार्य करते हैं। | ||
संलग्न प्लॉट | संलग्न प्लॉट प्रतिरूप आकार n ∈ {3,10,50}, सफलताओं s ∈ {n/2,n/4} और बीटा(α प्रायर,β प्रायर) ∈ {बीटा(0,0), बीटा (1/2,1/2), बीटा (1,1)}। n={4,12,40}, Success s={n/4} और बीटा(α प्रायर,β प्रायर) ∈ { बीटा(0,0),बीटा(1/2,1/2) के स्तिथियाँ भी दिखाए गए हैं , बीटा (1,1)}। पहला प्लॉट सक्सेस s ∈ {n/2} के लिए मीन = मोड = 1/2 के साथ सिमेट्रिक केस दिखाता है और दूसरा प्लॉट विषम केस s ∈ {n/4} दिखाता है। छवियों से पता चलता है कि 50 के प्रतिरूप के आकार के साथ पश्च के लिए पूर्वों के मध्य थोड़ा अंतर है (पी = 1/2 के पास अधिक स्पष्ट शिखर द्वारा विशेषता)। बहुत छोटे प्रतिरूप आकार के लिए महत्वपूर्ण अंतर दिखाई देते हैं (विशेष रूप से प्रतिरूप आकार के पतित स्तिथियों के लिए चापलूसी वितरण के लिए = 3)। इसलिए, विषम स्तिथियाँ , सफलताओं के साथ = {n/4}, सममित स्थितियों की तुलना में, छोटे प्रतिरूप के आकार में, पूर्व की पसंद से बड़ा प्रभाव दिखाते हैं। सममित वितरण के लिए, बेयस पूर्व बीटा (1,1) का परिणाम सबसे वेरिएबल म और उच्चतम पश्च वितरण में होता है और हाल्डेन पूर्व बीटा (0,0) का परिणाम सबसे सपाट और निम्नतम शिखर वितरण होता है। जेफरीज़ पूर्व बीटा (1/2,1/2) उनके मध्य में है। लगभग सममित, बहुत अधिक विषम वितरण के लिए, पुरोहितबं का प्रभाव समान होता है। बहुत छोटे प्रतिरूप के आकार के लिए (इस स्तिथियों में 3 के प्रतिरूप के आकार के लिए) और विषम वितरण (इस उदाहरण में s ∈ {n/4} के लिए) हाल्डेन पूर्व में विलक्षणता के साथ रिवर्स-j-आकार का वितरण हो सकता है बायाँ छोर। चूंकि, यह केवल पतित स्थितियों में होता है (इस उदाहरण में n = 3 और इसलिए s = 3/4 < 1, पतित मान क्योंकि हल्दाने के पश्च भाग के लिए s को एकता से अधिक होना चाहिए जिससे मध्य में मोड स्थित हो अंत, और क्योंकि s = 3/4 पूर्णांक संख्या नहीं है, इसलिए यह संभावना के लिए द्विपद वितरण की प्रारंभिक धारणा का उल्लंघन करता है) और यह उचित प्रतिरूप आकार के सामान्य स्थितियों में कोई समस्या नहीं है (जैसे कि स्थिति 1 < s < n − 1, मोड के दोनों सिरों के मध्य उपस्थितहोने के लिए आवश्यक है, पूरा हो गया है)। | ||
उनकी किताब जेनेस के अध्याय 12 (पृष्ठ 385) में<ref name=Jaynes/> | उनकी किताब जेनेस के अध्याय 12 (पृष्ठ 385) में<ref name=Jaynes/>प्रमाणित करता है कि हाल्डेन पूर्व बीटा (0,0) पूर्ण अज्ञानता के ज्ञान की पूर्व स्थिति का वर्णन करता है, जहां हम यह भी सुनिश्चित नहीं हैं कि किसी प्रयोग के लिए शारीरिक रूप से संभव है या तब सफलता या असफलता, जबकि बेयस (वर्दी) पूर्व बीटा (1,1) प्रयुक्त होता है यदि कोई जानता है कि दोनों बाइनरी परिणाम संभव हैं। जिन्हें जेनेस कहते हैं: बेयस-लाप्लास (बीटा (1,1)) की व्याख्या करने से पहले पूर्ण अज्ञानता की स्थिति का वर्णन नहीं करना चाहिए, किंतु ज्ञान की स्थिति जिसमें हमने सफलता और विफलता देखी है अनेक बार हमने कम से कम देखा है कि सफलता और असफलता तब हम जानते हैं कि प्रयोग भौतिक संभावना के अर्थ में वास्तविक द्विआधारी है। जेनेस <ref name=Jaynes/>विशेष रूप से जेफरीस के पूर्व बीटा (1/2,1/2) पर चर्चा नहीं करता है (पृष्ठ 181, 423 और जेनेस पुस्तक के अध्याय 12 पर जेफ्रीस के पूर्व की जेन्स चर्चा <ref name=Jaynes/>इसके अतिरिक्त जेफरीज़ द्वारा अपनी पुस्तक के 1939 संस्करण में प्रस्तुत किए गए अनुचित, गैर-सामान्यीकृत, पूर्व 1/p dp को संदर्भित करता है,<ref name=Jeffreys/>सात साल पहले उन्होंने प्रस्तुत किया था जिसे अब जेफरीस के अपरिवर्तनीय पूर्व के रूप में जाना जाता है: फिशर के सूचना आव्युह के निर्धारक का वर्गमूल। 1/p जेफरीज़' (1946) वेरिएबल घातांकी वितरण से पहले का अपरिवर्तनीय है, बर्नौली या द्विपद वितरणों के लिए नहीं)। चूंकि, उपरोक्त चर्चा से यह पता चलता है कि जेफरीस बीटा (1/2,1/2) पूर्व हल्दाने बीटा (0,0) और बेयस बीटा (1,1) पूर्व के मध्य ज्ञान की स्थिति का प्रतिनिधित्व करता है। | ||
इसी तरह, कार्ल पियर्सन ने अपनी 1892 की पुस्तक [[विज्ञान का व्याकरण]] में<ref name=PearsonGrammar>{{cite book| last=Pearson|first=Karl|title=विज्ञान का व्याकरण|year=1892|publisher=Walter Scott, London|url=https://books.google.com/books?id=IvdsEcFwcnsC&q=grammar+of+science&pg=PR19}}</ref><ref name=PearsnGrammar2009>{{cite book|last=Pearson|first=Karl|title=विज्ञान का व्याकरण|year=2009|publisher=BiblioLife|isbn=978-1110356119}}</ref> (1900 संस्करण का पृष्ठ 144) ने कहा कि बेज़ (बीटा (1,1) वर्दी पूर्व में पूर्ण अज्ञानता नहीं थी, और यह कि इसका उपयोग तब किया जाना चाहिए जब पूर्व सूचना हमारी अज्ञानता को समान रूप से वितरित करने के लिए उचित हो। के. पियर्सन ने लिखा: फिर भी ऐसा लगता है कि हमने जो एकमात्र अनुमान लगाया है वह यह है: | इसी तरह, कार्ल पियर्सन ने अपनी 1892 की पुस्तक [[विज्ञान का व्याकरण]] में<ref name=PearsonGrammar>{{cite book| last=Pearson|first=Karl|title=विज्ञान का व्याकरण|year=1892|publisher=Walter Scott, London|url=https://books.google.com/books?id=IvdsEcFwcnsC&q=grammar+of+science&pg=PR19}}</ref><ref name=PearsnGrammar2009>{{cite book|last=Pearson|first=Karl|title=विज्ञान का व्याकरण|year=2009|publisher=BiblioLife|isbn=978-1110356119}}</ref> (1900 संस्करण का पृष्ठ 144) ने कहा कि बेज़ (बीटा (1,1) वर्दी पूर्व में पूर्ण अज्ञानता नहीं थी, और यह कि इसका उपयोग तब किया जाना चाहिए जब पूर्व सूचना हमारी अज्ञानता को समान रूप से वितरित करने के लिए उचित हो। के. पियर्सन ने लिखा: फिर भी ऐसा लगता है कि हमने जो एकमात्र अनुमान लगाया है वह यह है: प्रकृतिक, दिनचर्या और विसंगति के बारे में कुछ भी नहीं जानना (ग्रीक ανομία से, अर्थात्: ए- बिना, और नोमोस नियम) को समान रूप से घटित होने की संभावना के रूप में माना जाता है। अब हम इस धारणा को बनाने में वास्तव में न्याय संगत नहीं थे, क्योंकि इसमें ऐसा ज्ञान सम्मिलित है जो हमारे पास प्रकृति के संबंध में नहीं है। हम सामान्य रूप से सिक्कों की संरचना और कार्रवाई के अपने अनुभव का उपयोग यह प्रमाणित करने के लिए करते हैं कि सिर और टेल समान रूप से संभावित हैं, किन्तु हमारे पास कोई नहीं है अनुभव से पहले प्रमाणित करने का अधिकार कि, जैसा कि हम प्रकृति के बारे में कुछ भी नहीं जानते हैं, दिनचर्या और उल्लंघन समान रूप से संभावित हैं। हमारी अज्ञानता में हमें अनुभव से पहले विचार करना चाहिए कि प्रकृति में सभी दिनचर्या , सभी विसंगतियाँ (सामान्यता), या दोनों का मिश्रण सम्मिलित हो सकता है। इसमें y का अनुपात जो भी हो, और यह कि सभी समान रूप से संभावित हैं। अनुभव के पश्चात् इनमें से कौन सा संविधान सबसे अधिक संभावित है, यह स्पष्ट रूप से इस बात पर निर्भर होना चाहिए कि वह अनुभव कैसा रहा है। | ||
यदि पर्याप्त | यदि पर्याप्त प्रतिरूप (सांख्यिकी) है, और पश्च संभाव्यता मोड डोमेन (x = 0 या x = 1) के वेरिएबल सीमाओं में से पर स्थित नहीं है, बेयस के तीन पूर्व (बीटा (1,1)), जेफरीस (बीटा(1/2,1/2)) और हाल्डेन (बीटा(0,0)) को समान पश्च संभाव्यता घनत्व प्राप्त करना चाहिए। अन्यथा, गेलमैन एट अल के रूप में।<ref name=Gelman>{{cite book|last=Gelman|first=A., Carlin, J. B., Stern, H. S., and Rubin, D. B.|title=बायेसियन डेटा विश्लेषण| year=2003|publisher=Chapman and Hall/CRC|isbn=978-1584883883}}</ref> (पृष्ठ 65) इंगित करें, यदि इतने कम डेटा उपलब्ध हैं कि गैर-सूचनात्मक पूर्व वितरण के विकल्प से फर्क पड़ता है, तब किसी को प्रासंगिक जानकारी को पूर्व वितरण में या बर्जर के रूप में रखना चाहिए<ref name=BergerDecisionTheory/>(पृ. 125) इंगित करता है कि जब अलग-अलग उचित प्राथमिकताएं पर्याप्त रूप से अलग-अलग उत्तर देती हैं, तब क्या यह कहना सही हो सकता है कि ही उत्तर है? क्या यह स्वीकार करना उत्तम नहीं होगा कि पूर्व मान्यताओं के आधार पर निष्कर्ष के साथ वैज्ञानिक अनिश्चितता है? | ||
== घटना और अनुप्रयोग == | == घटना और अनुप्रयोग == | ||
=== आदेश आँकड़े === | === आदेश आँकड़े === | ||
{{Main| | {{Main|आदेश आँकड़े}} | ||
ऑर्डर सांख्यिकी के सिद्धांत में बीटा वितरण का महत्वपूर्ण अनुप्रयोग है। मूल परिणाम यह है कि निरंतर समान वितरण (निरंतर) से आकार n के | ऑर्डर सांख्यिकी के सिद्धांत में बीटा वितरण का महत्वपूर्ण अनुप्रयोग है। मूल परिणाम यह है कि निरंतर समान वितरण (निरंतर) से आकार n के प्रतिरूप के सबसे छोटे kth के वितरण में बीटा वितरण होता है।<ref name=David1>David, H. A., Nagaraja, H. N. (2003) ''Order Statistics'' (3rd Edition). Wiley, New Jersey pp 458. {{ISBN|0-471-38926-9}}</ref> इस परिणाम का सारांश इस प्रकार है: | ||
:<math>U_{(k)} \sim \operatorname{Beta}(k,n+1-k).</math> | :<math>U_{(k)} \sim \operatorname{Beta}(k,n+1-k).</math> | ||
इससे, और [[संभाव्यता अभिन्न परिवर्तन]] से संबंधित सिद्धांत के अनुप्रयोग से, किसी भी [[निरंतर वितरण]] से किसी भी व्यक्तिगत ऑर्डर स्टेटिस्टिक का वितरण प्राप्त किया जा सकता है।<ref name=David1/> | इससे, और [[संभाव्यता अभिन्न परिवर्तन]] से संबंधित सिद्धांत के अनुप्रयोग से, किसी भी [[निरंतर वितरण]] से किसी भी व्यक्तिगत ऑर्डर स्टेटिस्टिक का वितरण प्राप्त किया जा सकता है।<ref name=David1/> | ||
=== विषयगत तर्क === | === विषयगत तर्क === | ||
{{Main| | {{Main|व्यक्तिपरक तर्क}} | ||
मानक तर्क में, प्रस्तावों को या तब सही या गलत माना जाता है। इसके विपरीत, [[व्यक्तिपरक तर्क]] यह मानता है कि मनुष्य पूर्ण निश्चितता के साथ यह निर्धारित नहीं कर सकता है कि वास्तविक विश्व के बारे में कोई प्रस्ताव बिल्कुल सही है या गलत। व्यक्तिपरक तर्क में द्विआधारी घटनाओं के a पश्चवर्ती संभाव्यता अनुमानों को बीटा वितरण द्वारा दर्शाया जा सकता है।<ref name="J01">A. Jøsang. A Logic for Uncertain Probabilities. ''[[International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems]].'' 9(3), pp.279-311, June 2001. [http://www.unik.no/people/josang/papers/Jos2001-IJUFKS.pdf PDF]{{Dead link|date=October 2019 |bot=InternetArchiveBot |fix-attempted=yes }}</ref> | |||
=== तरंगिका विश्लेषण === | === तरंगिका विश्लेषण === | ||
{{Main| | {{Main|बीटा वेवलेट}} | ||
एक तरंगिका तरंग-जैसा दोलन है जिसका [[आयाम]] शून्य से | एक तरंगिका तरंग-जैसा दोलन है जिसका [[आयाम]] शून्य से प्रारंभिक होता है, बढ़ता है, और फिर वापस शून्य हो जाता है। इसे सामान्यतः संक्षिप्त दोलन के रूप में देखा जा सकता है जो तुरंत क्षय हो जाता है। [[ छोटा लहर ]] का उपयोग अनेक अलग-अलग प्रकार के डेटा से जानकारी निकालने के लिए किया जा सकता है, जिसमें ऑडियो सिग्नल और छवियां सम्मिलित हैं, किन्तु निश्चित रूप से इन्हीं तक सीमित नहीं हैं। इस प्रकार, वेवलेट्स को विशिष्ट गुणों के लिए उद्देश्यपूर्ण रूप से तैयार किया जाता है जो उन्हें [[ संकेत आगे बढ़ाना ]] के लिए उपयोगी बनाते हैं। तरंगिकाएँ समय और [[आवृत्ति]] दोनों में स्थानीयकृत होती हैं जबकि मानक फूरियर रूपांतरण केवल आवृत्ति में स्थानीयकृत होता है। इसलिए, मानक फूरियर ट्रांसफ़ॉर्म केवल [[स्थिर प्रक्रिया]]ओं पर प्रयुक्त होते हैं, जबकि तरंगिकाएँ गैर-स्थिर प्रक्रियाओं पर प्रयुक्त होती हैं। बीटा वितरण के आधार पर निरंतर तरंगिकाओं का निर्माण किया जा सकता है। [[बीटा तरंगिका]]<ref name="wavelet oliveira">H.M. de Oliveira and G.A.A. Araújo,. Compactly Supported One-cyclic Wavelets Derived from Beta Distributions. ''Journal of Communication and Information Systems.'' vol.20, n.3, pp.27-33, 2005.</ref> हार तरंगों की नरम प्रकार के रूप में देखा जा सकता है जिसका आकार दो आकार के मापदंडों α और β द्वारा ठीक-ठीक है। | ||
=== | === संख्या आनुवंशिकी === | ||
{{main| | {{main|बैल्डिंग-निकोल्स मॉडल}} | ||
{{further| | {{further|एफ-स्टैटिक्स |निर्धारण सूचकांक|संबंध का गुणांक}} | ||
बैल्डिंग-निकोल्स मॉडल [[जनसंख्या आनुवंशिकी]] में उपयोग किए जाने वाले बीटा वितरण का दो- | बैल्डिंग-निकोल्स मॉडल [[जनसंख्या आनुवंशिकी|संख्या आनुवंशिकी]] में उपयोग किए जाने वाले बीटा वितरण का दो-मापदंड सांख्यिकीय मापदंड है।<ref name=Balding>{{cite journal |last1=Balding |first1=David J. |author-link1=David Balding |last2=Nichols |first2=Richard A. |year=1995 |title=पहचान और पितृत्व की जांच के लिए बहु-एलील लोकी और इसके प्रभावों पर आबादी के बीच भेदभाव को मापने के लिए एक विधि|journal=Genetica |volume=96 |issue=1–2 |pages=3–12 |publisher=Springer |doi=10.1007/BF01441146 |pmid=7607457|s2cid=30680826 }}</ref> यह उप-विभाजित संख्या के घटकों में [[एलील आवृत्तियों]] का सांख्यिकीय विवरण है: | ||
:<math> | :<math> | ||
| Line 1,612: | Line 1,630: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहाँ <math>\nu =\alpha+\beta= \frac{1-F}{F}</math> और <math>0 < F < 1</math>; जहाँ F दो संख्या के मध्य (राइट की) आनुवंशिक दूरी है। | |||
=== [[परियोजना प्रबंधन]]: कार्य | === [[परियोजना प्रबंधन]]: कार्य निवेश और अनुसूची मॉडलिंग === | ||
बीटा वितरण का उपयोग उन घटनाओं को मॉडल करने के लिए किया जा सकता है जो न्यूनतम और अधिकतम मान द्वारा परिभाषित अंतराल के | बीटा वितरण का उपयोग उन घटनाओं को मॉडल करने के लिए किया जा सकता है जो न्यूनतम और अधिकतम मान द्वारा परिभाषित अंतराल के अंदर होने के लिए विवश हैं। इस कारण से, बीटा वितरण - त्रिकोणीय वितरण के साथ - पीईआरटी, महत्वपूर्ण पथ विधि (सीपीएम), संयुक्त निवेश अनुसूची मॉडलिंग (जेसीएसएम) और अन्य परियोजना प्रबंधन/नियंत्रण प्रणालियों में बड़े पैमाने पर उपयोग किया जाता है जिससेपूरा होने में लगने वाले समय और निवेश का वर्णन किया जा सके किसी कार्य का। परियोजना प्रबंधन में, बीटा वितरण के माध्य और मानक विचलन का अनुमान लगाने के लिए आशुलिपि संगणनाओं का व्यापक रूप से उपयोग किया जाता है:<ref name=Malcolm>{{cite journal |last1=Malcolm |first1=D. G. |last2=Roseboom |first2=J. H. |last3=Clark |first3=C. E. |last4=Fazar |first4=W. |title=अनुसंधान और विकास कार्यक्रम मूल्यांकन के लिए एक तकनीक का अनुप्रयोग|journal=Operations Research |date=September–October 1958 |volume=7 |issue=5 |pages=646–669 |doi=10.1287/opre.7.5.646 |issn=0030-364X}}</ref> | ||
:<math> \begin{align} | :<math> \begin{align} | ||
\mu(X) & = \frac{a + 4b + c}{6} \\ | \mu(X) & = \frac{a + 4b + c}{6} \\ | ||
| Line 1,622: | Line 1,640: | ||
जहाँ a न्यूनतम है, c अधिकतम है, और b सबसे संभावित मान है (α > 1 और β > 1 के लिए बहुलक (सांख्यिकी)। | जहाँ a न्यूनतम है, c अधिकतम है, और b सबसे संभावित मान है (α > 1 और β > 1 के लिए बहुलक (सांख्यिकी)। | ||
माध्य के लिए उपरोक्त अनुमान <math>\mu(X)= \frac{a + 4b + c}{6}</math> PERT तीन-बिंदु अनुमान के रूप में जाना जाता है और यह β के निम्न मानों में से किसी के लिए | माध्य के लिए उपरोक्त अनुमान <math>\mu(X)= \frac{a + 4b + c}{6}</math> PERT तीन-बिंदु अनुमान के रूप में जाना जाता है और यह β के निम्न मानों में से किसी के लिए स्पष्ट है (इन सीमाओं के अंदर इच्छानुसार α के लिए): | ||
:β = α > 1 (सममित | :β = α > 1 (सममित स्तिथि ) मानक विचलन के साथ <math>\sigma(X) = \frac{c-a}{2 \sqrt {1+2\alpha}}</math>, विषमता = 0, और अतिरिक्त ककुदता = <math> \frac{-6}{3+2 \alpha}</math> | ||
फ़ाइल:बीटा वितरण बीटा=alpha from 1.05 to 4.95.svgया | '''फ़ाइल:बीटा वितरण बीटा=alpha from 1.05 to 4.95.svgया''' | ||
:β = 6 - α 5 के लिए > α > 1 ( | :β = 6 - α 5 के लिए > α > 1 (विषम स्तिथि ) मानक विचलन के साथ | ||
:<math>\sigma(X) = \frac{(c-a)\sqrt{\alpha(6-\alpha)}}{6 \sqrt 7},</math> | :<math>\sigma(X) = \frac{(c-a)\sqrt{\alpha(6-\alpha)}}{6 \sqrt 7},</math> | ||
विषमता = <math>\frac{(3-\alpha) \sqrt 7}{2\sqrt{\alpha(6-\alpha)}}</math>, और अतिरिक्त कर्टोसिस = <math>\frac{21}{\alpha (6- \alpha)} - 3</math> | |||
फ़ाइल:बीटा वितरण बीटा=6-alpha from 1.05 to 4.95. | |||
'''फ़ाइल:बीटा वितरण बीटा=6-alpha from 1.05 to 4.95.svg''' | |||
मानक विचलन σ(X) = (c - a)/6 के लिए उपरोक्त अनुमान α और β के निम्नलिखित मानों में से किसी के लिए स्पष्ट है: | |||
: α = β = 4 (सममित) विषमता = 0 के साथ, और अतिरिक्त कर्टोसिस = -6/11। | : α = β = 4 (सममित) विषमता = 0 के साथ, और अतिरिक्त कर्टोसिस = -6/11। | ||
:β = 6 - α और <math>\alpha = 3 - \sqrt2</math> (राइट-टेल्ड, पॉजिटिव | :β = 6 - α और <math>\alpha = 3 - \sqrt2</math> (राइट-टेल्ड, पॉजिटिव विषम) विषमता के साथ <math>=\frac{1}{\sqrt 2}</math>, और अतिरिक्त कर्टोसिस = 0 | ||
:β = 6 - α और <math>\alpha = 3 + \sqrt2</math> (बाएं- | :β = 6 - α और <math>\alpha = 3 + \sqrt2</math> (बाएं-टेल , ऋणात्मक विषम) विषमता के साथ <math>= \frac{-1}{\sqrt 2}</math>, और अतिरिक्त कर्टोसिस = 0 | ||
[[File:Beta Distribution for conjugate alpha beta.svg]]अन्यथा, ये α और β के अन्य मूल्यों के साथ बीटा वितरण के लिए खराब अनुमान हो सकते हैं, माध्य में 40% की औसत त्रुटि और विचरण में 549% प्रदर्शित करते हैं।<ref>Keefer, Donald L. and Verdini, William A. (1993). Better Estimation of PERT Activity Time Parameters. Management Science 39(9), p. 1086–1091.</ref><ref>Keefer, Donald L. and Bodily, Samuel E. (1983). Three-point Approximations for Continuous Random variables. Management Science 29(5), p. 595–609.</ref><ref>{{Cite web|url=https://www.nps.edu/web/drmi/|title=रक्षा संसाधन प्रबंधन संस्थान - नौसेना स्नातकोत्तर स्कूल|website=www.nps.edu}}</ref> | [[File:Beta Distribution for conjugate alpha beta.svg]]अन्यथा, ये α और β के अन्य मूल्यों के साथ बीटा वितरण के लिए खराब अनुमान हो सकते हैं, माध्य में 40% की औसत त्रुटि और विचरण में 549% प्रदर्शित करते हैं।<ref>Keefer, Donald L. and Verdini, William A. (1993). Better Estimation of PERT Activity Time Parameters. Management Science 39(9), p. 1086–1091.</ref><ref>Keefer, Donald L. and Bodily, Samuel E. (1983). Three-point Approximations for Continuous Random variables. Management Science 29(5), p. 595–609.</ref><ref>{{Cite web|url=https://www.nps.edu/web/drmi/|title=रक्षा संसाधन प्रबंधन संस्थान - नौसेना स्नातकोत्तर स्कूल|website=www.nps.edu}}</ref> | ||
== रैंडम वेरिएट जनरेशन == | == रैंडम वेरिएट जनरेशन == | ||
{{further| | {{further|गैर-समान यादृच्छिक विविधता पीढ़ी}} | ||
यदि X और Y स्वतंत्र हैं, साथ में <math>X \sim \Gamma(\alpha, \theta)</math> और <math>Y \sim \Gamma(\beta, \theta)</math> तब | यदि X और Y स्वतंत्र हैं, साथ में <math>X \sim \Gamma(\alpha, \theta)</math> और <math>Y \sim \Gamma(\beta, \theta)</math> तब | ||
:<math>\frac{X}{X+Y} \sim \Beta(\alpha, \beta).</math> | :<math>\frac{X}{X+Y} \sim \Beta(\alpha, \beta).</math> | ||
तब बीटा संस्करण उत्पन्न करने के लिए एल्गोरिदम उत्पन्न करना है <math>\frac{X}{X + Y}</math>, जहां X गामा वितरण है#मापदंड (α, 1) के साथ रैंडम वैरिएट जनरेशन और मापदंड (β, 1) के साथ Y स्वतंत्र गामा वेरिएट है।<ref>van der Waerden, B. L., "Mathematical Statistics", Springer, {{ISBN|978-3-540-04507-6}}.</ref> वास्तव में, यहाँ <math>\frac{X}{X+Y}</math> और <math>X+Y</math> स्वतंत्र हैं, और <math>X+Y \sim \Gamma(\alpha + \beta, \theta)</math>. यदि <math>Z \sim \Gamma(\gamma, \theta)</math> और <math>Z</math> से स्वतंत्र है <math>X</math> और <math>Y</math>, तब <math>\frac{X+Y}{X+Y+Z} \sim \Beta(\alpha+\beta,\gamma)</math> और <math>\frac{X+Y}{X+Y+Z}</math> से स्वतंत्र है <math>\frac{X}{X+Y}</math>. इससे पता चलता है कि स्वतंत्र का उत्पाद <math>\Beta(\alpha,\beta)</math> और <math>\Beta(\alpha+\beta,\gamma)</math> यादृच्छिक वेरिएबल है <math>\Beta(\alpha,\beta+\gamma)</math> अनियमित परिवर्तनशील वस्तु। | |||
साथ ही, n यूनिफ़ॉर्म डिस्ट्रीब्यूशन (सतत) वेरियेट्स का kth ऑर्डर स्टेटिस्टिक है <math>\Beta(k, n+1-k)</math>, इसलिए विकल्प यदि α और β छोटे पूर्णांक हैं | साथ ही, n यूनिफ़ॉर्म डिस्ट्रीब्यूशन (सतत) वेरियेट्स का kth ऑर्डर स्टेटिस्टिक है <math>\Beta(k, n+1-k)</math>, इसलिए विकल्प यदि α और β छोटे पूर्णांक हैं तब α + β - 1 समान वेरिएबल उत्पन्न करना है और α-th सबसे छोटा चुनना है।<ref name=David1/> | ||
बीटा वितरण उत्पन्न करने का दूसरा | बीटा वितरण उत्पन्न करने का दूसरा विधि पोल्या कलश मॉडल है। इस पद्धति के अनुसार, α काली गेंदों और β सफेद गेंदों के साथ कलश से शुरुआत की जाती है और प्रतिस्थापन के साथ समान रूप से खींचा जाता है। प्रत्येक परीक्षण में अतिरिक्त गेंद निकाली गई अंतिम गेंद के रंग के अनुसार जोड़ी जाती है। असीमित रूप से, काले और सफेद गेंदों का अनुपात बीटा वितरण के अनुसार वितरित किया जाएगा, जहां प्रयोग की प्रत्येक पुनरावृत्ति अलग मान उत्पन्न करेगी। | ||
उलटा रूपांतरण | उलटा रूपांतरण प्रतिरूप करण का उपयोग करना भी संभव है। | ||
== बीटा वितरण के लिए सामान्य सन्निकटन == | == बीटा वितरण के लिए सामान्य सन्निकटन == | ||
एक बीटा वितरण <math>\Beta(\alpha,\beta)</math> α ~ β और α और β >> 1 औसत 1/2 और विचरण 1/4 (2α + 1) के साथ लगभग सामान्य है। यदि α ≥ β के व्युत्क्रम के लघुगणक का घनमूल लेकर सामान्य सन्निकटन में सुधार किया जा सकता है <math>\Beta(\alpha,\beta)</math><ref>On normalizing the incomplete beta-function for fitting to dose-response curves M.E. Wise Biometrika vol 47, No. 1/2, June 1960, pp. 173-175</ref> | एक बीटा वितरण <math>\Beta(\alpha,\beta)</math> α ~ β और α और β >> 1 औसत 1/2 और विचरण 1/4 (2α + 1) के साथ लगभग सामान्य है। यदि α ≥ β के व्युत्क्रम के लघुगणक का घनमूल लेकर सामान्य सन्निकटन में सुधार किया जा सकता है <math>\Beta(\alpha,\beta)</math><ref>On normalizing the incomplete beta-function for fitting to dose-response curves M.E. Wise Biometrika vol 47, No. 1/2, June 1960, pp. 173-175</ref> | ||
== इतिहास == | |||
थॉमस बेयस, मरणोपरांत पेपर में <ref name="ThomasBayes">{{cite journal|last=Bayes|first=Thomas|author2=communicated by Richard Price|title=संभावना के सिद्धांत में एक समस्या को हल करने की दिशा में एक निबंध|journal=Philosophical Transactions of the Royal Society|year=1763|volume=53|pages=370–418|jstor=105741|doi=10.1098/rstl.1763.0053|doi-access=free}}</ref> [[रिचर्ड प्राइस|रिवेरिएबल ्ड प्राइस]] द्वारा 1763 में प्रकाशित, बर्नौली परीक्षणों में सफलता की संभावना के घनत्व के रूप में बीटा वितरण प्राप्त किया (देखें {{section link||अनुप्रयोग, बायेसियन अनुमान}}), किन्तुपेपर बीटा वितरण के किसी भी पल का विश्लेषण नहीं करता है या इसके किसी भी गुण पर चर्चा नहीं करता है। | |||
[[File:Karl Pearson 2.jpg|thumb|220px|कार्ल पियर्सन ने पियर्सन वितरण के समाधान प्रकार I के रूप में बीटा वितरण का विश्लेषण किया]]बीटा वितरण की पहली व्यवस्थित आधुनिक चर्चा संभवतः कार्ल पियर्सन के कारण है।<ref>{{Cite journal | last1 = Yule | first1 = G. U. | author-link1 = Udny Yule| last2 = Filon | first2 = L. N. G. | doi = 10.1098/rsbm.1936.0007 | title = Karl Pearson. 1857-1936 | journal = [[Obituary Notices of Fellows of the Royal Society]] | volume = 2 | issue = 5 | pages = 72 | year = 1936 | jstor = 769130| title-link = Karl Pearson }}</ref><ref name=rscat>{{cite web|url=http://www2.royalsociety.org/DServe/dserve.exe?dsqIni=Dserve.ini&dsqApp=Archive&dsqCmd=Show.tcl&dsqDb=Persons&dsqPos=0&dsqSearch=%28%28text%29%3D%27%20%20Pearson%3A%20Karl%20%281857%20-%201936%29%20%20%27%29%29|access-date=2011-07-01|title=पुस्तकालय और पुरालेख सूची|work=Sackler Digital Archive|publisher=Royal Society|archive-url=https://web.archive.org/web/20111025030931/http://www2.royalsociety.org/DServe/dserve.exe?dsqIni=Dserve.ini&dsqApp=Archive&dsqCmd=Show.tcl&dsqDb=Persons&dsqPos=0&dsqSearch=%28%28text%29%3D%27%20%20Pearson%3A%20Karl%20%281857%20-%201936%29%20%20%27%29)|archive-date=2011-10-25|url-status=dead}}</ref> पियर्सन के कागजात में<ref name=Pearson/><ref name=Pearson1895/>बीटा वितरण को अंतर समीकरण के समाधान के रूप में जोड़ा गया है: पियर्सन वितरण | पियर्सन का प्रकार I वितरण जो इच्छानुसार से स्थानांतरण और पुन: स्केलिंग को छोड़कर अनिवार्य रूप से समान है (बीटा और पियर्सन प्रकार I वितरण सदैव उचित विकल्प द्वारा सामान्तर किया जा सकता है मापदंड)। वास्तव में, द्वितीय विश्व युद्ध से पहले कुछ दशकों में अनेक अंग्रेजी पुस्तकों और जर्नल लेखों में, बीटा वितरण को पियर्सन के टाइप I वितरण के रूप में संदर्भित करना सामान्य बात थी। विलियम पॉलिन एल्डर्टन|(विलियम पी. एल्डर्टन) अपने 1906 मोनोग्राफ में आवृत्ति घटता और सहसंबंध<ref name=Elderton1906>{{cite book|last=Elderton|first=William Palin|title=आवृत्ति-वक्र और सहसंबंध|year=1906|publisher=Charles and Edwin Layton (London)|url=https://archive.org/details/frequencycurvesc00elderich}}</ref> पियर्सन के टाइप I वितरण के रूप में बीटा वितरण का और विश्लेषण करता है, जिसमें चार मापदंड स्तिथियों के लिए क्षणों की विधि की पूरी चर्चा सम्मिलित है, और आरेख (जो एल्डर्टन के रूप में वर्णित है) u-आकार, j-आकार, मुड़ j-आकार, कॉक्ड- टोपी के आकार, क्षैतिज और कोण वाली सीधी रेखा के स्तिथियाँ । एल्डर्टन ने लिखा है कि मैं मुख्य रूप से प्रोफेसर पियर्सन का ऋणी हूं, किन्तुऋण प्रकार का है जिसके लिए औपचारिक धन्यवाद देना असंभव है। [[विलियम पॉलिन एल्डर्टन]] ने अपने 1906 के मोनोग्राफ में <ref name=Elderton1906/>मोड के रूप में चुने गए वितरण की उत्पत्ति के लिए समीकरणों सहित बीटा वितरण पर प्रभावशाली जानकारी प्रदान करता है, साथ ही साथ अन्य पियर्सन वितरणों के लिए: प्रकार I से VII तक। एल्डर्टन ने बीटा और गामा कार्यों पर परिशिष्ट (II) सहित अनेक परिशिष्ट भी सम्मिलित किए। पश्चात् के संस्करणों में, एल्डर्टन ने माध्य के रूप में चुने गए वितरण की उत्पत्ति के लिए समीकरण जोड़े, और पियर्सन वितरण VIII से XII तक का विश्लेषण किया। | |||
= | जैसा कि बोमन और शेंटन ने टिप्पणी की है<ref name="BowmanShenton"/>फ़िशर और पियर्सन के मध्य (मापदंड) अनुमान के दृष्टिकोण में मतभेद था, विशेष रूप से (पियर्सन की विधि) क्षणों से संबंधित और (फ़िशर की विधि) बीटा वितरण के स्तिथियों में अधिकतम संभावना। साथ ही बोमन और शेंटन के अनुसार, प्रकार I (बीटा वितरण) मॉडल के विवाद का केंद्र होने का स्तिथि विशुद्ध संयोग था। 4 मापदंडों का अधिक कठिन मॉडल खोजना कठिन होता। कार्ल पियर्सन के साथ फिशर के लंबे समय से चल रहे सार्वजनिक संघर्ष को प्रतिष्ठित पत्रिकाओं में अनेक लेखों में देखा जा सकता है। उदाहरण के लिए, बीटा वितरण के लिए चार मापदंडों के अनुमान के संबंध में, और फिशर की पियर्सन की पलों की पद्धति की मनमानी के रूप में आलोचना, पियर्सन का लेख देखें क्षणों की विधि और अधिकतम संभावना की विधि <ref name=Pearson1936>{{cite journal|last=Pearson|first=Karl|title=क्षणों की विधि और अधिकतम संभावना की विधि|journal=Biometrika|date=June 1936|volume=28|issue=1/2|doi=10.2307/2334123|pages=34–59|jstor=2334123}}</ref> (यूनिवर्सिटी कॉलेज, लंदन से उनकी सेवानिवृत्ति के तीन साल पश्चात् प्रकाशित, जहां उनकी स्थिति फिशर और पियर्सन के बेटे एगॉन के मध्य विभाजित हो गई थी) जिसमें पियर्सन ने लिखा है कि मैंने पढ़ा (रॉयल स्टैटिस्टिकल सोसाइटी के जर्नल में कोशाई का पेपर, 1933) जो जहाँ तक है मुझे पता है कि वर्तमान में प्रोफेसर फिशर की विधि के आवेदन का एकमात्र स्तिथि प्रकाशित हुआ है। मेरे विस्मय के लिए यह विधि पहले (पियर्सन) मेथड ऑफ मोमेंट्स द्वारा फ़्रीक्वेंसी कर्व के कॉन्स्टेंट को काम करने पर निर्भर करती है और फिर उस पर सुपरपोज़िंग करती है, जिसे फ़िशर अधिकतम संभावना की विधि के अनुसार प्राप्त करने के लिए और सन्निकटन बताता है, वह क्या रखता है, वह इस प्रकार वक्र स्थिरांकों के अधिक कुशल मान प्राप्त होंगे। | ||
आंकड़ों के इतिहास पर डेविड और एडवर्ड्स का ग्रंथ<ref name="David History">{{cite book|last=David|first=H. A. and A.W.F. Edwards|title=सांख्यिकी के इतिहास में एनोटेट रीडिंग|year=2001|publisher=Springer; 1 edition|isbn=978-0387988443}}</ref> 1911 में, बीटा वितरण के पहले आधुनिक उपचार का हवाला देते हैं,<ref>{{cite journal |last=Gini |first=Corrado |title=Considerazioni Sulle Probabilità Posteriori e Applicazioni al Rapporto dei Sessi Nelle Nascite Umane |journal=Studi Economico-Giuridici della Università de Cagliari |year=1911 |volume=Anno III |issue=reproduced in Metron 15, 133,171, 1949 |pages=5–41}}</ref> इतालवी [[सांख्यिकीविद]]्, [[जनसांख्यिकी]] और समाजशास्त्र, [[ कॉनराड गिन्नी ]] के कारण बीटा पदनाम का उपयोग करना मानक बन गया है, जिन्होंने गिनी गुणांक विकसित किया था। नॉर्मन लॉयड जॉनसन|(एन.एल.जॉनसन) और सैमुअल कोटज़|(एस.कोट्ज़,) अपने व्यापक और बहुत ही सूचनात्मक मोनोग्राफ में<ref>{{cite book|editor-last=Johnson|editor-first=Norman L. and Samuel Kotz|title=Leading Personalities in Statistical Sciences: From the Seventeenth Century to the Present (Wiley Series in Probability and Statistics|year=1997|publisher=Wiley|isbn=978-0471163817}}</ref> सांख्यिकीय विज्ञान क्रेडिट कोराडो गिन्नी में प्रमुख ऐतिहासिक व्यक्तित्वों पर<ref>{{cite web|last=Metron journal. |title=कोराडो गिन्नी की जीवनी|url=http://www.metronjournal.it/storia/ginibio.htm |publisher=Metron Journal |access-date=2012-08-18 |url-status=dead|archive-url=https://web.archive.org/web/20120716202225/http://www.metronjournal.it/storia/ginibio.htm |archive-date=2012-07-16 }}</ref> प्रारंभिक बायेसियन के रूप में ... जिन्होंने प्रारंभिक बीटा वितरण के मापदंडों को अलग करने की समस्या से निपटा, एकल विधियों द्वारा जो तथाकथित अनुभवजन्य बेयस दृष्टिकोण के आगमन की आशंका थी। | |||
आंकड़ों के इतिहास पर डेविड और एडवर्ड्स का ग्रंथ<ref name="David History">{{cite book|last=David|first=H. A. and A.W.F. Edwards|title=सांख्यिकी के इतिहास में एनोटेट रीडिंग|year=2001|publisher=Springer; 1 edition|isbn=978-0387988443}}</ref> 1911 में, बीटा वितरण के पहले आधुनिक उपचार का हवाला देते हैं,<ref>{{cite journal |last=Gini |first=Corrado |title=Considerazioni Sulle Probabilità Posteriori e Applicazioni al Rapporto dei Sessi Nelle Nascite Umane |journal=Studi Economico-Giuridici della Università de Cagliari |year=1911 |volume=Anno III |issue=reproduced in Metron 15, 133,171, 1949 |pages=5–41}}</ref> इतालवी [[सांख्यिकीविद]]्, [[जनसांख्यिकी]] और समाजशास्त्र, [[ कॉनराड गिन्नी ]] के कारण बीटा पदनाम का उपयोग करना मानक बन गया है, जिन्होंने गिनी गुणांक विकसित किया था। नॉर्मन लॉयड जॉनसन|एन.एल.जॉनसन और सैमुअल कोटज़|एस.कोट्ज़, अपने व्यापक और बहुत ही सूचनात्मक मोनोग्राफ में<ref>{{cite book|editor-last=Johnson|editor-first=Norman L. and Samuel Kotz|title=Leading Personalities in Statistical Sciences: From the Seventeenth Century to the Present (Wiley Series in Probability and Statistics|year=1997|publisher=Wiley|isbn=978-0471163817}}</ref> सांख्यिकीय विज्ञान क्रेडिट कोराडो गिन्नी में प्रमुख ऐतिहासिक व्यक्तित्वों पर<ref>{{cite web|last=Metron journal. |title=कोराडो गिन्नी की जीवनी|url=http://www.metronjournal.it/storia/ginibio.htm |publisher=Metron Journal |access-date=2012-08-18 |url-status=dead|archive-url=https://web.archive.org/web/20120716202225/http://www.metronjournal.it/storia/ginibio.htm |archive-date=2012-07-16 }}</ref> | |||
==संदर्भ== | ==संदर्भ== | ||
| Line 1,673: | Line 1,692: | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
{{Commons category}} | {{Commons category}} | ||
*[http://demonstrations.wolfram.com/BetaDistribution/ " | *[http://demonstrations.wolfram.com/BetaDistribution/ "बीटा Distribution"] by Fiona Maclachlan, the [[Wolfram Demonstrations Project]], 2007. | ||
*[http://www.xycoon.com/beta.htm | *[http://www.xycoon.com/beta.htm बीटा Distribution – Overview and Example], xycoon.com | ||
*[https://web.archive.org/web/20120829140915/http://www.brighton-webs.co.uk/distributions/beta.htm | *[https://web.archive.org/web/20120829140915/http://www.brighton-webs.co.uk/distributions/beta.htm बीटा Distribution], brighton-webs.co.uk | ||
*[http://www.exstrom.com/blog/snark/posts/dancingbeta.html | *[http://www.exstrom.com/blog/snark/posts/dancingbeta.html बीटा Distribution Video], exstrom.com | ||
*{{springer|title=Beta-distribution|id=p/b015950}} | *{{springer|title=Beta-distribution|id=p/b015950}} | ||
*{{MathWorld|urlname=BetaDistribution|title=Beta Distribution}} | *{{MathWorld|urlname=BetaDistribution|title=Beta Distribution}} | ||
*[https://www.youtube.com/watch?v=UZjlBQbV1KU Harvard University Statistics 110 Lecture 23 | *[https://www.youtube.com/watch?v=UZjlBQbV1KU Harvard University Statistics 110 Lecture 23 बीटा Distribution, Prof. Joe Blitzstein] | ||
{{ProbDistributions|continuous-bounded}} | {{ProbDistributions|continuous-bounded}} | ||
{{DEFAULTSORT:Beta Distribution}} | {{DEFAULTSORT:Beta Distribution}} | ||
[[Category: | [[Category:All articles with dead external links]] | ||
[[Category:Created On 21/03/2023]] | [[Category:Articles with dead external links from October 2019]] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Beta Distribution]] | |||
[[Category:Articles with permanently dead external links]] | |||
[[Category:CS1]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 errors]] | |||
[[Category:CS1 maint]] | |||
[[Category:Collapse templates|Beta Distribution]] | |||
[[Category:Commons category link is the pagename|Beta Distribution]] | |||
[[Category:Created On 21/03/2023|Beta Distribution]] | |||
[[Category:Lua-based templates|Beta Distribution]] | |||
[[Category:Machine Translated Page|Beta Distribution]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Beta Distribution]] | |||
[[Category:Pages with script errors|Beta Distribution]] | |||
[[Category:Short description with empty Wikidata description|Beta Distribution]] | |||
[[Category:Sidebars with styles needing conversion|Beta Distribution]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Beta Distribution]] | |||
[[Category:Templates generating microformats|Beta Distribution]] | |||
[[Category:Templates that add a tracking category|Beta Distribution]] | |||
[[Category:Templates that are not mobile friendly|Beta Distribution]] | |||
[[Category:Templates that generate short descriptions|Beta Distribution]] | |||
[[Category:Templates using TemplateData|Beta Distribution]] | |||
[[Category:Wikipedia metatemplates|Beta Distribution]] | |||
[[Category:क्रमगुणित और द्विपद विषय|Beta Distribution]] | |||
[[Category:घातीय परिवार वितरण|Beta Distribution]] | |||
[[Category:निरंतर वितरण|Beta Distribution]] | |||
[[Category:पूर्व वितरण संयुग्मित करें|Beta Distribution]] | |||
Latest revision as of 09:52, 4 August 2023
|
Probability density function 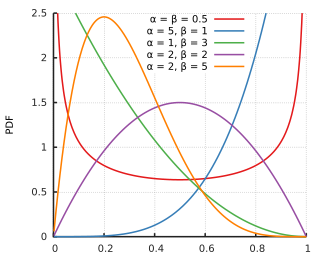 | |||
|
Cumulative distribution function 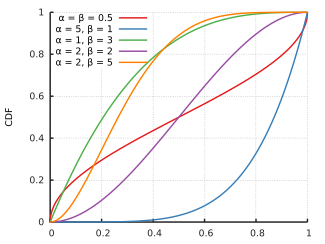 | |||
| Notation | Beta(α, β) | ||
|---|---|---|---|
| Parameters |
α > 0 shape (real) β > 0 shape (real) | ||
| Support | or | ||
|
where and is the Gamma function. | |||
| CDF |
(the regularized incomplete beta function) | ||
| Mean |
| ||
| Median | |||
| Mode |
for α, β > 1 any value in for α, β = 1 {0, 1} (bimodal) for α, β < 1 0 for α ≤ 1, β > 1 1 for α > 1, β ≤ 1 | ||
| Variance |
(see trigamma function and see section: Geometric variance) | ||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
| MGF | |||
| CF | (see Confluent hypergeometric function) | ||
| Fisher information |
see section: Fisher information matrix | ||
| Method of Moments |
| ||
संभाव्यता सिद्धांत और सांख्यिकी में, बीटा वितरण के दो धनात्मक सांख्यिकीय मापदंड होते है इसके संदर्भ में अंतराल [0,1] पर परिभाषित निरंतर संभाव्यता वितरण का परिवार है, जिसे 'अल्फा' (α) और बीटा (β) द्वारा दर्शाया गया है। जो वेरिएबल के घातांक और क्रमशः 1 के पूरक के रूप में दिखाई देते हैं, और वितरण के आकार मापदंड को नियंत्रित करते हैं।
विभिन्न प्रकार के विषयों में परिमित लंबाई के अंतराल तक सीमित यादृच्छिक वेरिएबल है जिन्हें उनके व्यवहार को मॉडल करने के लिए बीटा वितरण के रूप में प्रयुक्त किया गया है। बीटा वितरण प्रतिशत और अनुपात के यादृच्छिक व्यवहार के लिए उपयुक्त मॉडल है।
बायेसियन अनुमान में, बीटा वितरण बर्नौली वितरण, द्विपद वितरण, ऋणात्मक द्विपद वितरण और ज्यामितीय वितरण वितरण के लिए संयुग्मित पूर्व वितरण है।
यहां चर्चा किए गए बीटा वितरण के सूत्रीकरण को पहली तरह के बीटा वितरण के रूप में भी जाना जाता है, जबकि दूसरी तरह का बीटा वितरण बीटा प्राइम वितरण का वैकल्पिक नाम है। अनेक वेरिएबलों के सामान्यीकरण को डिरिचलेट वितरण कहा जाता है।
परिभाषाएँ
संभाव्यता घनत्व फलन
प्रायिकता घनत्व फलन (पीडीएफ) बीटा वितरण के लिए 0 ≤ x ≤ 1, और आकार मापदंड α, β > 0, वेरिएबल x और उसके प्रतिबिंब सूत्र का (1 − x) शक्ति कार्य है निम्नलिखित नुसार:
जहां Γ(z) गामा फलन है। बीटा फलन , , यह सुनिश्चित करने के लिए सामान्यीकरण स्थिरांक है कि कुल संभाव्यता 1 है। उपरोक्त समीकरणों में x यादृच्छिक वेरिएबल X का अहसास (संभावना) है—एक प्रेक्षित मान जो वास्तव में हुआ है।
इस परिभाषा में दोनों छोर सम्मिलित हैं x = 0 और x = 1, जो संभाव्यता वितरण की अन्य सूची के लिए परिभाषाओं के अनुरूप है, जो बीटा वितरण के विशेष स्तिथियाँ हैं, उदाहरण के लिए आर्क्सिन वितरण, और अनेक लेखकों के साथ संगत है, जैसे |एन। एल. जॉनसन और एस. कोटज़।[1][2][3][4] चूंकि, x = 0 और x = 1 का समावेश α, β < 1 के लिए काम नहीं करता है ; तदनुसार, विलियम फेलर सहित अनेक अन्य लेखक | डब्ल्यू। ,[5][6][7] x = 0 और x = 1, फलेर सिरों को बाहर करना चुनें (जिससे दो छोर वास्तव में घनत्व फलन के डोमेन का भाग न हों) और इसके अतिरिक्त 0 < x < 1 पर विचार करें .
नॉर्मन लॉयड जॉनसन सहित अनेक लेखक एन. एल. जॉनसन और सैमुअल कोट्ज़ (एस. कोटज़),[1] बीटा वितरण के आकार मापदंडों के लिए प्रतीकों p और q (α और β के अतिरिक्त) का उपयोग करें,तथा यह पारंपरिक रूप से बर्नौली वितरण के मापदंडों के लिए उपयोग किए जाने वाले प्रतीकों की याद दिलाते हैं, क्योंकि बीटा वितरण सीमा में बर्नौली वितरण तक पहुंचता है जब दोनों आकार मापदंड α और β शून्य के मान तक पहुंचते हैं।
निम्नलिखित में, मापदंड α और β के साथ यादृच्छिक वेरिएबल X बीटा-वितरित द्वारा निरूपित किया जाएगा:[8][9]
सांख्यिकीय साहित्य में प्रयुक्त बीटा-वितरित यादृच्छिक वेरिएबल के लिए अन्य अंकन [10] और हैं.[5]
संचयी वितरण फलन
संचयी वितरण फलन है
जहाँ बीटा फलन है और अधूरा बीटा फलन नियमित अधूरा बीटा फलन है।
वैकल्पिक मापदंडकरण
दो मापदंड
माध्य और प्रतिरूप आकार
बीटा वितरण को इसके औसत μ(0 < μ < 1) और दो आकार के मापदंडों का योग ν = α + β > 0( पी 83)[9]. के संदर्भ में भी पुनर्मूल्यांकित किया जा सकता है α पोस्टीरियर और β पोस्टीरियर द्वारा पोस्टीरियर बीटा डिस्ट्रीब्यूशन के शेप मापदंड्स को अस्वीकार करना , जिसके परिणाम स्वरूप बेयस प्रमेय को द्विपदीय संभावना फलन और पूर्व संभावना पर प्रयुक्त किया जाता है, प्रतिरूप आकार होने के लिए दोनों आकार मापदंडों के जोड़ की व्याख्या = ν = α·पोस्टीरियर + β· हाल्डेन पूर्व संभाव्यता बीटा (0,0) के लिए केवल पश्च भाग ही सही है। विशेष रूप से, बेयस (यूनिफ़ॉर्म) पूर्व बीटा (1,1) के लिए सही व्याख्या प्रतिरूप आकार = α·पोस्टीरियर + β पोस्टीरियर - 2, या ν = (प्रतिरूप आकार) + 2 होगी। 2 से बहुत बड़े सैंपल आकार के लिए, इन दो पूर्वों के मध्य का अंतर नगण्य हो जाता है। (अधिक विवरण के लिए अनुभाग या बायेसियन अनुमान देखें।) ν = α + β को बीटा वितरण के प्रतिरूप आकार के रूप में संदर्भित किया जाता है, किन्तु किसी को यह याद रखना चाहिए कि यह सख्ती से बोलना,जरुरी है तथा द्विपदीय संभावना फलन का प्रतिरूप आकार केवल उपयोग करते समय बेज़ प्रमेय से पहले हाल्डेन बीटा (0,0) होता है ।
यह पैरामीट्रिजेशन बायेसियन मापदंड आकलन में उपयोगी हो सकता है। उदाहरण के लिए, कोई व्यक्ति अनेक व्यक्तियों को परीक्षण दे सकता है। यदि यह मान लिया जाए कि प्रत्येक व्यक्ति का स्कोर (0 ≤ θ ≤ 1) संख्या -स्तर बीटा वितरण से लिया गया है, तब महत्वपूर्ण आँकड़ा इस संख्या -स्तर वितरण का माध्य है। माध्य और प्रतिरूप आकार मापदंड आकार मापदंड α और β के माध्यम से संबंधित हैं[9]
- α = μν, β = (1 - μ)ν
इस सांख्यिकीय मापदंड के अनुसार है , जिसको प्रतिरूप आकार के लिए धनात्मक वास्तविकताओं पर माध्य पर अनौपचारिक पूर्व संभावना, और अस्पष्ट पूर्व संभावना (जैसे घातीय या गामा वितरण) रख सकते हैं, यदि वे स्वतंत्र हैं, और पूर्व डेटा या विश्वासियें है तो इसे सही ठहराते हैं।
मोड और एकाग्रता
अवतल कार्य बीटा वितरण जिनके पास है मोड और एकाग्रता के संदर्भ में पैरामीट्रिज्ड किया जा सकता है। साधन, , और एकाग्रता, , का उपयोग सामान्य आकार के मापदंडों को निम्नानुसार परिभाषित करने के लिए किया जा सकता है:[11]
मोड के लिए, , अच्छी तरह से परिभाषित होने के लिए, हमें , या समकक्ष . की आवश्यकता है यदि इसके अतिरिक्त हम एकाग्रता को के रूप में परिभाषित करते हैं तो स्थिति सरल हो जाती है और और पर बीटा घनत्व पर इस प्रकार लिखा जा सकता है:
जहाँ सीधे पर्याप्त आँकड़ों और . को मापता है, यह भी ध्यान दें कि सीमा में, , वितरण सपाट हो जाता है।
माध्य और विचरण
उपरोक्त वर्गों में दिए गए (युग्मित) समीकरणों की प्रणाली को माध्य के समीकरणों के रूप में हल करना और मूल मापदंडों α और β के संदर्भ में बीटा वितरण का विचरण , माध्य के संदर्भ में α और β मापदंडों को व्यक्त कर सकता है ( μ) और विचरण (var):
बीटा वितरण का यह सांख्यिकीय मापदंड मूल मापदंड α और β के आधार पर से अधिक सहज ज्ञान युक्त समझ उत्पन्न कर सकता है। उदाहरण के लिए, माध्य और विचरण के संदर्भ में मोड, विषमता, अतिरिक्त कुर्टोसिस और अंतर एन्ट्रापी को व्यक्त करके:
चार मापदंड्स
दो आकार मापदंड α और β के साथ बीटा वितरण श्रेणी [0,1] या (0,1) पर समर्थित है। न्यूनतम, a, और अधिकतम c(c> a), वितरण के मूल्यों का प्रतिनिधित्व करने वाले दो और मापदंड प्रस्तुत करके वितरण के स्थान और पैमाने को बदलना संभव है,[1] गैर-आयामी वेरिएबल को प्रतिस्थापित करने वाले रैखिक परिवर्तन द्वारा x नए वेरिएबल y के संदर्भ में (समर्थन [a, c] या (a, c) के साथ) और मापदंड a और c होंगे :
चार मापदंड बीटा वितरण का प्रायिकता घनत्व फलन दो मापदंड वितरण के सामान्तर है, जिसे रेंज (c-a) द्वारा स्केल किया गया है, (जिससेघनत्व वक्र के अंतर्गत कुल क्षेत्रफल की संभावना के सामान्तर हो), और y वेरिएबल के साथ शिफ्ट हो गया और निम्नानुसार स्केल किया गया:
यह कि यादृच्छिक वेरिएबल Y को चार मापदंड α, β, a, और c हैं बीटा-वितरित है जिसे निम्न द्वारा दर्शाया गया है |
केंद्रीय स्थान के कुछ उपायों को स्केल किया गया है (द्वारा (सी-ए)) और स्थानांतरित (ए द्वारा), निम्नानुसार है:
नोट: ज्यामितीय माध्य और हार्मोनिक माध्य को रेखीय परिवर्तन द्वारा रूपांतरित नहीं किया जा सकता है, जिस तरह से माध्य, माध्यिका और मोड कर सकते हैं।
Y के आकार के मापदंडों को इसके माध्य और विचरण के रूप में लिखा जा सकता है
सांख्यिकीय फैलाव उपायों को बढ़ाया जाता है (उन्हें स्थानांतरित करने की आवश्यकता नहीं है क्योंकि वे पहले से ही माध्य पर केंद्रित हैं) सीमा (सी-ए) द्वारा, औसत विचलन के लिए रैखिक रूप से और भिन्नता के लिए गैर-रैखिक रूप से:
चूँकि विषमता और अतिरिक्त कर्टोसिस गैर-आयामी मात्राएँ हैं (जैसा कि क्षण (गणित) माध्य पर केंद्रित है और मानक विचलन द्वारा सामान्यीकृत है), वे मापदंड a और c से स्वतंत्र हैं, और इसलिए ऊपर दिए गए भावों के सामान्तर हैं x (समर्थन के साथ [0,1] या (0,1)):
गुण
केंद्रीय प्रवृत्ति के उपाय
मोड
α, β> 1 के साथ बीटा वितरित रैंडम वेरिएबल X का मोड (सांख्यिकी) वितरण का सबसे संभावित मान है (PDF में शिखर के अनुरूप), और निम्नलिखित अभिव्यक्ति द्वारा दिया गया है:[1]
जब दोनों मापदंड (α, β <1) से कम होते हैं, तब यह एंटी-मोड होता है: प्रायिकता घनत्व वक्र का निम्नतम बिंदु।[3]
Α = β देने पर, मोड के लिए अभिव्यक्ति 1/2 तक सरल हो जाती है, यह दिखाते हुए कि α = β> 1 के लिए मोड (प्रतिक्रिया विरोधी मोड जब α, β < 1), वितरण के केंद्र में है: यह उन स्थितियों में सममित है। α और β के इच्छानुसार मानों के लिए मोड स्थितियों की पूरी सूची के लिए इस आलेख में बीटा वितरण या आकार अनुभाग देखें, । इनमें से अनेक स्थितियों के लिए, घनत्व फलन का अधिकतम मान या दोनों सिरों पर होता है। कुछ स्थितियों में अंत में होने वाले घनत्व फलन का (अधिकतम) मान परिमित होता है। उदाहरण के लिए, α = 2, β = 1 (या α = 1, β = 2) के स्तिथियों में, घनत्व फलन त्रिकोणीय बंटन बन जाता है। समकोण-त्रिकोण वितरण जो दोनों सिरों पर परिमित है। अनेक अन्य स्थितियों में छोर पर गणितीय विलक्षणता होती है, जहां घनत्व फलन का मान अनंत तक पहुंचता है। उदाहरण के लिए, स्तिथियों में α = β = 1/2, बीटा वितरण आर्सेन वितरण बनने के लिए सरल हो जाता है। इनमें से कुछ स्थितियों को लेकर गणितज्ञों के मध्य बहस है और क्या छोरों (x = 0, और x = 1) को बहुलक कहा जा सकता है या नहीं।[6][8]
क्या सिरे घनत्व फलन के फलन के डोमेन का भाग हैं
- क्या गणितीय विलक्षणता को कभी भी विधा कहा जा सकता है
- क्या दो मैक्सिमा वाले स्थितियों को बिमॉडल कहा जाना चाहिए
मध्य
इसमें बीटा वितरण का माध्य अद्वितीय वास्तविक संख्या है जिसके लिए नियमित अधूरा बीटा फलन . α और β के इच्छानुसार मूल्यों के लिए बीटा वितरण के माध्यिका के लिए कोई सामान्य विवृत -रूप अभिव्यक्ति नहीं है। मापदंडों α और β के विशेष मूल्यों के लिए विवृत -रूप अभिव्यक्ति का पालन करें:
- सममित स्थितियों के लिए α = β, माध्यिका = 1/2।
- α = 1 और β > 0 के लिए माध्यिका (यह केस दर्पण छवि है | पावर फलन [0,1] डिस्ट्रीब्यूशन की मिरर-इमेज)
- α > 0 और β = 1 के लिए माध्यिका = (यह स्तिथि पावर फलन [0,1] वितरण है[6]
- α = 3 और β = 2 के लिए माध्यिका = 0.6142724318676105..., चतुर्थक फलन 1 − 8x3 + 6x4 = 0 का वास्तविक समाधान , जो [0,1] में है।
- α = 2 और β = 3 के लिए, माध्य = 0.38572756813238945... = 1−माध्यिका (बीटा (3, 2))
एक मापदंड परिमित (गैर-शून्य) के साथ निम्नलिखित सीमाएँ हैं और दूसरी इन सीमाओं तक पहुँच रही हैं:
α और β दोनों के लिए से अधिक या सामान्तर, बीटा वितरण के माध्यिका के मूल्य का उचित सन्निकटन सूत्र द्वारा दिया गया है[12]
जब α, β ≥ 1, इस सन्निकटन में सापेक्ष त्रुटि (माध्यिका द्वारा विभाजित सन्निकटन त्रुटि) 4% से कम है और α ≥ 2 और β ≥ 2 दोनों के लिए यह 1% से कम है। माध्य और मोड के मध्य के अंतर से विभाजित सन्निकटन त्रुटि समान रूप से छोटी है:
मीन ===
दो मापदंड α और β के साथ बीटा वितरण यादृच्छिक वेरिएबल X का अपेक्षित मान (माध्य) (μ) इन मापदंडों के केवल β/α का फलन है:[1]
उपरोक्त अभिव्यक्ति में α = β देने पर μ = 1/2 प्राप्त करता है α = β माध्य वितरण के केंद्र में है: यह सममित है। साथ ही, उपरोक्त अभिव्यक्ति से निम्नलिखित सीमाएँ प्राप्त की जा सकती हैं:
इसलिए, β/α → 0 , या α/β → ∞ के लिए, माध्य दाहिने छोर पर स्थित है, x = 1. इन सीमा अनुपातबं के लिए, बीटा वितरण डिराक डेल्टा फलन के साथ एक-बिंदु पतित वितरण बन जाता है, दाहिने छोर पर स्पाइक, x = 1, प्रायिकता 1 के साथ, और हर स्थान पर शून्य प्रायिकता पाई जाती है । 100% संभावना (पूर्ण निश्चितता) x = 1 सही छोर पर केंद्रित है| .
:
जबकि ठेठ एकरूप वितरण के लिए (केंद्रीय रूप से स्थित मोड के साथ, मोड के दोनों किनारों पर नतिकरण बिंदु, और लंबी टेल ) (बीटा (α, β) के साथ जैसे कि α, β > 2) यह ज्ञात है कि प्रतिरूप माध्य (स्थान के अनुमान के रूप में) प्रतिरूप माध्यिका के रूप में शक्तिशाली आँकड़े नहीं है, इसके विपरीत वर्दी या यू-आकार के बिमोडल वितरण (बीटा (α, β) के साथ) के स्तिथियों में है α, β ≤ 1), वितरण के अंत में स्थित मोड के साथ। मोस्टेलर और टुकी टिप्पणी के रूप में ([13] पी। 207) दो वेरिएबल म अवलोकनों का औसत सभी प्रतिरूप जानकारी का उपयोग करता है। यह दर्शाता है कि कैसे लघु-टेल वितरण के लिए, वेरिएबल म प्रेक्षणों को अधिक भार मिलना चाहिए। इसके विपरीत, यह वितरण के किनारे पर मोड के साथ यू-आकार के बिमोडल वितरण का माध्यिका है (बीटा (α, β) के साथ जैसे कि α, β ≤ 1) शक्तिशाली नहीं है, क्योंकि प्रतिरूप माध्यिका अत्यधिक प्रतिरूप टिप्पणियों को विचार से हटा देती है। इसका व्यावहारिक अनुप्रयोग उदाहरण के लिए यादृच्छिक चाल के लिए होता है, क्योंकि रैंडम वॉक में मूल स्थान पर अंतिम विज़िट के समय की संभावना आर्क्सिन वितरण बीटा (1/2, 1/2) के रूप में वितरित की जाती है:[5][14]एक यादृच्छिक चलने की अनेक प्राप्ति (संभावना) का कारणऔसत से अधिक शक्तिशाली अनुमानक है (जो इस स्तिथियों में अनुचित प्रतिरूप माप अनुमान है)।
ज्यामितीय माध्य
यादृच्छिक वेरिएबल X के साथ वितरण का ज्यामितीय माध्य GX का लघुगणक ln(X) का अंकगणितीय माध्य है, या, समतुल्य, इसका अपेक्षित मान है
बीटा वितरण के लिए, अपेक्षित मान अभिन्न देता है:
जहां ψ डिगामा फलन है।
इसलिए, इसका आकार मापदंड α और β के साथ बीटा वितरण का ज्यामितीय माध्य α और β के डिगामा कार्यों का घातांक निम्नानुसार है:
जबकि समान आकार के मापदंड α = β के साथ बीटा वितरण के लिए, यह इस प्रकार है कि विषमता = 0 और मोड = माध्य = औसत = 1/2, ज्यामितीय माध्य 1/2 से कम है: 0 < GX < 1/2. इसका कारण यह है कि लॉगरिदमिक परिवर्तन X के मूल्यों को शून्य के समीप दृढ़ता से भारित करता है, क्योंकि ln(X) दृढ़ता से ऋणात्मक अनन्तता की ओर जाता है क्योंकि X शून्य तक पहुंचता है, जबकि ln(X) X → 1 शून्य की ओर चपटा होता है .
एक पंक्ति के साथ α = β, निम्नलिखित सीमाएँ प्रयुक्त होती हैं:
निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं:
संलग्न आलेख शून्य से 2 तक आकृति मापदंड α और β उपयोग किये जाते है जिनके लिए माध्य और ज्यामितीय माध्य के मध्य अंतर दिखाता है। इस तथ्य के अतिरिक्त कि उनके मध्य का अंतर शून्य तक पहुंच जाता है क्योंकि α और β अनंत तक पहुंचते हैं और यह अंतर α के मानों के लिए बड़ा हो जाता है और β शून्य के समीप पहुंचने वाला होता है, आकार मापदंड α और β के संबंध में ज्यामितीय माध्य की स्पष्ट विषमता देखी जा सकती है। जब कि β और α के परिमाणों का आदान-प्रदान करने की तुलना में β के संबंध में α के छोटे मानों के लिए ज्यामितीय माध्य और माध्य के मध्य का अंतर बड़ा है।
नॉर्मन लॉयड जॉनसन|(एन. एल.जॉनसन) और सैमुअल कोटज़(एस. कोटज़)[1] डिगामा फलन ψ(α) ≈ ln(α − 1/2) के लिए लघुगणक सन्निकटन का सुझाव देते है , जिसके परिणामस्वरूप ज्यामितीय माध्य के लिए निम्नलिखित सन्निकटन होता है:
इस सन्निकटन में सापेक्ष त्रुटि के लिए संख्यात्मक मान अनुसरण करते हैं: [(α = β = 1): 9.39%]; [(α = β = 2): 1.29%]; [(α = 2, β = 3): 1.51%]; [(α = 3, β = 2): 0.44%]; [(α = β = 3): 0.51%]; [(α = β = 4): 0.26%]; [(α = 3, β = 4): 0.55%]; [(α = 4, β = 3): 0.24%]।
इसी तरह, ज्यामितीय माध्य के सामान्तर 1/2 के लिए आवश्यक आकार मापदंडों के मान की गणना कर सकते हैं। मापदंड β के मान को देखते हुए, 1/2 के सामान्तर ज्यामितीय माध्य के लिए आवश्यक अन्य मापदंड α का मान क्या होगा?. उत्तर यह है कि (β > 1 के लिए), आवश्यक α का मान β → ∞ के रूप में β + 1/2 की ओर बढ़ता है। उदाहरण के लिए, इन सभी जोड़ों का 1/2 का समान ज्यामितीय माध्य है: [β = 1, α = 1.4427], [β = 2, α = 2.46958], [β = 3, α = 3.47943], [β = 4, α = 4.48449], [β = 5, α = 5.48756], [β = 10, α = 10.4938], [β = 100, α = 100.499]।
ज्यामितीय माध्य का मौलिक गुण है जो किसी अन्य माध्य के लिए असत्य सिद्ध हो सकता है,
यह ज्यामितीय माध्य को एकमात्र सही माध्य बनाता है जब सामान्यीकृत परिणामों का औसत निकाला जाता है, अर्थात वे परिणाम जो संदर्भ मूल्यों के अनुपात के रूप में प्रस्तुत किए जाते हैं।[15] यह प्रासंगिक है क्योंकि बीटा वितरण प्रतिशत के यादृच्छिक व्यवहार के लिए उपयुक्त मॉडल है और यह अनुपात के सांख्यिकीय मॉडलिंग के लिए विशेष रूप से उपयुक्त है। ज्यामितीय माध्य अधिकतम संभावना अनुमान में केंद्रीय भूमिका निभाता है,जिससे कि खंड मापदंड के अनुमान, तथा अधिकतम संभावना देखें जा सके। दरअसल, अधिकतम संभावना का अनुमान लगाते समय, यादृच्छिक वेरिएबल X के आधार पर ज्यामितीय माध्य GX के अतिरिक्त , और ज्यामितीय माध्य भी स्वाभाविक रूप से प्रकट होता है: रैखिक परिवर्तन के आधार पर ज्यामितीय माध्य--(1 − X), X की दर्पण छवि, जिसे G(1−X) द्वारा निरूपित किया जाता है:
एक पंक्ति के साथ α = β, निम्नलिखित सीमाएँ प्रयुक्त होती हैं:
निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं:
इसका निम्नलिखित अनुमानित मूल्य है:
चूंकि दोनों GX और G(1−X) असममित हैं, इस स्तिथियों में इनकी दोनों की आकार मापदंड समान α = β हैं , ज्यामितीय साधन सामान्तर हैं: GX = G(1−X). यह समानता दोनों ज्यामितीय साधनों के मध्य प्रदर्शित निम्नलिखित समरूपता से होती है:
:
हार्मोनिक कारण
यादृच्छिक वेरिएबल X के साथ वितरण का हार्मोनिक माध्य HX का व्युत्क्रम 1/X का अंकगणितीय माध्य है या, समतुल्य, इसका अपेक्षित मान है। इसलिए, आकार मापदंड α और β के साथ बीटा वितरण का है:
α <1 के साथ बीटा वितरण का हार्मोनिक माध्य (HX) अपरिभाषित है, क्योंकि इसकी परिभाषित अभिव्यक्ति एकता से कम आकार मापदंड α के लिए [0, 1] में सीमित नहीं है।
उपरोक्त व्यंजक में α = β देने से प्राप्त होता है
दिखा रहा है कि α = β के लिए हार्मोनिक माध्य 0 से है, α = β = 1 के लिए, 1/2 के लिए, α = β → ∞ के लिए।
निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं:
ज्यामितीय माध्य के अतिरिक्त, हार्मोनिक माध्य चार मापदंड स्तिथियों के लिए अधिकतम संभावना अनुमान में भूमिका निभाता है। दरअसल, हार्मोनिक माध्य HX के अतिरिक्त, चार मापदंड स्तिथियों के लिए अधिकतम संभावना अनुमान लगाते समययादृच्छिक वेरिएबल X के आधार पर, अन्य हार्मोनिक माध्य भी स्वाभाविक रूप से प्रकट होता है: रैखिक परिवर्तन (1 − X) पर आधारित हार्मोनिक माध्य, X की दर्पण-छवि, H द्वारा निरूपित1 − X:
हार्मोनिक माध्य (एच(1 − X)β <1 के साथ बीटा वितरण अपरिभाषित है, क्योंकि इसकी परिभाषित अभिव्यक्ति [0, 1] में एकता से कम आकार मापदंड β के लिए बाध्य नहीं है।
उपरोक्त व्यंजक में α = β देने से प्राप्त होता है
दिखा रहा है कि α = β के लिए हार्मोनिक माध्य 0 से है, α = β = 1 के लिए, 1/2 के लिए, α = β → ∞ के लिए।
निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं:
चूंकि दोनों HX और H1−X असममित हैं, इस स्तिथियों में α = β कि दोनों आकार मापदंड सामान्तर हैं, HX = H1−X. हार्मोनिक साधन सामान्तर हैं: यह समानता दोनों हार्मोनिक साधनों के मध्य प्रदर्शित निम्नलिखित समरूपता से होती है:
सांख्यिकीय फैलाव के उपाय
विचरण
मापदंड α और β के साथ बीटा वितरण यादृच्छिक वेरिएबल X का विचरण (माध्य पर केंद्रित दूसरा क्षण) है:[1][16]
उपरोक्त व्यंजक में α = β देने से प्राप्त होता है
दिखा रहा है कि α = β के लिए जैसे जैसे α = β बढ़ती है। वैसे वैसे विचरण नीरस रूप से घटता है समुच्चयिंग α = β = 0 इस व्यंजक में, अधिकतम प्रसरण var(X) = 1/4 मिलता है[1]जो केवल α = β = 0. पर सीमा के निकट होता है,
बीटा वितरण को इसके माध्य μ (0 < μ < 1) और प्रतिरूप आकार ν = α + β (ν > 0) के संदर्भ में भी पैरामीट्रिज्ड किया जा सकता है (उपखंड माध्य और प्रतिरूप आकार देखें):
इस सांख्यिकीय मापदंड का उपयोग करते हुए, माध्य μ और प्रतिरूप आकार ν के संदर्भ में विचरण को निम्नानुसार व्यक्त किया जा सकता है:
तब से ν = α + β > 0, यह इस प्रकार है कि var(X) < μ(1 − μ).
एक सममित वितरण के लिए, माध्य वितरण के मध्य में है, μ = 1/2, और इसलिए:
साथ ही, उपरोक्त भावों से निम्नलिखित सीमाएँ प्राप्त की जा सकती हैं (केवल विख्यात वेरिएबल सीमा तक पहुँच रहे हैं):
ज्यामितीय विचरण और सहप्रसरण
ज्यामितीय विचरण का लघुगणक, ln(varGX), यादृच्छिक वेरिएबल X के साथ वितरण का X के लघुगणक का दूसरा क्षण X के ज्यामितीय माध्य ln(GX) पर केंद्रित है,
और इसलिए, ज्यामितीय विचरण है:
फिशर सूचना आव्युह में, और लॉग संभावना फलन की वक्रता, प्रतिबिंब सूत्र वेरिएबल 1 − X के ज्यामितीय भिन्नता का लघुगणक और X और 1 − X के मध्य ज्यामितीय सहप्रसरण का लघुगणक प्रकट होता है:
बीटा वितरण के लिए, दो गामा वितरणों के अनुपात के रूप में बीटा वितरण के प्रतिनिधित्व का उपयोग करके और अभिन्न के माध्यम से अंतर करके उच्च क्रम लॉगरिदमिक क्षण प्राप्त किए जा सकते हैं। उन्हें उच्च क्रम के पॉली-गामा कार्यों के संदर्भ में व्यक्त किया जा सकता है। अनुभाग देखें § लघुगणकीय रूप से परिवर्तित यादृच्छिक चर के क्षण. लघुगणकीय वेरिएबल का प्रसरण और ln X और ln(1−X) का सहप्रसरण हैं:
जहाँ त्रिगामा फलन, ψ1(α) निरूपित करता है, तथा बहुग्राम कार्यों का दूसरा फलन है और इसे डिगामा फलन के व्युत्पन्न के रूप में परिभाषित किया गया है:
इसलिए,
इसके साथ वाले प्लॉट लॉग ज्यामितीय प्रसरण दिखाते हैं और ज्यामितीय सहप्रसरण बनाम आकृति मापदंड α और β लॉग करते हैं। भूखंड दिखाते हैं कि लॉग ज्यामितीय संस्करण और लॉग ज्यामितीय सहप्रसरण आकार मापदंडों α और β 2 से अधिक के लिए शून्य के समीप हैं, और यह कि आकार मापदंड मान α और β एकता से कम के लिए लॉग ज्यामितीय संस्करण तेजी से मूल्य में वृद्धि करते हैं। आकार के मापदंडों के सभी मूल्यों के लिए लॉग ज्यामितीय संस्करण धनात्मक हैं। आकार के मापदंडों के सभी मूल्यों के लिए लॉग ज्यामितीय सहप्रसरण ऋणात्मक है, और यह एकता से कम α और β के लिए बड़े ऋणात्मक मूल्यों तक पहुंचता है।
निम्नलिखित मापदंड परिमित (गैर-शून्य) के साथ सीमाएँ हैं और अन्य इन सीमाओं के समीप हैं:
अलग-अलग दो मापदंड वाली सीमाएँ:
चूंकि दोनों ln(varGX) और ln(varG(1 − X)) असममित हैं, जब आकार मापदंड सामान्तर होते हैं, तब α = β, में होता है: ln(varGX) = ln(varG(1 − X). यह समानता दोनों लॉग ज्यामितीय भिन्नताओं के मध्य प्रदर्शित निम्नलिखित समरूपता से होती है:
लॉग ज्यामितीय सहप्रसरण सममित है:
माध्य के आस-पास निरपेक्ष विचलन
आकार मापदंडों α और β के साथ बीटा वितरण के लिए माध्य के आसपास औसत निरपेक्ष विचलन है:[6]
माध्य के चारों ओर औसत निरपेक्ष विचलन मोड के प्रत्येक पक्ष में टेल और विभक्ति बिंदुओं के साथ बीटा वितरण के लिए मानक विचलन की तुलना में सांख्यिकीय फैलाव का अधिक शक्तिशाली सांख्यिकी अनुमानक है, α,β > 2 के साथ बीटा(α, β) वितरण यह माध्य से वर्ग विचलन के अतिरिक्त रैखिक (पूर्ण) विचलन पर निर्भर करता है। इसलिए, माध्य से बहुत बड़े विचलन का प्रभाव उतना अधिक भारित नहीं होता है।
गामा फलन के लिए स्टर्लिंग के सन्निकटन का उपयोग करते हुए, नॉर्मन लॉयड जॉनसन|(एन.एल.जॉनसन) और सैमुअल कोटज़|(एस.कोट्ज़)[1]एकता से अधिक आकार के मापदंडों के मूल्यों के लिए निम्नलिखित सन्निकटन प्राप्त किया (इस सन्निकटन के लिए सापेक्ष त्रुटि α = β = 1 के लिए केवल -3.5% है, और यह α → ∞, β → ∞ के रूप में शून्य हो जाती है):
सीमा α → ∞, β → ∞ पर, मानक विचलन (बीटा वितरण के लिए) के औसत पूर्ण विचलन का अनुपात सामान्य वितरण के लिए समान उपायों के अनुपात के सामान्तर हो जाता है: . α = β = 1 के लिए यह अनुपात सामान्तर है , जिससे कि α = β = 1 से α, β → ∞ अनुपात 8.5% कम हो जाएगा। α = β = 0 के लिए मानक विचलन माध्य के चारों ओर पूर्ण विचलन के सामान्तर है। इसलिए, यह अनुपात α = β = 0 से α = β = 1 तक 15% कम हो जाता है, और α = β = 0 से α, β → ∞ तक 25% कम हो जाता है। चूंकि, विषम बीटा वितरण के लिए जैसे कि α → 0 या β → 0, मानक विचलन का औसत निरपेक्ष विचलन का अनुपात अनंत तक पहुंचता है (चूंकि उनमें से प्रत्येक, व्यक्तिगत रूप से, शून्य तक पहुंचता है) क्योंकि औसत निरपेक्ष विचलन शून्य की तुलना में तेजी से पहुंचता है मानक विचलन।
माध्य μ और प्रतिरूप आकार ν = α + β > 0 के संदर्भ में सांख्यिकीय मापदंड का उपयोग करना:
- α = μν, β = (1−μ)ν
माध्य μ और प्रतिरूप आकार ν के संदर्भ में माध्य के चारों ओर औसत निरपेक्ष विचलन को निम्नानुसार व्यक्त किया जा सकता है:
एक सममित वितरण के लिए, μ = 1/2, माध्य वितरण के मध्य में है,और इसलिए:
साथ ही, उपरोक्त भावों से निम्नलिखित सीमाएँ प्राप्त की जा सकती हैं (केवल विख्यात वेरिएबल सीमा तक पहुँच रहे हैं):
कारणपूर्ण अंतर
बीटा वितरण के लिए औसत निरपेक्ष अंतर है:
बीटा वितरण के लिए गिन्नी गुणांक सापेक्ष माध्य निरपेक्ष अंतर का आधा है:
विषमता
विषमता (बीटा वितरण का तीसरा क्षण माध्य पर केंद्रित, विचरण की 3/2 शक्ति द्वारा सामान्यीकृत) है[1]
उपरोक्त अभिव्यक्ति में α = β देने से γ1 = 0 प्राप्त होता है ,तथा बार फिर दिखा रहा है कि α = β के लिए वितरण सममित है और इसलिए विषमता शून्य है। α < β के लिए धनात्मक विषम (दायां-टेल), α> β के लिए ऋणात्मक विषम (बायां-टेल)।
और औसत μ और प्रतिरूप आकार ν = α + β के संदर्भ में सांख्यिकीय मापदंड का उपयोग करना:
माध्य μ और प्रतिरूप आकार ν के संदर्भ में विषमता व्यक्त किया जा सकता है:
विषमता केवल विचरण संस्करण और माध्य μ के रूप में निम्नानुसार व्यक्त किया जा सकता है:
विचरण और माध्य के कार्य के रूप में विषमता के साथ की साजिश से पता चलता है कि अधिकतम विचरण (1/4) शून्य विषमता और समरूपता की स्थिति (μ = 1/2) के साथ युग्मित है, और वह अधिकतम विषमता (धनात्मक या ऋणात्मक अनंत) तब होता है जब माध्य छोर या दूसरे छोर पर स्थित है, जिससे संभाव्यता वितरण का द्रव्यमान सिरों पर केंद्रित हो (न्यूनतम विचरण )।
प्रतिरूप के आकार ν = α + β और विचरण संस्करण के संदर्भ में विषमता के वर्ग के लिए निम्नलिखित अभिव्यक्ति, चार मापदंडों के क्षणों के आकलन की विधि के लिए उपयोगी है:
यह अभिव्यक्ति सही ढंग से α = β के लिए शून्य का विषमता देती है, क्योंकि उस स्तिथियाँ में (देखें § वरिएंस): .
सममित स्तिथियाँ के लिए (α = β), विषमता = 0 पूरी सीमा पर, और निम्नलिखित सीमाएँ प्रयुक्त होती हैं:
असममित स्थितियों के लिए (α ≠ β) निम्नलिखित सीमाएँ (केवल विख्यात वेरिएबल सीमा के समीप पहुंचकर) उपरोक्त अभिव्यक्तियों से प्राप्त की जा सकती हैं:
कुर्तबसिस
गियर के हानि का आकलन करने के लिए ध्वनिक विश्लेषण में बीटा वितरण प्रयुक्त किया गया है, क्योंकि बीटा वितरण के कर्टोसिस को गियर की स्थिति का अच्छा संकेतक बताया गया है।[17] कर्टोसिस का उपयोग किसी व्यक्ति के कदमों से उत्पन्न भूकंपीय संकेत को अन्य संकेत से अलग करने के लिए भी किया जाता है। जैसा कि जमीन पर चलने वाले व्यक्ति या अन्य लक्ष्य भूकंपीय तरंगों के रूप में निरंतर संकेत उत्पन्न करते हैं, उनके द्वारा उत्पन्न भूकंपीय तरंगों के आधार पर विभिन्न लक्ष्यों को अलग किया जा सकता है। कर्टोसिस आवेगी संकेतबं के प्रति संवेदनशील है, इसलिए यह वाहनों, हवाओं, ध्वनि आदि द्वारा उत्पन्न अन्य संकेत की तुलना में मानव पदचिन्हों द्वारा उत्पन्न संकेतबं के प्रति अधिक संवेदनशील है।[18] दुर्भाग्य से, ककुदता के लिए अंकन मानकीकृत नहीं किया गया है। अतिरिक्त कर्टोसिस के लिए केनी और कीपिंग में प्रतीक γ2 का प्रयोग करें [19], किन्तु अब्रामोवित्ज़ और स्टेगुन विभिन्न शब्दावली का प्रयोग करें।[20] भ्रम को रोकने के लिए कर्टोसिस के मध्य (माध्य पर केंद्रित चौथा क्षण, विचरण के वर्ग द्वारा सामान्यीकृत)[21] और अतिरिक्त कर्टोसिस, प्रतीकों का उपयोग करते समय, उन्हें निम्नानुसार लिखा जाएगा:[6][7]
उपरोक्त व्यंजक में α = β देने से प्राप्त होता है
- .
इसलिए, सममित बीटा वितरण के लिए, अतिरिक्त कर्टोसिस ऋणात्मक है, {α = β} → 0 के रूप में सीमा पर -2 के न्यूनतम मान से बढ़ रहा है, और शून्य के अधिकतम मान को {α = β} → ∞ के रूप में आ रहा है। तथा −2 का मान अतिरिक्त कर्टोसिस का न्यूनतम मूल्य है जिसे कोई भी वितरण (न केवल बीटा वितरण, किंतु किसी भी संभावित प्रकार का वितरण) कभी भी प्राप्त कर सकता है। यह न्यूनतम मूल्य तब प्राप्त होता है जब सभी प्रायिकता घनत्व पूरी तरह से प्रत्येक छोर x = 0 और x = 1 पर केंद्रित होते हैं, मध्य में कुछ भी नहीं होता है: प्रत्येक छोर पर समान संभावना 1/2 के साथ 2-बिंदु बर्नौली वितरण (एक सिक्का टॉस: देखें) आगे की चर्चा के लिए विषमता के वर्ग से घिरे कर्टोसिस के नीचे का खंड)। संभाव्यता वितरण के संभावित आउटलेयर (या संभावित दुर्लभ, वेरिएबल मान) के माप के रूप में कुकुदता का विवरण, बीटा वितरण सहित सभी वितरणों के लिए सही है। जब दुर्लभ, वेरिएबल म मान बीटा वितरण में हो सकते हैं, तब इसका कर्टोसिस जितना अधिक होगा; अन्यथा, कर्टोसिस कम होता है। α ≠ β, विषम बीटा वितरण के लिए, अतिरिक्त कर्टोसिस असीमित धनात्मक मूल्यों तक पहुंच सकता है (विशेष रूप से α → 0 के लिए परिमित β के लिए, या β → 0 के लिए परिमित α के लिए) क्योंकि मोड से दूर की ओर कभी-कभी चरम मान उत्पन्न होंगे। न्यूनतम कर्टोसिस तब होता है जब द्रव्यमान घनत्व प्रत्येक छोर पर समान रूप से केंद्रित होता है (और इसलिए माध्य केंद्र में होता है), और सिरों के मध्य द्रव्यमान घनत्व की कोई संभावना नहीं होती है।
औसत μ और प्रतिरूप आकार ν = α + β के संदर्भ में सांख्यिकीय मापदंड का उपयोग करना:
माध्य μ और प्रतिरूप आकार ν के संदर्भ में अतिरिक्त कर्टोसिस को निम्नानुसार व्यक्त किया जा सकता है:
अतिरिक्त कर्टोसिस को केवल निम्नलिखित दो मापदंडों के संदर्भ में भी व्यक्त किया जा सकता है: विचरण संस्करण, और प्रतिरूप आकार ν निम्नानुसार है:
और, भिन्नता संस्करण और माध्य μ के संदर्भ में निम्नानुसार है:
विचरण और माध्य के कार्य के रूप में अतिरिक्त कर्टोसिस की साजिश से पता चलता है कि अतिरिक्त कुर्तबसिस का न्यूनतम मूल्य (−2, जो किसी भी वितरण के लिए अतिरिक्त कर्टोसिस के लिए न्यूनतम संभव मूल्य है) अंतर के अधिकतम मूल्य के साथ घनिष्ठ रूप से जुड़ा हुआ है ( 1/4) और समरूपता की स्थिति: मध्य बिंदु पर होने वाली माध्य (μ = 1/2)। यह शून्य विषमता के साथ α = β = 0 के सममित स्तिथियाँ के लिए होता है। सीमा पर, यह 2 बिंदु बर्नौली वितरण है जिसमें समान संभावना 1/2 प्रत्येक डायराक डेल्टा फलन के अंत में x = 0 और x = 1 और हर स्थान शून्य संभावना है। (एक सिक्के का उछाल: सिक्के का फलक x = 0 और दूसरा फलक x = 1 है।) प्रसरण अधिकतम है क्योंकि वितरण के दो मोडल है और प्रत्येक छोर पर दो मोड (स्पाइक्स) के मध्य कुछ भी नहीं है। अतिरिक्त कर्टोसिस न्यूनतम है:क्योंकि संभाव्यता घनत्व द्रव्यमान माध्य पर शून्य है और यह प्रत्येक छोर पर दो चोटियों पर केंद्रित है। अतिरिक्त कर्टोसिस न्यूनतम संभव मान (किसी भी वितरण के लिए) तक पहुँच जाता है जब प्रायिकता घनत्व फलन के प्रत्येक छोर पर दो स्पाइक्स होते हैं: यह द्वि-शिखर होता है। और उनके मध्य में कुछ भी नहीं होता है
दूसरी ओर, प्लॉट से पता चलता है कि अत्यधिक विषम स्थितियों के लिए, जहां माध्य या दूसरे छोर (μ = 0 या μ = 1) के पास स्थित है, विचरण शून्य के समीप है, और अतिरिक्त कर्टोसिस तेजी से अनंत तक पहुंचता है जब बंटन का माध्य या तब अंत की ओर पहुंचता है।
वैकल्पिक रूप से, अतिरिक्त कर्टोसिस को केवल निम्नलिखित दो मापदंडों के संदर्भ में भी व्यक्त किया जा सकता है: विषमता का वर्ग, और प्रतिरूप आकार ν निम्नानुसार है:
इस अंतिम अभिव्यक्ति से, कार्ल पियर्सन द्वारा अपने पेपर में व्यावहारिक रूप से सदी पहले प्रकाशित समान सीमाएँ प्राप्त कर सकते हैं,[22]बीटा वितरण के लिए (विषमता के वर्ग से घिरा कर्टोसिस शीर्षक वाला नीचे दिया गया अनुभाग देखें)। उपरोक्त व्यंजक में α + β= ν = 0 समुच्चय करने पर, पियर्सन की निचली सीमा प्राप्त होती है (सीमा के नीचे विषमता और अतिरिक्त कर्टोसिस के लिए मान (अतिरिक्त कर्टोसिस + 2 - विषमता2 = 0) किसी भी वितरण के लिए नहीं हो सकता है, और इसलिए कार्ल पियर्सन ने उचित रूप से इस सीमा के नीचे के क्षेत्र को असंभव क्षेत्र कहा है)। α + β = ν → ∞ की सीमा पियर्सन की ऊपरी सीमा निर्धारित करती है।
इसलिए:
ν = α + β के मान जैसे कि ν शून्य से अनंत तक होता है, 0 < ν < ∞, बीटा वितरण के पूरे क्षेत्र को अतिरिक्त कर्टोसिस बनाम स्क्वायर विषमता के विमान में फैलाता है।
सममित स्तिथियाँ (α = β) के लिए, निम्नलिखित सीमाएं प्रयुक्त होती हैं:
असममित स्थितियों के लिए (α ≠ β) निम्नलिखित सीमाएँ (केवल विख्यात वेरिएबल सीमा के समीप पहुंचकर) उपरोक्त अभिव्यक्तियों से प्राप्त की जा सकती हैं:
विशेषता फलन
अभिलक्षणिक फलन (संभाव्यता सिद्धांत) प्रायिकता घनत्व फलन का फूरियर रूपांतरण है। बीटा डिस्ट्रीब्यूशन का विशिष्ट कार्य कंफ्लुएंट हाइपरजियोमेट्रिक फलन है। कुमेर का कंफ्लुएंट हाइपरजियोमेट्रिक फलन (पहली तरह का):[1][19][23]
जहाँ
उभरता हुआ भाज्य है, जिसे पोचममेर प्रतीक भी कहा जाता है। t = 0 के लिए अभिलाक्षणिक फलन का मान है:
- .
इसके अतिरिक्त, वेरिएबल टी की उत्पत्ति के संबंध में विशेषता फलन के वास्तविक और काल्पनिक भाग निम्नलिखित समरूपता का आनंद लेते हैं:
सममित स्तिथि α = β बेसेल फलन के लिए बीटा वितरण के विशिष्ट कार्य को सरल करता है, क्योंकि विशेष स्तिथियों में α + β = 2α संगम हाइपरज्यामितीय फलन पहली तरह ) (पहली तरह का) बेसेल फलन (संशोधित बेसेल फलन) को कम करता है अर्नस्ट कुमेर | कुमेर के दूसरे परिवर्तन का उपयोग इस प्रकार है:
बीमा रूपिंग अनुप्रयोगों के लिए सममित स्तिथियाँ α = β = n/2 का और उदाहरण चित्र 11 में पाया जा सकता है [24]
साथ वाले भूखंडों में, सममित (α = β) और विषम (α ≠ β) स्थितियों के लिए बीटा वितरण के विशेषता फलन (संभाव्यता सिद्धांत) की जटिल संख्या (Re) प्रदर्शित की जाती है।
अन्य क्षण
मोमेंट जनरेटिंग फलन
यह भी अनुसरण करता है[1][6] वह क्षण उत्पन्न करने वाला कार्य है
विशेष रूप से MX(α; β; 0) = 1.
उच्च क्षण
मोमेंट जनरेटिंग फलन का उपयोग करके, k-वें कारक कच्चा पल द्वारा दिया जाता है[1]
(घातीय श्रृंखला) शब्द को गुणा करना पल उत्पन्न करने वाले फलन की श्रृंखला में
जहाँ Xk पोचहैमर प्रतीक है जो बढ़ती फैक्टोरियल का प्रतिनिधित्व करता है। इसे पुनरावर्ती रूप में भी लिखा जा सकता है
क्षण उत्पन्न करने के कार्य के पश्चात् से अभिसरण का धनात्मक सीमाहै, बीटा वितरण मोमेंट समस्या है।[25]
परिवर्तित यादृच्छिक वेरिएबल के क्षण
रैखिक रूप से रूपांतरित, उत्पाद और उल्टे यादृच्छिक वेरिएबल के क्षण
एक परिवर्तित यादृच्छिक वेरिएबल के लिए निम्नलिखित अपेक्षाएँ भी दिखा सकते हैं,[1]जहां रैंडम वेरिएबल X को मापदंड α और β: X ~ बीटा (α, β) के साथ बीटा-वितरित किया गया है। वेरिएबल 1 − X का अपेक्षित मान X पर आधारित अपेक्षित मान का दर्पण-समरूपता है:
बीटा वितरण के प्रायिकता घनत्व फलन की दर्पण-समरूपता के कारण, वेरिएबल X और 1 − X पर आधारित प्रसरण समान हैं, और X(1 − X) पर सहप्रसरण प्रसरण का ऋणात्मक है:
इनवर्टेड वेरिएबल्स के लिए ये अपेक्षित मूल्य हैं, (ये हार्मोनिक साधनों से संबंधित हैं, देखें § हार्मोनिक माध्य):
निम्नलिखित परिवर्तन को वेरिएबल X को उसकी दर्पण-छवि X/(1 − X) से विभाजित करके उल्टे बीटा वितरण या बीटा प्राइम वितरण (जिसे दूसरी तरह के बीटा वितरण या पियर्सन वितरण के रूप में भी जाना जाता है) के अपेक्षित मूल्य में परिणाम मिलता है। पियर्सन का प्रकार छठी):[1]
इन रूपांतरित वेरिएबल के प्रसरणों को एकीकरण द्वारा प्राप्त किया जा सकता है, क्योंकि संबंधित वेरिएबल पर केंद्रित दूसरे क्षणों के अपेक्षित मान:
इसके दर्पण-छवि (X/1−X) द्वारा विभाजित वेरिएबल X का निम्नलिखित प्रसरण, उल्टे बीटा वितरण या बीटा प्राइम वितरण (जिसे दूसरी तरह के बीटा वितरण या पियर्सन वितरण के रूप में भी जाना जाता है) के विचरण में परिणाम देता है। पियर्सन का प्रकार छठी):[1]
सहप्रसरण हैं:
ये अपेक्षाएँ और भिन्नताएँ चार-मापदंड फ़िशर सूचना आव्युह में दिखाई देती हैं (§ फिशर जानकारी.)
लघुगणकीय रूप से परिवर्तित यादृच्छिक वेरिएबल के क्षण

लघुगणक परिवर्तन के लिए अपेक्षित मान (अधिकतम संभावना अनुमानों के लिए उपयोगी, देखें § पैरामीटर अनुमान, अधिकतम संभावना) इस खंड में चर्चा कर रहे हैं। निम्नलिखित लघुगणक रैखिक परिवर्तन ज्यामितीय माध्य GX और G(1−X) से संबंधित हैं(देखना § जियोमेट्रिक माध्य):
जहां डिगामा फलन ψ(α) को गामा फलन के लघुगणक व्युत्पन्न के रूप में परिभाषित किया गया है:[19]
लॉग परिवर्तन रोचक हैं,[26] जैसा कि वे सामान्यतः विभिन्न आकारों (जे-आकृतियों सहित) को (सामान्यतः विषम) घंटी के आकार के घनत्वों को लॉजिट वेरिएबल पर बदलते हैं, और वे मूल वेरिएबल पर अंत विलक्षणताओं को हटा सकते हैं:
जॉनसन[27] लॉगिट-रूपांतरित वेरिएबल ln(X/1−X) के वितरण पर विचार किया गया, जिसमें आकार मापदंड के बड़े मूल्यों के लिए इसके क्षण उत्पन्न करने वाले फलन और सन्निकटन सम्मिलित हैं। यह रूपांतरण वास्तविक रेखा (-∞, +∞) की दोनों दिशाओं में मूल वेरिएबल X के आधार पर परिमित समर्थन [0, 1] को अनंत समर्थन तक बढ़ाता है।
दो गामा वितरणों के अनुपात के रूप में बीटा वितरण के प्रतिनिधित्व का उपयोग करके और अभिन्न के माध्यम से अंतर करके उच्च क्रम लॉगरिदमिक क्षण प्राप्त किए जा सकते हैं। उन्हें उच्च क्रम के पॉली-गामा कार्यों के रूप में निम्नानुसार व्यक्त किया जा सकता है:
इसलिए लघुगणकीय चरो का प्रसरण और ln(X) और ln(1−X) का सहप्रसरण हैं:
जहाँ त्रिगामा फलन, ψ1(α) निरूपित करता है बहुग्राम कार्यों का दूसरा है, और इसे डिगामा फलन के व्युत्पन्न के रूप में परिभाषित किया गया है:
- .
लघुगणक रूप से रूपांतरित वेरिएबल X और (1−X) के प्रसरण और सहप्रसरण सामान्य रूप से भिन्न होते हैं, क्योंकि लघुगणक रूपांतरण मूल वेरिएबल X और (1−X) के दर्पण-समरूपता को नष्ट कर देता है, क्योंकि लघुगणक ऋणात्मक अनंतता तक पहुंचता है वेरिएबल शून्य के समीप पहुंच रहा है।
ये लघुगणक प्रसरण और सहप्रसरण बीटा वितरण के लिए फिशर सूचना आव्युह के तत्व हैं। वे लॉग संभावना फलन की वक्रता का माप भी हैं (अधिकतम संभावना अनुमान पर अनुभाग देखें)।
लॉग व्युत्क्रम वेरिएबल के प्रसरण लॉग वेरिएबल के प्रसरण के समान हैं:
यह भी अनुसरण करता है कि लॉगिट रूपांतरित वेरिएबल के संस्करण हैं:
जानकारी की मात्रा (एन्ट्रापी)
एक बीटा वितरित यादृच्छिक वेरिएबल , X ~ बीटा (α, β) को देखते हुए, X की सूचना एन्ट्रापी (नेट (यूनिट) में मापी गई है,[28] प्रायिकता घनत्व फलन के लघुगणक के ऋणात्मक का अपेक्षित मान:
जहाँ f(x; α, β) बीटा वितरण का प्रायिकता घनत्व फलन है:
डिगामा फलन ψ हार्मोनिक संख्याओं के लिए यूलर के अभिन्न सूत्र के परिणाम के रूप में अंतर एंट्रॉपी के सूत्र में प्रकट होता है जो अभिन्न से अनुसरण करता है:
जहाँ α = β = 1 है तो (जिन मूल्यों के लिए बीटा वितरण एक समान वितरण (निरंतर) के समान है) उनको को छोड़कर, शून्य से अधिक α और β के सभी मानों के लिए बीटा वितरण की सूचना एन्ट्रॉपी ऋणात्मक है, जहां सूचना एन्ट्रापी शून्य के अधिकतम और न्यूनतम मान तक पहुँच जाता है। यह उम्मीद की जानी चाहिए कि अधिकतम एन्ट्रापी तब होनी चाहिए जब बीटा वितरण समान वितरण के सामान्तर हो जाए, क्योंकि अनिश्चितता अधिकतम होती है जब सभी संभव घटनाएं परिवर्तनीय होती हैं।
जब α या β शून्य के समीप पहुंचने के लिए, सूचना एन्ट्रॉपी अपने मैक्सिमा और ऋणात्मक अनंतता के न्यूनतम मूल्य तक पहुंचती है। (या तब या दोनों) α या β शून्य के समीप पहुंचने के लिए, ऑर्डर की अधिकतम मात्रा होती है: सभी प्रायिकता घनत्व सिरों पर केंद्रित होते हैं, और सिरों के मध्य स्थित बिंदुओं पर शून्य प्रायिकता घनत्व होता है। इसी प्रकार (या तब या दोनों) α या β अनंत तक पहुंचने के लिए, अंतर एंट्रॉपी ऋणात्मक अनंतता के न्यूनतम मूल्य और ऑर्डर की अधिकतम मात्रा तक पहुंचता है। यदि या तब α या β अनंत तक पहुंचता है (और दूसरा परिमित है) सभी प्रायिकता घनत्व अंत में केंद्रित होते हैं, और प्रायिकता घनत्व हर स्थान शून्य होता है। यदि दोनों आकार मापदंड समान हैं (सममित स्तिथि ), α = β, और वे साथ अनंत तक पहुंचते हैं, तब प्रायिकता घनत्व मध्य x = 1/2 पर केंद्रित स्पाइक फलन (डायराक डेल्टा फलन) बन जाता है, और इसलिए 100% संभावना होती है मध्य में x = 1/2 और हर स्थान शून्य संभावना।

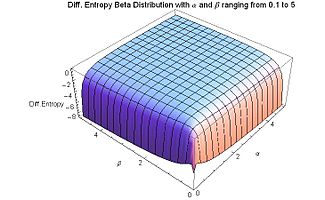 (निरंतर केस) सूचना एंट्रॉपी को शैनन ने अपने मूल पेपर में प्रस्तुत किया था (जहां उन्होंने इसे निरंतर वितरण की एंट्रॉपी नाम दिया था), उसी पेपर के समापन भाग के रूप में जहां उन्होंने सूचना एंट्रॉपी को परिभाषित किया था।[29] तब से यह ज्ञात है कि अंतर एंट्रॉपी असतत एंट्रॉपी की असीमित सीमा से अनंत ऑफ समुच्चय से भिन्न हो सकती है, इसलिए अंतर एन्ट्रॉपी ऋणात्मक हो सकती है (जैसा कि यह बीटा वितरण के लिए है)। एंट्रॉपी के सापेक्ष मूल्य वास्तव में क्या मायने रखता है।
(निरंतर केस) सूचना एंट्रॉपी को शैनन ने अपने मूल पेपर में प्रस्तुत किया था (जहां उन्होंने इसे निरंतर वितरण की एंट्रॉपी नाम दिया था), उसी पेपर के समापन भाग के रूप में जहां उन्होंने सूचना एंट्रॉपी को परिभाषित किया था।[29] तब से यह ज्ञात है कि अंतर एंट्रॉपी असतत एंट्रॉपी की असीमित सीमा से अनंत ऑफ समुच्चय से भिन्न हो सकती है, इसलिए अंतर एन्ट्रॉपी ऋणात्मक हो सकती है (जैसा कि यह बीटा वितरण के लिए है)। एंट्रॉपी के सापेक्ष मूल्य वास्तव में क्या मायने रखता है।
दो बीटा वितरित यादृच्छिक वेरिएबल दिए गए हैं, X1 ~ बीटा (α', β') और X2 ~ बीटा (α', β'), क्रॉस एन्ट्रापी है (नट्स में मापा जाता है)[30]
दो परिकल्पनाओं के मध्य की दूरी को मापने के लिए क्रॉस एन्ट्रॉपी का उपयोग त्रुटि मीट्रिक के रूप में किया गया है।[31][32] इसका निरपेक्ष मान न्यूनतम होता है जब दो वितरण समान होते हैं। तथा यह लॉग अधिकतम संभावना से सबसे अधिक निकटता से संबंधित सूचना उपाय है [30](मापदंड अनुमान पर अनुभाग देखें। अधिकतम संभावना अनुमान))।
सापेक्ष एन्ट्रॉपी, या कुल्बैक-लीब्लर विचलन DKL(X1 || X2), यह मानने की अक्षमता का उपाय है कि वितरण X2 है ~ बीटा (α', β') जब वितरण वास्तव में X1 है ~ बीटा (α, β)। इसे निम्नानुसार परिभाषित किया गया है (नट्स में मापा गया)।
सापेक्ष एन्ट्रापी, या कुल्बैक-लीब्लर विचलन, सदैव गैर-ऋणात्मक होता है। कुछ संख्यात्मक उदाहरण अनुसरण करते हैं:
- X1 ~ बीटा(1, 1) और X2 ~ बीटा(3, 3); DKL(X1 || X2) = 0.598803; DKL(X2 || X1) = 0.267864; h(X1) = 0; h(X2) = −0.2678
- X1 ~ बीटा(3, 0.5) और X2 ~ बीटा (0.5, 3); DKL(X1 || X2) = 7.21574; DKL(X2 || X1) = 7.21574; h(X1) = −1.10805; h(X2) = −1.10805.
कुल्बैक-लीब्लर विचलन सममित DKL(X1 || X2) ≠ DKL(X2 || X1) नहीं है उस स्तिथियों के लिए जिसमें व्यक्तिगत बीटा वितरण बीटा (1, 1) और बीटा (3, 3) सममित हैं, किन्तु अलग-अलग एंट्रॉपी h(x1) ≠ h(X2) हैं . कुलबैक डाइवर्जेंस का मान तय की गई दिशा पर निर्भर करता है: चाहे वह उच्च (डिफरेंशियल) एंट्रॉपी से लोअर (डिफरेंशियल) एंट्रॉपी में जा रहा हो या इसके विपरीत। उपरोक्त संख्यात्मक उदाहरण में, कुल्बैक विचलन यह मानने की अक्षमता को मापता है कि वितरण (घंटी के आकार का) बीटा (3, 3) है, बजाय (समान) बीटा (1, 1) के। बीटा (1, 1) की h एन्ट्रॉपी बीटा (3, 3) की h एन्ट्रॉपी से अधिक है क्योंकि समान वितरण बीटा (1, 1) में अधिकतम मात्रा में विकार है। कुलबैक डाइवर्जेंस दो गुना अधिक (0.267864 के अतिरिक्त 0.598803) से अधिक है, जब एंट्रॉपी घटने की दिशा में मापा जाता है: वह दिशा जो मानती है कि (समान) बीटा (1, 1) वितरण (घंटी के आकार का) बीटा (3,) है 3) इसके विपरीत नहीं। इस प्रतिबंधित अर्थ में, कुल्बैक विचलन ऊष्म प्रवैगिकी के दूसरे नियम के अनुरूप है।
कुल्बैक-लीब्लर विचलन सममित DKL(X1 || X2) = DKL(X2 || X1) है विषम स्थितियों के लिए बीटा (3, 0.5) और बीटा (0.5, 3) जिसमें समान अंतर एंट्रॉपी h(X1) = h(X2).है
समरूपता की स्थिति:
उपरोक्त परिभाषाओं से अनुसरण करता है और दर्पण-समरूपता f(x; α, β) = f(1−x; α, β) बीटा वितरण द्वारा आनंदित होता है।
सांख्यिकीय उपायों के मध्य संबंध
माध्य, विधा और मध्य संबंध
यदि 1 < α < β तब बहुलक ≤ माध्यिका ≤ माध्य।[12] मोड को (केवल α, β > 1 के लिए) व्यक्त करना , और α और β के संदर्भ में माध्य:
यदि 1 < β < α तब असमिकाओं का क्रम उल्टा हो जाता है। जहाँ α, β > 1 के लिए माध्य और माध्यिका के मध्य की पूर्ण दूरी x के अधिकतम और न्यूनतम मानों के मध्य की दूरी के 5% से कम है। दूसरी ओर, α = 1 और β = 1 के (पैथोलॉजिकल (गणित)) स्तिथियाँ के लिए, माध्य और मोड के मध्य की पूर्ण दूरी x के अधिकतम और न्यूनतम मानों के मध्य की दूरी के 50% तक पहुंच सकती है, जिसके लिए मान बीटा वितरण समान वितरण तक पहुंचता है और सूचना एन्ट्रापी अपने मैक्सिमा और मिनिमा मूल्य तक पहुंचता है, और इसलिए अधिकतम विकार।
उदाहरण के लिए, α = 1.0001 और β = 1.00000001 के लिए:
- मोड = 0.9999; पीडीएफ (मोड) = 1.00010
- माध्य = 0.500025; पीडीएफ (माध्य) = 1.00003
- माध्य = 0.500035; पीडीएफ (माध्यिका) = 1.00003
- माध्य - मोड = -0.499875
- माध्य − माध्यिका = −9.65538 × 10−6
जहाँ पीडीएफ प्रायिकता घनत्व फलन के मान के लिए है।
माध्य, ज्यामितीय माध्य और हार्मोनिक माध्य संबंध
अंकगणित और ज्यामितीय साधनों की असमानता से ज्ञात होता है कि ज्यामितीय माध्य माध्य से कम होता है। इसी तरह, हार्मोनिक माध्य ज्यामितीय माध्य से कम होता है। संलग्न प्लॉट से पता चलता है कि α = β के लिए, α = β के मान की परवाह किए बिना, माध्य और माध्यिका दोनों 1/2 के सामान्तर हैं, और α = β > 1 के लिए मोड भी 1/2 के सामान्तर है, चूँकि ज्यामितीय और हार्मोनिक साधन 1/2 से कम हैं और वे केवल α = β → ∞ के रूप में इस मान को स्पर्शोन्मुख रूप से प्राप्त करते हैं।
कुर्टोसिस विषमता के वर्ग से घिरा हुआ है
जैसा कि विलियम फेलर ने टिप्पणी की है,[5]पियर्सन वितरण में बीटा प्रायिकता घनत्व पियर्सन वितरण के रूप में प्रकट होता है (बीटा वितरण और पियर्सन के प्रकार I वितरण के मध्य कोई भी अंतर केवल सतही है और कुर्तबसिस और विषमता के मध्य संबंध के बारे में निम्नलिखित चर्चा के लिए कोई अंतर नहीं है)। कार्ल पियर्सन ने अपने पेपर के प्लेट 1 में दिखाया [22] 1916 में प्रकाशित, ऊर्ध्वाधर अक्ष (तालमेल) के रूप में कर्टोसिस के साथ ग्राफ और क्षैतिज अक्ष (सूच्याकार आकृति का भुज) के रूप में विषमता का वर्ग, जिसमें अनेक वितरण प्रदर्शित किए गए थे।[33] बीटा वितरण द्वारा कब्जा कर लिया गया क्षेत्र निम्नलिखित दो रेखा (ज्यामिति) से घिरा हुआ है (विषम2, कर्टोसिस) कार्तीय समन्वय प्रणाली, या (विषमता2, अतिरिक्त कर्टोसिस) कार्तीय समन्वय प्रणाली:
या, समकक्ष,
ऐसे समय में जब शक्तिशाली डिजिटल कंप्यूटर नहीं थे, तब कार्ल पियर्सन ने स्पष्ट रूप से आगे की सीमाओं की गणना की,[4][22]उदाहरण के लिए, U-आकार के वितरण को जे-आकार के वितरण से अलग करना। तथा निचली सीमा रेखा (अतिरिक्त कर्टोसिस + 2 - विषमता2 = 0) टेढ़े U-आकार के बीटा वितरण द्वारा निर्मित होता है, जिसमें आकृति मापदंड α और β शून्य के समीप दोनों मान होते हैं। ऊपरी सीमा रेखा (अतिरिक्त कर्टोसिस - (3/2) विषमता2 = 0) किसी मापदंड के बहुत बड़े मान और दूसरे मापदंड के बहुत छोटे मान के साथ अत्यधिक विषम वितरण द्वारा निर्मित होता है। जहाँ कार्ल पियर्सन ने दिखाया[22]कि यह ऊपरी सीमा रेखा (अतिरिक्त कर्टोसिस - (3/2) विषमता2 = 0) पियर्सन के वितरण III के साथ प्रतिच्छेदन भी है, जिसका दिशा में (धनात्मक अनंत की ओर) असीमित समर्थन है, और घंटी के आकार का या J- आकार का हो सकता है। उनके बेटे, एगॉन पियर्सन ने दिखाया[33]कि क्षेत्र (कर्टोसिस/स्क्वायर्ड-स्क्यूनेस प्लेन में) बीटा वितरण (समतुल्य रूप से, पियर्सन का वितरण) I द्वारा कब्जा कर लिया गया है क्योंकि यह इस सीमा तक पहुंचता है (अतिरिक्त कर्टोसिस - (3/2) विषमता2 = 0) गैर-केंद्रीय ची-वर्ग वितरण के साथ साझा किया गया है। कार्ल पियर्सन[34] (पियर्सन 1895, पीपी. 357, 360, 373–376) ने यह भी दिखाया कि गामा वितरण पियर्सन प्रकार III वितरण है। इसलिए पियर्सन के प्रकार III वितरण के लिए यह सीमा रेखा गामा रेखा के रूप में जानी जाती है। (यह इस तथ्य से दिखाया जा सकता है कि गामा वितरण का अतिरिक्त कर्टोसिस 6/k है और विषमता का वर्ग 4/k है, इसलिए (अतिरिक्त कुर्तबसिस - (3/2) विषमता)2 = 0) मापदंड k के मान की परवाह किए बिना गामा वितरण से समान रूप से संतुष्ट है)। पियर्सन ने पश्चात् में उल्लेख किया कि ची-स्क्वेर्ड वितरण पियर्सन के प्रकार III का विशेष स्तिथि है और इस सीमा रेखा को भी साझा करता है (जैसा कि इस तथ्य से स्पष्ट है कि ची-स्क्वेर्ड वितरण के लिए अतिरिक्त कर्टोसिस 12/के और वर्ग का वर्ग है। विषमता 8/k है, इसलिए (अतिरिक्त कर्टोसिस - (3/2) विषमता2 = 0) मापदंड k के मान की परवाह किए बिना समान रूप से संतुष्ट है)। ची-स्क्वेर्ड वितरण X ~ χ के पश्चात् से इसकी उम्मीद की जानी चाहिए2(k) पैरामीट्रिजेशन X ~ Γ(k/2, 1/2) के साथ गामा वितरण का विशेष स्तिथि है, जहां k धनात्मक पूर्णांक है जो ची-वर्ग की स्वतंत्रता की डिग्री की संख्या को निर्दिष्ट करता वितरण है।
ऊपरी सीमा के पास बीटा वितरण का उदाहरण (अतिरिक्त कर्टोसिस - (3/2) विषमता2 = 0) α = 0.1, β = 1000 द्वारा दिया जाता है, जिसके लिए अनुपात (अतिरिक्त कुर्तबसिस)/(विषमता)2) = 1.49835 नीचे से 1.5 की ऊपरी सीमा तक पहुंचता है। निचली सीमा के पास बीटा वितरण का उदाहरण (अतिरिक्त कर्टोसिस + 2 - विषमता2 = 0) α= 0.0001, β = 0.1 द्वारा दिया जाता है, जिसके लिए अभिव्यक्ति (अतिरिक्त कर्टोसिस + 2)/(विषमता)2) = 1.01621 ऊपर से 1 की निचली सीमा तक पहुंचता है। α और β दोनों के लिए अनंत सीमा में सममित रूप से शून्य पर पहुंचने पर, अतिरिक्त कर्टोसिस -2 पर अपने न्यूनतम मूल्य तक पहुंच जाता है। यह न्यूनतम मान उस बिंदु पर होता है जिस पर निचली सीमा रेखा ऊर्ध्वाधर अक्ष (समन्वय) को काटती है। (चूंकि, पियर्सन के मूल चार्ट में, अधिक कर्टोसिस के अतिरिक्त कोटि कर्टोसिस है, और यह ऊपर की बजाय नीचे की ओर बढ़ती है)।
विषमता और निचली सीमा के नीचे अतिरिक्त कर्टोसिस के लिए मान (अतिरिक्त कुर्तबसिस + 2 - विषमता2 = 0) किसी भी वितरण के लिए नहीं हो सकता है, और इसलिए कार्ल पियर्सन ने उचित रूप से इस सीमा के नीचे के क्षेत्र को असंभव क्षेत्र कहा जाता है। इस असंभव क्षेत्र के लिए सीमा (सममित या विषम) बिमोडल यू-आकार के वितरण द्वारा निर्धारित की जाती है जिसके लिए मापदंड α और β शून्य तक पहुंचते हैं और इसलिए सभी प्रायिकता घनत्व सिरों पर केंद्रित होते हैं: x = 0, 1 व्यावहारिक रूप से मध्य में कुछ भी नहीं उन्हें। चूंकि α ≈ β ≈ 0 के लिए प्रायिकता घनत्व दो सिरों x = 0 और x = 1 पर केंद्रित है, यह असंभव सीमा बर्नौली वितरण द्वारा निर्धारित की जाती है, जहां संबंधित संभावनाओं के साथ केवल दो संभावित परिणाम होते हैं p और q = के साथ होते है 1- p। समरूपता α = β, विषमता ≈ 0, अतिरिक्त कर्टोसिस ≈ −2 इस सीमा को सीमा तक पहुंचने वाले स्थितियों के लिए (यह किसी भी वितरण के लिए न्यूनतम अतिरिक्त कुर्तबसिस संभव है), और संभावनाएं p ≈ q ≈ 1/2 हैं। विषमता के साथ इस सीमा को सीमा तक पहुंचने वाले स्थितियों के लिए, अतिरिक्त कर्टोसिस ≈ −2 + विषमता2, और प्रायिकता घनत्व दूसरे छोर की तुलना में छोर पर अधिक केंद्रित है (व्यावहारिक रूप से मध्य में कुछ भी नहीं है), संभावनाओं के साथ बाएँ छोर पर x = 0 और दाएँ सिरे पर x = 1.
समरूपता
सभी कथन α, β > 0 पर सनियम हैं
- संभावना घनत्व फलन समरूपता है
- संचयी वितरण फलन होता है तथा समरूपता प्लस एकात्मक समरूपता है
- मोड समरूपता प्लस एकात्मक समरूपता है
- मेडियन समरूपता प्लस एकात्मक समरूपता है
- मीन समरूपता प्लस एकात्मक समरूपता है
- ज्यामितीय कारण प्रत्येक व्यक्तिगत रूप से असममित है, और निम्नलिखित समरूपता 'X' के आधार पर ज्यामितीय माध्य और इसके प्रतिबिंब सूत्र (1-X) के आधार पर ज्यामितीय माध्य के मध्य प्रयुक्त होती है।
- हार्मोनिक का अर्थ है कि प्रत्येक व्यक्तिगत रूप से असममित है, निम्नलिखित समरूपता 'X' पर आधारित हार्मोनिक माध्य और इसके प्रतिबिंब सूत्र (1-X) के आधार पर हार्मोनिक माध्य के मध्य प्रयुक्त होती है।
- .
- भिन्नता समरूपता
- प्रत्येक ज्यामितीय भिन्नता व्यक्तिगत रूप से असममित है, निम्नलिखित समरूपता X पर आधारित लॉग ज्यामितीय भिन्नता और इसके प्रतिबिंब सूत्र (1-X) के आधार पर लॉग ज्यामितीय भिन्नता के मध्य प्रयुक्त होती है।
- ज्यामितीय सहप्रसरण समरूपता है
- माध्य समरूपता के चारों ओर पूर्ण विचलन है
- विषमता समरूपता (गणित) | विषम-समरूपता
- अतिरिक्त कर्टोसिस समरूपता है
- वास्तविक भाग की विशेषता फलन (वेरिएबल टी की उत्पत्ति के संबंध में) समरूपता है
- विशेषता फलन समरूपता (गणित) है | काल्पनिक भाग (वेरिएबल टी की उत्पत्ति के संबंध ) की विषम-समरूपता है
- निरपेक्ष मूल्य की विशेषता फलन (वेरिएबल टी की उत्पत्ति के संबंध में) समरूपता है
- विभेदक एन्ट्रापी समरूपता
- सापेक्ष एन्ट्रॉपी (जिसे कुल्बैक-लीब्लर डाइवर्जेंस भी कहा जाता है) समरूपता है
- फिशर सूचना आव्युह समरूपता है
प्रायिकता घनत्व फलन की ज्यामिति
विभक्ति बिंदु
आकार मापदंड α और β के कुछ मूल्यों के लिए, संभाव्यता घनत्व फलन में विभक्ति बिंदु होते हैं, जिस पर वक्रता परिवर्तन चिन्ह होता है। इन मोड़ बिंदुओं की स्थिति सांख्यिकीय फैलाव या वितरण के फैलाव के माप के रूप में उपयोगी हो सकती है।
निम्नलिखित मात्रा को परिभाषित करना:
विभक्ति के बिंदु होते हैं,[1][3][6][7]आकृति मापदंड α और β के मान के आधार पर निम्नानुसार है:
- (α > 2, β > 2) वितरण घंटी के आकार का है (α = β के लिए सममित और अन्यथा विषम), दो विभक्ति बिंदुओं के साथ, मोड से समान दूरी पर:
- (α = 2, β > 2) वितरण असमान, धनात्मक रूप से विषम, दाएं-टेल वाला, विभक्ति बिंदु के साथ, मोड के दाईं ओर स्थित है:
- (α > 2, β = 2) वितरण असमान, ऋणात्मक रूप से विषम, बायां-पुच्छ, विभक्ति बिंदु के साथ, मोड के बाईं ओर स्थित है:
- (1 < α < 2, β > 2, α+β>2) वितरण असमान, धनात्मक रूप से विषम, दाएं-टेल वाला, विभक्ति बिंदु के साथ, मोड के दाईं ओर स्थित है:
- (0 < α < 1, 1 < β < 2) बंटन के बाएँ सिरे पर बहुलक x = 0 है और यह धनात्मक रूप से विषम, दाएँ-टेल वाला है। मोड के दाईं ओर स्थित 'एक विभक्ति बिंदु' है:
- (α > 2, 1 < β < 2) वितरण असमान ऋणात्मक रूप से विषम, बायां-टेल वाला, विभक्ति बिंदु के साथ, मोड के बाईं ओर स्थित है:
- (1 < α < 2, 0 < β < 1) बंटन के दायें सिरे पर बहुलक x=1 है और यह ऋणात्मक रूप से विषम, बायां-पुच्छ है। मोड के बाईं ओर स्थित 'एक विभक्ति बिंदु' है:
शेष (सममित और विषम) क्षेत्रों में कोई विभक्ति बिंदु नहीं हैं: U-आकार: (α, β <1) ऊपर-नीचे-U-आकार: (1 <α <2, 1 <β <2), रिवर्स- J- आकार (α < 1, β > 2) या J- आकार: (α > 2, β < 1)
साथ वाले भूखंडों में विभक्ति बिंदु स्थान को (0 से 1 तक लंबवत दिखाया गया है) बनाम α और β (क्षैतिज अक्ष 0 से 5 तक) के रूप में दिखाते हैं। α = 1, β = 1, α = 2, और β = 2 को काटने वाली सतहों पर बड़े कट हैं क्योंकि इन मूल्यों पर बीटा वितरण 2 मोड से और 1 मोड से नो मोड में बदल जाता है।
आकार
बीटा घनत्व फलन दो मापदंड α और β के मानों के आधार पर विभिन्न प्रकार के विभिन्न आकार ले सकता है। आकार की इस महान विविधता को लेने के लिए बीटा वितरण की क्षमता (केवल दो मापदंडों का उपयोग करके) मॉडलिंग वास्तविक माप के लिए व्यापक आवेदन खोजने के लिए आंशिक रूप से जिम्मेदार है:
= सममित (α = β)
- घनत्व फलन समरूपता लगभग 1/2 (नीला और टील भूखंड) है।
- माध्यिका = माध्य = 1/2।
- विषमता = 0।
- विचरण = 1/(4(2α + 1))
- 'α = β <1'
- u-आकार (नीला प्लॉट)।
- बाइमोडल: लेफ्ट मोड = 0, राइट मोड = 1, एंटी-मोड = 1/2
- 1/12 <वर (X) <1/4[1]
- −2 <अतिरिक्त कर्टोसिस (X) <−6/5
- α = β = 1/2 आर्क्साइन वितरण है
- वर (X) = 1/8
- अतिरिक्त कर्टोसिस (X) = -3/2
- CF = रिंक (टी) [35]
- α = β → 0 2-बिंदु बर्नौली वितरण है जिसमें प्रत्येक डायराक डेल्टा फलन अंत x = 0 और x = 1 पर समान संभावना 1/2 है और हर स्थान शून्य संभावना है। सिक्का टॉस: सिक्के का चेहरा x = 0 और दूसरा चेहरा x = 1 है।
- इससे कम मान किसी भी वितरण तक पहुंचना असंभव है।
- सूचना एन्ट्रापी मैक्सिमा और मिनिमा वैल्यू -∞ तक पहुंचती है
- α = β = 1
- समान वितरण (निरंतर)|समान [0, 1] वितरण
- कोई मोड नहीं
- var(X) = 1/12
- अतिरिक्त कर्टोसिस(X) = -6/5
- (कहीं भी ऋणात्मक ) सूचना एन्ट्रापी अपने अधिकतम और शून्य के न्यूनतम मान तक पहुँच जाती है
- सीएफ = सिंक (टी)
- α = β > 1
- सममित अनिमॉडल
- मोड = 1/2।
- 0 <var(X) <1/12[1]
- −6/5 <अतिरिक्त कर्टोसिस (X) <0
- α = β = 3/2 अर्ध-अण्डाकार [0, 1] वितरण है, देखें: विग्नर अर्धवृत्त वितरण[36]
- वार (एक्स) = 1/16।
- अतिरिक्त कर्टोसिस (X) = -1
- सीएफ = 2 जिंक (टी)
- α = β = 2 परवलयिक [0, 1] वितरण है
- वार (X) = 1/20
- अतिरिक्त कर्टोसिस (X) = -6/7
- सीएफ = 3 टिन (टी) [37]
- α = β > 2 घंटी के आकार का है, मोड के दोनों ओर स्थित विभक्ति बिंदु के साथ
- 0 <वर (एक्स) <1/20
- −6/7 <अतिरिक्त कर्टोसिस (X) <0
- α = β → ∞ मिडपॉइंट x = 1/2 पर डायराक डेल्टा फलन स्पाइक के साथ 1-पॉइंट डिजनरेट डिस्ट्रीब्यूशन है, प्रायिकता 1 के साथ, और हर स्थान शून्य प्रायिकता। एकल बिंदु x = 1/2 पर केंद्रित 100% संभावना (पूर्ण निश्चितता) है।
- सूचना एंट्रोपी −∞ के मैक्सिमा और मिनिमा वैल्यू तक पहुंचती है
विषम (α ≠ β)
घनत्व फलन विषमता है। मापदंड मानों का आदान-प्रदान प्रारंभिक वक्र की दर्पण छवि (विपरीत) उत्पन्न करता है, कुछ और विशिष्ट स्तिथियाँ :
- 'α <1, β <1'
- U-आकार
- α <β के लिए धनात्मक विषम, α> β के लिए ऋणात्मक विषम।
- बाइमोडल: लेफ्ट मोड = 0, राइट मोड = 1, एंटी-मोड =
- 0 <माध्यिका <1।
- 0 <वर (X) <1/4
- 'ए> 1, बी> 1'
- यूनिमोडल (मैजेंटा और सियान प्लॉट),
- α <β के लिए धनात्मक विषम, α> β के लिए ऋणात्मक विषम।
- 0 <माध्यिका <1
- 0 <वर (X) <1/12
- 'α <1, β ≥ 1'
- एक दाहिनी टेल के साथ रिवर्स j-आकार,
- धनात्मक रूप से विषम,
- कड़ाई से घटते हुए, उत्तल कार्य
- मोड = 0
- 0 <माध्यिका <1/2।
- (अधिकतम विचरण के लिए होता है , या α = Φ गोल्डन अनुपात)
- α ≥ 1, β <1
- J के आकार का बाईं टेल के साथ,
- ऋणात्मक विषम,
- सख्ती से बढ़ रहा है, उत्तल कार्य
- मोड = 1
- 1/2 <माध्यिका <1
- (अधिकतम विचरण के लिए होता है , या β = Φ गोल्डन अनुपात)
- α = 1, β > 1
- धनात्मक रूप से विषम,
- सख्ती से घट रहा है (लाल प्लॉट),
- एक उलटा (मिरर-इमेज) पावर फलन [0,1] वितरण
- माध्य = 1 / (β + 1)
- माध्यिका = 1 - 1/21/β
- मोड = 0
- α = 1, 1 <β <2
- अवतल कार्य
- 1/18 <वर (X) <1/12।
- α = 1, β = 2
- स्लोप के साथ सीधी रेखा -2, दाएं-त्रिकोणीय वितरण बाएं छोर पर समकोण के साथ, x = 0 पर
- वर (X) = 1/18
- α = 1, β> 2
- एक दाहिनी टेल के साथ रिवर्स जे-आकार,
- उत्तल कार्य
- 0 <वर (X) <1/18
- 'α > 1, β = 1'
- ऋणात्मक विषम,
- सख्ती से बढ़ रहा है (हरा प्लॉट),
- पावर फलन [0, 1] वितरण[6]
- माध्य = α / (α + 1)
- माध्यिका = 1/21/α
- मोड = 1
- 2> α> 1, बी = 1
- अवतल कार्य
- 1/18 <वर (X) <1/12
- α = 2, β = 1
- स्लोप +2 के साथ सीधी रेखा, दाहिने सिरे पर समकोण के साथ समकोण-त्रिकोणीय वितरण, x = 1 पर होता है
- वर (X) = 1/18
- α> 2, β = 1
- एक बाईं टेल के साथ जम्मू के आकार का, उत्तल कार्य
- 0 <वर (X) <1/18
संबंधित वितरण
रूपांतरण
- यदि X ~ बीटा (α, β) तब 1 − X ~ बीटा (β, α) दर्पण छवि समरूपता है |
- यदि X ~ बीटा (α, β) तब . बीटा प्राइम डिस्ट्रीब्यूशन, जिसे दूसरी तरह का बीटा डिस्ट्रीब्यूशन भी कहा जाता है।
- यदि , तब घनत्व के साथ सामान्यीकृत रसद वितरण है , जहाँ लॉजिस्टिक सिग्मॉइड है।
- यदि X ~ बीटा (α, β) तब होता है
- यदि X ~ बीटा (एन/2, एम/2) तब (एन > 0 और एम > 0 मानते हुए), एफ-वितरण | फिशर-स्नेडेकोर एफ वितरण।
- यदि फिर मिनट + X (अधिकतम - मिनट) ~ पीईआरटी (न्यूनतम, अधिकतम, एम, λ) जहां पीईआरटी पीईआरटी विश्लेषण में उपयोग किए जाने वाले पीईआरटी वितरण को दर्शाता है, और M = सबसे संभावित मूल्य होता है ।[38] पारंपरिक रूप से[39]PERT विश्लेषण में λ = 4 है ।
- यदि X ~ बीटा (1, β) तब X ~ कुमारस्वामी वितरण मापदंड (1, β) के साथ उपयोग किया जाता है
- यदि X ~ बीटा (α, 1) तब X ~ कुमारस्वामी वितरण मापदंड (α, 1) के साथ होता है
- यदि X ~ बीटा (α, 1) तब −ln(X) ~ एक्सपोनेंशियल (α) है|
विशेष और सीमित स्तिथियाँ

* बीटा(1, 1) ~ u(0, 1).समान वितरण (निरंतर) है |
- बीटा (n, 1) ~ अधिकतम n स्वतंत्र आरवीएस। समान वितरण के साथ (सतत)| U(0, 1), कभी-कभी उस अंतराल पर घनत्व n xn-1 के साथ a मानक पावर फलन वितरण कहा जाता है।
- बीटा (1, n) ~ न्यूनतम n स्वतंत्र आरवीएस। समान वितरण के साथ (निरंतर)| u(0, 1)
- यदि X ~ बीटा(3/2, 3/2) और r > 0 तब 2rX − r ~ विग्नेर अर्धवृत्त वितरण होता है ।
- बीटा(1/2, 1/2) आर्क्साइन वितरण के सामान्तर है। यह बंटन बर्नौली बंटन और द्विपद बंटन के लिए जेफरी की पूर्व प्रायिकता भी है। तथा आर्क्सिन संभाव्यता घनत्व वितरण है जो अनेक रैंडम-वॉक मौलिक प्रमेयों में प्रकट होता है। उचित सिक्के में बेतरतीब ढंग से चलना, और मूल स्थान की अंतिम यात्रा के समय की संभावना को (यू-आकार) चाप वितरण के रूप में वितरित किया जाता है।[5][14] दो खिलाड़ियों के फेयर-कॉइन-टॉस गेम में, खिलाड़ी को लीड में रहने कहा जाता है यदि रैंडम वॉक (जो मूल पर प्रारंभिक हुआ) मूल से ऊपर है। तो लंबाई 2N के खेल में किसी दिए गए खिलाड़ी के नेतृत्व में होने की सबसे संभावित संख्या N नहीं है। इसके विपरीत, N कम से कम संभावना है कि खिलाड़ी लीड में होगा। जब कि लीड में सबसे संभावित संख्या 0 या 2N (आर्क्सिन वितरण के पश्चात्) है।
- घातीय वितरण।
- गामा वितरण।
- बड़े के लिए , सामान्य वितरण। अधिक स्पष्ट, यदि है तब माध्य 0 और विचरण के साथ वितरण में सामान्य वितरण में परिवर्तित हो जाता है जैसे n बढ़ता है। वैसे हो जाता है|
अन्य वितरणों से प्राप्त
- समान वितरण (निरंतर) से आकार n के प्रतिरूप का kवां क्रम आँकड़ा बीटा यादृच्छिक वेरिएबल , U है(k) ~ बीटा (k, n+1−k)।[40]
- यदि x~गामा(α, θ) और y~गामा(β, θ) स्वतंत्र हैं, तब होगा .
- यदि और स्वतंत्र हैं, तब होगा .
- यदि X ~ U(0, 1) और α > 0 तब X1/α ~ बीटा(α, 1). पावर फलन वितरण होता है |
- यदि है तब n और k के असतत मानों के लिए होता है जहाँ और होगा .[41]
- यदि X ~ कॉची (0, 1) तब होगा
अन्य वितरणों के साथ संयोजन
- X ~ बीटा (α, β) और Y ~ F (2β, 2α) फिर सभी के लिए x> 0 होगा ।
अन्य वितरणों के साथ कंपाउंडिंग
- यदि p~ बीटा (α, β) और X ~ बिन (k, p) तब X ~ बीटा-द्विपद वितरण होता है
- यदि p~ बीटा (α, β) और X ~ एनबी (r, p) तब X~ बीटा ऋणात्मक द्विपद वितरण होता है
सामान्यीकरण
- अनेक वेरिएबल के लिए सामान्यीकरण, अर्थात डिरिचलेट वितरण, कहलाता है। डिरिचलेट वितरण के यूनीवेरिएट मार्जिनल में बीटा वितरण होता है। बीटा वितरण द्विपद और बर्नौली वितरण से ठीक उसी तरह संयुग्मित होता है जिस तरह डिरिचलेट वितरण बहुपद वितरण और श्रेणीबद्ध वितरण के लिए संयुग्मित होता है।
- पियर्सन वितरण या पियर्सन प्रकार वितरण बीटा वितरण के समान है (मनमानी स्थानांतरण और पुन: स्केलिंग को छोड़कर जिसे बीटा वितरण के चार मापदंड पैरामीट्रिजेशन के साथ भी पूरा किया जा सकता है)।
- बीटा वितरण गैर-केंद्रीय बीटा वितरण का विशेष स्तिथि है जहां : .होता है
- सामान्यीकृत बीटा वितरण पांच-मापदंड वितरण परिवार है जिसमें विशेष स्तिथियों के रूप में बीटा वितरण होता है।
- आव्युह वेरिएबल बीटा वितरण धनात्मक-निश्चित आव्यूहों का वितरण है।
सांख्यिकीय निष्कर्ष
मापदंड अनुमान
क्षणों की विधि
दो अज्ञात मापदंड
[0,1] अंतराल में समर्थित बीटा वितरण के दो अज्ञात मापदंड ( का अनुमान पहले दो क्षणों (प्रतिरूप माध्य और प्रतिरूप भिन्नता) के साथ क्षणों की विधि का उपयोग करके लगाया जा सकता है,जिसे निम्नानुसार किया जा सकता है।
प्रतिरूप औसत अनुमान हो और ये
प्रतिरूप विचरण अनुमान हो। तथा आघूर्णों की विधि के (सांख्यिकी)| ,आघूर्ण प्राचलों के अनुमान हैं
- यदि
- यदि
जब यादृच्छिक वेरिएबल X के साथ [0, 1] के अतिरिक्त किसी ज्ञात अंतराल पर वितरण की आवश्यकता होती है, तब कहें [a, c] यादृच्छिक वेरिएबल Y के साथ, फिर प्रतिस्थापित करें साथ और साथ आकार के मापदंडों के लिए उपरोक्त कुछ समीकरणों में (वैकल्पिक पैरामीट्रिजेशन देखें, नीचे चार मापदंड अनुभाग)।,[42] जहाँ :
चार अज्ञात मापदंड
सभी चार मापदंड ( [a, c] अंतराल में समर्थित बीटा वितरण का - खंड देखें तथा बीटा वितरण या चार मापदंड को दर्शाए | वैकल्पिक पैरामीट्रिजेशन, चार मापदंड -) का अनुमान लगाया जा सकता है, कार्ल पियर्सन द्वारा विकसित क्षणों की विधि का उपयोग करके, पहले चार केंद्रीय क्षणों (माध्य, विचरण , विषमता और अतिरिक्त कर्टोसिस) के प्रतिरूप और संख्या मूल्यों को समान करके।[1][43][44] अतिरिक्त कर्टोसिस को विषमता के वर्ग के संदर्भ में व्यक्त किया गया था, और प्रतिरूप आकार ν = α + β, (पिछला अनुभाग बीटा वितरण देखें या कर्टोसिस | ) इस प्रकार है:
इस समीकरण का उपयोग प्रतिरूप आकार ν = α + β को विषमता के वर्ग और अतिरिक्त कर्टोसिस के रूप में हल करने के लिए किया जा सकता है:[43]
यह अंतरिक्ष में बीटा वितरण के लिए पहले से व्युत्पन्न सीमा सीमाओं के मध्य अनुपात (3 के कारक से गुणा) है (जैसा कि मूल रूप से कार्ल पियर्सन द्वारा किया गया था)[22] अक्ष में विषमता के वर्ग के निर्देशांक और दूसरे अक्ष में अतिरिक्त कर्टोसिस के साथ परिभाषित किया गया है (देखें § कर्टोसिस विषमता के वर्ग से घिरा हुआ है):
शून्य विषमता का स्तिथि तुरंत हल किया जा सकता है क्योंकि शून्य विषमता के लिए, α = β और इसलिए ν = 2α = 2β, इसलिए α = β = ν/2
(अतिरिक्त कर्टोसिस बीटा वितरण के लिए शून्य विषमता के साथ ऋणात्मक है, -2 से 0 तक, जिससे -और इसलिए प्रतिरूप आकार मापदंड- धनात्मक है, शून्य से लेकर जब आकार मापदंड शून्य तक पहुंचते हैं और अतिरिक्त कर्टोसिस -2 तक पहुंचते हैं, अनंत तक जब आकार मापदंड अनंत तक पहुंचते हैं और अतिरिक्त कुर्तबसिस शून्य तक पहुंचते हैं)।
गैर-शून्य प्रतिरूप विषमता के लिए है जो कि जिसमे दो युग्मित समीकरणों की प्रणाली को हल करने की आवश्यकता होती है। चूंकि विषमता और अतिरिक्त कर्टोसिस मापदंडों से स्वतंत्र हैं तथा , मापदंड दो ज्ञात वेरिएबल (प्रतिरूप विषमता और प्रतिरूप अतिरिक्त कर्टोसिस) और दो अज्ञात (आकार मापदंड) के साथ युग्मित समीकरणों को हल करके प्रतिरूप विषमता और प्रतिरूप अतिरिक्त कर्टोसिस से विशिष्ट रूप से निर्धारित किया जा सकता है:
जिसके परिणामस्वरूप निम्नलिखित समाधान होता है:[43]
जहां निम्न प्रकार से उपाय करना चाहिए:जहाँ के लिए (ऋणात्मक ) प्रतिरूप विषम <0, और (धनात्मक) प्रतिरूप विषमता > 0 के लिए उपयोग किया जाता है ।
संलग्न प्लॉट इन दो समाधानों को अंतरिक्ष में सतहों के रूप में क्षैतिज अक्षों (प्रतिरूप अतिरिक्त कर्टोसिस) और (प्रतिरूप वर्ग विषमता) और ऊर्ध्वाधर अक्ष के रूप में आकार मापदंडों के साथ दिखाता है। सतहों को इस नियम से विवश किया जाता है कि प्रतिरूप अतिरिक्त कर्टोसिस उपरोक्त समीकरण में निर्धारित प्रतिरूप वर्ग विषमता से घिरा होना चाहिए। दो सतहें शून्य विषमता द्वारा परिभाषित दाहिने किनारे पर मिलती हैं। इस दाहिने किनारे के साथ,दोनों मापदंड समान हैं और वितरण α = β <1 के लिए सममित U- आकार का है, α = β = 1 के लिए समान है, 1 < α = β <2 के लिए उल्टा-U-आकार का है और बेल- α = β> 2 के लिए आकार। सतहें असंभव सीमा रेखा (अतिरिक्त कर्टोसिस + 2 - विषमता2) द्वारा परिभाषित सामने (निचले) किनारे पर भी मिलती हैं = 0). इस मोर्चे (निचली) सीमा के साथ दोनों आकार मापदंड शून्य तक पहुंचते हैं, और संभाव्यता घनत्व दूसरे छोर की तुलना में छोर पर अधिक केंद्रित होता है (व्यावहारिक रूप मध्य में कुछ भी नहीं होता है ),
संभावनाओं के साथ बाएँ छोर पर x = 0 और दाएँ सिरे पर x = 1। पीछे के किनारे की ओर दो सतहें और दूर हो जाती हैं। इस पिछले किनारे पर सतह के मापदंड दूसरे से अधिक अलग हैं। जैसा कि टिप्पणी की गई है, उदाहरण के लिए, बोमन और शेंटन द्वारा,[45] लाइन के निकटतम में प्रतिरूप करण (प्रतिरूप अतिरिक्त कुर्तबसिस - (3/2)(प्रतिरूप विषमता)2 = 0) (पीछे के किनारे का जस्ट-जे-आकार का भाग जहां नीला बेज रंग से मिलता है), खतरनाक रूप से अराजकता के समीप है, क्योंकि उस रेखा पर अनुमान के लिए उपरोक्त अभिव्यक्ति का भाजक ν = α + β शून्य हो जाता है और इसलिए ν अनंत तक पहुंचता है क्योंकि उस रेखा तक पहुंच जाती है। बोमन और शेंटन [45]लिखें कि उच्च क्षण के मापदंड (कर्टोसिस और विषमता) अत्यधिक नाजुक (उस रेखा के पास) हैं। चूंकि, माध्य और मानक विचलन अधिक विश्वसनीय हैं। इसलिए, समस्या बहुत विषम वितरणों के लिए चार मापदंड अनुमान के स्तिथियों के लिए है, जैसे कि अतिरिक्त कर्टोसिस विषमता के वर्ग (3/2) गुना तक पहुंचता है। यह सीमा रेखा मापदंड के बहुत बड़े मूल्यों और दूसरे मापदंड के बहुत छोटे मूल्यों के साथ अत्यंत विषम वितरणों द्वारा निर्मित होती है। देखना § कर्टोसिस विषमता के वर्ग से घिरा हुआ है संख्यात्मक उदाहरण के लिए और इस रियर एज सीमा रेखा के बारे में आगे की टिप्पणी (प्रतिरूप अतिरिक्त कर्टोसिस - (3/2) (प्रतिरूप विषमता)2 = 0). जैसा कि स्वयं कार्ल पियर्सन ने टिप्पणी की है [46]यह उद्देश्य अधिक व्यावहारिक महत्व का नहीं हो सकता है क्योंकि यह समस्या केवल बहुत विषम जे-आकार (या दर्पण-छवि जे-आकार) वितरण के लिए उत्पन्न होती है, जो आकार के मापदंडों के बहुत अलग मूल्यों के साथ होती है जो व्यवहार में बहुत अधिक होने की संभावना नहीं है)। अभ्यास में होने वाले सामान्य विषम-बेल-आकार के वितरण में यह मापदंड अनुमान समस्या नहीं होती है।
शेष दो मापदंड विभिन्न समीकरणों का उपयोग करके प्रतिरूप माध्य और प्रतिरूप भिन्नता का उपयोग करके निर्धारित किया जा सकता है।[1][43] विकल्प समर्थन अंतराल सीमा की गणना करना है प्रतिरूप विचरण और प्रतिरूप कर्टोसिस के आधार पर होता है। इस प्रयोजन के लिए कोई भी सीमा के संदर्भ में हल कर सकता है , प्रतिरूप विचरण और प्रतिरूप आकार ν के संदर्भ में अतिरिक्त कुर्तबसिस को व्यक्त करने वाला समीकरण (देखें § कर्टोसिस और § वैकल्पिक पैरामीट्रिज़ेशन, चार पैरामीटर):
प्राप्त करने के लिए:
एक अन्य विकल्प समर्थन में अंतराल सीमा की गणना करना है और प्रतिरूप विचरण और प्रतिरूप विषमता के आधार पर उपयोग किया जाता है ।[43] इस प्रयोजन के लिए कोई भी इसको सीमा के संदर्भ में प्रतिरूप विचरण के संदर्भ में वर्ग विषमता व्यक्त करने वाला समीकरण और प्रतिरूप आकार ν हल कर सकता है (विषमता और वैकल्पिक पैरामीट्रिजेशन शीर्षक वाला अनुभाग देखें, चार मापदंड):
प्राप्त करने के लिए:[43]
शेष मापदंड प्रतिरूप माध्य और पहले प्राप्त मापदंड से निर्धारित किया जा सकता है: :
और अंत में, .
उपरोक्त सूत्रों में, उदाहरण के लिए, प्रतिरूप क्षणों के अनुमान के रूप में लिया जा सकता है:
अनुमानक G1 विषमता और G2 के लिए कर्टोसिस के लिए डीएपी (सॉफ्टवेयर)/एसएएस प्रणाली , पीएसपीपी/एसपीएसएस और माइक्रोसॉफ्ट एक्सेल द्वारा उपयोग किया जाता है। चूँकि, उनका उपयोग बीएमडीपी द्वारा नहीं किया जाता है और (के अनुसार [47] वे 1998 में मिनीटैब द्वारा उपयोग नहीं किए गए थे। दरअसल, जोनेस और गिल ने 1998 के अपने अध्ययन में[47] निष्कर्ष निकाला कि बीएमडीपी और मिनीटैब (उस समय) में उपयोग किए जाने वाले विषमता और कर्टोसिस अनुमानक में सामान्य प्रतिरूपों में छोटा विचलन और माध्य-वर्ग त्रुटि थी, किन्तु DAP (सॉफ़्टवेयर)/SAS प्रणाली, PSPP/SPSS में उपयोग किए जाने वाले विषमता और कुर्तबसिस अनुमानक, अर्थात् G1 और G2, बहुत ही विषम वितरण से प्रतिरूपों में छोटी माध्य-वर्गीय त्रुटि थी। यह इस कारण से है कि हमने उपरोक्त सूत्रों में प्रतिरूप विषमता आदि को स्पष्ट किया है, जिससेयह स्पष्ट हो सके कि उपयोगकर्ता को समस्या के अनुसार सबसे अच्छा अनुमानक चुनना चाहिए, क्योंकि विषमता और कर्टोसिस के लिए सबसे अच्छा अनुमानक निर्भर करता है और विषमता की मात्रा बताता है (जैसा कि जोनेस और गिल द्वारा दिखाया गया है[47]).
अधिकतम संभावना
दो अज्ञात मापदंड
जैसा कि गामा वितरण के लिए अधिकतम संभावना अनुमानों के स्तिथियों में भी है, वैसे ही बीटा वितरण के लिए अधिकतम संभावना अनुमानों में आकृति मापदंडों के इच्छानुसार मूल्यों के लिए सामान्य विवृत रूप समाधान नहीं है। यदि स्वतंत्र यादृच्छिक वेरिएबल X1, ..., XN हैं जिनमें से प्रत्येक में बीटा वितरण है, N स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकनों के लिए संयुक्त लॉग संभावना कार्य करता है:
आकार मापदंड के संबंध में अधिकतम ढूँढना तथा आकार मापदंड के संबंध में आंशिक व्युत्पन्न लेना और अभिव्यक्ति मापदंड के अधिकतम संभावना अनुमानक को शून्य के सामान्तर अभिव्यक्ति समुच्चय करना सम्मिलित है:
जहाँ :
चूंकि डिगामा फलन ने ψ(α) को निरूपित किया है, इसे गामा फलन के लॉगरिदमिक व्युत्पन्न के रूप में परिभाषित किया गया है:[19]
यह सुनिश्चित करने के लिए कि शून्य स्पर्शरेखा स्लोप वाले मान वास्तव में अधिकतम हैं (एक सैडल-पॉइंट या न्यूनतम के अतिरिक्त) किसी को भी इस नियम को पूरा करना होगा कि वक्रता ऋणात्मक है। यह संतबषजनक है कि आकार के मापदंडों के संबंध में दूसरा आंशिक व्युत्पन्न ऋणात्मक है
पिछले समीकरणों का उपयोग करते हुए, यह इसके सामान्तर है:
जहां त्रिगामा फलन, ψ1(α) को निरूपित करता है,तथा बहुग्राम कार्यों का दूसरा है, और इसे डिगामा फलन के व्युत्पन्न के रूप में परिभाषित किया गया है:
ये स्थितियाँ यह बताने के सामान्तर हैं कि लघुगणक रूप से परिवर्तित वेरिएबल के प्रसरण धनात्मक हैं, क्योंकि:
इसलिए, अधिकतम ऋणात्मक वक्रता की स्थिति कथनों के सामान्तर है:
वैकल्पिक रूप से, अधिकतम पर ऋणात्मक वक्रता की स्थिति भी यह बताने के सामान्तर है कि ज्यामितीय के निम्न लघुगणकीय डेरिवेटिव का अर्थ GX और G(1−X) धनात्मक हैं, क्योंकि:
जबकि ये स्लोप वास्तव में धनात्मक हैं, अन्य स्लोप ऋणात्मक हैं:
α और β के संबंध में माध्य और माध्यिका के स्लोप समान संकेत व्यवहार प्रदर्शित करते हैं।
इस नियम के अनुसार अधिकतम आकार मापदंड के संबंध में आंशिक व्युत्पन्न शून्य के सामान्तर है, तथा हम युग्मित अधिकतम संभावना अनुमान समीकरणों की निम्नलिखित प्रणाली प्राप्त करते हैं (औसत लॉग-संभावना के लिए) जिसे (अज्ञात) प्राप्त करने के लिए उलटा करने की आवश्यकता होती है। आकार मापदंड अनुमान X1, ..., XN: प्रतिरूप के लॉगरिदम के (ज्ञात) औसत के संदर्भ में होते है [1]
जहां हम प्रतिरूप ज्यामितीय माध्य के लघुगणक के रूप में को पहचानते हैं और (को लघुगणक के रूप में पहचानते है 1 − X), आधारित प्रतिरूप ज्यामितीय माध्य । के लिए X की दर्पण छवि पर ,उपयोग किया जाता है यह इस प्रकार है कि .होगा
आकार मापदंड अनुमानों के डिगामा कार्यों वाले ये युग्मित समीकरण संख्यात्मक विधियों द्वारा हल किया जाना चाहिए, उदाहरण के लिए, बेकमैन एट अल द्वारा।[48] ज्ञानदेसिकन एट अल। कुछ स्थितियों के लिए संख्यात्मक समाधान दें।[49] नॉर्मन लॉयड जॉनसन|एन.एल.जॉनसन और सैमुअल कोटज़|एस.कोट्ज़[1]सुझाव है कि बहुत छोटे आकार के मापदंड अनुमानों के लिए नहीं , डिगामा फलन के लिए लॉगरिदमिक सन्निकटन पुनरावृत्त समाधान के लिए प्रारंभिक मान प्राप्त करने के लिए उपयोग किया जा सकता है, क्योंकि इस सन्निकटन से उत्पन्न समीकरणों को ठीक से हल किया जा सकता है:
जो पुनरावृत्त समाधान के लिए प्रारंभिक मानों (प्रतिरूप ज्यामितीय साधनों के संदर्भ में अनुमान आकार मापदंडों के) के लिए निम्नलिखित समाधान की ओर ले जाता है:
वैकल्पिक रूप से, क्षणों की विधि द्वारा प्रदान किए गए अनुमानों को डिगम्मा कार्यों के संदर्भ में अधिकतम संभावना युग्मित समीकरणों के पुनरावृत्त समाधान के लिए प्रारंभिक मानों के रूप में उपयोग किया जा सकता है।
जब किसी ज्ञात अंतराल पर वितरण की आवश्यकता होती है, [0, 1] यादृच्छिक वेरिएबल X के साथ के अतिरिक्त तब [a, c] को यादृच्छिक वेरिएबल Y के साथ कहें, फिर पहले समीकरण में ln(Xi) को बदलें |
और ln(1−Xi) के साथ दूसरे समीकरण में
(नीचे वैकल्पिक पैरामीट्रिजेशन, चार मापदंड अनुभाग देखें)।
यदि आकार के मापदंडों में से ज्ञात है, तब समस्या अधिक सरल हो जाती है। निम्नलिखित लॉग परिवर्तन का उपयोग अज्ञात आकार मापदंड के लिए हल करने के लिए किया जा सकता है (विषम स्थितियों के लिए जैसे कि , अन्यथा, यदि सममित, दोनों-सामान्तर-मापदंड ज्ञात होने पर ज्ञात होते हैं):
यह लॉगिट परिवर्तन का लघुगणक है जो वेरिएबल X को उसकी दर्पण-छवि (X/1 - X) से विभाजित करता है जिसके परिणाम स्वरूप उलटा बीटा वितरण या बीटा प्राइम वितरण होता है (जिसे दूसरी तरह के बीटा वितरण या पियर्सन के प्रकार VI के रूप में भी जाना जाता है) | समर्थन के साथ [0, +∞) जैसा कि पहले अनुभाग में लघुगणक रूप से परिवर्तित यादृच्छिक वेरिएबल के क्षण", की खण्ड में चर्चा की गई थी| जॉनसन द्वारा अध्ययन लघुगणक परिवर्तन , किया गया, के आधार पर परिमित समर्थन [0, 1] का विस्तार करता है।[27] वास्तविक रेखा (−∞, +∞) की दोनों दिशाओं में अनंत समर्थन के लिए मूल वेरिएबल X होता है |
यदि, उदाहरण के लिए, ज्ञात है, अज्ञात मापदंड प्रतिलोम के रूप में प्राप्त किया जा सकता है[50] इस समीकरण के दाहिने हाथ की ओर का डिगम्मा कार्य:
विशेष रूप से, यदि आकार के मापदंडों में से में एकता का मान है, उदाहरण के लिए (परिबद्ध समर्थन के साथ पावर फलन वितरण),[0,1] पहचान ψ(x + 1) का उपयोग करके = ψ(x) + 1/x समीकरण में , अज्ञात मापदंड के लिए अधिकतम संभावना अनुमानक है,[1]बिल्कुल:
बीटा का समर्थन [0, 1] है इसलिए , और इसलिए , और इसलिए
अंत में, बीटा वितरण के आकार मापदंडों के अधिकतम संभावना अनुमान (सामान्य रूप से) प्रतिरूप ज्यामितीय माध्य का जटिल कार्य है, और प्रतिरूप ज्यामितीय माध्य (1−X), X की दर्पण-छवि पर आधारित है। कोई पूछ सकता है, यदि क्षणों की विधि के साथ दो आकृति मापदंडों का अनुमान लगाने के लिए विचरण (माध्य के अतिरिक्त) आवश्यक है, तब अधिकतम संभावना विधि के साथ दो आकार के मापदंडों का अनुमान लगाने के लिए (लघुगणक या ज्यामितीय) विचरण क्यों आवश्यक नहीं है? कौन सा केवल ज्यामितीय का कारणपर्याप्त है? उत्तर इसलिए है क्योंकि माध्य उतनी जानकारी प्रदान नहीं करता जितनी कि ज्यामितीय माध्य। समान आकार के मापदंडों α = β के साथ बीटा वितरण के लिए, आकृति मापदंडों के मान की परवाह किए बिना, और इसलिए सांख्यिकीय फैलाव (भिन्नता) के मूल्य की परवाह किए बिना, माध्य ठीक 1/2 है। दूसरी ओर, समान आकार के मापदंड α=β के साथ बीटा वितरण का ज्यामितीय माध्य आकार मापदंड के मान पर निर्भर करता है, और इसलिए इसमें अधिक जानकारी होती है। इसके अतिरिक्त, बीटा वितरण का ज्यामितीय माध्य माध्य द्वारा संतुष्ट सममिति नियम को संतुष्ट नहीं करता है, इसलिए, X पर आधारित ज्यामितीय माध्य और (1 − X) पर आधारित ज्यामितीय माध्य दोनों को नियोजित करके, अधिकतम संभावना विधि प्रदान करने में सक्षम है दोनों मापदंड α=β के लिए सर्वोत्तम अनुमान, भिन्नता को नियोजित किए बिना।
कोई भी पर्याप्त आँकड़ों (प्रतिरूप ज्यामितीय साधनों) के संदर्भ में प्रति n स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल टिप्पणियों के संयुक्त लॉग संभावना को निम्नानुसार व्यक्त कर सकता है:
हम आकार मापदंड α और β के फलन के रूप में संभावना फलन के व्यवहार को देखने के लिए प्रतिरूप ज्यामितीय साधनों के निश्चित मूल्यों के लिए प्रति n अवलोकनों के संयुक्त लॉग संभावना को प्लॉट कर सकते हैं। ऐसी साजिश में, आकृति मापदंड अनुमानक संभावना फलन की अधिकतमता के अनुरूप। संलग्न ग्राफ़ देखें जो दर्शाता है कि सभी संभावित कार्य α = β = 1 पर प्रतिच्छेद करते हैं, जो आकार के मापदंडों के मूल्यों से मेल खाता है जो अधिकतम एन्ट्रापी देता है (एकता के सामान्तर आकृति मापदंडों के लिए अधिकतम एन्ट्रापी होती है: समान वितरण)। प्लॉट से यह स्पष्ट है कि संभावना फलन शून्य के समीप आकार मापदंड अनुमानकों के मूल्यों के लिए तेज चोटियां देता है, किन्तु आकार मापदंड अनुमानकों के मूल्यों के लिए से अधिक होने पर, कम परिभाषित चोटियों के साथ संभावना फलन अधिक सपाट हो जाता है। किन्तु है, आकार मापदंड अनुमानकों के बड़े मूल्यों के लिए बीटा वितरण के लिए अधिकतम संभावना मापदंड अनुमान विधि कम स्वीकार्य हो जाती है, क्योंकि शिखर परिभाषा में अनिश्चितता आकार मापदंड अनुमानकों के मूल्य के साथ बढ़ जाती है। ही निष्कर्ष पर यह ध्यान देकर पहुंचा जा सकता है कि संभावना फलन की वक्रता के लिए अभिव्यक्ति ज्यामितीय भिन्नताओं के संदर्भ में है
आकार मापदंड α और β के छोटे मानों के लिए ये भिन्नताएं (और इसलिए वक्रताएं) बहुत बड़ी हैं। चूँकि, आकार मापदंड मान α, β > 1 के लिए, प्रसरण (और इसलिए वक्रता) समतल हो जाते हैं। समतुल्य रूप से, यह परिणाम क्रैमर-राव बाउंड से आता है, क्योंकि बीटा वितरण के लिए फिशर सूचना आव्युह घटक ये लघुगणक प्रसरण हैं। क्रैमर-राव बाउंड बताता है कि किसी भी निष्पक्ष अनुमानक का प्रसरण α का फिशर जानकारी के गुणक व्युत्क्रम से घिरा है:
इसलिए अनुमानकों का प्रसरण बढ़ते हुए α और β के साथ बढ़ता है, क्योंकि लघुगणक प्रसरण घटते हैं।
प्रतिरूप ज्यामितीय साधनों के लघुगणक के लिए डिगामा फलन एक्सप्रेशंस के संदर्भ में एन स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल टिप्पणियों के प्रति संयुक्त लॉग संभावना को भी व्यक्त कर सकते हैं:
यह अभिव्यक्ति क्रॉस-एन्ट्रॉपी के ऋणात्मक के समान है (जानकारी की मात्रा (एन्ट्रॉपी) पर अनुभाग देखें)। इसलिए, आकार मापदंडों के संयुक्त लॉग संभावना की अधिकतम खोज, प्रति N स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकन, बीटा वितरण के लिए न्यूनतम क्रॉस-एन्ट्रॉपी खोजने के समान है, आकार मापदंडों के फलन के रूप में।
क्रॉस-एन्ट्रॉपी के साथ निम्नानुसार परिभाषित किया गया है:
चार अज्ञात मापदंड
प्रक्रिया दो अज्ञात मापदंड स्तिथियों में अपनाई गई प्रक्रिया के समान है। यदि y1, ...,yN और स्वतंत्र यादृच्छिक वेरिएबल हैं जिनमें से प्रत्येक में चार मापदंडों के साथ बीटा वितरण है, N स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल टिप्पणियों के लिए संयुक्त लॉग संभावना कार्य है:
आकार मापदंड के संबंध में अधिकतम ढूँढना तथा आकार मापदंड के संबंध में आंशिक व्युत्पन्न लेना और अभिव्यक्ति मापदंड के अधिकतम संभावना अनुमानक को शून्य के सामान्तर अभिव्यक्ति समुच्चय करना आदि सम्मिलित है:
इन समीकरणों को चार युग्मित समीकरणों की निम्नलिखित प्रणाली के रूप में फिर से व्यवस्थित किया जा सकता है (पहले दो समीकरण ज्यामितीय साधन हैं और दूसरे दो समीकरण हार्मोनिक साधन हैं चार मापदंडों के लिए अधिकतम संभावना अनुमानों के संदर्भ में :
प्रतिरूप ज्यामितीय साधनों के साथ:
मापदंड गैर-रैखिक तरीके से (शक्ति 1/n) में ज्यामितीय माध्य अभिव्यक्तियों के अंदर एम्बेडेड हैं। यह सामान्य रूप से, विवृत रूप समाधान को रोकता है, यहां तक कि पुनरावृति प्रयोजनों के लिए प्रारंभिक मूल्य सन्निकटन के लिए भी। विकल्प चार मापदंड स्तिथियों के लिए क्षणों के समाधान की विधि से प्राप्त मूल्यों को पुनरावृत्ति के लिए प्रारंभिक मानों के रूप में उपयोग करना है। इसके अतिरिक्त, हार्मोनिक साधनों के भाव केवल के लिए अच्छी तरह से परिभाषित हैं , जो चार-मापदंड स्तिथियों में एकता से कम आकार के मापदंडों के लिए अधिकतम संभावना समाधान को रोकता है। चार मापदंड स्तिथियों के लिए फिशर की सूचना आव्युह धनात्मक -निश्चित आव्युह है। धनात्मक -निश्चित केवल α, β> 2 के लिए (आगे की चर्चा के लिए, फिशर सूचना आव्युह पर अनुभाग देखें, चार मापदंड स्तिथि ), घंटी के आकार (सममित या असममित) बीटा वितरण, मोड के दोनों ओर स्थित विभक्ति बिंदुओं के साथ। निम्नलिखित फिशर सूचना घटकों (जो लॉग संभावना फलन की वक्रता की अपेक्षाओं का प्रतिनिधित्व करते हैं) में निम्नलिखित मानों पर गणितीय विलक्षणता है:
(आगे की चर्चा के लिए फिशर सूचना आव्युह पर अनुभाग देखें)। इस प्रकार, चार-मापदंड बीटा वितरण परिवार से संबंधित कुछ प्रसिद्ध वितरणों जैसे निरंतर समान वितरण (बीटा (1, 1, a, c)), और आर्क्साइन वितरण के लिए अधिकतम संभावना अनुमान को सख्ती से प्रयुक्त करना संभव नहीं है, (बीटा (1/2, 1/2, a, c))। नॉर्मन लॉयड जॉनसन|(एन.एल.जॉनसन) और सैमुअल कोटज़|(एस.कोट्ज़)[1]हार्मोनिक साधनों के लिए समीकरणों को अनदेखा करें और इसके अतिरिक्त सुझाव दें कि यदि a और c अज्ञात हैं, और a, c, α और β के अधिकतम संभावना अनुमानक आवश्यक हैं, तब उपरोक्त प्रक्रिया (दो अज्ञात मापदंड स्तिथियों के लिए, X को X साथ = Y − a)/(c − a)) के रूप में रूपांतरित किया गया है उत्तराधिकार का उपयोग करके दोहराया जा सकता है a और c के परीक्षण मूल्यों के , जब तक कि जोड़ी (a, c) जिसके लिए अधिकतम संभावना (दिया गया a और c) जितना अधिक हो सके, है प्राप्त (जहाँ, स्पष्टता के प्रयोजन के लिए, मापदंडों के लिए उनके अंकन को वर्तमान अंकन में अनुवादित किया गया है)।
फिशर सूचना आव्युह
मान लें कि यादृच्छिक वेरिएबल X का प्रायिकता घनत्व f(x;α) है। लॉग संभावना फलन के (अज्ञात, और अनुमानित) मापदंड α के संबंध में आंशिक व्युत्पन्न को स्कोर (सांख्यिकी) कहा जाता है। स्कोर के दूसरे क्षण को फिशर सूचना कहा जाता है:
स्कोर (सांख्यिकी) का अपेक्षित मूल्य शून्य है, इसलिए फिशर की जानकारी भी स्कोर के माध्य पर केंद्रित दूसरा क्षण है: स्कोर का विचरण ।
यदि लॉग संभावना फलन मापदंड α के संबंध में दो बार भिन्न होता है, और कुछ नियमितता नियम के अनुसार ,[51] तब फ़िशर जानकारी को निम्नानुसार भी लिखा जा सकता है (जो अधिकांशतः गणना उद्देश्यों के लिए अधिक सुविधाजनक रूप होता है):
इस प्रकार, फिशर की जानकारी लॉग संभावना फलन के मापदंड α के संबंध में दूसरे व्युत्पन्न की अपेक्षा का ऋणात्मक है। इसलिए, फिशर की जानकारी α के लॉग संभावना फलन की वक्रता का उपाय है। कम वक्रता (और इसलिए वक्रता (गणित) की उच्च त्रिज्या), चापलूसी लॉग संभावना फलन वक्र में कम फ़िशर जानकारी होती है; जबकि बड़ी वक्रता (और इसलिए वक्रता की कम त्रिज्या (गणित)) के साथ लॉग संभावना फलन वक्र में उच्च फ़िशर जानकारी होती है। जब फिशर सूचना आव्युह की गणना मापदंडों के मूल्यांकन पर की जाती है (देखा गया फिशर सूचना आव्युह) यह टेलर की श्रृंखला सन्निकटन द्वारा सही लॉग संभावना सतह के प्रतिस्थापन के सामान्तर है, जहाँ तक द्विघात शब्दों को लिया गया है।[52] शब्द सूचना, फिशर जानकारी के संदर्भ में, मापदंडों के बारे में जानकारी को संदर्भित करता है। जानकारी जैसे: अनुमान, पर्याप्तता और अनुमानकों के प्रसरण के गुण। क्रैमर-राव बाउंड बताता है कि फिशर सूचना का व्युत्क्रम मापदंड α के किसी भी अनुमानक के विचरण पर निचली सीमा है:
स्पष्टता जिसके लिए कोई मापदंड α के अनुमानक का अनुमान लगा सकता है, लॉग संभावना फलन के फ़िशर सूचना द्वारा सीमित है। फिशर जानकारी वितरण के मापदंड का अनुमान लगाने में सम्मिलित न्यूनतम त्रुटि का उपाय है और इसे मापदंड के दो वैकल्पिक परिकल्पनाओं के मध्य भेदभाव करने के लिए आवश्यक प्रयोग की संकल्प शक्ति के माप के रूप में देखा जा सकता है।[53]
जब एन मापदंड होते हैं
तब फिशर जानकारी विशिष्ट तत्व के साथ N× N धनात्मक अर्ध-निश्चित आव्युह सममित आव्युह, फिशर सूचना आव्युह का रूप लेती है:
कुछ नियमितता नियम के अनुसार ,[51]फिशर इंरूपेशन आव्युह को निम्नलिखित रूप में भी लिखा जा सकता है, जो अधिकांशतः गणना के लिए अधिक सुविधाजनक होता है:
X1 ..., XN iid यादृच्छिक वेरिएबल के साथ , पक्षों N-आयामी बॉक्स का निर्माण X1, ..., XN के साथ किया जा सकता है कोस्टा और आवरण [54] दिखाएँ कि (शैनन) डिफरेंशियल एन्ट्रापी h(X) विशिष्ट समुच्चय की मात्रा से संबंधित है (प्रतिरूप एन्ट्रापी को सही एन्ट्रापी के समीप होने पर), जबकि फिशर की जानकारी इस विशिष्ट समुच्चय की सतह से संबंधित है।
दो मापदंड
X1 ..., XN स्वतंत्र यादृच्छिक वेरिएबल के लिए प्रत्येक में जो आकार मापदंडों α और β के साथ पैरामीट्रिज्ड होता है N स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकनों के लिए संयुक्त लॉग संभावना फलन है:
इसलिए संयुक्त लॉग संभावना कार्य प्रति n स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकन है:
दो मापदंड स्तिथियों के लिए, फिशर जानकारी में 4 घटक होते हैं: 2 विकर्ण और 2 ऑफ-विकर्ण। चूंकि फिशर सूचना आव्युह सममित है, इनमें से विकर्ण घटक स्वतंत्र है। इसलिए, फिशर सूचना आव्युह में 3 स्वतंत्र घटक (2 विकर्ण और 1 विकर्ण) हैं।
आर्यल और नादराजा[55] चार-मापदंड स्तिथियों के लिए फिशर की सूचना आव्युह की गणना की गई, जिससे दो मापदंड स्तिथियाँनिम्नानुसार प्राप्त किए जा सकते हैं:
चूंकि फिशर सूचना आव्युह सममित है
फिशर सूचना घटक लॉग ज्यामितीय प्रसरण और लॉग ज्यामितीय सहप्रसरण के सामान्तर हैं। इसलिए, उन्हें त्रिगामा कार्यों के रूप में व्यक्त किया जा सकता है, जिसे ψ1(α) निरूपित किया जाता है, बहुग्राम कार्यों का दूसरा, डिगामा फलन के व्युत्पन्न के रूप में परिभाषित किया गया है:
- : : : : : : : : : : : : : : : : : : : : : : : :
ये डेरिवेटिव भी में व्युत्पन्न हैं § दो अज्ञात पैरामीटर और लॉग संभावना फलन के प्लॉट भी उस अनुभाग में दिखाए जाते हैं। § ज्यामितीय विचरण और सहप्रसरण में फिशर सूचना आव्युह घटकों के प्लॉट और आगे की चर्चा सम्मिलित है: लॉग ज्यामितीय प्रसरण और लॉग ज्यामितीय सहप्रसरण आकार मापदंड α और β के फलन के रूप में। § लघुगणकीय रूप से परिवर्तित यादृच्छिक चर के क्षण लघुगणक रूप से परिवर्तित यादृच्छिक वेरिएबल के क्षणों के लिए सूत्र सम्मिलित हैं। फिशर सूचना घटकों के लिए छवियां और में दर्शाए गए हैं § ज्यामितीय विचरण.
फ़िशर के सूचना आव्युह का निर्धारक रुचि का है (उदाहरण के लिए जेफ़रीज़ पूर्व संभाव्यता की गणना के लिए)। फिशर सूचना आव्युह के अलग-अलग घटकों के भावों से, यह इस प्रकार है कि बीटा वितरण के लिए फिशर (सममित) सूचना आव्युह का निर्धारक है:
सिल्वेस्टर की कसौटी से (यह जांचना कि क्या विकर्ण तत्व सभी धनात्मक हैं), यह इस प्रकार है कि दो मापदंड केस के लिए फिशर सूचना आव्युह धनात्मक -निश्चित आव्युह है। धनात्मक -निश्चित (मानक स्थिति के अनुसार α > 0 और β > 0आकार मापदंड धनात्मक हैं ).
चार मापदंड
यदि y1, ..., yNस्वतंत्र यादृच्छिक वेरिएबल हैं जिनमें से प्रत्येक में चार मापदंडों के साथ बीटा वितरण होता है: एक्सपोनेंट्स α और β, और a (वितरण सीमा का न्यूनतम), और c (वितरण सीमा का अधिकतम) (वैकल्पिक पैरामीट्रिजेशन शीर्षक वाला खंड, चार मापदंड) प्रायिकता घनत्व फलन के साथ:
संयुक्त लॉग संभावना फलन प्रति n स्वतंत्र और समान रूप से वितरित यादृच्छिक वेरिएबल अवलोकन है:
चार मापदंड केस के लिए, फिशर जानकारी में 4*4=16 घटक होते हैं। इसमें 12 ऑफ-डायगोनल घटक = (4 × 4 कुल - 4 विकर्ण) हैं। चूंकि फिशर सूचना आव्युह सममित है, इनमें से आधे घटक (12/2 = 6) स्वतंत्र हैं। इसलिए, फिशर सूचना आव्युह में 6 स्वतंत्र ऑफ-विकर्ण + 4 विकर्ण = 10 स्वतंत्र घटक हैं। आर्यल और नादराजा[55]निम्नानुसार चार मापदंड स्तिथियों के लिए फिशर की सूचना आव्युह की गणना:
उपरोक्त भावों में, भावों में Y के स्थान पर X का प्रयोग var[ln(X)] = ln(varGX) कोई त्रुटि नहीं है। लॉग ज्यामितीय प्रसरण और लॉग ज्यामितीय सहप्रसरण के संदर्भ में अभिव्यक्तियाँ दो मापदंड X ~ बीटा (α, β) पैरामीट्रिजेशन के कार्यों के रूप में होती हैं क्योंकि चार मापदंड स्तिथियों में घातांक (α, β) के संबंध में आंशिक डेरिवेटिव लेते समय , दो मापदंड स्तिथियों के लिए समान अभिव्यक्ति प्राप्त करता है: चार मापदंड फिशर सूचना आव्युह की ये नियम ें वितरण की सीमा के न्यूनतम ए और अधिकतम सी से स्वतंत्र हैं। घातांक α और β के संबंध में लॉग संभावना फलन के दोहरे विभेदन पर एकमात्र गैर-शून्य शब्द बीटा फलन के लॉग का दूसरा व्युत्पन्न है: ln(B(α, β))। यह शब्द वितरण की सीमा के न्यूनतम a और अधिकतम c से स्वतंत्र है। इस पद के दोहरे विभेदन के परिणामस्वरूप त्रिगामा फलन उत्पन्न होते हैं। अधिकतम संभावना, दो अज्ञात मापदंड और चार अज्ञात मापदंड शीर्षक वाले खंड भी इस तथ्य को दर्शाते हैं।
एन आई.डी. के लिए फिशर जानकारी प्रतिरूप व्यक्तिगत फिशर जानकारी का N गुना है (eq. 11.279, आवरण और थॉमस का पृष्ठ 394[30]). (आर्यल और नादराजा[55]फिशर जानकारी के निम्नलिखित घटकों की गणना करने के लिए एकल अवलोकन, एन = 1 लें, जो प्रति एन अवलोकन लॉग संभावना के डेरिवेटिव पर विचार करने के समान परिणाम की ओर जाता है। इसके अतिरिक्त, के लिए गलत अभिव्यक्ति के नीचे आर्यल और नादराजाह में सुधार किया गया है।)
फिशर सूचना आव्युह की निचली दो विकर्ण प्रविष्टियाँ, मापदंड a (वितरण की सीमा का न्यूनतम) के संबंध में: , और मापदंड c के संबंध में (वितरण की अधिकतम सीमा): क्रमशः घातांक α > 2 और β > 2 के लिए परिभाषित हैं। फिशर सूचना आव्युह घटक ऊपर से 2 तक पहुंचने वाले घातांक α के लिए न्यूनतम ए दृष्टिकोण अनंत और फिशर सूचना आव्युह घटक के लिए ऊपर से 2 की ओर आने वाले घातांक β के लिए अधिकतम c अनंत की ओर अग्रसर होता है।
चार मापदंड स्तिथियों के लिए फिशर सूचना आव्युह न्यूनतम a और अधिकतम c के व्यक्तिगत मूल्यों पर निर्भर नहीं करता है, किन्तु केवल कुल सीमा (c-a) पर निर्भर करता है। इसके अतिरिक्त, फिशर सूचना आव्युह के घटक जो रेंज (c-a) पर निर्भर करते हैं, केवल इसके व्युत्क्रम (या व्युत्क्रम के वर्ग) के माध्यम से निर्भर करते हैं, जैसे कि फिशर की जानकारी बढ़ती रेंज (c-a) के लिए घट जाती है।
संलग्न छवियां फिशर सूचना घटकों को दिखाती हैं और . फिशर सूचना घटकों के लिए छवियां और में दर्शाए गए हैं § ज्यामितीय विचरण. ये सभी फिशर सूचना घटक बेसिन की तरह दिखते हैं, जिसमें बेसिन की दीवारें मापदंडों के कम मूल्यों पर स्थित होती हैं।
निम्नलिखित चार-मापदंड-बीटा-वितरण फिशर जानकारी घटकों को दो-मापदंड के संदर्भ में व्यक्त किया जा सकता है: X ~ बीटा (α, β) रूपांतरित अनुपात ((1-X)/X) और इसकी दर्पण छवि की अपेक्षाएं (एक्स/(1-एक्स)), श्रेणी (c−a) द्वारा स्केल किया गया, जो व्याख्या के लिए सहायक हो सकता है:
ये इन्वर्टेड बीटा डिस्ट्रीब्यूशन या बीटा प्राइम डिस्ट्रीब्यूशन के अपेक्षित मूल्य भी हैं (जिसे दूसरी तरह के बीटा डिस्ट्रीब्यूशन या पियर्सन डिस्ट्रीब्यूशन के रूप में भी जाना जाता है। पियर्सन टाइप VI) [1]और इसकी दर्पण छवि, श्रेणी (c − a) द्वारा स्केल की गई।
साथ ही, निम्न फ़िशर सूचना घटकों को हार्मोनिक (1/X) प्रसरणों या अनुपात रूपांतरित चरो ((1-X)/X) के आधार पर प्रसरणों के रूप में निम्नानुसार व्यक्त किया जा सकता है:
इन अपेक्षाओं के लिए रैखिक रूप से रूपांतरित, उत्पाद और उल्टे यादृच्छिक वेरिएबल के क्षण देखें।
फ़िशर के सूचना आव्युह का निर्धारक रुचि का है (उदाहरण के लिए जेफ़रीज़ पूर्व संभाव्यता की गणना के लिए)। अलग-अलग घटकों के भावों से, यह अनुसरण करता है कि चार मापदंडों के साथ बीटा वितरण के लिए फिशर (सममित) सूचना आव्युह का निर्धारक है:
सिल्वेस्टर की कसौटी का उपयोग करना (जांच करना कि क्या विकर्ण तत्व सभी धनात्मक हैं), और विकर्ण घटकों के पश्चात् से और α=2 और β=2 पर गणितीय विलक्षणता है यह इस प्रकार है कि चार मापदंड स्तिथियों के लिए फिशर सूचना आव्युह धनात्मक -निश्चित आव्युह है। α>2 और β>2 के लिए धनात्मक -निश्चित है। चूंकि α > 2 और β > 2 के लिए बीटा वितरण (सममित या असममित) घंटी के आकार का है, यह अनुसरण करता है कि फिशर सूचना आव्युह केवल घंटी के आकार (सममित या असममित) बीटा वितरण के लिए धनात्मक -निश्चित है, जिसमें विभक्ति बिंदु स्थित हैं मोड के दोनों ओर। इस प्रकार, चार-मापदंड बीटा वितरण परिवार से संबंधित महत्वपूर्ण प्रसिद्ध वितरण, जैसे परवलयिक वितरण (बीटा (2,2, a, c)) और निरंतर समान वितरण (बीटा (1,1, a, c)) फिशर सूचना घटक () जो चार-मापदंड स्तिथियों में उड़ते हैं (अनंत तक पहुंचते हैं) (चूंकि उनके फिशर सूचना घटक सभी दो मापदंड स्तिथियों के लिए परिभाषित हैं)। चार-मापदंड विग्नर अर्धवृत्त वितरण (बीटा(3/2,3/2,a,c)) और आर्क्साइन वितरण (बीटा(1/2,1/2,a,c)) में चार के लिए ऋणात्मक फिशर सूचना निर्धारक हैं -मापदंड स्तिथि ।
बायेसियन अनुमान

बायेसियन अनुमान में बीटा वितरण का उपयोग इस तथ्य के कारण है कि वे द्विपद वितरण (बर्नौली वितरण सहित) और ज्यामितीय वितरण के लिए संयुग्मित पूर्व वितरण का परिवार प्रदान करते हैं। बीटा वितरण के क्षेत्र को प्रायिकता के रूप में देखा जा सकता है, और वास्तव में बीटा वितरण का उपयोग प्रायिकता मान p के वितरण का वर्णन करने के लिए किया जाता है:[26]
बेयसियन अनुमान में पूर्व मापदंड मानों की अज्ञानता का प्रतिनिधित्व करने के लिए पूर्व संभावनाओं के रूप में उपयोग किए जाने वाले बीटा वितरण के उदाहरण बीटा (1,1), बीटा (0,0) और बीटा (1/2,1/2) हैं।
उत्तराधिकार का नियम
बीटा वितरण का क्लासिक अनुप्रयोग उत्तराधिकार का नियम है, जिसे 18वीं शताब्दी में पियरे-साइमन लाप्लास द्वारा प्रस्तुत किया गया था।[56] सूर्योदय की समस्या के उपचार के दौरान। इसमें कहा गया है कि, n सनियम स्वतंत्रता बर्नौली परीक्षणों में संभाव्यता p के साथ सफलताओं को देखते हुए, कि अगले परीक्षण में अपेक्षित मूल्य का अनुमान है . यह अनुमान p, अर्थात् बीटा(s+1, n−s+1) पर पश्च वितरण का अपेक्षित मूल्य है, जो बेज़ के नियम द्वारा दिया जाता है यदि कोई p पर समान पूर्व संभावना मानता है (अर्थात, बीटा(1, 1)) और फिर देखता है कि p ने n परीक्षणों में सफलताएँ उत्पन्न की हैं। लाप्लास के उत्तराधिकार के नियम की प्रमुख वैज्ञानिकों ने आलोचना की है। R T कॉक्स ने लाप्लास के सूर्योदय समस्या के उत्तराधिकार के नियम के अनुप्रयोग का वर्णन किया जाता है ([57] पी। 89) इस सिद्धांत के उचित उपयोग के उपहास के रूप में। कीन्स टिप्पणी ([58] Ch.XXX, पी. 382) वास्तव में यह इतना मूर्खतापूर्ण प्रमेय है कि इसका मनोरंजन करना निंदनीय है। कार्ल पियर्सन[59] n परीक्षणों में n सफलताओं के पश्चात् अगले (n + 1) परीक्षणों के सफल होने की संभावना केवल 50% है, जिसे जेफरीज़ जैसे वैज्ञानिकों द्वारा बहुत कम और प्रयोग की वैज्ञानिक प्रक्रिया के प्रतिनिधित्व के रूप में अस्वीकार्य माना गया है। प्रस्तावित वैज्ञानिक नियम का परीक्षण करने के लिए। जैसा कि जेफरीस ने बताया है ([60]पी। 128) (सी. डी. ब्रॉड का श्रेय[61] ) लाप्लास के उत्तराधिकार का नियम अगले परीक्षण में सफलता की उच्च संभावना ((n+1)/(n+2)) स्थापित करता है, किन्तु केवल मध्यम संभावना (50%) कि और प्रतिरूप (n+1) आकार में तुलनीय है समान रूप से सफल होंगे। जैसा कि पर्क्स द्वारा बताया गया है,[62] उत्तराधिकार के नियम को ही स्वीकार करना कठिन है। यह अगले परीक्षण के लिए संभावना प्रदान करता है जिसका अर्थ है कि देखा गया वास्तविक रन औसत रन है और हम सदैव औसत रन के अंत में होते हैं। यह सोचना होगा, यह मान लेना अधिक उचित होगा कि हम औसत रन के मध्य में थे। स्पष्ट रूप से दोनों संभावनाओं के लिए उच्च मूल्य आवश्यक है यदि वे उचित विश्वास के अनुरूप हों। लाप्लास के उत्तराधिकार के नियम के साथ इन समस्याओं ने हाल्डेन, पर्क्स, जेफरीज़ और अन्य को पूर्व संभाव्यता के अन्य रूपों की खोज करने के लिए प्रेरित किया (अगला देखें) § बायेसियन अनुमान). जेनेस के अनुसार,[53]उत्तराधिकार के नियम के साथ मुख्य समस्या यह है कि यह मान्य नहीं है जब s=0 या s=n (इसकी वैधता के विश्लेषण के लिए उत्तराधिकार का नियम देखें)।
बेयस-लाप्लास पूर्व संभावना (बीटा(1,1))
बीटा वितरण बीटा (1,1) के लिए अधिकतम अंतर एंट्रॉपी प्राप्त करता है: समान घनत्व संभाव्यता घनत्व, जिसके लिए वितरण के डोमेन में सभी मूल्यों में समान घनत्व होता है। थॉमस बेयस द्वारा इस समान वितरण बीटा (1,1) का सुझाव दिया गया था (बहुत संदेह के साथ)।[63]पूर्व संभाव्यता वितरण के रूप में सही पूर्व वितरण के बारे में अज्ञानता व्यक्त करने के लिए। यह पूर्व वितरण अपनाया गया था (किन्तुा तौर पर, उनके लेखन से, संदेह के छोटे संकेत के साथ[56] पियरे-साइमन लाप्लास द्वारा, और इसलिए इसे 20 वीं शताब्दी के पहले छमाही के प्रकाशनों में बेयस-लाप्लास नियम या व्युत्क्रम संभाव्यता के लाप्लास नियम के रूप में भी जाना जाता था। 19वीं सदी के उत्तरार्ध और 20वीं सदी के प्रारंभिक भाग में, वैज्ञानिकों ने अनुभूत किया कि एकसमान समान संभाव्यता घनत्व की धारणा वास्तविक कार्यों पर निर्भर करती है (उदाहरण के लिए क्या रैखिक या लघुगणकीय मापदंड सबसे उपयुक्त था) और प्रयुक्त पैरामीट्रिजेशन। विशेष रूप से, परिमित समर्थन के साथ वितरण के सिरों के पास व्यवहार (उदाहरण के लिए x = 0 के पास, x = 0 पर प्रारंभिक समर्थन वाले वितरण के लिए) विशेष ध्यान देने की आवश्यकता है। कीन्स ([58]Ch.XXX, पी. 381) ने बेयस की समान पूर्व संभाव्यता (बीटा (1,1)) के उपयोग की आलोचना की, जो कि शून्य और के मध्य के सभी मूल्यों को परिवर्तनीय है, इस प्रकार है: इस प्रकार अनुभव, यदि यह कुछ भी दिखाता है, तब यह दर्शाता है कि सांख्यिकीय अनुपातबं का बहुत ही स्पष्ट क्लस्टरिंग है शून्य और एकता के निकटतम में, धनात्मक सिद्धांतबं के लिए और शून्य के निकटतम में धनात्मक गुणों के मध्य संबंध के लिए, और ऋणात्मक सिद्धांतबं के लिए और एकता के निकटतम में ऋणात्मक गुणों के मध्य संबंध के लिए।
==={{Anchor|Haldane prior}हल्डेन की पूर्व प्रायिकता (बीटा(0,0))

बीटा (0,0) वितरण J.B.S द्वारा प्रस्तावित किया गया था। हाल्डेन,[64] जिन्होंने सुझाव दिया कि पूर्ण अनिश्चितता का प्रतिनिधित्व करने वाली पूर्व संभाव्यता p−1(1−p)-1 के समानुपाती होनी चाहिए और फलन p−1(1−p)−1 को बीटा वितरण के अंश की सीमा के रूप में देखा जा सकता है क्योंकि दोनों आकार मापदंड शून्य तक पहुंचते हैं: α, β → 0. बीटा फलन (बीटा वितरण के हर में) दोनों मापदंड के लिए अनंत तक पहुंचता है अर्थात् यह शून्य की ओर अग्रसर, α, β → 0. इसलिए, p−1(1−p)−1 को बीटा फलन द्वारा विभाजित करने पर 0 और 1 पर प्राप्त होता है तथा प्रत्येक सिरे पर 1/2 की समान प्रायिकता के साथ 2-बिंदु बर्नौली वितरण प्राप्त होता है, और मध्य में कुछ भी नहीं होता है, जैसा कि α, β → 0. सिक्का-टॉस: सिक्के का फलक 0 पर है और दूसरा फलक 1 पर है। हाल्डेन पूर्व संभाव्यता वितरण बीटा (0,0) अनुचित पूर्व है क्योंकि इसका एकीकरण (0 से 1 तक) प्रत्येक छोर पर विशिष्टता के कारण 1 में सख्ती से अभिसरण करने में विफल रहता है चूँकि, जब तक प्रतिरूप आकार बहुत छोटा न हो, तब तक पश्च संभावनाओं की गणना के लिए यह कोई समस्या नहीं है। इसके अतिरिक्त, ज़ेलनर[65] बताते हैं कि लॉग-बाधाओं की स्केल पर, (लॉगिट ट्रांसफ़ॉर्मेशन ln(p/1−p)), हल्डेन पूर्व समान रूप से सपाट पूर्व है। तथ्य यह है कि लॉगिट रूपांतरित परिवर्तनीय ln(p/1−p) (डोमेन के साथ (-∞, ∞)) पर समान पूर्व संभावना, डोमेन [0, 1] से पहले हाल्डेन के सामान्तर है जिसे हेरोल्ड जेफरीस द्वारा इंगित किया गया था। उनकी पुस्तक थ्योरी ऑफ प्रॉबेबिलिटी के पहले संस्करण (1939) में ([60]पी। 123). जेफरीस लिखते हैं निश्चित रूप से यदि हम बेयस-लाप्लास नियम को वेरिएबल M सीमा तक ले जाते हैं तब हम ऐसे परिणामों की ओर अग्रसर होते हैं जो किसी के सोचने के तरीके के अनुरूप नहीं होते हैं। (हल्दाने) नियम dx/(x(1−x)) दूसरे तरीके से बहुत दूर जाता है। इससे यह निष्कर्ष निकलता है कि यदि किसी संपत्ति के संबंध में प्रतिरूप इस प्रकार का होता है तब संभावना 1 होती है जैसे कि पूरी संख्या उस प्रकार की ही है। तथ्य यह है कि वर्दी पैरामीट्रिजेशन पर निर्भर करती है, जेफ़रीज़ को पूर्व के रूप की तलाश करने के लिए प्रेरित करती है जो विभिन्न पैरामीट्रिज़ेशन के अनुसार अपरिवर्तनीय होगा।
जेफरी की पूर्व संभावना (बीटा (1/2,1/2) बर्नौली के लिए या द्विपद वितरण के लिए)


हेरोल्ड जेफरीस[60][66] गैर-सूचनात्मक पूर्व संभाव्यता माप का उपयोग करने का प्रस्ताव है जो पैरामीट्रिजेशन इनवेरिएंस होना चाहिए: फिशर की सूचना आव्युह के निर्धारक के वर्गमूल के समानुपाती। बर्नौली वितरण के लिए, इसे इस प्रकार दिखाया जा सकता है: एक सिक्के के लिए जो प्रायिकता p ∈ [0, 1] के साथ "हेड्स" है और दिए गए (H,T) ∈ { के लिए प्रायिकता 1 - p के साथ "टेल्स" है। (0,1), (1,0)} संभावना pH(1 − p)T है। चूँकि T = 1 - H, बर्नौली वितरण pH(1 - p)1 - H है। p को एकमात्र पैरामीटर मानते हुए, यह इस प्रकार है कि बर्नौली वितरण के लिए लॉग संभावना है
फिशर सूचना आव्युह में केवल घटक है (यह अदिश राशि है, क्योंकि केवल मापदंड है: p), इसलिए:
इसी तरह, n बर्नोली परीक्षणों के साथ द्विपद वितरण के लिए, यह दिखाया जा सकता है
इस प्रकार, बर्नोली बंटन, और द्विपद बंटन के लिए, जेफ्रेय्स पूर्व के लिए आनुपातिक है , जो डोमेन वेरिएबल x = p, और आकार मापदंड α = β = 1/2, आर्क्साइन वितरण के साथ बीटा वितरण के समानुपाती होता है:
यह अगले खंड में दिखाया जाएगा कि जेफ़रीज़ प्रायर के लिए सामान्यीकरण स्थिरांक अंतिम परिणाम के लिए सारहीन है क्योंकि बेयस प्रमेय में पश्च संभाव्यता के लिए सामान्यीकरण निरंतर रद्द हो जाता है। इसलिए बीटा (1/2,1/2) का उपयोग बर्नौली और द्विपद वितरण दोनों के लिए पहले जेफरीज़ के रूप में किया जाता है। जैसा कि अगले भाग में दिखाया गया है, जब इस अभिव्यक्ति का उपयोग बेयस प्रमेय में संभावना के पूर्व संभाव्यता गुणा के रूप में किया जाता है, तब पश्च संभाव्यता बीटा वितरण बन जाती है। चूंकि, यह अनुभूत करना महत्वपूर्ण है कि जेफ़रीज़ पूर्व के समानुपाती है बर्नोली और द्विपद वितरण के लिए होता है , किन्तु बीटा वितरण के लिए नहीं। बीटा वितरण के लिए जेफरीस पहले बीटा वितरण के लिए फिशर की जानकारी के निर्धारक द्वारा दिया गया है, जैसा कि दिखाया गया है § फिशर सूचना आव्युह त्रिगामा फलन ψ1 का फलन है आकार के मापदंड α और β निम्नानुसार हैं:
जैसा कि पहले चर्चा की गई थी, बर्नौली और द्विपद वितरण के लिए जेफरीस आर्क्सिन वितरण बीटा (1/2,1/2) के समानुपाती है, आयामी वक्र जो बर्नौली के मापदंड p के फलन के रूप में बेसिन की तरह दिखता है और द्विपद वितरण है। बेसिन की दीवारें p के सिरों p → 0 और p → 1 पर सिंग्युलेरिटी के समीप पहुंचने से बनती हैं, जहां बीटा (1/2,1/2) अनंत तक पहुंचता है। तथा बीटा वितरण से पहले जेफ़रीज़ 2-आयामी सतह (त्रि-आयामी अंतरिक्ष में एम्बेडेड) है जो बेसिन की तरह दिखती है जिसकी केवल दो दीवारें कोने α = β = 0 पर मिलती हैं (और अन्य दो दीवारों को गायब कर देती हैं) बीटा वितरण के आकार मापदंड α और β का कार्य है । इस 2-आयामी सतह की दो निकटवर्ती दीवारें α, β → 0 पर एकवचन (ट्राइगामा फलन के) के पास आकृति मापदंडों α और β द्वारा बनाई गई हैं। इसमें α, β → ∞ के लिए कोई दीवार नहीं है क्योंकि इस स्तिथियों में बीटा वितरण के लिए फिशर के सूचना आव्युह का निर्धारक शून्य तक पहुंचता है।
यह अगले खंड में दिखाया जाएगा कि जेफरी की पूर्व संभाव्यता का परिणाम पश्च संभाव्यता में होता है (जब द्विपद संभावना फलन द्वारा गुणा किया जाता है) जो हाल्डेन और बेयस पूर्व संभावनाओं के पश्च संभाव्यता परिणामों के मध्य मध्यवर्ती हैं।
जेफरीज़ पहले विश्लेषणात्मक रूप से प्राप्त करना जटिल हो सकता है, और कुछ स्थितियों के लिए यह उपस्थित नहीं है (असममित त्रिकोणीय वितरण जैसे सरल वितरण कार्यों के लिए भी)। बर्जर, बर्नार्डो और सन, 2009 के पेपर में[67] संदर्भ पूर्व संभाव्यता वितरण परिभाषित किया गया है जो (जेफ्रीस पूर्व के विपरीत) असममित त्रिकोणीय वितरण के लिए उपस्थित है। वे अपने संदर्भ के लिए पूर्व में विवृत -रूप अभिव्यक्ति प्राप्त नहीं कर सकते हैं, किन्तु संख्यात्मक गणना यह दर्शाती है कि यह पूर्व (उचित) द्वारा लगभग पूरी तरह से फिट है।
जहां θ समर्थन के साथ असममित त्रिकोणीय वितरण के लिए वेरिएबल है [0, 1] (त्रिकोणीय वितरण पर विकिपीडिया के आलेख में निम्नलिखित मापदंड मानों के अनुरूप: वर्टेक्स सी = θ, बाएं अंत = 0, और दायां अंत बी = 1 ). बर्जर एट अल। अनुमानी तर्क भी देते हैं कि बीटा (1/2,1/2) वास्तव में असममित त्रिकोणीय वितरण के लिए स्पष्ट बर्जर-बर्नार्डो-सन संदर्भ हो सकता है। इसलिए, बीटा (1/2,1/2) न केवल बर्नौली और द्विपद वितरण के लिए जेफ्रीस पूर्व है, किंतु असममित त्रिकोणीय वितरण के लिए बर्जर-बर्नार्डो-सूर्य संदर्भ भी प्रतीत होता है (जिसके लिए जेफ्रीस पूर्व नहीं करता है) उपस्थित है कि परियोजना प्रबंधन और परियोजना कार्यों की निवेश और अवधि का वर्णन करने के लिए पीईआरटी विश्लेषण में उपयोग किया जाने वाला वितरण।
क्लार्क और बैरोन[68] सिद्ध करें कि, निरंतर धनात्मक पुजारियों के मध्य, जेफ़रीज़ पूर्व (जब यह उपस्थितहै) आकार n और मापदंड के प्रतिरूप के मध्य शैनन की पारस्परिक जानकारी को स्पर्शोन्मुख रूप से अधिकतम करता है, और इसलिए जेफ़्रीज़ पूर्व सबसे असंक्रामक पूर्व है (शैनन जानकारी के रूप में जानकारी को मापना)। प्रमाण iid यादृच्छिक वेरिएबल के लिए संभाव्यता घनत्व कार्यों के मध्य कुल्बैक-लीब्लर विचलन की परीक्षा पर टिकी हुई है।
पश्च बीटा वितरण पर विभिन्न पूर्व संभाव्यता विकल्पों का प्रभाव
यदि यादृच्छिक वेरिएबल X की संख्या से प्रतिरूप लिए जाते हैं, जिसके परिणाम स्वरूप "n" बर्नौली में सफलताएँ और f विफलताएँ होती हैं तो परीक्षण n = s + f, फिर पैरामीटर s और f के लिए संभावना फलन x = p दिया गया है (नीचे दिए गए भावों में x = p संकेतन इस बात पर जोर देगा कि डोमेन x द्विपद वितरण में पैरामीटर p के मान को दर्शाता है), निम्नलिखित द्विपद वितरण है:
यदि पूर्व संभाव्यता जानकारी के बारे में मान्यताओं को α प्रायर और β प्रायर मापदंडों के साथ बीटा वितरण द्वारा यथोचित रूप से अच्छी तरह से अनुमानित किया गया है, तो:
एक निरंतर घटना स्थान के लिए बेयस के प्रमेय के अनुसार, पश्च संभाव्यता पूर्व संभाव्यता और संभावना फलन के उत्पाद द्वारा दी जाती है (दिए गए साक्ष्य s और f = n n − s), सामान्यीकृत है जिससे वक्र के नीचे का क्षेत्र सामान्तर हो होता है , निम्नलिखित नुसार:
पश्च संभाव्यता के अंश और भाजक दोनों में प्रकट होता है, और यह एकीकरण वेरिएबल x पर निर्भर नहीं करता है, इसलिए यह रद्द हो जाता है, और यह अंतिम परिणाम के लिए अप्रासंगिक है। इसी तरह पूर्व संभाव्यता के लिए सामान्य कारक, बीटा फलन बी (α प्रायर, β प्रायर) रद्द हो जाता है और यह अंतिम परिणाम के लिए सारहीन है। यदि कोई पूर्व-सामान्यीकृत पूर्व का उपयोग करता है तब समान पश्च संभाव्यता परिणाम प्राप्त किया जा सकता है
क्योंकि सामान्य करने वाले कारक सभी रद्द हो जाते हैं। अनेक लेखक (स्वयं जेफरीज़ सहित) इस प्रकार गैर-सामान्यीकृत पूर्व सूत्र का उपयोग करते हैं क्योंकि सामान्यीकरण निरंतर रद्द हो जाता है। पश्च संभाव्यता का अंश पूर्व संभाव्यता और संभावना कार्य के केवल (असामान्यीकृत) उत्पाद होने के कारण समाप्त होता है, और भाजक शून्य से तक इसका अभिन्न अंग है। भाजक में बीटा फलन B(s + α प्रायर, n − s + β प्रायर), यह सुनिश्चित करने के लिए सामान्यीकरण स्थिरांक के रूप में प्रकट होता है कि कुल पश्च संभाव्यता एकता में एकीकृत हो जाती है।
परीक्षणों की कुल संख्या के लिए सफलताओं की संख्या का अनुपात द्विपद स्तिथियों में पर्याप्त आंकड़ा है, जो निम्नलिखित परिणामों के लिए प्रासंगिक है।
'बेयस पूर्व संभाव्यता (बीटा (1,1)) के लिए, पश्च संभाव्यता है:
जेफरीज़ की पूर्व संभावना (बीटा (1/2,1/2)) के लिए, पश्च संभावना है:
और हाल्डेन पूर्व संभावना (बीटा (0,0)) के लिए, पश्च संभावना है:
उपरोक्त भावों से यह पता चलता है कि s/n = 1/2 के लिए) उपरोक्त सभी तीन पूर्व संभावनाओं का परिणाम पश्च संभाव्यता माध्य = मोड = 1/2 के लिए समान स्थान पर होता है। s/n < 1/2 के लिए, निम्नलिखित प्राथमिकताओं का उपयोग करते हुए,उपयोग किया जाता है इसके पश्चात् की संभावनाओं का कारण इस प्रकार है: बेयस पूर्व के लिए कारण जेफरीस पूर्व के लिए कारण हाल्डेन पूर्व के लिए कारण। s/n > 1/2 के लिए इन असमानताओं के क्रम को उलट दिया जाता है जैसे कि हाल्डेन पूर्व संभाव्यता का परिणाम सबसे बड़ा पश्च माध्य होता है। हाल्डेन पूर्व संभाव्यता बीटा (0,0) माध्य (अगले परीक्षण में सफलता की संभावना के लिए अपेक्षित मान) के साथ पश्च संभाव्यता घनत्व का परिणाम है, जो परीक्षणों की कुल संख्या के लिए सफलताओं की संख्या के अनुपात s/n के समान है। . इसलिए, हाल्डेन पूर्व परिणाम अगले परीक्षण में अपेक्षित मूल्य के साथ अधिकतम संभावना के सामान्तर पश्च संभाव्यता में परिणाम देता है। बेयस पूर्व संभाव्यता बीटा (1,1) अनुपात s/n (अधिकतम संभावना) के समान मोड के साथ पश्च संभाव्यता घनत्व में परिणाम देता है।
इस स्तिथियों में यह है कि 100% परीक्षण सफल रहे हैं s= n, बेयस पूर्व संभावना बीटा (1,1) के परिणामस्वरूप उत्तराधिकार के नियम (n + 1)/(n + 2) के सामान्तर पश्च प्रत्याशित मान होता है, जबकि हाल्डेन पूर्व बीटा (0,0) का परिणाम 1 के पश्चात् के अपेक्षित मूल्य (अगले परीक्षण में सफलता की पूर्ण निश्चितता) में होता है। जेफ़रीज़ पूर्व संभाव्यता के परिणामस्वरूप (n + 1/2)/(n + 1) के सामान्तर पश्च प्रत्याशित मान होता है। सुविधाएं[62](पृष्ठ 303) बताते हैं: यह उत्तराधिकार का नया नियम प्रदान करता है और लेने के लिए 'उचित' स्थिति को व्यक्त करता है, अर्थात्, एन सफलताओं के अटूट रन के पश्चात् हम अगले परीक्षण के लिए संभावना मानते हैं कि हम इस धारणा के सामान्तर हैं औसत रन के लगभग आधे रास्ते पर हैं, अर्थात हम (2n + 2) परीक्षणों में बार विफलता की उम्मीद करते हैं। बेयस-लाप्लास नियम का तात्पर्य है कि हम औसत रन के अंत के समीप हैं या हम (n + 2) परीक्षणों में बार विफलता की उम्मीद करते हैं। तुलना स्पष्ट रूप से 'तर्कसंगतता' के दृष्टिकोण से नए परिणाम (जिसे अब जेफ़रीज़ प्रायर कहा जाता है) का समर्थन करती है।
इसके विपरीत, इस स्तिथियों में है कि 100% परीक्षणों के परिणाम स्वरूप विफलता (s = 0) हुई है, बेज़ पूर्व संभाव्यता बीटा (1,1) के परिणाम 1/(n + के सामान्तर अगले परीक्षण में सफलता के लिए अपेक्षित मान हैं। 2), जबकि हाल्डेन पूर्व बीटा (0,0) का परिणाम 0 के अगले परीक्षण में सफलता के पश्चात् के अपेक्षित मूल्य में होता है (अगले परीक्षण में विफलता की पूर्ण निश्चितता)। जेफ़्रीज़ की पूर्व संभाव्यता का परिणाम अगले परीक्षण में सफलता के लिए अपेक्षित पश्चगामी मान होता है, जो (1/2)/(n + 1) के सामान्तर होता है, जिसका फ़ायदा होता है[62](पृष्ठ 303) बताते हैं: बेयस-लाप्लास परिणाम 1/(एन + 2) की तुलना में कहीं अधिक उचित रूप से दूरस्थ परिणाम है।
जेनेस[53]प्रश्न (वर्दी पूर्व बीटा (1,1) के लिए) स्थितियों के लिए इन सूत्रों का उपयोग s = 0 या s = n होगा क्योंकि इंटीग्रल अभिसरण नहीं करते हैं (बीटा (1,1) s = 0 या के लिए अनुचित पूर्व है s = n) होगा । व्यवहार में, पूर्व बेज़ के लिए दोनों सिरों के मध्य मोड के उपस्थित होने के लिए आवश्यक 0<s<n नियममों में सामान्यतः पूरी होती हैं, और इसलिए बेज़ पूर्व (0 < s < n तक) का परिणाम दोनों के मध्य स्थित पश्च मोड में होता है डोमेन के अंत तक होता है ।
जैसा कि उत्तराधिकार के नियम पर अनुभाग में टिप्पणी की गई है, के. पियर्सन ने दिखाया कि n परीक्षणों में n सफलताओं के पश्चात् पश्च संभाव्यता (पूर्व संभाव्यता के रूप में बेयस बीटा (1,1) वितरण के आधार पर) कि अगला (n + 1) परीक्षण सभी सफल होंगे,जो कि ठीक 1/2 है, चाहे n का मान कुछ भी हो। जिसके पूर्व संभाव्यता के रूप में हाल्डेन बीटा (0,0) वितरण के आधार पर होता है , यह पश्च संभाव्यता 1 है (पूर्ण निश्चितता है कि n परीक्षणों में n सफलताओं के पश्चात् अगला (n + 1) परीक्षण सभी सफल होंगे)। सुविधाएं[62](पृ. 303) दर्शाता है कि, जिसे अब जेफ़रीज़ प्रायर के नाम से जाना जाता है, उसके लिए यह प्रायिकता ((n + 1/2)/(n + 1))((n + 3/2)/(n + 2) है )...(2n + 1/2)/(2n + 1), जो n = 1, 2, 3 के लिए 15/24, 315/480, 9009/13440 देता है; तेजी से सीमित मूल्य के समीप पहुंच रहा है n के रूप में अनंत की ओर जाता है। पर्क्स टिप्पणी करते हैं कि जिसे अब जेफ़रीज़ प्रायर के रूप में जाना जाता है: स्पष्ट रूप से या तब बेज़-लाप्लास परिणाम या जेफ़रीज़ द्वारा अस्वीकार किए गए (हाल्डेन) वैकल्पिक नियम के परिणाम की तुलना में अधिक 'उचित' है जो संभाव्यता के रूप में निश्चितता देता है। यह स्पष्ट रूप से प्रेरण की प्रक्रिया के साथ बहुत उत्तम पत्राचार प्रदान करता है। क्या यह उद्देश्य के लिए 'बिल्कुल' उचित है, अर्थात क्या यह अभी तक अधिक बड़ा है, एकता तक पहुंचने की बेतुकापन के बिना, यह तय करने का स्तिथि है। किन्तु यह अनुभूत किया जाना चाहिए कि परिणाम प्रतिरूप करण प्रयोग से पहले पूर्ण उदासीनता और ज्ञान की अनुपस्थिति की धारणा पर निर्भर करता है।
इन तीन पूर्व संभाव्यता वितरणों के साथ प्राप्त पश्च वितरण के प्रसरण निम्नलिखित हैं:
बेयस की पूर्व संभावना (बीटा (1,1)) के लिए, पश्च विचरण है:
जेफरीज़ की पूर्व संभावना (बीटा (1/2,1/2)) के लिए, पश्च विचरण है:
और हाल्डेन पूर्व संभावना (बीटा (0,0)) के लिए, पश्च विचरण है:
तब, जैसा कि सिल्वे ने टिप्पणी की,[51]बड़े n के लिए, विचरण छोटा है और इसलिए पश्च वितरण अत्यधिक केंद्रित है, जबकि माना गया पूर्व वितरण बहुत फैला हुआ था। यह इस बात के अनुरूप है कि कोई क्या उम्मीद करेगा, क्योंकि अस्पष्ट पूर्व ज्ञान (बेयस प्रमेय के माध्यम से) सूचनात्मक प्रयोग द्वारा अधिक स्पष्ट पश्च ज्ञान में परिवर्तित हो जाता है। छोटे n के लिए हल्डेन बीटा (0,0) सबसे बड़े पश्च विचरण में पूर्व परिणाम जबकि बेयस बीटा (1,1) पूर्व परिणाम अधिक केंद्रित पश्च में। जेफ़्रीज़ पूर्व बीटा (1/2,1/2) के परिणाम स्वरूप अन्य दो के मध्य पश्च विचरण होता है। जैसे-जैसे n बढ़ता है, वैरियंस तेजी से घटता जाता है जिससे कि तीनों पूर्ववर्तियों के लिए पश्च विचरण लगभग समान मान में ही परिवर्तित हो जाता है (शून्य प्रसरण के रूप में n → ∞)। पिछले परिणाम को याद करते हुए कि हाल्डेन पूर्व संभाव्यता बीटा (0,0) का परिणाम माध्य के साथ पश्च संभाव्यता घनत्व (अगले परीक्षण में सफलता की संभावना के लिए अपेक्षित मूल्य) के समान सफलताओं की संख्या के अनुपात s/n के समान है। परीक्षणों की कुल संख्या, यह उपरोक्त अभिव्यक्ति से अनुसरण करता है कि हाल्डेन पूर्व बीटा (0,0) परिणाम भी अधिकतम के संदर्भ में व्यक्त भिन्नता के समान भिन्नता के साथ पश्च में होता है। संभावना अनुमान s/n और प्रतिरूप आकार (में § विचरण):
कारण μ=s/n और प्रतिरूप आकार ν=n के साथ।
बायेसियन अनुमान में, द्विपद वितरण से पहले पूर्व वितरण बीटा (α प्रायर, β प्रायर) का उपयोग करना सफलता की वास्तविक संख्या में (α प्रायर − 1) छद्म-अवलोकन और (β प्रायर − 1) विफलता की छद्म-अवलोकन जोड़ने के सामान्तर है और विफलताओं का अवलोकन किया जाता है ,उसके बाद फिर वास्तविक और छद्म-अवलोकन दोनों पर सफलताओं के अनुपात द्वारा द्विपद वितरण के मापदंड p का अनुमान लगाया जाता है । समान पूर्व बीटा(1,1) किसी छद्म अवलोकन को नहीं जोड़ता (या घटाता) है क्योंकि बीटा(1,1) के लिए यह (α प्रायर − 1) = 0 और (β प्रायर − 1) =0 का अनुसरण करता है। बीटा (0,0) प्रत्येक से छद्म अवलोकन घटाता है और जेफरीस पूर्व बीटा (1/2,1/2) सफलता के 1/2 छद्म-अवलोकन और विफलता की समान संख्या घटाता है। इस घटाव का पश्च वितरण को सुचारू करने का प्रभाव है। यदि सफलताओं का अनुपात αप्रायर और βप्रायर के 50% (s/n ≠ 1/2) मान 1 से कम नहीं है (और इसलिए ऋणात्मक (α प्रायर − 1) और (β प्रायर − 1)) स्पार्सिटी का पक्ष लेते हैं, अर्थात वितरण जहां मापदंड p या तब 0 या 1 के समीप है। वास्तव में, 0 और 1 के मध्य αप्रायर और βप्रायर के मान, साथ संचालन करते समय, एकाग्रता मापदंड के रूप में कार्य करते हैं।
संलग्न प्लॉट प्रतिरूप आकार n ∈ {3,10,50}, सफलताओं s ∈ {n/2,n/4} और बीटा(α प्रायर,β प्रायर) ∈ {बीटा(0,0), बीटा (1/2,1/2), बीटा (1,1)}। n={4,12,40}, Success s={n/4} और बीटा(α प्रायर,β प्रायर) ∈ { बीटा(0,0),बीटा(1/2,1/2) के स्तिथियाँ भी दिखाए गए हैं , बीटा (1,1)}। पहला प्लॉट सक्सेस s ∈ {n/2} के लिए मीन = मोड = 1/2 के साथ सिमेट्रिक केस दिखाता है और दूसरा प्लॉट विषम केस s ∈ {n/4} दिखाता है। छवियों से पता चलता है कि 50 के प्रतिरूप के आकार के साथ पश्च के लिए पूर्वों के मध्य थोड़ा अंतर है (पी = 1/2 के पास अधिक स्पष्ट शिखर द्वारा विशेषता)। बहुत छोटे प्रतिरूप आकार के लिए महत्वपूर्ण अंतर दिखाई देते हैं (विशेष रूप से प्रतिरूप आकार के पतित स्तिथियों के लिए चापलूसी वितरण के लिए = 3)। इसलिए, विषम स्तिथियाँ , सफलताओं के साथ = {n/4}, सममित स्थितियों की तुलना में, छोटे प्रतिरूप के आकार में, पूर्व की पसंद से बड़ा प्रभाव दिखाते हैं। सममित वितरण के लिए, बेयस पूर्व बीटा (1,1) का परिणाम सबसे वेरिएबल म और उच्चतम पश्च वितरण में होता है और हाल्डेन पूर्व बीटा (0,0) का परिणाम सबसे सपाट और निम्नतम शिखर वितरण होता है। जेफरीज़ पूर्व बीटा (1/2,1/2) उनके मध्य में है। लगभग सममित, बहुत अधिक विषम वितरण के लिए, पुरोहितबं का प्रभाव समान होता है। बहुत छोटे प्रतिरूप के आकार के लिए (इस स्तिथियों में 3 के प्रतिरूप के आकार के लिए) और विषम वितरण (इस उदाहरण में s ∈ {n/4} के लिए) हाल्डेन पूर्व में विलक्षणता के साथ रिवर्स-j-आकार का वितरण हो सकता है बायाँ छोर। चूंकि, यह केवल पतित स्थितियों में होता है (इस उदाहरण में n = 3 और इसलिए s = 3/4 < 1, पतित मान क्योंकि हल्दाने के पश्च भाग के लिए s को एकता से अधिक होना चाहिए जिससे मध्य में मोड स्थित हो अंत, और क्योंकि s = 3/4 पूर्णांक संख्या नहीं है, इसलिए यह संभावना के लिए द्विपद वितरण की प्रारंभिक धारणा का उल्लंघन करता है) और यह उचित प्रतिरूप आकार के सामान्य स्थितियों में कोई समस्या नहीं है (जैसे कि स्थिति 1 < s < n − 1, मोड के दोनों सिरों के मध्य उपस्थितहोने के लिए आवश्यक है, पूरा हो गया है)।
उनकी किताब जेनेस के अध्याय 12 (पृष्ठ 385) में[53]प्रमाणित करता है कि हाल्डेन पूर्व बीटा (0,0) पूर्ण अज्ञानता के ज्ञान की पूर्व स्थिति का वर्णन करता है, जहां हम यह भी सुनिश्चित नहीं हैं कि किसी प्रयोग के लिए शारीरिक रूप से संभव है या तब सफलता या असफलता, जबकि बेयस (वर्दी) पूर्व बीटा (1,1) प्रयुक्त होता है यदि कोई जानता है कि दोनों बाइनरी परिणाम संभव हैं। जिन्हें जेनेस कहते हैं: बेयस-लाप्लास (बीटा (1,1)) की व्याख्या करने से पहले पूर्ण अज्ञानता की स्थिति का वर्णन नहीं करना चाहिए, किंतु ज्ञान की स्थिति जिसमें हमने सफलता और विफलता देखी है अनेक बार हमने कम से कम देखा है कि सफलता और असफलता तब हम जानते हैं कि प्रयोग भौतिक संभावना के अर्थ में वास्तविक द्विआधारी है। जेनेस [53]विशेष रूप से जेफरीस के पूर्व बीटा (1/2,1/2) पर चर्चा नहीं करता है (पृष्ठ 181, 423 और जेनेस पुस्तक के अध्याय 12 पर जेफ्रीस के पूर्व की जेन्स चर्चा [53]इसके अतिरिक्त जेफरीज़ द्वारा अपनी पुस्तक के 1939 संस्करण में प्रस्तुत किए गए अनुचित, गैर-सामान्यीकृत, पूर्व 1/p dp को संदर्भित करता है,[60]सात साल पहले उन्होंने प्रस्तुत किया था जिसे अब जेफरीस के अपरिवर्तनीय पूर्व के रूप में जाना जाता है: फिशर के सूचना आव्युह के निर्धारक का वर्गमूल। 1/p जेफरीज़' (1946) वेरिएबल घातांकी वितरण से पहले का अपरिवर्तनीय है, बर्नौली या द्विपद वितरणों के लिए नहीं)। चूंकि, उपरोक्त चर्चा से यह पता चलता है कि जेफरीस बीटा (1/2,1/2) पूर्व हल्दाने बीटा (0,0) और बेयस बीटा (1,1) पूर्व के मध्य ज्ञान की स्थिति का प्रतिनिधित्व करता है।
इसी तरह, कार्ल पियर्सन ने अपनी 1892 की पुस्तक विज्ञान का व्याकरण में[69][70] (1900 संस्करण का पृष्ठ 144) ने कहा कि बेज़ (बीटा (1,1) वर्दी पूर्व में पूर्ण अज्ञानता नहीं थी, और यह कि इसका उपयोग तब किया जाना चाहिए जब पूर्व सूचना हमारी अज्ञानता को समान रूप से वितरित करने के लिए उचित हो। के. पियर्सन ने लिखा: फिर भी ऐसा लगता है कि हमने जो एकमात्र अनुमान लगाया है वह यह है: प्रकृतिक, दिनचर्या और विसंगति के बारे में कुछ भी नहीं जानना (ग्रीक ανομία से, अर्थात्: ए- बिना, और नोमोस नियम) को समान रूप से घटित होने की संभावना के रूप में माना जाता है। अब हम इस धारणा को बनाने में वास्तव में न्याय संगत नहीं थे, क्योंकि इसमें ऐसा ज्ञान सम्मिलित है जो हमारे पास प्रकृति के संबंध में नहीं है। हम सामान्य रूप से सिक्कों की संरचना और कार्रवाई के अपने अनुभव का उपयोग यह प्रमाणित करने के लिए करते हैं कि सिर और टेल समान रूप से संभावित हैं, किन्तु हमारे पास कोई नहीं है अनुभव से पहले प्रमाणित करने का अधिकार कि, जैसा कि हम प्रकृति के बारे में कुछ भी नहीं जानते हैं, दिनचर्या और उल्लंघन समान रूप से संभावित हैं। हमारी अज्ञानता में हमें अनुभव से पहले विचार करना चाहिए कि प्रकृति में सभी दिनचर्या , सभी विसंगतियाँ (सामान्यता), या दोनों का मिश्रण सम्मिलित हो सकता है। इसमें y का अनुपात जो भी हो, और यह कि सभी समान रूप से संभावित हैं। अनुभव के पश्चात् इनमें से कौन सा संविधान सबसे अधिक संभावित है, यह स्पष्ट रूप से इस बात पर निर्भर होना चाहिए कि वह अनुभव कैसा रहा है।
यदि पर्याप्त प्रतिरूप (सांख्यिकी) है, और पश्च संभाव्यता मोड डोमेन (x = 0 या x = 1) के वेरिएबल सीमाओं में से पर स्थित नहीं है, बेयस के तीन पूर्व (बीटा (1,1)), जेफरीस (बीटा(1/2,1/2)) और हाल्डेन (बीटा(0,0)) को समान पश्च संभाव्यता घनत्व प्राप्त करना चाहिए। अन्यथा, गेलमैन एट अल के रूप में।[71] (पृष्ठ 65) इंगित करें, यदि इतने कम डेटा उपलब्ध हैं कि गैर-सूचनात्मक पूर्व वितरण के विकल्प से फर्क पड़ता है, तब किसी को प्रासंगिक जानकारी को पूर्व वितरण में या बर्जर के रूप में रखना चाहिए[10](पृ. 125) इंगित करता है कि जब अलग-अलग उचित प्राथमिकताएं पर्याप्त रूप से अलग-अलग उत्तर देती हैं, तब क्या यह कहना सही हो सकता है कि ही उत्तर है? क्या यह स्वीकार करना उत्तम नहीं होगा कि पूर्व मान्यताओं के आधार पर निष्कर्ष के साथ वैज्ञानिक अनिश्चितता है?
घटना और अनुप्रयोग
आदेश आँकड़े
ऑर्डर सांख्यिकी के सिद्धांत में बीटा वितरण का महत्वपूर्ण अनुप्रयोग है। मूल परिणाम यह है कि निरंतर समान वितरण (निरंतर) से आकार n के प्रतिरूप के सबसे छोटे kth के वितरण में बीटा वितरण होता है।[40] इस परिणाम का सारांश इस प्रकार है:
इससे, और संभाव्यता अभिन्न परिवर्तन से संबंधित सिद्धांत के अनुप्रयोग से, किसी भी निरंतर वितरण से किसी भी व्यक्तिगत ऑर्डर स्टेटिस्टिक का वितरण प्राप्त किया जा सकता है।[40]
विषयगत तर्क
मानक तर्क में, प्रस्तावों को या तब सही या गलत माना जाता है। इसके विपरीत, व्यक्तिपरक तर्क यह मानता है कि मनुष्य पूर्ण निश्चितता के साथ यह निर्धारित नहीं कर सकता है कि वास्तविक विश्व के बारे में कोई प्रस्ताव बिल्कुल सही है या गलत। व्यक्तिपरक तर्क में द्विआधारी घटनाओं के a पश्चवर्ती संभाव्यता अनुमानों को बीटा वितरण द्वारा दर्शाया जा सकता है।[72]
तरंगिका विश्लेषण
एक तरंगिका तरंग-जैसा दोलन है जिसका आयाम शून्य से प्रारंभिक होता है, बढ़ता है, और फिर वापस शून्य हो जाता है। इसे सामान्यतः संक्षिप्त दोलन के रूप में देखा जा सकता है जो तुरंत क्षय हो जाता है। छोटा लहर का उपयोग अनेक अलग-अलग प्रकार के डेटा से जानकारी निकालने के लिए किया जा सकता है, जिसमें ऑडियो सिग्नल और छवियां सम्मिलित हैं, किन्तु निश्चित रूप से इन्हीं तक सीमित नहीं हैं। इस प्रकार, वेवलेट्स को विशिष्ट गुणों के लिए उद्देश्यपूर्ण रूप से तैयार किया जाता है जो उन्हें संकेत आगे बढ़ाना के लिए उपयोगी बनाते हैं। तरंगिकाएँ समय और आवृत्ति दोनों में स्थानीयकृत होती हैं जबकि मानक फूरियर रूपांतरण केवल आवृत्ति में स्थानीयकृत होता है। इसलिए, मानक फूरियर ट्रांसफ़ॉर्म केवल स्थिर प्रक्रियाओं पर प्रयुक्त होते हैं, जबकि तरंगिकाएँ गैर-स्थिर प्रक्रियाओं पर प्रयुक्त होती हैं। बीटा वितरण के आधार पर निरंतर तरंगिकाओं का निर्माण किया जा सकता है। बीटा तरंगिका[73] हार तरंगों की नरम प्रकार के रूप में देखा जा सकता है जिसका आकार दो आकार के मापदंडों α और β द्वारा ठीक-ठीक है।
संख्या आनुवंशिकी
बैल्डिंग-निकोल्स मॉडल संख्या आनुवंशिकी में उपयोग किए जाने वाले बीटा वितरण का दो-मापदंड सांख्यिकीय मापदंड है।[74] यह उप-विभाजित संख्या के घटकों में एलील आवृत्तियों का सांख्यिकीय विवरण है:
जहाँ और ; जहाँ F दो संख्या के मध्य (राइट की) आनुवंशिक दूरी है।
परियोजना प्रबंधन: कार्य निवेश और अनुसूची मॉडलिंग
बीटा वितरण का उपयोग उन घटनाओं को मॉडल करने के लिए किया जा सकता है जो न्यूनतम और अधिकतम मान द्वारा परिभाषित अंतराल के अंदर होने के लिए विवश हैं। इस कारण से, बीटा वितरण - त्रिकोणीय वितरण के साथ - पीईआरटी, महत्वपूर्ण पथ विधि (सीपीएम), संयुक्त निवेश अनुसूची मॉडलिंग (जेसीएसएम) और अन्य परियोजना प्रबंधन/नियंत्रण प्रणालियों में बड़े पैमाने पर उपयोग किया जाता है जिससेपूरा होने में लगने वाले समय और निवेश का वर्णन किया जा सके किसी कार्य का। परियोजना प्रबंधन में, बीटा वितरण के माध्य और मानक विचलन का अनुमान लगाने के लिए आशुलिपि संगणनाओं का व्यापक रूप से उपयोग किया जाता है:[39]
जहाँ a न्यूनतम है, c अधिकतम है, और b सबसे संभावित मान है (α > 1 और β > 1 के लिए बहुलक (सांख्यिकी)।
माध्य के लिए उपरोक्त अनुमान PERT तीन-बिंदु अनुमान के रूप में जाना जाता है और यह β के निम्न मानों में से किसी के लिए स्पष्ट है (इन सीमाओं के अंदर इच्छानुसार α के लिए):
- β = α > 1 (सममित स्तिथि ) मानक विचलन के साथ , विषमता = 0, और अतिरिक्त ककुदता =
फ़ाइल:बीटा वितरण बीटा=alpha from 1.05 to 4.95.svgया
- β = 6 - α 5 के लिए > α > 1 (विषम स्तिथि ) मानक विचलन के साथ
विषमता = , और अतिरिक्त कर्टोसिस =
फ़ाइल:बीटा वितरण बीटा=6-alpha from 1.05 to 4.95.svg
मानक विचलन σ(X) = (c - a)/6 के लिए उपरोक्त अनुमान α और β के निम्नलिखित मानों में से किसी के लिए स्पष्ट है:
- α = β = 4 (सममित) विषमता = 0 के साथ, और अतिरिक्त कर्टोसिस = -6/11।
- β = 6 - α और (राइट-टेल्ड, पॉजिटिव विषम) विषमता के साथ , और अतिरिक्त कर्टोसिस = 0
- β = 6 - α और (बाएं-टेल , ऋणात्मक विषम) विषमता के साथ , और अतिरिक्त कर्टोसिस = 0
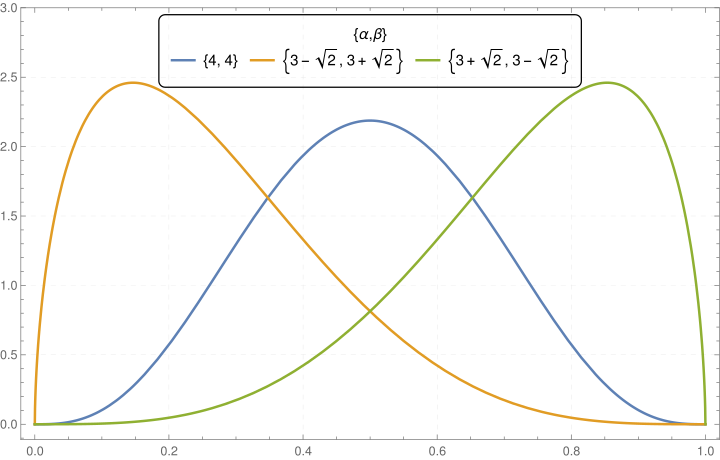 अन्यथा, ये α और β के अन्य मूल्यों के साथ बीटा वितरण के लिए खराब अनुमान हो सकते हैं, माध्य में 40% की औसत त्रुटि और विचरण में 549% प्रदर्शित करते हैं।[75][76][77]
अन्यथा, ये α और β के अन्य मूल्यों के साथ बीटा वितरण के लिए खराब अनुमान हो सकते हैं, माध्य में 40% की औसत त्रुटि और विचरण में 549% प्रदर्शित करते हैं।[75][76][77]
रैंडम वेरिएट जनरेशन
यदि X और Y स्वतंत्र हैं, साथ में और तब
तब बीटा संस्करण उत्पन्न करने के लिए एल्गोरिदम उत्पन्न करना है , जहां X गामा वितरण है#मापदंड (α, 1) के साथ रैंडम वैरिएट जनरेशन और मापदंड (β, 1) के साथ Y स्वतंत्र गामा वेरिएट है।[78] वास्तव में, यहाँ और स्वतंत्र हैं, और . यदि और से स्वतंत्र है और , तब और से स्वतंत्र है . इससे पता चलता है कि स्वतंत्र का उत्पाद और यादृच्छिक वेरिएबल है अनियमित परिवर्तनशील वस्तु।
साथ ही, n यूनिफ़ॉर्म डिस्ट्रीब्यूशन (सतत) वेरियेट्स का kth ऑर्डर स्टेटिस्टिक है , इसलिए विकल्प यदि α और β छोटे पूर्णांक हैं तब α + β - 1 समान वेरिएबल उत्पन्न करना है और α-th सबसे छोटा चुनना है।[40]
बीटा वितरण उत्पन्न करने का दूसरा विधि पोल्या कलश मॉडल है। इस पद्धति के अनुसार, α काली गेंदों और β सफेद गेंदों के साथ कलश से शुरुआत की जाती है और प्रतिस्थापन के साथ समान रूप से खींचा जाता है। प्रत्येक परीक्षण में अतिरिक्त गेंद निकाली गई अंतिम गेंद के रंग के अनुसार जोड़ी जाती है। असीमित रूप से, काले और सफेद गेंदों का अनुपात बीटा वितरण के अनुसार वितरित किया जाएगा, जहां प्रयोग की प्रत्येक पुनरावृत्ति अलग मान उत्पन्न करेगी।
उलटा रूपांतरण प्रतिरूप करण का उपयोग करना भी संभव है।
बीटा वितरण के लिए सामान्य सन्निकटन
एक बीटा वितरण α ~ β और α और β >> 1 औसत 1/2 और विचरण 1/4 (2α + 1) के साथ लगभग सामान्य है। यदि α ≥ β के व्युत्क्रम के लघुगणक का घनमूल लेकर सामान्य सन्निकटन में सुधार किया जा सकता है [79]
इतिहास
थॉमस बेयस, मरणोपरांत पेपर में [63] रिवेरिएबल ्ड प्राइस द्वारा 1763 में प्रकाशित, बर्नौली परीक्षणों में सफलता की संभावना के घनत्व के रूप में बीटा वितरण प्राप्त किया (देखें § अनुप्रयोग, बायेसियन अनुमान), किन्तुपेपर बीटा वितरण के किसी भी पल का विश्लेषण नहीं करता है या इसके किसी भी गुण पर चर्चा नहीं करता है।
बीटा वितरण की पहली व्यवस्थित आधुनिक चर्चा संभवतः कार्ल पियर्सन के कारण है।[80][81] पियर्सन के कागजात में[22][34]बीटा वितरण को अंतर समीकरण के समाधान के रूप में जोड़ा गया है: पियर्सन वितरण | पियर्सन का प्रकार I वितरण जो इच्छानुसार से स्थानांतरण और पुन: स्केलिंग को छोड़कर अनिवार्य रूप से समान है (बीटा और पियर्सन प्रकार I वितरण सदैव उचित विकल्प द्वारा सामान्तर किया जा सकता है मापदंड)। वास्तव में, द्वितीय विश्व युद्ध से पहले कुछ दशकों में अनेक अंग्रेजी पुस्तकों और जर्नल लेखों में, बीटा वितरण को पियर्सन के टाइप I वितरण के रूप में संदर्भित करना सामान्य बात थी। विलियम पॉलिन एल्डर्टन|(विलियम पी. एल्डर्टन) अपने 1906 मोनोग्राफ में आवृत्ति घटता और सहसंबंध[43] पियर्सन के टाइप I वितरण के रूप में बीटा वितरण का और विश्लेषण करता है, जिसमें चार मापदंड स्तिथियों के लिए क्षणों की विधि की पूरी चर्चा सम्मिलित है, और आरेख (जो एल्डर्टन के रूप में वर्णित है) u-आकार, j-आकार, मुड़ j-आकार, कॉक्ड- टोपी के आकार, क्षैतिज और कोण वाली सीधी रेखा के स्तिथियाँ । एल्डर्टन ने लिखा है कि मैं मुख्य रूप से प्रोफेसर पियर्सन का ऋणी हूं, किन्तुऋण प्रकार का है जिसके लिए औपचारिक धन्यवाद देना असंभव है। विलियम पॉलिन एल्डर्टन ने अपने 1906 के मोनोग्राफ में [43]मोड के रूप में चुने गए वितरण की उत्पत्ति के लिए समीकरणों सहित बीटा वितरण पर प्रभावशाली जानकारी प्रदान करता है, साथ ही साथ अन्य पियर्सन वितरणों के लिए: प्रकार I से VII तक। एल्डर्टन ने बीटा और गामा कार्यों पर परिशिष्ट (II) सहित अनेक परिशिष्ट भी सम्मिलित किए। पश्चात् के संस्करणों में, एल्डर्टन ने माध्य के रूप में चुने गए वितरण की उत्पत्ति के लिए समीकरण जोड़े, और पियर्सन वितरण VIII से XII तक का विश्लेषण किया।
जैसा कि बोमन और शेंटन ने टिप्पणी की है[45]फ़िशर और पियर्सन के मध्य (मापदंड) अनुमान के दृष्टिकोण में मतभेद था, विशेष रूप से (पियर्सन की विधि) क्षणों से संबंधित और (फ़िशर की विधि) बीटा वितरण के स्तिथियों में अधिकतम संभावना। साथ ही बोमन और शेंटन के अनुसार, प्रकार I (बीटा वितरण) मॉडल के विवाद का केंद्र होने का स्तिथि विशुद्ध संयोग था। 4 मापदंडों का अधिक कठिन मॉडल खोजना कठिन होता। कार्ल पियर्सन के साथ फिशर के लंबे समय से चल रहे सार्वजनिक संघर्ष को प्रतिष्ठित पत्रिकाओं में अनेक लेखों में देखा जा सकता है। उदाहरण के लिए, बीटा वितरण के लिए चार मापदंडों के अनुमान के संबंध में, और फिशर की पियर्सन की पलों की पद्धति की मनमानी के रूप में आलोचना, पियर्सन का लेख देखें क्षणों की विधि और अधिकतम संभावना की विधि [46] (यूनिवर्सिटी कॉलेज, लंदन से उनकी सेवानिवृत्ति के तीन साल पश्चात् प्रकाशित, जहां उनकी स्थिति फिशर और पियर्सन के बेटे एगॉन के मध्य विभाजित हो गई थी) जिसमें पियर्सन ने लिखा है कि मैंने पढ़ा (रॉयल स्टैटिस्टिकल सोसाइटी के जर्नल में कोशाई का पेपर, 1933) जो जहाँ तक है मुझे पता है कि वर्तमान में प्रोफेसर फिशर की विधि के आवेदन का एकमात्र स्तिथि प्रकाशित हुआ है। मेरे विस्मय के लिए यह विधि पहले (पियर्सन) मेथड ऑफ मोमेंट्स द्वारा फ़्रीक्वेंसी कर्व के कॉन्स्टेंट को काम करने पर निर्भर करती है और फिर उस पर सुपरपोज़िंग करती है, जिसे फ़िशर अधिकतम संभावना की विधि के अनुसार प्राप्त करने के लिए और सन्निकटन बताता है, वह क्या रखता है, वह इस प्रकार वक्र स्थिरांकों के अधिक कुशल मान प्राप्त होंगे।
आंकड़ों के इतिहास पर डेविड और एडवर्ड्स का ग्रंथ[82] 1911 में, बीटा वितरण के पहले आधुनिक उपचार का हवाला देते हैं,[83] इतालवी सांख्यिकीविद्, जनसांख्यिकी और समाजशास्त्र, कॉनराड गिन्नी के कारण बीटा पदनाम का उपयोग करना मानक बन गया है, जिन्होंने गिनी गुणांक विकसित किया था। नॉर्मन लॉयड जॉनसन|(एन.एल.जॉनसन) और सैमुअल कोटज़|(एस.कोट्ज़,) अपने व्यापक और बहुत ही सूचनात्मक मोनोग्राफ में[84] सांख्यिकीय विज्ञान क्रेडिट कोराडो गिन्नी में प्रमुख ऐतिहासिक व्यक्तित्वों पर[85] प्रारंभिक बायेसियन के रूप में ... जिन्होंने प्रारंभिक बीटा वितरण के मापदंडों को अलग करने की समस्या से निपटा, एकल विधियों द्वारा जो तथाकथित अनुभवजन्य बेयस दृष्टिकोण के आगमन की आशंका थी।
संदर्भ
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 1.25 Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1995). "Chapter 25:Beta Distributions". Continuous Univariate Distributions Vol. 2 (2nd ed.). Wiley. ISBN 978-0-471-58494-0.
- ↑ Keeping, E. S. (2010). सांख्यिकीय निष्कर्ष का परिचय. Dover Publications. ISBN 978-0486685021.
- ↑ 3.0 3.1 3.2 Wadsworth, George P. and Joseph Bryan (1960). संभाव्यता और यादृच्छिक चर का परिचय. McGraw-Hill.
- ↑ 4.0 4.1 Hahn, Gerald J.; Shapiro, S. (1994). इंजीनियरिंग में सांख्यिकीय मॉडल (विली क्लासिक्स लाइब्रेरी). Wiley-Interscience. ISBN 978-0471040651.
- ↑ 5.0 5.1 5.2 5.3 5.4 Feller, William (1971). An Introduction to Probability Theory and Its Applications, Vol. 2. Wiley. ISBN 978-0471257097.
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 Gupta, Arjun K., ed. (2004). हैंडबुक ऑफ़ बीटा डिस्ट्रीब्यूशन एंड इट्स एप्लीकेशन्स. CRC Press. ISBN 978-0824753962.
- ↑ 7.0 7.1 7.2 Panik, Michael J (2005). प्रारंभिक दृष्टिकोण से उन्नत सांख्यिकी. Academic Press. ISBN 978-0120884940.
- ↑ 8.0 8.1 Rose, Colin; Smith, Murray D. (2002). गणित के साथ गणितीय सांख्यिकी. Springer. ISBN 978-0387952345.
- ↑ 9.0 9.1 9.2 Kruschke, John K. (2011). Doing Bayesian data analysis: A tutorial with R and BUGS. p. 83: Academic Press / Elsevier. ISBN 978-0123814852.
{{cite book}}: CS1 maint: location (link) - ↑ 10.0 10.1 Berger, James O. (2010). सांख्यिकीय निर्णय सिद्धांत और बायेसियन विश्लेषण (2nd ed.). Springer. ISBN 978-1441930743.
- ↑ Kruschke, John K. (2015). Doing Bayesian Data Analysis: A Tutorial with R, JAGS and Stan. Academic Press / Elsevier. ISBN 978-0-12-405888-0.
- ↑ 12.0 12.1 Kerman J (2011) "A closed-form approximation for the median of the beta distribution". arXiv:1111.0433v1
- ↑ Mosteller, Frederick and John Tukey (1977). Data Analysis and Regression: A Second Course in Statistics. Addison-Wesley Pub. Co. Bibcode:1977dars.book.....M. ISBN 978-0201048544.
- ↑ 14.0 14.1 Feller, William (1968). प्रायिकता सिद्धांत और उसके आवेदन के लिए एक परिचय. Vol. 1 (3rd ed.). ISBN 978-0471257080.
- ↑ Philip J. Fleming and John J. Wallace. How not to lie with statistics: the correct way to summarize benchmark results. Communications of the ACM, 29(3):218–221, March 1986.
- ↑ "NIST/SEMATECH e-Handbook of Statistical Methods 1.3.6.6.17. Beta Distribution". National Institute of Standards and Technology Information Technology Laboratory. April 2012. Retrieved May 31, 2016.
- ↑ Oguamanam, D.C.D.; Martin, H. R.; Huissoon, J. P. (1995). "गियर क्षति विश्लेषण के लिए बीटा वितरण के अनुप्रयोग पर". Applied Acoustics. 45 (3): 247–261. doi:10.1016/0003-682X(95)00001-P.
- ↑ Zhiqiang Liang; Jianming Wei; Junyu Zhao; Haitao Liu; Baoqing Li; Jie Shen; Chunlei Zheng (27 August 2008). "कर्टोसिस का सांख्यिकीय अर्थ और भूकंपीय संकेतों के आधार पर व्यक्तियों की पहचान के लिए इसका नया अनुप्रयोग". Sensors. 8 (8): 5106–5119. Bibcode:2008Senso...8.5106L. doi:10.3390/s8085106. PMC 3705491. PMID 27873804.
- ↑ 19.0 19.1 19.2 19.3 Abramowitz, Milton and Irene A. Stegun (1965). सूत्र, रेखांकन और गणितीय तालिकाओं के साथ गणितीय कार्यों की पुस्तिका. Dover. ISBN 978-0-486-61272-0.
- ↑ Kenney, J. F., and E. S. Keeping (1951). Mathematics of Statistics Part Two, 2nd edition. D. Van Nostrand Company Inc.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Weisstein., Eric W. "कुकुदता". MathWorld--A Wolfram Web Resource. Retrieved 13 August 2012.
- ↑ 22.0 22.1 22.2 22.3 22.4 22.5 Pearson, Karl (1916). "Mathematical contributions to the theory of evolution, XIX: Second supplement to a memoir on skew variation". Philosophical Transactions of the Royal Society A. 216 (538–548): 429–457. Bibcode:1916RSPTA.216..429P. doi:10.1098/rsta.1916.0009. JSTOR 91092.
- ↑ Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich; Geronimus, Yuri Veniaminovich; Tseytlin, Michail Yulyevich; Jeffrey, Alan (2015) [October 2014]. Zwillinger, Daniel; Moll, Victor Hugo (eds.). इंटीग्रल्स, सीरीज़ और उत्पादों की तालिका (in English). Translated by Scripta Technica, Inc. (8 ed.). Academic Press, Inc. ISBN 978-0-12-384933-5. LCCN 2014010276.
- ↑ Buchanan, Kris; Wheeland, Sara; Flores, Carlos; Overturf, Drew; Adeyemi, Timi; Acevedo, Vincent; Huff, Gregory (2020). "Analysis of Collaborative Beamforming for Circularly Bound Random Antenna Array Distributions". doi:10.13140/RG.2.2.16399.71848.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Billingsley, Patrick (1995). "30". संभाव्यता और माप (3rd ed.). Wiley-Interscience. ISBN 978-0-471-00710-4.
- ↑ 26.0 26.1 MacKay, David (2003). सूचना सिद्धांत, अनुमान और लर्निंग एल्गोरिदम. Cambridge University Press; First Edition. Bibcode:2003itil.book.....M. ISBN 978-0521642989.
- ↑ 27.0 27.1 Johnson, N.L. (1949). "अनुवाद के तरीकों द्वारा उत्पन्न आवृत्ति वक्रों की प्रणाली" (PDF). Biometrika. 36 (1–2): 149–176. doi:10.1093/biomet/36.1-2.149. hdl:10338.dmlcz/135506. PMID 18132090.
- ↑ Verdugo Lazo, A. C. G.; Rathie, P. N. (1978). "निरंतर संभाव्यता वितरण की एन्ट्रापी पर". IEEE Trans. Inf. Theory. 24 (1): 120–122. doi:10.1109/TIT.1978.1055832.
- ↑ Shannon, Claude E. (1948). "संचार का एक गणितीय सिद्धांत". Bell System Technical Journal. 27 (4): 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x.
- ↑ 30.0 30.1 30.2 Cover, Thomas M. and Joy A. Thomas (2006). Elements of Information Theory 2nd Edition (Wiley Series in Telecommunications and Signal Processing). Wiley-Interscience; 2 edition. ISBN 978-0471241959.
- ↑ Plunkett, Kim, and Jeffrey Elman (1997). Exercises in Rethinking Innateness: A Handbook for Connectionist Simulations (Neural Network Modeling and Connectionism). A Bradford Book. p. 166. ISBN 978-0262661058.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Nallapati, Ramesh (2006). The smoothed dirichlet distribution: understanding cross-entropy ranking in information retrieval (Thesis). Computer Science Dept., University of Massachusetts Amherst.
- ↑ 33.0 33.1 Pearson, Egon S. (July 1969). "फ़्रीक्वेंसी कर्व्स के उपयोग के विकास के माध्यम से कुछ ऐतिहासिक प्रतिबिंबों का पता लगाया गया". THEMIS Statistical Analysis Research Program, Technical Report 38. Office of Naval Research, Contract N000014-68-A-0515 (Project NR 042–260).
- ↑ 34.0 34.1 Pearson, Karl (1895). "Contributions to the mathematical theory of evolution, II: Skew variation in homogeneous material". Philosophical Transactions of the Royal Society. 186: 343–414. Bibcode:1895RSPTA.186..343P. doi:10.1098/rsta.1895.0010. JSTOR 90649.
- ↑ Buchanan, K.; Rockway, J.; Sternberg, O.; Mai, N. N. (May 2016). "सर्कुलर पतला यादृच्छिक सरणी का उपयोग कर रडार अनुप्रयोगों के लिए सम-अंतर बीमफॉर्मिंग". 2016 IEEE Radar Conference (RadarConf): 1–5. doi:10.1109/RADAR.2016.7485289. ISBN 978-1-5090-0863-6. S2CID 32525626.
- ↑ Buchanan, K.; Flores, C.; Wheeland, S.; Jensen, J.; Grayson, D.; Huff, G. (May 2017). "राडार अनुप्रयोगों के लिए ट्रांसमिट बीमफॉर्मिंग गोलाकार टेपर्ड रैंडम ऐरे का उपयोग करते हुए". 2017 IEEE Radar Conference (RadarConf): 0112–0117. doi:10.1109/RADAR.2017.7944181. ISBN 978-1-4673-8823-8. S2CID 38429370.
- ↑ Ryan, Buchanan, Kristopher (2014-05-29). "एपेरियोडिक (यादृच्छिक) चरणबद्ध सारणियों का सिद्धांत और अनुप्रयोग" (in English).
{{cite journal}}: Cite journal requires|journal=(help)CS1 maint: multiple names: authors list (link) - ↑ Herrerías-Velasco, José Manuel and Herrerías-Pleguezuelo, Rafael and René van Dorp, Johan. (2011). Revisiting the PERT mean and Variance. European Journal of Operational Research (210), p. 448–451.
- ↑ 39.0 39.1 Malcolm, D. G.; Roseboom, J. H.; Clark, C. E.; Fazar, W. (September–October 1958). "अनुसंधान और विकास कार्यक्रम मूल्यांकन के लिए एक तकनीक का अनुप्रयोग". Operations Research. 7 (5): 646–669. doi:10.1287/opre.7.5.646. ISSN 0030-364X.
- ↑ 40.0 40.1 40.2 40.3 David, H. A., Nagaraja, H. N. (2003) Order Statistics (3rd Edition). Wiley, New Jersey pp 458. ISBN 0-471-38926-9
- ↑ "बीटा वितरण". www.statlect.com.
- ↑ "1.3.6.6.17. Beta Distribution". www.itl.nist.gov.
- ↑ 43.0 43.1 43.2 43.3 43.4 43.5 43.6 43.7 Elderton, William Palin (1906). आवृत्ति-वक्र और सहसंबंध. Charles and Edwin Layton (London).
- ↑ Elderton, William Palin and Norman Lloyd Johnson (2009). फ़्रीक्वेंसी कर्व्स की प्रणाली. Cambridge University Press. ISBN 978-0521093361.
- ↑ 45.0 45.1 45.2 Bowman, K. O.; Shenton, L. R. (2007). "बीटा वितरण, क्षण विधि, कार्ल पियर्सन और आर.ए. मछुआ" (PDF). Far East J. Theo. Stat. 23 (2): 133–164.
- ↑ 46.0 46.1 Pearson, Karl (June 1936). "क्षणों की विधि और अधिकतम संभावना की विधि". Biometrika. 28 (1/2): 34–59. doi:10.2307/2334123. JSTOR 2334123.
- ↑ 47.0 47.1 47.2 Joanes, D. N.; C. A. Gill (1998). "नमूना तिरछापन और कर्टोसिस के उपायों की तुलना करना". The Statistician. 47 (Part 1): 183–189. doi:10.1111/1467-9884.00122.
- ↑ Beckman, R. J.; G. L. Tietjen (1978). "बीटा वितरण के लिए अधिकतम संभावना अनुमान". Journal of Statistical Computation and Simulation. 7 (3–4): 253–258. doi:10.1080/00949657808810232.
- ↑ Gnanadesikan, R.,Pinkham and Hughes (1967). "सबसे छोटे क्रम के आँकड़ों से बीटा वितरण के मापदंडों का अधिकतम संभावना अनुमान". Technometrics. 9 (4): 607–620. doi:10.2307/1266199. JSTOR 1266199.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Fackler, Paul. "उलटा दिग्मा समारोह (मतलब)". Harvard University School of Engineering and Applied Sciences. Retrieved 2012-08-18.
- ↑ 51.0 51.1 51.2 Silvey, S.D. (1975). सांख्यिकीय निष्कर्ष. Chapman and Hal. p. 40. ISBN 978-0412138201.
- ↑ Edwards, A. W. F. (1992). संभावना. The Johns Hopkins University Press. ISBN 978-0801844430.
- ↑ 53.0 53.1 53.2 53.3 53.4 53.5 Jaynes, E.T. (2003). संभाव्यता सिद्धांत, विज्ञान का तर्क. Cambridge University Press. ISBN 978-0521592710.
- ↑ Costa, Max, and Cover, Thomas (September 1983). एंट्रॉपी पावर असमानता और ब्रून मिन्कोव्स्की असमानता की समानता पर (PDF). Tech.Report 48, Dept. Statistics, Stanford University.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ 55.0 55.1 55.2 Aryal, Gokarna; Saralees Nadarajah (2004). "बीटा वितरण के लिए सूचना मैट्रिक्स" (PDF). Serdica Mathematical Journal (Bulgarian Academy of Science). 30: 513–526.
- ↑ 56.0 56.1 Laplace, Pierre Simon, marquis de (1902). संभावनाओं पर एक दार्शनिक निबंध. New York : J. Wiley ; London : Chapman & Hall. ISBN 978-1-60206-328-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Cox, Richard T. (1961). संभावित अनुमान का बीजगणित. The Johns Hopkins University Press. ISBN 978-0801869822.
- ↑ 58.0 58.1 Keynes, John Maynard (2010) [1921]. A Treatise on Probability: The Connection Between Philosophy and the History of Science. Wildside Press. ISBN 978-1434406965.
- ↑ Pearson, Karl (1907). "भविष्य की अपेक्षाओं पर पिछले अनुभव के प्रभाव पर". Philosophical Magazine. 6 (13): 365–378.
- ↑ 60.0 60.1 60.2 60.3 Jeffreys, Harold (1998). संभाव्यता का सिद्धांत. Oxford University Press, 3rd edition. ISBN 978-0198503682.
- ↑ Broad, C. D. (October 1918). "प्रेरण और संभाव्यता के बीच संबंध पर". MIND, A Quarterly Review of Psychology and Philosophy. 27 (New Series) (108): 389–404. doi:10.1093/mind/XXVII.4.389. JSTOR 2249035.
- ↑ 62.0 62.1 62.2 62.3 Perks, Wilfred (January 1947). "व्युत्क्रम संभाव्यता पर कुछ अवलोकन जिसमें एक नया उदासीनता नियम शामिल है". Journal of the Institute of Actuaries. 73 (2): 285–334. doi:10.1017/S0020268100012270.
- ↑ 63.0 63.1 Bayes, Thomas; communicated by Richard Price (1763). "संभावना के सिद्धांत में एक समस्या को हल करने की दिशा में एक निबंध". Philosophical Transactions of the Royal Society. 53: 370–418. doi:10.1098/rstl.1763.0053. JSTOR 105741.
- ↑ Haldane, J.B.S. (1932). "व्युत्क्रम संभाव्यता पर एक नोट". Mathematical Proceedings of the Cambridge Philosophical Society. 28 (1): 55–61. Bibcode:1932PCPS...28...55H. doi:10.1017/s0305004100010495. S2CID 122773707.
- ↑ Zellner, Arnold (1971). अर्थमिति में बायेसियन अनुमान का परिचय. Wiley-Interscience. ISBN 978-0471169376.
- ↑ Jeffreys, Harold (September 1946). "अनुमान समस्याओं में पूर्व संभावना के लिए एक अपरिवर्तनीय प्रपत्र". Proceedings of the Royal Society. A 24. 186 (1007): 453–461. Bibcode:1946RSPSA.186..453J. doi:10.1098/rspa.1946.0056. PMID 20998741.
- ↑ Berger, James; Bernardo, Jose; Sun, Dongchu (2009). "संदर्भ पुरोहितों की औपचारिक परिभाषा". The Annals of Statistics. 37 (2): 905–938. arXiv:0904.0156. Bibcode:2009arXiv0904.0156B. doi:10.1214/07-AOS587. S2CID 3221355.
- ↑ Clarke, Bertrand S.; Andrew R. Barron (1994). "जेफरीज़ का पूर्व एन्ट्रापी जोखिम के तहत विषम रूप से कम से कम अनुकूल है" (PDF). Journal of Statistical Planning and Inference. 41: 37–60. doi:10.1016/0378-3758(94)90153-8.
- ↑ Pearson, Karl (1892). विज्ञान का व्याकरण. Walter Scott, London.
- ↑ Pearson, Karl (2009). विज्ञान का व्याकरण. BiblioLife. ISBN 978-1110356119.
- ↑ Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B. (2003). बायेसियन डेटा विश्लेषण. Chapman and Hall/CRC. ISBN 978-1584883883.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ A. Jøsang. A Logic for Uncertain Probabilities. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems. 9(3), pp.279-311, June 2001. PDF[permanent dead link]
- ↑ H.M. de Oliveira and G.A.A. Araújo,. Compactly Supported One-cyclic Wavelets Derived from Beta Distributions. Journal of Communication and Information Systems. vol.20, n.3, pp.27-33, 2005.
- ↑ Balding, David J.; Nichols, Richard A. (1995). "पहचान और पितृत्व की जांच के लिए बहु-एलील लोकी और इसके प्रभावों पर आबादी के बीच भेदभाव को मापने के लिए एक विधि". Genetica. Springer. 96 (1–2): 3–12. doi:10.1007/BF01441146. PMID 7607457. S2CID 30680826.
- ↑ Keefer, Donald L. and Verdini, William A. (1993). Better Estimation of PERT Activity Time Parameters. Management Science 39(9), p. 1086–1091.
- ↑ Keefer, Donald L. and Bodily, Samuel E. (1983). Three-point Approximations for Continuous Random variables. Management Science 29(5), p. 595–609.
- ↑ "रक्षा संसाधन प्रबंधन संस्थान - नौसेना स्नातकोत्तर स्कूल". www.nps.edu.
- ↑ van der Waerden, B. L., "Mathematical Statistics", Springer, ISBN 978-3-540-04507-6.
- ↑ On normalizing the incomplete beta-function for fitting to dose-response curves M.E. Wise Biometrika vol 47, No. 1/2, June 1960, pp. 173-175
- ↑ Yule, G. U.; Filon, L. N. G. (1936). "Karl Pearson. 1857-1936". Obituary Notices of Fellows of the Royal Society. 2 (5): 72. doi:10.1098/rsbm.1936.0007. JSTOR 769130.
- ↑ "पुस्तकालय और पुरालेख सूची". Sackler Digital Archive. Royal Society. Archived from the original on 2011-10-25. Retrieved 2011-07-01.
- ↑ David, H. A. and A.W.F. Edwards (2001). सांख्यिकी के इतिहास में एनोटेट रीडिंग. Springer; 1 edition. ISBN 978-0387988443.
- ↑ Gini, Corrado (1911). "Considerazioni Sulle Probabilità Posteriori e Applicazioni al Rapporto dei Sessi Nelle Nascite Umane". Studi Economico-Giuridici della Università de Cagliari. Anno III (reproduced in Metron 15, 133, 171, 1949): 5–41.
- ↑ Johnson, Norman L. and Samuel Kotz, ed. (1997). Leading Personalities in Statistical Sciences: From the Seventeenth Century to the Present (Wiley Series in Probability and Statistics. Wiley. ISBN 978-0471163817.
- ↑ Metron journal. "कोराडो गिन्नी की जीवनी". Metron Journal. Archived from the original on 2012-07-16. Retrieved 2012-08-18.
बाहरी संबंध
- "बीटा Distribution" by Fiona Maclachlan, the Wolfram Demonstrations Project, 2007.
- बीटा Distribution – Overview and Example, xycoon.com
- बीटा Distribution, brighton-webs.co.uk
- बीटा Distribution Video, exstrom.com
- "Beta-distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Beta Distribution". MathWorld.
- Harvard University Statistics 110 Lecture 23 बीटा Distribution, Prof. Joe Blitzstein




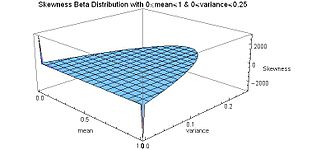

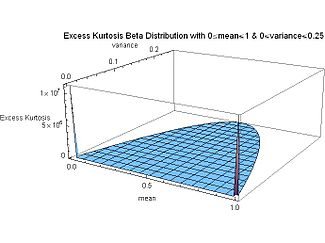



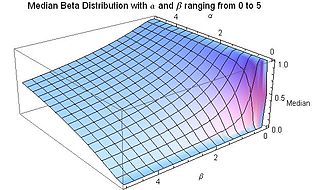

![1 ≤ α ≤ 5 और 1 ≤ β ≤ 5 के लिए बीटा वितरण के लिए ABS [(माध्यिका-Appr.)/मध्यिका]](https://upload.wikimedia.org/wikipedia/commons/thumb/a/af/Relative_Error_for_Approximation_to_Median_of_Beta_Distribution_for_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg/325px-Relative_Error_for_Approximation_to_Median_of_Beta_Distribution_for_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg)
![1≤α≤5 और 1≤β≤5 के लिए बीटा वितरण के लिए Abs[(माध्य-Appr.)/(मीन-मोड)]](https://upload.wikimedia.org/wikipedia/commons/thumb/e/e8/Error_in_Median_Apprx._relative_to_Mean-Mode_distance_for_Beta_Distribution_with_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg/325px-Error_in_Median_Apprx._relative_to_Mean-Mode_distance_for_Beta_Distribution_with_alpha_and_beta_from_1_to_5_-_J._Rodal.jpg)