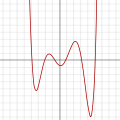बहुपद: Difference between revisions

Revision as of 16:04, 16 September 2022

बहुपद, गणित में वह व्यंजक है जिसमें अनिश्चित पद और गुणांक होते हैं, जिसमें केवल जोड़, घटाव, गुणा, और पद के गैर-ऋणात्मक पूर्णांक घातांक के संचालन सम्मिलित होते हैं। अनिश्चित $x$ के बहुपद का एक उदाहरण: $x 2 - 4 x + 7$ है। तीन चरों में एक उदाहरण: $x 3 + 2 xyz 2 - yz + 1$ है।

गणित और विज्ञान के कई क्षेत्रों में बहुपद उपस्थित होता है। उदाहरण: उनका उपयोग बहुपद समीकरण बनाने के लिए किया जाता है, जो प्राथमिक शब्द समस्याओं से लेकर जटिल वैज्ञानिक समस्याओं तक, समस्याओं की एक विस्तृत श्रृंखला को एन्कोड करते हैं;उनका उपयोग बहुपद फलनको परिभाषित करने के लिए किया जाता है, जो बुनियादी रसायन विज्ञान और भौतिकी से लेकर अर्थशास्त्र और सामाजिक विज्ञान तक की सेटिंग्स में दिखाई देते हैं;वे अन्य फलनको अनुमानित करने के लिए कैलकुलस और संख्यात्मक विश्लेषण में उपयोग किए जाते हैं। उन्नत गणित में, बहुपद का उपयोग बहुपद के वलय और बीजगणितीय विविधता के निर्माण के लिए किया जाता है, जो बीजगणित और बीजगणितीय ज्यामिति में केंद्रीय अवधारणाएं हैं।

व्युत्पत्ति

बहुपद शब्द दो विविध आधार को जोड़ता है: ग्रीक पॉली, जिसका अर्थ है "कई", और लैटिन नाम, या "नाम"। यह लैटिन मूल द्वि- को ग्रीक पॉली- के साथ बदलकर द्विपद शब्द से लिया गया था। अर्थात् इसका अर्थ अनेक पदों (एकपदी) का योग है। बहुपद शब्द का प्रयोग पहली बार 17वीं शताब्दी में किया गया था।^[1]

संकेतन और शब्दावली

ग्राफ 3 के बहुपद फलन का आलेख

बहुपद में होने वाले x को आमतौर पर एक चर या अनिश्चित कहा जाता है। जब बहुपद को व्यंजक के रूप में माना जाता है, तो x एक निश्चित प्रतीक है जिसका कोई मान नहीं है (इसका मान "अनिश्चित" है)। हालांकि, जब कोई बहुपद द्वारा परिभाषित फलन पर विचार करता है, तो x फलन के तर्क का प्रतिनिधित्व करता है, और इसलिए इसे "चर" कहा जाता है। कई लेखक इन दोनों शब्दों का परस्पर प्रयोग करते हैं।

अनिश्चित (इंडेटरमिनते) x में एक बहुपद P को आमतौर पर या तो P या P (x) के रूप में दर्शाया जाता है। औपचारिक रूप से, बहुपद का नाम P है, न कि P (x), लेकिन कार्यात्मक संकेतन P (x) का उपयोग उस समय से होता है जब बहुपद और संबंधित फलन के बीच का अंतर स्पष्ट नहीं था। इसके अलावा, कार्यात्मक संकेतन अक्सर एक वाक्यांश, एक बहुपद और उसके अनिश्चित में निर्दिष्ट करने के लिए उपयोगी होता है। उदाहरण के लिए, "मान लीजिए P (x) एक बहुपद है" के लिए एक आशुलिपि है" "मान लीजिए P अनिश्चित x में एक बहुपद है" के लिए एक आशुलिपि है। दूसरी ओर, जब अनिश्चित के नाम पर जोर देना आवश्यक नहीं है, तो कई सूत्र बहुत सरल और पढ़ने में आसान होते हैं यदि बहुपद की प्रत्येक घटना में अनिश्चित के नाम प्रकट नहीं होते हैं।

गणितीय वस्तु के लिए दो अंकन होने की अस्पष्टता को बहुपद के लिए कार्यात्मक संकेतन के सामान्य अर्थ पर विचार करके औपचारिक रूप से हल किया जा सकता है। यदि a एक संख्या, एक चर, एक अन्य बहुपद, या, अधिक सामान्य रूप से, किसी भी अभिव्यक्ति को दर्शाता है, तो P(a) परंपरा द्वारा, P में x के लिए a को प्रतिस्थापित करने के परिणाम को दर्शाता है। इस प्रकार, बहुपद P फलन को परिभाषित करता है।

$a\mapsto P(a),$

जो कि P से जुड़ा एक बहुपद फलन है। अक्सर, इस संकेतन का उपयोग करते समय, कोई यह मान लेता है कि a एक संख्या है। हालाँकि, कोई भी इसका उपयोग किसी भी डोमेन में कर सकता है जहाँ जोड़ और गुणा परिभाषित हैं (अर्थात कोई भी रिंग)। विशेष रूप से, यदि a एक बहुपद है तो P(a) भी एक बहुपद है।

अधिक विशेष रूप से, जब a अनिश्चित x है, तो इस फलन द्वारा x की छवि बहुपद P ही है (x के लिए x को प्रतिस्थापित करने से कुछ भी नहीं बदलता है)।

दूसरे शब्दों में,

$P(x)=P,$

जो औपचारिक रूप से एक ही बहुपद के लिए दो संकेतन के अस्तित्व को सही ठहराता है।

परिभाषा

बहुपद व्यंजक एक ऐसा व्यंजक है जो एक गैर-ऋणात्मक पूर्णांक घात के योग, गुणन और घातांक के माध्यम से स्थिरांक और प्रतीकों से बनाया जा सकता है जिन्हें चर या अनिश्चित कहा जाता है। स्थिरांक आम तौर पर संख्या होते हैं, लेकिन कोई भी अभिव्यक्ति हो सकती है जिसमें अनिश्चित शामिल नहीं होते हैं, और गणितीय वस्तुओं का प्रतिनिधित्व करते हैं जिन्हें जोड़ा और गुणा किया जा सकता है। दो बहुपद व्यंजकों को एक ही बहुपद को परिभाषित करने के रूप में माना जाता है, यदि वे रूपांतरित हो सकते हैं, एक से दूसरे में, जोड़ और गुणा के सामान्य गुणों को लागू करके कम्यूटेटिविटी, सहयोगीता और वितरण । उदाहरण के लिए $(x-1)(x-2)$ तथा $x^{2}-3x+2$ दो बहुपद व्यंजक हैं जो एक ही बहुपद को निरूपित करते हैं; तो, लिखा जाता है $(x-1)(x-2)=x^{2}-3x+2.$

एकल अनिश्चित $x$ में एक बहुपद को हमेशा फॉर्म में लिखा (या फिर से लिखा) जा सकता है:

$a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{2}x^{2}+a_{1}x+a_{0},$

जहाँ पे $a_{0},\ldots ,a_{n}$ अचर हैं जो बहुपद के गुणांक कहलाते हैं, और $x$ अनिश्चित है। ^[2] "अनिश्चित" शब्द का अर्थ है कि $x$ किसी विशेष मूल्य का प्रतिनिधित्व नहीं करता है, हालांकि इसके लिए किसी भी मूल्य को प्रतिस्थापित किया जा सकता है। मैपिंग जो इस प्रतिस्थापन के परिणाम को प्रतिस्थापित मान से जोड़ता है वह एक फलन है, जिसे बहुपद फलन कहा जाता है।

इसे और अधिक संक्षिप्त रूप से योग संकेतन का उपयोग करके व्यक्त किया जा सकता है:

$\sum _{k=0}^{n}a_{k}x^{k}$

अर्थात्, एक बहुपद या तो शून्य हो सकता है या गैर-शून्य पदों की एक परिमित संख्या के योग के रूप में लिखा जा सकता है। प्रत्येक पद में एक संख्या . का गुणनफल होता है – शब्द का गुणांक कहा जाता है ^{[lower-alpha 1]}और अनिश्चित की एक सीमित संख्या, गैर-ऋणात्मक पूर्णांक शक्तियों तक विस्तारित की गयी है।

वर्गीकरण

किसी पद में अनिश्चित काल के घातांक को उस पद में अनिश्चित काल की घात कहते हैं। किसी पद की घात उस पद की अनिश्चितताओं की घातों का योग है, और बहुपद की घात अशून्य गुणांक वाले पद की सबसे बड़ी घात है। क्योंकि $x = x 1$ , एक लिखित घातांक के बिना एक अनिश्चित की डिग्री एक है।

जिस पद में कोई अनिश्चितता न हो और एक बहुपद जिसमें कोई अनिश्चितता न हो, तो उसे क्रमशः अचर पद और अचर बहुपद कहते हैं।^{[lower-alpha 2]} अचर पद और अशून्य स्थिर बहुपद की घात 0 है। 0 की घात (जिसका कोई पद नहीं है) के लिए शून्य बहुपद को आमतौर पर परिभाषित नहीं माना जाता है (नीचे देखें)।^[3]

उदाहरण के लिए:

$-5x^{2}y$

यह एक पद है। गुणांक -5 है, अनिश्चित x और y हैं, x की डिग्री दो है, जबकि y की डिग्री एक है। संपूर्ण पद की घात इसमें प्रत्येक अनिश्चित की घातों का योग है, इसलिए इस उदाहरण में घात $2 + 1 = 3$ है।

अनेक पदों के योग से एक बहुपद बनता है। उदाहरण के लिए, निम्नलिखित एक बहुपद है:

$\underbrace {_{\,}3x^{2}} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {1} \end{smallmatrix}}\underbrace {-_{\,}5x} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {2} \end{smallmatrix}}\underbrace {+_{\,}4} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {3} \end{smallmatrix}}.$

इसके तीन पद हैं: पहली डिग्री दो है, दूसरी डिग्री एक है, और तीसरी डिग्री शून्य है।

छोटे भिन्नों के बहुपदों को विशेष नाम दिए गए हैं। शून्य घात वाला बहुपद एक अचर बहुपद या केवल एक अचर होता है। एक, दो या तीन घात वाले बहुपद क्रमशः रैखिक बहुपद, द्विघात बहुपद और घन बहुपद होते हैं।^[4] उच्च डिग्री के लिए, विशिष्ट नामों का आमतौर पर उपयोग नहीं किया जाता है, हालांकि कभी-कभी क्वार्टिक बहुपद (डिग्री चार के लिए) और क्विंटिक बहुपद (डिग्री पांच के लिए) का उपयोग किया जाता है। डिग्री के नाम बहुपद या इसकी शर्तों पर लागू हो सकते हैं। उदाहरण के लिए, $x 2 + 2 x + 1$ में पद $2 x$ एक द्विघात बहुपद में एक रैखिक पद है।

बहुपद 0, जिसे एक पद के रूप में नहीं माना जा सकता है, इसे शून्य बहुपद कहा जाता है। अन्य अचर बहुपदों के विपरीत, इसका घात शून्य नहीं होती है। बल्कि, शून्य बहुपद की डिग्री को या तो स्पष्ट रूप से अपरिभाषित छोड़ दिया जाता है, या ऋणात्मक (या तो -1 या −∞) के रूप में परिभाषित किया जाता है।^[5] शून्य बहुपद इस मायने में भी अद्वितीय है कि यह एक अनिश्चित में एकमात्र बहुपद है और साथ में जिसमें अनंत संख्या की मूलें होती हैं। शून्य बहुपद का ग्राफ, $f (x) = 0$ , x -अक्ष (एक्सिस) है।

एक से अधिक अनिश्चित बहुपदों के मामले में, एक बहुपद को degree $n$ का समघात (होमोजेनियस) कहा जाता है, यदि इसके सभी गैर-शून्य पदों में degree $n$ है। शून्य बहुपद समघात (होमोजेनियस पोलयनोमिअल) है, और एक सजातीय बहुपद के रूप में, इसकी डिग्री अपरिभाषित है।^{[lower-alpha 3]} उदाहरण के लिए, $x 3 y 2 + 7 x 2 y 3 - 3 x 5$ डिग्री 5 का समघात है। अधिक जानकारी के लिए, समघात बहुपद देखें।

जोड़ के क्रमविनिमेयता कम्यूटेटिव कानून का प्रयोग किसी भी पसंदीदा क्रम में शब्दों को पुनर्व्यवस्थित करने के लिए किया जा सकता है। एक अनिश्चित के साथ बहुपदों में, शर्तों को आमतौर पर डिग्री के अनुसार आदेश दिया जाता है, या तो " $x$ की अवरोही शक्तियों" में, पहले सबसे बड़ी डिग्री की अवधि के साथ, या " $x$ की आरोही शक्तियों" में। बहुपद $3 x 2 - 5 x + 4$ को $x$ के अवरोही घातों में लिखा जाता है। पहले पद का गुणांक $3$ , अनिश्चित $x$ , और घातांक $2$ है। दूसरे पद में, गुणांक is $-5$ । तीसरा पद एक स्थिरांक है। चूँकि गैर-शून्य बहुपद की घात किसी एक पद की सबसे बड़ी घात होती है, इसलिए इस बहुपद की घात दो होती है।^[6] समान अनिश्चितता वाले दो शब्दों को समान शक्तियों के लिए उठाया जाता है, उन्हें "समान चर " या "सदृश चर" कहा जाता है, और उन्हें वितरण नियम का उपयोग करके एक एकल पद में संयोजित किया जा सकता है जिसका गुणांक पदों के गुणांकों का योग है। ऐसा हो सकता है कि यह गुणांक 0 बनाता है।^[7]बहुपदों को अशून्य गुणांक वाले पदों की संख्या के आधार पर वर्गीकृत किया जा सकता है ताकि एक पद वाले बहुपद को एकपदी कहा जा सके,,^{[lower-alpha 4]} दो-पद वाले बहुपद को द्विपद कहा जाता है, और तीन-पद वाले बहुपद को त्रिपद कहा जाता है। शब्द "चतुर्भुज" का प्रयोग कभी-कभी चार-पद के बहुपद के लिए किया जाता है।

एक वास्तविक बहुपद वास्तविक गुणांक वाला बहुपद है। जब किसी फलन को परिभाषित करने के लिए इसका उपयोग किया जाता है, तो डोमेन इतना प्रतिबंधित नहीं होता है। हालाँकि, एक वास्तविक बहुपद फलन वास्तविक से वास्तविक तक का एक फलन है जिसे वास्तविक बहुपद द्वारा परिभाषित किया जाता है। इसी तरह, एक पूर्णांक बहुपद पूर्णांक गुणांक वाला बहुपद है, और एक जटिल बहुपद जटिल गुणांक वाला बहुपद है।

एक अनिश्चित बहुपद को एक अविभाज्य बहुपद कहा जाता है, और एक से अधिक अनिश्चित बहुपद को "बहुभिन्नरूपी बहुपद" कहा जाता है। दो अनिश्चितों वाले बहुपद को द्विपद बहुपद कहते हैं।^[8] ये धारणाएं आम तौर पर उन बहुपदों के प्रकारों को संदर्भित करती हैं जो अलग-अलग बहुपदों की तुलना में उन पर काम करती हैं; उदाहरण के लिए, जब अविभाज्य बहुपदों (univariate polynomials) के साथ काम करते हैं, तो कोई निरंतर बहुपद (जो गैर-स्थिर बहुपदों के घटाव के परिणामस्वरूप हो सकता है) को बाहर नहीं करता है, हालांकि कड़ाई से बोलते हुए, निरंतर बहुपद में कोई भी अनिश्चित नहीं होता है। अनुमत अनिश्चितताओं की अधिकतम संख्या के अनुसार, बहुभिन्नरूपी बहुपदों को द्विपद, त्रिपद, आदि के रूप में वर्गीकृत करना संभव है। फिर से, ताकि विचाराधीन वस्तुओं के सेट को घटाव के तहत बंद किया जा सके, ट्रिवेरिएट बहुपदों का एक अध्ययन आमतौर पर द्विचर बहुपदों की अनुमति देता है, और इसी तरह। यह कहना भी आम है कि " $x, y$ , और $z$ में बहुपद ", अनुमत अनिश्चितों को सूचीबद्ध करते हैं।

बहुपद के मूल्यांकन में प्रत्येक अनिश्चित के लिए एक संख्यात्मक मान को प्रतिस्थापित करना और संकेतित गुणन और परिवर्धन करना शामिल है। अनिश्चित बहुपद के लिए, हॉर्नर की विधि का उपयोग करके मूल्यांकन आम तौर पर अधिक कुशल होता है (प्रदर्शन करने के लिए अंकगणितीय संचालन की कम संख्या):

एक अनिश्चित बहुपद के लिए, मूल्यांकन आमतौर पर हॉर्नर की विधि का उपयोग करके अधिक कुशल होता है

$(((((a_{n}x+a_{n-1})x+a_{n-2})x+\dotsb +a_{3})x+a_{2})x+a_{1})x+a_{0}.$

अंकगणित

जोड़ और घटाव

जोड़ के साहचर्य नियम का उपयोग करकेबहुपदों को जोड़ के साहचर्य नियम का उपयोग करके जोड़ा जा सकता है (उनके सभी पदों को एक साथ योग में समूहित करना),संभवतः इसके बाद समान पदों (कम्यूटिव कानून का उपयोग करते हुए) का पुनर्क्रमण और संयोजन किया जाता है।

^[7]^[9]

उदाहरण के लिए, यदि

P=3x^{2}-2x+5xy-2

तथा

Q=-3x^{2}+3x+4y^{2}+8

फिर योग

P+Q=3x^{2}-2x+5xy-2-3x^{2}+3x+4y^{2}+8

के रूप में पुन: व्यवस्थित और पुन: समूहित किया जा सकता है

P+Q=(3x^{2}-3x^{2})+(-2x+3x)+5xy+4y^{2}+(8-2)

और फिर सरलीकृत करने के लिए

P+Q=x+5xy+4y^{2}+6.

जब बहुपदों को एक साथ जोड़ा जाता है, तो परिणाम एक और बहुपद होता है।^[10]

बहुपदों का घटाव समान होता है।

गुणन

बहुपदों को भी गुणा किया जा सकता है। दो बहुपदों के गुणनफल को पदों के योग में विस्तारित करने के लिए, वितरण नियम को बार-बार लागू किया जाता है, जिसके परिणामस्वरूप एक बहुपद के प्रत्येक पद को दूसरे के प्रत्येक पद से गुणा किया जाता है।^[7]उदाहरण के लिए, यदि

{\begin{aligned}\color {Red}P&\color {Red}{=2x+3y+5}\\\color {Blue}Q&\color {Blue}{=2x+5y+xy+1}\end{aligned}}

फिर

{\begin{array}{rccrcrcrcr}{\color {Red}{P}}{\color {Blue}{Q}}&{=}&&({\color {Red}{2x}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{1}})\\&&+&({\color {Red}{3y}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{1}})\\&&+&({\color {Red}{5}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{5}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{5}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{5}}\cdot {\color {Blue}{1}})\end{array}}

प्रत्येक पद में गुणा करने पर उत्पन्न होता है

{\begin{array}{rccrcrcrcr}PQ&=&&4x^{2}&+&10xy&+&2x^{2}y&+&2x\\&&+&6xy&+&15y^{2}&+&3xy^{2}&+&3y\\&&+&10x&+&25y&+&5xy&+&5.\end{array}}

समान पदों को मिलाने से उपज

{\begin{array}{rcccrcrcrcr}PQ&=&&4x^{2}&+&(10xy+6xy+5xy)&+&2x^{2}y&+&(2x+10x)\\&&+&15y^{2}&+&3xy^{2}&+&(3y+25y)&+&5\end{array}}

जिसे सरल बनाया जा सकता है

PQ=4x^{2}+21xy+2x^{2}y+12x+15y^{2}+3xy^{2}+28y+5.

उदाहरण के रूप में, बहुपद का उत्पाद हमेशा एक बहुपद होता है।^[10]^[3]

संयोजन

एक चर के एक बहुपद $f$ और किसी भी संख्या में चर के एक अन्य बहुपद $g$ को देखते हुए, पहले बहुपद के चर की प्रत्येक प्रति को दूसरे बहुपद द्वारा प्रतिस्थापित करके रचना $f\circ g$ प्राप्त की जाती है।^[3] उदाहरण के लिए, यदि $f(x)=x^{2}+2x$ तथा $g(x)=3x+2$ फिर

(f\circ g)(x)=f(g(x))=(3x+2)^{2}+2(3x+2).

(f\circ g)(x)=f(g(x))=(3x+2)^{2}+2(3x+2).

गुणन और बहुपदों के विभाजन के नियमों का उपयोग करके एक निर्माण को पदों के योग तक बढ़ाया जा सकता है। दो बहुपदों का संघटन एक अन्य बहुपद है।^[11]

विभाजन

एक बहुपद का दूसरे से विभाजन आमतौर पर बहुपद नहीं होता है। इसके बजाय, ऐसे अनुपात वस्तुओं का एक अधिक सामान्य परिवार हैं, जिन्हें संदर्भ के आधार पर तर्कसंगत अंश, तर्कसंगत अभिव्यक्ति या तर्कसंगत कार्य कहा जाता है।^[12] यह इस तथ्य के अनुरूप है कि दो पूर्णांक का अनुपात एक तर्कसंगत संख्या है, जरूरी नहीं कि एक पूर्णांक हो।^[13]^[14] उदाहरण के लिए, अंभिन्न 1/(x2 + 1) एक बहुपद नहीं है, और इसे चर x की घातों के परिमित योग के रूप में नहीं लिखा जा सकता है।

एक चर में बहुपद के लिए, बहुपदों के यूक्लिडियन विभाजन की एक धारणा है, जो पूर्णांकों के यूक्लिडियन विभाजन को सामान्यीकृत करता है।^{[lower-alpha 5]} विभाजन की यह धारणा $a (x)/ b (x)$ दो बहुपदों में परिणाम, एक भागफल $q (x)$ और एक शेष $r (x)$ , ऐसा है कि $a = b q + r$ तथा $degree(r) < degree(b)$ ।भागफल और शेष की गणना कई एल्गोरिदम में से किसी द्वारा की जा सकती है, जिसमें बहुपद लॉन्ग डिवीजन और सिंथेटिक डिवीजन शामिल हैं।^[15] जब हर $b (x)$ मोनिक और रैखिक है, अर्थात्, $b (x) = x - c$ कुछ स्थिर के लिए $c$ , फिर बहुपद शेष प्रमेय का दावा है कि शेष विभाजन के शेष $a (x)$ द्वारा $b (x)$ मूल्यांकन है $a (c)$ .^[14] इस मामले में, भागफल की गणना रफिनी के नियम द्वारा की जा सकती है, जो सिंथेटिक डिवीजन का एक विशेष मामला है।^[16]

फैक्टरिंग

एक अद्वितीय फैक्टरिंग डोमेन (उदाहरण के लिए, पूर्णांक या एक फ़ील्ड) में गुणांक वाले सभी बहुपदों का एक कारक रूप भी होता है जिसमें बहुपद को अघुलनशील बहुपद और एक स्थिरांक के गुणनफल के रूप में लिखा जाता है। यह गुणनखंड रूप में अद्वितीय है, कारकों का क्रम और व्युत्क्रम स्थिरांक से उनका गुणन है। सम्मिश्र संख्याओं के क्षेत्र के मामले में, अपूरणीय कारक रैखिक होते हैं। उनके पास एक या दो डिग्री है, जो वास्तविक संख्या से अधिक है। पूर्णांकों और परिमेय संख्याओं के ऊपर, अपरिमेय कारकों की कोई भी डिग्री हो सकती है।^[17] उदाहरण के लिए, भाज्य रूप पूर्णांकों

5x^{3}-5

और

5(x-1)\left(x^{2}+x+1\right)

वास्तविक और

5(x-1)\left(x+{\frac {1+i{\sqrt {3}}}{2}}\right)\left(x+{\frac {1-i{\sqrt {3}}}{2}}\right)

सम्मिश्र संख्याओं से बड़ा होता है।

गुणनखंड की गणना, जिसे फ़ैक्टराइज़ेशन कहा जाता है, सामान्य रूप से हस्तलिखित गणनाओं द्वारा किया जाना बहुत मुश्किल है। हालांकि, अधिकांश कंप्यूटर बीजगणित प्रणालियों में कुशल बहुपद गुणनखंड एल्गोरिदम उपलब्ध हैं।

गणना

अन्य प्रकार के फलन की तुलना में बहुपदों के व्युत्पन्न और समाकलन की गणना करना विशेष रूप से आसान है। बहुपद का व्युत्पन्न

P=a_{n}x^{n}+a_{n-1}x^{n-1}+\dots +a_{2}x^{2}+a_{1}x+a_{0}=\sum _{i=0}^{n}a_{i}x^{i}

इसके संबंध में

x

बहुपद है

 $na_{n}x^{n-1}+(n-1)a_{n-1}x^{n-2}+\dots +2a_{2}x+a_{1}=\sum _{i=1}^{n}ia_{i}x^{i-1}.$

इसी तरह, सामान्य एंटीडिवेटिव (या अनिश्चित अभिन्न) $P$ है

{\frac {a_{n}x^{n+1}}{n+1}}+{\frac {a_{n-1}x^{n}}{n}}+\dots +{\frac {a_{2}x^{3}}{3}}+{\frac {a_{1}x^{2}}{2}}+a_{0}x+c=c+\sum _{i=0}^{n}{\frac {a_{i}x^{i+1}}{i+1}}

कहाँ पे

c

एक मनमाना स्थिरांक है।उदाहरण के लिए, के प्रतिपक्ष

x 2 + 1

फार्म है

.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/3x3 + x + c

।

बहुपद के लिए जिनके गुणांक अधिक अमूर्त सेटिंग्स से आते हैं (उदाहरण के लिए, यदि गुणांक पूर्णांक हैं तो कुछ प्रमुख संख्या $p$ , या एक मनमानी अंगूठी के तत्व), व्युत्पन्न के लिए सूत्र अभी भी औपचारिक रूप से व्याख्या की जा सकती है, गुणांक के साथ $ka k$ का मतलब है कि योग $k$ की प्रतियां $a k$ ।उदाहरण के लिए, पूर्णांक मोडुलो पर $p$ , बहुपद का व्युत्पन्न $x p + x$ बहुपद है $1$ .^[18]

बहुपद फलन

एएक बहुपद फलन एक ऐसा फलन है जिसे बहुपद का मूल्यांकन करके परिभाषित किया जा सकता है। अधिक सटीक रूप से, किसी दिए गए डोमेन से एक तर्क का फलन $f$ एक बहुपद फलन होता है यदि कोई बहुपद मौजूद होता है

a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{2}x^{2}+a_{1}x+a_{0}

इसका मूल्यांकन करता है $f(x)$ सभी के लिए $x$ के डोमेन में $f$ (यहां, $n$ एक गैर-नकारात्मक पूर्णांक है और $a 0, a 1, a 2, ..., a n$ निरंतर गुणांक हैं)। आम तौर पर, जब तक कि अन्यथा निर्दिष्ट नहीं किया जाता है, बहुपद फलनमें जटिल गुणांक, तर्क और मूल्य होते हैं। विशेष रूप से, एक बहुपद, वास्तविक गुणांक के लिए प्रतिबंधित, जटिल संख्याओं से जटिल संख्याओं तक एक फलन को परिभाषित करता है। यदि इस फलन का डोमेन भी REALS तक ही सीमित है, तो परिणामी फलन एक वास्तविक फलन है जो वास्तविक को वास्तविक से मैप करता है।।

उदाहरण के लिए, फलन $f$ , द्वारा परिभाषित

f(x)=x^{3}-x,

एक चर का एक बहुपद कार्य है। कई चर के बहुपद फलनको समान रूप से परिभाषित किया जाता है, एक से अधिक अनिश्चित में बहुपद का उपयोग करते हुए, जैसा कि

f(x,y)=2x^{3}+4x^{2}y+xy^{5}+y^{2}-7.

बहुपद फलनकी परिभाषा के अनुसार, ऐसे भाव हो सकते हैं जो स्पष्ट रूप से बहुपद नहीं हैं, लेकिन फिर भी बहुपद फलनको परिभाषित करते हैं। उदाहरण अभिव्यक्ति है $\left({\sqrt {1-x^{2}}}\right)^{2},$ जो बहुपद के समान मान लेता है $1-x^{2}$ अंतराल पर $[-1,1]$ , और इस प्रकार दोनों भाव इस अंतराल पर एक ही बहुपद कार्य को परिभाषित करते हैं।

प्रत्येक बहुपद फलन संतत, सुचारू और पूर्ण होता है।

रेखांकन (ग्राफ

)

Polynomial of degree 0:
$f (x) = 2$
Polynomial of degree 1:
$f (x) = 2 x + 1$
Polynomial of degree 2:
$f (x) = x 2 - x - 2$
$= (x + 1)(x - 2)$
Polynomial of degree 3:
$f (x) = x 3 /4 + 3 x 2 /4 - 3 x /2 - 2$
$= 1/4 (x + 4)(x + 1)(x - 2)$
Polynomial of degree 4:
$f (x) = 1/14 (x + 4)(x + 1)(x - 1)(x - 3) + 0.5$
Polynomial of degree 5:
$f (x) = 1/20 (x + 4)(x + 2)(x + 1)(x - 1) (x - 3) + 2$
Polynomial of degree 6:
$f (x) = 1/100 (x 6 - 2 x 5 - 26 x 4 + 28 x 3$
$+ 145 x 2 - 26 x - 80)$
Polynomial of degree 7:
$f (x) = (x - 3)(x - 2)(x - 1)(x)(x + 1)(x + 2)$
$(x + 3)$

एक वास्तविक चर में एक बहुपद कार्य को एक ग्राफ द्वारा दर्शाया जा सकता है।

शून्य बहुपद का ग्राफ
$f (x) = 0$
है $x$ -एक्सिस।
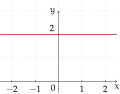
एक डिग्री 0 बहुपद का ग्राफ
$f (x) = a 0$ , where $a 0 \neq 0$ ,
के साथ एक क्षैतिज रेखा है $y$ -intercept $a 0$
एक डिग्री 1 बहुपद (या रैखिक फलन) का ग्राफ
$f (x) = a 0 + a 1 x$ , where $a 1 \neq 0$ ,
के साथ एक तिरछी रेखा है $y$ -intercept $a 0$ और ढलान $a 1$ ।
एक डिग्री 2 बहुपद का ग्राफ
$f (x) = a 0 + a 1 x + a 2 x 2$ , where $a 2 \neq 0$
एक परबोला है।
एक डिग्री 3 बहुपद का ग्राफ
$f (x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3$ , where $a 3 \neq 0$
एक क्यूबिक वक्र है।
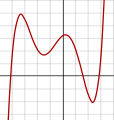
डिग्री 2 या उससे अधिक के साथ किसी भी बहुपद का ग्राफ
$f (x) = a 0 + a 1 x + a 2 x 2 + \dots + a n x n$ , where $a n \neq 0 and n \geq 2$
एक निरंतर गैर-रैखिक वक्र है।

जब चर अनिश्चित काल (निरपेक्ष मूल्य में) बढ़ता है तो एक गैर-स्थिर बहुपद कार्य अनंतता में जाता है।यदि डिग्री एक से अधिक है, तो ग्राफ में कोई स्पर्शोन्मुख नहीं है।इसमें ऊर्ध्वाधर दिशा के साथ दो परवलयिक शाखाएं हैं (सकारात्मक एक्स के लिए एक शाखा और नकारात्मक एक्स के लिए एक)।

बहुपद रेखांकन का विश्लेषण कैलकुलस में इंटरसेप्ट्स, ढलान, समवर्ती और अंत व्यवहार का उपयोग करके किया जाता है।

समीकरण

एक बहुपद समीकरण, जिसे बीजीय समीकरण भी कहा जाता है, फॉर्म का एक समीकरण है^[19]

a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{2}x^{2}+a_{1}x+a_{0}=0.

उदाहरण के लिए,

3x^{2}+4x-5=0

एक बहुपद समीकरण है।

समीकरणों पर विचार करते समय, बहुपद के अनिश्चितता (चर) को अज्ञात भी कहा जाता है, और समाधान उन अज्ञात के संभावित मूल्य हैं जिनके लिए समानता सत्य है (सामान्य रूप से एक से अधिक समाधान मौजूद हो सकते हैं)।एक बहुपद समीकरण एक बहुपद पहचान के विपरीत है $(x + y)(x - y) = x 2 - y 2$ , जहां दोनों अभिव्यक्तियाँ अलग -अलग रूपों में एक ही बहुपद का प्रतिनिधित्व करती हैं, और परिणामस्वरूप दोनों सदस्यों का कोई भी मूल्यांकन एक वैध समानता देता है।

प्राथमिक बीजगणित में, द्विघात सूत्र जैसे तरीकों को एक चर में सभी प्रथम डिग्री और दूसरी डिग्री बहुपद समीकरणों को हल करने के लिए सिखाया जाता है।क्यूबिक और क्वार्टिक समीकरणों के लिए भी सूत्र हैं।उच्च डिग्री के लिए, एबेल -रफिनी प्रमेय का दावा है कि कट्टरपंथी में एक सामान्य सूत्र मौजूद नहीं हो सकता है।हालांकि, रूट-फाइंडिंग एल्गोरिदम का उपयोग किसी भी डिग्री के बहुपद अभिव्यक्ति की मूलों के संख्यात्मक अनुमानों को खोजने के लिए किया जा सकता है।

वास्तविक गुणांक के साथ एक बहुपद समीकरण के समाधानों की संख्या डिग्री से अधिक नहीं हो सकती है, और जब जटिल समाधानों को उनकी बहुलता के साथ गिना जाता है तो डिग्री के बराबर होता है।इस तथ्य को बीजगणित का मौलिक प्रमेय कहा जाता है।

समीकरणों को हल करना

एक गैर-शून्य अविभाज्य बहुपद $P$ का एक मूल $a$ का x का मान इस प्रकार है कि $P (a) = 0$ है। दूसरे शब्दों में, $P$ का एक मूल बहुपद समीकरण $P (x) = 0$ या बहुपद का एक शून्य का हल है। $P$ द्वारा परिभाषित फलन है। शून्य बहुपद के मामले में, प्रत्येक संख्या संबंधित फलन का शून्य है, और रूट की अवधारणा पर शायद ही कभी विचार किया जाता है।

एक संख्या $a$ एक बहुपद की मूल है $P$ यदि और केवल अगर रैखिक बहुपद $x - a$ विभाजित $P$ , कि अगर कोई और बहुपद है $Q$ ऐसा है कि $P = (x - a) Q$ ।ऐसा हो सकता है कि एक शक्ति (से अधिक) $1$ ) का $x - a$ विभाजित $P$ ;इस मामले में, $a$ की एक कई मूल है $P$ , और अन्यथा $a$ की एक सरल मूल है $P$ ।यदि $P$ एक नॉनज़ेरो बहुपद है, एक उच्चतम शक्ति है $m$ ऐसा है कि $(x - a) m$ विभाजित $P$ , जिसे बहुलता कहा जाता है $a$ की मूल के रूप में $P$ ।एक नॉनज़ेरो बहुपद की मूलों की संख्या $P$ , उनके संबंधित गुणकों के साथ गिना जाता है, की डिग्री से अधिक नहीं हो सकता है $P$ ,^[20] और इस डिग्री के बराबर है यदि सभी जटिल मूलों पर विचार किया जाता है (यह बीजगणित के मौलिक प्रमेय का परिणाम है। एक बहुपद और उसकी मूलों के गुणांक विएता के सूत्रों से संबंधित हैं।

कुछ बहुपद, जैसे $x 2 + 1$ , वास्तविक संख्याओं के बीच कोई मूल नहीं है।यदि, हालांकि, स्वीकृत समाधानों के सेट को जटिल संख्याओं तक विस्तारित किया जाता है, तो प्रत्येक गैर-स्थिर बहुपद में कम से कम एक मूल होती है;यह बीजगणित का मौलिक प्रमेय है।क्रमिक रूप से कारकों को विभाजित करके $x - a$ , एक देखता है कि जटिल गुणांक के साथ किसी भी बहुपद को एक स्थिर (इसके प्रमुख गुणांक) के रूप में लिखा जा सकता है, जो डिग्री के ऐसे बहुपद कारकों के उत्पाद के एक उत्पाद & nbsp; 1;परिणामस्वरूप, उनकी गुणन के साथ गिने जाने वाली (जटिल) मूलों की संख्या वास्तव में बहुपद की डिग्री के बराबर है।

एक समीकरण को हल करने के कई अर्थ हो सकते हैं।कोई भी समाधानों को स्पष्ट संख्या के रूप में व्यक्त करना चाह सकता है; उदाहरण के लिए, का अनूठा समाधान $2 x - 1 = 0$ है $1/2$ । दुर्भाग्य से, यह सामान्य रूप से, एक से अधिक डिग्री के समीकरणों के लिए असंभव है, और, प्राचीन काल के बाद से, गणितज्ञों ने समाधानों को बीजगणितीय अभिव्यक्तियों के रूप में व्यक्त करने के लिए खोज की है;उदाहरण के लिए, स्वर्ण अनुपात $(1+{\sqrt {5}})/2$ का अनूठा सकारात्मक समाधान है $x^{2}-x-1=0.$ प्राचीन काल में, वे केवल एक और दो डिग्री के लिए सफल हुए। द्विघात समीकरणों के लिए, द्विघात सूत्र समाधानों के ऐसे भाव प्रदान करता है। 16 वीं शताब्दी के बाद से, समान सूत्र (वर्ग मूलों के अलावा क्यूब मूलों का उपयोग करके), हालांकि बहुत अधिक जटिल, डिग्री तीन और चार के समीकरणों के लिए जाने जाते हैं (क्यूबिक समीकरण और चतुर्थक समीकरण देखें)। लेकिन कई शताब्दियों के लिए डिग्री 5 और उच्चतर शोधकर्ताओं के लिए सूत्र। 1824 में, नील्स हेनरिक एबेल ने हड़ताली परिणाम साबित कर दिया कि डिग्री 5 के समीकरण हैं जिनके समाधानों को एक (परिमित) सूत्र द्वारा व्यक्त नहीं किया जा सकता है, जिसमें केवल अंकगणितीय संचालन और कट्टरपंथी शामिल हैं (एबेल -रफिनी प्रमेय देखें)। 1830 में, Évariste Galois ने साबित किया कि चार से अधिक डिग्री के अधिकांश समीकरणों को कट्टरपंथियों द्वारा हल नहीं किया जा सकता है, और दिखाया गया है कि प्रत्येक समीकरण के लिए, कोई यह तय कर सकता है कि क्या यह कट्टरपंथियों द्वारा हल करने योग्य है, और, यदि यह है, तो इसे हल करें। इस परिणाम ने गैलोइस सिद्धांत और समूह सिद्धांत, आधुनिक बीजगणित की दो महत्वपूर्ण शाखाओं की शुरुआत को चिह्नित किया। गैलोइस ने खुद नोट किया कि उनकी विधि द्वारा निहित गणना अव्यावहारिक थी। फिर भी, डिग्री 5 और 6 के हल करने योग्य समीकरणों के लिए सूत्र प्रकाशित किए गए हैं (देखें क्विंटिक फलन और सेक्स्टिक समीकरण)।

जब मूलों के लिए कोई बीजगणितीय अभिव्यक्ति नहीं होती है, और जब इस तरह की बीजीय अभिव्यक्ति मौजूद होती है, लेकिन उपयोगी होने के लिए बहुत जटिल होती है, तो इसे हल करने का अनूठा तरीका समाधानों के संख्यात्मक अनुमानों की गणना करना है।^[21] उसके लिए कई तरीके हैं; कुछ बहुपद तक सीमित हैं और अन्य किसी भी निरंतर कार्य पर लागू हो सकते हैं। सबसे कुशल एल्गोरिदम आसानी से (कंप्यूटर पर) 1,000 से अधिक डिग्री के बहुपद समीकरणों को हल करने की अनुमति देता है (रूट-फाइंडिंग एल्गोरिथ्म देखें)।

एक से अधिक अनिश्चित के साथ बहुपद के लिए, चर के लिए मानों के संयोजन जिसके लिए बहुपद कार्य मूल्य शून्य लेता है, आमतौर पर मूलों के बजाय शून्य कहा जाता है। बहुपद के शून्य के सेट का अध्ययन बीजगणितीय ज्यामिति का उद्देश्य है। कई अज्ञात के साथ बहुपद समीकरणों के एक सेट के लिए, यह तय करने के लिए एल्गोरिदम हैं कि क्या उनके पास जटिल समाधानों की एक परिमित संख्या है, और, यदि यह संख्या परिमित है, तो समाधानों की गणना के लिए। बहुपद समीकरणों की प्रणाली देखें।

विशेष मामला जहां सभी बहुपद डिग्री के होते हैं, को रैखिक समीकरणों की एक प्रणाली कहा जाता है, जिसके लिए शास्त्रीय गौसियन उन्मूलन सहित विभिन्न समाधान विधियों की एक और सीमा मौजूद है।

एक बहुपद समीकरण जिसके लिए कोई केवल समाधानों में रुचि रखता है जो पूर्णांक होते हैं इसे डायोफेंटाइन समीकरण कहा जाता है। डायोफेंटाइन समीकरणों को हल करना आम तौर पर एक बहुत कठिन काम है। यह साबित कर दिया गया है कि उन्हें हल करने के लिए कोई सामान्य एल्गोरिथ्म नहीं हो सकता है, या यहां तक कि यह तय करने के लिए कि समाधान का सेट खाली है (हिल्बर्ट की दसवीं समस्या देखें)। पिछले पचास वर्षों के दौरान हल की गई कुछ सबसे प्रसिद्ध समस्याएं डायफेंटाइन समीकरणों से संबंधित हैं, जैसे कि फर्मेट के अंतिम प्रमेय।

बहुपद व्यंजक

बहुपद जहां अनिश्चित को किसी अन्य गणितीय वस्तु के लिए प्रतिस्थापित किया जाता है,

त्रिकोणमितीय बहुपद

त्रिकोणमितीय बहुपद n के साथ sin(nx) और cos(nx) फलन का एक परिमित रैखिक संयोजन है।^[22] वास्तविक-मूल्यवान फलन के लिए गुणांकों को वास्तविक संख्याओं के रूप में लिया जा सकता है।

यदि sin(nx) और cos(nx) को sin(x) और cos(x) के पदों में विस्तारित किया जाता है, तो एक त्रिकोणमितीय बहुपद दो चर sin(x) और cos(x) में एक बहुपद बन जाता है (त्रिकोणमितीय सर्वसमिकाओं की सूची का उपयोग करके #मल्टीपल-एंगल फॉर्मूला)। इसके विपरीत, sin(x) और cos(x) में प्रत्येक बहुपद को sin(nx) और cos(nx) फलनों के एक रैखिक संयोजन में, उत्पाद-से-योग पहचान के साथ रूपांतरित किया जा सकता है। यह तुल्यता बताती है कि रैखिक संयोजनों को बहुपद क्यों कहा जाता है।

जटिल गुणांक के लिए, इस तरह के एक फलन और एक परिमित फूरियर श्रृंखला के बीच कोई अंतर नहीं है।

त्रिकोणमितीय बहुपद का व्यापक रूप से उपयोग किया जाता है, उदाहरण के लिए त्रिकोणमितीय प्रक्षेप में आवधिक फलनके प्रक्षेप पर लागू होता है।उनका उपयोग असतत फूरियर ट्रांसफॉर्म में भी किया जाता है।

मैट्रिक्स बहुपद

एक मैट्रिक्स बहुपद चर के रूप में वर्ग मैट्रिस के साथ एक बहुपद है।^[23] एक साधारण, स्केलर-मूल्यवान बहुपद को देखते हुए

P(x)=\sum _{i=0}^{n}{a_{i}x^{i}}=a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{n}x^{n},

यह बहुपद एक मैट्रिक्स A में मूल्यांकन किया गया है

P(A)=\sum _{i=0}^{n}{a_{i}A^{i}}=a_{0}I+a_{1}A+a_{2}A^{2}+\cdots +a_{n}A^{n},

जहां मैं पहचान मैट्रिक्स है।^[24] मैट्रिक्स बहुपद समीकरण दो मैट्रिक्स बहुपद के बीच एक समानता है, जो प्रश्न में विशिष्ट मैट्रिसेस के लिए रखता है।एक मैट्रिक्स बहुपद पहचान एक मैट्रिक्स बहुपद समीकरण है जो एक निर्दिष्ट मैट्रिक्स रिंग एम में सभी मैट्रिसेस ए 'के लिए रखती है_n(आर)।

घातीय बहुपद

एक द्विभाजित बहुपद जहां दूसरे चर को पहले चर पर लागू एक घातीय फलन के लिए प्रतिस्थापित किया जाता है, उदाहरण के लिए $P (x, e x)$ , एक घातीय बहुपद कहा जा सकता है।

बहुपद रिंग

एक बहुपद $f$ एक कम्यूटेटिव रिंग पर $R$ एक बहुपद है जिसके सभी गुणांक हैं $R$ ।यह सत्यापित करना सीधा है कि अनिश्चितता के एक सेट में बहुपद $R$ इन अनिश्चितताओं में बहुपद रिंग नामक एक कम्यूटेटिव रिंग बनाएं, जिसे निरूपित किया गया $R[x]$ अविभाज्य मामले में और $R[x_{1},\ldots ,x_{n}]$ बहुभिन्नरूपी मामले में।

किसी के पास

R[x_{1},\ldots ,x_{n}]=\left(R[x_{1},\ldots ,x_{n-1}]\right)[x_{n}].

इसलिए, बहुभिन्नरूपी मामले के अधिकांश सिद्धांत को एक पुनरावृत्त एकतरफा मामले में कम किया जा सकता है।

से नक्शा $R$ प्रति $R [x]$ भेजना $r$ खुद को एक निरंतर बहुपद के रूप में माना जाता है एक इंजेक्टिव रिंग होमोमोर्फिज्म है, जिसके द्वारा $R$ के एक सबरिंग के रूप में देखा जाता है $R [x]$ ।विशेष रूप से, $R [x]$ एक बीजगणित पर है $R$ ।

रिंग के बारे में सोच सकते हैं $R [x]$ के रूप में से उत्पन्न हो रहा है $R$ आर में एक नए तत्व एक्स जोड़कर, और एक रिंग के लिए न्यूनतम तरीके से विस्तार करना $x$ अनिवार्य लोगों की तुलना में कोई अन्य संबंध संतुष्ट नहीं करता है, साथ ही सभी तत्वों के साथ कम्यूटेशन $R$ (वह है $xr = rx$ )।ऐसा करने के लिए, किसी को सभी शक्तियों को जोड़ना होगा $x$ और उनके रैखिक संयोजन भी।

बहुपद रिंग का गठन, आदर्शों को फैक्टरिंग करके कारक के छल्ले बनाने के साथ, ज्ञात लोगों से बाहर नए छल्ले के निर्माण के लिए महत्वपूर्ण उपकरण हैं।उदाहरण के लिए, जटिल संख्याओं की अंगूठी (वास्तव में क्षेत्र में), जिसका निर्माण बहुपद रिंग से किया जा सकता है $R [x]$ बहुपद के गुणकों के आदर्श को फैक्टर करके वास्तविक संख्या पर $x 2 + 1$ ।एक अन्य उदाहरण परिमित क्षेत्रों का निर्माण है, जो समान रूप से आगे बढ़ता है, जो कि पूर्णांक के क्षेत्र के साथ शुरू होता है, गुणांक रिंग के रूप में कुछ प्रमुख संख्या $R$ (मॉड्यूलर अंकगणित देखें)।

यदि $R$ कम्यूटेटिव है, तो कोई हर बहुपद के साथ जुड़ सकता है $P$ में $R [x]$ एक बहुपद कार्य $f$ डोमेन और रेंज के बराबर $R$ ।(अधिक आम तौर पर, कोई भी डोमेन और रेंज ले सकता है जो किसी भी समान यूनिटल एसोसिएटिव बीजगणित हो सकता है $R$ ।) एक मूल्य प्राप्त करता है $f (r)$ मूल्य के प्रतिस्थापन द्वारा $r$ प्रतीक के लिए $x$ में $P$ ।बहुपद और बहुपद फलनके बीच अंतर करने का एक कारण यह है कि, कुछ छल्ले पर, अलग -अलग बहुपद एक ही बहुपद कार्य को जन्म दे सकते हैं (एक उदाहरण के लिए फ़र्मेट के छोटे प्रमेय को देखें जहां $R$ पूर्णांक modulo है $p$ )।यह मामला नहीं है $R$ क्या वास्तविक या जटिल संख्या है, जहां दो अवधारणाएं हमेशा विश्लेषण में प्रतिष्ठित नहीं होती हैं।बहुपद और बहुपद फलनके बीच अंतर करने का एक और भी महत्वपूर्ण कारण यह है कि बहुपदों पर कई संचालन (जैसे यूक्लिडियन डिवीजन) को यह देखने की आवश्यकता है कि एक बहुपद क्या है। $x$ ।

डिविसिबिलिटी

यदि $R$ एक अभिन्न डोमेन है और $f$ तथा $g$ में बहुपद हैं $R [x]$ , कहते है कि $f$ विभाजित $g$ या $f$ का भाजक है $g$ अगर वहाँ एक बहुपद मौजूद है $q$ में $R [x]$ ऐसा है कि $f q = g$ ।यदि $a\in R,$ फिर $a$ की मूल है $f$ अगर और केवल $x-a$ विभाजित $f$ ।इस मामले में, भागफल को बहुपद लॉन्ग डिवीजन का उपयोग करके गणना की जा सकती है।^[25]^[26] यदि $F$ एक क्षेत्र है और $f$ तथा $g$ में बहुपद हैं $F [x]$ साथ $g \neq 0$ , फिर अद्वितीय बहुपद मौजूद हैं $q$ तथा $r$ में $F [x]$ साथ

f=q\,g+r

और इस तरह की डिग्री $r$ की डिग्री से छोटा है $g$ (सम्मेलन का उपयोग करते हुए कि बहुपद 0 में एक नकारात्मक डिग्री है)।बहुपद $q$ तथा $r$ द्वारा विशिष्ट रूप से निर्धारित किए जाते हैं $f$ तथा $g$ ।इसे यूक्लिडियन डिवीजन कहा जाता है, शेष या बहुपद लॉन्ग डिवीजन के साथ डिवीजन और दिखाता है कि रिंग $F [x]$ एक यूक्लिडियन डोमेन है।

समान रूप से, अभाज्य बहुपद (अधिक सही ढंग से, इरेड्यूसिबल बहुपद) को गैर-शून्य बहुपद के रूप में परिभाषित किया जा सकता है, जिन्हें दो गैर-स्थिर बहुपदों के गुणनफल में विभाजित नहीं किया जा सकता है। एक अंगूठी में गुणांक के मामले में, "गैर-स्थिर" को "गैर-स्थिर या गैर-इकाई" द्वारा प्रतिस्थापित किया जाना चाहिए (दोनों परिभाषाएं एक क्षेत्र में गुणांक के मामले में सहमत हैं)। किसी भी बहुपद को अपरिवर्तनीय बहुपदों के उत्पाद द्वारा एक व्युत्क्रम स्थिरांक के गुणनफल में विघटित किया जा सकता है। यदि गुणांक एक क्षेत्र या एक अद्वितीय गुणनखंड डोमेन से संबंधित है, तो यह अपघटन कारकों के क्रम और किसी इकाई द्वारा किसी गैर-इकाई कारक के गुणन (और एक ही इकाई द्वारा इकाई कारक का विभाजन) तक अद्वितीय है। जब गुणांक पूर्णांकों, परिमेय संख्याओं या एक परिमित क्षेत्र से संबंधित होते हैं, तो इरेड्यूसिबिलिटी का परीक्षण करने और इरेड्यूसेबल बहुपदों में गुणनखंडन की गणना करने के लिए एल्गोरिदम होते हैं (देखें बहुपदों का गुणनखंड)। ये एल्गोरिदम हस्तलिखित गणना के लिए व्यावहारिक नहीं हैं, लेकिन किसी भी कंप्यूटर बीजगणित प्रणाली में उपलब्ध हैं। ईसेनस्टीन की कसौटी का उपयोग कुछ मामलों में इरेड्यूसिबिलिटी को निर्धारित करने के लिए भी किया जा सकता है।

अनुप्रयोग

पोजिशनल नोटेशन

आधुनिक स्थिति संख्या प्रणालियों में, जैसे कि दशमलव प्रणाली, अंक और एक पूर्णांक के प्रतिनिधित्व में उनके पद, उदाहरण के लिए, 45, रेडिक्स या आधार में एक बहुपद के लिए एक शॉर्टहैंड नोटेशन हैं, इस मामले में, इस मामले में, 4 × 10¹ + 5 × 10⁰।एक अन्य उदाहरण के रूप में, रेडिक्स 5 में, 132 जैसे अंकों की एक स्ट्रिंग (दशमलव) संख्या को दर्शाता है 1 × 5² + 3 × 5¹ + 2 × 5⁰ = 42. यह प्रतिनिधित्व अद्वितीय है।चलो बी 1 से अधिक एक सकारात्मक पूर्णांक हो। फिर प्रत्येक सकारात्मक पूर्णांक ए को रूप में विशिष्ट रूप से व्यक्त किया जा सकता है

a=r_{m}b^{m}+r_{m-1}b^{m-1}+\dotsb +r_{1}b+r_{0},

जहां एम एक गैर -नॉनगेटिव पूर्णांक है और आर के पूर्णांक ऐसे हैं

0 < r m < b

तथा

0 \leq r i < b

के लिये

i = 0, 1, . . . , m - 1

.^[27]

प्रक्षेप और सन्निकटन

बहुपद फलनकी सरल संरचना उन्हें बहुपद अनुमानों का उपयोग करके सामान्य फलनका विश्लेषण करने में काफी उपयोगी बनाती है।कैलकुलस में एक महत्वपूर्ण उदाहरण टेलर का प्रमेय है, जो मोटे तौर पर बताता है कि हर अलग -अलग कार्य स्थानीय रूप से एक बहुपद कार्य की तरह दिखता है, और पत्थर -वीरस्ट्रास प्रमेय, जो बताता है कि वास्तविक अक्ष के कॉम्पैक्ट अंतराल पर परिभाषित प्रत्येक निरंतर फलन का अनुमान लगाया जा सकता है।एक बहुपद समारोह द्वारा वांछित के रूप में पूरे अंतराल के रूप में।सन्निकटन के व्यावहारिक तरीकों में बहुपद प्रक्षेप और विभाजन का उपयोग शामिल है।^[28]

अन्य अनुप्रयोग

बहुपद का उपयोग अक्सर कुछ अन्य वस्तुओं के बारे में जानकारी को एन्कोड करने के लिए किया जाता है।एक मैट्रिक्स या रैखिक ऑपरेटर की विशेषता बहुपद में ऑपरेटर के eigenvalues के बारे में जानकारी होती है।एक बीजीय तत्व का न्यूनतम बहुपद उस तत्व द्वारा संतुष्ट सबसे सरल बीजगणितीय संबंध को रिकॉर्ड करता है।एक ग्राफ का रंगीन बहुपद उस ग्राफ के उचित रंगों की संख्या को गिनता है।

बहुपद शब्द, एक विशेषण के रूप में, का उपयोग उन मात्राओं या फलनके लिए भी किया जा सकता है जिन्हें बहुपद रूप में लिखा जा सकता है।उदाहरण के लिए, कम्प्यूटेशनल जटिलता सिद्धांत में वाक्यांश बहुपद समय का मतलब है कि एल्गोरिथ्म को पूरा करने में लगने वाला समय कुछ चर के बहुपद कार्य से बंधा होता है, जैसे कि इनपुट का आकार।

इतिहास

बहुपद की मूलों का निर्धारण, या बीजीय समीकरणों को हल करना, गणित में सबसे पुरानी समस्याओं में से एक है।हालाँकि, सुरुचिपूर्ण और व्यावहारिक संकेतन का उपयोग हम आज केवल 15 वीं शताब्दी में शुरू करते हैं।इससे पहले, समीकरणों को शब्दों में लिखा गया था।उदाहरण के लिए, नौ खंडों में चीनी अंकगणित से एक बीजगणित समस्या, 200 ईसा पूर्व, अच्छी फसल के तीन शीफ, दो शीफ के औसत दर्जे की फसल की शुरुआत होती है, और खराब फसल के एक शीफ को 29 डू के लिए बेचा जाता है।हम लिखेंगे $3 x + 2 y + z = 29$ ।

संकेतन का इतिहास

रॉबर्ट रिकार्डे की द वेटस्टोन ऑफ विट, 1557 में समता चिन्हह्न का सबसे पहला ज्ञात उपयोग है। जोड़ के लिए + चिह्न का उपयोग, - घटाव के लिए, और अज्ञात के लिए एक अक्षर माइकल स्टिफ़ेल के अरिथेमेटिका इंटेग्रा, 1544 में प्रकट होता है। रेने डेसकार्टेस ने 1637 में ला ज्योमेट्री में, एक बहुपद समीकरण के ग्राफ की अवधारणा को पेश किया। उन्होंने वर्णमाला की शुरुआत से अक्षरों के उपयोग को स्थिरांक को दर्शाने के लिए, और वर्णमाला के अंत से अक्षरों को चर को दर्शाने के लिए लोकप्रिय बनाया, जैसा कि ऊपर देखा जा सकता है, एक चर में बहुपद के लिए सामान्य सूत्र में, जहां $a$ एक स्थिरांक को दर्शाता है और $x$ एक चर को दर्शाता है। डेसकार्टेस ने प्रतिपादकों का प्रतिनिधित्व करने के लिए सुपरस्क्रिप्ट के उपयोग की भी शुरुआत की।^[29]

यह भी देखें

बहुपद विषयों की सूची

↑ See "polynomial" and "binomial", Compact Oxford English Dictionary
↑ Weisstein, Eric W. "Polynomial". mathworld.wolfram.com (in English). Retrieved 2020-08-28.
↑ ^3.0 ^3.1 ^3.2 Barbeau 2003, pp. 1–2
↑ "Polynomials | Brilliant Math & Science Wiki". brilliant.org (in English). Retrieved 2020-08-28.
↑ Weisstein, Eric W. "Zero Polynomial". MathWorld.
↑ Edwards 1995, p. 78
↑ ^7.0 ^7.1 ^7.2 Edwards, Harold M. (1995). Linear Algebra. Springer. p. 47. ISBN 978-0-8176-3731-6.
↑ Weisstein, Eric W. "Polynomial". mathworld.wolfram.com (in English). Retrieved 2020-08-28.
↑ Salomon, David (2006). Coding for Data and Computer Communications. Springer. p. 459. ISBN 978-0-387-23804-3.
↑ ^10.0 ^10.1 Introduction to Algebra (in English). Yale University Press. 1965. p. 621. Any two such polynomials can be added, subtracted, or multiplied. Furthermore , the result in each case is another polynomial
↑ Kriete, Hartje (1998-05-20). Progress in Holomorphic Dynamics (in English). CRC Press. p. 159. ISBN 978-0-582-32388-9. This class of endomorphisms is closed under composition,
↑ Marecek, Lynn; Mathis, Andrea Honeycutt (6 May 2020). Intermediate Algebra 2e. OpenStax. §7.1.
↑ Haylock, Derek; Cockburn, Anne D. (2008-10-14). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers (in English). SAGE. p. 49. ISBN 978-1-4462-0497-9. We find that the set of integers is not closed under this operation of division.
↑ ^14.0 ^14.1 Marecek & Mathis 2020, §5.4]
↑ Selby, Peter H.; Slavin, Steve (1991). Practical Algebra: A Self-Teaching Guide (2nd ed.). Wiley. ISBN 978-0-471-53012-1.
↑ Weisstein, Eric W. "Ruffini's Rule". mathworld.wolfram.com (in English). Retrieved 2020-07-25.
↑ Barbeau 2003, pp. 80–2
↑ Barbeau 2003, pp. 64–5
↑ Proskuryakov, I.V. (1994). "Algebraic equation". In Hazewinkel, Michiel (ed.). Encyclopaedia of Mathematics. Vol. 1. Springer. ISBN 978-1-55608-010-4.
↑ Leung, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. p. 134. ISBN 9789622092716.
↑ McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.
↑ Powell, Michael J. D. (1981). Approximation Theory and Methods. Cambridge University Press. ISBN 978-0-521-29514-7.
↑ Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. Vol. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-681-8. Zbl 1170.15300.
↑ Horn & Johnson 1990, p. 36.
↑ Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. Springer. p. 129. ISBN 978-0-387-20172-6.
↑ Jackson, Terrence H. (1995). From Polynomials to Sums of Squares. CRC Press. p. 143. ISBN 978-0-7503-0329-3.
↑ McCoy 1968, p. 75
↑ de Villiers, Johann (2012). Mathematics of Approximation. Springer. ISBN 9789491216503.
↑ Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Saunders. ISBN 0-03-029558-0.

↑ The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers modulo some prime number $p$ .
↑ This terminology dates from the time when the distinction was not clear between a polynomial and the function that it defines: a constant term and a constant polynomial define constant functions.^{[citation needed]}
↑ In fact, as a homogeneous function, it is homogeneous of every degree.^{[citation needed]}
↑ Some authors use "monomial" to mean "monic monomial". See Knapp, Anthony W. (2007). Advanced Algebra: Along with a Companion Volume Basic Algebra. Springer. p. 457. ISBN 978-0-8176-4522-9.
↑ This paragraph assumes that the polynomials have coefficients in a field.

संदर्भ

Barbeau, E.J. (2003). Polynomials. Springer. ISBN 978-0-387-40627-5.
Bronstein, Manuel; et al., eds. (2006). Solving Polynomial Equations: Foundations, Algorithms, and Applications. Springer. ISBN 978-3-540-27357-8.
Cahen, Paul-Jean; Chabert, Jean-Luc (1997). Integer-Valued Polynomials. American Mathematical Society. ISBN 978-0-8218-0388-2.
Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556. This classical book covers most of the content of this article.
Leung, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. ISBN 9789622092716.
Mayr, K. (1937). "Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen". Monatshefte für Mathematik und Physik. 45: 280–313. doi:10.1007/BF01707992. S2CID 197662587.
McCoy, Neal H. (1968), Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, LCCN 68015225
Prasolov, Victor V. (2005). Polynomials. Springer. ISBN 978-3-642-04012-2.
Sethuraman, B.A. (1997). "Polynomials". Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra Via Geometric Constructibility. Springer. ISBN 978-0-387-94848-5.
Umemura, H. (2012) [1984]. "Resolution of algebraic equations by theta constants". In Mumford, David (ed.). Tata Lectures on Theta II: Jacobian theta functions and differential equations. Springer. pp. 261–. ISBN 978-0-8176-4578-6.
von Lindemann, F. (1884). "Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen". Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1884: 245–8.
von Lindemann, F. (1892). "Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen. II". Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1892: 245–8.

बाहरी संबंध

"Polynomial", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
"Euler's Investigations on the Roots of Equations". Archived from the original on September 24, 2012.

[1] See "polynomial" and "binomial", Compact Oxford English Dictionary

[:12-2] Weisstein, Eric W. "Polynomial". mathworld.wolfram.com (in English). Retrieved 2020-08-28.

[Barbeau-2003-pp1-2-5] 3.0 ^3.1 ^3.2 Barbeau 2003, pp. 1–2

[:2-6] "Polynomials | Brilliant Math & Science Wiki". brilliant.org (in English). Retrieved 2020-08-28.

[7] Weisstein, Eric W. "Zero Polynomial". MathWorld.

[9] Edwards 1995, p. 78

[Edwards-1995-p47-10] 7.0 ^7.1 ^7.2 Edwards, Harold M. (1995). Linear Algebra. Springer. p. 47. ISBN 978-0-8176-3731-6.

[:1-12] Weisstein, Eric W. "Polynomial". mathworld.wolfram.com (in English). Retrieved 2020-08-28.

[13] Salomon, David (2006). Coding for Data and Computer Communications. Springer. p. 459. ISBN 978-0-387-23804-3.

[:0-14] 10.0 ^10.1 Introduction to Algebra (in English). Yale University Press. 1965. p. 621. Any two such polynomials can be added, subtracted, or multiplied. Furthermore , the result in each case is another polynomial

[15] Kriete, Hartje (1998-05-20). Progress in Holomorphic Dynamics (in English). CRC Press. p. 159. ISBN 978-0-582-32388-9. This class of endomorphisms is closed under composition,

[16] Marecek, Lynn; Mathis, Andrea Honeycutt (6 May 2020). Intermediate Algebra 2e. OpenStax. §7.1.

[17] Haylock, Derek; Cockburn, Anne D. (2008-10-14). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers (in English). SAGE. p. 49. ISBN 978-1-4462-0497-9. We find that the set of integers is not closed under this operation of division.

[openstax-18] 14.0 ^14.1 Marecek & Mathis 2020, §5.4]

[20] Selby, Peter H.; Slavin, Steve (1991). Practical Algebra: A Self-Teaching Guide (2nd ed.). Wiley. ISBN 978-0-471-53012-1.

[21] Weisstein, Eric W. "Ruffini's Rule". mathworld.wolfram.com (in English). Retrieved 2020-07-25.

[Barbeau-2003-pp80-82-22] Barbeau 2003, pp. 80–2

[Barbeau-2003-pp64-65-23] Barbeau 2003, pp. 64–5

[24] Proskuryakov, I.V. (1994). "Algebraic equation". In Hazewinkel, Michiel (ed.). Encyclopaedia of Mathematics. Vol. 1. Springer. ISBN 978-1-55608-010-4.

[25] Leung, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. p. 134. ISBN 9789622092716.

[26] McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.

[27] Powell, Michael J. D. (1981). Approximation Theory and Methods. Cambridge University Press. ISBN 978-0-521-29514-7.

[28] Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. Vol. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-681-8. Zbl 1170.15300.

[FOOTNOTEHornJohnson199036-29] Horn & Johnson 1990, p. 36.

[30] Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. Springer. p. 129. ISBN 978-0-387-20172-6.

[31] Jackson, Terrence H. (1995). From Polynomials to Sums of Squares. CRC Press. p. 143. ISBN 978-0-7503-0329-3.

[32] McCoy 1968, p. 75

[33] Villiers, Johann (2012). Mathematics of Approximation. Springer. ISBN 9789491216503.

[34] Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Saunders. ISBN 0-03-029558-0.

[3] The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers modulo some prime number $p$ .

[4] This terminology dates from the time when the distinction was not clear between a polynomial and the function that it defines: a constant term and a constant polynomial define constant functions.^{[citation needed]}

[8] In fact, as a homogeneous function, it is homogeneous of every degree.^{[citation needed]}

[11] Some authors use "monomial" to mean "monic monomial". See Knapp, Anthony W. (2007). Advanced Algebra: Along with a Companion Volume Basic Algebra. Springer. p. 457. ISBN 978-0-8176-4522-9.

[19] This paragraph assumes that the polynomials have coefficients in a field.

[1]

[2]

[lower-alpha 1]

[lower-alpha 2]

[3]

[4]

[5]

[lower-alpha 3]

[6]

[7]

[lower-alpha 4]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[lower-alpha 5]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

@@ Line 407: / Line 407: @@
 [[Category:बहुपद| बहुपद ]]
 [[Category:बीजगणित]]
+[[Category:Organic Articles]]

v t e बहुपद और बहुपद कार्य
डिग्री	शून्य बहुपद (डिग्री अपरिभाषित या −1 या and) निरंतर कार्य (0) रैखिक फ़ंक्शन (1) रेखीय समीकरण द्विघात कार्य (2) द्विघात समीकरण क्यूबिक फंक्शन (3) घन समीकरण चतुर्थक कार्य (4) चतुर्थक समीकरण क्विंटिक फंक्शन (5) सेक्स्टिक समीकरण (6) सेप्टिक समीकरण (7)
गुणों से	Univariate bivariate बहुभिन्नरूपी मोनोमियल बिनोमियल ट्रिनोमियल irreducible वर्ग-मुक्त सजातीय quasi-homogenous
औजार और एल्गोरिदम	कारक सबसे बड़ा आम भाजक डिवीजन हॉर्नर की मूल्यांकन की विधि परिणामी भेदभावपूर्ण Gröbner आधार

Anonymous

Search