प्रस्तावक सूत्र: Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Logic formula}} | {{Short description|Logic formula}} | ||
प्रस्तावपरक तर्क में, | प्रस्तावपरक तर्क में, '''प्रस्तावात्मक सूत्र''' प्रकार का वाक्य-विन्यास के [[सूत्र (गणितीय तर्क)|गणितीय तार्किक सूत्र]] पर निर्भर करता है, यह ऐसा निर्मित सूत्र होता है जिसका [[सत्य मूल्य|मान सदैव सही]] होता है। यदि किसी प्रस्तावात्मक सूत्र में सभी चरों के मान दिए जाते हैं, तो यह अद्वितीय सही मानों को निर्धारित करता है। प्रस्तावनात्मक सूत्र को प्रस्तावक अभिव्यक्ति, वाक्य या वाक्यात्मक सूत्र भी कहा जाता है। | ||
प्रस्तावनात्मक सूत्र विशेष रूप से सरल [[प्रस्ताव (तर्क)|तार्किक प्रस्ताव]] से निर्मित होता है, जैसे कि पाँच तीन से अधिक या प्रस्तावात्मक चर होता हैं जैसे उदाहरण के लिए ''p'' और ''q'', कनेक्टिव्स या [[तार्किक ऑपरेटर]] है जिसके लिए NOT, AND, OR गेट का उपयोग किया जाता हैं जैसे: | |||
: ('' | : (''p'' AND NOT ''q'') IMPLIES (''p'' OR ''q'') | ||
गणित में, | इस प्रकार गणित में, तर्कवाक्य सूत्र को अधिकांशतः अधिक संक्षिप्त रूप से प्रस्तावित करके संदर्भित किया जाता है, किन्तु अधिक त्रुटीहीन स्थिति में प्रस्तावक सूत्र प्रस्तावित नहीं होता हैं, इसके अतिरिक्त [[औपचारिक अभिव्यक्ति]] प्रस्तावित होती है जो [[प्रस्ताव (गणित)|प्रस्तावित गणितीय]] मान को दर्शाती हैं, इस मत के अनुसार [[औपचारिक वस्तु]], जैसे अभिव्यक्ति की तरह {{nowrap|''x'' + ''y''}} का मान निर्धारित नहीं होता है, किन्तु इसके मान को दर्शाया जा सकता है। कुछ संदर्भों में भेद होने के कारण इसके महत्व को निर्धारित किया जाता हैं। | ||
== प्रस्ताव == | == प्रस्ताव == | ||
प्रस्तावपरक कलन के प्रयोजनों के लिए, | '''प्रस्तावपरक कलन''' के प्रयोजनों के लिए, प्रस्तावित उच्चारण, वाक्य, अभिकथन को या तो सरल या यौगिक के रूप में मान लिया जाता है।<ref>Hamilton 1978:1</ref> इस प्रकार यौगिक तर्कवाक्यों को वाक्यात्मक संयोजकों द्वारा संयोजित किया जाता है, जिनमें से कुछ सबसे सामान्य हैं जैसें- AND , OR , IF ... THEN ... , NEITHER ... NOR ... , ... IS EQUIVALENT TO ... . लिंकिंग अर्धविराम इत्यादि, और इसी प्रकार संयोजी BUT को AND का व्यंजक माना जाता है। असतत वाक्यों के क्रम को AND से जुड़ा हुआ माना जाता है, और औपचारिक विश्लेषण पर सरल प्रस्तावों के अनुक्रमों के संबंध में पुनरावर्ती कोष्ठक के नियम को लागू किया जाता हैं ( इसके लिए बनाए गए सूत्रों के बारे में अच्छी तरह से अध्ययन करें)। | ||
: उदाहरण के लिए: कथन: यह गाय नीली है। वह घोड़ा नारंगी | : उदाहरण के लिए: कथन: यह गाय नीली है। वह घोड़ा नारंगी है किन्तु यहां का घोड़ा बैंगनी रंग का है। वास्तव में AND से संयोजित मिश्रित तर्कवाक्य है: ((यह गाय नीली है और वह घोड़ा नारंगी है) और यह घोड़ा यहाँ बैंगनी है)। | ||
सरल प्रस्ताव प्रकृति में घोषणात्मक होते हैं, अर्थात, वे किसी विशेष वस्तु की अनुभूति की स्थिति या प्रकृति के बारे में प्रमाणित करते हैं | इस प्रकार सरल प्रस्ताव प्रकृति में घोषणात्मक होते हैं, अर्थात, वे किसी विशेष वस्तु की अनुभूति की स्थिति या प्रकृति के बारे में प्रमाणित करते हैं, उदाहरण के लिए यह गाय नीली है, कोयोट है! (वह कोयोट वहाँ है।)<ref>[[Principia Mathematica]] (PM) p. 91 eschews "the" because they require a clear-cut "object of sensation"; they stipulate the use of "this"</ref> इस प्रकार सरल तार्किक कथन विशिष्ट वस्तुओं या मन की विशिष्ट अवस्थाओं के बारे में उपयोग किया जाना चाहिए। इस प्रकार प्रत्येक के पास कम से कम विषयों पर विचार या अवलोकन के तत्काल वस्तु, क्रिया (सक्रिय आवाज और वर्तमान काल में उपयोग के आधार पर), और संभवतः विशेषण या क्रिया विशेषण प्रकार की होनी चाहिए। कुत्ता! संभवतः इसका तात्पर्य है कि मैं कुत्ते को देखता हूं किन्तु इसे बहुत अस्पष्ट के रूप में अनुपयोगी कर दिया जाना चाहिए। | ||
: उदाहरण: वह बैंगनी कुत्ता दौड़ रहा है, यह गाय नीली है, स्विच M31 | : उदाहरण: वह बैंगनी कुत्ता दौड़ रहा है, यह गाय नीली है, स्विच M31 CLOSE है, यह टोपी CLOSE है, कल शुक्रवार है। | ||
तर्कवाक्य कलन के प्रयोजनों के लिए | इस प्रकार तर्कवाक्य कलन के प्रयोजनों के लिए यौगिक तर्कवाक्य को सामान्यतः सरल वाक्यों की श्रृंखला में फिर से लिखा जा सकता है, चूंकि इसका परिणाम संभवतः अधूरा लगेगा। | ||
=== प्रस्तावक और विधेय सूत्रों के बीच संबंध === | === प्रस्तावक और विधेय सूत्रों के बीच संबंध === | ||
प्रस्तावों की आंतरिक संरचना के विश्लेषण के लिए विधेय कलन प्रस्तावक कलन की तुलना में | प्रस्तावों की आंतरिक संरचना के विश्लेषण के लिए विधेय कलन प्रस्तावक कलन की तुलना में यह स्थिति आगे रहती हैं।<ref>(italics added) Reichenbach{{clarify|reason=There is no 'Reichenbach' entry under 'References', not even a link to an article about Reichenbach.|date=October 2013}} p.80.</ref> यह साधारण वाक्य को दो भागों में विभाजित करता है (i) इसका विषय ([[एकवचन शब्द]] या बहुवचन) और (ii) [[विधेय (व्याकरण)]] (एक क्रिया या संभवतः क्रिया-खंड जो गुण या विशेषता का प्रमाणित करता है)। इस प्रकार विधेय कलन इस स्थिति में विषय का सामान्यीकरण करता है। विधेय रूप (जहां प्रतीकों का साथ) निम्नलिखित रिक्त-विषय संरचना के साथ रूप में होता है। | ||
: उदाहरण: इस नीले सुअर के पंख हैं, प्रस्तावक कलन में दो वाक्य बन जाते हैं: इस सुअर के पंख | : उदाहरण: इस नीले सुअर के पंख हैं, प्रस्तावक कलन में दो वाक्य बन जाते हैं: इस सुअर के पंख हैं और यह सुअर नीले रंग का है, जिसकी आंतरिक संरचना पर विचार नहीं किया जाता है। इसके विपरीत, विधेय कलन में, पहला वाक्य इस सुअर में विषय के रूप में टूट जाता है, और विधेय के रूप में पंख होते हैं। इस प्रकार यह प्रमाणित करता है कि वस्तु यह सुअर पंखों वाली चीजों के वर्ग (सेट, संग्रह) का सदस्य है। दूसरा वाक्य इस बात पर जोर देता है कि वस्तु इस सुअर में नीले रंग की विशेषता है और इस प्रकार यह नीली चीजों की श्रेणी का सदस्य है। कोई भी AND से जुड़े दो वाक्यों को इस प्रकार लिखना चुन सकता है: | ||
:: | :: p|W AND p|B | ||
इस सुअर के दो वर्गों के (संभावित) सदस्य पंखों वाली चीजों और नीली चीजों के सामान्यीकरण का अर्थ है कि इसका इन दोनों वर्गों के साथ | इस सुअर के दो वर्गों के (संभावित) सदस्य पंखों वाली चीजों और नीली चीजों के सामान्यीकरण का अर्थ है कि इसका इन दोनों वर्गों के साथ सत्य-संबंध है। दूसरे शब्दों में, प्रवचन पंख वाली चीजों का डोमेन दिया गया है, P या तो इस डोमेन का सदस्य पाया जाता है या नहीं। इस प्रकार p (सुअर) और { T, F }, W (p) के बीच संबंध W (विंग्डनेस) है, जो { T, F } का मूल्यांकन करता है, जहाँ { T, F } [[बूलियन डेटा प्रकार]] सत्य और असत्य का सेट है। इसी प्रकार B (नीलापन) और P (सुअर) और {T, F} के लिए: B (p) {T, F} का मूल्यांकन करता है। तो अब कोई जुड़ा हुआ अभिकथन B(p) और W(p) का समग्र सत्य-मूल्य के लिए विश्लेषण कर सकता है, अर्थात: | ||
: ( | : ( B(p) AND W(p) ) evaluates to { T, F } | ||
विशेष रूप से, सरल वाक्य जो [[तार्किक परिमाणक]] कहलाने वाले सभी | इस प्रकार विशेष रूप से, सरल वाक्य जो [[तार्किक परिमाणक]] कहलाने वाले सभी या कुछ की धारणाओं को नियोजित करते हैं, विधेय कलन द्वारा व्यवहार किए जाते हैं। नए फ़ंक्शन को प्रतीक F(x) के साथ दो नए प्रतीक ∀ (सभी के लिए), और ∃ (वहाँ संलग्न है ..., कम से कम ... संलग्न है, आदि) प्रस्तुत किए गए हैं। विधेय कलन, किन्तु प्रस्तावक कलन नहीं, निम्नलिखित कथन की औपचारिक वैधता स्थापित कर सकता है: | ||
: सभी नीले सूअरों के पंख होते हैं किन्तु कुछ सूअरों के पंख नहीं होते हैं, इसलिए कुछ सूअर नीले नहीं होते हैं। | : सभी नीले सूअरों के पंख होते हैं किन्तु कुछ सूअरों के पंख नहीं होते हैं, इसलिए कुछ सूअर नीले नहीं होते हैं। | ||
=== पहचान === | === पहचान === | ||
तर्स्की का प्रमाणित है कि पहचान की धारणा (तार्किक समानता से अलग) प्रस्ताविक कलन के बाहर है | तर्स्की का प्रमाणित है कि पहचान की धारणा (तार्किक समानता से अलग) प्रस्ताविक कलन के बाहर है, चूंकि, वह नोट करता है कि यदि किसी तर्क को गणित और विज्ञान के लिए उपयोग करना है तो उसमें पहचान का सिद्धांत होना चाहिए।<ref>Tarski p.54-68. Suppes calls IDENTITY a "further rule of inference" and has a brief development around it; Robbin, Bender and Williamson, and Goodstein introduce the sign and its usage without comment or explanation. Hamilton p. 37 employs two signs ≠ and = with respect to the '''valuation''' of a formula in a formal calculus. Kleene p. 70 and Hamilton p. 52 place it in the predicate calculus, in particular with regards to the arithmetic of natural numbers.</ref> इस प्रकार कुछ लेखक इस विस्तार पर जोर देने के लिए पहचान के साथ विधेय तर्क का उल्लेख करते हैं। इसके बारे में नीचे देखें। | ||
== प्रस्तावों का | == प्रस्तावों का बीजगणित, प्रस्तावपरक कलन == | ||
बीजगणित (जिसमें कई मान अलग-अलग हैं), शिथिल रूप से परिभाषित की जाती हैं, यह ऐसी विधि है जिसके द्वारा कुछ अन्य प्रतीकों जैसे कोष्ठक (,) और कुछ उप-प्रतीकों जैसे कि *, +, ~ के साथ चर प्रतीकों , &, ∨, =, ≡, ∧, ¬ को संग्रहित किया जाता है। इन नियमों की प्रणाली के भीतर परिवर्तन किया जाता है। इस प्रकार हम कह सकते हैं कि ये प्रतीक और इनसे बनी हुई वस्तुओं का प्रतिनिधित्व करते हैं, किन्तु विशिष्ट बीजगणितीय प्रणाली में इन वस्तुओं का कोई अर्थ नहीं होता है। इस प्रकार बीजगणित के अंदर कार्य प्रतीकों के शब्दार्थ (अर्थ) के अतिरिक्त बीजगणित के [[वाक्य - विन्यास]] (प्रतीक-गठन) के कुछ नियमों का पालन करने का अभ्यास बन जाता है। यह मुख्य रूप से गणितीय बीजगणित के बाहर पाए जाते हैं। | |||
बीजगणित में प्रतीकों के | इस प्रकार बीजगणित में प्रतीकों के अच्छी तरह से गठित अनुक्रम के लिए - सूत्र - बीजगणित के बाहर कुछ उपयोगिता रखने के लिए प्रतीकों को अर्थ निर्दिष्ट किया जाता है और अंततः चर को मान निर्दिष्ट किया जाता है, फिर नियमों की श्रृंखला द्वारा सूत्र का मूल्यांकन किया जाता है। | ||
जब मान केवल दो तक सीमित होते हैं और साधारण वाक्यों (जैसे बोले गए उच्चारण या लिखित अभिकथन) की धारणा पर लागू होते हैं, जो प्रस्तावक संयोजकों से जुड़े होते हैं, तो प्रतीकों और नियमों और मूल्यांकन-पद्धतियों की इस पूरी बीजगणितीय प्रणाली को सामान्यतः प्रस्तावात्मक कलन या वाक्यगत कलन कहा जाता है। . | इस प्रकार जब मान केवल दो तक सीमित होते हैं और साधारण वाक्यों (जैसे बोले गए उच्चारण या लिखित अभिकथन) की धारणा पर लागू होते हैं, जो प्रस्तावक संयोजकों से जुड़े होते हैं, तो प्रतीकों और नियमों और मूल्यांकन-पद्धतियों की इस पूरी बीजगणितीय प्रणाली को सामान्यतः प्रस्तावात्मक कलन या वाक्यगत कलन कहा जाता है। . | ||
जबकि अंकगणित बीजगणित के कुछ परिचित नियम प्रस्तावों के बीजगणित में बने रहते | जबकि अंकगणित बीजगणित के कुछ परिचित नियम प्रस्तावों के बीजगणित में बने रहते हैं। इस प्रकार उदाहरण के लिए AND और OR के लिए क्रमविनिमेय और साहचर्य नियम), कुछ नहीं (उदाहरण के लिए AND, OR और NOT के लिए [[वितरण कानून|वितरण नियम]] इत्यादि। | ||
=== प्रस्तावात्मक सूत्रों की उपयोगिता === | === प्रस्तावात्मक सूत्रों की उपयोगिता === | ||
विश्लेषण: [[निगमनात्मक तर्क]] में, दार्शनिक, | विश्लेषण: [[निगमनात्मक तर्क]] में, दार्शनिक, वादविवाद करने वाले और गणितज्ञ तर्कों को सूत्रों तक कम करते हैं और फिर इस प्रकार शुद्धता (सुदृढ़ता) के लिए उनका (सामान्यतः सत्य तालिकाओं के साथ) अध्ययन करते हैं। उदाहरण के लिए: क्या निम्नलिखित तर्क सही है? | ||
: यह देखते हुए कि | : यह देखते हुए कि कृत्रिम बुद्धि के लिए चेतना पर्याप्त है और केवल सचेत संस्थाएं [[ट्यूरिंग टेस्ट|ट्यूरिंग जाँच]] पास कर सकती हैं, इस प्रकार इससे पहले कि हम यह निष्कर्ष निकाल सकें कि रोबोट कृत्रिम बुद्धि है, रोबोट को ट्यूरिंग टेस्ट पास करना होगा। | ||
इंजीनियर [[तर्क सर्किट]] का विश्लेषण करते हैं जिसे उन्होंने संश्लेषण तकनीकों का उपयोग करके डिजाइन किया है और फिर उनके डिजाइन को सरल बनाने के लिए विभिन्न कटौती और न्यूनीकरण तकनीकों को लागू करते हैं। | इंजीनियर [[तर्क सर्किट|तर्क परिपथ]] का विश्लेषण करते हैं इस प्रकार जिसे उन्होंने संश्लेषण तकनीकों का उपयोग करके डिजाइन किया है और फिर उनके डिजाइन को सरल बनाने के लिए विभिन्न कटौती और न्यूनीकरण तकनीकों को लागू करते हैं। | ||
संश्लेषण: इंजीनियर विशेष रूप से सत्य तालिकाओं से प्रस्तावन सूत्र (जो अंततः प्रतीकों के | संश्लेषण: इंजीनियर विशेष रूप से सत्य तालिकाओं से प्रस्तावन सूत्र (जो अंततः प्रतीकों के परिपथ के रूप में समाप्त होते हैं) को संश्लेषित करते हैं। इस प्रकार उदाहरण के लिए, सत्य तालिका लिख सकता है कि बाइनरी जोड़ को कैसे व्यवहार करना चाहिए, चर b और a और कैरी_इन सीआई के अतिरिक्त, और परिणाम carry_out सह और योग Σ: | ||
* उदाहरण: पंक्ति 5 में, (( | * उदाहरण: पंक्ति 5 में, ((B+A) + CI) = ((1+0) + 1) = 2, इसे बाइनरी नंबर के रूप में लिखा जाता है, यह 10<sub>2</sub> है, जहाँ co =1 और Σ=0 जैसा कि सबसे दाएँ कॉलम में दिखाया गया है। | ||
{| class="wikitable" style="text-align:center; margin-left: auto; margin-right: auto; border: none;" | {| class="wikitable" style="text-align:center; margin-left: auto; margin-right: auto; border: none;" | ||
|- | |- | ||
| Line 79: | Line 79: | ||
| 1 || 1 || 1 || || 3 || 1 || 1 | | 1 || 1 || 1 || || 3 || 1 || 1 | ||
|} | |} | ||
=== प्रस्ताव चर === | === प्रस्ताव चर === | ||
प्रस्तावात्मक सूत्र का सबसे सरल प्रकार | '''प्रस्तावात्मक सूत्र''' का सबसे सरल प्रकार प्रस्तावक चर है। इस प्रकार प्रस्ताव जो सरल ([[परमाणु सूत्र]]) हैं, प्रतीकात्मक अभिव्यक्ति अधिकांशतः ''p'', ''q'', या ''P'', ''Q'', आदि नाम के चर द्वारा दर्शाए जाते हैं। परमाणु प्रस्ताव (अभिकथन) का प्रतिनिधित्व करते हैं, जैसे कि यह शनिवार है = ''p'' (यहाँ प्रतीक = का अर्थ है ... नाम का चर निर्दिष्ट किया गया है ...) या मैं केवल सोमवार = ''q '' को फिल्मों में संयोजित किया जाता हैं। | ||
=== सत्य-मूल्य असाइनमेंट, सूत्र मूल्यांकन === | === सत्य-मूल्य असाइनमेंट, सूत्र मूल्यांकन === | ||
एक प्रस्तावक सूत्र का मूल्यांकन प्रत्येक चर के लिए | एक प्रस्तावक सूत्र का मूल्यांकन प्रत्येक चर के लिए सत्य मान के असाइनमेंट से प्रारंभ होता है। क्योंकि प्रत्येक चर सरल वाक्य का प्रतिनिधित्व करता है, इस प्रकार इन सरल वाक्यों की सत्यता या असत्यता पर सत्य मान लागू किए जा रहे हैं। | ||
==== वादविवाद, दर्शन और गणित में सत्य मूल्य ==== | |||
सत्य मान केवल दो हैं: {सत्य T, असत्य F}। [[अनुभववादी]] सभी प्रस्तावों को दो व्यापक वर्गों में रखता है: ''विश्लेषणात्मक''—सच्चा कोई फर्क नहीं पड़ता (उदाहरण के लिए [[टॉटोलॉजी (तर्क)]]), और ''सिंथेटिक''—अनुभव से व्युत्पन्न और इस तरह तीसरे पक्ष द्वारा पुष्टि के लिए अतिसंवेदनशील ([[सत्यापन सिद्धांत]]) अर्थ का)।<ref>Empiricits eschew the notion of ''a priori'' (built-in, born-with) knowledge. "Radical reductionists" such as [[John Locke]] and [[David Hume]] "held that every idea must either originate directly in sense experience or else be compounded of ideas thus originating"; quoted from Quine reprinted in 1996 ''The Emergence of Logical Empriricism'', Garland Publishing Inc. http://www.marxists.org/reference/subject/philosophy/works/us/quine.htm</ref> अनुभवजन्य मानते हैं कि, सामान्य रूप से, [[सिंथेटिक प्रस्ताव]] के सत्य-मूल्य पर पहुंचने के लिए, अर्थ को पहले शब्दों पर लागू किया जाना चाहिए, और फिर इन अर्थ-सांचे को जो कुछ भी हो रहा है, उसके विरुद्ध मिलान किया जाना चाहिए। इस प्रकार प्रमाणित भी किया जाना चाहिए। जैसे कि उक्त कथन है कि गाय है, क्या यह कथन सत्य है? सत्य में मैंने कहा था और संभवतः मैं नीली गाय को देख रहा हूं - जब तक कि मैं असत्य नहीं बोल रहा हूं, मेरा कथन मेरी (संभवतः त्रुटिपूर्ण) धारणा के उद्देश्य के सापेक्ष सत्य है। किन्तु क्या वाकई में नीली गाय होती है? जब आप उसी खिड़की से बाहर देखते हैं तो आप क्या देखते हैं? सत्यापन के साथ आगे बढ़ने के लिए, आपको गाय और गाय दोनों की पूर्व धारणा की आवश्यकता होगी और वस्तु के विरुद्ध टेम्पलेट्स से मिलान करने की क्षमता (यदि वास्तव में कोई है)। | |||
सत्य | ==== इंजीनियरिंग में सत्य मूल्य ==== | ||
इंजीनियर सत्य और असत्य की धारणाओं से बचने की प्रयास करते हैं जो दार्शनिकों को इंगित करते हैं, किन्तु अंतिम विश्लेषण में इंजीनियरों को अपने मापने वाले उपकरणों पर भरोसा करना चाहिए। इस प्रकार मजबूत आँकड़ों की अपनी खोज में, इंजीनियर छोटे पुस्तकालय से ज्ञात वस्तुओं को खींचना पसंद करते हैं - ऐसी वस्तुएँ जिनमें बड़े संयोजनों में भी अच्छी तरह से परिभाषित, पूर्वानुमेय व्यवहार होता है, (इसलिए उनका नाम प्रस्ताविक कलन के लिए है: संयोजक तर्क पर आधारित होते हैं। किसी वस्तु के सबसे कम व्यवहार दो हैं (जैसे {OFF, ON}, {OPEN, SHUT}, {UP, DOWN} आदि), और इन्हें {0, 1} के अनुरूप रखा गया है। ऐसे तत्वों को डिजिटल डेटा कहा जाता है, व्यवहारों की सतत श्रृंखला वाले [[एनालॉग संकेत]] कहलाते हैं। इस प्रकार जब भी किसी एनालॉग सिस्टम में निर्णय लेने होते हैं, तो अधिकांशतः इंजीनियर तुलनित्र के उपयोग से एनालॉग व्यवहार (दरवाजा 45.32146% UP है) को डिजिटल (जैसे DOWN=0 ) में परिवर्तित कर देगा।<ref>[[Neural net]] modelling offers a good mathematical model for a comparator as follows: Given a signal S and a threshold "thr", subtract "thr" from S and substitute this difference d to a [[sigmoid function]]: For large "gains" k, e.g. k=100, 1/( 1 + e<sup>−k*d</sup> ) = 1/( 1 + e<sup>−k*(S-thr)</sup> ) = { ≃0, ≃1 }.{{clarify|What is the meaning of the curly braces here? Denoting set comprehension wouldn't make sense.|date=October 2016}} For example, if "The door is DOWN" means "The door is less than 50% of the way up", then a threshold thr=0.5 corresponding to 0.5*5.0 = +2.50 volts could be applied to a "linear" measuring-device with an output of 0 volts when fully closed and +5.0 volts when fully open.</ref> | |||
इस प्रकार चर और दो मूल्य-प्रतीकों {0, 1} के अर्थ का असाइनमेंट सूत्र के बाहर से आता है जो (सामान्यतः) यौगिक वस्तु के व्यवहार का प्रतिनिधित्व करता है। उदाहरण गेराज दरवाजा है जिसमें दो सीमा स्विच हैं, UP लेबल वाले SW_U के लिए और नीचे लेबल वाले SW_D के लिए, और जो कुछ भी दरवाजे के सर्किटरी में है। इस प्रकार परिपथ का निरीक्षण (या तो आरेख या वास्तविक वस्तुएं स्वयं-दरवाजा, स्विच, तार, परिपथ बोर्ड इत्यादि) प्रकट कर सकता है कि परिपथ बोर्ड नोड 22 पर +0 वोल्ट जाता है। जब स्विच SW_D के संपर्क यांत्रिक रूप से होते हैं तब संपर्क (CLOSE) और दरवाजा नीचे की स्थिति में है (95% नीचे), और नोड 29 +0 वोल्ट पर जाता है जब दरवाजा 95% UP होता है और स्विच SW_U के संपर्क यांत्रिक संपर्क (CLOSE) में होते हैं।<ref>In actuality the digital 1 and 0 are defined over non-overlapping ranges e.g. { "1" = +5/+0.2/−1.0 volts, 0 = +0.5/−0.2 volts }{{clarify|Explain the meaning of curly braces and slash here.|date=October 2016}}. When a value falls outside the defined range(s) the value becomes "u" -- unknown; e.g. +2.3 would be "u".</ref> इस प्रकार इंजीनियर को इन वोल्टेज और सभी संभावित संयोजनों (उनमें से सभी 4) के अर्थ को परिभाषित करना चाहिए, जिसमें असत्य भी सम्मलित हैं (उदाहरण के लिए दोनों नोड्स 22 और 29 0 वोल्ट पर हैं, जिसका अर्थ है कि दरवाजा ही समय में OPEN और CLOSE है)। परिपथ सच्चाई या असत्य, सही या गलत, सुरक्षित या खतरनाक के बारे में किसी भी जागरूकता के बिना जो भी वोल्टेज का अनुभव करता है, बिना सोचे-समझे प्रतिक्रिया करता है। | |||
इस प्रकार चर और दो मूल्य-प्रतीकों {0, 1} के अर्थ का | |||
== प्रस्तावित संयोजक == | == प्रस्तावित संयोजक == | ||
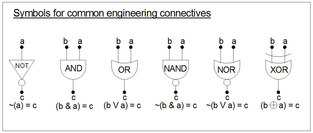
तर्कवाक्य चरों और [[तार्किक संयोजक]]ों का उपयोग करते हुए अन्य तर्कवाक्य सूत्रों से मनमाना तर्कवाक्य सूत्र बनाए जाते हैं। संयोजकों के उदाहरणों में सम्मलित हैं: | तर्कवाक्य चरों और [[तार्किक संयोजक]]ों का उपयोग करते हुए अन्य तर्कवाक्य सूत्रों से मनमाना तर्कवाक्य सूत्र बनाए जाते हैं। संयोजकों के उदाहरणों में सम्मलित हैं: | ||
* एकात्मक निषेध संयोजक। यदि <math>\alpha</math> | * एकात्मक निषेध संयोजक। यदि <math>\alpha</math> सूत्र है, तो <math>\lnot \alpha</math> सूत्र है। | ||
* मौलिक बाइनरी संयोजक <math>\land, \lor, \to, \leftrightarrow</math>. इस प्रकार, उदाहरण के लिए, यदि <math>\alpha</math> और <math>\beta</math> सूत्र हैं, इसलिए है <math>(\alpha \to \beta)</math>. | * मौलिक बाइनरी संयोजक <math>\land, \lor, \to, \leftrightarrow</math>. इस प्रकार, उदाहरण के लिए, यदि <math>\alpha</math> और <math>\beta</math> सूत्र हैं, इसलिए है <math>(\alpha \to \beta)</math>. | ||
* अन्य बाइनरी संयोजक, जैसे NAND, NOR, और XOR | * अन्य बाइनरी संयोजक, जैसे NAND, NOR, और XOR | ||
* त्रिक संयोजक | * त्रिक संयोजक IF ... THEN ... ELSE ... | ||
* | * निरंतर 0- संयोजक ⊤ और ⊥ (वैकल्पिक रूप से, स्थिरांक { T, F }, { 1, 0 } आदि।) | ||
* सिद्धांत-विस्तार संयोजक EQUALS (वैकल्पिक रूप से, पहचान, या चिन्ह = जैसा कि तार्किक संयोजक से अलग है <math>\leftrightarrow</math>) | * सिद्धांत-विस्तार संयोजक EQUALS (वैकल्पिक रूप से, पहचान, या चिन्ह = जैसा कि तार्किक संयोजक से अलग है <math>\leftrightarrow</math>) | ||
=== | === वादविवाद, दर्शन और गणित के संयोजक === | ||
वादविवाद, दर्शन और गणित के साथ-साथ उनके सत्य तालिकाओं के लिए सामान्य संयोजक निम्नलिखित हैं। इस प्रकार उपयोग किए गए प्रतीक लेखक से लेखक और प्रयास के क्षेत्रों के बीच भिन्न होंगे। सामान्यतः संक्षिप्त रूप T और F मूल्यांकनों के लिए खड़े होते हैं सत्य और असत्यता प्रस्तावक सूत्र में चरों पर लागू होते हैं (उदाहरण के लिए प्रमाणित: वह गाय नीली है, सत्य के लिए सत्य-मूल्य T या असत्यता के लिए F, जैसा भी मामला हो .). | |||
संयोजक कई अलग-अलग शब्द-प्रयोगों से चलते हैं, | संयोजक कई अलग-अलग शब्द-प्रयोगों से चलते हैं, उदाहरण के लिए a का अर्थ है b को IF a THEN b भी कहा जाता है। इनमें से कुछ तालिका में दिखाए गए हैं। | ||
{|class="wikitable" | {|class="wikitable" | ||
| Line 144: | Line 142: | ||
| | | | ||
|style="background-color:#E5E0EC" | {{not a typo|a}} IS NECESSARY FOR b | |style="background-color:#E5E0EC" | {{not a typo|a}} IS NECESSARY FOR b | ||
|style="background-color:#F2F2F2" | b IF AND ONLY IF a | |style="background-color:#F2F2F2" | b IF AND ONLY IF a, b IFF a | ||
| | | | ||
| | | | ||
| Line 256: | Line 254: | ||
=== इंजीनियरिंग संयोजक === | === इंजीनियरिंग संयोजक === | ||
[[File:Propositional formula connectives 1.png|313px|thumb|right| इंजीनियरिंग प्रतीकों में पिछले कुछ वर्षों में विविधता आई है, किन्तु ये सामान्य हैं। कभी-कभी वे प्रतीकों वाले बक्से के रूप में दिखाई देते हैं। ए और बी को इनपुट कहा जाता है और | [[File:Propositional formula connectives 1.png|313px|thumb|right| इंजीनियरिंग प्रतीकों में पिछले कुछ वर्षों में विविधता आई है, किन्तु ये सामान्य हैं। इस प्रकार कभी-कभी वे प्रतीकों वाले बक्से के रूप में दिखाई देते हैं। ए और बी को इनपुट कहा जाता है और C को आउटपुट कहा जाता है।]]सामान्यतः, इंजीनियरिंग संयोजक गणित के संयोजकों के समान ही होते हैं, इस प्रकार 1 = T और 0 = F के साथ मूल्यांकन करते हैं। इस प्रकार यह मध्य मान और कर्णघ तो मानचित्र (नीचे देखें) की धारणा के उपयोग से विश्लेषण/न्यूनीकरण और सूत्रों के संश्लेषण के उद्देश्यों के लिए किया जाता है। इंजीनियर [[बूलियन]] की धारणा (a*a = a) से 'तार्किक उत्पाद' और [[विलियम स्टेनली जेवन्स]] की धारणा (a+a = a) से 'तार्किक योग' शब्दों का भी उपयोग करते हैं।<ref>While the notion of logical product is not so peculiar (e.g. 0*0=0, 0*1=0, 1*0=0, 1*1=1), the notion of (1+1=1 ''is'' peculiar; in fact (a "+" b) = (a + (b - a*b)) where "+" is the "logical sum" but + and - are the true arithmetic counterparts. Occasionally all four notions do appear in a formula: A AND B = 1/2*( A plus B minus ( A XOR B ) ] (cf p. 146 in John Wakerly 1978, ''Error Detecting Codes, Self-Checking Circuits and Applications, North-Holland, New York, {{isbn|0-444-00259-6}} pbk.)</ref> | ||
{|class="wikitable" style="text-align:center" | {|class="wikitable" style="text-align:center" | ||
| Line 347: | Line 345: | ||
=== केस कनेक्टिव: | === केस कनेक्टिव: IF ... THEN ... ELSE ... === | ||
IF ... THEN ... ELSE ... संयोजी [[पुनरावर्तन सिद्धांत]] और [[संगणना सिद्धांत]] के CASE संचालक के सरलतम रूप के रूप में प्रकट होता है और सशर्त गोटो (कूदता है, शाखाओं) के लिए जिम्मेदार संयोजी है। इस | IF ... THEN ... ELSE ... संयोजी [[पुनरावर्तन सिद्धांत]] और [[संगणना सिद्धांत]] के CASE संचालक के सरलतम रूप के रूप में प्रकट होता है और सशर्त गोटो (कूदता है, शाखाओं) के लिए जिम्मेदार संयोजी है। इस संयोजी से अन्य सभी संयोजकों का निर्माण किया जा सकता है। इस प्रकार यद्यपि IF c THEN b ELSE a निहितार्थ की तरह लगता है, यह अपने सबसे कम रूप में है, स्विच जो निर्णय लेता है और परिणाम के रूप में केवल दो विकल्पों में से या b प्रदान करता है (इसलिए C में नाम [[स्विच स्टेटमेंट]] (प्रोग्रामिंग भाषा) ) प्रोग्रामिंग भाषा)।<ref>A careful look at its Karnaugh map shows that IF...THEN...ELSE can also be expressed, in a rather round-about way, in terms of two exclusive-ORs: ( (b AND (c XOR a)) OR (a AND (c XOR b)) ) = d.</ref> | ||
निम्नलिखित तीन तर्कवाक्य समतुल्य हैं (जैसा कि तार्किक तुल्यता चिह्न ≡ द्वारा इंगित किया गया है): | निम्नलिखित तीन तर्कवाक्य समतुल्य हैं (जैसा कि तार्किक तुल्यता चिह्न ≡ द्वारा इंगित किया गया है): | ||
# (यदि 'काउंटर शून्य है' तो 'निर्देश बी पर जाएं' या 'अनुदेश पर जाएं') ≡ | # (यदि 'काउंटर शून्य है' तो 'निर्देश बी पर जाएं' या 'अनुदेश पर जाएं') ≡ | ||
# (( | # ((C → B) और (~C → A)) ≡ ((यदि 'काउंटर शून्य है' तो 'निर्देश B' पर जाएं) और (यदि 'यह वह स्थिति नहीं है कि काउंटर शून्य है' तो 'पर जाएं निर्देश A) ≡ | ||
# (( | # ((C और B) ∨ (~C और A)) ≡ ('काउंटर शून्य है' और 'निर्देश B पर जाएं) या ('ऐसा नहीं है कि 'काउंटर शून्य है' और 'निर्देश A पर जाएं) | ||
इस प्रकार IF ... THEN ... ELSE - निहितार्थ के विपरीत - | इस प्रकार IF ... THEN ... ELSE - निहितार्थ के विपरीत - अस्पष्ट सत्य का मूल्यांकन नहीं करता है जब पहला प्रस्ताव असत्य होता है ,अर्थात c = F in (c → b)। उदाहरण के लिए, अधिकांश लोग निम्नलिखित संयुक्त तर्कवाक्य को निरर्थक गैर अनुगामी के रूप में अस्वीकार कर देंगे क्योंकि दूसरा वाक्य अर्थ में पहले से जुड़ा नहीं है।<ref>Robbin p. 3.</ref> | ||
: उदाहरण: प्रस्ताव यदि 'विंस्टन चर्चिल चीनी थे' तब 'सूरज पूर्व में उगता है' | : उदाहरण: प्रस्ताव यदि 'विंस्टन चर्चिल चीनी थे' तब 'सूरज पूर्व में उगता है' सत्य के रूप में मूल्यांकन करता है, इस प्रकार यह देखते हुए कि 'विंस्टन चर्चिल चीनी थे' इस प्रकार इसका मान असत्य होगा और 'सूर्य पूर्व में उगता है' सत्य के रूप में मूल्यांकन करता है। | ||
इस समस्या की पहचान में, प्रस्ताविक कलन में औपचारिक निहितार्थ के संकेत → को हर रोज़, सहज ज्ञान युक्त निहितार्थ से अलग करने के लिए [[सामग्री सशर्त]] कहा जाता है।{{efn|Rosenbloom discusses this problem of implication at some length. Most philosophers and mathematicians just accept the material definition as given above. But some do not, including the [[Intuitionism|intuitionists]]; they consider it a form of the law of excluded middle misapplied.{{sfn|Rosenbloom|1950|pp=30 and 54ff}}}} | इस समस्या की पहचान में, प्रस्ताविक कलन में औपचारिक निहितार्थ के संकेत → को हर रोज़, सहज ज्ञान युक्त निहितार्थ से अलग करने के लिए [[सामग्री सशर्त]] कहा जाता है।{{efn|Rosenbloom discusses this problem of implication at some length. Most philosophers and mathematicians just accept the material definition as given above. But some do not, including the [[Intuitionism|intuitionists]]; they consider it a form of the law of excluded middle misapplied.{{sfn|Rosenbloom|1950|pp=30 and 54ff}}}} | ||
IF ... THEN ... ELSE निर्माण विवाद से बचा जाता है क्योंकि यह दो घोषित विकल्पों के बीच पूरी तरह से निर्धारक विकल्प प्रदान करता है | IF ... THEN ... ELSE निर्माण विवाद से बचा जाता है क्योंकि यह दो घोषित विकल्पों के बीच पूरी तरह से निर्धारक विकल्प प्रदान करता है, यह दो वस्तुओं (दो विकल्प बी और ए) प्रदान करता है, और यह उनके बीच विस्तृत और स्पष्ट रूप से चयन करता है।<ref>Indeed, exhaustive selection between alternatives -- '''mutual exclusion''' -- is required by the definition that Kleene gives the CASE operator (Kleene 1952229)</ref> नीचे दी गई सत्य तालिका में, d1 सूत्र है: ((IF c THEN b) AND (IF NOT-c THEN a) ) का उपयोग देखा जा सकता हैं। इस प्रकार इसका पूरी तरह से घटता हुआ रूप d2 के लिए उक्त सूत्र है: ((c AND b) OR (NOT-c AND a)। कॉलम =d1 और =d2 द्वारा दिखाए गए दो सूत्र समकक्ष हैं। इलेक्ट्रिकल इंजीनियर पूरी तरह से कम किए गए फॉर्मूले को AND- कहते हैं। इस प्रकार OR-चयन ऑपरेटर या CASE (या स्विच) ऑपरेटर n संभव, किन्तु परस्पर अनन्य परिणामों के लिए ही विचार का विस्तार है। विद्युत इंजीनियर CASE ऑपरेटर को [[बहुसंकेतक]] कहते हैं। | ||
{| | {| | ||
| Line 778: | Line 777: | ||
=== पहचान और मूल्यांकन === | === पहचान और मूल्यांकन === | ||
इस खंड की पहली तालिका में *** प्रविष्टि तार्किक तुल्यता है जो इस तथ्य पर ध्यान देती है कि तार्किक तुल्यता पहचान के समान नहीं है। उदाहरण के लिए, अधिकांश लोग इस बात से सहमत होंगे कि यह कथन कि गाय नीली है, गाय के नीले होने के कथन के समान है। दूसरी ओर, तार्किक तुल्यता कभी-कभी भाषण में प्रकट होती है जैसे कि इस उदाहरण में: 'सूरज चमक रहा है' का अर्थ है 'मैं बाइक चला रहा हूं' | इस खंड की पहली तालिका में *** प्रविष्टि तार्किक तुल्यता है जो इस तथ्य पर ध्यान देती है कि तार्किक तुल्यता पहचान के समान नहीं है। उदाहरण के लिए, अधिकांश लोग इस बात से सहमत होंगे कि यह कथन कि गाय नीली है, गाय के नीले होने के कथन के समान है। दूसरी ओर, तार्किक तुल्यता कभी-कभी भाषण में प्रकट होती है जैसे कि इस उदाहरण में: 'सूरज चमक रहा है' का अर्थ है 'मैं बाइक चला रहा हूं' प्रस्तावक सूत्र में अनुवादित शब्द बन जाते हैं: यदि 'सूरज चमक रहा है' तो 'मैं' बाइकिंग', और यदि 'मैं बाइकिंग कर रहा हूं' तो 'सूरज चमक रहा है':<ref>The use of quote marks around the expressions is not accidental. Tarski comments on the use of quotes in his "18. Identity of things and identity of their designations; use of quotation marks" p. 58ff.</ref> | ||
: IF 's' THEN 'b' AND IF 'b' THEN 's' को ((s → b) & (b → s)) या संक्षिप्त रूप में (s ↔ b) लिखा जाता है। जैसा कि सबसे दाहिना प्रतीक स्ट्रिंग बाईं ओर के प्रतीकों के संदर्भ में | : IF 's' THEN 'b' AND IF 'b' THEN 's' को ((s → b) & (b → s)) या संक्षिप्त रूप में (s ↔ b) लिखा जाता है। जैसा कि सबसे दाहिना प्रतीक स्ट्रिंग बाईं ओर के प्रतीकों के संदर्भ में नए प्रतीक की परिभाषा है, पहचान चिह्न = का उपयोग उचित है: | ||
:: (( | :: ((S → B) और (B → S)) = (S ↔ B) | ||
विभिन्न लेखक तार्किक तुल्यता के लिए अलग-अलग चिह्नों का उपयोग करते हैं: ↔ ( | विभिन्न लेखक तार्किक तुल्यता के लिए अलग-अलग चिह्नों का उपयोग करते हैं: ↔ (उदाहरणतयः सप्पेस, गुडस्टीन, हैमिल्टन), ≡ (उदाहरणतयः रॉबिन), ⇔ (उदाहरणतयः बेंडर और विलियमसन)। इस प्रकार विशिष्ट पहचान को बराबर चिह्न = के रूप में लिखा जाता है। इस प्रकार इस नियम का अपवाद 'प्रिंसिपिया मैथेमेटिका' में पाया जाता है। पहचान की धारणा के दर्शन के बारे में अधिक जानकारी के लिए अविवेक की पहचान या लीबनिज का नियम देखें। | ||
जैसा कि ऊपर उल्लेख किया गया है, टार्स्की पहचान को प्रस्ताविक कलन के बाहर मानता है, किन्तु वह प्रमाणित करता है कि धारणा के बिना, गणित और निगमनात्मक विज्ञान के लिए तर्क अपर्याप्त है। वास्तव में जब किसी सूत्र का मूल्यांकन किया जाना होता है तो संकेत प्रमेय कलन में आता है।<ref>Hamilton p. 37. Bender and Williamson p. 29 state "In what follows, we'll replace "equals" with the symbol " ⇔ " (equivalence) which is usually used in logic. We use the more familiar " = " for assigning meaning and values."</ref> | जैसा कि ऊपर उल्लेख किया गया है, टार्स्की पहचान को प्रस्ताविक कलन के बाहर मानता है, किन्तु वह प्रमाणित करता है कि धारणा के बिना, गणित और निगमनात्मक विज्ञान के लिए तर्क अपर्याप्त है। इस प्रकार वास्तव में जब किसी सूत्र का मूल्यांकन किया जाना होता है तो संकेत प्रमेय कलन में आता है।<ref>Hamilton p. 37. Bender and Williamson p. 29 state "In what follows, we'll replace "equals" with the symbol " ⇔ " (equivalence) which is usually used in logic. We use the more familiar " = " for assigning meaning and values."</ref> | ||
उदाहरण के लिए, हैमिल्टन दो प्रतीकों = और ≠ का उपयोग करता है जब वह किसी भी [[अच्छी तरह से गठित सूत्र]] | कुछ प्रणालियों में कोई सत्य सारणी नहीं होती है, बल्कि केवल औपचारिक स्वयंसिद्ध (उदाहरण के लिए सेट से प्रतीकों के तार { ~, →, (, ), चर P<sub>1</sub>, P<sub>2</sub>, P<sub>3</sub>, ... } और सूत्र-गठन नियम (उदाहरण के लिए प्रतिस्थापन और [[मूड सेट करना]] के उपयोग से पिछले तारों से अधिक प्रतीक तार बनाने के नियम) पर आधारित हैं। इस प्रकार कलन का परिणाम अन्य सूत्र अर्थात अच्छी तरह से निर्मित प्रतीक स्ट्रिंग के रूप में होगा। इस प्रकार अंततः चूंकि, यदि कोई वैधता और सत्य की धारणाओं का अध्ययन करने के लिए कलन का उपयोग करना चाहता है, तो इस प्रकार उसे ऐसे स्वयंसिद्धों को जोड़ना होगा जो सत्य मान {T, F} (या {1, 0}, आदि) कहे जाने वाले प्रतीकों के व्यवहार को अन्य प्रतीकों के सापेक्ष परिभाषित करते हैं। | ||
उदाहरण के लिए, हैमिल्टन दो प्रतीकों = और ≠ का उपयोग करता है इस प्रकार जब वह किसी भी [[अच्छी तरह से गठित सूत्र]] (wffs) ''A'' और ''B'' के मूल्यांकन v की धारणा को अपने औपचारिक बयान कलन L में परिभाषित करता है। मूल्यांकन v है a ''फ़ंक्शन (गणित)'' उनके सिस्टम L के wffs से सीमा (output) {T, F} तक, दिया गया है कि प्रत्येक चर p<sub>1</sub>, p<sub>2</sub>, p<sub>3</sub> wff में सत्य मान {T, F} द्वारा इंगित किया जाता है। | |||
{{NumBlk|*| '''v'''(''A'') ≠ '''v'''(~''A'')|{{EquationRef|i}}}} | {{NumBlk|*| '''v'''(''A'') ≠ '''v'''(~''A'')|{{EquationRef|i}}}} | ||
{{NumBlk|*| '''v'''(''A'' → ''B'') {{=}} F if and only if '''v'''(''A'') {{=}} T and '''v'''(''B'') {{=}} F|{{EquationRef|ii}}}} | {{NumBlk|*| '''v'''(''A'' → ''B'') {{=}} F if and only if '''v'''(''A'') {{=}} T and '''v'''(''B'') {{=}} F|{{EquationRef|ii}}}} | ||
दो परिभाषाएँ ({{EquationNote|i}}) और ({{EquationNote|ii}}) अपने सिस्टम के ~ (NOT) और → (IMPLICATION) संयोजकों के लिए सत्य तालिकाओं के समतुल्य को परिभाषित | दो परिभाषाएँ ({{EquationNote|i}}) और ({{EquationNote|ii}}) अपने सिस्टम के ~ (NOT) और → (IMPLICATION) संयोजकों के लिए सत्य तालिकाओं के समतुल्य को परिभाषित करते हैं। इसके पहले वाला F ≠ T और T ≠ F प्राप्त करता है, दूसरे शब्दों में v(''A'') का अर्थ v(~''A'') नहीं है। परिभाषा ({{EquationNote|ii}}) सत्य तालिका में तीसरी पंक्ति निर्दिष्ट करता है, और इस प्रकार फिर अन्य तीन पंक्तियाँ परिभाषा के अनुप्रयोग से आती हैं ({{EquationNote|i}}). विशेष रूप से ({{EquationNote|ii}}) संपूर्ण व्यंजक को मान F (या F का अर्थ) प्रदान करता है। इस प्रकार परिभाषाएँ गठन नियमों के रूप में भी काम करती हैं जो पहले से सूत्र में प्राप्त मान के प्रतिस्थापन की अनुमति देती हैं: | ||
{| | {| | ||
|- style="font-size:9pt" align="center" | |- style="font-size:9pt" align="center" | ||
| Line 830: | Line 830: | ||
| | | | ||
|} | |} | ||
कुछ औपचारिक प्रणालियाँ प्रारंभ में इन मूल्यांकन सिद्धांतों को कुछ सूत्रों के रूप में निर्दिष्ट करती हैं जैसे कि [[विरोधाभास का कानून]] या पहचान और अशक्तता के | कुछ औपचारिक प्रणालियाँ प्रारंभ में इन मूल्यांकन सिद्धांतों को कुछ सूत्रों के रूप में निर्दिष्ट करती हैं जैसे कि [[विरोधाभास का कानून|विरोधाभास का नियम]] या पहचान और अशक्तता के नियम इसका मुख्य उदाहरण हैं। कम्यूटेशन और डिस्ट्रीब्यूशन जैसे नियमों के साथ किसका उपयोग करना है, इसका चुनाव सिस्टम के डिज़ाइनर पर निर्भर करता है, इस प्रकार जब तक कि स्वयंसिद्धों का सेट पूरा हो जाता है (अर्थात सिस्टम में बनाए गए किसी भी अच्छी तरह से तैयार किए गए फॉर्मूले का मूल्यांकन करने के लिए पर्याप्त है)। | ||
== अधिक जटिल सूत्र == | == अधिक जटिल सूत्र == | ||
जैसा कि ऊपर दिखाया गया है, CASE (IF c THEN b ELSE a ) संयोजक या तो 2-तर्क संयोजक IF ... THEN ... और AND या OR और AND और 1-तर्क नहीं से निर्मित होता है। n-तर्क AND (a & b & c & ... & n), OR (a ∨ b ∨ c ∨ ... ∨ n) जैसे संयोजक दो-तर्क AND और OR के तार से निर्मित होते हैं और इसमें | जैसा कि ऊपर दिखाया गया है, CASE (IF c THEN b ELSE a ) संयोजक या तो 2-तर्क संयोजक IF ... THEN ... और AND या OR और AND और 1-तर्क नहीं से निर्मित होता है। n-तर्क AND (a & b & c & ... & n), OR (a ∨ b ∨ c ∨ ... ∨ n) जैसे संयोजक दो-तर्क AND और OR के तार से निर्मित होते हैं और इसमें कोष्ठक के बिना संक्षिप्त रूप में लिखे जाते हैं। ये और अन्य संयोजक भी, फिर आगे के संयोजकों के लिए बिल्डिंग ब्लॉक्स के रूप में उपयोग किए जा सकते हैं। अलंकारिक, दार्शनिक और गणितज्ञ अपने सूत्रों का विश्लेषण और सरलीकरण करने के लिए सत्य तालिकाओं और विभिन्न प्रमेयों का उपयोग करते हैं। | ||
इस प्रकार विद्युत इंजीनियरिंग खींचे गए प्रतीकों का उपयोग करता है और उन्हें उन रेखाओं से जोड़ता है जो प्रतिस्थापन और प्रतिस्थापन के गणितीय कार्य के लिए खड़ी होती हैं। फिर वे अपने आरेखणों को सत्य तालिकाओं के साथ सत्यापित करते हैं और कर्णघ नक्शों या प्रमेयों के उपयोग द्वारा नीचे दिखाए गए भावों को सरल करते हैं। इस प्रकार से इंजीनियरों ने कॉम्बिनेटरियल तर्क (अर्थात फीडबैक के बिना कनेक्टिव्स) जैसे डिकोडर्स, एनकोडर्स, म्यूटिफंक्शन गेट्स, मेजॉरिटी तर्क, बाइनरी एडर्स, अंकगणितीय तर्क इकाई आदि का निर्माण किया है। | |||
=== परिभाषाएँ === | === परिभाषाएँ === | ||
इन परिभाषा को अधिकांशतः संक्षेप के प्रयोजनों के लिए नया प्रतीक और उसका व्यवहार बनाती है। इस प्रकार परिभाषा प्रस्तुत करने के बाद, समकक्ष प्रतीक या सूत्र के किसी भी रूप का उपयोग किया जा सकता है। निम्नलिखित प्रतीकवाद =<sub>Df</sub> रेइचेनबैच के सम्मेलन का पालन कर रहा है।<ref>Reichenbach p. 20-22 and follows the conventions of PM. The symbol =<sub>Df</sub> is in the [[metalanguage]] and is not a formal symbol with the following meaning: "by symbol ' s ' is to have the same meaning as the formula '(c & d)' ".</ref> प्रतीक समुच्चय { ~, &, (, ) } और चरों से निकाली गई सुविधाजनक परिभाषाओं के कुछ उदाहरण हैं। प्रत्येक परिभाषा तार्किक रूप से समतुल्य सूत्र का उत्पादन कर रही है जिसका उपयोग प्रतिस्थापन या प्रतिस्थापन के लिए किया जा सकता है। | |||
:* एक नए चर की परिभाषा: ( | :*एक नए चर की परिभाषा: (c & d) =<sub>Df</sub> s | ||
:* | :*OR: ~(~a & ~b) =<sub>Df</sub> (a ∨ b) | ||
:* | :*IMPLICATION: (~a ∨ b) =<sub>Df</sub> (a → b) | ||
:* | :*XOR: (~a & b) ∨ (a & ~b) =<sub>Df</sub> (a ⊕ b) | ||
:* | :*LOGICAL EQUIVALENCE: ( (a → b) & (b → a) ) =<sub>Df</sub> ( a ≡ b ) | ||
=== स्वयंसिद्ध और परिभाषा स्कीमा === | === स्वयंसिद्ध और परिभाषा स्कीमा === | ||
OR, IMPLICATION, XOR, और तार्किक तुल्यता के लिए उपरोक्त परिभाषाएँ वास्तव में स्वयंसिद्ध स्कीमा (या स्कीमाटा) हैं, अर्थात | OR, IMPLICATION, XOR, और तार्किक तुल्यता के लिए उपरोक्त परिभाषाएँ वास्तव में स्वयंसिद्ध स्कीमा (या स्कीमाटा) हैं, अर्थात इस प्रकार वे सामान्य सूत्र प्रारूप के लिए मॉडल (प्रदर्शन, उदाहरण) हैं, किन्तु विशिष्ट अक्षरों a के साथ (उदाहरण के उद्देश्यों के लिए) दिखाए गए हैं। b, c वेरिएबल्स के लिए, जबकि कोई भी वेरिएबल अक्षर उनके स्थान पर तब तक जा सकते हैं, इस प्रकार जब तक अक्षर प्रतिस्थापन नीचे प्रतिस्थापन के नियम का पालन करते हैं। | ||
: उदाहरण: परिभाषा में (~a ∨ b) =<sub>Df</sub> (ए → बी), अन्य चर-प्रतीकों जैसे कि SW2 और CON1 का उपयोग किया जा सकता है, अर्थात औपचारिक रूप से: | : उदाहरण: परिभाषा में (~a ∨ b) =<sub>Df</sub> (ए → बी), अन्य चर-प्रतीकों जैसे कि SW2 और CON1 का उपयोग किया जा सकता है, अर्थात औपचारिक रूप से: | ||
:: | :: a =<sub>Df</sub> SW2, b =<sub>Df</sub> CON1, इसलिए हमारे पास परिभाषा स्कीमा का उदाहरण होगा (~SW2 ∨ CON1) =<sub>Df</sub> (SW2 → CON1) | ||
=== प्रतिस्थापन बनाम प्रतिस्थापन === | === प्रतिस्थापन बनाम प्रतिस्थापन === | ||
प्रतिस्थापन: किसी अन्य चर, स्थिरांक या उप-सूत्र के साथ प्रतिस्थापित किए जाने वाले चर या उप-सूत्र को समग्र सूत्र में सभी उदाहरणों में प्रतिस्थापित किया जाना चाहिए। | प्रतिस्थापन: किसी अन्य चर, स्थिरांक या उप-सूत्र के साथ प्रतिस्थापित किए जाने वाले चर या उप-सूत्र को समग्र सूत्र में सभी उदाहरणों में प्रतिस्थापित किया जाना चाहिए। | ||
: उदाहरण: ( | : उदाहरण: (c & d) ∨ (p & ~(c & ~d)), किन्तु (q1 & ~q2) ≡ d। अब जहाँ भी चर d होता है, स्थानापन्न (q<sub>1</sub> & ~ q<sub>2</sub>): | ||
:: ( | :: (c & (q<sub>1</sub> & ~ q<sub>2</sub>)) ∨ (p & ~(c & ~(q<sub>1</sub> & ~ q<sub>2</sub>))) | ||
प्रतिस्थापन: (i) प्रतिस्थापित किया जाने वाला सूत्र | प्रतिस्थापन: (i) प्रतिस्थापित किया जाने वाला सूत्र तनातनी के भीतर होना चाहिए, अर्थात ''तार्किक रूप से समतुल्य'' (≡ या ↔ से जुड़ा हुआ) उस सूत्र से जुड़ा होना चाहिए जो इसे प्रतिस्थापित करता है, और (ii) प्रतिस्थापन के विपरीत प्रतिस्थापन होने के लिए इसकी अनुमति है। केवल ही स्थान पर अर्थात सूत्र के लिए उपयोग किया जाता हैं। | ||
: उदाहरण: फॉर्मूला स्कीमा/समतुल्यता के इस सेट का उपयोग करें: | : उदाहरण: फॉर्मूला स्कीमा/समतुल्यता के इस सेट का उपयोग करें: | ||
:# (( | :# ( (a ∨ 0) ≡ a ). | ||
:# (( | :# ( (a & ~a) ≡ 0 ). | ||
:# ((~a ∨ b) =<sub>Df</sub> ( | :# ( (~a ∨ b) =<sub>Df</sub> (a → b) ). | ||
:# | :# ( ~(~a) ≡ a ) | ||
:{{ordered list|list-style-type=lower-alpha | :{{ordered list|list-style-type=lower-alpha | ||
| start with "a": a | | start with "a": a | ||
| Line 870: | Line 870: | ||
== आगमनात्मक परिभाषा == | == आगमनात्मक परिभाषा == | ||
प्रस्तावपरक तर्क की मौलिक प्रस्तुति ([[हर्बर्ट एंडर्टन]] 2002 देखें) संयोजकों | प्रस्तावपरक तर्क की मौलिक प्रस्तुति ([[हर्बर्ट एंडर्टन]] 2002 देखें) संयोजकों <math>\lnot, \land, \lor, \to, \leftrightarrow</math> का उपयोग करती है, इस प्रकार प्रपोजल वेरिएबल्स के दिए गए सेट पर फॉर्मूलों का सेट की [[आगमनात्मक परिभाषा]] कहा जाता है जो एक्सप्रेशंस का सबसे छोटा सेट है: | ||
* सेट में प्रत्येक प्रस्तावक चर | * सेट में प्रत्येक प्रस्तावक चर सूत्र है, | ||
* <math>(\lnot \alpha)</math> | * <math>(\lnot \alpha)</math> सूत्र है जब भी <math>\alpha</math> है और | ||
* <math> (\alpha\,\Box\,\beta)</math> | * <math> (\alpha\,\Box\,\beta)</math> सूत्र है जब भी <math>\alpha</math> और <math>\beta</math> सूत्र हैं और <math>\Box</math> द्विआधारी संयोजकों <math>\land, \lor, \to, \leftrightarrow</math> में से है। | ||
अतिरिक्त संयोजकों को सम्मलित करने के लिए इस आगमनात्मक परिभाषा को आसानी से बढ़ाया जा सकता है। | अतिरिक्त संयोजकों को सम्मलित करने के लिए इस आगमनात्मक परिभाषा को आसानी से बढ़ाया जा सकता है। | ||
आगमनात्मक परिभाषा को क्लोजर (गणित) ऑपरेशन (एंडर्टन 2002) के संदर्भ में भी दोहराया जा सकता है। | आगमनात्मक परिभाषा को क्लोजर (गणित) ऑपरेशन (एंडर्टन 2002) के संदर्भ में भी दोहराया जा सकता है। इस प्रकार v<sub>V</sub> प्रस्तावित चर के सेट को निरूपित करते हैं और एक्स को जाने देते हैं, V, बाएँ और दाएँ कोष्ठकों में प्रतीकों, और विचाराधीन सभी तार्किक संयोजकों सहित वर्णमाला से सभी स्ट्रिंग्स के सेट को निरूपित करें। इस प्रकार प्रत्येक लॉजिकल कनेक्टिव फॉर्मूला बिल्डिंग ऑपरेशन, XX<sub>V</sub> से फ़ंक्शन X<sub>V</sub>X से मेल खाता है। | ||
* एक स्ट्रिंग z दिया गया है, ऑपरेशन <math>\mathcal{E}_\lnot(z)</math> रिटर्न <math>(\lnot z)</math>. | * एक स्ट्रिंग z दिया गया है, ऑपरेशन <math>\mathcal{E}_\lnot(z)</math> रिटर्न <math>(\lnot z)</math>. | ||
* दिए गए तार y और z, ऑपरेशन <math>\mathcal{E}_\land(y,z)</math> रिटर्न <math>(y\land z)</math>. इसी तरह के ऑपरेशन हैं <math>\mathcal{E}_\lor</math>, <math>\mathcal{E}_\to</math>, और <math>\mathcal{E}_\leftrightarrow</math> अन्य बाइनरी संयोजकों के | * दिए गए तार y और z, ऑपरेशन <math>\mathcal{E}_\land(y,z)</math> रिटर्न <math>(y\land z)</math>. इसी तरह के ऑपरेशन हैं <math>\mathcal{E}_\lor</math>, <math>\mathcal{E}_\to</math>, और <math>\mathcal{E}_\leftrightarrow</math> अन्य बाइनरी संयोजकों के अनुरूप उपयोग किए जाते हैं। | ||
V पर सूत्रों के सेट को XX | V पर सूत्रों के सेट को XX<sub>V</sub> का सबसे छोटा उपसमुच्चय माना जाता है, जिसमें V है और सभी फॉर्मूला बिल्डिंग ऑपरेशंस के अनुसार CLOSE है। | ||
== पार्सिंग सूत्र == | == पार्सिंग सूत्र == | ||
जटिल सूत्रों को कम करने के लिए प्रस्तावक कलन के निम्नलिखित नियमों का उपयोग किया जाता है। सत्य तालिकाओं के साथ | जटिल सूत्रों को कम करने के लिए प्रस्तावक कलन के निम्नलिखित नियमों का उपयोग किया जाता है। इस प्रकार सत्य तालिकाओं के साथ नियमों को आसानी से सत्यापित किया जा सकता है। प्रत्येक नियम के लिए, मुख्य (बाह्यतम) संयोजक तार्किक तुल्यता ≡ या तत्समक = से जुड़ा होता है। सभी का पूर्ण विश्लेषण 2<sup>n</sup> इसके n विशिष्ट चरों के लिए सत्य-मानों का संयोजन इस संयोजी के नीचे 1's (T's) के कॉलम में परिणत होगा। यह खोज प्रत्येक नियम को, परिभाषा के अनुसार, पुनरुक्ति बनाती है। इस प्रकार किसी दिए गए नियम के लिए, क्योंकि बाएँ और दाएँ पर इसके सूत्र समतुल्य (या समरूप) हैं, उन्हें दूसरे के लिए प्रतिस्थापित किया जा सकता है। | ||
* उदाहरण: निम्नलिखित सत्य तालिका OR से अधिक नहीं के व्यवहार के लिए डी मॉर्गन का नियम है: ~(a ∨ b) ≡ (~a & ~b) | * उदाहरण: निम्नलिखित सत्य तालिका OR से अधिक नहीं के व्यवहार के लिए डी मॉर्गन का नियम है: ~(a ∨ b) ≡ (~a & ~b), मुख्य संयोजक के बाईं ओर ≡ (उपयोग किए जाने वाले लेबल वाला पीला स्तंभ) सूत्र ~(b ∨ a) लेबल P के अंतर्गत (1, 0, 0, 0) का मूल्यांकन करता है। इस प्रकार इसेके दाईं ओर सूत्र (~(b) ∨ ~(a)) भी लेबल Q के अंतर्गत (1, 0, 0, 0) का मूल्यांकन करता है। चूंकि इस प्रकार दो स्तंभों में समतुल्य मूल्यांकन हैं, तार्किक तुल्यता ≡ के अनुसार तना हुआ मूल्यांकन (1, 1, 1, 1), अर्थात P ≡ Q. इस प्रकार या तो सूत्र को दूसरे के लिए प्रतिस्थापित किया जा सकता है यदि यह बड़े सूत्र में प्रकट होता है। | ||
{| style="margin-left: auto; margin-right: auto; border: none;" | {| style="margin-left: auto; margin-right: auto; border: none;" | ||
|- style="font-size:9pt; text-align:center" | |- style="font-size:9pt; text-align:center" | ||
| Line 1,030: | Line 1,030: | ||
| | | | ||
|} | |} | ||
उद्यमी पाठक खुद को | उद्यमी पाठक खुद को स्वयंसिद्ध प्रणाली का आविष्कार करने के लिए चुनौती दे सकते हैं जो प्रतीकों {∨, &, ~, (, ), चर a, b, c}, ऊपर निर्दिष्ट गठन नियमों का उपयोग करता है, और नीचे सूचीबद्ध नियमों में से जितना संभव हो उतना कम, और इस प्रकार प्रमेयों के रूप में अन्य के साथ-साथ ∨, &, और ~ के लिए सत्य-तालिका मूल्यांकन प्राप्त करें। हंटिंगटन (1904) (स्यूप्स: 204) के लिए जिम्मेदार सेट नीचे परिभाषित आठ नियमों का उपयोग करता है। | ||
यदि | यदि स्वयंसिद्ध प्रणाली में प्रयोग किया जाता है, तो प्रतीकों 1 और 0 (या T और F) को अच्छी तरह से गठित सूत्र माना जाता है और इस प्रकार चर के समान सभी नियमों का पालन करते हैं। इस प्रकार नीचे सूचीबद्ध नियम वास्तव में स्वयंसिद्ध स्कीमा हैं, अर्थात इस प्रकार इन अनंत संख्या में उदाहरणों के स्थान पर खड़े होते हैं। इस प्रकार ( x ∨ y ) ≡ ( y ∨ x ) का उपयोग उदाहरण में किया जा सकता है, ( p ∨ 0 ) ≡ ( 0 ∨ p ) और दूसरे उदाहरण में ( 1 ∨ q ) ≡ ( q ∨ 1 ), आदि। | ||
=== संयोजी वरिष्ठता (प्रतीक रैंक) === | === संयोजी वरिष्ठता (प्रतीक रैंक) === | ||
सामान्यतः, प्रस्तावात्मक सूत्रों के विश्लेषण और मूल्यांकन के समय भ्रम से बचने के लिए कोष्ठकों का उदारतापूर्वक उपयोग | सामान्यतः, प्रस्तावात्मक सूत्रों के विश्लेषण और मूल्यांकन के समय भ्रम से बचने के लिए कोष्ठकों का उदारतापूर्वक उपयोग करते हैं। चूंकि, अधिकांशतः लेखक उन्हें छोड़ देते हैं। जटिल सूत्र को पार्स करने के लिए सबसे पहले वरिष्ठता, या रैंक जानने की जरूरत है, कि प्रत्येक संयोजक (* को छोड़कर) अन्य संयोजकों पर है। इस प्रकार इस सूत्र को अच्छी तरह से बनाने के लिए, उच्चतम रैंक वाले संयोजी से प्रारंभ करें और इसके घटकों के चारों ओर कोष्ठक जोड़ें, फिर रैंक में नीचे जाएं (संयोजी के दायरे पर ध्यान दें जिस पर यह काम कर रहा है)। सबसे कम से कम वरिष्ठ तक, विधेय चिह्न ∀x और ∃x के साथ, पहचान = और अंकगणितीय संकेत पूर्णता के लिए जोड़े गए हैं:{{efn|Rosenbloom{{sfn|Rosenbloom|1950|p=32}} and Kleene 1952:73-74 ranks all 11 symbols.}} | ||
:; ≡: (तार्किक समानता) | :; ≡: (तार्किक समानता) | ||
:; →: (निहितार्थ) | :; →: (निहितार्थ) | ||
| Line 1,042: | Line 1,042: | ||
:; ~: (नहीं) | :; ~: (नहीं) | ||
:; ∀x: (सभी x के लिए) | :; ∀x: (सभी x के लिए) | ||
:; ∃x: (वहाँ | :; ∃x: (वहाँ एक्स संलग्न है) | ||
:; =: (पहचान) | :; =: (पहचान) | ||
:; +: (अंकगणितीय योग) | :; +: (अंकगणितीय योग) | ||
:;<nowiki>*</nowiki>: (अंकगणितीय गुणा) | :;<nowiki>*</nowiki>: (अंकगणितीय गुणा) | ||
:; ' : ( | :; ' : (अंकगणितीय उत्तराधिकारी)। | ||
इस प्रकार सूत्र को पार्स किया जा सकता है - किन्तु क्योंकि वितरण | इस प्रकार सूत्र को पार्स किया जा सकता है - किन्तु क्योंकि वितरण नियम का पालन नहीं करता है, आंतरिक सूत्र (~c & ~d) के चारों ओर कोष्ठक अनिवार्य है: | ||
: उदाहरण: d & c ∨ w को फिर से लिखा गया है ( (d & c) ∨ w ) | : उदाहरण: d & c ∨ w को फिर से लिखा गया है ( (d & c) ∨ w ) | ||
: उदाहरण: a & a → b ≡ a & ~a ∨ b पुनर्लेखित (कठोरता से) है | : उदाहरण: a & a → b ≡ a & ~a ∨ b पुनर्लेखित (कठोरता से) है | ||
::* ≡ में वरिष्ठता है: ( ( a & a → b ) ≡ ( a & ~a ∨ b ) ) | ::* ≡ में वरिष्ठता है: ( ( a & a → b ) ≡ ( a & ~a ∨ b ) ) | ||
::* → वरिष्ठता है: (( | ::* → वरिष्ठता है: ((a और (a → b)) ≡ (a और ~a ∨ b)) | ||
::* & दोनों पक्षों में वरिष्ठता है: (((( | ::* & दोनों पक्षों में वरिष्ठता है: ((((a) और (a → b)) ≡ (((a) और (~ए ∨ b))) | ||
::* ~ वरिष्ठता है: (((( | ::* ~ वरिष्ठता है: ((((a) और (a → b)) ≡ (((a) और (~(a) ∨ b))) | ||
::* चेक 9 (-कोष्ठक और 9) -कोष्ठक: (((( | ::* चेक 9 (-कोष्ठक और 9) -कोष्ठक: ((((a) और (a → b)) ≡ (((a) और (~(a) ∨ b))) | ||
: उदाहरण: | : उदाहरण: | ||
:: d & c ∨ p & ~(c & ~d) ≡ c & d ∨ p & c ∨ p & ~d फिर से लिखा गया है ( ( (d & c) ∨ ( p & ~((c & ~(d)) ) ) ) ≡ ( ( | :: d & c ∨ p & ~(c & ~d) ≡ c & d ∨ p & c ∨ p & ~d फिर से लिखा गया है ( ( (d & c) ∨ ( p & ~((c & ~(d)) ) ) ) ≡ ( (c और d) ∨ (p और c) ∨ (p और ~(d)) ) ) | ||
=== क्रमविनिमेय और साहचर्य | === क्रमविनिमेय और साहचर्य नियम === | ||
AND और OR दोनों क्रम[[विनिमेय कानून]] और साहचर्य | AND और OR दोनों क्रम[[विनिमेय कानून|विनिमेय नियम]] और '''साहचर्य नियम''' का पालन करते हैं: | ||
* OR के लिए क्रमविनिमेय नियम: ( a ∨ b ) ≡ ( b ∨ a ) | * OR के लिए क्रमविनिमेय नियम: ( a ∨ b ) ≡ ( b ∨ a ) | ||
* AND के लिए क्रमविनिमेय नियम: (a और b) ≡ (b और a) | * AND के लिए क्रमविनिमेय नियम: (a और b) ≡ (b और a) | ||
* OR के लिए साहचर्य नियम: ((a ∨ b ) ∨ c ) ≡ ( a ∨ (b ∨ c) ) | * OR के लिए साहचर्य नियम: ((a ∨ b ) ∨ c ) ≡ ( a ∨ (b ∨ c) ) | ||
* AND के लिए [[सहयोगी कानून]]: (( | * AND के लिए [[सहयोगी कानून|सहयोगी नियम]]: ((a और b) और c) ≡ (a और (b और c)) | ||
AND और OR के तार में कोष्ठकों को छोड़ना: संयोजकों को एकात्मक (एक-चर, जैसे नहीं) और बाइनरी (अर्थात दो-चर AND, OR, IMPLIES) माना जाता है। उदाहरण के लिए: | AND और OR के तार में कोष्ठकों को छोड़ना: संयोजकों को एकात्मक (एक-चर, जैसे नहीं) और बाइनरी (अर्थात दो-चर AND, OR, IMPLIES) माना जाता है। उदाहरण के लिए: | ||
: ( ((c & d) ∨ (p & c) ∨ (p & ~d) ) ऊपर लिखा जाना चाहिए ( ((c & d) ∨ (p & c)) ∨ (p & ~(d) ) ) या संभवतः (( | : ( ((c & d) ∨ (p & c) ∨ (p & ~d) ) ऊपर लिखा जाना चाहिए ( ((c & d) ∨ (p & c)) ∨ (p & ~(d) ) ) या संभवतः ((c और d) ∨ ((p और c) ∨ (p और ~(d)))) | ||
चूंकि | चूंकि इस प्रकार सत्य-सारणी प्रदर्शन दिखाता है कि अतिरिक्त कोष्ठकों के बिना प्रपत्र पूरी तरह से पर्याप्त है। | ||
एकल-चर के संबंध में कोष्ठकों को छोड़ना नहीं: जबकि ~(a) जहां a | एकल-चर के संबंध में कोष्ठकों को छोड़ना नहीं: जबकि ~(a) जहां a एकल चर है, इस प्रकार पूर्ण रूप से स्पष्ट है, ~a पर्याप्त है और यह [[शाब्दिक (गणितीय तर्क)]] प्रकट होने का सामान्य विधि है। जब NOT से अधिक प्रतीक वाले सूत्र के ऊपर हो, तब कोष्ठक अनिवार्य होते हैं, उदा. ~(a ∨ b). | ||
=== वितरण | === वितरण नियम === | ||
OR AND पर वितरित करता है और AND OR पर वितरित करता है। NOT AND या OR पर वितरित नहीं होता है। डी मॉर्गन के | OR AND पर वितरित करता है और AND OR पर वितरित करता है। इस प्रकार NOT AND या OR पर वितरित नहीं होता है। डी मॉर्गन के नियम के बारे में नीचे देखें: | ||
* OR के लिए वितरण नियम: ( c ∨ ( a & b) ) ≡ ( (c ∨ a) और (c ∨ b) ) | * OR के लिए वितरण नियम: ( c ∨ ( a & b) ) ≡ ( (c ∨ a) और (c ∨ b) ) | ||
* AND के लिए वितरण नियम: (c & (a ∨ b) ) ≡ ((c & a) ∨ (c & b) ) | * AND के लिए वितरण नियम: (c & (a ∨ b) ) ≡ ((c & a) ∨ (c & b) ) | ||
=== डी मॉर्गन के नियम === | === डी मॉर्गन के नियम === | ||
जब OR या AND पर वितरित नहीं किया जाता है, तो कुछ अलग सी स्थिति बनती है (फिर से, इन्हें सत्य-तालिका के साथ सत्यापित किया जा सकता है): | |||
* OR के लिए डी मॉर्गन का नियम: ¬(a ∨ b) ≡ (¬a ^ ¬b) | * OR के लिए डी मॉर्गन का नियम: ¬(a ∨ b) ≡ (¬a ^ ¬b) | ||
* AND के लिए डी मॉर्गन का नियम: ¬(a ^ b) ≡ (¬a ∨ ¬b) | * AND के लिए डी मॉर्गन का नियम: ¬(a ^ b) ≡ (¬a ∨ ¬b) | ||
| Line 1,086: | Line 1,086: | ||
अवशोषण, विशेष रूप से पहला, तर्क के नियमों को अंकगणित के नियमों से अलग करने का कारण बनता है: | अवशोषण, विशेष रूप से पहला, तर्क के नियमों को अंकगणित के नियमों से अलग करने का कारण बनता है: | ||
* OR: (a ∨ a) ≡ a के लिए अवशोषण (निष्क्रियता)। | * OR: (a ∨ a) ≡ a के लिए अवशोषण (निष्क्रियता)। | ||
* AND के लिए अवशोषण (निष्क्रियता): ( | * AND के लिए अवशोषण (निष्क्रियता): (a & a) ≡ a | ||
=== मूल्यांकन के नियम: पहचान, शून्यता, और पूरक === | === मूल्यांकन के नियम: पहचान, शून्यता, और पूरक === | ||
चिह्न = (तार्किक तुल्यता ≡ से अलग, वैकल्पिक रूप से ↔ या ⇔) मूल्य या अर्थ के असाइनमेंट का प्रतीक है। इस प्रकार स्ट्रिंग (a & ~(a)) 0 का प्रतीक है, अर्थात इसका | चिह्न = (तार्किक तुल्यता ≡ से अलग, वैकल्पिक रूप से ↔ या ⇔) मूल्य या अर्थ के असाइनमेंट का प्रतीक है। इस प्रकार स्ट्रिंग (a & ~(a)) 0 का प्रतीक है, अर्थात इसका तात्पर्य प्रतीक 0 जैसा ही है। कुछ प्रणालियों में यह स्वयंसिद्ध (परिभाषा) होगी जिसे संभवतः ((a & ~(a)) =<sub>Df</sub> 0 के रूप में दिखाया गया है), अन्य प्रणालियों में, इसे नीचे दी गई सत्य तालिका में प्राप्त किया जा सकता है: | ||
{| style="margin-left: auto; margin-right: auto; border: none;" | {| style="margin-left: auto; margin-right: auto; border: none;" | ||
|- style="font-size:9pt; text-align:center" | |- style="font-size:9pt; text-align:center" | ||
| Line 1,152: | Line 1,152: | ||
| | | | ||
|} | |} | ||
* समानता का रूपांतरण: ( | * समानता का रूपांतरण: (a = b) ≡ (b = a) | ||
* OR के लिए सर्वसमिका: (a ∨ 0) = a | * OR के लिए सर्वसमिका: (a ∨ 0) = a OR (a ∨ F) = a | ||
* AND के लिए सर्वसमिका: (a & 1) = a | * AND के लिए सर्वसमिका: (a & 1) = a OR (a & T) = a | ||
* OR के लिए शून्यता: (a ∨ 1) = 1 | * OR के लिए शून्यता: (a ∨ 1) = 1 OR (a ∨ T) = T | ||
* AND के लिए शून्यता: (a और 0) = 0 | * AND के लिए शून्यता: (a और 0) = 0 OR (a और F) = F | ||
* OR के लिए पूरक: (a ∨ ~a) = 1 | * OR के लिए पूरक: (a ∨ ~a) = 1 OR (a ∨ ~a) = T, बहिष्कृत मध्य का नियम | ||
* AND के लिए पूरक: (a & ~a) = 0 | * AND के लिए पूरक: (a & ~a) = 0 OR (a & ~a) = F, विरोधाभास का नियम | ||
=== डबल नेगेटिव (इनवोल्यूशन) === | === डबल नेगेटिव (इनवोल्यूशन) === | ||
* ¬( | * ¬(¬a) ≡ a | ||
== सुगठित सूत्र | == सुगठित सूत्र == | ||
सूत्रों की | सूत्रों की प्रमुख संपत्ति यह है कि इसके प्रस्ताविक चर और तार्किक संयोजकों के संदर्भ में सूत्र की संरचना का निर्धारण करने के लिए उन्हें विशिष्ट रूप से पार्स किया जा सकता है। जब सूत्रों को [[इंफिक्स नोटेशन]] में लिखा जाता है, तो सूत्रों की परिभाषा में कोष्ठकों के उचित उपयोग के माध्यम से अद्वितीय पठनीयता सुनिश्चित की जाती है। इस प्रकार वैकल्पिक रूप से, सूत्रों को [[पोलिश संकेतन]] या [[रिवर्स पोलिश नोटेशन]] में लिखा जा सकता है, जिससे कोष्ठकों की आवश्यकता पूरी तरह से समाप्त हो जाती है। | ||
पिछले खंड में इन्फिक्स सूत्रों की आगमनात्मक परिभाषा को [[बैकुस-नौर फॉर्म]] में | पिछले खंड में इन्फिक्स सूत्रों की आगमनात्मक परिभाषा को [[बैकुस-नौर फॉर्म]] में [[औपचारिक व्याकरण]] में परिवर्तित किया जा सकता है: | ||
<formula> ::= <propositional variable> | |||
| ( ¬ <formula> ) | |||
| ( <formula> ∧ <formula>) | |||
| (¬ < | | ( <formula> ∨ <formula> ) | ||
| ( < | | ( <formula> → <formula> ) | ||
| ( < | | ( <formula> ↔ <formula> ) | ||
| ( < | यह दिखाया जा सकता है कि व्याकरण से मेल खाने वाली किसी भी अभिव्यक्ति में बाएँ और दाएँ कोष्ठकों की संतुलित संख्या होती है, और सूत्र के किसी भी गैर-रिक्त प्रारंभिक खंड में दाएँ कोष्ठकों की तुलना में अधिक बाएँ होते हैं।<ref>cf Minsky 1967:75, section 4.2.3 "The method of parenthesis counting". Minsky presents a state machine that will do the job, and by use of induction (recursive definition) Minsky proves the "method" and presents a theorem as the result. A fully generalized "parenthesis grammar" requires an infinite state machine (e.g. a Turing machine) to do the counting.</ref> इस तथ्य का उपयोग फ़ार्मुलों को पार्स करने के लिए एल्गोरिथम देने के लिए किया जा सकता है। इस प्रकार उदाहरण के लिए, मान लीजिए कि एक्सप्रेशन x से प्रारंभ होता है <math>( \lnot</math>. दूसरे प्रतीक के बाद प्रारंभ करते हुए, x के सबसे छोटे उप-अभिव्यक्ति y का मिलान करें जिसमें संतुलित कोष्ठक हैं। इस प्रकार यदि x सूत्र है, तो इस व्यंजक के बाद ठीक प्रतीक शेष रह जाता है, यह प्रतीक समापन कोष्ठक है, और y स्वयं सूत्र है। इस विचार का उपयोग सूत्रों के लिए पुनरावर्ती मूल पार्सर उत्पन्न करने के लिए किया जा सकता है। | ||
| ( < | |||
यह दिखाया जा सकता है कि व्याकरण से मेल खाने वाली किसी भी अभिव्यक्ति में बाएँ और दाएँ कोष्ठकों की | |||
'कोष्ठकों की गिनती का उदाहरण': | 'कोष्ठकों की गिनती का उदाहरण': | ||
यह विधि 1 'प्रमुख संयोजक' के रूप में खोज करती है {{--}} संयोजी जिसके अनुसार सूत्र का समग्र मूल्यांकन सबसे बाहरी कोष्ठकों के लिए होता है (जो अधिकांशतः छोड़े जाते हैं)।<ref>Robbin p. 7</ref> यह सबसे भीतरी संयोजक का भी पता लगाता है जहां कोई सत्य तालिका के उपयोग के बिना सूत्र का मूल्यांकन प्रारंभ करेगा, उदा। स्तर 6 पर। | यह विधि 1 'प्रमुख संयोजक' के रूप में खोज करती है {{--}} संयोजी जिसके अनुसार सूत्र का समग्र मूल्यांकन सबसे बाहरी कोष्ठकों के लिए होता है (जो अधिकांशतः छोड़े जाते हैं)।<ref>Robbin p. 7</ref> इस प्रकार यह सबसे भीतरी संयोजक का भी पता लगाता है जहां कोई सत्य तालिका के उपयोग के बिना सूत्र का मूल्यांकन प्रारंभ करेगा, उदा। स्तर 6 पर। | ||
{|class="wikitable" | {|class="wikitable" | ||
|- style="font-size:9pt" align="center" valign="bottom" | |- style="font-size:9pt" align="center" valign="bottom" | ||
| Line 1,292: | Line 1,290: | ||
=== [[अनुमान|अनुमानों]] में मान्य सूत्रों बनाम अच्छी तरह से गठित सूत्र === | === [[अनुमान|अनुमानों]] में मान्य सूत्रों बनाम अच्छी तरह से गठित सूत्र === | ||
वैध तर्क की धारणा सामान्यतः तर्कों में अनुमानों पर लागू होती है, किन्तु तर्क प्रस्तावात्मक सूत्रों में कम हो जाते हैं और किसी अन्य प्रस्ताव सूत्र के समान मूल्यांकन किया जा सकता है। यहाँ | वैध तर्क की धारणा सामान्यतः तर्कों में अनुमानों पर लागू होती है, किन्तु तर्क प्रस्तावात्मक सूत्रों में कम हो जाते हैं और किसी अन्य प्रस्ताव सूत्र के समान मूल्यांकन किया जा सकता है। यहाँ मान्य अनुमान का अर्थ है: सूत्र जो अनुमान का प्रतिनिधित्व करता है, उसके प्रमुख संयोजक के नीचे सत्य का मूल्यांकन करता है, चाहे इसके चरों को कोई भी सत्य-मान सौंपा गया हो, अर्थात सूत्र पुनरुक्ति है।<ref>cf Reichenbach p. 68 for a more involved discussion: "If the inference is valid and the premises are true, the inference is called ''conclusive''.</ref> | ||
* उदाहरण 1: अनुसरण करने में कठिन निम्नलिखित कथनों से कोई क्या बनाता है? क्या यह वैध है? यदि धूप है, किन्तु यदि मेंढक टर्र-टर्र कर रहा है तो धूप नहीं है, तो यह कहने के समान है कि मेंढक टर्र-टर्र नहीं कर रहा है। इसे | इस प्रकार अधिक संभवतः सूत्र अच्छी तरह से बना होगा किन्तु मान्य नहीं होगा। इसे कहने का दूसरा विधि यह है: किसी सूत्र के मान्य होने के लिए अच्छी तरह से निर्मित होना आवश्यक है किन्तु यह पर्याप्त नहीं है। यह पता लगाने का एकमात्र विधि है कि यह अच्छी तरह से गठित और वैध दोनों है या नहीं, इसे सत्य तालिका या नियमों के उपयोग से सत्यापन के लिए जमा करना है: | ||
* उदाहरण 1: अनुसरण करने में कठिन निम्नलिखित कथनों से कोई क्या बनाता है? क्या यह वैध है? यदि धूप है, किन्तु यदि मेंढक टर्र-टर्र कर रहा है तो धूप नहीं है, तो यह कहने के समान है कि मेंढक टर्र-टर्र नहीं कर रहा है। इसे प्रस्तावक सूत्र में निम्नानुसार परिवर्तित करें: | |||
*:: IF (a AND (IF b THEN NOT-a) THEN NOT-a जहां a धूप का प्रतिनिधित्व करता है और b मेंढक टर्राने का प्रतिनिधित्व करता है : | *:: IF (a AND (IF b THEN NOT-a) THEN NOT-a जहां a धूप का प्रतिनिधित्व करता है और b मेंढक टर्राने का प्रतिनिधित्व करता है : | ||
*:: (( | *:: ((a) & ((b) → ~(a)) ≡ ~(b)) | ||
*: यह सुगठित है, किन्तु क्या यह मान्य है? दूसरे शब्दों में, जब मूल्यांकन किया जाएगा तो क्या यह तार्किक-तुल्यता प्रतीक ≡ के नीचे | *: यह सुगठित है, किन्तु क्या यह मान्य है? दूसरे शब्दों में, जब मूल्यांकन किया जाएगा तो क्या यह तार्किक-तुल्यता प्रतीक ≡ के नीचे पुनरुक्ति (सभी T) उत्पन्न करेगा? उत्तर नहीं है, यह मान्य नहीं है। चूंकि, यदि निहितार्थ के रूप में पुनर्निर्माण किया गया तो तर्क मान्य है। | ||
*: यह कहना धूप है, किन्तु यदि मेंढक टर्रा रहा है तो धूप नहीं है, इसका | *: यह कहना धूप है, किन्तु यदि मेंढक टर्रा रहा है तो धूप नहीं है, इसका तात्पर्य है कि मेंढक टर्रा नहीं रहा है। | ||
*: अन्य परिस्थितियाँ मेंढक को टेढ़े होने से रोक सकती हैं: संभवतः | *: अन्य परिस्थितियाँ मेंढक को टेढ़े होने से रोक सकती हैं: संभवतः क्रेन ने उसे खा लिया। | ||
* उदाहरण 2 (रीचेनबैक से बर्ट्रेंड रसेल के माध्यम से): | * उदाहरण 2 (रीचेनबैक से बर्ट्रेंड रसेल के माध्यम से): | ||
*: यदि सूअरों के पंख होते हैं, तो कुछ पंख वाले जानवर खाने में अच्छे होते हैं। कुछ पंखों वाले जानवर खाने में अच्छे होते हैं, तो सूअरों के पंख होते हैं। | *: यदि सूअरों के पंख होते हैं, तो कुछ पंख वाले जानवर खाने में अच्छे होते हैं। कुछ पंखों वाले जानवर खाने में अच्छे होते हैं, तो सूअरों के पंख होते हैं। | ||
*: (( | *: ((a) → (b)) और (b) → (a)) अच्छी तरह से गठित है, किन्तु अमान्य तर्क जैसा कि मुख्य निहितार्थ के अनुसार लाल मूल्यांकन द्वारा दिखाया गया है: | ||
{|style="margin-left: auto; margin-right: auto; border: none;" | {|style="margin-left: auto; margin-right: auto; border: none;" | ||
|- style="font-size:9pt" align="center" | |- style="font-size:9pt" align="center" | ||
| Line 1,412: | Line 1,411: | ||
== संयोजकों के घटे हुए सेट == | == संयोजकों के घटे हुए सेट == | ||
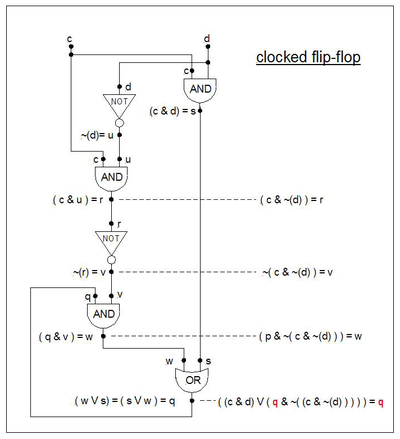
[[File:Propositional formula NANDs.png|400px|thumb|right|NAND संयोजी ('स्ट्रोक') के लिए अभियांत्रिकी चिह्न का उपयोग किसी भी प्रस्तावात्मक सूत्र के निर्माण के लिए किया जा सकता है। यह धारणा कि सत्य (1) और असत्य (0) को इस संबंध के संदर्भ में परिभाषित किया जा सकता है, बाईं ओर NANDs के अनुक्रम में दिखाया गया है, और NAND b के चार मूल्यांकनों की व्युत्पत्ति नीचे के साथ दिखाई गई है। सत्य तालिका से NAND की परिभाषा का उपयोग करना अधिक सामान्य विधि है।]]तार्किक संयोजकों के | [[File:Propositional formula NANDs.png|400px|thumb|right|NAND संयोजी ('स्ट्रोक') के लिए अभियांत्रिकी चिह्न का उपयोग किसी भी प्रस्तावात्मक सूत्र के निर्माण के लिए किया जा सकता है। यह धारणा कि सत्य (1) और असत्य (0) को इस संबंध के संदर्भ में परिभाषित किया जा सकता है, बाईं ओर NANDs के अनुक्रम में दिखाया गया है, और NAND b के चार मूल्यांकनों की व्युत्पत्ति नीचे के साथ दिखाई गई है। सत्य तालिका से NAND की परिभाषा का उपयोग करना अधिक सामान्य विधि है।]]तार्किक संयोजकों के सेट को पूर्ण कहा जाता है यदि प्रत्येक प्रस्ताव सूत्र उस सेट में केवल संयोजकों के साथ सूत्र के बराबर है। संयोजकों के कई पूर्ण सेट हैं, जिनमें सम्मलित हैं <math>\{\land, \lnot\}</math>, <math>\{\lor, \lnot\}</math>, और <math>\{\to, \lnot\}</math>, इस प्रकार इसमें दो बाइनरी संयोजक होते हैं जो क्रमशः NAND और NOR के अनुरूप अपने आप पूर्ण होते हैं।<ref>As well as the first three, Hamilton pp.19-22 discusses logics built from only | (NAND), and ↓ (NOR).</ref> उदाहरण के लिए, <math>\{\land, \lor\}</math> जोड़ पूर्ण नहीं हैं। | ||
=== स्ट्रोक (नंद) === | === स्ट्रोक (नंद) === | ||
एनएएनडी से संबंधित द्विआधारी संयोजक को [[शेफर लाइन]] कहा जाता है, और | एनएएनडी से संबंधित द्विआधारी संयोजक को [[शेफर लाइन]] कहा जाता है, और ऊर्ध्वाधर पट्टी के साथ लिखा जाता है या लंबवत तीर ↑. इस संयोजकता की पूर्णता प्रिन्सिपिया मैथेमेटिका (1927:xvii) में नोट की गई थी। चूँकि यह अपने आप में पूर्ण है, अन्य सभी संयोजकों को केवल आघात का प्रयोग करके व्यक्त किया जा सकता है। उदाहरण के लिए, जहां प्रतीक ≡ तार्किक तुल्यता का प्रतिनिधित्व करता है: | ||
: ~p ≡ p|p | : ~p ≡ p|p | ||
: | : p → q ≡ p | ~ q | ||
: p ∨ q ≡ ~p|~q | : p ∨ q ≡ ~p|~q | ||
: | : p & p ≡ ~ (p | q) | ||
विशेष रूप से, शून्य-ऐरी संयोजक <math>\top</math> (सच्चाई का प्रतिनिधित्व) और <math>\bot</math> ( | विशेष रूप से, शून्य-ऐरी संयोजक <math>\top</math> (सच्चाई का प्रतिनिधित्व) और <math>\bot</math> (असत्य का प्रतिनिधित्व) स्ट्रोक का उपयोग करके व्यक्त किया जा सकता है: | ||
: <math>\top \equiv (a|(a|a))</math> | : <math>\top \equiv (a|(a|a))</math> | ||
: <math>\bot \equiv (\top | \top)</math> | : <math>\bot \equiv (\top | \top)</math> | ||
=== IF ... THEN ... ELSE === | |||
यह संयोजक {0, 1}, (या {F, T} या { <math>\bot</math>, <math>\top</math> } ) पूर्ण सेट बनाता है। निम्नलिखित में IF...THEN...ELSE [[संबंध (गणित)]] (c, b, a) = d निरूपित करता है ((c → b) ∨ (~c → a) ) ≡ ( (c & b) ∨ ( ~ c & a)) = d | |||
: (c, b, a): | |||
: (c, 0, 1) ≡ ~ c | |||
: (c, b, 1) ≡ (c → b) | |||
: (c, c, a) ≡ (c ∨ a) | |||
: (c, b, c) ≡ (c & b) | |||
उदाहरण: निम्नलिखित दिखाता है कि (c, b, 1) ≡ (c → b) का प्रमेय-आधारित प्रमाण कैसे आगे बढ़ेगा, प्रमाण के नीचे इसका सत्य-सारणी सत्यापन है। (नोट: (c → b) को (~c ∨ b) के रूप में परिभाषित किया गया है): | |||
उदाहरण: निम्नलिखित दिखाता है कि (c, b, 1) ≡ (c → b) का | |||
:* घटाए गए रूप से प्रारंभ करें: ( (c & b) ∨ (~c & a) ) | :* घटाए गए रूप से प्रारंभ करें: ( (c & b) ∨ (~c & a) ) | ||
:* 1 को a से बदलें: ( (c & b) ∨ (~c & 1) ) | :* 1 को a से बदलें: ( (c & b) ∨ (~c & 1) ) | ||
| Line 1,445: | Line 1,442: | ||
:* ( ~c ∨ b ) को 'c → b' Q. E. D के रूप में परिभाषित किया गया है। | :* ( ~c ∨ b ) को 'c → b' Q. E. D के रूप में परिभाषित किया गया है। | ||
निम्नलिखित सत्य तालिका में टॉटोलॉजी के लिए तना हुआ लेबल वाला कॉलम d लेबल वाले दो स्तंभों के बीच तार्किक तुल्यता (यहाँ ≡ द्वारा चिन्हित) का मूल्यांकन करता है। क्योंकि तना हुआ के अंतर्गत सभी चार पंक्तियाँ 1 हैं, तुल्यता वास्तव में | निम्नलिखित सत्य तालिका में टॉटोलॉजी के लिए तना हुआ लेबल वाला कॉलम d लेबल वाले दो स्तंभों के बीच तार्किक तुल्यता (यहाँ ≡ द्वारा चिन्हित) का मूल्यांकन करता है। क्योंकि तना हुआ के अंतर्गत सभी चार पंक्तियाँ 1 हैं, तुल्यता वास्तव में पुनरुक्ति का प्रतिनिधित्व करती है। | ||
{|style="margin-left: auto; margin-right: auto; border: none;" | {|style="margin-left: auto; margin-right: auto; border: none;" | ||
|- style="font-size:9pt; text-align:center" | |- style="font-size:9pt; text-align:center" | ||
| Line 1,646: | Line 1,643: | ||
| | | | ||
|} | |} | ||
== सामान्य रूप == | == सामान्य रूप == | ||
एक | एक प्रस्तावित सूत्र में बहुत जटिल संरचना हो सकती है। ऐसे सूत्रों के साथ काम करना अधिकांशतः सुविधाजनक होता है जिनके सरल रूप होते हैं, जिन्हें सामान्य रूपों के रूप में जाना जाता है। कुछ सामान्य सामान्य रूपों में संयोजक सामान्य रूप और विघटनकारी सामान्य रूप सम्मलित हैं। किसी भी प्रस्तावनात्मक सूत्र को उसके संयोजक या वियोगी सामान्य रूप में घटाया जा सकता है। | ||
=== सामान्य रूप में कमी === | === सामान्य रूप में कमी === | ||
[[File:Propositional formula maps 1.png|450px|thumb|right| एक सत्य तालिका में 2 होंगे<sup>n</sup> पंक्तियाँ, जहाँ n चरों की संख्या है (उदाहरण के लिए तीन चर p , d , c 2 उत्पन्न करते हैं<sup>3</sup> पंक्तियाँ)। प्रत्येक पंक्ति | [[File:Propositional formula maps 1.png|450px|thumb|right| एक सत्य तालिका में 2 होंगे<sup>n</sup> पंक्तियाँ, जहाँ n चरों की संख्या है (उदाहरण के लिए तीन चर p , d , c 2 उत्पन्न करते हैं<sup>3</sup> पंक्तियाँ)। प्रत्येक पंक्ति minterm का प्रतिनिधित्व करती है। प्रत्येक मिंटर्म हास आरेख पर, वेइच आरेख पर और कर्णघ मानचित्र पर पाया जा सकता है। (सत्य तालिका में दिखाए गए पी के मूल्यांकन हस्से, वेइच और कर्णघ आरेखों में नहीं दिखाए गए हैं, ये निम्नलिखित खंड के कर्णघ मानचित्र में दिखाए गए हैं।)<!-- For example, row 2 represents the minterm (~p & d & ~c). If "~v" (where v is any variable) is thought of as "0" and "v" is thought of as "1", then the minterm can be thought of as a binary number, e.g. (~p & d & ~c) = 010<sub>2</sub> = 2<sub>10</sub>. A formula (e.g. the formula for q) evaluated for variabiles ''p'' = 0, ''d'' = 1, ''c'' = 0 will produce an output (e.g. q). -->]]सूत्र के लिए सत्य तालिका तैयार होने के बाद सामान्य रूप में कमी अपेक्षाकृत सरल होती है। किन्तु शाब्दिक संख्या को कम करने के लिए आगे के प्रयासों (नीचे देखें) के लिए कुछ उपकरणों की आवश्यकता होती है: डी मॉर्गन के नियमों और सत्य तालिकाओं द्वारा कमी करना जटिल हो सकता है, किन्तु कर्णघ के नक्शे चर की छोटी संख्या (5 या उससे कम) के लिए बहुत उपयुक्त हैं। कई आउटपुट वाले अधिक जटिल परिपथ के लिए कुछ परिष्कृत सारणीबद्ध तरीके संलग्न हैं किन्तु ये इस लेख के दायरे से बाहर हैं, अधिक जानकारी के लिए क्विन-मैक्लुस्की एल्गोरिथम देखें। | ||
==== शाब्दिक, पद और पर्याय ==== | ==== शाब्दिक, पद और पर्याय ==== | ||
इलेक्ट्रिकल इंजीनियरिंग में | इलेक्ट्रिकल इंजीनियरिंग में चर x या इसका निषेध ~(x) साथ एकल धारणा में साथ हो जाता है जिसे शाब्दिक (गणितीय तर्क) कहा जाता है। AND द्वारा जुड़े शाब्दिक शब्दों की स्ट्रिंग को शब्द कहा जाता है। OR से जुड़े शाब्दिक शब्दों की स्ट्रिंग को परिवर्तन कहा जाता है। विशिष्ट रूप से शाब्दिक ~(x) का संक्षिप्त रूप ~x है। कभी-कभी बीजगणितीय गुणन की विधियों में &-प्रतीक को पूर्ण रूप से छोड़ दिया जाता है। | ||
* उदाहरण | * उदाहरण | ||
*# | *# a, b, c, d चर हैं। ((( a & ~(b) ) & ~(c)) & d) पद है। इसे (a & ~b & ~c & d), या a~b~cd के रूप में संक्षिप्त किया जा सकता है। | ||
*# p, q, r, s चर हैं। (((p & ~(q) ) & r) & ~(s) ) | *# p, q, r, s चर हैं। (((p & ~(q) ) & r) & ~(s) ) परिवर्तन है। इसे (p ∨ ~q ∨ r ∨ ~s) के रूप में संक्षिप्त किया जा सकता है। | ||
==== मिनट्स ==== | ==== मिनट्स ==== | ||
इसी प्रकार | इसी प्रकार a 2<sup>n</sup>-पंक्ति सत्य तालिका सभी 2<sup>n</sup> मान के लिए प्रस्ताव सूत्र का मूल्यांकन प्रदर्शित करती है, इसके चरों के संभावित मान, n चर 2 उत्पन्न करते हैं<sup>n</sup>-स्क्वायर कर्णघ मानचित्र (यदि हम इसे इसके पूर्ण-आयामी बोध में नहीं बना सकते हैं)। उदाहरण के लिए, 3 चर 2<sup>3</sup>= 8 उत्पन्न करते हैं, इस प्रकार पंक्तियाँ और 8 कर्णघ वर्ग, 4 चर 16 सत्य-तालिका पंक्तियाँ और 16 वर्ग उत्पन्न करते हैं और इसलिए 16 [[minterms|मध्यमान]] होते हैं। प्रत्येक कर्णघ-नक्शा वर्ग और इसके संबंधित सत्य-तालिका मूल्यांकन मिनट का प्रतिनिधित्व करता है। | ||
किसी भी प्रस्तावित सूत्र को सक्रिय (अर्थात 1 - या | किसी भी प्रस्तावित सूत्र को सक्रिय (अर्थात 1 - या T-वैल्यूड) मिन्टरम्स के तार्किक योग (OR) तक कम किया जा सकता है। जब इस रूप में सूत्र को वियोगात्मक सामान्य रूप में कहा जाता है। किन्तु यदि यह इस रूप में है, यह आवश्यक नहीं कि शब्दों की संख्या या अक्षर की संख्या के संबंध में कम से कम हो। | ||
निम्नलिखित तालिका में, पंक्तियों की अजीबोगरीब संख्या देखें: (0, 1, 3, 2, 6, 7, 5, 4, 0)। पहला कॉलम अंक cba के बाइनरी समतुल्य का दशमलव समतुल्य है, दूसरे शब्दों में: | निम्नलिखित तालिका में, पंक्तियों की अजीबोगरीब संख्या देखें: (0, 1, 3, 2, 6, 7, 5, 4, 0)। पहला कॉलम अंक cba के बाइनरी समतुल्य का दशमलव समतुल्य है, दूसरे शब्दों में: | ||
* उदाहरण | * उदाहरण | ||
*: | *: cba<sub>2</sub> = c * 2<sup>2</sup> + b*2<sup>1</sup> + a*2<sup>0</sup>: | ||
*: | *: cba = (c=1, b=0, a=0) = 101<sub>2</sub> = 1*2<sup>2</sup> + 0*2<sup>1</sup> + 1*2<sup>0= 5<sub>10</sub> | ||
यह क्रमांकन इस बारे में आता है क्योंकि जैसे ही कोई पंक्ति से पंक्ति में तालिका को नीचे ले जाता है, | यह क्रमांकन इस बारे में आता है क्योंकि जैसे ही कोई पंक्ति से पंक्ति में तालिका को नीचे ले जाता है, समय में केवल चर इसके मूल्य को बदलता है। [[ग्रे कोड]] इस धारणा से लिया गया है। इस धारणा को तीन और चार-आयामी [[अतिविम]] तक बढ़ाया जा सकता है जिसे हस्से आरेख कहा जाता है, जहां प्रत्येक कोने के चर समय में केवल परिवर्तन करते हैं, क्योंकि घन के किनारों के चारों ओर घूमते हैं। हस्से आरेख (हाइपरक्यूब्स) दो आयामों में चपटा हुआ या तो [[वेच आरेख]] या कर्णघ मानचित्र हैं। | ||
कर्णघ नक्शों के साथ काम करते समय हमेशा यह ध्यान रखना चाहिए कि शीर्ष किनारा नीचे के किनारे के चारों ओर लपेटता है, और बायां किनारा दाएं किनारे के चारों ओर लपेटता है- कर्णघ आरेख वास्तव में | कर्णघ नक्शों के साथ काम करते समय हमेशा यह ध्यान रखना चाहिए कि शीर्ष किनारा नीचे के किनारे के चारों ओर लपेटता है, और बायां किनारा दाएं किनारे के चारों ओर लपेटता है- कर्णघ आरेख वास्तव में तीन- या चार- या n-आयामी वस्तु है। | ||
{|class="wikitable" | {|class="wikitable" | ||
| Line 1,689: | Line 1,685: | ||
| 0 | | 0 | ||
| 0 | | 0 | ||
|style="background-color:#FDE9D9" | (~c | |style="background-color:#FDE9D9" | (~c & ~b & ~a) | ||
|- style="font-size:9pt" align="center" valign="bottom" | |- style="font-size:9pt" align="center" valign="bottom" | ||
| Height="15" | 1 | | Height="15" | 1 | ||
| Line 1,695: | Line 1,691: | ||
| 0 | | 0 | ||
| 1 | | 1 | ||
|style="background-color:#FDE9D9" | (~c | |style="background-color:#FDE9D9" | (~c & ~b & a) | ||
|- style="font-size:9pt" align="center" valign="bottom" | |- style="font-size:9pt" align="center" valign="bottom" | ||
| Height="12" | 3 | | Height="12" | 3 | ||
| Line 1,701: | Line 1,697: | ||
| 1 | | 1 | ||
| 1 | | 1 | ||
|style="background-color:#FDE9D9" | (~c | |style="background-color:#FDE9D9" | (~c & b & a) | ||
|- style="font-size:9pt" align="center" valign="bottom" | |- style="font-size:9pt" align="center" valign="bottom" | ||
| Height="12" | 2 | | Height="12" | 2 | ||
| Line 1,707: | Line 1,703: | ||
| 1 | | 1 | ||
| 0 | | 0 | ||
|style="background-color:#FDE9D9" | (~c & | |style="background-color:#FDE9D9" | (~c & b & ~a) | ||
|- style="font-size:9pt" align="center" valign="bottom" | |- style="font-size:9pt" align="center" valign="bottom" | ||
| Height="12" | 6 | | Height="12" | 6 | ||
| Line 1,713: | Line 1,709: | ||
| 1 | | 1 | ||
| 0 | | 0 | ||
|style="background-color:#FDE9D9" | (c | |style="background-color:#FDE9D9" | (c & b & ~a) | ||
|- style="font-size:9pt" align="center" valign="bottom" | |- style="font-size:9pt" align="center" valign="bottom" | ||
| Height="12" | 7 | | Height="12" | 7 | ||
| Line 1,719: | Line 1,715: | ||
| 1 | | 1 | ||
| 1 | | 1 | ||
|style="background-color:#FDE9D9" | (c & | |style="background-color:#FDE9D9" | (c & b & a) | ||
|- style="font-size:9pt" align="center" valign="bottom" | |- style="font-size:9pt" align="center" valign="bottom" | ||
| Height="12" | 5 | | Height="12" | 5 | ||
| Line 1,725: | Line 1,721: | ||
| 0 | | 0 | ||
| 1 | | 1 | ||
|style="background-color:#FDE9D9" | (c | |style="background-color:#FDE9D9" | (c & ~b & a) | ||
|- style="font-size:9pt" align="center" valign="bottom" | |- style="font-size:9pt" align="center" valign="bottom" | ||
| Height="12" | 4 | | Height="12" | 4 | ||
| Line 1,731: | Line 1,727: | ||
| 0 | | 0 | ||
| 0 | | 0 | ||
|style="background-color:#FDE9D9" | (c | |style="background-color:#FDE9D9" | (c & ~b & ~a) | ||
|- style="font-size:9pt;color:#A5A5A5" align="center" valign="bottom" | |- style="font-size:9pt;color:#A5A5A5" align="center" valign="bottom" | ||
| Height="12" | 0 | | Height="12" | 0 | ||
| Line 1,737: | Line 1,733: | ||
| 0 | | 0 | ||
| 0 | | 0 | ||
| (~a | | (~a & ~b & ~c) | ||
|} | |} | ||
=== मानचित्र विधि (वीच, कर्णघ) के उपयोग से कमी === | === मानचित्र विधि (वीच, कर्णघ) के उपयोग से कमी === | ||
वेइच ने वृत्तों को संलग्न वर्गों में परिवर्तित करके [[वेन आरेख]] | वेइच ने वृत्तों को संलग्न वर्गों में परिवर्तित करके [[वेन आरेख|वेन आरेखों]] की धारणा में सुधार किया, और कर्णघ ने उनके शाब्दिक रूप (जैसे ~abc~d) में लिखे गए टकसालों को संख्याओं में परिवर्तित करके वेइच आरेख को सरल बनाया।<ref>Wickes 1967:36ff. Wickes offers a good example of 8 of the 2 x 4 (3-variable maps) and 16 of the 4 x 4 (4-variable) maps. As an arbitrary 3-variable map could represent any one of 2<sup>8</sup>=256 2x4 maps, and an arbitrary 4-variable map could represent any one of 2<sup>16</sup> = 65,536 different formula-evaluations, writing down every one is infeasible.</ref> विधि निम्नानुसार आगे बढ़ती है: | ||
==== सूत्र की सत्य तालिका तैयार करें ==== | ==== सूत्र की सत्य तालिका तैयार करें ==== | ||
सूत्र की सत्य तालिका तैयार करें। n चर के लिए चर के बाइनरी-समतुल्य (सामान्यतः सिर्फ क्रमिक रूप से 0 से n-1) का उपयोग करके इसकी पंक्तियों को संख्या | सूत्र की सत्य तालिका तैयार करें। n चर के लिए चर के बाइनरी-समतुल्य (सामान्यतः सिर्फ क्रमिक रूप से 0 से n-1) का उपयोग करके इसकी पंक्तियों को संख्या का मान दिया जाता हैं। | ||
: तकनीकी रूप से, [[प्रस्तावक समारोह]] को इसके (अन्यूनतम) संयोजन सामान्य रूप में कम कर दिया गया है: प्रत्येक पंक्ति में इसकी न्यूनतम अभिव्यक्ति होती है और इन्हें इसके (अन्यूनतम) संयोजन सामान्य रूप में सूत्र का उत्पादन करने के लिए OR'd किया जा सकता है। | : तकनीकी रूप से, [[प्रस्तावक समारोह]] को इसके (अन्यूनतम) संयोजन सामान्य रूप में कम कर दिया गया है: प्रत्येक पंक्ति में इसकी न्यूनतम अभिव्यक्ति होती है और इन्हें इसके (अन्यूनतम) संयोजन सामान्य रूप में सूत्र का उत्पादन करने के लिए OR'd किया जा सकता है। | ||
| Line 1,786: | Line 1,780: | ||
! width="10.5" | ) | ! width="10.5" | ) | ||
! {{Active}} minterms | ! {{Active}} minterms | ||
! | ! संयोजक सामान्य रूप में सूत्र | ||
|- style="font-size:9pt" | |- style="font-size:9pt" | ||
|style="background-color:#F2F2F2;font-weight:bold" Height="12" align="center" valign="bottom" | 0 | |style="background-color:#F2F2F2;font-weight:bold" Height="12" align="center" valign="bottom" | 0 | ||
| Line 2,071: | Line 2,065: | ||
==== सूत्र का कर्णघ नक्शा बनाएं ==== | ==== सूत्र का कर्णघ नक्शा बनाएं ==== | ||
[[File:Propositional formula maps 2.png|400px|thumb|right| कर्णघ मानचित्र का उपयोग करते हुए न्यूनीकरण के चरण। अंतिम परिणाम तीन घटे हुए शब्दों का OR (तार्किक योग) है।]]ट्रूथ-टेबल विधि द्वारा प्राप्त सूत्र (जैसे p) के मानों का उपयोग करें और उन्हें उनके संबंधित (संबद्ध) कर्णघ वर्गों में रखें (ये ग्रे कोड कन्वेंशन के अनुसार गिने जाते हैं)। यदि तालिका में परवाह नहीं करने के लिए d के मान दिखाई देते हैं, तो यह कमी चरण के समय | [[File:Propositional formula maps 2.png|400px|thumb|right| कर्णघ मानचित्र का उपयोग करते हुए न्यूनीकरण के चरण। अंतिम परिणाम तीन घटे हुए शब्दों का OR (तार्किक योग) है।]]ट्रूथ-टेबल विधि द्वारा प्राप्त सूत्र (जैसे p) के मानों का उपयोग करें और उन्हें उनके संबंधित (संबद्ध) कर्णघ वर्गों में रखें (ये ग्रे कोड कन्वेंशन के अनुसार गिने जाते हैं)। यदि तालिका में परवाह नहीं करने के लिए d के मान दिखाई देते हैं, तो यह कमी चरण के समय जोड़ता है। | ||
==== minterm कम करें ==== | ==== minterm कम करें ==== | ||
सन्निकट (संलग्न) 1-वर्गों ( | सन्निकट (संलग्न) 1-वर्गों (T-स्क्वायर) के न्यूनतम पदों को उनके शाब्दिक (गणितीय तर्क) की संख्या के संबंध में कम किया जा सकता है, और प्रक्रिया में संख्या शर्तों को भी घटाया जाएगा। दो जुड़े हुए वर्ग (2 x 1 क्षैतिज या 1 x 2 लंबवत, यहां तक कि किनारे भी संलग्न वर्गों का प्रतिनिधित्व करते हैं) 4 x 1 आयत (क्षैतिज या लंबवत) या 2 x 2 वर्ग में शाब्दिक, चार वर्ग खो देते हैं (यहां तक कि चार कोने संलग्न करने का प्रतिनिधित्व करते हैं) वर्ग) दो अक्षर खो देते हैं, आयत में आठ वर्ग 3 अक्षर खो देते हैं, आदि। (कोई सबसे बड़े वर्ग या आयत की तलाश करता है और छोटे वर्गों या आयतों को पूरी तरह से अनदेखा कर देता है।) यह प्रक्रिया तब तक जारी रहती है जब तक कि सभी संलग्न वर्गों का मान नहीं संलग्न होता हैं। जिस बिंदु पर '''प्रस्तावात्मक सूत्र''' को छोटा किया जाता है। | ||
उदाहरण के लिए, वर्ग | उदाहरण के लिए, वर्ग 3 और 7 के लिए ये दो संलग्न वर्ग शाब्दिक विलुप्त हो सकते हैं (उदाहरण के लिए वर्ग 3 और 7 से p), आयत या वर्ग में चार वर्ग दो शाब्दिक खो देते हैं, आयत में आठ वर्ग 3 अक्षर विलुप्त हो जाते हैं। (एक सबसे बड़े वर्ग की तलाश करता है या आयतें।) यह प्रक्रिया तब तक जारी रहती है जब तक कि सभी संलग्न वर्गों का मान नहीं लगाया जाता है, जिस बिंदु पर प्रस्तावक सूत्र को न्यूनतम कहा जाता है। | ||
उदाहरण: मानचित्र विधि सामान्यतः निरीक्षण द्वारा की जाती है। कर्णघ मानचित्र पर शब्दों के संयोजन के पीछे की चाल दिखाने के लिए निम्न उदाहरण बीजगणितीय पद्धति का विस्तार करता है: | उदाहरण: मानचित्र विधि सामान्यतः निरीक्षण द्वारा की जाती है। कर्णघ मानचित्र पर शब्दों के संयोजन के पीछे की चाल दिखाने के लिए निम्न उदाहरण बीजगणितीय पद्धति का विस्तार करता है: | ||
: मिन्टरम्स | : मिन्टरम्स 3 & 7, 7 & 6, और 4 & 6 अबाउट (क्योंकि टेबल के किनारे लपेटे जाते हैं)। तो इनमें से प्रत्येक जोड़े को कम किया जा सकता है। | ||
निरीक्षण करें कि कार्यकुशलता नियम (A ∨ A) = A द्वारा, हम और पद बना सकते हैं। फिर संघ और वितरण | निरीक्षण करें कि कार्यकुशलता नियम (A ∨ A) = A द्वारा, हम और पद बना सकते हैं। फिर संघ और वितरण नियमों द्वारा विलुप्त होने वाले चर जोड़े जा सकते हैं, और फिर विरोधाभास के नियम (x & ~x)=0 के साथ विलुप्त हो सकते हैं। निम्नलिखित केवल शब्दों का ट्रैक रखने के लिए कोष्ठक [ और ] का उपयोग करता है, उनका कोई विशेष महत्व नहीं है: | ||
* सूत्र को कम किए जाने वाले सूत्र के साथ संयोजन सामान्य रूप में रखें: | * सूत्र को कम किए जाने वाले सूत्र के साथ संयोजन सामान्य रूप में रखें: | ||
::: q = ((~p & d & c) ∨ (p & d & c) ∨ (p & d & ~c) ∨ (p & ~d & ~c) ) = ( #3 ∨ #7 ∨ #6 ∨ #4 ) | ::: q = ((~p & d & c) ∨ (p & d & c) ∨ (p & d & ~c) ∨ (p & ~d & ~c) ) = ( #3 ∨ #7 ∨ #6 ∨ #4 ) | ||
* उदासीनता (अवशोषण) [ | * '''उदासीनता (अवशोषण)''' [a ∨ a) = a: | ||
::: ( #3 ∨ [ #7 ∨ #7 ] ∨ [ #6 ∨ #6 ] ∨ #4 ) | ::: ( #3 ∨ [ #7 ∨ #7 ] ∨ [ #6 ∨ #6 ] ∨ #4 ) | ||
* साहचर्य नियम (x ∨ (y ∨ z)) = ((x ∨ y) ∨ z ) | * '''साहचर्य नियम''' (x ∨ (y ∨ z)) = ((x ∨ y) ∨ z ) | ||
::: ( [ #3 ∨ #7 ] ∨ [ #7 ∨ #6 ] ∨ [ #6 ∨ #4] ) | ::: ( [ #3 ∨ #7 ] ∨ [ #7 ∨ #6 ] ∨ [ #6 ∨ #4] ) | ||
::: [ (~ | ::: [ (~p & d & c) ∨ (p & d & c)] ∨ [(p & d & c) ∨ (p & & & ~c)] ∨ [ (p & d & ~c) ∨ (p & ~d & ~c)]। | ||
* वितरण नियम (x | * '''वितरण नियम''' (x & (y ∨ z) ) = ( (x & y) ∨ (x & z) ): | ||
::: ( [( | ::: ( [(d & c) ∨ (~p & p)] ∨ [(p & d) ∨ (~c & c) ] ∨ [ (p & ~c) ∨ (c & ~c) ] ) | ||
* क्रमविनिमेय नियम और विरोधाभास का नियम (x & ~x) = (~x & x) = 0: | * '''क्रमविनिमेय नियम और विरोधाभास का नियम''' (x & ~x) = (~x & x) = 0: | ||
::: ( [( | ::: ( [(d & c) ∨ (0) ] ∨ [ (p & d) ∨ (0) ] ∨ [ (p & ~c) ∨ (0) ] ) | ||
* पहचान का नियम ( x ∨ 0 ) = x सूत्र के घटे हुए रूप के लिए अग्रणी: | * '''पहचान का नियम''' ( x ∨ 0 ) = x सूत्र के घटे हुए रूप के लिए अग्रणी: | ||
::: | ::: q = ((d & c) ∨ (p & d) ∨ (p & ~c)) | ||
==== एक सत्य तालिका के साथ कमी को सत्यापित करें ==== | ==== एक सत्य तालिका के साथ कमी को सत्यापित करें ==== | ||
| Line 2,378: | Line 2,372: | ||
: (1) यह वाक्य सरल है। (2) यह वाक्य जटिल है, और यह AND से जुड़ा है। | : (1) यह वाक्य सरल है। (2) यह वाक्य जटिल है, और यह AND से जुड़ा है। | ||
फिर चर s को बाएँ-सबसे वाक्य में असाइन करें यह वाक्य सरल है। कंपाउंड c = सरल नहीं ~s को परिभाषित करें, और c = ~s को यह वाक्य कंपाउंड है | फिर चर s को बाएँ-सबसे वाक्य में असाइन करें यह वाक्य सरल है। कंपाउंड c = सरल नहीं ~s को परिभाषित करें, और c = ~s को यह वाक्य कंपाउंड है, इसे j का मान असाइन करके AND से संयोजित किया जाता है। दूसरे वाक्य को इस प्रकार व्यक्त किया जा सकता है: | ||
: ( | : (NO(S) & J) | ||
यदि सत्य मान वाक्यों c = ~s और j पर रखे जाने हैं, तो सभी स्पष्ट रूप से FALSEHOODS हैं: उदा। यह वाक्य जटिल है | यदि सत्य मान वाक्यों c = ~s और j पर रखे जाने हैं, तो सभी स्पष्ट रूप से FALSEHOODS हैं: उदा। यह वाक्य जटिल है FALSEHOOD है (यह सरल है, परिभाषा के अनुसार)। अतः उनका संयोजन (AND) असत्य है। किन्तु जब इसके एकत्रित रूप में लिया जाता है, तो वाक्य सत्य होता है। | ||
यह उन [[विरोधाभास]] | यह उन [[विरोधाभास]] का उदाहरण है जो '''अप्रतिबंधित''' परिभाषा से उत्पन्न होते हैं - अर्थात, जब किसी वस्तु m में गुण P होता है, किन्तु वस्तु m को गुण P के संदर्भ में परिभाषित किया जाता है।<ref>This definition is given by [[Stephen Kleene]]. Both [[Kurt Gödel]] and Kleene believed that the classical paradoxes are uniformly examples of this sort of definition. But Kleene went on to assert that the problem has not been solved satisfactorily and impredicative definitions can be found in [[analysis]]. He gives as example the definition of the [[least upper bound]] (l.u.b) '''u''' of '''M'''. Given a [[Dedekind cut]] of the number line '''C''' and the two parts into which the number line is cut, i.e. '''M''' and ('''C''' - '''M'''), l.u.b. = '''u''' is defined in terms of the notion '''M''', whereas '''M''' is defined in terms of '''C'''. Thus the definition of '''u''', an element of '''C''', is defined in terms of the totality '''C''' and this makes its definition impredicative. Kleene asserts that attempts to argue this away can be used to uphold the impredicative definitions in the paradoxes.(Kleene 1952:43).</ref> वादविवाद करने वाले या निगमनात्मक विश्लेषण में सम्मलित व्यक्ति के लिए सबसे अच्छी सलाह है कि वह अप्रतिबंधात्मक परिभाषाओं से बचें, किन्तु साथ ही साथ उनकी तलाश में रहें क्योंकि वे वास्तव में विरोधाभास उत्पन्न कर सकते हैं। दूसरी ओर, इंजीनियरों ने उन्हें प्रतिक्रिया के साथ प्रस्तावात्मक सूत्रों के रूप में काम करने के लिए रखा जाता हैं। | ||
== प्रतिक्रिया के साथ प्रस्ताव सूत्र == | == प्रतिक्रिया के साथ प्रस्ताव सूत्र == | ||
अपने स्वयं के चरों में से | अपने स्वयं के चरों में से के रूप में प्रकट होने वाले '''प्रस्तावनात्मक सूत्र''' की धारणा के लिए गठन नियम की आवश्यकता होती है जो सूत्र को चर के असाइनमेंट की अनुमति देता है। सामान्यतः ऐसी कोई शर्त नहीं है (वस्तुओं और संबंधों की स्वयंसिद्ध या सत्य-सारणी प्रणाली) जो ऐसा होने से मना करती है।<ref>McCluskey comments that "it could be argued that the analysis is still incomplete because the word statement "The outputs are equal to the previous values of the inputs" has not been obtained"; he goes on to dismiss such worries because "English is not a formal language in a mathematical sense, [and] it is not really possible to have a ''formal'' procedure for obtaining word statements" (p. 185).</ref> सबसे सरल मामला तब होता है जब OR सूत्र अपना स्वयं का इनपुट बन जाता है, उदाहरण के लिए p = q। (p ∨ s) = q से प्रारंभ करें, फिर मान लीजिए p = q, इस स्थिति में ध्यान दें कि q की परिभाषा स्वयं q के साथ-साथ s और OR संयोजक पर भी निर्भर करती है, क्यू की यह परिभाषा इस प्रकार अप्रतिबंधात्मक है। | ||
सबसे सरल मामला तब होता है जब | |||
दो स्थितियों में से कोई भी परिणाम हो सकता है:<ref>More precisely, given enough "loop gain", either oscillation or memory will occur (cf McCluskey p. 191-2). In abstract (idealized) mathematical systems adequate loop gain is not a problem.</ref> कंपन या स्मृति। | दो स्थितियों में से कोई भी परिणाम हो सकता है:<ref>More precisely, given enough "loop gain", either oscillation or memory will occur (cf McCluskey p. 191-2). In abstract (idealized) mathematical systems adequate loop gain is not a problem.</ref> कंपन या स्मृति। | ||
यह सूत्र को [[ब्लैक बॉक्स]] के रूप में सोचने में मदद करता है। सूत्र-बॉक्स के अंदर क्या चल रहा है, इसके ज्ञान के बिना बाहर से ऐसा प्रतीत होगा कि आउटपुट अब केवल इनपुट का | यह सूत्र को [[ब्लैक बॉक्स]] के रूप में सोचने में मदद करता है। सूत्र-बॉक्स के अंदर क्या चल रहा है, इसके ज्ञान के बिना बाहर से ऐसा प्रतीत होगा कि आउटपुट अब केवल इनपुट का फ़ंक्शन (गणित) नहीं है। अर्थात्, कभी कोई q को देखता है और 0 को देखता है और अन्य समय 1 को देखता है। इस समस्या से बचने के लिए किसी को बॉक्स के अंदर छिपे चर p की स्थिति (स्थिति) को जानना होगा (अर्थात q का मान वापस खिलाया गया और p को सौंपा गया) . जब यह ज्ञात हो जाता है तो स्पष्ट असंगति दूर हो जाती है। | ||
समझने के लिए | समझने के लिए प्रतिक्रिया के साथ सूत्रों के व्यवहार को [[अनुक्रमिक सर्किट|अनुक्रमिक परिपथ]] के अधिक परिष्कृत विश्लेषण की आवश्यकता होती है। इस प्रकार इन मशीनों के लिए, उनके सरलतम रूप में, फीडबैक लीड के साथ प्रस्तावक सूत्र, वे ट्यूरिंग टेप और काउंटर-मशीन काउंटर के रूप में यादों को भी जन्म देते हैं। इस प्रकार इन तत्वों के संयोजन से कोई भी किसी भी प्रकार के परिबद्ध कम्प्यूटेशनल मॉडल (जैसे [[ट्यूरिंग मशीन]], [[काउंटर मशीन]], [[रजिस्टर मशीन]], [[मैकिंटोश कंप्यूटर]], आदि) का निर्माण कर सकता है। | ||
=== दोलन === | === दोलन === | ||
सार (आदर्श) | सार (आदर्श) स्थिति में सबसे सरल दोलन सूत्र खुद को वापस नहीं खिलाया जाता है: ~(~(p=q)) = q, इस सत्य-सारणी में सार (आदर्श) तर्कवाक्य सूत्र का विश्लेषण p=1 और p=0 दोनों स्थितियों के लिए असंगति प्रकट करता है: जब p=1, q=0, यह नहीं हो सकता क्योंकि p=q, इसी तरह जब p = 0 और q = 1 के लिए इस सारणी को इस प्रकार अंकित किया जा सकता हैं। | ||
{| | {| | ||
| Line 2,438: | Line 2,432: | ||
|} | |} | ||
[[File:Propositional formula oscillator 1.png|400px|thumb|right]]विलंब के साथ दोलन: यदि विलंब हो<ref>The notion of delay and the principle of local causation as caused ultimately by the speed of light appears in Robin Gandy (1980), "Church's thesis and Principles for Mechanisms", in J. Barwise, H. J. Keisler and K. Kunen, eds., ''The Kleene Symposium'', North-Holland Publishing Company (1980) 123-148. Gandy considered this to be the most important of his principles: "Contemporary physics rejects the possibility of instantaneous action at a distance" (p. 135). Gandy was [[Alan Turing]]'s student and close friend.</ref> (आदर्श या गैर-आदर्श) p और q के बीच सार सूत्र में डाला जाता है तो p 1 और 0: 101010...101... अनंत के बीच दोलन करेगा। यदि देरी में से कोई भी और सार नहीं है (अर्थात आदर्श नहीं है), तो उपयोग किए जाने वाले विश्लेषण का प्रकार ऑसिलेटर बनाने वाली वस्तुओं की त्रुटीहीन प्रकृति पर निर्भर करेगा | [[File:Propositional formula oscillator 1.png|400px|thumb|right]]विलंब के साथ दोलन: यदि विलंब हो<ref>The notion of delay and the principle of local causation as caused ultimately by the speed of light appears in Robin Gandy (1980), "Church's thesis and Principles for Mechanisms", in J. Barwise, H. J. Keisler and K. Kunen, eds., ''The Kleene Symposium'', North-Holland Publishing Company (1980) 123-148. Gandy considered this to be the most important of his principles: "Contemporary physics rejects the possibility of instantaneous action at a distance" (p. 135). Gandy was [[Alan Turing]]'s student and close friend.</ref> (आदर्श या गैर-आदर्श) p और q के बीच सार सूत्र में डाला जाता है तो p 1 और 0: 101010...101... अनंत के बीच दोलन करेगा। यदि देरी में से कोई भी और सार नहीं है (अर्थात आदर्श नहीं है), तो उपयोग किए जाने वाले विश्लेषण का प्रकार ऑसिलेटर बनाने वाली वस्तुओं की त्रुटीहीन प्रकृति पर निर्भर करेगा, ऐसी चीजें गणित के बाहर और इंजीनियरिंग में आती हैं। | ||
विश्लेषण के लिए देरी डालने की आवश्यकता होती है और फिर देरी और इनपुट p के बीच लूप कट जाता है। विलंब को | विश्लेषण के लिए देरी डालने की आवश्यकता होती है और फिर देरी और इनपुट p के बीच लूप कट जाता है। विलंब को प्रकार के प्रस्ताव के रूप में देखा जाना चाहिए जिसमें इनपुट के रूप में q के आउटपुट के रूप में qd (q-delayed) है। यह नया प्रस्ताव सत्य तालिका में और स्तंभ जोड़ता है। असंगति अब qd और p के बीच है जैसा कि लाल रंग में दिखाया गया है, परिणामी दो स्थिर अवस्थाएँ: | ||
{| | {| | ||
| Line 2,507: | Line 2,501: | ||
=== मेमोरी === | === मेमोरी === | ||
[[File:Propositional formula flip flops 1.png|400px|thumb|right| सबसे सरल मेमोरी परिणामों के बारे में जब OR का आउटपुट उसके किसी | [[File:Propositional formula flip flops 1.png|400px|thumb|right| सबसे सरल मेमोरी परिणामों के बारे में जब OR का आउटपुट उसके किसी इनपुट पर वापस फीड होता है, इस मामले में आउटपुट q p में वापस फीड करता है। अगला सरलतम फ्लिप-फ्लॉप है जो वन्स-फ्लिप के नीचे दिखाया गया है। इस प्रकार के फ़ार्मुलों का विश्लेषण या तो फ़ीडबैक पाथ(पथों) को काट कर या पथ में (आदर्श) विलंब डालकर किया जा सकता है। कट पथ और धारणा है कि परिपथ में कहीं भी कोई देरी नहीं होती है, कुल राज्यों में से कुछ के लिए असंगतता होती है (इनपुट और आउटपुट का संयोजन, उदाहरण के लिए (पी = 0, एस = 1, आर = 1) असंगतता में परिणाम)। जब विलंब संलग्न होता है तो ये असंगतताएं केवल अस्थायी होती हैं और विलंब समाप्त होने पर समाप्त हो जाती हैं। दाईं ओर के रेखाचित्रों को [[राज्य आरेख]] कहा जाता है।]] | ||
[[File:Propositional formula 3.png|400px|thumb|right| क्लॉक्ड फ्लिप-फ्लॉप मेमोरी (c क्लॉक है और d डेटा है)। डेटा किसी भी समय बदल सकता है जब घड़ी c = 0 | [[File:Propositional formula 3.png|400px|thumb|right| क्लॉक्ड फ्लिप-फ्लॉप मेमोरी (c क्लॉक है और d डेटा है)। डेटा किसी भी समय बदल सकता है जब घड़ी c = 0, जब घड़ी c = 1 आउटपुट q डेटा d के मान को ट्रैक करता है। जब c 1 से 0 तक जाता है तो यह d = q के मान को पकड़ लेता है और यह q पर दिखाई देना जारी रखता है चाहे d कुछ भी करे (जब तक c 0 रहता है)।]]बिना देर किए, सत्य तालिका विश्लेषण से विसंगतियों को दूर किया जाना चाहिए। देरी की धारणा के साथ, यह स्थिति खुद को फेड-बैक आउटपुट वेरिएबल q और p = q <sub>delayed</sub>.के बीच क्षणिक असंगति के रूप में प्रस्तुत करती है | ||
एक सत्य तालिका उन पंक्तियों को प्रकट करती है जहाँ p = q | एक सत्य तालिका उन पंक्तियों को प्रकट करती है जहाँ p = q<sub>delayed</sub> के बीच इनपुट पर और q आउटपुट पर विसंगतियाँ होती हैं। फ़ीड-बैक को तोड़ने के बाद,<ref>McKlusky p. 194-5 discusses "breaking the loop" and inserts "amplifiers" to do this; Wickes (p. 118-121) discuss inserting delays. McCluskey p. 195ff discusses the problem of "races" caused by delays.</ref> सत्य तालिका निर्माण पारंपरिक तरीके से आगे बढ़ता है। किन्तु बाद में, प्रत्येक पंक्ति में आउटपुट q की तुलना अब-स्वतंत्र इनपुट p से की जाती है और p और q के बीच कोई भी विसंगतियां नोट की जाती हैं (अर्थात p = 0 q = 1, या p = 1 और q = 0 के साथ), जब लाइन को फिर से बनाया जाता है तो इस प्रकार विरोधाभास के नियम ~(p & ~p) द्वारा दोनों को असंभव बना दिया जाता है। विसंगतियों को प्रकट करने वाली पंक्तियों को या तो क्षणिक स्थिति माना जाता है या असंगत के रूप में समाप्त कर दिया जाता है और इसलिए असंभव है। | ||
==== वन्स-फ्लिप मेमोरी ==== | ==== वन्स-फ्लिप मेमोरी ==== | ||
सबसे सरल मेमोरी परिणामों के बारे में जब OR का आउटपुट इसके किसी | सबसे सरल मेमोरी परिणामों के बारे में जब OR का आउटपुट इसके किसी इनपुट को वापस फीड करता है, इस स्थिति में आउटपुट q p में वापस फीड करता है। इस प्रकार यह देखते हुए कि सूत्र का पहले p=0 और q=0 के साथ मूल्यांकन (प्रारंभिक) किया जाता है, यह s=1 द्वारा सेट किए जाने पर बार फ़्लिप करेगा। इसके बाद, आउटपुट q फ़्लिप की स्थिति में q को बनाए रखेगा (q = 1)। यह व्यवहार, जो अब समय-निर्भर है, इस आरेख द्वारा वंस-फ्लिप के दाईं ओर दिखाया गया है। | ||
{| | {| | ||
| Line 2,581: | Line 2,575: | ||
==== फ्लिप-फ्लॉप मेमोरी ==== | ==== फ्लिप-फ्लॉप मेमोरी ==== | ||
अगला सरल मामला है सेट-रीसेट [[फ्लिप-फ्लॉप (इलेक्ट्रॉनिक्स)]] | अगला सरल मामला है सेट-रीसेट [[फ्लिप-फ्लॉप (इलेक्ट्रॉनिक्स)]] या फ्लिप-फ्लॉप बार-फ्लिप के नीचे दिखाया गया है। यह देखते हुए कि r = 0 और s = 0 और q = 0 प्रारंभ में, यह बार-फ्लिप के समान तरीके से सेट (s = 1) है। चूंकि इसमें r = 1 होने पर q = 0 को रीसेट करने का प्रावधान है। और अतिरिक्त जटिलता तब होती है जब दोनों सेट = 1 और रीसेट = 1 का मान निर्धारित किया जाता हैं। इस सूत्र में, सेट = 1 आउटपुट q = 1 को बाध्य करता है, इसलिए कब और यदि (s = 0 और r = 1) फ्लिप-फ्लॉप रीसेट हो जाएगा। या, यदि (s=1 & r=0) फ्लिप-फ्लॉप सेट हो जाएगा। अमूर्त (आदर्श) उदाहरण में जिसमें s=1 ⇒ s=0 & r=1 ⇒ r=0 साथ, सूत्र q अनिश्चित (अनिश्चित) होगा। वास्तविक OR, AND और NOT में देरी के कारण परिणाम प्रारंभ में अज्ञात होगा किन्तु उसके बाद विधेय होगा। | ||
{| | {| | ||
| Line 2,768: | Line 2,762: | ||
==== क्लॉक फ्लिप-फ्लॉप मेमोरी ==== | ==== क्लॉक फ्लिप-फ्लॉप मेमोरी ==== | ||
क्लॉक्ड फ्लिप-फ्लॉप मेमोरी (c क्लॉक है और d डेटा है) के रूप में जाना जाने वाला सूत्र नीचे दिया गया है। यह निम्नानुसार कार्य करता है: जब c = 0 डेटा d (या तो 0 या 1) आउटपुट q को प्रभावित करने के लिए प्राप्त नहीं कर सकता है। जब c = 1 डेटा d के माध्यम से प्राप्त होता है और आउटपुट q d के मान का अनुसरण करता है। जब c 1 से 0 तक जाता है तो डेटा का अंतिम मान आउटपुट q पर फंसा रहता है। जब तक c = 0, d, q को बदले बिना मान बदल सकता है। | क्लॉक्ड फ्लिप-फ्लॉप मेमोरी (c क्लॉक है और d डेटा है) के रूप में जाना जाने वाला सूत्र नीचे दिया गया है। यह निम्नानुसार कार्य करता है: जब c = 0 डेटा d (या तो 0 या 1) आउटपुट q को प्रभावित करने के लिए प्राप्त नहीं कर सकता है। जब c = 1 डेटा d के माध्यम से प्राप्त होता है और आउटपुट q d के मान का अनुसरण करता है। इस प्रकार जब c 1 से 0 तक जाता है तो डेटा का अंतिम मान आउटपुट q पर फंसा रहता है। जब तक c = 0, d, q को बदले बिना मान बदल सकता है। | ||
* उदाहरण | * उदाहरण | ||
*# (( | *# ((c & d) ∨ (p & (~(c & ~(d))) = q, किन्तु अब p = q: | ||
*# (( | *# ((c & d) ∨ (q & (~(c & ~(d))) = q | ||
आरेख फ्लिप-फ्लॉप के आरेख के आकार के समान है, किन्तु संक्रमणों पर अलग-अलग लेबलिंग के साथ दर्शाया जा सकता हैं। | |||
{| | {| | ||
| Line 2,986: | Line 2,980: | ||
| | | | ||
|style="background-color:#FDE9D9" | 1 | |style="background-color:#FDE9D9" | 1 | ||
| state 1 with (d =0 & c=0 ), | | state 1 with (d =0 & c=0 ), 1 is trapped | ||
|- style="font-size:9pt" align="center" | |- style="font-size:9pt" align="center" | ||
|style="background-color:#BFBFBF;font-weight:bold" Height="12" | 5 | |style="background-color:#BFBFBF;font-weight:bold" Height="12" | 5 | ||
| Line 3,081: | Line 3,075: | ||
== ऐतिहासिक विकास == | == ऐतिहासिक विकास == | ||
[[बर्ट्रेंड रसेल]] (1912:74) [[अरस्तू]] से प्राप्त विचार के तीन नियमों को सूचीबद्ध करता है: (1) पहचान का नियम | [[बर्ट्रेंड रसेल]] (1912:74) [[अरस्तू]] से प्राप्त विचार के तीन नियमों को सूचीबद्ध करता है: (1) पहचान का नियम से प्राप्त मान पर निर्भर करता हैं। इस प्रकार (2) गैर-विरोधाभास का नियम: कुछ भी नहीं हो सकता है और न ही हो सकता है, और (3) बहिष्कृत मध्य का नियम: सब कुछ होना चाहिए या नहीं होना चाहिए। | ||
* उदाहरण: यहाँ O किसी वस्तु के होने या गुणवत्ता के बारे में | * उदाहरण: यहाँ O किसी वस्तु के होने या गुणवत्ता के बारे में अभिव्यक्ति है: | ||
*# पहचान का नियम: O = O | *# पहचान का नियम: O = O | ||
*#विरोधाभास का नियम: ~(O & ~(O)) | *#विरोधाभास का नियम: ~(O & ~(O)) | ||
*# बहिष्कृत मध्य का | *# बहिष्कृत मध्य का नियम: (O ∨ ~(O)) | ||
बहिष्कृत मध्य के | इस प्रकार बहिष्कृत मध्य के नियम में सब कुछ शब्द का उपयोग इस नियम की रसेल की अभिव्यक्ति को बहस के लिए OPEN करता है। यदि वस्तुओं के परिमित संग्रह (प्रवचन का परिमित ब्रह्मांड) के संदर्भ में BEING या QUALITY के बारे में अभिव्यक्ति तक सीमित है - जिसके सदस्यों की उपस्थिति या अनुपस्थिति के लिए के बाद जांच की जा सकती है - तो नियम माना जाता है सहज रूप से उपयुक्त। इस प्रकार अभिकथन जैसे: यह वस्तु या तो होनी चाहिए या नहीं होनी चाहिए (संग्रह में), या इस वस्तु में या तो यह गुणवत्ता होनी चाहिए या यह गुणवत्ता नहीं होनी चाहिए (संग्रह में वस्तुओं के सापेक्ष) स्वीकार्य है। इस स्थिति को वेन आरेख पर देखें। | ||
यद्यपि तर्कवाक्य कलन की उत्पत्ति अरस्तू के साथ हुई, फिर भी तर्कवाक्यों पर लागू बीजगणित की धारणा को 19वीं शताब्दी की प्रारंभ तक प्रतीक्षा करनी पड़ी। अरस्तू के न्यायवाक्य की 2000 वर्ष की परंपरा की | यद्यपि तर्कवाक्य कलन की उत्पत्ति अरस्तू के साथ हुई, फिर भी तर्कवाक्यों पर लागू बीजगणित की धारणा को 19वीं शताब्दी की प्रारंभ तक प्रतीक्षा करनी पड़ी। इस प्रकार अरस्तू के न्यायवाक्य की 2000 वर्ष की परंपरा की (प्रतिकूल) प्रतिक्रिया में, [[जॉन लोके]] के मानव समझ से संबंधित निबंध (1690) में लाक्षणिकता (प्रतीकों के उपयोग का सिद्धांत) शब्द का प्रयोग किया गया था। 1826 तक [[रिचर्ड व्हाटली]] ने लोके के लाक्षणिकता के प्रति सहानुभूति के साथ न्याय संगत तर्क का आलोचनात्मक विश्लेषण किया था। [[जॉर्ज बेंथम]] के कार्य (1827) के परिणामस्वरूप विधेय (1827) के परिमाणीकरण की धारणा उत्पन्न हुई (आजकल इसे सभी के लिए ∀ ≡ के रूप में दर्शाया जाता है)। [[ऑगस्टस डी मॉर्गन]] के साथ प्राथमिकता विवाद पर सर विलियम हैमिल्टन, 9वें बैरोनेट द्वारा उकसाए गए विवाद ने [[जॉर्ज बूले]] को तर्क पर अपने विचार लिखने और उन्हें 1847 में एमएएल [तर्क का गणितीय विश्लेषण] के रूप में प्रकाशित करने के लिए प्रेरित किया (ग्रैटिन-गिनीज और बोर्नेट 1997) :xxviii)। | ||
उनके योगदान के बारे में ग्रैटिन-गिनीज और बोर्नेट टिप्पणी: | उनके योगदान के बारे में ग्रैटिन-गिनीज और बोर्नेट टिप्पणी: | ||
: बोले का प्रमुख एकल नवाचार [द] | : बोले का प्रमुख एकल नवाचार [द] नियम [x] था<sup>n</sup> = x ] तर्क के लिए: यह कहा गया है कि गुण x को चुनने और x को बार-बार चुनने का मानसिक कार्य बार x को चुनने के समान है... इसके परिणामस्वरूप उसने समीकरण x•(1) बनाया -x)=0 और x+(1-x)=1 जो उसके लिए क्रमशः विरोधाभास के नियम और बहिष्कृत मध्य के नियम (p या xxviiff) को व्यक्त करता है। बूले के लिए 1 प्रवचन का ब्रह्मांड था और 0 कुछ भी नहीं था। | ||
[[भगवान फ्रीज का शुक्र है]] के बड़े पैमाने पर उपक्रम (1879) के परिणामस्वरूप प्रस्तावों की | [[भगवान फ्रीज का शुक्र है]] के बड़े पैमाने पर उपक्रम (1879) के परिणामस्वरूप प्रस्तावों की औपचारिक गणना हुई, किन्तु उनका प्रतीकवाद इतना कठिन था कि व्यक्ति को छोड़कर इसका बहुत कम प्रभाव था: बर्ट्रेंड रसेल। जिन्होंने सबसे पहले [[अल्फ्रेड नॉर्थ व्हाइटहेड]] के छात्र के रूप में उन्होंने फ्रीज के काम का अध्ययन किया और इस प्रकार इसके संबंध में (प्रसिद्ध और कुख्यात) संशोधन का सुझाव दिया (1904) [[अधिकार-विरोध]] की समस्या के आसपास जिसे उन्होंने फ्रेज के उपचार (cf रसेल के विरोधाभास) में खोजा। रसेल के काम ने व्हाइटहेड के साथ सहयोग का नेतृत्व किया, जिसने 1912 में प्रिंसिपिया मैथेमेटिका (पीएम) के पहले खंड का निर्माण किया। यही वह स्थान है जिसे हम आधुनिक तर्कवाक्य तर्क मानते हैं जो सबसे पहले प्रकट हुआ। विशेष रूप से, पीएम ने NOT और OR और अभिकथन प्रतीक ⊦ आदिम के रूप में परिचय दिया। इस प्रकार इन धारणाओं के संदर्भ में वे इम्प्लीकेशन को परिभाषित करते हैं → ( def. *1.01: ~p ∨ q), फिर AND (def. *3.01: ~(~p ∨ ~q) ), फिर EQUIVALENCE p ←→ q (*4.01: ( p → q) और (q → p))। | ||
* हेनरी एम. शेफ़र (1921) और [[जॉन निकोड]] प्रदर्शित करते हैं कि केवल | * हेनरी एम. शेफ़र (1921) और [[जॉन निकोड]] प्रदर्शित करते हैं कि केवल संयोजक, स्ट्रोक | सभी प्रस्तावित सूत्रों को व्यक्त करने के लिए पर्याप्त है। | ||
* [[एमिल पोस्ट]] (1921) ने प्रारंभिक प्रस्तावों के | * [[एमिल पोस्ट]] (1921) ने प्रारंभिक प्रस्तावों के सामान्य सिद्धांत के अपने परिचय में विश्लेषण की सत्य तालिका पद्धति विकसित की। उसने निकोद के स्ट्रोक को नोट किया | . | ||
* व्हाइटहेड और रसेल ने पीएम के अपने 1927 के पुनर्प्रकाशन में | * व्हाइटहेड और रसेल ने पीएम के अपने 1927 के पुनर्प्रकाशन में परिचय जोड़ा, जिसमें आंशिक रूप से आघात का अनुकूल उपचार जोड़ा गया। | ||
'गणना और स्विचिंग | 'गणना और स्विचिंग तर्क': | ||
* विलियम एक्लस (भौतिक विज्ञानी) और | * विलियम एक्लस (भौतिक विज्ञानी) और F W जॉर्डन (1919) वैक्यूम ट्यूब से बने ट्रिगर रिले का वर्णन करते हैं। | ||
* [[जॉर्ज स्टि[[अंश]] | * [[जॉर्ज स्टि[[अंश|अंशज]]]] (1937) ने यांत्रिक रिले का उपयोग करके बाइनरी योजक का आविष्कार किया। वह इसे अपनी रसोई की मेज पर बनाता है। | ||
: उदाहरण: दिए गए बाइनरी बिट्स | : उदाहरण: दिए गए बाइनरी बिट्स a<sub>i</sub> और b<sub>i</sub> और कैरी-इन ( c_in<sub>i</sub>), उनका योग Σ<sub>i</sub> और कैरी-आउट (c_out<sub>i</sub>) हैं: | ||
:* ( ( | :* ( ( a<sub>i</sub> XOR b<sub>i</sub> ) XOR c_in<sub>i</sub> )= s<sub>i</sub> | ||
:* ( | :* ( a<sub>i</sub> & b<sub>i</sub> ) ∨ c_in<sub>i</sub> ) = c_out<sub>i</sub>, | ||
* [[एलन ट्यूरिंग]] रिले (1937-1938) का उपयोग करके गुणक बनाता है। ऐसा करने के लिए उसे अपने स्वयं के रिले कॉइल्स को हाथ से हवा देना पड़ता है। | * [[एलन ट्यूरिंग]] रिले (1937-1938) का उपयोग करके गुणक बनाता है। ऐसा करने के लिए उसे अपने स्वयं के रिले कॉइल्स को हाथ से हवा देना पड़ता है। | ||
* स्विचिंग | * स्विचिंग परिपथ के बारे में पाठ्यपुस्तकें 1950 के दशक की प्रारंभ में दिखाई देती हैं। | ||
* [[विलार्ड क्वीन]] 1952 और 1955, एडवर्ड डब्ल्यू. वीच | * [[विलार्ड क्वीन]] 1952 और 1955, एडवर्ड डब्ल्यू. वीच, ई. डब्ल्यू. वीच 1952, और मौरिस कर्णघ, एम. कर्णघ (1953) प्रस्तावित कार्यों को सरल बनाने के लिए मानचित्र-विधियाँ विकसित करते हैं। | ||
* जॉर्ज एच. मीली (1955) और एडवर्ड | * जॉर्ज एच. मीली (1955) और एडवर्ड F. मूर (1956) अनुक्रमिक (अर्थात स्विचिंग-परिपथ) मशीनों के सिद्धांत को संबोधित करते हैं। | ||
* ई.जे. मैकक्लुस्की और एच. शोर ने प्रस्तावित (स्विचिंग) | * ई.जे. मैकक्लुस्की और एच. शोर ने प्रस्तावित (स्विचिंग) परिपथ (1962) को सरल बनाने के लिए विधि विकसित की। | ||
== फुटनोट्स == | == फुटनोट्स == | ||
| Line 3,124: | Line 3,118: | ||
* {{cite book |last= Kleene |first= Stephen |author-link= Stephen Cole Kleene |date=1952 |title=Introduction to metamathematics |location=Amsterdam |publisher=North-Holland Publishing Company}} | * {{cite book |last= Kleene |first= Stephen |author-link= Stephen Cole Kleene |date=1952 |title=Introduction to metamathematics |location=Amsterdam |publisher=North-Holland Publishing Company}} | ||
* {{aut|Bender, Edward A.}} and {{aut|Williamson, S. Gill}}, 2005, ''A Short Course in Discrete Mathematics'', Dover Publications, Mineola NY, {{isbn|0-486-43946-1}}. This text is used in a "lower division two-quarter [computer science] course" at UC San Diego. | * {{aut|Bender, Edward A.}} and {{aut|Williamson, S. Gill}}, 2005, ''A Short Course in Discrete Mathematics'', Dover Publications, Mineola NY, {{isbn|0-486-43946-1}}. This text is used in a "lower division two-quarter [computer science] course" at UC San Diego. | ||
* {{aut|[[Herbert Enderton|Enderton, H. B.]]}}, | * {{aut|[[Herbert Enderton|Enderton, H. B.]]}}, 2002, ''A Mathematical Introduction to Logic.'' Harcourt/Academic Press. {{isbn|0-12-238452-0}} | ||
* {{aut|Goodstein, R. L.}}, (Pergamon Press 1963), 1966, (Dover edition 2007), ''Boolean Algebra'', Dover Publications, Inc. Minola, New York, {{isbn|0-486-45894-6}}. Emphasis on the notion of "algebra of classes" with set-theoretic symbols such as ∩, ∪, ' (NOT), ⊂ (IMPLIES). Later Goldstein replaces these with &, ∨, ¬, → (respectively) in his treatment of "Sentence Logic" pp. 76–93. | * {{aut|Goodstein, R. L.}}, (Pergamon Press 1963), 1966, (Dover edition 2007), ''Boolean Algebra'', Dover Publications, Inc. Minola, New York, {{isbn|0-486-45894-6}}. Emphasis on the notion of "algebra of classes" with set-theoretic symbols such as ∩, ∪, ' (NOT), ⊂ (IMPLIES). Later Goldstein replaces these with &, ∨, ¬, → (respectively) in his treatment of "Sentence Logic" pp. 76–93. | ||
* {{aut|[[Ivor Grattan-Guinness]]}} and Gérard Bornet 1997, ''George Boole: Selected Manuscripts on Logic and its Philosophy'', Birkhäuser Verlag, Basil, {{isbn|978-0-8176-5456-6}} (Boston). | * {{aut|[[Ivor Grattan-Guinness]]}} and Gérard Bornet 1997, ''George Boole: Selected Manuscripts on Logic and its Philosophy'', Birkhäuser Verlag, Basil, {{isbn|978-0-8176-5456-6}} (Boston). | ||
| Line 3,144: | Line 3,138: | ||
{{Mathematical logic}} | {{Mathematical logic}} | ||
{{DEFAULTSORT:Propositional Formula}} | {{DEFAULTSORT:Propositional Formula}} | ||
[[Category: | [[Category:Articles with invalid date parameter in template]] | ||
[[Category:Created On 16/02/2023]] | [[Category:Collapse templates|Propositional Formula]] | ||
[[Category:Created On 16/02/2023|Propositional Formula]] | |||
[[Category:Lua-based templates|Propositional Formula]] | |||
[[Category:Machine Translated Page|Propositional Formula]] | |||
[[Category:Mathematics navigational boxes|Propositional Formula]] | |||
[[Category:Navbox orphans|Propositional Formula]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Propositional Formula]] | |||
[[Category:Pages with empty portal template|Propositional Formula]] | |||
[[Category:Pages with script errors|Propositional Formula]] | |||
[[Category:Philosophy and thinking navigational boxes|Propositional Formula]] | |||
[[Category:Portal-inline template with redlinked portals|Propositional Formula]] | |||
[[Category:Short description with empty Wikidata description|Propositional Formula]] | |||
[[Category:Sidebars with styles needing conversion|Propositional Formula]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi|Propositional Formula]] | |||
[[Category:Templates Vigyan Ready|Propositional Formula]] | |||
[[Category:Templates generating microformats|Propositional Formula]] | |||
[[Category:Templates that add a tracking category|Propositional Formula]] | |||
[[Category:Templates that are not mobile friendly|Propositional Formula]] | |||
[[Category:Templates that generate short descriptions|Propositional Formula]] | |||
[[Category:Templates using TemplateData|Propositional Formula]] | |||
[[Category:Wikipedia articles needing clarification from October 2013]] | |||
[[Category:Wikipedia articles needing clarification from October 2016]] | |||
[[Category:Wikipedia metatemplates|Propositional Formula]] | |||
[[Category:तार्किक भाव|Propositional Formula]] | |||
[[Category:प्रस्ताव|Propositional Formula]] | |||
[[Category:प्रस्तावक कलन|Propositional Formula]] | |||
[[Category:बयान|Propositional Formula]] | |||
[[Category:बूलियन बीजगणित|Propositional Formula]] | |||
[[Category:सिंटेक्स (तर्क)|Propositional Formula]] | |||
Latest revision as of 11:04, 23 February 2023
प्रस्तावपरक तर्क में, प्रस्तावात्मक सूत्र प्रकार का वाक्य-विन्यास के गणितीय तार्किक सूत्र पर निर्भर करता है, यह ऐसा निर्मित सूत्र होता है जिसका मान सदैव सही होता है। यदि किसी प्रस्तावात्मक सूत्र में सभी चरों के मान दिए जाते हैं, तो यह अद्वितीय सही मानों को निर्धारित करता है। प्रस्तावनात्मक सूत्र को प्रस्तावक अभिव्यक्ति, वाक्य या वाक्यात्मक सूत्र भी कहा जाता है।
प्रस्तावनात्मक सूत्र विशेष रूप से सरल तार्किक प्रस्ताव से निर्मित होता है, जैसे कि पाँच तीन से अधिक या प्रस्तावात्मक चर होता हैं जैसे उदाहरण के लिए p और q, कनेक्टिव्स या तार्किक ऑपरेटर है जिसके लिए NOT, AND, OR गेट का उपयोग किया जाता हैं जैसे:
- (p AND NOT q) IMPLIES (p OR q)
इस प्रकार गणित में, तर्कवाक्य सूत्र को अधिकांशतः अधिक संक्षिप्त रूप से प्रस्तावित करके संदर्भित किया जाता है, किन्तु अधिक त्रुटीहीन स्थिति में प्रस्तावक सूत्र प्रस्तावित नहीं होता हैं, इसके अतिरिक्त औपचारिक अभिव्यक्ति प्रस्तावित होती है जो प्रस्तावित गणितीय मान को दर्शाती हैं, इस मत के अनुसार औपचारिक वस्तु, जैसे अभिव्यक्ति की तरह x + y का मान निर्धारित नहीं होता है, किन्तु इसके मान को दर्शाया जा सकता है। कुछ संदर्भों में भेद होने के कारण इसके महत्व को निर्धारित किया जाता हैं।
प्रस्ताव
प्रस्तावपरक कलन के प्रयोजनों के लिए, प्रस्तावित उच्चारण, वाक्य, अभिकथन को या तो सरल या यौगिक के रूप में मान लिया जाता है।[1] इस प्रकार यौगिक तर्कवाक्यों को वाक्यात्मक संयोजकों द्वारा संयोजित किया जाता है, जिनमें से कुछ सबसे सामान्य हैं जैसें- AND , OR , IF ... THEN ... , NEITHER ... NOR ... , ... IS EQUIVALENT TO ... . लिंकिंग अर्धविराम इत्यादि, और इसी प्रकार संयोजी BUT को AND का व्यंजक माना जाता है। असतत वाक्यों के क्रम को AND से जुड़ा हुआ माना जाता है, और औपचारिक विश्लेषण पर सरल प्रस्तावों के अनुक्रमों के संबंध में पुनरावर्ती कोष्ठक के नियम को लागू किया जाता हैं ( इसके लिए बनाए गए सूत्रों के बारे में अच्छी तरह से अध्ययन करें)।
- उदाहरण के लिए: कथन: यह गाय नीली है। वह घोड़ा नारंगी है किन्तु यहां का घोड़ा बैंगनी रंग का है। वास्तव में AND से संयोजित मिश्रित तर्कवाक्य है: ((यह गाय नीली है और वह घोड़ा नारंगी है) और यह घोड़ा यहाँ बैंगनी है)।
इस प्रकार सरल प्रस्ताव प्रकृति में घोषणात्मक होते हैं, अर्थात, वे किसी विशेष वस्तु की अनुभूति की स्थिति या प्रकृति के बारे में प्रमाणित करते हैं, उदाहरण के लिए यह गाय नीली है, कोयोट है! (वह कोयोट वहाँ है।)[2] इस प्रकार सरल तार्किक कथन विशिष्ट वस्तुओं या मन की विशिष्ट अवस्थाओं के बारे में उपयोग किया जाना चाहिए। इस प्रकार प्रत्येक के पास कम से कम विषयों पर विचार या अवलोकन के तत्काल वस्तु, क्रिया (सक्रिय आवाज और वर्तमान काल में उपयोग के आधार पर), और संभवतः विशेषण या क्रिया विशेषण प्रकार की होनी चाहिए। कुत्ता! संभवतः इसका तात्पर्य है कि मैं कुत्ते को देखता हूं किन्तु इसे बहुत अस्पष्ट के रूप में अनुपयोगी कर दिया जाना चाहिए।
- उदाहरण: वह बैंगनी कुत्ता दौड़ रहा है, यह गाय नीली है, स्विच M31 CLOSE है, यह टोपी CLOSE है, कल शुक्रवार है।
इस प्रकार तर्कवाक्य कलन के प्रयोजनों के लिए यौगिक तर्कवाक्य को सामान्यतः सरल वाक्यों की श्रृंखला में फिर से लिखा जा सकता है, चूंकि इसका परिणाम संभवतः अधूरा लगेगा।
प्रस्तावक और विधेय सूत्रों के बीच संबंध
प्रस्तावों की आंतरिक संरचना के विश्लेषण के लिए विधेय कलन प्रस्तावक कलन की तुलना में यह स्थिति आगे रहती हैं।[3] यह साधारण वाक्य को दो भागों में विभाजित करता है (i) इसका विषय (एकवचन शब्द या बहुवचन) और (ii) विधेय (व्याकरण) (एक क्रिया या संभवतः क्रिया-खंड जो गुण या विशेषता का प्रमाणित करता है)। इस प्रकार विधेय कलन इस स्थिति में विषय का सामान्यीकरण करता है। विधेय रूप (जहां प्रतीकों का साथ) निम्नलिखित रिक्त-विषय संरचना के साथ रूप में होता है।
- उदाहरण: इस नीले सुअर के पंख हैं, प्रस्तावक कलन में दो वाक्य बन जाते हैं: इस सुअर के पंख हैं और यह सुअर नीले रंग का है, जिसकी आंतरिक संरचना पर विचार नहीं किया जाता है। इसके विपरीत, विधेय कलन में, पहला वाक्य इस सुअर में विषय के रूप में टूट जाता है, और विधेय के रूप में पंख होते हैं। इस प्रकार यह प्रमाणित करता है कि वस्तु यह सुअर पंखों वाली चीजों के वर्ग (सेट, संग्रह) का सदस्य है। दूसरा वाक्य इस बात पर जोर देता है कि वस्तु इस सुअर में नीले रंग की विशेषता है और इस प्रकार यह नीली चीजों की श्रेणी का सदस्य है। कोई भी AND से जुड़े दो वाक्यों को इस प्रकार लिखना चुन सकता है:
- p|W AND p|B
इस सुअर के दो वर्गों के (संभावित) सदस्य पंखों वाली चीजों और नीली चीजों के सामान्यीकरण का अर्थ है कि इसका इन दोनों वर्गों के साथ सत्य-संबंध है। दूसरे शब्दों में, प्रवचन पंख वाली चीजों का डोमेन दिया गया है, P या तो इस डोमेन का सदस्य पाया जाता है या नहीं। इस प्रकार p (सुअर) और { T, F }, W (p) के बीच संबंध W (विंग्डनेस) है, जो { T, F } का मूल्यांकन करता है, जहाँ { T, F } बूलियन डेटा प्रकार सत्य और असत्य का सेट है। इसी प्रकार B (नीलापन) और P (सुअर) और {T, F} के लिए: B (p) {T, F} का मूल्यांकन करता है। तो अब कोई जुड़ा हुआ अभिकथन B(p) और W(p) का समग्र सत्य-मूल्य के लिए विश्लेषण कर सकता है, अर्थात:
- ( B(p) AND W(p) ) evaluates to { T, F }
इस प्रकार विशेष रूप से, सरल वाक्य जो तार्किक परिमाणक कहलाने वाले सभी या कुछ की धारणाओं को नियोजित करते हैं, विधेय कलन द्वारा व्यवहार किए जाते हैं। नए फ़ंक्शन को प्रतीक F(x) के साथ दो नए प्रतीक ∀ (सभी के लिए), और ∃ (वहाँ संलग्न है ..., कम से कम ... संलग्न है, आदि) प्रस्तुत किए गए हैं। विधेय कलन, किन्तु प्रस्तावक कलन नहीं, निम्नलिखित कथन की औपचारिक वैधता स्थापित कर सकता है:
- सभी नीले सूअरों के पंख होते हैं किन्तु कुछ सूअरों के पंख नहीं होते हैं, इसलिए कुछ सूअर नीले नहीं होते हैं।
पहचान
तर्स्की का प्रमाणित है कि पहचान की धारणा (तार्किक समानता से अलग) प्रस्ताविक कलन के बाहर है, चूंकि, वह नोट करता है कि यदि किसी तर्क को गणित और विज्ञान के लिए उपयोग करना है तो उसमें पहचान का सिद्धांत होना चाहिए।[4] इस प्रकार कुछ लेखक इस विस्तार पर जोर देने के लिए पहचान के साथ विधेय तर्क का उल्लेख करते हैं। इसके बारे में नीचे देखें।
प्रस्तावों का बीजगणित, प्रस्तावपरक कलन
बीजगणित (जिसमें कई मान अलग-अलग हैं), शिथिल रूप से परिभाषित की जाती हैं, यह ऐसी विधि है जिसके द्वारा कुछ अन्य प्रतीकों जैसे कोष्ठक (,) और कुछ उप-प्रतीकों जैसे कि *, +, ~ के साथ चर प्रतीकों , &, ∨, =, ≡, ∧, ¬ को संग्रहित किया जाता है। इन नियमों की प्रणाली के भीतर परिवर्तन किया जाता है। इस प्रकार हम कह सकते हैं कि ये प्रतीक और इनसे बनी हुई वस्तुओं का प्रतिनिधित्व करते हैं, किन्तु विशिष्ट बीजगणितीय प्रणाली में इन वस्तुओं का कोई अर्थ नहीं होता है। इस प्रकार बीजगणित के अंदर कार्य प्रतीकों के शब्दार्थ (अर्थ) के अतिरिक्त बीजगणित के वाक्य - विन्यास (प्रतीक-गठन) के कुछ नियमों का पालन करने का अभ्यास बन जाता है। यह मुख्य रूप से गणितीय बीजगणित के बाहर पाए जाते हैं।
इस प्रकार बीजगणित में प्रतीकों के अच्छी तरह से गठित अनुक्रम के लिए - सूत्र - बीजगणित के बाहर कुछ उपयोगिता रखने के लिए प्रतीकों को अर्थ निर्दिष्ट किया जाता है और अंततः चर को मान निर्दिष्ट किया जाता है, फिर नियमों की श्रृंखला द्वारा सूत्र का मूल्यांकन किया जाता है।
इस प्रकार जब मान केवल दो तक सीमित होते हैं और साधारण वाक्यों (जैसे बोले गए उच्चारण या लिखित अभिकथन) की धारणा पर लागू होते हैं, जो प्रस्तावक संयोजकों से जुड़े होते हैं, तो प्रतीकों और नियमों और मूल्यांकन-पद्धतियों की इस पूरी बीजगणितीय प्रणाली को सामान्यतः प्रस्तावात्मक कलन या वाक्यगत कलन कहा जाता है। .
जबकि अंकगणित बीजगणित के कुछ परिचित नियम प्रस्तावों के बीजगणित में बने रहते हैं। इस प्रकार उदाहरण के लिए AND और OR के लिए क्रमविनिमेय और साहचर्य नियम), कुछ नहीं (उदाहरण के लिए AND, OR और NOT के लिए वितरण नियम इत्यादि।
प्रस्तावात्मक सूत्रों की उपयोगिता
विश्लेषण: निगमनात्मक तर्क में, दार्शनिक, वादविवाद करने वाले और गणितज्ञ तर्कों को सूत्रों तक कम करते हैं और फिर इस प्रकार शुद्धता (सुदृढ़ता) के लिए उनका (सामान्यतः सत्य तालिकाओं के साथ) अध्ययन करते हैं। उदाहरण के लिए: क्या निम्नलिखित तर्क सही है?
- यह देखते हुए कि कृत्रिम बुद्धि के लिए चेतना पर्याप्त है और केवल सचेत संस्थाएं ट्यूरिंग जाँच पास कर सकती हैं, इस प्रकार इससे पहले कि हम यह निष्कर्ष निकाल सकें कि रोबोट कृत्रिम बुद्धि है, रोबोट को ट्यूरिंग टेस्ट पास करना होगा।
इंजीनियर तर्क परिपथ का विश्लेषण करते हैं इस प्रकार जिसे उन्होंने संश्लेषण तकनीकों का उपयोग करके डिजाइन किया है और फिर उनके डिजाइन को सरल बनाने के लिए विभिन्न कटौती और न्यूनीकरण तकनीकों को लागू करते हैं।
संश्लेषण: इंजीनियर विशेष रूप से सत्य तालिकाओं से प्रस्तावन सूत्र (जो अंततः प्रतीकों के परिपथ के रूप में समाप्त होते हैं) को संश्लेषित करते हैं। इस प्रकार उदाहरण के लिए, सत्य तालिका लिख सकता है कि बाइनरी जोड़ को कैसे व्यवहार करना चाहिए, चर b और a और कैरी_इन सीआई के अतिरिक्त, और परिणाम carry_out सह और योग Σ:
- उदाहरण: पंक्ति 5 में, ((B+A) + CI) = ((1+0) + 1) = 2, इसे बाइनरी नंबर के रूप में लिखा जाता है, यह 102 है, जहाँ co =1 और Σ=0 जैसा कि सबसे दाएँ कॉलम में दिखाया गया है।
| row | b | a | ci | (b+a)+ci | co | Σ | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | |
| 2 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 3 | 0 | 1 | 1 | 2 | 1 | 0 | |
| 4 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 5 | 1 | 0 | 1 | 2 | 1 | 0 | |
| 6 | 1 | 1 | 0 | 2 | 1 | 0 | |
| 7 | 1 | 1 | 1 | 3 | 1 | 1 |
प्रस्ताव चर
प्रस्तावात्मक सूत्र का सबसे सरल प्रकार प्रस्तावक चर है। इस प्रकार प्रस्ताव जो सरल (परमाणु सूत्र) हैं, प्रतीकात्मक अभिव्यक्ति अधिकांशतः p, q, या P, Q, आदि नाम के चर द्वारा दर्शाए जाते हैं। परमाणु प्रस्ताव (अभिकथन) का प्रतिनिधित्व करते हैं, जैसे कि यह शनिवार है = p (यहाँ प्रतीक = का अर्थ है ... नाम का चर निर्दिष्ट किया गया है ...) या मैं केवल सोमवार = q को फिल्मों में संयोजित किया जाता हैं।
सत्य-मूल्य असाइनमेंट, सूत्र मूल्यांकन
एक प्रस्तावक सूत्र का मूल्यांकन प्रत्येक चर के लिए सत्य मान के असाइनमेंट से प्रारंभ होता है। क्योंकि प्रत्येक चर सरल वाक्य का प्रतिनिधित्व करता है, इस प्रकार इन सरल वाक्यों की सत्यता या असत्यता पर सत्य मान लागू किए जा रहे हैं।
वादविवाद, दर्शन और गणित में सत्य मूल्य
सत्य मान केवल दो हैं: {सत्य T, असत्य F}। अनुभववादी सभी प्रस्तावों को दो व्यापक वर्गों में रखता है: विश्लेषणात्मक—सच्चा कोई फर्क नहीं पड़ता (उदाहरण के लिए टॉटोलॉजी (तर्क)), और सिंथेटिक—अनुभव से व्युत्पन्न और इस तरह तीसरे पक्ष द्वारा पुष्टि के लिए अतिसंवेदनशील (सत्यापन सिद्धांत) अर्थ का)।[5] अनुभवजन्य मानते हैं कि, सामान्य रूप से, सिंथेटिक प्रस्ताव के सत्य-मूल्य पर पहुंचने के लिए, अर्थ को पहले शब्दों पर लागू किया जाना चाहिए, और फिर इन अर्थ-सांचे को जो कुछ भी हो रहा है, उसके विरुद्ध मिलान किया जाना चाहिए। इस प्रकार प्रमाणित भी किया जाना चाहिए। जैसे कि उक्त कथन है कि गाय है, क्या यह कथन सत्य है? सत्य में मैंने कहा था और संभवतः मैं नीली गाय को देख रहा हूं - जब तक कि मैं असत्य नहीं बोल रहा हूं, मेरा कथन मेरी (संभवतः त्रुटिपूर्ण) धारणा के उद्देश्य के सापेक्ष सत्य है। किन्तु क्या वाकई में नीली गाय होती है? जब आप उसी खिड़की से बाहर देखते हैं तो आप क्या देखते हैं? सत्यापन के साथ आगे बढ़ने के लिए, आपको गाय और गाय दोनों की पूर्व धारणा की आवश्यकता होगी और वस्तु के विरुद्ध टेम्पलेट्स से मिलान करने की क्षमता (यदि वास्तव में कोई है)।
इंजीनियरिंग में सत्य मूल्य
इंजीनियर सत्य और असत्य की धारणाओं से बचने की प्रयास करते हैं जो दार्शनिकों को इंगित करते हैं, किन्तु अंतिम विश्लेषण में इंजीनियरों को अपने मापने वाले उपकरणों पर भरोसा करना चाहिए। इस प्रकार मजबूत आँकड़ों की अपनी खोज में, इंजीनियर छोटे पुस्तकालय से ज्ञात वस्तुओं को खींचना पसंद करते हैं - ऐसी वस्तुएँ जिनमें बड़े संयोजनों में भी अच्छी तरह से परिभाषित, पूर्वानुमेय व्यवहार होता है, (इसलिए उनका नाम प्रस्ताविक कलन के लिए है: संयोजक तर्क पर आधारित होते हैं। किसी वस्तु के सबसे कम व्यवहार दो हैं (जैसे {OFF, ON}, {OPEN, SHUT}, {UP, DOWN} आदि), और इन्हें {0, 1} के अनुरूप रखा गया है। ऐसे तत्वों को डिजिटल डेटा कहा जाता है, व्यवहारों की सतत श्रृंखला वाले एनालॉग संकेत कहलाते हैं। इस प्रकार जब भी किसी एनालॉग सिस्टम में निर्णय लेने होते हैं, तो अधिकांशतः इंजीनियर तुलनित्र के उपयोग से एनालॉग व्यवहार (दरवाजा 45.32146% UP है) को डिजिटल (जैसे DOWN=0 ) में परिवर्तित कर देगा।[6]
इस प्रकार चर और दो मूल्य-प्रतीकों {0, 1} के अर्थ का असाइनमेंट सूत्र के बाहर से आता है जो (सामान्यतः) यौगिक वस्तु के व्यवहार का प्रतिनिधित्व करता है। उदाहरण गेराज दरवाजा है जिसमें दो सीमा स्विच हैं, UP लेबल वाले SW_U के लिए और नीचे लेबल वाले SW_D के लिए, और जो कुछ भी दरवाजे के सर्किटरी में है। इस प्रकार परिपथ का निरीक्षण (या तो आरेख या वास्तविक वस्तुएं स्वयं-दरवाजा, स्विच, तार, परिपथ बोर्ड इत्यादि) प्रकट कर सकता है कि परिपथ बोर्ड नोड 22 पर +0 वोल्ट जाता है। जब स्विच SW_D के संपर्क यांत्रिक रूप से होते हैं तब संपर्क (CLOSE) और दरवाजा नीचे की स्थिति में है (95% नीचे), और नोड 29 +0 वोल्ट पर जाता है जब दरवाजा 95% UP होता है और स्विच SW_U के संपर्क यांत्रिक संपर्क (CLOSE) में होते हैं।[7] इस प्रकार इंजीनियर को इन वोल्टेज और सभी संभावित संयोजनों (उनमें से सभी 4) के अर्थ को परिभाषित करना चाहिए, जिसमें असत्य भी सम्मलित हैं (उदाहरण के लिए दोनों नोड्स 22 और 29 0 वोल्ट पर हैं, जिसका अर्थ है कि दरवाजा ही समय में OPEN और CLOSE है)। परिपथ सच्चाई या असत्य, सही या गलत, सुरक्षित या खतरनाक के बारे में किसी भी जागरूकता के बिना जो भी वोल्टेज का अनुभव करता है, बिना सोचे-समझे प्रतिक्रिया करता है।
प्रस्तावित संयोजक
तर्कवाक्य चरों और तार्किक संयोजकों का उपयोग करते हुए अन्य तर्कवाक्य सूत्रों से मनमाना तर्कवाक्य सूत्र बनाए जाते हैं। संयोजकों के उदाहरणों में सम्मलित हैं:
- एकात्मक निषेध संयोजक। यदि सूत्र है, तो सूत्र है।
- मौलिक बाइनरी संयोजक . इस प्रकार, उदाहरण के लिए, यदि और सूत्र हैं, इसलिए है .
- अन्य बाइनरी संयोजक, जैसे NAND, NOR, और XOR
- त्रिक संयोजक IF ... THEN ... ELSE ...
- निरंतर 0- संयोजक ⊤ और ⊥ (वैकल्पिक रूप से, स्थिरांक { T, F }, { 1, 0 } आदि।)
- सिद्धांत-विस्तार संयोजक EQUALS (वैकल्पिक रूप से, पहचान, या चिन्ह = जैसा कि तार्किक संयोजक से अलग है )
वादविवाद, दर्शन और गणित के संयोजक
वादविवाद, दर्शन और गणित के साथ-साथ उनके सत्य तालिकाओं के लिए सामान्य संयोजक निम्नलिखित हैं। इस प्रकार उपयोग किए गए प्रतीक लेखक से लेखक और प्रयास के क्षेत्रों के बीच भिन्न होंगे। सामान्यतः संक्षिप्त रूप T और F मूल्यांकनों के लिए खड़े होते हैं सत्य और असत्यता प्रस्तावक सूत्र में चरों पर लागू होते हैं (उदाहरण के लिए प्रमाणित: वह गाय नीली है, सत्य के लिए सत्य-मूल्य T या असत्यता के लिए F, जैसा भी मामला हो .).
संयोजक कई अलग-अलग शब्द-प्रयोगों से चलते हैं, उदाहरण के लिए a का अर्थ है b को IF a THEN b भी कहा जाता है। इनमें से कुछ तालिका में दिखाए गए हैं।
| b only if a | |||||||||||
| b IS SUFFICIENT FOR a | b PRECISELY WHEN a | ||||||||||
| a IS NECESSARY FOR b | b IF AND ONLY IF a, b IFF a | ||||||||||
| inclusive OR | IF b THEN a | b IS NECESSARY AND SUFFICIENT FOR a | |||||||||
| negation | negation | conjunction | disjunction | implication | biconditional | ||||||
| variables | NOT b | NOT a | b AND a | b OR a | b IMPLIES a | b IS logically equivalent TO a *** | f IS A tautology | NEITHER a NOR b | b stroke a | exclusive OR | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| b | a | ¬(b) | ¬(a) | (b ∧ a) | (b ∨ a) | (b → a) | (b ↔ a) | (f = formula) | (a NOR b) | (b|a) | various |
| F | F | T | T | F | F | T | T | T | T | T | F |
| F | T | T | F | F | T | T | F | T | F | T | T |
| T | F | F | T | F | T | F | F | T | F | T | T |
| T | T | F | F | T | T | T | T | T | F | F | F |
इंजीनियरिंग संयोजक
सामान्यतः, इंजीनियरिंग संयोजक गणित के संयोजकों के समान ही होते हैं, इस प्रकार 1 = T और 0 = F के साथ मूल्यांकन करते हैं। इस प्रकार यह मध्य मान और कर्णघ तो मानचित्र (नीचे देखें) की धारणा के उपयोग से विश्लेषण/न्यूनीकरण और सूत्रों के संश्लेषण के उद्देश्यों के लिए किया जाता है। इंजीनियर बूलियन की धारणा (a*a = a) से 'तार्किक उत्पाद' और विलियम स्टेनली जेवन्स की धारणा (a+a = a) से 'तार्किक योग' शब्दों का भी उपयोग करते हैं।[8]
| logical product | logical sum | half-adder (no carry) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| exclusive OR | |||||||||
| row number | variables | NOT | NOT | AND | OR | NAND | NOR | XOR | |
| b*21+a*20 | b | a | ~(b) | ~(a) | (b & a) | (b ∨ a) | ~(b & a) | ~(b ∨ a) | ⊕ |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
केस कनेक्टिव: IF ... THEN ... ELSE ...
IF ... THEN ... ELSE ... संयोजी पुनरावर्तन सिद्धांत और संगणना सिद्धांत के CASE संचालक के सरलतम रूप के रूप में प्रकट होता है और सशर्त गोटो (कूदता है, शाखाओं) के लिए जिम्मेदार संयोजी है। इस संयोजी से अन्य सभी संयोजकों का निर्माण किया जा सकता है। इस प्रकार यद्यपि IF c THEN b ELSE a निहितार्थ की तरह लगता है, यह अपने सबसे कम रूप में है, स्विच जो निर्णय लेता है और परिणाम के रूप में केवल दो विकल्पों में से या b प्रदान करता है (इसलिए C में नाम स्विच स्टेटमेंट (प्रोग्रामिंग भाषा) ) प्रोग्रामिंग भाषा)।[9]
निम्नलिखित तीन तर्कवाक्य समतुल्य हैं (जैसा कि तार्किक तुल्यता चिह्न ≡ द्वारा इंगित किया गया है):
- (यदि 'काउंटर शून्य है' तो 'निर्देश बी पर जाएं' या 'अनुदेश पर जाएं') ≡
- ((C → B) और (~C → A)) ≡ ((यदि 'काउंटर शून्य है' तो 'निर्देश B' पर जाएं) और (यदि 'यह वह स्थिति नहीं है कि काउंटर शून्य है' तो 'पर जाएं निर्देश A) ≡
- ((C और B) ∨ (~C और A)) ≡ ('काउंटर शून्य है' और 'निर्देश B पर जाएं) या ('ऐसा नहीं है कि 'काउंटर शून्य है' और 'निर्देश A पर जाएं)
इस प्रकार IF ... THEN ... ELSE - निहितार्थ के विपरीत - अस्पष्ट सत्य का मूल्यांकन नहीं करता है जब पहला प्रस्ताव असत्य होता है ,अर्थात c = F in (c → b)। उदाहरण के लिए, अधिकांश लोग निम्नलिखित संयुक्त तर्कवाक्य को निरर्थक गैर अनुगामी के रूप में अस्वीकार कर देंगे क्योंकि दूसरा वाक्य अर्थ में पहले से जुड़ा नहीं है।[10]
- उदाहरण: प्रस्ताव यदि 'विंस्टन चर्चिल चीनी थे' तब 'सूरज पूर्व में उगता है' सत्य के रूप में मूल्यांकन करता है, इस प्रकार यह देखते हुए कि 'विंस्टन चर्चिल चीनी थे' इस प्रकार इसका मान असत्य होगा और 'सूर्य पूर्व में उगता है' सत्य के रूप में मूल्यांकन करता है।
इस समस्या की पहचान में, प्रस्ताविक कलन में औपचारिक निहितार्थ के संकेत → को हर रोज़, सहज ज्ञान युक्त निहितार्थ से अलग करने के लिए सामग्री सशर्त कहा जाता है।[lower-alpha 1]
IF ... THEN ... ELSE निर्माण विवाद से बचा जाता है क्योंकि यह दो घोषित विकल्पों के बीच पूरी तरह से निर्धारक विकल्प प्रदान करता है, यह दो वस्तुओं (दो विकल्प बी और ए) प्रदान करता है, और यह उनके बीच विस्तृत और स्पष्ट रूप से चयन करता है।[12] नीचे दी गई सत्य तालिका में, d1 सूत्र है: ((IF c THEN b) AND (IF NOT-c THEN a) ) का उपयोग देखा जा सकता हैं। इस प्रकार इसका पूरी तरह से घटता हुआ रूप d2 के लिए उक्त सूत्र है: ((c AND b) OR (NOT-c AND a)। कॉलम =d1 और =d2 द्वारा दिखाए गए दो सूत्र समकक्ष हैं। इलेक्ट्रिकल इंजीनियर पूरी तरह से कम किए गए फॉर्मूले को AND- कहते हैं। इस प्रकार OR-चयन ऑपरेटर या CASE (या स्विच) ऑपरेटर n संभव, किन्तु परस्पर अनन्य परिणामों के लिए ही विचार का विस्तार है। विद्युत इंजीनियर CASE ऑपरेटर को बहुसंकेतक कहते हैं।
| d1 | d2 | ||||||||||||||||||||||||||||||||||||||
| row | c | b | a | ( | ( | c | → | b | ) | & | ( | ~ | ( | c | ) | → | a | ) | ) | =d1 | ( | ( | c | & | b | ) | ∨ | ( | ~ | ( | c | ) | & | a | ) | ) | =d2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 2 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 3 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||||||||||||||||||
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | ||||||||||||||||||
| 6 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | ||||||||||||||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
पहचान और मूल्यांकन
इस खंड की पहली तालिका में *** प्रविष्टि तार्किक तुल्यता है जो इस तथ्य पर ध्यान देती है कि तार्किक तुल्यता पहचान के समान नहीं है। उदाहरण के लिए, अधिकांश लोग इस बात से सहमत होंगे कि यह कथन कि गाय नीली है, गाय के नीले होने के कथन के समान है। दूसरी ओर, तार्किक तुल्यता कभी-कभी भाषण में प्रकट होती है जैसे कि इस उदाहरण में: 'सूरज चमक रहा है' का अर्थ है 'मैं बाइक चला रहा हूं' प्रस्तावक सूत्र में अनुवादित शब्द बन जाते हैं: यदि 'सूरज चमक रहा है' तो 'मैं' बाइकिंग', और यदि 'मैं बाइकिंग कर रहा हूं' तो 'सूरज चमक रहा है':[13]
- IF 's' THEN 'b' AND IF 'b' THEN 's' को ((s → b) & (b → s)) या संक्षिप्त रूप में (s ↔ b) लिखा जाता है। जैसा कि सबसे दाहिना प्रतीक स्ट्रिंग बाईं ओर के प्रतीकों के संदर्भ में नए प्रतीक की परिभाषा है, पहचान चिह्न = का उपयोग उचित है:
- ((S → B) और (B → S)) = (S ↔ B)
विभिन्न लेखक तार्किक तुल्यता के लिए अलग-अलग चिह्नों का उपयोग करते हैं: ↔ (उदाहरणतयः सप्पेस, गुडस्टीन, हैमिल्टन), ≡ (उदाहरणतयः रॉबिन), ⇔ (उदाहरणतयः बेंडर और विलियमसन)। इस प्रकार विशिष्ट पहचान को बराबर चिह्न = के रूप में लिखा जाता है। इस प्रकार इस नियम का अपवाद 'प्रिंसिपिया मैथेमेटिका' में पाया जाता है। पहचान की धारणा के दर्शन के बारे में अधिक जानकारी के लिए अविवेक की पहचान या लीबनिज का नियम देखें।
जैसा कि ऊपर उल्लेख किया गया है, टार्स्की पहचान को प्रस्ताविक कलन के बाहर मानता है, किन्तु वह प्रमाणित करता है कि धारणा के बिना, गणित और निगमनात्मक विज्ञान के लिए तर्क अपर्याप्त है। इस प्रकार वास्तव में जब किसी सूत्र का मूल्यांकन किया जाना होता है तो संकेत प्रमेय कलन में आता है।[14]
कुछ प्रणालियों में कोई सत्य सारणी नहीं होती है, बल्कि केवल औपचारिक स्वयंसिद्ध (उदाहरण के लिए सेट से प्रतीकों के तार { ~, →, (, ), चर P1, P2, P3, ... } और सूत्र-गठन नियम (उदाहरण के लिए प्रतिस्थापन और मूड सेट करना के उपयोग से पिछले तारों से अधिक प्रतीक तार बनाने के नियम) पर आधारित हैं। इस प्रकार कलन का परिणाम अन्य सूत्र अर्थात अच्छी तरह से निर्मित प्रतीक स्ट्रिंग के रूप में होगा। इस प्रकार अंततः चूंकि, यदि कोई वैधता और सत्य की धारणाओं का अध्ययन करने के लिए कलन का उपयोग करना चाहता है, तो इस प्रकार उसे ऐसे स्वयंसिद्धों को जोड़ना होगा जो सत्य मान {T, F} (या {1, 0}, आदि) कहे जाने वाले प्रतीकों के व्यवहार को अन्य प्रतीकों के सापेक्ष परिभाषित करते हैं।
उदाहरण के लिए, हैमिल्टन दो प्रतीकों = और ≠ का उपयोग करता है इस प्रकार जब वह किसी भी अच्छी तरह से गठित सूत्र (wffs) A और B के मूल्यांकन v की धारणा को अपने औपचारिक बयान कलन L में परिभाषित करता है। मूल्यांकन v है a फ़ंक्शन (गणित) उनके सिस्टम L के wffs से सीमा (output) {T, F} तक, दिया गया है कि प्रत्येक चर p1, p2, p3 wff में सत्य मान {T, F} द्वारा इंगित किया जाता है।
-
v(A) ≠ v(~A)
(i)
-
v(A → B) = F if and only if v(A) = T and v(B) = F
(ii)
दो परिभाषाएँ (i) और (ii) अपने सिस्टम के ~ (NOT) और → (IMPLICATION) संयोजकों के लिए सत्य तालिकाओं के समतुल्य को परिभाषित करते हैं। इसके पहले वाला F ≠ T और T ≠ F प्राप्त करता है, दूसरे शब्दों में v(A) का अर्थ v(~A) नहीं है। परिभाषा (ii) सत्य तालिका में तीसरी पंक्ति निर्दिष्ट करता है, और इस प्रकार फिर अन्य तीन पंक्तियाँ परिभाषा के अनुप्रयोग से आती हैं (i). विशेष रूप से (ii) संपूर्ण व्यंजक को मान F (या F का अर्थ) प्रदान करता है। इस प्रकार परिभाषाएँ गठन नियमों के रूप में भी काम करती हैं जो पहले से सूत्र में प्राप्त मान के प्रतिस्थापन की अनुमति देती हैं:
| v(A→B) | ||||
| ( | v(A) | → | v(B) | ) |
| F | T | F | ||
| F | T | T | ||
| T | F | F | ||
| T | T | T |
कुछ औपचारिक प्रणालियाँ प्रारंभ में इन मूल्यांकन सिद्धांतों को कुछ सूत्रों के रूप में निर्दिष्ट करती हैं जैसे कि विरोधाभास का नियम या पहचान और अशक्तता के नियम इसका मुख्य उदाहरण हैं। कम्यूटेशन और डिस्ट्रीब्यूशन जैसे नियमों के साथ किसका उपयोग करना है, इसका चुनाव सिस्टम के डिज़ाइनर पर निर्भर करता है, इस प्रकार जब तक कि स्वयंसिद्धों का सेट पूरा हो जाता है (अर्थात सिस्टम में बनाए गए किसी भी अच्छी तरह से तैयार किए गए फॉर्मूले का मूल्यांकन करने के लिए पर्याप्त है)।
अधिक जटिल सूत्र
जैसा कि ऊपर दिखाया गया है, CASE (IF c THEN b ELSE a ) संयोजक या तो 2-तर्क संयोजक IF ... THEN ... और AND या OR और AND और 1-तर्क नहीं से निर्मित होता है। n-तर्क AND (a & b & c & ... & n), OR (a ∨ b ∨ c ∨ ... ∨ n) जैसे संयोजक दो-तर्क AND और OR के तार से निर्मित होते हैं और इसमें कोष्ठक के बिना संक्षिप्त रूप में लिखे जाते हैं। ये और अन्य संयोजक भी, फिर आगे के संयोजकों के लिए बिल्डिंग ब्लॉक्स के रूप में उपयोग किए जा सकते हैं। अलंकारिक, दार्शनिक और गणितज्ञ अपने सूत्रों का विश्लेषण और सरलीकरण करने के लिए सत्य तालिकाओं और विभिन्न प्रमेयों का उपयोग करते हैं।
इस प्रकार विद्युत इंजीनियरिंग खींचे गए प्रतीकों का उपयोग करता है और उन्हें उन रेखाओं से जोड़ता है जो प्रतिस्थापन और प्रतिस्थापन के गणितीय कार्य के लिए खड़ी होती हैं। फिर वे अपने आरेखणों को सत्य तालिकाओं के साथ सत्यापित करते हैं और कर्णघ नक्शों या प्रमेयों के उपयोग द्वारा नीचे दिखाए गए भावों को सरल करते हैं। इस प्रकार से इंजीनियरों ने कॉम्बिनेटरियल तर्क (अर्थात फीडबैक के बिना कनेक्टिव्स) जैसे डिकोडर्स, एनकोडर्स, म्यूटिफंक्शन गेट्स, मेजॉरिटी तर्क, बाइनरी एडर्स, अंकगणितीय तर्क इकाई आदि का निर्माण किया है।
परिभाषाएँ
इन परिभाषा को अधिकांशतः संक्षेप के प्रयोजनों के लिए नया प्रतीक और उसका व्यवहार बनाती है। इस प्रकार परिभाषा प्रस्तुत करने के बाद, समकक्ष प्रतीक या सूत्र के किसी भी रूप का उपयोग किया जा सकता है। निम्नलिखित प्रतीकवाद =Df रेइचेनबैच के सम्मेलन का पालन कर रहा है।[15] प्रतीक समुच्चय { ~, &, (, ) } और चरों से निकाली गई सुविधाजनक परिभाषाओं के कुछ उदाहरण हैं। प्रत्येक परिभाषा तार्किक रूप से समतुल्य सूत्र का उत्पादन कर रही है जिसका उपयोग प्रतिस्थापन या प्रतिस्थापन के लिए किया जा सकता है।
- एक नए चर की परिभाषा: (c & d) =Df s
- OR: ~(~a & ~b) =Df (a ∨ b)
- IMPLICATION: (~a ∨ b) =Df (a → b)
- XOR: (~a & b) ∨ (a & ~b) =Df (a ⊕ b)
- LOGICAL EQUIVALENCE: ( (a → b) & (b → a) ) =Df ( a ≡ b )
स्वयंसिद्ध और परिभाषा स्कीमा
OR, IMPLICATION, XOR, और तार्किक तुल्यता के लिए उपरोक्त परिभाषाएँ वास्तव में स्वयंसिद्ध स्कीमा (या स्कीमाटा) हैं, अर्थात इस प्रकार वे सामान्य सूत्र प्रारूप के लिए मॉडल (प्रदर्शन, उदाहरण) हैं, किन्तु विशिष्ट अक्षरों a के साथ (उदाहरण के उद्देश्यों के लिए) दिखाए गए हैं। b, c वेरिएबल्स के लिए, जबकि कोई भी वेरिएबल अक्षर उनके स्थान पर तब तक जा सकते हैं, इस प्रकार जब तक अक्षर प्रतिस्थापन नीचे प्रतिस्थापन के नियम का पालन करते हैं।
- उदाहरण: परिभाषा में (~a ∨ b) =Df (ए → बी), अन्य चर-प्रतीकों जैसे कि SW2 और CON1 का उपयोग किया जा सकता है, अर्थात औपचारिक रूप से:
- a =Df SW2, b =Df CON1, इसलिए हमारे पास परिभाषा स्कीमा का उदाहरण होगा (~SW2 ∨ CON1) =Df (SW2 → CON1)
प्रतिस्थापन बनाम प्रतिस्थापन
प्रतिस्थापन: किसी अन्य चर, स्थिरांक या उप-सूत्र के साथ प्रतिस्थापित किए जाने वाले चर या उप-सूत्र को समग्र सूत्र में सभी उदाहरणों में प्रतिस्थापित किया जाना चाहिए।
- उदाहरण: (c & d) ∨ (p & ~(c & ~d)), किन्तु (q1 & ~q2) ≡ d। अब जहाँ भी चर d होता है, स्थानापन्न (q1 & ~ q2):
- (c & (q1 & ~ q2)) ∨ (p & ~(c & ~(q1 & ~ q2)))
प्रतिस्थापन: (i) प्रतिस्थापित किया जाने वाला सूत्र तनातनी के भीतर होना चाहिए, अर्थात तार्किक रूप से समतुल्य (≡ या ↔ से जुड़ा हुआ) उस सूत्र से जुड़ा होना चाहिए जो इसे प्रतिस्थापित करता है, और (ii) प्रतिस्थापन के विपरीत प्रतिस्थापन होने के लिए इसकी अनुमति है। केवल ही स्थान पर अर्थात सूत्र के लिए उपयोग किया जाता हैं।
- उदाहरण: फॉर्मूला स्कीमा/समतुल्यता के इस सेट का उपयोग करें:
- ( (a ∨ 0) ≡ a ).
- ( (a & ~a) ≡ 0 ).
- ( (~a ∨ b) =Df (a → b) ).
- ( ~(~a) ≡ a )
- start with "a": a
- Use 1 to replace "a" with (a ∨ 0): (a ∨ 0)
- Use the notion of "schema" to substitute b for a in 2: ( (a & ~a) ≡ 0 )
- Use 2 to replace 0 with (b & ~b): ( a ∨ (b & ~b) )
- (see below for how to distribute "a ∨" over (b & ~b), etc.)
आगमनात्मक परिभाषा
प्रस्तावपरक तर्क की मौलिक प्रस्तुति (हर्बर्ट एंडर्टन 2002 देखें) संयोजकों का उपयोग करती है, इस प्रकार प्रपोजल वेरिएबल्स के दिए गए सेट पर फॉर्मूलों का सेट की आगमनात्मक परिभाषा कहा जाता है जो एक्सप्रेशंस का सबसे छोटा सेट है:
- सेट में प्रत्येक प्रस्तावक चर सूत्र है,
- सूत्र है जब भी है और
- सूत्र है जब भी और सूत्र हैं और द्विआधारी संयोजकों में से है।
अतिरिक्त संयोजकों को सम्मलित करने के लिए इस आगमनात्मक परिभाषा को आसानी से बढ़ाया जा सकता है।
आगमनात्मक परिभाषा को क्लोजर (गणित) ऑपरेशन (एंडर्टन 2002) के संदर्भ में भी दोहराया जा सकता है। इस प्रकार vV प्रस्तावित चर के सेट को निरूपित करते हैं और एक्स को जाने देते हैं, V, बाएँ और दाएँ कोष्ठकों में प्रतीकों, और विचाराधीन सभी तार्किक संयोजकों सहित वर्णमाला से सभी स्ट्रिंग्स के सेट को निरूपित करें। इस प्रकार प्रत्येक लॉजिकल कनेक्टिव फॉर्मूला बिल्डिंग ऑपरेशन, XXV से फ़ंक्शन XVX से मेल खाता है।
- एक स्ट्रिंग z दिया गया है, ऑपरेशन रिटर्न .
- दिए गए तार y और z, ऑपरेशन रिटर्न . इसी तरह के ऑपरेशन हैं , , और अन्य बाइनरी संयोजकों के अनुरूप उपयोग किए जाते हैं।
V पर सूत्रों के सेट को XXV का सबसे छोटा उपसमुच्चय माना जाता है, जिसमें V है और सभी फॉर्मूला बिल्डिंग ऑपरेशंस के अनुसार CLOSE है।
पार्सिंग सूत्र
जटिल सूत्रों को कम करने के लिए प्रस्तावक कलन के निम्नलिखित नियमों का उपयोग किया जाता है। इस प्रकार सत्य तालिकाओं के साथ नियमों को आसानी से सत्यापित किया जा सकता है। प्रत्येक नियम के लिए, मुख्य (बाह्यतम) संयोजक तार्किक तुल्यता ≡ या तत्समक = से जुड़ा होता है। सभी का पूर्ण विश्लेषण 2n इसके n विशिष्ट चरों के लिए सत्य-मानों का संयोजन इस संयोजी के नीचे 1's (T's) के कॉलम में परिणत होगा। यह खोज प्रत्येक नियम को, परिभाषा के अनुसार, पुनरुक्ति बनाती है। इस प्रकार किसी दिए गए नियम के लिए, क्योंकि बाएँ और दाएँ पर इसके सूत्र समतुल्य (या समरूप) हैं, उन्हें दूसरे के लिए प्रतिस्थापित किया जा सकता है।
- उदाहरण: निम्नलिखित सत्य तालिका OR से अधिक नहीं के व्यवहार के लिए डी मॉर्गन का नियम है: ~(a ∨ b) ≡ (~a & ~b), मुख्य संयोजक के बाईं ओर ≡ (उपयोग किए जाने वाले लेबल वाला पीला स्तंभ) सूत्र ~(b ∨ a) लेबल P के अंतर्गत (1, 0, 0, 0) का मूल्यांकन करता है। इस प्रकार इसेके दाईं ओर सूत्र (~(b) ∨ ~(a)) भी लेबल Q के अंतर्गत (1, 0, 0, 0) का मूल्यांकन करता है। चूंकि इस प्रकार दो स्तंभों में समतुल्य मूल्यांकन हैं, तार्किक तुल्यता ≡ के अनुसार तना हुआ मूल्यांकन (1, 1, 1, 1), अर्थात P ≡ Q. इस प्रकार या तो सूत्र को दूसरे के लिए प्रतिस्थापित किया जा सकता है यदि यह बड़े सूत्र में प्रकट होता है।
| P | taut | Q | ||||||||||||||||||||
| b | a | ( | ~ | ( | b | V | a | ) | ≡ | ( | ~ | ( | b | ) | & | ~ | ( | a | ) | ) | ) | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | |||||||||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |||||||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
उद्यमी पाठक खुद को स्वयंसिद्ध प्रणाली का आविष्कार करने के लिए चुनौती दे सकते हैं जो प्रतीकों {∨, &, ~, (, ), चर a, b, c}, ऊपर निर्दिष्ट गठन नियमों का उपयोग करता है, और नीचे सूचीबद्ध नियमों में से जितना संभव हो उतना कम, और इस प्रकार प्रमेयों के रूप में अन्य के साथ-साथ ∨, &, और ~ के लिए सत्य-तालिका मूल्यांकन प्राप्त करें। हंटिंगटन (1904) (स्यूप्स: 204) के लिए जिम्मेदार सेट नीचे परिभाषित आठ नियमों का उपयोग करता है।
यदि स्वयंसिद्ध प्रणाली में प्रयोग किया जाता है, तो प्रतीकों 1 और 0 (या T और F) को अच्छी तरह से गठित सूत्र माना जाता है और इस प्रकार चर के समान सभी नियमों का पालन करते हैं। इस प्रकार नीचे सूचीबद्ध नियम वास्तव में स्वयंसिद्ध स्कीमा हैं, अर्थात इस प्रकार इन अनंत संख्या में उदाहरणों के स्थान पर खड़े होते हैं। इस प्रकार ( x ∨ y ) ≡ ( y ∨ x ) का उपयोग उदाहरण में किया जा सकता है, ( p ∨ 0 ) ≡ ( 0 ∨ p ) और दूसरे उदाहरण में ( 1 ∨ q ) ≡ ( q ∨ 1 ), आदि।
संयोजी वरिष्ठता (प्रतीक रैंक)
सामान्यतः, प्रस्तावात्मक सूत्रों के विश्लेषण और मूल्यांकन के समय भ्रम से बचने के लिए कोष्ठकों का उदारतापूर्वक उपयोग करते हैं। चूंकि, अधिकांशतः लेखक उन्हें छोड़ देते हैं। जटिल सूत्र को पार्स करने के लिए सबसे पहले वरिष्ठता, या रैंक जानने की जरूरत है, कि प्रत्येक संयोजक (* को छोड़कर) अन्य संयोजकों पर है। इस प्रकार इस सूत्र को अच्छी तरह से बनाने के लिए, उच्चतम रैंक वाले संयोजी से प्रारंभ करें और इसके घटकों के चारों ओर कोष्ठक जोड़ें, फिर रैंक में नीचे जाएं (संयोजी के दायरे पर ध्यान दें जिस पर यह काम कर रहा है)। सबसे कम से कम वरिष्ठ तक, विधेय चिह्न ∀x और ∃x के साथ, पहचान = और अंकगणितीय संकेत पूर्णता के लिए जोड़े गए हैं:[lower-alpha 2]
- ≡
- (तार्किक समानता)
- →
- (निहितार्थ)
- &
- (और)
- ∨
- (या)
- ~
- (नहीं)
- ∀x
- (सभी x के लिए)
- ∃x
- (वहाँ एक्स संलग्न है)
- =
- (पहचान)
- +
- (अंकगणितीय योग)
- *
- (अंकगणितीय गुणा)
- '
- (अंकगणितीय उत्तराधिकारी)।
इस प्रकार सूत्र को पार्स किया जा सकता है - किन्तु क्योंकि वितरण नियम का पालन नहीं करता है, आंतरिक सूत्र (~c & ~d) के चारों ओर कोष्ठक अनिवार्य है:
- उदाहरण: d & c ∨ w को फिर से लिखा गया है ( (d & c) ∨ w )
- उदाहरण: a & a → b ≡ a & ~a ∨ b पुनर्लेखित (कठोरता से) है
- ≡ में वरिष्ठता है: ( ( a & a → b ) ≡ ( a & ~a ∨ b ) )
- → वरिष्ठता है: ((a और (a → b)) ≡ (a और ~a ∨ b))
- & दोनों पक्षों में वरिष्ठता है: ((((a) और (a → b)) ≡ (((a) और (~ए ∨ b)))
- ~ वरिष्ठता है: ((((a) और (a → b)) ≡ (((a) और (~(a) ∨ b)))
- चेक 9 (-कोष्ठक और 9) -कोष्ठक: ((((a) और (a → b)) ≡ (((a) और (~(a) ∨ b)))
- उदाहरण:
- d & c ∨ p & ~(c & ~d) ≡ c & d ∨ p & c ∨ p & ~d फिर से लिखा गया है ( ( (d & c) ∨ ( p & ~((c & ~(d)) ) ) ) ≡ ( (c और d) ∨ (p और c) ∨ (p और ~(d)) ) )
क्रमविनिमेय और साहचर्य नियम
AND और OR दोनों क्रमविनिमेय नियम और साहचर्य नियम का पालन करते हैं:
- OR के लिए क्रमविनिमेय नियम: ( a ∨ b ) ≡ ( b ∨ a )
- AND के लिए क्रमविनिमेय नियम: (a और b) ≡ (b और a)
- OR के लिए साहचर्य नियम: ((a ∨ b ) ∨ c ) ≡ ( a ∨ (b ∨ c) )
- AND के लिए सहयोगी नियम: ((a और b) और c) ≡ (a और (b और c))
AND और OR के तार में कोष्ठकों को छोड़ना: संयोजकों को एकात्मक (एक-चर, जैसे नहीं) और बाइनरी (अर्थात दो-चर AND, OR, IMPLIES) माना जाता है। उदाहरण के लिए:
- ( ((c & d) ∨ (p & c) ∨ (p & ~d) ) ऊपर लिखा जाना चाहिए ( ((c & d) ∨ (p & c)) ∨ (p & ~(d) ) ) या संभवतः ((c और d) ∨ ((p और c) ∨ (p और ~(d))))
चूंकि इस प्रकार सत्य-सारणी प्रदर्शन दिखाता है कि अतिरिक्त कोष्ठकों के बिना प्रपत्र पूरी तरह से पर्याप्त है।
एकल-चर के संबंध में कोष्ठकों को छोड़ना नहीं: जबकि ~(a) जहां a एकल चर है, इस प्रकार पूर्ण रूप से स्पष्ट है, ~a पर्याप्त है और यह शाब्दिक (गणितीय तर्क) प्रकट होने का सामान्य विधि है। जब NOT से अधिक प्रतीक वाले सूत्र के ऊपर हो, तब कोष्ठक अनिवार्य होते हैं, उदा. ~(a ∨ b).
वितरण नियम
OR AND पर वितरित करता है और AND OR पर वितरित करता है। इस प्रकार NOT AND या OR पर वितरित नहीं होता है। डी मॉर्गन के नियम के बारे में नीचे देखें:
- OR के लिए वितरण नियम: ( c ∨ ( a & b) ) ≡ ( (c ∨ a) और (c ∨ b) )
- AND के लिए वितरण नियम: (c & (a ∨ b) ) ≡ ((c & a) ∨ (c & b) )
डी मॉर्गन के नियम
जब OR या AND पर वितरित नहीं किया जाता है, तो कुछ अलग सी स्थिति बनती है (फिर से, इन्हें सत्य-तालिका के साथ सत्यापित किया जा सकता है):
- OR के लिए डी मॉर्गन का नियम: ¬(a ∨ b) ≡ (¬a ^ ¬b)
- AND के लिए डी मॉर्गन का नियम: ¬(a ^ b) ≡ (¬a ∨ ¬b)
अवशोषण के नियम
अवशोषण, विशेष रूप से पहला, तर्क के नियमों को अंकगणित के नियमों से अलग करने का कारण बनता है:
- OR: (a ∨ a) ≡ a के लिए अवशोषण (निष्क्रियता)।
- AND के लिए अवशोषण (निष्क्रियता): (a & a) ≡ a
मूल्यांकन के नियम: पहचान, शून्यता, और पूरक
चिह्न = (तार्किक तुल्यता ≡ से अलग, वैकल्पिक रूप से ↔ या ⇔) मूल्य या अर्थ के असाइनमेंट का प्रतीक है। इस प्रकार स्ट्रिंग (a & ~(a)) 0 का प्रतीक है, अर्थात इसका तात्पर्य प्रतीक 0 जैसा ही है। कुछ प्रणालियों में यह स्वयंसिद्ध (परिभाषा) होगी जिसे संभवतः ((a & ~(a)) =Df 0 के रूप में दिखाया गया है), अन्य प्रणालियों में, इसे नीचे दी गई सत्य तालिका में प्राप्त किया जा सकता है:
| c | taut | c | |||||||||||
| a | ( | ( | a | & | ~ | ( | a | ) | ) | ≡ | 0 | ) | |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | |||||||
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
- समानता का रूपांतरण: (a = b) ≡ (b = a)
- OR के लिए सर्वसमिका: (a ∨ 0) = a OR (a ∨ F) = a
- AND के लिए सर्वसमिका: (a & 1) = a OR (a & T) = a
- OR के लिए शून्यता: (a ∨ 1) = 1 OR (a ∨ T) = T
- AND के लिए शून्यता: (a और 0) = 0 OR (a और F) = F
- OR के लिए पूरक: (a ∨ ~a) = 1 OR (a ∨ ~a) = T, बहिष्कृत मध्य का नियम
- AND के लिए पूरक: (a & ~a) = 0 OR (a & ~a) = F, विरोधाभास का नियम
डबल नेगेटिव (इनवोल्यूशन)
- ¬(¬a) ≡ a
सुगठित सूत्र
सूत्रों की प्रमुख संपत्ति यह है कि इसके प्रस्ताविक चर और तार्किक संयोजकों के संदर्भ में सूत्र की संरचना का निर्धारण करने के लिए उन्हें विशिष्ट रूप से पार्स किया जा सकता है। जब सूत्रों को इंफिक्स नोटेशन में लिखा जाता है, तो सूत्रों की परिभाषा में कोष्ठकों के उचित उपयोग के माध्यम से अद्वितीय पठनीयता सुनिश्चित की जाती है। इस प्रकार वैकल्पिक रूप से, सूत्रों को पोलिश संकेतन या रिवर्स पोलिश नोटेशन में लिखा जा सकता है, जिससे कोष्ठकों की आवश्यकता पूरी तरह से समाप्त हो जाती है।
पिछले खंड में इन्फिक्स सूत्रों की आगमनात्मक परिभाषा को बैकुस-नौर फॉर्म में औपचारिक व्याकरण में परिवर्तित किया जा सकता है:
<formula> ::= <propositional variable>
| ( ¬ <formula> ) | ( <formula> ∧ <formula>) | ( <formula> ∨ <formula> ) | ( <formula> → <formula> ) | ( <formula> ↔ <formula> )
यह दिखाया जा सकता है कि व्याकरण से मेल खाने वाली किसी भी अभिव्यक्ति में बाएँ और दाएँ कोष्ठकों की संतुलित संख्या होती है, और सूत्र के किसी भी गैर-रिक्त प्रारंभिक खंड में दाएँ कोष्ठकों की तुलना में अधिक बाएँ होते हैं।[17] इस तथ्य का उपयोग फ़ार्मुलों को पार्स करने के लिए एल्गोरिथम देने के लिए किया जा सकता है। इस प्रकार उदाहरण के लिए, मान लीजिए कि एक्सप्रेशन x से प्रारंभ होता है . दूसरे प्रतीक के बाद प्रारंभ करते हुए, x के सबसे छोटे उप-अभिव्यक्ति y का मिलान करें जिसमें संतुलित कोष्ठक हैं। इस प्रकार यदि x सूत्र है, तो इस व्यंजक के बाद ठीक प्रतीक शेष रह जाता है, यह प्रतीक समापन कोष्ठक है, और y स्वयं सूत्र है। इस विचार का उपयोग सूत्रों के लिए पुनरावर्ती मूल पार्सर उत्पन्न करने के लिए किया जा सकता है।
'कोष्ठकों की गिनती का उदाहरण':
यह विधि 1 'प्रमुख संयोजक' के रूप में खोज करती है — संयोजी जिसके अनुसार सूत्र का समग्र मूल्यांकन सबसे बाहरी कोष्ठकों के लिए होता है (जो अधिकांशतः छोड़े जाते हैं)।[18] इस प्रकार यह सबसे भीतरी संयोजक का भी पता लगाता है जहां कोई सत्य तालिका के उपयोग के बिना सूत्र का मूल्यांकन प्रारंभ करेगा, उदा। स्तर 6 पर।
| start | ( | ( | ( | c | & | d | ) | V | ( | p | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | = | ( | ( | ( | c | & | d | ) | V | ( | p | & | d | ) | ) | V | ( | p | & | ~ | ( | c | ) | ) | ) | ) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 0 | 1 | 2 | 3 | 3 | 3 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 5 | 4 | 3 | 3 | 1 | 1 | 2 | 3 | 4 | 4 | 4 | 4 | 3 | 3 | 4 | 4 | 4 | 4 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 1 | 0 |
अनुमानों में मान्य सूत्रों बनाम अच्छी तरह से गठित सूत्र
वैध तर्क की धारणा सामान्यतः तर्कों में अनुमानों पर लागू होती है, किन्तु तर्क प्रस्तावात्मक सूत्रों में कम हो जाते हैं और किसी अन्य प्रस्ताव सूत्र के समान मूल्यांकन किया जा सकता है। यहाँ मान्य अनुमान का अर्थ है: सूत्र जो अनुमान का प्रतिनिधित्व करता है, उसके प्रमुख संयोजक के नीचे सत्य का मूल्यांकन करता है, चाहे इसके चरों को कोई भी सत्य-मान सौंपा गया हो, अर्थात सूत्र पुनरुक्ति है।[19]
इस प्रकार अधिक संभवतः सूत्र अच्छी तरह से बना होगा किन्तु मान्य नहीं होगा। इसे कहने का दूसरा विधि यह है: किसी सूत्र के मान्य होने के लिए अच्छी तरह से निर्मित होना आवश्यक है किन्तु यह पर्याप्त नहीं है। यह पता लगाने का एकमात्र विधि है कि यह अच्छी तरह से गठित और वैध दोनों है या नहीं, इसे सत्य तालिका या नियमों के उपयोग से सत्यापन के लिए जमा करना है:
- उदाहरण 1: अनुसरण करने में कठिन निम्नलिखित कथनों से कोई क्या बनाता है? क्या यह वैध है? यदि धूप है, किन्तु यदि मेंढक टर्र-टर्र कर रहा है तो धूप नहीं है, तो यह कहने के समान है कि मेंढक टर्र-टर्र नहीं कर रहा है। इसे प्रस्तावक सूत्र में निम्नानुसार परिवर्तित करें:
- IF (a AND (IF b THEN NOT-a) THEN NOT-a जहां a धूप का प्रतिनिधित्व करता है और b मेंढक टर्राने का प्रतिनिधित्व करता है :
- ((a) & ((b) → ~(a)) ≡ ~(b))
- यह सुगठित है, किन्तु क्या यह मान्य है? दूसरे शब्दों में, जब मूल्यांकन किया जाएगा तो क्या यह तार्किक-तुल्यता प्रतीक ≡ के नीचे पुनरुक्ति (सभी T) उत्पन्न करेगा? उत्तर नहीं है, यह मान्य नहीं है। चूंकि, यदि निहितार्थ के रूप में पुनर्निर्माण किया गया तो तर्क मान्य है।
- यह कहना धूप है, किन्तु यदि मेंढक टर्रा रहा है तो धूप नहीं है, इसका तात्पर्य है कि मेंढक टर्रा नहीं रहा है।
- अन्य परिस्थितियाँ मेंढक को टेढ़े होने से रोक सकती हैं: संभवतः क्रेन ने उसे खा लिया।
- उदाहरण 2 (रीचेनबैक से बर्ट्रेंड रसेल के माध्यम से):
- यदि सूअरों के पंख होते हैं, तो कुछ पंख वाले जानवर खाने में अच्छे होते हैं। कुछ पंखों वाले जानवर खाने में अच्छे होते हैं, तो सूअरों के पंख होते हैं।
- ((a) → (b)) और (b) → (a)) अच्छी तरह से गठित है, किन्तु अमान्य तर्क जैसा कि मुख्य निहितार्थ के अनुसार लाल मूल्यांकन द्वारा दिखाया गया है:
| W | G | arg | |||||||||||||
| a | b | ( | ( | ( | a | -> | b | ) | & | b | ) | -> | a | ) | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |||||||
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
संयोजकों के घटे हुए सेट

तार्किक संयोजकों के सेट को पूर्ण कहा जाता है यदि प्रत्येक प्रस्ताव सूत्र उस सेट में केवल संयोजकों के साथ सूत्र के बराबर है। संयोजकों के कई पूर्ण सेट हैं, जिनमें सम्मलित हैं , , और , इस प्रकार इसमें दो बाइनरी संयोजक होते हैं जो क्रमशः NAND और NOR के अनुरूप अपने आप पूर्ण होते हैं।[20] उदाहरण के लिए, जोड़ पूर्ण नहीं हैं।
स्ट्रोक (नंद)
एनएएनडी से संबंधित द्विआधारी संयोजक को शेफर लाइन कहा जाता है, और ऊर्ध्वाधर पट्टी के साथ लिखा जाता है या लंबवत तीर ↑. इस संयोजकता की पूर्णता प्रिन्सिपिया मैथेमेटिका (1927:xvii) में नोट की गई थी। चूँकि यह अपने आप में पूर्ण है, अन्य सभी संयोजकों को केवल आघात का प्रयोग करके व्यक्त किया जा सकता है। उदाहरण के लिए, जहां प्रतीक ≡ तार्किक तुल्यता का प्रतिनिधित्व करता है:
- ~p ≡ p|p
- p → q ≡ p | ~ q
- p ∨ q ≡ ~p|~q
- p & p ≡ ~ (p | q)
विशेष रूप से, शून्य-ऐरी संयोजक (सच्चाई का प्रतिनिधित्व) और (असत्य का प्रतिनिधित्व) स्ट्रोक का उपयोग करके व्यक्त किया जा सकता है:
IF ... THEN ... ELSE
यह संयोजक {0, 1}, (या {F, T} या { , } ) पूर्ण सेट बनाता है। निम्नलिखित में IF...THEN...ELSE संबंध (गणित) (c, b, a) = d निरूपित करता है ((c → b) ∨ (~c → a) ) ≡ ( (c & b) ∨ ( ~ c & a)) = d
- (c, b, a):
- (c, 0, 1) ≡ ~ c
- (c, b, 1) ≡ (c → b)
- (c, c, a) ≡ (c ∨ a)
- (c, b, c) ≡ (c & b)
उदाहरण: निम्नलिखित दिखाता है कि (c, b, 1) ≡ (c → b) का प्रमेय-आधारित प्रमाण कैसे आगे बढ़ेगा, प्रमाण के नीचे इसका सत्य-सारणी सत्यापन है। (नोट: (c → b) को (~c ∨ b) के रूप में परिभाषित किया गया है):
- घटाए गए रूप से प्रारंभ करें: ( (c & b) ∨ (~c & a) )
- 1 को a से बदलें: ( (c & b) ∨ (~c & 1) )
- सर्वसमिका (~c & 1) = ~c: ((c & b) ∨ (~c) )
- V के लिए परिवर्तन का नियम: ((~c) ∨ (c & b) )
- ~c V को (c और b) पर वितरित करें: ( ((~c) ∨ c ) और ((~c) ∨ b )
- अपवर्जित मध्य का नियम (((~c) ∨ c ) = 1 ): ( (1) & ((~c) ∨ b ) )
- वितरण (1) और अधिक ((~c) ∨ b): ( ((1) और (~c)) ∨ ((1) और b )) )
- कम्युटिविटी और आइडेंटिटी (( 1 & ~c) = (~c & 1) = ~c, and (( 1 & b) ≡ (b & 1) ≡ b: ( ~c ∨ b )
- ( ~c ∨ b ) को 'c → b' Q. E. D के रूप में परिभाषित किया गया है।
निम्नलिखित सत्य तालिका में टॉटोलॉजी के लिए तना हुआ लेबल वाला कॉलम d लेबल वाले दो स्तंभों के बीच तार्किक तुल्यता (यहाँ ≡ द्वारा चिन्हित) का मूल्यांकन करता है। क्योंकि तना हुआ के अंतर्गत सभी चार पंक्तियाँ 1 हैं, तुल्यता वास्तव में पुनरुक्ति का प्रतिनिधित्व करती है।
| d | taut | d | |||||||||||||||||||||||||||||
| rows | c | b | a | ( | ( | ( | c | & | b | ) | V | ( | ~ | ( | c | ) | & | a | ) | ) | ≡ | ( | ~ | ( | c | ) | V | b | ) | ) | |
| 0,1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | |||||||||||||||
| 2,3 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | |||||||||||||||
| 4,5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |||||||||||||||
| 6,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
सामान्य रूप
एक प्रस्तावित सूत्र में बहुत जटिल संरचना हो सकती है। ऐसे सूत्रों के साथ काम करना अधिकांशतः सुविधाजनक होता है जिनके सरल रूप होते हैं, जिन्हें सामान्य रूपों के रूप में जाना जाता है। कुछ सामान्य सामान्य रूपों में संयोजक सामान्य रूप और विघटनकारी सामान्य रूप सम्मलित हैं। किसी भी प्रस्तावनात्मक सूत्र को उसके संयोजक या वियोगी सामान्य रूप में घटाया जा सकता है।
सामान्य रूप में कमी

सूत्र के लिए सत्य तालिका तैयार होने के बाद सामान्य रूप में कमी अपेक्षाकृत सरल होती है। किन्तु शाब्दिक संख्या को कम करने के लिए आगे के प्रयासों (नीचे देखें) के लिए कुछ उपकरणों की आवश्यकता होती है: डी मॉर्गन के नियमों और सत्य तालिकाओं द्वारा कमी करना जटिल हो सकता है, किन्तु कर्णघ के नक्शे चर की छोटी संख्या (5 या उससे कम) के लिए बहुत उपयुक्त हैं। कई आउटपुट वाले अधिक जटिल परिपथ के लिए कुछ परिष्कृत सारणीबद्ध तरीके संलग्न हैं किन्तु ये इस लेख के दायरे से बाहर हैं, अधिक जानकारी के लिए क्विन-मैक्लुस्की एल्गोरिथम देखें।
शाब्दिक, पद और पर्याय
इलेक्ट्रिकल इंजीनियरिंग में चर x या इसका निषेध ~(x) साथ एकल धारणा में साथ हो जाता है जिसे शाब्दिक (गणितीय तर्क) कहा जाता है। AND द्वारा जुड़े शाब्दिक शब्दों की स्ट्रिंग को शब्द कहा जाता है। OR से जुड़े शाब्दिक शब्दों की स्ट्रिंग को परिवर्तन कहा जाता है। विशिष्ट रूप से शाब्दिक ~(x) का संक्षिप्त रूप ~x है। कभी-कभी बीजगणितीय गुणन की विधियों में &-प्रतीक को पूर्ण रूप से छोड़ दिया जाता है।
- उदाहरण
- a, b, c, d चर हैं। ((( a & ~(b) ) & ~(c)) & d) पद है। इसे (a & ~b & ~c & d), या a~b~cd के रूप में संक्षिप्त किया जा सकता है।
- p, q, r, s चर हैं। (((p & ~(q) ) & r) & ~(s) ) परिवर्तन है। इसे (p ∨ ~q ∨ r ∨ ~s) के रूप में संक्षिप्त किया जा सकता है।
मिनट्स
इसी प्रकार a 2n-पंक्ति सत्य तालिका सभी 2n मान के लिए प्रस्ताव सूत्र का मूल्यांकन प्रदर्शित करती है, इसके चरों के संभावित मान, n चर 2 उत्पन्न करते हैंn-स्क्वायर कर्णघ मानचित्र (यदि हम इसे इसके पूर्ण-आयामी बोध में नहीं बना सकते हैं)। उदाहरण के लिए, 3 चर 23= 8 उत्पन्न करते हैं, इस प्रकार पंक्तियाँ और 8 कर्णघ वर्ग, 4 चर 16 सत्य-तालिका पंक्तियाँ और 16 वर्ग उत्पन्न करते हैं और इसलिए 16 मध्यमान होते हैं। प्रत्येक कर्णघ-नक्शा वर्ग और इसके संबंधित सत्य-तालिका मूल्यांकन मिनट का प्रतिनिधित्व करता है।
किसी भी प्रस्तावित सूत्र को सक्रिय (अर्थात 1 - या T-वैल्यूड) मिन्टरम्स के तार्किक योग (OR) तक कम किया जा सकता है। जब इस रूप में सूत्र को वियोगात्मक सामान्य रूप में कहा जाता है। किन्तु यदि यह इस रूप में है, यह आवश्यक नहीं कि शब्दों की संख्या या अक्षर की संख्या के संबंध में कम से कम हो।
निम्नलिखित तालिका में, पंक्तियों की अजीबोगरीब संख्या देखें: (0, 1, 3, 2, 6, 7, 5, 4, 0)। पहला कॉलम अंक cba के बाइनरी समतुल्य का दशमलव समतुल्य है, दूसरे शब्दों में:
- उदाहरण
- cba2 = c * 22 + b*21 + a*20:
- cba = (c=1, b=0, a=0) = 1012 = 1*22 + 0*21 + 1*20= 510
यह क्रमांकन इस बारे में आता है क्योंकि जैसे ही कोई पंक्ति से पंक्ति में तालिका को नीचे ले जाता है, समय में केवल चर इसके मूल्य को बदलता है। ग्रे कोड इस धारणा से लिया गया है। इस धारणा को तीन और चार-आयामी अतिविम तक बढ़ाया जा सकता है जिसे हस्से आरेख कहा जाता है, जहां प्रत्येक कोने के चर समय में केवल परिवर्तन करते हैं, क्योंकि घन के किनारों के चारों ओर घूमते हैं। हस्से आरेख (हाइपरक्यूब्स) दो आयामों में चपटा हुआ या तो वेच आरेख या कर्णघ मानचित्र हैं।
कर्णघ नक्शों के साथ काम करते समय हमेशा यह ध्यान रखना चाहिए कि शीर्ष किनारा नीचे के किनारे के चारों ओर लपेटता है, और बायां किनारा दाएं किनारे के चारों ओर लपेटता है- कर्णघ आरेख वास्तव में तीन- या चार- या n-आयामी वस्तु है।
| decimal equivalent of (c, b, a) | c | b | a | minterm |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | (~c & ~b & ~a) |
| 1 | 0 | 0 | 1 | (~c & ~b & a) |
| 3 | 0 | 1 | 1 | (~c & b & a) |
| 2 | 0 | 1 | 0 | (~c & b & ~a) |
| 6 | 1 | 1 | 0 | (c & b & ~a) |
| 7 | 1 | 1 | 1 | (c & b & a) |
| 5 | 1 | 0 | 1 | (c & ~b & a) |
| 4 | 1 | 0 | 0 | (c & ~b & ~a) |
| 0 | 0 | 0 | 0 | (~a & ~b & ~c) |
मानचित्र विधि (वीच, कर्णघ) के उपयोग से कमी
वेइच ने वृत्तों को संलग्न वर्गों में परिवर्तित करके वेन आरेखों की धारणा में सुधार किया, और कर्णघ ने उनके शाब्दिक रूप (जैसे ~abc~d) में लिखे गए टकसालों को संख्याओं में परिवर्तित करके वेइच आरेख को सरल बनाया।[21] विधि निम्नानुसार आगे बढ़ती है:
सूत्र की सत्य तालिका तैयार करें
सूत्र की सत्य तालिका तैयार करें। n चर के लिए चर के बाइनरी-समतुल्य (सामान्यतः सिर्फ क्रमिक रूप से 0 से n-1) का उपयोग करके इसकी पंक्तियों को संख्या का मान दिया जाता हैं।
- तकनीकी रूप से, प्रस्तावक समारोह को इसके (अन्यूनतम) संयोजन सामान्य रूप में कम कर दिया गया है: प्रत्येक पंक्ति में इसकी न्यूनतम अभिव्यक्ति होती है और इन्हें इसके (अन्यूनतम) संयोजन सामान्य रूप में सूत्र का उत्पादन करने के लिए OR'd किया जा सकता है।
उदाहरण: ((c & d) ∨ (p & ~(c & (~d)))) = q संयोजक सामान्य रूप में है:
- ((~p & d & c) ∨ (p & d & c) ∨ (p & d & ~c) ∨ (p & ~d & ~c) ) = q
चूंकि, इस सूत्र को शब्दों की संख्या (4 से 3 तक) और इसके शाब्दिक (12 से 6) की कुल संख्या में घटाया जा सकता है।
| row | Minterms | p | d | c | ( | ( | c | & | d | ) | ∨ | ( | p | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | Active minterms | संयोजक सामान्य रूप में सूत्र |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ( ~p & ~d & ~c ) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | ||||||||||||||
| 1 | ( ~p & ~d & c) | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | ||||||||||||||
| 2 | ( ~p & d & ~c ) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||||||||||||||
| 3 | ( ~p & d & c ) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | (~p & d & c) | |||||||||||||
| 4 | ( p & ~d & ~c ) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | (~p & d & c) | |||||||||||||
| 5 | ( p & ~d & c ) | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | ||||||||||||||
| 6 | ( p & d & ~c ) | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | (p & d & ~c) | |||||||||||||
| 7 | ( p & d & c ) | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | ( p & d & c ) | |||||||||||||
| q | = (~p&d&c) ∨ (~p&d&c) ∨ (p&d&~c ) ∨ (p&d&c ) |
सूत्र का कर्णघ नक्शा बनाएं
ट्रूथ-टेबल विधि द्वारा प्राप्त सूत्र (जैसे p) के मानों का उपयोग करें और उन्हें उनके संबंधित (संबद्ध) कर्णघ वर्गों में रखें (ये ग्रे कोड कन्वेंशन के अनुसार गिने जाते हैं)। यदि तालिका में परवाह नहीं करने के लिए d के मान दिखाई देते हैं, तो यह कमी चरण के समय जोड़ता है।
minterm कम करें
सन्निकट (संलग्न) 1-वर्गों (T-स्क्वायर) के न्यूनतम पदों को उनके शाब्दिक (गणितीय तर्क) की संख्या के संबंध में कम किया जा सकता है, और प्रक्रिया में संख्या शर्तों को भी घटाया जाएगा। दो जुड़े हुए वर्ग (2 x 1 क्षैतिज या 1 x 2 लंबवत, यहां तक कि किनारे भी संलग्न वर्गों का प्रतिनिधित्व करते हैं) 4 x 1 आयत (क्षैतिज या लंबवत) या 2 x 2 वर्ग में शाब्दिक, चार वर्ग खो देते हैं (यहां तक कि चार कोने संलग्न करने का प्रतिनिधित्व करते हैं) वर्ग) दो अक्षर खो देते हैं, आयत में आठ वर्ग 3 अक्षर खो देते हैं, आदि। (कोई सबसे बड़े वर्ग या आयत की तलाश करता है और छोटे वर्गों या आयतों को पूरी तरह से अनदेखा कर देता है।) यह प्रक्रिया तब तक जारी रहती है जब तक कि सभी संलग्न वर्गों का मान नहीं संलग्न होता हैं। जिस बिंदु पर प्रस्तावात्मक सूत्र को छोटा किया जाता है।
उदाहरण के लिए, वर्ग 3 और 7 के लिए ये दो संलग्न वर्ग शाब्दिक विलुप्त हो सकते हैं (उदाहरण के लिए वर्ग 3 और 7 से p), आयत या वर्ग में चार वर्ग दो शाब्दिक खो देते हैं, आयत में आठ वर्ग 3 अक्षर विलुप्त हो जाते हैं। (एक सबसे बड़े वर्ग की तलाश करता है या आयतें।) यह प्रक्रिया तब तक जारी रहती है जब तक कि सभी संलग्न वर्गों का मान नहीं लगाया जाता है, जिस बिंदु पर प्रस्तावक सूत्र को न्यूनतम कहा जाता है।
उदाहरण: मानचित्र विधि सामान्यतः निरीक्षण द्वारा की जाती है। कर्णघ मानचित्र पर शब्दों के संयोजन के पीछे की चाल दिखाने के लिए निम्न उदाहरण बीजगणितीय पद्धति का विस्तार करता है:
- मिन्टरम्स 3 & 7, 7 & 6, और 4 & 6 अबाउट (क्योंकि टेबल के किनारे लपेटे जाते हैं)। तो इनमें से प्रत्येक जोड़े को कम किया जा सकता है।
निरीक्षण करें कि कार्यकुशलता नियम (A ∨ A) = A द्वारा, हम और पद बना सकते हैं। फिर संघ और वितरण नियमों द्वारा विलुप्त होने वाले चर जोड़े जा सकते हैं, और फिर विरोधाभास के नियम (x & ~x)=0 के साथ विलुप्त हो सकते हैं। निम्नलिखित केवल शब्दों का ट्रैक रखने के लिए कोष्ठक [ और ] का उपयोग करता है, उनका कोई विशेष महत्व नहीं है:
- सूत्र को कम किए जाने वाले सूत्र के साथ संयोजन सामान्य रूप में रखें:
- q = ((~p & d & c) ∨ (p & d & c) ∨ (p & d & ~c) ∨ (p & ~d & ~c) ) = ( #3 ∨ #7 ∨ #6 ∨ #4 )
- उदासीनता (अवशोषण) [a ∨ a) = a:
- ( #3 ∨ [ #7 ∨ #7 ] ∨ [ #6 ∨ #6 ] ∨ #4 )
- साहचर्य नियम (x ∨ (y ∨ z)) = ((x ∨ y) ∨ z )
- ( [ #3 ∨ #7 ] ∨ [ #7 ∨ #6 ] ∨ [ #6 ∨ #4] )
- [ (~p & d & c) ∨ (p & d & c)] ∨ [(p & d & c) ∨ (p & & & ~c)] ∨ [ (p & d & ~c) ∨ (p & ~d & ~c)]।
- वितरण नियम (x & (y ∨ z) ) = ( (x & y) ∨ (x & z) ):
- ( [(d & c) ∨ (~p & p)] ∨ [(p & d) ∨ (~c & c) ] ∨ [ (p & ~c) ∨ (c & ~c) ] )
- क्रमविनिमेय नियम और विरोधाभास का नियम (x & ~x) = (~x & x) = 0:
- ( [(d & c) ∨ (0) ] ∨ [ (p & d) ∨ (0) ] ∨ [ (p & ~c) ∨ (0) ] )
- पहचान का नियम ( x ∨ 0 ) = x सूत्र के घटे हुए रूप के लिए अग्रणी:
- q = ((d & c) ∨ (p & d) ∨ (p & ~c))
एक सत्य तालिका के साथ कमी को सत्यापित करें
| row | Minterms | p | d | c | ( | ( | d | & | c | ) | ∨ | ( | p | & | d | ) | ∨ | ( | p | & | ~ | ( | c | ) | ) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ( ~p & ~d & ~c ) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |||||||||
| 1 | ( ~p & ~d & c) | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||||||||
| 2 | ( ~p & d & ~c ) | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |||||||||
| 3 | ( ~p & d & c ) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||||
| 4 | ( p & ~d & ~c ) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |||||||||
| 5 | ( p & ~d & c ) | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |||||||||
| 6 | ( p & d & ~c ) | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||||
| 7 | ( p & d & c ) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |||||||||
| q |
अप्रतिबंधित प्रस्ताव
निम्नलिखित उदाहरणों को परिभाषाओं के रूप में देखते हुए, बाद के तर्कों से क्या बनता है:
- (1) यह वाक्य सरल है। (2) यह वाक्य जटिल है, और यह AND से जुड़ा है।
फिर चर s को बाएँ-सबसे वाक्य में असाइन करें यह वाक्य सरल है। कंपाउंड c = सरल नहीं ~s को परिभाषित करें, और c = ~s को यह वाक्य कंपाउंड है, इसे j का मान असाइन करके AND से संयोजित किया जाता है। दूसरे वाक्य को इस प्रकार व्यक्त किया जा सकता है:
- (NO(S) & J)
यदि सत्य मान वाक्यों c = ~s और j पर रखे जाने हैं, तो सभी स्पष्ट रूप से FALSEHOODS हैं: उदा। यह वाक्य जटिल है FALSEHOOD है (यह सरल है, परिभाषा के अनुसार)। अतः उनका संयोजन (AND) असत्य है। किन्तु जब इसके एकत्रित रूप में लिया जाता है, तो वाक्य सत्य होता है।
यह उन विरोधाभास का उदाहरण है जो अप्रतिबंधित परिभाषा से उत्पन्न होते हैं - अर्थात, जब किसी वस्तु m में गुण P होता है, किन्तु वस्तु m को गुण P के संदर्भ में परिभाषित किया जाता है।[22] वादविवाद करने वाले या निगमनात्मक विश्लेषण में सम्मलित व्यक्ति के लिए सबसे अच्छी सलाह है कि वह अप्रतिबंधात्मक परिभाषाओं से बचें, किन्तु साथ ही साथ उनकी तलाश में रहें क्योंकि वे वास्तव में विरोधाभास उत्पन्न कर सकते हैं। दूसरी ओर, इंजीनियरों ने उन्हें प्रतिक्रिया के साथ प्रस्तावात्मक सूत्रों के रूप में काम करने के लिए रखा जाता हैं।
प्रतिक्रिया के साथ प्रस्ताव सूत्र
अपने स्वयं के चरों में से के रूप में प्रकट होने वाले प्रस्तावनात्मक सूत्र की धारणा के लिए गठन नियम की आवश्यकता होती है जो सूत्र को चर के असाइनमेंट की अनुमति देता है। सामान्यतः ऐसी कोई शर्त नहीं है (वस्तुओं और संबंधों की स्वयंसिद्ध या सत्य-सारणी प्रणाली) जो ऐसा होने से मना करती है।[23] सबसे सरल मामला तब होता है जब OR सूत्र अपना स्वयं का इनपुट बन जाता है, उदाहरण के लिए p = q। (p ∨ s) = q से प्रारंभ करें, फिर मान लीजिए p = q, इस स्थिति में ध्यान दें कि q की परिभाषा स्वयं q के साथ-साथ s और OR संयोजक पर भी निर्भर करती है, क्यू की यह परिभाषा इस प्रकार अप्रतिबंधात्मक है।
दो स्थितियों में से कोई भी परिणाम हो सकता है:[24] कंपन या स्मृति।
यह सूत्र को ब्लैक बॉक्स के रूप में सोचने में मदद करता है। सूत्र-बॉक्स के अंदर क्या चल रहा है, इसके ज्ञान के बिना बाहर से ऐसा प्रतीत होगा कि आउटपुट अब केवल इनपुट का फ़ंक्शन (गणित) नहीं है। अर्थात्, कभी कोई q को देखता है और 0 को देखता है और अन्य समय 1 को देखता है। इस समस्या से बचने के लिए किसी को बॉक्स के अंदर छिपे चर p की स्थिति (स्थिति) को जानना होगा (अर्थात q का मान वापस खिलाया गया और p को सौंपा गया) . जब यह ज्ञात हो जाता है तो स्पष्ट असंगति दूर हो जाती है।
समझने के लिए प्रतिक्रिया के साथ सूत्रों के व्यवहार को अनुक्रमिक परिपथ के अधिक परिष्कृत विश्लेषण की आवश्यकता होती है। इस प्रकार इन मशीनों के लिए, उनके सरलतम रूप में, फीडबैक लीड के साथ प्रस्तावक सूत्र, वे ट्यूरिंग टेप और काउंटर-मशीन काउंटर के रूप में यादों को भी जन्म देते हैं। इस प्रकार इन तत्वों के संयोजन से कोई भी किसी भी प्रकार के परिबद्ध कम्प्यूटेशनल मॉडल (जैसे ट्यूरिंग मशीन, काउंटर मशीन, रजिस्टर मशीन, मैकिंटोश कंप्यूटर, आदि) का निर्माण कर सकता है।
दोलन
सार (आदर्श) स्थिति में सबसे सरल दोलन सूत्र खुद को वापस नहीं खिलाया जाता है: ~(~(p=q)) = q, इस सत्य-सारणी में सार (आदर्श) तर्कवाक्य सूत्र का विश्लेषण p=1 और p=0 दोनों स्थितियों के लिए असंगति प्रकट करता है: जब p=1, q=0, यह नहीं हो सकता क्योंकि p=q, इसी तरह जब p = 0 और q = 1 के लिए इस सारणी को इस प्रकार अंकित किया जा सकता हैं।
| q | |||||||
|---|---|---|---|---|---|---|---|
| p | ~ | ( | p | ) | = q | ||
| 0 | 1 | 0 | 1 | q & p inconsistent | |||
| 1 | 0 | 1 | 0 | q & p inconsistent |
विलंब के साथ दोलन: यदि विलंब हो[25] (आदर्श या गैर-आदर्श) p और q के बीच सार सूत्र में डाला जाता है तो p 1 और 0: 101010...101... अनंत के बीच दोलन करेगा। यदि देरी में से कोई भी और सार नहीं है (अर्थात आदर्श नहीं है), तो उपयोग किए जाने वाले विश्लेषण का प्रकार ऑसिलेटर बनाने वाली वस्तुओं की त्रुटीहीन प्रकृति पर निर्भर करेगा, ऐसी चीजें गणित के बाहर और इंजीनियरिंग में आती हैं।
विश्लेषण के लिए देरी डालने की आवश्यकता होती है और फिर देरी और इनपुट p के बीच लूप कट जाता है। विलंब को प्रकार के प्रस्ताव के रूप में देखा जाना चाहिए जिसमें इनपुट के रूप में q के आउटपुट के रूप में qd (q-delayed) है। यह नया प्रस्ताव सत्य तालिका में और स्तंभ जोड़ता है। असंगति अब qd और p के बीच है जैसा कि लाल रंग में दिखाया गया है, परिणामी दो स्थिर अवस्थाएँ:
| q | ||||||||
|---|---|---|---|---|---|---|---|---|
| qd | p | ( | ~ | ( | p | ) | = q | |
| 0 | 0 | 1 | 0 | 1 | state 1 | |||
| 0 | 1 | 0 | 1 | 0 | qd & p inconsistent | |||
| 1 | 0 | 1 | 0 | 1 | qd & p inconsistent | |||
| 1 | 1 | 0 | 1 | 0 | state 0 |
मेमोरी

बिना देर किए, सत्य तालिका विश्लेषण से विसंगतियों को दूर किया जाना चाहिए। देरी की धारणा के साथ, यह स्थिति खुद को फेड-बैक आउटपुट वेरिएबल q और p = q delayed.के बीच क्षणिक असंगति के रूप में प्रस्तुत करती है
एक सत्य तालिका उन पंक्तियों को प्रकट करती है जहाँ p = qdelayed के बीच इनपुट पर और q आउटपुट पर विसंगतियाँ होती हैं। फ़ीड-बैक को तोड़ने के बाद,[26] सत्य तालिका निर्माण पारंपरिक तरीके से आगे बढ़ता है। किन्तु बाद में, प्रत्येक पंक्ति में आउटपुट q की तुलना अब-स्वतंत्र इनपुट p से की जाती है और p और q के बीच कोई भी विसंगतियां नोट की जाती हैं (अर्थात p = 0 q = 1, या p = 1 और q = 0 के साथ), जब लाइन को फिर से बनाया जाता है तो इस प्रकार विरोधाभास के नियम ~(p & ~p) द्वारा दोनों को असंभव बना दिया जाता है। विसंगतियों को प्रकट करने वाली पंक्तियों को या तो क्षणिक स्थिति माना जाता है या असंगत के रूप में समाप्त कर दिया जाता है और इसलिए असंभव है।
वन्स-फ्लिप मेमोरी
सबसे सरल मेमोरी परिणामों के बारे में जब OR का आउटपुट इसके किसी इनपुट को वापस फीड करता है, इस स्थिति में आउटपुट q p में वापस फीड करता है। इस प्रकार यह देखते हुए कि सूत्र का पहले p=0 और q=0 के साथ मूल्यांकन (प्रारंभिक) किया जाता है, यह s=1 द्वारा सेट किए जाने पर बार फ़्लिप करेगा। इसके बाद, आउटपुट q फ़्लिप की स्थिति में q को बनाए रखेगा (q = 1)। यह व्यवहार, जो अब समय-निर्भर है, इस आरेख द्वारा वंस-फ्लिप के दाईं ओर दिखाया गया है।
| q | ||||||||
|---|---|---|---|---|---|---|---|---|
| p | s | ( | s | ∨ | p | ) | = q | |
| 0 | 0 | 0 | 0 | 0 | 0 | state 0, s=0 | ||
| 0 | 1 | 1 | 1 | 0 | q & p inconsistent | |||
| 1 | 0 | 0 | 1 | 1 | 1 | state 1 with s = 0 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | state 1 with s = 1 |
फ्लिप-फ्लॉप मेमोरी
अगला सरल मामला है सेट-रीसेट फ्लिप-फ्लॉप (इलेक्ट्रॉनिक्स) या फ्लिप-फ्लॉप बार-फ्लिप के नीचे दिखाया गया है। यह देखते हुए कि r = 0 और s = 0 और q = 0 प्रारंभ में, यह बार-फ्लिप के समान तरीके से सेट (s = 1) है। चूंकि इसमें r = 1 होने पर q = 0 को रीसेट करने का प्रावधान है। और अतिरिक्त जटिलता तब होती है जब दोनों सेट = 1 और रीसेट = 1 का मान निर्धारित किया जाता हैं। इस सूत्र में, सेट = 1 आउटपुट q = 1 को बाध्य करता है, इसलिए कब और यदि (s = 0 और r = 1) फ्लिप-फ्लॉप रीसेट हो जाएगा। या, यदि (s=1 & r=0) फ्लिप-फ्लॉप सेट हो जाएगा। अमूर्त (आदर्श) उदाहरण में जिसमें s=1 ⇒ s=0 & r=1 ⇒ r=0 साथ, सूत्र q अनिश्चित (अनिश्चित) होगा। वास्तविक OR, AND और NOT में देरी के कारण परिणाम प्रारंभ में अज्ञात होगा किन्तु उसके बाद विधेय होगा।
| q | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | s | r | ( | s | ∨ | ( | p | & | ~ | ( | r | ) | ) | ) | = q | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | state 0 with ( s=0 & r=0 ) | ||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | state 0 with ( s=0 & r=1 ) | ||||||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | q & p inconsistent | |||||||
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | q & p inconsistent | |||||||
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | state 1 with ( s=0 & r=0 ) | ||||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | q & p inconsistent | |||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | state 1 with ( s=1 & r=0 ) | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | state 1 with s & r simultaneously 1 |
क्लॉक फ्लिप-फ्लॉप मेमोरी
क्लॉक्ड फ्लिप-फ्लॉप मेमोरी (c क्लॉक है और d डेटा है) के रूप में जाना जाने वाला सूत्र नीचे दिया गया है। यह निम्नानुसार कार्य करता है: जब c = 0 डेटा d (या तो 0 या 1) आउटपुट q को प्रभावित करने के लिए प्राप्त नहीं कर सकता है। जब c = 1 डेटा d के माध्यम से प्राप्त होता है और आउटपुट q d के मान का अनुसरण करता है। इस प्रकार जब c 1 से 0 तक जाता है तो डेटा का अंतिम मान आउटपुट q पर फंसा रहता है। जब तक c = 0, d, q को बदले बिना मान बदल सकता है।
- उदाहरण
- ((c & d) ∨ (p & (~(c & ~(d))) = q, किन्तु अब p = q:
- ((c & d) ∨ (q & (~(c & ~(d))) = q
आरेख फ्लिप-फ्लॉप के आरेख के आकार के समान है, किन्तु संक्रमणों पर अलग-अलग लेबलिंग के साथ दर्शाया जा सकता हैं।
| s | q | w | v | r | u | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| row | q | d | c | ( | ( | c | & | d | ) | ∨ | ( | q | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | =q | Description |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | state 0 with ( s=0 & r=0 ), 0 is trapped | ||||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | state 0 with ( d=0 & c=1 ): q=0 is following d=0 | ||||||||||||
| 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | state 0 with ( d=1 & r=0 ), 0 is trapped | ||||||||||||
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | q & p inconsistent | |||||||||||||
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | state 1 with (d =0 & c=0 ), 1 is trapped | ||||||||||||
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | q & p inconsistent | |||||||||||||
| 6 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | state 1 with (d =1 & c=0 ), 1 is trapped | ||||||||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | state 1 with ( d=1 & c=1 ): q=1 is following d=1 |
ऐतिहासिक विकास
बर्ट्रेंड रसेल (1912:74) अरस्तू से प्राप्त विचार के तीन नियमों को सूचीबद्ध करता है: (1) पहचान का नियम से प्राप्त मान पर निर्भर करता हैं। इस प्रकार (2) गैर-विरोधाभास का नियम: कुछ भी नहीं हो सकता है और न ही हो सकता है, और (3) बहिष्कृत मध्य का नियम: सब कुछ होना चाहिए या नहीं होना चाहिए।
- उदाहरण: यहाँ O किसी वस्तु के होने या गुणवत्ता के बारे में अभिव्यक्ति है:
- पहचान का नियम: O = O
- विरोधाभास का नियम: ~(O & ~(O))
- बहिष्कृत मध्य का नियम: (O ∨ ~(O))
इस प्रकार बहिष्कृत मध्य के नियम में सब कुछ शब्द का उपयोग इस नियम की रसेल की अभिव्यक्ति को बहस के लिए OPEN करता है। यदि वस्तुओं के परिमित संग्रह (प्रवचन का परिमित ब्रह्मांड) के संदर्भ में BEING या QUALITY के बारे में अभिव्यक्ति तक सीमित है - जिसके सदस्यों की उपस्थिति या अनुपस्थिति के लिए के बाद जांच की जा सकती है - तो नियम माना जाता है सहज रूप से उपयुक्त। इस प्रकार अभिकथन जैसे: यह वस्तु या तो होनी चाहिए या नहीं होनी चाहिए (संग्रह में), या इस वस्तु में या तो यह गुणवत्ता होनी चाहिए या यह गुणवत्ता नहीं होनी चाहिए (संग्रह में वस्तुओं के सापेक्ष) स्वीकार्य है। इस स्थिति को वेन आरेख पर देखें।
यद्यपि तर्कवाक्य कलन की उत्पत्ति अरस्तू के साथ हुई, फिर भी तर्कवाक्यों पर लागू बीजगणित की धारणा को 19वीं शताब्दी की प्रारंभ तक प्रतीक्षा करनी पड़ी। इस प्रकार अरस्तू के न्यायवाक्य की 2000 वर्ष की परंपरा की (प्रतिकूल) प्रतिक्रिया में, जॉन लोके के मानव समझ से संबंधित निबंध (1690) में लाक्षणिकता (प्रतीकों के उपयोग का सिद्धांत) शब्द का प्रयोग किया गया था। 1826 तक रिचर्ड व्हाटली ने लोके के लाक्षणिकता के प्रति सहानुभूति के साथ न्याय संगत तर्क का आलोचनात्मक विश्लेषण किया था। जॉर्ज बेंथम के कार्य (1827) के परिणामस्वरूप विधेय (1827) के परिमाणीकरण की धारणा उत्पन्न हुई (आजकल इसे सभी के लिए ∀ ≡ के रूप में दर्शाया जाता है)। ऑगस्टस डी मॉर्गन के साथ प्राथमिकता विवाद पर सर विलियम हैमिल्टन, 9वें बैरोनेट द्वारा उकसाए गए विवाद ने जॉर्ज बूले को तर्क पर अपने विचार लिखने और उन्हें 1847 में एमएएल [तर्क का गणितीय विश्लेषण] के रूप में प्रकाशित करने के लिए प्रेरित किया (ग्रैटिन-गिनीज और बोर्नेट 1997) :xxviii)।
उनके योगदान के बारे में ग्रैटिन-गिनीज और बोर्नेट टिप्पणी:
- बोले का प्रमुख एकल नवाचार [द] नियम [x] थाn = x ] तर्क के लिए: यह कहा गया है कि गुण x को चुनने और x को बार-बार चुनने का मानसिक कार्य बार x को चुनने के समान है... इसके परिणामस्वरूप उसने समीकरण x•(1) बनाया -x)=0 और x+(1-x)=1 जो उसके लिए क्रमशः विरोधाभास के नियम और बहिष्कृत मध्य के नियम (p या xxviiff) को व्यक्त करता है। बूले के लिए 1 प्रवचन का ब्रह्मांड था और 0 कुछ भी नहीं था।
भगवान फ्रीज का शुक्र है के बड़े पैमाने पर उपक्रम (1879) के परिणामस्वरूप प्रस्तावों की औपचारिक गणना हुई, किन्तु उनका प्रतीकवाद इतना कठिन था कि व्यक्ति को छोड़कर इसका बहुत कम प्रभाव था: बर्ट्रेंड रसेल। जिन्होंने सबसे पहले अल्फ्रेड नॉर्थ व्हाइटहेड के छात्र के रूप में उन्होंने फ्रीज के काम का अध्ययन किया और इस प्रकार इसके संबंध में (प्रसिद्ध और कुख्यात) संशोधन का सुझाव दिया (1904) अधिकार-विरोध की समस्या के आसपास जिसे उन्होंने फ्रेज के उपचार (cf रसेल के विरोधाभास) में खोजा। रसेल के काम ने व्हाइटहेड के साथ सहयोग का नेतृत्व किया, जिसने 1912 में प्रिंसिपिया मैथेमेटिका (पीएम) के पहले खंड का निर्माण किया। यही वह स्थान है जिसे हम आधुनिक तर्कवाक्य तर्क मानते हैं जो सबसे पहले प्रकट हुआ। विशेष रूप से, पीएम ने NOT और OR और अभिकथन प्रतीक ⊦ आदिम के रूप में परिचय दिया। इस प्रकार इन धारणाओं के संदर्भ में वे इम्प्लीकेशन को परिभाषित करते हैं → ( def. *1.01: ~p ∨ q), फिर AND (def. *3.01: ~(~p ∨ ~q) ), फिर EQUIVALENCE p ←→ q (*4.01: ( p → q) और (q → p))।
- हेनरी एम. शेफ़र (1921) और जॉन निकोड प्रदर्शित करते हैं कि केवल संयोजक, स्ट्रोक | सभी प्रस्तावित सूत्रों को व्यक्त करने के लिए पर्याप्त है।
- एमिल पोस्ट (1921) ने प्रारंभिक प्रस्तावों के सामान्य सिद्धांत के अपने परिचय में विश्लेषण की सत्य तालिका पद्धति विकसित की। उसने निकोद के स्ट्रोक को नोट किया | .
- व्हाइटहेड और रसेल ने पीएम के अपने 1927 के पुनर्प्रकाशन में परिचय जोड़ा, जिसमें आंशिक रूप से आघात का अनुकूल उपचार जोड़ा गया।
'गणना और स्विचिंग तर्क':
- विलियम एक्लस (भौतिक विज्ञानी) और F W जॉर्डन (1919) वैक्यूम ट्यूब से बने ट्रिगर रिले का वर्णन करते हैं।
- [[जॉर्ज स्टिअंशज]] (1937) ने यांत्रिक रिले का उपयोग करके बाइनरी योजक का आविष्कार किया। वह इसे अपनी रसोई की मेज पर बनाता है।
- उदाहरण: दिए गए बाइनरी बिट्स ai और bi और कैरी-इन ( c_ini), उनका योग Σi और कैरी-आउट (c_outi) हैं:
- ( ( ai XOR bi ) XOR c_ini )= si
- ( ai & bi ) ∨ c_ini ) = c_outi,
- एलन ट्यूरिंग रिले (1937-1938) का उपयोग करके गुणक बनाता है। ऐसा करने के लिए उसे अपने स्वयं के रिले कॉइल्स को हाथ से हवा देना पड़ता है।
- स्विचिंग परिपथ के बारे में पाठ्यपुस्तकें 1950 के दशक की प्रारंभ में दिखाई देती हैं।
- विलार्ड क्वीन 1952 और 1955, एडवर्ड डब्ल्यू. वीच, ई. डब्ल्यू. वीच 1952, और मौरिस कर्णघ, एम. कर्णघ (1953) प्रस्तावित कार्यों को सरल बनाने के लिए मानचित्र-विधियाँ विकसित करते हैं।
- जॉर्ज एच. मीली (1955) और एडवर्ड F. मूर (1956) अनुक्रमिक (अर्थात स्विचिंग-परिपथ) मशीनों के सिद्धांत को संबोधित करते हैं।
- ई.जे. मैकक्लुस्की और एच. शोर ने प्रस्तावित (स्विचिंग) परिपथ (1962) को सरल बनाने के लिए विधि विकसित की।
फुटनोट्स
- ↑ Rosenbloom discusses this problem of implication at some length. Most philosophers and mathematicians just accept the material definition as given above. But some do not, including the intuitionists; they consider it a form of the law of excluded middle misapplied.[11]
- ↑ Rosenbloom[16] and Kleene 1952:73-74 ranks all 11 symbols.
उद्धरण
- ↑ Hamilton 1978:1
- ↑ Principia Mathematica (PM) p. 91 eschews "the" because they require a clear-cut "object of sensation"; they stipulate the use of "this"
- ↑ (italics added) Reichenbach[clarification needed] p.80.
- ↑ Tarski p.54-68. Suppes calls IDENTITY a "further rule of inference" and has a brief development around it; Robbin, Bender and Williamson, and Goodstein introduce the sign and its usage without comment or explanation. Hamilton p. 37 employs two signs ≠ and = with respect to the valuation of a formula in a formal calculus. Kleene p. 70 and Hamilton p. 52 place it in the predicate calculus, in particular with regards to the arithmetic of natural numbers.
- ↑ Empiricits eschew the notion of a priori (built-in, born-with) knowledge. "Radical reductionists" such as John Locke and David Hume "held that every idea must either originate directly in sense experience or else be compounded of ideas thus originating"; quoted from Quine reprinted in 1996 The Emergence of Logical Empriricism, Garland Publishing Inc. http://www.marxists.org/reference/subject/philosophy/works/us/quine.htm
- ↑ Neural net modelling offers a good mathematical model for a comparator as follows: Given a signal S and a threshold "thr", subtract "thr" from S and substitute this difference d to a sigmoid function: For large "gains" k, e.g. k=100, 1/( 1 + e−k*d ) = 1/( 1 + e−k*(S-thr) ) = { ≃0, ≃1 }.[clarification needed] For example, if "The door is DOWN" means "The door is less than 50% of the way up", then a threshold thr=0.5 corresponding to 0.5*5.0 = +2.50 volts could be applied to a "linear" measuring-device with an output of 0 volts when fully closed and +5.0 volts when fully open.
- ↑ In actuality the digital 1 and 0 are defined over non-overlapping ranges e.g. { "1" = +5/+0.2/−1.0 volts, 0 = +0.5/−0.2 volts }[clarification needed]. When a value falls outside the defined range(s) the value becomes "u" -- unknown; e.g. +2.3 would be "u".
- ↑ While the notion of logical product is not so peculiar (e.g. 0*0=0, 0*1=0, 1*0=0, 1*1=1), the notion of (1+1=1 is peculiar; in fact (a "+" b) = (a + (b - a*b)) where "+" is the "logical sum" but + and - are the true arithmetic counterparts. Occasionally all four notions do appear in a formula: A AND B = 1/2*( A plus B minus ( A XOR B ) ] (cf p. 146 in John Wakerly 1978, Error Detecting Codes, Self-Checking Circuits and Applications, North-Holland, New York, ISBN 0-444-00259-6 pbk.)
- ↑ A careful look at its Karnaugh map shows that IF...THEN...ELSE can also be expressed, in a rather round-about way, in terms of two exclusive-ORs: ( (b AND (c XOR a)) OR (a AND (c XOR b)) ) = d.
- ↑ Robbin p. 3.
- ↑ Rosenbloom 1950, pp. 30 and 54ff.
- ↑ Indeed, exhaustive selection between alternatives -- mutual exclusion -- is required by the definition that Kleene gives the CASE operator (Kleene 1952229)
- ↑ The use of quote marks around the expressions is not accidental. Tarski comments on the use of quotes in his "18. Identity of things and identity of their designations; use of quotation marks" p. 58ff.
- ↑ Hamilton p. 37. Bender and Williamson p. 29 state "In what follows, we'll replace "equals" with the symbol " ⇔ " (equivalence) which is usually used in logic. We use the more familiar " = " for assigning meaning and values."
- ↑ Reichenbach p. 20-22 and follows the conventions of PM. The symbol =Df is in the metalanguage and is not a formal symbol with the following meaning: "by symbol ' s ' is to have the same meaning as the formula '(c & d)' ".
- ↑ Rosenbloom 1950, p. 32.
- ↑ cf Minsky 1967:75, section 4.2.3 "The method of parenthesis counting". Minsky presents a state machine that will do the job, and by use of induction (recursive definition) Minsky proves the "method" and presents a theorem as the result. A fully generalized "parenthesis grammar" requires an infinite state machine (e.g. a Turing machine) to do the counting.
- ↑ Robbin p. 7
- ↑ cf Reichenbach p. 68 for a more involved discussion: "If the inference is valid and the premises are true, the inference is called conclusive.
- ↑ As well as the first three, Hamilton pp.19-22 discusses logics built from only | (NAND), and ↓ (NOR).
- ↑ Wickes 1967:36ff. Wickes offers a good example of 8 of the 2 x 4 (3-variable maps) and 16 of the 4 x 4 (4-variable) maps. As an arbitrary 3-variable map could represent any one of 28=256 2x4 maps, and an arbitrary 4-variable map could represent any one of 216 = 65,536 different formula-evaluations, writing down every one is infeasible.
- ↑ This definition is given by Stephen Kleene. Both Kurt Gödel and Kleene believed that the classical paradoxes are uniformly examples of this sort of definition. But Kleene went on to assert that the problem has not been solved satisfactorily and impredicative definitions can be found in analysis. He gives as example the definition of the least upper bound (l.u.b) u of M. Given a Dedekind cut of the number line C and the two parts into which the number line is cut, i.e. M and (C - M), l.u.b. = u is defined in terms of the notion M, whereas M is defined in terms of C. Thus the definition of u, an element of C, is defined in terms of the totality C and this makes its definition impredicative. Kleene asserts that attempts to argue this away can be used to uphold the impredicative definitions in the paradoxes.(Kleene 1952:43).
- ↑ McCluskey comments that "it could be argued that the analysis is still incomplete because the word statement "The outputs are equal to the previous values of the inputs" has not been obtained"; he goes on to dismiss such worries because "English is not a formal language in a mathematical sense, [and] it is not really possible to have a formal procedure for obtaining word statements" (p. 185).
- ↑ More precisely, given enough "loop gain", either oscillation or memory will occur (cf McCluskey p. 191-2). In abstract (idealized) mathematical systems adequate loop gain is not a problem.
- ↑ The notion of delay and the principle of local causation as caused ultimately by the speed of light appears in Robin Gandy (1980), "Church's thesis and Principles for Mechanisms", in J. Barwise, H. J. Keisler and K. Kunen, eds., The Kleene Symposium, North-Holland Publishing Company (1980) 123-148. Gandy considered this to be the most important of his principles: "Contemporary physics rejects the possibility of instantaneous action at a distance" (p. 135). Gandy was Alan Turing's student and close friend.
- ↑ McKlusky p. 194-5 discusses "breaking the loop" and inserts "amplifiers" to do this; Wickes (p. 118-121) discuss inserting delays. McCluskey p. 195ff discusses the problem of "races" caused by delays.
संदर्भ
- Rosenbloom, Paul (1950). The Elements of Mathematical Logic. Mineola, New York: Dover Publications, Inc. ISBN 0-486-44617-4.
- Kleene, Stephen (1952). Introduction to metamathematics. Amsterdam: North-Holland Publishing Company.
- Bender, Edward A. and Williamson, S. Gill, 2005, A Short Course in Discrete Mathematics, Dover Publications, Mineola NY, ISBN 0-486-43946-1. This text is used in a "lower division two-quarter [computer science] course" at UC San Diego.
- Enderton, H. B., 2002, A Mathematical Introduction to Logic. Harcourt/Academic Press. ISBN 0-12-238452-0
- Goodstein, R. L., (Pergamon Press 1963), 1966, (Dover edition 2007), Boolean Algebra, Dover Publications, Inc. Minola, New York, ISBN 0-486-45894-6. Emphasis on the notion of "algebra of classes" with set-theoretic symbols such as ∩, ∪, ' (NOT), ⊂ (IMPLIES). Later Goldstein replaces these with &, ∨, ¬, → (respectively) in his treatment of "Sentence Logic" pp. 76–93.
- Ivor Grattan-Guinness and Gérard Bornet 1997, George Boole: Selected Manuscripts on Logic and its Philosophy, Birkhäuser Verlag, Basil, ISBN 978-0-8176-5456-6 (Boston).
- A. G. Hamilton 1978, Logic for Mathematicians, Cambridge University Press, Cambridge UK, ISBN 0-521-21838-1.
- E. J. McCluskey 1965, Introduction to the Theory of Switching Circuits, McGraw-Hill Book Company, New York. No ISBN. Library of Congress Catalog Card Number 65-17394. McCluskey was a student of Willard Quine and developed some notable theorems with Quine and on his own. For those interested in the history, the book contains a wealth of references.
- Marvin L. Minsky 1967, Computation: Finite and Infinite Machines, Prentice-Hall, Inc, Englewood Cliffs, N.J.. No ISBN. Library of Congress Catalog Card Number 67-12342. Useful especially for computability, plus good sources.
- Joel W. Robbin 1969, 1997, Mathematical Logic: A First Course, Dover Publications, Inc., Mineola, New York, ISBN 0-486-45018-X (pbk.).
- Patrick Suppes 1957 (1999 Dover edition), Introduction to Logic, Dover Publications, Inc., Mineola, New York. ISBN 0-486-40687-3 (pbk.). This book is in print and readily available.
- On his page 204 in a footnote he references his set of axioms to E. V. Huntington, "Sets of Independent Postulates for the Algebra of Logic", Transactions of the American Mathematical Society, Vol. 5 91904) pp. 288-309.
- Alfred Tarski 1941 (1995 Dover edition), Introduction to Logic and to the Methodology of Deductive Sciences, Dover Publications, Inc., Mineola, New York. ISBN 0-486-28462-X (pbk.). This book is in print and readily available.
- Jean van Heijenoort 1967, 3rd printing with emendations 1976, From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931, Harvard University Press, Cambridge, Massachusetts. ISBN 0-674-32449-8 (pbk.) Translation/reprints of Frege (1879), Russell's letter to Frege (1902) and Frege's letter to Russell (1902), Richard's paradox (1905), Post (1921) can be found here.
- Alfred North Whitehead and Bertrand Russell 1927 2nd edition, paperback edition to *53 1962, Principia Mathematica, Cambridge University Press, no ISBN. In the years between the first edition of 1912 and the 2nd edition of 1927, H. M. Sheffer 1921 and M. Jean Nicod (no year cited) brought to Russell's and Whitehead's attention that what they considered their primitive propositions (connectives) could be reduced to a single |, nowadays known as the "stroke" or NAND (NOT-AND, NEITHER ... NOR...). Russell-Whitehead discuss this in their "Introduction to the Second Edition" and makes the definitions as discussed above.
- William E. Wickes 1968, Logic Design with Integrated Circuits, John Wiley & Sons, Inc., New York. No ISBN. Library of Congress Catalog Card Number: 68-21185. Tight presentation of engineering's analysis and synthesis methods, references McCluskey 1965. Unlike Suppes, Wickes' presentation of "Boolean algebra" starts with a set of postulates of a truth-table nature and then derives the customary theorems of them (p. 18ff).
बाहरी संबंध
 Media related to प्रस्तावक सूत्र at Wikimedia Commons
Media related to प्रस्तावक सूत्र at Wikimedia Commons