मैकडोनाल्ड बहुपद

गणित में, मैकडोनाल्ड बहुपद पी_λ(x; t,q) 1987 में इयान जी मैकडोनाल्ड द्वारा पेश किए गए कई चर में ऑर्थोगोनल बहुपद सममित बहुपद बहुपद का एक परिवार है। बाद में उन्होंने 1995 में एक गैर-सममित सामान्यीकरण पेश किया। मैकडोनाल्ड ने मूल रूप से अपने बहुपदों को परिमित के वजन λ के साथ जोड़ा। रूट सिस्टम और केवल एक वेरिएबल t का उपयोग किया, लेकिन बाद में महसूस किया कि परिमित रूट सिस्टम के बजाय उन्हें affine रूट सिस्टम से जोड़ना अधिक स्वाभाविक है, जिस स्थिति में वेरिएबल t को कई अलग-अलग वेरिएबल्स t=(t) से बदला जा सकता है₁,...,टी_k), affine रूट सिस्टम में जड़ों की प्रत्येक k कक्षाओं के लिए एक। मैकडोनाल्ड बहुपद n चर x = (x) में बहुपद हैं₁,...,एक्स_n), जहां n affine रूट सिस्टम का रैंक है। वे ऑर्थोगोनल बहुपदों के कई अन्य परिवारों को सामान्यीकृत करते हैं, जैसे कि जैक बहुपद और हॉल-लिटिलवुड बहुपद और आस्की-विल्सन बहुपद, जो विशेष मामलों के रूप में नामित 1-चर ऑर्थोगोनल बहुपदों में से अधिकांश को शामिल करते हैं। Koornwinder बहुपद कुछ गैर-कम रूट सिस्टम के Macdonald बहुपद हैं। उनके पास affine हेज बीजगणित और हिल्बर्ट योजनाओं के साथ गहरे संबंध हैं, जिनका उपयोग मैकडोनाल्ड द्वारा उनके बारे में किए गए कई अनुमानों को साबित करने के लिए किया गया था।

परिभाषा

पहले कुछ नोटेशन ठीक करें:

• R वास्तविक सदिश समष्टि V में एक परिमित मूल तंत्र है।
• आर⁺ रूट सिस्टम#पॉज़िटिव रूट्स और सिंपल रूट्स का एक विकल्प है, जो एक पॉज़िटिव वेइल कक्ष से मेल खाता है।
• W, R का वेइल समूह है।
• क्यू आर की जड़ जाली है (जड़ों द्वारा फैली जाली)।
• P, R (Q युक्त) का भार जालक है।
• एक वजन जाली # वजन के स्थान पर आदेश देना: $\mu \leq \lambda$ अगर और केवल अगर $\lambda -\mu$ रूट सिस्टम # पॉजिटिव रूट्स और सिंपल रूट्स का नॉन-नेगेटिव लीनियर कॉम्बिनेशन है।
• पी⁺ प्रमुख वज़न का सेट है: पॉज़िटिव वेइल चैंबर में P के तत्व।
• ρ वेइल वेक्टर है: सकारात्मक जड़ों का आधा योग; यह P का एक विशेष तत्व है⁺ सकारात्मक वेइल कक्ष के आंतरिक भाग में।
• F विशेषता 0 का एक क्षेत्र है, आमतौर पर परिमेय संख्याएँ।
• ए = एफ(पी) ई लिखा तत्वों के आधार के साथ, पी की समूह अंगूठी है^λ λ ∈ P के लिए।
• अगर एफ = ई^λ, तब f का अर्थ है ई^−λ, और यह रैखिकता द्वारा पूरे समूह बीजगणित तक विस्तारित है।
• एम_μ = एस_{λ ∈ Wμ}e^λ कक्षा योग है; ये तत्व सबलजेब्रा ए के लिए आधार बनाते हैं^W तत्वों का निर्धारण W द्वारा किया जाता है।
• $(a;q)_{\infty }=\prod _{r\geq 0}(1-aq^{r})$, क्यू-पोचममेर प्रतीक|अनंत क्यू-पोचममेर प्रतीक।
• $\Delta =\prod _{\alpha \in R}{(e^{\alpha };q)_{\infty } \over (te^{\alpha };q)_{\infty }}.$
• $\langle f,g\rangle =({\text{constant term of }}f{\overline {g}}\Delta )/|W|$ ए के दो तत्वों का आंतरिक उत्पाद है, कम से कम जब टी क्यू की सकारात्मक पूर्णांक शक्ति है।

'मैकडोनाल्ड बहुपद' पी_λ λ ∈ पी के लिए⁺ विशिष्ट रूप से निम्नलिखित दो शर्तों द्वारा परिभाषित हैं:

$P_{\lambda }=\sum _{\mu \leq \lambda }u_{\lambda \mu }m_{\mu }$ जहां तुम_λμ यू के साथ क्यू और टी का एक तर्कसंगत कार्य है_λλ = 1;

पी_λ और पी_μ ओर्थोगोनल हैं अगर λ<<μ।

दूसरे शब्दों में, मैकडोनाल्ड बहुपदों को ए के स्पष्ट आधार को ऑर्थोगोनलाइज़ करके प्राप्त किया जाता हैडब्ल्यू</सुप>. इन गुणों वाले बहुपदों का अस्तित्व दिखाना आसान है (किसी भी आंतरिक उत्पाद के लिए)। मैकडोनाल्ड बहुपदों की एक प्रमुख संपत्ति यह है कि वे 'ऑर्थोगोनल' हैं: 〈पी_λ, पी_μ〉 = 0 जब भी λ ≠ μ। यह परिभाषा का तुच्छ परिणाम नहीं है क्योंकि पी^{+ पूरी तरह से आदेशित नहीं है, और इसलिए इसमें बहुत सारे तत्व हैं जो अतुलनीय हैं। इस प्रकार किसी को यह जांचना चाहिए कि संबंधित बहुपद अभी भी ओर्थोगोनल हैं। ऑर्थोगोनलिटी को यह दिखा कर साबित किया जा सकता है कि मैकडोनाल्ड बहुपद ईजेनवेक्टर हैं 1-आयामी eigenspaces के साथ स्व-आसन्न ऑपरेटरों के आने-जाने के बीजगणित के लिए, और इस तथ्य का उपयोग करते हुए कि विभिन्न eigenvalues ​​​​के लिए eigenspaces ऑर्थोगोनल होना चाहिए।}

नॉन-सिंपली-लेस्ड रूट सिस्टम (बी, सी, एफ, जी) के मामले में, पैरामीटर टी को रूट की लंबाई के साथ बदलने के लिए चुना जा सकता है, जिससे मैकडोनाल्ड बहुपदों का तीन-पैरामीटर परिवार मिलता है। परिभाषा को गैर-घटित रूट सिस्टम बीसी तक भी बढ़ाया जा सकता है, जिस स्थिति में कोई छह-पैरामीटर परिवार (जड़ों की प्रत्येक कक्षा के लिए एक टी, प्लस क्यू) प्राप्त करता है, जिसे कोर्नविंदर बहुपद के रूप में जाना जाता है। मैकडोनाल्ड बहुपदों को कभी-कभी गैर-कम किए गए एफ़िन रूट सिस्टम के आधार पर मानना ​​​​बेहतर होता है। इस मामले में, affine रूट सिस्टम में जड़ों की प्रत्येक कक्षा से जुड़ा एक पैरामीटर t है, साथ ही एक पैरामीटर q भी है। जड़ों की कक्षाओं की संख्या 1 से 5 तक भिन्न हो सकती है।

उदाहरण

• यदि q = t मैकडोनाल्ड बहुपद जड़ प्रणाली के कॉम्पैक्ट समूह के प्रतिनिधित्व के वेइल वर्ण बन जाते हैं, या टाइप ए के रूट सिस्टम के मामले में शूर कार्य करता है।
• यदि q = 0 मैकडोनाल्ड बहुपद अर्ध-सरल पी-एडिक समूह, या हॉल-लिटिलवुड बहुपदों के लिए (पुनर्वर्धित) आंचलिक गोलाकार कार्य बन जाते हैं, जब रूट सिस्टम का प्रकार ए होता है।
• यदि t = 1 मैकडोनाल्ड बहुपद W कक्षाओं पर योग बन जाते हैं, जो रूट सिस्टम के प्रकार A होने पर मोनोमियल सममित कार्य होते हैं।
• यदि हम t = q रखें^α और मान लें कि q 1 की ओर जाता है तो मैकडोनाल्ड बहुपद जैक बहुपद बन जाते हैं जब रूट सिस्टम A प्रकार का होता है, और अधिक सामान्य रूट सिस्टम के लिए हेकमैन-ऑप्डम बहुपद।
• एफ़ाइन रूट सिस्टम के लिए A₁, मैकडोनाल्ड बहुपद रोजर्स बहुपद हैं।
• गैर-कम रैंक 1 के लिए प्रकार की जड़ प्रणाली (सी^∨
  ₁, सी₁), मैकडोनाल्ड बहुपद आस्की-विल्सन बहुपद हैं, जो बदले में 1 चर में ऑर्थोगोनल बहुपदों के अधिकांश नामित परिवारों को विशेष मामलों के रूप में शामिल करते हैं।
• गैर-कम किए गए एफाइन रूट सिस्टम के प्रकार के लिए (सी^∨
  _n, सी_n), मैकडोनाल्ड बहुपद कोर्नविंदर बहुपद हैं।

मैकडॉनल्ड कॉन्स्टेंट टर्म कंजेक्चर

अगर टी = क्यू^k किसी धनात्मक पूर्णांक k के लिए, तब मैकडोनाल्ड बहुपदों का मान दिया जाता है

$\langle P_{\lambda },P_{\lambda }\rangle =\prod _{\alpha \in R,\alpha >0}\prod _{0<i<k}{1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))+i} \over 1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))-i}}.$

यह मैकडोनाल्ड (1982) द्वारा डायसन अनुमान के सामान्यीकरण के रूप में अनुमान लगाया गया था, और चेरेडनिक (1995) द्वारा सभी (कम) रूट सिस्टम के लिए साबित किया गया था, जिसमें डबल एफाइन हेके बीजगणित के गुणों का उपयोग किया गया था। अनुमान पहले प्रकार ई को छोड़कर सभी जड़ प्रणालियों के लिए मामला-दर-मामला साबित हुआ था_n कई लेखकों द्वारा।

दो अन्य अनुमान हैं जो मानक अनुमान के साथ सामूहिक रूप से इस संदर्भ में मैकडोनाल्ड अनुमान के रूप में संदर्भित होते हैं: मानदंड के सूत्र के अतिरिक्त, मैकडोनाल्ड ने पी के मूल्य के लिए एक सूत्र का अनुमान लगाया_λ बिंदु पर टी^ρ, और एक सममिति

${\frac {P_{\lambda }(\dots ,q^{\mu _{i}}t^{\rho _{i}},\dots )}{P_{\lambda }(t^{\rho })}}={\frac {P_{\mu }(\dots ,q^{\lambda _{i}}t^{\rho _{i}},\dots )}{P_{\mu }(t^{\rho })}}.$

फिर से, ये सामान्य रूप से कम रूट सिस्टम के लिए सिद्ध हुए Cherednik (1995), वैन डायजेन, नौमी और साही के काम के माध्यम से शीघ्र ही बाद में बीसी मामले के विस्तार के साथ डबल एफाइन हेके बीजगणित का उपयोग करते हुए।

मैकडोनाल्ड सकारात्मकता अनुमान

प्रकार ए की जड़ प्रणालियों के मामले में_n−1 मैकडोनाल्ड बहुपद गुणांक वाले n चरों में केवल सममित बहुपद हैं जो q और t के परिमेय फलन हैं। एक निश्चित रूपांतरित संस्करण ${\widetilde {H}}_{\mu }$ मैकडोनाल्ड बहुपदों के (नीचे मैकडोनाल्ड बहुपदों के लिए #combinatorial सूत्र देखें) सममित कार्यों के स्थान का एक ऑर्थोगोनल आधार बनाते हैं $\mathbb {Q} (q,t)$, और इसलिए शूर बहुपद के संदर्भ में व्यक्त किया जा सकता है $s_{\lambda }$. गुणांक के_λμ(q,t) इन संबंधों को 'कोस्तका-मैकडोनाल्ड गुणांक' या qt-कोस्तका गुणांक कहा जाता है। मैकडोनाल्ड ने अनुमान लगाया कि कोस्तका-मैकडोनाल्ड गुणांक गैर-नकारात्मक पूर्णांक गुणांक वाले क्यू और टी में बहुपद थे। ये अनुमान अब सिद्ध हो गए हैं; सबसे कठिन और अंतिम कदम सकारात्मकता को साबित करना था, जो मार्क हाईमन (2001) द्वारा किया गया था, एन साबित करके! अनुमान|एन! अनुमान।

क्यूटी-कोस्टका गुणांक के लिए एक संयोजक सूत्र खोजने के लिए यह अभी भी बीजगणितीय संयोजक में एक केंद्रीय खुली समस्या है।

एन! अनुमान

तब! अनुमान|एन! एड्रियन गार्सिया और मार्क हैमैन के अनुमान में कहा गया है कि प्रत्येक विभाजन के लिए n स्थान का μ है

$D_{\mu }=C[\partial x,\partial y]\,\Delta _{\mu }$

के सभी उच्च आंशिक डेरिवेटिव द्वारा फैलाया गया

$\Delta _{\mu }=\det(x_{i}^{p_{j}}y_{i}^{q_{j}})_{1\leq i,j,\leq n}$

इसका आयाम n है !, जहाँ (p_j, क्यू_j) विभाजन μ के आरेख के n तत्वों के माध्यम से चलाया जाता है, जिसे गैर-ऋणात्मक पूर्णांकों के जोड़े के सबसेट के रूप में माना जाता है। उदाहरण के लिए, यदि μ n = 3 का विभाजन 3 = 2 + 1 है तो जोड़े (p_j, क्यू_j) हैं (0, 0), (0, 1), (1, 0), और स्पेस डी_μ द्वारा फैलाया जाता है

$\Delta _{\mu }=x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}$

$y_{2}-y_{3}$

$y_{3}-y_{1}$

$x_{3}-x_{2}$

$x_{1}-x_{3}$

$1$

जिसका आयाम 6 = 3! है।

मैकडोनाल्ड सकारात्मकता अनुमान और n का हैमन का प्रमाण! अनुमान में शामिल है कि एक विमान में n बिंदुओं की आइसोस्पेक्ट्रल हिल्बर्ट योजना कोहेन-मैकाले (और यहां तक ​​कि गोरेंस्टीन की अंगूठी) थी। हैमन और गार्सिया के पहले के परिणाम पहले ही दिखा चुके थे कि इसका मतलब n! अनुमान, और वह एन! अनुमान का तात्पर्य है कि कोस्तका-मैकडोनाल्ड गुणांक मॉड्यूल डी के लिए चरित्र बहुगुणों को वर्गीकृत किया गया था_μ. यह तुरंत मैकडोनाल्ड सकारात्मकता अनुमान का तात्पर्य है क्योंकि चरित्र गुणकों को गैर-ऋणात्मक पूर्णांक होना चाहिए।

इयान ग्रोजनोव्स्की और मार्क हैमन ने एलएलटी बहुपदों के लिए सकारात्मकता अनुमान को साबित करके मैकडोनाल्ड सकारात्मकता अनुमान का एक और प्रमाण पाया।

मैकडोनाल्ड बहुपदों के लिए संयोजन सूत्र

2005 में, जे. हागलंड, एम. हैमन और एन. लोहरकी मिश्रित व्याख्या का पहला प्रमाण दिया मैकडोनाल्ड बहुपद। 1988 में, आई.जी. macdonaldमैकडोनाल्ड बहुपदों (समीकरण (4.11) और (5.13)) की संयोजन व्याख्या का दूसरा प्रमाण दिया। मैकडोनाल्ड का सूत्र हैगलंड, हैमन और लोहर के काम से अलग है, बहुत कम शर्तों के साथ (यह सूत्र मैकडोनाल्ड के मूल कार्य में भी सिद्ध होता है,च। VI (7.13))। जबकि संगणना के लिए बहुत उपयोगी और अपने आप में दिलचस्प है, उनके संयोजक सूत्र तुरंत कोस्तका-मैकडोनाल्ड गुणांकों की सकारात्मकता का संकेत नहीं देते हैं। $K_{\lambda \mu }(q,t),$ जैसा कि मैकडोनाल्ड बहुपदों के अपघटन को शूर कार्यों के बजाय मोनोमियल सममित कार्यों में दिया जाता है।

रूपांतरित मैकडोनाल्ड बहुपदों में लिखा गया ${\widetilde {H}}_{\mu }$ सामान्य के बजाय $P_{\lambda }$, वे हैं

${\widetilde {H}}_{\mu }(x;q,t)=\sum _{\sigma :\mu \to \mathbb {Z} _{+}}q^{inv(\sigma )}t^{maj(\sigma )}x^{\sigma }$

जहां σ आकार μ, inv और maj की युवा झांकी की फिलिंग है, फिलिंग σ पर परिभाषित कुछ कॉम्बीनेटरियल स्टैटिस्टिक्स (फंक्शंस) हैं। यह सूत्र Macdonald बहुपदों को अपरिमित रूप से अनेक चरों में व्यक्त करता है। n चरों में बहुपद प्राप्त करने के लिए, सूत्र को केवल उन भरणों तक सीमित करें जो केवल पूर्णांकों 1, 2, ..., n का उपयोग करते हैं। शब्द एक्स^σ की व्याख्या की जानी चाहिए $x_{1}^{\sigma _{1}}x_{2}^{\sigma _{2}}\cdots$ जहां प_iसामग्री i के साथ μ भरने में बक्सों की संख्या है।

यह यंग आरेख के एक वर्ग के हाथ और पैर को दर्शाता है। भुजा उसके दायीं ओर के वर्गों की संख्या है, और पैर उसके ऊपर के वर्गों की संख्या है।

रूपांतरित मैकडोनाल्ड बहुपद ${\widetilde {H}}_{\mu }(x;q,t)$ उपर्युक्त सूत्र में शास्त्रीय मैकडोनाल्ड बहुपदों से संबंधित हैं $P_{\lambda }$ परिवर्तनों के एक क्रम के माध्यम से। सबसे पहले, मैकडोनाल्ड बहुपदों का अभिन्न रूप, निरूपित $J_{\lambda }(x;q,t)$, का पुन: स्केलिंग है $P_{\lambda }(x;q,t)$ जो गुणांकों के हरों को साफ करता है:

$J_{\lambda }(x;q,t)=\prod _{s\in D(\lambda )}(1-q^{a(s)}t^{1+l(s)})\cdot P_{\lambda }(x;q,t)$

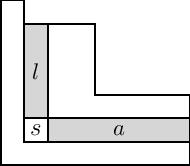
कहाँ $D(\lambda )$ के यंग आरेख में वर्गों का संग्रह है $\lambda$, और $a(s)$ और $l(s)$ वर्ग के हाथ और पैर को निरूपित करें $s$, जैसा कि चित्र में दिखाया गया है। ध्यान दें: दाहिनी ओर का चित्र झाँकी के लिए फ्रेंच संकेतन का उपयोग करता है, जो यंग आरेखों के लिए विकिपीडिया पृष्ठ पर उपयोग किए गए अंग्रेजी अंकन से लंबवत रूप से फ़्लिप किया गया है। मैकडोनाल्ड बहुपदों के अध्ययन में फ्रांसीसी संकेतन का अधिक सामान्यतः उपयोग किया जाता है।

रूपांतरित मैकडोनाल्ड बहुपद ${\widetilde {H}}_{\mu }(x;q,t)$ के रूप में परिभाषित किया जा सकता है $J_{\mu }$'एस। अपने पास

${\widetilde {H}}_{\mu }(x;q,t)=t^{-n(\mu )}J_{\mu }\left[{\frac {X}{1-t^{-1}}};q,t^{-1}\right]$

कहाँ

$n(\mu )=\sum _{i}\mu _{i}\cdot (i-1).$

उपरोक्त कोष्ठक संकेतन बहुतायत प्रतिस्थापन को दर्शाता है।

जैक फलन के लिए नोप और साही के सूत्र को सिद्ध करने के लिए इस सूत्र का उपयोग किया जा सकता है।

गैर-सममित मैकडोनाल्ड बहुपद

1995 में, मैकडोनाल्ड ने सममित मैकडोनाल्ड बहुपदों का एक गैर-सममित एनालॉग पेश किया, और सममित मैकडोनाल्ड बहुपद गैर-सममित समकक्ष से आसानी से पुनर्प्राप्त किए जा सकते हैं। अपनी मूल परिभाषा में, वह दिखाता है कि गैर-सममित मैकडोनाल्ड बहुपद का एक अनूठा परिवार है एक निश्चित आंतरिक उत्पाद के लिए बहुपद ऑर्थोगोनल, साथ ही संतोषजनक ए त्रिकोणीय संपत्ति जब मोनोमियल आधार में विस्तारित होती है।

2007 में, हैगलंड, हैमन और लोहर ने गैर-सममित मैकडोनाल्ड बहुपदों के लिए एक संयोजक सूत्र दिया।

गैर-सममित मैकडोनाल्ड बहुपद q = t = 0 लेकर Demazure वर्णों के विशेषज्ञ हैं, और प्रमुख बहुपदों के लिए जब q=t=∞.

बहिष्करण प्रक्रिया के आधार पर मिश्रित सूत्र

2018 में, सिल्वी कॉर्टील|एस. कॉर्टील, ओ. मैंडेलश्टम, और लॉरेन विलियम्स (गणितज्ञ)|एल. विलियम्स ने बहिष्करण प्रक्रिया का उपयोग सममित और गैर-सममित मैकडोनाल्ड बहुपद दोनों के प्रत्यक्ष दहनशील लक्षण वर्णन के लिए किया।उनके परिणाम हाग्लंड के पहले के काम से अलग हैं क्योंकि वे मैकडोनाल्ड बहुपदों के लिए एक रूपांतरण के बजाय सीधे एक सूत्र देते हैं। वे एक बहुपंक्ति कतार की अवधारणा विकसित करते हैं, जो गेंदों और उनके पड़ोसियों के बीच एक मानचित्रण और संयोजन लेबलिंग तंत्र के साथ गेंदों या खाली कोशिकाओं वाली एक मैट्रिक्स है। असममित मैकडोनाल्ड बहुपद तब संतुष्ट करता है:

$E_{\lambda }({\textbf {x}};q,t)=\sum _{Q}\mathrm {wt} (Q)$

जहां योग सब खत्म हो गया है $L\times n$ मल्टीलाइन प्रकार की कतारें $\lambda$ और $\mathrm {wt}$ विशिष्ट बहुपदों के लिए उन कतारों का मानचित्रण करने वाला एक भारोत्तोलन कार्य है। सममित मैकडोनाल्ड बहुपद संतुष्ट करता है:

$P_{\lambda }({\textbf {x}};q,t)=\sum _{\mu }E_{\mu }(x_{1},...,x_{n};q,t)=\sum _{\mu }\sum _{Q}\mathrm {wt} (Q)$

जहां बाहरी योग सभी विशिष्ट रचनाओं पर है $\mu$ जो के क्रमपरिवर्तन हैं $\lambda$, और आंतरिक योग पहले जैसा है।

ग्रन्थसूची

• Cherednik, Ivan (1995), "Double Affine Hecke Algebras and Macdonald's Conjectures", Annals of Mathematics, Second Series, Annals of Mathematics, 141 (1): 191–216, doi:10.2307/2118632, ISSN 0003-486X, JSTOR 2118632
• Garsia, Adriano; Remmel, Jeffrey B. (March 15, 2005), "Breakthroughs in the theory of Macdonald polynomials", PNAS, 102 (11): 3891–3894, Bibcode:2005PNAS..102.3891G, doi:10.1073/pnas.0409705102, PMC 554818, PMID 15753285
• Mark Haiman Combinatorics, symmetric functions, and Hilbert schemes Current Developments in Mathematics 2002, no. 1 (2002), 39–111.
• Haiman, Mark Notes on Macdonald polynomials and the geometry of Hilbert schemes. Symmetric functions 2001: surveys of developments and perspectives, 1–64, NATO Sci. Ser. II Math. Phys. Chem., 74, Kluwer Acad. Publ., Dordrecht, 2002.MR2059359
• Haiman, Mark (2001), "Hilbert schemes, polygraphs, and the Macdonald positivity conjecture", J. Amer. Math. Soc., 14 (4): 941–1006, arXiv:math.AG/0010246, doi:10.1090/S0894-0347-01-00373-3, S2CID 9253880
• Kirillov, A. A. (1997), "Lectures on affine Hecke algebras and Macdonald's conjectures", Bull. Amer. Math. Soc., 34 (3): 251–292, doi:10.1090/S0273-0979-97-00727-1
• Macdonald, I. G. (1982), "Some conjectures for root systems", SIAM Journal on Mathematical Analysis, 13 (6): 988–1007, doi:10.1137/0513070, ISSN 0036-1410, MR 0674768
• Macdonald, I. G. Symmetric functions and Hall polynomials. Second edition. Oxford Mathematical Monographs. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1995. x+475 pp. ISBN 0-19-853489-2 MR1354144
• Macdonald, I. G. Symmetric functions and orthogonal polynomials. Dean Jacqueline B. Lewis Memorial Lectures presented at Rutgers University, New Brunswick, NJ. University Lecture Series, 12. American Mathematical Society, Providence, RI, 1998. xvi+53 pp. ISBN 0-8218-0770-6 MR1488699
• Macdonald, I. G. Affine Hecke algebras and orthogonal polynomials. Séminaire Bourbaki 797 (1995).
• Macdonald, I. G. (2000–2001), "Orthogonal polynomials associated with root systems", Séminaire Lotharingien de Combinatoire, 45: Art. B45a, arXiv:math.QA/0011046, MR 1817334
• Macdonald, I. G. (2003), Affine Hecke algebras and orthogonal polynomials, Cambridge Tracts in Mathematics, vol. 157, Cambridge: Cambridge University Press, pp. x+175, ISBN 978-0-521-82472-9, MR 1976581

बाहरी संबंध

• Mike Zabrocki's page about Macdonald polynomials.
• Some of Haiman's papers about Macdonald polynomials.