ट्यूरिंग मशीन: Difference between revisions
(Created page with "{{Short description|Computation model defining an abstract machine}} {{other uses}} {{turing}} File:Turing Machine Model Davey 2012.jpg|alt=A physical Turing machine constru...") |
No edit summary |
||
| Line 2: | Line 2: | ||
{{other uses}} | {{other uses}} | ||
{{turing}} | {{turing}} | ||
[[File:Turing Machine Model Davey 2012.jpg|alt=A physical Turing machine constructed by Mike Davey|thumb|एक भौतिक ट्यूरिंग मशीन मॉडल। | [[File:Turing Machine Model Davey 2012.jpg|alt=A physical Turing machine constructed by Mike Davey|thumb|एक भौतिक ट्यूरिंग मशीन मॉडल। सच्चे ट्यूरिंग मशीन में दोनों तरफ असीमित टेप होगा, हालांकि, भौतिक मॉडल में केवल सीमित मात्रा में टेप हो सकता है।]] | ||
{{Automata theory}} | {{Automata theory}} | ||
एक ट्यूरिंग मशीन | एक ट्यूरिंग मशीन [[अमूर्त मशीन]] का वर्णन करने वाली संगणना का गणितीय मॉडल है<ref>Minsky 1967:107 "In his 1936 paper, A. M. Turing defined the class of abstract machines that now bear his name. A Turing machine is a finite-state machine associated with a special kind of environment -- its tape -- in which it can store (and later recover) sequences of symbols," also Stone 1972:8 where the word "machine" is in quotation marks.</ref> जो नियमों की तालिका के अनुसार टेप की पट्टी पर प्रतीकों में हेरफेर करता है।<ref>Stone 1972:8 states "This "machine" is an abstract mathematical model", also cf. Sipser 2006:137ff that describes the "Turing machine model". Rogers 1987 (1967):13 refers to "Turing's characterization", Boolos Burgess and Jeffrey 2002:25 refers to a "specific kind of idealized machine".</ref> मॉडल की सादगी के बावजूद, यह किसी भी [[कंप्यूटर एल्गोरिथ्म]] को लागू करने में सक्षम है।<ref>Sipser 2006:137 "A Turing machine can do everything that a real computer can do".</ref> | ||
ट्यूरिंग मशीन का आविष्कार 1936 में [[एलन ट्यूरिंग]] ने किया था।<ref name=Hodges-2012>{{cite book |first=Andrew | last=Hodges |author-link =Andrew Hodges |year = 2012 |title =Alan Turing: The Enigma |publisher =[[Princeton University Press]] |isbn=978-0-691-15564-7 |edition=The Centenary }}</ref><ref>The idea came to him in mid-1935 (perhaps, see more in the History section) after a question posed by [[M. H. A. Newman]] in his lectures: "Was there a definite method, or as Newman put it, a "mechanical process" which could be applied to a mathematical statement, and which would come up with the answer as to whether it was provable" (Hodges 1983:93). Turing submitted his paper on 31 May 1936 to the London Mathematical Society for its ''Proceedings'' (cf. Hodges 1983:112), but it was published in early 1937 and offprints were available in February 1937 (cf. Hodges 1983:129).</ref> जिन्होंने इसे ए-मशीन (स्वचालित मशीन) कहा।<ref>See footnote in Davis 2000:151.</ref> यह ट्यूरिंग के डॉक्टरेट सलाहकार [[अलोंजो चर्च]] थे, जिन्होंने बाद में | मशीन अनंत पर काम करती है<ref>Cf. Sipser 2002:137. Also, Rogers 1987 (1967):13 describes "a paper tape of infinite length in both directions". Minsky 1967:118 states "The tape is regarded as infinite in both directions". Boolos Burgess and Jeffrey 2002:25 include the possibility of "there is someone stationed at each end to add extra blank squares as needed".</ref> असतत गणित कोशिकाओं में विभाजित मेमोरी टेप,<ref>Cf. Rogers 1987 (1967):13. Other authors use the word "square" e.g. Boolos Burgess Jeffrey 2002:35, Minsky 1967:117, Penrose 1989:37.</ref> जिनमें से प्रत्येक मशीन के वर्णमाला (औपचारिक भाषा) कहे जाने वाले प्रतीकों के [[परिमित सेट]] से खींचे गए एकल प्रतीक को धारण कर सकता है। इसका सिर होता है, जो मशीन के संचालन के किसी भी बिंदु पर, इन कोशिकाओं में से पर स्थित होता है, और राज्य राज्यों के सीमित सेट से चुना जाता है। इसके संचालन के प्रत्येक चरण में, सिर अपने सेल में प्रतीक को पढ़ता है। फिर, प्रतीक और मशीन की अपनी वर्तमान स्थिति के आधार पर, मशीन उसी सेल में प्रतीक लिखती है, और सिर को कदम बाईं या दाईं ओर ले जाती है,<ref>Boolos Burgess Jeffry 2002:25 illustrate the machine as moving along the tape. Penrose 1989:36-37 describes himself as "uncomfortable" with an infinite tape observing that it "might be hard to shift!"; he "prefer[s] to think of the tape as representing some external environment through which our finite device can move" and after observing that the " 'movement' is a convenient way of picturing things" and then suggests that "the device receives all its input from this environment. Some variations of the Turing machine model also allow the head to stay in the same position instead of moving or halting.</ref> या गणना को रोक देता है। किस प्रतिस्थापन प्रतीक को लिखना है और किस दिशा में जाना है, यह परिमित तालिका पर आधारित है जो निर्दिष्ट करती है कि वर्तमान स्थिति के प्रत्येक संयोजन और पढ़े जाने वाले प्रतीक के लिए क्या करना है। | ||
ट्यूरिंग मशीन का आविष्कार 1936 में [[एलन ट्यूरिंग]] ने किया था।<ref name="Hodges-2012">{{cite book |first=Andrew | last=Hodges |author-link =Andrew Hodges |year = 2012 |title =Alan Turing: The Enigma |publisher =[[Princeton University Press]] |isbn=978-0-691-15564-7 |edition=The Centenary }}</ref><ref>The idea came to him in mid-1935 (perhaps, see more in the History section) after a question posed by [[M. H. A. Newman]] in his lectures: "Was there a definite method, or as Newman put it, a "mechanical process" which could be applied to a mathematical statement, and which would come up with the answer as to whether it was provable" (Hodges 1983:93). Turing submitted his paper on 31 May 1936 to the London Mathematical Society for its ''Proceedings'' (cf. Hodges 1983:112), but it was published in early 1937 and offprints were available in February 1937 (cf. Hodges 1983:129).</ref> जिन्होंने इसे ए-मशीन (स्वचालित मशीन) कहा।<ref>See footnote in Davis 2000:151.</ref> यह ट्यूरिंग के डॉक्टरेट सलाहकार [[अलोंजो चर्च]] थे, जिन्होंने बाद में समीक्षा में ट्यूरिंग मशीन शब्द गढ़ा।<ref>see note in forward to The Collected Works of Alonzo Church ({{Cite book |url=https://mitpress.mit.edu/books/collected-works-alonzo-church |title=The Collected Works of Alonzo Church |date=2019-04-23 |publisher=MIT Press |isbn=978-0-262-02564-5 |editor-last=Burge |editor-first=Tyler |location=Cambridge, MA, USA |language=en |editor-last2=Enderton |editor-first2=Herbert}})</ref> इस मॉडल के साथ, ट्यूरिंग नकारात्मक में दो प्रश्नों का उत्तर देने में सक्षम था: | |||
* क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन गोलाकार है (उदाहरण के लिए, फ्रीज, या उसके कम्प्यूटेशनल कार्य को जारी रखने में विफल)? | * क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन गोलाकार है (उदाहरण के लिए, फ्रीज, या उसके कम्प्यूटेशनल कार्य को जारी रखने में विफल)? | ||
* क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन कभी किसी दिए गए प्रतीक को प्रिंट करती है या नहीं?<ref>Turing 1936 in ''The Undecidable'' 1965:132-134; Turing's definition of "circular" is found on page 119.</ref><ref>{{cite journal |first=Alan Mathison |last=Turing |title=On Computable Numbers, with an Application to the ''Entscheidungsproblem'' |journal=Proceedings of the London Mathematical Society |series=Series 2 |volume=42 |number=1 |pages=230–265 |year=1937 | doi=10.1112/plms/s2-42.1.230 |s2cid=73712 }} — Reprint at: {{cite web | * क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन कभी किसी दिए गए प्रतीक को प्रिंट करती है या नहीं?<ref>Turing 1936 in ''The Undecidable'' 1965:132-134; Turing's definition of "circular" is found on page 119.</ref><ref>{{cite journal |first=Alan Mathison |last=Turing |title=On Computable Numbers, with an Application to the ''Entscheidungsproblem'' |journal=Proceedings of the London Mathematical Society |series=Series 2 |volume=42 |number=1 |pages=230–265 |year=1937 | doi=10.1112/plms/s2-42.1.230 |s2cid=73712 }} — Reprint at: {{cite web | ||
|url=http://www.turingarchive.org/viewer/?id=466&title=01e |access-date=9 July 2020 |first=Alan |last=Turing |title=On computable numbers, with an application to the Entscheidungsproblem |website=The Turing Digital Archive }}</ref> | |url=http://www.turingarchive.org/viewer/?id=466&title=01e |access-date=9 July 2020 |first=Alan |last=Turing |title=On computable numbers, with an application to the Entscheidungsproblem |website=The Turing Digital Archive }}</ref> | ||
इस प्रकार मनमाना संगणना करने में सक्षम | इस प्रकार मनमाना संगणना करने में सक्षम बहुत ही सरल उपकरण का गणितीय विवरण प्रदान करके, वह सामान्य रूप से संगणना के गुणों को साबित करने में सक्षम था - और विशेष रूप से, Entscheidungsproblem ('[[निर्णय समस्या]]') की संगणनीयता।<ref>Turing 1936 in ''The Undecidable'' 1965:145</ref> | ||
ट्यूरिंग मशीनों ने यांत्रिक संगणना की शक्ति पर मौलिक सीमाओं के अस्तित्व को सिद्ध किया।<ref>Sipser 2006:137 observes that "A Turing machine can do everything that a real computer can do. Nevertheless, even a Turing machine cannot solve certain problems. In a very real sense, these problems are beyond the theoretical limits of computation."</ref> जबकि वे मनमाना संगणना व्यक्त कर सकते हैं, उनका न्यूनतम डिजाइन उन्हें व्यवहार में गणना के लिए अनुपयुक्त बनाता है: वास्तविक दुनिया के [[संगणक]] विभिन्न डिजाइनों पर आधारित होते हैं, जो ट्यूरिंग मशीनों के विपरीत, [[रैंडम एक्सेस मेमोरी]] का उपयोग करते हैं। | ट्यूरिंग मशीनों ने यांत्रिक संगणना की शक्ति पर मौलिक सीमाओं के अस्तित्व को सिद्ध किया।<ref>Sipser 2006:137 observes that "A Turing machine can do everything that a real computer can do. Nevertheless, even a Turing machine cannot solve certain problems. In a very real sense, these problems are beyond the theoretical limits of computation."</ref> जबकि वे मनमाना संगणना व्यक्त कर सकते हैं, उनका न्यूनतम डिजाइन उन्हें व्यवहार में गणना के लिए अनुपयुक्त बनाता है: वास्तविक दुनिया के [[संगणक]] विभिन्न डिजाइनों पर आधारित होते हैं, जो ट्यूरिंग मशीनों के विपरीत, [[रैंडम एक्सेस मेमोरी]] का उपयोग करते हैं। | ||
[[ट्यूरिंग पूर्णता]] | [[ट्यूरिंग पूर्णता]] ट्यूरिंग मशीन का अनुकरण करने के लिए निर्देशों की प्रणाली की क्षमता है। प्रोग्रामिंग भाषा जो ट्यूरिंग पूर्ण है, सैद्धांतिक रूप से कंप्यूटर द्वारा पूरा किए जाने वाले सभी कार्यों को व्यक्त करने में सक्षम है; यदि परिमित स्मृति की सीमाओं को नजरअंदाज कर दिया जाए तो लगभग सभी प्रोग्रामिंग भाषाएं ट्यूरिंग पूर्ण हैं। | ||
== सिंहावलोकन == | == सिंहावलोकन == | ||
एक ट्यूरिंग मशीन | एक ट्यूरिंग मशीन केंद्रीय प्रसंस्करण इकाई (सीपीयू) का सामान्य उदाहरण है जो डेटा को स्टोर करने के लिए अनुक्रमिक मेमोरी का उपयोग करके कैननिकल मशीन के साथ कंप्यूटर द्वारा किए गए सभी डेटा हेरफेर को नियंत्रित करता है। अधिक विशेष रूप से, यह मशीन ([[आटोमैटिक मशीन]]) है जो वर्णमाला (औपचारिक भाषाओं) के वैध स्ट्रिंग्स के कुछ मनमाने उपसमुच्चय की [[[[गणना]]]] करने में सक्षम है; ये तार [[पुनरावर्ती गणना योग्य सेट]] का हिस्सा हैं। ट्यूरिंग मशीन में अनंत लंबाई का टेप होता है जिस पर यह पढ़ने और लिखने का कार्य कर सकता है। | ||
एक [[ब्लैक बॉक्स]] मानकर, ट्यूरिंग मशीन यह नहीं जान सकती है कि क्या यह अंततः किसी दिए गए प्रोग्राम के साथ सबसेट के किसी | एक [[ब्लैक बॉक्स]] मानकर, ट्यूरिंग मशीन यह नहीं जान सकती है कि क्या यह अंततः किसी दिए गए प्रोग्राम के साथ सबसेट के किसी विशिष्ट स्ट्रिंग की गणना करेगी। यह इस तथ्य के कारण है कि हॉल्टिंग समस्या हल नहीं हो सकती है, जिसका कंप्यूटिंग की सैद्धांतिक सीमाओं के लिए प्रमुख निहितार्थ है। | ||
ट्यूरिंग मशीन | ट्यूरिंग मशीन [[अप्रतिबंधित व्याकरण]] को संसाधित करने में सक्षम है, जिसका अर्थ है कि यह अनंत तरीकों से पहले क्रम के [[तर्क]] का मजबूती से मूल्यांकन करने में सक्षम है। यह लैम्ब्डा कैलकुस के माध्यम से प्रसिद्ध रूप से प्रदर्शित होता है। | ||
एक ट्यूरिंग मशीन जो किसी अन्य ट्यूरिंग मशीन का अनुकरण करने में सक्षम है, उसे [[यूनिवर्सल ट्यूरिंग मशीन]] (UTM, या बस | एक ट्यूरिंग मशीन जो किसी अन्य ट्यूरिंग मशीन का अनुकरण करने में सक्षम है, उसे [[यूनिवर्सल ट्यूरिंग मशीन]] (UTM, या बस यूनिवर्सल मशीन) कहा जाता है। समान सार्वभौमिक प्रकृति के साथ अधिक गणितीय रूप से उन्मुख परिभाषा अलोंजो चर्च द्वारा पेश की गई थी, जिसका [[लैम्ब्डा कैलकुलस]] पर काम [[चर्च-ट्यूरिंग थीसिस]] के रूप में ज्ञात गणना के औपचारिक सिद्धांत में ट्यूरिंग के साथ जुड़ा हुआ है। थीसिस में कहा गया है कि ट्यूरिंग मशीनें वास्तव में तर्क और गणित में प्रभावी तरीकों की अनौपचारिक धारणा को पकड़ती हैं, और मॉडल प्रदान करती हैं जिसके माध्यम से कोई [[कलन विधि]] या यांत्रिक प्रक्रिया के बारे में तर्क कर सकता है। उनकी अमूर्त मशीन का अध्ययन करने से [[कंप्यूटर विज्ञान]] और [[कम्प्यूटेशनल जटिलता सिद्धांत]] में कई अंतर्दृष्टि प्राप्त होती है। | ||
=== भौतिक विवरण === | === भौतिक विवरण === | ||
| Line 41: | Line 43: | ||
== विवरण == | == विवरण == | ||
{{for|visualizations of Turing machines|Turing machine gallery}} | {{for|visualizations of Turing machines|Turing machine gallery}} | ||
ट्यूरिंग मशीन गणितीय रूप से | ट्यूरिंग मशीन गणितीय रूप से मशीन का मॉडल बनाती है जो यांत्रिक रूप से टेप पर चलती है। इस टेप पर प्रतीक होते हैं, जिन्हें मशीन बार में टेप हेड का उपयोग करके पढ़ और लिख सकती है। ऑपरेशन पूरी तरह से प्राथमिक निर्देशों के परिमित सेट द्वारा निर्धारित किया जाता है जैसे कि राज्य 42 में, यदि देखा गया प्रतीक 0 है, तो 1 लिखें; यदि देखा गया प्रतीक 1 है, तो स्थिति 17 में बदलें; स्थिति 17 में, यदि देखा गया प्रतीक 0 है, तो 1 लिखें और स्थिति 6 में बदलें; आदि मूल लेख में (संगणनीय संख्याओं पर, Entscheidungsproblem के लिए आवेदन के साथ, #The Entscheidungsproblem (निर्णय समस्या) भी देखें): हिल्बर्ट का 1900 का दसवां प्रश्न), ट्यूरिंग तंत्र की कल्पना नहीं करता है, लेकिन व्यक्ति जिसे वह कंप्यूटर कहता है , जो इन नियतात्मक यांत्रिक नियमों को गुलामी से निष्पादित करता है (या जैसा कि ट्यूरिंग इसे कहते हैं, अपमानजनक तरीके से)। | ||
[[File:Turing machine 2a.svg|thumb|right|300px|सिर हमेशा टेप के | [[File:Turing machine 2a.svg|thumb|right|300px|सिर हमेशा टेप के विशेष वर्ग के ऊपर होता है; वर्गों का केवल परिमित विस्तार दिखाया गया है। प्रदर्शन करने का निर्देश (q<sub>4</sub>) स्कैन किए गए वर्ग पर दिखाया गया है। (ड्राइंग आफ्टर क्लेन (1952) पृष्ठ 375।)]] | ||
[[File:Turing machine 2b.svg|thumb|right|300px|यहाँ, आंतरिक स्थिति (q<sub>1</sub>) सिर के अंदर दिखाया गया है, और चित्रण टेप को अनंत और 0 से पहले से भरे हुए के रूप में वर्णित करता है, प्रतीक रिक्त के रूप में कार्य करता है। सिस्टम की पूर्ण स्थिति (इसकी पूर्ण कॉन्फ़िगरेशन) में आंतरिक स्थिति, टेप पर कोई भी गैर-रिक्त प्रतीक (इस चित्रण 11B में), और रिक्त स्थान सहित उन प्रतीकों के सापेक्ष सिर की स्थिति, यानी 011B शामिल हैं। (मिंस्की के बाद का चित्र (1967) पृष्ठ 121।)]]अधिक स्पष्ट रूप से, | [[File:Turing machine 2b.svg|thumb|right|300px|यहाँ, आंतरिक स्थिति (q<sub>1</sub>) सिर के अंदर दिखाया गया है, और चित्रण टेप को अनंत और 0 से पहले से भरे हुए के रूप में वर्णित करता है, प्रतीक रिक्त के रूप में कार्य करता है। सिस्टम की पूर्ण स्थिति (इसकी पूर्ण कॉन्फ़िगरेशन) में आंतरिक स्थिति, टेप पर कोई भी गैर-रिक्त प्रतीक (इस चित्रण 11B में), और रिक्त स्थान सहित उन प्रतीकों के सापेक्ष सिर की स्थिति, यानी 011B शामिल हैं। (मिंस्की के बाद का चित्र (1967) पृष्ठ 121।)]]अधिक स्पष्ट रूप से, ट्यूरिंग मशीन में निम्न शामिल हैं: | ||
* कोशिकाओं में विभाजित | * कोशिकाओं में विभाजित टेप, दूसरे के बगल में। प्रत्येक कोशिका में कुछ परिमित वर्णमाला से प्रतीक होता है। वर्णमाला में विशेष रिक्त प्रतीक (यहाँ '0' के रूप में लिखा गया है) और या अधिक अन्य प्रतीक हैं। यह माना जाता है कि टेप मनमाने ढंग से बायीं ओर और दायीं ओर बढ़ाया जा सकता है, ताकि ट्यूरिंग मशीन को हमेशा उतनी ही टेप की आपूर्ति की जा सके जितनी इसकी गणना के लिए आवश्यक है। जिन कक्षों को पहले नहीं लिखा गया है उन्हें रिक्त प्रतीक से भरा माना जाता है। कुछ मॉडलों में टेप का बायां सिरा विशेष प्रतीक के साथ चिह्नित होता है; टेप फैली हुई है या अनिश्चित रूप से दाईं ओर फैली हुई है। | ||
* एक सिर जो टेप पर प्रतीकों को पढ़ और लिख सकता है और टेप को | * एक सिर जो टेप पर प्रतीकों को पढ़ और लिख सकता है और टेप को बार में (और केवल एक) सेल को बाएं और दाएं घुमा सकता है। कुछ मॉडलों में सिर हिलता है और टेप स्थिर रहता है। | ||
* एक राज्य रजिस्टर जो ट्यूरिंग मशीन की स्थिति को संग्रहीत करता है, बहुत से में से एक। इनमें से | * एक राज्य रजिस्टर जो ट्यूरिंग मशीन की स्थिति को संग्रहीत करता है, बहुत से में से एक। इनमें से स्पेशल स्टार्ट स्टेट है जिसके साथ स्टेट रजिस्टर को इनिशियलाइज़ किया जाता है। ये राज्य, ट्यूरिंग लिखते हैं, मन की उस स्थिति को प्रतिस्थापित करते हैं जो संगणना करने वाला व्यक्ति सामान्य रूप से होगा। | ||
* एक परिमित तालिका<ref>Occasionally called an ''action table'' or ''transition function''.</ref> निर्देशों का<ref>Usually quintuples [5-tuples]: q<sub>i</sub>a<sub>j</sub>→q<sub>i1</sub>a<sub>j1</sub>d<sub>k</sub>, but sometimes quadruples [4-tuples].</ref> वह, दिया गया राज्य (q<sub>i</sub>) मशीन वर्तमान में है और प्रतीक (a<sub>j</sub>) यह टेप पर पढ़ रहा है (प्रतीक वर्तमान में सिर के नीचे), मशीन को अनुक्रम में निम्नलिखित करने के लिए कहता है (5-ट्यूपल मॉडल के लिए): | * एक परिमित तालिका<ref>Occasionally called an ''action table'' or ''transition function''.</ref> निर्देशों का<ref>Usually quintuples [5-tuples]: q<sub>i</sub>a<sub>j</sub>→q<sub>i1</sub>a<sub>j1</sub>d<sub>k</sub>, but sometimes quadruples [4-tuples].</ref> वह, दिया गया राज्य (q<sub>i</sub>) मशीन वर्तमान में है और प्रतीक (a<sub>j</sub>) यह टेप पर पढ़ रहा है (प्रतीक वर्तमान में सिर के नीचे), मशीन को अनुक्रम में निम्नलिखित करने के लिए कहता है (5-ट्यूपल मॉडल के लिए): | ||
# या तो मिटा दें या | # या तो मिटा दें या प्रतीक लिखें (ए की जगह<sub>j</sub> के साथ<sub>j1</sub>). | ||
# सिर को हिलाएं (जो डी द्वारा वर्णित है<sub>k</sub> और मान हो सकते हैं: 'L' | # सिर को हिलाएं (जो डी द्वारा वर्णित है<sub>k</sub> और मान हो सकते हैं: 'L' कदम बाएं के लिए या 'R' कदम दाएं के लिए या 'N' ही स्थान पर रहने के लिए)। | ||
# निर्धारित के अनुसार समान या नई स्थिति मान लें (राज्य q पर जाएं<sub>i1</sub>). | # निर्धारित के अनुसार समान या नई स्थिति मान लें (राज्य q पर जाएं<sub>i1</sub>). | ||
4-ट्यूपल मॉडल में, किसी प्रतीक को मिटाना या लिखना (a<sub>j1</sub>) और सिर को बाएँ या दाएँ घुमाना (d<sub>k</sub>) अलग निर्देशों के रूप में निर्दिष्ट हैं। तालिका मशीन को (ia) मिटाने या | 4-ट्यूपल मॉडल में, किसी प्रतीक को मिटाना या लिखना (a<sub>j1</sub>) और सिर को बाएँ या दाएँ घुमाना (d<sub>k</sub>) अलग निर्देशों के रूप में निर्दिष्ट हैं। तालिका मशीन को (ia) मिटाने या प्रतीक लिखने या (ib) सिर को बाएँ या दाएँ ले जाने के लिए कहती है, और फिर (ii) उसी या नई स्थिति को निर्धारित करती है, लेकिन दोनों क्रियाओं (ia) और (ib) को नहीं ) उसी निर्देश में। कुछ मॉडलों में, यदि प्रतीक और स्थिति के वर्तमान संयोजन के लिए तालिका में कोई प्रविष्टि नहीं है, तो मशीन रुक जाएगी; अन्य मॉडलों को भरने के लिए सभी प्रविष्टियों की आवश्यकता होती है। | ||
मशीन का प्रत्येक भाग (अर्थात इसकी स्थिति, प्रतीक-संग्रह, और किसी भी समय प्रयुक्त टेप) और इसकी क्रियाएं (जैसे मुद्रण, मिटाना और टेप गति) परिमित, असतत और विशिष्ट है; यह असीमित मात्रा में टेप और रनटाइम है जो इसे [[कंप्यूटर भंडारण]] की असीमित मात्रा देता है। | मशीन का प्रत्येक भाग (अर्थात इसकी स्थिति, प्रतीक-संग्रह, और किसी भी समय प्रयुक्त टेप) और इसकी क्रियाएं (जैसे मुद्रण, मिटाना और टेप गति) परिमित, असतत और विशिष्ट है; यह असीमित मात्रा में टेप और रनटाइम है जो इसे [[कंप्यूटर भंडारण]] की असीमित मात्रा देता है। | ||
== औपचारिक परिभाषा == | == औपचारिक परिभाषा == | ||
अगले {{harvtxt|Hopcroft|Ullman|1979|p=148}}, | अगले {{harvtxt|Hopcroft|Ullman|1979|p=148}}, (एक-टेप) ट्यूरिंग मशीन को औपचारिक रूप से 7-[[टपल]] के रूप में परिभाषित किया जा सकता है <math>M = \langle Q, \Gamma, b, \Sigma, \delta, q_0, F \rangle</math> कहाँ पे | ||
* <math>\Gamma</math> टेप वर्णमाला प्रतीकों का | * <math>\Gamma</math> टेप वर्णमाला प्रतीकों का परिमित, गैर-खाली सेट है; | ||
* <math>b \in \Gamma</math> रिक्त प्रतीक है (गणना के दौरान किसी भी चरण में असीम रूप से अक्सर टेप पर होने की अनुमति देने वाला एकमात्र प्रतीक); | * <math>b \in \Gamma</math> रिक्त प्रतीक है (गणना के दौरान किसी भी चरण में असीम रूप से अक्सर टेप पर होने की अनुमति देने वाला एकमात्र प्रतीक); | ||
* <math>\Sigma\subseteq\Gamma\setminus\{b\}</math> इनपुट प्रतीकों का सेट है, यानी, प्रारंभिक टेप सामग्री में दिखाई देने वाले प्रतीकों का सेट; | * <math>\Sigma\subseteq\Gamma\setminus\{b\}</math> इनपुट प्रतीकों का सेट है, यानी, प्रारंभिक टेप सामग्री में दिखाई देने वाले प्रतीकों का सेट; | ||
* <math>Q</math> राज्यों का | * <math>Q</math> राज्यों का परिमित, गैर-रिक्त सेट है; | ||
* <math>q_0 \in Q</math> प्रारंभिक अवस्था है; | * <math>q_0 \in Q</math> प्रारंभिक अवस्था है; | ||
* <math>F \subseteq Q</math> अंतिम राज्यों या स्वीकार करने वाले राज्यों का सेट है। कहा जाता है कि प्रारंभिक टेप की सामग्री द्वारा स्वीकार की जाती है <math>M</math> अगर यह अंततः | * <math>F \subseteq Q</math> अंतिम राज्यों या स्वीकार करने वाले राज्यों का सेट है। कहा जाता है कि प्रारंभिक टेप की सामग्री द्वारा स्वीकार की जाती है <math>M</math> अगर यह अंततः राज्य में रुकता है <math>F</math>. | ||
* <math>\delta: (Q \setminus F) \times \Gamma \not\to Q \times \Gamma \times \{L,R\}</math> | * <math>\delta: (Q \setminus F) \times \Gamma \not\to Q \times \Gamma \times \{L,R\}</math> आंशिक कार्य है जिसे [[राज्य संक्रमण प्रणाली]] कहा जाता है, जहाँ L लेफ्ट शिफ्ट है, R राइट शिफ्ट है। अगर <math>\delta</math> वर्तमान स्थिति और वर्तमान टेप प्रतीक पर परिभाषित नहीं है, तो मशीन रुक जाती है;<ref>p.149; in particular, Hopcroft and Ullman assume that <math>\delta</math> is undefined on all states from <math>F</math></ref> सहजता से, संक्रमण फ़ंक्शन वर्तमान स्थिति से प्रेषित अगले राज्य को निर्दिष्ट करता है, जो प्रतीक सिर द्वारा इंगित वर्तमान प्रतीक को अधिलेखित करता है, और अगला सिर आंदोलन। | ||
[[File:Busy Beaver 3 State.png|thumb|3-राज्य व्यस्त ऊदबिलाव। ब्लैक आइकन स्थान और सिर की स्थिति का प्रतिनिधित्व करते हैं; वर्ग रंग 1s (नारंगी) और 0s (सफेद) का प्रतिनिधित्व करते हैं; समय नीचे की ओर HALT अवस्था तक ऊपर से लंबवत रूप से आगे बढ़ता है।]]इसके अलावा, अस्वीकृति को और अधिक स्पष्ट करने के लिए ट्यूरिंग मशीन में | [[File:Busy Beaver 3 State.png|thumb|3-राज्य व्यस्त ऊदबिलाव। ब्लैक आइकन स्थान और सिर की स्थिति का प्रतिनिधित्व करते हैं; वर्ग रंग 1s (नारंगी) और 0s (सफेद) का प्रतिनिधित्व करते हैं; समय नीचे की ओर HALT अवस्था तक ऊपर से लंबवत रूप से आगे बढ़ता है।]]इसके अलावा, अस्वीकृति को और अधिक स्पष्ट करने के लिए ट्यूरिंग मशीन में अस्वीकार स्थिति भी हो सकती है। उस स्थिति में तीन संभावनाएँ हैं: स्वीकार करना, अस्वीकार करना और हमेशा के लिए दौड़ना। अन्य संभावना यह है कि टेप पर अंतिम मानों को आउटपुट माना जाए। हालाँकि, यदि एकमात्र आउटपुट अंतिम स्थिति है, तो मशीन समाप्त हो जाती है (या कभी रुकती नहीं है), मशीन अभी भी प्रभावी रूप से पूर्णांक में ले कर लंबी स्ट्रिंग का उत्पादन कर सकती है जो यह बताती है कि आउटपुट के लिए स्ट्रिंग का कौन सा हिस्सा है। | ||
दिशाओं के सेट के तीसरे तत्व के रूप में | दिशाओं के सेट के तीसरे तत्व के रूप में अपेक्षाकृत असामान्य संस्करण कोई बदलाव की अनुमति नहीं देता है, एन कहते हैं <math>\{L,R\}</math>. | ||
3-राज्य व्यस्त बीवर के लिए 7-ट्यूपल इस तरह दिखता है ([[ट्यूरिंग मशीन के उदाहरण]] | 3-राज्य व्यस्त बीवर के लिए 7-ट्यूपल इस तरह दिखता है ([[ट्यूरिंग मशीन के उदाहरण]] में इस व्यस्त बीवर के बारे में और देखें): | ||
* <math>Q = \{ \mbox{A}, \mbox{B}, \mbox{C}, \mbox{HALT} \}</math> (राज्य); | * <math>Q = \{ \mbox{A}, \mbox{B}, \mbox{C}, \mbox{HALT} \}</math> (राज्य); | ||
* <math>\Gamma = \{ 0, 1 \}</math> (टेप वर्णमाला प्रतीक); | * <math>\Gamma = \{ 0, 1 \}</math> (टेप वर्णमाला प्रतीक); | ||
| Line 127: | Line 129: | ||
उदाहरण के लिए, | उदाहरण के लिए, | ||
* प्रतीकों को वास्तव में कैसा दिखता है, और प्रतीकों को अनिश्चित काल तक पढ़ने और लिखने का | * प्रतीकों को वास्तव में कैसा दिखता है, और प्रतीकों को अनिश्चित काल तक पढ़ने और लिखने का असफल तरीका है, इस पर कई निर्णय लेने की आवश्यकता होगी। | ||
* बाएँ और दाएँ शिफ्ट करने से टेप हेड को टेप पर शिफ्ट किया जा सकता है, लेकिन जब वास्तव में ट्यूरिंग मशीन का निर्माण किया जाता है तो टेप को हेड के नीचे आगे और पीछे स्लाइड करना अधिक व्यावहारिक होता है। | * बाएँ और दाएँ शिफ्ट करने से टेप हेड को टेप पर शिफ्ट किया जा सकता है, लेकिन जब वास्तव में ट्यूरिंग मशीन का निर्माण किया जाता है तो टेप को हेड के नीचे आगे और पीछे स्लाइड करना अधिक व्यावहारिक होता है। | ||
* टेप परिमित हो सकता है, और स्वचालित रूप से आवश्यकतानुसार रिक्त स्थान के साथ विस्तारित हो सकता है (जो गणितीय परिभाषा के सबसे करीब है), लेकिन यह सोचना अधिक सामान्य है कि | * टेप परिमित हो सकता है, और स्वचालित रूप से आवश्यकतानुसार रिक्त स्थान के साथ विस्तारित हो सकता है (जो गणितीय परिभाषा के सबसे करीब है), लेकिन यह सोचना अधिक सामान्य है कि या दोनों सिरों पर असीम रूप से फैला हुआ है और रिक्त स्थान को छोड़कर पहले से भरा हुआ है स्पष्ट रूप से दिया गया परिमित टुकड़ा टेप हेड चालू है। (यह, निश्चित रूप से, व्यवहार में लागू करने योग्य नहीं है।) टेप को लंबाई में तय नहीं किया जा सकता है, क्योंकि यह दी गई परिभाषा के अनुरूप नहीं होगा और गंभीर रूप से संगणना की सीमा को सीमित कर देगा जो मशीन रैखिक परिबद्ध ऑटोमेटन के लिए कर सकती है यदि टेप इनपुट आकार, या परिमित-राज्य मशीन के समानुपाती था यदि यह सख्ती से निश्चित-लंबाई थी। | ||
=== वैकल्पिक परिभाषाएं === | === वैकल्पिक परिभाषाएं === | ||
तर्कों या प्रमाणों को आसान या स्पष्ट बनाने के लिए साहित्य में परिभाषाएँ कभी-कभी थोड़ी भिन्न होती हैं, लेकिन यह हमेशा इस तरह से किया जाता है कि परिणामी मशीन में समान कम्प्यूटेशनल शक्ति हो। उदाहरण के लिए, सेट से बदला जा सकता है <math>\{L,R\}</math> को <math>\{L,R,N\}</math>, जहाँ N (कोई नहीं या कोई ऑपरेशन नहीं) मशीन को बाएँ या दाएँ चलने के बजाय उसी टेप सेल पर रहने की अनुमति देगा। इससे मशीन की कम्प्यूटेशनल शक्ति में वृद्धि नहीं होगी। | तर्कों या प्रमाणों को आसान या स्पष्ट बनाने के लिए साहित्य में परिभाषाएँ कभी-कभी थोड़ी भिन्न होती हैं, लेकिन यह हमेशा इस तरह से किया जाता है कि परिणामी मशीन में समान कम्प्यूटेशनल शक्ति हो। उदाहरण के लिए, सेट से बदला जा सकता है <math>\{L,R\}</math> को <math>\{L,R,N\}</math>, जहाँ N (कोई नहीं या कोई ऑपरेशन नहीं) मशीन को बाएँ या दाएँ चलने के बजाय उसी टेप सेल पर रहने की अनुमति देगा। इससे मशीन की कम्प्यूटेशनल शक्ति में वृद्धि नहीं होगी। | ||
ट्यूरिंग/डेविस के सम्मेलन के अनुसार, ट्यूरिंग टेबल में प्रत्येक ट्यूरिंग निर्देश को नौ 5-टुपल्स में से | ट्यूरिंग/डेविस के सम्मेलन के अनुसार, ट्यूरिंग टेबल में प्रत्येक ट्यूरिंग निर्देश को नौ 5-टुपल्स में से द्वारा सबसे आम परंपरा का प्रतिनिधित्व करता है (ट्यूरिंग (1936) द अनडिसिडेबल में, पृष्ठ 126–127 और डेविस (2000) पृष्ठ 152) : | ||
: (परिभाषा 1): '(क्यू<sub>i</sub>, एस<sub>j</sub>, एस<sub>k</sub>/ई/एन, एल/आर/एन, क्यू<sub>m</sub>) | : (परिभाषा 1): '(क्यू<sub>i</sub>, एस<sub>j</sub>, एस<sub>k</sub>/ई/एन, एल/आर/एन, क्यू<sub>m</sub>) | ||
:: (वर्तमान स्थिति क्यू<sub>i</sub>, प्रतीक स्कैन एस<sub>j</sub>, प्रिंट प्रतीक एस<sub>k</sub>/erase E/none N , Move_tape_one_square बाएँ L/दाएँ R/none N , नई अवस्था q<sub>m</sub>) | :: (वर्तमान स्थिति क्यू<sub>i</sub>, प्रतीक स्कैन एस<sub>j</sub>, प्रिंट प्रतीक एस<sub>k</sub>/erase E/none N , Move_tape_one_square बाएँ L/दाएँ R/none N , नई अवस्था q<sub>m</sub>) | ||
अन्य लेखक (मिंस्की (1967) पृष्ठ 119, होपक्रॉफ्ट और उल्मैन (1979) पृष्ठ 158, स्टोन (1972) पृष्ठ 9) नए राज्य क्यू के साथ | अन्य लेखक (मिंस्की (1967) पृष्ठ 119, होपक्रॉफ्ट और उल्मैन (1979) पृष्ठ 158, स्टोन (1972) पृष्ठ 9) नए राज्य क्यू के साथ अलग सम्मेलन को अपनाते हैं<sub>m</sub>स्कैन किए गए प्रतीक S के तुरंत बाद सूचीबद्ध<sub>j</sub>: | ||
: (परिभाषा 2): (क्यू<sub>i</sub>, एस<sub>j</sub>, क्यू<sub>m</sub>, एस<sub>k</sub>/ई/एन, एल/आर/एन) | : (परिभाषा 2): (क्यू<sub>i</sub>, एस<sub>j</sub>, क्यू<sub>m</sub>, एस<sub>k</sub>/ई/एन, एल/आर/एन) | ||
:: (वर्तमान स्थिति क्यू<sub>i</sub>, प्रतीक स्कैन एस<sub>j</sub>, नया राज्य क्यू<sub>m</sub>, प्रिंट प्रतीक एस<sub>k</sub>/मिटाना ई/कोई नहीं एन, चाल_टेप_एक_वर्ग बाएं एल/दाएं आर/कोई नहीं एन) | :: (वर्तमान स्थिति क्यू<sub>i</sub>, प्रतीक स्कैन एस<sub>j</sub>, नया राज्य क्यू<sub>m</sub>, प्रिंट प्रतीक एस<sub>k</sub>/मिटाना ई/कोई नहीं एन, चाल_टेप_एक_वर्ग बाएं एल/दाएं आर/कोई नहीं एन) | ||
| Line 309: | Line 311: | ||
किसी भी ट्यूरिंग टेबल (निर्देशों की सूची) का निर्माण उपरोक्त नौ 5-टुपल्स से किया जा सकता है। तकनीकी कारणों से, तीन गैर-मुद्रण या एन निर्देश (4, 5, 6) को आमतौर पर समाप्त किया जा सकता है। उदाहरण के लिए ट्यूरिंग मशीन के उदाहरण देखें। | किसी भी ट्यूरिंग टेबल (निर्देशों की सूची) का निर्माण उपरोक्त नौ 5-टुपल्स से किया जा सकता है। तकनीकी कारणों से, तीन गैर-मुद्रण या एन निर्देश (4, 5, 6) को आमतौर पर समाप्त किया जा सकता है। उदाहरण के लिए ट्यूरिंग मशीन के उदाहरण देखें। | ||
कम अक्सर 4-ट्यूपल्स का उपयोग होता है: ये ट्यूरिंग निर्देशों (cf. पोस्ट (1947), बूलोस और जेफरी (1974, 1999), डेविस-सिगल-वेयुकर (1994)) के | कम अक्सर 4-ट्यूपल्स का उपयोग होता है: ये ट्यूरिंग निर्देशों (cf. पोस्ट (1947), बूलोस और जेफरी (1974, 1999), डेविस-सिगल-वेयुकर (1994)) के और परमाणुकरण का प्रतिनिधित्व करते हैं; पोस्ट-ट्यूरिंग मशीन पर और देखें। | ||
=== राज्य === | === राज्य === | ||
ट्यूरिंग मशीनों के संदर्भ में प्रयुक्त राज्य शब्द भ्रम का स्रोत हो सकता है, क्योंकि इसका अर्थ दो चीजें हो सकता है। ट्यूरिंग के बाद के अधिकांश टिप्पणीकारों ने प्रदर्शन करने के लिए वर्तमान निर्देश के नाम / पदनाम के लिए राज्य का उपयोग किया है - अर्थात। राज्य रजिस्टर की सामग्री। लेकिन ट्यूरिंग (1936) ने मशीन के एम-कॉन्फ़िगरेशन और मशीन की (या व्यक्ति की) गणना के माध्यम से प्रगति की स्थिति - कुल प्रणाली की वर्तमान स्थिति के रिकॉर्ड के बीच | ट्यूरिंग मशीनों के संदर्भ में प्रयुक्त राज्य शब्द भ्रम का स्रोत हो सकता है, क्योंकि इसका अर्थ दो चीजें हो सकता है। ट्यूरिंग के बाद के अधिकांश टिप्पणीकारों ने प्रदर्शन करने के लिए वर्तमान निर्देश के नाम / पदनाम के लिए राज्य का उपयोग किया है - अर्थात। राज्य रजिस्टर की सामग्री। लेकिन ट्यूरिंग (1936) ने मशीन के एम-कॉन्फ़िगरेशन और मशीन की (या व्यक्ति की) गणना के माध्यम से प्रगति की स्थिति - कुल प्रणाली की वर्तमान स्थिति के रिकॉर्ड के बीच मजबूत अंतर बनाया। जिसे ट्यूरिंग ने राज्य सूत्र कहा है उसमें वर्तमान निर्देश और टेप पर सभी प्रतीक शामिल हैं: | ||
{{quote|Thus the state of progress of the computation at any stage is completely determined by the note of instructions and the symbols on the tape. That is, the ''state of the system'' may be described by a single expression (sequence of symbols) consisting of the symbols on the tape followed by Δ (which is supposed to not to appear elsewhere) and then by the note of instructions. This expression is called the "state formula".|''The Undecidable'', pp. 139–140, emphasis added}} | {{quote|Thus the state of progress of the computation at any stage is completely determined by the note of instructions and the symbols on the tape. That is, the ''state of the system'' may be described by a single expression (sequence of symbols) consisting of the symbols on the tape followed by Δ (which is supposed to not to appear elsewhere) and then by the note of instructions. This expression is called the "state formula".|''The Undecidable'', pp. 139–140, emphasis added}} | ||
इससे पहले अपने पेपर में ट्यूरिंग ने इसे और भी आगे बढ़ाया: वह | इससे पहले अपने पेपर में ट्यूरिंग ने इसे और भी आगे बढ़ाया: वह उदाहरण देता है जहां उसने वर्तमान एम-कॉन्फ़िगरेशन का प्रतीक रखा है - निर्देश का लेबल - स्कैन किए गए वर्ग के नीचे, टेप पर सभी प्रतीकों के साथ (अनिर्णायक, पृष्ठ 121) ); इसे वह पूर्ण विन्यास कहते हैं (अनिर्णायक, पृ. 118)। पूर्ण कॉन्फ़िगरेशन को लाइन पर प्रिंट करने के लिए, वह स्कैन किए गए प्रतीक के बाईं ओर स्थिति-लेबल/एम-कॉन्फ़िगरेशन रखता है। | ||
इसका | इसका रूप क्लेन (1952) में देखा गया है जहां [[स्टीफन कोल क्लेन]] दिखाता है कि मशीन की स्थिति का गोडेल नंबर कैसे लिखा जाता है: वह एम-कॉन्फ़िगरेशन प्रतीक क्यू रखता है।<sub>4</sub> स्कैन किए गए वर्ग के ऊपर मोटे तौर पर टेप पर 6 गैर-रिक्त वर्गों के केंद्र में (इस लेख में ट्यूरिंग-टेप का आंकड़ा देखें) और इसे स्कैन किए गए वर्ग के दाईं ओर रखता है। लेकिन क्लेन क्यू को संदर्भित करता है<sub>4</sub>मशीन स्थिति के रूप में ही (क्लीन, पृष्ठ 374-375)। हॉपक्रॉफ्ट और उलमैन इस संयोजन को तात्कालिक विवरण कहते हैं और वर्तमान स्थिति (निर्देश-लेबल, एम-कॉन्फ़िगरेशन) को स्कैन किए गए प्रतीक (पृष्ठ 149) के बाईं ओर रखने के ट्यूरिंग सम्मेलन का पालन करते हैं, यानी, तात्कालिक विवरण समग्र है बाईं ओर गैर-रिक्त प्रतीकों की संख्या, मशीन की स्थिति, सिर द्वारा स्कैन किया गया वर्तमान प्रतीक और दाईं ओर गैर-रिक्त प्रतीक। | ||
उदाहरण: 3 चालों के बाद 3-राज्य 2-प्रतीक व्यस्त ऊदबिलाव की कुल स्थिति (उदाहरण से लिया गया चित्र नीचे दिखाया गया है): | उदाहरण: 3 चालों के बाद 3-राज्य 2-प्रतीक व्यस्त ऊदबिलाव की कुल स्थिति (उदाहरण से लिया गया चित्र नीचे दिखाया गया है): | ||
:: 1'ए'1 | :: 1'ए'1 | ||
इसका मतलब है: तीन चालों के बाद टेप में ... 000110000 ... होता है, सिर सबसे दाहिनी ओर 1 स्कैन कर रहा है, और स्थिति ए है। कुल राज्य जैसा कि यहाँ दिखाया गया है: B01; टेप पर केवल | इसका मतलब है: तीन चालों के बाद टेप में ... 000110000 ... होता है, सिर सबसे दाहिनी ओर 1 स्कैन कर रहा है, और स्थिति ए है। कुल राज्य जैसा कि यहाँ दिखाया गया है: B01; टेप पर केवल 1 है, लेकिन हेड 0 (रिक्त) को उसके बाईं ओर स्कैन कर रहा है और स्थिति B है। | ||
ट्यूरिंग मशीनों के संदर्भ में राज्य को स्पष्ट किया जाना चाहिए कि किसका वर्णन किया जा रहा है: वर्तमान निर्देश, या वर्तमान निर्देश के साथ टेप पर प्रतीकों की सूची, या टेप पर प्रतीकों की सूची को वर्तमान निर्देश के साथ रखा गया है स्कैन किए गए प्रतीक के बाईं ओर या स्कैन किए गए प्रतीक के दाईं ओर। | ट्यूरिंग मशीनों के संदर्भ में राज्य को स्पष्ट किया जाना चाहिए कि किसका वर्णन किया जा रहा है: वर्तमान निर्देश, या वर्तमान निर्देश के साथ टेप पर प्रतीकों की सूची, या टेप पर प्रतीकों की सूची को वर्तमान निर्देश के साथ रखा गया है स्कैन किए गए प्रतीक के बाईं ओर या स्कैन किए गए प्रतीक के दाईं ओर। | ||
| Line 371: | Line 373: | ||
|} | |} | ||
[[File:State diagram 3 state busy beaver 2B.svg|thumb|500px|right|3-राज्य व्यस्त ऊदबिलाव ट्यूरिंग मशीन | [[File:State diagram 3 state busy beaver 2B.svg|thumb|500px|right|3-राज्य व्यस्त ऊदबिलाव ट्यूरिंग मशीन परिमित-राज्य मशीन में परिमित-राज्य प्रतिनिधित्व। प्रत्येक वृत्त तालिका की स्थिति का प्रतिनिधित्व करता है - एम-कॉन्फ़िगरेशन या निर्देश। राज्य संक्रमण की दिशा तीर द्वारा दर्शाई गई है। आउटगोइंग स्थिति (तीर के अंत में) के पास लेबल (जैसे 0/P, R) स्कैन किए गए प्रतीक को निर्दिष्ट करता है जो विशेष संक्रमण (जैसे 0) के बाद स्लैश / का कारण बनता है, जिसके बाद मशीन के बाद के व्यवहार होते हैं, उदा. P प्रिंट करें फिर टेप R को दाएँ ले जाएँ। कोई सामान्य स्वीकृत प्रारूप मौजूद नहीं है। दिखाया गया सम्मेलन मैकक्लस्की (1965), बूथ (1967), हिल और पीटरसन (1974) के बाद है।]]दाईं ओर: ऊपर दी गई तालिका को राज्य संक्रमण आरेख के रूप में व्यक्त किया गया है। | ||
आम तौर पर बड़ी टेबल को टेबल के रूप में छोड़ देना बेहतर होता है (बूथ, पृ. 74)। वे कंप्यूटर द्वारा सारणीबद्ध रूप में अधिक आसानी से सिम्युलेट किए जाते हैं (बूथ, पृ. 74)। हालाँकि, कुछ अवधारणाएँ- उदा। रीसेट स्थिति वाली मशीनें और दोहराए जाने वाले पैटर्न वाली मशीनें (cf. हिल और पीटरसन पृष्ठ 244ff)—चित्रकारी के रूप में देखे जाने पर अधिक आसानी से देखी जा सकती हैं। | आम तौर पर बड़ी टेबल को टेबल के रूप में छोड़ देना बेहतर होता है (बूथ, पृ. 74)। वे कंप्यूटर द्वारा सारणीबद्ध रूप में अधिक आसानी से सिम्युलेट किए जाते हैं (बूथ, पृ. 74)। हालाँकि, कुछ अवधारणाएँ- उदा। रीसेट स्थिति वाली मशीनें और दोहराए जाने वाले पैटर्न वाली मशीनें (cf. हिल और पीटरसन पृष्ठ 244ff)—चित्रकारी के रूप में देखे जाने पर अधिक आसानी से देखी जा सकती हैं। | ||
क्या | क्या चित्र अपनी तालिका में सुधार का प्रतिनिधित्व करता है, यह पाठक द्वारा विशेष संदर्भ के लिए तय किया जाना चाहिए। | ||
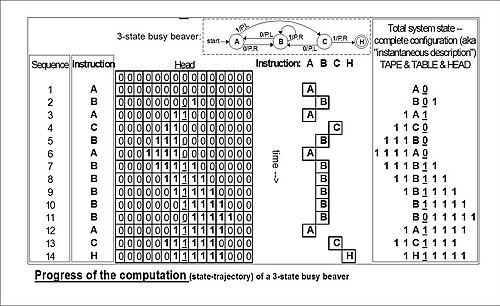
[[File:Moves of a 3-state Busy Beaver.jpg|thumbnail|500px|right|व्यस्त ऊदबिलाव की संगणना का विकास शीर्ष पर शुरू होता है और नीचे की ओर बढ़ता है।]]पाठक को फिर से सावधान किया जाना चाहिए कि इस तरह के चित्र समय और स्थान के माध्यम से गणना के पाठ्यक्रम (प्रक्षेपवक्र) नहीं, समय में जमे हुए उनकी तालिका के | [[File:Moves of a 3-state Busy Beaver.jpg|thumbnail|500px|right|व्यस्त ऊदबिलाव की संगणना का विकास शीर्ष पर शुरू होता है और नीचे की ओर बढ़ता है।]]पाठक को फिर से सावधान किया जाना चाहिए कि इस तरह के चित्र समय और स्थान के माध्यम से गणना के पाठ्यक्रम (प्रक्षेपवक्र) नहीं, समय में जमे हुए उनकी तालिका के स्नैपशॉट का प्रतिनिधित्व करते हैं। जबकि हर बार व्यस्त बीवर मशीन चलती है, यह हमेशा ही राज्य-प्रक्षेपवक्र का पालन करेगी, यह कॉपी मशीन के लिए सही नहीं है जिसे चर इनपुट मापदंडों के साथ प्रदान किया जा सकता है। | ||
गणना की आरेख प्रगति शुरू से अंत तक इसकी गणना के माध्यम से तीन-राज्य व्यस्त बीवर की स्थिति (निर्देश) की प्रगति को दर्शाती है। दायीं ओर ट्यूरिंग पूर्ण विन्यास है (क्लीन स्थिति | गणना की आरेख प्रगति शुरू से अंत तक इसकी गणना के माध्यम से तीन-राज्य व्यस्त बीवर की स्थिति (निर्देश) की प्रगति को दर्शाती है। दायीं ओर ट्यूरिंग पूर्ण विन्यास है (क्लीन स्थिति, होपक्रॉफ्ट-उलमैन तात्कालिक विवरण ) प्रत्येक चरण पर। अगर मशीन को रोका जाना था और राज्य रजिस्टर और पूरे टेप दोनों को खाली करने के लिए साफ़ किया जाना था, तो इन कॉन्फ़िगरेशन का उपयोग इसकी प्रगति में कहीं भी संगणना को फिर से शुरू करने के लिए किया जा सकता है (cf. ट्यूरिंग (1936) द अनडेसिडेबल, पीपी। 139-140)। | ||
== समतुल्य मॉडल == | == समतुल्य मॉडल == | ||
{{See also|Turing machine equivalents|Register machine|Post–Turing machine}} | {{See also|Turing machine equivalents|Register machine|Post–Turing machine}} | ||
कई मशीनें जिनके बारे में सोचा जा सकता है कि | कई मशीनें जिनके बारे में सोचा जा सकता है कि साधारण यूनिवर्सल ट्यूरिंग मशीन की तुलना में अधिक कम्प्यूटेशनल क्षमता है, उन्हें और अधिक शक्ति नहीं दिखाया जा सकता है (हॉपक्रॉफ्ट और उल्मैन पृष्ठ 159, cf. Minsky (1967))। वे तेजी से गणना कर सकते हैं, शायद, या कम मेमोरी का उपयोग कर सकते हैं, या उनका निर्देश सेट छोटा हो सकता है, लेकिन वे अधिक शक्तिशाली रूप से गणना नहीं कर सकते (यानी अधिक गणितीय कार्य)। (चर्च-ट्यूरिंग थीसिस किसी भी प्रकार की मशीन के लिए इसे सच मानती है: कि किसी भी चीज़ की गणना किसी ट्यूरिंग मशीन द्वारा की जा सकती है।) | ||
एक ट्यूरिंग मशीन सिंगल-स्टैक [[पुशडाउन ऑटोमेटन]] (पीडीए) के बराबर है जिसे एलआईएफओ (कंप्यूटिंग) | लास्ट-इन-फर्स्ट-आउट (एलआईएफओ) आवश्यकता को आराम देकर अधिक लचीला और संक्षिप्त बनाया गया है। इसके अलावा, | एक ट्यूरिंग मशीन सिंगल-स्टैक [[पुशडाउन ऑटोमेटन]] (पीडीए) के बराबर है जिसे एलआईएफओ (कंप्यूटिंग) | लास्ट-इन-फर्स्ट-आउट (एलआईएफओ) आवश्यकता को आराम देकर अधिक लचीला और संक्षिप्त बनाया गया है। इसके अलावा, ट्यूरिंग मशीन मानक LIFO शब्दार्थ के साथ दो-स्टैक पीडीए के बराबर भी है, स्टैक का उपयोग सिर के बाईं ओर टेप के लिए और दूसरे स्टैक को दाईं ओर टेप के लिए किया जाता है। | ||
दूसरे चरम पर, कुछ बहुत ही सरल मॉडल ट्यूरिंग पूर्णता के रूप में सामने आते हैं | ट्यूरिंग-समतुल्य, यानी ट्यूरिंग मशीन मॉडल के समान कम्प्यूटेशनल शक्ति रखने के लिए। | दूसरे चरम पर, कुछ बहुत ही सरल मॉडल ट्यूरिंग पूर्णता के रूप में सामने आते हैं | ट्यूरिंग-समतुल्य, यानी ट्यूरिंग मशीन मॉडल के समान कम्प्यूटेशनल शक्ति रखने के लिए। | ||
सामान्य समकक्ष मॉडल [[मल्टी-टेप ट्यूरिंग मशीन]], [[मल्टी-ट्रैक ट्यूरिंग मशीन]], इनपुट और आउटपुट वाली मशीनें, और गैर-नियतात्मक ट्यूरिंग मशीन | गैर-नियतात्मक ट्यूरिंग मशीन (एनडीटीएम) हैं, जो नियतात्मक ट्यूरिंग मशीन (डीटीएम) के विपरीत जिसमें प्रतीक और स्थिति के प्रत्येक संयोजन के लिए क्रिया तालिका में अधिक से अधिक | सामान्य समकक्ष मॉडल [[मल्टी-टेप ट्यूरिंग मशीन]], [[मल्टी-ट्रैक ट्यूरिंग मशीन]], इनपुट और आउटपुट वाली मशीनें, और गैर-नियतात्मक ट्यूरिंग मशीन | गैर-नियतात्मक ट्यूरिंग मशीन (एनडीटीएम) हैं, जो नियतात्मक ट्यूरिंग मशीन (डीटीएम) के विपरीत जिसमें प्रतीक और स्थिति के प्रत्येक संयोजन के लिए क्रिया तालिका में अधिक से अधिक प्रविष्टि हो। | ||
रीड-ओनली राइट मूविंग ट्यूरिंग मशीन | रीड-ओनली, राइट-मूविंग ट्यूरिंग मशीन नियतात्मक परिमित ऑटोमेटन (साथ ही एनडीएफए से डीएफए रूपांतरण एल्गोरिथ्म का उपयोग करके रूपांतरण द्वारा | रीड-ओनली राइट मूविंग ट्यूरिंग मशीन | रीड-ओनली, राइट-मूविंग ट्यूरिंग मशीन नियतात्मक परिमित ऑटोमेटन (साथ ही एनडीएफए से डीएफए रूपांतरण एल्गोरिथ्म का उपयोग करके रूपांतरण द्वारा गैर [[नियतात्मक परिमित automaton]] के बराबर हैं। | ||
व्यावहारिक और व्यावहारिक उद्देश्यों के लिए समतुल्य [[रजिस्टर मशीन]] का उपयोग सामान्य असेंबली भाषा [[प्रोग्रामिंग भाषा]] के रूप में किया जा सकता है। | व्यावहारिक और व्यावहारिक उद्देश्यों के लिए समतुल्य [[रजिस्टर मशीन]] का उपयोग सामान्य असेंबली भाषा [[प्रोग्रामिंग भाषा]] के रूप में किया जा सकता है। | ||
एक प्रासंगिक प्रश्न यह है कि ठोस प्रोग्रामिंग भाषाओं द्वारा प्रस्तुत अभिकलन मॉडल ट्यूरिंग समकक्ष है या नहीं। जबकि | एक प्रासंगिक प्रश्न यह है कि ठोस प्रोग्रामिंग भाषाओं द्वारा प्रस्तुत अभिकलन मॉडल ट्यूरिंग समकक्ष है या नहीं। जबकि वास्तविक कंप्यूटर की गणना परिमित अवस्थाओं पर आधारित होती है और इस प्रकार ट्यूरिंग मशीन का अनुकरण करने में सक्षम नहीं होती है, स्वयं प्रोग्रामिंग भाषाओं में यह सीमा नहीं होती है। किरनर और अन्य, 2009 ने दिखाया है कि सामान्य प्रयोजन की प्रोग्रामिंग भाषाओं में से कुछ ट्यूरिंग पूर्ण हैं जबकि अन्य नहीं हैं। उदाहरण के लिए, [[एएनएसआई सी]] ट्यूरिंग-समतुल्य नहीं है, क्योंकि एएनएसआई सी के सभी तात्कालिकताएं संभव हैं (विभिन्न तात्कालिकताएं संभव हैं क्योंकि मानक जानबूझकर कुछ व्यवहारों को विरासत कारणों से अपरिभाषित छोड़ देता है) परिमित-अंतरिक्ष स्मृति का अर्थ है। ऐसा इसलिए है क्योंकि स्मृति संदर्भ डेटा प्रकारों का आकार, जिसे पॉइंटर्स कहा जाता है, भाषा के अंदर पहुंच योग्य है। हालाँकि, [[पास्कल (प्रोग्रामिंग भाषा)]] जैसी अन्य प्रोग्रामिंग भाषाओं में यह सुविधा नहीं है, जो उन्हें सिद्धांत रूप में ट्यूरिंग पूर्ण होने की अनुमति देती है। | ||
सिद्धांत रूप में यह केवल ट्यूरिंग पूर्ण है, क्योंकि | सिद्धांत रूप में यह केवल ट्यूरिंग पूर्ण है, क्योंकि प्रोग्रामिंग भाषा में मेमोरी आवंटन को विफल होने दिया जाता है, जिसका अर्थ है कि विफल मेमोरी आवंटन की अनदेखी करते समय प्रोग्रामिंग भाषा ट्यूरिंग पूर्ण हो सकती है, लेकिन वास्तविक कंप्यूटर पर निष्पादन योग्य संकलित प्रोग्राम नहीं हो सकते। | ||
== च्वाइस सी-मशीन, ऑरेकल ओ-मशीन == | == च्वाइस सी-मशीन, ऑरेकल ओ-मशीन == | ||
अपने पेपर के आरंभ में (1936) ट्यूरिंग | अपने पेपर के आरंभ में (1936) ट्यूरिंग स्वचालित मशीन के बीच अंतर करता है - इसकी गति ... पूरी तरह से कॉन्फ़िगरेशन और पसंद मशीन द्वारा निर्धारित: | ||
{{quote|...whose motion is only partially determined by the configuration ... When such a machine reaches one of these ambiguous configurations, it cannot go on until some arbitrary choice has been made by an external operator. This would be the case if we were using machines to deal with axiomatic systems.|''The Undecidable'', p. 118}} | {{quote|...whose motion is only partially determined by the configuration ... When such a machine reaches one of these ambiguous configurations, it cannot go on until some arbitrary choice has been made by an external operator. This would be the case if we were using machines to deal with axiomatic systems.|''The Undecidable'', p. 118}} | ||
ट्यूरिंग (1936) | ट्यूरिंग (1936) फुटनोट को छोड़कर आगे विस्तृत नहीं करता है जिसमें वह वर्णन करता है कि [हिल्बर्ट] कैलकुलस के सभी सिद्ध सूत्रों को खोजने के लिए ए-मशीन का उपयोग कैसे किया जाए, बजाय इसके कि वह विकल्प मशीन का उपयोग करे। उनका मानना है कि विकल्प हमेशा दो संभावनाओं 0 और 1 के बीच होते हैं। प्रत्येक प्रमाण तब विकल्पों के अनुक्रम द्वारा निर्धारित किया जाएगा I<sub>1</sub>, मैं<sub>2</sub>, ..., मैं<sub>n</sub> (मैं<sub>1</sub> = 0 या 1, मैं<sub>2</sub> = 0 या 1, ..., i<sub>n</sub> = 0 या 1), और इसलिए संख्या 2<sup>एन</sup> + मैं<sub>1</sub>2<sup>n-1</sup> + i<sub>2</sub>2<sup>n-2</sup> + ... +i<sub>n</sub> पूरी तरह से प्रमाण निर्धारित करता है। स्वचालित मशीन क्रमिक रूप से प्रूफ 1, प्रूफ 2, प्रूफ 3, ... (फुटनोट ‡, द अनडेसिडेबल, पृष्ठ 138) करती है। | ||
यह वास्तव में वह तकनीक है जिसके द्वारा | यह वास्तव में वह तकनीक है जिसके द्वारा निर्धारक ट्यूरिंग मशीन की कार्रवाई की नकल करने के लिए नियतात्मक (यानी, ए-) ट्यूरिंग मशीन का उपयोग किया जा सकता है; ट्यूरिंग ने फुटनोट में मामले को सुलझाया और इसे आगे के विचार से खारिज कर दिया। | ||
एक [[ओरेकल मशीन]] या ओ-मशीन | एक [[ओरेकल मशीन]] या ओ-मशीन ट्यूरिंग मशीन है जो अपनी गणना को स्थिति 'ओ' पर रोक देती है, जबकि अपनी गणना पूरी करने के लिए, यह ऑरेकल के निर्णय की प्रतीक्षा करती है - अनिर्दिष्ट इकाई यह कहने के अलावा कि यह मशीन नहीं हो सकती ( ट्यूरिंग (1939), द अनडिसीडेबल, पृष्ठ 166-168)। | ||
== यूनिवर्सल ट्यूरिंग मशीन == | == यूनिवर्सल ट्यूरिंग मशीन == | ||
| Line 416: | Line 418: | ||
{{quote|Turing's paper ... contains, in essence, the invention of the modern computer and some of the programming techniques that accompanied it.|Minsky (1967), p. 104}} | {{quote|Turing's paper ... contains, in essence, the invention of the modern computer and some of the programming techniques that accompanied it.|Minsky (1967), p. 104}} | ||
कम्प्यूटेशनल जटिलता सिद्धांत के संदर्भ में, | कम्प्यूटेशनल जटिलता सिद्धांत के संदर्भ में, मल्टी-टेप यूनिवर्सल ट्यूरिंग मशीन को केवल उन मशीनों की तुलना में लॉगरिदमिक फैक्टर द्वारा धीमा होना चाहिए जो इसे अनुकरण करती हैं। यह परिणाम 1966 में F. C. हेनी और R. E. स्टर्न्स द्वारा प्राप्त किया गया था। (अरोड़ा और बराक, 2009, प्रमेय 1.9) | ||
== वास्तविक मशीनों के साथ तुलना == | == वास्तविक मशीनों के साथ तुलना == | ||
[[File:Lego Turing Machine.jpg|thumb|[[लेगो]] टुकड़ों का उपयोग करके | [[File:Lego Turing Machine.jpg|thumb|[[लेगो]] टुकड़ों का उपयोग करके ट्यूरिंग मशीन की प्राप्ति]]प्राय: माना जाता है कि ट्यूरिंग मशीनें, सरल ऑटोमेटा के विपरीत, वास्तविक मशीनों की तरह शक्तिशाली हैं, और किसी भी ऑपरेशन को निष्पादित करने में सक्षम हैं जो वास्तविक प्रोग्राम कर सकता है। इस कथन में जो उपेक्षित है, वह यह है कि, क्योंकि वास्तविक मशीन में केवल सीमित संख्या में विन्यास हो सकते हैं, यह परिमित-राज्य मशीन के अलावा और कुछ नहीं है, जबकि ट्यूरिंग मशीन में इसकी संगणनाओं के लिए असीमित मात्रा में भंडारण स्थान उपलब्ध है। | ||
यह समझाने के कई तरीके हैं कि ट्यूरिंग मशीन वास्तविक कंप्यूटर के उपयोगी मॉडल क्यों हैं: | यह समझाने के कई तरीके हैं कि ट्यूरिंग मशीन वास्तविक कंप्यूटर के उपयोगी मॉडल क्यों हैं: | ||
* एक वास्तविक कंप्यूटर कुछ भी गणना कर सकता है, | * एक वास्तविक कंप्यूटर कुछ भी गणना कर सकता है, ट्यूरिंग मशीन भी गणना कर सकती है। उदाहरण के लिए: ट्यूरिंग मशीन प्रोग्रामिंग भाषाओं में पाए जाने वाले किसी भी प्रकार के सबरूटीन का अनुकरण कर सकती है, जिसमें पुनरावर्ती प्रक्रियाएं और ज्ञात पैरामीटर-पासिंग मैकेनिज्म (हॉपक्रॉफ्ट और उल्मैन पृष्ठ 157) शामिल हैं। बड़ा पर्याप्त FSA IO की अवहेलना करते हुए किसी भी वास्तविक कंप्यूटर को भी मॉडल कर सकता है। इस प्रकार, ट्यूरिंग मशीनों की सीमाओं के बारे में बयान वास्तविक कंप्यूटरों पर भी लागू होगा। | ||
* अंतर केवल ट्यूरिंग मशीन की असीमित मात्रा में डेटा में हेरफेर करने की क्षमता के साथ है। हालाँकि, | * अंतर केवल ट्यूरिंग मशीन की असीमित मात्रा में डेटा में हेरफेर करने की क्षमता के साथ है। हालाँकि, सीमित समय दिया गया है, ट्यूरिंग मशीन (एक वास्तविक मशीन की तरह) केवल डेटा की सीमित मात्रा में हेरफेर कर सकती है। | ||
* एक ट्यूरिंग मशीन की तरह, | * एक ट्यूरिंग मशीन की तरह, वास्तविक मशीन में अधिक डिस्क या अन्य स्टोरेज मीडिया प्राप्त करके, इसकी स्टोरेज स्पेस को आवश्यकतानुसार बढ़ाया जा सकता है। | ||
* ट्यूरिंग मशीनों का उपयोग करने वाले विवरणों की तुलना में सरल अमूर्त मॉडल का उपयोग करने वाले वास्तविक मशीन प्रोग्राम के विवरण अक्सर अधिक जटिल होते हैं। उदाहरण के लिए, | * ट्यूरिंग मशीनों का उपयोग करने वाले विवरणों की तुलना में सरल अमूर्त मॉडल का उपयोग करने वाले वास्तविक मशीन प्रोग्राम के विवरण अक्सर अधिक जटिल होते हैं। उदाहरण के लिए, एल्गोरिथ्म का वर्णन करने वाली ट्यूरिंग मशीन में कुछ सौ अवस्थाएँ हो सकती हैं, जबकि किसी वास्तविक मशीन पर समतुल्य नियतात्मक परिमित ऑटोमेटन (DFA) में क्वाड्रिलियन होते हैं। यह डीएफए प्रतिनिधित्व का विश्लेषण करने के लिए अक्षम बनाता है। | ||
* ट्यूरिंग मशीनें एल्गोरिदम का वर्णन करती हैं जो इस बात से स्वतंत्र हैं कि वे कितनी मेमोरी का उपयोग करते हैं। किसी भी मौजूदा मशीन के पास मेमोरी की | * ट्यूरिंग मशीनें एल्गोरिदम का वर्णन करती हैं जो इस बात से स्वतंत्र हैं कि वे कितनी मेमोरी का उपयोग करते हैं। किसी भी मौजूदा मशीन के पास मेमोरी की सीमा होती है, लेकिन यह सीमा समय के साथ मनमाने ढंग से बढ़ सकती है। ट्यूरिंग मशीन हमें एल्गोरिदम के बारे में बयान देने की अनुमति देती है जो (सैद्धांतिक रूप से) पारंपरिक कंप्यूटिंग मशीन आर्किटेक्चर में प्रगति की परवाह किए बिना हमेशा के लिए बनी रहेगी। | ||
* ट्यूरिंग मशीन एल्गोरिदम के कथन को सरल बनाती है। | * ट्यूरिंग मशीन एल्गोरिदम के कथन को सरल बनाती है। ट्यूरिंग-समतुल्य अमूर्त मशीनों पर चलने वाले एल्गोरिदम आमतौर पर वास्तविक मशीनों पर चलने वाले उनके समकक्षों की तुलना में अधिक सामान्य होते हैं, क्योंकि उनके पास मनमाने ढंग से सटीक डेटा प्रकार उपलब्ध होते हैं और उन्हें कभी भी अप्रत्याशित परिस्थितियों से निपटना नहीं पड़ता है ([[स्मृति से बाहर]] चलने सहित, लेकिन सीमित नहीं) . | ||
[[File:Turingmachine.jpg|thumb|एक और ट्यूरिंग मशीन की प्राप्ति]] | [[File:Turingmachine.jpg|thumb|एक और ट्यूरिंग मशीन की प्राप्ति]] | ||
| Line 436: | Line 438: | ||
==== कम्प्यूटेशनल जटिलता सिद्धांत ==== | ==== कम्प्यूटेशनल जटिलता सिद्धांत ==== | ||
{{further|Computational complexity theory}} | {{further|Computational complexity theory}} | ||
ट्यूरिंग मशीनों की | ट्यूरिंग मशीनों की सीमा यह है कि वे किसी विशेष व्यवस्था की ताकत को अच्छी तरह से मॉडल नहीं करते हैं। उदाहरण के लिए, आधुनिक संग्रहीत प्रोग्राम कंप्यूटर वास्तव में अमूर्त मशीन के अधिक विशिष्ट रूप के उदाहरण हैं जिन्हें [[रैंडम-एक्सेस संग्रहित प्रोग्राम मशीन]] मशीन या आरएएसपी मशीन मॉडल के रूप में जाना जाता है। यूनिवर्सल ट्यूरिंग मशीन की तरह, आरएएसपी अपने कार्यक्रम को अपनी परिमित-राज्य मशीन के निर्देशों के बाहर स्मृति में संग्रहीत करता है। यूनिवर्सल ट्यूरिंग मशीन के विपरीत, RASP में अलग-अलग, क्रमांकित लेकिन असीमित रजिस्टरों की अनंत संख्या होती है - मेमोरी सेल जिसमें कोई भी पूर्णांक हो सकता है (cf. Elgot और रॉबिन्सन (1964), हार्टमैनिस (1971), और विशेष रूप से कुक-रेचो (1973) ); [[रैंडम-एक्सेस मशीन]] पर संदर्भ)। आरएएसपी की परिमित-राज्य मशीन अप्रत्यक्ष पते की क्षमता से लैस है (उदाहरण के लिए, रजिस्टर की सामग्री को दूसरे रजिस्टर को निर्दिष्ट करने के लिए पते के रूप में इस्तेमाल किया जा सकता है); इस प्रकार आरएएसपी का कार्यक्रम रजिस्टर-अनुक्रम में किसी भी रजिस्टर को संबोधित कर सकता है। इस अंतर का परिणाम यह है कि ऐसे कम्प्यूटेशनल ऑप्टिमाइजेशन हैं जो मेमोरी इंडेक्स के आधार पर किए जा सकते हैं, जो सामान्य ट्यूरिंग मशीन में संभव नहीं हैं; इस प्रकार जब ट्यूरिंग मशीनों को बाउंडिंग रनिंग टाइम के आधार के रूप में उपयोग किया जाता है, तो कुछ एल्गोरिदम के चलने के समय (ट्यूरिंग मशीन की झूठी सरलीकृत धारणा के कारण) पर झूठी निचली सीमा सिद्ध की जा सकती है। इसका उदाहरण [[द्विआधारी खोज]] है, एल्गोरिदम जिसे ट्यूरिंग मशीन मॉडल के बजाय गणना के आरएएसपी मॉडल का उपयोग करते समय अधिक तेज़ी से प्रदर्शन करने के लिए दिखाया जा सकता है। | ||
==== समवर्ती ==== | ==== समवर्ती ==== | ||
ट्यूरिंग मशीनों की और सीमा यह है कि वे Concurrency_(कंप्यूटर_साइंस) को अच्छी तरह से मॉडल नहीं करती हैं। उदाहरण के लिए, पूर्णांक के आकार पर सीमा होती है जिसकी गणना खाली टेप पर शुरू होने वाली हमेशा रुकने वाली गैर-नियतात्मक ट्यूरिंग मशीन द्वारा की जा सकती है। ([[असीमित nondeterminism]] पर लेख देखें।) इसके विपरीत, बिना किसी इनपुट के हमेशा रुकने वाली समवर्ती प्रणालियाँ होती हैं जो असीमित आकार के पूर्णांक की गणना कर सकती हैं। (स्थानीय भंडारण के साथ प्रक्रिया बनाई जा सकती है जिसे 0 की गिनती के साथ आरंभ किया जाता है जो समवर्ती रूप से स्टॉप और गो संदेश दोनों भेजता है। जब इसे गो संदेश प्राप्त होता है, तो यह 1 से अपनी गिनती बढ़ाता है और खुद को संदेश भेजता है। जब यह स्टॉप संदेश प्राप्त करता है, यह अपने स्थानीय भंडारण में असीमित संख्या के साथ बंद हो जाता है।) | |||
ट्यूरिंग मशीनों की | |||
==== इंटरेक्शन ==== | ==== इंटरेक्शन ==== | ||
कंप्यूटिंग के शुरुआती दिनों में, कंप्यूटर का उपयोग आमतौर पर [[प्रचय संसाधन]] तक सीमित था, यानी, गैर-संवादात्मक कार्य, प्रत्येक दिए गए इनपुट डेटा से आउटपुट डेटा का उत्पादन करता था। कम्प्यूटेबिलिटी सिद्धांत, जो इनपुट से आउटपुट तक कार्यों की कम्प्यूटेबिलिटी का अध्ययन करता है, और जिसके लिए ट्यूरिंग मशीनों का आविष्कार किया गया था, इस अभ्यास को दर्शाता है। | कंप्यूटिंग के शुरुआती दिनों में, कंप्यूटर का उपयोग आमतौर पर [[प्रचय संसाधन]] तक सीमित था, यानी, गैर-संवादात्मक कार्य, प्रत्येक दिए गए इनपुट डेटा से आउटपुट डेटा का उत्पादन करता था। कम्प्यूटेबिलिटी सिद्धांत, जो इनपुट से आउटपुट तक कार्यों की कम्प्यूटेबिलिटी का अध्ययन करता है, और जिसके लिए ट्यूरिंग मशीनों का आविष्कार किया गया था, इस अभ्यास को दर्शाता है। | ||
1970 के दशक के बाद से, कंप्यूटरों का [[अन्तरक्रियाशीलता]] उपयोग बहुत अधिक सामान्य हो गया। सिद्धांत रूप में, | 1970 के दशक के बाद से, कंप्यूटरों का [[अन्तरक्रियाशीलता]] उपयोग बहुत अधिक सामान्य हो गया। सिद्धांत रूप में, बाहरी एजेंट को टेप से पढ़ने और ट्यूरिंग मशीन के रूप में ही समय में लिखने के द्वारा इसे मॉडल करना संभव है, लेकिन यह शायद ही कभी मेल खाता है कि बातचीत वास्तव में कैसे होती है; इसलिए, अन्तरक्रियाशीलता का वर्णन करते समय, इनपुट/आउटपुट ऑटोमेटन|I/O ऑटोमेटा जैसे विकल्प आमतौर पर पसंद किए जाते हैं। | ||
== इतिहास == | == इतिहास == | ||
| Line 452: | Line 453: | ||
=== ऐतिहासिक पृष्ठभूमि: कम्प्यूटेशनल मशीनरी === | === ऐतिहासिक पृष्ठभूमि: कम्प्यूटेशनल मशीनरी === | ||
[[रॉबिन गैंडी]] (1919-1995) - एलन ट्यूरिंग (1912-1954) के | [[रॉबिन गैंडी]] (1919-1995) - एलन ट्यूरिंग (1912-1954) के छात्र, और उनके आजीवन दोस्त - [[चार्ल्स बैबेज]] (लगभग 1834) में गणना मशीन की धारणा के वंश का पता लगाते हैं और वास्तव में बैबेज की थीसिस का प्रस्ताव देते हैं: | ||
{{quote|''That the whole of development and operations of analysis are now capable of being executed by machinery''.|(italics in Babbage as cited by Gandy, p. 54)}} | {{quote|''That the whole of development and operations of analysis are now capable of being executed by machinery''.|(italics in Babbage as cited by Gandy, p. 54)}} | ||
बैबेज के [[विश्लेषणात्मक इंजन]] का गैंडी का विश्लेषण निम्नलिखित पांच कार्यों का वर्णन करता है (cf. p. 52–53): | बैबेज के [[विश्लेषणात्मक इंजन]] का गैंडी का विश्लेषण निम्नलिखित पांच कार्यों का वर्णन करता है (cf. p. 52–53): | ||
* अंकगणितीय फलन +, -, ×, जहाँ - उचित घटाव दर्शाता है {{nowrap|''x'' − ''y'' {{=}} 0}} अगर {{nowrap|''y'' ≥ ''x''}}. | * अंकगणितीय फलन +, -, ×, जहाँ - उचित घटाव दर्शाता है {{nowrap|''x'' − ''y'' {{=}} 0}} अगर {{nowrap|''y'' ≥ ''x''}}. | ||
* संचालन का कोई भी क्रम | * संचालन का कोई भी क्रम ऑपरेशन है। | ||
* एक ऑपरेशन का पुनरावृत्ति (एन बार | * एक ऑपरेशन का पुनरावृत्ति (एन बार ऑपरेशन पी दोहराना)। | ||
* सशर्त पुनरावृत्ति (परीक्षण टी की सफलता पर एन बार | * सशर्त पुनरावृत्ति (परीक्षण टी की सफलता पर एन बार ऑपरेशन पी सशर्त दोहराना)। | ||
* सशर्त स्थानांतरण (यानी, सशर्त [[के लिए जाओ]])। | * सशर्त स्थानांतरण (यानी, सशर्त [[के लिए जाओ]])। | ||
| Line 468: | Line 469: | ||
=== Entscheidungsproblem (निर्णय समस्या): हिल्बर्ट का 1900 का दसवां प्रश्न=== | === Entscheidungsproblem (निर्णय समस्या): हिल्बर्ट का 1900 का दसवां प्रश्न=== | ||
1900 में प्रसिद्ध गणितज्ञ [[डेविड हिल्बर्ट]] द्वारा पेश की गई हिल्बर्ट की समस्याओं के संबंध में, समस्या #10 का | 1900 में प्रसिद्ध गणितज्ञ [[डेविड हिल्बर्ट]] द्वारा पेश की गई हिल्बर्ट की समस्याओं के संबंध में, समस्या #10 का पहलू लगभग 30 वर्षों से चल रहा था, जब तक कि इसे सटीक रूप से तैयार नहीं किया गया था। नंबर 10 के लिए हिल्बर्ट की मूल अभिव्यक्ति इस प्रकार है: | ||
{{quote|''10. Determination of the solvability of a Diophantine equation''. Given a [[Diophantine equation]] with any number of unknown quantities and with rational integral coefficients: To devise a process according to which it can be determined in a finite number of operations whether the equation is solvable in rational integers. | {{quote|''10. Determination of the solvability of a Diophantine equation''. Given a [[Diophantine equation]] with any number of unknown quantities and with rational integral coefficients: To devise a process according to which it can be determined in a finite number of operations whether the equation is solvable in rational integers. | ||
| Line 481: | Line 482: | ||
1928 में गणितज्ञों की अंतर्राष्ट्रीय कांग्रेस द्वारा, हिल्बर्ट ने अपने प्रश्नों को काफी सटीक बनाया। पहला, गणित [[पूर्णता (तर्क)]] था ... दूसरा, गणित [[संगति प्रमाण]] था ... और तीसरा, गणित [[निर्णायकता (तर्क)]] था? (होजेस पृष्ठ 91, हॉकिंग पृष्ठ 1121)। पहले दो सवालों का जवाब 1930 में कर्ट गोडेल ने उसी बैठक में दिया था, जहां हिल्बर्ट ने अपना सेवानिवृत्ति भाषण दिया था (हिल्बर्ट को बहुत दुख हुआ था); तीसरी- Entscheidungsproblem- को 1930 के दशक के मध्य तक प्रतीक्षा करनी पड़ी। | 1928 में गणितज्ञों की अंतर्राष्ट्रीय कांग्रेस द्वारा, हिल्बर्ट ने अपने प्रश्नों को काफी सटीक बनाया। पहला, गणित [[पूर्णता (तर्क)]] था ... दूसरा, गणित [[संगति प्रमाण]] था ... और तीसरा, गणित [[निर्णायकता (तर्क)]] था? (होजेस पृष्ठ 91, हॉकिंग पृष्ठ 1121)। पहले दो सवालों का जवाब 1930 में कर्ट गोडेल ने उसी बैठक में दिया था, जहां हिल्बर्ट ने अपना सेवानिवृत्ति भाषण दिया था (हिल्बर्ट को बहुत दुख हुआ था); तीसरी- Entscheidungsproblem- को 1930 के दशक के मध्य तक प्रतीक्षा करनी पड़ी। | ||
समस्या यह थी कि | समस्या यह थी कि उत्तर के लिए पहले निश्चित सामान्य लागू नुस्खे की सटीक परिभाषा की आवश्यकता होती थी, जिसे प्रिंसटन के प्रोफेसर अलोंजो चर्च [[प्रभावी गणना]]त्मकता कहते थे, और 1928 में ऐसी कोई परिभाषा मौजूद नहीं थी। लेकिन अगले 6-7 वर्षों में [[एमिल पोस्ट]] ने निर्देशों की सूची (1936 के बाद) के अनुसार कमरे से दूसरे कमरे में लिखने और निशान मिटाने वाले कार्यकर्ता की अपनी परिभाषा विकसित की, जैसा कि चर्च और उनके दो छात्रों [[स्टीफन क्लेन]] और जे.बी. रोसेर ने किया था। चर्च का लैम्ब्डा-कैलकुलस और गोडेल का [[पुनरावर्तन सिद्धांत]] (1934)। चर्च के पेपर (15 अप्रैल 1936 को प्रकाशित) ने दिखाया कि एंट्सचेइडुंग्सप्रोब्लेम वास्तव में अनिर्णीत था और ट्यूरिंग को लगभग साल तक हरा दिया (ट्यूरिंग का पेपर 28 मई 1936 को प्रस्तुत किया गया, जनवरी 1937 को प्रकाशित हुआ)। इस बीच, एमिल पोस्ट ने 1936 के पतन में संक्षिप्त पत्र प्रस्तुत किया, इसलिए ट्यूरिंग को कम से कम पोस्ट पर प्राथमिकता मिली। जबकि चर्च ने ट्यूरिंग के पेपर को रेफर किया था, ट्यूरिंग के पास चर्च के पेपर का अध्ययन करने और परिशिष्ट जोड़ने का समय था जहां उन्होंने प्रमाण को स्केच किया कि चर्च का लैम्ब्डा-कैलकुलस और उनकी मशीनें समान कार्यों की गणना करेंगी। | ||
{{quote|But what Church had done was something rather different, and in a certain sense weaker. ... the Turing construction was more direct, and provided an argument from first principles, closing the gap in Church's demonstration.|Hodges p. 112}} | {{quote|But what Church had done was something rather different, and in a certain sense weaker. ... the Turing construction was more direct, and provided an argument from first principles, closing the gap in Church's demonstration.|Hodges p. 112}} | ||
| Line 487: | Line 488: | ||
=== एलन ट्यूरिंग की ए-मशीन === | === एलन ट्यूरिंग की ए-मशीन === | ||
1935 के वसंत में, कैम्ब्रिज के किंग्स कॉलेज में मास्टर के | 1935 के वसंत में, कैम्ब्रिज के किंग्स कॉलेज में मास्टर के युवा छात्र के रूप में ट्यूरिंग ने चुनौती ली; वह तर्कशास्त्री एम. एच. ए. न्यूमैन के व्याख्यानों से प्रेरित हुए थे और उनसे गोडेल के काम और एंट्सचेइडुंग्सप्रोब्लेम के बारे में सीखा ... न्यूमैन ने 'मैकेनिकल' शब्द का इस्तेमाल किया ... ट्यूरिंग 1955 के अपने मृत्युलेख में न्यूमैन लिखते हैं: | ||
{{quote|To the question 'what is a "mechanical" process?' Turing returned the characteristic answer 'Something that can be done by a machine' and he embarked on the highly congenial task of analysing the general notion of a computing machine.|Gandy, p. 74}} | {{quote|To the question 'what is a "mechanical" process?' Turing returned the characteristic answer 'Something that can be done by a machine' and he embarked on the highly congenial task of analysing the general notion of a computing machine.|Gandy, p. 74}} | ||
| Line 493: | Line 494: | ||
{{quote|I suppose, but do not know, that Turing, right from the start of his work, had as his goal a proof of the undecidability of the Entscheidungsproblem. He told me that the 'main idea' of the paper came to him when he was lying in Grantchester meadows in the summer of 1935. The 'main idea' might have either been his analysis of computation or his realization that there was a universal machine, and so a [[Cantor's diagonal argument|diagonal argument]] to prove unsolvability.|''ibid.'', p. 76}} | {{quote|I suppose, but do not know, that Turing, right from the start of his work, had as his goal a proof of the undecidability of the Entscheidungsproblem. He told me that the 'main idea' of the paper came to him when he was lying in Grantchester meadows in the summer of 1935. The 'main idea' might have either been his analysis of computation or his realization that there was a universal machine, and so a [[Cantor's diagonal argument|diagonal argument]] to prove unsolvability.|''ibid.'', p. 76}} | ||
जबकि गैंडी का मानना था कि ऊपर न्यूमैन का बयान भ्रामक है, यह राय सभी के द्वारा साझा नहीं की जाती है। मशीनों में ट्यूरिंग की आजीवन रुचि थी: एलन ने | जबकि गैंडी का मानना था कि ऊपर न्यूमैन का बयान भ्रामक है, यह राय सभी के द्वारा साझा नहीं की जाती है। मशीनों में ट्यूरिंग की आजीवन रुचि थी: एलन ने लड़के के रूप में टाइपराइटर का आविष्कार करने का सपना देखा था; [उनकी मां] श्रीमती ट्यूरिंग के पास टाइपराइटर था; और वह अच्छी तरह से खुद से पूछकर शुरू कर सकता था कि टाइपराइटर को 'मैकेनिकल' कहने का क्या मतलब है (होजेस पी. 96)। प्रिंसटन में अपनी पीएचडी की पढ़ाई के दौरान, ट्यूरिंग ने बूलियन-लॉजिक मल्टीप्लायर बनाया (नीचे देखें)। उनकी पीएचडी थीसिस, जिसका शीर्षक [[ऑर्डिनल्स पर आधारित लॉजिक सिस्टम्स]] है, में संगणनीय कार्य की निम्नलिखित परिभाषा शामिल है: | ||
{{quote|It was stated above that 'a function is effectively calculable if its values can be found by some purely mechanical process'. We may take this statement literally, understanding by a purely mechanical process one which could be carried out by a machine. It is possible to give a mathematical description, in a certain normal form, of the structures of these machines. The development of these ideas leads to the author's definition of a computable function, and to an identification of computability with effective calculability. It is not difficult, though somewhat laborious, to prove that these three definitions [the 3rd is the λ-calculus] are equivalent.|Turing (1939) in ''The Undecidable'', p. 160}} | {{quote|It was stated above that 'a function is effectively calculable if its values can be found by some purely mechanical process'. We may take this statement literally, understanding by a purely mechanical process one which could be carried out by a machine. It is possible to give a mathematical description, in a certain normal form, of the structures of these machines. The development of these ideas leads to the author's definition of a computable function, and to an identification of computability with effective calculability. It is not difficult, though somewhat laborious, to prove that these three definitions [the 3rd is the λ-calculus] are equivalent.|Turing (1939) in ''The Undecidable'', p. 160}} | ||
एलन ट्यूरिंग ने 1936 में ए-मशीन (स्वचालित मशीन) का आविष्कार किया।<ref name=Hodges-2012/>ट्यूरिंग ने अपना पेपर 31 मई 1936 को लंदन मैथमेटिकल सोसाइटी फॉर इट्स प्रोसीडिंग्स (cf. हॉजेस 1983: 112) को प्रस्तुत किया, लेकिन यह 1937 की शुरुआत में प्रकाशित हुआ था और ऑफप्रिंट फरवरी 1937 में उपलब्ध थे (cf. हॉजेस 1983: 129) यह ट्यूरिंग का था डॉक्टरेट सलाहकार, अलोंजो चर्च, जिन्होंने बाद में | एलन ट्यूरिंग ने 1936 में ए-मशीन (स्वचालित मशीन) का आविष्कार किया।<ref name=Hodges-2012/> ट्यूरिंग ने अपना पेपर 31 मई 1936 को लंदन मैथमेटिकल सोसाइटी फॉर इट्स प्रोसीडिंग्स (cf. हॉजेस 1983: 112) को प्रस्तुत किया, लेकिन यह 1937 की शुरुआत में प्रकाशित हुआ था और ऑफप्रिंट फरवरी 1937 में उपलब्ध थे (cf. हॉजेस 1983: 129) यह ट्यूरिंग का था डॉक्टरेट सलाहकार, अलोंजो चर्च, जिन्होंने बाद में समीक्षा में ट्यूरिंग मशीन शब्द गढ़ा।<ref>see note in forward to The Collected Works of Alonzo Church ({{Cite book |url=https://mitpress.mit.edu/books/collected-works-alonzo-church |title=The Collected Works of Alonzo Church |date=2019-04-23 |publisher=MIT Press |isbn=978-0-262-02564-5 |editor-last=Burge |editor-first=Tyler |location=Cambridge, MA, USA |language=en |editor-last2=Enderton |editor-first2=Herbert}})</ref> इस मॉडल के साथ, ट्यूरिंग नकारात्मक में दो प्रश्नों का उत्तर देने में सक्षम था: | ||
* क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन गोलाकार है (उदाहरण के लिए, फ्रीज, या उसके कम्प्यूटेशनल कार्य को जारी रखने में विफल)? | * क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन गोलाकार है (उदाहरण के लिए, फ्रीज, या उसके कम्प्यूटेशनल कार्य को जारी रखने में विफल)? | ||
* क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन कभी किसी दिए गए प्रतीक को प्रिंट करती है या नहीं?<ref>Turing 1936 in ''The Undecidable'' 1965:132-134; Turing's definition of "circular" is found on page 119.</ref><ref>{{cite journal |first=Alan Mathison |last=Turing |title=On Computable Numbers, with an Application to the ''Entscheidungsproblem'' |journal=Proceedings of the London Mathematical Society |series=Series 2 |volume=42 |number=1 |pages=230–265 |year=1937 | doi=10.1112/plms/s2-42.1.230 |s2cid=73712 }} — Reprint at: {{cite web | * क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन कभी किसी दिए गए प्रतीक को प्रिंट करती है या नहीं?<ref>Turing 1936 in ''The Undecidable'' 1965:132-134; Turing's definition of "circular" is found on page 119.</ref><ref>{{cite journal |first=Alan Mathison |last=Turing |title=On Computable Numbers, with an Application to the ''Entscheidungsproblem'' |journal=Proceedings of the London Mathematical Society |series=Series 2 |volume=42 |number=1 |pages=230–265 |year=1937 | doi=10.1112/plms/s2-42.1.230 |s2cid=73712 }} — Reprint at: {{cite web | ||
|url=http://www.turingarchive.org/viewer/?id=466&title=01e |access-date=9 July 2020 |first=Alan |last=Turing |title=On computable numbers, with an application to the Entscheidungsproblem |website=The Turing Digital Archive }}</ref> | |url=http://www.turingarchive.org/viewer/?id=466&title=01e |access-date=9 July 2020 |first=Alan |last=Turing |title=On computable numbers, with an application to the Entscheidungsproblem |website=The Turing Digital Archive }}</ref> | ||
इस प्रकार मनमाना संगणना करने में सक्षम | इस प्रकार मनमाना संगणना करने में सक्षम बहुत ही सरल उपकरण का गणितीय विवरण प्रदान करके, वह सामान्य रूप से संगणना के गुणों को साबित करने में सक्षम था - और विशेष रूप से, Entscheidungsproblem ('निर्णय समस्या') की संगणनीयता।<ref>Turing 1936 in ''The Undecidable'' 1965:145</ref> | ||
जब ट्यूरिंग यूके लौटे तो अंततः वे एनिग्मा नामक एन्क्रिप्शन मशीनों द्वारा बनाए गए जर्मन गुप्त कोड को तोड़ने के लिए संयुक्त रूप से जिम्मेदार हो गए; वह एसीई ([[स्वचालित कंप्यूटिंग इंजन]]) के डिजाइन में भी शामिल हो गया, [ट्यूरिंग] एसीई प्रस्ताव प्रभावी रूप से आत्मनिर्भर था, और इसकी जड़ें ईडीवीएसी [यूएसए की पहल] में नहीं थीं, बल्कि अपनी सार्वभौमिक मशीन (होजेस पी) में थीं। . 318)। क्लेन (1952) ट्यूरिंग की थीसिस द्वारा जो नाम दिया गया है, उसकी उत्पत्ति और प्रकृति के संबंध में तर्क अभी भी जारी हैं। लेकिन ट्यूरिंग ने अपने कम्प्यूटेशनल-मशीन मॉडल के साथ जो साबित किया, वह उनके पेपर ऑन कंप्यूटेबल नंबर्स में | |||
जब ट्यूरिंग यूके लौटे तो अंततः वे एनिग्मा नामक एन्क्रिप्शन मशीनों द्वारा बनाए गए जर्मन गुप्त कोड को तोड़ने के लिए संयुक्त रूप से जिम्मेदार हो गए; वह एसीई ([[स्वचालित कंप्यूटिंग इंजन]]) के डिजाइन में भी शामिल हो गया, [ट्यूरिंग] एसीई प्रस्ताव प्रभावी रूप से आत्मनिर्भर था, और इसकी जड़ें ईडीवीएसी [यूएसए की पहल] में नहीं थीं, बल्कि अपनी सार्वभौमिक मशीन (होजेस पी) में थीं। . 318)। क्लेन (1952) ट्यूरिंग की थीसिस द्वारा जो नाम दिया गया है, उसकी उत्पत्ति और प्रकृति के संबंध में तर्क अभी भी जारी हैं। लेकिन ट्यूरिंग ने अपने कम्प्यूटेशनल-मशीन मॉडल के साथ जो साबित किया, वह उनके पेपर ऑन कंप्यूटेबल नंबर्स में एप्लीकेशन टू द एंट्सचिडंगस्प्रोब्लेम (1937) के साथ दिखाई देता है: | |||
{{quote|[that] the Hilbert Entscheidungsproblem can have no solution ... I propose, therefore to show that there can be no general process for determining whether a given formula U of the functional calculus K is provable, i.e. that there can be no machine which, supplied with any one U of these formulae, will eventually say whether U is provable.|from Turing's paper as reprinted in ''The Undecidable'', p. 145}} | {{quote|[that] the Hilbert Entscheidungsproblem can have no solution ... I propose, therefore to show that there can be no general process for determining whether a given formula U of the functional calculus K is provable, i.e. that there can be no machine which, supplied with any one U of these formulae, will eventually say whether U is provable.|from Turing's paper as reprinted in ''The Undecidable'', p. 145}} | ||
ट्यूरिंग का उदाहरण (उनका दूसरा प्रमाण): यदि कोई हमें यह बताने के लिए | ट्यूरिंग का उदाहरण (उनका दूसरा प्रमाण): यदि कोई हमें यह बताने के लिए सामान्य प्रक्रिया के बारे में पूछता है: क्या यह मशीन कभी 0 प्रिंट करती है, तो यह प्रश्न अनिर्णीत है। | ||
=== 1937-1970: डिजिटल कंप्यूटर, कंप्यूटर विज्ञान का जन्म === | === 1937-1970: डिजिटल कंप्यूटर, कंप्यूटर विज्ञान का जन्म === | ||
1937 में, प्रिंसटन में अपनी पीएचडी थीसिस पर काम करते हुए, ट्यूरिंग ने स्क्रैच से | 1937 में, प्रिंसटन में अपनी पीएचडी थीसिस पर काम करते हुए, ट्यूरिंग ने स्क्रैच से डिजिटल (बूलियन-लॉजिक) मल्टीप्लायर बनाया, जिससे अपना खुद का इलेक्ट्रोमैकेनिकल [[रिले]] (होजेस पृष्ठ 138) बना। एलन का कार्य रिले-संचालित स्विचों के नेटवर्क में ट्यूरिंग मशीन के तार्किक डिजाइन को मूर्त रूप देना था ... (होजेस पी। 138)। जबकि ट्यूरिंग शुरू में जिज्ञासु और प्रयोग करने वाला हो सकता था, उसी दिशा में जर्मनी ([[कोनराड ज़्यूस]] (1938)), और संयुक्त राज्य अमेरिका (हावर्ड ऐकेन) और [[जॉर्ज स्टिबिट्ज़]] (1937) में काफी ईमानदारी से काम चल रहा था; [[द्वितीय विश्व युद्ध]] में एक्सिस और मित्र देशों की सेनाओं द्वारा उनके मजदूरों के फलों का उपयोग किया गया था (cf. हॉजेस पृष्ठ 298-299)। 1950 के दशक के मध्य में हाओ वांग (अकादमिक) और [[मार्विन मिंस्की]] ने ट्यूरिंग मशीन को सरल रूप में कम कर दिया ([[मार्टिन डेविस (गणितज्ञ)]] की पोस्ट-ट्यूरिंग मशीन का अग्रदूत); साथ ही साथ यूरोपीय शोधकर्ता नए-फंसे हुए [[इलेक्ट्रॉनिक कंप्यूटर]] को कंप्यूटर जैसी सैद्धांतिक वस्तु के बराबर बना रहे थे जिसे अब ट्यूरिंग मशीन कहा जा रहा है। 1950 के दशक के अंत और 1960 के दशक के प्रारंभ में, संयोग से मेलज़क और लैम्बेक (1961), मिन्स्की (1961), और शेफर्डसन और स्टर्गिस (1961) के समानांतर विकास ने यूरोपीय कार्य को आगे बढ़ाया और ट्यूरिंग मशीन को अधिक अनुकूल, कंप्यूटर की तरह कम कर दिया। सार मॉडल जिसे [[काउंटर मशीन]] कहा जाता है; एलगोट और रॉबिन्सन (1964), हार्टमैनिस (1971), कुक और रेक्हो (1973) ने रजिस्टर मशीन और रैंडम-एक्सेस मशीन मॉडल के साथ इस काम को और आगे बढ़ाया- लेकिन मूल रूप से सभी अंकगणितीय निर्देश वाली मल्टी-टेप ट्यूरिंग मशीन हैं। तय करना। | ||
=== 1970-वर्तमान: गणना के | === 1970-वर्तमान: गणना के मॉडल के रूप में === | ||
आज, काउंटर, रजिस्टर और रैंडम-एक्सेस मशीन और उनकी जननी ट्यूरिंग मशीन अभिकलन के सिद्धांत में सवालों की जांच करने वाले सिद्धांतकारों के लिए पसंद के मॉडल बने हुए हैं। विशेष रूप से, कम्प्यूटेशनल जटिलता सिद्धांत ट्यूरिंग मशीन का उपयोग करता है: | आज, काउंटर, रजिस्टर और रैंडम-एक्सेस मशीन और उनकी जननी ट्यूरिंग मशीन अभिकलन के सिद्धांत में सवालों की जांच करने वाले सिद्धांतकारों के लिए पसंद के मॉडल बने हुए हैं। विशेष रूप से, कम्प्यूटेशनल जटिलता सिद्धांत ट्यूरिंग मशीन का उपयोग करता है: | ||
| Line 554: | Line 556: | ||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist}} | {{Reflist}} | ||
=== प्राथमिक साहित्य, पुनर्मुद्रण और संकलन === | === प्राथमिक साहित्य, पुनर्मुद्रण और संकलन === | ||
* बी [[जैक कोपलैंड]] एड। (2004), द एसेंशियल ट्यूरिंग: सेमिनल राइटिंग्स इन कम्प्यूटिंग, लॉजिक, फिलॉसफी, आर्टिफिशियल इंटेलिजेंस, एंड आर्टिफिशियल लाइफ प्लस द सीक्रेट्स ऑफ एनिग्मा, क्लेरेंडन प्रेस (ऑक्सफोर्ड यूनिवर्सिटी प्रेस), ऑक्सफोर्ड यूके, {{isbn|0-19-825079-7}}. ट्यूरिंग पेपर्स के साथ-साथ एमिल पोस्ट को ट्यूरिंग के सम्मेलन की उनकी आलोचना, और ट्यूरिंग की यूनिवर्सल कंप्यूटिंग मशीन के लिए डोनाल्ड डब्ल्यू डेविस के सुधारों के लिए | * बी [[जैक कोपलैंड]] एड। (2004), द एसेंशियल ट्यूरिंग: सेमिनल राइटिंग्स इन कम्प्यूटिंग, लॉजिक, फिलॉसफी, आर्टिफिशियल इंटेलिजेंस, एंड आर्टिफिशियल लाइफ प्लस द सीक्रेट्स ऑफ एनिग्मा, क्लेरेंडन प्रेस (ऑक्सफोर्ड यूनिवर्सिटी प्रेस), ऑक्सफोर्ड यूके, {{isbn|0-19-825079-7}}. ट्यूरिंग पेपर्स के साथ-साथ एमिल पोस्ट को ट्यूरिंग के सम्मेलन की उनकी आलोचना, और ट्यूरिंग की यूनिवर्सल कंप्यूटिंग मशीन के लिए डोनाल्ड डब्ल्यू डेविस के सुधारों के लिए मसौदा पत्र शामिल है | ||
* मार्टिन डेविस (गणितज्ञ) (संपा.) (1965), द अनडिसीडेबल, रेवेन प्रेस, हेवलेट, एनवाई। | * मार्टिन डेविस (गणितज्ञ) (संपा.) (1965), द अनडिसीडेबल, रेवेन प्रेस, हेवलेट, एनवाई। | ||
* एमिल पोस्ट (1936), फाइनाइट कॉम्बिनेटरी प्रोसेसेस-फॉर्मूलेशन 1, जर्नल ऑफ़ सिंबॉलिक लॉजिक, 1, 103-105, 1936। | * एमिल पोस्ट (1936), फाइनाइट कॉम्बिनेटरी प्रोसेसेस-फॉर्मूलेशन 1, जर्नल ऑफ़ सिंबॉलिक लॉजिक, 1, 103-105, 1936। | ||
| Line 572: | Line 570: | ||
* {{cite book | last = Boolos | first = George |author2=Richard Jeffrey | title = संगणना और तर्क| url = https://archive.org/details/computabilitylog0000bool_r8y9 | url-access = registration | edition = 3rd | publisher = Cambridge University Press | location = Cambridge UK | orig-year = 1989| year = 1999| isbn = 0-521-20402-X }} | * {{cite book | last = Boolos | first = George |author2=Richard Jeffrey | title = संगणना और तर्क| url = https://archive.org/details/computabilitylog0000bool_r8y9 | url-access = registration | edition = 3rd | publisher = Cambridge University Press | location = Cambridge UK | orig-year = 1989| year = 1999| isbn = 0-521-20402-X }} | ||
* {{cite book | last = Boolos | first = George |author2=John Burgess |author3=Richard Jeffrey | title = संगणना और तर्क| edition = 4th | publisher = Cambridge University Press | location = Cambridge UK | year = 2002 | isbn = 0-521-00758-5 }} बर्गेस द्वारा कुछ हिस्सों को महत्वपूर्ण रूप से फिर से लिखा गया है। लैम्बेक अबैकस मशीन (cf. रजिस्टर मशीन) और [[संगणनीय समारोह]] के संदर्भ में ट्यूरिंग मशीनों की प्रस्तुति, उनकी समानता दर्शाती है। | * {{cite book | last = Boolos | first = George |author2=John Burgess |author3=Richard Jeffrey | title = संगणना और तर्क| edition = 4th | publisher = Cambridge University Press | location = Cambridge UK | year = 2002 | isbn = 0-521-00758-5 }} बर्गेस द्वारा कुछ हिस्सों को महत्वपूर्ण रूप से फिर से लिखा गया है। लैम्बेक अबैकस मशीन (cf. रजिस्टर मशीन) और [[संगणनीय समारोह]] के संदर्भ में ट्यूरिंग मशीनों की प्रस्तुति, उनकी समानता दर्शाती है। | ||
* टेलर एल बूथ (1967), अनुक्रमिक मशीनें और ऑटोमेटा थ्योरी, जॉन विली एंड संस, इंक, न्यूयॉर्क। स्नातक स्तर का इंजीनियरिंग पाठ; विषयों की | * टेलर एल बूथ (1967), अनुक्रमिक मशीनें और ऑटोमेटा थ्योरी, जॉन विली एंड संस, इंक, न्यूयॉर्क। स्नातक स्तर का इंजीनियरिंग पाठ; विषयों की विस्तृत विविधता से अधिक है, अध्याय IX ट्यूरिंग मशीन में कुछ पुनरावर्तन सिद्धांत शामिल हैं। | ||
* {{cite book|author = Martin Davis | year = 1958| title = संगणनीयता और अघुलनशीलता| publisher = McGraw-Hill Book Company, Inc, New York | author-link = Martin Davis (mathematician)}}. पृष्ठ 12-20 पर वह जोड़, उत्तरवर्ती फलन, घटाव (x ≥ y), उचित घटाव (0 यदि x < y), पहचान फलन और विभिन्न पहचान फलन, और गुणन के लिए 5-ट्यूपल तालिकाओं का उदाहरण देता है। | * {{cite book|author = Martin Davis | year = 1958| title = संगणनीयता और अघुलनशीलता| publisher = McGraw-Hill Book Company, Inc, New York | author-link = Martin Davis (mathematician)}}. पृष्ठ 12-20 पर वह जोड़, उत्तरवर्ती फलन, घटाव (x ≥ y), उचित घटाव (0 यदि x < y), पहचान फलन और विभिन्न पहचान फलन, और गुणन के लिए 5-ट्यूपल तालिकाओं का उदाहरण देता है। | ||
* {{cite book | last = Davis| first = Martin |author2=Ron Sigal |author3=Elaine J. Weyuker|author3-link=Elaine Weyuker | title = संगणनीयता, जटिलता, और भाषाएँ और तर्क: सैद्धांतिक कंप्यूटर विज्ञान के मूल तत्व| edition = 2nd | publisher = Academic Press, Harcourt, Brace & Company| location = San Diego | year = 1994 | isbn = 0-12-206382-1}} | * {{cite book | last = Davis| first = Martin |author2=Ron Sigal |author3=Elaine J. Weyuker|author3-link=Elaine Weyuker | title = संगणनीयता, जटिलता, और भाषाएँ और तर्क: सैद्धांतिक कंप्यूटर विज्ञान के मूल तत्व| edition = 2nd | publisher = Academic Press, Harcourt, Brace & Company| location = San Diego | year = 1994 | isbn = 0-12-206382-1}} | ||
| Line 594: | Line 592: | ||
=== छोटी ट्यूरिंग मशीनें === | === छोटी ट्यूरिंग मशीनें === | ||
* रोगोज़िन, यूरी, 1998, [https://web.archive.org/web/20050308141040/http://www.imt.ro/Romjist/Volum1/Vol1_3/turing.htm 22 राज्यों और 2 के साथ | * रोगोज़िन, यूरी, 1998, [https://web.archive.org/web/20050308141040/http://www.imt.ro/Romjist/Volum1/Vol1_3/turing.htm 22 राज्यों और 2 के साथ यूनिवर्सल ट्यूरिंग मशीन प्रतीकों], सूचना विज्ञान और प्रौद्योगिकी के रोमानियाई जर्नल, 1(3), 259–265, 1998. (छोटे सार्वभौमिक ट्यूरिंग मशीनों के बारे में ज्ञात परिणामों का सर्वेक्षण) | ||
* [[स्टीफन वोल्फ्राम]], 2002, [http://www.wolframscience.com/nksonline/page-707 विज्ञान का | * [[स्टीफन वोल्फ्राम]], 2002, [http://www.wolframscience.com/nksonline/page-707 विज्ञान का नया प्रकार], वोल्फ्राम मीडिया, {{isbn|1-57955-008-8}} | ||
* ब्रुनफिल, ज्योफ, [http://www.nature.com/news/2007/071024/full/news.2007.190.html स्टूडेंट स्नैग मैथ्स प्राइज], नेचर, 24 अक्टूबर 2007। | * ब्रुनफिल, ज्योफ, [http://www.nature.com/news/2007/071024/full/news.2007.190.html स्टूडेंट स्नैग मैथ्स प्राइज], नेचर, 24 अक्टूबर 2007। | ||
* जिम जाइल्स (2007), [https://www.newscientist.com/article/dn12826-simplest-universal-computer-wins-student-25000.html सिंपलेस्ट 'यूनिवर्सल कंप्यूटर' ने छात्र को $25,000 जीता], न्यू साइंटिस्ट, 24 अक्टूबर , 2007. | * जिम जाइल्स (2007), [https://www.newscientist.com/article/dn12826-simplest-universal-computer-wins-student-25000.html सिंपलेस्ट 'यूनिवर्सल कंप्यूटर' ने छात्र को $25,000 जीता], न्यू साइंटिस्ट, 24 अक्टूबर , 2007. | ||
| Line 604: | Line 602: | ||
* हेक्टर जेनिल (वोल्फ्राम रिसर्च), 2007 [http://cs.nyu.edu/pipermail/fom/2007-October/012163.html सबसे छोटी यूनिवर्सल मशीन], एफओएम ईमेल सूची। 29 अक्टूबर, 2007। | * हेक्टर जेनिल (वोल्फ्राम रिसर्च), 2007 [http://cs.nyu.edu/pipermail/fom/2007-October/012163.html सबसे छोटी यूनिवर्सल मशीन], एफओएम ईमेल सूची। 29 अक्टूबर, 2007। | ||
* टोड रोलैंड, 2007, [http://forum.wolframscience.com/showthread.php?s=&threadid=1472 FOM पर भ्रम], वोल्फ्राम विज्ञान संदेश बोर्ड, 30 अक्टूबर, 2007। | * टोड रोलैंड, 2007, [http://forum.wolframscience.com/showthread.php?s=&threadid=1472 FOM पर भ्रम], वोल्फ्राम विज्ञान संदेश बोर्ड, 30 अक्टूबर, 2007। | ||
* ओलिवियर और मार्क रेनॉड, 2014, [http://www.machinedeturing.com/ang_default.asp ट्यूरिंग मशीन हासिल करने के लिए | * ओलिवियर और मार्क रेनॉड, 2014, [http://www.machinedeturing.com/ang_default.asp ट्यूरिंग मशीन हासिल करने के लिए प्रोग्रामेबल प्रोटोटाइप] ब्लेज़ पास्कल यूनिवर्सिटी की लिमोस लेबोरेटरी (फ्रांस में क्लेरमोंट-फेरैंड)। | ||
=== अन्य === | === अन्य === | ||
| Line 611: | Line 609: | ||
* [[स्टीफन हॉकिंग]] (संपादक), 2005, गॉड क्रिएटेड द इंटीजर: द मैथमेटिकल ब्रेकथ्रूज़ दैट चेंज्ड हिस्ट्री, रनिंग प्रेस, फिलाडेल्फिया, {{isbn|978-0-7624-1922-7}}. हॉकिंग द्वारा लिखित ट्यूरिंग की संक्षिप्त टिप्पणी और जीवनी के साथ ट्यूरिंग का 1936-1937 का पेपर शामिल है। | * [[स्टीफन हॉकिंग]] (संपादक), 2005, गॉड क्रिएटेड द इंटीजर: द मैथमेटिकल ब्रेकथ्रूज़ दैट चेंज्ड हिस्ट्री, रनिंग प्रेस, फिलाडेल्फिया, {{isbn|978-0-7624-1922-7}}. हॉकिंग द्वारा लिखित ट्यूरिंग की संक्षिप्त टिप्पणी और जीवनी के साथ ट्यूरिंग का 1936-1937 का पेपर शामिल है। | ||
* {{cite book | author = Rolf Herken | title = द यूनिवर्सल ट्यूरिंग मशीन-ए हाफ-सेंचुरी सर्वे| publisher = Springer Verlag | isbn = 978-3-211-82637-9 | year = 1995}} | * {{cite book | author = Rolf Herken | title = द यूनिवर्सल ट्यूरिंग मशीन-ए हाफ-सेंचुरी सर्वे| publisher = Springer Verlag | isbn = 978-3-211-82637-9 | year = 1995}} | ||
* [[एंड्रयू हॉजेस]], एलन ट्यूरिंग: द एनिग्मा, [[साइमन और शूस्टर]], न्यूयॉर्क। सी एफ अध्याय द स्पिरिट ऑफ ट्रूथ | * [[एंड्रयू हॉजेस]], एलन ट्यूरिंग: द एनिग्मा, [[साइमन और शूस्टर]], न्यूयॉर्क। सी एफ अध्याय द स्पिरिट ऑफ ट्रूथ ऐसे इतिहास के लिए जो उसके प्रमाण की ओर ले जाता है और उसकी चर्चा करता है। | ||
* {{cite book|author = Ivars Peterson | year = 1988| title = गणितीय पर्यटक: आधुनिक गणित का स्नैपशॉट|url = https://archive.org/details/mathematicaltour00pete |url-access = registration | publisher = W. H. Freeman and Company, New York| edition = 1st | isbn = 978-0-7167-2064-5 | author-link = Ivars Peterson}} | * {{cite book|author = Ivars Peterson | year = 1988| title = गणितीय पर्यटक: आधुनिक गणित का स्नैपशॉट|url = https://archive.org/details/mathematicaltour00pete |url-access = registration | publisher = W. H. Freeman and Company, New York| edition = 1st | isbn = 978-0-7167-2064-5 | author-link = Ivars Peterson}} | ||
* [[रोजर पेनरोज़]], द एम्परर्स न्यू माइंड: कन्सर्निंग कंप्यूटर्स, माइंड्स एंड द लॉज़ ऑफ़ फ़िज़िक्स, [[ऑक्सफोर्ड यूनिवरसिटि प्रेस]], ऑक्सफोर्ड एंड न्यूयॉर्क, 1989 (1990 सुधार), {{isbn|0-19-851973-7}}. | * [[रोजर पेनरोज़]], द एम्परर्स न्यू माइंड: कन्सर्निंग कंप्यूटर्स, माइंड्स एंड द लॉज़ ऑफ़ फ़िज़िक्स, [[ऑक्सफोर्ड यूनिवरसिटि प्रेस]], ऑक्सफोर्ड एंड न्यूयॉर्क, 1989 (1990 सुधार), {{isbn|0-19-851973-7}}. | ||
* {{cite book | author = Paul Strathern | title = ट्यूरिंग एंड द कंप्यूटर-द बिग आइडिया| publisher = Anchor Books/Doubleday | isbn = 978-0-385-49243-0 | year = 1997 | url = https://archive.org/details/turingcomputer00stra | author-link = Paul Strathern }} | * {{cite book | author = Paul Strathern | title = ट्यूरिंग एंड द कंप्यूटर-द बिग आइडिया| publisher = Anchor Books/Doubleday | isbn = 978-0-385-49243-0 | year = 1997 | url = https://archive.org/details/turingcomputer00stra | author-link = Paul Strathern }} | ||
* हाओ वांग (अकादमिक), कंप्यूटिंग मशीनों के ट्यूरिंग के सिद्धांत का | * हाओ वांग (अकादमिक), कंप्यूटिंग मशीनों के ट्यूरिंग के सिद्धांत का प्रकार, जर्नल ऑफ़ द एसोसिएशन फॉर कंप्यूटिंग मशीनरी (JACM) 4, 63–92 (1957)। | ||
* [[चार्ल्स पेटज़ोल्ड]], [http://www.theannotatedturing.com/ पेटज़ोल्ड, चार्ल्स, द एनोटेटेड ट्यूरिंग], जॉन विले एंड संस, इंक। {{isbn|0-470-22905-5}} | * [[चार्ल्स पेटज़ोल्ड]], [http://www.theannotatedturing.com/ पेटज़ोल्ड, चार्ल्स, द एनोटेटेड ट्यूरिंग], जॉन विले एंड संस, इंक। {{isbn|0-470-22905-5}} | ||
* अरोड़ा, संजीव; बराक, बोअज़, [http://www.cs.princeton.edu/theory/complexity/ कॉम्प्लेक्सिटी थ्योरी: ए मॉडर्न अप्रोच], कैम्ब्रिज यूनिवर्सिटी प्रेस, 2009, {{isbn|978-0-521-42426-4}}, खंड 1.4, तार के रूप में मशीनें और सार्वभौमिक ट्यूरिंग मशीन और 1.7, प्रमेय 1.9 का प्रमाण | * अरोड़ा, संजीव; बराक, बोअज़, [http://www.cs.princeton.edu/theory/complexity/ कॉम्प्लेक्सिटी थ्योरी: ए मॉडर्न अप्रोच], कैम्ब्रिज यूनिवर्सिटी प्रेस, 2009, {{isbn|978-0-521-42426-4}}, खंड 1.4, तार के रूप में मशीनें और सार्वभौमिक ट्यूरिंग मशीन और 1.7, प्रमेय 1.9 का प्रमाण | ||
| Line 631: | Line 629: | ||
{{Mathematical logic}} | {{Mathematical logic}} | ||
{{Alan Turing}} | {{Alan Turing}} | ||
{{DEFAULTSORT:Turing machine}}[[Category: ट्यूरिंग मशीन | ट्यूरिंग मशीन ]] [[Category: कंप्यूटिंग में 1936]] [[Category: कंप्यूटिंग में 1937]] [[Category: शैक्षिक सार मशीनें]] [[Category: सैद्धांतिक कंप्यूटर विज्ञान]] [[Category: एलन ट्यूरिंग]] [[Category: गणना के मॉडल]] [[Category: औपचारिक तरीके]] [[Category: संगणनीयता सिद्धांत]] [[Category: अंग्रेजी आविष्कार]] [[Category: ऑटोमेटा (गणना)]] [[Category: औपचारिक भाषाएँ]] [[Category: सार मशीनें]] | {{DEFAULTSORT:Turing machine}}[[Category: ट्यूरिंग मशीन | ट्यूरिंग मशीन ]] [[Category: कंप्यूटिंग में 1936]] [[Category: कंप्यूटिंग में 1937]] [[Category: शैक्षिक सार मशीनें]] [[Category: सैद्धांतिक कंप्यूटर विज्ञान]] [[Category: एलन ट्यूरिंग]] [[Category: गणना के मॉडल]] [[Category: औपचारिक तरीके]] [[Category: संगणनीयता सिद्धांत]] [[Category: अंग्रेजी आविष्कार]] [[Category: ऑटोमेटा (गणना)]] [[Category: औपचारिक भाषाएँ]] [[Category: सार मशीनें]] | ||
Revision as of 12:44, 2 August 2023
Error: Image is invalid or non-existent.
एक ट्यूरिंग मशीन अमूर्त मशीन का वर्णन करने वाली संगणना का गणितीय मॉडल है[1] जो नियमों की तालिका के अनुसार टेप की पट्टी पर प्रतीकों में हेरफेर करता है।[2] मॉडल की सादगी के बावजूद, यह किसी भी कंप्यूटर एल्गोरिथ्म को लागू करने में सक्षम है।[3]
मशीन अनंत पर काम करती है[4] असतत गणित कोशिकाओं में विभाजित मेमोरी टेप,[5] जिनमें से प्रत्येक मशीन के वर्णमाला (औपचारिक भाषा) कहे जाने वाले प्रतीकों के परिमित सेट से खींचे गए एकल प्रतीक को धारण कर सकता है। इसका सिर होता है, जो मशीन के संचालन के किसी भी बिंदु पर, इन कोशिकाओं में से पर स्थित होता है, और राज्य राज्यों के सीमित सेट से चुना जाता है। इसके संचालन के प्रत्येक चरण में, सिर अपने सेल में प्रतीक को पढ़ता है। फिर, प्रतीक और मशीन की अपनी वर्तमान स्थिति के आधार पर, मशीन उसी सेल में प्रतीक लिखती है, और सिर को कदम बाईं या दाईं ओर ले जाती है,[6] या गणना को रोक देता है। किस प्रतिस्थापन प्रतीक को लिखना है और किस दिशा में जाना है, यह परिमित तालिका पर आधारित है जो निर्दिष्ट करती है कि वर्तमान स्थिति के प्रत्येक संयोजन और पढ़े जाने वाले प्रतीक के लिए क्या करना है।
ट्यूरिंग मशीन का आविष्कार 1936 में एलन ट्यूरिंग ने किया था।[7][8] जिन्होंने इसे ए-मशीन (स्वचालित मशीन) कहा।[9] यह ट्यूरिंग के डॉक्टरेट सलाहकार अलोंजो चर्च थे, जिन्होंने बाद में समीक्षा में ट्यूरिंग मशीन शब्द गढ़ा।[10] इस मॉडल के साथ, ट्यूरिंग नकारात्मक में दो प्रश्नों का उत्तर देने में सक्षम था:
- क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन गोलाकार है (उदाहरण के लिए, फ्रीज, या उसके कम्प्यूटेशनल कार्य को जारी रखने में विफल)?
- क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन कभी किसी दिए गए प्रतीक को प्रिंट करती है या नहीं?[11][12]
इस प्रकार मनमाना संगणना करने में सक्षम बहुत ही सरल उपकरण का गणितीय विवरण प्रदान करके, वह सामान्य रूप से संगणना के गुणों को साबित करने में सक्षम था - और विशेष रूप से, Entscheidungsproblem ('निर्णय समस्या') की संगणनीयता।[13]
ट्यूरिंग मशीनों ने यांत्रिक संगणना की शक्ति पर मौलिक सीमाओं के अस्तित्व को सिद्ध किया।[14] जबकि वे मनमाना संगणना व्यक्त कर सकते हैं, उनका न्यूनतम डिजाइन उन्हें व्यवहार में गणना के लिए अनुपयुक्त बनाता है: वास्तविक दुनिया के संगणक विभिन्न डिजाइनों पर आधारित होते हैं, जो ट्यूरिंग मशीनों के विपरीत, रैंडम एक्सेस मेमोरी का उपयोग करते हैं।
ट्यूरिंग पूर्णता ट्यूरिंग मशीन का अनुकरण करने के लिए निर्देशों की प्रणाली की क्षमता है। प्रोग्रामिंग भाषा जो ट्यूरिंग पूर्ण है, सैद्धांतिक रूप से कंप्यूटर द्वारा पूरा किए जाने वाले सभी कार्यों को व्यक्त करने में सक्षम है; यदि परिमित स्मृति की सीमाओं को नजरअंदाज कर दिया जाए तो लगभग सभी प्रोग्रामिंग भाषाएं ट्यूरिंग पूर्ण हैं।
सिंहावलोकन
एक ट्यूरिंग मशीन केंद्रीय प्रसंस्करण इकाई (सीपीयू) का सामान्य उदाहरण है जो डेटा को स्टोर करने के लिए अनुक्रमिक मेमोरी का उपयोग करके कैननिकल मशीन के साथ कंप्यूटर द्वारा किए गए सभी डेटा हेरफेर को नियंत्रित करता है। अधिक विशेष रूप से, यह मशीन (आटोमैटिक मशीन) है जो वर्णमाला (औपचारिक भाषाओं) के वैध स्ट्रिंग्स के कुछ मनमाने उपसमुच्चय की [[गणना]] करने में सक्षम है; ये तार पुनरावर्ती गणना योग्य सेट का हिस्सा हैं। ट्यूरिंग मशीन में अनंत लंबाई का टेप होता है जिस पर यह पढ़ने और लिखने का कार्य कर सकता है।
एक ब्लैक बॉक्स मानकर, ट्यूरिंग मशीन यह नहीं जान सकती है कि क्या यह अंततः किसी दिए गए प्रोग्राम के साथ सबसेट के किसी विशिष्ट स्ट्रिंग की गणना करेगी। यह इस तथ्य के कारण है कि हॉल्टिंग समस्या हल नहीं हो सकती है, जिसका कंप्यूटिंग की सैद्धांतिक सीमाओं के लिए प्रमुख निहितार्थ है।
ट्यूरिंग मशीन अप्रतिबंधित व्याकरण को संसाधित करने में सक्षम है, जिसका अर्थ है कि यह अनंत तरीकों से पहले क्रम के तर्क का मजबूती से मूल्यांकन करने में सक्षम है। यह लैम्ब्डा कैलकुस के माध्यम से प्रसिद्ध रूप से प्रदर्शित होता है।
एक ट्यूरिंग मशीन जो किसी अन्य ट्यूरिंग मशीन का अनुकरण करने में सक्षम है, उसे यूनिवर्सल ट्यूरिंग मशीन (UTM, या बस यूनिवर्सल मशीन) कहा जाता है। समान सार्वभौमिक प्रकृति के साथ अधिक गणितीय रूप से उन्मुख परिभाषा अलोंजो चर्च द्वारा पेश की गई थी, जिसका लैम्ब्डा कैलकुलस पर काम चर्च-ट्यूरिंग थीसिस के रूप में ज्ञात गणना के औपचारिक सिद्धांत में ट्यूरिंग के साथ जुड़ा हुआ है। थीसिस में कहा गया है कि ट्यूरिंग मशीनें वास्तव में तर्क और गणित में प्रभावी तरीकों की अनौपचारिक धारणा को पकड़ती हैं, और मॉडल प्रदान करती हैं जिसके माध्यम से कोई कलन विधि या यांत्रिक प्रक्रिया के बारे में तर्क कर सकता है। उनकी अमूर्त मशीन का अध्ययन करने से कंप्यूटर विज्ञान और कम्प्यूटेशनल जटिलता सिद्धांत में कई अंतर्दृष्टि प्राप्त होती है।
भौतिक विवरण
अपने 1948 के निबंध, इंटेलिजेंट मशीनरी में, ट्यूरिंग ने लिखा है कि उनकी मशीन में शामिल हैं:
...an unlimited memory capacity obtained in the form of an infinite tape marked out into squares, on each of which a symbol could be printed. At any moment there is one symbol in the machine; it is called the scanned symbol. The machine can alter the scanned symbol, and its behavior is in part determined by that symbol, but the symbols on the tape elsewhere do not affect the behavior of the machine. However, the tape can be moved back and forth through the machine, this being one of the elementary operations of the machine. Any symbol on the tape may therefore eventually have an innings.[15]
— Turing 1948, p. 3[16]
विवरण
ट्यूरिंग मशीन गणितीय रूप से मशीन का मॉडल बनाती है जो यांत्रिक रूप से टेप पर चलती है। इस टेप पर प्रतीक होते हैं, जिन्हें मशीन बार में टेप हेड का उपयोग करके पढ़ और लिख सकती है। ऑपरेशन पूरी तरह से प्राथमिक निर्देशों के परिमित सेट द्वारा निर्धारित किया जाता है जैसे कि राज्य 42 में, यदि देखा गया प्रतीक 0 है, तो 1 लिखें; यदि देखा गया प्रतीक 1 है, तो स्थिति 17 में बदलें; स्थिति 17 में, यदि देखा गया प्रतीक 0 है, तो 1 लिखें और स्थिति 6 में बदलें; आदि मूल लेख में (संगणनीय संख्याओं पर, Entscheidungsproblem के लिए आवेदन के साथ, #The Entscheidungsproblem (निर्णय समस्या) भी देखें): हिल्बर्ट का 1900 का दसवां प्रश्न), ट्यूरिंग तंत्र की कल्पना नहीं करता है, लेकिन व्यक्ति जिसे वह कंप्यूटर कहता है , जो इन नियतात्मक यांत्रिक नियमों को गुलामी से निष्पादित करता है (या जैसा कि ट्यूरिंग इसे कहते हैं, अपमानजनक तरीके से)।
अधिक स्पष्ट रूप से, ट्यूरिंग मशीन में निम्न शामिल हैं:
- कोशिकाओं में विभाजित टेप, दूसरे के बगल में। प्रत्येक कोशिका में कुछ परिमित वर्णमाला से प्रतीक होता है। वर्णमाला में विशेष रिक्त प्रतीक (यहाँ '0' के रूप में लिखा गया है) और या अधिक अन्य प्रतीक हैं। यह माना जाता है कि टेप मनमाने ढंग से बायीं ओर और दायीं ओर बढ़ाया जा सकता है, ताकि ट्यूरिंग मशीन को हमेशा उतनी ही टेप की आपूर्ति की जा सके जितनी इसकी गणना के लिए आवश्यक है। जिन कक्षों को पहले नहीं लिखा गया है उन्हें रिक्त प्रतीक से भरा माना जाता है। कुछ मॉडलों में टेप का बायां सिरा विशेष प्रतीक के साथ चिह्नित होता है; टेप फैली हुई है या अनिश्चित रूप से दाईं ओर फैली हुई है।
- एक सिर जो टेप पर प्रतीकों को पढ़ और लिख सकता है और टेप को बार में (और केवल एक) सेल को बाएं और दाएं घुमा सकता है। कुछ मॉडलों में सिर हिलता है और टेप स्थिर रहता है।
- एक राज्य रजिस्टर जो ट्यूरिंग मशीन की स्थिति को संग्रहीत करता है, बहुत से में से एक। इनमें से स्पेशल स्टार्ट स्टेट है जिसके साथ स्टेट रजिस्टर को इनिशियलाइज़ किया जाता है। ये राज्य, ट्यूरिंग लिखते हैं, मन की उस स्थिति को प्रतिस्थापित करते हैं जो संगणना करने वाला व्यक्ति सामान्य रूप से होगा।
- एक परिमित तालिका[17] निर्देशों का[18] वह, दिया गया राज्य (qi) मशीन वर्तमान में है और प्रतीक (aj) यह टेप पर पढ़ रहा है (प्रतीक वर्तमान में सिर के नीचे), मशीन को अनुक्रम में निम्नलिखित करने के लिए कहता है (5-ट्यूपल मॉडल के लिए):
- या तो मिटा दें या प्रतीक लिखें (ए की जगहj के साथj1).
- सिर को हिलाएं (जो डी द्वारा वर्णित हैk और मान हो सकते हैं: 'L' कदम बाएं के लिए या 'R' कदम दाएं के लिए या 'N' ही स्थान पर रहने के लिए)।
- निर्धारित के अनुसार समान या नई स्थिति मान लें (राज्य q पर जाएंi1).
4-ट्यूपल मॉडल में, किसी प्रतीक को मिटाना या लिखना (aj1) और सिर को बाएँ या दाएँ घुमाना (dk) अलग निर्देशों के रूप में निर्दिष्ट हैं। तालिका मशीन को (ia) मिटाने या प्रतीक लिखने या (ib) सिर को बाएँ या दाएँ ले जाने के लिए कहती है, और फिर (ii) उसी या नई स्थिति को निर्धारित करती है, लेकिन दोनों क्रियाओं (ia) और (ib) को नहीं ) उसी निर्देश में। कुछ मॉडलों में, यदि प्रतीक और स्थिति के वर्तमान संयोजन के लिए तालिका में कोई प्रविष्टि नहीं है, तो मशीन रुक जाएगी; अन्य मॉडलों को भरने के लिए सभी प्रविष्टियों की आवश्यकता होती है।
मशीन का प्रत्येक भाग (अर्थात इसकी स्थिति, प्रतीक-संग्रह, और किसी भी समय प्रयुक्त टेप) और इसकी क्रियाएं (जैसे मुद्रण, मिटाना और टेप गति) परिमित, असतत और विशिष्ट है; यह असीमित मात्रा में टेप और रनटाइम है जो इसे कंप्यूटर भंडारण की असीमित मात्रा देता है।
औपचारिक परिभाषा
अगले Hopcroft & Ullman (1979, p. 148), (एक-टेप) ट्यूरिंग मशीन को औपचारिक रूप से 7-टपल के रूप में परिभाषित किया जा सकता है कहाँ पे
- टेप वर्णमाला प्रतीकों का परिमित, गैर-खाली सेट है;
- रिक्त प्रतीक है (गणना के दौरान किसी भी चरण में असीम रूप से अक्सर टेप पर होने की अनुमति देने वाला एकमात्र प्रतीक);
- इनपुट प्रतीकों का सेट है, यानी, प्रारंभिक टेप सामग्री में दिखाई देने वाले प्रतीकों का सेट;
- राज्यों का परिमित, गैर-रिक्त सेट है;
- प्रारंभिक अवस्था है;
- अंतिम राज्यों या स्वीकार करने वाले राज्यों का सेट है। कहा जाता है कि प्रारंभिक टेप की सामग्री द्वारा स्वीकार की जाती है अगर यह अंततः राज्य में रुकता है .
- आंशिक कार्य है जिसे राज्य संक्रमण प्रणाली कहा जाता है, जहाँ L लेफ्ट शिफ्ट है, R राइट शिफ्ट है। अगर वर्तमान स्थिति और वर्तमान टेप प्रतीक पर परिभाषित नहीं है, तो मशीन रुक जाती है;[19] सहजता से, संक्रमण फ़ंक्शन वर्तमान स्थिति से प्रेषित अगले राज्य को निर्दिष्ट करता है, जो प्रतीक सिर द्वारा इंगित वर्तमान प्रतीक को अधिलेखित करता है, और अगला सिर आंदोलन।
इसके अलावा, अस्वीकृति को और अधिक स्पष्ट करने के लिए ट्यूरिंग मशीन में अस्वीकार स्थिति भी हो सकती है। उस स्थिति में तीन संभावनाएँ हैं: स्वीकार करना, अस्वीकार करना और हमेशा के लिए दौड़ना। अन्य संभावना यह है कि टेप पर अंतिम मानों को आउटपुट माना जाए। हालाँकि, यदि एकमात्र आउटपुट अंतिम स्थिति है, तो मशीन समाप्त हो जाती है (या कभी रुकती नहीं है), मशीन अभी भी प्रभावी रूप से पूर्णांक में ले कर लंबी स्ट्रिंग का उत्पादन कर सकती है जो यह बताती है कि आउटपुट के लिए स्ट्रिंग का कौन सा हिस्सा है।
दिशाओं के सेट के तीसरे तत्व के रूप में अपेक्षाकृत असामान्य संस्करण कोई बदलाव की अनुमति नहीं देता है, एन कहते हैं .
3-राज्य व्यस्त बीवर के लिए 7-ट्यूपल इस तरह दिखता है (ट्यूरिंग मशीन के उदाहरण में इस व्यस्त बीवर के बारे में और देखें):
- (राज्य);
- (टेप वर्णमाला प्रतीक);
- (खाली प्रतीक);
- (इनपुट प्रतीक);
- (प्रारम्भिक अवस्था);
- (अंतिम स्थिति);
- नीचे राज्य-तालिका देखें (संक्रमण समारोह)।
प्रारंभ में सभी टेप कोशिकाओं को चिह्नित किया जाता है .
| Tape symbol | Current state A | Current state B | Current state C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Write symbol | Move tape | Next state | Write symbol | Move tape | Next state | Write symbol | Move tape | Next state | |
| 0 | 1 | R | B | 1 | L | A | 1 | L | B |
| 1 | 1 | L | C | 1 | R | B | 1 | R | HALT |
ट्यूरिंग मशीनों की कल्पना या कार्यान्वयन के लिए आवश्यक अतिरिक्त विवरण
वैन एम्डे बोस (1990) के शब्दों में, पी। 6: सेट-सैद्धांतिक वस्तु [उसका औपचारिक सात-टुपल विवरण ऊपर के समान है] केवल आंशिक जानकारी प्रदान करता है कि मशीन कैसे व्यवहार करेगी और इसकी संगणना कैसी दिखेगी।
उदाहरण के लिए,
- प्रतीकों को वास्तव में कैसा दिखता है, और प्रतीकों को अनिश्चित काल तक पढ़ने और लिखने का असफल तरीका है, इस पर कई निर्णय लेने की आवश्यकता होगी।
- बाएँ और दाएँ शिफ्ट करने से टेप हेड को टेप पर शिफ्ट किया जा सकता है, लेकिन जब वास्तव में ट्यूरिंग मशीन का निर्माण किया जाता है तो टेप को हेड के नीचे आगे और पीछे स्लाइड करना अधिक व्यावहारिक होता है।
- टेप परिमित हो सकता है, और स्वचालित रूप से आवश्यकतानुसार रिक्त स्थान के साथ विस्तारित हो सकता है (जो गणितीय परिभाषा के सबसे करीब है), लेकिन यह सोचना अधिक सामान्य है कि या दोनों सिरों पर असीम रूप से फैला हुआ है और रिक्त स्थान को छोड़कर पहले से भरा हुआ है स्पष्ट रूप से दिया गया परिमित टुकड़ा टेप हेड चालू है। (यह, निश्चित रूप से, व्यवहार में लागू करने योग्य नहीं है।) टेप को लंबाई में तय नहीं किया जा सकता है, क्योंकि यह दी गई परिभाषा के अनुरूप नहीं होगा और गंभीर रूप से संगणना की सीमा को सीमित कर देगा जो मशीन रैखिक परिबद्ध ऑटोमेटन के लिए कर सकती है यदि टेप इनपुट आकार, या परिमित-राज्य मशीन के समानुपाती था यदि यह सख्ती से निश्चित-लंबाई थी।
वैकल्पिक परिभाषाएं
तर्कों या प्रमाणों को आसान या स्पष्ट बनाने के लिए साहित्य में परिभाषाएँ कभी-कभी थोड़ी भिन्न होती हैं, लेकिन यह हमेशा इस तरह से किया जाता है कि परिणामी मशीन में समान कम्प्यूटेशनल शक्ति हो। उदाहरण के लिए, सेट से बदला जा सकता है को , जहाँ N (कोई नहीं या कोई ऑपरेशन नहीं) मशीन को बाएँ या दाएँ चलने के बजाय उसी टेप सेल पर रहने की अनुमति देगा। इससे मशीन की कम्प्यूटेशनल शक्ति में वृद्धि नहीं होगी।
ट्यूरिंग/डेविस के सम्मेलन के अनुसार, ट्यूरिंग टेबल में प्रत्येक ट्यूरिंग निर्देश को नौ 5-टुपल्स में से द्वारा सबसे आम परंपरा का प्रतिनिधित्व करता है (ट्यूरिंग (1936) द अनडिसिडेबल में, पृष्ठ 126–127 और डेविस (2000) पृष्ठ 152) :
- (परिभाषा 1): '(क्यूi, एसj, एसk/ई/एन, एल/आर/एन, क्यूm)
- (वर्तमान स्थिति क्यूi, प्रतीक स्कैन एसj, प्रिंट प्रतीक एसk/erase E/none N , Move_tape_one_square बाएँ L/दाएँ R/none N , नई अवस्था qm)
अन्य लेखक (मिंस्की (1967) पृष्ठ 119, होपक्रॉफ्ट और उल्मैन (1979) पृष्ठ 158, स्टोन (1972) पृष्ठ 9) नए राज्य क्यू के साथ अलग सम्मेलन को अपनाते हैंmस्कैन किए गए प्रतीक S के तुरंत बाद सूचीबद्धj:
- (परिभाषा 2): (क्यूi, एसj, क्यूm, एसk/ई/एन, एल/आर/एन)
- (वर्तमान स्थिति क्यूi, प्रतीक स्कैन एसj, नया राज्य क्यूm, प्रिंट प्रतीक एसk/मिटाना ई/कोई नहीं एन, चाल_टेप_एक_वर्ग बाएं एल/दाएं आर/कोई नहीं एन)
इस लेख के शेष भाग के लिए परिभाषा 1 (ट्यूरिंग/डेविस सम्मेलन) का उपयोग किया जाएगा।
| Current state | Scanned symbol | Print symbol | Move tape | Final (i.e. next) state | 5-tuples | |
|---|---|---|---|---|---|---|
| A | 0 | 1 | R | B | (A, 0, 1, R, B) | |
| A | 1 | 1 | L | C | (A, 1, 1, L, C) | |
| B | 0 | 1 | L | A | (B, 0, 1, L, A) | |
| B | 1 | 1 | R | B | (B, 1, 1, R, B) | |
| C | 0 | 1 | L | B | (C, 0, 1, L, B) | |
| C | 1 | 1 | N | H | (C, 1, 1, N, H) |
निम्नलिखित तालिका में, ट्यूरिंग के मूल मॉडल ने केवल पहली तीन पंक्तियों की अनुमति दी जिसे उन्होंने N1, N2, N3 कहा (cf. ट्यूरिंग इन द अनडेकिडेबल, पृष्ठ 126)। उन्होंने 0वें प्रतीक S का नाम देकर स्कैन किए गए वर्ग को मिटाने की अनुमति दी0 = इरेज़ या ब्लैंक, आदि। हालाँकि, उन्होंने गैर-मुद्रण की अनुमति नहीं दी, इसलिए प्रत्येक निर्देश-पंक्ति में प्रिंट प्रतीक S शामिल हैkया मिटाना (cf. फुटनोट 12 इन पोस्ट (1947), द अनडिसीडेबल, पृष्ठ 300)। संक्षिप्ताक्षर ट्यूरिंग हैं (द अनडिसिडेबल, पृष्ठ 119)। 1936-1937 में ट्यूरिंग के मूल पेपर के बाद, मशीन-मॉडल ने सभी नौ संभावित प्रकार के पांच-टुपल्स की अनुमति दी है:
| Current m-configuration (Turing state) |
Tape symbol | Print-operation | Tape-motion | Final m-configuration (Turing state) |
5-tuple | 5-tuple comments | 4-tuple | |
|---|---|---|---|---|---|---|---|---|
| N1 | qi | Sj | Print(Sk) | Left L | qm | (qi, Sj, Sk, L, qm) | "blank" = S0, 1=S1, etc. | |
| N2 | qi | Sj | Print(Sk) | Right R | qm | (qi, Sj, Sk, R, qm) | "blank" = S0, 1=S1, etc. | |
| N3 | qi | Sj | Print(Sk) | None N | qm | (qi, Sj, Sk, N, qm) | "blank" = S0, 1=S1, etc. | (qi, Sj, Sk, qm) |
| 4 | qi | Sj | None N | Left L | qm | (qi, Sj, N, L, qm) | (qi, Sj, L, qm) | |
| 5 | qi | Sj | None N | Right R | qm | (qi, Sj, N, R, qm) | (qi, Sj, R, qm) | |
| 6 | qi | Sj | None N | None N | qm | (qi, Sj, N, N, qm) | Direct "jump" | (qi, Sj, N, qm) |
| 7 | qi | Sj | Erase | Left L | qm | (qi, Sj, E, L, qm) | ||
| 8 | qi | Sj | Erase | Right R | qm | (qi, Sj, E, R, qm) | ||
| 9 | qi | Sj | Erase | None N | qm | (qi, Sj, E, N, qm) | (qi, Sj, E, qm) |
किसी भी ट्यूरिंग टेबल (निर्देशों की सूची) का निर्माण उपरोक्त नौ 5-टुपल्स से किया जा सकता है। तकनीकी कारणों से, तीन गैर-मुद्रण या एन निर्देश (4, 5, 6) को आमतौर पर समाप्त किया जा सकता है। उदाहरण के लिए ट्यूरिंग मशीन के उदाहरण देखें।
कम अक्सर 4-ट्यूपल्स का उपयोग होता है: ये ट्यूरिंग निर्देशों (cf. पोस्ट (1947), बूलोस और जेफरी (1974, 1999), डेविस-सिगल-वेयुकर (1994)) के और परमाणुकरण का प्रतिनिधित्व करते हैं; पोस्ट-ट्यूरिंग मशीन पर और देखें।
राज्य
ट्यूरिंग मशीनों के संदर्भ में प्रयुक्त राज्य शब्द भ्रम का स्रोत हो सकता है, क्योंकि इसका अर्थ दो चीजें हो सकता है। ट्यूरिंग के बाद के अधिकांश टिप्पणीकारों ने प्रदर्शन करने के लिए वर्तमान निर्देश के नाम / पदनाम के लिए राज्य का उपयोग किया है - अर्थात। राज्य रजिस्टर की सामग्री। लेकिन ट्यूरिंग (1936) ने मशीन के एम-कॉन्फ़िगरेशन और मशीन की (या व्यक्ति की) गणना के माध्यम से प्रगति की स्थिति - कुल प्रणाली की वर्तमान स्थिति के रिकॉर्ड के बीच मजबूत अंतर बनाया। जिसे ट्यूरिंग ने राज्य सूत्र कहा है उसमें वर्तमान निर्देश और टेप पर सभी प्रतीक शामिल हैं:
Thus the state of progress of the computation at any stage is completely determined by the note of instructions and the symbols on the tape. That is, the state of the system may be described by a single expression (sequence of symbols) consisting of the symbols on the tape followed by Δ (which is supposed to not to appear elsewhere) and then by the note of instructions. This expression is called the "state formula".
— The Undecidable, pp. 139–140, emphasis added
इससे पहले अपने पेपर में ट्यूरिंग ने इसे और भी आगे बढ़ाया: वह उदाहरण देता है जहां उसने वर्तमान एम-कॉन्फ़िगरेशन का प्रतीक रखा है - निर्देश का लेबल - स्कैन किए गए वर्ग के नीचे, टेप पर सभी प्रतीकों के साथ (अनिर्णायक, पृष्ठ 121) ); इसे वह पूर्ण विन्यास कहते हैं (अनिर्णायक, पृ. 118)। पूर्ण कॉन्फ़िगरेशन को लाइन पर प्रिंट करने के लिए, वह स्कैन किए गए प्रतीक के बाईं ओर स्थिति-लेबल/एम-कॉन्फ़िगरेशन रखता है।
इसका रूप क्लेन (1952) में देखा गया है जहां स्टीफन कोल क्लेन दिखाता है कि मशीन की स्थिति का गोडेल नंबर कैसे लिखा जाता है: वह एम-कॉन्फ़िगरेशन प्रतीक क्यू रखता है।4 स्कैन किए गए वर्ग के ऊपर मोटे तौर पर टेप पर 6 गैर-रिक्त वर्गों के केंद्र में (इस लेख में ट्यूरिंग-टेप का आंकड़ा देखें) और इसे स्कैन किए गए वर्ग के दाईं ओर रखता है। लेकिन क्लेन क्यू को संदर्भित करता है4मशीन स्थिति के रूप में ही (क्लीन, पृष्ठ 374-375)। हॉपक्रॉफ्ट और उलमैन इस संयोजन को तात्कालिक विवरण कहते हैं और वर्तमान स्थिति (निर्देश-लेबल, एम-कॉन्फ़िगरेशन) को स्कैन किए गए प्रतीक (पृष्ठ 149) के बाईं ओर रखने के ट्यूरिंग सम्मेलन का पालन करते हैं, यानी, तात्कालिक विवरण समग्र है बाईं ओर गैर-रिक्त प्रतीकों की संख्या, मशीन की स्थिति, सिर द्वारा स्कैन किया गया वर्तमान प्रतीक और दाईं ओर गैर-रिक्त प्रतीक।
उदाहरण: 3 चालों के बाद 3-राज्य 2-प्रतीक व्यस्त ऊदबिलाव की कुल स्थिति (उदाहरण से लिया गया चित्र नीचे दिखाया गया है):
- 1'ए'1
इसका मतलब है: तीन चालों के बाद टेप में ... 000110000 ... होता है, सिर सबसे दाहिनी ओर 1 स्कैन कर रहा है, और स्थिति ए है। कुल राज्य जैसा कि यहाँ दिखाया गया है: B01; टेप पर केवल 1 है, लेकिन हेड 0 (रिक्त) को उसके बाईं ओर स्कैन कर रहा है और स्थिति B है।
ट्यूरिंग मशीनों के संदर्भ में राज्य को स्पष्ट किया जाना चाहिए कि किसका वर्णन किया जा रहा है: वर्तमान निर्देश, या वर्तमान निर्देश के साथ टेप पर प्रतीकों की सूची, या टेप पर प्रतीकों की सूची को वर्तमान निर्देश के साथ रखा गया है स्कैन किए गए प्रतीक के बाईं ओर या स्कैन किए गए प्रतीक के दाईं ओर।
ट्यूरिंग के जीवनी लेखक एंड्रयू होजेस (1983: 107) ने इस भ्रम को नोट किया और उस पर चर्चा की।
राज्य आरेख
| Tape symbol | Current state A | Current state B | Current state C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Write symbol | Move tape | Next state | Write symbol | Move tape | Next state | Write symbol | Move tape | Next state | |
| 0 | P | R | B | P | L | A | P | L | B |
| 1 | P | L | C | P | R | B | P | R | HALT |
दाईं ओर: ऊपर दी गई तालिका को राज्य संक्रमण आरेख के रूप में व्यक्त किया गया है।
आम तौर पर बड़ी टेबल को टेबल के रूप में छोड़ देना बेहतर होता है (बूथ, पृ. 74)। वे कंप्यूटर द्वारा सारणीबद्ध रूप में अधिक आसानी से सिम्युलेट किए जाते हैं (बूथ, पृ. 74)। हालाँकि, कुछ अवधारणाएँ- उदा। रीसेट स्थिति वाली मशीनें और दोहराए जाने वाले पैटर्न वाली मशीनें (cf. हिल और पीटरसन पृष्ठ 244ff)—चित्रकारी के रूप में देखे जाने पर अधिक आसानी से देखी जा सकती हैं।
क्या चित्र अपनी तालिका में सुधार का प्रतिनिधित्व करता है, यह पाठक द्वारा विशेष संदर्भ के लिए तय किया जाना चाहिए।
पाठक को फिर से सावधान किया जाना चाहिए कि इस तरह के चित्र समय और स्थान के माध्यम से गणना के पाठ्यक्रम (प्रक्षेपवक्र) नहीं, समय में जमे हुए उनकी तालिका के स्नैपशॉट का प्रतिनिधित्व करते हैं। जबकि हर बार व्यस्त बीवर मशीन चलती है, यह हमेशा ही राज्य-प्रक्षेपवक्र का पालन करेगी, यह कॉपी मशीन के लिए सही नहीं है जिसे चर इनपुट मापदंडों के साथ प्रदान किया जा सकता है।
गणना की आरेख प्रगति शुरू से अंत तक इसकी गणना के माध्यम से तीन-राज्य व्यस्त बीवर की स्थिति (निर्देश) की प्रगति को दर्शाती है। दायीं ओर ट्यूरिंग पूर्ण विन्यास है (क्लीन स्थिति, होपक्रॉफ्ट-उलमैन तात्कालिक विवरण ) प्रत्येक चरण पर। अगर मशीन को रोका जाना था और राज्य रजिस्टर और पूरे टेप दोनों को खाली करने के लिए साफ़ किया जाना था, तो इन कॉन्फ़िगरेशन का उपयोग इसकी प्रगति में कहीं भी संगणना को फिर से शुरू करने के लिए किया जा सकता है (cf. ट्यूरिंग (1936) द अनडेसिडेबल, पीपी। 139-140)।
समतुल्य मॉडल
कई मशीनें जिनके बारे में सोचा जा सकता है कि साधारण यूनिवर्सल ट्यूरिंग मशीन की तुलना में अधिक कम्प्यूटेशनल क्षमता है, उन्हें और अधिक शक्ति नहीं दिखाया जा सकता है (हॉपक्रॉफ्ट और उल्मैन पृष्ठ 159, cf. Minsky (1967))। वे तेजी से गणना कर सकते हैं, शायद, या कम मेमोरी का उपयोग कर सकते हैं, या उनका निर्देश सेट छोटा हो सकता है, लेकिन वे अधिक शक्तिशाली रूप से गणना नहीं कर सकते (यानी अधिक गणितीय कार्य)। (चर्च-ट्यूरिंग थीसिस किसी भी प्रकार की मशीन के लिए इसे सच मानती है: कि किसी भी चीज़ की गणना किसी ट्यूरिंग मशीन द्वारा की जा सकती है।)
एक ट्यूरिंग मशीन सिंगल-स्टैक पुशडाउन ऑटोमेटन (पीडीए) के बराबर है जिसे एलआईएफओ (कंप्यूटिंग) | लास्ट-इन-फर्स्ट-आउट (एलआईएफओ) आवश्यकता को आराम देकर अधिक लचीला और संक्षिप्त बनाया गया है। इसके अलावा, ट्यूरिंग मशीन मानक LIFO शब्दार्थ के साथ दो-स्टैक पीडीए के बराबर भी है, स्टैक का उपयोग सिर के बाईं ओर टेप के लिए और दूसरे स्टैक को दाईं ओर टेप के लिए किया जाता है।
दूसरे चरम पर, कुछ बहुत ही सरल मॉडल ट्यूरिंग पूर्णता के रूप में सामने आते हैं | ट्यूरिंग-समतुल्य, यानी ट्यूरिंग मशीन मॉडल के समान कम्प्यूटेशनल शक्ति रखने के लिए।
सामान्य समकक्ष मॉडल मल्टी-टेप ट्यूरिंग मशीन, मल्टी-ट्रैक ट्यूरिंग मशीन, इनपुट और आउटपुट वाली मशीनें, और गैर-नियतात्मक ट्यूरिंग मशीन | गैर-नियतात्मक ट्यूरिंग मशीन (एनडीटीएम) हैं, जो नियतात्मक ट्यूरिंग मशीन (डीटीएम) के विपरीत जिसमें प्रतीक और स्थिति के प्रत्येक संयोजन के लिए क्रिया तालिका में अधिक से अधिक प्रविष्टि हो।
रीड-ओनली राइट मूविंग ट्यूरिंग मशीन | रीड-ओनली, राइट-मूविंग ट्यूरिंग मशीन नियतात्मक परिमित ऑटोमेटन (साथ ही एनडीएफए से डीएफए रूपांतरण एल्गोरिथ्म का उपयोग करके रूपांतरण द्वारा गैर नियतात्मक परिमित automaton के बराबर हैं।
व्यावहारिक और व्यावहारिक उद्देश्यों के लिए समतुल्य रजिस्टर मशीन का उपयोग सामान्य असेंबली भाषा प्रोग्रामिंग भाषा के रूप में किया जा सकता है।
एक प्रासंगिक प्रश्न यह है कि ठोस प्रोग्रामिंग भाषाओं द्वारा प्रस्तुत अभिकलन मॉडल ट्यूरिंग समकक्ष है या नहीं। जबकि वास्तविक कंप्यूटर की गणना परिमित अवस्थाओं पर आधारित होती है और इस प्रकार ट्यूरिंग मशीन का अनुकरण करने में सक्षम नहीं होती है, स्वयं प्रोग्रामिंग भाषाओं में यह सीमा नहीं होती है। किरनर और अन्य, 2009 ने दिखाया है कि सामान्य प्रयोजन की प्रोग्रामिंग भाषाओं में से कुछ ट्यूरिंग पूर्ण हैं जबकि अन्य नहीं हैं। उदाहरण के लिए, एएनएसआई सी ट्यूरिंग-समतुल्य नहीं है, क्योंकि एएनएसआई सी के सभी तात्कालिकताएं संभव हैं (विभिन्न तात्कालिकताएं संभव हैं क्योंकि मानक जानबूझकर कुछ व्यवहारों को विरासत कारणों से अपरिभाषित छोड़ देता है) परिमित-अंतरिक्ष स्मृति का अर्थ है। ऐसा इसलिए है क्योंकि स्मृति संदर्भ डेटा प्रकारों का आकार, जिसे पॉइंटर्स कहा जाता है, भाषा के अंदर पहुंच योग्य है। हालाँकि, पास्कल (प्रोग्रामिंग भाषा) जैसी अन्य प्रोग्रामिंग भाषाओं में यह सुविधा नहीं है, जो उन्हें सिद्धांत रूप में ट्यूरिंग पूर्ण होने की अनुमति देती है। सिद्धांत रूप में यह केवल ट्यूरिंग पूर्ण है, क्योंकि प्रोग्रामिंग भाषा में मेमोरी आवंटन को विफल होने दिया जाता है, जिसका अर्थ है कि विफल मेमोरी आवंटन की अनदेखी करते समय प्रोग्रामिंग भाषा ट्यूरिंग पूर्ण हो सकती है, लेकिन वास्तविक कंप्यूटर पर निष्पादन योग्य संकलित प्रोग्राम नहीं हो सकते।
च्वाइस सी-मशीन, ऑरेकल ओ-मशीन
अपने पेपर के आरंभ में (1936) ट्यूरिंग स्वचालित मशीन के बीच अंतर करता है - इसकी गति ... पूरी तरह से कॉन्फ़िगरेशन और पसंद मशीन द्वारा निर्धारित:
...whose motion is only partially determined by the configuration ... When such a machine reaches one of these ambiguous configurations, it cannot go on until some arbitrary choice has been made by an external operator. This would be the case if we were using machines to deal with axiomatic systems.
— The Undecidable, p. 118
ट्यूरिंग (1936) फुटनोट को छोड़कर आगे विस्तृत नहीं करता है जिसमें वह वर्णन करता है कि [हिल्बर्ट] कैलकुलस के सभी सिद्ध सूत्रों को खोजने के लिए ए-मशीन का उपयोग कैसे किया जाए, बजाय इसके कि वह विकल्प मशीन का उपयोग करे। उनका मानना है कि विकल्प हमेशा दो संभावनाओं 0 और 1 के बीच होते हैं। प्रत्येक प्रमाण तब विकल्पों के अनुक्रम द्वारा निर्धारित किया जाएगा I1, मैं2, ..., मैंn (मैं1 = 0 या 1, मैं2 = 0 या 1, ..., in = 0 या 1), और इसलिए संख्या 2एन + मैं12n-1 + i22n-2 + ... +in पूरी तरह से प्रमाण निर्धारित करता है। स्वचालित मशीन क्रमिक रूप से प्रूफ 1, प्रूफ 2, प्रूफ 3, ... (फुटनोट ‡, द अनडेसिडेबल, पृष्ठ 138) करती है।
यह वास्तव में वह तकनीक है जिसके द्वारा निर्धारक ट्यूरिंग मशीन की कार्रवाई की नकल करने के लिए नियतात्मक (यानी, ए-) ट्यूरिंग मशीन का उपयोग किया जा सकता है; ट्यूरिंग ने फुटनोट में मामले को सुलझाया और इसे आगे के विचार से खारिज कर दिया।
एक ओरेकल मशीन या ओ-मशीन ट्यूरिंग मशीन है जो अपनी गणना को स्थिति 'ओ' पर रोक देती है, जबकि अपनी गणना पूरी करने के लिए, यह ऑरेकल के निर्णय की प्रतीक्षा करती है - अनिर्दिष्ट इकाई यह कहने के अलावा कि यह मशीन नहीं हो सकती ( ट्यूरिंग (1939), द अनडिसीडेबल, पृष्ठ 166-168)।
यूनिवर्सल ट्यूरिंग मशीन
जैसा कि ट्यूरिंग ने द अनडिसीडेबल में लिखा है, पृ. 128 (इटैलिक जोड़े गए):
It is possible to invent a single machine which can be used to compute any computable sequence. If this machine U is supplied with the tape on the beginning of which is written the string of quintuples separated by semicolons of some computing machine M, then U will compute the same sequence as M.
इस खोज को अब मान लिया गया है, लेकिन उस समय (1936) इसे आश्चर्यजनक माना गया था।[citation needed] कम्प्यूटेशन का मॉडल जिसे ट्यूरिंग ने अपनी सार्वभौमिक मशीन कहा - यू शॉर्ट के लिए - कुछ (cf. डेविस (2000)) द्वारा माना जाता है कि यह मौलिक सैद्धांतिक सफलता है जिसने संग्रहीत प्रोग्राम कंप्यूटर की धारणा को जन्म दिया।
Turing's paper ... contains, in essence, the invention of the modern computer and some of the programming techniques that accompanied it.
— Minsky (1967), p. 104
कम्प्यूटेशनल जटिलता सिद्धांत के संदर्भ में, मल्टी-टेप यूनिवर्सल ट्यूरिंग मशीन को केवल उन मशीनों की तुलना में लॉगरिदमिक फैक्टर द्वारा धीमा होना चाहिए जो इसे अनुकरण करती हैं। यह परिणाम 1966 में F. C. हेनी और R. E. स्टर्न्स द्वारा प्राप्त किया गया था। (अरोड़ा और बराक, 2009, प्रमेय 1.9)
वास्तविक मशीनों के साथ तुलना
प्राय: माना जाता है कि ट्यूरिंग मशीनें, सरल ऑटोमेटा के विपरीत, वास्तविक मशीनों की तरह शक्तिशाली हैं, और किसी भी ऑपरेशन को निष्पादित करने में सक्षम हैं जो वास्तविक प्रोग्राम कर सकता है। इस कथन में जो उपेक्षित है, वह यह है कि, क्योंकि वास्तविक मशीन में केवल सीमित संख्या में विन्यास हो सकते हैं, यह परिमित-राज्य मशीन के अलावा और कुछ नहीं है, जबकि ट्यूरिंग मशीन में इसकी संगणनाओं के लिए असीमित मात्रा में भंडारण स्थान उपलब्ध है।
यह समझाने के कई तरीके हैं कि ट्यूरिंग मशीन वास्तविक कंप्यूटर के उपयोगी मॉडल क्यों हैं:
- एक वास्तविक कंप्यूटर कुछ भी गणना कर सकता है, ट्यूरिंग मशीन भी गणना कर सकती है। उदाहरण के लिए: ट्यूरिंग मशीन प्रोग्रामिंग भाषाओं में पाए जाने वाले किसी भी प्रकार के सबरूटीन का अनुकरण कर सकती है, जिसमें पुनरावर्ती प्रक्रियाएं और ज्ञात पैरामीटर-पासिंग मैकेनिज्म (हॉपक्रॉफ्ट और उल्मैन पृष्ठ 157) शामिल हैं। बड़ा पर्याप्त FSA IO की अवहेलना करते हुए किसी भी वास्तविक कंप्यूटर को भी मॉडल कर सकता है। इस प्रकार, ट्यूरिंग मशीनों की सीमाओं के बारे में बयान वास्तविक कंप्यूटरों पर भी लागू होगा।
- अंतर केवल ट्यूरिंग मशीन की असीमित मात्रा में डेटा में हेरफेर करने की क्षमता के साथ है। हालाँकि, सीमित समय दिया गया है, ट्यूरिंग मशीन (एक वास्तविक मशीन की तरह) केवल डेटा की सीमित मात्रा में हेरफेर कर सकती है।
- एक ट्यूरिंग मशीन की तरह, वास्तविक मशीन में अधिक डिस्क या अन्य स्टोरेज मीडिया प्राप्त करके, इसकी स्टोरेज स्पेस को आवश्यकतानुसार बढ़ाया जा सकता है।
- ट्यूरिंग मशीनों का उपयोग करने वाले विवरणों की तुलना में सरल अमूर्त मॉडल का उपयोग करने वाले वास्तविक मशीन प्रोग्राम के विवरण अक्सर अधिक जटिल होते हैं। उदाहरण के लिए, एल्गोरिथ्म का वर्णन करने वाली ट्यूरिंग मशीन में कुछ सौ अवस्थाएँ हो सकती हैं, जबकि किसी वास्तविक मशीन पर समतुल्य नियतात्मक परिमित ऑटोमेटन (DFA) में क्वाड्रिलियन होते हैं। यह डीएफए प्रतिनिधित्व का विश्लेषण करने के लिए अक्षम बनाता है।
- ट्यूरिंग मशीनें एल्गोरिदम का वर्णन करती हैं जो इस बात से स्वतंत्र हैं कि वे कितनी मेमोरी का उपयोग करते हैं। किसी भी मौजूदा मशीन के पास मेमोरी की सीमा होती है, लेकिन यह सीमा समय के साथ मनमाने ढंग से बढ़ सकती है। ट्यूरिंग मशीन हमें एल्गोरिदम के बारे में बयान देने की अनुमति देती है जो (सैद्धांतिक रूप से) पारंपरिक कंप्यूटिंग मशीन आर्किटेक्चर में प्रगति की परवाह किए बिना हमेशा के लिए बनी रहेगी।
- ट्यूरिंग मशीन एल्गोरिदम के कथन को सरल बनाती है। ट्यूरिंग-समतुल्य अमूर्त मशीनों पर चलने वाले एल्गोरिदम आमतौर पर वास्तविक मशीनों पर चलने वाले उनके समकक्षों की तुलना में अधिक सामान्य होते हैं, क्योंकि उनके पास मनमाने ढंग से सटीक डेटा प्रकार उपलब्ध होते हैं और उन्हें कभी भी अप्रत्याशित परिस्थितियों से निपटना नहीं पड़ता है (स्मृति से बाहर चलने सहित, लेकिन सीमित नहीं) .
सीमाएं
कम्प्यूटेशनल जटिलता सिद्धांत
ट्यूरिंग मशीनों की सीमा यह है कि वे किसी विशेष व्यवस्था की ताकत को अच्छी तरह से मॉडल नहीं करते हैं। उदाहरण के लिए, आधुनिक संग्रहीत प्रोग्राम कंप्यूटर वास्तव में अमूर्त मशीन के अधिक विशिष्ट रूप के उदाहरण हैं जिन्हें रैंडम-एक्सेस संग्रहित प्रोग्राम मशीन मशीन या आरएएसपी मशीन मॉडल के रूप में जाना जाता है। यूनिवर्सल ट्यूरिंग मशीन की तरह, आरएएसपी अपने कार्यक्रम को अपनी परिमित-राज्य मशीन के निर्देशों के बाहर स्मृति में संग्रहीत करता है। यूनिवर्सल ट्यूरिंग मशीन के विपरीत, RASP में अलग-अलग, क्रमांकित लेकिन असीमित रजिस्टरों की अनंत संख्या होती है - मेमोरी सेल जिसमें कोई भी पूर्णांक हो सकता है (cf. Elgot और रॉबिन्सन (1964), हार्टमैनिस (1971), और विशेष रूप से कुक-रेचो (1973) ); रैंडम-एक्सेस मशीन पर संदर्भ)। आरएएसपी की परिमित-राज्य मशीन अप्रत्यक्ष पते की क्षमता से लैस है (उदाहरण के लिए, रजिस्टर की सामग्री को दूसरे रजिस्टर को निर्दिष्ट करने के लिए पते के रूप में इस्तेमाल किया जा सकता है); इस प्रकार आरएएसपी का कार्यक्रम रजिस्टर-अनुक्रम में किसी भी रजिस्टर को संबोधित कर सकता है। इस अंतर का परिणाम यह है कि ऐसे कम्प्यूटेशनल ऑप्टिमाइजेशन हैं जो मेमोरी इंडेक्स के आधार पर किए जा सकते हैं, जो सामान्य ट्यूरिंग मशीन में संभव नहीं हैं; इस प्रकार जब ट्यूरिंग मशीनों को बाउंडिंग रनिंग टाइम के आधार के रूप में उपयोग किया जाता है, तो कुछ एल्गोरिदम के चलने के समय (ट्यूरिंग मशीन की झूठी सरलीकृत धारणा के कारण) पर झूठी निचली सीमा सिद्ध की जा सकती है। इसका उदाहरण द्विआधारी खोज है, एल्गोरिदम जिसे ट्यूरिंग मशीन मॉडल के बजाय गणना के आरएएसपी मॉडल का उपयोग करते समय अधिक तेज़ी से प्रदर्शन करने के लिए दिखाया जा सकता है।
समवर्ती
ट्यूरिंग मशीनों की और सीमा यह है कि वे Concurrency_(कंप्यूटर_साइंस) को अच्छी तरह से मॉडल नहीं करती हैं। उदाहरण के लिए, पूर्णांक के आकार पर सीमा होती है जिसकी गणना खाली टेप पर शुरू होने वाली हमेशा रुकने वाली गैर-नियतात्मक ट्यूरिंग मशीन द्वारा की जा सकती है। (असीमित nondeterminism पर लेख देखें।) इसके विपरीत, बिना किसी इनपुट के हमेशा रुकने वाली समवर्ती प्रणालियाँ होती हैं जो असीमित आकार के पूर्णांक की गणना कर सकती हैं। (स्थानीय भंडारण के साथ प्रक्रिया बनाई जा सकती है जिसे 0 की गिनती के साथ आरंभ किया जाता है जो समवर्ती रूप से स्टॉप और गो संदेश दोनों भेजता है। जब इसे गो संदेश प्राप्त होता है, तो यह 1 से अपनी गिनती बढ़ाता है और खुद को संदेश भेजता है। जब यह स्टॉप संदेश प्राप्त करता है, यह अपने स्थानीय भंडारण में असीमित संख्या के साथ बंद हो जाता है।)
इंटरेक्शन
कंप्यूटिंग के शुरुआती दिनों में, कंप्यूटर का उपयोग आमतौर पर प्रचय संसाधन तक सीमित था, यानी, गैर-संवादात्मक कार्य, प्रत्येक दिए गए इनपुट डेटा से आउटपुट डेटा का उत्पादन करता था। कम्प्यूटेबिलिटी सिद्धांत, जो इनपुट से आउटपुट तक कार्यों की कम्प्यूटेबिलिटी का अध्ययन करता है, और जिसके लिए ट्यूरिंग मशीनों का आविष्कार किया गया था, इस अभ्यास को दर्शाता है।
1970 के दशक के बाद से, कंप्यूटरों का अन्तरक्रियाशीलता उपयोग बहुत अधिक सामान्य हो गया। सिद्धांत रूप में, बाहरी एजेंट को टेप से पढ़ने और ट्यूरिंग मशीन के रूप में ही समय में लिखने के द्वारा इसे मॉडल करना संभव है, लेकिन यह शायद ही कभी मेल खाता है कि बातचीत वास्तव में कैसे होती है; इसलिए, अन्तरक्रियाशीलता का वर्णन करते समय, इनपुट/आउटपुट ऑटोमेटन|I/O ऑटोमेटा जैसे विकल्प आमतौर पर पसंद किए जाते हैं।
इतिहास
ऐतिहासिक पृष्ठभूमि: कम्प्यूटेशनल मशीनरी
रॉबिन गैंडी (1919-1995) - एलन ट्यूरिंग (1912-1954) के छात्र, और उनके आजीवन दोस्त - चार्ल्स बैबेज (लगभग 1834) में गणना मशीन की धारणा के वंश का पता लगाते हैं और वास्तव में बैबेज की थीसिस का प्रस्ताव देते हैं:
That the whole of development and operations of analysis are now capable of being executed by machinery.
— (italics in Babbage as cited by Gandy, p. 54)
बैबेज के विश्लेषणात्मक इंजन का गैंडी का विश्लेषण निम्नलिखित पांच कार्यों का वर्णन करता है (cf. p. 52–53):
- अंकगणितीय फलन +, -, ×, जहाँ - उचित घटाव दर्शाता है x − y = 0 अगर y ≥ x.
- संचालन का कोई भी क्रम ऑपरेशन है।
- एक ऑपरेशन का पुनरावृत्ति (एन बार ऑपरेशन पी दोहराना)।
- सशर्त पुनरावृत्ति (परीक्षण टी की सफलता पर एन बार ऑपरेशन पी सशर्त दोहराना)।
- सशर्त स्थानांतरण (यानी, सशर्त के लिए जाओ)।
गैंडी का कहना है कि जिन कार्यों की गणना (1), (2), और (4) द्वारा की जा सकती है, वे ठीक वही हैं जो ट्यूरिंग संगणनीय हैं। (पृष्ठ 53)। वह पर्सी लुडगेट (1909), लियोनार्डो टोरेस और क्यूवेदो (1914), मौरिस डी'ओकग्ने (1922), लुइस कॉफिग्नल (1933), वन्नेवर बुश (1936), हावर्ड ऐकेन (1937) सहित सार्वभौमिक गणना मशीनों के लिए अन्य प्रस्तावों का हवाला देते हैं। . हालाँकि:
… the emphasis is on programming a fixed iterable sequence of arithmetical operations. The fundamental importance of conditional iteration and conditional transfer for a general theory of calculating machines is not recognized…
— Gandy p. 55
Entscheidungsproblem (निर्णय समस्या): हिल्बर्ट का 1900 का दसवां प्रश्न
1900 में प्रसिद्ध गणितज्ञ डेविड हिल्बर्ट द्वारा पेश की गई हिल्बर्ट की समस्याओं के संबंध में, समस्या #10 का पहलू लगभग 30 वर्षों से चल रहा था, जब तक कि इसे सटीक रूप से तैयार नहीं किया गया था। नंबर 10 के लिए हिल्बर्ट की मूल अभिव्यक्ति इस प्रकार है:
10. Determination of the solvability of a Diophantine equation. Given a Diophantine equation with any number of unknown quantities and with rational integral coefficients: To devise a process according to which it can be determined in a finite number of operations whether the equation is solvable in rational integers. The Entscheidungsproblem [decision problem for first-order logic] is solved when we know a procedure that allows for any given logical expression to decide by finitely many operations its validity or satisfiability ... The Entscheidungsproblem must be considered the main problem of mathematical logic.
— quoted, with this translation and the original German, in Dershowitz and Gurevich, 2008
1922 तक, Entscheidungsproblem की यह धारणा थोड़ी विकसित हो गई थी, और हेनरिक बेहमन | एच। बेहमन ने कहा
... most general form of the Entscheidungsproblem [is] as follows:
A quite definite generally applicable prescription is required which will allow one to decide in a finite number of steps the truth or falsity of a given purely logical assertion ...
— Gandy p. 57, quoting Behmann
Behmann remarks that ... the general problem is equivalent to the problem of deciding which mathematical propositions are true.
— ibid.
If one were able to solve the Entscheidungsproblem then one would have a "procedure for solving many (or even all) mathematical problems".
— ibid., p. 92
1928 में गणितज्ञों की अंतर्राष्ट्रीय कांग्रेस द्वारा, हिल्बर्ट ने अपने प्रश्नों को काफी सटीक बनाया। पहला, गणित पूर्णता (तर्क) था ... दूसरा, गणित संगति प्रमाण था ... और तीसरा, गणित निर्णायकता (तर्क) था? (होजेस पृष्ठ 91, हॉकिंग पृष्ठ 1121)। पहले दो सवालों का जवाब 1930 में कर्ट गोडेल ने उसी बैठक में दिया था, जहां हिल्बर्ट ने अपना सेवानिवृत्ति भाषण दिया था (हिल्बर्ट को बहुत दुख हुआ था); तीसरी- Entscheidungsproblem- को 1930 के दशक के मध्य तक प्रतीक्षा करनी पड़ी।
समस्या यह थी कि उत्तर के लिए पहले निश्चित सामान्य लागू नुस्खे की सटीक परिभाषा की आवश्यकता होती थी, जिसे प्रिंसटन के प्रोफेसर अलोंजो चर्च प्रभावी गणनात्मकता कहते थे, और 1928 में ऐसी कोई परिभाषा मौजूद नहीं थी। लेकिन अगले 6-7 वर्षों में एमिल पोस्ट ने निर्देशों की सूची (1936 के बाद) के अनुसार कमरे से दूसरे कमरे में लिखने और निशान मिटाने वाले कार्यकर्ता की अपनी परिभाषा विकसित की, जैसा कि चर्च और उनके दो छात्रों स्टीफन क्लेन और जे.बी. रोसेर ने किया था। चर्च का लैम्ब्डा-कैलकुलस और गोडेल का पुनरावर्तन सिद्धांत (1934)। चर्च के पेपर (15 अप्रैल 1936 को प्रकाशित) ने दिखाया कि एंट्सचेइडुंग्सप्रोब्लेम वास्तव में अनिर्णीत था और ट्यूरिंग को लगभग साल तक हरा दिया (ट्यूरिंग का पेपर 28 मई 1936 को प्रस्तुत किया गया, जनवरी 1937 को प्रकाशित हुआ)। इस बीच, एमिल पोस्ट ने 1936 के पतन में संक्षिप्त पत्र प्रस्तुत किया, इसलिए ट्यूरिंग को कम से कम पोस्ट पर प्राथमिकता मिली। जबकि चर्च ने ट्यूरिंग के पेपर को रेफर किया था, ट्यूरिंग के पास चर्च के पेपर का अध्ययन करने और परिशिष्ट जोड़ने का समय था जहां उन्होंने प्रमाण को स्केच किया कि चर्च का लैम्ब्डा-कैलकुलस और उनकी मशीनें समान कार्यों की गणना करेंगी।
But what Church had done was something rather different, and in a certain sense weaker. ... the Turing construction was more direct, and provided an argument from first principles, closing the gap in Church's demonstration.
— Hodges p. 112
और पोस्ट ने केवल चर्च-ट्यूरिंग थीसिस की परिभाषा प्रस्तावित की थी और चर्च की परिभाषा की आलोचना की थी, लेकिन कुछ भी साबित नहीं किया था।
एलन ट्यूरिंग की ए-मशीन
1935 के वसंत में, कैम्ब्रिज के किंग्स कॉलेज में मास्टर के युवा छात्र के रूप में ट्यूरिंग ने चुनौती ली; वह तर्कशास्त्री एम. एच. ए. न्यूमैन के व्याख्यानों से प्रेरित हुए थे और उनसे गोडेल के काम और एंट्सचेइडुंग्सप्रोब्लेम के बारे में सीखा ... न्यूमैन ने 'मैकेनिकल' शब्द का इस्तेमाल किया ... ट्यूरिंग 1955 के अपने मृत्युलेख में न्यूमैन लिखते हैं:
To the question 'what is a "mechanical" process?' Turing returned the characteristic answer 'Something that can be done by a machine' and he embarked on the highly congenial task of analysing the general notion of a computing machine.
— Gandy, p. 74
गैंडी कहते हैं कि:
I suppose, but do not know, that Turing, right from the start of his work, had as his goal a proof of the undecidability of the Entscheidungsproblem. He told me that the 'main idea' of the paper came to him when he was lying in Grantchester meadows in the summer of 1935. The 'main idea' might have either been his analysis of computation or his realization that there was a universal machine, and so a diagonal argument to prove unsolvability.
— ibid., p. 76
जबकि गैंडी का मानना था कि ऊपर न्यूमैन का बयान भ्रामक है, यह राय सभी के द्वारा साझा नहीं की जाती है। मशीनों में ट्यूरिंग की आजीवन रुचि थी: एलन ने लड़के के रूप में टाइपराइटर का आविष्कार करने का सपना देखा था; [उनकी मां] श्रीमती ट्यूरिंग के पास टाइपराइटर था; और वह अच्छी तरह से खुद से पूछकर शुरू कर सकता था कि टाइपराइटर को 'मैकेनिकल' कहने का क्या मतलब है (होजेस पी. 96)। प्रिंसटन में अपनी पीएचडी की पढ़ाई के दौरान, ट्यूरिंग ने बूलियन-लॉजिक मल्टीप्लायर बनाया (नीचे देखें)। उनकी पीएचडी थीसिस, जिसका शीर्षक ऑर्डिनल्स पर आधारित लॉजिक सिस्टम्स है, में संगणनीय कार्य की निम्नलिखित परिभाषा शामिल है:
It was stated above that 'a function is effectively calculable if its values can be found by some purely mechanical process'. We may take this statement literally, understanding by a purely mechanical process one which could be carried out by a machine. It is possible to give a mathematical description, in a certain normal form, of the structures of these machines. The development of these ideas leads to the author's definition of a computable function, and to an identification of computability with effective calculability. It is not difficult, though somewhat laborious, to prove that these three definitions [the 3rd is the λ-calculus] are equivalent.
— Turing (1939) in The Undecidable, p. 160
एलन ट्यूरिंग ने 1936 में ए-मशीन (स्वचालित मशीन) का आविष्कार किया।[7] ट्यूरिंग ने अपना पेपर 31 मई 1936 को लंदन मैथमेटिकल सोसाइटी फॉर इट्स प्रोसीडिंग्स (cf. हॉजेस 1983: 112) को प्रस्तुत किया, लेकिन यह 1937 की शुरुआत में प्रकाशित हुआ था और ऑफप्रिंट फरवरी 1937 में उपलब्ध थे (cf. हॉजेस 1983: 129) यह ट्यूरिंग का था डॉक्टरेट सलाहकार, अलोंजो चर्च, जिन्होंने बाद में समीक्षा में ट्यूरिंग मशीन शब्द गढ़ा।[20] इस मॉडल के साथ, ट्यूरिंग नकारात्मक में दो प्रश्नों का उत्तर देने में सक्षम था:
- क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन गोलाकार है (उदाहरण के लिए, फ्रीज, या उसके कम्प्यूटेशनल कार्य को जारी रखने में विफल)?
- क्या कोई मशीन मौजूद है जो यह निर्धारित कर सकती है कि उसके टेप पर कोई मनमानी मशीन कभी किसी दिए गए प्रतीक को प्रिंट करती है या नहीं?[21][22]
इस प्रकार मनमाना संगणना करने में सक्षम बहुत ही सरल उपकरण का गणितीय विवरण प्रदान करके, वह सामान्य रूप से संगणना के गुणों को साबित करने में सक्षम था - और विशेष रूप से, Entscheidungsproblem ('निर्णय समस्या') की संगणनीयता।[23]
जब ट्यूरिंग यूके लौटे तो अंततः वे एनिग्मा नामक एन्क्रिप्शन मशीनों द्वारा बनाए गए जर्मन गुप्त कोड को तोड़ने के लिए संयुक्त रूप से जिम्मेदार हो गए; वह एसीई (स्वचालित कंप्यूटिंग इंजन) के डिजाइन में भी शामिल हो गया, [ट्यूरिंग] एसीई प्रस्ताव प्रभावी रूप से आत्मनिर्भर था, और इसकी जड़ें ईडीवीएसी [यूएसए की पहल] में नहीं थीं, बल्कि अपनी सार्वभौमिक मशीन (होजेस पी) में थीं। . 318)। क्लेन (1952) ट्यूरिंग की थीसिस द्वारा जो नाम दिया गया है, उसकी उत्पत्ति और प्रकृति के संबंध में तर्क अभी भी जारी हैं। लेकिन ट्यूरिंग ने अपने कम्प्यूटेशनल-मशीन मॉडल के साथ जो साबित किया, वह उनके पेपर ऑन कंप्यूटेबल नंबर्स में एप्लीकेशन टू द एंट्सचिडंगस्प्रोब्लेम (1937) के साथ दिखाई देता है:
[that] the Hilbert Entscheidungsproblem can have no solution ... I propose, therefore to show that there can be no general process for determining whether a given formula U of the functional calculus K is provable, i.e. that there can be no machine which, supplied with any one U of these formulae, will eventually say whether U is provable.
— from Turing's paper as reprinted in The Undecidable, p. 145
ट्यूरिंग का उदाहरण (उनका दूसरा प्रमाण): यदि कोई हमें यह बताने के लिए सामान्य प्रक्रिया के बारे में पूछता है: क्या यह मशीन कभी 0 प्रिंट करती है, तो यह प्रश्न अनिर्णीत है।
1937-1970: डिजिटल कंप्यूटर, कंप्यूटर विज्ञान का जन्म
1937 में, प्रिंसटन में अपनी पीएचडी थीसिस पर काम करते हुए, ट्यूरिंग ने स्क्रैच से डिजिटल (बूलियन-लॉजिक) मल्टीप्लायर बनाया, जिससे अपना खुद का इलेक्ट्रोमैकेनिकल रिले (होजेस पृष्ठ 138) बना। एलन का कार्य रिले-संचालित स्विचों के नेटवर्क में ट्यूरिंग मशीन के तार्किक डिजाइन को मूर्त रूप देना था ... (होजेस पी। 138)। जबकि ट्यूरिंग शुरू में जिज्ञासु और प्रयोग करने वाला हो सकता था, उसी दिशा में जर्मनी (कोनराड ज़्यूस (1938)), और संयुक्त राज्य अमेरिका (हावर्ड ऐकेन) और जॉर्ज स्टिबिट्ज़ (1937) में काफी ईमानदारी से काम चल रहा था; द्वितीय विश्व युद्ध में एक्सिस और मित्र देशों की सेनाओं द्वारा उनके मजदूरों के फलों का उपयोग किया गया था (cf. हॉजेस पृष्ठ 298-299)। 1950 के दशक के मध्य में हाओ वांग (अकादमिक) और मार्विन मिंस्की ने ट्यूरिंग मशीन को सरल रूप में कम कर दिया (मार्टिन डेविस (गणितज्ञ) की पोस्ट-ट्यूरिंग मशीन का अग्रदूत); साथ ही साथ यूरोपीय शोधकर्ता नए-फंसे हुए इलेक्ट्रॉनिक कंप्यूटर को कंप्यूटर जैसी सैद्धांतिक वस्तु के बराबर बना रहे थे जिसे अब ट्यूरिंग मशीन कहा जा रहा है। 1950 के दशक के अंत और 1960 के दशक के प्रारंभ में, संयोग से मेलज़क और लैम्बेक (1961), मिन्स्की (1961), और शेफर्डसन और स्टर्गिस (1961) के समानांतर विकास ने यूरोपीय कार्य को आगे बढ़ाया और ट्यूरिंग मशीन को अधिक अनुकूल, कंप्यूटर की तरह कम कर दिया। सार मॉडल जिसे काउंटर मशीन कहा जाता है; एलगोट और रॉबिन्सन (1964), हार्टमैनिस (1971), कुक और रेक्हो (1973) ने रजिस्टर मशीन और रैंडम-एक्सेस मशीन मॉडल के साथ इस काम को और आगे बढ़ाया- लेकिन मूल रूप से सभी अंकगणितीय निर्देश वाली मल्टी-टेप ट्यूरिंग मशीन हैं। तय करना।
1970-वर्तमान: गणना के मॉडल के रूप में
आज, काउंटर, रजिस्टर और रैंडम-एक्सेस मशीन और उनकी जननी ट्यूरिंग मशीन अभिकलन के सिद्धांत में सवालों की जांच करने वाले सिद्धांतकारों के लिए पसंद के मॉडल बने हुए हैं। विशेष रूप से, कम्प्यूटेशनल जटिलता सिद्धांत ट्यूरिंग मशीन का उपयोग करता है:
Depending on the objects one likes to manipulate in the computations (numbers like nonnegative integers or alphanumeric strings), two models have obtained a dominant position in machine-based complexity theory:
the off-line multitape Turing machine..., which represents the standard model for string-oriented computation, and the random access machine (RAM) as introduced by Cook and Reckhow ..., which models the idealized Von Neumann-style computer.
— van Emde Boas 1990:4
Only in the related area of analysis of algorithms this role is taken over by the RAM model.
— van Emde Boas 1990:16
यह भी देखें
- अंकगणितीय पदानुक्रम
- बेकनस्टीन बाध्य, परिमित आकार और बाउंड एनर्जी की अनंत-टेप ट्यूरिंग मशीनों की असंभवता को दर्शाता है
- ब्लूपी और फ्लूपी
- हॉल्टिंग प्रॉब्लम से संबंधित जानकारी के लिए चैटिन कांस्टेंट या ओमेगा (कंप्यूटर साइंस)।
- चीनी कमरा
- कॉनवे का गेम ऑफ लाइफ, एक ट्यूरिंग-पूर्ण सेलुलर ऑटोमेटन
- डिजिटल अनंत
- सम्राट का नया मन
- प्रगणक (सैद्धांतिक कंप्यूटर विज्ञान में)
- जेनेटिक्स
- गोडेल, एस्चर, बाख: एक शाश्वत स्वर्णिम चोटी, एक प्रसिद्ध पुस्तक जो अन्य विषयों के साथ-साथ चर्च-ट्यूरिंग थीसिस पर चर्चा करती है
- रुकने की समस्या, अधिक संदर्भों के लिए
- हार्वर्ड वास्तुकला
- अनिवार्य प्रोग्रामिंग
- लैंगटन की चींटी और जेलें, ट्यूरिंग मशीन के सरल द्वि-आयामी अनुरूप
- एलन ट्यूरिंग के नाम पर रखी गई चीजों की सूची
- संशोधित हार्वर्ड वास्तुकला
- क्वांटम ट्यूरिंग मशीन
- क्लाउड शैनन, सूचना सिद्धांत में एक अन्य प्रमुख विचारक
- ट्यूरिंग मशीन के उदाहरण
- ट्यूरिंग स्विच
- ट्यूरिंग टैरपिट, कोई भी कंप्यूटिंग सिस्टम या भाषा, जो ट्यूरिंग पूर्ण होने के बावजूद, व्यावहारिक कंप्यूटिंग के लिए आमतौर पर बेकार मानी जाती है
- तंत्रिका नेटवर्क पर ट्यूरिंग के शुरुआती विचारों के लिए असंगठित मशीन
- वॉन न्यूमैन वास्तुकला
टिप्पणियाँ
- ↑ Minsky 1967:107 "In his 1936 paper, A. M. Turing defined the class of abstract machines that now bear his name. A Turing machine is a finite-state machine associated with a special kind of environment -- its tape -- in which it can store (and later recover) sequences of symbols," also Stone 1972:8 where the word "machine" is in quotation marks.
- ↑ Stone 1972:8 states "This "machine" is an abstract mathematical model", also cf. Sipser 2006:137ff that describes the "Turing machine model". Rogers 1987 (1967):13 refers to "Turing's characterization", Boolos Burgess and Jeffrey 2002:25 refers to a "specific kind of idealized machine".
- ↑ Sipser 2006:137 "A Turing machine can do everything that a real computer can do".
- ↑ Cf. Sipser 2002:137. Also, Rogers 1987 (1967):13 describes "a paper tape of infinite length in both directions". Minsky 1967:118 states "The tape is regarded as infinite in both directions". Boolos Burgess and Jeffrey 2002:25 include the possibility of "there is someone stationed at each end to add extra blank squares as needed".
- ↑ Cf. Rogers 1987 (1967):13. Other authors use the word "square" e.g. Boolos Burgess Jeffrey 2002:35, Minsky 1967:117, Penrose 1989:37.
- ↑ Boolos Burgess Jeffry 2002:25 illustrate the machine as moving along the tape. Penrose 1989:36-37 describes himself as "uncomfortable" with an infinite tape observing that it "might be hard to shift!"; he "prefer[s] to think of the tape as representing some external environment through which our finite device can move" and after observing that the " 'movement' is a convenient way of picturing things" and then suggests that "the device receives all its input from this environment. Some variations of the Turing machine model also allow the head to stay in the same position instead of moving or halting.
- ↑ 7.0 7.1 Hodges, Andrew (2012). Alan Turing: The Enigma (The Centenary ed.). Princeton University Press. ISBN 978-0-691-15564-7.
- ↑ The idea came to him in mid-1935 (perhaps, see more in the History section) after a question posed by M. H. A. Newman in his lectures: "Was there a definite method, or as Newman put it, a "mechanical process" which could be applied to a mathematical statement, and which would come up with the answer as to whether it was provable" (Hodges 1983:93). Turing submitted his paper on 31 May 1936 to the London Mathematical Society for its Proceedings (cf. Hodges 1983:112), but it was published in early 1937 and offprints were available in February 1937 (cf. Hodges 1983:129).
- ↑ See footnote in Davis 2000:151.
- ↑ see note in forward to The Collected Works of Alonzo Church (Burge, Tyler; Enderton, Herbert, eds. (2019-04-23). The Collected Works of Alonzo Church (in English). Cambridge, MA, USA: MIT Press. ISBN 978-0-262-02564-5.)
- ↑ Turing 1936 in The Undecidable 1965:132-134; Turing's definition of "circular" is found on page 119.
- ↑ Turing, Alan Mathison (1937). "On Computable Numbers, with an Application to the Entscheidungsproblem". Proceedings of the London Mathematical Society. Series 2. 42 (1): 230–265. doi:10.1112/plms/s2-42.1.230. S2CID 73712. — Reprint at: Turing, Alan. "On computable numbers, with an application to the Entscheidungsproblem". The Turing Digital Archive. Retrieved 9 July 2020.
- ↑ Turing 1936 in The Undecidable 1965:145
- ↑ Sipser 2006:137 observes that "A Turing machine can do everything that a real computer can do. Nevertheless, even a Turing machine cannot solve certain problems. In a very real sense, these problems are beyond the theoretical limits of computation."
- ↑ See the definition of "innings" on Wiktionary
- ↑ A.M. Turing (Jul 1948). Intelligent Machinery (Report). National Physical Laboratory. Here: p.3-4
- ↑ Occasionally called an action table or transition function.
- ↑ Usually quintuples [5-tuples]: qiaj→qi1aj1dk, but sometimes quadruples [4-tuples].
- ↑ p.149; in particular, Hopcroft and Ullman assume that is undefined on all states from
- ↑ see note in forward to The Collected Works of Alonzo Church (Burge, Tyler; Enderton, Herbert, eds. (2019-04-23). The Collected Works of Alonzo Church (in English). Cambridge, MA, USA: MIT Press. ISBN 978-0-262-02564-5.)
- ↑ Turing 1936 in The Undecidable 1965:132-134; Turing's definition of "circular" is found on page 119.
- ↑ Turing, Alan Mathison (1937). "On Computable Numbers, with an Application to the Entscheidungsproblem". Proceedings of the London Mathematical Society. Series 2. 42 (1): 230–265. doi:10.1112/plms/s2-42.1.230. S2CID 73712. — Reprint at: Turing, Alan. "On computable numbers, with an application to the Entscheidungsproblem". The Turing Digital Archive. Retrieved 9 July 2020.
- ↑ Turing 1936 in The Undecidable 1965:145
संदर्भ
प्राथमिक साहित्य, पुनर्मुद्रण और संकलन
- बी जैक कोपलैंड एड। (2004), द एसेंशियल ट्यूरिंग: सेमिनल राइटिंग्स इन कम्प्यूटिंग, लॉजिक, फिलॉसफी, आर्टिफिशियल इंटेलिजेंस, एंड आर्टिफिशियल लाइफ प्लस द सीक्रेट्स ऑफ एनिग्मा, क्लेरेंडन प्रेस (ऑक्सफोर्ड यूनिवर्सिटी प्रेस), ऑक्सफोर्ड यूके, ISBN 0-19-825079-7. ट्यूरिंग पेपर्स के साथ-साथ एमिल पोस्ट को ट्यूरिंग के सम्मेलन की उनकी आलोचना, और ट्यूरिंग की यूनिवर्सल कंप्यूटिंग मशीन के लिए डोनाल्ड डब्ल्यू डेविस के सुधारों के लिए मसौदा पत्र शामिल है
- मार्टिन डेविस (गणितज्ञ) (संपा.) (1965), द अनडिसीडेबल, रेवेन प्रेस, हेवलेट, एनवाई।
- एमिल पोस्ट (1936), फाइनाइट कॉम्बिनेटरी प्रोसेसेस-फॉर्मूलेशन 1, जर्नल ऑफ़ सिंबॉलिक लॉजिक, 1, 103-105, 1936।
- एमिल पोस्ट (1947), रिकर्सिव अनसॉल्वेबिलिटी ऑफ़ ए प्रॉब्लम ऑफ़ थू, जर्नल ऑफ़ सिंबॉलिक लॉजिक, वॉल्यूम। 12, पीपी। 1-11। द अनडिसीडेबल में पुनर्मुद्रित, पीपी. 293ff। इस पेपर के परिशिष्ट में टिप्पणी पोस्ट करें और ट्यूरिंग के 1936-1937 के पेपर में सुधार करें। विशेष रूप से फ़ुटनोट्स 11 को यूनिवर्सल कंप्यूटिंग मशीन कोडिंग में सुधार के साथ और फ़ुटनोट 14 को ट्यूरिंग के प्रमाण पर टिप्पणी के साथ देखें। ट्यूरिंग का पहला और दूसरा प्रमाण।
- Turing, A.M. (1936). "कम्प्यूटेबल नंबरों पर, Entscheidungsproblem के लिए एक एप्लिकेशन के साथ". Proceedings of the London Mathematical Society. 2 (published 1937). 42: 230–265. doi:10.1112/plms/s2-42.1.230. S2CID 73712. (और Turing, A.M. (1938). "Entscheidungsproblem के लिए एक आवेदन के साथ कम्प्यूटेबल नंबरों पर: एक सुधार". Proceedings of the London Mathematical Society. 2 (published 1937). 43 (6): 544–6. doi:10.1112/plms/s2-43.6.544.). कई संग्रहों में पुनर्मुद्रित, उदा। द अनडिसीडेबल में, पीपी. 115–154; वेब पर कई जगहों पर उपलब्ध है।
- एलन ट्यूरिंग, 1948, इंटेलिजेंट मशीनरी। साइबरनेटिक्स में पुनर्मुद्रित: प्रमुख कागजात। ईडी। सी.आर. इवांस और ए.डी.जे. रॉबर्टसन। बाल्टीमोर: यूनिवर्सिटी पार्क प्रेस, 1968. पी। 31. में पुनर्मुद्रित Turing, A. M. (1996). "इंटेलिजेंट मशीनरी, ए हेरेटिकल थ्योरी". Philosophia Mathematica. 4 (3): 256–260. doi:10.1093/philmat/4.3.256.
- एफ. सी. हेनी और आर. ई. स्टर्न्स। मल्टीटेप ट्यूरिंग मशीनों का दो-टेप सिमुलेशन। जेएसीएम, 13(4):533–546, 1966।
संगणनीयता सिद्धांत
- Boolos, George; Richard Jeffrey (1999) [1989]. संगणना और तर्क (3rd ed.). Cambridge UK: Cambridge University Press. ISBN 0-521-20402-X.
- Boolos, George; John Burgess; Richard Jeffrey (2002). संगणना और तर्क (4th ed.). Cambridge UK: Cambridge University Press. ISBN 0-521-00758-5. बर्गेस द्वारा कुछ हिस्सों को महत्वपूर्ण रूप से फिर से लिखा गया है। लैम्बेक अबैकस मशीन (cf. रजिस्टर मशीन) और संगणनीय समारोह के संदर्भ में ट्यूरिंग मशीनों की प्रस्तुति, उनकी समानता दर्शाती है।
- टेलर एल बूथ (1967), अनुक्रमिक मशीनें और ऑटोमेटा थ्योरी, जॉन विली एंड संस, इंक, न्यूयॉर्क। स्नातक स्तर का इंजीनियरिंग पाठ; विषयों की विस्तृत विविधता से अधिक है, अध्याय IX ट्यूरिंग मशीन में कुछ पुनरावर्तन सिद्धांत शामिल हैं।
- Martin Davis (1958). संगणनीयता और अघुलनशीलता. McGraw-Hill Book Company, Inc, New York.. पृष्ठ 12-20 पर वह जोड़, उत्तरवर्ती फलन, घटाव (x ≥ y), उचित घटाव (0 यदि x < y), पहचान फलन और विभिन्न पहचान फलन, और गुणन के लिए 5-ट्यूपल तालिकाओं का उदाहरण देता है।
- Davis, Martin; Ron Sigal; Elaine J. Weyuker (1994). संगणनीयता, जटिलता, और भाषाएँ और तर्क: सैद्धांतिक कंप्यूटर विज्ञान के मूल तत्व (2nd ed.). San Diego: Academic Press, Harcourt, Brace & Company. ISBN 0-12-206382-1.
- Hennie, Fredrick (1977). कम्प्यूटेबिलिटी का परिचय. Addison–Wesley, Reading, Mass. QA248.5H4 1977.. 90-103 पृष्ठों पर हेनी उदाहरणों और प्रवाह-चार्ट के साथ UTM की चर्चा करती है, लेकिन कोई वास्तविक 'कोड' नहीं है।
- John Hopcroft and Jeffrey Ullman (1979). ऑटोमेटा सिद्धांत, भाषाएं और संगणना का परिचय (1st ed.). Addison–Wesley, Reading Mass. ISBN 0-201-02988-X. भाषाओं की मशीन-व्याख्या, एनपी-पूर्णता, आदि के मुद्दों पर केंद्रित है।
- Hopcroft, John E.; Rajeev Motwani; Jeffrey D. Ullman (2001). ऑटोमेटा सिद्धांत, भाषाएं और संगणना का परिचय (2nd ed.). Reading Mass: Addison–Wesley. ISBN 0-201-44124-1.
- स्टीफन क्लेन (1952), मेटामैथमैटिक्स का परिचय, नॉर्थ-हॉलैंड पब्लिशिंग कंपनी, एम्स्टर्डम नीदरलैंड्स, 10वीं छाप (6वें पुनर्मुद्रण 1971 के सुधार के साथ)। स्नातक स्तर का पाठ; अध्याय XIII के अधिकांश संगणनीय कार्य पुनरावर्ती कार्यों की संगणना के ट्यूरिंग मशीन प्रमाणों आदि पर हैं।
- Knuth, Donald E. (1973). खंड 1/मौलिक एल्गोरिदम: कंप्यूटर प्रोग्रामिंग की कला (2nd ed.). Reading, Mass.: Addison–Wesley Publishing Company.. कम्प्यूटेशन (हार्डवेयर और सॉफ्टवेयर दोनों) के विकास में ट्यूरिंग मशीनों की भूमिका के संदर्भ में 1.4.5 इतिहास और ग्रंथ सूची पीपी। 225ff और 2.6 इतिहास और ग्रंथ सूची पीपी देखें। 456फ।
- जौहर मन्ना, 1974, संगणना का गणितीय सिद्धांत। पुनर्मुद्रित, डोवर, 2003। ISBN 978-0-486-43238-0
- मार्विन मिन्स्की, कम्प्यूटेशन: परिमित और अनंत मशीनें, प्रेंटिस-हॉल, इंक।, एन.जे., 1967। अध्याय 8 देखें, खंड 8.2 रुकने की समस्या का समाधान नहीं।
- Christos Papadimitriou (1993). अभिकलनात्मक जटिलता (1st ed.). Addison Wesley. ISBN 0-201-53082-1. अध्याय 2: ट्यूरिंग मशीन, पीपी। 19–56।
- हार्टले रोजर्स, जूनियर, पुनरावर्ती कार्यों और प्रभावी संगणनीयता का सिद्धांत, एमआईटी प्रेस, कैम्ब्रिज एमए, पेपरबैक संस्करण 1987, मूल मैकग्रा-हिल संस्करण 1967, ISBN 0-262-68052-1 (पीबीके।)
- Michael Sipser (1997). संगणना के सिद्धांत का परिचय. PWS Publishing. ISBN 0-534-94728-X. अध्याय 3: चर्च-ट्यूरिंग थीसिस, पीपी। 125-149।
- Stone, Harold S. (1972). कंप्यूटर संगठन और डेटा संरचनाओं का परिचय (1st ed.). New York: McGraw–Hill Book Company. ISBN 0-07-061726-0.
- पीटर वैन एम्डे बोस 1990, मशीन मॉडल और सिमुलेशन, पीपी। 3–66, जॉन वैन लीउवेन में, एड।, सैद्धांतिक कंप्यूटर विज्ञान की हैंडबुक, वॉल्यूम ए: एल्गोरिदम और जटिलता, एमआईटी प्रेस/एल्सेवियर, [स्थान?], ISBN 0-444-88071-2 (वॉल्यूम ए)। QA76.H279 1990।
चर्च की थीसिस
- Nachum Dershowitz; Yuri Gurevich (September 2008). "कम्प्यूटेबिलिटी और चर्च की थीसिस के प्रमाण का एक प्राकृतिक स्वयंसिद्ध" (PDF). Bulletin of Symbolic Logic. 14 (3). Retrieved 2008-10-15.
- Roger Penrose (1990) [1989]. सम्राट का नया मन (2nd ed.). Oxford University Press, New York. ISBN 0-19-851973-7.
छोटी ट्यूरिंग मशीनें
- रोगोज़िन, यूरी, 1998, 22 राज्यों और 2 के साथ यूनिवर्सल ट्यूरिंग मशीन प्रतीकों, सूचना विज्ञान और प्रौद्योगिकी के रोमानियाई जर्नल, 1(3), 259–265, 1998. (छोटे सार्वभौमिक ट्यूरिंग मशीनों के बारे में ज्ञात परिणामों का सर्वेक्षण)
- स्टीफन वोल्फ्राम, 2002, विज्ञान का नया प्रकार, वोल्फ्राम मीडिया, ISBN 1-57955-008-8
- ब्रुनफिल, ज्योफ, स्टूडेंट स्नैग मैथ्स प्राइज, नेचर, 24 अक्टूबर 2007।
- जिम जाइल्स (2007), सिंपलेस्ट 'यूनिवर्सल कंप्यूटर' ने छात्र को $25,000 जीता, न्यू साइंटिस्ट, 24 अक्टूबर , 2007.
- एलेक्स स्मिथ, यूनिवर्सलिटी ऑफ वोल्फ्राम 2, 3 ट्यूरिंग मशीन, वोल्फ्राम 2, 3 ट्यूरिंग मशीन रिसर्च प्राइज के लिए सबमिशन।
- वॉन प्रैट, 2007, सिंपल ट्यूरिंग मशीन, यूनिवर्सलिटी, एनकोडिंग आदि , FOM ईमेल लिस्ट। 29 अक्टूबर, 2007।
- मार्टिन डेविस, 2007, स्मॉलेस्ट यूनिवर्सल मशीन, और -October/012145.html यूनिवर्सल ट्यूरिंग मशीन की परिभाषा FOM ईमेल सूची। अक्टूबर 26-27, 2007।
- अलास्डेयर उर्कहार्ट, 2007 सबसे छोटी यूनिवर्सल मशीन, एफओएम ईमेल सूची। 26 अक्टूबर, 2007।
- हेक्टर जेनिल (वोल्फ्राम रिसर्च), 2007 सबसे छोटी यूनिवर्सल मशीन, एफओएम ईमेल सूची। 29 अक्टूबर, 2007।
- टोड रोलैंड, 2007, FOM पर भ्रम, वोल्फ्राम विज्ञान संदेश बोर्ड, 30 अक्टूबर, 2007।
- ओलिवियर और मार्क रेनॉड, 2014, ट्यूरिंग मशीन हासिल करने के लिए प्रोग्रामेबल प्रोटोटाइप ब्लेज़ पास्कल यूनिवर्सिटी की लिमोस लेबोरेटरी (फ्रांस में क्लेरमोंट-फेरैंड)।
अन्य
- Martin Davis (2000). तर्क के इंजन: गणितज्ञ और कंप्यूटर की उत्पत्ति (1st ed.). W. W. Norton & Company, New York. ISBN 978-0-393-32229-3.
- रॉबिन गैंडी, द कंफ्लुएंस ऑफ आइडियाज इन 1936, पीपी. 51–102 रॉल्फ पहचानो में, नीचे देखें।
- स्टीफन हॉकिंग (संपादक), 2005, गॉड क्रिएटेड द इंटीजर: द मैथमेटिकल ब्रेकथ्रूज़ दैट चेंज्ड हिस्ट्री, रनिंग प्रेस, फिलाडेल्फिया, ISBN 978-0-7624-1922-7. हॉकिंग द्वारा लिखित ट्यूरिंग की संक्षिप्त टिप्पणी और जीवनी के साथ ट्यूरिंग का 1936-1937 का पेपर शामिल है।
- Rolf Herken (1995). द यूनिवर्सल ट्यूरिंग मशीन-ए हाफ-सेंचुरी सर्वे. Springer Verlag. ISBN 978-3-211-82637-9.
- एंड्रयू हॉजेस, एलन ट्यूरिंग: द एनिग्मा, साइमन और शूस्टर, न्यूयॉर्क। सी एफ अध्याय द स्पिरिट ऑफ ट्रूथ ऐसे इतिहास के लिए जो उसके प्रमाण की ओर ले जाता है और उसकी चर्चा करता है।
- Ivars Peterson (1988). गणितीय पर्यटक: आधुनिक गणित का स्नैपशॉट (1st ed.). W. H. Freeman and Company, New York. ISBN 978-0-7167-2064-5.
- रोजर पेनरोज़, द एम्परर्स न्यू माइंड: कन्सर्निंग कंप्यूटर्स, माइंड्स एंड द लॉज़ ऑफ़ फ़िज़िक्स, ऑक्सफोर्ड यूनिवरसिटि प्रेस, ऑक्सफोर्ड एंड न्यूयॉर्क, 1989 (1990 सुधार), ISBN 0-19-851973-7.
- Paul Strathern (1997). ट्यूरिंग एंड द कंप्यूटर-द बिग आइडिया. Anchor Books/Doubleday. ISBN 978-0-385-49243-0.
- हाओ वांग (अकादमिक), कंप्यूटिंग मशीनों के ट्यूरिंग के सिद्धांत का प्रकार, जर्नल ऑफ़ द एसोसिएशन फॉर कंप्यूटिंग मशीनरी (JACM) 4, 63–92 (1957)।
- चार्ल्स पेटज़ोल्ड, पेटज़ोल्ड, चार्ल्स, द एनोटेटेड ट्यूरिंग, जॉन विले एंड संस, इंक। ISBN 0-470-22905-5
- अरोड़ा, संजीव; बराक, बोअज़, कॉम्प्लेक्सिटी थ्योरी: ए मॉडर्न अप्रोच, कैम्ब्रिज यूनिवर्सिटी प्रेस, 2009, ISBN 978-0-521-42426-4, खंड 1.4, तार के रूप में मशीनें और सार्वभौमिक ट्यूरिंग मशीन और 1.7, प्रमेय 1.9 का प्रमाण
- Kantorovitz, Isaiah Pinchas (December 1, 2005). "नियम संचालित प्रणालियों की ट्यूरिंग मशीन की संगणना पर एक नोट". SIGACT News. 36 (4): 109–110. doi:10.1145/1107523.1107525. S2CID 31117713.
- किरनेर, रायमुंड; ज़िम्मरमैन, वुल्फ; रिक्टर, डिर्क: चालू रियल प्रोग्रामिंग लैंग्वेज के अनिर्णीत परिणाम, 15वीं कोलोक्वियम प्रोग्रामिंग लैंग्वेज एंड फंडामेंटल ऑफ प्रोग्रामिंग (केपीएस'09) में, मारिया टैफरल, ऑस्ट्रिया, अक्टूबर। 2009
बाहरी संबंध
- "Turing machine", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Turing Machine – Stanford Encyclopedia of Philosophy
- Turing Machine Causal Networks by Enrique Zeleny as part of the Wolfram Demonstrations Project.
- Turing Machines at Curlie