विश्लेषणात्मक यांत्रिकी

सैद्धांतिक भौतिकी और गणितीय भौतिकी में, विश्लेषणात्मक यांत्रिकी, या सैद्धांतिक यांत्रिकी शास्त्रीय यांत्रिकी के निकट संबंधित वैकल्पिक योगों का एक संग्रह है।यह 18 वीं शताब्दी के दौरान और न्यूटोनियन यांत्रिकी के बाद कई वैज्ञानिकों और गणितज्ञों द्वारा विकसित किया गया था।चूंकि न्यूटोनियन यांत्रिकी वेक्टर मात्रा को गति, विशेष रूप से त्वरण, क्षण, बलों, सिस्टम के घटकों के, न्यूटन के कानूनों और यूलर के कानूनों द्वारा शासित यांत्रिकी के लिए एक वैकल्पिक नाम वेक्टरियल मैकेनिक्स पर मानते हैं।

इसके विपरीत, विश्लेषणात्मक यांत्रिकी गति के स्केलर गुणों का उपयोग करता है जो सिस्टम को एक पूरे के रूप में दर्शाता है - आमतौर पर इसकी कुल गतिज ऊर्जा और संभावित ऊर्जा - न्यूटन के व्यक्तिगत कणों के वेक्टरियल बलों को नहीं। एक स्केलर एक मात्रा है, जबकि एक वेक्टर को मात्रा और दिशा द्वारा दर्शाया जाता है। गति के समीकरण स्केलर की भिन्नता के बारे में कुछ अंतर्निहित सिद्धांत द्वारा स्केलर मात्रा से प्राप्त होते हैं।

विश्लेषणात्मक यांत्रिकी समस्याओं को हल करने के लिए एक प्रणाली की बाधाओं का लाभ उठाता है। बाधाएं स्वतंत्रता की डिग्री को सीमित करती हैं जो सिस्टम में हो सकती है, और इसका उपयोग गति के लिए हल करने के लिए आवश्यक निर्देशांक की संख्या को कम करने के लिए किया जा सकता है। औपचारिकता अच्छी तरह से निर्देशांक के मनमाने विकल्पों के लिए अनुकूल है, जिसे संदर्भ में सामान्यीकृत निर्देशांक के रूप में जाना जाता है। सिस्टम की गतिज और संभावित ऊर्जा को इन सामान्यीकृत निर्देशांक या मोमेंट का उपयोग करके व्यक्त किया जाता है, और गति के समीकरणों को आसानी से स्थापित किया जा सकता है, इस प्रकार विश्लेषणात्मक यांत्रिकी कई यांत्रिक समस्याओं को पूरी तरह से वेक्टोरियल तरीकों की तुलना में अधिक दक्षता के साथ हल करने की अनुमति देता है। यह हमेशा गैर-रूढ़िवादी बलों या घर्षण जैसे विघटनकारी बलों के लिए काम नहीं करता है, जिस स्थिति में कोई न्यूटोनियन यांत्रिकी में वापस आ सकता है।

विश्लेषणात्मक यांत्रिकी की दो प्रमुख शाखाएं लैग्रैन्जियन मैकेनिक्स (सामान्यीकृत निर्देशांक और कॉन्फ़िगरेशन स्पेस में इसी सामान्यीकृत वेगों का उपयोग करके) और हैमिल्टनियन यांत्रिकी (चरण अंतरिक्ष में निर्देशांक और इसी क्षण का उपयोग करके) हैं। दोनों फॉर्मुलेशन एक लीजेंड्रे ट्रांसफॉर्मेशन#हैमिल्टन -लाग्रेंज मैकेनिक्स के बराबर हैं। सामान्यीकृत निर्देशांक, वेग और मोमेंट पर किंवदंती परिवर्तन, इसलिए दोनों में एक प्रणाली की गतिशीलता का वर्णन करने के लिए समान जानकारी होती है। हैमिल्टन -जैकोबी थ्योरी, राउथियन मैकेनिक्स, और एपेल के मोशन के समीकरण जैसे अन्य फॉर्मूलेशन हैं। कणों और क्षेत्रों के लिए गति के सभी समीकरण, किसी भी औपचारिकता में, व्यापक रूप से लागू परिणाम से प्राप्त किए जा सकते हैं जिन्हें कम से कम कार्रवाई का सिद्धांत कहा जाता है। एक परिणाम नूथर का प्रमेय है, एक बयान जो संरक्षण कानूनों को उनके संबद्ध समरूपता से जोड़ता है।

विश्लेषणात्मक यांत्रिकी नए भौतिकी का परिचय नहीं देता है और न्यूटोनियन यांत्रिकी से अधिक सामान्य नहीं है। बल्कि यह समकक्ष औपचारिकताओं का एक संग्रह है जिसमें व्यापक अनुप्रयोग है। वास्तव में समान सिद्धांतों और औपचारिकताओं का उपयोग सापेक्ष यांत्रिकी और सामान्य सापेक्षता में और कुछ संशोधनों, क्वांटम यांत्रिकी और क्वांटम क्षेत्र सिद्धांत के साथ किया जा सकता है।

विश्लेषणात्मक यांत्रिकी का व्यापक रूप से उपयोग किया जाता है, मौलिक भौतिकी से लेकर लागू गणित, विशेष रूप से अराजकता सिद्धांत तक।

विश्लेषणात्मक यांत्रिकी के तरीके असतत कणों पर लागू होते हैं, प्रत्येक स्वतंत्रता की डिग्री की एक सीमित संख्या के साथ। उन्हें निरंतर क्षेत्रों या तरल पदार्थों का वर्णन करने के लिए संशोधित किया जा सकता है, जिनमें स्वतंत्रता की अनंत डिग्री होती है। परिभाषाओं और समीकरणों में यांत्रिकी के साथ एक करीबी सादृश्य है।

विश्लेषणात्मक यांत्रिकी का विषय

यांत्रिक सिद्धांत का सबसे स्पष्ट लक्ष्य यांत्रिक समस्याओं को हल करना है जो भौतिकी या खगोल विज्ञान में उत्पन्न होते हैं। एक भौतिक अवधारणा से शुरू, जैसे कि एक तंत्र या एक स्टार प्रणाली, एक गणितीय अवधारणा, या मॉडल, एक अंतर समीकरण या समीकरणों के रूप में विकसित किया जाता है और फिर उन्हें हल करने का प्रयास किया जाता है।

यांत्रिकी के लिए वेक्टर दृष्टिकोण, जैसा कि न्यूटन द्वारा स्थापित किया गया है, न्यूटन के कानूनों पर आधारित है, जो बल, वेग, त्वरण जैसे वेक्टर मात्रा की मदद से गति का वर्णन करते हैं। ये मात्रा एक शरीर की गति को चिह्नित करती है जो एक द्रव्यमान बिंदु के रूप में आदर्शित होती है या एक कण को ​​एक एकल बिंदु के रूप में समझा जाता है, जिसमें एक द्रव्यमान संलग्न होता है। न्यूटन की विधि सफल रही और उन्हें भौतिक समस्याओं की एक विस्तृत श्रृंखला पर लागू किया गया, जो पृथ्वी के गुरुत्वाकर्षण क्षेत्र में एक कण की गति से शुरू हुआ और फिर सूर्य की कार्रवाई के तहत ग्रहों की गति तक बढ़ाया गया। इस दृष्टिकोण में, न्यूटन के कानून एक अंतर समीकरण द्वारा गति का वर्णन करते हैं और फिर समस्या उस समीकरण को हल करने के लिए कम हो जाती है।

जब कण कणों की एक प्रणाली का एक हिस्सा होता है, जैसे कि एक ठोस शरीर या एक द्रव, जिसमें कण स्वतंत्र रूप से नहीं चलते हैं, लेकिन एक दूसरे के साथ बातचीत करते हैं, तो न्यूटन का दृष्टिकोण अभी भी उचित सावधानियों के तहत लागू होता है जैसे कि प्रत्येक एकल कण को ​​अलग करना अन्य, और उस पर काम करने वाले सभी बलों का निर्धारण करना: सिस्टम पर एक पूरे के रूप में सिस्टम पर काम करने वाले लोग सिस्टम में अन्य सभी कणों के साथ प्रत्येक कण की बातचीत के बलों को भी। इस तरह का विश्लेषण अपेक्षाकृत सरल प्रणालियों में भी बोझिल हो सकता है। एक नियम के रूप में, इंटरैक्शन फोर्स अज्ञात या कठिन हैं जो नए पोस्टुलेट्स को पेश करने के लिए आवश्यक बनाने के लिए निर्धारित करते हैं। न्यूटन ने सोचा कि न्यूटन का तीसरा कानून | उनकी तीसरी कानून कार्रवाई के बराबर प्रतिक्रिया सभी जटिलताओं का ध्यान रखेगी। यह एक ठोस शरीर के घुमाव के रूप में ऐसी सरल प्रणाली के लिए भी नहीं है। अधिक जटिल प्रणालियों में, वेक्टरियल दृष्टिकोण पर्याप्त विवरण नहीं दे सकता है।

गति की समस्या के लिए विश्लेषणात्मक दृष्टिकोण कण को ​​एक पृथक इकाई के रूप में नहीं बल्कि एक यांत्रिक प्रणाली के एक हिस्से के रूप में देखा जाता है, जो कणों के एक विधानसभा के रूप में समझा जाता है जो एक दूसरे के साथ बातचीत करते हैं। जैसा कि पूरी प्रणाली ध्यान में आती है, एकल कण अपना महत्व खो देता है; गतिशील समस्या में पूरे सिस्टम को भागों में तोड़े बिना शामिल किया जाता है। यह गणना को काफी सरल बनाता है क्योंकि वेक्टरियल दृष्टिकोण में बलों को प्रत्येक कण के लिए व्यक्तिगत रूप से निर्धारित किया जाता है, जबकि विश्लेषणात्मक दृष्टिकोण में यह एक एकल फ़ंक्शन को जानने के लिए पर्याप्त है, जिसमें सिस्टम में और सिस्टम में अभिनय करने वाले सभी बल शामिल हैं। इस तरह के सरलीकरण को अक्सर कुछ कीनेमेटिकल स्थितियों का उपयोग करके किया जाता है जो एक प्राथमिकता कहा जाता है; वे पहले से मौजूद हैं और कुछ मजबूत बलों की कार्रवाई के कारण हैं। हालांकि, विश्लेषणात्मक उपचार के लिए इन बलों के ज्ञान की आवश्यकता नहीं है और इन कीनेमेटिक परिस्थितियों को दी गई है। यह देखते हुए कि उन्हें बनाए रखने वाली ताकतों की भीड़ की तुलना में ये स्थितियां कितनी सरल हैं, वेक्टर एक पर विश्लेषणात्मक दृष्टिकोण की श्रेष्ठता स्पष्ट हो जाती है।

फिर भी, एक जटिल यांत्रिक प्रणाली की गति के समीकरणों को बड़ी संख्या में अलग -अलग अंतर समीकरणों की आवश्यकता होती है, जिन्हें कुछ एकीकृत आधार के बिना प्राप्त नहीं किया जा सकता है, जहां से वे अनुसरण करते हैं। यह आधार वैरिएबल सिद्धांत हैं: समीकरणों के प्रत्येक सेट के पीछे एक सिद्धांत है जो पूरे सेट के अर्थ को व्यक्त करता है। 'एक्शन' नामक एक मौलिक और सार्वभौमिक मात्रा को देखते हुए, यह सिद्धांत कि यह कार्रवाई कुछ अन्य यांत्रिक मात्रा के छोटे बदलाव के तहत स्थिर हो सकती है, अंतर समीकरणों के आवश्यक सेट को उत्पन्न करती है। सिद्धांत के विवरण को किसी विशेष समन्वय प्रणाली की आवश्यकता नहीं होती है, और सभी परिणाम सामान्यीकृत निर्देशांक में व्यक्त किए जाते हैं। इसका मतलब है कि एम के विश्लेषणात्मक समीकरणविकल्प एक समन्वय परिवर्तन पर नहीं बदलते हैं, एक इनवेरियन संपत्ति जो गति के वेक्टरियल समीकरण में कमी है। यह पूरी तरह से स्पष्ट नहीं है कि अंतर समीकरणों के एक सेट को 'हल' करने का क्या मतलब है। एक समस्या को हल किया जाता है जब कणों को समय पर निर्देशांक होता है, टी के सरल कार्यों के रूप में व्यक्त किया जाता है और प्रारंभिक पदों और वेगों को परिभाषित करने वाले मापदंडों के रूप में। हालांकि, 'सिंपल फ़ंक्शन' एक अच्छी तरह से परिभाषित अवधारणा नहीं है: आजकल, एक फ़ंक्शन f (t) को T (प्राथमिक फ़ंक्शन) में एक औपचारिक अभिव्यक्ति के रूप में नहीं माना जाता है, जैसा कि न्यूटन के समय में है, लेकिन आमतौर पर टी द्वारा निर्धारित मात्रा के रूप में। , और 'सरल' और 'सरल' कार्यों के बीच एक तेज रेखा खींचना संभव नहीं है। यदि कोई केवल 'कार्यों' के बारे में बोलता है, तो हर यांत्रिक समस्या को हल किया जाता है जैसे ही यह अंतर समीकरणों में अच्छी तरह से कहा गया है, क्योंकि प्रारंभिक शर्तों को देखते हुए और टी टी पर निर्देशांक निर्धारित करते हैं। यह विशेष रूप से कंप्यूटर मॉडलिंग के आधुनिक तरीकों के साथ एक तथ्य है जो किसी भी वांछित सटीकता के लिए यांत्रिक समस्याओं के लिए अंकगणितीय समाधान प्रदान करता है, अंतर समीकरणों को अंतर समीकरणों द्वारा प्रतिस्थापित किया जा रहा है।

फिर भी, हालांकि सटीक परिभाषाओं की कमी है, यह स्पष्ट है कि दो-शरीर की समस्या का एक सरल समाधान है, जबकि तीन-शरीर की समस्या नहीं है। दो-शरीर की समस्या को मापदंडों से जुड़े सूत्रों द्वारा हल किया जाता है; उनके मूल्यों को सभी समाधानों के वर्ग का अध्ययन करने के लिए बदला जा सकता है, अर्थात् समस्या की गणितीय संरचना। इसके अलावा, एक सटीक मानसिक या खींची गई तस्वीर दो निकायों की गति के लिए बनाई जा सकती है, और यह वास्तविक और सटीक हो सकता है जैसे कि वास्तविक शरीर चलते और बातचीत करते हैं। तीन-शरीर की समस्या में, मापदंडों को विशिष्ट मान भी सौंपा जा सकता है; हालांकि, इन असाइन किए गए मूल्यों पर समाधान या इस तरह के समाधानों का संग्रह समस्या के गणितीय संरचना को प्रकट नहीं करता है। कई अन्य समस्याओं के रूप में, गणितीय संरचना को केवल अंतर समीकरणों की जांच करके केवल स्पष्ट किया जा सकता है।

विश्लेषणात्मक यांत्रिकी का उद्देश्य और भी अधिक है: एक एकल यांत्रिक समस्या की गणितीय संरचना को समझने में नहीं, लेकिन समस्याओं के एक वर्ग के इतने व्यापक हैं कि वे अधिकांश यांत्रिकी को शामिल करते हैं। यह उन प्रणालियों पर ध्यान केंद्रित करता है, जिन पर Lagrangian या हैमिल्टनियन समीकरण गति के लागू होते हैं और इसमें वास्तव में समस्याओं की एक विस्तृत श्रृंखला शामिल है। विश्लेषणात्मक यांत्रिकी के विकास के दो उद्देश्य हैं: (i) प्रयोज्यता की एक विस्तृत श्रृंखला के साथ मानक तकनीकों को विकसित करके हल करने योग्य समस्याओं की सीमा को बढ़ाते हैं, और (ii) यांत्रिकी की गणितीय संरचना को समझते हैं।लंबे समय में, हालांकि, (ii) विशिष्ट समस्याओं पर एक एकाग्रता से अधिक (i) मदद कर सकता है, जिसके लिए पहले से ही डिज़ाइन किए गए हैं।

आंतरिक गति

सामान्यीकृत निर्देशांक और बाधाएं

न्यूटोनियन यांत्रिकी में, एक कस्टम रूप से सभी तीन कार्टेशियन निर्देशांक, या अन्य 3 डी समन्वय प्रणाली का उपयोग करता है, इसकी गति के दौरान एक शरीर की स्थिति का उल्लेख करने के लिए।भौतिक प्रणालियों में, हालांकि, कुछ संरचना या अन्य प्रणाली आमतौर पर शरीर की गति को कुछ दिशाओं और मार्गों को लेने से रोकती है।इसलिए कार्टेशियन निर्देशांक का एक पूरा सेट अक्सर अनावश्यक होता है, क्योंकि बाधाएं निर्देशांक के बीच विकसित संबंधों को निर्धारित करती हैं, कि संबंधों को बाधाओं के अनुरूप समीकरणों द्वारा मॉडल किया जा सकता है।Lagrangian और हैमिल्टनियन औपचारिकताओं में, बाधाओं को गति की ज्यामिति में शामिल किया जाता है, जिससे गति को मॉडल करने के लिए आवश्यक न्यूनतम तक निर्देशांक की संख्या को कम किया जाता है।इन्हें सामान्यीकृत निर्देशांक के रूप में जाना जाता है, निरूपित क्यू_i(i = 1, 2, 3 ...)।

वक्रता और सामान्यीकृत निर्देशांक के बीच अंतर

सामान्यीकृत निर्देशांक सिस्टम पर बाधाओं को शामिल करते हैं।एक सामान्यीकृत समन्वय क्यू है_iस्वतंत्रता की प्रत्येक डिग्री के लिए (एक सूचकांक I = 1, 2 ... n) द्वारा लेबल की गई सुविधा के लिए, यानी प्रत्येक तरह से सिस्टम अपने कॉन्फ़िगरेशन को बदल सकता है;वक्रता की लंबाई या रोटेशन के कोण के रूप में।सामान्यीकृत निर्देशांक वक्रता के निर्देशांक के समान नहीं हैं।वक्रता के निर्देशांक की संख्या प्रश्न में स्थिति स्थान के आयाम के बराबर होती है (आमतौर पर 3 डी स्पेस के लिए 3), जबकि सामान्यीकृत निर्देशांक की संख्या इस आयाम के बराबर नहीं है;बाधाएं स्वतंत्रता की डिग्री की संख्या को कम कर सकती हैं (इसलिए सिस्टम के कॉन्फ़िगरेशन को परिभाषित करने के लिए आवश्यक सामान्यीकृत निर्देशांक की संख्या), सामान्य नियम के बाद:

[dimension of position space (usually 3)] × [number of constituents of system ("particles")] − (number of constraints)

= (number of degrees of freedom) = (number of generalized coordinates)

स्वतंत्रता की एन डिग्री के साथ एक प्रणाली के लिए, सामान्यीकृत निर्देशांक को एन-टपल में एकत्र किया जा सकता है:

$$\mathbf {q} =(q_{1},q_{2},\dots ,q_{N})$$

और इस टपल के समय व्युत्पन्न (यहाँ एक ओवरडॉट द्वारा निरूपित) सामान्यीकृत वेग देते हैं:

$${\frac {d\mathbf {q} }{dt}}=\left({\frac {dq_{1}}{dt}},{\frac {dq_{2}}{dt}},\dots ,{\frac {dq_{N}}{dt}}\right)\equiv \mathbf {\dot {q}} =({\dot {q}}_{1},{\dot {q}}_{2},\dots ,{\dot {q}}_{N}).$$

D'Alembert का सिद्धांत

जिस नींव पर विषय बनाया गया है, वह है D'Alembert का सिद्धांत।

इस सिद्धांत में कहा गया है कि प्रतिवर्ती विस्थापन में एक बल द्वारा किए गए इनफिनिटिमल वर्चुअल वर्क शून्य है, जो सिस्टम के आदर्श बाधाओं के अनुरूप बल द्वारा किया गया काम है।एक बाधा का विचार उपयोगी है - चूंकि यह सीमित है कि सिस्टम क्या कर सकता है, और सिस्टम की गति के लिए हल करने के लिए कदम प्रदान कर सकता है।D'Alembert के सिद्धांत के लिए समीकरण है:

$$\delta W={\boldsymbol {\mathcal {Q}}}\cdot \delta \mathbf {q} =0\,,$$

कहाँ पे

$${\boldsymbol {\mathcal {Q}}}=({\mathcal {Q}}_{1},{\mathcal {Q}}_{2},\dots ,{\mathcal {Q}}_{N})$$

सामान्यीकृत बल हैं (साधारण क्यू के बजाय स्क्रिप्ट क्यू का उपयोग यहां विहित परिवर्तनों के साथ संघर्ष को रोकने के लिए किया जाता है) और q सामान्यीकृत निर्देशांक हैं।यह विश्लेषणात्मक यांत्रिकी की भाषा में न्यूटन के कानूनों के सामान्यीकृत रूप की ओर जाता है:

$${\boldsymbol {\mathcal {Q}}}={\frac {d}{dt}}\left({\frac {\partial T}{\partial \mathbf {\dot {q}} }}\right)-{\frac {\partial T}{\partial \mathbf {q} }}\,,$$

जहां टी सिस्टम की कुल गतिज ऊर्जा है, और संकेतन

$${\frac {\partial }{\partial \mathbf {q} }}=\left({\frac {\partial }{\partial q_{1}}},{\frac {\partial }{\partial q_{2}}},\dots ,{\frac {\partial }{\partial q_{N}}}\right)$$

एक उपयोगी शॉर्टहैंड है (मैट्रिक्स कैलकुलस#स्केलर-बाय-वेक्टर देखें। इस संकेतन के लिए मैट्रिक्स कैलकुलस)।

होलोनोमिक बाधाएं

यदि वक्रता समन्वय प्रणाली मानक स्थिति वेक्टर द्वारा परिभाषित की जाती है r, और यदि स्थिति वेक्टर सामान्यीकृत निर्देशांक के संदर्भ में लिखा जा सकता है q और समय t फार्म में:

$$\mathbf {r} =\mathbf {r} (\mathbf {q} (t),t)$$

और यह संबंध सभी समय के लिए है t, फिर q होलोनोमिक बाधाएं कहा जाता है। Vector r is explicitly dependent on t in cases when the constraints vary with time, not just because of q(t). For time-independent situations, the constraints are also called scleronomic, for time-dependent cases they are called rheonomic.

Lagrangian यांत्रिकी

Lagrangian और Euler -Lagrange समीकरण

सामान्यीकृत निर्देशांक और मौलिक lagrangian फ़ंक्शन की शुरूआत:

$L(\mathbf {q} ,\mathbf {\dot {q}} ,t)=T(\mathbf {q} ,\mathbf {\dot {q}} ,t)-V(\mathbf {q} ,\mathbf {\dot {q}} ,t)$

जहां टी कुल काइनेटिक ऊर्जा है और वी पूरे सिस्टम की कुल संभावित ऊर्जा है, तो या तो भिन्नताओं की पथरी का पालन करना या उपरोक्त सूत्र का उपयोग करना - यूलर -लग्रांज समीकरणों का नेतृत्व करना;

${\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\right)={\frac {\partial L}{\partial \mathbf {q} }}\,,$

जो एन सेकंड-ऑर्डर साधारण डिफरेंशियल इक्वेशन का एक सेट है, प्रत्येक क्यू के लिए एक_i(टी)।

यह सूत्रीकरण उस पथ के चयन के रूप में गति के बाद वास्तविक पथ की पहचान करता है, जिस पर काइनेटिक ऊर्जा का समय कम से कम है, कुल ऊर्जा को तय करने के लिए, और पारगमन के समय पर कोई स्थिति नहीं है।

'कॉन्फ़िगरेशन स्पेस'

Lagrangian सूत्रीकरण सिस्टम के कॉन्फ़िगरेशन स्थान का उपयोग करता है, सभी संभावित सामान्यीकृत निर्देशांक का सेट:

${\mathcal {C}}=\{\mathbf {q} \in \mathbb {R} ^{N}\}\,,$

कहाँ पे $\mathbb {R} ^{N}$ एन-डायमेंशनल रियल स्पेस है (सेट-बिल्डर नोटेशन भी देखें)।Euler -Lagrange समीकरणों के विशेष समाधान को A (कॉन्फ़िगरेशन) पथ या प्रक्षेपवक्र कहा जाता है, यानी आवश्यक प्रारंभिक शर्तों के अधीन एक विशेष 'q' (t)।सामान्य समाधान समय के कार्यों के रूप में संभावित कॉन्फ़िगरेशन का एक सेट बनाते हैं:

$\{\mathbf {q} (t)\in \mathbb {R} ^{N}\,:\,t\geq 0,t\in \mathbb {R} \}\subseteq {\mathcal {C}}\,,$

कॉन्फ़िगरेशन स्पेस को अधिक आम तौर पर परिभाषित किया जा सकता है, और वास्तव में अधिक गहराई से, टोपोलॉजिकल मैनिफोल्ड्स और स्पर्शरेखा बंडल के संदर्भ में।

हैमिल्टन मैकेनिक्स

हैमिल्टन और हैमिल्टन के समीकरण

Lagrangian के किंवदंती परिवर्तन सामान्यीकृत निर्देशांक और वेग (q, q̇) को (q, p) के साथ बदल देता है;सामान्यीकृत निर्देशांक और सामान्यीकृत क्षण सामान्यीकृत निर्देशांक के लिए संयुग्म:

$\mathbf {p} ={\frac {\partial L}{\partial \mathbf {\dot {q}} }}=\left({\frac {\partial L}{\partial {\dot {q}}_{1}}},{\frac {\partial L}{\partial {\dot {q}}_{2}}},\cdots {\frac {\partial L}{\partial {\dot {q}}_{N}}}\right)=(p_{1},p_{2}\cdots p_{N})\,,$

और हैमिल्टनियन का परिचय देता है (जो सामान्यीकृत निर्देशांक और मोमेंट के संदर्भ में है):

$H(\mathbf {q} ,\mathbf {p} ,t)=\mathbf {p} \cdot \mathbf {\dot {q}} -L(\mathbf {q} ,\mathbf {\dot {q}} ,t)$

जहां • डॉट उत्पाद को दर्शाता है, भी हैमिल्टन के समीकरणों के लिए अग्रणी है:

$\mathbf {\dot {p}} =-{\frac {\partial H}{\partial \mathbf {q} }}\,,\quad \mathbf {\dot {q}} =+{\frac {\partial H}{\partial \mathbf {p} }}\,,$

जो अब 2n प्रथम-क्रम साधारण अंतर समीकरणों का एक सेट है, प्रत्येक क्यू के लिए एक_i(t) and p_i(टी)।लीजेंड्रे ट्रांसफॉर्मेशन से एक अन्य परिणाम लैग्रैन्जियन और हैमिल्टन के समय के व्युत्पन्न से संबंधित है:

${\frac {dH}{dt}}=-{\frac {\partial L}{\partial t}}\,,$

जिसे अक्सर हैमिल्टन के गति के समीकरणों में से एक माना जाता है।सामान्यीकृत मोमेंट को सामान्यीकृत बलों के संदर्भ में उसी तरह से लिखा जा सकता है जैसे न्यूटन के दूसरे कानून:

$\mathbf {\dot {p}} ={\boldsymbol {\mathcal {Q}}}\,.$

सामान्यीकृत गति का स्थान

कॉन्फ़िगरेशन स्पेस के अनुरूप, सभी मोमेंट का सेट मोमेंटम स्पेस है (तकनीकी रूप से इस संदर्भ में; सामान्यीकृत मोमेंटम स्पेस ):

${\mathcal {M}}=\{\mathbf {p} \in \mathbb {R} ^{N}\}\,.$

मोमेंटम स्पेस के-स्पेस को भी संदर्भित करता है;क्वांटम यांत्रिकी और तरंगों के सिद्धांत में उपयोग किए जाने वाले सभी तरंग वैक्टर (डी ब्रोगली संबंधों द्वारा दिया गया) का सेट: यह इस संदर्भ में संदर्भित नहीं है।

चरण स्थान

सभी पदों और क्षणों का सेट चरण स्थान बनाता है;

${\mathcal {P}}={\mathcal {C}}\times {\mathcal {M}}=\{(\mathbf {q} ,\mathbf {p} )\in \mathbb {R} ^{2N}\}\,,$

अर्थात्, कॉन्फ़िगरेशन स्पेस के कार्टेशियन उत्पाद × और सामान्यीकृत गति स्थान।

हैमिल्टन के समीकरणों के लिए एक विशेष समाधान को एक चरण पथ कहा जाता है, एक विशेष वक्र ('q' (t), 'p' (t)) आवश्यक प्रारंभिक स्थितियों के अधीन है।सभी चरण पथों का सेट, अंतर समीकरणों का सामान्य समाधान, चरण चित्र है:

$\{(\mathbf {q} (t),\mathbf {p} (t))\in \mathbb {R} ^{2N}\,:\,t\geq 0,t\in \mathbb {R} \}\subseteq {\mathcal {P}}\,,$

पॉइसन ब्रैकेट

सभी डायनेमिक वैरिएबल को स्थिति आर, मोमेंटम पी, और टाइम टी से लिया जा सकता है, और इन के एक समारोह के रूप में लिखा जा सकता है: ए = )।यदि (q, p, t ) और b (q, p, t ) दो स्केलर वैल्यूड डायनेमिक वैरिएबल हैं,सामान्यीकृत निर्देशांक और क्षण द्वारा:

${\begin{aligned}\{A,B\}\equiv \{A,B\}_{\mathbf {q} ,\mathbf {p} }&={\frac {\partial A}{\partial \mathbf {q} }}\cdot {\frac {\partial B}{\partial \mathbf {p} }}-{\frac {\partial A}{\partial \mathbf {p} }}\cdot {\frac {\partial B}{\partial \mathbf {q} }}\\&\equiv \sum _{k}{\frac {\partial A}{\partial q_{k}}}{\frac {\partial B}{\partial p_{k}}}-{\frac {\partial A}{\partial p_{k}}}{\frac {\partial B}{\partial q_{k}}}\,,\end{aligned}}$

इनमें से किसी एक के कुल व्युत्पन्न की गणना करना, ए, और परिणाम में हैमिल्टन के समीकरणों को प्रतिस्थापित करना एक के समय के विकास की ओर जाता है:

${\frac {dA}{dt}}=\{A,H\}+{\frac {\partial A}{\partial t}}\,.$

ए में यह समीकरण क्वांटम मैकेनिक्स के हाइजेनबर्ग तस्वीर में गति के समीकरण से निकटता से संबंधित है, जिसमें शास्त्रीय डायनेमिक वैरिएबल क्वांटम ऑपरेटर बन जाते हैं (हैट्स (^) द्वारा इंगित), और पॉइसन ब्रैकेट को डिरैक के माध्यम से ऑपरेटरों के कम्यूटेटर द्वारा बदल दिया जाता है।कैनोनिकल परिमाणीकरण:

$\{A,B\}\rightarrow {\frac {1}{i\hbar }}[{\hat {A}},{\hat {B}}]\,.$

Lagrangian और Hamiltonian कार्यों के गुण

Lagrangian और Hamiltonian कार्यों के बीच अतिव्यापी गुण निम्नलिखित हैं।

• सभी व्यक्तिगत सामान्यीकृत निर्देशांक q_i(t), velocities q̇_i(t) and momenta p_i(टी) स्वतंत्रता की हर डिग्री के लिए परस्पर स्वतंत्र हैं।किसी फ़ंक्शन के स्पष्ट समय-निर्भरता का अर्थ है कि फ़ंक्शन में वास्तव में 'q' (t), 'p' (t) के अलावा एक चर के रूप में समय t शामिल है, न कि केवल 'Q' (t) और 'P के माध्यम से एक पैरामीटर के रूप में'(टी), जिसका अर्थ स्पष्ट समय-स्वतंत्रता होगा।
• Lagrangian 'Q' और T के किसी भी कार्य के कुल समय व्युत्पन्न के अलावा अपरिवर्तनीय है, अर्थात:
  $$L'=L+{\frac {d}{dt}}F(\mathbf {q} ,t)\,,$$
  तो प्रत्येक Lagrangian l और l 'बिल्कुल उसी गति का वर्णन करते हैं।दूसरे शब्दों में, एक प्रणाली का लैग्रैन्जियन अद्वितीय नहीं है।
• एनालॉग रूप से, हैमिल्टनियन 'क्यू', 'पी' और टी के किसी भी कार्य के आंशिक समय व्युत्पन्न के अलावा अपरिवर्तनीय है: अर्थात:
  $$K=H+{\frac {\partial }{\partial t}}G(\mathbf {q} ,\mathbf {p} ,t)\,,$$
  (K इस मामले में अक्सर इस्तेमाल किया जाने वाला पत्र है)।इस संपत्ति का उपयोग विहित परिवर्तनों (नीचे देखें) में किया जाता है।
• यदि Lagrangian कुछ सामान्यीकृत निर्देशांक से स्वतंत्र है, तो उन निर्देशांक के लिए सामान्यीकृत मोमेंटा संयुग्म गति के स्थिरांक हैं, यानी संरक्षित हैं, यह तुरंत Lagrange के समीकरणों से अनुसरण करता है:
  $${\frac {\partial L}{\partial q_{j}}}=0\,\rightarrow \,{\frac {dp_{j}}{dt}}={\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}=0$$
  इस तरह के निर्देशांक चक्रीय या अज्ञानी हैं।यह दिखाया जा सकता है कि हैमिल्टन भी ठीक उसी सामान्यीकृत निर्देशांक में चक्रीय है।
• यदि लैग्रैजियन समय-स्वतंत्र है तो हैमिल्टनियन भी समय-स्वतंत्र है (यानी दोनों समय में स्थिर हैं)।
• यदि काइनेटिक ऊर्जा सामान्यीकृत वेगों के डिग्री 2 का एक सजातीय कार्य है, और लैग्रैन्जियन स्पष्ट रूप से समय-स्वतंत्र है, तो: फिर:
  $$T((\lambda {\dot {q}}_{i})^{2},(\lambda {\dot {q}}_{j}\lambda {\dot {q}}_{k}),\mathbf {q} )=\lambda ^{2}T(({\dot {q}}_{i})^{2},{\dot {q}}_{j}{\dot {q}}_{k},\mathbf {q} )\,,\quad L(\mathbf {q} ,\mathbf {\dot {q}} )\,,$$
  जहां λ एक स्थिर है, तो हैमिल्टनियन कुल संरक्षित ऊर्जा होगी, जो सिस्टम की कुल गतिज और संभावित ऊर्जा के बराबर है:
  $$H=T+V=E\,.$$
  यह श्रोडिंगर समीकरण के लिए आधार है, क्वांटम ऑपरेटरों को सम्मिलित करना सीधे इसे प्राप्त करता है।

कम से कम कार्रवाई का सिद्धांत

जैसा कि सिस्टम विकसित होता है, क्यू कॉन्फ़िगरेशन स्पेस के माध्यम से एक पथ का पता लगाता है (केवल कुछ दिखाए गए हैं)।सिस्टम (RED) द्वारा लिए गए पथ में सिस्टम के कॉन्फ़िगरेशन में छोटे परिवर्तनों के तहत एक स्थिर कार्रवाई (ΔS = 0) होती है () q)।

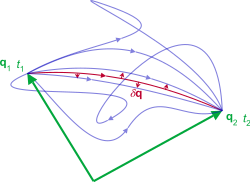
कार्रवाई विश्लेषणात्मक यांत्रिकी में एक और मात्रा है जिसे लैग्रैन्जियन के कार्यात्मक के रूप में परिभाषित किया गया है:

${\mathcal {S}}=\int _{t_{1}}^{t_{2}}L(\mathbf {q} ,\mathbf {\dot {q}} ,t)dt\,.$

कार्रवाई से गति के समीकरणों को खोजने का एक सामान्य तरीका कम से कम कार्रवाई का सिद्धांत है:

$\delta {\mathcal {S}}=\delta \int _{t_{1}}^{t_{2}}L(\mathbf {q} ,\mathbf {\dot {q}} ,t)dt=0\,,$

where the departure t₁ and arrival t₂ times are fixed. शब्द पथ या प्रक्षेपवक्र कॉन्फ़िगरेशन स्थान के माध्यम से एक पथ के रूप में सिस्टम के समय के विकास को संदर्भित करता है${\mathcal {C}}$, दूसरे शब्दों में q ( t ) में एक पथ का पता लगाना ${\mathcal {C}}$।जिस मार्ग के लिए कार्रवाई कम से कम सिस्टम द्वारा लिया गया मार्ग है।

इस सिद्धांत से, शास्त्रीय यांत्रिकी में गति के सभी समीकरण प्राप्त किए जा सकते हैं।इस दृष्टिकोण को कणों की एक प्रणाली (नीचे देखें) के बजाय क्षेत्रों में बढ़ाया जा सकता है, और क्वांटम यांत्रिकी के पथ अभिन्न सूत्रीकरण को रेखांकित करता है, और सामान्य सापेक्षता में जियोडेसिक गति की गणना के लिए उपयोग किया जाता है।

हैमिल्टन-जैकोबी यांत्रिकी

कैनोनिकल ट्रांसफॉर्मेशन

हैमिल्टनियन का आक्रमण (पी, क्यू, और टी के एक मनमाना कार्य के आंशिक समय के व्युत्पन्न के अलावा) हैमिल्टन को निर्देशांक के एक सेट में क्यू और मोमेंट पी को एक नए सेट क्यू = में परिवर्तित करने की अनुमति देता है।Q (q, p, t ) और p = p (q, p, t ), चार संभावित तरीकों से:

${\begin{aligned}&K(\mathbf {Q} ,\mathbf {P} ,t)=H(\mathbf {q} ,\mathbf {p} ,t)+{\frac {\partial }{\partial t}}G_{1}(\mathbf {q} ,\mathbf {Q} ,t)\\&K(\mathbf {Q} ,\mathbf {P} ,t)=H(\mathbf {q} ,\mathbf {p} ,t)+{\frac {\partial }{\partial t}}G_{2}(\mathbf {q} ,\mathbf {P} ,t)\\&K(\mathbf {Q} ,\mathbf {P} ,t)=H(\mathbf {q} ,\mathbf {p} ,t)+{\frac {\partial }{\partial t}}G_{3}(\mathbf {p} ,\mathbf {Q} ,t)\\&K(\mathbf {Q} ,\mathbf {P} ,t)=H(\mathbf {q} ,\mathbf {p} ,t)+{\frac {\partial }{\partial t}}G_{4}(\mathbf {p} ,\mathbf {P} ,t)\\\end{aligned}}$

P और Q पर प्रतिबंध के साथ जैसे कि रूपांतरित हैमिल्टन सिस्टम है:

$\mathbf {\dot {P}} =-{\frac {\partial K}{\partial \mathbf {Q} }}\,,\quad \mathbf {\dot {Q}} =+{\frac {\partial K}{\partial \mathbf {P} }}\,,$

उपरोक्त परिवर्तनों को विहित परिवर्तन कहा जाता है, प्रत्येक फ़ंक्शन जी_nnth प्रकार या टाइप-एन का एक जनरेटिंग फ़ंक्शन कहा जाता है।निर्देशांक और मोमेंट का परिवर्तन किसी दिए गए समस्या के लिए हैमिल्टन के समीकरणों को हल करने के लिए सरलीकरण की अनुमति दे सकता है।

'क्यू' और 'पी' की पसंद पूरी तरह से मनमानी है, लेकिन हर विकल्प एक विहित परिवर्तन की ओर नहीं जाता है।एक परिवर्तन के लिए एक सरल मानदंड 'q' → 'q' और 'p' → 'p' होने के लिए कैनोनिकल है पोइसन ब्रैकेट एकता हो,

$\{Q_{i},P_{i}\}=1$

सभी के लिए i = 1, 2, ... n।यदि यह पकड़ में नहीं आता है तो परिवर्तन विहित नहीं है।

हैमिल्टन -जैकोबी समीकरण

कैनोनिक रूप से रूपांतरित हैमिल्टनियन के = 0, और टाइप -2 जनरेटिंग फ़ंक्शन को 'हैमिल्टन के प्रमुख फ़ंक्शन' के बराबर सेट करके (एक्शन भी${\mathcal {S}}$) प्लस एक मनमाना निरंतर सी:

$G_{2}(\mathbf {q} ,t)={\mathcal {S}}(\mathbf {q} ,t)+C\,,$

सामान्यीकृत क्षण बन जाता है:

$\mathbf {p} ={\frac {\partial {\mathcal {S}}}{\partial \mathbf {q} }}$

और P स्थिर है, फिर हैमिल्टन-जैकोबी समीकरण (HJE) टाइप -2 कैनोनिकल परिवर्तन से प्राप्त किया जा सकता है:

$H=-{\frac {\partial {\mathcal {S}}}{\partial t}}$

जहां एच हैमिल्टनियन पहले की तरह है:

$H=H(\mathbf {q} ,\mathbf {p} ,t)=H\left(\mathbf {q} ,{\frac {\partial {\mathcal {S}}}{\partial \mathbf {q} }},t\right)$

एक अन्य संबंधित कार्य हैमिल्टन का विशिष्ट कार्य है

$W(\mathbf {q} )={\mathcal {S}}(\mathbf {q} ,t)+Et$

एक समय-स्वतंत्र हैमिल्टनियन एच के लिए चर के योज्य पृथक्करण द्वारा HJE को हल करने के लिए उपयोग किया जाता है।

हैमिल्टन -जैकोबी समीकरणों के समाधानों का अध्ययन स्वाभाविक रूप से सहानुभूति के कई गुना और सहानुभूति टोपोलॉजी के अध्ययन की ओर जाता है। इस सूत्रीकरण में, हैमिल्टन -जैकोबी समीकरणों के समाधान हैमिल्टनियन वेक्टर क्षेत्रों के अभिन्न घटता हैं।

राउथियन मैकेनिक्स

Routhian यांत्रिकी Lagrangian और Hamiltonian यांत्रिकी का एक संकर सूत्रीकरण है, जिसका उपयोग अक्सर नहीं किया जाता है, लेकिन विशेष रूप से चक्रीय निर्देशांक को हटाने के लिए उपयोगी है।यदि किसी प्रणाली के लैग्रैन्जियन के पास 'चक्रीय निर्देशांक Q =' 'Q' 'है₁, q₂, ... q_s with conjugate momenta p = p₁, p₂, ... p_s, with the rest of the coordinates non-cyclic and denoted ζ = ζ₁, ζ₁, ..., ζ_{N − s}, उन्हें राउथियन का परिचय देकर हटाया जा सकता है:

$R=\mathbf {p} \cdot \mathbf {\dot {q}} -L(\mathbf {q} ,\mathbf {p} ,{\boldsymbol {\zeta }},{\dot {\boldsymbol {\zeta }}})\,,$

जो चक्रीय निर्देशांक 'क्यू' के लिए 2 एस हैमिल्टन के समीकरणों के एक सेट की ओर जाता है,

${\dot {\mathbf {q} }}=+{\frac {\partial R}{\partial \mathbf {p} }}\,,\quad {\dot {\mathbf {p} }}=-{\frac {\partial R}{\partial \mathbf {q} }}\,,$

और N - S Lagrangian समीकरण गैर चक्रीय निर्देशांक 'ζ' में।

${\frac {d}{dt}}{\frac {\partial R}{\partial {\dot {\boldsymbol {\zeta }}}}}={\frac {\partial R}{\partial {\boldsymbol {\zeta }}}}\,.$

इस तरह से सेट करें, हालांकि राउथियन में हैमिल्टनियन का रूप है, यह स्वतंत्रता के एन - एस डिग्री के साथ एक लैग्रैन्जियन के बारे में सोचा जा सकता है।

निर्देशांक 'क्यू' को चक्रीय होने की आवश्यकता नहीं है, जिसके बीच का विभाजन है कि समन्वय हैमिल्टन के समीकरणों में प्रवेश करता है और जो लैग्रैन्जियन समीकरणों में प्रवेश करते हैं, वे मनमाना हैं।यह केवल हैमिल्टनियन समीकरणों को चक्रीय निर्देशांक को हटाने के लिए सुविधाजनक है, गैर चक्रीय निर्देशांक को गति के लैग्रैन्जियन समीकरणों के लिए छोड़ देता है।

अपीलीय यांत्रिकी

गति के अपील के समीकरण में सामान्यीकृत त्वरण शामिल हैं, सामान्यीकृत निर्देशांक के दूसरी बार डेरिवेटिव:

$\alpha _{r}={\ddot {q}}_{r}={\frac {d^{2}q_{r}}{dt^{2}}}\,,$

साथ ही सामान्यीकृत बलों ने डी'एलबर्ट के सिद्धांत में ऊपर उल्लेख किया है।समीकरण हैं

${\mathcal {Q}}_{r}={\frac {\partial S}{\partial \alpha _{r}}}\,,\quad S={\frac {1}{2}}\sum _{k=1}^{N}m_{k}\mathbf {a} _{k}^{2}\,,$

कहाँ पे

$\mathbf {a} _{k}={\ddot {\mathbf {r} }}_{k}={\frac {d^{2}\mathbf {r} _{k}}{dt^{2}}}$

K कण का त्वरण है, दूसरी बार इसकी स्थिति वेक्टर का व्युत्पन्न है।प्रत्येक त्वरण 'ए'_k is expressed in terms of the generalized accelerations α_r, likewise each r_k are expressed in terms the generalized coordinates q_r।

शास्त्रीय क्षेत्र सिद्धांत के लिए एक्सटेंशन

लैग्रैन्जियन फील्ड थ्योरी

सामान्यीकृत निर्देशांक असतत कणों पर लागू होते हैं।एन स्केलर फ़ील्ड के लिए φ_i('r', t) जहाँ i = 1, 2, ... n, 'lagrangian घनत्व' इन क्षेत्रों और उनके स्थान और समय डेरिवेटिव का एक कार्य है, और संभवतः अंतरिक्ष और समय खुद को समन्वित करता है:

$${\mathcal {L}}={\mathcal {L}}(\phi _{1},\phi _{2},\dots ,\nabla \phi _{1},\nabla \phi _{2},\dots ,\partial _{t}\phi _{1},\partial _{t}\phi _{2},\ldots ,\mathbf {r} ,t)\,.$$

और Euler -Lagrange समीकरणों में क्षेत्रों के लिए एक एनालॉग है:

$$\partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\phi _{i})}}\right)={\frac {\partial {\mathcal {L}}}{\partial \phi _{i}}}\,,$$

जहां ∂_μ4-ग्रेडिएंट को दर्शाता है और योग सम्मेलन का उपयोग किया गया है।एन स्केलर फ़ील्ड के लिए, ये लैग्रैन्जियन फील्ड समीकरण क्षेत्रों में एन सेकंड ऑर्डर आंशिक अंतर समीकरणों का एक सेट हैं, जो सामान्य रूप से युग्मित और नॉनलाइनियर होंगे।

इस स्केलर फ़ील्ड फॉर्मुलेशन को वेक्टर फ़ील्ड, टेंसर फ़ील्ड और स्पिनर फ़ील्ड तक बढ़ाया जा सकता है।

Lagrangian Lagrangian घनत्व का आयतन अभिन्न है:

$$L=\int _{\mathcal {V}}{\mathcal {L}}\,dV\,.$$

Originally developed for classical fields, the above formulation is applicable to all physical fields in classical, quantum, and relativistic situations: such as Newtonian gravity, classical electromagnetism, general relativity, and quantum field theory. It is a question of determining the correct Lagrangian density to generate the correct field equation.

Hamiltonian field theory

The corresponding "momentum" field densities conjugate to the N scalar fields φ_i(r, t) are:

$$\pi _{i}(\mathbf {r} ,t)={\frac {\partial {\mathcal {L}}}{\partial {\dot {\phi }}_{i}}}\,\quad {\dot {\phi }}_{i}\equiv {\frac {\partial \phi _{i}}{\partial t}}$$

जहां इस संदर्भ में ओवरडॉट एक आंशिक समय व्युत्पन्न को दर्शाता है, कुल समय व्युत्पन्न नहीं।हैमिल्टनियन घनत्व${\mathcal {H}}$ यांत्रिकी के साथ सादृश्य द्वारा परिभाषित किया गया है:

$${\mathcal {H}}(\phi _{1},\phi _{2},\ldots ,\pi _{1},\pi _{2},\ldots ,\mathbf {r} ,t)=\sum _{i=1}^{N}{\dot {\phi }}_{i}(\mathbf {r} ,t)\pi _{i}(\mathbf {r} ,t)-{\mathcal {L}}\,.$$

गति के समीकरण हैं:

$${\dot {\phi }}_{i}=+{\frac {\delta {\mathcal {H}}}{\delta \pi _{i}}}\,,\quad {\dot {\pi }}_{i}=-{\frac {\delta {\mathcal {H}}}{\delta \phi _{i}}}\,,$$

जहां वैरिएशनल व्युत्पन्न

$${\frac {\delta }{\delta \phi _{i}}}={\frac {\partial }{\partial \phi _{i}}}-\partial _{\mu }{\frac {\partial }{\partial (\partial _{\mu }\phi _{i})}}$$

केवल आंशिक डेरिवेटिव के बजाय उपयोग किया जाना चाहिए।एन फील्ड्स के लिए, ये हैमिल्टन फील्ड समीकरण 2 एन फर्स्ट ऑर्डर आंशिक अंतर समीकरणों का एक सेट हैं, जो सामान्य रूप से युग्मित और नॉनलाइनियर होंगे।

फिर, हैमिल्टनियन घनत्व का वॉल्यूम अभिन्न है हैमिल्टनियन है

$$H=\int _{\mathcal {V}}{\mathcal {H}}\,dV\,.$$

समरूपता, संरक्षण, और नूथर के प्रमेय

शास्त्रीय अंतरिक्ष और समय में समरूपता परिवर्तन

प्रत्येक परिवर्तन को एक ऑपरेटर द्वारा वर्णित किया जा सकता है (यानी उन्हें बदलने के लिए स्थिति आर या गति पी चर पर कार्य करने वाला कार्य)।निम्नलिखित मामले हैं जब ऑपरेटर आर या पी को नहीं बदलता है, यानी समरूपता।

Transformation	Operator	Position	Momentum
Translational symmetry	$X(\mathbf {a} )$	$\mathbf {r} \rightarrow \mathbf {r} +\mathbf {a}$	$\mathbf {p} \rightarrow \mathbf {p}$
Time translation	$U(t_{0})$	$\mathbf {r} (t)\rightarrow \mathbf {r} (t+t_{0})$	$\mathbf {p} (t)\rightarrow \mathbf {p} (t+t_{0})$
Rotational invariance	$R(\mathbf {\hat {n}} ,\theta )$	$\mathbf {r} \rightarrow R(\mathbf {\hat {n}} ,\theta )\mathbf {r}$	$\mathbf {p} \rightarrow R(\mathbf {\hat {n}} ,\theta )\mathbf {p}$
Galilean transformations	$G(\mathbf {v} )$	$\mathbf {r} \rightarrow \mathbf {r} +\mathbf {v} t$	$\mathbf {p} \rightarrow \mathbf {p} +m\mathbf {v}$
Parity	$P$	$\mathbf {r} \rightarrow -\mathbf {r}$	$\mathbf {p} \rightarrow -\mathbf {p}$
T-symmetry	$T$	$\mathbf {r} \rightarrow \mathbf {r} (-t)$	$\mathbf {p} \rightarrow -\mathbf {p} (-t)$

जहां r ('n̂', θ) यूनिट वेक्टर 'n̂' और कोण θ द्वारा परिभाषित अक्ष के बारे में रोटेशन मैट्रिक्स है।

नथर का प्रमेय

नूथर के प्रमेय में कहा गया है कि कार्रवाई का एक निरंतर समरूपता परिवर्तन एक संरक्षण कानून से मेल खाता है, अर्थात् कार्रवाई (और इसलिए लैग्रैन्जियन) एक पैरामीटर एस द्वारा एक परिवर्तन के तहत नहीं बदलता है:

$$L[q(s,t),{\dot {q}}(s,t)]=L[q(t),{\dot {q}}(t)]$$

Lagrangian S से स्वतंत्र एक ही गति का वर्णन करता है, जो लंबाई, रोटेशन का कोण, या समय हो सकता है।क्यू के लिए संबंधित मोमेंट का संरक्षण किया जाएगा।

यह भी देखें

• लैग्रैन्जियन मैकेनिक्स
• हैमिल्टन मैकेनिक्स
• सैद्धांतिक यांत्रिकी
• शास्त्रीय यांत्रिकी
• गतिशीलता
• नज़री मेक्सानिका
• हैमिल्टन -जैकोबी समीकरण
• हैमिल्टन का सिद्धांत
• गतिकी
• कैनेटीक्स (भौतिकी)
• गैर-स्वायत्त यांत्रिकी
• Udwadia -kalaba समीकरण

संदर्भ और नोट्स

श्रेणी: गणितीय भौतिकी श्रेणी: सैद्धांतिक भौतिकी श्रेणी: गतिशील प्रणाली