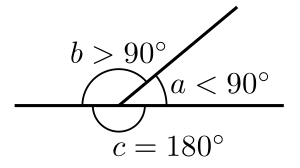ज्यामिति: Difference between revisions

Latest revision as of 22:02, 11 August 2022

Desargus 'प्रमेय का एक चित्रण, यूक्लिडियन और प्रोजेक्टिव ज्यामिति में एक परिणाम

ज्यामिती (प्राचीन ग्रीक भाषा से) भू-आकृति (भूगोल मापन) गणित की सबसे पुरानी शाखाओं में से एक है। यह अंतरिक्ष के गुणों जैसे दूरी, आकार, माप और आंकड़ों की सापेक्ष स्थिति से संबंधित हैं।^[1] ज्यामिति के क्षेत्र में काम करने वाले गणितज्ञ को भूमापी (जियोमीटर) कहा जाता है।

19 वीं शताब्दी तक, ज्यामिति लगभग विशेष रूप से यूक्लिडियन ज्यामिति (Euclidean geometry) के लिए समर्पित थी,^{[lower-alpha 1]} जिसमें मूलभूत अवधारणाओं के रूप में बिंदु, रेखा, विमान, दूरी, कोण, सतह और वक्र की धारणाएं शामिल हैं।^[2]

19 वीं शताब्दी के दौरान कई खोजों ने नाटकीय रूप से ज्यामिति के दायरे को बढ़ाया। इस तरह की सबसे पुरानी खोजों में से एक गॉस 'प्रमेमा एग्रेगियम (Gauss' Theorema Egregium ) (उल्लेखनीय प्रमेय) है जो मोटे तौर पर दावा करता है कि सतह की गाऊसी वक्रता यूक्लिडियन अंतरिक्ष में किसी भी विशिष्ट एम्बेडिंग से स्वतंत्र है। इसका तात्पर्य यह है कि सतहों का आंतरिक रूप से अध्ययन किया जा सकता है, अर्थात् स्टैंड-अलोन रिक्त स्थान के रूप में, और इसे मैनिफोल्ड्स और रीमैनियन ज्यामिति (manifolds and Riemannian geometry) के सिद्धांत में विस्तारित किया गया है।

बाद में 19 वीं शताब्दी में, यह प्रतीत हुआ कि समानांतर अभिधारणा (गैर-यूक्लिडियन ज्यामिति) को बिना किसी विरोधाभास के विकसित किया जा सकता है। सामान्य सापेक्षता को रेखांकित करने वाली गैर-यूक्लिडियन ज्यामिति एक प्रसिद्ध अनुप्रयोग है।

तब से, ज्यामिति के दायरे का बहुत विस्तार किया गया है, और इस क्षेत्र को कई उपक्षेत्रों में विभाजित किया गया है, जो अंतर्निहित तरीकों पर निर्भर करते हैं- ज्यामिति, बीजगणितीय ज्यामिति, कम्प्यूटेशनल ज्यामिति, बीजगणितीय टोपोलॉजी, असतत ज्यामिति (जिसे कॉम्बीनेटरियल ज्यामिति के रूप में भी जाना जाता है) आदि यूक्लिडियन रिक्त स्थान के गुणों पर जिनकी अवहेलना की जाती है, जो केवल बिंदुओं के संरेखण पर विचार करते हैं, लेकिन दूरी और समानांतरता पर नहीं, सममित ज्यामिति जो कोण और दूरी की अवधारणा को छोड़ देती है और परिमित ज्यामिति जो निरंतरता को छोड़ देती है।

मूल रूप से विकसित भौतिक दुनिया को मॉडल करने के लिए, ज्यामिति में लगभग सभी विज्ञानों, कला, वास्तुकला और ग्राफिक्स से संबंधित अन्य गतिविधियों में भी अनुप्रयोग हैं।^[3] ज्यामिति में गणित के उन क्षेत्रों में भी अनुप्रयोग हैं जो स्पष्ट रूप से असंबंधित हैं। उदाहरण के लिए, बीजगणितीय ज्यामिति के तरीके विल्स के फ़र्मेट के अंतिम प्रमेय के प्रमाण प्रमुख हैं, एक समस्या जो प्राथमिक अंकगणित के संदर्भ में कही गई थी, और कई शताब्दियों तक समाधान नहीं किया गया।

इतिहास

15 वीं शताब्दी में एक यूरोपीय और एक अरब प्रैक्टिस करने वाला ज्यामिति

दूसरी सहस्राब्दी ईसा पूर्व में ज्यामिति की सबसे प्रारंभिक शुरुआत प्राचीन मेसोपोटामिया और मिस्र से की जा सकती है।^[4]^[5] प्रारंभिक ज्यामिति लंबाई, कोण, क्षेत्रों और संस्करणों से संबंधित अनुभवजन्य रूप से खोजे गए सिद्धांतों का एक संग्रह था, जिन्हें सर्वेक्षण, निर्माण, खगोल विज्ञान और विभिन्न शिल्पों में कुछ व्यावहारिक आवश्यकताओं को पूरा करने के लिए विकसित किया गया था। ज्यामिति पर सबसे पहले ज्ञात ग्रंथ मिस्र के राइंड पपीरस (Egyptian Rhind Papyrus ) (2000-1800 ईसा पूर्व), मॉस्को पपीरस (Moscow Papyrus) (1890 ईसा पूर्व), बेबीलोनियन क्ले टैबलेट (Babylonian clay tablets) और प्लिम्पटन 322 (Plimpton 322) (1900 ईसा पूर्व) शामिल हैं। उदाहरण के लिए, मॉस्को पेपिरस एक काटे गए पिरामिड के आयतन की गणना के लिए एक सूत्र देता है।Cite error: Invalid <ref> tag; invalid names, e.g. too many बाद में मिट्टी की गोलियां (350-50 ईसा पूर्व) यह प्रदर्शित करती हैं कि बेबीलोन के खगोलविदों ने समय-वेग के अंतरिक्ष के भीतर बृहस्पति की स्थिति और गति की गणना के लिए समलम्बाकार (trapezoid) प्रक्रियाओं को लागू किया। इन ज्यामितीय प्रक्रियाओं ने ने 14 शताब्दियों तक औसत गति प्रमेय सहित ऑक्सफोर्ड कैलकुलेटर का अनुमान लगाया था।^[6] मिस्र के दक्षिण में प्राचीन नूबियों ने सूर्य घड़ियों के शुरुआती संस्करणों सहित ज्यामिति की एक प्रणाली की स्थापना की।^[7]^[8]

7 वीं शताब्दी ईसा पूर्व में, मिलिटस के ग्रीक गणितज्ञ थेल्स ने पिरामिडों की ऊंचाई और किनारे से जहाजों की दूरी की गणना जैसी समस्याओं को हल करने के लिए ज्यामिति का उपयोग किया। उन्हें थेल्स के प्रमेय के चार उपफलों की व्युत्पत्ति करके, ज्यामिति पर लागू निगमनात्मक तर्क के पहले उपयोग का श्रेय दिया जाता है। पाइथागोरस ने पाइथागोरियन स्कूल की स्थापना की, जिसे पाइथागोरियन प्रमेय के पहले प्रमाण का श्रेय दिया जाता है,^[9] हालांकि प्रमेय के कथन का एक लंबा इतिहास है।^[10]^[11] यूडोक्सस (Eudoxus) (408-c) 355 ईसा पूर्व ने निकास की विधि विकसित की, जिसने क्यूविलिनियर आकृतियों के क्षेत्रों और संस्करणों की गणना की,^[12] साथ ही अनुपातों का एक सिद्धांत जो असंगत परिमाणों की समस्या से बचता था, जिसने बाद के जियोमेटरों को महत्वपूर्ण प्रगति करने में सक्षम बनाया। लगभग 300 ईसा पूर्व, यूक्लिड द्वारा ज्यामिति में क्रांति ला दी गई थी, जिसके तत्वों को व्यापक रूप से अब तक की सबसे सफल और प्रभावशाली पाठ्यपुस्तक माना जाता है,^[13] स्वयंसिद्ध विधि के माध्यम से गणितीय कठोरता का परिचय दिया और आज भी गणित में उपयोग किए जाने वाले प्रारूप का सबसे पहला उदाहरण है, जो कि परिभाषा, स्वयंसिद्ध, प्रमेय और प्रमाण है। यद्यपि तत्वों की अधिकांश सामग्री पहले से ही ज्ञात थी, यूक्लिड ने उन्हें एक सुसंगत तार्किक ढांचे में व्यवस्थित किया।Cite error: Invalid <ref> tag; invalid names, e.g. too many पश्चिम के सभी शिक्षित लोगों को 20वीं शताब्दी के मध्य तक तत्व ज्ञात थे और इसकी सामग्री आज भी ज्यामिति कक्षाओं में सिखाई जाती है।^[14] सिरैक्यूज़ के आर्किमिडीज़ (c 287-212 ईसा पूर्व) ने एक अनंत श्रृंखला के योग के साथ एक परवलय के चाप के तहत क्षेत्र की गणना करने के लिए निकास की विधि का उपयोग किया, और पीआई (pi) के उल्लेखनीय सटीक अनुमान दिए।^[15] उन्होंने अपने नाम वाले सर्पिल का भी अध्ययन किया और क्रांति की सतहों के संस्करणों के लिए सूत्र प्राप्त किए।

भारतीय गणितज्ञों ने भी ज्यामिति में कई महत्वपूर्ण योगदान दिया। सतापथ ब्राह्मण (तीसरी शताब्दी ईसा पूर्व) में अनुष्ठान ज्यामितीय निर्माणों के नियम शामिल हैं जो सुलबा सूत्र के समान हैं।^[16] (हयाशी 2005, पृष्ठ 363) के अनुसार, सुल्बा सूत्रों में "दुनिया में पाइथागोरस प्रमेय की सबसे पुरानी मौजूदा मौखिक अभिव्यक्ति है, हालांकि यह पुराने बेबीलोनियों को पहले से ही ज्ञात था। उनमें पाइथागोरियन त्रिगुणों की सूची है,^[17] जो डायफेंटाइन समीकरणों के विशेष मामले हैं।^[18] बखमली पांडुलिपि (Bakhshali manuscript) में, कुछ हद तक ज्यामितीय समस्याएं हैं (अनियमित ठोस पदार्थों के संस्करणों की समस्याओं सहित)। बखमली पांडुलिपि शून्य के लिए एक डॉट के साथ दशमलव स्थान मूल्य प्रणाली भी नियुक्त करती है।^[19] आर्यभट्ट के आर्यभटीय (499) में क्षेत्रों और संस्करणों की गणना शामिल है। ब्रह्मगुप्त ने अपना खगोलीय कार्य ब्रह्म स्फुता सिद्धांत 628 में लिखा था। अध्याय 12, जिसमें 66 संस्कृत छंद को दो खंडों में विभाजित किया गया था: बुनियादी संचालन (घनमूल, अंश, भिन्न, अनुपात, और वस्तु विनिमय ) और व्यावहारिक गणित (मिश्रण, गणितीय श्रृंखला, विमान के आंकड़े, पत्थर की ईंटें, लकड़ी की सलाई और अनाज का पाइलिंग)।^[20] बाद के खंड में, उन्होंने चक्रीय चतुर्भुज के विकर्णों पर अपने प्रसिद्ध प्रमेय को बताया। बाद के खंड में, उन्होंने एक साइक्लिक चतुर्भुज के विकर्णों पर अपने प्रसिद्ध प्रमेय का उल्लेख किया। अध्याय 12 में चक्रीय चतुर्भुज के क्षेत्रफल के लिए एक सूत्र भी शामिल था (हेरॉन के सूत्र का सामान्यीकरण) , साथ ही साथ तर्कसंगत त्रिभुजों (यानी तर्कसंगत पक्षों और तर्कसंगत क्षेत्रों के साथ त्रिकोण) का एक पूर्ण विवरण भी शामिल था।^[20]

मध्ययुगीन इस्लाम में गणित ने ज्यामिति, विशेष रूप से बीजगणितीय ज्यामिति के विकास में योगदान दिया।^[21]^[22] अल-महानी (b 853) ने ज्यामितीय समस्याओं को कम करने के विचार की कल्पना की जैसे कि बीजगणित में समस्याओं के लिए क्यूब को डुप्लिकेट करना।^[23] थबिट इब्न कुर्रा (लैटिन में थैब के रूप में जाना जाता है) (836–901) ज्यामितीय मात्राओं के अनुपात में लागू अंकगणितीय संक्रियाओं के साथ पेश किया, और विश्लेषणात्मक ज्यामिति के विकास में योगदान दिया।^[24] उमर खायम (1048–1131) ने घन समीकरणों के ज्यामितीय हल खोजे।^[25] इब्न अल-हयथम (अलहाज़ेन), उमर खय्याम और नासिर अल-दीन अल-तूसी के चतुष्कोण, लैंबर्ट चतुर्भुज और सैचरी चतुर्भुज सहित, हाइपरबोलिक ज्यामिति में शुरुआती परिणाम थे, और उनके वैकल्पिक अभिधारणाओं के साथ, जैसे प्लेफेयरका स्वयंसिद्ध, इन कार्यों का विटेलो (c 12-30), गेर्सोनाइड्स (1288-1344), अल्फोंसो, जॉन वालिस, और गियोवन्नी गिरोलामो सैचेरी सहित बाद के यूरोपीय भूमापियों के बीच गैर-यूक्लिडियन ज्यामिति के विकास पर काफी प्रभाव पड़ा।^[26]

17 वीं शताब्दी की शुरुआत में, ज्यामिति में दो महत्वपूर्ण विकास हुए। पहले रेने डेसकार्टेस (René Descartes) (1596-1650) और पियरे डे फर्मेट (Pierre de Fermat) (1601-1665) द्वारा निर्देशांक और समीकरणों के साथ विश्लेषणात्मक ज्यामिति, या ज्यामिति का निर्माण हुआ था।^[27] यह कैलकुलस के विकास और भौतिकी के सटीक मात्रात्मक विज्ञान के लिए एक आवश्यक अग्रदूत था।^[28] इस अवधि का दूसरा ज्यामितीय विकास गिरार्ड देसार्गस (1591-1661) द्वारा प्रोजेक्टिव ज्यामिति का व्यवस्थित अध्ययन था।^[29] प्रोजेक्टिव ज्यामिति आकृतियों के गुणों का अध्ययन करता है जो अनुमानों और वर्गों के तहत अपरिवर्तित होते हैं, विशेष रूप से जब वे कलात्मक परिप्रेक्ष्य से संबंधित होते हैं।^[30]

19 वीं शताब्दी में ज्यामिति में दो घटनाक्रमों ने उस तरीके को बदल दिया जिस तरह से पहले अध्ययन किया गया था।^[31] ये निकोलाई इवानोविच लोबाचेवस्की, जानोस बोल्याई और कार्ल फ्रेडरिक गॉस द्वारा गैर-यूक्लिडियन ज्यामिति की खोज और फेलिक्स क्लेन के एर्लांगेन कार्यक्रम में केंद्रीय विचार के रूप में समरूपता के निर्माण की खोज थी। उस समय के दो मास्टर जियोमेटर बर्नहार्ड रीमैन (1826-1866) थे, जो मुख्य रूप से गणितीय विश्लेषण से उपकरणों के साथ काम कर रहे थे, रीमैन सतह का परिचय देते थे और हेनरी पोंकारे, बीजगणितीय टोपोलॉजी के संस्थापक और गतिशील प्रणालियों के ज्यामितीय सिद्धांत थे। ज्यामिति की अवधारणा में इन प्रमुख परिवर्तनों के परिणामस्वरूप, अंतरिक्ष की अवधारणा कुछ समृद्ध और विविध हो गई और सिद्धांतों की प्राकृतिक पृष्ठभूमि जटिल विश्लेषण और शास्त्रीय यांत्रिकी के रूप में भिन्न हो गई।^[32]

मुख्य अवधारणाएं

ज्यामिति में सबसे महत्वपूर्ण अवधारणाओं में से कुछ निम्नलिखित हैं।^[2]^[33]^[34]

स्वयंसिद्ध (Axioms)

यूक्लिड के समानांतर पोस्टुलेट का एक चित्रण

यूक्लिड ने अपने तत्वों में ज्यामिति के लिए एक अमूर्त दृष्टिकोण अपनाया,^[35] जो अब तक लिखी गई सबसे प्रभावशाली पुस्तकों में से एक थी। ^[36] यूक्लिड ने बिंदुओं, रेखाओं और तलों के प्राथमिक या स्व-स्पष्ट गुणों को व्यक्त करते हुए कुछ स्वयंसिद्ध या अभिधारणाएँ प्रस्तुत कीं।^[37] उन्होंने गणितीय तर्क द्वारा अन्य गुणों की कठोरता से कटौती की। ज्यामिति के लिए यूक्लिड के दृष्टिकोण की विशिष्ट विशेषता इसकी कठोरता थी, और इसे स्वयंसिद्ध या सिंथेटिक ज्यामिति के रूप में जाना जाता है।^[38] 19 वीं शताब्दी की शुरुआत में, निकोलाई इवानोविच लोबचेवस्की (1792-1856), जनोस बोलवाई (1802-1860), कार्ल फ्रेडरिक गॉस (1777-1855) और अन्य द्वारा ^[39] गैर-यूक्लिडियन ज्यामिति की खोज ने एक पुनरुद्धार का नेतृत्व किया। 20 वीं शताब्दी में, डेविड हिल्बर्ट (1862-1943) ने ज्यामिति की एक आधुनिक नींव प्रदान करने के प्रयास में स्वयंसिद्ध तर्क को नियोजित किया।^[40]

वस्तुएँ (Objects)

अंक

बिंदुओं को आमतौर पर ज्यामिति के निर्माण के लिए मूल वस्तुएं माना जाता है। यूक्लिड की परिभाषा के अनुसार, "जिसका कोई हिस्सा नहीं है",^[41] या सिंथेटिक ज्यामिति के रूप में उनके पास मौजूद गुणों से उन्हें परिभाषित किया जा सकता है। आधुनिक गणित में, उन्हें आम तौर पर अंतरिक्ष नामक एक सेट के तत्वों के स्वयंसिद्ध रूप से परिभाषित होता है।

इन आधुनिक परिभाषाओं के साथ, प्रत्येक ज्यामितीय आकृति को बिंदुओं के एक समूह के रूप में परिभाषित किया जाता है; सिंथेटिक ज्यामिति में यह मामला नहीं है, जहां एक रेखा एक और मौलिक वस्तु है जिसे उन बिंदुओं के सेट के रूप में नहीं देखा जाता है जिनसे वह गुजरती है।

हालांकि, आधुनिक ज्यामितीय हैं, जिसमें बिंदु आदिम वस्तुएं नहीं हैं, या यहां तक कि बिना बिंदुओं के भी हैं।^[42]^[43] इस तरह की सबसे पुरानी ज्यामिति में से एक व्हाइटहेड की पॉइंट-फ्री ज्यामिति है, जिसे अल्फ्रेड नॉर्थ व्हाइटहेड द्वारा 1919-1920 में तैयार किया गया था।

रेखा

यूक्लिड ने एक रेखा को चौड़ाई रहित लंबाई के रूप में वर्णित किया अपने आप में बिंदुओं के संबंध में समान रूप से स्थित है।^[41] आधुनिक गणित में, ज्यामिति की बहुतायत को देखते हुए, एक रेखा की अवधारणा ज्यामिति के वर्णन के तरीके से बारीकी से जुड़ी हुई है। उदाहरण के लिए, विश्लेषणात्मक ज्यामिति में, समतल में एक रेखा को अक्सर उन बिंदुओं के समुच्चय के रूप में परिभाषित किया जाता है, जिनके निर्देशांक किसी दिए गए रैखिक समीकरण को संतुष्ट करते हैं,^[44] लेकिन अधिकतर स्थान में, जैसे कि घटना ज्यामिति, रेखा एक स्वतंत्र वस्तु हो सकती है, जो बिंदुओं के सेट से अलग होती है।^[45] अंतर ज्यामिति में, एक जियोडेसिक (geodesic) एक लाइन से लेकर घुमावदार स्पेस तक की धारणा का एक सामान्यीकरण है।^[46]

समतल

यूक्लिडियन ज्यामिति में एक समतल, दो-आयामी सतह है जो असीम रूप से फैली हुई है;^[41] अन्य प्रकार के ज्यामितीयों के लिए परिभाषाएँ उसी का सामान्यीकरण हैं। ज्यामिति के कई क्षेत्रों में समतल का उपयोग किया जाता है। उदाहरण के लिए, समतल को दूरियों या कोणों के संदर्भ के बिना एक टोपोलॉजिकल सतह के रूप में अध्ययन किया जा सकता है;^[47] जहां समरैखिकता और अनुपात का अध्ययन किया जा सकता है, लेकिन दूरियों का अध्ययन नहीं किया जा सकता है।^[48] इसी तरह जटिल विश्लेषण की तकनीकों का उपयोग करके जटिल समतल के रूप में अध्ययन किया जा सकता है।^[49]

कोण

यूक्लिड एक समतल कोण को एक दूसरे के प्रति झुकाव के रूप में परिभाषित करता है, एक समतल में दो रेखाएं जो एक दूसरे से मिलती हैं, और एक दूसरे के संबंध में सीधी नहीं होती हैं।^[41] आधुनिक शब्दों में, एक कोण दो किरणों द्वारा बनाई गई आकृति है, जिसे कोण की भुजाएँ कहा जाता है, एक सामान्य अंतबिंदु साझा करते हैं, जिसे कोण का शीर्ष कहा जाता है।^[50]

तीव्र (ए), ओब्यूस (बी), और सीधे (सी) कोण।तीव्र और obtuse कोणों को तिरछे कोणों के रूप में भी जाना जाता है।

यूक्लिडियन ज्यामिति में, कोणों का उपयोग बहुभुज और त्रिकोणों का अध्ययन करने के साथ ही साथ अपने स्वयं में अध्ययन का एक उद्देश्य बनाने के लिए भी किया जाता है।^[41]एक त्रिभुज के कोणों का अध्ययन या एक इकाई वृत्त में कोणों के अध्ययन से त्रिकोणमिति का आधार बनाता है।^[51]

अंतर ज्यामिति और कैलकुलस में, समतल वक्र और दूरी वक्र या सतहों के बीच के कोणों की गणना व्युत्पन्न का उपयोग करके की जा सकती है।^[52]^[53]

वक्र

वक्र 1- आयामी वस्तु है जो सीधा हो सकता है (एक रेखा की तरह) या नहीं; 2- आयामी स्थान में वक्र को समतल वक्र कहा जाता है और 3- आयामी स्थान में वक्रों को स्थान वक्र कहा कहा जाता है।^[54]

टोपोलॉजी में, एक वक्र को वास्तविक संख्याओं के अंतराल से दूसरे स्थान पर एक फ़ंक्शन द्वारा परिभाषित किया जाता है।^[47] अंतर ज्यामिति में, एक ही परिभाषा का उपयोग किया जाता है, लेकिन परिभाषित फ़ंक्शन को अलग -अलग होना आवश्यक है ^[55] बीजीय ज्यामिति बीजीय वक्रों का अध्ययन करती है, जिन्हें एक आयाम की बीजीय किस्मों के रूप में परिभाषित किया जाता है।^[56]

सतहों

एक गोला एक सतह है जिसे पैरामीट्रिक रूप से परिभाषित किया जा सकता है (द्वारा) x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ) या निहित रूप से (द्वारा) x² + y² + z² − r² = 0।)

सतह एक द्वि-आयामी वस्तु है, जैसे कि एक गोला या पराबोलॉइड।^[57] अंतर ज्यामिति^[55] और टोपोलॉजी में,^[47]सतहों को दो-आयामी 'पैच' द्वारा वर्णित किया जाता है जो क्रमशः डिफोमोर्फिज्म या होमोमोर्फिज्म द्वारा इकट्ठे होते हैं। बीजगणितीय ज्यामिति में, सतहों को बहुपद समीकरणों द्वारा वर्णित किया जाता है।^[56]

बहुविध

अनेक वक्र और सतह की अवधारणाओं का एक सामान्यीकरण है। टोपोलॉजी में, बहुविध टोपोलॉजिकल स्पेस है जहां हर बिंदु का एक पड़ोस होता है जो यूक्लिडियन स्पेस के लिए होमोमोर्फिक होता है।^[47] अंतर ज्यामिति में, एक विभेदनीय बहुविध ऐसा स्थान है जहां प्रत्येक पड़ोस यूक्लिडियन अंतरिक्ष के लिए अलग है।^[55]

सामान्य सापेक्षता और स्ट्रिंग सिद्धांत सहित भौतिकी में बहुविध का व्यापक रूप से उपयोग किया जाता है।^[58]

लंबाई, क्षेत्र, और मात्रा

लंबाई, क्षेत्रफल और मात्रा क्रमशः एक आयाम, दो आयाम और तीन आयामों में किसी वस्तु के आकार या विस्तार का वर्णन करते हैं।^[59]

यूक्लिडियन ज्यामिति और विश्लेषणात्मक ज्यामिति में, एक लाइन सेगमेंट की लंबाई की गणना अक्सर पाइथागोरियन प्रमेय द्वारा की जा सकती है।^[60]

क्षेत्रफल और आयतन को लंबाई से अलग मूल मात्रा के रूप में परिभाषित किया जा सकता है, या उन्हें समतल या आयामी स्थान में लंबाई के रूप में वर्णित और गणना की जा सकती है।^[59] गणितज्ञों ने क्षेत्रफल और विभिन्न ज्यामितीय वस्तुओं के आयतन के लिए कई सूत्र खोजे हैं। कैलकुलस में, क्षेत्रफल और आयतन को पूर्ण रूप में परिभाषित किया जा सकता है, जैसे कि रीमैन इंटीग्रल ^[61] या लेब्सोग इंटीग्रल।^[62]

मापीय और उपाय

पाइथागोरियन प्रमेय की विज़ुअल चेकिंग (3, 4, 5) त्रिभुज के लिए, जैसा कि झोउबी सुआजिंग में 500-200 & nbsp; bc।पाइथागोरियन प्रमेय यूक्लिडियन मीट्रिक का एक परिणाम है।

लंबाई या दूरी की अवधारणा को सामान्यीकृत किया जा सकता है, जिससे मापीय का विचार सामने आता है।^[63] उदाहरण के लिए, यूक्लिडियन मापीय यूक्लिडियन समतल में बिंदुओं के बीच की दूरी को मापता है, जबकि हाइपरबोलिक मापीय हाइपरबोलिक समतल में दूरी को मापता है। मापीय के अन्य महत्वपूर्ण उदाहरणों में विशेष सापेक्षता के लोरेंत्ज़ मापीय और सामान्य सापेक्षता के अर्ध-रीमैनियन मापीय शामिल हैं।^[64]

एक अलग दिशा में, लंबाई,क्षेत्रफल और आयतन की अवधारणाओं को माप सिद्धांत द्वारा विस्तारित किया जाता है, जो सेट को आकार या माप निर्दिष्ट करने के तरीकों का अध्ययन करता है, जहां उपाय शास्त्रीय क्षेत्र और मात्रा के समान नियमों का पालन करते हैं।^[65]

अनुरूपता और समानता

जब दो आकारों की एक जैसी विशेषताएँ होती हैं, तब अनुरूपता और समानता की अवधारणाएं होती हैं।^[66] यूक्लिडियन ज्यामिति में, समानता का उपयोग उन वस्तुओं का वर्णन करने के लिए किया जाता है जिनके आकार समान होते है, जबकि अनुरूपता का उपयोग उन वस्तुओं का वर्णन करने के लिए किया जाता है जिनके आकार और रूप दोनों समान होते हैं।^[67] हिल्बर्ट ने ज्यामिति के लिए अधिक कठोर आधार तैयार करने के अपने काम में, अनुरूपता को एक अपरिभाषित शब्द के रूप में माना, जिसके गुण स्वयंसिद्धों द्वारा परिभाषित किए गए हैं।

अनुरूपता और समानता को परिवर्तन ज्यामिति में सामान्यीकृत किया जाता है, जो विभिन्न प्रकार के परिवर्तनों द्वारा संरक्षित ज्यामितीय वस्तुओं के गुणों का अध्ययन करता है।^[68]

परिध् और किनारे बनाना

शास्त्रीय ज्यामिति ने ज्यामितीय वस्तुओं के निर्माण पर विशेष ध्यान दिया, जिन्हें किसी अन्य तरीके से वर्णित किया गया था। शास्त्रीय रूप से, अधिकांश ज्यामितीय निर्माणों में उपयोग किए जाने वाले एकमात्र उपकरण परिध् और किनारे हैं।^{[lower-alpha 2]} इसके अलावा, प्रत्येक निर्माण को चरणों की एक सीमित संख्या में पूरा करना था। हालांकि, कुछ समस्याएं अकेले इन माध्यमों से हल करना मुश्किल या असंभव साबित हुईं, और नेसिस, अनुवृत्त और अन्य कर्व, या यांत्रिक उपकरणों का उपयोग करके सरल निर्माण किया गया।

आयाम

कोच स्नोफ्लेक, फ्रैक्टल आयाम के साथ = log4/log3 और टोपोलॉजिकल आयाम = 1

जहां पारंपरिक ज्यामिति ने आयाम 1 (एक रेखा), 2 (एक समतल) और 3 (हमारी परिवेश की दुनिया की कल्पना त्रि-आयामी स्थान के रूप में माना जाता है), गणितज्ञों और भौतिकविदों ने लगभग दो शताब्दियों के लिए उच्च आयामों का उपयोग किया है।^[69] उच्च आयामों के लिए एक गणितीय उपयोग का एक उदाहरण एक भौतिक प्रणाली का समाकृति स्थान है, जिसमें सिस्टम की स्वतंत्रता की डिग्री के बराबर आयाम है। उदाहरण के लिए, एक स्क्रू की समाकृति का वर्णन पांच निर्देशांक द्वारा किया जा सकता है।^[70]

सामान्य टोपोलॉजी में, आयाम की अवधारणा को प्राकृतिक संख्याओं से, अनंत आयाम (हिल्बर्ट स्पेस, उदाहरण के लिए) और घनात्मक वास्तविक संख्या (आंशिक ज्यामिति में) तक विस्तारित किया गया है।^[71] बीजगणितीय ज्यामिति में, एक बीजीय विविधता के आयाम को स्पष्ट रूप से विभिन्न परिभाषाएं प्राप्त हुई हैं, जो सभी सामान्य मामलों में समान हैं।^[72]

समरूपता

हाइपरबोलिक समतल की टाइलिंग

ज्यामिति में समरूपता का विषय लगभग उतना ही पुराना है जितना कि ज्यामिति का विज्ञान।^[73] वृत्त, नियमित बहुभुज और प्लेटोनिक ठोस जैसी सममित आकृतिया कई प्राचीन दार्शनिकों के लिए बहुत महत्वपूर्ण थी^[74] और यूक्लिड के समय से पहले विस्तार से जांच की गई।^[37] सममित पैटर्न प्रकृति में होते हैं और लियोनार्डो दा विंची, एम.सी. एस्चर और अन्य के ग्राफिक्स सहित कई रूपों में कलात्मक रूप से प्रस्तुत किए गए थे।^[75] 19 वीं शताब्दी के उत्तरार्ध में, समरूपता और ज्यामिति के बीच संबंध जांच के दायरे में आया। फेलिक्स क्लेन के एर्लांगेन कार्यक्रम ने बहुत ही सटीक अर्थ में घोषणा की कि, समरूपता, एक परिवर्तन समूह की धारणा के माध्यम से निर्धारित करता है कि ज्यामिति क्या है।^[76] शास्त्रीय यूक्लिडियन ज्यामिति में समरूपता को सर्वांगसमता और कठोर गतियों द्वारा दर्शाया जाता है, जबकि प्रोजेक्टर ज्यामिति में एक अनुरूप भूमिका निभाई जाती है, जो सीधी रेखाओं को सीधी रेखाओं में ले जाती है।^[77] हालांकि, बोल्याई और लोबाचेव्स्की, रीमैन, क्लिफोर्ड, क्लेन और सोफस लाई की नई ज्यामिति में ही क्लेन के विचार को इसकी समरूपता समूह के माध्यम से ज्यामिति को परिभाषित करने की प्रेरणा मिली।^[78] पूर्व में टोपोलॉजी और ज्यामितीय समूह सिद्धांत, लाई थ्योरी और रीमैनियन ज्यामिति में,^[79]^[80] असतत और निरंतर समरूपता दोनों प्रमुख भूमिका निभाते हैं।^[81]^[82]

एक अलग प्रकार की समरूपता अन्य क्षेत्रों के बीच प्रोजेक्टिव ज्यामिति में द्वंद्व का सिद्धांत है। इस मेटा-घटना को मोटे तौर पर निम्नानुसार वर्णित किया जा सकता है: किसी भी प्रमेय में, समतल के साथ विनिमय बिंदु, मिलान के साथ निहित होता हैं, और परिणाम एक समान रूप से सही प्रमेय है।^[83] एक सदिश स्थान और उसके दोहरे स्थान के बीच द्वंद्व एक समान और निकटता से संबंधित रूप मौजूद है।^[84]

समकालीन ज्यामिति

यूक्लिडियन ज्यामिति

यूक्लिडियन ज्यामिति अपने शास्त्रीय अर्थों में ज्यामिति है।^[85] जैसा कि यह भौतिक दुनिया के स्थान को मॉडल करता है, इसका उपयोग कई वैज्ञानिक क्षेत्रों में किया जाता है, जैसे कि यांत्रिकी, खगोल विज्ञान, क्रिस्टलोग्राफी,^[86] और कई तकनीकी क्षेत्र, जैसे इंजीनियरिंग,^[87] वास्तुकला,^[88] भूगणित, ^[89] वायुगतिकी और नेविगेशन। अधिकांश राष्ट्रों के अनिवार्य शैक्षिक पाठ्यक्रम में अंक, रेखाएँ, समतल, कोण, त्रिकोण, सर्वांगसमता, समानता, ठोस आंकड़े, वृत्त और विश्लेषणात्मक ज्यामिति जैसी यूक्लिडियन अवधारणाओं का अध्ययन शामिल है।

अंतर ज्यामिति

अंतर ज्यामिति वक्रता से जुड़ी समस्याओं का अध्ययन करने के लिए पथरी से उपकरणों का उपयोग करती है।

अंतर ज्यामिति में समस्याओं का अध्ययन करने के लिए कैलकुलस और रैखिक बीजगणित की तकनीकों का उपयोग करती है।^[90] इसके पास भौतिक,^[91] अर्थमिति,^[92] और जैव सूचना विज्ञान,^[93] में अनुप्रयोग हैं।

विशेष रूप से, अल्बर्ट आइंस्टीन के सामान्य सापेक्षता की धारणा के कारण अंतर ज्यामिति गणितीय भौतिकी के लिए महत्वपूर्ण है कि ब्रह्मांड वक्र है।^[94] अंतर ज्यामिति या तो आंतरिक हो सकती है (जिसका अर्थ है कि रिक्त स्थान यह मानते हैं कि वे चिकनी कई गुना हैं जिनकी ज्यामितीय संरचना एक रीमैनियन मीट्रिक द्वारा शासित है, जो यह निर्धारित करती है कि प्रत्येक बिंदु के पास दूरी कैसे मापा जाता है) या बाहरी ( जहां अध्ययन के तहत वस्तु परिवेशी फ्लैट यूक्लिडियन स्पेस का हिस्सा है)।^[95]

गैर-यूक्लिडियन ज्यामिति

यूक्लिडियन ज्यामिति अध्ययन किए गए ज्यामिति का एकमात्र ऐतिहासिक रूप नहीं था। गोलाकार ज्यामिति का उपयोग लंबे समय से खगोलविदों, ज्योतिषियों और नाविकों द्वारा किया गया है।^[96]

इमैनुएल कांत ने तर्क दिया कि केवल निरपेक्ष ज्यामिति है, जिसे मन के एक आंतरिक संकाय द्वारा एक प्राथमिकता के रूप में जाना जाता है: यूक्लिडियन ज्यामिति कृत्रिम थी।^[97] इस विचार को शुरू में सैकेरी जैसे विचारकों ने कुछ हद तक चुनौती दी थी, फिर बोलवाई, लोबचेवस्की और गॉस (जिन्होंने अपने सिद्धांत को प्रकाशित नहीं किया) के कार्यों में गैर-यूक्लिडियन ज्यामिति की क्रांतिकारी खोज से उलट दिया।^[98] उन्होंने प्रदर्शित किया कि सामान्य यूक्लिडियन स्थान ज्यामिति के विकास के लिए केवल एक संभावना है। ज्यामिति के विषय की एक व्यापक दृष्टि तब रीमैन ने अपने 1867 के उद्घाटन व्याख्यान में व्यक्त की गई थी, डाई हाइपोथेसन, वेलचे डेर जियोमेट्री ज़ू ग्रुंडे लीजेन (जिस परिकल्पना पर ज्यामिति आधारित है),^[99] उनकी मृत्यु के बाद ही प्रकाशित हुआ। अल्बर्ट आइंस्टीन के सामान्य सापेक्षता सिद्धांत में रिमैन का नया विचार महत्वपूर्ण साबित हुआ। रीमैनियन ज्यामिति, जो बहुत सामान्य स्थानों पर विचार करती है जिसमें लंबाई की धारणा को परिभाषित किया गया है, आधुनिक ज्यामिति का एक मुख्य आधार है।^[78]

टोपोलॉजी

ट्रेफिल गाँठ का एक मोटा होना

टोपोलॉजी निरंतर मानचित्रण के गुणों से संबंधित क्षेत्र है,^[100] और इसे यूक्लिडियन ज्यामिति का सामान्यीकरण माना जा सकता है।^[101] अभ्यास में, टोपोलॉजी का अर्थ रिक्त स्थान के बड़े पैमाने पर गुणों जैसे कि जुड़ाव और ठोसपन से निपटना होता है।^[47]

टोपोलॉजी का क्षेत्र, जिसने 20 वीं शताब्दी में बड़े पैमाने पर विकास देखा, एक तकनीकी अर्थ में एक प्रकार का परिवर्तन ज्यामिति है, जिसमें परिवर्तन होमोमोर्फिज्म हैं।^[102] इसे अक्सर 'टोपोलॉजी रबर-शीट ज्योमेट्री है' कहावत के रूप में व्यक्त किया गया है। टोपोलॉजी के उपक्षेत्रों में ज्यामितीय टोपोलॉजी, अंतर टोपोलॉजी, बीजगणितीय टोपोलॉजी और सामान्य टोपोलॉजी शामिल हैं।^[103]

बीजीय ज्यामिति

कुइंतिन - टोडा थ्री फोल्ड

बीजीय ज्यामिति का क्षेत्र निर्देशांकों की कार्तीय ज्यामिति से विकसित हुआ।^[104] यह अन्य विषयों के अलावा प्रक्षेपी ज्यामिति, बायरेशनल ज्योमेट्री, बीजीय किस्मों, और क्रमविनिमेय बीजगणित के निर्माण और अध्ययन के साथ-साथ विकास की आवधिक अवधियों से गुजरा।^[105] 1950 के दशक के उत्तरार्ध से 1970 के दशक के मध्य तक जीन-पियरे सेरे और अलेक्जेंडर ग्रोथेंडिक के काम के कारण इसमें आधारभूत विकास हुआ।^[105] इसके कारण योजनाओं की शुरुआत हुई और विभिन्न सह-विज्ञान सिद्धांतों सहित टोपोलॉजिकल तरीकों पर अधिक जोर दिया गया। सात मिलेनियम पुरस्कार समस्याओं में से एक, हॉज अनुमान, बीजगणितीय ज्यामिति में एक सवाल है।^[106] फर्मेट के अंतिम प्रमेय के विल्स का प्रमाण संख्या सिद्धांत की एक लंबे समय से चली आ रही समस्या को हल करने के लिए बीजगणितीय ज्यामिति के उन्नत तरीकों का उपयोग करता है।

सामान्य तौर पर, बीजगणितीय ज्यामिति बहुभिन्नरूपी बहुपदों जैसे क्रमपरिवर्तनीय बीजगणित में अवधारणाओं के उपयोग के माध्यम से ज्यामिति का अध्ययन करती है।।^[107] इसमें क्रिप्टोग्राफी ^[108] और स्ट्रिंग सिद्धांत सहित कई क्षेत्रों में आवेदन हैं।^[109]

जटिल ज्यामिति

जटिल ज्यामिति समतल पर निर्मित या उससे उत्पन्न ज्यामितीय संरचनाओं की प्रकृति का अध्ययन करती है।^[110]^[111]^[112] जटिल ज्यामिति अवकल ज्यामिति, बीजगणितीय ज्यामिति और कई जटिल चर के विश्लेषण के प्रतिच्छेदन पर स्थित है, और स्ट्रिंग सिद्धांत और दर्पण समरूपता के लिए अनुप्रयोगों को पाया गया हैं।^[113]

जटिल ज्यामिति पहली बार रीमैन सतहों के अध्ययन और बर्नहार्ड रीमैन के काम में अध्ययन को एक अलग क्षेत्र के रूप में देखा।^[114]^[115]^[116] 1900 के दशक की शुरुआत में इटैलियन स्कूल ऑफ बीजीब्रेक ने ज्यामिति द्वारा रीमैन की भावना में काम किया गया था। जटिल ज्यामिति का समकालीन निरूपण जीन-पियरे सेरे के काम के साथ शुरू हुआ, जिन्होंने इस विषय के लिए शीशों की अवधारणा को पेश किया, जटिल ज्यामिति और बीजगणितीय ज्यामिति के बीच संबंधों को प्रकाशित किया।^[117]^[118] जटिल ज्यामिति में अध्ययन की प्राथमिक वस्तुएं जटिल बहुविध, जटिल बीजीय किस्में, जटिल विश्लेषणात्मक किस्में, और इन स्थानों पर होलोमोर्फिक वेक्टर बंडलों और सुसंगत पुलिंदा हैं। जटिल ज्यामिति में अध्ययन किए गए रिक्त स्थान के विशेष उदाहरणों में रिमैन सतहों और कैलाबी -यौ मैनिफोल्ड्स शामिल हैं और इन स्थानों का उपयोग स्ट्रिंग सिद्धांत में होता है। विशेष रूप से, वर्ल्डशीट ऑफ स्ट्रिंग्स को रीमैन सतहों द्वारा मॉडलिंग की जाती है, और सुपरस्ट्रिंग सिद्धांत भविष्यवाणी करता है कि 10 आयामी स्पेसटाइम के अतिरिक्त 6 आयामों को कैलाबी -यौ द्वारा मॉडल किया जा सकता है।

असतत ज्यामिति

असतत ज्यामिति में विभिन्न क्षेत्र पैकिंग का अध्ययन शामिल है।

असतत ज्यामिति एक ऐसा विषय है जिसका उत्तल ज्यामिति के साथ घनिष्ठ संबंध है। ^[119]^[120]^[121] यह मुख्य रूप से सरल ज्यामितीय वस्तुओं जैसे बिंदुओं, रेखाओं और वृत्तों की सापेक्ष स्थिति के प्रश्नों से संबंधित है। उदाहरणों में उदाहरण में वृत्त की पैकिंग, त्रिकोणमिति, केनेसर-पुएलसेन अनुमान आदि का अध्ययन शामिल है।^[122]^[123] यह संयोजन के साथ कई तरीकों और सिद्धांतों को साझा करता है।

संगणनात्मक ज्यामिति

संगणनात्मक ज्यामिति एल्गोरिदम और ज्यामितीय वस्तुओं में हेरफेर करने के कार्यान्वयन से संबंधित है। महत्वपूर्ण समस्याओं में ऐतिहासिक रूप से यात्रा करने वाले सेल्समैन की समस्या, न्यूनतम फैले हुए पेड़, छिपी हुई लाइन हटाने और रैखिक प्रोग्रामिंग शामिल हैं।^[124]

हालांकि ज्यामिति का एक युवा क्षेत्र होने के नाते, इसमें कंप्यूटर विजन, छवि प्रसंस्करण, कंप्यूटर सहायता प्राप्त डिजाइन, मेडिकल इमेजिंग, आदि में कई अनुप्रयोग हैं।^[125]

ज्यामितीय समूह सिद्धांत

दो जनरेटर ए और बी पर मुक्त समूह का केली ग्राफ

ज्यामितीय समूह सिद्धांत बारीक रूप से उत्पन्न समूहों का अध्ययन करने के लिए बड़े पैमाने पर ज्यामितीय तकनीकों का उपयोग करता है। ^[126] यह कम-आयामी टोपोलॉजी से निकटता से जुड़ा हुआ है, जैसे कि ग्रिगोरी पेरेलमैन के ज्यामितीय अनुमान के प्रमाण में, जिसमें एक सहस्राब्दी पुरस्कार समस्या का प्रमाण शामिल था।

ज्यामितीय समूह सिद्धांत अक्सर केले ग्राफ के चारों ओर घूमता है, जो एक समूह का ज्यामितीय प्रतिनिधित्व है।अन्य महत्वपूर्ण विषयों में अर्ध-सममिति, ग्रोमोव-हाइपरबोलिक समूह,और समकोण आर्टिन समूह शामिल हैं।

उत्तल ज्यामिति

उत्तल ज्यामिति वास्तविक विश्लेषण और असतत गणित की तकनीकों का उपयोग करते हुए, यूक्लिडियन स्थान में उत्तल आकृतियों और इसके अधिक अमूर्त अनुरूपों की जांच करती है।^[127] यह उत्तल विश्लेषण, अनुकूलन, कार्यात्मक विश्लेषण और संख्या सिद्धांत में महत्वपूर्ण अनुप्रयोगों के साथ घनिष्ठ संबंध है।

उत्तल ज्यामिति प्राचीन काल की है।^[127] आर्किमिडीज़ ने उत्तलता की पहली ज्ञात सटीक परिभाषा दी। उत्तल ज्यामिति में एक आवर्ती अवधारणा, आइसोपेरिमेट्रिक समस्या का ग्रीक लोगों द्वारा भी अध्ययन किया गया था, जिसमें ज़ेनोडोरस भी शामिल है। आर्किमिडीज, प्लेटो, यूक्लिड, और बाद में केप्लर और कॉक्सेटर सभी ने उत्तल पोलीटोप्स और उनके गुणों का अध्ययन किया। 19 वीं शताब्दी से, गणितज्ञों ने उत्तल गणित के अन्य क्षेत्रों का अध्ययन किया है, जिसमें उच्च-आयामी पॉलीटोप्स, उत्तल निकायों का आयतन, सतह क्षेत्र, गाऊसी वक्रता, एल्गोरिदम, झुकाव और जाली शामिल हैं।

अनुप्रयोग

ज्यामिति में कई क्षेत्रों में अनुप्रयोग पाए हैं, जिनमें से कुछ का वर्णन नीचे किया गया है।

कला

बुउ इनानिया मद्रासा, FES, MOROCCO, Zellige मोज़ेक टाइलें जो विस्तृत ज्यामितीय tessellations बनाते हैं

गणित और कला विभिन्न तरीकों से जुड़े हुए हैं। उदाहरण के लिए, परिप्रेक्ष्य के सिद्धांत ने दिखाया कि आंकड़ों के मीट्रिक गुणों की तुलना में ज्यामिति में और भी बहुत कुछ है: परिप्रेक्ष्य प्रक्षेप्य ज्यामिति की उत्पत्ति है।^[128]

कलाकारों ने लंबे समय से डिजाइन में अनुपात की अवधारणाओं का उपयोग किया है। विट्रुवियस (Vitruvius) ने मानव आकृति के लिए आदर्श अनुपात का एक जटिल सिद्धांत विकसित किया।^[129] इन अवधारणाओं को माइकल एंजेलो के कलाकारों द्वारा आधुनिक कॉमिक बुक कलाकारों के लिए उपयोग और रूपांतरित किया गया है।^[130]

स्वर्ण अनुपात एक विशेष अनुपात है जिसकी कला में विवादास्पद भूमिका है। अक्सर लंबाई का सबसे प्रेय अनुपात होने का दावा किया जाता है, इसे अक्सर कला के प्रसिद्ध कार्यों में शामिल करने के लिए कहा जाता है, हालांकि सबसे विश्वसनीय और स्पष्ट उदाहरण इस किंवदंती से अवगत कलाकारों द्वारा जानबूझकर बनाए गए थे।^[131]

पूरे इतिहास में कला में टिलिंग्स और टेससेलेशन का उपयोग किया गया है। इस्लामिक कला ने टेससेलेशन का लगातार उपयोग किया, जैसा कि एम. सी. एस्चर (M. C. Escher) की कला ने किया था।^[132] एस्चर के काम ने अतिपरवलयिक ज्यामिति का भी उपयोग किया।

सेज़ेन (Cézanne) ने इस सिद्धांत को आगे बढ़ाया कि सभी छवियों को गोले, शंकु और सिलेंडर से बनाया जा सकता है। यह आज भी कला सिद्धांत में उपयोग किया जाता है, हालांकि आकृतियों की सटीक सूची लेखक से लेखक में भिन्न होती है।^[133]^[134]

वास्तुकला

ज्यामिति में वास्तुकला के कई अनुप्रयोग हैं। वास्तव में, यह कहा गया है कि ज्यामिति वास्तुशिल्प डिजाइन के मूल में निहित है।^[135]^[136] वास्तुकला के लिए ज्यामिति के अनुप्रयोगों में मजबूत परिप्रेक्ष्य बनाने के लिए प्रक्षेपी ज्यामिति का उपयोग,^[137] गुंबदों और समान वस्तुओं के निर्माण में शंकु वर्गों का उपयोग,^[88] टेस्टसेलेशन का उपयोग,^[88]और समरूपता का उपयोग शामिल है।^[88]

भौतिकी

खगोल विज्ञान का क्षेत्र, विशेष रूप से जब यह आकाशीय क्षेत्र पर सितारों और ग्रहों की स्थिति के मानचित्रण से संबंधित है और आकाशीय पिंडों की गति के बीच संबंध का वर्णन करता है, पूरे इतिहास में ज्यामितीय ने समस्याओं के एक महत्वपूर्ण स्रोत के रूप में कार्य किया है।^[138]

सामान्य सापेक्षता में रीमैनियन ज्यामिति (Riemannian Geometry) और कृत्रिम रीमैनियन ज्यामिति (Pseudo-Riemannian Geometry) का उपयोग किया जाता है। प्रमात्रा सूचना सिद्धांत के रूप में, स्ट्रिंग सिद्धांत ज्यामिति के कई रूपों का उपयोग करता है।

गणित के अन्य क्षेत्र

पाइथागोरस ने पाया कि एक त्रिभुज के किनारों में असंगत लंबाई हो सकती है।

कैलकुलस ज्यामिति से अत्यधिक प्रभावित था।^[27] उदाहरण के लिए, रेने डेसकार्टेस द्वारा निर्देशांक की शुरूआत और बीजगणित के समवर्ती विकास ने ज्यामिति के लिए एक नया चरण चिह्नित किया, क्योंकि ज्यामितीय आंकड़े जैसे कि समतल वक्रों को अब कार्यों, समीकरणों और विश्लेषणात्मक रूप से प्रदर्शित किए जा सकते है। 17 वीं शताब्दी में अतिसूक्ष्म कैलकुलस के उद्भव में इसने महत्वपूर्ण भूमिका निभाई। विश्लेषणात्मक ज्यामिति पूर्व-कैलकुलस और कैलकुलस पाठ्यक्रम का एक मुख्य आधार है।^[139]^[140]

अनुप्रयोग का एक अन्य महत्वपूर्ण क्षेत्र संख्या सिद्धांत है।^[141] प्राचीन ग्रीस में पाइथागोरस ने ज्यामिति में संख्याओं की भूमिका पर विचार किया। हालांकि, अतुलनीय लंबाई की खोज ने उनके दार्शनिक विचारों का खंडन किया।^[142] 19 वीं शताब्दी से, ज्यामिति का उपयोग संख्या सिद्धांत में समस्याओं को हल करने के लिए किया गया है, उदाहरण के लिए, संख्याओं की ज्यामिति के माध्यम से योजना सिद्धांत, जिसका उपयोग फर्मेट के अंतिम प्रमेय के विल्स के प्रमाण में किया जाता है।^[143]

यह भी देखें

सूची

जियोमेटरों की सूची
- श्रेणी: बीजीय जियोमेटर्स
  
  श्रेणी: विभेदक जियोमेटर्स
  
  श्रेणी: जियोमेटर्स
  
  श्रेणी: टोपोलॉजिस्ट
प्राथमिक ज्यामिति में सूत्रों की सूची
ज्यामिति विषयों की सूची
ज्यामिति में महत्वपूर्ण प्रकाशनों की सूची
गणित के विषयों की सूची

अन्य फ़ील्ड

आणविक ज्यामिति

↑ Until the 19th century, geometry was dominated by the assumption that all geometric constructions were Euclidean. In the 19th century and later, this was challenged by the development of hyperbolic geometry by Lobachevsky and other non-Euclidean geometries by Gauss and others. It was then realised that implicitly non-Euclidean geometry had appeared throughout history, including the work of Desargues in the 17th century, all the way back to the implicit use of spherical geometry to understand the Earth geodesy and to navigate the oceans since antiquity.
↑ The ancient Greeks had some constructions using other instruments.

↑ Vincenzo De Risi (2015). Mathematizing Space: The Objects of Geometry from Antiquity to the Early Modern Age. Birkhäuser. pp. 1–. ISBN 978-3-319-12102-4.
↑ ^2.0 ^2.1 Tabak, John (2014). Geometry: the language of space and form. Infobase Publishing. p. xiv. ISBN 978-0-8160-4953-0.
↑ Walter A. Meyer (2006). Geometry and Its Applications. Elsevier. ISBN 978-0-08-047803-6.
↑ J. Friberg, Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations , Historia Mathematica, 8, 1981, pp. 277–318.
↑ "Chap. IV Egyptian Mathematics and Astronomy". The Exact Sciences in Antiquity (2 ed.). last = Neugebauer. 1969 [1957]. pp. 71–96. ISBN 978-0-486-22332-2. {{cite book}}: |first= missing |last= (help); Missing pipe in: |publisher= (help).
↑ Ossendrijver, Mathieu (29 January 2016). "Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph". Science. 351 (6272): 482–484. Bibcode:2016Sci...351..482O. doi:10.1126/science.aad8085. PMID 26823423. S2CID 206644971.
↑ Depuydt, Leo (1 January 1998). "Gnomons at Meroë and Early Trigonometry". The Journal of Egyptian Archaeology. 84: 171–180. doi:10.2307/3822211. JSTOR 3822211.
↑ Slayman, Andrew (27 May 1998). "Neolithic Skywatchers". Archaeology Magazine Archive. Archived from the original on 5 June 2011. Retrieved 17 April 2011.
↑ Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0.
↑ Kurt Von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics.
↑ James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal.
↑ (Boyer 1991, The Age of Plato and Aristotle p. 92)
↑ (Boyer 1991, Euclid of Alexandria p. 119)
↑ Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0 p. 141: No work, except The Bible, has been more widely used....
↑ O'Connor, J.J.; Robertson, E.F. (February 1996). "A history of calculus". url = http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/The_rise_of_calculus.html. {{cite web}}: |access-date= requires |url= (help); |archive-url= requires |url= (help); External link in |publisher= (help); Missing or empty |url= (help); Missing pipe in: |publisher= (help)
↑ Staal, Frits (1999). "Greek and Vedic Geometry". Journal of Indian Philosophy. 27 (1–2): 105–127. doi:10.1023/A:1004364417713. S2CID 170894641.
↑ Pythagorean triples are triples of integers $(a,b,c)$ with the property: $a^{2}+b^{2}=c^{2}$ . Thus, $3^{2}+4^{2}=5^{2}$ , $8^{2}+15^{2}=17^{2}$ , $12^{2}+35^{2}=37^{2}$ etc.
↑ (Cooke 2005, p. 198): "The arithmetic content of the Śulva Sūtras consists of rules for finding Pythagorean triples such as (3, 4, 5), (5, 12, 13), (8, 15, 17), and (12, 35, 37). It is not certain what practical use these arithmetic rules had. The best conjecture is that they were part of religious ritual. A Hindu home was required to have three fires burning at three different altars. The three altars were to be of different shapes, but all three were to have the same area. These conditions led to certain "Diophantine" problems, a particular case of which is the generation of Pythagorean triples, so as to make one square integer equal to the sum of two others."
↑ (Hayashi 2005, p. 371)
↑ ^20.0 ^20.1 (Hayashi 2003, pp. 121–122)
↑ R. Rashed (1994), The development of Arabic mathematics: between arithmetic and algebra, p. 35 London
↑ (Boyer 1991, "The Arabic Hegemony" pp. 241–242) "Omar Khayyam (c. 1050–1123), the "tent-maker," wrote an Algebra that went beyond that of al-Khwarizmi to include equations of third degree. Like his Arab predecessors, Omar Khayyam provided for quadratic equations both arithmetic and geometric solutions; for general cubic equations, he believed (mistakenly, as the 16th century later showed), arithmetic solutions were impossible; hence he gave only geometric solutions. The scheme of using intersecting conics to solve cubics had been used earlier by Menaechmus, Archimedes, and Alhazan, but Omar Khayyam took the praiseworthy step of generalizing the method to cover all third-degree equations (having positive roots). .. For equations of higher degree than three, Omar Khayyam evidently did not envision similar geometric methods, for space does not contain more than three dimensions, ... One of the most fruitful contributions of Arabic eclecticism was the tendency to close the gap between numerical and geometric algebra. The decisive step in this direction came much later with Descartes, but Omar Khayyam was moving in this direction when he wrote, "Whoever thinks algebra is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and geometry are different in appearance. Algebras are geometric facts which are proved."".
↑ O'Connor, John J.; Robertson, Edmund F. "Al-Mahani". MacTutor History of Mathematics archive. University of St Andrews.
↑ O'Connor, John J.; Robertson, Edmund F. "Al-Sabi Thabit ibn Qurra al-Harrani". MacTutor History of Mathematics archive. University of St Andrews.
↑ O'Connor, John J.; Robertson, Edmund F. "Omar Khayyam". MacTutor History of Mathematics archive. University of St Andrews.
↑ Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, pp. 447–494 [470], Routledge, London and New York:
"Three scientists, Ibn al-Haytham, Khayyam, and al-Tusi, had made the most considerable contribution to this branch of geometry whose importance came to be completely recognized only in the 19th century. In essence, their propositions concerning the properties of quadrangles which they considered, assuming that some of the angles of these figures were acute of obtuse, embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between this postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investigations of their European counterparts. The first European attempt to prove the postulate on parallel lines—made by Witelo, the Polish scientists of the 13th century, while revising Ibn al-Haytham's Book of Optics (Kitab al-Manazir)—was undoubtedly prompted by Arabic sources. The proofs put forward in the 14th century by the Jewish scholar Levi ben Gerson, who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that Pseudo-Tusi's Exposition of Euclid had stimulated both J. Wallis's and G. Saccheri's studies of the theory of parallel lines."
↑ ^27.0 ^27.1 Carl B. Boyer (2012). History of Analytic Geometry. Courier Corporation. ISBN 978-0-486-15451-0.
↑ C.H. Edwards Jr. (2012). The Historical Development of the Calculus. Springer Science & Business Media. p. 95. ISBN 978-1-4612-6230-5.
↑ Judith V. Field; Jeremy Gray (2012). The Geometrical Work of Girard Desargues. Springer Science & Business Media. p. 43. ISBN 978-1-4613-8692-6.
↑ C. R. Wylie (2011). Introduction to Projective Geometry. Courier Corporation. ISBN 978-0-486-14170-1.
↑ Jeremy Gray (2011). Worlds Out of Nothing: A Course in the History of Geometry in the 19th Century. Springer Science & Business Media. ISBN 978-0-85729-060-1.
↑ Eduardo Bayro-Corrochano (2018). Geometric Algebra Applications Vol. I: Computer Vision, Graphics and Neurocomputing. Springer. p. 4. ISBN 978-3-319-74830-6.
↑ Cite error: Invalid <ref> tag; no text was provided for refs named Schmidt, W. 2002
↑ Morris Kline (1990). Mathematical Thought From Ancient to Modern Times: Volume 3. US: Oxford University Press. pp. 1010–. ISBN 978-0-19-506137-6.
↑ Victor J. Katz (2000). Using History to Teach Mathematics: An International Perspective. Cambridge University Press. pp. 45–. ISBN 978-0-88385-163-0.
↑ David Berlinski (2014). The King of Infinite Space: Euclid and His Elements. Basic Books. ISBN 978-0-465-03863-3.
↑ ^37.0 ^37.1 Robin Hartshorne (2013). Geometry: Euclid and Beyond. Springer Science & Business Media. pp. 29–. ISBN 978-0-387-22676-7.
↑ Pat Herbst; Taro Fujita; Stefan Halverscheid; Michael Weiss (2017). The Learning and Teaching of Geometry in Secondary Schools: A Modeling Perspective. Taylor & Francis. pp. 20–. ISBN 978-1-351-97353-3.
↑ I.M. Yaglom (2012). A Simple Non-Euclidean Geometry and Its Physical Basis: An Elementary Account of Galilean Geometry and the Galilean Principle of Relativity. Springer Science & Business Media. pp. 6–. ISBN 978-1-4612-6135-3.
↑ Audun Holme (2010). Geometry: Our Cultural Heritage. Springer Science & Business Media. pp. 254–. ISBN 978-3-642-14441-7.
↑ ^41.0 ^41.1 ^41.2 ^41.3 ^41.4 Euclid's Elements – All thirteen books in one volume, Based on Heath's translation, Green Lion Press ISBN 1-888009-18-7.
↑ Gerla, G. (1995). "Pointless Geometries" (PDF). In Buekenhout, F.; Kantor, W. (eds.). Handbook of incidence geometry: buildings and foundations. North-Holland. pp. 1015–1031. Archived from the original (PDF) on 17 July 2011.
↑ Clark, Bowman L. (Jan 1985). "Individuals and Points". Notre Dame Journal of Formal Logic. 26 (1): 61–75. doi:10.1305/ndjfl/1093870761.
↑ John Casey (1885). Analytic Geometry of the Point, Line, Circle, and Conic Sections.
↑ Buekenhout, Francis (1995), Handbook of Incidence Geometry: Buildings and Foundations, Elsevier B.V.
↑ "geodesic – definition of geodesic in English from the Oxford dictionary". OxfordDictionaries.com. Archived from the original on 15 July 2016. Retrieved 2016-01-20.
↑ ^47.0 ^47.1 ^47.2 ^47.3 ^47.4 Munkres, James R. Topology. Vol. 2. Upper Saddle River: Prentice Hall, 2000.
↑ Szmielew, Wanda. From affine to Euclidean geometry: An axiomatic approach. Springer, 1983.
↑ Ahlfors, Lars V. Complex analysis: an introduction to the theory of analytic functions of one complex variable. New York; London (1953).
↑ Sidorov, L.A. (2001) [1994]. "Angle". Encyclopedia of Mathematics. EMS Press.
↑ Gelʹfand, Izrailʹ Moiseevič, and Mark Saul. "Trigonometry." Trigonometry. Birkhäuser Boston, 2001. 1–20.
↑ Stewart, James (2012). Calculus: Early Transcendentals, 7th ed., Brooks Cole Cengage Learning. ISBN 978-0-538-49790-9
↑ Jost, Jürgen (2002). Riemannian Geometry and Geometric Analysis. Berlin: Springer-Verlag. ISBN 978-3-540-42627-1..
↑ Baker, Henry Frederick. Principles of geometry. Vol. 2. CUP Archive, 1954.
↑ ^55.0 ^55.1 ^55.2 Do Carmo, Manfredo Perdigao, and Manfredo Perdigao Do Carmo. Differential geometry of curves and surfaces. Vol. 2. Englewood Cliffs: Prentice-hall, 1976.
↑ ^56.0 ^56.1 Mumford, David (1999). The Red Book of Varieties and Schemes Includes the Michigan Lectures on Curves and Their Jacobians (2nd ed.). Springer-Verlag. ISBN 978-3-540-63293-1. Zbl 0945.14001.
↑ Briggs, William L., and Lyle Cochran Calculus. "Early Transcendentals." ISBN 978-0-321-57056-7.
↑ Yau, Shing-Tung; Nadis, Steve (2010). The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions. Basic Books. ISBN 978-0-465-02023-2.
↑ ^59.0 ^59.1 Steven A. Treese (2018). History and Measurement of the Base and Derived Units. Springer International Publishing. pp. 101–. ISBN 978-3-319-77577-7.
↑ James W. Cannon (2017). Geometry of Lengths, Areas, and Volumes. American Mathematical Soc. p. 11. ISBN 978-1-4704-3714-5.
↑ Gilbert Strang (1991). Calculus. SIAM. ISBN 978-0-9614088-2-4.
↑ H. S. Bear (2002). A Primer of Lebesgue Integration. Academic Press. ISBN 978-0-12-083971-1.
↑ Dmitri Burago, Yu D Burago, Sergei Ivanov, A Course in Metric Geometry, American Mathematical Society, 2001, ISBN 0-8218-2129-6.
↑ Wald, Robert M. (1984). General Relativity. University of Chicago Press. ISBN 978-0-226-87033-5.
↑ Terence Tao (2011). An Introduction to Measure Theory. American Mathematical Soc. ISBN 978-0-8218-6919-2.
↑ Shlomo Libeskind (2008). Euclidean and Transformational Geometry: A Deductive Inquiry. Jones & Bartlett Learning. p. 255. ISBN 978-0-7637-4366-6.
↑ Mark A. Freitag (2013). Mathematics for Elementary School Teachers: A Process Approach. Cengage Learning. p. 614. ISBN 978-0-618-61008-2.
↑ George E. Martin (2012). Transformation Geometry: An Introduction to Symmetry. Springer Science & Business Media. ISBN 978-1-4612-5680-9.
↑ Mark Blacklock (2018). The Emergence of the Fourth Dimension: Higher Spatial Thinking in the Fin de Siècle. Oxford University Press. ISBN 978-0-19-875548-7.
↑ Charles Jasper Joly (1895). Papers. The Academy. pp. 62–.
↑ Roger Temam (2013). Infinite-Dimensional Dynamical Systems in Mechanics and Physics. Springer Science & Business Media. p. 367. ISBN 978-1-4612-0645-3.
↑ Bill Jacob; Tsit-Yuen Lam (1994). Recent Advances in Real Algebraic Geometry and Quadratic Forms: Proceedings of the RAGSQUAD Year, Berkeley, 1990–1991. American Mathematical Soc. p. 111. ISBN 978-0-8218-5154-8.
↑ Ian Stewart (2008). Why Beauty Is Truth: A History of Symmetry. Basic Books. p. 14. ISBN 978-0-465-08237-7.
↑ Stakhov Alexey (2009). Mathematics Of Harmony: From Euclid To Contemporary Mathematics And Computer Science. World Scientific. p. 144. ISBN 978-981-4472-57-9.
↑ Werner Hahn (1998). Symmetry as a Developmental Principle in Nature and Art. World Scientific. ISBN 978-981-02-2363-2.
↑ Brian J. Cantwell (2002). Introduction to Symmetry Analysis. Cambridge University Press. p. 34. ISBN 978-1-139-43171-2.
↑ B. Rosenfeld; Bill Wiebe (2013). Geometry of Lie Groups. Springer Science & Business Media. pp. 158ff. ISBN 978-1-4757-5325-7.
↑ ^78.0 ^78.1 Peter Pesic (2007). Beyond Geometry: Classic Papers from Riemann to Einstein. Courier Corporation. ISBN 978-0-486-45350-7.
↑ Michio Kaku (2012). Strings, Conformal Fields, and Topology: An Introduction. Springer Science & Business Media. p. 151. ISBN 978-1-4684-0397-8.
↑ Mladen Bestvina; Michah Sageev; Karen Vogtmann (2014). Geometric Group Theory. American Mathematical Soc. p. 132. ISBN 978-1-4704-1227-2.
↑ W-H. Steeb (1996). Continuous Symmetries, Lie Algebras, Differential Equations and Computer Algebra. World Scientific Publishing Company. ISBN 978-981-310-503-4.
↑ Charles W. Misner (2005). Directions in General Relativity: Volume 1: Proceedings of the 1993 International Symposium, Maryland: Papers in Honor of Charles Misner. Cambridge University Press. p. 272. ISBN 978-0-521-02139-5.
↑ Linnaeus Wayland Dowling (1917). Projective Geometry. McGraw-Hill book Company, Incorporated. p. 10.
↑ G. Gierz (2006). Bundles of Topological Vector Spaces and Their Duality. Springer. p. 252. ISBN 978-3-540-39437-2.
↑ Robert E. Butts; J.R. Brown (2012). Constructivism and Science: Essays in Recent German Philosophy. Springer Science & Business Media. pp. 127–. ISBN 978-94-009-0959-5.
↑ Science. Moses King. 1886. pp. 181–.
↑ W. Abbot (2013). Practical Geometry and Engineering Graphics: A Textbook for Engineering and Other Students. Springer Science & Business Media. pp. 6–. ISBN 978-94-017-2742-6.
↑ ^88.0 ^88.1 ^88.2 ^88.3 George L. Hersey (2001). Architecture and Geometry in the Age of the Baroque. University of Chicago Press. ISBN 978-0-226-32783-9.
↑ P. Vanícek; E.J. Krakiwsky (2015). Geodesy: The Concepts. Elsevier. p. 23. ISBN 978-1-4832-9079-9.
↑ Gerard Walschap (2015). Multivariable Calculus and Differential Geometry. De Gruyter. ISBN 978-3-11-036954-0.
↑ Harley Flanders (2012). Differential Forms with Applications to the Physical Sciences. Courier Corporation. ISBN 978-0-486-13961-6.
↑ Paul Marriott; Mark Salmon (2000). Applications of Differential Geometry to Econometrics. Cambridge University Press. ISBN 978-0-521-65116-5.
↑ Matthew He; Sergey Petoukhov (2011). Mathematics of Bioinformatics: Theory, Methods and Applications. John Wiley & Sons. p. 106. ISBN 978-1-118-09952-0.
↑ P.A.M. Dirac (2016). General Theory of Relativity. Princeton University Press. ISBN 978-1-4008-8419-3.
↑ Nihat Ay; Jürgen Jost; Hông Vân Lê; Lorenz Schwachhöfer (2017). Information Geometry. Springer. p. 185. ISBN 978-3-319-56478-4.
↑ Boris A. Rosenfeld (2012). A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space. Springer Science & Business Media. ISBN 978-1-4419-8680-1.
↑ Kline (1972) "Mathematical thought from ancient to modern times", Oxford University Press, p. 1032. Kant did not reject the logical (analytic a priori) possibility of non-Euclidean geometry, see Jeremy Gray, "Ideas of Space Euclidean, Non-Euclidean, and Relativistic", Oxford, 1989; p. 85. Some have implied that, in light of this, Kant had in fact predicted the development of non-Euclidean geometry, cf. Leonard Nelson, "Philosophy and Axiomatics," Socratic Method and Critical Philosoph, Dover, 1965, p. 164.
↑ Duncan M'Laren Young Sommerville (1919). Elements of Non-Euclidean Geometry ... Open Court. pp. 15ff.
↑ "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen". Archived from the original on 18 March 2016.
↑ Martin D. Crossley (2011). Essential Topology. Springer Science & Business Media. ISBN 978-1-85233-782-7.
↑ Charles Nash; Siddhartha Sen (1988). Topology and Geometry for Physicists. Elsevier. p. 1. ISBN 978-0-08-057085-3.
↑ George E. Martin (1996). Transformation Geometry: An Introduction to Symmetry. Springer Science & Business Media. ISBN 978-0-387-90636-2.
↑ J. P. May (1999). A Concise Course in Algebraic Topology. University of Chicago Press. ISBN 978-0-226-51183-2.
↑ The Encyclopedia Americana: A Universal Reference Library Comprising the Arts and Sciences, Literature, History, Biography, Geography, Commerce, Etc., of the World. Scientific American Compiling Department. 1905. pp. 489–.
↑ ^105.0 ^105.1 Suzanne C. Dieudonne (1985). History Algebraic Geometry. CRC Press. ISBN 978-0-412-99371-8.
↑ James Carlson; James A. Carlson; Arthur Jaffe; Andrew Wiles (2006). The Millennium Prize Problems. American Mathematical Soc. ISBN 978-0-8218-3679-8.
↑ Robin Hartshorne (2013). Algebraic Geometry. Springer Science & Business Media. ISBN 978-1-4757-3849-0.
↑ Everett W. Howe; Kristin E. Lauter; Judy L. Walker (2017). Algebraic Geometry for Coding Theory and Cryptography: IPAM, Los Angeles, CA, February 2016. Springer. ISBN 978-3-319-63931-4.
↑ Marcos Marino; Michael Thaddeus; Ravi Vakil (2008). Enumerative Invariants in Algebraic Geometry and String Theory: Lectures given at the C.I.M.E. Summer School held in Cetraro, Italy, June 6–11, 2005. Springer. ISBN 978-3-540-79814-9.
↑ Huybrechts, D. (2006). Complex geometry: an introduction. Springer Science & Business Media.
↑ Griffiths, P., & Harris, J. (2014). Principles of algebraic geometry. John Wiley & Sons.
↑ Wells, R. O. N., & García-Prada, O. (1980). Differential analysis on complex manifolds (Vol. 21980). New York: Springer.
↑ Hori, K., Thomas, R., Katz, S., Vafa, C., Pandharipande, R., Klemm, A., ... & Zaslow, E. (2003). Mirror symmetry (Vol. 1). American Mathematical Soc.
↑ Forster, O. (2012). Lectures on Riemann surfaces (Vol. 81). Springer Science & Business Media.
↑ Miranda, R. (1995). Algebraic curves and Riemann surfaces (Vol. 5). American Mathematical Soc.
↑ Donaldson, S. (2011). Riemann surfaces. Oxford University Press.
↑ Serre, J. P. (1955). Faisceaux algébriques cohérents. Annals of Mathematics, 197–278.
↑ Serre, J. P. (1956). Géométrie algébrique et géométrie analytique. In Annales de l'Institut Fourier (vol. 6, pp. 1–42).
↑ Jiří Matoušek (2013). Lectures on Discrete Geometry. Springer Science & Business Media. ISBN 978-1-4613-0039-7.
↑ Chuanming Zong (2006). The Cube – A Window to Convex and Discrete Geometry. Cambridge University Press. ISBN 978-0-521-85535-8.
↑ Peter M. Gruber (2007). Convex and Discrete Geometry. Springer Science & Business Media. ISBN 978-3-540-71133-9.
↑ Satyan L. Devadoss; Joseph O'Rourke (2011). Discrete and Computational Geometry. Princeton University Press. ISBN 978-1-4008-3898-1.
↑ Károly Bezdek (2010). Classical Topics in Discrete Geometry. Springer Science & Business Media. ISBN 978-1-4419-0600-7.
↑ Franco P. Preparata; Michael I. Shamos (2012). Computational Geometry: An Introduction. Springer Science & Business Media. ISBN 978-1-4612-1098-6.
↑ Xianfeng David Gu; Shing-Tung Yau (2008). Computational Conformal Geometry. International Press. ISBN 978-1-57146-171-1.
↑ Clara Löh (2017). Geometric Group Theory: An Introduction. Springer. ISBN 978-3-319-72254-2.
↑ ^127.0 ^127.1 Gerard Meurant (2014). Handbook of Convex Geometry. Elsevier Science. ISBN 978-0-08-093439-6.
↑ Jürgen Richter-Gebert (2011). Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Geometry. Springer Science & Business Media. ISBN 978-3-642-17286-1.
↑ Kimberly Elam (2001). Geometry of Design: Studies in Proportion and Composition. Princeton Architectural Press. ISBN 978-1-56898-249-6.
↑ Brad J. Guigar (2004). The Everything Cartooning Book: Create Unique And Inspired Cartoons For Fun And Profit. Adams Media. pp. 82–. ISBN 978-1-4405-2305-2.
↑ Mario Livio (2008). The Golden Ratio: The Story of PHI, the World's Most Astonishing Number. Crown/Archetype. p. 166. ISBN 978-0-307-48552-6.
↑ Michele Emmer; Doris Schattschneider (2007). M. C. Escher's Legacy: A Centennial Celebration. Springer. p. 107. ISBN 978-3-540-28849-7.
↑ Robert Capitolo; Ken Schwab (2004). Drawing Course 101. Sterling Publishing Company, Inc. p. 22. ISBN 978-1-4027-0383-6.
↑ Phyllis Gelineau (2011). Integrating the Arts Across the Elementary School Curriculum. Cengage Learning. p. 55. ISBN 978-1-111-30126-2.
↑ Cristiano Ceccato; Lars Hesselgren; Mark Pauly; Helmut Pottmann, Johannes Wallner (2016). Advances in Architectural Geometry 2010. Birkhäuser. p. 6. ISBN 978-3-99043-371-3.
↑ Helmut Pottmann (2007). Architectural geometry. Bentley Institute Press. ISBN 978-1-934493-04-5.
↑ Marian Moffett; Michael W. Fazio; Lawrence Wodehouse (2003). A World History of Architecture. Laurence King Publishing. p. 371. ISBN 978-1-85669-371-4.
↑ Robin M. Green; Robin Michael Green (1985). Spherical Astronomy. Cambridge University Press. p. 1. ISBN 978-0-521-31779-5.
↑ Harley Flanders; Justin J. Price (2014). Calculus with Analytic Geometry. Elsevier Science. ISBN 978-1-4832-6240-6.
↑ Jon Rogawski; Colin Adams (2015). Calculus. W. H. Freeman. ISBN 978-1-4641-7499-5.
↑ Álvaro Lozano-Robledo (2019). Number Theory and Geometry: An Introduction to Arithmetic Geometry. American Mathematical Soc. ISBN 978-1-4704-5016-8.
↑ Arturo Sangalli (2009). Pythagoras' Revenge: A Mathematical Mystery. Princeton University Press. p. 57. ISBN 978-0-691-04955-7.
↑ Gary Cornell; Joseph H. Silverman; Glenn Stevens (2013). Modular Forms and Fermat's Last Theorem. Springer Science & Business Media. ISBN 978-1-4612-1974-3.

सूत्रों का कहना है

Boyer, C.B. (1991) [1989]. A History of Mathematics (Second edition, revised by Uta C. Merzbach ed.). New York: Wiley. ISBN 978-0-471-54397-8.
Cooke, Roger (2005). The History of Mathematics. New York: Wiley-Interscience. ISBN 978-0-471-44459-6.
Hayashi, Takao (2003). "Indian Mathematics". In Grattan-Guinness, Ivor (ed.). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. Vol. 1. Baltimore, MD: The Johns Hopkins University Press. pp. 118–130. ISBN 978-0-8018-7396-6.
Hayashi, Takao (2005). "Indian Mathematics". In Flood, Gavin (ed.). The Blackwell Companion to Hinduism. Oxford: Basil Blackwell. pp. 360–375. ISBN 978-1-4051-3251-0.
Nikolai I. Lobachevsky (2010). Pangeometry. Heritage of European Mathematics Series. Vol. 4. translator and editor: A. Papadopoulos. European Mathematical Society.

अग्रिम पठन

Jay Kappraff (2014). A Participatory Approach to Modern Geometry. World Scientific Publishing. doi:10.1142/8952. ISBN 978-981-4556-70-5.
Leonard Mlodinow (2002). Euclid's Window – The Story of Geometry from Parallel Lines to Hyperspace (UK ed.). Allen Lane. ISBN 978-0-7139-9634-0.

बाहरी संबंध

"Geometry" . Encyclopædia Britannica (in English). Vol. 11 (11th ed.). 1911. pp. 675–736.

A geometry course from Wikiversity
Unusual Geometry Problems
The Math Forum – Geometry
Nature Precedings – Pegs and Ropes Geometry at Stonehenge
The Mathematical Atlas – Geometric Areas of Mathematics
"4000 Years of Geometry", lecture by Robin Wilson given at Gresham College, 3 October 2007 (available for MP3 and MP4 download as well as a text file)
- Finitism in Geometry at the Stanford Encyclopedia of Philosophy
The Geometry Junkyard
Interactive geometry reference with hundreds of applets
Dynamic Geometry Sketches (with some Student Explorations)
Geometry classes at Khan Academy

{{Navbox

| name =गणित के क्षेत्र

|state = collapsed

| title =अंक शास्त्र | bodyclass = hlist

|above =

| group1 = नींव | list1 =* श्रेणी सिद्धांत

| group2 =बीजगणित | list2 =* सार

| group3 = विश्लेषण | list3 =* पथरी

| group4 = असतत | list4 =* कॉम्बीनेटरिक्स

| group5 =ज्यामिति | list5 =* बीजगणितीय

| group6 =संख्या सिद्धांत | list6 =* अंकगणित

| group7 =टोपोलॉजी | list7 =* सामान्य

| group8 = लागू | list8 =* इंजीनियरिंग गणित

| group9 = कम्प्यूटेशनल | list9 =* कंप्यूटर विज्ञान

| group10 = संबंधित विषय | list10 =* अनौपचारिक गणित

| below =* '

' श्रेणी' '
' कॉमन्स'
[[gikewikipedia: wikiproject matics | wikiproject]

}}

[2] Until the 19th century, geometry was dominated by the assumption that all geometric constructions were Euclidean. In the 19th century and later, this was challenged by the development of hyperbolic geometry by Lobachevsky and other non-Euclidean geometries by Gauss and others. It was then realised that implicitly non-Euclidean geometry had appeared throughout history, including the work of Desargues in the 17th century, all the way back to the implicit use of spherical geometry to understand the Earth geodesy and to navigate the oceans since antiquity.

[70] The ancient Greeks had some constructions using other instruments.

[Risi2015-1] Vincenzo De Risi (2015). Mathematizing Space: The Objects of Geometry from Antiquity to the Early Modern Age. Birkhäuser. pp. 1–. ISBN 978-3-319-12102-4.

[Tabak_2014_xiv-3] 2.0 ^2.1 Tabak, John (2014). Geometry: the language of space and form. Infobase Publishing. p. xiv. ISBN 978-0-8160-4953-0.

[Meyer2006-4] Walter A. Meyer (2006). Geometry and Its Applications. Elsevier. ISBN 978-0-08-047803-6.

[5] J. Friberg, Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations , Historia Mathematica, 8, 1981, pp. 277–318.

[6] "Chap. IV Egyptian Mathematics and Astronomy". The Exact Sciences in Antiquity (2 ed.). last = Neugebauer. 1969 [1957]. pp. 71–96. ISBN 978-0-486-22332-2. {{cite book}}: |first= missing |last= (help); Missing pipe in: |publisher= (help).

[7] Ossendrijver, Mathieu (29 January 2016). "Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph". Science. 351 (6272): 482–484. Bibcode:2016Sci...351..482O. doi:10.1126/science.aad8085. PMID 26823423. S2CID 206644971.

[8] Depuydt, Leo (1 January 1998). "Gnomons at Meroë and Early Trigonometry". The Journal of Egyptian Archaeology. 84: 171–180. doi:10.2307/3822211. JSTOR 3822211.

[9] Slayman, Andrew (27 May 1998). "Neolithic Skywatchers". Archaeology Magazine Archive. Archived from the original on 5 June 2011. Retrieved 17 April 2011.

[10] Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0.

[11] Kurt Von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics.

[12] James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal.

[13] (Boyer 1991, The Age of Plato and Aristotle p. 92)

[14] (Boyer 1991, Euclid of Alexandria p. 119)

[15] Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0 p. 141: No work, except The Bible, has been more widely used....

[16] O'Connor, J.J.; Robertson, E.F. (February 1996). "A history of calculus". url = http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/The_rise_of_calculus.html. {{cite web}}: |access-date= requires |url= (help); |archive-url= requires |url= (help); External link in |publisher= (help); Missing or empty |url= (help); Missing pipe in: |publisher= (help)

[Staal_1999-17] Staal, Frits (1999). "Greek and Vedic Geometry". Journal of Indian Philosophy. 27 (1–2): 105–127. doi:10.1023/A:1004364417713. S2CID 170894641.

[18] Pythagorean triples are triples of integers $(a,b,c)$ with the property: $a^{2}+b^{2}=c^{2}$ . Thus, $3^{2}+4^{2}=5^{2}$ , $8^{2}+15^{2}=17^{2}$ , $12^{2}+35^{2}=37^{2}$ etc.

[cooke198-19] (Cooke 2005, p. 198): "The arithmetic content of the Śulva Sūtras consists of rules for finding Pythagorean triples such as (3, 4, 5), (5, 12, 13), (8, 15, 17), and (12, 35, 37). It is not certain what practical use these arithmetic rules had. The best conjecture is that they were part of religious ritual. A Hindu home was required to have three fires burning at three different altars. The three altars were to be of different shapes, but all three were to have the same area. These conditions led to certain "Diophantine" problems, a particular case of which is the generation of Pythagorean triples, so as to make one square integer equal to the sum of two others."

[hayashi2005-371-20] (Hayashi 2005, p. 371)

[hayashi2003-p121-122-21] 20.0 ^20.1 (Hayashi 2003, pp. 121–122)

[22] R. Rashed (1994), The development of Arabic mathematics: between arithmetic and algebra, p. 35 London

[23] (Boyer 1991, "The Arabic Hegemony" pp. 241–242) "Omar Khayyam (c. 1050–1123), the "tent-maker," wrote an Algebra that went beyond that of al-Khwarizmi to include equations of third degree. Like his Arab predecessors, Omar Khayyam provided for quadratic equations both arithmetic and geometric solutions; for general cubic equations, he believed (mistakenly, as the 16th century later showed), arithmetic solutions were impossible; hence he gave only geometric solutions. The scheme of using intersecting conics to solve cubics had been used earlier by Menaechmus, Archimedes, and Alhazan, but Omar Khayyam took the praiseworthy step of generalizing the method to cover all third-degree equations (having positive roots). .. For equations of higher degree than three, Omar Khayyam evidently did not envision similar geometric methods, for space does not contain more than three dimensions, ... One of the most fruitful contributions of Arabic eclecticism was the tendency to close the gap between numerical and geometric algebra. The decisive step in this direction came much later with Descartes, but Omar Khayyam was moving in this direction when he wrote, "Whoever thinks algebra is a trick in obtaining unknowns has thought it in vain. No attention should be paid to the fact that algebra and geometry are different in appearance. Algebras are geometric facts which are proved."".

[24] O'Connor, John J.; Robertson, Edmund F. "Al-Mahani". MacTutor History of Mathematics archive. University of St Andrews.

[ReferenceA-25] O'Connor, John J.; Robertson, Edmund F. "Al-Sabi Thabit ibn Qurra al-Harrani". MacTutor History of Mathematics archive. University of St Andrews.

[26] O'Connor, John J.; Robertson, Edmund F. "Omar Khayyam". MacTutor History of Mathematics archive. University of St Andrews.

[27] Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, pp. 447–494 [470], Routledge, London and New York:
"Three scientists, Ibn al-Haytham, Khayyam, and al-Tusi, had made the most considerable contribution to this branch of geometry whose importance came to be completely recognized only in the 19th century. In essence, their propositions concerning the properties of quadrangles which they considered, assuming that some of the angles of these figures were acute of obtuse, embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between this postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investigations of their European counterparts. The first European attempt to prove the postulate on parallel lines—made by Witelo, the Polish scientists of the 13th century, while revising Ibn al-Haytham's Book of Optics (Kitab al-Manazir)—was undoubtedly prompted by Arabic sources. The proofs put forward in the 14th century by the Jewish scholar Levi ben Gerson, who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that Pseudo-Tusi's Exposition of Euclid had stimulated both J. Wallis's and G. Saccheri's studies of the theory of parallel lines."

[Boyer2012-28] 27.0 ^27.1 Carl B. Boyer (2012). History of Analytic Geometry. Courier Corporation. ISBN 978-0-486-15451-0.

[Edwards2012-29] C.H. Edwards Jr. (2012). The Historical Development of the Calculus. Springer Science & Business Media. p. 95. ISBN 978-1-4612-6230-5.

[FieldGray2012-30] Judith V. Field; Jeremy Gray (2012). The Geometrical Work of Girard Desargues. Springer Science & Business Media. p. 43. ISBN 978-1-4613-8692-6.

[Wylie2011-31] C. R. Wylie (2011). Introduction to Projective Geometry. Courier Corporation. ISBN 978-0-486-14170-1.

[Gray2011-32] Jeremy Gray (2011). Worlds Out of Nothing: A Course in the History of Geometry in the 19th Century. Springer Science & Business Media. ISBN 978-0-85729-060-1.

[Bayro-Corrochano2018-33] Eduardo Bayro-Corrochano (2018). Geometric Algebra Applications Vol. I: Computer Vision, Graphics and Neurocomputing. Springer. p. 4. ISBN 978-3-319-74830-6.

[Schmidt,_W._2002-34] Cite error: Invalid <ref> tag; no text was provided for refs named Schmidt, W. 2002

[Kline1990-35] Morris Kline (1990). Mathematical Thought From Ancient to Modern Times: Volume 3. US: Oxford University Press. pp. 1010–. ISBN 978-0-19-506137-6.

[Katz2000-36] Victor J. Katz (2000). Using History to Teach Mathematics: An International Perspective. Cambridge University Press. pp. 45–. ISBN 978-0-88385-163-0.

[Berlinski2014-37] David Berlinski (2014). The King of Infinite Space: Euclid and His Elements. Basic Books. ISBN 978-0-465-03863-3.

[Hartshorne2013-38] 37.0 ^37.1 Robin Hartshorne (2013). Geometry: Euclid and Beyond. Springer Science & Business Media. pp. 29–. ISBN 978-0-387-22676-7.

[HerbstFujita2017-39] Pat Herbst; Taro Fujita; Stefan Halverscheid; Michael Weiss (2017). The Learning and Teaching of Geometry in Secondary Schools: A Modeling Perspective. Taylor & Francis. pp. 20–. ISBN 978-1-351-97353-3.

[Yaglom2012-40] I.M. Yaglom (2012). A Simple Non-Euclidean Geometry and Its Physical Basis: An Elementary Account of Galilean Geometry and the Galilean Principle of Relativity. Springer Science & Business Media. pp. 6–. ISBN 978-1-4612-6135-3.

[Holme2010-41] Audun Holme (2010). Geometry: Our Cultural Heritage. Springer Science & Business Media. pp. 254–. ISBN 978-3-642-14441-7.

[EuclidAll-42] 41.0 ^41.1 ^41.2 ^41.3 ^41.4 Euclid's Elements – All thirteen books in one volume, Based on Heath's translation, Green Lion Press ISBN 1-888009-18-7.

[43] Gerla, G. (1995). "Pointless Geometries" (PDF). In Buekenhout, F.; Kantor, W. (eds.). Handbook of incidence geometry: buildings and foundations. North-Holland. pp. 1015–1031. Archived from the original (PDF) on 17 July 2011.

[44] Clark, Bowman L. (Jan 1985). "Individuals and Points". Notre Dame Journal of Formal Logic. 26 (1): 61–75. doi:10.1305/ndjfl/1093870761.

[45] John Casey (1885). Analytic Geometry of the Point, Line, Circle, and Conic Sections.

[46] Buekenhout, Francis (1995), Handbook of Incidence Geometry: Buildings and Foundations, Elsevier B.V.

[47] "geodesic – definition of geodesic in English from the Oxford dictionary". OxfordDictionaries.com. Archived from the original on 15 July 2016. Retrieved 2016-01-20.

[Munkres-48] 47.0 ^47.1 ^47.2 ^47.3 ^47.4 Munkres, James R. Topology. Vol. 2. Upper Saddle River: Prentice Hall, 2000.

[49] Szmielew, Wanda. From affine to Euclidean geometry: An axiomatic approach. Springer, 1983.

[50] Ahlfors, Lars V. Complex analysis: an introduction to the theory of analytic functions of one complex variable. New York; London (1953).

[51] Sidorov, L.A. (2001) [1994]. "Angle". Encyclopedia of Mathematics. EMS Press.

[52] Gelʹfand, Izrailʹ Moiseevič, and Mark Saul. "Trigonometry." Trigonometry. Birkhäuser Boston, 2001. 1–20.

[Stewart-53] Stewart, James (2012). Calculus: Early Transcendentals, 7th ed., Brooks Cole Cengage Learning. ISBN 978-0-538-49790-9

[54] Jost, Jürgen (2002). Riemannian Geometry and Geometric Analysis. Berlin: Springer-Verlag. ISBN 978-3-540-42627-1..

[55] Baker, Henry Frederick. Principles of geometry. Vol. 2. CUP Archive, 1954.

[Carmo-56] 55.0 ^55.1 ^55.2 Do Carmo, Manfredo Perdigao, and Manfredo Perdigao Do Carmo. Differential geometry of curves and surfaces. Vol. 2. Englewood Cliffs: Prentice-hall, 1976.

[mumford-57] 56.0 ^56.1 Mumford, David (1999). The Red Book of Varieties and Schemes Includes the Michigan Lectures on Curves and Their Jacobians (2nd ed.). Springer-Verlag. ISBN 978-3-540-63293-1. Zbl 0945.14001.

[58] Briggs, William L., and Lyle Cochran Calculus. "Early Transcendentals." ISBN 978-0-321-57056-7.

[59] Yau, Shing-Tung; Nadis, Steve (2010). The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions. Basic Books. ISBN 978-0-465-02023-2.

[Treese2018-60] 59.0 ^59.1 Steven A. Treese (2018). History and Measurement of the Base and Derived Units. Springer International Publishing. pp. 101–. ISBN 978-3-319-77577-7.

[Cannon2017-61] James W. Cannon (2017). Geometry of Lengths, Areas, and Volumes. American Mathematical Soc. p. 11. ISBN 978-1-4704-3714-5.

[Strang1991-62] Gilbert Strang (1991). Calculus. SIAM. ISBN 978-0-9614088-2-4.

[Bear2002-63] H. S. Bear (2002). A Primer of Lebesgue Integration. Academic Press. ISBN 978-0-12-083971-1.

[64] Dmitri Burago, Yu D Burago, Sergei Ivanov, A Course in Metric Geometry, American Mathematical Society, 2001, ISBN 0-8218-2129-6.

[65] Wald, Robert M. (1984). General Relativity. University of Chicago Press. ISBN 978-0-226-87033-5.

[Tao2011-66] Terence Tao (2011). An Introduction to Measure Theory. American Mathematical Soc. ISBN 978-0-8218-6919-2.

[Libeskind2008-67] Shlomo Libeskind (2008). Euclidean and Transformational Geometry: A Deductive Inquiry. Jones & Bartlett Learning. p. 255. ISBN 978-0-7637-4366-6.

[Freitag2013-68] Mark A. Freitag (2013). Mathematics for Elementary School Teachers: A Process Approach. Cengage Learning. p. 614. ISBN 978-0-618-61008-2.

[Martin2012-69] George E. Martin (2012). Transformation Geometry: An Introduction to Symmetry. Springer Science & Business Media. ISBN 978-1-4612-5680-9.

[Blacklock2018-71] Mark Blacklock (2018). The Emergence of the Fourth Dimension: Higher Spatial Thinking in the Fin de Siècle. Oxford University Press. ISBN 978-0-19-875548-7.

[Joly1895-72] Charles Jasper Joly (1895). Papers. The Academy. pp. 62–.

[Temam2013-73] Roger Temam (2013). Infinite-Dimensional Dynamical Systems in Mechanics and Physics. Springer Science & Business Media. p. 367. ISBN 978-1-4612-0645-3.

[JacobLam1994-74] Bill Jacob; Tsit-Yuen Lam (1994). Recent Advances in Real Algebraic Geometry and Quadratic Forms: Proceedings of the RAGSQUAD Year, Berkeley, 1990–1991. American Mathematical Soc. p. 111. ISBN 978-0-8218-5154-8.

[Stewart2008-75] Ian Stewart (2008). Why Beauty Is Truth: A History of Symmetry. Basic Books. p. 14. ISBN 978-0-465-08237-7.

[Alexey2009-76] Stakhov Alexey (2009). Mathematics Of Harmony: From Euclid To Contemporary Mathematics And Computer Science. World Scientific. p. 144. ISBN 978-981-4472-57-9.

[Hahn1998-77] Werner Hahn (1998). Symmetry as a Developmental Principle in Nature and Art. World Scientific. ISBN 978-981-02-2363-2.

[Cantwell2002-78] Brian J. Cantwell (2002). Introduction to Symmetry Analysis. Cambridge University Press. p. 34. ISBN 978-1-139-43171-2.

[RosenfeldWiebe2013-79] B. Rosenfeld; Bill Wiebe (2013). Geometry of Lie Groups. Springer Science & Business Media. pp. 158ff. ISBN 978-1-4757-5325-7.

[Pesic2007-80] 78.0 ^78.1 Peter Pesic (2007). Beyond Geometry: Classic Papers from Riemann to Einstein. Courier Corporation. ISBN 978-0-486-45350-7.

[Kaku2012-81] Michio Kaku (2012). Strings, Conformal Fields, and Topology: An Introduction. Springer Science & Business Media. p. 151. ISBN 978-1-4684-0397-8.

[BestvinaSageev2014-82] Mladen Bestvina; Michah Sageev; Karen Vogtmann (2014). Geometric Group Theory. American Mathematical Soc. p. 132. ISBN 978-1-4704-1227-2.

[Steeb1996-83] W-H. Steeb (1996). Continuous Symmetries, Lie Algebras, Differential Equations and Computer Algebra. World Scientific Publishing Company. ISBN 978-981-310-503-4.

[Misner2005-84] Charles W. Misner (2005). Directions in General Relativity: Volume 1: Proceedings of the 1993 International Symposium, Maryland: Papers in Honor of Charles Misner. Cambridge University Press. p. 272. ISBN 978-0-521-02139-5.

[Dowling1917-85] Linnaeus Wayland Dowling (1917). Projective Geometry. McGraw-Hill book Company, Incorporated. p. 10.

[Gierz2006-86] G. Gierz (2006). Bundles of Topological Vector Spaces and Their Duality. Springer. p. 252. ISBN 978-3-540-39437-2.

[ButtsBrown2012-87] Robert E. Butts; J.R. Brown (2012). Constructivism and Science: Essays in Recent German Philosophy. Springer Science & Business Media. pp. 127–. ISBN 978-94-009-0959-5.

[88] Science. Moses King. 1886. pp. 181–.

[Abbot2013-89] W. Abbot (2013). Practical Geometry and Engineering Graphics: A Textbook for Engineering and Other Students. Springer Science & Business Media. pp. 6–. ISBN 978-94-017-2742-6.

[HerseyHersey2001-90] 88.0 ^88.1 ^88.2 ^88.3 George L. Hersey (2001). Architecture and Geometry in the Age of the Baroque. University of Chicago Press. ISBN 978-0-226-32783-9.

[vanicekkrakisky2015-91] P. Vanícek; E.J. Krakiwsky (2015). Geodesy: The Concepts. Elsevier. p. 23. ISBN 978-1-4832-9079-9.

[Walschap2015-92] Gerard Walschap (2015). Multivariable Calculus and Differential Geometry. De Gruyter. ISBN 978-3-11-036954-0.

[Flanders2012-93] Harley Flanders (2012). Differential Forms with Applications to the Physical Sciences. Courier Corporation. ISBN 978-0-486-13961-6.

[MarriottSalmon2000-94] Paul Marriott; Mark Salmon (2000). Applications of Differential Geometry to Econometrics. Cambridge University Press. ISBN 978-0-521-65116-5.

[HePetoukhov2011-95] Matthew He; Sergey Petoukhov (2011). Mathematics of Bioinformatics: Theory, Methods and Applications. John Wiley & Sons. p. 106. ISBN 978-1-118-09952-0.

[Dirac2016-96] P.A.M. Dirac (2016). General Theory of Relativity. Princeton University Press. ISBN 978-1-4008-8419-3.

[AyJost2017-97] Nihat Ay; Jürgen Jost; Hông Vân Lê; Lorenz Schwachhöfer (2017). Information Geometry. Springer. p. 185. ISBN 978-3-319-56478-4.

[Rosenfeld2012-98] Boris A. Rosenfeld (2012). A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space. Springer Science & Business Media. ISBN 978-1-4419-8680-1.

[99] Kline (1972) "Mathematical thought from ancient to modern times", Oxford University Press, p. 1032. Kant did not reject the logical (analytic a priori) possibility of non-Euclidean geometry, see Jeremy Gray, "Ideas of Space Euclidean, Non-Euclidean, and Relativistic", Oxford, 1989; p. 85. Some have implied that, in light of this, Kant had in fact predicted the development of non-Euclidean geometry, cf. Leonard Nelson, "Philosophy and Axiomatics," Socratic Method and Critical Philosoph, Dover, 1965, p. 164.

[Sommerville1919-100] Duncan M'Laren Young Sommerville (1919). Elements of Non-Euclidean Geometry ... Open Court. pp. 15ff.

[101] "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen". Archived from the original on 18 March 2016.

[Crossley2011-102] Martin D. Crossley (2011). Essential Topology. Springer Science & Business Media. ISBN 978-1-85233-782-7.

[NashSen1988-103] Charles Nash; Siddhartha Sen (1988). Topology and Geometry for Physicists. Elsevier. p. 1. ISBN 978-0-08-057085-3.

[Martin1996-104] George E. Martin (1996). Transformation Geometry: An Introduction to Symmetry. Springer Science & Business Media. ISBN 978-0-387-90636-2.

[May1999-105] J. P. May (1999). A Concise Course in Algebraic Topology. University of Chicago Press. ISBN 978-0-226-51183-2.

[inc1905-106] The Encyclopedia Americana: A Universal Reference Library Comprising the Arts and Sciences, Literature, History, Biography, Geography, Commerce, Etc., of the World. Scientific American Compiling Department. 1905. pp. 489–.

[Dieudonne1985-107] 105.0 ^105.1 Suzanne C. Dieudonne (1985). History Algebraic Geometry. CRC Press. ISBN 978-0-412-99371-8.

[CarlsonCarlson2006-108] James Carlson; James A. Carlson; Arthur Jaffe; Andrew Wiles (2006). The Millennium Prize Problems. American Mathematical Soc. ISBN 978-0-8218-3679-8.

[AHartshorne2013-109] Robin Hartshorne (2013). Algebraic Geometry. Springer Science & Business Media. ISBN 978-1-4757-3849-0.

[HoweLauter2017-110] Everett W. Howe; Kristin E. Lauter; Judy L. Walker (2017). Algebraic Geometry for Coding Theory and Cryptography: IPAM, Los Angeles, CA, February 2016. Springer. ISBN 978-3-319-63931-4.

[MarinoThaddeus2008-111] Marcos Marino; Michael Thaddeus; Ravi Vakil (2008). Enumerative Invariants in Algebraic Geometry and String Theory: Lectures given at the C.I.M.E. Summer School held in Cetraro, Italy, June 6–11, 2005. Springer. ISBN 978-3-540-79814-9.

[112] Huybrechts, D. (2006). Complex geometry: an introduction. Springer Science & Business Media.

[113] Griffiths, P., & Harris, J. (2014). Principles of algebraic geometry. John Wiley & Sons.

[114] Wells, R. O. N., & García-Prada, O. (1980). Differential analysis on complex manifolds (Vol. 21980). New York: Springer.

[115] Hori, K., Thomas, R., Katz, S., Vafa, C., Pandharipande, R., Klemm, A., ... & Zaslow, E. (2003). Mirror symmetry (Vol. 1). American Mathematical Soc.

[116] Forster, O. (2012). Lectures on Riemann surfaces (Vol. 81). Springer Science & Business Media.

[117] Miranda, R. (1995). Algebraic curves and Riemann surfaces (Vol. 5). American Mathematical Soc.

[118] Donaldson, S. (2011). Riemann surfaces. Oxford University Press.

[119] Serre, J. P. (1955). Faisceaux algébriques cohérents. Annals of Mathematics, 197–278.

[120] Serre, J. P. (1956). Géométrie algébrique et géométrie analytique. In Annales de l'Institut Fourier (vol. 6, pp. 1–42).

[Matoušek2013-121] Jiří Matoušek (2013). Lectures on Discrete Geometry. Springer Science & Business Media. ISBN 978-1-4613-0039-7.

[Zong2006-122] Chuanming Zong (2006). The Cube – A Window to Convex and Discrete Geometry. Cambridge University Press. ISBN 978-0-521-85535-8.

[Gruber2007-123] Peter M. Gruber (2007). Convex and Discrete Geometry. Springer Science & Business Media. ISBN 978-3-540-71133-9.

[DevadossO'Rourke2011-124] Satyan L. Devadoss; Joseph O'Rourke (2011). Discrete and Computational Geometry. Princeton University Press. ISBN 978-1-4008-3898-1.

[Bezdek2010-125] Károly Bezdek (2010). Classical Topics in Discrete Geometry. Springer Science & Business Media. ISBN 978-1-4419-0600-7.

[PreparataShamos2012-126] Franco P. Preparata; Michael I. Shamos (2012). Computational Geometry: An Introduction. Springer Science & Business Media. ISBN 978-1-4612-1098-6.

[GuYau2008-127] Xianfeng David Gu; Shing-Tung Yau (2008). Computational Conformal Geometry. International Press. ISBN 978-1-57146-171-1.

[Löh2017-128] Clara Löh (2017). Geometric Group Theory: An Introduction. Springer. ISBN 978-3-319-72254-2.

[Meurant2014-129] 127.0 ^127.1 Gerard Meurant (2014). Handbook of Convex Geometry. Elsevier Science. ISBN 978-0-08-093439-6.

[Richter-Gebert2011-130] Jürgen Richter-Gebert (2011). Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Geometry. Springer Science & Business Media. ISBN 978-3-642-17286-1.

[Elam2001-131] Kimberly Elam (2001). Geometry of Design: Studies in Proportion and Composition. Princeton Architectural Press. ISBN 978-1-56898-249-6.

[Guigar2004-132] Brad J. Guigar (2004). The Everything Cartooning Book: Create Unique And Inspired Cartoons For Fun And Profit. Adams Media. pp. 82–. ISBN 978-1-4405-2305-2.

[Livio2008-133] Mario Livio (2008). The Golden Ratio: The Story of PHI, the World's Most Astonishing Number. Crown/Archetype. p. 166. ISBN 978-0-307-48552-6.

[EmmerSchattschneider2007-134] Michele Emmer; Doris Schattschneider (2007). M. C. Escher's Legacy: A Centennial Celebration. Springer. p. 107. ISBN 978-3-540-28849-7.

[CapitoloSchwab2004-135] Robert Capitolo; Ken Schwab (2004). Drawing Course 101. Sterling Publishing Company, Inc. p. 22. ISBN 978-1-4027-0383-6.

[Gelineau2011-136] Phyllis Gelineau (2011). Integrating the Arts Across the Elementary School Curriculum. Cengage Learning. p. 55. ISBN 978-1-111-30126-2.

[CeccatoHesselgren2016-137] Cristiano Ceccato; Lars Hesselgren; Mark Pauly; Helmut Pottmann, Johannes Wallner (2016). Advances in Architectural Geometry 2010. Birkhäuser. p. 6. ISBN 978-3-99043-371-3.

[Pottmann2007-138] Helmut Pottmann (2007). Architectural geometry. Bentley Institute Press. ISBN 978-1-934493-04-5.

[MoffettFazio2003-139] Marian Moffett; Michael W. Fazio; Lawrence Wodehouse (2003). A World History of Architecture. Laurence King Publishing. p. 371. ISBN 978-1-85669-371-4.

[GreenGreen1985-140] Robin M. Green; Robin Michael Green (1985). Spherical Astronomy. Cambridge University Press. p. 1. ISBN 978-0-521-31779-5.

[FlandersPrice2014-141] Harley Flanders; Justin J. Price (2014). Calculus with Analytic Geometry. Elsevier Science. ISBN 978-1-4832-6240-6.

[RogawskiAdams2015-142] Jon Rogawski; Colin Adams (2015). Calculus. W. H. Freeman. ISBN 978-1-4641-7499-5.

[Lozano-Robledo2019-143] Álvaro Lozano-Robledo (2019). Number Theory and Geometry: An Introduction to Arithmetic Geometry. American Mathematical Soc. ISBN 978-1-4704-5016-8.

[Sangalli2009-144] Arturo Sangalli (2009). Pythagoras' Revenge: A Mathematical Mystery. Princeton University Press. p. 57. ISBN 978-0-691-04955-7.

[CornellSilverman2013-145] Gary Cornell; Joseph H. Silverman; Glenn Stevens (2013). Modular Forms and Fermat's Last Theorem. Springer Science & Business Media. ISBN 978-1-4612-1974-3.

[1]

[lower-alpha 1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[lower-alpha 2]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

@@ Line 287: / Line 287: @@
 {{Authority control}}
-[[Category: ज्यामिति | ज्यामिति ]]
+[[Category:Machine Translated Page]]
+[[Category:AC with 0 elements]]
-[[Category: Machine Translated Page]]
+[[Category:Articles with short description]]
+[[Category:CS1 English-language sources (en)]]
+[[Category:CS1 errors]]
+[[Category:Pages using Sister project links with default search|v]]
+[[Category:Pages with empty portal template]]
+[[Category:Pages with reference errors]]
+[[Category:Portal-inline template with redlinked portals]]
+[[Category:Portal templates with redlinked portals]]
+[[Category:Short description with empty Wikidata description]]
+[[Category:Wikipedia articles incorporating a citation from the 1911 Encyclopaedia Britannica with Wikisource reference]]
+[[Category:ज्यामिति| ज्यामिति ]]

v t e Major topics in Geometry
Euclidean geometry	Combinatorial Convex Discrete Plane geometry Polygon Solid geometry
Non-Euclidean geometry	Elliptic Hyperbolic Symplectic Spherical Affine Projective Riemannian
Other	Trigonometry Lie group Algebraic geometry Differential geometry
Lists	Shape Lists List of geometry topics List of differential geometry topics

Anonymous

Search