रैखिक विभेदक विश्लेषण: Difference between revisions
No edit summary |
No edit summary |
||
| (41 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Method used in statistics, pattern recognition, and other fields}} | {{Short description|Method used in statistics, pattern recognition, and other fields}} | ||
[[अव्यक्त डिरिचलेट आवंटन]] के साथ भ्रमित न हों। | |||
एलडीए | रेखीय विवेचक विश्लेषण (एलडीए) सामान्य विभेदक विश्लेषण (एनडीए) या विवेचक कार्य विश्लेषण फिशर के रेखीय विवेचक का एक सामान्यीकरण है, यह विधि सांख्यिकी और अन्य क्षेत्रों में प्रयुक्त होती है। जो दो या दो से अधिक वर्गों को चिह्नित या भिन्न करने वाली विशेषताओं का एक [[रैखिक संयोजन]] खोजने के लिए किया जाता है। वस्तुओं या घटनाओं का परिणामस्वरूप संयोजन का प्रयोग रेखीय वर्गीकारक के रूप में किया जा सकता है, या बाद में [[सांख्यिकीय वर्गीकरण]] से पहले [[आयामीता में कमी]] के लिए अधिक सामान्यतः के रूप में किया जा सकता है। | ||
एलडीए | एलडीए विचरण (एनोवा) और [[प्रतिगमन विश्लेषण]] निकटता से संबंधित है, जो एक आश्रित चर के रूप में होता है, जो कि अन्य विशेषताओं या मापों के रैखिक संयोजन के रूप में व्यक्त करने का प्रयास करता है।<ref name="Fisher:1936">{{cite journal |last=Fisher |first=R. A. |author-link=Ronald Fisher |title=टैक्सोनोमिक समस्याओं में एकाधिक मापन का उपयोग|journal=[[Annals of Eugenics]] |volume=7 |pages=179–188 |year=1936 |hdl=2440/15227|doi=10.1111/j.1469-1809.1936.tb02137.x |issue=2|url=https://digital.library.adelaide.edu.au/dspace/bitstream/2440/15227/1/138.pdf |hdl-access=free }} | ||
</ref><ref name="McLachlan:2004">{{cite book |title=विभेदक विश्लेषण और सांख्यिकीय पैटर्न पहचान|first1=G. J. |last1=McLachlan |publisher=Wiley Interscience |isbn=978-0-471-69115-0 |year=2004 |mr=1190469}}</ref> चूंकि, एनोवा श्रेणीबद्ध चर स्वतंत्र चर और एक सतत चर आश्रित चर के रूप में उपयोग करता है, जबकि विवेचक विश्लेषण में निरंतर स्वतंत्र चर होता है और एक श्रेणीबद्ध आश्रित चर अर्थात वर्ग लेबल के रूप में होता है।<ref>Analyzing Quantitative Data: An Introduction for Social Researchers, Debra Wetcher-Hendricks, p.288</ref> लॉजिस्टिक प्रतिगमन और [[प्रोबिट प्रतिगमन]] एनोवा की तुलना में एलडीए से अधिक मिलते-जुलते हैं, क्योंकि ये निरंतर स्वतंत्र चर के मूल्यों द्वारा एक श्रेणीगत चर की व्याख्या भी करते हैं। ये अन्य विधि उन अनुप्रयोगों में उत्तम हैं, जहां यह मान लेना उचित नहीं है, कि स्वतंत्र चर सामान्य रूप से वितरित किए जाते हैं, जो एलडीए पद्धति की एक मौलिक धारणा है। | |||
एलडीए | एलडीए [[ प्रमुख कंपोनेंट विश्लेषण | प्रमुख घटक विश्लेषण]] (पीसीए) और [[ कारक विश्लेषण | कारक विश्लेषण]] से काफी निकटता से संबंधित है, जिसमें वे दोनों चर के रैखिक संयोजनों की तलाश करते हैं, जो डेटा को सर्वोत्तम रूप से समझते हैं।।<ref name="Martinez:2001">{{cite journal |last1=Martinez |first1=A. M. |last2=Kak |first2=A. C. |title=पीसीए बनाम एलडीए|journal=[[IEEE Transactions on Pattern Analysis and Machine Intelligence]] |volume=23| issue = 2 |pages=228–233 |year=2001 |url=http://www.ece.osu.edu/~aleix/pami01.pdf |doi=10.1109/34.908974}}</ref> एलडीए स्पष्ट रूप से डेटा की कक्षाओं के बीच अंतर को मॉडल करने का प्रयास करता है। इसके विपरीत, पीसीए वर्ग किसी भी अंतर को ध्यान में नहीं रखता है और गुणक विश्लेषण समानता के बजाय मतभेदों पर आधारित फीचर संयोजन बनाता है।। विभेदक विश्लेषण भी कारक विश्लेषण से भिन्न है, क्योंकि यह एक अन्योन्याश्रित प्रद्योगिकी नहीं है:स्वतंत्र चरों तथा आश्रित चरों के बीच भेद को भी मानक चर कहा जाता है। | ||
एलडीए काम करता है जब प्रत्येक अवलोकन के लिए स्वतंत्र चर पर किए गए माप निरंतर मात्रा के रूप में होते हैं। स्पष्ट स्वतंत्र चर के साथ काम करते समय, समतुल्य प्रद्योगिकी भेदभावपूर्ण पत्राचार विश्लेषण के रूप में है।<ref name="Abdi 2007">Abdi, H. (2007) [http://www.utdallas.edu/~herve/Abdi-DCA2007-pretty.pdf "Discriminant correspondence analysis."] In: N.J. Salkind (Ed.): ''Encyclopedia of Measurement and Statistic''. Thousand Oaks (CA): Sage. pp. 270–275.</ref><ref name="Perriere 2003">{{cite journal | last1 = Perriere | first1 = G. | last2 = Thioulouse | first2 = J. | year = 2003 | title = बैक्टीरियल प्रोटीन के उपकोशिकीय स्थान की भविष्यवाणी करने के लिए पत्राचार विभेदक विश्लेषण का उपयोग| journal = Computer Methods and Programs in Biomedicine | volume = 70 | issue = 2| pages = 99–105 | doi=10.1016/s0169-2607(02)00011-1| pmid = 12507786 }}</ref> | |||
भेदभावपूर्ण विश्लेषण उस समय उपयोग किया जाता है, जब समूहों को प्राथमिकता [[क्लस्टर विश्लेषण]] के रूप में जाना जाता है। प्रत्येक मामले में एक मात्रात्मक भविष्यवक्ता उपायों पर एक अंक और एक समूह माप पर एक अंक होना चाहिए।<ref name="buy">Büyüköztürk, Ş. & Çokluk-Bökeoğlu, Ö. (2008). [https://ejer.com.tr/wp-content/uploads/2021/01/ejer_2008_issue_33.pdf Discriminant function analysis: Concept and application]. Egitim Arastirmalari - Eurasian Journal of Educational Research, 33, 73-92. </ref> सरल शब्दों में विवेचक संकल्पना विश्लेषण के रूप में चीजों को समूह वर्गों या एक ही प्रकार की श्रेणियों में बांटने की क्रिया का वर्गीकरण है। | |||
== इतिहास == | |||
1936 में सर [[रोनाल्ड फिशर]] द्वारा मूल द्विभाजित विभेदक विश्लेषण विकसित किया गया था।<ref name="cohen">Cohen et al. Applied Multiple Regression/Correlation Analysis for the Behavioural Sciences 3rd ed. (2003). Taylor & Francis Group.</ref> यह एक [[एनोवा]] या [[ परिवर्तन | मनोवा]] से भिन्न है, जिसका उपयोग एक या एक से अधिक स्वतंत्र श्रेणीबद्ध चर के रूप में किया जाता है। एक एनोवा या बहु मनोवा के निरंतर आश्रित चर की भविष्यवाणी करने के लिए किया जाता है। भेदभावपूर्ण कार्य विश्लेषण यह निर्धारित करने में उपयोगी है, कि श्रेणी सदस्यता की भविष्यवाणी करने में चर का एक सेट प्रभावी है या नहीं।<ref name="green">Green, S.B. Salkind, N. J. & Akey, T. M. (2008). [https://www.tandfonline.com/doi/pdf/10.1198/tas.2005.s139 Using SPSS for Windows and Macintosh: Analyzing and understanding data]. New Jersey: Prentice Hall.</ref> | |||
== दो वर्गों के लिए एलडीए == | == दो वर्गों के लिए एलडीए == | ||
टिप्पणियों के एक सेट पर विचार करें <math> { \vec x } </math> ज्ञात वर्ग के साथ किसी वस्तु या घटना के प्रत्येक नमूने के लिए (जिसे विशेषताएं | टिप्पणियों के एक सेट पर विचार करें <math> { \vec x } </math> ज्ञात वर्ग के साथ किसी वस्तु या घटना के प्रत्येक नमूने के लिए (जिसे विशेषताएं, चर या माप भी कहा जाता है)। <math>y</math>. नमूनों के इस सेट को [[ प्रशिक्षण सेट ]] कहा जाता है। वर्गीकरण समस्या तब वर्ग के लिए एक अच्छा भविष्यवक्ता खोजने की है <math>y</math> एक ही वितरण के किसी भी नमूने का आवश्यक नहीं कि प्रशिक्षण सेट से मात्र एक अवलोकन दिया गया हो <math> \vec x </math>.<ref name="Venables:2002">{{cite book |title=एस के साथ आधुनिक एप्लाइड सांख्यिकी|first1=W. N. |last1=Venables |first2=B. D. |last2=Ripley |author-link2=Brian Ripley |publisher=Springer Verlag |isbn=978-0-387-95457-8 |year=2002 |edition=4th}} | ||
</ref>{{rp|338}} | </ref>{{rp|338}} | ||
| Line 25: | Line 25: | ||
किसी और धारणा के बिना, परिणामी वर्गीकारक को [[द्विघात वर्गीकारक]] (QDA) के रूप में संदर्भित किया जाता है। | किसी और धारणा के बिना, परिणामी वर्गीकारक को [[द्विघात वर्गीकारक]] (QDA) के रूप में संदर्भित किया जाता है। | ||
एलडीए इसके अतिरिक्त | एलडीए इसके अतिरिक्त सरलीकृत समरूपता धारणा बनाता है अर्थात कि वर्ग सहप्रसरण समान हैं, इसलिए <math>\Sigma_0 = \Sigma_1 = \Sigma</math>) और यह कि सहप्रसरण की पूरी रैंक है। | ||
इस मामले में | |||
इस मामले में कई शर्तें रद्द: | |||
:<math> {\vec x}^\mathrm{T} \Sigma_0^{-1} \vec x = {\vec x}^\mathrm{T} \Sigma_1^{-1} \vec x</math> | :<math> {\vec x}^\mathrm{T} \Sigma_0^{-1} \vec x = {\vec x}^\mathrm{T} \Sigma_1^{-1} \vec x</math> | ||
:<math>{\vec x}^\mathrm{T} {\Sigma_i}^{-1} \vec{\mu}_i = {\vec{\mu}_i}^\mathrm{T}{\Sigma_i}^{-1} \vec x</math> क्योंकि <math>\Sigma_i</math> [[हर्मिटियन मैट्रिक्स]] | :<math>{\vec x}^\mathrm{T} {\Sigma_i}^{-1} \vec{\mu}_i = {\vec{\mu}_i}^\mathrm{T}{\Sigma_i}^{-1} \vec x</math> क्योंकि <math>\Sigma_i</math> [[हर्मिटियन मैट्रिक्स|हर्मिटियन आव्यूह]] है। | ||
और उपरोक्त निर्णय मानदंड के रूप में है। | |||
[[डॉट उत्पाद]] पर दहलीज बन जाता है। | |||
[[डॉट उत्पाद]] पर दहलीज बन जाता | |||
:<math> {\vec w}^\mathrm{T} \vec x > c </math> | :<math> {\vec w}^\mathrm{T} \vec x > c </math> | ||
| Line 39: | Line 41: | ||
:<math>\vec w = \Sigma^{-1} (\vec \mu_1 - \vec \mu_0)</math> | :<math>\vec w = \Sigma^{-1} (\vec \mu_1 - \vec \mu_0)</math> | ||
:<math> c = \frac12 \, {\vec w}^\mathrm{T} (\vec \mu_1 + \vec \mu_0)</math> | :<math> c = \frac12 \, {\vec w}^\mathrm{T} (\vec \mu_1 + \vec \mu_0)</math> | ||
इसका मतलब है कि एक इनपुट की कसौटी <math> \vec{ x }</math> एक कक्षा में होना <math>y</math> विशुद्ध रूप से ज्ञात प्रेक्षणों के इस रैखिक संयोजन का | इसका मतलब है कि एक इनपुट की कसौटी <math> \vec{ x }</math> एक कक्षा में होना <math>y</math> विशुद्ध रूप से ज्ञात प्रेक्षणों के इस रैखिक संयोजन के संकल्पना का रूप है। | ||
इस निष्कर्ष को ज्यामितीय दृष्टि से देखना अधिकांशतः उपयोगी होता है | वाई पूरी तरह से ज्ञात टिप्पणियों के इस रैखिक संयोजन का एक रूप है। | ||
इस निष्कर्ष को ज्यामितीय दृष्टि से देखना अधिकांशतः उपयोगी होता है, एक इनपुट की कसौटी <math> \vec{ x }</math> एक कक्षा में होना <math>y</math> विशुद्ध रूप से बहुआयामी अंतरिक्ष बिंदु के प्रक्षेपण का कार्य है <math> \vec{ x }</math> सदिश पर <math> \vec{ w }</math> इस प्रकार हम मात्र इसकी दिशा पर विचार करते हैं। दूसरे शब्दों में अवलोकन का है <math>y</math> यदि संगत है <math> \vec{ x }</math> के लंबवत अधिसमतल के एक निश्चित तरफ स्थित है। <math> \vec{ w }</math>. विमान का स्थान दहलीज द्वारा परिभाषित किया गया है <math>c</math>.जो कि के रूप में है। | |||
== अनुमान == | == अनुमान == | ||
विवेचक विश्लेषण की धारणाएं मनोवा के समान ही हैं। विश्लेषण आउटलेयर के प्रति पर्याप्त संवेदनशील है और सबसे छोटे समूह का | विवेचक विश्लेषण की धारणाएं मनोवा के समान ही हैं। विश्लेषण आउटलेयर के प्रति पर्याप्त संवेदनशील है और सबसे छोटे समूह का आकार भविष्यवाणी करने वाले चरों की संख्या से बड़ा होना चाहिए।।<ref name="buy"/> | ||
* बहुभिन्नरूपी सामान्य वितरण: समूहीकरण चर के प्रत्येक स्तर के लिए स्वतंत्र चर सामान्य होते हैं।<ref name="green"/><ref name="buy"/>*प्रसरण/सहप्रसरण की एकरूपता (समरूपता): | * बहुभिन्नरूपी सामान्य वितरण: समूहीकरण चर के प्रत्येक स्तर के लिए स्वतंत्र चर सामान्य होते हैं।<ref name="green"/><ref name="buy"/> | ||
*प्रसरण/सहप्रसरण की एकरूपता (समरूपता): सभी चरों के बीच भिन्नताएँ भविष्यवक्ताओं के स्तरों पर समान होती हैं।।बॉक्स के एम आंकड़ों के साथ परीक्षण किया जा सकता है ।<ref name="green" /> | |||
*चूंकि यह सुझाव दिया गया है कि सहप्रसरण समान होने पर रैखिक विभेदक विश्लेषण का उपयोग किया जाता है, और जब सहप्रसरण समान नहीं होते हैं तो द्विघात क्लासिफायर क्वाड्रैटिक विवेचक विश्लेषण का उपयोग किया जा सकता है।<ref name="buy" /> | |||
*बहुसंरेखता: पूर्वसूचक चरों के बीच बढ़े हुए सहसंबंध के साथ भविष्य कहनेवाला शक्ति घट सकती है।<ref name="buy" /> | |||
*[[सांख्यिकीय स्वतंत्रता|सांख्यिकीय स्वतंत्र]]: प्रतिभागियों को यादृच्छिक नमूना माना जाता है और एक चर पर एक प्रतिभागी का स्कोर अन्य सभी प्रतिभागियों के लिए उस चर पर स्कोर से स्वतंत्र माना जाता है।<ref name="green" /><ref name="buy" /> | |||
यह सुझाव दिया गया है कि भेदभावपूर्ण विश्लेषण इन मान्यताओं के | यह सुझाव दिया गया है कि भेदभावपूर्ण विश्लेषण इन मान्यताओं के मामूली उल्लंघनों के लिए अपेक्षाकृत मजबूत है,<ref>Lachenbruch, P. A. (1975). ''Discriminant analysis''. NY: Hafner</ref> और यह भी दिखाया गया है कि द्विबीजपत्री चरों का उपयोग करते समय विभेदक विश्लेषण अभी भी विश्वसनीय हो सकता है। जहां बहुभिन्नरूपी सामान्यता का अधिकांशतः उल्लंघन किया जाता है।<ref>Klecka, William R. (1980). ''Discriminant analysis''. Quantitative Applications in the Social Sciences Series, No. 19. Thousand Oaks, CA: Sage Publications.</ref> | ||
== भेदभावपूर्ण कार्य == | |||
विवेकशील विश्लेषण भविष्यवक्ताओं के एक या अधिक रैखिक संयोजन बनाकर काम करता है, प्रत्येक संकल्पना के लिए एक नया [[अव्यक्त चर]] बन जाता है। इन कार्यों को विभेदक कार्य कहा जाता है। संभव कार्यों की संख्या या तो है <math>N_g-1</math> जहाँ <math>N_g</math> = समूहों की संख्या, या <math>p</math> भविष्यवक्ताओं की संख्या है, जो कि छोटा हैइस संकल्पना ने बनाया है। पहला संकल्पना उस संकल्पना के समूहों के बीच के अंतर को अधिकतम करता है। दूसरा संकल्पना उस संकल्पना के अंतर को अधिकतम करता है, लेकिन पिछले संकल्पना के साथ सहसंबद्ध भी नहीं होना चाहिए। यह बाद के कार्यों के साथ इन आवश्यकता के साथ जारी रहता है, कि नया कार्य पिछले कार्यों में से किसी के साथ सहसंबद्ध न हो सके । | |||
दिया गया समूह <math>j</math>, साथ <math>\mathbb{R}_j</math> नमूना स्थान के सेट, एक भेदभावपूर्ण नियम है जैसे कि यदि <math>x \in\mathbb{R}_j</math>, तब <math>x\in j</math>. भेदभावपूर्ण विश्लेषण तब, के "भोजन" क्षेत्रों को खोजें <math>\mathbb{R}_j</math> वर्गीकरण त्रुटि को कम करने के लिए, इसलिए वर्गीकरण तालिका में उच्च प्रतिशत सही वर्गीकृत करने के लिए अग्रणी होता है।<ref>Hardle, W., Simar, L. (2007). ''Applied Multivariate Statistical Analysis''. Springer Berlin Heidelberg. pp. 289–303.</ref> | |||
प्रत्येक संकल्पना को एक विवेकशील स्कोर दिया जाता है,{{clarify|date=April 2019}} यह निर्धारित करने के लिए कि यह समूह प्लेसमेंट की कितनी अच्छी भविष्यवाणी करता है। | |||
प्रत्येक | *संरचना सहसंबंध गुणांक: प्रत्येक भविष्यवक्ता और प्रत्येक संकल्पना के विवेचक स्कोर के बीच सहसंबंध होता है। यह एक शून्य क्रम सहसंबंध है अर्थात अन्य भविष्यवक्ताओं के लिए सही नहीं होता है ।<ref>Garson, G. D. (2008). Discriminant function analysis. https://web.archive.org/web/20080312065328/http://www2.chass.ncsu.edu/garson/pA765/discrim.htm.</ref> | ||
*संरचना सहसंबंध गुणांक: प्रत्येक भविष्यवक्ता और प्रत्येक | *मानकीकृत गुणांक: रैखिक संयोजन में प्रत्येक भविष्यवक्ता का वजन जो कि विभेदक कार्य है। एक प्रतिगमन समीकरण की तरह ये गुणांक आंशिक हैं अर्थात अन्य भविष्यवक्ताओं के लिए सही हैं। समूह असाइनमेंट की भविष्यवाणी करने में प्रत्येक भविष्यवक्ता के अद्वितीय योगदान को इंगित करता है। | ||
*मानकीकृत गुणांक: रैखिक संयोजन में प्रत्येक भविष्यवक्ता का वजन जो कि विभेदक कार्य है। एक प्रतिगमन समीकरण की | *ग्रुप सेंट्रोइड्स पर कार्य: प्रत्येक संकल्पना के लिए ग्रुपिंग चर के लिए औसत विभेदक के रूप में स्कोर दिए गए हैं।। साधन जितने दूर होंगे, वर्गीकरण में त्रुटि उतनी ही कम होगी। | ||
*ग्रुप सेंट्रोइड्स पर कार्य: प्रत्येक ग्रुपिंग | |||
== | == डिस्क्रिमिनेशननियम == | ||
*अधिकतम संभावना: असाइन करें <math>x</math> उस समूह के लिए जो जनसंख्या (समूह) घनत्व को अधिकतम करता है।<ref name="har">Hardle, W., Simar, L. (2007). ''[https://pdfs.semanticscholar.org/e49a/3ed1560a0979f5ca0146c1aca7ef98e64af7.pdf Applied Multivariate Statistical Analysis]''. Springer Berlin Heidelberg. pp. 289-303.</ref> | *अधिकतम संभावना: असाइन करें <math>x</math> उस समूह के लिए जो जनसंख्या (समूह) घनत्व को अधिकतम करता है।<ref name="har">Hardle, W., Simar, L. (2007). ''[https://pdfs.semanticscholar.org/e49a/3ed1560a0979f5ca0146c1aca7ef98e64af7.pdf Applied Multivariate Statistical Analysis]''. Springer Berlin Heidelberg. pp. 289-303.</ref> | ||
*बेयस डिस्क्रिमिनेंट रूल: असाइन करता है <math>x</math> | *बेयस डिस्क्रिमिनेंट रूल: असाइन करता है <math>x</math> उस समूह के लिए जो अधिकतम करता है, <math>\pi_i f_i(x)</math> जहां πi उस वर्गीकरण की [[पूर्व संभावना]] का प्रतिनिधित्व करता है, और <math>f_i(x)</math> जनसंख्या घनत्व का प्रतिनिधित्व करता है।<ref name="har"/> | ||
*फिशर का रेखीय विविक्तकर नियम: एसएस के बीच अनुपात को अधिकतम करता है और एस.एस समूह की भविष्यवाणी करने के लिए भविष्यवक्ताओं का एक रैखिक संयोजन पाता है।<ref name="har" /> | |||
== अभिलक्षणिक मान == | |||
विवेचक विश्लेषण में एक अभिलाक्षणिक मान प्रत्येक संकल्पना की विशेष जड़ होती है।{{clarify|date=April 2012}} यह इस बात का संकेत है, कि यह संकल्पना समूहों को कितनी अच्छी प्रकार से भिन्न करता है, जहां अभिलाक्षणिक मान जितना बड़ा होता है, उतना ही उत्तम संकल्पना को भिन्न करता है।<ref name="buy"/>चूंकि इसे सावधानी के साथ समझा जाना चाहिए, क्योंकि अभिलाक्षणिक मान की कोई ऊपरी सीमा नहीं है।<ref name="green"/><ref name="buy"/> | |||
इस प्रकार अभिलाक्षणिक मान को एनोवा के रूप में एसएस के बीच में और एस.एस के अंदर अनुपात के रूप में देखा जा सकता है,जब आश्रित चर विवेकशील के रूप में कार्य करता है, और समूह [[वाद्य चर]] स्तर के रूप में होते हैं,{{clarify|date=April 2012}}.<ref name="green" />इसका मतलब यह है कि सबसे बड़ा अभिलाक्षणिक मान पहले संकल्पनाके साथ जुड़ा हुआ है, दूसरा सबसे बड़ा दूसरे के साथ आदि। | |||
== प्रभाव बनावट == | == प्रभाव बनावट == | ||
कुछ सुझाव देते हैं कि | कुछ सुझाव देते हैं कि प्रभावी आकार उपायों के रूप में अभिलाक्षणिक मान उपयोग किया जाता है, चूंकि, यह सामान्यतः समर्थित नहीं है।<ref name="green"/>इसके अतिरिक्त, [[विहित सहसंबंध]] प्रभावी आकार का पसंदीदा उपाय है। यह अभिलाक्षणिक मान के समान है, लेकिन एस.एस के बीच और एस.एस के कुल अनुपात का वर्गमूल है।. यह समूहों और कार्यों के बीच संबंध है।<ref name="green"/> | ||
प्रभाव आकार का एक अन्य लोकप्रिय उपाय प्रत्येक संकल्पना के लिए विचरण स्पष्टीकरण आवश्यकता का प्रतिशत है।{{clarify|date=April 2012}} प्रत्येक संकल्पना के लिए इसकी गणना इस प्रकार की जाती है: (λ<sub>x</sub>/ क्रम<sub>i</sub>) एक्स 100 जहां λ<sub>x</sub>फ़ंक्शन और Σλ के लिए अभिलाक्षणिक मान है, और Σλi सभी अभिलाक्षणिक मान का योग है। यह हमें बताता है कि अन्य कार्यों की तुलना में उस विशेष कार्य के लिए भविष्यवाणी कितनी मजबूत है।<ref name="green" /> | |||
सही ढंग से वर्गीकृत प्रतिशत का प्रभाव आकार के रूप में भी विश्लेषण किया जा सकता है। कप्पा मूल्य इस बात का वर्णन कर सकता है, कि आकस्मिक करार में सुधार होता है।कप्पा एक बहुत अच्छे या खराब प्रदर्शन वाले वर्गों द्वारा पक्षपातपूर्ण होने के बजाय सभी श्रेणियों में सामान्य बनाता है। स्पष्टीकरण की आवश्यकता होती है।<ref name="green" />{{clarify|date=April 2012|reason=Kappa normalizes across all categorizes rather than biased by a significantly good or poorly performing classes|text=Kappa normalizes across all categorizes rather than biased by a significantly good or poorly performing classes.|pre-text=|post-text=}}<ref>{{Cite journal|last=Israel|first=Steven A.|date=June 2006|title=Performance Metrics: How and When|journal=Geocarto International|volume=21|issue=2|pages=23–32|doi=10.1080/10106040608542380|s2cid=122376081|issn=1010-6049}}</ref> | |||
== के वर्गों के लिए विहित विभेदक विश्लेषण == | == के वर्गों के लिए विहित विभेदक विश्लेषण == | ||
कैनोनिकल डिस्क्रिमिनेंट एनालिसिस ( | कैनोनिकल डिस्क्रिमिनेंट एनालिसिस (सीडीए) अक्षों को पाता है, (k − 1 कैनोनिकल निर्देशांक, k वर्गों की संख्या है) जो श्रेणियों को उत्तम प्रकार से भिन्न करते हैं। ये रैखिक कार्य असंबद्ध हैं और वास्तव में डेटा के एन आयामी बादल के माध्यम से एक इष्टतम k − 1 स्थान को प्रभावी रूप से परिभाषित करते हैं, जो k समूहों के उस स्थान में अनुमानों को सबसे अच्छी प्रकार से भिन्न करता है। नीचे विवरण के लिए "मल्टीक्लास एलडीए"के रूप में देखें। | ||
== फिशर का रैखिक विवेचक == | == फिशर का रैखिक विवेचक == | ||
फ़िशर के रैखिक विवेचक और | फ़िशर के रैखिक विवेचक और एलडीए शब्द अधिकांशतः एक दूसरे के स्थान पर उपयोग किया जाता है, चूंकि रोनाल्ड ए फ़िशर का मूल लेख होता है <ref name="Fisher:1936" />वास्तव में थोड़ा भिन्न डिस्क्रिमिनेशनका वर्णन करता है, जो एलडीए की कुछ धारणाओं को नहीं बनाता है, जैसे कि [[सामान्य वितरण]] वर्ग या समान वर्ग सहप्रसरण होता है। | ||
मान लीजिए कि टिप्पणियों के दो वर्गों का मतलब है <math> \vec \mu_0, \vec \mu_1 </math> और सहप्रसरण <math>\Sigma_0,\Sigma_1 </math>. फिर सुविधाओं का रैखिक संयोजन <math> {\vec w}^\mathrm{T} \vec x </math> साधन होंगे <math> {\vec w}^\mathrm{T} \vec \mu_i </math> और प्रसरण <math> {\vec w}^\mathrm{T} \Sigma_i \vec w </math> के लिए <math> i=0,1 </math>. फिशर ने इन दो संभाव्यता वितरण के बीच भिन्नता के वर्गों के बीच भिन्नता के अनुपात के रूप में परिभाषित किया जाता है। | |||
:<math>S=\frac{\sigma_{\text{between}}^2}{\sigma_{\text{within}}^2}= \frac{(\vec w \cdot \vec \mu_1 - \vec w \cdot \vec \mu_0)^2}{{\vec w}^\mathrm{T} \Sigma_1 \vec w + {\vec w}^\mathrm{T} \Sigma_0 \vec w} = \frac{(\vec w \cdot (\vec \mu_1 - \vec \mu_0))^2}{{\vec w}^\mathrm{T} (\Sigma_0+\Sigma_1) \vec w} </math> | :<math>S=\frac{\sigma_{\text{between}}^2}{\sigma_{\text{within}}^2}= \frac{(\vec w \cdot \vec \mu_1 - \vec w \cdot \vec \mu_0)^2}{{\vec w}^\mathrm{T} \Sigma_1 \vec w + {\vec w}^\mathrm{T} \Sigma_0 \vec w} = \frac{(\vec w \cdot (\vec \mu_1 - \vec \mu_0))^2}{{\vec w}^\mathrm{T} (\Sigma_0+\Sigma_1) \vec w} </math> | ||
यह उपाय, कुछ अर्थों में, | यह उपाय, कुछ अर्थों में, वर्ग लेबलिंग के लिए संकेत-ध्वनि अनुपात का माप होता है। यह दिखाया जा सकता है कि अधिकतम पृथक्करण तब होता है, | ||
:<math> \vec w \propto (\Sigma_0+\Sigma_1)^{-1}(\vec \mu_1 - \vec \mu_0) </math> | :<math> \vec w \propto (\Sigma_0+\Sigma_1)^{-1}(\vec \mu_1 - \vec \mu_0) </math> | ||
जब एलडीए की धारणाएं संतुष्ट होती हैं, तो उपरोक्त समीकरण एलडीए के समतुल्य होता है। | जब एलडीए की धारणाएं संतुष्ट होती हैं, तो उपरोक्त समीकरण एलडीए के समतुल्य होता है। | ||
[[File:Fisher2classes.png|thumb|फिशर का रेखीय विभेदक एक अक्ष के रूप में देखा गया]]ध्यान दें कि | [[File:Fisher2classes.png|thumb|फिशर का रेखीय विभेदक एक अक्ष के रूप में देखा गया]]ध्यान दें कि सदिश <math>\vec w</math> विवेचक [[ hyperplane | हाइपरप्लेन]] के लिए [[सतह सामान्य]] है। एक उदाहरण के रूप में, दो आयामी समस्या में, दो समूहों को विभाजित करने वाली रेखा लंबवत होती है <math>\vec w</math>. | ||
सामान्यतः, | सामान्यतः, डिस्क्रिमिनेशनकिए जाने वाले डेटा बिंदुओं को प्रक्षेपित किया जाता है, <math>\vec w</math>; फिर एक आयामी वितरण के विश्लेषण से डेटा को सबसे भिन्न करने वाली सीमा को चुना जाता है। दहलीज के लिए कोई सामान्य नियम नहीं है। चूंकि, यदि दोनों कक्षाओं के बिंदुओं के अनुमान लगभग समान वितरण प्रदर्शित करता है, तो एक अच्छा विकल्प दो साधनों के अनुमानों के बीच हाइपरप्लेन होगा, <math>\vec w \cdot \vec \mu_0 </math> और <math>\vec w \cdot \vec \mu_1 </math>. इस स्थिति में पैरामीटर c दहलीज स्थिति में है <math> \vec w \cdot \vec x > c </math> स्पष्ट रूप से पाया जा सकता है। | ||
:<math> c = \vec w \cdot \frac12 (\vec \mu_0 + \vec \mu_1) = \frac{1}{2} \vec\mu_1^\mathrm{T} \Sigma^{-1}_{1} \vec\mu_1 - \frac{1}{2} \vec\mu_0^\mathrm{T} \Sigma^{-1}_{0} \vec\mu_0 </math>. | :<math> c = \vec w \cdot \frac12 (\vec \mu_0 + \vec \mu_1) = \frac{1}{2} \vec\mu_1^\mathrm{T} \Sigma^{-1}_{1} \vec\mu_1 - \frac{1}{2} \vec\mu_0^\mathrm{T} \Sigma^{-1}_{0} \vec\mu_0 </math>. | ||
ओत्सु की विधि फिशर के रेखीय विवेचक से संबंधित है, और एक ग्रेस्केल छवि में पिक्सेल के हिस्टोग्राम को | ओत्सु की विधि फिशर के रेखीय विवेचक से संबंधित है, और एक ग्रेस्केल छवि में पिक्सेल के हिस्टोग्राम को एक काली/सफेद थ्रेसहोल्ड को चुनने के लिए बनाया गया है, जो कि इंट्रा-क्लास विचरण को कम करता है और काले और सफेद पिक्सेल कक्षाओं को दिये गये होते है, ग्रेस्केल के भीतर / बीच अंतर-वर्ग विचरण को अधिकतम करता है। | ||
== मल्टीक्लास एलडीए == | == मल्टीक्लास एलडीए == | ||
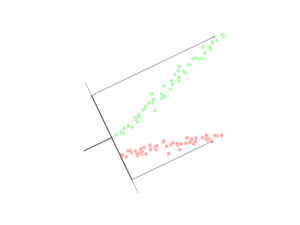
[[File:4class3ddiscriminant.png|thumb|3डी में 4 वर्गों के लिए एक-बनाम-सभी एलडीए अक्षों के लिए विज़ुअलाइज़ेशन]] | [[File:4class3ddiscriminant.png|thumb|3डी में 4 वर्गों के लिए एक-बनाम-सभी एलडीए अक्षों के लिए विज़ुअलाइज़ेशन]] | ||
[[File:3dProjections.png|thumb|4 वर्गों के लिए रेखीय विवेचक अक्षों के साथ प्रक्षेपण]]ऐसे मामले में जहां दो से अधिक वर्ग हैं, फिशर विवेचक की व्युत्पत्ति में उपयोग किए गए विश्लेषण को एक रेखीय उप | [[File:3dProjections.png|thumb|4 वर्गों के लिए रेखीय विवेचक अक्षों के साथ प्रक्षेपण]]ऐसे मामले में जहां दो से अधिक वर्ग हैं, फिशर विवेचक की व्युत्पत्ति में उपयोग किए गए विश्लेषण को एक रेखीय उप स्थान खोजने के लिए विस्तारित किया जा सकता है, जो कि सभी वर्ग परिवर्तनशीलता को समाहित करता प्रतीत होता है।<ref name="garson">Garson, G. D. (2008). Discriminant function analysis. {{cite web |url=http://www2.chass.ncsu.edu/garson/pa765/discrim.htm |title=PA 765: Discriminant Function Analysis |access-date=2008-03-04 |url-status=dead |archive-url=https://web.archive.org/web/20080312065328/http://www2.chass.ncsu.edu/garson/pA765/discrim.htm |archive-date=2008-03-12 }} .</ref> यह सामान्यीकरण सी. आर. राव के कारण है।<ref name="Rao:1948">{{cite journal |last=Rao |first=R. C. |author-link=Calyampudi Radhakrishna Rao |title=जैविक वर्गीकरण की समस्याओं में बहु मापन का उपयोग|journal=Journal of the Royal Statistical Society, Series B |volume=10 |issue=2 |pages=159–203 |year=1948 |jstor=2983775}}</ref> मान लीजिए कि प्रत्येक C वर्ग का माध्य है <math> \mu_i </math> और वही सहप्रसरण <math> \Sigma </math> .के साथ तब वर्ग परिवर्तनशीलता के बीच बिखराव को वर्ग माध्य के नमूना सहप्रसरण द्वारा परिभाषित किया जा सकता है। | ||
:<math> \Sigma_b = \frac{1}{C} \sum_{i=1}^C (\mu_i-\mu) (\mu_i-\mu)^\mathrm{T} </math> | :<math> \Sigma_b = \frac{1}{C} \sum_{i=1}^C (\mu_i-\mu) (\mu_i-\mu)^\mathrm{T} </math> | ||
जहां <math> \mu </math> वर्ग का माध्य है। एक दिशा में वर्ग जुदाई <math> \vec w </math> इस मामले में दिया जाएगा | |||
:<math> S = \frac{{\vec w}^\mathrm{T} \Sigma_b \vec w}{{\vec w}^\mathrm{T} \Sigma \vec w} </math> | :<math> S = \frac{{\vec w}^\mathrm{T} \Sigma_b \vec w}{{\vec w}^\mathrm{T} \Sigma \vec w} </math> | ||
इसका मतलब है कि जब <math> \vec w </math> का [[आइजन्वेक्टर]] है <math> \Sigma^{-1} \Sigma_b </math> पृथक्करण संगत | इसका मतलब है कि जब <math> \vec w </math> का [[आइजन्वेक्टर|अभिलक्षणिक सदिश]] है <math> \Sigma^{-1} \Sigma_b </math> पृथक्करण संगत अभिलाक्षणिक मान के समतुल्य होगा। | ||
चूंकि <math> \Sigma^{-1} \Sigma_b </math> विकर्णीय है, सुविधाओं के बीच परिवर्तनशीलता सी − 1 सबसे बड़े | चूंकि <math> \Sigma^{-1} \Sigma_b </math> का विकर्णीय किया जा सकता है, सुविधाओं के बीच परिवर्तनशीलता सी − 1 सबसे बड़े अभिलाक्षणिक मान के अनुरूप पैरामीटर के आकार में समाहित किया जाएगा. चूंकि <math> \Sigma_b </math> अधिक से अधिक रैंक C − 1 का है। ये ईगेन सदिश मुख्य रूप से पीसीए के प्रकार के फीचर रिडक्शन में उपयोग किए जाते हैं। छोटे अभिलाक्षणिक मान के अनुरूप ईगेंवैक्टर प्रशिक्षण डेटा की उपयुक्त पसंद के प्रति बहुत संवेदनशील होते हैं, और अगले खंड में वर्णित नियमितीकरण का उपयोग करना अधिकांशतः आवश्यक होता है. | ||
यदि | यदि [[आयाम में कमी]] के अतिरिक्त, वर्गीकरण की आवश्यकता होती है, तो कई वैकल्पिक प्रद्योगिकी के रूप में उपलब्ध हैं। उदाहरण के लिए, वर्गों को विभाजित किया जा सकता है, और प्रत्येक विभाजन को वर्गीकृत करने के लिए एक मानक फिशर डिस्क्रिमिनेंट या एलडीए का उपयोग किया जाता है। इसका एक सामान्य उदाहरण "एक बनाम बाकी" है, जहां एक वर्ग के अंक एक समूह में रखे जाते हैं, और बाकी सब दूसरे में और फिर एलडीए लागू होता है। इसका परिणाम सी क्लासिफायर होगा, जिसके परिणाम संयुक्त होंगे। | ||
एक अन्य सामान्य विधि जोड़ीदार वर्गीकरण है जहां प्रत्येक वर्ग के जोड़े के लिए एक नया वर्गीकारक बनाया जाता है,जिसमें कुल मिलाकर कुल C(C − 1)/2 वर्गीकारक होते हैं। एक अंतिम वर्गीकरण तैयार करने के लिए भिन्न-भिन्न वर्गीकारकों संयोजन के साथ होते हैं। | |||
== इंक्रीमेंटल एलडीए == | == इंक्रीमेंटल एलडीए == | ||
एलडीए | एलडीए प्रद्योगिकी के विशिष्ट कार्यान्वयन के लिए सभी नमूने अग्रिम में उपलब्ध होने की आवश्यकता होती है.। चूंकि ऐसी स्थितियाँ होती हैं जहाँ संपूर्ण डेटा सेट उपलब्ध नहीं होता है और इनपुट डेटा को एक धारा के रूप में देखा जाता है। इस स्थिति में यह एलडीए सुविधा निष्कर्षण के लिए यह वांछनीय है कि पूरे डेटा सेट पर एल्गोरिथ्म को चलाए बिना नए नमूनों को देखकर गणना की गई है,एलडीए विशेषताओं को अद्यतन करने की क्षमता रखने के लिए वांछनीय होती है। उदाहरण के लिए, वास्तविक समय में मोबाइल रोबोटिक्स जैसे अनुप्रयोगों में नए प्रेक्षण उपलब्ध होते ही एक्सट्रेक्ट किए गए एवास्तविक समय में मोबाइल रोबोटिक्स जैसे अनुप्रयोगों में नए प्रेक्षण उपलब्ध होते ही एक्सट्रेक्ट किए गए एल. डी. ए. फीचर को अपडेट करना महत्वपूर्ण है। एक एल. डी. ए. विशेषता निष्कर्षण प्रद्योगिकी जो सिर्फ नए नमूने देख कर एल. डी. ए. सुविधाओं को अद्यतन कर सकते हैं, एक वृद्धिशील एल. डी. ए. एल्गोरिथ्म है और इस विचार का पिछले दो दशकों में बड़े पैमाने पर अध्ययन किया गया है।<ref name=":0">{{Cite journal|title = तेजी से वृद्धिशील एलडीए सुविधा निष्कर्षण|journal = Pattern Recognition|date = 2015-06-01|pages = 1999–2012|volume = 48|issue = 6|doi = 10.1016/j.patcog.2014.12.012|first1 = Youness|last1 = Aliyari Ghassabeh|first2 = Frank|last2 = Rudzicz|first3 = Hamid Abrishami|last3 = Moghaddam|bibcode = 2015PatRe..48.1999A}}</ref> चटर्जी और रॉयचौधरी ने एलडीए सुविधाओं को अद्यतन करने के लिए एक वृद्धिशील स्वयं संगठित एलडीए कलन विधिप्रस्तावित किया।<ref name=":1">{{Cite journal|title = वर्ग-विभाजन सुविधाओं के लिए स्व-संगठित एल्गोरिदम और नेटवर्क पर|journal = IEEE Transactions on Neural Networks|date = 1997-05-01|issn = 1045-9227|pages = 663–678|volume = 8|issue = 3|doi = 10.1109/72.572105|pmid = 18255669|first1 = C.|last1 = Chatterjee|first2 = V.P.|last2 = Roychowdhury}}</ref> अन्य कार्य में, डेमिर और ओजमेमेट ने त्रुटि-सुधार और हेब्बियन सीखने के नियमों का उपयोग करते हुए एलडीए सुविधाओं को अद्यतन करने के लिए ऑनलाइन स्थानीय शिक्षण एल्गोरिदम प्रस्तावित किया।<ref>{{Cite journal|title = रैखिक विभेदक विश्लेषण के लिए ऑनलाइन स्थानीय शिक्षण एल्गोरिदम|journal = Pattern Recognit. Lett.|date = 2005-03-01|issn = 0167-8655|pages = 421–431|volume = 26|issue = 4|doi = 10.1016/j.patrec.2004.08.005|first1 = G. K.|last1 = Demir|first2 = K.|last2 = Ozmehmet|bibcode = 2005PaReL..26..421D}}</ref> बाद में, अलियारी एट अल के नए नमूने देखकर एलडीए सुविधाओं को अद्यतन करने के लिए तेजी से वृद्धिशील एल्गोरिदम व्युत्पन्न किया गया था ।<ref name=":0" /> | ||
== व्यावहारिक उपयोग == | |||
व्यवहार में वर्ग का अर्थ और सहप्रसरण ज्ञात नहीं हैं। चूंकि,प्रशिक्षण सेट से इनका अनुमान लगाया जा सकता है। उपरोक्त समीकरणों में उपयुक्त मान के स्थान पर या तो [[अधिकतम संभावना अनुमान]] या अधिकतम पश्च अनुमान का उपयोग किया जा सकता है। चूंकि सहप्रसरण के अनुमानों को कुछ अर्थों में इष्टतम माना जा सकता है, इसका मतलब यह नहीं है कि इन मूल्यों को प्रतिस्थापित करके प्राप्त परिणामी विवेचक किसी भी अर्थ में इष्टतम है, भले ही सामान्य रूप से वितरित वर्गों की धारणा सही हो सकती है। | |||
एलडीए और फिशर के विवेचक को वास्तविक डेटा पर लागू करने में एक और जटिलता तब होती है, जब प्रत्येक नमूने के माप की संख्या अर्थात प्रत्येक डेटा सदिश की आयाम प्रत्येक कक्षा में नमूनों की संख्या से अधिक हो जाती है।<ref name="Martinez:2001" />इस मामले में सहप्रसरण अनुमानों की पूरी रैंक नहीं होती है और इसलिए इसे उल्टा नहीं किया जा सकता है। इससे निपटने के कई तरीके हैं। उपरोक्त सूत्रों में सामान्य आव्यूह व्युत्क्रम के अतिरिक्त छद्म व्युत्क्रम का उपयोग करना है। चूंकि, उत्तम संख्यात्मक स्थिरता प्राप्त करने के लिए सबसे पहले समस्या के सबस्पेस को प्रक्षेपित करते हुए किया जा सकता है।<math> \Sigma_b </math>.<ref>{{cite journal | last1 = Yu | first1 = H. | last2 = Yang | first2 = J. | year = 2001 | title = A direct LDA algorithm for high-dimensional data — with application to face recognition | journal = Pattern Recognition | volume = 34 | issue = 10| pages = 2067–2069 | doi=10.1016/s0031-3203(00)00162-x| bibcode = 2001PatRe..34.2067Y | citeseerx = 10.1.1.70.3507 }}</ref> | |||
छोटे नमूने के बनावट से निपटने के लिए एक अन्य रणनीति सहप्रसरण आव्यूह के [[संकोचन अनुमानक]] का उपयोग होता है। | |||
जिसे गणितीय रूप में व्यक्त किया जा सकता है। | |||
गणितीय रूप में व्यक्त किया जा सकता | |||
:<math> \Sigma = (1-\lambda) \Sigma+\lambda I\,</math><!-- TeX --> | :<math> \Sigma = (1-\lambda) \Sigma+\lambda I\,</math><!-- TeX --> | ||
जहाँ <math> I </math> आइडेंटिटीआव्यूह है, और <math> \lambda </math> संकोचन तीव्रता या नियमितीकरण पैरामीटर है। | |||
यह नियमित विभेदक विश्लेषण के ढांचे की ओर जाता | |||
यह नियमित विभेदक विश्लेषण के ढांचे की ओर ले जाता है।<ref name="Friedman:2001">{{cite journal |last=Friedman |first=J. H. |title=नियमित विभेदक विश्लेषण|journal=[[Journal of the American Statistical Association]] |volume=84 |issue=405 |pages=165–175 |year=1989 |url=http://www.slac.stanford.edu/cgi-wrap/getdoc/slac-pub-4389.pdf |doi=10.2307/2289860 |jstor=2289860 |mr=0999675|citeseerx=10.1.1.382.2682 }}</ref> या संकोचन विभेदक विश्लेषण होता है ।<ref>{{cite journal | last1 = Ahdesmäki | first1 = M. | last2 = Strimmer | first2 = K. | year = 2010 | title = कैट स्कोर और फाल्स नॉनडिस्कवरी रेट कंट्रोल का उपयोग करते हुए ओमिक्स भविष्यवाणी समस्याओं में फीचर चयन| journal = Annals of Applied Statistics | volume = 4 | issue = 1| pages = 503–519 | doi=10.1214/09-aoas277| arxiv = 0903.2003 | s2cid = 2508935 }}</ref> | |||
कई व्यावहारिक मामलों में रैखिक विवेचक उपयुक्त नहीं होते हैं। एलडीए और फिशर के विवेचक को [[कर्नेल चाल]] के माध्यम से गैर-रैखिक वर्गीकरण में उपयोग के लिए बढ़ाया जा सकता है। यहां, मूल प्रेक्षणों को प्रभावी रूप से एक उच्च आयामी गैर रैखिक अंतरिक्ष में प्रतिचित्रित किया गया है। इस गैर रैखिक स्थान में रैखिक वर्गीकरण फिर मूल स्थान में गैर रैखिक वर्गीकरण के समतुल्य होता है। इसका सबसे अधिक उपयोग किया जाने वाला उदाहरण कर्नेल [[एकाधिक विभेदक विश्लेषण]] होता है। | |||
एलडीए को कई विभेदक विश्लेषणों के लिए सामान्यीकृत किया जा सकता है, जहां सी मात्र दो के अतिरिक्त एन संभावित राज्यों के साथ एक श्रेणीबद्ध चर बन जाता है। अनुरूप रूप से | एलडीए को कई विभेदक विश्लेषणों के लिए सामान्यीकृत किया जा सकता है, जहां सी मात्र दो के अतिरिक्त एन संभावित राज्यों के साथ एक श्रेणीबद्ध चर बन जाता है। जिसे अनुरूप रूप से यदि वर्ग-सशर्त घनत्व <math>p(\vec x\mid c=i)</math> साझा सहप्रसरण के साथ सामान्य होता हैं, [[पर्याप्त आँकड़ा]] <math>P(c\mid\vec x)</math> एन अनुमानों के मूल्य हैं, जो एन साधनों द्वारा फैलाए गए रैखिक उप-स्थान हैं, व्युत्क्रम सहप्रसरण आव्यूह द्वारा परिशोधित परिवर्तन। इन अनुमानों को एक आव्यूह सामान्यीकृत अभिलाक्षणिक मान समस्या को हल करके पाया जा सकता है, ईजेन डीकंपोजीशन होता है, जो नमूनों के माध्यम से मापन से तैयार किया जाता है, और हर भाग में साझा सहप्रसविताआव्यूह होता है। विवरण के लिए ऊपर "मल्टीक्लास एलडीए" के रूप में देखें। | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
नीचे दिए गए उदाहरणों के अतिरिक्त, एलडीए को [[ स्थिति (विपणन) ]] और [[उत्पाद प्रबंधन]] में लागू किया जाता है। | नीचे दिए गए उदाहरणों के अतिरिक्त, एलडीए को [[ स्थिति (विपणन) | स्थिति (मार्केटिंग)]] और [[उत्पाद प्रबंधन]] में लागू किया जाता है। | ||
=== दिवालियापन की भविष्यवाणी === | === दिवालियापन की भविष्यवाणी === | ||
लेखा अनुपात और अन्य वित्तीय चर के आधार पर दिवालियापन की भविष्यवाणी में, रैखिक विभेदक विश्लेषण व्यवस्थित रूप से यह समझाने के लिए लागू किया गया | लेखा अनुपात और अन्य वित्तीय चर के आधार पर दिवालियापन की भविष्यवाणी में, रैखिक विभेदक विश्लेषण व्यवस्थित रूप से यह समझाने के लिए था। कि प्रथम सांख्यिकीय पद्धति के रूप में लागू किया गया था।जिसका इस्तेमाल दिवालियापन बनाम अस्तित्व में था।एलडीए के सामान्य वितरण मान्यताओं के अनुरूप लेखा करण अनुपात की अनदेखी के बावजूद, [[एडवर्ड ऑल्टमैन]] का [[जेड-स्कोर वित्तीय विश्लेषण उपकरण]] अभी भी व्यावहारिक उपयोग में अभी भी अग्रणी मॉडल के रूप में है। | ||
=== | === फेसेस की पहचान === | ||
कम्प्यूटरीकृत [[चेहरे की पहचान प्रणाली]] में, प्रत्येक | कम्प्यूटरीकृत [[चेहरे की पहचान प्रणाली|फेसेस की आइडेंटिटी प्रणाली]] में, प्रत्येक फेसेस को बड़ी संख्या में पिक्सेल मानों द्वारा प्रदर्शित किया जाता है। रेखीय डिस्क्रिमिनेशन विश्लेषण का प्रमुख रूप से प्रयोग वर्गीकरण से पूर्व लक्षणों की संख्या को अधिक प्रबंधनीय संख्या में घटाने के लिए किया जाता है। प्रत्येक नया आयाम पिक्सेल मानों का एक रैखिक संयोजन है, जो एक टेम्पलेट का निर्माण करता है। फिशर के रैखिक विवेचक का उपयोग करके प्राप्त रैखिक संयोजनों को फिशर फेसेस कहा जाता है, जबकि संबंधित प्रमुख घटक विश्लेषण के उपयोग से प्राप्त रेखीय संयोजनों को ईजीफेसेस कहा जाता है। | ||
=== मार्केटिंग === | === मार्केटिंग === | ||
मार्केटिंगमें, भेदभावपूर्ण विश्लेषण का उपयोग अधिकांशतः उन कारकों को निर्धारित करने के लिए किया जाता था, जो विभिन्न प्रकार के ग्राहकों और उत्पादों को सर्वेक्षण या अन्य प्रकार के एकत्रित डेटा के आधार पर भिन्न करते हैं। लॉजिस्टिक रिग्रेशन या अन्य विधि अब अधिक सामान्य रूप से उपयोग किए जाते हैं। मार्केटिंग में विभेदक विश्लेषण के उपयोग को निम्नलिखित चरणों द्वारा वर्णित किया जा सकता है: | |||
#समस्या तैयार | #समस्या तैयार करना और डेटा एकत्र करना- इस श्रेणी में उत्पादों का मूल्यांकन करने के लिए उपयोग किए जाने वाले सामाजिक गुणों की आइडेंटिटी करना [[मात्रात्मक विपणन अनुसंधान|मात्रात्मक मार्केटिंग अनुसंधान]] प्रद्योगिक के रूप में है। जैसे [[सांख्यिकीय सर्वेक्षण]] का उपयोग करें जिससे की सभी उत्पाद विशेषताओं की रेटिंग के संबंध में संभावित ग्राहकों के नमूने से डेटा एकत्र किए जा सकते है, डेटा संग्रह चरण सामान्यतः मार्केटिंग अनुसंधान पेशेवरों द्वारा की जाती है। सर्वेक्षण के प्रश्न प्रतिवादी को शोधकर्ता द्वारा चुनी गई विशेषताओं की एक श्रृंखला पर उत्पाद को एक से पांच (या 1 से 7, या 1 से 10) तक रेट करने के लिए कहते हैं। कहीं भी पाँच से बीस विशेषताओं का चयन किया जाता है। उनमें निम्न चीज़ें सम्मलित हो सकती हैं: उपयोग में आसानी, वजन, उपयुक्तता, टिकाऊपन, रंगीनता, कीमत या बनावट के रूप में हो सकती है। और इस प्रकार गुण अध्ययन किए जा रहे है। उत्पाद के आधार पर गुण भिन्न-भिन्न होंगे। अध्ययन में सभी उत्पादों के बारे में एक ही प्रश्न पूछा गया है। कई उत्पादों के डेटा को संहिताबद्ध किया जाता है और एक सांख्यिकीय कार्यक्रम जैसे [[आर भाषा]], [[एसपीएसएस]] या [[एसएएस प्रोग्रामिंग भाषा]] में इनपुट किया जाता है। यह चरण कारक विश्लेषण के समान है। | ||
#डिस्क्रिमिनेंट | #डिस्क्रिमिनेंट संकल्पना गुणांक का अनुमान लगाएं और सांख्यिकीय महत्व और वैधता निर्धारित करें उपयुक्त डिस्क्रिमिनेंट विश्लेषण विधि चुनें। प्रत्यक्ष विधि में विवेचक संकल्पना का आकलन करना सम्मलित है, जिससे की सभी भविष्यवक्ताओं का एक साथ मूल्यांकन किया जा सके। स्टेप [[चरणबद्ध प्रतिगमन]] भविष्यवाणियों में क्रमिक रूप से प्रवेश करता है। दो-समूह विधि का उपयोग तब किया जाना चाहिए जब आश्रित चर में दो श्रेणियां या अवस्थाएँ हों। एकाधिक विभेदक विधि का उपयोग तब किया जाता है जब आश्रित चर में तीन या अधिक श्रेणीबद्ध अवस्थाएँ होती हैं। विल्क्स लैम्ब्डा डिस्ट्रीब्यूशन का प्रयोग करें। एसपीएसएस में महत्व या एसएएस में एफ स्टेट के परीक्षण के लिए विल्क्स लैम्ब्डा का उपयोग करें। वैधता का परीक्षण करने के लिए उपयोग की जाने वाली सबसे आम विधि नमूने को एक अनुमान या विश्लेषण नमूने और एक सत्यापन या होल्डआउट नमूने में विभाजित करना है। अनुमान नमूना का उपयोग विवेचक संकल्पना के निर्माण में किया जाता है। सत्यापन नमूने का उपयोग एक वर्गीकरण आव्यूह के निर्माण के लिए किया जाता है जिसमें सही ढंग से वर्गीकृत और गलत वर्गीकृत मामलों की संख्या सम्मलित होती है। सही ढंग से वर्गीकृत मामलों के प्रतिशत को हिट अनुपात कहा जाता है। | ||
# परिणामों को दो आयामी मानचित्र पर प्लॉट करें, आयामों को परिभाषित करें और परिणामों की व्याख्या करें। सांख्यिकीय कार्यक्रम | # परिणामों को दो आयामी मानचित्र पर प्लॉट करें, आयामों को परिभाषित करें और परिणामों की व्याख्या करें। सांख्यिकीय कार्यक्रम या संबंधित मॉड्यूल परिणामों को प्रतिचित्रित करता है। प्रत्येक उत्पाद को सामान्यतया दो-आयामी स्थान में मानचित्र से ग्रथित किया जायेगा।एक दूसरे से उत्पादों की दूरी या तो वे कितने अलग हैं संकेत मिलता है.आयामों को शोधकर्ता द्वारा लेबल किया जाना चाहिए। इसके लिए व्यक्तिपरक निर्णय की आवश्यकता होती है और अक्सर यह बहुत ही चुनौतीपूर्ण होता है। [[अवधारणात्मक मानचित्रण]] देखें। | ||
=== बायोमेडिकल अध्ययन === | === बायोमेडिकल अध्ययन === | ||
चिकित्सा में विभेदक विश्लेषण का मुख्य | चिकित्सा में विभेदक विश्लेषण का मुख्य उपयोग रोगी की तीक्ष्णता की स्थिति और रोग के परिणाम का पूर्वानुमान है। उदाहरण के लिए, पूर्वव्यापी विश्लेषण के दौरान रोगी को बीमारी की गंभीरता के अनुसार हल्के, मध्यम और गंभीर रूप में समूहों में विभाजित किया जाता है। इसके बाद नैदानिक और प्रयोगशाला के विश्लेषणों का अध्ययन किया जाता है, जिससे की आंकड़ों के आधार पर विभिन्न स्तरों का पता लगाया जा सके।इन चर भेदभावपूर्ण कार्यों का उपयोग करते हुए, भेदभावपूर्ण कार्यों का निर्माण किया जाता है जो रोग को किसी भावी रोगी में हल्के, मध्यम या गंभीर रूप में वर्गीकृत करने में सहायक होता है। | ||
जीव विज्ञान में, समान सिद्धांतों का उपयोग विभिन्न जैविक वस्तुओं के समूहों को वर्गीकृत करने और परिभाषित करने के लिए किया जाता है, उदाहरण के लिए, फूरियर ट्रांसफॉर्म इन्फ्रारेड स्पेक्ट्रा के आधार पर साल्मोनेला एंटरिटिडिस के फेज प्रकारों को परिभाषित करने के लिए,<ref>{{cite journal | last1 = Preisner | first1 = O | last2 = Guiomar | first2 = R | last3 = Machado | first3 = J | last4 = Menezes | first4 = JC | last5 = Lopes | first5 = JA | year = 2010 | title = साल्मोनेला एंटरिका सेरोवर एंटरिटिडिस फेज प्रकारों के विभेदन के लिए फूरियर ट्रांसफॉर्म इंफ्रारेड स्पेक्ट्रोस्कोपी और केमोमेट्रिक्स का अनुप्रयोग| journal = Appl Environ Microbiol | volume = 76 | issue = 11| pages = 3538–3544 | doi=10.1128/aem.01589-09| pmid = 20363777 | pmc = 2876429 | bibcode = 2010ApEnM..76.3538P }}</ref> एस्चेरिचिया कोलाई के पशु स्रोत का पता लगाने के लिए इसके विषाणु कारकों का अध्ययन करना<ref>{{cite journal | last1 = David | first1 = DE | last2 = Lynne | first2 = AM | last3 = Han | first3 = J | last4 = Foley | first4 = SL | year = 2010 | title = पशु चिकित्सा Escherichia कोलाई आइसोलेट्स के लक्षण वर्णन में विषाणु कारक प्रोफाइलिंग का मूल्यांकन| journal = Appl Environ Microbiol | volume = 76 | issue = 22| pages = 7509–7513 | doi=10.1128/aem.00726-10| pmid = 20889790 | pmc = 2976202 | bibcode = 2010ApEnM..76.7509D }}</ref> वगैरह के रूप में होता है। | |||
===एर्थ विज्ञान=== | |||
इस विधि का उपयोग परिवर्तन ज़ोनस्क्रीरिफिकेशन को आवश्यक अलग-अलग करने के लिए किया जा सकता है{{clarify|date=May 2021 |reason=separate what, where?|text=separate the alteration zones}}. उदाहरण के लिए, जब विभिन्न क्षेत्रों से भिन्न-भिन्न डेटा उपलब्ध होते हैं, तो विवेकशील विश्लेषण डेटा के पैटर्न को ढूंढ सकता है और इसे प्रभावी ढंग से वर्गीकृत कर सकता है।<ref>{{cite journal | last1 = Tahmasebi | first1 = P. | last2 = Hezarkhani | first2 = A. | last3 = Mortazavi | first3 = M. | year = 2010 | title = Application of discriminant analysis for alteration separation; sungun copper deposit, East Azerbaijan, Iran. Australian | url = http://ajbasweb.com/old/ajbas/2010/564-576.pdf | journal = Journal of Basic and Applied Sciences | volume = 6 | issue = 4| pages = 564–576 }}</ref> | |||
== रसद प्रतिगमन की तुलना == | == रसद प्रतिगमन की तुलना == | ||
विभेदक कार्य विश्लेषण रसद प्रतिगमन के समान है, और दोनों का उपयोग समान शोध प्रश्नों के उत्तर देने के लिए किया जा सकता है।<ref name="green"/>तार्किक प्रतिगमन में विवेकपूर्ण विश्लेषण के रूप में कई धारणाएं और प्रतिबंध नहीं हैं। | विभेदक कार्य विश्लेषण रसद प्रतिगमन के समान है, और दोनों का उपयोग समान शोध प्रश्नों के उत्तर देने के लिए किया जा सकता है।<ref name="green"/>तार्किक प्रतिगमन में विवेकपूर्ण विश्लेषण के रूप में कई धारणाएं और प्रतिबंध नहीं हैं। चूंकि, जब डिस्क्रिमिनेंट एनालिसिस की धारणाएँ पूरी होती हैं, तो यह लॉजिस्टिक रिग्रेशन से अधिक शक्तिशाली होता है।<ref>{{cite book|author1=Trevor Hastie|author2=Robert Tibshirani|author3=Jerome Friedman|title=सांख्यिकीय सबक के तत्व। डेटा खनन, अनुमान और भविष्यवाणी|edition=second|publisher=Springer|page=128}}</ref> लॉजिस्टिक प्रतिगमन के विपरीत, विभेदक विश्लेषण का उपयोग छोटे नमूना बनावटों के साथ किया जा सकता है। यह दिखाया गया है कि जब नमूना बनावट समान होते हैं, और विचरण सहप्रसरण की एकरूपता हो, तो विवेचक विश्लेषण अधिक उपयुक्त होता है।<ref name="buy"/>इन सभी फायदों के अतिरिक्त, लॉजिस्टिक रिग्रेशन कम से कम आम पसंद बन गया है, क्योंकि भेदभावपूर्ण विश्लेषण की धारणाएं संभवतः ही कभी पूरी होती हैं।<ref name="cohen"/><ref name="buy"/> | ||
== उच्च आयाम में रैखिक विवेचक == | == उच्च आयाम में रैखिक विवेचक == | ||
उच्च आयामों में ज्यामितीय विसंगतियाँ आयामीता के प्रसिद्ध अभिशाप | उच्च आयामों में ज्यामितीय विसंगतियाँ आयामीता के प्रसिद्ध अभिशाप को जन्म देती हैं। फिर भी, माप की घटना की एकाग्रता के उचित उपयोग से अभिकलन आसान हो सकता है।।<ref>Kainen P.C. (1997) [https://web.archive.org/web/20190226172352/http://pdfs.semanticscholar.org/708f/8e0a95ba5977072651c0681f3c7b8f09eca3.pdf Utilizing geometric anomalies of high dimension: When complexity makes computation easier]. In: Kárný M., Warwick K. (eds) Computer Intensive Methods in Control and Signal Processing: The Curse of Dimensionality, Springer, 1997, pp. 282–294.</ref> आयामीता के इन अभिशाप का एक महत्वपूर्ण स्थिति डोनो और टैनर द्वारा प्रकाश में लाया गया था, यदि एक नमूना अनिवार्य रूप से उच्च आयामी है, तो प्रत्येक बिंदु को रेखीय असमानता के द्वारा, यहां तक कि अत्यधिक बड़ी नमूनों के लिए भी, शेष बिंदु से अलग किया जा सकता है। ।<ref>Donoho, D., Tanner, J. (2009) [https://arxiv.org/abs/0906.2530 Observed universality of phase transitions in high-dimensional geometry, with implications for modern data analysis and signal processing], Phil. Trans. R. Soc. A 367, 4273–4293.</ref> इन रैखिक असमानताओं को संभाव्यता वितरण के एक समृद्ध परिवार के लिए रैखिक विवेचक के मानक (फिशर) रूप में चुना जा सकता है।<ref>{{cite journal |last1= Gorban| first1= Alexander N.|last2= Golubkov |first2 = Alexander |last3= Grechuck|first3 = Bogdan |last4= Mirkes|first4 = Evgeny M.|last5= Tyukin |first5 = Ivan Y. | year= 2018 |title= Correction of AI systems by linear discriminants: Probabilistic foundations|journal= Information Sciences |volume=466|pages= 303–322|doi= 10.1016/j.ins.2018.07.040| arxiv= 1811.05321| s2cid= 52876539}}</ref> विशेष रूप से, इस प्रकार के प्रमेय लॉगरिदमिक रूप से अवतल माप के लिए सिद्ध होते हैं। बहुभिन्नरूपी सामान्य वितरण सहित लॉग-अवतल वितरण प्रमाण लॉग अवतल माध्यमों के लिए एकाग्रता असमानताओं पर आधारित है<ref>Guédon, O., Milman, E. (2011) [https://arxiv.org/abs/1011.0943 Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures], Geom. Funct. Anal. 21 (5), 1043–1068.</ref> और एक बहुआयामी घन पर उत्पाद के माध्यमों के लिए यह उत्पाद संभाव्यता रिक्त स्थान के लिए तालग्रैंड की एकाग्रता असमानता का उपयोग करके सिद्ध होता है। मौलिक रेखीय विभेदकों द्वारा डेटा पृथक्करण उच्च आयाम में कृत्रिम बुद्धिमत्ता प्रणालियों के लिए त्रुटि सुधार की समस्या को सरल करता है।<ref name=GMT2019>{{cite journal |last1= Gorban|first1= Alexander N.|last2= Makarov|first2= Valeri A.|last3= Tyukin |first3= Ivan Y.|date= July 2019|title= उच्च-आयामी मस्तिष्क में छोटे तंत्रिका टुकड़ियों की अनुचित प्रभावशीलता|journal= Physics of Life Reviews|volume= 29 |pages= 55–88|doi= 10.1016/j.plrev.2018.09.005|doi-access=free|arxiv= 1809.07656| pmid= 30366739|bibcode= 2019PhLRv..29...55G}}</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
*[[डेटा खनन]] | *[[डेटा खनन|डेटा माइनिंग]] | ||
* [[निर्णय वृक्ष सीखना]] | * [[निर्णय वृक्ष सीखना|निर्णय ट्री सीखना]] | ||
*कारक विश्लेषण | *कारक विश्लेषण | ||
*कर्नेल फिशर डिस्क्रिमिनेंट एनालिसिस | *कर्नेल फिशर डिस्क्रिमिनेंट एनालिसिस | ||
| Line 194: | Line 200: | ||
{{Wikiversity|Discriminant function analysis}} | {{Wikiversity|Discriminant function analysis}} | ||
* [https://github.com/mhaghighat/dcaFuse Discriminant Correlation Analysis (DCA) of the Haghighat article (see above)] | * [https://github.com/mhaghighat/dcaFuse Discriminant Correlation Analysis (DCA) of the Haghighat article (see above)] | ||
* [http://www.alglib.net/dataanalysis/lineardiscriminantanalysis.php ALGLIB] contains open-source | * [http://www.alglib.net/dataanalysis/lineardiscriminantanalysis.php ALGLIB] contains open-source एल. डी. ए. implementation in C# / C++ / Pascal / VBA. | ||
* [https://www.mltut.com/linear-discriminant-analysis-python-complete-and-easy-guide/ | * [https://www.mltut.com/linear-discriminant-analysis-python-complete-and-easy-guide/ एल. डी. ए. in Python]- एल. डी. ए. implementation in Python | ||
* [http://people.revoledu.com/kardi/tutorial/LDA/index.html | * [http://people.revoledu.com/kardi/tutorial/LDA/index.html एल. डी. ए. tutorial using MS Excel] | ||
* [https://web.archive.org/web/20150405124836/http://biostat.katerynakon.in.ua/en/prognosis/discriminant-analysis.html Biomedical statistics. Discriminant analysis] | * [https://web.archive.org/web/20150405124836/http://biostat.katerynakon.in.ua/en/prognosis/discriminant-analysis.html Biomedical statistics. Discriminant analysis] | ||
* {{YouTube|azXCzI57Yfc|StatQuest: Linear Discriminant Analysis (LDA) clearly explained}} | * {{YouTube|azXCzI57Yfc|StatQuest: Linear Discriminant Analysis (LDA) clearly explained}} | ||
| Line 207: | Line 213: | ||
{{Authority control}} | {{Authority control}} | ||
{{DEFAULTSORT:Linear Discriminant Analysis}} | {{DEFAULTSORT:Linear Discriminant Analysis}} | ||
[[Category: | [[Category:Collapse templates|Linear Discriminant Analysis]] | ||
[[Category:Created On 31/05/2023]] | [[Category:Created On 31/05/2023|Linear Discriminant Analysis]] | ||
[[Category:Lua-based templates|Linear Discriminant Analysis]] | |||
[[Category:Machine Translated Page|Linear Discriminant Analysis]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Linear Discriminant Analysis]] | |||
[[Category:Pages with empty portal template|Linear Discriminant Analysis]] | |||
[[Category:Pages with script errors|Linear Discriminant Analysis]] | |||
[[Category:Portal-inline template with redlinked portals|Linear Discriminant Analysis]] | |||
[[Category:Sidebars with styles needing conversion|Linear Discriminant Analysis]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Linear Discriminant Analysis]] | |||
[[Category:Templates generating microformats|Linear Discriminant Analysis]] | |||
[[Category:Templates that add a tracking category|Linear Discriminant Analysis]] | |||
[[Category:Templates that are not mobile friendly|Linear Discriminant Analysis]] | |||
[[Category:Templates that generate short descriptions|Linear Discriminant Analysis]] | |||
[[Category:Templates using TemplateData|Linear Discriminant Analysis]] | |||
[[Category:Wikipedia articles needing clarification from April 2012|Linear Discriminant Analysis]] | |||
[[Category:Wikipedia articles needing clarification from April 2019|Linear Discriminant Analysis]] | |||
[[Category:Wikipedia articles needing clarification from May 2021|Linear Discriminant Analysis]] | |||
[[Category:Wikipedia metatemplates|Linear Discriminant Analysis]] | |||
[[Category:बाजार अनुसंधान|Linear Discriminant Analysis]] | |||
[[Category:बाजार विभाजन|Linear Discriminant Analysis]] | |||
[[Category:वर्गीकरण एल्गोरिदम|Linear Discriminant Analysis]] | |||
[[Category:सांख्यिकीय वर्गीकरण|Linear Discriminant Analysis]] | |||
Latest revision as of 20:44, 5 July 2023
अव्यक्त डिरिचलेट आवंटन के साथ भ्रमित न हों।
रेखीय विवेचक विश्लेषण (एलडीए) सामान्य विभेदक विश्लेषण (एनडीए) या विवेचक कार्य विश्लेषण फिशर के रेखीय विवेचक का एक सामान्यीकरण है, यह विधि सांख्यिकी और अन्य क्षेत्रों में प्रयुक्त होती है। जो दो या दो से अधिक वर्गों को चिह्नित या भिन्न करने वाली विशेषताओं का एक रैखिक संयोजन खोजने के लिए किया जाता है। वस्तुओं या घटनाओं का परिणामस्वरूप संयोजन का प्रयोग रेखीय वर्गीकारक के रूप में किया जा सकता है, या बाद में सांख्यिकीय वर्गीकरण से पहले आयामीता में कमी के लिए अधिक सामान्यतः के रूप में किया जा सकता है।
एलडीए विचरण (एनोवा) और प्रतिगमन विश्लेषण निकटता से संबंधित है, जो एक आश्रित चर के रूप में होता है, जो कि अन्य विशेषताओं या मापों के रैखिक संयोजन के रूप में व्यक्त करने का प्रयास करता है।[1][2] चूंकि, एनोवा श्रेणीबद्ध चर स्वतंत्र चर और एक सतत चर आश्रित चर के रूप में उपयोग करता है, जबकि विवेचक विश्लेषण में निरंतर स्वतंत्र चर होता है और एक श्रेणीबद्ध आश्रित चर अर्थात वर्ग लेबल के रूप में होता है।[3] लॉजिस्टिक प्रतिगमन और प्रोबिट प्रतिगमन एनोवा की तुलना में एलडीए से अधिक मिलते-जुलते हैं, क्योंकि ये निरंतर स्वतंत्र चर के मूल्यों द्वारा एक श्रेणीगत चर की व्याख्या भी करते हैं। ये अन्य विधि उन अनुप्रयोगों में उत्तम हैं, जहां यह मान लेना उचित नहीं है, कि स्वतंत्र चर सामान्य रूप से वितरित किए जाते हैं, जो एलडीए पद्धति की एक मौलिक धारणा है।
एलडीए प्रमुख घटक विश्लेषण (पीसीए) और कारक विश्लेषण से काफी निकटता से संबंधित है, जिसमें वे दोनों चर के रैखिक संयोजनों की तलाश करते हैं, जो डेटा को सर्वोत्तम रूप से समझते हैं।।[4] एलडीए स्पष्ट रूप से डेटा की कक्षाओं के बीच अंतर को मॉडल करने का प्रयास करता है। इसके विपरीत, पीसीए वर्ग किसी भी अंतर को ध्यान में नहीं रखता है और गुणक विश्लेषण समानता के बजाय मतभेदों पर आधारित फीचर संयोजन बनाता है।। विभेदक विश्लेषण भी कारक विश्लेषण से भिन्न है, क्योंकि यह एक अन्योन्याश्रित प्रद्योगिकी नहीं है:स्वतंत्र चरों तथा आश्रित चरों के बीच भेद को भी मानक चर कहा जाता है।
एलडीए काम करता है जब प्रत्येक अवलोकन के लिए स्वतंत्र चर पर किए गए माप निरंतर मात्रा के रूप में होते हैं। स्पष्ट स्वतंत्र चर के साथ काम करते समय, समतुल्य प्रद्योगिकी भेदभावपूर्ण पत्राचार विश्लेषण के रूप में है।[5][6]
भेदभावपूर्ण विश्लेषण उस समय उपयोग किया जाता है, जब समूहों को प्राथमिकता क्लस्टर विश्लेषण के रूप में जाना जाता है। प्रत्येक मामले में एक मात्रात्मक भविष्यवक्ता उपायों पर एक अंक और एक समूह माप पर एक अंक होना चाहिए।[7] सरल शब्दों में विवेचक संकल्पना विश्लेषण के रूप में चीजों को समूह वर्गों या एक ही प्रकार की श्रेणियों में बांटने की क्रिया का वर्गीकरण है।
इतिहास
1936 में सर रोनाल्ड फिशर द्वारा मूल द्विभाजित विभेदक विश्लेषण विकसित किया गया था।[8] यह एक एनोवा या मनोवा से भिन्न है, जिसका उपयोग एक या एक से अधिक स्वतंत्र श्रेणीबद्ध चर के रूप में किया जाता है। एक एनोवा या बहु मनोवा के निरंतर आश्रित चर की भविष्यवाणी करने के लिए किया जाता है। भेदभावपूर्ण कार्य विश्लेषण यह निर्धारित करने में उपयोगी है, कि श्रेणी सदस्यता की भविष्यवाणी करने में चर का एक सेट प्रभावी है या नहीं।[9]
दो वर्गों के लिए एलडीए
टिप्पणियों के एक सेट पर विचार करें ज्ञात वर्ग के साथ किसी वस्तु या घटना के प्रत्येक नमूने के लिए (जिसे विशेषताएं, चर या माप भी कहा जाता है)। . नमूनों के इस सेट को प्रशिक्षण सेट कहा जाता है। वर्गीकरण समस्या तब वर्ग के लिए एक अच्छा भविष्यवक्ता खोजने की है एक ही वितरण के किसी भी नमूने का आवश्यक नहीं कि प्रशिक्षण सेट से मात्र एक अवलोकन दिया गया हो .[10]: 338
एलडीए सशर्त संभाव्यता घनत्व कार्यों को मानकर समस्या का समाधान करता है और माध्य और सहप्रसरण मापदंडों के साथ दोनों बहुभिन्नरूपी सामान्य वितरण हैं और , क्रमश। इस धारणा के अनुसार, बेयस वर्गीकारक | बेयस-इष्टतम समाधान अंक को दूसरी श्रेणी से होने की भविष्यवाणी करना है यदि संभावना अनुपात का लॉग कुछ थ्रेशोल्ड टी से बड़ा है, जिससे की:
किसी और धारणा के बिना, परिणामी वर्गीकारक को द्विघात वर्गीकारक (QDA) के रूप में संदर्भित किया जाता है।
एलडीए इसके अतिरिक्त सरलीकृत समरूपता धारणा बनाता है अर्थात कि वर्ग सहप्रसरण समान हैं, इसलिए ) और यह कि सहप्रसरण की पूरी रैंक है।
इस मामले में कई शर्तें रद्द:
- क्योंकि हर्मिटियन आव्यूह है।
और उपरोक्त निर्णय मानदंड के रूप में है।
डॉट उत्पाद पर दहलीज बन जाता है।
कुछ दहलीज स्थिर सी के लिए, जहां
इसका मतलब है कि एक इनपुट की कसौटी एक कक्षा में होना विशुद्ध रूप से ज्ञात प्रेक्षणों के इस रैखिक संयोजन के संकल्पना का रूप है।
वाई पूरी तरह से ज्ञात टिप्पणियों के इस रैखिक संयोजन का एक रूप है।
इस निष्कर्ष को ज्यामितीय दृष्टि से देखना अधिकांशतः उपयोगी होता है, एक इनपुट की कसौटी एक कक्षा में होना विशुद्ध रूप से बहुआयामी अंतरिक्ष बिंदु के प्रक्षेपण का कार्य है सदिश पर इस प्रकार हम मात्र इसकी दिशा पर विचार करते हैं। दूसरे शब्दों में अवलोकन का है यदि संगत है के लंबवत अधिसमतल के एक निश्चित तरफ स्थित है। . विमान का स्थान दहलीज द्वारा परिभाषित किया गया है .जो कि के रूप में है।
अनुमान
विवेचक विश्लेषण की धारणाएं मनोवा के समान ही हैं। विश्लेषण आउटलेयर के प्रति पर्याप्त संवेदनशील है और सबसे छोटे समूह का आकार भविष्यवाणी करने वाले चरों की संख्या से बड़ा होना चाहिए।।[7]
- बहुभिन्नरूपी सामान्य वितरण: समूहीकरण चर के प्रत्येक स्तर के लिए स्वतंत्र चर सामान्य होते हैं।[9][7]
- प्रसरण/सहप्रसरण की एकरूपता (समरूपता): सभी चरों के बीच भिन्नताएँ भविष्यवक्ताओं के स्तरों पर समान होती हैं।।बॉक्स के एम आंकड़ों के साथ परीक्षण किया जा सकता है ।[9]
- चूंकि यह सुझाव दिया गया है कि सहप्रसरण समान होने पर रैखिक विभेदक विश्लेषण का उपयोग किया जाता है, और जब सहप्रसरण समान नहीं होते हैं तो द्विघात क्लासिफायर क्वाड्रैटिक विवेचक विश्लेषण का उपयोग किया जा सकता है।[7]
- बहुसंरेखता: पूर्वसूचक चरों के बीच बढ़े हुए सहसंबंध के साथ भविष्य कहनेवाला शक्ति घट सकती है।[7]
- सांख्यिकीय स्वतंत्र: प्रतिभागियों को यादृच्छिक नमूना माना जाता है और एक चर पर एक प्रतिभागी का स्कोर अन्य सभी प्रतिभागियों के लिए उस चर पर स्कोर से स्वतंत्र माना जाता है।[9][7]
यह सुझाव दिया गया है कि भेदभावपूर्ण विश्लेषण इन मान्यताओं के मामूली उल्लंघनों के लिए अपेक्षाकृत मजबूत है,[11] और यह भी दिखाया गया है कि द्विबीजपत्री चरों का उपयोग करते समय विभेदक विश्लेषण अभी भी विश्वसनीय हो सकता है। जहां बहुभिन्नरूपी सामान्यता का अधिकांशतः उल्लंघन किया जाता है।[12]
भेदभावपूर्ण कार्य
विवेकशील विश्लेषण भविष्यवक्ताओं के एक या अधिक रैखिक संयोजन बनाकर काम करता है, प्रत्येक संकल्पना के लिए एक नया अव्यक्त चर बन जाता है। इन कार्यों को विभेदक कार्य कहा जाता है। संभव कार्यों की संख्या या तो है जहाँ = समूहों की संख्या, या भविष्यवक्ताओं की संख्या है, जो कि छोटा हैइस संकल्पना ने बनाया है। पहला संकल्पना उस संकल्पना के समूहों के बीच के अंतर को अधिकतम करता है। दूसरा संकल्पना उस संकल्पना के अंतर को अधिकतम करता है, लेकिन पिछले संकल्पना के साथ सहसंबद्ध भी नहीं होना चाहिए। यह बाद के कार्यों के साथ इन आवश्यकता के साथ जारी रहता है, कि नया कार्य पिछले कार्यों में से किसी के साथ सहसंबद्ध न हो सके ।
दिया गया समूह , साथ नमूना स्थान के सेट, एक भेदभावपूर्ण नियम है जैसे कि यदि , तब . भेदभावपूर्ण विश्लेषण तब, के "भोजन" क्षेत्रों को खोजें वर्गीकरण त्रुटि को कम करने के लिए, इसलिए वर्गीकरण तालिका में उच्च प्रतिशत सही वर्गीकृत करने के लिए अग्रणी होता है।[13]
प्रत्येक संकल्पना को एक विवेकशील स्कोर दिया जाता है,[clarification needed] यह निर्धारित करने के लिए कि यह समूह प्लेसमेंट की कितनी अच्छी भविष्यवाणी करता है।
- संरचना सहसंबंध गुणांक: प्रत्येक भविष्यवक्ता और प्रत्येक संकल्पना के विवेचक स्कोर के बीच सहसंबंध होता है। यह एक शून्य क्रम सहसंबंध है अर्थात अन्य भविष्यवक्ताओं के लिए सही नहीं होता है ।[14]
- मानकीकृत गुणांक: रैखिक संयोजन में प्रत्येक भविष्यवक्ता का वजन जो कि विभेदक कार्य है। एक प्रतिगमन समीकरण की तरह ये गुणांक आंशिक हैं अर्थात अन्य भविष्यवक्ताओं के लिए सही हैं। समूह असाइनमेंट की भविष्यवाणी करने में प्रत्येक भविष्यवक्ता के अद्वितीय योगदान को इंगित करता है।
- ग्रुप सेंट्रोइड्स पर कार्य: प्रत्येक संकल्पना के लिए ग्रुपिंग चर के लिए औसत विभेदक के रूप में स्कोर दिए गए हैं।। साधन जितने दूर होंगे, वर्गीकरण में त्रुटि उतनी ही कम होगी।
डिस्क्रिमिनेशननियम
- अधिकतम संभावना: असाइन करें उस समूह के लिए जो जनसंख्या (समूह) घनत्व को अधिकतम करता है।[15]
- बेयस डिस्क्रिमिनेंट रूल: असाइन करता है उस समूह के लिए जो अधिकतम करता है, जहां πi उस वर्गीकरण की पूर्व संभावना का प्रतिनिधित्व करता है, और जनसंख्या घनत्व का प्रतिनिधित्व करता है।[15]
- फिशर का रेखीय विविक्तकर नियम: एसएस के बीच अनुपात को अधिकतम करता है और एस.एस समूह की भविष्यवाणी करने के लिए भविष्यवक्ताओं का एक रैखिक संयोजन पाता है।[15]
अभिलक्षणिक मान
विवेचक विश्लेषण में एक अभिलाक्षणिक मान प्रत्येक संकल्पना की विशेष जड़ होती है।[clarification needed] यह इस बात का संकेत है, कि यह संकल्पना समूहों को कितनी अच्छी प्रकार से भिन्न करता है, जहां अभिलाक्षणिक मान जितना बड़ा होता है, उतना ही उत्तम संकल्पना को भिन्न करता है।[7]चूंकि इसे सावधानी के साथ समझा जाना चाहिए, क्योंकि अभिलाक्षणिक मान की कोई ऊपरी सीमा नहीं है।[9][7]
इस प्रकार अभिलाक्षणिक मान को एनोवा के रूप में एसएस के बीच में और एस.एस के अंदर अनुपात के रूप में देखा जा सकता है,जब आश्रित चर विवेकशील के रूप में कार्य करता है, और समूह वाद्य चर स्तर के रूप में होते हैं,[clarification needed].[9]इसका मतलब यह है कि सबसे बड़ा अभिलाक्षणिक मान पहले संकल्पनाके साथ जुड़ा हुआ है, दूसरा सबसे बड़ा दूसरे के साथ आदि।
प्रभाव बनावट
कुछ सुझाव देते हैं कि प्रभावी आकार उपायों के रूप में अभिलाक्षणिक मान उपयोग किया जाता है, चूंकि, यह सामान्यतः समर्थित नहीं है।[9]इसके अतिरिक्त, विहित सहसंबंध प्रभावी आकार का पसंदीदा उपाय है। यह अभिलाक्षणिक मान के समान है, लेकिन एस.एस के बीच और एस.एस के कुल अनुपात का वर्गमूल है।. यह समूहों और कार्यों के बीच संबंध है।[9]
प्रभाव आकार का एक अन्य लोकप्रिय उपाय प्रत्येक संकल्पना के लिए विचरण स्पष्टीकरण आवश्यकता का प्रतिशत है।[clarification needed] प्रत्येक संकल्पना के लिए इसकी गणना इस प्रकार की जाती है: (λx/ क्रमi) एक्स 100 जहां λxफ़ंक्शन और Σλ के लिए अभिलाक्षणिक मान है, और Σλi सभी अभिलाक्षणिक मान का योग है। यह हमें बताता है कि अन्य कार्यों की तुलना में उस विशेष कार्य के लिए भविष्यवाणी कितनी मजबूत है।[9]
सही ढंग से वर्गीकृत प्रतिशत का प्रभाव आकार के रूप में भी विश्लेषण किया जा सकता है। कप्पा मूल्य इस बात का वर्णन कर सकता है, कि आकस्मिक करार में सुधार होता है।कप्पा एक बहुत अच्छे या खराब प्रदर्शन वाले वर्गों द्वारा पक्षपातपूर्ण होने के बजाय सभी श्रेणियों में सामान्य बनाता है। स्पष्टीकरण की आवश्यकता होती है।[9]Kappa normalizes across all categorizes rather than biased by a significantly good or poorly performing classes.[clarification needed][16]
के वर्गों के लिए विहित विभेदक विश्लेषण
कैनोनिकल डिस्क्रिमिनेंट एनालिसिस (सीडीए) अक्षों को पाता है, (k − 1 कैनोनिकल निर्देशांक, k वर्गों की संख्या है) जो श्रेणियों को उत्तम प्रकार से भिन्न करते हैं। ये रैखिक कार्य असंबद्ध हैं और वास्तव में डेटा के एन आयामी बादल के माध्यम से एक इष्टतम k − 1 स्थान को प्रभावी रूप से परिभाषित करते हैं, जो k समूहों के उस स्थान में अनुमानों को सबसे अच्छी प्रकार से भिन्न करता है। नीचे विवरण के लिए "मल्टीक्लास एलडीए"के रूप में देखें।
फिशर का रैखिक विवेचक
फ़िशर के रैखिक विवेचक और एलडीए शब्द अधिकांशतः एक दूसरे के स्थान पर उपयोग किया जाता है, चूंकि रोनाल्ड ए फ़िशर का मूल लेख होता है [1]वास्तव में थोड़ा भिन्न डिस्क्रिमिनेशनका वर्णन करता है, जो एलडीए की कुछ धारणाओं को नहीं बनाता है, जैसे कि सामान्य वितरण वर्ग या समान वर्ग सहप्रसरण होता है।
मान लीजिए कि टिप्पणियों के दो वर्गों का मतलब है और सहप्रसरण . फिर सुविधाओं का रैखिक संयोजन साधन होंगे और प्रसरण के लिए . फिशर ने इन दो संभाव्यता वितरण के बीच भिन्नता के वर्गों के बीच भिन्नता के अनुपात के रूप में परिभाषित किया जाता है।
यह उपाय, कुछ अर्थों में, वर्ग लेबलिंग के लिए संकेत-ध्वनि अनुपात का माप होता है। यह दिखाया जा सकता है कि अधिकतम पृथक्करण तब होता है,
जब एलडीए की धारणाएं संतुष्ट होती हैं, तो उपरोक्त समीकरण एलडीए के समतुल्य होता है।
ध्यान दें कि सदिश विवेचक हाइपरप्लेन के लिए सतह सामान्य है। एक उदाहरण के रूप में, दो आयामी समस्या में, दो समूहों को विभाजित करने वाली रेखा लंबवत होती है .
सामान्यतः, डिस्क्रिमिनेशनकिए जाने वाले डेटा बिंदुओं को प्रक्षेपित किया जाता है, ; फिर एक आयामी वितरण के विश्लेषण से डेटा को सबसे भिन्न करने वाली सीमा को चुना जाता है। दहलीज के लिए कोई सामान्य नियम नहीं है। चूंकि, यदि दोनों कक्षाओं के बिंदुओं के अनुमान लगभग समान वितरण प्रदर्शित करता है, तो एक अच्छा विकल्प दो साधनों के अनुमानों के बीच हाइपरप्लेन होगा, और . इस स्थिति में पैरामीटर c दहलीज स्थिति में है स्पष्ट रूप से पाया जा सकता है।
- .
ओत्सु की विधि फिशर के रेखीय विवेचक से संबंधित है, और एक ग्रेस्केल छवि में पिक्सेल के हिस्टोग्राम को एक काली/सफेद थ्रेसहोल्ड को चुनने के लिए बनाया गया है, जो कि इंट्रा-क्लास विचरण को कम करता है और काले और सफेद पिक्सेल कक्षाओं को दिये गये होते है, ग्रेस्केल के भीतर / बीच अंतर-वर्ग विचरण को अधिकतम करता है।
मल्टीक्लास एलडीए
ऐसे मामले में जहां दो से अधिक वर्ग हैं, फिशर विवेचक की व्युत्पत्ति में उपयोग किए गए विश्लेषण को एक रेखीय उप स्थान खोजने के लिए विस्तारित किया जा सकता है, जो कि सभी वर्ग परिवर्तनशीलता को समाहित करता प्रतीत होता है।[17] यह सामान्यीकरण सी. आर. राव के कारण है।[18] मान लीजिए कि प्रत्येक C वर्ग का माध्य है और वही सहप्रसरण .के साथ तब वर्ग परिवर्तनशीलता के बीच बिखराव को वर्ग माध्य के नमूना सहप्रसरण द्वारा परिभाषित किया जा सकता है।
जहां वर्ग का माध्य है। एक दिशा में वर्ग जुदाई इस मामले में दिया जाएगा
इसका मतलब है कि जब का अभिलक्षणिक सदिश है पृथक्करण संगत अभिलाक्षणिक मान के समतुल्य होगा।
चूंकि का विकर्णीय किया जा सकता है, सुविधाओं के बीच परिवर्तनशीलता सी − 1 सबसे बड़े अभिलाक्षणिक मान के अनुरूप पैरामीटर के आकार में समाहित किया जाएगा. चूंकि अधिक से अधिक रैंक C − 1 का है। ये ईगेन सदिश मुख्य रूप से पीसीए के प्रकार के फीचर रिडक्शन में उपयोग किए जाते हैं। छोटे अभिलाक्षणिक मान के अनुरूप ईगेंवैक्टर प्रशिक्षण डेटा की उपयुक्त पसंद के प्रति बहुत संवेदनशील होते हैं, और अगले खंड में वर्णित नियमितीकरण का उपयोग करना अधिकांशतः आवश्यक होता है.
यदि आयाम में कमी के अतिरिक्त, वर्गीकरण की आवश्यकता होती है, तो कई वैकल्पिक प्रद्योगिकी के रूप में उपलब्ध हैं। उदाहरण के लिए, वर्गों को विभाजित किया जा सकता है, और प्रत्येक विभाजन को वर्गीकृत करने के लिए एक मानक फिशर डिस्क्रिमिनेंट या एलडीए का उपयोग किया जाता है। इसका एक सामान्य उदाहरण "एक बनाम बाकी" है, जहां एक वर्ग के अंक एक समूह में रखे जाते हैं, और बाकी सब दूसरे में और फिर एलडीए लागू होता है। इसका परिणाम सी क्लासिफायर होगा, जिसके परिणाम संयुक्त होंगे।
एक अन्य सामान्य विधि जोड़ीदार वर्गीकरण है जहां प्रत्येक वर्ग के जोड़े के लिए एक नया वर्गीकारक बनाया जाता है,जिसमें कुल मिलाकर कुल C(C − 1)/2 वर्गीकारक होते हैं। एक अंतिम वर्गीकरण तैयार करने के लिए भिन्न-भिन्न वर्गीकारकों संयोजन के साथ होते हैं।
इंक्रीमेंटल एलडीए
एलडीए प्रद्योगिकी के विशिष्ट कार्यान्वयन के लिए सभी नमूने अग्रिम में उपलब्ध होने की आवश्यकता होती है.। चूंकि ऐसी स्थितियाँ होती हैं जहाँ संपूर्ण डेटा सेट उपलब्ध नहीं होता है और इनपुट डेटा को एक धारा के रूप में देखा जाता है। इस स्थिति में यह एलडीए सुविधा निष्कर्षण के लिए यह वांछनीय है कि पूरे डेटा सेट पर एल्गोरिथ्म को चलाए बिना नए नमूनों को देखकर गणना की गई है,एलडीए विशेषताओं को अद्यतन करने की क्षमता रखने के लिए वांछनीय होती है। उदाहरण के लिए, वास्तविक समय में मोबाइल रोबोटिक्स जैसे अनुप्रयोगों में नए प्रेक्षण उपलब्ध होते ही एक्सट्रेक्ट किए गए एवास्तविक समय में मोबाइल रोबोटिक्स जैसे अनुप्रयोगों में नए प्रेक्षण उपलब्ध होते ही एक्सट्रेक्ट किए गए एल. डी. ए. फीचर को अपडेट करना महत्वपूर्ण है। एक एल. डी. ए. विशेषता निष्कर्षण प्रद्योगिकी जो सिर्फ नए नमूने देख कर एल. डी. ए. सुविधाओं को अद्यतन कर सकते हैं, एक वृद्धिशील एल. डी. ए. एल्गोरिथ्म है और इस विचार का पिछले दो दशकों में बड़े पैमाने पर अध्ययन किया गया है।[19] चटर्जी और रॉयचौधरी ने एलडीए सुविधाओं को अद्यतन करने के लिए एक वृद्धिशील स्वयं संगठित एलडीए कलन विधिप्रस्तावित किया।[20] अन्य कार्य में, डेमिर और ओजमेमेट ने त्रुटि-सुधार और हेब्बियन सीखने के नियमों का उपयोग करते हुए एलडीए सुविधाओं को अद्यतन करने के लिए ऑनलाइन स्थानीय शिक्षण एल्गोरिदम प्रस्तावित किया।[21] बाद में, अलियारी एट अल के नए नमूने देखकर एलडीए सुविधाओं को अद्यतन करने के लिए तेजी से वृद्धिशील एल्गोरिदम व्युत्पन्न किया गया था ।[19]
व्यावहारिक उपयोग
व्यवहार में वर्ग का अर्थ और सहप्रसरण ज्ञात नहीं हैं। चूंकि,प्रशिक्षण सेट से इनका अनुमान लगाया जा सकता है। उपरोक्त समीकरणों में उपयुक्त मान के स्थान पर या तो अधिकतम संभावना अनुमान या अधिकतम पश्च अनुमान का उपयोग किया जा सकता है। चूंकि सहप्रसरण के अनुमानों को कुछ अर्थों में इष्टतम माना जा सकता है, इसका मतलब यह नहीं है कि इन मूल्यों को प्रतिस्थापित करके प्राप्त परिणामी विवेचक किसी भी अर्थ में इष्टतम है, भले ही सामान्य रूप से वितरित वर्गों की धारणा सही हो सकती है।
एलडीए और फिशर के विवेचक को वास्तविक डेटा पर लागू करने में एक और जटिलता तब होती है, जब प्रत्येक नमूने के माप की संख्या अर्थात प्रत्येक डेटा सदिश की आयाम प्रत्येक कक्षा में नमूनों की संख्या से अधिक हो जाती है।[4]इस मामले में सहप्रसरण अनुमानों की पूरी रैंक नहीं होती है और इसलिए इसे उल्टा नहीं किया जा सकता है। इससे निपटने के कई तरीके हैं। उपरोक्त सूत्रों में सामान्य आव्यूह व्युत्क्रम के अतिरिक्त छद्म व्युत्क्रम का उपयोग करना है। चूंकि, उत्तम संख्यात्मक स्थिरता प्राप्त करने के लिए सबसे पहले समस्या के सबस्पेस को प्रक्षेपित करते हुए किया जा सकता है।.[22]
छोटे नमूने के बनावट से निपटने के लिए एक अन्य रणनीति सहप्रसरण आव्यूह के संकोचन अनुमानक का उपयोग होता है।
जिसे गणितीय रूप में व्यक्त किया जा सकता है।
जहाँ आइडेंटिटीआव्यूह है, और संकोचन तीव्रता या नियमितीकरण पैरामीटर है।
यह नियमित विभेदक विश्लेषण के ढांचे की ओर ले जाता है।[23] या संकोचन विभेदक विश्लेषण होता है ।[24]
कई व्यावहारिक मामलों में रैखिक विवेचक उपयुक्त नहीं होते हैं। एलडीए और फिशर के विवेचक को कर्नेल चाल के माध्यम से गैर-रैखिक वर्गीकरण में उपयोग के लिए बढ़ाया जा सकता है। यहां, मूल प्रेक्षणों को प्रभावी रूप से एक उच्च आयामी गैर रैखिक अंतरिक्ष में प्रतिचित्रित किया गया है। इस गैर रैखिक स्थान में रैखिक वर्गीकरण फिर मूल स्थान में गैर रैखिक वर्गीकरण के समतुल्य होता है। इसका सबसे अधिक उपयोग किया जाने वाला उदाहरण कर्नेल एकाधिक विभेदक विश्लेषण होता है।
एलडीए को कई विभेदक विश्लेषणों के लिए सामान्यीकृत किया जा सकता है, जहां सी मात्र दो के अतिरिक्त एन संभावित राज्यों के साथ एक श्रेणीबद्ध चर बन जाता है। जिसे अनुरूप रूप से यदि वर्ग-सशर्त घनत्व साझा सहप्रसरण के साथ सामान्य होता हैं, पर्याप्त आँकड़ा एन अनुमानों के मूल्य हैं, जो एन साधनों द्वारा फैलाए गए रैखिक उप-स्थान हैं, व्युत्क्रम सहप्रसरण आव्यूह द्वारा परिशोधित परिवर्तन। इन अनुमानों को एक आव्यूह सामान्यीकृत अभिलाक्षणिक मान समस्या को हल करके पाया जा सकता है, ईजेन डीकंपोजीशन होता है, जो नमूनों के माध्यम से मापन से तैयार किया जाता है, और हर भाग में साझा सहप्रसविताआव्यूह होता है। विवरण के लिए ऊपर "मल्टीक्लास एलडीए" के रूप में देखें।
अनुप्रयोग
नीचे दिए गए उदाहरणों के अतिरिक्त, एलडीए को स्थिति (मार्केटिंग) और उत्पाद प्रबंधन में लागू किया जाता है।
दिवालियापन की भविष्यवाणी
लेखा अनुपात और अन्य वित्तीय चर के आधार पर दिवालियापन की भविष्यवाणी में, रैखिक विभेदक विश्लेषण व्यवस्थित रूप से यह समझाने के लिए था। कि प्रथम सांख्यिकीय पद्धति के रूप में लागू किया गया था।जिसका इस्तेमाल दिवालियापन बनाम अस्तित्व में था।एलडीए के सामान्य वितरण मान्यताओं के अनुरूप लेखा करण अनुपात की अनदेखी के बावजूद, एडवर्ड ऑल्टमैन का जेड-स्कोर वित्तीय विश्लेषण उपकरण अभी भी व्यावहारिक उपयोग में अभी भी अग्रणी मॉडल के रूप में है।
फेसेस की पहचान
कम्प्यूटरीकृत फेसेस की आइडेंटिटी प्रणाली में, प्रत्येक फेसेस को बड़ी संख्या में पिक्सेल मानों द्वारा प्रदर्शित किया जाता है। रेखीय डिस्क्रिमिनेशन विश्लेषण का प्रमुख रूप से प्रयोग वर्गीकरण से पूर्व लक्षणों की संख्या को अधिक प्रबंधनीय संख्या में घटाने के लिए किया जाता है। प्रत्येक नया आयाम पिक्सेल मानों का एक रैखिक संयोजन है, जो एक टेम्पलेट का निर्माण करता है। फिशर के रैखिक विवेचक का उपयोग करके प्राप्त रैखिक संयोजनों को फिशर फेसेस कहा जाता है, जबकि संबंधित प्रमुख घटक विश्लेषण के उपयोग से प्राप्त रेखीय संयोजनों को ईजीफेसेस कहा जाता है।
मार्केटिंग
मार्केटिंगमें, भेदभावपूर्ण विश्लेषण का उपयोग अधिकांशतः उन कारकों को निर्धारित करने के लिए किया जाता था, जो विभिन्न प्रकार के ग्राहकों और उत्पादों को सर्वेक्षण या अन्य प्रकार के एकत्रित डेटा के आधार पर भिन्न करते हैं। लॉजिस्टिक रिग्रेशन या अन्य विधि अब अधिक सामान्य रूप से उपयोग किए जाते हैं। मार्केटिंग में विभेदक विश्लेषण के उपयोग को निम्नलिखित चरणों द्वारा वर्णित किया जा सकता है:
- समस्या तैयार करना और डेटा एकत्र करना- इस श्रेणी में उत्पादों का मूल्यांकन करने के लिए उपयोग किए जाने वाले सामाजिक गुणों की आइडेंटिटी करना मात्रात्मक मार्केटिंग अनुसंधान प्रद्योगिक के रूप में है। जैसे सांख्यिकीय सर्वेक्षण का उपयोग करें जिससे की सभी उत्पाद विशेषताओं की रेटिंग के संबंध में संभावित ग्राहकों के नमूने से डेटा एकत्र किए जा सकते है, डेटा संग्रह चरण सामान्यतः मार्केटिंग अनुसंधान पेशेवरों द्वारा की जाती है। सर्वेक्षण के प्रश्न प्रतिवादी को शोधकर्ता द्वारा चुनी गई विशेषताओं की एक श्रृंखला पर उत्पाद को एक से पांच (या 1 से 7, या 1 से 10) तक रेट करने के लिए कहते हैं। कहीं भी पाँच से बीस विशेषताओं का चयन किया जाता है। उनमें निम्न चीज़ें सम्मलित हो सकती हैं: उपयोग में आसानी, वजन, उपयुक्तता, टिकाऊपन, रंगीनता, कीमत या बनावट के रूप में हो सकती है। और इस प्रकार गुण अध्ययन किए जा रहे है। उत्पाद के आधार पर गुण भिन्न-भिन्न होंगे। अध्ययन में सभी उत्पादों के बारे में एक ही प्रश्न पूछा गया है। कई उत्पादों के डेटा को संहिताबद्ध किया जाता है और एक सांख्यिकीय कार्यक्रम जैसे आर भाषा, एसपीएसएस या एसएएस प्रोग्रामिंग भाषा में इनपुट किया जाता है। यह चरण कारक विश्लेषण के समान है।
- डिस्क्रिमिनेंट संकल्पना गुणांक का अनुमान लगाएं और सांख्यिकीय महत्व और वैधता निर्धारित करें उपयुक्त डिस्क्रिमिनेंट विश्लेषण विधि चुनें। प्रत्यक्ष विधि में विवेचक संकल्पना का आकलन करना सम्मलित है, जिससे की सभी भविष्यवक्ताओं का एक साथ मूल्यांकन किया जा सके। स्टेप चरणबद्ध प्रतिगमन भविष्यवाणियों में क्रमिक रूप से प्रवेश करता है। दो-समूह विधि का उपयोग तब किया जाना चाहिए जब आश्रित चर में दो श्रेणियां या अवस्थाएँ हों। एकाधिक विभेदक विधि का उपयोग तब किया जाता है जब आश्रित चर में तीन या अधिक श्रेणीबद्ध अवस्थाएँ होती हैं। विल्क्स लैम्ब्डा डिस्ट्रीब्यूशन का प्रयोग करें। एसपीएसएस में महत्व या एसएएस में एफ स्टेट के परीक्षण के लिए विल्क्स लैम्ब्डा का उपयोग करें। वैधता का परीक्षण करने के लिए उपयोग की जाने वाली सबसे आम विधि नमूने को एक अनुमान या विश्लेषण नमूने और एक सत्यापन या होल्डआउट नमूने में विभाजित करना है। अनुमान नमूना का उपयोग विवेचक संकल्पना के निर्माण में किया जाता है। सत्यापन नमूने का उपयोग एक वर्गीकरण आव्यूह के निर्माण के लिए किया जाता है जिसमें सही ढंग से वर्गीकृत और गलत वर्गीकृत मामलों की संख्या सम्मलित होती है। सही ढंग से वर्गीकृत मामलों के प्रतिशत को हिट अनुपात कहा जाता है।
- परिणामों को दो आयामी मानचित्र पर प्लॉट करें, आयामों को परिभाषित करें और परिणामों की व्याख्या करें। सांख्यिकीय कार्यक्रम या संबंधित मॉड्यूल परिणामों को प्रतिचित्रित करता है। प्रत्येक उत्पाद को सामान्यतया दो-आयामी स्थान में मानचित्र से ग्रथित किया जायेगा।एक दूसरे से उत्पादों की दूरी या तो वे कितने अलग हैं संकेत मिलता है.आयामों को शोधकर्ता द्वारा लेबल किया जाना चाहिए। इसके लिए व्यक्तिपरक निर्णय की आवश्यकता होती है और अक्सर यह बहुत ही चुनौतीपूर्ण होता है। अवधारणात्मक मानचित्रण देखें।
बायोमेडिकल अध्ययन
चिकित्सा में विभेदक विश्लेषण का मुख्य उपयोग रोगी की तीक्ष्णता की स्थिति और रोग के परिणाम का पूर्वानुमान है। उदाहरण के लिए, पूर्वव्यापी विश्लेषण के दौरान रोगी को बीमारी की गंभीरता के अनुसार हल्के, मध्यम और गंभीर रूप में समूहों में विभाजित किया जाता है। इसके बाद नैदानिक और प्रयोगशाला के विश्लेषणों का अध्ययन किया जाता है, जिससे की आंकड़ों के आधार पर विभिन्न स्तरों का पता लगाया जा सके।इन चर भेदभावपूर्ण कार्यों का उपयोग करते हुए, भेदभावपूर्ण कार्यों का निर्माण किया जाता है जो रोग को किसी भावी रोगी में हल्के, मध्यम या गंभीर रूप में वर्गीकृत करने में सहायक होता है।
जीव विज्ञान में, समान सिद्धांतों का उपयोग विभिन्न जैविक वस्तुओं के समूहों को वर्गीकृत करने और परिभाषित करने के लिए किया जाता है, उदाहरण के लिए, फूरियर ट्रांसफॉर्म इन्फ्रारेड स्पेक्ट्रा के आधार पर साल्मोनेला एंटरिटिडिस के फेज प्रकारों को परिभाषित करने के लिए,[25] एस्चेरिचिया कोलाई के पशु स्रोत का पता लगाने के लिए इसके विषाणु कारकों का अध्ययन करना[26] वगैरह के रूप में होता है।
एर्थ विज्ञान
इस विधि का उपयोग परिवर्तन ज़ोनस्क्रीरिफिकेशन को आवश्यक अलग-अलग करने के लिए किया जा सकता हैseparate the alteration zones[clarification needed]. उदाहरण के लिए, जब विभिन्न क्षेत्रों से भिन्न-भिन्न डेटा उपलब्ध होते हैं, तो विवेकशील विश्लेषण डेटा के पैटर्न को ढूंढ सकता है और इसे प्रभावी ढंग से वर्गीकृत कर सकता है।[27]
रसद प्रतिगमन की तुलना
विभेदक कार्य विश्लेषण रसद प्रतिगमन के समान है, और दोनों का उपयोग समान शोध प्रश्नों के उत्तर देने के लिए किया जा सकता है।[9]तार्किक प्रतिगमन में विवेकपूर्ण विश्लेषण के रूप में कई धारणाएं और प्रतिबंध नहीं हैं। चूंकि, जब डिस्क्रिमिनेंट एनालिसिस की धारणाएँ पूरी होती हैं, तो यह लॉजिस्टिक रिग्रेशन से अधिक शक्तिशाली होता है।[28] लॉजिस्टिक प्रतिगमन के विपरीत, विभेदक विश्लेषण का उपयोग छोटे नमूना बनावटों के साथ किया जा सकता है। यह दिखाया गया है कि जब नमूना बनावट समान होते हैं, और विचरण सहप्रसरण की एकरूपता हो, तो विवेचक विश्लेषण अधिक उपयुक्त होता है।[7]इन सभी फायदों के अतिरिक्त, लॉजिस्टिक रिग्रेशन कम से कम आम पसंद बन गया है, क्योंकि भेदभावपूर्ण विश्लेषण की धारणाएं संभवतः ही कभी पूरी होती हैं।[8][7]
उच्च आयाम में रैखिक विवेचक
उच्च आयामों में ज्यामितीय विसंगतियाँ आयामीता के प्रसिद्ध अभिशाप को जन्म देती हैं। फिर भी, माप की घटना की एकाग्रता के उचित उपयोग से अभिकलन आसान हो सकता है।।[29] आयामीता के इन अभिशाप का एक महत्वपूर्ण स्थिति डोनो और टैनर द्वारा प्रकाश में लाया गया था, यदि एक नमूना अनिवार्य रूप से उच्च आयामी है, तो प्रत्येक बिंदु को रेखीय असमानता के द्वारा, यहां तक कि अत्यधिक बड़ी नमूनों के लिए भी, शेष बिंदु से अलग किया जा सकता है। ।[30] इन रैखिक असमानताओं को संभाव्यता वितरण के एक समृद्ध परिवार के लिए रैखिक विवेचक के मानक (फिशर) रूप में चुना जा सकता है।[31] विशेष रूप से, इस प्रकार के प्रमेय लॉगरिदमिक रूप से अवतल माप के लिए सिद्ध होते हैं। बहुभिन्नरूपी सामान्य वितरण सहित लॉग-अवतल वितरण प्रमाण लॉग अवतल माध्यमों के लिए एकाग्रता असमानताओं पर आधारित है[32] और एक बहुआयामी घन पर उत्पाद के माध्यमों के लिए यह उत्पाद संभाव्यता रिक्त स्थान के लिए तालग्रैंड की एकाग्रता असमानता का उपयोग करके सिद्ध होता है। मौलिक रेखीय विभेदकों द्वारा डेटा पृथक्करण उच्च आयाम में कृत्रिम बुद्धिमत्ता प्रणालियों के लिए त्रुटि सुधार की समस्या को सरल करता है।[33]
यह भी देखें
- डेटा माइनिंग
- निर्णय ट्री सीखना
- कारक विश्लेषण
- कर्नेल फिशर डिस्क्रिमिनेंट एनालिसिस
- लोगिट (लॉजिस्टिक रिग्रेशन के लिए)
- रेखीय प्रतिगमन
- एकाधिक विभेदक विश्लेषण
- बहुआयामी स्केलिंग
- पैटर्न मान्यता
- वरीयता प्रतिगमन
- द्विघात वर्गीकारक
- सांख्यिकीय वर्गीकरण
संदर्भ
- ↑ 1.0 1.1 Fisher, R. A. (1936). "टैक्सोनोमिक समस्याओं में एकाधिक मापन का उपयोग" (PDF). Annals of Eugenics. 7 (2): 179–188. doi:10.1111/j.1469-1809.1936.tb02137.x. hdl:2440/15227.
- ↑ McLachlan, G. J. (2004). विभेदक विश्लेषण और सांख्यिकीय पैटर्न पहचान. Wiley Interscience. ISBN 978-0-471-69115-0. MR 1190469.
- ↑ Analyzing Quantitative Data: An Introduction for Social Researchers, Debra Wetcher-Hendricks, p.288
- ↑ 4.0 4.1 Martinez, A. M.; Kak, A. C. (2001). "पीसीए बनाम एलडीए" (PDF). IEEE Transactions on Pattern Analysis and Machine Intelligence. 23 (2): 228–233. doi:10.1109/34.908974.
- ↑ Abdi, H. (2007) "Discriminant correspondence analysis." In: N.J. Salkind (Ed.): Encyclopedia of Measurement and Statistic. Thousand Oaks (CA): Sage. pp. 270–275.
- ↑ Perriere, G.; Thioulouse, J. (2003). "बैक्टीरियल प्रोटीन के उपकोशिकीय स्थान की भविष्यवाणी करने के लिए पत्राचार विभेदक विश्लेषण का उपयोग". Computer Methods and Programs in Biomedicine. 70 (2): 99–105. doi:10.1016/s0169-2607(02)00011-1. PMID 12507786.
- ↑ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8 7.9 Büyüköztürk, Ş. & Çokluk-Bökeoğlu, Ö. (2008). Discriminant function analysis: Concept and application. Egitim Arastirmalari - Eurasian Journal of Educational Research, 33, 73-92.
- ↑ 8.0 8.1 Cohen et al. Applied Multiple Regression/Correlation Analysis for the Behavioural Sciences 3rd ed. (2003). Taylor & Francis Group.
- ↑ 9.00 9.01 9.02 9.03 9.04 9.05 9.06 9.07 9.08 9.09 9.10 Green, S.B. Salkind, N. J. & Akey, T. M. (2008). Using SPSS for Windows and Macintosh: Analyzing and understanding data. New Jersey: Prentice Hall.
- ↑ Venables, W. N.; Ripley, B. D. (2002). एस के साथ आधुनिक एप्लाइड सांख्यिकी (4th ed.). Springer Verlag. ISBN 978-0-387-95457-8.
- ↑ Lachenbruch, P. A. (1975). Discriminant analysis. NY: Hafner
- ↑ Klecka, William R. (1980). Discriminant analysis. Quantitative Applications in the Social Sciences Series, No. 19. Thousand Oaks, CA: Sage Publications.
- ↑ Hardle, W., Simar, L. (2007). Applied Multivariate Statistical Analysis. Springer Berlin Heidelberg. pp. 289–303.
- ↑ Garson, G. D. (2008). Discriminant function analysis. https://web.archive.org/web/20080312065328/http://www2.chass.ncsu.edu/garson/pA765/discrim.htm.
- ↑ 15.0 15.1 15.2 Hardle, W., Simar, L. (2007). Applied Multivariate Statistical Analysis. Springer Berlin Heidelberg. pp. 289-303.
- ↑ Israel, Steven A. (June 2006). "Performance Metrics: How and When". Geocarto International. 21 (2): 23–32. doi:10.1080/10106040608542380. ISSN 1010-6049. S2CID 122376081.
- ↑ Garson, G. D. (2008). Discriminant function analysis. "PA 765: Discriminant Function Analysis". Archived from the original on 2008-03-12. Retrieved 2008-03-04. .
- ↑ Rao, R. C. (1948). "जैविक वर्गीकरण की समस्याओं में बहु मापन का उपयोग". Journal of the Royal Statistical Society, Series B. 10 (2): 159–203. JSTOR 2983775.
- ↑ 19.0 19.1 Aliyari Ghassabeh, Youness; Rudzicz, Frank; Moghaddam, Hamid Abrishami (2015-06-01). "तेजी से वृद्धिशील एलडीए सुविधा निष्कर्षण". Pattern Recognition. 48 (6): 1999–2012. Bibcode:2015PatRe..48.1999A. doi:10.1016/j.patcog.2014.12.012.
- ↑ Chatterjee, C.; Roychowdhury, V.P. (1997-05-01). "वर्ग-विभाजन सुविधाओं के लिए स्व-संगठित एल्गोरिदम और नेटवर्क पर". IEEE Transactions on Neural Networks. 8 (3): 663–678. doi:10.1109/72.572105. ISSN 1045-9227. PMID 18255669.
- ↑ Demir, G. K.; Ozmehmet, K. (2005-03-01). "रैखिक विभेदक विश्लेषण के लिए ऑनलाइन स्थानीय शिक्षण एल्गोरिदम". Pattern Recognit. Lett. 26 (4): 421–431. Bibcode:2005PaReL..26..421D. doi:10.1016/j.patrec.2004.08.005. ISSN 0167-8655.
- ↑ Yu, H.; Yang, J. (2001). "A direct LDA algorithm for high-dimensional data — with application to face recognition". Pattern Recognition. 34 (10): 2067–2069. Bibcode:2001PatRe..34.2067Y. CiteSeerX 10.1.1.70.3507. doi:10.1016/s0031-3203(00)00162-x.
- ↑ Friedman, J. H. (1989). "नियमित विभेदक विश्लेषण" (PDF). Journal of the American Statistical Association. 84 (405): 165–175. CiteSeerX 10.1.1.382.2682. doi:10.2307/2289860. JSTOR 2289860. MR 0999675.
- ↑ Ahdesmäki, M.; Strimmer, K. (2010). "कैट स्कोर और फाल्स नॉनडिस्कवरी रेट कंट्रोल का उपयोग करते हुए ओमिक्स भविष्यवाणी समस्याओं में फीचर चयन". Annals of Applied Statistics. 4 (1): 503–519. arXiv:0903.2003. doi:10.1214/09-aoas277. S2CID 2508935.
- ↑ Preisner, O; Guiomar, R; Machado, J; Menezes, JC; Lopes, JA (2010). "साल्मोनेला एंटरिका सेरोवर एंटरिटिडिस फेज प्रकारों के विभेदन के लिए फूरियर ट्रांसफॉर्म इंफ्रारेड स्पेक्ट्रोस्कोपी और केमोमेट्रिक्स का अनुप्रयोग". Appl Environ Microbiol. 76 (11): 3538–3544. Bibcode:2010ApEnM..76.3538P. doi:10.1128/aem.01589-09. PMC 2876429. PMID 20363777.
- ↑ David, DE; Lynne, AM; Han, J; Foley, SL (2010). "पशु चिकित्सा Escherichia कोलाई आइसोलेट्स के लक्षण वर्णन में विषाणु कारक प्रोफाइलिंग का मूल्यांकन". Appl Environ Microbiol. 76 (22): 7509–7513. Bibcode:2010ApEnM..76.7509D. doi:10.1128/aem.00726-10. PMC 2976202. PMID 20889790.
- ↑ Tahmasebi, P.; Hezarkhani, A.; Mortazavi, M. (2010). "Application of discriminant analysis for alteration separation; sungun copper deposit, East Azerbaijan, Iran. Australian" (PDF). Journal of Basic and Applied Sciences. 6 (4): 564–576.
- ↑ Trevor Hastie; Robert Tibshirani; Jerome Friedman. सांख्यिकीय सबक के तत्व। डेटा खनन, अनुमान और भविष्यवाणी (second ed.). Springer. p. 128.
- ↑ Kainen P.C. (1997) Utilizing geometric anomalies of high dimension: When complexity makes computation easier. In: Kárný M., Warwick K. (eds) Computer Intensive Methods in Control and Signal Processing: The Curse of Dimensionality, Springer, 1997, pp. 282–294.
- ↑ Donoho, D., Tanner, J. (2009) Observed universality of phase transitions in high-dimensional geometry, with implications for modern data analysis and signal processing, Phil. Trans. R. Soc. A 367, 4273–4293.
- ↑ Gorban, Alexander N.; Golubkov, Alexander; Grechuck, Bogdan; Mirkes, Evgeny M.; Tyukin, Ivan Y. (2018). "Correction of AI systems by linear discriminants: Probabilistic foundations". Information Sciences. 466: 303–322. arXiv:1811.05321. doi:10.1016/j.ins.2018.07.040. S2CID 52876539.
- ↑ Guédon, O., Milman, E. (2011) Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures, Geom. Funct. Anal. 21 (5), 1043–1068.
- ↑ Gorban, Alexander N.; Makarov, Valeri A.; Tyukin, Ivan Y. (July 2019). "उच्च-आयामी मस्तिष्क में छोटे तंत्रिका टुकड़ियों की अनुचित प्रभावशीलता". Physics of Life Reviews. 29: 55–88. arXiv:1809.07656. Bibcode:2019PhLRv..29...55G. doi:10.1016/j.plrev.2018.09.005. PMID 30366739.
अग्रिम पठन
- Duda, R. O.; Hart, P. E.; Stork, D. H. (2000). Pattern Classification (2nd ed.). Wiley Interscience. ISBN 978-0-471-05669-0. MR 1802993.
- Hilbe, J. M. (2009). Logistic Regression Models. Chapman & Hall/CRC Press. ISBN 978-1-4200-7575-5.
- Mika, S.; et al. (1999). "Fisher Discriminant Analysis with Kernels". Neural Networks for Signal Processing IX: Proceedings of the 1999 IEEE Signal Processing Society Workshop (Cat. No.98TH8468). pp. 41–48. CiteSeerX 10.1.1.35.9904. doi:10.1109/NNSP.1999.788121. ISBN 978-0-7803-5673-3. S2CID 8473401.
{{cite book}}:|journal=ignored (help) - McFarland, H. Richard; Donald, St. P. Richards (2001). "Exact Misclassification Probabilities for Plug-In Normal Quadratic Discriminant Functions. I. The Equal-Means Case". Journal of Multivariate Analysis. 77 (1): 21–53. doi:10.1006/jmva.2000.1924.
- McFarland, H. Richard; Donald, St. P. Richards (2002). "Exact Misclassification Probabilities for Plug-In Normal Quadratic Discriminant Functions. II. The Heterogeneous Case". Journal of Multivariate Analysis. 82 (2): 299–330. doi:10.1006/jmva.2001.2034.
- Haghighat, M.; Abdel-Mottaleb, M.; Alhalabi, W. (2016). "Discriminant Correlation Analysis: Real-Time Feature Level Fusion for Multimodal Biometric Recognition". IEEE Transactions on Information Forensics and Security. 11 (9): 1984–1996. doi:10.1109/TIFS.2016.2569061. S2CID 15624506.
बाहरी संबंध
- Discriminant Correlation Analysis (DCA) of the Haghighat article (see above)
- ALGLIB contains open-source एल. डी. ए. implementation in C# / C++ / Pascal / VBA.
- एल. डी. ए. in Python- एल. डी. ए. implementation in Python
- एल. डी. ए. tutorial using MS Excel
- Biomedical statistics. Discriminant analysis
- StatQuest: Linear Discriminant Analysis (LDA) clearly explained on YouTube
- Course notes, Discriminant function analysis by G. David Garson, NC State University
- Discriminant analysis tutorial in Microsoft Excel by Kardi Teknomo
- Course notes, Discriminant function analysis by David W. Stockburger, Missouri State University
- Discriminant function analysis (DA) by John Poulsen and Aaron French, San Francisco State University