पथ अभिन्न सूत्रीकरण

This article is about क्वांटम यांत्रिकी का सूत्रीकरण. For एक पथ के साथ समाकलन, जिसे रेखा या समोच्च समाकल के रूप में भी जाना जाता है, see रेखा अभिन्न.

पथ अभिन्न सूत्रीकरण क्वांटम यांत्रिकी में ऐसा सूत्रीकरण है जो मौलिक यांत्रिकी की भौतिक क्रिया को सामान्य करने में सहायक होता है। यह संभाव्यता आयाम की गणना करने के लिए क्वांटम यांत्रिकी के उपयोग से संभव प्रक्षेपवक्र की अनंतता के योग या अभिन्न फलन के साथ किसी प्रणाली के लिए एकल, अद्वितीय मौलिक प्रक्षेपवक्र की मौलिक धारणाओं को प्रतिस्थापित करने में सहायक होता हैं।

यह सूत्रीकरण सैद्धांतिक भौतिकी के बाद में किये गए विकासों के अनुरूप महत्वपूर्ण रूप से प्रमाणित हुआ है, क्योंकि इस प्रकार से प्रकट किए जाने वाले लोरेंत्ज़ सहप्रसरण (मात्राओं के समय और स्थान के घटक उसी प्रकार से समीकरणों में प्रवेश करते हैं) विहित परिमाणीकरण के संचालक औपचारिकता की तुलना में प्राप्त करना सरल है। इस प्रकार पिछली विधियों के विपरीत, पथ अभिन्न अंग ही क्वांटम सिस्टम के बहुत भिन्न विहित निर्देशांक विवरणों के बीच निर्देशांक को सरली से परिवर्तित करने की अनुमति देता है। इस प्रकार अन्य लाभ यह है कि किसी सिद्धांत के लैग्रैंगियन (क्षेत्र सिद्धांत) के सही रूप का अनुमान लगाना व्यवहार में सरल है, जो स्वाभाविक रूप से पथ अभिन्न में प्रवेश करता है (एक निश्चित प्रकार की बातचीत के लिए, ये समन्वय स्थान या हैं फेनमैन पथ समाकलन ), हैमिल्टनियन (क्वांटम यांत्रिकी) की तुलना में उपयोग किया जाता हैं। दृष्टिकोण के संभावित डाउनसाइड्स में सम्मिलित है कि एस आव्यूह की एकात्मकता (यह संभाव्यता के संरक्षण से संबंधित है, इस प्रकार सभी भौतिक रूप से संभावित परिणामों की संभावनाओं को तक जोड़ना चाहिए) के सूत्रीकरण में अस्पष्ट रहता है। इस प्रकार पथ-अभिन्न दृष्टिकोण क्वांटम यांत्रिकी और क्वांटम क्षेत्र सिद्धांत के अन्य औपचारिकताओं के समान प्रमाणित हुआ है। इस प्रकार इसके द्वारा प्राप्त होने वाले या तो दूसरे दृष्टिकोण से देखने पर इससे जुड़ी समस्याएं (जैसा कि लोरेंत्ज़ सहप्रसरण या एकात्मकता द्वारा उदाहरण दिया गया है) दूर हो जाती हैं।

पाथ समाकलन भी क्वांटम और स्टोकेस्टिक प्रक्रियाओं से संबंधित है, और इसने 1970 के दशक के भव्य संश्लेषण के लिए आधार प्रदान किया, जिसने क्वांटम क्षेत्र सिद्धांत को दूसरे क्रम के चरण संक्रमण के पास उतार-चढ़ाव वाले क्षेत्र के सांख्यिकीय क्षेत्र सिद्धांत के साथ एकीकृत किया। श्रोडिंगर समीकरण काल्पनिक प्रसार स्थिरांक के साथ प्रसार समीकरण है, और पथ अभिन्न सभी संभावित यादृच्छिक चलने के योग के लिए विधि का विश्लेषणात्मक निरंतरता को प्रकट करता है।

इस पथ अभिन्न सूत्रीकरण का मूल विचार नॉर्बर्ट वीनर के लिए वापस खोजा जा सकता है, जिन्होंने प्रसार और ब्राउनियन गति में समस्याओं को हल करने के लिए वीनर अभिन्न को प्रस्तुत किया। यह विचार पॉल डिराक द्वारा अपने 1933 के लेख में क्वांटम यांत्रिकी में लैगरैंगियन (क्षेत्र सिद्धांत) के उपयोग के लिए विस्तारित किया गया था। पूरी विधि 1948 में रिचर्ड फेनमैन द्वारा विकसित की गई थी। जॉन आर्चीबाल्ड व्हीलर की देखरेख में उनके डॉक्टरेट के कार्य में कुछ प्रारंभिक कार्य किए गए थे। मूल प्रेरणा व्हीलर-फेनमैन अवशोषक सिद्धांत के लिए क्वांटम-यांत्रिक सूत्र प्राप्त करने की इच्छा से उत्पन्न हुई थी, जो प्रारंभिक बिंदु के रूप में लैग्रैंगियन (क्षेत्र सिद्धांत) (हैमिल्टनियन (क्वांटम यांत्रिकी) के अतिरिक्त) का उपयोग कर रही थी।

ये कण के लिए समय t पर बिंदु A से समय t'(>t) पर बिंदु B तक जाने के लिए उपलब्ध अनंत पथों में से पांच हैं। पथ जो स्वयं-प्रतिच्छेद करते हैं या समय में पीछे की ओर जाते हैं, की अनुमति नहीं है।

क्वांटम क्रिया सिद्धांत

क्वांटम यांत्रिकी में, मौलिक यांत्रिकी की प्रकार, हैमिल्टनियन (क्वांटम यांत्रिकी) समय के अनुवाद का जनक है। इसका अर्थ यह है कि हैमिल्टनियन ऑपरेटर (ऋणात्मक काल्पनिक इकाई द्वारा गुणा) के साथ कार्य करने के परिणाम से थोड़ी देर बाद −i की स्थिति वर्तमान समय में स्थिति से भिन्न होती है। इस कारण निश्चित ऊर्जा वाले स्थितियों के लिए, यह आवृत्ति और ऊर्जा के बीच डी ब्रोगली संबंध का प्रमाण है, और सामान्य संबंध उस प्लस सुपरपोजिशन सिद्धांत के अनुरूप है।

मौलिक यांत्रिकी में हेमिल्टनियन लैग्रैंगियन क्षेत्र सिद्धांत से लिया गया है, जो विशेष सापेक्षता के सापेक्ष अधिक मौलिक मात्रा है। हैमिल्टनियन इंगित करता है कि समय में कैसे आगे बढ़ना है, किन्तु इस संदर्भ के विभिन्न फ्रेम में समय अलग है। इस प्रकार लैगरैंगियन लोरेंत्ज़ अदिश है, इसके अतिरिक्त है, मिल्टन चार-वेक्टर का समय घटक है। तो हैमिल्टन विभिन्न फ्रेमों में भिन्न है, और क्वांटम यांत्रिकी के मूल सूत्रीकरण में इस प्रकार की समरूपता स्पष्ट नहीं है।

हैमिल्टनियन समय में स्थिति और गति का कार्य है, और यह थोड़ी देर पश्चात इस स्थिति और गति को निर्धारित करने में सहायक होता हैं। इस प्रकार लैगरैंगियन अभी की स्थिति और थोड़ी देर बाद की स्थिति का कार्य है (या, समान रूप से अनन्त समय के अलगाव के लिए, यह स्थिति और वेग का कार्य है)। इस प्रकार दोनों के बीच का संबंध लीजेंड्रे परिवर्तन द्वारा है, और गति के मौलिक समीकरणों (यूलर-लग्रेंज समीकरणों) को निर्धारित करने वाली स्थिति यह है कि क्रिया (भौतिकी) में अत्यधिक है।

क्वांटम यांत्रिकी में, लीजेंड्रे परिवर्तन की व्याख्या करना कठिन है, क्योंकि गति निश्चित प्रक्षेपवक्र से अधिक नहीं है। इस प्रकार मौलिक यांत्रिकी में, समय में विवेक के साथ, लीजेंड्रे परिवर्तन बन जाता है

$\varepsilon H=p(t){\big (}q(t+\varepsilon )-q(t){\big )}-\varepsilon L$

और

$p={\frac {\partial L}{\partial {\dot {q}}}},$

जहाँ इसके संबंध में आंशिक व्युत्पन्न ${\dot {q}}$ रखती है जिसे q(t + ε) द्वारा हल करके प्राप्त किया जाता हैं। इस प्रकार व्युत्क्रम लीजेंड्रे रूपांतरण है

$\varepsilon L=\varepsilon p{\dot {q}}-\varepsilon H,$

जहाँ

${\dot {q}}={\frac {\partial H}{\partial p}},$

और आंशिक व्युत्पन्न अब के संबंध में p पर q को सेट किया गया हैं।

क्वांटम यांत्रिकी में, स्थिति जितना अध्यारोपण है जिसमें q का मान विभिन्न मानों को प्रकट करता है, इसके विभिन्न मान p, और मात्राएँ p और q नॉनकम्यूटिंग ऑपरेटरों के रूप में व्याख्या की जा सकती है। इस कारण परिचालक p केवल उन स्थितियों पर निश्चित है जो q के लिए अनिश्चित हैं, तो इस प्रकार इस समय में अलग-अलग दो स्थितियों पर विचार करें और लैग्रैंगियन के अनुरूप ऑपरेटर के साथ कार्य करते हैं:

$e^{i{\big [}p{\big (}q(t+\varepsilon )-q(t){\big )}-\varepsilon H(p,q){\big ]}}.$

यदि इस सूत्र में निहित गुणा को आव्यूह गुणन के रूप में पुनर्व्याख्या की जाती है, तो पहला कारक है

$e^{-ipq(t)},$

और अगर इसे आव्यूह गुणन के रूप में भी समझा जाता है, तो सभी स्थितियों का योग सभी पर एकीकृत हो जाता है q(t), और इसलिए यह फूरियर को रूपांतरित करता है q(t) आधार परिवर्तित करने के लिए p(t). वह हिल्बर्ट अंतरिक्ष पर प्रतिक्रिया है - इस परिवर्तन के आधार पर p समय पर t को प्रकट करता हैं।

अगला आता है

$e^{-i\varepsilon H(p,q)},$

या भविष्य में अतिसूक्ष्म समय विकसित करें।

अंत में, इस व्याख्या में अंतिम कारक है

$e^{ipq(t+\varepsilon )},$

जिसका अर्थ है, इसका आधार को वापस बदलकर q को इसके पश्चात प्राप्त किया जाता हैं।

यह साधारण समय के विकास से बहुत अलग नहीं है: द H कारक में सभी गतिशील जानकारी होती है - यह स्थिति को समय पर आगे बढ़ाती है। पहला भाग और अंतिम भाग शुद्ध रूप में परिवर्तित करने के लिए सिर्फ फूरियर रूपांतरण हैं, इस प्रकार इसके फलस्वरूप q मध्यवर्ती से आधार p आधार पर उपयोग किया जाता हैं।

...हम देखते हैं कि (11) में समाकलन रूप का होना चाहिए e^iF/h, जहाँ F का फंक्शन q_T, q₁, q₂, … q_m, q_t हैं, जो परिमित रहता है h शून्य हो जाता है। आइए अब हम मध्यवर्ती में से एक को चित्रित करें qs, say q_k,के रूप में निरंतर परिवर्तित करते रहते हैं जबकि अन्य स्थिर होते हैं। लघुता के कारण h, तब हमारे पास सामान्य रूप से होगा F/h बहुत तेजी से बदल रहा है। इसका अर्थ है कि e^iF/h मूल्य शून्य के बारे में बहुत उच्च आवृत्ति के साथ समय-समय पर भिन्न होगा, जिसके परिणामस्वरूप इसका अभिन्न व्यावहारिक रूप से शून्य होगा। के एकीकरण के क्षेत्र में एकमात्र महत्वपूर्ण भाग है q_k इस प्रकार वह है जिसके लिए तुलनात्मक रूप से बड़ी भिन्नता है q_k में बहुत कम भिन्नता उत्पन्न करता है F। यह भाग एक बिंदु का पड़ोस है जिसके लिए F में छोटे बदलावों के संबंध में स्थिर है q_k। हम इस तर्क को एकीकरण के प्रत्येक चर के लिए लागू कर सकते हैं और परिणाम प्राप्त कर सकते हैं कि एकीकरण के क्षेत्र में एकमात्र महत्वपूर्ण परिवर्तन वह है जिसके लिए F सभी मध्यवर्ती में छोटे परिवर्तनों के लिए स्थिर है qs. ... हम यहाँ देखते हैं कि F इसके मौलिक समकक्ष के लिए है ∫^t
_T L dt, जो केवल क्रिया फलन है, जिसके मौलिक यांत्रिकी को सभी मध्यवर्ती में छोटे परिवर्तनों के लिए स्थिर होने की आवश्यकता होती है qs. इससे पता चलता है कि किस प्रकार से समीकरण (11) मौलिक परिणामों में परिवर्तित कर देता है h अत्यधिक छोटा हो जाता है।

Dirac (1933), p. 69

इसे संदर्भित करने की दूसरी विधि यह है कि हैमिल्टनियन स्वाभाविक रूप से p और q के मध्य कार्य करता है, इस मात्रा का घातांक और से बदलकर इसके आधार p को q के प्रत्येक चरण में आव्यूह तत्व की अनुमति देता है, इस प्रकार H प्रत्येक पथ के साथ साधारण कार्य के रूप में व्यक्त किया जाना है। यह कार्य मौलिक क्रिया का क्वांटम एनालॉग है। यह अवलोकन पॉल डिराक के कारण है। डिराक ने आगे कहा कि कोई समय-विकास संचालिका को वर्गाकार कर सकता है जो S प्रतिनिधित्व को प्रकट करता हैं:

$e^{i\varepsilon S},$

और यह समय-विकास संचालक को समय के बीच देता है, जो विशेषतः t और समय t + 2ε के समान रहता हैं। इसके अतिरिक्त में H मध्यवर्ती स्थितियों पर अभिव्यक्त की जाने वाली मात्रा का प्रतिनिधित्व अस्पष्ट आव्यूह तत्व है S प्रतिनिधित्व पथ से जुड़ी मात्रा के रूप में इसकी पुनर्व्याख्या की जाती है। इस प्रकार इस ऑपरेटर की बड़ी शक्ति लेने की सीमा में, दो स्थितियों के बीच पूर्ण क्वांटम विकास का पुनर्निर्माण करता है, प्रारंभिक निश्चित मान के साथ q(0) और इसके बाद निश्चित मान के साथ q(t) का परिणाम इस प्रकार से प्राप्त होने वाले विभिन्न चरणों के साथ इनके पथों के योग के समान होता हैं, जो क्वांटम क्रिया द्वारा प्राप्त किया जाता है। इस प्रकार महत्वपूर्ण रूप से डिराक ने इस लेख में मौलिक सीमा को नियंत्रित करने वाली कम से कम प्रतिक्रिया के सिद्धांत के गहरे क्वांटम-यांत्रिक कारण की समरूपता की (उद्धरण बॉक्स देखें) जाती हैं।

फेनमैन की व्याख्या

डिराक के कार्य ने पथों के योग की गणना करने के लिए इस विधि को उपयोग नहीं किया था, और उन्होंने यह नहीं दिखाया कि कोई इस नियम से श्रोडिंगर समीकरण विहित रूपान्तरण संबंध संबंधों को पुनर्प्राप्त कर सकता है। यह फेनमैन द्वारा किया गया था। अर्थात् मौलिक मार्ग स्वाभाविक रूप से मौलिक सीमा में उत्पन्न होता है।

फेनमैन ने दिखाया कि डिराक की क्वांटम प्रतिक्रिया, ब्याज के अधिकतम स्थितियों के लिए, मौलिक प्रतिक्रिया के समान, उचित रूप से अलग थी। इस प्रकार इसका अर्थ यह है कि मौलिक क्रिया दो निश्चित समापन बिंदुओं के बीच क्वांटम विकास द्वारा प्राप्त चरण है। उन्होंने सभी क्वांटम यांत्रिकी को निम्नलिखित अभिधारणाओं से पुनर्प्राप्त करने का प्रस्ताव दिया था:

1. किसी घटना की संभावना जटिल संख्या के वर्ग मापांक द्वारा दी जाती है, जिसे प्रायिकता आयाम कहा जाता है।
2. कॉन्फ़िगरेशन स्पेस में सभी पथों के योगदान को साथ जोड़कर संभाव्यता आयाम दिया जाता है।
3. पथ का योगदान आनुपातिक e^iS/ħ है , इस प्रकार जहाँ S पथ के साथ लैगरैंगियन यांत्रिकी के अभिन्न समय द्वारा दी गई क्रिया (भौतिकी) है।

किसी दिए गए प्रक्रिया के लिए समग्र संभाव्यता आयाम खोजने के लिए, प्रारंभिक और अंतिम स्थितियों के बीच सिस्टम के सभी संभावित पथों के स्थान पर तीसरे पद के आयाम को जोड़ता है, या अभिन्न, उन सहित जो हैं मौलिक मानकों से अलग हैं। इस प्रकार कण के लिए अंतरिक्ष-समय समन्वय से दूसरे में जाने के लिए संभाव्यता आयाम की गणना करने में, उन पथों को सम्मिलित करना सही होता है जिनमें कण विस्तृत वक्रता का वर्णन करता है, वक्र जिसमें कण बाहरी अंतरिक्ष में गोली मारता है और फिर से वापस उड़ता है, और इसके आगे यह 'समय अभिन्न' इन सभी आयामों को समान भार किन्तु अलग-अलग चरण (तरंगें), या जटिल संख्या का तर्क प्रदान करता है। इस प्रकार मौलिक प्रक्षेपवक्र से अधकतम रूप में भिन्न-भिन्न पथों से प्राप्त होने वाले मानों को हस्तक्षेप (तरंग प्रसार) (नीचे देखें) करके दबाया जाता है।

फेनमैन ने दिखाया कि क्वांटम यांत्रिकी का यह सूत्रीकरण क्वांटिज़ेशन (भौतिकी) के समान है जब हैमिल्टन गति में सबसे अधिक द्विघात है। इस प्रकार फेनमैन के सिद्धांतों के अनुसार गणना की गई आयाम दी गई क्रिया के अनुरूप हैमिल्टनियन (क्वांटम यांत्रिकी) के लिए श्रोडिंगर समीकरण का भी पालन करेगा।

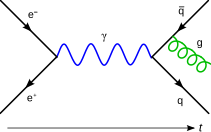
क्वांटम क्षेत्र सिद्धांत का पथ अभिन्न सूत्रीकरण प्रारंभिक से अंतिम अवस्था तक सिस्टम के सभी संभावित इतिहासों के भारित योग के रूप में संक्रमण आयाम (मौलिक सहसंबंध फलन के अनुरूप) का प्रतिनिधित्व करता है। फेनमैन आरेख संक्रमण आयाम में विक्षोभ योगदान का चित्रमय प्रतिनिधित्व है।

क्वांटम यांत्रिकी में पथ अभिन्न

टाइम-स्लाइसिंग व्युत्पत्ति

Main article: श्रोडिंगर% 27s समीकरण और क्वांटम यांत्रिकी के पथ अभिन्न सूत्रीकरण के बीच संबंध

पथ अभिन्न सूत्र प्राप्त करने के लिए सामान्य दृष्टिकोण समय अंतराल को छोटे टुकड़ों में विभाजित करना है। बार यह हो जाने के पश्चात लाई उत्पाद सूत्र हमें बताता है कि गतिज और संभावित ऊर्जा ऑपरेटरों की गैर-अनुक्रमणीयता को अनदेखा किया जा सकता है।

एक चिकनी क्षमता में कण के लिए, पथ समाकलन को ज़िगज़ैग पथों द्वारा अनुमानित किया जाता है, जो इस प्रकार आयाम में साधारण समाकलन का उत्पाद है। इस स्थिति से कण की गति के लिए x_a समय पर t_a को x_b समय पर t_b, समय क्रम में प्रकट होता हैं-

$t_{a}=t_{0}<t_{1}<\cdots <t_{n-1}<t_{n}<t_{n+1}=t_{b}$

में विभाजित किया जा सकता है। इस प्रकार n + 1 छोटे खंड t_j − t_{j − 1}, जहाँ j = 1, ..., n + 1, निश्चित अवधि का मान प्रकट होता हैं-

$\varepsilon =\Delta t={\frac {t_{b}-t_{a}}{n+1}}.$

इस प्रक्रिया को टाइम-स्लाइसिंग कहा जाता है।

पथ समाकल के लिए समीपता की गणना समानुपाती के रूप में की जा सकती है।

$\int \limits _{-\infty }^{+\infty }\cdots \int \limits _{-\infty }^{+\infty }\exp \left({\frac {i}{\hbar }}\int _{t_{a}}^{t_{b}}L{\big (}x(t),v(t){\big )}\,dt\right)\,dx_{0}\,\cdots \,dx_{n},$

जहाँ L(x, v) स्थिति चर के साथ एक-आयामी प्रणाली का लैग्रेंजियन है। इस प्रकार x(t) और वेग v = ẋ(t) माना जाता है, और dx_j की स्थिति से मेल खाता है jवें समय कदम, अगर समय अभिन्न का योग द्वारा n शर्तें अनुमानित है । इस सीमा में n → ∞, यह फलन अभिन्न अंग बन जाता है, जो गैर-आवश्यक कारक के अतिरिक्त, संभाव्यता आयाम का सीधे उत्पाद ⟨x_b, t_b|x_a, t_a⟩ है, ( इस प्रकार अधिक सही रूप प्राप्त करने के लिए किसी को निरंतर स्पेक्ट्रम, संबंधित घनत्व के साथ कार्य करना चाहिए) क्वांटम यांत्रिक कण को ​​​​खोजने के लिए t_a प्रारंभिक अवस्था में x_a और कम से t_b अंतिम अवस्था में x_b के रूप में हैं।

वास्तव में L माना जाता है कि एक-आयामी प्रणाली का मौलिक लैग्रैन्जियन यांत्रिकी है,

$L(x,{\dot {x}})=T-V={\frac {1}{2}}m|{\dot {x}}|^{2}-V(x)$

और उपर्युक्त ज़िगज़ैगिंग शर्तों की उपस्थिति से मेल खाती है

$\exp \left({\frac {i}{\hbar }}\varepsilon \sum _{j=1}^{n+1}L\left({\tilde {x}}_{j},{\frac {x_{j}-x_{j-1}}{\varepsilon }},j\right)\right)$

रीमैन योग में समय के अभिन्न अंग का अनुमान लगाया जाता है, जो इस प्रकार अंत में एकीकृत होते हैं। इस कारण x₁ को x_n एकीकरण के उपाय के साथ dx₁...dx_n, x̃_j के संगत अंतराल j का मान है, उदाहरण के रूप में इसका केंद्र, x_j + x_j−1/2 उक्त मान उत्पन्न करता हैं।

इस प्रकार, मौलिक यांत्रिकी के विपरीत, न केवल स्थिर पथ योगदान देता है, इसके अतिरिक्त वास्तव में प्रारंभिक और अंतिम बिंदु के बीच के सभी आभासी पथ भी योगदान करते हैं।

पथ अभिन्न

स्थिति प्रतिनिधित्व में तरंग फलन के संदर्भ में, पथ अभिन्न सूत्र निम्नानुसार पढ़ता है:

$\psi (x,t)={\frac {1}{Z}}\int _{\mathbf {x} (0)=x}{\mathcal {D}}\mathbf {x} \,e^{iS[\mathbf {x} ,{\dot {\mathbf {x} }}]}\psi _{0}(\mathbf {x} (t))\,$

जहाँ ${\mathcal {D}}\mathbf {x}$ सभी रास्तों पर एकीकरण को दर्शाता है $\mathbf {x}$ साथ $\mathbf {x} (0)=x$ और जहाँ $Z$ सामान्यीकरण कारक है। यहां $S$ द्वारा दी गई क्रिया है

$S[\mathbf {x} ,{\dot {\mathbf {x} }}]=\int dt\,L(\mathbf {x} (t),{\dot {\mathbf {x} }}(t))$

आरेख पथों के समूह के लिए मुक्त कण के पथ अभिन्न अंग में योगदान को दर्शाता है, अंततः सर्पिल हॉर्न को चित्रित करता है।

मुक्त कण

पथ अभिन्न प्रतिनिधित्व बिंदु से जाने के लिए क्वांटम आयाम देता है, इस प्रकार x इंगित करने के लिए y सभी रास्तों पर अभिन्न के रूप में मुक्त-कण क्रिया के लिए (सरलता के लिए आइए m = 1, ħ = 1) करता हैं।

$S=\int {\frac {{\dot {x}}^{2}}{2}}\,dt,$

अभिन्न का स्पष्ट रूप से मानांकन किया जा सकता है।

ऐसा करने के लिए, कारक के बिना प्रारंभ करना सुविधाजनक है, इस प्रकार i घातांक में, जिससे कि बड़े विचलन को छोटी संख्या से दबा दिया जाए, न कि दोलन योगदान को निरस्त करके प्राप्त होता हैं। यह आयाम (या कर्नेल) पढ़ता है:

$K(x-y;T)=\int _{x(0)=x}^{x(T)=y}\exp \left(-\int _{0}^{T}{\frac {{\dot {x}}^{2}}{2}}\,dt\right)\,Dx.$

समाकलन को टाइम स्लाइस में विभाजित करना:

$K(x,y;T)=\int _{x(0)=x}^{x(T)=y}\prod _{t}\exp \left(-{\tfrac {1}{2}}\left({\frac {x(t+\varepsilon )-x(t)}{\varepsilon }}\right)^{2}\varepsilon \right)\,Dx,$

जहाँ Dx के प्रत्येक पूर्णांक पर एकीकरण के परिमित संग्रह ε के रूप में व्याख्या की जाती है। इस प्रकार उत्पाद में प्रत्येक कारक के कार्य के रूप में गाऊसी है x(t + ε) पर केंद्रित है x(t) विचरण के साथ ε. मल्टीपल समाकलन इस गॉसियन का बार-बार होने वाला घुमाव है। इस कारण G_ε आसन्न समय पर स्वयं की प्रतियों के साथ किया जाता हैं:

$K(x-y;T)=G_{\varepsilon }*G_{\varepsilon }*\cdots *G_{\varepsilon },$

जहाँ संकल्पों की संख्या T/ε है। इस प्रकार दोनों पक्षों के फूरियर रूपांतरण को लेकर परिणाम का मानांकन करना सरल है, जिससे कि कनवल्शन गुणन बन जाए:

${\tilde {K}}(p;T)={\tilde {G}}_{\varepsilon }(p)^{T/\varepsilon }.$

गॉसियन का फूरियर रूपांतरण G पारस्परिक भिन्नता का और गॉसियन है:

${\tilde {G}}_{\varepsilon }(p)=e^{-{\frac {\varepsilon p^{2}}{2}}},$

और परिणाम है

${\tilde {K}}(p;T)=e^{-{\frac {Tp^{2}}{2}}}.$

फूरियर रूपांतरण देता है K, और यह पारस्परिक विचरण के साथ फिर से गाऊसी है:

$K(x-y;T)\propto e^{-{\frac {(x-y)^{2}}{2T}}}.$

आनुपातिकता स्थिरांक वास्तव में टाइम-स्लाइसिंग दृष्टिकोण द्वारा निर्धारित नहीं किया जाता है, केवल विभिन्न समापन बिंदु विकल्पों के लिए मानों का अनुपात निर्धारित किया जाता है। आनुपातिकता स्थिरांक को यह सुनिश्चित करने के लिए चुना जाना चाहिए कि प्रत्येक दो समय के स्लाइस के बीच समय का विकास क्वांटम-यांत्रिक रूप से एकात्मक है, किन्तु इस प्रकार सामान्यीकरण को ठीक करने का अधिक उपयोगी विधि यह है कि स्टोकेस्टिक प्रक्रिया के विवरण के रूप में पथ अभिन्न पर विचार किया जाता हैं।

परिणाम की संभाव्यता व्याख्या है। घातीय कारक के सभी पथों के योग को उस पथ के चयन की प्रायिकता के प्रत्येक पथ के योग के रूप में देखा जा सकता है। संभाव्यता उस खंड को चुनने की संभावना के प्रत्येक खंड पर उत्पाद है, जिससे कि प्रत्येक खंड संभावित रूप से स्वतंत्र रूप से चुना जा सके। इसका तथ्य यह है कि उत्तर गॉसियन है जो समय में रैखिक रूप से फैल रहा है, इस प्रकार केंद्रीय सीमा प्रमेय है, जिसे सांख्यिकीय पथ अभिन्न के पहले ऐतिहासिक मानांकन के रूप में व्याख्या किया जा सकता है।

संभाव्यता व्याख्या प्राकृतिक सामान्यीकरण विकल्प देती है। इस प्रकार इस पथ अभिन्न परिभाषित किया जाना चाहिए जिससे कि उक्त समीकरण प्राप्त होता हैं।

$\int K(x-y;T)\,dy=1.$

यह स्थिति गॉसियन को सामान्यीकृत करती है और कर्नेल उत्पन्न करती है जो इस प्रकार प्रसार समीकरण का पालन करती है:

${\frac {d}{dt}}K(x;T)={\frac {\nabla ^{2}}{2}}K.$

ऑसिलेटरी पथ समाकलन के लिए, के साथ i अंश में, समय का टुकड़ा करने से पहले की प्रकार दृढ़ गाऊसी उत्पन्न होते हैं। अब, चूंकि, कनवल्शन उत्पाद मामूली रूप से एकवचन है, क्योंकि इसमें ऑसिलेटिंग समाकलन का मानांकन करने के लिए सावधानीपूर्वक सीमा की आवश्यकता होती है। इस प्रकार इन कारकों को अच्छी प्रकार से परिभाषित करने के लिए, समय वृद्धि में छोटा सा काल्पनिक भाग ε जोड़ने की सबसे सरल विधि है। इसके घूर्णन से समीपता से संबंधित है। फिर पहले जैसा ही कनवल्शन तर्क प्रचार कर्नेल देता है:

$K(x-y;T)\propto e^{\frac {i(x-y)^{2}}{2T}},$

जो, पहले के समान सामान्यीकरण के साथ (सम-स्क्वायर सामान्यीकरण नहीं - इस फ़ंक्शन का भिन्न मानदंड है), मुक्त श्रोडिंगर समीकरण का पालन करता है:

${\frac {d}{dt}}K(x;T)=i{\frac {\nabla ^{2}}{2}}K.$

इसका अर्थ यह है कि किसी भी सुपरपोजिशन Ks भी समान समीकरण का पालन करेगा, रैखिकता द्वारा प्रकट होती हैं। इस परिभाषा के अनुसार यह समीकरण प्राप्त होता हैं।

$\psi _{t}(y)=\int \psi _{0}(x)K(x-y;t)\,dx=\int \psi _{0}(x)\int _{x(0)=x}^{x(t)=y}e^{iS}\,Dx,$

तब ψ_t मुक्त श्रोडिंगर समीकरण का पालन K द्वारा किया जाता है:

$i{\frac {\partial }{\partial t}}\psi _{t}=-{\frac {\nabla ^{2}}{2}}\psi _{t}.$

साधारण आवर्त दोलित्र

साधारण आवर्त दोलित्र का लैगरैंगियन है

${\mathcal {L}}={\tfrac {1}{2}}m{\dot {x}}^{2}-{\tfrac {1}{2}}m\omega ^{2}x^{2}.$

इसका प्रक्षेपवक्र लिखिए x(t) मौलिक प्रक्षेपवक्र और कुछ त्रुटि के रूप में, x(t) = x_c(t) + δx(t) और प्रतिक्रिया के रूप में S = S_c + δS. मौलिक प्रक्षेपवक्र के रूप में लिखा जा सकता है

$x_{\text{c}}(t)=x_{i}{\frac {\sin \omega (t_{f}-t)}{\sin \omega (t_{f}-t_{i})}}+x_{f}{\frac {\sin \omega (t-t_{i})}{\sin \omega (t_{f}-t_{i})}}.$

यह प्रक्षेपवक्र मौलिक क्रिया उत्पन्न करता है

${\begin{aligned}S_{\text{c}}&=\int _{t_{i}}^{t_{f}}{\mathcal {L}}\,dt=\int _{t_{i}}^{t_{f}}\left({\tfrac {1}{2}}m{\dot {x}}^{2}-{\tfrac {1}{2}}m\omega ^{2}x^{2}\right)\,dt\\[6pt]&={\frac {1}{2}}m\omega \left({\frac {(x_{i}^{2}+x_{f}^{2})\cos \omega (t_{f}-t_{i})-2x_{i}x_{f}}{\sin \omega (t_{f}-t_{i})}}\right)~.\end{aligned}}$

अगला, फूरियर श्रृंखला के रूप में मौलिक पथ से विचलन का विस्तार करें, और इस प्रकार प्रतिक्रिया में योगदान की गणना δS द्वारा करते हैं, जो उक्त समीकरण देता है

$S=S_{\text{c}}+\sum _{n=1}^{\infty }{\tfrac {1}{2}}a_{n}^{2}{\frac {m}{2}}\left({\frac {(n\pi )^{2}}{t_{f}-t_{i}}}-\omega ^{2}(t_{f}-t_{i})\right).$

इसका अर्थ है कि प्रचारक है

${\begin{aligned}K(x_{f},t_{f};x_{i},t_{i})&=Qe^{\frac {iS_{\text{c}}}{\hbar }}\prod _{j=1}^{\infty }{\frac {j\pi }{\sqrt {2}}}\int da_{j}\exp {\left({\frac {i}{2\hbar }}a_{j}^{2}{\frac {m}{2}}\left({\frac {(j\pi )^{2}}{t_{f}-t_{i}}}-\omega ^{2}(t_{f}-t_{i})\right)\right)}\\[6pt]&=e^{\frac {iS_{\text{c}}}{\hbar }}Q\prod _{j=1}^{\infty }\left(1-\left({\frac {\omega (t_{f}-t_{i})}{j\pi }}\right)^{2}\right)^{-{\frac {1}{2}}}\end{aligned}}$

कुछ सामान्यीकरण के लिए

$Q={\sqrt {\frac {m}{2\pi i\hbar (t_{f}-t_{i})}}}~.$

sinc फलन के अनंत-गुणन निरूपण का उपयोग करके प्राप्त होता हैं,

$\prod _{j=1}^{\infty }\left(1-{\frac {x^{2}}{j^{2}}}\right)={\frac {\sin \pi x}{\pi x}},$

प्रचारक के रूप में लिखा जा सकता है

$K(x_{f},t_{f};x_{i},t_{i})=Qe^{\frac {iS_{\text{c}}}{\hbar }}{\sqrt {\frac {\omega (t_{f}-t_{i})}{\sin \omega (t_{f}-t_{i})}}}=e^{\frac {iS_{c}}{\hbar }}{\sqrt {\frac {m\omega }{2\pi i\hbar \sin \omega (t_{f}-t_{i})}}}.$

इस प्रकार T = t_f − t_i. कोई इस प्रचारक को ऊर्जा ईजेनस्टेट्स के रूप में लिख सकता है

${\begin{aligned}K(x_{f},t_{f};x_{i},t_{i})&=\left({\frac {m\omega }{2\pi i\hbar \sin \omega T}}\right)^{\frac {1}{2}}\exp {\left({\frac {i}{\hbar }}{\tfrac {1}{2}}m\omega {\frac {(x_{i}^{2}+x_{f}^{2})\cos \omega T-2x_{i}x_{f}}{\sin \omega T}}\right)}\\[6pt]&=\sum _{n=0}^{\infty }\exp {\left(-{\frac {iE_{n}T}{\hbar }}\right)}\psi _{n}(x_{f})\psi _{n}(x_{i})^{*}~.\end{aligned}}$

इस प्रकार समरूपता का उपयोग करना i sin ωT = 1/2e^iωT (1 − e^−2iωT) और इस प्रकार cos ωT = 1/2e^iωT (1 + e^−2iωT), यह समान है

$K(x_{f},t_{f};x_{i},t_{i})=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{2}}e^{\frac {-i\omega T}{2}}\left(1-e^{-2i\omega T}\right)^{-{\frac {1}{2}}}\exp {\left(-{\frac {m\omega }{2\hbar }}\left(\left(x_{i}^{2}+x_{f}^{2}\right){\frac {1+e^{-2i\omega T}}{1-e^{-2i\omega T}}}-{\frac {4x_{i}x_{f}e^{-i\omega T}}{1-e^{-2i\omega T}}}\right)\right)}.$

इस प्रकार सभी शर्तों को अवशोषित कर सकता है e^−iωT/2 में R(T), जिससे प्राप्त हो रहा है

$K(x_{f},t_{f};x_{i},t_{i})=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{2}}e^{\frac {-i\omega T}{2}}\cdot R(T).$

कोई अंत में विस्तार कर सकता है R(T) की पावर में e^−iωT द्वारा प्रकट होता हैं: इस प्रकार इस विस्तार में सभी पदों का गुणा e^−iωT/2 द्वारा प्राप्त किया जाता है, इस प्रकार सामने कारक के लिए इस फॉर्म की कुछ शर्ते इस समीकरण द्वारा पूर्ण होती हैं।

$e^{\frac {-i\omega T}{2}}e^{-in\omega T}=e^{-i\omega T\left({\frac {1}{2}}+n\right)}\quad {\text{for }}n=0,1,2,\ldots .$

उपरोक्त ईजेनस्टेट विस्तार की तुलना सरल आवर्त दोलित्र के लिए मानक ऊर्जा स्पेक्ट्रम उत्पन्न करती है,

$E_{n}=\left(n+{\tfrac {1}{2}}\right)\hbar \omega ~.$

See also: प्रोपेगेटर § बुनियादी उदाहरण: फ्री पार्टिकल के प्रोपेगेटर और हार्मोनिक ऑसिलेटर, and मेहलर कर्नेल

कूलम्ब क्षमता

फेनमैन का टाइम-स्लाइस्ड समीपता, चूंकि, परमाणुओं के सबसे महत्वपूर्ण क्वांटम-यांत्रिक पथ समाकलन के लिए सम्मिलित नहीं है, इस प्रकार कूलम्ब क्षमता की विलक्षणता के कारण e²/r मूल में प्राप्त होता हैं। समय परिवर्तित करने के बाद ही t अन्य पथ-निर्भर छद्म-समय पैरामीटर द्वारा किया जाता हैं।

$s=\int {\frac {dt}{r(t)}}$

विलक्षणता को हटा दिया गया है और समय-कटा हुआ समीपता सम्मिलित है, जो बिल्कुल पूर्णांक है, क्योंकि इसे साधारण समन्वय परिवर्तन द्वारा हार्मोनिक बनाया जा सकता है, जैसा कि 1979 में इस्माइल हक्की दुरू और हेगन क्लेनर्ट द्वारा खोजा गया था। इस प्रकार पथ-निर्भर समय परिवर्तन और समन्वय परिवर्तन का संयोजन कई पथ समाकलन को हल करने के लिए महत्वपूर्ण उपकरण है और इसे सामान्य रूप से ड्यूरू-क्लिनर्ट परिवर्तन कहा जाता है।

श्रोडिंगर समीकरण

Main article: श्रोडिंगर के समीकरण और क्वांटम यांत्रिकी के पथ अभिन्न सूत्रीकरण के बीच संबंध

पथ समाकल प्रारंभिक और अंतिम स्थिति के लिए श्रोडिंगर समीकरण को पुन: उत्पन्न करता है, इस प्रकार तब भी जब कोई संभावित सम्मिलित होता हैं। इसकी उच्च सीमा को प्राप्त करने के फलस्वरूप इसे अलग-अलग समयों पर पथ-अभिन्न को ले कर इसे देखना सबसे सरल है।

$\psi (y;t+\varepsilon )=\int _{-\infty }^{\infty }\psi (x;t)\int _{x(t)=x}^{x(t+\varepsilon )=y}e^{i\int _{t}^{t+\varepsilon }{\bigl (}{\frac {1}{2}}{\dot {x}}^{2}-V(x){\bigr )}dt}Dx(t)\,dx\qquad (1)$

चूँकि समय पृथक्करण अतिसूक्ष्म है और बड़े मानों के लिए निरस्त करने वाले दोलन गंभीर हो जाते हैं ẋ, पथ समाकल के लिए सबसे अधिक भार है, इस प्रकार y के पास x उपस्थित रहता हैं। इस स्थिति में, सबसे कम क्रम में संभावित ऊर्जा स्थिर है, और केवल गतिज ऊर्जा का योगदान अनुपयोगी है। (घातांक में गतिज और संभावित ऊर्जा शब्दों का यह पृथक्करण अनिवार्य रूप से लाई उत्पाद सूत्र है।) इसका क्रिया घातांक इस प्रकार हैं-

$e^{-i\varepsilon V(x)}e^{i{\frac {{\dot {x}}^{2}}{2}}\varepsilon }$

पहला पद के चरण को घुमाता है ψ(x) स्थानीय रूप से संभावित ऊर्जा के आनुपातिक राशि से। दूसरा शब्द मुक्त कण प्रचारक है, इस प्रकार i प्रसार प्रक्रिया का समय जिसके अनुरूप है। निम्नतम क्रम में ε वे योज्य हैं; किसी भी स्थिति में किसी के पास (1) है:

$\psi (y;t+\varepsilon )\approx \int \psi (x;t)e^{-i\varepsilon V(x)}e^{\frac {i(x-y)^{2}}{2\varepsilon }}\,dx\,.$

जैसा कि उल्लेख किया गया है, में फैल गया ψ मुक्त कण प्रसार से विसारक है, इस प्रकार इस चरण में अतिरिक्त अनंत घूर्णन के साथ जो धीरे-धीरे संभावित से बिंदु से भिन्न होता है:

${\frac {\partial \psi }{\partial t}}=i\cdot \left({\tfrac {1}{2}}\nabla ^{2}-V(x)\right)\psi \,$

और यह श्रोडिंगर समीकरण है। पथ अभिन्न के सामान्यीकरण को ठीक उसी प्रकार तय करने की आवश्यकता है जैसे मुक्त कण स्थिति में इसका उपयोग किया जाता हैं। अनियंत्रित निरंतर क्षमता सामान्यीकरण को प्रभावित नहीं करती है, चूंकि विलक्षण क्षमता के लिए सावधानीपूर्वक उपचार की आवश्यकता होती है।

गति के समीकरण

चूंकि स्थिति श्रोडिंगर समीकरण का पालन करते हैं, पथ समाकल को औसत के लिए गति के हाइजेनबर्ग समीकरणों को पुन: उत्पन्न करना चाहिए x और ẋ चर, किन्तु इसे सीधे देखना शिक्षाप्रद है। इस प्रकार प्रत्यक्ष दृष्टिकोण से पता चलता है कि पथ समाकलन से गणना किए गए अपेक्षा मान क्वांटम यांत्रिकी के सामान्य लोगों को पुन: उत्पन्न करते हैं।

कुछ निश्चित प्रारंभिक अवस्था के साथ अभिन्न पथ पर विचार करके प्रारंभ करते हैं-

$\int \psi _{0}(x)\int _{x(0)=x}e^{iS(x,{\dot {x}})}\,Dx\,$

अभी x(t) प्रत्येक अलग समय पर अलग एकीकरण चर होता है। इसलिए शिफ्टिंग द्वारा समाकलन में वेरिएबल्स को परिवर्तित करना वैध है: x(t) = u(t) + ε(t) जहाँ ε(t) हर बार अलग बदलाव होता है किन्तु ε(0) = ε(T) = 0, चूंकि समापन बिंदु एकीकृत नहीं हैं:

$\int \psi _{0}(x)\int _{u(0)=x}e^{iS(u+\varepsilon ,{\dot {u}}+{\dot {\varepsilon }})}\,Du\,$

शिफ्ट से समाकलन में परिवर्तन, पहले अपरिमेय क्रम ε में है :

$\int \psi _{0}(x)\int _{u(0)=x}\left(\int {\frac {\partial S}{\partial u}}\varepsilon +{\frac {\partial S}{\partial {\dot {u}}}}{\dot {\varepsilon }}\,dt\right)e^{iS}\,Du\,$

जो, भागों द्वारा एकीकृत t, देता है:

$\int \psi _{0}(x)\int _{u(0)=x}-\left(\int \left({\frac {d}{dt}}{\frac {\partial S}{\partial {\dot {u}}}}-{\frac {\partial S}{\partial u}}\right)\varepsilon (t)\,dt\right)e^{iS}\,Du\,$

किन्तु यह सिर्फ एकीकरण चर का बदलाव था, जो किसी भी विकल्प के लिए अभिन्न का मान ε(t) परिवर्तित नहीं होता है। इस प्रकार इसका निष्कर्ष यह है कि यह पहला क्रम भिन्नता प्रारंभिक अवस्था के लिए शून्य है और समय पर एक बिंदु है:

$\left\langle \psi _{0}\left|{\frac {\delta S}{\delta x}}(t)\right|\psi _{0}\right\rangle =0$

यह गति का हाइजेनबर्ग समीकरण है।

यदि क्रिया में ऐसे पद हैं जो गुणा करते हैं ẋ और x, ही समय में, ऊपर दिए गए जोड़-तोड़ केवल अनुमानी हैं, क्योंकि इन मात्राओं के लिए गुणन नियम पथ के अभिन्न अंग के रूप में गैर-आगंतुक हैं क्योंकि यह ऑपरेटर औपचारिकता में किया जाता है।

स्थिर-चरण समीपता

यदि क्रिया में भिन्नता अधिक हो जाती है ħ परिमाण के कई आदेशों से, हमारे पास सामान्यतः यूलर-लग्रेंज समीकरण को संतुष्ट करने वाले उन प्रक्षेपवक्रों के आसपास के अतिरिक्त विनाशकारी हस्तक्षेप होता है, जिसे अब रचनात्मक हस्तक्षेप की स्थिति के रूप में पुनर्व्याख्या की जाती है। इसे प्रचारक पर लागू स्थिर चरण की विधि का उपयोग करके दिखाया जा सकता है। इस प्रकार जैसे-जैसे ħ घटता है, इस प्रकार क्रिया में किसी भी परिवर्तन के लिए अभिन्न अंग में घातांक जटिल डोमेन में तेजी से दोलन करता है। इस प्रकार, उस सीमा में ħ शून्य पर जाता है, केवल उन बिंदुओं पर जहाँ मौलिक क्रिया भिन्न नहीं होती है, प्रचारक के लिए योगदान करती है।

कैनोनिकल कम्यूटरीकृत संबंध

पथ अभिन्न का सूत्रीकरण प्रारंभ में यह स्पष्ट नहीं करता है कि मात्राएँ x और p यात्रा नहीं करते हैं। पथ अभिन्न में, ये केवल एकीकरण चर हैं और उनका कोई स्पष्ट क्रम नहीं है। फेनमैन ने पाया कि गैर-कम्यूटेटिविटी अभी भी सम्मिलित है। इसे देखने के लिए, सबसे सरल अभिन्न पथ, ब्राउनियन वॉक पर विचार करते हैं। यह अभी तक क्वांटम यांत्रिकी नहीं है, इसलिए पथ-अभिन्न में क्रिया को i द्वारा गुणा नहीं किया जाता है :

$S=\int \left({\frac {dx}{dt}}\right)^{2}\,dt$

मात्रा x(t) उतार-चढ़ाव होता है, और व्युत्पन्न को असतत अंतर की सीमा के रूप में परिभाषित किया जाता है।

${\frac {dx}{dt}}={\frac {x(t+\varepsilon )-x(t)}{\varepsilon }}$

एक यादृच्छिक चाल चलने वाली दूरी √t के समानुपाती होती है , जिससे कि:

$x(t+\varepsilon )-x(t)\approx {\sqrt {\varepsilon }}$

इससे पता चलता है कि रैंडम वॉक अवकलन नहीं है, क्योंकि अनुपात जो डेरिवेटिव डायवर्ज को प्रायिकता के साथ परिभाषित करता है।

मात्रा xẋ अस्पष्ट है, दो संभावित अर्थों के साथ:

$[1]=x{\frac {dx}{dt}}=x(t){\frac {x(t+\varepsilon )-x(t)}{\varepsilon }}$

$[2]=x{\frac {dx}{dt}}=x(t+\varepsilon ){\frac {x(t+\varepsilon )-x(t)}{\varepsilon }}$

प्रारंभिक कलन में, दोनों केवल उस राशि से भिन्न होते हैं जो 0 के रूप में जाती है ε 0 पर जाता है। किन्तु इस स्थिति में, दोनों के बीच का अंतर 0 नहीं है:

$[2]-[1]={\frac {{\big (}x(t+\varepsilon )-x(t){\big )}^{2}}{\varepsilon }}\approx {\frac {\varepsilon }{\varepsilon }}$

इस प्रकार

$f(t)={\frac {{\big (}x(t+\varepsilon )-x(t){\big )}^{2}}{\varepsilon }}$

फिर f(t) तेजी से उतार-चढ़ाव वाली सांख्यिकीय मात्रा है, जिसका औसत मान 1 है, अर्ताथ सामान्यीकृत गॉसियन प्रक्रिया के समान हैं। इस प्रकार की मात्रा के उतार-चढ़ाव को सांख्यिकीय लैग्रेंजियन द्वारा वर्णित किया जा सकता है।

${\mathcal {L}}=(f(t)-1)^{2}\,,$

और गति के समीकरण के लिए f क्रिया को अत्यधिक पर पहुँचाने से प्राप्त होता है S तदनुसार L बस इसे 1 के समान समूह करके उपयोग होते हैं। भौतिकी में, संकारक समरूपता के रूप में ऐसी मात्रा 1 के समान होती है। गणित में, यह कमजोर रूप से 1 में अभिसरण करता है। किसी भी स्थिति में, यह किसी भी अपेक्षा मान में 1 है, या जब किसी अंतराल पर औसत होता है, या सभी व्यावहारिक उद्देश्यों के लिए किया जाता हैं।

ऑपरेटर ऑर्डर होने के लिए समय आदेश को परिभाषित करना:

$[x,{\dot {x}}]=x{\frac {dx}{dt}}-{\frac {dx}{dt}}x=1$

इसे स्टोकेस्टिक कलन में इटो लेम्मा कहा जाता है, और भौतिकी में (यूक्लिडियनकृत) विहित रूपान्तरण संबंध स्थापित करता हैं।

एक सामान्य सांख्यिकीय क्रिया के लिए, समान तर्क यह दर्शाता है।

$\left[x,{\frac {\partial S}{\partial {\dot {x}}}}\right]=1$

और क्वांटम यांत्रिकी में, क्रिया में अतिरिक्त काल्पनिक इकाई इसे कैनोनिकल कम्यूटेशन संबंध में परिवर्तित करती है,

$[x,p]=i$

घुमावदार क्षेत्रों में कण

घुमावदार स्थान में कण के लिए गतिज शब्द स्थिति पर निर्भर करता है, और उपरोक्त टाइम स्लाइसिंग को लागू नहीं किया जा सकता है, यह इस प्रकार श्रोडिंगर क्वांटम यांत्रिकी में कुख्यात ऑपरेटर ऑर्डरिंग समस्या का प्रकटीकरण है। चूंकि, बहु-मानवान समन्वय परिवर्तन (नॉनहोलोनोमिक मैपिंग समझाया का उपयोग करके समय-कटा हुआ फ्लैट-स्पेस पथ अभिन्न को घुमावदार स्थान में बदलकर इस समस्या को हल कर सकता है। /psfiles/pthic10.pdf यहाँ)।

माप-सैद्धांतिक कारक

कभी-कभी (उदाहरण के लिए घुमावदार स्थान में घूर्णन वाला कण) हमारे पास फलन अभिन्न में माप-सिद्धांत संबंधी कारक भी होते हैं:

$\int \mu [x]e^{iS[x]}\,{\mathcal {D}}x.$

एकता को बहाल करने के लिए इस कारक की आवश्यकता है।

उदाहरण के लिए, अगर

$S=\int \left({\frac {m}{2}}g_{ij}{\dot {x}}^{i}{\dot {x}}^{j}-V(x)\right)\,dt,$

तो इसका अर्थ है कि प्रत्येक स्थानिक टुकड़ा माप को √g से गुणा किया जाता है, इस उपाय को फलन गुणन के रूप में व्यक्त नहीं किया जा सकता है, इस प्रकार Dx उपाय करें क्योंकि वे पूरी प्रकार से अलग वर्गों से संबंधित हैं।

अपेक्षा मान और आव्यूह तत्व

प्रकार के आव्यूह तत्व $\langle x_{f}|e^{-{\frac {i}{\hbar }}{\hat {H}}(t-t')}F({\hat {x}})e^{-{\frac {i}{\hbar }}{\hat {H}}(t')}|x_{i}\rangle$ प्रपत्र ले जाने पर-

$\int _{x(0)=x_{i}}^{x(t)=x_{f}}{\mathcal {D}}[x]F(x(t'))e^{{\frac {i}{\hbar }}\int dtL(x(t),{\dot {x}}(t))}$.

उदाहरण के लिए, यह कई ऑपरेटरों के लिए सामान्यीकरण करता है

$\langle x_{f}|e^{-{\frac {i}{\hbar }}{\hat {H}}(t-t_{1})}F_{1}({\hat {x}})e^{-{\frac {i}{\hbar }}{\hat {H}}(t_{1}-t_{2})}F_{2}({\hat {x}})e^{-{\frac {i}{\hbar }}{\hat {H}}(t_{2})}|x_{i}\rangle =\int _{x(0)=x_{i}}^{x(t)=x_{f}}{\mathcal {D}}[x]F_{1}(x(t_{1}))F_{2}(x(t_{2}))e^{{\frac {i}{\hbar }}\int dtL(x(t),{\dot {x}}(t))}$,

और सामान्य अपेक्षा मान के लिए

$\langle F\rangle ={\frac {\int {\mathcal {D}}[\phi ]F(\phi )e^{{\frac {i}{\hbar }}S[\phi ]}}{\int {\mathcal {D}}[\phi ]e^{{\frac {i}{\hbar }}S[\phi ]}}}$.

यूक्लिडियन पथ अभिन्नता

वास्तविक से काल्पनिक समय तक विक घूर्णन करने के लिए पथ समाकलन में यह बहुत सरल है। इस प्रकार क्वांटम क्षेत्र सिद्धांत की समूहिंग में, विक घूर्णन अंतरिक्ष-समय की ज्यामिति को लोरेंट्ज़ियन से यूक्लिडियन में बदल देता है; परिणामस्वरूप, विक-रोटेटेड पाथ समाकलन को अधिकांशतः यूक्लिडियन पथ समाकलन कहा जाता है।

प्रकाष का घुमाव और फेनमैन-केएसी सूत्र

यदि हम प्रतिस्थापित करते हैं $t$ द्वारा $-it$, समय-विकास ऑपरेटर $e^{-it{\hat {H}}/\hbar }$ द्वारा प्रतिस्थापित किया जाता है, इस प्रकार $e^{-t{\hat {H}}/\hbar }$(इस परिवर्तन को विक घूर्णन के रूप में जाना जाता है।) यदि हम इस समूहिंग में पथ-अभिन्न सूत्र की व्युत्पत्ति को दोहराते हैं, तो हम प्राप्त करते हैं

$\psi (x,t)={\frac {1}{Z}}\int _{\mathbf {x} (0)=x}e^{-S_{\mathrm {Euclidean} }(\mathbf {x} ,{\dot {\mathbf {x} }})/\hbar }\psi _{0}(\mathbf {x} (t))\,{\mathcal {D}}\mathbf {x} \,$,

जहाँ $S_{\mathrm {Euclidean} }$ द्वारा दी गई यूक्लिडियन क्रिया है

$S_{\mathrm {Euclidean} }(\mathbf {x} ,{\dot {\mathbf {x} }})=\int \left[{\frac {m}{2}}|{\dot {\mathbf {x} }}(t)|^{2}+V(\mathbf {x} (t))\right]\,dt$.

इस और सामान्य क्रिया के बीच संकेत परिवर्तन पर ध्यान दें, जहाँ स्थितिज ऊर्जा शब्द ऋणात्मक है। (यूक्लिडियन शब्द क्वांटम फील्ड सिद्धांत के संदर्भ में है, जहाँ वास्तविक से काल्पनिक समय में परिवर्तन अंतरिक्ष-समय की ज्यामिति को लोरेंट्ज़ियन से यूक्लिडियन में परिवर्तित कर देता है।)

अब, अभिन्न पथ में गतिज ऊर्जा का योगदान इस प्रकार है:

${\frac {1}{Z}}\int _{\mathbf {x} (0)=x}f(\mathbf {x} )e^{-{\frac {m}{2}}\int |{\dot {\mathbf {x} }}|^{2}dt}\,{\mathcal {D}}\mathbf {x} \,$

जहाँ $f(\mathbf {x} )$ पथ पर इंटीग्रैंड की शेष सभी निर्भरता सम्मिलित है। वीनर प्रक्रिया के खिलाफ एकीकरण के रूप में इस समाकलन की कठोर गणितीय व्याख्या है, जिसे निरूपित किया गया है $\mu _{x}$. नॉर्बर्ट वीनर द्वारा निर्मित वीनर माप, ब्राउनियन गति#आइंस्टीन.27एस सिद्धांत या आइंस्टीन के ब्राउनियन गति के गणितीय प्रारूप को कठोर आधार देता है। इस प्रकार सबस्क्रिप्ट $x$ उपाय बताता है $\mu _{x}$ पथों पर समर्थित है $\mathbf {x}$ साथ $\mathbf {x} (0)=x$.

फिर हमारे पास फेनमैन पाथ समाकलन का कठोर संस्करण है, जिसे फेनमैन-केएसी सूत्र के रूप में जाना जाता है:

$\psi (x,t)=\int e^{-\int V(\mathbf {x} (t)\,dt/\hbar }\,\psi _{0}(\mathbf {x} (t))\,d\mu _{x}(\mathbf {x} )$,

जहाँ $\psi (x,t)$ श्रोडिंगर समीकरण के विक-रोटेटेड संस्करण को संतुष्ट करता है,

$\hbar {\frac {\partial }{\partial t}}\psi (x,t)=-{\hat {H}}\psi (x,t)$.

चूंकि विक-रोटेटेड श्रोडिंगर समीकरण का प्रत्यक्ष भौतिक अर्थ नहीं है, श्रोडिंगर ऑपरेटर के दिलचस्प गुण ${\hat {H}}$ इसका अध्ययन कर निकाला जा सकता है।

इस प्रकार गणित और भौतिकी साहित्य दोनों में पथ-अभिन्न परिप्रेक्ष्य से क्वांटम क्षेत्र सिद्धांतों का अधिकांश अध्ययन यूक्लिडियन समूहिंग में किया जाता है, जो कि विक घूर्णन के बाद होता है। विशेष रूप से, विभिन्न परिणाम दिखा रहे हैं कि यदि उपयुक्त गुणों के साथ यूक्लिडियन क्षेत्र सिद्धांत का निर्माण किया जा सकता है, तो भौतिक, लोरेंत्ज़ियन सिद्धांत को पुनर्प्राप्त करने के लिए विक घूर्णन को पूर्ववत किया जा सकता है। दूसरी ओर, क्वांटम यांत्रिकी की तुलना में क्वांटम क्षेत्र सिद्धांत में पथ समाकलन (यहां तक ​​​​कि यूक्लिडियन पथ समाकलन) को अर्थ देना अधिक कठिन है।

पथ अभिन्न और विभाजन फलन

पथ अभिन्न सभी क्वांटम यांत्रिक समस्याओं के ऊपर अभिन्न अंग का सामान्यीकरण है-

$Z=\int e^{\frac {i{\mathcal {S}}[\mathbf {x} ]}{\hbar }}\,{\mathcal {D}}\mathbf {x} \quad {\text{where }}{\mathcal {S}}[\mathbf {x} ]=\int _{0}^{t_{f}}L[\mathbf {x} (t),{\dot {\mathbf {x} }}(t)]\,dt$

मौलिक समस्या की क्रिया (भौतिकी) है जिसमें व्यक्ति समय से प्रारंभ होने वाले पथ की जांच करता है t = 0 और समय पर समाप्त हो रहा है t = t_f, और ${\mathcal {D}}\mathbf {x}$ सभी रास्तों पर एकीकरण माप को दर्शाता है। मौलिक सीमा में, ${\mathcal {S}}[\mathbf {x} ]\gg \hbar$, न्यूनतम क्रिया का मार्ग अभिन्न पर हावी है, क्योंकि इससे दूर किसी भी पथ का चरण तेजी से उतार-चढ़ाव करता है और विभिन्न योगदान निरस्त हो जाते हैं। सांख्यिकीय यांत्रिकी के साथ संबंध इस प्रकार है। केवल उन्हीं रास्तों को ध्यान में रखते हुए जो ही कॉन्फ़िगरेशन में प्रारंभ और समाप्त होते हैं, it = ħβ द्वारा विक घूर्णन प्राप्त करें, अर्ताथ इस प्रकार समय को काल्पनिक बनाया जाता हैं, और सभी संभव आरंभ-समाप्ति कॉन्फ़िगरेशन पर एकीकृत करें। विक-रोटेटेड पाथ समाकलन - पिछले उपखंड में वर्णित, इसके यूक्लिडियन समकक्ष द्वारा प्रतिस्थापित सामान्य क्रिया के साथ - अब काल्पनिक समय के आनुपातिक तापमान के साथ कैनोनिकल स्थिति में परिभाषित सांख्यिकीय यांत्रिकी के विभाजन फ़ंक्शन (सांख्यिकीय यांत्रिकी) जैसा दिखता है। इस प्रकार 1/T = ik_Bt/ħ. कड़ाई से बोलते हुए, चूंकि, यह सांख्यिकीय क्षेत्र सिद्धांत के लिए विभाजन कार्य है।

इस प्रकार क्वांटम यांत्रिकी और सांख्यिकीय यांत्रिकी के बीच इतना गहरा सादृश्य सूत्रीकरण पर निर्भर नहीं हो सकता हैं। इस प्रकार विहित सूत्रीकरण में, कोई देखता है कि स्थिति के एकात्मक विकास संचालिका द्वारा दिया गया है

$|\alpha ;t\rangle =e^{-{\frac {iHt}{\hbar }}}|\alpha ;0\rangle$

जहाँ स्थिति α समय से विकसित होता है t = 0. यदि कोई यहां विक घूर्णन करता है, और किसी भी स्थिति से जाने के लिए आयाम पाता है, उसी स्थिति में वापस (काल्पनिक) समय में iβ द्वारा दिया गया है

$Z=\operatorname {Tr} \left[e^{-H\beta }\right]$

जो ठीक उसी प्रणाली के लिए सांख्यिकीय यांत्रिकी का विभाजन कार्य है जो पहले उद्धृत तापमान पर है। इस तुल्यता का पहलू इरविन श्रोडिंगर को भी ज्ञात था जिन्होंने टिप्पणी की थी कि उनके नाम का समीकरण विक घूर्णन के बाद विसरण समीकरण जैसा दिखता था। यहाँ पर ध्यान दें, चूंकि, यूक्लिडियन पथ अभिन्न वास्तव में मौलिक सांख्यिकीय यांत्रिकी प्रारूप के रूप में है।

क्वांटम क्षेत्र सिद्धांत

श्रोडिंगर और हाइजेनबर्ग दोनों क्वांटम यांत्रिकी के लिए एकल समय का दृष्टिकोण रखते हैं और सापेक्षता की भावना में नहीं हैं। उदाहरण के लिए, हाइजेनबर्ग दृष्टिकोण के लिए आवश्यक है कि स्केलर फील्ड ऑपरेटर कम्यूटेशन संबंध का पालन करते हैं-

$[\varphi (x),\partial _{t}\varphi (y)]=i\delta ^{3}(x-y)$

दो साथ स्थानिक पदों के लिए x और y, और यह सापेक्षिक रूप से अपरिवर्तनीय अवधारणा नहीं है। गणना के परिणाम सहसंयोजक हैं, किन्तु मध्यवर्ती चरणों में समरूपता स्पष्ट नहीं है। यदि भोले-भाले क्षेत्र-सिद्धांत की गणनाओं ने सातत्य सीमा में अनंत उत्तर नहीं दिए होते, तो यह इतनी बड़ी समस्या नहीं होती हैं- यह सिर्फ निर्देशांक का बुरा विकल्प होता। किन्तु समरूपता की कमी का अर्थ है कि अनंत मात्राओं को काट दिया जाना चाहिए, और इस प्रकार के अनुपयोगी निर्देशांक समरूपता को खराब किए बिना सिद्धांत को काटना लगभग असंभव बना देता है। इससे भौतिक भविष्यवाणियों को निकालना मुश्किल हो जाता है, जिसके लिए पुनर्सामान्यीकरण की आवश्यकता होती है।

खोई हुई समरूपता की समस्या मौलिक यांत्रिकी में भी दिखाई देती है, जहाँ हैमिल्टनियन सूत्र भी सतही रूप से एकल समय निकाल देता है। लैगरैंगियन सूत्रीकरण आपेक्षिकीय निश्चरता स्पष्ट बनाता है। उसी प्रकार, अभिन्न पथ स्पष्ट रूप से सापेक्षवादी है। यह श्रोडिंगर समीकरण, गति के हाइजेनबर्ग समीकरण, और विहित रूपांतरण संबंधों को पुन: उत्पन्न करता है और दिखाता है कि वे सापेक्षता के साथ संगत हैं। यह हाइजेनबर्ग-प्रकार के ऑपरेटर बीजगणित को ऑपरेटर उत्पाद विस्तार तक बढ़ाता है, जो पुराने औपचारिकता में देखने के लिए नए संबंध हैं।

इसके अतिरिक्त, विहित चर के विभिन्न विकल्प ही सिद्धांत के बहुत भिन्न-प्रतीत होने वाले योगों की ओर ले जाते हैं। चर के बीच परिवर्तन बहुत जटिल हो सकते हैं, किन्तु पथ अभिन्न उन्हें एकीकरण चर के यथोचित सीधे परिवर्तन में परिवर्तित कर देता है। इस प्रकार इन कारणों से, फेनमैन पाथ समाकलन ने पहले की औपचारिकताओं को काफी हद तक अप्रचलित बना दिया है।

एक पथ अभिन्न प्रतिनिधित्व की कीमत यह है कि सिद्धांत की एकात्मकता अब स्वयं स्पष्ट नहीं है, किन्तु यह चर को कुछ विहित प्रतिनिधित्व में बदलकर सिद्ध किया जा सकता है। पाथ समाकलन स्वयं भी सामान्य से अधिक बड़े गणितीय रिक्त स्थान से संबंधित है, जिसके लिए अधिक सावधान गणित की आवश्यकता होती है, जिनमें से सभी को पूरी प्रकार से कार्य नहीं किया गया है। ऐतिहासिक रूप से अभिन्न पथ को तुरंत स्वीकार नहीं किया गया था, इस प्रकार आंशिक रूप से क्योंकि फर्मों को ठीक से सम्मिलित करने में कई साल लग गए थे। इसके लिए भौतिकविदों को पूरी प्रकार से नई गणितीय वस्तु - ग्रासमैन चर - का आविष्कार करने की आवश्यकता थी - जिसने चर के परिवर्तन को स्वाभाविक रूप से करने की अनुमति दी, साथ ही फदीव-पोपोव भूत को अनुमति दी जाती हैं।

पथ अभिन्न में एकीकरण चर सूक्ष्म रूप से गैर-आगमन कर रहे हैं। इस बिंदु के समान दिखने वाले दो फील्ड ऑपरेटरों के उत्पाद का मान इस बात पर निर्भर करता है कि अंतरिक्ष और समय में दो बिंदुओं का क्रम कैसे दिया जाता है। यह कुछ भोली समरूपता को विसंगति (भौतिकी) बनाता है।

प्रचारक

सापेक्षतावादी सिद्धांतों में, प्रत्येक सिद्धांत के लिए कण और क्षेत्र दोनों का प्रतिनिधित्व होता है। क्षेत्र प्रतिनिधित्व सभी क्षेत्र विन्यासों पर योग है, और कण प्रतिनिधित्व विभिन्न कण पथों पर योग है।

गैर-सापेक्षवादी सूत्रीकरण पारंपरिक रूप से कण पथों के संदर्भ में दिया जाता है, न कि क्षेत्र्स के रूप में संदर्भित होते हैं। वहां, निश्चित सीमा शर्तों के साथ, सामान्य चरों में अभिन्न पथ, कण के लिए बिंदु से जाने की संभावना आयाम देता है, इस x इंगित करने के लिए y समय के भीतर का मान इस प्रकार हैं- T:

$K(x,y;T)=\langle y;T\mid x;0\rangle =\int _{x(0)=x}^{x(T)=y}e^{iS[x]}\,Dx.$

इसे प्रचारक कहा जाता है। प्रारंभिक स्थिति के विभिन्न मानों को सुपरपोज़ करना x प्रारंभिक अवस्था के साथ ψ₀(x) अंतिम स्थिति का निर्माण करता है:

$\psi _{T}(y)=\int _{x}\psi _{0}(x)K(x,y;T)\,dx=\int ^{x(T)=y}\psi _{0}(x(0))e^{iS[x]}\,Dx.$

एक स्थानिक सजातीय प्रणाली के लिए, जहाँ K(x, y) का कार्य मात्र है (x − y), अभिन्न कनवल्शन है, इस प्रकार अंतिम अवस्था प्रचारक के साथ आरंभिक अवस्था है:

$\psi _{T}=\psi _{0}*K(;T).$

द्रव्यमान के मुक्त कण के लिए m, प्रोपेगेटर का मानांकन या तो स्पष्ट रूप से पथ अभिन्न से किया जा सकता है या यह देखते हुए कि श्रोडिंगर समीकरण काल्पनिक समय में प्रसार समीकरण है, और समाधान सामान्यीकृत गॉसियन होना चाहिए:

$K(x,y;T)\propto e^{\frac {im(x-y)^{2}}{2T}}.$

फूरियर ट्रांसफॉर्म को अंदर ले जाना (x − y) और गाऊसी उत्पन्न करता है:

$K(p;T)=e^{\frac {iTp^{2}}{2m}},$

और इसमें p-अंतरिक्ष यहाँ आनुपातिकता कारक समय में स्थिर है, जैसा कि क्षण में सत्यापित किया जाता हैं। इस प्रकार फूरियर समय के साथ रूपांतरित होता है, विस्तार करता है K(p; T) ऋणात्मक समय के लिए शून्य होने के लिए, ग्रीन का कार्य, या आवृत्ति-स्थान प्रचारक देता है:

$G_{\text{F}}(p,E)={\frac {-i}{E-{\frac {{\vec {p}}^{2}}{2m}}+i\varepsilon }},$

जो ऑपरेटर का पारस्परिक है जो श्रोडिंगर समीकरण में वेवफंक्शन को खत्म कर देता है, जो आनुपातिकता कारक स्थिर नहीं होने पर सही नहीं होता p-अंतरिक्ष प्रतिनिधित्व करता हैं।

इस कारण किसी भाजक में अतिसूक्ष्म शब्द छोटी धनात्मक संख्या है, जो निर्णय करता है कि व्युत्क्रम फूरियर में रूपांतरित होता है E केवल भविष्य के समय के लिए अशून्य होगा। पिछले समय के लिए, व्युत्क्रम फूरियर रूपांतरण समुच्चय E के मानों की ओर बंद हो जाता है जहाँ कोई विलक्षणता नहीं है। इस प्रकार यह इसकी गारंटी देता है K कण को ​​​​भविष्य में प्रचारित करता है और G सबस्क्रिप्ट एफ का कारण प्रकट करता है। इस प्रकार अनन्तसूक्ष्म शब्द की व्याख्या काल्पनिक समय की ओर अतिसूक्ष्म घुमाव के रूप में की जा सकती है।

अतीत की ओर जाने वाले प्रचारकों के संदर्भ में गैर-सापेक्षवादी समय के विकास को फिर से व्यक्त करना भी संभव है, क्योंकि श्रोडिंगर समीकरण समय-प्रतिवर्ती है। पिछला प्रचारक भविष्य के प्रचारकर्ता के समान है, स्पष्ट अंतर को छोड़कर कि यह भविष्य में विलुप्त हो जाता है, और इस प्रकार गॉसियन में t द्वारा प्रतिस्थापित किया जाता है −t. इस स्थिति में, व्याख्या यह है कि प्रारंभिक तरंग प्राप्त करने के लिए अंतिम तरंग को हल करने के लिए ये मात्राएं हैं:

$G_{\text{B}}(p,E)={\frac {-i}{-E-{\frac {i{\vec {p}}^{2}}{2m}}+i\varepsilon }}.$

इस प्रकार दिया गया समीकरण लगभग समान परिवर्तन ही परिवर्तन का संकेत E और ε है , इस कारण पैरामीटर E ग्रीन के कार्य में या तो ऊर्जा हो सकती है यदि रास्ते भविष्य की ओर जा रहे हैं, या ऋणात्मक ऊर्जा हो सकती है, यदि इस चरण को भविष्य की ओर उपयोग करते है।

एक गैर-सापेक्षवादी सिद्धांत के लिए, गतिमान कण के पथ के साथ मापा गया समय और बाहरी पर्यवेक्षक द्वारा मापा गया समय समान होता है। इस प्रकार इसकी सापेक्षता में, यह अब सत्य नहीं है। इस प्रकार सापेक्षतावादी सिद्धांत के लिए प्रचारक को उन सभी रास्तों के योग के रूप में परिभाषित किया जाना चाहिए जो इस प्रकार निश्चित रूप से उचित समय में दो बिंदुओं के बीच यात्रा करते हैं, जैसा कि पथ के साथ मापा जाता है (ये पथ अंतरिक्ष में और समय में कण के प्रक्षेपवक्र का वर्णन करते हैं):

$K(x-y,\mathrm {T} )=\int _{x(0)=x}^{x(\mathrm {T} )=y}e^{i\int _{0}^{\mathrm {T} }{\sqrt {{\dot {x}}^{2}}}-\alpha \,d\tau }.$

उपरोक्त समाकल वर्गमूल के कारण व्याख्या करने के लिए तुच्छ नहीं है। इस प्रकार सौभाग्य से अनुमानी चाल प्राप्त होती है। इस प्रकार योग दोलनशील मात्रा के पथ की सापेक्षतावादी चाप लंबाई से अधिक है, और इस कारण गैर-सापेक्षतावादी पथ अभिन्न की प्रकार काल्पनिक समय में थोड़ा घुमाए जाने के रूप में व्याख्या की जानी चाहिए। कार्यक्रम K(x − y, τ) मानांकन किया जा सकता है जब योग यूक्लिडियन अंतरिक्ष में पथ से अधिक हो:

$K(x-y,\mathrm {T} )=e^{-\alpha \mathrm {T} }\int _{x(0)=x}^{x(\mathrm {T} )=y}e^{-L}.$

यह लंबाई के सभी पथों के योग का वर्णन करता है Τ माइनस लंबाई के घातांक का। इसे संभाव्यता व्याख्या दी जा सकती है। सभी पथों का योग चरण दर चरण निर्मित पथ पर प्रायिकता औसत है। इस प्रकार चरणों की कुल संख्या Τ के समानुपाती होती है, और इस प्रकार प्रत्येक चरण के लंबे होने की संभावना कम होती है। केंद्रीय सीमा प्रमेय के अनुसार, कई स्वतंत्र चरणों का परिणाम समानुपातिक प्रसरण Τ का गॉसियन रूप है:

$K(x-y,\mathrm {T} )=e^{-\alpha \mathrm {T} }e^{-{\frac {(x-y)^{2}}{\mathrm {T} }}}.$

सापेक्षवादी प्रचारक की सामान्य परिभाषा केवल उस आयाम के लिए पूछती है जिससे यात्रा करना है, इस प्रकार x को y, इसमें लगने वाले सभी संभावित उचित समयों का योग करने के पश्चात उक्त समीकरण प्राप्त होता हैं:

$K(x-y)=\int _{0}^{\infty }K(x-y,\mathrm {T} )W(\mathrm {T} )\,d\mathrm {T} ,$

जहाँ W(Τ) भार कारक है, विभिन्न उचित समय के पथों का सापेक्ष महत्व प्रदान होता हैं। इस प्रकार अनुवाद समरूपता द्वारा उचित समय में, यह भार केवल घातीय कारक हो सकता है और α को निरंतरता में अवशोषित किया जा सकता है :

$K(x-y)=\int _{0}^{\infty }e^{-{\frac {(x-y)^{2}}{\mathrm {T} }}-\alpha \mathrm {T} }\,d\mathrm {T} .$

यह फेनमैन आरेख श्विंगर प्रतिनिधित्व है। वेरिएबल पर फूरियर ट्रांसफॉर्म लेना (x − y) के प्रत्येक मान के लिए किया जा सकता है, इस प्रकार Τ अलग-अलग, और क्योंकि प्रत्येक अलग-अलग Τ योगदान गॉसियन है, देता है जिसका फूरियर रूपांतरण पारस्परिक चौड़ाई वाला और गॉसियन है। इस प्रकार p-स्पेस के लिए इस प्रचारक को फिर से व्यक्त किया जा सकता है:

$K(p)=\int _{0}^{\infty }e^{-\mathrm {T} p^{2}-\mathrm {T} \alpha }\,d\mathrm {T} ={\frac {1}{p^{2}+\alpha }},$

जो अदिश कण के लिए यूक्लिडियन प्रचारक है। इस प्रकार घूर्णन p₀ काल्पनिक होना सामान्य सापेक्षवादी प्रचारक देता है, इसके कारक की सीमा तक −i का मान और अस्पष्टता, जिसे नीचे स्पष्ट किया जाएगा:

$K(p)={\frac {i}{p_{0}^{2}-{\vec {p}}^{2}-m^{2}}}.$

इस अभिव्यक्ति की व्याख्या गैर-सापेक्षतावादी सीमा में की जा सकती है, जहाँ इस प्रकार इसे आंशिक अंशों द्वारा विभाजित करना सुविधाजनक है:

$2p_{0}K(p)={\frac {i}{p_{0}-{\sqrt {{\vec {p}}^{2}+m^{2}}}}}+{\frac {i}{p_{0}+{\sqrt {{\vec {p}}^{2}+m^{2}}}}}.$

उन स्थितियों के लिए जहाँ गैर-सापेक्षिक कण सम्मिलित है, प्रारंभिक तरंग फलन में आवृत्ति वितरण p₀ = m के पास केंद्रित होता है। इस प्रकार प्रचारक के साथ बातचीत करते समय, जिसमें p स्पेस का अर्थ केवल प्रचारकर्ता द्वारा गुणा करना है, दूसरा पद दबा दिया जाता है और पहला पद बढ़ा दिया जाता है। इस प्रकार निकट आवृत्तियों के लिए p₀ = m प्रभावी प्रथम पद का रूप है।

$2mK_{\text{NR}}(p)={\frac {i}{(p_{0}-m)-{\frac {{\vec {p}}^{2}}{2m}}}}.$

यह मुक्त श्रोडिंगर कण के गैर-सापेक्षवादी ग्रीन के कार्य के लिए अभिव्यक्ति है।

इस प्रकार किसी दूसरे पद की गैर-सापेक्षतावादी सीमा भी है, किन्तु यह सीमा ऋणात्मक आवृत्तियों पर केंद्रित है। दूसरे ध्रुव पर पथों के योगदान का प्रभुत्व है जहाँ उचित समय और समन्वय समय विपरीत अर्थ में टिक रहे हैं, जिसका अर्थ है कि दूसरे शब्द को एंटीपार्टिकल के रूप में व्याख्या किया जाना है। इस प्रकार गैर-सापेक्षवादी विश्लेषण से पता चलता है कि इस रूप के साथ एंटीपार्टिकल में अभी भी धनात्मक ऊर्जा है।

इसे गणितीय रूप से व्यक्त करने का उचित विधि यह है कि उचित समय में छोटा दमन कारक जोड़कर, सीमा जहाँ t → −∞ है, जिसका पहला कार्यकाल विलुप्त हो जाना चाहिए, इसके अतिरिक्त t → +∞ दूसरे कार्यकाल की सीमा समाप्त हो जाना चाहिए। फूरियर रूपांतरण में, इसका अर्थ है पोल p₀ को थोड़ा सा अंदर ले जाना आवश्यक होता हैं, जिससे कि इस प्रकार व्युत्क्रम फूरियर रूपांतरण समय दिशाओं में छोटा क्षय कारक उठाएगा:

$K(p)={\frac {i}{p_{0}-{\sqrt {{\vec {p}}^{2}+m^{2}}}+i\varepsilon }}+{\frac {i}{p_{0}-{\sqrt {{\vec {p}}^{2}+m^{2}}}-i\varepsilon }}.$

इन शर्तों के बिना, के व्युत्क्रम फूरियर रूपांतरण को लेते समय ध्रुव योगदान p₀ का स्पष्ट रूप से मानांकन नहीं किया जा सकता है। इस प्रकार उक्त शर्तों को पुनर्संयोजित किया जा सकता है:

$K(p)={\frac {i}{p^{2}-m^{2}+i\varepsilon }},$

जो गुणनखंडित होने पर, प्रत्येक गुणनखंड में विपरीत-चिह्न वाले अतिसूक्ष्म शब्द उत्पन्न करता है। इस प्रकार यह सापेक्षतावादी कण प्रचारक का गणितीय रूप से सटीक रूप है, जो किसी भी अस्पष्टता से मुक्त है। ε }} शब्द छोटे से काल्पनिक भाग α = m² का परिचय देता है, जो मिन्कोव्स्की संस्करण में लंबे रास्तों का छोटा घातीय विलोप हो जाता है।

तो सापेक्षवादी स्थिति में, प्रचारक के फेनमैन पथ-अभिन्न प्रतिनिधित्व में समय में पीछे की ओर जाने वाले पथ सम्मिलित हैं, जो एंटीपार्टिकल्स का वर्णन करते हैं। इस प्रकार सापेक्षवादी प्रचारक में योगदान करने वाले पथ समय में आगे और पीछे जाते हैं, और फेनमैन-स्ट्यूकेलबर्ग की व्याख्या यह है कि दो बिंदुओं के बीच यात्रा करने के लिए मुक्त कण के आयाम में कण के एंटीपार्टिकल में उतार-चढ़ाव करने के लिए आयाम सम्मिलित हैं, वापस यात्रा करते हैं।

गैर-सापेक्षतावादी स्थिति के विपरीत, एंटीपार्टिकल्स को सम्मिलित किए बिना स्थानीय कण प्रसार के सापेक्षवादी सिद्धांत का उत्पादन करना असंभव है। इस प्रकार सभी स्थानीय अंतर ऑपरेटरों के व्युत्क्रम होते हैं जो प्रकाश शंकु के बाहर अशून्य होते हैं, जिसका अर्थ है कि कण को ​​​​प्रकाश की तुलना में तेजी से यात्रा करने से रोकना असंभव है। इस प्रकार के कण में ग्रीन का कार्य नहीं हो सकता है जो कि भविष्य में सापेक्षिक रूप से अपरिवर्तनीय सिद्धांत में केवल अशून्य है।

क्षेत्रों के कार्य

चूंकि, क्वांटम क्षेत्र सिद्धांत के प्रत्यक्ष अनुप्रयोग में पथ अभिन्न सूत्रीकरण भी अत्यधिक महत्वपूर्ण है, जिसमें माना जा रहा मार्ग या इतिहास कण की गति नहीं है, इसके अतिरिक्त पूरे स्थान पर क्षेत्र (भौतिकी) के संभावित समय के विकास हैं। क्रिया को तकनीकी रूप से क्षेत्र के फलन (गणित) के रूप में संदर्भित किया जाता है: S[ϕ], जहाँ इस प्रकार मैदान ϕ(x^μ) स्वयं स्थान और समय का कार्य है, और वर्गाकार कोष्ठक अनुस्मारक हैं कि क्रिया हर जगह सभी क्षेत्रों के मानों पर निर्भर करती है, न कि केवल कुछ विशेष मानों पर। ऐसा ही दिया गया कार्य ϕ(x^μ) अंतरिक्ष समय के क्षेत्र विन्यास को कहा जाता है। इस प्रकार सैद्धांतिक रूप में, फेनमैन के आयाम को सभी संभावित क्षेत्र विन्यासों के वर्ग पर एकीकृत करता है।

इस प्रकार QFT का अधिकांश औपचारिक अध्ययन परिणामी फलन अभिन्न के गुणों के लिए समर्पित है, और इन फलन अभिन्नों को गणितीय रूप से सटीक बनाने के लिए बहुत प्रयास (अभी तक पूरी प्रकार से सफल नहीं) किए गए हैं।

ऐसा फलन अभिन्न सांख्यिकीय यांत्रिकी में विभाजन फलन (सांख्यिकीय यांत्रिकी) के समान ही है। वास्तव में, इसे कभी-कभी विभाजन फलन (क्वांटम क्षेत्र सिद्धांत) कहा जाता है, और दो अनिवार्य रूप से गणितीय रूप से समान होते हैं सिवाय इसके कारक के i फेनमैन के अभिधारणा में प्रतिपादक में 3 मान प्राप्त होता है। इस प्रकार विश्लेषणात्मक निरंतरता काल्पनिक समय चर (जिसे विक घूर्णन कहा जाता है) का अभिन्न अंग सांख्यिकीय विभाजन फलन की प्रकार फलन अभिन्न को और भी अधिक बनाता है और इन अभिन्नों के साथ कार्य करने की कुछ गणितीय कठिनाइयों को भी दूर करता है।

अपेक्षा मान

क्वांटम क्षेत्र सिद्धांत में, यदि क्रिया (भौतिकी) फलन (गणित) द्वारा दी गई है S क्षेत्रीय विकास (जो केवल स्थानीय रूप से क्षेत्र पर निर्भर करता है), फिर इस प्रकार बहुपद रूप से बंधे फलन का समय-आदेशित वैक्यूम अपेक्षा मान F, ⟨F⟩, द्वारा दिया गया है

$\langle F\rangle ={\frac {\int {\mathcal {D}}\varphi F[\varphi ]e^{i{\mathcal {S}}[\varphi ]}}{\int {\mathcal {D}}\varphi e^{i{\mathcal {S}}[\varphi ]}}}.$

इस प्रतीक ∫Dϕ के आधार पर यहां सभी स्पेस-टाइम पर सभी संभावित क्षेत्रीय विकास पर अनंत-आयामी समाकलन का प्रतिनिधित्व करने का संक्षिप्त विधि है। जैसा कि ऊपर कहा गया है, भाजक में इस प्रकार अभिन्न पथ का अभिन्न अंग उचित सामान्यीकरण सुनिश्चित करता है।

संभावना के रूप में

इस प्रकार भौतिकी में एकमात्र प्रश्न पूछा जा सकता है: स्थिति को संतुष्ट करने वाले स्थितियों का कौन सा अंश A तथा B की शर्त भी पूरी करते हैं ? इस प्रकार इसका उत्तर 0 और 1 के बीच की संख्या है, जिसे सशर्त संभावना P(B|A)के रूप में लिखा जा सकता है ।पइस प्रकार थ एकीकरण के संदर्भ में, चूंकि P(B|A) = P(A∩B) / P(A), इसका अर्थ इस प्रकार हैं-

$\operatorname {P} (B\mid A)={\frac {\sum _{F\subset A\cap B}\left|\int {\mathcal {D}}\varphi O_{\text{in}}[\varphi ]e^{i{\mathcal {S}}[\varphi ]}F[\varphi ]\right|^{2}}{\sum _{F\subset A}\left|\int {\mathcal {D}}\varphi O_{\text{in}}[\varphi ]e^{i{\mathcal {S}}[\varphi ]}F[\varphi ]\right|^{2}}},$

जहाँ फलन O_in[ϕ] आने वाले सभी स्थितियों का सुपरपोजिशन है जो उन स्थितियों की ओर ले जा सकता है जिनमें हम रुचि रखते हैं। इस प्रकार विशेष रूप से, यह महा विस्फोट के ठीक बाद ब्रह्मांड की स्थिति के अनुरूप स्थिति हो सकता है, चूंकि इस प्रकार इसकी वास्तविक गणना के लिए इसे हेयुरिस्टिक विधियों का उपयोग करके सरल बनाया जा सकता है। चूँकि इस प्रकार यह व्यंजक पथ समाकलनों का भागफल है, यह स्वाभाविक रूप से सामान्यीकृत होता है।

श्विंगर-डायसन समीकरण

Main article: श्विंगर-डायसन समीकरण

चूँकि क्वांटम यांत्रिकी का यह सूत्रीकरण मौलिक क्रिया सिद्धांत के अनुरूप है, कोई उम्मीद कर सकता है कि मौलिक यांत्रिकी में इस प्रकार प्रतिक्रिया से संबंधित समरूपता में फलन अभिन्न से व्युत्पन्न क्वांटम समकक्ष होंगे। अधिकांशतः ऐसा होता है।

प्रफलन विश्लेषण की भाषा में, हम यूलर-लैग्रेंज समीकरणों को इस प्रकार लिख सकते हैं

${\frac {\delta {\mathcal {S}}[\varphi ]}{\delta \varphi }}=0$

(बाईं ओर फलन व्युत्पन्न है; समीकरण का अर्थ है कि क्षेत्र विन्यास में छोटे परिवर्तनों के तहत क्रिया स्थिर है)। इस प्रकार इन समीकरणों के क्वांटम अनुरूपों को श्विंगर-डायसन समीकरण कहा जाता है।

यदि फलन उपाय Dϕ अनुवादिक समरूपता निकला (हम इस लेख के अतिरिक्त भागों के लिए इसे मानेंगे, चूंकि इस प्रकार यह इसकी सीमा में नहीं आता है, मान लें कि गैर रेखीय सिग्मा प्रारूप), और अगर हम मानते हैं कि विक घूर्णन के बाद प्राप्त होता हैं-

$e^{i{\mathcal {S}}[\varphi ]},$

जो अब बन गया है

$e^{-H[\varphi ]}$

कुछ के लिए H, यह के बड़े मानों के लिए किसी भी बहुपद के गुणक व्युत्क्रम की तुलना में तेजी से शून्य हो जाता है φ, तो हम उम्मीद के लिए निम्नलिखित श्विंगर-डायसन समीकरण प्राप्त करने के लिए भागों द्वारा एकीकरण कर सकते हैं (एक विक घूर्णन के बाद, विक घूर्णन के पश्चात वापस करते हैं):

$\left\langle {\frac {\delta F[\varphi ]}{\delta \varphi }}\right\rangle =-i\left\langle F[\varphi ]{\frac {\delta {\mathcal {S}}[\varphi ]}{\delta \varphi }}\right\rangle$

किसी भी बहुपद-सीमित फलन के लिए F. डेविट संकेतन में ऐसा दिखता है।

$\left\langle F_{,i}\right\rangle =-i\left\langle F{\mathcal {S}}_{,i}\right\rangle .$

ये समीकरण ऑन-शैल EL समीकरणों के अनुरूप हैं। इस प्रकार टाइम ऑर्डरिंग अंदर टाइम डेरिवेटिव्स S_,i से पहले लिया जाता है-

यदि J (स्रोत क्षेत्र कहा जाता है) क्षेत्रीय विकास के दोहरे स्थान का तत्व है (जिसमें फलन माप के लिए अनुवाद संबंधी व्युत्क्रम की धारणा के कारण कम से कम एफ़िन संरचना होती है), फिर उत्पन्न करने वाला फलन Z स्रोत क्षेत्र के रूप में परिभाषित किया गया है

$Z[J]=\int {\mathcal {D}}\varphi e^{i\left({\mathcal {S}}[\varphi ]+\langle J,\varphi \rangle \right)}.$

ध्यान दें कि

${\frac {\delta ^{n}Z}{\delta J(x_{1})\cdots \delta J(x_{n})}}[J]=i^{n}\,Z[J]\,\left\langle \varphi (x_{1})\cdots \varphi (x_{n})\right\rangle _{J},$

या

$Z^{,i_{1}\cdots i_{n}}[J]=i^{n}Z[J]\left\langle \varphi ^{i_{1}}\cdots \varphi ^{i_{n}}\right\rangle _{J},$

जहाँ

$\langle F\rangle _{J}={\frac {\int {\mathcal {D}}\varphi F[\varphi ]e^{i\left({\mathcal {S}}[\varphi ]+\langle J,\varphi \rangle \right)}}{\int {\mathcal {D}}\varphi e^{i\left({\mathcal {S}}[\varphi ]+\langle J,\varphi \rangle \right)}}}.$

मूल रूप से, अगर Dφ e^iS[φ] फलन वितरण के रूप में देखा जाता है (इसे क्वांटम क्षेत्र सिद्धांत की व्याख्या के रूप में शाब्दिक रूप से नहीं लिया जाना चाहिए, इसके विक-रोटेट स्टैटिस्टिकल मैकेनिक्स एनालॉग के विपरीत, क्योंकि हमारे पास यहां समय-समय पर जटिलताएं हैं!), फिर ⟨φ(x₁) ... φ(x_n)⟩ इसके क्षण (गणित) हैं, और Z इसका फूरियर रूपांतरण है।

यदि F का क्रियात्मक है φ, फिर ऑपरेटर (गणित) के लिए K, F[K] ऑपरेटर के रूप में परिभाषित किया गया है जो इस प्रकार स्थानापन्न करता है K के लिए φ को प्रकट करने के लिए इसे उदाहरण के रूप में प्रकट कर सकते हैं-

$F[\varphi ]={\frac {\partial ^{k_{1}}}{\partial x_{1}^{k_{1}}}}\varphi (x_{1})\cdots {\frac {\partial ^{k_{n}}}{\partial x_{n}^{k_{n}}}}\varphi (x_{n}),$

और G का क्रियात्मक J है, इस प्रकार प्राप्त होने वाला समीकरण इस प्रकार होगा-

$F\left[-i{\frac {\delta }{\delta J}}\right]G[J]=(-i)^{n}{\frac {\partial ^{k_{1}}}{\partial x_{1}^{k_{1}}}}{\frac {\delta }{\delta J(x_{1})}}\cdots {\frac {\partial ^{k_{n}}}{\partial x_{n}^{k_{n}}}}{\frac {\delta }{\delta J(x_{n})}}G[J].$

फिर, फलन अभिन्न के गुणों से किया जाता हैं-

$\left\langle {\frac {\delta {\mathcal {S}}}{\delta \varphi (x)}}[\varphi ]+J(x)\right\rangle _{J}=0$

हमें मास्टर श्विंगर-डायसन समीकरण मिलता है:

${\frac {\delta {\mathcal {S}}}{\delta \varphi (x)}}\left[-i{\frac {\delta }{\delta J}}\right]Z[J]+J(x)Z[J]=0,$

या

${\mathcal {S}}_{,i}[-i\partial ]Z+J_{i}Z=0.$

यदि फलन उपाय पारभासी रूप से अपरिवर्तनीय नहीं है, तो इसे उत्पाद के रूप में व्यक्त करना संभव हो सकता है M[φ] Dφ, जहाँ M फलन और है, इस प्रकार Dφ अनुवादात्मक रूप से अपरिवर्तनीय उपाय है। यह सच है, उदाहरण के लिए, गैर-रैखिक सिग्मा प्रारूप के लिए जहाँ लक्षित स्थान Rⁿ अलग-अलग प्राप्त होते है। चूंकि इस प्रकार यदि लक्ष्य कई गुना कुछ स्थैतिक रूप से अनुपयोगी स्थान है, तो अनुवाद की अवधारणा का कोई अर्थ नहीं है।

उस स्थिति में, हमें इसे परिवर्तित करना होगा S इस समीकरण में अन्य फलन द्वारा प्राप्त किया जाता हैं।

${\hat {\mathcal {S}}}={\mathcal {S}}-i\ln M.$

यदि हम जे के बारे में टेलर श्रृंखला के रूप में इस समीकरण का विस्तार करते हैं, इस प्रकार हमें श्विंगर-डायसन समीकरणों का पूरा समूह मिलता है।

स्थानीयकरण

पथ समाकलन को सामान्यतः अनंत स्थान-समय के माध्यम से सभी पथों का योग माना जाता है। चूंकि इस प्रकार स्थानीय क्वांटम क्षेत्र सिद्धांत में हम सब कुछ परिमित रूप से पूर्ण क्षेत्र के भीतर असत्य बोलने के लिए प्रतिबंधित करेंगे, उदाहरण के लिए डबल लाइट-शंकु के अंदर। स्थानीय क्वांटम क्षेत्र सिद्धांत की अधिक गणितीय रूप से सटीक और भौतिक रूप से कठोर परिभाषा देता है।

वार्ड-ताकाहाशी समरूपता

Main article: वार्ड-ताकाहाशी पहचान

अब कैसे मौलिक स्थिति के लिए शेल नोएदर के प्रमेय के बारे में? क्या इसका क्वांटम एनालॉग भी है? हाँ, किन्तु चेतावनी के साथ उपयोग होता हैं। इस प्रकार समरूपता परिवर्तन के पैरामीटर समूह के तहत फलन माप को भी अपरिवर्तनीय होना होगा।

आइए यहां सरलता के लिए मान लें कि प्रश्न में समरूपता स्थानीय है (गेज समरूपता के अर्थ में स्थानीय नहीं है, किन्तु इस अर्थ में कि किसी भी बिंदु पर असीम परिवर्तन के तहत क्षेत्र का रूपांतरित मान केवल क्षेत्रीय विकास पर निर्भर करेगा विचाराधीन बिंदु के स्वयं की इस विधि से छोटे समीप पर)। आइए यह भी मान लें कि क्रिया स्थानीय है इस अर्थ में कि यह लैग्रैंगियन (क्षेत्र सिद्धांत) के स्पेसटाइम पर अभिन्न अंग है, और वह

$Q[{\mathcal {L}}(x)]=\partial _{\mu }f^{\mu }(x)$

किसी फलन के लिए f जहाँ f केवल स्थानीय रूप φ (और संभवतः स्पेसटाइम स्थिति) से निर्भर करता है।

यदि हम कोई विशेष सीमा स्थिति नहीं मानते हैं, तो यह सामान्य रूप से शब्द के सही अर्थों में सही समरूपता नहीं होगी जब तक कि f = 0 या कुछ और। यहां, Q व्युत्पत्ति (अमूर्त बीजगणित) है जो प्रश्न में पैरामीटर समूह उत्पन्न करता है। इस प्रकार हमारे पास बीआरएसटी परिमाणीकरण और सुपरसिमेट्री जैसे प्रतिपक्षी भी हो सकते हैं।

चलिये मान लेते हैं-

$\int {\mathcal {D}}\varphi \,Q[F][\varphi ]=0$

किसी भी बहुपद-सीमित फलन के लिए F को इस प्रकार इस संपत्ति को माप का व्युत्क्रम कहा जाता है। और यह सामान्य तौर पर नहीं होता है। अधिक विवरण के लिए विसंगति (भौतिकी) देखें।

फिर,

$\int {\mathcal {D}}\varphi \,Q\left[Fe^{iS}\right][\varphi ]=0,$

जो ये दर्शाता हे

$\langle Q[F]\rangle +i\left\langle F\int _{\partial V}f^{\mu }\,ds_{\mu }\right\rangle =0$

जहाँ अभिन्न सीमा से अधिक है। यह नोएदर के प्रमेय का क्वांटम एनालॉग है।

अब, इससे भी आगे मान लेते हैं Q स्थानीय अभिन्न है

$Q=\int d^{d}x\,q(x)$

जहाँ

$q(x)[\varphi (y)]=\delta ^{(d)}(X-y)Q[\varphi (y)]\,$

जिससे कि

$q(x)[S]=\partial _{\mu }j^{\mu }(x)\,$

जहाँ

$j^{\mu }(x)=f^{\mu }(x)-{\frac {\partial }{\partial (\partial _{\mu }\varphi )}}{\mathcal {L}}(x)Q[\varphi ]\,$

(यह माना जा रहा है कि लैगरैंगियन केवल इस पर निर्भर करता है φ और इसका पहला आंशिक डेरिवेटिव अधिक सामान्य लैगरैंगियनs को इस परिभाषा में संशोधन की आवश्यकता होगी!) हम उस पर जोर नहीं दे रहे हैं q(x) समरूपता का जनरेटर है (अर्ताथ हम गेज सिद्धांत पर जोर नहीं दे रहे हैं), किन्तु बस इतना ही Q है। और इस प्रकार हम यह भी मानते हैं कि फलन माप स्थानीय रूप से अपरिवर्तनीय है:

$\int {\mathcal {D}}\varphi \,q(x)[F][\varphi ]=0.$

तब,

हमारे पास कुछ इस प्रकार समीकरण प्राप्त होगा।

$\langle q(x)[F]\rangle +i\langle Fq(x)[S]\rangle =\langle q(x)[F]\rangle +i\left\langle F\partial _{\mu }j^{\mu }(x)\right\rangle =0.$

वैकल्पिक रूप से,

$q(x)[S]\left[-i{\frac {\delta }{\delta J}}\right]Z[J]+J(x)Q[\varphi (x)]\left[-i{\frac {\delta }{\delta J}}\right]Z[J]=\partial _{\mu }j^{\mu }(x)\left[-i{\frac {\delta }{\delta J}}\right]Z[J]+J(x)Q[\varphi (x)]\left[-i{\frac {\delta }{\delta J}}\right]Z[J]=0.$

उपरोक्त दो समीकरण वार्ड-ताकाहाशी समरूपता हैं।

अब जहाँ स्थिति के लिए f = 0, हम सभी सीमा शर्तों और क्षेत्र की धारणाओं के बारे में भूल सकते हैं। हमारे पास कुछ इस प्रकार समीकरण प्राप्त होगा।

$\left\langle Q[F]\right\rangle =0.$

वैकल्पिक रूप से,

$\int d^{d}x\,J(x)Q[\varphi (x)]\left[-i{\frac {\delta }{\delta J}}\right]Z[J]=0.$

चेतावनी

नियामकों और पुनर्सामान्यीकरण की आवश्यकता

पथ समाकलन, जैसा कि यहां परिभाषित किया गया है, जिसको नियमितीकरण (भौतिकी) की प्रारंभ की आवश्यकता है। नियामक के पैमाने को परिवर्तित करने से पुनर्सामान्यीकरण समूह होता है। वास्तव में, पथ समाकलन को अच्छी प्रकार से परिभाषित करने के लिए पुनर्सामान्यीकरण प्रमुख बाधा है।

आदेश

इस प्रकार भले ही किसी कॉन्फ़िगरेशन स्पेस या फेज़ स्पेस में कार्य करता हो, इस प्रकार जब क्वांटम यांत्रिकी के गणितीय सूत्रीकरण और पथ समाकलन सूत्र की बराबरी करते हैं, तो गैर-कम्यूटेटिव ऑपरेटरों और कम्यूटेटिव फ़ंक्शंस के बीच पत्राचार में अस्पष्टता को हल करने के लिए ऑर्डरिंग प्रिस्क्रिप्शन की आवश्यकता होती है। जो इस प्रकार पथ एकीकृत के लिए उपयोग करता हैं। उदाहरण के लिए, ऑपरेटर ${\frac {1}{2}}({\hat {q}}{\hat {p}}+{\hat {p}}{\hat {q}})$ या तो वापस अनुवादित किया जा सकता है $qp-{\frac {i\hbar }{2}}$, $qp+{\frac {i\hbar }{2}}$, या $qp$ इस पर निर्भर करता है कि कोई चुनता है या नहीं इसका निर्णय ${\hat {q}}{\hat {p}}$, ${\hat {p}}{\hat {q}}$, या वेइल ऑर्डरिंग प्रिस्क्रिप्शन; इसके विपरीत, $qp$ दोनों में अनुवाद किया जा सकता है ${\hat {q}}{\hat {p}}$, ${\hat {p}}{\hat {q}}$, या ${\frac {1}{2}}({\hat {q}}{\hat {p}}+{\hat {p}}{\hat {q}})$ ऑर्डर करने की विधि के समान संबंधित विकल्प के लिए उपयोग करता हैं।

क्वांटम यांत्रिक व्याख्या में पथ अभिन्न

क्वांटम यांत्रिकी की व्याख्या में, इतिहास की व्याख्या पर योग, पथ अभिन्न को मौलिक माना जाता है, और वास्तविकता को पथों के एकल अप्रभेद्य वर्ग के रूप में देखा जाता है, जो सभी समान घटनाओं को साझा करते हैं। इस व्याख्या के लिए, यह समझना महत्वपूर्ण है कि वास्तव में कोई घटना क्या है। इस प्रकार सम-ओवर-इतिहास विधि विहित क्वांटम यांत्रिकी, और सिन्हा और सॉर्किन को समान परिणाम देती है। इस प्रकार प्रमाण व्याख्या दूरी पर प्रतिक्रिया का सहारा लिए बिना आइंस्टीन-पोडॉल्स्की-रोसेन विरोधाभास की व्याख्या करती है।

इस प्रकार कुछ क्वांटम यांत्रिकी की व्याख्याओं के पैरोकारों ने सभी संभव इतिहासों के स्थान से मौलिक-समान मोटे अनाज वाले इतिहास को निकालने की धारणा को और अधिक कठोर बनाने का प्रयास किया है।

क्वांटम गुरुत्व

इसके अतिरिक्त क्वांटम यांत्रिकी में पथ अभिन्न सूत्रीकरण अन्य योगों के लिए पूरी प्रकार से समतुल्य है, यह हो सकता है कि इसे क्वांटम गुरुत्व तक बढ़ाया जा सकता है, जो इसे हिल्बर्ट अंतरिक्ष प्रारूप से अलग बना देगा। फेनमैन को इस दिशा में कुछ सफलता मिली, और इस प्रकार उनके कार्य को स्टीफन हॉकिंग और अन्य लोगों ने आगे बढ़ाया था। इस पद्धति का उपयोग करने वाले दृष्टिकोणों में कारण गतिशील त्रिभुज और स्पिनफोम प्रारूप सम्मिलित हैं।

क्वांटम टनलिंग

एक संभावित बाधा के माध्यम से प्रक्षेपवक्र की प्रतिक्रिया निर्धारित करने के लिए पथ अभिन्न गठन का उपयोग करके क्वांटम टनलिंग का प्रारूप तैयार किया जा सकता है। इस प्रकार WKB समीपता का उपयोग करते हुए, टनलिंग दर (Γ) के रूप में निर्धारित किया जा सकता है

$\Gamma =A_{\mathrm {o} }\exp \left(-{\frac {S_{\mathrm {eff} }}{\hbar }}\right)$

प्रभावी प्रतिक्रिया के साथ S_eff और पूर्व घातीय कारक A_o हैं। इस प्रकार यह प्रपत्र विघटनकारी प्रणाली में विशेष रूप से उपयोगी है, जिसमें सिस्टम और परिवेश को साथ प्रारूप किया जाना चाहिए। इस प्रकार ब्राउनियन गति को प्रारूप करने के लिए लैंग्विन समीकरण का उपयोग करते हुए, टनलिंग पर अपव्यय के प्रभाव को देखने के लिए प्रभावी प्रतिक्रिया और पूर्व-घातीय प्रारूप को निर्धारित करने के लिए पथ अभिन्न गठन का उपयोग किया जा सकता है। इस प्रारूप से, मैक्रोस्कोपिक सिस्टम (परिमित तापमान पर) की टनलिंग दरों का अनुमान लगाया जा सकता है।

यह भी देखें

• श्रोडिंगर समीकरण के लिए सैद्धांतिक और प्रायोगिक औचित्य
• स्थैतिक बल और आभासी-कण विनिमय
• फेनमैन चेकरबोर्ड
• बेरेज़िन अभिन्न
• प्रचारक
• व्हीलर-फेनमैन अवशोषक सिद्धांत
• फेनमैन-केएसी सूत्र
• बहुलक विज्ञान में पाथ इंटीग्रल

संदर्भ

• Ahmad, Ishfaq (1971). Mathematical Integrals in Quantum Nature. The Nucleus. pp. 189–209.
• Albeverio, S.; Hoegh-Krohn., R. & Mazzucchi, S (2008). Mathematical Theory of Feynman Path Integral. Lecture Notes in Mathematics 523. Springer-Verlag. ISBN 9783540769569.
• Caldeira, A. O.; Leggett, A. J. (1983). "Quantum tunnelling in a dissipative system". Annals of Physics. 149 (2): 374–456. Bibcode:1983AnPhy.149..374C. doi:10.1016/0003-4916(83)90202-6.
• Cartier, P; DeWitt-Morette, Cécile (1995). "A new perspective on Functional Integration". Journal of Mathematical Physics. 36 (5): 2137–2340. arXiv:funct-an/9602005. Bibcode:1995JMP....36.2237C. doi:10.1063/1.531039. S2CID 119581543.
• Chaichian, M.; Demichev, A. P. (2001). "Introduction". Path Integrals in Physics Volume 1: Stochastic Process & Quantum Mechanics. Taylor & Francis. p. 1ff. ISBN 978-0-7503-0801-4.
• DeWitt-Morette, C. (1972). "Feynman's path integral: Definition without limiting procedure". Communications in Mathematical Physics. 28 (1): 47–67. Bibcode:1972CMaPh..28...47D. doi:10.1007/BF02099371. MR 0309456. S2CID 119669964.
• Dirac, Paul A. M. (1933). "The Lagrangian in Quantum Mechanics" (PDF). Physikalische Zeitschrift der Sowjetunion. 3: 64–72.
• Duru, İ. H.; Kleinert, Hagen (1979). "Solution of the path integral for the H-atom" (PDF). Physics Letters. 84B (2): 185–188. Bibcode:1979PhLB...84..185D. doi:10.1016/0370-2693(79)90280-6. Retrieved 2007-11-25.
• Etingof, P (2002). "Geometry and Quantum Field Theory". MIT OpenCourseWare. This course, designed for mathematicians, is a rigorous introduction to perturbative quantum field theory, using the language of functional integrals.
• Feynman, R. P. (2005) [1942/1948]. Brown, L. M. (ed.). Feynman's Thesis — A New Approach to Quantum Theory. World Scientific. Bibcode:2005ftna.book.....B. doi:10.1142/5852. ISBN 978-981-256-366-8. The 1942 thesis. Also includes Dirac's 1933 paper and Feynman's 1948 publication.
• Feynman, R. P. (1948). "Space-Time Approach to Non-Relativistic Quantum Mechanics" (PDF). Reviews of Modern Physics. 20 (2): 367–387. Bibcode:1948RvMP...20..367F. doi:10.1103/RevModPhys.20.367.
• Feynman, R. P.; Hibbs, A. R. (1965). Quantum Mechanics and Path Integrals. New York: McGraw-Hill. ISBN 978-0-07-020650-2. The historical reference, written by the inventor of the path integral formulation himself and one of his students.
• Feynman, R. P.; Hibbs, A. R.; Styer, D. F. (2010). Quantum Mechanics and Path Integrals. Mineola, NY: Dover Publications. pp. 29–31. ISBN 978-0-486-47722-0.
• Gell-Mann, Murray (1993). "Most of the Good Stuff". In Brown, Laurie M.; Rigden, John S. (eds.). Memories Of Richard Feynman. American Institute of Physics. ISBN 978-0883188705.
• Glimm, J. & Jaffe, A. (1981). Quantum Physics: A Functional Integral Point of View. New York: Springer-Verlag. ISBN 978-0-387-90562-4.
• Grosche, Christian & Steiner, Frank (1998). Handbook of Feynman Path Integrals. Springer Tracts in Modern Physics 145. Springer-Verlag. ISBN 978-3-540-57135-3.
• Grosche, Christian (1992). "An Introduction into the Feynman Path Integral". arXiv:hep-th/9302097.
• Hall, Brian C. (2013). Quantum Theory for Mathematicians. Graduate Texts in Mathematics. Vol. 267. Springer. doi:10.1007/978-1-4614-7116-5. ISBN 978-1-4614-7115-8. S2CID 117837329.
• Inomata, Akira; Kuratsuji, Hiroshi; Gerry, Christopher (1992). Path Integrals and Coherent States of SU(2) and SU(1,1). Singapore: World Scientific. ISBN 978-981-02-0656-7.
• Janke, W.; Pelster, Axel, eds. (2008). Path Integrals--New Trends And Perspectives. Proceedings Of The 9Th International Conference. World Scientific Publishing. ISBN 978-981-283-726-4.
• Johnson, Gerald W.; Lapidus, Michel L. (2002). The Feynman Integral and Feynman's Operational Calculus. Oxford Mathematical Monographs. Oxford University Press. ISBN 978-0-19-851572-2.
• Klauder, John R. (2010). A Modern Approach to Functional Integration. New York: Birkhäuser. ISBN 978-0-8176-4790-2.
• Kleinert, Hagen (2004). Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets (4th ed.). Singapore: World Scientific. ISBN 978-981-238-107-1.
• MacKenzie, Richard (2000). "Path Integral Methods and Applications". arXiv:quant-ph/0004090.
• Mazzucchi, S. (2009). Mathematical Feynman path integrals and their applications. World Scientific. ISBN 978-981-283-690-8.
• Müller-Kirsten, Harald J. W. (2012). Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral (2nd ed.). Singapore: World Scientific.
• Rivers, R. J. (1987). Path Integrals Methods in Quantum Field Theory. Cambridge University Press. ISBN 978-0-521-25979-8.
• Ryder, Lewis H. (1985). Quantum Field Theory. Cambridge University Press. ISBN 978-0-521-33859-2. Highly readable textbook; introduction to relativistic QFT for particle physics.
• Schulman, L S. (1981). Techniques & Applications of Path Integration. New York: John Wiley & Sons. ISBN 978-0-486-44528-1.
• Simon, B. (1979). Functional Integration and Quantum Physics. New York: Academic Press. ISBN 978-0-8218-6941-3.
• Sinha, Sukanya; Sorkin, Rafael D. (1991). "A Sum-over-histories Account of an EPR(B) Experiment" (PDF). Foundations of Physics Letters. 4 (4): 303–335. Bibcode:1991FoPhL...4..303S. doi:10.1007/BF00665892. S2CID 121370426.
• Tomé, W. A. (1998). Path Integrals on Group Manifolds. Singapore: World Scientific. ISBN 978-981-02-3355-6. Discusses the definition of Path Integrals for systems whose kinematical variables are the generators of a real separable, connected Lie group with irreducible, square integrable representations.
• Van Vleck, J. H. (1928). "The correspondence principle in the statistical interpretation of quantum mechanics". Proceedings of the National Academy of Sciences of the United States of America. 14 (2): 178–188. Bibcode:1928PNAS...14..178V. doi:10.1073/pnas.14.2.178. PMC 1085402. PMID 16577107.
• Weinberg, S. (2002) [1995], Foundations, The Quantum Theory of Fields, vol. 1, Cambridge: Cambridge University Press, ISBN 978-0-521-55001-7
• Zee, A. (2010-02-21). Quantum Field Theory in a Nutshell (Second ed.). Princeton University Press. ISBN 978-0-691-14034-6. A great introduction to Path Integrals (Chapter 1) and QFT in general.
• Zinn Justin, J. (2004). Path Integrals in Quantum Mechanics. Oxford University Press. ISBN 978-0-19-856674-8.

बाहरी कड़ियाँ

• Path integral on Scholarpedia
• Path Integrals in Quantum Theories: A Pedagogic 1st Step
• A mathematically rigorous approach to perturbative path integrals via animation on YouTube
• Feynman's Infinite Quantum Paths | PBS Space Time. July 7, 2017. (Video, 15:48)