समुचित अनुक्रम

समुचित अनुक्रम वस्तुओं के बीच आकारिकी का एक क्रम है, उदाहरण के लिए, समूह (गणित), वृत्त (गणित), मापदंड (गणित), और अधिक सामान्यतः एक एबेलियन श्रेणी की वस्तुएं इत्यादि। समुचित अनुक्रम में एक आकारिकी की छवि कर्नेल की अगली छवि के बराबर होती है।
परिभाषा
समूह सिद्धांत के संदर्भ में, एक अनुक्रम
अगर है तो समूहों और समूह समरूपताओं को पर समुचित कहा जाता है। अनुक्रम को तब भी समुचित कहा जाता है यदि सभी के लिए प्रत्येक ,पर समुचित हो यानी, यदि प्रत्येक समरूपता की छवि अगले छवि के कर्नेल के बराबर हो।
समूहों और समरूपताओं का क्रम या तो सीमित या अनंत हो सकता है।
इसी तरह की परिभाषा अन्य बीजगणितीय संरचनाओं के लिए भी बनाई जा सकती है। उदाहरण के लिए, किसी के पास रेखीय स्थान और रैखिक मानचित्र, या मापदंड और मापदंड समरूपता का समुचित अनुक्रम हो सकता है। विशेष रूप से एबेलियन श्रेणियों में इसका उपयोग व्यापक रूप से किया जाता है और सामान्यतौर पर, एक समुचित अनुक्रम की धारणा किसी भी श्रेणी में कर्नेल श्रेणी सिद्धांत और कोकर्नेल के साथ अधिक अर्थपूर्ण होती है।
सामान्य स्तिथियाँ
परिभाषा को समझने के लिए, अपेक्षाकृत सरल स्तिथियों पर विचार करना सहायक होता है जहां समूह समरूपता का अनुक्रम सीमित है, और शून्य समूह के साथ शुरू या समाप्त होता है। परंपरागत रूप से,सामान्यतौर पर जब समूह एबेलियन होते हैं तब एकल समरूपता तत्व के साथ योगात्मक संकेतन '0' को दर्शाया जाता है, या गुणात्मक संकेतन '1' को दर्शाया जाता है।
- अनुक्रम 0 → A→ B पर विचार करें। सबसे बाएं मानचित्र की छवि 0 है, अगर और केवल अगर सबसे दाहिने मानचित्र (A से B तक) में कर्नेल {0} है तो यह अनुक्रम समुचित है ; यानी, अगर और केवल अगर वह नक्शा एकरूपता अंतःक्षेपक, या एक-से-एक है।
- दोहरे अनुक्रम B → C → 0 पर विचार करें। सबसे दाहिने मानचित्र का कर्नेल C है, अगर और केवल अगर बाईं ओर के मानचित्र की छवि (B से C तक) सभी C की है तो यह अनुक्रम समुचित है; यानी, अगर और केवल अगर वह मानचित्र एक अधिरूपता प्रक्षेपण या एक पर एक है।
- इसलिए, अनुक्रम 0 → X → Y → 0 समुचित है अगर और केवल अगर X से Y तक का मानचित्र एक एकरूपता और अधिरूपता यानी, एक द्विरूपता है, और इसलिए सामान्यतौर पर X से Y तक एक समरूपता 'समुच्चय' जैसी समुचित श्रेणियों में आता है।
लघु समुचित अनुक्रम
लघु समुचित अनुक्रम प्रपत्र के समुचित अनुक्रम हैं
ऊपर स्थापित किये गए सूत्र के अनुसार, किसी भी छोटे समुचित अनुक्रम के लिए, f एक एकरूपता है और g एक अधिरूपता है। इसके अतिरिक्त , f की छवि g के कर्नेल के बराबर है। A को f के साथ B के उपवस्तु के रूप में और A को B और C को संबंधित कारक वस्तु (या भागफल वस्तु) में अन्तः स्थापित करने के साथ, B/A के रूप में सोचना मददगार होता है, जिसमें g एक समरूपता को प्रेरित करता है।
लघु समुचित अनुक्रम
यदि h : C → B समरूपता मौजूद है जैसे कि रचना g ∘ h C पर समरूपता मानचित्र है तो इसे विभाजित समुचित अनुक्रम कहा जाता है। यह इस प्रकार है कि यदि ये एबेलियन समूह का अनुसरण करता हैं, तो A और C के प्रत्यक्ष योग के लिए B समरूपता है:
दीर्घ समुचित अनुक्रम
एक लघु
समुचित अनुक्रम के विशेष स्तिथियों से अलग करने के लिए, एक सामान्य समुचित अनुक्रम को कभी-कभी एक दीर्घ समुचित अनुक्रम कहा जाता है।[1]
एक दीर्घ समुचित अनुक्रम निम्नलिखित अर्थों में लघु समुचित अनुक्रमों के श्रेणी के बराबर है: एक दीर्घ अनुक्रम दिया गया है
(1)
n ≥ 2 के साथ, हम इसे लघु अनुक्रमों में विभाजित कर सकते हैं
(2)
जहाँ प्रत्येक के लिए , सूत्र संरचना के द्वारा, पर अनुक्रम (2) समुचित हैं। इसके अतिरिक्त, (1) एक दीर्घ समुचित अनुक्रम है अगर और केवल अगर सभी (2) लघु समुचित अनुक्रम हैं।
उदाहरण
दो पूर्णांक गुणनखंड
एबेलियन समूहों के निम्नलिखित अनुक्रम पर विचार करें:
पहला समरूपता पूर्णांक 'Z' के समुच्चय में प्रत्येक तत्व i को 'Z' के तत्व 2i में मानचित्र करता है। दूसरा समरूपता 'Z' के प्रत्येक तत्व i को भागफल समूह के एक तत्व j में मानचित्र करता है; वह है, j = i mod 2. यहाँ अंकुश निशान इंगित करता है कि Z से Z तक का मानचित्र 2× एक एकरूपता है, और दो-सिरे वाला निशान इंगित करता है कि मानचित्र मॉड 2 एक अधिरूपता है। यह एक समुचित क्रम है क्योंकि एकरूपता की छवि 2Z अधिरूपता का कर्नेल है। अनिवार्य रूप से उसी क्रम को इस रूप में भी लिखा जा सकता है
इस स्तिथियों में एकरूपता 2n ↦ 2n है और यद्यपि यह एक समरूपता कार्य की तरह दिखता है, पर यह आच्छादित नहीं है अर्थात, अधिरूपता नहीं है क्योंकि विषम संख्याएँ 2'Z' से संबंधित नहीं हैं। हालांकि, इस एकरूपता के माध्यम से 2'Z' की छवि 'Z' का बिल्कुल वही उपसमुच्चय है, जो पिछले अनुक्रम में प्रयुक्त n ↦ 2n के माध्यम से 'Z' की छवि है। यह बाद वाला क्रम पिछले एक से अपनी पहली वस्तु की ठोस प्रकृति में भिन्न होता है क्योंकि 2'Z' 'Z' के समान समुच्चय नहीं है, भले ही दोनों समूह के रूप में समरूपी हों।
एकरूपता और अधिरूपता के लिए विशेष प्रतीकों का उपयोग किए बिना भी पहला अनुक्रम लिखा जा सकता है:
यहाँ 0 शून्य समूह को दर्शाता है, Z से Z का मानचित्र 2 से गुणा है, और Z से कारक समूह Z/2Z का मानचित्र पूर्णांक गुणनखंड 2 को कम करके दिया गया है। यह वास्तव में एक समुचित क्रम है:
- मानचित्र 0 → Z की छवि {0} है, और 2 से गुणन का कर्नेल भी {0} है, इसलिए अनुक्रम पहले Z पर समुचित है।
- 2 से गुणन की छवि 2Z है, और गुणनखंड 2 को कम करने का कर्नल भी 2Z है, इसलिए अनुक्रम दूसरे Z पर समुचित है।
- गुणनखंड 2 को कम करने की छवि Z/2Z है, और शून्य मानचित्र का कर्नेल भी Z/2Z है, इसलिए अनुक्रम Z/2Z की स्थिति पर समुचित है।
Z की अनंत प्रकृति के कारण पहला और तीसरा क्रम कुछ विशेष स्तिथि है। एक सीमित समूह के लिए स्वयम के एक उचित उपसमूह के रूप में समावेशन (अर्थात, एक एकरूपता) द्वारा मानचित्र किया जाना संभव नहीं है। सबसे पहले समरूपता सिद्धांत से निकलने वाला क्रम है
सीमित समूहों पर एक समुचित अनुक्रम के अधिक ठोस उदाहरण के रूप में:
जहाँ क्रम n और का चक्रीय समूह है और क्रम 2n का द्वितल समूह है, जो एक गैर-अबेलियन समूह है।
प्रतिच्छेदन और मापदंड का योग
माना की I और J एक सिद्धांत R के दो आदर्श (घेरा सिद्धांत) हों
तब
R-मापदंड का समुचित क्रम है, जहां मापदंड समरूपता , x के प्रत्येक तत्व को (x,x) के प्रत्यक्ष योग के साथ मानचित्र करता है और समरूपता , के प्रत्येक तत्व को . के साथ मानचित्र करता है।
ये समरूपता समान रूप से परिभाषित समरूपता के प्रतिबंध हैं जो लघु समुचित अनुक्रम बनाते हैं
- भागफल मापदंड के पास स्थानांतरित करने से एक और समुचित अनुक्रम प्राप्त होता है
अंतरात्मक रेखागणित में ग्रेड, कर्ल और डिव
विशेष रूप से मैक्सवेल समीकरण पर काम के लिए अनुरूप एक और उदाहरण अंतरात्मक रेखागणित से प्राप्त किया जा सकता है।
हिल्बर्ट रिक्त स्थान के तीन आकारों पर अदिश-मान वर्ग-अभिन्न कार्य पर विचार करें, किसी फलन का ग्रेडियेंट लेना के उपसमुच्चय में ले जाता है , सदिश मान का स्थान, स्थिर रूप से वर्ग-अभिन्न कार्य पर एक ही कार्यक्षेत्र है - विशेष रूप से, ऐसे फलन का समुच्चय जो संरक्षी सदिश क्षेत्रों का प्रतिनिधित्व करते हैं। सामान्यीकृत स्टोक्स सिद्धांत ने पूर्णता को संरक्षित रखा है।
सबसे पहले, ध्यान दें कि ऐसे सभी क्षेत्रों का कर्ल (गणित) शून्य है - चूंकि ऐसे सभी f के लिए
- हालाँकि, यह केवल यह सिद्ध करता है कि ग्रेडियेंट की छवि कर्ल के कर्नेल का एक उपसमुच्चय है। यह सिद्ध करने के लिए कि वे वास्तव में एक ही समुच्चय हैं, इसका विपरीत सिद्ध करें कि यदि एक सदिश क्षेत्र का कर्ल 0 है, तो कुछ अदिश फलन का ग्रेडिएंट है। यह स्टोक्स के सिद्धांत का लगभग समीपता से अनुसरण करता है जिसे संरक्षी बल समर्थित करता है। अगर ग्रेडिएंट की छवि कर्ल की सटीक कर्नेल है तो के उपसमुच्चय के लिए कर्ल को अपना अगला आकारिकी के रूप ले सकते हैं।
इसी तरह, हम ध्यान दें
तो कर्ल की छवि विस्तार के कर्नेल का एक उपसमुच्चय है। इसमें भी कुछ हद तक विपरीत सम्मिलित है:
| Proof that = 0 implies for some |
|---|
| We shall proceed by construction: given a vector field such that , we produce a field such that
First, note that since as proved above , we can add the gradient of any scalar function to without changing the curl. We can use this gauge freedom to set any one component of to zero without changing its curl; choosing arbitrarily the z-component, we thus require simply that Then by simply integrating the first two components, and noting that the 'constant' of integration may still depend on any variable not integrated over, we find that Note that since the two integration terms both depend only on x and y and not on z, then we can add another gradient of some function that also does not depend on z. This permits us to eliminate either of the terms in favor of the other, without spoiling our earlier work that set to zero. Choosing to eliminate and applying the last component as a constraint, we have By assumption, , and so Since the fundamental theorem of calculus requires that the first term above be precisely plus a constant in z, a solution to the above system of equations is guaranteed to exist. |
इस प्रकार यह सिद्ध करने के बाद कि कर्ल की छवि वास्तव में विस्तार की कर्नेल है, यह आकारिकी हमें पर वापस ले जाती है जहां से हमने शुरू किया था. चूंकि निश्चित रूप से हम अभिन्न कार्यों के एक स्थान पर पहुंचे हैं, औपचारिक रूप से ऐसा कोई भी कार्य एक सदिश क्षेत्र का निर्माण करने के लिए एकीकृत किया जा सकता है जो फलन का विस्तार है - इसलिए विस्तार की छवि पूरी तरह से है, और हम अपना क्रम पूरा कर सकते हैं:
समतुल्य रूप से, हम इसके विपरीत तर्क दे सकते हैं कि: सरल रूप से जुड़े हुए स्थान में, एक कर्ल-मुक्त सदिश क्षेत्र को हमेशा एक संरक्षी सदिश क्षेत्र को ग्रेडियेंट की छवि के रूप में लिखा जा सकता है, इसी प्रकार, विस्तार रहित क्षेत्र को दूसरे क्षेत्र के कर्ल के रूप में लिखा जा सकता है।[2] इस दिशा में तर्क इस तथ्य का उपयोग करता है कि 3-आकारीय स्थान सांस्थितिक रूप से शून्य है।
यह लघु समुचित अनुक्रम भी हेल्महोल्ट्ज़ अपघटन की वैधता के एक बहुत छोटे प्रमाण की अनुमति देता है जो ब्रूट-बल सदिश गणना पर निर्भर नहीं करता है। अनुवर्ती पर विचार करें
वर्ग-अभिन्न कार्यों के हिल्बर्ट स्थान को लाप्लासियन के अभिलक्षणिक फलन द्वारा विस्तार किया जा सकता है, क्योंकि ग्रेडियेंट का विस्तार लाप्लासियन है। हम पहले से ही देखते हैं कि कुछ विपरीत मानचित्रण सम्मिलित होना चाहिए। स्पष्ट रूप से इस तरह के व्युत्क्रम का निर्माण करने के लिए, हम सदिश लाप्लासियन की परिभाषा से शुरू कर सकते हैं
चूंकि हम ग्रेडियेंट के साथ कुछ फलन बनाकर एक समरूपता मानचित्रण बनाने की कोशिश कर रहे हैं, हमारी स्तिथि में . फिर अगर हम दोनों पक्षों का विस्तार करते हैं तो
हम देखते हैं कि यदि कोई फलन सदिश लाप्लासियन का एक अभिलक्षणिक फलन है, तो इसका विस्तार उसी अभिलक्षणिक मान के साथ अदिश लाप्लासियन का एक अभिलक्षणिक फलन होना चाहिए। तब हम अपने के किसी भी फलन का विभाजन करके सदिश-लाप्लासियन अभिलक्षणिक आधार में विपरीत फलन का निर्माण कर सकते हैं और उनके प्रत्येक विपरीत को अभिलक्षणिक मान के द्वारा माप कर विस्तार करने के बाद परिणामस्वरूप स्पष्ट रूप से समरूपता होगा। इस प्रकार विभाजन लेम्मा द्वारा,
- ,
या समतुल्य रूप से हम सिद्ध करने के लिए निर्धारित करते हैं कि कोई भी वर्ग-पूर्णांक सदिश क्षेत्र पर को एक ग्रेडियेंट और एक कर्ल के योग में विभाजन किया जा सकता है।
गुण
विभाजन लेम्मा में उल्लेख किया गया है कि यदि लघु समुचित अनुक्रम
t : B → A आकारिता को स्वीकृति देता है तो A पर t ∘ f समरूपता है या u: C → B आकारिता को स्वीकृति देता है तो C पर g ∘ u समरूपता है, तब अविनिमेय समूहों के लिए B का प्रत्यक्ष योग A और C है और यह एक अर्ध-प्रत्यक्ष उत्पाद है। कुछ गणितज्ञ के अनुसार इतना लघु समुचित क्रम विभाजित हो जाता है।
स्नेक लेम्मा दिखाता है कि कैसे दो समुचित पंक्तियों वाला एक क्रमविनिमेय चित्र एक दीर्घ समुचित अनुक्रम को विकसित करता है। नौ लेम्मा एक विशेष स्तिथि है।
पांच लेम्मा ऐसी स्थितियाँ देती है जिसके तहत 5 लंबाई की समुचित पंक्तियों के साथ एक क्रमविनिमेय चित्र में मध्य मानचित्र एक समरूपता है; लघु पांच लेम्मा इसकी एक विशेष स्तिथि है जो लघु समुचित अनुक्रमों पर लागू होती है।
लघु समुचित अनुक्रमों के महत्व को इस तथ्य से रेखांकित किया जाता है कि प्रत्येक समुचित अनुक्रम कई अतिव्यापी लघु समुचित अनुक्रमों के अंतर्गत उत्पन्न होता है। उदाहरण के लिए समुचित क्रम पर विचार करें
जिसका तात्पर्य है कि श्रेणी में वस्तु Ck सम्मिलित है
- .
इसके अतिरिक्त मान लीजिए कि प्रत्येक आकारिता का कोकर्नेल सम्मिलित है, और अनुक्रम में अगले आकारिकी की छवि के लिए समरूप है:
यह विभिन्न रुचिकर श्रेणियों के लिए सही है, जिसमें एबेलियन समूह जैसे कोई भी एबेलियन श्रेणी सम्मिलित है; लेकिन यह उन सभी श्रेणियों के लिए सही नहीं है जो समुचित अनुक्रमों की अनुमति देते हैं, और विशेष रूप से समूहों की श्रेणी के लिए सही नहीं है, जिसमें कोकर ( f) : G → H, H/im(f) नहीं है लेकिन H का भागफल im(f) के संयुग्मन समापन द्वारा है। तब हमें एक क्रमविनिमेय चित्र प्राप्त होता है जिसमें सभी विकर्ण लघु समुचित क्रम होते हैं:
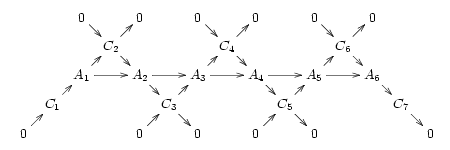 इस चित्र का एकमात्र भाग जो कोकरनेल की स्थिति पर निर्भर करता है वह वस्तु और आकारिता की निर्णायक समरूप हैं। अगर कोई वस्तु और आकृतिवाद सम्मिलित है तो समुचित है, तो की समुचितता को सुनिश्चित किया जाता है। फिर से समूहों की श्रेणी का उदाहरण लेते हुए, तथ्य यह है कि H पर im(f)) कुछ समरूपता का कर्नेल है, जो यह दर्शाता है कि यह एक सामान्य उपसमूह है, इसके संयुग्मित समापन के साथ एक मत होता है; इस प्रकार आकारिकी की अगली छवि H/im(f) के लिए coker(f)) समरूपी है।
इस चित्र का एकमात्र भाग जो कोकरनेल की स्थिति पर निर्भर करता है वह वस्तु और आकारिता की निर्णायक समरूप हैं। अगर कोई वस्तु और आकृतिवाद सम्मिलित है तो समुचित है, तो की समुचितता को सुनिश्चित किया जाता है। फिर से समूहों की श्रेणी का उदाहरण लेते हुए, तथ्य यह है कि H पर im(f)) कुछ समरूपता का कर्नेल है, जो यह दर्शाता है कि यह एक सामान्य उपसमूह है, इसके संयुग्मित समापन के साथ एक मत होता है; इस प्रकार आकारिकी की अगली छवि H/im(f) के लिए coker(f)) समरूपी है।
इसके विपरीत, अतिव्यापी लघु समुचित अनुक्रमों की किसी भी सूची को देखते हुए, उनके मध्य शब्द उसी तरह एक समुचित अनुक्रम बनाते हैं।
समुचित अनुक्रमों के अनुप्रयोग
एबेलियन श्रेणियों के सिद्धांत में, लघु समुचित अनुक्रमों को प्रायः उप-वस्तु और कारक वस्तुओं के बारे में बात करने के लिए एक सुविधाजनक भाषा के रूप में उपयोग किया जाता है।
एक लघु समुचित अनुक्रम की अंत स्तिथि A और C को देखते हुए विस्तार की समस्या अनिवार्य रूप से प्रश्न है मध्य अवधि B के लिए क्या संभावनाएं उपलब्ध हैं? समूहों की श्रेणी में, यह प्रश्न के समतुल्य है, कौन से समूह B में सामान्य उपसमूह के रूप में A और संबंधित कारक समूह के रूप में C है? सीमित सरल समूहों के वर्गीकरण में यह समस्या महत्वपूर्ण है। बाहरी प्रतिधारण समूह भी देखें।
ध्यान दें कि एक समुचित क्रम में रचना f i +1 ∘ f i , A i +2 में A i से 0 को मानचित्र करता है, इसलिए प्रत्येक समुचित क्रम एक श्रृंखला परिसर है। इसके अतिरिक्त , केवल Ai के तत्वों की छवि को f i द्वारा 0 से fi+1 पर मानचित्र किया जाता है इसलिए इस श्रृंखला परिसर की समरूपता (गणित) शून्य है। अधिक संक्षेप में:
- समुचित अनुक्रम समुचित रूप से वे श्रृंखला परिसर हैं जो चक्रीय परिसर हैं।
किसी भी श्रृंखला परिसर को देखते हुए, इसकी समरूपता को उस डिग्री के माप के रूप में माना जा सकता है जिस पर यह समुचित नहीं हो पाता है।
यदि हम श्रृंखला परिसरों से लघु समुचित अनुक्रमों की एक श्रृंखला लेते हैं, तो हम ज़िगज़ैग लेम्मा के अनुप्रयोग द्वारा एक दीर्घ समुचित अनुक्रम प्राप्त कर सकते हैं। यह सापेक्ष समरूपता के अध्ययन में बीजगणितीय टोपोलॉजी में आता है; इसका अन्य उदाहरण मेयर-विटोरिस अनुक्रम है। लघु समुचित अनुक्रमों से प्रेरित दीर्घ समुचित अनुक्रम भी व्युत्पन्न कारक की विशेषता हैं।
समुचित संचालक ऐसे कारक हैं जो समुचित अनुक्रमों को समुचित अनुक्रमों में बदलते हैं।
संदर्भ
- Citations
- ↑ "exact sequence in nLab, Remark 2.3". ncatlab.org. Retrieved 2021-09-05.
{{cite web}}: CS1 maint: url-status (link) - ↑ "विचलन रहित क्षेत्र". December 6, 2009.
- Sources
- Spanier, Edwin Henry (1995). Algebraic Topology. Berlin: Springer. p. 179. ISBN 0-387-94426-5.
- Eisenbud, David (1995). Commutative Algebra: with a View Toward Algebraic Geometry. Springer-Verlag New York. p. 785. ISBN 0-387-94269-6.