बलोच क्षेत्र

बलोच क्षेत्र

परिमाण यांत्रिकी और परिमाण संगणना में, बलोच क्षेत्र एक दो-स्तरीय प्रणाली के शुद्ध अवस्था स्थान का एक ज्यामितीय प्रतिनिधित्व है। दो-स्तरीय परिमाण यांत्रिक तन्त्र (क्विबिट), जिसका नाम भौतिक विज्ञानी फेलिक्स बलोच के नाम पर रखा गया है।

परिमाण यांत्रिकी गणितीय रूप से हिल्बर्ट स्थल अथवा प्रक्षेपीय हिल्बर्ट स्थल में तैयार की गई है। एक परिमाण प्रणाली की शुद्ध अवस्था संबंधित हिल्बर्ट स्थल (और प्रक्षेपीय हिल्बर्ट स्थल के बिंदु) के एक आयामी उप-स्थान के अनुरूप होती है। द्वि-आयामी हिल्बर्ट स्थल के लिए, ऐसे सभी दिक् का स्थान जटिल प्रक्षेपण रेखा $\mathbb {CP} ^{1}$ है यह बलोच क्षेत्र है, जिसे रीमैन क्षेत्र में मानचित्र किया जा सकता है।

बलोच क्षेत्र एक इकाई n-क्षेत्र 2-वृत्त है, जिसमें पारस्परिक रूप से आयतीय स्थिति सदिश की एक जोड़ी के अनुरूप प्रतिव्यासांत बिंदु होते हैं। बलोच क्षेत्र के उत्तरी और दक्षिणी ध्रुवों को सामान्यतः मानक आधार सदिश $|0\rangle$ और $|1\rangle$ के अनुरूप चुना जाता है, क्रमशः, जो बदले में एक इलेक्ट्रॉन की चक्रण (भौतिकी)-ऊपर और चक्रण (भौतिकी)-नीचे अवस्थाओं के लिए उदा. हो सकता है। हालाँकि यह चुनाव स्वेच्छाचारी है। गोले की सतह पर बिंदु प्रणाली की शुद्ध अवस्थाओं की परिमाण अवस्था के अनुरूप होते हैं, जबकि आंतरिक बिंदु मिश्रित अवस्थाओं के अनुरूप होते हैं। बलोच वृत्त को n-स्तर परिमाण प्रणाली के लिए सामान्यीकृत किया जा सकता है, लेकिन तब मानसिक चित्रण कम उपयोगी होता है।

ऐतिहासिक कारणों से, प्रकाशिकी में बलोच क्षेत्र को पोंकारे क्षेत्र (दृग्विद्या) के रूप में भी जाना जाता है और विशेष रूप से विभिन्न प्रकार के ध्रुवीकरण (तरंगों) का प्रतिनिधित्व करता है। छह सामान्य ध्रुवीकरण प्रकार उपस्थित हैं और उन्हें जोन्स सदिश कहा जाता है। वास्तव में हेनरी पोंकारे 19वीं शताब्दी के अंत में स्टोक्स मापदंडों के त्रि-आयामी प्रतिनिधित्व के रूप में इस तरह के ज्यामितीय प्रतिनिधित्व के उपयोग का सुझाव देने वाले पहले व्यक्ति थे।

बलोच क्षेत्र पर प्राकृतिक मापीय (गणित) फ़ुबिनी-अध्ययन मापीय है। द्वि-आयामी स्थिति अंतरिक्ष में इकाई 3-क्षेत्र से मानचित्रण $\mathbb {C} ^{2}$ बलोच क्षेत्र के लिए हॉप फ़िब्रेशन है, जिसमें घूर्णक के प्रत्येक प्रक्षेपीय हिल्बर्ट स्थल के साथ बलोच क्षेत्र पर एक बिंदु पर मानचित्रण होता है।

परिभाषा

एक अलौकिक आधार दिया गया है, दो-स्तरीय क्वांटम प्रणाली के किसी भी शुद्ध अवस्था $|\psi \rangle$ को आधार सदिशों $|0\rangle$ और $|1\rangle$ के अधिस्थापन के रूप में लिखा जा सकता है , जहां दो आधार सदिशों में से प्रत्येक का गुणांक (या योगदान) एक सम्मिश्र संख्या है। इसका अर्थ है कि स्थिति को चार वास्तविक संख्याओं द्वारा वर्णित किया गया है। हालाँकि दो आधार सदिश के गुणांक के बीच केवल सापेक्ष चरण का कोई भौतिक अर्थ है (परिमाण प्रणाली का चरण सीधे परिमाण यांत्रिकी में माप नहीं है), ताकि इस विवरण में अतिरेक हो सके। हम $|0\rangle$ का गुणांक वास्तविक और गैर-नकारात्मक ले सकते हैं। यह बलोच क्षेत्र के तीन आयामों को उत्पन्न करते हुए स्थिति को केवल तीन वास्तविक संख्याओं द्वारा वर्णित करने की अनुमति देता है।

हम परिमाण यांत्रिकी से यह भी जानते हैं कि प्रणाली की कुल संभावना एक होनी चाहिए:

$\langle \psi |\psi \rangle =1$, या समकक्ष ${\big \|}|\psi \rangle {\big \|}^{2}=1$.

इस बाधा को देखते हुए हम निम्नलिखित प्रतिनिधित्व का उपयोग करके $|\psi \rangle$ लिख सकते हैं:

$|\psi \rangle =\cos \left(\theta /2\right)|0\rangle \,+\,e^{i\phi }\sin \left(\theta /2\right)|1\rangle =\cos \left(\theta /2\right)|0\rangle \,+\,(\cos \phi +i\sin \phi )\,\sin \left(\theta /2\right)|1\rangle$, जहाँ $0\leq \theta \leq \pi$ और $0\leq \phi <2\pi$.

प्रतिनिधित्व हमेशा अनूठा होता है, क्योंकि, भले ही $\phi$ का मूल्य अद्वितीय नहीं है जब $|\psi \rangle$ स्तिथि में से एक (ब्रा-केट चिन्हांकन देखें) $|0\rangle$ या $|1\rangle$ है, $\theta$ और $\phi$ द्वारा दर्शाया गया बिंदु अद्वितीय है।

मापदण्ड $\theta \,$ और $\phi \,$, गोलाकार समन्वय प्रणाली में क्रमशः z-अक्ष के संबंध में समांतरता और x-अक्ष के संबंध में देशांतर के रूप में फिर से व्याख्या की गई, निम्नलिखित में एक बिंदु निर्दिष्ट करें

${\vec {a}}=(\sin \theta \cos \phi ,\;\sin \theta \sin \phi ,\;\cos \theta )=(u,v,w)$

$\mathbb {R} ^{3}$ इकाई क्षेत्र पर बिंदु निर्दिष्ट करें।

मिश्रित अवस्था (भौतिकी) के लिए, एक घनत्व संचालक पर विचार करता है। कोई द्वि-आयामी घनत्व संचालक ρ I और हर्मिटियन आव्यूह, ट्रेस (रैखिक बीजगणित) पॉल आव्यूह ${\vec {\sigma }}$ अस्मिता का उपयोग करके विस्तारित किया जा सकता है,

${\begin{aligned}\rho &={\frac {1}{2}}\left(I+{\vec {a}}\cdot {\vec {\sigma }}\right)\\&={\frac {1}{2}}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+{\frac {a_{x}}{2}}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}+{\frac {a_{y}}{2}}{\begin{pmatrix}0&-i\\i&0\end{pmatrix}}+{\frac {a_{z}}{2}}{\begin{pmatrix}1&0\\0&-1\end{pmatrix}}\\&={\frac {1}{2}}{\begin{pmatrix}1+a_{z}&a_{x}-ia_{y}\\a_{x}+ia_{y}&1-a_{z}\end{pmatrix}}\end{aligned}}$,

जहाँ ${\vec {a}}\in \mathbb {R} ^{3}$ बलोच सदिश कहा जाता है।

यह सदिश क्षेत्र के भीतर उस बिंदु को इंगित करता है जो किसी दिए गए मिश्रित स्थिति से मेल खाता है। विशेष रूप से, पाउली सदिश की मूल विशेषता के रूप में, ${\frac {1}{2}}\left(1\pm |{\vec {a}}|\right)$ के अभिलक्षणिक मान ρ हैं। घनत्व संचालकों को सकारात्मक-अर्ध-परिमित होना चाहिए, इसलिए यह उसी $\left|{\vec {a}}\right|\leq 1$ का अनुसरण करता है।

शुद्ध अवस्था के लिए, एक के पास निम्न है

$\operatorname {tr} \left(\rho ^{2}\right)={\frac {1}{2}}\left(1+\left|{\vec {a}}\right|^{2}\right)=1\quad \Leftrightarrow \quad \left|{\vec {a}}\right|=1~,$

उपरोक्त के अनुरूप।

नतीजतन, बलोच क्षेत्र की सतह द्वि-आयामी परिमाण प्रणाली के सभी शुद्ध अवस्था का प्रतिनिधित्व करती है, जबकि आंतरिक सभी मिश्रित अवस्था से मेल खाती है।

u, v, w प्रतिनिधित्व

बलोच सदिश ${\vec {a}}=(u,v,w)$ घनत्व संचालक के संदर्भ में निम्नलिखित आधार $\rho$ पर प्रतिनिधित्व किया जा सकता है :

$u=\rho _{10}+\rho _{01}=2\operatorname {Re} (\rho _{01})$

$v=i(\rho _{01}-\rho _{10})=2\operatorname {Im} (\rho _{10})$

$w=\rho _{00}-\rho _{11}$

जहाँ

$\rho ={\begin{pmatrix}\rho _{00}&\rho _{01}\\\rho _{10}&\rho _{11}\end{pmatrix}}={\frac {1}{2}}{\begin{pmatrix}1+w&u-iv\\u+iv&1-w\end{pmatrix}}.$

यह आधार प्रायः लेज़र सिद्धांत में प्रयोग किया जाता है, जहां $w$ जनसंख्या व्युत्क्रमण के रूप में जाना जाता है। इस आधार पर, संख्याएँ $u,v,w$ तीन पाउली आव्यूह की अपेक्षाएं $X,Y,Z$ हैं, एक को xy और z अक्षों के साथ तीन निर्देशांकों की सर्वसमिका की अनुमति देता है।

शुद्ध अवस्थाएँ

एक n-स्तर परिमाण यांत्रिक प्रणाली पर विचार करें। इस प्रणाली का वर्णन n-विमीय हिल्बर्ट अन्तराल h_n द्वारा किया गया है परिभाषा के अनुसार शुद्ध अवस्था स्थान H_n की 1-आयामी अर्धरेखा का समुच्चय है।

प्रमेय. U(N)|U(n) आकार n के एकात्मक आव्यूह का लाइ समूह होने दें। फिर 'H_n' का शुद्ध स्थिति स्थान सघन सह समुच्चय स्थल के साथ पहचाना जा सकता है

$\operatorname {U} (n)/(\operatorname {U} (n-1)\times \operatorname {U} (1)).$

इस तथ्य को सिद्ध करने के लिए, ध्यान दें कि H_n की अवस्थाओं के समुच्चय पर U(n) की एक प्राकृतिक रूपांतरण समूह क्रिया (गणित) है। यह क्रिया शुद्ध अवस्थाओं पर निरंतर और सकर्मक समूह क्रिया है। किसी भी स्थिति $|\psi \rangle$ के लिए, का समदैशिकता समूह $|\psi \rangle$, (तत्वों के सम्मुच्चय के रूप में परिभाषित $g$ u (n) की ऐसी है कि $g|\psi \rangle =|\psi \rangle$) उत्पाद समूह के लिए समरूपी है

$\operatorname {U} (n-1)\times \operatorname {U} (1).$

रैखिक बीजगणित के संदर्भ में, इसे निम्नानुसार उचित ठहराया जा सकता है। कोई $g$ u (n) का जो $|\psi \rangle$ छोड़ देता है। एक अभिलक्षणिक सदिश के रूप में अपरिवर्तनीय $|\psi \rangle$ होना चाहिए। चूंकि संबंधित अभिलक्षणिक मान मापांक 1 की एक सम्मिश्र संख्या होनी चाहिए, यह समदैशिकता समूह का U(1) कारक देता है। समदैशिकता समूह के दूसरे भाग को आयतीय पूरक पर एकात्मक आव्यूह द्वारा $|\psi \rangle$ प्राचलीकरण किया गया है, जो U(n − 1) के लिए तुल्याकारी है। इससे प्रमेय का अभिकथन सघन समूहों के सकर्मक समूह कार्यों के बारे में बुनियादी तथ्यों से होता है।

ऊपर ध्यान देने योग्य महत्वपूर्ण तथ्य यह है कि एकात्मक समूह शुद्ध अवस्थाओं पर सकर्मक रूप से कार्य करता है।

अब U(n) का (वास्तविक) आयाम n^{2 है। घातीय मानचित्र के बाद से यह देखना आसान है}

$A\mapsto e^{iA}$

स्व-संलग्न जटिल आव्यूह के स्थान से u (n) तक एक स्थानीय होमोमोर्फिज्म है। स्व-संलग्न जटिल आव्यूहों के स्थान का वास्तविक आयाम n^{2 है।}

परिणाम. 'H_n' के शुद्ध स्थिति स्थान का वास्तविक आयाम 2n - 2 है।

वास्तव में,

$n^{2}-\left((n-1)^{2}+1\right)=2n-2.\quad$

आइए इसे m क्यूबिट परिमाण क्यूबिट के वास्तविक आयाम पर विचार करने के लिए लागू करें। संबंधित हिल्बर्ट स्पेस का आयाम 2 है।

परिमाण क्यूबिट के शुद्ध अवस्था स्थान का वास्तविक आयाम 2^m+1 − 2 है।

त्रिविम प्रक्षेपण के माध्यम से शुद्ध दो-चक्रण स्थिति आलेखन करना

$\mathbb {R} ^{3}$ बलोच क्षेत्र के मूल पर केंद्रित है। उस पर बिंदुओं की एक जोड़ी, $\left|\uparrow \right\rangle$ और $\left|\downarrow \right\rangle$ आधार के रूप में चुना गया है। गणितीय रूप से वे आयतीय हैं, हालांकि लेखाचित्रीय रूप से उनके बीच का कोण π है। $\mathbb {R} ^{3}$ में उन बिंदुओं के निर्देशांक (0,0,1) और (0,0,−1) हैं। एक स्वेच्छाचारी स्पाइनर $\left|\nearrow \right\rangle$ बलोच क्षेत्र पर दो आधार घूर्णक के एक अद्वितीय रैखिक संयोजन के रूप में प्रतिनिधित्व करने योग्य है, जिसमें गुणांक जटिल संख्याओं की एक जोड़ी है; उन्हें α और β कहते हैं। उनका अनुपात $u={\beta \over \alpha }$ होने दें, जो एक सम्मिश्र संख्या $u_{x}+iu_{y}$ भी है। समतल z = 0 पर विचार करें, गोले का विषुवतीय तल, जैसा कि यह था, एक जटिल तल है और बिंदु u को इस रूप में क्षेत्रक किया गया है $(u_{x},u_{y},0)$. परियोजना बिन्दु u स्टैरियोग्राफिक रूप से बलोच क्षेत्र पर दक्षिण ध्रुव से दूर - जैसा कि - (0,0,-1) था। प्रक्षेपण गोले पर चिह्नित बिंदु $\left|\nearrow \right\rangle$ पर है .

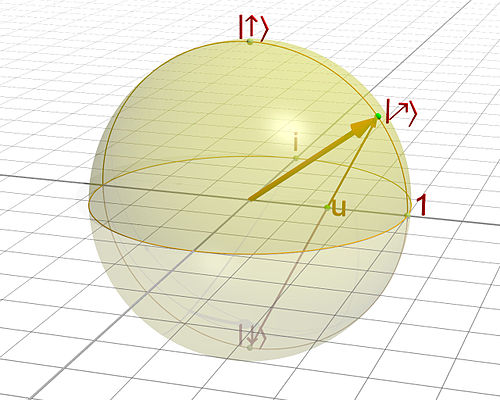
शुद्ध अवस्था प्रदान की

$\alpha \left|\uparrow \right\rangle +\beta \left|\downarrow \right\rangle =\left|\nearrow \right\rangle$

जहाँ $\alpha$ और $\beta$ जटिल संख्याएँ हैं जिन्हें सामान्यीकृत किया जाता है ताकि

$|\alpha |^{2}+|\beta |^{2}=\alpha ^{*}\alpha +\beta ^{*}\beta =1$

और ऐसा है $\langle \downarrow |\uparrow \rangle =0$ और $\langle \downarrow |\downarrow \rangle =\langle \uparrow |\uparrow \rangle =1$,

अर्थात्, ऐसा कि $\left|\uparrow \right\rangle$ और $\left|\downarrow \right\rangle$ एक आधार बनाते हैं और बलोच क्षेत्र पर बिल्कुल विपरीत प्रतिनिधित्व करते हैं, फिर मान लीजिये

$u={\beta \over \alpha }={\alpha ^{*}\beta \over \alpha ^{*}\alpha }={\alpha ^{*}\beta \over |\alpha |^{2}}=u_{x}+iu_{y}$

उनका अनुपात हो।

यदि बलोच क्षेत्र $\mathbb {R} ^{3}$ को अंतर्निहित माना जाता है। मूल में इसके केंद्र के साथ और त्रिज्या एक के साथ, फिर तल z = 0 (जो बलोच क्षेत्र को एक बड़े वृत्त पर काटता है; गोले का भूमध्य रेखा, जैसा कि था) को अरगंड आरेख के रूप में माना जा सकता है। इस तल में क्षेत्रक बिंदु u - ताकि अंदर $\mathbb {R} ^{3}$ इसके निर्देशांक $(u_{x},u_{y},0)$ हैं।

u के माध्यम से और प्रतिनिधित्व करने वाले गोले पर बिंदु के माध्यम से एक सीधी रेखा $\left|\downarrow \right\rangle$ खींचें। (चलो (0,0,1) प्रतिनिधित्व करते हैं $\left|\uparrow \right\rangle$ और (0,0,−1) $\left|\downarrow \right\rangle$ प्रतिनिधित्व करते हैं .) यह रेखा गोले को इसके अलावा एक अन्य बिंदु पर काटती है $\left|\downarrow \right\rangle$। (एकमात्र अपवाद है जब $u=\infty$, यानी जब $\alpha =0$ और $\beta \neq 0$।) इस बिंदु को P कहते हैं। समतल z = 0 पर बिंदु u बलोच क्षेत्र पर बिंदु P का त्रिविमीय प्रक्षेपण है। मूल बिंदु पर पूंछ और पी पर टिप वाला सदिश स्पाइनर के अनुरूप 3-डी अंतरिक्ष में दिशा है $\left|\nearrow \right\rangle$. P के निर्देशांक हैं

$P_{x}={2u_{x} \over 1+u_{x}^{2}+u_{y}^{2}}$

$P_{y}={2u_{y} \over 1+u_{x}^{2}+u_{y}^{2}}$

$P_{z}={1-u_{x}^{2}-u_{y}^{2} \over 1+u_{x}^{2}+u_{y}^{2}}$.

गणितीय रूप से दो-स्पाइनर स्थिति के लिए बलोच क्षेत्र को रीमैन क्षेत्र या एक जटिल 2-आयामी प्रक्षेपीय हिल्बर्ट स्पेस में मानचित्र किया जा सकता है, जिसे $\mathbb {P} \mathbf {H} ^{2}$ निरूपित किया जा सकता है जटिल द्वि-आयामी हिल्बर्ट स्थल $\mathbf {H} ^{2}$ (जिसका कि $\mathbb {P} \mathbf {H} ^{2}$ एक प्रक्षेपण है) SO(3) का प्रतिनिधित्व स्थान है।

घनत्व संचालक

पृथक प्रणालियों के लिए शुद्ध अवस्थाओं के संदर्भ में परिमाण यांत्रिकी के सूत्रीकरण पर्याप्त हैं; घनत्व आव्यूह के संदर्भ में सामान्य परिमाण यांत्रिक प्रणालियों में वर्णित करने की आवश्यकता है। बलोच क्षेत्र न केवल शुद्ध अवस्थाओं बल्कि 2-स्तरीय प्रणालियों के लिए मिश्रित अवस्थाओं का प्राचलिक करता है। 2-स्तरीय परिमाण प्रणाली (क्यूबिट) के मिश्रित-स्थिति का वर्णन करने वाला घनत्व संचालक निम्नलिखित निर्देशांक के साथ बलोच क्षेत्र के अंदर एक बिंदु से मेल खाता है:

$\left(\sum p_{i}x_{i},\sum p_{i}y_{i},\sum p_{i}z_{i}\right),$

जहाँ $p_{i}$ समुच्चय के भीतर अलग-अलग स्तिथि की संभावना है और $x_{i},y_{i},z_{i}$ अलग-अलग स्तिथि के निर्देशांक हैं (बलोच क्षेत्र की सतह पर)। बलोच वृत्त पर और अंदर सभी बिंदुओं के सम्मुच्चय को बलोच गोलक के रूप में जाना जाता है।

उच्च आयाम वाले स्तिथि के लिए इसे मिश्रित स्तिथि तक विस्तारित करने में कठिनाई होती है। सांस्थितिक विवरण इस तथ्य से जटिल है कि एकात्मक समूह घनत्व संचालकों पर सकर्मक रूप से कार्य नहीं करता है। इसके अलावा, कक्षाएँ अत्यंत विविध हैं, जैसा कि निम्नलिखित अवलोकन से पता चलता है:

प्रमेय. मान लीजिए A एक n स्तर परिमाण यांत्रिक प्रणाली पर घनत्व संचालक है जिसका अलग-अलग आइगेनमान μ₁, ..., μ_k गुणन के साथ n₁, ..., n_k हैं।

फिर एकात्मक संकारकों का समूह V ऐसा कि V A V* = A समरूपी (एक लाइ समूह के रूप में) है

$\operatorname {U} (n_{1})\times \cdots \times \operatorname {U} (n_{k}).$

विशेष रूप से a की कक्षा समरूपी है

$\operatorname {U} (n)/\left(\operatorname {U} (n_{1})\times \cdots \times \operatorname {U} (n_{k})\right).$

बलोच गेंद के निर्माण को 2 से बड़े आयामों के लिए सामान्यीकृत करना संभव है, लेकिन ऐसे बलोच शरीर की ज्यामिति गेंद की तुलना में अधिक जटिल होती है।

परिक्रमण

बलोच क्षेत्र के प्रतिनिधित्व का एक उपयोगी लाभ यह है कि बलोच क्षेत्र के घुमावों द्वारा क्वबिट स्थिति का विकास वर्णित है। ऐसा क्यों है, इसकी सबसे संक्षिप्त व्याख्या यह है कि एकात्मक और हर्मिटियन आव्यूह के समूह के लिए लाइ बीजगणित $SU(2)$ तीन आयामी घुमावों के समूह के लाई बीजगणित $SO(3)$ के लिए समरूपी है।

बलोच आधार के बारे में क्रमावर्तन संचालक

बलोच आधार में कार्तीय अक्ष के बारे में बलोच क्षेत्र के क्रमावर्तन द्वारा दिया जाता है

${\begin{aligned}R_{x}(\theta )&=e^{(-i\theta X/2)}=\cos(\theta /2)I-i\sin(\theta /2)X={\begin{bmatrix}\cos \theta /2&-i\sin \theta /2\\-i\sin \theta /2&\cos \theta /2\end{bmatrix}}\\R_{y}(\theta )&=e^{(-i\theta Y/2)}=\cos(\theta /2)I-i\sin(\theta /2)Y={\begin{bmatrix}\cos \theta /2&-\sin \theta /2\\\sin \theta /2&\cos \theta /2\end{bmatrix}}\\R_{z}(\theta )&=e^{(-i\theta Z/2)}=\cos(\theta /2)I-i\sin(\theta /2)Z={\begin{bmatrix}e^{-i\theta /2}&0\\0&e^{i\theta /2}\end{bmatrix}}\end{aligned}}$

एक सामान्य अक्ष के चारों ओर घूर्णन

अगर ${\hat {n}}=(n_{x},n_{y},n_{z})$ तीन आयामों में एक वास्तविक इकाई सदिश है, इस अक्ष के बारे में बलोच क्षेत्र का क्रमावर्तन निम्न द्वारा दिया गया है:

$R_{\hat {n}}(\theta )=\exp \left(-i\theta {\hat {n}}\cdot {\frac {1}{2}}{\vec {\sigma }}\right)$

ध्यान देने वाली एक रोचक बात यह है कि यह अभिव्यक्ति चतुष्कोणों और स्थानिक घुमाव के लिए विस्तारित यूलर सूत्र के पुन: वर्गीकरण के समान है।

$\mathbf {q} =e^{{\frac {1}{2}}\theta (u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )}=\cos {\frac {\theta }{2}}+(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )\sin {\frac {\theta }{2}}$

बलोच क्रमावर्तन जनित्र की व्युत्पत्ति

बैलेंटाइन अतिसूक्ष्म एकात्मक परिवर्तन के लिए एक सहज व्युत्पत्ति प्रस्तुत करता है। यह समझने के लिए महत्वपूर्ण है कि बलोच क्षेत्रों के घूर्णन पाउली आव्यूह के रैखिक संयोजनों के घातीय क्यों हैं। अतः इसका संक्षिप्त उपचार यहाँ दिया जा रहा है। परिमाण यांत्रिक संदर्भ में एक अधिक पूर्ण विवरण क्रमावर्तन संचालक (परिमाण यांत्रिकी) पाया जा सकता है।

एकात्मक संचालकों के एक वर्ग पर विचार करें $U$ किसी अक्ष के परितः घूर्णन को निरूपित करता है। चूंकि क्रमावर्तन में स्वतंत्रता की एक घात होती है, संचालक अदिश $S$ के क्षेत्र में इस प्रकार कार्य करता है कि:

$U(0)=I$

$U(s_{1}+s_{2})=U(s_{1})U(s_{2})$

जहाँ $0,s_{1},s_{2},\in S$

हम असीम एकात्मक को परिभाषित करते हैं क्योंकि टेलर का विस्तार दूसरे क्रम में छोटा है।

$U(s)=I+{\frac {dU}{ds}}{\Bigg |}_{s=0}s+O\left(s^{2}\right)$

एकात्मक स्थिति से:

$U^{\dagger }U=I$

इस तरह

$U^{\dagger }U=I+s\left({\frac {dU}{ds}}{\Bigg |}_{s=0}+{\frac {dU^{\dagger }}{ds}}{\Bigg |}_{s=0}\right)+O\left(s^{2}\right)=I$

इस समानता को सत्य मानने के लिए (यह मानते हुए कि $O\left(s^{2}\right)$ नगण्य है), हमें चाहिए

${\frac {dU}{ds}}{\Bigg |}_{s=0}+{\frac {dU^{\dagger }}{ds}}{\Bigg |}_{s=0}=0$.

इसका परिणाम स्वरुप के समाधान में होता है:

${\frac {dU}{ds}}{\Bigg |}_{s=0}=iK$

जहाँ $K$ कोई हर्मिटियन परिवर्तन है, और इसे एकात्मक वर्ग का जनक कहा जाता है।

इस तरह:

$U(s)=e^{iKs}$

पाउली आव्यूह के बाद से $(\sigma _{x},\sigma _{y},\sigma _{z})$ एकात्मक हर्मिटियन आव्यूह हैं और बलोच आधार $({\hat {x}},{\hat {y}},{\hat {z}})$ के अनुरूप अभिलक्षणिक सदिश हैं, हम स्वाभाविक रूप से देख सकते हैं कि कैसे बलोच का घूर्णन एक स्वेच्छाचारी अक्ष ${\hat {n}}$ के बारे में निम्नलिखित द्वारा वर्णित है

$R_{\hat {n}}(\theta )=\exp(-i\theta {\hat {n}}\cdot {\vec {\sigma }}/2)$

$K={\hat {n}}\cdot {\vec {\sigma }}/2$ द्वारा दिए गए क्रमावर्तन जनित्र के साथ वर्णित है।

यह भी देखें

• परमाणु इलेक्ट्रॉन संक्रमण
• घूर्णिका सदिश स्थल
• पोंकारे क्षेत्र (प्रकाशिकी)
• वर्सेज
• बलोच क्षेत्र के विशिष्ट कार्यान्वयनों की गणना भौतिक कार्यान्वयन लेख के अंतर्गत की गई है।