| फलन
|
अवकलज
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|
त्रिकोणमितीय फलनों का विभेदन,एक त्रिकोणमितीय फलन के अवकलज या एक चर के संबंध में उसके परिवर्तन की दर का पता लगाने की गणितीय प्रक्रिया है।उदाहरण के लिए,ज्या फलन का अवकलज sin'(a) = cos(a) के रूप में लिखा जाता है,इसका अर्थ है कि एक विशेष कोण x = a पर sin(x) की परिवर्तन दर को उस कोण के कोज्या से दिया जाता है।
वृत्तीय त्रिकोणमितीय फलनों के सभी अवकलज sin(x) और cos(x) से tan(x) = sin(x)/cos(x) जैसे फलनों पर लागू होने वाले भागफल नियम के माध्यम से पाए जा सकते हैं।इन अवकलजों को जानने के लिए,प्रतिलोम त्रिकोणमितीय फलनों के अवकलजों को अप्रत्य्क्ष विभेदन का उपयोग करके पाया जाता है।
त्रिकोणमितीय फलनों के अवकलजों के प्रमाण
जब θ,0 की ओर प्रवृत्त होता है,तो sin(θ)/θ की सीमा

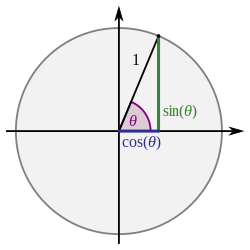
वृत्त, केंद्रO, त्रिज्या 1
दायीं ओर आरेख केंद्र o और त्रिज्या r = 1 के साथ एक वृत्त दिखाता है।दो त्रिज्याएँ OA और OB,θ रेडियन का एक चाप बनाते हैं।चूंकि हम सीमा को शून्य मान रहे हैं,इसलिए हम मान सकते हैं कि θ एक छोटी धनात्मक संख्या है,अर्थात्,0 < θ < ½ π पहले चतुर्थांश में है।
आरेख में,OAB त्रिभुज को R1,OAB वृत्तीय क्षेत्र को R2 और OAC त्रिभुज को R3 लें।OAB त्रिभुज का क्षेत्रफल है:

OAB वृत्तीय क्षेत्र का क्षेत्रफल  है,जबकि OAC त्रिभुज का क्षेत्रफल दिया गया है
है,जबकि OAC त्रिभुज का क्षेत्रफल दिया गया है

चूँकि प्रत्येक क्षेत्र अगले क्षेत्र में निहित है,इसलिए एक निम्न विधि होती है:
इसके अतिरिक्त,चूँकि पहले चतुर्थांश में sin θ > 0 होता है,हम ½ sin θ से भाग कर सकते हैं:

अंतिम चरण में,असमिका को उलटते हुए,हमने तीन सकारात्मक मानों के प्रतिलोम मान लिए हैं।

संकुचन: वक्र y = 1 और y = cos θ लाल रंग में दिखाए गए हैं, वक्र y = sin(θ)/θ नीले लाल रंग में दिखाए गए हैं।
हम इस निष्कर्ष पर पहुंचते हैं कि 0 < θ < ½ π के लिए,राशि sin(θ)/θ हमेशा 1 से कम और हमेशा cos(θ) से अधिक होती है। इस प्रकार,जब θ,0 के नजदीक जाता है, sin(θ)/θ को 1 ऊँचाई पर छत और cos θ ऊँचाई पर फर्श के बीच "संकुचित" किया जाता है,जो 1 की ओर उठता है;इसलिए θ के धनात्मक दिशा से 0 की ओर पहुंचते ही sin(θ)/θ 1 की ओर प्रवृत्त होना चाहिए:

इस मामले के लिए जहां θ एक छोटी ऋणात्मक संख्या हो -½ π < θ < 0,तब हम इस तथ्य का उपयोग करते हैं कि साइन एक विषम फलन है:
जब θ,0 की ओर प्रवृत्त होता है,तो (cos(θ)-1)/θ की सीमा
अंतिम खंड हमें इस नई सीमा की अपेक्षाकृत आसानी से गणना करने में सक्षम बनाता है।इसे एक सरल चाल का उपयोग करके किया जाता है।इस गणना में, θ का चिह्न महत्त्वहीन है।

cos2θ – 1 = –sin2θ का उपयोग करते हुए,तथ्य यह है कि एक गुणांक की सीमा सीमाओं का गुणांक होती है,और पिछले खंड से सीमा परिणाम मिलता है,हम पाते हैं कि:
जब θ,0 की ओर प्रवृत्त होता है,तो tan(θ)/θ की सीमा
ज्या फलन के लिए सीमा,स्पर्शज्या फलन विषम होने के तथ्य,और एक गुणांक की सीमा सीमाओं का गुणांक के तथ्य का उपयोग करते हुए,हम पाते हैं:

ज्या फलन का अवकलज
हम ज्या फलन के अवकलज की गणना सीमा परिभाषा से करते हैं:

कोण जोड़ सूत्र sin(α+β) = sin α cos β + sin β cos α का उपयोग करते हुए,हमें मिलता है:

ज्या और कोज्या फलनों के लिए सीमाओं का उपयोग करते हुए:

कोज्या फलन का अवकलज
अवकलज की परिभाषा से
हम पुनः सीमा परिभाषा से कोज्या फलन के अवकलज की गणना करते हैं:

कोण जोड़ सूत्र cos(α+β) = cos α cos β – sin α sin β का उपयोग करते हुए,हमें मिलता है:

ज्या और कोज्या फलनों के लिए सीमाओं का उपयोग करते हुए:

श्रृंखला नियम से
कोज्या फलन के अवकलज की गणना श्रृंखला नियम से करने के लिए,पहले निम्नलिखित तीन तथ्यों का ध्यान दें:



पहला और दूसरा तथ्य त्रिकोणमितीय सर्वसमिकाएं है,और तीसरा ऊपर प्रमाणित है।इन तीन तथ्यों का उपयोग करके हम निम्नलिखित लिख सकते हैं,

हम इसका श्रृंखला नियम का उपयोग करके विभेदन कर सकते हैं।यदि  ,तो हमें मिलता है:
,तो हमें मिलता है:
 .
.
इसलिए,हमने यह सिद्ध किया है कि
 .
.
स्पर्शज्या फलन का अवकलज
अवकलज की परिभाषा से
हम पहले सिद्धांतों का उपयोग स्पर्शज्या फलन tan θ के अवकलज की गणना करने के लिए करते हैं। परिभाषा के अनुसार:

प्रसिद्ध कोण सूत्र tan(α+β) = (tan α + tan β) / (1 - tan α tan β) का उपयोग करते हुए,हमें मिलता है:![{\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =\lim _{\delta \to 0}\left[{\frac {{\frac {\tan \theta +\tan \delta }{1-\tan \theta \tan \delta }}-\tan \theta }{\delta }}\right]=\lim _{\delta \to 0}\left[{\frac {\tan \theta +\tan \delta -\tan \theta +\tan ^{2}\theta \tan \delta }{\delta \left(1-\tan \theta \tan \delta \right)}}\right].}](/index.php?title=Special:MathShowImage&hash=a5893fd35d613ee50fc17749fe02252d&mode=mathml)
इस तथ्य एक गुणांक की सीमा सीमाओं का गुणांक होती है का उपयोग करते हुए:

स्पर्शज्या फलन के लिए सीमा और तथ्य का उपयोग करते हुए कि जैसे δ 0 की ओर प्रवृत्त होता है tan δ 0 की ओर प्रवृत्त होता है:

हम तुरंत देखते हैं कि:

भागफल नियम से
एक भागफल नियम का उपयोग करके स्पर्शज्या फलन के अवकलज की भी गणना कर सकते है।

अंश को 1 के रूप में पायथागॉरियन सर्वसमिका द्वारा सरलित किया जा सकता है,जिससे हमें मिलता है:

इसलिए,

प्रतिलोम त्रिकोणमितीय फलनों के अवकलजों का प्रमाण
निम्नलिखित अवकलजों को एक चर y को उस प्रतिलोम त्रिकोणमितीय फलन के बराबर रखकर प्राप्त करते हैं जिसे हम अवकलज लेना चाहते हैं।अप्रत्य्क्ष विभेदन का उपयोग करके और फिर dy/dx के लिए हल करके,प्रतिलोम फलन के अवकलज y के रूप में प्राप्त किया जाता है।dy/dx को पुनः x के रूप में प्रकट करने के लिए,हम एक इकाई वृत्त पर संदर्भ त्रिकोण बना सकते हैं,जहां y को θ के रूप में लेते हैं।पाइथागोरस प्रमेय और नियमित त्रिकोणमितीय फलन की परिभाषा का उपयोग करके,हम अंततः dy/dx को x के संदर्भ में व्यक्त कर सकते हैं।
प्रतिलोम ज्या फलन का विभेदन करना
हम

लेते हैं,जहां

फिर

दोनों ओर से  के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:
के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:


प्रतिस्थापन  ऊपर से,
ऊपर से,

प्रतिस्थापन  ऊपर से,
ऊपर से,


प्रतिलोम कोज्या फलन का विभेदन करना
हम

लेते हैं,जहां

फिर

दोनों पक्षों से  के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:
के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:


प्रतिस्थापन  ऊपर से,
ऊपर से,

प्रतिस्थापन  ऊपर से,
ऊपर से,


वैकल्पिक रूप से,एक बार जब  का अवकलज स्थापित हो जाता है,तो सर्वसमिका
का अवकलज स्थापित हो जाता है,तो सर्वसमिका  का विभेदन करने से
का विभेदन करने से  का अवकलज तुरंत अनुसरण करता है,ताकि
का अवकलज तुरंत अनुसरण करता है,ताकि  हो।
हो।
प्रतिलोम स्पर्शज्या फलन का विभेदन करना
हम

लेते हैं,जहां

फिर,

दोनों पक्षों से  के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:
के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:

बाईं तरफ:
 ,पायथागॉरियन सर्वसमिका का उपयोग करके
,पायथागॉरियन सर्वसमिका का उपयोग करके
दाईं तरफ:

इसलिए,

प्रतिस्थापन  ऊपर से, हमें मिलता है
ऊपर से, हमें मिलता है


प्रतिलोम कोस्पर्शज्या फलन का विभेदन करना
हम

लेते हैं,जहां 
फिर,

दोनों पक्षों से  के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:
के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:

बाईं तरफ:
 ,पायथागॉरियन सर्वसमिका का उपयोग करके
,पायथागॉरियन सर्वसमिका का उपयोग करके
दाईं तरफ:

इसलिए,

 प्रतिस्थापन करते हुए,
प्रतिस्थापन करते हुए,


वैकल्पिक रूप से,जैसा कि ऊपर दिखाया गया है वैसे ही  का अवकलज व्युत्पन्न किया गया,फिर सर्वसमिका
का अवकलज व्युत्पन्न किया गया,फिर सर्वसमिका  का उपयोग करके उसका तुरंत अनुसरण करता है
का उपयोग करके उसका तुरंत अनुसरण करता है

प्रतिलोम व्युत्क्रम-कोज्या फलन का विभेदन करना
अप्रत्य्क्ष विभेदन का उपयोग करना
माना

लेते हैं,जहां
![{\displaystyle x=\sec y\mid \ y\in \left[0,{\frac {\pi }{2}}\right)\cup \left({\frac {\pi }{2}},\pi \right]}](/index.php?title=Special:MathShowImage&hash=6837f27c6ded7ea86cf61108dc195276&mode=mathml) फिर,
फिर,
(अभिव्यक्ति में निरपेक्ष मान आवश्यक है क्योंकि y के अंतराल में व्युत्क्रम-कोज्या और स्पर्शज्या का गुणांक हमेशा गैर-ऋणात्मक होता है,जबकि प्रमुख वर्गमूल की परिभाषा के अनुसार करणी  हमेशा गैर-ऋणात्मक होती है,इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए,जो x के निरपेक्ष मान का उपयोग करके प्राप्त किये जाते हैं।)
हमेशा गैर-ऋणात्मक होती है,इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए,जो x के निरपेक्ष मान का उपयोग करके प्राप्त किये जाते हैं।)

श्रृंखला नियम का उपयोग करना
वैकल्पिक रूप से,प्रतिलोम व्युत्क्रम-कोज्या का अवकलज श्रृंखला नियम का उपयोग करके प्रतिलोम कोज्या के अवकलज से व्युत्पन्न किया जा सकता है।
माना

लेते हैं,जहां
 और
और ![{\displaystyle y\in \left[0,{\frac {\pi }{2}}\right)\cup \left({\frac {\pi }{2}},\pi \right]}](/index.php?title=Special:MathShowImage&hash=1165087dee67405c9eda3fb48e7f1199&mode=mathml)
फिर,  के लिए श्रृंखला नियम का उपयोग करते हुए:
के लिए श्रृंखला नियम का उपयोग करते हुए:

प्रतिलोम व्युत्क्रमज्या फलन का विभेदन करना
अप्रत्य्क्ष विभेदन का उपयोग करना
माना

लेते हैं,जहां
![{\displaystyle x=\csc y\ \mid \ y\in \left[-{\frac {\pi }{2}},0\right)\cup \left(0,{\frac {\pi }{2}}\right]}](/index.php?title=Special:MathShowImage&hash=1ceced66968453312f098771f63a1a25&mode=mathml)
- फिर,

(अभिव्यक्ति में निरपेक्ष मान आवश्यक है क्योंकि y के अंतराल में व्युत्क्रमज्या और कोस्पर्शज्या का गुणांक हमेशा गैर-ऋणात्मक होता है,जबकि प्रमुख वर्गमूल की परिभाषा के अनुसार करणी  हमेशा गैर-ऋणात्मक होता है,इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए,जो x के निरपेक्ष मान का उपयोग करके प्राप्त किये जाते हैं।)
हमेशा गैर-ऋणात्मक होता है,इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए,जो x के निरपेक्ष मान का उपयोग करके प्राप्त किये जाते हैं।)

श्रृंखला नियम का उपयोग करना
वैकल्पिक रूप से,प्रतिलोम व्युत्क्रमज्या का अवकलज श्रृंखला नियम का उपयोग करके प्रतिलोम-ज्या के अवकलज से व्युत्पन्न किया जा सकता है।
माना

लेते हैं,जहां
 और
और ![{\displaystyle y\in \left[-{\frac {\pi }{2}},0\right)\cup \left(0,{\frac {\pi }{2}}\right]}](/index.php?title=Special:MathShowImage&hash=e9af644a6253e4ceca8d081478dd764b&mode=mathml)
फिर,  के लिए श्रृंखला नियम को लागू करके
के लिए श्रृंखला नियम को लागू करके

यह भी देखें
संदर्भ
ग्रन्थसूची