हॉर्नर की विधि: Difference between revisions
No edit summary |
No edit summary |
||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Algorithm for polynomial evaluation}} | {{short description|Algorithm for polynomial evaluation}}गणित और [[कंप्यूटर विज्ञान]] में, हॉर्नर की विधि या हॉर्नर की योजना [[बहुपद मूल्यांकन]] के लिए एक कलन विधि के रूप में होती है। यद्यपि [[विलियम जॉर्ज हॉर्नर]] के नाम पर इसका नाम रखा गया, यह बहुत पुरानी विधि के रूप में है और इसका श्रेय हॉर्नर द्वारा [[जोसेफ-लुई लाग्रेंज]] को दिया गया है तथा चीनी और फ़ारसी गणितज्ञों को कई सैकड़ों वर्षों में खोजा गया है।<ref>600 years earlier, by the Chinese mathematician [[Qin Jiushao]] and 700 years earlier, by the Persian mathematician [[Sharaf al-Dīn al-Ṭūsī]]</ref> कंप्यूटरों के आगमन के बाद, यह कलन विधि बहुपदों के साथ कुशलतापूर्वक गणना करने के लिए मूलभूत रूप बन गया। | ||
गणित और [[कंप्यूटर विज्ञान]] में, हॉर्नर की विधि या हॉर्नर की योजना [[बहुपद मूल्यांकन]] के लिए एक | |||
कलन विधि हॉर्नर के नियम पर आधारित है, जिसमें एक बहुपद को 'नेस्टेड फॉर्म' में लिखा गया है | कलन विधि हॉर्नर के नियम पर आधारित है, जिसमें एक बहुपद को 'नेस्टेड फॉर्म' में लिखा गया है | ||
| Line 20: | Line 17: | ||
:<math>p(x) = \sum_{i=0}^n a_i x^i = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots + a_n x^n,</math> | :<math>p(x) = \sum_{i=0}^n a_i x^i = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots + a_n x^n,</math> | ||
जहाँ | जहाँ <math>a_0, \ldots, a_n</math> निरंतर गुणांक के रूप में होता है, समस्या <math>x_0</math> के एक विशिष्ट मान <math>x.</math>पर बहुपद का मूल्यांकन करना है। | ||
इसके लिए, अचरों के एक नए अनुक्रम का पुनरावर्तन संबंध इस प्रकार परिभाषित किया जाता है। | इसके लिए, अचरों के एक नए अनुक्रम का पुनरावर्तन संबंध इस प्रकार परिभाषित किया जाता है। | ||
| Line 31: | Line 28: | ||
b_0 & := a_0 + b_1 x_0. | b_0 & := a_0 + b_1 x_0. | ||
\end{align}</math> | \end{align}</math> | ||
तब <math>b_0</math> का मूल्य | तब <math>b_0</math> का मूल्य <math>p(x_0)</math>.है | ||
यह देखने के लिए कि यह क्यों काम करता है, बहुपद के रूप में लिखा जा सकता है | यह देखने के लिए कि यह क्यों काम करता है, बहुपद के रूप में लिखा जा सकता है | ||
| Line 54: | Line 51: | ||
p(x)/(x-x_0) | p(x)/(x-x_0) | ||
</math> | </math> | ||
<math>b_0</math> के साथ जो <math>p(x_0)</math> के बराबर है, जो कि विभाजन का शेषफल है, जैसा कि नीचे दिए गए उदाहरणों द्वारा प्रदर्शित होता है। यदि | <math>b_0</math> के साथ जो <math>p(x_0)</math> के बराबर है, जो कि विभाजन का शेषफल है, जैसा कि नीचे दिए गए उदाहरणों द्वारा प्रदर्शित होता है। यदि <math>x_0</math> की रूट् <math>p(x)</math> है, तब <math>b_0 = 0</math> का मतलब शेष <math>0</math> है, जिसका अर्थ है कि आप <math>p(x)</math> को <math>x-x_0</math>.के रूप में गुणनखंडित कर सकते हैं। | ||
लगातार <math>b</math>-मूल्य खोजने के लिए, आप <math>b_n</math> निर्धारण के साथ प्रारंभ | लगातार <math>b</math>-मूल्य खोजने के लिए, आप <math>b_n</math> निर्धारण के साथ प्रारंभ करते हैं, जो कि एक <math>a_n</math>के बराबर होता है। फिर आप सूत्र का उपयोग करके पुनरावर्ती रूप से कार्य करते हैं। | ||
:<math> | :<math> | ||
b_{n-1}=a_{n-1}+b_{n}x_0 | b_{n-1}=a_{n-1}+b_{n}x_0 | ||
| Line 68: | Line 65: | ||
हम निम्नानुसार [[सिंथेटिक विभाजन]] का उपयोग करते हैं, | हम निम्नानुसार [[सिंथेटिक विभाजन]] का उपयोग करते हैं, | ||
<math>x_0</math>│<math>x^3</math> | <math>x_0</math>│<math>x^3</math> <math>x^2</math> <math>x^1</math> <math>x^0</math>3 │ 2 −6 2 −1 | ||
│ 6 0 6 | |||
└──────────────────────── | |||
2 0 2 5 | |||
तीसरी पंक्ति की प्रविष्टियाँ पहले दो की प्रविष्टियों का योग हैं। दूसरी पंक्ति में प्रत्येक प्रविष्टि का उत्पाद <math>x</math>-मान है, इस उदाहरण में 3 तीसरी-पंक्ति प्रविष्टि के साथ तुरंत बाईं ओर होती है। पहली पंक्ति में प्रविष्टियाँ मूल्यांकन किए जाने वाले बहुपद के गुणांक हैं। तब <math>x-3</math> से भाग देने पर <math>f(x)</math> का शेषफल 5 होता है। | तीसरी पंक्ति की प्रविष्टियाँ पहले दो की प्रविष्टियों का योग हैं। दूसरी पंक्ति में प्रत्येक प्रविष्टि का उत्पाद <math>x</math>-मान है, इस उदाहरण में 3 तीसरी-पंक्ति प्रविष्टि के साथ तुरंत बाईं ओर होती है। पहली पंक्ति में प्रविष्टियाँ मूल्यांकन किए जाने वाले बहुपद के गुणांक हैं। तब <math>x-3</math> से भाग देने पर <math>f(x)</math> का शेषफल 5 होता है। | ||
| Line 84: | Line 81: | ||
2 │ 1 −6 11 −6 | 2 │ 1 −6 11 −6 | ||
│ 2 −8 6 | |||
└──────────────────────── | |||
1 −4 3 0 | |||
भागफल <math>x^2-4x+3</math> है | भागफल <math>x^2-4x+3</math> है | ||
| Line 94: | Line 91: | ||
0.5 │ 4 -6 0 3 -5 | |||
│ 2 -2 -1 1 | |||
└─────────────────────── | |||
2 -2 -1 1 -4 | |||
तीसरी पंक्ति पहली दो पंक्तियों का योग है, जिसे 2 से विभाजित किया गया है। दूसरी पंक्ति में प्रत्येक प्रविष्टि 1 का गुणनफल है और बाईं ओर तीसरी पंक्ति की प्रविष्टि उत्तर है | तीसरी पंक्ति पहली दो पंक्तियों का योग है, जिसे 2 से विभाजित किया गया है। दूसरी पंक्ति में प्रत्येक प्रविष्टि 1 का गुणनफल है और बाईं ओर तीसरी पंक्ति की प्रविष्टि उत्तर है | ||
| Line 106: | Line 103: | ||
=== दक्षता === | === दक्षता === | ||
घात के | घात के एकपद रूप का उपयोग करके मूल्यांकन <math>n</math> बहुपद की अधिकतम आवश्यकता होती है <math>n</math> अतिरिक्त और <math>(n^2+n)/2</math> गुणन, यदि बार-बार गुणन द्वारा शक्तियों की गणना की जाती है और प्रत्येक एकपद का व्यक्तिगत रूप से मूल्यांकन किया जाता है। पुनरावृत्ति द्वारा <math>x</math> की शक्तियों का मूल्यांकन करके लागत को <math>n</math> जोड़ और <math>2n-1</math> गुणा तक कम किया जा सकता है। | ||
यह मानता है कि बहुपद का मूल्यांकन | यदि संख्यात्मक डेटा अंकों या बिट्स के संदर्भ में प्रस्तुत किया जाता है, तो सहज कलन विधि भी <math>x</math> के बिट्स की संख्या का लगभग <math>2n</math> गुना स्टोर करने पर जोर देता है, मूल्यांकित बहुपद का परिमाण <math>x^n</math>अनुमानित है और किसी <math>x^n</math>को अपने आप में स्टोर करना चाहिए। इसके विपरीत, हॉर्नर की विधि को केवल <math>n</math> जोड़ और <math>n</math> गुणन की आवश्यकता होती है,और इसकी भंडारण आवश्यकताएं केवल <math>n</math> के बिट्स की संख्या का केवल <math>x</math> गुना होती हैं। वैकल्पिक रूप से, हॉर्नर की विधि की गणना <math>n</math> फ़्यूज्ड गुणा-जोड़ों के साथ की जा सकती है। हॉर्नर की विधि को <math>kn</math> योग और गुणन के साथ बहुपद के पहले <math>k</math> डेरिवेटिव का मूल्यांकन करने के लिए भी बढ़ाया जा सकता है।<ref>{{harvnb|Pankiewicz|1968}}.</ref> | ||
हॉर्नर की विधि इष्टतम रूप में होती है, इस अर्थ में किसी भी कलन विधि को यादृच्छिक ढंग से बहुपद का मूल्यांकन करने के लिए कम से कम कई परिचालनों का उपयोग करना चाहिए। [[अलेक्जेंडर ओस्ट्रोव्स्की]] ने 1954 में सिद्ध किया कि आवश्यक परिवर्धन की संख्या न्यूनतम रूप में होती है।<ref>{{harvnb|Ostrowski|1954}}.</ref> [[विक्टर पैन]] ने 1966 में सिद्ध किया कि गुणन की संख्या न्यूनतम होती है।<ref>{{harvnb|Pan|1966}}.</ref> चूँकि, कब <math>x</math> एक मैट्रिक्स के रूप में होता है, बहुपद मूल्यांकन हॉर्नर की विधि इष्टतम रूप में नहीं होती है। | |||
यह मानता है कि बहुपद का मूल्यांकन एकपद रूप में किया जाता है और प्रतिनिधित्व की कोई पूर्व [[शर्त]] की अनुमति नहीं होती है, जो समझ में आता है कि बहुपद का मूल्यांकन केवल एक बार किया जाता है। चूंकि, यदि पूर्व शर्त की अनुमति होती है और बहुपद का कई बार मूल्यांकन किया जाता है, तो तेज़ कलन विधि संभव हैं। उनमें बहुपद के प्रतिनिधित्व का परिवर्तन सम्मलित है। सामान्यतः, एक घात -<math>n</math> बहुपद का मूल्यांकन केवल {{floor|''n''/2}}+2 गुणा और <math>n</math> जोड़ का उपयोग करके किया जा सकता है।<ref>{{harvnb|Knuth|1997}}.</ref> | |||
==== समानांतर मूल्यांकन ==== | ==== समानांतर मूल्यांकन ==== | ||
{{see also| | {{see also|एस्ट्रिन की योजना}} | ||
हॉर्नर के नियम का एक नुकसान यह है कि सभी ऑपरेशन डेटा पर निर्भर | हॉर्नर के नियम का एक नुकसान यह है कि सभी ऑपरेशन डेटा पर निर्भर होते है, इसलिए आधुनिक कंप्यूटरों पर निर्देश स्तर की समानता का लाभ उठाना संभव नहीं होता है। अधिकांश अनुप्रयोगों में जहां बहुपद मूल्यांकन की दक्षता मायने रखती है, कई निम्न-क्रम वाले बहुपदों का एक साथ मूल्यांकन किया जाता है, कंप्यूटर ग्राफिक्स में प्रत्येक पिक्सेल या बहुभुज के लिए या प्रत्येक ग्रिड वर्ग के लिए एक संख्यात्मक सिमुलेशन के रूप में होता है, इसलिए एकल बहुपद मूल्यांकन के भीतर समानता खोजना आवश्यक नहीं है। | ||
चूंकि , यदि कोई बहुत उच्च क्रम के एकल बहुपद का मूल्यांकन कर रहा है, तो इसे निम्न प्रकार से | चूंकि, यदि कोई बहुत उच्च क्रम के एकल बहुपद का मूल्यांकन कर रहा है, तो इसे निम्न प्रकार से विभाजित किया सकता है, | ||
:<math>\begin{align} | :<math>\begin{align} | ||
p(x) & = \sum_{i=0}^n a_i x^i \\ | p(x) & = \sum_{i=0}^n a_i x^i \\ | ||
| Line 126: | Line 125: | ||
& = p_0(x^2) + x p_1(x^2). \\ | & = p_0(x^2) + x p_1(x^2). \\ | ||
\end{align}</math> | \end{align}</math> | ||
अधिक सामान्यतः, योग को k भागों में | अधिक सामान्यतः, योग को k भागों में विभाजित किया जा सकता है | ||
:<math>\begin{align} | :<math>\begin{align} | ||
p(x) & = \sum_{i=0}^n a_i x^i \\ | p(x) & = \sum_{i=0}^n a_i x^i \\ | ||
| Line 132: | Line 131: | ||
& = \sum_{j=0}^{k-1} x^j p_j(x^k) \\ | & = \sum_{j=0}^{k-1} x^j p_j(x^k) \\ | ||
\end{align}</math> | \end{align}</math> | ||
जहां हॉर्नर की विधि के अलग-अलग समानांतर उदाहरणों का उपयोग करके आंतरिक योग का मूल्यांकन किया जा सकता है। इसके लिए मूल हॉर्नर विधि की तुलना में थोड़े अधिक संचालन की आवश्यकता होती है, लेकिन उनमें से अधिकांश के | जहां हॉर्नर की विधि के अलग-अलग समानांतर उदाहरणों का उपयोग करके आंतरिक योग का मूल्यांकन किया जा सकता है। इसके लिए मूल हॉर्नर विधि की तुलना में थोड़े अधिक संचालन की आवश्यकता होती है, लेकिन उनमें से अधिकांश के के-वे [[सिमड]] निष्पादन की अनुमति देता है। आधुनिक संकलक सामान्यतः इस तरह से बहुपदों का मूल्यांकन करते हैं, जब फायदेमंद होता है, चूंकि [[तैरनेवाला स्थल|फ्लोटिंग-पॉइंट]] गणनाओं के लिए इसके लिए असुरक्षित पुनर्संरचनात्मक गणित को सक्षम करने की आवश्यकता होती है।{{Citation needed|date=February 2022}}. | ||
=== फ़्लोटिंग-पॉइंट गुणा और भाग के लिए आवेदन === | === फ़्लोटिंग-पॉइंट गुणा और भाग के लिए आवेदन === | ||
{{main| | {{main|गुणन कलन विधि शिफ्ट और जोड़ें}} | ||
हॉर्नर की विधि बिना किसी [[बाइनरी गुणक]] वाले [[ microcontroller ]] पर बाइनरी संख्याओं के गुणन और विभाजन के लिए एक तेज़, कोड-कुशल विधि है। गुणा की जाने वाली द्विआधारी संख्याओं में से एक को तुच्छ बहुपद के रूप में दर्शाया गया है, जहाँ | हॉर्नर की विधि बिना किसी [[बाइनरी गुणक]] वाले [[ microcontroller |माइक्रोकंट्रोलर]] पर बाइनरी संख्याओं के गुणन और विभाजन के लिए एक तेज़, कोड-कुशल विधि के रूप में होती है। गुणा की जाने वाली द्विआधारी संख्याओं में से एक को तुच्छ बहुपद के रूप में दर्शाया गया है, जहाँ उपरोक्त संकेतन का उपयोग करके <math>a_i = 1</math>, और <math>x = 2</math>. फिर, x या x से कुछ शक्ति को बार-बार फैक्टर आउट किया जाता है। इस बाइनरी अंक प्रणाली आधार 2 में, <math>x = 2</math>, इसलिए 2 की घातें बार-बार फ़ैक्टर आउट की जाती हैं। | ||
==== उदाहरण ==== | ==== उदाहरण ==== | ||
उदाहरण के लिए, दो संख्याओं (0.15625) और m का गुणनफल ज्ञात करने के लिए | उदाहरण के लिए, दो संख्याओं (0.15625) और m का गुणनफल ज्ञात करने के लिए हैं | ||
:<math> | :<math> | ||
| Line 151: | Line 150: | ||
==== तरीका ==== | ==== तरीका ==== | ||
दो बाइनरी नंबरों d और m का गुणनफल ज्ञात करने के लिए | दो बाइनरी नंबरों d और m का गुणनफल ज्ञात करने के लिए इस प्रकार किया है | ||
:1. इंटरमीडिएट परिणाम रखने वाले एक रजिस्टर को डी में प्रारंभ किया जाता है। | :1. इंटरमीडिएट परिणाम रखने वाले एक रजिस्टर को डी में प्रारंभ किया जाता है। | ||
:2. मीटर में कम से कम महत्वपूर्ण | :2. मीटर में कम से कम महत्वपूर्ण दाहिनी ओर गैर-शून्य बिट से प्रारंभ करते है। | ||
::2बी। गिनती | ::2बी। गिनती बाईं ओर अगले सबसे महत्वपूर्ण गैर-शून्य बिट के लिए बिट पदों की संख्या के रूप में होती है। यदि अधिक महत्वपूर्ण बिट नहीं होती है, तो वर्तमान बिट स्थिति का मान लेते है। | ||
::2सी। उस मान का उपयोग करते हुए, इंटरमीडिएट परिणाम रखने वाले रजिस्टर पर बिट्स की संख्या से बाएं-शिफ्ट ऑपरेशन | ::2सी। उस मान का उपयोग करते हुए, इंटरमीडिएट परिणाम रखने वाले रजिस्टर पर बिट्स की संख्या से बाएं-शिफ्ट ऑपरेशन प्रारंभ करते है। | ||
:3. यदि सभी गैर-शून्य बिट्स गिने जाते हैं, तो मध्यवर्ती परिणाम रजिस्टर अब अंतिम परिणाम रखता है। अन्यथा, मध्यवर्ती परिणाम में d जोड़ें | :3. यदि सभी गैर-शून्य बिट्स गिने जाते हैं, तो मध्यवर्ती परिणाम रजिस्टर अब अंतिम परिणाम रखता है। अन्यथा, मध्यवर्ती परिणाम में d जोड़ें और m में अगले सबसे महत्वपूर्ण बिट के साथ चरण 2 में जारी रखते है। | ||
==== व्युत्पत्ति ==== | ==== व्युत्पत्ति ==== | ||
सामान्यतः , बिट वैल्यू वाले बाइनरी नंबर के लिए (<math> d_3 d_2 d_1 d_0 </math>) उत्पाद है | सामान्यतः , बिट वैल्यू वाले बाइनरी नंबर के लिए (<math> d_3 d_2 d_1 d_0 </math>) उत्पाद है | ||
:<math> (d_3 2^3 + d_2 2^2 + d_1 2^1 + d_0 2^0)m = d_3 2^3 m + d_2 2^2 m + d_1 2^1 m + d_0 2^0 m. </math> | :<math> (d_3 2^3 + d_2 2^2 + d_1 2^1 + d_0 2^0)m = d_3 2^3 m + d_2 2^2 m + d_1 2^1 m + d_0 2^0 m. </math> | ||
कलन विधि में इस स्तर पर, यह आवश्यक है कि शून्य-मूल्य वाले गुणांक वाले पदों को हटा दिया जाए, जिससे कि | कलन विधि में इस स्तर पर, यह आवश्यक है कि शून्य-मूल्य वाले गुणांक वाले पदों को हटा दिया जाए, जिससे कि केवल एक के बराबर द्विआधारी गुणांक की गणना की जा सके, इस प्रकार शून्य से गुणा या विभाजन की समस्या कोई समस्या नहीं है, इस निहितार्थ के बावजूद कारक समीकरण के रूप में होते है | ||
:<math> = d_0\left(m + 2 \frac{d_1}{d_0} \left(m + 2 \frac{d_2}{d_1} \left(m + 2 \frac{d_3}{d_2} (m)\right)\right)\right). </math> | :<math> = d_0\left(m + 2 \frac{d_1}{d_0} \left(m + 2 \frac{d_2}{d_1} \left(m + 2 \frac{d_3}{d_2} (m)\right)\right)\right). </math> | ||
हर सभी बराबर एक | हर सभी बराबर एक या शब्द अनुपस्थित है, तो यह कम हो जाता है | ||
:<math> = d_0(m + 2 {d_1} (m + 2 {d_2} (m + 2 {d_3} (m)))),</math> | :<math> = d_0(m + 2 {d_1} (m + 2 {d_2} (m + 2 {d_3} (m)))),</math> | ||
या समकक्ष | या समकक्ष ऊपर वर्णित विधि के अनुरूप होते है | ||
:<math> = d_3(m + 2^{-1} {d_2} (m + 2^{-1}{d_1} (m + {d_0} (m)))). </math> | :<math> = d_3(m + 2^{-1} {d_2} (m + 2^{-1}{d_1} (m + {d_0} (m)))). </math> | ||
बाइनरी | बाइनरी बेस -2 गणित में, 2 की शक्ति से गुणा केवल एक अंकगणितीय शिफ्ट ऑपरेशन के रूप में होते है। इस प्रकार, 2 से गुणा करने पर आधार-2 में एक अंकगणितीय शिफ्ट द्वारा गणना की जाती है। कारक (2<sup>−1</sup>) एक सही अंकगणितीय बदलाव है, a (0) के परिणामस्वरूप कोई संक्रिया नहीं होती 2<sup>0</sup> = 1 के बाद से गुणात्मक [[पहचान तत्व]] है और एक (2<sup>1</sup>) का परिणाम बाएं अंकगणितीय बदलाव में होता है। गुणन गुणनफल अब केवल अंकगणितीय पारी संचालन जोड़ और घटाव का उपयोग करके जल्दी से गणना की जा सकती है। | ||
गुणन गुणनफल अब केवल अंकगणितीय पारी संचालन | |||
एकल-निर्देश शिफ्ट-एंड-एडिशन-संचय का समर्थन करने वाले प्रोसेसर पर विधि विशेष रूप से तेज़ है, सी फ्लोटिंग-पॉइंट लाइब्रेरी की तुलना में, | |||
हॉर्नर की विधि कुछ यथार्थ ता का त्याग करती है, चूंकि यह नाममात्र रूप से 13 गुना तेज है, 16 गुना तेज जब कैनोनिकल हस्ताक्षरित अंक सीएसडी फॉर्म का उपयोग किया जाता है और कोड स्थान का केवल 20% उपयोग करता है।<ref>{{harvnb|Kripasagar|2008|p=62}}.</ref> | |||
=== अन्य अनुप्रयोग === | === अन्य अनुप्रयोग === | ||
हॉर्नर की विधि का उपयोग विभिन्न स्थितीय अंक प्रणालियों के बीच रूपांतरण के लिए किया जा सकता है | हॉर्नर की विधि का उपयोग विभिन्न स्थितीय अंक प्रणालियों के बीच रूपांतरण के लिए किया जा सकता है, इस स्थिति में x संख्या प्रणाली का आधार है और a<sub>''i''</sub> गुणांक किसी दिए गए नंबर के बेस-एक्स प्रतिनिधित्व के अंक हैं और इसका उपयोग तब भी किया जा सकता है जब एक्स एक [[मैट्रिक्स (गणित)]] के रूप में होता है, इस स्थिति में कम्प्यूटेशनल दक्षता में लाभ और भी अधिक है। चूँकि, ऐसे स्थितियों के लिए बहुपद मूल्यांकन के लिए तेज़ तरीके ज्ञात हैं।।<ref>{{harvnb|Higham|2002|loc=Section 5.4}}.</ref> | ||
== बहुपद रूट् ढूँढना == | |||
न्यूटन की विधि के संयोजन में दीर्घ विभाजन कलन विधि का उपयोग करके, बहुपद की वास्तविक रूट्स का अनुमान लगाना संभव होता है। यह कलन विधि इस प्रकार काम करता है। एक बहुपद <math>p_n(x)</math>दिया घात का <math>n</math> शून्य के साथ <math> z_n < z_{n-1} < \cdots < z_1,</math> कुछ प्रारंभिक अनुमान लगाएं <math> x_0 </math> ऐसा है कि <math> z_1 < x_0 </math>. अब निम्नलिखित दो चरणों को दोहराता है,. | |||
#न्यूटन की विधि का उपयोग करते हुए, अनुमान <math>x_0</math> का उपयोग करके <math>p_n(x)</math> का सबसे बड़ा शून्य <math>z_1</math> ज्ञात करते है | |||
# हॉर्नर की विधि का उपयोग करके <math>p_{n-1}</math> प्राप्त करने के लिए <math>(x-z_1)</math> को विभाजित करते है, चरण 1 पर लौटते है लेकिन बहुपद <math>p_{n-1}</math> और प्रारंभिक अनुमान <math>z_1</math>.का उपयोग करते है | |||
इन दो चरणों को तब तक दोहराया जाता है जब तक कि बहुपद के लिए सभी वास्तविक शून्य नहीं मिल जाते। यदि अनुमानित शून्य पर्याप्त यथार्थ रूप में नहीं होते है, तो प्राप्त मूल्यों को न्यूटन की विधि के लिए प्रारंभिक अनुमानों के रूप में उपयोग किया जा सकता है, लेकिन कम बहुपदों के अतिरिक्त पूर्ण बहुपद का उपयोग किया जा सकता है।<ref>{{harvnb|Kress|1991|p=112}}.</ref> | |||
इन दो चरणों को तब तक दोहराया जाता है जब तक कि बहुपद के लिए सभी वास्तविक शून्य नहीं मिल जाते। यदि अनुमानित शून्य पर्याप्त यथार्थ | |||
=== उदाहरण === | === उदाहरण === | ||
[[File:HornerandNewton.gif|thumb|right|400px|हॉर्नर की विधि का उपयोग करते हुए बहुपद मूल खोज]]बहुपद पर विचार | [[File:HornerandNewton.gif|thumb|right|400px|हॉर्नर की विधि का उपयोग करते हुए बहुपद मूल खोज]]बहुपद पर विचार करते है | ||
: <math> | : <math> | ||
| Line 205: | Line 200: | ||
p_5(x) = x^5 + 11x^4 + 5x^3 - 179x^2 - 126x + 720 | p_5(x) = x^5 + 11x^4 + 5x^3 - 179x^2 - 126x + 720 | ||
</math> | </math> | ||
जो दाईं ओर की आकृति में लाल रंग से खींचा गया है। 7 के प्रारंभिक अनुमान के साथ इस बहुपद का सबसे बड़ा शून्य खोजने के लिए न्यूटन की विधि का उपयोग किया जाता है। इस बहुपद का सबसे बड़ा शून्य जो मूल बहुपद के दूसरे सबसे बड़े शून्य से मेल खाता है, 3 पर पाया जाता है और लाल रंग में घेरा जाता है। घात 5 बहुपद अब से विभाजित | जो दाईं ओर की आकृति में लाल रंग से खींचा गया है। 7 के प्रारंभिक अनुमान के साथ इस बहुपद का सबसे बड़ा शून्य खोजने के लिए न्यूटन की विधि का उपयोग किया जाता है। इस बहुपद का सबसे बड़ा शून्य जो मूल बहुपद के दूसरे सबसे बड़े शून्य से मेल खाता है, 3 पर पाया जाता है और लाल रंग में घेरा जाता है। घात 5 बहुपद अब से विभाजित <math>(x-3)</math> प्राप्त करने के लिए है | ||
: <math> | : <math> | ||
| Line 220: | Line 215: | ||
p_2(x) = x^2 + 13x + 40 | p_2(x) = x^2 + 13x + 40 | ||
</math> | </math> | ||
जो नीले रंग में दिखाया गया है और -5 का शून्य देता है। न्यूटन की विधि के प्रारंभिक अनुमान के रूप में अंतिम शून्य का उपयोग करके या घटाकर मूल बहुपद का अंतिम मूल पाया जा सकता है <math>p_2(x)</math> और रैखिक समीकरण को हल करना। जैसा कि देखा जा सकता है, -8, -5, -3, 2, 3 और 7 की अपेक्षित | जो नीले रंग में दिखाया गया है और -5 का शून्य देता है। न्यूटन की विधि के प्रारंभिक अनुमान के रूप में अंतिम शून्य का उपयोग करके या घटाकर मूल बहुपद का अंतिम मूल पाया जा सकता है <math>p_2(x)</math> और रैखिक समीकरण को हल करना। जैसा कि देखा जा सकता है, -8, -5, -3, 2, 3 और 7 की अपेक्षित रुट के रूप में पाई गईं है। | ||
== एक बहुपद का विभाजित अंतर == | == एक बहुपद का विभाजित अंतर == | ||
| Line 242: | Line 237: | ||
\end{align}</math> | \end{align}</math> | ||
विभाजित अंतर की यह गणना कम के अधीन है | विभाजित अंतर की यह गणना कम के अधीन है | ||
मूल्यांकन की तुलना में राउंड-ऑफ़ त्रुटि <math>p(x)</math> और <math>p(y)</math> अलग से, विशेष रूप से | मूल्यांकन की तुलना में राउंड-ऑफ़ त्रुटि <math>p(x)</math> और <math>p(y)</math> अलग से, विशेष रूप से जब | ||
<math> x \approx y</math>. स्थानापन्न | <math> x \approx y</math>. स्थानापन्न | ||
<math>y = x</math> इस विधि में देता है <math>d_1 = p'(x)</math>, का व्युत्पन्न <math>p(x)</math>. | <math>y = x</math> इस विधि में देता है <math>d_1 = p'(x)</math>, का व्युत्पन्न <math>p(x)</math>. | ||
== इतिहास == | == इतिहास == | ||
[[File:Qingjiushaoquad1.GIF|thumb|right|200px|द्विघात बहुपद समीकरण को हल करने के लिए [[जे आईयू में क्यू कम]] का | [[File:Qingjiushaoquad1.GIF|thumb|right|200px|द्विघात बहुपद समीकरण को हल करने के लिए [[जे आईयू में क्यू कम]] का कलनविधि<math>-x^4+763200x^2-40642560000=0</math><br />परिणाम: x=840<ref>{{harvnb|Libbrecht|2005|pages=181–191}}.</ref>]]निरंतर सन्निकटन द्वारा सभी आदेशों के संख्यात्मक समीकरणों को हल करने की एक नई विधि शीर्षक वाला हॉर्नर का पेपर, 1 जुलाई 1819 को रॉयल सोसाइटी ऑफ लंदन की बैठक में 1823 में अगली कड़ी के साथ [[पढ़ा गया]] था।<ref name="Horner">{{harvnb|Horner|1819}}.</ref> 1819 के लिए लंदन की रॉयल सोसाइटी के दार्शनिक लेनदेन के भाग II में हॉर्नर के पेपर का अप्रैल, 1820 के द मंथली रिव्यू या लिटरेरी जर्नल के अंक में एक [[समीक्षक]] स्थायी डेड लिंक द्वारा गर्मजोशी और विस्तार से स्वागत किया गया था; इसकी तुलना में [[चार्ल्स बैबेज]] के एक तकनीकी पेपर को इस समीक्षा में स्पष्ट रूप से खारिज कर दिया गया है। सितंबर, 1821 के लिए द मंथली रिव्यू में समीक्षाओं का क्रम यह निष्कर्ष निकालता है कि होल्डर संख्यात्मक समीकरणों के प्रत्यक्ष और सामान्य व्यावहारिक समाधान की खोज करने वाले पहले व्यक्ति थे। <ref>{{harvnb|Fuller|1999|pages=29–51}}.</ref> फुलर दिखाया कि हॉर्नर के 1819 के पेपर की विधि बाद की विधि" के रूप में जानी जाने वाली पेपर विधि से भिन्न है और इसके परिणामस्वरूप इस पद्धति की प्राथमिकता होल्ड्रेड (1820) को मिलनी चाहिए थी। | ||
अपने अंग्रेजी समकालीनों के विपरीत, हॉर्नर ने महाद्वीपीय साहित्य पर विशेष रूप से लुइस फ्रांकोइस एंटोनी अर्बोगैस्ट के काम को आकर्षित किया। हॉर्नर को बीजगणित पर जॉन बोनीकैसल की पुस्तक का गहन अध्ययन करने के लिए भी जाना जाता है, चूंकि | अपने अंग्रेजी समकालीनों के विपरीत, हॉर्नर ने महाद्वीपीय साहित्य पर विशेष रूप से लुइस फ्रांकोइस एंटोनी अर्बोगैस्ट के काम को आकर्षित किया। हॉर्नर को बीजगणित पर जॉन बोनीकैसल की पुस्तक का गहन अध्ययन करने के लिए भी जाना जाता है, चूंकि उन्होंने पाओलो रफिनी (गणितज्ञ) के काम की उपेक्षा की थी। | ||
चूँकि | चूँकि, हॉर्नर को इस विधि को सुलभ और व्यावहारिक बनाने का श्रेय दिया जाता है, लेकिन यह हॉर्नर से बहुत पहले से जाना जाता था। रिवर्स कालानुक्रमिक क्रम में हॉर्नर की विधि पहले से ही ज्ञात थी | ||
* 1809 में पाओलो रफ़िनी (गणितज्ञ) | * 1809 में पाओलो रफ़िनी (गणितज्ञ) रुफ़िनी का नियम देखें<ref name="Cajori">{{harvnb|Cajori|1911}}.</ref><ref name="St Andrews">{{MacTutor|id=Horner}}</ref> | ||
* [[आइजैक न्यूटन]] ने 1669 में<ref>Analysis Per Quantitatum Series, Fluctiones ac Differentias : Cum Enumeratione Linearum Tertii Ordinis, Londini. Ex Officina Pearsoniana. Anno MDCCXI, p. 10, 4th paragraph.</ref><ref>Newton's collected papers, the edition 1779, in a footnote, vol. I, p. 270-271</ref> | * [[आइजैक न्यूटन]] ने 1669 में<ref>Analysis Per Quantitatum Series, Fluctiones ac Differentias : Cum Enumeratione Linearum Tertii Ordinis, Londini. Ex Officina Pearsoniana. Anno MDCCXI, p. 10, 4th paragraph.</ref><ref>Newton's collected papers, the edition 1779, in a footnote, vol. I, p. 270-271</ref> | ||
* 14वीं शताब्दी में [[चीनी गणित]] [[मिस जेड टाइगर]]<ref name="St Andrews" />* 13वीं शताब्दी में चीनी गणित किन जियुशाओ ने अपने गणितीय ग्रंथ नौ खंडों में | * 14वीं शताब्दी में [[चीनी गणित]] [[मिस जेड टाइगर]] के रूप में थे<ref name="St Andrews" /> | ||
* [[फारसी लोग]] [[मध्यकालीन इस्लाम में गणित]] शराफ अल-दीन अल-यूसी 12वीं शताब्दी में | *13वीं शताब्दी में चीनी गणित किन जियुशाओ ने अपने गणितीय ग्रंथ नौ खंडों में प्रस्तुत किया था | ||
* 11वीं शताब्दी में चीनी गणितज्ञ [[जे आइए एक्स इयान]] | * [[फारसी लोग]] [[मध्यकालीन इस्लाम में गणित]] शराफ अल-दीन अल-यूसी 12वीं शताब्दी में घन समीकरण के सामान्य स्थिति में उस पद्धति का उपयोग करने वाले पहले व्यक्ति के रूप में थे <ref>{{harvnb|Berggren|1990|pages=304–309}}.</ref> | ||
* [[गणितीय कला पर नौ अध्याय]], हान राजवंश | * 11वीं शताब्दी में चीनी गणितज्ञ [[जे आइए एक्स इयान]] सांग राजवंश के रूप में थे | ||
किन जिउशाओ, अपने शू शू जिउ झांग | * [[गणितीय कला पर नौ अध्याय]], हान राजवंश की एक चीनी कृति 202 ईसा पूर्व - 220 ईस्वी, तीसरी शताब्दी में लियू हुई फ़्ल द्वारा संपादित हुई है।<ref>{{harvnb|Temple|1986|p=142}}.</ref>किन जिउशाओ, अपने शू शू जिउ झांग मैथमेटिकल ट्रीटिस इन नाइन सेक्शन्स, 1247 में बहुपद समीकरणों को हल करने के लिए हॉर्नर प्रकार के विधि का एक पोर्टफोलियो प्रस्तुत करता है, जो 11 वीं शताब्दी के सांग वंश के गणितज्ञ जिया जियान के पहले के कार्यों पर आधारित था, उदाहरण के लिए एक विधि बाय-क्विंटिक्स के अनुकूल विशेष रूप से है, जिसमें से केस स्टडीज के तत्कालीन चीनी रिवाज को ध्यान में रखते हुए किन एक उदाहरण देता है। चीन और जापान में गणित के विकास में योशियो मिकामी लीपज़िग 1913 ने लिखा गया है।{{Blockquote | style=font-size:100% | text=यूरोप की तुलना में कम से कम छह लंबी शताब्दियों पहले चीन में हॉर्नर की शानदार प्रक्रिया का उपयोग करने के तथ्य से कौन इंकार कर सकता है, हम निश्चित रूप से किसी भी तरह से हॉर्नर के आविष्कार को चीनी मूल के रूप में वर्णित करने का इरादा नहीं रखते हैं, लेकिन समय की कमी पर्याप्त रूप से बनाती है यह पूरी तरह से असंभव नहीं था कि यूरोपीय लोग प्रत्यक्ष या अप्रत्यक्ष रूप से चीनी पद्धति के बारे में जान सकते थे}} | ||
[[उलरिच लिब्रेब्रेच]] ने निष्कर्ष निकाला | [[उलरिच लिब्रेब्रेच]] ने निष्कर्ष निकाला यह स्पष्ट है कि यह प्रक्रिया एक चीनी आविष्कार के रूप में है, यह विधि भारत में ज्ञात नहीं थी। उन्होंने कहा, फिबोनाची ने संभवतः इसके बारे में अरबों से सीखा, जिन्होंने संभवतः चीनियों से उधार लिया था।<ref>{{harvnb|Libbrecht|2005|p=208}}.</ref> जिउ झांग सुआन शू में समस्या IV.16 और 22 के संबंध में समान रेखाओं के साथ वर्ग और घन रूट्स की निकासी पर पहले से ही लियू हुई द्वारा चर्चा की गई है, जबकि 7 वीं शताब्दी में [[वांग ξए ओ टोंग|वांग शियाओतोंग]] का मानना है कि उनके पाठक क्यूबिक्स को उनके द्वारा वर्णित एक सन्निकटन विधि द्वारा हल कर सकते हैं। उनकी किताब [[जिगू सुंजिंग]] में दिखाया गया है | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[चेबिशेव रूप]] में बहुपदों का मूल्यांकन करने के लिए [[क्लेंशॉ | * [[चेबिशेव रूप]] में बहुपदों का मूल्यांकन करने के लिए [[क्लेंशॉ कलन विधि]] का प्रयोग करते है | ||
*[[बी-पट्टी]] फॉर्म में [[तख़्ता वक्र]] का मूल्यांकन करने के लिए डी बूर का | *[[बी-पट्टी]] फॉर्म में [[तख़्ता वक्र]] का मूल्यांकन करने के लिए डी बूर का कलन विधि का प्रयोग करते है | ||
*बेज़ियर रूप में बहुपदों का मूल्यांकन करने के लिए डी कैस्टेलजौ का | *बेज़ियर रूप में बहुपदों का मूल्यांकन करने के लिए डी कैस्टेलजौ का कलन विधि का प्रयोग करते है | ||
*एस्ट्रिन की योजना आधुनिक कंप्यूटर आर्किटेक्चर पर समानांतरकरण की सुविधा के | *एस्ट्रिन की योजना आधुनिक कंप्यूटर आर्किटेक्चर पर समानांतरकरण की सुविधा के रूप में होता है | ||
*लील की विधि से रूट्स का रेखांकन किया जा सकता है | *लील की विधि से रूट्स का रेखांकन किया जा सकता है | ||
* रफ़िनी का नियम और सिंथेटिक विभाजन एक बहुपद को x - r के रूप में एक द्विपद से विभाजित करने के लिए | * रफ़िनी का नियम और सिंथेटिक विभाजन एक बहुपद को x - r के रूप में एक द्विपद से विभाजित करने के लिए करते है | ||
== टिप्पणियाँ == | == टिप्पणियाँ == | ||
| Line 511: | Line 506: | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* {{springer|title=Horner scheme|id=p/h048030}} | * {{springer|title=Horner scheme|id=p/h048030}} | ||
* Qiu Jin-Shao, [https://web.archive.org/web/20140106040413/http://turing.une.edu.au/~ernie/Chinese/SSJZ.pdf Shu Shu Jiu Zhang] (Cong Shu Ji Cheng ed.) | * Qiu Jin-Shao, [https://web.archive.org/web/20140106040413/http://turing.une.edu.au/~ernie/Chinese/SSJZ.pdf Shu Shu Jiu Zhang] (Cong Shu Ji Cheng ed.) | ||
| Line 517: | Line 511: | ||
{{Polynomials}} | {{Polynomials}} | ||
[[Category: | [[Category:All articles with unsourced statements]] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with unsourced statements from February 2022]] | |||
[[Category:CS1]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 03/03/2023]] | [[Category:Created On 03/03/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:बहुपदों]] | |||
[[Category:बीजगणित]] | |||
[[Category:संख्यात्मक विश्लेषण]] | |||
Latest revision as of 13:31, 17 March 2023
गणित और कंप्यूटर विज्ञान में, हॉर्नर की विधि या हॉर्नर की योजना बहुपद मूल्यांकन के लिए एक कलन विधि के रूप में होती है। यद्यपि विलियम जॉर्ज हॉर्नर के नाम पर इसका नाम रखा गया, यह बहुत पुरानी विधि के रूप में है और इसका श्रेय हॉर्नर द्वारा जोसेफ-लुई लाग्रेंज को दिया गया है तथा चीनी और फ़ारसी गणितज्ञों को कई सैकड़ों वर्षों में खोजा गया है।[1] कंप्यूटरों के आगमन के बाद, यह कलन विधि बहुपदों के साथ कुशलतापूर्वक गणना करने के लिए मूलभूत रूप बन गया।
कलन विधि हॉर्नर के नियम पर आधारित है, जिसमें एक बहुपद को 'नेस्टेड फॉर्म' में लिखा गया है
यह केवल n गुणन और n जोड़ के साथ घात n के बहुपद के मूल्यांकन की अनुमति देता है। यह इष्टतम है, क्योंकि घात n के बहुपद हैं जिनका मूल्यांकन कम अंकगणितीय परिचालनों के साथ नहीं किया जा सकता है[2]
वैकल्पिक रूप से, हॉर्नर की विधि 1819 में हॉर्नर द्वारा वर्णित बहुपदों की रूट्स का अनुमान लगाने के लिए एक विधि को संदर्भित करती है। यह न्यूटन रैप्सन विधि का एक प्रकार है, जो हॉर्नर के नियम के अनुप्रयोग द्वारा हाथ की गणना के लिए अधिक कुशल रूप में होती है। 1970 के आसपास कंप्यूटर के सामान्य उपयोग में आने तक इसका व्यापक रूप से उपयोग किया जाता था।
बहुपद मूल्यांकन और दीर्घ विभाजन
बहुपद दिया है
जहाँ निरंतर गुणांक के रूप में होता है, समस्या के एक विशिष्ट मान पर बहुपद का मूल्यांकन करना है।
इसके लिए, अचरों के एक नए अनुक्रम का पुनरावर्तन संबंध इस प्रकार परिभाषित किया जाता है।
तब का मूल्य .है
यह देखने के लिए कि यह क्यों काम करता है, बहुपद के रूप में लिखा जा सकता है
इस प्रकार, पुनरावृत्त रूप से को प्रतिस्थापित करके अभिव्यक्ति इस प्रकार किया है,
अब, यह सिद्ध किया जा सकता है कि
यह अभिव्यक्ति हॉर्नर के व्यावहारिक अनुप्रयोग का गठन करती है, क्योंकि यह परिणाम का निर्धारण करने का एक बहुत तेज़ विधि प्रदान करती है;
के साथ जो के बराबर है, जो कि विभाजन का शेषफल है, जैसा कि नीचे दिए गए उदाहरणों द्वारा प्रदर्शित होता है। यदि की रूट् है, तब का मतलब शेष है, जिसका अर्थ है कि आप को .के रूप में गुणनखंडित कर सकते हैं।
लगातार -मूल्य खोजने के लिए, आप निर्धारण के साथ प्रारंभ करते हैं, जो कि एक के बराबर होता है। फिर आप सूत्र का उपयोग करके पुनरावर्ती रूप से कार्य करते हैं।
जब तक आप पर नहीं पहुंच जाते हैं।
उदाहरण
मूल्यांकन करना के लिए .
हम निम्नानुसार सिंथेटिक विभाजन का उपयोग करते हैं,
│ 3 │ 2 −6 2 −1
│ 6 0 6 └──────────────────────── 2 0 2 5
तीसरी पंक्ति की प्रविष्टियाँ पहले दो की प्रविष्टियों का योग हैं। दूसरी पंक्ति में प्रत्येक प्रविष्टि का उत्पाद -मान है, इस उदाहरण में 3 तीसरी-पंक्ति प्रविष्टि के साथ तुरंत बाईं ओर होती है। पहली पंक्ति में प्रविष्टियाँ मूल्यांकन किए जाने वाले बहुपद के गुणांक हैं। तब से भाग देने पर का शेषफल 5 होता है।
लेकिन बहुपद शेष प्रमेय द्वारा हम जानते हैं कि शेषफल इस प्रकार है
इस उदाहरण में, यदि हम देख सकते हैं कि , तीसरी पंक्ति में प्रविष्टियाँ के रूप में होते है। अतः संश्लेषित विभाजन हॉर्नर विधि पर आधारित होती है।
बहुपद शेष प्रमेय के परिणाम के रूप में, तीसरी पंक्ति में प्रविष्टियां दूसरी घात बहुपद के गुणांक के रूप में होते है, और इसका भागफल विभाजन .पर शेष है यह हॉर्नर की विधि को बहुपद लंबे विभाजन के लिए उपयोगी बनाता है।
को से विभाजित करें
2 │ 1 −6 11 −6 │ 2 −8 6 └──────────────────────── 1 −4 3 0
भागफल है
माना और , को से विभाजित करना है हॉर्नर की विधि का उपयोग करके।
0.5 │ 4 -6 0 3 -5 │ 2 -2 -1 1 └─────────────────────── 2 -2 -1 1 -4
तीसरी पंक्ति पहली दो पंक्तियों का योग है, जिसे 2 से विभाजित किया गया है। दूसरी पंक्ति में प्रत्येक प्रविष्टि 1 का गुणनफल है और बाईं ओर तीसरी पंक्ति की प्रविष्टि उत्तर है
दक्षता
घात के एकपद रूप का उपयोग करके मूल्यांकन बहुपद की अधिकतम आवश्यकता होती है अतिरिक्त और गुणन, यदि बार-बार गुणन द्वारा शक्तियों की गणना की जाती है और प्रत्येक एकपद का व्यक्तिगत रूप से मूल्यांकन किया जाता है। पुनरावृत्ति द्वारा की शक्तियों का मूल्यांकन करके लागत को जोड़ और गुणा तक कम किया जा सकता है।
यदि संख्यात्मक डेटा अंकों या बिट्स के संदर्भ में प्रस्तुत किया जाता है, तो सहज कलन विधि भी के बिट्स की संख्या का लगभग गुना स्टोर करने पर जोर देता है, मूल्यांकित बहुपद का परिमाण अनुमानित है और किसी को अपने आप में स्टोर करना चाहिए। इसके विपरीत, हॉर्नर की विधि को केवल जोड़ और गुणन की आवश्यकता होती है,और इसकी भंडारण आवश्यकताएं केवल के बिट्स की संख्या का केवल गुना होती हैं। वैकल्पिक रूप से, हॉर्नर की विधि की गणना फ़्यूज्ड गुणा-जोड़ों के साथ की जा सकती है। हॉर्नर की विधि को योग और गुणन के साथ बहुपद के पहले डेरिवेटिव का मूल्यांकन करने के लिए भी बढ़ाया जा सकता है।[3]
हॉर्नर की विधि इष्टतम रूप में होती है, इस अर्थ में किसी भी कलन विधि को यादृच्छिक ढंग से बहुपद का मूल्यांकन करने के लिए कम से कम कई परिचालनों का उपयोग करना चाहिए। अलेक्जेंडर ओस्ट्रोव्स्की ने 1954 में सिद्ध किया कि आवश्यक परिवर्धन की संख्या न्यूनतम रूप में होती है।[4] विक्टर पैन ने 1966 में सिद्ध किया कि गुणन की संख्या न्यूनतम होती है।[5] चूँकि, कब एक मैट्रिक्स के रूप में होता है, बहुपद मूल्यांकन हॉर्नर की विधि इष्टतम रूप में नहीं होती है।
यह मानता है कि बहुपद का मूल्यांकन एकपद रूप में किया जाता है और प्रतिनिधित्व की कोई पूर्व शर्त की अनुमति नहीं होती है, जो समझ में आता है कि बहुपद का मूल्यांकन केवल एक बार किया जाता है। चूंकि, यदि पूर्व शर्त की अनुमति होती है और बहुपद का कई बार मूल्यांकन किया जाता है, तो तेज़ कलन विधि संभव हैं। उनमें बहुपद के प्रतिनिधित्व का परिवर्तन सम्मलित है। सामान्यतः, एक घात - बहुपद का मूल्यांकन केवल ⌊n/2⌋+2 गुणा और जोड़ का उपयोग करके किया जा सकता है।[6]
समानांतर मूल्यांकन
हॉर्नर के नियम का एक नुकसान यह है कि सभी ऑपरेशन डेटा पर निर्भर होते है, इसलिए आधुनिक कंप्यूटरों पर निर्देश स्तर की समानता का लाभ उठाना संभव नहीं होता है। अधिकांश अनुप्रयोगों में जहां बहुपद मूल्यांकन की दक्षता मायने रखती है, कई निम्न-क्रम वाले बहुपदों का एक साथ मूल्यांकन किया जाता है, कंप्यूटर ग्राफिक्स में प्रत्येक पिक्सेल या बहुभुज के लिए या प्रत्येक ग्रिड वर्ग के लिए एक संख्यात्मक सिमुलेशन के रूप में होता है, इसलिए एकल बहुपद मूल्यांकन के भीतर समानता खोजना आवश्यक नहीं है।
चूंकि, यदि कोई बहुत उच्च क्रम के एकल बहुपद का मूल्यांकन कर रहा है, तो इसे निम्न प्रकार से विभाजित किया सकता है,
अधिक सामान्यतः, योग को k भागों में विभाजित किया जा सकता है
जहां हॉर्नर की विधि के अलग-अलग समानांतर उदाहरणों का उपयोग करके आंतरिक योग का मूल्यांकन किया जा सकता है। इसके लिए मूल हॉर्नर विधि की तुलना में थोड़े अधिक संचालन की आवश्यकता होती है, लेकिन उनमें से अधिकांश के के-वे सिमड निष्पादन की अनुमति देता है। आधुनिक संकलक सामान्यतः इस तरह से बहुपदों का मूल्यांकन करते हैं, जब फायदेमंद होता है, चूंकि फ्लोटिंग-पॉइंट गणनाओं के लिए इसके लिए असुरक्षित पुनर्संरचनात्मक गणित को सक्षम करने की आवश्यकता होती है।[citation needed].
फ़्लोटिंग-पॉइंट गुणा और भाग के लिए आवेदन
हॉर्नर की विधि बिना किसी बाइनरी गुणक वाले माइक्रोकंट्रोलर पर बाइनरी संख्याओं के गुणन और विभाजन के लिए एक तेज़, कोड-कुशल विधि के रूप में होती है। गुणा की जाने वाली द्विआधारी संख्याओं में से एक को तुच्छ बहुपद के रूप में दर्शाया गया है, जहाँ उपरोक्त संकेतन का उपयोग करके , और . फिर, x या x से कुछ शक्ति को बार-बार फैक्टर आउट किया जाता है। इस बाइनरी अंक प्रणाली आधार 2 में, , इसलिए 2 की घातें बार-बार फ़ैक्टर आउट की जाती हैं।
उदाहरण
उदाहरण के लिए, दो संख्याओं (0.15625) और m का गुणनफल ज्ञात करने के लिए हैं
तरीका
दो बाइनरी नंबरों d और m का गुणनफल ज्ञात करने के लिए इस प्रकार किया है
- 1. इंटरमीडिएट परिणाम रखने वाले एक रजिस्टर को डी में प्रारंभ किया जाता है।
- 2. मीटर में कम से कम महत्वपूर्ण दाहिनी ओर गैर-शून्य बिट से प्रारंभ करते है।
- 2बी। गिनती बाईं ओर अगले सबसे महत्वपूर्ण गैर-शून्य बिट के लिए बिट पदों की संख्या के रूप में होती है। यदि अधिक महत्वपूर्ण बिट नहीं होती है, तो वर्तमान बिट स्थिति का मान लेते है।
- 2सी। उस मान का उपयोग करते हुए, इंटरमीडिएट परिणाम रखने वाले रजिस्टर पर बिट्स की संख्या से बाएं-शिफ्ट ऑपरेशन प्रारंभ करते है।
- 3. यदि सभी गैर-शून्य बिट्स गिने जाते हैं, तो मध्यवर्ती परिणाम रजिस्टर अब अंतिम परिणाम रखता है। अन्यथा, मध्यवर्ती परिणाम में d जोड़ें और m में अगले सबसे महत्वपूर्ण बिट के साथ चरण 2 में जारी रखते है।
व्युत्पत्ति
सामान्यतः , बिट वैल्यू वाले बाइनरी नंबर के लिए () उत्पाद है
कलन विधि में इस स्तर पर, यह आवश्यक है कि शून्य-मूल्य वाले गुणांक वाले पदों को हटा दिया जाए, जिससे कि केवल एक के बराबर द्विआधारी गुणांक की गणना की जा सके, इस प्रकार शून्य से गुणा या विभाजन की समस्या कोई समस्या नहीं है, इस निहितार्थ के बावजूद कारक समीकरण के रूप में होते है
हर सभी बराबर एक या शब्द अनुपस्थित है, तो यह कम हो जाता है
या समकक्ष ऊपर वर्णित विधि के अनुरूप होते है
बाइनरी बेस -2 गणित में, 2 की शक्ति से गुणा केवल एक अंकगणितीय शिफ्ट ऑपरेशन के रूप में होते है। इस प्रकार, 2 से गुणा करने पर आधार-2 में एक अंकगणितीय शिफ्ट द्वारा गणना की जाती है। कारक (2−1) एक सही अंकगणितीय बदलाव है, a (0) के परिणामस्वरूप कोई संक्रिया नहीं होती 20 = 1 के बाद से गुणात्मक पहचान तत्व है और एक (21) का परिणाम बाएं अंकगणितीय बदलाव में होता है। गुणन गुणनफल अब केवल अंकगणितीय पारी संचालन जोड़ और घटाव का उपयोग करके जल्दी से गणना की जा सकती है।
एकल-निर्देश शिफ्ट-एंड-एडिशन-संचय का समर्थन करने वाले प्रोसेसर पर विधि विशेष रूप से तेज़ है, सी फ्लोटिंग-पॉइंट लाइब्रेरी की तुलना में,
हॉर्नर की विधि कुछ यथार्थ ता का त्याग करती है, चूंकि यह नाममात्र रूप से 13 गुना तेज है, 16 गुना तेज जब कैनोनिकल हस्ताक्षरित अंक सीएसडी फॉर्म का उपयोग किया जाता है और कोड स्थान का केवल 20% उपयोग करता है।[7]
अन्य अनुप्रयोग
हॉर्नर की विधि का उपयोग विभिन्न स्थितीय अंक प्रणालियों के बीच रूपांतरण के लिए किया जा सकता है, इस स्थिति में x संख्या प्रणाली का आधार है और ai गुणांक किसी दिए गए नंबर के बेस-एक्स प्रतिनिधित्व के अंक हैं और इसका उपयोग तब भी किया जा सकता है जब एक्स एक मैट्रिक्स (गणित) के रूप में होता है, इस स्थिति में कम्प्यूटेशनल दक्षता में लाभ और भी अधिक है। चूँकि, ऐसे स्थितियों के लिए बहुपद मूल्यांकन के लिए तेज़ तरीके ज्ञात हैं।।[8]
बहुपद रूट् ढूँढना
न्यूटन की विधि के संयोजन में दीर्घ विभाजन कलन विधि का उपयोग करके, बहुपद की वास्तविक रूट्स का अनुमान लगाना संभव होता है। यह कलन विधि इस प्रकार काम करता है। एक बहुपद दिया घात का शून्य के साथ कुछ प्रारंभिक अनुमान लगाएं ऐसा है कि . अब निम्नलिखित दो चरणों को दोहराता है,.
- न्यूटन की विधि का उपयोग करते हुए, अनुमान का उपयोग करके का सबसे बड़ा शून्य ज्ञात करते है
- हॉर्नर की विधि का उपयोग करके प्राप्त करने के लिए को विभाजित करते है, चरण 1 पर लौटते है लेकिन बहुपद और प्रारंभिक अनुमान .का उपयोग करते है
इन दो चरणों को तब तक दोहराया जाता है जब तक कि बहुपद के लिए सभी वास्तविक शून्य नहीं मिल जाते। यदि अनुमानित शून्य पर्याप्त यथार्थ रूप में नहीं होते है, तो प्राप्त मूल्यों को न्यूटन की विधि के लिए प्रारंभिक अनुमानों के रूप में उपयोग किया जा सकता है, लेकिन कम बहुपदों के अतिरिक्त पूर्ण बहुपद का उपयोग किया जा सकता है।[9]
उदाहरण
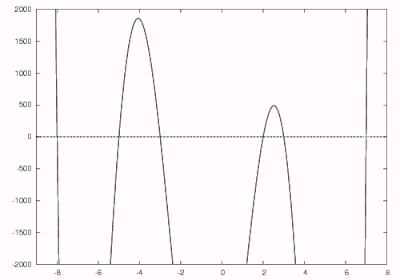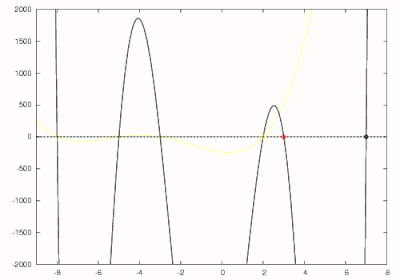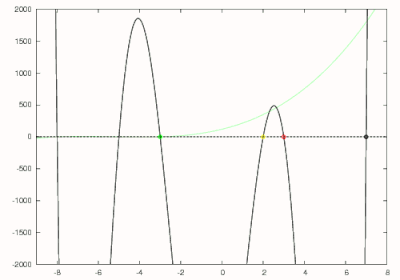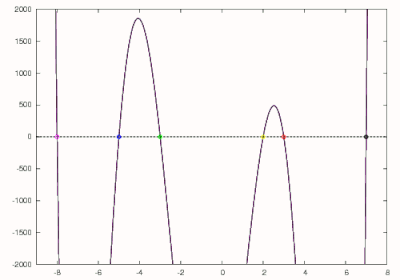
बहुपद पर विचार करते है
जिसे बढ़ाया जा सकता है
ऊपर से हम जानते हैं कि इस बहुपद का सबसे बड़ा मूल 7 है इसलिए हम 8 का प्रारंभिक अनुमान लगाने में सक्षम हैं। न्यूटन की विधि का उपयोग करके 7 का पहला शून्य पाया जाता है जैसा कि दाईं ओर की आकृति में काले रंग में दिखाया गया है। अगला से विभाजित है प्राप्त करने के लिए
जो दाईं ओर की आकृति में लाल रंग से खींचा गया है। 7 के प्रारंभिक अनुमान के साथ इस बहुपद का सबसे बड़ा शून्य खोजने के लिए न्यूटन की विधि का उपयोग किया जाता है। इस बहुपद का सबसे बड़ा शून्य जो मूल बहुपद के दूसरे सबसे बड़े शून्य से मेल खाता है, 3 पर पाया जाता है और लाल रंग में घेरा जाता है। घात 5 बहुपद अब से विभाजित प्राप्त करने के लिए है
जो पीले रंग में दिखाया गया है। न्यूटन की विधि का उपयोग करके इस बहुपद के लिए शून्य फिर से 2 पर पाया जाता है और पीले रंग में घेरा जाता है। प्राप्त करने के लिए हॉर्नर विधि का उपयोग किया जाता है
जो हरे रंग में दिखाया गया है और -3 पर शून्य पाया गया है। इस बहुपद को और घटाया जाता है
जो नीले रंग में दिखाया गया है और -5 का शून्य देता है। न्यूटन की विधि के प्रारंभिक अनुमान के रूप में अंतिम शून्य का उपयोग करके या घटाकर मूल बहुपद का अंतिम मूल पाया जा सकता है और रैखिक समीकरण को हल करना। जैसा कि देखा जा सकता है, -8, -5, -3, 2, 3 और 7 की अपेक्षित रुट के रूप में पाई गईं है।
एक बहुपद का विभाजित अंतर
विभाजित अंतर की गणना करने के लिए हॉर्नर की विधि को संशोधित किया जा सकता है बहुपद को देखते हुए (पहले की तरह)
निम्नलिखित के रूप में आगे बढ़ें[10]
पूरा होने पर, हमारे पास है
विभाजित अंतर की यह गणना कम के अधीन है मूल्यांकन की तुलना में राउंड-ऑफ़ त्रुटि और अलग से, विशेष रूप से जब . स्थानापन्न इस विधि में देता है , का व्युत्पन्न .
इतिहास
निरंतर सन्निकटन द्वारा सभी आदेशों के संख्यात्मक समीकरणों को हल करने की एक नई विधि शीर्षक वाला हॉर्नर का पेपर, 1 जुलाई 1819 को रॉयल सोसाइटी ऑफ लंदन की बैठक में 1823 में अगली कड़ी के साथ पढ़ा गया था।[12] 1819 के लिए लंदन की रॉयल सोसाइटी के दार्शनिक लेनदेन के भाग II में हॉर्नर के पेपर का अप्रैल, 1820 के द मंथली रिव्यू या लिटरेरी जर्नल के अंक में एक समीक्षक स्थायी डेड लिंक द्वारा गर्मजोशी और विस्तार से स्वागत किया गया था; इसकी तुलना में चार्ल्स बैबेज के एक तकनीकी पेपर को इस समीक्षा में स्पष्ट रूप से खारिज कर दिया गया है। सितंबर, 1821 के लिए द मंथली रिव्यू में समीक्षाओं का क्रम यह निष्कर्ष निकालता है कि होल्डर संख्यात्मक समीकरणों के प्रत्यक्ष और सामान्य व्यावहारिक समाधान की खोज करने वाले पहले व्यक्ति थे। [13] फुलर दिखाया कि हॉर्नर के 1819 के पेपर की विधि बाद की विधि" के रूप में जानी जाने वाली पेपर विधि से भिन्न है और इसके परिणामस्वरूप इस पद्धति की प्राथमिकता होल्ड्रेड (1820) को मिलनी चाहिए थी।
अपने अंग्रेजी समकालीनों के विपरीत, हॉर्नर ने महाद्वीपीय साहित्य पर विशेष रूप से लुइस फ्रांकोइस एंटोनी अर्बोगैस्ट के काम को आकर्षित किया। हॉर्नर को बीजगणित पर जॉन बोनीकैसल की पुस्तक का गहन अध्ययन करने के लिए भी जाना जाता है, चूंकि उन्होंने पाओलो रफिनी (गणितज्ञ) के काम की उपेक्षा की थी।
चूँकि, हॉर्नर को इस विधि को सुलभ और व्यावहारिक बनाने का श्रेय दिया जाता है, लेकिन यह हॉर्नर से बहुत पहले से जाना जाता था। रिवर्स कालानुक्रमिक क्रम में हॉर्नर की विधि पहले से ही ज्ञात थी
- 1809 में पाओलो रफ़िनी (गणितज्ञ) रुफ़िनी का नियम देखें[14][15]
- आइजैक न्यूटन ने 1669 में[16][17]
- 14वीं शताब्दी में चीनी गणित मिस जेड टाइगर के रूप में थे[15]
- 13वीं शताब्दी में चीनी गणित किन जियुशाओ ने अपने गणितीय ग्रंथ नौ खंडों में प्रस्तुत किया था
- फारसी लोग मध्यकालीन इस्लाम में गणित शराफ अल-दीन अल-यूसी 12वीं शताब्दी में घन समीकरण के सामान्य स्थिति में उस पद्धति का उपयोग करने वाले पहले व्यक्ति के रूप में थे [18]
- 11वीं शताब्दी में चीनी गणितज्ञ जे आइए एक्स इयान सांग राजवंश के रूप में थे
- गणितीय कला पर नौ अध्याय, हान राजवंश की एक चीनी कृति 202 ईसा पूर्व - 220 ईस्वी, तीसरी शताब्दी में लियू हुई फ़्ल द्वारा संपादित हुई है।[19]किन जिउशाओ, अपने शू शू जिउ झांग मैथमेटिकल ट्रीटिस इन नाइन सेक्शन्स, 1247 में बहुपद समीकरणों को हल करने के लिए हॉर्नर प्रकार के विधि का एक पोर्टफोलियो प्रस्तुत करता है, जो 11 वीं शताब्दी के सांग वंश के गणितज्ञ जिया जियान के पहले के कार्यों पर आधारित था, उदाहरण के लिए एक विधि बाय-क्विंटिक्स के अनुकूल विशेष रूप से है, जिसमें से केस स्टडीज के तत्कालीन चीनी रिवाज को ध्यान में रखते हुए किन एक उदाहरण देता है। चीन और जापान में गणित के विकास में योशियो मिकामी लीपज़िग 1913 ने लिखा गया है।
यूरोप की तुलना में कम से कम छह लंबी शताब्दियों पहले चीन में हॉर्नर की शानदार प्रक्रिया का उपयोग करने के तथ्य से कौन इंकार कर सकता है, हम निश्चित रूप से किसी भी तरह से हॉर्नर के आविष्कार को चीनी मूल के रूप में वर्णित करने का इरादा नहीं रखते हैं, लेकिन समय की कमी पर्याप्त रूप से बनाती है यह पूरी तरह से असंभव नहीं था कि यूरोपीय लोग प्रत्यक्ष या अप्रत्यक्ष रूप से चीनी पद्धति के बारे में जान सकते थे
उलरिच लिब्रेब्रेच ने निष्कर्ष निकाला यह स्पष्ट है कि यह प्रक्रिया एक चीनी आविष्कार के रूप में है, यह विधि भारत में ज्ञात नहीं थी। उन्होंने कहा, फिबोनाची ने संभवतः इसके बारे में अरबों से सीखा, जिन्होंने संभवतः चीनियों से उधार लिया था।[20] जिउ झांग सुआन शू में समस्या IV.16 और 22 के संबंध में समान रेखाओं के साथ वर्ग और घन रूट्स की निकासी पर पहले से ही लियू हुई द्वारा चर्चा की गई है, जबकि 7 वीं शताब्दी में वांग शियाओतोंग का मानना है कि उनके पाठक क्यूबिक्स को उनके द्वारा वर्णित एक सन्निकटन विधि द्वारा हल कर सकते हैं। उनकी किताब जिगू सुंजिंग में दिखाया गया है
यह भी देखें
- चेबिशेव रूप में बहुपदों का मूल्यांकन करने के लिए क्लेंशॉ कलन विधि का प्रयोग करते है
- बी-पट्टी फॉर्म में तख़्ता वक्र का मूल्यांकन करने के लिए डी बूर का कलन विधि का प्रयोग करते है
- बेज़ियर रूप में बहुपदों का मूल्यांकन करने के लिए डी कैस्टेलजौ का कलन विधि का प्रयोग करते है
- एस्ट्रिन की योजना आधुनिक कंप्यूटर आर्किटेक्चर पर समानांतरकरण की सुविधा के रूप में होता है
- लील की विधि से रूट्स का रेखांकन किया जा सकता है
- रफ़िनी का नियम और सिंथेटिक विभाजन एक बहुपद को x - r के रूप में एक द्विपद से विभाजित करने के लिए करते है
टिप्पणियाँ
- ↑ 600 years earlier, by the Chinese mathematician Qin Jiushao and 700 years earlier, by the Persian mathematician Sharaf al-Dīn al-Ṭūsī
- ↑ Pan 1966
- ↑ Pankiewicz 1968.
- ↑ Ostrowski 1954.
- ↑ Pan 1966.
- ↑ Knuth 1997.
- ↑ Kripasagar 2008, p. 62.
- ↑ Higham 2002, Section 5.4.
- ↑ Kress 1991, p. 112.
- ↑ Fateman & Kahan 2000
- ↑ Libbrecht 2005, pp. 181–191.
- ↑ Horner 1819.
- ↑ Fuller 1999, pp. 29–51.
- ↑ Cajori 1911.
- ↑ 15.0 15.1 O'Connor, John J.; Robertson, Edmund F., "हॉर्नर की विधि", MacTutor History of Mathematics archive, University of St Andrews
- ↑ Analysis Per Quantitatum Series, Fluctiones ac Differentias : Cum Enumeratione Linearum Tertii Ordinis, Londini. Ex Officina Pearsoniana. Anno MDCCXI, p. 10, 4th paragraph.
- ↑ Newton's collected papers, the edition 1779, in a footnote, vol. I, p. 270-271
- ↑ Berggren 1990, pp. 304–309.
- ↑ Temple 1986, p. 142.
- ↑ Libbrecht 2005, p. 208.
संदर्भ
- Berggren, J. L. (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat". Journal of the American Oriental Society. 110 (2): 304–309. doi:10.2307/604533. JSTOR 604533.
- Cajori, Florian (1911). "Horner's method of approximation anticipated by Ruffini". Bulletin of the American Mathematical Society. 17 (8): 409–414. doi:10.1090/s0002-9904-1911-02072-9. Read before the Southwestern Section of the American Mathematical Society on November 26, 1910.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein10.1016/0315-0860(81)90069-0, Clifford (2009). "Introduction to Algorithms". Historia Mathematica (3rd ed.). MIT Press. 8 (3): 277–318. doi:10.1016/0315-0860(81)90069-0.
- Fateman, R. J.; Kahan, W. (2000). Improving exact integrals from symbolic algebra systems (PDF) (Report). PAM. University of California, Berkeley: Center for Pure and Applied Mathematics. Archived from the original (PDF) on 2017-08-14. Retrieved 2018-05-17.
- Fuller, A. T. (1999). "Horner versus Holdred: An Episode in the History of Root Computation". Historia Mathematica. 26: 29–51. doi:10.1006/hmat.1998.2214.
- Higham, Nicholas (2002). Accuracy and Stability of Numerical Algorithms. SIAM. ISBN 978-0-89871-521-7.
- Holdred, T. (1820). A New Method of Solving Equations with Ease and Expedition; by which the True Value of the Unknown Quantity is Found Without Previous Reduction. With a Supplement, Containing Two Other Methods of Solving Equations, Derived from the Same Principle (PDF). Richard Watts. Archived from the original (PDF) on 2014-01-06. Retrieved 2012-12-10.
- Holdred's method is in the supplement following page numbered 45 (which is the 52nd page of the pdf version).
- Horner, William George (July 1819). "A new method of solving numerical equations of all orders, by continuous approximation". Philosophical Transactions. Royal Society of London. 109: 308–335. doi:10.1098/rstl.1819.0023. JSTOR 107508. S2CID 186210512.
- Directly available online via the link, but also reprinted with appraisal in D.E. Smith: A Source Book in Mathematics, McGraw-Hill, 1929; Dover reprint, 2 vols, 1959.
- Knuth, Donald (1997). The Art of Computer Programming. Vol. 2: Seminumerical Algorithms (3rd ed.). Addison-Wesley. pp. 486–488 in section 4.6.4. ISBN 978-0-201-89684-8.
- Kress, Rainer (1991). Numerical Analysis. Springer.
- Kripasagar, Venkat (March 2008). "Efficient Micro Mathematics – Multiplication and Division Techniques for MCUs". Circuit Cellar Magazine (212).
- Libbrecht, Ulrich (2005). "Chapter 13". Chinese Mathematics in the Thirteenth Century (2nd ed.). Dover. ISBN 978-0-486-44619-6. Archived from the original on 2017-06-06. Retrieved 2016-08-23.
- Mikami, Yoshio (1913). "Chapter 11. Ch'in Chiu-Shao". The Development of Mathematics in China and Japan (1st ed.). Chelsea Publishing Co reprint. pp. 74–77.
- Ostrowski, Alexander M. (1954). "On two problems in abstract algebra connected with Horner's rule". Studies in Mathematics and Mechanics presented to Richard von Mises. Academic Press. pp. 40–48. ISBN 978-1-4832-3272-0.
- Pan, Y. Ja (1966). "On means of calculating values of polynomials". Russian Math. Surveys. 21: 105–136. doi:10.1070/rm1966v021n01abeh004147. S2CID 250869179.
- Pankiewicz, W. (1968). "Algorithm 337: calculation of a polynomial and its derivative values by Horner scheme". Communications of the ACM. ACM. 11 (9): 633. doi:10.1145/364063.364089. S2CID 52859619.
- Spiegel, Murray R. (1956). Schaum's Outline of Theory and Problems of College Algebra. McGraw-Hill.
- Temple, Robert (1986). The Genius of China: 3,000 Years of Science, Discovery, and Invention. Simon and Schuster. ISBN 978-0-671-62028-8.
- Whittaker, E.T.; Robinson, G. (1924). The Calculus of Observations. London: Blackie.
- Wylie, Alexander (1897). "Jottings on the Science of Chinese Arithmetic". Chinese Researches. Shanghai. pp. 159–194.
{{cite book}}: CS1 maint: location missing publisher (link)- Reprinted from issues of The North China Herald (1852).
बाहरी संबंध
- "Horner scheme", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Qiu Jin-Shao, Shu Shu Jiu Zhang (Cong Shu Ji Cheng ed.)
- For more on the root-finding application see [1]