प्वासों बिंदु प्रक्रिया: Difference between revisions
No edit summary |
(Work done) |
||
| Line 1: | Line 1: | ||
{{Short description|Type of random mathematical object}} | {{Short description|Type of random mathematical object}} | ||
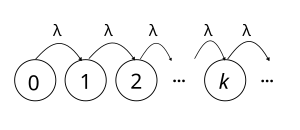
[[File:Poisson process.svg|thumb|alt=Poisson point process| | [[File:Poisson process.svg|thumb|alt=Poisson point process|पॉइसन बिंदु प्रक्रिया की एक दृश्यानुकरणिका, जिसमें 0 से शुरू होते हुए वृद्धि λ दर पर सतत और स्वतंत्र रूप से होती हैं।]]प्रायिकता, सांख्यिकी और संबंधित क्षेत्रों में, '''पॉइसन बिंदु प्रक्रिया''' एक प्रकार का यादृच्छिक [[गणितीय वस्तु|गणितीय प्रयोजन]] है जो [[गणितीय स्थान|गणितीय समष्टि]] पर यादृच्छिक रूप से स्थानांतरित होने वाले [[बिंदु (ज्यामिति)|बिन्दुओं]] से मिलकर बनता है, जहां महत्वपूर्ण विशेषता यह है कि ये बिन्दु एक दूसरे से स्वतंत्र रूप से होते हैं।<ref name="ChiuStoyan2013">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3}}</ref> पॉइसन बिंदु प्रक्रिया को सामान्यतः '''पॉइसन प्रक्रिया''' कहा जाता है, लेकिन इसे '''पॉइसन यादृच्छिक माप''', '''पॉइसन यादृच्छिक बिन्दु फ़ील्ड''' या '''पॉइसन बिंदु फ़ील्ड''' भी कहा जाता है। यह [[बिंदु प्रक्रिया]] उचित गणितीय गुणों के साथ होती है,<ref name="Kingman1992">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2}}</ref> जिसके कारण इसे [[यूक्लिडियन अंतरिक्ष|यूक्लिडीयन समष्टि]] में प्रायः परिभाषित किया जाता है और यह [[खगोल|खगोल शास्त्र]],<ref name="babu1996spatial">G. J. Babu and E. D. Feigelson. Spatial point processes in astronomy. ''Journal of statistical planning and inference'', 50(3):311–326, 1996.</ref> जीव-विज्ञान,<ref name="othmer1988models">H. G. Othmer, S. R. Dunbar, and W. Alt. Models of dispersal in biological systems. ''Journal of mathematical biology'', 26(3):263–298, 1988.</ref> पारिस्थितिकी,<ref name="thompson1955spatial">H. Thompson. Spatial point processes, with applications to ecology. ''Biometrika'', 42(1/2):102–115, 1955.</ref> भूविज्ञान,<ref name="connor1995three">C. B. Connor and B. E. Hill. Three nonhomogeneous poisson models for the probability of basaltic volcanism: application to the yucca mountain region, nevada. ''Journal of Geophysical Research: Solid Earth (1978–2012)'', 100(B6):10107–10125, 1995.</ref> [[भूकंप विज्ञान]],<ref>{{Cite journal|last1=Gardner|first1=J. K.|last2=Knopoff|first2=L.|date=1974|title=Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian?|url=https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/64/5/1363/117341/is-the-sequence-of-earthquakes-in-southern|journal=Bulletin of the Seismological Society of America|volume=64|issue=5 |pages=1363–1367|doi=10.1785/BSSA0640051363 |bibcode=1974BuSSA..64.1363G |s2cid=131035597 }}</ref> [[भौतिक विज्ञान]],<ref name="scargle1998studies">J. D. Scargle. Studies in astronomical time series analysis. v. bayesian blocks, a new method to analyze structure in photon counting data. ''The Astrophysical Journal'', 504(1):405, 1998.</ref> अर्थशास्त्र,<ref name="AghionHowitt1992">P. Aghion and P. Howitt. A Model of Growth through Creative Destruction. ''Econometrica'', 60(2). 323–351, 1992.</ref> [[मूर्ति प्रोद्योगिकी|छवि प्रसंस्करण]],<ref name="bertero2009image">M. Bertero, P. Boccacci, G. Desidera, and G. Vicidomini. Image deblurring with poisson data: from cells to galaxies. ''Inverse Problems'', 25(12):123006, 2009.</ref><ref>{{cite web | url=https://caseymuratori.com/blog_0010 | title=The Color of Noise }}</ref> और दूरसंचार जैसे विभिन्न शास्त्रों में आपूर्ति-मांग मॉडल के रूप में उपयोग किया जाता है।<ref name="baccelli2009stochastic2">F. Baccelli and B. Błaszczyszyn. ''Stochastic Geometry and Wireless Networks, Volume II- Applications'', volume 4, No 1–2 of ''Foundations and Trends in Networking''. NoW Publishers, 2009.</ref><ref name="Haenggi2009">M. Haenggi, J. Andrews, F. Baccelli, O. Dousse, and M. Franceschetti. Stochastic geometry and random graphs for the analysis and design of wireless networks. ''IEEE JSAC'', 27(7):1029–1046, September 2009.</ref> | ||
यह प्रक्रिया फ्रांसीसी गणितज्ञ शिमोन डेनिस | यह प्रक्रिया फ्रांसीसी गणितज्ञ शिमोन डेनिस पॉइसन के नाम पर रखी गई है, हालांकि पॉइसन ने कभी इस प्रक्रिया का अध्ययन नहीं किया। इसका नाम इस तथ्य से जुड़ा है कि यदि किसी स्थान में यादृच्छिक बिन्दुओं का संग्रह पॉइसन प्रक्रिया बनाता है, तो एक परिमित आकार क्षेत्र में बिन्दुओं की संख्या यादृच्छिक प्रायस्थानिकी संगणना के साथ [[पॉसों वितरण|पॉइसन बंटन]] होती है। इस प्रक्रिया की खोज अलग-अलग सेटिंग्स पर स्वतंत्र रूप से और अनेक बार की गई, जिसमें रेडियोधर्मी क्षय, टेलीफोन कॉल आगमन और इनश्योरेंस गणित पर प्रयोग सम्मिलित हैं।<ref name="Stirzaker2000">{{cite journal|last1=Stirzaker|first1=David|title=हाथी को सलाह, या स्थिरांक भिन्न हो सकते हैं|journal=The Mathematical Gazette|volume=84|issue=500|year=2000|pages=197–210|issn=0025-5572|doi=10.2307/3621649|jstor=3621649|s2cid=125163415}}</ref><ref name="GuttorpThorarinsdottir2012">{{cite journal|last1=Guttorp|first1=Peter|last2=Thorarinsdottir|first2=Thordis L.|title=What Happened to Discrete Chaos, the Quenouille Process, and the Sharp Markov Property? Some History of Stochastic Point Processes|journal=International Statistical Review|volume=80|issue=2|year=2012|pages=253–268|issn=0306-7734|doi=10.1111/j.1751-5823.2012.00181.x|s2cid=80836 }}</ref> | ||
पॉइसन बिंदु प्रक्रिया सामान्यतः [[वास्तविक रेखा]] पर परिभाषित की जाती है, जहां इसे प्रसंभाव्य प्रक्रम (स्टोकेस्टिक प्रोसेस) के रूप में माना जा सकता है। इस सेटिंग में, यह उदाहरण के लिए, [[ कतार सिद्धांत |कतारबद्ध सिद्धांत]] में उपयोग होती है<ref name="Kleinrock1976">{{cite book|author=Leonard Kleinrock|title=Queueing Systems: Theory|url=https://archive.org/details/queueingsystems01klei|url-access=registration|year=1976|publisher=Wiley|isbn=978-0-471-49110-1}}</ref> जहां यादृच्छिक घटनाओं का मॉडलिंग किया जाता है, जैसे कि किसी संग्रहागार में ग्राहकों के आगमन, प्रतिदान में फोन कॉल, या भूकंप की घटना, जो समय के आधार पर वितरित होती हैं। समतल में, बिन्दु प्रक्रिया, जिसे '''स्थानिक पॉइसन प्रक्रिया''' भी कहा जाता है,<ref name="BaddeleyBárány2006page102"><nowiki>{{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=</nowiki>https://books.google.com/books?id=X-m5BQAAQBAJ|date=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4|page=10}</ref> प्रकीर्णित [[ बेतार तंत्र |वायरलेस नेटवर्क]] में प्रेषकों के स्थानों,<ref name="baccelli2009stochastic2" /><ref name="andrews2010primer">J. G. Andrews, R. K. Ganti, M. Haenggi, N. Jindal, and S. Weber. A primer on spatial modeling and analysis in wireless networks. ''Communications Magazine, IEEE'', 48(11):156–163, 2010.</ref><ref name="baccelli2009stochastic1">F. Baccelli and B. Błaszczyszyn. ''Stochastic Geometry and Wireless Networks, Volume I – Theory'', volume 3, No 3–4 of ''Foundations and Trends in Networking''. NoW Publishers, 2009.</ref><ref name="Haenggi2013">{{cite book|author=Martin Haenggi|title=वायरलेस नेटवर्क के लिए स्टोचैस्टिक ज्योमेट्री|url=https://books.google.com/books?id=CLtDhblwWEgC|year=2013|publisher=Cambridge University Press|isbn=978-1-107-01469-5}}</ref> संवेदक में टकराने वाले [[कण|कणों]] के, या जंगल में पेड़ों के आवास के स्थानों का प्रतिनिधित्व कर सकती है।<ref name="ChiuStoyan2013page51">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=51–52}}</ref> इस संदर्भ में, प्रक्रिया प्रायः गणितीय मॉडलों में और स्थानिक बिन्दु प्रक्रियाओं,<ref name="BaddeleyBárány2006"><nowiki>{{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=</nowiki>https://books.google.com/books?id=X-m5BQAAQBAJ|date=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4}</ref> [[स्टोकेस्टिक ज्यामिति|प्रसंभाव्य ज्यामिति]],<ref name="ChiuStoyan2013" /> [[स्थानिक आँकड़े|स्थानिक सांख्यिकी]]<ref name="BaddeleyBárány2006" /><ref name="MollerWaagepetersen2003">{{cite book|author1=Jesper Moller|author2=Rasmus Plenge Waagepetersen|title=स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण|url=https://books.google.com/books?id=dBNOHvElXZ4C|date=25 September 2003|publisher=CRC Press|isbn=978-0-203-49693-0}}</ref> और [[सातत्य रिसाव सिद्धांत|नियतांत्रण प्रक्षेपण सिद्धांत]]<ref name="meester1996continuum">R. Meester and R. Roy. Continuum percolation, volume 119 of cambridge tracts in mathematics, 1996.</ref> के संबंधित क्षेत्रों में उपयोग होती है। पॉइसन बिंदु प्रक्रिया को अधिक एब्स्ट्रैक्ट समष्टि पर परिभाषित किया जा सकता है। अनुप्रयोगों से परे, पॉइसन बिंदु प्रक्रिया स्वयं में गणितीय अध्ययन का विषय है।<ref name="Kingman1992" /> सभी सेटिंग में, पॉइसन बिंदु प्रक्रिया का एक मुख्य गुण यह है कि प्रत्येक बिंदु प्रक्रिया में सभी अन्य बिंदुओं के प्रति यादृच्छिक रूप से अव्यवस्थित होता है, इसलिए कभी-कभी इसे ''पूरी रूप से'' या ''पूर्णतः'' यादृच्छिक प्रक्रिया कहा जाता है।{{sfnp|Daley|Vere-Jones|2003|page=27}} किसी प्रणाली को पॉइसन प्रक्रिया के रूप मॉडलिंग करना पर्याप्त नहीं होता है जब बिंदु से बिंदु के संवेदनशील संबंध अत्यधिक प्रबल होते हैं (अर्थात बिंदु प्रसंभाव्य रूप से स्वतंत्र नहीं हैं)। ऐसी प्रणाली को भिन्न बिंदु प्रक्रिया के साथ अपेक्षाकृत अधिक श्रेष्ठता से मॉडलिंग किया जा सकता है।<ref name="ChiuStoyan2013page35">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=35–36}}</ref> | |||
बिंदु प्रक्रिया एकल गणितीय प्रयोजन पर निर्भर करती है, जो परिस्थिति के आधार पर किसी स्थिरांक, स्थानिक समाकलित फलन या अधिक सामान्य संदर्भ में [[रेडॉन माप]] हो सकती है।<ref name="ChiuStoyan2013page41and51">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=41 and 51 }}</ref> प्राथमिक स्थिति में, जिसे दर या इंटेंसिटी कहा जाता है, समष्टि के किसी क्षेत्र में | बिंदु प्रक्रिया एकल गणितीय प्रयोजन पर निर्भर करती है, जो परिस्थिति के आधार पर किसी स्थिरांक, स्थानिक समाकलित फलन या अधिक सामान्य संदर्भ में [[रेडॉन माप]] हो सकती है।<ref name="ChiuStoyan2013page41and51">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=41 and 51 }}</ref> प्राथमिक स्थिति में, जिसे '''दर''' या '''तीव्रता (इंटेंसिटी)''' कहा जाता है, समष्टि के किसी क्षेत्र में पॉइसन प्रक्रिया के बिंदुओं की औसत [[घनत्व]] होती है। इस परिणामक बिंदु प्रक्रिया को '''समघातीय''' या '''स्थिर पॉइसन बिंदु प्रक्रिया''' कहा जाता है।<ref name="ChiuStoyan2013page412">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=41–42}}</ref> द्वितीय स्थिति में, बिंदु प्रक्रिया को '''असमघातीय''' या '''असमघातीय पॉइसन बिंदु प्रक्रिया''' कहा जाता है, और बिंदु प्रक्रिया की मूलभूत स्थान के स्थान पर बिंदुओं की औसत घनत्व पर निर्भर करती है।{{sfnp|Daley|Vere-Jones|2003|page=22}} शब्द "बिंदु" प्रायः छोड़ दिया जाता है,<ref name="Kingman1992" /> लेकिन वस्तुओं की अन्य ''पॉइसन प्रक्रियाएं'' भी होती हैं, जिनमें बिंदुओं की बजाय [[रेखा (ज्यामिति)|रेखाएं]] और [[बहुभुज]] जैसी जटिल गणितीय प्रयोजन सम्मिलित होते हैं, और ऐसी प्रक्रियाएं पॉइसन बिंदु प्रक्रिया पर आधारित हो सकती हैं।<ref name="Kingman1992page73to76">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|pages=73–76}}</ref> समघाती और असमघाती पॉइसन बिंदु प्रक्रियाएँ विशेषित मुद्रण प्रक्रिया की विशेष स्थिति हैं। | ||
{{toclimit|limit=3}} | {{toclimit|limit=3}} | ||
== परिभाषाओं का अवलोकन == | == परिभाषाओं का अवलोकन == | ||
सेटिंग के आधार पर, इस प्रक्रिया के कई समकक्ष परिभाषाएं<ref name="Tijms2003page1">{{cite book|author=H. C. Tijms|title=स्टोकेस्टिक मॉडल में पहला कोर्स|url=https://books.google.com/books?id=RK9yFrNxom8C|date=18 April 2003|publisher=John Wiley & Sons|isbn=978-0-471-49880-3|pages=1–2}}</ref> हो सकती हैं, साथ ही इसके कई अनुप्रयोगों और विशेषताओं के कारण विभिन्न व्यापकता की परिभाषाएं भी हो सकती हैं।{{sfnp|Daley|Vere-Jones|2003|pages=26–37}} | सेटिंग के आधार पर, इस प्रक्रिया के कई समकक्ष परिभाषाएं<ref name="Tijms2003page1">{{cite book|author=H. C. Tijms|title=स्टोकेस्टिक मॉडल में पहला कोर्स|url=https://books.google.com/books?id=RK9yFrNxom8C|date=18 April 2003|publisher=John Wiley & Sons|isbn=978-0-471-49880-3|pages=1–2}}</ref> हो सकती हैं, साथ ही इसके कई अनुप्रयोगों और विशेषताओं के कारण विभिन्न व्यापकता की परिभाषाएं भी हो सकती हैं।{{sfnp|Daley|Vere-Jones|2003|pages=26–37}} पॉइसन बिंदु प्रक्रिया को एक विमा में परिभाषित, अध्ययन और उपयोग किया जा सकता है, उदाहरण के लिए, वास्तविक रेखा पर, जहां इसे गणना प्रक्रिया या कतारबद्ध मॉडल के भाग के रूप में व्याख्या किया जा सकता है;<ref name="Tijms2003page1and9">{{cite book|author=H. C. Tijms|title=स्टोकेस्टिक मॉडल में पहला कोर्स|url=https://books.google.com/books?id=RK9yFrNxom8C|date=18 April 2003|publisher=John Wiley & Sons|isbn=978-0-471-49880-3|pages=1 and 9}}</ref><ref name="Ross1996page59">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|pages=59–60}}</ref> उच्च विमाओं में जैसे कि समतल जहां इसकी प्रसंभाव्य ज्यामिति<ref name="ChiuStoyan2013"/> और स्थानिक सांख्यिकी<ref name="baddeley1999crash">A. Baddeley. A crash course in stochastic geometry. ''Stochastic Geometry: Likelihood and Computation Eds OE Barndorff-Nielsen, WS Kendall, HNN van Lieshout (London: Chapman and Hall)'', pages 1–35, 1999.</ref> में महत्वपूर्ण भूमिका निभाता है; या और अधिक सामान्य गणितीय समष्टि पर।<ref name="DaleyVere-Jones2007page1">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=1–2}}</ref> इसलिए, पॉइसन बिंदु प्रक्रिया और बिंदु प्रक्रियाओं की परिभाषा और अध्ययन करने के लिए उपयोग की जाने वाली नोटेशन, शब्दावली और गणितीय सावधानी का स्तर आधार के अनुसार भिन्न होते हैं।<ref name="ChiuStoyan2013page110to111">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=110–111 }}</ref> | ||
इसके अतिरिक्त, | इसके अतिरिक्त, पॉइसन बिंदु प्रक्रिया में दो प्रमुख गुण हैं- पॉइसन गुणधर्म और स्वतंत्रता गुणधर्म- जो सभी सेटिंग्स में एक आवश्यक भूमिका निभाती है जहां पॉइसन बिंदु प्रक्रिया का उपयोग किया जाता है।<ref name="ChiuStoyan2013page41and51" /><ref name="Kingman1992page11">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|pages=11–12}}</ref> दो गुणधर्म तार्किक रूप से स्वतंत्र नहीं होते हैं; वास्तव में, स्वतंत्रता का तात्पर्य बिंदु गणना के पॉइसन बंटन से है, लेकिन इसके विपरीत नहीं।{{efn|See Section 2.3.2 of Chiu, Stoyan, Kendall, Mecke<ref name="ChiuStoyan2013"/> or Section 1.3 of Kingman.<ref name="Kingman1992"/>}} | ||
=== बिंदु संख्या का | === बिंदु संख्या का पॉइसन बंटन === | ||
पॉइसन बिंदु प्रक्रिया को पॉइसन बंटन के माध्यम से अभिलक्षित किया जाता है। पॉइसन बंटन यादृच्छिक चर <math display="inline"> N</math> का (''पॉइसन यादृच्छिक चर'' के नाम से जाना जाता है) प्रायिकता बंटन होता है, जिसमें <math>\textstyle N</math> बराबर <math>\textstyle n</math> होने की प्रायिकता निम्नलिखित प्राप्त होती है: | |||
:<math> \Pr \{N=n\}=\frac{\Lambda^n}{n!} e^{-\Lambda} </math> | :<math> \Pr \{N=n\}=\frac{\Lambda^n}{n!} e^{-\Lambda} </math> | ||
जहाँ <math display="inline"> n!</math> गुणांक को [[ कारख़ाने का |क्रमगुणितअ]] (फैक्टोरियल) को दर्शाने के लिए है और पैरामीटर <math display="inline"> \Lambda</math> बंटन के आकार को निर्धारित करता है। (वास्तव में, <math display="inline"> \Lambda</math> को <math display="inline"> N</math> की प्रत्याशित मान के बराबर होने वाले मान के रूप में लिया जाता है।) | जहाँ <math display="inline"> n!</math> गुणांक को [[ कारख़ाने का |क्रमगुणितअ]] (फैक्टोरियल) को दर्शाने के लिए है और पैरामीटर <math display="inline"> \Lambda</math> बंटन के आकार को निर्धारित करता है। (वास्तव में, <math display="inline"> \Lambda</math> को <math display="inline"> N</math> की प्रत्याशित मान के बराबर होने वाले मान के रूप में लिया जाता है।) | ||
परिभाषा के अनुसार, | परिभाषा के अनुसार, पॉइसन बिंदु प्रक्रिया का एक गुण है कि प्रक्रिया के अन्तर्निहित समष्टि के सीमित क्षेत्र में बिंदुओं की संख्या पॉइसन बंटन का यादृच्छिक चर होती है।<ref name="Kingman1992page11" /> | ||
=== पूर्ण स्वतंत्रता === | === पूर्ण स्वतंत्रता === | ||
अंतर्निहित समष्टि के असंयुक्त और परिबद्ध उपक्षेत्रों के संग्रह पर विचार करें। परिभाषा के अनुसार, प्रत्येक परिबद्ध उपक्षेत्र में | अंतर्निहित समष्टि के असंयुक्त और परिबद्ध उपक्षेत्रों के संग्रह पर विचार करें। परिभाषा के अनुसार, प्रत्येक परिबद्ध उपक्षेत्र में पॉइसन बिंदु प्रक्रिया के बिंदुओं की संख्या सभी अन्य से पूर्णतः स्वतंत्र होगी। | ||
इस गुणधर्म को कई नामों से जाना जाता है जैसे पूर्ण यादृच्छिकता, पूर्ण स्वतंत्रता,<ref name="DaleyVere-Jones2007page26">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=26}}</ref> या स्वतंत्र प्रकीर्णन<ref name="MollerWaagepetersen2003page15">{{cite book|author1=Jesper Moller|author2=Rasmus Plenge Waagepetersen|title=स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण|url=https://books.google.com/books?id=dBNOHvElXZ4C|date=25 September 2003|publisher=CRC Press|isbn=978-0-203-49693-0|pages=15–16}}</ref><ref name="Streit2010page7">{{cite book|author=Roy L. Streit|title=Poisson Point Processes: Imaging, Tracking, and Sensing|url=https://books.google.com/books?id=KAWmFYUJ5zsC|date=15 September 2010|publisher=Springer Science & Business Media|isbn=978-1-4419-6923-1|pages=7–8}}</ref> और यह सभी | इस गुणधर्म को कई नामों से जाना जाता है जैसे ''पूर्ण यादृच्छिकता'', ''पूर्ण स्वतंत्रता'',<ref name="DaleyVere-Jones2007page26">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=26}}</ref> या ''स्वतंत्र प्रकीर्णन''<ref name="MollerWaagepetersen2003page15">{{cite book|author1=Jesper Moller|author2=Rasmus Plenge Waagepetersen|title=स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण|url=https://books.google.com/books?id=dBNOHvElXZ4C|date=25 September 2003|publisher=CRC Press|isbn=978-0-203-49693-0|pages=15–16}}</ref><ref name="Streit2010page7">{{cite book|author=Roy L. Streit|title=Poisson Point Processes: Imaging, Tracking, and Sensing|url=https://books.google.com/books?id=KAWmFYUJ5zsC|date=15 September 2010|publisher=Springer Science & Business Media|isbn=978-1-4419-6923-1|pages=7–8}}</ref> और यह सभी पॉइसन बिंदु प्रक्रियाओं में सामान्य होता है। दूसरे शब्दों में, विभिन्न क्षेत्रों और बिंदुओं के बीच परस्पर क्रिया की कमी होती है,<ref name="feller1974introduction">W. Feller. Introduction to probability theory and its applications, vol. ii pod. 1974.</ref> जिसके कारण पॉइसन प्रक्रिया को कभी-कभी ''पूर्णतः'' या ''पूर्ण रूप से'' यादृच्छिक प्रक्रिया कहा जाता है।<ref name="DaleyVere-Jones2007page26" /> | ||
== समघाती | == समघाती पॉइसन बिंदु प्रक्रिया == | ||
यदि किसी | यदि किसी पॉइसन बिंदु प्रक्रिया का पैरामीटर <math display="inline"> \Lambda=\nu \lambda</math> के रूप में होता है, जहां <math display="inline"> \nu </math> लेबेस्ग माप होती है (अर्थात, यह समुच्चय के लिए लम्बाई, क्षेत्रफल या आयतन निर्दिष्ट करता है) और <math display="inline"> \lambda</math> एक स्थिरांक होता है, तो बिंदु प्रक्रिया को समघाती या स्थायी पॉइसन बिंदु प्रक्रिया कहा जाता है। इस पैरामीटर को '''दर''' या '''तीव्रता''' कहा जाता है और यह किसी सीमित क्षेत्र में विद्यमान पॉइसन बिंदुओं की अपेक्षित (या औसत) संख्या से संबंधित होता है,<ref name="Kingman1992page13">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=13}}</ref><ref name="MollerWaagepetersen2003page14">{{cite book|author1=Jesper Moller|author2=Rasmus Plenge Waagepetersen|title=स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण|url=https://books.google.com/books?id=dBNOHvElXZ4C|date=25 September 2003|publisher=CRC Press|isbn=978-0-203-49693-0|page=14}}</ref> जहां दर उस अंतर्निहित समष्टि के लिए उपयोग होती है जिसके एक विमा होती है।<ref name="Kingman1992page13" /> पैरामीटर <math display="inline"> \lambda</math> को मानचित्रित किया जा सकता है जैसे कि [[लंबाई]], क्षेत्रफल, [[आयतन]] या समय के कुछ इकाई पर प्रति औसत बिंदुओं की औसत संख्या, यहां तक कि इसे ''माध्य घनत्व'' या ''माध्य दर'' भी कहा जाता है;{{sfnp|Daley|Vere-Jones|2003|page=20}} टर्मिनोलॉजी देखें। | ||
=== गणना प्रक्रिया के रूप में व्याख्या === | === गणना प्रक्रिया के रूप में व्याख्या === | ||
धनात्मक अर्ध-रेखा पर विचारित होने पर, समघाती | धनात्मक अर्ध-रेखा पर विचारित होने पर, समघाती पॉइसन बिंदु प्रक्रिया को गणना प्रक्रिया के रूप में परिभाषित किया जा सकता है, जो एक प्रकार की प्रसंभाव्य प्रक्रिया होती है, जिसे <math display="inline"> \{N(t), t\geq 0\}</math> के रूप में दर्शाया जा सकता है।<ref name="Tijms2003page1" /><ref name="Ross1996page59" /> गणना प्रक्रिया समय <math display="inline"> t</math> तक हुए घटनाओं की कुल संख्या का प्रतिनिधित्व करती है। यदि गणना प्रक्रिया में निम्नलिखित तीन गुण हों, तो वह समघाती पॉइसन गणना प्रक्रिया दर <math display="inline"> \lambda>0</math> के साथ होती है, तीन गुण निम्नलिखित है:<ref name="Tijms2003page1" /><ref name="Ross1996page59" /> | ||
* <math display="inline"> N(0)=0;</math> | * <math display="inline"> N(0)=0;</math> | ||
*स्वतंत्र वृद्धि होती है; और | *स्वतंत्र वृद्धि होती है; और | ||
*लंबाई <math display="inline"> t</math> के किसी भी अंतराल में घटनाओं (या अंक) की संख्या पैरामीटर (या माध्य) <math display="inline"> \lambda t</math> के साथ | *लंबाई <math display="inline"> t</math> के किसी भी अंतराल में घटनाओं (या अंक) की संख्या पैरामीटर (या माध्य) <math display="inline"> \lambda t</math> के साथ पॉइसन यादृच्छिक चर है। | ||
अंतिम गुणधर्म का अर्थ है: | अंतिम गुणधर्म का अर्थ है: | ||
| Line 44: | Line 44: | ||
:<math> \Pr \{N(t)=n\}=\frac{(\lambda t)^n}{n!} e^{-\lambda t}. </math> | :<math> \Pr \{N(t)=n\}=\frac{(\lambda t)^n}{n!} e^{-\lambda t}. </math> | ||
पॉइसन गणना प्रक्रिया को यह कहते हुए भी परिभाषित किया जा सकता है कि गणना प्रक्रिया की घटनाओं के बीच समय का अंतर माध्य <math display="inline"> 1/\lambda</math> के साथ घातांकी चर होता हैं।<ref name="Tijms2003">{{cite book|author=H. C. Tijms|title=स्टोकेस्टिक मॉडल में पहला कोर्स|url=https://books.google.com/books?id=RK9yFrNxom8C|date=18 April 2003|publisher=John Wiley & Sons|isbn=978-0-471-49880-3}}</ref> घटनाओं या आमंद के बीच समय के अंतर को '''अंतर आमंद'''<ref name="Ross1996page64">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|page=64}}</ref> या '''अंतःक्रिया''' समय के रूप में जाना जाता है।<ref name="Tijms2003" /> | |||
=== वास्तविक रेखा पर एक बिंदु प्रक्रिया के रूप में व्याख्या === | === वास्तविक रेखा पर एक बिंदु प्रक्रिया के रूप में व्याख्या === | ||
पॉइसन बिंदु प्रक्रिया को वास्तविक रेखा पर परिभाषित किया जा सकता है इस प्रक्रिया के बिंदुओं की संख्या को <math display="inline"> (a,b]</math> के अंतराल में विचार करके, बिंदु प्रक्रिया के रूप में व्याख्या किया जाता है। वास्तविक रेखा पर सामान्य पॉइसन बिंदु प्रक्रिया के पैरामीटर <math display="inline"> \lambda>0</math> के साथ, इस यादृच्छिक संख्या के बिंदुओं की संख्या, जिसे यहां <math display="inline"> N(a,b]</math> के रूप में लिखा गया है, किसी [[गिनती संख्या|गणना संख्या]] <math display="inline"> n</math> के बराबर होने की प्रायिकता निम्नलिखित रूप में दी गई है:<ref name="DaleyVere-Jones2007page19">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=19}}</ref> | |||
:<math> \Pr \{N(a,b]=n\}=\frac{[\lambda(b-a)]^n}{n!} e^{-\lambda (b-a)}, </math> | :<math> \Pr \{N(a,b]=n\}=\frac{[\lambda(b-a)]^n}{n!} e^{-\lambda (b-a)}, </math> | ||
कुछ धनात्मक पूर्णांक 11 के लिए, समघाती | कुछ धनात्मक पूर्णांक 11 के लिए, समघाती पॉइसन बिंदु प्रक्रिया का परिमित-विमीय बंटन होता है:<ref name="DaleyVere-Jones2007page19" /> | ||
:<math> \Pr \{N(a_i,b_i]=n_i, i=1, \dots, k\} = \prod_{i=1}^k\frac{[\lambda(b_i-a_i)]^{n_i}}{n_i!} e^{-\lambda(b_i-a_i)}, </math> | :<math> \Pr \{N(a_i,b_i]=n_i, i=1, \dots, k\} = \prod_{i=1}^k\frac{[\lambda(b_i-a_i)]^{n_i}}{n_i!} e^{-\lambda(b_i-a_i)}, </math> | ||
जहाँ वास्तविक संख्याएँ <math display="inline"> a_i<b_i\leq a_{i+1}</math> हैं। | जहाँ वास्तविक संख्याएँ <math display="inline"> a_i<b_i\leq a_{i+1}</math> हैं। | ||
दूसरे शब्दों में, <math display="inline"> N(a,b]</math> माध्य <math display="inline"> \lambda(b-a)</math> के साथ | दूसरे शब्दों में, <math display="inline"> N(a,b]</math> माध्य <math display="inline"> \lambda(b-a)</math> के साथ पॉइसन यादृच्छिक चर होता है, जहां <math display="inline"> a\le b</math> है। इसके अतिरिक्त, किन्हीं दो असंयुक्त अंतरालों में बिंदुओं की संख्या, मान लीजिए, <math display="inline"> (a_1,b_1]</math> और <math display="inline"> (a_2,b_2]</math>, एक-दूसरे के स्वतंत्र हैं, और यह असंयुक्त अंतरालों की किसी भी परिमित संख्या तक विस्तारित होता है।<ref name="DaleyVere-Jones2007page19" /> कतारबद्ध सिद्धांत के संदर्भ में, एक बिंदु अस्तित्व (एक अंतराल में) होने को किसी ''घटना'' के रूप में विचार किया जा सकता है, लेकिन यह प्रायिकता सिद्धांत के अर्थ में घटना शब्द से भिन्न होता है।{{efn|For example, it is possible for an event ''not'' happening in the queueing theory sense to be an event in the probability theory sense.}} यह इस प्रकार है कि <math display="inline"> \lambda</math> ''एराइवल'' की अपेक्षित संख्या है जो प्रति इकाई समय में होती है।<ref name="Ross1996page59" /> | ||
==== प्रमुख गुण ==== | ==== प्रमुख गुण ==== | ||
पूर्व परिभाषा के अनुसार सामान्यतः | पूर्व परिभाषा के अनुसार सामान्यतः पॉइसन बिंदु प्रक्रियाओं के समग्र में दो महत्वपूर्ण विशेषताएं हैं जो निम्नलिखित है:<ref name="DaleyVere-Jones2007page19"/><ref name="ChiuStoyan2013page41and51"/> | ||
* प्रत्येक परिमित अंतराल में होने वाले एराइवल की संख्या में | * प्रत्येक परिमित अंतराल में होने वाले एराइवल की संख्या में पॉइसन बंटन होता है। | ||
* असयुंक्त अंतरालों में होने वाले एराइवल की संख्या एक-दूसरे के निर्पेक्ष यादृच्छिक चर होते हैं। | * असयुंक्त अंतरालों में होने वाले एराइवल की संख्या एक-दूसरे के निर्पेक्ष यादृच्छिक चर होते हैं। | ||
इसके अतिरिक्त, इसमें केवल समान्य | इसके अतिरिक्त, इसमें केवल समान्य पॉइसन बिंदु प्रक्रिया से संबंधित तृतीय विशेषता निम्नलिखित है:{{sfnp|Daley|Vere-Jones|2003|pages=19–23}} | ||
* प्रत्येक अंतराल <math display="inline"> (a+t,b+t]</math> में एराइवल की संख्या का | * प्रत्येक अंतराल <math display="inline"> (a+t,b+t]</math> में एराइवल की संख्या का पॉइसन बंटन केवल अंतराल की लंबाई <math display="inline"> b-a</math> पर निर्भर करता है। | ||
दूसरे शब्दों में, किसी भी परिमित <math display="inline"> t>0</math> के लिए, यादृच्छिक चर <math display="inline"> N(a+t,b+t]</math> और <math display="inline"> t</math> स्वयं में स्वतंत्र होते हैं, अतः इसे स्थायी | दूसरे शब्दों में, किसी भी परिमित <math display="inline"> t>0</math> के लिए, यादृच्छिक चर <math display="inline"> N(a+t,b+t]</math> और <math display="inline"> t</math> स्वयं में स्वतंत्र होते हैं, अतः इसे स्थायी पॉइसन प्रक्रिया भी कहा जाता है।<ref name="DaleyVere-Jones2007page19" /> | ||
==== बड़ी संख्याओं का नियम ==== | ==== बड़ी संख्याओं का नियम ==== | ||
| Line 72: | Line 72: | ||
:<math> \operatorname E[N(a_i,b_i]] =\lambda(b_i-a_i), </math> | :<math> \operatorname E[N(a_i,b_i]] =\lambda(b_i-a_i), </math> | ||
जहाँ <math>\operatorname E</math> [[अपेक्षित मूल्य|अपेक्षाओं]] के ऑपरेटर को दर्शाता है। दूसरे शब्दों में, | जहाँ <math>\operatorname E</math> [[अपेक्षित मूल्य|अपेक्षाओं]] के ऑपरेटर को दर्शाता है। दूसरे शब्दों में, पॉइसन प्रक्रिया के पैरामीटर <math display="inline"> \lambda</math> बिंदुओं की घनत्व के सामान होता है। इसके अतिरिक्त, समान्य पॉइसन बिंदु प्रक्रिया (प्रबल) बड़े आंकड़ों के नियम का अनुपालन करती है।<ref name="Kingman1992page42">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=42}}</ref> अधिक विशेष रूप से, एक प्रायिकता के साथ: | ||
:<math> \lim_{t\rightarrow \infty} \frac{N(t)}{t} =\lambda, </math> | :<math> \lim_{t\rightarrow \infty} \frac{N(t)}{t} =\lambda, </math> | ||
| Line 78: | Line 78: | ||
====मेमोरीलेस गुणधर्म ==== | ====मेमोरीलेस गुणधर्म ==== | ||
वास्तविक रेखा पर बिंदु प्रक्रिया के दो क्रमागत बिंदुओं के बीच की दूरी [[घातीय यादृच्छिक चर|घातांकी यादृच्छिक चर]] होगा जिसका पैरामीटर <math display="inline"> \lambda</math> होता है (अथवा समानांतर, औसत <math display="inline"> 1/\lambda</math> होता है)। इसका तात्पर्य है कि बिंदुओं का [[स्मृतिहीनता|मेमोरीलेस]] गुणधर्म होता है: किसी परिमित अंतराल में किसी बिंदु का अस्तित्व, अन्य बिंदुओं के अस्तित्व की प्रायिकता (बंटन) प्रासंगिकता को प्रभावित नहीं करता है,<ref name="Tijms2003page2">{{cite book|author=Henk C. Tijms|title=स्टोकेस्टिक मॉडल में पहला कोर्स|url=https://books.google.com/books?id=eBeNngEACAAJ|date=6 May 2003|publisher=Wiley|isbn=978-0-471-49881-0|pages=2–3}}</ref><ref name="Ross1996page35">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|pages=35–36}}</ref> लेकिन जब | वास्तविक रेखा पर बिंदु प्रक्रिया के दो क्रमागत बिंदुओं के बीच की दूरी [[घातीय यादृच्छिक चर|घातांकी यादृच्छिक चर]] होगा जिसका पैरामीटर <math display="inline"> \lambda</math> होता है (अथवा समानांतर, औसत <math display="inline"> 1/\lambda</math> होता है)। इसका तात्पर्य है कि बिंदुओं का [[स्मृतिहीनता|मेमोरीलेस]] गुणधर्म होता है: किसी परिमित अंतराल में किसी बिंदु का अस्तित्व, अन्य बिंदुओं के अस्तित्व की प्रायिकता (बंटन) प्रासंगिकता को प्रभावित नहीं करता है,<ref name="Tijms2003page2">{{cite book|author=Henk C. Tijms|title=स्टोकेस्टिक मॉडल में पहला कोर्स|url=https://books.google.com/books?id=eBeNngEACAAJ|date=6 May 2003|publisher=Wiley|isbn=978-0-471-49881-0|pages=2–3}}</ref><ref name="Ross1996page35">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|pages=35–36}}</ref> लेकिन जब पॉइसन प्रक्रिया को उच्चतम विमाओं वाले समष्टि पर परिभाषित किया जाता है, अतः इस गुणधर्म का कोई प्राकृतिक समरूपता नहीं होती है।<ref name="Kingman1992page38">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|pages=38–39}}</ref> | ||
==== क्रमबद्धता और | ==== क्रमबद्धता और साधारणता ==== | ||
[[स्थिर वृद्धि|स्थैतिक वृद्धियों]] वाली एक बिंदु प्रक्रिया को कभी-कभी क्रमित{{sfnp|Daley|Vere-Jones|2003|pages=29–30}} या नियमित<ref name="Ross1996page151">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|page=151}}</ref> कहा जाता है, यदि: | [[स्थिर वृद्धि|स्थैतिक वृद्धियों]] वाली एक बिंदु प्रक्रिया को कभी-कभी क्रमित{{sfnp|Daley|Vere-Jones|2003|pages=29–30}} या नियमित<ref name="Ross1996page151">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|page=151}}</ref> कहा जाता है, यदि: | ||
:<math> \Pr \{ N(t,t+\delta]>1 \} = o(\delta), </math> | :<math> \Pr \{ N(t,t+\delta]>1 \} = o(\delta), </math> | ||
यहां छोटे-o संकेतन का उपयोग किया जा रहा है। जब किसी बिंदु प्रक्रिया में दो बिंदुओं का अंतर्निहित समष्टि पर एक ही स्थिति में संयोग की प्रायिकता शून्य होती है, अतः उसे एक साधारण बिंदु प्रक्रिया कहा जाता है। वास्तविक रेखा पर सामान्य बिंदु प्रक्रियाओं के लिए, क्रमबद्धता की गुणवत्ता यह सिद्ध करती है कि प्रक्रिया | यहां छोटे-o संकेतन का उपयोग किया जा रहा है। जब किसी बिंदु प्रक्रिया में दो बिंदुओं का अंतर्निहित समष्टि पर एक ही स्थिति में संयोग की प्रायिकता शून्य होती है, अतः उसे एक '''साधारण बिंदु प्रक्रिया''' कहा जाता है। वास्तविक रेखा पर सामान्य बिंदु प्रक्रियाओं के लिए, क्रमबद्धता की गुणवत्ता यह सिद्ध करती है कि प्रक्रिया साधारण होती है,{{sfnp|Cox|Isham|1980|page=25}} जो समघाती पॉइसन बिंदु प्रक्रिया के लिए सत्य होता है।<ref name="DaleyVere-Jones2007page29">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=29}}</ref> | ||
==== मार्टिंगेल विशेषण ==== | ==== मार्टिंगेल विशेषण ==== | ||
वास्तविक रेखा पर, समघाती | वास्तविक रेखा पर, समघाती पॉइसन बिंदु प्रक्रिया का मार्टिंगेल सिद्धांत के साथ एक संबंध होता है निम्नलिखित विशेषण के माध्यम से: बिंदु प्रक्रिया समघाती पॉइसन बिंदु प्रक्रिया होती है यदि और केवल यदि | ||
:<math> N(-\infty,t]-\lambda t, </math> | :<math> N(-\infty,t]-\lambda t, </math> | ||
मार्टिंगेल है।<ref name="merzbach1986characterization">E. Merzbach and D. Nualart. A characterization of the spatial poisson process and changing time. ''The Annals of Probability'', 14(4):1380–1390, 1986.</ref><ref>{{cite journal | url=https://www.jstor.org/stable/3212898 | jstor=3212898 | title=ऑर्डर स्टेटिस्टिक प्रॉपर्टी के साथ पॉइंट प्रोसेस के कैरेक्टराइजेशन पर| last1=Feigin | first1=Paul D. | journal=Journal of Applied Probability | year=1979 | volume=16 | issue=2 | pages=297–304 | doi=10.2307/3212898 | s2cid=123904407 }}</ref> | मार्टिंगेल है।<ref name="merzbach1986characterization">E. Merzbach and D. Nualart. A characterization of the spatial poisson process and changing time. ''The Annals of Probability'', 14(4):1380–1390, 1986.</ref><ref>{{cite journal | url=https://www.jstor.org/stable/3212898 | jstor=3212898 | title=ऑर्डर स्टेटिस्टिक प्रॉपर्टी के साथ पॉइंट प्रोसेस के कैरेक्टराइजेशन पर| last1=Feigin | first1=Paul D. | journal=Journal of Applied Probability | year=1979 | volume=16 | issue=2 | pages=297–304 | doi=10.2307/3212898 | s2cid=123904407 }}</ref> | ||
==== अन्य प्रक्रियाओं से संबंध ==== | ==== अन्य प्रक्रियाओं से संबंध ==== | ||
वास्तविक रेखा पर, | वास्तविक रेखा पर, पॉइसन प्रक्रिया एक प्रकार की सतत-समय [[मार्कोव प्रक्रिया]] है जिसे [[जन्म प्रक्रिया]] के रूप में जाना जाता है, जन्म-मृत्यु प्रक्रिया के एक विशेष प्रकार (केवल जन्म और शून्य मृत्यु के साथ)।<ref name="Ross1996page2352">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|page=235}}</ref><ref name="papoulis2002probability2">A. Papoulis and S. U. Pillai. ''Probability, random variables, and stochastic processes''. Tata McGraw-Hill Education, 2002.</ref> [[मार्कोव संपत्ति|मार्कोव गुणधर्म]] के साथ अधिक जटिल प्रक्रियाएँ, जैसे [[मार्कोव आगमन प्रक्रिया|मार्कोव एराइवल प्रक्रियाएँ]], परिभाषित की गई हैं जहां पॉइसन प्रक्रिया एक विशेष स्थिति हैं।<ref name="Tijms2003" /> | ||
==== अर्ध-रेखा पर प्रतिबंध ==== | ==== अर्ध-रेखा पर प्रतिबंध ==== | ||
यदि समघाती | यदि समघाती पॉइसन प्रक्रिया केवल अर्ध-रेखा पर <math display="inline"> [0,\infty)</math> के रूप में विचार की जाती है, जब <math display="inline"> t</math> समय को दर्शाता है,<ref name="Tijms2003page1" /> अतः परिणामस्वरूप प्रक्रिया स्थानांतरण के अंतर्गत वास्तव में स्थानांतरण के प्रति समान नहीं होती है।<ref name="Kingman1992page38" /> उस स्थिति में, कुछ स्थानिकता की परिभाषाओं के अनुसार पॉइसन प्रक्रिया स्थायी नहीं रहती है।<ref name="ChiuStoyan2013page41">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=41–42}}</ref> | ||
==== अनुप्रयोग ==== | ==== अनुप्रयोग ==== | ||
समघाती | समघाती पॉइसन प्रक्रिया का वास्तविक रेखा पर कई अनुप्रयोग हुए हैं जो प्रतीत होने वाले यादृच्छिक और स्वतंत्र घटनाओं के मॉडलिंग का प्रयास करते हैं। यह कतारबद्ध सिद्धांत में मौलिक भूमिका निभाता है, जो कुछ घटनाओं के यादृच्छिक एराइवल और अपक्रम को प्रतिष्ठानुसार प्रतिष्ठापित करने के लिए उपयुक्त प्रसंभाव्य मॉडल विकसित करने का प्रायिकता क्षेत्र है।<ref name="Kleinrock1976"/><ref name="Tijms2003"/> उदाहरण के लिए, कतारबद्ध सिद्धांत के तकनीकों का उपयोग करके ग्राहकों के आगमन और सेवा प्राप्ति या फोन कॉल के आगमन का अध्ययन किया जा सकता है जो फोन विनियम में होते हैं। | ||
==== सामान्यीकरण ==== | ==== सामान्यीकरण ==== | ||
वास्तविक रेखा पर, समघाती | वास्तविक रेखा पर, समघाती पॉइसन प्रक्रिया को यादृच्छिक बिंदुओं की संख्या की गणना के लिए साधारणतम प्रसंभाव्य प्रक्रियाओं में से एक माना जाता है।{{sfnp|Cox|Isham|1980|page=3}}<ref name="snyder1991random">D. Snyder and M. Miller. Random point processes in time and space 2e springer-verlag. ''New York, NY'', 1991.</ref> इस प्रक्रिया को कई विधियों से सामान्यीकृत किया जा सकता है। संभावित सामान्यीकरण है कि अंतर-आगमन समय के बंटन को घातांकी बंटन से अन्य बंटनों तक विस्तारित किया जाए, जो पुनर्नवीनीकरण प्रक्रिया के रूप में जानी जाती है। एक अन्य सामान्यीकरण यह है कि पॉइसन बिंदु प्रक्रिया को समतल जैसे उच्च विमीय समष्टियों पर परिभाषित किया जाए।<ref name="DaleyVere-Jones2007">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378}}</ref> | ||
=== स्थानिक | === स्थानिक पॉइसन बिंदु प्रक्रिया === | ||
{{further|पूर्ण स्थानिक अनियमितता}} | {{further|पूर्ण स्थानिक अनियमितता}} | ||
स्थानिक | '''स्थानिक पॉइसन प्रक्रिया''' समतल <math>\textstyle \mathbb{R}^2</math> में परिभाषित पॉइसन बिंदु प्रक्रिया है।<ref name="merzbach1986characterization" /><ref name="lawson1993deviance">{{cite journal |first=A. B. |last=Lawson |title=विषम स्थानिक जहर प्रक्रियाओं के लिए अवशिष्ट अवशिष्ट|journal=Biometrics |volume=49 |issue=3 |pages=889–897 |year=1993 |doi=10.2307/2532210 |jstor=2532210 }}</ref> इसकी गणितीय परिभाषा के लिए, सबसे पहले समतल के परिबद्ध, विवृत या संवृत (या अधिक यथार्थ रूप से, बोरेल मापनीय) क्षेत्र <math display="inline"> B</math> पर विचार किया जाता है। इस क्षेत्र <math>\textstyle B\subset \mathbb{R}^2</math> में विद्यमान बिंदु प्रक्रिया <math>\textstyle N</math> के बिंदुओं की संख्या एक यादृच्छिक चर है, जिसे <math>\textstyle N(B)</math> द्वारा निरूपित किया जाता है। यदि अंक <math>\textstyle \lambda>0</math> के पैरामीटर के साथ एक समघाती पॉइसन प्रक्रिया से संबंधित हैं, तो <math>\textstyle B</math> में विद्यमान <math>\textstyle n</math> बिंदुओं की प्रायिकता निम्न द्वारा दी गई है: | ||
:<math> \Pr \{N(B)=n\}=\frac{(\lambda|B|)^n}{n!} e^{-\lambda|B|} </math> | :<math> \Pr \{N(B)=n\}=\frac{(\lambda|B|)^n}{n!} e^{-\lambda|B|} </math> | ||
जहाँ <math>\textstyle |B|</math> के क्षेत्र को दर्शाता है <math>\textstyle B</math>. | जहाँ <math>\textstyle |B|</math> के क्षेत्र को दर्शाता है <math>\textstyle B</math>. | ||
कुछ परिमित पूर्णांक <math>\textstyle k\geq 1</math> के लिए, हम पहले असम्बद्ध, परिबद्ध बोरेल (मापने योग्य) सेट <math>\textstyle B_1,\dots,B_k</math> के संग्रह पर विचार करके समघाती | कुछ परिमित पूर्णांक <math>\textstyle k\geq 1</math> के लिए, हम पहले असम्बद्ध, परिबद्ध बोरेल (मापने योग्य) सेट <math>\textstyle B_1,\dots,B_k</math> के संग्रह पर विचार करके समघाती पॉइसन बिंदु प्रक्रिया का परिमित-विमीय बंटन प्रदान कर सकते हैं। बिंदु प्रक्रिया के बिंदुओं की संख्या <math>\textstyle N </math> <math>\textstyle B_i</math> में विद्यमान <math>\textstyle N(B_i)</math> के रूप में लिखी जा सकती है। अतः पैरामीटर <math>\textstyle \lambda>0</math> के साथ समघाती पॉइसन बिंदु प्रक्रिया का परिमित-विमीय बंटन है:<ref name="DaleyVere-Jones2007page19to23">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=19–23}}</ref> | ||
:<math> \Pr \{N(B_i)=n_i, i=1, \dots, k\}=\prod_{i=1}^k\frac{(\lambda|B_i|)^{n_i}}{n_i!}e^{-\lambda|B_i|}. </math> | :<math> \Pr \{N(B_i)=n_i, i=1, \dots, k\}=\prod_{i=1}^k\frac{(\lambda|B_i|)^{n_i}}{n_i!}e^{-\lambda|B_i|}. </math> | ||
==== अनुप्रयोग ==== | ==== अनुप्रयोग ==== | ||
[[File:Sydney skyline at dusk - Dec 2008.jpg|thumb|400px|right|alt=Sydney at night time| | [[File:Sydney skyline at dusk - Dec 2008.jpg|thumb|400px|right|alt=Sydney at night time|सांख्यिकीय अध्ययन के अनुसार, ऑस्ट्रेलियाई शहर [[सिडनी]] में सेल्युलर या मोबाइल फोन बेस स्टेशनों की स्थितियां, ऊपर चित्रित की गई हैं, समानियोजित पॉइसन बिंदु प्रक्रिया के एक प्राप्ति की तरह हैं, जबकि दुनिया भर के कई अन्य शहरों में ऐसा नहीं होता है और अन्य बिंदु प्रक्रियाएँ आवश्यक होती हैं।<ref name="lee2012stochastic">{{cite journal |first1=C.-H. |last1=Lee |first2=C.-Y. |last2=Shih |first3=Y.-S. |last3=Chen |title=शहरी क्षेत्रों में सेलुलर नेटवर्क मॉडलिंग के लिए स्टोकेस्टिक ज्यामिति आधारित मॉडल|journal=Wireless Networks |volume=19 |pages=1063–1072 |year=2012 |issue=6 |doi=10.1007/s11276-012-0518-0 |s2cid=8409538 }}</ref>]]स्थानिक पॉइसन बिंदु प्रक्रिया स्थानिक सांख्यिकी में प्रमुखता से दिखाई देती है,<ref name="BaddeleyBárány2006"/><ref name="MollerWaagepetersen2003"/> प्रसंभाव्य ज्यामिति, और सातत्य सिद्धांत।<ref name="meester1996continuum"/> इस बिंदु प्रक्रिया को विभिन्न भौतिक विज्ञानों में लागू किया जाता है जैसे अल्फा कणों का पता लगाने के लिए विकसित एक मॉडल होता है। हाल के वर्षों में, यह प्रायः कुछ वायरलेस संचार नेटवर्कों के प्रतीत होने वाले अव्यवस्थित स्थानिक विन्यासों के मॉडल के लिए उपयोग किया गया है।<ref name="andrews2010primer"/><ref name="baccelli2009stochastic1"/><ref name="Haenggi2013"/> उदाहरण के लिए, सेलुलर या मोबाइल फोन नेटवर्क के मॉडल विकसित किए गए हैं जहां यह माना जाता है कि फोन नेटवर्क ट्रांसमीटर, जिन्हें बेस स्टेशन के रूप में जाना जाता है, समघाती पॉइसन बिंदु प्रक्रिया के अनुसार स्थित हैं। | ||
=== उच्च विमाओं में परिभाषित === | === उच्च विमाओं में परिभाषित === | ||
पूर्व समघाती | पूर्व समघाती पॉइसन बिंदु प्रक्रिया को क्षेत्र की धारणा को (उच्च विमीय) आयतन के साथ बदलकर उच्च विमाओं में विस्तारित किया जाता है। यदि यूक्लिडियन समष्टि <math>\textstyle \mathbb{R}^d</math>, के किसी परिबद्ध क्षेत्र <math>\textstyle B</math> के बिंदु एक समघाती पॉइसन प्रक्रिया बनाते हैं जिसका पैरामीटर <math>\textstyle \lambda>0</math> होता है, अतः <math>\textstyle B\subset \mathbb{R}^d</math> में विद्यमान <math>\textstyle n</math> बिंदुओं की प्रायिकता निम्नलिखित होती है: | ||
:<math> \Pr \{N(B)=n\}=\frac{(\lambda|B|)^n}{n!}e^{-\lambda|B|} </math> | :<math> \Pr \{N(B)=n\}=\frac{(\lambda|B|)^n}{n!}e^{-\lambda|B|} </math> | ||
जहां <math>\textstyle |B|</math> अब <math>\textstyle B</math> के <math>\textstyle d</math>-विमीय आयतन को दर्शाता है। इसके अतिरिक्त, असंयुक्त, परिबद्ध बोरेल समुच्चय <math>\textstyle B_1,\dots,B_k \subset \mathbb{R}^d</math> के संग्रह के लिए, <math>\textstyle N(B_i)</math> को <math>\textstyle B_i</math> में विद्यमान <math>\textstyle N</math> के बिंदुओं की संख्या को दर्शाता है। फिर पैरामीटर <math>\textstyle \lambda>0</math> के साथ संबंधित समघाती | जहां <math>\textstyle |B|</math> अब <math>\textstyle B</math> के <math>\textstyle d</math>-विमीय आयतन को दर्शाता है। इसके अतिरिक्त, असंयुक्त, परिबद्ध बोरेल समुच्चय <math>\textstyle B_1,\dots,B_k \subset \mathbb{R}^d</math> के संग्रह के लिए, <math>\textstyle N(B_i)</math> को <math>\textstyle B_i</math> में विद्यमान <math>\textstyle N</math> के बिंदुओं की संख्या को दर्शाता है। फिर पैरामीटर <math>\textstyle \lambda>0</math> के साथ संबंधित समघाती पॉइसन बिंदु प्रक्रिया का परिमित-विमीय बंटन होता है:<ref name="DaleyVere-Jones2007IIpage31">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|page=31}}</ref> | ||
:<math> \Pr \{N(B_i)=n_i, i=1, \dots, k\}=\prod_{i=1}^k\frac{(\lambda|B_i|)^{n_i}}{n_i!} e^{-\lambda|B_i|}. </math> | :<math> \Pr \{N(B_i)=n_i, i=1, \dots, k\}=\prod_{i=1}^k\frac{(\lambda|B_i|)^{n_i}}{n_i!} e^{-\lambda|B_i|}. </math> | ||
समघाती | समघाती पॉइसन बिंदु प्रक्रियाएँ स्वयं के पैरामीटर <math>\textstyle \lambda</math> के माध्यम से अंतर्निहित समष्टि की स्थिति पर निर्भर नहीं होती हैं, जिससे यह स्पष्ट होता है कि यह एक स्थिर प्रक्रिया (स्थानांतरण के लिए अपरिवर्तनीय) और आइसोट्रोपिक (घूर्णन के लिए अपरिवर्तनीय) प्रसंभाव्य प्रक्रिया है।<ref name="ChiuStoyan2013page41" /> एकल-विमीय स्थिति की तरह, समघाती बिंदु प्रक्रिया को कुछ परिबद्ध उपसमुच्चय <math display="inline"> \mathbb{R}^d</math> के लिए प्रतिबंधित किया जाता है, अतः स्थिरता की कुछ परिभाषाओं के अनुसार, प्रक्रिया अब स्थायी नहीं रहती है।<ref name="ChiuStoyan2013page41" /><ref name="Kingman1992page38" /> | ||
=== बिंदुओं का समान रूप से बंटन === | === बिंदुओं का समान रूप से बंटन === | ||
यदि समघाती बिंदु प्रक्रिया को वास्तविक रेखा पर किसी प्रयोजन की घटनाओं के लिए गणितीय मॉडल के रूप में परिभाषित किया जाता है, अतः इसकी विशेषताऐं इस प्रकार है कि वास्तविक रेखा पर इन घटनाओं की स्थितियों का बंटन समानतापूर्व होता है (जिसे प्रायः समय के रूप में व्याख्या किया जाता है)। विशेष रूप से, यदि किसी घटना (इस प्रक्रिया के अनुसार) किसी अंतराल <math>\textstyle (a,b]</math> में होती है जहां <math>\textstyle a \leq b</math> है, तो उसकी स्थानांतरिता उस अंतराल पर परिभाषित एक समान यादृच्छिक चर होगा।<ref name="DaleyVere-Jones2007page19to232">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=19–23}}</ref> इसके अतिरिक्त, समघाती बिंदु प्रक्रिया को | यदि समघाती बिंदु प्रक्रिया को वास्तविक रेखा पर किसी प्रयोजन की घटनाओं के लिए गणितीय मॉडल के रूप में परिभाषित किया जाता है, अतः इसकी विशेषताऐं इस प्रकार है कि वास्तविक रेखा पर इन घटनाओं की स्थितियों का बंटन समानतापूर्व होता है (जिसे प्रायः समय के रूप में व्याख्या किया जाता है)। विशेष रूप से, यदि किसी घटना (इस प्रक्रिया के अनुसार) किसी अंतराल <math>\textstyle (a,b]</math> में होती है जहां <math>\textstyle a \leq b</math> है, तो उसकी स्थानांतरिता उस अंतराल पर परिभाषित एक समान यादृच्छिक चर होगा।<ref name="DaleyVere-Jones2007page19to232">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=19–23}}</ref> इसके अतिरिक्त, समघाती बिंदु प्रक्रिया को ''एकसमान'' पॉइसन बिंदु प्रक्रिया भी कहा जाता है (टर्मिनोलॉजी देखें)। यह समानता गुण कार्तीय निर्देशांक में उच्च विमाओं तक विस्तारित होता है, लेकिन उदाहरण के लिए ध्रुवीय निर्देशांक में नहीं होता है।<ref name="ChiuStoyan2013page38to40and53">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=38–40 and 53–54}}</ref><ref name="DaleyVere-Jones2007page25">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|page=25}}</ref> | ||
== असमघाती | == असमघाती पॉइसन बिंदु प्रक्रिया == | ||
[[File:Inhomogeneouspoissonprocess.svg|thumb|वास्तविक रेखा पर एक विषम | [[File:Inhomogeneouspoissonprocess.svg|thumb|वास्तविक रेखा पर एक विषम पॉइसन बिंदु प्रक्रिया का ग्राफ। घटनाओं को काले क्रॉस, समय-निर्भर दर के साथ चिह्नित किया गया है <math> \lambda(t) </math> लाल रंग से चिह्नित फलन द्वारा दिया जाता है।]]'''असमघाती''' या '''असमघाती पॉइसन बिंदु प्रक्रिया''' (शब्दावली देखें) एक पॉइसन बिंदु प्रक्रिया है जिसमें पॉइसन पैरामीटर अंतर्निहित स्थान में कुछ स्थान-निर्भर फलन के रूप में सेट किया गया है, जिस पर पॉइसन प्रक्रिया परिभाषित है। यूक्लिडियन समष्टि <math>\textstyle \mathbb{R}^d</math> के लिए, यह स्थानीय रूप से पूर्णांक धनात्मक फलन <math>\lambda\colon\mathbb{R}^d\to[0,\infty)</math> को शुरू करके प्राप्त किया जाता है, जैसे कि प्रत्येक परिबद्ध क्षेत्र <math>\textstyle B</math> के लिए (<math>\textstyle d</math>-विमीय) आयतन <math>\textstyle \lambda (x)</math> से अधिक क्षेत्र <math>\textstyle B</math> का समाकल भाग है। दूसरे शब्दों में, यदि यह समाकल, <math>\textstyle \Lambda (B)</math> द्वारा निरूपित किया जाता है, अतः यह निम्न प्रकार है:<ref name="MollerWaagepetersen2003page14" /> | ||
:<math> \Lambda (B)=\int_B \lambda(x)\,\mathrm dx < \infty, </math> | :<math> \Lambda (B)=\int_B \lambda(x)\,\mathrm dx < \infty, </math> | ||
जहां <math>\textstyle{\mathrm dx}</math>, (<math>\textstyle d</math>-विमीय) आयतन अंश है,{{efn|Instead of <math>\textstyle \lambda(x)</math> and <math>\textstyle{\mathrm d}x</math>, one could write, for example, in (two-dimensional) polar coordinates <math>\textstyle \lambda(r,\theta)</math> and <math display="inline"> r\,dr\,d\theta</math> , where <math>\textstyle r</math> and <math>\textstyle \theta</math> denote the radial and angular coordinates respectively, and so <math>\textstyle{\mathrm d}x</math> would be an area element in this example.}} फिर असंयुक्त परिबद्ध बोरेल मापने योग्य समुच्चयों <math>\textstyle B_1,\dots,B_k</math> के प्रत्येक संग्रह के लिए, ( | जहां <math>\textstyle{\mathrm dx}</math>, (<math>\textstyle d</math>-विमीय) आयतन अंश है,{{efn|Instead of <math>\textstyle \lambda(x)</math> and <math>\textstyle{\mathrm d}x</math>, one could write, for example, in (two-dimensional) polar coordinates <math>\textstyle \lambda(r,\theta)</math> and <math display="inline"> r\,dr\,d\theta</math> , where <math>\textstyle r</math> and <math>\textstyle \theta</math> denote the radial and angular coordinates respectively, and so <math>\textstyle{\mathrm d}x</math> would be an area element in this example.}} फिर असंयुक्त परिबद्ध बोरेल मापने योग्य समुच्चयों <math>\textstyle B_1,\dots,B_k</math> के प्रत्येक संग्रह के लिए, (तीव्रता) फलन <math>\textstyle \lambda(x)</math> के साथ असमघातीय पॉइसन प्रक्रिया का परिमित-विमीय बंटन है:<ref name="DaleyVere-Jones2007IIpage31" /> | ||
:<math> \Pr \{N(B_i)=n_i, i=1, \dots, k\}=\prod_{i=1}^k\frac{(\Lambda(B_i))^{n_i}}{n_i!} e^{-\Lambda(B_i)}. </math> | :<math> \Pr \{N(B_i)=n_i, i=1, \dots, k\}=\prod_{i=1}^k\frac{(\Lambda(B_i))^{n_i}}{n_i!} e^{-\Lambda(B_i)}. </math> | ||
इसके अतिरिक्त, <math>\textstyle \Lambda (B)</math> की व्याख्या परिबद्ध क्षेत्र <math>\textstyle B</math> में स्थित | इसके अतिरिक्त, <math>\textstyle \Lambda (B)</math> की व्याख्या परिबद्ध क्षेत्र <math>\textstyle B</math> में स्थित पॉइसन प्रक्रिया के बिंदुओं की अपेक्षित संख्या होने की है, अर्थात् | ||
:<math> \Lambda (B)= \operatorname E[N(B)] . </math> | :<math> \Lambda (B)= \operatorname E[N(B)] . </math> | ||
=== वास्तविक रेखा पर परिभाषित === | === वास्तविक रेखा पर परिभाषित === | ||
वास्तविक रेखा पर, गैर-समघातीय या असमघातीय | वास्तविक रेखा पर, गैर-समघातीय या असमघातीय पॉइसन बिंदु प्रक्रिया का औसत माप एकल विमीय समाकल योग के द्वारा दी जाती है। दो वास्तविक संख्याओं <math>\textstyle a</math> और <math>\textstyle b</math> के लिए, जहां <math>\textstyle a\leq b</math>, <math>\textstyle (a,b]</math> में होने वाले असमघातीय पॉइसन प्रक्रिया के संख्या बिंदु को <math>\textstyle N(a,b]</math> द्वारा चिह्नित किया जाता है, जिसमें तीव्रता फलन <math>\textstyle \lambda(t)</math> सम्मिलित होता है।उपरोक्त अंतराल <math>\textstyle (a,b]</math> में विद्यमान <math>\textstyle n</math> बिंदुओं की प्रायिकता निम्न द्वारा दिया गया है: | ||
:<math> \Pr \{N(a,b]=n\}=\frac{[\Lambda(a,b)]^n}{n!} e^{-\Lambda(a,b)}. </math> | :<math> \Pr \{N(a,b]=n\}=\frac{[\Lambda(a,b)]^n}{n!} e^{-\Lambda(a,b)}. </math> | ||
जहां माध्य या | जहां माध्य या तीव्रता माप है: | ||
:<math> \Lambda(a,b)=\int_a^b \lambda (t)\,\mathrm dt, </math> | :<math> \Lambda(a,b)=\int_a^b \lambda (t)\,\mathrm dt, </math> | ||
जिसका अर्थ है कि यादृच्छिक चर <math>\textstyle N(a,b]</math> माध्य <math>\textstyle \operatorname E[N(a,b]] = \Lambda(a,b)</math> के साथ एक | जिसका अर्थ है कि यादृच्छिक चर <math>\textstyle N(a,b]</math> माध्य <math>\textstyle \operatorname E[N(a,b]] = \Lambda(a,b)</math> के साथ एक पॉइसन यादृच्छिक चर है। | ||
एक-विमा सेटिंग की एक विशेषता यह है कि किसी असमघातीय | एक-विमा सेटिंग की एक विशेषता यह है कि किसी असमघातीय पॉइसन प्रक्रिया को [[मोनोटोनिक फ़ंक्शन|एकदिष्ट (मोनोटोन)]] परिवर्तन या मानचित्रण द्वारा सजातीय में रूपांतरित किया जा सकता है, जिसे <math>\textstyle \Lambda </math> के प्रतिलोम के साथ प्राप्त किया जाता है।<ref name="Kingman1992pageX">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=X}}</ref><ref name="Streit2010page6">{{cite book|author=Roy L. Streit|title=Poisson Point Processes: Imaging, Tracking, and Sensing|url=https://books.google.com/books?id=KAWmFYUJ5zsC|date=15 September 2010|publisher=Springer Science & Business Media|isbn=978-1-4419-6923-1|page=6}}</ref> | ||
==== गणना प्रक्रिया की व्याख्या ==== | ==== गणना प्रक्रिया की व्याख्या ==== | ||
जब धनात्मक अर्ध-रेखा पर विचार किया जाता है, अतः असमघातीय | जब धनात्मक अर्ध-रेखा पर विचार किया जाता है, अतः असमघातीय पॉइसन बिंदु प्रक्रिया को कई बार गणना प्रक्रिया के रूप में भी परिभाषित किया जाता है। इस व्याख्यान के साथ, प्रक्रिया, जिसे कभी-कभी <math>\textstyle \{N(t), t\geq 0\}</math> के रूप में लिखा जाता है, <math>\textstyle t</math> समय तक हुई प्रत्येक घटनाओं की कुल संख्या का प्रतिनिधित्व किया जाता है। गणना प्रक्रिया को असमघातीय पॉइसन गणना प्रक्रिया कहा जाता है यदि इसके चार गुण होते हैं:<ref name="Ross1996page59" /><ref name="Tijms2003page22">{{cite book|author=H. C. Tijms|title=स्टोकेस्टिक मॉडल में पहला कोर्स|url=https://books.google.com/books?id=RK9yFrNxom8C|date=18 April 2003|publisher=John Wiley & Sons|isbn=978-0-471-49880-3|pages=22–23}}</ref> | ||
* <math>\textstyle N(0)=0;</math> | * <math>\textstyle N(0)=0;</math> | ||
* स्वतंत्र वृद्धि होती है; | * स्वतंत्र वृद्धि होती है; | ||
| Line 151: | Line 151: | ||
यहां <math>\textstyle o(h)</math>, <math>\textstyle h\rightarrow 0</math> के लिए <math>\textstyle o(h)/h\rightarrow 0</math> के अनन्तस्पर्शी या छोटे-o नोटेशन है। अपवर्तकता के साथ बिंदु प्रक्रियाओं की स्थिति में (जैसे कि न्यूरल स्पाइक ट्रेन), प्रगुण 4 का एक अन्य प्रबल संस्करण लागू होता है:<ref>{{cite journal|author1=L. Citi |author2=D. Ba |author3=E.N. Brown |author4=R. Barbieri |name-list-style=amp |title = अपवर्तकता के साथ बिंदु प्रक्रियाओं के लिए संभावना विधियाँ|journal=Neural Computation|volume=26 |issue=2 |pages=237–263 |year=2014|doi=10.1162/NECO_a_00548|pmid=24206384 |url=https://dspace.mit.edu/bitstream/1721.1/85015/2/Citi-2013-Likelihood%20Methods%20f.pdf |hdl=1721.1/85015 |s2cid=1436173 |hdl-access=free }}</ref> <math>\Pr \{N(t+h)-N(t) \ge 2\} = o(h^2)</math>. | यहां <math>\textstyle o(h)</math>, <math>\textstyle h\rightarrow 0</math> के लिए <math>\textstyle o(h)/h\rightarrow 0</math> के अनन्तस्पर्शी या छोटे-o नोटेशन है। अपवर्तकता के साथ बिंदु प्रक्रियाओं की स्थिति में (जैसे कि न्यूरल स्पाइक ट्रेन), प्रगुण 4 का एक अन्य प्रबल संस्करण लागू होता है:<ref>{{cite journal|author1=L. Citi |author2=D. Ba |author3=E.N. Brown |author4=R. Barbieri |name-list-style=amp |title = अपवर्तकता के साथ बिंदु प्रक्रियाओं के लिए संभावना विधियाँ|journal=Neural Computation|volume=26 |issue=2 |pages=237–263 |year=2014|doi=10.1162/NECO_a_00548|pmid=24206384 |url=https://dspace.mit.edu/bitstream/1721.1/85015/2/Citi-2013-Likelihood%20Methods%20f.pdf |hdl=1721.1/85015 |s2cid=1436173 |hdl-access=free }}</ref> <math>\Pr \{N(t+h)-N(t) \ge 2\} = o(h^2)</math>. | ||
उपरोक्त गुणों का अर्थ है कि <math>\textstyle N(t+h) - N(t)</math> पैरामीटर (या माध्य) के साथ एक | उपरोक्त गुणों का अर्थ है कि <math>\textstyle N(t+h) - N(t)</math> पैरामीटर (या माध्य) के साथ एक पॉइसन यादृच्छिक चर है। | ||
:<math> \operatorname E[N(t+h) - N(t)] = \int_t^{t+h}\lambda (s) \, ds, </math> | :<math> \operatorname E[N(t+h) - N(t)] = \int_t^{t+h}\lambda (s) \, ds, </math> | ||
| Line 157: | Line 157: | ||
:<math> \operatorname E[N(h)]=\int_0^h \lambda (s) \, ds. </math> | :<math> \operatorname E[N(h)]=\int_0^h \lambda (s) \, ds. </math> | ||
=== स्थानिक | === स्थानिक पॉइसन प्रक्रिया === | ||
समतल <math>\textstyle \mathbb{R}^2</math> में परिभाषित असमघातीय | समतल <math>\textstyle \mathbb{R}^2</math> में परिभाषित असमघातीय पॉइसन प्रक्रिया को '''स्थानिक पॉइसन प्रक्रिया''' कहा जाता है<ref name="BaddeleyBárány2006page10"><nowiki>{{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=</nowiki>https://books.google.com/books?id=X-m5BQAAQBAJ|date=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4|page=10}</ref> इसे तीव्रता फलन के साथ परिभाषित किया जाता है और इसकी तीव्रता की माप कुछ क्षेत्र में इसकी तीव्रता फलन का सतह समाकलन करके प्राप्त किया जाता है।<ref name="ChiuStoyan2013page51" /><ref name="BaddeleyBárány2006page12"><nowiki>{{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=</nowiki>https://books.google.com/books?id=X-m5BQAAQBAJ|date=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4|page=12}</ref> उदाहरण के लिए, इसका तीव्रता फलन (कार्तीय निर्देशांक <math display="inline"> x</math> और <math>\textstyle y</math> के एक फलन के रूप में) हो सकता है | ||
:<math> \lambda(x,y)= e^{-(x^2+y^2)}, </math> | :<math> \lambda(x,y)= e^{-(x^2+y^2)}, </math> | ||
इसलिए संगत | इसलिए संगत तीव्रता माप सतह समाकल द्वारा निम्नलिखित रूप दिया जाता है | ||
:<math> \Lambda(B)= \int_B e^{-(x^2+y^2)}\,\mathrm dx\,\mathrm dy, </math> | :<math> \Lambda(B)= \int_B e^{-(x^2+y^2)}\,\mathrm dx\,\mathrm dy, </math> | ||
| Line 173: | Line 173: | ||
=== अनुप्रयोग === | === अनुप्रयोग === | ||
जब वास्तविक रेखा को समय के रूप में व्याख्या किया जाता है, अतः असमान्य प्रक्रिया को गणना प्रक्रियाओं और कतारबद्ध सिद्धांत के क्षेत्रों में उपयोग किया जाता है।<ref name="Tijms2003page22"/><ref name="Ross1996page78">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|pages=78–81}}</ref> असमान्य | जब वास्तविक रेखा को समय के रूप में व्याख्या किया जाता है, अतः असमान्य प्रक्रिया को गणना प्रक्रियाओं और कतारबद्ध सिद्धांत के क्षेत्रों में उपयोग किया जाता है।<ref name="Tijms2003page22"/><ref name="Ross1996page78">{{cite book|author=Sheldon M. Ross|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=ImUPAQAAMAAJ|year=1996|publisher=Wiley|isbn=978-0-471-12062-9|pages=78–81}}</ref> असमान्य पॉइसन बिंदु प्रक्रिया द्वारा प्रतिष्ठित या अपेक्षित होने वाली घटनाओं के उदाहरणों में निम्नलिखित सम्मिलित होते हैं: | ||
* फ़ुटबॉल के खेल में किए जा रहे गोल।<ref name="heuer2010soccer">A. Heuer, C. Mueller, and O. Rubner. Soccer: Is scoring goals a predictable Poissonian process? ''EPL'', 89(3):38007, 2010.</ref> | * फ़ुटबॉल के खेल में किए जा रहे गोल।<ref name="heuer2010soccer">A. Heuer, C. Mueller, and O. Rubner. Soccer: Is scoring goals a predictable Poissonian process? ''EPL'', 89(3):38007, 2010.</ref> | ||
* सर्किट बोर्ड में दोष<ref name="hwang2011modeling">J. Y. Hwang, W. Kuo, and C. Ha. Modeling of integrated circuit yield using a spatial nonhomogeneous poisson process. ''Semiconductor Manufacturing, IEEE Transactions on'', 24(3):377–384, 2011.</ref> | * सर्किट बोर्ड में दोष<ref name="hwang2011modeling">J. Y. Hwang, W. Kuo, and C. Ha. Modeling of integrated circuit yield using a spatial nonhomogeneous poisson process. ''Semiconductor Manufacturing, IEEE Transactions on'', 24(3):377–384, 2011.</ref> | ||
समतल में, प्रसंभाव्य ज्यामिति<ref name="ChiuStoyan2013"/><ref name="baddeley1999crash"/> और स्थानिक आंकड़ों<ref name="BaddeleyBárány2006"/><ref name="MollerWaagepetersen2003"/> के संबंधित शाखाओं में महत्वपूर्ण होती है। इस बिंदु प्रक्रिया की | समतल में, प्रसंभाव्य ज्यामिति<ref name="ChiuStoyan2013"/><ref name="baddeley1999crash"/> और स्थानिक आंकड़ों<ref name="BaddeleyBárány2006"/><ref name="MollerWaagepetersen2003"/> के संबंधित शाखाओं में महत्वपूर्ण होती है। इस बिंदु प्रक्रिया की तीव्रता माप अंतर्निहित समष्टि के स्थान पर निर्भर करती है, जिसका तात्पर्य है कि इसका उपयोग किसी क्षेत्र में भिन्नता वाली घटनाओं के मॉडलिंग के लिए किया जा सकता है। दूसरे शब्दों में, ये घटनाएं ऐसे बिंदुओं के रूप में प्रतिष्ठित की जा सकती हैं जिनका स्थान-निर्भर घनत्व है।<ref name="ChiuStoyan2013page51"/> यह प्रक्रियाएँ विभिन्न क्षेत्रों में उपयोग की जाती हैं और उनमें महासागरों में सैल्मन और समुद्री जीवाणुओं का अध्ययन,<ref name="krkovsek2005transmission">M. Krko{\vs}ek, M. A. Lewis, and J. P. Volpe. Transmission dynamics of parasitic sea lice from farm to wild salmon. ''Proceedings of the Royal Society B: Biological Sciences'', 272(1564):689–696, 2005.</ref> वानिकी,<ref name="thompson1955spatial"/> और खोज समस्याओं<ref name="lewis1979simulation">P. A. Lewis and G. S. Shedler. Simulation of nonhomogeneous Poisson processes by thinning. ''Naval Research Logistics Quarterly'', 26(3):403–413, 1979.</ref> का अध्ययन सम्मिलित होता है। | ||
=== | === तीव्रता फलन की व्याख्या === | ||
पॉइसन तीव्रता फलन <math display="inline"> \lambda(x)</math> की व्याख्या, जो सहज रूप में मानी जाती है,<ref name="ChiuStoyan2013page51"/> अत्यल्पिक रूप में आयतन घटक <math display="inline">\mathrm dx</math> के साथ संबंधित होती है: <math display="inline"> \lambda(x)\,\mathrm dx</math> पॉइसन बिंदु प्रक्रिया के किसी बिंदु की अत्यल्पिक प्रायिकता है जो समष्टि के किसी क्षेत्र में विद्यमान होता है और जिसका आयतन <math display="inline">\mathrm dx</math> पर नियत होता है। यह क्षेत्र <math display="inline"> x</math> पर नियत होता है।<ref name="ChiuStoyan2013page51"/> इस व्याख्या से पॉइसन प्रक्रिया में बिंदुओं का अस्तित्व और बंटन का ज्ञान प्राप्त होता है। | |||
उदाहरण के लिए, वास्तविक रेखा पर किसी सजातीय | उदाहरण के लिए, वास्तविक रेखा पर किसी सजातीय पॉइसन बिंदु प्रक्रिया को देखते हुए, चौड़ाई <math display="inline"> \delta</math> के एक छोटे अंतराल में प्रक्रिया के एक बिंदु को प्राप्त करने की प्रायिकता लगभग <math display="inline"> \lambda \delta</math> है। वास्तव में, इस तरह के अंतर्ज्ञान से पॉइसन बिंदु प्रक्रिया को कभी-कभी प्रस्तुत किया जाता है और इसका बंटन प्राप्त होता है।<ref name="Kingman1992page9">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|pages=10}}</ref><ref name="feller1974introduction" />{{sfnp|Cox|Isham|1980|pages=3–6}} | ||
=== | === साधारण बिंदु प्रक्रिया === | ||
यदि किसी | यदि किसी पॉइसन बिंदु प्रक्रिया में तीव्रता माप स्थानिक रूप से परिमित और असंगठित (या गैर-परमाणु) होती है, अतः वह एक साधारण बिंदु प्रक्रिया होती है। '''साधारण बिंदु प्रक्रिया''' के लिए, अंतर्निहित (स्थिति) समष्टि में एकल बिंदु या स्थान पर बिंदु के अस्तित्व की प्रायिकता शून्य या एक होती है। इसका अर्थ है कि पॉइसन बिंदु प्रक्रिया के दो (या अधिक) बिंदु अंतर्निहित समष्टि में स्थान के सामान होता हैं।<ref name="ChiuStoyan2013page44">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|page=44}}</ref><ref name="baccelli2009stochastic1"/><ref name="Haenggi2013page11">{{cite book|author=Martin Haenggi|title=वायरलेस नेटवर्क के लिए स्टोचैस्टिक ज्योमेट्री|url=https://books.google.com/books?id=CLtDhblwWEgC|year=2013|publisher=Cambridge University Press|isbn=978-1-107-01469-5|page=11}}</ref> | ||
== अनुकरण == | == अनुकरण == | ||
कंप्यूटर पर | कंप्यूटर पर पॉइसन बिंदु प्रक्रिया का अनुकरण करना सामान्यतः किसी परिमित स्थानिक क्षेत्र में, जिसे अनुकरण ''विंडो'' के रूप में जाना जाता है, किया जाता है और इसके लिए दो चरणों की आवश्यक होती हैं: उचित रूप से किसी यादृच्छिक संख्या के बिंदुओं को बनाना और फिर उन बिंदुओं को एक यादृच्छिक विधि से उचित रूप से स्थानित करना। दोनों इन दो चरणों का प्रयोग किए जाने वाली अनुकरण प्रक्रिया पर निर्भर करते हैं जो वर्तमान में अनुकरणित की जा रही है।<ref name="ChiuStoyan2013page53to55">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=53–55}}</ref><ref name="Streit2010page13">{{cite book|author=Roy L. Streit|title=Poisson Point Processes: Imaging, Tracking, and Sensing|url=https://books.google.com/books?id=KAWmFYUJ5zsC|date=15 September 2010|publisher=Springer Science & Business Media|isbn=978-1-4419-6923-1|pages=13–14}}</ref> | ||
===चरण 1: बिंदुओं की संख्या=== | ===चरण 1: बिंदुओं की संख्या=== | ||
विंडो में बिंदुओं की संख्या <math display="inline"> N</math>, जिसे यहां <math display="inline"> W</math> से चिह्नित किया गया है, को अनुकरणित करने की आवश्यकता है, जो एक (छद्म)-[[रैंडम संख्या जनरेटर|यादृच्छिक संख्या उत्पन्न]] करने वाले फलन का उपयोग करके किया जाता है जो | विंडो में बिंदुओं की संख्या <math display="inline"> N</math>, जिसे यहां <math display="inline"> W</math> से चिह्नित किया गया है, को अनुकरणित करने की आवश्यकता है, जो एक (छद्म)-[[रैंडम संख्या जनरेटर|यादृच्छिक संख्या उत्पन्न]] करने वाले फलन का उपयोग करके किया जाता है जो पॉइसन यादृच्छिक चर का अनुकरण करने में सक्षम है। | ||
==== समघाती स्थिति ==== | ==== समघाती स्थिति ==== | ||
समघातीय स्थिति के लिए नियतांक <math display="inline"> \lambda</math> के साथ, | समघातीय स्थिति के लिए नियतांक <math display="inline"> \lambda</math> के साथ, पॉइसन यादृच्छिक परिमाण <math display="inline"> N</math> का औसत <math display="inline"> \lambda |W|</math> पर सेट किया जाता है जहां <math display="inline"> |W|</math> लंबाई, क्षेत्रफल या ( <math display="inline"> d</math>-विमीय) आयतन <math display="inline"> W</math> है। | ||
====असमान स्थिति==== | ====असमान स्थिति==== | ||
| Line 207: | Line 207: | ||
एकल विमा में समघातीय स्थिति के लिए, सभी बिंदुओं को विंडो या अंतराल <math>\textstyle W</math> में एकसमान और स्वतंत्र रूप से स्थानित किया जाता है। कार्तीय निर्देशांक प्रणाली में अधिकतर विमाओं के लिए, प्रत्येक निर्देशांक को एकसमान और स्वतंत्र रूप से विंडो <math>\textstyle W</math> में स्थानित किया जाता है। तथापि, यदि विंडो कार्तीय समष्टि का उपअंश नहीं है (उदाहरण के लिए, किसी इकाई स्फीयर के अंदर या किसी इकाई स्फीयर की सतह पर), अतः बिंदुओं को <math>\textstyle W</math> में एकसमान रूप से नहीं रखा जाएगा, और ऐसे स्थितियों में कार्तीय से उचित निर्देशांकों की आवश्यकता होती है।<ref name="ChiuStoyan2013page53to55" /> | एकल विमा में समघातीय स्थिति के लिए, सभी बिंदुओं को विंडो या अंतराल <math>\textstyle W</math> में एकसमान और स्वतंत्र रूप से स्थानित किया जाता है। कार्तीय निर्देशांक प्रणाली में अधिकतर विमाओं के लिए, प्रत्येक निर्देशांक को एकसमान और स्वतंत्र रूप से विंडो <math>\textstyle W</math> में स्थानित किया जाता है। तथापि, यदि विंडो कार्तीय समष्टि का उपअंश नहीं है (उदाहरण के लिए, किसी इकाई स्फीयर के अंदर या किसी इकाई स्फीयर की सतह पर), अतः बिंदुओं को <math>\textstyle W</math> में एकसमान रूप से नहीं रखा जाएगा, और ऐसे स्थितियों में कार्तीय से उचित निर्देशांकों की आवश्यकता होती है।<ref name="ChiuStoyan2013page53to55" /> | ||
====असमान स्थिति==== | ====असमान स्थिति==== | ||
असमघातीय स्थानिकता वाली स्थितियों में, | असमघातीय स्थानिकता वाली स्थितियों में, तीव्रता फलन की प्रकृति पर निर्भर करते हुए कुछ अलग-अलग विधियाँ उपयोग की जा सकती हैं जो तीव्रता फलन <math>\textstyle \lambda(x)</math> की प्रकृति पर निर्भर करती हैं।<ref name="ChiuStoyan2013page53to55" /> यदि तीव्रता फलन पर्याप्त रूप से साधारण हो, तो बिना एक-दूसरे के स्वतंत्र और यादृच्छिक असमान (कार्तीय या अन्य) निर्देशांकों को उत्पन्न किया जा सकता है। उदाहरण के लिए, वृत्ताकार विंडो पर पॉइसन बिंदु प्रक्रिया का अनुकरण एक ऐसी आइसोटोपिक तीव्रता फलन (ध्रुवीय निर्देशांकों <math>\textstyle r</math> और <math>\textstyle \theta</math> में) के लिए किया जा सकता है, जिसका अर्थ है कि यह घूर्णी रूप से भिन्न या <math>\textstyle \theta</math> से स्वतंत्र है, लेकिन <math>\textstyle r</math> पर निर्भर होती है, <math>\textstyle r</math> में चर के परिवर्तन के द्वारा यदि तीव्रता फलन पर्याप्त रूप से साधारण होता है।<ref name="ChiuStoyan2013page53to55" /> | ||
अधिक जटिल | अधिक जटिल तीव्रता फलनों के लिए, [[अस्वीकृति नमूनाकरण|स्वीकृति-अस्वीकृति पद्धति]] का उपयोग किया जा सकता है, जिसमें अनुपात के आधार पर केवल कुछ यादृच्छिक बिंदुओं का उपयोग (या 'स्वीकार') करना और अन्य बिंदुओं का उपयोग नहीं करना (या 'अस्वीकार करना') सम्मिलित है:<ref name="Streit2010page14">{{cite book|author=Roy L. Streit|title=Poisson Point Processes: Imaging, Tracking, and Sensing|url=https://books.google.com/books?id=KAWmFYUJ5zsC|date=15 September 2010|publisher=Springer Science & Business Media|isbn=978-1-4419-6923-1|pages=14–16}}</ref> | ||
:<math> \frac{\lambda(x_i)}{\Lambda(W)}=\frac{\lambda(x_i)}{\int_W\lambda(x)\,\mathrm dx. } </math> | :<math> \frac{\lambda(x_i)}{\Lambda(W)}=\frac{\lambda(x_i)}{\int_W\lambda(x)\,\mathrm dx. } </math> | ||
जहाँ <math>\textstyle x_i</math> स्वीकृति या अस्वीकृति के लिए विचाराधीन बिंदु है। | जहाँ <math>\textstyle x_i</math> स्वीकृति या अस्वीकृति के लिए विचाराधीन बिंदु है। | ||
== सामान्य | == सामान्य पॉइसन बिंदु प्रक्रिया == | ||
रेडॉन माप <math>\textstyle \Lambda</math> का उपयोग करके | रेडॉन माप <math>\textstyle \Lambda</math> का उपयोग करके पॉइसन बिंदु प्रक्रिया को कभी-कभी '''सामान्य पॉइसन बिंदु प्रक्रिया'''<ref name="ChiuStoyan2013page51"/><ref name="Haenggi2013page18">{{cite book|author=Martin Haenggi|title=वायरलेस नेटवर्क के लिए स्टोचैस्टिक ज्योमेट्री|url=https://books.google.com/books?id=CLtDhblwWEgC&pg=PA18|year=2013|publisher=Cambridge University Press|isbn=978-1-107-01469-5|pages=18–19}}</ref> या '''सामान्य पॉइसन प्रक्रिया'''<ref name="BaddeleyBárány2006page12"/> के रूप में जाना जाता है, जो कि स्थानीय-परिमित माप है। सामान्य तौर पर, यह रेडॉन माप <math>\textstyle \Lambda</math> परमाणु हो सकता है, जिसका अर्थ है कि पॉसों बिंदु प्रक्रिया के कई बिंदु अंतर्निहित समष्टि के एक ही स्थान पर विद्यमान हो सकते हैं। इस स्थिति में, <math>\textstyle x </math> पर बिंदुओं की संख्या <math>\textstyle \Lambda({x})</math> माध्य के साथ एक पॉइसन यादृच्छिक चर होता है।<ref name="Haenggi2013page18" /> लेकिन कभी-कभी विपरीत मान लिया जाता है, इसलिए रेडॉन माप <math>\textstyle \Lambda</math> विसरित या गैर-परमाणु है।<ref name="ChiuStoyan2013page51"/> | ||
बिंदु प्रक्रिया <math>\textstyle {N}</math>, | बिंदु प्रक्रिया <math>\textstyle {N}</math>, तीव्रता <math>\textstyle \Lambda</math> के साथ सामान्य पॉइसन बिंदु प्रक्रिया है, यदि इसमें निम्नलिखित दो गुण हैं:<ref name="ChiuStoyan2013page51"/> | ||
* परिबद्ध [[बोरेल सेट|बोरेल समुच्चय]] <math>\textstyle B</math> में अंकों की संख्या माध्य <math>\textstyle \Lambda(B)</math> के साथ एक | * परिबद्ध [[बोरेल सेट|बोरेल समुच्चय]] <math>\textstyle B</math> में अंकों की संख्या माध्य <math>\textstyle \Lambda(B)</math> के साथ एक पॉइसन यादृच्छिक चर है। दूसरे शब्दों में, <math>\textstyle {N}(B)</math> द्वारा <math>\textstyle B</math> में स्थित अंकों की कुल संख्या को निरूपित करें, फिर यादृच्छिक चर <math>\textstyle {N}(B)</math> के <math>\textstyle n</math> के बराबर होने की प्रायिकता इस प्रकार दी गई है: | ||
:: <math> \Pr \{ N(B)=n\}=\frac{(\Lambda(B))^n}{n!} e^{-\Lambda(B)} </math> | :: <math> \Pr \{ N(B)=n\}=\frac{(\Lambda(B))^n}{n!} e^{-\Lambda(B)} </math> | ||
* <math>\textstyle n</math> असंयुक्त बोरेल समुच्चय में बिंदुओं की संख्या <math>\textstyle n</math> स्वतंत्र यादृच्छिक चर बनाती है। | * <math>\textstyle n</math> असंयुक्त बोरेल समुच्चय में बिंदुओं की संख्या <math>\textstyle n</math> स्वतंत्र यादृच्छिक चर बनाती है। | ||
| Line 229: | Line 229: | ||
:<math> \Lambda (B)=\int_B \lambda(x)\,\mathrm dx, </math> | :<math> \Lambda (B)=\int_B \lambda(x)\,\mathrm dx, </math> | ||
जहां घनत्व <math>\textstyle \lambda(x)</math> को अन्य पदों के साथ-साथ | जहां घनत्व <math>\textstyle \lambda(x)</math> को अन्य पदों के साथ-साथ तीव्रता फलन के रूप में जाना जाता है। | ||
== इतिहास == | == इतिहास == | ||
=== | === पॉइसन बंटन === | ||
इसके नाम के अतिरिक्त, | इसके नाम के अतिरिक्त, पॉइसन बिंदु प्रक्रिया की न तो खोज की गई और न ही फ्रांसीसी गणितज्ञ सिमोन डेनिस पॉइसन द्वारा इसका अध्ययन किया गया; स्टिग्लर के नियम के उदाहरण के रूप में नाम का उल्लेख किया गया है।<ref name="Stirzaker2000"/><ref name="GuttorpThorarinsdottir2012"/> यह नाम पॉइसन बंटन के साथ इसके अंतर्निहित संबंध से प्राप्त हुआ, जो पॉइसन द्वारा द्विपद बंटन के किसी परिमित स्थिति के रूप में प्राप्त किया गया है।<ref name="Good1986">{{cite journal|last1=Good|first1=I. J.|title=प्वासों के कार्य के कुछ सांख्यिकीय अनुप्रयोग|journal=Statistical Science|volume=1|issue=2|year=1986|pages=157–170|issn=0883-4237|doi=10.1214/ss/1177013690|doi-access=free}}</ref> यह प्रायिकता <math>\textstyle p</math> के साथ <math>\textstyle n</math> बर्नौली परीक्षणों के योग की प्रायिकता का वर्णन करता है, जिसकी तुलना प्रायः हेड (या टेल) की संख्या के साथ की जाती है, जो एक सिक्के के <math>\textstyle n</math> पक्षपाती फ़्लिप के बाद हेड (या टेल) की प्रायिकता <math>\textstyle p</math> होती है। कुछ धनात्मक नियतांक <math>\textstyle \Lambda>0</math> के लिए, जैसे-जैसे <math>\textstyle n</math> अनंत की ओर बढ़ता है और <math>\textstyle p</math> शून्य की ओर घटता जाता है जैसे कि उत्पाद <math>\textstyle np=\Lambda</math> नियत हो जाता है, पॉइसन बंटन द्विपद के अधिक निकट आ जाता है।<ref name="grimmett2001probability">{{cite book |first1=G. |last1=Grimmett |first2=D. |last2=Stirzaker |title=संभाव्यता और यादृच्छिक प्रक्रियाएं|publisher=Oxford University Press |edition=3rd |year=2001 |isbn=0-19-857222-0 }}</ref> | ||
पॉइसन ने <math>\textstyle p</math> (शून्य से) और <math>\textstyle n</math> (अनंत तक) की सीमा में द्विपद बंटन की जांच करके, 1841 में प्रकाशित, पॉइसन बंटन को व्युत्पन्न किया। पॉइसन के सभी फलनों में यह केवल एक बार प्रकट होता है,<ref name="stigler1982poisson">{{cite journal |first=S. M. |last=Stigler |title=पॉसॉन वितरण पर पॉसॉन|journal=Statistics & Probability Letters |volume=1 |issue=1 |pages=33–35 |year=1982 |doi=10.1016/0167-7152(82)90010-4 }}</ref> और उनके समय में परिणाम अच्छी तरह से ज्ञात नहीं था। बाद के वर्षों में [[फिलिप लुडविग वॉन सेडेल]] और [[अर्नेस्ट अब्बे]] सहित कई लोगों ने पॉइसन का हवाला दिए बिना बंटन का उपयोग किया।{{sfnp|Daley|Vere-Jones|2003|pages=8–9}}<ref name="Stirzaker2000" /> उन्नीसवीं शताब्दी के अंत में, [[लैडिसलॉस बोर्टकिविक्ज़]] बंटन का फिर से अलग सेटिंग में अध्ययन करेगा (पॉइसन का उल्लेखन करते हुए), वास्तविक डेटा के साथ बंटन का उपयोग करके प्रशिया सेना में हॉर्स किक से होने वाली मौतों की संख्या का अध्ययन करने के लिए।<ref name="Good1986" /><ref name="quine1987bortkiewicz">{{cite journal |first1=M. |last1=Quine |first2=E. |last2=Seneta |title=Bortkiewicz डेटा और छोटी संख्या का नियम|journal=International Statistical Review |volume=55 |issue=2 |pages=173–181 |year=1987 |doi=10.2307/1403193 |jstor=1403193 }}</ref> | |||
=== खोज === | === खोज === | ||
पॉइसन बिंदु प्रक्रिया के पहले उपयोग या खोज के लिए कई दावे हैं।<ref name="Stirzaker2000"/><ref name="GuttorpThorarinsdottir2012"/> उदाहरण के लिए, 1767 में पॉइसन के जन्म से दस साल पहले, [[जॉन मिशेल]] ने एक सितारे के एक निश्चित क्षेत्र में दूसरे सितारे की प्रायिकता की रुपरेखा के बारे में रुचि दिखाई, असुमंगल या "केवल संयोग के द्वारा बिखेरे गए" सितारों की अनुमानित संख्या का अध्ययन किया और [[प्लीएडेस|प्लेयडीज़]] में छह सबसे चमकदार सितारों, पॉइसन बंटन प्राप्त किए बिना। इस काम ने [[साइमन न्यूकॉम्ब]] को प्रभावित किया और उन्हें समस्या का अध्ययन करने और 1860 में द्विपद बंटन के लिए वर्गीकरण के रूप में पॉइसन बंटन की गणना करने के लिए प्रेरित किया।<ref name="GuttorpThorarinsdottir2012"/> | |||
20वीं शताब्दी की शुरुआत में पोइसन प्रक्रिया (एक आयाम में) विभिन्न स्थितियों में स्वतंत्र रूप से उत्पन्न होगी।<ref name="Stirzaker2000"/><ref name="GuttorpThorarinsdottir2012"/> स्वीडन 1903 में, [[फिलिप लुंडबर्ग]] ने एक थीसिस प्रकाशित की जिसमें कार्य शामिल था, जिसे अब मौलिक और अग्रणी माना जाता है, जहां उन्होंने एक सजातीय पॉइसन प्रक्रिया के साथ बीमा दावों को मॉडल करने का प्रस्ताव दिया।<ref name="EmbrechtsFrey2001page367">{{cite book|last1=Embrechts|first1=Paul|title=Stochastic Processes: Theory and Methods|last2=Frey|first2=Rüdiger|last3=Furrer|first3=Hansjörg|chapter=Stochastic processes in insurance and finance|volume=19|year=2001|page=367|issn=0169-7161|doi=10.1016/S0169-7161(01)19014-0|series=Handbook of Statistics|isbn=9780444500144}}</ref><ref name="Cramér1969">{{cite journal|last1=Cramér|first1=Harald|title=जोखिम सिद्धांत पर फ़िलिप लुंडबर्ग के कार्यों की ऐतिहासिक समीक्षा|journal=Scandinavian Actuarial Journal|volume=1969|issue=sup3|year=1969|pages=6–12|issn=0346-1238|doi=10.1080/03461238.1969.10404602}}</ref> | 20वीं शताब्दी की शुरुआत में पोइसन प्रक्रिया (एक आयाम में) विभिन्न स्थितियों में स्वतंत्र रूप से उत्पन्न होगी।<ref name="Stirzaker2000"/><ref name="GuttorpThorarinsdottir2012"/> स्वीडन 1903 में, [[फिलिप लुंडबर्ग]] ने एक थीसिस प्रकाशित की जिसमें कार्य शामिल था, जिसे अब मौलिक और अग्रणी माना जाता है, जहां उन्होंने एक सजातीय पॉइसन प्रक्रिया के साथ बीमा दावों को मॉडल करने का प्रस्ताव दिया।<ref name="EmbrechtsFrey2001page367">{{cite book|last1=Embrechts|first1=Paul|title=Stochastic Processes: Theory and Methods|last2=Frey|first2=Rüdiger|last3=Furrer|first3=Hansjörg|chapter=Stochastic processes in insurance and finance|volume=19|year=2001|page=367|issn=0169-7161|doi=10.1016/S0169-7161(01)19014-0|series=Handbook of Statistics|isbn=9780444500144}}</ref><ref name="Cramér1969">{{cite journal|last1=Cramér|first1=Harald|title=जोखिम सिद्धांत पर फ़िलिप लुंडबर्ग के कार्यों की ऐतिहासिक समीक्षा|journal=Scandinavian Actuarial Journal|volume=1969|issue=sup3|year=1969|pages=6–12|issn=0346-1238|doi=10.1080/03461238.1969.10404602}}</ref> | ||
1909 में [[डेनमार्क]] में एक अन्य खोज हुई जब ए.के. अर्लांग ने सीमित समय अंतराल में आने वाले फोन कॉलों की संख्या के लिए एक गणितीय मॉडल विकसित करते समय | 1909 में [[डेनमार्क]] में एक अन्य खोज हुई जब ए.के. अर्लांग ने सीमित समय अंतराल में आने वाले फोन कॉलों की संख्या के लिए एक गणितीय मॉडल विकसित करते समय पॉइसन बंटन की खोज की। उस समय अर्लांग को पॉइसन के पहले के काम की जानकारी नहीं थी और उन्होंने माना कि प्रत्येक समय अंतराल में आने वाले फोन कॉलों की संख्या एक दूसरे के अन्यान्य हैं। फिर उन्होंने सीमित स्थिति को खोजा, जो प्रभावी रूप से पॉइसन बंटन को द्विपद बंटन की सीमा के रूप में पुनर्स्थापित कर रही है।<ref name="Stirzaker2000"/> | ||
1910 में [[अर्नेस्ट रदरफोर्ड]] और [[हंस गीजर]] ने अल्फा कणों की गणना पर प्रयोगात्मक परिणाम प्रकाशित किए। उनके प्रायोगिक कार्य में [[हैरी बेटमैन]] से गणितीय योगदान था, जिन्होंने अंतर समीकरणों के परिवार के समाधान के रूप में | 1910 में [[अर्नेस्ट रदरफोर्ड]] और [[हंस गीजर]] ने अल्फा कणों की गणना पर प्रयोगात्मक परिणाम प्रकाशित किए। उनके प्रायोगिक कार्य में [[हैरी बेटमैन]] से गणितीय योगदान था, जिन्होंने अंतर समीकरणों के परिवार के समाधान के रूप में पॉइसन प्रायिकताओं को व्युत्पन्न किया था, हालांकि समाधान पहले प्राप्त किया गया था, जिसके परिणामस्वरूप पॉइसन प्रक्रिया की स्वतंत्र खोज हुई।<ref name="Stirzaker2000"/> इस समय के बाद पॉइसन प्रक्रिया के कई अध्ययन और अनुप्रयोग हुए, लेकिन इसका प्रारंभिक इतिहास जटिल है, जिसे जीवविज्ञानियों, पारिस्थितिकीविदों, इंजीनियरों और विभिन्न भौतिक वैज्ञानिकों द्वारा कई क्षेत्रों में प्रक्रिया के विभिन्न अनुप्रयोगों द्वारा समझाया गया है।<ref name="Stirzaker2000"/> | ||
=== प्रारंभिक अनुप्रयोग === | === प्रारंभिक अनुप्रयोग === | ||
1909 के बाद के वर्षों में | 1909 के बाद के वर्षों में पॉइसन बिंदु प्रक्रिया के कई अध्ययन और अनुप्रयोग हुए, हालांकि, इसका प्रारंभिक इतिहास जटिल है, जिसे [[जीव|बायोलॉजिस्ट]], पारिस्थितिकीविद, अभियंता और अन्य [[भौतिक विज्ञान]] में काम करने वाले लोगों ने इस प्रक्रिया के कई क्षेत्रों में अनेक अनुप्रयोगों के द्वारा समझाया है। प्रारंभिक परिणामों को विभिन्न भाषाओं और विभिन्न संस्करणों में प्रकाशित किया गया, जहां कोई मानक शब्दावली और नोटेशन का उपयोग नहीं हुआ।<ref name="Stirzaker2000"/> उदाहरण के लिए, 1922 में स्वीडिश रसायनविद और [[नोबेल पुरस्कार विजेता|नोबेल पुरस्कार प्राप्तकर्ता]] [[ थिओडोर स्वेडबर्ग |थिओडोर स्वेडबर्ग]] ने एक मॉडल प्रस्तावित किया, जिसमें एक स्थानिक पॉइसन बिंदु प्रक्रिया पौधों को अध्ययन करने के लिए उपयोगी है जो वनस्पति समुदायों में वितरित होते हैं।<ref name="illian2008statistical">{{cite book |first1=J. |last1=Illian |first2=A. |last2=Penttinen |first3=H. |last3=Stoyan |first4=D. |last4=Stoyan |title=स्थानिक बिंदु पैटर्न का सांख्यिकीय विश्लेषण और मॉडलिंग|volume=70 |publisher=John Wiley & Sons |year=2008 |isbn=978-0-470-01491-2 }}</ref> कई गणितज्ञों ने 1930 के दशक में प्रक्रिया का अध्ययन शुरू किया और इसमें [[एंड्री कोलमोगोरोव]], [[विलियम फेलर]] और [[अलेक्सांद्र खींचीं]],<ref name="Stirzaker2000"/> सहित अन्यों ने महत्वपूर्ण योगदान दिया।<ref name="kingman2009first">{{cite journal |first=J. |last=Kingman |title=The first Erlang century—and the next |journal=Queueing Systems |volume=63 |issue=1–4 |pages=3–12 |year=2009 |doi=10.1007/s11134-009-9147-4 |s2cid=38588726 }}</ref> [[टेलीट्रैफिक इंजीनियरिंग|टेलीट्रैफिक अभियतंत्रिकी]] के क्षेत्र में, गणितज्ञों और सांख्यिकीयज्ञों ने पॉइसन और अन्य बिंदु प्रक्रियाओं का अध्ययन किया और उन्हें उपयोग किया।<ref name="haugen1995life">{{cite journal |first=R. B. |last=Haugen |title=कोनी पाम का जीवन और कार्य। कुछ व्यक्तिगत टिप्पणियाँ और अनुभव|journal=VTT Symposium |volume=154 |pages=207 |publisher=Valtion teknillinen tutkimuskeskus |year=1995 |issn=0357-9387 }}</ref> | ||
=== शब्दावली का इतिहास === | === शब्दावली का इतिहास === | ||
1943 में स्वीडिश विद्वान [[कोनी पाम]] ने अपने विधानिका में [[एक आयामी|एक विमीय]] स्थानिकता में | 1943 में स्वीडिश विद्वान [[कोनी पाम]] ने अपने विधानिका में [[एक आयामी|एक विमीय]] स्थानिकता में पॉइसन और अन्य बिंदु प्रक्रियाओं का अध्ययन किया, जहां उन्होंने समय के संबंध में बिंदु के बीच आपसी सांख्यिक या प्रसंभाव्य आधिपत्य की परीक्षा की।।<ref name="DaleyVere-Jones2007page13">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=13–14}}</ref><ref name="haugen1995life"/> उनके कार्य में पहली ज्ञात रूप से टर्म बिंदु प्रक्रियाओं का प्रयोग हुआ, जैसे कि जर्मन में ''पंकटप्रोज़ेस'' के रूप में शब्द ''बिंदु प्रक्रियाओं'' का पहला ज्ञात रिकॉर्ड विद्यमान है।<ref name="DaleyVere-Jones2007page13"/><ref name="GuttorpThorarinsdottir2012"/> | ||
यह माना जाता है<ref name="Stirzaker2000"/> कि 1940 में विलियम फेलर ने इसे | यह माना जाता है<ref name="Stirzaker2000"/> कि 1940 में विलियम फेलर ने इसे ''पॉइसन प्रक्रिया'' के रूप में प्रिंट में पहली बार संदर्भित किया था। हालांकि, स्वीडिश विद्वान ओवे लुंडबर्ग ने अपने 1940 के डॉक्टरेट पेपर में भी इस शब्द का प्रयोग किया था,<ref name="GuttorpThorarinsdottir2012"/> जिसमें फेलर को प्रभावित करने के रूप में स्वीकार किया गया था,<ref name="grandell1997mixed">J. Grandell. ''Mixed poisson processes'', volume 77. CRC Press, 1997.</ref> लेकिन कहा गया है कि फेलर ने 1940 से पहले ही इस शब्द की सृजनशीलता की थी।<ref name="grimmett2001probability"/> यह बात बताई गई है कि फेलर और लुंडबर्ग दोनों ने इस शब्द का उपयोग ऐसे किया, जैसे यह पहले से प्रसिद्ध हो, इससे इसका अर्थ है कि यह तब से पहले ही बोली जाने वाली थी।<ref name="GuttorpThorarinsdottir2012"/> फेलर 1936 से 1939 तक [[स्टॉकहोम विश्वविद्यालय]] में हराल्ड क्रामर के साथ काम कर रहे थे, जहां लुंडबर्ग क्रामर के निर्देशन में एक डॉक्टरेट छात्र थे, जिन्होंने इस शब्द का उपयोग नहीं किया था, जिसकी पुस्तक को वे 1936 में पूरा कर चुके थे, लेकिन इसके बाद की संस्करणों में किया, जिससे यह संकेत मिला है कि ''पॉइसन प्रक्रिया'' शब्द का निर्माण स्टॉकहोम विश्वविद्यालय में 1936 से 1939 के बीच किया गया था।<ref name="GuttorpThorarinsdottir2012"/> | ||
== शब्दावली == | == शब्दावली == | ||
बिंदु प्रक्रिया सिद्धांत की शब्दावली सामान्य रूप से बहुत असमघातीय मानी जाती है।<ref name="GuttorpThorarinsdottir2012"/> बिंदु शब्द को छोड़ दिया जाना एक साधारण बात है,<ref name="DaleyVere-Jones2007"/><ref name="Kingman1992"/> समान | बिंदु प्रक्रिया सिद्धांत की शब्दावली सामान्य रूप से बहुत असमघातीय मानी जाती है।<ref name="GuttorpThorarinsdottir2012"/> बिंदु शब्द को छोड़ दिया जाना एक साधारण बात है,<ref name="DaleyVere-Jones2007"/><ref name="Kingman1992"/> समान पॉइसन (बिंदु) प्रक्रिया को समघातीय पॉइसन (बिंदु) प्रक्रिया के रूप में भी कहा जाता है,<ref name="DaleyVere-Jones2007page19"/> साथ ही यह ''स्थायी'' पॉइसन (बिंदु) प्रक्रिया भी कहलाती है।<ref name="Kingman1992page13"/> असमघातीय पॉइसन बिंदु प्रक्रिया, ''असमघातीय'' के रूप के साथ ही,<ref name="DaleyVere-Jones2007page19"/> ''स्थायी'' पॉइसन प्रक्रिया के रूप में भी उल्लेख की जाती है।<ref name="Tijms2003page22"/>{{sfnp|Cox|Isham|1980|page=X}} | ||
शब्द बिंदु प्रक्रिया की आलोचना की गई है, क्योंकि शब्द प्रक्रिया समय और स्थान के साथ सुझाव दे सकती है, इसलिए यादृच्छिक बिंदु क्षेत्र,<ref name="ChiuStoyan2013page109">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|page=109}}</ref> जिसके परिणामस्वरूप पोइसन यादृच्छिक बिंदु क्षेत्र या पॉइसन बिंदु क्षेत्र का भी उपयोग किया जाता है।<ref name="mikhailov2010statistical">G. Mikhailov and T. Averina. Statistical modeling of inhomogeneous random functions on the basis of poisson point fields. In ''Doklady Mathematics'', volume 82, pages 701–704. Springer, 2010.</ref> एक बिंदु प्रक्रिया को माना जाता है, और कभी-कभी इसे एक यादृच्छिक गिनती माप कहा जाता है,<ref name="molchanov2006theory">I. Molchanov. ''Theory of random sets''. Springer Science \& Business Media, 2006.</ref> इसलिए पॉसॉन बिंदु प्रक्रिया को एक पॉइसन यादृच्छिक माप के रूप में भी जाना जाता है,<ref name="sato1999levy">K. Sato. Lévy processes and infinite divisibility, 1999.</ref> लेवी प्रक्रियाओं के अध्ययन में प्रयुक्त शब्द,<ref name="sato1999levy"/><ref name="mandrekar2015stochastic">V. Mandrekar and B. Rüdiger. ''Stochastic Integration in Banach Spaces''. Springer, 2015.</ref> लेकिन कुछ लोग दो अलग-अलग अंतर्निहित स्थानों पर परिभाषित प्वासों बिंदु प्रक्रियाओं के लिए दो शब्दों का उपयोग करना चुनते हैं।<ref name="applebaum2009levy">D. Applebaum. ''Lévy processes and stochastic calculus''. Cambridge university press, 2009.</ref> | शब्द ''बिंदु प्रक्रिया'' की आलोचना की गई है, क्योंकि शब्द ''प्रक्रिया'' समय और स्थान के साथ सुझाव दे सकती है, इसलिए ''यादृच्छिक बिंदु क्षेत्र'',<ref name="ChiuStoyan2013page109">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|page=109}}</ref> जिसके परिणामस्वरूप ''पोइसन यादृच्छिक बिंदु क्षेत्र'' या ''पॉइसन बिंदु क्षेत्र'' का भी उपयोग किया जाता है।<ref name="mikhailov2010statistical">G. Mikhailov and T. Averina. Statistical modeling of inhomogeneous random functions on the basis of poisson point fields. In ''Doklady Mathematics'', volume 82, pages 701–704. Springer, 2010.</ref> एक बिंदु प्रक्रिया को माना जाता है, और कभी-कभी इसे एक यादृच्छिक गिनती माप कहा जाता है,<ref name="molchanov2006theory">I. Molchanov. ''Theory of random sets''. Springer Science \& Business Media, 2006.</ref> इसलिए पॉसॉन बिंदु प्रक्रिया को एक ''पॉइसन यादृच्छिक'' ''माप'' के रूप में भी जाना जाता है,<ref name="sato1999levy">K. Sato. Lévy processes and infinite divisibility, 1999.</ref> लेवी प्रक्रियाओं के अध्ययन में प्रयुक्त शब्द,<ref name="sato1999levy"/><ref name="mandrekar2015stochastic">V. Mandrekar and B. Rüdiger. ''Stochastic Integration in Banach Spaces''. Springer, 2015.</ref> लेकिन कुछ लोग दो अलग-अलग अंतर्निहित स्थानों पर परिभाषित प्वासों बिंदु प्रक्रियाओं के लिए दो शब्दों का उपयोग करना चुनते हैं।<ref name="applebaum2009levy">D. Applebaum. ''Lévy processes and stochastic calculus''. Cambridge university press, 2009.</ref> | ||
पॉइसन बिंदु प्रक्रिया की आधारभूत गणितीय स्थान को "'''कैरियर समष्टि'''",<ref name="harding1974stochastic">E. F. Harding and R. Davidson. ''Stochastic geometry: a tribute to the memory of Rollo Davidson''. Wiley, 1974.</ref><ref name="chen2004stein">L. H. Chen and A. Xia. Stein's method, Palm theory and Poisson process approximation. ''Annals of probability'', pages 2545–2569, 2004.</ref> या "'''स्थिति समष्टि'''" कहा जाता है, हालांकि इस्पात संदर्भ में दूसरा शब्द अलग अर्थ रखता है। बिंदु प्रक्रियाओं के संदर्भ में, "स्थिति समष्टि" शब्द का उपयोग बिंदु प्रक्रिया के परिभाषित स्थान को दर्शाने के लिए किया जा सकता है, जैसे वास्तविक रेखा,<ref name="Kingman1992page8">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=8}}</ref><ref name="MollerWaagepetersen2003page7">{{cite book|author1=Jesper Moller|author2=Rasmus Plenge Waagepetersen|title=स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण|url=https://books.google.com/books?id=dBNOHvElXZ4C|date=25 September 2003|publisher=CRC Press|isbn=978-0-203-49693-0|page=7}}</ref> जो प्रसंभाव्य प्रक्रिया की शब्दावली में अनुक्रमणिका समुच्चय<ref name="Parzen1999page7and29">{{cite book|author=Emanuel Parzen|title=स्टचास्तिक प्रोसेसेज़|url=https://books.google.com/books?id=0mB2CQAAQBAJ|date=17 June 2015|publisher=Courier Dover Publications|isbn=978-0-486-79688-8|pages=7–8 and 29–30}}</ref>या पैरामीटर समुच्चय<ref name="Lamperti1977page1and10">{{cite book|author=John Lamperti|title=Stochastic processes: a survey of the mathematical theory|url=https://books.google.com/books?id=Pd4cvgAACAAJ|year=1977|publisher=Springer-Verlag|isbn=978-3-540-90275-1|pages=1 and 10–11}}</ref> के समर्थन स्थान के तौर पर प्रतिष्ठित होती है। | |||
माप <math>\textstyle \Lambda</math> को | माप <math>\textstyle \Lambda</math> को ''तीव्रता माप'' कहा जाता है,<ref name="ChiuStoyan2013page112">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|page=112}}</ref> ''औसत माप'',<ref name="Kingman1992page11" /> या ''पैरामीटर माप'',<ref name="DaleyVere-Jones2007IIpage31" /> क्योंकि इसमें कोई मानक शब्द नहीं हैं।<ref name="Kingman1992page11" /> यदि <math>\textstyle \Lambda</math> का व्युत्पन्न या घनत्व है, जिसे <math>\textstyle \lambda(x)</math> द्वारा निरूपित किया जाता है, तो पॉइसन बिंदु प्रक्रिया का ''तीव्रता फलन'' कहा जाता है।<ref name="ChiuStoyan2013page51" /> समघातीय पोइसन बिंदु प्रक्रिया के लिए, तीव्रता माप का व्युत्पन्न केवल स्थिर <math>\textstyle \lambda>0</math> है, जिसे दर के रूप में संदर्भित किया जा सकता है, आमतौर पर जब अंतर्निहित समष्टि वास्तविक रेखा या ''तीव्रता'' होती है।<ref name="Kingman1992page13" /> इसे ''औसत दर'' या ''औसत घनत्व''<ref name="DaleyVere-Jones2007page20">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=20}}</ref> या ''दर'' भी कहा जाता है।<ref name="Ross1996page59" /> <math>\textstyle \lambda=1</math> के लिए, संबंधित प्रक्रिया को कभी-कभी ''मानक पॉइसन'' (बिंदु) प्रक्रिया के रूप में जाना जाता है।<ref name="MollerWaagepetersen2003page14" /><ref name="merzbach1986characterization" /><ref name="grandell1977point">J. Grandell. Point processes and random measures. ''Advances in Applied Probability'', pages 502–526, 1977.</ref> | ||
पॉइसन बिंदु प्रक्रिया की सीमा को कभी-कभी ''एक्सपोजर'' कहा जाता है।<ref name="Vose">{{Citation | title = Some Poisson models | publisher = Vose Software | |||
| url = http://www.vosesoftware.com/ModelRiskHelp/index.htm#Probability_theory_and_statistics/Stochastic_processes/Some_Poisson_models.htm | | url = http://www.vosesoftware.com/ModelRiskHelp/index.htm#Probability_theory_and_statistics/Stochastic_processes/Some_Poisson_models.htm | ||
| access-date = 18 January 2016}}</ref><ref name="Jouni">{{Citation | | access-date = 18 January 2016}}</ref><ref name="Jouni">{{Citation | ||
| Line 284: | Line 284: | ||
{{main|बिंदु प्रक्रिया अंकन}} | {{main|बिंदु प्रक्रिया अंकन}} | ||
पॉइसन बिंदु प्रक्रिया की नोटेशन इसकी स्थापना और उस क्षेत्र पर निर्भर करती है जिसमें इसका उपयोग हो रहा है। उदाहरण के लिए, वास्तविक रेखा पर, पॉइसन प्रक्रिया, समरूपी या असमरूपी दोनों, कभी-कभी एक गिनती प्रक्रिया के रूप में व्याख्या की जाती है, और नोटेशन <math>\textstyle \{N(t), t\geq 0\}</math> का प्रयोग पॉइसन प्रक्रिया को प्रतिष्ठान करने के लिए किया जाता है।<ref name="Tijms2003page1" /><ref name="Ross1996page59" /> | |||
विभिन्न नोटेशन के लिए एक अन्य कारण बिंदु प्रक्रिया के सिद्धांत का हो सकता है, जिसके कुछ गणितीय व्याख्यान होते हैं। उदाहरण के लिए, | विभिन्न नोटेशन के लिए एक अन्य कारण बिंदु प्रक्रिया के सिद्धांत का हो सकता है, जिसके कुछ गणितीय व्याख्यान होते हैं। उदाहरण के लिए, साधारण पॉइसन बिंदु प्रक्रिया को किसी यादृच्छिक समुच्चय के रूप में विचार किया जा सकता है, जिससे संकेतन <math>\textstyle x\in N</math> दर्शाते है, जो प्रस्तावित करता है कि <math>\textstyle x</math> पॉइसन बिंदु प्रक्रिया <math>\textstyle N</math> का एक यादृच्छिक बिंदु होता है या इसका तत्व होता है। एक अन्य अधिक सामान्य, व्याख्या यह है कि पॉइसन या किसी अन्य बिंदु प्रक्रिया को किसी यादृच्छिक गणना माप के रूप में विचार किया जा सकता है, ताकि हम किसी (बोरेल माप्य) क्षेत्र <math>\textstyle B</math> में पाए जाने वाले बिंदुओं की संख्या <math>\textstyle {N}</math> को <math>\textstyle N(B)</math> के रूप में लिख सकें, जो एक यादृच्छिक परिवर्तन है। इन विभिन्न व्याख्याओं के परिणामस्वरूप गणितीय क्षेत्रों जैसे माप सिद्धांत और सेट सिद्धांत से संकेतन का उपयोग किया जाता है।<ref name="ChiuStoyan2013page110" /> | ||
सामान्य बिंदु प्रक्रियाओं के लिए, कभी-कभी बिंदु प्रतीक पर सबस्क्रिप्ट, उदाहरण के लिए <math>\textstyle x</math>, सम्मिलित होता है अतः किसी व्यष्टि बिंदु को इसे छोड़कर (समुच्चय अंकन के साथ) <math>\textstyle x_i\in N</math> के स्थान पर <math>\textstyle x\in N</math> के रूप में लिखा जाता है, और ऐसे समाकल व्यंजकों में [[बाध्य चर|परिमित चर]] के लिए <math>\textstyle x</math> का प्रयोग किया जा सकता है, जैसे कैम्पबेल के सिद्धांत में, जो यादृच्छिक बिंदुओं का प्रतिनिधित्व नहीं करता है।<ref name="baccelli2009stochastic1" /> कभी-कभी बड़ा अक्षर बिंदु प्रक्रिया को दर्शाता है, जबकि छोटा अक्षर प्रक्रिया से एक बिंदु को दर्शाता है, इसलिए, उदाहरण के लिए, बिंदु <math>\textstyle x</math> या <math>\textstyle x_i</math> बिंदु प्रक्रिया <math>\textstyle X</math> का भाग होता है या उसका बिंदु होता है, और समुच्चय अंकन के साथ <math>\textstyle x\in X</math> या <math>\textstyle x_i\in X</math> के रूप में लिखा जा सकता है।<ref name="MollerWaagepetersen2003page7" /> | सामान्य बिंदु प्रक्रियाओं के लिए, कभी-कभी बिंदु प्रतीक पर सबस्क्रिप्ट, उदाहरण के लिए <math>\textstyle x</math>, सम्मिलित होता है अतः किसी व्यष्टि बिंदु को इसे छोड़कर (समुच्चय अंकन के साथ) <math>\textstyle x_i\in N</math> के स्थान पर <math>\textstyle x\in N</math> के रूप में लिखा जाता है, और ऐसे समाकल व्यंजकों में [[बाध्य चर|परिमित चर]] के लिए <math>\textstyle x</math> का प्रयोग किया जा सकता है, जैसे कैम्पबेल के सिद्धांत में, जो यादृच्छिक बिंदुओं का प्रतिनिधित्व नहीं करता है।<ref name="baccelli2009stochastic1" /> कभी-कभी बड़ा अक्षर बिंदु प्रक्रिया को दर्शाता है, जबकि छोटा अक्षर प्रक्रिया से एक बिंदु को दर्शाता है, इसलिए, उदाहरण के लिए, बिंदु <math>\textstyle x</math> या <math>\textstyle x_i</math> बिंदु प्रक्रिया <math>\textstyle X</math> का भाग होता है या उसका बिंदु होता है, और समुच्चय अंकन के साथ <math>\textstyle x\in X</math> या <math>\textstyle x_i\in X</math> के रूप में लिखा जा सकता है।<ref name="MollerWaagepetersen2003page7" /> | ||
| Line 298: | Line 298: | ||
प्रायिकता सिद्धांत में, विभिन्न उद्देश्यों के लिए यादृच्छिक संख्याओं पर संचालित किए जाते हैं। कभी-कभी ये संक्रियाएँ नियमित आपेक्षिक होती हैं जो किसी यादृच्छिक संख्या के औसत या प्रसारण का निर्माण करते हैं। अन्य, यादृच्छिक संख्या की विशेषता-कारक (या लाप्लास रूपांतरण) के रूप में उपयोग किए जा सकते हैं, जो यादृच्छिक संख्याओं की अद्वितीय पहचान करने या वर्गमूल सीमा सिद्धांत जैसे परिणामों को सिद्ध करने में सहायता प्रदान करते हैं।<ref name="karr1993probability">A. Karr. ''Probability''. Springer Texts in Statistics Series. Springer-Verlag, 1993.</ref> बिंदु प्रक्रिया के सिद्धांत में, इसी तरह के गणितीय साधन होते हैं जो सामान्यतः किसी माप और कार्यात्मक के रूप में होते हैं और किसी भी प्रकार के मोमेंट और फलन के के स्थान पर विद्यमान होते हैं।<ref name="ChiuStoyan2013page120to126">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=120–126}}</ref><ref name="DaleyVere-Jones2007page52to75">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=52–75}}</ref> | प्रायिकता सिद्धांत में, विभिन्न उद्देश्यों के लिए यादृच्छिक संख्याओं पर संचालित किए जाते हैं। कभी-कभी ये संक्रियाएँ नियमित आपेक्षिक होती हैं जो किसी यादृच्छिक संख्या के औसत या प्रसारण का निर्माण करते हैं। अन्य, यादृच्छिक संख्या की विशेषता-कारक (या लाप्लास रूपांतरण) के रूप में उपयोग किए जा सकते हैं, जो यादृच्छिक संख्याओं की अद्वितीय पहचान करने या वर्गमूल सीमा सिद्धांत जैसे परिणामों को सिद्ध करने में सहायता प्रदान करते हैं।<ref name="karr1993probability">A. Karr. ''Probability''. Springer Texts in Statistics Series. Springer-Verlag, 1993.</ref> बिंदु प्रक्रिया के सिद्धांत में, इसी तरह के गणितीय साधन होते हैं जो सामान्यतः किसी माप और कार्यात्मक के रूप में होते हैं और किसी भी प्रकार के मोमेंट और फलन के के स्थान पर विद्यमान होते हैं।<ref name="ChiuStoyan2013page120to126">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=120–126}}</ref><ref name="DaleyVere-Jones2007page52to75">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=52–75}}</ref> | ||
=== लाप्लास प्रकार्य === | === लाप्लास प्रकार्य === | ||
किसी स्थान <math>X</math> पर | किसी स्थान <math>X</math> पर तीव्रता माप <math>\textstyle \Lambda</math> के साथ किसी पॉइसन बिंदु प्रक्रिया <math>\textstyle N</math> के लिए, [[लाप्लास कार्यात्मक|लाप्लास प्रकार्य]] निम्नलिखित द्वारा दिया जाता है:<ref name="baccelli2009stochastic1"/> | ||
:<math> L_N(f)= \mathbb{E} e^{-\int_X f(x)\, N(\mathrm dx)} = e^{-\int_{X}(1-e^{-f(x)})\Lambda(\mathrm dx)}, </math> | :<math> L_N(f)= \mathbb{E} e^{-\int_X f(x)\, N(\mathrm dx)} = e^{-\int_{X}(1-e^{-f(x)})\Lambda(\mathrm dx)}, </math> | ||
कैंपबेल के प्रमेय के एक संस्करण में | कैंपबेल के प्रमेय के एक संस्करण में पॉइसन बिंदु प्रक्रिया के लाप्लास प्रकार्य सम्मिलित है। | ||
=== प्रायिकता जनित्र फलन === | === प्रायिकता जनित्र फलन === | ||
गैर-ऋणात्मक पूर्णांक-मूल्यवान यादृच्छिक चर का प्रायिकता जनित्र फलन किसी भी गैर- | गैर-ऋणात्मक पूर्णांक-मूल्यवान यादृच्छिक चर का प्रायिकता जनित्र फलन किसी भी गैर-ऋणात्मक परिबद्ध फलन <math>\textstyle v</math> पर <math>\textstyle \mathbb{R}^d</math> जैसे कि <math>\textstyle 0\leq v(x) \leq 1</math> के संबंध में समान रूप से परिभाषित प्रायिकता जनित्र फलन की ओर जाता है। किसी बिंदु प्रक्रिया के लिए <math>\textstyle {N}</math> प्रायिकता जनित्र फलन को परिभाषित किया गया है :<ref name="ChiuStoyan2013page125">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=125–126}}</ref> | ||
:<math> G(v)=\operatorname E \left[\prod_{x\in N} v(x) \right] </math> | :<math> G(v)=\operatorname E \left[\prod_{x\in N} v(x) \right] </math> | ||
जहां गुणनफल <math display="inline"> N </math> में सभी बिंदुओं के लिए किया जाता है। यदि <math>\textstyle {N}</math> की | जहां गुणनफल <math display="inline"> N </math> में सभी बिंदुओं के लिए किया जाता है। यदि <math>\textstyle {N}</math> की तीव्रता माप <math>\textstyle \Lambda</math> स्थानीय रूप से परिमित है, अतः <math display="inline"> G</math>, <math>\textstyle \mathbb{R}^d</math> पर किसी भी मापनीय फलन <math>\textstyle u</math> के लिए अच्छी तरह से परिभाषित है। तीव्रता माप <math>\textstyle \Lambda</math> के साथ किसी पॉइसन बिंदु प्रक्रिया के लिए जनित्र फलन द्वारा दिया गया है: | ||
:<math> G(v)=e^{-\int_{\mathbb{R}^d} [1-v(x)]\,\Lambda(\mathrm dx)}, </math> | :<math> G(v)=e^{-\int_{\mathbb{R}^d} [1-v(x)]\,\Lambda(\mathrm dx)}, </math> | ||
| Line 314: | Line 314: | ||
:<math> G(v)=e^{-\lambda\int_{\mathbb{R}^d} [1-v(x)]\,\mathrm dx}. </math> | :<math> G(v)=e^{-\lambda\int_{\mathbb{R}^d} [1-v(x)]\,\mathrm dx}. </math> | ||
=== मोमेंट माप === | === मोमेंट माप === | ||
तीव्रता माप <math>\textstyle \Lambda</math> के साथ एक सामान्य पॉइसन बिंदु प्रक्रिया के लिए प्रथम मोमेंट माप इसकी तीव्रता माप है:<ref name="baccelli2009stochastic1"/><ref name="Haenggi2013"/> | |||
:<math> M^1(B)=\Lambda(B), </math> | :<math> M^1(B)=\Lambda(B), </math> | ||
जो सतत | जो सतत तीव्रता <math>\textstyle \lambda</math> के साथ समघातीय पॉइसन बिंदु प्रक्रिया के लिए है: | ||
:<math> M^1(B)=\lambda|B|, </math> | :<math> M^1(B)=\lambda|B|, </math> | ||
| Line 323: | Line 323: | ||
=== मेके समीकरण === | === मेके समीकरण === | ||
मेके समीकरण | मेके समीकरण पॉइसन बिंदु प्रक्रिया की विशेषता बताता है। <math>\mathbb{N}_\sigma</math> को कुछ सामान्य स्थान <math>\mathcal{Q}</math> पर सभी <math>\sigma</math>-परिमित उपायों का स्थान दें। <math>\mathcal{Q}</math> पर तीव्रता <math>\lambda</math> के साथ बिंदु प्रक्रिया <math>\eta</math> पॉइसन बिंदु प्रक्रिया है यदि और केवल यदि सभी मापनीय फलनों के लिए <math>f:\mathcal{Q}\times\mathbb{N}_\sigma\to \mathbb{R}_+</math> निम्नलिखित धारण करता है | ||
:<math>\Pr \left[\int f(x,\eta)\eta(\mathrm{d}x)\right]=\int \Pr \left[ f(x,\eta+\delta_x) \right] \lambda(\mathrm{d}x)</math> | :<math>\Pr \left[\int f(x,\eta)\eta(\mathrm{d}x)\right]=\int \Pr \left[ f(x,\eta+\delta_x) \right] \lambda(\mathrm{d}x)</math> | ||
अधिक जानकारी के लिए देखें।<ref name="Proper Point Process">{{cite book|author1=Günter Last|author2=Mathew Penrose|title=प्वासों प्रक्रिया पर व्याख्यान|url=http://www.math.kit.edu/stoch/~last/seite/lectures_on_the_poisson_process/media/lastpenrose2017.pdf|date=8 August 2017}}</ref> | अधिक जानकारी के लिए देखें।<ref name="Proper Point Process">{{cite book|author1=Günter Last|author2=Mathew Penrose|title=प्वासों प्रक्रिया पर व्याख्यान|url=http://www.math.kit.edu/stoch/~last/seite/lectures_on_the_poisson_process/media/lastpenrose2017.pdf|date=8 August 2017}}</ref> | ||
=== क्रमगुणित मोमेंट माप === | === क्रमगुणित मोमेंट माप === | ||
तीव्रता माप <math>\textstyle \Lambda</math> के साथ सामान्य पॉइसन बिंदु प्रक्रिया के लिए <math>\textstyle n</math>-वाँ तथ्यात्मक मोमेंट माप व्यंजक द्वारा दिया जाता है:<ref name="ChiuStoyan2013page47">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=47–48}}</ref> | |||
:<math> M^{(n)}(B_1\times\cdots\times B_n)=\prod_{i=1}^n[\Lambda(B_i)], </math> | :<math> M^{(n)}(B_1\times\cdots\times B_n)=\prod_{i=1}^n[\Lambda(B_i)], </math> | ||
जहां <math>\textstyle \Lambda</math> | जहां <math>\textstyle \Lambda</math> तीव्रता माप या <math>\textstyle {N}</math> का प्रथम मोमेंट माप है, जो कि कुछ बोरेल समुच्चय <math>\textstyle B</math> के द्वारा दिया जाता है | ||
:<math> \Lambda(B)=M^1(B)=\operatorname E[N(B)]. </math> | :<math> \Lambda(B)=M^1(B)=\operatorname E[N(B)]. </math> | ||
किसी समघातीय | किसी समघातीय पॉइसन बिंदु प्रक्रिया के लिए <math>\textstyle n</math>-वां क्रमगुणित मोमेंट मात्र है:<ref name="baccelli2009stochastic1"/><ref name="Haenggi2013"/> | ||
:<math> M^{(n)}(B_1\times\cdots\times B_n)=\lambda^n \prod_{i=1}^n |B_i|, </math> | :<math> M^{(n)}(B_1\times\cdots\times B_n)=\lambda^n \prod_{i=1}^n |B_i|, </math> | ||
| Line 339: | Line 339: | ||
== परिवर्जन फलन == | == परिवर्जन फलन == | ||
परिवर्जन फलन <ref name="DaleyVere-Jones2007page25"/>या | '''परिवर्जन फलन''' <ref name="DaleyVere-Jones2007page25"/>या '''वोयड प्रायिकता''' <ref name="ChiuStoyan2013page110">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|page=100}}</ref> <math>\textstyle v</math> बिंदु प्रक्रिया का <math>\textstyle {N}</math> कुछ सेट के संबंध में परिभाषित किया गया है <math>\textstyle B</math>, जो अंतर्निहित स्थान का सबसेट है <math>\textstyle \mathbb{R}^d</math>, बिना अंक की प्रायिकता के रूप में <math>\textstyle {N}</math> में विद्यमान है <math>\textstyle B</math>. ज्यादा ठीक,<ref name="ChiuStoyan2013page42">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|page=42}}</ref> एक परीक्षण सेट के लिए <math>\textstyle B</math> परिवर्जन फलन द्वारा दिया जाता है: | ||
:<math> v(B)=\Pr \{N(B)=0\}. </math> | :<math> v(B)=\Pr \{N(B)=0\}. </math> | ||
तीव्रता माप <math>\textstyle \Lambda</math> के साथ सामान्य पॉइसन बिंदु प्रक्रिया <math>\textstyle {N}</math> के लिए, इसका परिवर्जन फलन निम्न द्वारा दिया जाता है: | |||
:<math> v(B)=e^{-\Lambda(B)} </math> | :<math> v(B)=e^{-\Lambda(B)} </math> | ||
=== रेनी की प्रमेय === | === रेनी की प्रमेय === | ||
साधारण बिंदु प्रक्रियाएं अपनी शून्यता प्रायिकताओं द्वारा पूर्ण रूप से वर्णीय होती हैं।<ref name="ChiuStoyan2013page43">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|page=43}}</ref> अन्य शब्दों में, साधारण बिंदु प्रक्रिया की पूर्ण जानकारी शून्यता प्रायिकताओं में पूरी तरह से प्रतिष्ठित होती है, और यदि और केवल यदि दो साधारण बिंदु प्रक्रियाएं एक ही बिंदु प्रक्रियाएं हैं तो वे एक ही शून्यता प्रायिकताएं रखती हैं। पॉइसन प्रक्रिया के लिए स्थिति को कभी-कभी ''रेनी के सिद्धांत'' के रूप में जाना जाता है, जो अल्फ्रेड रेनी द्वारा एक-विमा में समान प्रकार की किसी समानांतर बिंदु प्रक्रिया के स्थिति के लिए परिणाम की खोज करने के बाद नामित किया गया है।<ref name="Kingman1992page33">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|pages=34}}</ref> | |||
एक रूप में,<ref name="Kingman1992page33" /> रेनी के सिद्धांत के अनुसार किसी विस्तरित (या गैर-अणुगत) रेडोन माप <math>\textstyle \Lambda</math> पर <math>\textstyle \mathbb{R}^d</math> और एक समुच्चय <math>\textstyle A</math> है जो वर्गों के परिमित संघ है (इसलिए बोरेल{{efn|This set <math>\textstyle A</math> is formed by a finite number of unions, whereas a Borel set is formed by a countable number of set operations.<ref name="DaleyVere-Jones2007page384">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=384–385}}</ref> | एक रूप में,<ref name="Kingman1992page33" /> रेनी के सिद्धांत के अनुसार किसी विस्तरित (या गैर-अणुगत) रेडोन माप <math>\textstyle \Lambda</math> पर <math>\textstyle \mathbb{R}^d</math> और एक समुच्चय <math>\textstyle A</math> है जो वर्गों के परिमित संघ है (इसलिए बोरेल{{efn|This set <math>\textstyle A</math> is formed by a finite number of unions, whereas a Borel set is formed by a countable number of set operations.<ref name="DaleyVere-Jones2007page384">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=384–385}}</ref> | ||
| Line 353: | Line 353: | ||
:<math> \Pr \{N(A)=0\} = v(A) = e^{-\Lambda(A)} </math> | :<math> \Pr \{N(A)=0\} = v(A) = e^{-\Lambda(A)} </math> | ||
तो <math>\textstyle {N}</math> | तो <math>\textstyle {N}</math> तीव्रता माप <math>\textstyle \Lambda</math> के साथ पॉइसन बिंदु प्रक्रिया है। | ||
== बिंदु प्रक्रिया संक्रियाएँ == | == बिंदु प्रक्रिया संक्रियाएँ == | ||
| Line 361: | Line 361: | ||
=== विरलन === | === विरलन === | ||
पॉइसन प्रक्रिया के लिए, स्वतंत्र <math>\textstyle p(x)</math>-विरलन संक्रिया के परिणामस्वरूप एक और पॉइसन बिंदु प्रक्रिया होती है। अधिक विशेष रूप से, तीव्रता माप <math>\textstyle \Lambda</math> के साथ एक पॉइसन बिंदु प्रक्रिया पर लागू एक <math>\textstyle p(x)</math>-विरलन संक्रिया हटाए गए बिंदुओं की एक बिंदु प्रक्रिया देता है जो पॉइसन बिंदु प्रक्रिया <math>\textstyle {N}_p</math> की तीव्रता माप <math>\textstyle \Lambda_p</math> के साथ भी है, जो परिबद्ध बोरेल समुच्चय <math>\textstyle B</math> के लिए दिया गया है: | |||
:<math> \Lambda_p(B)= \int_B p(x)\,\Lambda(\mathrm dx) </math> | :<math> \Lambda_p(B)= \int_B p(x)\,\Lambda(\mathrm dx) </math> | ||
यह | यह पॉइसन बिंदु प्रक्रिया के विरलन का परिणाम कभी-कभी '''प्रेकोपा के सिद्धांत''' के रूप में जाना जाता है।<ref name="ChiuStoyan2013page160">{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|pages=160}}</ref> इसके अतिरिक्त, पॉइसन बिंदु प्रक्रिया को यादृच्छिक रूप से विरलन के बाद, शेष बिंदुओं भी पॉइसन बिंदु प्रक्रिया बनाते हैं, जिसका तीव्रता माप है | ||
:<math> \Lambda_p(B)= \int_B (1-p(x))\,\Lambda(\mathrm dx). </math> | :<math> \Lambda_p(B)= \int_B (1-p(x))\,\Lambda(\mathrm dx). </math> | ||
हटाए गए और रखे गए बिंदुओं से क्रमशः बनने वाली दो अलग-अलग | हटाए गए और रखे गए बिंदुओं से क्रमशः बनने वाली दो अलग-अलग पॉइसन बिंदु प्रक्रियाएं एक दूसरे से प्रसंभाव्य रूप से स्वतंत्र हैं।<ref name="ChiuStoyan2013page158" /> दूसरे शब्दों में, यदि किसी क्षेत्र को <math>\textstyle n</math> रखे हुए बिंदुओं (मूल पॉइसन बिंदु प्रक्रिया से) के लिए जाना जाता है, तो उसी क्षेत्र में हटाए गए बिंदुओं की यादृच्छिक संख्या पर इसका कोई प्रभाव नहीं पड़ेगा। यादृच्छिक रूप से एक से दो स्वतंत्र पॉइसन बिंदु प्रक्रियाओं को बनाने की इस क्षमता को कभी-कभी ''विभाजन''<ref name="bertsekas2008introduction">[[Dimitri Bertsekas|D. Bertsekas]] and [[John Tsitsiklis|J. Tsitsiklis]]. Introduction to probability, ser. ''Athena Scientific optimization and computation series. Athena Scientific'', 2008.</ref><ref name="hayes1984modeling">J. F. Hayes. ''Modeling and analysis of computer communications networks''. Perseus Publishing, 1984.</ref> पॉइसन बिंदु प्रक्रिया के रूप में जाना जाता है। | ||
=== अध्यारोपण === | === अध्यारोपण === | ||
| Line 377: | Line 377: | ||
==== अध्यारोपण प्रमेय ==== | ==== अध्यारोपण प्रमेय ==== | ||
पॉइसन बिंदु प्रक्रिया के '''अध्यारोपण प्रमेय''' का कहना है कि औसत माप <math>\textstyle \Lambda_1,\Lambda_2,\dots</math> के साथ स्वतंत्र पॉइसन बिंदु प्रक्रिया <math>\textstyle N_1,N_2\dots</math> का अध्यारोपण भी औसत माप के साथ एक पॉइसन बिंदु प्रक्रिया होगी<ref name="Kingman1992page16">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=16}}</ref><ref name="grimmett2001probability" /> | |||
:<math> \Lambda=\sum_{i=1}^\infty \Lambda_i. </math> | :<math> \Lambda=\sum_{i=1}^\infty \Lambda_i. </math> | ||
दूसरे शब्दों में, दो (या गणनीय रूप से अधिक) | दूसरे शब्दों में, दो (या गणनीय रूप से अधिक) पॉइसन प्रक्रियाओं का यूनियन अन्य पॉइसन प्रक्रिया है। यदि बिंदु <math display="inline"> x</math> को पॉइसन प्रक्रियाओं के गणनीय <math display="inline"> n</math> यूनियन से सैंपल लिया जाता है, अतः प्रायिकता है कि बिंदु <math>\textstyle x</math>, <math display="inline"> j</math> यूनियन प्रक्रिया <math display="inline"> N_j</math> के अंतर्गत आता है: | ||
:<math> \Pr \{x\in N_j\}=\frac{\Lambda_j}{\sum_{i=1}^n\Lambda_i}. </math> | :<math> \Pr \{x\in N_j\}=\frac{\Lambda_j}{\sum_{i=1}^n\Lambda_i}. </math> | ||
तीव्रता <math display="inline"> \lambda_1,\lambda_2\dots</math> के साथ दो समघातीय पॉइसन प्रक्रियाओं के लिए, पूर्व दो व्यंजक निम्नलिखित परिवर्तित हो जाते है | |||
:<math> \lambda=\sum_{i=1}^\infty \lambda_i, </math> | :<math> \lambda=\sum_{i=1}^\infty \lambda_i, </math> | ||
| Line 391: | Line 391: | ||
=== क्लस्टरिंग === | === क्लस्टरिंग === | ||
जब किसी बिंदु प्रक्रिया <math>\textstyle {N}</math> के प्रत्येक बिंदु <math>\textstyle x</math> को दूसरे (संभवतः अलग) बिंदु प्रक्रिया से प्रतिस्थापित किया जाता है, तब ऑपरेशन क्लस्टरिंग का उपयोग किया जाता है। यदि मूल प्रक्रिया <math>\textstyle {N}</math> | जब किसी बिंदु प्रक्रिया <math>\textstyle {N}</math> के प्रत्येक बिंदु <math>\textstyle x</math> को दूसरे (संभवतः अलग) बिंदु प्रक्रिया से प्रतिस्थापित किया जाता है, तब ऑपरेशन क्लस्टरिंग का उपयोग किया जाता है। यदि मूल प्रक्रिया <math>\textstyle {N}</math> पॉइसन बिंदु प्रक्रिया है, तो परिणामस्वरूपी प्रक्रिया <math>\textstyle {N}_c</math> को पॉइसन क्लस्टर बिंदु प्रक्रिया कहा जाता है। | ||
===यादृच्छिक विस्थापन=== | ===यादृच्छिक विस्थापन=== | ||
गणितीय मॉडल को कभी-कभी यादृच्छिक रूप से गतिमान बिंदुओं की आवश्यकता होती है ताकि उन्हें मूल गणितीय समष्टि पर अन्य स्थानों पर ले जाया जा सके, जिससे बिंदु प्रक्रिया संक्रिया का उत्पन्न होता है जिसे 'स्थानांतरण'<ref name="Kingman1992page61">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=61}}</ref> या 'स्थानांकन'<ref name="DaleyVere-Jones2007page166">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=166–167}}</ref> के नाम से जाना जाता है। | गणितीय मॉडल को कभी-कभी यादृच्छिक रूप से गतिमान बिंदुओं की आवश्यकता होती है ताकि उन्हें मूल गणितीय समष्टि पर अन्य स्थानों पर ले जाया जा सके, जिससे बिंदु प्रक्रिया संक्रिया का उत्पन्न होता है जिसे 'स्थानांतरण'<ref name="Kingman1992page61">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=61}}</ref> या 'स्थानांकन'<ref name="DaleyVere-Jones2007page166">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=166–167}}</ref> के नाम से जाना जाता है। पॉइसन बिंदु प्रक्रिया का उपयोग करके, उदाहरण के लिए, पौधों के पीढ़ियों के बीच चलने का मॉडल बनाने के लिए उपयोग किया गया है, जो 'स्थानांतरण सिद्धांत'<ref name="Kingman1992page61"/> के कारण है, जिसका ठीक-ठीक अर्थ होता है कि पॉइसन बिंदु प्रक्रिया के बिंदुओं का यादृच्छिक स्वतंत्र स्थानांतरण (एक ही मूल समष्टि पर) दूसरी पॉइसन बिंदु प्रक्रिया बनाता है। | ||
==== विस्थापन प्रमेय ==== | ==== विस्थापन प्रमेय ==== | ||
किसी संस्करण में, स्थानांतरण सिद्धांत<ref name="Kingman1992page61"/> में | किसी संस्करण में, स्थानांतरण सिद्धांत<ref name="Kingman1992page61"/> में पॉइसन बिंदु प्रक्रिया <math>\textstyle {N}</math> को <math>\textstyle \mathbb{R}^d</math> पर तीव्रता फलन <math>\textstyle \lambda(x)</math> के साथ निर्धारित किया जाता है। इसके बाद माना जाता है कि <math>\textstyle {N}</math> के बिंदुओं को यादृच्छिक रूप से <math>\textstyle \mathbb{R}^d</math> में कहीं और स्थानांतरित किया जाता है, जिससे प्रत्येक बिंदु का स्थानांतरण स्वतंत्र होता है और एक का विस्थापन पूर्व में <math>\textstyle x</math> पर बिंदु प्रायिकता घनत्व <math>\textstyle \rho(x,\cdot)</math> के साथ यादृच्छिक सदिश होता है।{{efn|Kingman<ref name="Kingman1992page61"/> calls this a probability density, but in other resources this is called a ''probability kernel''.<ref name="baccelli2009stochastic1"/>}} इसके बाद स्थानांतरण से प्राप्त होने वाली नई बिंदु प्रक्रिया, जिसे <math>\textstyle N_D</math> के रूप में चिह्नित किया जाता है, भी पॉइसन बिंदु प्रक्रिया होती है जिसका तीव्रता फलन | ||
:<math> \lambda_D(y)=\int_{\mathbb{R}^d} \lambda(x) \rho(x,y)\,\mathrm dx. </math> | :<math> \lambda_D(y)=\int_{\mathbb{R}^d} \lambda(x) \rho(x,y)\,\mathrm dx. </math> | ||
यदि | यदि पॉइसन प्रक्रिया <math>\textstyle\lambda(x) = \lambda > 0</math> के साथ समघातीय है और यदि <math>\rho(x, y)</math>, <math>y-x</math> का फलन है, अतः | ||
:<math> \lambda_D(y)=\lambda. </math> | :<math> \lambda_D(y)=\lambda. </math> | ||
दूसरे शब्दों में, बिंदुओं के प्रत्येक यादृच्छिक और स्वतंत्र विस्थापन के बाद, मूल | दूसरे शब्दों में, बिंदुओं के प्रत्येक यादृच्छिक और स्वतंत्र विस्थापन के बाद, मूल पॉइसन बिंदु प्रक्रिया अभी भी विद्यमान है। | ||
विस्थापन प्रमेय को विस्थापित किया जा सकता है ताकि | विस्थापन प्रमेय को विस्थापित किया जा सकता है ताकि पॉइसन बिंदुओं को यूक्लिडियन समष्टि <math>\textstyle \mathbb{R}^d</math> से यूक्लिडियन समष्टि <math>\textstyle \mathbb{R}^{d'}</math> में यादृच्छिक रूप से विस्थापित किया जाए, जहां <math>\textstyle d'\geq 1</math>, <math>\textstyle d</math> के बराबर नहीं होता है।<ref name="baccelli2009stochastic1"/> | ||
=== मैपिंग === | === मैपिंग === | ||
अन्य गुणधर्म जिसे उपयोगी माना जाता है वह अंतर्निहित समष्टि से दूसरे स्थान पर | अन्य गुणधर्म जिसे उपयोगी माना जाता है वह अंतर्निहित समष्टि से दूसरे स्थान पर पॉइसन बिंदु प्रक्रिया को मैप करने की क्षमता है।<ref name="Kingman1992page17">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|pages=18}}</ref> | ||
==== मैपिंग प्रमेय ==== | ==== मैपिंग प्रमेय ==== | ||
{{main|मैपिंग प्रमेय (बिंदु प्रक्रिया)}} | {{main|मैपिंग प्रमेय (बिंदु प्रक्रिया)}} | ||
यदि मैपिंग (या परिवर्तन) कुछ शर्तों का पालन करता है, तो परिणामस्वरूप मैप किए गए (या परिवर्तित) बिंदुओं का संग्रह भी | यदि मैपिंग (या परिवर्तन) कुछ शर्तों का पालन करता है, तो परिणामस्वरूप मैप किए गए (या परिवर्तित) बिंदुओं का संग्रह भी पॉइसन बिंदु प्रक्रिया बनाता है, और इस परिणाम को कभी-कभी '''मैपिंग''' '''सिद्धांत''' के रूप में संदर्भित किया जाता है।<ref name="Kingman1992page17"/><ref name="GrimmettStirzaker2001page284">{{cite book|author1=Geoffrey Grimmett|author2=David Stirzaker|title=संभाव्यता और यादृच्छिक प्रक्रियाएं|url=https://books.google.com/books?id=G3ig-0M4wSIC|date=31 May 2001|publisher=OUP Oxford|isbn=978-0-19-857222-0|page=284}}</ref> यह सिद्धांत किसी मूलभूत स्थान पर कुछ पॉइसन बिंदु प्रक्रिया के साथ संबंधित होता है जिसमें माध्यम माप <math>\textstyle \Lambda</math> होती है। यदि बिंदुओं की स्थानों को किसी फलन के अनुसार (अर्थात बिंदु प्रक्रिया परिवर्तित की जाती है) किसी अन्य मूलभूत स्थान में मैप किया जाता है, तो परिणामस्वरूप बिंदु प्रक्रिया भी एक पॉइसन बिंदु प्रक्रिया होती है, लेकिन एक अलग माध्यम माप <math>\textstyle \Lambda'</math> के साथ। | ||
अधिक विशेष रूप से, (बोरेल मापने योग्य) फलन <math>\textstyle f</math> पर विचार किया जा सकता है जो बिंदु प्रक्रिया <math>\textstyle {N}</math> को | अधिक विशेष रूप से, (बोरेल मापने योग्य) फलन <math>\textstyle f</math> पर विचार किया जा सकता है जो बिंदु प्रक्रिया <math>\textstyle {N}</math> को तीव्रता माप <math>\textstyle \Lambda</math> के साथ किसी स्थान <math>\textstyle S</math> से दूसरे स्थान <math>\textstyle T</math> तक इस तरह से मैप करता है ताकि नई बिंदु प्रक्रिया <math>\textstyle {N}'</math> में तीव्रता का माप हो: | ||
:<math> \Lambda(B)'=\Lambda(f^{-1}(B)) </math> | :<math> \Lambda(B)'=\Lambda(f^{-1}(B)) </math> | ||
जहां <math>\textstyle B</math> बोरेल समुच्चय है और <math>\textstyle f^{-1}</math> फलन <math>\textstyle f</math> का व्युत्क्रम होता है, जहाँ कोई अणु नहीं होते हैं। यदि <math>\textstyle {N}</math> | जहां <math>\textstyle B</math> बोरेल समुच्चय है और <math>\textstyle f^{-1}</math> फलन <math>\textstyle f</math> का व्युत्क्रम होता है, जहाँ कोई अणु नहीं होते हैं। यदि <math>\textstyle {N}</math> पॉइसन बिंदु प्रक्रिया है, तो नवीन प्रक्रिया <math>\textstyle {N}'</math> भी पॉइसन बिंदु प्रक्रिया है जिसमें घनत्व माप <math>\textstyle \Lambda'</math> होती है। | ||
== पॉइसन बिंदु प्रक्रियाओं के साथ सन्निकटन == | |||
पॉइसन प्रक्रिया की अनुकरणीयता का अर्थ है कि कभी-कभी गैर-पॉइसन बिंदु प्रक्रिया को पॉइसन प्रक्रिया से अनुमानित करना सुविधाजनक होता है। समग्र उद्देश्य है किसी बिंदु प्रक्रिया के बिंदुओं की संख्या और प्रत्येक बिंदु के स्थान को पॉइसन बिंदु प्रक्रिया से अनुमानित करना।<ref name="chen2013approximating">L. H. Chen, A. Röllin, et al. Approximating dependent rare events. ''Bernoulli'', 19(4):1243–1267, 2013.</ref> ऐसे कई तरीके हैं जो प्रायोगिक या कठोर रूप से उचित पोइसन बिंदु प्रक्रियाओं के साथ यादृच्छिक घटनाओं या घटनाओं की घटना का अनुमान लगाने के लिए किया जा सकता है। अधिक कठोर रूप से पॉइसन और गैर-पॉइसन बिंदु प्रक्रियाओं के बीच प्रायोगिक मेट्रिक्स के बारे में ऊपरी सीमाओं को प्राप्त करने में संलग्न होते हैं, जबकि अन्य विधियों को कम औपचारिक अनुमानों द्वारा तार्किकतापूर्वक विवर्णित किया जा सकता है।<ref name="arratia1993review">R. Arratia, S. Tavare, et al. {Review: D. Aldous, Probability Approximations via the Poisson Clumping Heuristic; AD Barbour, L. Holst, S. Janson, Poisson Approximation}. ''The Annals of Probability'', 21(4):2269–2279, 1993.</ref> | |||
=== क्लंपिंग ह्यूरिस्टिक === | === क्लंपिंग ह्यूरिस्टिक === | ||
पॉइसन प्रक्रियाओं के साथ यादृच्छिक घटनाओं या परिघटनाओं का पूर्वानुमान के लिए एक विधि को '''क्लंपिंग ह्यूरिस्टिक''' कहा जाता है।<ref name="aldous1989poisson">D. Aldous. ''Poisson Clumping Heuristic''. Wiley Online Library, 1989.</ref> सामान्य हेयुरिस्टिक या सिद्धांत में पॉइसन बिंदु प्रक्रिया (या पॉइसन बंटन) का उपयोग अनुमानित घटनाओं के लिए करना सम्मिलित है, जिन्हें कुछ प्रसंभाव प्रक्रिया के दुर्लभ या असंभावित माना जाता है। कुछ स्थितियों में ये दुर्लभ घटनाएं स्वतंत्र होने के निकट हैं, इसलिए पॉइसन बिंदु प्रक्रिया का उपयोग किया जा सकता है। जब घटनाएँ स्वतंत्र नहीं होती हैं, लेकिन ''क्लंपस'' या क्लस्टर में घटित होती हैं, तो यदि इन क्लस्टर को उपयुक्त रूप से इस तरह परिभाषित किया जाता है कि वे लगभग दूसरे से स्वतंत्र हैं, अतः घटित होने वाले क्लस्टर की संख्या पॉइसन यादृच्छिक चर के निकट होगी<ref name="arratia1993review" /> और क्लस्टर का स्थान पॉइसन प्रक्रिया के समीप होगा।<ref name="aldous1989poisson" /> | |||
=== स्टीन की विधि === | === स्टीन की विधि === | ||
स्टीन की विधि एक गणितीय तकनीक है जिसे मूल रूप से [[ गाऊसी ]] और | स्टीन की विधि एक गणितीय तकनीक है जिसे मूल रूप से [[ गाऊसी |गॉसियन]] और पॉइसन चर जैसे यादृच्छिक चर के अनुमान के लिए विकसित किया गया था, जिसे बिंदु प्रक्रियाओं पर भी लागू किया गया है। स्टीन की विधि का उपयोग प्रायिकता आव्यूह पर ऊपरी परिबंध को प्राप्त करने के लिए किया जा सकता है, जो यह निर्धारित करने की विधि प्रदान करता है कि दो भिन्न-भिन्न यादृच्छिक गणितीय वस्तुएं प्रसंभाव्य रूप से कैसे परिवर्तित हैं।<ref name="chen2013approximating2">L. H. Chen, A. Röllin, et al. Approximating dependent rare events. ''Bernoulli'', 19(4):1243–1267, 2013.</ref><ref name="barbour1992stein2">A. D. Barbour and T. C. Brown. Stein's method and point process approximation. ''Stochastic Processes and their Applications'', 43(1):9–31, 1992.</ref> प्रायिकता आव्यूह पर ऊपरी परिबंध जैसे कि [[कुल भिन्नता]] और [[वासेरस्टीन दूरी]] को व्युत्पन्न किया गया है।<ref name="chen2013approximating"/> | ||
शोधकर्ताओं ने स्टीन की विधि को | शोधकर्ताओं ने स्टीन की विधि को कई तरीकों से पॉइसन बिंदु प्रक्रियाओं पर लागू किया है,<ref name="chen2013approximating"/> जैसे कि [[हथेली की पथरी|पाम कैलकुलस]] का उपयोग करना।<ref name="chen2004stein"/> स्टीन की विधि पर आधारित तकनीकों को ऊपरी परिबंध में विरलन और अध्यारोपण जैसे कुछ [[बिंदु प्रक्रिया संचालन|बिंदु प्रक्रिया संक्रिया]] के प्रभावों को प्रभावित करने के लिए विकसित किया गया है।<ref name="schuhmacher2005super">D. Schuhmacher. Distance estimates for dependent superpositions of point processes. ''Stochastic processes and their applications'', 115(11):1819–1837, 2005.</ref><ref name="schuhmacher2005thinnings">D. Schuhmacher. Distance estimates for poisson process approximations of dependent thinnings. ''Electronic Journal of Probability'', 10:165–201, 2005.</ref> स्टीन की विधि का उपयोग पॉइसन के आव्यूह और [[कॉक्स प्वाइंट प्रक्रिया|कॉक्स बिंदु प्रक्रिया]] जैसी अन्य प्रक्रियाओं पर ऊपरी परिबंध को प्राप्त करने के लिए भी किया गया है, जो यादृच्छिक तीव्रता माप के साथ पॉइसन प्रक्रिया है।<ref name="chen2013approximating"/> | ||
== पॉइसन बिंदु प्रक्रिया के लिए कन्वर्जेन्स == | |||
सामान्यतः, जब किसी साधारण बिंदु प्रक्रिया पर कोई आपरेशन लागू किया जाता है, तो परिणामस्वरूप प्रक्रिया आमतौर पर एक पॉइसन पॉइंट प्रक्रिया नहीं होती है। उदाहरण के लिए, यदि किसी बिंदु प्रक्रिया को, पॉइसन के अतिरिक्त, इसके बिंदुओं को यादृच्छिक और स्वतंत्र रूप से विस्थापित किया जाता है, तो प्रक्रिया आवश्यकतापूर्वक एक पॉइसन बिंदु प्रक्रिया नहीं होगी। हालांकि, मूल बिंदु प्रक्रिया और यादृच्छिक विस्थापन के लिए निश्चित गणितीय शर्तों के तहत, सीमा सिद्धांतों के माध्यम से दिखाया गया है कि यदि एक बिंदु प्रक्रिया के बिंदुओं को यादृच्छिक और स्वतंत्र रूप से बार-बार विस्थापित किया जाए, तो बिंदु प्रक्रिया की सीमित बंटन (दुर्बल रूप से) पॉइसन बिंदु प्रक्रिया के बराबर होगी।<ref name="DaleyVere-Jones2007page131">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=131–132}}</ref> | |||
== | विरलन और अध्यारोपण संक्रियाओं के लिए भी ऐसे संघटकता परिणाम विकसित किए गए हैं<ref name="DaleyVere-Jones2007page131" /> जो दिखाते हैं कि ऐसी पुनरावृत्त संक्रियाओं को बिंदु प्रक्रियाओं पर अनुमानित करने पर यदि उचित तीव्रता माप का संगठन किया जाए (अन्यथा परिणामस्वरूप बिंदु प्रक्रियाओं के तीव्रता माप के मान शून्य या अनंत की ओर पहुंचेंगे), तो प्रक्रिया पॉइसन बिंदु प्रक्रियाओं के संगत बराबर हो सकती है। ऐसी संघटना कार्य सीधे उन परिणामों से संबंधित होती है जिन्हें पाम-खिंचिन{{efn|Also spelt Palm–Khintchine in, for example, ''[[Point Processes]]'' by {{harvtxt|Cox|Isham|1980|page=41}}}} समीकरण के रूप में जाना जाता है, जिसकी उत्पत्ति कॉनी पाम और अलेक्सांदर खिंचिन के कार्य में हुई है,<ref name="DaleyVere-Jones2007page146">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|page=146}}</ref> और यह समझने में मदद करती है कि पॉइसन प्रक्रिया अकस्मात घटित होने वाले विभिन्न यादृच्छिक प्रभावों के गणितीय मॉडल के रूप में प्रायः उपयोग की जा सकती है।<ref name="DaleyVere-Jones2007page131" /> | ||
== पॉइसन बिंदु प्रक्रियाओं का सामान्यीकरण == | |||
पॉइसन बिंदु प्रक्रिया को विस्तारित किया जा सकता है, उदाहरण के लिए, तीव्रता माप को परिवर्तित करके या अधिक सामान्य गणितीय स्थानों पर परिभाषित करके। इन सामान्यीकरणों का गणितीय अध्ययन किया जा सकता है साथ ही इनका उपयोग गणितीय रूप से भौतिक प्रभावों के मॉडल बनाने या प्रतिष्ठित करने के लिए किया जा सकता है। | |||
=== पॉइसन-प्रकार का यादृच्छिक माप === | |||
[[पॉइसन-प्रकार के यादृच्छिक उपाय|पॉइसन प्रकार के यादृच्छिक माप]] (पीटी) विविधता यादृच्छिक गणना माप के समूह होते हैं जो उपगणमें सीमित करने के अंतर्गत होते हैं, अर्थात् बिन्दु प्रक्रिया आपरेशन#थिनिंग के अंतर्गत सीमित होते हैं। ये यादृच्छिक माप [[मिश्रित द्विपद प्रक्रिया]] के उदाहरण हैं और पॉइसन यादृच्छिक माप की बंटनात्मक स्व-समानता गुणधर्म साझा करते हैं। ये बंटनात्मक स्व-समानता गुणधर्म वाले बंटनों के कैननिक गैर-ऋणात्मक श्रेणी के अद्यावधिक सदस्य हैं और पॉइसन बंटन, [[नकारात्मक द्विपद वितरण|ऋणात्मक द्विपद बंटन]] और द्विपद बंटन को सम्मिलित करते हैं। पॉइसन यादृच्छिक माप अलग-अलग उपगणों पर स्वतंत्र होता है, जबकि अन्य पीटी यादृच्छिक माप (ऋणात्मक द्विपद और द्विपद) का धनात्मक और ऋणात्मक सह-संयोजन होता है। पीटी यादृच्छिक माप पर चर्चा की जाती है<ref>Caleb Bastian, Gregory Rempala. Throwing stones and collecting bones: Looking for Poisson-like random measures, Mathematical Methods in the Applied Sciences, 2020. [[doi:10.1002/mma.6224]]</ref> और इसमें पॉइसन यादृच्छिक माप, ऋणात्मक द्विपद यादृच्छिक माप और द्विपद यादृच्छिक माप सम्मिलित होते हैं। | |||
=== अधिक सामान्य समष्टियों पर पॉइसन बिंदु प्रक्रियाएं === | |||
=== | गणितीय मॉडल के लिए पॉइसन बिंदु प्रक्रिया को प्रायः यूक्लिडियन समष्टि में परिभाषित किया जाता है,<ref name="ChiuStoyan2013"/><ref name="Kingman1992page11"/> लेकिन इसे अधिक ऑब्स्ट्रक्ट समष्टियों के लिए सामान्यीकृत किया गया है और यादृच्छिक मापों के अध्ययन में मौलिक भूमिका निभाता है,<ref name="Kallenberg1983">{{cite book|author=Olav Kallenberg|title=यादृच्छिक उपाय|url=https://books.google.com/books?id=bBnvAAAAMAAJ|year=1983|publisher=Akademie-Verlag|isbn=978-0-12-394960-8}}</ref><ref name="Kingman1992page79to84">{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|pages=79–84}}</ref> जिसके लिए प्रायिकता सिद्धांत, माप सिद्धांत और टोपोलॉजी जैसे गणितीय क्षेत्रों की समझ आवश्यक है।<ref name="DaleyVere-Jones2007page368to413">{{cite book|author1=D.J. Daley|author2=David Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|url=https://books.google.com/books?id=nPENXKw5kwcC|date=12 November 2007|publisher=Springer Science & Business Media|isbn=978-0-387-21337-8|pages=368–413}}</ref> | ||
सामान्य तौर पर, दूरी की अवधारणा अनुप्रयोगों के लिए व्यावहारिक रुचि की है, जबकि पाम वितरण के लिए टोपोलॉजिकल संरचना की आवश्यकता होती है, जिसका अर्थ है कि बिंदु प्रक्रियाओं को सामान्यतः आव्यूह के साथ गणितीय समष्टि पर परिभाषित किया जाता है।<ref name="gelfand2010handbook">A. E. Gelfand, P. Diggle, P. Guttorp, and M. Fuentes. ''Handbook of spatial statistics'', Chapter 9. CRC press, 2010.</ref> इसके अतिरिक्त, बिंदु प्रक्रिया की प्राप्ति को गणना की माप के रूप में माना जा सकता है, इसलिए बिंदु प्रक्रियाएं एक प्रकार के यादृच्छिक उपाय हैं जिन्हें यादृच्छिक गणना के माप के रूप में जाना जाता है।<ref name="grandell1977point" /> इस संदर्भ में, पॉइसन और अन्य बिंदु प्रक्रियाओं का अध्ययन स्थानीय रूप से सघन द्वितीय गणनीय हॉउसडॉर्फ स्थान पर किया गया है।<ref name="kallenberg1983random">O. Kallenberg. ''Random measures''. Academic Pr, 1983.</ref> | |||
=== कॉक्स बिंदु प्रक्रिया === | |||
{{main|कॉक्स प्रक्रिया}} | |||
'''कॉक्स बिंदु प्रक्रिया''', '''कॉक्स प्रक्रिया''' या '''दोगुनी प्रसंभाव्य पॉइसन प्रक्रिया''' पॉइसन बिंदु प्रक्रिया का सामान्यीकरण है, इसकी तीव्रता माप <math>\textstyle \Lambda</math> को भी यादृच्छिक और अंतर्निहित पॉइसन प्रक्रिया से स्वतंत्र होने की अनुमति देती है। इस प्रक्रिया का नाम डेविड कॉक्स के नाम पर रखा गया है, जिन्होंने इसे 1955 में प्रस्तुत किया था, हालांकि अन्य पॉइसन प्रक्रियाओं को यादृच्छिक तीव्रता के साथ स्वतंत्र रूप से लुसिएन ले कैम और मौरिस क्वेनौइल द्वारा पहले ही प्रस्तुत किया गया था।<ref name="GuttorpThorarinsdottir2012"/> तीव्रता माप यादृच्छिक चर या यादृच्छिक क्षेत्र की प्राप्ति हो सकती है। उदाहरण के लिए, यदि तीव्रता माप का लघुगणक गॉसियन यादृच्छिक क्षेत्र है, तो परिणामी प्रक्रिया को ''लघुगणक गॉसियन कॉक्स प्रक्रिया'' के रूप में जाना जाता है।<ref name="moller1998log">J. Møller, A. R. Syversveen, and R. P. Waagepetersen. Log Gaussian Cox Processes. ''Scandinavian journal of statistics'', 25(3):451–482, 1998.</ref> अधिक सामान्यतः, तीव्रता के उपाय एक गैर-ऋणात्मक स्थानीय परिमित यादृच्छिक माप की प्राप्ति है। कॉक्स बिंदु प्रक्रियाएं बिंदुओं के ''क्लस्टरिंग'' को प्रदर्शित करती हैं, जिन्हें गणितीय रूप से पॉइसन बिंदु प्रक्रियाओं की तुलना में बड़ा दिखाया जा सकता है। कॉक्स प्रक्रियाओं की व्यापकता और सुवाह्यता के परिणामस्वरूप उन्हें स्थानिक सांख्यिकी<ref name="moller2007modern">J. Møller and R. P. Waagepetersen. Modern statistics for spatial point processes. ''Scandinavian Journal of Statistics'', 34(4):643–684, 2007.</ref> और वायरलेस नेटवर्क<ref name="Haenggi2013"/> जैसे क्षेत्रों में मॉडल के रूप में उपयोग किया जा रहा है। | |||
===चिह्नित पॉइसन बिंदु प्रक्रिया=== | |||
[[File:Marked point process.png|thumb|600px|एक चिह्नित बिंदु प्रक्रिया का एक उदाहरण, जहां अचिह्नित बिंदु प्रक्रिया को सकारात्मक वास्तविक रेखा पर परिभाषित किया गया है, जो अक्सर समय का प्रतिनिधित्व करती है। यादृच्छिक चिह्न स्थिति समष्टि में मान लेते हैं <math>S</math> मार्क स्पेस के रूप में जाना जाता है। ऐसी किसी भी चिह्नित बिंदु प्रक्रिया की व्याख्या अंतरिक्ष पर एक अचिह्नित बिंदु प्रक्रिया के रूप में की जा सकती है <math>[0,\infty]\times S </math>. अंकन प्रमेय का कहना है कि यदि मूल अचिह्नित बिंदु प्रक्रिया एक पॉसॉन बिंदु प्रक्रिया है और निशान प्रसंभाव्य रूप से स्वतंत्र हैं, तो चिह्नित बिंदु प्रक्रिया भी एक पॉइसन बिंदु प्रक्रिया है <math>[0,\infty]\times S </math>. यदि पॉसों बिंदु प्रक्रिया समघाती है, तो अंतराल <math>\tau_i</math> आरेख में एक घातीय बंटन से तैयार किए गए हैं।]]दिए गए बिन्दु प्रक्रिया के लिए, प्रत्येक यादृच्छिक बिंदु के साथ एक यादृच्छिक गणितीय वस्तु, जिसे अंकित कहा जाता है, यादृच्छिक रूप से समर्पित किया जा सकता है। ये अंक अभिविन्यासी रूप से पूर्णांक, वास्तविक संख्याएँ, रेखाएँ, ज्यामिति वस्तुएँ या अन्य बिंदु प्रक्रियाएं हो सकती हैं। [156][157] बिंदु प्रक्रिया का बिंदु और इसके संबंधित अंक का योग होने पर मर्किंग बिंदु कहलाता है, और सभी मार्किंग बिंदु परिक्रिया को एक मार्किंग बिंदु प्रक्रिया बनाते हैं। [158] यह आमतौर पर माना जाता है कि यादृच्छिक अंक एक दूसरे के निरपेक्ष होते हैं और समान वितरित होते हैं, हालांकि, बिंदु का अंक अपने अंतर्निहित (स्थिति) समष्टि में उसके संबंधित बिंदु की स्थान पर भी निर्भर कर सकता है।<ref name="MollerWaagepetersen2003page8">{{cite book|author1=Jesper Moller|author2=Rasmus Plenge Waagepetersen|title=स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण|url=https://books.google.com/books?id=dBNOHvElXZ4C|date=25 September 2003|publisher=CRC Press|isbn=978-0-203-49693-0|page=8}}</ref> यदि अंतर्निहित बिंदु प्रक्रिया पॉयसन बिंदु प्रक्रिया है, तो परिणामस्वरूपी बिंदु प्रक्रिया एक मार्किंग पॉयसन बिंदु प्रक्रिया होती है।<ref name="Haenggi2013page138">{{cite book|author=Martin Haenggi|title=वायरलेस नेटवर्क के लिए स्टोचैस्टिक ज्योमेट्री|url=https://books.google.com/books?id=CLtDhblwWEgC|year=2013|publisher=Cambridge University Press|isbn=978-1-107-01469-5|pages=138–140}}</ref> बिंदु प्रक्रिया के एक बिंदु और उसके संबंधित चिह्न वाली जोड़ी को एक चिह्नित बिंदु कहा जाता है, और सभी चिह्नित बिंदु एक चिह्नित बिंदु प्रक्रिया बनाते हैं।<ref name="BaddeleyBárány2006page19">{{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=https://books.google.com/books?id=X-m5BQAAQBAJ|date=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4|pages=19–21}</ref> अक्सर यह माना जाता है कि यादृच्छिक अंक एक दूसरे से स्वतंत्र होते हैं और समान रूप से वितरित होते हैं, फिर भी एक बिंदु का निशान अंतर्निहित (राज्य) स्थान में इसके संबंधित बिंदु के स्थान पर निर्भर हो सकता है। रेफरी नाम= किंगमैन 1992पृष्ठ55 >{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=55}</ref> यदि अंतर्निहित बिंदु प्रक्रिया एक प्वॉइसन बिंदु प्रक्रिया है, तो परिणामी बिंदु प्रक्रिया एक चिन्हित पॉइसन बिंदु प्रक्रिया है। रेफ नाम = बेसेलीब्लास्ज़ज़ीस्ज़िन2009पृष्ठ291 >{{cite book|author1=François Baccelli|author2=Bartlomiej Blaszczyszyn|title=स्टोचैस्टिक ज्यामिति और वायरलेस नेटवर्क|url=https://books.google.com/books?id=H3ZkTN2pYS4C|year=2009|publisher=Now Publishers Inc|isbn=978-1-60198-264-3|pages=291–293}}</ref> | |||
===चिह्नित | |||
[[File:Marked point process.png|thumb|600px|एक चिह्नित बिंदु प्रक्रिया का एक उदाहरण, जहां अचिह्नित बिंदु प्रक्रिया को सकारात्मक वास्तविक रेखा पर परिभाषित किया गया है, जो अक्सर समय का प्रतिनिधित्व करती है। यादृच्छिक चिह्न स्थिति समष्टि में मान लेते हैं <math>S</math> मार्क स्पेस के रूप में जाना जाता है। ऐसी किसी भी चिह्नित बिंदु प्रक्रिया की व्याख्या अंतरिक्ष पर एक अचिह्नित बिंदु प्रक्रिया के रूप में की जा सकती है <math>[0,\infty]\times S </math>. अंकन प्रमेय का कहना है कि यदि मूल अचिह्नित बिंदु प्रक्रिया एक पॉसॉन बिंदु प्रक्रिया है और निशान प्रसंभाव्य रूप से स्वतंत्र हैं, तो चिह्नित बिंदु प्रक्रिया भी एक | |||
{{See also|Markov renewal process}} | {{See also|Markov renewal process}} | ||
==== अंकन प्रमेय ==== | ==== अंकन प्रमेय ==== | ||
यदि | यदि किसी साधारण बिंदु प्रक्रिया को किसी गणितीय समष्टि पर परिभाषित किया जाता है और यादृच्छिक अंक किसी अन्य गणितीय समष्टि पर परिभाषित किए जाते हैं, तो अंकन बिंदु प्रक्रिया उन दोनों स्थानों के कार्तीय गुणांक पर परिभाषित होती है। यदि अंकन पॉइसन बिंदु प्रक्रिया में यादृच्छिक और समान वितरित अंक हों, तो '''अंकन सिद्धांत'''<ref name="Kingman1992page55" /><ref name="Streit2010page205">{{cite book|author=Roy L. Streit|title=Poisson Point Processes: Imaging, Tracking, and Sensing|url=https://books.google.com/books?id=KAWmFYUJ5zsC|date=15 September 2010|publisher=Springer Science & Business Media|isbn=978-1-4419-6923-1|pages=205–206}}</ref> कहता है कि यह अंकन बिंदु प्रक्रिया उसी उपरोक्त गणितीय स्थानों के कार्तीय गुणांक पर परिभाषित (गैर-अंकन) पॉइसन बिंदु प्रक्रिया भी होती है, जो साधारण बिंदु प्रक्रियाओं के लिए सत्य नहीं है। | ||
=== | === संयुक्त पॉइसन बिंदु प्रक्रिया === | ||
'''संयुक्त पॉइसन बिंदु प्रक्रिया''' या '''संयुक्त पॉइसन प्रक्रिया''', किसी अंतर्निहित समष्टि पर परिभाषित पॉइसन बिंदु प्रक्रिया के प्रत्येक बिंदु में यादृच्छिक मान या वजन को जोड़कर बनाई जाती है, इस प्रक्रिया को अंकन पॉइसन बिंदु प्रक्रिया से निर्मित किया जाता है, जहां अंक संग्रह स्वतंत्र और समान वितरित गैर-ऋणात्मक स्थिरांक होते हैं। अन्य शब्दों में, मूल पॉइसन प्रक्रिया के प्रत्येक बिंदु के लिए एक स्वतंत्र और समान वितरित गैर-ऋणात्मक स्थिरांक होता है, और फिर संयुक्त पॉइसन प्रक्रिया को निर्मित किया जाता है जो उपर्युक्त गणितीय स्थान के कुछ क्षेत्र में स्थित पॉइसन प्रक्रिया के बिंदुओं के सभी स्वतंत्र और समान वितरित गैर-ऋणात्मक स्थिरांकों के योग से बनी होती है।{{sfnp|Daley|Vere-Jones|2003|pages=198–199}} | |||
यदि | यदि किसी पॉइसन पॉइंट प्रक्रिया <math>\textstyle N</math> (जो, उदाहरण के लिए, <math>\textstyle \mathbb{R}^d</math> पर परिभाषित होती है) और स्वतंत्र और समान वितरित गैर-ऋणात्मक बिंदु <math>\textstyle \{M_i\}</math> के एक संग्रह के बिंदुगामी पॉइसन बिंदु प्रक्रिया के रूप में निर्मित किया जाता है, जिसके लिए पॉइसन प्रक्रिया <math>\textstyle N</math> के प्रत्येक बिंदु <math>\textstyle x_i</math> के लिए एक गैर-ऋणात्मक यादृच्छिक परिवर्तन <math>\textstyle M_i</math> होता है, तो परिणामस्वरूपी संयुक्त पॉइसन प्रक्रिया निम्नलिखित होती है:<ref name="DaleyVere-Jones2007page198">{{cite book |last1=Daley |first1=Daryl J. |last2=Vere-Jones |first2=David |year=2007 |title=An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure|publisher=Springer|isbn=978-0387213378|pages=198}}</ref> | ||
:<math> C(B)=\sum_{i=1}^{N(B)} M_i ,</math> | :<math> C(B)=\sum_{i=1}^{N(B)} M_i ,</math> | ||
जहां <math>\textstyle B\subset \mathbb{R}^d</math> बोरेल मापनीय समुच्चय है। | |||
=== | यदि सामान्य यादृच्छिक चर <math>\textstyle \{M_i\}</math> मान लेते हैं, उदाहरण के लिए, <math>\textstyle d</math>-विमीय यूक्लिडियन समष्टि <math>\textstyle \mathbb{R}^d</math>, परिणामी यौगिक पॉइसन प्रक्रिया लेवी प्रक्रिया का एक उदाहरण है, बशर्ते कि यह गैर-नकारात्मक संख्या <math>\textstyle [0, \infty) </math> पर परिभाषित एक समघातीय बिंदु प्रक्रिया <math>\textstyle N</math> से बनाई गई हो<ref name="ApplebaumBook2004page46">{{cite book|author=David Applebaum|title=Lévy Processes and Stochastic Calculus|url=https://books.google.com/books?id=q7eDUjdJxIkC|date=5 July 2004|publisher=Cambridge University Press|isbn=978-0-521-83263-2|pages=46–47}}</ref> | ||
=== तीव्रता फलनों का घातीय संरेखण के साथ विफलता प्रक्रिया === | |||
अविस्मरण त्रुटि प्रक्रिया जिसमें आंतरिकता समीकरणों की व्यापक स्मूदन साथ एकाधिक की प्रकार होती है (एफपी-ईएसआई), गैरसमग्र पॉइसन प्रक्रिया का विस्तार है। एफपी-ईएसआई की आंतरिकता समीकरण एक समीकरण की तरह होती है जिसमें घटना घटनाओं के अंतिम समय बिंदुओं पर आंतरिकता समीकरणों की संरेखण फलन होती है और यह मॉडल डेटासेट्स को फिट करने के लिए उपयोग किए जाने पर 8 वास्तविक दुनिया के असफलता डेटासेट पर अन्य नौ स्टोकेस्टिक प्रक्रियाओं से बेहतर प्रदर्शन करती है, जहां मॉडल की प्रदर्शन का माप एआईसी (अकयके सूचना माप) और बीआईसी ([[बायेसियन सूचना मानदंड]]) के माध्यम से किया जाता है।<ref name="Wu2019">Wu, S. (2019). [https://doi.org/10.1016/j.ejor.2018.11.045 A failure process model with the exponential smoothing of intensity functions]. ''European Journal of Operational Research'', 275(2), 502–513</ref> | |||
== यह भी देखें == | == यह भी देखें == | ||
* [[बूलियन मॉडल (संभाव्यता सिद्धांत)]] | * [[बूलियन मॉडल (संभाव्यता सिद्धांत)|बूलियन मॉडल (प्रायिकता सिद्धांत)]] | ||
*सातत्य | *सातत्य अंत:स्त्राव सिद्धांत | ||
* [[यौगिक पॉइसन | * [[यौगिक पॉइसन प्रक्रिया]] | ||
* [[कॉक्स प्रक्रिया]] | * [[कॉक्स प्रक्रिया]] | ||
* बिंदु प्रक्रिया | * बिंदु प्रक्रिया | ||
* | * प्रसंभाव्य ज्यामिति | ||
* [[वायरलेस नेटवर्क के स्टोचैस्टिक ज्यामिति मॉडल|वायरलेस नेटवर्क के प्रसंभाव्य ज्यामिति मॉडल]] | * [[वायरलेस नेटवर्क के स्टोचैस्टिक ज्यामिति मॉडल|वायरलेस नेटवर्क के प्रसंभाव्य ज्यामिति मॉडल]] | ||
* [[मार्कोवियन आगमन प्रक्रियाएं]] | * [[मार्कोवियन आगमन प्रक्रियाएं|मार्कोवियन एराइवल प्रक्रियाएं]] | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
Revision as of 21:58, 18 June 2023
प्रायिकता, सांख्यिकी और संबंधित क्षेत्रों में, पॉइसन बिंदु प्रक्रिया एक प्रकार का यादृच्छिक गणितीय प्रयोजन है जो गणितीय समष्टि पर यादृच्छिक रूप से स्थानांतरित होने वाले बिन्दुओं से मिलकर बनता है, जहां महत्वपूर्ण विशेषता यह है कि ये बिन्दु एक दूसरे से स्वतंत्र रूप से होते हैं।[1] पॉइसन बिंदु प्रक्रिया को सामान्यतः पॉइसन प्रक्रिया कहा जाता है, लेकिन इसे पॉइसन यादृच्छिक माप, पॉइसन यादृच्छिक बिन्दु फ़ील्ड या पॉइसन बिंदु फ़ील्ड भी कहा जाता है। यह बिंदु प्रक्रिया उचित गणितीय गुणों के साथ होती है,[2] जिसके कारण इसे यूक्लिडीयन समष्टि में प्रायः परिभाषित किया जाता है और यह खगोल शास्त्र,[3] जीव-विज्ञान,[4] पारिस्थितिकी,[5] भूविज्ञान,[6] भूकंप विज्ञान,[7] भौतिक विज्ञान,[8] अर्थशास्त्र,[9] छवि प्रसंस्करण,[10][11] और दूरसंचार जैसे विभिन्न शास्त्रों में आपूर्ति-मांग मॉडल के रूप में उपयोग किया जाता है।[12][13]
यह प्रक्रिया फ्रांसीसी गणितज्ञ शिमोन डेनिस पॉइसन के नाम पर रखी गई है, हालांकि पॉइसन ने कभी इस प्रक्रिया का अध्ययन नहीं किया। इसका नाम इस तथ्य से जुड़ा है कि यदि किसी स्थान में यादृच्छिक बिन्दुओं का संग्रह पॉइसन प्रक्रिया बनाता है, तो एक परिमित आकार क्षेत्र में बिन्दुओं की संख्या यादृच्छिक प्रायस्थानिकी संगणना के साथ पॉइसन बंटन होती है। इस प्रक्रिया की खोज अलग-अलग सेटिंग्स पर स्वतंत्र रूप से और अनेक बार की गई, जिसमें रेडियोधर्मी क्षय, टेलीफोन कॉल आगमन और इनश्योरेंस गणित पर प्रयोग सम्मिलित हैं।[14][15]
पॉइसन बिंदु प्रक्रिया सामान्यतः वास्तविक रेखा पर परिभाषित की जाती है, जहां इसे प्रसंभाव्य प्रक्रम (स्टोकेस्टिक प्रोसेस) के रूप में माना जा सकता है। इस सेटिंग में, यह उदाहरण के लिए, कतारबद्ध सिद्धांत में उपयोग होती है[16] जहां यादृच्छिक घटनाओं का मॉडलिंग किया जाता है, जैसे कि किसी संग्रहागार में ग्राहकों के आगमन, प्रतिदान में फोन कॉल, या भूकंप की घटना, जो समय के आधार पर वितरित होती हैं। समतल में, बिन्दु प्रक्रिया, जिसे स्थानिक पॉइसन प्रक्रिया भी कहा जाता है,[17] प्रकीर्णित वायरलेस नेटवर्क में प्रेषकों के स्थानों,[12][18][19][20] संवेदक में टकराने वाले कणों के, या जंगल में पेड़ों के आवास के स्थानों का प्रतिनिधित्व कर सकती है।[21] इस संदर्भ में, प्रक्रिया प्रायः गणितीय मॉडलों में और स्थानिक बिन्दु प्रक्रियाओं,[22] प्रसंभाव्य ज्यामिति,[1] स्थानिक सांख्यिकी[22][23] और नियतांत्रण प्रक्षेपण सिद्धांत[24] के संबंधित क्षेत्रों में उपयोग होती है। पॉइसन बिंदु प्रक्रिया को अधिक एब्स्ट्रैक्ट समष्टि पर परिभाषित किया जा सकता है। अनुप्रयोगों से परे, पॉइसन बिंदु प्रक्रिया स्वयं में गणितीय अध्ययन का विषय है।[2] सभी सेटिंग में, पॉइसन बिंदु प्रक्रिया का एक मुख्य गुण यह है कि प्रत्येक बिंदु प्रक्रिया में सभी अन्य बिंदुओं के प्रति यादृच्छिक रूप से अव्यवस्थित होता है, इसलिए कभी-कभी इसे पूरी रूप से या पूर्णतः यादृच्छिक प्रक्रिया कहा जाता है।[25] किसी प्रणाली को पॉइसन प्रक्रिया के रूप मॉडलिंग करना पर्याप्त नहीं होता है जब बिंदु से बिंदु के संवेदनशील संबंध अत्यधिक प्रबल होते हैं (अर्थात बिंदु प्रसंभाव्य रूप से स्वतंत्र नहीं हैं)। ऐसी प्रणाली को भिन्न बिंदु प्रक्रिया के साथ अपेक्षाकृत अधिक श्रेष्ठता से मॉडलिंग किया जा सकता है।[26]
बिंदु प्रक्रिया एकल गणितीय प्रयोजन पर निर्भर करती है, जो परिस्थिति के आधार पर किसी स्थिरांक, स्थानिक समाकलित फलन या अधिक सामान्य संदर्भ में रेडॉन माप हो सकती है।[27] प्राथमिक स्थिति में, जिसे दर या तीव्रता (इंटेंसिटी) कहा जाता है, समष्टि के किसी क्षेत्र में पॉइसन प्रक्रिया के बिंदुओं की औसत घनत्व होती है। इस परिणामक बिंदु प्रक्रिया को समघातीय या स्थिर पॉइसन बिंदु प्रक्रिया कहा जाता है।[28] द्वितीय स्थिति में, बिंदु प्रक्रिया को असमघातीय या असमघातीय पॉइसन बिंदु प्रक्रिया कहा जाता है, और बिंदु प्रक्रिया की मूलभूत स्थान के स्थान पर बिंदुओं की औसत घनत्व पर निर्भर करती है।[29] शब्द "बिंदु" प्रायः छोड़ दिया जाता है,[2] लेकिन वस्तुओं की अन्य पॉइसन प्रक्रियाएं भी होती हैं, जिनमें बिंदुओं की बजाय रेखाएं और बहुभुज जैसी जटिल गणितीय प्रयोजन सम्मिलित होते हैं, और ऐसी प्रक्रियाएं पॉइसन बिंदु प्रक्रिया पर आधारित हो सकती हैं।[30] समघाती और असमघाती पॉइसन बिंदु प्रक्रियाएँ विशेषित मुद्रण प्रक्रिया की विशेष स्थिति हैं।
परिभाषाओं का अवलोकन
सेटिंग के आधार पर, इस प्रक्रिया के कई समकक्ष परिभाषाएं[31] हो सकती हैं, साथ ही इसके कई अनुप्रयोगों और विशेषताओं के कारण विभिन्न व्यापकता की परिभाषाएं भी हो सकती हैं।[32] पॉइसन बिंदु प्रक्रिया को एक विमा में परिभाषित, अध्ययन और उपयोग किया जा सकता है, उदाहरण के लिए, वास्तविक रेखा पर, जहां इसे गणना प्रक्रिया या कतारबद्ध मॉडल के भाग के रूप में व्याख्या किया जा सकता है;[33][34] उच्च विमाओं में जैसे कि समतल जहां इसकी प्रसंभाव्य ज्यामिति[1] और स्थानिक सांख्यिकी[35] में महत्वपूर्ण भूमिका निभाता है; या और अधिक सामान्य गणितीय समष्टि पर।[36] इसलिए, पॉइसन बिंदु प्रक्रिया और बिंदु प्रक्रियाओं की परिभाषा और अध्ययन करने के लिए उपयोग की जाने वाली नोटेशन, शब्दावली और गणितीय सावधानी का स्तर आधार के अनुसार भिन्न होते हैं।[37]
इसके अतिरिक्त, पॉइसन बिंदु प्रक्रिया में दो प्रमुख गुण हैं- पॉइसन गुणधर्म और स्वतंत्रता गुणधर्म- जो सभी सेटिंग्स में एक आवश्यक भूमिका निभाती है जहां पॉइसन बिंदु प्रक्रिया का उपयोग किया जाता है।[27][38] दो गुणधर्म तार्किक रूप से स्वतंत्र नहीं होते हैं; वास्तव में, स्वतंत्रता का तात्पर्य बिंदु गणना के पॉइसन बंटन से है, लेकिन इसके विपरीत नहीं।[lower-alpha 1]
बिंदु संख्या का पॉइसन बंटन
पॉइसन बिंदु प्रक्रिया को पॉइसन बंटन के माध्यम से अभिलक्षित किया जाता है। पॉइसन बंटन यादृच्छिक चर का (पॉइसन यादृच्छिक चर के नाम से जाना जाता है) प्रायिकता बंटन होता है, जिसमें बराबर होने की प्रायिकता निम्नलिखित प्राप्त होती है:
जहाँ गुणांक को क्रमगुणितअ (फैक्टोरियल) को दर्शाने के लिए है और पैरामीटर बंटन के आकार को निर्धारित करता है। (वास्तव में, को की प्रत्याशित मान के बराबर होने वाले मान के रूप में लिया जाता है।)
परिभाषा के अनुसार, पॉइसन बिंदु प्रक्रिया का एक गुण है कि प्रक्रिया के अन्तर्निहित समष्टि के सीमित क्षेत्र में बिंदुओं की संख्या पॉइसन बंटन का यादृच्छिक चर होती है।[38]
पूर्ण स्वतंत्रता
अंतर्निहित समष्टि के असंयुक्त और परिबद्ध उपक्षेत्रों के संग्रह पर विचार करें। परिभाषा के अनुसार, प्रत्येक परिबद्ध उपक्षेत्र में पॉइसन बिंदु प्रक्रिया के बिंदुओं की संख्या सभी अन्य से पूर्णतः स्वतंत्र होगी।
इस गुणधर्म को कई नामों से जाना जाता है जैसे पूर्ण यादृच्छिकता, पूर्ण स्वतंत्रता,[39] या स्वतंत्र प्रकीर्णन[40][41] और यह सभी पॉइसन बिंदु प्रक्रियाओं में सामान्य होता है। दूसरे शब्दों में, विभिन्न क्षेत्रों और बिंदुओं के बीच परस्पर क्रिया की कमी होती है,[42] जिसके कारण पॉइसन प्रक्रिया को कभी-कभी पूर्णतः या पूर्ण रूप से यादृच्छिक प्रक्रिया कहा जाता है।[39]
समघाती पॉइसन बिंदु प्रक्रिया
यदि किसी पॉइसन बिंदु प्रक्रिया का पैरामीटर के रूप में होता है, जहां लेबेस्ग माप होती है (अर्थात, यह समुच्चय के लिए लम्बाई, क्षेत्रफल या आयतन निर्दिष्ट करता है) और एक स्थिरांक होता है, तो बिंदु प्रक्रिया को समघाती या स्थायी पॉइसन बिंदु प्रक्रिया कहा जाता है। इस पैरामीटर को दर या तीव्रता कहा जाता है और यह किसी सीमित क्षेत्र में विद्यमान पॉइसन बिंदुओं की अपेक्षित (या औसत) संख्या से संबंधित होता है,[43][44] जहां दर उस अंतर्निहित समष्टि के लिए उपयोग होती है जिसके एक विमा होती है।[43] पैरामीटर को मानचित्रित किया जा सकता है जैसे कि लंबाई, क्षेत्रफल, आयतन या समय के कुछ इकाई पर प्रति औसत बिंदुओं की औसत संख्या, यहां तक कि इसे माध्य घनत्व या माध्य दर भी कहा जाता है;[45] टर्मिनोलॉजी देखें।
गणना प्रक्रिया के रूप में व्याख्या
धनात्मक अर्ध-रेखा पर विचारित होने पर, समघाती पॉइसन बिंदु प्रक्रिया को गणना प्रक्रिया के रूप में परिभाषित किया जा सकता है, जो एक प्रकार की प्रसंभाव्य प्रक्रिया होती है, जिसे के रूप में दर्शाया जा सकता है।[31][34] गणना प्रक्रिया समय तक हुए घटनाओं की कुल संख्या का प्रतिनिधित्व करती है। यदि गणना प्रक्रिया में निम्नलिखित तीन गुण हों, तो वह समघाती पॉइसन गणना प्रक्रिया दर के साथ होती है, तीन गुण निम्नलिखित है:[31][34]
- स्वतंत्र वृद्धि होती है; और
- लंबाई के किसी भी अंतराल में घटनाओं (या अंक) की संख्या पैरामीटर (या माध्य) के साथ पॉइसन यादृच्छिक चर है।
अंतिम गुणधर्म का अर्थ है:
दूसरे शब्दों में, यादृच्छिक चर के के बराबर होने की प्रायिकता निम्नलिखित प्रकार दी गई है:
पॉइसन गणना प्रक्रिया को यह कहते हुए भी परिभाषित किया जा सकता है कि गणना प्रक्रिया की घटनाओं के बीच समय का अंतर माध्य के साथ घातांकी चर होता हैं।[46] घटनाओं या आमंद के बीच समय के अंतर को अंतर आमंद[47] या अंतःक्रिया समय के रूप में जाना जाता है।[46]
वास्तविक रेखा पर एक बिंदु प्रक्रिया के रूप में व्याख्या
पॉइसन बिंदु प्रक्रिया को वास्तविक रेखा पर परिभाषित किया जा सकता है इस प्रक्रिया के बिंदुओं की संख्या को के अंतराल में विचार करके, बिंदु प्रक्रिया के रूप में व्याख्या किया जाता है। वास्तविक रेखा पर सामान्य पॉइसन बिंदु प्रक्रिया के पैरामीटर के साथ, इस यादृच्छिक संख्या के बिंदुओं की संख्या, जिसे यहां के रूप में लिखा गया है, किसी गणना संख्या के बराबर होने की प्रायिकता निम्नलिखित रूप में दी गई है:[48]
कुछ धनात्मक पूर्णांक 11 के लिए, समघाती पॉइसन बिंदु प्रक्रिया का परिमित-विमीय बंटन होता है:[48]
जहाँ वास्तविक संख्याएँ हैं।
दूसरे शब्दों में, माध्य के साथ पॉइसन यादृच्छिक चर होता है, जहां है। इसके अतिरिक्त, किन्हीं दो असंयुक्त अंतरालों में बिंदुओं की संख्या, मान लीजिए, और , एक-दूसरे के स्वतंत्र हैं, और यह असंयुक्त अंतरालों की किसी भी परिमित संख्या तक विस्तारित होता है।[48] कतारबद्ध सिद्धांत के संदर्भ में, एक बिंदु अस्तित्व (एक अंतराल में) होने को किसी घटना के रूप में विचार किया जा सकता है, लेकिन यह प्रायिकता सिद्धांत के अर्थ में घटना शब्द से भिन्न होता है।[lower-alpha 2] यह इस प्रकार है कि एराइवल की अपेक्षित संख्या है जो प्रति इकाई समय में होती है।[34]
प्रमुख गुण
पूर्व परिभाषा के अनुसार सामान्यतः पॉइसन बिंदु प्रक्रियाओं के समग्र में दो महत्वपूर्ण विशेषताएं हैं जो निम्नलिखित है:[48][27]
- प्रत्येक परिमित अंतराल में होने वाले एराइवल की संख्या में पॉइसन बंटन होता है।
- असयुंक्त अंतरालों में होने वाले एराइवल की संख्या एक-दूसरे के निर्पेक्ष यादृच्छिक चर होते हैं।
इसके अतिरिक्त, इसमें केवल समान्य पॉइसन बिंदु प्रक्रिया से संबंधित तृतीय विशेषता निम्नलिखित है:[49]
- प्रत्येक अंतराल में एराइवल की संख्या का पॉइसन बंटन केवल अंतराल की लंबाई पर निर्भर करता है।
दूसरे शब्दों में, किसी भी परिमित के लिए, यादृच्छिक चर और स्वयं में स्वतंत्र होते हैं, अतः इसे स्थायी पॉइसन प्रक्रिया भी कहा जाता है।[48]
बड़ी संख्याओं का नियम
मात्रा की व्याख्या अंतराल में होने वाली अपेक्षित या औसत बिंदुओं की संख्या के रूप में की जा सकती है, अर्थात्:
जहाँ अपेक्षाओं के ऑपरेटर को दर्शाता है। दूसरे शब्दों में, पॉइसन प्रक्रिया के पैरामीटर बिंदुओं की घनत्व के सामान होता है। इसके अतिरिक्त, समान्य पॉइसन बिंदु प्रक्रिया (प्रबल) बड़े आंकड़ों के नियम का अनुपालन करती है।[50] अधिक विशेष रूप से, एक प्रायिकता के साथ:
जहां एक फलन की सीमा को दर्शाता है, और समय की प्रति यूनिट एराइवल अपेक्षित संख्या है।
मेमोरीलेस गुणधर्म
वास्तविक रेखा पर बिंदु प्रक्रिया के दो क्रमागत बिंदुओं के बीच की दूरी घातांकी यादृच्छिक चर होगा जिसका पैरामीटर होता है (अथवा समानांतर, औसत होता है)। इसका तात्पर्य है कि बिंदुओं का मेमोरीलेस गुणधर्म होता है: किसी परिमित अंतराल में किसी बिंदु का अस्तित्व, अन्य बिंदुओं के अस्तित्व की प्रायिकता (बंटन) प्रासंगिकता को प्रभावित नहीं करता है,[51][52] लेकिन जब पॉइसन प्रक्रिया को उच्चतम विमाओं वाले समष्टि पर परिभाषित किया जाता है, अतः इस गुणधर्म का कोई प्राकृतिक समरूपता नहीं होती है।[53]
क्रमबद्धता और साधारणता
स्थैतिक वृद्धियों वाली एक बिंदु प्रक्रिया को कभी-कभी क्रमित[54] या नियमित[55] कहा जाता है, यदि:
यहां छोटे-o संकेतन का उपयोग किया जा रहा है। जब किसी बिंदु प्रक्रिया में दो बिंदुओं का अंतर्निहित समष्टि पर एक ही स्थिति में संयोग की प्रायिकता शून्य होती है, अतः उसे एक साधारण बिंदु प्रक्रिया कहा जाता है। वास्तविक रेखा पर सामान्य बिंदु प्रक्रियाओं के लिए, क्रमबद्धता की गुणवत्ता यह सिद्ध करती है कि प्रक्रिया साधारण होती है,[56] जो समघाती पॉइसन बिंदु प्रक्रिया के लिए सत्य होता है।[57]
मार्टिंगेल विशेषण
वास्तविक रेखा पर, समघाती पॉइसन बिंदु प्रक्रिया का मार्टिंगेल सिद्धांत के साथ एक संबंध होता है निम्नलिखित विशेषण के माध्यम से: बिंदु प्रक्रिया समघाती पॉइसन बिंदु प्रक्रिया होती है यदि और केवल यदि
अन्य प्रक्रियाओं से संबंध
वास्तविक रेखा पर, पॉइसन प्रक्रिया एक प्रकार की सतत-समय मार्कोव प्रक्रिया है जिसे जन्म प्रक्रिया के रूप में जाना जाता है, जन्म-मृत्यु प्रक्रिया के एक विशेष प्रकार (केवल जन्म और शून्य मृत्यु के साथ)।[60][61] मार्कोव गुणधर्म के साथ अधिक जटिल प्रक्रियाएँ, जैसे मार्कोव एराइवल प्रक्रियाएँ, परिभाषित की गई हैं जहां पॉइसन प्रक्रिया एक विशेष स्थिति हैं।[46]
अर्ध-रेखा पर प्रतिबंध
यदि समघाती पॉइसन प्रक्रिया केवल अर्ध-रेखा पर के रूप में विचार की जाती है, जब समय को दर्शाता है,[31] अतः परिणामस्वरूप प्रक्रिया स्थानांतरण के अंतर्गत वास्तव में स्थानांतरण के प्रति समान नहीं होती है।[53] उस स्थिति में, कुछ स्थानिकता की परिभाषाओं के अनुसार पॉइसन प्रक्रिया स्थायी नहीं रहती है।[62]
अनुप्रयोग
समघाती पॉइसन प्रक्रिया का वास्तविक रेखा पर कई अनुप्रयोग हुए हैं जो प्रतीत होने वाले यादृच्छिक और स्वतंत्र घटनाओं के मॉडलिंग का प्रयास करते हैं। यह कतारबद्ध सिद्धांत में मौलिक भूमिका निभाता है, जो कुछ घटनाओं के यादृच्छिक एराइवल और अपक्रम को प्रतिष्ठानुसार प्रतिष्ठापित करने के लिए उपयुक्त प्रसंभाव्य मॉडल विकसित करने का प्रायिकता क्षेत्र है।[16][46] उदाहरण के लिए, कतारबद्ध सिद्धांत के तकनीकों का उपयोग करके ग्राहकों के आगमन और सेवा प्राप्ति या फोन कॉल के आगमन का अध्ययन किया जा सकता है जो फोन विनियम में होते हैं।
सामान्यीकरण
वास्तविक रेखा पर, समघाती पॉइसन प्रक्रिया को यादृच्छिक बिंदुओं की संख्या की गणना के लिए साधारणतम प्रसंभाव्य प्रक्रियाओं में से एक माना जाता है।[63][64] इस प्रक्रिया को कई विधियों से सामान्यीकृत किया जा सकता है। संभावित सामान्यीकरण है कि अंतर-आगमन समय के बंटन को घातांकी बंटन से अन्य बंटनों तक विस्तारित किया जाए, जो पुनर्नवीनीकरण प्रक्रिया के रूप में जानी जाती है। एक अन्य सामान्यीकरण यह है कि पॉइसन बिंदु प्रक्रिया को समतल जैसे उच्च विमीय समष्टियों पर परिभाषित किया जाए।[65]
स्थानिक पॉइसन बिंदु प्रक्रिया
स्थानिक पॉइसन प्रक्रिया समतल में परिभाषित पॉइसन बिंदु प्रक्रिया है।[58][66] इसकी गणितीय परिभाषा के लिए, सबसे पहले समतल के परिबद्ध, विवृत या संवृत (या अधिक यथार्थ रूप से, बोरेल मापनीय) क्षेत्र पर विचार किया जाता है। इस क्षेत्र में विद्यमान बिंदु प्रक्रिया के बिंदुओं की संख्या एक यादृच्छिक चर है, जिसे द्वारा निरूपित किया जाता है। यदि अंक के पैरामीटर के साथ एक समघाती पॉइसन प्रक्रिया से संबंधित हैं, तो में विद्यमान बिंदुओं की प्रायिकता निम्न द्वारा दी गई है:
जहाँ के क्षेत्र को दर्शाता है .
कुछ परिमित पूर्णांक के लिए, हम पहले असम्बद्ध, परिबद्ध बोरेल (मापने योग्य) सेट के संग्रह पर विचार करके समघाती पॉइसन बिंदु प्रक्रिया का परिमित-विमीय बंटन प्रदान कर सकते हैं। बिंदु प्रक्रिया के बिंदुओं की संख्या में विद्यमान के रूप में लिखी जा सकती है। अतः पैरामीटर के साथ समघाती पॉइसन बिंदु प्रक्रिया का परिमित-विमीय बंटन है:[67]
अनुप्रयोग
स्थानिक पॉइसन बिंदु प्रक्रिया स्थानिक सांख्यिकी में प्रमुखता से दिखाई देती है,[22][23] प्रसंभाव्य ज्यामिति, और सातत्य सिद्धांत।[24] इस बिंदु प्रक्रिया को विभिन्न भौतिक विज्ञानों में लागू किया जाता है जैसे अल्फा कणों का पता लगाने के लिए विकसित एक मॉडल होता है। हाल के वर्षों में, यह प्रायः कुछ वायरलेस संचार नेटवर्कों के प्रतीत होने वाले अव्यवस्थित स्थानिक विन्यासों के मॉडल के लिए उपयोग किया गया है।[18][19][20] उदाहरण के लिए, सेलुलर या मोबाइल फोन नेटवर्क के मॉडल विकसित किए गए हैं जहां यह माना जाता है कि फोन नेटवर्क ट्रांसमीटर, जिन्हें बेस स्टेशन के रूप में जाना जाता है, समघाती पॉइसन बिंदु प्रक्रिया के अनुसार स्थित हैं।
उच्च विमाओं में परिभाषित
पूर्व समघाती पॉइसन बिंदु प्रक्रिया को क्षेत्र की धारणा को (उच्च विमीय) आयतन के साथ बदलकर उच्च विमाओं में विस्तारित किया जाता है। यदि यूक्लिडियन समष्टि , के किसी परिबद्ध क्षेत्र के बिंदु एक समघाती पॉइसन प्रक्रिया बनाते हैं जिसका पैरामीटर होता है, अतः में विद्यमान बिंदुओं की प्रायिकता निम्नलिखित होती है:
जहां अब के -विमीय आयतन को दर्शाता है। इसके अतिरिक्त, असंयुक्त, परिबद्ध बोरेल समुच्चय के संग्रह के लिए, को में विद्यमान के बिंदुओं की संख्या को दर्शाता है। फिर पैरामीटर के साथ संबंधित समघाती पॉइसन बिंदु प्रक्रिया का परिमित-विमीय बंटन होता है:[69]
समघाती पॉइसन बिंदु प्रक्रियाएँ स्वयं के पैरामीटर के माध्यम से अंतर्निहित समष्टि की स्थिति पर निर्भर नहीं होती हैं, जिससे यह स्पष्ट होता है कि यह एक स्थिर प्रक्रिया (स्थानांतरण के लिए अपरिवर्तनीय) और आइसोट्रोपिक (घूर्णन के लिए अपरिवर्तनीय) प्रसंभाव्य प्रक्रिया है।[62] एकल-विमीय स्थिति की तरह, समघाती बिंदु प्रक्रिया को कुछ परिबद्ध उपसमुच्चय के लिए प्रतिबंधित किया जाता है, अतः स्थिरता की कुछ परिभाषाओं के अनुसार, प्रक्रिया अब स्थायी नहीं रहती है।[62][53]
बिंदुओं का समान रूप से बंटन
यदि समघाती बिंदु प्रक्रिया को वास्तविक रेखा पर किसी प्रयोजन की घटनाओं के लिए गणितीय मॉडल के रूप में परिभाषित किया जाता है, अतः इसकी विशेषताऐं इस प्रकार है कि वास्तविक रेखा पर इन घटनाओं की स्थितियों का बंटन समानतापूर्व होता है (जिसे प्रायः समय के रूप में व्याख्या किया जाता है)। विशेष रूप से, यदि किसी घटना (इस प्रक्रिया के अनुसार) किसी अंतराल में होती है जहां है, तो उसकी स्थानांतरिता उस अंतराल पर परिभाषित एक समान यादृच्छिक चर होगा।[70] इसके अतिरिक्त, समघाती बिंदु प्रक्रिया को एकसमान पॉइसन बिंदु प्रक्रिया भी कहा जाता है (टर्मिनोलॉजी देखें)। यह समानता गुण कार्तीय निर्देशांक में उच्च विमाओं तक विस्तारित होता है, लेकिन उदाहरण के लिए ध्रुवीय निर्देशांक में नहीं होता है।[71][72]
असमघाती पॉइसन बिंदु प्रक्रिया
असमघाती या असमघाती पॉइसन बिंदु प्रक्रिया (शब्दावली देखें) एक पॉइसन बिंदु प्रक्रिया है जिसमें पॉइसन पैरामीटर अंतर्निहित स्थान में कुछ स्थान-निर्भर फलन के रूप में सेट किया गया है, जिस पर पॉइसन प्रक्रिया परिभाषित है। यूक्लिडियन समष्टि के लिए, यह स्थानीय रूप से पूर्णांक धनात्मक फलन को शुरू करके प्राप्त किया जाता है, जैसे कि प्रत्येक परिबद्ध क्षेत्र के लिए (-विमीय) आयतन से अधिक क्षेत्र का समाकल भाग है। दूसरे शब्दों में, यदि यह समाकल, द्वारा निरूपित किया जाता है, अतः यह निम्न प्रकार है:[44]
जहां , (-विमीय) आयतन अंश है,[lower-alpha 3] फिर असंयुक्त परिबद्ध बोरेल मापने योग्य समुच्चयों के प्रत्येक संग्रह के लिए, (तीव्रता) फलन के साथ असमघातीय पॉइसन प्रक्रिया का परिमित-विमीय बंटन है:[69]
इसके अतिरिक्त, की व्याख्या परिबद्ध क्षेत्र में स्थित पॉइसन प्रक्रिया के बिंदुओं की अपेक्षित संख्या होने की है, अर्थात्
वास्तविक रेखा पर परिभाषित
वास्तविक रेखा पर, गैर-समघातीय या असमघातीय पॉइसन बिंदु प्रक्रिया का औसत माप एकल विमीय समाकल योग के द्वारा दी जाती है। दो वास्तविक संख्याओं और के लिए, जहां , में होने वाले असमघातीय पॉइसन प्रक्रिया के संख्या बिंदु को द्वारा चिह्नित किया जाता है, जिसमें तीव्रता फलन सम्मिलित होता है।उपरोक्त अंतराल में विद्यमान बिंदुओं की प्रायिकता निम्न द्वारा दिया गया है:
जहां माध्य या तीव्रता माप है:
जिसका अर्थ है कि यादृच्छिक चर माध्य के साथ एक पॉइसन यादृच्छिक चर है।
एक-विमा सेटिंग की एक विशेषता यह है कि किसी असमघातीय पॉइसन प्रक्रिया को एकदिष्ट (मोनोटोन) परिवर्तन या मानचित्रण द्वारा सजातीय में रूपांतरित किया जा सकता है, जिसे के प्रतिलोम के साथ प्राप्त किया जाता है।[73][74]
गणना प्रक्रिया की व्याख्या
जब धनात्मक अर्ध-रेखा पर विचार किया जाता है, अतः असमघातीय पॉइसन बिंदु प्रक्रिया को कई बार गणना प्रक्रिया के रूप में भी परिभाषित किया जाता है। इस व्याख्यान के साथ, प्रक्रिया, जिसे कभी-कभी के रूप में लिखा जाता है, समय तक हुई प्रत्येक घटनाओं की कुल संख्या का प्रतिनिधित्व किया जाता है। गणना प्रक्रिया को असमघातीय पॉइसन गणना प्रक्रिया कहा जाता है यदि इसके चार गुण होते हैं:[34][75]
- स्वतंत्र वृद्धि होती है;
- और
यहां , के लिए के अनन्तस्पर्शी या छोटे-o नोटेशन है। अपवर्तकता के साथ बिंदु प्रक्रियाओं की स्थिति में (जैसे कि न्यूरल स्पाइक ट्रेन), प्रगुण 4 का एक अन्य प्रबल संस्करण लागू होता है:[76] .
उपरोक्त गुणों का अर्थ है कि पैरामीटर (या माध्य) के साथ एक पॉइसन यादृच्छिक चर है।
जो ये दर्शाता हे
स्थानिक पॉइसन प्रक्रिया
समतल में परिभाषित असमघातीय पॉइसन प्रक्रिया को स्थानिक पॉइसन प्रक्रिया कहा जाता है[77] इसे तीव्रता फलन के साथ परिभाषित किया जाता है और इसकी तीव्रता की माप कुछ क्षेत्र में इसकी तीव्रता फलन का सतह समाकलन करके प्राप्त किया जाता है।[21][78] उदाहरण के लिए, इसका तीव्रता फलन (कार्तीय निर्देशांक और के एक फलन के रूप में) हो सकता है
इसलिए संगत तीव्रता माप सतह समाकल द्वारा निम्नलिखित रूप दिया जाता है
जहाँ समतल में कुछ घिरा क्षेत्र है।
उच्च विमाओं में
समतल में, सतह समाकलन के सामान प्रतीत होता है जबकि में (-विमीय) आयतन समाकलन में परिवर्तित हो जाता है।
अनुप्रयोग
जब वास्तविक रेखा को समय के रूप में व्याख्या किया जाता है, अतः असमान्य प्रक्रिया को गणना प्रक्रियाओं और कतारबद्ध सिद्धांत के क्षेत्रों में उपयोग किया जाता है।[75][79] असमान्य पॉइसन बिंदु प्रक्रिया द्वारा प्रतिष्ठित या अपेक्षित होने वाली घटनाओं के उदाहरणों में निम्नलिखित सम्मिलित होते हैं:
समतल में, प्रसंभाव्य ज्यामिति[1][35] और स्थानिक आंकड़ों[22][23] के संबंधित शाखाओं में महत्वपूर्ण होती है। इस बिंदु प्रक्रिया की तीव्रता माप अंतर्निहित समष्टि के स्थान पर निर्भर करती है, जिसका तात्पर्य है कि इसका उपयोग किसी क्षेत्र में भिन्नता वाली घटनाओं के मॉडलिंग के लिए किया जा सकता है। दूसरे शब्दों में, ये घटनाएं ऐसे बिंदुओं के रूप में प्रतिष्ठित की जा सकती हैं जिनका स्थान-निर्भर घनत्व है।[21] यह प्रक्रियाएँ विभिन्न क्षेत्रों में उपयोग की जाती हैं और उनमें महासागरों में सैल्मन और समुद्री जीवाणुओं का अध्ययन,[82] वानिकी,[5] और खोज समस्याओं[83] का अध्ययन सम्मिलित होता है।
तीव्रता फलन की व्याख्या
पॉइसन तीव्रता फलन की व्याख्या, जो सहज रूप में मानी जाती है,[21] अत्यल्पिक रूप में आयतन घटक के साथ संबंधित होती है: पॉइसन बिंदु प्रक्रिया के किसी बिंदु की अत्यल्पिक प्रायिकता है जो समष्टि के किसी क्षेत्र में विद्यमान होता है और जिसका आयतन पर नियत होता है। यह क्षेत्र पर नियत होता है।[21] इस व्याख्या से पॉइसन प्रक्रिया में बिंदुओं का अस्तित्व और बंटन का ज्ञान प्राप्त होता है।
उदाहरण के लिए, वास्तविक रेखा पर किसी सजातीय पॉइसन बिंदु प्रक्रिया को देखते हुए, चौड़ाई के एक छोटे अंतराल में प्रक्रिया के एक बिंदु को प्राप्त करने की प्रायिकता लगभग है। वास्तव में, इस तरह के अंतर्ज्ञान से पॉइसन बिंदु प्रक्रिया को कभी-कभी प्रस्तुत किया जाता है और इसका बंटन प्राप्त होता है।[84][42][85]
साधारण बिंदु प्रक्रिया
यदि किसी पॉइसन बिंदु प्रक्रिया में तीव्रता माप स्थानिक रूप से परिमित और असंगठित (या गैर-परमाणु) होती है, अतः वह एक साधारण बिंदु प्रक्रिया होती है। साधारण बिंदु प्रक्रिया के लिए, अंतर्निहित (स्थिति) समष्टि में एकल बिंदु या स्थान पर बिंदु के अस्तित्व की प्रायिकता शून्य या एक होती है। इसका अर्थ है कि पॉइसन बिंदु प्रक्रिया के दो (या अधिक) बिंदु अंतर्निहित समष्टि में स्थान के सामान होता हैं।[86][19][87]
अनुकरण
कंप्यूटर पर पॉइसन बिंदु प्रक्रिया का अनुकरण करना सामान्यतः किसी परिमित स्थानिक क्षेत्र में, जिसे अनुकरण विंडो के रूप में जाना जाता है, किया जाता है और इसके लिए दो चरणों की आवश्यक होती हैं: उचित रूप से किसी यादृच्छिक संख्या के बिंदुओं को बनाना और फिर उन बिंदुओं को एक यादृच्छिक विधि से उचित रूप से स्थानित करना। दोनों इन दो चरणों का प्रयोग किए जाने वाली अनुकरण प्रक्रिया पर निर्भर करते हैं जो वर्तमान में अनुकरणित की जा रही है।[88][89]
चरण 1: बिंदुओं की संख्या
विंडो में बिंदुओं की संख्या , जिसे यहां से चिह्नित किया गया है, को अनुकरणित करने की आवश्यकता है, जो एक (छद्म)-यादृच्छिक संख्या उत्पन्न करने वाले फलन का उपयोग करके किया जाता है जो पॉइसन यादृच्छिक चर का अनुकरण करने में सक्षम है।
समघाती स्थिति
समघातीय स्थिति के लिए नियतांक के साथ, पॉइसन यादृच्छिक परिमाण का औसत पर सेट किया जाता है जहां लंबाई, क्षेत्रफल या ( -विमीय) आयतन है।
असमान स्थिति
विषम स्थितियों के लिए, के साथ प्रतिस्थापित किया गया है (-विमीय) आयतन समाकल
चरण 2: बिंदुओं की स्थिति
दूसरे चरण में, विंडो में बिंदुओं को यादृच्छिक रूप से स्थानित करना आवश्यक होता है।
समघाती स्थिति
एकल विमा में समघातीय स्थिति के लिए, सभी बिंदुओं को विंडो या अंतराल में एकसमान और स्वतंत्र रूप से स्थानित किया जाता है। कार्तीय निर्देशांक प्रणाली में अधिकतर विमाओं के लिए, प्रत्येक निर्देशांक को एकसमान और स्वतंत्र रूप से विंडो में स्थानित किया जाता है। तथापि, यदि विंडो कार्तीय समष्टि का उपअंश नहीं है (उदाहरण के लिए, किसी इकाई स्फीयर के अंदर या किसी इकाई स्फीयर की सतह पर), अतः बिंदुओं को में एकसमान रूप से नहीं रखा जाएगा, और ऐसे स्थितियों में कार्तीय से उचित निर्देशांकों की आवश्यकता होती है।[88]
असमान स्थिति
असमघातीय स्थानिकता वाली स्थितियों में, तीव्रता फलन की प्रकृति पर निर्भर करते हुए कुछ अलग-अलग विधियाँ उपयोग की जा सकती हैं जो तीव्रता फलन की प्रकृति पर निर्भर करती हैं।[88] यदि तीव्रता फलन पर्याप्त रूप से साधारण हो, तो बिना एक-दूसरे के स्वतंत्र और यादृच्छिक असमान (कार्तीय या अन्य) निर्देशांकों को उत्पन्न किया जा सकता है। उदाहरण के लिए, वृत्ताकार विंडो पर पॉइसन बिंदु प्रक्रिया का अनुकरण एक ऐसी आइसोटोपिक तीव्रता फलन (ध्रुवीय निर्देशांकों और में) के लिए किया जा सकता है, जिसका अर्थ है कि यह घूर्णी रूप से भिन्न या से स्वतंत्र है, लेकिन पर निर्भर होती है, में चर के परिवर्तन के द्वारा यदि तीव्रता फलन पर्याप्त रूप से साधारण होता है।[88]
अधिक जटिल तीव्रता फलनों के लिए, स्वीकृति-अस्वीकृति पद्धति का उपयोग किया जा सकता है, जिसमें अनुपात के आधार पर केवल कुछ यादृच्छिक बिंदुओं का उपयोग (या 'स्वीकार') करना और अन्य बिंदुओं का उपयोग नहीं करना (या 'अस्वीकार करना') सम्मिलित है:[90]
जहाँ स्वीकृति या अस्वीकृति के लिए विचाराधीन बिंदु है।
सामान्य पॉइसन बिंदु प्रक्रिया
रेडॉन माप का उपयोग करके पॉइसन बिंदु प्रक्रिया को कभी-कभी सामान्य पॉइसन बिंदु प्रक्रिया[21][91] या सामान्य पॉइसन प्रक्रिया[78] के रूप में जाना जाता है, जो कि स्थानीय-परिमित माप है। सामान्य तौर पर, यह रेडॉन माप परमाणु हो सकता है, जिसका अर्थ है कि पॉसों बिंदु प्रक्रिया के कई बिंदु अंतर्निहित समष्टि के एक ही स्थान पर विद्यमान हो सकते हैं। इस स्थिति में, पर बिंदुओं की संख्या माध्य के साथ एक पॉइसन यादृच्छिक चर होता है।[91] लेकिन कभी-कभी विपरीत मान लिया जाता है, इसलिए रेडॉन माप विसरित या गैर-परमाणु है।[21]
बिंदु प्रक्रिया , तीव्रता के साथ सामान्य पॉइसन बिंदु प्रक्रिया है, यदि इसमें निम्नलिखित दो गुण हैं:[21]
- परिबद्ध बोरेल समुच्चय में अंकों की संख्या माध्य के साथ एक पॉइसन यादृच्छिक चर है। दूसरे शब्दों में, द्वारा में स्थित अंकों की कुल संख्या को निरूपित करें, फिर यादृच्छिक चर के के बराबर होने की प्रायिकता इस प्रकार दी गई है:
- असंयुक्त बोरेल समुच्चय में बिंदुओं की संख्या स्वतंत्र यादृच्छिक चर बनाती है।
राडोन माप परिबद्ध क्षेत्र में स्थित के बिंदुओं की अपेक्षित संख्या होने की अपनी पूर्व व्याख्या को बनाए रखता है, अर्थात्
इसके अतिरिक्त, यदि पूरी तरह से सतत होता है जैसे कि लेबेस्गु माप के संबंध में इसका घनत्व (जो रेडॉन-निकोडीम घनत्व या व्युत्पन्न है) है, तो सभी बोरेल समुच्चय के लिए इसे इस प्रकार लिखा जा सकता है:
जहां घनत्व को अन्य पदों के साथ-साथ तीव्रता फलन के रूप में जाना जाता है।
इतिहास
पॉइसन बंटन
इसके नाम के अतिरिक्त, पॉइसन बिंदु प्रक्रिया की न तो खोज की गई और न ही फ्रांसीसी गणितज्ञ सिमोन डेनिस पॉइसन द्वारा इसका अध्ययन किया गया; स्टिग्लर के नियम के उदाहरण के रूप में नाम का उल्लेख किया गया है।[14][15] यह नाम पॉइसन बंटन के साथ इसके अंतर्निहित संबंध से प्राप्त हुआ, जो पॉइसन द्वारा द्विपद बंटन के किसी परिमित स्थिति के रूप में प्राप्त किया गया है।[92] यह प्रायिकता के साथ बर्नौली परीक्षणों के योग की प्रायिकता का वर्णन करता है, जिसकी तुलना प्रायः हेड (या टेल) की संख्या के साथ की जाती है, जो एक सिक्के के पक्षपाती फ़्लिप के बाद हेड (या टेल) की प्रायिकता होती है। कुछ धनात्मक नियतांक के लिए, जैसे-जैसे अनंत की ओर बढ़ता है और शून्य की ओर घटता जाता है जैसे कि उत्पाद नियत हो जाता है, पॉइसन बंटन द्विपद के अधिक निकट आ जाता है।[93]
पॉइसन ने (शून्य से) और (अनंत तक) की सीमा में द्विपद बंटन की जांच करके, 1841 में प्रकाशित, पॉइसन बंटन को व्युत्पन्न किया। पॉइसन के सभी फलनों में यह केवल एक बार प्रकट होता है,[94] और उनके समय में परिणाम अच्छी तरह से ज्ञात नहीं था। बाद के वर्षों में फिलिप लुडविग वॉन सेडेल और अर्नेस्ट अब्बे सहित कई लोगों ने पॉइसन का हवाला दिए बिना बंटन का उपयोग किया।[95][14] उन्नीसवीं शताब्दी के अंत में, लैडिसलॉस बोर्टकिविक्ज़ बंटन का फिर से अलग सेटिंग में अध्ययन करेगा (पॉइसन का उल्लेखन करते हुए), वास्तविक डेटा के साथ बंटन का उपयोग करके प्रशिया सेना में हॉर्स किक से होने वाली मौतों की संख्या का अध्ययन करने के लिए।[92][96]
खोज
पॉइसन बिंदु प्रक्रिया के पहले उपयोग या खोज के लिए कई दावे हैं।[14][15] उदाहरण के लिए, 1767 में पॉइसन के जन्म से दस साल पहले, जॉन मिशेल ने एक सितारे के एक निश्चित क्षेत्र में दूसरे सितारे की प्रायिकता की रुपरेखा के बारे में रुचि दिखाई, असुमंगल या "केवल संयोग के द्वारा बिखेरे गए" सितारों की अनुमानित संख्या का अध्ययन किया और प्लेयडीज़ में छह सबसे चमकदार सितारों, पॉइसन बंटन प्राप्त किए बिना। इस काम ने साइमन न्यूकॉम्ब को प्रभावित किया और उन्हें समस्या का अध्ययन करने और 1860 में द्विपद बंटन के लिए वर्गीकरण के रूप में पॉइसन बंटन की गणना करने के लिए प्रेरित किया।[15]
20वीं शताब्दी की शुरुआत में पोइसन प्रक्रिया (एक आयाम में) विभिन्न स्थितियों में स्वतंत्र रूप से उत्पन्न होगी।[14][15] स्वीडन 1903 में, फिलिप लुंडबर्ग ने एक थीसिस प्रकाशित की जिसमें कार्य शामिल था, जिसे अब मौलिक और अग्रणी माना जाता है, जहां उन्होंने एक सजातीय पॉइसन प्रक्रिया के साथ बीमा दावों को मॉडल करने का प्रस्ताव दिया।[97][98]
1909 में डेनमार्क में एक अन्य खोज हुई जब ए.के. अर्लांग ने सीमित समय अंतराल में आने वाले फोन कॉलों की संख्या के लिए एक गणितीय मॉडल विकसित करते समय पॉइसन बंटन की खोज की। उस समय अर्लांग को पॉइसन के पहले के काम की जानकारी नहीं थी और उन्होंने माना कि प्रत्येक समय अंतराल में आने वाले फोन कॉलों की संख्या एक दूसरे के अन्यान्य हैं। फिर उन्होंने सीमित स्थिति को खोजा, जो प्रभावी रूप से पॉइसन बंटन को द्विपद बंटन की सीमा के रूप में पुनर्स्थापित कर रही है।[14]
1910 में अर्नेस्ट रदरफोर्ड और हंस गीजर ने अल्फा कणों की गणना पर प्रयोगात्मक परिणाम प्रकाशित किए। उनके प्रायोगिक कार्य में हैरी बेटमैन से गणितीय योगदान था, जिन्होंने अंतर समीकरणों के परिवार के समाधान के रूप में पॉइसन प्रायिकताओं को व्युत्पन्न किया था, हालांकि समाधान पहले प्राप्त किया गया था, जिसके परिणामस्वरूप पॉइसन प्रक्रिया की स्वतंत्र खोज हुई।[14] इस समय के बाद पॉइसन प्रक्रिया के कई अध्ययन और अनुप्रयोग हुए, लेकिन इसका प्रारंभिक इतिहास जटिल है, जिसे जीवविज्ञानियों, पारिस्थितिकीविदों, इंजीनियरों और विभिन्न भौतिक वैज्ञानिकों द्वारा कई क्षेत्रों में प्रक्रिया के विभिन्न अनुप्रयोगों द्वारा समझाया गया है।[14]
प्रारंभिक अनुप्रयोग
1909 के बाद के वर्षों में पॉइसन बिंदु प्रक्रिया के कई अध्ययन और अनुप्रयोग हुए, हालांकि, इसका प्रारंभिक इतिहास जटिल है, जिसे बायोलॉजिस्ट, पारिस्थितिकीविद, अभियंता और अन्य भौतिक विज्ञान में काम करने वाले लोगों ने इस प्रक्रिया के कई क्षेत्रों में अनेक अनुप्रयोगों के द्वारा समझाया है। प्रारंभिक परिणामों को विभिन्न भाषाओं और विभिन्न संस्करणों में प्रकाशित किया गया, जहां कोई मानक शब्दावली और नोटेशन का उपयोग नहीं हुआ।[14] उदाहरण के लिए, 1922 में स्वीडिश रसायनविद और नोबेल पुरस्कार प्राप्तकर्ता थिओडोर स्वेडबर्ग ने एक मॉडल प्रस्तावित किया, जिसमें एक स्थानिक पॉइसन बिंदु प्रक्रिया पौधों को अध्ययन करने के लिए उपयोगी है जो वनस्पति समुदायों में वितरित होते हैं।[99] कई गणितज्ञों ने 1930 के दशक में प्रक्रिया का अध्ययन शुरू किया और इसमें एंड्री कोलमोगोरोव, विलियम फेलर और अलेक्सांद्र खींचीं,[14] सहित अन्यों ने महत्वपूर्ण योगदान दिया।[100] टेलीट्रैफिक अभियतंत्रिकी के क्षेत्र में, गणितज्ञों और सांख्यिकीयज्ञों ने पॉइसन और अन्य बिंदु प्रक्रियाओं का अध्ययन किया और उन्हें उपयोग किया।[101]
शब्दावली का इतिहास
1943 में स्वीडिश विद्वान कोनी पाम ने अपने विधानिका में एक विमीय स्थानिकता में पॉइसन और अन्य बिंदु प्रक्रियाओं का अध्ययन किया, जहां उन्होंने समय के संबंध में बिंदु के बीच आपसी सांख्यिक या प्रसंभाव्य आधिपत्य की परीक्षा की।।[102][101] उनके कार्य में पहली ज्ञात रूप से टर्म बिंदु प्रक्रियाओं का प्रयोग हुआ, जैसे कि जर्मन में पंकटप्रोज़ेस के रूप में शब्द बिंदु प्रक्रियाओं का पहला ज्ञात रिकॉर्ड विद्यमान है।[102][15]
यह माना जाता है[14] कि 1940 में विलियम फेलर ने इसे पॉइसन प्रक्रिया के रूप में प्रिंट में पहली बार संदर्भित किया था। हालांकि, स्वीडिश विद्वान ओवे लुंडबर्ग ने अपने 1940 के डॉक्टरेट पेपर में भी इस शब्द का प्रयोग किया था,[15] जिसमें फेलर को प्रभावित करने के रूप में स्वीकार किया गया था,[103] लेकिन कहा गया है कि फेलर ने 1940 से पहले ही इस शब्द की सृजनशीलता की थी।[93] यह बात बताई गई है कि फेलर और लुंडबर्ग दोनों ने इस शब्द का उपयोग ऐसे किया, जैसे यह पहले से प्रसिद्ध हो, इससे इसका अर्थ है कि यह तब से पहले ही बोली जाने वाली थी।[15] फेलर 1936 से 1939 तक स्टॉकहोम विश्वविद्यालय में हराल्ड क्रामर के साथ काम कर रहे थे, जहां लुंडबर्ग क्रामर के निर्देशन में एक डॉक्टरेट छात्र थे, जिन्होंने इस शब्द का उपयोग नहीं किया था, जिसकी पुस्तक को वे 1936 में पूरा कर चुके थे, लेकिन इसके बाद की संस्करणों में किया, जिससे यह संकेत मिला है कि पॉइसन प्रक्रिया शब्द का निर्माण स्टॉकहोम विश्वविद्यालय में 1936 से 1939 के बीच किया गया था।[15]
शब्दावली
बिंदु प्रक्रिया सिद्धांत की शब्दावली सामान्य रूप से बहुत असमघातीय मानी जाती है।[15] बिंदु शब्द को छोड़ दिया जाना एक साधारण बात है,[65][2] समान पॉइसन (बिंदु) प्रक्रिया को समघातीय पॉइसन (बिंदु) प्रक्रिया के रूप में भी कहा जाता है,[48] साथ ही यह स्थायी पॉइसन (बिंदु) प्रक्रिया भी कहलाती है।[43] असमघातीय पॉइसन बिंदु प्रक्रिया, असमघातीय के रूप के साथ ही,[48] स्थायी पॉइसन प्रक्रिया के रूप में भी उल्लेख की जाती है।[75][104]
शब्द बिंदु प्रक्रिया की आलोचना की गई है, क्योंकि शब्द प्रक्रिया समय और स्थान के साथ सुझाव दे सकती है, इसलिए यादृच्छिक बिंदु क्षेत्र,[105] जिसके परिणामस्वरूप पोइसन यादृच्छिक बिंदु क्षेत्र या पॉइसन बिंदु क्षेत्र का भी उपयोग किया जाता है।[106] एक बिंदु प्रक्रिया को माना जाता है, और कभी-कभी इसे एक यादृच्छिक गिनती माप कहा जाता है,[107] इसलिए पॉसॉन बिंदु प्रक्रिया को एक पॉइसन यादृच्छिक माप के रूप में भी जाना जाता है,[108] लेवी प्रक्रियाओं के अध्ययन में प्रयुक्त शब्द,[108][109] लेकिन कुछ लोग दो अलग-अलग अंतर्निहित स्थानों पर परिभाषित प्वासों बिंदु प्रक्रियाओं के लिए दो शब्दों का उपयोग करना चुनते हैं।[110]
पॉइसन बिंदु प्रक्रिया की आधारभूत गणितीय स्थान को "कैरियर समष्टि",[111][112] या "स्थिति समष्टि" कहा जाता है, हालांकि इस्पात संदर्भ में दूसरा शब्द अलग अर्थ रखता है। बिंदु प्रक्रियाओं के संदर्भ में, "स्थिति समष्टि" शब्द का उपयोग बिंदु प्रक्रिया के परिभाषित स्थान को दर्शाने के लिए किया जा सकता है, जैसे वास्तविक रेखा,[113][114] जो प्रसंभाव्य प्रक्रिया की शब्दावली में अनुक्रमणिका समुच्चय[115]या पैरामीटर समुच्चय[116] के समर्थन स्थान के तौर पर प्रतिष्ठित होती है।
माप को तीव्रता माप कहा जाता है,[117] औसत माप,[38] या पैरामीटर माप,[69] क्योंकि इसमें कोई मानक शब्द नहीं हैं।[38] यदि का व्युत्पन्न या घनत्व है, जिसे द्वारा निरूपित किया जाता है, तो पॉइसन बिंदु प्रक्रिया का तीव्रता फलन कहा जाता है।[21] समघातीय पोइसन बिंदु प्रक्रिया के लिए, तीव्रता माप का व्युत्पन्न केवल स्थिर है, जिसे दर के रूप में संदर्भित किया जा सकता है, आमतौर पर जब अंतर्निहित समष्टि वास्तविक रेखा या तीव्रता होती है।[43] इसे औसत दर या औसत घनत्व[118] या दर भी कहा जाता है।[34] के लिए, संबंधित प्रक्रिया को कभी-कभी मानक पॉइसन (बिंदु) प्रक्रिया के रूप में जाना जाता है।[44][58][119]
पॉइसन बिंदु प्रक्रिया की सीमा को कभी-कभी एक्सपोजर कहा जाता है।[120][121]
अंकन (नोटेशन)
पॉइसन बिंदु प्रक्रिया की नोटेशन इसकी स्थापना और उस क्षेत्र पर निर्भर करती है जिसमें इसका उपयोग हो रहा है। उदाहरण के लिए, वास्तविक रेखा पर, पॉइसन प्रक्रिया, समरूपी या असमरूपी दोनों, कभी-कभी एक गिनती प्रक्रिया के रूप में व्याख्या की जाती है, और नोटेशन का प्रयोग पॉइसन प्रक्रिया को प्रतिष्ठान करने के लिए किया जाता है।[31][34]
विभिन्न नोटेशन के लिए एक अन्य कारण बिंदु प्रक्रिया के सिद्धांत का हो सकता है, जिसके कुछ गणितीय व्याख्यान होते हैं। उदाहरण के लिए, साधारण पॉइसन बिंदु प्रक्रिया को किसी यादृच्छिक समुच्चय के रूप में विचार किया जा सकता है, जिससे संकेतन दर्शाते है, जो प्रस्तावित करता है कि पॉइसन बिंदु प्रक्रिया का एक यादृच्छिक बिंदु होता है या इसका तत्व होता है। एक अन्य अधिक सामान्य, व्याख्या यह है कि पॉइसन या किसी अन्य बिंदु प्रक्रिया को किसी यादृच्छिक गणना माप के रूप में विचार किया जा सकता है, ताकि हम किसी (बोरेल माप्य) क्षेत्र में पाए जाने वाले बिंदुओं की संख्या को के रूप में लिख सकें, जो एक यादृच्छिक परिवर्तन है। इन विभिन्न व्याख्याओं के परिणामस्वरूप गणितीय क्षेत्रों जैसे माप सिद्धांत और सेट सिद्धांत से संकेतन का उपयोग किया जाता है।[122]
सामान्य बिंदु प्रक्रियाओं के लिए, कभी-कभी बिंदु प्रतीक पर सबस्क्रिप्ट, उदाहरण के लिए , सम्मिलित होता है अतः किसी व्यष्टि बिंदु को इसे छोड़कर (समुच्चय अंकन के साथ) के स्थान पर के रूप में लिखा जाता है, और ऐसे समाकल व्यंजकों में परिमित चर के लिए का प्रयोग किया जा सकता है, जैसे कैम्पबेल के सिद्धांत में, जो यादृच्छिक बिंदुओं का प्रतिनिधित्व नहीं करता है।[19] कभी-कभी बड़ा अक्षर बिंदु प्रक्रिया को दर्शाता है, जबकि छोटा अक्षर प्रक्रिया से एक बिंदु को दर्शाता है, इसलिए, उदाहरण के लिए, बिंदु या बिंदु प्रक्रिया का भाग होता है या उसका बिंदु होता है, और समुच्चय अंकन के साथ या के रूप में लिखा जा सकता है।[114]
इसके अतिरिक्त, समुच्चय सिद्धांत और समाकल या माप सिद्धांत अंकन का परस्पर उपयोग किया जा सकता है। उदाहरण के लिए, यूक्लिडियन स्टेट स्पेस पर परिभाषित बिंदु प्रक्रिया और पर (मापने योग्य) फलन के लिए, व्यंजक
दो विभिन्न विधियों को दिखाता है बिंदु प्रक्रिया पर एक योग को लिखने के लिए (कैम्पबेल की प्रमेय भी देखें (प्रायिकता))। अधिक विशेष रूप से, बाएं हाथ की ओर समाकल अंकन बिंदु प्रक्रिया को यादृच्छिक गणना माप के रूप में व्याख्या कर रहा है जबकि दाएं हाथ की ओर सम किसी यादृच्छिक समुच्चय व्याख्या प्रस्तावित करता है।[122]
प्रकार्य और मोमेंट माप
प्रायिकता सिद्धांत में, विभिन्न उद्देश्यों के लिए यादृच्छिक संख्याओं पर संचालित किए जाते हैं। कभी-कभी ये संक्रियाएँ नियमित आपेक्षिक होती हैं जो किसी यादृच्छिक संख्या के औसत या प्रसारण का निर्माण करते हैं। अन्य, यादृच्छिक संख्या की विशेषता-कारक (या लाप्लास रूपांतरण) के रूप में उपयोग किए जा सकते हैं, जो यादृच्छिक संख्याओं की अद्वितीय पहचान करने या वर्गमूल सीमा सिद्धांत जैसे परिणामों को सिद्ध करने में सहायता प्रदान करते हैं।[123] बिंदु प्रक्रिया के सिद्धांत में, इसी तरह के गणितीय साधन होते हैं जो सामान्यतः किसी माप और कार्यात्मक के रूप में होते हैं और किसी भी प्रकार के मोमेंट और फलन के के स्थान पर विद्यमान होते हैं।[124][125]
लाप्लास प्रकार्य
किसी स्थान पर तीव्रता माप के साथ किसी पॉइसन बिंदु प्रक्रिया के लिए, लाप्लास प्रकार्य निम्नलिखित द्वारा दिया जाता है:[19]
कैंपबेल के प्रमेय के एक संस्करण में पॉइसन बिंदु प्रक्रिया के लाप्लास प्रकार्य सम्मिलित है।
प्रायिकता जनित्र फलन
गैर-ऋणात्मक पूर्णांक-मूल्यवान यादृच्छिक चर का प्रायिकता जनित्र फलन किसी भी गैर-ऋणात्मक परिबद्ध फलन पर जैसे कि के संबंध में समान रूप से परिभाषित प्रायिकता जनित्र फलन की ओर जाता है। किसी बिंदु प्रक्रिया के लिए प्रायिकता जनित्र फलन को परिभाषित किया गया है :[126]
जहां गुणनफल में सभी बिंदुओं के लिए किया जाता है। यदि की तीव्रता माप स्थानीय रूप से परिमित है, अतः , पर किसी भी मापनीय फलन के लिए अच्छी तरह से परिभाषित है। तीव्रता माप के साथ किसी पॉइसन बिंदु प्रक्रिया के लिए जनित्र फलन द्वारा दिया गया है:
जो समघाती स्थितियों में कम हो जाता है
मोमेंट माप
तीव्रता माप के साथ एक सामान्य पॉइसन बिंदु प्रक्रिया के लिए प्रथम मोमेंट माप इसकी तीव्रता माप है:[19][20]
जो सतत तीव्रता के साथ समघातीय पॉइसन बिंदु प्रक्रिया के लिए है:
जहां , की लंबाई, क्षेत्रफल या आयतन (या अधिक सामान्यतः, लेबेस्ग माप) है।
मेके समीकरण
मेके समीकरण पॉइसन बिंदु प्रक्रिया की विशेषता बताता है। को कुछ सामान्य स्थान पर सभी -परिमित उपायों का स्थान दें। पर तीव्रता के साथ बिंदु प्रक्रिया पॉइसन बिंदु प्रक्रिया है यदि और केवल यदि सभी मापनीय फलनों के लिए निम्नलिखित धारण करता है
अधिक जानकारी के लिए देखें।[127]
क्रमगुणित मोमेंट माप
तीव्रता माप के साथ सामान्य पॉइसन बिंदु प्रक्रिया के लिए -वाँ तथ्यात्मक मोमेंट माप व्यंजक द्वारा दिया जाता है:[128]
जहां तीव्रता माप या का प्रथम मोमेंट माप है, जो कि कुछ बोरेल समुच्चय के द्वारा दिया जाता है
किसी समघातीय पॉइसन बिंदु प्रक्रिया के लिए -वां क्रमगुणित मोमेंट मात्र है:[19][20]
जहां , की लंबाई, क्षेत्रफल, या आयतन (या अधिक सामान्य रूप से, लेबेस्ग माप) है। इसके अतिरिक्त, -वां क्रमगुणित मोमेंट घनत्व है:[128]
परिवर्जन फलन
परिवर्जन फलन [72]या वोयड प्रायिकता [122] बिंदु प्रक्रिया का कुछ सेट के संबंध में परिभाषित किया गया है , जो अंतर्निहित स्थान का सबसेट है , बिना अंक की प्रायिकता के रूप में में विद्यमान है . ज्यादा ठीक,[129] एक परीक्षण सेट के लिए परिवर्जन फलन द्वारा दिया जाता है:
तीव्रता माप के साथ सामान्य पॉइसन बिंदु प्रक्रिया के लिए, इसका परिवर्जन फलन निम्न द्वारा दिया जाता है:
रेनी की प्रमेय
साधारण बिंदु प्रक्रियाएं अपनी शून्यता प्रायिकताओं द्वारा पूर्ण रूप से वर्णीय होती हैं।[130] अन्य शब्दों में, साधारण बिंदु प्रक्रिया की पूर्ण जानकारी शून्यता प्रायिकताओं में पूरी तरह से प्रतिष्ठित होती है, और यदि और केवल यदि दो साधारण बिंदु प्रक्रियाएं एक ही बिंदु प्रक्रियाएं हैं तो वे एक ही शून्यता प्रायिकताएं रखती हैं। पॉइसन प्रक्रिया के लिए स्थिति को कभी-कभी रेनी के सिद्धांत के रूप में जाना जाता है, जो अल्फ्रेड रेनी द्वारा एक-विमा में समान प्रकार की किसी समानांतर बिंदु प्रक्रिया के स्थिति के लिए परिणाम की खोज करने के बाद नामित किया गया है।[131]
एक रूप में,[131] रेनी के सिद्धांत के अनुसार किसी विस्तरित (या गैर-अणुगत) रेडोन माप पर और एक समुच्चय है जो वर्गों के परिमित संघ है (इसलिए बोरेल[lower-alpha 4] नहीं है) तब यदि ऐसा एक गणनीय उपसमुच्चय है जो का एक संख्यात्मक उपसमुच्चय होता है, जिसकी शर्तें हैं:
तो तीव्रता माप के साथ पॉइसन बिंदु प्रक्रिया है।
बिंदु प्रक्रिया संक्रियाएँ
नई बिंदु प्रक्रियाओं को प्राप्त करने और कुछ वस्तुओं के स्थानों के लिए नए गणितीय मॉडल विकसित करने के लिए गणितीय संक्रिया बिंदु प्रक्रियाओं पर किया जा सकता है। ऑपरेशन के एक उदाहरण को थिनिंग के रूप में जाना जाता है, जिसमें एक नियम के अनुसार कुछ बिंदु प्रक्रिया के बिंदुओं को हटाना सम्मिलित है, शेष बिंदुओं के साथ नई प्रक्रिया का निर्माण करना (हटाए गए बिंदु भी एक बिंदु प्रक्रिया बनाते हैं)।[133]
विरलन
पॉइसन प्रक्रिया के लिए, स्वतंत्र -विरलन संक्रिया के परिणामस्वरूप एक और पॉइसन बिंदु प्रक्रिया होती है। अधिक विशेष रूप से, तीव्रता माप के साथ एक पॉइसन बिंदु प्रक्रिया पर लागू एक -विरलन संक्रिया हटाए गए बिंदुओं की एक बिंदु प्रक्रिया देता है जो पॉइसन बिंदु प्रक्रिया की तीव्रता माप के साथ भी है, जो परिबद्ध बोरेल समुच्चय के लिए दिया गया है:
यह पॉइसन बिंदु प्रक्रिया के विरलन का परिणाम कभी-कभी प्रेकोपा के सिद्धांत के रूप में जाना जाता है।[134] इसके अतिरिक्त, पॉइसन बिंदु प्रक्रिया को यादृच्छिक रूप से विरलन के बाद, शेष बिंदुओं भी पॉइसन बिंदु प्रक्रिया बनाते हैं, जिसका तीव्रता माप है
हटाए गए और रखे गए बिंदुओं से क्रमशः बनने वाली दो अलग-अलग पॉइसन बिंदु प्रक्रियाएं एक दूसरे से प्रसंभाव्य रूप से स्वतंत्र हैं।[133] दूसरे शब्दों में, यदि किसी क्षेत्र को रखे हुए बिंदुओं (मूल पॉइसन बिंदु प्रक्रिया से) के लिए जाना जाता है, तो उसी क्षेत्र में हटाए गए बिंदुओं की यादृच्छिक संख्या पर इसका कोई प्रभाव नहीं पड़ेगा। यादृच्छिक रूप से एक से दो स्वतंत्र पॉइसन बिंदु प्रक्रियाओं को बनाने की इस क्षमता को कभी-कभी विभाजन[135][136] पॉइसन बिंदु प्रक्रिया के रूप में जाना जाता है।
अध्यारोपण
यदि बिंदु प्रक्रियाओं का गणनीय संग्रह है, तो उनका अध्यारोपण, या, समुच्चय सिद्धांत लैंग्वेज में, उनका संघ, जो निम्नलिखित है[137]
बिंदु प्रक्रिया भी बनाता है। दूसरे शब्दों में, किसी भी बिंदु प्रक्रिया में स्थित कोई भी बिंदु इन बिंदु प्रक्रियाओं के अध्यारोपण में स्थित होगा।
अध्यारोपण प्रमेय
पॉइसन बिंदु प्रक्रिया के अध्यारोपण प्रमेय का कहना है कि औसत माप के साथ स्वतंत्र पॉइसन बिंदु प्रक्रिया का अध्यारोपण भी औसत माप के साथ एक पॉइसन बिंदु प्रक्रिया होगी[138][93]
दूसरे शब्दों में, दो (या गणनीय रूप से अधिक) पॉइसन प्रक्रियाओं का यूनियन अन्य पॉइसन प्रक्रिया है। यदि बिंदु को पॉइसन प्रक्रियाओं के गणनीय यूनियन से सैंपल लिया जाता है, अतः प्रायिकता है कि बिंदु , यूनियन प्रक्रिया के अंतर्गत आता है:
तीव्रता के साथ दो समघातीय पॉइसन प्रक्रियाओं के लिए, पूर्व दो व्यंजक निम्नलिखित परिवर्तित हो जाते है
और
क्लस्टरिंग
जब किसी बिंदु प्रक्रिया के प्रत्येक बिंदु को दूसरे (संभवतः अलग) बिंदु प्रक्रिया से प्रतिस्थापित किया जाता है, तब ऑपरेशन क्लस्टरिंग का उपयोग किया जाता है। यदि मूल प्रक्रिया पॉइसन बिंदु प्रक्रिया है, तो परिणामस्वरूपी प्रक्रिया को पॉइसन क्लस्टर बिंदु प्रक्रिया कहा जाता है।
यादृच्छिक विस्थापन
गणितीय मॉडल को कभी-कभी यादृच्छिक रूप से गतिमान बिंदुओं की आवश्यकता होती है ताकि उन्हें मूल गणितीय समष्टि पर अन्य स्थानों पर ले जाया जा सके, जिससे बिंदु प्रक्रिया संक्रिया का उत्पन्न होता है जिसे 'स्थानांतरण'[139] या 'स्थानांकन'[140] के नाम से जाना जाता है। पॉइसन बिंदु प्रक्रिया का उपयोग करके, उदाहरण के लिए, पौधों के पीढ़ियों के बीच चलने का मॉडल बनाने के लिए उपयोग किया गया है, जो 'स्थानांतरण सिद्धांत'[139] के कारण है, जिसका ठीक-ठीक अर्थ होता है कि पॉइसन बिंदु प्रक्रिया के बिंदुओं का यादृच्छिक स्वतंत्र स्थानांतरण (एक ही मूल समष्टि पर) दूसरी पॉइसन बिंदु प्रक्रिया बनाता है।
विस्थापन प्रमेय
किसी संस्करण में, स्थानांतरण सिद्धांत[139] में पॉइसन बिंदु प्रक्रिया को पर तीव्रता फलन के साथ निर्धारित किया जाता है। इसके बाद माना जाता है कि के बिंदुओं को यादृच्छिक रूप से में कहीं और स्थानांतरित किया जाता है, जिससे प्रत्येक बिंदु का स्थानांतरण स्वतंत्र होता है और एक का विस्थापन पूर्व में पर बिंदु प्रायिकता घनत्व के साथ यादृच्छिक सदिश होता है।[lower-alpha 5] इसके बाद स्थानांतरण से प्राप्त होने वाली नई बिंदु प्रक्रिया, जिसे के रूप में चिह्नित किया जाता है, भी पॉइसन बिंदु प्रक्रिया होती है जिसका तीव्रता फलन
यदि पॉइसन प्रक्रिया के साथ समघातीय है और यदि , का फलन है, अतः
दूसरे शब्दों में, बिंदुओं के प्रत्येक यादृच्छिक और स्वतंत्र विस्थापन के बाद, मूल पॉइसन बिंदु प्रक्रिया अभी भी विद्यमान है।
विस्थापन प्रमेय को विस्थापित किया जा सकता है ताकि पॉइसन बिंदुओं को यूक्लिडियन समष्टि से यूक्लिडियन समष्टि में यादृच्छिक रूप से विस्थापित किया जाए, जहां , के बराबर नहीं होता है।[19]
मैपिंग
अन्य गुणधर्म जिसे उपयोगी माना जाता है वह अंतर्निहित समष्टि से दूसरे स्थान पर पॉइसन बिंदु प्रक्रिया को मैप करने की क्षमता है।[141]
मैपिंग प्रमेय
यदि मैपिंग (या परिवर्तन) कुछ शर्तों का पालन करता है, तो परिणामस्वरूप मैप किए गए (या परिवर्तित) बिंदुओं का संग्रह भी पॉइसन बिंदु प्रक्रिया बनाता है, और इस परिणाम को कभी-कभी मैपिंग सिद्धांत के रूप में संदर्भित किया जाता है।[141][142] यह सिद्धांत किसी मूलभूत स्थान पर कुछ पॉइसन बिंदु प्रक्रिया के साथ संबंधित होता है जिसमें माध्यम माप होती है। यदि बिंदुओं की स्थानों को किसी फलन के अनुसार (अर्थात बिंदु प्रक्रिया परिवर्तित की जाती है) किसी अन्य मूलभूत स्थान में मैप किया जाता है, तो परिणामस्वरूप बिंदु प्रक्रिया भी एक पॉइसन बिंदु प्रक्रिया होती है, लेकिन एक अलग माध्यम माप के साथ।
अधिक विशेष रूप से, (बोरेल मापने योग्य) फलन पर विचार किया जा सकता है जो बिंदु प्रक्रिया को तीव्रता माप के साथ किसी स्थान से दूसरे स्थान तक इस तरह से मैप करता है ताकि नई बिंदु प्रक्रिया में तीव्रता का माप हो:
जहां बोरेल समुच्चय है और फलन का व्युत्क्रम होता है, जहाँ कोई अणु नहीं होते हैं। यदि पॉइसन बिंदु प्रक्रिया है, तो नवीन प्रक्रिया भी पॉइसन बिंदु प्रक्रिया है जिसमें घनत्व माप होती है।
पॉइसन बिंदु प्रक्रियाओं के साथ सन्निकटन
पॉइसन प्रक्रिया की अनुकरणीयता का अर्थ है कि कभी-कभी गैर-पॉइसन बिंदु प्रक्रिया को पॉइसन प्रक्रिया से अनुमानित करना सुविधाजनक होता है। समग्र उद्देश्य है किसी बिंदु प्रक्रिया के बिंदुओं की संख्या और प्रत्येक बिंदु के स्थान को पॉइसन बिंदु प्रक्रिया से अनुमानित करना।[143] ऐसे कई तरीके हैं जो प्रायोगिक या कठोर रूप से उचित पोइसन बिंदु प्रक्रियाओं के साथ यादृच्छिक घटनाओं या घटनाओं की घटना का अनुमान लगाने के लिए किया जा सकता है। अधिक कठोर रूप से पॉइसन और गैर-पॉइसन बिंदु प्रक्रियाओं के बीच प्रायोगिक मेट्रिक्स के बारे में ऊपरी सीमाओं को प्राप्त करने में संलग्न होते हैं, जबकि अन्य विधियों को कम औपचारिक अनुमानों द्वारा तार्किकतापूर्वक विवर्णित किया जा सकता है।[144]
क्लंपिंग ह्यूरिस्टिक
पॉइसन प्रक्रियाओं के साथ यादृच्छिक घटनाओं या परिघटनाओं का पूर्वानुमान के लिए एक विधि को क्लंपिंग ह्यूरिस्टिक कहा जाता है।[145] सामान्य हेयुरिस्टिक या सिद्धांत में पॉइसन बिंदु प्रक्रिया (या पॉइसन बंटन) का उपयोग अनुमानित घटनाओं के लिए करना सम्मिलित है, जिन्हें कुछ प्रसंभाव प्रक्रिया के दुर्लभ या असंभावित माना जाता है। कुछ स्थितियों में ये दुर्लभ घटनाएं स्वतंत्र होने के निकट हैं, इसलिए पॉइसन बिंदु प्रक्रिया का उपयोग किया जा सकता है। जब घटनाएँ स्वतंत्र नहीं होती हैं, लेकिन क्लंपस या क्लस्टर में घटित होती हैं, तो यदि इन क्लस्टर को उपयुक्त रूप से इस तरह परिभाषित किया जाता है कि वे लगभग दूसरे से स्वतंत्र हैं, अतः घटित होने वाले क्लस्टर की संख्या पॉइसन यादृच्छिक चर के निकट होगी[144] और क्लस्टर का स्थान पॉइसन प्रक्रिया के समीप होगा।[145]
स्टीन की विधि
स्टीन की विधि एक गणितीय तकनीक है जिसे मूल रूप से गॉसियन और पॉइसन चर जैसे यादृच्छिक चर के अनुमान के लिए विकसित किया गया था, जिसे बिंदु प्रक्रियाओं पर भी लागू किया गया है। स्टीन की विधि का उपयोग प्रायिकता आव्यूह पर ऊपरी परिबंध को प्राप्त करने के लिए किया जा सकता है, जो यह निर्धारित करने की विधि प्रदान करता है कि दो भिन्न-भिन्न यादृच्छिक गणितीय वस्तुएं प्रसंभाव्य रूप से कैसे परिवर्तित हैं।[146][147] प्रायिकता आव्यूह पर ऊपरी परिबंध जैसे कि कुल भिन्नता और वासेरस्टीन दूरी को व्युत्पन्न किया गया है।[143]
शोधकर्ताओं ने स्टीन की विधि को कई तरीकों से पॉइसन बिंदु प्रक्रियाओं पर लागू किया है,[143] जैसे कि पाम कैलकुलस का उपयोग करना।[112] स्टीन की विधि पर आधारित तकनीकों को ऊपरी परिबंध में विरलन और अध्यारोपण जैसे कुछ बिंदु प्रक्रिया संक्रिया के प्रभावों को प्रभावित करने के लिए विकसित किया गया है।[148][149] स्टीन की विधि का उपयोग पॉइसन के आव्यूह और कॉक्स बिंदु प्रक्रिया जैसी अन्य प्रक्रियाओं पर ऊपरी परिबंध को प्राप्त करने के लिए भी किया गया है, जो यादृच्छिक तीव्रता माप के साथ पॉइसन प्रक्रिया है।[143]
पॉइसन बिंदु प्रक्रिया के लिए कन्वर्जेन्स
सामान्यतः, जब किसी साधारण बिंदु प्रक्रिया पर कोई आपरेशन लागू किया जाता है, तो परिणामस्वरूप प्रक्रिया आमतौर पर एक पॉइसन पॉइंट प्रक्रिया नहीं होती है। उदाहरण के लिए, यदि किसी बिंदु प्रक्रिया को, पॉइसन के अतिरिक्त, इसके बिंदुओं को यादृच्छिक और स्वतंत्र रूप से विस्थापित किया जाता है, तो प्रक्रिया आवश्यकतापूर्वक एक पॉइसन बिंदु प्रक्रिया नहीं होगी। हालांकि, मूल बिंदु प्रक्रिया और यादृच्छिक विस्थापन के लिए निश्चित गणितीय शर्तों के तहत, सीमा सिद्धांतों के माध्यम से दिखाया गया है कि यदि एक बिंदु प्रक्रिया के बिंदुओं को यादृच्छिक और स्वतंत्र रूप से बार-बार विस्थापित किया जाए, तो बिंदु प्रक्रिया की सीमित बंटन (दुर्बल रूप से) पॉइसन बिंदु प्रक्रिया के बराबर होगी।[150]
विरलन और अध्यारोपण संक्रियाओं के लिए भी ऐसे संघटकता परिणाम विकसित किए गए हैं[150] जो दिखाते हैं कि ऐसी पुनरावृत्त संक्रियाओं को बिंदु प्रक्रियाओं पर अनुमानित करने पर यदि उचित तीव्रता माप का संगठन किया जाए (अन्यथा परिणामस्वरूप बिंदु प्रक्रियाओं के तीव्रता माप के मान शून्य या अनंत की ओर पहुंचेंगे), तो प्रक्रिया पॉइसन बिंदु प्रक्रियाओं के संगत बराबर हो सकती है। ऐसी संघटना कार्य सीधे उन परिणामों से संबंधित होती है जिन्हें पाम-खिंचिन[lower-alpha 6] समीकरण के रूप में जाना जाता है, जिसकी उत्पत्ति कॉनी पाम और अलेक्सांदर खिंचिन के कार्य में हुई है,[151] और यह समझने में मदद करती है कि पॉइसन प्रक्रिया अकस्मात घटित होने वाले विभिन्न यादृच्छिक प्रभावों के गणितीय मॉडल के रूप में प्रायः उपयोग की जा सकती है।[150]
पॉइसन बिंदु प्रक्रियाओं का सामान्यीकरण
पॉइसन बिंदु प्रक्रिया को विस्तारित किया जा सकता है, उदाहरण के लिए, तीव्रता माप को परिवर्तित करके या अधिक सामान्य गणितीय स्थानों पर परिभाषित करके। इन सामान्यीकरणों का गणितीय अध्ययन किया जा सकता है साथ ही इनका उपयोग गणितीय रूप से भौतिक प्रभावों के मॉडल बनाने या प्रतिष्ठित करने के लिए किया जा सकता है।
पॉइसन-प्रकार का यादृच्छिक माप
पॉइसन प्रकार के यादृच्छिक माप (पीटी) विविधता यादृच्छिक गणना माप के समूह होते हैं जो उपगणमें सीमित करने के अंतर्गत होते हैं, अर्थात् बिन्दु प्रक्रिया आपरेशन#थिनिंग के अंतर्गत सीमित होते हैं। ये यादृच्छिक माप मिश्रित द्विपद प्रक्रिया के उदाहरण हैं और पॉइसन यादृच्छिक माप की बंटनात्मक स्व-समानता गुणधर्म साझा करते हैं। ये बंटनात्मक स्व-समानता गुणधर्म वाले बंटनों के कैननिक गैर-ऋणात्मक श्रेणी के अद्यावधिक सदस्य हैं और पॉइसन बंटन, ऋणात्मक द्विपद बंटन और द्विपद बंटन को सम्मिलित करते हैं। पॉइसन यादृच्छिक माप अलग-अलग उपगणों पर स्वतंत्र होता है, जबकि अन्य पीटी यादृच्छिक माप (ऋणात्मक द्विपद और द्विपद) का धनात्मक और ऋणात्मक सह-संयोजन होता है। पीटी यादृच्छिक माप पर चर्चा की जाती है[152] और इसमें पॉइसन यादृच्छिक माप, ऋणात्मक द्विपद यादृच्छिक माप और द्विपद यादृच्छिक माप सम्मिलित होते हैं।
अधिक सामान्य समष्टियों पर पॉइसन बिंदु प्रक्रियाएं
गणितीय मॉडल के लिए पॉइसन बिंदु प्रक्रिया को प्रायः यूक्लिडियन समष्टि में परिभाषित किया जाता है,[1][38] लेकिन इसे अधिक ऑब्स्ट्रक्ट समष्टियों के लिए सामान्यीकृत किया गया है और यादृच्छिक मापों के अध्ययन में मौलिक भूमिका निभाता है,[153][154] जिसके लिए प्रायिकता सिद्धांत, माप सिद्धांत और टोपोलॉजी जैसे गणितीय क्षेत्रों की समझ आवश्यक है।[155]
सामान्य तौर पर, दूरी की अवधारणा अनुप्रयोगों के लिए व्यावहारिक रुचि की है, जबकि पाम वितरण के लिए टोपोलॉजिकल संरचना की आवश्यकता होती है, जिसका अर्थ है कि बिंदु प्रक्रियाओं को सामान्यतः आव्यूह के साथ गणितीय समष्टि पर परिभाषित किया जाता है।[156] इसके अतिरिक्त, बिंदु प्रक्रिया की प्राप्ति को गणना की माप के रूप में माना जा सकता है, इसलिए बिंदु प्रक्रियाएं एक प्रकार के यादृच्छिक उपाय हैं जिन्हें यादृच्छिक गणना के माप के रूप में जाना जाता है।[119] इस संदर्भ में, पॉइसन और अन्य बिंदु प्रक्रियाओं का अध्ययन स्थानीय रूप से सघन द्वितीय गणनीय हॉउसडॉर्फ स्थान पर किया गया है।[157]
कॉक्स बिंदु प्रक्रिया
कॉक्स बिंदु प्रक्रिया, कॉक्स प्रक्रिया या दोगुनी प्रसंभाव्य पॉइसन प्रक्रिया पॉइसन बिंदु प्रक्रिया का सामान्यीकरण है, इसकी तीव्रता माप को भी यादृच्छिक और अंतर्निहित पॉइसन प्रक्रिया से स्वतंत्र होने की अनुमति देती है। इस प्रक्रिया का नाम डेविड कॉक्स के नाम पर रखा गया है, जिन्होंने इसे 1955 में प्रस्तुत किया था, हालांकि अन्य पॉइसन प्रक्रियाओं को यादृच्छिक तीव्रता के साथ स्वतंत्र रूप से लुसिएन ले कैम और मौरिस क्वेनौइल द्वारा पहले ही प्रस्तुत किया गया था।[15] तीव्रता माप यादृच्छिक चर या यादृच्छिक क्षेत्र की प्राप्ति हो सकती है। उदाहरण के लिए, यदि तीव्रता माप का लघुगणक गॉसियन यादृच्छिक क्षेत्र है, तो परिणामी प्रक्रिया को लघुगणक गॉसियन कॉक्स प्रक्रिया के रूप में जाना जाता है।[158] अधिक सामान्यतः, तीव्रता के उपाय एक गैर-ऋणात्मक स्थानीय परिमित यादृच्छिक माप की प्राप्ति है। कॉक्स बिंदु प्रक्रियाएं बिंदुओं के क्लस्टरिंग को प्रदर्शित करती हैं, जिन्हें गणितीय रूप से पॉइसन बिंदु प्रक्रियाओं की तुलना में बड़ा दिखाया जा सकता है। कॉक्स प्रक्रियाओं की व्यापकता और सुवाह्यता के परिणामस्वरूप उन्हें स्थानिक सांख्यिकी[159] और वायरलेस नेटवर्क[20] जैसे क्षेत्रों में मॉडल के रूप में उपयोग किया जा रहा है।
चिह्नित पॉइसन बिंदु प्रक्रिया

दिए गए बिन्दु प्रक्रिया के लिए, प्रत्येक यादृच्छिक बिंदु के साथ एक यादृच्छिक गणितीय वस्तु, जिसे अंकित कहा जाता है, यादृच्छिक रूप से समर्पित किया जा सकता है। ये अंक अभिविन्यासी रूप से पूर्णांक, वास्तविक संख्याएँ, रेखाएँ, ज्यामिति वस्तुएँ या अन्य बिंदु प्रक्रियाएं हो सकती हैं। [156][157] बिंदु प्रक्रिया का बिंदु और इसके संबंधित अंक का योग होने पर मर्किंग बिंदु कहलाता है, और सभी मार्किंग बिंदु परिक्रिया को एक मार्किंग बिंदु प्रक्रिया बनाते हैं। [158] यह आमतौर पर माना जाता है कि यादृच्छिक अंक एक दूसरे के निरपेक्ष होते हैं और समान वितरित होते हैं, हालांकि, बिंदु का अंक अपने अंतर्निहित (स्थिति) समष्टि में उसके संबंधित बिंदु की स्थान पर भी निर्भर कर सकता है।[160] यदि अंतर्निहित बिंदु प्रक्रिया पॉयसन बिंदु प्रक्रिया है, तो परिणामस्वरूपी बिंदु प्रक्रिया एक मार्किंग पॉयसन बिंदु प्रक्रिया होती है।[161] बिंदु प्रक्रिया के एक बिंदु और उसके संबंधित चिह्न वाली जोड़ी को एक चिह्नित बिंदु कहा जाता है, और सभी चिह्नित बिंदु एक चिह्नित बिंदु प्रक्रिया बनाते हैं।[162] अक्सर यह माना जाता है कि यादृच्छिक अंक एक दूसरे से स्वतंत्र होते हैं और समान रूप से वितरित होते हैं, फिर भी एक बिंदु का निशान अंतर्निहित (राज्य) स्थान में इसके संबंधित बिंदु के स्थान पर निर्भर हो सकता है। रेफरी नाम= किंगमैन 1992पृष्ठ55 >{{cite book|author=J. F. C. Kingman|title=पोइसन प्रक्रियाएं|url=https://books.google.com/books?id=VEiM-OtwDHkC%7Cdate=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=55}</ref> यदि अंतर्निहित बिंदु प्रक्रिया एक प्वॉइसन बिंदु प्रक्रिया है, तो परिणामी बिंदु प्रक्रिया एक चिन्हित पॉइसन बिंदु प्रक्रिया है। रेफ नाम = बेसेलीब्लास्ज़ज़ीस्ज़िन2009पृष्ठ291 >François Baccelli; Bartlomiej Blaszczyszyn (2009). स्टोचैस्टिक ज्यामिति और वायरलेस नेटवर्क. Now Publishers Inc. pp. 291–293. ISBN 978-1-60198-264-3.</ref>
अंकन प्रमेय
यदि किसी साधारण बिंदु प्रक्रिया को किसी गणितीय समष्टि पर परिभाषित किया जाता है और यादृच्छिक अंक किसी अन्य गणितीय समष्टि पर परिभाषित किए जाते हैं, तो अंकन बिंदु प्रक्रिया उन दोनों स्थानों के कार्तीय गुणांक पर परिभाषित होती है। यदि अंकन पॉइसन बिंदु प्रक्रिया में यादृच्छिक और समान वितरित अंक हों, तो अंकन सिद्धांत[163][164] कहता है कि यह अंकन बिंदु प्रक्रिया उसी उपरोक्त गणितीय स्थानों के कार्तीय गुणांक पर परिभाषित (गैर-अंकन) पॉइसन बिंदु प्रक्रिया भी होती है, जो साधारण बिंदु प्रक्रियाओं के लिए सत्य नहीं है।
संयुक्त पॉइसन बिंदु प्रक्रिया
संयुक्त पॉइसन बिंदु प्रक्रिया या संयुक्त पॉइसन प्रक्रिया, किसी अंतर्निहित समष्टि पर परिभाषित पॉइसन बिंदु प्रक्रिया के प्रत्येक बिंदु में यादृच्छिक मान या वजन को जोड़कर बनाई जाती है, इस प्रक्रिया को अंकन पॉइसन बिंदु प्रक्रिया से निर्मित किया जाता है, जहां अंक संग्रह स्वतंत्र और समान वितरित गैर-ऋणात्मक स्थिरांक होते हैं। अन्य शब्दों में, मूल पॉइसन प्रक्रिया के प्रत्येक बिंदु के लिए एक स्वतंत्र और समान वितरित गैर-ऋणात्मक स्थिरांक होता है, और फिर संयुक्त पॉइसन प्रक्रिया को निर्मित किया जाता है जो उपर्युक्त गणितीय स्थान के कुछ क्षेत्र में स्थित पॉइसन प्रक्रिया के बिंदुओं के सभी स्वतंत्र और समान वितरित गैर-ऋणात्मक स्थिरांकों के योग से बनी होती है।[165]
यदि किसी पॉइसन पॉइंट प्रक्रिया (जो, उदाहरण के लिए, पर परिभाषित होती है) और स्वतंत्र और समान वितरित गैर-ऋणात्मक बिंदु के एक संग्रह के बिंदुगामी पॉइसन बिंदु प्रक्रिया के रूप में निर्मित किया जाता है, जिसके लिए पॉइसन प्रक्रिया के प्रत्येक बिंदु के लिए एक गैर-ऋणात्मक यादृच्छिक परिवर्तन होता है, तो परिणामस्वरूपी संयुक्त पॉइसन प्रक्रिया निम्नलिखित होती है:[166]
जहां बोरेल मापनीय समुच्चय है।
यदि सामान्य यादृच्छिक चर मान लेते हैं, उदाहरण के लिए, -विमीय यूक्लिडियन समष्टि , परिणामी यौगिक पॉइसन प्रक्रिया लेवी प्रक्रिया का एक उदाहरण है, बशर्ते कि यह गैर-नकारात्मक संख्या पर परिभाषित एक समघातीय बिंदु प्रक्रिया से बनाई गई हो[167]
तीव्रता फलनों का घातीय संरेखण के साथ विफलता प्रक्रिया
अविस्मरण त्रुटि प्रक्रिया जिसमें आंतरिकता समीकरणों की व्यापक स्मूदन साथ एकाधिक की प्रकार होती है (एफपी-ईएसआई), गैरसमग्र पॉइसन प्रक्रिया का विस्तार है। एफपी-ईएसआई की आंतरिकता समीकरण एक समीकरण की तरह होती है जिसमें घटना घटनाओं के अंतिम समय बिंदुओं पर आंतरिकता समीकरणों की संरेखण फलन होती है और यह मॉडल डेटासेट्स को फिट करने के लिए उपयोग किए जाने पर 8 वास्तविक दुनिया के असफलता डेटासेट पर अन्य नौ स्टोकेस्टिक प्रक्रियाओं से बेहतर प्रदर्शन करती है, जहां मॉडल की प्रदर्शन का माप एआईसी (अकयके सूचना माप) और बीआईसी (बायेसियन सूचना मानदंड) के माध्यम से किया जाता है।[168]
यह भी देखें
- बूलियन मॉडल (प्रायिकता सिद्धांत)
- सातत्य अंत:स्त्राव सिद्धांत
- यौगिक पॉइसन प्रक्रिया
- कॉक्स प्रक्रिया
- बिंदु प्रक्रिया
- प्रसंभाव्य ज्यामिति
- वायरलेस नेटवर्क के प्रसंभाव्य ज्यामिति मॉडल
- मार्कोवियन एराइवल प्रक्रियाएं
टिप्पणियाँ
- ↑ See Section 2.3.2 of Chiu, Stoyan, Kendall, Mecke[1] or Section 1.3 of Kingman.[2]
- ↑ For example, it is possible for an event not happening in the queueing theory sense to be an event in the probability theory sense.
- ↑ Instead of and , one could write, for example, in (two-dimensional) polar coordinates and , where and denote the radial and angular coordinates respectively, and so would be an area element in this example.
- ↑ This set is formed by a finite number of unions, whereas a Borel set is formed by a countable number of set operations.[132]
- ↑ Kingman[139] calls this a probability density, but in other resources this is called a probability kernel.[19]
- ↑ Also spelt Palm–Khintchine in, for example, Point Processes by Cox & Isham (1980, p. 41)
संदर्भ
विशिष्ट
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. ISBN 978-1-118-65825-3.
- ↑ 2.0 2.1 2.2 2.3 2.4 J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. ISBN 978-0-19-159124-2.
- ↑ G. J. Babu and E. D. Feigelson. Spatial point processes in astronomy. Journal of statistical planning and inference, 50(3):311–326, 1996.
- ↑ H. G. Othmer, S. R. Dunbar, and W. Alt. Models of dispersal in biological systems. Journal of mathematical biology, 26(3):263–298, 1988.
- ↑ 5.0 5.1 H. Thompson. Spatial point processes, with applications to ecology. Biometrika, 42(1/2):102–115, 1955.
- ↑ C. B. Connor and B. E. Hill. Three nonhomogeneous poisson models for the probability of basaltic volcanism: application to the yucca mountain region, nevada. Journal of Geophysical Research: Solid Earth (1978–2012), 100(B6):10107–10125, 1995.
- ↑ Gardner, J. K.; Knopoff, L. (1974). "Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian?". Bulletin of the Seismological Society of America. 64 (5): 1363–1367. Bibcode:1974BuSSA..64.1363G. doi:10.1785/BSSA0640051363. S2CID 131035597.
- ↑ J. D. Scargle. Studies in astronomical time series analysis. v. bayesian blocks, a new method to analyze structure in photon counting data. The Astrophysical Journal, 504(1):405, 1998.
- ↑ P. Aghion and P. Howitt. A Model of Growth through Creative Destruction. Econometrica, 60(2). 323–351, 1992.
- ↑ M. Bertero, P. Boccacci, G. Desidera, and G. Vicidomini. Image deblurring with poisson data: from cells to galaxies. Inverse Problems, 25(12):123006, 2009.
- ↑ "The Color of Noise".
- ↑ 12.0 12.1 F. Baccelli and B. Błaszczyszyn. Stochastic Geometry and Wireless Networks, Volume II- Applications, volume 4, No 1–2 of Foundations and Trends in Networking. NoW Publishers, 2009.
- ↑ M. Haenggi, J. Andrews, F. Baccelli, O. Dousse, and M. Franceschetti. Stochastic geometry and random graphs for the analysis and design of wireless networks. IEEE JSAC, 27(7):1029–1046, September 2009.
- ↑ 14.00 14.01 14.02 14.03 14.04 14.05 14.06 14.07 14.08 14.09 14.10 Stirzaker, David (2000). "हाथी को सलाह, या स्थिरांक भिन्न हो सकते हैं". The Mathematical Gazette. 84 (500): 197–210. doi:10.2307/3621649. ISSN 0025-5572. JSTOR 3621649. S2CID 125163415.
- ↑ 15.00 15.01 15.02 15.03 15.04 15.05 15.06 15.07 15.08 15.09 15.10 Guttorp, Peter; Thorarinsdottir, Thordis L. (2012). "What Happened to Discrete Chaos, the Quenouille Process, and the Sharp Markov Property? Some History of Stochastic Point Processes". International Statistical Review. 80 (2): 253–268. doi:10.1111/j.1751-5823.2012.00181.x. ISSN 0306-7734. S2CID 80836.
- ↑ 16.0 16.1 Leonard Kleinrock (1976). Queueing Systems: Theory. Wiley. ISBN 978-0-471-49110-1.
- ↑ {{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=https://books.google.com/books?id=X-m5BQAAQBAJ%7Cdate=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4|page=10}
- ↑ 18.0 18.1 J. G. Andrews, R. K. Ganti, M. Haenggi, N. Jindal, and S. Weber. A primer on spatial modeling and analysis in wireless networks. Communications Magazine, IEEE, 48(11):156–163, 2010.
- ↑ 19.0 19.1 19.2 19.3 19.4 19.5 19.6 19.7 19.8 F. Baccelli and B. Błaszczyszyn. Stochastic Geometry and Wireless Networks, Volume I – Theory, volume 3, No 3–4 of Foundations and Trends in Networking. NoW Publishers, 2009.
- ↑ 20.0 20.1 20.2 20.3 20.4 Martin Haenggi (2013). वायरलेस नेटवर्क के लिए स्टोचैस्टिक ज्योमेट्री. Cambridge University Press. ISBN 978-1-107-01469-5.
- ↑ 21.0 21.1 21.2 21.3 21.4 21.5 21.6 21.7 21.8 Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 51–52. ISBN 978-1-118-65825-3.
- ↑ 22.0 22.1 22.2 22.3 {{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=https://books.google.com/books?id=X-m5BQAAQBAJ%7Cdate=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4}
- ↑ 23.0 23.1 23.2 Jesper Moller; Rasmus Plenge Waagepetersen (25 September 2003). स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण. CRC Press. ISBN 978-0-203-49693-0.
- ↑ 24.0 24.1 R. Meester and R. Roy. Continuum percolation, volume 119 of cambridge tracts in mathematics, 1996.
- ↑ Daley & Vere-Jones (2003), p. 27.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 35–36. ISBN 978-1-118-65825-3.
- ↑ 27.0 27.1 27.2 Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 41 and 51. ISBN 978-1-118-65825-3.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 41–42. ISBN 978-1-118-65825-3.
- ↑ Daley & Vere-Jones (2003), p. 22.
- ↑ J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. pp. 73–76. ISBN 978-0-19-159124-2.
- ↑ 31.0 31.1 31.2 31.3 31.4 H. C. Tijms (18 April 2003). स्टोकेस्टिक मॉडल में पहला कोर्स. John Wiley & Sons. pp. 1–2. ISBN 978-0-471-49880-3.
- ↑ Daley & Vere-Jones (2003), pp. 26–37.
- ↑ H. C. Tijms (18 April 2003). स्टोकेस्टिक मॉडल में पहला कोर्स. John Wiley & Sons. pp. 1 and 9. ISBN 978-0-471-49880-3.
- ↑ 34.0 34.1 34.2 34.3 34.4 34.5 34.6 Sheldon M. Ross (1996). स्टचास्तिक प्रोसेसेज़. Wiley. pp. 59–60. ISBN 978-0-471-12062-9.
- ↑ 35.0 35.1 A. Baddeley. A crash course in stochastic geometry. Stochastic Geometry: Likelihood and Computation Eds OE Barndorff-Nielsen, WS Kendall, HNN van Lieshout (London: Chapman and Hall), pages 1–35, 1999.
- ↑ D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. pp. 1–2. ISBN 978-0-387-21337-8.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 110–111. ISBN 978-1-118-65825-3.
- ↑ 38.0 38.1 38.2 38.3 38.4 J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. pp. 11–12. ISBN 978-0-19-159124-2.
- ↑ 39.0 39.1 Daley, Daryl J.; Vere-Jones, David (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer. p. 26. ISBN 978-0387213378.
- ↑ Jesper Moller; Rasmus Plenge Waagepetersen (25 September 2003). स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण. CRC Press. pp. 15–16. ISBN 978-0-203-49693-0.
- ↑ Roy L. Streit (15 September 2010). Poisson Point Processes: Imaging, Tracking, and Sensing. Springer Science & Business Media. pp. 7–8. ISBN 978-1-4419-6923-1.
- ↑ 42.0 42.1 W. Feller. Introduction to probability theory and its applications, vol. ii pod. 1974.
- ↑ 43.0 43.1 43.2 43.3 J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. 13. ISBN 978-0-19-159124-2.
- ↑ 44.0 44.1 44.2 Jesper Moller; Rasmus Plenge Waagepetersen (25 September 2003). स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण. CRC Press. p. 14. ISBN 978-0-203-49693-0.
- ↑ Daley & Vere-Jones (2003), p. 20.
- ↑ 46.0 46.1 46.2 46.3 H. C. Tijms (18 April 2003). स्टोकेस्टिक मॉडल में पहला कोर्स. John Wiley & Sons. ISBN 978-0-471-49880-3.
- ↑ Sheldon M. Ross (1996). स्टचास्तिक प्रोसेसेज़. Wiley. p. 64. ISBN 978-0-471-12062-9.
- ↑ 48.0 48.1 48.2 48.3 48.4 48.5 48.6 Daley, Daryl J.; Vere-Jones, David (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer. p. 19. ISBN 978-0387213378.
- ↑ Daley & Vere-Jones (2003), pp. 19–23.
- ↑ J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. 42. ISBN 978-0-19-159124-2.
- ↑ Henk C. Tijms (6 May 2003). स्टोकेस्टिक मॉडल में पहला कोर्स. Wiley. pp. 2–3. ISBN 978-0-471-49881-0.
- ↑ Sheldon M. Ross (1996). स्टचास्तिक प्रोसेसेज़. Wiley. pp. 35–36. ISBN 978-0-471-12062-9.
- ↑ 53.0 53.1 53.2 J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. pp. 38–39. ISBN 978-0-19-159124-2.
- ↑ Daley & Vere-Jones (2003), pp. 29–30.
- ↑ Sheldon M. Ross (1996). स्टचास्तिक प्रोसेसेज़. Wiley. p. 151. ISBN 978-0-471-12062-9.
- ↑ Cox & Isham (1980), p. 25.
- ↑ Daley, Daryl J.; Vere-Jones, David (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer. p. 29. ISBN 978-0387213378.
- ↑ 58.0 58.1 58.2 E. Merzbach and D. Nualart. A characterization of the spatial poisson process and changing time. The Annals of Probability, 14(4):1380–1390, 1986.
- ↑ Feigin, Paul D. (1979). "ऑर्डर स्टेटिस्टिक प्रॉपर्टी के साथ पॉइंट प्रोसेस के कैरेक्टराइजेशन पर". Journal of Applied Probability. 16 (2): 297–304. doi:10.2307/3212898. JSTOR 3212898. S2CID 123904407.
- ↑ Sheldon M. Ross (1996). स्टचास्तिक प्रोसेसेज़. Wiley. p. 235. ISBN 978-0-471-12062-9.
- ↑ A. Papoulis and S. U. Pillai. Probability, random variables, and stochastic processes. Tata McGraw-Hill Education, 2002.
- ↑ 62.0 62.1 62.2 Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 41–42. ISBN 978-1-118-65825-3.
- ↑ Cox & Isham (1980), p. 3.
- ↑ D. Snyder and M. Miller. Random point processes in time and space 2e springer-verlag. New York, NY, 1991.
- ↑ 65.0 65.1 Daley, Daryl J.; Vere-Jones, David (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer. ISBN 978-0387213378.
- ↑ Lawson, A. B. (1993). "विषम स्थानिक जहर प्रक्रियाओं के लिए अवशिष्ट अवशिष्ट". Biometrics. 49 (3): 889–897. doi:10.2307/2532210. JSTOR 2532210.
- ↑ Daley, Daryl J.; Vere-Jones, David (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer. pp. 19–23. ISBN 978-0387213378.
- ↑ Lee, C.-H.; Shih, C.-Y.; Chen, Y.-S. (2012). "शहरी क्षेत्रों में सेलुलर नेटवर्क मॉडलिंग के लिए स्टोकेस्टिक ज्यामिति आधारित मॉडल". Wireless Networks. 19 (6): 1063–1072. doi:10.1007/s11276-012-0518-0. S2CID 8409538.
- ↑ 69.0 69.1 69.2 D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. p. 31. ISBN 978-0-387-21337-8.
- ↑ Daley, Daryl J.; Vere-Jones, David (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer. pp. 19–23. ISBN 978-0387213378.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 38–40 and 53–54. ISBN 978-1-118-65825-3.
- ↑ 72.0 72.1 D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. p. 25. ISBN 978-0-387-21337-8.
- ↑ J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. X. ISBN 978-0-19-159124-2.
- ↑ Roy L. Streit (15 September 2010). Poisson Point Processes: Imaging, Tracking, and Sensing. Springer Science & Business Media. p. 6. ISBN 978-1-4419-6923-1.
- ↑ 75.0 75.1 75.2 H. C. Tijms (18 April 2003). स्टोकेस्टिक मॉडल में पहला कोर्स. John Wiley & Sons. pp. 22–23. ISBN 978-0-471-49880-3.
- ↑ L. Citi; D. Ba; E.N. Brown & R. Barbieri (2014). "अपवर्तकता के साथ बिंदु प्रक्रियाओं के लिए संभावना विधियाँ" (PDF). Neural Computation. 26 (2): 237–263. doi:10.1162/NECO_a_00548. hdl:1721.1/85015. PMID 24206384. S2CID 1436173.
- ↑ {{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=https://books.google.com/books?id=X-m5BQAAQBAJ%7Cdate=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4|page=10}
- ↑ 78.0 78.1 {{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=https://books.google.com/books?id=X-m5BQAAQBAJ%7Cdate=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4|page=12}
- ↑ Sheldon M. Ross (1996). स्टचास्तिक प्रोसेसेज़. Wiley. pp. 78–81. ISBN 978-0-471-12062-9.
- ↑ A. Heuer, C. Mueller, and O. Rubner. Soccer: Is scoring goals a predictable Poissonian process? EPL, 89(3):38007, 2010.
- ↑ J. Y. Hwang, W. Kuo, and C. Ha. Modeling of integrated circuit yield using a spatial nonhomogeneous poisson process. Semiconductor Manufacturing, IEEE Transactions on, 24(3):377–384, 2011.
- ↑ M. Krko{\vs}ek, M. A. Lewis, and J. P. Volpe. Transmission dynamics of parasitic sea lice from farm to wild salmon. Proceedings of the Royal Society B: Biological Sciences, 272(1564):689–696, 2005.
- ↑ P. A. Lewis and G. S. Shedler. Simulation of nonhomogeneous Poisson processes by thinning. Naval Research Logistics Quarterly, 26(3):403–413, 1979.
- ↑ J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. 10. ISBN 978-0-19-159124-2.
- ↑ Cox & Isham (1980), pp. 3–6.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 44. ISBN 978-1-118-65825-3.
- ↑ Martin Haenggi (2013). वायरलेस नेटवर्क के लिए स्टोचैस्टिक ज्योमेट्री. Cambridge University Press. p. 11. ISBN 978-1-107-01469-5.
- ↑ 88.0 88.1 88.2 88.3 Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 53–55. ISBN 978-1-118-65825-3.
- ↑ Roy L. Streit (15 September 2010). Poisson Point Processes: Imaging, Tracking, and Sensing. Springer Science & Business Media. pp. 13–14. ISBN 978-1-4419-6923-1.
- ↑ Roy L. Streit (15 September 2010). Poisson Point Processes: Imaging, Tracking, and Sensing. Springer Science & Business Media. pp. 14–16. ISBN 978-1-4419-6923-1.
- ↑ 91.0 91.1 Martin Haenggi (2013). वायरलेस नेटवर्क के लिए स्टोचैस्टिक ज्योमेट्री. Cambridge University Press. pp. 18–19. ISBN 978-1-107-01469-5.
- ↑ 92.0 92.1 Good, I. J. (1986). "प्वासों के कार्य के कुछ सांख्यिकीय अनुप्रयोग". Statistical Science. 1 (2): 157–170. doi:10.1214/ss/1177013690. ISSN 0883-4237.
- ↑ 93.0 93.1 93.2 Grimmett, G.; Stirzaker, D. (2001). संभाव्यता और यादृच्छिक प्रक्रियाएं (3rd ed.). Oxford University Press. ISBN 0-19-857222-0.
- ↑ Stigler, S. M. (1982). "पॉसॉन वितरण पर पॉसॉन". Statistics & Probability Letters. 1 (1): 33–35. doi:10.1016/0167-7152(82)90010-4.
- ↑ Daley & Vere-Jones (2003), pp. 8–9.
- ↑ Quine, M.; Seneta, E. (1987). "Bortkiewicz डेटा और छोटी संख्या का नियम". International Statistical Review. 55 (2): 173–181. doi:10.2307/1403193. JSTOR 1403193.
- ↑ Embrechts, Paul; Frey, Rüdiger; Furrer, Hansjörg (2001). "Stochastic processes in insurance and finance". Stochastic Processes: Theory and Methods. Handbook of Statistics. Vol. 19. p. 367. doi:10.1016/S0169-7161(01)19014-0. ISBN 9780444500144. ISSN 0169-7161.
- ↑ Cramér, Harald (1969). "जोखिम सिद्धांत पर फ़िलिप लुंडबर्ग के कार्यों की ऐतिहासिक समीक्षा". Scandinavian Actuarial Journal. 1969 (sup3): 6–12. doi:10.1080/03461238.1969.10404602. ISSN 0346-1238.
- ↑ Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. (2008). स्थानिक बिंदु पैटर्न का सांख्यिकीय विश्लेषण और मॉडलिंग. Vol. 70. John Wiley & Sons. ISBN 978-0-470-01491-2.
- ↑ Kingman, J. (2009). "The first Erlang century—and the next". Queueing Systems. 63 (1–4): 3–12. doi:10.1007/s11134-009-9147-4. S2CID 38588726.
- ↑ 101.0 101.1 Haugen, R. B. (1995). "कोनी पाम का जीवन और कार्य। कुछ व्यक्तिगत टिप्पणियाँ और अनुभव". VTT Symposium. Valtion teknillinen tutkimuskeskus. 154: 207. ISSN 0357-9387.
- ↑ 102.0 102.1 D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. pp. 13–14. ISBN 978-0-387-21337-8.
- ↑ J. Grandell. Mixed poisson processes, volume 77. CRC Press, 1997.
- ↑ Cox & Isham (1980), p. X.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 109. ISBN 978-1-118-65825-3.
- ↑ G. Mikhailov and T. Averina. Statistical modeling of inhomogeneous random functions on the basis of poisson point fields. In Doklady Mathematics, volume 82, pages 701–704. Springer, 2010.
- ↑ I. Molchanov. Theory of random sets. Springer Science \& Business Media, 2006.
- ↑ 108.0 108.1 K. Sato. Lévy processes and infinite divisibility, 1999.
- ↑ V. Mandrekar and B. Rüdiger. Stochastic Integration in Banach Spaces. Springer, 2015.
- ↑ D. Applebaum. Lévy processes and stochastic calculus. Cambridge university press, 2009.
- ↑ E. F. Harding and R. Davidson. Stochastic geometry: a tribute to the memory of Rollo Davidson. Wiley, 1974.
- ↑ 112.0 112.1 L. H. Chen and A. Xia. Stein's method, Palm theory and Poisson process approximation. Annals of probability, pages 2545–2569, 2004.
- ↑ J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. 8. ISBN 978-0-19-159124-2.
- ↑ 114.0 114.1 Jesper Moller; Rasmus Plenge Waagepetersen (25 September 2003). स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण. CRC Press. p. 7. ISBN 978-0-203-49693-0.
- ↑ Emanuel Parzen (17 June 2015). स्टचास्तिक प्रोसेसेज़. Courier Dover Publications. pp. 7–8 and 29–30. ISBN 978-0-486-79688-8.
- ↑ John Lamperti (1977). Stochastic processes: a survey of the mathematical theory. Springer-Verlag. pp. 1 and 10–11. ISBN 978-3-540-90275-1.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 112. ISBN 978-1-118-65825-3.
- ↑ Daley, Daryl J.; Vere-Jones, David (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer. p. 20. ISBN 978-0387213378.
- ↑ 119.0 119.1 J. Grandell. Point processes and random measures. Advances in Applied Probability, pages 502–526, 1977.
- ↑ Some Poisson models, Vose Software, retrieved 18 January 2016
- ↑ Helske, Jouni (25 June 2015), "KFAS: Exponential Family State Space Models in R" (PDF), Journal of Statistical Software, Comprehensive R Archive Network, 78 (10), arXiv:1612.01907, doi:10.18637/jss.v078.i10, S2CID 14379617, retrieved 18 January 2016
- ↑ 122.0 122.1 122.2 Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 100. ISBN 978-1-118-65825-3.
- ↑ A. Karr. Probability. Springer Texts in Statistics Series. Springer-Verlag, 1993.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 120–126. ISBN 978-1-118-65825-3.
- ↑ D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. pp. 52–75. ISBN 978-0-387-21337-8.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 125–126. ISBN 978-1-118-65825-3.
- ↑ Günter Last; Mathew Penrose (8 August 2017). प्वासों प्रक्रिया पर व्याख्यान (PDF).
- ↑ 128.0 128.1 Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. pp. 47–48. ISBN 978-1-118-65825-3.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 42. ISBN 978-1-118-65825-3.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 43. ISBN 978-1-118-65825-3.
- ↑ 131.0 131.1 J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. 34. ISBN 978-0-19-159124-2.
- ↑ D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. pp. 384–385. ISBN 978-0-387-21337-8.
- ↑ 133.0 133.1 Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 158. ISBN 978-1-118-65825-3.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 160. ISBN 978-1-118-65825-3.
- ↑ D. Bertsekas and J. Tsitsiklis. Introduction to probability, ser. Athena Scientific optimization and computation series. Athena Scientific, 2008.
- ↑ J. F. Hayes. Modeling and analysis of computer communications networks. Perseus Publishing, 1984.
- ↑ Sung Nok Chiu; Dietrich Stoyan; Wilfrid S. Kendall; Joseph Mecke (27 June 2013). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. John Wiley & Sons. p. 165. ISBN 978-1-118-65825-3.
- ↑ J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. 16. ISBN 978-0-19-159124-2.
- ↑ 139.0 139.1 139.2 139.3 J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. 61. ISBN 978-0-19-159124-2.
- ↑ D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. pp. 166–167. ISBN 978-0-387-21337-8.
- ↑ 141.0 141.1 J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. p. 18. ISBN 978-0-19-159124-2.
- ↑ Geoffrey Grimmett; David Stirzaker (31 May 2001). संभाव्यता और यादृच्छिक प्रक्रियाएं. OUP Oxford. p. 284. ISBN 978-0-19-857222-0.
- ↑ 143.0 143.1 143.2 143.3 L. H. Chen, A. Röllin, et al. Approximating dependent rare events. Bernoulli, 19(4):1243–1267, 2013.
- ↑ 144.0 144.1 R. Arratia, S. Tavare, et al. {Review: D. Aldous, Probability Approximations via the Poisson Clumping Heuristic; AD Barbour, L. Holst, S. Janson, Poisson Approximation}. The Annals of Probability, 21(4):2269–2279, 1993.
- ↑ 145.0 145.1 D. Aldous. Poisson Clumping Heuristic. Wiley Online Library, 1989.
- ↑ L. H. Chen, A. Röllin, et al. Approximating dependent rare events. Bernoulli, 19(4):1243–1267, 2013.
- ↑ A. D. Barbour and T. C. Brown. Stein's method and point process approximation. Stochastic Processes and their Applications, 43(1):9–31, 1992.
- ↑ D. Schuhmacher. Distance estimates for dependent superpositions of point processes. Stochastic processes and their applications, 115(11):1819–1837, 2005.
- ↑ D. Schuhmacher. Distance estimates for poisson process approximations of dependent thinnings. Electronic Journal of Probability, 10:165–201, 2005.
- ↑ 150.0 150.1 150.2 D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. pp. 131–132. ISBN 978-0-387-21337-8.
- ↑ D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. p. 146. ISBN 978-0-387-21337-8.
- ↑ Caleb Bastian, Gregory Rempala. Throwing stones and collecting bones: Looking for Poisson-like random measures, Mathematical Methods in the Applied Sciences, 2020. doi:10.1002/mma.6224
- ↑ Olav Kallenberg (1983). यादृच्छिक उपाय. Akademie-Verlag. ISBN 978-0-12-394960-8.
- ↑ J. F. C. Kingman (17 December 1992). पोइसन प्रक्रियाएं. Clarendon Press. pp. 79–84. ISBN 978-0-19-159124-2.
- ↑ D.J. Daley; David Vere-Jones (12 November 2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer Science & Business Media. pp. 368–413. ISBN 978-0-387-21337-8.
- ↑ A. E. Gelfand, P. Diggle, P. Guttorp, and M. Fuentes. Handbook of spatial statistics, Chapter 9. CRC press, 2010.
- ↑ O. Kallenberg. Random measures. Academic Pr, 1983.
- ↑ J. Møller, A. R. Syversveen, and R. P. Waagepetersen. Log Gaussian Cox Processes. Scandinavian journal of statistics, 25(3):451–482, 1998.
- ↑ J. Møller and R. P. Waagepetersen. Modern statistics for spatial point processes. Scandinavian Journal of Statistics, 34(4):643–684, 2007.
- ↑ Jesper Moller; Rasmus Plenge Waagepetersen (25 September 2003). स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण. CRC Press. p. 8. ISBN 978-0-203-49693-0.
- ↑ Martin Haenggi (2013). वायरलेस नेटवर्क के लिए स्टोचैस्टिक ज्योमेट्री. Cambridge University Press. pp. 138–140. ISBN 978-1-107-01469-5.
- ↑ {{cite book|author1=A. Baddeley|author2=I. Bárány|author3=R. Schneider|title=स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल|url=https://books.google.com/books?id=X-m5BQAAQBAJ%7Cdate=26 October 2006|publisher=Springer|isbn=978-3-540-38175-4|pages=19–21}
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedKingman1992page55 - ↑ Roy L. Streit (15 September 2010). Poisson Point Processes: Imaging, Tracking, and Sensing. Springer Science & Business Media. pp. 205–206. ISBN 978-1-4419-6923-1.
- ↑ Daley & Vere-Jones (2003), pp. 198–199.
- ↑ Daley, Daryl J.; Vere-Jones, David (2007). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Springer. p. 198. ISBN 978-0387213378.
- ↑ David Applebaum (5 July 2004). Lévy Processes and Stochastic Calculus. Cambridge University Press. pp. 46–47. ISBN 978-0-521-83263-2.
- ↑ Wu, S. (2019). A failure process model with the exponential smoothing of intensity functions. European Journal of Operational Research, 275(2), 502–513
सामान्य
किताबें
- A. Baddeley; I. Bárány; R. Schneider (26 October 2006). स्टोचैस्टिक ज्योमेट्री: C.I.M.E में दिए गए व्याख्यान। मार्टिना फ्रांका, इटली में 13-18 सितंबर, 2004 को आयोजित समर स्कूल. Springer. ISBN 978-3-540-38175-4.
- Cox, D. R.; Isham, Valerie (1980). बिंदु प्रक्रियाएं. Chapman & Hall. ISBN 978-0-412-21910-8.
- Daley, Daryl J.; Vere-Jones, David (2003). बिंदु प्रक्रियाओं के सिद्धांत का परिचय: खंड I: प्राथमिक सिद्धांत और तरीके. Springer. ISBN 978-1475781090.
- Daley, Daryl J.; Vere-Jones, David (2007). बिंदु प्रक्रियाओं के सिद्धांत का परिचय: खंड II: सामान्य सिद्धांत और संरचना. Springer. ISBN 978-0387213378.
- Kingman, John Frank (1992). पॉसों प्रक्रियाएं. Clarendon Press. ISBN 978-0198536932.
- Moller, Jesper; Waagepetersen, Rasmus P. (2003). स्थानिक बिंदु प्रक्रियाओं के लिए सांख्यिकीय अनुमान और अनुकरण. CRC Press. ISBN 978-1584882657.
- Ross, S. M. (1996). स्टचास्तिक प्रोसेसेज़. Wiley. ISBN 978-0-471-12062-9.
- Snyder, D. L.; Miller, M. I. (1991). समय और स्थान में यादृच्छिक बिंदु प्रक्रियाएँ. Springer-Verlag. ISBN 978-0-387-97577-1.
- Stoyan, Dietrich; Kendall, Wilfred S.; Mecke, Joseph (1995). स्टोचैस्टिक ज्यामिति और इसके अनुप्रयोग. Wiley. ISBN 978-0471950998.
- Streit, Streit (2010). पॉइसन प्वाइंट प्रक्रियाएं: इमेजिंग, ट्रैकिंग और सेंसिंग. Springer Science& Business Media. ISBN 978-1441969224.
- H. C. Tijms (18 April 2003). स्टोकेस्टिक मॉडल में पहला कोर्स. John Wiley & Sons. pp. 22–23. ISBN 978-0-471-49880-3.
लेख
- Stirzaker, David (2000). "Hedgehogs, या स्थिरांक के लिए सलाह अलग-अलग हो सकती है". The Mathematical Gazette.
- Guttorp, Peter; Thorarinsdottir, Thordis L. (2012). "असतत अराजकता, क्वेनौइल प्रक्रिया और तेज मार्कोव संपत्ति का क्या हुआ? स्टोकेस्टिक बिंदु प्रक्रियाओं का कुछ इतिहास". International Statistical Review.
श्रेणी:प्वाइंट प्रक्रियाएं श्रेणी:मार्कोव प्रक्रियाएं श्रेणी:प्वाइसन बिंदु प्रक्रियाएं श्रेणी:स्थानिक प्रक्रियाएँ श्रेणी:लेवी प्रक्रियाएँ