द्विघात समीकरण

This article is about algebraic equations of degree two and their solutions. For the formula used to find solutions to such equations, see Quadratic formula. For functions defined by polynomials of degree two, see Quadratic function.

द्विघात सूत्र

बीजगणित में, एक द्विघात समीकरण (from Latin quadratus 'वर्ग') कोई भी समीकरण है जिसे मानक रूप में पुन: व्यवस्थित किया जा सकता है: <गणित प्रदर्शन=ब्लॉक>कुल्हाड़ी^2 + बीएक्स + सी = 0</गणित> कहाँ पे x एक अज्ञात का प्रतिनिधित्व करता है, और a, b, तथा c ज्ञात संख्याओं का प्रतिनिधित्व करते हैं, जहां a ≠ 0. यदि a = 0, तो समीकरण रैखिक है, द्विघात नहीं है, क्योंकि कोई नहीं है $ax^{2}$ टर्म। संख्या a, b, तथा c समीकरण के गुणांक हैं और उन्हें क्रमशः द्विघात गुणांक, रैखिक गुणांक और स्थिर या मुक्त पद कहकर अलग किया जा सकता है।

के मान x जो समीकरण को संतुष्ट करते हैं, समीकरण के हल कहलाते हैं, और इसके बायीं ओर व्यंजक के मूल या शून्य कहलाते हैं। एक द्विघात समीकरण के अधिकतम दो हल होते हैं। यदि केवल एक ही समाधान है, तो कोई कहता है कि यह दोहरी जड़ है। यदि सभी गुणांक वास्तविक संख्याएँ हैं, तो या तो दो वास्तविक समाधान हैं, या एक एकल वास्तविक दोहरा मूल, या दो जटिल समाधान हैं। एक द्विघात समीकरण के हमेशा दो मूल होते हैं, यदि सम्मिश्र जड़ों को शामिल किया जाए; और एक डबल रूट दो के लिए गिना जाता है। एक द्विघात समीकरण को एक समान समीकरण में विभाजित किया जा सकता है

$$ax^{2}+bx+c=a(x-r)(x-s)=0$$

कहाँ पे r तथा s के लिए समाधान हैं x.

द्विघात सूत्र <गणित प्रदर्शन=ब्लॉक>x=\frac{-b\pm\sqrt{b^2-4ac} }{2a}</math> के संदर्भ में समाधान व्यक्त करता है a, b, तथा c. वर्ग को पूरा करना इसे प्राप्त करने के कई तरीकों में से एक है।

द्विघात समीकरणों के रूप में व्यक्त की जा सकने वाली समस्याओं के समाधान 2000 ईसा पूर्व के रूप में जाने जाते थे।

चूँकि द्विघात समीकरण में केवल एक अज्ञात शामिल होता है, इसलिए इसे अविभाज्य कहा जाता है। द्विघात समीकरण में केवल की शक्तियां होती हैं x जो गैर-ऋणात्मक पूर्णांक हैं, और इसलिए यह एक बहुपद समीकरण है। विशेष रूप से, यह दूसरी डिग्री बहुपद समीकरण है, क्योंकि सबसे बड़ी शक्ति दो है।

द्विघात समीकरण को हल करना

igure 1. द्विघात फलन के प्लॉट y = ax² + bx + c, प्रत्येक गुणांक को अलग-अलग बदलते हैं जबकि अन्य गुणांक स्थिर होते हैं (मान a = 1, b = 0, c = 0)

परवलय नीचे की ओर खुलता है। वास्तविक या जटिल गुणांक वाले द्विघात समीकरण के दो हल होते हैं, जिन्हें मूल कहते हैं। ये दो समाधान भिन्न हो सकते हैं या नहीं भी हो सकते हैं, और वे वास्तविक हो भी सकते हैं और नहीं भी।

निरीक्षण द्वारा फैक्टरिंग

द्विघात समीकरण को व्यक्त करना संभव हो सकता है ax² + bx + c = 0 एक उत्पाद के रूप में {गणित|(पीएक्स + क्यू)(आरएक्स + एस) = 0}}. कुछ मामलों में, सरल निरीक्षण द्वारा, p, q, r, और s के मानों को निर्धारित करना संभव है जो दो रूपों को एक दूसरे के बराबर बनाते हैं। यदि द्विघात समीकरण को दूसरे रूप में लिखा जाता है, तो शून्य गुणनखंड गुण बताता है कि द्विघात समीकरण संतुष्ट होता है यदि px + q = 0 या {गणित|आरएक्स + एस = 0}}. इन दो रैखिक समीकरणों को हल करने से द्विघात के मूल प्राप्त होते हैं।

अधिकांश छात्रों के लिए, निरीक्षण द्वारा फैक्टरिंग द्विघात समीकरणों को हल करने का पहला तरीका है जिससे वे उजागर होते हैं। यदि किसी को द्विघात समीकरण के रूप में दिया जाता है x² + bx + c = 0, मांगे गए गुणनखंड का रूप है (x + q)(x + s), और एक को दो नंबर खोजने होंगे q तथा s जो तक जोड़ता है b और जिसका उत्पाद है c (इसे कभी-कभी विएटा का नियम कहा जाता हैऔर विएटा के सूत्रों से संबंधित है)। उदाहरण के तौर पे, x² + 5x + 6 कारक के रूप में (x + 3)(x + 2). अधिक सामान्य मामला जहां a बराबर नही हैं 1 परीक्षण और त्रुटि अनुमान-और-जांच में काफी प्रयास की आवश्यकता हो सकती है, यह मानते हुए कि निरीक्षण द्वारा इसे बिल्कुल भी शामिल किया जा सकता है।

विशेष मामलों को छोड़कर जहां b = 0 या {गणित|सी = 0}}, निरीक्षण द्वारा फैक्टरिंग केवल द्विघात समीकरणों के लिए काम करता है जिनमें तर्कसंगत जड़ें होती हैं। इसका मतलब यह है कि व्यावहारिक अनुप्रयोगों में उत्पन्न होने वाले द्विघात समीकरणों का बड़ा हिस्सा निरीक्षण द्वारा फैक्टरिंग द्वारा हल नहीं किया जा सकता है।

वर्ग को पूरा करना

Main article: Completing the square

igure 2. द्विघात फलन के लिए y = x² - x - 2, वे बिंदु जहां ग्राफ़ x-अक्ष को पार करता है, x = −1 और x = 2, द्विघात समीकरण के हल हैं x² − एक्स -2 = 0।

वर्ग को पूरा करने की प्रक्रिया बीजीय सर्वसमिका का उपयोग करती है

$x^{2}+2hx+h^{2}=(x+h)^{2},$

जो एक अच्छी तरह से परिभाषित एल्गोरिथम का प्रतिनिधित्व करता है जिसका उपयोग किसी भी द्विघात समीकरण को हल करने के लिए किया जा सकता है। मानक रूप में द्विघात समीकरण से शुरू करते हुए, ax² + bx + c = 0

1. प्रत्येक पक्ष को विभाजित करें {math|a}}, वर्ग पद का गुणांक।
2. स्थिर पद घटाएं c/a दोनों तरफ से।
3. आधे के वर्ग को जोड़ें b/a, का गुणांक x, दोनों पक्षों को। यह वर्ग को पूरा करता है, बाईं ओर को एक पूर्ण वर्ग में परिवर्तित करता है।
4. बाईं ओर को एक वर्ग के रूप में लिखें और यदि आवश्यक हो तो दाईं ओर को सरल करें।
5. बाईं ओर के वर्गमूल को दाईं ओर के धनात्मक और ऋणात्मक वर्गमूल से बराबर करके दो रैखिक समीकरण तैयार करें।
6. दो रैखिक समीकरणों में से प्रत्येक को हल करें।

हम हल करके इस एल्गोरिथम के उपयोग का वर्णन करते हैं 2x² + 4x − 4 = 0

$1)\ x^{2}+2x-2=0$

$2)\ x^{2}+2x=2$

$3)\ x^{2}+2x+1=2+1$

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "ब" found.in 1:22"): {\displaystyle 4) \ \बाएं(x+1 \दाएं)^2=3}

$5)\ x+1=\pm {\sqrt {3}}$

$6)\ x=-1\pm {\sqrt {3}}$

धन-ऋण चिह्न|धन-ऋण चिह्न ± इंगित करता है कि दोनों x = −1 + √3 तथा {गणित|x = −1 − √3}} द्विघात समीकरण के हल हैं।

द्विघात सूत्र और उसकी व्युत्पत्ति

Main article: Quadratic formula

वर्ग को पूरा करने का उपयोग द्विघात समीकरणों को हल करने के लिए एक सामान्य सूत्र प्राप्त करने के लिए किया जा सकता है, जिसे द्विघात सूत्र कहा जाता है।गणितीय प्रमाण को अब संक्षेप में प्रस्तुत किया जाएगा। बहुपद विस्तार द्वारा यह आसानी से देखा जा सकता है कि निम्नलिखित समीकरण द्विघात समीकरण के बराबर है:

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "ब" found.in 1:17"): {\displaystyle \बाएं(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}.}

दोनों पक्षों का वर्गमूल लेना और पृथक करना x, देता है:

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.$

कुछ स्रोत, विशेष रूप से पुराने वाले, द्विघात समीकरण के वैकल्पिक मापदंडों का उपयोग करते हैं जैसे कि ax² + 2bx + c = 0 या {गणित|कुल्हाड़ी²− 2बीएक्स + सी = 0}} ,कहाँ पे b अधिक सामान्य का आधा परिमाण है, संभवतः विपरीत संकेत के साथ। ये समाधान के लिए थोड़े अलग रूपों में परिणत होते हैं, लेकिन अन्यथा समकक्ष होते हैं।

साहित्य में कई वैकल्पिक व्युत्पत्तियां पाई जा सकती हैं। ये प्रमाण वर्ग विधि को पूरा करने वाले मानक की तुलना में सरल हैं, बीजगणित में अक्सर उपयोग की जाने वाली अन्य तकनीकों के दिलचस्प अनुप्रयोगों का प्रतिनिधित्व करते हैं, या गणित के अन्य क्षेत्रों में अंतर्दृष्टि प्रदान करते हैं।

एक कम ज्ञात द्विघात सूत्र, जैसा कि मुलर की विधि में प्रयोग किया जाता है, समीकरण के माध्यम से समान मूल प्रदान करता है

$x={\frac {2c}{-b\pm {\sqrt {b^{2}-4ac}}}}.$

इसे वियत के सूत्रों द्वारा मानक द्विघात सूत्र से घटाया जा सकता है, जो यह दावा करता है कि जड़ों का उत्पाद है c/a.

इस फॉर्म का एक गुण यह है कि यह एक वैध रूट देता है जब a = 0, जबकि दूसरी जड़ में शून्य से विभाजन होता है, क्योंकि जब a = 0, द्विघात समीकरण एक रैखिक समीकरण बन जाता है, जिसका एक मूल होता है। इसके विपरीत, इस मामले में, अधिक सामान्य सूत्र में एक मूल और एक अनिश्चित रूप के लिए शून्य से विभाजन होता है 0/0 दूसरी जड़ के लिए। दूसरी ओर, जब c = 0, अधिक सामान्य सूत्र से दो सही मूल प्राप्त होते हैं जबकि इस रूप से शून्य मूल और एक अनिश्चित रूप प्राप्त होता है 0/0.

घटा हुआ द्विघात समीकरण

द्विघात समीकरण को कम करना कभी-कभी सुविधाजनक होता है ताकि इसका अग्रणी गुणांक एक हो। यह दोनों पक्षों को द्वारा विभाजित करके किया जाता है a, जो हमेशा से संभव है a गैर-शून्य है। यह घटा हुआ द्विघात समीकरण उत्पन्न करता है:

$x^{2}+px+q=0,$

कहाँ पे p = बी/ए और {गणित|क्यू = सीए}}। इस मोनिक बहुपद समीकरण के मूल के समान ही समाधान हैं।

घटे हुए द्विघात समीकरण के हल के लिए द्विघात सूत्र, इसके गुणांकों के रूप में लिखा गया है:

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "ब" found.in 1:33"): {\displaystyle x = \frac{1}{2} \बाएं(- p \pm \sqrt{p^2 - 4q} \right),}

या समकक्ष:

$x=-{\frac {p}{2}}\pm {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}.$

भेदभावपूर्ण

igure 3. विभेदक चिन्ह

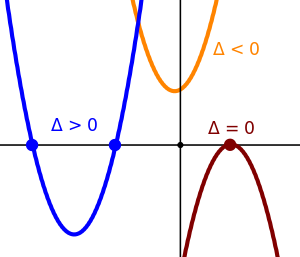
-अक्ष बिल्कुल। द्विघात सूत्र में, वर्गमूल चिह्न के नीचे के व्यंजक को द्विघात समीकरण का विभेदक कहा जाता है, और इसे अक्सर अपर केस का उपयोग करके दर्शाया जाता है D या अपर केस ग्रीक डेल्टा::$\Delta =b^{2}-4ac.$ वास्तविक गुणांक वाले द्विघात समीकरण में एक या दो भिन्न वास्तविक मूल या दो भिन्न जटिल मूल हो सकते हैं। इस मामले में विवेचक जड़ों की संख्या और प्रकृति को निर्धारित करता है। तीन मामले हैं:

• यदि विवेचक धनात्मक है, तो दो भिन्न मूल हैं

${\frac {-b+{\sqrt {\Delta }}}{2a}}\quad {\text{and}}\quad {\frac {-b-{\sqrt {\Delta }}}{2a}},$

दोनों वास्तविक संख्याएँ हैं। परिमेय गुणांक वाले द्विघात समीकरणों के लिए, यदि विवेचक एक वर्ग संख्या है, तो मूल परिमेय होते हैं—अन्य मामलों में वे द्विघात अपरिमेय हो सकते हैं।

• यदि विवेचक शून्य है, तो वास्तव में एक वास्तविक मूल है

$-{\frac {b}{2a}},$

कभी-कभी दोहराया या दोहरा रूट कहा जाता है।

• यदि विवेचक ऋणात्मक है, तो कोई वास्तविक मूल नहीं है। बल्कि, दो अलग (गैर-वास्तविक) जटिल जड़ें हैं::$-{\frac {b}{2a}}+i{\frac {\sqrt {-\Delta }}{2a}}\quad {\text{and}}\quad -{\frac {b}{2a}}-i{\frac {\sqrt {-\Delta }}{2a}},$

जो एक दूसरे के जटिल संयुग्म हैं। इन भावों में i काल्पनिक इकाई है।

इस प्रकार जड़ें अलग होती हैं यदि और केवल अगर विवेचक गैर-शून्य है, और जड़ें वास्तविक हैं यदि और केवल अगर विवेचक गैर-नकारात्मक है।

ज्यामितीय व्याख्या

Graph of y = ax² + bx + c, where a and the discriminant b² − 4ac are positive, with

• Roots and y-intercept in red
• Vertex and axis of symmetry in blue
• Focus and directrix in pink

Visualisation of the complex roots of y = ax² + bx + c: the parabola is rotated 180° about its vertex (orange). Its x-intercepts are rotated 90° around their mid-point, and the Cartesian plane is interpreted as the complex plane (green).

कार्यक्रम f(x) = कुल्हाड़ी²+ bx + c एक द्विघात फलन है।किसी भी द्विघात फलन के ग्राफ का सामान्य आकार समान होता है, जिसे परवलय कहते हैं। परवलय का स्थान और आकार, और यह कैसे खुलता है, के मानों पर निर्भर करता है a, b, तथा c. जैसा कि चित्र 1 में दिखाया गया है, यदि a > 0, परवलय का एक न्यूनतम बिंदु होता है और ऊपर की ओर खुलता है। यदि a < 0, परवलय का अधिकतम बिंदु होता है और नीचे की ओर खुलता है। परवलय का चरम बिंदु, चाहे वह न्यूनतम हो या अधिकतम, इसके शीर्ष से मेल खाता है।x-शीर्ष का निर्देशांक स्थित होगा $\scriptstyle x={\tfrac {-b}{2a}}$, औरy-शीर्ष का निर्देशांक इसे प्रतिस्थापित करके पाया जा सकता हैx- फ़ंक्शन में मान।y-अवरोधन बिंदु पर स्थित है (0, c).

द्विघात समीकरण के हल ax² + bx + c = 0 फ़ंक्शन की जड़ों के अनुरूप है {गणित | एफ (एक्स) = कुल्हाड़ी²+ bx + c}}, क्योंकि वे के मान हैं x जिसके लिए f(x) = 0. जैसा कि चित्र 2 में दिखाया गया है, यदि a, b, तथा c वास्तविक संख्याएँ हैं और का डोमेन हैं f वास्तविक संख्याओं का समुच्चय है, तो के मूल f बिल्कुल वही हैं x-उन बिंदुओं के निर्देशांक जहां ग्राफ स्पर्श करता है x-एक्सिस। जैसा कि चित्र 3 में दिखाया गया है, यदि विवेचक धनात्मक है, तो ग्राफ़ x-अक्ष को स्पर्श करता है|x-अक्ष दो बिंदुओं पर; यदि शून्य है, तो आलेख एक बिंदु पर स्पर्श करता है; और यदि ऋणात्मक है, तो ग्राफ को स्पर्श नहीं करता है x-एक्सिस।

द्विघात गुणनखंड

शब्द

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "ए" found.in 1:16"): {\displaystyle एक्स - आर</गणित> बहुपद का एक गुणनखंड है : <math>ax^2+bx+c}

अगर और केवल अगर r द्विघात समीकरण का मूल है

$ax^{2}+bx+c=0.$

यह द्विघात सूत्र से निम्नानुसार है कि

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "द" found.in 1:126"): {\displaystyle ax^2+bx+c = a \left( x - \frac{-b + \sqrt {b^2-4ac}}{2a} \right) \left( x - \frac{-b - \sqrt { b^2-4ac}}{2a} \दाएं)।}

विशेष मामले में b² = 4ac जहां द्विघात का केवल एक अलग मूल है (अर्थात विवेचक शून्य है), द्विघात बहुपद को इस प्रकार गुणनखंडित किया जा सकता है

$ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}.$

ग्राफिकल हल

File:Graphical calculation of root of quadratic equation.png

igure 4. द्विघात समीकरण 2x² + 4x − 4 = 0 के दो मूलों में से एक का रेखांकन कैलकुलेटर गणना। हालांकि प्रदर्शन सटीकता के केवल पांच महत्वपूर्ण आंकड़े दिखाता है, xc का पुनर्प्राप्त मूल्य 0.732050807569 है, जो बारह के लिए सटीक है

महत्वपूर्ण आंकड़े।

वास्तविक मूल के बिना द्विघात फलन: y = (x - 5)² + 9। 3 x-अवरोधन का काल्पनिक भाग है। वास्तविक भाग शीर्ष का x-निर्देशांक है। इस प्रकार जड़ें हैं

अब्रैप|5 ± 3i}}.

द्विघात समीकरण के हल

$ax^{2}+bx+c=0$

द्विघात फलन के ग्राफ से निकाला जा सकता है

$y=ax^{2}+bx+c,$

जो एक परवलय है।

यदि परवलय प्रतिच्छेद करता है x-अक्ष दो बिंदुओं में, दो वास्तविक मूल हैं, जो हैं x-इन दो बिंदुओं के निर्देशांक (जिन्हें भी कहा जाता है) x-अवरोधन)।

यदि परवलय स्पर्शरेखा है x-अक्ष, एक दोहरी जड़ है, जो है x-ग्राफ और परवलय के बीच संपर्क बिंदु का निर्देशांक।

यदि परवलय प्रतिच्छेद नहीं करता है x-अक्ष, दो जटिल संयुग्म जड़ें हैं। हालांकि इन जड़ों को ग्राफ पर नहीं देखा जा सकता है, लेकिन इनके वास्तविक और काल्पनिक हिस्से हो सकते हैं।

होने देना h तथा k क्रमशः हो x-समन्वय और y-परवलय के शीर्ष का निर्देशांक (जो कि अधिकतम या न्यूनतम वाला बिंदु है y-समन्वय। द्विघात फलन को फिर से लिखा जा सकता है

$y=a(x-h)^{2}+k.$

होने देना d के बिंदु के बीच की दूरी हो y-समन्वय 2k परवलय की धुरी पर, और उसी के साथ परवलय पर एक बिंदु y-निर्देशांक (आकृति देखें; परवलय की समरूपता के कारण दो ऐसे बिंदु हैं, जो समान दूरी देते हैं)। तब जड़ों का वास्तविक भाग होता है h, और उनका काल्पनिक हिस्सा हैं ±d. यानी जड़ें हैं

$h+id\quad {\text{and}}\quad x-id,$

या आकृति के उदाहरण के मामले में

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "म" found.in 1:24"): {\displaystyle x + p \ मई \ txt {जब } \ हो सकता है।</ क्या> === महत्व के नुकसान से बचना === हालांकि द्विघात सूत्र एक सटीक समाधान प्रदान करता है, परिणाम सटीक नहीं है यदि गणना के दौरान वास्तविक संख्याओं का अनुमान लगाया जाता है, हमेशा की तरह संख्यात्मक विश्लेषण में, जहां वास्तविक संख्याओं को फ्लोटिंग पॉइंट नंबरों (कई प्रोग्रामिंग भाषाओं में वास्तविक कहा जाता है) द्वारा अनुमानित किया जाता है। इस संदर्भ में द्विघात सूत्र पूरी तरह से स्थिर नहीं है। यह तब होता है जब जड़ों में परिमाण का भिन्न क्रम होता है, या, समान रूप से, जब {{math|''b''²}} तथा {{math|''b''² − 4''ac''}} परिमाण के करीब हैं। इस मामले में, दो लगभग समान संख्याओं का घटाव महत्व की हानि या छोटी जड़ में विनाशकारी रद्दीकरण का कारण होगा। इससे बचने के लिए जो जड़ परिमाण में छोटी होती है, {{math|''r''}}, के रूप में गणना की जा सकती है <math>(सी/ए)/आर} जहां R वह जड़ है जो परिमाण में बड़ी है।

रद्दीकरण का दूसरा रूप शर्तों के बीच हो सकता है b² तथा 4ac विवेचक का, वह तब होता है जब दो जड़ें बहुत करीब होती हैं। इससे जड़ों में सही महत्वपूर्ण आंकड़ों के आधे तक का नुकसान हो सकता है।

उदाहरण और अनुप्रयोग

वह चट्टान जम्पर का प्रक्षेपवक्र परवलयिक है क्योंकि क्षैतिज विस्थापन समय का एक रैखिक कार्य है $x=v_{x}t$, जबकि ऊर्ध्वाधर विस्थापन समय का एक द्विघात फलन है $y={\tfrac {1}{2}}^{2}+v_{y}t+h$ पर। परिणामस्वरूप, पथ द्विघात समीकरण $y={\tfrac {a}{2v_{x}^{2}}}x^{2}+{\tfrac {v_{y}}{v_{x}}}x+h$ का अनुसरण करता है, जहां Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "औ" found.in 1:28"): {\displaystyle v_x< /math> और <math>v_y} मूल वेग के क्षैतिज और लंबवत घटक हैं, a गुरुत्वाकर्षण त्वरण है और h मूल ऊंचाई है। a मान को यहां ऋणात्मक माना जाना चाहिए, क्योंकि इसकी दिशा (नीचे की ओर) h के विपरीत है।

ght माप (ऊपर की ओर)। स्वर्णिम अनुपात द्विघात समीकरण के धनात्मक हल के रूप में पाया जाता है $x^{2}-x-1=0.$

वृत्त और अन्य शंकु वर्गों के समीकरण- दीर्घवृत्त, परवलय और अतिपरवलय- दो चरों में द्विघात समीकरण हैं।

किसी कोण की कोज्या या ज्या को देखते हुए, आधे बड़े कोण की कोज्या या ज्या ज्ञात करने में द्विघात समीकरण को हल करना शामिल है।

एक व्यंजक के वर्गमूल को शामिल करने वाले व्यंजकों को सरल बनाने की प्रक्रिया में किसी अन्य व्यंजक के वर्गमूल को शामिल करना एक द्विघात समीकरण के दो हल खोजना शामिल है।

डेसकार्टेस के प्रमेय में कहा गया है कि प्रत्येक चार चुंबन (पारस्परिक रूप से स्पर्शरेखा) मंडलियों के लिए, उनकी त्रिज्या एक विशेष द्विघात समीकरण को संतुष्ट करती है।

फ्यूस के प्रमेय द्वारा दिए गए समीकरण, एक द्विकेन्द्रीय चतुर्भुज के खुदा वृत्त की त्रिज्या, उसके परिबद्ध वृत्त की त्रिज्या और उन वृत्तों के केंद्रों के बीच की दूरी के बीच संबंध देते हुए, एक द्विघात समीकरण के रूप में व्यक्त किया जा सकता है जिसके बीच की दूरी दो वृत्तों के केंद्र उनकी त्रिज्या के संदर्भ में समाधानों में से एक है। प्रासंगिक त्रिज्या के संदर्भ में समान समीकरण का दूसरा समाधान परिबद्ध वृत्त के केंद्र और एक पूर्व-स्पर्शरेखा चतुर्भुज के वृत्त के केंद्र के बीच की दूरी देता है।

एक द्विघात समीकरण को हल करके एक क्यूबिक फ़ंक्शन के महत्वपूर्ण बिंदु और एक क्वार्टिक फ़ंक्शन के विभक्ति बिंदु पाए जाते हैं।

इतिहास

बेबीलोन के गणितज्ञ, 2000 ईसा पूर्व (पुरानी बेबीलोन की मिट्टी की गोलियों पर प्रदर्शित) आयतों के क्षेत्रों और पक्षों से संबंधित समस्याओं को हल कर सकते थे। इस एल्गोरिथम को उर के तीसरे राजवंश के रूप में डेटिंग करने के प्रमाण हैं।आधुनिक संकेतन में, समस्याओं में आम तौर पर फॉर्म के एक साथ समीकरणों की एक जोड़ी को हल करना शामिल होता है:

$x+y=p,\ \ xy=q,$

जो इस कथन के समतुल्य है कि x तथा y समीकरण की जड़ें हैं:

$z^{2}+q=pz.$

उपरोक्त आयत समस्या को हल करने के लिए बेबीलोन के शास्त्रियों द्वारा दिए गए कदम, के संदर्भ में x तथा y, इस प्रकार थे:

1. पी का आधा कंप्यूट करें।
2. परिणाम को बराबर करें।
3. घटाना क्यू।
4. वर्गों की तालिका का उपयोग करके (सकारात्मक) वर्गमूल ज्ञात कीजिए।
5. देने के लिए चरण (1) और (4) के परिणामों को एक साथ जोड़ें x.

आधुनिक संकेतन में इसका अर्थ है गणना करना $x=\left({\frac {p}{2}}\right)+{\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}$, जो आधुनिक के बराबर है बड़े वास्तविक मूल के लिए दिन द्विघात सूत्र (यदि कोई हो) $x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}$ के साथ a = 1, b = −p, तथा c = q.

बेबीलोनिया, मिस्र, ग्रीस, चीन और भारत में द्विघात समीकरणों को हल करने के लिए ज्यामितीय विधियों का उपयोग किया गया था। मिस्र के बर्लिन पेपिरस 6619|बर्लिन पेपिरस, मध्य साम्राज्य (2050 ईसा पूर्व से 1650 ईसा पूर्व) में वापस डेटिंग करते हुए, दो-अवधि के द्विघात समीकरण का समाधान शामिल है।लगभग 400 ईसा पूर्व के बेबीलोन के गणितज्ञों और लगभग 200 ईसा पूर्व के चीनी गणितज्ञों ने सकारात्मक जड़ों वाले द्विघात समीकरणों को हल करने के लिए विच्छेदन के ज्यामितीय तरीकों का इस्तेमाल किया।द्विघात समीकरणों के नियम गणितीय कला पर नौ अध्याय, गणित पर एक चीनी ग्रंथ में दिए गए थे।ऐसा लगता है कि इन प्रारंभिक ज्यामितीय विधियों का कोई सामान्य सूत्र नहीं था। यूनानी गणितज्ञ यूक्लिड ने लगभग 300 ईसा पूर्व एक अधिक अमूर्त ज्यामितीय पद्धति का निर्माण किया। पूरी तरह से ज्यामितीय दृष्टिकोण के साथ पाइथागोरस और यूक्लिड ने द्विघात समीकरण के समाधान खोजने के लिए एक सामान्य प्रक्रिया बनाई। अपने काम अंकगणित में, ग्रीक गणितज्ञ डायोफैंटस ने द्विघात समीकरण को हल किया, लेकिन केवल एक मूल दिया, भले ही दोनों जड़ें सकारात्मक हों।

628 ईस्वी में, एक भारतीय गणितज्ञ ब्रह्मगुप्त ने द्विघात समीकरण का पहला स्पष्ट (हालांकि अभी भी पूरी तरह से सामान्य नहीं) हल दिया। ax² + bx = c इस प्रकार है: निरपेक्ष संख्या को [द गुणांक] के चार गुणा से गुणा करने पर, मध्य पद के [गुणांक] का वर्ग जोड़ें; उसी का वर्गमूल, मध्य पद का [गुणांक] कम, [गुणांक] के दोगुने से विभाजित होने का मान है। (ब्रह्मस्फुटसिद्धांत, कोलब्रुक अनुवाद, 1817, पृष्ठ 346) यह बराबर है

$x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}.$

7 वीं शताब्दी ईस्वी में भारत में लिखी गई बख्शाली पांडुलिपि में द्विघात समीकरणों को हल करने के लिए एक बीजीय सूत्र के साथ-साथ द्विघात अनिश्चित समीकरण (मूल रूप से प्रकार के) शामिल थे ax/c = वाई) मुहम्मद इब्न मूसा अल-ख्वारिज्मी (देश बिल्ली), मेरे द्वारा प्रेरित होकर, सकारात्मक समाधानों के लिए काम करने वाले सूत्रों का एक सेट विकसित किया। अल-ख्वारिज्मी सामान्य द्विघात समीकरण का पूर्ण समाधान प्रदान करने में आगे बढ़ता है, प्रक्रिया में ज्यामितीय प्रमाण प्रदान करते हुए प्रत्येक द्विघात समीकरण के लिए एक या दो संख्यात्मक उत्तरों को स्वीकार करता है।उन्होंने वर्ग को पूरा करने की विधि का भी वर्णन किया और माना कि विवेचक सकारात्मक होना चाहिए, जो उनके समकालीन 'अब्द अल-हमीद इब्न तुर्क (मध्य एशिया, 9वीं शताब्दी) द्वारा सिद्ध किया गया था, जिन्होंने यह साबित करने के लिए ज्यामितीय आंकड़े दिए कि यदि विवेचक नकारात्मक है, तो द्विघात समीकरण का कोई समाधान नहीं है। जबकि अल-ख्वारिज्मी ने स्वयं नकारात्मक समाधानों को स्वीकार नहीं किया, बाद में उनके उत्तराधिकारी इस्लामी गणितज्ञों ने नकारात्मक समाधान स्वीकार किए, साथ ही अपरिमेय संख्या और समाधान।अबू कामिल शुजा इब्न असलम (मिस्र, 10वीं शताब्दी) विशेष रूप से अपरिमेय संख्याओं (अक्सर वर्गमूल, घनमूल या चौथे मूल के रूप में) को द्विघात समीकरणों के समाधान के रूप में या किसी समीकरण में गुणांक के रूप में स्वीकार करने वाले पहले व्यक्ति थे।9वीं शताब्दी के भारतीय गणितज्ञ श्रीधर ने द्विघात समीकरणों को हल करने के नियम लिखे।

यहूदी गणितज्ञ अब्राहम बार हिया हा-नसी (12वीं शताब्दी, स्पेन) ने सामान्य द्विघात समीकरण के पूर्ण समाधान को शामिल करने वाली पहली यूरोपीय पुस्तक लिखी।उनका समाधान काफी हद तक अल-ख्वारिज्मी के काम पर आधारित था।चीनी गणितज्ञ यांग हुई (1238-1298 ईस्वी) का लेखन पहला ज्ञात है जिसमें 'x' के नकारात्मक गुणांक वाले द्विघात समीकरण दिखाई देते हैं, हालांकि वह इसका श्रेय पहले के लियू यी को देते हैं।1545 तक गेरोलामो कार्डानो ने द्विघात समीकरणों से संबंधित कार्यों को संकलित किया। सभी मामलों को कवर करने वाला द्विघात सूत्र पहली बार 1594 में साइमन स्टीविन द्वारा प्राप्त किया गया था।1637 में रेने डेसकार्टेस ने ला जियोमेट्री को प्रकाशित किया जिसमें द्विघात सूत्र उस रूप में था जिसे हम आज जानते हैं।

उन्नत विषय

मूल गणना के वैकल्पिक तरीके

स्थान के सूत्र

Main article: Vieta's formulas

द्विघात समीकरण x² + bx + c = 0 के सबसे छोटे मूल के लिए Vieta के सन्निकटन के बीच अंतर का रफ़ द्विघात सूत्र का उपयोग करके परिकलित मान की तुलना में

वियत के सूत्र (फ्रांकोइस वियत के नाम पर) संबंध हैं

$x_{1}+x_{2}=-{\frac {b}{a}},\quad x_{1}x_{2}={\frac {c}{a}}$

द्विघात बहुपद की जड़ों और उसके गुणांकों के बीच। वे संबंध द्वारा शब्द की तुलना करने के परिणामस्वरूप होते हैं

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "ब" found.in 1:17"): {\displaystyle \बाएं(x - x_1 \दाएं) \बाएं(x-x_2 \दाएं) = x^2 - \बाएं(x_1+x_2 \दाएं)x +x_1 x_2 = 0</गणित> समीकरण के साथ :<math>x^2 + \frac ba x +\frac ca = 0.}

पहला विएटा का सूत्र द्विघात फलन को रेखांकन करने के लिए उपयोगी है। चूंकि ग्राफ शीर्ष के माध्यम से एक ऊर्ध्वाधर रेखा के संबंध में सममित है, शीर्ष का x-कोऑर्डिनेट जड़ों (या इंटरसेप्ट्स) के औसत पर स्थित होता है। इस प्रकार x-शीर्ष का निर्देशांक है

$x_{V}={\frac {x_{1}+x_{2}}{2}}=-{\frac {b}{2a}}.$

y-निर्देशांक उपरोक्त परिणाम को दिए गए द्विघात समीकरण में प्रतिस्थापित करके प्राप्त किया जा सकता है

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "।" found.in 1:69"): {\displaystyle y_V = - \frac{b^2}{4a} + c = - \frac{ b^2 - 4ac} {4a}।}

शीर्ष के लिए ये सूत्र सीधे सूत्र से भी निकाले जा सकते हैं (वर्ग को पूरा करना देखें)

$ax^{2}+bx+c=a\left(\left(x-{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}-4ac}{4a}}\right).$

संख्यात्मक गणना के लिए, विएटा के सूत्र उस स्थिति में द्विघात समीकरण की जड़ों को खोजने के लिए एक उपयोगी विधि प्रदान करते हैं जहां एक जड़ दूसरे की तुलना में बहुत छोटी होती है। यदि |x₂| << |x₁|, then x₁ + x₂ ≈ x₁, और हमारे पास अनुमान है:

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "ल" found.in 1:21"): {\displaystyle x_1 \लगभग -\frac{b}{a} .}

दूसरा विएटा का सूत्र तब प्रदान करता है:

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "ल" found.in 1:39"): {\displaystyle x_2 = \frac{c}{a x_1} \लगभग -\frac{c}{b} .}

एक बड़ी और एक छोटी जड़ की स्थिति में द्विघात सूत्र की तुलना में इन सूत्रों का मूल्यांकन करना बहुत आसान है, क्योंकि द्विघात सूत्र छोटे मूल का मूल्यांकन दो बहुत ही लगभग समान संख्याओं के अंतर के रूप में करता है (बड़े का मामला) b), जो एक संख्यात्मक मूल्यांकन में राउंड-ऑफ त्रुटि का कारण बनता है। आंकड़ा के बीच का अंतर दिखाता है (i) द्विघात सूत्र का उपयोग करके एक प्रत्यक्ष मूल्यांकन (सटीक जब जड़ें एक-दूसरे के पास मूल्य में होती हैं) और (ii) विएटा के सूत्रों के उपरोक्त अनुमान पर आधारित एक मूल्यांकन (सटीक जब जड़ें व्यापक रूप से दूरी पर होती हैं)। रैखिक गुणांक के रूप में b बढ़ता है, शुरू में द्विघात सूत्र सटीक होता है, और अनुमानित सूत्र सटीकता में सुधार करता है, जिससे विधियों के बीच एक छोटा अंतर होता है b बढ़ती है। हालांकि, कुछ बिंदु पर राउंड ऑफ एरर के कारण द्विघात सूत्र सटीकता खोना शुरू कर देता है, जबकि अनुमानित विधि में सुधार जारी है। नतीजतन, विधियों के बीच का अंतर बढ़ने लगता है क्योंकि द्विघात सूत्र बदतर और बदतर होता जाता है।

यह स्थिति आमतौर पर एम्पलीफायर डिजाइन में उत्पन्न होती है, जहां एक स्थिर संचालन सुनिश्चित करने के लिए व्यापक रूप से अलग जड़ों को वांछित किया जाता है (चरण प्रतिक्रिया देखें)।

त्रिकोणमितीय हल

कैलकुलेटर से पहले के दिनों में, लोग गणितीय तालिकाओं का उपयोग करते थे - गणना के परिणामों को अलग-अलग तर्कों के साथ दिखाने वाली संख्याओं की सूची - गणना को सरल और तेज करने के लिए। गणित और विज्ञान की पाठ्यपुस्तकों में लघुगणक और त्रिकोणमितीय कार्यों की तालिकाएँ आम थीं। खगोल विज्ञान, आकाशीय नेविगेशन और सांख्यिकी जैसे अनुप्रयोगों के लिए विशिष्ट तालिकाओं को प्रकाशित किया गया था। संख्यात्मक सन्निकटन के तरीके मौजूद थे, जिन्हें प्रोस्थफेरेसिस कहा जाता था, जो समय लेने वाले कार्यों जैसे गुणा और शक्तियों और जड़ों को लेने के आसपास शॉर्टकट पेश करते थे।खगोलविद, विशेष रूप से, उन तरीकों से चिंतित थे जो आकाशीय यांत्रिकी गणनाओं में शामिल गणनाओं की लंबी श्रृंखला को गति दे सकते थे।

इस संदर्भ में हम त्रिकोणमितीय प्रतिस्थापन की सहायता से द्विघात समीकरणों को हल करने के साधनों के विकास को समझ सकते हैं। द्विघात समीकरण के निम्नलिखित वैकल्पिक रूप पर विचार करें,

[1] $ax^{2}+bx\pm c=0,$

जहां ± प्रतीक का चिन्ह चुना जाता है ताकि a तथा c दोनों सकारात्मक हो सकते हैं। प्रतिस्थापित करके

[2] $x={\sqrt {c/a}}\tan \theta$

और फिर से गुणा करके cos²θ, हमने प्राप्त किया

[3] Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "।" found.in 1:95"): {\displaystyle \sin^2\theta + \frac{b}{\sqrt {ac}} \sin\theta \cos\theta \pm \cos^2\theta = 0 ।}

के कार्यों का परिचय {math|2θ}} और पुनर्व्यवस्थित करने पर, हम प्राप्त करते हैं

'[4]' $\tan 2\theta _{n}=+2{\frac {\sqrt {ac}}{b}},$

[5] $\sin 2\theta _{p}=-2{\frac {\sqrt {ac}}{b}},$

जहां सबस्क्रिप्ट n तथा p समीकरण [1] में ऋणात्मक या धनात्मक चिह्न के प्रयोग से क्रमशः मेल खाते हैं। के दो मानों को प्रतिस्थापित करना θ_n या θ_p समीकरण [4] या [5] से [2] में पाया जाता है, [1] की आवश्यक जड़ें देता है। समीकरण के आधार पर समाधान में जटिल जड़ें होती हैं [5] यदि का निरपेक्ष मान sin 2θ_p एकता से अधिक है। इस मिश्रित त्रिकोणमितीय और लॉगरिदमिक तालिका लुक-अप रणनीति का उपयोग करके द्विघात समीकरणों को हल करने में शामिल प्रयास की मात्रा अकेले लॉगरिदमिक तालिकाओं का उपयोग करके दो-तिहाई प्रयास थी।जटिल जड़ों की गणना के लिए एक अलग त्रिकोणमितीय रूप का उपयोग करने की आवश्यकता होगी।

उदाहरण के लिए, मान लें कि हमारे पास सात-स्थानीय लघुगणक और त्रिकोणमितीय तालिकाएँ उपलब्ध थीं, और हम निम्नलिखित को छह-महत्वपूर्ण-अंक सटीकता के लिए हल करना चाहते थे:

$4.16130x^{2}+9.15933x-11.4207=0$

1. सात-स्थान वाली लुकअप तालिका में केवल 100,000 प्रविष्टियाँ हो सकती हैं, और सात स्थानों पर मध्यवर्ती परिणामों की गणना करने के लिए आम तौर पर आसन्न प्रविष्टियों के बीच प्रक्षेप की आवश्यकता होगी।
2. $\log a=0.6192290,\log b=0.9618637,\log c=1.0576927$
3. $2{\sqrt {ac}}/b=2\times 10^{(0.6192290+1.0576927)/2-0.9618637}=1.505314$
4. Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "थ" found.in 1:17"): {\displaystyle \थीटा = (\tan^{-1}1.505314)/2 = 28.20169^{\circ} \text{ या } -61.79831^{\circ} }
5. Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "ल" found.in 1:17"): {\displaystyle \लॉग | \ तन \ थीटा | = -0.2706462 \पाठ{ या } 0.2706462}
6. $\log {\sqrt {c/a}}=(1.0576927-0.6192290)/2=0.2192318$
7. $x_{1}=10^{0.2192318-0.2706462}=0.888353$ (छह सार्थक अंकों तक गोल)

$x_{2}=-10^{0.2192318+0.2706462}=-3.08943$

ध्रुवीय निर्देशांक में जटिल जड़ों के लिए समाधान

यदि द्विघात समीकरण $ax^{2}+bx+c=0$ वास्तविक गुणांकों के साथ दो जटिल मूल होते हैं—वह स्थिति जहां $b^{2}-4ac<0,$ के लिए a और c का एक दूसरे के समान चिह्न होना आवश्यक है—तब जड़ों के समाधान को ध्रुवीय रूप में व्यक्त किया जा सकता है

$x_{1},\,x_{2}=r(\cos \theta \pm i\sin \theta ),$

कहाँ पे $r={\sqrt {\tfrac {c}{a}}}$ और Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "थ" found.in 1:17"): {\displaystyle \थीटा =\cos ^{-1}\बाएं(\frac{-b}{2\sqrt{ac}}\right).}

ज्यामितीय समाधान

igure 6. लिल की विधि का उपयोग करके ax² + bx + c = 0 का ज्यामितीय समाधान। समाधान हैं −AX1/SA, −AX2/SA

एह एक्स 2 एस एह द्वारा विभाजित।

द्विघात समीकरण को कई तरीकों से ज्यामितीय रूप से हल किया जा सकता है। एक तरीका है लिल की विधि के माध्यम से। तीन गुणांक a, b, c उनके बीच समकोण के साथ चित्र 6 में SA, AB और BC के रूप में खींचे गए हैं। प्रारंभ और अंत बिंदु SC को व्यास के रूप में लेकर एक वृत्त खींचा गया है। यदि यह तीनों की मध्य रेखा AB को काटता है तो समीकरण का एक हल होता है, और समाधान इस रेखा के साथ दूरी के ऋणात्मक द्वारा दिया जाता है जो पहले गुणांक से विभाजित होता है। a या एसए. यदि a है 1 गुणांक सीधे पढ़ा जा सकता है। इस प्रकार आरेख में समाधान −AX1/SA और −AX2/SA हैं।

द्विघात समीकरण का अर्ली सर्कल x² − sx + p = 0.

थॉमस कार्लाइल के नाम पर कार्लाइल सर्कल में संपत्ति है कि द्विघात समीकरण के समाधान क्षैतिज अक्ष के साथ सर्कल के चौराहे के क्षैतिज निर्देशांक हैं।नियमित बहुभुजों के शासक-और-कम्पास निर्माण को विकसित करने के लिए कार्लाइल सर्कल का उपयोग किया गया है।

द्विघात समीकरण का सामान्यीकरण

गुणांक . होने पर सूत्र और उसकी व्युत्पत्ति सही रहती है a, b तथा c सम्मिश्र संख्याएँ हैं, या अधिक सामान्यतः किसी भी क्षेत्र के सदस्य हैं जिनकी विशेषता नहीं है 2. (विशेषता 2 के क्षेत्र में, तत्व 2a शून्य है और इसे विभाजित करना असंभव है।)

प्रतीक

$\pm {\sqrt {b^{2}-4ac}}$

सूत्र में दो तत्वों में से किसी एक के रूप में समझा जाना चाहिए जिसका वर्ग है b² − 4ac, यदि ऐसे तत्व मौजूद हैं। कुछ क्षेत्रों में, कुछ तत्वों के वर्गमूल नहीं होते और कुछ में दो होते हैं; विशेषता के क्षेत्रों को छोड़कर, केवल शून्य में केवल एक वर्गमूल होता है 2. भले ही किसी फ़ील्ड में किसी संख्या का वर्गमूल न हो, हमेशा एक द्विघात विस्तार क्षेत्र होता है, इसलिए द्विघात सूत्र हमेशा उस विस्तार क्षेत्र में एक सूत्र के रूप में समझ में आता है।

विशेषता 2

विशेषता के क्षेत्र में 2, द्विघात सूत्र, जो पर निर्भर करता है 2 एक इकाई होने के नाते, धारण नहीं करता है। मोनिक द्विघात बहुपद पर विचार करें

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "ए" found.in 1:16"): {\displaystyle एक्स^{2} + बीएक्स + सी}

विशेषता के क्षेत्र में 2. यदि b = 0, तो समाधान एक वर्गमूल निकालने के लिए कम हो जाता है, इसलिए समाधान है

$x={\sqrt {c}}$

और तब से केवल एक ही जड़ है

$-{\sqrt {c}}=-{\sqrt {c}}+2{\sqrt {c}}={\sqrt {c}}.$

सारांश,

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "।" found.in 1:60"): {\displaystyle \displaystyle x^{2} + c = (x + \sqrt{c})^{2}।}

परिमित क्षेत्रों में वर्गमूल निकालने के बारे में अधिक जानकारी के लिए द्विघात अवशेष देखें।

मामले में कि b ≠ 0, दो अलग-अलग मूल हैं, लेकिन यदि बहुपद अपरिवर्तनीय है, तो उन्हें गुणांक क्षेत्र में संख्याओं के वर्गमूल के रूप में व्यक्त नहीं किया जा सकता है। इसके बजाय, 2-रूट को परिभाषित करें R(c) का c बहुपद का मूल होना x² + x + c, उस बहुपद के विभाजन क्षेत्र का एक तत्व। एक सत्यापित करता है कि R(c) + 1 एक जड़ भी है। 2-रूट ऑपरेशन के संदर्भ में, (गैर-मोनिक) द्विघात की दो जड़ें ax² + bx + c हैं

${\frac {b}{a}}R\left({\frac {ac}{b^{2}}}\right)$

तथा

Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected [, ;!_#%$&], [a-zA-Z], or [{}|] but "ब" found.in 1:28"): {\displaystyle \frac{b}{a}\बाएं(R\बाएं(\frac{ac}{b^2}\right)+1\right).}

उदाहरण के लिए, चलो a इकाइयों के समूह के गुणक जनरेटर को निरूपित करें F₄, क्रम चार का गैल्वा क्षेत्र (इस प्रकार) a तथा a + 1 की जड़ें हैं x² + x + 1 ऊपर F₄. इसलिये (a + 1)² = एक, a + 1 द्विघात समीकरण का अद्वितीय हल है x² + a = 0. दूसरी ओर, बहुपद x² + ax + 1 इरेड्यूसबल ओवर है F₄, लेकिन यह अलग हो जाता है F₁₆, जहां इसकी दो जड़ें हैं ab तथा ab + a, कहाँ पे b की जड़ है x² + x + a में F₁₆.

यह आर्टिन-श्रेयर सिद्धांत का एक विशेष मामला है।

यह भी देखें

• निरंतर भिन्नों के साथ द्विघात समीकरणों को हल करना
• रेखीय समीकरण
• क्यूबिक फंक्शन
• चतुर्थक समीकरण
• क्विंटिक समीकरण
• बीजगणित की मौलिक प्रमेय

बाहरी संबंध

• "Quadratic equation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Quadratic equations". MathWorld.
• 101 uses of a quadratic equation
• 101 uses of a quadratic equation: Part II