सेप्टिक समीकरण: Difference between revisions

Revision as of 21:33, 28 November 2022

डिग्री 7 के एक बहुपद का ग्राफ, 7 वास्तविक संख्या के साथ एक बहुपद का मूल (क्रॉसिंग)

x

अक्ष) और 6 महत्वपूर्ण बिंदु (गणित)। न्यूनतम की संख्या और ऊर्ध्वाधर स्थान के आधार पर, सेप्टिक में उनकी बहुलता के साथ 7, 5, 3, या 1 वास्तविक रूट गिना जा सकता है; जटिल संख्या गैर-वास्तविक जड़ों की संख्या 7 माइनस वास्तविक जड़ों की संख्या है।

बीजगणित में, एक सेप्टिक समीकरण , नीचे लिखे रूप का एक समीकरण है

ax^{7}+bx^{6}+cx^{5}+dx^{4}+ex^{3}+fx^{2}+gx+h=0,\,

जहाँ पर $a \neq 0$ .

एक सेप्टिक फलन, निम्नलिखित रूप का एक फलन है

f(x)=ax^{7}+bx^{6}+cx^{5}+dx^{4}+ex^{3}+fx^{2}+gx+h\,

जहाँ पर $a \neq 0$ । दूसरे शब्दों में, यह 7 की घात का एक बहुपद है। यदि $a = 0$ , तो f, 6 घात का एक फलन है ( $b \neq 0$ ), 5 घात का फलन ( $b = 0, c \neq 0$ ), आदि।

$f (x) = 0$ रखकर फलन से समीकरण प्राप्त किया जा सकता है :

गुणांक $a, b, c, d, e, f, g, h$ या तो पूर्णांक, परिमेय संख्या, वास्तविक संख्या, जटिल संख्या या, अधिक सामान्यतः, किसी भी क्षेत्र के सदस्य हो सकते हैं।

क्योंकि उनके पास एक विषम डिग्री है। जब ग्राफ़ किया जाता है तो सेप्टिक फलन, क्विंटिक फलन या घन फलन के समान दिखाई देते हैं, केवल इसके कि उनके पास अतिरिक्त उच्चतम और निम्नतम और स्थानीय निम्न (तीन उच्च और तीन निम्न तक) हो सकते हैं। सेप्टिक फलन का व्युत्पन्न एक सेक्स्टिक फलन (6 घात का एक फलन) है।

हल करने योग्य सेप्टिक्स

कुछ सातवीं डिग्री के समीकरणों को मूल अभिव्यक्ति में गुणनखंड बनाकर हल किया जा सकता है, लेकिन अन्य सेप्टिक्स नहीं कर सकते। इवरिस्ट गैलोइस ने यह निर्धारित करने के लिए तकनीक विकसित की कि क्या किसी दिए गए समीकरण को रेडिकल्स द्वारा हल किया जा सकता है जिसने गैलोइस सिद्धांत के क्षेत्र को जन्म दिया। एक अलघुकरणीय लेकिन हल करने योग्य सेप्टिक का उदाहरण देने के लिए, कोई हल करने योग्य डे मोइवर क्विंटिक को प्राप्त करने के लिए सामान्य कर सकता है,

x^{7}+7\alpha x^{5}+14\alpha ^{2}x^{3}+7\alpha ^{3}x+\beta =0\,

,

जहाँ सहायक समीकरण है

y^{2}+\beta y-\alpha ^{7}=0\,

.

इसका अर्थ है कि सेप्टिक को $u$ तथा $v$ के बीच $x = u + v$ , $uv + α = 0$ तथा $u 7 + v 7 + β = 0$ से प्राप्त किया जाता है।

यह इस प्रकार है जिससे कि सेप्टिक की सात मूल को प्राप्त किया जा सकता है

x_{k}=\omega _{k}{\sqrt[{7}]{y_{1}}}+\omega _{k}^{6}{\sqrt[{7}]{y_{2}}}

जहाँ पर $ω k$ एकता के 7 सातवें मूल में से कोई भी है। इस सेप्टिक का गैलोज़ समूह क्रम 42 का अधिकतम हल करने योग्य समूह है। इसे आसानी से किसी भी अन्य डिग्री $k$ के लिए सामान्यीकृत किया जाता है, जरूरी नहीं है कि प्रधान हो।

एक और समाधान परिवार है,

x^{7}-2x^{6}+(\alpha +1)x^{5}+(\alpha -1)x^{4}-\alpha x^{3}-(\alpha +5)x^{2}-6x-4=0\,

जिसके सदस्य संख्या क्षेत्रों के क्लूनर के डेटाबेस में दिखाई देते हैं। इसका विवेचक है

\Delta =-4^{4}\left(4\alpha ^{3}+99\alpha ^{2}-34\alpha +467\right)^{3}\,

इन सेप्टिक्स का गैलोज़ समूह ऑर्डर 14 का डायहेड्रल समूह है।

सामान्य सेप्टिक समीकरण को वैकल्पिक समूह या सममित समूह गैलोइस समूह के साथ हल किया जा सकता है $A 7$ या $S 7$ .^[1]इस तरह के समीकरणों को उनके समाधान के लिए जीनस (गणित) 3 के हाइपरेलिप्टिक फलन और संबंधित थीटा कार्यों की आवश्यकता होती है।^[1]हालाँकि, इन समीकरणों का विशेष रूप से उन्नीसवीं शताब्दी के गणितज्ञों द्वारा बीजीय समीकरणों के समाधान का अध्ययन नहीं किया गया था, क्योंकि सेक्स्टिक समीकरणों के समाधान पहले से ही कंप्यूटर के बिना उनकी कम्प्यूटेशनल क्षमताओं की सीमा पर थे।^[1] सेप्टिक्स निम्नतम क्रम के समीकरण हैं जिनके लिए यह स्पष्ट नहीं है कि उनके समाधान दो चरों के निरंतर कार्यों को अध्यारोपित करके प्राप्त किए जा सकते हैं। हिल्बर्ट की तेरहवीं समस्या|हिल्बर्ट की 13वीं समस्या अनुमान था, यह सातवें डिग्री के समीकरणों के सामान्य मामले में संभव नहीं था। व्लादिमीर अर्नोल्ड ने 1957 में यह प्रदर्शित करते हुए इसे हल किया कि यह हमेशा संभव था।^[2] हालांकि, अर्नोल्ड ने खुद को वास्तविक हिल्बर्ट समस्या माना कि क्या सेप्टिक्स के लिए उनके समाधान दो चर के बीजगणितीय कार्यों को सुपरइम्पोज़ करके प्राप्त किए जा सकते हैं (समस्या अभी भी खुली है)।^[3]

गैलोइस समूह

फानो विमान

रेडिकल्स द्वारा हल किए जा सकने वाले सेप्टिक समीकरणों में गैलोज़ समूह होता है जो या तो ऑर्डर 7 का चक्रीय समूह होता है, या ऑर्डर 14 का डायहेड्रल समूह या ऑर्डर 21 या 42 का मेटासाइक्लिक समूह होता है।^[1]

$L (3, 2)$ }} गाल्वा समूह (क्रम 168 का) 7 वर्टेक्स लेबल के क्रमपरिवर्तन से बनता है जो फ़ानो विमान में 7 पंक्तियों को संरक्षित करता है।^[1]इस गैलोज़ समूह के साथ सेप्टिक समीकरण $L (3, 2)$ उनके समाधान के लिए अण्डाकार कार्यों की आवश्यकता होती है, लेकिन हाइपरलिप्टिक कार्यों की नहीं।^[1]*अन्यथा एक सेप्टिक का गैलोज़ समूह या तो क्रम 2520 का वैकल्पिक समूह है या क्रम 5040 का सममित समूह है।

एक चक्रीय पंचभुज या षट्भुज के वर्ग क्षेत्र के लिए सेप्टिक समीकरण

चक्रीय पेंटागन के क्षेत्रफल का वर्ग एक सेप्टिक समीकरण का एक मूल है, जिसके गुणांक पंचभुज की भुजाओं के सममित फलन होते हैं।^[4] चक्रीय षट्भुज के क्षेत्रफल के वर्ग के बारे में भी यही सच है।^[5]

यह भी देखें

क्यूबिक फलन
चतुर्थक समारोह
क्विंटिक फंक्शन
सेक्सेटिक समीकरण
लैब्स सेप्टिक

संदर्भ

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 R. Bruce King (16 January 2009), Beyond the Quartic Equation, Birkhaüser, p. 143 and 144, ISBN 9780817648497
↑ Vasco Brattka (13 September 2007), "Kolmogorov's Superposition Theorem", Kolmogorov's heritage in mathematics, Springer, ISBN 9783540363514
↑ V.I. Arnold, From Hilbert's Superposition Problem to Dynamical Systems, p. 4
↑ Weisstein, Eric W. "Cyclic Pentagon." From MathWorld--A Wolfram Web Resource. [1]
↑ Weisstein, Eric W. "Cyclic Hexagon." From MathWorld--A Wolfram Web Resource. [2]

[BeyondQuartic-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 R. Bruce King (16 January 2009), Beyond the Quartic Equation, Birkhaüser, p. 143 and 144, ISBN 9780817648497

[2] Vasco Brattka (13 September 2007), "Kolmogorov's Superposition Theorem", Kolmogorov's heritage in mathematics, Springer, ISBN 9783540363514

[3] V.I. Arnold, From Hilbert's Superposition Problem to Dynamical Systems, p. 4

[4] Weisstein, Eric W. "Cyclic Pentagon." From MathWorld--A Wolfram Web Resource. [1]

[5] Weisstein, Eric W. "Cyclic Hexagon." From MathWorld--A Wolfram Web Resource. [2]

[1]

[2]

[3]

[4]

[5]

@@ Line 1: / Line 1: @@
 {{short description|Polynomial equation of degree 7}}
-{{Other uses|Septic (disambiguation)}}
+{{Other uses|सेप्टिक ( विसंदिग्धीकरण)}}
-[[Image:Septic graph.svg|thumb|right|233px|डिग्री 7 के एक बहुपद का ग्राफ, 7 [[वास्तविक संख्या]] के साथ एक बहुपद का मूल (क्रॉसिंग) {{math|''x''}} अक्ष) और 6 [[महत्वपूर्ण बिंदु (गणित)]]। [[न्यूनतम]] की संख्या और ऊर्ध्वाधर स्थान के आधार पर, सेप्टिक में उनकी बहुलता के साथ 7, 5, 3, या 1 वास्तविक रूट गिना जा सकता है; [[जटिल संख्या]] गैर-वास्तविक जड़ों की संख्या 7 माइनस वास्तविक जड़ों की संख्या है।]][[बीजगणित]] में, एक सेप्टिक [[समीकरण]] रूप का एक समीकरण है
+[[Image:Septic graph.svg|thumb|right|233px|डिग्री 7 के एक बहुपद का ग्राफ, 7 [[वास्तविक संख्या]] के साथ एक बहुपद का मूल (क्रॉसिंग) {{math|''x''}} अक्ष) और 6 [[महत्वपूर्ण बिंदु (गणित)]]। [[न्यूनतम]] की संख्या और ऊर्ध्वाधर स्थान के आधार पर, सेप्टिक में उनकी बहुलता के साथ 7, 5, 3, या 1 वास्तविक रूट गिना जा सकता है; [[जटिल संख्या]] गैर-वास्तविक जड़ों की संख्या 7 माइनस वास्तविक जड़ों की संख्या है।]][[बीजगणित]] में, एक सेप्टिक [[समीकरण]] , नीचे लिखे रूप का एक समीकरण है
 :<math>ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h=0,\,</math>
-कहाँ पे {{math|''a'' ≠ 0}}.
+जहाँ पर {{math|''a'' ≠ 0}}.
-एक सेप्टिक फ़ंक्शन फॉर्म का एक फ़ंक्शन (गणित) है
+एक सेप्टिक फलन, निम्नलिखित रूप का एक फलन है
 :<math>f(x)=ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h\,</math>
-कहाँ पे {{math|''a'' ≠ 0}}. दूसरे शब्दों में, यह एक [[बहुपद]] सात की घात का बहुपद है। यदि {{math|1=''a'' = 0}}, तो f एक यौन कार्य है ({{math|''b'' ≠ 0}}), [[पंचक समारोह]] ({{math|1=''b'' = 0, ''c'' ≠ 0}}), आदि।
+जहाँ पर {{math|''a'' ≠ 0}}।  दूसरे शब्दों में, यह 7 की घात का एक [[बहुपद]] है। यदि {{math|1=''a'' = 0}}, तो f, 6 घात का एक फलन है ({{math|''b'' ≠ 0}}), [[पंचक समारोह|5 घात का फलन]]  ({{math|1=''b'' = 0, ''c'' ≠ 0}}), आदि।
-सेटिंग द्वारा फ़ंक्शन से समीकरण प्राप्त किया जा सकता है {{math|1=''f''(''x'') = 0}}.
+{{math|1=''f''(''x'') = 0}} रखकर फलन से समीकरण प्राप्त किया जा सकता है :
-गुणांक {{math|''a'', ''b'', ''c'', ''d'', ''e'', ''f'', ''g'', ''h''}} या तो पूर्णांक, [[परिमेय संख्या]], वास्तविक संख्या, जटिल संख्या या, अधिक सामान्यतः, किसी भी [[क्षेत्र (गणित)]] के सदस्य हो सकते हैं।
+गुणांक {{math|''a'', ''b'', ''c'', ''d'', ''e'', ''f'', ''g'', ''h''}} या तो पूर्णांक, [[परिमेय संख्या]], वास्तविक संख्या, जटिल संख्या या, अधिक सामान्यतः, किसी भी [[क्षेत्र (गणित)|क्षेत्र]] के सदस्य हो सकते हैं।
-क्योंकि उनके पास एक विषम डिग्री है, सेप्टिक फ़ंक्शन क्विंटिक फ़ंक्शन या [[घन समारोह]] के समान दिखाई देते हैं, जब ग्राफ़ किया जाता है, सिवाय इसके कि उनके पास अतिरिक्त [[मैक्सिमा और मिनिमा]] और स्थानीय मिनिमा (तीन मैक्सिमा और तीन मिनिमा तक) हो सकते हैं। सेप्टिक फ़ंक्शन का व्युत्पन्न एक सेक्स्टिक फ़ंक्शन है।
+क्योंकि उनके पास एक विषम डिग्री है। जब ग्राफ़ किया जाता है तो सेप्टिक फलन, क्विंटिक फलन या [[घन समारोह|घन फलन]] के समान दिखाई देते हैं, केवल इसके कि उनके पास अतिरिक्त [[मैक्सिमा और मिनिमा|उच्चतम और निम्नतम]] और स्थानीय निम्न (तीन उच्च और तीन निम्न तक) हो सकते हैं। सेप्टिक फलन का व्युत्पन्न एक सेक्स्टिक फलन (6 घात का एक फलन) है।
-== सॉल्वेबल सेप्टिक्स ==
+== हल करने योग्य सेप्टिक्स ==
-कुछ सातवीं डिग्री के समीकरणों को मूल अभिव्यक्ति में कारक बनाकर हल किया जा सकता है, लेकिन अन्य सेप्टिक्स नहीं कर सकते। इवरिस्ट गैलोइस ने यह निर्धारित करने के लिए तकनीक विकसित की कि क्या किसी दिए गए समीकरण को रेडिकल्स द्वारा हल किया जा सकता है जिसने गैलोइस सिद्धांत के क्षेत्र को जन्म दिया। एक इरेड्यूसिबल लेकिन सॉल्व करने योग्य सेप्टिक का उदाहरण देने के लिए, कोई सॉल्वेबल डे मोइवर [[क्विंटिक]] को प्राप्त करने के लिए सामान्य कर सकता है,
+कुछ सातवीं डिग्री के समीकरणों को मूल अभिव्यक्ति में गुणनखंड बनाकर हल किया जा सकता है, लेकिन अन्य सेप्टिक्स नहीं कर सकते। इवरिस्ट गैलोइस ने यह निर्धारित करने के लिए तकनीक विकसित की कि क्या किसी दिए गए समीकरण को रेडिकल्स द्वारा हल किया जा सकता है जिसने गैलोइस सिद्धांत के क्षेत्र को जन्म दिया। एक अलघुकरणीय लेकिन हल करने योग्य सेप्टिक का उदाहरण देने के लिए, कोई हल करने योग्य डे मोइवर [[क्विंटिक]] को प्राप्त करने के लिए सामान्य कर सकता है,
 :<math>x^7+7\alpha x^5+14\alpha^2x^3+7\alpha^3x+\beta = 0\,</math>,
-जहां सहायक समीकरण है
+जहाँ सहायक समीकरण है
 :<math>y^2+\beta y-\alpha^7 = 0\,</math>.
-इसका मतलब है कि सेप्टिक को खत्म करके प्राप्त किया जाता है {{math|''u''}} तथा {{math|''v''}} के बीच {{math|1=''x'' = ''u'' + ''v''}},  {{math|1=''uv'' + ''α'' = 0}} तथा {{math|1=''u''<sup>7</sup> + ''v''<sup>7</sup> + ''β'' = 0}}.
+इसका अर्थ है कि सेप्टिक को {{math|''u''}} तथा {{math|''v''}} के बीच {{math|1=''x'' = ''u'' + ''v''}},  {{math|1=''uv'' + ''α'' = 0}} तथा {{math|1=''u''<sup>7</sup> + ''v''<sup>7</sup> + ''β'' = 0}} से प्राप्त किया जाता है।
-यह इस प्रकार है कि सेप्टिक की सात जड़ें किसके द्वारा दी गई हैं
+यह इस प्रकार है जिससे कि सेप्टिक की सात मूल को प्राप्त किया जा सकता है
 :<math>x_k = \omega_k\sqrt[7]{y_1} + \omega_k^6\sqrt[7]{y_2}</math>
-कहाँ पे {{math|''ω<sub>k</sub>''}} एकता के 7 सातवें मूल में से कोई भी है। इस सेप्टिक का गैलोज़ समूह क्रम 42 का अधिकतम हल करने योग्य समूह है। इसे आसानी से किसी भी अन्य डिग्री के लिए सामान्यीकृत किया जाता है {{math|''k''}}, जरूरी नहीं कि प्रधान हो।
+जहाँ पर {{math|''ω<sub>k</sub>''}} एकता के 7 सातवें मूल में से कोई भी है। इस सेप्टिक का गैलोज़ समूह क्रम 42 का अधिकतम हल करने योग्य समूह है। इसे आसानी से किसी भी अन्य डिग्री {{math|''k''}} के लिए सामान्यीकृत किया जाता है, जरूरी नहीं  है कि प्रधान हो।
-एक और समाधान योग्य परिवार है,
+एक और समाधान परिवार है,
 :<math>x^7-2x^6+(\alpha+1)x^5+(\alpha-1)x^4-\alpha x^3-(\alpha+5)x^2-6x-4 = 0\,</math>
@@ Line 39: / Line 39: @@
 इन सेप्टिक्स का गैलोज़ समूह ऑर्डर 14 का [[डायहेड्रल समूह]] है।
-सामान्य सेप्टिक समीकरण को [[वैकल्पिक समूह]] या [[सममित समूह]] गैलोइस समूह के साथ हल किया जा सकता है {{math|''A''<sub>7</sub>}} या {{math|''S''<sub>7</sub>}}.<ref name="BeyondQuartic"/>इस तरह के समीकरणों को उनके समाधान के लिए [[जीनस (गणित)]] 3 के [[हाइपरेलिप्टिक फ़ंक्शन]] और संबंधित थीटा कार्यों की आवश्यकता होती है।<ref name="BeyondQuartic"/>हालाँकि, इन समीकरणों का विशेष रूप से उन्नीसवीं शताब्दी के गणितज्ञों द्वारा बीजीय समीकरणों के समाधान का अध्ययन नहीं किया गया था, क्योंकि सेक्स्टिक समीकरणों के समाधान पहले से ही कंप्यूटर के बिना उनकी कम्प्यूटेशनल क्षमताओं की सीमा पर थे।<ref name="BeyondQuartic">{{citation|url=https://books.google.com/books?id=9cKX_9zkeg4C&q=septic+equation&pg=PA143 |author=R. Bruce King |title=Beyond the Quartic Equation |date=16 January 2009 |publisher= Birkhaüser|page=  143 and 144|isbn=9780817648497 }}</ref>
+सामान्य सेप्टिक समीकरण को [[वैकल्पिक समूह]] या [[सममित समूह]] गैलोइस समूह के साथ हल किया जा सकता है {{math|''A''<sub>7</sub>}} या {{math|''S''<sub>7</sub>}}.<ref name="BeyondQuartic"/>इस तरह के समीकरणों को उनके समाधान के लिए [[जीनस (गणित)]] 3 के [[हाइपरेलिप्टिक फ़ंक्शन|हाइपरेलिप्टिक फलन]] और संबंधित थीटा कार्यों की आवश्यकता होती है।<ref name="BeyondQuartic"/>हालाँकि, इन समीकरणों का विशेष रूप से उन्नीसवीं शताब्दी के गणितज्ञों द्वारा बीजीय समीकरणों के समाधान का अध्ययन नहीं किया गया था, क्योंकि सेक्स्टिक समीकरणों के समाधान पहले से ही कंप्यूटर के बिना उनकी कम्प्यूटेशनल क्षमताओं की सीमा पर थे।<ref name="BeyondQuartic">{{citation|url=https://books.google.com/books?id=9cKX_9zkeg4C&q=septic+equation&pg=PA143 |author=R. Bruce King |title=Beyond the Quartic Equation |date=16 January 2009 |publisher= Birkhaüser|page=  143 and 144|isbn=9780817648497 }}</ref>
 सेप्टिक्स निम्नतम क्रम के समीकरण हैं जिनके लिए यह स्पष्ट नहीं है कि उनके समाधान दो चरों के निरंतर कार्यों को अध्यारोपित करके प्राप्त किए जा सकते हैं। हिल्बर्ट की तेरहवीं समस्या|हिल्बर्ट की 13वीं समस्या अनुमान था, यह सातवें डिग्री के समीकरणों के सामान्य मामले में संभव नहीं था। [[व्लादिमीर अर्नोल्ड]] ने 1957 में यह प्रदर्शित करते हुए इसे हल किया कि यह हमेशा संभव था।<ref>{{citation |chapter-url=https://books.google.com/books?id=SpTv44Ia-J0C&pg=PA254 |title=Kolmogorov's heritage in mathematics |author=Vasco Brattka |chapter=Kolmogorov's Superposition Theorem|date=13 September 2007 |publisher=Springer|isbn=9783540363514 }}</ref> हालांकि, अर्नोल्ड ने खुद को वास्तविक हिल्बर्ट समस्या माना कि क्या सेप्टिक्स के लिए उनके समाधान दो चर के बीजगणितीय कार्यों को सुपरइम्पोज़ करके प्राप्त किए जा सकते हैं (समस्या अभी भी खुली है)।<ref>{{citation |url=http://www.pdmi.ras.ru/~arnsem/Arnold/arnlect1.ps.gz |title=From Hilbert's Superposition Problem to Dynamical Systems |author=V.I. Arnold |page=4}}</ref>
 == गैलोइस समूह ==
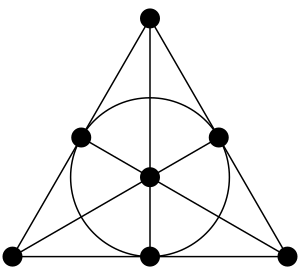
-[[Image:Fano plane.svg|thumb|[[फानो विमान]]]]*रेडिकल्स द्वारा हल किए जा सकने वाले सेप्टिक समीकरणों में गैलोज़ समूह होता है जो या तो ऑर्डर 7 का [[चक्रीय समूह]] होता है, या ऑर्डर 14 का डायहेड्रल समूह या ऑर्डर 21 या 42 का [[मेटासाइक्लिक समूह]] होता है।<ref name="BeyondQuartic"/>* {{math|''L''(3, 2)}} }} गाल्वा समूह (क्रम 168 का) 7 वर्टेक्स लेबल के [[क्रमपरिवर्तन]] से बनता है जो फ़ानो विमान में 7 पंक्तियों को संरक्षित करता है।<ref name="BeyondQuartic"/>इस गैलोज़ समूह के साथ सेप्टिक समीकरण {{math|''L''(3, 2)}} उनके समाधान के लिए अण्डाकार कार्यों की आवश्यकता होती है, लेकिन हाइपरलिप्टिक कार्यों की नहीं।<ref name="BeyondQuartic"/>*अन्यथा एक सेप्टिक का गैलोज़ समूह या तो क्रम 2520 का वैकल्पिक समूह है या क्रम 5040 का सममित समूह है।
+[[Image:Fano plane.svg|thumb|[[फानो विमान]]]]रेडिकल्स द्वारा हल किए जा सकने वाले सेप्टिक समीकरणों में गैलोज़ समूह होता है जो या तो ऑर्डर 7 का [[चक्रीय समूह]] होता है, या ऑर्डर 14 का डायहेड्रल समूह या ऑर्डर 21 या 42 का [[मेटासाइक्लिक समूह]] होता है।<ref name="BeyondQuartic"/>
-== एक चक्रीय पेंटागन या षट्भुज के वर्ग क्षेत्र के लिए सेप्टिक समीकरण ==
+{{math|''L''(3, 2)}}<nowiki> }} गाल्वा समूह (क्रम 168 का) 7 वर्टेक्स लेबल के </nowiki>[[क्रमपरिवर्तन]] से बनता है जो फ़ानो विमान में 7 पंक्तियों को संरक्षित करता है।<ref name="BeyondQuartic" />इस गैलोज़ समूह के साथ सेप्टिक समीकरण {{math|''L''(3, 2)}} उनके समाधान के लिए अण्डाकार कार्यों की आवश्यकता होती है, लेकिन हाइपरलिप्टिक कार्यों की नहीं।<ref name="BeyondQuartic" />*अन्यथा एक सेप्टिक का गैलोज़ समूह या तो क्रम 2520 का वैकल्पिक समूह है या क्रम 5040 का सममित समूह है।
+== एक चक्रीय पंचभुज या षट्भुज के वर्ग क्षेत्र के लिए सेप्टिक समीकरण ==
+चक्रीय पेंटागन के क्षेत्रफल का वर्ग एक सेप्टिक समीकरण का एक मूल है, जिसके गुणांक पंचभुज की भुजाओं के सममित फलन होते हैं।<ref>Weisstein, Eric W. "Cyclic Pentagon." From MathWorld--A Wolfram Web Resource. [http://mathworld.wolfram.com/CyclicPentagon.html]</ref> चक्रीय षट्भुज के क्षेत्रफल के वर्ग के बारे में भी यही सच है।<ref>Weisstein, Eric W. "Cyclic Hexagon." From MathWorld--A Wolfram Web Resource. [http://mathworld.wolfram.com/CyclicHexagon.html]</ref>
-पेंटागन#चक्रीय पेंटागन के क्षेत्रफल का वर्ग एक सेप्टिक समीकरण का एक मूल है, जिसके गुणांक पेंटागन की भुजाओं के सममित फलन होते हैं।<ref>Weisstein, Eric W. "Cyclic Pentagon." From MathWorld--A Wolfram Web Resource. [http://mathworld.wolfram.com/CyclicPentagon.html]</ref> षट्भुज#चक्रीय षट्भुज के क्षेत्रफल के वर्ग के बारे में भी यही सच है।<ref>Weisstein, Eric W. "Cyclic Hexagon." From MathWorld--A Wolfram Web Resource. [http://mathworld.wolfram.com/CyclicHexagon.html]</ref>
 == यह भी देखें ==
-* क्यूबिक फ़ंक्शन
+* क्यूबिक फलन
 * [[चतुर्थक समारोह]]
 *क्विंटिक फंक्शन

v t e बहुपद और बहुपद कार्य
डिग्री	शून्य बहुपद (डिग्री अपरिभाषित या −1 या and) निरंतर कार्य (0) रैखिक फ़ंक्शन (1) रेखीय समीकरण द्विघात कार्य (2) द्विघात समीकरण क्यूबिक फंक्शन (3) घन समीकरण चतुर्थक कार्य (4) चतुर्थक समीकरण क्विंटिक फंक्शन (5) सेक्स्टिक समीकरण (6) सेप्टिक समीकरण (7)
गुणों से	Univariate bivariate बहुभिन्नरूपी मोनोमियल बिनोमियल ट्रिनोमियल irreducible वर्ग-मुक्त सजातीय quasi-homogenous
औजार और एल्गोरिदम	कारक सबसे बड़ा आम भाजक डिवीजन हॉर्नर की मूल्यांकन की विधि परिणामी भेदभावपूर्ण Gröbner आधार

Anonymous

Search

सेप्टिक समीकरण: Difference between revisions

Namespaces

More

Page actions

Revision as of 21:33, 28 November 2022

Contents

हल करने योग्य सेप्टिक्स

गैलोइस समूह

एक चक्रीय पंचभुज या षट्भुज के वर्ग क्षेत्र के लिए सेप्टिक समीकरण

यह भी देखें

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

सेप्टिक समीकरण: Difference between revisions

Revision as of 21:33, 28 November 2022

हल करने योग्य सेप्टिक्स

गैलोइस समूह

एक चक्रीय पंचभुज या षट्भुज के वर्ग क्षेत्र के लिए सेप्टिक समीकरण

यह भी देखें

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Categories