ब्रोवर फिक्स्ड-पॉइंट प्रमेय: Difference between revisions
No edit summary |
|||
| (42 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Theorem in topology}} | {{Short description|Theorem in topology}} | ||
'''ब्रोवर फिक्स्ड-पॉइंट प्रमेय''' [[टोपोलॉजी|संस्थिति]] में निश्चित-बिंदु प्रमेय है, जिसका नामकरण लुइट्ज़ेन एगबर्टस जन ब्रोवर के नाम पर किया गया है। यह बताता है कि किसी भी [[निरंतर कार्य|निरंतर फलन]] के लिए <math>f</math>[[ सघनता ]][[उत्तल सेट|उत्तल समूह]] को मापने के लिए <math>x_0</math>बिंदु जैसे कि <math>f(x_0)=x_0</math> है। निरंतर कार्यों के लिए है <math>f</math> बंद अंतराल से <math>I</math> से स्वयं का वास्तविक संख्या में या बंद डिस्क से <math>D</math> का स्वयं से कार्य करना, ब्रोवर के प्रमेय का सबसे सरलतम रूप है। उत्तल संकुचित उपसमुच्चय से निरंतर फलन के लिए उत्तरार्द्ध की समानता में <math>K | |||
</math> [[Index.php?title=यूक्लिडियन स्पेस|यूक्लिडियन स्पेस]] अत्यधिक सामान्य रूप है। | |||
आंशिक रूप से गणित के कई क्षेत्रों में इसके उपयोग के कारण ब्रोवर का निश्चित बिंदु प्रमेय सैकड़ो अन्य निश्चित बिंदु प्रमेयो के मध्य सर्वाधिक प्रसिद्ध है। अपने मूल क्षेत्र में, [[जॉर्डन वक्र प्रमेय]], [[बालों वाली गेंद प्रमेय|हेयरी बॉल प्रमेय]], [[आयाम का व्युत्क्रम]] और बोरसुक-उलम प्रमेय के साथ ही यह युक्लेडियन स्पेस संस्थिति की विशेस्ता वाले प्रमेयो में से एक है।<ref>See page 15 of: D. Leborgne ''Calcul différentiel et géométrie'' Puf (1982) {{ISBN|2-13-037495-6}}</ref> यह इसे संस्थिति के मूलभूत प्रमेयों में स्थान देता है।<ref>More exactly, according to Encyclopédie Universalis: ''Il en a démontré l'un des plus beaux théorèmes, le théorème du point fixe, dont les applications et généralisations, de la théorie des jeux aux équations différentielles, se sont révélées fondamentales.'' [http://www.universalis.fr/encyclopedie/T705705/BROUWER_L.htm Luizen Brouwer] by G. Sabbagh</ref> इस प्रमेय का उपयोग [[अंतर समीकरण|अवकल समीकरणों]] के बारे में गहरे परिणाम प्रमाणित करने के लिए भी किया जाता है और [[अंतर ज्यामिति|अवकल ज्यामिति]] पर अधिकांश परिचयात्मक पाठ्यक्रमों में सम्मलित किया जाता है। यह [[Index.php?title=क्रीड़ा सिद्धांत|क्रीड़ा सिद्धांत]] जैसे असंभावित क्षेत्रों में प्रकट होता है। अर्थशास्त्र में, ब्रौवर की निश्चित-बिंदु प्रमेय और इसका विस्तार, काकुटानी निश्चित-बिंदु प्रमेय, 1950 के दशक में अर्थशास्त्र नोबेल पुरस्कार विजेता [[केनेथ एरो]] और जेरार्ड डेब्रू द्वारा विकसित बाजार अर्थव्यवस्थाओं में [[सामान्य संतुलन]] के अस्तित्व के प्रमाण में एक केंद्रीय भूमिका निभाते हैं। | |||
फ़्रांसिसी गणितज्ञों हेनरी पॉइनकेयर और चार्ल्स एमिल पिकार्ड के द्वारा अवकल समीकरणों पर फलन को ध्यान में रखते हुए प्रमेय का सबसे पहले अध्ययन किया गया था। पॉइंकेयर-बेंडिक्ससन प्रमेय जैसे परिणाम प्रमाणित करने के लिए संस्थितिक विधियों के उपयोग की आवश्यकता होती है। 19वीं शताब्दी के अंत में यह कार्य प्रमेय के कई क्रमिक संस्करणों के रूप में खुल गया। {{mvar|''n''}}-डायमेंशनल क्लोज्ड बॉल को अलग-अलग मापने के कथन को पहली बार 1910 में [[जैक्स हैडमार्ड]] ने सिद्ध किया था<ref name="hadamard-1910">[[Jacques Hadamard]]: ''[https://archive.org/stream/introductionla02tannuoft#page/436/mode/2up Note sur quelques applications de l’indice de Kronecker]'' in [[Jules Tannery]]: ''Introduction à la théorie des fonctions d’une variable'' (Volume 2), 2nd edition, A. Hermann & Fils, Paris 1910, pp. 437–477 (French)</ref> और 1911 में ब्रोवर द्वारा निरंतर मानचित्रण के सामान्य घटना को सिद्ध किया गया है। <ref name="brouwer-1910">{{cite journal | last1 = Brouwer | first1 = L. E. J. | author-link = Luitzen Egbertus Jan Brouwer | year = 1911| title = Über Abbildungen von Mannigfaltigkeiten | url = http://resolver.sub.uni-goettingen.de/purl?GDZPPN002264021 | journal = [[Mathematische Annalen]] | volume = 71 | pages = 97–115 | doi = 10.1007/BF01456931 | s2cid = 177796823 | language = de }}</ref> | |||
== कथन == | == कथन == | ||
प्रमेय के कई सूत्र हैं, यह इसके उपयोग और इसके सामान्यीकरण की परिमाण के सन्दर्भ पर निर्भर करता है। सबसे सरलतम निम्नानुसार दिया गया है: | प्रमेय के कई सूत्र हैं, यह इसके उपयोग और इसके सामान्यीकरण की परिमाण के सन्दर्भ पर निर्भर करता है। सबसे सरलतम निम्नानुसार दिया गया है: | ||
:; समतल में: | :; समतल में: [[बंद सेट|बंद समूह]] से प्रत्येक [[निरंतर कार्य (टोपोलॉजी)|निरंतर फलन टोपोलॉजी (संस्थिति)]] में कम से कम एक निश्चित बिंदु होता है।<ref>D. Violette ''[http://newton.mat.ulaval.ca/amq/bulletins/dec06/sperner.pdf Applications du lemme de Sperner pour les triangles]'' Bulletin AMQ, V. XLVI N° 4, (2006) p 17. {{webarchive |url=https://web.archive.org/web/20110608214059/http://newton.mat.ulaval.ca/amq/bulletins/dec06/sperner.pdf |date=June 8, 2011 }}</ref> | ||
यह | यह विवेकाधीन परिमित आयाम के लिए सामान्यीकृत किया जा सकता है: | ||
:;यूक्लिडियन स्पेस में: यूक्लिडियन स्पेस की | :;यूक्लिडियन स्पेस में: यूक्लिडियन स्पेस की [[बंद गेंद]] से प्रत्येक निरंतर फलन में एक निश्चित बिंदु होता है।<ref>Page 15 of: D. Leborgne ''Calcul différentiel et géométrie'' Puf (1982) {{ISBN|2-13-037495-6}}.</ref> | ||
थोड़ा और सामान्य संस्करण इस प्रकार है:<ref>This version follows directly from the previous one because every convex compact subset of a Euclidean space is homeomorphic to a closed ball of the same dimension as the subset; see {{cite book|title=General Equilibrium Analysis: Existence and Optimality Properties of Equilibria|first=Monique|last=Florenzano|publisher=Springer|year=2003|isbn=9781402075124|page=7|url=https://books.google.com/books?id=cNBMfxPQlvEC&pg=PA7|access-date=2016-03-08}}</ref> | थोड़ा और सामान्य संस्करण इस प्रकार है:<ref>This version follows directly from the previous one because every convex compact subset of a Euclidean space is homeomorphic to a closed ball of the same dimension as the subset; see {{cite book|title=General Equilibrium Analysis: Existence and Optimality Properties of Equilibria|first=Monique|last=Florenzano|publisher=Springer|year=2003|isbn=9781402075124|page=7|url=https://books.google.com/books?id=cNBMfxPQlvEC&pg=PA7|access-date=2016-03-08}}</ref> | ||
:;उत्तल | :;उत्तल सघन समुच्चय: यूक्लिडियन स्पेस के [[ कॉम्पैक्ट जगह |उत्तल सघन]] उपसमुच्चय K से लेकर K तक सभी निरंतर फलन में एक निश्चित बिंदु होता है।<ref>V. & F. Bayart ''[http://www.bibmath.net/dico/index.php3?action=affiche&quoi=./p/pointfixe.html Point fixe, et théorèmes du point fixe ]'' on Bibmath.net. {{webarchive|url=https://web.archive.org/web/20081226200755/http://www.bibmath.net/dico/index.php3?action=affiche&quoi=.%2Fp%2Fpointfixe.html |date=December 26, 2008 }}</ref> | ||
एक और भी सामान्य रूप | एक और भी सामान्य रूप अलग नाम के द्वारा जाना जाता है: | ||
:;स्काउडर निश्चित बिंदु प्रमेय: बैनक स्पेस के उत्तल सघन उपसमुच्चय K से K तक प्रत्येक निरंतर फलन में एक निश्चित बिंदु होता है।<ref>C. Minazzo K. Rider ''[http://math1.unice.fr/~eaubry/Enseignement/M1/memoire.pdf Théorèmes du Point Fixe et Applications aux Equations Différentielles] {{Webarchive|url=https://web.archive.org/web/20180404001651/http://math1.unice.fr/~eaubry/Enseignement/M1/memoire.pdf |date=2018-04-04 }}'' Université de Nice-Sophia Antipolis.</ref> | |||
== पूर्व शर्तों का महत्व == | == पूर्व शर्तों का महत्व == | ||
प्रमेय | प्रमेय सिर्फ उन फलनों के लिए है जो अंतःरूपता हैं (फलन जो प्रान्त और सहप्रांत के समान समुच्चय हैं) और उन समुच्चयो के लिए जो सघन (इस प्रकार, विशेष रूप से, बंधे और बंद) और उत्तल (या [[होमोमोर्फिज्म]] से उत्तल) है निम्नलिखित उदाहरण बताते हैं कि पूर्व-शर्तें क्यों महत्वपूर्ण हैं। | ||
'''एक एंडोमोर्फिज्म के रूप में फलन f''' | '''एक एंडोमोर्फिज्म (अन्तःरूपता) के रूप में फलन f''' | ||
:<math>f(x) = x+1</math> | :<math>f(x) = x+1</math> | ||
प्रान्त [-1,1] के साथ फलन पर विचार करे। फलन का परिसर [0,2] है। इस प्रकार, f एंडोमोर्फिज्म नहीं है। | |||
=== सीमाबद्धता === | === सीमाबद्धता === | ||
फलन पर विचार करे | फलन पर विचार करे | ||
:<math>f(x) = x+1,</math> | :<math>f(x) = x+1,</math> | ||
जो | जो <math>\mathbb{R}</math> सतत फलन है। चूंकि यह सभी बिंदु को दाईं ओर स्थानांतरित करता है, इसलिए इसका कोई निश्चित बिंदु नहीं हो सकता है। स्पेस <math>\mathbb{R}</math> उत्तल और बंद है, परन्तु बद्ध नहीं है। | ||
=== बंद स्तिथि === | === बंद स्तिथि === | ||
फलन पर विचार करे | फलन पर विचार करे | ||
:<math>f(x) = \frac{x+1}{2},</math> | :<math>f(x) = \frac{x+1}{2},</math> | ||
जो मुक्त अंतराल (-1,1) से स्वयं | जो मुक्त अंतराल (-1,1) से स्वयं एक सतत फलन है। चूंकि x = 1 अंतराल का भाग नहीं है, f(x) = x का कोई निश्चित बिंदु नहीं है। स्पेस (−1,1) उत्तल और घिरा हुआ है, परन्तु बंद नहीं है। दूसरी तरफ, फलन f का बंद अंतराल [−1,1] के लिए एक निश्चित बिंदु है, अर्थात् f(1) = 1 है। | ||
=== उत्तलता === | === उत्तलता === | ||
बीएफपीटी के लिए उत्तलता अत्यधिक आवश्यक नहीं है। क्योंकि सम्मलित गुण (निरंतरता, एक निश्चित बिंदु होने की वजह से) होमोमोर्फिज्म के अनुसार | बीएफपीटी के लिए उत्तलता अत्यधिक आवश्यक नहीं है। क्योंकि सम्मलित गुण (निरंतरता, एक निश्चित बिंदु होने की वजह से) होमोमोर्फिज्म के अनुसार अपरिवर्तनीय हैं, बीएफपीटी उन रूपों के बराबर है जिनमें प्रान्त को बंद इकाई बॉल '''<math>D^n</math> का''' होना आवश्यक है। समान कारण से यह प्रत्येक समुच्चय जो बंद बॉल के लिए होमोमॉर्फिक है के लिए क्रियान्वित होता है (और इसलिए बंद समूह, सीमित, [[ जुड़ा हुआ स्थान |जुड़ा हुआ स्थान]], बिना छिद्र का इत्यादि उपस्थित है)। | ||
निम्नलिखित उदाहरण से पता चलता है कि बीएफपीटी छिद्र वाले प्रान्त के लिए कार्य नहीं करता है। फलन <math>f(x)=-x</math> पर विचार करे, जो इकाई वृत्त से स्वयं तक सतत कार्य है। चूंकि इकाई वृत्त के किसी भी बिंदु के लिए -x≠x है, f का कोई निश्चित बिंदु नहीं है। अनुरूप उदाहरण एन-आयामी क्षेत्र (या कोई सममित प्रान्त जिसमें मूल उपस्थित नहीं है) के लिए कार्य करता है। इकाई वृत्त बंद और घिरा हुआ है, परन्तु इसमें एक छिद्र है (और इसलिए यह उत्तल नहीं है)। फलन f इकाई डिस्क के लिए एक निश्चित बिंदु है, क्योकि ये इसी से उत्पन्न होता है । | |||
"छिद्र-मुक्त" (होल -फ्री) प्रान्त के लिए बीएफपीटी का एक औपचारिक सामान्यीकरण [[Index.php?title=लेफ्सेटज़ फिक्स्ड-पॉइंट प्रमेय|लेफ्सेटज़ निश्चित-बिंदु प्रमेय]] से प्राप्त किया जा सकता है।<ref>{{cite web | url=https://math.stackexchange.com/q/323841 | title=Why is convexity a requirement for Brouwer fixed points? | publisher=Math StackExchange | access-date=22 May 2015 | author=Belk, Jim}}</ref> | |||
===टिप्पणियाँ=== | ===टिप्पणियाँ=== | ||
इस प्रमेय में फलन का [[Index.php?title=द्विभाजित|द्विभाजित]] या फिर [[Index.php?title=विशिस्ट|विशिस्ट]] होना आवश्यक नहीं है। | इस प्रमेय में फलन का [[Index.php?title=द्विभाजित|द्विभाजित]] या फिर [[Index.php?title=विशिस्ट|विशिस्ट]] होना आवश्यक नहीं है। | ||
== चित्र == | == चित्र == | ||
प्रमेय में वास्तविक दुनिया के कई उदाहरण हैं। यहां कुछ उदाहरण दिए गए हैं। | प्रमेय में वास्तविक दुनिया के कई उदाहरण हैं। यहां कुछ उदाहरण दिए गए हैं। | ||
# समान आकार के ग्राफ पेपर की दो पन्ने लें, उन पर समन्वय प्रणाली के साथ, टेबल पर समतल बिछाएं और दूसरे को (बिना चीर-फाड़ या फाड़े) समेट लें और इसे किसी भी | # समान आकार के ग्राफ पेपर की दो पन्ने लें, उन पर समन्वय प्रणाली के साथ, टेबल पर समतल बिछाएं और दूसरे को (बिना चीर-फाड़ या फाड़े) समेट लें और इसे किसी भी प्रकार से पहले के ऊपर रखना है। क्रुम्प्लेड कागज समतल वाले के बाहर नहीं पहुंचता है। तब क्रुम्प्लेड (तुड़ा मुड़ा) पन्ने का कम से कम एक बिंदु होगा जो समतल पन्ने के संबंधित बिंदु (अर्थात समान निर्देशांक वाला बिंदु) के ठीक ऊपर स्थित होगा। यह ब्रौवर के प्रमेय के ''n = 2'' कथन का परिणाम है जो निरंतर मानचित्र पर क्रियान्वित होता है जो क्रुम्प्लेड पन्ने के प्रत्येक बिंदु के निर्देशांक को उसके ठीक नीचे समतल पन्ने के बिंदु के निर्देशांक प्रदान करता है। | ||
# किसी देश का | # किसी देश का साधारण मानचित्र लें, और मान लें कि वह मानचित्र उस देश के अंदर एक मेज पर रखा हुआ है। मानचित्र पर निरंतर आप यहां हैं बिंदु होगा जो देश में उसी बिंदु का प्रतिनिधित्व करता है। | ||
# तीन आयामों में ब्रोवर फिक्स्ड-पॉइंट प्रमेय का | # तीन आयामों में ब्रोवर फिक्स्ड-पॉइंट प्रमेय का परिणाम यह है कि, भले आप एक गिलास में स्वादिष्ट कॉकटेल को कितना भी हिलाएं (या मिल्क शेक के बारे में सोचें), जब तरल को स्थिर अवस्था में आना होगा, तरल में कुछ बिंदु होगा यह मानते हुए कि प्रत्येक बिंदु की अंतिम स्थिति अपनी मूल स्थिति का निरंतर फलन है, कि ग्लॉस हिलाने के बाद तरल मूल रूप से इसके द्वारा लिए गए स्थान के भीतर समाहित है, यह मानते हुए ग्लास में ठीक उसी स्थान पर समाप्त होता है, जैसा कि आपने कोई कार्य करने से पहले पाया था, तथा कांच (और हिलाई हुई सतह का आकार) उत्तल आयतन बनाए रखता है। कॉकटेल को हिलाना, हिलाया नहीं जाना उत्तलता की स्थिति में गलत सिद्ध हो जाता है (झटकों को ढक्कन के नीचे खाली हेडस्पेस में गैर-उत्तल जड़त्वीय रोकथाम की गतिशील श्रृंखला के रूप में परिभाषित किया जाता है)। उस स्थिति में, प्रमेय क्रियान्वित नहीं होगा, और इस प्रकार तरल स्वभाव के सभी बिंदु मूल अवस्था से संभावित रूप से विस्थापित हो जाते हैं। | ||
== सहज दृष्टिकोण == | == सहज दृष्टिकोण == | ||
===ब्रूवर को दिया गया स्पष्टीकरण === | ===ब्रूवर को दिया गया स्पष्टीकरण === | ||
माना जाता है कि प्रमेय की उत्पत्ति एक कप गोरमेट कॉफी के ब्रौवर के अवलोकन से हुई है।<ref>The interest of this anecdote rests in its intuitive and didactic character, but its accuracy is dubious. As the history section shows, the origin of the theorem is not Brouwer's work. More than 20 years earlier [[Henri Poincaré]] had proved an equivalent result, and 5 years before Brouwer P. Bohl had proved the three-dimensional case.</ref> | माना जाता है कि प्रमेय की उत्पत्ति एक कप गोरमेट कॉफी के ब्रौवर के अवलोकन से हुई है।<ref>The interest of this anecdote rests in its intuitive and didactic character, but its accuracy is dubious. As the history section shows, the origin of the theorem is not Brouwer's work. More than 20 years earlier [[Henri Poincaré]] had proved an equivalent result, and 5 years before Brouwer P. Bohl had proved the three-dimensional case.</ref> यदि कोई चीनी की गांठ को घोलता है, तो ऐसा प्रतीत होता है कि निरंतर गतिहीन बिंदु होता है। उन्होंने निष्कर्ष निकाला कि किसी भी समय, सतह पर बिंदु है जो गतिमान नहीं है।<ref name=Arte>This citation comes originally from a television broadcast: ''[https://archive.today/20130113210953/http://archives.arte.tv/hebdo/archimed/19990921/ftext/sujet5.html Archimède]'', [[Arte]], 21 septembre 1999</ref> निश्चित बिंदु अनिवार्य रूप से वह बिंदु नहीं है जो गतिहीन प्रतीत होता है, क्योंकि विक्षोभ का केंद्र थोड़ा हिलता है। परिणाम सहज नहीं है, क्योंकि एक और निश्चित बिंदु दिखाई देने पर मूल निश्चित बिंदु गतिमान हो सकता है। | ||
यदि कोई चीनी की गांठ को | |||
उन्होंने निष्कर्ष निकाला कि किसी भी समय, सतह पर | |||
निश्चित बिंदु अनिवार्य रूप से वह बिंदु नहीं है जो गतिहीन प्रतीत होता है, क्योंकि विक्षोभ का केंद्र थोड़ा हिलता | |||
ब्रोवर ने कहा है की : मैं इस | ब्रोवर ने कहा है की: मैं इस अद्भुत परिणाम को अलग-अलग बना सकता हूं, मैं एक क्षैतिज पन्ने लेता हूं, और एक दूसरा समान जिसे मैं समेटता हूं, चपटा करता हूं और दूसरे पर रखता हूं। तब क्रुम्प्लेड पन्ना का बिंदु उसी स्थान पर होता है जैसे दूसरी पन्ने पर होता है।<ref name=Arte /> ब्रौवर सिलवटों को हटाए बिना अपनी चादर को सपाट लोहे की तरह चपटा कर देता है। कॉफी कप उदाहरण के विपरीत, क्रुम्प्लेड पन्ना उदाहरण भी दर्शाता है कि एक से अत्यधिक निश्चित बिंदु स्थित हो सकते हैं। यह ब्रोवर के परिणाम को अन्य निश्चित-बिंदु प्रमेयों से भिन्न है, जैसे कि [[स्टीफन बानाच]], जो अद्वितीयता का आश्वासन देता है। | ||
=== एक विमीय प्रकरण === | === एक विमीय प्रकरण === | ||
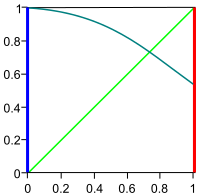
[[File:Théorème-de-Brouwer-dim-1.svg|200px|right]] | [[File:Théorème-de-Brouwer-dim-1.svg|200px|right]]विमीय में, परिणाम सहज और सिद्ध करने में सरल है। सतत फलन f को बंद अंतराल [a, b] पर परिभाषित किया गया है और उसी अंतराल में स्थान लेता है। यह कहना कि इस फलन का निश्चित बिंदु है, यह कहने के बराबर है कि इसका ग्राफ़ (दाहिने तरफ की आकृति में गहरा हरा) समान अंतराल [a, b] पर परिभाषित फलन को काटता है जो x से x (हल्का हरा) मापता है। | ||
सहज रूप से, वर्ग के बाएँ किनारे से दाएँ किनारे तक कोई भी निरंतर रेखा आवश्यक रूप से हरे रंग के विकर्ण को काटती है। इसे सिद्ध करने के लिए, फलन g पर विचार करें जो x को f(x) − x से मापता है। यह a पर ≥ 0 और b पर ≤ 0 है। मध्यवर्ती मान प्रमेय के अनुसार, g का [a, b] में एक फलन का मूल है; यह शून्य एक निश्चित बिंदु है। | सहज रूप से, वर्ग के बाएँ किनारे से दाएँ किनारे तक कोई भी निरंतर रेखा आवश्यक रूप से हरे रंग के विकर्ण को काटती है। इसे सिद्ध करने के लिए, फलन g पर विचार करें जो x को f(x) − x से मापता है। यह a पर ≥ 0 और b पर ≤ 0 है। मध्यवर्ती मान प्रमेय के अनुसार, g का [a, b] में एक फलन का मूल है; यह शून्य एक निश्चित बिंदु है। | ||
कहा जाता है कि ब्रोवर ने इसे इस प्रकार व्यक्त किया: सतह की जांच करने के | कहा जाता है कि ब्रोवर ने इसे इस प्रकार व्यक्त किया: सतह की जांच करने के बदले, हम प्रमेय को स्ट्रिंग के टुकड़े के बारे में सिद्ध करेंगे। स्ट्रिंग को बिना मुड़ी हुई अवस्था में प्रारम्भ करें, फिर इसे दोबारा मोड़ देना है। हम दोबारा मोड़ी गयी स्ट्रिंग को चपटा करेंगे। स्ट्रिंग के बिंदु ने बिना मुड़ी हुई स्ट्रिंग पर अपनी मूल स्थिति के संबंध में अपनी स्थिति नहीं बदलती है।<ref name=Arte /> | ||
== इतिहास == | == इतिहास == | ||
ब्रौवर [[निश्चित बिंदु प्रमेय]] [[बीजगणितीय टोपोलॉजी]] की | ब्रौवर [[निश्चित बिंदु प्रमेय]] [[बीजगणितीय टोपोलॉजी|बीजगणितीय संस्थिति]] की प्रारंभिक उपलब्धियों में से एक था, और अत्यधिक सामान्य निश्चित बिंदु प्रमेयों का आधार है जो [[कार्यात्मक विश्लेषण]] में महत्वपूर्ण हैं। कथन n = 3 पहली बार 1904 में [[पियर्स बोहल]] द्वारा सिद्ध किया गया था (फुर्र दे रिने युन्द एंगेवैनदते माथेमैटिक नामक पत्रिका में प्रकाशित)।<ref name=Bohl1904>{{cite journal |first=P. |last=Bohl |title= Über die Bewegung eines mechanischen Systems in der Nähe einer Gleichgewichtslage |journal=J. Reine Angew. Math. |volume=127 |issue=3/4 |pages=179–276 |year=1904 }}</ref> इसे बाद में लुइट्ज़ेन एगबर्टस जान ब्रोवर एल द्वारा 1909 में सिद्ध किया गया था।1910 में जैक्स हैडमार्ड ने सामान्य कथनो को सिद्ध किया है,<ref name="hadamard-1910" />और उसी वर्ष ब्रोवर को एक अलग प्रमाण मिला था।<ref name="brouwer-1910" /> चूँकि ये प्रारंभिक प्रमाण सभी [[रचनात्मक प्रमाण]] थेl चूँकि रचनावाद (गणित) के अर्थ में एक निश्चित बिंदु का अस्तित्व रचनात्मक नहीं है, ब्रोवर के प्रमेय द्वारा निश्चित अनुमानित सिद्धांत निश्चित बिंदुओं के प्रकारो के नाम से जाना जाता है।<ref name=Karamardian1977>{{cite book|last1=Karamardian|first1=Stephan|title=Fixed points: algorithms and applications|date=1977|publisher=Academic Press|location=New York|isbn=978-0-12-398050-2}}</ref><ref name=Istratescu1981>{{cite book|last1=Istrăţescu|first1=Vasile|title=निश्चित बिंदु सिद्धांत|date=1981|publisher=D. Reidel Publishing Co.|location=Dordrecht-Boston, Mass.|isbn=978-90-277-1224-0}}</ref> | ||
=== प्रागितिहास === | === प्रागितिहास === | ||
[[File:Théorème-de-Brouwer-(cond-1).jpg|thumb|right|एक असीमित क्षेत्र में प्रवाह के लिए, या एक छेद वाले क्षेत्र में, प्रमेय लागू नहीं होता है।]] | [[File:Théorème-de-Brouwer-(cond-1).jpg|thumb|right|एक असीमित क्षेत्र में प्रवाह के लिए, या एक छेद वाले क्षेत्र में, प्रमेय लागू नहीं होता है।]] | ||
[[File:Théorème-de-Brouwer-(cond-2).jpg|thumb|left|प्रमेय किसी भी डिस्क के आकार के क्षेत्र पर प्रयुक्त होता है, जहां यह निश्चित बिंदु के अस्तित्व का अस्वासन देता है।]]ब्रोवर के निश्चित बिंदु प्रमेय के प्रागितिहास को समझने के लिए अवकल समीकरणों को ध्यान देने की आवश्यक्ता है। 19 वीं सदी के अंत में, पुरानी समस्या<ref>See F. Brechenmacher ''[https://arxiv.org/abs/0704.2931 L'identité algébrique d'une pratique portée par la discussion sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des planètes]'' CNRS Fédération de Recherche Mathématique du Nord-Pas-de-Calais</ref> [[सौर मंडल की स्थिरता]] गणितीय समुदाय के ध्यान में लौट | [[File:Théorème-de-Brouwer-(cond-2).jpg|thumb|left|प्रमेय किसी भी डिस्क के आकार के क्षेत्र पर प्रयुक्त होता है, जहां यह निश्चित बिंदु के अस्तित्व का अस्वासन देता है।]]ब्रोवर के निश्चित बिंदु प्रमेय के प्रागितिहास को समझने के लिए अवकल समीकरणों को ध्यान देने की आवश्यक्ता है। 19 वीं सदी के अंत में, पुरानी समस्या<ref>See F. Brechenmacher ''[https://arxiv.org/abs/0704.2931 L'identité algébrique d'une pratique portée par la discussion sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des planètes]'' CNRS Fédération de Recherche Mathématique du Nord-Pas-de-Calais</ref> [[सौर मंडल की स्थिरता]] गणितीय समुदाय के ध्यान में लौट आई है।<ref>[[Henri Poincaré]] won the [[Oscar II, King of Sweden|King of Sweden]]'s mathematical competition in 1889 for his work on the related [[three-body problem]]: [[Jacques Tits]] ''[http://www.culture.gouv.fr/culture/actualites/celebrations2004/poincare.htm Célébrations nationales 2004]'' Site du Ministère Culture et Communication</ref> | ||
इसके समाधान के लिए नए | इसके समाधान के लिए नए प्रकारों की आवश्यकता थी। जैसा कि [[Index.php?title=तीन-पिंड की समस्या|तीन-पिंड की समस्या]] पर कार्य करने वाले हेनरी पोंकारे ने उल्लेख किया है, सही समाधान ढूंढने की कोई आशा नहीं है: हमें तीन-पिंड की समस्या की कठोरता और साधारणतया सभी समस्याओं के बारे में विचार देने के लिए कुछ भी अत्यधिक उचित नहीं है। गतिकी जहां कोई समान अभिन्न नहीं है और बोहलिन श्रृंखला विचलन करती है।<ref name=methodes>[[Henri Poincaré]] ''Les méthodes nouvelles de la mécanique céleste'' T Gauthier-Villars, Vol 3 p 389 (1892) new edition Paris: Blanchard, 1987.</ref> उन्होंने यह भी कहा कि अनुमानित समाधान की खोज अत्यधिक कुशल नहीं है: जितना अत्यधिक हम लगभग बिलकुल ठीक प्राप्त करना चाहते हैं, उतना ही अत्यधिक परिणाम बढ़ती हुई अशुद्धि की ओर बढ़ जाएगा।<ref>Quotation from [[Henri Poincaré]] taken from: P. A. Miquel ''[http://www.arches.ro/revue/no03/no3art03.htm La catégorie de désordre] {{Webarchive|url=https://web.archive.org/web/20160303205947/http://www.arches.ro/revue/no03/no3art03.htm# |date=2016-03-03 }}'', on the website of l'Association roumaine des chercheurs francophones en sciences humaines</ref> उन्होंने एक कप कॉफी में सतह की गति के समान प्रश्न का अध्ययन किया है। सामान्य रूप से, हम निरंतर [[प्रवाह (गणित)]] द्वारा अनुप्राणित सतह पर प्रक्षेपवक्र के बारे में क्या कह सकते हैं?<ref>This question was studied in: {{cite journal |first=H. |last=Poincaré |title=Sur les courbes définies par les équations différentielles |journal=[[Journal de Mathématiques Pures et Appliquées]] |volume=2 |issue=4 |pages=167–244 |year=1886 }}</ref> पोनकारे ने पाया कि उत्तर उस क्षेत्र में पाया जा सकता है जिसे अब हम प्रक्षेपवक्र वाले क्षेत्र में संस्थिति गुण कहते हैं। यदि यह क्षेत्र सघन स्थान है, अर्थात बंद समूह और [[Index.php?title=बंधा हुआ समूह|बंधा हुआ समूह]] दोनों, तो प्रक्षेपवक्र या तो स्थिर हो जाता है, या यह एक [[सीमा चक्र]] तक पहुंच जाता है।<ref>This follows from the [[Poincaré–Bendixson theorem]].</ref> पोंकारे और आगे बढ़े; यदि क्षेत्र डिस्क के समान प्रकार का है, जैसा कि कॉफी के कप के स्थिति में है, तो निश्चित रूप से एक निश्चित बिंदु होना चाहिए। यह निश्चित बिंदु उन सभी कार्यों के अंतर्गत अपरिवर्तनीय है जो मूल सतह के प्रत्येक बिंदु से इसकी स्थिति को थोड़े समय के अंतराल t के बाद जोड़ते हैं। यदि क्षेत्र एक गोलाकार पट्टी है, या यह बंद नहीं है,<ref>Multiplication by {{sfrac|1|2}} on ]0, 1[<sup>2</sup> has no fixed point.</ref> तो यह आवश्यक नहीं है। | ||
अवकल समीकरणों को | अवकल समीकरणों को सही ढंग से समझने के लिए गणित की एक नई शाखा का जन्म हुआ। पॉइनकेयर ने इसे एनालिसिस साइटस कहा है। फ्रांसीसी एनसाइक्लोपीडिया यूनिवर्सलिस इसे उस शाखा के रूप में परिभाषित करता है जो किसी वस्तु के गुणों का इलाज करता है जो अपरिवर्तनीय है। यदि यह किसी भी निरंतर प्रकार से बिना फाडे विकृत होता है।<ref>"concerne les propriétés invariantes d'une figure lorsqu’on la déforme de manière continue quelconque, sans déchirure (par exemple, dans le cas de la déformation de la sphère, les propriétés corrélatives des objets tracés sur sa surface". From C. Houzel M. Paty ''[http://www.scientiaestudia.org.br/associac/paty/pdf/Paty,M_1997g-PoincareEU.pdf Poincaré, Henri (1854–1912)] {{webarchive|url=https://web.archive.org/web/20101008232932/http://www.scientiaestudia.org.br/associac/paty/pdf/Paty%2CM_1997g-PoincareEU.pdf |archive-url=https://ghostarchive.org/archive/20221009/http://www.scientiaestudia.org.br/associac/paty/pdf/Paty%2CM_1997g-PoincareEU.pdf |archive-date=2022-10-09 |url-status=live |date=2010-10-08 }}'' Encyclopædia Universalis Albin Michel, Paris, 1999, p. 696–706</ref> 1886 में, पोंकारे ने एक परिणाम सिद्ध किया जो ब्रोवर के निश्चित-बिंदु प्रमेय के समान है,<ref>Poincaré's theorem is stated in: V. I. Istratescu ''Fixed Point Theory an Introduction'' Kluwer Academic Publishers (réédition de 2001) p 113 {{isbn|1-4020-0301-3}}</ref> चूँकि इस लेख के विषय के साथ संबंध अभी तक स्पष्ट नहीं हुआ था।<ref>{{SpringerEOM|title=Brouwer theorem |first=M.I. |last=Voitsekhovskii |isbn=1-4020-0609-8}}</ref> थोड़ी देर बाद, उन्होंने विश्लेषण साइटस को सही ढंग से समझने के लिए मूलभूत उपकरणों में से विकसित किया, जिसे अब मूल [[मौलिक समूह|समूह]] या कभी-कभी पोंकारे समूह के रूप में जाना जाता है।<ref>{{cite book |first=Jean |last=Dieudonné |author-link=Jean Dieudonné |title=A History of Algebraic and Differential Topology, 1900–1960 |location=Boston |publisher=Birkhäuser |year=1989 |isbn=978-0-8176-3388-2 |pages=[https://archive.org/details/historyofalgebra0000dieu_g9a3/page/17 17–24] |url=https://archive.org/details/historyofalgebra0000dieu_g9a3/page/17 }}</ref> इस पद्धति का उपयोग चर्चा के अंतर्गत प्रमेय के एक बहुत ही संक्षिप्त प्रमाण के लिए किया जा सकता है पोनकारे की पद्धति चार्ल्स एमिल पिकार्ड के अनुरूप थी, जो उनके समकालीन गणितज्ञ थे जिन्होंने कॉची-लिप्सचिट्ज़ प्रमेय को सामान्यीकृत किया था।<ref>See for example: [[Charles Émile Picard|Émile Picard]] ''[http://portail.mathdoc.fr/JMPA/PDF/JMPA_1893_4_9_A4_0.pdf Sur l'application des méthodes d'approximations successives à l'étude de certaines équations différentielles ordinaires] {{Webarchive|url=https://web.archive.org/web/20110716055143/http://portail.mathdoc.fr/JMPA/PDF/JMPA_1893_4_9_A4_0.pdf# |archive-url=https://web.archive.org/web/20110716055143/http://portail.mathdoc.fr/JMPA/PDF/JMPA_1893_4_9_A4_0.pdf |archive-date=2011-07-16 |url-status=live |date=2011-07-16 }}'' Journal de Mathématiques p 217 (1893)</ref> पिकार्ड का दृष्टिकोण एक परिणाम पर आधारित है जिसे बाद में [[बानाच फिक्स्ड-पॉइंट प्रमेय]] द्वारा औपचारिक रूप दिया गया है, जिसका नाम स्टीफन बानाच के नाम पर रखा गया है। प्रान्त के सामयिक गुणों के अतिरिक्त, यह प्रमेय इस तथ्य का उपयोग करता है कि विचाराधीन कार्य [[संकुचन मानचित्रण|सघन मानचित्रण]] है। | ||
=== पहला प्रमाण === | === पहला प्रमाण === | ||
[[Image:Hadamard2.jpg|thumb|right|जैक्स हैडमार्ड ने अपने विचारों को औपचारिक रूप देने में ब्रोवर की मदद की।]]20वीं सदी की प्रारम्भ में, विश्लेषण विपरीत स्थान किसी का ध्यान नहीं गया है। चूँकि, इस आलेख में बताई गई प्रमेय के बराबर प्रमेय की आवश्यकता अभी तक स्पष्ट नहीं थी। [[लातविया]]ई गणितज्ञ पियर्स बोहल ने अंतर समीकरणों के अध्ययन के लिए सांस्थितिकीय विधियों को क्रियान्वित किया है।<ref>J. J. O'Connor E. F. Robertson ''[http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Bohl.html Piers Bohl]''</ref> 1904 में उन्होंने हमारे प्रमेय के त्रि-आयामी सन्दर्भों को सिद्ध किया है,<ref name="Bohl1904" /> परन्तु उनके प्रकाशन पर ध्यान नहीं दिया गया है।<ref>{{cite journal |first1=A. D. |last1=Myskis |first2=I. M. |last2=Rabinovic |title=Первое доказательство теоремы о неподвижной точке при непрерывном отображении шара в себя, данное латышским математиком П.Г.Болем |trans-title=The first proof of a fixed-point theorem for a continuous mapping of a sphere into itself, given by the Latvian mathematician P. G. Bohl |language=ru |journal=Успехи математических наук |volume=10 |issue=3 |year=1955 |pages=188–192 |url=http://mi.mathnet.ru/eng/umn/v10/i3/p179 }}</ref> | [[Image:Hadamard2.jpg|thumb|right|जैक्स हैडमार्ड ने अपने विचारों को औपचारिक रूप देने में ब्रोवर की मदद की।]]20वीं सदी की प्रारम्भ में, विश्लेषण विपरीत स्थान किसी का ध्यान नहीं गया है। चूँकि, इस आलेख में बताई गई प्रमेय के बराबर प्रमेय की आवश्यकता अभी तक स्पष्ट नहीं थी। [[लातविया]]ई गणितज्ञ पियर्स बोहल ने अंतर समीकरणों के अध्ययन के लिए सांस्थितिकीय विधियों को क्रियान्वित किया है।<ref>J. J. O'Connor E. F. Robertson ''[http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Bohl.html Piers Bohl]''</ref> 1904 में उन्होंने हमारे प्रमेय के त्रि-आयामी सन्दर्भों को सिद्ध किया है,<ref name="Bohl1904" /> परन्तु उनके प्रकाशन पर ध्यान नहीं दिया गया है।<ref>{{cite journal |first1=A. D. |last1=Myskis |first2=I. M. |last2=Rabinovic |title=Первое доказательство теоремы о неподвижной точке при непрерывном отображении шара в себя, данное латышским математиком П.Г.Болем |trans-title=The first proof of a fixed-point theorem for a continuous mapping of a sphere into itself, given by the Latvian mathematician P. G. Bohl |language=ru |journal=Успехи математических наук |volume=10 |issue=3 |year=1955 |pages=188–192 |url=http://mi.mathnet.ru/eng/umn/v10/i3/p179 }}</ref> | ||
यह ब्रौवर था, अंत में, जिसने प्रमेय को श्रेष्ठता का प्रथम अधिकार दिया है। उनके लक्ष्य पोंकारे से भिन्न थे। यह गणितज्ञ गणित की आधार, विशेष प्रकार से [[गणितीय तर्क]] और टोपोलॉजी से प्रेरित था। उनकी प्रारंभिक रुझान हिल्बर्ट की पांचवीं समस्या को सिद्ध करने के प्रयास में थी।<ref>J. J. O'Connor E. F. Robertson ''[http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Brouwer.html Luitzen Egbertus Jan Brouwer]''</ref> 1909 में, पेरिस की यात्रा के समय, उनकी मुलाकात हेनरी पोंकारे, जैक्स हैडमार्ड और एमिल बोरेल से हुई। भविष्य में होने वाले बातचीत यूक्लिडियन स्पेस की सही समझ के महत्व के ब्रोवर को प्रोत्साहित किया, और हैडमार्ड के साथ पत्रों के उपयोगी आदान-प्रदान की उत्पत्ति थी। अगले चार वर्षों तक, उन्होंने इस प्रश्न पर विशेष प्रमेयों के प्रमाण पर ध्यान केंद्रित किया है। 1912 में उन्होंने द्वि-आयामी क्षेत्र के लिए हेरी बॉल प्रमेय को सिद्ध किया, साथ ही इस तथ्य को भी सिद्ध किया कि द्वि-आयामी गेंद से लेकर स्वयं तक प्रत्येक निरंतर मानचित्र का निश्चित बिंदु होता है।<ref>{{cite journal |first=Hans |last=Freudenthal |author-link=Hans Freudenthal | title=ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल|journal=[[Historia Mathematica]] |volume=2 |issue=4 |pages=495–502 [p. 495] |year=1975 |doi=10.1016/0315-0860(75)90111-1 |doi-access=free }}</ref> अपने आप में ये दो परिणाम वास्तव में नए नहीं थे। जैसा कि हैडमार्ड ने देखा, पोंकारे ने बालों वाली गेंद प्रमेय के बराबर एक प्रमेय दिखाया था।<ref>{{cite journal |first=Hans |last=Freudenthal |author-link=Hans Freudenthal | title=ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल|journal=[[Historia Mathematica]] |volume=2 |issue=4 |pages=495–502 [p. 495] |year=1975 |doi=10.1016/0315-0860(75)90111-1 |quote=... cette dernière propriété, bien que sous des hypothèses plus grossières, ait été démontré par H. Poincaré |doi-access=free }}</ref> ब्रौवर के दृष्टिकोण का क्रांतिकारी परिणाम वर्तमान में ही विकसित उपकरण जैसे [[होमोटॉपी]], पोंकारे समूह की अंतर्निहित अवधारणा का उनका व्यवस्थित उपयोग था। अगले वर्ष में, हैडमर्ड ने प्रमेय को स्वेच्छाकारी परिमित आयाम पर बातचीत के अंतर्गत सामान्यीकृत किया गया है, परन्तु उन्होंने विभिन्न प्रकारों को नियोजित किया है। [[हंस फ्रायडेंथल]] संबंधित आधारों पर निम्नानुसार टिप्पणी करते हैं: ब्रोवर के क्रांतिकारी प्रकारों के सामान में, हैडमर्ड के लोग बहुत पारंपरिक थे, परन्तु ब्रोवर के विचारों के जन्म में हैडमार्ड की का सिद्धांत एक धाय की तरह महत्वपूर्ण भूमिका निभाया है।<ref>{{cite journal |first=Hans |last=Freudenthal |author-link=Hans Freudenthal | title=ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल|journal=[[Historia Mathematica]] |volume=2 |issue=4 |pages=495–502 [p. 501] |year=1975 |doi=10.1016/0315-0860(75)90111-1 |doi-access=free }}</ref> ब्रोवर के दृष्टिकोण ने अपना फल दिया, और 1910 में उन्हें प्रमाण भी मिला जो किसी भी परिमित आयाम के लिए मान्य था,<ref name="brouwer-1910" />साथ ही अन्य प्रमुख प्रमेय जैसे कि आयाम का व्युत्क्रम हैं।<ref>If an open subset of a [[manifold]] is [[homeomorphism|homeomorphic]] to an open subset of a Euclidean space of dimension ''n'', and if ''p'' is a positive integer other than ''n'', then the open set is never homeomorphic to an open subset of a Euclidean space of dimension ''p''.</ref> इस कार्य के संदर्भ में, ब्रौवर ने स्वेच्छारी आयाम के लिए जॉर्डन वक्र प्रमेय को भी सामान्यीकृत किया और [[निरंतर मानचित्रण की डिग्री]] से जुड़े गुणों को स्थापित किया है।<ref>J. J. O'Connor E. F. Robertson ''[http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Brouwer.html Luitzen Egbertus Jan Brouwer]''.</ref> गणित की इस शाखा, मुख्य प्रकार से पॉइनकेयर द्वारा परिकल्पित और ब्रौवर द्वारा विकसित, ने अपना नाम बदल दिया है। 1930 के दशक में, विश्लेषण स्थल बीजगणितीय टोपोलॉजी बन गया है।<ref>The term ''algebraic topology'' first appeared 1931 under the pen of David van Dantzig: J. Miller ''[http://jeff560.tripod.com/t.html Topological algebra]'' on the site Earliest Known Uses of Some of the Words of Mathematics (2007)</ref> | यह ब्रौवर था, अंत में, जिसने प्रमेय को श्रेष्ठता का प्रथम अधिकार दिया है। उनके लक्ष्य पोंकारे से भिन्न थे। यह गणितज्ञ गणित की आधार, विशेष प्रकार से [[गणितीय तर्क]] और टोपोलॉजी से प्रेरित था। उनकी प्रारंभिक रुझान हिल्बर्ट की पांचवीं समस्या को सिद्ध करने के प्रयास में थी।<ref>J. J. O'Connor E. F. Robertson ''[http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Brouwer.html Luitzen Egbertus Jan Brouwer]''</ref> 1909 में, पेरिस की यात्रा के समय, उनकी मुलाकात हेनरी पोंकारे, जैक्स हैडमार्ड और एमिल बोरेल से हुई। भविष्य में होने वाले बातचीत यूक्लिडियन स्पेस की सही समझ के महत्व के ब्रोवर को प्रोत्साहित किया, और हैडमार्ड के साथ पत्रों के उपयोगी आदान-प्रदान की उत्पत्ति थी। अगले चार वर्षों तक, उन्होंने इस प्रश्न पर विशेष प्रमेयों के प्रमाण पर ध्यान केंद्रित किया है। 1912 में उन्होंने द्वि-आयामी क्षेत्र के लिए हेरी बॉल प्रमेय को सिद्ध किया, साथ ही इस तथ्य को भी सिद्ध किया कि द्वि-आयामी गेंद से लेकर स्वयं तक प्रत्येक निरंतर मानचित्र का निश्चित बिंदु होता है।<ref>{{cite journal |first=Hans |last=Freudenthal |author-link=Hans Freudenthal | title=ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल|journal=[[Historia Mathematica]] |volume=2 |issue=4 |pages=495–502 [p. 495] |year=1975 |doi=10.1016/0315-0860(75)90111-1 |doi-access=free }}</ref> अपने आप में ये दो परिणाम वास्तव में नए नहीं थे। जैसा कि हैडमार्ड ने देखा, पोंकारे ने बालों वाली गेंद प्रमेय के बराबर एक प्रमेय दिखाया था।<ref>{{cite journal |first=Hans |last=Freudenthal |author-link=Hans Freudenthal | title=ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल|journal=[[Historia Mathematica]] |volume=2 |issue=4 |pages=495–502 [p. 495] |year=1975 |doi=10.1016/0315-0860(75)90111-1 |quote=... cette dernière propriété, bien que sous des hypothèses plus grossières, ait été démontré par H. Poincaré |doi-access=free }}</ref> ब्रौवर के दृष्टिकोण का क्रांतिकारी परिणाम वर्तमान में ही विकसित उपकरण जैसे [[होमोटॉपी]], पोंकारे समूह की अंतर्निहित अवधारणा का उनका व्यवस्थित उपयोग था। अगले वर्ष में, हैडमर्ड ने प्रमेय को स्वेच्छाकारी परिमित आयाम पर बातचीत के अंतर्गत सामान्यीकृत किया गया है, परन्तु उन्होंने विभिन्न प्रकारों को नियोजित किया है। [[हंस फ्रायडेंथल]] संबंधित आधारों पर निम्नानुसार टिप्पणी करते हैं: ब्रोवर के क्रांतिकारी प्रकारों के सामान में, हैडमर्ड के लोग बहुत पारंपरिक थे, परन्तु ब्रोवर के विचारों के जन्म में हैडमार्ड की का सिद्धांत एक धाय की तरह महत्वपूर्ण भूमिका निभाया है।<ref>{{cite journal |first=Hans |last=Freudenthal |author-link=Hans Freudenthal | title=ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल|journal=[[Historia Mathematica]] |volume=2 |issue=4 |pages=495–502 [p. 501] |year=1975 |doi=10.1016/0315-0860(75)90111-1 |doi-access=free }}</ref> ब्रोवर के दृष्टिकोण ने अपना फल दिया, और 1910 में उन्हें प्रमाण भी मिला जो किसी भी परिमित आयाम के लिए मान्य था,<ref name="brouwer-1910" />साथ ही अन्य प्रमुख प्रमेय जैसे कि आयाम का व्युत्क्रम हैं।<ref>If an open subset of a [[manifold]] is [[homeomorphism|homeomorphic]] to an open subset of a Euclidean space of dimension ''n'', and if ''p'' is a positive integer other than ''n'', then the open set is never homeomorphic to an open subset of a Euclidean space of dimension ''p''.</ref> इस कार्य के संदर्भ में, ब्रौवर ने स्वेच्छारी आयाम के लिए जॉर्डन वक्र प्रमेय को भी सामान्यीकृत किया और [[निरंतर मानचित्रण की डिग्री]] से जुड़े गुणों को स्थापित किया है।<ref>J. J. O'Connor E. F. Robertson ''[http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Brouwer.html Luitzen Egbertus Jan Brouwer]''.</ref> गणित की इस शाखा, मुख्य प्रकार से पॉइनकेयर द्वारा परिकल्पित और ब्रौवर द्वारा विकसित, ने अपना नाम बदल दिया है। 1930 के दशक में, विश्लेषण स्थल बीजगणितीय टोपोलॉजी बन गया है।<ref>The term ''algebraic topology'' first appeared 1931 under the pen of David van Dantzig: J. Miller ''[http://jeff560.tripod.com/t.html Topological algebra]'' on the site Earliest Known Uses of Some of the Words of Mathematics (2007)</ref> | ||
=== रिसेप्शन === | === रिसेप्शन === | ||
[[Image:John f nash 20061102 2.jpg|thumb|220px|left|[[जॉन फोर्ब्स नैश]] ने एक संतुलन रणनीति प्रोफ़ाइल के अस्तित्व को साबित करने के लिए गेम थ्योरी में प्रमेय का इस्तेमाल किया।]]प्रमेय ने एक से अत्यधिक प्रकारों से अपना मूल्य सिद्ध किया है। 20वीं शताब्दी के समय कई निश्चित-बिंदु प्रमेय विकसित किए गए थे, और यहां तक कि गणित की शाखा को [[निश्चित-बिंदु सिद्धांत]] कहा जाता है।<ref>V. I. Istratescu ''Fixed Point Theory. An Introduction'' Kluwer Academic Publishers (new edition 2001) {{isbn|1-4020-0301-3}}.</ref> | [[Image:John f nash 20061102 2.jpg|thumb|220px|left|[[जॉन फोर्ब्स नैश]] ने एक संतुलन रणनीति प्रोफ़ाइल के अस्तित्व को साबित करने के लिए गेम थ्योरी में प्रमेय का इस्तेमाल किया।]]प्रमेय ने एक से अत्यधिक प्रकारों से अपना मूल्य सिद्ध किया है। 20वीं शताब्दी के समय कई निश्चित-बिंदु प्रमेय विकसित किए गए थे, और यहां तक कि गणित की शाखा को [[निश्चित-बिंदु सिद्धांत]] कहा जाता है।<ref>V. I. Istratescu ''Fixed Point Theory. An Introduction'' Kluwer Academic Publishers (new edition 2001) {{isbn|1-4020-0301-3}}.</ref> | ||
ब्रौवर प्रमेय संभवतः सबसे महत्वपूर्ण है।<ref>"... Brouwer's fixed point theorem, perhaps the most important fixed point theorem." p xiii V. I. Istratescu ''Fixed Point Theory an Introduction'' Kluwer Academic Publishers (new edition 2001) {{isbn|1-4020-0301-3}}.</ref> यह | ब्रौवर प्रमेय संभवतः सबसे महत्वपूर्ण है।<ref>"... Brouwer's fixed point theorem, perhaps the most important fixed point theorem." p xiii V. I. Istratescu ''Fixed Point Theory an Introduction'' Kluwer Academic Publishers (new edition 2001) {{isbn|1-4020-0301-3}}.</ref> यह संस्थिति मूलभूत प्रमेयों में से एक है और अधिकांशतः जॉर्डन वक्र प्रमेय जैसे महत्वपूर्ण परिणामो को प्रमाणित करने के लिए प्रयोग जाता है।<ref>E.g.: S. Greenwood J. Cao'' [http://www.math.auckland.ac.nz/class750/section5.pdf Brouwer’s Fixed Point Theorem and the Jordan Curve Theorem]'' University of Auckland, New Zealand.</ref> अत्यधिक या कम संकुचन मानचित्रण फलन के लिए निश्चित-बिंदु प्रमेय के अतिरिक्त, कई ऐसे हैं जो प्रत्यक्ष या अप्रत्यक्ष रूप से बातचीत के परिणाम से सामने आये हैं। युक्लीडियन स्पेस की बंद गेंद से इसकी सीमा से सतत नक्शा सीमा पर पहचान नहीं हो सकता है। इसी प्रकार बोरसुक-उलम प्रमेय कहता है की एन-आयामी क्षेत्र से '''R'''''<sup>n</sup>'' तक सतत नक्शा में प्रतिलोम-संबंधी बिंदुओं की एक जोड़ी होती है जो एक ही बिंदु पर मैप की जाती है। परिमित-आयामी कथन में, 1926 से लेफ्शेट्ज़ के नियत-बिंदु प्रमेय निश्चित बिंदुओं की गणना के लिए विधि प्रदान करता है। | ||
== | 1930 में, ब्रौवर के निश्चित-बिंदु प्रमेय को बांच स्पेस के लिए सामान्यीकृत किया गया है।<ref>{{cite journal |first=J. |last=Schauder |title=Der Fixpunktsatz in Funktionsräumen |journal=[[Studia Mathematica]] |volume=2 |year=1930 |pages=171–180 |doi= 10.4064/sm-2-1-171-180|doi-access=free }}</ref> इस सामान्यीकरण को अनंत-आयामी स्थानों में निश्चित-बिंदु प्रमेय के रूप में जाना जाता है। शाउडर की निश्चित-बिंदु प्रमेय, एस. काकुटानी द्वारा समूह-मूल्य फलन के लिए सामान्यीकृत परिणाम होता है।<ref>{{cite journal |first=S. |last=Kakutani |title=ब्राउवर के निश्चित बिंदु प्रमेय का एक सामान्यीकरण|journal= Duke Mathematical Journal|volume=8 |year=1941 |issue=3 |pages=457–459 |doi=10.1215/S0012-7094-41-00838-4 }}</ref> संस्थिति के बाहर प्रमेय और इसके रूपों से भी मिलता है। इसका उपयोग [[हार्टमैन-ग्रोबमैन प्रमेय]] को प्रमाणित करने के लिए किया जा सकता है, जो निश्चित संतुलन के पास कुछ अंतर समीकरणों के गुणात्मक व्यवहार का वर्णन करता है। इसी प्रकार, [[केंद्रीय सीमा प्रमेय]] के प्रमाण के लिए ब्रोवर के प्रमेय का उपयोग किया जाता है। कुछ आंशिक अंतर समीकरणों के समाधान के लिए प्रमेय को अस्तित्व प्रमाण में भी पाया जा सकता है।<ref>These examples are taken from: F. Boyer ''[http://www.cmi.univ-mrs.fr/~fboyer/ter_fboyer2.pdf Théorèmes de point fixe et applications]'' CMI Université Paul Cézanne (2008–2009) [https://www.webcitation.org/5refXIDvI?url=http://www.cmi.univ-mrs.fr/%7Efboyer/ter_fboyer2.pdf Archived copy] at [[WebCite]] (August 1, 2010).</ref> अन्य क्षेत्रों को भी ध्यान में रखा जाता है। गेम सिद्धांत में, जॉन फोर्ब्स नैश ने यह प्रमाणित करने के लिए प्रमेय का उपयोग किया कि [[हेक्स (बोर्ड गेम)]] के खेल में सफेद के लिए जीतने की रणनीति है।<ref>For context and references see the article [[Hex (board game)]].</ref> अर्थशास्त्र में, पी. बिच बताते हैं कि प्रमेय के कुछ सामान्यीकरण से पता चलता है कि इसका उपयोग गेम प्रमेय में कुछ प्रतिष्ठित समस्याओं और सामान्यतौर पर संतुलन (होटेलिंग का नियम), वित्तीय संतुलन और अपूर्ण बाजारों के लिए सहायक है।<ref>P. Bich ''[http://www.ann.jussieu.fr/~plc/code2007/bich.pdf Une extension discontinue du théorème du point fixe de Schauder, et quelques applications en économie] {{webarchive |url=https://web.archive.org/web/20110611140634/http://www.ann.jussieu.fr/~plc/code2007/bich.pdf |date=June 11, 2011 }}'' Institut Henri Poincaré, Paris (2007)</ref> ब्रौवर की पहचान विशेष रूप से उनके सांस्थितिकीय कार्य के कारण नहीं है। उनके महान सामयिक प्रमेय के प्रमाण रचनात्मक प्रमाण हैं,<ref>For a long explanation, see: {{cite journal |first=J. P. |last=Dubucs |url=http://www.persee.fr/web/revues/home/prescript/article/rhs_0151-4105_1988_num_41_2_4094 |title=L. J. E. Brouwer : Topologie et constructivisme |journal=Revue d'Histoire des Sciences |volume=41 |issue=2 |pages=133–155 |year=1988 |doi=10.3406/rhs.1988.4094 }}</ref> और ब्रोवर के इस पर असंतोष ने आंशिक रूप से उन्हें रचनावाद (गणित) के विचार को स्पष्ट करने के लिए प्रेरित किया है। वह गणित को औपचारिक रूप देने के प्रकार के प्रवर्तक और उत्साहपूर्वक समर्थक बन गए, जिसे [[अंतर्ज्ञानवादी तर्क]] के रूप में जाना जाता है, जिसने उस समय निर्धारित सिद्धांत के विरोध में कारण दिया था।<ref>Later it would be shown that the formalism that was combatted by Brouwer can also serve to formalise intuitionism, with some modifications. For further details see [[constructive set theory]].</ref> ब्रोवर ने निश्चित-बिंदु प्रमेय के अपने मूल प्रमाण को अस्वीकार कर दिया था। निश्चित बिंदु का अनुमान लगाने वाला पहला एल्गोरिथम [[हर्बर्ट स्कार्फ]] द्वारा प्रस्तावित किया गया था।<ref>H. Scarf found the first algorithmic proof: {{SpringerEOM|title=Brouwer theorem |first=M.I. |last=Voitsekhovskii |isbn=1-4020-0609-8}}.</ref> स्कार्फ के बीजगणित का सूक्ष्म कारण यह है कि यह एक बिंदु पाता है जो है जो लगभग निश्चित फलन एफ द्वारा, परन्तु सामान्य प्रकार से बिंदु नहीं मिल सकता है जो वास्तविक निश्चित बिंदु के निकट है। गणितीय भाषा में, यदि {{mvar|ε}} को बहुत छोटा चुना गया है, स्कार्फ के बीजगणित का उपयोग बिंदु x को ढूंढने के लिए किया जा सकता है जैसे कि f(x) x के बहुत निकट है, अर्थात, <math>d(f(x),x) < \varepsilon </math> है, परन्तु स्कार्फ के बीजगणित का उपयोग बिंदु x को ढूंढने के लिए नहीं किया जा सकता है जैसे कि x एक निश्चित बिंदु के बहुत निकट है: हम आश्वाशन नहीं दे सकते <math>d(x,y) < \varepsilon,</math> जहाँ <math>f(y)=y</math> है अधिकांशतः यह बाद की स्थिति एक निश्चित बिंदु का अनुमान लगाने वाले अनौपचारिक वाक्यांश का अर्थ है। | ||
== प्रमाण की रूपरेखा == | |||
=== अंश का उपयोग करके एक प्रमाण === | === अंश का उपयोग करके एक प्रमाण === | ||
ब्रौवर का मूल 1911 का प्रमाण एक निरंतर मानचित्रण की डिग्री की धारणा पर निर्भर करता है, जो विभेदक टोपोलॉजी में विचारों से उपजा है। प्रमाण के कई आधुनिक अभिलेख साहित्य में पाए जा सकते हैं, विशेष रूप से {{harvtxt|मिलनर|1965}}.<ref name="Milnor">{{harvnb|Milnor|1965|pages=1–19}}</ref><ref>{{cite book | last = Teschl| first = Gerald| author-link = Gerald Teschl| title = रेखीय और अरैखिक कार्यात्मक विश्लेषण में विषय|url=https://www.mat.univie.ac.at/~gerald/ftp/book-fa/fa.pdf |archive-url=https://ghostarchive.org/archive/20221009/https://www.mat.univie.ac.at/~gerald/ftp/book-fa/fa.pdf |archive-date=2022-10-09 |url-status=live|chapter=10. The Brouwer mapping degree|access-date=1 February 2022|year=2019|publisher=[[American Mathematical Society]]|series=Graduate Studies in Mathematics}}</ref>माना की <math>K=\overline{B(0)}</math> बंद इकाई बॉल को निरूपित करें <math>\mathbb R^n</math> मूल पर केन्द्रित है। संकुचित करने के लिए माना कि <math>f:K\to K</math> निरन्तर अवकलनीय है। | ब्रौवर का मूल 1911 का प्रमाण एक निरंतर मानचित्रण की डिग्री की धारणा पर निर्भर करता है, जो विभेदक टोपोलॉजी में विचारों से उपजा है। प्रमाण के कई आधुनिक अभिलेख साहित्य में पाए जा सकते हैं, विशेष रूप से {{harvtxt|मिलनर|1965}}.<ref name="Milnor">{{harvnb|Milnor|1965|pages=1–19}}</ref><ref>{{cite book | last = Teschl| first = Gerald| author-link = Gerald Teschl| title = रेखीय और अरैखिक कार्यात्मक विश्लेषण में विषय|url=https://www.mat.univie.ac.at/~gerald/ftp/book-fa/fa.pdf |archive-url=https://ghostarchive.org/archive/20221009/https://www.mat.univie.ac.at/~gerald/ftp/book-fa/fa.pdf |archive-date=2022-10-09 |url-status=live|chapter=10. The Brouwer mapping degree|access-date=1 February 2022|year=2019|publisher=[[American Mathematical Society]]|series=Graduate Studies in Mathematics}}</ref>माना की <math>K=\overline{B(0)}</math> बंद इकाई बॉल को निरूपित करें <math>\mathbb R^n</math> मूल पर केन्द्रित है। संकुचित करने के लिए माना कि <math>f:K\to K</math> निरन्तर अवकलनीय है। [[नियमित मूल्य]] <math>f</math> बिन्दु <math>p\in B(0)</math> है जैसे कि [[जेकोबियन मैट्रिक्स और निर्धारक]] <math>f</math> की पूर्वकल्पना के प्रत्येक बिंदु p पर एकल नहीं है। विशेष रूप से, व्युत्क्रम कार्य प्रमेय द्वारा, प्रत्येक बिंदु की पूर्वकल्पना <math>f</math> में <math>B(0)</math> निहित है | | ||
(आंतरिक भाग <math>K</math>) अंश का नियमित मूल्य पर <math>p\in B(0)</math> के जैकोबियन निर्धारक के संकेतों के योग के रूप में परिभाषित किया गया है <math>f</math> के पूर्वापेक्षाओं पर <math>p</math> के अंतर्गत <math>f</math>: | |||
:<math>\operatorname{deg}_p(f) = \sum_{x\in f^{-1}(p)} \operatorname{sign}\,\det (df_x).</math> | :<math>\operatorname{deg}_p(f) = \sum_{x\in f^{-1}(p)} \operatorname{sign}\,\det (df_x).</math> | ||
डिग्री, सामान्यतया यह दर्शा रही है की, p के चारों ओर प्राइमेज f का एक छोटे से खुले समुच्चय पर रखे गए पन्नो की संख्या, विपरीत दिशा में गिने जाने वाली पन्नो के साथ होती है। इस प्रकार यह उच्च आयामों के लिए वाइंडिंग संख्या का सामान्यीकरण है। | डिग्री, सामान्यतया यह दर्शा रही है की, p के चारों ओर प्राइमेज f का एक छोटे से खुले समुच्चय पर रखे गए पन्नो की संख्या, विपरीत दिशा में गिने जाने वाली पन्नो के साथ होती है। इस प्रकार यह उच्च आयामों के लिए वाइंडिंग संख्या का सामान्यीकरण है। | ||
डिग्री होमोटॉपी इनवेरियन की निर्देशों को संतुष्ट करती है: माना <math>f</math> और <math>g</math> दो लगातार अलग-अलग कार्य हो, और <math>H_t(x)=tf+(1-t)g</math> के लिए <math>0\le t\le 1</math>. मान लीजिए कि बिंदु <math>p</math>, सभी t के लिए | डिग्री होमोटॉपी इनवेरियन की निर्देशों को संतुष्ट करती है: माना <math>f</math> और <math>g</math> दो लगातार अलग-अलग कार्य हो, और <math>H_t(x)=tf+(1-t)g</math> के लिए <math>0\le t\le 1</math>. मान लीजिए कि बिंदु <math>p</math>, सभी t के लिए का नियमित मान <math>H_t</math> है। तब <math>\deg_p f = \deg_p g</math> होता है। | ||
यदि की सीमा का कोई निश्चित बिंदु <math>K</math> नहीं है ,तब फलन | यदि की सीमा का कोई निश्चित बिंदु <math>K</math> नहीं है ,तब फलन | ||
| Line 114: | Line 98: | ||
अच्छे से परिभाषित है, और | अच्छे से परिभाषित है, और | ||
<math>H(t,x) = \frac{x-tf(x)}{\sup_{x\in K}\left|x-tf(x)\right|}</math>तत्समक फलन से समरूपता को परिभाषित करता | <math>H(t,x) = \frac{x-tf(x)}{\sup_{x\in K}\left|x-tf(x)\right|}</math>तत्समक फलन से समरूपता को परिभाषित करता है। विशेषतः तत्समक फलन मूल में डिग्री एक है, इसलिए <math>g</math> मूल में डिग्री भी है। जिस कारण से, प्रीइमेज <math>g^{-1}(0)</math> खाली नहीं है। <math>g^{-1}(0)</math> के तत्त्व वास्तविक फलन के निश्चित बिंदु के रूप में होते है। | ||
डिग्री की परिभाषा को च के एकवचन मूल्यों और फिर निरंतर कार्यों तक विस्तारित किया जाना चाहिए। [[समरूपता सिद्धांत]] का अधिक आधुनिक आगमन डिग्री के निर्माण को सरल करता है, और इसलिए यह साहित्य में एक मानक प्रमाण बन गया है। | डिग्री की परिभाषा को च के एकवचन मूल्यों और फिर निरंतर कार्यों तक विस्तारित किया जाना चाहिए। [[समरूपता सिद्धांत]] का अधिक आधुनिक आगमन डिग्री के निर्माण को सरल करता है, और इसलिए यह साहित्य में एक मानक प्रमाण बन गया है। | ||
'''हेयरी बॉल प्रमेय का उपयोग करके सिद्ध करना''' | '''हेयरी बॉल प्रमेय का उपयोग करके सिद्ध करना''' | ||
हेयरी बॉल प्रमेय के अनुसार इकाई क्षेत्र पर {{mvar|''S''}} एक विषम-आयामी यूक्लिडियन स्पेस में, कहीं नहीं गायब होने वाला निरंतर स्पर्शरेखा सदिश क्षेत्र {{mvar|'''w'''}} पर {{mvar|''S''}} नहीं है। (स्पर्श स्थिति का अर्थ है कि {{mvar|'''w'''('''x''') ⋅ '''x'''}} = 0 प्रत्येक इकाई वेक्टर के लिए {{mvar|'''x'''}}।) कभी-कभी प्रमेय को इस कथन द्वारा व्यक्त किया जाता है कि ग्लोब पर हमेशा एक जगह होती है जिसमें हवा नहीं होती है। हेयरी बॉल प्रमेय का एक प्रारंभिक प्रमाण {{harvtxt|Milnor|1978}}के सिद्धांत में पाया जा सकता है। | हेयरी बॉल प्रमेय के अनुसार इकाई क्षेत्र पर {{mvar|''S''}} एक विषम-आयामी यूक्लिडियन स्पेस में, कहीं नहीं गायब होने वाला निरंतर स्पर्शरेखा सदिश क्षेत्र {{mvar|'''w'''}} पर {{mvar|''S''}} नहीं है। (स्पर्श स्थिति का अर्थ है कि {{mvar|'''w'''('''x''') ⋅ '''x'''}} = 0 प्रत्येक इकाई वेक्टर के लिए {{mvar|'''x'''}}।) कभी-कभी प्रमेय को इस कथन द्वारा व्यक्त किया जाता है कि ग्लोब पर हमेशा एक जगह होती है जिसमें हवा नहीं होती है। हेयरी बॉल प्रमेय का एक प्रारंभिक प्रमाण {{harvtxt|Milnor|1978}} के सिद्धांत में पाया जा सकता है। | ||
वास्तव में, पहले मान लीजिए {{mvar|'''w'''}} निरंतर अवकलनीय है। स्केलिंग करके, यह माना जा सकता है {{mvar|'''w'''}} | वास्तव में, पहले मान लीजिए {{mvar|'''w'''}} निरंतर अवकलनीय है। स्केलिंग करके, यह माना जा सकता है {{mvar|'''w'''}} सतत अवकलनीय इकाई स्पर्शरेखा सदिश {{mvar|'''S'''}} है। इसे रेडियल रूप से {{mvar|''A''}} का {{mvar|''S''}} छोटे गोलाकार खोल तक बढ़ाया जा सकता है। {{mvar|''t''}} के लिए पर्याप्त रूप से छोटा, नियमित संगणना से पता चलता है कि मैपिंग {{mvar|'''f'''<sub>''t''</sub>}}({{mvar|'''x'''}}) = {{mvar|''t'' '''x'''}} + {{mvar|'''w'''('''x''')}} एक संकुचन मानचित्रण है {{mvar|''A''}} और इसकी इमेज का आयतन बहुपद {{mvar|''t''}} है। दूसरी तरफ, संकुचन मानचित्रण के रूप में, {{mvar|'''f'''<sub>''t''</sub>}} के सामान्य स्तर तक ही {{mvar|''S''}} पर सीमित होना चाहिए (1 + {{mvar|''t''<sup>2</sup>}})<sup>½ {{mvar|''S''}} और {{mvar|''A''}} पर (1 + {{mvar|''t''<sup>2</sup>}})<sup>½ {{mvar|''A''}}. यह एक विरोधाभास देता है, क्योंकि यदि आयाम ''n'' यूक्लिडियन स्थान का विषम है, (1 + {{mvar|''t''<sup>2</sup>}})<sup>{{mvar|''n''}}/2 बहुपद नहीं है। | ||
यदि {{mvar|'''w'''}} सिर्फ S पर निरंतर इकाई स्पर्शरेखा सदिश है, वेअरस्ट्रास लगभग प्रमेय के द्वारा, इसे बहुपद मानचित्र द्वारा समान रूप से {{mvar|'''u'''}} को {{mvar|''A''}} यूक्लिडियन स्पेस में अनुमानित किया जाता है। स्पर्शरेखीय स्पेस पर समकोणीय निरूपण द्वारा {{mvar|'''v'''}}({{mvar|'''x'''}}) = {{mvar|'''u'''}}({{mvar|'''x'''}}) - {{mvar|'''u'''}}({{mvar|'''x'''}}) ⋅ {{mvar|'''x'''}} दिया गया है। इस प्रकार {{mvar|'''v'''}} बहुपद है और A पर कही स्थान नहीं पाता है; निर्माण द्वारा {{mvar|'''v'''}}/||{{mvar|'''v'''}}|| एक निरंतर इकाई स्पर्शरेखा S का खंडन सदिश क्षेत्र है। | |||
हेयरी बॉल प्रमेय का निरंतर संस्करण अब ब्रौवर निश्चित बिंदु प्रमेय सिद्ध करने के लिए उपयोग किया जा सकता है। मान लीजिए {{mvar|''n''}} विसम है। यदि कोई निश्चित-बिंदु-मुक्त निरंतर स्व-मानचित्रण होता {{mvar|'''f'''}} बंद इकाई बॉल की {{mvar|''B''}} की {{mvar|''n''}}-आयामी यूक्लिडियन स्थान {{mvar|''V''}}, तय करना है: | |||
:<math>{\mathbf w}({\mathbf x}) = (1 - {\mathbf x}\cdot {\mathbf f}({\mathbf x}))\, {\mathbf x} - (1 - {\mathbf x}\cdot {\mathbf x})\, {\mathbf f}({\mathbf x}).</math> | :<math>{\mathbf w}({\mathbf x}) = (1 - {\mathbf x}\cdot {\mathbf f}({\mathbf x}))\, {\mathbf x} - (1 - {\mathbf x}\cdot {\mathbf x})\, {\mathbf f}({\mathbf x}).</math> | ||
चुकी {{mvar|'''f'''}} का कोई निश्चित बिंदु नहीं है, यह इस प्रकार है, के लिए {{mvar|'''x'''}} के [[इंटीरियर (टोपोलॉजी)]] में {{mvar|''B''}}, वेक्टर {{mvar|'''w'''}}({{mvar|'''x'''}}) शून्य नहीं है; और S के लिए {{mvar|'''x'''}} में, स्केलर उत्पाद <br/> {{mvar|'''x'''}} ⋅ {{mvar|'''w'''}}({{mvar|'''x'''}}) = 1 – {{mvar|'''x'''}} ⋅ {{mvar|'''f'''}}({{mvar|'''x'''}}) से धनात्मक है। मूल से {{mvar|''n''}}-आयामी यूक्लिडियन स्पेस {{mvar|''V''}}, ({{mvar|''n'' + 1}})-विमीय स्थान {{mvar|''W''}} = {{mvar|''V''}} x R, निर्देशांक के साथ {{mvar|''y''}} = ({{mvar|'''x'''}}, {{mvar|''t''}}) के साथ एक नया सहायक '''X( x,t ) = ( -t w(x), x.w(x))''' निर्मित करता है। | |||
निर्माण द्वारा {{mvar|'''X'''}} के इकाई क्षेत्र पर सतत सदिश {{mvar|''W''}} क्षेत्र है, स्पर्शरेखा की स्थिति {{mvar|'''y'''}} ⋅ {{mvar|'''X'''}}({{mvar|'''y'''}}) = 0 को संतुष्ट करना है। इसके अतिरिक्त {{mvar|'''X'''}}({{mvar|'''y'''}}) कहीं अदृष्ट नहीं है (क्योंकि, यदि {{var|'''x'''}} का मानदंड 1 है, तो {{mvar|'''x'''}} ⋅ {{mvar|'''w'''}}({{mvar|''x''}}) शून्य नहीं है; जबकि यदि {{mvar|'''x'''}} का मानदंड वास्तव में 1 से कम है, तो {{mvar|''t''}} और {{mvar|'''w'''}}({{mvar|'''x'''}}) दोनों शून्य नहीं हैं)। यह खंडन निश्चित बिंदु प्रमेय को सिद्ध करता है जब {{mvar|''n''}} विषम है। यहां तक कि {{mvar|''n''}} के लिए, निश्चित बिंदु प्रमेय को बंद इकाई गेंद पर क्रियान्वित किया जा सकता है {{mvar|''B''}} में {{mvar|''n'' + 1}} आयाम और मानचित्रण {{mvar|'''F'''}}({{mvar|'''x'''}},{{mvar|''y''}}) = ({{mvar|'''f'''}}({{mvar|'''x'''}}), 0) है। इस प्रमाण का लाभ यह है कि यह सिर्फ प्रारंभिक तकनीकों का उपयोग करता है; [[बोरसुक-उलम प्रमेय]] जैसे अत्यधिक सामान्य परिणामों के लिए बीजगणितीय संस्थिति से उपकरणों की आवश्यकता होती है।<ref name="Milnor78">{{harvnb|Milnor|1978}}</ref> | |||
'''होमोलॉजी या कोहोलॉजी का उपयोग करते हुए एक प्रमाण''' | |||
समरूपता या कोहोलॉजी का उपयोग करते हुए प्रमाण अवलोकन का उपयोग करता है कि एन-डिस्क D<sup>n</sup> की [[सीमा (टोपोलॉजी)|सीमा (संस्थिति)]] S<sup>n−1</sup> है, (n − 1)-गोला है। | |||
[[Image:Brouwer fixed point theorem retraction.svg|thumb|right|रिट्रेक्शन एफ का चित्रण]]मान लीजिए, खंडन के लिए, सतत फलन {{nowrap|''f'' : ''D''<sup>''n''</sup> → ''D''<sup>''n''</sup>}} का कोई निश्चित बिंदु नहीं है। इसका अर्थ है कि, D में प्रत्येक बिंदु x<sup>n</sup> के लिए, बिंदु x और f(x) भिन्न हैं। क्योंकि वे अलग-अलग हैं, D में प्रत्येक बिंदु x<sup>n</sup> के लिए, हम f(x) से x तक अद्वितीय किरण का निर्माण कर सकते हैं और किरण का अनुसरण तब तक कर सकते हैं जब तक कि यह सीमा S<sup>n−1</sup> को काट न दे (उदाहरण देखें)। इस प्रतिच्छेदन बिंदु F(x) को प्रयोग करके, हम फलन F : D<sup>n</sup> को परिभाषित करते हैं→ S<sup>n−1</sup> डिस्क में प्रत्येक बिंदु को सीमा पर उसके संबंधित प्रतिच्छेदन बिंदु पर भेज रहा है। विशेष कथन के रूप में, जब भी x स्वयं सीमा पर होता है, तो प्रतिच्छेदन बिंदु F(x) x होना चाहिए। | |||
इसीलिए, f एक विशेष प्रकार का निरंतर फलन है जिसे रिट्रेक्शन (संस्थिति) के रूप में जाना जाता है: [[कोडोमेन]] के सभी बिंदु (इस कथन S<sup>n−1</sup> में) F का निश्चित बिंदु है। | |||
सहज रूप से ऐसा प्रतीत नहीं होता है कि D<sup>n</sup> की S<sup>n−1</sup> पर रिट्रैक्शन हो सकती है, और इस कथन में n = 1, असंभवता अत्यधिक मूलभूत है, क्योंकि S<sup>0</sup> (अर्थात, बंद अंतराल डी<sup>1</sup> के अंत बिंदु) जुड़ा हुआ नहीं है। कथन n = 2 कम स्पष्ट है, परन्तु संबंधित स्थानों के मूलभूत समूहों को सम्मिलित करते हुए मूलभूत तर्कों का उपयोग करके सिद्ध किया जा सकता है: प्रत्यावर्तन D<sup>2</sup> के मूल समूह से विशेषण [[समूह समरूपता]] को S<sup>1</sup> के लिए प्रेरित करेगा, परन्तु बाद वाला समूह Z के लिए समरूप है जबकि पहला समूह छोटा है, इसलिए यह असंभव है। कथन ''n'' = 2 [[वेक्टर क्षेत्र|जिसे लुप्त न किया जा सके क्षेत्रों]] के बारे में प्रमेय के आधार पर खंडन द्वारा भी सिद्ध किया जा सकता है। | |||
''n'' > 2 के लिए, चूँकि, प्रत्यावर्तन की असंभवता को प्रमाणित करना अत्यधिक कठिन है। सजातीय (गणित) का उपयोग करने का विधि है: समरूपता H<sub>''n''−1</sub>(D<sup>n</sup>) निम्न है, जबकि H<sub>''n''−1</sub>(S<sup>n−1</sup>) अनंत [[चक्रीय समूह]] है। इससे पता चलता है कि प्रत्यावर्तन असंभव है, क्योंकि फिर से प्रत्यावर्तन बाद वाले समूह से पूर्व समूह के लिए द्वीअंतःक्षेपण समूह समरूपता को प्रेरित करेगा। | |||
यूक्लिडियन स्पेस E<sup>n</sup> के खुले उपसमुच्चय के [[डॉ कहलमज गर्भाशय|डॉ कहलमज कोहोलॉजी]] का उपयोग करके रिट्रैक्शन की असंभवता भी दिखायी जा सकती है n ≥ 2 के लिए, U = E<sup>n</sup> - (0) की डी रम कोहोलॉजी डिग्री 0 और n - 1 में आयामी है, और अन्यथा लुप्त हो जाता है। यदि प्रत्यावर्तन अस्तित्व में है, तो U को संविदात्मक होना होगा और n-1 डिग्री में इसके डी राम कोहोलॉजी को खंडन में लुप्त होना होगा।<ref>{{harvnb|Madsen|Tornehave |1997|pages=39–48}}</ref> | |||
=== स्टोक्स के प्रमेय का प्रयोग करके एक उपपत्ति === | === स्टोक्स के प्रमेय का प्रयोग करके एक उपपत्ति === | ||
समरूपता का उपयोग करते हुए निरंतर नक्शों के लिए ब्रोवर के निश्चित-बिंदु प्रमेय के प्रमाण के रूप में, यह | समरूपता का उपयोग करते हुए निरंतर नक्शों के लिए ब्रोवर के निश्चित-बिंदु प्रमेय के प्रमाण के रूप में, यह प्रमाणित करने के लिए कम किया गया है की गेंद B से इसकी सीमा ∂B पर कोई निरंतर रिट्रैक्शन F नहीं है। ऐसे में यह माना जा सकता है {{mvar|''F''}} सहज है, क्योंकि इसे वीयरस्ट्रैस लगभग प्रमेय का उपयोग करके या पर्याप्त रूप से छोटे सहायता और अभिन्न (अर्थात शिथिल [[शमन करनेवाला|करनेवाला]]) के अऋणात्मक निरंतर उभार फलन के साथ [[कनवल्शन|संवलन]] द्वारा अनुमानित किया जा सकता है। यदि {{mvar|ω}} स्टोक्स के प्रमेय द्वारा सीमा पर आयतन रूप है, | ||
:<math>0<\int_{\partial B}\omega = \int_{\partial B}F^*(\omega) = \int_BdF^*(\omega)= \int_BF^*(d\omega)=\int_BF^*(0) = 0,</math> | :<math>0<\int_{\partial B}\omega = \int_{\partial B}F^*(\omega) = \int_BdF^*(\omega)= \int_BF^*(d\omega)=\int_BF^*(0) = 0,</math> | ||
खंडन रहा है।<ref>{{harvnb|Boothby|1971}}</ref><ref>{{harvnb|Boothby|1986}}</ref> | |||
अत्यधिक समान्यतौर पर, यह दर्शाता है कि किसी भी भरी हुई निरंतर उन्मुख सघन विविध से कोई निरंतर रिट्रैक्शन {{mvar|''M''}} इसकी सीमा पर नहीं होता है। स्टोक्स के प्रमेय का उपयोग करने वाला प्रमाण सजातीय का उपयोग करने वाले प्रमाण से निकटता से संबंधित है, क्योंकि {{mvar|ω}} डी रम कोहोलॉजी उत्पन्न करता है {{mvar|''H''<sup>''n''-1</sup>}}(∂{{mvar|''M''}}) जो डी रम कोहोलॉजी द्वारा सजातीय समूह {{mvar|''H''<sub>''n''-1</sub>}}(∂{{mvar|''M''}}) के लिए समरूप है।<ref>{{harvnb|Dieudonné|1982}}</ref> | |||
=== एक संयोजन प्रमाण === | === एक संयोजन प्रमाण === | ||
स्पर्नर लेम्मा का उपयोग करके | स्पर्नर लेम्मा का उपयोग करके बीइपीटी को सिद्ध किया जा सकता है। अब हम विशेष कथन के लिए प्रमाणित रूपरेखा देते हैं जिसमें f मानक [[संकेतन]] से फ़ंक्शन है, <math>\Delta^n,</math> जहाँ | ||
:<math>\Delta^n = \left\{P\in\mathbb{R}^{n+1}\mid\sum_{i = 0}^{n}{P_i} = 1 \text{ and } P_i \ge 0 \text{ for all } i\right\}.</math> | :<math>\Delta^n = \left\{P\in\mathbb{R}^{n+1}\mid\sum_{i = 0}^{n}{P_i} = 1 \text{ and } P_i \ge 0 \text{ for all } i\right\}.</math> | ||
सभी बिंदु के लिए <math>P\in \Delta^n,</math> भी <math>f(P)\in \Delta^n.</math> इसलिए उनके निर्देशांकों का योग बराबर है: | |||
:<math>\sum_{i = 0}^{n}{P_i} = 1 = \sum_{i = 0}^{n}{f(P)_i}</math> | :<math>\sum_{i = 0}^{n}{P_i} = 1 = \sum_{i = 0}^{n}{f(P)_i}</math> | ||
इसलिए, | इसलिए, पीजेनहोल सिद्धांत द्वारा, हर <math>P\in \Delta^n</math> के लिए <math>j \in \{0, \ldots, n\}</math> सूचकांक होना चाहिए ऐसा कि <math>j</math> वें का समन्वय <math>P</math> से अत्यधिक या उसके बराबर है <math>j</math>f के अंतर्गत इसकी इमेज के निर्देशांक: | ||
:<math>P_j \geq f(P)_j.</math> | :<math>P_j \geq f(P)_j.</math> | ||
इसके | इसके अतिरिक्त, यदि <math>P</math> के k-आयामी <math>\Delta^n</math> के ऊपरी सतह पर स्थित है, फिर उसी तर्क से, निर्देशिका <math>j</math> में से चुना जा सकता है {{nowrap|''k'' + 1}} निर्देशांक जो इस ऊपरी सतह पर शून्य नहीं हैं। | ||
अब हम इस तथ्य का उपयोग स्पर्नर रंग बनाने के लिए करते हैं। | अब हम इस तथ्य का उपयोग स्पर्नर रंग बनाने के लिए करते हैं। सभी <math>\Delta^n</math> त्रिभुज के लिए प्रत्येक शीर्ष '''p''' का रंग निर्देशांक <math>j</math> है जैसे की <math>f(P)_j \leq P_j</math>। रचना के अनुसार, यह एक स्पर्नर रंग है। इसलिए, स्पर्नर की लेम्मा द्वारा, n-विमीय सिम्प्लेक्स है, जिसके कोने के पुरे समूह के साथ उपलब्ध रंग {{nowrap|''n'' + 1}} है। | ||
रचना के अनुसार, यह एक स्पर्नर रंग है। इसलिए, स्पर्नर की लेम्मा द्वारा, | |||
चूँकि f निरंतर है, इस | चूँकि f निरंतर है, इस संकेतन को स्वेच्छचरित प्रकार से सूक्ष्म त्रिकोण का चयन करके छोटा बनाया जा सकता है। इसलिए, <math>P</math> बिंदु होना चाहिए जो सभी निर्देशांकों में <math>f(P)_j \leq P_j</math> लेबलिंग शर्त को पूरा करता है: सभी के लिए <math>j</math> क्योंकि के निर्देशांक का योग <math>P</math> और <math>f(P)</math> समान होना चाहिए, ये सभी असमानताएँ वास्तव में समानताएँ होनी चाहिए। परन्तु इसका अर्थ यह है कि: | ||
क्योंकि के निर्देशांक का योग <math>P</math> और <math>f(P)</math> समान होना चाहिए, ये सभी असमानताएँ वास्तव में समानताएँ होनी चाहिए। | |||
:<math>f(P) = P.</math> | :<math>f(P) = P.</math> | ||
वह | वह <math>P</math> का निश्चित बिन्दु <math>f</math> हैl | ||
'''हिर्श द्वारा उपयोग करके''' | |||
हिर्श द्वारा प्रमाण अलग-अलग रिट्रैक्शन की असंभवता के आधार पर [[मॉरिस हिर्श]] द्वारा त्वरित प्रमाण भी है। अप्रत्यक्ष प्रमाण यह देखते हुए प्रारम्भ होता है कि मानचित्र f को बिंदु को ठीक न करने की गुण को बनाए रखते हुए सहज मानचित्र द्वारा अनुमानित किया जा सकता है; यह वेएरस्ट्रास लगभग प्रमेय का उपयोग करके साधारण उठे हुए फंक्शन्स के साथ संवलन द्वारा किया जा सकता है। ऊपर के रूप में रिट्रैक्शन को परिभाषित करता है जो अब भिन्न होना चाहिए। सार्ड के प्रमेय के अनुसार इस प्रकार के प्रत्यावर्तन का व्युत्क्रमणीय मूल्य होना चाहिए, जो सीमा के प्रतिबंध के लिए व्युत्क्रमणीय है (जो कि सिर्फ पहचान है)। इस प्रकार विपरीत इमेज सीमा के साथ एक गुना होगी। सीमा में कम से कम दो अंतिम बिंदु सम्मिलित होने चाहिए, दोनों को मूल गेंद की सीमा पर होना चाहिए जो वापसी में असंभव है।<ref>{{harvnb|Hirsch|1988}}</ref> आर. ब्रूस केलॉग, टीएन-यीन ली, और जेम्स ए. यॉर्क ने हिर्श के प्रमाण को संगणनीयता प्रमाण में बदल दिया, यह देखते हुए कि निश्चित बिंदुओं को छोड़कर सभी जगह वास्तव में वापस लेना परिभाषित किया गया है।{{sfn|Kellogg|Li|Yorke|1976}} लगभग किसी भी बिंदु के लिए, q, सीमा पर, (यह मानते हुए कि यह एक निश्चित बिंदु नहीं है) ऊपर उल्लिखित सीमा के साथ कई गुना उपस्थित है और एकमात्र संभावना यह है कि यह q से एक निश्चित बिंदु तक ले जाती है। q से निश्चित बिंदु तक इस प्रकार के पथ का पालन करना आसान संख्यात्मक कार्य है, इसलिए विधि अनिवार्य रूप से गणना योग्य है।{{sfn|Chow|Mallet-Paret|Yorke|1978}} संकल्पनात्मक रूप से समरूपता प्रमाण समान पथ-अनुवर्ती संस्करण दिया जो विभिन्न प्रकार की संबंधित समस्याओं तक फैला हुआ है। | |||
अलग-अलग | |||
आर. ब्रूस केलॉग, टीएन-यीन ली, और जेम्स ए. यॉर्क ने हिर्श के प्रमाण को | |||
=== उन्मुख क्षेत्र का प्रयोग करते हुए एक प्रमाण === | === उन्मुख क्षेत्र का प्रयोग करते हुए एक प्रमाण === | ||
पूर्ववर्ती प्रमाण की भिन्नता सार्ड के प्रमेय को नियोजित नहीं करती है, और निम्नानुसार जाती है। यदि <math>r\colon B\to \partial B</math> | पूर्ववर्ती प्रमाण की भिन्नता सार्ड के प्रमेय को नियोजित नहीं करती है, और निम्नानुसार जाती है। यदि <math>r\colon B\to \partial B</math> सुचारू रिट्रैक्शन है, सहज विकृति पर विचार करता है <math>g^t(x):=t r(x)+(1-t)x,</math> और सुचारू कार्य | ||
:<math>\varphi(t):=\int_B \det D g^t(x) \, dx.</math> | :<math>\varphi(t):=\int_B \det D g^t(x) \, dx.</math> | ||
समाकल के चिह्न के अंतर्गत अंतर करना यह जाँचना कठिन नहीं है {{prime|φ}}(t) = 0 सभी t के लिए, इसलिए φ स्थिर | समाकल के चिह्न के अंतर्गत अंतर करना यह जाँचना कठिन नहीं है {{prime|φ}}(t) = 0 सभी t के लिए, इसलिए φ स्थिर फलन है, जो खंडन है क्योंकि φ(0) गेंद का n-आयामी आयतन है, जबकि φ(1) शून्य है। ज्यामितीय विचार यह है कि φ(t) g<sup>t</sup>(B) का उन्मुख क्षेत्र है (अर्थात, g<sup>t</sup> के माध्यम से गेंद की इमेज का लेब्सग्यु माप, बहुलता और अभिविन्यास को ध्यान में रखते हुए), और स्थिर रहना चाहिए (क्योंकि यह आयामी कथन में बहुत स्पष्ट है)। दूसरी तरफ, पैरामीटर ''t'' के रूप में 0 से 1 नक्शा g<sup>t</sup> पास होता है निरंतर गेंद के पहचान मानचित्र से रिट्रैक्शन r में रूपांतरित होता है, जो खंडन है क्योंकि पहचान का उन्मुख क्षेत्र गेंद के आयतन के साथ मिलता है, जबकि r का उन्मुख क्षेत्र आवश्यक रूप से 0 है, जैसा कि इसकी इमेज गेंद की सीमा है, अशक्त माप का समूह है।<ref>{{harvnb|Kulpa|1989}}</ref> | ||
'''खेल हेक्स का उपयोग कर एक प्रमाण''' | |||
खेल हेक्स का उपयोग कर [[डेविड गेल]] द्वारा दिया गया बिल्कुल अलग प्रमाण हेक्स (बोर्ड गेम) के खेल पर आधारित है। हेक्स के बारे में मूल प्रमेय, जो पहले जॉन नैश द्वारा सिद्ध किया गया था, यह है कि हेक्स का कोई भी गेम ड्रा में समाप्त नहीं हो सकता है; पहले खिलाड़ी के पास निरंतर जीतने की रणनीति होती है (चूँकि यह प्रमेय रचनात्मक नहीं है, और 10 x 10 या अत्यधिक आयामों के बोर्ड आकार के लिए स्पष्ट रणनीतियों को पूर्ण प्रकार से विकसित नहीं किया गया है)। यह आयाम 2 के लिए ब्रौवर नियत बिंदु प्रमेय के बराबर निकला है। हेक्स के एन-आयामी संस्करणों पर विचार करके, सामान्य प्रकार से प्रमाणित कर सकता है कि ब्रौवर का प्रमेय हेक्स के लिए निर्धारक प्रमेय के बराबर है।<ref>{{cite journal|author=David Gale |year=1979|title=हेक्स और ब्रोवर फिक्स्ड-प्वाइंट प्रमेय का खेल| journal=The American Mathematical Monthly | volume=86 | pages=818–827|doi=10.2307/2320146|jstor=2320146|issue=10}}</ref> | |||
=== | === लेफ्शेट्ज़ निश्चित-बिंदु प्रमेय का उपयोग करके एक प्रमाण === | ||
लेफ्शेट्ज़ निश्चित-बिंदु प्रमेय का कहना है कि यदि परिमित साधारण परिसर B से निरंतर मानचित्र f में सिर्फ अलग-अलग निश्चित बिंदु हैं, तो गुणकों के साथ गिने गए निश्चित बिंदुओं की संख्या (जो ऋणात्मक हो सकती है) लेफ्शेट्ज़ संख्या के बराबर है | लेफ्शेट्ज़ निश्चित-बिंदु प्रमेय का कहना है कि यदि परिमित साधारण परिसर B से निरंतर मानचित्र f में सिर्फ अलग-अलग निश्चित बिंदु हैं, तो गुणकों के साथ गिने गए निश्चित बिंदुओं की संख्या (जो ऋणात्मक हो सकती है) लेफ्शेट्ज़ संख्या के बराबर है | ||
:<math>\displaystyle \sum_n(-1)^n\operatorname{Tr}(f|H_n(B))</math> | :<math>\displaystyle \sum_n(-1)^n\operatorname{Tr}(f|H_n(B))</math> | ||
और विशेष रूप से यदि लेफ्सहेट्ज़ संख्या अऋणात्मक है तो f का एक निश्चित बिंदु होना चाहिए। यदि ''B'' एक गेंद है (या अत्यधिक सामान्यतौर पर सिकुड़ा जा सकता है) तो लेफ्शेट्ज़ संख्या एक है क्योंकि सिर्फ अऋणात्मक साधारण समरूपता समूह है: <math>H_0(B)</math> और f इस समूह पर तत्समक के रूप में कार्य करता है, इसलिए f का एक निश्चित बिंदु है।<ref>{{harvnb|Hilton|Wylie|1960}}</ref><ref>{{harvnb|Spanier|1966}}</ref> | और विशेष रूप से यदि लेफ्सहेट्ज़ संख्या अऋणात्मक है तो f का एक निश्चित बिंदु होना चाहिए। यदि ''B'' एक गेंद है (या अत्यधिक सामान्यतौर पर सिकुड़ा जा सकता है) तो लेफ्शेट्ज़ संख्या एक है क्योंकि सिर्फ अऋणात्मक साधारण समरूपता समूह है: <math>H_0(B)</math> और f इस समूह पर तत्समक के रूप में कार्य करता है, इसलिए f का एक निश्चित बिंदु है।<ref>{{harvnb|Hilton|Wylie|1960}}</ref><ref>{{harvnb|Spanier|1966}}</ref> | ||
=== अप्रभावी तार्किक प्रणाली में एक प्रमाण === | |||
=== | |||
विपरीत गणित में, ब्रौवर के प्रमेय को प्रणाली WKL<sub>0</sub> में सिद्ध किया जा सकता है, और इसके विपरीत आधार प्रणाली पर वर्ग के लिए RCA<sub>0</sub> ब्रौवर प्रमेय कमजोर कोनिग लेम्मा को दर्शाता है, इसलिए यह ब्रौवर के प्रमेय की ताकत का उपयुक्त विवरण देता है। | विपरीत गणित में, ब्रौवर के प्रमेय को प्रणाली WKL<sub>0</sub> में सिद्ध किया जा सकता है, और इसके विपरीत आधार प्रणाली पर वर्ग के लिए RCA<sub>0</sub> ब्रौवर प्रमेय कमजोर कोनिग लेम्मा को दर्शाता है, इसलिए यह ब्रौवर के प्रमेय की ताकत का उपयुक्त विवरण देता है। | ||
| Line 212: | Line 184: | ||
स्पेस के बड़े वर्ग के लिए परिमित-आयामी सामान्यीकरण भी है: यदि <math>X</math> परिमित रूप से कई श्रृंखला योग्य निरंतरता का प्रोडक्ट है, फिर प्रत्येक निरंतर कार्य <math>f:X\rightarrow X</math> निश्चित बिंदु है,<ref>{{cite journal|author=Eldon Dyer |year=1956|title=एक निश्चित बिंदु प्रमेय| journal=Proceedings of the American Mathematical Society| volume=7 | pages=662–672|doi=10.1090/S0002-9939-1956-0078693-4|issue=4|doi-access=free}}</ref> जहां श्रृंखला योग्य सातत्य (सामान्य तौर पर परन्तु इस कथन में जरूरी नहीं कि [[मीट्रिक स्थान]]) सघन स्पेस [[हॉसडॉर्फ स्पेस]] है, जिसमें हर खुले कवर में परिमित खुला शोधन होता है <math>\{U_1,\ldots,U_m\}</math>, जैसे <math>U_i \cap U_j \neq \emptyset</math> और सिर्फ <math>|i-j| \leq 1</math>है। श्रृंखला योग्य निरंतरता के उदाहरणों में सघन आनुषंगिक रैखिक क्रम किए गए स्थान और विशेष रूप से वास्तविक संख्याओं के बंद अंतराल सम्मिलित हैं। | स्पेस के बड़े वर्ग के लिए परिमित-आयामी सामान्यीकरण भी है: यदि <math>X</math> परिमित रूप से कई श्रृंखला योग्य निरंतरता का प्रोडक्ट है, फिर प्रत्येक निरंतर कार्य <math>f:X\rightarrow X</math> निश्चित बिंदु है,<ref>{{cite journal|author=Eldon Dyer |year=1956|title=एक निश्चित बिंदु प्रमेय| journal=Proceedings of the American Mathematical Society| volume=7 | pages=662–672|doi=10.1090/S0002-9939-1956-0078693-4|issue=4|doi-access=free}}</ref> जहां श्रृंखला योग्य सातत्य (सामान्य तौर पर परन्तु इस कथन में जरूरी नहीं कि [[मीट्रिक स्थान]]) सघन स्पेस [[हॉसडॉर्फ स्पेस]] है, जिसमें हर खुले कवर में परिमित खुला शोधन होता है <math>\{U_1,\ldots,U_m\}</math>, जैसे <math>U_i \cap U_j \neq \emptyset</math> और सिर्फ <math>|i-j| \leq 1</math>है। श्रृंखला योग्य निरंतरता के उदाहरणों में सघन आनुषंगिक रैखिक क्रम किए गए स्थान और विशेष रूप से वास्तविक संख्याओं के बंद अंतराल सम्मिलित हैं। | ||
काकुटानी निश्चित बिंदु प्रमेय ब्रोवर निश्चित बिंदु प्रमेय को अलग दिशा में सामान्यीकृत करता है: यह R<sup>n</sup> में रहता है, परन्तु ऊपरी [[अर्ध-निरंतर]] समूह-मूल्य | काकुटानी निश्चित बिंदु प्रमेय ब्रोवर निश्चित बिंदु प्रमेय को अलग दिशा में सामान्यीकृत करता है: यह R<sup>n</sup> में रहता है, परन्तु ऊपरी [[अर्ध-निरंतर]] समूह-मूल्य फलन (फलन जो समूह के प्रत्येक बिंदु को समूह का उपसमुच्चय निर्दिष्ट करते हैं) पर विचार करता है। इसमें समूह की सघनता और उत्तलता की भी आवश्यकता होती है। | ||
लेफ्सहेट्ज़ निश्चित-बिंदु प्रमेय (लगभग) स्वैच्छिक सघन संस्थिति स्पेस पर क्रियान्वित होता है, और एकवचन समजतता के संदर्भ में शर्त देता है जो निश्चित बिंदुओं के अस्तित्व निश्चित होता है; D''<sup>n</sup>'' के कथन में किसी भी मानचित्र के लिए यह स्थिति नगण्य रूप से संतुष्ट है। | लेफ्सहेट्ज़ निश्चित-बिंदु प्रमेय (लगभग) स्वैच्छिक सघन संस्थिति स्पेस पर क्रियान्वित होता है, और एकवचन समजतता के संदर्भ में शर्त देता है जो निश्चित बिंदुओं के अस्तित्व निश्चित होता है; D''<sup>n</sup>'' के कथन में किसी भी मानचित्र के लिए यह स्थिति नगण्य रूप से संतुष्ट है। | ||
| Line 220: | Line 192: | ||
== यह भी देखें == | == यह भी देखें == | ||
* बैनाच | * बैनाच निश्चित-बिंदु प्रमेय | ||
* [[विश्लेषणात्मक कार्यों की अनंत रचनाएँ]] | * [[विश्लेषणात्मक कार्यों की अनंत रचनाएँ|विश्लेषणात्मक फलन की अनंत रचनाएँ]] | ||
* नैश | * नैश समतुल्यता | ||
* पोंकारे-मिरांडा प्रमेय - ब्रोवर | * पोंकारे-मिरांडा प्रमेय-ब्रोवर निश्चित-बिंदु प्रमेय के बराबर | ||
* [[टोपोलॉजिकल कॉम्बिनेटरिक्स]] | * [[टोपोलॉजिकल कॉम्बिनेटरिक्स|संस्थितिकी साहचर्य]] | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
| Line 267: | Line 239: | ||
{{Authority control}} | {{Authority control}} | ||
{{DEFAULTSORT:Brouwer Fixed Point Theorem}} | {{DEFAULTSORT:Brouwer Fixed Point Theorem}} | ||
[[Category: | [[Category:CS1 Deutsch-language sources (de)|Brouwer Fixed Point Theorem]] | ||
[[Category:Created On 28/02/2023]] | [[Category:CS1 français-language sources (fr)|Brouwer Fixed Point Theorem]] | ||
[[Category:CS1 русский-language sources (ru)|Brouwer Fixed Point Theorem]] | |||
[[Category:Created On 28/02/2023|Brouwer Fixed Point Theorem]] | |||
[[Category:Fixed points (mathematics)|Brouwer Fixed Point Theorem]] | |||
[[Category:Lua-based templates|Brouwer Fixed Point Theorem]] | |||
[[Category:Machine Translated Page|Brouwer Fixed Point Theorem]] | |||
[[Category:Pages with script errors|Brouwer Fixed Point Theorem]] | |||
[[Category:Short description with empty Wikidata description|Brouwer Fixed Point Theorem]] | |||
[[Category:Templates Vigyan Ready|Brouwer Fixed Point Theorem]] | |||
[[Category:Templates that add a tracking category|Brouwer Fixed Point Theorem]] | |||
[[Category:Templates that generate short descriptions|Brouwer Fixed Point Theorem]] | |||
[[Category:Templates using TemplateData|Brouwer Fixed Point Theorem]] | |||
[[Category:Webarchive template wayback links|Brouwer Fixed Point Theorem]] | |||
[[Category:उत्तल ज्यामिति में प्रमेय|Brouwer Fixed Point Theorem]] | |||
[[Category:टोपोलॉजी में प्रमेय|Brouwer Fixed Point Theorem]] | |||
[[Category:निरंतर कार्यों का सिद्धांत|Brouwer Fixed Point Theorem]] | |||
[[Category:फिक्स्ड-पॉइंट प्रमेय|Brouwer Fixed Point Theorem]] | |||
Latest revision as of 17:14, 29 August 2023
ब्रोवर फिक्स्ड-पॉइंट प्रमेय संस्थिति में निश्चित-बिंदु प्रमेय है, जिसका नामकरण लुइट्ज़ेन एगबर्टस जन ब्रोवर के नाम पर किया गया है। यह बताता है कि किसी भी निरंतर फलन के लिए सघनता उत्तल समूह को मापने के लिए बिंदु जैसे कि है। निरंतर कार्यों के लिए है बंद अंतराल से से स्वयं का वास्तविक संख्या में या बंद डिस्क से का स्वयं से कार्य करना, ब्रोवर के प्रमेय का सबसे सरलतम रूप है। उत्तल संकुचित उपसमुच्चय से निरंतर फलन के लिए उत्तरार्द्ध की समानता में यूक्लिडियन स्पेस अत्यधिक सामान्य रूप है।
आंशिक रूप से गणित के कई क्षेत्रों में इसके उपयोग के कारण ब्रोवर का निश्चित बिंदु प्रमेय सैकड़ो अन्य निश्चित बिंदु प्रमेयो के मध्य सर्वाधिक प्रसिद्ध है। अपने मूल क्षेत्र में, जॉर्डन वक्र प्रमेय, हेयरी बॉल प्रमेय, आयाम का व्युत्क्रम और बोरसुक-उलम प्रमेय के साथ ही यह युक्लेडियन स्पेस संस्थिति की विशेस्ता वाले प्रमेयो में से एक है।[1] यह इसे संस्थिति के मूलभूत प्रमेयों में स्थान देता है।[2] इस प्रमेय का उपयोग अवकल समीकरणों के बारे में गहरे परिणाम प्रमाणित करने के लिए भी किया जाता है और अवकल ज्यामिति पर अधिकांश परिचयात्मक पाठ्यक्रमों में सम्मलित किया जाता है। यह क्रीड़ा सिद्धांत जैसे असंभावित क्षेत्रों में प्रकट होता है। अर्थशास्त्र में, ब्रौवर की निश्चित-बिंदु प्रमेय और इसका विस्तार, काकुटानी निश्चित-बिंदु प्रमेय, 1950 के दशक में अर्थशास्त्र नोबेल पुरस्कार विजेता केनेथ एरो और जेरार्ड डेब्रू द्वारा विकसित बाजार अर्थव्यवस्थाओं में सामान्य संतुलन के अस्तित्व के प्रमाण में एक केंद्रीय भूमिका निभाते हैं।
फ़्रांसिसी गणितज्ञों हेनरी पॉइनकेयर और चार्ल्स एमिल पिकार्ड के द्वारा अवकल समीकरणों पर फलन को ध्यान में रखते हुए प्रमेय का सबसे पहले अध्ययन किया गया था। पॉइंकेयर-बेंडिक्ससन प्रमेय जैसे परिणाम प्रमाणित करने के लिए संस्थितिक विधियों के उपयोग की आवश्यकता होती है। 19वीं शताब्दी के अंत में यह कार्य प्रमेय के कई क्रमिक संस्करणों के रूप में खुल गया। n-डायमेंशनल क्लोज्ड बॉल को अलग-अलग मापने के कथन को पहली बार 1910 में जैक्स हैडमार्ड ने सिद्ध किया था[3] और 1911 में ब्रोवर द्वारा निरंतर मानचित्रण के सामान्य घटना को सिद्ध किया गया है। [4]
कथन
प्रमेय के कई सूत्र हैं, यह इसके उपयोग और इसके सामान्यीकरण की परिमाण के सन्दर्भ पर निर्भर करता है। सबसे सरलतम निम्नानुसार दिया गया है:
- समतल में
- बंद समूह से प्रत्येक निरंतर फलन टोपोलॉजी (संस्थिति) में कम से कम एक निश्चित बिंदु होता है।[5]
यह विवेकाधीन परिमित आयाम के लिए सामान्यीकृत किया जा सकता है:
थोड़ा और सामान्य संस्करण इस प्रकार है:[7]
एक और भी सामान्य रूप अलग नाम के द्वारा जाना जाता है:
- स्काउडर निश्चित बिंदु प्रमेय
- बैनक स्पेस के उत्तल सघन उपसमुच्चय K से K तक प्रत्येक निरंतर फलन में एक निश्चित बिंदु होता है।[9]
पूर्व शर्तों का महत्व
प्रमेय सिर्फ उन फलनों के लिए है जो अंतःरूपता हैं (फलन जो प्रान्त और सहप्रांत के समान समुच्चय हैं) और उन समुच्चयो के लिए जो सघन (इस प्रकार, विशेष रूप से, बंधे और बंद) और उत्तल (या होमोमोर्फिज्म से उत्तल) है निम्नलिखित उदाहरण बताते हैं कि पूर्व-शर्तें क्यों महत्वपूर्ण हैं।
एक एंडोमोर्फिज्म (अन्तःरूपता) के रूप में फलन f
प्रान्त [-1,1] के साथ फलन पर विचार करे। फलन का परिसर [0,2] है। इस प्रकार, f एंडोमोर्फिज्म नहीं है।
सीमाबद्धता
फलन पर विचार करे
जो सतत फलन है। चूंकि यह सभी बिंदु को दाईं ओर स्थानांतरित करता है, इसलिए इसका कोई निश्चित बिंदु नहीं हो सकता है। स्पेस उत्तल और बंद है, परन्तु बद्ध नहीं है।
बंद स्तिथि
फलन पर विचार करे
जो मुक्त अंतराल (-1,1) से स्वयं एक सतत फलन है। चूंकि x = 1 अंतराल का भाग नहीं है, f(x) = x का कोई निश्चित बिंदु नहीं है। स्पेस (−1,1) उत्तल और घिरा हुआ है, परन्तु बंद नहीं है। दूसरी तरफ, फलन f का बंद अंतराल [−1,1] के लिए एक निश्चित बिंदु है, अर्थात् f(1) = 1 है।
उत्तलता
बीएफपीटी के लिए उत्तलता अत्यधिक आवश्यक नहीं है। क्योंकि सम्मलित गुण (निरंतरता, एक निश्चित बिंदु होने की वजह से) होमोमोर्फिज्म के अनुसार अपरिवर्तनीय हैं, बीएफपीटी उन रूपों के बराबर है जिनमें प्रान्त को बंद इकाई बॉल का होना आवश्यक है। समान कारण से यह प्रत्येक समुच्चय जो बंद बॉल के लिए होमोमॉर्फिक है के लिए क्रियान्वित होता है (और इसलिए बंद समूह, सीमित, जुड़ा हुआ स्थान, बिना छिद्र का इत्यादि उपस्थित है)।
निम्नलिखित उदाहरण से पता चलता है कि बीएफपीटी छिद्र वाले प्रान्त के लिए कार्य नहीं करता है। फलन पर विचार करे, जो इकाई वृत्त से स्वयं तक सतत कार्य है। चूंकि इकाई वृत्त के किसी भी बिंदु के लिए -x≠x है, f का कोई निश्चित बिंदु नहीं है। अनुरूप उदाहरण एन-आयामी क्षेत्र (या कोई सममित प्रान्त जिसमें मूल उपस्थित नहीं है) के लिए कार्य करता है। इकाई वृत्त बंद और घिरा हुआ है, परन्तु इसमें एक छिद्र है (और इसलिए यह उत्तल नहीं है)। फलन f इकाई डिस्क के लिए एक निश्चित बिंदु है, क्योकि ये इसी से उत्पन्न होता है ।
"छिद्र-मुक्त" (होल -फ्री) प्रान्त के लिए बीएफपीटी का एक औपचारिक सामान्यीकरण लेफ्सेटज़ निश्चित-बिंदु प्रमेय से प्राप्त किया जा सकता है।[10]
टिप्पणियाँ
इस प्रमेय में फलन का द्विभाजित या फिर विशिस्ट होना आवश्यक नहीं है।
चित्र
प्रमेय में वास्तविक दुनिया के कई उदाहरण हैं। यहां कुछ उदाहरण दिए गए हैं।
- समान आकार के ग्राफ पेपर की दो पन्ने लें, उन पर समन्वय प्रणाली के साथ, टेबल पर समतल बिछाएं और दूसरे को (बिना चीर-फाड़ या फाड़े) समेट लें और इसे किसी भी प्रकार से पहले के ऊपर रखना है। क्रुम्प्लेड कागज समतल वाले के बाहर नहीं पहुंचता है। तब क्रुम्प्लेड (तुड़ा मुड़ा) पन्ने का कम से कम एक बिंदु होगा जो समतल पन्ने के संबंधित बिंदु (अर्थात समान निर्देशांक वाला बिंदु) के ठीक ऊपर स्थित होगा। यह ब्रौवर के प्रमेय के n = 2 कथन का परिणाम है जो निरंतर मानचित्र पर क्रियान्वित होता है जो क्रुम्प्लेड पन्ने के प्रत्येक बिंदु के निर्देशांक को उसके ठीक नीचे समतल पन्ने के बिंदु के निर्देशांक प्रदान करता है।
- किसी देश का साधारण मानचित्र लें, और मान लें कि वह मानचित्र उस देश के अंदर एक मेज पर रखा हुआ है। मानचित्र पर निरंतर आप यहां हैं बिंदु होगा जो देश में उसी बिंदु का प्रतिनिधित्व करता है।
- तीन आयामों में ब्रोवर फिक्स्ड-पॉइंट प्रमेय का परिणाम यह है कि, भले आप एक गिलास में स्वादिष्ट कॉकटेल को कितना भी हिलाएं (या मिल्क शेक के बारे में सोचें), जब तरल को स्थिर अवस्था में आना होगा, तरल में कुछ बिंदु होगा यह मानते हुए कि प्रत्येक बिंदु की अंतिम स्थिति अपनी मूल स्थिति का निरंतर फलन है, कि ग्लॉस हिलाने के बाद तरल मूल रूप से इसके द्वारा लिए गए स्थान के भीतर समाहित है, यह मानते हुए ग्लास में ठीक उसी स्थान पर समाप्त होता है, जैसा कि आपने कोई कार्य करने से पहले पाया था, तथा कांच (और हिलाई हुई सतह का आकार) उत्तल आयतन बनाए रखता है। कॉकटेल को हिलाना, हिलाया नहीं जाना उत्तलता की स्थिति में गलत सिद्ध हो जाता है (झटकों को ढक्कन के नीचे खाली हेडस्पेस में गैर-उत्तल जड़त्वीय रोकथाम की गतिशील श्रृंखला के रूप में परिभाषित किया जाता है)। उस स्थिति में, प्रमेय क्रियान्वित नहीं होगा, और इस प्रकार तरल स्वभाव के सभी बिंदु मूल अवस्था से संभावित रूप से विस्थापित हो जाते हैं।
सहज दृष्टिकोण
ब्रूवर को दिया गया स्पष्टीकरण
माना जाता है कि प्रमेय की उत्पत्ति एक कप गोरमेट कॉफी के ब्रौवर के अवलोकन से हुई है।[11] यदि कोई चीनी की गांठ को घोलता है, तो ऐसा प्रतीत होता है कि निरंतर गतिहीन बिंदु होता है। उन्होंने निष्कर्ष निकाला कि किसी भी समय, सतह पर बिंदु है जो गतिमान नहीं है।[12] निश्चित बिंदु अनिवार्य रूप से वह बिंदु नहीं है जो गतिहीन प्रतीत होता है, क्योंकि विक्षोभ का केंद्र थोड़ा हिलता है। परिणाम सहज नहीं है, क्योंकि एक और निश्चित बिंदु दिखाई देने पर मूल निश्चित बिंदु गतिमान हो सकता है।
ब्रोवर ने कहा है की: मैं इस अद्भुत परिणाम को अलग-अलग बना सकता हूं, मैं एक क्षैतिज पन्ने लेता हूं, और एक दूसरा समान जिसे मैं समेटता हूं, चपटा करता हूं और दूसरे पर रखता हूं। तब क्रुम्प्लेड पन्ना का बिंदु उसी स्थान पर होता है जैसे दूसरी पन्ने पर होता है।[12] ब्रौवर सिलवटों को हटाए बिना अपनी चादर को सपाट लोहे की तरह चपटा कर देता है। कॉफी कप उदाहरण के विपरीत, क्रुम्प्लेड पन्ना उदाहरण भी दर्शाता है कि एक से अत्यधिक निश्चित बिंदु स्थित हो सकते हैं। यह ब्रोवर के परिणाम को अन्य निश्चित-बिंदु प्रमेयों से भिन्न है, जैसे कि स्टीफन बानाच, जो अद्वितीयता का आश्वासन देता है।
एक विमीय प्रकरण
विमीय में, परिणाम सहज और सिद्ध करने में सरल है। सतत फलन f को बंद अंतराल [a, b] पर परिभाषित किया गया है और उसी अंतराल में स्थान लेता है। यह कहना कि इस फलन का निश्चित बिंदु है, यह कहने के बराबर है कि इसका ग्राफ़ (दाहिने तरफ की आकृति में गहरा हरा) समान अंतराल [a, b] पर परिभाषित फलन को काटता है जो x से x (हल्का हरा) मापता है।
सहज रूप से, वर्ग के बाएँ किनारे से दाएँ किनारे तक कोई भी निरंतर रेखा आवश्यक रूप से हरे रंग के विकर्ण को काटती है। इसे सिद्ध करने के लिए, फलन g पर विचार करें जो x को f(x) − x से मापता है। यह a पर ≥ 0 और b पर ≤ 0 है। मध्यवर्ती मान प्रमेय के अनुसार, g का [a, b] में एक फलन का मूल है; यह शून्य एक निश्चित बिंदु है।
कहा जाता है कि ब्रोवर ने इसे इस प्रकार व्यक्त किया: सतह की जांच करने के बदले, हम प्रमेय को स्ट्रिंग के टुकड़े के बारे में सिद्ध करेंगे। स्ट्रिंग को बिना मुड़ी हुई अवस्था में प्रारम्भ करें, फिर इसे दोबारा मोड़ देना है। हम दोबारा मोड़ी गयी स्ट्रिंग को चपटा करेंगे। स्ट्रिंग के बिंदु ने बिना मुड़ी हुई स्ट्रिंग पर अपनी मूल स्थिति के संबंध में अपनी स्थिति नहीं बदलती है।[12]
इतिहास
ब्रौवर निश्चित बिंदु प्रमेय बीजगणितीय संस्थिति की प्रारंभिक उपलब्धियों में से एक था, और अत्यधिक सामान्य निश्चित बिंदु प्रमेयों का आधार है जो कार्यात्मक विश्लेषण में महत्वपूर्ण हैं। कथन n = 3 पहली बार 1904 में पियर्स बोहल द्वारा सिद्ध किया गया था (फुर्र दे रिने युन्द एंगेवैनदते माथेमैटिक नामक पत्रिका में प्रकाशित)।[13] इसे बाद में लुइट्ज़ेन एगबर्टस जान ब्रोवर एल द्वारा 1909 में सिद्ध किया गया था।1910 में जैक्स हैडमार्ड ने सामान्य कथनो को सिद्ध किया है,[3]और उसी वर्ष ब्रोवर को एक अलग प्रमाण मिला था।[4] चूँकि ये प्रारंभिक प्रमाण सभी रचनात्मक प्रमाण थेl चूँकि रचनावाद (गणित) के अर्थ में एक निश्चित बिंदु का अस्तित्व रचनात्मक नहीं है, ब्रोवर के प्रमेय द्वारा निश्चित अनुमानित सिद्धांत निश्चित बिंदुओं के प्रकारो के नाम से जाना जाता है।[14][15]
प्रागितिहास
ब्रोवर के निश्चित बिंदु प्रमेय के प्रागितिहास को समझने के लिए अवकल समीकरणों को ध्यान देने की आवश्यक्ता है। 19 वीं सदी के अंत में, पुरानी समस्या[16] सौर मंडल की स्थिरता गणितीय समुदाय के ध्यान में लौट आई है।[17]
इसके समाधान के लिए नए प्रकारों की आवश्यकता थी। जैसा कि तीन-पिंड की समस्या पर कार्य करने वाले हेनरी पोंकारे ने उल्लेख किया है, सही समाधान ढूंढने की कोई आशा नहीं है: हमें तीन-पिंड की समस्या की कठोरता और साधारणतया सभी समस्याओं के बारे में विचार देने के लिए कुछ भी अत्यधिक उचित नहीं है। गतिकी जहां कोई समान अभिन्न नहीं है और बोहलिन श्रृंखला विचलन करती है।[18] उन्होंने यह भी कहा कि अनुमानित समाधान की खोज अत्यधिक कुशल नहीं है: जितना अत्यधिक हम लगभग बिलकुल ठीक प्राप्त करना चाहते हैं, उतना ही अत्यधिक परिणाम बढ़ती हुई अशुद्धि की ओर बढ़ जाएगा।[19] उन्होंने एक कप कॉफी में सतह की गति के समान प्रश्न का अध्ययन किया है। सामान्य रूप से, हम निरंतर प्रवाह (गणित) द्वारा अनुप्राणित सतह पर प्रक्षेपवक्र के बारे में क्या कह सकते हैं?[20] पोनकारे ने पाया कि उत्तर उस क्षेत्र में पाया जा सकता है जिसे अब हम प्रक्षेपवक्र वाले क्षेत्र में संस्थिति गुण कहते हैं। यदि यह क्षेत्र सघन स्थान है, अर्थात बंद समूह और बंधा हुआ समूह दोनों, तो प्रक्षेपवक्र या तो स्थिर हो जाता है, या यह एक सीमा चक्र तक पहुंच जाता है।[21] पोंकारे और आगे बढ़े; यदि क्षेत्र डिस्क के समान प्रकार का है, जैसा कि कॉफी के कप के स्थिति में है, तो निश्चित रूप से एक निश्चित बिंदु होना चाहिए। यह निश्चित बिंदु उन सभी कार्यों के अंतर्गत अपरिवर्तनीय है जो मूल सतह के प्रत्येक बिंदु से इसकी स्थिति को थोड़े समय के अंतराल t के बाद जोड़ते हैं। यदि क्षेत्र एक गोलाकार पट्टी है, या यह बंद नहीं है,[22] तो यह आवश्यक नहीं है।
अवकल समीकरणों को सही ढंग से समझने के लिए गणित की एक नई शाखा का जन्म हुआ। पॉइनकेयर ने इसे एनालिसिस साइटस कहा है। फ्रांसीसी एनसाइक्लोपीडिया यूनिवर्सलिस इसे उस शाखा के रूप में परिभाषित करता है जो किसी वस्तु के गुणों का इलाज करता है जो अपरिवर्तनीय है। यदि यह किसी भी निरंतर प्रकार से बिना फाडे विकृत होता है।[23] 1886 में, पोंकारे ने एक परिणाम सिद्ध किया जो ब्रोवर के निश्चित-बिंदु प्रमेय के समान है,[24] चूँकि इस लेख के विषय के साथ संबंध अभी तक स्पष्ट नहीं हुआ था।[25] थोड़ी देर बाद, उन्होंने विश्लेषण साइटस को सही ढंग से समझने के लिए मूलभूत उपकरणों में से विकसित किया, जिसे अब मूल समूह या कभी-कभी पोंकारे समूह के रूप में जाना जाता है।[26] इस पद्धति का उपयोग चर्चा के अंतर्गत प्रमेय के एक बहुत ही संक्षिप्त प्रमाण के लिए किया जा सकता है पोनकारे की पद्धति चार्ल्स एमिल पिकार्ड के अनुरूप थी, जो उनके समकालीन गणितज्ञ थे जिन्होंने कॉची-लिप्सचिट्ज़ प्रमेय को सामान्यीकृत किया था।[27] पिकार्ड का दृष्टिकोण एक परिणाम पर आधारित है जिसे बाद में बानाच फिक्स्ड-पॉइंट प्रमेय द्वारा औपचारिक रूप दिया गया है, जिसका नाम स्टीफन बानाच के नाम पर रखा गया है। प्रान्त के सामयिक गुणों के अतिरिक्त, यह प्रमेय इस तथ्य का उपयोग करता है कि विचाराधीन कार्य सघन मानचित्रण है।
पहला प्रमाण
20वीं सदी की प्रारम्भ में, विश्लेषण विपरीत स्थान किसी का ध्यान नहीं गया है। चूँकि, इस आलेख में बताई गई प्रमेय के बराबर प्रमेय की आवश्यकता अभी तक स्पष्ट नहीं थी। लातवियाई गणितज्ञ पियर्स बोहल ने अंतर समीकरणों के अध्ययन के लिए सांस्थितिकीय विधियों को क्रियान्वित किया है।[28] 1904 में उन्होंने हमारे प्रमेय के त्रि-आयामी सन्दर्भों को सिद्ध किया है,[13] परन्तु उनके प्रकाशन पर ध्यान नहीं दिया गया है।[29]
यह ब्रौवर था, अंत में, जिसने प्रमेय को श्रेष्ठता का प्रथम अधिकार दिया है। उनके लक्ष्य पोंकारे से भिन्न थे। यह गणितज्ञ गणित की आधार, विशेष प्रकार से गणितीय तर्क और टोपोलॉजी से प्रेरित था। उनकी प्रारंभिक रुझान हिल्बर्ट की पांचवीं समस्या को सिद्ध करने के प्रयास में थी।[30] 1909 में, पेरिस की यात्रा के समय, उनकी मुलाकात हेनरी पोंकारे, जैक्स हैडमार्ड और एमिल बोरेल से हुई। भविष्य में होने वाले बातचीत यूक्लिडियन स्पेस की सही समझ के महत्व के ब्रोवर को प्रोत्साहित किया, और हैडमार्ड के साथ पत्रों के उपयोगी आदान-प्रदान की उत्पत्ति थी। अगले चार वर्षों तक, उन्होंने इस प्रश्न पर विशेष प्रमेयों के प्रमाण पर ध्यान केंद्रित किया है। 1912 में उन्होंने द्वि-आयामी क्षेत्र के लिए हेरी बॉल प्रमेय को सिद्ध किया, साथ ही इस तथ्य को भी सिद्ध किया कि द्वि-आयामी गेंद से लेकर स्वयं तक प्रत्येक निरंतर मानचित्र का निश्चित बिंदु होता है।[31] अपने आप में ये दो परिणाम वास्तव में नए नहीं थे। जैसा कि हैडमार्ड ने देखा, पोंकारे ने बालों वाली गेंद प्रमेय के बराबर एक प्रमेय दिखाया था।[32] ब्रौवर के दृष्टिकोण का क्रांतिकारी परिणाम वर्तमान में ही विकसित उपकरण जैसे होमोटॉपी, पोंकारे समूह की अंतर्निहित अवधारणा का उनका व्यवस्थित उपयोग था। अगले वर्ष में, हैडमर्ड ने प्रमेय को स्वेच्छाकारी परिमित आयाम पर बातचीत के अंतर्गत सामान्यीकृत किया गया है, परन्तु उन्होंने विभिन्न प्रकारों को नियोजित किया है। हंस फ्रायडेंथल संबंधित आधारों पर निम्नानुसार टिप्पणी करते हैं: ब्रोवर के क्रांतिकारी प्रकारों के सामान में, हैडमर्ड के लोग बहुत पारंपरिक थे, परन्तु ब्रोवर के विचारों के जन्म में हैडमार्ड की का सिद्धांत एक धाय की तरह महत्वपूर्ण भूमिका निभाया है।[33] ब्रोवर के दृष्टिकोण ने अपना फल दिया, और 1910 में उन्हें प्रमाण भी मिला जो किसी भी परिमित आयाम के लिए मान्य था,[4]साथ ही अन्य प्रमुख प्रमेय जैसे कि आयाम का व्युत्क्रम हैं।[34] इस कार्य के संदर्भ में, ब्रौवर ने स्वेच्छारी आयाम के लिए जॉर्डन वक्र प्रमेय को भी सामान्यीकृत किया और निरंतर मानचित्रण की डिग्री से जुड़े गुणों को स्थापित किया है।[35] गणित की इस शाखा, मुख्य प्रकार से पॉइनकेयर द्वारा परिकल्पित और ब्रौवर द्वारा विकसित, ने अपना नाम बदल दिया है। 1930 के दशक में, विश्लेषण स्थल बीजगणितीय टोपोलॉजी बन गया है।[36]
रिसेप्शन

प्रमेय ने एक से अत्यधिक प्रकारों से अपना मूल्य सिद्ध किया है। 20वीं शताब्दी के समय कई निश्चित-बिंदु प्रमेय विकसित किए गए थे, और यहां तक कि गणित की शाखा को निश्चित-बिंदु सिद्धांत कहा जाता है।[37]
ब्रौवर प्रमेय संभवतः सबसे महत्वपूर्ण है।[38] यह संस्थिति मूलभूत प्रमेयों में से एक है और अधिकांशतः जॉर्डन वक्र प्रमेय जैसे महत्वपूर्ण परिणामो को प्रमाणित करने के लिए प्रयोग जाता है।[39] अत्यधिक या कम संकुचन मानचित्रण फलन के लिए निश्चित-बिंदु प्रमेय के अतिरिक्त, कई ऐसे हैं जो प्रत्यक्ष या अप्रत्यक्ष रूप से बातचीत के परिणाम से सामने आये हैं। युक्लीडियन स्पेस की बंद गेंद से इसकी सीमा से सतत नक्शा सीमा पर पहचान नहीं हो सकता है। इसी प्रकार बोरसुक-उलम प्रमेय कहता है की एन-आयामी क्षेत्र से Rn तक सतत नक्शा में प्रतिलोम-संबंधी बिंदुओं की एक जोड़ी होती है जो एक ही बिंदु पर मैप की जाती है। परिमित-आयामी कथन में, 1926 से लेफ्शेट्ज़ के नियत-बिंदु प्रमेय निश्चित बिंदुओं की गणना के लिए विधि प्रदान करता है।
1930 में, ब्रौवर के निश्चित-बिंदु प्रमेय को बांच स्पेस के लिए सामान्यीकृत किया गया है।[40] इस सामान्यीकरण को अनंत-आयामी स्थानों में निश्चित-बिंदु प्रमेय के रूप में जाना जाता है। शाउडर की निश्चित-बिंदु प्रमेय, एस. काकुटानी द्वारा समूह-मूल्य फलन के लिए सामान्यीकृत परिणाम होता है।[41] संस्थिति के बाहर प्रमेय और इसके रूपों से भी मिलता है। इसका उपयोग हार्टमैन-ग्रोबमैन प्रमेय को प्रमाणित करने के लिए किया जा सकता है, जो निश्चित संतुलन के पास कुछ अंतर समीकरणों के गुणात्मक व्यवहार का वर्णन करता है। इसी प्रकार, केंद्रीय सीमा प्रमेय के प्रमाण के लिए ब्रोवर के प्रमेय का उपयोग किया जाता है। कुछ आंशिक अंतर समीकरणों के समाधान के लिए प्रमेय को अस्तित्व प्रमाण में भी पाया जा सकता है।[42] अन्य क्षेत्रों को भी ध्यान में रखा जाता है। गेम सिद्धांत में, जॉन फोर्ब्स नैश ने यह प्रमाणित करने के लिए प्रमेय का उपयोग किया कि हेक्स (बोर्ड गेम) के खेल में सफेद के लिए जीतने की रणनीति है।[43] अर्थशास्त्र में, पी. बिच बताते हैं कि प्रमेय के कुछ सामान्यीकरण से पता चलता है कि इसका उपयोग गेम प्रमेय में कुछ प्रतिष्ठित समस्याओं और सामान्यतौर पर संतुलन (होटेलिंग का नियम), वित्तीय संतुलन और अपूर्ण बाजारों के लिए सहायक है।[44] ब्रौवर की पहचान विशेष रूप से उनके सांस्थितिकीय कार्य के कारण नहीं है। उनके महान सामयिक प्रमेय के प्रमाण रचनात्मक प्रमाण हैं,[45] और ब्रोवर के इस पर असंतोष ने आंशिक रूप से उन्हें रचनावाद (गणित) के विचार को स्पष्ट करने के लिए प्रेरित किया है। वह गणित को औपचारिक रूप देने के प्रकार के प्रवर्तक और उत्साहपूर्वक समर्थक बन गए, जिसे अंतर्ज्ञानवादी तर्क के रूप में जाना जाता है, जिसने उस समय निर्धारित सिद्धांत के विरोध में कारण दिया था।[46] ब्रोवर ने निश्चित-बिंदु प्रमेय के अपने मूल प्रमाण को अस्वीकार कर दिया था। निश्चित बिंदु का अनुमान लगाने वाला पहला एल्गोरिथम हर्बर्ट स्कार्फ द्वारा प्रस्तावित किया गया था।[47] स्कार्फ के बीजगणित का सूक्ष्म कारण यह है कि यह एक बिंदु पाता है जो है जो लगभग निश्चित फलन एफ द्वारा, परन्तु सामान्य प्रकार से बिंदु नहीं मिल सकता है जो वास्तविक निश्चित बिंदु के निकट है। गणितीय भाषा में, यदि ε को बहुत छोटा चुना गया है, स्कार्फ के बीजगणित का उपयोग बिंदु x को ढूंढने के लिए किया जा सकता है जैसे कि f(x) x के बहुत निकट है, अर्थात, है, परन्तु स्कार्फ के बीजगणित का उपयोग बिंदु x को ढूंढने के लिए नहीं किया जा सकता है जैसे कि x एक निश्चित बिंदु के बहुत निकट है: हम आश्वाशन नहीं दे सकते जहाँ है अधिकांशतः यह बाद की स्थिति एक निश्चित बिंदु का अनुमान लगाने वाले अनौपचारिक वाक्यांश का अर्थ है।
प्रमाण की रूपरेखा
अंश का उपयोग करके एक प्रमाण
ब्रौवर का मूल 1911 का प्रमाण एक निरंतर मानचित्रण की डिग्री की धारणा पर निर्भर करता है, जो विभेदक टोपोलॉजी में विचारों से उपजा है। प्रमाण के कई आधुनिक अभिलेख साहित्य में पाए जा सकते हैं, विशेष रूप से मिलनर (1965).[48][49]माना की बंद इकाई बॉल को निरूपित करें मूल पर केन्द्रित है। संकुचित करने के लिए माना कि निरन्तर अवकलनीय है। नियमित मूल्य बिन्दु है जैसे कि जेकोबियन मैट्रिक्स और निर्धारक की पूर्वकल्पना के प्रत्येक बिंदु p पर एकल नहीं है। विशेष रूप से, व्युत्क्रम कार्य प्रमेय द्वारा, प्रत्येक बिंदु की पूर्वकल्पना में निहित है |
(आंतरिक भाग ) अंश का नियमित मूल्य पर के जैकोबियन निर्धारक के संकेतों के योग के रूप में परिभाषित किया गया है के पूर्वापेक्षाओं पर के अंतर्गत :
डिग्री, सामान्यतया यह दर्शा रही है की, p के चारों ओर प्राइमेज f का एक छोटे से खुले समुच्चय पर रखे गए पन्नो की संख्या, विपरीत दिशा में गिने जाने वाली पन्नो के साथ होती है। इस प्रकार यह उच्च आयामों के लिए वाइंडिंग संख्या का सामान्यीकरण है।
डिग्री होमोटॉपी इनवेरियन की निर्देशों को संतुष्ट करती है: माना और दो लगातार अलग-अलग कार्य हो, और के लिए . मान लीजिए कि बिंदु , सभी t के लिए का नियमित मान है। तब होता है।
यदि की सीमा का कोई निश्चित बिंदु नहीं है ,तब फलन
अच्छे से परिभाषित है, और
तत्समक फलन से समरूपता को परिभाषित करता है। विशेषतः तत्समक फलन मूल में डिग्री एक है, इसलिए मूल में डिग्री भी है। जिस कारण से, प्रीइमेज खाली नहीं है। के तत्त्व वास्तविक फलन के निश्चित बिंदु के रूप में होते है।
डिग्री की परिभाषा को च के एकवचन मूल्यों और फिर निरंतर कार्यों तक विस्तारित किया जाना चाहिए। समरूपता सिद्धांत का अधिक आधुनिक आगमन डिग्री के निर्माण को सरल करता है, और इसलिए यह साहित्य में एक मानक प्रमाण बन गया है।
हेयरी बॉल प्रमेय का उपयोग करके सिद्ध करना
हेयरी बॉल प्रमेय के अनुसार इकाई क्षेत्र पर S एक विषम-आयामी यूक्लिडियन स्पेस में, कहीं नहीं गायब होने वाला निरंतर स्पर्शरेखा सदिश क्षेत्र w पर S नहीं है। (स्पर्श स्थिति का अर्थ है कि w(x) ⋅ x = 0 प्रत्येक इकाई वेक्टर के लिए x।) कभी-कभी प्रमेय को इस कथन द्वारा व्यक्त किया जाता है कि ग्लोब पर हमेशा एक जगह होती है जिसमें हवा नहीं होती है। हेयरी बॉल प्रमेय का एक प्रारंभिक प्रमाण Milnor (1978) के सिद्धांत में पाया जा सकता है।
वास्तव में, पहले मान लीजिए w निरंतर अवकलनीय है। स्केलिंग करके, यह माना जा सकता है w सतत अवकलनीय इकाई स्पर्शरेखा सदिश S है। इसे रेडियल रूप से A का S छोटे गोलाकार खोल तक बढ़ाया जा सकता है। t के लिए पर्याप्त रूप से छोटा, नियमित संगणना से पता चलता है कि मैपिंग ft(x) = t x + w(x) एक संकुचन मानचित्रण है A और इसकी इमेज का आयतन बहुपद t है। दूसरी तरफ, संकुचन मानचित्रण के रूप में, ft के सामान्य स्तर तक ही S पर सीमित होना चाहिए (1 + t2)½ S और A पर (1 + t2)½ A. यह एक विरोधाभास देता है, क्योंकि यदि आयाम n यूक्लिडियन स्थान का विषम है, (1 + t2)n/2 बहुपद नहीं है।
यदि w सिर्फ S पर निरंतर इकाई स्पर्शरेखा सदिश है, वेअरस्ट्रास लगभग प्रमेय के द्वारा, इसे बहुपद मानचित्र द्वारा समान रूप से u को A यूक्लिडियन स्पेस में अनुमानित किया जाता है। स्पर्शरेखीय स्पेस पर समकोणीय निरूपण द्वारा v(x) = u(x) - u(x) ⋅ x दिया गया है। इस प्रकार v बहुपद है और A पर कही स्थान नहीं पाता है; निर्माण द्वारा v/||v|| एक निरंतर इकाई स्पर्शरेखा S का खंडन सदिश क्षेत्र है।
हेयरी बॉल प्रमेय का निरंतर संस्करण अब ब्रौवर निश्चित बिंदु प्रमेय सिद्ध करने के लिए उपयोग किया जा सकता है। मान लीजिए n विसम है। यदि कोई निश्चित-बिंदु-मुक्त निरंतर स्व-मानचित्रण होता f बंद इकाई बॉल की B की n-आयामी यूक्लिडियन स्थान V, तय करना है:
चुकी f का कोई निश्चित बिंदु नहीं है, यह इस प्रकार है, के लिए x के इंटीरियर (टोपोलॉजी) में B, वेक्टर w(x) शून्य नहीं है; और S के लिए x में, स्केलर उत्पाद
x ⋅ w(x) = 1 – x ⋅ f(x) से धनात्मक है। मूल से n-आयामी यूक्लिडियन स्पेस V, (n + 1)-विमीय स्थान W = V x R, निर्देशांक के साथ y = (x, t) के साथ एक नया सहायक X( x,t ) = ( -t w(x), x.w(x)) निर्मित करता है।
निर्माण द्वारा X के इकाई क्षेत्र पर सतत सदिश W क्षेत्र है, स्पर्शरेखा की स्थिति y ⋅ X(y) = 0 को संतुष्ट करना है। इसके अतिरिक्त X(y) कहीं अदृष्ट नहीं है (क्योंकि, यदि x का मानदंड 1 है, तो x ⋅ w(x) शून्य नहीं है; जबकि यदि x का मानदंड वास्तव में 1 से कम है, तो t और w(x) दोनों शून्य नहीं हैं)। यह खंडन निश्चित बिंदु प्रमेय को सिद्ध करता है जब n विषम है। यहां तक कि n के लिए, निश्चित बिंदु प्रमेय को बंद इकाई गेंद पर क्रियान्वित किया जा सकता है B में n + 1 आयाम और मानचित्रण F(x,y) = (f(x), 0) है। इस प्रमाण का लाभ यह है कि यह सिर्फ प्रारंभिक तकनीकों का उपयोग करता है; बोरसुक-उलम प्रमेय जैसे अत्यधिक सामान्य परिणामों के लिए बीजगणितीय संस्थिति से उपकरणों की आवश्यकता होती है।[50]
होमोलॉजी या कोहोलॉजी का उपयोग करते हुए एक प्रमाण
समरूपता या कोहोलॉजी का उपयोग करते हुए प्रमाण अवलोकन का उपयोग करता है कि एन-डिस्क Dn की सीमा (संस्थिति) Sn−1 है, (n − 1)-गोला है।
मान लीजिए, खंडन के लिए, सतत फलन f : Dn → Dn का कोई निश्चित बिंदु नहीं है। इसका अर्थ है कि, D में प्रत्येक बिंदु xn के लिए, बिंदु x और f(x) भिन्न हैं। क्योंकि वे अलग-अलग हैं, D में प्रत्येक बिंदु xn के लिए, हम f(x) से x तक अद्वितीय किरण का निर्माण कर सकते हैं और किरण का अनुसरण तब तक कर सकते हैं जब तक कि यह सीमा Sn−1 को काट न दे (उदाहरण देखें)। इस प्रतिच्छेदन बिंदु F(x) को प्रयोग करके, हम फलन F : Dn को परिभाषित करते हैं→ Sn−1 डिस्क में प्रत्येक बिंदु को सीमा पर उसके संबंधित प्रतिच्छेदन बिंदु पर भेज रहा है। विशेष कथन के रूप में, जब भी x स्वयं सीमा पर होता है, तो प्रतिच्छेदन बिंदु F(x) x होना चाहिए।
इसीलिए, f एक विशेष प्रकार का निरंतर फलन है जिसे रिट्रेक्शन (संस्थिति) के रूप में जाना जाता है: कोडोमेन के सभी बिंदु (इस कथन Sn−1 में) F का निश्चित बिंदु है।
सहज रूप से ऐसा प्रतीत नहीं होता है कि Dn की Sn−1 पर रिट्रैक्शन हो सकती है, और इस कथन में n = 1, असंभवता अत्यधिक मूलभूत है, क्योंकि S0 (अर्थात, बंद अंतराल डी1 के अंत बिंदु) जुड़ा हुआ नहीं है। कथन n = 2 कम स्पष्ट है, परन्तु संबंधित स्थानों के मूलभूत समूहों को सम्मिलित करते हुए मूलभूत तर्कों का उपयोग करके सिद्ध किया जा सकता है: प्रत्यावर्तन D2 के मूल समूह से विशेषण समूह समरूपता को S1 के लिए प्रेरित करेगा, परन्तु बाद वाला समूह Z के लिए समरूप है जबकि पहला समूह छोटा है, इसलिए यह असंभव है। कथन n = 2 जिसे लुप्त न किया जा सके क्षेत्रों के बारे में प्रमेय के आधार पर खंडन द्वारा भी सिद्ध किया जा सकता है।
n > 2 के लिए, चूँकि, प्रत्यावर्तन की असंभवता को प्रमाणित करना अत्यधिक कठिन है। सजातीय (गणित) का उपयोग करने का विधि है: समरूपता Hn−1(Dn) निम्न है, जबकि Hn−1(Sn−1) अनंत चक्रीय समूह है। इससे पता चलता है कि प्रत्यावर्तन असंभव है, क्योंकि फिर से प्रत्यावर्तन बाद वाले समूह से पूर्व समूह के लिए द्वीअंतःक्षेपण समूह समरूपता को प्रेरित करेगा।
यूक्लिडियन स्पेस En के खुले उपसमुच्चय के डॉ कहलमज कोहोलॉजी का उपयोग करके रिट्रैक्शन की असंभवता भी दिखायी जा सकती है n ≥ 2 के लिए, U = En - (0) की डी रम कोहोलॉजी डिग्री 0 और n - 1 में आयामी है, और अन्यथा लुप्त हो जाता है। यदि प्रत्यावर्तन अस्तित्व में है, तो U को संविदात्मक होना होगा और n-1 डिग्री में इसके डी राम कोहोलॉजी को खंडन में लुप्त होना होगा।[51]
स्टोक्स के प्रमेय का प्रयोग करके एक उपपत्ति
समरूपता का उपयोग करते हुए निरंतर नक्शों के लिए ब्रोवर के निश्चित-बिंदु प्रमेय के प्रमाण के रूप में, यह प्रमाणित करने के लिए कम किया गया है की गेंद B से इसकी सीमा ∂B पर कोई निरंतर रिट्रैक्शन F नहीं है। ऐसे में यह माना जा सकता है F सहज है, क्योंकि इसे वीयरस्ट्रैस लगभग प्रमेय का उपयोग करके या पर्याप्त रूप से छोटे सहायता और अभिन्न (अर्थात शिथिल करनेवाला) के अऋणात्मक निरंतर उभार फलन के साथ संवलन द्वारा अनुमानित किया जा सकता है। यदि ω स्टोक्स के प्रमेय द्वारा सीमा पर आयतन रूप है,
अत्यधिक समान्यतौर पर, यह दर्शाता है कि किसी भी भरी हुई निरंतर उन्मुख सघन विविध से कोई निरंतर रिट्रैक्शन M इसकी सीमा पर नहीं होता है। स्टोक्स के प्रमेय का उपयोग करने वाला प्रमाण सजातीय का उपयोग करने वाले प्रमाण से निकटता से संबंधित है, क्योंकि ω डी रम कोहोलॉजी उत्पन्न करता है Hn-1(∂M) जो डी रम कोहोलॉजी द्वारा सजातीय समूह Hn-1(∂M) के लिए समरूप है।[54]
एक संयोजन प्रमाण
स्पर्नर लेम्मा का उपयोग करके बीइपीटी को सिद्ध किया जा सकता है। अब हम विशेष कथन के लिए प्रमाणित रूपरेखा देते हैं जिसमें f मानक संकेतन से फ़ंक्शन है, जहाँ
सभी बिंदु के लिए भी इसलिए उनके निर्देशांकों का योग बराबर है:
इसलिए, पीजेनहोल सिद्धांत द्वारा, हर के लिए सूचकांक होना चाहिए ऐसा कि वें का समन्वय से अत्यधिक या उसके बराबर है f के अंतर्गत इसकी इमेज के निर्देशांक:
इसके अतिरिक्त, यदि के k-आयामी के ऊपरी सतह पर स्थित है, फिर उसी तर्क से, निर्देशिका में से चुना जा सकता है k + 1 निर्देशांक जो इस ऊपरी सतह पर शून्य नहीं हैं।
अब हम इस तथ्य का उपयोग स्पर्नर रंग बनाने के लिए करते हैं। सभी त्रिभुज के लिए प्रत्येक शीर्ष p का रंग निर्देशांक है जैसे की । रचना के अनुसार, यह एक स्पर्नर रंग है। इसलिए, स्पर्नर की लेम्मा द्वारा, n-विमीय सिम्प्लेक्स है, जिसके कोने के पुरे समूह के साथ उपलब्ध रंग n + 1 है।
चूँकि f निरंतर है, इस संकेतन को स्वेच्छचरित प्रकार से सूक्ष्म त्रिकोण का चयन करके छोटा बनाया जा सकता है। इसलिए, बिंदु होना चाहिए जो सभी निर्देशांकों में लेबलिंग शर्त को पूरा करता है: सभी के लिए क्योंकि के निर्देशांक का योग और समान होना चाहिए, ये सभी असमानताएँ वास्तव में समानताएँ होनी चाहिए। परन्तु इसका अर्थ यह है कि:
वह का निश्चित बिन्दु हैl
हिर्श द्वारा उपयोग करके
हिर्श द्वारा प्रमाण अलग-अलग रिट्रैक्शन की असंभवता के आधार पर मॉरिस हिर्श द्वारा त्वरित प्रमाण भी है। अप्रत्यक्ष प्रमाण यह देखते हुए प्रारम्भ होता है कि मानचित्र f को बिंदु को ठीक न करने की गुण को बनाए रखते हुए सहज मानचित्र द्वारा अनुमानित किया जा सकता है; यह वेएरस्ट्रास लगभग प्रमेय का उपयोग करके साधारण उठे हुए फंक्शन्स के साथ संवलन द्वारा किया जा सकता है। ऊपर के रूप में रिट्रैक्शन को परिभाषित करता है जो अब भिन्न होना चाहिए। सार्ड के प्रमेय के अनुसार इस प्रकार के प्रत्यावर्तन का व्युत्क्रमणीय मूल्य होना चाहिए, जो सीमा के प्रतिबंध के लिए व्युत्क्रमणीय है (जो कि सिर्फ पहचान है)। इस प्रकार विपरीत इमेज सीमा के साथ एक गुना होगी। सीमा में कम से कम दो अंतिम बिंदु सम्मिलित होने चाहिए, दोनों को मूल गेंद की सीमा पर होना चाहिए जो वापसी में असंभव है।[55] आर. ब्रूस केलॉग, टीएन-यीन ली, और जेम्स ए. यॉर्क ने हिर्श के प्रमाण को संगणनीयता प्रमाण में बदल दिया, यह देखते हुए कि निश्चित बिंदुओं को छोड़कर सभी जगह वास्तव में वापस लेना परिभाषित किया गया है।[56] लगभग किसी भी बिंदु के लिए, q, सीमा पर, (यह मानते हुए कि यह एक निश्चित बिंदु नहीं है) ऊपर उल्लिखित सीमा के साथ कई गुना उपस्थित है और एकमात्र संभावना यह है कि यह q से एक निश्चित बिंदु तक ले जाती है। q से निश्चित बिंदु तक इस प्रकार के पथ का पालन करना आसान संख्यात्मक कार्य है, इसलिए विधि अनिवार्य रूप से गणना योग्य है।[57] संकल्पनात्मक रूप से समरूपता प्रमाण समान पथ-अनुवर्ती संस्करण दिया जो विभिन्न प्रकार की संबंधित समस्याओं तक फैला हुआ है।
उन्मुख क्षेत्र का प्रयोग करते हुए एक प्रमाण
पूर्ववर्ती प्रमाण की भिन्नता सार्ड के प्रमेय को नियोजित नहीं करती है, और निम्नानुसार जाती है। यदि सुचारू रिट्रैक्शन है, सहज विकृति पर विचार करता है और सुचारू कार्य
समाकल के चिह्न के अंतर्गत अंतर करना यह जाँचना कठिन नहीं है φ′(t) = 0 सभी t के लिए, इसलिए φ स्थिर फलन है, जो खंडन है क्योंकि φ(0) गेंद का n-आयामी आयतन है, जबकि φ(1) शून्य है। ज्यामितीय विचार यह है कि φ(t) gt(B) का उन्मुख क्षेत्र है (अर्थात, gt के माध्यम से गेंद की इमेज का लेब्सग्यु माप, बहुलता और अभिविन्यास को ध्यान में रखते हुए), और स्थिर रहना चाहिए (क्योंकि यह आयामी कथन में बहुत स्पष्ट है)। दूसरी तरफ, पैरामीटर t के रूप में 0 से 1 नक्शा gt पास होता है निरंतर गेंद के पहचान मानचित्र से रिट्रैक्शन r में रूपांतरित होता है, जो खंडन है क्योंकि पहचान का उन्मुख क्षेत्र गेंद के आयतन के साथ मिलता है, जबकि r का उन्मुख क्षेत्र आवश्यक रूप से 0 है, जैसा कि इसकी इमेज गेंद की सीमा है, अशक्त माप का समूह है।[58]
खेल हेक्स का उपयोग कर एक प्रमाण
खेल हेक्स का उपयोग कर डेविड गेल द्वारा दिया गया बिल्कुल अलग प्रमाण हेक्स (बोर्ड गेम) के खेल पर आधारित है। हेक्स के बारे में मूल प्रमेय, जो पहले जॉन नैश द्वारा सिद्ध किया गया था, यह है कि हेक्स का कोई भी गेम ड्रा में समाप्त नहीं हो सकता है; पहले खिलाड़ी के पास निरंतर जीतने की रणनीति होती है (चूँकि यह प्रमेय रचनात्मक नहीं है, और 10 x 10 या अत्यधिक आयामों के बोर्ड आकार के लिए स्पष्ट रणनीतियों को पूर्ण प्रकार से विकसित नहीं किया गया है)। यह आयाम 2 के लिए ब्रौवर नियत बिंदु प्रमेय के बराबर निकला है। हेक्स के एन-आयामी संस्करणों पर विचार करके, सामान्य प्रकार से प्रमाणित कर सकता है कि ब्रौवर का प्रमेय हेक्स के लिए निर्धारक प्रमेय के बराबर है।[59]
लेफ्शेट्ज़ निश्चित-बिंदु प्रमेय का उपयोग करके एक प्रमाण
लेफ्शेट्ज़ निश्चित-बिंदु प्रमेय का कहना है कि यदि परिमित साधारण परिसर B से निरंतर मानचित्र f में सिर्फ अलग-अलग निश्चित बिंदु हैं, तो गुणकों के साथ गिने गए निश्चित बिंदुओं की संख्या (जो ऋणात्मक हो सकती है) लेफ्शेट्ज़ संख्या के बराबर है
और विशेष रूप से यदि लेफ्सहेट्ज़ संख्या अऋणात्मक है तो f का एक निश्चित बिंदु होना चाहिए। यदि B एक गेंद है (या अत्यधिक सामान्यतौर पर सिकुड़ा जा सकता है) तो लेफ्शेट्ज़ संख्या एक है क्योंकि सिर्फ अऋणात्मक साधारण समरूपता समूह है: और f इस समूह पर तत्समक के रूप में कार्य करता है, इसलिए f का एक निश्चित बिंदु है।[60][61]
अप्रभावी तार्किक प्रणाली में एक प्रमाण
विपरीत गणित में, ब्रौवर के प्रमेय को प्रणाली WKL0 में सिद्ध किया जा सकता है, और इसके विपरीत आधार प्रणाली पर वर्ग के लिए RCA0 ब्रौवर प्रमेय कमजोर कोनिग लेम्मा को दर्शाता है, इसलिए यह ब्रौवर के प्रमेय की ताकत का उपयुक्त विवरण देता है।
सामान्यीकरण
ब्रौवर निश्चित-बिंदु प्रमेय अत्यधिक सामान्य निश्चित-बिंदु प्रमेयों का प्रारंभिक बिंदु बनाता है।
अनंत आयामों के लिए सीधा सामान्यीकरण, अर्थात यूक्लिडियन स्पेस के स्थान पर हिल्बर्ट स्पेस की इकाई गेंद का उपयोग करना सही नहीं है। यहां मुख्य समस्या यह है कि अनंत-आयामी हिल्बर्ट स्पेस की इकाई गेंदें सघन स्थान नहीं हैं। उदाहरण के लिए, हिल्बर्ट स्पेस एलपी स्पेस ℓ2 वर्ग-संकलन योग्य वास्तविक (या जटिल) क्रम, मानचित्र पर विचार करें f : ℓ2 → ℓ2 जो ℓ2 की बंद इकाई गेंद से अनुक्रम (yn) द्वारा परिभाषित अनुक्रम (xn) भेजता है।
यह जाँचना कठिन नहीं है कि यह मानचित्र निरंतर है, इसकी इमेज ℓ2 के इकाई क्षेत्र में है, परन्तु इसका कोई निश्चित बिंदु नहीं है।
ब्रौवर निश्चित-बिंदु प्रमेय के अनंत आयामी स्पेस के सामान्यीकरण इसलिए सभी में किसी प्रकार की सघनता धारणा सम्मिलित है, और अधिकांशतः उत्तल समूह की धारणा भी सम्मिलित है। इन प्रमेयों की चर्चा के लिए अनंत-आयामी स्थानों में निश्चित-बिंदु प्रमेय देखना अनिवार्य है।
स्पेस के बड़े वर्ग के लिए परिमित-आयामी सामान्यीकरण भी है: यदि परिमित रूप से कई श्रृंखला योग्य निरंतरता का प्रोडक्ट है, फिर प्रत्येक निरंतर कार्य निश्चित बिंदु है,[62] जहां श्रृंखला योग्य सातत्य (सामान्य तौर पर परन्तु इस कथन में जरूरी नहीं कि मीट्रिक स्थान) सघन स्पेस हॉसडॉर्फ स्पेस है, जिसमें हर खुले कवर में परिमित खुला शोधन होता है , जैसे और सिर्फ है। श्रृंखला योग्य निरंतरता के उदाहरणों में सघन आनुषंगिक रैखिक क्रम किए गए स्थान और विशेष रूप से वास्तविक संख्याओं के बंद अंतराल सम्मिलित हैं।
काकुटानी निश्चित बिंदु प्रमेय ब्रोवर निश्चित बिंदु प्रमेय को अलग दिशा में सामान्यीकृत करता है: यह Rn में रहता है, परन्तु ऊपरी अर्ध-निरंतर समूह-मूल्य फलन (फलन जो समूह के प्रत्येक बिंदु को समूह का उपसमुच्चय निर्दिष्ट करते हैं) पर विचार करता है। इसमें समूह की सघनता और उत्तलता की भी आवश्यकता होती है।
लेफ्सहेट्ज़ निश्चित-बिंदु प्रमेय (लगभग) स्वैच्छिक सघन संस्थिति स्पेस पर क्रियान्वित होता है, और एकवचन समजतता के संदर्भ में शर्त देता है जो निश्चित बिंदुओं के अस्तित्व निश्चित होता है; Dn के कथन में किसी भी मानचित्र के लिए यह स्थिति नगण्य रूप से संतुष्ट है।
समतुल्य परिणाम
There are several fixed-point theorems which come in three equivalent variants: an algebraic topology variant, a combinatorial variant and a set-covering variant. Each variant can be proved separately using totally different arguments, but each variant can also be reduced to the other variants in its row. Additionally, each result in the top row can be deduced from the one below it in the same column.[63]
| Algebraic topology | Combinatorics | Set covering |
|---|---|---|
| Brouwer fixed-point theorem | Sperner's lemma | Knaster–Kuratowski–Mazurkiewicz lemma |
| Borsuk–Ulam theorem | Tucker's lemma | Lusternik–Schnirelmann theorem |
यह भी देखें
- बैनाच निश्चित-बिंदु प्रमेय
- विश्लेषणात्मक फलन की अनंत रचनाएँ
- नैश समतुल्यता
- पोंकारे-मिरांडा प्रमेय-ब्रोवर निश्चित-बिंदु प्रमेय के बराबर
- संस्थितिकी साहचर्य
टिप्पणियाँ
- ↑ See page 15 of: D. Leborgne Calcul différentiel et géométrie Puf (1982) ISBN 2-13-037495-6
- ↑ More exactly, according to Encyclopédie Universalis: Il en a démontré l'un des plus beaux théorèmes, le théorème du point fixe, dont les applications et généralisations, de la théorie des jeux aux équations différentielles, se sont révélées fondamentales. Luizen Brouwer by G. Sabbagh
- ↑ 3.0 3.1 Jacques Hadamard: Note sur quelques applications de l’indice de Kronecker in Jules Tannery: Introduction à la théorie des fonctions d’une variable (Volume 2), 2nd edition, A. Hermann & Fils, Paris 1910, pp. 437–477 (French)
- ↑ 4.0 4.1 4.2 Brouwer, L. E. J. (1911). "Über Abbildungen von Mannigfaltigkeiten". Mathematische Annalen (in Deutsch). 71: 97–115. doi:10.1007/BF01456931. S2CID 177796823.
- ↑ D. Violette Applications du lemme de Sperner pour les triangles Bulletin AMQ, V. XLVI N° 4, (2006) p 17. Archived June 8, 2011, at the Wayback Machine
- ↑ Page 15 of: D. Leborgne Calcul différentiel et géométrie Puf (1982) ISBN 2-13-037495-6.
- ↑ This version follows directly from the previous one because every convex compact subset of a Euclidean space is homeomorphic to a closed ball of the same dimension as the subset; see Florenzano, Monique (2003). General Equilibrium Analysis: Existence and Optimality Properties of Equilibria. Springer. p. 7. ISBN 9781402075124. Retrieved 2016-03-08.
- ↑ V. & F. Bayart Point fixe, et théorèmes du point fixe on Bibmath.net. Archived December 26, 2008, at the Wayback Machine
- ↑ C. Minazzo K. Rider Théorèmes du Point Fixe et Applications aux Equations Différentielles Archived 2018-04-04 at the Wayback Machine Université de Nice-Sophia Antipolis.
- ↑ Belk, Jim. "Why is convexity a requirement for Brouwer fixed points?". Math StackExchange. Retrieved 22 May 2015.
- ↑ The interest of this anecdote rests in its intuitive and didactic character, but its accuracy is dubious. As the history section shows, the origin of the theorem is not Brouwer's work. More than 20 years earlier Henri Poincaré had proved an equivalent result, and 5 years before Brouwer P. Bohl had proved the three-dimensional case.
- ↑ 12.0 12.1 12.2 This citation comes originally from a television broadcast: Archimède, Arte, 21 septembre 1999
- ↑ 13.0 13.1 Bohl, P. (1904). "Über die Bewegung eines mechanischen Systems in der Nähe einer Gleichgewichtslage". J. Reine Angew. Math. 127 (3/4): 179–276.
- ↑ Karamardian, Stephan (1977). Fixed points: algorithms and applications. New York: Academic Press. ISBN 978-0-12-398050-2.
- ↑ Istrăţescu, Vasile (1981). निश्चित बिंदु सिद्धांत. Dordrecht-Boston, Mass.: D. Reidel Publishing Co. ISBN 978-90-277-1224-0.
- ↑ See F. Brechenmacher L'identité algébrique d'une pratique portée par la discussion sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des planètes CNRS Fédération de Recherche Mathématique du Nord-Pas-de-Calais
- ↑ Henri Poincaré won the King of Sweden's mathematical competition in 1889 for his work on the related three-body problem: Jacques Tits Célébrations nationales 2004 Site du Ministère Culture et Communication
- ↑ Henri Poincaré Les méthodes nouvelles de la mécanique céleste T Gauthier-Villars, Vol 3 p 389 (1892) new edition Paris: Blanchard, 1987.
- ↑ Quotation from Henri Poincaré taken from: P. A. Miquel La catégorie de désordre Archived 2016-03-03 at the Wayback Machine, on the website of l'Association roumaine des chercheurs francophones en sciences humaines
- ↑ This question was studied in: Poincaré, H. (1886). "Sur les courbes définies par les équations différentielles". Journal de Mathématiques Pures et Appliquées. 2 (4): 167–244.
- ↑ This follows from the Poincaré–Bendixson theorem.
- ↑ Multiplication by 1/2 on ]0, 1[2 has no fixed point.
- ↑ "concerne les propriétés invariantes d'une figure lorsqu’on la déforme de manière continue quelconque, sans déchirure (par exemple, dans le cas de la déformation de la sphère, les propriétés corrélatives des objets tracés sur sa surface". From C. Houzel M. Paty Poincaré, Henri (1854–1912) Archived 2010-10-08 at the Wayback Machine Encyclopædia Universalis Albin Michel, Paris, 1999, p. 696–706
- ↑ Poincaré's theorem is stated in: V. I. Istratescu Fixed Point Theory an Introduction Kluwer Academic Publishers (réédition de 2001) p 113 ISBN 1-4020-0301-3
- ↑ Voitsekhovskii, M.I. (2001) [1994], "Brouwer theorem", Encyclopedia of Mathematics, EMS Press, ISBN 1-4020-0609-8
- ↑ Dieudonné, Jean (1989). A History of Algebraic and Differential Topology, 1900–1960. Boston: Birkhäuser. pp. 17–24. ISBN 978-0-8176-3388-2.
- ↑ See for example: Émile Picard Sur l'application des méthodes d'approximations successives à l'étude de certaines équations différentielles ordinaires Archived 2011-07-16 at the Wayback Machine Journal de Mathématiques p 217 (1893)
- ↑ J. J. O'Connor E. F. Robertson Piers Bohl
- ↑ Myskis, A. D.; Rabinovic, I. M. (1955). "Первое доказательство теоремы о неподвижной точке при непрерывном отображении шара в себя, данное латышским математиком П.Г.Болем" [The first proof of a fixed-point theorem for a continuous mapping of a sphere into itself, given by the Latvian mathematician P. G. Bohl]. Успехи математических наук (in русский). 10 (3): 188–192.
- ↑ J. J. O'Connor E. F. Robertson Luitzen Egbertus Jan Brouwer
- ↑ Freudenthal, Hans (1975). "ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल". Historia Mathematica. 2 (4): 495–502 [p. 495]. doi:10.1016/0315-0860(75)90111-1.
- ↑ Freudenthal, Hans (1975). "ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल". Historia Mathematica. 2 (4): 495–502 [p. 495]. doi:10.1016/0315-0860(75)90111-1.
... cette dernière propriété, bien que sous des hypothèses plus grossières, ait été démontré par H. Poincaré
- ↑ Freudenthal, Hans (1975). "ब्रौवर के इनएडिटा के अनुसार, आधुनिक टोपोलॉजी का उद्गम स्थल". Historia Mathematica. 2 (4): 495–502 [p. 501]. doi:10.1016/0315-0860(75)90111-1.
- ↑ If an open subset of a manifold is homeomorphic to an open subset of a Euclidean space of dimension n, and if p is a positive integer other than n, then the open set is never homeomorphic to an open subset of a Euclidean space of dimension p.
- ↑ J. J. O'Connor E. F. Robertson Luitzen Egbertus Jan Brouwer.
- ↑ The term algebraic topology first appeared 1931 under the pen of David van Dantzig: J. Miller Topological algebra on the site Earliest Known Uses of Some of the Words of Mathematics (2007)
- ↑ V. I. Istratescu Fixed Point Theory. An Introduction Kluwer Academic Publishers (new edition 2001) ISBN 1-4020-0301-3.
- ↑ "... Brouwer's fixed point theorem, perhaps the most important fixed point theorem." p xiii V. I. Istratescu Fixed Point Theory an Introduction Kluwer Academic Publishers (new edition 2001) ISBN 1-4020-0301-3.
- ↑ E.g.: S. Greenwood J. Cao Brouwer’s Fixed Point Theorem and the Jordan Curve Theorem University of Auckland, New Zealand.
- ↑ Schauder, J. (1930). "Der Fixpunktsatz in Funktionsräumen". Studia Mathematica. 2: 171–180. doi:10.4064/sm-2-1-171-180.
- ↑ Kakutani, S. (1941). "ब्राउवर के निश्चित बिंदु प्रमेय का एक सामान्यीकरण". Duke Mathematical Journal. 8 (3): 457–459. doi:10.1215/S0012-7094-41-00838-4.
- ↑ These examples are taken from: F. Boyer Théorèmes de point fixe et applications CMI Université Paul Cézanne (2008–2009) Archived copy at WebCite (August 1, 2010).
- ↑ For context and references see the article Hex (board game).
- ↑ P. Bich Une extension discontinue du théorème du point fixe de Schauder, et quelques applications en économie Archived June 11, 2011, at the Wayback Machine Institut Henri Poincaré, Paris (2007)
- ↑ For a long explanation, see: Dubucs, J. P. (1988). "L. J. E. Brouwer : Topologie et constructivisme". Revue d'Histoire des Sciences. 41 (2): 133–155. doi:10.3406/rhs.1988.4094.
- ↑ Later it would be shown that the formalism that was combatted by Brouwer can also serve to formalise intuitionism, with some modifications. For further details see constructive set theory.
- ↑ H. Scarf found the first algorithmic proof: Voitsekhovskii, M.I. (2001) [1994], "Brouwer theorem", Encyclopedia of Mathematics, EMS Press, ISBN 1-4020-0609-8.
- ↑ Milnor 1965, pp. 1–19
- ↑ Teschl, Gerald (2019). "10. The Brouwer mapping degree". रेखीय और अरैखिक कार्यात्मक विश्लेषण में विषय (PDF). Graduate Studies in Mathematics. American Mathematical Society. Archived (PDF) from the original on 2022-10-09. Retrieved 1 February 2022.
- ↑ Milnor 1978
- ↑ Madsen & Tornehave 1997, pp. 39–48
- ↑ Boothby 1971
- ↑ Boothby 1986
- ↑ Dieudonné 1982
- ↑ Hirsch 1988
- ↑ Kellogg, Li & Yorke 1976.
- ↑ Chow, Mallet-Paret & Yorke 1978.
- ↑ Kulpa 1989
- ↑ David Gale (1979). "हेक्स और ब्रोवर फिक्स्ड-प्वाइंट प्रमेय का खेल". The American Mathematical Monthly. 86 (10): 818–827. doi:10.2307/2320146. JSTOR 2320146.
- ↑ Hilton & Wylie 1960
- ↑ Spanier 1966
- ↑ Eldon Dyer (1956). "एक निश्चित बिंदु प्रमेय". Proceedings of the American Mathematical Society. 7 (4): 662–672. doi:10.1090/S0002-9939-1956-0078693-4.
- ↑ Nyman, Kathryn L.; Su, Francis Edward (2013), "A Borsuk–Ulam equivalent that directly implies Sperner's lemma", The American Mathematical Monthly, 120 (4): 346–354, doi:10.4169/amer.math.monthly.120.04.346, JSTOR 10.4169/amer.math.monthly.120.04.346, MR 3035127
संदर्भ
- Boothby, William M. (1971). "On two classical theorems of algebraic topology". Amer. Math. Monthly. 78: 237–249. JSTOR 2317520. MR 0283792.
- Boothby, William M. (1986). An introduction to differentiable manifolds and Riemannian geometry. Pure and Applied Mathematics. Vol. 120 (Second ed.). Academic Press. ISBN 0-12-116052-1. MR 0861409.
- Bredon, Glen E. (1993). Topology and geometry. Graduate Texts in Mathematics. Vol. 139. Springer-Verlag. ISBN 0-387-97926-3. MR 1224675.
- Chow, Shui Nee; Mallet-Paret, John; Yorke, James A. (1978). "Finding zeroes of maps: Homotopy methods that are constructive with probability one". Mathematics of Computation. 32 (143): 887–899. doi:10.1090/S0025-5718-1978-0492046-9. MR 0492046.
- Dieudonné, Jean (1982). "8. Les théorèmes de Brouwer". Éléments d'analyse. Cahiers Scientifiques (in français). Vol. IX. Paris: Gauthier-Villars. pp. 44–47. ISBN 2-04-011499-8. MR 0658305.
- Dieudonné, Jean (1989). A history of algebraic and differential topology, 1900–1960. Birkhäuser. pp. 166–203. ISBN 0-8176-3388-X. MR 0995842.
- Gale, D. (1979). "The Game of Hex and Brouwer Fixed-Point Theorem". The American Mathematical Monthly. 86 (10): 818–827. doi:10.2307/2320146. JSTOR 2320146.
- Hirsch, Morris W. (1988). Differential Topology. New York: Springer. ISBN 978-0-387-90148-0. (see p. 72–73 for Hirsch's proof utilizing non-existence of a differentiable retraction)
- Hilton, Peter J.; Wylie, Sean (1960). Homology theory: An introduction to algebraic topology. New York: Cambridge University Press. ISBN 0521094224. MR 0115161.
- Istrăţescu, Vasile I. (1981). Fixed Point Theory. Mathematics and its Applications. Vol. 7. Dordrecht–Boston, MA: D. Reidel. ISBN 978-90-277-1224-0. MR 0620639.
- Karamardian, S., ed. (1977). Fixed Points: Algorithms and Applications. Academic Press. ISBN 978-0-12-398050-2.
- Kellogg, R. Bruce; Li, Tien-Yien; Yorke, James A. (1976). "A constructive proof of the Brouwer fixed point theorem and computational results". SIAM Journal on Numerical Analysis. 13 (4): 473–483. Bibcode:1976SJNA...13..473K. doi:10.1137/0713041. MR 0416010.
- Kulpa, Władysław (1989). "An integral theorem and its applications to coincidence theorems". Acta Universitatis Carolinae. Mathematica et Physica. 30 (2): 83–90.
- Leoni, Giovanni (2017). A First Course in Sobolev Spaces: Second Edition. Graduate Studies in Mathematics. 181. American Mathematical Society. pp. 734. ISBN 978-1-4704-2921-8
- Madsen, Ib; Tornehave, Jørgen (1997). From calculus to cohomology: de Rham cohomology and characteristic classes. Cambridge University Press. ISBN 0-521-58059-5. MR 1454127.
- Milnor, John W. (1965). Topology from the differentiable viewpoint. Charlottesville: University Press of Virginia. MR 0226651.
- Milnor, John W. (1978). "Analytic proofs of the 'hairy ball theorem' and the Brouwer fixed-point theorem" (PDF). Amer. Math. Monthly. 85 (7): 521–524. JSTOR 2320860. MR 0505523. Archived (PDF) from the original on 2022-10-09.
- Sobolev, Vladimir I. (2001) [1994], "Brouwer theorem", Encyclopedia of Mathematics, EMS Press
- Spanier, Edwin H. (1966). Algebraic topology. New York-Toronto-London: McGraw-Hill.
बाहरी संबंध
- Brouwer's Fixed Point Theorem for Triangles at cut-the-knot
- Brouwer theorem, from PlanetMath with attached proof.
- Reconstructing Brouwer at MathPages
- Brouwer Fixed Point Theorem at Math Images.