त्रिकोणमितीय फलनों का विभेदन: Difference between revisions
No edit summary |
No edit summary |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
{|class="wikitable" style="background-color:#FFFFFF; margin:1em 0 1em 1em" align="right" hspace="3" | {|class="wikitable" style="background-color:#FFFFFF; margin:1em 0 1em 1em" align="right" hspace="3" | ||
! '''फलन''' | ! '''फलन''' | ||
! ''' | ! '''अवकलज''' | ||
|- | |- | ||
| <math>\sin(x)</math> | | <math>\sin(x)</math> | ||
| Line 42: | Line 42: | ||
|} | |} | ||
'''त्रिकोणमितीय फलनों का विभेदन''',एक त्रिकोणमितीय फलन के | '''त्रिकोणमितीय फलनों का विभेदन''',एक [[त्रिकोणमितीय फलन]] के [[अवकलज]] या एक चर के संबंध में उसके परिवर्तन की दर का पता लगाने की गणितीय प्रक्रिया है।उदाहरण के लिए,ज्या फलन का अवकलज sin'(a) = cos(a) के रूप में लिखा जाता है,इसका अर्थ है कि एक विशेष कोण x = a पर sin(x) की परिवर्तन दर को उस कोण के कोज्या से दिया जाता है। | ||
वृत्तीय त्रिकोणमितीय फलनों के सभी | वृत्तीय त्रिकोणमितीय फलनों के सभी अवकलज sin(x) और cos(x) से tan(x) = sin(x)/cos(x) जैसे फलनों पर लागू होने वाले [[भागफल नियम]] के माध्यम से पाए जा सकते हैं।इन अवकलजों को जानने के लिए,[[प्रतिलोम त्रिकोणमितीय फलनों]] के अवकलजों को [[अंतर्निहित अवकलन|अप्रत्य्क्ष विभेदन]] का उपयोग करके पाया जाता है। | ||
==त्रिकोणमितीय फलनों के अवकलजों के प्रमाण== | ==त्रिकोणमितीय फलनों के अवकलजों के प्रमाण== | ||
=== sin(θ)/θ की सीमा | === जब θ,0 की ओर प्रवृत्त होता है,तो sin(θ)/θ की सीमा === | ||
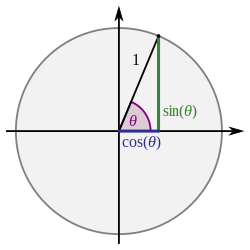
[[File:limit circle FbN.jpeg | [[File:limit circle FbN.jpeg|{{center|वृत्त, केंद्र''O'', त्रिज्या 1}}|frame]]दायीं ओर आरेख केंद्र o और त्रिज्या r = 1 के साथ एक वृत्त दिखाता है।दो त्रिज्याएँ OA और OB,θ रेडियन का एक चाप बनाते हैं।चूंकि हम सीमा को शून्य मान रहे हैं,इसलिए हम मान सकते हैं कि θ एक छोटी धनात्मक संख्या है,अर्थात्,0 < θ < ½ π पहले चतुर्थांश में है। | ||
आरेख में,त्रिभुज | आरेख में,OAB त्रिभुज को R1,OAB [[वृत्तीय क्षेत्र]] को R2 और OAC त्रिभुज को R3 लें।OAB [[त्रिभुज का क्षेत्रफल]] है: | ||
:<math> \mathrm{Area}(R_1 | :<math> \mathrm{Area}(R_1 | ||
) | ) | ||
=\tfrac{1}{2} \ |OA| \ |OB| \sin\theta = \tfrac{1}{2}\sin\theta \, . </math> | =\tfrac{1}{2} \ |OA| \ |OB| \sin\theta = \tfrac{1}{2}\sin\theta \, . </math> | ||
[[वृत्तीय क्षेत्र | OAB [[वृत्तीय क्षेत्र का क्षेत्रफल]] <math>\mathrm{Area}(R_2) | ||
=\tfrac{1}{2}\theta</math>,जबकि त्रिभुज | =\tfrac{1}{2}\theta</math> है,जबकि OAC त्रिभुज का क्षेत्रफल दिया गया है | ||
:<math> \mathrm{Area}(R_3 | :<math> \mathrm{Area}(R_3 | ||
) | ) | ||
=\tfrac{1}{2} \ |OA| \ |AC| = \tfrac{1}{2} \tan\theta \, . </math> | =\tfrac{1}{2} \ |OA| \ |AC| = \tfrac{1}{2} \tan\theta \, . </math> | ||
चूँकि प्रत्येक क्षेत्र अगले क्षेत्र में | चूँकि प्रत्येक क्षेत्र अगले क्षेत्र में निहित है,इसलिए एक निम्न विधि होती है:<math>\text{Area}(R_1) < \text{Area}(R_2) < \text{Area}(R_3) \implies | ||
\tfrac{1}{2}\sin\theta < \tfrac{1}{2}\theta < \tfrac{1}{2}\tan\theta \, . </math> | |||
इसके अतिरिक्त,चूँकि पहले चतुर्थांश में sin θ > 0 होता है,हम ½ sin θ से भाग कर सकते हैं: | |||
:<math>1 < \frac{\theta}{\sin\theta} < \frac{1}{\cos\theta} \implies 1 > \frac{\sin\theta}{\theta} > \cos\theta \, . </math> | :<math>1 < \frac{\theta}{\sin\theta} < \frac{1}{\cos\theta} \implies 1 > \frac{\sin\theta}{\theta} > \cos\theta \, . </math> | ||
अंतिम चरण में | अंतिम चरण में,असमिका को उलटते हुए,हमने तीन सकारात्मक मानों के प्रतिलोम मान लिए हैं। | ||
[[File:Squeeze FbN.png|thumb|{{center| | [[File:Squeeze FbN.png|thumb|{{center|संकुचन: वक्र {{nowrap|1=''y'' = 1}} और {{nowrap|1=''y'' = cos ''θ''}} लाल रंग में दिखाए गए हैं, वक्र {{nowrap|1=''y'' = sin(''θ'')/''θ''}} नीले लाल रंग में दिखाए गए हैं।}}]]हम इस निष्कर्ष पर पहुंचते हैं कि 0 < θ < ½ π के लिए,राशि sin(θ)/θ हमेशा 1 से कम और हमेशा cos(θ) से अधिक होती है। इस प्रकार,जब θ,0 के नजदीक जाता है, sin(θ)/θ को 1 ऊँचाई पर छत और cos θ ऊँचाई पर फर्श के बीच "[[संकुचित]]" किया जाता है,जो 1 की ओर उठता है;इसलिए θ के धनात्मक दिशा से 0 की ओर पहुंचते ही sin(θ)/θ 1 की ओर प्रवृत्त होना चाहिए: | ||
<math>\lim_{\theta \to 0^+} \frac{\sin\theta}{\theta} = 1 \, . </math> | |||
:<math>\lim_{\theta \to 0^-}\! \frac{\sin\theta}{\theta} | इस मामले के लिए जहां θ एक छोटी ऋणात्मक संख्या हो -½ π < θ < 0,तब हम इस तथ्य का उपयोग करते हैं कि साइन एक [[विषम फलन|विषम]] [[फलन]] है:<math>\lim_{\theta \to 0^-}\! \frac{\sin\theta}{\theta} | ||
\ =\ | \ =\ | ||
\lim_{\theta\to 0^+}\!\frac{\sin(-\theta)}{-\theta} | \lim_{\theta\to 0^+}\!\frac{\sin(-\theta)}{-\theta} | ||
| Line 81: | Line 80: | ||
\lim_{\theta\to 0^+}\!\frac{\sin\theta}{\theta} \ =\ | \lim_{\theta\to 0^+}\!\frac{\sin\theta}{\theta} \ =\ | ||
1 \, . </math> | 1 \, . </math> | ||
===(cos(θ)-1)/θ की सीमा | ===जब θ,0 की ओर प्रवृत्त होता है,तो (cos(θ)-1)/θ की सीमा === | ||
अंतिम खंड | अंतिम खंड हमें इस नई सीमा की अपेक्षाकृत आसानी से गणना करने में सक्षम बनाता है।इसे एक सरल चाल का उपयोग करके किया जाता है।इस गणना में, θ का चिह्न महत्त्वहीन है। | ||
<math> \lim_{\theta \to 0}\, \frac{\cos\theta - 1}{\theta} | |||
\ =\ | \ =\ | ||
\lim_{\theta \to 0} \left( \frac{\cos\theta - 1}{\theta} \right)\!\! \left( \frac{\cos\theta + 1}{\cos\theta + 1} \right) | \lim_{\theta \to 0} \left( \frac{\cos\theta - 1}{\theta} \right)\!\! \left( \frac{\cos\theta + 1}{\cos\theta + 1} \right) | ||
\ =\ | \ =\ | ||
\lim_{\theta \to 0}\, \frac{\cos^2\!\theta - 1}{\theta\,(\cos\theta + 1)} . </math> | \lim_{\theta \to 0}\, \frac{\cos^2\!\theta - 1}{\theta\,(\cos\theta + 1)} . </math> | ||
:<math> \lim_{\theta \to 0}\,\frac{\cos\theta - 1}{\theta} | {{nowrap|1=cos<sup>2</sup>''θ'' – 1 = –sin<sup>2</sup>''θ''}} का उपयोग करते हुए,तथ्य यह है कि एक गुणांक की सीमा सीमाओं का गुणांक होती है,और पिछले खंड से सीमा परिणाम मिलता है,हम पाते हैं कि:<math> \lim_{\theta \to 0}\,\frac{\cos\theta - 1}{\theta} | ||
\ =\ | \ =\ | ||
\lim_{\theta \to 0}\, \frac{-\sin^2\theta}{\theta(\cos\theta+1)} | \lim_{\theta \to 0}\, \frac{-\sin^2\theta}{\theta(\cos\theta+1)} | ||
| Line 98: | Line 95: | ||
\left( -\lim_{\theta \to 0} \frac{\sin\theta}{\theta}\right)\! \left( \lim_{\theta \to 0}\,\frac{\sin\theta}{\cos\theta + 1} \right) | \left( -\lim_{\theta \to 0} \frac{\sin\theta}{\theta}\right)\! \left( \lim_{\theta \to 0}\,\frac{\sin\theta}{\cos\theta + 1} \right) | ||
\ =\ | \ =\ | ||
(-1)\left(\frac{0}{2}\right) = 0 \, . </math> | (-1)\left(\frac{0}{2}\right) = 0 \, . </math> | ||
=== tan(θ)/θ की सीमा | === जब θ,0 की ओर प्रवृत्त होता है,तो tan(θ)/θ की सीमा === | ||
[[ज्या]] फलन के लिए सीमा | [[ज्या]] फलन के लिए सीमा,स्पर्शज्या फलन विषम होने के तथ्य,और एक गुणांक की सीमा सीमाओं का गुणांक के तथ्य का उपयोग करते हुए,हम पाते हैं: | ||
:<math> | :<math> | ||
\lim_{\theta\to 0} \frac{\tan\theta}{\theta} | \lim_{\theta\to 0} \frac{\tan\theta}{\theta} | ||
| Line 111: | Line 108: | ||
\ =\ | \ =\ | ||
1 \, . </math> | 1 \, . </math> | ||
===ज्या फलन का अवकलज=== | ===ज्या फलन का अवकलज === | ||
हम | हम [[ज्या फलन|ज्या]] फलन के अवकलज की गणना [[सीमा परिभाषा]] से करते हैं: | ||
:<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\sin\theta = \lim_{\delta \to 0} \frac{\sin(\theta + \delta) - \sin \theta}{\delta} . </math> | :<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\sin\theta = \lim_{\delta \to 0} \frac{\sin(\theta + \delta) - \sin \theta}{\delta} . </math> | ||
[[कोण समीकरण सूत्र]] sin(α+β) = sin α cos β + sin β cos α का उपयोग करते हुए,हमें | [[कोण समीकरण सूत्र|कोण जोड़ सूत्र]] sin(α+β) = sin α cos β + sin β cos α का उपयोग करते हुए,हमें मिलता है: | ||
<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\sin\theta | |||
= | = | ||
\lim_{\delta \to 0} \frac{\sin\theta\cos\delta + \sin\delta\cos\theta-\sin\theta}{\delta} | \lim_{\delta \to 0} \frac{\sin\theta\cos\delta + \sin\delta\cos\theta-\sin\theta}{\delta} | ||
| Line 121: | Line 119: | ||
\lim_{\delta \to 0} \left( \frac{\sin\delta}{\delta} \cos\theta | \lim_{\delta \to 0} \left( \frac{\sin\delta}{\delta} \cos\theta | ||
+ \frac{\cos\delta -1}{\delta}\sin\theta \right) . </math> | + \frac{\cos\delta -1}{\delta}\sin\theta \right) . </math> | ||
[[Sine|ज्या]] और [[ | |||
[[Sine|ज्या]] और [[कोज्या]] फलनों के लिए सीमाओं का उपयोग करते हुए: | |||
:<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\sin\theta | :<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\sin\theta | ||
= | = | ||
| Line 127: | Line 126: | ||
= | = | ||
\cos\theta \, . </math> | \cos\theta \, . </math> | ||
===कोज्या फलन का अवकलज=== | ===कोज्या फलन का अवकलज === | ||
====अवकलज की परिभाषा से==== | ====अवकलज की परिभाषा से==== | ||
हम | हम पुनः सीमा परिभाषा से [[कोसाइन फ़ंक्शन|कोज्या]] फलन के अवकलज की गणना करते हैं: | ||
:<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\cos\theta | :<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\cos\theta | ||
= | = | ||
\lim_{\delta \to 0} \frac{\cos(\theta+\delta)-\cos\theta}{\delta} . </math> | \lim_{\delta \to 0} \frac{\cos(\theta+\delta)-\cos\theta}{\delta} . </math> | ||
कोण जोड़ सूत्र {{nowrap|1=cos(α+β) = cos α cos β – sin α sin β}} का उपयोग करते हुए,हमें | कोण जोड़ सूत्र {{nowrap|1=cos(α+β) = cos α cos β – sin α sin β}} का उपयोग करते हुए,हमें मिलता है: | ||
<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\cos\theta | |||
= | = | ||
\lim_{\delta \to 0} \frac{\cos\theta\cos\delta - \sin\theta\sin\delta-\cos\theta}{\delta} | \lim_{\delta \to 0} \frac{\cos\theta\cos\delta - \sin\theta\sin\delta-\cos\theta}{\delta} | ||
= | = | ||
\lim_{\delta \to 0} \left(\frac{\cos\delta -1}{\delta}\cos\theta \,-\, \frac{\sin\delta}{\delta} \sin\theta \right) . </math> | \lim_{\delta \to 0} \left(\frac{\cos\delta -1}{\delta}\cos\theta \,-\, \frac{\sin\delta}{\delta} \sin\theta \right) . </math> | ||
[[ज्या]] और [[कोज्या]] फलनों | |||
[[ज्या]] और [[कोज्या]] फलनों के लिए सीमाओं का उपयोग करते हुए: | |||
:<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\cos\theta | :<math> \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\cos\theta | ||
= (0) \cos\theta - (1) \sin\theta = -\sin\theta \, . </math> | = (0) \cos\theta - (1) \sin\theta = -\sin\theta \, . </math> | ||
====श्रृंखला नियम से==== | ====श्रृंखला नियम से==== | ||
कोज्या फलन के अवकलज की गणना श्रृंखला नियम से करने के लिए,पहले निम्नलिखित तीन तथ्यों का ध्यान दें: | |||
:<math>\cos\theta = \sin\left(\tfrac{\pi}{2}-\theta\right)</math> | :<math>\cos\theta = \sin\left(\tfrac{\pi}{2}-\theta\right)</math> | ||
:<math>\sin\theta = \cos\left(\tfrac{\pi}{2}-\theta\right)</math> | :<math>\sin\theta = \cos\left(\tfrac{\pi}{2}-\theta\right)</math> | ||
:<math>\tfrac{\operatorname{d}}{\operatorname{d}\!\theta} \sin\theta = \cos\theta</math> | :<math>\tfrac{\operatorname{d}}{\operatorname{d}\!\theta} \sin\theta = \cos\theta</math> | ||
पहला और दूसरा तथ्य [[त्रिकोणमितीय सर्वसमिकाओं]] | पहला और दूसरा तथ्य [[त्रिकोणमितीय सर्वसमिकाओं|त्रिकोणमितीय सर्वसमिकाएं]] है,और तीसरा ऊपर प्रमाणित है।इन तीन तथ्यों का उपयोग करके हम निम्नलिखित लिख सकते हैं, | ||
:<math>\tfrac{\operatorname{d}}{\operatorname{d}\!\theta} \cos\theta = \tfrac{\operatorname{d}}{\operatorname{d}\!\theta} \sin\left(\tfrac{\pi}{2}-\theta\right)</math> | :<math>\tfrac{\operatorname{d}}{\operatorname{d}\!\theta} \cos\theta = \tfrac{\operatorname{d}}{\operatorname{d}\!\theta} \sin\left(\tfrac{\pi}{2}-\theta\right)</math> | ||
हम [[श्रृंखला नियम]] का उपयोग करके | हम इसका [[श्रृंखला नियम]] का उपयोग करके विभेदन कर सकते हैं।यदि <math>f(x) = \sin x,\ \ g(\theta) =\tfrac{\pi}{2}-\theta</math>,तो हमें मिलता है: | ||
:<math>\tfrac{\operatorname{d}}{\operatorname{d}\!\theta} f\!\left(g\!\left(\theta\right)\right) = f^\prime\!\left(g\!\left(\theta\right)\right) \cdot g^\prime\!\left(\theta\right) = \cos\left(\tfrac{\pi}{2}-\theta\right) \cdot (0-1) = -\sin\theta</math>. | :<math>\tfrac{\operatorname{d}}{\operatorname{d}\!\theta} f\!\left(g\!\left(\theta\right)\right) = f^\prime\!\left(g\!\left(\theta\right)\right) \cdot g^\prime\!\left(\theta\right) = \cos\left(\tfrac{\pi}{2}-\theta\right) \cdot (0-1) = -\sin\theta</math>. | ||
इसलिए,हमने सिद्ध किया है कि | इसलिए,हमने यह सिद्ध किया है कि | ||
:<math>\tfrac{\operatorname{d}}{\operatorname{d}\!\theta} \cos\theta = -\sin\theta</math>. | :<math>\tfrac{\operatorname{d}}{\operatorname{d}\!\theta} \cos\theta = -\sin\theta</math>. | ||
===स्पर्शज्या फलन का अवकलज=== | ===स्पर्शज्या फलन का अवकलज === | ||
====अवकलज की परिभाषा से==== | ====अवकलज की परिभाषा से==== | ||
[[ | हम [[पहले सिद्धांतों]] का उपयोग [[स्पर्शज्या फलन]] tan θ के अवकलज की गणना करने के लिए करते हैं। परिभाषा के अनुसार: | ||
:<math> | :<math> | ||
\frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\tan\theta | \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\tan\theta | ||
= \lim_{\delta \to 0} \left( \frac{\tan(\theta+\delta)-\tan\theta}{\delta} \right) . | = \lim_{\delta \to 0} \left( \frac{\tan(\theta+\delta)-\tan\theta}{\delta} \right) . | ||
</math> | </math> | ||
प्रसिद्ध कोण | प्रसिद्ध कोण सूत्र {{nowrap|1=tan(α+β) = (tan α + tan β) / (1 - tan α tan β)}} का उपयोग करते हुए,हमें मिलता है:<math> | ||
:<math> | |||
\frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\tan\theta | \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\tan\theta | ||
= \lim_{\delta \to 0} \left[ \frac{\frac{\tan\theta + \tan\delta}{1 - \tan\theta\tan\delta} - \tan\theta}{\delta} \right] | = \lim_{\delta \to 0} \left[ \frac{\frac{\tan\theta + \tan\delta}{1 - \tan\theta\tan\delta} - \tan\theta}{\delta} \right] | ||
= \lim_{\delta \to 0} \left[ \frac{\tan\theta + \tan\delta - \tan\theta + \tan^2\theta\tan\delta}{\delta \left( 1 - \tan\theta\tan\delta \right)} \right] . | = \lim_{\delta \to 0} \left[ \frac{\tan\theta + \tan\delta - \tan\theta + \tan^2\theta\tan\delta}{\delta \left( 1 - \tan\theta\tan\delta \right)} \right] . | ||
</math> | </math> | ||
इस तथ्य | |||
इस तथ्य एक गुणांक की सीमा सीमाओं का गुणांक होती है का उपयोग करते हुए: | |||
:<math> | :<math> | ||
\frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\tan\theta | \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\tan\theta | ||
= \lim_{\delta \to 0} \frac{\tan\delta}{\delta} \times \lim_{\delta \to 0} \left( \frac{1 + \tan^2\theta}{1 - \tan\theta\tan\delta} \right) . | = \lim_{\delta \to 0} \frac{\tan\delta}{\delta} \times \lim_{\delta \to 0} \left( \frac{1 + \tan^2\theta}{1 - \tan\theta\tan\delta} \right) . | ||
</math> | </math> | ||
[[स्पर्शज्या]] फलन | [[स्पर्शज्या]] फलन के लिए सीमा और तथ्य का उपयोग करते हुए कि जैसे δ 0 की ओर प्रवृत्त होता है tan δ 0 की ओर प्रवृत्त होता है: | ||
:<math> | :<math> | ||
\frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\tan\theta | \frac{\operatorname{d}}{\operatorname{d}\!\theta}\,\tan\theta | ||
| Line 191: | Line 192: | ||
</math> | </math> | ||
====भागफल नियम से==== | ====भागफल नियम से==== | ||
एक [[भागफल नियम]] का उपयोग करके स्पर्शज्या फलन के अवकलज की भी गणना कर सकते है। | |||
<math>\frac{\operatorname{d}}{\operatorname{d}\!\theta} \tan\theta | |||
= \frac{\operatorname{d}}{\operatorname{d}\!\theta} \frac{\sin\theta}{\cos\theta} | = \frac{\operatorname{d}}{\operatorname{d}\!\theta} \frac{\sin\theta}{\cos\theta} | ||
= \frac{\left(\sin\theta\right)^\prime \cdot \cos\theta - \sin\theta \cdot \left(\cos\theta\right)^\prime}{ \cos^2 \theta } | = \frac{\left(\sin\theta\right)^\prime \cdot \cos\theta - \sin\theta \cdot \left(\cos\theta\right)^\prime}{ \cos^2 \theta } | ||
| Line 197: | Line 200: | ||
</math> | </math> | ||
पायथागॉरियन | अंश को 1 के रूप में [[पायथागॉरियन सर्वसमिका]] द्वारा सरलित किया जा सकता है,जिससे हमें मिलता है: | ||
:<math>\frac{1}{\cos^2 \theta} = \sec^2 \theta</math> | :<math>\frac{1}{\cos^2 \theta} = \sec^2 \theta</math> | ||
इसलिए, | इसलिए, | ||
| Line 203: | Line 206: | ||
== प्रतिलोम त्रिकोणमितीय फलनों के अवकलजों का प्रमाण == | == प्रतिलोम त्रिकोणमितीय फलनों के अवकलजों का प्रमाण == | ||
निम्नलिखित अवकलजों को | निम्नलिखित अवकलजों को एक [[चर (गणित)|चर]] y को उस [[प्रतिलोम त्रिकोणमितीय फलन]] के बराबर रखकर प्राप्त करते हैं जिसे हम अवकलज लेना चाहते हैं।[[अंतर्निहित अवकलन|अप्रत्य्क्ष विभेदन]] का उपयोग करके और फिर dy/dx के लिए हल करके,प्रतिलोम फलन के अवकलज y के रूप में प्राप्त किया जाता है।dy/dx को पुनः x के रूप में प्रकट करने के लिए,हम एक इकाई वृत्त पर संदर्भ त्रिकोण बना सकते हैं,जहां y को θ के रूप में लेते हैं।[[पाइथागोरस प्रमेय]] और नियमित त्रिकोणमितीय फलन की परिभाषा का उपयोग करके,हम अंततः dy/dx को x के संदर्भ में व्यक्त कर सकते हैं। | ||
===प्रतिलोम ज्या फलन | ===प्रतिलोम ज्या फलन का विभेदन करना=== | ||
हम | हम | ||
:<math>y=\arcsin x\,\!</math> | :<math>y=\arcsin x\,\!</math> | ||
लेते हैं,जहां | |||
:<math>-\frac{\pi}{2}\le y \le \frac{\pi}{2}</math> | :<math>-\frac{\pi}{2}\le y \le \frac{\pi}{2}</math> | ||
फिर | |||
:<math>\sin y=x\,\!</math> | :<math>\sin y=x\,\!</math> | ||
दोनों | दोनों ओर से <math>x</math> के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए: | ||
:<math>{d \over dx}\sin y={d \over dx}x</math> | :<math>{d \over dx}\sin y={d \over dx}x</math> | ||
:<math>\cos y \cdot {dy \over dx} = 1\,\!</math> | :<math>\cos y \cdot {dy \over dx} = 1\,\!</math> | ||
प्रतिस्थापन <math> \cos y = \sqrt{1-\sin^2 y}</math> ऊपर से, | |||
:<math>\sqrt{1-\sin^2 y} \cdot {dy \over dx} =1</math> | :<math>\sqrt{1-\sin^2 y} \cdot {dy \over dx} =1</math> | ||
प्रतिस्थापन <math>x=\sin y</math> ऊपर से, | |||
:<math>\sqrt{1-x^2} \cdot {dy \over dx} =1</math> | :<math>\sqrt{1-x^2} \cdot {dy \over dx} =1</math> | ||
:<math>{dy \over dx}=\frac{1}{\sqrt{1-x^2}}</math> | :<math>{dy \over dx}=\frac{1}{\sqrt{1-x^2}}</math> | ||
===प्रतिलोम कोज्या फलन | ===प्रतिलोम कोज्या फलन का विभेदन करना=== | ||
हम | हम | ||
:<math>y=\arccos x\,\!</math> | :<math>y=\arccos x\,\!</math> | ||
लेते हैं,जहां | |||
:<math>0 \le y \le \pi</math> | :<math>0 \le y \le \pi</math> | ||
फिर | |||
:<math>\cos y=x\,\!</math> | :<math>\cos y=x\,\!</math> | ||
दोनों पक्षों से <math>x</math> के संबंध में अवकलज | दोनों पक्षों से <math>x</math> के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए: | ||
:<math>{d \over dx}\cos y={d \over dx}x</math> | :<math>{d \over dx}\cos y={d \over dx}x</math> | ||
:<math>-\sin y \cdot {dy \over dx} =1</math> | :<math>-\sin y \cdot {dy \over dx} =1</math> | ||
प्रतिस्थापन <math>\sin y = \sqrt{1-\cos^2 y}\,\!</math> ऊपर से, | |||
:<math>-\sqrt{1-\cos^2 y} \cdot {dy \over dx} =1</math> | :<math>-\sqrt{1-\cos^2 y} \cdot {dy \over dx} =1</math> | ||
प्रतिस्थापन <math>x=\cos y\,\!</math> ऊपर से, | |||
:<math>-\sqrt{1-x^2} \cdot {dy \over dx} =1</math> | :<math>-\sqrt{1-x^2} \cdot {dy \over dx} =1</math> | ||
:<math>{dy \over dx} = -\frac{1}{\sqrt{1-x^2}}</math> | :<math>{dy \over dx} = -\frac{1}{\sqrt{1-x^2}}</math> | ||
वैकल्पिक रूप से,एक बार जब <math>\arcsin x</math> का अवकलज स्थापित हो जाता है,तो | वैकल्पिक रूप से,एक बार जब <math>\arcsin x</math> का अवकलज स्थापित हो जाता है,तो सर्वसमिका <math>\arcsin x+\arccos x=\pi/2</math> का विभेदन करने से <math>\arccos x</math> का अवकलज तुरंत अनुसरण करता है,ताकि <math>(\arccos x)'=-(\arcsin x)'</math>हो। | ||
===प्रतिलोम स्पर्शज्या फलन | ===प्रतिलोम स्पर्शज्या फलन का विभेदन करना=== | ||
हम | हम | ||
:<math>y=\arctan x\,\!</math> | :<math>y=\arctan x\,\!</math> | ||
लेते हैं,जहां | |||
:<math>-\frac{\pi}{2} < y < \frac{\pi}{2}</math> | :<math>-\frac{\pi}{2} < y < \frac{\pi}{2}</math> | ||
फिर, | |||
:<math>\tan y=x\,\!</math> | :<math>\tan y=x\,\!</math> | ||
दोनों पक्षों से <math>x</math> के संबंध में अवकलज | दोनों पक्षों से <math>x</math> के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए: | ||
:<math>{d \over dx}\tan y={d \over dx}x</math> | :<math>{d \over dx}\tan y={d \over dx}x</math> | ||
| Line 269: | Line 272: | ||
= \sec^2 y \cdot {dy \over dx} | = \sec^2 y \cdot {dy \over dx} | ||
= (1 + \tan^2 y) {dy \over dx} | = (1 + \tan^2 y) {dy \over dx} | ||
</math>,पायथागॉरियन सर्वसमिका का उपयोग | </math>,पायथागॉरियन सर्वसमिका का उपयोग करके | ||
दाईं तरफ: | दाईं तरफ: | ||
| Line 277: | Line 280: | ||
:<math>(1+\tan^2 y){dy \over dx}=1</math> | :<math>(1+\tan^2 y){dy \over dx}=1</math> | ||
प्रतिस्थापन <math>x=\tan y\,\!</math> ऊपर से, हमें मिलता है | |||
:<math>(1+x^2){dy \over dx}=1</math> | :<math>(1+x^2){dy \over dx}=1</math> | ||
:<math>{dy \over dx}=\frac{1}{1+x^2}</math> | :<math>{dy \over dx}=\frac{1}{1+x^2}</math> | ||
===प्रतिलोम | ===प्रतिलोम कोस्पर्शज्या फलन का विभेदन करना === | ||
हम | हम | ||
:<math>y=\arccot x</math> | :<math>y=\arccot x</math> | ||
लेते हैं,जहां <math>0<y<\pi</math> | |||
फिर, | |||
:<math>\cot y=x</math> | :<math>\cot y=x</math> | ||
दोनों पक्षों से <math>x</math> के संबंध में अवकलज | दोनों पक्षों से <math>x</math> के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए: | ||
:<math>\frac{d}{dx}\cot y=\frac{d}{dx}x</math> | :<math>\frac{d}{dx}\cot y=\frac{d}{dx}x</math> | ||
| Line 308: | Line 311: | ||
:<math>-(1+\cot^2y)\frac{dy}{dx}=1</math> | :<math>-(1+\cot^2y)\frac{dy}{dx}=1</math> | ||
<math>x=\cot y</math> | <math>x=\cot y</math> प्रतिस्थापन करते हुए, | ||
:<math>-(1+x^2)\frac{dy}{dx}=1</math> | :<math>-(1+x^2)\frac{dy}{dx}=1</math> | ||
:<math>\frac{dy}{dx}=-\frac{1}{1+x^2}</math> | :<math>\frac{dy}{dx}=-\frac{1}{1+x^2}</math> | ||
वैकल्पिक रूप से,जैसा कि ऊपर दिखाया गया है | वैकल्पिक रूप से,जैसा कि ऊपर दिखाया गया है वैसे ही <math>\arctan x</math> का अवकलज व्युत्पन्न किया गया,फिर सर्वसमिका <math>\arctan x+\arccot x=\dfrac{\pi}{2}</math> का उपयोग करके उसका तुरंत अनुसरण करता है<math display="block">\begin{align} | ||
\dfrac{d}{dx}\arccot x | \dfrac{d}{dx}\arccot x | ||
&=\dfrac{d}{dx}\left(\dfrac{\pi}{2}-\arctan x\right)\\ | &=\dfrac{d}{dx}\left(\dfrac{\pi}{2}-\arctan x\right)\\ | ||
&=-\dfrac{1}{1+x^2} | &=-\dfrac{1}{1+x^2} | ||
\end{align} </math> | \end{align} </math> | ||
===प्रतिलोम | |||
===प्रतिलोम व्युत्क्रम-कोज्या फलन का विभेदन करना=== | |||
==== | ====अप्रत्य्क्ष विभेदन का उपयोग करना ==== | ||
माना | माना | ||
:<math> y = \arcsec x\ \mid |x| \geq 1</math> | :<math> y = \arcsec x\ \mid |x| \geq 1</math> | ||
लेते हैं,जहां | |||
:<math> x = \sec y \mid \ y \in \left [0,\frac{\pi}{2} \right )\cup \left (\frac{\pi}{2},\pi \right] | :<math> x = \sec y \mid \ y \in \left [0,\frac{\pi}{2} \right )\cup \left (\frac{\pi}{2},\pi \right] | ||
</math> | </math>फिर, | ||
:<math> \frac{dx}{dy} = \sec y \tan y = |x|\sqrt{x^2-1}</math> | :<math> \frac{dx}{dy} = \sec y \tan y = |x|\sqrt{x^2-1}</math> | ||
(अभिव्यक्ति में | (अभिव्यक्ति में निरपेक्ष मान आवश्यक है क्योंकि y के अंतराल में व्युत्क्रम-कोज्या और स्पर्शज्या का गुणांक हमेशा गैर-ऋणात्मक होता है,जबकि प्रमुख वर्गमूल की परिभाषा के अनुसार करणी <math>\sqrt{x^2-1}</math> हमेशा गैर-ऋणात्मक होती है,इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए,जो x के निरपेक्ष मान का उपयोग करके प्राप्त किये जाते हैं।) | ||
:<math> \frac{dy}{dx} = \frac{1}{|x|\sqrt{x^2-1}}</math> | :<math> \frac{dy}{dx} = \frac{1}{|x|\sqrt{x^2-1}}</math> | ||
====श्रृंखला नियम का उपयोग करना==== | ====श्रृंखला नियम का उपयोग करना==== | ||
वैकल्पिक रूप से,[[श्रृंखला नियम]] का उपयोग करके | वैकल्पिक रूप से,प्रतिलोम व्युत्क्रम-कोज्या का अवकलज [[श्रृंखला नियम]] का उपयोग करके प्रतिलोम कोज्या के अवकलज से व्युत्पन्न किया जा सकता है। | ||
माना | माना | ||
:<math> y = \arcsec x = \arccos \left(\frac{1}{x}\right) </math> | :<math> y = \arcsec x = \arccos \left(\frac{1}{x}\right) </math> | ||
लेते हैं,जहां | |||
:<math> |x| \geq 1 </math> और <math> y \in \left[0, \frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \pi\right] </math> | :<math> |x| \geq 1 </math> और <math> y \in \left[0, \frac{\pi}{2}\right) \cup \left(\frac{\pi}{2}, \pi\right] </math> | ||
फिर, <math> \arccos \left(\frac{1}{x}\right) </math>के लिए श्रृंखला नियम का उपयोग करते हुए: | |||
:<math> \frac{dy}{dx} = -\frac{1}{\sqrt{1-(\frac{1}{x})^2}} \cdot \left(-\frac{1}{x^2}\right) | :<math> \frac{dy}{dx} = -\frac{1}{\sqrt{1-(\frac{1}{x})^2}} \cdot \left(-\frac{1}{x^2}\right) | ||
| Line 346: | Line 350: | ||
= \frac{1}{\sqrt{x^2}\sqrt{x^2-1}} | = \frac{1}{\sqrt{x^2}\sqrt{x^2-1}} | ||
= \frac{1}{|x|\sqrt{x^2-1}} </math> | = \frac{1}{|x|\sqrt{x^2-1}} </math> | ||
===प्रतिलोम | ===प्रतिलोम व्युत्क्रमज्या फलन का विभेदन करना=== | ||
==== | ====अप्रत्य्क्ष विभेदन का उपयोग करना ==== | ||
माना | माना | ||
:<math>y = \arccsc x\ \mid |x| \geq 1</math> | :<math>y = \arccsc x\ \mid |x| \geq 1</math> | ||
लेते हैं,जहां | |||
:<math> x = \csc y\ \mid \ y \in \left [-\frac{\pi}{2},0 \right )\cup \left (0,\frac{\pi}{2} \right]</math> | :<math> x = \csc y\ \mid \ y \in \left [-\frac{\pi}{2},0 \right )\cup \left (0,\frac{\pi}{2} \right]</math> | ||
: | :फिर, | ||
:<math> \frac{dx}{dy} = -\csc y \cot y = -|x|\sqrt{x^2-1}</math> | :<math> \frac{dx}{dy} = -\csc y \cot y = -|x|\sqrt{x^2-1}</math> | ||
(अभिव्यक्ति में | (अभिव्यक्ति में निरपेक्ष मान आवश्यक है क्योंकि y के अंतराल में व्युत्क्रमज्या और कोस्पर्शज्या का गुणांक हमेशा गैर-ऋणात्मक होता है,जबकि प्रमुख वर्गमूल की परिभाषा के अनुसार करणी <math>\sqrt{x^2-1}</math> हमेशा गैर-ऋणात्मक होता है,इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए,जो x के निरपेक्ष मान का उपयोग करके प्राप्त किये जाते हैं।) | ||
:<math> \frac{dy}{dx} = \frac{-1}{|x|\sqrt{x^2-1}}</math> | :<math> \frac{dy}{dx} = \frac{-1}{|x|\sqrt{x^2-1}}</math> | ||
====श्रृंखला नियम का उपयोग करना==== | ====श्रृंखला नियम का उपयोग करना==== | ||
वैकल्पिक रूप से,[[श्रृंखला नियम]] का उपयोग करके | वैकल्पिक रूप से,प्रतिलोम व्युत्क्रमज्या का अवकलज [[श्रृंखला नियम]] का उपयोग करके प्रतिलोम-ज्या के अवकलज से व्युत्पन्न किया जा सकता है। | ||
माना | माना | ||
:<math> y = \arccsc x = \arcsin \left(\frac{1}{x}\right) </math> | :<math> y = \arccsc x = \arcsin \left(\frac{1}{x}\right) </math> | ||
लेते हैं,जहां | |||
:<math> |x| \geq 1 </math> और <math> y \in \left[-\frac{\pi}{2}, 0\right) \cup \left(0, \frac{\pi}{2}\right] </math> | :<math> |x| \geq 1 </math> और <math> y \in \left[-\frac{\pi}{2}, 0\right) \cup \left(0, \frac{\pi}{2}\right] </math> | ||
फिर, <math> \arcsin \left(\frac{1}{x}\right) </math>के लिए श्रृंखला नियम को लागू करके | |||
:<math> \frac{dy}{dx} =\frac{1}{\sqrt{1-(\frac{1}{x})^2}} \cdot \left(-\frac{1}{x^2}\right) | :<math> \frac{dy}{dx} =\frac{1}{\sqrt{1-(\frac{1}{x})^2}} \cdot \left(-\frac{1}{x^2}\right) | ||
| Line 397: | Line 401: | ||
{{DEFAULTSORT:Differentiation Of Trigonometric Functions}} | {{DEFAULTSORT:Differentiation Of Trigonometric Functions}} | ||
[[Category: Machine Translated Page]] | [[Category:Created On 04/07/2023|Differentiation Of Trigonometric Functions]] | ||
[[Category: | [[Category:Lua-based templates|Differentiation Of Trigonometric Functions]] | ||
[[Category:Machine Translated Page|Differentiation Of Trigonometric Functions]] | |||
[[Category:Mathematics sidebar templates|Differentiation Of Trigonometric Functions]] | |||
[[Category:Pages with broken file links|Differentiation Of Trigonometric Functions]] | |||
[[Category:Pages with script errors|Differentiation Of Trigonometric Functions]] | |||
[[Category:Sidebars with styles needing conversion|Differentiation Of Trigonometric Functions]] | |||
[[Category:Templates Vigyan Ready|Differentiation Of Trigonometric Functions]] | |||
[[Category:Templates that add a tracking category|Differentiation Of Trigonometric Functions]] | |||
[[Category:Templates that generate short descriptions|Differentiation Of Trigonometric Functions]] | |||
[[Category:Templates using TemplateData|Differentiation Of Trigonometric Functions]] | |||
[[Category:अंतर कलन|Differentiation Of Trigonometric Functions]] | |||
[[Category:गणितीय पहचान|Differentiation Of Trigonometric Functions]] | |||
[[Category:प्रमाण युक्त लेख|Differentiation Of Trigonometric Functions]] | |||
[[Category:विभेदक समीकरण|Differentiation Of Trigonometric Functions]] | |||
Latest revision as of 10:42, 15 July 2023
| त्रिकोणमिति |
|---|
 |
| संदर्भ |
| कानून और सिद्धांत |
| पथरी |
| फलन | अवकलज |
|---|---|
त्रिकोणमितीय फलनों का विभेदन,एक त्रिकोणमितीय फलन के अवकलज या एक चर के संबंध में उसके परिवर्तन की दर का पता लगाने की गणितीय प्रक्रिया है।उदाहरण के लिए,ज्या फलन का अवकलज sin'(a) = cos(a) के रूप में लिखा जाता है,इसका अर्थ है कि एक विशेष कोण x = a पर sin(x) की परिवर्तन दर को उस कोण के कोज्या से दिया जाता है।
वृत्तीय त्रिकोणमितीय फलनों के सभी अवकलज sin(x) और cos(x) से tan(x) = sin(x)/cos(x) जैसे फलनों पर लागू होने वाले भागफल नियम के माध्यम से पाए जा सकते हैं।इन अवकलजों को जानने के लिए,प्रतिलोम त्रिकोणमितीय फलनों के अवकलजों को अप्रत्य्क्ष विभेदन का उपयोग करके पाया जाता है।
त्रिकोणमितीय फलनों के अवकलजों के प्रमाण
जब θ,0 की ओर प्रवृत्त होता है,तो sin(θ)/θ की सीमा
दायीं ओर आरेख केंद्र o और त्रिज्या r = 1 के साथ एक वृत्त दिखाता है।दो त्रिज्याएँ OA और OB,θ रेडियन का एक चाप बनाते हैं।चूंकि हम सीमा को शून्य मान रहे हैं,इसलिए हम मान सकते हैं कि θ एक छोटी धनात्मक संख्या है,अर्थात्,0 < θ < ½ π पहले चतुर्थांश में है।
आरेख में,OAB त्रिभुज को R1,OAB वृत्तीय क्षेत्र को R2 और OAC त्रिभुज को R3 लें।OAB त्रिभुज का क्षेत्रफल है:
OAB वृत्तीय क्षेत्र का क्षेत्रफल है,जबकि OAC त्रिभुज का क्षेत्रफल दिया गया है
चूँकि प्रत्येक क्षेत्र अगले क्षेत्र में निहित है,इसलिए एक निम्न विधि होती है:
इसके अतिरिक्त,चूँकि पहले चतुर्थांश में sin θ > 0 होता है,हम ½ sin θ से भाग कर सकते हैं:
अंतिम चरण में,असमिका को उलटते हुए,हमने तीन सकारात्मक मानों के प्रतिलोम मान लिए हैं।
हम इस निष्कर्ष पर पहुंचते हैं कि 0 < θ < ½ π के लिए,राशि sin(θ)/θ हमेशा 1 से कम और हमेशा cos(θ) से अधिक होती है। इस प्रकार,जब θ,0 के नजदीक जाता है, sin(θ)/θ को 1 ऊँचाई पर छत और cos θ ऊँचाई पर फर्श के बीच "संकुचित" किया जाता है,जो 1 की ओर उठता है;इसलिए θ के धनात्मक दिशा से 0 की ओर पहुंचते ही sin(θ)/θ 1 की ओर प्रवृत्त होना चाहिए:
इस मामले के लिए जहां θ एक छोटी ऋणात्मक संख्या हो -½ π < θ < 0,तब हम इस तथ्य का उपयोग करते हैं कि साइन एक विषम फलन है:
जब θ,0 की ओर प्रवृत्त होता है,तो (cos(θ)-1)/θ की सीमा
अंतिम खंड हमें इस नई सीमा की अपेक्षाकृत आसानी से गणना करने में सक्षम बनाता है।इसे एक सरल चाल का उपयोग करके किया जाता है।इस गणना में, θ का चिह्न महत्त्वहीन है।
cos2θ – 1 = –sin2θ का उपयोग करते हुए,तथ्य यह है कि एक गुणांक की सीमा सीमाओं का गुणांक होती है,और पिछले खंड से सीमा परिणाम मिलता है,हम पाते हैं कि:
जब θ,0 की ओर प्रवृत्त होता है,तो tan(θ)/θ की सीमा
ज्या फलन के लिए सीमा,स्पर्शज्या फलन विषम होने के तथ्य,और एक गुणांक की सीमा सीमाओं का गुणांक के तथ्य का उपयोग करते हुए,हम पाते हैं:
ज्या फलन का अवकलज
हम ज्या फलन के अवकलज की गणना सीमा परिभाषा से करते हैं:
कोण जोड़ सूत्र sin(α+β) = sin α cos β + sin β cos α का उपयोग करते हुए,हमें मिलता है:
ज्या और कोज्या फलनों के लिए सीमाओं का उपयोग करते हुए:
कोज्या फलन का अवकलज
अवकलज की परिभाषा से
हम पुनः सीमा परिभाषा से कोज्या फलन के अवकलज की गणना करते हैं:
कोण जोड़ सूत्र cos(α+β) = cos α cos β – sin α sin β का उपयोग करते हुए,हमें मिलता है:
ज्या और कोज्या फलनों के लिए सीमाओं का उपयोग करते हुए:
श्रृंखला नियम से
कोज्या फलन के अवकलज की गणना श्रृंखला नियम से करने के लिए,पहले निम्नलिखित तीन तथ्यों का ध्यान दें:
पहला और दूसरा तथ्य त्रिकोणमितीय सर्वसमिकाएं है,और तीसरा ऊपर प्रमाणित है।इन तीन तथ्यों का उपयोग करके हम निम्नलिखित लिख सकते हैं,
हम इसका श्रृंखला नियम का उपयोग करके विभेदन कर सकते हैं।यदि ,तो हमें मिलता है:
- .
इसलिए,हमने यह सिद्ध किया है कि
- .
स्पर्शज्या फलन का अवकलज
अवकलज की परिभाषा से
हम पहले सिद्धांतों का उपयोग स्पर्शज्या फलन tan θ के अवकलज की गणना करने के लिए करते हैं। परिभाषा के अनुसार:
प्रसिद्ध कोण सूत्र tan(α+β) = (tan α + tan β) / (1 - tan α tan β) का उपयोग करते हुए,हमें मिलता है:
इस तथ्य एक गुणांक की सीमा सीमाओं का गुणांक होती है का उपयोग करते हुए:
स्पर्शज्या फलन के लिए सीमा और तथ्य का उपयोग करते हुए कि जैसे δ 0 की ओर प्रवृत्त होता है tan δ 0 की ओर प्रवृत्त होता है:
हम तुरंत देखते हैं कि:
भागफल नियम से
एक भागफल नियम का उपयोग करके स्पर्शज्या फलन के अवकलज की भी गणना कर सकते है।
अंश को 1 के रूप में पायथागॉरियन सर्वसमिका द्वारा सरलित किया जा सकता है,जिससे हमें मिलता है:
इसलिए,
प्रतिलोम त्रिकोणमितीय फलनों के अवकलजों का प्रमाण
निम्नलिखित अवकलजों को एक चर y को उस प्रतिलोम त्रिकोणमितीय फलन के बराबर रखकर प्राप्त करते हैं जिसे हम अवकलज लेना चाहते हैं।अप्रत्य्क्ष विभेदन का उपयोग करके और फिर dy/dx के लिए हल करके,प्रतिलोम फलन के अवकलज y के रूप में प्राप्त किया जाता है।dy/dx को पुनः x के रूप में प्रकट करने के लिए,हम एक इकाई वृत्त पर संदर्भ त्रिकोण बना सकते हैं,जहां y को θ के रूप में लेते हैं।पाइथागोरस प्रमेय और नियमित त्रिकोणमितीय फलन की परिभाषा का उपयोग करके,हम अंततः dy/dx को x के संदर्भ में व्यक्त कर सकते हैं।
प्रतिलोम ज्या फलन का विभेदन करना
हम
लेते हैं,जहां
फिर
दोनों ओर से के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:
प्रतिस्थापन ऊपर से,
प्रतिस्थापन ऊपर से,
प्रतिलोम कोज्या फलन का विभेदन करना
हम
लेते हैं,जहां
फिर
दोनों पक्षों से के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:
प्रतिस्थापन ऊपर से,
प्रतिस्थापन ऊपर से,
वैकल्पिक रूप से,एक बार जब का अवकलज स्थापित हो जाता है,तो सर्वसमिका का विभेदन करने से का अवकलज तुरंत अनुसरण करता है,ताकि हो।
प्रतिलोम स्पर्शज्या फलन का विभेदन करना
हम
लेते हैं,जहां
फिर,
दोनों पक्षों से के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:
बाईं तरफ:
- ,पायथागॉरियन सर्वसमिका का उपयोग करके
दाईं तरफ:
इसलिए,
प्रतिस्थापन ऊपर से, हमें मिलता है
प्रतिलोम कोस्पर्शज्या फलन का विभेदन करना
हम
लेते हैं,जहां
फिर,
दोनों पक्षों से के संबंध में अवकलज लेते हुए और dy/dx के लिए हल करते हुए:
बाईं तरफ:
- ,पायथागॉरियन सर्वसमिका का उपयोग करके
दाईं तरफ:
इसलिए,
प्रतिस्थापन करते हुए,
वैकल्पिक रूप से,जैसा कि ऊपर दिखाया गया है वैसे ही का अवकलज व्युत्पन्न किया गया,फिर सर्वसमिका का उपयोग करके उसका तुरंत अनुसरण करता है
प्रतिलोम व्युत्क्रम-कोज्या फलन का विभेदन करना
अप्रत्य्क्ष विभेदन का उपयोग करना
माना
लेते हैं,जहां
- फिर,
(अभिव्यक्ति में निरपेक्ष मान आवश्यक है क्योंकि y के अंतराल में व्युत्क्रम-कोज्या और स्पर्शज्या का गुणांक हमेशा गैर-ऋणात्मक होता है,जबकि प्रमुख वर्गमूल की परिभाषा के अनुसार करणी हमेशा गैर-ऋणात्मक होती है,इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए,जो x के निरपेक्ष मान का उपयोग करके प्राप्त किये जाते हैं।)
श्रृंखला नियम का उपयोग करना
वैकल्पिक रूप से,प्रतिलोम व्युत्क्रम-कोज्या का अवकलज श्रृंखला नियम का उपयोग करके प्रतिलोम कोज्या के अवकलज से व्युत्पन्न किया जा सकता है।
माना
लेते हैं,जहां
- और
फिर, के लिए श्रृंखला नियम का उपयोग करते हुए:
प्रतिलोम व्युत्क्रमज्या फलन का विभेदन करना
अप्रत्य्क्ष विभेदन का उपयोग करना
माना
लेते हैं,जहां
- फिर,
(अभिव्यक्ति में निरपेक्ष मान आवश्यक है क्योंकि y के अंतराल में व्युत्क्रमज्या और कोस्पर्शज्या का गुणांक हमेशा गैर-ऋणात्मक होता है,जबकि प्रमुख वर्गमूल की परिभाषा के अनुसार करणी हमेशा गैर-ऋणात्मक होता है,इसलिए शेष गुणक भी गैर-ऋणात्मक होना चाहिए,जो x के निरपेक्ष मान का उपयोग करके प्राप्त किये जाते हैं।)
श्रृंखला नियम का उपयोग करना
वैकल्पिक रूप से,प्रतिलोम व्युत्क्रमज्या का अवकलज श्रृंखला नियम का उपयोग करके प्रतिलोम-ज्या के अवकलज से व्युत्पन्न किया जा सकता है।
माना
लेते हैं,जहां
- और
फिर, के लिए श्रृंखला नियम को लागू करके
यह भी देखें
- Calculus – Branch of mathematics
- Derivative – Instantaneous rate of change (mathematics)
- Differentiation rules – Rules for computing derivatives of functions
- General Leibniz rule – Generalization of the product rule in calculus
- Inverse functions and differentiation
- Linearity of differentiation – Calculus property
- List of integrals of inverse trigonometric functions
- List of trigonometric identities – Equalities that involve trigonometric functions
- Table of derivatives
- Trigonometry
संदर्भ
ग्रन्थसूची
- Handbook of Mathematical Functions, Edited by Abramowitz and Stegun, National Bureau of Standards, Applied Mathematics Series, 55 (1964)

