फैराडे का प्रेरण का नियम: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
{{Use American English|date=March 2019}}{{Short description|Basic law of electromagnetism of magnetic fields inducing a potential difference}} | {{Use American English|date=March 2019}}{{Short description|Basic law of electromagnetism of magnetic fields inducing a potential difference}} | ||
[[Image:Induction experiment.png|thumb|upright=1.3|फैराडे का प्रयोग तार के कॉइल के बीच प्रेरण दिखा रहा है: तरल बैटरी (दाएं) एक करंट प्रदान करती है जो छोटे कॉइल (ए) के माध्यम से प्रवाहित होती है, जिससे एक चुंबकीय क्षेत्र बनता है। जब कुण्डलियाँ स्थिर होती हैं, तो कोई धारा प्रेरित नहीं होती है। लेकिन जब छोटे कॉइल को बड़े कॉइल (B) के अंदर या बाहर ले जाया जाता है, तो बड़े कॉइल के माध्यम से चुंबकीय प्रवाह बदल जाता है, जिससे करंट उत्पन्न होता है जिसे गैल्वेनोमीटर (G) द्वारा पता लगाया जाता है।<ref>{{cite book|last=Poyser|first=Arthur William|url=https://archive.org/details/bub_gb_JzBAAAAAYAAJ|title=Magnetism and Electricity: A manual for students in advanced classes|date=1892|publisher=Longmans, Green, & Co.|location=London and New York|at=Fig. 248, p. 245|access-date=2009-08-06}}</ref>]]फैराडे का इंडक्शन (प्रेरण) का नियम (संक्षेप में, फैराडे का नियम) विद्युत् चुम्बकत्व का एक बुनियादी नियम है, जो अभिरुचि करता है कि एक [[ वैद्युतवाहक बल ]] (ईएमएफ) उत्पन्न करने के लिए एक [[ चुंबकीय क्षेत्र ]] एक [[Index.php?title=विद्युत परिपथ|विद्युत परिपथ]] के साथ कैसे परस्पर प्रभाव करेगा - एक घटना जिसे [[Index.php?title=विद्युत चुंबकीय प्रेरण|विद्युत चुंबकीय प्रेरण]] के रूप में जाना जाता है। यह [[Index.php?title=रूपांतरक|रूपांतरक]] (ट्रांसफार्मर), कुचालक और कई प्रकार के[[ बिजली की मोटर | बिजली की मोटर]], [[ [[ विद्युत ]] जनरेटर ]] और [[Index.php?title=परिनालिका|परिनालिका]] का मूलभूत संचालन सिद्धांत है।<ref name="Sadiku386">{{cite book|last=Sadiku|first=M. N. O.|title=Elements of Electromagnetics|year=2007|page=386|publisher=Oxford University Press|edition=4th|location=New York & Oxford|url=https://books.google.com/books?id=w2ITHQAACAAJ|isbn=978-0-19-530048-2}}</ref><ref>{{cite web|date=1999-07-22|title=Applications of electromagnetic induction|url=http://physics.bu.edu/~duffy/py106/Electricgenerators.html|publisher=[[Boston University]]}}</ref> | [[Image:Induction experiment.png|thumb|upright=1.3|फैराडे का प्रयोग तार के कॉइल के बीच प्रेरण दिखा रहा है: तरल बैटरी (दाएं) एक करंट प्रदान करती है जो छोटे कॉइल (ए) के माध्यम से प्रवाहित होती है, जिससे एक चुंबकीय क्षेत्र बनता है। जब कुण्डलियाँ स्थिर होती हैं, तो कोई धारा प्रेरित नहीं होती है। लेकिन जब छोटे कॉइल को बड़े कॉइल (B) के अंदर या बाहर ले जाया जाता है, तो बड़े कॉइल के माध्यम से चुंबकीय प्रवाह बदल जाता है, जिससे करंट उत्पन्न होता है जिसे गैल्वेनोमीटर (G) द्वारा पता लगाया जाता है।<ref>{{cite book|last=Poyser|first=Arthur William|url=https://archive.org/details/bub_gb_JzBAAAAAYAAJ|title=Magnetism and Electricity: A manual for students in advanced classes|date=1892|publisher=Longmans, Green, & Co.|location=London and New York|at=Fig. 248, p. 245|access-date=2009-08-06}}</ref>]]फैराडे का इंडक्शन (प्रेरण) का नियम (संक्षेप में, फैराडे का नियम) विद्युत् चुम्बकत्व का एक बुनियादी नियम है, जो अभिरुचि करता है कि एक [[ वैद्युतवाहक बल ]] (ईएमएफ) उत्पन्न करने के लिए एक [[ चुंबकीय क्षेत्र ]] एक [[Index.php?title=विद्युत परिपथ|विद्युत परिपथ]] के साथ कैसे परस्पर प्रभाव करेगा - एक घटना जिसे [[Index.php?title=विद्युत चुंबकीय प्रेरण|विद्युत चुंबकीय प्रेरण]] के रूप में जाना जाता है। यह [[Index.php?title=रूपांतरक|रूपांतरक]] (ट्रांसफार्मर), कुचालक और कई प्रकार के[[ बिजली की मोटर | बिजली की मोटर]], [[ [[ विद्युत ]] जनरेटर ]] और [[Index.php?title=परिनालिका|परिनालिका]] का मूलभूत संचालन सिद्धांत है।<ref name="Sadiku386">{{cite book|last=Sadiku|first=M. N. O.|title=Elements of Electromagnetics|year=2007|page=386|publisher=Oxford University Press|edition=4th|location=New York & Oxford|url=https://books.google.com/books?id=w2ITHQAACAAJ|isbn=978-0-19-530048-2}}</ref><ref>{{cite web|date=1999-07-22|title=Applications of electromagnetic induction|url=http://physics.bu.edu/~duffy/py106/Electricgenerators.html|publisher=[[Boston University]]}}</ref> | ||
मैक्सवेल-फैराडे समीकरण (मैक्सवेल के समीकरणों में से एक के रूप में सूचीबद्ध) इस तथ्य का वर्णन करता है कि एक स्थानिक रूप से भिन्न (और संभवतः समय-भिन्न भी, इस पर निर्भर करता है कि एक चुंबकीय क्षेत्र समय में कैसे भिन्न होता है) विद्युत क्षेत्र हमेशा एक समय-भिन्न चुंबकीय क्षेत्र के साथ होता है, जबकि फैराडे के | मैक्सवेल-फैराडे समीकरण (मैक्सवेल के समीकरणों में से एक के रूप में सूचीबद्ध) इस तथ्य का वर्णन करता है कि एक स्थानिक रूप से भिन्न (और संभवतः समय-भिन्न भी, इस पर निर्भर करता है कि एक चुंबकीय क्षेत्र समय में कैसे भिन्न होता है) विद्युत क्षेत्र हमेशा एक समय-भिन्न चुंबकीय क्षेत्र के साथ होता है, जबकि फैराडे के नियम में कहा गया है कि प्रवाहकीय लूप पर ईएमएफ (वैद्युतवाहक बल, एक यूनिट चार्ज पर किए गए विद्युत चुम्बकीय कार्य के रूप में परिभाषित किया जाता है) प्रवाहकीय लूप पर होता है, जब लूप द्वारा संलग्न सतह के माध्यम से चुंबकीय प्रवाह समय में भिन्न होता है। | ||
फैराडे के नियम की खोज की जा चुकी थी और इसके एक पहलू (रूपांतरक ईएमएफ) को बाद में मैक्सवेल-फैराडे समीकरण के रूप में तैयार किया गया था। फैराडे के | फैराडे के नियम की खोज की जा चुकी थी और इसके एक पहलू (रूपांतरक ईएमएफ) को बाद में मैक्सवेल-फैराडे समीकरण के रूप में तैयार किया गया था। फैराडे के नियम का समीकरण मैक्सवेल-फैराडे समीकरण (रूपांतरक ईएमएफ का वर्णन) और [[ लोरेंत्ज़ बल ]] (गतिशील ईएमएफ का वर्णन) द्वारा प्राप्त किया जा सकता है। मैक्सवेल-फैराडे समीकरण का अभिन्न रूप केवल रूपांतरक ईएमएफ का वर्णन करता है, जबकि फैराडे के नियम का समीकरण रूपांतरक ईएमएफ और गतिक ईएमएफ दोनों का वर्णन करता है। | ||
{{electromagnetism|cTopic=Electrodynamics}} | {{electromagnetism|cTopic=Electrodynamics}} | ||
| Line 10: | Line 10: | ||
== इतिहास == | == इतिहास == | ||
[[File:Faraday emf experiment.svg|thumb|upright=1.3|फैराडे के लौह वलय उपकरण का आरेख। बाएं कॉइल का बदलता चुंबकीय प्रवाह दाएं कॉइल में करंट को प्रेरित करता है।<ref name=Giancoli>{{cite book|last=Giancoli|first=Douglas C.|title=Physics: Principles with Applications|url=https://archive.org/details/physicsprinciple00gian|url-access=registration|year=1998|pages=[https://archive.org/details/physicsprinciple00gian/page/623 623–624]|edition=5th}}</ref>]]1831 में [[ माइकल फैराडे ]] और 1832 में [[ जोसेफ हेनरी ]] द्वारा स्वतंत्र रूप से विद्युत चुम्बकीय प्रेरण की खोज की गई थी।<ref>{{cite web|title=A Brief History of Electromagnetism|url=http://web.hep.uiuc.edu/home/serrede/P435/Lecture_Notes/A_Brief_History_of_Electromagnetism.pdf}}</ref> फैराडे अपने प्रयोगों के परिणामों को प्रकाशित करने वाले पहले व्यक्ति थे।<ref>{{cite book|last=Ulaby|first=Fawwaz|title=Fundamentals of applied electromagnetics|edition=5th|year=2007|url=https://www.amazon.com/exec/obidos/tg/detail/-/0132413264/ref=ord_cart_shr?%5Fencoding=UTF8&m=ATVPDKIKX0DER&v=glance|publisher=Pearson:Prentice Hall|isbn=978-0-13-241326-8|page=255}}</ref><ref>{{cite web|url=http://www.nasonline.org/member-directory/deceased-members/20001467.html |title=Joseph Henry |access-date=2016-12-30 |work=Member Directory, National Academy of Sciences}}</ref> फैराडे के विद्युत चुम्बकीय प्रेरण के पहले प्रायोगिक प्रदर्शन में (29 अगस्त, 1831),<ref name="FaradayDay1999">{{cite book|last1=Faraday|first1=Michael|last2=Day|first2=P.|title=The philosopher's tree: a selection of Michael Faraday's writings|url=https://books.google.com/books?id=ur6iKVmzYhcC&pg=PA71|access-date=28 August 2011|date=1999-02-01|publisher=CRC Press|isbn=978-0-7503-0570-9|page=71}}</ref> उन्होंने एक लोहे की अंगूठी ([[ टोरस्र्स ]]) (एक आधुनिक [[ टॉरॉयडल ट्रांसफार्मर | टॉरॉयडल रूपांतरक]] के समान व्यवस्था) के विपरीत दिशा में दो तारों को लपेटा। विद्युत चुम्बक के हाल ही में खोजे गए गुणों के अपने आकलन के आधार पर, उन्होंने उम्मीद की कि जब एक तार में करंट प्रवाहित होना | [[File:Faraday emf experiment.svg|thumb|upright=1.3|फैराडे के लौह वलय उपकरण का आरेख। बाएं कॉइल का बदलता चुंबकीय प्रवाह दाएं कॉइल में करंट को प्रेरित करता है।<ref name=Giancoli>{{cite book|last=Giancoli|first=Douglas C.|title=Physics: Principles with Applications|url=https://archive.org/details/physicsprinciple00gian|url-access=registration|year=1998|pages=[https://archive.org/details/physicsprinciple00gian/page/623 623–624]|edition=5th}}</ref>]]1831 में [[ माइकल फैराडे ]] और 1832 में [[ जोसेफ हेनरी ]] द्वारा स्वतंत्र रूप से विद्युत चुम्बकीय प्रेरण की खोज की गई थी।<ref>{{cite web|title=A Brief History of Electromagnetism|url=http://web.hep.uiuc.edu/home/serrede/P435/Lecture_Notes/A_Brief_History_of_Electromagnetism.pdf}}</ref> फैराडे अपने प्रयोगों के परिणामों को प्रकाशित करने वाले पहले व्यक्ति थे।<ref>{{cite book|last=Ulaby|first=Fawwaz|title=Fundamentals of applied electromagnetics|edition=5th|year=2007|url=https://www.amazon.com/exec/obidos/tg/detail/-/0132413264/ref=ord_cart_shr?%5Fencoding=UTF8&m=ATVPDKIKX0DER&v=glance|publisher=Pearson:Prentice Hall|isbn=978-0-13-241326-8|page=255}}</ref><ref>{{cite web|url=http://www.nasonline.org/member-directory/deceased-members/20001467.html |title=Joseph Henry |access-date=2016-12-30 |work=Member Directory, National Academy of Sciences}}</ref> फैराडे के विद्युत चुम्बकीय प्रेरण के पहले प्रायोगिक प्रदर्शन में (29 अगस्त, 1831),<ref name="FaradayDay1999">{{cite book|last1=Faraday|first1=Michael|last2=Day|first2=P.|title=The philosopher's tree: a selection of Michael Faraday's writings|url=https://books.google.com/books?id=ur6iKVmzYhcC&pg=PA71|access-date=28 August 2011|date=1999-02-01|publisher=CRC Press|isbn=978-0-7503-0570-9|page=71}}</ref> उन्होंने एक लोहे की अंगूठी ([[ टोरस्र्स ]]) (एक आधुनिक [[ टॉरॉयडल ट्रांसफार्मर | टॉरॉयडल रूपांतरक]] के समान व्यवस्था) के विपरीत दिशा में दो तारों को लपेटा। विद्युत चुम्बक के हाल ही में खोजे गए गुणों के अपने आकलन के आधार पर, उन्होंने उम्मीद की कि जब एक तार में करंट प्रवाहित होना प्रारंभ होता है, तो एक तरह की तरंग रिंग के माध्यम से यात्रा करेगी और विपरीत दिशा में कुछ विद्युत प्रभाव पैदा करेगी। उसने एक तार को [[ बिजली की शक्ति नापने का यंत्र ]] में प्लग किया, और दूसरे तार को बैटरी से जोड़ते हुए उसे देखा। वास्तव में, जब उन्होंने तार को बैटरी से संसक्त, और जब उन्होंने इसे असंगत किया, तो उन्होंने एक क्षणिक धारा (जिसे उन्होंने बिजली की लहर कहा) देखा।<ref name=Williams>{{cite book|title=Michael Faraday|url=https://archive.org/details/michaelfaradaybi00will|url-access=registration|first=L. Pearce|last=Williams|year=1965|publisher=New York, Basic Books}}{{full citation needed|date=September 2018}}</ref>{{rp|182–183}} यह प्रेरण बैटरी के संसक्त और असंगत होने पर होने वाले [[ चुंबकीय प्रवाह ]] में बदलाव के कारण था।<ref name=Giancoli/>दो महीनों के भीतर, फैराडे ने विद्युत चुम्बकीय प्रेरण की कई अन्य अभिव्यक्तियाँ पाईं। उदाहरण के लिए, उन्होंने क्षणिक धाराओं को देखा जब उन्होंने तारों के तार के अंदर और बाहर एक बार चुंबक को जल्दी से सर्पण किया, और उन्होंने एक सर्पण विद्युत चालक तार (फैराडे की डिस्क) के साथ बार चुंबक के पास एक तांबे की डिस्क को घुमाकर एक स्थिर (प्रत्यक्ष धारा) धारा उत्पन्न किया था।.<ref name=Williams/>{{rp|191–195}} | ||
[[File:Faraday disk generator.jpg|thumb|फैराडे की डिस्क, पहला विद्युत जनरेटर, एक प्रकार का [[ एकध्रुवीय जनरेटर ]]।|बायां]]माइकल फैराडे ने एक अवधारणा का उपयोग करते हुए विद्युत चुम्बकीय प्रेरण की व्याख्या की जिसे उन्होंने बल की रेखाएं कहा। | [[File:Faraday disk generator.jpg|thumb|फैराडे की डिस्क, पहला विद्युत जनरेटर, एक प्रकार का [[ एकध्रुवीय जनरेटर ]]।|बायां]]माइकल फैराडे ने एक अवधारणा का उपयोग करते हुए विद्युत चुम्बकीय प्रेरण की व्याख्या की जिसे उन्होंने बल की रेखाएं कहा। चूंकि, उस समय के वैज्ञानिकों ने उनके सैद्धांतिक विचारों को व्यापक रूप से खारिज कर दिया, मुख्यतः क्योंकि वे गणितीय रूप से तैयार नहीं किए गए थे।<ref name=Williams/>{{rp|510}} एक अपवाद [[ जेम्स क्लर्क मैक्सवेल ]] थे, जिन्होंने 1861-62 में फैराडे के विचारों को अपने मात्रात्मक विद्युत चुम्बकीय सिद्धांत के आधार के रूप में उपयोग किया।<ref name=Williams/>{{rp|510}}<ref>{{cite book|last=Clerk Maxwell |first=James |date=1904 |title=A Treatise on Electricity and Magnetism |volume=2 |edition=3rd |publisher=Oxford University Press |pages=178–179, 189}}</ref><ref name="IEEUK">{{cite web|url=http://www.theiet.org/resources/library/archives/biographies/faraday.cfm |title=Archives Biographies: Michael Faraday |publisher=The Institution of Engineering and Technology}}</ref> मैक्सवेल के कागजात में, विद्युत चुम्बकीय प्रेरण के समय-भिन्न पहलू को एक अंतर समीकरण के रूप में व्यक्त किया जाता है, जिसे [[ ओलिवर हीविसाइड ]] ने फैराडे के नियम के रूप में संदर्भित किया है, चूंकि यह फैराडे के नियम के मूल संस्करण से अलग है, और #दो घटनाओं का वर्णन नहीं करता है। हीविसाइड का संस्करण (#मैक्सवेल-फैराडे समीकरण|नीचे मैक्सवेल-फैराडे समीकरण देखें) वह रूप है जिसे आज मैक्सवेल के समीकरणों के रूप में ज्ञात समीकरणों के समूह में मान्यता प्राप्त है। | ||
1834 में [[ एमिल लेनज़ ]] द्वारा प्रतिपादित लेनज़ का नियम,<ref>{{cite journal|last=Lenz |first=Emil |date=1834 |url=http://gallica.bnf.fr/ark:/12148/bpt6k151161/f499.image.r=lenz.langEN |title=Ueber<!--[sic]--> die Bestimmung der Richtung der durch elektodynamische Vertheilung erregten galvanischen Ströme |journal=Annalen der Physik und Chemie |volume=107 |issue=31 |pages=483–494|bibcode=1834AnP...107..483L |doi=10.1002/andp.18341073103 }}<br>A partial translation of the paper is available in {{cite book|last=Magie |first=W. M. |date=1963 |title=A Source Book in Physics |publisher=Harvard Press |location=Cambridge, MA |pages=511–513}}</ref> | 1834 में [[ एमिल लेनज़ ]] द्वारा प्रतिपादित लेनज़ का नियम,<ref>{{cite journal|last=Lenz |first=Emil |date=1834 |url=http://gallica.bnf.fr/ark:/12148/bpt6k151161/f499.image.r=lenz.langEN |title=Ueber<!--[sic]--> die Bestimmung der Richtung der durch elektodynamische Vertheilung erregten galvanischen Ströme |journal=Annalen der Physik und Chemie |volume=107 |issue=31 |pages=483–494|bibcode=1834AnP...107..483L |doi=10.1002/andp.18341073103 }}<br>A partial translation of the paper is available in {{cite book|last=Magie |first=W. M. |date=1963 |title=A Source Book in Physics |publisher=Harvard Press |location=Cambridge, MA |pages=511–513}}</ref> परिपथ के माध्यम से प्रवाह का वर्णन करता है, और विद्युत चुम्बकीय प्रेरण से उत्पन्न प्रेरित ईएमएफ और वर्तमान की दिशा देता है (नीचे दिए गए उदाहरणों में विस्तृत)। | ||
{{clear}} | {{clear}} | ||
| Line 23: | Line 23: | ||
===गणितीय कथन=== | ===गणितीय कथन=== | ||
[[Image:Surface integral illustration.svg|right|thumb|सतह अभिन्न की परिभाषा सतह को विभाजित करने पर निर्भर करती है {{math|Σ}} छोटे सतह तत्वों में। प्रत्येक तत्व एक | [[Image:Surface integral illustration.svg|right|thumb|सतह अभिन्न की परिभाषा सतह को विभाजित करने पर निर्भर करती है {{math|Σ}} छोटे सतह तत्वों में। प्रत्येक तत्व एक सदिश से जुड़ा होता है {{math|d'''A'''}} तत्व के क्षेत्र के बराबर परिमाण और तत्व के लिए सामान्य दिशा के साथ और बाहर की ओर इशारा करते हुए (सतह के अभिविन्यास के संबंध में)।]]चुंबकीय क्षेत्र में तार के एक लूप के लिए, चुंबकीय प्रवाह {{math|Φ<sub>''B''</sub>}} किसी भी [[ सतह (गणित) ]] के लिए परिभाषित किया गया है {{math|Σ}} जिसकी [[ सीमा (टोपोलॉजी) ]] दिया गया लूप है। चूँकि वायर लूप गतिमान हो सकता है, हम लिखते हैं {{math|Σ(''t'')}} सतह के लिए। चुंबकीय प्रवाह [[ सतह अभिन्न ]] है: | ||
<math display="block"> \Phi_B = \iint_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d} \mathbf{A}\, , </math> | <math display="block"> \Phi_B = \iint_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d} \mathbf{A}\, , </math> | ||
जहाँ पे {{math|d'''A'''}} चलती सतह के सतह क्षेत्र का एक तत्व है {{math|Σ(''t'')}}, {{math|'''B'''}} चुंबकीय क्षेत्र है, और {{math|'''B''' · d'''A'''}} एक [[ डॉट उत्पाद ]] है जो प्रवाह के तत्व का प्रतिनिधित्व करता है {{math|d'''A'''}}. अधिक दृश्य शब्दों में, वायर लूप के माध्यम से चुंबकीय प्रवाह लूप से गुजरने वाली [[ फील्ड लाइन ]] की संख्या के समानुपाती होता है। | जहाँ पे {{math|d'''A'''}} चलती सतह के सतह क्षेत्र का एक तत्व है {{math|Σ(''t'')}}, {{math|'''B'''}} चुंबकीय क्षेत्र है, और {{math|'''B''' · d'''A'''}} एक [[ डॉट उत्पाद ]] है जो प्रवाह के तत्व का प्रतिनिधित्व करता है {{math|d'''A'''}}. अधिक दृश्य शब्दों में, वायर लूप के माध्यम से चुंबकीय प्रवाह लूप से गुजरने वाली [[ फील्ड लाइन ]] की संख्या के समानुपाती होता है। | ||
जब प्रवाह बदलता है—क्योंकि {{math|'''B'''}} परिवर्तन, या क्योंकि वायर लूप को स्थानांतरित या विकृत किया जाता है, या दोनों - फैराडे के प्रेरण के नियम का कहना है कि वायर लूप एक वैद्युतवाहक बल प्राप्त करता है, जिसे यूनिट चार्ज से उपलब्ध ऊर्जा के रूप में परिभाषित किया जाता है जो वायर लूप के चारों ओर एक बार यात्रा करता है।<ref name="Feynman">{{Cite web| last=Feynman|first=Richard P. |title=The Feynman Lectures on Physics Vol. II |url=https://feynmanlectures.caltech.edu/II_toc.html|access-date=2020-11-07 |website=feynmanlectures.caltech.edu}}</ref>{{Rp|ch17}}<ref name=Griffiths2>{{cite book|last=Griffiths|first=David J. | title=Introduction to Electrodynamics | url=https://archive.org/details/introductiontoel00grif_0/page/301 | edition=3rd |pages=[https://archive.org/details/introductiontoel00grif_0/page/301 301–303] | publisher=Prentice Hall| year=1999 | location=Upper Saddle River, NJ | isbn=0-13-805326-X}}</ref><ref>{{cite book |last1=Tipler|last2=Mosca |title=Physics for Scientists and Engineers |year=2004|page=795|isbn=9780716708100 |url=https://books.google.com/books?id=R2Nuh3Ux1AwC&pg=PA795}}</ref> ( | जब प्रवाह बदलता है—क्योंकि {{math|'''B'''}} परिवर्तन, या क्योंकि वायर लूप को स्थानांतरित या विकृत किया जाता है, या दोनों - फैराडे के प्रेरण के नियम का कहना है कि वायर लूप एक वैद्युतवाहक बल प्राप्त करता है, जिसे यूनिट चार्ज से उपलब्ध ऊर्जा के रूप में परिभाषित किया जाता है जो वायर लूप के चारों ओर एक बार यात्रा करता है।<ref name="Feynman">{{Cite web| last=Feynman|first=Richard P. |title=The Feynman Lectures on Physics Vol. II |url=https://feynmanlectures.caltech.edu/II_toc.html|access-date=2020-11-07 |website=feynmanlectures.caltech.edu}}</ref>{{Rp|ch17}}<ref name=Griffiths2>{{cite book|last=Griffiths|first=David J. | title=Introduction to Electrodynamics | url=https://archive.org/details/introductiontoel00grif_0/page/301 | edition=3rd |pages=[https://archive.org/details/introductiontoel00grif_0/page/301 301–303] | publisher=Prentice Hall| year=1999 | location=Upper Saddle River, NJ | isbn=0-13-805326-X}}</ref><ref>{{cite book |last1=Tipler|last2=Mosca |title=Physics for Scientists and Engineers |year=2004|page=795|isbn=9780716708100 |url=https://books.google.com/books?id=R2Nuh3Ux1AwC&pg=PA795}}</ref> (चूंकि कुछ स्रोत परिभाषा को अलग तरीके से बताते हैं, इस अभिव्यक्ति को [[ विशेष सापेक्षता ]] के समीकरणों के साथ संगतता के लिए चुना गया था।) समान रूप से, यह वह वोल्टेज है जिसे इलेक्ट्रिक परिपथ बनाने के लिए तार को काटकर और चालक तार में [[ वाल्टमीटर ]] जोड़कर मापा जाएगा। . | ||
फैराडे के | फैराडे के नियम में कहा गया है कि ईएमएफ भी चुंबकीय प्रवाह के [[ समय व्युत्पन्न ]] द्वारा दिया जाता है: | ||
<math display="block">\mathcal{E} = -\frac{\mathrm{d}\Phi_B}{\mathrm{d}t}, </math> | <math display="block">\mathcal{E} = -\frac{\mathrm{d}\Phi_B}{\mathrm{d}t}, </math> | ||
जहाँ पे <math>\mathcal{E}</math> वैद्युतवाहक बल (ईएमएफ) है और {{math|Φ<sub>''B''</sub>}} चुंबकीय प्रवाह है। | जहाँ पे <math>\mathcal{E}</math> वैद्युतवाहक बल (ईएमएफ) है और {{math|Φ<sub>''B''</sub>}} चुंबकीय प्रवाह है। | ||
| Line 35: | Line 35: | ||
वैद्युतवाहक बल की दिशा लेंज़ के नियम द्वारा दी गई है। | वैद्युतवाहक बल की दिशा लेंज़ के नियम द्वारा दी गई है। | ||
1845 में [[ फ्रांज अर्न्स्ट न्यूमैन ]] द्वारा गणितीय रूप में विद्युत धाराओं को | 1845 में [[ फ्रांज अर्न्स्ट न्यूमैन ]] द्वारा गणितीय रूप में विद्युत धाराओं को सम्मलित करने के नियम स्थापित किए गए थे।<ref>{{cite journal|first=Franz Ernst|last=Neumann |title=Allgemeine Gesetze der inducirten elektrischen Ströme|journal=Annalen der Physik |volume=143|number=1|pages=31–44 |year=1846|doi=10.1002/andp.18461430103 |url=https://isidore.co/misc/Physics%20papers%20and%20books/Zotero/storage/3UM3CRQ2/18461430103_ftp.pdf |archive-url=https://web.archive.org/web/20200312012028/https://isidore.co/misc/Physics%20papers%20and%20books/Zotero/storage/3UM3CRQ2/18461430103_ftp.pdf |archive-date=12 March 2020 |bibcode=1846AnP...143...31N}}</ref> | ||
फैराडे के नियम में दोनों परिमाणों और इसके चरों की दिशाओं के बीच संबंधों के बारे में जानकारी | फैराडे के नियम में दोनों परिमाणों और इसके चरों की दिशाओं के बीच संबंधों के बारे में जानकारी सम्मलित है। चूंकि, दिशाओं के बीच संबंध स्पष्ट नहीं हैं; वे गणितीय सूत्र में छिपे हैं। | ||
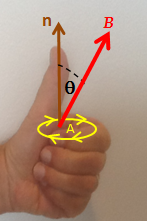
[[File:Salu's left-hand rule (magnetic induction).png|thumb|फैराडे के कानून के लिए एक बाएं हाथ का नियम। का चिह्न {{math|ΔΦ<sub>''B''</sub>}}, फ्लक्स में परिवर्तन, चुंबकीय क्षेत्र के बीच संबंध के आधार पर पाया जाता है {{math|'''B'''}}, लूप का क्षेत्र {{mvar|A}}, और उस क्षेत्र का सामान्य n, जैसा कि बाएं हाथ की उंगलियों द्वारा दर्शाया गया है। यदि {{math|ΔΦ<sub>''B''</sub>}} सकारात्मक है, ईएमएफ की दिशा घुमावदार उंगलियों (पीले तीर) के समान है। यदि {{math|ΔΦ<sub>''B''</sub>}} नकारात्मक है, ईएमएफ की दिशा तीर के निशान के खिलाफ है।<ref name=Salu2014/>|ऑल्ट=]]लेन्ज़ के नियम का प्रयोग किए बिना, फैराडे के नियम से सीधे वैद्युतवाहक बल (ईएमएफ) की दिशा का पता लगाना संभव है। बाएं हाथ का नियम ऐसा करने में मदद करता है, जो इस प्रकार है:<ref name="Salu2014">{{cite journal|year=2014 |url=https://www.researchgate.net/publication/262986189 |title=A Left Hand Rule for Faraday's Law | journal=[[The Physics Teacher]] | volume=52|pages=48 |doi=10.1119/1.4849156 |author=Yehuda Salu| issue=1 |bibcode=2014PhTea..52...48S}} [https://www.youtube.com/watch?v=ipUD9VcAd9o Video Explanation] </ref><ref>{{cite web |url=http://Physicsforarchitects.com/bypassing-lenzs-rule |archive-url=https://web.archive.org/web/20200507170609/http://physicsforarchitects.com/bypassing-lenzs-rule |archive-date=7 May 2020 |title=Bypassing Lenz's Rule - A Left Hand Rule for Faraday's Law |website=www.PhysicsForArchitects.com |last1=Salu|first1=Yehuda |access-date=30 July 2017}}</ref> | [[File:Salu's left-hand rule (magnetic induction).png|thumb|फैराडे के कानून के लिए एक बाएं हाथ का नियम। का चिह्न {{math|ΔΦ<sub>''B''</sub>}}, फ्लक्स में परिवर्तन, चुंबकीय क्षेत्र के बीच संबंध के आधार पर पाया जाता है {{math|'''B'''}}, लूप का क्षेत्र {{mvar|A}}, और उस क्षेत्र का सामान्य n, जैसा कि बाएं हाथ की उंगलियों द्वारा दर्शाया गया है। यदि {{math|ΔΦ<sub>''B''</sub>}} सकारात्मक है, ईएमएफ की दिशा घुमावदार उंगलियों (पीले तीर) के समान है। यदि {{math|ΔΦ<sub>''B''</sub>}} नकारात्मक है, ईएमएफ की दिशा तीर के निशान के खिलाफ है।<ref name=Salu2014/>|ऑल्ट=]]लेन्ज़ के नियम का प्रयोग किए बिना, फैराडे के नियम से सीधे वैद्युतवाहक बल (ईएमएफ) की दिशा का पता लगाना संभव है। बाएं हाथ का नियम ऐसा करने में मदद करता है, जो इस प्रकार है:<ref name="Salu2014">{{cite journal|year=2014 |url=https://www.researchgate.net/publication/262986189 |title=A Left Hand Rule for Faraday's Law | journal=[[The Physics Teacher]] | volume=52|pages=48 |doi=10.1119/1.4849156 |author=Yehuda Salu| issue=1 |bibcode=2014PhTea..52...48S}} [https://www.youtube.com/watch?v=ipUD9VcAd9o Video Explanation] </ref><ref>{{cite web |url=http://Physicsforarchitects.com/bypassing-lenzs-rule |archive-url=https://web.archive.org/web/20200507170609/http://physicsforarchitects.com/bypassing-lenzs-rule |archive-date=7 May 2020 |title=Bypassing Lenz's Rule - A Left Hand Rule for Faraday's Law |website=www.PhysicsForArchitects.com |last1=Salu|first1=Yehuda |access-date=30 July 2017}}</ref> | ||
* बाएं हाथ की मुड़ी हुई उंगलियों को लूप (पीली रेखा) से संरेखित करें। | * बाएं हाथ की मुड़ी हुई उंगलियों को लूप (पीली रेखा) से संरेखित करें। | ||
| Line 50: | Line 50: | ||
===मैक्सवेल–फैराडे समीकरण=== | ===मैक्सवेल–फैराडे समीकरण=== | ||
{{anchor|Faraday equation}} | {{anchor|Faraday equation}} | ||
[[Image:Stokes' Theorem.svg|thumb|right|सतह के साथ केल्विन-स्टोक्स प्रमेय का एक उदाहरण {{math|'''Σ'''}}, इसकी सीमा {{math|∂'''Σ'''}}, और अभिविन्यास {{math|'''n'''}} दाहिने हाथ के नियम द्वारा निर्धारित।]]मैक्सवेल-फैराडे समीकरण बताता है कि एक समय-भिन्न चुंबकीय क्षेत्र हमेशा एक स्थानिक रूप से भिन्न (संभवतः समय-भिन्न), गैर-[[ रूढ़िवादी वेक्टर क्षेत्र ]] विद्युत क्षेत्र, और इसके विपरीत के साथ होता है। मैक्सवेल-फैराडे समीकरण है | [[Image:Stokes' Theorem.svg|thumb|right|सतह के साथ केल्विन-स्टोक्स प्रमेय का एक उदाहरण {{math|'''Σ'''}}, इसकी सीमा {{math|∂'''Σ'''}}, और अभिविन्यास {{math|'''n'''}} दाहिने हाथ के नियम द्वारा निर्धारित।]]मैक्सवेल-फैराडे समीकरण बताता है कि एक समय-भिन्न चुंबकीय क्षेत्र हमेशा एक स्थानिक रूप से भिन्न (संभवतः समय-भिन्न), गैर-[[ रूढ़िवादी वेक्टर क्षेत्र | रूढ़िवादी सदिश क्षेत्र]] विद्युत क्षेत्र, और इसके विपरीत के साथ होता है। मैक्सवेल-फैराडे समीकरण है | ||
{{Equation box 1 | {{Equation box 1 | ||
| Line 61: | Line 61: | ||
(एसआई इकाइयों में) जहां {{math|∇ ×}} [[ कर्ल (गणित) ]] रैखिक संकारक है और फिर से {{math|'''E'''('''r''', ''t'')}} विद्युत क्षेत्र है और {{math|'''B'''('''r''', ''t'')}} चुंबकीय क्षेत्र है। ये क्षेत्र | (एसआई इकाइयों में) जहां {{math|∇ ×}} [[ कर्ल (गणित) ]] रैखिक संकारक है और फिर से {{math|'''E'''('''r''', ''t'')}} विद्युत क्षेत्र है और {{math|'''B'''('''r''', ''t'')}} चुंबकीय क्षेत्र है। ये क्षेत्र सामान्यत: स्थिति के कार्य हो सकते हैं {{math|'''r'''}} और समय {{mvar|t}}.<ref name="Griffiths">{{cite book | ||
|last = Griffiths | |last = Griffiths | ||
|first = David J. | |first = David J. | ||
| Line 84: | Line 84: | ||
जहां, जैसा कि चित्र में दिखाया गया है, {{math|'''Σ'''}} बंद समोच्च से घिरा सतह है {{math|∂'''Σ'''}}, {{math|d'''l'''}} समोच्च का एक अतिसूक्ष्म सदिश तत्व है {{math|'''∂Σ'''}}, और {{math|d'''A'''}} सतह का एक अतिसूक्ष्म सदिश तत्व है {{math|'''Σ'''}}. इसकी दिशा उस सतह के पैच के लिए [[Index.php?title=लांबिक|लांबिक]] है, परिमाण सतह के एक अतिसूक्ष्म पैच का क्षेत्र है। | जहां, जैसा कि चित्र में दिखाया गया है, {{math|'''Σ'''}} बंद समोच्च से घिरा सतह है {{math|∂'''Σ'''}}, {{math|d'''l'''}} समोच्च का एक अतिसूक्ष्म सदिश तत्व है {{math|'''∂Σ'''}}, और {{math|d'''A'''}} सतह का एक अतिसूक्ष्म सदिश तत्व है {{math|'''Σ'''}}. इसकी दिशा उस सतह के पैच के लिए [[Index.php?title=लांबिक|लांबिक]] है, परिमाण सतह के एक अतिसूक्ष्म पैच का क्षेत्र है। | ||
दोनों {{math|d'''l'''}} और {{math|d'''A'''}} एक संकेत अस्पष्टता है; सही संकेत प्राप्त करने के लिए, दाहिने हाथ के नियम का उपयोग किया जाता है, जैसा कि लेख केल्विन-स्टोक्स प्रमेय में बताया गया है। | दोनों {{math|d'''l'''}} और {{math|d'''A'''}} एक संकेत अस्पष्टता है; सही संकेत प्राप्त करने के लिए, दाहिने हाथ के नियम का उपयोग किया जाता है, जैसा कि लेख केल्विन-स्टोक्स प्रमेय में बताया गया है। एक तलीय सतह Σ के लिए, वक्र ∂Σ का एक सकारात्मक पथ तत्व dl दाएँ हाथ के नियम द्वारा परिभाषित किया जाता है, जो दाहिने हाथ की उंगलियों से इंगित करता है जब अंगूठा सामान्य n की दिशा में सतह Σ की ओर इंगित करता है। | ||
चारों ओर [[ रेखा अभिन्न ]] | ∂Σ के चारों ओर [[ रेखा अभिन्न |रेखा अभिन्न]] को [[ परिसंचरण (भौतिकी) |परिसंचरण (भौतिकी)]] कहा जाता है। [15]: ch3 E का एक अशून्य संचलन स्थिर आवेशों द्वारा उत्पन्न विद्युत क्षेत्र के व्यवहार से भिन्न होता है। एक चार्ज-जनित E-फ़ील्ड को [[ अदिश क्षेत्र |अदिश क्षेत्र]] के ढाल के रूप में व्यक्त किया जा सकता है जो पोइसन के समीकरण का समाधान है, और शून्य पथ अभिन्न है। ढाल प्रमेय देखें। | ||
अभिन्न समीकरण समष्टि के माध्यम से किसी भी पथ ∂Σ के लिए सही है, और कोई भी सतह Σ जिसके लिए वह पथ एक सीमा है। | |||
यदि सतह | यदि सतह Σ समय के साथ नहीं बदल रही है, तो समीकरण को फिर से लिखा जा सकता है: | ||
<math display="block"> \oint_{\partial \Sigma} \mathbf{E} \cdot \mathrm{d}\mathbf{l} = - \frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma} \mathbf{B} \cdot \mathrm{d}\mathbf{A}. </math> | <math display="block"> \oint_{\partial \Sigma} \mathbf{E} \cdot \mathrm{d}\mathbf{l} = - \frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma} \mathbf{B} \cdot \mathrm{d}\mathbf{A}. </math> | ||
दाहिनी ओर सतह समाकल चुंबकीय प्रवाह के लिए स्पष्ट अभिव्यक्ति | दाहिनी ओर सतह समाकल चुंबकीय प्रवाह ΦB से Σ के लिए स्पष्ट अभिव्यक्ति है। | ||
एक बदलते चुंबकीय प्रवाह से प्रेरित विद्युत सदिश क्षेत्र, समग्र विद्युत क्षेत्र के | एक बदलते चुंबकीय प्रवाह से प्रेरित विद्युत सदिश क्षेत्र, समग्र विद्युत क्षेत्र के परिनालिकीय घटक, आयतन अभिन्न समीकरण द्वारा गैर-सापेक्षतावादी सीमा में अनुमानित किया जा सकता है।<ref name="Griffiths"/>{{Rp|321}} | ||
<math display="block"> \mathbf E_s (\mathbf r,t) \approx -\frac{1}{4\pi}\iiint_V \ \frac{\left(\frac{\partial \mathbf{B}(\mathbf{r}',t)}{\partial t} \right) \times \left(\mathbf{r}-\mathbf{r}' \right) }{|\mathbf {r} - \mathbf{r}'|^3} d^3\mathbf{r'}</math> | <math display="block"> \mathbf E_s (\mathbf r,t) \approx -\frac{1}{4\pi}\iiint_V \ \frac{\left(\frac{\partial \mathbf{B}(\mathbf{r}',t)}{\partial t} \right) \times \left(\mathbf{r}-\mathbf{r}' \right) }{|\mathbf {r} - \mathbf{r}'|^3} d^3\mathbf{r'}</math> | ||
| Line 109: | Line 109: | ||
== प्रमाण == | == प्रमाण == | ||
मैक्सवेल के चार समीकरण (मैक्सवेल-फैराडे समीकरण सहित), लोरेंत्ज़ बल नियम के साथ, शास्त्रीय विद्युत चुंबकत्व में सब कुछ प्राप्त करने के लिए पर्याप्त आधार हैं।<ref name=Feynman/><ref name=Griffiths2/>इसलिए, इन समीकरणों से प्रारंभ करके फैराडे के नियम को सिद्ध करना संभव है।<ref name=Davison>{{Cite journal | last1 = Davison | first1 = M. E. | title = A Simple Proof that the Lorentz Force, Law Implied Faraday's Law of Induction, when '''B''' is Time Independent | doi = 10.1119/1.1987339 | journal = American Journal of Physics | volume = 41 | issue = 5 | page = 713| year = 1973 |bibcode = 1973AmJPh..41..713D }}</ref><ref name=Krey>{{cite book|title=Basic Theoretical Physics: A Concise Overview |last1=Krey |last2=Owen |date=14 August 2007 |page=155 |isbn=9783540368052 | url=https://books.google.com/books?id=xZ_QelBmkxYC&pg=PA155}}</ref> | |||
प्रारंभिक बिंदु एक | प्रारंभिक बिंदु एक यादृच्छिक सतह के माध्यम से प्रवाह का समय-व्युत्पन्न है {{math|Σ}} (जिसे स्थानांतरित या विकृत किया जा सकता है) समष्टि में: | ||
<math display="block">\frac{\mathrm{d}\Phi_B}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t}\int_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d}\mathbf{A}</math> | <math display="block">\frac{\mathrm{d}\Phi_B}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t}\int_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d}\mathbf{A}</math> | ||
(परिभाषा से)। मैक्सवेल-फैराडे समीकरण और कुछ सदिश सर्वसमिकाओं की सहायता से इस कुल समय व्युत्पन्न का मूल्यांकन और सरलीकरण किया जा सकता है; विवरण नीचे दिए गए बॉक्स में हैं: | (परिभाषा से)। मैक्सवेल-फैराडे समीकरण और कुछ सदिश सर्वसमिकाओं की सहायता से इस कुल समय व्युत्पन्न का मूल्यांकन और सरलीकरण किया जा सकता है; विवरण नीचे दिए गए बॉक्स में हैं: | ||
{| class="wikitable" | {| class="wikitable" | ||
| | |एक बंद सीमा (लूप) के माध्यम से चुंबकीय प्रवाह के समय-व्युत्पन्न पर विचार करें जो गतिमान या विकृत हो सकता है। लूप से घिरे क्षेत्र को Σ(t) के रूप में निरूपित किया जाता है, तो समय-व्युत्पन्न के रूप में व्यक्त किया जा सकता है | ||
<math display="block">\frac{\mathrm{d}\Phi_B}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t}\int_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d}\mathbf{A}</math> | <math display="block">\frac{\mathrm{d}\Phi_B}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t}\int_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d}\mathbf{A}</math> | ||
समाकल समय के साथ दो कारणों से बदल सकता है: समाकलन बदल सकता है, या समाकलन क्षेत्र बदल सकता है। इसलिए ये रैखिक रूप से जोड़ते हैं: | |||
<!-- not clear at all how to derive such formula from the previous one! --><math display="block">\left. \frac{\mathrm{d}\Phi_B}{\mathrm{d}t}\right|_{t=t_0} = \left( \int_{\Sigma(t_0)} \left. \frac{\partial\mathbf{B}}{\partial t}\right|_{t=t_0} \cdot \mathrm{d}\mathbf{A}\right) + \left( \frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d}\mathbf{A} \right)</math> | <!-- not clear at all how to derive such formula from the previous one! --><math display="block">\left. \frac{\mathrm{d}\Phi_B}{\mathrm{d}t}\right|_{t=t_0} = \left( \int_{\Sigma(t_0)} \left. \frac{\partial\mathbf{B}}{\partial t}\right|_{t=t_0} \cdot \mathrm{d}\mathbf{A}\right) + \left( \frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d}\mathbf{A} \right)</math> | ||
जहाँ t<sub>0</sub> कोई निश्चित समय है। हम दिखाएंगे कि दाईं ओर का पहला शब्द ट्रांसफॉर्मर ईएमएफ से मेल खाता है, दूसरा गतिमान ईएमएफ (चुंबकीय लोरेंत्ज़ बल से आवेश वाहक पर चुंबकीय क्षेत्र में संवाहक पाश की गति या विकृति के कारण)। मैक्सवेल-फैराडे समीकरण के अभिन्न रूप का उपयोग करके दाईं ओर का पहला शब्द फिर से लिखा जा सकता है: | |||
<math display="block"> \int_{\Sigma(t_0)} \left. \frac{\partial \mathbf{B}}{\partial t}\right|_{t=t_0} \cdot \mathrm{d}\mathbf{A} = - \oint_{\partial \Sigma(t_0)} \mathbf{E}(t_0) \cdot \mathrm{d}\mathbf{l} </math> | <math display="block"> \int_{\Sigma(t_0)} \left. \frac{\partial \mathbf{B}}{\partial t}\right|_{t=t_0} \cdot \mathrm{d}\mathbf{A} = - \oint_{\partial \Sigma(t_0)} \mathbf{E}(t_0) \cdot \mathrm{d}\mathbf{l} </math> | ||
इसके बाद, हम दाहिनी ओर दूसरे पद का विश्लेषण करते हैं: | |||
<math display="block">\frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d}\mathbf{A}</math> | <math display="block">\frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d}\mathbf{A}</math> | ||
[[File:Derivation of Faraday Equation Wikipedia 20181127 - 4.png|alt=|thumb|upright=1.2|The area swept out by a vector element {{math|d'''l'''}} of a loop {{math|∂'''Σ'''}} in time {{math|d''t''}} when it has moved with velocity {{math|'''v'''<sub>'''l'''</sub>}} .]] | [[File:Derivation of Faraday Equation Wikipedia 20181127 - 4.png|alt=|thumb|upright=1.2|The area swept out by a vector element {{math|d'''l'''}} of a loop {{math|∂'''Σ'''}} in time {{math|d''t''}} when it has moved with velocity {{math|'''v'''<sub>'''l'''</sub>}} .]]इसका प्रमाण पहले पद की तुलना में थोड़ा अधिक कठिन है; प्रमाण के लिए अधिक विवरण और वैकल्पिक दृष्टिकोण संदर्भों में पाए जा सकते हैं। जैसे ही लूप चलता है और/या विकृत होता है, यह एक सतह को साफ करता है (सही चित्र देखें)। चूंकि लूप dl का एक छोटा सा हिस्सा वेग vl के साथ थोड़े समय dt पर चलता है, यह एक ऐसे क्षेत्र को स्वीप करता है जिसका सदिश dAsweep = vl dt × dl है (ध्यान दें कि यह सदिश सही आकृति में प्रदर्शन से बाहर की ओर है)। इसलिए, समय dt पर लूप की विकृति या गति के कारण लूप के माध्यम से चुंबकीय प्रवाह का परिवर्तन होता है <math display="block">\mathrm{d}\Phi_B = \int \mathbf{B} \cdot \mathrm{d}\mathbf{A}_\text{sweep} = \int \mathbf{B} \cdot (\mathbf{v}_{\mathbf{l}} \mathrm{d}t \times \mathrm{d}\mathbf{l}) = -\int \mathrm{d}t \, \mathrm{d}\mathbf{l} \cdot (\mathbf{v}_{\mathbf{l}}\times\mathbf{B})</math> | ||
यहां ट्रिपल स्केलर उत्पादों की पहचान का उपयोग किया जाता है। इसलिए, | |||
<math display="block">\frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d}\mathbf{A} = -\oint_{\partial \Sigma(t_0)} (\mathbf{v}_{\mathbf{l}}(t_0)\times \mathbf{B}(t_0))\cdot \mathrm{d}\mathbf{l}</math> | <math display="block">\frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d}\mathbf{A} = -\oint_{\partial \Sigma(t_0)} (\mathbf{v}_{\mathbf{l}}(t_0)\times \mathbf{B}(t_0))\cdot \mathrm{d}\mathbf{l}</math> | ||
जहां vl पाश ∂Σ के एक भाग का वेग है। | |||
इन्हें एक साथ रखने का परिणाम होता है,<math display="block">\left. \frac{\mathrm{d}\Phi_B}{\mathrm{d}t}\right|_{t=t_0} = \left(- \oint_{\partial \Sigma(t_0)} \mathbf{E}(t_0) \cdot \mathrm{d}\mathbf{l}\right) + \left(- \oint_{\partial \Sigma(t_0)} \bigl(\mathbf{v}_{\mathbf{l}}(t_0)\times \mathbf{B}(t_0)\bigr)\cdot \mathrm{d}\mathbf{l} \right)</math> | |||
<math display="block">\left. \frac{\mathrm{d}\Phi_B}{\mathrm{d}t}\right|_{t=t_0} = \left(- \oint_{\partial \Sigma(t_0)} \mathbf{E}(t_0) \cdot \mathrm{d}\mathbf{l}\right) + \left(- \oint_{\partial \Sigma(t_0)} \bigl(\mathbf{v}_{\mathbf{l}}(t_0)\times \mathbf{B}(t_0)\bigr)\cdot \mathrm{d}\mathbf{l} \right)</math> | |||
<math display="block">\left. \frac{\mathrm{d}\Phi_B}{\mathrm{d}t}\right|_{t=t_0} = - \oint_{\partial \Sigma(t_0)} \bigl( \mathbf{E}(t_0) + \mathbf{v}_{\mathbf{l}}(t_0)\times \mathbf{B}(t_0) \bigr) \cdot \mathrm{d}\mathbf{l}.</math> | <math display="block">\left. \frac{\mathrm{d}\Phi_B}{\mathrm{d}t}\right|_{t=t_0} = - \oint_{\partial \Sigma(t_0)} \bigl( \mathbf{E}(t_0) + \mathbf{v}_{\mathbf{l}}(t_0)\times \mathbf{B}(t_0) \bigr) \cdot \mathrm{d}\mathbf{l}.</math> | ||
|} | |} | ||
परिणाम है: | परिणाम है: | ||
<math display="block">\frac{\mathrm{d}\Phi_B}{\mathrm{d}t} = - \oint_{\partial \Sigma} \left( \mathbf{E} + \mathbf{v}_{\mathbf{l}} \times \mathbf{B} \right) \cdot \mathrm{d}\mathbf{l}.</math> | <math display="block">\frac{\mathrm{d}\Phi_B}{\mathrm{d}t} = - \oint_{\partial \Sigma} \left( \mathbf{E} + \mathbf{v}_{\mathbf{l}} \times \mathbf{B} \right) \cdot \mathrm{d}\mathbf{l}.</math> | ||
जहाँ पे {{math|∂Σ}} सतह की सीमा (लूप) है {{math|Σ}}, और {{math|'''v'''<sub>'''l'''</sub>}} सीमा के एक भाग का वेग है। | |||
एक प्रवाहकीय लूप | एक प्रवाहकीय लूप की स्थिति में, ईएमएफ (वैद्युतवाहक बल) एक यूनिट चार्ज पर किया जाने वाला विद्युत चुम्बकीय कार्य है, जब यह लूप के चारों ओर एक बार घूम चुका होता है, और यह काम [[ लोरेंत्ज़ बल कानून | लोरेंत्ज़ बल नियम]] द्वारा किया जाता है। इसलिए, ईएमएफ के रूप में व्यक्त किया जाता है | ||
<math display="block">\mathcal{E} = \oint \left(\mathbf{E} + \mathbf{v}\times\mathbf{B}\right) \cdot \mathrm{d}\mathbf{l}</math> | <math display="block">\mathcal{E} = \oint \left(\mathbf{E} + \mathbf{v}\times\mathbf{B}\right) \cdot \mathrm{d}\mathbf{l}</math> | ||
जहाँ पे <math>\mathcal{E}</math> ईएमएफ है और {{math|'''v'''}} इकाई आवेश वेग है। | |||
मैक्रोस्कोपिक दृश्य में, लूप के एक खंड पर | मैक्रोस्कोपिक दृश्य में, लूप के एक खंड पर प्रभार के लिए, {{math|'''v'''}} औसत में दो घटक होते हैं; एक खंड के साथ आवेश का वेग है {{math|'''v'''<sub>'''t'''</sub>}}, और दूसरा खंड का वेग है {{math|'''v'''<sub>'''l'''</sub>}} (लूप विकृत या स्थानांतरित हो गया है)। {{math|'''v'''<sub>'''t'''</sub>}} के निर्देशन के बाद से प्रभार पर किए गए कार्य में योगदान नहीं करता है {{math|'''v'''<sub>'''t'''</sub>}} की दिशा के समान है <math>\mathrm{d}\mathbf{l}</math>. गणितीय रूप से, | ||
<math display="block">(\mathbf{v}\times \mathbf{B})\cdot \mathrm{d}\mathbf{l} = ((\mathbf{v}_t + \mathbf{v}_l) \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l}=(\mathbf{v}_t\times \mathbf{B}+\mathbf{v}_l\times \mathbf{B})\cdot \mathrm{d}\mathbf{l} = (\mathbf{v}_l\times \mathbf{B})\cdot \mathrm{d}\mathbf{l}</math> | <math display="block">(\mathbf{v}\times \mathbf{B})\cdot \mathrm{d}\mathbf{l} = ((\mathbf{v}_t + \mathbf{v}_l) \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l}=(\mathbf{v}_t\times \mathbf{B}+\mathbf{v}_l\times \mathbf{B})\cdot \mathrm{d}\mathbf{l} = (\mathbf{v}_l\times \mathbf{B})\cdot \mathrm{d}\mathbf{l}</math> | ||
जब से <math>(\mathbf{v}_t\times \mathbf{B})</math> के लंबवत है <math>\mathrm{d}\mathbf{l}</math> जैसा <math>\mathbf{v}_t</math> और <math>\mathrm{d}\mathbf{l}</math> उसी दिशा में हैं। अब हम देख सकते हैं कि, प्रवाहकीय लूप के लिए, ईएमएफ उस पर हस्ताक्षर को छोड़कर लूप के माध्यम से चुंबकीय प्रवाह के समय-व्युत्पन्न के समान है। इसलिए, अब हम फैराडे के नियम (प्रवाहकीय पाश के लिए) के समीकरण तक पहुँचते हैं | |||
<math display="block">\frac{\mathrm{d}\Phi_B}{\mathrm{d}t} = -\mathcal{E}</math> | <math display="block">\frac{\mathrm{d}\Phi_B}{\mathrm{d}t} = -\mathcal{E}</math> | ||
जहाँ पे <math display="inline">\mathcal{E} = \oint \left(\mathbf{E} + \mathbf{v}\times\mathbf{B}\right) \cdot \mathrm{d}\mathbf{l}</math>. इस अभिन्न को तोड़कर, <math display="inline">\oint\mathbf{E}\cdot\mathrm{d}\mathbf{l}</math> रूपांतरक ईएमएफ के लिए है (समय-भिन्न चुंबकीय क्षेत्र के कारण) और <math display="inline">\oint \left(\mathbf{v}\times\mathbf{B}\right) \cdot \mathrm{d}\mathbf{l} = \oint \left(\mathbf{v}_l\times\mathbf{B}\right) \cdot \mathrm{d}\mathbf{l}</math> गतिमान ईएमएफ के लिए है (चुंबकीय क्षेत्र में लूप की गति या विरूपण द्वारा आवेशों पर चुंबकीय लोरेंत्ज़ बल के कारण)। | |||
== अपवाद == | == अपवाद == | ||
{{See also| | {{See also|फैराडे विरोधाभास}} | ||
फैराडे के नियम का सामान्यीकरण यह बताने के लिए आकर्षक है कि: यदि{{math|∂Σ}} | |||
फैराडे के नियम का सामान्यीकरण यह बताने के लिए आकर्षक है कि: यदि {{math|∂Σ}} समष्टि में कोई भी यादृच्छिक बंद लूप है, फिर चुंबकीय प्रवाह का कुल समय व्युत्पन्न {{math|Σ}} चारों ओर ईएमएफ के बराबर है {{math|∂Σ}}। यह कथन, चूंकि, हमेशा सत्य नहीं होता है और इसका कारण केवल स्पष्ट कारण से नहीं है, जब कोई संवाहक सम्मलित नहीं होता है तो ईएमएफ रिक्त स्थान में अपरिभाषित होता है। जैसा कि पिछले खंड में उल्लेख किया गया है, फैराडे के नियम को तब तक काम करने की गारंटी नहीं है जब तक कि अमूर्त वक्र का वेग न हो {{math|∂Σ}} बिजली का संचालन करने वाली सामग्री के वास्तविक वेग से मेल खाता है।<ref name=Stewart>{{cite book |title=Intermediate Electromagnetic Theory |first1=Joseph V. |last1=Stewart |page=396 |quote=This example of Faraday's Law [the homopolar generator] makes it very clear that in the case of extended bodies care must be taken that the boundary used to determine the flux must not be stationary but must be moving with respect to the body.}}</ref> नीचे दिए गए दो उदाहरणों से पता चलता है कि जब ∂Σ की गति को सामग्री की गति से अलग किया जाता है तो अधिकांशत: गलत परिणाम प्राप्त होते हैं।<ref name=Feynman/> | |||
<gallery widths="300"> | <gallery widths="300"> | ||
File:Faraday's disc.PNG| | File:Index.php?title=File:Faraday's disc.PNG|फैराडे का एकध्रुवीय जनरेटर। डिस्क कोणीय दर ω के साथ घूमती है, स्थिर चुंबकीय क्षेत्र B (जो दिशा डिस्क की सतह के साथ सामान्य है) में परिपत्र त्रिज्या को व्यापक रूप से घुमाती है। चुंबकीय लोरेंत्ज़ बल v × B प्रवाहकीय त्रिज्या के साथ प्रवाहकीय रिम तक एक धारा चलाता है, और वहां से परिपथ निचले ब्रश और डिस्क का समर्थन करने वाले एक्सल के माध्यम से पूरा होता है। यह उपकरण एक ईएमएफ और करंट उत्पन्न करता है, चूंकि "परिपथ" का आकार स्थिर है और इस प्रकार परिपथ के माध्यम से प्रवाह समय के साथ नहीं बदलता है। | ||
File:FaradaysLawWithPlates.gif| | File:Index.php?title=File:FaradaysLawWithPlates.gif|एक तार (ठोस लाल रेखाएँ) एक परिपथ बनाने के लिए दो स्पर्श करने वाली धातु की प्लेटों (चाँदी) से जुड़ती हैं। संपूर्ण प्रणाली एक समान चुंबकीय क्षेत्र में बैठती है, जो पृष्ठ के लिए सामान्य है। यदि सार पथ ∂Σ वर्तमान प्रवाह (लाल रंग में चिह्नित) के प्राथमिक पथ का अनुसरण करता है, तो इस पथ के माध्यम से चुंबकीय प्रवाह नाटकीय रूप से बदल जाता है क्योंकि प्लेटें घुमाई जाती हैं, फिर भी ईएमएफ लगभग शून्य है। भौतिकी पर फेनमैन व्याख्यान के बाद<ref name=Feynman />{{Rp|ch17}} | ||
</gallery> | </gallery> | ||
इस तरह के उदाहरणों का विश्लेषण पथ का ध्यान रखकर किया जा सकता है {{math|∂Σ}} पदार्थ के समान वेग से गति करता है।<ref name=Stewart/>वैकल्पिक रूप से, मैक्सवेल-फैराडे समीकरण के साथ लोरेंत्ज़ बल | इस तरह के उदाहरणों का विश्लेषण पथ का ध्यान रखकर किया जा सकता है {{math|∂Σ}} पदार्थ के समान वेग से गति करता है।<ref name=Stewart/>वैकल्पिक रूप से, मैक्सवेल-फैराडे समीकरण के साथ लोरेंत्ज़ बल नियम को जोड़कर कोई भी ईएमएफ की सही गणना कर सकता है:<ref name=Feynman/>{{Rp|ch17}}<ref name=HughesYoung>{{cite book|title=The Electromagnetodynamics of Fluid|first1=W. F.|last1=Hughes|first2=F. J.|last2=Young|publisher=John Wiley|date=1965|at=Eq. (2.6–13) p. 53}}</ref> | ||
:<math>\mathcal{E} = \int_{\partial \Sigma} (\mathbf{E} + \mathbf{v}_m \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l} = -\int_\Sigma \frac{\partial \mathbf{B}}{\partial t} \cdot \mathrm{d}\Sigma + \oint_{\partial \Sigma} (\mathbf{v}_m\times\mathbf{B}) \cdot \mathrm{d}\mathbf{l}</math> | :<math>\mathcal{E} = \int_{\partial \Sigma} (\mathbf{E} + \mathbf{v}_m \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l} = -\int_\Sigma \frac{\partial \mathbf{B}}{\partial t} \cdot \mathrm{d}\Sigma + \oint_{\partial \Sigma} (\mathbf{v}_m\times\mathbf{B}) \cdot \mathrm{d}\mathbf{l}</math> | ||
जहां यह ध्यान रखना बहुत महत्वपूर्ण है कि (1) {{math|['''v'''<sub>''m''</sub>]}} | जहां यह ध्यान रखना बहुत महत्वपूर्ण है कि (1) {{math|['''v'''<sub>''m''</sub>]}} संवाहक का वेग है ... पथ तत्व का वेग नहीं {{math|d'''l'''}} और (2) सामान्य तौर पर, समय के संबंध में आंशिक व्युत्पन्न को अभिन्न के बाहर नहीं ले जाया जा सकता क्योंकि क्षेत्र समय का एक कार्य है।<ref name=HughesYoung/> | ||
== फैराडे का नियम और सापेक्षता == | == फैराडे का नियम और सापेक्षता == | ||
{{Further| | {{Further|चुंबकीय और कंडक्टर की समस्या}} | ||
=== दो घटनाएं === | === दो घटनाएं === | ||
फैराडे का नियम दो अलग-अलग घटनाओं का वर्णन करने वाला एक समीकरण है: गतिमान तार पर एक चुंबकीय बल द्वारा उत्पन्न गतिमान ईएमएफ (वर्तमान-वाही तार पर लोरेंत्ज़ बल # बल देखें), और एक विद्युत बल द्वारा उत्पन्न रूपांतरक ईएमएफ बदलते चुंबकीय क्षेत्र (#मैक्सवेल-फैराडे समीकरण | फैराडे का नियम दो अलग-अलग घटनाओं का वर्णन करने वाला एक समीकरण है: गतिमान तार पर एक चुंबकीय बल द्वारा उत्पन्न गतिमान ईएमएफ (वर्तमान-वाही तार पर लोरेंत्ज़ बल # बल देखें), और एक विद्युत बल द्वारा उत्पन्न रूपांतरक ईएमएफ बदलते चुंबकीय क्षेत्र (#मैक्सवेल-फैराडे समीकरण मैक्सवेल-फैराडे समीकरण द्वारा वर्णित) है। | ||
जेम्स क्लर्क मैक्सवेल ने अपने 1861 के पेपर | जेम्स क्लर्क मैक्सवेल ने अपने 1861 के पेपर ऑन फिजिकल लाइन्स ऑफ फोर्स में इस तथ्य की ओर ध्यान आकर्षित किया। [30] उस पेपर के भाग II के उत्तरार्ध में, मैक्सवेल दो घटनाओं में से प्रत्येक के लिए एक अलग भौतिक विवरण देता है।। | ||
कुछ आधुनिक पाठ्यपुस्तकों में विद्युत चुम्बकीय प्रेरण के इन दो पहलुओं का संदर्भ दिया गया है।<ref name=Griffiths1>{{cite book|last=Griffiths|first=David J.|title=Introduction to Electrodynamics|url=https://archive.org/details/introductiontoel00grif_0/page/301|edition=3rd|pages=[https://archive.org/details/introductiontoel00grif_0/page/301 301–3]|publisher=Prentice Hall|year=1999|location=Upper Saddle River, NJ|isbn=0-13-805326-X}}<br>Note that the law relating flux to emf, which this article calls "Faraday's law", is referred to in Griffiths' terminology as the "universal flux rule". Griffiths uses the term "Faraday's law" to refer to what this article calls the "Maxwell–Faraday equation". So in fact, in the textbook, Griffiths' statement is about the "universal flux rule".</ref> जैसा कि रिचर्ड फेनमैन कहते हैं: | कुछ आधुनिक पाठ्यपुस्तकों में विद्युत चुम्बकीय प्रेरण के इन दो पहलुओं का संदर्भ दिया गया है।<ref name=Griffiths1>{{cite book|last=Griffiths|first=David J.|title=Introduction to Electrodynamics|url=https://archive.org/details/introductiontoel00grif_0/page/301|edition=3rd|pages=[https://archive.org/details/introductiontoel00grif_0/page/301 301–3]|publisher=Prentice Hall|year=1999|location=Upper Saddle River, NJ|isbn=0-13-805326-X}}<br>Note that the law relating flux to emf, which this article calls "Faraday's law", is referred to in Griffiths' terminology as the "universal flux rule". Griffiths uses the term "Faraday's law" to refer to what this article calls the "Maxwell–Faraday equation". So in fact, in the textbook, Griffiths' statement is about the "universal flux rule".</ref> जैसा कि रिचर्ड फेनमैन कहते हैं: | ||
{{Quotation| | {{Quotation|"फ्लक्स नियम" कि एक सर्किट में ईएमएफ सर्किट के माध्यम से चुंबकीय प्रवाह के परिवर्तन की दर के बराबर होता है, चाहे फ्लक्स बदलता है क्योंकि क्षेत्र बदलता है या क्योंकि सर्किट चलता है (या दोनों)... | ||
फिर भी नियम की अपनी व्याख्या में हमने दो मामलों के लिए दो पूरी तरह से भिन्न कानूनों का उपयोग किया है – {{math|'''v''' × '''B'''}} for "सर्किट चाल" और {{math|∇ × '''E''' {{=}} −∂<sub>''t''</sub>'''B'''}} क्षेत्र परिवर्तन के लिए". | |||
हम भौतिकी में किसी अन्य स्थान के बारे में नहीं जानते हैं जहाँ इस तरह के एक सरल और सटीक सामान्य सिद्धांत को इसकी वास्तविक समझ के लिए "दो अलग-अलग घटनाओं" के संदर्भ में एक विश्लेषण की आवश्यकता होती है।''.|रिचर्ड पी. फेनमैन, ''[[भौतिकी पर फेनमैन व्याख्यान]]''<ref>[https://feynmanlectures.caltech.edu/II_17.html#Ch17-S1-p10 The Feynman Lectures on Physics Vol. II Ch. 17: The Laws of Induction]</ref>}} | |||
=== चार आयामी औपचारिकता के आधार पर व्याख्या === | === चार आयामी औपचारिकता के आधार पर व्याख्या === | ||
सामान्य स्थिति में, गतिमान तार में आवेशों पर चुंबकीय बल की क्रिया द्वारा या इसके क्षेत्र को बदलने वाले | सामान्य स्थिति में, गतिमान तार में आवेशों पर चुंबकीय बल की क्रिया द्वारा या इसके क्षेत्र को बदलने वाले परिपथ में गतिमान ईएमएफ उपस्थिति की व्याख्या असंतोषजनक है। तथ्य की बात के रूप में, तार या परिपथ में चार्ज पूरी तरह से अनुपस्थित हो सकते हैं, तो क्या इस स्थिति में विद्युत चुम्बकीय प्रेरण प्रभाव गायब हो जाएगा? इस स्थिति का लेख में विश्लेषण किया गया है, जिसमें फैराडे के नियम में चार-आयामी सहसंयोजक रूप में विद्युत चुम्बकीय क्षेत्र के अभिन्न समीकरणों को लिखते समय आंशिक समय व्युत्पन्न के अतिरिक्त परिपथ के माध्यम से चुंबकीय प्रवाह का कुल समय व्युत्पन्न दिखाई देता है। . <ref>{{cite journal | last1 = Fedosin | first1 = Sergey G. | title = On the Covariant Representation of Integral Equations of the Electromagnetic Field | journal = Progress in Electromagnetics Research C | volume = 96 | pages = 109–122| year = 2019 | url = https://rdcu.be/ccV9o| doi = 10.2528/PIERC19062902|arxiv=1911.11138| bibcode=2019arXiv191111138F| s2cid = 208095922 }}</ref> इस प्रकार, विद्युत चुम्बकीय प्रेरण तब प्रकट होता है जब चुंबकीय क्षेत्र समय के साथ बदलता है या जब परिपथ का क्षेत्र बदलता है। भौतिक दृष्टिकोण से, प्रेरण ईएमएफ के बारे में नहीं, बल्कि प्रेरित विद्युत क्षेत्र की ताकत के बारे में बात करना बेहतर है <math display="inline"> \mathbf E = - \nabla \mathcal{E} - \frac{ \partial \mathbf A}{ \partial t}</math>, जो परिपथ में तब होता है जब चुंबकीय प्रवाह बदलता है। इस स्थिति में योगदान <math> \mathbf E</math> शब्द के माध्यम से चुंबकीय क्षेत्र में परिवर्तन से किया जाता है <math display="inline"> - \frac{ \partial \mathbf A}{ \partial t}</math> , कहाँ पे <math> \mathbf A</math> सदिश क्षमता है। यदि निरंतर चुंबकीय क्षेत्र की स्थिति में परिपथ क्षेत्र बदल रहा है, तो परिपथ का कुछ हिस्सा अनिवार्य रूप से चल रहा है, और विद्युत क्षेत्र <math> \mathbf E</math> चुंबकीय क्षेत्र के लोरेंत्ज़ परिवर्तन के परिणामस्वरूप आने वाले संदर्भ फ्रेम K' में परिपथ के इस हिस्से में उभरता है <math> \mathbf B</math>, स्थिर संदर्भ फ्रेम K में सम्मलित है, जो परिपथ से होकर गुजरता है। क्षेत्र की उपस्थिति <math> \mathbf E</math> इन K' को चल परिपथ में प्रेरण प्रभाव के परिणामस्वरूप माना जाता है, भले ही परिपथ में चार्ज सम्मलित हों या नहीं। संचालन परिपथ में, क्षेत्र <math> \mathbf E</math> आरोपों की गति का कारण बनता है। संदर्भ फ्रेम K में, यह प्रेरण के ईएमएफ की तरह दिखता है <math> \mathcal{E} </math>, जिसके रूप में ढाल <math> - \nabla \mathcal{E} </math>, परिपथ के साथ लिया गया, ऐसा लगता है कि <math> \mathbf E</math>. क्षेत्र उत्पन्न होता है। | ||
===आइंस्टीन के विचार=== | ===आइंस्टीन के विचार=== | ||
इस स्पष्ट द्विभाजन पर चिंतन प्रमुख मार्गों में से एक था जिसने [[ अल्बर्ट आइंस्टीन ]] को विशेष सापेक्षता विकसित करने के लिए प्रेरित किया: | इस स्पष्ट द्विभाजन पर चिंतन प्रमुख मार्गों में से एक था जिसने [[ अल्बर्ट आइंस्टीन ]] को विशेष सापेक्षता विकसित करने के लिए प्रेरित किया: | ||
{{Quotation| | {{Quotation|यह ज्ञात है कि मैक्सवेल के विद्युतगतिकी - जैसा कि वर्तमान समय में आम तौर पर समझा जाता है - जब गतिमान पिंडों पर लागू किया जाता है, तो असममितता की ओर जाता है जो घटना में निहित प्रतीत नहीं होता है। उदाहरण के लिए, चुंबक और संवाहक की पारस्परिक विद्युत क्रिया को लें। | ||
यहां देखने योग्य घटना केवल संवाहक और चुंबक की सापेक्ष गति पर निर्भर करती है, जबकि प्रथागत दृश्य दो मामलों के बीच एक तेज अंतर खींचता है जिसमें इनमें से एक या दूसरा गति में है। यदि चुंबक गति में है और संवाहक आराम पर है, तो चुंबक के पड़ोस में एक निश्चित निश्चित ऊर्जा के साथ एक विद्युत क्षेत्र उत्पन्न होता है, जहां संवाहक के हिस्से स्थित होते हैं।. | |||
लेकिन अगर चुंबक स्थिर है और चालक गति में है, तो चुंबक के पड़ोस में कोई विद्युत क्षेत्र उत्पन्न नहीं होता है। संवाहक में, हालांकि, हम एक वैद्युतवाहक बल पाते हैं, जिसमें स्वयं कोई संबंधित ऊर्जा नहीं होती है, लेकिन जो उत्पन्न होती है - दो मामलों में सापेक्ष गति की समानता को मानते हुए - समान पथ और तीव्रता के विद्युत धाराओं को उत्पादित किया जाता है। | |||
इस तरह के उदाहरण, "प्रकाश माध्यम" के सापेक्ष पृथ्वी की किसी भी गति को खोजने के असफल प्रयासों के साथ, यह सुझाव देते हैं कि वैद्युतगतिकी के साथ-साथ यांत्रिकी की घटनाओं में पूर्ण आराम के विचार के अनुरूप कोई गुण नहीं है। | |||
| [[ | | [[अल्बर्ट आइंस्टीन]], ''[[मूविंग बॉडीज के वैद्युतगतिकी पर]]''<ref>{{cite web|first=Albert|last=Einstein|author-link=Albert Einstein|url=http://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf|title=On the Electrodynamics of Moving Bodies}}</ref>}} | ||
Revision as of 22:12, 1 June 2023
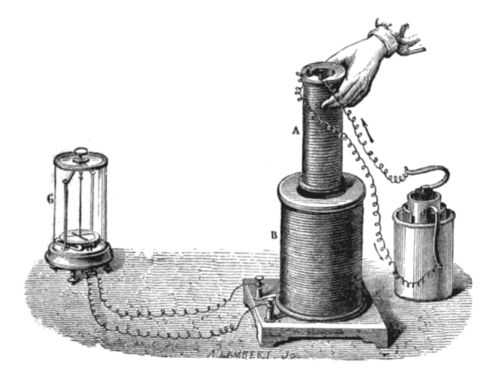
फैराडे का इंडक्शन (प्रेरण) का नियम (संक्षेप में, फैराडे का नियम) विद्युत् चुम्बकत्व का एक बुनियादी नियम है, जो अभिरुचि करता है कि एक वैद्युतवाहक बल (ईएमएफ) उत्पन्न करने के लिए एक चुंबकीय क्षेत्र एक विद्युत परिपथ के साथ कैसे परस्पर प्रभाव करेगा - एक घटना जिसे विद्युत चुंबकीय प्रेरण के रूप में जाना जाता है। यह रूपांतरक (ट्रांसफार्मर), कुचालक और कई प्रकार के बिजली की मोटर, [[ विद्युत जनरेटर ]] और परिनालिका का मूलभूत संचालन सिद्धांत है।[2][3]
मैक्सवेल-फैराडे समीकरण (मैक्सवेल के समीकरणों में से एक के रूप में सूचीबद्ध) इस तथ्य का वर्णन करता है कि एक स्थानिक रूप से भिन्न (और संभवतः समय-भिन्न भी, इस पर निर्भर करता है कि एक चुंबकीय क्षेत्र समय में कैसे भिन्न होता है) विद्युत क्षेत्र हमेशा एक समय-भिन्न चुंबकीय क्षेत्र के साथ होता है, जबकि फैराडे के नियम में कहा गया है कि प्रवाहकीय लूप पर ईएमएफ (वैद्युतवाहक बल, एक यूनिट चार्ज पर किए गए विद्युत चुम्बकीय कार्य के रूप में परिभाषित किया जाता है) प्रवाहकीय लूप पर होता है, जब लूप द्वारा संलग्न सतह के माध्यम से चुंबकीय प्रवाह समय में भिन्न होता है।
फैराडे के नियम की खोज की जा चुकी थी और इसके एक पहलू (रूपांतरक ईएमएफ) को बाद में मैक्सवेल-फैराडे समीकरण के रूप में तैयार किया गया था। फैराडे के नियम का समीकरण मैक्सवेल-फैराडे समीकरण (रूपांतरक ईएमएफ का वर्णन) और लोरेंत्ज़ बल (गतिशील ईएमएफ का वर्णन) द्वारा प्राप्त किया जा सकता है। मैक्सवेल-फैराडे समीकरण का अभिन्न रूप केवल रूपांतरक ईएमएफ का वर्णन करता है, जबकि फैराडे के नियम का समीकरण रूपांतरक ईएमएफ और गतिक ईएमएफ दोनों का वर्णन करता है।
| Articles about |
| Electromagnetism |
|---|
 |
इतिहास

1831 में माइकल फैराडे और 1832 में जोसेफ हेनरी द्वारा स्वतंत्र रूप से विद्युत चुम्बकीय प्रेरण की खोज की गई थी।[5] फैराडे अपने प्रयोगों के परिणामों को प्रकाशित करने वाले पहले व्यक्ति थे।[6][7] फैराडे के विद्युत चुम्बकीय प्रेरण के पहले प्रायोगिक प्रदर्शन में (29 अगस्त, 1831),[8] उन्होंने एक लोहे की अंगूठी (टोरस्र्स ) (एक आधुनिक टॉरॉयडल रूपांतरक के समान व्यवस्था) के विपरीत दिशा में दो तारों को लपेटा। विद्युत चुम्बक के हाल ही में खोजे गए गुणों के अपने आकलन के आधार पर, उन्होंने उम्मीद की कि जब एक तार में करंट प्रवाहित होना प्रारंभ होता है, तो एक तरह की तरंग रिंग के माध्यम से यात्रा करेगी और विपरीत दिशा में कुछ विद्युत प्रभाव पैदा करेगी। उसने एक तार को बिजली की शक्ति नापने का यंत्र में प्लग किया, और दूसरे तार को बैटरी से जोड़ते हुए उसे देखा। वास्तव में, जब उन्होंने तार को बैटरी से संसक्त, और जब उन्होंने इसे असंगत किया, तो उन्होंने एक क्षणिक धारा (जिसे उन्होंने बिजली की लहर कहा) देखा।[9]: 182–183 यह प्रेरण बैटरी के संसक्त और असंगत होने पर होने वाले चुंबकीय प्रवाह में बदलाव के कारण था।[4]दो महीनों के भीतर, फैराडे ने विद्युत चुम्बकीय प्रेरण की कई अन्य अभिव्यक्तियाँ पाईं। उदाहरण के लिए, उन्होंने क्षणिक धाराओं को देखा जब उन्होंने तारों के तार के अंदर और बाहर एक बार चुंबक को जल्दी से सर्पण किया, और उन्होंने एक सर्पण विद्युत चालक तार (फैराडे की डिस्क) के साथ बार चुंबक के पास एक तांबे की डिस्क को घुमाकर एक स्थिर (प्रत्यक्ष धारा) धारा उत्पन्न किया था।.[9]: 191–195
माइकल फैराडे ने एक अवधारणा का उपयोग करते हुए विद्युत चुम्बकीय प्रेरण की व्याख्या की जिसे उन्होंने बल की रेखाएं कहा। चूंकि, उस समय के वैज्ञानिकों ने उनके सैद्धांतिक विचारों को व्यापक रूप से खारिज कर दिया, मुख्यतः क्योंकि वे गणितीय रूप से तैयार नहीं किए गए थे।[9]: 510 एक अपवाद जेम्स क्लर्क मैक्सवेल थे, जिन्होंने 1861-62 में फैराडे के विचारों को अपने मात्रात्मक विद्युत चुम्बकीय सिद्धांत के आधार के रूप में उपयोग किया।[9]: 510 [10][11] मैक्सवेल के कागजात में, विद्युत चुम्बकीय प्रेरण के समय-भिन्न पहलू को एक अंतर समीकरण के रूप में व्यक्त किया जाता है, जिसे ओलिवर हीविसाइड ने फैराडे के नियम के रूप में संदर्भित किया है, चूंकि यह फैराडे के नियम के मूल संस्करण से अलग है, और #दो घटनाओं का वर्णन नहीं करता है। हीविसाइड का संस्करण (#मैक्सवेल-फैराडे समीकरण|नीचे मैक्सवेल-फैराडे समीकरण देखें) वह रूप है जिसे आज मैक्सवेल के समीकरणों के रूप में ज्ञात समीकरणों के समूह में मान्यता प्राप्त है।
1834 में एमिल लेनज़ द्वारा प्रतिपादित लेनज़ का नियम,[12] परिपथ के माध्यम से प्रवाह का वर्णन करता है, और विद्युत चुम्बकीय प्रेरण से उत्पन्न प्रेरित ईएमएफ और वर्तमान की दिशा देता है (नीचे दिए गए उदाहरणों में विस्तृत)।
फैराडे का नियम
फैराडे के कानून का सबसे व्यापक संस्करण कहता है:
The electromotive force around a closed path is equal to the negative of the time rate of change of the magnetic flux enclosed by the path.[13][14]
गणितीय कथन
चुंबकीय क्षेत्र में तार के एक लूप के लिए, चुंबकीय प्रवाह ΦB किसी भी सतह (गणित) के लिए परिभाषित किया गया है Σ जिसकी सीमा (टोपोलॉजी) दिया गया लूप है। चूँकि वायर लूप गतिमान हो सकता है, हम लिखते हैं Σ(t) सतह के लिए। चुंबकीय प्रवाह सतह अभिन्न है:
जब प्रवाह बदलता है—क्योंकि B परिवर्तन, या क्योंकि वायर लूप को स्थानांतरित या विकृत किया जाता है, या दोनों - फैराडे के प्रेरण के नियम का कहना है कि वायर लूप एक वैद्युतवाहक बल प्राप्त करता है, जिसे यूनिट चार्ज से उपलब्ध ऊर्जा के रूप में परिभाषित किया जाता है जो वायर लूप के चारों ओर एक बार यात्रा करता है।[15]: ch17 [16][17] (चूंकि कुछ स्रोत परिभाषा को अलग तरीके से बताते हैं, इस अभिव्यक्ति को विशेष सापेक्षता के समीकरणों के साथ संगतता के लिए चुना गया था।) समान रूप से, यह वह वोल्टेज है जिसे इलेक्ट्रिक परिपथ बनाने के लिए तार को काटकर और चालक तार में वाल्टमीटर जोड़कर मापा जाएगा। .
फैराडे के नियम में कहा गया है कि ईएमएफ भी चुंबकीय प्रवाह के समय व्युत्पन्न द्वारा दिया जाता है:
वैद्युतवाहक बल की दिशा लेंज़ के नियम द्वारा दी गई है।
1845 में फ्रांज अर्न्स्ट न्यूमैन द्वारा गणितीय रूप में विद्युत धाराओं को सम्मलित करने के नियम स्थापित किए गए थे।[18] फैराडे के नियम में दोनों परिमाणों और इसके चरों की दिशाओं के बीच संबंधों के बारे में जानकारी सम्मलित है। चूंकि, दिशाओं के बीच संबंध स्पष्ट नहीं हैं; वे गणितीय सूत्र में छिपे हैं।
लेन्ज़ के नियम का प्रयोग किए बिना, फैराडे के नियम से सीधे वैद्युतवाहक बल (ईएमएफ) की दिशा का पता लगाना संभव है। बाएं हाथ का नियम ऐसा करने में मदद करता है, जो इस प्रकार है:[19][20]
- बाएं हाथ की मुड़ी हुई उंगलियों को लूप (पीली रेखा) से संरेखित करें।
- अपना अंगूठा तानें फैला हुआ अंगूठा किस दिशा को इंगित करता है n (भूरा), पाश से घिरे क्षेत्र के लिए सामान्य
- का चिह्न खोजें ΔΦBप्रवाह में परिवर्तन, प्रारंभिक और अंतिम अपशिष्टों निर्धारित करें (जिसका अंतर है ΔΦB) सामान्य के संबंध में n, जैसा कि फैला हुआ अंगूठा दिखाता है।
- यदि प्रवाह में परिवर्तन, ΔΦB, सकारात्मक है, घुमावदार उंगलियां वैद्युतवाहक बल (पीले तीर) की दिशा दिखाती हैं।
- यदि ΔΦB ऋणात्मक है, वैद्युतवाहक बल की दिशा घुमावदार उंगलियों (पीले तीर के विपरीत) की दिशा के विपरीत है।
N समरूप घुमावों से बने तार के कसकर लपेटे गए कुंडल के लिए, प्रत्येक समान ΦB के साथ, फैराडे के प्रेरण के नियम में कहा गया है कि[21][22]
मैक्सवेल–फैराडे समीकरण
मैक्सवेल-फैराडे समीकरण बताता है कि एक समय-भिन्न चुंबकीय क्षेत्र हमेशा एक स्थानिक रूप से भिन्न (संभवतः समय-भिन्न), गैर- रूढ़िवादी सदिश क्षेत्र विद्युत क्षेत्र, और इसके विपरीत के साथ होता है। मैक्सवेल-फैराडे समीकरण है
(एसआई इकाइयों में) जहां ∇ × कर्ल (गणित) रैखिक संकारक है और फिर से E(r, t) विद्युत क्षेत्र है और B(r, t) चुंबकीय क्षेत्र है। ये क्षेत्र सामान्यत: स्थिति के कार्य हो सकते हैं r और समय t.[23]
मैक्सवेल-फैराडे समीकरण मैक्सवेल के चार समीकरणों में से एक है, और इसलिए चिरसम्मत विद्युत चुंबकत्व के सिद्धांत में एक मौलिक भूमिका निभाता है। यह केल्विन-स्टोक्स प्रमेय द्वारा एक अभिन्न रूप में भी लिखा जा सकता है,[24] इस प्रकार फैराडे के नियम का पुनरुत्पादन:
जहां, जैसा कि चित्र में दिखाया गया है, Σ बंद समोच्च से घिरा सतह है ∂Σ, dl समोच्च का एक अतिसूक्ष्म सदिश तत्व है ∂Σ, और dA सतह का एक अतिसूक्ष्म सदिश तत्व है Σ. इसकी दिशा उस सतह के पैच के लिए लांबिक है, परिमाण सतह के एक अतिसूक्ष्म पैच का क्षेत्र है।
दोनों dl और dA एक संकेत अस्पष्टता है; सही संकेत प्राप्त करने के लिए, दाहिने हाथ के नियम का उपयोग किया जाता है, जैसा कि लेख केल्विन-स्टोक्स प्रमेय में बताया गया है। एक तलीय सतह Σ के लिए, वक्र ∂Σ का एक सकारात्मक पथ तत्व dl दाएँ हाथ के नियम द्वारा परिभाषित किया जाता है, जो दाहिने हाथ की उंगलियों से इंगित करता है जब अंगूठा सामान्य n की दिशा में सतह Σ की ओर इंगित करता है।
∂Σ के चारों ओर रेखा अभिन्न को परिसंचरण (भौतिकी) कहा जाता है। [15]: ch3 E का एक अशून्य संचलन स्थिर आवेशों द्वारा उत्पन्न विद्युत क्षेत्र के व्यवहार से भिन्न होता है। एक चार्ज-जनित E-फ़ील्ड को अदिश क्षेत्र के ढाल के रूप में व्यक्त किया जा सकता है जो पोइसन के समीकरण का समाधान है, और शून्य पथ अभिन्न है। ढाल प्रमेय देखें।
अभिन्न समीकरण समष्टि के माध्यम से किसी भी पथ ∂Σ के लिए सही है, और कोई भी सतह Σ जिसके लिए वह पथ एक सीमा है।
यदि सतह Σ समय के साथ नहीं बदल रही है, तो समीकरण को फिर से लिखा जा सकता है:
एक बदलते चुंबकीय प्रवाह से प्रेरित विद्युत सदिश क्षेत्र, समग्र विद्युत क्षेत्र के परिनालिकीय घटक, आयतन अभिन्न समीकरण द्वारा गैर-सापेक्षतावादी सीमा में अनुमानित किया जा सकता है।[23]: 321
प्रमाण
मैक्सवेल के चार समीकरण (मैक्सवेल-फैराडे समीकरण सहित), लोरेंत्ज़ बल नियम के साथ, शास्त्रीय विद्युत चुंबकत्व में सब कुछ प्राप्त करने के लिए पर्याप्त आधार हैं।[15][16]इसलिए, इन समीकरणों से प्रारंभ करके फैराडे के नियम को सिद्ध करना संभव है।[25][26] प्रारंभिक बिंदु एक यादृच्छिक सतह के माध्यम से प्रवाह का समय-व्युत्पन्न है Σ (जिसे स्थानांतरित या विकृत किया जा सकता है) समष्टि में:
| एक बंद सीमा (लूप) के माध्यम से चुंबकीय प्रवाह के समय-व्युत्पन्न पर विचार करें जो गतिमान या विकृत हो सकता है। लूप से घिरे क्षेत्र को Σ(t) के रूप में निरूपित किया जाता है, तो समय-व्युत्पन्न के रूप में व्यक्त किया जा सकता है
समाकल समय के साथ दो कारणों से बदल सकता है: समाकलन बदल सकता है, या समाकलन क्षेत्र बदल सकता है। इसलिए ये रैखिक रूप से जोड़ते हैं:
जहाँ t0 कोई निश्चित समय है। हम दिखाएंगे कि दाईं ओर का पहला शब्द ट्रांसफॉर्मर ईएमएफ से मेल खाता है, दूसरा गतिमान ईएमएफ (चुंबकीय लोरेंत्ज़ बल से आवेश वाहक पर चुंबकीय क्षेत्र में संवाहक पाश की गति या विकृति के कारण)। मैक्सवेल-फैराडे समीकरण के अभिन्न रूप का उपयोग करके दाईं ओर का पहला शब्द फिर से लिखा जा सकता है:
इसके बाद, हम दाहिनी ओर दूसरे पद का विश्लेषण करते हैं: इसका प्रमाण पहले पद की तुलना में थोड़ा अधिक कठिन है; प्रमाण के लिए अधिक विवरण और वैकल्पिक दृष्टिकोण संदर्भों में पाए जा सकते हैं। जैसे ही लूप चलता है और/या विकृत होता है, यह एक सतह को साफ करता है (सही चित्र देखें)। चूंकि लूप dl का एक छोटा सा हिस्सा वेग vl के साथ थोड़े समय dt पर चलता है, यह एक ऐसे क्षेत्र को स्वीप करता है जिसका सदिश dAsweep = vl dt × dl है (ध्यान दें कि यह सदिश सही आकृति में प्रदर्शन से बाहर की ओर है)। इसलिए, समय dt पर लूप की विकृति या गति के कारण लूप के माध्यम से चुंबकीय प्रवाह का परिवर्तन होता है यहां ट्रिपल स्केलर उत्पादों की पहचान का उपयोग किया जाता है। इसलिए,
जहां vl पाश ∂Σ के एक भाग का वेग है।
इन्हें एक साथ रखने का परिणाम होता है, |
परिणाम है:
एक प्रवाहकीय लूप की स्थिति में, ईएमएफ (वैद्युतवाहक बल) एक यूनिट चार्ज पर किया जाने वाला विद्युत चुम्बकीय कार्य है, जब यह लूप के चारों ओर एक बार घूम चुका होता है, और यह काम लोरेंत्ज़ बल नियम द्वारा किया जाता है। इसलिए, ईएमएफ के रूप में व्यक्त किया जाता है
मैक्रोस्कोपिक दृश्य में, लूप के एक खंड पर प्रभार के लिए, v औसत में दो घटक होते हैं; एक खंड के साथ आवेश का वेग है vt, और दूसरा खंड का वेग है vl (लूप विकृत या स्थानांतरित हो गया है)। vt के निर्देशन के बाद से प्रभार पर किए गए कार्य में योगदान नहीं करता है vt की दिशा के समान है . गणितीय रूप से,
अपवाद
फैराडे के नियम का सामान्यीकरण यह बताने के लिए आकर्षक है कि: यदि ∂Σ समष्टि में कोई भी यादृच्छिक बंद लूप है, फिर चुंबकीय प्रवाह का कुल समय व्युत्पन्न Σ चारों ओर ईएमएफ के बराबर है ∂Σ। यह कथन, चूंकि, हमेशा सत्य नहीं होता है और इसका कारण केवल स्पष्ट कारण से नहीं है, जब कोई संवाहक सम्मलित नहीं होता है तो ईएमएफ रिक्त स्थान में अपरिभाषित होता है। जैसा कि पिछले खंड में उल्लेख किया गया है, फैराडे के नियम को तब तक काम करने की गारंटी नहीं है जब तक कि अमूर्त वक्र का वेग न हो ∂Σ बिजली का संचालन करने वाली सामग्री के वास्तविक वेग से मेल खाता है।[27] नीचे दिए गए दो उदाहरणों से पता चलता है कि जब ∂Σ की गति को सामग्री की गति से अलग किया जाता है तो अधिकांशत: गलत परिणाम प्राप्त होते हैं।[15]
- Index.php?title=File:Faraday's disc.PNG
फैराडे का एकध्रुवीय जनरेटर। डिस्क कोणीय दर ω के साथ घूमती है, स्थिर चुंबकीय क्षेत्र B (जो दिशा डिस्क की सतह के साथ सामान्य है) में परिपत्र त्रिज्या को व्यापक रूप से घुमाती है। चुंबकीय लोरेंत्ज़ बल v × B प्रवाहकीय त्रिज्या के साथ प्रवाहकीय रिम तक एक धारा चलाता है, और वहां से परिपथ निचले ब्रश और डिस्क का समर्थन करने वाले एक्सल के माध्यम से पूरा होता है। यह उपकरण एक ईएमएफ और करंट उत्पन्न करता है, चूंकि "परिपथ" का आकार स्थिर है और इस प्रकार परिपथ के माध्यम से प्रवाह समय के साथ नहीं बदलता है।
- Index.php?title=File:FaradaysLawWithPlates.gif
एक तार (ठोस लाल रेखाएँ) एक परिपथ बनाने के लिए दो स्पर्श करने वाली धातु की प्लेटों (चाँदी) से जुड़ती हैं। संपूर्ण प्रणाली एक समान चुंबकीय क्षेत्र में बैठती है, जो पृष्ठ के लिए सामान्य है। यदि सार पथ ∂Σ वर्तमान प्रवाह (लाल रंग में चिह्नित) के प्राथमिक पथ का अनुसरण करता है, तो इस पथ के माध्यम से चुंबकीय प्रवाह नाटकीय रूप से बदल जाता है क्योंकि प्लेटें घुमाई जाती हैं, फिर भी ईएमएफ लगभग शून्य है। भौतिकी पर फेनमैन व्याख्यान के बाद[15]: ch17
इस तरह के उदाहरणों का विश्लेषण पथ का ध्यान रखकर किया जा सकता है ∂Σ पदार्थ के समान वेग से गति करता है।[27]वैकल्पिक रूप से, मैक्सवेल-फैराडे समीकरण के साथ लोरेंत्ज़ बल नियम को जोड़कर कोई भी ईएमएफ की सही गणना कर सकता है:[15]: ch17 [28]
जहां यह ध्यान रखना बहुत महत्वपूर्ण है कि (1) [vm] संवाहक का वेग है ... पथ तत्व का वेग नहीं dl और (2) सामान्य तौर पर, समय के संबंध में आंशिक व्युत्पन्न को अभिन्न के बाहर नहीं ले जाया जा सकता क्योंकि क्षेत्र समय का एक कार्य है।[28]
फैराडे का नियम और सापेक्षता
दो घटनाएं
फैराडे का नियम दो अलग-अलग घटनाओं का वर्णन करने वाला एक समीकरण है: गतिमान तार पर एक चुंबकीय बल द्वारा उत्पन्न गतिमान ईएमएफ (वर्तमान-वाही तार पर लोरेंत्ज़ बल # बल देखें), और एक विद्युत बल द्वारा उत्पन्न रूपांतरक ईएमएफ बदलते चुंबकीय क्षेत्र (#मैक्सवेल-फैराडे समीकरण मैक्सवेल-फैराडे समीकरण द्वारा वर्णित) है।
जेम्स क्लर्क मैक्सवेल ने अपने 1861 के पेपर ऑन फिजिकल लाइन्स ऑफ फोर्स में इस तथ्य की ओर ध्यान आकर्षित किया। [30] उस पेपर के भाग II के उत्तरार्ध में, मैक्सवेल दो घटनाओं में से प्रत्येक के लिए एक अलग भौतिक विवरण देता है।।
कुछ आधुनिक पाठ्यपुस्तकों में विद्युत चुम्बकीय प्रेरण के इन दो पहलुओं का संदर्भ दिया गया है।[29] जैसा कि रिचर्ड फेनमैन कहते हैं:
"फ्लक्स नियम" कि एक सर्किट में ईएमएफ सर्किट के माध्यम से चुंबकीय प्रवाह के परिवर्तन की दर के बराबर होता है, चाहे फ्लक्स बदलता है क्योंकि क्षेत्र बदलता है या क्योंकि सर्किट चलता है (या दोनों)...
फिर भी नियम की अपनी व्याख्या में हमने दो मामलों के लिए दो पूरी तरह से भिन्न कानूनों का उपयोग किया है – v × B for "सर्किट चाल" और ∇ × E = −∂tB क्षेत्र परिवर्तन के लिए".
हम भौतिकी में किसी अन्य स्थान के बारे में नहीं जानते हैं जहाँ इस तरह के एक सरल और सटीक सामान्य सिद्धांत को इसकी वास्तविक समझ के लिए "दो अलग-अलग घटनाओं" के संदर्भ में एक विश्लेषण की आवश्यकता होती है।.
— रिचर्ड पी. फेनमैन, भौतिकी पर फेनमैन व्याख्यान[30]
चार आयामी औपचारिकता के आधार पर व्याख्या
सामान्य स्थिति में, गतिमान तार में आवेशों पर चुंबकीय बल की क्रिया द्वारा या इसके क्षेत्र को बदलने वाले परिपथ में गतिमान ईएमएफ उपस्थिति की व्याख्या असंतोषजनक है। तथ्य की बात के रूप में, तार या परिपथ में चार्ज पूरी तरह से अनुपस्थित हो सकते हैं, तो क्या इस स्थिति में विद्युत चुम्बकीय प्रेरण प्रभाव गायब हो जाएगा? इस स्थिति का लेख में विश्लेषण किया गया है, जिसमें फैराडे के नियम में चार-आयामी सहसंयोजक रूप में विद्युत चुम्बकीय क्षेत्र के अभिन्न समीकरणों को लिखते समय आंशिक समय व्युत्पन्न के अतिरिक्त परिपथ के माध्यम से चुंबकीय प्रवाह का कुल समय व्युत्पन्न दिखाई देता है। . [31] इस प्रकार, विद्युत चुम्बकीय प्रेरण तब प्रकट होता है जब चुंबकीय क्षेत्र समय के साथ बदलता है या जब परिपथ का क्षेत्र बदलता है। भौतिक दृष्टिकोण से, प्रेरण ईएमएफ के बारे में नहीं, बल्कि प्रेरित विद्युत क्षेत्र की ताकत के बारे में बात करना बेहतर है , जो परिपथ में तब होता है जब चुंबकीय प्रवाह बदलता है। इस स्थिति में योगदान शब्द के माध्यम से चुंबकीय क्षेत्र में परिवर्तन से किया जाता है , कहाँ पे सदिश क्षमता है। यदि निरंतर चुंबकीय क्षेत्र की स्थिति में परिपथ क्षेत्र बदल रहा है, तो परिपथ का कुछ हिस्सा अनिवार्य रूप से चल रहा है, और विद्युत क्षेत्र चुंबकीय क्षेत्र के लोरेंत्ज़ परिवर्तन के परिणामस्वरूप आने वाले संदर्भ फ्रेम K' में परिपथ के इस हिस्से में उभरता है , स्थिर संदर्भ फ्रेम K में सम्मलित है, जो परिपथ से होकर गुजरता है। क्षेत्र की उपस्थिति इन K' को चल परिपथ में प्रेरण प्रभाव के परिणामस्वरूप माना जाता है, भले ही परिपथ में चार्ज सम्मलित हों या नहीं। संचालन परिपथ में, क्षेत्र आरोपों की गति का कारण बनता है। संदर्भ फ्रेम K में, यह प्रेरण के ईएमएफ की तरह दिखता है , जिसके रूप में ढाल , परिपथ के साथ लिया गया, ऐसा लगता है कि . क्षेत्र उत्पन्न होता है।
आइंस्टीन के विचार
इस स्पष्ट द्विभाजन पर चिंतन प्रमुख मार्गों में से एक था जिसने अल्बर्ट आइंस्टीन को विशेष सापेक्षता विकसित करने के लिए प्रेरित किया:
यह ज्ञात है कि मैक्सवेल के विद्युतगतिकी - जैसा कि वर्तमान समय में आम तौर पर समझा जाता है - जब गतिमान पिंडों पर लागू किया जाता है, तो असममितता की ओर जाता है जो घटना में निहित प्रतीत नहीं होता है। उदाहरण के लिए, चुंबक और संवाहक की पारस्परिक विद्युत क्रिया को लें।
यहां देखने योग्य घटना केवल संवाहक और चुंबक की सापेक्ष गति पर निर्भर करती है, जबकि प्रथागत दृश्य दो मामलों के बीच एक तेज अंतर खींचता है जिसमें इनमें से एक या दूसरा गति में है। यदि चुंबक गति में है और संवाहक आराम पर है, तो चुंबक के पड़ोस में एक निश्चित निश्चित ऊर्जा के साथ एक विद्युत क्षेत्र उत्पन्न होता है, जहां संवाहक के हिस्से स्थित होते हैं।.
लेकिन अगर चुंबक स्थिर है और चालक गति में है, तो चुंबक के पड़ोस में कोई विद्युत क्षेत्र उत्पन्न नहीं होता है। संवाहक में, हालांकि, हम एक वैद्युतवाहक बल पाते हैं, जिसमें स्वयं कोई संबंधित ऊर्जा नहीं होती है, लेकिन जो उत्पन्न होती है - दो मामलों में सापेक्ष गति की समानता को मानते हुए - समान पथ और तीव्रता के विद्युत धाराओं को उत्पादित किया जाता है।
इस तरह के उदाहरण, "प्रकाश माध्यम" के सापेक्ष पृथ्वी की किसी भी गति को खोजने के असफल प्रयासों के साथ, यह सुझाव देते हैं कि वैद्युतगतिकी के साथ-साथ यांत्रिकी की घटनाओं में पूर्ण आराम के विचार के अनुरूप कोई गुण नहीं है।
यह भी देखें
संदर्भ
- ↑ Poyser, Arthur William (1892). Magnetism and Electricity: A manual for students in advanced classes. London and New York: Longmans, Green, & Co. Fig. 248, p. 245. Retrieved 2009-08-06.
- ↑ Sadiku, M. N. O. (2007). Elements of Electromagnetics (4th ed.). New York & Oxford: Oxford University Press. p. 386. ISBN 978-0-19-530048-2.
- ↑ "Applications of electromagnetic induction". Boston University. 1999-07-22.
- ↑ 4.0 4.1 Giancoli, Douglas C. (1998). Physics: Principles with Applications (5th ed.). pp. 623–624.
- ↑ "A Brief History of Electromagnetism" (PDF).
- ↑ Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson:Prentice Hall. p. 255. ISBN 978-0-13-241326-8.
- ↑ "Joseph Henry". Member Directory, National Academy of Sciences. Retrieved 2016-12-30.
- ↑ Faraday, Michael; Day, P. (1999-02-01). The philosopher's tree: a selection of Michael Faraday's writings. CRC Press. p. 71. ISBN 978-0-7503-0570-9. Retrieved 28 August 2011.
- ↑ 9.0 9.1 9.2 9.3 Williams, L. Pearce (1965). Michael Faraday. New York, Basic Books.[full citation needed]
- ↑ Clerk Maxwell, James (1904). A Treatise on Electricity and Magnetism. Vol. 2 (3rd ed.). Oxford University Press. pp. 178–179, 189.
- ↑ "Archives Biographies: Michael Faraday". The Institution of Engineering and Technology.
- ↑ Lenz, Emil (1834). "Ueber die Bestimmung der Richtung der durch elektodynamische Vertheilung erregten galvanischen Ströme". Annalen der Physik und Chemie. 107 (31): 483–494. Bibcode:1834AnP...107..483L. doi:10.1002/andp.18341073103.
A partial translation of the paper is available in Magie, W. M. (1963). A Source Book in Physics. Cambridge, MA: Harvard Press. pp. 511–513. - ↑ Jordan, Edward; Balmain, Keith G. (1968). Electromagnetic Waves and Radiating Systems (2nd ed.). Prentice-Hall. p. 100.
Faraday's Law, which states that the electromotive force around a closed path is equal to the negative of the time rate of change of magnetic flux enclosed by the path.
- ↑ Hayt, William (1989). Engineering Electromagnetics (5th ed.). McGraw-Hill. p. 312. ISBN 0-07-027406-1.
The magnetic flux is that flux which passes through any and every surface whose perimeter is the closed path.
- ↑ 15.0 15.1 15.2 15.3 15.4 Feynman, Richard P. "The Feynman Lectures on Physics Vol. II". feynmanlectures.caltech.edu. Retrieved 2020-11-07.
- ↑ 16.0 16.1 Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Upper Saddle River, NJ: Prentice Hall. pp. 301–303. ISBN 0-13-805326-X.
- ↑ Tipler; Mosca (2004). Physics for Scientists and Engineers. p. 795. ISBN 9780716708100.
- ↑ Neumann, Franz Ernst (1846). "Allgemeine Gesetze der inducirten elektrischen Ströme" (PDF). Annalen der Physik. 143 (1): 31–44. Bibcode:1846AnP...143...31N. doi:10.1002/andp.18461430103. Archived from the original (PDF) on 12 March 2020.
- ↑ 19.0 19.1 Yehuda Salu (2014). "A Left Hand Rule for Faraday's Law". The Physics Teacher. 52 (1): 48. Bibcode:2014PhTea..52...48S. doi:10.1119/1.4849156. Video Explanation
- ↑ Salu, Yehuda. "Bypassing Lenz's Rule - A Left Hand Rule for Faraday's Law". www.PhysicsForArchitects.com. Archived from the original on 7 May 2020. Retrieved 30 July 2017.
- ↑ Whelan, P. M.; Hodgeson, M. J. (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1.
- ↑ Nave, Carl R. "Faraday's Law". HyperPhysics. Georgia State University. Retrieved 2011-08-29.
- ↑ 23.0 23.1 Griffiths, David J. (2017). Introduction to Electrodynamics. 4 (Fourth ed.). Cambridge University Press. ISBN 978-1-108-42041-9. OCLC 965197645.
- ↑ Harrington, Roger F. (2003). Introduction to electromagnetic engineering. Mineola, NY: Dover Publications. p. 56. ISBN 0-486-43241-6.
- ↑ Davison, M. E. (1973). "A Simple Proof that the Lorentz Force, Law Implied Faraday's Law of Induction, when B is Time Independent". American Journal of Physics. 41 (5): 713. Bibcode:1973AmJPh..41..713D. doi:10.1119/1.1987339.
- ↑ Krey; Owen (14 August 2007). Basic Theoretical Physics: A Concise Overview. p. 155. ISBN 9783540368052.
- ↑ 27.0 27.1 Stewart, Joseph V. Intermediate Electromagnetic Theory. p. 396.
This example of Faraday's Law [the homopolar generator] makes it very clear that in the case of extended bodies care must be taken that the boundary used to determine the flux must not be stationary but must be moving with respect to the body.
- ↑ 28.0 28.1 Hughes, W. F.; Young, F. J. (1965). The Electromagnetodynamics of Fluid. John Wiley. Eq. (2.6–13) p. 53.
- ↑ Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Upper Saddle River, NJ: Prentice Hall. pp. 301–3. ISBN 0-13-805326-X.
Note that the law relating flux to emf, which this article calls "Faraday's law", is referred to in Griffiths' terminology as the "universal flux rule". Griffiths uses the term "Faraday's law" to refer to what this article calls the "Maxwell–Faraday equation". So in fact, in the textbook, Griffiths' statement is about the "universal flux rule". - ↑ The Feynman Lectures on Physics Vol. II Ch. 17: The Laws of Induction
- ↑ Fedosin, Sergey G. (2019). "On the Covariant Representation of Integral Equations of the Electromagnetic Field". Progress in Electromagnetics Research C. 96: 109–122. arXiv:1911.11138. Bibcode:2019arXiv191111138F. doi:10.2528/PIERC19062902. S2CID 208095922.
- ↑ Einstein, Albert. "On the Electrodynamics of Moving Bodies" (PDF).
आगे की पढाई
- Clerk Maxwell, James (1881). A treatise on electricity and magnetism, Vol. II. Oxford: Clarendon Press. ch. III, sec. 530, p. 178. ISBN 0-486-60637-6.
a treatise on electricity and magnetism.
बाहरी कड़ियाँ
 Media related to फैराडे का प्रेरण का नियम at Wikimedia Commons
Media related to फैराडे का प्रेरण का नियम at Wikimedia Commons- A simple interactive tutorial on electromagnetic induction (click and drag magnet back and forth) National High Magnetic Field Laboratory
- Roberto Vega. Induction: Faraday's law and Lenz's law – Highly animated lecture, with sound effects, Electricity and Magnetism course page
- Notes from Physics and Astronomy HyperPhysics at Georgia State University
- Tankersley and Mosca: Introducing Faraday's law
- A free simulation on motional emf