Rational Triangles
A rational triangle can be defined as one having all sides with rational length.
Rational Right Triangles - Early Solutions
In Śulba solution for the equation -------(1) is available[1]. Baudhāyana[2] (c. 800 B.C.), Āpastamba[3] and Kātyāyana[4] (c. 500 B.C.) gave a method for the transformation of a rectangle into a square, which is the equivalent of the algebraical identity.
where m, n are any two arbitrary numbers. Thus we get
substituting p2,q2 for m, n respectively in order to eliminate the irrational quantities, we get
which gives the rational solution of (1).
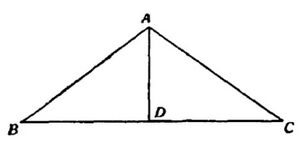
Kātyāyana gives a very simple method for finding a square equal to the sum of a number of other squares of the same size which gives us with another solution of the rational right triangle.
Kātyāyana says: "As many squares (of equal size) as you wish to combine into one, the transverse line will be (equal to) one less than that; twice a side will be (equal to) one more than that; (thus) form (an isosceles) triangle. Its arrow (i.e., altitude) will do that."
For combining n squares of sides a each we form the isosceles triangle ABC such that and
Then which gives the formula
put m2 for n in order to make the sides of the right angled triangle without the radical, we have
which gives the rational solution of (1).
Later Rational Solutions
Brahmagupta (628) says : "The square of the optional (iṣṭa) side is divided and then diminished by an optional number; half the
result is the upright, and that increased by the optional number gives the hypotenuse of a rectangle."
If m, n be any rational numbers then the sides of a right triangle will be
Iṣṭa the sanskrit word is understood as "given" as well as "optional".
A similar rule is given by Śrīpati (1039): "Any optional number is the side; the square of that divided and then diminished by an optional number and halved is the upright; that added with the previous divisor is the hypotenuse of a right-angled triangle. For, so it has been explained by the learned in the matter of the rules of geometry."
Integral Solutions
Brahmagupta was the first to give a solution of the equation in integers. It is m and n being any two unequal integers.
Mahāvīra (850) says: "The difference of the squares (of two elements) is the upright, twice their product is the base and the sum of their squares is the diagonal of a generated rectangle. "
Mahāvīra's Definitions
Mahāvīra[5] says A triangle or a quadrilateral whose sides, altitudes and other dimensions can be expressed in terms of rational numbers is called janya which means generated, formed or that which is generated or formed. Numbers which are involved in forming a particular figure are called its bīja-saṃkhyā (element-numbers) or simply bīja (element or seed).
See Also
External Links
- A Study on the Properties of Rational Triangles
- Rational Triangles with the same perimeter and the same area
References
- ↑ Datta, Bibhutibhusan; Narayan Singh, Avadhesh (1962). History of Hindu Mathematics. Mumbai: Asia Publishing House.
- ↑ "Baudhāyana".
- ↑ "Āpastamba".
- ↑ "Kātyāyana".
- ↑ "Mahāvīra".