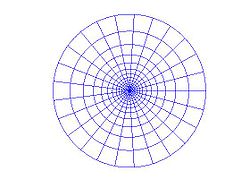
लॉग-ध्रुवीय निर्देशांक

गणित में, लॉग-ध्रुवीय निर्देशांक (या लघुगणकीय ध्रुवीय निर्देशांक) दो विमाओं वाला एक ऐसा निर्देशांक निकाय है, जहाँ एक बिंदु को दो संख्याओं द्वारा निरूपित किया जाता है, जिनमें से एक संख्या निश्चित बिंदु की दूरी के लघुगणक के लिए जबकि दूसरी संख्या एक कोण के लिए प्रयुक्त होती है। लॉग-ध्रुवीय निर्देशांक, ऐसे ध्रुवीय निर्देशांकों से घनिष्ठता से जुड़े होते हैं, जो सामान्यतः किसी प्रकार की घूर्णी समरूपता के साथ समतल में प्रांतों का वर्णन करने के लिए उपयोग किए जाते हैं। लॉग-ध्रुवीय निर्देशांक हार्मोनिक और सम्मिश्र विश्लेषण जैसे क्षेत्रों में ध्रुवीय निर्देशांकों की तुलना में अधिक विहित हैं।

परिभाषा और निर्देशांक रूपांतरण

समतल में लॉग-ध्रुवीय निर्देशांक वास्तविक संख्याओं (ρ,θ) के एक युग्म से मिलकर बने होते हैं, जहाँ ρ किसी दिए गए बिंदु और मूल बिंदु के बीच की दूरी का लघुगणक और θ निर्देश रेखा (x-अक्ष) और मूलबिंदु एवं उस बिंदु से होकर जाने वाली रेखा के बीच का कोण है। कोणीय निर्देशांक, ध्रुवीय निर्देशांकों के समान हैं, जबकि त्रिज्यीय निर्देशांक निम्न नियम के अनुसार रूपांतरित होते हैं

$r=e^{\rho }$.

जहाँ $r$ मूलबिंदु से दूरी है। कार्तीय निर्देशांक से लॉग-ध्रुवीय निर्देशांकों में परिवर्तन के सूत्र इस प्रकार दिए गए हैं

${\begin{cases}\rho =\ln \left({\sqrt {x^{2}+y^{2}}}\right),\\\theta =\operatorname {atan2} (y,\,x).\end{cases}}$

और लॉग-ध्रुवीय से कार्तीय निर्देशांकों में परिवर्तन के सूत्र इस प्रकार हैं

${\begin{cases}x=e^{\rho }\cos \theta ,\\y=e^{\rho }\sin \theta .\end{cases}}$

सम्मिश्र संख्याओं (x, y) = x + iy का उपयोग करके, बाद वाले परिवर्तन को निम्न रूप में लिखा जा सकता है

$x+iy=e^{\rho +i\theta }$

अर्थात् सम्मिश्र चरघातांकीय फलन। इससे यह पता चलता है कि हार्मोनिक और सम्मिश्र विश्लेषण में मौलिक समीकरणों का रूप कार्तीय निर्देशांकों के समान सरल होता है। ध्रुवीय निर्देशांकों के लिए ऐसा नहीं है।

लॉग-ध्रुवीय निर्देशांक में कुछ महत्वपूर्ण समीकरण

लाप्लास का समीकरण

द्विविमीय कार्तीय निर्देशांक में लाप्लास का समीकरण निम्न द्वारा दिया जाता है

${\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0$

समान समीकरण को ध्रुवीय निर्देशांकों में लिखने से अधिक जटिल समीकरण प्राप्त होता है

$r{\frac {\partial }{\partial r}}\left(r{\frac {\partial u}{\partial r}}\right)+{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0$

या समतुल्य रूप से

$\left(r{\frac {\partial }{\partial r}}\right)^{2}u+{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0$

हालाँकि, सम्बन्ध $r=e^{\rho }$ से यह इस प्रकार है कि $r{\frac {\partial }{\partial r}}={\frac {\partial }{\partial \rho }}$, तब लॉग-ध्रुवीय निर्देशांक में लाप्लास के समीकरण,

${\frac {\partial ^{2}u}{\partial \rho ^{2}}}+{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0$

में कार्तीय निर्देशांकों के समान ही सरल व्यंजक है। यह सभी ऐसे निर्देशांक निकायों के लिए सत्य है जहाँ कार्तीय निर्देशांक में परिवर्तन एक अनुकोणी प्रतिचित्रण द्वारा दिया जाता है। इस प्रकार, एक गोलाकार डिस्क जैसे घूर्णन सममिति वाले समतल के एक भाग के लिए लाप्लास के समीकरण पर विचार करते समय, लॉग-ध्रुवीय निर्देशांकों का चयन स्वाभाविक है।

कैशी-रीमैन समीकरण

विश्लेषणात्मक फलनों पर विचार करते समय एक समान स्थिति उत्पन्न होती है। कार्तीय निर्देशांकों में लिखित एक विश्लेषणात्मक फलन $f(x,y)=u(x,y)+iv(x,y)$, निम्न कैशी-रीमैन समीकरणों को संतुष्ट करता है:

${\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}},\ \ \ \ \ \ {\frac {\partial u}{\partial y}}=-{\frac {\partial v}{\partial x}}$

यदि इस फलन को इसके स्थान पर ध्रुवीय रूप $f(re^{i\theta })=Re^{i\Phi }$ में व्यक्त किया जाता है, तो कैशी-रीमैन समीकरण अधिक जटिल रूप ग्रहण करते हैं

$r{\frac {\partial \log R}{\partial r}}={\frac {\partial \Phi }{\partial \theta }},\ \ \ \ \ \ {\frac {\partial \log R}{\partial \theta }}=-r{\frac {\partial \Phi }{\partial r}},$

लाप्लास की समीकरण की स्थिति में, ध्रुवीय निर्देशांकों को लॉग-ध्रुवीय निर्देशांकों में परिवर्तित करके कार्तीय निर्देशांकों के सरल रूप को पुनर्प्राप्त किया जाता है (माना $P=\log R$):

${\frac {\partial P}{\partial \rho }}={\frac {\partial \Phi }{\partial \theta }},\ \ \ \ \ \ {\frac {\partial P}{\partial \theta }}=-{\frac {\partial \Phi }{\partial \rho }}$

कैशी-रिमैन समीकरणों को एक एकल समीकरण में भी इस प्रकार लिखा जा सकता है

$\left({\frac {\partial }{\partial x}}+i{\frac {\partial }{\partial y}}\right)f(x+iy)=0$

${\frac {\partial }{\partial x}}$ और ${\frac {\partial }{\partial y}}$ को ${\frac {\partial }{\partial \rho }}$ और ${\frac {\partial }{\partial \theta }}$ के पदों में व्यक्त करके इस समीकरण को निम्न समतुल्य रूप में लिखा जा सकता है

$\left({\frac {\partial }{\partial \rho }}+i{\frac {\partial }{\partial \theta }}\right)f(e^{\rho +i\theta })=0$

यूलर का समीकरण

जब घूर्णी सममिति वाले प्रांत में डिरिक्ले समस्या को हल करने की आवश्यकता होती है, तो ध्रुवीय रूप में लाप्लास के समीकरण के लिए आंशिक अवकल समीकरणों के लिए चरों के पृथक्करण की विधि का उपयोग करना सामान्य है। इसका अर्थ है कि $u(r,\theta )=R(r)\Theta (\theta )$ लिखा जाता है। तब लाप्लास के समीकरण को निम्न दो साधारण अवकल समीकरणों में विभाजित किया जाता है

${\begin{cases}\Theta ''(\theta )+\nu ^{2}\Theta (\theta )=0\\r^{2}R''(r)+rR'(r)-\nu ^{2}R(r)=0\end{cases}}$

जहाँ $\nu$ एक स्थिरांक है। इनमें से पहली समीकरण में स्थिर गुणांक होते हैं जो आसानी से हल हो जाते हैं। दूसरी समीकरण यूलर के समीकरण की एक विशेष स्थिति है

$r^{2}R''(r)+crR'(r)+dR(r)=0$

जहाँ $c,d$ स्थिरांक हैं। यह समीकरण सामान्यतः $R(r)=r^{\lambda }$ दृष्टिकोण द्वारा हल की जाती है, लेकिन इसे लॉग-ध्रुवीय त्रिज्या के उपयोग के माध्यम से स्थिर गुणांक वाले समीकरण में परिवर्तित किया जा सकता है:

$P''(\rho )+(c-1)P'(\rho )+dP(\rho )=0$

लाप्लास के समीकरण पर विचार करने पर, $c=1$ और $d=-\nu ^{2}$, इसलिए $r$ के लिए समीकरण निम्न सरल रूप धारण करता है

$P''(\rho )-\nu ^{2}P(\rho )=0$

कार्तीय निर्देशांक में डिरिक्ले समस्या को हल करने पर, ये $x$ और $y$ के लिए यथार्थ समीकरणें हैं। इस प्रकार, एक बार पुनः घूर्णी सममिति वाले प्रान्त के लिए स्वाभाविक चयन ध्रुवीय निर्देशांक नहीं, बल्कि लॉग-ध्रुवीय निर्देशांक हैं।

असतत ज्यामिति

लॉग-ध्रुवीय निर्देशांक (n = 25) द्वारा दी गयी एक वृत्ताकार डिस्क में असतत निर्देशांक निकाय

एक वृत्ताकार डिस्क में असतत निर्देशांक निकाय, जिसे लॉग-ध्रुवीय निर्देशांक (n = 25) में आसानी से व्यक्त किया जा सकता है

सर्पिल व्यवहार दर्शाता मैंडलब्रॉट फ्रैक्टल का एक हिस्सा

एक प्रांत में पीडीई को संख्यात्मक रूप से हल करने के लिए, इस प्रांत में एक असतत निर्देशांक निकाय प्रस्तावित किया जाना चाहिए। यदि प्रांत में घूर्णी सममिति है और आयतों से युक्त एक ग्रिड वांछित हैं, तो ध्रुवीय निर्देशांक एक खराब विकल्प है, क्योंकि यह वृत्त के केंद्र में आयतों के स्थान पर त्रिभुजों का निर्माण करता है। हालाँकि, निम्न विधि से लॉग-ध्रुवीय निर्देशांक प्रस्तुत करके इसका समस्या को हल किया जा सकता है। समतल को 2$\pi$/n लम्बी भुजा वाले वर्गों के एक ग्रिड में विभाजित करें, जहाँ n एक धनात्मक पूर्णांक है। समतल में लॉग-ध्रुवीय ग्रिड के निर्माण के लिए सम्मिश्र चरघातांकीय फलन का उपयोग करें। बाएँ अर्द्ध-तल को इकाई डिस्क पर प्रतिचित्रित किया जाता है, जिसमें त्रिज्याओं की संख्या n के बराबर होती है। इसके स्थान पर इन वर्गों में विकर्णों को प्रतिचित्रित करना और भी अधिक लाभदायक हो सकता है, जो इकाई डिस्क में कुण्डलीयुक्त एक असतत निर्देशांक निकाय प्रदान करता है, दाईं ओर का चित्र देखें।

डिरिक्ले-से-न्यूमैन संकारक

उदाहरण के लिए बाद वाला निर्देशांक निकाय डिरिक्ले और न्यूमैन समस्याओं को हल करने के लिए उपयुक्त है। यदि असतत निर्देशांक निकाय की व्याख्या इकाई डिस्क में एक अप्रत्यक्ष आलेख के रूप में की जाती है, तो इसे विद्युत नेटवर्क के लिए एक मॉडल के रूप में माना जा सकता है। आलेख में प्रत्येक रेखा खंड के लिए, फलन $\gamma$ द्वारा दिया गया एक चालकत्व सम्बद्ध है। तब विद्युत नेटवर्क इकाई डिस्क में डिरिक्ले समस्या के लिए असतत मॉडल के रूप में कार्य करता है, जहाँ लाप्लास समीकरण किरचॉफ के नियम का रूप लेती है। वृत्त की परिसीमा पर नोडों पर, एक विद्युत विभव (डिरिक्ले डेटा) परिभाषित किया जाता है, जो सीमा नोडों के माध्यम से विद्युत धारा (न्यूमैन डेटा) को प्रेरित करती है। डिरिक्ले डेटा से न्यूमैन डेटा तक रैखिक संकारक $\Lambda _{\gamma }$, डिरिक्ले-से-न्यूमैन संकारक कहलाता है, जो नेटवर्क की सांस्थिति और चालकत्व पर निर्भर करता है।

सतत डिस्क की स्थिति में, यह इस प्रकार है कि यदि चालकत्व सजातीय, माना $\gamma =1$ सर्वत्र, है, तो डिरिक्ले-से-न्यूमैन संकारक निम्नलिखित समीकरण को संतुष्ट करता है

$\Lambda _{\gamma }^{2}+{\frac {\partial ^{2}\ }{\partial \theta ^{2}}}=0$

डिरिक्ले समस्या का एक अच्छा असतत मॉडल प्राप्त करने के लिए, इकाई डिस्क में एक ऐसा आलेख प्राप्त करना उपयोगी होता है, जिसके (असतत) डिरिक्ले-से-न्यूमैन संकारक में समान गुण हैं। यद्यपि ध्रुवीय निर्देशांक हमें कोई उत्तर नहीं देते हैं, फिर भी यह अनुमानित/अप्रत्यक्ष है, जो हमें लॉग-ध्रुवीय निर्देशांक द्वारा दिया गया घूर्णी सममित नेटवर्क प्रदान करता है।

प्रतिबिम्ब विश्लेषण

वर्ष 1970 के दशक के अंत तक प्रतिबिम्ब विश्लेषण (प्रतिबिम्ब संपातन) में असतत सर्पिल निर्देशांक निकाय के अनुप्रयोग पहले से ही दिए गए थे। एक प्रतिबिम्ब को कार्तीय निर्देशांकों के स्थान पर इस निर्देशांक निकाय में निरूपित करने लिए, एक प्रतिबिम्ब को घुमाने या आकार-परिवर्तन करने पर यह संगणनीय लाभ प्रदान करता है। इसके अतिरिक्त, मानव नेत्र के रेटिना में प्रकाश ग्राहियों को इस प्रकार वितरित किया जाता है जिसमें सर्पिल निर्देशांक निकाय के साथ बड़ी समानताएँ होती हैं। यह मैंडेलब्रॉट फ्रैक्टल में भी पाया जा सकता है (दाईं ओर चित्र देखें)।

लॉग-ध्रुवीय निर्देशांक का उपयोग रेडॉन रूपांतरण और इसके व्युत्क्रम हेतु तीव्र विधियों के निर्माण के लिए भी किया जा सकता है।

यह भी देखें

• धुवीय निर्देशांक
• कार्तीय निर्देशांक
• बेलनाकार निर्देशांक
• गोलाकार निर्देशांक
• रेटिनोटॉपी में लॉग-ध्रुवीय प्रतिचित्रण

बाहरी संबंध

• Non-Newtonian calculus website