बर्स्ट त्रुटि-सुधार करने वाले कोड
कोडिंग सिद्धांत में, बर्स्ट त्रुटि-सुधार करने वाले कोड बर्स्ट त्रुटियों को ठीक करने के विधियों को नियोजित करते हैं, जो त्रुटियां हैं जो एक-दूसरे से स्वतंत्र रूप से बिट्स में होने के अतिरिक्त निरंतर अनेक बिट्स में होती हैं।
यादृच्छिक त्रुटियों को ठीक करने के लिए अनेक कोड डिज़ाइन किए गए हैं। चूँकि, कभी-कभी चैनल त्रुटियाँ प्रस्तुत कर सकते हैं जो अल्प अंतराल में स्थानीयकृत होती हैं। ऐसी त्रुटियाँ बर्स्ट में होती हैं (जिन्हें बर्स्ट त्रुटियाँ कहा जाता है) क्योंकि वह निरंतर अनेक बिट्स में होती हैं। बर्स्ट त्रुटियों के उदाहरण संग्रहण माध्यमों में बड़े मापदंड पर पाए जा सकते हैं। ये त्रुटियाँ शारीरिक क्षति जैसे डिस्क पर खरोंच या वायरलेस चैनलों के उपस्थिति में विद्युत के झटके के कारण हो सकती हैं। वह स्वतंत्र नहीं हैं; वह स्थानिक रूप से केंद्रित होते हैं। यदि बिट में कोई त्रुटि है, तो संभावना है कि आसन्न बिट्स भी दूषित हो सकते हैं। यादृच्छिक त्रुटियों को ठीक करने के लिए उपयोग की जाने वाली विधियाँ बर्स्ट त्रुटियों को ठीक करने में अक्षम हैं।
परिभाषाएँ
इस प्रकार की लम्बाई का बर्स्ट ℓ[1] कोडवर्ड बोलो प्रसारित किया जाता है, और इसे प्राप्त किया जाता है फिर, त्रुटि सदिश लम्बाई का बर्स्ट कहलाता है यदि के गैर-शून्य अवयव तक निरंतर अवयव ही सीमित हैं . उदाहरण के लिए, लम्बाई का बर्स्ट है
चूँकि यह परिभाषा यह बताने के लिए पर्याप्त है कि बर्स्ट त्रुटि क्या है, बर्स्ट त्रुटि सुधार के लिए विकसित अधिकांश उपकरण चक्रीय कोड पर निर्भर करते हैं। यह हमारी अगली परिभाषा को प्रेरित करता है।
त्रुटि सदिश को लंबाई की चक्रीय बर्स्ट त्रुटि कहलाती है यदि इसके गैरशून्य अवयव चक्रीय रूप से निरंतर अवयव तक ही सीमित हैं। उदाहरण के लिए, पहले माना गया त्रुटि सदिश , लंबाई का चक्रीय बर्स्ट है , चूंकि हम स्थिति से प्रारंभ होने वाली त्रुटि पर विचार करते हैं और स्थिति पर समाप्त हो रहा है. ध्यान दें कि सूचकांक हैं -आधारित, अर्थात पहला अवयव पर स्थिति है .
इस लेख के शेष भाग के लिए, हम चक्रीय बर्स्ट को संदर्भित करने के लिए बर्स्ट शब्द का उपयोग करेंगे, जब तक कि अन्यथा उल्लेख न किया गया हो।
बर्स्ट विवरण
बर्स्ट त्रुटि की संक्षिप्त परिभाषा रखना अधिकांशतः उपयोगी होता है, जिसमें न केवल इसकी लंबाई, किंतु ऐसी त्रुटि का पैटर्न और स्थान भी सम्मिलित होता है। हम बर्स्ट विवरण को टुपल के रूप में परिभाषित करते हैं जहाँ त्रुटि का पैटर्न है (जो कि त्रुटि पैटर्न में पहली गैर-शून्य प्रविष्टि से प्रारंभ होने वाले और अंतिम गैर-शून्य प्रतीक के साथ समाप्त होने वाले प्रतीकों की स्ट्रिंग है), और कोडवर्ड पर वह स्थान है, जहां बर्स्ट पाया जा सकता है।[1]
उदाहरण के लिए, त्रुटि पैटर्न का बर्स्ट विवरण है ध्यान दें कि ऐसा वर्णन अद्वितीय नहीं है, क्योंकि उसी बर्स्ट त्रुटि का वर्णन करता है। सामान्यतः , यदि में गैर-शून्य अवयव की संख्या है , तब में भिन्न -भिन्न बर्स्ट विवरण होगा, जिनमें से प्रत्येक भिन्न गैर-शून्य प्रविष्टि पर प्रारंभ होता है . नीचे दिए गए प्रमेय के साथ बर्स्ट विवरण की अस्पष्टता से उत्पन्न होने वाले विवादों को हल करने के लिए, चूंकि ऐसा करने से पहले हमें पहले परिभाषा की आवश्यकता है।
परिभाषा। किसी दिए गए त्रुटि पैटर्न में प्रतीकों की संख्या द्वारा निरूपित किया जाता है
Theorem (Uniqueness of burst descriptions) — मान लीजिए लंबाई का त्रुटि सदिश है दो बर्स्ट विवरण के साथ and . If तो दोनों विवरण समान हैं अर्थात् उनके अवयव समतुल्य हैं.[2]
{{math proof | proof = हैमिंग वज़न (या गैर-शून्य प्रविष्टियों की संख्या) हो . तब बिलकुल है त्रुटि विवरण. के लिए साबित करने के लिए कुछ भी नहीं है. तो हम ऐसा मान लेते हैं और यह कि विवरण समान नहीं हैं। हम देखते हैं कि प्रत्येक गैर-शून्य प्रविष्टि wमैं पैटर्न में दिखाई दूंगा, और इसी तरह, इसके अवयव भी पैटर्न में सम्मिलित नहीं किए जाने पर शून्यों का चक्रीय क्रम बनेगा, जो अंतिम गैर-शून्य प्रविष्टि के पश्चात प्रारंभ होगा, और पैटर्न की पहली गैर-शून्य प्रविष्टि से ठीक पहले जारी रहेगा। हम इस रन के अनुरूप सूचकांकों के सेट को शून्य रन कहते हैं। हमने तुरंत देखा कि प्रत्येक बर्स्ट विवरण के साथ एक शून्य रन जुड़ा हुआ है और प्रत्येक शून्य रन असंयुक्त है। चूंकि हमारे पास है शून्य रन, और प्रत्येक असंयुक्त है, हमारे पास कुल है सभी शून्य रन में विशिष्ट तत्व। दूसरी ओर हमारे पास है:
उपरोक्त प्रमेय का परिणाम यह है कि हमारे पास लंबाई के बर्स्ट के लिए दो भिन्न -भिन्न बर्स्ट विवरण नहीं हो सकते हैं
बर्स्ट त्रुटि सुधार के लिए चक्रीय कोड
चक्रीय कोड को इस प्रकार परिभाषित किया गया है: प्रतीक को के अवयव के रूप के बारे में सोचें. अब, हम शब्दों को से अधिक बहुपद के रूप में सोच सकते हैं जहां किसी शब्द के भिन्न -भिन्न प्रतीक बहुपद के विभिन्न गुणांकों से मेल खाते हैं। चक्रीय कोड को परिभाषित करने के लिए, हम निश्चित बहुपद चुनते हैं, जिसे जनरेटर बहुपद कहा जाता है। इस चक्रीय कोड के कोडवर्ड वह सभी बहुपद हैं जो इस जनरेटर बहुपद से विभाज्य हैं।
कोडवर्ड डिग्री के बहुपद हैं. मान लीजिए कि जनरेटर बहुपद की डिग्री है . तथा डिग्री के बहुपद जिनसे विभाज्य होते हैं को घात के बहुपदों से गुणा करने से परिणाम प्राप्त होते है . अपने पास ऐसे बहुपद है. उनमें से प्रत्येक कोडवर्ड से मेल खाता है। इसलिए, चक्रीय कोड के लिए उपयोग किये जाते है .
चक्रीय कोड तक की लंबाई के सभी बर्स्ट का पता लगा सकते हैं . हम पश्चात में देखेंगे कि किसी की बर्स्ट त्रुटि का पता लगाने की क्षमता कोड ऊपर से तक सीमित है। . बर्स्ट त्रुटि का पता लगाने के लिए चक्रीय कोड को इष्टतम माना जाता है क्योंकि वह इस ऊपरी सीमा को पूरा करते हैं:
Theorem (Cyclic burst correction capability) — डिग्री के जनरेटर बहुपद के साथ प्रत्येक चक्रीय कोड लंबाई के सभी विस्फोटों का पता लगा सकता है
{{math proof | proof = कोडवर्ड के लिए (अर्थात एक बहुपद के लिए जो विभाज्य है ), तब परिणाम कोई कोडवर्ड नहीं होगा (अर्थात संबंधित बहुपद इससे विभाज्य नहीं है) ). यह दिखाने के लिए पर्याप्त है कि लंबाई में कोई उछाल नहीं है से विभाज्य है .ऐसे फूटने का रूप होता है , जहाँ इसलिए, से विभाज्य नहीं है (क्योंकि पश्चात वाले के पास डिग्री है). से विभाज्य नहीं है (अन्यथा, सभी कोडवर्ड से प्रारंभ होंगे ). इसलिए, से विभाज्य नहीं है as well.}}
उपरोक्त प्रमाण चक्रीय कोड में बर्स्ट त्रुटि का पता लगाने/सुधार के लिए सरल एल्गोरिदम का सुझाव देता है: संचरित शब्द (अर्थात डिग्री का बहुपद) दिया गया है ), जो कि से विभाजित करने पर इस शब्द के शेषफल की गणना करता और यदि शेषफल शून्य है (अर्थात् यदि शब्द विभाज्य है ), तो यह वैध कोडवर्ड है। अन्यथा, त्रुटि की रिपोर्ट करें. इस त्रुटि को ठीक करने के लिए, इस शेषफल को प्रेषित शब्द से घटाएँ। घटाव का परिणाम व से िभाजित होने वाला है (अर्थात यह वैध कोडवर्ड होगा)।
बर्स्ट त्रुटि का पता लगाने पर की ऊपरी सीमा द्वारा हम जानते हैं कि चक्रीय कोड लंबाई के सभी बर्स्ट का पता नहीं लगा सकता है. चूँकि चक्रीय कोड वास्तव में लंबाई के अधिकांश बर्स्ट का पता लगा सकते हैं .जिसका कारण यह है कि पता लगाना तभी विफल होता है जब बर्स्ट विभाज्य हो . द्विआधारी वर्णमाला से अधिक, वहाँ उपस्थित हैं लंबाई का फटना . उनमें से ही से विभाज्य हैं . इसलिए,) लंबाई के सभी बर्स्ट पर समान वितरण मानते हुए पता लगाने में विफलता की संभावना बहुत कम ( है
अब हम चक्रीय कोड के बारे में मौलिक प्रमेय पर विचार करते हैं जो बर्स्ट को भिन्न -भिन्न सहसमुच्चय में वर्गीकृत करके कुशल बर्स्ट-त्रुटि सुधार कोड को डिजाइन करने में सहायता करेगा।
Theorem (Distinct Cosets) — एक रेखीय कोडएक-बर्स्ट-एरर-सही कोड यदि लंबाई की सभी बर्स्ट त्रुटियां भिन्न -भिन्न उपसमुच्चय में झूठ बोलें.
{{math proof | proof =लंबाई की भिन्न -भिन्न बर्स्ट त्रुटियाँ हों जो कोड के एक ही कोसेट में स्थित हैं . Then कोडवर्ड है. इसलिए, यदि हम प्राप्त करते हैं हम इसे या तो डिकोड कर सकते हैं or . इसके विपरीत, यदि सभी विस्फोट त्रुटियाँ and एक ही कोसेट में न रहें, तो प्रत्येक बर्स्ट त्रुटि उसके सिंड्रोम द्वारा निर्धारित होती है। फिर त्रुटि को उसके सिंड्रोम के माध्यम से ठीक किया जा सकता है। इस प्रकार, एक रैखिक कोड is an -बर्स्ट-त्रुटि-सही कोड यदि और केवल यदि लंबाई की सभी बर्स्ट त्रुटियां के भिन्न-भिन्न कोसेट में स्थित हैं.}}
Theorem (Burst error codeword classification) — मान लीजिये एक रेखीय हो -विस्फोट-त्रुटि-सुधार कोड। फिर लंबाई का कोई शून्येतर विस्फोट नहीं कोडवर्ड हो सकता है.
लंबाई में वृद्धि के साथ एक कोडवर्ड बनें . इस प्रकार इसका पैटर्न है , जहाँ and लंबाई के शब्द हैं इसलिए, शब्द and लंबाई के दो विस्फोट हैं . बाइनरी रैखिक कोड के लिए, वे एक ही कोसेट से संबंधित हैं। यह विशिष्ट कोसेट प्रमेय का खंडन करता है, इसलिए लंबाई का कोई गैर-शून्य विस्फोट नहीं होता हैएक कोडवर्ड हो सकता है
बर्स्ट त्रुटि सुधार सीमा
बर्स्ट त्रुटि का पता लगाने और सुधार पर ऊपरी सीमा
ऊपरी सीमा से हमारा तात्पर्य हमारी त्रुटि पता लगाने की क्षमता की सीमा से है जिसे हम कभी भी पार नहीं कर सकते। मान लीजिए कि हम डिज़ाइन बनाना चाहते हैं कोड जो लंबाई की सभी बर्स्ट त्रुटियों का पता लगा सकता है पूछने के लिए स्वाभाविक प्रश्न है: दिया गया और , अधिकतम क्या है कि हम इससे आगे कभी हासिल नहीं कर सकते? दूसरे शब्दों में, लंबाई की ऊपरी सीमा क्या है हम किसी भी बर्स्ट का पता लगा सकते हैं कोड? निम्नलिखित प्रमेय इस प्रश्न का उत्तर प्रदान करता है।
Theorem (Burst error detection ability) — किसी की भी बर्स्ट त्रुटि का पता लगाने की क्षमता code is
पहले हम देखते हैं कि एक कोड लंबाई के सभी विस्फोटों का पता लगा सकता है यदि और केवल यदि कोई भी दो कोडवर्ड लंबाई के हिसाब से भिन्न न हों . मान लीजिए कि हमारे पास दो कोड वर्ड हैं and जो विस्फोट से भिन्न होता है लम्बाई का . प्राप्त करने पर , हम यह नहीं बता सकते कि प्रेषित शब्द वास्तव में है या नहीं बिना किसी ट्रांसमिशन त्रुटि के, या चाहे वह हो बर्स्ट त्रुटि के साथजो प्रसारण के दौरान घटित हुआ। अब, मान लीजिए कि प्रत्येक दो कोडवर्ड की लंबाई में बहुत अधिक अंतर होता है भले ही प्रेषित कोडवर्ड विस्फोट की चपेट में आ गया है लम्बाई का ,यह किसी अन्य वैध कोडवर्ड में परिवर्तित नहीं होगा. इसे प्राप्त करने पर, हम बता सकते हैं कि यह है विस्फोट के साथ उपरोक्त अवलोकन से, हम जानते हैं कि कोई भी दो कोडवर्ड पहले को साझा नहीं कर सकते हैं प्रतीक. कारण यह है कि भले ही वे सभी में भिन्न हों प्रतीक, वे अभी भी लंबाई के आधार पर भिन्न होंगे इसलिए, कोडवर्ड की संख्या संतुष्ट को प्रयुक्त करने दोनों तरफ और पुनर्व्यवस्थित करके, हम इसे देख सकते हैं .
अब, हम वही प्रश्न दोहराते हैं किन्तु त्रुटि सुधार के लिए: दिया गया है और , लंबाई पर ऊपरी सीमा क्या है बर्स्ट का जिन्हें हम किसी का उपयोग करके ठीक कर सकते हैं कोड? निम्नलिखित प्रमेय इस प्रश्न का प्रारंभिक उत्तर प्रदान करता है:
Theorem (Burst error correction ability) — किसी की भी बर्स्ट त्रुटि सुधार क्षमता कोड संतुष्ट करता है
पहले हम देखते हैं कि एक कोड लंबाई के सभी विस्फोटों को ठीक कर सकता है यदि और केवल यदि कोई भी दो कोडवर्ड लंबाई के दो बर्स्ट के योग से भिन्न न हों मान लीजिए कि दो कोडवर्ड और विस्फोट से भिन्न and लम्बाई का each.प्राप्त करने परविस्फोट से मारा गया, हम इसकी व्याख्या ऐसे कर सकते हैं जैसे कि यह था विस्फोट से मारा गया . हम यह नहीं बता सकते कि प्रेषित शब्द है या नहीं or . अब, मान लीजिए कि प्रत्येक दो कोडवर्ड की लंबाई दो से अधिक भिन्न होती है . तदपि प्रेषित कोडवर्ड लम्बाई के विस्फोट से मारा जाता है , यह किसी अन्य कोडवर्ड की तरह नहीं दिखने वाला है जो एक और विस्फोट से प्रभावित हुआ है. For each codeword मान लीजिये से भिन्न सभी शब्दों के समुच्चय को निरूपित करें bआप लंबाई का एक विस्फोट नोटिस जो सम्मिलित अपने आप। उपरोक्त अवलोकन से, हम जानते हैं कि दो भिन्न-भिन्न कोडवर्ड के लिए और और असंयुक्त हैं. अपने पास कोडवर्ड इसलिए हम ऐसा कह सकते हैं. इसके अतिरिक्त, हमारे पास है. पश्चात वाली असमानता को पहले वाली असमानता से जोड़कर, फिर आधार लेकर लघुगणक और पुनर्व्यवस्थित करने पर, हमें उपरोक्त प्रमेय प्राप्त होता है।
रीगर बाउंड द्वारा सशक्त परिणाम दिया गया है:
Theorem (Rieger bound) — यदि की बर्स्ट त्रुटि सुधार करने की क्षमता है रैखिक ब्लॉक कोड, फिर.
कोई भी रैखिक कोड जो लंबाई के किसी भी विस्फोट पैटर्न को सही कर सकता है लम्बाई का विस्फोट नहीं हो सकता एक कोडवर्ड के रूप में. यदि इसकी लम्बाई में वृद्धि होती एक कोडवर्ड के रूप में, फिर लंबाई का विस्फोट कोडवर्ड को लंबाई के बर्स्ट पैटर्न में बदल सकता है , जिसे लंबाई की बर्स्ट त्रुटि बनाकर भी प्राप्त किया जा सकता है बिल्कुल शून्य कोडवर्ड में. यदि सदिश पहले शून्येतर हैं प्रतीकों, तो सदिश एक सरणी के विभिन्न उपसमूहों से होने चाहिए ताकि उनका अंतर लंबाई के फटने का कोडवर्ड न हो. इस शर्त को सुनिश्चित करते हुए, ऐसे उपसमुच्चय की संख्या कम से कम सदिश की संख्या के समान्तर है। इस प्रकार, उपसमुच्चय की संख्या कम से कम होगी.इसलिए, हमारे पास कम से कम है अलग-अलग प्रतीक, अन्यथा, ऐसे दो बहुपदों का अंतर एक कोडवर्ड होगा जो लंबाई के दो विस्फोटों का योग है इस प्रकार, यह रीगर बाउंड सिद्ध होता है।
परिभाषा। उपरोक्त रीगर सीमा को प्राप्त करने वाले रैखिक बर्स्ट-त्रुटि-सुधार करने वाले कोड को इष्टतम बर्स्ट-त्रुटि-सुधार करने वाला कोड कहा जाता है।
बर्स्ट त्रुटि सुधार पर आगे की सीमाएं
एकाधिक चरणबद्ध-बर्स्ट सुधार (एमपीबीसी) के लिए रैखिक ब्लॉक कोड की प्राप्त कोड दर पर से अधिक ऊपरी सीमा होती है। ऐसी सीमा प्रत्येक उपब्लॉक के अंदर अधिकतम सुधार योग्य चक्रीय बर्स्ट लंबाई तक सीमित है, या समकक्ष रूप से प्रत्येक चरण-बर्स्ट के अंदर न्यूनतम त्रुटि मुक्त लंबाई या अंतराल पर बाधा है। यह सीमा, जब एकल बर्स्ट सुधार के लिए बाध्य के विशेष उपस्थितियां में कम हो जाती है, अब्रामसन बाध्य (बर्स्ट -त्रुटि सुधार के लिए हैमिंग बाध्य का परिणाम) है जब चक्रीय बर्स्ट की लंबाई ब्लॉक लंबाई के आधे से कम होती है।[3]
Theorem (number of bursts) — इसके लिए एक द्विआधारी वर्णमाला पर, वहाँ हैं लंबाई के सदिश जो लम्बाई के विस्फोट हैं .[1]
चूंकि बर्स्ट की लंबाई हैविस्फोट के साथ एक अनोखा विस्फोट वर्णन जुड़ा हुआ है। विस्फोट इनमें से किसी पर भी प्रारंभ हो सकता है पैटर्न की स्थिति. प्रत्येक पैटर्न की प्रारंभिक होती है और की लंबाई सम्मलित है . हम इसे प्रारंभ होने वाली सभी स्ट्रिंग्स के समूह के रूप में सोच सकते हैं और लंबाई है . इस प्रकार, कुल हैंऐसे पैटर्न संभव हैं, और कुल लंबाई का फटनायदि हम सर्व-शून्य विस्फोट को सम्मिलित करते हैं, तो हमारे पास है सदिश लंबाई के विस्फोट का प्रतिनिधित्व करते हैं
Theorem (Bound on the number of codewords) — यदि बाइनरी -विस्फोट त्रुटि सुधार कोड में अधिकतम है कूटशब्द.
Since , हम जानते हैं कि वहाँ हैं लंबाई का फटना. कहो कोड है कोडवर्ड, तो वहाँ हैं ऐसे कोडवर्ड जो लंबाई की दृष्टि से कोडवर्ड से भिन्न होते हैं .हरेक शब्द भिन्न-भिन्न होने चाहिए, अन्यथा कोड में दूरी होगी. इसलिए, तात्पर्य
Theorem (Abramson's bounds) — यदि एक बाइनरी है रैखिक -बर्स्ट त्रुटि सुधार कोड, इसकी ब्लॉक-लंबाई को संतुष्ट करना होगा:
For a linear कोड, वहाँ हैं कोडवर्ड हमारे पिछले परिणाम से, हम यह जानते हैं
टिप्पणी। कोड की अतिरेक कहा जाता है और अब्रामसन की सीमा के लिए वैकल्पिक सूत्रीकरण में है
अग्नि कोड[3][4][5]
जबकि सामान्यतः चक्रीय कोड बर्स्ट त्रुटियों का पता लगाने के लिए शक्तिशाली उपकरण होते हैं, अब हम फायर कोड नामक बाइनरी चक्रीय कोड के वर्ग पर विचार करते हैं, जिसमें अच्छी एकल बर्स्ट त्रुटि सुधार क्षमताएं होती हैं। एकल बर्स्ट से, लंबाई के बारे में कहें , हमारा अर्थ है कि प्राप्त कोडवर्ड में उपस्थित सभी त्रुटियां निश्चित अवधि के अंदर होती हैं अंक है .
मान लीजिये डिग्री का अपरिवर्तनीय बहुपद बनें ऊपर , और जाने की अवधि हो . की अवधि , और वास्तव में किसी भी बहुपद को सबसे कम धनात्मक पूर्णांक के रूप में परिभाषित किया गया है ऐसा है कि होने देना धनात्मक पूर्णांक और संतोषजनक हो तथा से विभाज्य नहीं है , जहाँ की अवधि है . अग्नि संहिता को परिभाषित करें निम्नलिखित जनरेटर बहुपद द्वारा:
Lemma 1 —
Let दो बहुपदों का सबसे बड़ा सामान्य भाजक बनें। तब से अपरिवर्तनीय है, या .मान लीजिए तब for कुछ स्थिर. किन्तु, का भाजक है तब से का भाजक है.किन्तु यह हमारी धारणा का खंडन करता है विभाजित नहीं करता यद्यपि, प्रमेयिका सिद्ध करना.
Lemma 2 — यदि काल का एक बहुपद है, तब यदि और केवल यदि
यदि , तब . इस प्रकार,
अब मान लीजिए . तब , . हम वो दिखाते हैंसे विभाज्य है पर प्रेरण द्वारा . आधार स्तिथि अनुसरण करता है। इसलिए, मान लीजिए.हम वह जानते हैं दोनों को विभाजित करता है (क्योंकि इसमें आवर्त है)
लेम्मा 2 का एक परिणाम यह है कि तब से अवधि है , तब विभाजित यदि और केवल यदि .
यदि हम यह दिखा सकें कि लंबाई के सभी बर्स्ट या कम भिन्न -भिन्न सह समुच्चय में होते हैं, हम उन्हें सहसमुच्चय लीडर के रूप में उपयोग कर सकते हैं जो सुधार योग्य त्रुटि पैटर्न बनाते हैं। कारण सरल है: हम जानते हैं कि प्रत्येक सहसमुच्चय में अद्वितीय सिंड्रोम डिकोडिंग जुड़ी होती है, और यदि भिन्न -भिन्न लंबाई के सभी बर्स्ट भिन्न -भिन्न सहसमुच्चय में होते हैं, तो सभी में अद्वितीय सिंड्रोम होते हैं, जिससे त्रुटि सुधार की सुविधा मिलती है।
प्रमेय का प्रमाण
मान लीजिए कि और डिग्री और के साथ बहुपद हैं, जो क्रमशः के साथ लंबाई और के विस्फोट का प्रतिनिधित्व करते हैं, पूर्णांक प्रारंभिक का प्रतिनिधित्व करते हैं बर्स्ट की स्थिति, और कोड की ब्लॉक लंबाई से कम होते हैं। विरोधाभास के लिए, यह मान लें और ही सहसमुच्चय में हैं. तब, वैध कोडवर्ड है (क्योंकि दोनों पद ही सहसमुच्चय में हैं)। व्यापकता की हानि के बिना, .चुनें विभाजन प्रमेय द्वारा हम लिख सकते हैं: पूर्णांकों और के लिए | हम बहुपद को फिर से लिखते हैं निम्नलिखित नुसार:
ध्यान दें कि दूसरे परिवर्तन में, हमने शब्द प्रस्तुत किया . हमें ऐसा करने की अनुमति है, क्योंकि फायर कोड क्रियान्वित हैं . और हमारी धारणा से, वैध कोडवर्ड है, तथा इस प्रकार, इसका गुणज होना चाहिए . जैसा कि पहले उल्लेख किया गया है, कि कारकों के पश्चात से अपेक्षाकृत प्रमुख हैं, जो कि से विभाज्य होना चाहिए . के लिए व्युत्पन्न अंतिम अभिव्यक्ति को समीप से देख रहे हैं हम उस पर ध्यान देते हैं कि , (लेम्मा 2 के परिणाम द्वारा ) से विभाज्य है। इसलिए, या तो विभाज्य है विभाजन प्रमेय को दोबारा प्रयुक्त करने पर, हम देखते हैं कि वाला बहुपद पर इस प्रकार उपस्थित है
तब से , अपने पास . किन्तु इसलिए, अपरिवर्तनीय है और अपेक्षाकृत प्रधान होना चाहिए। तब से कोडवर्ड है, से विभाज्य होना चाहिए , क्योंकि इसे विभाज्य नहीं किया जा सकता . इसलिए, का गुणज होना चाहिए . किन्तु इसका गुणज भी होना चाहिए , जिसका अर्थ है कि यह का गुणज होना चाहिए किन्तु वह बिल्कुल कोड की ब्लॉक-लंबाई है। इसलिए, का गुणज नहीं हो सकता चूँकि वह दोनों इससे कम हैं . इस प्रकार, हमारी धारणा कोडवर्ड होना गलत है, और इसलिए और अद्वितीय सिंड्रोम के साथ भिन्न -भिन्न सहसमुच्चय में हैं, और इसलिए सुधार योग्य हैं।
उदाहरण: फायर कोड को सही करने में 5-बर्स्ट त्रुटि
उपरोक्त अनुभाग में प्रस्तुत सिद्धांत के साथ, के निर्माण पर विचार करें -फ़ायर कोड को सही करने में बर्स्ट त्रुटि। याद रखें कि फायर कोड बनाने के लिए, हमें अपरिवर्तनीय बहुपद की आवश्यकता होती है , पूर्णांक , हमारे कोड की बर्स्ट त्रुटि सुधार क्षमता का प्रतिनिधित्व करता है, और हमें उस संपत्ति को संतुष्ट करने की आवश्यकता है की अवधि से विभाज्य नहीं है . इन आवश्यकताओं को ध्यान में रखते हुए, अपरिवर्तनीय बहुपद पर विचार करें , और जाने . तब से आदिम बहुपद है, इसका आवर्त है . हम इसकी पुष्टि करते हैं से विभाज्य नहीं है . इस प्रकार,
इस प्रकार फायर कोड जनरेटर है. हम न्यूनतम समापवर्त्य का मूल्यांकन करके कोड की ब्लॉक-लंबाई की गणना कर सकते हैं और . दूसरे शब्दों में, . इस प्रकार, उपरोक्त फायर कोड चक्रीय कोड है जो लंबाई के किसी भी बर्स्ट को ठीक करने में सक्षम है या कम।
बाइनरी रीड-सोलोमन कोड
कोड के कुछ वर्ग , जैसे रीड-सोलोमन त्रुटि सुधार|रीड-सोलोमन, बाइनरी से बड़े वर्णमाला आकार पर काम करते हैं। यह संपत्ति ऐसे कोड को शक्तिशाली बर्स्ट त्रुटि सुधार क्षमताएं प्रदान करती है। उस कोड पर विचार करें जिस पर कार्य चल रहा है . वर्णमाला के प्रत्येक प्रतीक को बिट्स द्वारा दर्शाया जा सकता है? यदि के ऊपर रीड-सोलोमन कोड ख़त्म है, हम को के ऊपर कोड के रूप में सोच सकते हैं .
बर्स्ट त्रुटि सुधार के लिए ऐसे कोड शक्तिशाली होने का कारण यह है कि प्रत्येक प्रतीक बिट्स का प्रतिनिधित्व किया जाता है , और सामान्यतः , यह अप्रासंगिक है कि उनमें से कितने हैं बिट्स ग़लत हैं; चाहे बिट, या सभी बिट्स में त्रुटियाँ हैं, डिकोडिंग परिप्रेक्ष्य से यह अभी भी एकल प्रतीक त्रुटि है। दूसरे शब्दों में, चूंकि क्लस्टर में बर्स्ट त्रुटियां होती हैं, इसलिए एकल प्रतीक त्रुटि में अनेक बाइनरी त्रुटियों के योगदान की प्रबल संभावना होती है।
ध्यान दें कि बर्स्ट त्रुटियाँ अधिकतम प्रभावित कर सकती हैं प्रतीकों, और का बर्स्ट अधिक से अधिक प्रभावित कर सकता है प्रतीक. फिर, बर्स्ट अधिक से अधिक प्रभावित कर सकता है प्रतीक; इसका तात्पर्य यह है कि ए -प्रतीक-त्रुटि सुधार कोड अधिकतम लंबाई के बर्स्ट को ठीक कर सकता है .
सामान्यतः , a -रीड-सोलोमन कोड को सही करने में त्रुटि के किसी भी संयोजन को ठीक कर सकता है
बाइनरी आरएस कोड का उदाहरण
मान लीजिये हो आरएस कोड ख़त्म . इस कोड को नासा ने अपने कैसिनी-हुय्गेंस अंतरिक्ष यान में नियोजित किया था।[6] यह ठीक करने में सक्षम है प्रतीक त्रुटियाँ. अब हम बाइनरी आरएस कोड बनाते हैं से . प्रत्येक चिन्ह का प्रयोग करके लिखा जायेगा बिट्स इसलिए, बाइनरी आरएस कोड होगा इसके मापदंड के रूप में। यह लंबाई के किसी भी बर्स्ट को ठीक करने में सक्षम है .
इंटरलीव्ड कोड
इंटरलीविंग का उपयोग कनवल्शनल कोड को यादृच्छिक त्रुटि सुधारकों से बर्स्ट त्रुटि सुधारकों में परिवर्तित करने के लिए किया जाता है। इंटरलीव्ड कोड के उपयोग के पीछे मूल विचार ट्रांसमीटर पर प्रतीकों को मिलाना है। इससे प्राप्त त्रुटियों के बर्स्ट का यादृच्छिककरण होता है जो निकट स्थित होते हैं और फिर हम यादृच्छिक चैनल के लिए विश्लेषण प्रयुक्त कर सकते हैं। इस प्रकार, ट्रांसमीटर पर इंटरलीवर द्वारा किया जाने वाला मुख्य कार्य इनपुट प्रतीक अनुक्रम को परिवर्तित करना है। रिसीवर पर, डिइंटरलीवर ट्रांसमीटर पर मूल अपरिवर्तित अनुक्रम को वापस पाने के लिए प्राप्त अनुक्रम को परिवर्तित कर देगा।
इंटरलीवर की बर्स्ट त्रुटि सुधार क्षमता
Theorem — यदि बर्स्ट एरर को कुछ कोड की सही करने की क्षमता है फिर बर्स्ट त्रुटि को ठीक करने की क्षमता -वे इंटरलीव है
मान लीजिए कि हमारे पास एक कोड जो लंबाई के सभी विस्फोटों को ठीक कर सकता है इंटरलीविंग हमें प्रदान कर सकता है कोड जो लंबाई के सभी विस्फोटों को ठीक कर सकता है किसी भी दिए गए के लिए.यदि हम इंटरलीविंग का उपयोग करके अपनी इच्छानुसार लंबाई के संदेश को एन्कोड करना चाहते हैं, तो पहले हम इसे लंबाई के ब्लॉक में विभाजित करते हैं .हम लिखते हैं प्रत्येक ब्लॉक की प्रविष्टियाँ a पंक्ति-प्रमुख क्रम का उपयोग कर मैट्रिक्स। फिर, हम प्रत्येक पंक्ति का उपयोग करके एन्कोड करते हैं कोड. हमें जो मिलेगा वह है a आव्यूह। अब, इस आव्यूह को कॉलम-प्रमुख क्रम में पढ़ा और प्रसारित किया जाता है। विधि यह है कि यदि लम्बाई का विस्फोट होता है प्रेषित शब्द में, तो प्रत्येक पंक्ति में लगभग शामिल होगालगातार त्रुटियाँ (अधिक विशेष रूप से, प्रत्येक पंक्ति में कम से कम लंबाई का विस्तार होगा और अधिक से अधिक).यदि तब और यह कोड प्रत्येक पंक्ति को सही कर सकता है। इसलिए, इंटरलीव्ड कोड लंबाई के विस्फोट को ठीक कर सकता है .इसके विपरीत, यदितो कम से कम एक पंक्ति में इससे अधिक होंगे निरंतर त्रुटियाँ, और कोड उन्हें ठीक करने में विफल हो सकता है। इसलिए, इंटरलीव्ड की त्रुटि सुधार क्षमता कोड बिल्कुल सही है इंटरलीव्ड कोड की बीईसी दक्षता मूल के समान ही रहती है कोड. यह सच है क्योंकि:
ब्लॉक इंटरलीवर
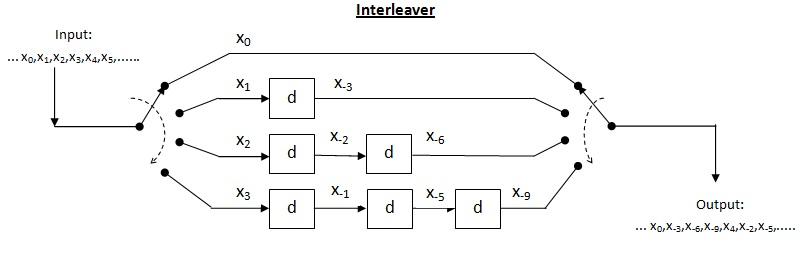
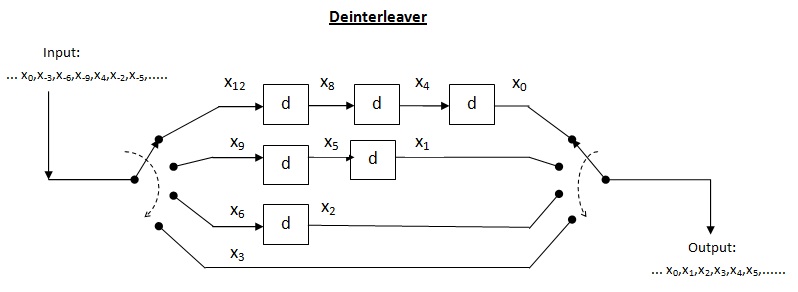
नीचे दिया गया चित्र 4 द्वारा 3 इंटरलीवर दिखाता है।
उपरोक्त इंटरलीवर को ब्लॉक इंटरलीवर कहा जाता है। यहां, इनपुट प्रतीकों को पंक्तियों में क्रमिक रूप से लिखा जाता है और आउटपुट प्रतीकों को स्तम्भ को क्रमिक रूप से पढ़कर प्राप्त किया जाता है। इस प्रकार, यह इस रूप में है सरणी. सामान्यतः , कोडवर्ड की लंबाई है.
ब्लॉक इंटरलीवर की क्षमता: के लिए ब्लॉक इंटरलीवर और लंबाई का फटना त्रुटियों की संख्या की ऊपरी सीमा है यह इस तथ्य से स्पष्ट है कि हम आउटपुट को स्तम्भ के अनुसार पढ़ रहे हैं और पंक्तियों की संख्या है . उपरोक्त प्रमेय के अनुसार त्रुटि सुधार क्षमता तक अनुमत अधिकतम बर्स्ट लंबाई है की बर्स्ट लंबाई के लिए , डिकोडर विफल हो सकता है।
ब्लॉक इंटरलीवर की दक्षता (): यह बर्स्ट लंबाई का अनुपात लेकर पाया जाता है जहां डिकोडर इंटरलीवर मेमोरी में विफल हो सकता है। इस प्रकार, हम सूत्रीकरण कर सकते हैं जैसा
कन्वेंशनल इंटरलीवर
क्रॉस इंटरलीवर प्रकार का मल्टीप्लेक्सर-डेमल्टीप्लेक्सर प्रणाली है। इस प्रणाली में, लंबाई को उत्तरोत्तर बढ़ाने के लिए विलंब रेखाओं का उपयोग किया जाता है। विलंब रेखा मूल रूप से इलेक्ट्रॉनिक परिपथ है जिसका उपयोग सिग्नल को निश्चित समय अवधि तक विलंबित करने के लिए किया जाता है। होने देना विलंब रेखाओं की संख्या हो और प्रत्येक विलंब रेखा द्वारा प्रस्तुत प्रतीकों की संख्या हो। इस प्रकार, निरंतर इनपुट के बीच भिन्नता = प्रतीक. कोडवर्ड की लंबाई बताएं इस प्रकार, इनपुट कोडवर्ड में प्रत्येक प्रतीक भिन्न विलंब रेखा पर होगा। लंबाई की बर्स्ट त्रुटि दें घटित होना। चूँकि क्रमागत प्रतीकों के बीच पृथक्करण है डीइंटरलीव्ड आउटपुट में त्रुटियों की संख्या हो सकती है उपरोक्त प्रमेय के अनुसार, त्रुटि सुधार क्षमता तक, अनुमत अधिकतम बर्स्ट लंबाई है तथा इसकी बर्स्ट लंबाई के लिए डिकोडर विफल हो सकता है.
क्रॉस इंटरलीवर की दक्षता (): यह बर्स्ट लंबाई के अनुपात को लेकर पाया जाता है जहां डिकोडर इंटरलीवर मेमोरी में विफल हो सकता है। इस उपस्थितियों में, इंटरलीवर की मेमोरी की गणना इस प्रकार की जा सकती है
अनुप्रयोग
कॉम्पैक्ट डिस्क
त्रुटि सुधार कोड के बिना, डिजिटल ऑडियो तकनीकी रूप से संभव नहीं होगा।[7] रीड-सोलोमन त्रुटि सुधार|रीड-सोलोमन कोड एकल बिट त्रुटि वाले दूषित प्रतीक को उतनी ही सरलता से ठीक कर सकते हैं जितनी सरलता से यह सभी बिट गलत वाले प्रतीक को ठीक कर सकता है। यह आरएस कोड को बर्स्ट त्रुटियों को ठीक करने के लिए विशेष रूप से उपयुक्त बनाता है।[5] अब तक, आरएस कोड का सबसे सामान्य अनुप्रयोग कॉम्पैक्ट डिस्क में है। आरएस कोड द्वारा प्रदान की गई मूलभूत त्रुटि सुधार के अलावा, डिस्क पर खरोंच के कारण होने वाली बर्स्ट त्रुटियों से सुरक्षा क्रॉस इंटरलीवर द्वारा प्रदान की जाती है।[3]
वर्तमान कॉम्पैक्ट डिस्क डिजिटल ऑडियो प्रणाली नीदरलैंड के एन. वी. फिलिप्स और जापान के सोनी कॉरपोरेशन (1979 में हस्ताक्षरित समझौते) द्वारा विकसित किया गया था।
कॉम्पैक्ट डिस्क में स्पष्ट प्लास्टिक कोटिंग के साथ लेपित 120 मिमी एल्युमिनाइज्ड डिस्क होती है, जिसमें सर्पिल ट्रैक होता है, जिसकी लंबाई लगभग 5 किमी होती है, जिसे ~ 0.8 माइक्रोमीटर तरंग दैर्ध्य के लेजर द्वारा ~ 1.25 मीटर/सेकेंड की निरंतर गति से ऑप्टिकली स्कैन किया जाता है। इस स्थिर गति को प्राप्त करने के लिए, ट्रैक के आंतरिक भाग पर स्कैन करते समय डिस्क का घुमाव ~8 रेव/सेकेंड से लेकर बाहरी भाग पर ~3.5 रेव/सेकेंड तक भिन्न होता है। गड्ढे और भूमि अवसाद (0.12 माइक्रोमीटर गहरे) और समतल खंड हैं जो ट्रैक के साथ बाइनरी डेटा बनाते हैं (0.6 माइक्रोमीटर चौड़ाई)।[8]
सीडी प्रक्रिया को निम्नलिखित उप-प्रक्रियाओं के अनुक्रम के रूप में समझा जा सकता है:
- सिग्नल के स्रोत का चैनल एन्कोडिंग
- मास्टर डिस्क तैयार करने, उपयोगकर्ता डिस्क का उत्पादन करने और खेलते समय उपयोगकर्ता डिस्क पर एम्बेडेड संकेतों को अनुभूत करने की यांत्रिक उप-प्रक्रियाएँ - चैनल
- उपयोगकर्ता डिस्क से प्राप्त संकेतों को डिकोड करना
यह प्रक्रिया बर्स्ट त्रुटियों और यादृच्छिक त्रुटियों दोनों के अधीन है।[7] बर्स्ट त्रुटियों में डिस्क सामग्री (एल्यूमीनियम प्रतिबिंबित फिल्म के दोष, पारदर्शी डिस्क सामग्री का व्यर्थ प्रतिबिंबित सूचकांक), डिस्क उत्पादन (डिस्क बनाने और डिस्क काटने आदि के समय दोष), डिस्क हैंडलिंग (स्क्रैच - सामान्यतः पतली, रेडियल और रिकॉर्डिंग की दिशा में ऑर्थोगोनल) और प्ले-बैक तंत्र में भिन्नताएं सम्मिलित हैं। यादृच्छिक त्रुटियों में पुनर्निर्मित सिग्नल तरंग की घबराहट और सिग्नल में हस्तक्षेप के कारण होने वाली त्रुटियां सम्मिलित हैं। सीआईआरसी (क्रॉस-इंटरलीव्ड रीड-सोलोमन कोडिंग|क्रॉस-इंटरलीव्ड रीड-सोलोमन कोड) सीडी प्रक्रिया में त्रुटि का पता लगाने और सुधार का आधार है। यह क्रमिक रूप से 3,500 बिट्स (सीडी सतह पर देखी गई लंबाई में 2.4 मिमी) तक त्रुटि बर्स्ट को ठीक करता है और 12,000 बिट्स (8.5 मिमी) तक त्रुटि बर्स्ट की भरपाई करता है जो सामान्य खरोंच के कारण हो सकते हैं।
एन्कोडिंग: ध्वनि-तरंगों का प्रतिरूप लिया जाता है और ए/डी कनवर्टर द्वारा डिजिटल रूप में परिवर्तित किया जाता है। ध्वनि तरंग का प्रतिरूप आयाम के लिए लिया जाता है (44.1 kHz या 44,100 जोड़े पर, स्टीरियो ध्वनि के बाएँ और दाएँ चैनलों के लिए एक-एक)। उदाहरण पर आयाम को लंबाई 16 की बाइनरी स्ट्रिंग सौंपी गई है। इस प्रकार, प्रत्येक प्रतिरूप दो बाइनरी सदिश या 4 डेटा के बाइट्स उत्पन्न करता है. रिकॉर्ड की गई ध्वनि के प्रत्येक सेकंड में 44,100 × 32 = 1,411,200 बिट्स (176,400 बाइट्स) डेटा प्राप्त होता है।[5] 1.41 एमबिट्स/एस प्रतिरूप डेटा स्ट्रीम त्रुटि सुधार प्रणाली से होकर निकलती है और अंततः 1.88 एमबिट्स/एस की स्ट्रीम में परिवर्तित हो जाती है।
एनकोडर के लिए इनपुट में 24 8-बिट प्रतीकों (ए/डी कनवर्टर से 12 16-बिट नमूने, बाएं और दाएं डेटा (ध्वनि) स्रोतों से 6 प्रत्येक) के इनपुट फ्रेम होते हैं। फ़्रेम का प्रतिनिधित्व किया जा सकता है जहाँ और से बाएँ और दाएँ फ़्रेम का प्रतिरूप चैनल से बाइट्स हैं .
प्रारंभ में, बाइट्स को नए फ़्रेम बनाने के लिए क्रमपरिवर्तित किया जाता है जहाँ प्रतिनिधित्व करना -2 मध्यवर्ती फ़्रेमों के पश्चात फ़्रेम से बाएँ और दाएँ नमूने।
इसके पश्चात , इन 24 संदेश प्रतीकों को C2 (28,24,5) रीड-सोलोमन कोड का उपयोग करके एन्कोड किया गया है जो कि संक्षिप्त RS कोड है . यह दो-त्रुटि-सुधार करने वाला है, न्यूनतम दूरी 5 का है। यह अतिरेक के 4 बाइट्स जोड़ता है, नया फ्रेम बनाना: . परिणामी 28-प्रतीक कोडवर्ड को (28.4) क्रॉस इंटरलीवर के माध्यम से पारित किया जाता है, जिससे 28 इंटरलीव्ड प्रतीक बन जाते हैं। फिर इन्हें C1 (32,28,5) RS कोड से निकला जाता है, जिसके परिणामस्वरूप 32 कोडित आउटपुट प्रतीकों के कोडवर्ड प्राप्त होते हैं। किसी कोडवर्ड के विषम संख्या वाले प्रतीकों को अगले कोडवर्ड के सम संख्या वाले प्रतीकों के साथ फिर से समूहीकृत किया जाता है ताकि किसी भी छोटे बर्स्ट को तोड़ा जा सके जो उपरोक्त 4-फ्रेम विलंब इंटरलीविंग के पश्चात भी उपस्थित हो सकता है। इस प्रकार, प्रत्येक 24 इनपुट प्रतीकों के लिए 32 आउटपुट प्रतीक होंगे . अंत में नियंत्रण और प्रदर्शन जानकारी की बाइट जोड़ी जाती है।[5] 33 बाइट्स में से प्रत्येक को ईएफएम (आठ से चौदह मॉड्यूलेशन) के माध्यम से 17 बिट्स में परिवर्तित किया जाता है और 3 मर्ज बिट्स को जोड़ा जाता है। इसलिए, छह नमूनों के फ्रेम का परिणाम 33 बाइट्स × 17 बिट्स (561 बिट्स) होता है, जिसमें 24 सिंक्रोनाइज़ेशन बिट्स और 3 मर्जिंग बिट्स जोड़े जाते हैं, जिससे कुल 588 बिट्स प्राप्त होते हैं।
डिकोडिंग: सीडी प्लेयर (सीआईआरसी डिकोडर) 32 आउटपुट सिंबल डेटा स्ट्रीम प्राप्त करता है। यह धारा पहले डिकोडर D1 से होकर निकलती है। डिकोडिंग विधियों पर निर्णय लेना और अपने उत्पाद प्रदर्शन को अनुकूलित करना सीडी प्रणाली के व्यक्तिगत डिजाइनरों पर निर्भर है। न्यूनतम दूरी 5 होने के कारण D1, D2 डिकोडर प्रत्येक के संयोजन को सही कर सकते हैं त्रुटियाँ और ऐसे मिटाता है .[5] अधिकांश डिकोडिंग समाधानों में, D1 को एकल त्रुटि को ठीक करने के लिए डिज़ाइन किया गया है। और 1 से अधिक त्रुटि के उपस्थितियां में, यह डिकोडर 28 इरेज़र आउटपुट करता है। अगले चरण में डीइंटरलीवर इन विलोपनों को 28 डी2 कोडवर्ड में वितरित करता है। पुनः अधिकांश समाधानों में, D2 को केवल मिटाने से निपटने के लिए सेट किया गया है ( सरल और कम महंगा समाधान)। यदि 4 से अधिक विलोपन का सामना करना पड़ता है, तो 24 विलोपन D2 द्वारा आउटपुट होते हैं। इसके पश्चात , त्रुटि छुपाने वाली प्रणाली अचूक प्रतीकों के उपस्थितियां में (पड़ोसी प्रतीकों से) प्रक्षेप करने का प्रयास करती है, जिसमें विफल रहने पर ऐसे गलत प्रतीकों के अनुरूप ध्वनियाँ म्यूट हो जाती हैं।
सीआईआरसी का प्रदर्शन:[7] सीआईआरसी सरल रैखिक प्रक्षेप द्वारा लंबी बस्ट त्रुटियों को छुपाता है। 2.5 मिमी ट्रैक लंबाई (4000 बिट्स) अधिकतम पूरी तरह से सुधार योग्य बर्स्ट लंबाई है। 7.7 मिमी ट्रैक लंबाई (12,300 बिट्स) अधिकतम बर्स्ट लंबाई है जिसे इंटरपोल किया जा सकता है। बिट त्रुटि दर (बीईआर) पर प्रतिरूप प्रक्षेप दर हर 10 घंटे में होती है इस प्रकार और बीईआर पर प्रति मिनट 1000 नमूने = अज्ञात त्रुटि नमूने (क्लिक): बीईआर = पर प्रत्येक 750 घंटे में से कम और BER = पर नगण्य है
यह भी देखें
- त्रुटि का पता लगाना और सुधार करना
- प्रतिक्रिया के साथ त्रुटि-सुधार कोड
- कोड दर
- रीड-सोलोमन त्रुटि सुधार
संदर्भ
- ↑ 1.0 1.1 1.2 Coding Bounds for Multiple Phased-Burst Correction and Single Burst Correction Codes
- ↑ सूचना और कोडिंग का सिद्धांत: छात्र संस्करण,आर जे मैकलीस द्वारा
- ↑ 3.0 3.1 3.2 Ling, San, and Chaoping Xing. Coding Theory: A First Course. Cambridge, UK: Cambridge UP, 2004. Print
- ↑ 4.0 4.1 Moon, Todd K. Error Correction Coding: Mathematical Methods and Algorithms. Hoboken, NJ: Wiley-Interscience, 2005. Print
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Lin, Shu, and Daniel J. Costello. Error Control Coding: Fundamentals and Applications. Upper Saddle River, NJ: Pearson-Prentice Hall, 2004. Print
- ↑ quest.arc.nasa.gov https://web.archive.org/web/20120627022807/http://quest.arc.nasa.gov/saturn/qa/cassini/Error_correction.txt. Archived from the original on 2012-06-27.
{{cite web}}: Missing or empty|title=(help) - ↑ 7.0 7.1 7.2 Algebraic Error Control Codes (Autumn 2012) – Handouts from Stanford University
- ↑ McEliece, Robert J. The Theory of Information and Coding: A Mathematical Framework for Communication. Reading, MA: Addison-Wesley Pub., Advanced Book Program, 1977. Print