कक्षा (गतिकी)
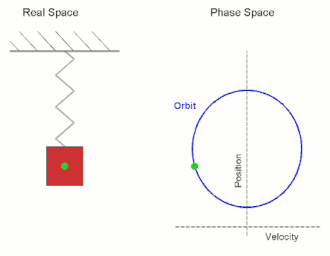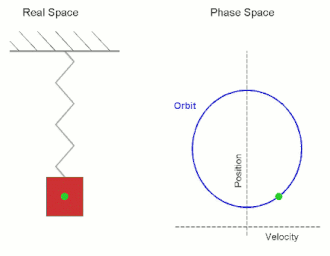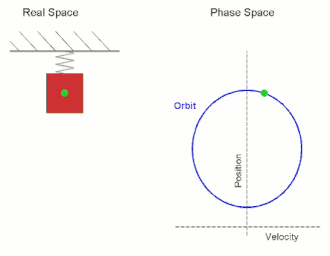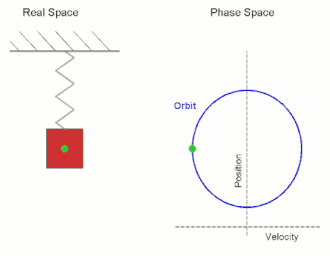
गणित में विशेष रूप से गतिशील प्रणालियों के अध्ययन में चरण स्थान (गतिशील प्रणाली) के विकास कार्य से संबंधित बिंदुओं का एक संग्रह है। इसे प्रारंभिक स्थितियों के एक विशेष समुच्चय के अनुसार डायनेमिक प्रणाली के प्रक्षेप वक्र द्वारा कवर किए गए फेज स्पेस (डायनेमिक प्रणाली) के सबसेट के रूप में समझा जा सकता है क्योंकि प्रणाली विकसित होता है। एक चरण अंतरिक्ष प्रक्षेप वक्र के रूप में चरण अंतरिक्ष निर्देशांक के किसी भी समुच्चय के लिए विशिष्ट रूप से निर्धारित किया जाता है। विभिन्न कक्षाओं के लिए चरण अंतरिक्ष में अंतर करना संभव नहीं है। इसलिए एक गतिशील प्रणाली की सभी कक्षाओं का समुच्चय चरण का एक विभाजन (समुच्चय सिद्धांत) है। सामयिक गतिकी का उपयोग करके कक्षाओं के गुणों को समझना डायनेमिक प्रणाली के आधुनिक सिद्धांत के उद्देश्यों में से एक है।
असतत-समय गतिशील प्रणालियों के लिए कक्षाएँ अनुक्रम हैं। वास्तविक गतिशील प्रणाली के लिए कक्षाएँ वक्र हैं और होलोमॉर्फिक फ़ंक्शन डायनेमिक प्रणालीके लिए कक्षाएँ रीमैन सतह हैं।
परिभाषा
T समूह (गणित), M समुच्चय (गणित) और Φ विकास समारोह के साथ गतिशील प्रणाली (T, M, Φ) को देखते हुए
- जहाँ साथ
हम परिभाषित करते हैं-
फिर समुच्चय-
x के माध्यम से कक्षा कहा जाता है। एक कक्षा जिसमें एक बिंदु होता है, वह स्थिर कक्षा कहलाती है। एक गैर-निरंतर कक्षा को बंद या आवधिक कहा जाता है। यदि उपस्थित हो
में
ऐसा है कि-
- .
वास्तविक गतिशील प्रणाली
वास्तविक गतिशील प्रणाली (R, M, Φ) को देखते हुए (x) वास्तविक संख्या में खुला अंतराल है। जो . M में किसी भी x के लिए
'x' और के माध्यम से सकारात्मक अर्ध-कक्षा कहा जाता है।
x से होकर ऋणात्मक अर्ध-कक्षा कहलाती है।
असतत समय गतिशील प्रणाली
असतत समय गतिशील प्रणाली के लिए x की आगे की कक्षा समुच्चय है।
x की पश्च कक्षा समुच्चय है।
और x की कक्षा समुच्चय है।
जहां:
- एक विकास कार्य है। जो यहाँ एक पुनरावृत्त कार्य है।
- गतिशील स्थान निश्चित करता है।
- पुनरावृत्ति की संख्या है। जो प्राकृतिक संख्या है और
- प्रणाली की प्रारंभिक अवस्था है और
सामान्यतः अलग संकेतन प्रयोग किया जाता है।
- के रूप में लिखा गया है।
- उपरोक्त अंकन में जहां है।
सामान्य गतिशील प्रणाली
सामान्य गतिशील प्रणाली के लिए विशेष रूप से सजातीय गतिशीलता में जब किसी के पास एक अच्छा समूह होता है। संभाव्यता स्थान पर कार्य करना