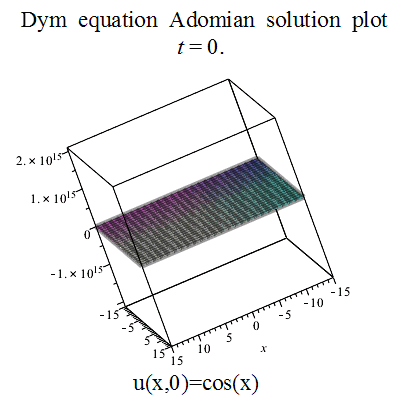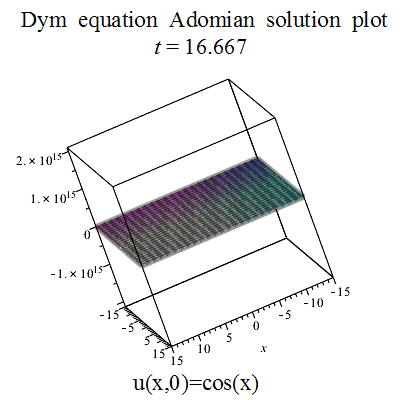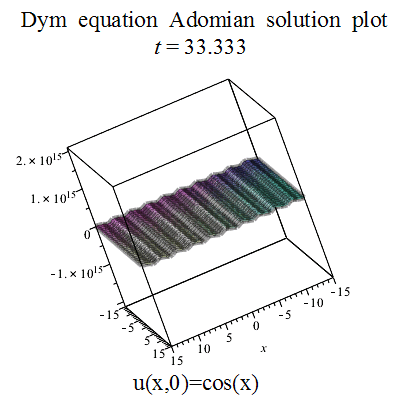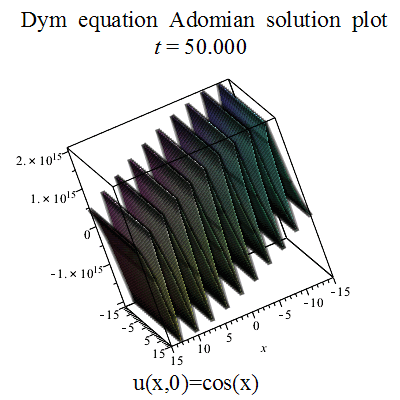
एडोमियन अपघटन विधि
एडोमियन वियोजन विधि (एडीएम) साधारण और आंशिक अरैखिक अवकल समीकरणों को हल करने के लिए एक अर्ध-विश्लेषणात्मक विधि है। जॉर्जिया विश्वविद्यालय में अनुप्रयुक्त गणित केंद्र के अध्यक्ष जॉर्ज एडोमियन द्वारा 1970 से 1990 के दशक में इस पद्धति को विकसित किया गया था।[1] यह इटो समाकल का उपयोग करके स्टोकेस्टिक पद्धति के लिए और अधिक विस्तार योग्य है।[2] इस विधि का उद्देश्य आंशिक अवकल समीकरणों (पीडीई) के हल के लिए एकीकृत सिद्धांत की ओर है; एक लक्ष्य जिसे होमोटॉपी विश्लेषण पद्धति के अधिक सामान्य सिद्धांत द्वारा अधिक्रमित कर दिया गया है।[3] विधि का महत्वपूर्ण दृष्टिकोण "एडोमियन बहुपद" की नियुक्ति है जो समीकरण के अरैखिक भाग के हल कन्वर्जेन्स की अनुमति प्रदान करता है, पद्धति को केवल रैखिक बनाने के बिना। ये बहुपद गणितीय रूप से एक मैकलॉरिन श्रेणी के लिए एक यादृच्छिक बाह्य पैरामीटर के क्रमानुसार सामान्यीकृत करते हैं; जो सीधे टेलर श्रेणी के विस्तार की तुलना में हल विधि को अधिक उपयोग क्षमता प्रदान करता है।[4]
साधारण अवकल समीकरण
एडोमियन पद्धति कॉची समस्याओं को हल करने के लिए उपयुक्त है, समस्याओं का एक महत्वपूर्ण वर्ग जिसमें प्रारंभिक स्थितियों की समस्याएं सम्मिलित होती हैं।
प्रथम कोटि की अरैखिक पद्धति के लिए अनुप्रयोग
एक साधारण अवकल समीकरण के लिए प्रारंभिक स्थिति समस्या का एक उदाहरण निम्नलिखित है:
समस्या को हल करने के लिए, उच्चतम कोटि अवकल संक्रियक (यहाँ L के रूप में लिखा गया है) को बाईं ओर रखा गया है, निम्नलिखित रूप से:
L = d/dt और के साथ। अब हल को निम्नअंशो की अनंत श्रेणी माना जाता है:
पूर्व व्यंजक में प्रतिस्थापित करने पर, हम निम्नलिखित प्राप्त करते हैं:
अब हम y0 को दाईं ओर कुछ स्पष्ट व्यंजक के साथ पहचानते हैं, और yi, i = 1, 2, 3, ..., दाईं ओर कुछ व्यंजक के साथ i की तुलना में निम्न क्रम के पदों को रखते हैं। उदाहरण के लिए :
इस प्रकार, किसी भी कोटि में किसी भी अंश की स्पष्ट रूप से गणना की जा सकती है। यदि हम प्राथमिक चार पदों के लिए हल करते हैं, तो सन्निकट निम्नलिखित है:
ब्लासियस समीकरण का अनुप्रयोग
एक अन्य उदाहरण, अधिक जटिल सीमा स्थितियों के साथ किसी परिसीमा स्तर में प्रवाह के लिए ब्लासियस समीकरण है:
निम्नलिखित शर्तों के साथ सीमाओं पर:
रैखिक और अरैखिक संक्रियकों को अब क्रमशः और रूप में प्रदर्शित किया जाता है। तब अभिव्यक्ति बन जाती है:
और इस स्थिति में हल निम्नलिखित सरल रूप में व्यक्त किया जा सकता है:
जहाँ: यदि:
और:
अरैखिक पद को रेखीयकृत करने के लिए एडोमियन के बहुपदों को व्यवस्थित रूप से निम्नलिखित नियम का उपयोग करके प्राप्त किया जा सकता है:
जहाँ:
सामान्य रूप से, प्रत्येक सन्निकटन के अंत में, सीमा शर्तों को लागू किया जाना चाहिए। इस स्थिति में, एकीकरण स्थिरांकों को तीन अंतिम स्वतंत्र स्थिरांकों में समूहीकृत किया जाना चाहिए। हालांकि, हमारे उदाहरण में, तीन स्थिरांक ऊपर औपचारिक हल में दिखाए गए रूप में प्रारम्भ से समूहीकृत दिखाई देते हैं। दो पहली सीमा शर्तों को लागू करने के बाद हम तथाकथित ब्लासियस श्रेणी प्राप्त करते हैं:
γ प्राप्त करने के लिए हमें ∞ पर सीमा शर्तों को लागू करना होगा, जो कि श्रेणी को पैड सन्निकट के रूप में लिखकर किया जा सकता है:
जहाँ L = M। इस व्यंजक की की सीमा aL/bM है।
यदि हम b0 = 1 चयनित करते हैं, अतः b गुणांकों के लिए M रेखीय समीकरण प्राप्त होते हैं:
इसके पश्चात, हम निम्नलिखित अनुक्रम के माध्यम से a गुणांक प्राप्त करते हैं:
हमारे उदाहरण में:
जो जब γ = 0.0408 हो जाता है:
सीमा के साथ:
जो लगभग 4/1000 की यथार्थता के साथ 1 (सीमा की स्थिति (3) से) के बराबर है।
आंशिक अवकल समीकरण
अरैखिकता के साथ एक आयताकार प्रणाली का अनुप्रयोग
भौतिक विज्ञान में सबसे अधिक बार आने वाली समस्याओं में से एक (रैखिक या अरैखिक) आंशिक अवकल समीकरण का हल प्राप्त करना है जो एक आयताकार सीमा पर कार्यात्मक मूल्यों के एक समुच्चय को संतुष्ट करता है। निम्नलिखित समस्या का एक उदाहरण है:
आयत पर परिभाषित निम्न सीमा शर्तों के साथ:
इस प्रकार का आंशिक अवकल समीकरण प्रायः विज्ञान और अभियांत्रिकी में दूसरों के साथ युग्मित हो कर दिखाई देता है I उदाहरण के लिए, असंपीड्य द्रव प्रवाह समस्या में, नेवियर-स्टोक्स समीकरणों को दाब के लिए पॉइज़न समीकरण के साथ समानांतर में हल किया जाना चाहिए।
प्रणाली का वियोजन
आइए हम समस्या के लिए निम्नलिखित संकेतन का उपयोग करें (1):
जहाँ Lx, Ly द्विक अवकलज संक्रियक हैं और N एक अरैखिक संक्रियक है।
(2) का औपचारिक हल है:
हमारे पास हल के लिए योगदानों के एक समुच्चय के रूप में अब u का विस्तार करना:
(3) में प्रतिस्थापन करके और बाईं ओर के योगदानों और दाईं ओर की शर्तों के बीच एक-से-एक समतुल्य करके हम निम्नलिखित पुनरावृत्त योजना प्राप्त करते हैं:
जहाँ युग्म {an(y), bn(y)} निम्नलिखित समीकरणों के प्रणाली का हल है:
यहाँ हल का nवाँ क्रम सन्निकट है और N u को एडोमियन बहुपदों में निरंतर विस्तारित किया गया है:
जहाँ और f(u) = u2 उदाहरण (1) में हैं।
यहाँ C(ν, n) u के ν घटकों के गुणनफल (या गुणनफलों का योग) हैं, जिनके सबस्क्रिप्ट का योग n तक होता है, जो बार-बार सबस्क्रिप्ट की संख्या के भाज्य द्वारा विभाजित है। यह सुनिश्चित करने के लिए व्यवस्थित रूप से वियोजन को क्रमित करने के लिए केवल एक अंगुष्ठ-नियम है कि प्रदर्शित होने वाले सभी संयोजनों का शीघ्र या बाद में उपयोग किया जाता है।
u0 के क्रमानुसार सामान्यीकृत टेलर श्रेणी के योग के बराबर है।[1]
उदाहरण के लिए (1) एडोमियन बहुपद इस प्रकार हैं:
अन्य संभावित विकल्प भी An के व्यंजक के लिए संभव हैं।
श्रेणी हल
चेरौल्ट ने स्थापित किया कि एडोमियन की विधि द्वारा प्राप्त श्रेणी की शर्तें शून्य के रूप में 1/(mn)! तक पहुंचती हैं यदि m उच्चतम रैखिक अवकल संकारक की कोटि है और वह है।[5]
इस पद्धति के साथ दो दिशाओं में से किसी भी दिशा में व्यवस्थित रूप से एकीकृत करके हल प्राप्त किया जा सकता है: x-दिशा में हम व्यंजक (3) का उपयोग करेंगे; वैकल्पिक y-दिशा में हम निम्नलिखित व्यंजक का उपयोग करेंगे:
जहाँ: c(x), d(x) सीमा स्थितियों से y = - yl और y = yl पर प्राप्त किया जाता है:
यदि हम दो संबंधित हलों को x-आंशिक हल और y-आंशिक हल कहते हैं, अतः विधि के सबसे रोचक परिणामों में से एक यह है कि x-आंशिक हल केवल दो सीमा शर्तों (1-a) का उपयोग करता है और y-आंशिक हल केवल स्थितियों (1-b) का उपयोग करता है।
इस प्रकार, परिसीमा फलनों के दो समुच्चय {f1, f2} या {g1, g2} में से एक आधिक्य बोधक है, और इसका तात्पर्य यह है कि एक आयत पर परिसीमा शर्तों के साथ आंशिक अवकल समीकरण की सीमाओं पर यादृच्छिक रूप से परिसीमा शर्तें नहीं हो सकती हैं, क्योंकि x = x1, x = x2 पर शर्तें y = y1 और y = y2 पर लगाई गई शर्तों के साथ संगत होनी चाहिए।
इस बिंदु को स्पष्ट करने के लिए एक उदाहरण निम्न सीमा शर्तों के साथ पॉइज़न समस्या का हल है:
एडोमियन की विधि और एक प्रतीकात्मक प्रोसेसर (जैसे मेथेमेटिका या मेपल) का उपयोग करके हल के लिए अनुमानित तीसरी कोटि प्राप्त करना सरल है। इस सन्निकटन में किसी भी बिंदु पर 5×10−16 से कम त्रुटि है, क्योंकि इसे प्रारंभिक समस्या में प्रतिस्थापन द्वारा और (x, y) के फलन के रूप में प्राप्त अवशिष्ट के निरपेक्ष मान को प्रदर्शित करके सिद्ध किया जा सकता है।[6]
y = -0.25 और y = 0.25 पर हल विशिष्ट फलनों द्वारा दिया जाता है जो इस स्थिति में हैं:
और g2(x) = g1(x) क्रमशः।
यदि एक (द्विक) एकीकरण अब इन दो परिसीमा फलनों का उपयोग करके y-दिशा में किया जाता है तो एक ही हल प्राप्त होगा, जो u(x=0, y) = 0 और u(x=0.5, y) = 0 को संतुष्ट करते हैं और इन सीमाओं पर किसी भी अन्य शर्त को पूरा नहीं कर सकते हैं।
इन परिणामों से कुछ लोग हैरान हैं; यह अजीब लगता है कि एक अवकल प्रणाली को हल करने के लिए सभी प्रारंभिक-सीमा शर्तों का स्पष्ट रूप से उपयोग नहीं किया जाना चाहिए। हालाँकि, यह एक अच्छी तरह से स्थापित तथ्य है कि किसी भी दीर्घवृत्तीय समीकरण का आयत के चारों पक्षों में किसी भी कार्यात्मक स्थितियों के लिए एक और केवल एक ही हल होता है, बशर्ते कि किनारों पर कोई असंततता न हो। गलत धारणा का कारण यह है कि वैज्ञानिक और अभियांत्रिक सामान्यतः एक हिल्बर्ट समष्टि में दुर्बल कन्वर्जेन्स के संदर्भ में एक सीमा की स्थिति में सोचते हैं (सीमा फलन की दूरी व्यावहारिक उद्देश्यों के लिए काफी छोटी है)। इसके विपरीत, कॉची समस्याएँ किसी दिए गए परिसीमा फलन और इसके सभी अवकलजों के लिए बिंदु-से-बिंदु कन्वर्जेन्स लागू करती हैं (और यह एक बहुत मजबूत स्थिति है!)। पहले वाले के लिए, एक फलन एक सीमा स्थिति को संतुष्ट करता है जब इसके बीच का क्षेत्र (या अन्य कार्यात्मक दूरी) और सीमा में लगाया गया वास्तविक फलन वांछित के रूप में बहुत छोटा होता है; हालांकि, दूसरे वाले के लिए, फलन को अंतराल के किसी भी और हर बिंदु पर लगाए गए सत्य फलन के लिए जाना चाहिए।
टिप्पणी की गई पॉइज़न समस्या में किसी कार्यात्मक सीमा स्थिति f1, f2, g1, g2 का हल नहीं है; हालांकि, दिए गए f1, f2 परिसीमा फलनों g1*, g2* को वांछित के रूप में g1, g2 के इतने निकट खोजना हमेशा संभव है (दुर्बल कन्वर्जेन्स अर्थ में) जिसके लिए समस्या का हल है। यह संपत्ति यादृच्छिक रूप से सीमा शर्तों के साथ पॉइज़न और कई अन्य समस्याओं को हल करना संभव बनाती है लेकिन कभी भी विश्लेषणात्मक फलनों के लिए बिल्कुल सीमाओं पर निर्दिष्ट नहीं होती है। पाठक x-दिशा के साथ एकीकृत होने वाली इस समस्या को हल करके सीमा स्थितियों में छोटे परिवर्तनों के लिए पीडीई हलों की उच्च संवेदनशीलता के बारे में खुद को (स्वयं को) मना सकता है, परिसीमा फलनों के साथ थोड़ा अलग भले ही दृष्टिगत रूप से अलग नहीं हो। उदाहरण के लिए, सीमा की स्थिति के साथ हल:
x = 0 और x = 0.5 पर, और सीमा शर्तों के साथ हल:
x = 0 और x = 0.5 पर, अलग-अलग संकेत उत्तलता के साथ पार्श्व फलन उत्पन्न करते हैं, भले ही दोनों फलन दृष्टिगत रूप से भिन्न न हों।
दीर्घवृत्तीय समस्याओं के हल और अन्य आंशिक अवकल समीकरण केवल दो पक्षों का उपयोग किए जाने पर लगाए गए परिसीमा फलन में छोटे परिवर्तनों के प्रति अत्यधिक संवेदनशील होते हैं। और यह संवेदनशीलता उन मॉडलों के साथ आसानी से संगत नहीं है जो वास्तविक प्रणालियों का प्रतिनिधित्व करने वाले हैं, जिन्हें प्रयोगात्मक त्रुटियों वाले मापों के माध्यम से वर्णित किया गया है और सामान्यतः हिल्बर्ट समष्टि में प्रारंभिक-सीमा मूल्य समस्याओं के रूप में व्यक्त किया जाता है।
वियोजन विधि में संशोधन
कम से कम तीन तरीकों की सूचना दी गई है[6][7][8] परिसीमा फलन g1*, g2* प्राप्त करने के लिए जो लगाए गए शर्तों के किसी भी पार्श्व समुच्चय के साथ संगत हैं {f1, f2}। यह आवश्यक सटीकता के साथ एक बंद आयत पर किसी भी पीडीई सीमा समस्या का विश्लेषणात्मक हल खोजना संभव बनाता है, जिससे उन समस्याओं की एक विस्तृत श्रेणी को हल करने की अनुमति प्राप्त होती है जो मानक एडोमियन की पद्धति को संबोधित करने में सक्षम नहीं थी।
पहले वाले ने x = 0 और x = x1 (शर्त 1-a) पर लगाए गए दो परिसीमा फलनों को y: p1, p2 में Nवां-क्रम बहुपद के साथ इस तरह से परेशान किया है कि: f1' = f1 + p1, f2' = f2 + p2, जहां दो प्रक्षोभ फलनों के मानदंड सीमाओं पर आवश्यक सटीकता से छोटे होते हैं। ये p1, p2 बहुपद गुणांक ci, i = 1, ..., N के एक समुच्चय पर निर्भर करते हैं। फिर, एडोमियन पद्धति को लागू किया जाता है और चार सीमाओं पर फलन प्राप्त किए जाते हैं जो ci, i = 1, ..., N के समुच्चय पर निर्भर करते हैं। अंत में, एक परिसीमा फलन F(c1, c2, ..., cN) को इन चार फलनों के योग के रूप में परिभाषित किया गया है, और F(c1, c2, ..., cN) और वास्तविक परिसीमा फलनों ((1-a) और (1-b)) के बीच की दूरी को कम किया गया है। समस्या को कम कर दिया गया है, इस प्रकार, फलन F(c1, c2, ..., cN) के वैश्विक न्यूनीकरण के लिए, जिसमें ci, i = 1, ..., N के पैरामीटर के कुछ संयोजन के लिए वैश्विक न्यूनतम है। यह न्यूनतम एक आनुवंशिक एल्गोरिथम के माध्यम से या कुछ अन्य अनुकूलन विधि का उपयोग करके पाया जा सकता है, जैसा कि चेरौल्ट (1999) द्वारा प्रस्तावित किया गया है।[9]
आरंभिक-सीमा समस्याओं के विश्लेषणात्मक सन्निकटन प्राप्त करने का दूसरा तरीका है, एडोमियन वियोजन को वर्णक्रमीय विधियों के साथ संयोजित करना।[7]
अंत में, गार्सिया-ओलिवारेस द्वारा प्रस्तावित तीसरी विधि चार सीमाओं पर विश्लेषणात्मक हल लगाने पर आधारित है, लेकिन मूल अवकल संकारक को इस प्रकार से संशोधित करना है कि यह सीमाओं के निकट एक संकीर्ण क्षेत्र में ही मूल से अलग है, और यह हल को चार सीमाओं पर सटीक विश्लेषणात्मक स्थितियों को संतुष्ट करने के लिए बाध्य करता है।[8]
समाकल समीकरण
एडोमियन वियोजन विधि को हल प्राप्त करने के लिए रैखिक और अरैखिक समाकल समीकरणों पर भी लागू किया जा सकता है।[10] यह इस तथ्य के सामान प्रतीत होता है कि कई अवकल समीकरणों को समाकल समीकरणों में परिवर्तित किया जा सकता है।[10]
एडोमियन वियोजन विधि
दूसरे प्रकार के गैर-समरूप फ्रेडहोम समाकल समीकरण के लिए एडोमियन वियोजन विधि निम्नानुसार है:[10]
निम्नलिखित रूप का एक समाकल समीकरण दिया गया है:
हम मानते हैं कि हम श्रेणी के रूप में हल व्यक्त कर सकते हैं:
श्रेणी के रूप को समाकल समीकरण में प्लग करता है अतः निम्नलिखित प्राप्त होता है:
यह मानते हुए कि योग पूर्ण रूप से में परिवर्तित होता है, हम योग और समाकलन को इस प्रकार पूर्णांकित कर सकते हैं
दोनों पक्षों पर योग का विस्तार करने पर प्राप्त होता है:
इसलिए हम प्रत्येक को निम्नलिखित आवर्ती तरीके से संबद्ध कर सकते हैं:
जो हमें ऊपर दिए गए हल के रूप में हल प्रदान करता है।
उदाहरण
फ्रेडहोम समाकल समीकरण दिया गया है:
तब से , हम सेट कर सकते हैं:
- ...
इसलिए हल को इस प्रकार लिखा जा सकता है:
चूंकि यह एक टेलिस्कोपिंग श्रेणी है, हम देख सकते हैं कि के बाद प्रत्येक पद रद्द हो जाता है और इसे "नॉइज़" माना जा सकता है,[10] इस प्रकार, बन जाता है:
गैलरी
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 Adomian, G. (1994). भौतिकी की सीमांत समस्याओं का समाधान: अपघटन विधि. Kluwer Academic Publishers.
- ↑ Adomian, G. (1986). नॉनलाइनियर स्टोकेस्टिक ऑपरेटर समीकरण. Kluwer Academic Publishers. ISBN 978-0-12-044375-8.
- ↑ Liao, S.J. (2012), Homotopy Analysis Method in Nonlinear Differential Equation, Berlin & Beijing: Springer & Higher Education Press, ISBN 978-3642251313
- ↑ Wazwaz, Abdul-Majid (2009). आंशिक विभेदक समीकरण और एकान्त तरंग सिद्धांत. Higher Education Press. p. 15. ISBN 978-90-5809-369-1.
- ↑ Cherruault, Y. (1989), "Convergence of Adomian's Method", Kybernetes, 18 (2): 31–38, doi:10.1108/eb005812
- ↑ 6.0 6.1 García-Olivares, A. (2003), "Analytic solution of partial differential equations with Adomian's decomposition", Kybernetes, 32 (3): 354–368, doi:10.1108/03684920310458584 [1]
- ↑ 7.0 7.1 García-Olivares, A. (2002), "Analytical approximants of time-dependent partial differential equations with tau methods", Mathematics and Computers in Simulation, 61: 35–45, doi:10.1016/s0378-4754(02)00133-7, hdl:10261/51182 [2]
- ↑ 8.0 8.1 García-Olivares, A. (2003), "Analytical solution of nonlinear partial differential equations of physics", Kybernetes, 32 (4): 548–560, doi:10.1108/03684920310463939, hdl:10261/51176 [DOI: 10.1108/03684920310463939] [3]
- ↑ Cherruault, Y. (1999). अनुकूलन, स्थानीय और वैश्विक तरीके. Presses Universitaires de France. ISBN 978-2-13-049910-7.
- ↑ 10.0 10.1 10.2 10.3 Wazwaz, Abdul-majid (2015). इंटीग्रल इक्वेशन में पहला कोर्स, ए. World Scientific Publishing Company. ISBN 978-981-4675-16-1. OCLC 1020691303.