नवीकरण सिद्धांत: Difference between revisions
m (9 revisions imported from alpha:नवीकरण_सिद्धांत) |
No edit summary |
||
| Line 336: | Line 336: | ||
{{Stochastic processes}} | {{Stochastic processes}} | ||
{{DEFAULTSORT:Renewal theory}} | {{DEFAULTSORT:Renewal theory}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Renewal theory]] | |||
[[Category:Collapse templates|Renewal theory]] | |||
[[Category: | [[Category:Created On 01/06/2023|Renewal theory]] | ||
[[Category:Created On 01/06/2023]] | [[Category:Lua-based templates|Renewal theory]] | ||
[[Category:Vigyan Ready]] | [[Category:Machine Translated Page|Renewal theory]] | ||
[[Category:Multi-column templates|Renewal theory]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Renewal theory]] | |||
[[Category:Pages using div col with small parameter|Renewal theory]] | |||
[[Category:Pages with script errors|Renewal theory]] | |||
[[Category:Sidebars with styles needing conversion|Renewal theory]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Renewal theory]] | |||
[[Category:Templates generating microformats|Renewal theory]] | |||
[[Category:Templates that add a tracking category|Renewal theory]] | |||
[[Category:Templates that are not mobile friendly|Renewal theory]] | |||
[[Category:Templates that generate short descriptions|Renewal theory]] | |||
[[Category:Templates using TemplateData|Renewal theory]] | |||
[[Category:Templates using under-protected Lua modules|Renewal theory]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates|Renewal theory]] | |||
[[Category:बिंदु प्रक्रियाएं|Renewal theory]] | |||
Latest revision as of 16:56, 19 June 2023
नवीकरण सिद्धांत संभाव्यता सिद्धांत की शाखा है जो धारण समय के लिए पॉइसन प्रक्रिया को सामान्य करता है। घातांकी रूप से वितरण होल्डिंग समय के अतिरिक्त, नवीनीकरण प्रक्रिया में कोई भी स्वतंत्र और समान रूप से वितरित आईआईडी होल्डिंग समय हो सकता है जिसका परिमित माध्य हो। नवीनीकरण-रिवॉर्ड प्रक्रिया में अतिरिक्त रूप से प्रत्येक होल्डिंग समय पर किए गए रिवॉर्ड का यादृच्छिक क्रम होता है, जो आईआईडी हैं किंतु होल्डिंग समय से स्वतंत्र होने की आवश्यकता नहीं है।
नवीकरण प्रक्रिया में बड़ी संख्या और केंद्रीय सीमा प्रमेय के स्थिर नियम के समान स्पर्शोन्मुख गुण होते हैं। नवीनीकरण फलन (आगमन की अपेक्षित संख्या) और रिवॉर्ड फलन (अपेक्षित रिवॉर्ड मान) नवीकरण सिद्धांत में महत्वपूर्ण हैं। नवीकरण फलन पुनरावर्ती अभिन्न समीकरण को संतुष्ट करता है। प्रमुख नवीनीकरण समीकरण के कनवल्शन का सीमित मान देता है उपयुक्त गैर-नकारात्मक फलन के साथ मार्कोव नवीनीकरण प्रक्रियाओं की विशेष स्थति के रूप में नवीकरण प्रक्रियाओं के सुपरपोजिशन का अध्ययन किया जा सकता है।
अनुप्रयोगों के माध्यम से कारखाने में व्यर्थ हो चुकी मशीनरी को परिवर्तित करने के लिए सर्वोत्तम रणनीति की गणना करना और विभिन्न बीमा पॉलिसियों के दीर्घकालिक लाभों की तुलना करना सम्मिलित है। निरीक्षण विरोधाभास इस तथ्य से संबंधित है कि समय t पर नवीकरण अंतराल का अवलोकन औसत नवीनीकरण अंतराल की तुलना में औसत मान के साथ अंतराल देता है।
नवीनीकरण प्रक्रिया
परिचय
नवीनीकरण प्रक्रिया प्वासों प्रक्रिया का सामान्यीकरण है। संक्षेप में, पॉइसन प्रक्रिया सकारात्मक पूर्णांकों (सामान्यतः शून्य से प्रारंभ) पर निरंतर-समय की मार्कोव प्रक्रिया है, जिसमें प्रत्येक पूर्णांक पर स्वतंत्र रूप से वितरित होल्डिंग समय होता है। अगले पूर्णांक तक जाने से पहले, नवीनीकरण प्रक्रिया में, होल्डिंग समय का घातीय वितरण होना आवश्यक नहीं है; अन्यथा, होल्डिंग समय का सकारात्मक संख्याओं पर वितरण हो सकता है, जब तक कि होल्डिंग समय स्वतंत्र और समान रूप से वितरित (आईआईडी) और परिमित माध्य हो।
औपचारिक परिभाषा
परिमित अपेक्षित मान के साथ समान रूप से वितरित सकारात्मक स्वतंत्र समान रूप से वितरित रैंडम चर का अनुक्रम हो
हम यादृच्छिक चर का उल्लेख करते हैं के रूप में -वें होल्डिंग समय है,
प्रत्येक n > 0 के लिए परिभाषित करें:
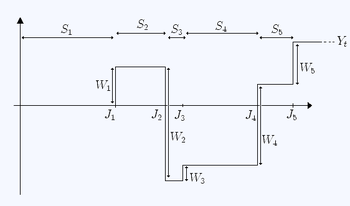
प्रत्येक के रूप में जाना जाता है -वें जम्प का समय और अंतराल को "नवीनीकरण अंतराल" कहा जाता है।
तब यादृच्छिक चर द्वारा दिया जाता है
जहाँ यादृच्छिक चर द्वारा दिया जाता है
समय t द्वारा हुई जम्प की संख्या का प्रतिनिधित्व करता है, और इसे नवीनीकरण प्रक्रिया कहा जाता है।
व्याख्या
यदि कोई यादृच्छिक समय पर होने वाली घटनाओं पर विचार करता है, तो कोई होल्डिंग समय के बारे में सोच सकता है निरन्तर दो घटनाओं के मध्य बीता हुआ यादृच्छिक समय है। उदाहरण के लिए, यदि नवीनीकरण प्रक्रिया विभिन्न मशीनों के विभक्त होने की संख्या को मॉडलिंग कर रही है, तो होल्डिंग समय मशीन के विभक्त होने से पहले दूसरी मशीन के विभक्त होने के मध्य के समय का प्रतिनिधित्व करता है।
पोइसन प्रक्रिया मार्कोव संपत्ति के साथ अद्वितीय नवीनीकरण प्रक्रिया है,[1]क्योंकि घातीय वितरण मेमोरी लेस्स की संपत्ति के साथ अद्वितीय निरंतर यादृच्छिक चर है।
नवीनीकरण-रिवॉर्ड प्रक्रिया
संतोषजनक आईआईडी यादृच्छिक चर (पुरस्कार) का क्रम हो,
फिर यादृच्छिक चर
नवीनीकरण-रिवॉर्ड प्रक्रिया में कहा जाता है कि विपरीत , प्रत्येक नकारात्मक मान के साथ-साथ सकारात्मक मान भी ले सकते हैं।
यादृच्छिक चर दो अनुक्रमों पर निर्भर करता है: होल्डिंग समय और रिवॉर्ड इन दो अनुक्रमों को स्वतंत्र होने की आवश्यकता नहीं है। विशेष रूप से, फलन हो सकता है।
व्याख्या
मशीन के निरन्तर व्यर्थ होने के मध्य के समय के रूप में होल्डिंग समय की उपरोक्त व्याख्या के संदर्भ में, रिवॉर्ड (जो इस स्थिति में नकारात्मक होता है) को क्रमिक व्यर्थ के परिणामस्वरूप होने वाली क्रमिक त्रुटिनिवारण व्यय के रूप में देखा जा सकता है।
वैकल्पिक सादृश्य यह है कि हमारे निकट मैजिक गूस है जो अंतराल पर संख्या देते है (होल्डिंग समय) के रूप में वितरित किया जाता है, कभी-कभी यह यादृच्छिक भार के रूप में संख्या देते है, (यादृच्छिक भार का भी) जिसके लिए उत्तरदायी (और उचित मूल्य) निवारण की आवश्यकता होती है। रिवॉर्ड उत्तरोत्तर संख्या (i = 1,2,3,...) और समय t पर कुल वित्तीय रिवॉर्ड रिकॉर्ड करता है।
नवीनीकरण फलन
हम नवीनीकरण फलन को कुछ समय तक देखी गई जम्प की संख्या के अपेक्षित मान के रूप में परिभाषित करते हैं:
एलीमेंट्री नवीनीकरण प्रमेय
नवीनीकरण फलन संतुष्ट करता है
Proof The strong law of large numbers for renewal processes implies To prove the elementary renewal theorem, it is sufficient to show that is uniformly integrable.
To do this, consider some truncated renewal process where the holding times are defined by where is a point such that which exists for all non-deterministic renewal processes. This new renewal process is an upper bound on and its renewals can only occur on the lattice . Furthermore, the number of renewals at each time is geometric with parameter . So we have
नवीनीकरण रिवॉर्ड प्रक्रियाओं के लिए प्राथमिक नवीनीकरण प्रमेय
हम रिवॉर्ड फलन को परिभाषित करते हैं:
रिवॉर्ड फलन संतुष्ट करता है
नवीकरण समीकरण
नवीनीकरण फलन संतुष्ट करता है
जहाँ का संचयी बंटन फलन है और संगत प्रायिकता घनत्व फलन है।
सिद्ध We may iterate the expectation about the first holding time: From the definition of the renewal process, we have
So
as required.
प्रमुख नवीकरण प्रमेय
बता दें कि X नवीनीकरण फलन के साथ नवीनीकरण प्रक्रिया और अंतराल का अर्थ है। फलन संतोषजनक हो:
- g मोनोटोन और न बढ़ने वाला है
प्रमुख नवीकरण प्रमेय बताता है कि, जैसा कि :[2]
नवीनीकरण प्रमेय
किसी के लिए की विशेष स्थिति के रूप में नवीकरण प्रमेय देता है:[3]
- जैसा
परिणाम को अभिन्न समीकरणों का उपयोग करके या युग्मन (संभाव्यता) तर्क द्वारा सिद्ध किया जा सकता है।[4]चूँकि प्रमुख नवीकरण प्रमेय की विशेष स्थिति है, इसका उपयोग चरण कार्यों पर विचार करके और फिर चरण कार्यों के अनुक्रमों को बढ़ाकर पूर्ण प्रमेय को निकालने के लिए किया जा सकता है।[2]
स्पर्शोन्मुख गुण
नवीकरण प्रक्रियाओं और नवीकरण-रिवॉर्ड प्रक्रियाओं में बड़ी संख्या के स्थिर नियम के समान गुण होते हैं, जो एक ही प्रमेय से प्राप्त किए जा सकते हैं। यदि नवीनीकरण प्रक्रिया है और नवीनीकरण-रिवॉर्ड प्रक्रिया है तो:
लगभग निश्चित रूप से,
सिद्ध First consider . By definition we have: for all and so
for all t ≥ 0.
Now since we have:
as almost surely (with probability 1). Hence:
almost surely (using the strong law of large numbers); similarly:
almost surely.
Thus (since is sandwiched between the two terms)
almost surely.[2]
Next consider . We have
almost surely (using the first result and using the law of large numbers on ).
नवीनीकरण प्रक्रियाओं में अतिरिक्त रूप से केंद्रीय सीमा प्रमेय के समान गुण होते हैं:[5]
निरीक्षण विरोधाभास
नवीकरण प्रक्रियाओं की लोकप्रिय विशेषता यह है कि यदि हम कुछ पूर्व निर्धारित समय t की प्रतीक्षा करते हैं और फिर निरीक्षण करते हैं कि t युक्त नवीकरण अंतराल कितना बड़ा है, तो हमें आशा करनी चाहिए कि यह औसत आकार के नवीनीकरण अंतराल से सामान्यतः बड़ा होगा।
गणितीय रूप से 'निरीक्षण विरोधाभास' कहता है: किसी भी t > 0 के लिए t युक्त नवीकरण अंतराल पहले नवीनीकरण अंतराल की तुलना में स्टोचैस्टिक रूप से बड़ा है। अर्थात्, सभी x > 0 और t > 0 के लिए:
जहां FS आईआईडी होल्डिंग समय Si का संचयी वितरण फलन है, ज्वलंत उदाहरण 'बस प्रतीक्षा समय विरोधाभास' है: बस आगमन के दिए गए यादृच्छिक वितरण के लिए, बस स्टॉप पर औसत सवार बसों के औसत ऑपरेटर की तुलना में अधिक देरी देखता है।
विरोधाभास का संकल्प यह है कि समय t पर हमारा प्रारूप वितरण आकार-पक्षपाती है (प्रारूप पूर्वाग्रह देखें), इसमें अंतराल चयन की जाने की संभावना इसके आकार के समानुपाती होती है। चूँकि, औसत आकार का नवीनीकरण अंतराल आकार-पक्षपाती नहीं है।
सिद्ध Observe that the last jump-time before t is ; and that the renewal interval containing t is . Then since both and are greater than or equal to for all values of s.
सुपरपोजिशन
जब तक नवीनीकरण प्रक्रिया पोइसन प्रक्रिया नहीं है, दो स्वतंत्र नवीनीकरण प्रक्रियाओं का सुपरपोजिशन (योग) नवीनीकरण प्रक्रिया नहीं है।[6] चूँकि, ऐसी प्रक्रियाओं को मार्कोव नवीनीकरण प्रक्रियाओं नामक प्रक्रियाओं के एक बड़े वर्ग के भीतर वर्णित किया जा सकता है।[7] चूँकि, सुपरपोज़िशन प्रक्रिया में पहली इंटर-इवेंट समय का संचयी वितरण फलन द्वारा दिया गया है[8]
जहां Rk(t) और αk> 0 इंटर-इवेंट समय का सीडीएफ है और प्रक्रिया की आगमन दर k है।[9]
उदाहरण अनुप्रयोग
एरिक उद्यमी के निकट n मशीनें हैं, जिनमें से प्रत्येक का परिचालन जीवनकाल समान रूप से शून्य और दो वर्षों के मध्य वितरित किया गया है। एरिक प्रत्येक मशीन को तब तक चलने दे सकता है जब तक कि वह विफल न हो जाए और प्रतिस्थापन व्यय €2600; वैकल्पिक रूप से वह €200 की व्यय से किसी भी समय मशीन को परिवर्तित कर सकता है जबकि यह अभी भी कार्यात्मक है।
उसकी इष्टतम प्रतिस्थापन नीति क्या है?
समाधान The lifetime of the n machines can be modeled as n independent concurrent renewal-reward processes, so it is sufficient to consider the case n=1. Denote this process by . The successive lifetimes S of the replacement machines are independent and identically distributed, so the optimal policy is the same for all replacement machines in the process. If Eric decides at the start of a machine's life to replace it at time 0 < t < 2 but the machine happens to fail before that time then the lifetime S of the machine is uniformly distributed on [0, t] and thus has expectation 0.5t. So the overall expected lifetime of the machine is:
and the expected cost W per machine is:
So by the strong law of large numbers, his long-term average cost per unit time is:
then differentiating with respect to t:
this implies that the turning points satisfy:
and thus
We take the only solution t in [0, 2]: t = 2/3. This is indeed a minimum (and not a maximum) since the cost per unit time tends to infinity as t tends to zero, meaning that the cost is decreasing as t increases, until the point 2/3 where it starts to increase.
यह भी देखें
- कैम्पबेल प्रमेय (प्रायिकता)
- यौगिक पॉइसन प्रक्रिया
- सतत समय मार्कोव प्रक्रिया
- लिटिल लेम्मा
- लोटका का अभिन्न समीकरण
- हथेली-खिन्चाइन प्रमेय
- पोइसन प्रक्रिया
- केउटिंग सिद्धांत
- अवशिष्ट समय
- व्यर्थ सिद्धांत
- सेमी-मार्कोव प्रक्रिया
टिप्पणियाँ
- ↑ Grimmett & Stirzaker (1992), p. 393.
- ↑ 2.0 2.1 2.2 Grimmett & Stirzaker (1992), p. 395.
- ↑ Feller (1971), p. 347–351.
- ↑ Grimmett & Stirzaker (1992), p. 394–5.
- ↑ 5.0 5.1 Grimmett & Stirzaker (1992), p. 394.
- ↑ Grimmett & Stirzaker (1992), p. 405.
- ↑ Çinlar, Erhan (1969). "मार्कोव नवीकरण सिद्धांत". Advances in Applied Probability. Applied Probability Trust. 1 (2): 123–187. doi:10.2307/1426216. JSTOR 1426216.
- ↑ Lawrence, A. J. (1973). "सुपरपोजिशन प्रक्रियाओं में घटनाओं के बीच अंतराल की निर्भरता". Journal of the Royal Statistical Society. Series B (Methodological). 35 (2): 306–315. doi:10.1111/j.2517-6161.1973.tb00960.x. JSTOR 2984914. formula 4.1
- ↑ Choungmo Fofack, Nicaise; Nain, Philippe; Neglia, Giovanni; Towsley, Don (6 March 2012). टीटीएल-आधारित कैश नेटवर्क का विश्लेषण. Proceedings of 6th International Conference on Performance Evaluation Methodologies and Tools (report). Retrieved Nov 15, 2012.
संदर्भ
- Cox, David (1970). Renewal Theory. London: Methuen & Co. p. 142. ISBN 0-412-20570-X.
- Doob, J. L. (1948). "Renewal Theory From the Point of View of the Theory of Probability" (PDF). Transactions of the American Mathematical Society. 63 (3): 422–438. doi:10.2307/1990567. JSTOR 1990567.
- Feller, William (1971). An introduction to probability theory and its applications. Vol. 2 (second ed.). Wiley.
- Grimmett, G. R.; Stirzaker, D. R. (1992). Probability and Random Processes (second ed.). Oxford University Press. ISBN 0198572220.
- Smith, Walter L. (1958). "Renewal Theory and Its Ramifications". Journal of the Royal Statistical Society, Series B. 20 (2): 243–302. JSTOR 2983891.
- Wanli Wang, Johannes H. P. Schulz, Weihua Deng, and Eli Barkai (2018). "Renewal theory with fat-tailed distributed sojourn times: Typical versus rare". Phys. Rev. E. 98 (4): 042139. arXiv:1809.05856. Bibcode:2018PhRvE..98d2139W. doi:10.1103/PhysRevE.98.042139. S2CID 54727926.
{{cite journal}}: CS1 maint: multiple names: authors list (link)