परिमित-अंतर समय-डोमेन विधि

परिमित-अंतर समय-कार्यक्षेत्र पद्धति में, अंतरिक्ष में मैक्सवेल के समीकरणों को असतत करने के लिए यी जाली का उपयोग किया जाता है। इस योजना में कंपित ग्रिड पर विद्युत क्षेत्र और चुंबकीय क्षेत्र की नियुक्ति शामिल है।

परिमित-अंतर समय-कार्यक्षेत्र (एफडीटीडी) एक संख्यात्मक विश्लेषण तकनीक है। इसे यी की विधि के रूप में भी जाना जाता है क्योंकि इसका आविष्कार चीनी अमेरिकी व्यावहारिक गणितज्ञ केन एस यी ने किया था जिनका जन्म 1934 में हुआ था। इसका उपयोग अंतर समीकरण की संबंधित प्रणाली के अनुमानित समाधान खोजने के लिए संगणात्मक विद्युतीय गतिविज्ञान प्रतिरूपण के लिए किया जाता है। चूंकि यह एक समय-कार्यक्षेत्र पद्धति है, इसलिए एफडीटीडी समाधान एकल कंप्यूटर सिमुलेशन रन के साथ एक व्यापक आवृत्ति सीमा को सम्मिलित कर सकते हैं और गैर-रैखिक भौतिक गुणों से प्राकृतिक तरीके से व्यवहार कर सकते हैं।

एफडीटीडी विधि ग्रिड-आधारित अंतर संख्यात्मक प्रतिरूपण विधियों (परिमित अंतर विधियों) के सामान्य वर्ग से संबंधित है। समय-अधीन मैक्सवेल के समीकरण आंशिक अंतर समीकरण के रूप में स्थान और समय आंशिक व्युत्पन्न के लिए केंद्रीय अंतर का उपयोग करके अलग-अलग किये जाते है। परिणामी परिमित अंतर समीकरणों को या तो सॉफ्टवेयर या हार्डवेयर में लीपफ्रॉग एकीकरण तरीके से हल किया जाता है: स्थान की मात्रा में विद्युत क्षेत्र सदिश घटको को एक निश्चित समय पर हल किया जाता है फिर उसी स्थानिक आयतन में चुंबकीय क्षेत्र सदिश घटकों को अगले समय में हल किया जाता है और जब तक कि वांछित क्षणिक या स्थिर-स्थिति विद्युत चुम्बकीय क्षेत्र गतिविधि पूरी तरह से विकसित नहीं हो जाती तब तक प्रक्रिया को बार-बार दोहराया जाता है।

इतिहास

दूसरे क्रम की सटीकता प्राप्त करने के लिए स्थान और समय में संगणात्मक द्रव गतिकी समस्याओं में समय-निर्भर आंशिक अंतर समीकरणों (पीडीई) के लिए परिमित अंतर योजनाओं के साथ साथ कंपित ग्रिड पर केंद्रित परिमित अंतर संचालकों का उपयोग करने का विचार सम्मिलित करके कई वर्षों से नियोजित किया गया था। केन यी की एफडीटीडी योजना की नवीनता,मैक्सवेल के कर्ल समीकरणों में प्रत्येक विद्युत और चुंबकीय वेक्टर क्षेत्र घटक के लिए अंतरिक्ष और समय में कंपित ग्रिड पर केंद्रित परिमित अंतर संचालको को लागू करना था जो उनके प्राथमिक 1966 के पत्र में प्रस्तुत की गई थी।

वर्णनकर्ता "परिमित-अंतर समय-डोमेन" और इसके संबंधित एफडीटीडी संक्षिप्त नाम की उत्पत्ति 1980 में एलन टैफ्लोव द्वारा की गई थी।लगभग 1990 के बाद से, एफडीटीडी तकनीक भौतिक संरचनाओं के साथ विद्युत चुम्बकीय तरंगो की परस्पर क्रिया से सुलझाने वाली कई वैज्ञानिक और इंजीनियरिंग समस्याओं को संगणात्मक रूप से प्रतिरूपण करने के लिए प्राथमिक साधन के रूप में उभरी है। वर्तमान एफडीटीडी प्रतिरूपण अनुप्रयोग माइक्रोवेव (रडार हस्ताक्षर प्रौद्योगिकी, एंटीना (रेडियो), तार रहित संचार उपकरण, डिजिटल इंटरकनेक्ट, बायोमेडिकल इमेजिंग/ट्रीटमेंट) के माध्यम से दृश्य प्रकाश के माध्यम से एकदिश धारा (पराबैंगनी-आवृत्ति भूभौतिकी जिसमें संपूर्ण पृथ्वी-आयनमंडल वेवगाइड शामिल है) से लेकर है। (फोटोनिक क्रिस्टल, नैनोप्लाज्मोनिक्स, सॉलिटॉन्स और बायोफोटोनिक्स)। 2006 में, अनुमानित 2,000 एफडीटीडी से संबंधित प्रकाशन विज्ञान और इंजीनियरिंग साहित्य में प्रकाशित हुए (#लोकप्रियता देखें)। 2013 तक, कम से कम 25 वाणिज्यिक/मालिकाना एफडीटीडी सॉफ़्टवेयर विक्रेता हैं; 13 फ्री-सॉफ्टवेयर/ खुला स्त्रोत |ओपन-सोर्स-सॉफ्टवेयर एफडीटीडी प्रोजेक्ट; और 2 फ्रीवेयर/बंद-स्रोत एफडीटीडी परियोजनाएं, कुछ व्यावसायिक उपयोग के लिए नहीं हैं (#बाहरी लिंक देखें)।

एफडीटीडी और मैक्सवेल के समीकरणों का विकास

मैक्सवेल के समीकरणों के लिए एफडीटीडी संख्यात्मक तकनीकों के आधार, तकनीकी विकास और संभावित भविष्य की सराहना पहले उनके इतिहास पर विचार करके विकसित की जा सकती है। निम्नलिखित इस क्षेत्र के कुछ प्रमुख प्रकाशनों को सूचीबद्ध करता है।

मैक्सवेल के समीकरणों के लिए एफडीटीडी तकनीकों और अनुप्रयोगों का आंशिक कालक्रम।
वर्ष	आयोजन
1928	कुरेंट, फ्रेडरिक्स, और लेवी (सीएफएल) स्पष्ट समय-निर्भर परिमित अंतर योजनाओं की सशर्त स्थिरता की खोज के साथ-साथ 1-डी और 2-डी में द्वितीय-क्रम तरंग समीकरण को हल करने के लिए क्लासिक एफडी योजना के साथ सेमिनल पेपर प्रकाशित करते हैं।
1950	निहित/स्पष्ट समय-निर्भर परिमित अंतर विधियों के लिए वॉन न्यूमैन की स्थिरता विश्लेषण की पहली उपस्थिति।
1966	यी ने अंतरिक्ष और समय में कंपित ग्रिडों पर मैक्सवेल के कर्ल समीकरणों को हल करने के लिए एफडीटीडी संख्यात्मक तकनीक का वर्णन किया।
1969	लैम ने वॉन न्यूमैन स्थिरता विश्लेषण को नियोजित करके यी के एल्गोरिदम के लिए सही संख्यात्मक सीएफएल स्थिरता की स्थिति की सूचना दी।
1975	टैफ्लोव और ब्रोडविन ने सामग्री संरचनाओं के साथ दो- और तीन-आयामी विद्युत चुम्बकीय तरंग इंटरैक्शन के पहले साइनसोइडल स्थिर-राज्य एफडीटीडी समाधान की सूचना दी;  और पहला बायोइलेक्ट्रोमैग्नेटिक मॉडल।
1977	हॉलैंड और कुंज और ली ने ईएमपी समस्याओं के लिए यी के एल्गोरिद्म को लागू किया।
1980	टैफ्लोव ने एफडीटीडी परिवर्णी शब्द गढ़ा और तीन आयामी धातु गुहा में साइनसोइडल स्थिर-राज्य विद्युत चुम्बकीय तरंग पैठ के पहले मान्य एफडीटीडी मॉडल प्रकाशित किए।
1981	म्यूर ने यी के ग्रिड के लिए पहला संख्यात्मक रूप से स्थिर, दूसरा क्रम सटीक, अवशोषित सीमा स्थिति (एबीसी) प्रकाशित किया।
1982-83	टैफ्लोव और उमाशंकर ने दो और तीन आयामी संरचनाओं के लिए साइनसोइडल स्थिर-स्थिति निकट-क्षेत्रों, दूर-क्षेत्रों और रडार क्रॉस-सेक्शन की गणना करने वाला पहला एफडीटीडी विद्युत चुम्बकीय तरंग बिखरने वाला मॉडल विकसित किया।
1984	लियाओ एट अल ने बाहरी ग्रिड सीमा से सटे क्षेत्र के स्पेस-टाइम एक्सट्रपलेशन के आधार पर एक बेहतर एबीसी की सूचना दी।
1985	ग्वेयरेक ने एफडीटीडी के एकमुश्त समकक्ष सर्किट फॉर्मूलेशन की शुरुआत की।
1986	चोई और होफ़र ने वेवगाइड संरचनाओं का पहला एफडीटीडी अनुकरण प्रकाशित किया।
1987-88	Kriegsmann et al और मूर et al ने एंटेना और प्रसार पर IEEE लेनदेन में ABC सिद्धांत पर पहला लेख प्रकाशित किया ।
1987-88, 1992	पतले तारों और तार बंडलों के एफडीटीडी प्रतिरूपण की अनुमति देने के लिए उमाशंकर एट अल द्वारा कंटूर-पाथ सबसेल तकनीक पेश की गई थी ,  टैफ्लोव एट अल द्वारा कंडक्टिंग स्क्रीन में दरार के माध्यम से मॉडल पैठ बनाने के लिए,  और जर्गेंस एट अल द्वारा अनुरूप रूप से मॉडल बनाने के लिए सुचारू रूप से घुमावदार स्कैटर की सतह।
1988	सुलिवन एट अल ने एक पूर्ण मानव शरीर द्वारा साइनसोइडल स्थिर-राज्य विद्युत चुम्बकीय तरंग अवशोषण का पहला 3-डी एफडीटीडी मॉडल प्रकाशित किया।
1988	झांग एट अल द्वारा माइक्रोस्ट्रिप्स की एफडीटीडी प्रतिरूपण पेश की गई थी ।
1990-91	ल्यूबर्स एट अल ,  और जोसेफ एट अल द्वारा आवृत्ति-निर्भर डाइइलेक्ट्रिक परमिटिटिविटी की एफडीटीडी प्रतिरूपण पेश की गई थी ।
1990-91	एंटेना के एफडीटीडी प्रतिरूपण को मैलोनी एट अल ,  काट्ज़ एट अल ,  और तिर्कस और बालानीस द्वारा पेश किया गया था।
1990	सानो और शिबाता,  और अल-गज़ाली एट अल द्वारा पिकोसेकंड ऑप्टोइलेक्ट्रॉनिक स्विच की एफडीटीडी प्रतिरूपण पेश की गई थी ।
1992–94	नॉनलाइनियर डिस्पर्सिव मीडिया में ऑप्टिकल दालों के प्रसार की एफडीटीडी प्रतिरूपण पेश की गई, जिसमें गोर्जियन और टैफ्लोव द्वारा एक आयाम में पहला टेम्पोरल सॉलिटॉन शामिल है;  जिओल्कोव्स्की और जुडकिंस द्वारा बीम सेल्फ-फोकसिंग;  जोसेफ एट अल द्वारा दो आयामों में पहला टेम्पोरल सॉलिटॉन ;  और जोसेफ और टैफ्लोव द्वारा दो आयामों में पहला स्थानिक सॉलिटॉन।
1992	गांठ वाले इलेक्ट्रॉनिक सर्किट तत्वों की एफडीटीडी प्रतिरूपण सुई एट अल द्वारा पेश की गई थी ।
1993	टोलैंड एट अल ने लाभ उपकरणों (सुरंग डायोड और गन डायोड) रोमांचक गुहाओं और एंटेना के पहले एफडीटीडी मॉडल प्रकाशित किए।
1993	आओयागी और अन्य एक हाइब्रिड यी एल्गोरिथम/स्केलर-वेव समीकरण प्रस्तुत करते हैं और विद्युत चुम्बकीय तरंग समीकरण के लिए यी योजना के परिमित अंतर योजना की समानता प्रदर्शित करते हैं ।
1994	थॉमस एट अल ने एफडीटीडी स्पेस लैटिस के लिए नॉर्टन के समतुल्य सर्किट की शुरुआत की, जो स्पाइस सर्किट विश्लेषण टूल को नॉनलाइनियर इलेक्ट्रॉनिक घटकों के सटीक सबग्रिड मॉडल या लैटिस के भीतर एम्बेडेड पूर्ण सर्किट को लागू करने की अनुमति देता है।
1994	बेरेंजर ने द्वि-आयामी एफडीटीडी ग्रिड के लिए अत्यधिक प्रभावी, पूरी तरह से मेल खाने वाली परत (PML) ABC की शुरुआत की,  जिसे नवारो एट अल द्वारा गैर-ऑर्थोगोनल मेश तक बढ़ाया गया था ,  और काट्ज़ एट अल द्वारा तीन आयाम ,  और रेउटर एट अल द्वारा वेवगाइड टर्मिनेशन फैलाने के लिए ।
1994	च्यू और वीडॉन ने समन्वय स्ट्रेचिंग पीएमएल पेश किया जो आसानी से तीन आयामों, अन्य समन्वय प्रणालियों और अन्य भौतिक समीकरणों तक बढ़ाया जाता है।
1995-96	Sacks et al और Gedney ने एक शारीरिक रूप से प्राप्य, एक-अक्षीय पूरी तरह से मेल खाने वाली परत (UPML) ABC की शुरुआत की।
1997	लियू ने स्यूडोस्पेक्ट्रल टाइम-डोमेन (PSTD) पद्धति की शुरुआत की, जो Nyquist सीमा पर विद्युत चुम्बकीय क्षेत्र के अत्यधिक मोटे स्थानिक नमूने की अनुमति देती है।
1997	रमाही ने अत्यधिक प्रभावी विश्लेषणात्मक एबीसी को लागू करने के लिए पूरक संचालक विधि (COM) की शुरुआत की।
1998	एफडीटीडी अंतरिक्ष जाली में आवधिक संरचनाओं का विश्लेषण करने के लिए मैलोनी और केसलर ने कई उपन्यास पेश किए।
1998	नागरा और यॉर्क ने इलेक्ट्रोमैग्नेटिक वेव इंटरेक्शन का एक हाइब्रिड एफडीटीडी-क्वांटम मैकेनिक्स मॉडल पेश किया, जिसमें कई ऊर्जा स्तरों के बीच इलेक्ट्रॉनों का संक्रमण होता है।
1998	हेगनेस एट अल ने अल्ट्रावाइडबैंड रडार तकनीकों का उपयोग करके स्तन कैंसर का पता लगाने के लिए एफडीटीडी प्रतिरूपण की शुरुआत की।
1999	श्नाइडर और वैगनर ने जटिल तरंगों के आधार पर एफडीटीडी ग्रिड फैलाव का व्यापक विश्लेषण पेश किया।
2000–01	झेंग, चेन और झांग ने सिद्ध बिना शर्त संख्यात्मक स्थिरता के साथ पहला त्रि-आयामी वैकल्पिक-दिशा अंतर्निहित (एडीआई) एफडीटीडी एल्गोरिदम पेश किया।
2000	रोडेन और गेडनी ने उन्नत दृढ़ पीएमएल (सीपीएमएल) एबीसी की शुरुआत की।
2000	रायलैंडर और बॉन्डसन ने एक सिद्ध रूप से स्थिर एफडीटीडी - परिमित-तत्व टाइम-डोमेन हाइब्रिड तकनीक पेश की।
2002	हयाकावा एट अल और सिम्पसन और टैफ्लोव ने स्वतंत्र रूप से बेहद कम आवृत्ति वाली भूभौतिकीय घटनाओं के लिए वैश्विक पृथ्वी-आयनमंडल वेवगाइड के एफडीटीडी प्रतिरूपण की शुरुआत की।
2003	DeRaedt ने बिना शर्त स्थिर, "वन-स्टेप" एफडीटीडी तकनीक पेश की।
2004	सोरियानो और नवारो ने क्वांटम एफडीटीडी तकनीक के लिए स्थिरता की स्थिति का पता लगाया।
2008	अहमद, चुआ, ली और चेन ने त्रि-आयामी स्थानीय रूप से एक-आयामी (LOD) एफडीटीडी पद्धति की शुरुआत की और बिना शर्त संख्यात्मक स्थिरता साबित की।
2008	तानिगुची, बाबा, नागाओका और अमेतानी ने प्रवाहकीय मीडिया के लिए एफडीटीडी संगणनाओं के लिए थिन वायर प्रतिनिधित्व पेश किया
2009	ओलिविरा और सोब्रिन्हो ने बिजली सबस्टेशन में बिजली के झटके का अनुकरण करने के लिए एफडीटीडी विधि लागू की
2012	मोक्सले एट अल ने एन-बॉडी इंटरेक्टिंग हैमिल्टनियन के लिए एक सामान्यीकृत परिमित-अंतर समय-डोमेन क्वांटम विधि विकसित की।
2013	Moxley et al ने अरेखीय श्रोडिंगर समीकरणों को हल करने के लिए एक सामान्यीकृत परिमित-अंतर समय-डोमेन योजना विकसित की।
2014	Moxley et al ने अरेखीय श्रोडिंगर समीकरणों को हल करने के लिए एक अंतर्निहित सामान्यीकृत परिमित-अंतर समय-डोमेन योजना विकसित की।
2021	ओलिविरा और पाइवा ने एफडीटीडी सीएफएल सीमा से परे समय कदमों का उपयोग करने के लिए लीस्ट स्क्वायर फाइनाइट-डिफरेंस टाइम-डोमेन विधि (एलएस-एफडीटीडी) विकसित की।

एफडीटीडी मॉडल और तरीके

जब मैक्सवेल के विभेदक समीकरणों की जांच की जाती है, तो यह देखा जा सकता है कि समय में ई-क्षेत्र में परिवर्तन (समय व्युत्पन्न) अंतरिक्ष में एच-क्षेत्र में परिवर्तन (कर्ल (गणित)) पर निर्भर है। इसका परिणाम मूल एफडीटीडी समय-स्टेपिंग संबंध में होता है, जो अंतरिक्ष में किसी भी बिंदु पर, समय में ई-फ़ील्ड का अद्यतन मान ई-फ़ील्ड के संग्रहीत मान और H के स्थानीय वितरण के संख्यात्मक कर्ल पर निर्भर होता है। अंतरिक्ष में क्षेत्र।

एच-फ़ील्ड एक समान तरीके से समयबद्ध है। अंतरिक्ष में किसी भी बिंदु पर, समय में एच-फ़ील्ड का अद्यतन मान एच-फ़ील्ड के संग्रहीत मान और अंतरिक्ष में ई-फ़ील्ड के स्थानीय वितरण के संख्यात्मक कर्ल पर निर्भर होता है। ई-फ़ील्ड और एच-फ़ील्ड अपडेट को बदलने से एक मार्चिंग-इन-समय प्रक्रिया होती है जिसमें विचाराधीन निरंतर विद्युत चुम्बकीय तरंगों के नमूना-डेटा एनालॉग कंप्यूटर मेमोरी में संग्रहीत एक संख्यात्मक ग्रिड में प्रचारित होते हैं।

एफडीटीडी के लिए उपयोग किए जाने वाले एक मानक कार्तीय यी सेल का उदाहरण, जिसके बारे में विद्युत और चुंबकीय क्षेत्र वेक्टर घटक वितरित किए जाते हैं।एक घन स्वर के रूप में देखा गया, विद्युत क्षेत्र के घटक घन के किनारों का निर्माण करते हैं, और चुंबकीय क्षेत्र के घटक घन के चेहरों के लिए सामान्य बनाते हैं। त्रि-आयामी अंतरिक्ष जाली में ऐसी यी कोशिकाओं की बहुलता होती है। प्रत्येक विद्युत क्षेत्र घटक के लिए परमिटिटिविटी के उचित मान और प्रत्येक चुंबकीय क्षेत्र घटक के लिए पारगम्यता निर्दिष्ट करके एक विद्युत चुम्बकीय तरंग इंटरैक्शन संरचना को अंतरिक्ष जाली में मैप किया जाता है।

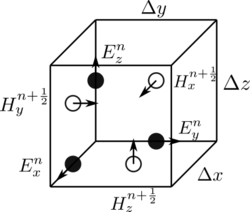
यह विवरण 1-डी, 2-डी और 3-डी एफडीटीडी तकनीकों के लिए सही है। जब कई आयामों पर विचार किया जाता है, तो संख्यात्मक कर्ल की गणना करना जटिल हो सकता है। केन यी के सेमिनल 1966 के पेपर ने कार्टेसियन कम्प्यूटेशनल ग्रिड की आयताकार इकाई कोशिकाओं के बारे में ई-फील्ड और एच-फील्ड के वेक्टर घटकों को स्थानिक रूप से चौंका देने वाला प्रस्ताव दिया ताकि प्रत्येक ई-फील्ड वेक्टर घटक एच-फील्ड वेक्टर घटकों की एक जोड़ी के बीच में स्थित हो, और इसके विपरीत। यह योजना, जिसे अब यी जाली के रूप में जाना जाता है, बहुत मजबूत साबित हुई है, और कई मौजूदा एफडीटीडी सॉफ्टवेयर निर्माणों के मूल में बनी हुई है।

इसके अलावा, यी ने समय में मार्चिंग के लिए एक लीपफ्रॉग योजना प्रस्तावित की जिसमें ई-फील्ड और एच-फील्ड अपडेट कंपित हैं ताकि ई-फील्ड अपडेट लगातार एच-फील्ड अपडेट के बीच प्रत्येक समय-चरण के दौरान बीच में आयोजित किए जाएं, और इसके विपरीत।प्लस साइड पर, यह स्पष्ट समय-स्टेपिंग योजना एक साथ समीकरणों को हल करने की आवश्यकता से बचाती है, और इसके अलावा अपव्यय-मुक्त संख्यात्मक तरंग प्रसार उत्पन्न करती है। नकारात्मक पक्ष पर, यह योजना संख्यात्मक स्थिरता सुनिश्चित करने के लिए समय-कदम पर एक ऊपरी सीमा को अनिवार्य करती है।नतीजतन, सिमुलेशन के कुछ वर्गों को पूरा करने के लिए हजारों समय-चरणों की आवश्यकता हो सकती है।

एफडीटीडी पद्धति का उपयोग करना

मैक्सवेल के समीकरणों के एफडीटीडी समाधान को लागू करने के लिए, एक कम्प्यूटेशनल कार्यक्षेत्र को पहले स्थापित किया जाना चाहिए। कम्प्यूटेशनल कार्यक्षेत्र केवल भौतिक क्षेत्र है जिस पर अनुकरण किया जाएगा। उस कम्प्यूटेशनल कार्यक्षेत्र के भीतर अंतरिक्ष में हर बिंदु पर ई और एच फ़ील्ड निर्धारित किए जाते हैं। कम्प्यूटेशनल कार्यक्षेत्र के भीतर प्रत्येक सेल की सामग्री निर्दिष्ट होनी चाहिए। आमतौर पर, सामग्री या तो फ्री-स्पेस (वायु), धातु या ढांकता हुआ है। किसी भी सामग्री का उपयोग तब तक किया जा सकता है जब तक कि पारगम्यता (विद्युत चुंबकत्व), पारगम्यता और विद्युत चालकता निर्दिष्ट हो।

सारणीबद्ध रूप में फैलाने वाली सामग्रियों की पारगम्यता को एफडीटीडी योजना में सीधे प्रतिस्थापित नहीं किया जा सकता है। इसके बजाय, इसे कई डेबी, ड्रूड, लॉरेंत्ज़ या महत्वपूर्ण बिंदु शब्दों का उपयोग करके अनुमानित किया जा सकता है। यह सन्निकटन ओपन फिटिंग प्रोग्राम का उपयोग करके प्राप्त किया जा सकता हैऔर जरूरी नहीं कि इसका भौतिक अर्थ हो।

कम्प्यूटेशनल कार्यक्षेत्र और ग्रिड सामग्री स्थापित होने के बाद, एक स्रोत निर्दिष्ट किया जाता है। स्रोत एक तार, लागू विद्युत क्षेत्र या समतल तरंग पर करंट हो सकता है। पिछले मामले में एफडीटीडी का उपयोग मनमाना आकार की वस्तुओं, विभिन्न घटना कोणों पर प्लानर आवधिक संरचनाओं से प्रकाश बिखरने का अनुकरण करने के लिए किया जा सकता है,और अनंत आवधिक संरचनाओं की फोटोनिक बैंड संरचना।

चूंकि ई और एच फ़ील्ड सीधे निर्धारित किए जाते हैं, सिमुलेशन का आउटपुट आमतौर पर कम्प्यूटेशनल कार्यक्षेत्र के भीतर एक बिंदु या बिंदुओं की एक श्रृंखला पर ई या एच फ़ील्ड होता है। सिमुलेशन समय में ई और एच क्षेत्रों को आगे बढ़ाता है।

सिमुलेशन द्वारा लौटाए गए ई और एच क्षेत्रों पर प्रसंस्करण किया जा सकता है। सिम्युलेशन चालू रहने के दौरान डेटा प्रोसेसिंग भी हो सकती है।

जबकि एफडीटीडी तकनीक एक कॉम्पैक्ट स्थानिक क्षेत्र के भीतर विद्युत चुम्बकीय क्षेत्रों की गणना करती है, बिखरे हुए और / या विकीर्ण दूर के क्षेत्रों को निकट-से-दूर-क्षेत्र परिवर्तनों के माध्यम से प्राप्त किया जा सकता है।

एफडीटीडी प्रतिरूपण की ताकत

हर प्रतिरूपण तकनीक में ताकत और कमजोरियां होती हैं, और एफडीटीडी पद्धति अलग नहीं है।

• एफडीटीडी मैक्सवेल के समीकरणों को हल करने के लिए उपयोग की जाने वाली एक बहुमुखी प्रतिरूपण तकनीक है। यह सहज है, इसलिए उपयोगकर्ता आसानी से समझ सकते हैं कि इसका उपयोग कैसे करना है और किसी दिए गए मॉडल से क्या उम्मीद करनी है।
• एफडीटीडी एक समय-कार्यक्षेत्र तकनीक है, और जब एक ब्रॉडबैंड पल्स (जैसे गॉसियन पल्स) का उपयोग स्रोत के रूप में किया जाता है, तो एक ही सिमुलेशन के साथ आवृत्तियों की एक विस्तृत श्रृंखला पर सिस्टम की प्रतिक्रिया प्राप्त की जा सकती है। यह उन अनुप्रयोगों में उपयोगी है जहां गुंजयमान आवृत्तियों को सटीक रूप से ज्ञात नहीं है, या किसी भी समय ब्रॉडबैंड परिणाम वांछित है।
• चूंकि एफडीटीडी कम्प्यूटेशनल कार्यक्षेत्र में हर जगह ई और एच क्षेत्रों की गणना करता है क्योंकि वे समय में विकसित होते हैं, यह मॉडल के माध्यम से विद्युत चुम्बकीय क्षेत्र आंदोलन के एनिमेटेड डिस्प्ले प्रदान करने के लिए खुद को उधार देता है। इस प्रकार का प्रदर्शन यह समझने में उपयोगी होता है कि मॉडल में क्या हो रहा है, और यह सुनिश्चित करने में मदद करता है कि मॉडल ठीक से काम कर रहा है।
• एफडीटीडी तकनीक उपयोगकर्ता को कम्प्यूटेशनल कार्यक्षेत्र के भीतर सभी बिंदुओं पर सामग्री निर्दिष्ट करने की अनुमति देती है। रैखिक और गैर-रैखिक ढांकता हुआ और चुंबकीय सामग्री की एक विस्तृत विविधता स्वाभाविक रूप से और आसानी से प्रतिरूपण की जा सकती है।
• एफडीटीडी एपर्चर के प्रभाव को सीधे निर्धारित करने की अनुमति देता है। परिरक्षण प्रभाव पाया जा सकता है, और एक संरचना के अंदर और बाहर दोनों क्षेत्रों को प्रत्यक्ष या अप्रत्यक्ष रूप से पाया जा सकता है।
• एफडीटीडी सीधे E और H फ़ील्ड का उपयोग करता है। चूंकि अधिकांश ईएमआई/ईएमसी प्रतिरूपण एप्लिकेशन ई और एच क्षेत्रों में रुचि रखते हैं, इसलिए यह सुविधाजनक है कि इन मूल्यों को प्राप्त करने के लिए सिमुलेशन चलने के बाद कोई रूपांतरण नहीं किया जाना चाहिए।

एफडीटीडी प्रतिरूपण की कमजोरियां

एक साधारण एक-आयामी एफडीटीडी योजना में एक वर्ग पल्स सिग्नल का संख्यात्मक फैलाव। नाड़ी के किनारों के चारों ओर बजने वाली कलाकृतियों को भारी रूप से उच्चारण किया जाता है (गिब्स घटना) और सिग्नल विकृत हो जाता है क्योंकि यह फैलाव (ऑप्टिक्स) की अनुपस्थिति में भी फैलता है। यह आर्टिफैक्ट विवेकीकरण योजना का प्रत्यक्ष परिणाम है।

* चूँकि एफडीटीडी के लिए आवश्यक है कि संपूर्ण कम्प्यूटेशनल कार्यक्षेत्र को ग्रिड किया जाए, और मॉडल में सबसे छोटी इलेक्ट्रोमैग्नेटिक वेवलेंथ और सबसे छोटी ज्यामितीय विशेषता दोनों को हल करने के लिए ग्रिड स्थानिक विवेक पर्याप्त रूप से ठीक होना चाहिए, बहुत बड़े कम्प्यूटेशनल कार्यक्षेत्र विकसित किए जा सकते हैं, जिसके परिणामस्वरूप बहुत लंबा परिणाम होता है समाधान समय। अत्यधिक बड़े कम्प्यूटेशनल कार्यक्षेत्र की आवश्यकता के कारण एफडीटीडी में लंबे, पतले फीचर्स (जैसे तार) वाले मॉडल को मॉडल करना मुश्किल है। ईजेनमोड विस्तार जैसे तरीके एक अधिक कुशल विकल्प प्रदान कर सकते हैं क्योंकि उन्हें जेड-दिशा के साथ ठीक ग्रिड की आवश्यकता नहीं होती है।* सामग्री इंटरफ़ेस पर पारगम्यता और पारगम्यता के लिए अद्वितीय मान निर्धारित करने का कोई तरीका नहीं है।

• अंतरिक्ष और समय के कदमों को कुरेंट-फ्रेडरिक-लेवी की स्थिति को पूरा करना चाहिए, या आंशिक अंतर समीकरण को हल करने के लिए उपयोग किए जाने वाले लीपफ्रॉग एकीकरण के अस्थिर होने की संभावना है।
• एफडीटीडी कम्प्यूटेशनल कार्यक्षेत्र में हर जगह सीधे E/H फ़ील्ड ढूंढता है। यदि कुछ दूरी पर क्षेत्र मान वांछित हैं, तो संभावना है कि यह दूरी कम्प्यूटेशनल कार्यक्षेत्र को अत्यधिक बड़ा होने के लिए मजबूर करेगी। एफडीटीडी के लिए फार-फील्ड एक्सटेंशन उपलब्ध हैं, लेकिन कुछ पोस्टप्रोसेसिंग की आवश्यकता होती है।* चूंकि एफडीटीडी सिमुलेशन कम्प्यूटेशनल कार्यक्षेत्र के भीतर सभी बिंदुओं पर ई और एच फ़ील्ड की गणना करता है, कम्प्यूटेशनल कार्यक्षेत्र को कंप्यूटर मेमोरी में अपने निवास की अनुमति देने के लिए परिमित होना चाहिए। कई मामलों में यह अनुकरण स्थान में कृत्रिम सीमाओं को सम्मिलित करके प्राप्त किया जाता है। ऐसी सीमाओं द्वारा शुरू की गई त्रुटियों को कम करने के लिए सावधानी बरतनी चाहिए। असीमित असीमित कम्प्यूटेशनल कार्यक्षेत्र को अनुकरण करने के लिए कई उपलब्ध अत्यधिक प्रभावी अवशोषित सीमा स्थितियां (एबीसी) हैं। इसके बजाय अधिकांश आधुनिक एफडीटीडी कार्यान्वयन एक विशेष अवशोषित सामग्री का उपयोग करते हैं, जिसे अवशोषित सीमाओं को लागू करने के लिए पूरी तरह से मिलान वाली परत (पीएमएल) कहा जाता है।* क्योंकि एफडीटीडी को समय कार्यक्षेत्र में फील्ड्स को आगे बढ़ाकर हल किया जाता है, माध्यम के इलेक्ट्रोमैग्नेटिक समय रिस्पांस को स्पष्ट रूप से मॉडल किया जाना चाहिए। मनमाने ढंग से प्रतिक्रिया के लिए, इसमें कम्प्यूटेशनल रूप से महंगा समय संकल्प शामिल है, हालांकि ज्यादातर मामलों में माध्यम (या फैलाव (ऑप्टिक्स)) की समय प्रतिक्रिया पर्याप्त रूप से हो सकती है और रिकर्सिव दृढ़ संकल्प (आरसी) तकनीक, सहायक अंतर समीकरण का उपयोग करके आसानी से तैयार की जा सकती है। (एडीई) तकनीक, या जेड-ट्रांसफॉर्म तकनीक। मैक्सवेल के समीकरणों को हल करने का एक वैकल्पिक तरीका जो मनमाना फैलाव का आसानी से इलाज कर सकता है, वह है कम्प्यूटेशनल इलेक्ट्रोडायनामिक्स#स्यूडो-स्पेक्ट्रल स्थानिक कार्यक्षेत्र .28PSSD.29|छद्म-स्पेक्ट्रल स्थानिक कार्यक्षेत्र (PSSD), जो इसके बजाय अंतरिक्ष में फ़ील्ड्स को आगे बढ़ाता है।

ग्रिड ट्रंकेशन तकनीक

खुले क्षेत्र की एफडीटीडी प्रतिरूपण समस्याओं के लिए सबसे अधिक इस्तेमाल की जाने वाली ग्रिड ट्रंकेशन तकनीकें मुर अवशोषित सीमा स्थिति (एबीसी) हैं,लियाओ एबीसी,और विभिन्न पूरी तरह से मेल खाने वाली परत (पीएमएल) फॉर्मूलेशन।मुर और लियाओ तकनीकें पीएमएल की तुलना में सरल हैं। हालांकि, पीएमएल (जो तकनीकी रूप से सीमा की स्थिति के बजाय एक अवशोषित क्षेत्र है) ऑर्डर-ऑफ-परिमाण कम प्रतिबिंब प्रदान कर सकता है। पीएमएल अवधारणा जे.पी. द्वारा पेश की गई थी। 1994 के जर्नल ऑफ कम्प्यूटेशनल फिजिक्स में एक सेमिनल पेपर में बेरेन्जर। 1994 के बाद से, बेरेंजर के मूल विभाजन-क्षेत्र कार्यान्वयन को संशोधित किया गया है और इसे एक अक्षीय पीएमएल (यूपीएमएल), दृढ़ पीएमएल (सीपीएमएल) और उच्च-क्रम पीएमएल तक बढ़ाया गया है। बाद के दो पीएमएल योगों में क्षणभंगुर तरंगों को अवशोषित करने की क्षमता में वृद्धि हुई है, और इसलिए सिद्धांत रूप में बेरेंजर के मूल सूत्रीकरण की तुलना में एक सिम्युलेटेड स्कैटरिंग या रेडिएटिंग संरचना के करीब रखा जा सकता है।

पीएमएल से अवांछित संख्यात्मक प्रतिबिंब को कम करने के लिए अतिरिक्त बैक अब्ज़ॉर्बिंग लेयर्स तकनीक का उपयोग किया जा सकता है।

लोकप्रियता

अकादमिक प्रकाशन में सामान्य वृद्धि दोनों के बावजूद उसी अवधि के दौरान थ्रूपुट और ब्याज का समग्र विस्तार सभी कम्प्यूटेशनल इलेक्ट्रोमैग्नेटिक्स (CEM) तकनीकों में, हैं एफडीटीडी में रुचि के जबरदस्त विस्तार के सात प्राथमिक कारण मैक्सवेल के समीकरणों के लिए कम्प्यूटेशनल समाधान दृष्टिकोण:

1. एफडीटीडी को मैट्रिक्स व्युत्क्रम की आवश्यकता नहीं है। पूरी तरह से स्पष्ट संगणना होने के नाते, एफडीटीडी मैट्रिक्स व्युत्क्रम के साथ कठिनाइयों से बचा जाता है जो आवृत्ति-कार्यक्षेत्र अभिन्न-समीकरण और परिमित-तत्व इलेक्ट्रोमैग्नेटिक्स मॉडल के आकार को आम तौर पर 10 से कम तक सीमित करता है।⁹ विद्युत चुम्बकीय क्षेत्र अज्ञात।एफडीटीडी मॉडल 10 के साथ⁹ फ़ील्ड अज्ञात चलाए गए हैं; इस संख्या के लिए कोई आंतरिक ऊपरी सीमा नहीं है।# एफडीटीडी सटीक और मजबूत है। एफडीटीडी गणनाओं में त्रुटि के स्रोत अच्छी तरह से समझे जाते हैं, और विद्युत चुम्बकीय तरंग अंतःक्रियात्मक समस्याओं की एक बहुत बड़ी विविधता के लिए सटीक मॉडल की अनुमति देने के लिए बाध्य किए जा सकते हैं।# एफडीटीडी आवेगी व्यवहार का स्वाभाविक रूप से इलाज करता है। समय-कार्यक्षेत्र तकनीक होने के नाते, एफडीटीडी सीधे विद्युत चुम्बकीय प्रणाली की आवेग प्रतिक्रिया की गणना करता है। इसलिए, एक एकल एफडीटीडी सिमुलेशन उत्तेजना स्पेक्ट्रम के भीतर किसी भी आवृत्ति पर या तो अल्ट्रावाइडबैंड टेम्पोरल वेवफॉर्म या साइनसोइडल स्थिर-राज्य प्रतिक्रिया प्रदान कर सकता है।# एफडीटीडी अरेखीय व्यवहार को स्वाभाविक रूप से व्यवहार करता है। समय-कार्यक्षेत्र तकनीक होने के नाते, एफडीटीडी सीधे इलेक्ट्रोमैग्नेटिक सिस्टम की गैर-रैखिक प्रतिक्रिया की गणना करता है। यह एफडीटीडी के सहायक अंतर समीकरणों के सेट के साथ प्राकृतिक संकरण की अनुमति देता है जो शास्त्रीय या अर्ध-शास्त्रीय दृष्टिकोण से गैर-रैखिकताओं का वर्णन करता है। एक अनुसंधान फ्रंटियर हाइब्रिड एल्गोरिदम का विकास है जो क्वांटम इलेक्ट्रोडायनामिक्स, विशेष रूप से वैक्यूम उतार-चढ़ाव, जैसे कासिमिर प्रभाव से उत्पन्न होने वाली घटनाओं के साथ एफडीटीडी शास्त्रीय इलेक्ट्रोडायनामिक्स मॉडल में शामिल होता है।
2. एफडीटीडी एक व्यवस्थित दृष्टिकोण है। एफडीटीडी के साथ, एक नई संरचना को मॉडल करने के लिए निर्दिष्ट करना एक अभिन्न समीकरण के संभावित जटिल सुधार की बजाय जाल पीढ़ी की समस्या को कम कर दिया गया है। उदाहरण के लिए, एफडीटीडी को संरचना-निर्भर ग्रीन फ़ंक्शंस की गणना की आवश्यकता नहीं है।# समानांतर-प्रसंस्करण कंप्यूटर आर्किटेक्चर सुपरकंप्यूटिंग पर हावी हो गए हैं। एफडीटीडी समानांतर-प्रसंस्करण सीपीयू-आधारित कंप्यूटरों पर उच्च दक्षता के साथ, और हाल ही में विकसित जीपीयू-आधारित त्वरक तकनीक पर बहुत अच्छी तरह से काम करता है।# कंप्यूटर विज़ुअलाइज़ेशन क्षमताएं तेजी से बढ़ रही हैं। हालांकि यह प्रवृत्ति सभी संख्यात्मक तकनीकों को सकारात्मक रूप से प्रभावित करती है, यह एफडीटीडी विधियों के लिए विशेष रूप से फायदेमंद है, जो क्षेत्र की गतिशीलता को चित्रित करने के लिए रंगीन वीडियो में उपयोग के लिए उपयुक्त फ़ील्ड मात्राओं के समय-मार्चेड एरे उत्पन्न करते हैं।

टैफ्लोव ने तर्क दिया है कि ये कारक मिलकर सुझाव देते हैं कि एफडीटीडी इनमें से एक रहेगा

प्रमुख कम्प्यूटेशनल इलेक्ट्रोडायनामिक्स तकनीक (साथ ही संभावित रूप से अन्य बहु-भौतिकी समस्याएं)।

कार्यान्वयन

सैकड़ों सिमुलेशन उपकरण हैं (जैसे ओमनीसिम, एक्सएफडीटीडी, ल्यूमेरिकल, सीएसटी स्टूडियो सूट, ऑप्टीएफडीटीडी आदि) जो एफडीटीडी एल्गोरिदम को लागू करते हैं, कई समानांतर-प्रसंस्करण समूहों पर चलने के लिए अनुकूलित हैं।

यह भी देखें

• कम्प्यूटेशनल इलेक्ट्रोमैग्नेटिक्स
• ईजेनमोड विस्तार
• बीम प्रसार विधि
• परिमित-अंतर आवृत्ति-कार्यक्षेत्र
• सीमित तत्व विधि
• बिखराव-मैट्रिक्स विधि
• असतत द्विध्रुवीय सन्निकटन

अग्रिम पठन

The following article in Nature Milestones: Photons illustrates the historical significance of the FDTD method as related to Maxwell's equations:

• David Pile (May 2010). "Milestone 2 (1861) Maxwell's equations". Nature Milestones: Photons. doi:10.1038/nmat2639. Retrieved 17 June 2010.

Allen Taflove's interview, "Numerical Solution," in the January 2015 focus issue of Nature Photonics honoring the 150th anniversary of the publication of Maxwell's equations. This interview touches on how the development of FDTD ties into the century and one-half history of Maxwell's theory of electrodynamics:

• Nature Photonics interview

The following university-level textbooks provide a good general introduction to the FDTD method:

• Karl S. Kunz; Raymond J. Luebbers (1993). The Finite Difference Time Domain Method for Electromagnetics. CRC Press. ISBN 978-0-8493-8657-2. Archived from the original on 2007-12-10. Retrieved 2006-08-05.

• Allen Taflove; Susan C. Hagness (2005). Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed. Artech House Publishers. ISBN 978-1-58053-832-9.

• Wenhua Yu; Raj Mittra; Tao Su; Yongjun Liu; Xiaoling Yang (2006). Parallel Finite-Difference Time-Domain Method. Artech House Publishers. ISBN 978-1-59693-085-8.

• John B. Schneider (2010). Understanding the FDTD Method. available online.

बाहरी संबंध

Free software/Open-source software एफडीटीडी projects:

• एफडीटीडी++: advanced, fully featured एफडीटीडी software, along with sophisticated material models and predefined fits as well as discussion/support forums and email support
• openEMS (Fully 3D Cartesian & Cylindrical graded mesh EC-एफडीटीडी Solver, written in C++, using a Matlab/Octave-Interface)
• pएफडीटीडी (3D C++ एफडीटीडी codes developed by Se-Heon Kim)
• Jएफडीटीडी (2D/3D C++ एफडीटीडी codes developed for nanophotonics by Jeffrey M. McMahon)
• WOLFSIM Archived 2008-07-02 at the Wayback Machine (NCSU) (2-D)
• Meep (MIT, 2D/3D/cylindrical parallel एफडीटीडी)
• (Geo-) Radar FDTD
• bigboy (unmaintained, no release files. must get source from cvs)
• Parallel (MPI&OpenMP) FDTD codes in C++ (developed by Zs. Szabó)
• FDTD code in Fortran 90
• FDTD code in C for 2D EM Wave simulation
• Angora (3D parallel FDTD software package, maintained by Ilker R. Capoglu)
• GSvit (3D FDTD solver with graphics card computing support, written in C, graphical user interface XSvit available)
• gprMax (Open Source (GPLv3), 3D/2D FDTD modelling code in Python/Cython developed for GPR but can be used for general EM modelling.)

Freeware/Closed source FDTD projects (some not for commercial use):

• EMTL (Electromagnetic Template Library) (Free С++ library for electromagnetic simulations. The current version implements mainly the FDTD).