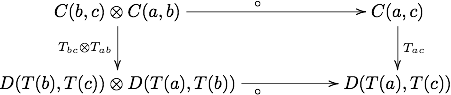समृद्ध श्रेणी: Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
 
(6 intermediate revisions by 4 users not shown)
Line 1: Line 1:
<nowiki>{{Short description|Category whose hom sets have algebraic structure}</nowiki>[[श्रेणी सिद्धांत]] में, गणित की शाखा, एक समृद्ध श्रेणी सामान्य [[मोनोइडल श्रेणी]] से वस्तुओं के साथ [[ होम सेट ]] को बदलकर [[श्रेणी (गणित)]] के विचार को सामान्यीकृत करती है। यह अवलोकन से प्रेरित है कि, कई व्यावहारिक अनुप्रयोगों में, होम-सेट में अक्सर अतिरिक्त संरचना होती है जिसका सम्मान किया जाना चाहिए, उदाहरण के लिए, आकारिकी का सदिश स्थान या आकारिकी का स्थलीय स्थान होना।  समृद्ध श्रेणी में, वस्तुओं की प्रत्येक जोड़ी के साथ जुड़े [[morphism]]s (होम-सेट) का सेट  ऑब्जेक्ट (श्रेणी सिद्धांत) द्वारा होम-ऑब्जेक्ट्स की कुछ निश्चित मोनोइडल श्रेणी में बदल दिया जाता है। सामान्य श्रेणी में morphisms की (सहयोगी) संरचना का अनुकरण करने के लिए, गृह-श्रेणी में होम-ऑब्जेक्ट्स को सहयोगी तरीके से बनाने का साधन होना चाहिए: यानी, हमें कम से कम देने वाली वस्तुओं पर बाइनरी ऑपरेशन होना चाहिए मोनोइडल श्रेणी की संरचना, हालांकि कुछ संदर्भों में ऑपरेशन को क्रमविनिमेय होने की आवश्यकता हो सकती है और शायद  सही आसन्न होने की भी (यानी, श्रेणी को [[सममित मोनोइडल श्रेणी]] या यहां तक ​​​​कि [[बंद मोनोइडल श्रेणी]] बनाना, क्रमशः)।
[[श्रेणी सिद्धांत]] में, गणित की एक शाखा, एक '''समृद्ध श्रेणी''' एक सामान्य [[मोनोइडल श्रेणी]] से वस्तुओं के साथ [[ होम सेट |होम सेट]] को बदलकर एक [[श्रेणी (गणित)]] के विचार को सामान्यीकृत करती है। यह अवलोकन से प्रेरित है कि, कई व्यावहारिक अनुप्रयोगों में, होम-सेट में अधिकांशतः अतिरिक्त संरचना होती है जिसका सम्मान किया जाना चाहिए, उदाहरण के लिए, आकारिकी का सदिश स्थान या आकारिकी का एक स्थलीय स्थान होना है। एक समृद्ध श्रेणी में, वस्तुओं की प्रत्येक जोड़ी से जुड़े [[morphism|रूपवाद]] (होम-सेट) का समुच्चय "होम-ऑब्जेक्ट्स" की कुछ निश्चित मोनोइडल श्रेणी में ऑब्जेक्ट द्वारा प्रतिस्थापित किया जाता है। एक सामान्य श्रेणी में रूपवाद की (सहयोगी) संरचना का अनुकरण करने के लिए, गृह-श्रेणी में होम-ऑब्जेक्ट्स को सहयोगी विधि से बनाने का एक साधन होना चाहिए: अर्थात, हमें कम से कम देने वाली वस्तुओं पर एक बाइनरी ऑपरेशन होना चाहिए एक मोनोइडल श्रेणी की संरचना, चूँकि कुछ संदर्भों में ऑपरेशन को क्रमविनिमेय होने की भी आवश्यकता हो सकती है और संभवतः एक सही आसन्न होने की भी आवश्यकता हो सकती है (अर्थात, श्रेणी को [[सममित मोनोइडल श्रेणी]] या यहां तक ​​​​कि [[बंद मोनोइडल श्रेणी]] बनाना)।  


समृद्ध श्रेणी सिद्धांत इस प्रकार एक ही ढांचे के भीतर विभिन्न प्रकार की संरचनाओं को शामिल करता है
समृद्ध श्रेणी सिद्धांत इस प्रकार एक ही ढांचे के अन्दर विभिन्न प्रकार की संरचनाओं को सम्मिलित करता है
* सामान्य श्रेणियां जहां होम-सेट में सेट होने के अलावा अतिरिक्त संरचना होती है। यही है, आकारिकी के ऐसे संचालन या गुण होते हैं जिन्हें संरचना द्वारा सम्मानित करने की आवश्यकता होती है (उदाहरण के लिए, [[2-श्रेणी]] में morphisms और क्षैतिज संरचना के बीच 2-कोशिकाओं का अस्तित्व, या [[एबेलियन श्रेणी]] में morphisms पर अतिरिक्त संचालन )
* सामान्य श्रेणियां जहां होम-सेट में समुच्चय होने के अतिरिक्त अतिरिक्त संरचना होती है। यही है, आकारिकी के ऐसे संचालन या गुण होते हैं जिन्हें संरचना द्वारा सम्मानित करने की आवश्यकता होती है (उदाहरण के लिए, [[2-श्रेणी]] में रूपवाद और क्षैतिज संरचना के मध्य 2-कोशिकाओं का अस्तित्व, या [[एबेलियन श्रेणी]] में रूपवाद पर अतिरिक्त संचालन ) |
* श्रेणी-जैसी संस्थाएँ जिनके पास स्वयं व्यक्तिगत रूपवाद की कोई धारणा नहीं है, लेकिन जिनके होम-ऑब्जेक्ट्स में समान रचना संबंधी पहलू हैं (उदाहरण के लिए, पूर्व-आदेश जहाँ रचना नियम ट्रांज़िटिविटी, या स्यूडोक्वासिमेट्रिक स्पेस सुनिश्चित करता है। लॉवर के मेट्रिक स्पेस, जहाँ होम-ऑब्जेक्ट्स हैं संख्यात्मक दूरियाँ और रचना नियम त्रिभुज असमानता प्रदान करता है)।
* श्रेणी-जैसी संस्थाएँ जिनके पास स्वयं व्यक्तिगत रूपवाद की कोई धारणा नहीं है, किन्तु जिनके होम-ऑब्जेक्ट्स में समान रचना संबंधी पहलू हैं (उदाहरण के लिए, पूर्व-आदेश जहाँ रचना नियम संक्रामकता, या स्यूडोक्वासिआव्यूह स्पेस सुनिश्चित करता है। लॉवर के आव्यूह स्पेस, जहाँ होम-ऑब्जेक्ट्स हैं संख्यात्मक दूरियाँ और रचना नियम त्रिभुज असमानता प्रदान करता है)।


ऐसे मामले में जहां होम-ऑब्जेक्ट श्रेणी सामान्य कार्टेशियन उत्पाद के साथ [[सेट की श्रेणी]] होती है, समृद्ध श्रेणी की परिभाषाएं, समृद्ध फ़ैक्टर इत्यादि ... सामान्य श्रेणी सिद्धांत से मूल परिभाषाओं को कम करती हैं।
ऐसे स्थिति में जहां होम-ऑब्जेक्ट श्रेणी सामान्य कार्टेशियन उत्पाद के साथ [[सेट की श्रेणी|समुच्चय की श्रेणी]] होती है, समृद्ध श्रेणी की परिभाषाएं, समृद्ध फ़ैक्टर इत्यादि सामान्य श्रेणी सिद्धांत से मूल परिभाषाओं को कम करती हैं।
 
मोनोइडल श्रेणी एम से होम-ऑब्जेक्ट्स के साथ  समृद्ध श्रेणी को एम से अधिक समृद्ध श्रेणी या एम में समृद्ध श्रेणी या केवल एम-श्रेणी कहा जाता है। मोनोइडल श्रेणी के संदर्भ में वी अक्षर के लिए मैक लेन की वरीयता के कारण, समृद्ध श्रेणियों को कभी-कभी आम तौर पर वी-श्रेणियों के रूप में भी संदर्भित किया जाता है।
 
'''मोनोइडल श्रेणी एम से होम-ऑब्जेक्ट्स के साथ  समृद्ध श्रेणी को एम से अधिक समृद्ध श्रेणी या एम में समृद्ध श्रेणी या केवल एम-श्रेणी कहा जाता है। मोनोइडल श्रेणी के संदर्भ में वी अक्षर के लिए मैक लेन'''


मोनोइडल श्रेणी M से होम-ऑब्जेक्ट्स के साथ समृद्ध श्रेणी को M से अधिक समृद्ध श्रेणी या M में समृद्ध श्रेणी या केवल M-श्रेणी कहा जाता है। मोनोइडल श्रेणी के संदर्भ में V अक्षर के लिए मैक लेन की वरीयता के कारण, समृद्ध श्रेणियों को कभी-कभी सामान्यतः V-श्रेणियों के रूप में भी संदर्भित किया जाता है।
== परिभाषा ==
== परिभाषा ==
होने देना {{math|('''M''', ⊗, ''I'', ''α'', ''λ'', ''ρ'')}} monoidal श्रेणी हो। फिर समृद्ध श्रेणी 'सी' (वैकल्पिक रूप से, ऐसी स्थितियों में जहां मोनोइडल श्रेणी की पसंद स्पष्ट होनी चाहिए, 'एम', या 'एम' श्रेणी से समृद्ध श्रेणी), में शामिल हैं
{{math|('''M''', ⊗, ''I'', ''α'', ''λ'', ''ρ'')}} एक मोनोइडल श्रेणी हो। फिर एक समृद्ध श्रेणी C (वैकल्पिक रूप से उन स्थितियों में जहां मोनोइडल श्रेणी की पसंद को स्पष्ट रूप से M, या M-श्रेणी से समृद्ध श्रेणी की आवश्यकता होती है) में सम्मिलित हैं
* 'सी' की वस्तुओं का [[वर्ग (सेट सिद्धांत)]] ओबी ('सी'),
* 'C' की वस्तुओं का [[वर्ग (सेट सिद्धांत)|वर्ग (समुच्चय सिद्धांत)]] OB ('C'),है |
* <nowiki>वस्तु {{math|</nowiki>''C''(''a'', ''b'')}वस्तुओं की प्रत्येक जोड़ी के लिए M का } ''a'', ''b'' C में, तीर को परिभाषित करने के लिए उपयोग किया जाता है <math>f:a\rightarrow b</math> सी में  तीर के रूप में <math>f:I\rightarrow C(a,b)</math> एम में,
* वस्तु ''C''(''a'', ''b'') वस्तुओं की प्रत्येक जोड़ी के लिए M का ऑब्जेक्ट ''a'', ''b'' C में, तीर <math>f:a\rightarrow b</math> को परिभाषित करने के लिए उपयोग किया जाता है | <math>f:I\rightarrow C(a,b)</math> M में तीर के रूप में परिभाषित करने के लिए प्रयोग किया जाता है,|
* तीर {{math|id<sub>''a''</sub> : ''I'' → ''C''(''a'', ''a'')}} M में C में प्रत्येक वस्तु ''a'' के लिए ''पहचान'' निर्दिष्ट करता है, और
* तीर {{math|id<sub>''a''</sub> : ''I'' → ''C''(''a'', ''a'')}} M में C में प्रत्येक वस्तु ''a'' के लिए ''पहचान'' निर्दिष्ट करता है,|
* तीर {{math|°<sub>''abc''</sub> : ''C''(''b'', ''c'') ⊗ ''C''(''a'', ''b'') → ''C''(''a'', ''c'')}} एम में वस्तुओं के प्रत्येक ट्रिपल ''ए'', ''बी'', ''सी'' के लिए ''कंपोजीशन'' को नामित करते हुए सी में, की संरचना को परिभाषित करने के लिए उपयोग किया जाता है <math>f:a\rightarrow b</math> और <math>g:b\rightarrow c</math> इंका <math>g \circ_{\textbf{C}} f = {^\circ}_{abc}(g\otimes f)</math> साथ तीन आने वाले आरेखों के साथ, नीचे चर्चा की गई।
* तीर {{math|°<sub>''abc''</sub> : ''C''(''b'', ''c'') ⊗ ''C''(''a'', ''b'') → ''C''(''a'', ''c'')}} M ''C'' में वस्तुओं के प्रत्येक ट्रिपल a, b, c के लिए ''रचना'' को निर्दिष्ट करता है, जिसका उपयोग संरचना को परिभाषित करने के लिए उपयोग किया जाता है <math>f:a\rightarrow b</math> और <math>g:b\rightarrow c</math> ''C'' में <math>g \circ_{\textbf{C}} f = {^\circ}_{abc}(g\otimes f)</math> साथ तीन आने वाले आरेखों के साथ, नीचे चर्चा की गई।


पहला आरेख रचना की साहचर्यता को व्यक्त करता है:
पहला आरेख रचना की साहचर्यता को व्यक्त करता है:


:[[Image:Math-enriched category associativity.svg]]यही है, [[सहयोगी]] श्रेणी एम के सहयोगी द्वारा अब सहयोगीता आवश्यकता को ले लिया गया है।
:[[Image:Math-enriched category associativity.svg]]
:यही है, [[सहयोगी]] श्रेणी M के सहयोगी द्वारा अब सहयोगीता आवश्यकता को ले लिया गया है। स्थिति के लिए कि M समुच्चय की श्रेणी है और {{math|(⊗, ''I'', ''α'', ''λ'', ''ρ'')}} कार्टेशियन उत्पाद द्वारा दिया गया, मोनोइडल संरचना {{math|(×, {•}, &hellip;)}} है | टर्मिनल सिंगल-पॉइंट समुच्चय, और कैनोनिकल आइसोमोर्फिज्म जो वे प्रेरित करते हैं, फिर प्रत्येक {{math|''C''(''a'', ''b'')}} ऐसा समुच्चय है जिसके तत्वों को C के अलग-अलग आकारिकी के रूप में माना जा सकता है, जबकि °, जो अब फलन है, यह परिभाषित करता है कि क्रमागत रूप कैसे बनते हैं। इस स्थिति में, पहले आरेख में {{math|''C''(''a'', ''d'')}} लगातार तीन अलग-अलग रूपवाद बनाने के दो विधियों में से एक से मेल खाता है | {{math|''a'' → ''b'' → ''c'' → ''d''}}, अर्थात तत्वों से {{math|''C''(''a'', ''b'')}}, {{math|''C''(''b'', ''c'')}} और {{math|''C''(''c'', ''d'')}}. आरेख की क्रमविनिमेयता तब केवल यह कथन है कि रचना के दोनों क्रम समान परिणाम देते हैं, जैसा कि सामान्य श्रेणियों के लिए आवश्यक है।


मामले के लिए कि एम सेट की श्रेणी है और {{math|(⊗, ''I'', ''α'', ''λ'', ''ρ'')}} monoidal संरचना है {{math|(×, {•}, &hellip;)}} कार्टेशियन उत्पाद द्वारा दिया गया, टर्मिनल सिंगल-पॉइंट सेट, और कैनोनिकल आइसोमोर्फिज्म जो वे प्रेरित करते हैं, फिर प्रत्येक {{math|''C''(''a'', ''b'')}}  ऐसा समुच्चय है जिसके तत्वों को C के अलग-अलग आकारिकी के रूप में माना जा सकता है, जबकि °, जो अब  फलन है, यह परिभाषित करता है कि क्रमागत रूप कैसे बनते हैं। इस स्थिति में, प्रत्येक पथ की ओर जाता है {{math|''C''(''a'', ''d'')}} पहले आरेख में लगातार तीन अलग-अलग morphisms बनाने के दो तरीकों में से एक से मेल खाता है {{math|''a'' → ''b'' → ''c'' → ''d''}}, यानी तत्वों से {{math|''C''(''a'', ''b'')}}, {{math|''C''(''b'', ''c'')}} और {{math|''C''(''c'', ''d'')}}. आरेख की क्रमविनिमेयता तब केवल यह कथन है कि रचना के दोनों क्रम समान परिणाम देते हैं, जैसा कि सामान्य श्रेणियों के लिए आवश्यक है।


यहाँ जो नया है वह यह है कि उपरोक्त समृद्ध श्रेणी सी में अलग-अलग morphisms के किसी भी स्पष्ट संदर्भ के बिना सहयोगीता के लिए आवश्यकता व्यक्त करता है - फिर से, ये आरेख monoidal श्रेणी एम में morphisms के लिए हैं, और सी में नहीं - इस प्रकार की सहयोगीता की अवधारणा बना रही है रचना सामान्य मामले में सार्थक है जहाँ होम-ऑब्जेक्ट्स {{math|''C''(''a'', ''b'')}} अमूर्त हैं, और स्वयं C को व्यक्तिगत रूपवाद की किसी भी धारणा के '' होने '' की भी आवश्यकता नहीं है।
यहाँ जो नया है वह यह है कि उपरोक्त समृद्ध श्रेणी C में अलग-अलग रूपवाद के किसी भी स्पष्ट संदर्भ के बिना सहयोगीता के लिए आवश्यकता व्यक्त करता है - फिर से, ये आरेख मोनोइडल श्रेणी M में रूपवाद के लिए हैं, और C में नहीं - इस प्रकार की सहयोगीता की अवधारणा बना रही है रचना सामान्य स्थिति में सार्थक है जहाँ होम-ऑब्जेक्ट्स {{math|''C''(''a'', ''b'')}} अमूर्त हैं, और स्वयं C को व्यक्तिगत रूपवाद की किसी भी धारणा के ''होने'' की भी आवश्यकता नहीं है।


यह धारणा कि सामान्य श्रेणी में पहचान आकारिकी होनी चाहिए, को दूसरे और तीसरे आरेखों द्वारा प्रतिस्थापित किया जाता है, जो बाएँ और दाएँ एककों के संदर्भ में पहचान व्यक्त करते हैं:
यह धारणा कि सामान्य श्रेणी में पहचान आकारिकी होनी चाहिए, को दूसरे और तीसरे आरेखों द्वारा प्रतिस्थापित किया जाता है, जो बाएँ और दाएँ एककों के संदर्भ में पहचान व्यक्त करते हैं:


:[[File:Math-enriched category identity1.svg]]और
:[[File:Math-enriched category identity1.svg]]और
:[[File:Math-enriched category identity2.svg]]उस मामले पर वापस लौटना जहां एम कार्टेशियन उत्पाद, आकारिकी के साथ सेट की श्रेणी है {{math|id<sub>''a''</sub>: ''I'' → ''C''(''a'', ''a'')}} एक-बिंदु सेट I से कार्य बन जाता है और फिर, किसी दिए गए ऑब्जेक्ट के लिए, प्रत्येक सेट के किसी विशेष तत्व की पहचान करता है {{math|''C''(''a'', ''a'')}}, कुछ ऐसा जिसे हम 'C' में a के लिए पहचान रूपवाद के रूप में सोच सकते हैं। बाद के दो आरेखों की क्रमविनिमेयता तब कथन है कि 'C' में इन विशिष्ट व्यक्तिगत पहचान रूपवादों को शामिल करने वाली रचनाएँ (जैसा कि कार्यों ° द्वारा परिभाषित है) सामान्य श्रेणियों के लिए पहचान नियमों के अनुसार बिल्कुल व्यवहार करती हैं।
:[[File:Math-enriched category identity2.svg]]
:उस स्थिति पर वापस लौटना जहां M कार्टेशियन उत्पाद, आकारिकी के साथ समुच्चय की श्रेणी है | एक-बिंदु समुच्चय {{math|id<sub>''a''</sub>: ''I'' → ''C''(''a'', ''a'')}} से कार्य बन जाता है और फिर, किसी दिए गए ऑब्जेक्ट के लिए, प्रत्येक समुच्चय के किसी विशेष तत्व {{math|''C''(''a'', ''a'')}} की पहचान करता है , कुछ ऐसा जिसे हम 'C' में a के लिए पहचान रूपवाद के रूप में सोच सकते हैं। बाद के दो आरेखों की क्रमविनिमेयता तब कथन है कि 'C' में इन विशिष्ट व्यक्तिगत पहचान रूपवादों को सम्मिलित करने वाली रचनाएँ (जैसा कि कार्यों ° द्वारा परिभाषित है) सामान्य श्रेणियों के लिए पहचान नियमों के अनुसार बिल्कुल व्यवहार करती हैं।


ध्यान दें कि यहां पहचान की कई अलग-अलग धारणाओं को संदर्भित किया जा रहा है:
ध्यान दें कि यहां पहचान की कई अलग-अलग धारणाओं को संदर्भित किया जा रहा है:
* <nowiki>मोनोइडल पहचान वस्तु {{mvar|I}एम का }, केवल मोनॉइड-सैद्धांतिक अर्थ में ⊗ के लिए पहचान होने के नाते, और फिर भी केवल विहित समरूपता तक </nowiki>{{math|(''λ'', ''ρ'')}}.
* M का मोनोइडल पहचान वस्तु केवल मोनॉइड-सैद्धांतिक अर्थ में ⊗ के लिए पहचान होने के सम्बन्ध में , और फिर भी केवल विहित समरूपता {{math|(''λ'', ''ρ'')}} तक होती है |.
* पहचान रूपवाद {{math|1<sub>''C''(''a'', ''b'')</sub> : ''C''(''a'', ''b'') → ''C''(''a'', ''b'')}} कि M के पास इसकी प्रत्येक वस्तु के लिए (कम से कम) सामान्य श्रेणी होने के कारण है।
* पहचान रूपवाद {{math|1<sub>''C''(''a'', ''b'')</sub> : ''C''(''a'', ''b'') → ''C''(''a'', ''b'')}} कि M के पास इसकी प्रत्येक वस्तु के लिए (कम से कम) सामान्य श्रेणी होने के कारण है।
* ''समृद्ध श्रेणी पहचान'' {{math|id<sub>''a''</sub> : ''I'' → ''C''(''a'', ''a'')}} प्रत्येक वस्तु के लिए 'सी' में, जो फिर से 'एम' का रूपवाद है, यहां तक ​​​​कि उस मामले में भी जहां 'सी' को अपने स्वयं के अलग-अलग रूपों के रूप में समझा जाता है, जरूरी नहीं कि वह किसी विशिष्ट व्यक्ति की पहचान करे।
* ''समृद्ध श्रेणी पहचान'' {{math|id<sub>''a''</sub> : ''I'' → ''C''(''a'', ''a'')}} प्रत्येक वस्तु के लिए 'C' में, जो फिर से 'M' का रूपवाद है, यहां तक ​​​​कि उस स्थिति में भी जहां 'C' को अपने स्वयं के अलग-अलग रूपों के रूप में समझा जाता है, आवश्यक नहीं कि वह किसी विशिष्ट व्यक्ति की पहचान करे।


== समृद्ध श्रेणियों के उदाहरण ==
== समृद्ध श्रेणियों के उदाहरण ==


* साधारण श्रेणियां (सेट, ×, {•}) से समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ सेट की श्रेणी मोनोइडल ऑपरेशन के रूप में, जैसा कि ऊपर बताया गया है।
* साधारण श्रेणियां (समुच्चय, ×, {•}) से समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ समुच्चय की श्रेणी मोनोइडल ऑपरेशन के रूप में, जैसा कि ऊपर बताया गया है।
* 2-श्रेणी|2-श्रेणियाँ कैट से अधिक समृद्ध श्रेणियां हैं, [[छोटी श्रेणियों की श्रेणी]], जिसमें कार्तीय उत्पाद द्वारा मोनोइडल संरचना दी जा रही है। इस मामले में आकारिकी ''a'' → ''b'' के बीच 2-कोशिकाएं और उनसे संबंधित लंबवत-रचना नियम सामान्य श्रेणी ''C''(''a'', ' 'बी'') और इसका अपना रचना नियम।
* 2-श्रेणियाँ कैट से अधिक समृद्ध श्रेणियां हैं, [[छोटी श्रेणियों की श्रेणी|छोT श्रेणियों की श्रेणी]], जिसमें कार्तीय उत्पाद द्वारा मोनोइडल संरचना दी जा रही है। इस स्थिति में आकारिकी ''a'' → ''b'' के मध्य 2-कोशिकाएं और उनसे संबंधित लंबवत-रचना नियम सामान्य श्रेणी ''C''(''a'', ' 'B'') और इसका अपना रचना नियम है।''
* [[स्थानीय रूप से छोटी श्रेणी]] (SmSet, ×) पर समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ मोनोइडल ऑपरेशन के रूप में छोटे सेट (श्रेणी सिद्धांत) की श्रेणी। (स्थानीय रूप से छोटी श्रेणी वह है जिसकी होम-ऑब्जेक्ट्स छोटे सेट हैं।)
* [[स्थानीय रूप से छोटी श्रेणी|स्थानीय रूप से छोT श्रेणी]] (स्मसमुच्चय, ×) पर समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ मोनोइडल ऑपरेशन के रूप में छोटे समुच्चय (श्रेणी सिद्धांत) की श्रेणी है। (स्थानीय रूप से छोT श्रेणी वह है जिसकी होम-ऑब्जेक्ट्स छोटे समुच्चय हैं।)
* [[स्थानीय रूप से परिमित श्रेणी]], सादृश्य द्वारा, (फ़िनसेट, ×) पर समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ मोनोइडल ऑपरेशन के रूप में [[परिमित सेट]] की श्रेणी।
* [[स्थानीय रूप से परिमित श्रेणी]], सादृश्य द्वारा, (फ़िनसमुच्चय, ×) पर समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ मोनोइडल ऑपरेशन के रूप में [[परिमित सेट|परिमित समुच्चय]] की श्रेणी है।
* यदि 'सी' बंद मोनोइडल श्रेणी है तो 'सी' अपने आप में समृद्ध है।
* यदि 'C' बंद मोनोइडल श्रेणी है तो 'C' अपने आप में समृद्ध है।
* पूर्व-आदेशित सेट  निश्चित मोनोइडल श्रेणी में समृद्ध श्रेणियां हैं, 2, जिसमें दो ऑब्जेक्ट और उनके बीच  गैर-पहचान वाला तीर शामिल है, जिसे हम '' FALSE'' → ''TRUE'' के रूप में लिख सकते हैं, मोनोइड ऑपरेशन के रूप में संयोजन, और ' 'TRUE'' इसकी मोनोइडल पहचान के रूप में। होम-ऑब्जेक्ट्स 2(''a'', ''b'') फिर वस्तुओं की दी गई जोड़ी (''a'', ''b'') पर एक विशेष द्विआधारी संबंध को अस्वीकार या पुष्टि करते हैं; अधिक परिचित अंकन के लिए हम इस संबंध को इस प्रकार लिख सकते हैं {{math|''a'' ≤ ''b''}}. 2 से अधिक समृद्ध श्रेणी के लिए आवश्यक रचनाओं और पहचान का अस्तित्व क्रमशः निम्नलिखित स्वयंसिद्धों में अनुवाद करता है
* पूर्व-आदेशित समुच्चय निश्चित मोनोइडल श्रेणी में समृद्ध श्रेणियां हैं, 2, जिसमें दो ऑब्जेक्ट और उनके मध्य गैर-पहचान वाला तीर सम्मिलित है, जिसे हम असत्य → सत्य के रूप में लिख सकते हैं, मोनोइड ऑपरेशन के रूप में संयोजन, और ' 'सत्य'' इसकी मोनोइडल पहचान के रूप में। होम-ऑब्जेक्ट्स 2(''a'', ''b'') फिर वस्तुओं की दी गई जोड़ी (''a'', ''b'') पर एक विशेष द्विआधारी संबंध को अस्वीकार या पुष्टि करते हैं; अधिक परिचित अंकन के लिए हम इस संबंध को इस प्रकार लिख सकते हैं {{math|''a'' ≤ ''b''}}. 2 से अधिक समृद्ध श्रेणी के लिए आवश्यक रचनाओं और पहचान का अस्तित्व क्रमशः निम्नलिखित स्वयंसिद्धों में अनुवाद करता है
::''b'' ≤ ''c'' और ''a'' ≤ ''b'' ⇒ ''a'' ≤ ''c'' (संक्रमण)
::''b'' ≤ ''c'' और ''a'' ≤ ''b'' ⇒ ''a'' ≤ ''c'' (संक्रमण)
::''TRUE'' ⇒ ''a'' ≤ ''a'' (रिफ्लेक्सिविटी)
::''सत्य'' ⇒ ''a'' ≤ ''a'' (रिफ्लेक्सिविT)
: जो ≤ एक पूर्व आदेश होने के स्वयंसिद्ध सिद्धांतों के अलावा और कोई नहीं हैं। और चूंकि 2 कम्यूट में सभी आरेख, यह 2 से अधिक समृद्ध श्रेणियों के लिए समृद्ध श्रेणी स्वयंसिद्धों की ''एकमात्र'' सामग्री है।
: जो ≤ एक पूर्व आदेश होने के स्वयंसिद्ध सिद्धांतों के अतिरिक्त और कोई नहीं हैं। और चूंकि 2 में सभी आरेख लघुकरण करते है, यह 2 से अधिक समृद्ध श्रेणियों के लिए समृद्ध श्रेणी स्वयंसिद्धों की ''एकमात्र'' सामग्री है।
* [[विलियम लॉवरे]] के सामान्यीकृत मीट्रिक रिक्त स्थान, जिन्हें मीट्रिक (गणित) Pseudoquasimetrics के रूप में भी जाना जाता है, वे श्रेणियां हैं जो गैर-नकारात्मक विस्तारित वास्तविक संख्याओं से समृद्ध हैं {{math|'''R'''<sup>+∞</sup>}}, जहां बाद वाले को अपने सामान्य क्रम के व्युत्क्रम के माध्यम से सामान्य श्रेणी की संरचना दी जाती है (यानी, आकृतिवाद r → s iff r ≥ s) और जोड़ (+) और शून्य (0) के माध्यम से मोनोइडल संरचना मौजूद है। होम-ऑब्जेक्ट्स {{math|'''R'''<sup>+∞</sup>(''a'', ''b'')}} अनिवार्य रूप से दूरी d(a,-b) हैं, और संरचना और पहचान का अस्तित्व अनुवाद करता है
* [[विलियम लॉवरे]] के सामान्यीकृत आव्यूह रिक्त स्थान, जिन्हें आव्यूह (गणित) स्यूडोक्वासिमेट्रिक्स के रूप में भी जाना जाता है, वे श्रेणियां हैं जो गैर-नकारात्मक विस्तारित वास्तविक संख्याओं {{math|'''R'''<sup>+∞</sup>}} से समृद्ध हैं , जहां बाद वाले को अपने सामान्य क्रम के व्युत्क्रम के माध्यम से सामान्य श्रेणी की संरचना दी जाती है (अर्थात, आकृतिवाद r → s iff r ≥ s) और जोड़ (+) और शून्य (0) के माध्यम से मोनोइडल संरचना उपस्थित है। होम-ऑब्जेक्ट्स {{math|'''R'''<sup>+∞</sup>(''a'', ''b'')}} अनिवार्य रूप से दूरी d(a,-b) हैं, और संरचना और पहचान का अस्तित्व अनुवाद करता है
::d(b, c) + d(a, b) ≥ d(a, c) (त्रिकोण असमानता)
::d(b, c) + d(a, b) ≥ d(a, c) (त्रिकोण असमानता)
::0 ≥ डी(ए, ए)
::0 ≥ D(A, A)
* शून्य मोर्फिज्म वाली श्रेणियां ('सेट *', ∧) से समृद्ध श्रेणियां हैं, मोनोइडल ऑपरेशन के रूप में स्मैश उत्पाद के साथ नुकीले सेटों की श्रेणी; होम-ऑब्जेक्ट होम (ए,-बी) का विशेष बिंदु ए से बी तक शून्य आकारिकी से मेल खाता है।
* शून्य मोर्फिज्म वाली श्रेणियां ('समुच्चय *', ∧) से समृद्ध श्रेणियां हैं, मोनोइडल ऑपरेशन के रूप में स्मैश उत्पाद के साथ नुकीले समुच्चयों की श्रेणी; होम-ऑब्जेक्ट होम (A,-B) का विशेष बिंदु A से B तक शून्य आकारिकी से मेल खाता है।
* [[एबेलियन समूह]]ों की श्रेणी 'एबी' और क्रमविनिमेय रिंग पर [[मॉड्यूल (गणित)]] की श्रेणी 'आर-मॉड', और किसी दिए गए [[क्षेत्र (गणित)]] पर वेक्टर रिक्त स्थान की श्रेणी 'वेक्ट' स्वयं से समृद्ध होती है, जहां morphisms बीजगणितीय संरचना बिंदुवार प्राप्त करते हैं। अधिक आम तौर पर, प्रीएडिटिव श्रेणी वे श्रेणियां होती हैं जो ('एबी', ⊗) से अधिक समृद्ध होती हैं, जिसमें मोनोइडल ऑपरेशन के रूप में [[टेंसर उत्पाद]] होता है (एबेलियन समूहों को 'जेड'-मॉड्यूल के रूप में सोचना)।
* [[एबेलियन समूह]] की श्रेणी 'AB' और क्रमविनिमेय रिंग पर [[मॉड्यूल (गणित)]] की श्रेणी 'आर-मॉड', और किसी दिए गए [[क्षेत्र (गणित)]] पर वेक्टर रिक्त स्थान की श्रेणी 'वेक्ट' स्वयं से समृद्ध होती है, जहां रूपवाद बीजगणितीय संरचना बिंदुवार प्राप्त करते हैं। अधिक सामान्यतः, प्रीएडिटिव श्रेणी वे श्रेणियां होती हैं जो ('AB', ⊗) से अधिक समृद्ध होती हैं, जिसमें मोनोइडल ऑपरेशन के रूप में [[टेंसर उत्पाद]] होता है (एबेलियन समूहों को 'जेड'-मॉड्यूल के रूप में सोचना)।


== monoidal functors के साथ संबंध ==
== मोनोइडल functors के साथ संबंध ==
यदि मोनोइडल श्रेणी एम से मोनोइडल श्रेणी एन तक [[मोनोइडल फ़ैक्टर]] है, तो एम से अधिक समृद्ध किसी भी श्रेणी को एन से समृद्ध श्रेणी के रूप में दोबारा परिभाषित किया जा सकता है। प्रत्येक मोनोइडल श्रेणी एम में मोनोइडल फ़ंक्शनर एम (''आई'', - ) सेट की श्रेणी में, इसलिए किसी भी समृद्ध श्रेणी में अंतर्निहित सामान्य श्रेणी होती है। कई उदाहरणों में (जैसे ऊपर वाले) यह फ़ैक्टर वफादार फ़ंक्टर है, इसलिए एम से समृद्ध श्रेणी को कुछ अतिरिक्त संरचना या गुणों के साथ सामान्य श्रेणी के रूप में वर्णित किया जा सकता है।
यदि मोनोइडल श्रेणी M से मोनोइडल श्रेणी n तक [[मोनोइडल फ़ैक्टर]] है, तो M से अधिक समृद्ध किसी भी श्रेणी को n से समृद्ध श्रेणी के रूप में दोबारा परिभाषित किया जा सकता है। प्रत्येक मोनोइडल श्रेणी M में मोनोइडल फ़ंक्शनर M (''I'', - ) समुच्चय की श्रेणी में, इसलिए किसी भी समृद्ध श्रेणी में अंतर्निहित सामान्य श्रेणी होती है। कई उदाहरणों में (जैसे ऊपर वाले) यह फ़ैक्टर वफादार फ़ंक्टर है, इसलिए M से समृद्ध श्रेणी को कुछ अतिरिक्त संरचना या गुणों के साथ सामान्य श्रेणी के रूप में वर्णित किया जा सकता है।


== समृद्ध कारक ==
== समृद्ध कारक ==


समृद्ध [[ऑपरेटर]] समृद्ध श्रेणियों के लिए फ़नकार की धारणा का उपयुक्त सामान्यीकरण है। समृद्ध कारक तब समृद्ध श्रेणियों के बीच मानचित्र होते हैं जो समृद्ध संरचना का सम्मान करते हैं।
समृद्ध [[ऑपरेटर|संचालक]] समृद्ध श्रेणियों के लिए फ़नकार की धारणा का उपयुक्त सामान्यीकरण है। समृद्ध कारक तब समृद्ध श्रेणियों के मध्य मानचित्र होते हैं जो समृद्ध संरचना का सम्मान करते हैं।


अगर ''सी'' और ''डी'' एम-श्रेणियां हैं (यानी, मोनोइडल श्रेणी एम पर समृद्ध श्रेणियां), एम-समृद्ध फ़ंक्टर ''टी'': ''सी'' → ''डी'' मानचित्र है जो ''सी'' की प्रत्येक वस्तु को ''डी'' की वस्तु प्रदान करता है और ''सी'' में ''ए'' और ''बी'' वस्तुओं की प्रत्येक जोड़ी के लिए एम में रूपवाद प्रदान करता है ''टी<sub>ab</sub>: सी (ए, बी) → डी (टी (ए), टी (बी)) सी और डी (जो 'एम' में वस्तुएं हैं) के होम-ऑब्जेक्ट्स के बीच, मज़ेदार के सिद्धांतों के समृद्ध संस्करणों को संतुष्ट करते हैं, जैसे पहचान और संरचना का संरक्षण।''
अगर ''C'' और ''D'' M-श्रेणियां हैं (अर्थात, मोनोइडल श्रेणी M पर समृद्ध श्रेणियां), M-समृद्ध फ़ंक्टर ''T'': ''C'' → ''D'' मानचित्र है जो ''C'' की प्रत्येक वस्तु को ''D'' की वस्तु प्रदान करता है और ''C'' में ''A'' और ''B'' वस्तुओं की प्रत्येक जोड़ी के लिए M में रूपवाद प्रदान करता है ''T<sub>ab</sub>: C (A, B) → D (T (A), T (B)) C और D (जो 'M' में वस्तुएं हैं) के होम-ऑब्जेक्ट्स के मध्य, रोचक के सिद्धांतों के समृद्ध संस्करणों को संतुष्ट करते हैं, जैसे पहचान और संरचना का संरक्षण है।''


चूंकि होम-ऑब्जेक्ट्स को समृद्ध श्रेणी में सेट करने की आवश्यकता नहीं है, इसलिए कोई विशेष रूपवाद के बारे में बात नहीं कर सकता है। पहचान रूपवाद की अब कोई धारणा नहीं है, न ही दो आकारिकी के किसी विशेष संयोजन की। इसके बजाय, इकाई से होम-ऑब्जेक्ट के आकारिकी को एक पहचान का चयन करने के बारे में सोचा जाना चाहिए, और मोनोइडल उत्पाद से आकारिकी को संरचना के रूप में सोचा जाना चाहिए। सामान्य क्रियात्मक स्वयंसिद्धों को इन morphisms से जुड़े संगत क्रमविनिमेय आरेखों से बदल दिया जाता है।
चूंकि होम-ऑब्जेक्ट्स को समृद्ध श्रेणी में समुच्चय करने की आवश्यकता नहीं है, इसलिए कोई विशेष रूपवाद के बारे में बात नहीं कर सकता है। पहचान रूपवाद की अब कोई धारणा नहीं है, न ही दो आकारिकी के किसी विशेष संयोजन की इसके अतिरिक्त, इकाई से होम-ऑब्जेक्ट के आकारिकी को एक पहचान का चयन करने के बारे में सोचा जाना चाहिए, और मोनोइडल उत्पाद से आकारिकी को संरचना के रूप में सोचा जाना चाहिए। सामान्य क्रियात्मक स्वयंसिद्धों को इन रूपवाद से जुड़े संगत क्रमविनिमेय आरेखों से बदल दिया जाता है।


विस्तार से, किसी के पास वह आरेख है
विस्तार से, किसी के पास वह आरेख है
[[Image:Enrichedidentity.png|center|300px]]कम्यूट करता है, जो समीकरण के बराबर है
[[Image:Enrichedidentity.png|center|300px]]लघुकरण करता है, जो समीकरण के सामान है
:<math>T_{aa}\circ \operatorname{id}_a=\operatorname{id}_{T(a)},</math>
:<math>T_{aa}\circ \operatorname{id}_a=\operatorname{id}_{T(a)},</math>
जहां मैं 'एम' की इकाई वस्तु है। यह नियम F(id<sub>''a''</sub>) = आईडी<sub>''F''(''a'')</sub> साधारण कार्यकर्ताओं के लिए। इसके अतिरिक्त, एक मांग करता है कि Diagram
जहां I 'M' की इकाई वस्तु है। यह नियम F(id<sub>''a''</sub>) = ID<sub>''F''(''a'')</sub> साधारण कार्यकर्ताओं के लिए। इसके अतिरिक्त, एक मांग करता है कि आरेख
  [[Image:Enrichedmult.png|center]]कम्यूट, जो साधारण फ़ैक्टरों के लिए F(fg)=F(f)F(g) नियम के अनुरूप है।
  [[Image:Enrichedmult.png|center]]लघुकरण, जो साधारण फ़ैक्टरों के लिए F(fg)=F(f)F(g) नियम के अनुरूप है।


== यह भी देखें ==
== यह भी देखें ==
Line 83: Line 81:
{{Category theory}}
{{Category theory}}


{{DEFAULTSORT:Enriched Category}}[[Category: श्रेणी सिद्धांत]] [[Category: मोनोइडल श्रेणियां]]
{{DEFAULTSORT:Enriched Category}}
 
 


[[Category: Machine Translated Page]]
[[Category:Collapse templates|Enriched Category]]
[[Category:Created On 24/04/2023]]
[[Category:Created On 24/04/2023|Enriched Category]]
[[Category:Machine Translated Page|Enriched Category]]
[[Category:Navigational boxes| ]]
[[Category:Navigational boxes without horizontal lists|Enriched Category]]
[[Category:Pages with empty portal template|Enriched Category]]
[[Category:Pages with script errors|Enriched Category]]
[[Category:Portal templates with redlinked portals|Enriched Category]]
[[Category:Sidebars with styles needing conversion|Enriched Category]]
[[Category:Template documentation pages|Documentation/doc]]
[[Category:Templates Vigyan Ready|Enriched Category]]
[[Category:Templates generating microformats|Enriched Category]]
[[Category:Templates that are not mobile friendly|Enriched Category]]
[[Category:Templates using TemplateData|Enriched Category]]
[[Category:Wikipedia metatemplates|Enriched Category]]
[[Category:मोनोइडल श्रेणियां|Enriched Category]]
[[Category:श्रेणी सिद्धांत|Enriched Category]]

Latest revision as of 14:55, 25 September 2023

श्रेणी सिद्धांत में, गणित की एक शाखा, एक समृद्ध श्रेणी एक सामान्य मोनोइडल श्रेणी से वस्तुओं के साथ होम सेट को बदलकर एक श्रेणी (गणित) के विचार को सामान्यीकृत करती है। यह अवलोकन से प्रेरित है कि, कई व्यावहारिक अनुप्रयोगों में, होम-सेट में अधिकांशतः अतिरिक्त संरचना होती है जिसका सम्मान किया जाना चाहिए, उदाहरण के लिए, आकारिकी का सदिश स्थान या आकारिकी का एक स्थलीय स्थान होना है। एक समृद्ध श्रेणी में, वस्तुओं की प्रत्येक जोड़ी से जुड़े रूपवाद (होम-सेट) का समुच्चय "होम-ऑब्जेक्ट्स" की कुछ निश्चित मोनोइडल श्रेणी में ऑब्जेक्ट द्वारा प्रतिस्थापित किया जाता है। एक सामान्य श्रेणी में रूपवाद की (सहयोगी) संरचना का अनुकरण करने के लिए, गृह-श्रेणी में होम-ऑब्जेक्ट्स को सहयोगी विधि से बनाने का एक साधन होना चाहिए: अर्थात, हमें कम से कम देने वाली वस्तुओं पर एक बाइनरी ऑपरेशन होना चाहिए एक मोनोइडल श्रेणी की संरचना, चूँकि कुछ संदर्भों में ऑपरेशन को क्रमविनिमेय होने की भी आवश्यकता हो सकती है और संभवतः एक सही आसन्न होने की भी आवश्यकता हो सकती है (अर्थात, श्रेणी को सममित मोनोइडल श्रेणी या यहां तक ​​​​कि बंद मोनोइडल श्रेणी बनाना)।

समृद्ध श्रेणी सिद्धांत इस प्रकार एक ही ढांचे के अन्दर विभिन्न प्रकार की संरचनाओं को सम्मिलित करता है

  • सामान्य श्रेणियां जहां होम-सेट में समुच्चय होने के अतिरिक्त अतिरिक्त संरचना होती है। यही है, आकारिकी के ऐसे संचालन या गुण होते हैं जिन्हें संरचना द्वारा सम्मानित करने की आवश्यकता होती है (उदाहरण के लिए, 2-श्रेणी में रूपवाद और क्षैतिज संरचना के मध्य 2-कोशिकाओं का अस्तित्व, या एबेलियन श्रेणी में रूपवाद पर अतिरिक्त संचालन ) |
  • श्रेणी-जैसी संस्थाएँ जिनके पास स्वयं व्यक्तिगत रूपवाद की कोई धारणा नहीं है, किन्तु जिनके होम-ऑब्जेक्ट्स में समान रचना संबंधी पहलू हैं (उदाहरण के लिए, पूर्व-आदेश जहाँ रचना नियम संक्रामकता, या स्यूडोक्वासिआव्यूह स्पेस सुनिश्चित करता है। लॉवर के आव्यूह स्पेस, जहाँ होम-ऑब्जेक्ट्स हैं संख्यात्मक दूरियाँ और रचना नियम त्रिभुज असमानता प्रदान करता है)।

ऐसे स्थिति में जहां होम-ऑब्जेक्ट श्रेणी सामान्य कार्टेशियन उत्पाद के साथ समुच्चय की श्रेणी होती है, समृद्ध श्रेणी की परिभाषाएं, समृद्ध फ़ैक्टर इत्यादि सामान्य श्रेणी सिद्धांत से मूल परिभाषाओं को कम करती हैं।

मोनोइडल श्रेणी M से होम-ऑब्जेक्ट्स के साथ समृद्ध श्रेणी को M से अधिक समृद्ध श्रेणी या M में समृद्ध श्रेणी या केवल M-श्रेणी कहा जाता है। मोनोइडल श्रेणी के संदर्भ में V अक्षर के लिए मैक लेन की वरीयता के कारण, समृद्ध श्रेणियों को कभी-कभी सामान्यतः V-श्रेणियों के रूप में भी संदर्भित किया जाता है।

परिभाषा

(M, ⊗, I, α, λ, ρ) एक मोनोइडल श्रेणी हो। फिर एक समृद्ध श्रेणी C (वैकल्पिक रूप से उन स्थितियों में जहां मोनोइडल श्रेणी की पसंद को स्पष्ट रूप से M, या M-श्रेणी से समृद्ध श्रेणी की आवश्यकता होती है) में सम्मिलित हैं

  • 'C' की वस्तुओं का वर्ग (समुच्चय सिद्धांत) OB ('C'),है |
  • वस्तु C(a, b) वस्तुओं की प्रत्येक जोड़ी के लिए M का ऑब्जेक्ट a, b C में, तीर को परिभाषित करने के लिए उपयोग किया जाता है | M में तीर के रूप में परिभाषित करने के लिए प्रयोग किया जाता है,|
  • तीर ida : I → C(a, a) M में C में प्रत्येक वस्तु a के लिए पहचान निर्दिष्ट करता है,|
  • तीर °abc : C(b, c) ⊗ C(a, b) → C(a, c) M C में वस्तुओं के प्रत्येक ट्रिपल a, b, c के लिए रचना को निर्दिष्ट करता है, जिसका उपयोग संरचना को परिभाषित करने के लिए उपयोग किया जाता है और C में साथ तीन आने वाले आरेखों के साथ, नीचे चर्चा की गई।

पहला आरेख रचना की साहचर्यता को व्यक्त करता है:

File:Math-enriched category associativity.svg
यही है, सहयोगी श्रेणी M के सहयोगी द्वारा अब सहयोगीता आवश्यकता को ले लिया गया है। स्थिति के लिए कि M समुच्चय की श्रेणी है और (⊗, I, α, λ, ρ) कार्टेशियन उत्पाद द्वारा दिया गया, मोनोइडल संरचना (×, {•}, …) है | टर्मिनल सिंगल-पॉइंट समुच्चय, और कैनोनिकल आइसोमोर्फिज्म जो वे प्रेरित करते हैं, फिर प्रत्येक C(a, b) ऐसा समुच्चय है जिसके तत्वों को C के अलग-अलग आकारिकी के रूप में माना जा सकता है, जबकि °, जो अब फलन है, यह परिभाषित करता है कि क्रमागत रूप कैसे बनते हैं। इस स्थिति में, पहले आरेख में C(a, d) लगातार तीन अलग-अलग रूपवाद बनाने के दो विधियों में से एक से मेल खाता है | a → b → c → d, अर्थात तत्वों से C(a, b), C(b, c) और C(c, d). आरेख की क्रमविनिमेयता तब केवल यह कथन है कि रचना के दोनों क्रम समान परिणाम देते हैं, जैसा कि सामान्य श्रेणियों के लिए आवश्यक है।


यहाँ जो नया है वह यह है कि उपरोक्त समृद्ध श्रेणी C में अलग-अलग रूपवाद के किसी भी स्पष्ट संदर्भ के बिना सहयोगीता के लिए आवश्यकता व्यक्त करता है - फिर से, ये आरेख मोनोइडल श्रेणी M में रूपवाद के लिए हैं, और C में नहीं - इस प्रकार की सहयोगीता की अवधारणा बना रही है रचना सामान्य स्थिति में सार्थक है जहाँ होम-ऑब्जेक्ट्स C(a, b) अमूर्त हैं, और स्वयं C को व्यक्तिगत रूपवाद की किसी भी धारणा के होने की भी आवश्यकता नहीं है।

यह धारणा कि सामान्य श्रेणी में पहचान आकारिकी होनी चाहिए, को दूसरे और तीसरे आरेखों द्वारा प्रतिस्थापित किया जाता है, जो बाएँ और दाएँ एककों के संदर्भ में पहचान व्यक्त करते हैं:

File:Math-enriched category identity1.svgऔर
Math-enriched category identity2.svg
उस स्थिति पर वापस लौटना जहां M कार्टेशियन उत्पाद, आकारिकी के साथ समुच्चय की श्रेणी है | एक-बिंदु समुच्चय ida: I → C(a, a) से कार्य बन जाता है और फिर, किसी दिए गए ऑब्जेक्ट के लिए, प्रत्येक समुच्चय के किसी विशेष तत्व C(a, a) की पहचान करता है , कुछ ऐसा जिसे हम 'C' में a के लिए पहचान रूपवाद के रूप में सोच सकते हैं। बाद के दो आरेखों की क्रमविनिमेयता तब कथन है कि 'C' में इन विशिष्ट व्यक्तिगत पहचान रूपवादों को सम्मिलित करने वाली रचनाएँ (जैसा कि कार्यों ° द्वारा परिभाषित है) सामान्य श्रेणियों के लिए पहचान नियमों के अनुसार बिल्कुल व्यवहार करती हैं।

ध्यान दें कि यहां पहचान की कई अलग-अलग धारणाओं को संदर्भित किया जा रहा है:

  • M का मोनोइडल पहचान वस्तु केवल मोनॉइड-सैद्धांतिक अर्थ में ⊗ के लिए पहचान होने के सम्बन्ध में , और फिर भी केवल विहित समरूपता (λ, ρ) तक होती है |.
  • पहचान रूपवाद 1C(a, b) : C(a, b) → C(a, b) कि M के पास इसकी प्रत्येक वस्तु के लिए (कम से कम) सामान्य श्रेणी होने के कारण है।
  • समृद्ध श्रेणी पहचान ida : I → C(a, a) प्रत्येक वस्तु के लिए 'C' में, जो फिर से 'M' का रूपवाद है, यहां तक ​​​​कि उस स्थिति में भी जहां 'C' को अपने स्वयं के अलग-अलग रूपों के रूप में समझा जाता है, आवश्यक नहीं कि वह किसी विशिष्ट व्यक्ति की पहचान करे।

समृद्ध श्रेणियों के उदाहरण

  • साधारण श्रेणियां (समुच्चय, ×, {•}) से समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ समुच्चय की श्रेणी मोनोइडल ऑपरेशन के रूप में, जैसा कि ऊपर बताया गया है।
  • 2-श्रेणियाँ कैट से अधिक समृद्ध श्रेणियां हैं, छोT श्रेणियों की श्रेणी, जिसमें कार्तीय उत्पाद द्वारा मोनोइडल संरचना दी जा रही है। इस स्थिति में आकारिकी a → b के मध्य 2-कोशिकाएं और उनसे संबंधित लंबवत-रचना नियम सामान्य श्रेणी C(a, ' 'B) और इसका अपना रचना नियम है।
  • स्थानीय रूप से छोT श्रेणी (स्मसमुच्चय, ×) पर समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ मोनोइडल ऑपरेशन के रूप में छोटे समुच्चय (श्रेणी सिद्धांत) की श्रेणी है। (स्थानीय रूप से छोT श्रेणी वह है जिसकी होम-ऑब्जेक्ट्स छोटे समुच्चय हैं।)
  • स्थानीय रूप से परिमित श्रेणी, सादृश्य द्वारा, (फ़िनसमुच्चय, ×) पर समृद्ध श्रेणियां हैं, कार्टेशियन उत्पाद के साथ मोनोइडल ऑपरेशन के रूप में परिमित समुच्चय की श्रेणी है।
  • यदि 'C' बंद मोनोइडल श्रेणी है तो 'C' अपने आप में समृद्ध है।
  • पूर्व-आदेशित समुच्चय निश्चित मोनोइडल श्रेणी में समृद्ध श्रेणियां हैं, 2, जिसमें दो ऑब्जेक्ट और उनके मध्य गैर-पहचान वाला तीर सम्मिलित है, जिसे हम असत्य → सत्य के रूप में लिख सकते हैं, मोनोइड ऑपरेशन के रूप में संयोजन, और ' 'सत्य इसकी मोनोइडल पहचान के रूप में। होम-ऑब्जेक्ट्स 2(a, b) फिर वस्तुओं की दी गई जोड़ी (a, b) पर एक विशेष द्विआधारी संबंध को अस्वीकार या पुष्टि करते हैं; अधिक परिचित अंकन के लिए हम इस संबंध को इस प्रकार लिख सकते हैं a ≤ b. 2 से अधिक समृद्ध श्रेणी के लिए आवश्यक रचनाओं और पहचान का अस्तित्व क्रमशः निम्नलिखित स्वयंसिद्धों में अनुवाद करता है
b ≤ c और a ≤ b ⇒ a ≤ c (संक्रमण)
सत्य ⇒ a ≤ a (रिफ्लेक्सिविT)
जो ≤ एक पूर्व आदेश होने के स्वयंसिद्ध सिद्धांतों के अतिरिक्त और कोई नहीं हैं। और चूंकि 2 में सभी आरेख लघुकरण करते है, यह 2 से अधिक समृद्ध श्रेणियों के लिए समृद्ध श्रेणी स्वयंसिद्धों की एकमात्र सामग्री है।
  • विलियम लॉवरे के सामान्यीकृत आव्यूह रिक्त स्थान, जिन्हें आव्यूह (गणित) स्यूडोक्वासिमेट्रिक्स के रूप में भी जाना जाता है, वे श्रेणियां हैं जो गैर-नकारात्मक विस्तारित वास्तविक संख्याओं R+∞ से समृद्ध हैं , जहां बाद वाले को अपने सामान्य क्रम के व्युत्क्रम के माध्यम से सामान्य श्रेणी की संरचना दी जाती है (अर्थात, आकृतिवाद r → s iff r ≥ s) और जोड़ (+) और शून्य (0) के माध्यम से मोनोइडल संरचना उपस्थित है। होम-ऑब्जेक्ट्स R+∞(a, b) अनिवार्य रूप से दूरी d(a,-b) हैं, और संरचना और पहचान का अस्तित्व अनुवाद करता है
d(b, c) + d(a, b) ≥ d(a, c) (त्रिकोण असमानता)
0 ≥ D(A, A)
  • शून्य मोर्फिज्म वाली श्रेणियां ('समुच्चय *', ∧) से समृद्ध श्रेणियां हैं, मोनोइडल ऑपरेशन के रूप में स्मैश उत्पाद के साथ नुकीले समुच्चयों की श्रेणी; होम-ऑब्जेक्ट होम (A,-B) का विशेष बिंदु A से B तक शून्य आकारिकी से मेल खाता है।
  • एबेलियन समूह की श्रेणी 'AB' और क्रमविनिमेय रिंग पर मॉड्यूल (गणित) की श्रेणी 'आर-मॉड', और किसी दिए गए क्षेत्र (गणित) पर वेक्टर रिक्त स्थान की श्रेणी 'वेक्ट' स्वयं से समृद्ध होती है, जहां रूपवाद बीजगणितीय संरचना बिंदुवार प्राप्त करते हैं। अधिक सामान्यतः, प्रीएडिटिव श्रेणी वे श्रेणियां होती हैं जो ('AB', ⊗) से अधिक समृद्ध होती हैं, जिसमें मोनोइडल ऑपरेशन के रूप में टेंसर उत्पाद होता है (एबेलियन समूहों को 'जेड'-मॉड्यूल के रूप में सोचना)।

मोनोइडल functors के साथ संबंध

यदि मोनोइडल श्रेणी M से मोनोइडल श्रेणी n तक मोनोइडल फ़ैक्टर है, तो M से अधिक समृद्ध किसी भी श्रेणी को n से समृद्ध श्रेणी के रूप में दोबारा परिभाषित किया जा सकता है। प्रत्येक मोनोइडल श्रेणी M में मोनोइडल फ़ंक्शनर M (I, - ) समुच्चय की श्रेणी में, इसलिए किसी भी समृद्ध श्रेणी में अंतर्निहित सामान्य श्रेणी होती है। कई उदाहरणों में (जैसे ऊपर वाले) यह फ़ैक्टर वफादार फ़ंक्टर है, इसलिए M से समृद्ध श्रेणी को कुछ अतिरिक्त संरचना या गुणों के साथ सामान्य श्रेणी के रूप में वर्णित किया जा सकता है।

समृद्ध कारक

समृद्ध संचालक समृद्ध श्रेणियों के लिए फ़नकार की धारणा का उपयुक्त सामान्यीकरण है। समृद्ध कारक तब समृद्ध श्रेणियों के मध्य मानचित्र होते हैं जो समृद्ध संरचना का सम्मान करते हैं।

अगर C और D M-श्रेणियां हैं (अर्थात, मोनोइडल श्रेणी M पर समृद्ध श्रेणियां), M-समृद्ध फ़ंक्टर T: C → D मानचित्र है जो C की प्रत्येक वस्तु को D की वस्तु प्रदान करता है और C में A और B वस्तुओं की प्रत्येक जोड़ी के लिए M में रूपवाद प्रदान करता है Tab: C (A, B) → D (T (A), T (B)) C और D (जो 'M' में वस्तुएं हैं) के होम-ऑब्जेक्ट्स के मध्य, रोचक के सिद्धांतों के समृद्ध संस्करणों को संतुष्ट करते हैं, जैसे पहचान और संरचना का संरक्षण है।

चूंकि होम-ऑब्जेक्ट्स को समृद्ध श्रेणी में समुच्चय करने की आवश्यकता नहीं है, इसलिए कोई विशेष रूपवाद के बारे में बात नहीं कर सकता है। पहचान रूपवाद की अब कोई धारणा नहीं है, न ही दो आकारिकी के किसी विशेष संयोजन की इसके अतिरिक्त, इकाई से होम-ऑब्जेक्ट के आकारिकी को एक पहचान का चयन करने के बारे में सोचा जाना चाहिए, और मोनोइडल उत्पाद से आकारिकी को संरचना के रूप में सोचा जाना चाहिए। सामान्य क्रियात्मक स्वयंसिद्धों को इन रूपवाद से जुड़े संगत क्रमविनिमेय आरेखों से बदल दिया जाता है।

विस्तार से, किसी के पास वह आरेख है

File:Enrichedidentity.png

लघुकरण करता है, जो समीकरण के सामान है

जहां I 'M' की इकाई वस्तु है। यह नियम F(ida) = IDF(a) साधारण कार्यकर्ताओं के लिए। इसके अतिरिक्त, एक मांग करता है कि आरेख

Enrichedmult.png

लघुकरण, जो साधारण फ़ैक्टरों के लिए F(fg)=F(f)F(g) नियम के अनुरूप है।

यह भी देखें

संदर्भ

  • Kelly,G.M. (2005) [1982]. Basic Concepts of Enriched Category Theory. Reprints in Theory and Applications of Categories. Vol. 10.
  • Mac Lane, Saunders (September 1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5 (2nd ed.). Springer. ISBN 0-387-98403-8.
  • Lawvere, F.W. (2002) [1973]. Metric Spaces, Generalized Logic, and Closed Categories. Reprints in Theory and Applications of Categories. Vol. 1.
  • Enriched category at the nLab
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=समृद्ध_श्रेणी&oldid=259847’