परिमेय त्रिभुज: Difference between revisions
(Content Modified) |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 33: | Line 33: | ||
== पश्चातवर्ती परिमेय समाधान == | == पश्चातवर्ती परिमेय समाधान == | ||
[[ब्रह्मगुप्त]] (628) कहते हैं: "वैकल्पिक (''इष्ट | [[ब्रह्मगुप्त]] (628) कहते हैं: "वैकल्पिक (''इष्ट'') पक्ष के वर्ग को विभाजित किया जाता है, और फिर एक वैकल्पिक संख्या से कम किया जाता है; आधा परिणाम उर्ध्वाधर होता है, और वैकल्पिक संख्या से बढ़ने पर एक आयत का कर्ण मिलता है।" | ||
यदि m, n कोई परिमेय संख्या हो तो एक समकोण त्रिभुज की भुजाएँ होंगी | यदि m, n कोई परिमेय संख्या हो तो, एक समकोण त्रिभुज की भुजाएँ इस प्रकार होंगी | ||
<math>m, \quad \frac{1}{2}\left( \frac{m^2}{n}-n \right), \quad \frac{1}{2}\left( \frac{m^2}{n}+n \right) </math> | <math>m, \quad \frac{1}{2}\left( \frac{m^2}{n}-n \right), \quad \frac{1}{2}\left( \frac{m^2}{n}+n \right) </math> | ||
''इष्ट | ''इष्ट'' संस्कृत शब्द को "दिया" के साथ-साथ "वैकल्पिक", के रूप में समझा जाता है। | ||
इसी तरह का एक नियम श्रीपति (1039) द्वारा दिया गया है: "कोई भी वैकल्पिक संख्या पक्ष है; उस का वर्ग विभाजित और फिर एक वैकल्पिक संख्या से छोटा और आधा उर्ध्वाधर है; पिछले भाजक के साथ जोड़ा गया एक समकोण का कर्ण है त्रिकोण। इसलिए, इसे ज्यामिति के नियमों के | इसी तरह का एक नियम श्रीपति (1039) द्वारा दिया गया है: "कोई भी वैकल्पिक संख्या पक्ष है; उस का वर्ग विभाजित और फिर एक वैकल्पिक संख्या से छोटा और आधा उर्ध्वाधर है; पिछले भाजक के साथ जोड़ा गया एक समकोण का कर्ण है त्रिकोण। इसलिए, इसे ज्यामिति के नियमों के संबंध में विद्वानों द्वारा इसकी व्याख्या की गई है।" | ||
== समाकल/ पूर्णांकीय समाधान == | == समाकल/ पूर्णांकीय समाधान == | ||
ब्रह्मगुप्त ने सबसे पहले समीकरण का हल दिया था <math>x^2+y^2=z^2</math> | ब्रह्मगुप्त ने सबसे पहले समीकरण का हल पूर्णांकों में दिया था <math>x^2+y^2=z^2</math> । यह <math>m^2-n^2,2mn, m^2+n^2</math> है। m और n कोई दो असमान पूर्णांक हैं। | ||
महावीर (850) कहते हैं: "वर्गों (दो तत्वों) का अंतर उर्ध्वाधर है, उनके | महावीर (850) कहते हैं: "वर्गों (दो तत्वों) का अंतर उर्ध्वाधर है, उनके गुणनफल का दोगुना आधार है और उनके वर्गों का योग एक उत्पन्न आयत का विकर्ण है।" | ||
== महावीर की परिभाषाएं == | == महावीर की परिभाषाएं == | ||
| Line 53: | Line 53: | ||
== बाहरी संपर्क == | == बाहरी संपर्क == | ||
*"परिमेय त्रिभुजों के गुणों पर एक अध्ययन"([http://www.irphouse.com/ijmr/ijmrv6n1_12.pdf A Study on the Properties of Rational Triangles]) | *"परिमेय त्रिभुजों के गुणों पर एक अध्ययन"([http://www.irphouse.com/ijmr/ijmrv6n1_12.pdf A Study on the Properties of Rational Triangles]) | ||
*"समान परिमाप और समान क्षेत्रफल वाले परिमेय त्रिभुज"([https://hrj.episciences.org/158/pdf Rational Triangles with the same perimeter and the same area]) | *"समान परिमाप और समान क्षेत्रफल वाले परिमेय त्रिभुज"([https://hrj.episciences.org/158/pdf Rational Triangles with the same perimeter and the same area]) | ||
| Line 62: | Line 61: | ||
== संदर्भ == | == संदर्भ == | ||
<references /> | <references /> | ||
[[Category:Organic Articles]] | |||
[[Category:गणित]] | [[Category:गणित]] | ||
[[Category:बीजगणित]] | [[Category:बीजगणित]] | ||
Latest revision as of 09:52, 16 December 2022
एक परिमेय त्रिभुज को उस त्रिभुज के रूप में परिभाषित किया जा सकता है जिसकी सभी भुजाएँ परिमेय लंबाई के साथ हों।
परिमेय समकोण त्रिभुज - प्रारंभिक समाधान
समीकरण के लिए शुल्बसूत्र (Śulba) समाधान में -------(1) उपलब्ध है।[1] बौधायन (सी 800 ईसा पूर्व)[2], आपस्तंब [3]और कात्यायन [4](सी 500 ईसा पूर्व) ने एक आयत को एक वर्ग में बदलने की एक विधि दी, जो बीजगणितीय पहचान के बराबर है।
जहाँ m, n कोई दो यादृच्छिक संख्याएँ हैं। इस प्रकार हम प्राप्त करते हैं
अपरिमेय मात्राओं को समाप्त करने के लिए क्रमशः m, n के लिए p2,q2 को प्रतिस्थापित करने पर, हम प्राप्त करते हैं:
जो (1) का परिमेय समाधान देता है।
कात्यायन, एक ही आकार के कई अन्य वर्गों के योग के बराबर एक वर्ग खोजने के लिए, एक बहुत ही सरल विधि देते हैं , जो हमें परिमेय समकोण त्रिभुज का एक और समाधान देता है।
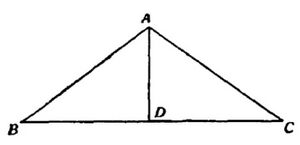
कात्यायन कहते हैं: "जितने वर्ग (बराबर आकार के) आप एक में जोड़ना चाहते हैं, अनुप्रस्थ रेखा उससे एक कम (बराबर) होगी; एक भुजा का दुगना (बराबर) उससे एक अधिक होगा; (इस प्रकार) रूप (एक समद्विबाहु) त्रिभुज। इसका तीर चिह्न (यानी, ऊंचाई) ऐसा करेगा।"
प्रत्येक भुजा a के n वर्गों को संयोजित करने के लिए, हम एक समद्विबाहु त्रिभुज ABC इस प्रकार बनाते हैं और
फिर जो सूत्र देता है
करणी(radicals) के बिना समकोण त्रिभुज की भुजाएँ बनाने के लिए n के लिए m2 रखें, तब हमारे पास है-
जो (1) का परिमेय समाधान देता है।
पश्चातवर्ती परिमेय समाधान
ब्रह्मगुप्त (628) कहते हैं: "वैकल्पिक (इष्ट) पक्ष के वर्ग को विभाजित किया जाता है, और फिर एक वैकल्पिक संख्या से कम किया जाता है; आधा परिणाम उर्ध्वाधर होता है, और वैकल्पिक संख्या से बढ़ने पर एक आयत का कर्ण मिलता है।"
यदि m, n कोई परिमेय संख्या हो तो, एक समकोण त्रिभुज की भुजाएँ इस प्रकार होंगी
इष्ट संस्कृत शब्द को "दिया" के साथ-साथ "वैकल्पिक", के रूप में समझा जाता है।
इसी तरह का एक नियम श्रीपति (1039) द्वारा दिया गया है: "कोई भी वैकल्पिक संख्या पक्ष है; उस का वर्ग विभाजित और फिर एक वैकल्पिक संख्या से छोटा और आधा उर्ध्वाधर है; पिछले भाजक के साथ जोड़ा गया एक समकोण का कर्ण है त्रिकोण। इसलिए, इसे ज्यामिति के नियमों के संबंध में विद्वानों द्वारा इसकी व्याख्या की गई है।"
समाकल/ पूर्णांकीय समाधान
ब्रह्मगुप्त ने सबसे पहले समीकरण का हल पूर्णांकों में दिया था । यह है। m और n कोई दो असमान पूर्णांक हैं।
महावीर (850) कहते हैं: "वर्गों (दो तत्वों) का अंतर उर्ध्वाधर है, उनके गुणनफल का दोगुना आधार है और उनके वर्गों का योग एक उत्पन्न आयत का विकर्ण है।"
महावीर की परिभाषाएं
महावीर [5]कहते हैं कि जिस त्रिभुज या चतुर्भुज की भुजाओं, ऊँचाइयों और अन्य आयामों को परिमेय संख्याओं के रूप में व्यक्त किया जा सकता है, उसे जन्य /जनित कहा जाता है, जिसका अर्थ है उत्पन्न, निर्मित या वह जो उत्पन्न या निर्मित होता है। वे संख्याएँ जो किसी विशेष आकृति को बनाने में शामिल होती हैं, उसकी बीज-सांख्य (तत्व-संख्याएँ) या मात्र बीज (तत्व या बीज) कहलाती हैं।
बाहरी संपर्क
- "परिमेय त्रिभुजों के गुणों पर एक अध्ययन"(A Study on the Properties of Rational Triangles)
- "समान परिमाप और समान क्षेत्रफल वाले परिमेय त्रिभुज"(Rational Triangles with the same perimeter and the same area)
यह भी देखें
संदर्भ
- ↑ दत्ता, विभूतिभूषण; नारायण सिंह, अवधेश (1962)। हिंदू गणित का इतिहास। मुंबई: एशिया पब्लिशिंग हाउस (Datta, Bibhutibhusan; Narayan Singh, Avadhesh (1962). History of Hindu Mathematics. Mumbai: Asia Publishing House.)
- ↑ "बौधायन"("Baudhayana")
- ↑ "आपस्तम्बा"("Apastamba")
- ↑ "कात्यायन"("Katyayana")
- ↑ "महावीर"("Mahavira")