विद्युत द्विध्रुव आघूर्ण: Difference between revisions
No edit summary |
m (13 revisions imported from alpha:विद्युत_द्विध्रुव_आघूर्ण) |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Measure of positive and negative charges}} | {{Short description|Measure of positive and negative charges}} | ||
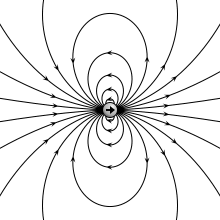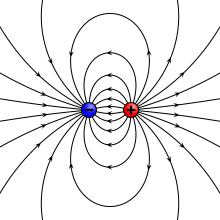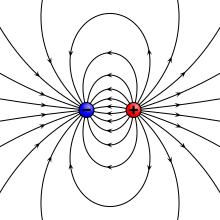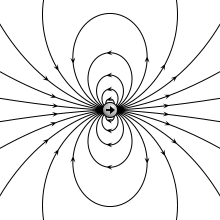
[[File:VFPt_dipoles_electric.svg|thumb|350px|'''[[विद्युत क्षेत्र]] ''बिंदु द्विध्रुव'' (ऊपरी बाएँ), विद्युत आवेशों के ''भौतिक द्विध्रुव'' (ऊपरी दाएँ), पतली ध्रुवीकृत शीट (निचला बाएँ) या प्लेट [[संधारित्र]] (निचला दाएँ) के कारण होता है। जब व्यवस्था अत्यंत छोटी होती है तब सभी समान क्षेत्र प्रोफ़ाइल उत्पन्न करते हैं।''']] | [[File:VFPt_dipoles_electric.svg|thumb|350px|'''[[विद्युत क्षेत्र]] ''बिंदु द्विध्रुव'' (ऊपरी बाएँ), विद्युत आवेशों के ''भौतिक द्विध्रुव'' (ऊपरी दाएँ), पतली ध्रुवीकृत शीट (निचला बाएँ) या प्लेट [[संधारित्र]] (निचला दाएँ) के कारण होता है। जब व्यवस्था अत्यंत छोटी होती है तब सभी समान क्षेत्र प्रोफ़ाइल उत्पन्न करते हैं।''']] | ||
'''विद्युत द्विध्रुव आघूर्ण''' प्रणाली के अंदर धनात्मक और ऋणात्मक [[विद्युत आवेश]] के पृथक्करण का माप है, अर्थात, प्रणाली की समग्र [[रासायनिक ध्रुवता]] का माप है। इस प्रकार विद्युत द्विध्रुव आघूर्ण के लिए [[इकाइयों की अंतर्राष्ट्रीय प्रणाली]] [[कूलम्ब]]-[[मीटर]] (C⋅m) है। डिबाई (डी) परमाणु भौतिकी और रसायन विज्ञान में उपयोग की जाने वाली माप की और इकाई है। | |||
'''विद्युत द्विध्रुव आघूर्ण''' प्रणाली के अंदर धनात्मक और ऋणात्मक [[विद्युत आवेश]] के पृथक्करण का माप है, अर्थात, प्रणाली की समग्र [[रासायनिक ध्रुवता]] का माप है। विद्युत द्विध्रुव आघूर्ण के लिए [[इकाइयों की अंतर्राष्ट्रीय प्रणाली]] [[कूलम्ब]]-[[मीटर]] (C⋅m) है। डिबाई (डी) परमाणु भौतिकी और रसायन विज्ञान में उपयोग की जाने वाली माप की और इकाई है। | |||
सैद्धांतिक रूप से, विद्युत द्विध्रुव को बहुध्रुव विस्तार के प्रथम-क्रम पद द्वारा परिभाषित किया जाता है; इसमें दो समान और विपरीत आवेश होते हैं जो एक-दूसरे के बहुत करीब होते हैं, चूंकि वास्तविक द्विध्रुवों में भिन्न-भिन्न आवेश होते हैं। | सैद्धांतिक रूप से, विद्युत द्विध्रुव को बहुध्रुव विस्तार के प्रथम-क्रम पद द्वारा परिभाषित किया जाता है; इसमें दो समान और विपरीत आवेश होते हैं जो एक-दूसरे के बहुत करीब होते हैं, चूंकि वास्तविक द्विध्रुवों में भिन्न-भिन्न आवेश होते हैं। | ||
| Line 17: | Line 16: | ||
}} | }} | ||
अधिकांशतः भौतिकी में किसी विशाल वस्तु के आयामों को नजरअंदाज किया जा सकता है और उसे बिंदु जैसी वस्तु, अर्थात [[बिंदु कण]] के रूप में माना जा सकता है। विद्युत आवेश वाले बिंदु कणों को बिंदु आवेश कहा जाता है। दो बिंदु आवेश, आवेश सहित {{math|+''q''}} और दूसरा आवेश वाला {{math|−''q''}} दूरी से भिन्न हो गया {{mvar|d}}, विद्युत द्विध्रुव (मल्टीपोल विस्तार का साधारण | अधिकांशतः भौतिकी में किसी विशाल वस्तु के आयामों को नजरअंदाज किया जा सकता है और उसे बिंदु जैसी वस्तु, अर्थात [[बिंदु कण]] के रूप में माना जा सकता है। इस प्रकार विद्युत आवेश वाले बिंदु कणों को बिंदु आवेश कहा जाता है। दो बिंदु आवेश, आवेश सहित {{math|+''q''}} और दूसरा आवेश वाला {{math|−''q''}} दूरी से भिन्न हो गया {{mvar|d}}, विद्युत द्विध्रुव (मल्टीपोल विस्तार का साधारण स्थिति) का गठन करता है। इस स्थितियों के लिए, विद्युत द्विध्रुव आघूर्ण का परिमाण होता है<math display="block">p = qd</math>और ऋणात्मक आवेश से धनात्मक आवेश की ओर निर्देशित होता है। कुछ लेखक भिन्न हो सकते हैं {{mvar|d}} आधे में और उपयोग करें {{math|1=''s'' = ''d''/2}} चूँकि यह मात्रा किसी भी आवेश और द्विध्रुव के केंद्र के मध्य की दूरी है, जिससे परिभाषा में दो का कारक बनता है। इस प्रकार एक शक्तिशाली गणितीय परिभाषा [[वेक्टर बीजगणित|सदिश बीजगणित]] का उपयोग करना है, क्योंकि परिमाण और दिशा वाली मात्रा, जैसे दो बिंदु आवेशों के द्विध्रुव क्षण को सदिश रूप में व्यक्त किया जा सकता है<math display="block">\mathbf{p} = q \mathbf{d}</math>कहाँ {{math|'''d'''}} ऋणात्मक आवेश से धनात्मक आवेश की ओर इंगित करने वाला [[विस्थापन (वेक्टर)|विस्थापन (सदिश)]] है। विद्युत द्विध्रुव आघूर्ण सदिश {{math|'''p'''}} ऋणात्मक आवेश से धनात्मक आवेश की ओर भी इंगित करता है। इस प्रकार इस परिभाषा के साथ द्विध्रुव दिशा स्वयं को बाहरी विद्युत क्षेत्र के साथ संरेखित करती है (और ध्यान दें कि द्विध्रुव के आवेशों द्वारा निर्मित विद्युत प्रवाह रेखाएं, जो धनात्मक आवेश से ऋणात्मक आवेश की ओर इंगित करती हैं, बाहरी विद्युत क्षेत्र की प्रवाह रेखाओं का विरोध करती हैं मैदान)। इस प्रकार ध्यान दें कि इस संकेत परंपरा का उपयोग भौतिकी में किया जाता है, जबकि धनात्मक आवेश से ऋणात्मक आवेश तक द्विध्रुव के लिए विपरीत संकेत परंपरा का उपयोग रसायन विज्ञान में किया जाता है।<ref name="Atkins"> | ||
एक शक्तिशाली गणितीय परिभाषा [[वेक्टर बीजगणित|सदिश बीजगणित]] का उपयोग करना है, क्योंकि परिमाण और दिशा वाली मात्रा, जैसे दो बिंदु आवेशों के द्विध्रुव क्षण को सदिश रूप में व्यक्त किया जा सकता है<math display="block">\mathbf{p} = q \mathbf{d}</math>कहाँ {{math|'''d'''}} ऋणात्मक आवेश से धनात्मक आवेश की ओर इंगित करने वाला [[विस्थापन (वेक्टर)|विस्थापन (सदिश)]] है। विद्युत द्विध्रुव आघूर्ण सदिश {{math|'''p'''}} ऋणात्मक आवेश से धनात्मक आवेश की ओर भी इंगित करता है। इस परिभाषा के साथ द्विध्रुव दिशा स्वयं को बाहरी विद्युत क्षेत्र के साथ संरेखित करती है (और ध्यान दें कि द्विध्रुव के आवेशों द्वारा निर्मित विद्युत प्रवाह रेखाएं, जो धनात्मक आवेश से ऋणात्मक आवेश की ओर इंगित करती हैं, बाहरी विद्युत क्षेत्र की प्रवाह रेखाओं का विरोध करती हैं मैदान)। ध्यान दें कि इस संकेत परंपरा का उपयोग भौतिकी में किया जाता है, जबकि धनात्मक आवेश से ऋणात्मक आवेश तक द्विध्रुव के लिए विपरीत संकेत परंपरा का उपयोग रसायन विज्ञान में किया जाता है।<ref name="Atkins"> | |||
{{cite book | {{cite book | ||
| title=Chemical principles: the quest for insight | | title=Chemical principles: the quest for insight | ||
| Line 28: | Line 25: | ||
| year=2016 | | year=2016 | ||
| publisher=Macmillan Learning | | publisher=Macmillan Learning | ||
| edition = 7th }}</ref> इस दो-आवेश प्रणाली का आदर्शीकरण विद्युत बिंदु द्विध्रुव है जिसमें दो (अनंत) आवेश होते हैं जो केवल अनंत रूप से भिन्न होते हैं, किन्तु सीमित सीमा के साथ {{math|'''p'''}}. इस मात्रा का उपयोग [[ध्रुवीकरण घनत्व]] की परिभाषा में किया जाता है। | | edition = 7th }}</ref> इस प्रकार दो-आवेश प्रणाली का आदर्शीकरण विद्युत बिंदु द्विध्रुव है जिसमें दो (अनंत) आवेश होते हैं जो केवल अनंत रूप से भिन्न होते हैं, किन्तु सीमित सीमा के साथ {{math|'''p'''}}. इस मात्रा का उपयोग [[ध्रुवीकरण घनत्व]] की परिभाषा में किया जाता है। | ||
=='''ऊर्जा और आघूर्ण'''== | =='''ऊर्जा और आघूर्ण'''== | ||
[[File:Electric dipole torque uniform field.svg|thumb|187x187px| | [[File:Electric dipole torque uniform field.svg|thumb|187x187px|एक समान ई क्षेत्र में विद्युत द्विध्रुव P और इसका आघूर्ण τ।]]विद्युत द्विध्रुव आघूर्ण p वाली कोई वस्तु बाह्य विद्युत क्षेत्र E में रखे जाने पर बलाघूर्ण ''τ'' के अधीन होती है। बलाघूर्ण द्विध्रुव को क्षेत्र के साथ संरेखित करता है। विद्युत क्षेत्र के समानांतर संरेखित द्विध्रुव में उसके साथ कुछ कोण बनाने वाले द्विध्रुव की तुलना में कम [[संभावित ऊर्जा]] होती है। इस प्रकार द्विध्रुव द्वारा व्याप्त छोटे क्षेत्र में स्थानिक रूप से समान विद्युत क्षेत्र के लिए, ऊर्जा ''U'' और [[ टॉर्कः |आघूर्णः]] <math>\boldsymbol{\tau}</math> द्वारा दिए गए हैं<ref name="Seaway">{{cite book | title=Physics for Scientists and Engineers, Volume 2 | author1=Raymond A. Serway | author2=John W. Jewett Jr. | url = https://books.google.com/books?id=1D4VJrWY9ikC&pg=PA756 | isbn=978-1439048399 | pages=756–757 | year=2009 | publisher=Cengage Learning | edition = 8th}}</ref><math display="block">U = - \mathbf{p} \cdot \mathbf{E},\qquad\ \boldsymbol{\tau} = \mathbf{p} \times \mathbf{E},</math>अदिश बिंदु{{math|⋅}} उत्पाद और ऋणात्मक चिह्न दर्शाता है कि जब द्विध्रुव क्षेत्र के समानांतर होता है तब स्थितिज ऊर्जा न्यूनतम हो जाती है और प्रतिसमानांतर होने पर अधिकतम होती है जबकि लंबवत होने पर शून्य होती है। इस प्रकार प्रतीक{{math|×}} [[वेक्टर क्रॉस उत्पाद|सदिश क्रॉस उत्पाद]] को संदर्भित करता है। E-क्षेत्र सदिश और द्विध्रुव सदिश विमान को परिभाषित करते हैं, और टोक़ को दाहिने हाथ के नियम द्वारा दी गई दिशा के साथ उस विमान के सामान्य रूप से निर्देशित किया जाता है। इस प्रकार ध्यान दें कि ऐसे समान क्षेत्र में द्विध्रुव मुड़ सकता है और दोलन कर सकता है किन्तु द्विध्रुव के कोई रैखिक त्वरण के साथ कोई समग्र शुद्ध बल प्राप्त नहीं करता है। द्विध्रुव बाहरी क्षेत्र के साथ संरेखित होने के लिए मुड़ता है। | ||
चूँकि गैर-समान विद्युत क्षेत्र में द्विध्रुव वास्तव में शुद्ध बल प्राप्त कर सकता है क्योंकि द्विध्रुव के छोर पर बल वर्तमान दूसरे छोर पर संतुलित नहीं होता है। यह दिखाया जा सकता है कि यह शुद्ध बल सामान्यतः द्विध्रुवीय क्षण के समानांतर होता है। | चूँकि गैर-समान विद्युत क्षेत्र में द्विध्रुव वास्तव में शुद्ध बल प्राप्त कर सकता है क्योंकि द्विध्रुव के छोर पर बल वर्तमान दूसरे छोर पर संतुलित नहीं होता है। यह दिखाया जा सकता है कि यह शुद्ध बल सामान्यतः द्विध्रुवीय क्षण के समानांतर होता है। | ||
=='''अभिव्यक्ति (सामान्य स्थिति)'''== | =='''अभिव्यक्ति (सामान्य स्थिति)'''== | ||
अधिक सामान्यतः, आयतन V तक सीमित आवेश के निरंतर वितरण के लिए, द्विध्रुव क्षण के लिए संगत अभिव्यक्ति है:<math display="block">\mathbf{p}(\mathbf{r}) = \int_{V} \rho(\mathbf{r}') \left(\mathbf{r}' - \mathbf{r}\right) d^3 \mathbf{r}',</math>अवलोकन बिंदु और '' | अधिक सामान्यतः, आयतन V तक सीमित आवेश के निरंतर वितरण के लिए, द्विध्रुव क्षण के लिए संगत अभिव्यक्ति है:<math display="block">\mathbf{p}(\mathbf{r}) = \int_{V} \rho(\mathbf{r}') \left(\mathbf{r}' - \mathbf{r}\right) d^3 \mathbf{r}',</math>जहां r अवलोकन के बिंदु का पता लगाता है और ''d''<sup>3</sup>'''r'''′ V में एक प्राथमिक आयतन को दर्शाता है। इस प्रकार बिंदु आवेशों की एक सरणी के लिए, आवेश घनत्व [[डिराक डेल्टा फ़ंक्शन|डिराक डेल्टा]] [[डिराक डेल्टा फ़ंक्शन|वेरिएबल]] का योग बन जाता है:<math display="block">\rho(\mathbf{r}) = \sum_{i=1}^N \, q_i \, \delta \left(\mathbf{r} - \mathbf{r}_i\right),</math>जहां प्रत्येक आर<sub>''i''</sub> किसी संदर्भ बिंदु से आवेश q<sub>i</sub>. तक सदिश है उपरोक्त एकीकरण सूत्र में प्रतिस्थापन प्रदान करता है: | ||
<math display="block">\mathbf{p}(\mathbf{r}) = | <math display="block">\mathbf{p}(\mathbf{r}) = | ||
\sum_{i=1}^N \, q_i \int_V \delta\left(\mathbf{r}_0 - \mathbf{r}_i\right)\, \left(\mathbf{r}_0 - \mathbf{r}\right)\, d^3 \mathbf{r}_0 = | \sum_{i=1}^N \, q_i \int_V \delta\left(\mathbf{r}_0 - \mathbf{r}_i\right)\, \left(\mathbf{r}_0 - \mathbf{r}\right)\, d^3 \mathbf{r}_0 = | ||
| Line 50: | Line 47: | ||
द्विध्रुव आघूर्ण आवेशों की समग्र तटस्थ प्रणाली के संदर्भ में विशेष रूप से उपयोगी है, उदाहरण के लिए विपरीत आवेशों की जोड़ी, या समान विद्युत क्षेत्र में तटस्थ कंडक्टर। | द्विध्रुव आघूर्ण आवेशों की समग्र तटस्थ प्रणाली के संदर्भ में विशेष रूप से उपयोगी है, उदाहरण के लिए विपरीत आवेशों की जोड़ी, या समान विद्युत क्षेत्र में तटस्थ कंडक्टर। | ||
आवेशों की ऐसी प्रणाली के लिए, जिसे युग्मित विपरीत आवेशों की श्रृंखला के रूप में देखा जाता है, विद्युत द्विध्रुव आघूर्ण का संबंध है: | आवेशों की ऐसी प्रणाली के लिए, जिसे युग्मित विपरीत आवेशों की श्रृंखला के रूप में देखा जाता है, विद्युत द्विध्रुव आघूर्ण का संबंध है: | ||
| Line 58: | Line 56: | ||
&= \sum_{i=1}^N q_i \mathbf{d}_i = \sum_{i=1}^{N} \mathbf{p}_i \, , | &= \sum_{i=1}^N q_i \mathbf{d}_i = \sum_{i=1}^{N} \mathbf{p}_i \, , | ||
\end{align}</math> | \end{align}</math> | ||
जहां r अवलोकन का बिंदु है, और d<sub>''i''</sub> = | जहां r अवलोकन का बिंदु है, और '''d'''<sub>''i''</sub> = '''r''''<sub>''i''</sub> − '''r'''<sub>''i''</sub>, '''r'''<sub>''i''</sub> द्विध्रुव i, और 'r में ऋणात्मक आवेश की स्थिति होना{{'}}<sub>''i''</sub> धनात्मक आवेश की स्थिति. | ||
यह तटस्थ आवेश युग्मों के व्यक्तिगत द्विध्रुव आघूर्णों का सदिश योग है। (समग्र आवेश तटस्थता के कारण , द्विध्रुव क्षण पर्यवेक्षक की स्थिति आर से स्वतंत्र है।) इस प्रकार, पी का मान संदर्भ बिंदु की पसंद से स्वतंत्र है, परंतु प्रणाली का समग्र आवेश शून्य हो। | यह तटस्थ आवेश युग्मों के व्यक्तिगत द्विध्रुव आघूर्णों का सदिश योग है। (समग्र आवेश तटस्थता के कारण , द्विध्रुव क्षण पर्यवेक्षक की स्थिति आर से स्वतंत्र है।) इस प्रकार, पी का मान संदर्भ बिंदु की पसंद से स्वतंत्र है, परंतु प्रणाली का समग्र आवेश शून्य हो। | ||
| Line 72: | Line 70: | ||
| edition= 2nd | | edition= 2nd | ||
| page=307 | | page=307 | ||
}}</ref> यह विकल्प केवल परंपरा का विषय नहीं है: द्विध्रुव क्षण की धारणा अनिवार्य रूप से टोक़ की यांत्रिक धारणा से ली गई है, और यांत्रिकी की तरह, अवलोकन बिंदु के रूप में द्रव्यमान के केंद्र को चुनना कम्प्यूटेशनल और सैद्धांतिक रूप से उपयोगी है। किसी आवेशित अणु के लिए द्रव्यमान के केंद्र के अतिरिक्त आवेश का केंद्र संदर्भ बिंदु होना चाहिए। तटस्थ प्रणालियों के लिए संदर्भ बिंदु महत्वपूर्ण नहीं है, और द्विध्रुवीय क्षण प्रणाली का आंतरिक गुण है। | }}</ref> यह विकल्प केवल परंपरा का विषय नहीं है: द्विध्रुव क्षण की धारणा अनिवार्य रूप से टोक़ की यांत्रिक धारणा से ली गई है, और यांत्रिकी की तरह, अवलोकन बिंदु के रूप में द्रव्यमान के केंद्र को चुनना कम्प्यूटेशनल और सैद्धांतिक रूप से उपयोगी है। किसी आवेशित अणु के लिए द्रव्यमान के केंद्र के अतिरिक्त आवेश का केंद्र संदर्भ बिंदु होना चाहिए। इस प्रकार तटस्थ प्रणालियों के लिए संदर्भ बिंदु महत्वपूर्ण नहीं है, और द्विध्रुवीय क्षण प्रणाली का आंतरिक गुण है। | ||
=='''विद्युत द्विध्रुव की क्षमता और क्षेत्र'''== | =='''विद्युत द्विध्रुव की क्षमता और क्षेत्र'''== | ||
एक आदर्श द्विध्रुव में अनंत सूक्ष्म पृथक्करण वाले दो विपरीत आवेश होते हैं। इस प्रकार हम ऐसे आदर्श द्विध्रुव की क्षमता और क्षेत्र की गणना करते हैं, जो पृथक्करण d > 0 पर दो विपरीत आवेशों से प्रारंभ होता है, और सीमा को d → 0 के रूप में लेता है। | |||
एक आदर्श द्विध्रुव में अनंत सूक्ष्म पृथक्करण वाले दो विपरीत आवेश होते हैं। हम ऐसे आदर्श द्विध्रुव की क्षमता और क्षेत्र की गणना करते हैं, जो पृथक्करण d > 0 पर दो विपरीत आवेशों से प्रारंभ होता है, और सीमा को d → 0 के रूप में लेता है। | |||
दो निकट दूरी वाले विपरीत आवेशों ±q की क्षमता इस प्रकार है: | दो निकट दूरी वाले विपरीत आवेशों ±q की क्षमता इस प्रकार है: | ||
| Line 86: | Line 82: | ||
<math display="block">\rho(\mathbf{r}) \ =\ -\varepsilon_0\nabla^2\phi \ =\ q\delta\left(\mathbf{r} - | <math display="block">\rho(\mathbf{r}) \ =\ -\varepsilon_0\nabla^2\phi \ =\ q\delta\left(\mathbf{r} - | ||
\mathbf{r}_+\right) - q\delta\left(\mathbf{r} - \mathbf{r}_-\right)</math> | \mathbf{r}_+\right) - q\delta\left(\mathbf{r} - \mathbf{r}_-\right)</math> | ||
कूलम्ब के नियम | कूलम्ब के नियम के अनुसार, जहां आवेश पृथक्करण है: | ||
<math display="block">\mathbf{d} = \mathbf{r}_+ - \mathbf{r}_- \, , | <math display="block">\mathbf{d} = \mathbf{r}_+ - \mathbf{r}_- \, , | ||
\quad d = |\mathbf{d}|\,. </math> | \quad d = |\mathbf{d}|\,. </math>मान लीजिए कि R मध्यबिंदु के सापेक्ष स्थिति सदिश को दर्शाता है <math>\frac{\mathbf{r}_+ + \mathbf{r}_-}{2}</math>, और <math>\hat\mathbf{R}</math> संबंधित इकाई सदिश:<math display="block">\mathbf{R} = \mathbf{r} - \frac{\mathbf{r}_+ + \mathbf{r}_-}{2}, \quad \hat{\mathbf{R}} = \frac{\mathbf{R}}{R}\, ,</math>टेलर का विस्तार <math>\tfrac dR</math> (मल्टीपोल विस्तार और क्वाड्रुपोल इलेक्ट्रिक क्वाड्रुपोल देखें) इस क्षमता को श्रृंखला के रूप में व्यक्त करता है।<ref name="Dugdale">{{cite book |title=विद्युत चुम्बकत्व की अनिवार्यताएँ|author=David E Dugdale |pages= 80–81 |url=https://books.google.com/books?id=LIwBcIwrwv4C&pg=PA81 |isbn=978-1-56396-253-0 |year=1993 |publisher=Springer}}</ref><ref name="Hirose">{{cite book |title=वास्तविक-अंतरिक्ष औपचारिकता में प्रथम-सिद्धांत गणना|author1=Kikuji Hirose |author2=Tomoya Ono |author3=Yoshitaka Fujimoto |url=https://books.google.com/books?id=TkvogLqVrqwC&pg=PA18 |page=18 |publisher=Imperial College Press |year=2005 |isbn=978-1-86094-512-0}}</ref><math display="block">\phi(\mathbf{R}) \ =\ | ||
मान लीजिए कि R मध्यबिंदु के सापेक्ष स्थिति सदिश को दर्शाता है <math>\frac{\mathbf{r}_+ + \mathbf{r}_-}{2}</math>, और <math>\hat\mathbf{R}</math> संबंधित इकाई सदिश: | |||
<math display="block">\mathbf{R} = \mathbf{r} - \frac{\mathbf{r}_+ + \mathbf{r}_-}{2}, \quad \hat{\mathbf{R}} = \frac{\mathbf{R}}{R}\, ,</math> | |||
टेलर का विस्तार <math>\tfrac dR</math> (मल्टीपोल विस्तार और क्वाड्रुपोल | |||
<math display="block">\phi(\mathbf{R}) \ =\ | |||
\frac{1}{4 \pi \varepsilon _0} \frac{q\mathbf{d} \cdot \hat{\mathbf{R}}}{R^2} + \mathcal O\left(\frac{d^3}{R^3}\right) | \frac{1}{4 \pi \varepsilon _0} \frac{q\mathbf{d} \cdot \hat{\mathbf{R}}}{R^2} + \mathcal O\left(\frac{d^3}{R^3}\right) | ||
\ \approx\ | \ \approx\ | ||
\frac{1}{4 \pi \varepsilon _0} \frac{\mathbf{p} \cdot \hat{\mathbf{R}}}{R^2}\, ,</math> | \frac{1}{4 \pi \varepsilon _0} \frac{\mathbf{p} \cdot \hat{\mathbf{R}}}{R^2}\, ,</math>जहां श्रृंखला में उच्च क्रम के पद बड़ी दूरी पर गायब हो रहे हैं, आर, डी की तुलना में। यहां, विद्युत द्विध्रुव आघूर्ण p उपरोक्तानुसार है:<math display="block">\mathbf{p} = q\mathbf{d}\, .</math>द्विध्रुव विभव का परिणाम इस प्रकार भी व्यक्त किया जा सकता है:<ref name="Laud">{{cite book |author=BB Laud |title=विद्युत चुम्बकीय|url=https://books.google.com/books?id=XtgFvbd9F2UC&pg=PA25 |page=25 |isbn=978-0-85226-499-7 |year=1987 |edition= 2nd |publisher=New Age International}}</ref><math display="block">\phi(\mathbf{R}) \approx -\mathbf{p} \cdot \mathbf{\nabla} \frac{1}{4 \pi \varepsilon _0 R}\, ,</math>जो बिंदु आवेश के द्विध्रुवीय विभव से संबंधित है। मुख्य बिंदु यह है कि द्विध्रुव की क्षमता बिंदु आवेश की तुलना में दूरी आर के साथ तेजी से गिरती है। | ||
जहां श्रृंखला में उच्च क्रम के पद बड़ी दूरी पर गायब हो रहे हैं, आर, डी की तुलना में। यहां, विद्युत द्विध्रुव आघूर्ण p उपरोक्तानुसार है: | द्विध्रुव का विद्युत क्षेत्र विभव की ऋणात्मक प्रवणता है, जिसके कारण :<ref name=Laud/><math display="block">\mathbf E\left(\mathbf R\right) = \frac{3\left(\mathbf{p} \cdot \hat{\mathbf{R}}\right) \hat{\mathbf{R}} - \mathbf{p}}{4 \pi \varepsilon_0 R^3}\, .</math>इस प्रकार, चूंकि दो निकट दूरी वाले विपरीत आवेश बिल्कुल आदर्श विद्युत द्विध्रुव नहीं हैं (क्योंकि कम दूरी पर उनकी क्षमता द्विध्रुव की तरह नहीं है), उनके पृथक्करण से बहुत बड़ी दूरी पर, उनका द्विध्रुव क्षण 'पी' सीधे उनकी क्षमता में दिखाई देता है और मैदान। | ||
<math display="block">\mathbf{p} = q\mathbf{d}\, .</math> | |||
द्विध्रुव विभव का परिणाम इस प्रकार भी व्यक्त किया जा सकता है:<ref name=Laud>{{cite book |author=BB Laud |title=विद्युत चुम्बकीय|url=https://books.google.com/books?id=XtgFvbd9F2UC&pg=PA25 |page=25 |isbn=978-0-85226-499-7 |year=1987 |edition= 2nd |publisher=New Age International}}</ref> | |||
<math display="block">\phi(\mathbf{R}) \approx -\mathbf{p} \cdot \mathbf{\nabla} \frac{1}{4 \pi \varepsilon _0 R}\, ,</math> | |||
जो बिंदु आवेश के द्विध्रुवीय विभव से संबंधित है। मुख्य बिंदु यह है कि द्विध्रुव की क्षमता बिंदु आवेश की तुलना में दूरी आर के साथ तेजी से गिरती है। | |||
द्विध्रुव का विद्युत क्षेत्र विभव की ऋणात्मक प्रवणता है, जिसके कारण :<ref name=Laud/> | |||
<math display="block">\mathbf E\left(\mathbf R\right) = \frac{3\left(\mathbf{p} \cdot \hat{\mathbf{R}}\right) \hat{\mathbf{R}} - \mathbf{p}}{4 \pi \varepsilon_0 R^3}\, .</math> | |||
इस प्रकार, चूंकि दो निकट दूरी वाले विपरीत आवेश बिल्कुल आदर्श विद्युत द्विध्रुव नहीं हैं (क्योंकि कम दूरी पर उनकी क्षमता द्विध्रुव की तरह नहीं है), उनके पृथक्करण से बहुत बड़ी दूरी पर, उनका द्विध्रुव क्षण 'पी' सीधे उनकी क्षमता में दिखाई देता है और मैदान। | |||
जैसे ही दोनों आवेशों को साथ करीब लाया जाता है (d को छोटा कर दिया जाता है), अनुपात d/R के आधार पर बहुध्रुव विस्तार में द्विध्रुव पद निकटतम दूरी R पर एकमात्र महत्वपूर्ण पद बन जाता है, और अनंत पृथक्करण की सीमा में द्विध्रुव पद इस विस्तार में ही सब कुछ मायने रखता है। चूँकि, चूँकि d को अतिसूक्ष्म बनाया गया है, इसलिए 'p' स्थिरांक को बनाए रखने के लिए द्विध्रुव आवेश को बढ़ाना होगा। इस सीमित प्रक्रिया का परिणाम बिंदु द्विध्रुव होता है। | जैसे ही दोनों आवेशों को साथ करीब लाया जाता है (d को छोटा कर दिया जाता है), अनुपात d/R के आधार पर बहुध्रुव विस्तार में द्विध्रुव पद निकटतम दूरी R पर एकमात्र महत्वपूर्ण पद बन जाता है, और अनंत पृथक्करण की सीमा में द्विध्रुव पद इस विस्तार में ही सब कुछ मायने रखता है। चूँकि, चूँकि d को अतिसूक्ष्म बनाया गया है, इसलिए 'p' स्थिरांक को बनाए रखने के लिए द्विध्रुव आवेश को बढ़ाना होगा। इस सीमित प्रक्रिया का परिणाम बिंदु द्विध्रुव होता है। | ||
| Line 113: | Line 95: | ||
आवेशों की श्रृंखला का द्विध्रुव आघूर्ण,<math display="block">\mathbf p = \sum_{i=1}^N q_i \mathbf {d_i} \, , </math>सरणी की ध्रुवीयता की डिग्री निर्धारित करता है, किन्तु तटस्थ सरणी के लिए यह केवल सरणी का सदिश गुण है जिसमें सरणी के पूर्ण स्थान के बारे में कोई जानकारी नहीं होती है। सरणी 'p'('r') के द्विध्रुव आघूर्ण घनत्व में सरणी का स्थान और उसका द्विध्रुव आघूर्ण दोनों सम्मिलित होते हैं। जब सरणी वाले किसी क्षेत्र में विद्युत क्षेत्र की गणना करने का समय आता है, तब मैक्सवेल के समीकरण हल हो जाते हैं, और आवेश सरणी के बारे में जानकारी मैक्सवेल के समीकरणों के ध्रुवीकरण घनत्व 'पी' ('आर') में निहित होती है। इस बात पर निर्भर करते हुए कि विद्युत क्षेत्र का कितना बारीक मूल्यांकन आवश्यक है, आवेश सरणी के बारे में अधिक या कम जानकारी 'पी' ('आर') द्वारा व्यक्त की जानी होगी। जैसा कि नीचे बताया गया है, कभी-कभी 'पी'('आर') = 'पी'('आर') लेना पर्याप्त रूप से त्रुटिहीन होता है। कभी-कभी अधिक विस्तृत विवरण की आवश्यकता होती है (उदाहरण के लिए, अतिरिक्त चतुर्भुज घनत्व के साथ द्विध्रुव क्षण घनत्व को पूरक करना) और कभी-कभी 'पी' ('आर') के और भी अधिक विस्तृत संस्करण आवश्यक होते हैं। | आवेशों की श्रृंखला का द्विध्रुव आघूर्ण,<math display="block">\mathbf p = \sum_{i=1}^N q_i \mathbf {d_i} \, , </math>सरणी की ध्रुवीयता की डिग्री निर्धारित करता है, किन्तु तटस्थ सरणी के लिए यह केवल सरणी का सदिश गुण है जिसमें सरणी के पूर्ण स्थान के बारे में कोई जानकारी नहीं होती है। सरणी 'p'('r') के द्विध्रुव आघूर्ण घनत्व में सरणी का स्थान और उसका द्विध्रुव आघूर्ण दोनों सम्मिलित होते हैं। जब सरणी वाले किसी क्षेत्र में विद्युत क्षेत्र की गणना करने का समय आता है, तब मैक्सवेल के समीकरण हल हो जाते हैं, और आवेश सरणी के बारे में जानकारी मैक्सवेल के समीकरणों के ध्रुवीकरण घनत्व 'पी' ('आर') में निहित होती है। इस बात पर निर्भर करते हुए कि विद्युत क्षेत्र का कितना बारीक मूल्यांकन आवश्यक है, आवेश सरणी के बारे में अधिक या कम जानकारी 'पी' ('आर') द्वारा व्यक्त की जानी होगी। जैसा कि नीचे बताया गया है, कभी-कभी 'पी'('आर') = 'पी'('आर') लेना पर्याप्त रूप से त्रुटिहीन होता है। कभी-कभी अधिक विस्तृत विवरण की आवश्यकता होती है (उदाहरण के लिए, अतिरिक्त चतुर्भुज घनत्व के साथ द्विध्रुव क्षण घनत्व को पूरक करना) और कभी-कभी 'पी' ('आर') के और भी अधिक विस्तृत संस्करण आवश्यक होते हैं। | ||
वर्तमान यह पता लगाया जा रहा है कि मैक्सवेल के समीकरणों में प्रवेश करने वाला ध्रुवीकरण घनत्व 'पी' ('आर') किस तरह से आवेशों के समग्र तटस्थ सरणी के द्विध्रुव क्षण 'पी' से संबंधित है, और द्विध्रुव क्षण घनत्व 'पी' से भी संबंधित है। ('आर') (जो न केवल द्विध्रुवीय क्षण का वर्णन करता है, किंतु सरणी स्थान का भी वर्णन करता है)। निम्नलिखित में केवल स्थिर स्थितियों पर विचार किया जाता है, इसलिए 'पी'('आर') पर कोई समय निर्भरता नहीं है, और कोई [[विस्थापन धारा]] नहीं है। सबसे पहले ध्रुवीकरण घनत्व 'पी'('आर') की कुछ चर्चा है। उस चर्चा का अनुसरण अनेक विशिष्ट उदाहरणों के साथ किया जाता है। | वर्तमान यह पता लगाया जा रहा है कि मैक्सवेल के समीकरणों में प्रवेश करने वाला ध्रुवीकरण घनत्व 'पी' ('आर') किस तरह से आवेशों के समग्र तटस्थ सरणी के द्विध्रुव क्षण 'पी' से संबंधित है, और द्विध्रुव क्षण घनत्व 'पी' से भी संबंधित है। ('आर') (जो न केवल द्विध्रुवीय क्षण का वर्णन करता है, किंतु सरणी स्थान का भी वर्णन करता है)। निम्नलिखित में केवल स्थिर स्थितियों पर विचार किया जाता है, इसलिए 'पी'('आर') पर कोई समय निर्भरता नहीं है, और कोई [[विस्थापन धारा]] नहीं है। सबसे पहले ध्रुवीकरण घनत्व 'पी'('आर') की कुछ चर्चा है। उस चर्चा का अनुसरण अनेक विशिष्ट उदाहरणों के साथ किया जाता है। | ||
मुक्त और बाध्य आवेशों और धाराओं में आवेशों और धाराओं के विभाजन के आधार पर मैक्सवेल के समीकरणों का सूत्रीकरण 'डी'- और 'पी'-क्षेत्रों की प्रारंभआत की ओर ले जाता है: | मुक्त और बाध्य आवेशों और धाराओं में आवेशों और धाराओं के विभाजन के आधार पर मैक्सवेल के समीकरणों का सूत्रीकरण 'डी'- और 'पी'-क्षेत्रों की प्रारंभआत की ओर ले जाता है:<math display="block"> \mathbf{D} = \varepsilon _0 \mathbf{E} + \mathbf{P}\, , </math>जहाँ P को ध्रुवीकरण घनत्व कहा जाता है। इस सूत्रीकरण में, इस समीकरण का विचलन उत्पन्न होता है:<math display="block">\nabla \cdot \mathbf{D} = \rho_f = \varepsilon _0 \nabla \cdot \mathbf{E} +\nabla \cdot \mathbf{P}\, , </math>और जैसा कि ई में विचलन शब्द ''कुल'' आवेश है, और ''ρ'' है<sub>f</sub>निःशुल्क शुल्क है, हमारे पास संबंध शेष है:<math display="block">\nabla \cdot \mathbf{P} = -\rho_b \, , </math>ρ के साथ<sub>b</sub>बाउंड आवेश के रूप में, जिसका कारण कुल और मुक्त आवेश घनत्व के मध्य का अंतर है। | ||
<math display="block"> \mathbf{D} = \varepsilon _0 \mathbf{E} + \mathbf{P}\, , </math> | एक तरफ, चुंबकीय प्रभाव की अनुपस्थिति में, मैक्सवेल के समीकरण इसे निर्दिष्ट करते हैं<math display="block">\nabla \times \mathbf{E} = \boldsymbol{0}\, ,</math>जो यह दर्शाता हे<math display="block">\nabla \times \left( \mathbf{D} - \mathbf{P} \right) = \boldsymbol{0}\, ,</math>[[हेल्महोल्ट्ज़ अपघटन]] प्रयुक्त करना:<ref name="Wu">{{cite book | title=भंवर और भंवर गतिशीलता| author1=Jie-Zhi Wu | author2=Hui-Yang Ma | author3=Ming-De Zhou | pages=36 ''ff'' | chapter-url=https://books.google.com/books?id=P5yNCu44PiwC&pg=PA36 | chapter=§2.3.1 Functionally Orthogonal Decomposition | isbn=978-3-540-29027-8 | year=200 | publisher=Springer }}</ref><math display="block"> \mathbf{D} - \mathbf{P} = -\nabla \varphi \, , </math>कुछ अदिश क्षमता के लिए φ, और:<math display="block">\nabla \cdot (\mathbf{D} - \mathbf{P}) = \varepsilon_0 \nabla \cdot \mathbf{E} = \rho_f + \rho_b = - \nabla^2 \varphi\, .</math>मान लीजिए कि आवेशों को मुक्त और बाध्य में विभाजित किया गया है, और क्षमता को विभाजित किया गया है<math display="block">\varphi = \varphi_f + \varphi_b\, .</math>φ पर सीमा शर्तों की संतुष्टि को φ के मध्य इच्छानुसार से विभाजित किया जा सकता है<sub>f</sub>और φ<sub>b</sub>क्योंकि केवल योग φ को ही इन शर्तों को पूरा करना होगा। इससे यह निष्कर्ष निकलता है कि 'पी' विद्युत क्षेत्र के समानुपाती होता है क्योंकि आवेशों को सीमा के रूप में चुना जाता है, सीमा की स्थितियाँ सुविधाजनक सिद्ध होती हैं। विशेष रूप से, जब कोई निःशुल्क शुल्क उपस्तिथ नहीं है, तब संभावित विकल्प 'पी' = ε है<sub>0</sub> इ। | ||
जहाँ P को ध्रुवीकरण घनत्व कहा जाता है। इस सूत्रीकरण में, इस समीकरण का विचलन उत्पन्न होता है: | |||
<math display="block">\nabla \cdot \mathbf{D} = \rho_f = \varepsilon _0 \nabla \cdot \mathbf{E} +\nabla \cdot \mathbf{P}\, , </math> | |||
और जैसा कि ई में विचलन शब्द ''कुल'' आवेश है, और ''ρ'' है<sub>f</sub>निःशुल्क शुल्क है, हमारे पास संबंध शेष है: | |||
<math display="block">\nabla \cdot \mathbf{P} = -\rho_b \, , </math> | |||
ρ के साथ<sub>b</sub>बाउंड आवेश के रूप में, जिसका कारण कुल और मुक्त आवेश घनत्व के मध्य का अंतर है। | |||
एक तरफ, चुंबकीय प्रभाव की अनुपस्थिति में, मैक्सवेल के समीकरण इसे निर्दिष्ट करते हैं | |||
<math display="block">\nabla \times \mathbf{E} = \boldsymbol{0}\, ,</math> | |||
जो यह दर्शाता हे | |||
<math display="block">\nabla \times \left( \mathbf{D} - \mathbf{P} \right) = \boldsymbol{0}\, ,</math> | |||
[[हेल्महोल्ट्ज़ अपघटन]] प्रयुक्त करना:<ref name=Wu>{{cite book | title=भंवर और भंवर गतिशीलता| author1=Jie-Zhi Wu | author2=Hui-Yang Ma | author3=Ming-De Zhou | pages=36 ''ff'' | chapter-url=https://books.google.com/books?id=P5yNCu44PiwC&pg=PA36 | chapter=§2.3.1 Functionally Orthogonal Decomposition | isbn=978-3-540-29027-8 | year=200 | publisher=Springer }}</ref> | |||
<math display="block"> \mathbf{D} - \mathbf{P} = -\nabla \varphi \, , </math> | |||
कुछ अदिश क्षमता के लिए φ, और: | |||
<math display="block">\nabla \cdot (\mathbf{D} - \mathbf{P}) = \varepsilon_0 \nabla \cdot \mathbf{E} = \rho_f + \rho_b = - \nabla^2 \varphi\, .</math> | |||
मान लीजिए कि आवेशों को मुक्त और बाध्य में विभाजित किया गया है, और क्षमता को विभाजित किया गया है | |||
<math display="block">\varphi = \varphi_f + \varphi_b\, .</math> | |||
φ पर सीमा शर्तों की संतुष्टि को φ के मध्य इच्छानुसार से विभाजित किया जा सकता है<sub>f</sub>और φ<sub>b</sub>क्योंकि केवल योग φ को ही इन शर्तों को पूरा करना होगा। इससे यह निष्कर्ष निकलता है कि 'पी' विद्युत क्षेत्र के समानुपाती होता है क्योंकि आवेशों को सीमा के रूप में चुना जाता है, सीमा की स्थितियाँ सुविधाजनक सिद्ध होती हैं। विशेष रूप से, जब कोई निःशुल्क शुल्क उपस्तिथ नहीं है, तब संभावित विकल्प 'पी' = ε है<sub>0</sub> इ। | |||
आगे चर्चा की गई है कि माध्यम के अनेक भिन्न-भिन्न द्विध्रुव क्षण विवरण मैक्सवेल के समीकरणों में प्रवेश करने वाले ध्रुवीकरण से कैसे संबंधित हैं। | आगे चर्चा की गई है कि माध्यम के अनेक भिन्न-भिन्न द्विध्रुव क्षण विवरण मैक्सवेल के समीकरणों में प्रवेश करने वाले ध्रुवीकरण से कैसे संबंधित हैं। | ||
===आवेश और द्विध्रुव घनत्व वाला माध्यम=== | ===आवेश और द्विध्रुव घनत्व वाला माध्यम=== | ||
जैसा कि आगे बताया गया है, ध्रुवीकरण क्षण घनत्व पी(आर) के लिए मॉडल के परिणामस्वरूप ध्रुवीकरण होता है | जैसा कि आगे बताया गया है, ध्रुवीकरण क्षण घनत्व पी(आर) के लिए मॉडल के परिणामस्वरूप ध्रुवीकरण होता है<math display="block">\mathbf{P}(\mathbf{r}) = \mathbf{p}(\mathbf{r}) </math>एक ही मॉडल तक सीमित। सुचारु रूप से भिन्न द्विध्रुव आघूर्ण वितरण पी(आर) के लिए, संबंधित बाध्य आवेश घनत्व बस है<math display="block">\nabla \cdot \mathbf{p} (\mathbf{r}) = -\rho_b,</math>जैसा कि हम [[भागों द्वारा एकीकरण]] के माध्यम से शीघ्र ही स्थापित करेंगे। चूँकि, यदि p(r) दो क्षेत्रों के मध्य की सीमा पर द्विध्रुव आघूर्ण में अचानक कदम प्रदर्शित करता है, तब ∇·p(r) के परिणामस्वरूप बाध्य आवेश का सतही आवेश घटक बनता है। इस सतह आवेश को [[सतह अभिन्न]] के माध्यम से, या सीमा पर असंततता स्थितियों का उपयोग करके इलाज किया जा सकता है, जैसा कि नीचे दिए गए विभिन्न उदाहरणों में दिखाया गया है। | ||
<math display="block">\mathbf{P}(\mathbf{r}) = \mathbf{p}(\mathbf{r}) </math> | |||
एक ही मॉडल तक सीमित। सुचारु रूप से भिन्न द्विध्रुव आघूर्ण वितरण पी(आर) के लिए, संबंधित बाध्य आवेश घनत्व बस है | |||
<math display="block">\nabla \cdot \mathbf{p} (\mathbf{r}) = -\rho_b,</math> | |||
जैसा कि हम [[भागों द्वारा एकीकरण]] के माध्यम से शीघ्र ही स्थापित करेंगे। चूँकि, यदि p(r) दो क्षेत्रों के मध्य की सीमा पर द्विध्रुव आघूर्ण में अचानक कदम प्रदर्शित करता है, तब ∇·p(r) के परिणामस्वरूप बाध्य आवेश का सतही आवेश घटक बनता है। इस सतह आवेश को [[सतह अभिन्न]] के माध्यम से, या सीमा पर असंततता स्थितियों का उपयोग करके इलाज किया जा सकता है, जैसा कि नीचे दिए गए विभिन्न उदाहरणों में दिखाया गया है। | |||
द्विध्रुव आघूर्ण को ध्रुवीकरण से संबंधित पहले उदाहरण के रूप में, सतत आवेश घनत्व ''ρ''(r) और सतत द्विध्रुव आघूर्ण वितरण p(r) से बने माध्यम पर विचार करें। स्थिति r पर क्षमता है:<ref name=Krey>{{cite book |title=Basic Theoretical Physics: A Concise Overview |author1=Uwe Krey |author2=Anthony Owen |pages = 138–143 |isbn=978-3-540-36804-5 |publisher=Springer | year=2007 |url=https://books.google.com/books?id=xZ_QelBmkxYC&pg=PA327 }}</ref><ref name=Tsang>{{cite book |title=शास्त्रीय इलेक्ट्रोडायनामिक्स|url=https://books.google.com/books?id=KQe5QJ9PJwMC&pg=PA59 |page=59 |author=T Tsang |isbn=978-981-02-3041-8 |publisher=World Scientific |year=1997 }}</ref> | द्विध्रुव आघूर्ण को ध्रुवीकरण से संबंधित पहले उदाहरण के रूप में, सतत आवेश घनत्व ''ρ''(r) और सतत द्विध्रुव आघूर्ण वितरण p(r) से बने माध्यम पर विचार करें। स्थिति r पर क्षमता है:<ref name=Krey>{{cite book |title=Basic Theoretical Physics: A Concise Overview |author1=Uwe Krey |author2=Anthony Owen |pages = 138–143 |isbn=978-3-540-36804-5 |publisher=Springer | year=2007 |url=https://books.google.com/books?id=xZ_QelBmkxYC&pg=PA327 }}</ref><ref name=Tsang>{{cite book |title=शास्त्रीय इलेक्ट्रोडायनामिक्स|url=https://books.google.com/books?id=KQe5QJ9PJwMC&pg=PA59 |page=59 |author=T Tsang |isbn=978-981-02-3041-8 |publisher=World Scientific |year=1997 }}</ref> | ||
<math display="block">\phi (\mathbf{r}) = \frac{1}{4 \pi \varepsilon_0} \int \frac{\rho \left(\mathbf{r}_0\right)}{\left|\mathbf{r} - \mathbf{r}_0\right|} d^3 \mathbf{r}_0 \ + \frac {1}{4 \pi \varepsilon_0}\int \frac{\mathbf{p} \left(\mathbf{r}_0\right) \cdot \left(\mathbf{r} - \mathbf{r}_0\right)} {| \mathbf{r} - \mathbf{r}_0 |^3 } d^3 \mathbf{ r}_0 , </math> | <math display="block">\phi (\mathbf{r}) = \frac{1}{4 \pi \varepsilon_0} \int \frac{\rho \left(\mathbf{r}_0\right)}{\left|\mathbf{r} - \mathbf{r}_0\right|} d^3 \mathbf{r}_0 \ + \frac {1}{4 \pi \varepsilon_0}\int \frac{\mathbf{p} \left(\mathbf{r}_0\right) \cdot \left(\mathbf{r} - \mathbf{r}_0\right)} {| \mathbf{r} - \mathbf{r}_0 |^3 } d^3 \mathbf{ r}_0 , </math> | ||
| Line 160: | Line 117: | ||
\end{align}</math> | \end{align}</math> | ||
जहां सदिश पहचान <math display="block"> \nabla\cdot(\mathbf{A}{B}) = (\nabla\cdot\mathbf{A}){B} + \mathbf{A}\cdot(\nabla{B}) \implies \mathbf{A}\cdot(\nabla{B}) = \nabla\cdot(\mathbf{A}{B}) - (\nabla\cdot\mathbf{A}){B} </math> अंतिम चरण में प्रयोग किया गया। पहले शब्द को एकीकरण की मात्रा को सीमित करने वाली सतह पर अभिन्न में परिवर्तित किया जा सकता है, और सतह आवेश घनत्व में योगदान देता है, जिस पर पश्चात् में चर्चा की गई है। इस परिणाम को संभावित में वापस लाना, और सतही आवेश को अभी के लिए अनदेखा करना: | जहां सदिश पहचान <math display="block"> \nabla\cdot(\mathbf{A}{B}) = (\nabla\cdot\mathbf{A}){B} + \mathbf{A}\cdot(\nabla{B}) \implies \mathbf{A}\cdot(\nabla{B}) = \nabla\cdot(\mathbf{A}{B}) - (\nabla\cdot\mathbf{A}){B} </math> अंतिम चरण में प्रयोग किया गया। पहले शब्द को एकीकरण की मात्रा को सीमित करने वाली सतह पर अभिन्न में परिवर्तित किया जा सकता है, और सतह आवेश घनत्व में योगदान देता है, जिस पर पश्चात् में चर्चा की गई है। इस परिणाम को संभावित में वापस लाना, और सतही आवेश को अभी के लिए अनदेखा करना: | ||
<math display="block">\phi (\mathbf{r}) = \frac{1}{4 \pi \varepsilon_0} \int \frac{\rho \left(\mathbf{r}_0\right) - \nabla_{\mathbf{r}_0} \cdot \mathbf{p} \left(\mathbf{r}_0\right)}{\left|\mathbf{r} - \mathbf{r}_0\right|} d^3 \mathbf{r}_0\, ,</math> | <math display="block">\phi (\mathbf{r}) = \frac{1}{4 \pi \varepsilon_0} \int \frac{\rho \left(\mathbf{r}_0\right) - \nabla_{\mathbf{r}_0} \cdot \mathbf{p} \left(\mathbf{r}_0\right)}{\left|\mathbf{r} - \mathbf{r}_0\right|} d^3 \mathbf{r}_0\, ,</math>जहां वॉल्यूम एकीकरण केवल बाउंडिंग सतह तक फैला हुआ है, और इसमें यह सतह सम्मिलित नहीं है। | ||
जहां वॉल्यूम एकीकरण केवल बाउंडिंग सतह तक फैला हुआ है, और इसमें यह सतह सम्मिलित नहीं है। | क्षमता कुल आवेश द्वारा निर्धारित की जाती है, जिसमें उपरोक्त शो सम्मिलित हैं:<math display="block">\rho_\text{total} \left(\mathbf{r}_0\right) = \rho\left(\mathbf{r}_0\right) - \nabla_{\mathbf{r}_0} \cdot \mathbf{p} \left(\mathbf{r}_0\right)\, ,</math>वह दिखा रहा हूँ:<math display="block">-\nabla_{\mathbf{r}_0} \cdot \mathbf{p} \left(\mathbf{r}_0\right) = \rho_b\, .</math>संक्षेप में, द्विध्रुव आघूर्ण घनत्व p(r) इस माध्यम के लिए ध्रुवीकरण घनत्व P की भूमिका निभाता है। ध्यान दें, पी(आर) में बाध्य आवेश घनत्व के सामान्तर गैर-शून्य विचलन है (जैसा कि इस सन्निकटन में दर्शाया गया है)। | ||
यह ध्यान दिया जा सकता है कि इस दृष्टिकोण को सभी बहुध्रुवों को सम्मिलित करने के लिए बढ़ाया जा सकता है: द्विध्रुव, चतुर्ध्रुव, आदि।<ref name=Owen>{{cite book |title= विद्युत चुम्बकीय सिद्धांत का परिचय|author=George E Owen |url=https://books.google.com/books?id=VLm_dqhZUOYC&pg=PA80 |page=80 |isbn=978-0-486-42830-7 |publisher=Courier Dover Publications |year=2003 |edition= republication of the 1963 Allyn & Bacon }}</ref><ref name=Brevet>{{cite book |title=सतह दूसरी हार्मोनिक पीढ़ी|author=Pierre-François Brevet |url=https://books.google.com/books?id=_clt5ZowQYsC&pg=PA24 |page=24 |isbn=978-2-88074-345-1 |year=1997 |publisher=[[Presses polytechniques et universitaires romandes]] }}</ref> संबंध का उपयोग करना: | यह ध्यान दिया जा सकता है कि इस दृष्टिकोण को सभी बहुध्रुवों को सम्मिलित करने के लिए बढ़ाया जा सकता है: द्विध्रुव, चतुर्ध्रुव, आदि।<ref name=Owen>{{cite book |title= विद्युत चुम्बकीय सिद्धांत का परिचय|author=George E Owen |url=https://books.google.com/books?id=VLm_dqhZUOYC&pg=PA80 |page=80 |isbn=978-0-486-42830-7 |publisher=Courier Dover Publications |year=2003 |edition= republication of the 1963 Allyn & Bacon }}</ref><ref name=Brevet>{{cite book |title=सतह दूसरी हार्मोनिक पीढ़ी|author=Pierre-François Brevet |url=https://books.google.com/books?id=_clt5ZowQYsC&pg=PA24 |page=24 |isbn=978-2-88074-345-1 |year=1997 |publisher=[[Presses polytechniques et universitaires romandes]] }}</ref> संबंध का उपयोग करना:<math display="block">\nabla \cdot \mathbf{D} = \rho_f \, ,</math>ध्रुवीकरण घनत्व पाया जाता है:<math display="block">\mathbf{P}(\mathbf{r}) = \mathbf{p}_\text{dip} - \nabla \cdot \mathbf{p}_\text{quad} + \cdots\, ,</math>जहां जोड़े गए शब्द उच्च बहुध्रुवों से योगदान को इंगित करने के लिए हैं। प्रकट है, उच्च मल्टीपोल को सम्मिलित करने से पता चलता है कि ध्रुवीकरण घनत्व पी वर्तमान अकेले द्विध्रुवीय क्षण घनत्व पी द्वारा निर्धारित नहीं होता है। उदाहरण के लिए, आवेश ऐरे से बिखरने पर विचार करते समय, भिन्न-भिन्न मल्टीपोल विद्युत चुम्बकीय तरंग को भिन्न-भिन्न और स्वतंत्र रूप से प्रसारित करते हैं, जिसके लिए उन आवेशों के प्रतिनिधित्व की आवश्यकता होती है जो द्विध्रुव सन्निकटन से परे जाते हैं।<ref name="multipole2">{{cite book |isbn=978-981-02-3325-9 |url=https://books.google.com/books?id=NUv5csOQBGAC&pg=PA219 |title=नई सामग्रियों का कम्प्यूटेशनल अध्ययन|author1=Daniel A. Jelski |author2=Thomas F. George |page=219 |year=1999 |publisher=World Scientific}}</ref><ref name="multipole3">{{cite journal |author1=EM Purcell |author2=CR Pennypacker |journal=Astrophysical Journal |title= गैरगोलाकार ढांकता हुआ अनाज द्वारा प्रकाश का प्रकीर्णन और अवशोषण|volume=186 |pages= 705–714 |year=1973 |bibcode=1973ApJ...186..705P |doi=10.1086/152538 }}</ref> | ||
<math display="block">\nabla \cdot \mathbf{D} = \rho_f \, ,</math>ध्रुवीकरण घनत्व पाया जाता है: | |||
<math display="block">\mathbf{P}(\mathbf{r}) = \mathbf{p}_\text{dip} - \nabla \cdot \mathbf{p}_\text{quad} + \cdots\, ,</math>जहां जोड़े गए शब्द उच्च बहुध्रुवों से योगदान को इंगित करने के लिए हैं। प्रकट है, उच्च मल्टीपोल को सम्मिलित करने से पता चलता है कि ध्रुवीकरण घनत्व पी वर्तमान अकेले द्विध्रुवीय क्षण घनत्व पी द्वारा निर्धारित नहीं होता है। उदाहरण के लिए, आवेश ऐरे से बिखरने पर विचार करते समय, भिन्न-भिन्न मल्टीपोल विद्युत चुम्बकीय तरंग को भिन्न-भिन्न और स्वतंत्र रूप से प्रसारित करते हैं, जिसके लिए उन आवेशों के प्रतिनिधित्व की आवश्यकता होती है जो द्विध्रुव सन्निकटन से परे जाते हैं।<ref name="multipole2">{{cite book |isbn=978-981-02-3325-9 |url=https://books.google.com/books?id=NUv5csOQBGAC&pg=PA219 |title=नई सामग्रियों का कम्प्यूटेशनल अध्ययन|author1=Daniel A. Jelski |author2=Thomas F. George |page=219 |year=1999 |publisher=World Scientific}}</ref><ref name="multipole3">{{cite journal |author1=EM Purcell |author2=CR Pennypacker |journal=Astrophysical Journal |title= गैरगोलाकार ढांकता हुआ अनाज द्वारा प्रकाश का प्रकीर्णन और अवशोषण|volume=186 |pages= 705–714 |year=1973 |bibcode=1973ApJ...186..705P |doi=10.1086/152538 }}</ref> | |||
====सतह प्रभार==== | ====सतह प्रभार==== | ||
[[File:Dipole polarization.JPG|thumb| | [[File:Dipole polarization.JPG|thumb|समान द्विध्रुवों की समान सारणी सतह आवेश के सामान्तर होती है।]]ऊपर, द्विध्रुव के कारण विभव के व्यंजक में पहले पद के लिए चर्चा स्थगित कर दी गई थी। विचलन को एकीकृत करने से सतही आवेश उत्पन्न होता है। दाईं ओर का चित्र सहज विचार प्रदान करता है कि सतही आवेश क्यों उत्पन्न होता है। चित्र दो सतहों के मध्य समान द्विध्रुवों की समान सरणी दिखाता है। आंतरिक रूप से, द्विध्रुवों के शीर्ष और पूंछ आसन्न और रद्द होते हैं। चूँकि, बाउंडिंग सतहों पर कोई निरस्तता नहीं होता है। इसके अतिरिक्त, सतह पर द्विध्रुव सिर धनात्मक सतह आवेश बनाते हैं, जबकि विपरीत सतह पर द्विध्रुव सिर ऋणात्मक सतह आवेश बनाते हैं। यह दो विपरीत सतह आवेश द्विध्रुवों की दिशा के विपरीत दिशा में शुद्ध विद्युत क्षेत्र बनाते हैं। | ||
उपरोक्त संभावित अभिव्यक्ति का उपयोग करके इस विचार को गणितीय रूप दिया गया है। मुफ़्त शुल्क को नज़रअंदाज करते हुए, संभावना यह है: | उपरोक्त संभावित अभिव्यक्ति का उपयोग करके इस विचार को गणितीय रूप दिया गया है। मुफ़्त शुल्क को नज़रअंदाज करते हुए, संभावना यह है: | ||
| Line 185: | Line 135: | ||
<math display="block"> \frac{1}{4 \pi \varepsilon_0} \int \nabla_{\mathbf{r}_0} \cdot \left(\mathbf{p} \left(\mathbf{r}_0\right) \frac{1}{\left|\mathbf{r} - \mathbf{r}_0\right|}\right) d^3\mathbf{r}_0 | <math display="block"> \frac{1}{4 \pi \varepsilon_0} \int \nabla_{\mathbf{r}_0} \cdot \left(\mathbf{p} \left(\mathbf{r}_0\right) \frac{1}{\left|\mathbf{r} - \mathbf{r}_0\right|}\right) d^3\mathbf{r}_0 | ||
= \frac{1}{4 \pi \varepsilon_0} \int \frac{\mathbf{p} \left(\mathbf{r}_0\right) \cdot d \mathbf{A}_0}\left|\mathbf{r} - \mathbf{r}_0\right| \, ,</math> | = \frac{1}{4 \pi \varepsilon_0} \int \frac{\mathbf{p} \left(\mathbf{r}_0\right) \cdot d \mathbf{A}_0}\left|\mathbf{r} - \mathbf{r}_0\right| \, ,</math> | ||
डीए<sub>0</sub> के साथ आयतन के सतह क्षेत्र का तत्व। इस घटना में कि पी(आर) स्थिरांक है, केवल सतही पद ही जीवित रहता है: | डीए<sub>0</sub> के साथ आयतन के सतह क्षेत्र का तत्व। इस घटना में कि पी(आर) स्थिरांक है, केवल सतही पद ही जीवित रहता है:<math display="block">\phi(\mathbf{r}) = \frac{1}{4 \pi \varepsilon_0} \int \frac{1}{\left|\mathbf{r} - \mathbf{r}_0\right|}\ \mathbf{p} \cdot d\mathbf{A}_0 \, ,</math>डीए<sub>0</sub> के साथ आवेशों को घेरने वाली सतह का प्राथमिक क्षेत्र मेंं शब्दों के रूप में सतह के अंदर स्थिरांक p के कारण क्षमता ''सतह आवेश'' के सामान्तर होती है<math display="block">\sigma = \mathbf{p} \cdot d \mathbf{A}</math>जो पी की दिशा में घटक वाले सतह तत्वों के लिए धनात्मक है और विपरीत दिशा में निर्देशित सतह तत्वों के लिए ऋणात्मक है। (सामान्यतः किसी सतह तत्व की दिशा को तत्व के स्थान पर सतह के बाहरी सामान्य दिशा के रूप में लिया जाता है।) | ||
<math display="block">\phi(\mathbf{r}) = \frac{1}{4 \pi \varepsilon_0} \int \frac{1}{\left|\mathbf{r} - \mathbf{r}_0\right|}\ \mathbf{p} \cdot d\mathbf{A}_0 \, ,</math> | यदि सीमाबद्ध सतह गोला है, और अवलोकन का बिंदु इस गोले के केंद्र में है, तब गोले की सतह पर एकीकरण शून्य है: संभावित निरस्तता में धनात्मक और ऋणात्मक सतह आवेश योगदान करते हैं। चूँकि, यदि अवलोकन का बिंदु केंद्र से बाहर है, तब शुद्ध क्षमता का परिणाम हो सकता है (स्थिति के आधार पर) क्योंकि धनात्मक और ऋणात्मक आवेश अवलोकन के बिंदु से भिन्न-भिन्न दूरी पर हैं। पृष्ठीय आवेश के कारण क्षेत्र है:<math display="block">\mathbf{E}\left(\mathbf{r}\right) = -\frac{1}{4 \pi \varepsilon_0} \nabla_\mathbf{r} \int \frac{1}{\left|\mathbf{r} - \mathbf{r}_0\right|}\ \mathbf{p} \cdot d\mathbf{A}_0\, ,</math>जो, गोलाकार सीमा सतह के केंद्र में शून्य नहीं है (केंद्र के विपरीत पक्षों पर ऋणात्मक और धनात्मक आवेश के क्षेत्र जुड़ते हैं क्योंकि दोनों क्षेत्र ही तरह से इंगित करते हैं) किंतु इसके अतिरिक्त है:<ref name="Ibach" /><math display="block">\mathbf{E} = -\frac{\mathbf{p}}{3 \varepsilon_0}\, .</math>यदि हम मानते हैं कि द्विध्रुव का ध्रुवीकरण किसी बाहरी क्षेत्र से प्रेरित था, तब ध्रुवीकरण क्षेत्र प्रयुक्त क्षेत्र का विरोध करता है और कभी-कभी इसे विध्रुवण क्षेत्र कहा जाता है।<ref name="Takagahara">{{cite book | title=Semiconductor quantum dots: physics, spectroscopy, and applications | author1=Yasuaki Masumoto | author2=Toshihide Takagahara | publisher=Springer | year=2002 | isbn=978-3-540-42805-3 | page=72 | url=https://books.google.com/books?id=eacszlpNisgC&pg=PA72 }}</ref><ref name="Toyozawa">{{cite book | author=Yutaka Toyozawa | title=ठोसों में ऑप्टिकल प्रक्रियाएँ| url=https://books.google.com/books?id=IGkSP2y8V7MC&pg=PA96 | page=96 | isbn=978-0-521-55605-7 | publisher=Cambridge University Press | year=2003 }}</ref> ऐसे स्थितियों में जब ध्रुवीकरण गोलाकार गुहा के बाहर होता है, आसपास के द्विध्रुवों के कारण गुहा में क्षेत्र ध्रुवीकरण के समान दिशा में होता है। | ||
डीए<sub>0</sub> के साथ आवेशों को घेरने वाली सतह का प्राथमिक क्षेत्र मेंं शब्दों के रूप में सतह के अंदर स्थिरांक p के कारण क्षमता ''सतह आवेश'' के सामान्तर होती है | विशेष रूप से, यदि [[विद्युत संवेदनशीलता]] को सन्निकटन के माध्यम से प्रस्तुतकिया जाता है:<math display="block">\mathbf{p}(\mathbf{r}) = \varepsilon_0 \chi(\mathbf{r}) \mathbf{E}(\mathbf{r})\, ,</math>कहाँ {{mvar|'''E'''}}, इस स्थितियों में और निम्नलिखित में, बाहरी क्षेत्र का प्रतिनिधित्व करते हैं जो ध्रुवीकरण को प्रेरित करता है। | ||
<math display="block">\sigma = \mathbf{p} \cdot d \mathbf{A}</math> | तब:<math display="block">\nabla \cdot \mathbf{p}(\mathbf{r}) = \nabla \cdot \left(\chi(\mathbf{r}) \varepsilon_0 \mathbf{E}(\mathbf{r})\right) = -\rho_b\, .</math>जब भी χ('r') का उपयोग दो क्षेत्रों के मध्य की सीमा पर चरण असंततता को मॉडल करने के लिए किया जाता है, तब चरण सतह आवेश परत उत्पन्न करता है। उदाहरण के लिए, सतह के ठीक अंदर वाले बिंदु से बाहरी सतह के दूसरे बिंदु तक सामान्य से बाउंडिंग सतह तक एकीकृत करना:<math display="block">\varepsilon_0 \hat{\mathbf{n}} \cdot \left[\chi\left(\mathbf{r}_+\right) \mathbf{E}\left(\mathbf{r}_+\right) - \chi\left(\mathbf{r}_-\right) \mathbf{E}\left(\mathbf{r}_-\right)\right] = \frac{1}{A_n} \int d \Omega_n\ \rho_b = 0 \, ,</math>जहाँ ''A''<sub>n</sub>, Ω<sub>n</sub> क्षेत्रों के मध्य की सीमा तक फैले प्रारंभिक क्षेत्र के क्षेत्र और आयतन को इंगित करें, और <math>\hat{\mathbf{n}}</math> सतह पर सामान्य इकाई. जैसे ही आयतन घटता है, दाहिना भाग गायब हो जाता है, यहाँ तक कि ρ तक<sub>b</sub> परिमित है, जो ''ई'' में असंततता को दर्शाता है, और इसलिए सतही आवेश है। अर्थात्, जहां प्रतिरूपित माध्यम में पारगम्यता का चरण सम्मिलित होता है, वहां द्विध्रुव आघूर्ण घनत्व के अनुरूप ध्रुवीकरण घनत्व होता है<math display="block">\mathbf{p}(\mathbf{r}) = \chi(\mathbf{r}) \mathbf{E}(\mathbf{r})</math>इसमें आवश्यक रूप से सतही आवेश का योगदान सम्मिलित होता है।<ref name="Chen">{{cite book | title=इलेक्ट्रिकल इंजीनियरिंग हैंडबुक| page=502 | author=Wai-Kai Chen | url=https://books.google.com/books?id=qhHsSlazGrQC&pg=PA502 | isbn=978-0-12-170960-0 | year=2005 | publisher=Academic Press }}</ref><ref name="Stratton2">{{cite book | title=विद्युत चुम्बकीय सिद्धांत| url=https://books.google.com/books?id=zFeWdS2luE4C&pg=PA184 | author=Julius Adams Stratton | page= 184 | year=2007 | isbn=978-0-470-13153-4 | publisher=Wiley-IEEE | edition= reprint of 1941 }}</ref><ref name="Cloud">{{cite book | url=https://books.google.com/books?id=jCqv1UygjA4C&pg=PA68 | page=68 | author1=Edward J. Rothwell | author2=Michael J. Cloud | title=विद्युत चुम्बकीय| isbn=978-0-8493-1397-4 | year=2001 | publisher=CRC Press }}</ref> | ||
जो पी की दिशा में घटक वाले सतह तत्वों के लिए धनात्मक है और विपरीत दिशा में निर्देशित सतह तत्वों के लिए ऋणात्मक है। (सामान्यतः किसी सतह तत्व की दिशा को तत्व के स्थान पर सतह के बाहरी सामान्य दिशा के रूप में लिया जाता है।) | |||
पी(आर) के भौतिक रूप से अधिक यथार्थवादी मॉडलिंग में द्विध्रुव क्षण घनत्व तेजी से गिर जाएगा, किन्तु शून्य घनत्व की ओर अचानक कदम उठाने के अतिरिक्त, सीमित क्षेत्र की सीमा पर आसानी से शून्य हो जाएगा। तब सतह आवेश उच्चतम रूप से पतली सतह में केंद्रित नहीं होगा, किंतु इसके अतिरिक्त, सुचारू रूप से भिन्न द्विध्रुवीय क्षण घनत्व का विचलन होने के कारण, स्वयं को पतली, किन्तु सीमित संक्रमण परत में वितरित कर देगा। | |||
====एक समान बाह्य विद्युत क्षेत्र में अचालक क्षेत्र==== | |||
[[File:Dielectric sphere.svg|thumb|250px|ई-क्षेत्र (दिखाया नहीं गया) हर स्थान डी-क्षेत्र के साथ मेल खाता है, किन्तु गोले के अंदर, उनका घनत्व कम है, इस तथ्य के अनुरूप कि ई-क्षेत्र क्षेत्र के अंदर अशक्त है बाहर से. अनेक बाहरी ई-क्षेत्र रेखाएँ गोले की सतह पर समाप्त होती हैं, जहाँ बाध्य आवेश होता है।]]सतह आवेश के बारे में उपरोक्त सामान्य टिप्पणियाँ समान विद्युत क्षेत्र में ढांकता हुआ क्षेत्र के उदाहरण पर विचार करके अधिक ठोस बनाई गई हैं।<ref name=Wyld> | |||
[[File:Dielectric sphere.svg|thumb|250px| | |||
{{cite book | {{cite book | ||
| title=Mathematical Methods for Physics | | title=Mathematical Methods for Physics | ||
| Line 243: | Line 175: | ||
<math display="block">\phi_> = \left(Br + \frac{C}{r^2} \right) \cos\theta \, .</math> | <math display="block">\phi_> = \left(Br + \frac{C}{r^2} \right) \cos\theta \, .</math> | ||
बड़ी दूरी पर, φ<sub>></sub> → एफ<sub>∞</sub> इसलिए बी = −ई<sub>∞ </sub>. विभव की निरंतरता और विस्थापन के रेडियल घटक 'डी' = κε<sub>0</sub>''ई'' अन्य दो स्थिरांक निर्धारित करते हैं। मान लीजिए कि गोले की त्रिज्या ''R'' है, | बड़ी दूरी पर, φ<sub>></sub> → एफ<sub>∞</sub> इसलिए बी = −ई<sub>∞ </sub>. विभव की निरंतरता और विस्थापन के रेडियल घटक 'डी' = κε<sub>0</sub>''ई'' अन्य दो स्थिरांक निर्धारित करते हैं। मान लीजिए कि गोले की त्रिज्या ''R'' है, | ||
<math display="block">A = -\frac{3}{\kappa + 2} E_\infty\ ;\ C = \frac{\kappa - 1}{\kappa + 2} E_\infty R^3\, ,</math> | <math display="block">A = -\frac{3}{\kappa + 2} E_\infty\ ;\ C = \frac{\kappa - 1}{\kappa + 2} E_\infty R^3\, ,</math>परिणामस्वरूप, संभावना यह है: | ||
परिणामस्वरूप, संभावना यह है: | <math display="block">\phi_> = \left(-r + \frac{\kappa - 1}{\kappa + 2} \frac{R^3}{r^2}\right) E_\infty \cos\theta\, ,</math>जो प्रयुक्त क्षेत्र के कारण संभावित है और, इसके अतिरिक्त, प्रयुक्त क्षेत्र की दिशा में द्विध्रुवीय (जेड-दिशा) द्विध्रुव क्षण का है: | ||
<math display="block">\phi_> = \left(-r + \frac{\kappa - 1}{\kappa + 2} \frac{R^3}{r^2}\right) E_\infty \cos\theta\, ,</math> | <math display="block">\mathbf{p} = 4 \pi \varepsilon_0 \left(\frac{\kappa - 1}{\kappa + 2} R^3\right) \mathbf{E}_\infty\, ,</math>या, प्रति इकाई आयतन: | ||
जो प्रयुक्त क्षेत्र के कारण संभावित है और, इसके अतिरिक्त, प्रयुक्त क्षेत्र की दिशा में द्विध्रुवीय (जेड-दिशा) द्विध्रुव क्षण का है: | <math display="block">\frac{\mathbf{p}}{V} = 3 \varepsilon_0 \left(\frac{\kappa - 1}{\kappa + 2}\right) \mathbf{E}_\infty\, .</math>कारक (κ - 1)/(κ + 2) को क्लॉसियस-मोसोटी संबंध कहा जाता है | क्लॉसियस-मोसोटी कारक और दिखाता है कि प्रेरित ध्रुवीकरण संकेत फ़्लिप करता है यदि κ < 1. इस उदाहरण में ऐसा नहीं हो सकता है, किन्तु दो भिन्न-भिन्न डाइलेक्ट्रिक्स के साथ उदाहरण κ को आंतरिक और बाहरी क्षेत्र के ढांकता हुआ स्थिरांक के अनुपात से प्रतिस्थापित किया जाता है, जो से अधिक या छोटा हो सकता है। गोले के अंदर की क्षमता है: | ||
<math display="block">\mathbf{p} = 4 \pi \varepsilon_0 \left(\frac{\kappa - 1}{\kappa + 2} R^3\right) \mathbf{E}_\infty\, ,</math> | |||
या, प्रति इकाई आयतन: | |||
<math display="block">\frac{\mathbf{p}}{V} = 3 \varepsilon_0 \left(\frac{\kappa - 1}{\kappa + 2}\right) \mathbf{E}_\infty\, .</math> | |||
कारक (κ - 1)/(κ + 2) को क्लॉसियस-मोसोटी संबंध कहा जाता है | क्लॉसियस-मोसोटी कारक और दिखाता है कि प्रेरित ध्रुवीकरण संकेत फ़्लिप करता है यदि κ < 1. इस उदाहरण में ऐसा नहीं हो सकता है, किन्तु दो भिन्न-भिन्न डाइलेक्ट्रिक्स के साथ उदाहरण κ को आंतरिक और बाहरी क्षेत्र के ढांकता हुआ स्थिरांक के अनुपात से प्रतिस्थापित किया जाता है, जो से अधिक या छोटा हो सकता है। गोले के अंदर की क्षमता है: | |||
<math display="block">\phi_< = -\frac{3}{\kappa + 2} E_\infty r \cos\theta\, ,</math> | <math display="block">\phi_< = -\frac{3}{\kappa + 2} E_\infty r \cos\theta\, ,</math> | ||
गोले के अंदर मैदान की ओर ले जाना: | गोले के अंदर मैदान की ओर ले जाना: | ||
<math display="block">-\nabla \phi_< = \frac{3}{\kappa + 2} \mathbf{E}_\infty = \left(1 - \frac{\kappa - 1}{\kappa + 2}\right)\mathbf{ E}_\infty\, ,</math> | <math display="block">-\nabla \phi_< = \frac{3}{\kappa + 2} \mathbf{E}_\infty = \left(1 - \frac{\kappa - 1}{\kappa + 2}\right)\mathbf{ E}_\infty\, ,</math>द्विध्रुव का विध्रुवण प्रभाव दिखा रहा है। ध्यान दें कि गोले के अंदर का क्षेत्र समान है और प्रयुक्त क्षेत्र के समानांतर है। द्विध्रुव आघूर्ण गोले के संपूर्ण आंतरिक भाग में समान होता है। गोले पर सतह आवेश घनत्व रेडियल क्षेत्र घटकों के मध्य का अंतर है: | ||
द्विध्रुव का विध्रुवण प्रभाव दिखा रहा है। ध्यान दें कि गोले के अंदर का क्षेत्र समान है और प्रयुक्त क्षेत्र के समानांतर है। द्विध्रुव आघूर्ण गोले के संपूर्ण आंतरिक भाग में समान होता है। गोले पर सतह आवेश घनत्व रेडियल क्षेत्र घटकों के मध्य का अंतर है: | <math display="block">\sigma = 3 \varepsilon_0 \frac{\kappa - 1}{\kappa + 2} E_\infty \cos\theta = \frac{1}{V} \mathbf{p} \cdot \hat{\mathbf{R}}\, .</math>यह रैखिक ढांकता हुआ उदाहरण दर्शाता है कि ढांकता हुआ निरंतर उपचार एकसमान द्विध्रुव क्षण मॉडल के सामान्तर है और गोले की सीमा पर सतह आवेश को छोड़कर हर स्थान शून्य आवेश होता है। | ||
<math display="block">\sigma = 3 \varepsilon_0 \frac{\kappa - 1}{\kappa + 2} E_\infty \cos\theta = \frac{1}{V} \mathbf{p} \cdot \hat{\mathbf{R}}\, .</math> | |||
यह रैखिक ढांकता हुआ उदाहरण दर्शाता है कि ढांकता हुआ निरंतर उपचार एकसमान द्विध्रुव क्षण मॉडल के सामान्तर है और गोले की सीमा पर सतह आवेश को छोड़कर हर स्थान शून्य आवेश होता है। | |||
===सामान्य मीडिया=== | ===सामान्य मीडिया=== | ||
यदि अवलोकन आवेशों की प्रणाली से पर्याप्त रूप से दूर के क्षेत्रों तक ही सीमित है, तब त्रुटिहीन ध्रुवीकरण घनत्व का बहुध्रुवीय विस्तार किया जा सकता है। इस विस्तार को छोटा करके (उदाहरण के लिए, केवल द्विध्रुव पदों को, या केवल द्विध्रुव और चतुष्कोण पदों को, या आदि को बनाए रखते हुए), पिछले अनुभाग के परिणाम पुनः प्राप्त हो जाते हैं। विशेष रूप से, द्विध्रुवीय पद पर विस्तार को छोटा करते हुए, परिणाम आवेश क्षेत्र तक सीमित समान द्विध्रुवीय क्षण द्वारा उत्पन्न ध्रुवीकरण घनत्व से अप्रभेद्य होता है। इस द्विध्रुव सन्निकटन की त्रुटिहीनता के लिए, जैसा कि पिछले अनुभाग में दिखाया गया है, द्विध्रुव क्षण घनत्व 'पी'('आर') (जिसमें न केवल 'पी' किंतु 'पी' का स्थान भी सम्मिलित है) 'पी'(' आर')। | यदि अवलोकन आवेशों की प्रणाली से पर्याप्त रूप से दूर के क्षेत्रों तक ही सीमित है, तब त्रुटिहीन ध्रुवीकरण घनत्व का बहुध्रुवीय विस्तार किया जा सकता है। इस विस्तार को छोटा करके (उदाहरण के लिए, केवल द्विध्रुव पदों को, या केवल द्विध्रुव और चतुष्कोण पदों को, या आदि को बनाए रखते हुए), पिछले अनुभाग के परिणाम पुनः प्राप्त हो जाते हैं। विशेष रूप से, द्विध्रुवीय पद पर विस्तार को छोटा करते हुए, परिणाम आवेश क्षेत्र तक सीमित समान द्विध्रुवीय क्षण द्वारा उत्पन्न ध्रुवीकरण घनत्व से अप्रभेद्य होता है। इस द्विध्रुव सन्निकटन की त्रुटिहीनता के लिए, जैसा कि पिछले अनुभाग में दिखाया गया है, द्विध्रुव क्षण घनत्व 'पी'('आर') (जिसमें न केवल 'पी' किंतु 'पी' का स्थान भी सम्मिलित है) 'पी'(' आर')। | ||
आवेश सरणी के अंदर के स्थानों पर, युग्मित आवेश की सरणी को केवल द्विध्रुवीय क्षण घनत्व 'पी' ('आर') वाले सन्निकटन से जोड़ने के लिए अतिरिक्त विचारों की आवश्यकता होती है। सबसे सरल सन्निकटन आवेश सारणी को आदर्श (असीमित दूरी वाले) द्विध्रुवों के मॉडल से बदलना है। विशेष रूप से, जैसा कि ऊपर दिए गए उदाहरण में परिमित क्षेत्र तक सीमित निरंतर द्विध्रुव आघूर्ण घनत्व का उपयोग किया जाता है, सतह आवेश और विध्रुवण क्षेत्र का परिणाम होता है। इस मॉडल का अधिक सामान्य संस्करण (जो स्थिति के साथ ध्रुवीकरण को भिन्न-भिन्न करने की अनुमति देता है) विद्युत संवेदनशीलता या [[विद्युत पारगम्यता]] का उपयोग करने वाला पारंपरिक दृष्टिकोण है। | आवेश सरणी के अंदर के स्थानों पर, युग्मित आवेश की सरणी को केवल द्विध्रुवीय क्षण घनत्व 'पी' ('आर') वाले सन्निकटन से जोड़ने के लिए अतिरिक्त विचारों की आवश्यकता होती है। सबसे सरल सन्निकटन आवेश सारणी को आदर्श (असीमित दूरी वाले) द्विध्रुवों के मॉडल से बदलना है। विशेष रूप से, जैसा कि ऊपर दिए गए उदाहरण में परिमित क्षेत्र तक सीमित निरंतर द्विध्रुव आघूर्ण घनत्व का उपयोग किया जाता है, सतह आवेश और विध्रुवण क्षेत्र का परिणाम होता है। इस प्रकार मॉडल का अधिक सामान्य संस्करण (जो स्थिति के साथ ध्रुवीकरण को भिन्न-भिन्न करने की अनुमति देता है) विद्युत संवेदनशीलता या [[विद्युत पारगम्यता]] का उपयोग करने वाला पारंपरिक दृष्टिकोण है। | ||
बिंदु आवेश सारणी का अधिक समष्टि मॉडल सूक्ष्म आवेशों के औसत द्वारा [[प्रभावी माध्यम सन्निकटन]] प्रस्तुत करता है;<ref name=Toyozawa/> उदाहरण के लिए, औसत यह व्यवस्था कर सकता है कि केवल द्विध्रुवीय क्षेत्र ही भूमिका निभाते हैं।<ref name=Shalaev> | बिंदु आवेश सारणी का अधिक समष्टि मॉडल सूक्ष्म आवेशों के औसत द्वारा [[प्रभावी माध्यम सन्निकटन]] प्रस्तुत करता है;<ref name=Toyozawa/> उदाहरण के लिए, औसत यह व्यवस्था कर सकता है कि केवल द्विध्रुवीय क्षेत्र ही भूमिका निभाते हैं।<ref name=Shalaev> | ||
| Line 347: | Line 273: | ||
}}</ref> | }}</ref> | ||
=='''मौलिक कणों के विद्युत द्विध्रुव आघूर्ण'''== | =='''मौलिक कणों के विद्युत द्विध्रुव आघूर्ण'''== | ||
[[स्पिन (भौतिकी)]] के साथ भ्रमित न हों जो कणों के चुंबकीय द्विध्रुव क्षणों को संदर्भित करता है, मौलिक और मिश्रित कणों, अर्थात् इलेक्ट्रॉन के विद्युत द्विध्रुव क्षणों (ईडीएम; या विषम विद्युत द्विध्रुव क्षण) को मापने पर बहुत प्रयोगात्मक कार्य जारी है। क्रमशः विद्युत द्विध्रुव आघूर्ण और [[न्यूट्रॉन विद्युत द्विध्रुव आघूर्ण]]। चूंकि ईडीएम [[समता (भौतिकी)]] (पी) और टी-समरूपता | [[स्पिन (भौतिकी)]] के साथ भ्रमित न हों जो कणों के चुंबकीय द्विध्रुव क्षणों को संदर्भित करता है, मौलिक और मिश्रित कणों, अर्थात् इलेक्ट्रॉन के विद्युत द्विध्रुव क्षणों (ईडीएम; या विषम विद्युत द्विध्रुव क्षण) को मापने पर बहुत प्रयोगात्मक कार्य जारी है। इस प्रकार क्रमशः विद्युत द्विध्रुव आघूर्ण और [[न्यूट्रॉन विद्युत द्विध्रुव आघूर्ण]]। चूंकि ईडीएम [[समता (भौतिकी)]] (पी) और टी-समरूपता समय-उत्क्रमण (टी) समरूपता दोनों का उल्लंघन करते हैं, उनके मूल्य प्रकृति में [[सीपी-उल्लंघन]] का अधिकतर मॉडल-स्वतंत्र माप उत्पन्न करते हैं (सीपी[[टी समरूपता]] वैध है)।<ref>{{cite book|last1=Khriplovich|first1=Iosip B.|last2=Lamoreaux|first2=Steve K.|title=CP violation without strangeness : electric dipole moments of particles, atoms, and molecules.|date=2012|publisher=Springer|location=[S.l.]|isbn=978-3-642-64577-8}}</ref> इसलिए, इन ईडीएम के मान सीपी-उल्लंघन के पैमाने पर शक्तिशाली बाधाएं डालते हैं जो [[कण भौतिकी]] के [[मानक मॉडल]] के विस्तार की अनुमति दे सकते हैं। प्रयोगों की वर्तमान पीढ़ियों को ईडीएम की [[अतिसममिति]] रेंज के प्रति संवेदनशील बनाने के लिए डिज़ाइन किया गया है, जो [[एलएचसी]] पर किए गए पूरक प्रयोगों को प्रदान करता है।<ref>{{Cite journal|last1=Ibrahim|first1=Tarik|last2=Itani|first2=Ahmad|last3=Nath|first3=Pran|title=पीईवी स्केल भौतिकी की एक संवेदनशील जांच के रूप में इलेक्ट्रॉन ईडीएम|journal=Physical Review D|volume=90|issue=5|pages=055006|date=2014 |arxiv=1406.0083|doi=10.1103/PhysRevD.90.055006|bibcode=2014PhRvD..90e5006I|s2cid=118880896}}</ref> | ||
वास्तव में, अनेक सिद्धांत वर्तमान सीमाओं के साथ असंगत हैं और उन्हें प्रभावी ढंग से खारिज कर दिया गया है, और स्थापित सिद्धांत इन सीमाओं से कहीं अधिक बड़े मूल्य की अनुमति देता है, जिससे [[मजबूत सीपी समस्या|शक्तिशाली सीपी समस्या]] उत्पन्न होती है और [[ अक्षतंतु |अक्षतंतु]] जैसे नए कणों की खोज को बढ़ावा मिलता है।<ref>{{cite journal|last1=Kim|first1=Jihn E.|last2=Carosi|first2=Gianpaolo|title=एक्सियन्स और मजबूत सीपी समस्या|journal=Reviews of Modern Physics|date=2010|volume=82|issue=1|pages=557–602|doi=10.1103/RevModPhys.82.557 |arxiv = 0807.3125 |bibcode = 2010RvMP...82..557K }}</ref> | वास्तव में, अनेक सिद्धांत वर्तमान सीमाओं के साथ असंगत हैं और उन्हें प्रभावी ढंग से खारिज कर दिया गया है, और स्थापित सिद्धांत इन सीमाओं से कहीं अधिक बड़े मूल्य की अनुमति देता है, जिससे [[मजबूत सीपी समस्या|शक्तिशाली सीपी समस्या]] उत्पन्न होती है और [[ अक्षतंतु |अक्षतंतु]] जैसे नए कणों की खोज को बढ़ावा मिलता है।<ref>{{cite journal|last1=Kim|first1=Jihn E.|last2=Carosi|first2=Gianpaolo|title=एक्सियन्स और मजबूत सीपी समस्या|journal=Reviews of Modern Physics|date=2010|volume=82|issue=1|pages=557–602|doi=10.1103/RevModPhys.82.557 |arxiv = 0807.3125 |bibcode = 2010RvMP...82..557K }}</ref> | ||
| Line 354: | Line 280: | ||
=='''अणुओं के द्विध्रुव आघूर्ण'''== | =='''अणुओं के द्विध्रुव आघूर्ण'''== | ||
द्विध्रुव#आण्विक द्विध्रुव बाहरी विद्युत क्षेत्रों की उपस्थिति में किसी पदार्थ के व्यवहार के लिए उत्तरदायी होते हैं। द्विध्रुव बाहरी क्षेत्र से संरेखित होते हैं जो स्थिर या समय पर निर्भर हो सकते हैं। यह प्रभाव [[ढांकता हुआ स्पेक्ट्रोस्कोपी]] नामक आधुनिक प्रायोगिक विधि का आधार बनता है। | द्विध्रुव#आण्विक द्विध्रुव बाहरी विद्युत क्षेत्रों की उपस्थिति में किसी पदार्थ के व्यवहार के लिए उत्तरदायी होते हैं। इस प्रकार द्विध्रुव बाहरी क्षेत्र से संरेखित होते हैं जो स्थिर या समय पर निर्भर हो सकते हैं। यह प्रभाव [[ढांकता हुआ स्पेक्ट्रोस्कोपी]] नामक आधुनिक प्रायोगिक विधि का आधार बनता है। | ||
द्विध्रुव क्षण पानी जैसे सामान्य अणुओं और प्रोटीन जैसे जैव अणुओं में भी पाए जा सकते हैं।<ref name="ojeda">{{cite journal |author1=Ojeda, P. |author2=Garcia, M. |title=मूल बीटा-शीट प्रोटीन संरचना का विद्युत क्षेत्र-चालित विघटन और हेलिक्स-संरचना का निर्माण|journal=Biophysical Journal |volume=99 |issue=2 |pages=595–599 |year=2010 |pmid=20643079 |pmc=2905109 |doi= 10.1016/j.bpj.2010.04.040 |bibcode = 2010BpJ....99..595O }}</ref> | द्विध्रुव क्षण पानी जैसे सामान्य अणुओं और प्रोटीन जैसे जैव अणुओं में भी पाए जा सकते हैं।<ref name="ojeda">{{cite journal |author1=Ojeda, P. |author2=Garcia, M. |title=मूल बीटा-शीट प्रोटीन संरचना का विद्युत क्षेत्र-चालित विघटन और हेलिक्स-संरचना का निर्माण|journal=Biophysical Journal |volume=99 |issue=2 |pages=595–599 |year=2010 |pmid=20643079 |pmc=2905109 |doi= 10.1016/j.bpj.2010.04.040 |bibcode = 2010BpJ....99..595O }}</ref> | ||
| Line 360: | Line 286: | ||
किसी सामग्री के कुल द्विध्रुव क्षण के माध्यम से कोई ढांकता हुआ स्थिरांक की गणना कर सकता है जो चालकता की अधिक सहज अवधारणा से संबंधित है। यदि <math> \mathcal{M}_{\rm Tot} </math> नमूने का कुल द्विध्रुव आघूर्ण है, तब ढांकता हुआ स्थिरांक द्वारा दिया जाता है, | किसी सामग्री के कुल द्विध्रुव क्षण के माध्यम से कोई ढांकता हुआ स्थिरांक की गणना कर सकता है जो चालकता की अधिक सहज अवधारणा से संबंधित है। यदि <math> \mathcal{M}_{\rm Tot} </math> नमूने का कुल द्विध्रुव आघूर्ण है, तब ढांकता हुआ स्थिरांक द्वारा दिया जाता है, | ||
<math display="block">\varepsilon = 1 + k \left\langle \mathcal{M}_\text{Tot}^2 \right\rangle</math> | <math display="block">\varepsilon = 1 + k \left\langle \mathcal{M}_\text{Tot}^2 \right\rangle</math> | ||
जहाँ k स्थिरांक है और <math>\left\langle \mathcal{M}_\text{Tot}^2 \right\rangle = \left\langle \mathcal{M}_\text{Tot} (t = 0) \mathcal{M}_\text{Tot}(t = 0) \right\rangle</math> कुल द्विध्रुव आघूर्ण का समय सहसंबंध फलन है। सामान्यतः कुल द्विध्रुव आघूर्ण में योगदान आता रहता है | जहाँ k स्थिरांक है और <math>\left\langle \mathcal{M}_\text{Tot}^2 \right\rangle = \left\langle \mathcal{M}_\text{Tot} (t = 0) \mathcal{M}_\text{Tot}(t = 0) \right\rangle</math> कुल द्विध्रुव आघूर्ण का समय सहसंबंध फलन है। इस प्रकार सामान्यतः कुल द्विध्रुव आघूर्ण में योगदान आता रहता है | ||
नमूने में अणुओं के अनुवाद और घूर्णन से, | नमूने में अणुओं के अनुवाद और घूर्णन से, | ||
<math display="block">\mathcal{M}_\text{Tot} = \mathcal{M}_\text{Trans} + \mathcal{M}_\text{Rot}.</math> | <math display="block">\mathcal{M}_\text{Tot} = \mathcal{M}_\text{Trans} + \mathcal{M}_\text{Rot}.</math>इसलिए, ढांकता हुआ स्थिरांक (और चालकता) में दोनों पदों का योगदान होता है। आवृत्ति पर निर्भर ढांकता हुआ वेरिएबल की गणना करने के लिए इस दृष्टिकोण को सामान्यीकृत किया जा सकता है।<ref name="kim">{{cite journal |author1=Y. Shim |author2=H. Kim |title=कमरे के तापमान वाले आयनिक तरल में ढांकता हुआ विश्राम, आयन चालकता, विलायक रोटेशन, और विलायक गतिशीलता|journal=J. Phys. Chem. B |volume=112 |issue=35 |pages=11028–11038 |year=2008 |pmid=18693693 |doi=10.1021/jp802595r}}</ref>[[इलेक्ट्रॉनिक संरचना]] से द्विध्रुव क्षणों की गणना करना संभव है, या तब निरंतर विद्युत क्षेत्रों की प्रतिक्रिया के रूप में या घनत्व आव्युह से।<ref>{{Cite book|title=कम्प्यूटेशनल रसायन विज्ञान का परिचय|last=Frank.|first=Jensen|date=2007|publisher=John Wiley & Sons|isbn=9780470011874|edition= 2nd|location=Chichester, England|oclc=70707839}}</ref> चूँकि, परमाणु क्वांटम प्रभावों की संभावित उपस्थिति के कारण ऐसे मूल्य सीधे प्रयोग के लिए तुलनीय नहीं हैं, जो अमोनिया अणु जैसी सरल प्रणालियों के लिए भी पर्याप्त हो सकते हैं।<ref>{{Cite journal|last=Puzzarini|first=Cristina|date=2008-09-01|title=Ab initio characterization of XH3 (X = N,P). Part II. Electric, magnetic and spectroscopic properties of ammonia and phosphine|journal=Theoretical Chemistry Accounts|language=en|volume=121|issue=1–2|pages=1–10|doi=10.1007/s00214-008-0409-8|s2cid=98782005|issn=1432-881X}}</ref> [[युग्मित क्लस्टर]] (विशेषकर सीसीएसडी(टी)<ref>{{Cite journal|last1=Raghavachari|first1=Krishnan| last2=Trucks|first2=Gary W.| last3=Pople|first3=John A.|last4=Head-Gordon|first4=Martin|title=इलेक्ट्रॉन सहसंबंध सिद्धांतों की पांचवें क्रम की गड़बड़ी तुलना|journal=Chemical Physics Letters|volume=157|issue=6|pages=479–483 |doi=10.1016/s0009-2614(89)87395-6 |bibcode=1989CPL...157..479R|year=1989}}</ref>) बहुत त्रुटिहीन द्विध्रुव आघूर्ण दे सकता है,<ref>{{Cite book|title=आणविक इलेक्ट्रॉनिक-संरचना सिद्धांत|last1=Helgaker|first1=Trygve|last2=Jørgensen|first2=Poul|last3=Olsen|first3=Jeppe|language=en|doi=10.1002/9781119019572|year=2000|isbn=9781119019572|url=https://cds.cern.ch/record/1529252|type=Submitted manuscript|publisher=Wiley}}{{Dead link|date=August 2022 |bot=InternetArchiveBot |fix-attempted=yes }}</ref> यद्यपि घनत्व कार्यात्मक सिद्धांत से उचित अनुमान (लगभग 5% के अंदर) प्राप्त करना संभव है, मुख्य रूप से यदि [[हाइब्रिड कार्यात्मक]] या डबल हाइब्रिड कार्यात्मक कार्यरत हैं।<ref>{{Cite journal|last1=Hait|first1=Diptarka|last2=Head-Gordon|first2=Martin|date=2018-03-21|title=How Accurate Is Density Functional Theory at Predicting Dipole Moments? An Assessment Using a New Database of 200 Benchmark Values|journal=Journal of Chemical Theory and Computation|language=en|volume=14|issue=4|pages=1969–1981 |doi=10.1021/acs.jctc.7b01252|pmid=29562129 |arxiv=1709.05075|s2cid=4391272}}</ref> इस प्रकार किसी अणु के द्विध्रुव क्षण की गणना समूह योगदान विधियों की अवधारणा का उपयोग करके आणविक संरचना के आधार पर भी की जा सकती है।<ref name="mueller">{{cite journal |author1=K. Müller |author2=L. Mokrushina |author3=W. Arlt |title=द्विध्रुवीय क्षण के निर्धारण के लिए द्वितीय-क्रम समूह योगदान विधि|journal=J. Chem. Eng. Data |volume=57 |issue=4 |pages=1231–1236 |year=2012 |doi=10.1021/je2013395 }}</ref> | ||
इसलिए, ढांकता हुआ स्थिरांक (और चालकता) में दोनों पदों का योगदान होता है। आवृत्ति पर निर्भर ढांकता हुआ वेरिएबल की गणना करने के लिए इस दृष्टिकोण को सामान्यीकृत किया जा सकता है।<ref name="kim">{{cite journal |author1=Y. Shim |author2=H. Kim |title=कमरे के तापमान वाले आयनिक तरल में ढांकता हुआ विश्राम, आयन चालकता, विलायक रोटेशन, और विलायक गतिशीलता|journal=J. Phys. Chem. B |volume=112 |issue=35 |pages=11028–11038 |year=2008 |pmid=18693693 |doi=10.1021/jp802595r}}</ref> | |||
[[इलेक्ट्रॉनिक संरचना]] से द्विध्रुव क्षणों की गणना करना संभव है, या तब निरंतर विद्युत क्षेत्रों की प्रतिक्रिया के रूप में या घनत्व आव्युह से।<ref>{{Cite book|title=कम्प्यूटेशनल रसायन विज्ञान का परिचय|last=Frank.|first=Jensen|date=2007|publisher=John Wiley & Sons|isbn=9780470011874|edition= 2nd|location=Chichester, England|oclc=70707839}}</ref> चूँकि, परमाणु क्वांटम प्रभावों की संभावित उपस्थिति के कारण ऐसे मूल्य सीधे प्रयोग के लिए तुलनीय नहीं हैं, जो अमोनिया अणु जैसी सरल प्रणालियों के लिए भी पर्याप्त हो सकते हैं।<ref>{{Cite journal|last=Puzzarini|first=Cristina|date=2008-09-01|title=Ab initio characterization of XH3 (X = N,P). Part II. Electric, magnetic and spectroscopic properties of ammonia and phosphine|journal=Theoretical Chemistry Accounts|language=en|volume=121|issue=1–2|pages=1–10|doi=10.1007/s00214-008-0409-8|s2cid=98782005|issn=1432-881X}}</ref> [[युग्मित क्लस्टर]] (विशेषकर सीसीएसडी(टी)<ref>{{Cite journal|last1=Raghavachari|first1=Krishnan| last2=Trucks|first2=Gary W.| last3=Pople|first3=John A.|last4=Head-Gordon|first4=Martin|title=इलेक्ट्रॉन सहसंबंध सिद्धांतों की पांचवें क्रम की गड़बड़ी तुलना|journal=Chemical Physics Letters|volume=157|issue=6|pages=479–483 |doi=10.1016/s0009-2614(89)87395-6 |bibcode=1989CPL...157..479R|year=1989}}</ref>) बहुत त्रुटिहीन द्विध्रुव आघूर्ण दे सकता है,<ref>{{Cite book|title=आणविक इलेक्ट्रॉनिक-संरचना सिद्धांत|last1=Helgaker|first1=Trygve|last2=Jørgensen|first2=Poul|last3=Olsen|first3=Jeppe|language=en|doi=10.1002/9781119019572|year=2000|isbn=9781119019572|url=https://cds.cern.ch/record/1529252|type=Submitted manuscript|publisher=Wiley}}{{Dead link|date=August 2022 |bot=InternetArchiveBot |fix-attempted=yes }}</ref> यद्यपि घनत्व कार्यात्मक सिद्धांत से उचित अनुमान (लगभग 5% के अंदर) प्राप्त करना संभव है, मुख्य रूप से यदि [[हाइब्रिड कार्यात्मक]] या डबल हाइब्रिड कार्यात्मक कार्यरत हैं।<ref>{{Cite journal|last1=Hait|first1=Diptarka|last2=Head-Gordon|first2=Martin|date=2018-03-21|title=How Accurate Is Density Functional Theory at Predicting Dipole Moments? An Assessment Using a New Database of 200 Benchmark Values|journal=Journal of Chemical Theory and Computation|language=en|volume=14|issue=4|pages=1969–1981 |doi=10.1021/acs.jctc.7b01252|pmid=29562129 |arxiv=1709.05075|s2cid=4391272}}</ref> किसी अणु के द्विध्रुव क्षण की गणना समूह योगदान विधियों की अवधारणा का उपयोग करके आणविक संरचना के आधार पर भी की जा सकती है।<ref name="mueller">{{cite journal |author1=K. Müller |author2=L. Mokrushina |author3=W. Arlt |title=द्विध्रुवीय क्षण के निर्धारण के लिए द्वितीय-क्रम समूह योगदान विधि|journal=J. Chem. Eng. Data |volume=57 |issue=4 |pages=1231–1236 |year=2012 |doi=10.1021/je2013395 }}</ref> | |||
=='''यह भी देखें'''== | =='''यह भी देखें'''== | ||
{{div col|colwidth=22em}} | {{div col|colwidth=22em}} | ||
| Line 400: | Line 323: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 12/08/2023]] | [[Category:Created On 12/08/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 22:57, 10 October 2023

विद्युत द्विध्रुव आघूर्ण प्रणाली के अंदर धनात्मक और ऋणात्मक विद्युत आवेश के पृथक्करण का माप है, अर्थात, प्रणाली की समग्र रासायनिक ध्रुवता का माप है। इस प्रकार विद्युत द्विध्रुव आघूर्ण के लिए इकाइयों की अंतर्राष्ट्रीय प्रणाली कूलम्ब-मीटर (C⋅m) है। डिबाई (डी) परमाणु भौतिकी और रसायन विज्ञान में उपयोग की जाने वाली माप की और इकाई है।
सैद्धांतिक रूप से, विद्युत द्विध्रुव को बहुध्रुव विस्तार के प्रथम-क्रम पद द्वारा परिभाषित किया जाता है; इसमें दो समान और विपरीत आवेश होते हैं जो एक-दूसरे के बहुत करीब होते हैं, चूंकि वास्तविक द्विध्रुवों में भिन्न-भिन्न आवेश होते हैं।
प्रारंभिक परिभाषा
अधिकांशतः भौतिकी में किसी विशाल वस्तु के आयामों को नजरअंदाज किया जा सकता है और उसे बिंदु जैसी वस्तु, अर्थात बिंदु कण के रूप में माना जा सकता है। इस प्रकार विद्युत आवेश वाले बिंदु कणों को बिंदु आवेश कहा जाता है। दो बिंदु आवेश, आवेश सहित +q और दूसरा आवेश वाला −q दूरी से भिन्न हो गया d, विद्युत द्विध्रुव (मल्टीपोल विस्तार का साधारण स्थिति) का गठन करता है। इस स्थितियों के लिए, विद्युत द्विध्रुव आघूर्ण का परिमाण होता है
ऊर्जा और आघूर्ण
विद्युत द्विध्रुव आघूर्ण p वाली कोई वस्तु बाह्य विद्युत क्षेत्र E में रखे जाने पर बलाघूर्ण τ के अधीन होती है। बलाघूर्ण द्विध्रुव को क्षेत्र के साथ संरेखित करता है। विद्युत क्षेत्र के समानांतर संरेखित द्विध्रुव में उसके साथ कुछ कोण बनाने वाले द्विध्रुव की तुलना में कम संभावित ऊर्जा होती है। इस प्रकार द्विध्रुव द्वारा व्याप्त छोटे क्षेत्र में स्थानिक रूप से समान विद्युत क्षेत्र के लिए, ऊर्जा U और आघूर्णः द्वारा दिए गए हैं[2]
चूँकि गैर-समान विद्युत क्षेत्र में द्विध्रुव वास्तव में शुद्ध बल प्राप्त कर सकता है क्योंकि द्विध्रुव के छोर पर बल वर्तमान दूसरे छोर पर संतुलित नहीं होता है। यह दिखाया जा सकता है कि यह शुद्ध बल सामान्यतः द्विध्रुवीय क्षण के समानांतर होता है।
अभिव्यक्ति (सामान्य स्थिति)
अधिक सामान्यतः, आयतन V तक सीमित आवेश के निरंतर वितरण के लिए, द्विध्रुव क्षण के लिए संगत अभिव्यक्ति है:
द्विध्रुव आघूर्ण आवेशों की समग्र तटस्थ प्रणाली के संदर्भ में विशेष रूप से उपयोगी है, उदाहरण के लिए विपरीत आवेशों की जोड़ी, या समान विद्युत क्षेत्र में तटस्थ कंडक्टर।
आवेशों की ऐसी प्रणाली के लिए, जिसे युग्मित विपरीत आवेशों की श्रृंखला के रूप में देखा जाता है, विद्युत द्विध्रुव आघूर्ण का संबंध है:
यह तटस्थ आवेश युग्मों के व्यक्तिगत द्विध्रुव आघूर्णों का सदिश योग है। (समग्र आवेश तटस्थता के कारण , द्विध्रुव क्षण पर्यवेक्षक की स्थिति आर से स्वतंत्र है।) इस प्रकार, पी का मान संदर्भ बिंदु की पसंद से स्वतंत्र है, परंतु प्रणाली का समग्र आवेश शून्य हो।
गैर-तटस्थ प्रणाली के द्विध्रुवीय क्षण, जैसे कि प्रोटोन के द्विध्रुवीय क्षण, पर चर्चा करते समय संदर्भ बिंदु की पसंद पर निर्भरता उत्पन्न होती है। ऐसे स्थितियों में यह पारंपरिक है कि संदर्भ बिंदु को प्रणाली के द्रव्यमान का केंद्र चुना जाए, न कि किसी मनमाने मूल को।[3] यह विकल्प केवल परंपरा का विषय नहीं है: द्विध्रुव क्षण की धारणा अनिवार्य रूप से टोक़ की यांत्रिक धारणा से ली गई है, और यांत्रिकी की तरह, अवलोकन बिंदु के रूप में द्रव्यमान के केंद्र को चुनना कम्प्यूटेशनल और सैद्धांतिक रूप से उपयोगी है। किसी आवेशित अणु के लिए द्रव्यमान के केंद्र के अतिरिक्त आवेश का केंद्र संदर्भ बिंदु होना चाहिए। इस प्रकार तटस्थ प्रणालियों के लिए संदर्भ बिंदु महत्वपूर्ण नहीं है, और द्विध्रुवीय क्षण प्रणाली का आंतरिक गुण है।
विद्युत द्विध्रुव की क्षमता और क्षेत्र
एक आदर्श द्विध्रुव में अनंत सूक्ष्म पृथक्करण वाले दो विपरीत आवेश होते हैं। इस प्रकार हम ऐसे आदर्श द्विध्रुव की क्षमता और क्षेत्र की गणना करते हैं, जो पृथक्करण d > 0 पर दो विपरीत आवेशों से प्रारंभ होता है, और सीमा को d → 0 के रूप में लेता है।
दो निकट दूरी वाले विपरीत आवेशों ±q की क्षमता इस प्रकार है:
द्विध्रुव आघूर्ण घनत्व और ध्रुवीकरण घनत्व
आवेशों की श्रृंखला का द्विध्रुव आघूर्ण,
वर्तमान यह पता लगाया जा रहा है कि मैक्सवेल के समीकरणों में प्रवेश करने वाला ध्रुवीकरण घनत्व 'पी' ('आर') किस तरह से आवेशों के समग्र तटस्थ सरणी के द्विध्रुव क्षण 'पी' से संबंधित है, और द्विध्रुव क्षण घनत्व 'पी' से भी संबंधित है। ('आर') (जो न केवल द्विध्रुवीय क्षण का वर्णन करता है, किंतु सरणी स्थान का भी वर्णन करता है)। निम्नलिखित में केवल स्थिर स्थितियों पर विचार किया जाता है, इसलिए 'पी'('आर') पर कोई समय निर्भरता नहीं है, और कोई विस्थापन धारा नहीं है। सबसे पहले ध्रुवीकरण घनत्व 'पी'('आर') की कुछ चर्चा है। उस चर्चा का अनुसरण अनेक विशिष्ट उदाहरणों के साथ किया जाता है।
मुक्त और बाध्य आवेशों और धाराओं में आवेशों और धाराओं के विभाजन के आधार पर मैक्सवेल के समीकरणों का सूत्रीकरण 'डी'- और 'पी'-क्षेत्रों की प्रारंभआत की ओर ले जाता है:
आवेश और द्विध्रुव घनत्व वाला माध्यम
जैसा कि आगे बताया गया है, ध्रुवीकरण क्षण घनत्व पी(आर) के लिए मॉडल के परिणामस्वरूप ध्रुवीकरण होता है
यह ध्यान दिया जा सकता है कि इस दृष्टिकोण को सभी बहुध्रुवों को सम्मिलित करने के लिए बढ़ाया जा सकता है: द्विध्रुव, चतुर्ध्रुव, आदि।[10][11] संबंध का उपयोग करना:
सतह प्रभार
ऊपर, द्विध्रुव के कारण विभव के व्यंजक में पहले पद के लिए चर्चा स्थगित कर दी गई थी। विचलन को एकीकृत करने से सतही आवेश उत्पन्न होता है। दाईं ओर का चित्र सहज विचार प्रदान करता है कि सतही आवेश क्यों उत्पन्न होता है। चित्र दो सतहों के मध्य समान द्विध्रुवों की समान सरणी दिखाता है। आंतरिक रूप से, द्विध्रुवों के शीर्ष और पूंछ आसन्न और रद्द होते हैं। चूँकि, बाउंडिंग सतहों पर कोई निरस्तता नहीं होता है। इसके अतिरिक्त, सतह पर द्विध्रुव सिर धनात्मक सतह आवेश बनाते हैं, जबकि विपरीत सतह पर द्विध्रुव सिर ऋणात्मक सतह आवेश बनाते हैं। यह दो विपरीत सतह आवेश द्विध्रुवों की दिशा के विपरीत दिशा में शुद्ध विद्युत क्षेत्र बनाते हैं।
उपरोक्त संभावित अभिव्यक्ति का उपयोग करके इस विचार को गणितीय रूप दिया गया है। मुफ़्त शुल्क को नज़रअंदाज करते हुए, संभावना यह है:
पी(आर) के भौतिक रूप से अधिक यथार्थवादी मॉडलिंग में द्विध्रुव क्षण घनत्व तेजी से गिर जाएगा, किन्तु शून्य घनत्व की ओर अचानक कदम उठाने के अतिरिक्त, सीमित क्षेत्र की सीमा पर आसानी से शून्य हो जाएगा। तब सतह आवेश उच्चतम रूप से पतली सतह में केंद्रित नहीं होगा, किंतु इसके अतिरिक्त, सुचारू रूप से भिन्न द्विध्रुवीय क्षण घनत्व का विचलन होने के कारण, स्वयं को पतली, किन्तु सीमित संक्रमण परत में वितरित कर देगा।
एक समान बाह्य विद्युत क्षेत्र में अचालक क्षेत्र
सतह आवेश के बारे में उपरोक्त सामान्य टिप्पणियाँ समान विद्युत क्षेत्र में ढांकता हुआ क्षेत्र के उदाहरण पर विचार करके अधिक ठोस बनाई गई हैं।[20][21] यह पाया गया है कि गोला अपने आंतरिक भाग के द्विध्रुवीय क्षण से संबंधित सतह आवेश को अपनाता है।
एक समान बाहरी विद्युत क्षेत्र को z-दिशा में इंगित करना माना जाता है, और गोलाकार-ध्रुवीय निर्देशांक प्रस्तुतकिए जाते हैं, इसलिए इस क्षेत्र द्वारा बनाई गई क्षमता है:
सामान्य मीडिया
यदि अवलोकन आवेशों की प्रणाली से पर्याप्त रूप से दूर के क्षेत्रों तक ही सीमित है, तब त्रुटिहीन ध्रुवीकरण घनत्व का बहुध्रुवीय विस्तार किया जा सकता है। इस विस्तार को छोटा करके (उदाहरण के लिए, केवल द्विध्रुव पदों को, या केवल द्विध्रुव और चतुष्कोण पदों को, या आदि को बनाए रखते हुए), पिछले अनुभाग के परिणाम पुनः प्राप्त हो जाते हैं। विशेष रूप से, द्विध्रुवीय पद पर विस्तार को छोटा करते हुए, परिणाम आवेश क्षेत्र तक सीमित समान द्विध्रुवीय क्षण द्वारा उत्पन्न ध्रुवीकरण घनत्व से अप्रभेद्य होता है। इस द्विध्रुव सन्निकटन की त्रुटिहीनता के लिए, जैसा कि पिछले अनुभाग में दिखाया गया है, द्विध्रुव क्षण घनत्व 'पी'('आर') (जिसमें न केवल 'पी' किंतु 'पी' का स्थान भी सम्मिलित है) 'पी'(' आर')।
आवेश सरणी के अंदर के स्थानों पर, युग्मित आवेश की सरणी को केवल द्विध्रुवीय क्षण घनत्व 'पी' ('आर') वाले सन्निकटन से जोड़ने के लिए अतिरिक्त विचारों की आवश्यकता होती है। सबसे सरल सन्निकटन आवेश सारणी को आदर्श (असीमित दूरी वाले) द्विध्रुवों के मॉडल से बदलना है। विशेष रूप से, जैसा कि ऊपर दिए गए उदाहरण में परिमित क्षेत्र तक सीमित निरंतर द्विध्रुव आघूर्ण घनत्व का उपयोग किया जाता है, सतह आवेश और विध्रुवण क्षेत्र का परिणाम होता है। इस प्रकार मॉडल का अधिक सामान्य संस्करण (जो स्थिति के साथ ध्रुवीकरण को भिन्न-भिन्न करने की अनुमति देता है) विद्युत संवेदनशीलता या विद्युत पारगम्यता का उपयोग करने वाला पारंपरिक दृष्टिकोण है।
बिंदु आवेश सारणी का अधिक समष्टि मॉडल सूक्ष्म आवेशों के औसत द्वारा प्रभावी माध्यम सन्निकटन प्रस्तुत करता है;[16] उदाहरण के लिए, औसत यह व्यवस्था कर सकता है कि केवल द्विध्रुवीय क्षेत्र ही भूमिका निभाते हैं।[22][23] संबंधित दृष्टिकोण यह है कि आवेशों को अवलोकन बिंदु के निकट के आवेशों में विभाजित किया जाए, और उन आवेशों को जो बहुध्रुवीय विस्तार की अनुमति देने के लिए पर्याप्त दूर हों। फिर निकटवर्ती आवेश स्थानीय क्षेत्र प्रभावों को जन्म देते हैं।[14][24] इस प्रकार के सामान्य मॉडल में, दूर के आवेशों को ढांकता हुआ स्थिरांक का उपयोग करके सजातीय माध्यम के रूप में माना जाता है, और पास के आवेशों को केवल द्विध्रुवीय सन्निकटन में माना जाता है।[25] केवल द्विध्रुवों और उनसे संबंधित द्विध्रुव आघूर्ण घनत्व द्वारा किसी माध्यम या आवेशों की सारणी के सन्निकटन को कभी-कभी बिंदु द्विध्रुव सन्निकटन, असतत द्विध्रुव सन्निकटन, या केवल द्विध्रुव सन्निकटन कहा जाता है।[26][27][28]
मौलिक कणों के विद्युत द्विध्रुव आघूर्ण
स्पिन (भौतिकी) के साथ भ्रमित न हों जो कणों के चुंबकीय द्विध्रुव क्षणों को संदर्भित करता है, मौलिक और मिश्रित कणों, अर्थात् इलेक्ट्रॉन के विद्युत द्विध्रुव क्षणों (ईडीएम; या विषम विद्युत द्विध्रुव क्षण) को मापने पर बहुत प्रयोगात्मक कार्य जारी है। इस प्रकार क्रमशः विद्युत द्विध्रुव आघूर्ण और न्यूट्रॉन विद्युत द्विध्रुव आघूर्ण। चूंकि ईडीएम समता (भौतिकी) (पी) और टी-समरूपता समय-उत्क्रमण (टी) समरूपता दोनों का उल्लंघन करते हैं, उनके मूल्य प्रकृति में सीपी-उल्लंघन का अधिकतर मॉडल-स्वतंत्र माप उत्पन्न करते हैं (सीपीटी समरूपता वैध है)।[29] इसलिए, इन ईडीएम के मान सीपी-उल्लंघन के पैमाने पर शक्तिशाली बाधाएं डालते हैं जो कण भौतिकी के मानक मॉडल के विस्तार की अनुमति दे सकते हैं। प्रयोगों की वर्तमान पीढ़ियों को ईडीएम की अतिसममिति रेंज के प्रति संवेदनशील बनाने के लिए डिज़ाइन किया गया है, जो एलएचसी पर किए गए पूरक प्रयोगों को प्रदान करता है।[30]
वास्तव में, अनेक सिद्धांत वर्तमान सीमाओं के साथ असंगत हैं और उन्हें प्रभावी ढंग से खारिज कर दिया गया है, और स्थापित सिद्धांत इन सीमाओं से कहीं अधिक बड़े मूल्य की अनुमति देता है, जिससे शक्तिशाली सीपी समस्या उत्पन्न होती है और अक्षतंतु जैसे नए कणों की खोज को बढ़ावा मिलता है।[31]
हम कम से कम सेतो युकावा में तटस्थ काओन दोलनों से जानते हैं कि सीपी टूट गया है। इलेक्ट्रॉन और न्यूट्रॉन जैसे विभिन्न कणों के विद्युत द्विध्रुव क्षण को मापने के लिए प्रयोग किए गए हैं। इसके अतिरिक्त सीपी-उल्लंघन शर्तों के साथ मानक मॉडल से परे अनेक मॉडल सामान्य रूप से गैर-शून्य विद्युत द्विध्रुवीय क्षण की भविष्यवाणी करते हैं और इसलिए ऐसी नई भौतिकी के प्रति संवेदनशील होते हैं। क्वांटम क्रोमोडायनामिक्स में गैर-शून्य θ शब्द से पल सुधार न्यूट्रॉन और प्रोटॉन के लिए गैर-शून्य विद्युत द्विध्रुवीय क्षण की भविष्यवाणी करते हैं, जो प्रयोगों में नहीं देखा गया है (जहां सबसे अच्छी सीमाएं न्यूट्रॉन के विश्लेषण से आती हैं)। यह शक्तिशाली सीपी समस्या है और चिरल अस्तव्यस्तता सिद्धांत की भविष्यवाणी है।
अणुओं के द्विध्रुव आघूर्ण
द्विध्रुव#आण्विक द्विध्रुव बाहरी विद्युत क्षेत्रों की उपस्थिति में किसी पदार्थ के व्यवहार के लिए उत्तरदायी होते हैं। इस प्रकार द्विध्रुव बाहरी क्षेत्र से संरेखित होते हैं जो स्थिर या समय पर निर्भर हो सकते हैं। यह प्रभाव ढांकता हुआ स्पेक्ट्रोस्कोपी नामक आधुनिक प्रायोगिक विधि का आधार बनता है।
द्विध्रुव क्षण पानी जैसे सामान्य अणुओं और प्रोटीन जैसे जैव अणुओं में भी पाए जा सकते हैं।[32]
किसी सामग्री के कुल द्विध्रुव क्षण के माध्यम से कोई ढांकता हुआ स्थिरांक की गणना कर सकता है जो चालकता की अधिक सहज अवधारणा से संबंधित है। यदि नमूने का कुल द्विध्रुव आघूर्ण है, तब ढांकता हुआ स्थिरांक द्वारा दिया जाता है,
नमूने में अणुओं के अनुवाद और घूर्णन से,
यह भी देखें
- विषम चुंबकीय द्विध्रुव आघूर्ण
- बंध द्विध्रुव आघूर्ण
- न्यूट्रॉन विद्युत द्विध्रुव आघूर्ण
- इलेक्ट्रॉन विद्युत द्विध्रुव आघूर्ण
- टोरॉयडल क्षण
- मल्टीपोल विस्तार
- बहुध्रुव क्षण
- ठोस हार्मोनिक्स
- अक्षीय बहुध्रुव क्षण
- बेलनाकार बहुध्रुव क्षण
- गोलाकार बहुध्रुव क्षण
- लाप्लास विस्तार (संभावित)
- दिग्गज बहुपद
टिप्पणियाँ
संदर्भ
- ↑ Peter W. Atkins; Loretta Jones (2016). Chemical principles: the quest for insight (7th ed.). Macmillan Learning. ISBN 978-1464183959.
- ↑ Raymond A. Serway; John W. Jewett Jr. (2009). Physics for Scientists and Engineers, Volume 2 (8th ed.). Cengage Learning. pp. 756–757. ISBN 978-1439048399.
- ↑ Christopher J. Cramer (2004). Essentials of computational chemistry (2nd ed.). Wiley. p. 307. ISBN 978-0-470-09182-1.
- ↑ David E Dugdale (1993). विद्युत चुम्बकत्व की अनिवार्यताएँ. Springer. pp. 80–81. ISBN 978-1-56396-253-0.
- ↑ Kikuji Hirose; Tomoya Ono; Yoshitaka Fujimoto (2005). वास्तविक-अंतरिक्ष औपचारिकता में प्रथम-सिद्धांत गणना. Imperial College Press. p. 18. ISBN 978-1-86094-512-0.
- ↑ 6.0 6.1 BB Laud (1987). विद्युत चुम्बकीय (2nd ed.). New Age International. p. 25. ISBN 978-0-85226-499-7.
- ↑ Jie-Zhi Wu; Hui-Yang Ma; Ming-De Zhou (200). "§2.3.1 Functionally Orthogonal Decomposition". भंवर और भंवर गतिशीलता. Springer. pp. 36 ff. ISBN 978-3-540-29027-8.
- ↑ Uwe Krey; Anthony Owen (2007). Basic Theoretical Physics: A Concise Overview. Springer. pp. 138–143. ISBN 978-3-540-36804-5.
- ↑ T Tsang (1997). शास्त्रीय इलेक्ट्रोडायनामिक्स. World Scientific. p. 59. ISBN 978-981-02-3041-8.
- ↑ George E Owen (2003). विद्युत चुम्बकीय सिद्धांत का परिचय (republication of the 1963 Allyn & Bacon ed.). Courier Dover Publications. p. 80. ISBN 978-0-486-42830-7.
- ↑ Pierre-François Brevet (1997). सतह दूसरी हार्मोनिक पीढ़ी. Presses polytechniques et universitaires romandes. p. 24. ISBN 978-2-88074-345-1.
- ↑ Daniel A. Jelski; Thomas F. George (1999). नई सामग्रियों का कम्प्यूटेशनल अध्ययन. World Scientific. p. 219. ISBN 978-981-02-3325-9.
- ↑ EM Purcell; CR Pennypacker (1973). "गैरगोलाकार ढांकता हुआ अनाज द्वारा प्रकाश का प्रकीर्णन और अवशोषण". Astrophysical Journal. 186: 705–714. Bibcode:1973ApJ...186..705P. doi:10.1086/152538.
- ↑ 14.0 14.1 H. Ibach; Hans Lüth (2003). Solid-state Physics: an introduction to principles of materials science (3rd ed.). Springer. p. 361. ISBN 978-3-540-43870-0.
- ↑ Yasuaki Masumoto; Toshihide Takagahara (2002). Semiconductor quantum dots: physics, spectroscopy, and applications. Springer. p. 72. ISBN 978-3-540-42805-3.
- ↑ 16.0 16.1 Yutaka Toyozawa (2003). ठोसों में ऑप्टिकल प्रक्रियाएँ. Cambridge University Press. p. 96. ISBN 978-0-521-55605-7.
- ↑ Wai-Kai Chen (2005). इलेक्ट्रिकल इंजीनियरिंग हैंडबुक. Academic Press. p. 502. ISBN 978-0-12-170960-0.
- ↑ Julius Adams Stratton (2007). विद्युत चुम्बकीय सिद्धांत (reprint of 1941 ed.). Wiley-IEEE. p. 184. ISBN 978-0-470-13153-4.
- ↑ Edward J. Rothwell; Michael J. Cloud (2001). विद्युत चुम्बकीय. CRC Press. p. 68. ISBN 978-0-8493-1397-4.
- ↑ HW Wyld (1999). Mathematical Methods for Physics (2nd ed.). Westview Press. pp. 233 ff. ISBN 978-0-7382-0125-2.
- ↑ Julius Adams Stratton (2007). Electromagnetic theory (Wiley-IEEE reissue ed.). Piscataway, NJ: IEEE Press. p. 205 ff. ISBN 978-0-470-13153-4.
- ↑ John E Swipe; RW Boyd (2002). "Nanocomposite materials for nonlinear optics based upon local field effects". In Vladimir M Shalaev (ed.). Optical properties of nanostructured random media. Springer. p. 3. ISBN 978-3-540-42031-6.
- ↑ Emil Wolf (1977). Progress in Optics. Elsevier. p. 288. ISBN 978-0-7204-1515-5.
- ↑ Mark Fox (2006). Optical Properties of Solids. Oxford University Press. p. 39. ISBN 978-0-19-850612-6.
- ↑ Lev Kantorovich (2004). "§8.2.1 The local field". Quantum theory of the solid state. Springer. p. 426. ISBN 978-1-4020-2153-4.
- ↑ Pierre Meystre (2001). Atom Optics. Springer. p. 5. ISBN 978-0-387-95274-1.
- ↑ Bruce T Draine (2001). "The discrete dipole approximation for light scattering by irregular targets". In Michael I. Mishchenko (ed.). Light scattering by nonspherical particles. Academic Press. p. 132. ISBN 978-0-12-498660-2.
- ↑ MA Yurkin; AG Hoekstra (2007). "The discrete dipole approximation: an overview and recent developments". Journal of Quantitative Spectroscopy and Radiative Transfer. 106 (1–3): 558–589. arXiv:0704.0038. Bibcode:2007JQSRT.106..558Y. doi:10.1016/j.jqsrt.2007.01.034. S2CID 119572857.
- ↑ Khriplovich, Iosip B.; Lamoreaux, Steve K. (2012). CP violation without strangeness : electric dipole moments of particles, atoms, and molecules. [S.l.]: Springer. ISBN 978-3-642-64577-8.
- ↑ Ibrahim, Tarik; Itani, Ahmad; Nath, Pran (2014). "पीईवी स्केल भौतिकी की एक संवेदनशील जांच के रूप में इलेक्ट्रॉन ईडीएम". Physical Review D. 90 (5): 055006. arXiv:1406.0083. Bibcode:2014PhRvD..90e5006I. doi:10.1103/PhysRevD.90.055006. S2CID 118880896.
- ↑ Kim, Jihn E.; Carosi, Gianpaolo (2010). "एक्सियन्स और मजबूत सीपी समस्या". Reviews of Modern Physics. 82 (1): 557–602. arXiv:0807.3125. Bibcode:2010RvMP...82..557K. doi:10.1103/RevModPhys.82.557.
- ↑ Ojeda, P.; Garcia, M. (2010). "मूल बीटा-शीट प्रोटीन संरचना का विद्युत क्षेत्र-चालित विघटन और हेलिक्स-संरचना का निर्माण". Biophysical Journal. 99 (2): 595–599. Bibcode:2010BpJ....99..595O. doi:10.1016/j.bpj.2010.04.040. PMC 2905109. PMID 20643079.
- ↑ Y. Shim; H. Kim (2008). "कमरे के तापमान वाले आयनिक तरल में ढांकता हुआ विश्राम, आयन चालकता, विलायक रोटेशन, और विलायक गतिशीलता". J. Phys. Chem. B. 112 (35): 11028–11038. doi:10.1021/jp802595r. PMID 18693693.
- ↑ Frank., Jensen (2007). कम्प्यूटेशनल रसायन विज्ञान का परिचय (2nd ed.). Chichester, England: John Wiley & Sons. ISBN 9780470011874. OCLC 70707839.
- ↑ Puzzarini, Cristina (2008-09-01). "Ab initio characterization of XH3 (X = N,P). Part II. Electric, magnetic and spectroscopic properties of ammonia and phosphine". Theoretical Chemistry Accounts (in English). 121 (1–2): 1–10. doi:10.1007/s00214-008-0409-8. ISSN 1432-881X. S2CID 98782005.
- ↑ Raghavachari, Krishnan; Trucks, Gary W.; Pople, John A.; Head-Gordon, Martin (1989). "इलेक्ट्रॉन सहसंबंध सिद्धांतों की पांचवें क्रम की गड़बड़ी तुलना". Chemical Physics Letters. 157 (6): 479–483. Bibcode:1989CPL...157..479R. doi:10.1016/s0009-2614(89)87395-6.
- ↑ Helgaker, Trygve; Jørgensen, Poul; Olsen, Jeppe (2000). आणविक इलेक्ट्रॉनिक-संरचना सिद्धांत (Submitted manuscript) (in English). Wiley. doi:10.1002/9781119019572. ISBN 9781119019572.[permanent dead link]
- ↑ Hait, Diptarka; Head-Gordon, Martin (2018-03-21). "How Accurate Is Density Functional Theory at Predicting Dipole Moments? An Assessment Using a New Database of 200 Benchmark Values". Journal of Chemical Theory and Computation (in English). 14 (4): 1969–1981. arXiv:1709.05075. doi:10.1021/acs.jctc.7b01252. PMID 29562129. S2CID 4391272.
- ↑ K. Müller; L. Mokrushina; W. Arlt (2012). "द्विध्रुवीय क्षण के निर्धारण के लिए द्वितीय-क्रम समूह योगदान विधि". J. Chem. Eng. Data. 57 (4): 1231–1236. doi:10.1021/je2013395.
अग्रिम पठन
- मेल्विन श्वार्ट्ज (1987). "विद्युत द्विध्रुव आघूर्ण". इलेक्ट्रोडायनामिक्स के सिद्धांत (1972 का पुनर्मुद्रण ed.). कूरियर डोवर प्रकाशन. p. 49ff. ISBN 978-0-486-65493-5.