अपक्षय बल: Difference between revisions
(Created page with "{{Other uses|Depletion (disambiguation)}} एक अवक्षय बल एक प्रभावी आकर्षक बल है जो बड़े कोला...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Other uses|Depletion (disambiguation)}} | {{Other uses|Depletion (disambiguation)}} | ||
अवक्षय बल प्रभावी आकर्षक बल है जो बड़े [[ कोलाइडयन का ]] कणों के बीच उत्पन्न होता है जो 'डिप्लेटेंट्स' के तनु विलयन में निलंबित होते हैं, जो छोटे विलेय होते हैं जिन्हें बड़े कणों के आसपास से अधिमानतः बाहर रखा जाता है।<ref name=physicaa>{{cite journal |last=Mao |first=Y. |author2=M. E. Cates |author3=H. N. W. Lekkerkerker |title=कोलाइडल सिस्टम में अवक्षय बल|journal=Physica A |date=May 1995 |volume=222 |issue=1–4 |pages=10–24 |doi=10.1016/0378-4371(95)00206-5 |bibcode=1995PhyA..222...10M |hdl=1874/22114 |s2cid=121387079 |hdl-access=free}}</ref><ref name=Lekkerkerker>{{cite book |last=Lekkerkerker |first=H. N. W. |author2=Tuinier, R. |title=कोलाइड्स और डिप्लेशन इंटरेक्शन|publisher=Springer: Heidelberg |year=2011}}</ref> कणों के जमाव की ओर ले जाने वाली कमी बलों की शुरुआती रिपोर्टों में से बॉन्डी की है, जिन्होंने समाधान के लिए बहुलक अपक्षय अणुओं ([[सोडियम alginate]]) के अलावा रबर लेटेक्स के पृथक्करण या क्रीमिंग को देखा।<ref name="Bondy">{{cite journal |last=Bondy |first=C. |title=रबर लेटेक्स की क्रीमिंग|journal=Trans. Faraday Soc. |date=1939 |volume=35 |pages=1093 |doi=10.1039/TF9393501093}}</ref> आम तौर पर, क्षीणकों में [[पॉलिमर]], मिसेल, [[osmolytes]], स्याही, कीचड़, या विकट में बिखरे हुए पेंट शामिल हो सकते हैं: निरंतर चरण।<ref name=physicaa /><ref name=textbook>{{cite book |last=Butt |first=Hans-Jürgen |title=इंटरफेस के भौतिकी और रसायन विज्ञान|year=2006 |publisher=Wiley-VCH-Verl. |location=Weinheim |isbn=978-3-527-40629-6 |pages=116–117 |edition=2nd., rev. and enl. |author2=Graf, Karlheinz |author3=Kappl, Michael }}</ref> | |||
कमी बलों को अक्सर [[एंट्रोपिक बल]]ों के रूप में माना जाता है, जैसा कि पहले स्थापित असाकुरा-ओसावा मॉडल द्वारा समझाया गया था।<ref name="AsakuraOosawa">{{cite journal |last=Asakura |first=Sho |author2=Oosawa, F. |title=मैक्रोमोलेक्युलस के घोल में डूबे दो निकायों के बीच परस्पर क्रिया पर|journal=The Journal of Chemical Physics |date=1 January 1954 |volume=22 |issue=7 |pages=1255 |doi=10.1063/1.1740347 |bibcode = 1954JChPh..22.1255A }}</ref><रे च चाट = "2" आसाकुरा>{{cite journal |last=Asakura |first=Sho |author2=Oosawa, F. |title=मैक्रोमोलेक्युलस के समाधान में निलंबित कणों के बीच सहभागिता|journal=Journal of Polymer Science |year=1958 |volume=33 |issue=126 |pages=183–192 |doi=10.1002/pol.1958.1203312618 |bibcode=1958JPoSc..33..183A }</ref> इस सिद्धांत में अवक्षय बल आसपास के विलयन के आसमाटिक दबाव में वृद्धि से उत्पन्न होता है जब कोलाइडल कण इतने करीब हो जाते हैं कि बहिष्कृत कोसोल्यूट्स (डिप्लेटेंट्स) उनके बीच फिट नहीं हो सकते।<ref name= seminar />क्योंकि कणों को हार्ड-कोर (पूरी तरह से कठोर) कणों के रूप में माना जाता था, बल को प्रेरित करने वाले अंतर्निहित तंत्र की उभरती हुई तस्वीर आवश्यक रूप से एंट्रोपिक थी। | कमी बलों को अक्सर [[एंट्रोपिक बल]]ों के रूप में माना जाता है, जैसा कि पहले स्थापित असाकुरा-ओसावा मॉडल द्वारा समझाया गया था।<ref name="AsakuraOosawa">{{cite journal |last=Asakura |first=Sho |author2=Oosawa, F. |title=मैक्रोमोलेक्युलस के घोल में डूबे दो निकायों के बीच परस्पर क्रिया पर|journal=The Journal of Chemical Physics |date=1 January 1954 |volume=22 |issue=7 |pages=1255 |doi=10.1063/1.1740347 |bibcode = 1954JChPh..22.1255A }}</ref><रे च चाट = "2" आसाकुरा>{{cite journal |last=Asakura |first=Sho |author2=Oosawa, F. |title=मैक्रोमोलेक्युलस के समाधान में निलंबित कणों के बीच सहभागिता|journal=Journal of Polymer Science |year=1958 |volume=33 |issue=126 |pages=183–192 |doi=10.1002/pol.1958.1203312618 |bibcode=1958JPoSc..33..183A }</ref> इस सिद्धांत में अवक्षय बल आसपास के विलयन के आसमाटिक दबाव में वृद्धि से उत्पन्न होता है जब कोलाइडल कण इतने करीब हो जाते हैं कि बहिष्कृत कोसोल्यूट्स (डिप्लेटेंट्स) उनके बीच फिट नहीं हो सकते।<ref name= seminar />क्योंकि कणों को हार्ड-कोर (पूरी तरह से कठोर) कणों के रूप में माना जाता था, बल को प्रेरित करने वाले अंतर्निहित तंत्र की उभरती हुई तस्वीर आवश्यक रूप से एंट्रोपिक थी। | ||
| Line 8: | Line 8: | ||
=== स्टेरिक्स === | === स्टेरिक्स === | ||
विलयन में कोलाइड्स और डिप्लेटेंट्स की प्रणाली को आम तौर पर बड़े कोलाइड्स और छोटे डिप्लेटेंट्स को अलग-अलग आकार के कठोर क्षेत्रों के रूप में मानकर तैयार किया जाता है।<ref name=physicaa />कठोर क्षेत्रों को गैर-अंतःक्रियात्मक और अभेद्य क्षेत्रों के रूप में जाना जाता है। कठिन क्षेत्रों के इन दो मूलभूत गुणों को गणितीय रूप से कठिन क्षेत्र की क्षमता द्वारा वर्णित किया गया है। हार्ड-स्फेयर पोटेंशिअल बड़े क्षेत्रों के चारों ओर स्टेरिक अवरोध लगाता है जो बदले में बहिष्कृत मात्रा को जन्म देता है, यानी वह वॉल्यूम जो छोटे क्षेत्रों के कब्जे के लिए अनुपलब्ध है।<ref name=seminar /> | विलयन में कोलाइड्स और डिप्लेटेंट्स की प्रणाली को आम तौर पर बड़े कोलाइड्स और छोटे डिप्लेटेंट्स को अलग-अलग आकार के कठोर क्षेत्रों के रूप में मानकर तैयार किया जाता है।<ref name=physicaa />कठोर क्षेत्रों को गैर-अंतःक्रियात्मक और अभेद्य क्षेत्रों के रूप में जाना जाता है। कठिन क्षेत्रों के इन दो मूलभूत गुणों को गणितीय रूप से कठिन क्षेत्र की क्षमता द्वारा वर्णित किया गया है। हार्ड-स्फेयर पोटेंशिअल बड़े क्षेत्रों के चारों ओर स्टेरिक अवरोध लगाता है जो बदले में बहिष्कृत मात्रा को जन्म देता है, यानी वह वॉल्यूम जो छोटे क्षेत्रों के कब्जे के लिए अनुपलब्ध है।<ref name=seminar /> | ||
==== हार्ड-क्षेत्र क्षमता ==== | ==== हार्ड-क्षेत्र क्षमता ==== | ||
कोलाइडल फैलाव में, कोलाइड-कोलॉइड इंटरेक्शन क्षमता को दो कठोर क्षेत्रों के बीच इंटरेक्शन क्षमता के रूप में अनुमानित किया जाता है। व्यास के दो कठोर गोलों के लिए <math>\sigma</math>, इंटरपार्टिकल सेपरेशन के | कोलाइडल फैलाव में, कोलाइड-कोलॉइड इंटरेक्शन क्षमता को दो कठोर क्षेत्रों के बीच इंटरेक्शन क्षमता के रूप में अनुमानित किया जाता है। व्यास के दो कठोर गोलों के लिए <math>\sigma</math>, इंटरपार्टिकल सेपरेशन के फंक्शन के रूप में इंटरेक्शन पोटेंशिअल है: | ||
:<math>V(h)=\left\{ \begin{matrix}0 & \mbox{if}\quad h\geq \sigma \\ \infty & \mbox{if}\quad h< \sigma \end{matrix} \right.</math> | :<math>V(h)=\left\{ \begin{matrix}0 & \mbox{if}\quad h\geq \sigma \\ \infty & \mbox{if}\quad h< \sigma \end{matrix} \right.</math> | ||
जहां हार्ड-क्षेत्र क्षमता कहा जाता है <math>h</math> गोले के बीच केंद्र से केंद्र की दूरी है।<ref name=binary>{{cite journal|last=Biben|first=Thierry|author2=Peter Bladon |author3=Daan Frenkel |title=बाइनरी हार्ड-स्फेयर तरल पदार्थों में कमी के प्रभाव|journal=Journal of Physics: Condensed Matter|year=1996|volume=8|issue=50|pages=10799–10800|bibcode = 1996JPCM....810799B |doi = 10.1088/0953-8984/8/50/008 |hdl=1874/10416|s2cid=250884220 |hdl-access=free}}</ref> | जहां हार्ड-क्षेत्र क्षमता कहा जाता है <math>h</math> गोले के बीच केंद्र से केंद्र की दूरी है।<ref name=binary>{{cite journal|last=Biben|first=Thierry|author2=Peter Bladon |author3=Daan Frenkel |title=बाइनरी हार्ड-स्फेयर तरल पदार्थों में कमी के प्रभाव|journal=Journal of Physics: Condensed Matter|year=1996|volume=8|issue=50|pages=10799–10800|bibcode = 1996JPCM....810799B |doi = 10.1088/0953-8984/8/50/008 |hdl=1874/10416|s2cid=250884220 |hdl-access=free}}</ref> | ||
यदि कोलाइड्स और डेप्लेटेंट दोनों | यदि कोलाइड्स और डेप्लेटेंट दोनों [[फैलाव (रसायन विज्ञान)]] में हैं, तो कोलाइडल कणों और घटिया कणों के बीच परस्पर क्रिया क्षमता होती है जिसे हार्ड-स्फीयर क्षमता द्वारा समान रूप से वर्णित किया जाता है।<ref name=seminar />फिर से, कणों को कठोर-गोले होने का अनुमान लगाते हुए, व्यास के कोलाइड्स के बीच परस्पर क्रिया क्षमता <math>D</math> और व्यास के घटिया सॉल <math>d</math> है: | ||
:<math>V(h)=\left\{ \begin{matrix}0 & \mbox{if}\quad h\geq \Big( \frac{D+d}{2} \Big)\\ \infty & \mbox{if}\quad h< \Big( \frac{D+d}{2} \Big) \end{matrix} \right. </math> | :<math>V(h)=\left\{ \begin{matrix}0 & \mbox{if}\quad h\geq \Big( \frac{D+d}{2} \Big)\\ \infty & \mbox{if}\quad h< \Big( \frac{D+d}{2} \Big) \end{matrix} \right. </math> | ||
कहाँ <math>h</math> गोले के बीच केंद्र से केंद्र की दूरी है। आमतौर पर, कोलाइड्स की तुलना में क्षीण कण बहुत छोटे होते हैं <math>d \ll D</math> | कहाँ <math>h</math> गोले के बीच केंद्र से केंद्र की दूरी है। आमतौर पर, कोलाइड्स की तुलना में क्षीण कण बहुत छोटे होते हैं <math>d \ll D</math> | ||
कठोर क्षेत्र की क्षमता का अंतर्निहित परिणाम यह है कि छितरे हुए कोलाइड | कठोर क्षेत्र की क्षमता का अंतर्निहित परिणाम यह है कि छितरे हुए कोलाइड दूसरे में प्रवेश नहीं कर सकते हैं और उनमें कोई पारस्परिक आकर्षण या प्रतिकर्षण नहीं है। | ||
==== बहिष्कृत मात्रा ==== | ==== बहिष्कृत मात्रा ==== | ||
{{Main article|Excluded volume}} | {{Main article|Excluded volume}} | ||
[[File:Overlap volume between hard spheres.png|thumb|हार्ड स्फेयर्स की अपवर्जित मात्रा ओवरलैप करती है जिसके परिणामस्वरूप क्षीणकों के लिए उपलब्ध कुल मात्रा में वृद्धि होती है। यह प्रणाली की एन्ट्रापी को बढ़ाता है और हेल्महोल्ट्ज़ मुक्त ऊर्जा को कम करता है]]जब बड़े कोलाइडल कण और छोटे अवक्षेपक दोनों | [[File:Overlap volume between hard spheres.png|thumb|हार्ड स्फेयर्स की अपवर्जित मात्रा ओवरलैप करती है जिसके परिणामस्वरूप क्षीणकों के लिए उपलब्ध कुल मात्रा में वृद्धि होती है। यह प्रणाली की एन्ट्रापी को बढ़ाता है और हेल्महोल्ट्ज़ मुक्त ऊर्जा को कम करता है]]जब बड़े कोलाइडल कण और छोटे अवक्षेपक दोनों [[निलंबन (रसायन विज्ञान)]] में होते हैं, तो ऐसा क्षेत्र होता है जो हर बड़े कोलाइडल कण को घेरता है जो कि अपक्षय के केंद्रों पर कब्जा करने के लिए अनुपलब्ध होता है। यह स्टेरिक प्रतिबंध कोलाइड-डेप्लेटेंट हार्ड-स्फीयर क्षमता के कारण है।<ref name=seminar>{{cite web|last=Mravlak|first=Marko|title=अपक्षय बल|publisher=University of Ljubljana department of physics|url=http://mafija.fmf.uni-lj.si/seminar/files/2007_2008/depletion.pdf|access-date=26 May 2013}}</ref><ref name=binary /> अपवर्जित क्षेत्र का आयतन है | ||
:<math>V_\mathrm{E}= \frac{\pi \big(D+d \big)^3}{3}</math> | :<math>V_\mathrm{E}= \frac{\pi \big(D+d \big)^3}{3}</math> | ||
| Line 35: | Line 32: | ||
:<math>V_\mathrm{A}=\left\{ \begin{matrix}V-V_\mathrm{E} & \mbox{if}\quad h\geq D+d\\V-V'_\mathrm{E} & \mbox{if}\quad h< D+d \end{matrix} \right. </math> | :<math>V_\mathrm{A}=\left\{ \begin{matrix}V-V_\mathrm{E} & \mbox{if}\quad h\geq D+d\\V-V'_\mathrm{E} & \mbox{if}\quad h< D+d \end{matrix} \right. </math> | ||
बाद वाले मामले में बड़े क्षेत्रों के बीच इंटरपार्टिकल क्षेत्र से छोटे गोले समाप्त हो जाते हैं और | बाद वाले मामले में बड़े क्षेत्रों के बीच इंटरपार्टिकल क्षेत्र से छोटे गोले समाप्त हो जाते हैं और कमी बल लागू होता है। | ||
=== ऊष्मप्रवैगिकी === | === ऊष्मप्रवैगिकी === | ||
अवक्षय बल को [[एन्ट्रोपिक]] बल के रूप में वर्णित किया गया है क्योंकि यह मौलिक रूप से ऊष्मप्रवैगिकी के दूसरे नियम का प्रकटीकरण है, जो बताता है कि | अवक्षय बल को [[एन्ट्रोपिक]] बल के रूप में वर्णित किया गया है क्योंकि यह मौलिक रूप से ऊष्मप्रवैगिकी के दूसरे नियम का प्रकटीकरण है, जो बताता है कि प्रणाली अपनी [[एन्ट्रापी]] को बढ़ाने की प्रवृत्ति रखती है।<ref name=seminar />उपलब्ध आयतन में वृद्धि के कारण डेप्लेंटेंट्स की ट्रांसलेशनल एन्ट्रापी में लाभ, कोलाइड्स के फ्लोक्यूलेशन से एन्ट्रापी के नुकसान से बहुत अधिक है।<ref name=textbook />एन्ट्रापी में सकारात्मक परिवर्तन [[हेल्महोल्ट्ज़ मुक्त ऊर्जा]] को कम करता है और कोलाइडल फ्लोकुलेशन को अनायास होने का कारण बनता है। समाधान में कोलाइड्स और डेप्लेटेंट्स की प्रणाली को थर्मोडायनामिक मात्राओं के सांख्यिकीय निर्धारण के लिए कठोर क्षेत्रों के विहित पहनावे के रूप में तैयार किया गया है।<ref name=seminar /> | ||
हालाँकि, हाल के प्रयोग<ref name="Politi2010">{{cite journal|last=Politi|first=R|author2=Harries, D.|title=सुरक्षात्मक ऑस्मोलिट्स द्वारा उत्साहपूर्वक संचालित पेप्टाइड स्थिरीकरण|journal=Chem. Commun.|year=2010|volume=46|issue=35|pages=6449–6451|doi=10.1039/c0cc01763a|pmid=20657920}}</ref><ref name="Benton2012">{{cite journal|last=Benton|first=L.A.|author2=Smith, A.E.|author3=Young, G.B.|author4=Pielak, G.J.|title=प्रोटीन स्थिरता पर मैक्रोमोलेक्युलर क्राउडिंग का अप्रत्याशित प्रभाव।|journal=Biochemistry|year=2012|volume=51|issue=49|pages=9773–9775|doi=10.1021/bi300909q|pmid=23167542}}</ref><ref name="Sukenik2013">{{cite journal|last=Sukenik|first=S|author2=Sapir, L. |author3=Harries, D. |title=क्षय बलों में एन्थैल्पी और एंट्रॉपी का संतुलन।|journal=Curr. Opin. Colloid Interface Sci.|year=2013|volume=18|issue=6|pages=495–501|doi=10.1016/j.cocis.2013.10.002|arxiv=1310.2100|s2cid=18847346}}</ref> और सैद्धांतिक मॉडल<ref name="Sapir2014">{{cite journal|last=Sapir|first=L|author2=Harries, D.|title=एन्थैल्पिक डिप्लेशन फोर्स की उत्पत्ति।|journal=J. Phys. Chem. Lett.|year=2014|volume=5|issue=7|pages=1061–1065|doi=10.1021/jz5002715|pmid=26274449}}</ref><ref name="COCIS2015">{{cite journal|last=Sapir|first=L|author2=Harries, D.|title=Is the depletion force entropic? Molecular crowding beyond steric interactions.|journal=Curr. Opin. Colloid Interface Sci.|year=2015|volume=20|pages=3–10|doi=10.1016/j.cocis.2014.12.003}}</ref> पाया गया कि अवक्षय बलों को उत्साहपूर्वक संचालित किया जा सकता है। इन उदाहरणों में, समाधान घटकों के बीच बातचीत के जटिल संतुलन के परिणामस्वरूप मैक्रोमोलेक्यूल से कोसोल्यूट का शुद्ध बहिष्करण होता है। इस बहिष्करण के परिणामस्वरूप मैक्रोमोलेक्यूल सेल्फ-एसोसिएशन का | हालाँकि, हाल के प्रयोग<ref name="Politi2010">{{cite journal|last=Politi|first=R|author2=Harries, D.|title=सुरक्षात्मक ऑस्मोलिट्स द्वारा उत्साहपूर्वक संचालित पेप्टाइड स्थिरीकरण|journal=Chem. Commun.|year=2010|volume=46|issue=35|pages=6449–6451|doi=10.1039/c0cc01763a|pmid=20657920}}</ref><ref name="Benton2012">{{cite journal|last=Benton|first=L.A.|author2=Smith, A.E.|author3=Young, G.B.|author4=Pielak, G.J.|title=प्रोटीन स्थिरता पर मैक्रोमोलेक्युलर क्राउडिंग का अप्रत्याशित प्रभाव।|journal=Biochemistry|year=2012|volume=51|issue=49|pages=9773–9775|doi=10.1021/bi300909q|pmid=23167542}}</ref><ref name="Sukenik2013">{{cite journal|last=Sukenik|first=S|author2=Sapir, L. |author3=Harries, D. |title=क्षय बलों में एन्थैल्पी और एंट्रॉपी का संतुलन।|journal=Curr. Opin. Colloid Interface Sci.|year=2013|volume=18|issue=6|pages=495–501|doi=10.1016/j.cocis.2013.10.002|arxiv=1310.2100|s2cid=18847346}}</ref> और सैद्धांतिक मॉडल<ref name="Sapir2014">{{cite journal|last=Sapir|first=L|author2=Harries, D.|title=एन्थैल्पिक डिप्लेशन फोर्स की उत्पत्ति।|journal=J. Phys. Chem. Lett.|year=2014|volume=5|issue=7|pages=1061–1065|doi=10.1021/jz5002715|pmid=26274449}}</ref><ref name="COCIS2015">{{cite journal|last=Sapir|first=L|author2=Harries, D.|title=Is the depletion force entropic? Molecular crowding beyond steric interactions.|journal=Curr. Opin. Colloid Interface Sci.|year=2015|volume=20|pages=3–10|doi=10.1016/j.cocis.2014.12.003}}</ref> पाया गया कि अवक्षय बलों को उत्साहपूर्वक संचालित किया जा सकता है। इन उदाहरणों में, समाधान घटकों के बीच बातचीत के जटिल संतुलन के परिणामस्वरूप मैक्रोमोलेक्यूल से कोसोल्यूट का शुद्ध बहिष्करण होता है। इस बहिष्करण के परिणामस्वरूप मैक्रोमोलेक्यूल सेल्फ-एसोसिएशन का प्रभावी स्थिरीकरण होता है, जो न केवल उत्साहपूर्वक हावी हो सकता है, बल्कि एंट्रोपिक रूप से प्रतिकूल भी हो सकता है। | ||
==== एन्ट्रॉपी और हेल्महोल्ट्ज़ ऊर्जा ==== | ==== एन्ट्रॉपी और हेल्महोल्ट्ज़ ऊर्जा ==== | ||
छोटे गोलों के लिए उपलब्ध कुल आयतन तब बढ़ जाता है जब बड़े गोलों के आस-पास बहिष्कृत आयतन ओवरलैप होते हैं। छोटे क्षेत्रों के लिए आवंटित बढ़ी हुई मात्रा उन्हें अधिक अनुवाद संबंधी स्वतंत्रता देती है जो उनकी एन्ट्रापी को बढ़ाती है।<ref name=physicaa />क्योंकि विहित पहनावा | छोटे गोलों के लिए उपलब्ध कुल आयतन तब बढ़ जाता है जब बड़े गोलों के आस-पास बहिष्कृत आयतन ओवरलैप होते हैं। छोटे क्षेत्रों के लिए आवंटित बढ़ी हुई मात्रा उन्हें अधिक अनुवाद संबंधी स्वतंत्रता देती है जो उनकी एन्ट्रापी को बढ़ाती है।<ref name=physicaa />क्योंकि विहित पहनावा विकट है: स्थिर आयतन पर तात्विक प्रणाली हेल्महोल्ट्ज़ मुक्त ऊर्जा लिखी जाती है | ||
:<math>A=-TS</math> | :<math>A=-TS</math> | ||
| Line 62: | Line 59: | ||
कुछ मामलों में कमी बलों की एन्ट्रोपिक प्रकृति प्रयोगात्मक रूप से सिद्ध हुई थी। उदाहरण के लिए, कुछ पॉलिमरिक क्राउडर एन्ट्रोपिक डिप्लेशन बलों को प्रेरित करते हैं जो प्रोटीन को उनके मूल राज्य में स्थिर करते हैं।<ref name="Minton1981">{{cite journal|last=Minton|first=A.|title=मैक्रोमोलेक्युलर स्ट्रक्चर और रिएक्टिविटी के निर्धारक के रूप में एक्सक्लूडेड वॉल्यूम|journal=Biopolymers|year=1981|volume=20|issue=10|pages=2093–2120|doi=10.1002/bip.1981.360201006|s2cid=97753189}}</ref><ref name="Kim2013">{{cite journal|last=Kim|first=Y.C.|author2=Mittal, J.|title=क्राउडिंग इंड्यूस्ड एंट्रॉपी-एन्थैल्पी कम्पेंसेशन इन प्रोटीन एसोसिएशन इक्विलिब्रिया|journal=Phys. Rev. Lett.|year=2013|volume=110|issue=20|pages=208102|doi=10.1103/PhysRevLett.110.208102|arxiv = 1209.6379 |bibcode = 2013PhRvL.110t8102K|pmid=25167454|s2cid=17966492}}</ref><ref name="Cheung2005">{{cite journal|last=Cheung|first=M.S.|author2=Klimov, D. |author3=Thirumalai, D. |title=मॉलिक्यूलर क्राउडिंग नेटिव स्टेट स्टेबिलिटी और ग्लोबुलर प्रोटीन की रीफोल्डिंग रेट को बढ़ाता है|journal=Proc. Natl. Acad. Sci. |year=2005|volume=102|issue=13|pages=4753–4758|doi=10.1073/pnas.0409630102|pmid=15781864|bibcode = 2005PNAS..102.4753C |pmc=555696|doi-access=free}}</ref> | कुछ मामलों में कमी बलों की एन्ट्रोपिक प्रकृति प्रयोगात्मक रूप से सिद्ध हुई थी। उदाहरण के लिए, कुछ पॉलिमरिक क्राउडर एन्ट्रोपिक डिप्लेशन बलों को प्रेरित करते हैं जो प्रोटीन को उनके मूल राज्य में स्थिर करते हैं।<ref name="Minton1981">{{cite journal|last=Minton|first=A.|title=मैक्रोमोलेक्युलर स्ट्रक्चर और रिएक्टिविटी के निर्धारक के रूप में एक्सक्लूडेड वॉल्यूम|journal=Biopolymers|year=1981|volume=20|issue=10|pages=2093–2120|doi=10.1002/bip.1981.360201006|s2cid=97753189}}</ref><ref name="Kim2013">{{cite journal|last=Kim|first=Y.C.|author2=Mittal, J.|title=क्राउडिंग इंड्यूस्ड एंट्रॉपी-एन्थैल्पी कम्पेंसेशन इन प्रोटीन एसोसिएशन इक्विलिब्रिया|journal=Phys. Rev. Lett.|year=2013|volume=110|issue=20|pages=208102|doi=10.1103/PhysRevLett.110.208102|arxiv = 1209.6379 |bibcode = 2013PhRvL.110t8102K|pmid=25167454|s2cid=17966492}}</ref><ref name="Cheung2005">{{cite journal|last=Cheung|first=M.S.|author2=Klimov, D. |author3=Thirumalai, D. |title=मॉलिक्यूलर क्राउडिंग नेटिव स्टेट स्टेबिलिटी और ग्लोबुलर प्रोटीन की रीफोल्डिंग रेट को बढ़ाता है|journal=Proc. Natl. Acad. Sci. |year=2005|volume=102|issue=13|pages=4753–4758|doi=10.1073/pnas.0409630102|pmid=15781864|bibcode = 2005PNAS..102.4753C |pmc=555696|doi-access=free}}</ref> | ||
अन्य उदाहरणों में हार्ड-कोर केवल इंटरैक्शन वाली कई प्रणालियाँ शामिल हैं।<ref name="Biben1996">{{cite journal|last1=Biben|first1=Thierry|last2=Bladon|first2=Peter|last3=Frenkel|first3=Daan|title=बाइनरी हार्ड-स्फेयर तरल पदार्थों में कमी के प्रभाव|journal=Journal of Physics: Condensed Matter|volume=8|issue=50|year=1996|pages=10799–10821|issn=0953-8984|doi=10.1088/0953-8984/8/50/008|bibcode = 1996JPCM....810799B |hdl=1874/10416|s2cid=250884220 |hdl-access=free}}</ref> | अन्य उदाहरणों में हार्ड-कोर केवल इंटरैक्शन वाली कई प्रणालियाँ शामिल हैं।<ref name="Biben1996">{{cite journal|last1=Biben|first1=Thierry|last2=Bladon|first2=Peter|last3=Frenkel|first3=Daan|title=बाइनरी हार्ड-स्फेयर तरल पदार्थों में कमी के प्रभाव|journal=Journal of Physics: Condensed Matter|volume=8|issue=50|year=1996|pages=10799–10821|issn=0953-8984|doi=10.1088/0953-8984/8/50/008|bibcode = 1996JPCM....810799B |hdl=1874/10416|s2cid=250884220 |hdl-access=free}}</ref> | ||
=== आसमाटिक दबाव === | === आसमाटिक दबाव === | ||
कमी बल आसपास के समाधान में बढ़े हुए आसमाटिक दबाव का प्रभाव है। | कमी बल आसपास के समाधान में बढ़े हुए आसमाटिक दबाव का प्रभाव है। | ||
जब कोलाइड्स पर्याप्त रूप से पास हो जाते हैं, अर्थात जब उनका बहिष्कृत आयतन ओवरलैप हो जाता है, तो अवक्षेपकों को अंतरकण क्षेत्र से बाहर निकाल दिया जाता है। कोलाइड्स के बीच का यह क्षेत्र तब शुद्ध विलायक का | जब कोलाइड्स पर्याप्त रूप से पास हो जाते हैं, अर्थात जब उनका बहिष्कृत आयतन ओवरलैप हो जाता है, तो अवक्षेपकों को अंतरकण क्षेत्र से बाहर निकाल दिया जाता है। कोलाइड्स के बीच का यह क्षेत्र तब शुद्ध विलायक का [[चरण (पदार्थ)]] बन जाता है। जब ऐसा होता है, तो इंटरपार्टिकल क्षेत्र की तुलना में आसपास के समाधान में उच्च कमी वाली एकाग्रता होती है।<ref name=textbook /><ref name= seminar />परिणामी घनत्व ढाल आसमाटिक दबाव को जन्म देता है जो प्रकृति में [[एनिस्ट्रोपिक]] है, कोलाइड्स के बाहरी किनारों पर कार्य करता है और फ्लोकुलेशन को बढ़ावा देता है। <रेफरी नाम = [2] भौतिक। रेव लेट। 83, 3960–3963 (1999) /> यदि हार्ड-स्फेयर सन्निकटन नियोजित है, आसमाटिक दबाव है: | ||
:<math>p_0= \rho k_\mathrm{B} T</math> | :<math>p_0= \rho k_\mathrm{B} T</math> | ||
| Line 76: | Line 71: | ||
=== कमी बल के कारण मुक्त ऊर्जा परिवर्तन === | === कमी बल के कारण मुक्त ऊर्जा परिवर्तन === | ||
अवक्षय बलों के लिए असाकुरा-ओसावा मॉडल में, | अवक्षय बलों के लिए असाकुरा-ओसावा मॉडल में, बहिष्कृत कोसोल्यूट द्वारा लगाए गए मुक्त-ऊर्जा में परिवर्तन, <math>\Delta G</math>, है: | ||
: <math>\Delta G(r)= \Pi \Delta V_{exclusion}</math> | : <math>\Delta G(r)= \Pi \Delta V_{exclusion}</math> | ||
कहाँ <math>\Pi</math> आसमाटिक दबाव है, और <math>\Delta V_{exclusion}</math> बहिष्कृत मात्रा में परिवर्तन है (जो आणविक आकार और आकार से संबंधित है)। [[किर्कवुड-बफ समाधान सिद्धांत]] का उपयोग करके | कहाँ <math>\Pi</math> आसमाटिक दबाव है, और <math>\Delta V_{exclusion}</math> बहिष्कृत मात्रा में परिवर्तन है (जो आणविक आकार और आकार से संबंधित है)। [[किर्कवुड-बफ समाधान सिद्धांत]] का उपयोग करके ही परिणाम प्राप्त किया जा सकता है।<ref name="COCIS2015"/> | ||
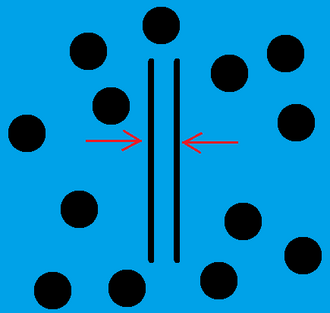
===स्थूल अणुओं के विलयन में ठोस प्लेटें === | ===स्थूल अणुओं के विलयन में ठोस प्लेटें === | ||
पहले मामले में, दो ठोस प्लेटों को कठोर गोलाकार मैक्रोमोलेक्यूल्स के घोल में रखा जाता है।<ref name="AsakuraOosawa"/> यदि दो प्लेटों के बीच की दूरी, <math>a</math>, विलेय अणुओं के व्यास से छोटा होता है, <math>d</math>, तब कोई भी विलेय प्लेटों के बीच प्रवेश नहीं कर सकता है। इसके परिणामस्वरूप प्लेटों के बीच विद्यमान शुद्ध [[विलायक]] होता है। प्लेटों और थोक समाधान के बीच समाधान में मैक्रोमोलेक्युलस की एकाग्रता में अंतर प्लेटों पर कार्य करने के लिए आसमाटिक दबाव के बराबर बल का कारण बनता है। | पहले मामले में, दो ठोस प्लेटों को कठोर गोलाकार मैक्रोमोलेक्यूल्स के घोल में रखा जाता है।<ref name="AsakuraOosawa"/> यदि दो प्लेटों के बीच की दूरी, <math>a</math>, विलेय अणुओं के व्यास से छोटा होता है, <math>d</math>, तब कोई भी विलेय प्लेटों के बीच प्रवेश नहीं कर सकता है। इसके परिणामस्वरूप प्लेटों के बीच विद्यमान शुद्ध [[विलायक]] होता है। प्लेटों और थोक समाधान के बीच समाधान में मैक्रोमोलेक्युलस की एकाग्रता में अंतर प्लेटों पर कार्य करने के लिए आसमाटिक दबाव के बराबर बल का कारण बनता है। बहुत ही तनु और मोनोडिस्पर्स समाधान में बल द्वारा परिभाषित किया गया है | ||
:<math>p=k_\mathrm{B}TN \left( \frac{\partial \ln Q}{\partial a} \right)</math> | :<math>p=k_\mathrm{B}TN \left( \frac{\partial \ln Q}{\partial a} \right)</math> | ||
| Line 90: | Line 83: | ||
=== रॉड की तरह मैक्रोमोलेक्युलस === | === रॉड की तरह मैक्रोमोलेक्युलस === | ||
असाकुरा और ओसावा ने दूसरे मामले का वर्णन किया जिसमें मैक्रोमोलेक्यूल्स जैसी छड़ के घोल में दो प्लेटें शामिल थीं। रॉड जैसे मैक्रोमोलेक्यूल्स को लंबाई के रूप में वर्णित किया गया है, <math>l</math>, कहाँ <math>l^2 \ll A</math>, प्लेटों का क्षेत्र। जैसे-जैसे छड़ों की लंबाई बढ़ती है, प्लेटों के बीच छड़ों की सघनता कम होती जाती है क्योंकि स्टीरिक बाधा के कारण छड़ों के लिए प्लेटों के बीच प्रवेश करना अधिक कठिन हो जाता है। नतीजतन, प्लेटों पर कार्य करने वाला बल छड़ की लंबाई के साथ बढ़ता है जब तक कि यह आसमाटिक दबाव के बराबर नहीं हो जाता।<ref name="AsakuraOosawa" />इस संदर्भ में, यह उल्लेखनीय है कि [[लियोट्रोपिक लिक्विड क्रिस्टल]] के आइसोट्रोपिक-नेमैटिक संक्रमण, जैसा कि पहली बार ऑनसेजर के सिद्धांत में समझाया गया है,<ref>{{cite journal| journal=Annals of the New York Academy of Sciences|volume = 51| issue =4|year = 1949| pages = 627–659| doi =10.1111/j.1749-6632.1949.tb27296.x|title=कोलाइडल कणों की परस्पर क्रिया पर आकार का प्रभाव|bibcode = 1949NYASA..51..627O| last1=Onsager| first1=Lars |s2cid = 84562683}}</ref> अपने आप में कमी बलों का | असाकुरा और ओसावा ने दूसरे मामले का वर्णन किया जिसमें मैक्रोमोलेक्यूल्स जैसी छड़ के घोल में दो प्लेटें शामिल थीं। रॉड जैसे मैक्रोमोलेक्यूल्स को लंबाई के रूप में वर्णित किया गया है, <math>l</math>, कहाँ <math>l^2 \ll A</math>, प्लेटों का क्षेत्र। जैसे-जैसे छड़ों की लंबाई बढ़ती है, प्लेटों के बीच छड़ों की सघनता कम होती जाती है क्योंकि स्टीरिक बाधा के कारण छड़ों के लिए प्लेटों के बीच प्रवेश करना अधिक कठिन हो जाता है। नतीजतन, प्लेटों पर कार्य करने वाला बल छड़ की लंबाई के साथ बढ़ता है जब तक कि यह आसमाटिक दबाव के बराबर नहीं हो जाता।<ref name="AsakuraOosawa" />इस संदर्भ में, यह उल्लेखनीय है कि [[लियोट्रोपिक लिक्विड क्रिस्टल]] के आइसोट्रोपिक-नेमैटिक संक्रमण, जैसा कि पहली बार ऑनसेजर के सिद्धांत में समझाया गया है,<ref>{{cite journal| journal=Annals of the New York Academy of Sciences|volume = 51| issue =4|year = 1949| pages = 627–659| doi =10.1111/j.1749-6632.1949.tb27296.x|title=कोलाइडल कणों की परस्पर क्रिया पर आकार का प्रभाव|bibcode = 1949NYASA..51..627O| last1=Onsager| first1=Lars |s2cid = 84562683}}</ref> अपने आप में कमी बलों का विशेष मामला माना जा सकता है।<ref name="Forsyth1977">{{cite journal|last=Forsyth|first=P.A.|author2=Marčelja, S. |author3=Mitchell, D.J. |author4= Ninham, B.W. |title=हार्ड प्लेट द्रव में ऑनसेजर संक्रमण|journal=J. Chem. Soc., Faraday Trans. 2 |year=1977|volume=73|pages=84–88|doi=10.1039/F29777300084}}</ref> | ||
=== पॉलिमर के घोल में प्लेट्स === | === पॉलिमर के घोल में प्लेट्स === | ||
असाकुरा और ओसावा द्वारा वर्णित तीसरा मामला पॉलिमर के घोल में दो प्लेटें हैं। पॉलिमर के आकार के कारण, प्लेटों के पड़ोस में पॉलिमर की सघनता कम हो जाती है, जिसके परिणामस्वरूप पॉलिमर की [[गठनात्मक एंट्रॉपी]] कम हो जाती है। मामले को दीवारों के साथ | असाकुरा और ओसावा द्वारा वर्णित तीसरा मामला पॉलिमर के घोल में दो प्लेटें हैं। पॉलिमर के आकार के कारण, प्लेटों के पड़ोस में पॉलिमर की सघनता कम हो जाती है, जिसके परिणामस्वरूप पॉलिमर की [[गठनात्मक एंट्रॉपी]] कम हो जाती है। मामले को दीवारों के साथ बर्तन में प्रसार के रूप में मॉडलिंग करके अनुमानित किया जा सकता है जो फैलाने वाले कणों को अवशोषित करता है। बल, <math>p</math>, के अनुसार गणना की जा सकती है: | ||
:<math>p= -Ap_o \Bigg\{(1-f)- a \left( \frac{\partial f}{\partial a} \right) \Bigg\}</math> | :<math>p= -Ap_o \Bigg\{(1-f)- a \left( \frac{\partial f}{\partial a} \right) \Bigg\}</math> | ||
इस समीकरण में <math> 1-f </math> आसमाटिक प्रभाव से आकर्षण है। <math>\frac{\partial f}{\partial a}</math> प्लेटों के बीच सीमित श्रृंखला अणुओं के कारण प्रतिकर्षण है। <math>p</math> के आदेश पर है <math>\langle r \rangle</math>, मुक्त स्थान में श्रृंखला अणुओं की औसत अंत-से-अंत दूरी।<ref name=seminar /> | इस समीकरण में <math> 1-f </math> आसमाटिक प्रभाव से आकर्षण है। <math>\frac{\partial f}{\partial a}</math> प्लेटों के बीच सीमित श्रृंखला अणुओं के कारण प्रतिकर्षण है। <math>p</math> के आदेश पर है <math>\langle r \rangle</math>, मुक्त स्थान में श्रृंखला अणुओं की औसत अंत-से-अंत दूरी।<ref name=seminar /> | ||
=== छोटे कठोर गोले के समाधान में बड़े कठोर गोले === | === छोटे कठोर गोले के समाधान में बड़े कठोर गोले === | ||
असाकुरा और ओसावा द्वारा वर्णित अंतिम मामला व्यास के दो बड़े, कठिन क्षेत्रों का वर्णन करता है <math>D</math>, व्यास के छोटे, कठोर गोले के घोल में <math>d</math>. यदि गोले के केंद्र के बीच की दूरी, <math>h</math>, मै रुक जाना <math>(D + d)</math>, तब छोटे गोलों को बड़े गोलों के बीच के स्थान से बाहर कर दिया जाता है। इसका परिणाम छोटे क्षेत्रों की कम सांद्रता वाले बड़े क्षेत्रों के बीच के क्षेत्र में होता है और इसलिए एंट्रॉपी कम हो जाती है। यह घटी हुई एन्ट्रापी बड़े गोलों को | असाकुरा और ओसावा द्वारा वर्णित अंतिम मामला व्यास के दो बड़े, कठिन क्षेत्रों का वर्णन करता है <math>D</math>, व्यास के छोटे, कठोर गोले के घोल में <math>d</math>. यदि गोले के केंद्र के बीच की दूरी, <math>h</math>, मै रुक जाना <math>(D + d)</math>, तब छोटे गोलों को बड़े गोलों के बीच के स्थान से बाहर कर दिया जाता है। इसका परिणाम छोटे क्षेत्रों की कम सांद्रता वाले बड़े क्षेत्रों के बीच के क्षेत्र में होता है और इसलिए एंट्रॉपी कम हो जाती है। यह घटी हुई एन्ट्रापी बड़े गोलों को साथ धकेलने के लिए बल का कारण बनती है।<ref name=seminar />इस आशय को वाइब्रोफ्लुइडाइज्ड दानेदार सामग्री के प्रयोगों में स्पष्ट रूप से प्रदर्शित किया गया था जहां आकर्षण को प्रत्यक्ष रूप से देखा जा सकता है।<ref name="Urbach2007">{{cite journal|last=Melby|first=P.|author2=Prevost, A. |author3=Egolf, D.A. |author4= Urbach, J.A. |title=द्विस्पर्श दानेदार परत में अवक्षय बल|journal=Phys. Rev. E|year=2007|volume=76|issue=5|pages=051307|doi=10.1103/PhysRevE.76.051307|pmid=18233652|bibcode = 2007PhRvE..76e1307M |arxiv=cond-mat/0507623}}</ref><ref name="Galanis2010">{{cite journal|last=Galanis|first=J.|author2=Nossal, R. |author3=Harries, D. |title=डिप्लेशन फोर्स पॉलीमर-जैसे सेल्फ-असेंबली को वाइब्रोफ्लुइडाइज्ड ग्रेन्युलर मटीरियल में ड्राइव करते हैं|journal=Soft Matter|year=2010|volume=6|issue=5|pages=1026–1034|doi=10.1039/b918034f|pmid=22039392|bibcode = 2010SMat....6.1026G |pmc=3203952}}</ref> | ||
| Line 109: | Line 98: | ||
==== सिद्धांत ==== | ==== सिद्धांत ==== | ||
असाकुरा और ओसावा ने मैक्रोमोलेक्यूल्स की कम सांद्रता ग्रहण की। हालांकि, मैक्रोमोलेक्युलस की उच्च सांद्रता पर, मैक्रोमोलेक्युलर तरल में संरचनात्मक सहसंबंध प्रभाव महत्वपूर्ण हो जाते हैं। इसके अतिरिक्त, के बड़े मूल्यों के लिए प्रतिकारक संपर्क शक्ति दृढ़ता से बढ़ जाती है <math>R/r</math> (बड़ा दायरा/छोटा दायरा)। <रेफरी नाम = [2] भौतिकी। रेव लेट। 83, 3960–3963 (1999) /> इन मुद्दों को ध्यान में रखते हुए, [[Derjaguin सन्निकटन]], जो किसी भी प्रकार के बल कानून के लिए मान्य है, को कमी बलों पर लागू किया गया है। Derjaguin सन्निकटन दो क्षेत्रों के बीच बल को दो प्लेटों के बीच बल से संबंधित करता है। बल तब | असाकुरा और ओसावा ने मैक्रोमोलेक्यूल्स की कम सांद्रता ग्रहण की। हालांकि, मैक्रोमोलेक्युलस की उच्च सांद्रता पर, मैक्रोमोलेक्युलर तरल में संरचनात्मक सहसंबंध प्रभाव महत्वपूर्ण हो जाते हैं। इसके अतिरिक्त, के बड़े मूल्यों के लिए प्रतिकारक संपर्क शक्ति दृढ़ता से बढ़ जाती है <math>R/r</math> (बड़ा दायरा/छोटा दायरा)। <रेफरी नाम = [2] भौतिकी। रेव लेट। 83, 3960–3963 (1999) /> इन मुद्दों को ध्यान में रखते हुए, [[Derjaguin सन्निकटन]], जो किसी भी प्रकार के बल कानून के लिए मान्य है, को कमी बलों पर लागू किया गया है। Derjaguin सन्निकटन दो क्षेत्रों के बीच बल को दो प्लेटों के बीच बल से संबंधित करता है। बल तब सतह और विपरीत सतह पर छोटे क्षेत्रों के बीच एकीकृत होता है, जिसे स्थानीय रूप से सपाट माना जाता है।<ref name=seminar /> [[File:Derjaguin Approximation.png|thumb|Derjaguin सन्निकटन दो क्षेत्रों के बीच बल को दो प्लेटों के बीच बल से संबंधित करता है।]] | ||
==== समीकरण ==== | ==== समीकरण ==== | ||
| Line 121: | Line 110: | ||
:<math>F(h)=- \pi \epsilon \left(R_B+R_S \right) \big [p( \rho )(2R_S-h)+ \gamma ( \rho , \infty) \big ]</math> | :<math>F(h)=- \pi \epsilon \left(R_B+R_S \right) \big [p( \rho )(2R_S-h)+ \gamma ( \rho , \infty) \big ]</math> | ||
इस समीकरण में, <math>\epsilon</math> ज्यामितीय कारक है, जो 1 पर सेट है, और <math>\gamma ( \rho , \infty) = 2 \gamma (\rho)</math>, दीवार-द्रव इंटरफ़ेस पर इंटरफेशियल तनाव।<ref name=seminar /> | इस समीकरण में, <math>\epsilon</math> ज्यामितीय कारक है, जो 1 पर सेट है, और <math>\gamma ( \rho , \infty) = 2 \gamma (\rho)</math>, दीवार-द्रव इंटरफ़ेस पर इंटरफेशियल तनाव।<ref name=seminar /> | ||
=== घनत्व कार्यात्मक सिद्धांत === | === घनत्व कार्यात्मक सिद्धांत === | ||
==== सिद्धांत ==== | ==== सिद्धांत ==== | ||
असाकुरा और ओसावा ने | असाकुरा और ओसावा ने समान कण घनत्व ग्रहण किया, जो सजातीय समाधान में सच है। हालांकि, यदि किसी समाधान पर बाहरी क्षमता लागू की जाती है, तो समान कण घनत्व बाधित हो जाता है, जिससे असकुरा और ओसावा की धारणा अमान्य हो जाती है। घनत्व कार्यात्मक सिद्धांत [[भव्य विहित क्षमता]] का उपयोग करके कण घनत्व में भिन्नता के लिए खाता है। भव्य विहित क्षमता, जो [[भव्य विहित पहनावा]] के लिए राज्य कार्य है, का उपयोग मैक्रोस्कोपिक अवस्था में सूक्ष्म राज्यों के लिए प्रायिकता घनत्व की गणना करने के लिए किया जाता है। जब कमी बलों पर लागू किया जाता है, तो भव्य विहित क्षमता समाधान में स्थानीय कण घनत्व की गणना करती है।<ref name=seminar /> | ||
==== समीकरण ==== | ==== समीकरण ==== | ||
घनत्व कार्यात्मक सिद्धांत कहता है कि जब किसी तरल पदार्थ को बाहरी क्षमता के संपर्क में लाया जाता है, <math>V(R)</math>, तब सभी संतुलन मात्राएँ संख्या घनत्व प्रोफ़ाइल के कार्य बन जाती हैं, <math>\rho(R)</math>. नतीजतन, कुल मुक्त ऊर्जा कम हो जाती है। ग्रैंड कैनोनिकल क्षमता, <math> \Omega \left( \big[ \rho (R) \big] ; \mu , T \right)</math>, फिर लिखा जाता है | घनत्व कार्यात्मक सिद्धांत कहता है कि जब किसी तरल पदार्थ को बाहरी क्षमता के संपर्क में लाया जाता है, <math>V(R)</math>, तब सभी संतुलन मात्राएँ संख्या घनत्व प्रोफ़ाइल के कार्य बन जाती हैं, <math>\rho(R)</math>. नतीजतन, कुल मुक्त ऊर्जा कम हो जाती है। ग्रैंड कैनोनिकल क्षमता, <math> \Omega \left( \big[ \rho (R) \big] ; \mu , T \right)</math>, फिर लिखा जाता है | ||
| Line 136: | Line 121: | ||
== एन्थैल्पिक कमी बल == | == एन्थैल्पिक कमी बल == | ||
मूल असाकुरा-ओसावा मॉडल को केवल हार्ड-कोर इंटरैक्शन माना जाता है। इस तरह के | मूल असाकुरा-ओसावा मॉडल को केवल हार्ड-कोर इंटरैक्शन माना जाता है। इस तरह के ऊष्मीय मिश्रण में कमी बलों की उत्पत्ति आवश्यक रूप से एंट्रोपिक है। यदि इंटरमॉलिक्युलर पोटेंशियल में प्रतिकारक और / या आकर्षक शब्द भी शामिल हैं, और यदि विलायक को स्पष्ट रूप से माना जाता है, तो कमी की बातचीत में अतिरिक्त थर्मोडायनामिक योगदान हो सकते हैं। | ||
यह धारणा कि अवक्षय बलों को भी उत्साहपूर्वक संचालित किया जा सकता है, संगत ऑस्मोलाइट्स, जैसे [[trehalose]], [[ग्लिसरॉल]], और [[सोर्बिटोल]] द्वारा प्रेरित प्रोटीन स्थिरीकरण के संबंध में हाल के प्रयोगों के कारण सामने आया है। प्रोटीन के चारों ओर तरजीही जलयोजन की परत बनाते हुए, इन ऑस्मोलिट्स को प्रोटीन सतहों से अधिमानतः बाहर रखा गया है। जब प्रोटीन मुड़ता है - यह बहिष्करण मात्रा कम हो जाती है, जिससे मुड़ी हुई अवस्था मुक्त ऊर्जा में कम हो जाती है। इसलिए बहिष्कृत ऑस्मोलिट्स तह संतुलन को तह अवस्था की ओर स्थानांतरित कर देता है। मूल असाकुरा-ओसावा मॉडल और [[मैक्रोमोलेक्युलर भीड़]] की भावना में, इस प्रभाव को आम तौर पर एंट्रोपिक बल माना जाता था। हालांकि, परासरणी जोड़ के कारण मुक्त-ऊर्जा लाभ के थर्मोडायनामिक ब्रेकडाउन से पता चलता है कि प्रभाव वास्तव में उत्साहपूर्वक संचालित होता है, जबकि एन्ट्रापी प्रतिकूल भी हो सकता है।<ref name="Politi2010"/><ref name="Benton2012"/><ref name="Sukenik2013"/><ref name="COCIS2015"/><ref name="Sukenik2013_b">{{cite journal|last=Sukenik|first=S|author2=Sapir, L. |author3=Gilman-Politi, R. |author4= Harries, D. |title=बायोमोलेक्यूलर प्रक्रियाओं पर कोसोल्यूट एक्शन के तंत्र में विविधता।|journal=Faraday Discussions|year=2013|volume=160|pages=225–237|doi=10.1039/C2FD20101A|pmid=23795502|bibcode = 2013FaDi..160..225S }}</ref> | |||
कई मामलों के लिए, इस उत्साही रूप से संचालित कमी बल की आणविक उत्पत्ति को मैक्रोमोलेक्यूल और कोसोल्यूट के बीच औसत बल की क्षमता में प्रभावी नरम प्रतिकर्षण का पता लगाया जा सकता है। मोंटे-कार्लो सिमुलेशन और सरल विश्लेषणात्मक मॉडल दोनों प्रदर्शित करते हैं कि जब हार्ड-कोर क्षमता (असाकुरा और ओसावा के मॉडल के रूप में) को अतिरिक्त प्रतिकारक नरम बातचीत के साथ पूरक किया जाता है, तो कमी बल जबरदस्त रूप से हावी हो सकता है।<ref name="Sapir2014"/> | |||
== मापन और प्रयोग == | == मापन और प्रयोग == | ||
[[परमाणु बल माइक्रोस्कोपी]], [[ऑप्टिकल चिमटी]], और हाइड्रोडायनामिक बल संतुलन मशीनों सहित विभिन्न प्रकार के उपकरणों का उपयोग करके अवक्षेपण बलों को देखा और मापा गया है। | [[परमाणु बल माइक्रोस्कोपी]], [[ऑप्टिकल चिमटी]], और हाइड्रोडायनामिक बल संतुलन मशीनों सहित विभिन्न प्रकार के उपकरणों का उपयोग करके अवक्षेपण बलों को देखा और मापा गया है। | ||
=== परमाणु बल माइक्रोस्कोपी === | === परमाणु बल माइक्रोस्कोपी === | ||
परमाणु बल माइक्रोस्कोपी (AFM) का उपयोग आमतौर पर कमी बलों के परिमाण को सीधे मापने के लिए किया जाता है। यह विधि | परमाणु बल माइक्रोस्कोपी (AFM) का उपयोग आमतौर पर कमी बलों के परिमाण को सीधे मापने के लिए किया जाता है। यह विधि नमूने से संपर्क करने वाले बहुत छोटे ब्रैकट के विक्षेपण का उपयोग करती है जिसे लेज़र द्वारा मापा जाता है। बीम विक्षेपण की निश्चित मात्रा का कारण बनने के लिए आवश्यक बल को लेजर के कोण में परिवर्तन से निर्धारित किया जा सकता है। एएफएम का छोटा पैमाना फैलाव (रसायन विज्ञान) के कणों को सीधे तौर पर मापने की अनुमति देता है जिससे कमी बलों की अपेक्षाकृत सटीक माप होती है।<ref>Milling, A. J.; Kendall, K. "Depletion, Adsorption, and Structuring of Sodium Poly(acrylate) at the Water-Silica Interface: An Atomic Force Microscopy Force Study" Langmuir. 2000. 16: pp. 5106-5115.</ref> | ||
===ऑप्टिकल चिमटी === | ===ऑप्टिकल चिमटी === | ||
दो [[कोलाइड]] कणों को अलग करने के लिए आवश्यक बल को ऑप्टिकल चिमटी का उपयोग करके मापा जा सकता है। यह विधि ढांकता हुआ सूक्ष्म और नैनोकणों पर | दो [[कोलाइड]] कणों को अलग करने के लिए आवश्यक बल को ऑप्टिकल चिमटी का उपयोग करके मापा जा सकता है। यह विधि ढांकता हुआ सूक्ष्म और नैनोकणों पर आकर्षक या प्रतिकारक बल लगाने के लिए केंद्रित लेजर बीम का उपयोग करती है। इस तकनीक का उपयोग फैलाव (रसायन विज्ञान) कणों के साथ बल लगाकर किया जाता है जो कमी बलों का विरोध करता है। कणों के विस्थापन को तब मापा जाता है और कणों के बीच आकर्षक बल का पता लगाने के लिए उपयोग किया जाता है। | ||
=== हाइड्रोडायनामिक बल संतुलन === | === हाइड्रोडायनामिक बल संतुलन === | ||
एचएफबी मशीनें कणों को अलग करने के लिए तरल प्रवाह का उपयोग करके कण परस्पर क्रियाओं की ताकत को मापती हैं। इस विधि का उपयोग | एचएफबी मशीनें कणों को अलग करने के लिए तरल प्रवाह का उपयोग करके कण परस्पर क्रियाओं की ताकत को मापती हैं। इस विधि का उपयोग स्थिर प्लेट कण को फैलाव (रसायन विज्ञान) कण डबलट का पालन करके और द्रव प्रवाह के माध्यम से कतरनी बल लागू करके कमी बल शक्ति का पता लगाने के लिए किया जाता है। फैलाव कणों द्वारा बनाया गया ड्रैग (भौतिकी) उनके बीच घटते बल का विरोध करता है, मुक्त कण को पालने वाले कण से दूर खींचता है। पृथक्करण पर कणों के बल संतुलन का उपयोग कणों के बीच घटते बल को निर्धारित करने के लिए किया जा सकता है।<ref>Piech, M.; Weronski, P.; Wu, X.; Walz, J.Y. "Prediction and Measurement of the Interparticle Depletion Interaction Next to a Flat Wall" Journal of Colloid and Interface Science. 2002. 247: pp. 327-341.</ref> | ||
== कोलाइडल अस्थिरता == | == कोलाइडल अस्थिरता == | ||
=== तंत्र === | === तंत्र === | ||
[[कोलाइड]]्स को अस्थिर करने की | [[कोलाइड]]्स को अस्थिर करने की विधि के रूप में अवक्षय बलों का बड़े पैमाने पर उपयोग किया जाता है। कोलाइडल फैलाव (रसायन विज्ञान) में कणों को पेश करके, बिखरे हुए कणों के बीच आकर्षक कमी बलों को प्रेरित किया जा सकता है। ये आकर्षक अन्योन्य क्रियाएँ बिखरे हुए कणों को साथ लाती हैं जिसके परिणामस्वरूप [[flocculation]] होता है।<ref name="Casey">Casey, T.J. "Unit Treatment Processes in Water and Wastewater Engineering". Aquavarra Research Ltd. 2006. Chp. 3, pp. 28-29.</ref><ref name="Roth">Roth, R.; Gotzelmann, B.; Dietrich, S. "Depletion Forces Near Curved Surfaces". American Physical Society. 1998. 82:2 pp. 448-451.</ref> यह कोलाइड को अस्थिर करता है क्योंकि कण अब तरल में बिखरे नहीं हैं, लेकिन फ्लोक्यूलेशन संरचनाओं में केंद्रित हैं। फ़्लॉक्स को फिर छानने की प्रक्रिया के माध्यम से आसानी से हटा दिया जाता है और गैर-छितरी हुई, शुद्ध तरल को पीछे छोड़ दिया जाता है।<ref name="Bratby">Bratby, J. "Coagulation and Flocculation in Water and Wastewater Treatment". IWA Publishing. London: 2006. pp. 3-6.</ref> | ||
=== जल उपचार === | === जल उपचार === | ||
फ्लोकुलेशन आरंभ करने के लिए अवक्षय बलों का उपयोग जल उपचार में | फ्लोकुलेशन आरंभ करने के लिए अवक्षय बलों का उपयोग जल उपचार में सामान्य प्रक्रिया है। अपशिष्ट जल में छितरे हुए कणों का अपेक्षाकृत छोटा आकार विशिष्ट निस्पंदन विधियों को अप्रभावी बना देता है। हालांकि, अगर फैलाव को अस्थिर करना था और फ्लोक्यूलेशन होता है, तो शुद्ध पानी का उत्पादन करने के लिए कणों को फ़िल्टर किया जा सकता है। इसलिए, कौयगुलांट और [[flocculants]] को आम तौर पर अपशिष्ट जल में पेश किया जाता है जो बिखरे हुए कणों के बीच इन कमी बलों को बनाते हैं।<ref name="Casey" /><ref name="Bratby" /> | ||
=== वाइनमेकिंग === | === वाइनमेकिंग === | ||
वाइन से बिखरे हुए कणों को हटाने के लिए कुछ शराब उत्पादन विधियों में कमी बलों का भी उपयोग किया जाता है। वाइन बनाने की प्रक्रिया के दौरान [[अवश्य]] या उत्पादित वाइन में अवांछित कोलाइडल कण पाए जा सकते हैं। इन कणों में आमतौर पर [[कार्बोहाइड्रेट]], रंजकता के अणु या [[प्रोटीन]] होते हैं जो शराब के स्वाद और शुद्धता पर प्रतिकूल प्रभाव डाल सकते हैं।<ref>Moreno, Juan; Peinado, Rafael. "Enological Chemistry". Elsevier Inc. San Diego: 2012. pp. 325-326.</ref> इसलिए, आसान निस्पंदन के लिए फ्लोक [[वर्षा (रसायन विज्ञान)]] को प्रेरित करने के लिए अक्सर फ्लोक्यूलेंट्स जोड़े जाते हैं। | वाइन से बिखरे हुए कणों को हटाने के लिए कुछ शराब उत्पादन विधियों में कमी बलों का भी उपयोग किया जाता है। वाइन बनाने की प्रक्रिया के दौरान [[अवश्य]] या उत्पादित वाइन में अवांछित कोलाइडल कण पाए जा सकते हैं। इन कणों में आमतौर पर [[कार्बोहाइड्रेट]], रंजकता के अणु या [[प्रोटीन]] होते हैं जो शराब के स्वाद और शुद्धता पर प्रतिकूल प्रभाव डाल सकते हैं।<ref>Moreno, Juan; Peinado, Rafael. "Enological Chemistry". Elsevier Inc. San Diego: 2012. pp. 325-326.</ref> इसलिए, आसान निस्पंदन के लिए फ्लोक [[वर्षा (रसायन विज्ञान)]] को प्रेरित करने के लिए अक्सर फ्लोक्यूलेंट्स जोड़े जाते हैं। | ||
| Line 186: | Line 161: | ||
| Polyethylene oxide || C<sub>2''n''</sub>H<sub>4''n''+2</sub>O<sub>''n''+1</sub> || Nonionic || 4–8 million|| Paper production | | Polyethylene oxide || C<sub>2''n''</sub>H<sub>4''n''+2</sub>O<sub>''n''+1</sub> || Nonionic || 4–8 million|| Paper production | ||
|} | |} | ||
== जैविक प्रणाली == | == जैविक प्रणाली == | ||
| Line 192: | Line 166: | ||
== सामान्यीकरण: अनिसोट्रोपिक कोलाइड्स और सिस्टम बिना पॉलिमर == | == सामान्यीकरण: अनिसोट्रोपिक कोलाइड्स और सिस्टम बिना पॉलिमर == | ||
कोलाइड-बहुलक मिश्रण में अवक्षेपण बल कोलाइड को समुच्चय बनाने के लिए प्रेरित करते हैं जो स्थानीय रूप से घनी रूप से भरे होते हैं। यह स्थानीय सघन संकुलन कोलाइडी तंत्रों में बिना बहुलक क्षीणकों के भी देखा जाता है। पॉलीमर क्षीणकों के बिना तंत्र समान है, क्योंकि घने कोलाइडल निलंबन में कण प्रभावी रूप से | कोलाइड-बहुलक मिश्रण में अवक्षेपण बल कोलाइड को समुच्चय बनाने के लिए प्रेरित करते हैं जो स्थानीय रूप से घनी रूप से भरे होते हैं। यह स्थानीय सघन संकुलन कोलाइडी तंत्रों में बिना बहुलक क्षीणकों के भी देखा जाता है। पॉलीमर क्षीणकों के बिना तंत्र समान है, क्योंकि घने कोलाइडल निलंबन में कण प्रभावी रूप से दूसरे के लिए क्षीणकों के रूप में कार्य करते हैं<ref name="vanAndersPNAS2014">{{cite journal|last1=van Anders| first1=Greg| last2=Klotsa| first2=Daphne| last3=Ahmed| first3=N. Khalid| last4=Engel| first4=Michael| last5=Glotzer| first5=Sharon C.| date=2014| title=स्थानीय सघन संकुलन के माध्यम से आकार एन्ट्रॉपी को समझना|journal=Proc Natl Acad Sci USA|volume=111| issue=45|pages=E4812–E4821|doi=10.1073/pnas.1418159111|arxiv=1309.1187| pmid=25344532| pmc=4234574|bibcode=2014PNAS..111E4812V| doi-access=free}}</ref> यह प्रभाव विशेष रूप से अनिसोट्रोपिक रूप से आकार के कोलाइडल कणों के लिए हड़ताली है, जहां आकार की अनिसोट्रॉपी दिशात्मक एन्ट्रोपिक बलों के उद्भव की ओर ले जाती है।<ref name="vanAndersPNAS2014" /><ref>{{cite journal|last1=Damasceno|first1=Pablo F.|last2=Engel|first2=Michael|last3=Glotzer|first3=Sharon C.|date=2012| title=क्रिस्टलीय असेंबली और ट्रंकेटेड टेट्राहेड्रा के एक परिवार की सबसे घनी पैकिंग और दिशात्मक एंट्रोपिक बलों की भूमिका|journal=ACS Nano|volume=6|issue=1|pages=609–614| doi=10.1021/nn204012y| arxiv=1109.1323| pmid=22098586|s2cid=12785227}}</ref> जो क्रिस्टल संरचनाओं की विस्तृत श्रृंखला में कठोर अनिसोट्रोपिक कोलाइड्स के क्रम के लिए जिम्मेदार हैं।<ref name="DamascenoScience2012">{{cite journal|last1=Damasceno| first1=Pablo F.|last2=Engel|first2=Michael|last3=Glotzer|first3=Sharon C.|date=2012| title=जटिल संरचनाओं में पॉलीहेड्रा की भविष्यवाणिय स्व-असेंबली|journal=Science|volume=337| issue=6093|pages=453–457|doi=10.1126/science.1220869|arxiv=1202.2177|pmid=22837525|bibcode=2012Sci...337..453D| s2cid=7177740}}</ref> | ||
== संदर्भ == | == संदर्भ == | ||
{{reflist|30em}} | {{reflist|30em}} | ||
Revision as of 16:28, 25 June 2023
अवक्षय बल प्रभावी आकर्षक बल है जो बड़े कोलाइडयन का कणों के बीच उत्पन्न होता है जो 'डिप्लेटेंट्स' के तनु विलयन में निलंबित होते हैं, जो छोटे विलेय होते हैं जिन्हें बड़े कणों के आसपास से अधिमानतः बाहर रखा जाता है।[1][2] कणों के जमाव की ओर ले जाने वाली कमी बलों की शुरुआती रिपोर्टों में से बॉन्डी की है, जिन्होंने समाधान के लिए बहुलक अपक्षय अणुओं (सोडियम alginate) के अलावा रबर लेटेक्स के पृथक्करण या क्रीमिंग को देखा।[3] आम तौर पर, क्षीणकों में पॉलिमर, मिसेल, osmolytes, स्याही, कीचड़, या विकट में बिखरे हुए पेंट शामिल हो सकते हैं: निरंतर चरण।[1][4] कमी बलों को अक्सर एंट्रोपिक बलों के रूप में माना जाता है, जैसा कि पहले स्थापित असाकुरा-ओसावा मॉडल द्वारा समझाया गया था।[5]<रे च चाट = "2" आसाकुरा>{{cite journal |last=Asakura |first=Sho |author2=Oosawa, F. |title=मैक्रोमोलेक्युलस के समाधान में निलंबित कणों के बीच सहभागिता|journal=Journal of Polymer Science |year=1958 |volume=33 |issue=126 |pages=183–192 |doi=10.1002/pol.1958.1203312618 |bibcode=1958JPoSc..33..183A }</ref> इस सिद्धांत में अवक्षय बल आसपास के विलयन के आसमाटिक दबाव में वृद्धि से उत्पन्न होता है जब कोलाइडल कण इतने करीब हो जाते हैं कि बहिष्कृत कोसोल्यूट्स (डिप्लेटेंट्स) उनके बीच फिट नहीं हो सकते।[6]क्योंकि कणों को हार्ड-कोर (पूरी तरह से कठोर) कणों के रूप में माना जाता था, बल को प्रेरित करने वाले अंतर्निहित तंत्र की उभरती हुई तस्वीर आवश्यक रूप से एंट्रोपिक थी।
कारण
स्टेरिक्स
विलयन में कोलाइड्स और डिप्लेटेंट्स की प्रणाली को आम तौर पर बड़े कोलाइड्स और छोटे डिप्लेटेंट्स को अलग-अलग आकार के कठोर क्षेत्रों के रूप में मानकर तैयार किया जाता है।[1]कठोर क्षेत्रों को गैर-अंतःक्रियात्मक और अभेद्य क्षेत्रों के रूप में जाना जाता है। कठिन क्षेत्रों के इन दो मूलभूत गुणों को गणितीय रूप से कठिन क्षेत्र की क्षमता द्वारा वर्णित किया गया है। हार्ड-स्फेयर पोटेंशिअल बड़े क्षेत्रों के चारों ओर स्टेरिक अवरोध लगाता है जो बदले में बहिष्कृत मात्रा को जन्म देता है, यानी वह वॉल्यूम जो छोटे क्षेत्रों के कब्जे के लिए अनुपलब्ध है।[6]
हार्ड-क्षेत्र क्षमता
कोलाइडल फैलाव में, कोलाइड-कोलॉइड इंटरेक्शन क्षमता को दो कठोर क्षेत्रों के बीच इंटरेक्शन क्षमता के रूप में अनुमानित किया जाता है। व्यास के दो कठोर गोलों के लिए , इंटरपार्टिकल सेपरेशन के फंक्शन के रूप में इंटरेक्शन पोटेंशिअल है:
जहां हार्ड-क्षेत्र क्षमता कहा जाता है गोले के बीच केंद्र से केंद्र की दूरी है।[7] यदि कोलाइड्स और डेप्लेटेंट दोनों फैलाव (रसायन विज्ञान) में हैं, तो कोलाइडल कणों और घटिया कणों के बीच परस्पर क्रिया क्षमता होती है जिसे हार्ड-स्फीयर क्षमता द्वारा समान रूप से वर्णित किया जाता है।[6]फिर से, कणों को कठोर-गोले होने का अनुमान लगाते हुए, व्यास के कोलाइड्स के बीच परस्पर क्रिया क्षमता और व्यास के घटिया सॉल है:
कहाँ गोले के बीच केंद्र से केंद्र की दूरी है। आमतौर पर, कोलाइड्स की तुलना में क्षीण कण बहुत छोटे होते हैं कठोर क्षेत्र की क्षमता का अंतर्निहित परिणाम यह है कि छितरे हुए कोलाइड दूसरे में प्रवेश नहीं कर सकते हैं और उनमें कोई पारस्परिक आकर्षण या प्रतिकर्षण नहीं है।
बहिष्कृत मात्रा
जब बड़े कोलाइडल कण और छोटे अवक्षेपक दोनों निलंबन (रसायन विज्ञान) में होते हैं, तो ऐसा क्षेत्र होता है जो हर बड़े कोलाइडल कण को घेरता है जो कि अपक्षय के केंद्रों पर कब्जा करने के लिए अनुपलब्ध होता है। यह स्टेरिक प्रतिबंध कोलाइड-डेप्लेटेंट हार्ड-स्फीयर क्षमता के कारण है।[6][7] अपवर्जित क्षेत्र का आयतन है
कहाँ बड़े गोले का व्यास है और छोटे गोले का व्यास है।
जब बड़े गोले पर्याप्त रूप से पास हो जाते हैं, तो गोले के चारों ओर बहिष्कृत आयतन प्रतिच्छेद करते हैं। ओवरलैपिंग वॉल्यूम के परिणामस्वरूप कम बहिष्कृत वॉल्यूम होता है, यानी छोटे क्षेत्रों के लिए उपलब्ध कुल मुक्त मात्रा में वृद्धि होती है।[1][4]कम बहिष्कृत मात्रा, लिखा जा सकता है
कहाँ गोलाकार टोपियों द्वारा गठित ओवरलैप वॉल्यूम के लेंस के आकार के क्षेत्र की आधी चौड़ाई है। उपलब्ध मात्रा छोटे क्षेत्रों के लिए सिस्टम की कुल मात्रा और बहिष्कृत मात्रा के बीच का अंतर है। छोटे गोले के लिए उपलब्ध आयतन निर्धारित करने के लिए, दो अलग-अलग मामले हैं: पहला, बड़े गोले का पृथक्करण इतना बड़ा है कि छोटे गोले उनके बीच में प्रवेश कर सकें; दूसरा, बड़े गोले इतने निकट होते हैं कि छोटे गोले उनके बीच प्रवेश नहीं कर सकते।[6]प्रत्येक मामले के लिए, छोटे गोले के लिए उपलब्ध आयतन द्वारा दिया गया है
बाद वाले मामले में बड़े क्षेत्रों के बीच इंटरपार्टिकल क्षेत्र से छोटे गोले समाप्त हो जाते हैं और कमी बल लागू होता है।
ऊष्मप्रवैगिकी
अवक्षय बल को एन्ट्रोपिक बल के रूप में वर्णित किया गया है क्योंकि यह मौलिक रूप से ऊष्मप्रवैगिकी के दूसरे नियम का प्रकटीकरण है, जो बताता है कि प्रणाली अपनी एन्ट्रापी को बढ़ाने की प्रवृत्ति रखती है।[6]उपलब्ध आयतन में वृद्धि के कारण डेप्लेंटेंट्स की ट्रांसलेशनल एन्ट्रापी में लाभ, कोलाइड्स के फ्लोक्यूलेशन से एन्ट्रापी के नुकसान से बहुत अधिक है।[4]एन्ट्रापी में सकारात्मक परिवर्तन हेल्महोल्ट्ज़ मुक्त ऊर्जा को कम करता है और कोलाइडल फ्लोकुलेशन को अनायास होने का कारण बनता है। समाधान में कोलाइड्स और डेप्लेटेंट्स की प्रणाली को थर्मोडायनामिक मात्राओं के सांख्यिकीय निर्धारण के लिए कठोर क्षेत्रों के विहित पहनावे के रूप में तैयार किया गया है।[6]
हालाँकि, हाल के प्रयोग[8][9][10] और सैद्धांतिक मॉडल[11][12] पाया गया कि अवक्षय बलों को उत्साहपूर्वक संचालित किया जा सकता है। इन उदाहरणों में, समाधान घटकों के बीच बातचीत के जटिल संतुलन के परिणामस्वरूप मैक्रोमोलेक्यूल से कोसोल्यूट का शुद्ध बहिष्करण होता है। इस बहिष्करण के परिणामस्वरूप मैक्रोमोलेक्यूल सेल्फ-एसोसिएशन का प्रभावी स्थिरीकरण होता है, जो न केवल उत्साहपूर्वक हावी हो सकता है, बल्कि एंट्रोपिक रूप से प्रतिकूल भी हो सकता है।
एन्ट्रॉपी और हेल्महोल्ट्ज़ ऊर्जा
छोटे गोलों के लिए उपलब्ध कुल आयतन तब बढ़ जाता है जब बड़े गोलों के आस-पास बहिष्कृत आयतन ओवरलैप होते हैं। छोटे क्षेत्रों के लिए आवंटित बढ़ी हुई मात्रा उन्हें अधिक अनुवाद संबंधी स्वतंत्रता देती है जो उनकी एन्ट्रापी को बढ़ाती है।[1]क्योंकि विहित पहनावा विकट है: स्थिर आयतन पर तात्विक प्रणाली हेल्महोल्ट्ज़ मुक्त ऊर्जा लिखी जाती है
कहाँ हेल्महोल्ट्ज़ मुक्त ऊर्जा है, एंट्रॉपी है और तापमान है। एंट्रॉपी में सिस्टम का शुद्ध लाभ बढ़ी हुई मात्रा से सकारात्मक है, इस प्रकार हेल्महोल्ट्ज़ मुक्त ऊर्जा नकारात्मक है और कमी फ्लोकुलेशन अनायास होता है।
सिस्टम की मुक्त ऊर्जा हेल्महोल्ट्ज़ मुक्त ऊर्जा की सांख्यिकीय परिभाषा से प्राप्त की जाती है
कहाँ विहित पहनावा के लिए विभाजन कार्य (सांख्यिकीय यांत्रिकी) है। विभाजन समारोह में सांख्यिकीय जानकारी होती है जो कैनोनिकल समेकन का वर्णन करती है जिसमें इसकी कुल मात्रा, छोटे क्षेत्रों की कुल संख्या, छोटे क्षेत्रों के लिए उपलब्ध मात्रा, और डी ब्रोगली तरंगदैर्ध्य शामिल है।[6]यदि कठोर क्षेत्रों को मान लिया जाए, तो विभाजन कार्य करता है है
छोटे गोले के लिए उपलब्ध मात्रा, ऊपर गणना की गई। छोटे गोले की संख्या है और डी ब्रोगली तरंग दैर्ध्य है। स्थानापन्न सांख्यिकीय परिभाषा में, हेल्महोल्ट्ज़ मुक्त ऊर्जा अब पढ़ती है
कमी बल का परिमाण, दो बड़े क्षेत्रों के बीच की दूरी के साथ हेल्महोल्ट्ज़ मुक्त ऊर्जा में परिवर्तन के बराबर है और इसके द्वारा दिया जाता है[6]
कुछ मामलों में कमी बलों की एन्ट्रोपिक प्रकृति प्रयोगात्मक रूप से सिद्ध हुई थी। उदाहरण के लिए, कुछ पॉलिमरिक क्राउडर एन्ट्रोपिक डिप्लेशन बलों को प्रेरित करते हैं जो प्रोटीन को उनके मूल राज्य में स्थिर करते हैं।[13][14][15] अन्य उदाहरणों में हार्ड-कोर केवल इंटरैक्शन वाली कई प्रणालियाँ शामिल हैं।[16]
आसमाटिक दबाव
कमी बल आसपास के समाधान में बढ़े हुए आसमाटिक दबाव का प्रभाव है। जब कोलाइड्स पर्याप्त रूप से पास हो जाते हैं, अर्थात जब उनका बहिष्कृत आयतन ओवरलैप हो जाता है, तो अवक्षेपकों को अंतरकण क्षेत्र से बाहर निकाल दिया जाता है। कोलाइड्स के बीच का यह क्षेत्र तब शुद्ध विलायक का चरण (पदार्थ) बन जाता है। जब ऐसा होता है, तो इंटरपार्टिकल क्षेत्र की तुलना में आसपास के समाधान में उच्च कमी वाली एकाग्रता होती है।[4][6]परिणामी घनत्व ढाल आसमाटिक दबाव को जन्म देता है जो प्रकृति में एनिस्ट्रोपिक है, कोलाइड्स के बाहरी किनारों पर कार्य करता है और फ्लोकुलेशन को बढ़ावा देता है। <रेफरी नाम = [2] भौतिक। रेव लेट। 83, 3960–3963 (1999) /> यदि हार्ड-स्फेयर सन्निकटन नियोजित है, आसमाटिक दबाव है:
कहाँ आसमाटिक दबाव है और छोटे क्षेत्रों की संख्या घनत्व है और बोल्ट्जमैन स्थिरांक है।
आसाकुरा-ओसावा मॉडल
1954 में शो असाकुरा और फुमियो ओसावा द्वारा पहली बार डिप्लेशन बलों का वर्णन किया गया था। उनके मॉडल में, बल को हमेशा आकर्षक माना जाता है। इसके अतिरिक्त, बल को आसमाटिक दबाव के समानुपाती माना जाता है। असाकुरा-ओसावा मॉडल कम मैक्रो मोलेक्यूल घनत्व मानता है और घनत्व वितरण, , मैक्रोमोलेक्युलस का स्थिर है। असाकुरा और ओसावा ने चार मामलों का वर्णन किया है जिसमें घटती ताकतें होंगी। उन्होंने सबसे पहले मैक्रोमोलेक्युलस के समाधान (रसायन विज्ञान) में दो ठोस प्लेटों के रूप में सबसे सामान्य मामले का वर्णन किया। पहले मामले के सिद्धांतों को फिर तीन अतिरिक्त मामलों तक बढ़ा दिया गया। <रेफरी नाम = [2] भौतिकी। रेव लेट। 83, 3960–3963 (1999) />
कमी बल के कारण मुक्त ऊर्जा परिवर्तन
अवक्षय बलों के लिए असाकुरा-ओसावा मॉडल में, बहिष्कृत कोसोल्यूट द्वारा लगाए गए मुक्त-ऊर्जा में परिवर्तन, , है:
कहाँ आसमाटिक दबाव है, और बहिष्कृत मात्रा में परिवर्तन है (जो आणविक आकार और आकार से संबंधित है)। किर्कवुड-बफ समाधान सिद्धांत का उपयोग करके ही परिणाम प्राप्त किया जा सकता है।[12]
स्थूल अणुओं के विलयन में ठोस प्लेटें
पहले मामले में, दो ठोस प्लेटों को कठोर गोलाकार मैक्रोमोलेक्यूल्स के घोल में रखा जाता है।[5] यदि दो प्लेटों के बीच की दूरी, , विलेय अणुओं के व्यास से छोटा होता है, , तब कोई भी विलेय प्लेटों के बीच प्रवेश नहीं कर सकता है। इसके परिणामस्वरूप प्लेटों के बीच विद्यमान शुद्ध विलायक होता है। प्लेटों और थोक समाधान के बीच समाधान में मैक्रोमोलेक्युलस की एकाग्रता में अंतर प्लेटों पर कार्य करने के लिए आसमाटिक दबाव के बराबर बल का कारण बनता है। बहुत ही तनु और मोनोडिस्पर्स समाधान में बल द्वारा परिभाषित किया गया है
कहाँ बल है, और विलेय अणुओं की कुल संख्या है। बल मैक्रोमोलेक्युलस की एन्ट्रापी को बढ़ाने का कारण बनता है और जब आकर्षक होता है <रेफरी नाम = [2] भौतिक। रेव लेट। 83, 3960–3963 (1999) >Bechinger, C.; Rudhardt, D.; Leiderer, P.; Roth, R.; Dietrich, S. (1 November 1999). "एन्ट्रापी से परे अवक्षय बलों को समझना". Physical Review Letters. 83 (19): 3960–3963. arXiv:cond-mat/9908350. Bibcode:1999PhRvL..83.3960B. doi:10.1103/PhysRevLett.83.3960. S2CID 14043180.</ref>
रॉड की तरह मैक्रोमोलेक्युलस
असाकुरा और ओसावा ने दूसरे मामले का वर्णन किया जिसमें मैक्रोमोलेक्यूल्स जैसी छड़ के घोल में दो प्लेटें शामिल थीं। रॉड जैसे मैक्रोमोलेक्यूल्स को लंबाई के रूप में वर्णित किया गया है, , कहाँ , प्लेटों का क्षेत्र। जैसे-जैसे छड़ों की लंबाई बढ़ती है, प्लेटों के बीच छड़ों की सघनता कम होती जाती है क्योंकि स्टीरिक बाधा के कारण छड़ों के लिए प्लेटों के बीच प्रवेश करना अधिक कठिन हो जाता है। नतीजतन, प्लेटों पर कार्य करने वाला बल छड़ की लंबाई के साथ बढ़ता है जब तक कि यह आसमाटिक दबाव के बराबर नहीं हो जाता।[5]इस संदर्भ में, यह उल्लेखनीय है कि लियोट्रोपिक लिक्विड क्रिस्टल के आइसोट्रोपिक-नेमैटिक संक्रमण, जैसा कि पहली बार ऑनसेजर के सिद्धांत में समझाया गया है,[17] अपने आप में कमी बलों का विशेष मामला माना जा सकता है।[18]
पॉलिमर के घोल में प्लेट्स
असाकुरा और ओसावा द्वारा वर्णित तीसरा मामला पॉलिमर के घोल में दो प्लेटें हैं। पॉलिमर के आकार के कारण, प्लेटों के पड़ोस में पॉलिमर की सघनता कम हो जाती है, जिसके परिणामस्वरूप पॉलिमर की गठनात्मक एंट्रॉपी कम हो जाती है। मामले को दीवारों के साथ बर्तन में प्रसार के रूप में मॉडलिंग करके अनुमानित किया जा सकता है जो फैलाने वाले कणों को अवशोषित करता है। बल, , के अनुसार गणना की जा सकती है:
इस समीकरण में आसमाटिक प्रभाव से आकर्षण है। प्लेटों के बीच सीमित श्रृंखला अणुओं के कारण प्रतिकर्षण है। के आदेश पर है , मुक्त स्थान में श्रृंखला अणुओं की औसत अंत-से-अंत दूरी।[6]
छोटे कठोर गोले के समाधान में बड़े कठोर गोले
असाकुरा और ओसावा द्वारा वर्णित अंतिम मामला व्यास के दो बड़े, कठिन क्षेत्रों का वर्णन करता है , व्यास के छोटे, कठोर गोले के घोल में . यदि गोले के केंद्र के बीच की दूरी, , मै रुक जाना , तब छोटे गोलों को बड़े गोलों के बीच के स्थान से बाहर कर दिया जाता है। इसका परिणाम छोटे क्षेत्रों की कम सांद्रता वाले बड़े क्षेत्रों के बीच के क्षेत्र में होता है और इसलिए एंट्रॉपी कम हो जाती है। यह घटी हुई एन्ट्रापी बड़े गोलों को साथ धकेलने के लिए बल का कारण बनती है।[6]इस आशय को वाइब्रोफ्लुइडाइज्ड दानेदार सामग्री के प्रयोगों में स्पष्ट रूप से प्रदर्शित किया गया था जहां आकर्षण को प्रत्यक्ष रूप से देखा जा सकता है।[19][20]
==इम्प लोमेन टीएस अपॉन ते आसाकुरा - ओसावा मोड l==
Derjaguin सन्निकटन
सिद्धांत
असाकुरा और ओसावा ने मैक्रोमोलेक्यूल्स की कम सांद्रता ग्रहण की। हालांकि, मैक्रोमोलेक्युलस की उच्च सांद्रता पर, मैक्रोमोलेक्युलर तरल में संरचनात्मक सहसंबंध प्रभाव महत्वपूर्ण हो जाते हैं। इसके अतिरिक्त, के बड़े मूल्यों के लिए प्रतिकारक संपर्क शक्ति दृढ़ता से बढ़ जाती है (बड़ा दायरा/छोटा दायरा)। <रेफरी नाम = [2] भौतिकी। रेव लेट। 83, 3960–3963 (1999) /> इन मुद्दों को ध्यान में रखते हुए, Derjaguin सन्निकटन, जो किसी भी प्रकार के बल कानून के लिए मान्य है, को कमी बलों पर लागू किया गया है। Derjaguin सन्निकटन दो क्षेत्रों के बीच बल को दो प्लेटों के बीच बल से संबंधित करता है। बल तब सतह और विपरीत सतह पर छोटे क्षेत्रों के बीच एकीकृत होता है, जिसे स्थानीय रूप से सपाट माना जाता है।[6]
समीकरण
यदि त्रिज्या के दो गोले हैं और पर अक्ष, और गोले हैं दूरी अलग, कहाँ से बहुत छोटा है और , फिर बल, , में दिशा है
इस समीकरण में, , और दो समतल सतहों की दूरी के बीच प्रति इकाई क्षेत्रफल पर लगने वाला सामान्य बल है अलग।
जब Derjaguin सन्निकटन अवक्षय बलों पर लागू होता है, और 0<h<2Rs, तो Derjaguin सन्निकटन द्वारा दिया गया अवक्षय बल है
इस समीकरण में, ज्यामितीय कारक है, जो 1 पर सेट है, और , दीवार-द्रव इंटरफ़ेस पर इंटरफेशियल तनाव।[6]
घनत्व कार्यात्मक सिद्धांत
सिद्धांत
असाकुरा और ओसावा ने समान कण घनत्व ग्रहण किया, जो सजातीय समाधान में सच है। हालांकि, यदि किसी समाधान पर बाहरी क्षमता लागू की जाती है, तो समान कण घनत्व बाधित हो जाता है, जिससे असकुरा और ओसावा की धारणा अमान्य हो जाती है। घनत्व कार्यात्मक सिद्धांत भव्य विहित क्षमता का उपयोग करके कण घनत्व में भिन्नता के लिए खाता है। भव्य विहित क्षमता, जो भव्य विहित पहनावा के लिए राज्य कार्य है, का उपयोग मैक्रोस्कोपिक अवस्था में सूक्ष्म राज्यों के लिए प्रायिकता घनत्व की गणना करने के लिए किया जाता है। जब कमी बलों पर लागू किया जाता है, तो भव्य विहित क्षमता समाधान में स्थानीय कण घनत्व की गणना करती है।[6]
समीकरण
घनत्व कार्यात्मक सिद्धांत कहता है कि जब किसी तरल पदार्थ को बाहरी क्षमता के संपर्क में लाया जाता है, , तब सभी संतुलन मात्राएँ संख्या घनत्व प्रोफ़ाइल के कार्य बन जाती हैं, . नतीजतन, कुल मुक्त ऊर्जा कम हो जाती है। ग्रैंड कैनोनिकल क्षमता, , फिर लिखा जाता है
कहाँ रासायनिक क्षमता है, तापमान है, और हेल्महोल्ट्ज़ मुक्त ऊर्जा है। <रेफरी नाम = [4]भौतिक। रेव. ई 57, 6785–6800 (1998) >Götzelmann, B.; Evans, R.; Dietrich, S. (1998). "द्रवों में अवक्षय बल". Physical Review E. 57 (6): 6785–6800. Bibcode:1998PhRvE..57.6785G. doi:10.1103/PhysRevE.57.6785.</ref>
एन्थैल्पिक कमी बल
मूल असाकुरा-ओसावा मॉडल को केवल हार्ड-कोर इंटरैक्शन माना जाता है। इस तरह के ऊष्मीय मिश्रण में कमी बलों की उत्पत्ति आवश्यक रूप से एंट्रोपिक है। यदि इंटरमॉलिक्युलर पोटेंशियल में प्रतिकारक और / या आकर्षक शब्द भी शामिल हैं, और यदि विलायक को स्पष्ट रूप से माना जाता है, तो कमी की बातचीत में अतिरिक्त थर्मोडायनामिक योगदान हो सकते हैं।
यह धारणा कि अवक्षय बलों को भी उत्साहपूर्वक संचालित किया जा सकता है, संगत ऑस्मोलाइट्स, जैसे trehalose, ग्लिसरॉल, और सोर्बिटोल द्वारा प्रेरित प्रोटीन स्थिरीकरण के संबंध में हाल के प्रयोगों के कारण सामने आया है। प्रोटीन के चारों ओर तरजीही जलयोजन की परत बनाते हुए, इन ऑस्मोलिट्स को प्रोटीन सतहों से अधिमानतः बाहर रखा गया है। जब प्रोटीन मुड़ता है - यह बहिष्करण मात्रा कम हो जाती है, जिससे मुड़ी हुई अवस्था मुक्त ऊर्जा में कम हो जाती है। इसलिए बहिष्कृत ऑस्मोलिट्स तह संतुलन को तह अवस्था की ओर स्थानांतरित कर देता है। मूल असाकुरा-ओसावा मॉडल और मैक्रोमोलेक्युलर भीड़ की भावना में, इस प्रभाव को आम तौर पर एंट्रोपिक बल माना जाता था। हालांकि, परासरणी जोड़ के कारण मुक्त-ऊर्जा लाभ के थर्मोडायनामिक ब्रेकडाउन से पता चलता है कि प्रभाव वास्तव में उत्साहपूर्वक संचालित होता है, जबकि एन्ट्रापी प्रतिकूल भी हो सकता है।[8][9][10][12][21]
कई मामलों के लिए, इस उत्साही रूप से संचालित कमी बल की आणविक उत्पत्ति को मैक्रोमोलेक्यूल और कोसोल्यूट के बीच औसत बल की क्षमता में प्रभावी नरम प्रतिकर्षण का पता लगाया जा सकता है। मोंटे-कार्लो सिमुलेशन और सरल विश्लेषणात्मक मॉडल दोनों प्रदर्शित करते हैं कि जब हार्ड-कोर क्षमता (असाकुरा और ओसावा के मॉडल के रूप में) को अतिरिक्त प्रतिकारक नरम बातचीत के साथ पूरक किया जाता है, तो कमी बल जबरदस्त रूप से हावी हो सकता है।[11]
मापन और प्रयोग
परमाणु बल माइक्रोस्कोपी, ऑप्टिकल चिमटी, और हाइड्रोडायनामिक बल संतुलन मशीनों सहित विभिन्न प्रकार के उपकरणों का उपयोग करके अवक्षेपण बलों को देखा और मापा गया है।
परमाणु बल माइक्रोस्कोपी
परमाणु बल माइक्रोस्कोपी (AFM) का उपयोग आमतौर पर कमी बलों के परिमाण को सीधे मापने के लिए किया जाता है। यह विधि नमूने से संपर्क करने वाले बहुत छोटे ब्रैकट के विक्षेपण का उपयोग करती है जिसे लेज़र द्वारा मापा जाता है। बीम विक्षेपण की निश्चित मात्रा का कारण बनने के लिए आवश्यक बल को लेजर के कोण में परिवर्तन से निर्धारित किया जा सकता है। एएफएम का छोटा पैमाना फैलाव (रसायन विज्ञान) के कणों को सीधे तौर पर मापने की अनुमति देता है जिससे कमी बलों की अपेक्षाकृत सटीक माप होती है।[22]
ऑप्टिकल चिमटी
दो कोलाइड कणों को अलग करने के लिए आवश्यक बल को ऑप्टिकल चिमटी का उपयोग करके मापा जा सकता है। यह विधि ढांकता हुआ सूक्ष्म और नैनोकणों पर आकर्षक या प्रतिकारक बल लगाने के लिए केंद्रित लेजर बीम का उपयोग करती है। इस तकनीक का उपयोग फैलाव (रसायन विज्ञान) कणों के साथ बल लगाकर किया जाता है जो कमी बलों का विरोध करता है। कणों के विस्थापन को तब मापा जाता है और कणों के बीच आकर्षक बल का पता लगाने के लिए उपयोग किया जाता है।
हाइड्रोडायनामिक बल संतुलन
एचएफबी मशीनें कणों को अलग करने के लिए तरल प्रवाह का उपयोग करके कण परस्पर क्रियाओं की ताकत को मापती हैं। इस विधि का उपयोग स्थिर प्लेट कण को फैलाव (रसायन विज्ञान) कण डबलट का पालन करके और द्रव प्रवाह के माध्यम से कतरनी बल लागू करके कमी बल शक्ति का पता लगाने के लिए किया जाता है। फैलाव कणों द्वारा बनाया गया ड्रैग (भौतिकी) उनके बीच घटते बल का विरोध करता है, मुक्त कण को पालने वाले कण से दूर खींचता है। पृथक्करण पर कणों के बल संतुलन का उपयोग कणों के बीच घटते बल को निर्धारित करने के लिए किया जा सकता है।[23]
कोलाइडल अस्थिरता
तंत्र
कोलाइड्स को अस्थिर करने की विधि के रूप में अवक्षय बलों का बड़े पैमाने पर उपयोग किया जाता है। कोलाइडल फैलाव (रसायन विज्ञान) में कणों को पेश करके, बिखरे हुए कणों के बीच आकर्षक कमी बलों को प्रेरित किया जा सकता है। ये आकर्षक अन्योन्य क्रियाएँ बिखरे हुए कणों को साथ लाती हैं जिसके परिणामस्वरूप flocculation होता है।[24][25] यह कोलाइड को अस्थिर करता है क्योंकि कण अब तरल में बिखरे नहीं हैं, लेकिन फ्लोक्यूलेशन संरचनाओं में केंद्रित हैं। फ़्लॉक्स को फिर छानने की प्रक्रिया के माध्यम से आसानी से हटा दिया जाता है और गैर-छितरी हुई, शुद्ध तरल को पीछे छोड़ दिया जाता है।[26]
जल उपचार
फ्लोकुलेशन आरंभ करने के लिए अवक्षय बलों का उपयोग जल उपचार में सामान्य प्रक्रिया है। अपशिष्ट जल में छितरे हुए कणों का अपेक्षाकृत छोटा आकार विशिष्ट निस्पंदन विधियों को अप्रभावी बना देता है। हालांकि, अगर फैलाव को अस्थिर करना था और फ्लोक्यूलेशन होता है, तो शुद्ध पानी का उत्पादन करने के लिए कणों को फ़िल्टर किया जा सकता है। इसलिए, कौयगुलांट और flocculants को आम तौर पर अपशिष्ट जल में पेश किया जाता है जो बिखरे हुए कणों के बीच इन कमी बलों को बनाते हैं।[24][26]
वाइनमेकिंग
वाइन से बिखरे हुए कणों को हटाने के लिए कुछ शराब उत्पादन विधियों में कमी बलों का भी उपयोग किया जाता है। वाइन बनाने की प्रक्रिया के दौरान अवश्य या उत्पादित वाइन में अवांछित कोलाइडल कण पाए जा सकते हैं। इन कणों में आमतौर पर कार्बोहाइड्रेट, रंजकता के अणु या प्रोटीन होते हैं जो शराब के स्वाद और शुद्धता पर प्रतिकूल प्रभाव डाल सकते हैं।[27] इसलिए, आसान निस्पंदन के लिए फ्लोक वर्षा (रसायन विज्ञान) को प्रेरित करने के लिए अक्सर फ्लोक्यूलेंट्स जोड़े जाते हैं।
आम गुच्छे
नीचे दी गई तालिका में उनके रासायनिक सूत्रों, शुद्ध विद्युत आवेश, आणविक भार और वर्तमान अनुप्रयोगों के साथ आम फ़्लोक्युलेंट्स सूचीबद्ध हैं।
| Flocculant | Chemical formula | Charge | Molecular mass (Da) | Application |
|---|---|---|---|---|
| Aluminum sulfate (alum) | Al2(SO4)3 | Ionic | 342.15 | Water treatment |
| Ferrous sulfate | FeSO4 | Ionic | 151.91 | Water treatment |
| Polyvinylpolypyrrolidone (PVPP) | (C6H9NO)n | Nonionic | 2.5 | Wine and beer clarification |
| Poly(acrylamide-co-sodium acrylate) | (C6H9NO3Na3 | Anionic | 10,000 – 1 million | Water treatment and paper production |
| Polyethylene oxide | C2nH4n+2On+1 | Nonionic | 4–8 million | Paper production |
जैविक प्रणाली
ऐसे सुझाव हैं कि कुछ जैविक प्रणालियों में कमी बलों का महत्वपूर्ण योगदान हो सकता है, विशेष रूप से सेल (जीव विज्ञान) या किसी झिल्लीदार संरचना के बीच झिल्ली की बातचीत में।[25]बाह्य मैट्रिक्स में प्रोटीन या कार्बोहाइड्रेट जैसे बड़े अणुओं की सांद्रता के साथ, यह संभावना है कि कोशिकाओं या पुटिका (जीव विज्ञान) के बीच कुछ कमी बल प्रभाव देखे जाते हैं जो बहुत करीब हैं। हालांकि, अधिकांश जैविक प्रणालियों की जटिलता के कारण, यह निर्धारित करना मुश्किल है कि ये कमी बल झिल्ली की बातचीत को कितना प्रभावित करते हैं।[25]कमी बलों के साथ वेसिकल इंटरैक्शन के मॉडल विकसित किए गए हैं, लेकिन ये बहुत सरल हैं और वास्तविक जैविक प्रणालियों के लिए उनकी प्रयोज्यता संदिग्ध है।
सामान्यीकरण: अनिसोट्रोपिक कोलाइड्स और सिस्टम बिना पॉलिमर
कोलाइड-बहुलक मिश्रण में अवक्षेपण बल कोलाइड को समुच्चय बनाने के लिए प्रेरित करते हैं जो स्थानीय रूप से घनी रूप से भरे होते हैं। यह स्थानीय सघन संकुलन कोलाइडी तंत्रों में बिना बहुलक क्षीणकों के भी देखा जाता है। पॉलीमर क्षीणकों के बिना तंत्र समान है, क्योंकि घने कोलाइडल निलंबन में कण प्रभावी रूप से दूसरे के लिए क्षीणकों के रूप में कार्य करते हैं[28] यह प्रभाव विशेष रूप से अनिसोट्रोपिक रूप से आकार के कोलाइडल कणों के लिए हड़ताली है, जहां आकार की अनिसोट्रॉपी दिशात्मक एन्ट्रोपिक बलों के उद्भव की ओर ले जाती है।[28][29] जो क्रिस्टल संरचनाओं की विस्तृत श्रृंखला में कठोर अनिसोट्रोपिक कोलाइड्स के क्रम के लिए जिम्मेदार हैं।[30]
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 1.4 Mao, Y.; M. E. Cates; H. N. W. Lekkerkerker (May 1995). "कोलाइडल सिस्टम में अवक्षय बल". Physica A. 222 (1–4): 10–24. Bibcode:1995PhyA..222...10M. doi:10.1016/0378-4371(95)00206-5. hdl:1874/22114. S2CID 121387079.
- ↑ Lekkerkerker, H. N. W.; Tuinier, R. (2011). कोलाइड्स और डिप्लेशन इंटरेक्शन. Springer: Heidelberg.
- ↑ Bondy, C. (1939). "रबर लेटेक्स की क्रीमिंग". Trans. Faraday Soc. 35: 1093. doi:10.1039/TF9393501093.
- ↑ 4.0 4.1 4.2 4.3 Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2006). इंटरफेस के भौतिकी और रसायन विज्ञान (2nd., rev. and enl. ed.). Weinheim: Wiley-VCH-Verl. pp. 116–117. ISBN 978-3-527-40629-6.
- ↑ 5.0 5.1 5.2 Asakura, Sho; Oosawa, F. (1 January 1954). "मैक्रोमोलेक्युलस के घोल में डूबे दो निकायों के बीच परस्पर क्रिया पर". The Journal of Chemical Physics. 22 (7): 1255. Bibcode:1954JChPh..22.1255A. doi:10.1063/1.1740347.
- ↑ 6.00 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.10 6.11 6.12 6.13 6.14 Mravlak, Marko. "अपक्षय बल" (PDF). University of Ljubljana department of physics. Retrieved 26 May 2013.
- ↑ 7.0 7.1 Biben, Thierry; Peter Bladon; Daan Frenkel (1996). "बाइनरी हार्ड-स्फेयर तरल पदार्थों में कमी के प्रभाव". Journal of Physics: Condensed Matter. 8 (50): 10799–10800. Bibcode:1996JPCM....810799B. doi:10.1088/0953-8984/8/50/008. hdl:1874/10416. S2CID 250884220.
- ↑ 8.0 8.1 Politi, R; Harries, D. (2010). "सुरक्षात्मक ऑस्मोलिट्स द्वारा उत्साहपूर्वक संचालित पेप्टाइड स्थिरीकरण". Chem. Commun. 46 (35): 6449–6451. doi:10.1039/c0cc01763a. PMID 20657920.
- ↑ 9.0 9.1 Benton, L.A.; Smith, A.E.; Young, G.B.; Pielak, G.J. (2012). "प्रोटीन स्थिरता पर मैक्रोमोलेक्युलर क्राउडिंग का अप्रत्याशित प्रभाव।". Biochemistry. 51 (49): 9773–9775. doi:10.1021/bi300909q. PMID 23167542.
- ↑ 10.0 10.1 Sukenik, S; Sapir, L.; Harries, D. (2013). "क्षय बलों में एन्थैल्पी और एंट्रॉपी का संतुलन।". Curr. Opin. Colloid Interface Sci. 18 (6): 495–501. arXiv:1310.2100. doi:10.1016/j.cocis.2013.10.002. S2CID 18847346.
- ↑ 11.0 11.1 Sapir, L; Harries, D. (2014). "एन्थैल्पिक डिप्लेशन फोर्स की उत्पत्ति।". J. Phys. Chem. Lett. 5 (7): 1061–1065. doi:10.1021/jz5002715. PMID 26274449.
- ↑ 12.0 12.1 12.2 Sapir, L; Harries, D. (2015). "Is the depletion force entropic? Molecular crowding beyond steric interactions". Curr. Opin. Colloid Interface Sci. 20: 3–10. doi:10.1016/j.cocis.2014.12.003.
- ↑ Minton, A. (1981). "मैक्रोमोलेक्युलर स्ट्रक्चर और रिएक्टिविटी के निर्धारक के रूप में एक्सक्लूडेड वॉल्यूम". Biopolymers. 20 (10): 2093–2120. doi:10.1002/bip.1981.360201006. S2CID 97753189.
- ↑ Kim, Y.C.; Mittal, J. (2013). "क्राउडिंग इंड्यूस्ड एंट्रॉपी-एन्थैल्पी कम्पेंसेशन इन प्रोटीन एसोसिएशन इक्विलिब्रिया". Phys. Rev. Lett. 110 (20): 208102. arXiv:1209.6379. Bibcode:2013PhRvL.110t8102K. doi:10.1103/PhysRevLett.110.208102. PMID 25167454. S2CID 17966492.
- ↑ Cheung, M.S.; Klimov, D.; Thirumalai, D. (2005). "मॉलिक्यूलर क्राउडिंग नेटिव स्टेट स्टेबिलिटी और ग्लोबुलर प्रोटीन की रीफोल्डिंग रेट को बढ़ाता है". Proc. Natl. Acad. Sci. 102 (13): 4753–4758. Bibcode:2005PNAS..102.4753C. doi:10.1073/pnas.0409630102. PMC 555696. PMID 15781864.
- ↑ Biben, Thierry; Bladon, Peter; Frenkel, Daan (1996). "बाइनरी हार्ड-स्फेयर तरल पदार्थों में कमी के प्रभाव". Journal of Physics: Condensed Matter. 8 (50): 10799–10821. Bibcode:1996JPCM....810799B. doi:10.1088/0953-8984/8/50/008. hdl:1874/10416. ISSN 0953-8984. S2CID 250884220.
- ↑ Onsager, Lars (1949). "कोलाइडल कणों की परस्पर क्रिया पर आकार का प्रभाव". Annals of the New York Academy of Sciences. 51 (4): 627–659. Bibcode:1949NYASA..51..627O. doi:10.1111/j.1749-6632.1949.tb27296.x. S2CID 84562683.
- ↑ Forsyth, P.A.; Marčelja, S.; Mitchell, D.J.; Ninham, B.W. (1977). "हार्ड प्लेट द्रव में ऑनसेजर संक्रमण". J. Chem. Soc., Faraday Trans. 2. 73: 84–88. doi:10.1039/F29777300084.
- ↑ Melby, P.; Prevost, A.; Egolf, D.A.; Urbach, J.A. (2007). "द्विस्पर्श दानेदार परत में अवक्षय बल". Phys. Rev. E. 76 (5): 051307. arXiv:cond-mat/0507623. Bibcode:2007PhRvE..76e1307M. doi:10.1103/PhysRevE.76.051307. PMID 18233652.
- ↑ Galanis, J.; Nossal, R.; Harries, D. (2010). "डिप्लेशन फोर्स पॉलीमर-जैसे सेल्फ-असेंबली को वाइब्रोफ्लुइडाइज्ड ग्रेन्युलर मटीरियल में ड्राइव करते हैं". Soft Matter. 6 (5): 1026–1034. Bibcode:2010SMat....6.1026G. doi:10.1039/b918034f. PMC 3203952. PMID 22039392.
- ↑ Sukenik, S; Sapir, L.; Gilman-Politi, R.; Harries, D. (2013). "बायोमोलेक्यूलर प्रक्रियाओं पर कोसोल्यूट एक्शन के तंत्र में विविधता।". Faraday Discussions. 160: 225–237. Bibcode:2013FaDi..160..225S. doi:10.1039/C2FD20101A. PMID 23795502.
- ↑ Milling, A. J.; Kendall, K. "Depletion, Adsorption, and Structuring of Sodium Poly(acrylate) at the Water-Silica Interface: An Atomic Force Microscopy Force Study" Langmuir. 2000. 16: pp. 5106-5115.
- ↑ Piech, M.; Weronski, P.; Wu, X.; Walz, J.Y. "Prediction and Measurement of the Interparticle Depletion Interaction Next to a Flat Wall" Journal of Colloid and Interface Science. 2002. 247: pp. 327-341.
- ↑ 24.0 24.1 Casey, T.J. "Unit Treatment Processes in Water and Wastewater Engineering". Aquavarra Research Ltd. 2006. Chp. 3, pp. 28-29.
- ↑ 25.0 25.1 25.2 Roth, R.; Gotzelmann, B.; Dietrich, S. "Depletion Forces Near Curved Surfaces". American Physical Society. 1998. 82:2 pp. 448-451.
- ↑ 26.0 26.1 Bratby, J. "Coagulation and Flocculation in Water and Wastewater Treatment". IWA Publishing. London: 2006. pp. 3-6.
- ↑ Moreno, Juan; Peinado, Rafael. "Enological Chemistry". Elsevier Inc. San Diego: 2012. pp. 325-326.
- ↑ 28.0 28.1 van Anders, Greg; Klotsa, Daphne; Ahmed, N. Khalid; Engel, Michael; Glotzer, Sharon C. (2014). "स्थानीय सघन संकुलन के माध्यम से आकार एन्ट्रॉपी को समझना". Proc Natl Acad Sci USA. 111 (45): E4812–E4821. arXiv:1309.1187. Bibcode:2014PNAS..111E4812V. doi:10.1073/pnas.1418159111. PMC 4234574. PMID 25344532.
- ↑ Damasceno, Pablo F.; Engel, Michael; Glotzer, Sharon C. (2012). "क्रिस्टलीय असेंबली और ट्रंकेटेड टेट्राहेड्रा के एक परिवार की सबसे घनी पैकिंग और दिशात्मक एंट्रोपिक बलों की भूमिका". ACS Nano. 6 (1): 609–614. arXiv:1109.1323. doi:10.1021/nn204012y. PMID 22098586. S2CID 12785227.
- ↑ Damasceno, Pablo F.; Engel, Michael; Glotzer, Sharon C. (2012). "जटिल संरचनाओं में पॉलीहेड्रा की भविष्यवाणिय स्व-असेंबली". Science. 337 (6093): 453–457. arXiv:1202.2177. Bibcode:2012Sci...337..453D. doi:10.1126/science.1220869. PMID 22837525. S2CID 7177740.