मॉडल श्रेणी: Difference between revisions

Revision as of 09:37, 7 May 2023

गणित में, विशेष रूप से समस्थेयता (होमोटॉपी) सिद्धांत में, मॉडल श्रेणी एक ऐसी श्रेणी है जिसमें आकारिकी ('तीर') के विशिष्ट वर्ग होते हैं जिन्हें 'दुर्बल समतुल्यता', 'फाइब्रेशन' और 'सह-संयोजन' कहा जाता है जो उनसे संबंधित कुछ सिद्धांतों को पूरा करते हैं। ये सांस्थितिक समष्टि या श्रृंखला सम्मिश्र (व्युत्पन्न श्रेणी सिद्धांत) की श्रेणी से अमूर्त हैं। यह अवधारणा डेनियल जी. क्विलेन (1967) द्वारा प्रस्तुत की गई थी।

हाल के दशकों में, मॉडल श्रेणियों की भाषा का उपयोग बीजगणितीय K-सिद्धांत और बीजगणितीय ज्यामिति के कुछ भागों में किया गया है, जहां समस्थेयता-सैद्धांतिक दृष्टिकोण ने स्थायी परिणाम दिए हैं।

कारण

मॉडल श्रेणियां समस्थेयता सिद्धांत के लिए एक प्राकृतिक समायोजन प्रदान कर सकती हैं: सांस्थितिक समष्टि की श्रेणी एक मॉडल श्रेणी है जिसमें समस्थेयता सामान्य सिद्धांत के अनुरूप है। इसी तरह, जिन वस्तुओं को समष्टि के रूप में माना जाता है, वे प्रायः एक मॉडल श्रेणी संरचना को स्वीकार करते हैं, जैसे कि साधारण समुच्चय की श्रेणी है।

अन्य मॉडल श्रेणी क्रमविनिमेय वलय R के लिए R-मॉड्यूल की श्रृंखला सम्मिश्र की श्रेणी है। इस संदर्भ में समस्थेयता सिद्धांत समजातीय बीजगणित है। समरूपता को तब एक प्रकार के समस्थेयता के रूप में देखा जा सकता है, जो अन्य वस्तुओं, जैसे कि समूह (गणित) और R-बीजगणित, सिद्धांत के पहले प्रमुख अनुप्रयोगों में से एक के लिए समरूपता के सामान्यीकरण की स्वीकृति देता है। समरूपता के संबंध में उपरोक्त उदाहरण के कारण, संवृत मॉडल श्रेणियों के अध्ययन को कभी-कभी समप्ररूपी बीजगणित के रूप में माना जाता है।

औपचारिक परिभाषा

क्विलेन द्वारा प्रारंभ में दी गई परिभाषा एक संवृत मॉडल श्रेणी की थी, जिसकी धारणा उस समय प्रबल लग रही थी, दूसरों को एक मॉडल श्रेणी को परिभाषित करने के लिए कुछ धारणाओं को दुर्बल करने के लिए प्रेरित कर रही थी। व्यवहार में यह अंतर महत्वपूर्ण प्रमाणित नहीं हुआ है और सबसे हाल के लेखक (जैसे, मार्क होवे और फिलिप हिर्शहॉर्न) संवृत मॉडल श्रेणियों के साथ कार्य करते हैं और केवल 'संवृत' विशेषण को छोड़ देते हैं।

परिभाषा को एक श्रेणी पर एक मॉडल संरचना के रूप में अलग किया गया है और फिर उस श्रेणी पर आगे की श्रेणीबद्ध शर्तें, जिसकी आवश्यकता पहले अप्रचलित लग सकती है लेकिन बाद में महत्वपूर्ण हो जाती है। निम्नलिखित परिभाषा इस प्रकार है जो होवी द्वारा दी गई है।

श्रेणी 'C' पर एक मॉडल संरचना में आकारिकी के तीन विशिष्ट वर्ग होते हैं (समान रूप से उपश्रेणियाँ) दुर्बल समतुल्यता (समस्थेयता सिद्धांत), फ़िब्रेशन, और सह-संयोजन, और दो कार्यात्मक कारक $(\alpha ,\beta )$ और $(\gamma ,\delta )$ निम्नलिखित अभिगृहीत के अधीन होते है। फ़िब्रेशन जो एक दुर्बल समतुल्यता भी है, उसे अनावर्ती (या सामान्य) फ़िब्रेशन कहा जाता है^[1] और एक सह-संयोजन जो एक दुर्बल समतुल्यता भी है, उसे अनावर्ती (या सामान्य) सह-संयोजन (या कभी-कभी एनोडीन आकारिकी कहा जाता है) कहा जाता है।

अभिगृहीत:

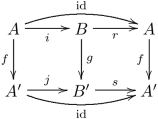
रिट्रेक्ट्स: यदि जी विशिष्ट वर्गों में से एक से संबंधित आकारिकी है, और एफजी का एक रिट्रेक्ट (श्रेणी सिद्धांत) है (तीर श्रेणी में वस्तुओं के रूप में) $C^{2}$ , जहां 2 2-तत्व आदेशित सेट है), तो f उसी विशिष्ट वर्ग से संबंधित है। स्पष्ट रूप से, आवश्यकता है कि एफ जी का एक वापसी है इसका मतलब है कि वहां मौजूद है i, j, r, और s, जैसे कि निम्न आरेख कम्यूट करता है:
# 2 का 3: यदि एफ और जी सी में मानचित्र हैं जैसे कि जीएफ परिभाषित है और इनमें से कोई भी दो दुर्बल समकक्ष हैं तो तीसरा भी है।
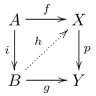
लिफ्टिंग: अनावर्ती सह-संयोजन में फाइब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है, और सह-संयोजन में अनावर्ती फाइब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है। स्पष्ट रूप से, यदि निम्नलिखित आरेख का बाहरी वर्ग कम्यूट करता है, जहां i एक कोफ़िब्रेशन है और p एक फ़िब्रेशन है, और i या p अनावर्ती है, तो आरेख को पूरा करने वाला h मौजूद है।
# गुणनखंडन:
- C में प्रत्येक आकारिकी f को इस रूप में लिखा जा सकता है $p\circ i$ एक फ़िब्रेशन p और एक अनावर्ती कोफ़िब्रेशन i के लिए;
- C में प्रत्येक आकारिकी f को इस रूप में लिखा जा सकता है $p\circ i$ अनावर्ती फाइब्रेशन पी और सह-संयोजन आई के लिए।

एक 'मॉडल श्रेणी' एक ऐसी श्रेणी है जिसमें एक मॉडल संरचना होती है और सभी (छोटी) सीमा (श्रेणी सिद्धांत) और सीमा (श्रेणी सिद्धांत)#Colimits, यानी मॉडल संरचना के साथ एक पूर्ण श्रेणी।

दुर्बल गुणनखंड प्रणाली के माध्यम से परिभाषा

उपरोक्त परिभाषा को संक्षेप में निम्नलिखित समतुल्य परिभाषा द्वारा व्यक्त किया जा सकता है: एक मॉडल श्रेणी एक श्रेणी सी है और तीन वर्ग (तथाकथित) दुर्बल समतुल्यता डब्ल्यू, फाइब्रेशन एफ और सह-संयोजन सी हैं। ताकि

C की सभी सीमाएँ और सीमाएँ हैं,

$(C\cap W,F)$ एक दुर्बल गुणनखंड प्रणाली है,

$(C,F\cap W)$ एक दुर्बल कारककरण प्रणाली है
$W$ 3 में से 2 संपत्ति को संतुष्ट करता है।^[2]

परिभाषा के पहले परिणाम

स्वयंसिद्धों का अर्थ है कि मानचित्रों के तीन वर्गों में से कोई भी दो तीसरे का निर्धारण करते हैं (उदाहरण के लिए, सह-संयोजन और दुर्बल समतुल्य फाइब्रेशन निर्धारित करते हैं)।

साथ ही, परिभाषा स्व-द्वैत है: यदि C एक मॉडल श्रेणी है, तो इसकी विपरीत श्रेणी ${\mathcal {C}}^{op}$ एक मॉडल संरचना को भी स्वीकार करता है ताकि दुर्बल तुल्यताएं उनके विरोधों के अनुरूप हों, तंतुकरणों के विपरीत तंतु और तंतुओं के विपरीत सह-संरचनाएं।

उदाहरण

सांस्थितिक स्पेस

सांस्थितिक स्पेस की श्रेणी, टॉप, सामान्य फ़िब्रेशन के साथ एक मानक मॉडल श्रेणी संरचना को स्वीकार करता है। (सेरे) फ़िब्रेशन और दुर्बल समरूपता के साथ दुर्बल समरूपता के रूप में। कोफ़िब्रेशन सामान्य धारणा नहीं है जो कोफ़िब्रेशन पाया जाता है, बल्कि नक्शों का संकरा वर्ग होता है, जिसमें अनावर्ती सेरे फ़िब्रेशन के संबंध में बाईं ओर उठाने वाली संपत्ति होती है। समान रूप से, वे आपेक्षिक कोशिका सम्मिश्र के प्रत्याहार हैं, जैसा कि उदाहरण के लिए होवी के मॉडल श्रेणियाँ में बताया गया है। यह संरचना अद्वितीय नहीं है; सामान्य तौर पर दी गई श्रेणी पर कई मॉडल श्रेणी संरचनाएँ हो सकती हैं। सांस्थितिक समष्टि की श्रेणी के लिए, इस तरह की एक अन्य संरचना ह्यूरेविक्ज़ फ़िब्रेशन और मानक सह-संयोजन द्वारा दी गई है, और दुर्बल समानताएँ (प्रबल) समस्थेयता # होमोटोपी_समतुल्यता हैं।

चेन कॉम्प्लेक्स

R-मॉड्यूल की (गैर-नकारात्मक रूप से वर्गीकृत) श्रृंखला सम्मिश्र की श्रेणी में कम से कम दो मॉडल संरचनाएं होती हैं, जो दोनों होमोलॉजिकल बीजगणित में प्रमुख रूप से प्रदर्शित होती हैं:

दुर्बल समतुल्यता ऐसे नक्शे हैं जो समरूपता में समरूपता को प्रेरित करते हैं;
सह-संयोजन वे मानचित्र होते हैं जो प्रोजेक्टिव cokernel के साथ प्रत्येक डिग्री में समाकृतिकता होते हैं; और
तंतु ऐसे मानचित्र हैं जो प्रत्येक गैर-शून्य डिग्री में एपीमोर्फिज्म हैं

या

दुर्बल समतुल्यता ऐसे नक्शे हैं जो समरूपता में समरूपता को प्रेरित करते हैं;
तंतु वे मानचित्र हैं जो इंजेक्शन कर्नेल (श्रेणी सिद्धांत) के साथ प्रत्येक डिग्री में अधिरूपता हैं; और
सह-संयोजन वे मानचित्र होते हैं जो प्रत्येक अशून्य डिग्री में एकरूपता होते हैं।

यह बताता है कि क्यों R-मॉड्यूल के एक्सट-ग्रुप्स की गणना या तो स्रोत को अनुमानित रूप से हल करके या लक्ष्य को इंजेक्ट करके की जा सकती है। ये संबंधित मॉडल संरचनाओं में कोफाइब्रेंट या फाइब्रेंट प्रतिस्थापन हैं।

R-मॉड्यूल की मनमानी श्रृंखला-सम्मिश्र की श्रेणी में एक मॉडल संरचना होती है जिसे परिभाषित किया जाता है

दुर्बल तुल्यताएं श्रृंखला-सम्मिश्र की श्रृंखला समरूपताएं हैं;
सह-संयोजन मोनोमोर्फिज्म हैं जो अंतर्निहित R-मॉड्यूल के आकारिकी के रूप में विभाजित हैं; और
तंतु एपिमोर्फिज्म हैं जो अंतर्निहित R-मॉड्यूल के आकारिकी के रूप में विभाजित हैं।

अन्य उदाहरण

मॉडल संरचनाओं को स्वीकार करने वाली श्रेणियों के अन्य उदाहरणों में सभी छोटी श्रेणियों की श्रेणी, किसी भी छोटे ग्रोथेंडिक साइट पर सिंपलियल सेट या सिंपल प्रीशेफ की श्रेणी, सांस्थितिक स्पेक्ट्रा की श्रेणी और छोटे ग्रोथेंडिक साइट पर सिंपल स्पेक्ट्रा या स्पेक्ट्रा के शीफ की श्रेणियां शामिल हैं। .

किसी श्रेणी में साधारण वस्तुएँ मॉडल श्रेणियों का लगातार स्रोत हैं; उदाहरण के लिए, साधारण क्रमविनिमेय छल्ले या साधारण R-मॉड्यूल प्राकृतिक मॉडल संरचनाओं को स्वीकार करते हैं। यह इस प्रकार है क्योंकि साधारण सेट और साधारण कम्यूटेटिव रिंग्स (भुलक्कड़ और मुक्त फ़ैक्टरों द्वारा दिए गए) के बीच एक संयोजन है, और अच्छे मामलों में कोई एक संयोजन के तहत मॉडल संरचनाओं को उठा सकता है।

एक साधारण मॉडल श्रेणी एक सरल रूप से समृद्ध श्रेणी है जिसमें एक मॉडल संरचना होती है जो सरल संरचना के अनुकूल होती है।^[3] किसी भी श्रेणी सी और एक मॉडल श्रेणी एम को देखते हुए, कुछ अतिरिक्त परिकल्पनाओं के तहत फ़ैक्टर्स फन (सी, एम) (एम में सी-आरेख भी कहा जाता है) की श्रेणी भी एक मॉडल श्रेणी है। वास्तव में, अलग-अलग मॉडल संरचनाओं के लिए हमेशा दो उम्मीदवार होते हैं: एक में, तथाकथित प्रक्षेपी मॉडल संरचना, फ़िब्रेशन और दुर्बल समतुल्यताएं ऑपरेटर के वे मानचित्र हैं जो सी के प्रत्येक ऑब्जेक्ट पर मूल्यांकन किए जाने पर फ़िब्रेशन और कमज़ोर समकक्ष हैं। इंजेक्टिव मॉडल संरचना इसके बजाय कॉफिब्रेशन और दुर्बल समकक्षों के समान है। दोनों ही मामलों में आकारिकी का तीसरा वर्ग उठाने की स्थिति (नीचे देखें) द्वारा दिया जाता है। कुछ मामलों में, जब श्रेणी सी एक रेडी श्रेणी है, तो प्रोजेक्टिव और इंजेक्शन के बीच एक तीसरी मॉडल संरचना होती है।

एक ही अंतर्निहित श्रेणी पर एक नई मॉडल श्रेणी संरचना में कुछ नक्शों को दुर्बल समतुल्यता बनने के लिए मजबूर करने की प्रक्रिया को बोसफील्ड स्थानीयकरण के रूप में जाना जाता है। उदाहरण के लिए, साधारण शीफ (गणित) की श्रेणी को साधारण presheaf के मॉडल श्रेणी के बोसफील्ड स्थानीयकरण के रूप में प्राप्त किया जा सकता है।

डेनिस-चार्ल्स सिसिंस्की ने विकसित किया है^[4] प्रीशेफ श्रेणियों पर मॉडल संरचनाओं का एक सामान्य सिद्धांत (सरलीकृत सेटों का सामान्यीकरण, जो सिम्प्लेक्स श्रेणी पर प्रीशेव हैं)।

यदि सी एक मॉडल श्रेणी है, तो सी में समर्थक वस्तु ्स की श्रेणी प्रो (सी) भी है। हालांकि, प्रो (सी) पर एक मॉडल संरचना भी सी के स्वयंसिद्धों के एक दुर्बल सेट को लागू करके बनाई जा सकती है।^[5]

कुछ निर्माण

प्रत्येक संवृत मॉडल श्रेणी में पूर्णता से एक टर्मिनल वस्तु और सह-पूर्णता द्वारा एक प्रारंभिक वस्तु होती है, क्योंकि ये वस्तुएं खाली आरेख की क्रमशः सीमा और कोलिमिट हैं। मॉडल श्रेणी में किसी वस्तु X को देखते हुए, यदि प्रारंभिक वस्तु से X तक का अद्वितीय मानचित्र एक सह-संयोजन है, तो X को 'कोफ़िब्रेंट' कहा जाता है। अनुरूप रूप से, यदि एक्स से टर्मिनल ऑब्जेक्ट का अद्वितीय नक्शा एक फ़िब्रेशन है तो एक्स को 'फ़ाइब्रेंट' कहा जाता है।

यदि Z और X एक मॉडल श्रेणी की वस्तुएँ हैं जैसे कि Z कोफ़िब्रेंट है और Z से X तक एक दुर्बल समतुल्यता है तो Z को X के लिए एक 'कॉफ़िब्रेंट प्रतिस्थापन' कहा जाता है। इसी तरह, यदि Z फ़िब्रेंट है और एक दुर्बल है X से Z तक समतुल्यता तब Z को X के लिए एक 'फाइब्रेंट रिप्लेसमेंट' कहा जाता है। सामान्य तौर पर, सभी वस्तुएं रेशेदार या कोफाइब्रेंट नहीं होती हैं, हालांकि यह कभी-कभी मामला होता है। उदाहरण के लिए, सभी ऑब्जेक्ट सरलीकृत सेट के मानक मॉडल श्रेणी में कोफ़ाइब्रेंट हैं और सभी ऑब्जेक्ट सांस्थितिक स्पेस के लिए ऊपर दी गई मानक मॉडल श्रेणी संरचना के लिए फ़िब्रेंट हैं।

लेफ्ट होमोटोपी को सिलिंडर ऑब्जेक्ट्स के संबंध में परिभाषित किया गया है और राइट समस्थेयता को [2] के संबंध में परिभाषित किया गया है + वस्तु पथ अंतरिक्ष वस्तुओं]। ये धारणाएं मेल खाती हैं जब डोमेन कॉफिब्रेंट होता है और कोडोमेन फाइब्रेंट होता है। उस स्थिति में, समस्थेयता मॉडल श्रेणी में होम सेट पर समतुल्य संबंध को परिभाषित करता है जिससे समस्थेयता क्लासेस को जन्म मिलता है।

गुणों को उठाने से फाइब्रेशन और कॉफिब्रेशन के लक्षण

कोफ़िब्रेशन को उन नक्शों के रूप में चित्रित किया जा सकता है, जिनमें अनावर्ती फ़ाइब्रेशन के संबंध में बाईं ओर उठाने वाली संपत्ति होती है, और अनावर्ती कोफ़िब्रेशन को उन मानचित्रों के रूप में चित्रित किया जाता है, जिनमें फ़िब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है। इसी तरह, फ़िब्रेशन को उन नक्शों के रूप में चित्रित किया जा सकता है जिनके पास अनावर्ती कोफ़िब्रेशन के संबंध में सही उठाने वाली संपत्ति है, और अनावर्ती फ़िब्रेशन को उन मानचित्रों के रूप में चित्रित किया जाता है जिनके पास कोफ़िब्रेशन के संबंध में सही उठाने की संपत्ति है।

समरूपता और समरूपता श्रेणी

एक मॉडल श्रेणी C की होमोटोपी श्रेणी दुर्बल समतुल्यता के वर्ग के संबंध में C की श्रेणी का स्थानीयकरण है। समस्थेयता श्रेणी की यह परिभाषा फ़िब्रेशन और सह-संयोजन की पसंद पर निर्भर नहीं करती है। हालांकि, फ़िब्रेशन और सह-संयोजन की कक्षाएं एक अलग तरीके से होमोटोपी श्रेणी का वर्णन करने और विशेष रूप से श्रेणियों के सामान्य स्थानीयकरणों में उत्पन्न होने वाले सेट-सैद्धांतिक मुद्दों से बचने में उपयोगी होती हैं। अधिक सटीक रूप से, मॉडल श्रेणियों के मौलिक प्रमेय में कहा गया है कि C की होमोटोपी श्रेणी उस श्रेणी के समतुल्य है, जिसकी वस्तुएं C की वस्तुएं हैं, जो कि रेशेदार और कोफिब्रेंट दोनों हैं, और जिनके आकारिकी मानचित्रों के समस्थेयता वर्ग हैं (समकक्ष रूप से, सही समस्थेयता वर्ग) मानचित्रों का) जैसा कि ऊपर परिभाषित किया गया है। (उदाहरण के लिए होवी द्वारा मॉडल श्रेणियाँ देखें, Thm 1.2.10)

इसे ऊपर दिए गए मॉडल संरचना के साथ सांस्थितिक समष्टि की श्रेणी में लागू करना, परिणामी समस्थेयता श्रेणी सीडब्ल्यू सम्मिश्र की श्रेणी और निरंतर मानचित्रों के होमोटोपी वर्गों के बराबर है, जहां से नाम है।

क्विलन एडजंक्शन

आसन्न फ़ैक्टरों की एक जोड़ी

F:C\leftrightarrows D:G

दो मॉडल श्रेणियों सी और डी के बीच एक क्विलन संयोजन कहा जाता है यदि एफ कॉफिब्रेशन और अनावर्ती सह-संयोजन को संरक्षित करता है या, समकक्ष रूप से संवृत मॉडल स्वयंसिद्धों द्वारा, जैसे कि जी फाइब्रेशन और अनावर्ती फाइब्रेशन को संरक्षित करता है। इस मामले में एफ और जी एक संयोजन को प्रेरित करते हैं

LF:Ho(C)\leftrightarrows Ho(D):RG

समस्थेयता श्रेणियों के बीच। उत्तरार्द्ध के लिए एक समानता होने के लिए एक स्पष्ट मानदंड भी है (फिर एफ और जी को क्विलन समकक्ष कहा जाता है)।

एक विशिष्ट उदाहरण साधारण सेट और सांस्थितिक समष्टि के बीच मानक संयोजन है:

|-|:\mathbf {sSet} \leftrightarrows \mathbf {Top} :Sing

कुछ सामयिक स्थान में एक साधारण सेट और एकवचन श्रृंखला के ज्यामितीय अहसास को शामिल करना। श्रेणियाँ sSet और Top समतुल्य नहीं हैं, लेकिन उनकी समस्थेयता श्रेणियां हैं। इसलिए, समस्थेयता श्रेणियों की इस समानता के कारण सरल सेटों को प्रायः सांस्थितिक स्पेस के लिए मॉडल के रूप में उपयोग किया जाता है।

यह भी देखें

(∞,1)-श्रेणी
कोसायकल श्रेणी
स्थिर मॉडल श्रेणी

↑ Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".
↑ Riehl (2014, §11.3)
↑ Definition 2.1. of [1].
↑ Cisinski, Denis-Charles. Les préfaisceaux comme modèles des types d'homotopie. (French) [Presheaves as models for homotopy types] Astérisque No. 308 (2006), xxiv+390 pp. ISBN 978-2-85629-225-9 MR2294028
↑ Barnea, Ilan; Schlank, Tomer M. (2016), "A projective model structure on pro-simplicial sheaves, and the relative étale homotopy type", Advances in Mathematics, 291: 784–858, arXiv:1109.5477, Bibcode:2011arXiv1109.5477B, doi:10.1016/j.aim.2015.11.014, MR 3459031

संदर्भ

Denis-Charles Cisinski: Les préfaisceaux commes modèles des types d'homotopie, Astérisque, (308) 2006, xxiv+392 pp.
Dwyer, William G.; Spaliński, Jan (1995), "Homotopy theories and model categories" (PDF), Handbook of algebraic topology, Amsterdam: North-Holland, pp. 73–126, doi:10.1016/B978-044481779-2/50003-1, MR 1361887
Philip S. Hirschhorn: Model Categories and Their Localizations, 2003, ISBN 0-8218-3279-4.
Mark Hovey: Model Categories, 1999, ISBN 0-8218-1359-5.
Klaus Heiner Kamps and Timothy Porter: Abstract homotopy and simple homotopy theory, 1997, World Scientific, ISBN 981-02-1602-5.
Georges Maltsiniotis: La théorie de l'homotopie de Grothendieck. Astérisque, (301) 2005, vi+140 pp.

Riehl, Emily (2014), Categorical homotopy theory, Cambridge University Press, doi:10.1017/CBO9781107261457, ISBN 978-1-107-04845-4, MR 3221774

Quillen, Daniel G. (1967), Homotopical algebra, Lecture Notes in Mathematics, No. 43, vol. 43, Berlin, New York: Springer-Verlag, doi:10.1007/BFb0097438, MR 0223432

Balchin, Scott (2021), A Handbook of Model Categories, Springer, doi:10.1007/978-3-030-75035-0, ISBN 978-3-030-75034-3, MR 4385504

अग्रिम पठन

"Do we still need model categories?"
"(infinity,1)-categories directly from model categories"
Paul Goerss and Kristen Schemmerhorn, Model Categories and Simplicial Methods

बाहरी संबंध

Model category at the nLab
Model category in Joyal's catlab

[1] Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".

[2] Riehl (2014, §11.3)

[3] Definition 2.1. of [1].

[4] Cisinski, Denis-Charles. Les préfaisceaux comme modèles des types d'homotopie. (French) [Presheaves as models for homotopy types] Astérisque No. 308 (2006), xxiv+390 pp. ISBN 978-2-85629-225-9 MR2294028

[5] Barnea, Ilan; Schlank, Tomer M. (2016), "A projective model structure on pro-simplicial sheaves, and the relative étale homotopy type", Advances in Mathematics, 291: 784–858, arXiv:1109.5477, Bibcode:2011arXiv1109.5477B, doi:10.1016/j.aim.2015.11.014, MR 3459031

[1]

[2]

[3]

[4]

[5]

@@ Line 1: / Line 1: @@
 {{Short description|Mathematical category with weak equivalences, fibrations and cofibrations}}
-गणित में, विशेष रूप से [[होमोटॉपी सिद्धांत]] में, एक मॉडल श्रेणी एक [[श्रेणी सिद्धांत]] है जिसमें आकारिकी ('तीर') के विशिष्ट वर्ग होते हैं, जिन्हें 'कमजोर समकक्ष (होमोटोपी सिद्धांत)', '[[ कंपन ]]' और '[[cofibration]]' कहा जाता है, जो उनसे संबंधित कुछ सिद्धांतों को संतुष्ट करते हैं। [[टोपोलॉजिकल स्पेस]] या [[चेन कॉम्प्लेक्स]] ([[व्युत्पन्न श्रेणी]] सिद्धांत) की श्रेणी से ये सार। अवधारणा द्वारा पेश किया गया था {{harvs|txt|first=Daniel G. |last=Quillen|authorlink=Daniel  Quillen|year=1967}}.
+गणित में, विशेष रूप से समस्थेयता (होमोटॉपी) सिद्धांत में,  '''मॉडल श्रेणी''' एक ऐसी श्रेणी है जिसमें आकारिकी ('तीर') के विशिष्ट वर्ग होते हैं जिन्हें 'दुर्बल समतुल्यता', 'फाइब्रेशन' और 'सह-संयोजन' कहा जाता है जो उनसे संबंधित कुछ सिद्धांतों को पूरा करते हैं। ये सांस्थितिक समष्टि या श्रृंखला सम्मिश्र (व्युत्पन्न श्रेणी सिद्धांत) की श्रेणी से अमूर्त हैं। यह अवधारणा डेनियल जी. क्विलेन (1967) द्वारा प्रस्तुत की गई थी।
-हाल के दशकों में, बीजगणितीय के-सिद्धांत के कुछ हिस्सों में मॉडल श्रेणियों की भाषा का उपयोग किया गया है। बीजगणितीय के-सिद्धांत और [[बीजगणितीय ज्यामिति]], जहां होमोटॉपी-सैद्धांतिक दृष्टिकोण ने गहरे परिणाम दिए।
+हाल के दशकों में, मॉडल श्रेणियों की भाषा का उपयोग बीजगणितीय K-सिद्धांत और बीजगणितीय ज्यामिति के कुछ भागों में किया गया है, जहां समस्थेयता-सैद्धांतिक दृष्टिकोण ने स्थायी परिणाम दिए हैं।
-== प्रेरणा ==
+== कारण ==
-मॉडल श्रेणियां होमोटॉपी सिद्धांत के लिए एक प्राकृतिक सेटिंग प्रदान कर सकती हैं: टोपोलॉजिकल रिक्त स्थान की श्रेणी एक मॉडल श्रेणी है, सामान्य सिद्धांत के अनुरूप समरूपता के साथ। इसी तरह, जिन वस्तुओं को रिक्त स्थान के रूप में माना जाता है, वे अक्सर एक मॉडल श्रेणी संरचना को स्वीकार करते हैं, जैसे कि साधारण सेट की श्रेणी।
+मॉडल श्रेणियां समस्थेयता सिद्धांत के लिए एक प्राकृतिक समायोजन प्रदान कर सकती हैं: सांस्थितिक समष्टि की श्रेणी एक मॉडल श्रेणी है जिसमें समस्थेयता सामान्य सिद्धांत के अनुरूप है। इसी तरह, जिन वस्तुओं को समष्टि के रूप में माना जाता है, वे प्रायः एक मॉडल श्रेणी संरचना को स्वीकार करते हैं, जैसे कि साधारण समुच्चय की श्रेणी है।
-एक अन्य मॉडल श्रेणी क्रमविनिमेय वलय आर के लिए आर-मॉड्यूल की श्रृंखला परिसरों की श्रेणी है। इस संदर्भ में होमोटॉपी सिद्धांत समजातीय बीजगणित है। समरूपता को तब समरूपता के एक प्रकार के रूप में देखा जा सकता है, जो अन्य वस्तुओं, जैसे कि [[समूह (गणित)]] और साहचर्य बीजगणित | आर-बीजगणित, सिद्धांत के पहले प्रमुख अनुप्रयोगों में से एक के लिए समरूपता के सामान्यीकरण की अनुमति देता है। समरूपता के संबंध में उपरोक्त उदाहरण के कारण, बंद मॉडल श्रेणियों के अध्ययन को कभी-कभी समस्थानिक बीजगणित के रूप में माना जाता है।
+अन्य मॉडल श्रेणी क्रमविनिमेय वलय R के लिए R-मॉड्यूल की श्रृंखला सम्मिश्र की श्रेणी है। इस संदर्भ में समस्थेयता सिद्धांत समजातीय बीजगणित है। समरूपता को तब एक प्रकार के  समस्थेयता के रूप में देखा जा सकता है, जो अन्य वस्तुओं, जैसे कि [[समूह (गणित)]] और R-बीजगणित, सिद्धांत के पहले प्रमुख अनुप्रयोगों में से एक के लिए समरूपता के सामान्यीकरण की स्वीकृति देता है। समरूपता के संबंध में उपरोक्त उदाहरण के कारण, संवृत मॉडल श्रेणियों के अध्ययन को कभी-कभी  समप्ररूपी बीजगणित के रूप में माना जाता है।
 == औपचारिक परिभाषा ==
-क्विलेन द्वारा शुरू में दी गई परिभाषा एक बंद मॉडल श्रेणी की थी, जिसकी धारणा उस समय मजबूत लग रही थी, दूसरों को एक मॉडल श्रेणी को परिभाषित करने के लिए कुछ धारणाओं को कमजोर करने के लिए प्रेरित कर रही थी। व्यवहार में यह अंतर महत्वपूर्ण साबित नहीं हुआ है और सबसे हाल के लेखक (जैसे, मार्क होवे और फिलिप हिर्शहॉर्न) बंद मॉडल श्रेणियों के साथ काम करते हैं और केवल 'बंद' विशेषण को छोड़ देते हैं।
+क्विलेन द्वारा प्रारंभ में दी गई परिभाषा एक संवृत मॉडल श्रेणी की थी, जिसकी धारणा उस समय प्रबल लग रही थी, दूसरों को एक मॉडल श्रेणी को परिभाषित करने के लिए कुछ धारणाओं को दुर्बल करने के लिए प्रेरित कर रही थी। व्यवहार में यह अंतर महत्वपूर्ण प्रमाणित नहीं हुआ है और सबसे हाल के लेखक (जैसे, मार्क होवे और फिलिप हिर्शहॉर्न) संवृत मॉडल श्रेणियों के साथ कार्य करते हैं और केवल 'संवृत' विशेषण को छोड़ देते हैं।
 परिभाषा को एक श्रेणी पर एक मॉडल संरचना के रूप में अलग किया गया है और फिर उस श्रेणी पर आगे की श्रेणीबद्ध शर्तें, जिसकी आवश्यकता पहले अप्रचलित लग सकती है लेकिन बाद में महत्वपूर्ण हो जाती है। निम्नलिखित परिभाषा इस प्रकार है जो होवी द्वारा दी गई है।
-एक श्रेणी 'सी' पर एक मॉडल संरचना में आकारिकी के तीन विशिष्ट वर्ग होते हैं (समान रूप से उपश्रेणियाँ): कमजोर तुल्यता (होमोटोपी सिद्धांत), फ़िब्रेशन, और कॉफ़िब्रेशन, और दो कार्यात्मक कारक <math>(\alpha , \beta)</math> और <math> (\gamma, \delta)</math> निम्नलिखित स्वयंसिद्धों के अधीन। एक फ़िब्रेशन जो एक कमजोर तुल्यता भी है, उसे एसाइक्लिक (या तुच्छ) फ़िब्रेशन कहा जाता है<ref>Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".</ref> और एक कोफिब्रेशन जो एक कमजोर तुल्यता भी है, उसे एसाइक्लिक (या ट्रिवियल) कोफिब्रेशन (या कभी-कभी एनोडीन मोर्फिज्म कहा जाता है) कहा जाता है।
+श्रेणी 'C' पर एक मॉडल संरचना में आकारिकी के तीन विशिष्ट वर्ग होते हैं (समान रूप से उपश्रेणियाँ) दुर्बल समतुल्यता (समस्थेयता सिद्धांत), फ़िब्रेशन, और सह-संयोजन, और दो कार्यात्मक कारक <math>(\alpha , \beta)</math> और <math> (\gamma, \delta)</math> निम्नलिखित अभिगृहीत के अधीन होते है। फ़िब्रेशन जो एक दुर्बल समतुल्यता भी है, उसे अनावर्ती (या सामान्य) फ़िब्रेशन कहा जाता है<ref>Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".</ref> और एक सह-संयोजन जो एक दुर्बल समतुल्यता भी है, उसे अनावर्ती (या सामान्य) सह-संयोजन (या कभी-कभी एनोडीन आकारिकी कहा जाता है) कहा जाता है।
 अभिगृहीत:
-# ''रिट्रेक्ट्स'': यदि ''जी'' विशिष्ट वर्गों में से एक से संबंधित आकारिकी है, और ''एफ'''जी'' का एक रिट्रेक्ट (श्रेणी सिद्धांत) है (तीर श्रेणी में वस्तुओं के रूप में) <math>C^2</math>, जहां 2 2-तत्व आदेशित सेट है), तो f उसी विशिष्ट वर्ग से संबंधित है। स्पष्ट रूप से, आवश्यकता है कि एफ जी का एक वापसी है इसका मतलब है कि वहां मौजूद है i, j, r, और s, जैसे कि निम्न आरेख कम्यूट करता है:
+# ''रिट्रेक्ट्स'': यदि ''जी'' विशिष्ट वर्गों में से एक से संबंधित आकारिकी है, और ''एफ''जी का एक रिट्रेक्ट (श्रेणी सिद्धांत) है (तीर श्रेणी में वस्तुओं के रूप में) <math>C^2</math>, जहां 2 2-तत्व आदेशित सेट है), तो f उसी विशिष्ट वर्ग से संबंधित है। स्पष्ट रूप से, आवश्यकता है कि एफ जी का एक वापसी है इसका मतलब है कि वहां मौजूद है i, j, r, और s, जैसे कि निम्न आरेख कम्यूट करता है:
-#:[[Image:Model category retract.png]]# 2 का 3: यदि एफ और जी सी में मानचित्र हैं जैसे कि जीएफ परिभाषित है और इनमें से कोई भी दो कमजोर समकक्ष हैं तो तीसरा भी है।
+#:[[Image:Model category retract.png]]# 2 का 3: यदि एफ और जी सी में मानचित्र हैं जैसे कि जीएफ परिभाषित है और इनमें से कोई भी दो दुर्बल समकक्ष हैं तो तीसरा भी है।
-# लिफ्टिंग: एसाइक्लिक कोफिब्रेशन में फाइब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है, और कोफिब्रेशन में एसाइक्लिक फाइब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है। स्पष्ट रूप से, यदि निम्नलिखित आरेख का बाहरी वर्ग कम्यूट करता है, जहां i एक कोफ़िब्रेशन है और p एक फ़िब्रेशन है, और i या p एसाइक्लिक है, तो आरेख को पूरा करने वाला h मौजूद है।
+# लिफ्टिंग: अनावर्ती सह-संयोजन में फाइब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है, और सह-संयोजन में अनावर्ती फाइब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है। स्पष्ट रूप से, यदि निम्नलिखित आरेख का बाहरी वर्ग कम्यूट करता है, जहां i एक कोफ़िब्रेशन है और p एक फ़िब्रेशन है, और i या p अनावर्ती है, तो आरेख को पूरा करने वाला h मौजूद है।
 #:[[Image:Model category lifting.png]]# गुणनखंडन:
-#* C में प्रत्येक आकारिकी f को इस रूप में लिखा जा सकता है <math>p\circ i</math> एक फ़िब्रेशन p और एक एसाइक्लिक कोफ़िब्रेशन i के लिए;
+#* C में प्रत्येक आकारिकी f को इस रूप में लिखा जा सकता है <math>p\circ i</math> एक फ़िब्रेशन p और एक अनावर्ती कोफ़िब्रेशन i के लिए;
-#* C में प्रत्येक आकारिकी f को इस रूप में लिखा जा सकता है <math>p\circ i</math> एसाइक्लिक फाइब्रेशन पी और कोफिब्रेशन आई के लिए।
+#* C में प्रत्येक आकारिकी f को इस रूप में लिखा जा सकता है <math>p\circ i</math> अनावर्ती फाइब्रेशन पी और सह-संयोजन आई के लिए।
 एक 'मॉडल श्रेणी' एक ऐसी श्रेणी है जिसमें एक मॉडल संरचना होती है और सभी (छोटी) [[सीमा (श्रेणी सिद्धांत)]] और सीमा (श्रेणी सिद्धांत)#Colimits, यानी मॉडल संरचना के साथ एक पूर्ण श्रेणी।
-=== कमजोर गुणनखंड प्रणाली के माध्यम से परिभाषा ===
+=== दुर्बल गुणनखंड प्रणाली के माध्यम से परिभाषा ===
-उपरोक्त परिभाषा को संक्षेप में निम्नलिखित समतुल्य परिभाषा द्वारा व्यक्त किया जा सकता है: एक मॉडल श्रेणी एक श्रेणी सी है और तीन वर्ग (तथाकथित) कमजोर तुल्यता ''डब्ल्यू'', फाइब्रेशन ''एफ'' और कोफिब्रेशन ''सी'' हैं। ताकि
+उपरोक्त परिभाषा को संक्षेप में निम्नलिखित समतुल्य परिभाषा द्वारा व्यक्त किया जा सकता है: एक मॉडल श्रेणी एक श्रेणी सी है और तीन वर्ग (तथाकथित) दुर्बल समतुल्यता ''डब्ल्यू'', फाइब्रेशन ''एफ'' और सह-संयोजन ''सी'' हैं। ताकि
 * C की सभी सीमाएँ और सीमाएँ हैं,
-* <math>(C \cap W, F)</math> एक कमजोर गुणनखंड प्रणाली है,
+* <math>(C \cap W, F)</math> एक दुर्बल गुणनखंड प्रणाली है,
-* <math>(C, F \cap W)</math> एक कमजोर कारककरण प्रणाली है
+* <math>(C, F \cap W)</math> एक दुर्बल कारककरण प्रणाली है
 * <math>W</math> 3 में से 2 संपत्ति को संतुष्ट करता है।<ref>{{harvtxt|Riehl|2014|loc=§11.3}}</ref>
@@ Line 43: / Line 43: @@
 === परिभाषा के पहले परिणाम ===
-स्वयंसिद्धों का अर्थ है कि मानचित्रों के तीन वर्गों में से कोई भी दो तीसरे का निर्धारण करते हैं (उदाहरण के लिए, कोफिब्रेशन और कमजोर समतुल्य फाइब्रेशन निर्धारित करते हैं)।
+स्वयंसिद्धों का अर्थ है कि मानचित्रों के तीन वर्गों में से कोई भी दो तीसरे का निर्धारण करते हैं (उदाहरण के लिए, सह-संयोजन और दुर्बल समतुल्य फाइब्रेशन निर्धारित करते हैं)।
-साथ ही, परिभाषा स्व-द्वैत है: यदि C एक मॉडल श्रेणी है, तो इसकी [[विपरीत श्रेणी]] <math>\mathcal{C}^{op}</math> एक मॉडल संरचना को भी स्वीकार करता है ताकि कमजोर तुल्यताएं उनके विरोधों के अनुरूप हों, तंतुकरणों के विपरीत तंतु और तंतुओं के विपरीत सह-संरचनाएं।
+साथ ही, परिभाषा स्व-द्वैत है: यदि C एक मॉडल श्रेणी है, तो इसकी [[विपरीत श्रेणी]] <math>\mathcal{C}^{op}</math> एक मॉडल संरचना को भी स्वीकार करता है ताकि दुर्बल तुल्यताएं उनके विरोधों के अनुरूप हों, तंतुकरणों के विपरीत तंतु और तंतुओं के विपरीत सह-संरचनाएं।
 == उदाहरण ==
-=== टोपोलॉजिकल स्पेस ===
+=== सांस्थितिक स्पेस ===
-[[टोपोलॉजिकल स्पेस की श्रेणी]], टॉप, सामान्य फ़िब्रेशन के साथ एक मानक मॉडल श्रेणी संरचना को स्वीकार करता है। (सेरे) फ़िब्रेशन और कमजोर समरूपता के साथ कमजोर समरूपता के रूप में। कोफ़िब्रेशन सामान्य धारणा नहीं है जो कोफ़िब्रेशन पाया जाता है, बल्कि नक्शों का संकरा वर्ग होता है, जिसमें एसाइक्लिक सेरे फ़िब्रेशन के संबंध में बाईं ओर उठाने वाली संपत्ति होती है।
+[[टोपोलॉजिकल स्पेस की श्रेणी|सांस्थितिक स्पेस की श्रेणी]], टॉप, सामान्य फ़िब्रेशन के साथ एक मानक मॉडल श्रेणी संरचना को स्वीकार करता है। (सेरे) फ़िब्रेशन और दुर्बल समरूपता के साथ दुर्बल समरूपता के रूप में। कोफ़िब्रेशन सामान्य धारणा नहीं है जो कोफ़िब्रेशन पाया जाता है, बल्कि नक्शों का संकरा वर्ग होता है, जिसमें अनावर्ती सेरे फ़िब्रेशन के संबंध में बाईं ओर उठाने वाली संपत्ति होती है।
-समान रूप से, वे आपेक्षिक कोशिका परिसरों के प्रत्याहार हैं, जैसा कि उदाहरण के लिए होवी के ''मॉडल श्रेणियाँ'' में बताया गया है। यह संरचना अद्वितीय नहीं है; सामान्य तौर पर दी गई श्रेणी पर कई मॉडल श्रेणी संरचनाएँ हो सकती हैं। टोपोलॉजिकल रिक्त स्थान की श्रेणी के लिए, इस तरह की एक अन्य संरचना [[ह्यूरेविक्ज़ फ़िब्रेशन]] और मानक कॉफ़िब्रेशन द्वारा दी गई है, और कमजोर समानताएँ (मजबूत) होमोटॉपी # होमोटोपी_समतुल्यता हैं।
+समान रूप से, वे आपेक्षिक कोशिका सम्मिश्र के प्रत्याहार हैं, जैसा कि उदाहरण के लिए होवी के ''मॉडल श्रेणियाँ'' में बताया गया है। यह संरचना अद्वितीय नहीं है; सामान्य तौर पर दी गई श्रेणी पर कई मॉडल श्रेणी संरचनाएँ हो सकती हैं। सांस्थितिक समष्टि की श्रेणी के लिए, इस तरह की एक अन्य संरचना [[ह्यूरेविक्ज़ फ़िब्रेशन]] और मानक सह-संयोजन द्वारा दी गई है, और दुर्बल समानताएँ (प्रबल) समस्थेयता # होमोटोपी_समतुल्यता हैं।
 === चेन कॉम्प्लेक्स ===
-आर-मॉड्यूल की (गैर-नकारात्मक रूप से वर्गीकृत) श्रृंखला परिसरों की श्रेणी में कम से कम दो मॉडल संरचनाएं होती हैं, जो दोनों होमोलॉजिकल बीजगणित में प्रमुख रूप से प्रदर्शित होती हैं:
+R-मॉड्यूल की (गैर-नकारात्मक रूप से वर्गीकृत) श्रृंखला सम्मिश्र की श्रेणी में कम से कम दो मॉडल संरचनाएं होती हैं, जो दोनों होमोलॉजिकल बीजगणित में प्रमुख रूप से प्रदर्शित होती हैं:
-*कमजोर समतुल्यता ऐसे नक्शे हैं जो समरूपता में समरूपता को प्रेरित करते हैं;
+*दुर्बल समतुल्यता ऐसे नक्शे हैं जो समरूपता में समरूपता को प्रेरित करते हैं;
-*कोफिब्रेशन वे मानचित्र होते हैं जो प्रोजेक्टिव [[cokernel]] के साथ प्रत्येक डिग्री में [[समाकृतिकता]] होते हैं; और
+*सह-संयोजन वे मानचित्र होते हैं जो प्रोजेक्टिव [[cokernel]] के साथ प्रत्येक डिग्री में [[समाकृतिकता]] होते हैं; और
 *तंतु ऐसे मानचित्र हैं जो प्रत्येक गैर-शून्य डिग्री में एपीमोर्फिज्म हैं
 या
-*कमजोर समतुल्यता ऐसे नक्शे हैं जो समरूपता में समरूपता को प्रेरित करते हैं;
+*दुर्बल समतुल्यता ऐसे नक्शे हैं जो समरूपता में समरूपता को प्रेरित करते हैं;
 *तंतु वे मानचित्र हैं जो इंजेक्शन [[कर्नेल (श्रेणी सिद्धांत)]] के साथ प्रत्येक डिग्री में [[अधिरूपता]] हैं; और
-*कोफिब्रेशन वे मानचित्र होते हैं जो प्रत्येक अशून्य डिग्री में [[एकरूपता]] होते हैं।
+*सह-संयोजन वे मानचित्र होते हैं जो प्रत्येक अशून्य डिग्री में [[एकरूपता]] होते हैं।
-यह बताता है कि क्यों आर-मॉड्यूल के एक्सट-ग्रुप्स की गणना या तो स्रोत को अनुमानित रूप से हल करके या लक्ष्य को इंजेक्ट करके की जा सकती है। ये संबंधित मॉडल संरचनाओं में कोफाइब्रेंट या फाइब्रेंट प्रतिस्थापन हैं।
+यह बताता है कि क्यों R-मॉड्यूल के एक्सट-ग्रुप्स की गणना या तो स्रोत को अनुमानित रूप से हल करके या लक्ष्य को इंजेक्ट करके की जा सकती है। ये संबंधित मॉडल संरचनाओं में कोफाइब्रेंट या फाइब्रेंट प्रतिस्थापन हैं।
-आर-मॉड्यूल की मनमानी श्रृंखला-परिसरों की श्रेणी में एक मॉडल संरचना होती है जिसे परिभाषित किया जाता है
+R-मॉड्यूल की मनमानी श्रृंखला-सम्मिश्र की श्रेणी में एक मॉडल संरचना होती है जिसे परिभाषित किया जाता है
-* कमजोर तुल्यताएं श्रृंखला-परिसरों की श्रृंखला समरूपताएं हैं;
+* दुर्बल तुल्यताएं श्रृंखला-सम्मिश्र की श्रृंखला समरूपताएं हैं;
-* कोफिब्रेशन मोनोमोर्फिज्म हैं जो अंतर्निहित आर-मॉड्यूल के आकारिकी के रूप में विभाजित हैं; और
+* सह-संयोजन मोनोमोर्फिज्म हैं जो अंतर्निहित R-मॉड्यूल के आकारिकी के रूप में विभाजित हैं; और
-* तंतु एपिमोर्फिज्म हैं जो अंतर्निहित आर-मॉड्यूल के आकारिकी के रूप में विभाजित हैं।
+* तंतु एपिमोर्फिज्म हैं जो अंतर्निहित R-मॉड्यूल के आकारिकी के रूप में विभाजित हैं।
 === अन्य उदाहरण ===
-मॉडल संरचनाओं को स्वीकार करने वाली श्रेणियों के अन्य उदाहरणों में सभी छोटी श्रेणियों की श्रेणी, किसी भी छोटे [[ग्रोथेंडिक साइट]] पर सिंपलियल सेट या सिंपल प्रीशेफ की श्रेणी, टोपोलॉजिकल स्पेक्ट्रा की श्रेणी और छोटे ग्रोथेंडिक साइट पर सिंपल स्पेक्ट्रा या स्पेक्ट्रा के शीफ की श्रेणियां शामिल हैं। .
+मॉडल संरचनाओं को स्वीकार करने वाली श्रेणियों के अन्य उदाहरणों में सभी छोटी श्रेणियों की श्रेणी, किसी भी छोटे [[ग्रोथेंडिक साइट]] पर सिंपलियल सेट या सिंपल प्रीशेफ की श्रेणी, सांस्थितिक स्पेक्ट्रा की श्रेणी और छोटे ग्रोथेंडिक साइट पर सिंपल स्पेक्ट्रा या स्पेक्ट्रा के शीफ की श्रेणियां शामिल हैं। .
-किसी श्रेणी में साधारण वस्तुएँ मॉडल श्रेणियों का लगातार स्रोत हैं; उदाहरण के लिए, साधारण क्रमविनिमेय छल्ले या साधारण आर-मॉड्यूल प्राकृतिक मॉडल संरचनाओं को स्वीकार करते हैं। यह इस प्रकार है क्योंकि साधारण सेट और साधारण कम्यूटेटिव रिंग्स (भुलक्कड़ और मुक्त फ़ैक्टरों द्वारा दिए गए) के बीच एक संयोजन है, और अच्छे मामलों में कोई एक संयोजन के तहत मॉडल संरचनाओं को उठा सकता है।
+किसी श्रेणी में साधारण वस्तुएँ मॉडल श्रेणियों का लगातार स्रोत हैं; उदाहरण के लिए, साधारण क्रमविनिमेय छल्ले या साधारण R-मॉड्यूल प्राकृतिक मॉडल संरचनाओं को स्वीकार करते हैं। यह इस प्रकार है क्योंकि साधारण सेट और साधारण कम्यूटेटिव रिंग्स (भुलक्कड़ और मुक्त फ़ैक्टरों द्वारा दिए गए) के बीच एक संयोजन है, और अच्छे मामलों में कोई एक संयोजन के तहत मॉडल संरचनाओं को उठा सकता है।
 एक साधारण मॉडल श्रेणी एक सरल रूप से समृद्ध श्रेणी है जिसमें एक मॉडल संरचना होती है जो सरल संरचना के अनुकूल होती है।<ref>Definition 2.1. of [https://arxiv.org/abs/math/0101162].</ref>
-किसी भी श्रेणी सी और एक मॉडल श्रेणी एम को देखते हुए, कुछ अतिरिक्त परिकल्पनाओं के तहत फ़ैक्टर्स फन (सी, एम) (एम में सी-आरेख भी कहा जाता है) की श्रेणी भी एक मॉडल श्रेणी है। वास्तव में, अलग-अलग मॉडल संरचनाओं के लिए हमेशा दो उम्मीदवार होते हैं: एक में, तथाकथित प्रक्षेपी मॉडल संरचना, फ़िब्रेशन और कमजोर समतुल्यताएं [[ऑपरेटर]] के वे मानचित्र हैं जो सी के प्रत्येक ऑब्जेक्ट पर मूल्यांकन किए जाने पर फ़िब्रेशन और कमज़ोर समकक्ष हैं। इंजेक्टिव मॉडल संरचना इसके बजाय कॉफिब्रेशन और कमजोर समकक्षों के समान है। दोनों ही मामलों में मोर्फिज्म का तीसरा वर्ग उठाने की स्थिति (नीचे देखें) द्वारा दिया जाता है। कुछ मामलों में, जब श्रेणी सी एक [[रेडी श्रेणी]] है, तो प्रोजेक्टिव और इंजेक्शन के बीच एक तीसरी मॉडल संरचना होती है।
+किसी भी श्रेणी सी और एक मॉडल श्रेणी एम को देखते हुए, कुछ अतिरिक्त परिकल्पनाओं के तहत फ़ैक्टर्स फन (सी, एम) (एम में सी-आरेख भी कहा जाता है) की श्रेणी भी एक मॉडल श्रेणी है। वास्तव में, अलग-अलग मॉडल संरचनाओं के लिए हमेशा दो उम्मीदवार होते हैं: एक में, तथाकथित प्रक्षेपी मॉडल संरचना, फ़िब्रेशन और दुर्बल समतुल्यताएं [[ऑपरेटर]] के वे मानचित्र हैं जो सी के प्रत्येक ऑब्जेक्ट पर मूल्यांकन किए जाने पर फ़िब्रेशन और कमज़ोर समकक्ष हैं। इंजेक्टिव मॉडल संरचना इसके बजाय कॉफिब्रेशन और दुर्बल समकक्षों के समान है। दोनों ही मामलों में आकारिकी का तीसरा वर्ग उठाने की स्थिति (नीचे देखें) द्वारा दिया जाता है। कुछ मामलों में, जब श्रेणी सी एक [[रेडी श्रेणी]] है, तो प्रोजेक्टिव और इंजेक्शन के बीच एक तीसरी मॉडल संरचना होती है।
-एक ही अंतर्निहित श्रेणी पर एक नई मॉडल श्रेणी संरचना में कुछ नक्शों को कमजोर तुल्यता बनने के लिए मजबूर करने की प्रक्रिया को बोसफील्ड स्थानीयकरण के रूप में जाना जाता है। उदाहरण के लिए, साधारण [[शीफ (गणित)]] की श्रेणी को साधारण [[presheaf]] के मॉडल श्रेणी के बोसफील्ड स्थानीयकरण के रूप में प्राप्त किया जा सकता है।
+एक ही अंतर्निहित श्रेणी पर एक नई मॉडल श्रेणी संरचना में कुछ नक्शों को दुर्बल समतुल्यता बनने के लिए मजबूर करने की प्रक्रिया को बोसफील्ड स्थानीयकरण के रूप में जाना जाता है। उदाहरण के लिए, साधारण [[शीफ (गणित)]] की श्रेणी को साधारण [[presheaf]] के मॉडल श्रेणी के बोसफील्ड स्थानीयकरण के रूप में प्राप्त किया जा सकता है।
 डेनिस-चार्ल्स सिसिंस्की ने विकसित किया है<ref>Cisinski, Denis-Charles. Les préfaisceaux comme modèles des types d'homotopie. (French) [Presheaves as models for homotopy types] Astérisque No. 308 (2006), xxiv+390 pp. {{isbn|978-2-85629-225-9}} {{MR|2294028}}</ref> प्रीशेफ श्रेणियों पर मॉडल संरचनाओं का एक सामान्य सिद्धांत (सरलीकृत सेटों का सामान्यीकरण, जो सिम्प्लेक्स श्रेणी पर प्रीशेव हैं)।
-यदि सी एक मॉडल श्रेणी है, तो सी में [[ समर्थक वस्तु ]]्स की श्रेणी प्रो (सी) भी है। हालांकि, प्रो (सी) पर एक मॉडल संरचना भी सी के स्वयंसिद्धों के एक कमजोर सेट को लागू करके बनाई जा सकती है।<ref>{{citation|
+यदि सी एक मॉडल श्रेणी है, तो सी में [[ समर्थक वस्तु ]]्स की श्रेणी प्रो (सी) भी है। हालांकि, प्रो (सी) पर एक मॉडल संरचना भी सी के स्वयंसिद्धों के एक दुर्बल सेट को लागू करके बनाई जा सकती है।<ref>{{citation|
 mr=3459031|author1=Barnea, Ilan|author2=Schlank, Tomer M.|title=A projective model structure on pro-simplicial sheaves, and the relative étale homotopy type |journal= [[Advances in Mathematics]]|volume=291|year=2016|pages=784–858|arxiv=1109.5477|bibcode=2011arXiv1109.5477B|doi=10.1016/j.aim.2015.11.014|doi-access=free}}</ref>
@@ Line 90: / Line 90: @@
 == कुछ निर्माण ==
-प्रत्येक बंद मॉडल श्रेणी में पूर्णता से एक [[टर्मिनल वस्तु]] और सह-पूर्णता द्वारा एक [[प्रारंभिक वस्तु]] होती है, क्योंकि ये वस्तुएं खाली आरेख की क्रमशः सीमा और कोलिमिट हैं। मॉडल श्रेणी में किसी वस्तु X को देखते हुए, यदि प्रारंभिक वस्तु से X तक का अद्वितीय मानचित्र एक कोफिब्रेशन है, तो X को 'कोफ़िब्रेंट' कहा जाता है। अनुरूप रूप से, यदि एक्स से टर्मिनल ऑब्जेक्ट का अद्वितीय नक्शा एक फ़िब्रेशन है तो एक्स को 'फ़ाइब्रेंट' कहा जाता है।
+प्रत्येक संवृत मॉडल श्रेणी में पूर्णता से एक [[टर्मिनल वस्तु]] और सह-पूर्णता द्वारा एक [[प्रारंभिक वस्तु]] होती है, क्योंकि ये वस्तुएं खाली आरेख की क्रमशः सीमा और कोलिमिट हैं। मॉडल श्रेणी में किसी वस्तु X को देखते हुए, यदि प्रारंभिक वस्तु से X तक का अद्वितीय मानचित्र एक सह-संयोजन है, तो X को 'कोफ़िब्रेंट' कहा जाता है। अनुरूप रूप से, यदि एक्स से टर्मिनल ऑब्जेक्ट का अद्वितीय नक्शा एक फ़िब्रेशन है तो एक्स को 'फ़ाइब्रेंट' कहा जाता है।
-यदि Z और X एक मॉडल श्रेणी की वस्तुएँ हैं जैसे कि Z कोफ़िब्रेंट है और Z से X तक एक कमजोर तुल्यता है तो Z को X के लिए एक 'कॉफ़िब्रेंट प्रतिस्थापन' कहा जाता है। इसी तरह, यदि Z फ़िब्रेंट है और एक कमजोर है X से Z तक तुल्यता तब Z को X के लिए एक 'फाइब्रेंट रिप्लेसमेंट' कहा जाता है। सामान्य तौर पर, सभी वस्तुएं रेशेदार या कोफाइब्रेंट नहीं होती हैं, हालांकि यह कभी-कभी मामला होता है। उदाहरण के लिए, सभी ऑब्जेक्ट सरलीकृत सेट के मानक मॉडल श्रेणी में कोफ़ाइब्रेंट हैं और सभी ऑब्जेक्ट टोपोलॉजिकल स्पेस के लिए ऊपर दी गई मानक मॉडल श्रेणी संरचना के लिए फ़िब्रेंट हैं।
+यदि Z और X एक मॉडल श्रेणी की वस्तुएँ हैं जैसे कि Z कोफ़िब्रेंट है और Z से X तक एक दुर्बल समतुल्यता है तो Z को X के लिए एक 'कॉफ़िब्रेंट प्रतिस्थापन' कहा जाता है। इसी तरह, यदि Z फ़िब्रेंट है और एक दुर्बल है X से Z तक समतुल्यता तब Z को X के लिए एक 'फाइब्रेंट रिप्लेसमेंट' कहा जाता है। सामान्य तौर पर, सभी वस्तुएं रेशेदार या कोफाइब्रेंट नहीं होती हैं, हालांकि यह कभी-कभी मामला होता है। उदाहरण के लिए, सभी ऑब्जेक्ट सरलीकृत सेट के मानक मॉडल श्रेणी में कोफ़ाइब्रेंट हैं और सभी ऑब्जेक्ट सांस्थितिक स्पेस के लिए ऊपर दी गई मानक मॉडल श्रेणी संरचना के लिए फ़िब्रेंट हैं।
-लेफ्ट होमोटोपी को [http://ncatlab.org/nlab/show/Cylinder+object सिलिंडर ऑब्जेक्ट्स] के संबंध में परिभाषित किया गया है और राइट होमोटॉपी को [http://ncatlab.org/nlab/show/path+space] के संबंध में परिभाषित किया गया है + वस्तु पथ अंतरिक्ष वस्तुओं]। ये धारणाएं मेल खाती हैं जब डोमेन कॉफिब्रेंट होता है और कोडोमेन फाइब्रेंट होता है। उस स्थिति में, होमोटॉपी मॉडल श्रेणी में होम सेट पर समतुल्य संबंध को परिभाषित करता है जिससे होमोटॉपी क्लासेस को जन्म मिलता है।
+लेफ्ट होमोटोपी को [http://ncatlab.org/nlab/show/Cylinder+object सिलिंडर ऑब्जेक्ट्स] के संबंध में परिभाषित किया गया है और राइट समस्थेयता को [http://ncatlab.org/nlab/show/path+space] के संबंध में परिभाषित किया गया है + वस्तु पथ अंतरिक्ष वस्तुओं]। ये धारणाएं मेल खाती हैं जब डोमेन कॉफिब्रेंट होता है और कोडोमेन फाइब्रेंट होता है। उस स्थिति में, समस्थेयता मॉडल श्रेणी में होम सेट पर समतुल्य संबंध को परिभाषित करता है जिससे समस्थेयता क्लासेस को जन्म मिलता है।
 == गुणों को उठाने से फाइब्रेशन और कॉफिब्रेशन के लक्षण ==
-कोफ़िब्रेशन को उन नक्शों के रूप में चित्रित किया जा सकता है, जिनमें एसाइक्लिक फ़ाइब्रेशन के संबंध में बाईं ओर उठाने वाली संपत्ति होती है, और एसाइक्लिक कोफ़िब्रेशन को उन मानचित्रों के रूप में चित्रित किया जाता है, जिनमें फ़िब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है। इसी तरह, फ़िब्रेशन को उन नक्शों के रूप में चित्रित किया जा सकता है जिनके पास एसाइक्लिक कोफ़िब्रेशन के संबंध में सही उठाने वाली संपत्ति है, और एसाइक्लिक फ़िब्रेशन को उन मानचित्रों के रूप में चित्रित किया जाता है जिनके पास कोफ़िब्रेशन के संबंध में [[सही उठाने की संपत्ति]] है।
+कोफ़िब्रेशन को उन नक्शों के रूप में चित्रित किया जा सकता है, जिनमें अनावर्ती फ़ाइब्रेशन के संबंध में बाईं ओर उठाने वाली संपत्ति होती है, और अनावर्ती कोफ़िब्रेशन को उन मानचित्रों के रूप में चित्रित किया जाता है, जिनमें फ़िब्रेशन के संबंध में लेफ्ट लिफ्टिंग प्रॉपर्टी होती है। इसी तरह, फ़िब्रेशन को उन नक्शों के रूप में चित्रित किया जा सकता है जिनके पास अनावर्ती कोफ़िब्रेशन के संबंध में सही उठाने वाली संपत्ति है, और अनावर्ती फ़िब्रेशन को उन मानचित्रों के रूप में चित्रित किया जाता है जिनके पास कोफ़िब्रेशन के संबंध में [[सही उठाने की संपत्ति]] है।
 == समरूपता और समरूपता श्रेणी ==
-एक मॉडल श्रेणी C की होमोटोपी श्रेणी कमजोर तुल्यता के वर्ग के संबंध में C की श्रेणी का स्थानीयकरण है। होमोटॉपी श्रेणी की यह परिभाषा फ़िब्रेशन और कॉफ़िब्रेशन की पसंद पर निर्भर नहीं करती है। हालांकि, फ़िब्रेशन और कॉफ़िब्रेशन की कक्षाएं एक अलग तरीके से होमोटोपी श्रेणी का वर्णन करने और विशेष रूप से श्रेणियों के सामान्य स्थानीयकरणों में उत्पन्न होने वाले सेट-सैद्धांतिक मुद्दों से बचने में उपयोगी होती हैं। अधिक सटीक रूप से, मॉडल श्रेणियों के मौलिक प्रमेय में कहा गया है कि C की होमोटोपी श्रेणी उस श्रेणी के समतुल्य है, जिसकी वस्तुएं C की वस्तुएं हैं, जो कि रेशेदार और कोफिब्रेंट दोनों हैं, और जिनके आकारिकी मानचित्रों के होमोटॉपी वर्ग हैं (समकक्ष रूप से, सही होमोटॉपी वर्ग) मानचित्रों का) जैसा कि ऊपर परिभाषित किया गया है। (उदाहरण के लिए होवी द्वारा मॉडल श्रेणियाँ देखें, Thm 1.2.10)
+एक मॉडल श्रेणी C की होमोटोपी श्रेणी दुर्बल समतुल्यता के वर्ग के संबंध में C की श्रेणी का स्थानीयकरण है। समस्थेयता श्रेणी की यह परिभाषा फ़िब्रेशन और सह-संयोजन की पसंद पर निर्भर नहीं करती है। हालांकि, फ़िब्रेशन और सह-संयोजन की कक्षाएं एक अलग तरीके से होमोटोपी श्रेणी का वर्णन करने और विशेष रूप से श्रेणियों के सामान्य स्थानीयकरणों में उत्पन्न होने वाले सेट-सैद्धांतिक मुद्दों से बचने में उपयोगी होती हैं। अधिक सटीक रूप से, मॉडल श्रेणियों के मौलिक प्रमेय में कहा गया है कि C की होमोटोपी श्रेणी उस श्रेणी के समतुल्य है, जिसकी वस्तुएं C की वस्तुएं हैं, जो कि रेशेदार और कोफिब्रेंट दोनों हैं, और जिनके आकारिकी मानचित्रों के समस्थेयता वर्ग हैं (समकक्ष रूप से, सही समस्थेयता वर्ग) मानचित्रों का) जैसा कि ऊपर परिभाषित किया गया है। (उदाहरण के लिए होवी द्वारा मॉडल श्रेणियाँ देखें, Thm 1.2.10)
-इसे ऊपर दिए गए मॉडल संरचना के साथ टोपोलॉजिकल रिक्त स्थान की श्रेणी में लागू करना, परिणामी होमोटॉपी श्रेणी सीडब्ल्यू परिसरों की श्रेणी और निरंतर मानचित्रों के होमोटोपी वर्गों के बराबर है, जहां से नाम है।
+इसे ऊपर दिए गए मॉडल संरचना के साथ सांस्थितिक समष्टि की श्रेणी में लागू करना, परिणामी समस्थेयता श्रेणी सीडब्ल्यू सम्मिश्र की श्रेणी और निरंतर मानचित्रों के होमोटोपी वर्गों के बराबर है, जहां से नाम है।
 === क्विलन एडजंक्शन ===
 आसन्न फ़ैक्टरों की एक जोड़ी
 :<math>F: C \leftrightarrows D : G</math>
-दो मॉडल श्रेणियों सी और डी के बीच एक [[ क्विलन संयोजन ]] कहा जाता है यदि एफ कॉफिब्रेशन और एसाइक्लिक कोफिब्रेशन को संरक्षित करता है या, समकक्ष रूप से बंद मॉडल स्वयंसिद्धों द्वारा, जैसे कि जी फाइब्रेशन और एसाइक्लिक फाइब्रेशन को संरक्षित करता है। इस मामले में एफ और जी एक संयोजन को प्रेरित करते हैं
+दो मॉडल श्रेणियों सी और डी के बीच एक [[ क्विलन संयोजन ]] कहा जाता है यदि एफ कॉफिब्रेशन और अनावर्ती सह-संयोजन को संरक्षित करता है या, समकक्ष रूप से संवृत मॉडल स्वयंसिद्धों द्वारा, जैसे कि जी फाइब्रेशन और अनावर्ती फाइब्रेशन को संरक्षित करता है। इस मामले में एफ और जी एक संयोजन को प्रेरित करते हैं
 :<math>LF: Ho(C) \leftrightarrows Ho(D) : RG</math>
-होमोटॉपी श्रेणियों के बीच। उत्तरार्द्ध के लिए एक समानता होने के लिए एक स्पष्ट मानदंड भी है (फिर एफ और जी को क्विलन समकक्ष कहा जाता है)।
+समस्थेयता श्रेणियों के बीच। उत्तरार्द्ध के लिए एक समानता होने के लिए एक स्पष्ट मानदंड भी है (फिर एफ और जी को क्विलन समकक्ष कहा जाता है)।
-एक विशिष्ट उदाहरण साधारण सेट और टोपोलॉजिकल रिक्त स्थान के बीच मानक संयोजन है:
+एक विशिष्ट उदाहरण साधारण सेट और सांस्थितिक समष्टि के बीच मानक संयोजन है:
 :<math>|-|: \mathbf{sSet} \leftrightarrows \mathbf{Top} : Sing</math>
-कुछ सामयिक स्थान में एक साधारण सेट और एकवचन श्रृंखला के ज्यामितीय अहसास को शामिल करना। श्रेणियाँ sSet और Top समतुल्य नहीं हैं, लेकिन उनकी होमोटॉपी श्रेणियां हैं। इसलिए, होमोटॉपी श्रेणियों की इस समानता के कारण सरल सेटों को अक्सर टोपोलॉजिकल स्पेस के लिए मॉडल के रूप में उपयोग किया जाता है।
+कुछ सामयिक स्थान में एक साधारण सेट और एकवचन श्रृंखला के ज्यामितीय अहसास को शामिल करना। श्रेणियाँ sSet और Top समतुल्य नहीं हैं, लेकिन उनकी समस्थेयता श्रेणियां हैं। इसलिए, समस्थेयता श्रेणियों की इस समानता के कारण सरल सेटों को प्रायः सांस्थितिक स्पेस के लिए मॉडल के रूप में उपयोग किया जाता है।
 == यह भी देखें ==

Anonymous

Search

मॉडल श्रेणी: Difference between revisions

Namespaces

More

Page actions

Revision as of 09:37, 7 May 2023

Contents

कारण

औपचारिक परिभाषा