सममित अंतर

Symmetric difference

Venn diagram of $A\triangle B$. The symmetric difference is the union without the intersection: $~\setminus ~$ $~=~$
Type	Set operation
Field	Set theory
Statement	The symmetric difference is the set of elements that are in either set, but not in the intersection.
Symbolic statement	$A\,\triangle \,B=\left(A\setminus B\right)\cup \left(B\setminus A\right)$

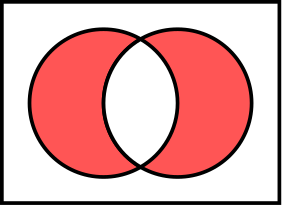
गणित में, दो सेटों (गणित) का सममित अंतर, जिसे वियोगात्मक संघ के रूप में भी जाना जाता है, उन तत्वों का सेट होता है जो किसी भी सेट में होते हैं, लेकिन उनके चौराहा (सेट सिद्धांत) में नहीं होते हैं। उदाहरण के लिए, सेट का सममित अंतर $\{1,2,3\}$ और $\{3,4\}$ है $\{1,2,4\}$.

समुच्चय A और B के सममितीय अंतर को सामान्यतया निरूपित किया जाता है $A\ominus B,$ या $A\operatorname {\triangle } B.$

सममित अंतर के संचालन के तहत किसी भी सेट का घात समुच्चय समूह के तटस्थ तत्व के रूप में खाली सेट के साथ एक एबेलियन समूह बन जाता है और इस समूह में प्रत्येक तत्व का अपना व्युत्क्रम होता है। किसी भी सेट का घात समुच्चय एक बूलियन रिंग बन जाता है, जिसमें रिंग के गुणन के रूप में रिंग और चौराहा (सेट सिद्धांत) के जोड़ के रूप में सममित अंतर होता है।

गुण

का वेन आरेख $~(A\triangle B)\triangle C$ $~\triangle ~$ $~=~$

सममित अंतर दोनों पूरक (सेट सिद्धांत) के संघ (सेट सिद्धांत) के बराबर है, अर्थात:

$A\,\triangle \,B=\left(A\setminus B\right)\cup \left(B\setminus A\right),$

सेट-बिल्डर नोटेशन में दो सेटों का वर्णन करने वाले विधेय (गणितीय तर्क) पर एक्सक्लूसिव डिसजंक्शन एक तार्किक ऑपरेशन ⊕ का उपयोग करके सममित अंतर भी व्यक्त किया जा सकता है:

$A\mathbin {\triangle } B=\{x:(x\in A)\oplus (x\in B)\}.$

उसी तथ्य को संकेतक फ़ंक्शन के रूप में कहा जा सकता है (यहाँ द्वारा दर्शाया गया है $\chi$) सममित अंतर का, इसके दो तर्कों के सूचक कार्यों का एक्सओआर (या अतिरिक्त मॉड्यूलर अंकगणितय प्रणाली) होने के नाते: $\chi _{(A\,\triangle \,B)}=\chi _{A}\oplus \chi _{B}$ या आइवरसन ब्रैकेट नोटेशन का उपयोग करना $[x\in A\,\triangle \,B]=[x\in A]\oplus [x\in B]$.

सममित अंतर को दो सेटों के मिलन के रूप में भी व्यक्त किया जा सकता है, उनके प्रतिच्छेदन (सेट सिद्धांत) को घटाकर:

$A\,\triangle \,B=(A\cup B)\setminus (A\cap B),$

विशेष रूप से, $A\mathbin {\triangle } B\subseteq A\cup B$; इस गैर-सख्त सबसेट में समानता तब होती है जब और केवल अगर $A$ और $B$ असंयुक्त समुच्चय हैं। इसके अलावा, निरूपण $D=A\mathbin {\triangle } B$ और $I=A\cap B$, तब $D$ और $I$ हमेशा अलग होते हैं, इसलिए $D$ और $I$ एक सेट का विभाजन $A\cup B$. नतीजतन, चौराहे और सममित अंतर को आदिम संचालन के रूप में मानते हुए, दो सेटों के मिलन को समानता के दाईं ओर सममित अंतर के संदर्भ में अच्छी तरह से परिभाषित किया जा सकता है

$A\,\cup \,B=(A\,\triangle \,B)\,\triangle \,(A\cap B)$.

सममित अंतर क्रमविनिमेयता और साहचर्य है:

${\begin{aligned}A\,\triangle \,B&=B\,\triangle \,A,\\(A\,\triangle \,B)\,\triangle \,C&=A\,\triangle \,(B\,\triangle \,C).\end{aligned}}$

रिक्त समुच्चय पहचान तत्व होता है, और प्रत्येक सेट का अपना व्युत्क्रम होता है:

${\begin{aligned}A\,\triangle \,\varnothing &=A,\\A\,\triangle \,A&=\varnothing .\end{aligned}}$

इस प्रकार, सममित अंतर ऑपरेशन के तहत किसी भी सेट X का घात समुच्चय एक एबेलियन समूह बन जाता है। (अधिक सामान्यतः, सेट का कोई भी क्षेत्र संक्रिया के रूप में सममितीय अंतर के साथ एक समूह बनाता है।) एक समूह जिसमें प्रत्येक तत्व का अपना व्युत्क्रम होता है (या, समतुल्य रूप से, जिसमें प्रत्येक तत्व का क्रम (समूह सिद्धांत) 2 होता है) को कभी-कभी बूलियन समूह कहा जाता है; सममित अंतर ऐसे समूहों का एक आदिरूप उदाहरण प्रदान करता है। कभी-कभी बूलियन समूह को वास्तव में समुच्चय पर सममित अंतर ऑपरेशन के रूप में परिभाषित किया जाता है। ऐसे स्थितिय में जहां X में केवल दो तत्व हैं, इस प्रकार प्राप्त समूह क्लेन चार-समूह होता है।

समतुल्य रूप से, एक बूलियन समूह एक प्राथमिक एबेलियन समूह है | प्राथमिक एबेलियन 2-समूह। नतीजतन, सममित अंतर से प्रेरित समूह वास्तव में परिमित क्षेत्र 'Z' पर एक सदिश स्थान है₂. यदि X परिमित है, तो सिंगलटन (गणित) इस सदिश स्थान का एक आधार (रैखिक बीजगणित) बनाता है, और इसका हेमल आयाम इसलिए X के तत्वों की संख्या के बराबर है। यह निर्माण ग्राफ सिद्धांत में उपयोग किया जाता है, परिभाषित करने के लिए एक ग्राफ का चक्र स्थान।

एक बूलियन समूह में व्युत्क्रम की संपत्ति से, यह निम्नानुसार है कि दो दोहराए गए सममित अंतरों का सममित अंतर मल्टीसेट के दोहराए गए सममित अंतर के बराबर है # दो मल्टीसेट्स के संचालन, जहां प्रत्येक डबल सेट के लिए दोनों को हटाया जा सकता है। विशेष रूप से:

$(A\,\triangle \,B)\,\triangle \,(B\,\triangle \,C)=A\,\triangle \,C.$

इसका तात्पर्य त्रिभुज असमानता है: A और C का सममित अंतर A और B के सममित अंतर और B और C के सममित अंतर के मिलन में निहित है।

सममित अंतर पर चौराहा वितरण:

$A\cap (B\,\triangle \,C)=(A\cap B)\,\triangle \,(A\cap C),$

और इससे पता चलता है कि X का पावर सेट एक वलय (गणित) बन जाता है, जिसमें सममित अंतर योग के रूप में और प्रतिच्छेदन गुणन के रूप में होता है। यह बूलियन रिंग का प्रोटोटाइपिक उदाहरण है।

सममित अंतर के और गुणों में शामिल हैं:

• $A\mathbin {\triangle } B=\emptyset$ अगर और केवल अगर $A=B$.
• $A\mathbin {\triangle } B=A^{c}\mathbin {\triangle } B^{c}$, कहाँ $A^{c}$, $B^{c}$ है $A$का पूरक, $B$के पूरक, क्रमशः, किसी भी (निश्चित) सेट के सापेक्ष जिसमें दोनों शामिल हैं।
• $\left(\bigcup _{\alpha \in {\mathcal {I}}}A_{\alpha }\right)\triangle \left(\bigcup _{\alpha \in {\mathcal {I}}}B_{\alpha }\right)\subseteq \bigcup _{\alpha \in {\mathcal {I}}}\left(A_{\alpha }\mathbin {\triangle } B_{\alpha }\right)$, कहाँ ${\mathcal {I}}$ एक मनमाना गैर-खाली इंडेक्स सेट है।
• अगर $f:S\rightarrow T$ कोई कार्य है और $A,B\subseteq T$ क्या कोई सेट है $f$का कोडोमेन, फिर $f^{-1}\left(A\mathbin {\triangle } B\right)=f^{-1}\left(A\right)\mathbin {\triangle } f^{-1}\left(B\right).$

सममित अंतर को किसी भी बूलियन बीजगणित (संरचना) में लिखकर परिभाषित किया जा सकता है

$x\,\triangle \,y=(x\lor y)\land \lnot (x\land y)=(x\land \lnot y)\lor (y\land \lnot x)=x\oplus y.$

इस ऑपरेशन में सेट के सममित अंतर के समान गुण हैं।

एन-एरी सममित अंतर

बार-बार सममित अंतर सेट के एक बहुसेट पर एक ऑपरेशन के बराबर होता है जो तत्वों के सेट को देता है जो विषम संख्या में सेट होते हैं।

ऊपर के रूप में, सेट के संग्रह के सममित अंतर में केवल तत्व होते हैं जो संग्रह में सेट की विषम संख्या में होते हैं:

$$\triangle M=\left\{a\in \bigcup M:\left|\{A\in M:a\in A\}\right|{\text{ is odd}}\right\}.$$

जाहिर है, यह केवल तभी अच्छी तरह से परिभाषित होता है जब संघ के प्रत्येक तत्व ${\textstyle \bigcup M}$ के तत्वों की एक सीमित संख्या द्वारा योगदान दिया जाता है $M$.

कल्पना करना $M=\left\{M_{1},M_{2},\ldots ,M_{n}\right\}$ एक मल्टीसेट है और $n\geq 2$. फिर इसके लिए एक सूत्र है $|\triangle M|$, में तत्वों की संख्या $\triangle M$, केवल के तत्वों के प्रतिच्छेदन के संदर्भ में दिया गया है $M$:

$$|\triangle M|=\sum _{l=1}^{n}(-2)^{l-1}\sum _{1\leq i_{1}<i_{2}<\ldots <i_{l}\leq n}\left|M_{i_{1}}\cap M_{i_{2}}\cap \ldots \cap M_{i_{l}}\right|.$$

माप रिक्त स्थान पर सममित अंतर

जब तक कोई धारणा है कि एक सेट कितना बड़ा है, दो सेटों के बीच सममित अंतर को एक उपाय माना जा सकता है कि वे कितने दूर हैं।

पहले एक परिमित समुच्चय S पर विचार करें और उनके आकार द्वारा दिए गए उपसमुच्चय पर गणना माप। अब S के दो उपसमुच्चयों पर विचार करें और उनकी दूरी को उनके सममित अंतर के आकार के रूप में सेट करें। यह दूरी वास्तव में एक मीट्रिक (गणित) है, जो एस पर सेट की गई शक्ति को एक मीट्रिक स्थान बनाती है। यदि S में n तत्व हैं, तो खाली सेट से S तक की दूरी n है, और यह किसी भी उपसमुच्चय की अधिकतम दूरी है। माप सिद्धांत के विचारों का उपयोग करते हुए, मापने योग्य सेटों के पृथक्करण को उनके सममित अंतर के माप के रूप में परिभाषित किया जा सकता है। यदि μ एक सिग्मा-परिमित है|σ-परिमित माप स्थान एक सिग्मा-बीजगणित|σ-बीजगणित Σ पर परिभाषित है, तो फ़ंक्शन

$d_{\mu }(X,Y)=\mu (X\,\triangle \,Y)$

Σ पर छद्ममितीय स्थान है। डी_μएक मीट्रिक स्थान बन जाता है अगर Σ को तुल्यता संबंध X ~ Y माना जाता है यदि और केवल यदि $\mu (X\,\triangle \,Y)=0$. इसे कभी-कभी फ्रेचेट-निकोडीम मीट्रिक कहा जाता है। परिणामी मीट्रिक स्थान वियोज्य स्थान है यदि और केवल यदि L^2|L²(μ) वियोज्य है।

अगर $\mu (X),\mu (Y)<\infty$, अपने पास: $|\mu (X)-\mu (Y)|\leq \mu (X\,\triangle \,Y)$. वास्तव में,

${\begin{aligned}|\mu (X)-\mu (Y)|&=\left|\left(\mu \left(X\setminus Y\right)+\mu \left(X\cap Y\right)\right)-\left(\mu \left(X\cap Y\right)+\mu \left(Y\setminus X\right)\right)\right|\\&=\left|\mu \left(X\setminus Y\right)-\mu \left(Y\setminus X\right)\right|\\&\leq \left|\mu \left(X\setminus Y\right)\right|+\left|\mu \left(Y\setminus X\right)\right|\\&=\mu \left(X\setminus Y\right)+\mu \left(Y\setminus X\right)\\&=\mu \left(\left(X\setminus Y\right)\cup \left(Y\setminus X\right)\right)\\&=\mu \left(X\,\triangle \,Y\right)\end{aligned}}$

अगर $S=\left(\Omega ,{\mathcal {A}},\mu \right)$ एक माप स्थान है और $F,G\in {\mathcal {A}}$ मापने योग्य सेट हैं, तो उनका सममित अंतर भी औसत दर्जे का है: $F\triangle G\in {\mathcal {A}}$. मापने योग्य सेटों पर एक समतुल्य संबंध को परिभाषित कर सकते हैं $F$ और $G$ संबंधित हो अगर $\mu \left(F\triangle G\right)=0$. इस संबंध को दर्शाया गया है $F=G\left[{\mathcal {A}},\mu \right]$.

दिया गया ${\mathcal {D}},{\mathcal {E}}\subseteq {\mathcal {A}}$, एक लिखता है ${\mathcal {D}}\subseteq {\mathcal {E}}\left[{\mathcal {A}},\mu \right]$ यदि प्रत्येक को $D\in {\mathcal {D}}$ वहाँ कुछ हैं $E\in {\mathcal {E}}$ ऐसा है कि $D=E\left[{\mathcal {A}},\mu \right]$. रिश्ता$\subseteq \left[{\mathcal {A}},\mu \right]$के उपसमुच्चयों के परिवार पर आंशिक क्रम है ${\mathcal {A}}$.

हम लिखते हैं ${\mathcal {D}}={\mathcal {E}}\left[{\mathcal {A}},\mu \right]$ अगर ${\mathcal {D}}\subseteq {\mathcal {E}}\left[{\mathcal {A}},\mu \right]$ और ${\mathcal {E}}\subseteq {\mathcal {D}}\left[{\mathcal {A}},\mu \right]$. रिश्ता$=\left[{\mathcal {A}},\mu \right]$के उपसमुच्चयों के बीच एक तुल्यता संबंध है ${\mathcal {A}}$.

का सममित समापन ${\mathcal {D}}$ सबका संग्रह है ${\mathcal {A}}$-मापने योग्य सेट जो हैं $=\left[{\mathcal {A}},\mu \right]$ कुछ करने के लिए $D\in {\mathcal {D}}$. का सममित समापन ${\mathcal {D}}$ रोकना ${\mathcal {D}}$. अगर ${\mathcal {D}}$ एक उप है$\sigma$-बीजगणित का ${\mathcal {A}}$, तो सममित बंद है ${\mathcal {D}}$.

$F=G\left[{\mathcal {A}},\mu \right]$ आईएफएफ $\left|\mathbf {1} _{F}-\mathbf {1} _{G}\right|=0$ $\left[{\mathcal {A}},\mu \right]$ लगभग हर जगह।

हॉसडॉर्फ दूरी बनाम सममित अंतर

हॉसडॉर्फ दूरी और (क्षेत्र) सममित अंतर मापने योग्य ज्यामितीय आकृतियों के सेट पर दोनों छद्म-मेट्रिक्स हैं। हालांकि, वे काफी अलग व्यवहार करते हैं। दाईं ओर की आकृति आकृतियों के दो क्रमों को दिखाती है, लाल और लाल ∪ हरा। जब उनके बीच हॉसडॉर्फ की दूरी कम हो जाती है, तो उनके बीच सममित अंतर का क्षेत्र बड़ा हो जाता है, और इसके विपरीत। इन अनुक्रमों को दोनों दिशाओं में जारी रखते हुए, दो अनुक्रम प्राप्त करना संभव है जैसे कि उनके बीच हॉसडॉर्फ की दूरी 0 में परिवर्तित हो जाती है और उनके बीच की सममित दूरी अलग हो जाती है, या इसके विपरीत।

यह भी देखें

• सेट का बीजगणित
• बूलियन समारोह
• पूरक (सेट सिद्धांत)
• अंतर (सेट सिद्धांत)
• एकमात्र
• फजी सेट
• चौराहा (सेट सिद्धांत)
• जैकार्ड इंडेक्स
• निर्धारित पहचान और संबंधों की सूची
• तार्किक ग्राफ
• सिग्मा-बीजगणित # वियोज्य .CF.83-बीजगणित
• समुच्चय सिद्धान्त
• समरूपता
• संघ (सेट सिद्धांत)
• समावेश-बहिष्करण सिद्धांत

ग्रन्थसूची

• Halmos, Paul R. (1960). Naive set theory. The University Series in Undergraduate Mathematics. van Nostrand Company. Zbl 0087.04403.
• Symmetric difference of sets. In Encyclopaedia of Mathematics