मध्य वोटर प्रमेय
मध्य वोटर प्रमेय 1948 में डंकन ब्लैक द्वारा प्रस्तुत रैंकिंग मतदातािंग वरीयता वोटर से संबंधित एक प्रस्ताव है।[1] इसमें कहा गया है कि यदि वोटर और नीतियों को एक आयामी स्पेक्ट्रम के साथ वितरित किया जाता है, जिसमें वोटर को निकटता के क्रम में विकल्पों की रैंकिंग की जाती है, तो कोई भी वोटर पद्धति जो कोंडोरसेट मानदंड को पूरा करती है, उम्मीदवार को औसत मतदाता के निकटतम उम्मीदवार का चुनाव करेगी। विशेष रूप से, दो विकल्पों के बीच बहुमत मतदाता ऐसा करेगा।
प्रमेय सार्वजनिक विकल्प और सांख्यिकीय राजनीति विज्ञान से जुड़ा है। पार्थ दासगुप्ता और एरिक मस्किन ने तर्क दिया है कि यह कॉन्डोर्सेट मानदंड के आधार पर वोटर की विधियों के लिए एक शक्तिशाली औचित्य प्रदान करता है।[2] प्लॉट का बहुमत नियम संतुलन प्रमेय इसे दो आयामों तक बढ़ाता है।
हेरोल्ड होटलिंग द्वारा पहले (1929 में) एक ढीला-ढाला प्रमाणित किया गया था।[3] यह एक वास्तविक प्रमेय नहीं है और इसे औसत मतदाता सिद्धांत या औसत मतदाता मॉडल के रूप में जाना जाता है। इसमें कहा गया है कि एक प्रतिनिधि लोकतंत्र में, राजनेता औसत मतदाता के दृष्टिकोण से अभिसरण करेंगे।[4]
प्रमेय का कथन और प्रमाण
मान लें कि विषम संख्या में मतदाता हैं और कम से कम दो उम्मीदवार हैं, और मान लें कि राय एक स्पेक्ट्रम के साथ वितरित की जाती है। मान लें कि प्रत्येक मतदाता उम्मीदवारों को निकटता के क्रम में रैंक करता है जैसे कि मतदाता के निकटतम उम्मीदवार को उनकी पहली वरीयता प्राप्त होती है, अगले निकटतम को उनकी दूसरी वरीयता प्राप्त होती है, और आगे भी। फिर एक औसत मतदाता है और हम दिखाएंगे कि चुनाव उस उम्मीदवार द्वारा जीता जाएगा जो उसके सबसे निकट होगा।
कोंडोरसेट मानदंड को किसी भी वोटर पद्धति से संतुष्ट होने के रूप में परिभाषित किया गया है जो यह सुनिश्चित करता है कि एक उम्मीदवार जो अधिकांश वोटर द्वारा हर दूसरे उम्मीदवार को विकल्प दिया जाता है, वह विजेता होगा, और यहाँ चार्ल्स के साथ ठीक यही स्थिति है;; इसलिए इस प्रकार है से चार्ल्स कॉन्डोर्सेट मानदंड को संतोषजनक करने वाली विधि को संचालित करके किसी भी चुनाव को जीतेंगे।
इसलिए किसी भी वोटर पद्धति के अनुसार जो कोंडोरसेट मानदंड को पूरा करता है, विजेता वह उम्मीदवार होगा जो औसत मतदाता द्वारा विकल्प दिया जाता है। द्विआधारी निर्णय के लिए बहुमत मतदाता मानदंड पर खरे उतरते हैं; बहुमार्गीय मतदाता के लिए कई विधियाँ इसे संतोषजनक बनाते हैं (देखें कोंडोरसेट विधि)।
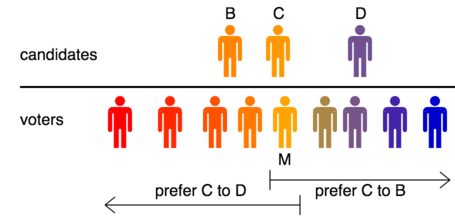
प्रमाण - बता दें कि माध्यिका मतदाता मार्लीन है। जो उम्मीदवार उसके सबसे निकटतम होगा उसे उसकी पहली वरीयता का मतदाता मिलेगा। मान लीजिए कि यह उम्मीदवार चार्ल्स है और वह उसके बाईं ओर झूठ बोलता है। तब मार्लीन और उसके बाईं ओर के सभी मतदाता (वोटर का बहुमत सम्मलित) चार्ल्स को उसके दाईं ओर के सभी उम्मीदवारों को विकल्प मिलेगे, और मार्लीन और उसके दाईं ओर के सभी मतदाता चार्ल्स को उसके बाईं ओर के सभी उम्मीदवारों को विकल्प मिलेगे।
अनुमान
प्रमेय तब भी लागू होता है जब वोटर की संख्या सम होती है, लेकिन विवरण इस बात पर निर्भर करता है कि संबंधों को कैसे सुलझाया जाता है।
यह धारणा कि वरीयताएँ निकटता के क्रम में डाली जाती हैं, केवल यह कहने में ढील दी जा सकती है कि वे एकल अस्वस्थ वाली प्राथमिकताएँ हैं।[5]
यह धारणा कि विचार एक वास्तविक रेखा के साथ स्थित हैं, को अधिक सामान्य टोपोलॉजी की अनुमति देने के लिए शिथिल किया जा सकता है।[6]
स्थानिक / वैलेंस मॉडल: मान लीजिए कि प्रत्येक उम्मीदवार के पास अन्तराल में उसकी स्थिति के अतिरिक्त एक वैलेंस पॉलिटिक्स (आकर्षण) है, और मान लीजिए कि मतदाता i उम्मीदवारों j को vj – dij के घटते क्रम में रैंक करता है, जहाँ vj j की संयोजकता है और dij, i से jकी दूरी है। तब माध्यिका मतदाता प्रमेय अभी भी लागू होता है: कोंडोरसेट विधियाँ माध्यिका मतदाता द्वारा वोटर किए गए उम्मीदवार का चुनाव करेंगी।
इतिहास
प्रमेय पहली बार 1948 में डंकन ब्लैक द्वारा निर्धारित किया गया था। उन्होंने लिखा है कि आर्थिक सिद्धांत में एक बड़ा अंतर देखा कि कैसे वोटर राजनीतिक निर्णयों सहित निर्णयों के परिणाम को निर्धारित करता है। ब्लैक के पेपर ने शोध को गति दी कि कैसे अर्थशास्त्र वोटिंग सिस्टम की व्याख्या कर सकता है। 1957 में एंथोनी डाउन्स ने अपनी पुस्तक एन इकोनॉमिक थ्योरी ऑफ डेमोक्रेसी में माध्यिका मतदाता प्रमेय पर विस्तार से बताया है।[7]
औसत मतदाता विशेशता
हम कहेंगे कि एक वोटर पद्धति में एक आयाम में औसत मतदाता विशेशता होती है यदि यह हमेशा एक आयामी स्थानिक मॉडल के अनुसार औसत मतदाता के निकटतम उम्मीदवार का चुनाव करती है। हम औसत मतदाता प्रमेय को संक्षेप में कह सकते हैं कि सभी कॉन्डोर्सेट विधियों में एक आयाम में औसत मतदाता विशेशता होती है।
यह पता चला है कि कॉन्डोर्सेट के विधियाँ इस स्थितियो में अद्वितीय नहीं हैं: कॉम्ब्स की विधि कॉन्डोर्सेट-संगत नहीं है, लेकिन फिर भी एक आयाम में औसत मतदाता विशेशता को संतुष्ट करती है।[8]
एक से अधिक आयामों में वितरण का विस्तार
मध्य मतदाता प्रमेय किसी भी आयाम के रिक्त स्थान में मतदाता राय के वितरण के लिए प्रतिबंधित रूप में लागू होता है।एक से अधिक आयामों में वितरण के लिए जरूरी नहीं कि सभी दिशाओं में एक माध्यिका हो (जिसे 'सर्वदिशात्मक माध्यिका' कहा जा सकता है); चूँकि बहुभिन्नरूपी सामान्य वितरण गॉसियन समेत घूर्णी रूप से सममित वितरण के एक व्यापक वर्ग में इस प्रकार का माध्यिका होता है।[9] जब भी वोटर के वितरण का सभी दिशाओं में एक अनूठा माध्यिका होता है, और मतदाता निकटता के क्रम में उम्मीदवारों को रैंक करते हैं, तो मध्यिका मतदाता प्रमेय लागू होता है: माध्यिका के निकटतम उम्मीदवार को अपने सभी प्रतिद्वंद्वियों पर बहुमत वरीयता प्राप्त होगी और किसी भी वोटर पद्धति द्वारा एक आयाम में मध्यिका मतदाता विशेशता को एक आयाम में संतुष्ट करना होता है।[10] (यहाँ अद्वितीयता एक ही आयाम में नमूना आकार की विषमता द्वारा गारंटीकृत संपत्ति को सामान्य बनाती है।)
यह इस प्रकार है कि सभी कॉन्डोर्सेट विधियां - और कूम्ब्स भी - सर्वदिशात्मक मध्यस्थों के साथ मतदाता वितरण के लिए किसी भी आयाम के रिक्त स्थान में औसत मतदाता विशेशता को संतुष्ट करती हैं।
मतदाता वितरण का निर्माण करना आसान है, जिसमें सभी दिशाओं में माध्यिका नहीं है। सबसे सरल उदाहरण में 3 बिंदुओं तक सीमित वितरण होता है जो एक सीधी रेखा में नहीं होता है, जैसे कि दूसरे आरेख में 1, 2 और 3। प्रत्येक मतदाता स्थान एक-आयामी अनुमानों के एक निश्चित सेट के अनुसार माध्यिका के साथ मेल खाता है। यदि ए, बी और सी उम्मीदवार हैं, तो '1' वोट ए-बी-सी, '2' वोट बी-सी-ए, और '3' सी-ए-बी वोट देगा, एक कॉन्डोर्सेट चक्र दे रहा है। यह मैककेल्वे-शोफिल्ड प्रमेय का विषय है।
प्रमाण । आरेख देखें, जिसमें ग्रे डिस्क एक वृत्त के ऊपर समान रूप से मतदाता वितरण का प्रतिनिधित्व करती है और M सभी दिशाओं में माध्यिका है। बता दें कि ए और बी दो उम्मीदवार हैं, जिनमें से ए माध्यिका के सबसे करीब है। तब मतदाता जो A को B से ऊपर रैंक करते हैं, ठीक वही हैं जो ठोस लाल रेखा के बाईं ओर (अर्थात 'A' पक्ष) हैं; और चूँकि A, B से M के अधिक निकट है, माध्यिका भी इस रेखा के बाईं ओर है।
अब, चूंकि M सभी दिशाओं में एक माध्यिका है, यह नीले तीर द्वारा दिखाए गए दिशा के विशेष स्थितियो में एक आयामी माध्यिका के साथ मेल खाता है, जो ठोस लाल रेखा के लंबवत है। इस प्रकार यदि हम नीले तीर के लंबवत M से होकर एक टूटी हुई लाल रेखा खींचते हैं, तो हम कह सकते हैं कि आधे मतदाता इस रेखा के बाईं ओर स्थित हैं। लेकिन चूँकि यह रेखा स्वयं ठोस लाल रेखा के बायीं ओर है, इसका अर्थ यह है कि आधे से अधिक मतदाता A को B से ऊपर स्थान देंगे।
सभी दिशाओं में माध्यिका और ज्यामितीय माध्यिका के बीच संबंध
जब भी कोई अद्वितीय सर्वदिशात्मक मध्यिका उपस्थित होती है, तो यह कॉन्डोर्सेट वोटर विधियों के परिणाम को निर्धारित करती है। उसी समय ज्यामितीय माध्यिका को वरीयता वाले चुनाव के आदर्श विजेता के रूप में पहचाना जा सकता है (चुनाव प्रणालियों की तुलना देखें)। इसलिए दोनों के बीच के संबंध को जानना जरूरी है। वास्तव में जब भी सभी दिशाओं में एक माध्यिका सम्मलित होती है (कम से कम असतत वितरण के मामले में), यह ज्यामितीय माध्यिका के साथ मेल खाता है।
लेम्मा । जब भी एक असतत वितरण में सभी दिशाओं में माध्य M होता है, तो M पर स्थित नहीं होने वाले डेटा बिंदुओं को M के दोनों ओर संतुलित जोड़े (A,A ') में इस संपत्ति के साथ आना चाहिए कि A - M - A' एक सीधी रेखा है ( अर्थात आरेख में ए 0 - M - ए 2 की तरह नहीं)।
प्रमाण । इस परिणाम को 1967 में चार्ल्स प्लॉट द्वारा बीजगणितीय रूप से सिद्ध किया गया था।[11] यहां हम दो विमाओं में विरोधाभास द्वारा सरल ज्यामितीय प्रमाण देते हैं।
मान लीजिए, इसके विपरीत, बिंदुओं का एक समूह A हैiजिनके पास सभी दिशाओं में माध्य के रूप में M है, लेकिन जिनके लिए बिंदु M के साथ मेल नहीं खाता है, वे संतुलित जोड़े में नहीं आते हैं। फिर हम इस सेट से M पर किसी भी बिंदु को हटा सकते हैं, और M के बारे में किसी भी संतुलित जोड़े को M के बिना किसी भी दिशा में माध्यिका बना सकते हैं; अतः M एक सर्वदिशात्मक माध्यक बना रहता है।
यदि शेष बिंदुओं की संख्या विषम है, तो M के माध्यम से आसानी से रेखा खींच सकते हैं, जैसे कि अधिकांश बिंदु इसके एक तरफ हों, जो M की माध्यिका विशेशता के विपरीत होता है।
यदि संख्या सम है, मान लीजिए 2n, तो हम बिंदुओं को A 0, A1,... को दक्षिणावर्त क्रम में M के बारे में किसी भी बिंदु से शुरू कर सकते हैं (आरेख देखें)। मान लीजिए θ चाप द्वारा M –A 0 से M –A n तक अंतरित कोण है। फिर यदि θ <180° जैसा कि दिखाया गया है, हम एम के माध्यम से टूटी हुई लाल रेखा के समान एक रेखा खींच सकते हैं, जिसके एक तरफ अधिकांश डेटा बिंदु हैं, फिर से एम की औसत संपत्ति का खंडन करते हैं; जबकि यदि θ > 180° वही दूसरी ओर के अधिकांश बिंदुओं पर लागू होता है। और यदि θ = 180°, तो A 0 और A n एक संतुलित युग्म बनाते हैं, जो एक अन्य धारणा का खंडन करता है।
प्रमेय। जब भी एक असतत वितरण में सभी दिशाओं में माध्य M होता है, तो यह अपने ज्यामितीय माध्यिका के साथ मेल खाता है।
प्रमाण । संतुलित जोड़े (ए, ए ') में डेटा बिंदुओं के किसी भी बिंदु पी से दूरी का योग लंबाई ए - पी - ए 'का योग है। जब रेखा सीधी होती है, तो इस रूप की प्रत्येक व्यक्तिगत लंबाई P पर कम से कम हो जाती है, जैसा कि तब होता है जब P, M के साथ मेल खाता है। P से M पर स्थित किसी भी डेटा बिंदु की दूरी इसी तरह कम हो जाती है जब P और M मेल खाते हैं। इस प्रकार जब P, M के साथ मेल खाता है, तो डेटा बिंदुओं से P तक की दूरी कम हो जाती है।
होटलिंग का नियम
अधिक अनौपचारिक अभिकथन - औसत मतदाता मॉडल - हेरोल्ड होटलिंग से संबंधित है । इसमें कहा गया है कि नीतिज्ञ औसत मतदाता के कब्जे वाली स्थिति की ओर बढ़ते हैं, या सामान्यतः चुनावी प्रणाली द्वारा समर्थित स्थिति की ओर बढ़ते हैं। 1929 में होटलिंग द्वारा इसे पहली बार (एक अवलोकन के रूप में, बिना किसी कठोरता के दावे के) सामने रखा गया था।[3]
होटललिंग ने राजनीतिज्ञों के व्यवहार को एक अर्थशास्त्री की दृष्टि से देखा। वह इस तथ्य से चकित थे कि एक विशेष सामान बेचने वाली दुकानें अधिकांशतः कस्बे के एक ही हिस्से में एकत्रित होती हैं, और उन्होंने इसे राजनीतिक दलों के अभिसरण के रूप में देखा। दोनों ही स्थितियों में यह बाजार हिस्सेदारी को अधिकतम करने के लिए एक तर्कसंगत नीति हो सकती है।
मानव प्रेरणा के किसी भी लक्षण वर्णन के साथ यह मनोवैज्ञानिक कारकों पर निर्भर करता है जो आसानी से अनुमानित नहीं होते हैं, और कई अपवादों के अधीन होते हैं। यह वोटर प्रणाली पर भी निर्भर है: जब तक चुनावी प्रक्रिया ऐसा नहीं करती है, तब तक राजनेता औसत मतदाता के साथ अभिसरण नहीं करेंगे।
माध्यिका मतदाता प्रमेय का उपयोग
प्रमेय उस प्रकाश के लिए मूल्यवान है जो यह कुछ वोटर प्रणालियों की इष्टतमता (और इष्टतमता की सीमा) पर डालता है।
वेलेरियो डोट्टी आवेदन के व्यापक क्षेत्रों की ओर इशारा करते हैं:
मेडियन वोटर थ्योरम पॉलिटिकल इकोनॉमी साहित्य में बहुत लोकप्रिय प्रमाणित हुआ है। इसका मुख्य कारण यह है कि इसे राजनीतिक प्रक्रिया की अन्य विशेषताओं से अलग करते हुए वोटर आबादी की कुछ विशेषताओं और नीतिगत परिणामों के बीच संबंध के परीक्षण योग्य निहितार्थ प्राप्त करने के लिए अपनाया जा सकता है। ।[10]
वह कहते हैं कि...
औसत मतदाता परिणाम अविश्वसनीय किस्म के प्रश्नों पर लागू किया गया है। पुनर्वितरण नीतियों (मेल्टज़र और रिचर्ड, 1981) में आय असमानता और सरकारी हस्तक्षेप के आकार के बीच संबंधों का विश्लेषण,[12]आप्रवासन नीतियों के निर्धारकों का अध्ययन (रज़ीन और सदका, 1999),[13] के उदाहरण हैं। आय के विभिन्न प्रकारों पर कराधान की सीमा (बैसेटो और बेन्हाबिब, 2006),[14] और भी बहुत कुछ।
यह भी देखें
- तीर की असंभवता प्रमेय
- मैककेल्वे-शोफिल्ड कैओस प्रमेय
- मध्य तंत्र
- रैंक मतदातािंग
संदर्भ
- ↑ Duncan Black, "On the Rationale of Group Decision-making" (1948).
- ↑ P. Dasgupta and E. Maskin, "The fairest vote of all" (2004); "On the Robustness of Majority Rule" (2008).
- ↑ 3.0 3.1 Hotelling, Harold (1929). "प्रतियोगिता में स्थिरता". The Economic Journal. 39 (153): 41–57. doi:10.2307/2224214. JSTOR 2224214.
- ↑ Holcombe, Randall G. (2006). Public Sector Economics: The Role of Government in the American Economy. p. 155. ISBN 9780131450424.
- ↑ See Black's paper.
- ↑ Berno Buechel, "Condorcet winners on median spaces" (2014).
- ↑ Anthony Downs, "An Economic Theory of Democracy" (1957).
- ↑ B. Grofman and S. L. Feld, "If you like the alternative vote (a.k.a. the instant runoff), then you ought to know about the Coombs rule" (2004).
- ↑ To be precise, it is the sample distribution of voter opinions which is relevant, and this is necessarily discrete. Results on continuous distributions are of interest only as indicating idealised or approximate behaviour of large samples.
- ↑ 10.0 10.1 See Valerio Dotti's thesis "Multidimensional Voting Models" (2016).
- ↑ C. R. Plott, "A Notion of Equilibrium and its Possibility Under Majority Rule" (1967).
- ↑ A. H. Meltzer and S. F. Richard, "A Rational Theory of the Size of Government" (1981).
- ↑ A. Razin and E. Sadka "Migration and Pension with International Capital Mobility" (1999).
- ↑ M. Bassetto and J. Benhabib, "Redistribution, Taxes, and the Median Voter" (2006).
अग्रिम पठन
- Buchanan, James M.; Tollison, Robert D. (1984). The Theory of Public Choice. Vol. II. Ann Arbor: University of Michigan Press. ISBN 0472080415.
- Clinton, Joshua D. (2006). "Representation in Congress: Constituents and the Roll Calls in the 106th House". Journal of Politics. 68 (2): 397–409. doi:10.1111/j.1468-2508.2006.00415.x.
- Congleton, Roger (2003). "The Median Voter Model" (PDF). In Rowley, C. K.; Schneider, F. (eds.). The Encyclopedia of Public Choice. Kluwer Academic Press. ISBN 978-0-7923-8607-0.
- Dasgupta, Partha and Eric Maskin, "On the Robustness of Majority Rule", Journal of the European Economic Association, 2008.
- Downs, Anthony (1957). "An Economic Theory of Political Action in a Democracy". Journal of Political Economy. 65 (2): 135–150. doi:10.1086/257897.
- Holcombe, Randall G. (1980). "An Empirical Test of the Median Voter Model". Economic Inquiry. 18 (2): 260–275. doi:10.1111/j.1465-7295.1980.tb00574.x.
- Holcombe, Randall G.; Sobel, Russell S. (1995). "Empirical Evidence on the Publicness of State Legislative Activities". Public Choice. 83 (1–2): 47–58. doi:10.1007/BF01047682. S2CID 44831293.
- Husted, Thomas A.; Kenny, Lawrence W. (1997). "The Effect of the Expansion of the Voting Franchise on the Size of Government". Journal of Political Economy. 105 (1): 54–82. doi:10.1086/262065.
- Krehbiel, Keith (2004). "Legislative Organization". Journal of Economic Perspectives. 18 (1): 113–128. doi:10.1257/089533004773563467.
- McKelvey, Richard D. (1976). "Intransitives in Multidimensional Voting Models and Some Implications for Agenda Control". Journal of Economic Theory. 12 (3): 472–482. doi:10.1016/0022-0531(76)90040-5.
- Schummer, James; Vohra, Rakesh V. (2013). "Mechanism Design Without Money". In Nisan, Noam; Roughgarden, Tim; Tardos, Eva; Vazirani, Vijay (eds.). Algorithmic Game Theory. New York: Cambridge University Press. pp. 246–252. ISBN 978-0-521-87282-9.
- Rice, Tom W. (1985). "An Examination of the Median Voter Hypothesis". Western Political Quarterly. 38 (2): 211–223. doi:10.2307/448625. JSTOR 448625.
- Romer, Thomas; Rosenthal, Howard (1979). "The Elusive Median Voter". Journal of Public Economics. 12 (2): 143–170. doi:10.1016/0047-2727(79)90010-0.
- Sobel, Russell S.; Holcombe, Randall G. (2001). "The Unanimous Voting Rule is not the Political Equivalent to Market Exchange". Public Choice. 106 (3–4): 233–242. doi:10.1023/A:1005298607876. S2CID 16736216.
- Waldfogel, Joel (2008). "The Median Voter and the Median Consumer: Local Private Goods and Population Composition". Journal of Urban Economics. 63 (2): 567–582. doi:10.1016/j.jue.2007.04.002. SSRN 878059.
बाहरी लिंक
श्रेणी:राजनीति विज्ञान के सिद्धांत श्रेणी:सार्वजनिक विकल्प [ सिद्धांत श्रेणी:वोटर सिद्धांत श्रेणी:गेम थ्योरी श्रेणी:गणितीय अर्थशास्त्र