दो नए विज्ञान

This article is about यह लेख गैलीलियो के काम के बारे में है।. For फ़ायर फ़्लाइज़ के एल्बम के लिए,, see दो नए विज्ञान देखें।.

दो नए विज्ञानों से संबंधित भाषण और गणितीय प्रदर्शन

Author	गैलीलियो गैलीली
Language	Italian, Latin
Published	1638

1638 में प्रकाशित दो नए विज्ञानों से संबंधित प्रवचन और गणितीय प्रदर्शन गैलीलियो गैलीली की अंतिम पुस्तक थी और [डी स्कॉर्सी इ डीडीमोस्ट्राटे टस्जो नी मेट म टिके इन टर्बो अड़ डुए नवो वी ईंटसे ] पिछले तीस वर्षों में भौतिकी में उनके अधिकांश कार्य को कवर करने वाला एक वैज्ञानिक वसीयतनामा था। यह आंशिक रूप से इतालवी और आंशिक रूप से लैटिन में लिखा गया था।

विश्व की दो प्रमुख प्रणालियों के विषय में उनकी बातचीत के बाद रोमन न्यायपालिका ने गैलीलियो की पुस्तक के प्रकाशन पर प्रतिबंध लगा दिया जिसमें कि वे भविष्य में लिख सकते थे। फ्रांस , जर्मनी तथा पोलैंड में अपने शुरुआती दो नए विज्ञानों की विफलता के बाद लॉडेविच एल्जिवर ने प्रकाशित किया जो लीडेन में कार्य कर रहे थे, दक्षिण हालैंड में, जहां न्यायालय की खोज के परिणाम के रूप में था (एल्ज़ेविर का घर देखें). वेनिस गणराज्य के आधिकारिक धर्मशास्त्री फ्रा फुलगेन्ज़ियो माइकान्ज़ियो ने शुरू में गैलीलियो को वेनिस में नए काम को प्रकाशित करने में मदद करने का प्रस्ताव रखा था, लेकिन उन्होंने बताया कि वेनिस में दो नए विज्ञानों को प्रकाशित करने से गैलीलियो को अनावश्यक परेशानी हो सकती है; इस प्रकार पुस्तक को अंततः हॉलैंड में प्रकाशित किया गया। ऐसा नहीं लगता कि गैलीलियो को इस पुस्तक के प्रकाशन की जांच से कोई क्षति हुई थी 1639 में रोम सरकार की पुस्तक स्टोर में पहुँची और सभी उपलब्ध प्रतियां लगभग 50 शीघ्र बिक गयीं।

भाषण की शैली को संवादों की तरह लिखे गए थे जिसमें तीन पुरुष (सिम्पलिसियो, साग्रेडो, तथा साल्वती) गैलीलियो के उत्तर देने वाले विभिन्न प्रश्नों पर चर्चा तथा बहस करते थे। चूंकि पुरुषों में उल्लेखनीय परिवर्तन किया जाता है सिंपलिसियो, विशेष रूप से आज भी उतनी ही सामान्य विचारधारा वाले जिद्दी तथा एस्थलियन नहीं होते है जैसा कि उसके नाम का अर्थ है। उनके तर्क गैलीलियो की अपनी शुरुआती मान्यताओं के प्रतिनिधि करते हैं, जैसा कि सग्रीडो उनके मध्य काल का प्रतिनिधित्व करता है, तथा सल्विती ने गैलीलियो के नवीनतम मॉडल का प्रस्ताव किया।

परिचय

पुस्तक को चार दिनों में बांटा गया है, प्रत्येक भौतिकी के विभिन्न क्षेत्रों को संबोधित करता है। गैलीलियो ने नोआइल्स के लॉर्ड काउंट को दो नए विज्ञान समर्पित किए।

पहले दिन के खंड में गैलीलियो के दो नए विज्ञानों में से चित्र 1

पहले गैलीलियो ने ऐसे विषयों को संबोधित किया, जिन पर अरस्तू की भौतिकी तथा एस्थेलियन स्कूल यांत्रिकी में चर्चा हुई। इसमें नये विज्ञान के बारे में परिचय दिया गया है। जिन विषयों पर विचार किया गया है उन विषयों के बीच समानता होती है ऐसी विशिष्ट प्रश्नों की परिकल्पना की गई है तथा शैली स्त्रोत ने सभी को अपने पहले दिन के लिए बैक-बोन प्रदान की है। पहले दिन वार्ता में वक्ताओं का परिचय देता है वही बातचीत में साल्विटी सग्रीडो तथा सालिसीयो ये तीनों व्यक्ति अपने जीवन के विभिन्न चरणों में गैलीलियो वक्ताओं का परिचय देता है। नये विज्ञानों के बारे में चर्चा का परिचय भी दिया गया है। दूसरे दिन पदार्थ के सवालों के बारे में संबोधित किया है

तीसरे तथा चौथे दिन गति विज्ञान को संबोधित करते हैं। तीसरे दिन प्रकृति रूप से त्वरित गति की चर्चा की जाती है, पहले दिन टर्मिनल वेग के अंक की चर्चा की जाती है चौथे दिन प्रक्षेप्य गति की चर्चा की जाती है

विज्ञान में समान गति को गति के रूप में परिभाषित किया गया है, जो किसी भी समान अवधि में समान दूरी को दर्शाता है। प्रमात्रक "किसी" के प्रयोग से पूर्व की परिभाषाओं की तुलना में एकरूपता का प्रवर्तन किया जाता है तथा स्पष्ट रूप से अभिव्यक्त किया जाता है।

गैलीलियो ने टकराव के बल पर अतिरिक्त दिन शुरू किया लेकिन अपनी संतुष्टि के लिए इसे पूरा नहीं कर पाए थे। चर्चा के पहले चार दिनों में इस खंड को अधिकांशतः उल्लेख किया गया था। यह अंततः केवल गैलीली के 1718 संस्करण में प्रकाशित हुआ। तथा यह प्रायः 1898 के संस्करण में संख्यांकन के बाद "छठे दिन" के रूप में उद्धृत किया जाता है। इस अतिरिक्त दिन के दौरान सिम्पलिसियो का स्थान पूर्व विद्वान तथा पडुआ में गैलीलियो के सहायक एप्रोइनो द्वारा ले लिया था।

सारांश

प्रत्येक पैराग्राफ की शुरुआत में पृष्ठ संख्या 1898 संस्करण से हैं, जिसे मानक मान लिया गया है तथा क्रू तथा ड्रेक अनुवादों में पाया जाता है।

पहला दिन: अलग होने के लिए शरीरों का प्रतिरोध

[50] प्रारंभिक चर्चा सग्रीदो को छोटा गैलीलियो समझ में नहीं आता कि मशीनों के कारण छोटे से बड़े में तर्क क्यों नहीं हो सकता "मुझे नहीं लगता कि मंडलियों, त्रिकोणों के गुण ठोस आंकड़े अपने आकार के साथ बदलना चाहिए। गैलीलियो के बोलते हुए सल्वती सामान्य रूप से गलत है। स्केल के स्थिति: 3 या 4 घन मीटर की ऊंचाई से गिरने वाला घोड़ा अपनी हड्डियों को तोड़ देता है जबकि बिल्ली दुगुनी ऊंचाई से गिरती है और किसी टावर से गिरने वाला कोई टिड्डा होता है।

[56] इसका पहला उदाहरण हैम्प रस्सी, जिसे छोटे रेशों से बनाया जाता है, जो एक-दूसरे से इस प्रकार बंधे होते हैं कि रस्सी विंडलास के इर्द-गिर्द तथा अधिक मज़बूत बनाने के लिए होती है। तब वैक्यूम से दो उच्च पालिश की गयी प्लेटों को अलग करने से बचा जा सकता है। सरग्रीदो ने वास्तव में यह देखा था कि सेजोड पम्प 18 हाथ से अधिक पानी नहीं उठा सकता तथा साल्विती का कहना है कि सक्शन पम्प शून्य के प्रति प्रतिरोधक मात्रा है। यह चर्चा तांबे के तार की ताकत पर बदल जाती है तथा धातु के भीतर सूक्ष्म रिक्त स्थान होते हैं या इसकी ताकत का कुछ तथा स्पष्टीकरण पर बदल जाती है।

[68] इसके फलस्वरूप अनन्तता तथा सातत्य का विवेचन होता है तथा तब यह देखने में आता है कि वर्गाकार की संख्या मूलों की संख्या के बराबर होती है।वे अंततः इस दृष्टिकोण से सहमत होते हैं कि 'यदि कोई संख़्या को अनंत कहा जा सके तो यह एकता होनी चाहिए' तथा यह ऐसी रचना को प्रदर्शित करता है जिसमें अनंत चक्र तक पहुंचता है तथा रेखा को विभाजित करता है।

[85] महीन धूल तथा तरल के बीच का अंतर प्रकाश की चर्चा की ओर ले जाता है तथा कैसे सूर्य की केंद्रित शक्ति धातुओं को पिघला सकती है। उन्होंने कहा कि प्रकाश में गति है तथा इसकी गति को मापने के असफल प्रयास का वर्णन करता है।

[106] अरस्तू का मानना था कि शरीर भार के अनुपात में तेजी से गिरता है परंतु इस संदेह में कि अरस्तू ने इसका परीक्षण किया था।उसकी यह भी मान्यता नहीं थी कि शून्य में गति संभव है, लेकिन हवा पानी की तुलना में काफी कम घनी होती है इसलिए साल्विती का कहना है कि किसी माध्यम के बिना ही निर्वात शरीर में ऊन का गोला अथवा थोड़ा-सा सीसा एक-सा ही गति से गिरेगा। बड़े तथा छोटे शरीर ही गति पर वायु या पानी के माध्यम से गिर जाते हैं। चूंकि आबनूस का वजन हजार गुना हवा होता है जिसे उसने मापा था यह सीसे बहुत कम धीरे धीरे ही गिरता है, जिसका वजन 10 गुना होता है। लेकिन आकार भी महत्वपूर्ण है-यहां तक कि सोने की पत्ती का टुकड़ा जो सब पदार्थों में सबसे अधिक गहरा होता है सल्विति हवा में तैरता है तथा वायु से भरा हुआ मूत्राशय सीसा की अपेक्षा धीरे-धीरे कम होता है।

[128] गिरने की गति को मापना मुश्किल है क्योंकि इसमें सम्मलित छोटे समय अंतराल तथा उसके पहले तरीके में समान लंबाई के पेंडुलम का उपयोग किया गया था लेकिन सीसा या कॉर्क वज़न के साथ दोलन की अवधि समान थी, भले ही कॉर्क को इस तथ्य की भरपाई के लिए अधिक व्यापक रूप से घुमाया गया था कि यह जल्द ही बंद हो गया।

[139] इससे तार के कंपन की चर्चा होती है तथा वह सुझाव देते हैं कि न केवल तार की लंबाई पिच के लिए महत्वपूर्ण है बल्कि तनाव तथा तार का वजन भी महत्वपूर्ण होता है।

दूसरा दिन: सामंजस्य का कारण

[151] साल्वती साबित करती है कि संतुलन का उपयोग न केवल समान भुजाओं के साथ किया जा सकता है, बल्कि असमान भुजाओं के साथ वजन के साथ आधार से दूरियों के व्युत्क्रमानुपाती के साथ भी किया जा सकता है। इसके बाद वह दिखाता है कि छोर पर समर्थित बीम द्वारा निलंबित भार का क्षण लंबाई के वर्ग के समानुपाती होता है। विभिन्न आकारों तथा मोटाई के बीमों के फ्रैक्चर के प्रतिरोध का प्रदर्शन किया जाता है, जो या दोनों सिरों पर समर्थित होता है।

[169] वह दिखाता है कि बड़े जानवरों के लिए जानवरों की हड्डियाँ आनुपातिक रूप से बड़ी होनी चाहिए तथा बेलन की लंबाई जो अपने वजन के नीचे टूट जाएगी। वह साबित करता है कि घुटने पर रखी छड़ी को तोड़ने का सबसे अच्छा स्थान मध्य है तथा यह दर्शाता है कि बीम के साथ कितनी दूर तक बड़ा वजन बिना तोड़े रखा जा सकता है।

[178] वह साबित करता है कि छोर पर समर्थित बीम तथा दूसरे पर भार वहन करने के लिए इष्टतम आकार परवलयिक है। वह यह भी दर्शाता है कि खोखले बेलन समान भार के ठोस बेलनों से अधिक मजबूत होते हैं।

तीन दिन: स्वाभाविक रूप से त्वरित गति

[191] वह पहले समान स्थिर गति को परिभाषित करता है तथा गति, समय तथा दूरी के बीच के संबंध को दर्शाता है। इसके बाद वह समान त्वरित गति को परिभाषित करता है जहां गति समय की वृद्धि में समान राशि से बढ़ जाती है।शरीर का पतन बहुत धीरे-धीरे शुरू होता है तथा वह यह दिखाने के लिए निकलता है कि उनका वेग समय के साथ सरल अनुपात में बढ़ता है, न कि दूरी जिसे वह दिखाता है असंभव है।

[208] उन्होंने दिखाया है कि प्राकृतिक रूप से त्वरित गति से की जाने वाली दूरी, समय के वर्ग के अनुपात में होती है। उन्होंने ऐसे प्रयोग का वर्णन किया है जिसमें ओर लकड़ी के ढलाई के टुकड़े की सिलाई में स्टील की गेंद को लपेटकर 4.5 मीटर लंबी तथा एक-दो हाथ में ले जाया जाता है।यह बड़ी जग के पानी के नीचे से जेट के पतले पाइप में से निकला पानी की मात्रा का सही नाप कर मापने के समय को दोहराया गया था। इस दृष्टि से वे समान रूप से त्वरित गति के सत्यापन में सफल रहे। तब वह दिखाता है कि विमान का झुकाव चाहे जो भी हो किसी दी गई ऊर्ध्वाधर ऊंचाई को गिरने में लगने वाले समय का वर्ग झुकी हुई दूरी के समानुपाती होता है।

[221] इसके बाद वह वृत्त के साथ अवतरण को भी मानता है तथा यह भी दर्शाता है कि समय बिल्कुल वैसा ही है जैसा कि उस समय का समय होता है जो शिखर से नीचे गिरता है तथा विमानों के अन्य प्रकार के संयोग से मिल जाता है। वह ब्रेकिस्टोक्रोन समस्या का गलत समाधान देता है जिसमें यह सिद्ध करने का दावा है कि वृत्त-चाप सबसे तेज वंश है। 16 हल के साथ समस्याओं को दिया जाता हैं।

चौथा दिन: प्रक्षेप्य की गति

गैलीलियो के दो नए विज्ञानों के चौथे दिन का अंतिम आंकड़ा

[268] प्रक्षेप्य की गति में समान क्षैतिज गति तथा स्वाभाविक रूप से त्वरित ऊर्ध्वाधर गति का संयोजन होता है जो परवलय वक्र का निर्माण करता है। समकोण पर दो गतियों की गणना वर्गों के योग का उपयोग करके की जा सकती है। वह विस्तार से दिखाता है कि विभिन्न स्थितियों में परवलय का निर्माण कैसे किया जाता है तथा प्रक्षेपित कोण के आधार पर ऊँचाई तथा सीमा के लिए तालिकाएँ को दर्शाता है।

[274] वायु प्रतिरोध खुद को दो तरह से दिखाता है: कम घने पिंडों को अधिक प्रभावित करके तथा तेज़ पिंडों को अधिक प्रतिरोध देकर। लीड बॉल ओक बॉल की तुलना में थोड़ी तेजी से गिरेगी, लेकिन स्टोन बॉल के साथ अंतर नगण्य है। चूंकि गति अनिश्चित काल तक नहीं बढ़ती है लेकिन अधिकतम तक पहुँच जाती है। यद्यपि छोटी गति पर वायु प्रतिरोध का प्रभाव कम होता है, यह विचार करते समय अधिक होता है तथा कहते हैं की तोप से दागी गई गेंद के रूप में होता है।

[292] यदि लक्ष्य को स्थानांतरित करने के लिए स्वतंत्र है तो लक्ष्य को मारने वाले प्रक्षेप्य का प्रभाव कम हो जाता है। गतिमान पिंड का वेग बड़े पिंड के वेग को पार कर सकता है यदि इसकी गति प्रतिरोध से आनुपातिक रूप से अधिक होती है।

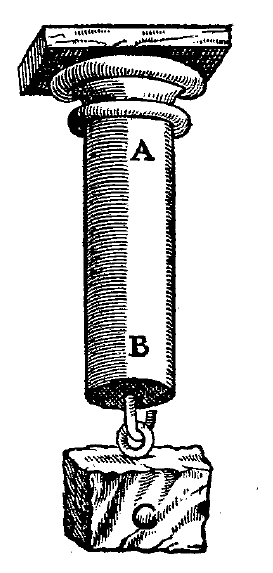
[310] खींची गई रस्सी या जंजीर कभी भी समतल नहीं होती, बल्कि परवलय के समान होती है। लेकिन ज़ंजीर को चित्र में देखें।

अतिरिक्त दिन: टक्कर का बल

[323] तुला भुजा पर लटकी बाल्टी से उसी भुजा पर लटकी दूसरी बाल्टी पर गिरने वाले पानी का भार कितना होता है।

[325] नींव के लिए लकड़ी के खंभों का जमाव हथौड़ों तथा टक्कर की ताकत होता है।

[336] झुके हुए विमानों के साथ गिरने की गति; फिर से जड़ता के सिद्धांत पर आधारित होती है।

कार्यप्रणाली

कई समकालीन वैज्ञानिक, जैसे कि पियरे गैसेंडी , गिरने वाले निकायों के अपने कानून की अवधारणा के लिए गैलीलियो की पद्धति का विवाद करते हैं। मुख्य तर्कों में से दो यह हैं कि उनकी ज्ञानमीमांसा ने प्लैटोनिस्ट विचार या हाइपोथेटिको-डिडक्टिविस्ट के उदाहरण का अनुसरण किया। भविष्य में इसी तरह के प्रभावों के उत्पादन के लिए आवश्यकताओं को निर्धारित करने के लिए इसे अब भूतपूर्व माना जाता है, या अतीत की घटनाओं से कैसे तथा क्यों प्रभावों को जानने के लिए माना जाता है। गैलीलियन पद्धति ने अरिस्टोटेलियन तथा आर्किमिडीयन ज्ञानमीमांसा को प्रतिबिम्बित किया। 1615 में कार्डिनल बेलार्माइन के पत्र के बाद गैलीलियो ने अपने तर्कों तथा कोपरनिकस को 'प्राकृतिक अनुमानों' के रूप में प्रतिष्ठित किया, जो कि केवल खगोलीय संगणनाओं के लिए पेश किए गए कल्पित के विपरीत है, जैसे कि विलक्षणता तथा समीकरणों पर प्लेटो की परिकल्पना।

गैलीलियो के पहले के लेखन को जुवेनिलिया, या युवा लेखन माना जाता है, पडुआ विश्वविद्यालय में अध्यापन के दौरान आकाशीय गति के अपने पाठ्यक्रम की परिकल्पना के लिए व्याख्यान नोट्स बनाने का उनका पहला प्रयास माना जाता है। इन नोटों ने कोलेजियो में उनके समकालीनों के साथ-साथ निश्चित थॉमिस्टिक सेंट थॉमस एक्विनास ओवरटोन के साथ अरिस्टोटेलियन संदर्भ को भी सम्मलित किया। ऐसा माना जाता है कि इन पहले के पत्रों ने गति पर उनकी खोजों को वैधता देने के लिए उन्हें प्रदर्शनकारी सबूत लागू करने के लिए प्रोत्साहित किया था।

फोलियो 116 वी की खोज से उन प्रयोगों के साक्ष्यदेती है जिनकी रिपोर्ट पहले नहींकिए गए थे तथा इस प्रकार गिरने वाले निकायों के कानून के बारे में गैलीलियो की वास्तविक गणना का प्रदर्शन किया गया था.

जेम्स मैकलाचलन, स्टिलमैन ड्रेक, आर.एच. टेलर तथा अन्य जैसे वैज्ञानिकों द्वारा की गई रिकॉर्डिंग तथा मनोरंजन से उनके प्रयोग के तरीकों को साबित किया गया है ताकि यह साबित किया जा सके कि जैसा कि इतिहासकार एलेक्जेंडर कोयरे ने तर्क दिया था, उन्होंने न केवल अपने विचारों की कल्पना की थी, बल्कि उन्हें गणितीय रूप से साबित करने की कोशिश की थी। .

गैलीलियो का मानना ​​था कि ज्ञान तर्क के माध्यम से प्राप्त किया जा सकता है, तथा अवलोकन तथा प्रयोग के माध्यम से प्रबलित किया जा सकता है। इस प्रकार, यह तर्क दिया जा सकता है कि गैलीलियो बुद्धिवादी थे, तथा यह भी कि वे अनुभववादी थे।

दो नए विज्ञान

शीर्षक में वर्णित दो विज्ञान सामग्री की ताकत तथा वस्तुओं की गति (आधुनिक सामग्री विज्ञान तथा गतिकी के अग्रदूत) हैं। पुस्तक के शीर्षक में यांत्रिकी तथा गति भिन्न-भिन्न हैं, क्योंकि गैलीलियो के समय में यांत्रिकी का अर्थ केवल सामग्री की स्थिति तथा शक्ति था।

सामग्री का विज्ञान

चर्चा उन कारणों के प्रदर्शन के साथ शुरू होती है कि बड़ी संरचना ठीक उसी तरह से आनुपातिक होती है जिस तरह छोटी संरचना को आवश्यक रूप से वर्ग-घन कानून के रूप में जाना जाता है। बाद में चर्चा में इस सिद्धांत को बड़े जानवर की हड्डियों के लिए आवश्यक मोटाई पर लागू किया जाता है, संभवतः जीव विज्ञान में पहला मात्रात्मक परिणाम, जॉन मेनार्ड स्मिथ द्वारा संपादित जे.बी.एस.

वस्तुओं की गति

गैलीलियो पहली बार गिरते हुए पिंड के निरंतर त्वरण को स्पष्ट रूप से व्यक्त करता है जिसे वह झुके हुए विमान का उपयोग करके इसे धीमा करके सटीक रूप से मापने में सक्षम था।

दो नए विज्ञानों में, गैलीलियो (सल्विती उसके लिए बोलती है) ने लकड़ी की ढलाई (सजावटी), 12 हाथ लंबी, आधा हाथ चौड़ी तथा तीन अंगुल-चौड़ाई सीधी, चिकनी, पॉलिश नाली (इंजीनियरिंग) के साथ झुके हुए विमान के रूप में उपयोग की। रोलिंग बॉल्स ( कठोर, चिकनी तथा बहुत गोल कांस्य गेंद) का अध्ययन करें। उन्होंने चर्मपत्र के साथ खांचे को पंक्तिबद्ध किया, जितना संभव हो उतना चिकना तथा पॉलिश किया। उन्होंने रैंप को विभिन्न कोणों पर झुकाया, प्रभावी रूप से त्वरण को काफी धीमा कर दिया ताकि वह बीता हुआ समय माप सके। वह गेंद को रैंप के नीचे ज्ञात दूरी पर लुढ़कने देगा, तथा ज्ञात दूरी को स्थानांतरित करने में लगने वाले समय को मापने के लिए पानी की घड़ी का उपयोग करेगा। यह घड़ी थी

ऊंचे स्थान पर रखा गया पानी का बड़ा बर्तन; इस बर्तन के तल में पानी की पतली धारा देने वाले छोटे व्यास का पाइप मिलाप किया गया था, जिसे हमने प्रत्येक अवतरण के समय छोटे गिलास में एकत्र किया, चाहे वह चैनल की पूरी लंबाई के लिए हो या उसकी लंबाई के हिस्से के लिए। एकत्र किए गए पानी का वजन किया गया था, तथा प्रत्येक वंश के बाद बहुत ही सटीक संतुलन पर, इन भारों के अंतर तथा अनुपात ने उन्हें समय के अंतर तथा अनुपात दिए। यह इतनी सटीकता के साथ किया गया था कि यद्यपि ऑपरेशन को कई बार दोहराया गया था, परिणामों में कोई उल्लेखनीय विसंगति नहीं थी।

गिरने वाले निकायों का कानून

जबकि अरस्तू ने देखा था कि भारी वस्तुएं हल्की वस्तुओं की तुलना में अधिक तेजी से गिरती हैं, दो नए विज्ञानों में गैलीलियो ने कहा कि यह भारी वस्तुओं पर कार्य करने वाली स्वाभाविक रूप से मजबूत ताकतों के कारण नहीं था, बल्कि वायु प्रतिरोध तथा घर्षण की प्रतिकारक शक्तियों के कारण था। क्षतिपूर्ति करने के लिए, उन्होंने उथले झुकाव वाले रैंप का उपयोग करते हुए प्रयोग किए, जितना संभव हो उतना घर्षण को खत्म करने के लिए चिकना किया, जिस पर उन्होंने विभिन्न भारों की गेंदों को लुढ़का दिया। इस तरह, वह अनुभवजन्य साक्ष्य प्रदान करने में सक्षम था कि द्रव्यमान गुरुत्वाकर्षण के प्रभाव के कारण द्रव्यमान की परवाह किए बिना स्थिर दर पर लंबवत रूप से नीचे की ओर बढ़ता है। फोलियो 116V में पाया गया अप्रमाणित प्रयोग गुरुत्वाकर्षण के कारण गिरने वाले पिंडों में त्वरण की निरंतर दर का परीक्षण करता है। इस प्रयोग में गेंद को निर्दिष्ट ऊंचाई से डिफ्लेक्टर पर गिराना सम्मलित था ताकि इसकी गति को लंबवत से क्षैतिज तक स्थानांतरित किया जा सके। अपेक्षित क्षैतिज गति की गणना करने के लिए इच्छुक विमान प्रयोगों के डेटा का उपयोग किया गया था। चूंकि , प्रयोग के परिणामों में विसंगतियाँ पाई गईं: देखी गई क्षैतिज दूरियाँ त्वरण की स्थिर दर के लिए अपेक्षित परिकलित दूरियों से असहमत थीं। गैलीलियो ने असंगत प्रयोग में वायु प्रतिरोध तथा झुकाव वाले विमान प्रयोग में घर्षण के लिए विसंगतियों को जिम्मेदार ठहराया। इन विसंगतियों ने गैलीलियो को यह दावा करने के लिए मजबूर किया कि सिद्धांत केवल आदर्श परिस्थितियों में आयोजित किया जाता है, अर्थात घर्षण तथा /या वायु प्रतिरोध की अनुपस्थिति में।

गतिशील निकाय

अरिस्टोटेलियन भौतिकी ने तर्क दिया कि पृथ्वी को गति नहीं करनी चाहिए क्योंकि मनुष्य इस गति के प्रभावों को समझने में असमर्थ हैं। इसका लोकप्रिय औचित्य तीरंदाज द्वारा सीधे हवा में तीर मारने का प्रयोग है। अरस्तू ने तर्क दिया कि यदि पृथ्वी गति कर रही थी, तो तीर को प्रक्षेपण बिंदु से भिन्न स्थान पर गिरना चाहिए। गैलीलियो ने दो प्रमुख विश्व प्रणालियों के संबंध में संवादों में इस तर्क का खंडन किया। उन्होंने समुद्र में नाव पर सवार नाविकों का उदाहरण दिया। नाव स्पष्ट रूप से गति में है, लेकिन मल्लाह इस गति को महसूस करने में असमर्थ हैं। यदि नाविक मस्तूल से भारित वस्तु को गिराता है, तो यह वस्तु मस्तूल के पीछे की बजाय (जहाज की आगे की गति के कारण) के आधार पर गिर जाएगी। यह साथ जहाज, नाविकों तथा गेंद की क्षैतिज तथा ऊर्ध्वाधर गति का परिणाम था।

गतियों की सापेक्षता

गैलीलियो डिस्कोर्सी (1638) में चित्र गतियों की सापेक्षता को दर्शाता है

गिरने वाले पिंडों के संबंध में गैलीलियो के प्रयोगों में से यह था कि गतियों की सापेक्षता का वर्णन करते हुए, यह समझाते हुए कि, सही परिस्थितियों में, गति को दूसरे पर बिना किसी प्रभाव के आरोपित किया जा सकता है ...। दो नए विज्ञानों में, गैलीलियो ने इस तर्क के लिए अपना पक्ष रखा तथा यह न्यूटन के पहले नियम, जड़ता के नियम का आधार बन गया।

वह सवाल उठाता है कि नौकायन जहाज के मस्तूल से गिराई गई गेंद या डेक पर हवा में फेंके गए तीर का क्या होता है। अरस्तू की भौतिकी के अनुसार, गिराई गई गेंद को जहाज के स्टर्न पर उतरना चाहिए क्योंकि यह मूल बिंदु से सीधे नीचे गिरती है। इसी तरह यदि जहाज चल रहा हो तो तीर को सीधा ऊपर की ओर फेंके जाने पर उसी स्थान पर नहीं गिरना चाहिए। गैलीलियो की पेशकश है कि खेल में दो स्वतंत्र गतियाँ हैं। गुरुत्वाकर्षण के कारण होने वाली त्वरित ऊर्ध्वाधर गति है, जबकि दूसरी गतिमान जहाज के कारण एकसमान क्षैतिज गति है जो जड़ता के सिद्धांत के माध्यम से गेंद के प्रक्षेपवक्र को प्रभावित करती रहती है। इन दो गतियों के संयोजन से परवलयिक वक्र बनता है। प्रेक्षक इस परवलयिक वक्र की पहचान नहीं कर सकता क्योंकि गेंद तथा प्रेक्षक जहाज द्वारा उन्हें प्रदान की गई क्षैतिज गति को साझा करते हैं, जिसका अर्थ है कि केवल लंबवत, ऊर्ध्वाधर गति ही बोधगम्य है। आश्चर्यजनक रूप से, किसी ने भी इस सिद्धांत का परीक्षण निर्णायक परिणाम प्राप्त करने के लिए आवश्यक सरल प्रयोगों के साथ नहीं किया था जब तक कि पियरे गसेन्डी ने डी मोटू इम्प्रेसो ए मोटोर ट्रांसलेटो (1642) नामक अपने पत्रों में उक्त प्रयोगों के परिणामों को प्रकाशित नहीं किया था।

अनंत

Main article: गैलीलियो का विरोधाभास

पुस्तक में अनंत की चर्चा भी है। गैलीलियो संख्या तथा वर्ग संख्या का उदाहरण देते हैं। वह यह ध्यान देकर शुरू करता है

इस बात से इंकार नहीं किया जा सकता है कि जितनी संख्याएँ हैं उतने वर्ग हैं क्योंकि प्रत्येक संख्या किसी न किसी वर्ग का मूल होता है

1 ↔ 1, 2 ↔ 4, 3 ↔ 9, 4 ↔ 16, तथा इसी तरह।

(आधुनिक भाषा में, धनात्मक पूर्णांक N के समुच्चय तथा वर्ग S के समुच्चय के तत्वों के बीच आपत्ति है, तथा S प्राकृतिक घनत्व का उचित उपसमुच्चय है।) लेकिन वह ध्यान देता है कि विरोधाभास क्या प्रतीत होता है:

फिर भी शुरुआत में हमने कहा कि वर्गों की तुलना में कई अधिक संख्याएँ हैं, क्योंकि उनमें से बड़ा हिस्सा वर्ग नहीं है। इतना ही नहीं, बल्कि जैसे-जैसे हम बड़ी संख्या में बढ़ते हैं, वर्गों की आनुपातिक संख्या कम होती जाती है।

वह अनंत संख्याओं की तुलना ( तथा अनंत तथा परिमित संख्याओं की तुलना करने) की संभावना को नकार कर विरोधाभास का समाधान करता है:

हम केवल यह अनुमान लगा सकते हैं कि सभी संख्याओं का योग अनंत है, कि वर्गों की संख्या अनंत है, तथा उनकी जड़ों की संख्या अनंत है; न तो वर्गों की संख्या सभी संख्याओं की समग्रता से कम है, तथा न ही बाद वाला पूर्व से अधिक है; तथा अंत में गुण समान, अधिक तथा कम, अनंत पर लागू नहीं होते, बल्कि केवल परिमित, मात्राओं पर लागू होते हैं।

इस निष्कर्ष ने, असीम सेटों को वर्णित करते हुए, असंभव को निर्धारित किया है, क़्योंकि इन दोनों स्वाभाविक तरीकों से प्राप्त परस्पर-विरोधी परिणाम इस समस्या के समाधान के लिए उपयोगी हैं जो कि आधुनिक गणित में प्रयोग की विधियों के समान है, परंतु उससे कम शक्तिशाली है.इस समस्या का समाधान गैलीलियो की पहली परिभाषा को देखते हुए सामान्यीकृत किया जा सकता है कि इस सेट का आकार से दूसरे के पत्राचार में क्या अर्थ है। इससे स्पष्ट हो जाता है कि अनन्त सेटों के आकार की तुलना विरोधाभासी परिणामों से की जा सकती है।

अनंतता के ये मुद्दे रोलिंग चक्र की समस्याओं से उत्पन्न होते हैं। यदि दो संकेन्द्रित वृत्तों की रेखा के साथ-साथ दो संकेन्द्रित वृत्त हों, तब यदि बड़ी रेखा फिसलने न लगे तो यह स्पष्ट हो जाता है कि छोटी गेंद फिसलनी चाहिए। लेकिन किस तरह से?गैलीलियो ने मामले को षट्भुज पर विचार करते हुए तथा उसके बाद उसे 100 हजार भुजों या एन-गनों की बालियां बताते हुए स्पष्ट करने का प्रयास किया है.अन्त में, वे समापन करते हैं, तब अंत में बड़े वृत्त से गुजरने वाली रेखा में अनंत अंकों की संख्या होती है जो उसे पूर्णतया भर देती है;जिस बिंदु को छोटे वृत्त द्वारा खोजा जाता है, उसमें अनंत संख्या में वे बिंदु हैं जो खाली स्थानों को छोड़ते हैं तथा केवल आंशिक रूप से रेखा को भर देते हैं।

टिप्पणीकारों द्वारा प्रतिक्रियाएं

भौतिकी में इतना बड़ा योगदान 'दो नए विज्ञान' का था कि विद्वानों ने लंबे समय तक बनाए रखा है कि पुस्तक ने आइजैक न्यूटन के गति के नियमों का अनुमान लगाया था।

— स्टीफन हॉकिंग पी. 397, ऑन द शोल्डर ऑफ जिअंट्स।

गैलीलियो वास्तव में आधुनिक विज्ञान के आधुनिक भौतिकी के जनक हैं

— अल्बर्ट आइंस्टीन पी 398, जिअंट्स के कंधों पर है।

गणित के दो नये विज्ञानों का भाग शुद्ध गणित था, जैसा कि गणितज्ञ अल्फ्रेड रेन्ययी ने बताया था कि यह गणित पर 2000 से अधिक वर्षों में सर्वाधिक महत्वपूर्ण पुस्तक थी: यूनानी गणित ने गति से संबंधित नहीं था, तथा इसलिए उन्होंने गणितीय नियमों की रचना नहीं की, हालांकि आर्किमिडीज में विभेदन तथा एकीकरण का विकास हुआ। दो नये विज्ञानों ने पहली बार गणितीय गति को गणितीय ढंग से रखकर भौतिकी के इलाज का मार्ग प्रशस्त किया। ग्रीक गणितज्ञ जेनो ने अपने विरोधाभासों को इस बात के प्रमाण के लिए तैयार किया था कि इस प्रस्ताव को गणितीय तरीके से नहीं समझा जा सकता तथा ऐसा करने के किसी भी प्रयास से विरोधाभासी पैदा हो सकते हैं। इसे वह गणित की अनिवार्य सीमा मानते हैं। अरस्तू ने इस विश्वास को बल दिया था कि गणित अपरिवर्तनीय वस्तुओं से ही निपट सकता था। गैलीलियो ने ग्रीक लोगों के पद्धति का उपयोग यह दिखाने के लिए किया कि उस प्रस्ताव का गणित के साथ इलाज किया जा सकता है। उनका विचार था-जीन की विरोधाभासों से अनंत के विरोधाभासों को अलग करना.यह कार्य उन्होंने अनेक चरणों में किया।पहले, उन्होंने दिखाया कि 1, 4, 9, 16, वर्गों की अनंत अनुक्रम एसभी सकारात्मक पूर्णांक (अनंत) के अनुक्रम N के रूप में कई तत्वों के रूप में निहित;अब इसे गैलीलियो का विरोधाभास कहा जाता है। फिर, ग्रीक शैली ज्यामिति का उपयोग करते हुए, उन्होंने छोटी लाइन अंतराल दिखाया जिसमें लंबे अंतराल के रूप में कई बिंदु सम्मलित थे.किसी न किसी समय वे छोटे अनन्त समूह के जितने भी बिंदुएं इसमें समाहित हैं उतनी ही अधिक हो सकते हैं।

गैसेंदी के विचार

पियरे गैसेंडी ने गैलीलियो की अपनी पुस्तक द मोटु इंप्रेस में उनके विचारों का बचाव किया। हॉवर्ड जोंस के लेख में गैससेदी ने गैलीलियो की रक्षा विवेक की राजनीति में जोंस ने गैलीलियो के तर्कों को समझना तथा पृथ्वी के प्रस्ताव पर शारीरिक आपत्तियों के उनके फलितयों को स्पष्ट रूप से समझ लिया।

कोयरे के विचार

शरीर गिरने का नियम 1638 में गैलीलियो द्वारा प्रकाशित किया गया था। परन्तु 20 वीं सदी में कुछ अधिकारियों ने गैलीलियो के प्रयोगों की वास्तविकता को चुनौती दी।विशेष रूप से, विज्ञान एलेक्जेंडर कोयरे के फ्रांसीसी इतिहासकार ने अपने इस तथ्य पर संदेह व्यक्त किया कि जिन प्रयोगों के बारे में दो नये विज्ञानों में गिरते हुए निकायों के कानून को बढ़ाने के लिए उल्लेख किया गया है, उनके लिए समय की सही-सही माप आवश्यक है जो 1600 की प्रौद्योगिकी के साथ असंभव लगता है।कोयरे के अनुसार, कानून की कटौती कर ली गई थी तथा ये प्रयोग केवल उदाहरण के तौर पर किए गए थे। वास्तव में ऊपर वर्णित गैलीलियो के पानी की घड़ी ने उनके अनुमानों की पुष्टि के लिए काफी सही समय प्रदान किया।

चूंकि, बाद में किये गये शोध के आधार पर इस प्रयोग की पुष्टि हो गयी है। गैलीलियो द्वारा वर्णित विधियों का प्रयोग कर गिरते हुए पिंड वास्तव में रोलिंग बॉल्स के प्रयोगों की पुनरावृत्ति की गई।, तथा परिणामों की सटीकता गैलीलियो की रिपोर्ट के अनुरूप थी। बाद में 1604 से गैलीलियो के अप्रकाशित वर्किंग पेपर्स में शोध ने स्पष्ट रूप से प्रयोगों की वास्तविकता को दिखाया तथा यहां तक ​​कि उन विशेष परिणामों को भी इंगित किया जो समय-वर्ग कानून का नेतृत्व करते थे।

यह भी देखें

• डी मोटू एंटिकियोरा गैलीलियो की गिरते निकायों की गति की प्रारंभिक जांच

टिप्पणियाँ

संदर्भ

• Drake, Stillman, translator (1974). Two New Sciences, University of Wisconsin Press, 1974. ISBN 0-299-06404-2. A new translation including sections on centers of gravity and the force of percussion.
• Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN 978-0-226-16226-3.
• Henry Crew and Alfonso de Salvio, translators, [1914] (1954). Dialogues Concerning Two New Sciences, Dover Publications Inc., New York, NY. ISBN 978-0-486-60099-4. The classic source in English, originally published by McMillan (1914).
• Jones, Howard, "Gassendi's Defense of Galileo: The Politics of Discretion", Medieval Renaissance Texts and Studies, 1988.
• Titles of the first editions taken from Leonard C. Bruno 1989, The Landmarks of Science: from the Collections of the Library of Congress. ISBN 0-8160-2137-6 Q125.B87
• Galileo Galilei, Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti la meccanica e i movimenti locali (pag.664, of Claudio Pierini) publication Cierre, Simeoni Arti Grafiche, Verona, 2011, ISBN 9788895351049.
• Wallace, Willian, A. Galileo and Reasoning Ex Suppositione: The Methodology of the Two New Sciences. PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association, Vol. 1974, (1974), pp. 79–104
• Salvia, Stafano (2014). "'Galileo's Machine': Late Notes on Free Fall, Projectile Motion, and the Force of Percussion (ca. 1638–1639)". Physics in Perspective. 16 (4): 440–460. Bibcode:2014PhP....16..440S. doi:10.1007/s00016-014-0149-1. S2CID 122967350.
• De Angelis, Alessandro (2021). Discorsi e Dimostrazioni Matematiche di Galileo Galilei per il Lettore Moderno (in italiano). Torino: Codice. ISBN 978-8875789305.
• De Angelis, Alessandro (2021). Galilei's Two New Sciences for Modern Readers (in English). Heidelberg: Springer Nature. ISBN 978-3030719524. With prefaces by Ugo Amaldi and Telmo Pievani.

बाहरी कड़ियाँ

• (in Italian) Italian text with figures
• English translation by Crew and de Salvio, with original figures
• Another on-line copy of Crew and de Salvio's translation