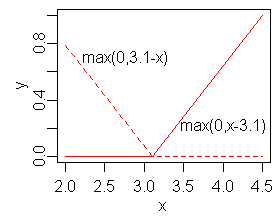रैंप फंक्शन

रैंप फ़ंक्शन के एक फ़ंक्शन का ग्राफ़

बढ़ाना फ़ंक्शन एक एकात्मक समारोह वास्तविक फ़ंक्शन है, जिसका फ़ंक्शन का ग्राफ़ रैंप के आकार का होता है। इसे कई #परिभाषाओं द्वारा व्यक्त किया जा सकता है, उदाहरण के लिए नकारात्मक इनपुट के लिए 0, आउटपुट गैर-नकारात्मक इनपुट के लिए इनपुट के बराबर है। रैंप शब्द का उपयोग स्केलिंग और स्थानांतरण द्वारा प्राप्त अन्य कार्यों के लिए भी किया जा सकता है, और इस लेख में फ़ंक्शन यूनिट रैंप फ़ंक्शन (ढलान 1, 0 से शुरू) है।

गणित में, रैम्प फलन को धनात्मक भाग के रूप में भी जाना जाता है।

यंत्र अधिगम में, इसे आमतौर पर रेक्टिफायर_(न्यूरल_नेटवर्क्स) सक्रियण समारोह के रूप में जाना जाता है या विद्युत अभियन्त्रण में आधा लहर सुधार के अनुरूप एक रेक्टिफायर (तंत्रिका नेटवर्क)। आँकड़ों में (जब संभावना कार्य के रूप में उपयोग किया जाता है) इसे टोबिट मॉडल के रूप में जाना जाता है।

इस फ़ंक्शन में गणित और इंजीनियरिंग में कई #अनुप्रयोग हैं, और संदर्भ के आधार पर विभिन्न नामों से जाना जाता है। रैंप फ़ंक्शन के रेक्टीफायर_ (तंत्रिका_नेटवर्क) # अन्य_गैर-रैखिक_वेरिएंट हैं।

परिभाषाएँ

रैंप समारोह (R(x) : R → R₀⁺) विश्लेषणात्मक रूप से कई तरीकों से परिभाषित किया जा सकता है। संभावित परिभाषाएँ हैं:

• एक टुकड़े का कार्य:
  $$R(x):={\begin{cases}x,&x\geq 0;\\0,&x<0\end{cases}}$$
• मैक्सिमा और मिनिमा:
  $$R(x):=\max(x,0)$$
• एक स्वतंत्र चर और उसके निरपेक्ष मूल्य का अंकगणितीय माध्य (एकता ढाल और उसके मापांक के साथ एक सीधी रेखा):
  $$R(x):={\frac {x+|x|}{2}}$$
  यह निम्नलिखित परिभाषा को ध्यान में रखते हुए प्राप्त किया जा सकता है max(a, b),
  $$\max(a,b)={\frac {a+b+|a-b|}{2}}$$
  जिसके लिए a = x और b = 0
• हैवीसाइड स्टेप फंक्शन को एकता ग्रेडिएंट के साथ एक सीधी रेखा से गुणा किया जाता है:
  $$R\left(x\right):=xH(x)$$
• खुद के साथ हीविसाइड स्टेप फंक्शन का कनवल्शन:
  $$R\left(x\right):=H(x)*H(x)$$
• हैविसाइड स्टेप फंक्शन का अभिन्न अंग:
  $$R(x):=\int _{-\infty }^{x}H(\xi )\,d\xi$$
• मैकाले कोष्ठक:
  $$R(x):=\langle x\rangle$$
• पहचान कार्य के सकारात्मक और नकारात्मक भाग:
  $$R:=\operatorname {id} ^{+}$$

अनुप्रयोग

रैंप फ़ंक्शन में इंजीनियरिंग में कई अनुप्रयोग हैं, जैसे कि अंकीय संकेत प्रक्रिया के सिद्धांत में।

अदायगी और कॉल विकल्प खरीदने से मुनाफा।

वित्त में, कॉल विकल्प का भुगतान एक रैंप (स्ट्राइक प्राइस द्वारा स्थानांतरित) है। रैम्प को क्षैतिज रूप से फ़्लिप करने से एक पुट विकल्प प्राप्त होता है, जबकि लंबवत रूप से फ़्लिप करना (नकारात्मक लेना) एक विकल्प को बेचने या छोटा करने से मेल खाता है। वित्त में, आकार को [[आइस हाँकी स्टिक ]] के समान होने के कारण व्यापक रूप से हॉकी स्टिक कहा जाता है।

x=3.1 पर एक गांठ के साथ बहुभिन्नरूपी अनुकूली प्रतिगमन स्प्लाइन#हिंज फ़ंक्शंस की एक मिरर की गई जोड़ी

आँकड़ों में, बहुभिन्नरूपी अनुकूली प्रतिगमन splines # बहुभिन्नरूपी अनुकूली प्रतिगमन splines (MARS) के काज कार्य रैंप हैं, और प्रतिगमन मॉडल बनाने के लिए उपयोग किए जाते हैं।

विश्लेषणात्मक गुण

गैर-नकारात्मकता

किसी फलन के पूरे क्षेत्र में फलन गैर-ऋणात्मक होता है, इसलिए इसका निरपेक्ष मान स्वयं ही होता है, अर्थात

$$\forall x\in \mathbb {R} :R(x)\geq 0$$

और

$$\left|R(x)\right|=R(x)$$

Proof

by the mean of definition 2, it is non-negative in the first quarter, and zero in the second; so everywhere it is non-negative.

व्युत्पन्न

इसका व्युत्पन्न हीविसाइड स्टेप फंक्शन है:

$$R'(x)=H(x)\quad {\mbox{for }}x\neq 0.$$

दूसरा व्युत्पन्न

रैंप फ़ंक्शन अंतर समीकरण को संतुष्ट करता है:

$${\frac {d^{2}}{dx^{2}}}R(x-x_{0})=\delta (x-x_{0}),$$

कहाँ δ(x) डिराक डेल्टा है। इस का मतलब है कि R(x) दूसरे डेरिवेटिव ऑपरेटर के लिए ग्रीन का कार्य है। इस प्रकार, कोई भी कार्य, f(x), एक पूर्णांक द्वितीय व्युत्पन्न के साथ, f″(x), समीकरण को संतुष्ट करेगा:

$$f(x)=f(a)+(x-a)f'(a)+\int _{a}^{b}R(x-s)f''(s)\,ds\quad {\mbox{for }}a<x<b.$$

फूरियर रूपांतरण

$${\mathcal {F}}{\big \{}R(x){\big \}}(f)=\int _{-\infty }^{\infty }R(x)e^{-2\pi ifx}\,dx={\frac {i\delta '(f)}{4\pi }}-{\frac {1}{4\pi ^{2}f^{2}}},$$

कहाँ δ(x) डिराक डेल्टा है (इस सूत्र में, इसका व्युत्पन्न प्रकट होता है)।

लाप्लास रूपांतरण

एक तरफा लाप्लास का रूपांतरण R(x) इस प्रकार दिया गया है,

$${\mathcal {L}}{\big \{}R(x){\big \}}(s)=\int _{0}^{\infty }e^{-sx}R(x)dx={\frac {1}{s^{2}}}.$$

बीजगणितीय गुण

पुनरावृत्ति आक्रमण

रैंप मैपिंग का प्रत्येक पुनरावृत्त कार्य स्वयं ही है

$$R{\big (}R(x){\big )}=R(x).$$

Proof

$$R{\big (}R(x){\big )}:={\frac {R(x)+|R(x)|}{2}}={\frac {R(x)+R(x)}{2}}=R(x).$$

This applies the non-negative property.

यह भी देखें

• टोबिट मॉडल