K-माध्यम क्लस्टरिंग

Not to be confused with k-निकटतम परस्पर एल्गोरिदम.

K-अर्थात समूह संचालन परिमाणीकरण की विधि है, जो मूल रूप से संकेत आगे बढ़ाना से है, जिसका उद्देश्य उपसमुच्चय N अवलोकनों को K समूहों में विभाजित करना है जिसमें प्रत्येक अवलोकन समूह (सांख्यिकी) से संबंधित हैI निकटतम माध्य (समूह केंद्र या समूह केन्द्रक) के साथ, समूह के प्रोटोटाइप के रूप में कार्य करता है। इसका परिणाम वोरोनोई कोशिकाओं में डेटा स्थान के विभाजन में होता है। k-अर्थात समूहिंग अंदर-समूह भिन्नता (यूक्लिडियन दूरियों को चुकता) को अल्प करता है, किन्तु नियमित यूक्लिडियन दूरियों को नहीं, जो कि अधिक कठिन वेबर समस्या होगी I माध्य चुकता त्रुटियों का अनुकूलन करता है, जबकि केवल ज्यामितीय माध्य यूक्लिडियन दूरी को अल्प करता है। उदाहरण के लिए, K-मीडियन समूहिंग k-मेडियंस एवं k-मेडोइड्स k-मेडॉयड्स का उपयोग करके उत्तम यूक्लिडियन समाधान संशोधित किये जा सकते हैं।

समस्या कम्प्यूटेशनल रूप से कठिन है (एनपी-कठोरता) चूंकि, कुशल अनुमानी एल्गोरिदम स्थानीय इष्टतम में परिवर्तित हो जाते हैं। ये सामान्यतः 'K-साधन' एवं 'गाऊसी मिश्रण प्रारूपो' दोनों द्वारा नियोजित पुनरावृत्त शोधन दृष्टिकोण के माध्यम से गॉसियन वितरण के मिश्रण प्रारूप के लिए अपेक्षा-अधिकतमकरण एल्गोरिथ्म के समान हैं। वे दोनों डेटा को प्रारूप करने के लिए समूह केंद्रों का उपयोग करते हैं; चूंकि, k - का अर्थ है समूहिंग तुलनीय स्थानिक सीमा के समूहों का शोध करने के लिए किया जाता है, जबकि गॉसियन मिश्रण प्रारूप समूह्स को अलग-अलग आकार देने की अनुमति देता है।

अनियंत्रित k-अर्थात एल्गोरिदम का k-निकटतम परस्पर से ढीला संबंध है, k-निकटतम परस्पर वर्गीकारक, के लिए लोकप्रिय पर्यवेक्षित यंत्र अधिगम प्रविधि है जिसे अक्सर के के साथ भ्रमित किया जाता है- अर्थात नाम के कारण। K द्वारा प्राप्त समूह केंद्रों में 1-निकटतम परस्पर क्लासिफायरियर को लागू करने का अर्थात मौजूदा समूह में नए डेटा को वर्गीकृत करना है। इसे निकटतम सेंट्रोइड क्लासिफायरियर या रोक्चियो एल्गोरिथम के रूप में जाना जाता है।

विवरण

टिप्पणियों के उपसमुच्चय को देखते हुए (x₁, x₂, ..., x_n), जहां प्रत्येक अवलोकन डी-आयामी वास्तविक वेक्टर है, k-अर्थात समूहिंग का उद्देश्य nअवलोकनों को k (≤ n) समुच्चय 's' = {s में विभाजित करना है₁, s₂, ..., s_k} जिससे वर्गों के अंदर-समूह योग (WCSS) (अर्थात विचरण) को अल्प किया जा सके। औपचारिक रूप से इस उद्देश्य का शोध करना हैI

${\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}={\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}|S_{i}|\operatorname {Var} S_{i}$

जहां μ_iमें बिंदुओं का माध्य (जिसे केन्द्रक भी कहा जाता है) है $S_{i}$, अर्थात। <डिव वर्ग = केंद्र>${\boldsymbol {\mu _{i}}}={\frac {1}{|S_{i}|}}\sum _{\mathbf {x} \in S_{i}}\mathbf {x} ,$ $|S_{i}|$ का आकार है $S_{i}$, एवं $\|\cdot \|$ सामान्य मानदंड (गणित) है|एल

2 </सुप> मानक । यह एक ही समूह में बिंदुओं के जोड़ीदार वर्ग विचलन को अल्प करने के बराबर है:

${\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}\,{\frac {1}{|S_{i}|}}\,\sum _{\mathbf {x} ,\mathbf {y} \in S_{i}}\left\|\mathbf {x} -\mathbf {y} \right\|^{2}$

समरूपता को सर्वसमिका से निकाला जा सकता है $|S_{i}|\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}={\frac {1}{2}}\sum _{\mathbf {x} ,\mathbf {y} \in S_{i}}\left\|\mathbf {x} -\mathbf {y} \right\|^{2}$. चूंकि कुल भिन्नता स्थिर है, यह विभिन्न समूहों (वर्गों के बीच-समूह योग, बीसीएसएस) में बिंदुओं के बीच वर्ग विचलन के योग को अधिकतम करने के बराबर है। यह नियतात्मक संबंध प्रायिकता सिद्धांत में कुल विचरण के नियम से भी संबंधित है।

इतिहास

के-मीन्स शब्द का पहली बार इस्तेमाल जेम्स मैकक्वीन ने 1967 में किया था। हालांकि यह विचार 1956 में ह्यूगो स्टीनहॉस के पास वापस चला गया। मानक एल्गोरिथम पहली बार 1957 में बेल लैब्स के स्टुअर्ट लॉयड द्वारा पल्स कोड मॉडुलेशन के लिए एक तकनीक के रूप में प्रस्तावित किया गया था, हालांकि इसे 1982 तक एक जर्नल लेख के रूप में प्रकाशित नहीं किया गया था। 1965 में, एडवर्ड डब्ल्यू फोर्गी ने अनिवार्य रूप से एक ही विधि प्रकाशित की, यही कारण है कि इसे कभी-कभी लॉयड-फोर्गी एल्गोरिथम कहा जाता है।

एल्गोरिदम

मानक एल्गोरिदम (बेवकूफ के-साधन)

के-साधनों का अभिसरण

सबसे आम एल्गोरिथ्म पुनरावृत्त शोधन तकनीक का उपयोग करता है। इसकी सर्वव्यापकता के कारण, इसे अक्सर k-means एल्गोरिथम कहा जाता है; इसे विशेष रूप से कंप्यूटर विज्ञान समुदाय में लॉयड्स एल्गोरिथम के रूप में भी जाना जाता है। इसे कभी-कभी भोली के-साधन के रूप में भी जाना जाता है, क्योंकि बहुत तेज़ विकल्प मौजूद हैं।

k के प्रारंभिक सेट को देखते हुए m का अर्थ है₁^{(1)</सुप>, ..., म_k(1) (नीचे देखें), एल्गोरिथ्म दो चरणों के बीच बारी-बारी से आगे बढ़ता है:}

असाइनमेंट चरण: प्रत्येक अवलोकन को क्लस्टर को निकटतम माध्य के साथ असाइन करें: कम से कम वर्ग यूक्लिडियन दूरी के साथ। (गणितीय रूप से, इसका अर्थ है साधनों द्वारा उत्पन्न वोरोनोई आरेख के अनुसार अवलोकनों को विभाजित करना।)

$S_{i}^{(t)}=\left\{x_{p}:\left\|x_{p}-m_{i}^{(t)}\right\|^{2}\leq \left\|x_{p}-m_{j}^{(t)}\right\|^{2}\ \forall j,1\leq j\leq k\right\},$

जहां प्रत्येक $x_{p}$ ठीक एक को सौंपा गया है $S^{(t)}$, भले ही यह उनमें से दो या अधिक को सौंपा जा सकता है।

अपडेट चरण: प्रत्येक क्लस्टर को असाइन किए गए अवलोकनों के लिए पुनर्गणना का मतलब (केन्द्रक)।

$m_{i}^{(t+1)}={\frac {1}{\left|S_{i}^{(t)}\right|}}\sum _{x_{j}\in S_{i}^{(t)}}x_{j}$

एल्गोरिथम अभिसरण तब होता है जब असाइनमेंट अब नहीं बदलते हैं। इष्टतम खोजने के लिए एल्गोरिदम की गारंटी नहीं है। एल्गोरिथम को अक्सर दूरी के आधार पर निकटतम क्लस्टर में ऑब्जेक्ट असाइन करने के रूप में प्रस्तुत किया जाता है। (स्क्वायर) यूक्लिडियन दूरी के अलावा किसी भिन्न दूरी फ़ंक्शन का उपयोग करने से एल्गोरिथम को अभिसरण से रोका जा सकता है। के-मीन्स के विभिन्न संशोधन जैसे गोलाकार के-मीन्स और के-मेडोइड्स | के-मेडोइड्स को अन्य दूरी उपायों का उपयोग करने की अनुमति देने के लिए प्रस्तावित किया गया है।

आरंभीकरण के तरीके

आमतौर पर इस्तेमाल की जाने वाली इनिशियलाइज़ेशन विधियाँ फोर्जी और रैंडम पार्टीशन हैं। Forgy विधि यादृच्छिक रूप से डेटासेट से k अवलोकन चुनती है और प्रारंभिक साधनों के रूप में इनका उपयोग करती है। रैंडम पार्टिशन विधि पहले बेतरतीब ढंग से प्रत्येक अवलोकन के लिए एक क्लस्टर प्रदान करती है और फिर अद्यतन चरण पर आगे बढ़ती है, इस प्रकार प्रारंभिक माध्य की गणना क्लस्टर के यादृच्छिक रूप से असाइन किए गए बिंदुओं के केन्द्रक के रूप में की जाती है। फोर्जी विधि प्रारंभिक साधनों को फैलाने की प्रवृत्ति रखती है, जबकि रैंडम विभाजन उन सभी को डेटा सेट के केंद्र के करीब रखता है। हैमरली एट अल। के अनुसार,यादृच्छिक विभाजन विधि आम तौर पर एल्गोरिदम जैसे के-हार्मोनिक साधनों और फ़ज़ी के-साधनों के लिए बेहतर होती है। अपेक्षा अधिकतमकरण और मानक के-साधन एल्गोरिदम के लिए, प्रारंभिकरण की फोर्जी विधि बेहतर है। सेलेबी एट अल द्वारा एक व्यापक अध्ययन। हालाँकि, पाया गया कि फोर्जी, रैंडम पार्टीशन और मैक्सिमिन जैसे लोकप्रिय इनिशियलाइज़ेशन तरीके अक्सर खराब प्रदर्शन करते हैं, जबकि ब्रैडली और फ़य्यद का दृष्टिकोण सर्वश्रेष्ठ समूह में लगातार प्रदर्शन करता है और K-means++|k-means++ आमतौर पर अच्छा प्रदर्शन करता है।

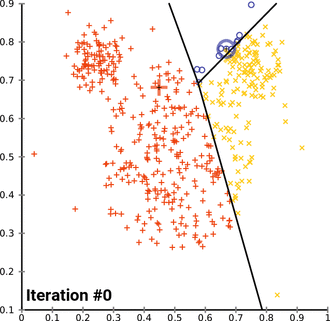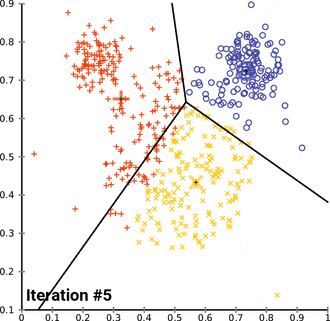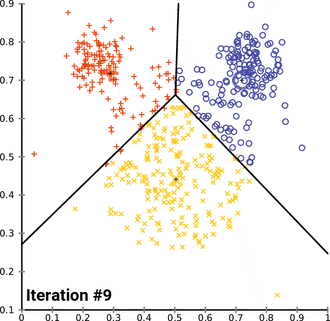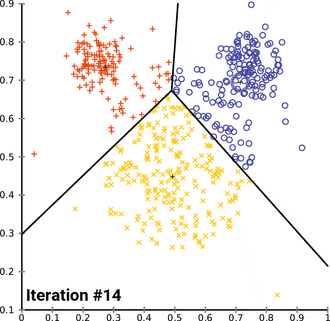
• Demonstration of the standard algorithm
• 

  1. के प्रारंभिक साधन (इस मामले में के = 3) डेटा डोमेन (रंग में दिखाया गया) के भीतर यादृच्छिक रूप से उत्पन्न होते हैं।

• 

  2. k क्लस्टर प्रत्येक अवलोकन को निकटतम माध्य से जोड़कर बनाया जाता है। यहां के विभाजन माध्यम से उत्पन्न वोरोनोई आरेख का प्रतिनिधित्व करते हैं।

• 

  3. प्रत्येक k क्लस्टर का केन्द्रक नया माध्य बन जाता है।

• 

  4. अभिसरण होने तक चरण 2 और 3 दोहराए जाते हैं।

एल्गोरिथ्म वैश्विक इष्टतम के अभिसरण की गारंटी नहीं देता है। परिणाम प्रारंभिक समूहों पर निर्भर हो सकता है। जैसा कि एल्गोरिथ्म आमतौर पर तेज़ होता है, इसे अलग-अलग शुरुआती स्थितियों के साथ कई बार चलाना आम बात है। हालांकि, सबसे खराब स्थिति का प्रदर्शन धीमा हो सकता है: विशेष रूप से निश्चित बिंदु सेट, दो आयामों में भी, घातीय समय में अभिसरण करते हैं, अर्थात 2^Ω(n). ये बिंदु सेट व्यवहार में उत्पन्न नहीं होते हैं: यह इस तथ्य से पुष्ट होता है कि के-मीन्स का स्मूथेड विश्लेषण चलने का समय बहुपद है। <रेफरी नाम = आर्थर, डेविड; मंथे, बी.; रोगलिन, एच. 20092 >Arthur, David; Manthey, B.; Roeglin, H. (2009). "के-साधन में बहुपद चिकनी जटिलता है". Proceedings of the 50th Symposium on Foundations of Computer Science (FOCS). arXiv:0904.1113.</ref>

असाइनमेंट स्टेप को एक्सपेक्टेशन स्टेप कहा जाता है, जबकि अपडेट स्टेप एक मैक्सिमाइज़ेशन स्टेप है, जो इस एल्गोरिथम को सामान्यीकृत एक्सपेक्टेशन-मैक्सिमाइज़ेशन एल्गोरिथम का एक वेरिएंट बनाता है।

जटिलता

डी आयामों में अवलोकन के लिए के-साधन क्लस्टरिंग समस्या का इष्टतम समाधान ढूँढना है:

• दो समूहों के लिए भी सामान्य यूक्लिडियन अंतरिक्ष (डी आयामों में) में एनपी कठिन ,
• एनपी-हार्ड सामान्य संख्या में क्लस्टर के लिए विमान में भी,
• यदि k और d (आयाम) निश्चित हैं, तो समस्या को समय पर ठीक से हल किया जा सकता है $O(n^{dk+1})$, जहां n क्लस्टर होने वाली संस्थाओं की संख्या है।

इस प्रकार, ऊपर दिए गए लॉयड के एल्गोरिथम जैसे विभिन्न अनुमानी एल्गोरिदम का आमतौर पर उपयोग किया जाता है।

लॉयड्स एल्गोरिथम (और अधिकांश वेरिएंट) का रनिंग टाइम है $O(nkdi)$, कहाँ:

• n डी-डायमेंशनल वैक्टर की संख्या है (क्लस्टर किया जाना है)
• कश्मीर समूहों की संख्या
• मैं अभिसरण तक आवश्यक पुनरावृत्तियों की संख्या।

क्लस्टरिंग संरचना वाले डेटा पर, अभिसरण तक पुनरावृत्तियों की संख्या अक्सर छोटी होती है, और परिणाम केवल पहले दर्जन पुनरावृत्तियों के बाद थोड़ा सुधार करते हैं। इसलिए लॉयड के एल्गोरिथ्म को व्यवहार में अक्सर रैखिक जटिलता वाला माना जाता है, हालांकि अभिसरण तक किए जाने पर यह वर्स्ट-केस जटिलता सुपरपोलिनोमियल में होता है।

• सबसे खराब स्थिति में, लॉयड के एल्गोरिथ्म की जरूरत है $i=2^{\Omega ({\sqrt {n}})}$ पुनरावृत्तियों, ताकि लॉयड के एल्गोरिथम की सबसे खराब स्थिति समय जटिलता#सुपरपोलिनोमियल समय हो।* लॉयड के के-मीन्स एल्गोरिदम में बहुपद स्मूथ रनिंग टाइम है। यह दिखाया गया है कि <रेफरी नाम = आर्थर, डेविड; मंथे, बी.; Roeglin, H. 20092 /> n बिंदुओं के मनमाने सेट के लिए $[0,1]^{d}$, यदि प्रत्येक बिंदु माध्य के साथ एक सामान्य वितरण द्वारा स्वतंत्र रूप से परेशान है 0 और विचरण $\sigma ^{2}$, फिर अपेक्षित चलने का समय k-मतलब एल्गोरिद्म बाउंडेड है $O(n^{34}k^{34}d^{8}\log ^{4}(n)/\sigma ^{6})$, जो एक बहुपद है n, k, d और $1/\sigma$.
• साधारण मामलों के लिए बेहतर सीमाएँ सिद्ध होती हैं। उदाहरण के लिए, यह दिखाया गया है कि k- साधन एल्गोरिथम का चलने का समय सीमाबद्ध है $O(dn^{4}M^{2})$ के लिए n एक पूर्णांक जाली में अंक $\{1,\dots ,M\}^{d}$.

लॉयड्स एल्गोरिद्म इस समस्या के लिए मानक दृष्टिकोण है। हालाँकि, यह प्रत्येक k क्लस्टर केंद्रों और n डेटा बिंदुओं के बीच की दूरी की गणना करने में बहुत अधिक समय व्यतीत करता है। चूंकि अंक आमतौर पर कुछ पुनरावृत्तियों के बाद समान समूहों में रहते हैं, इसलिए यह अधिकांश कार्य अनावश्यक है, जिससे भोले-भाले कार्यान्वयन बहुत अक्षम हो जाते हैं। लॉयड के एल्गोरिदम को गति देने और सीमा बनाने के लिए कुछ कार्यान्वयन कैशिंग और त्रिकोण असमानता का उपयोग करते हैं।

रूपांतर

• Jenks प्राकृतिक टूटता अनुकूलन: के-मीन्स यूनीवेट डेटा पर लागू होता है
• के-मेडियंस क्लस्टरिंग | के-मेडियंस क्लस्टरिंग औसत के बजाय प्रत्येक आयाम में औसत का उपयोग करता है, और इस तरह कम करता है $L_{1}$ मानदंड (टैक्सीकैब ज्यामिति)।
• के-मेडोइड्स | के-मेडोइड्स (यह भी: मेडोइड्स के आसपास विभाजन, पीएएम) माध्य के बजाय मेडॉइड का उपयोग करता है, और इस तरह मनमाना दूरी कार्यों के लिए दूरी का योग कम करता है।
• फ़ज़ी क्लस्टरिंग # फ़ज़ी सी-मीन्स क्लस्टरिंग। फ़ज़ी सी-मीन्स क्लस्टरिंग के-मीन्स का एक सॉफ्ट वर्जन है, जहाँ प्रत्येक डेटा पॉइंट में प्रत्येक क्लस्टर से संबंधित फ़ज़ी डिग्री होती है।
• मिश्रण मॉडल # गॉसियन मिश्रण मॉडल मॉडल उम्मीद-अधिकतमकरण एल्गोरिदम (ईएम एल्गोरिदम) के साथ प्रशिक्षित नियतात्मक असाइनमेंट के बजाय समूहों के लिए संभाव्य असाइनमेंट बनाए रखता है, और साधनों के बजाय बहुभिन्नरूपी गॉसियन वितरण करता है।
• K-means++|k-means++ प्रारंभिक केंद्रों को इस तरह से चुनता है जो WCSS उद्देश्य पर एक सिद्ध ऊपरी सीमा देता है।
• फ़िल्टरिंग एल्गोरिथ्म प्रत्येक k- साधन चरण को गति देने के लिए kd- ट्री का उपयोग करता है।
• कुछ विधियाँ त्रिभुज असमानता का उपयोग करके प्रत्येक k- साधन चरण को गति देने का प्रयास करती हैं।* समूहों के बीच बिंदुओं की अदला-बदली करके स्थानीय ऑप्टिमा से बचें।* गोलाकार k- साधन क्लस्टरिंग एल्गोरिथ्म शाब्दिक डेटा के लिए उपयुक्त है।
• पदानुक्रमित संस्करण जैसे द्विभाजित k- साधन, एक्स-मतलब क्लस्टरिंग और जी-मतलब क्लस्टरिंग पदानुक्रमित क्लस्टरिंग # विभाजक क्लस्टरिंग, और डेटासेट में क्लस्टर की इष्टतम संख्या को स्वचालित रूप से निर्धारित करने का प्रयास भी कर सकता है।
• क्लस्टर विश्लेषण # आंतरिक मूल्यांकन उपाय जैसे सिल्हूट (क्लस्टरिंग) डेटा सेट में क्लस्टर की संख्या निर्धारित करने में सहायक हो सकते हैं।
• Minkowski भारित k-means स्वचालित रूप से क्लस्टर विशिष्ट फीचर वेट की गणना करता है, सहज विचार का समर्थन करता है कि एक फीचर में अलग-अलग सुविधाओं पर प्रासंगिकता की अलग-अलग डिग्री हो सकती है। इन भारों का उपयोग किसी दिए गए डेटा सेट को फिर से स्केल करने के लिए भी किया जा सकता है, जिससे क्लस्टर की अपेक्षित संख्या में क्लस्टर वैधता सूचकांक को अनुकूलित करने की संभावना बढ़ जाती है।
• मिनी-बैच k- साधन: k- साधन डेटा सेट के लिए मिनी बैच नमूने का उपयोग करके भिन्नता जो मेमोरी में फिट नहीं होती है।
• ओत्सु की विधि

हार्टिगन-वोंग विधि

हार्टिगन और वोंग की विधिके-मीन्स एल्गोरिदम की विविधता प्रदान करता है जो विभिन्न समाधान अद्यतनों के साथ न्यूनतम योग-स्क्वायर समस्या के स्थानीय न्यूनतम की ओर बढ़ता है। विधि एक स्थानीय खोज (अनुकूलन) है जो एक नमूने को एक अलग क्लस्टर में स्थानांतरित करने का प्रयास करती है जब तक कि यह प्रक्रिया उद्देश्य समारोह में सुधार करती है। जब उद्देश्य में सुधार के साथ किसी भिन्न क्लस्टर में कोई नमूना स्थानांतरित नहीं किया जा सकता है, तो विधि बंद हो जाती है (स्थानीय न्यूनतम में)। शास्त्रीय के-साधन के समान ही, दृष्टिकोण एक अनुमानी बना हुआ है क्योंकि यह आवश्यक रूप से गारंटी नहीं देता है कि अंतिम समाधान विश्व स्तर पर इष्टतम है।

होने देना $\varphi (S_{j})$ की व्यक्तिगत लागत हो $S_{j}$ द्वारा परिभाषित $\sum _{x\in S_{j}}(x-\mu _{j})^{2}$, साथ $\mu _{j}$ क्लस्टर का केंद्र।

असाइनमेंट स्टेप: हार्टिगन और वोंग की विधि बिंदुओं को यादृच्छिक समूहों में विभाजित करके शुरू होती है $\{S_{j}\}_{j\in \{1,\cdots k\}}$.

अद्यतन चरण: अगला यह निर्धारित करता है $n,m\in \{1,\ldots ,k\}$ और $x\in S_{n}$ जिसके लिए निम्नलिखित कार्य अधिकतम तक पहुँचता है

$\Delta (m,n,x)=\varphi (S_{n})+\varphi (S_{m})-\varphi (S_{n}\smallsetminus \{x\})-\varphi (S_{m}\cup \{x\}).$

के लिए $x,n,m$ जो इस अधिकतम तक पहुँचे, $x$ क्लस्टर से चलता है $S_{n}$ क्लस्टर को $S_{m}$.

टर्मिनेशन: एल्गोरिथम एक बार टर्मिनेट होता है $\Delta (m,n,x)$ सभी के लिए शून्य से कम है $x,n,m$.

विभिन्न चाल स्वीकृति रणनीतियों का उपयोग किया जा सकता है। पहले-सुधार की रणनीति में, किसी भी सुधार के स्थानांतरण को लागू किया जा सकता है, जबकि सर्वोत्तम-सुधार की रणनीति में, सभी संभव स्थानांतरणों का पुनरावृत्त रूप से परीक्षण किया जाता है और प्रत्येक पुनरावृत्ति पर केवल सर्वश्रेष्ठ को लागू किया जाता है। पूर्व दृष्टिकोण गति का समर्थन करता है, चाहे बाद वाला दृष्टिकोण आम तौर पर अतिरिक्त कम्प्यूटेशनल समय की कीमत पर समाधान की गुणवत्ता का पक्ष लेता है। कार्यक्रम $\Delta$ एक स्थानांतरण के परिणाम की गणना करने के लिए उपयोग किया जाता है, समानता का उपयोग करके भी कुशलतापूर्वक मूल्यांकन किया जा सकता है

$\Delta (x,n,m)={\frac {\mid S_{n}\mid }{\mid S_{n}\mid -1}}\cdot \lVert \mu _{n}-x\rVert ^{2}-{\frac {\mid S_{m}\mid }{\mid S_{m}\mid +1}}\cdot \lVert \mu _{m}-x\rVert ^{2}.$

वैश्विक अनुकूलन और मेटाह्यूरिस्टिक्स

शास्त्रीय k- साधन एल्गोरिथ्म एवं इसकी विविधताओं को

के रूप में परिभाषित न्यूनतम-योग-स्क्वायर क्लस्टरिंग समस्या के केवल स्थानीय मिनीमा में परिवर्तित करने के लिए जाना जाता है। ${\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}.$

कई अध्ययनों ने एल्गोरिथम के अभिसरण व्यवहार में सुधार करने एवं वैश्विक इष्टतम (या अल्प से अल्प, उत्तम गुणवत्ता के स्थानीय न्यूनतम) प्राप्त करने की संभावना को अधिकतम करने का प्रयास किया है। पिछले अनुभागों में चर्चा की गई आरंभीकरण एवं पुनः आरंभ करने की तकनीकें उत्तम समाधान खोजने के लिए एक विकल्प हैं। हाल ही में, शाखा एवं बंधन एवं अर्ध निश्चित प्रोग्रामिंग पर आधारित वैश्विक अनुकूलन एल्गोरिदम ने 4,177 संस्थाओं एवं 20,531 सुविधाओं के साथ डेटासमुच्चय के लिए सिद्ध रूप से इष्टतम समाधान तैयार किए हैं। जैसा कि अपेक्षित था, उपजात अनुकूलन समस्या की एनपी-कठोरता के कारण, के-साधनों के लिए इष्टतम एल्गोरिदम का अल्प्प्यूटेशनल समय इस आकार से तेजी से बढ़ता है। अन्य अनुमानों की गुणवत्ता का मूल्यांकन करने के लिए, छोटे एवं मध्यम पैमाने के लिए इष्टतम समाधान अभी भी बेंचमार्क टूल के रूप में मूल्यवान हैं। एक नियंत्रित अल्प्प्यूटेशनल समय के अंदर उच्च-गुणवत्ता वाले स्थानीय मिनिमा को खोजने के लिए, किन्तु इष्टतमता की गारंटी के बिना, अन्य कार्यों ने मेटाह्यूरिस्टिक्स एवं अन्य वैश्विक अनुकूलन तकनीकों का पता लगाया है, उदाहरण के लिए, वृद्धिशील दृष्टिकोण एवं उत्तल अनुकूलन के आधार पर, यादृच्छिक अदला-बदली (यानी, पुनरावृत्त स्थानीय खोज), परिवर्तनशील पड़ोस खोज एवं आनुवंशिक एल्गोरिदम। यह वास्तव में ज्ञात है कि न्यूनतम सम-स्क्वायर समूहिंग समस्या का उत्तम स्थानीय मिनिमा खोजने से उच्च आयाम वाले फ़ीचर स्पेस में समूह संरचनाओं को पुनर्प्राप्त करने में विफलता एवं सफलता के बीच अंतर हो सकता है।

चर्चा

के-साधन अभिसरण का स्थानीय न्यूनतम का एक विशिष्ट उदाहरण। इस उदाहरण में, k- साधन क्लस्टरिंग (सही आंकड़ा) का परिणाम डेटा सेट की स्पष्ट क्लस्टर संरचना के विपरीत है। छोटे वृत्त डेटा बिंदु हैं, चार किरण तारे केन्द्रक (साधन) हैं। प्रारंभिक विन्यास बाईं आकृति पर है। एल्गोरिथम आंकड़ों पर प्रस्तुत पांच पुनरावृत्तियों के बाद, बाएं से दाएं की ओर अभिसरण करता है। उदाहरण Mirkes Java एप्लेट के साथ तैयार किया गया था।

के-मीन्स आइरिस फूल डेटा सेट के लिए क्लस्टरिंग परिणाम और सूचकांक-संरचनाओं द्वारा समर्थित केडीडी-अनुप्रयोगों के विकास के लिए पर्यावरण का उपयोग करके वास्तविक प्रजातियों की कल्पना की गई। क्लस्टर साधनों को बड़े, अर्ध-पारदर्शी प्रतीकों का उपयोग करके चिह्नित किया जाता है।

k-मतलब क्लस्टरिंग बनाम कृत्रिम डेटासेट (माउस) पर ईएम क्लस्टरिंग समान आकार के समूहों का उत्पादन करने के लिए के-साधन की प्रवृत्ति यहां खराब परिणामों की ओर ले जाती है, जबकि ईएम डेटा सेट में मौजूद विभिन्न त्रिज्या वाले गॉसियन वितरण से लाभान्वित होता है।

के-मीन्स की तीन प्रमुख विशेषताएं जो इसे कुशल बनाती हैं, अक्सर इसकी सबसे बड़ी अल्पियां मानी जाती हैं:

• यूक्लिडियन दूरी का उपयोग मीट्रिक (गणित) के रूप में किया जाता है और विचरण का उपयोग क्लस्टर स्कैटर के माप के रूप में किया जाता है।
• क्लस्टर k की संख्या एक इनपुट पैरामीटर है: k का अनुचित विकल्प खराब परिणाम दे सकता है। इसीलिए, k-means करते समय, डेटा सेट में क्लस्टर्स की संख्या निर्धारित करने के लिए डायग्नोस्टिक चेक चलाना महत्वपूर्ण है।
• एक स्थानीय न्यूनतम के अभिसरण से विपरीत (गलत) परिणाम उत्पन्न हो सकते हैं (चित्र में उदाहरण देखें)।

K- साधन की एक प्रमुख सीमा इसका क्लस्टर मॉडल है। अवधारणा गोलाकार समूहों पर आधारित है जो वियोज्य हैं ताकि माध्य क्लस्टर केंद्र की ओर अभिसरण हो। क्लस्टर समान आकार के होने की उम्मीद है, ताकि निकटतम क्लस्टर केंद्र को असाइनमेंट सही असाइनमेंट हो। उदाहरण के लिए जब k- साधन को मान के साथ लागू किया जाता है $k=3$ प्रसिद्ध आइरिस फूल डेटा सेट पर, परिणाम अक्सर डेटा सेट में निहित तीन आइरिस (पौधे) प्रजातियों को अलग करने में विफल रहता है। साथ $k=2$, दो दृश्य समूहों (दो प्रजातियों वाला एक) की खोज की जाएगी, जबकि साथ में $k=3$ दो समूहों में से एक को दो समान भागों में विभाजित किया जाएगा। वास्तव में, $k=2$ डेटा सेट में 3 वर्ग होने के बावजूद, इस डेटा सेट के लिए अधिक उपयुक्त है। किसी भी अन्य क्लस्टरिंग एल्गोरिदम के साथ, के-साधन परिणाम यह मानते हैं कि डेटा कुछ मानदंडों को पूरा करता है। यह कुछ डेटा सेट पर अच्छा काम करता है और दूसरों पर विफल रहता है।

के-साधनों का नतीजा क्लस्टर साधनों के वोरोनोई आरेख के रूप में देखा जा सकता है। चूंकि डेटा क्लस्टर माध्यमों के बीच आधे रास्ते में विभाजित होता है, इससे उप-इष्टतम विभाजन हो सकता है जैसा कि माउस उदाहरण में देखा जा सकता है। अपेक्षा-अधिकतमकरण एल्गोरिथ्म (तर्कसंगत रूप से k-साधनों का एक सामान्यीकरण) द्वारा उपयोग किए जाने वाले गॉसियन मॉडल प्रसरण और सहप्रसरण दोनों होने के कारण अधिक लचीले होते हैं। इस प्रकार EM परिणाम चर आकार के समूहों को k-साधनों के साथ-साथ सहसंबद्ध समूहों (इस उदाहरण में नहीं) से बेहतर समायोजित करने में सक्षम है। प्रतिपक्ष में, EM को बड़ी संख्या में मुक्त मापदंडों के अनुकूलन की आवश्यकता होती है और लुप्त हो रहे समूहों या बुरी तरह से वातानुकूलित सहप्रसरण मैट्रिक्स के कारण कुछ पद्धतिगत मुद्दों को प्रस्तुत करता है। K- साधन गैर-पैरामीट्रिक बायेसियन अनुमान से निकटता से संबंधित है।

अनुप्रयोग

k-means क्लस्टरिंग अपेक्षाकृत बड़े डेटा सेट पर लागू करना आसान है, खासकर जब ह्यूरिस्टिक्स जैसे कि लॉयड्स एल्गोरिथम का उपयोग करते हैं। इसे कई अन्य डोमेन के बीच बाजार विभाजन, कंप्यूटर दृष्टि और खगोल विज्ञान में सफलतापूर्वक उपयोग किया गया है। यह अक्सर अन्य एल्गोरिदम के लिए प्रीप्रोसेसिंग चरण के रूप में उपयोग किया जाता है, उदाहरण के लिए प्रारंभिक कॉन्फ़िगरेशन खोजने के लिए।

वेक्टर परिमाणीकरण

Main article: Vector quantization

दो-चैनल (चित्रण उद्देश्यों के लिए - केवल लाल और हरे रंग के चैनल) रंगीन छवि

के-मीन्स का उपयोग करके वोरोनोई कोशिकाओं में ऊपर की छवि में मौजूद रंगों का वेक्टर परिमाणीकरण

के-साधन सिग्नल प्रोसेसिंग से उत्पन्न होता है, एवं अभी भी इस डोमेन में उपयोग पाता है। उदाहरण के लिए, कंप्यूटर चित्रलेख में, रंग परिमाणीकरण एक छवि के पैलेट (कंप्यूटिंग) को रंगों की एक निश्चित संख्या में अल्प करने का कार्य है। इस कार्य के लिए के-मीन्स एल्गोरिदम का आसानी से उपयोग किया जा सकता है एवं प्रतिस्पर्धी परिणाम उत्पन्न करता है। इस दृष्टिकोण के लिए उपयोग का मामला छवि विभाजन है। सदिश परिमाणीकरण के अन्य उपयोगों में नमूनाकरण (सांख्यिकी) | गैर-यादृच्छिक नमूनाकरण शामिल है, क्योंकि k-साधन का उपयोग आगे के विश्लेषण के लिए एक बड़े डेटा समुच्चय से k भिन्न किन्तु प्रोटोटाइपिक वस्तुओं को चुनने के लिए आसानी से किया जा सकता है।

क्लस्टर विश्लेषण

Main article: Cluster analysis

समूह विश्लेषण में, k- साधन एल्गोरिथ्म का उपयोग इनपुट डेटा समुच्चय को k विभाजन (समूह) में विभाजित करने के लिए किया जा सकता है।

हालांकि, शुद्ध के-साधन एल्गोरिदम बहुत लचीला नहीं है, और जैसा कि सीमित उपयोग का है (सिवाय इसके कि जब ऊपर के रूप में वेक्टर क्वांटिज़ेशन वास्तव में वांछित उपयोग मामला है)। विशेष रूप से, पैरामीटर k को चुनना कठिन माना जाता है (जैसा कि ऊपर चर्चा की गई है) जब बाहरी बाधाओं द्वारा नहीं दिया जाता है। एक और सीमा यह है कि इसका उपयोग मनमाने दूरी के कार्यों या गैर-संख्यात्मक डेटा के साथ नहीं किया जा सकता है। इन उपयोग मामलों के लिए, कई अन्य एल्गोरिदम श्रेष्ठ हैं।

फीचर लर्निंग

k-means क्लस्टरिंग का उपयोग फीचर लर्निंग (या शब्दकोश सीखना ) स्टेप के रूप में किया गया है, या तो (सेमी-पर्यवेक्षित अध्ययन |सेमी-) सुपरवाइज्ड लर्निंग या अनियंत्रित शिक्षा । मूल दृष्टिकोण सबसे पहले इनपुट प्रशिक्षण डेटा (जिसे लेबल करने की आवश्यकता नहीं है) का उपयोग करके k- साधन क्लस्टरिंग प्रतिनिधित्व को प्रशिक्षित करना है। फिर, किसी भी इनपुट डेटम को नए फीचर स्पेस में प्रोजेक्ट करने के लिए, एक एन्कोडिंग फ़ंक्शन, जैसे कि सेंट्रोइड स्थानों के साथ डेटम का थ्रेशोल्ड मैट्रिक्स-उत्पाद, डेटम से प्रत्येक सेंट्रोइड तक की दूरी की गणना करता है, या बस निकटतम के लिए एक संकेतक फ़ंक्शन केन्द्रक, या दूरी का कुछ सहज परिवर्तन। वैकल्पिक रूप से, रेडियल आधार फ़ंक्शन के माध्यम से नमूना-क्लस्टर दूरी को बदलने से रेडियल आधार समारोह नेटवर्क की छिपी हुई परत प्राप्त होती है। प्राकृतिक भाषा प्रसंस्करण (विशेष रूप से नामित इकाई पहचान के लिए) में अर्ध-पर्यवेक्षित सीखने के लिए के-साधनों के इस उपयोग को सरल, रैखिक वर्गीकरण के साथ सफलतापूर्वक जोड़ा गया है। और कंप्यूटर दृष्टि में। ऑब्जेक्ट रिकग्निशन टास्क पर, autoencoder और प्रतिबंधित बोल्ट्जमैन मशीनों जैसे अधिक परिष्कृत फीचर लर्निंग दृष्टिकोण के साथ तुलनात्मक प्रदर्शन प्रदर्शित करने के लिए पाया गया।हालांकि, समान प्रदर्शन के लिए इसे आम तौर पर अधिक डेटा की आवश्यकता होती है, क्योंकि प्रत्येक डेटा बिंदु केवल एक सुविधा में योगदान देता है।

अन्य एल्गोरिदम से संबंध

गॉसियन मिश्रण मॉडल

Main article: Gaussian mixture model

के-मीन्स क्लस्टरिंग के लिए धीमी मानक एल्गोरिथ्म, और इसके संबद्ध अपेक्षा-अधिकतमकरण एल्गोरिथ्म | अपेक्षा-अधिकतमकरण एल्गोरिथ्म, गॉसियन मिश्रण मॉडल का एक विशेष मामला है, विशेष रूप से, सीमित मामला जब सभी सहप्रसरणों को विकर्ण, समान और अपरिमेय होने के लिए तय किया जाता है छोटा अंतर। छोटे प्रसरणों के बजाय, कठिन गॉसियन मिश्रण मॉडलिंग के एक विशेष मामले में k-साधन क्लस्टरिंग की एक और तुल्यता दिखाने के लिए एक कठिन क्लस्टर असाइनमेंट का भी उपयोग किया जा सकता है। इसका मतलब यह नहीं है कि के-साधनों की गणना करने के लिए गॉसियन मिश्रण मॉडलिंग का उपयोग करना कुशल है, लेकिन सिर्फ एक सैद्धांतिक संबंध है, और गॉसियन मिश्रण मॉडलिंग को के-साधनों के सामान्यीकरण के रूप में व्याख्या किया जा सकता है; इसके विपरीत, कठिन डेटा पर गॉसियन मिश्रण मॉडलिंग के लिए शुरुआती बिंदुओं को खोजने के लिए k- साधन क्लस्टरिंग का उपयोग करने का सुझाव दिया गया है।

के-एसवीडी

Main article: k-SVD

K- साधन एल्गोरिथ्म का एक अन्य सामान्यीकरण k-SVD एल्गोरिथ्म है, जो कोडबुक वैक्टर के विरल रैखिक संयोजन के रूप में डेटा बिंदुओं का अनुमान लगाता है। के-साधन 1 के वजन के साथ एकल कोडबुक वेक्टर का उपयोग करने के विशेष मामले से मेल खाता है।

प्रधान घटक विश्लेषण

Main article: Principal component analysis

का सुकून भरा उपाय k-मतलब क्लस्टरिंग, क्लस्टर संकेतकों द्वारा निर्दिष्ट, प्रमुख घटक विश्लेषण (पीसीए) द्वारा दिया जाता है। अंतर्ज्ञान यह है कि k- साधन गोलाकार आकार (गेंद की तरह) समूहों का वर्णन करते हैं। यदि डेटा में 2 क्लस्टर हैं, तो दो सेंट्रोइड्स को जोड़ने वाली रेखा सबसे अच्छी 1-आयामी प्रक्षेपण दिशा है, जो कि पहली पीसीए दिशा भी है। द्रव्यमान के केंद्र में रेखा को काटना समूहों को अलग करता है (यह असतत क्लस्टर संकेतक की निरंतर छूट है)। यदि डेटा में तीन क्लस्टर हैं, तो तीन क्लस्टर सेंट्रोइड्स द्वारा फैला हुआ 2-आयामी विमान सबसे अच्छा 2-डी प्रोजेक्शन है। यह विमान पहले दो पीसीए आयामों द्वारा भी परिभाषित किया गया है। अच्छी तरह से अलग किए गए समूहों को गेंद के आकार के समूहों द्वारा प्रभावी ढंग से तैयार किया जाता है और इस प्रकार के-साधनों द्वारा खोजा जाता है। गैर-गेंद के आकार के गुच्छों को पास होने पर अलग करना कठिन होता है। उदाहरण के लिए, अंतरिक्ष में आपस में गुंथे हुए दो आधे-चंद्रमा के आकार के गुच्छे पीसीए उप-स्थान पर प्रक्षेपित होने पर अच्छी तरह से अलग नहीं होते हैं। के-मीन्स से इस डेटा पर अच्छा प्रदर्शन करने की उम्मीद नहीं की जानी चाहिए। इस कथन के प्रति उदाहरण प्रस्तुत करना सीधा है कि क्लस्टर केन्द्रक उप-स्थान मुख्य दिशाओं द्वारा फैला हुआ है।

मीन शिफ्ट क्लस्टरिंग

Main article: Mean shift

बेसिक मीन शिफ्ट क्लस्टरिंग एल्गोरिदम इनपुट डेटा सेट के समान आकार के डेटा बिंदुओं का एक सेट बनाए रखता है। प्रारंभ में, इस सेट को इनपुट सेट से कॉपी किया जाता है। फिर इस सेट को पुनरावृत्त रूप से सेट में उन बिंदुओं के माध्यम से बदल दिया जाता है जो उस बिंदु की दी गई दूरी के भीतर हैं। इसके विपरीत, k-means इस अपडेटेड सेट को k पॉइंट्स तक सीमित करता है जो आमतौर पर इनपुट डेटा सेट में पॉइंट्स की संख्या से बहुत कम होता है, और इस सेट में प्रत्येक पॉइंट को इनपुट सेट में सभी पॉइंट्स के माध्यम से बदल देता है जो उस बिंदु के करीब हैं। किसी अन्य की तुलना में (उदाहरण के लिए प्रत्येक अद्यतन बिंदु के वोरोनोई विभाजन के भीतर)। एक मीन शिफ्ट एल्गोरिदम जो कि के-मीन्स के समान है, संभावना माध्य शिफ्ट कहा जाता है, इनपुट सेट में सभी बिंदुओं के माध्यम से प्रतिस्थापन के दौर से गुजरने वाले बिंदुओं के सेट को बदल देता है जो बदलते सेट की दी गई दूरी के भीतर हैं। के-साधनों पर औसत बदलाव के फायदों में से एक यह है कि समूहों की संख्या पूर्व-निर्दिष्ट नहीं है, क्योंकि औसत बदलाव केवल कुछ समूहों को खोजने की संभावना है यदि केवल एक छोटी संख्या मौजूद है। हालांकि, औसत बदलाव के-साधनों की तुलना में बहुत धीमा हो सकता है, और फिर भी बैंडविड्थ पैरामीटर के चयन की आवश्यकता होती है। मीन शिफ्ट में सॉफ्ट वेरिएंट हैं।

स्वतंत्र घटक विश्लेषण

Main article: Independent component analysis

स्पार्सिटी मान्यताओं के तहत और जब इनपुट डेटा को सफेदी परिवर्तन के साथ प्री-प्रोसेस किया जाता है, तो k-means रैखिक स्वतंत्र घटक विश्लेषण (ICA) कार्य का समाधान तैयार करता है। यह #फीचर लर्निंग के लिए के-मीन्स के सफल अनुप्रयोग की व्याख्या करने में सहायता करता है।

द्विपक्षीय फ़िल्टरिंग

Main article: Bilateral filter

के-साधन स्पष्ट रूप से मानता है कि इनपुट डेटा सेट का क्रम कोई फर्क नहीं पड़ता। द्विपक्षीय फिल्टर के-मीन्स और औसत पारी के समान है, जिसमें यह डेटा पॉइंट्स का एक सेट बनाए रखता है जो कि माध्यमों द्वारा प्रतिस्थापित किया जाता है। हालाँकि, द्विपक्षीय फ़िल्टर (कर्नेल भारित) की गणना को प्रतिबंधित करता है, केवल उन बिंदुओं को शामिल करने के लिए जो इनपुट डेटा के क्रम में करीब हैं।यह इसे इमेज डिनोइजिंग जैसी समस्याओं पर लागू करता है, जहां छवि में पिक्सेल की स्थानिक व्यवस्था महत्वपूर्ण महत्व की है।

समान समस्याएं

क्लस्टर फ़ंक्शंस को कम करने वाली चुकता त्रुटि के सेट में K-medoids | k-मेडोइड्स एल्गोरिथ्म भी शामिल है, एक दृष्टिकोण जो प्रत्येक क्लस्टर के केंद्र बिंदु को वास्तविक बिंदुओं में से एक होने के लिए मजबूर करता है, अर्थात, यह सेंट्रोइड्स के स्थान पर मेडोइड्स का उपयोग करता है।

सॉफ्टवेयर कार्यान्वयन

एल्गोरिथम के विभिन्न कार्यान्वयन प्रदर्शन अंतर प्रदर्शित करते हैं, परीक्षण डेटा सेट पर सबसे तेज़ 10 सेकंड में समाप्त होता है, सबसे धीमा 25,988 सेकंड (~ 7 घंटे) लेता है।अंतर को कार्यान्वयन गुणवत्ता, भाषा और संकलक अंतर, विभिन्न समाप्ति मानदंड और सटीक स्तर, और त्वरण के लिए अनुक्रमणिका के उपयोग के लिए जिम्मेदार ठहराया जा सकता है।

मुफ़्त सॉफ़्टवेयर/ओपन सोर्स

नि: शुल्क और ओपन-सोर्स सॉफ़्टवेयर के तहत निम्नलिखित कार्यान्वयन उपलब्ध हैं। सार्वजनिक रूप से उपलब्ध स्रोत कोड के साथ मुफ़्त/ओपन सोर्स सॉफ़्टवेयर लाइसेंस।

• Accord.NET में k-means, k-means++ और k-modes के लिए C# कार्यान्वयन शामिल हैं।
• ALGLIB में k-means और k-means++ के लिए समानांतर C++ और C# कार्यान्वयन शामिल हैं।
• एंड्रॉइड (ऑपरेटिंग सिस्टम) # ओपन-सोर्स समुदाय में के-साधनों के लिए जावा कार्यान्वयन शामिल है।
• क्राइमस्टैट दो स्थानिक के-मीन्स एल्गोरिदम को लागू करता है, जिनमें से एक उपयोगकर्ता को शुरुआती स्थानों को परिभाषित करने की अनुमति देता है।
• ईएलकेआई में के-मीन्स (लॉयड और मैकक्वीन पुनरावृत्ति के साथ-साथ विभिन्न इनिशियलाइज़ेशन जैसे कि के-मीन्स ++ इनिशियलाइज़ेशन) और विभिन्न अधिक उन्नत क्लस्टरिंग एल्गोरिदम शामिल हैं।
• मुस्कान में के-मीन्स और कई अन्य एल्गोरिदम और परिणाम विज़ुअलाइज़ेशन (जावा, कोटलिन और स्कैला के लिए) शामिल हैं।
• जूलिया भाषा में जूलियास्टैट्स क्लस्टरिंग पैकेज में के-साधन कार्यान्वयन शामिल है।
• KNIME में k-means और k-medoids के लिए नोड होते हैं।
• Apache Mahout में MapReduce आधारित k-means शामिल है।
• mypack में के-साधनों का सी ++ कार्यान्वयन शामिल है।
• जीएनयू ऑक्टेव में के-मीन्स शामिल हैं।
• OpenCV में k- साधन कार्यान्वयन शामिल है।
• ऑरेंज (सॉफ्टवेयर) में के-मीन्स क्लस्टरिंग के लिए एक घटक शामिल है जिसमें के और क्लस्टर सिल्हूट स्कोरिंग का स्वत: चयन होता है।
• PSPP में k- साधन शामिल हैं, QUICK CLUSTER कमांड डेटासेट पर k- साधन क्लस्टरिंग करता है।
• R (प्रोग्रामिंग लैंग्वेज) में तीन k-मीन वेरिएशन होते हैं।
• SciPy और scikit-learn में कई k- साधन कार्यान्वयन शामिल हैं।
• Apache Spark MLlib एक वितरित k- साधन एल्गोरिथम लागू करता है।
• टॉर्च (मशीन लर्निंग) में एक अन-अप पैकेज होता है जो k- साधन क्लस्टरिंग प्रदान करता है।
• वीका (मशीन लर्निंग) में के-मीन्स और एक्स-मीन्स शामिल हैं।

मालिकाना

निम्नलिखित कार्यान्वयन मालिकाना सॉफ्टवेयर लाइसेंस शर्तों के तहत उपलब्ध हैं, और सार्वजनिक रूप से उपलब्ध स्रोत कोड नहीं हो सकते हैं।

• ायस्डि
• मेथेमेटिका
• मतलब
• ओरिजिन (डाटा एनालिसिस सॉफ्टवेयर)
• रपीडमीनेर
• सैप हाना
• एसएएस सिस्टम
• सपसस
• सताता

यह भी देखें

• बीएफआर एल्गोरिदम
• सेंट्रोइडल वोरोनोई टेसलेशन
• सिर/पूंछ टूट जाती है
• के क्यू-फ्लैट्स|के क्यू-फ्लैट्स
• के-मीन्स++|के-मीन्स++
• लिंडे-बुजो-ग्रे एल्गोरिदम
• स्व-आयोजन मानचित्र

संदर्भ