ठोस प्रतिमन: Difference between revisions
(Created page with "{{Short description|Set of principles for modeling solid geometry}} {{Technical|date=January 2021}} {{Use dmy dates|date=February 2020}} File:Jack-in-cube solid model, light...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Set of principles for modeling solid geometry}} | {{Short description|Set of principles for modeling solid geometry}} | ||
[[File:Jack-in-cube solid model, light background.gif|thumb|right|ठोस मॉडलिंग में ज्यामिति पूरी तरह से 3 में वर्णित है{{nbhyph}}डी स्थान; वस्तुओं को किसी भी कोण से देखा जा सकता है।]][[3 डी मॉडलिंग]] (या सॉलिड मॉडलिंग) त्रि-आयामी आकार ''[[solid (mathematics)]]|(solid)'' के गणितीय और कंप्यूटर मॉडलिंग के लिए सिद्धांतों का सुसंगत सेट है। ठोस प्रतिरूपण ज्यामितीय प्रतिरूपण और [[कंप्यूटर चित्रलेख]] के संबंधित क्षेत्रों से अलग है, जैसे कि ''3डी प्रतिरूपण'', भौतिक निष्ठा पर जोर देने के कारण।<ref name = "Solid Modeling">{{cite book |url=http://sal-cnc.me.wisc.edu/index.php?option=com_remository&Itemid=143&func=fileinfo&id=53 |title= Solid Modeling|author= Shapiro, Vadim |year= 2001 |publisher= Elsevier |access-date=20 April 2010}}</ref> साथ में, ज्यामितीय और ठोस मॉडलिंग के सिद्धांत [[कंप्यूटर एडेड डिजाइन]] की नींव बनाते हैं और सामान्य रूप से भौतिक वस्तुओं के डिजिटल मॉडल के निर्माण, विनिमय, दृश्य, एनीमेशन, पूछताछ और एनोटेशन का समर्थन करते हैं। | |||
[[File:Jack-in-cube solid model, light background.gif|thumb|right|ठोस मॉडलिंग में ज्यामिति पूरी तरह से 3 में वर्णित है{{nbhyph}}डी स्थान; वस्तुओं को किसी भी कोण से देखा जा सकता है।]][[3 डी मॉडलिंग]] (या सॉलिड मॉडलिंग) त्रि-आयामी आकार ''[[solid (mathematics)]]|(solid)'' के गणितीय और कंप्यूटर मॉडलिंग के लिए सिद्धांतों का | |||
== सिंहावलोकन == | == सिंहावलोकन == | ||
ठोस मॉडलिंग तकनीकों का उपयोग डिजाइन प्रक्रिया के | ठोस मॉडलिंग तकनीकों का उपयोग डिजाइन प्रक्रिया के भाग के रूप में की जाने वाली कई कठिन इंजीनियरिंग गणनाओं की स्वचालन प्रक्रिया की अनुमति देता है। [[मशीनिंग]] और [[समनुक्रम]] जैसी प्रक्रियाओं का अनुकरण, योजना और सत्यापन ठोस मॉडलिंग के विकास के लिए मुख्य उत्प्रेरकों में से एक थे। हाल ही में, [[धातु की चादर]] [[उत्पादन]], [[अंतः क्षेपण ढलाई]], [[वेल्डिंग]], [[पाइपलाइन]] रूटिंग आदि को शामिल करने के लिए समर्थित निर्माण अनुप्रयोगों की सीमा का विस्तार किया गया है। पारंपरिक निर्माण से परे, ठोस मॉडलिंग तकनीकें तेजी [[तीव्र प्रोटोटाइपिंग]], डिजिटल डेटा अभिलेखीय और [[रिवर्स इंजीनियरिंग]] के लिए नींव के रूप में काम करती हैं। भौतिक वस्तुओं पर नमूना बिंदुओं से ठोस पदार्थों का पुनर्निर्माण करके, [[परिमित तत्व]] का उपयोग करके यांत्रिक विश्लेषण, [[गति योजना]] और एनसी पथ सत्यापन, [[तंत्र (इंजीनियरिंग)]] के [[गतिकी]] और गतिशीलता (भौतिकी), और इसी तरह। इन सभी अनुप्रयोगों में केंद्रीय समस्या वास्तविक कलाकृतियों के भौतिक व्यवहार के अनुरूप तीन आयामी ज्यामिति का प्रभावी ढंग से प्रतिनिधित्व और हेरफेर करने की क्षमता है। ठोस मॉडलिंग अनुसंधान और विकास ने इनमें से कई मुद्दों को प्रभावी ढंग से संबोधित किया है, और कंप्यूटर एडेड इंजीनियरिंग का केंद्रीय फोकस बना हुआ है। | ||
== गणितीय नींव == | == गणितीय नींव == | ||
आज प्रचलित ठोस मॉडलिंग की धारणा यांत्रिक ज्यामितीय मॉडलिंग प्रणालियों में सूचनात्मक पूर्णता की विशिष्ट आवश्यकता पर निर्भर करती है, इस अर्थ में कि किसी भी कंप्यूटर मॉडल को सभी ज्यामितीय प्रश्नों का समर्थन करना चाहिए जो इसके संबंधित भौतिक वस्तु से पूछे जा सकते हैं। आवश्यकता स्पष्ट रूप से एक ही भौतिक वस्तु के कई कंप्यूटर अभ्यावेदन की संभावना को पहचानती है जब तक कि कोई भी दो अभ्यावेदन सुसंगत हैं। | आज प्रचलित ठोस मॉडलिंग की धारणा यांत्रिक ज्यामितीय मॉडलिंग प्रणालियों में सूचनात्मक पूर्णता की विशिष्ट आवश्यकता पर निर्भर करती है, इस अर्थ में कि किसी भी कंप्यूटर मॉडल को सभी ज्यामितीय प्रश्नों का समर्थन करना चाहिए जो इसके संबंधित भौतिक वस्तु से पूछे जा सकते हैं। आवश्यकता स्पष्ट रूप से एक ही भौतिक वस्तु के कई कंप्यूटर अभ्यावेदन की संभावना को पहचानती है जब तक कि कोई भी दो अभ्यावेदन सुसंगत हैं। प्रतिनिधित्व की सूचनात्मक पूर्णता को कम्प्यूटेशनल रूप से सत्यापित करना असंभव है जब तक कि किसी भौतिक वस्तु की धारणा को गणना योग्य गणितीय गुणों और किसी विशेष प्रतिनिधित्व से स्वतंत्र के रूप में परिभाषित नहीं किया जाता है। इस तरह के तर्क ने मॉडलिंग प्रतिमान के विकास को जन्म दिया जिसने ठोस मॉडलिंग के क्षेत्र को आकार दिया है जैसा कि आज हम जानते हैं।<ref name = "First Principles">{{cite journal |title= Solid Modeling: Current Status and Research Directions|journal = IEEE Computer Graphics and Applications|volume = 3|issue = 7|pages = 25–37|author1=Requicha, A.A.G |author2=Voelcker, H. |name-list-style=amp |year= 1983 |publisher= IEEE Computer Graphics |doi= 10.1109/MCG.1983.263271|s2cid = 14462567}}</ref> | ||
सभी निर्मित घटकों में परिमित आकार और अच्छी तरह से व्यवहार वाली [[सीमा (टोपोलॉजी)]] है, इसलिए शुरू में सजातीय [[समदैशिक]] सामग्री से बने कठोर भागों को गणितीय रूप से मॉडलिंग करने पर ध्यान केंद्रित किया गया था जिसे जोड़ा या हटाया जा सकता था। इन अभिगृहीत गुणों को क्षेत्रों के गुणों में अनुवादित किया जा सकता है, त्रि-आयामी [[यूक्लिडियन अंतरिक्ष]] के सबसेट। दृढ़ता को परिभाषित करने के लिए दो सामान्य दृष्टिकोण क्रमशः [[बिंदु-सेट टोपोलॉजी]] और [[बीजगणितीय टोपोलॉजी]] पर निर्भर करते हैं। दोनों मॉडल निर्दिष्ट करते हैं कि सरल टुकड़ों या कोशिकाओं से ठोस कैसे बनाया जा सकता है। | सभी निर्मित घटकों में परिमित आकार और अच्छी तरह से व्यवहार वाली [[सीमा (टोपोलॉजी)]] है, इसलिए शुरू में सजातीय [[समदैशिक]] सामग्री से बने कठोर भागों को गणितीय रूप से मॉडलिंग करने पर ध्यान केंद्रित किया गया था जिसे जोड़ा या हटाया जा सकता था। इन अभिगृहीत गुणों को क्षेत्रों के गुणों में अनुवादित किया जा सकता है, त्रि-आयामी [[यूक्लिडियन अंतरिक्ष]] के सबसेट। दृढ़ता को परिभाषित करने के लिए दो सामान्य दृष्टिकोण क्रमशः [[बिंदु-सेट टोपोलॉजी]] और [[बीजगणितीय टोपोलॉजी]] पर निर्भर करते हैं। दोनों मॉडल निर्दिष्ट करते हैं कि सरल टुकड़ों या कोशिकाओं से ठोस कैसे बनाया जा सकता है। | ||
[[File:Regularize1.png|thumb|right|450px| | [[File:Regularize1.png|thumb|right|450px|2-डी समुच्चय के आंतरिक भाग को बंद करके उसका नियमितीकरण]]दृढ़ता के सातत्य बिंदु-सेट मॉडल के अनुसार, किसी भी X ⊂ ℝ के सभी बिंदु<sup>3</sup> को उनके [[पड़ोस (टोपोलॉजी)]] के अनुसार एक्स के संबंध में आंतरिक (टोपोलॉजी), [[बाहरी (टोपोलॉजी)]], या सीमा (टोपोलॉजी) बिंदुओं के रूप में वर्गीकृत किया जा सकता है। मान लीजिए<sup>3</sup> विशिष्ट [[यूक्लिडियन मीट्रिक]] से संपन्न है, बिंदु p ∈X का पड़ोस [[गेंद (गणित)]] का रूप ले लेता है। X को ठोस माने जाने के लिए, किसी भी p ∈X का प्रत्येक पड़ोस लगातार त्रिविमीय होना चाहिए; निम्न-आयामी पड़ोस वाले बिंदु दृढ़ता की कमी का संकेत देते हैं। पड़ोस की आयामी एकरूपता की गारंटी 'बंद नियमित सेट' के वर्ग के लिए है, जिसे उनके इंटीरियर के [[क्लोजर (टोपोलॉजी)]] के बराबर सेट के रूप में परिभाषित किया गया है। कोई एक्स ⊂ ℝ<sup>3</sup> को बंद नियमित सेट में बदला जा सकता है या इसके इंटीरियर को बंद करके नियमित किया जा सकता है, और इस प्रकार ठोस पदार्थों के मॉडलिंग स्थान को गणितीय रूप से ℝ के बंद नियमित उपसमुच्चय के स्थान के रूप में परिभाषित किया जाता है।<sup>3</sup> (हेइन-बोरेल प्रमेय द्वारा | हेइन-बोरेल प्रमेय यह निहित है कि सभी ठोस [[कॉम्पैक्ट जगह]] सेट हैं)। इसके अलावा, सेट यूनियन, चौराहे और अंतर के बूलियन संचालन के तहत ठोस पदार्थों को बंद करना आवश्यक है (सामग्री को जोड़ने और हटाने के बाद ठोसता की गारंटी देने के लिए)। मानक बूलियन संचालन को बंद नियमित सेट पर लागू करने से बंद नियमित सेट का उत्पादन नहीं हो सकता है, लेकिन मानक बूलियन संचालन को लागू करने के परिणाम को नियमित करके इस समस्या को हल किया जा सकता है।<ref name = "Regularized operations">{{citation|doi=10.1016/0010-4485(80)90025-1|title=Closure of Boolean operations on geometric entities|journal=Computer-Aided Design|volume=12|issue=5|pages=219–220|year=1980|last1=Tilove|first1=R.B.|last2=Requicha|first2=A.A.G.}}</ref> नियमित सेट संचालन को ∪ दर्शाया जाता है<sup>∗</sup>, ∩<sup>∗</sup>, और −<sup>∗</sup>. | ||
सेट X ⊂ ℝ का संयोजी लक्षण वर्णन<sup>3</sup> ठोस के रूप में एक्स को ओरिएंटेबल [[सीडब्ल्यू कॉम्प्लेक्स]] के रूप में प्रस्तुत करना शामिल है ताकि कोशिकाएं अन्यथा असंख्य सातत्य में बिंदुओं के लिए परिमित स्थानिक पते प्रदान कर सकें।<ref name="Solid Modeling"/>यूक्लिडियन अंतरिक्ष के [[अर्ध-विश्लेषणात्मक]] [[घिरा हुआ सेट]] उपसमुच्चय का वर्ग बूलियन संचालन (मानक और नियमित) के तहत बंद है और अतिरिक्त संपत्ति प्रदर्शित करता है कि प्रत्येक अर्ध-विश्लेषणात्मक सेट [[स्तरीकरण (गणित)]] हो सकता है जो आयामों के असंबद्ध कोशिकाओं के संग्रह में हो सकता है 0,1 ,2,3. बिंदुओं, [[रेखा खंड]], त्रिकोणीय चेहरे (ज्यामिति), और [[चतुष्फलकीय]] तत्वों के संग्रह में अर्ध-विश्लेषणात्मक सेट का त्रिभुज (टोपोलॉजी) स्तरीकरण का उदाहरण है जो आमतौर पर उपयोग किया जाता है। ठोसता के संयोजी मॉडल को यह कहते हुए संक्षेप में प्रस्तुत किया जाता है कि अर्ध-विश्लेषणात्मक बाध्य उपसमुच्चय होने के अलावा, ठोस त्रि-आयामी [[टोपोलॉजिकल पॉलीहेड्रा]] हैं, विशेष रूप से सीमा के साथ तीन-आयामी ओरिएंटेबल मैनिफोल्ड।<ref name = "Representations">{{cite journal |title= Representations for Rigid Solids: Theory, Methods, and Systems|journal= ACM Computing Surveys|volume= 12|issue= 4|pages= 437–464|author= Requicha, A.A.G. |year= 1980 |doi= 10.1145/356827.356833|s2cid= 207568300}}</ref> विशेष रूप से इसका तात्पर्य संयोजी सीमा की [[यूलर विशेषता]] से है<ref name = "Hatcher">{{cite book |url=http://www.math.cornell.edu/~hatcher/AT/ATpage.html |title= Algebraic Topology|author= Hatcher, A. |year= 2002 |publisher= Cambridge University Press |access-date=20 April 2010}}</ref> पॉलीहेड्रॉन का 2 है। सॉलिडिटी का कॉम्बिनेटरियल मैनिफोल्ड मॉडल भी [[जॉर्डन वक्र प्रमेय]] के परिणाम के रूप में ठोस अलग स्थान की सीमा को ठीक दो घटकों में गारंटी देता है। निर्माण करना असंभव है। | |||
ठोस पदार्थों के बिंदु-सेट और संयोजी मॉडल पूरी तरह से एक-दूसरे के साथ संगत होते हैं, एक दूसरे के स्थान पर उपयोग किए जा सकते हैं, निरंतर या संयोजी गुणों पर निर्भर करते हुए आवश्यकतानुसार, और n आयामों तक बढ़ाया जा सकता है। इस स्थिरता को सुविधाजनक बनाने वाली प्रमुख संपत्ति यह है कि ℝ के बंद नियमित उपसमुच्चय का वर्ग<sup>n</sup> सजातीय रूप से n-आयामी टोपोलॉजिकल पॉलीहेड्रा के साथ सटीक रूप से मेल खाता है। इसलिए, प्रत्येक एन-आयामी ठोस को इसकी सीमा द्वारा स्पष्ट रूप से दर्शाया जा सकता है और सीमा में | ठोस पदार्थों के बिंदु-सेट और संयोजी मॉडल पूरी तरह से एक-दूसरे के साथ संगत होते हैं, एक दूसरे के स्थान पर उपयोग किए जा सकते हैं, निरंतर या संयोजी गुणों पर निर्भर करते हुए आवश्यकतानुसार, और n आयामों तक बढ़ाया जा सकता है। इस स्थिरता को सुविधाजनक बनाने वाली प्रमुख संपत्ति यह है कि ℝ के बंद नियमित उपसमुच्चय का वर्ग<sup>n</sup> सजातीय रूप से n-आयामी टोपोलॉजिकल पॉलीहेड्रा के साथ सटीक रूप से मेल खाता है। इसलिए, प्रत्येक एन-आयामी ठोस को इसकी सीमा द्वारा स्पष्ट रूप से दर्शाया जा सकता है और सीमा में एन-1-आयामी पॉलीहेड्रॉन की मिश्रित संरचना होती है जिसमें सजातीय रूप से एन-1-आयामी पड़ोस होते हैं। | ||
== ठोस प्रतिनिधित्व योजनाएँ == | == ठोस प्रतिनिधित्व योजनाएँ == | ||
अनुमानित गणितीय गुणों के आधार पर, ठोस पदार्थों का प्रतिनिधित्व करने की कोई भी योजना यूक्लिडियन अंतरिक्ष के अर्ध-विश्लेषणात्मक उपसमुच्चय के वर्ग के बारे में जानकारी प्राप्त करने की | अनुमानित गणितीय गुणों के आधार पर, ठोस पदार्थों का प्रतिनिधित्व करने की कोई भी योजना यूक्लिडियन अंतरिक्ष के अर्ध-विश्लेषणात्मक उपसमुच्चय के वर्ग के बारे में जानकारी प्राप्त करने की विधि है। इसका मतलब है कि सभी प्रतिनिधित्व एक ही ज्यामितीय और सामयिक डेटा को [[डेटा संरचना]] के रूप में व्यवस्थित करने के विभिन्न तरीके हैं। सभी प्रतिनिधित्व योजनाओं को प्रिमिटिव के सेट पर परिमित संख्या में संचालन के संदर्भ में व्यवस्थित किया जाता है। इसलिए, किसी विशेष प्रतिनिधित्व का मॉडलिंग स्थान परिमित है, और कोई एकल प्रतिनिधित्व योजना सभी प्रकार के ठोस पदार्थों का प्रतिनिधित्व करने के लिए पूरी तरह से पर्याप्त नहीं हो सकती है। उदाहरण के लिए, [[रचनात्मक ठोस ज्यामिति]] के माध्यम से परिभाषित ठोस को बहुत ही सरल मामलों को छोड़कर, अंतरिक्ष प्रक्षेपवक्र के अनुसार आदिम गति के [[ठोस झाडू]] के रूप में प्रस्तुत नहीं किया जा सकता है। यह आधुनिक ज्यामितीय मॉडलिंग प्रणालियों को ठोस पदार्थों की कई प्रतिनिधित्व योजनाओं को बनाए रखने और प्रतिनिधित्व योजनाओं के बीच कुशल रूपांतरण की सुविधा प्रदान करने के लिए मजबूर करता है। | ||
नीचे ठोस मॉडल बनाने या प्रस्तुत करने के लिए उपयोग की जाने वाली सामान्य तकनीकों की सूची दी गई है।<ref name="Representations"/>आधुनिक मॉडलिंग सॉफ़्टवेयर ठोस का प्रतिनिधित्व करने के लिए इन योजनाओं के संयोजन का उपयोग कर सकता है। | नीचे ठोस मॉडल बनाने या प्रस्तुत करने के लिए उपयोग की जाने वाली सामान्य तकनीकों की सूची दी गई है।<ref name="Representations"/>आधुनिक मॉडलिंग सॉफ़्टवेयर ठोस का प्रतिनिधित्व करने के लिए इन योजनाओं के संयोजन का उपयोग कर सकता है। | ||
=== आदिम उदाहरण === | === आदिम उदाहरण === | ||
यह योजना वस्तु के परिवारों की धारणा पर आधारित है, परिवार के प्रत्येक सदस्य को कुछ मापदंडों द्वारा दूसरे से अलग किया जाता है। प्रत्येक वस्तु परिवार को | यह योजना वस्तु के परिवारों की धारणा पर आधारित है, परिवार के प्रत्येक सदस्य को कुछ मापदंडों द्वारा दूसरे से अलग किया जाता है। प्रत्येक वस्तु परिवार को सामान्य आदिम कहा जाता है, और परिवार के भीतर अलग-अलग वस्तुओं को आदिम उदाहरण कहा जाता है। उदाहरण के लिए, बोल्ट का परिवार सामान्य आदिम है, और मापदंडों के विशेष सेट द्वारा निर्दिष्ट एकल बोल्ट आदिम उदाहरण है। शुद्ध पैरामीटरयुक्त इंस्टेंसिंग योजनाओं की विशिष्ट विशेषता नई संरचनाओं को बनाने के लिए उदाहरणों के संयोजन के साधनों की कमी है जो नई और अधिक जटिल वस्तुओं का प्रतिनिधित्व करती हैं। इस योजना का अन्य मुख्य दोष प्रस्तुत ठोस पदार्थों के कंप्यूटिंग गुणों के लिए [[कलन विधि]] लिखने में कठिनाई है। एल्गोरिदम में काफी मात्रा में परिवार-विशिष्ट जानकारी का निर्माण किया जाना चाहिए और इसलिए प्रत्येक सामान्य आदिम को विशेष मामले के रूप में माना जाना चाहिए, जिससे कोई समान समग्र उपचार नहीं हो सके। | ||
=== स्थानिक अधिभोग गणना === | === स्थानिक अधिभोग गणना === | ||
यह योजना अनिवार्य रूप से ठोस द्वारा व्याप्त स्थानिक कोशिकाओं की | यह योजना अनिवार्य रूप से ठोस द्वारा व्याप्त स्थानिक कोशिकाओं की सूची है। कोशिकाएँ, जिन्हें स्वर भी कहा जाता है, निश्चित आकार के घन होते हैं और निश्चित स्थानिक ग्रिड में व्यवस्थित होते हैं (अन्य बहुफलकीय व्यवस्थाएँ भी संभव हैं लेकिन घन सबसे सरल हैं)। प्रत्येक सेल को बिंदु के निर्देशांक द्वारा दर्शाया जा सकता है, जैसे कि सेल का केन्द्रक। आम तौर पर विशिष्ट स्कैनिंग ऑर्डर लगाया जाता है और निर्देशांक के संबंधित ऑर्डर किए गए सेट को स्थानिक सरणी कहा जाता है। स्थानिक सरणियाँ असंदिग्ध और अद्वितीय ठोस निरूपण हैं लेकिन 'मास्टर' या निश्चित अभ्यावेदन के रूप में उपयोग के लिए बहुत अधिक वर्बोज़ हैं। हालांकि, वे भागों के मोटे अनुमानों का प्रतिनिधित्व कर सकते हैं और ज्यामितीय एल्गोरिदम के प्रदर्शन को बेहतर बनाने के लिए इस्तेमाल किया जा सकता है, खासकर जब [[रचनात्मक ठोस ज्यामिति]] जैसे अन्य अभ्यावेदन के साथ प्रयोग किया जाता है। | ||
=== सेल अपघटन === | === सेल अपघटन === | ||
यह योजना ऊपर वर्णित ठोस पदार्थों के संयोजी (बीजीय सांस्थितिकीय) विवरणों से अनुसरण करती है। | यह योजना ऊपर वर्णित ठोस पदार्थों के संयोजी (बीजीय सांस्थितिकीय) विवरणों से अनुसरण करती है। ठोस को उसके अपघटन द्वारा कई कोशिकाओं में दर्शाया जा सकता है। स्थानिक अधिभोग गणना योजनाएँ कोशिका अपघटन का विशेष मामला है जहाँ सभी कोशिकाएँ घनाकार होती हैं और नियमित ग्रिड में स्थित होती हैं। सेल अपघटन ठोस के कुछ [[टोपोलॉजिकल गुण]] की गणना के लिए सुविधाजनक तरीके प्रदान करते हैं जैसे कि इसके [[जुड़ा हुआ स्थान]] (टुकड़ों की संख्या) और [[जीनस (गणित)]] (छिद्रों की संख्या)। त्रिकोणीय के रूप में सेल अपघटन आंशिक अंतर समीकरणों के संख्यात्मक समाधान के लिए 3डी परिमित तत्वों में उपयोग किए जाने वाले प्रतिनिधित्व हैं। रोबोट मोशन प्लानिंग में अनुप्रयोगों के लिए अन्य सेल अपघटन जैसे व्हिटनी नियमित रूप से स्तरीकृत स्थान या मोर्स अपघटन का उपयोग किया जा सकता है।<ref name = "Complexity_planning">{{cite book |url=http://mitpress.mit.edu/catalog/item/default.asp?tid=4749&ttype=2 |title= रोबोट मोशन प्लानिंग की जटिलता|author= Canny, John F. |year= 1987 |publisher= MIT press, ACM doctoral dissertation award |access-date=20 April 2010}}</रेफरी> | ||
=== सरफेस मेश मॉडलिंग === | === सरफेस मेश मॉडलिंग === | ||
| Line 40: | Line 39: | ||
=== स्वीपिंग === | === स्वीपिंग === | ||
व्यापक योजनाओं में सन्निहित मूल धारणा सरल है। अंतरिक्ष के माध्यम से चलने वाला | व्यापक योजनाओं में सन्निहित मूल धारणा सरल है। अंतरिक्ष के माध्यम से चलने वाला सेट वॉल्यूम (ठोस) का पता लगा सकता है या स्वीप कर सकता है जिसे मूविंग सेट और उसके प्रक्षेपवक्र द्वारा दर्शाया जा सकता है। इस तरह का प्रतिनिधित्व अनुप्रयोगों के संदर्भ में महत्वपूर्ण है जैसे कटर से निकाली गई सामग्री का पता लगाने के रूप में यह निर्दिष्ट प्रक्षेपवक्र के साथ चलता है, सापेक्ष गति से गुजरने वाले दो ठोस पदार्थों के गतिशील हस्तक्षेप की गणना, गति योजना, और यहां तक कि कंप्यूटर ग्राफिक्स अनुप्रयोगों जैसे अनुरेखण में भी ब्रश की गति कैनवास पर चलती है। अधिकांश वाणिज्यिक सीएडी प्रणालियां स्वेप्ट सॉलिड्स के निर्माण के लिए (सीमित) कार्यक्षमता प्रदान करती हैं, जो ज्यादातर दो आयामी क्रॉस सेक्शन के रूप में होती हैं, जो स्पेस ट्रैजेक्टरी ट्रांसवर्सल पर सेक्शन में चलती हैं। हालाँकि, वर्तमान शोध ने तीन आयामी आकृतियों के पैरामीटर और यहां तक कि बहु-पैरामीटर गतियों के कई अनुमानों को दिखाया है। | ||
=== अंतर्निहित प्रतिनिधित्व === | === अंतर्निहित प्रतिनिधित्व === | ||
{{Main|Function representation}} | {{Main|Function representation}} | ||
अंक X के | अंक X के सेट को परिभाषित करने का बहुत ही सामान्य तरीका [[विधेय (गणितीय तर्क)]] निर्दिष्ट करना है जिसका मूल्यांकन अंतरिक्ष में किसी भी बिंदु पर किया जा सकता है। दूसरे शब्दों में, एक्स को निहित रूप से परिभाषित किया गया है जिसमें वे सभी बिंदु शामिल हैं जो विधेय द्वारा निर्दिष्ट शर्तों को पूरा करते हैं। विधेय का सबसे सरल रूप वास्तविक मूल्यवान फ़ंक्शन के संकेत पर स्थिति है जिसके परिणामस्वरूप समानता और असमानताओं द्वारा सेट का परिचित प्रतिनिधित्व होता है। उदाहरण के लिए, अगर <math>f= ax + by + cz + d</math> शर्तें <math>f(p) =0</math>, <math> f(p) > 0</math>, और <math>f(p) < 0</math> प्रतिनिधित्व करते हैं, क्रमशः, एक विमान और दो खुले रैखिक अर्ध-स्थान (ज्यामिति)। सरल विधेय के बूलियन संयोजनों द्वारा अधिक जटिल कार्यात्मक आदिम परिभाषित किए जा सकते हैं। इसके अलावा, [[रवाचेव समारोह]] का सिद्धांत | आर-फ़ंक्शंस ऐसे प्रतिनिधित्वों के रूपांतरण को किसी भी बंद अर्ध विश्लेषणात्मक सेट के लिए एकल फ़ंक्शन असमानता में बदलने की अनुमति देते हैं। इस तरह के प्रतिनिधित्व को बहुभुजीकरण एल्गोरिदम का उपयोग करके सीमा प्रतिनिधित्व में परिवर्तित किया जा सकता है, उदाहरण के लिए, [[मार्चिंग क्यूब्स]] एल्गोरिदम। | ||
=== पैरामीट्रिक और फीचर-आधारित मॉडलिंग === | === पैरामीट्रिक और फीचर-आधारित मॉडलिंग === | ||
सुविधाओं को आंतरिक ज्यामितीय मापदंडों (लंबाई, चौड़ाई, गहराई आदि), स्थिति और अभिविन्यास, [[ज्यामितीय सहिष्णुता]], भौतिक गुणों और अन्य विशेषताओं के संदर्भ जैसी विशेषताओं से जुड़े पैरामीट्रिक आकार के रूप में परिभाषित किया गया है।<ref name = "Features">{{cite journal |title= Challenges in feature based manufacturing research |journal= Communications of the ACM |volume= 39 |issue= 2 |pages= 77–85 |author= Mantyla, M., Nau, D. , and Shah, J.|year= 1996|doi= 10.1145/230798.230808 |s2cid= 3340804 |doi-access= free }}</ref> सुविधाएँ संबंधित उत्पादन प्रक्रियाओं और संसाधन मॉडल तक पहुँच भी प्रदान करती हैं। इस प्रकार, आदिम बंद नियमित सेटों की तुलना में सुविधाओं का शब्दार्थ उच्च स्तर है। सुविधाओं से आम तौर पर सीएडी को डाउनस्ट्रीम मैन्युफैक्चरिंग एप्लिकेशन के साथ जोड़ने और डिजाइन डेटा के पुन: उपयोग के लिए [[डेटाबेस]] को व्यवस्थित करने के लिए | सुविधाओं को आंतरिक ज्यामितीय मापदंडों (लंबाई, चौड़ाई, गहराई आदि), स्थिति और अभिविन्यास, [[ज्यामितीय सहिष्णुता]], भौतिक गुणों और अन्य विशेषताओं के संदर्भ जैसी विशेषताओं से जुड़े पैरामीट्रिक आकार के रूप में परिभाषित किया गया है।<ref name = "Features">{{cite journal |title= Challenges in feature based manufacturing research |journal= Communications of the ACM |volume= 39 |issue= 2 |pages= 77–85 |author= Mantyla, M., Nau, D. , and Shah, J.|year= 1996|doi= 10.1145/230798.230808 |s2cid= 3340804 |doi-access= free }}</ref> सुविधाएँ संबंधित उत्पादन प्रक्रियाओं और संसाधन मॉडल तक पहुँच भी प्रदान करती हैं। इस प्रकार, आदिम बंद नियमित सेटों की तुलना में सुविधाओं का शब्दार्थ उच्च स्तर है। सुविधाओं से आम तौर पर सीएडी को डाउनस्ट्रीम मैन्युफैक्चरिंग एप्लिकेशन के साथ जोड़ने और डिजाइन डेटा के पुन: उपयोग के लिए [[डेटाबेस]] को व्यवस्थित करने के लिए आधार बनाने की उम्मीद की जाती है। इंजीनियरिंग में जटिल वस्तुओं की प्रणालियों का पूरी तरह से वर्णन करने के लिए पैरामीट्रिक फीचर आधारित मॉडलिंग को अक्सर रचनात्मक बाइनरी सॉलिड ज्योमेट्री (CSG) के साथ जोड़ा जाता है। | ||
== ठोस मॉडलर्स का इतिहास == | == ठोस मॉडलर्स का इतिहास == | ||
सॉलिड मॉडलर्स के ऐतिहासिक विकास को पूरे कंप्यूटर-एडेड डिज़ाइन के संदर्भ में देखा जाना चाहिए, प्रमुख मील के पत्थर अनुसंधान प्रणाली BUILD के विकास के बाद इसके वाणिज्यिक स्पिन-ऑफ रोमुलस (बी-रेप सॉलिड मॉडलर) के रूप में आगे बढ़े। [[पैरासॉलिड]], एसीआईएस और [[ठोस मॉडलिंग समाधान]] के विकास को प्रभावित करते हैं। [[स्वतंत्र राष्ट्रों का राष्ट्रमंडल]] (CIS) में पहले सीएडी डेवलपर्स में से एक, ASCON ने 1990 के दशक में अपने स्वयं के ठोस मॉडलर का आंतरिक विकास शुरू किया।<ref>{{cite journal | |||
सॉलिड मॉडलर्स के ऐतिहासिक विकास को पूरे कंप्यूटर-एडेड डिज़ाइन के संदर्भ में देखा जाना चाहिए, प्रमुख मील के पत्थर अनुसंधान प्रणाली BUILD के विकास के बाद इसके वाणिज्यिक स्पिन-ऑफ रोमुलस (बी-रेप सॉलिड मॉडलर) के रूप में आगे बढ़े। [[पैरासॉलिड]], एसीआईएस और [[ठोस मॉडलिंग समाधान]] के विकास को प्रभावित करते हैं। [[स्वतंत्र राष्ट्रों का राष्ट्रमंडल]] (CIS) में पहले | |||
|last = Yares | |last = Yares | ||
|first = Evan | |first = Evan | ||
| Line 67: | Line 64: | ||
|archive-date = 30 January 2015 | |archive-date = 30 January 2015 | ||
|df = dmy-all | |df = dmy-all | ||
}}</ref> नवंबर 2012 में, ASCON का गणितीय प्रभाग | }}</ref> नवंबर 2012 में, ASCON का गणितीय प्रभाग अलग कंपनी बन गया, और इसका नाम [[C3D]] रखा गया। इसे C3D [[ज्यामितीय मॉडलिंग कर्नेल]] को स्टैंडअलोन उत्पाद के रूप में विकसित करने का कार्य सौंपा गया था - रूस से एकमात्र वाणिज्यिक 3D मॉडलिंग कर्नेल।<ref>{{cite book | ||
|last = Golovanov | |last = Golovanov | ||
|first = Nikolay | |first = Nikolay | ||
| Line 78: | Line 75: | ||
== कंप्यूटर एडेड डिजाइन == | == कंप्यूटर एडेड डिजाइन == | ||
{{Main|Computer-aided design}} | {{Main|Computer-aided design}} | ||
ठोस पदार्थों की मॉडलिंग कंप्यूटर-एडेड डिजाइन#क्षमताओं|सीएडी प्रणाली की क्षमताओं की केवल न्यूनतम आवश्यकता है। पिछले दस वर्षों में इंजीनियरिंग विभागों में ठोस मॉडलर आम हो गए हैं{{When|date=December 2011}} तेज कंप्यूटर और प्रतिस्पर्धी सॉफ्टवेयर मूल्य निर्धारण के कारण। ठोस मॉडलिंग सॉफ्टवेयर मशीन डिजाइन और विश्लेषण के लिए घटकों का आभासी 3डी प्रतिनिधित्व बनाता है।<ref name="LaCourse Handbook">{{cite book|last=LaCourse|first=Donald|title=Handbook of Solid Modeling|publisher=McGraw Hill|year=1995|pages=2.5|chapter=2|isbn=978-0-07-035788-4}}</ref> विशिष्ट [[जीयूआई]] में प्रोग्रामेबल मैक्रोज़, कीबोर्ड शॉर्टकट और डायनेमिक मॉडल हेरफेर शामिल हैं। रीयल-टाइम छायांकित 3-डी में मॉडल को गतिशील रूप से पुन: उन्मुख करने की क्षमता पर जोर दिया जाता है और डिजाइनर को मानसिक 3-डी छवि बनाए रखने में मदद मिलती है। | |||
ठोस पदार्थों की मॉडलिंग कंप्यूटर-एडेड डिजाइन#क्षमताओं|सीएडी प्रणाली की क्षमताओं की केवल न्यूनतम आवश्यकता है। पिछले दस वर्षों में इंजीनियरिंग विभागों में ठोस मॉडलर आम हो गए हैं{{When|date=December 2011}} तेज कंप्यूटर और प्रतिस्पर्धी सॉफ्टवेयर मूल्य निर्धारण के कारण। ठोस मॉडलिंग सॉफ्टवेयर मशीन डिजाइन और विश्लेषण के लिए घटकों का | |||
ठोस भाग मॉडल में आमतौर पर सुविधाओं का समूह होता है, जब तक कि मॉडल पूरा नहीं हो जाता, तब तक एक-एक करके जोड़ा जाता है। इंजीनियरिंग ठोस मॉडल ज्यादातर स्केचर-आधारित सुविधाओं के साथ बनाए जाते हैं; 2-डी रेखाचित्र जो 3-डी बनने के मार्ग के साथ बह गए हैं। उदाहरण के लिए ये कट या एक्सट्रूज़न हो सकते हैं। घटकों पर डिजाइन का काम आमतौर पर पूरे उत्पाद के संदर्भ में [[असेंबली मॉडलिंग]] विधियों का उपयोग करके किया जाता है। असेंबली मॉडल में अलग-अलग भाग मॉडल के संदर्भ शामिल होते हैं जिनमें उत्पाद शामिल होता है।<ref name="LaCourse Handbook 11.3">{{cite book|last=LaCourse|first=Donald|title=Handbook of Solid Modeling|publisher=McGraw Hill|year=1995|pages=111.2|chapter=11|isbn=978-0-07-035788-4}}</ref> | |||
अन्य प्रकार की मॉडलिंग तकनीक 'सरफेसिंग' ([[फ्रीफॉर्म सतह मॉडलिंग]]) है। यहाँ, सतहों को परिभाषित, छंटनी और विलय किया जाता है, और ठोस बनाने के लिए भरा जाता है। सतहों को आमतौर पर अंतरिक्ष में डेटम कर्व्स और कई तरह के जटिल कमांड के साथ परिभाषित किया जाता है। सरफेसिंग अधिक कठिन है, लेकिन इंजेक्शन मोल्डिंग जैसी कुछ निर्माण तकनीकों के लिए बेहतर है। इंजेक्शन ढाले भागों के लिए ठोस मॉडल में आमतौर पर सरफेसिंग और स्केचर आधारित विशेषताएं होती हैं। | |||
इंजीनियरिंग चित्र अर्ध-स्वचालित रूप से बनाए जा सकते हैं और ठोस मॉडल को संदर्भित कर सकते हैं। | इंजीनियरिंग चित्र अर्ध-स्वचालित रूप से बनाए जा सकते हैं और ठोस मॉडल को संदर्भित कर सकते हैं। | ||
=== पैरामीट्रिक मॉडलिंग === | === पैरामीट्रिक मॉडलिंग === | ||
पैरामीट्रिक मॉडलिंग | पैरामीट्रिक मॉडलिंग मॉडल को परिभाषित करने के लिए पैरामीटर का उपयोग करता है (उदाहरण के लिए आयाम)। मापदंडों के उदाहरण हैं: मॉडल सुविधाओं को बनाने के लिए उपयोग किए जाने वाले आयाम, सामग्री घनत्व, स्वेप्ट सुविधाओं का वर्णन करने के लिए सूत्र, आयातित डेटा (उदाहरण के लिए, संदर्भ सतह का वर्णन)। पैरामीटर को बाद में संशोधित किया जा सकता है, और संशोधन को दर्शाने के लिए मॉडल अपडेट होगा। आमतौर पर, भागों, विधानसभाओं और रेखाचित्रों के बीच संबंध होता है। एक भाग में कई विशेषताएं होती हैं, और असेंबली में कई भाग होते हैं। चित्र या तो भागों या विधानसभाओं से बनाए जा सकते हैं। | ||
उदाहरण: 100 मिमी के | उदाहरण: 100 मिमी के वृत्त को एक्सट्रूड करके शाफ़्ट बनाया जाता है। शाफ्ट के अंत में हब इकट्ठा किया जाता है। बाद में, शाफ्ट को 200 मिमी लंबा करने के लिए संशोधित किया गया है (शाफ्ट पर क्लिक करें, लंबाई आयाम का चयन करें, 200 में संशोधित करें)। जब मॉडल को अपडेट किया जाता है तो शाफ्ट 200 मिमी लंबा हो जाएगा, हब उस शाफ्ट के अंत में स्थानांतरित हो जाएगा जहां इसे इकट्ठा किया गया था, और इंजीनियरिंग चित्र और द्रव्यमान गुण स्वचालित रूप से सभी परिवर्तनों को दर्शाएंगे। | ||
मापदंडों से संबंधित, लेकिन थोड़ा अलग, [[बाधा (कंप्यूटर एडेड डिजाइन)]] हैं। प्रतिबन्ध संस्थाओं के बीच संबंध हैं जो | मापदंडों से संबंधित, लेकिन थोड़ा अलग, [[बाधा (कंप्यूटर एडेड डिजाइन)]] हैं। प्रतिबन्ध संस्थाओं के बीच संबंध हैं जो विशेष आकार बनाते हैं। खिड़की के लिए, पक्षों को समानांतर और समान लंबाई के रूप में परिभाषित किया जा सकता है। पैरामीट्रिक मॉडलिंग स्पष्ट और सहज है। लेकिन सीएडी के पहले तीन दशकों में ऐसा नहीं था। संशोधन का अर्थ है फिर से खींचना, या पुराने के ऊपर नया कट या फलाव जोड़ना। दिखाए जाने के बजाय इंजीनियरिंग ड्रॉइंग पर आयाम बनाए गए। पैरामीट्रिक मॉडलिंग बहुत शक्तिशाली है, लेकिन मॉडल निर्माण में अधिक कौशल की आवश्यकता होती है। इंजेक्शन मोल्डिंग भाग के लिए जटिल मॉडल में एक हजार विशेषताएं हो सकती हैं, और शुरुआती विशेषता को संशोधित करने से बाद की विशेषताएं विफल हो सकती हैं। कुशलता से बनाए गए पैरामीट्रिक मॉडल को बनाए रखना और संशोधित करना आसान है। पैरामीट्रिक मॉडलिंग भी खुद को डेटा के पुन: उपयोग के लिए उधार देती है। उदाहरण के लिए, [[पेंच]] का पूरा परिवार मॉडल में समाहित हो सकता है। | ||
=== मेडिकल ठोस मॉडलिंग === | === मेडिकल ठोस मॉडलिंग === | ||
आधुनिक [[गणना अक्षीय टोमोग्राफी]] और चुंबकीय अनुनाद इमेजिंग स्कैनर का उपयोग वोक्सल-आधारित मॉडल नामक आंतरिक शरीर सुविधाओं के ठोस मॉडल बनाने के लिए किया जा सकता है, जिसमें [[मात्रा प्रतिपादन]] का उपयोग करके छवियां उत्पन्न होती हैं। ऑप्टिकल [[3डी स्कैनर]] का उपयोग पॉइंट क्लाउड या बाह्य शरीर सुविधाओं के [[बहुभुज जाल]] मॉडल बनाने के लिए किया जा सकता है। | आधुनिक [[गणना अक्षीय टोमोग्राफी]] और चुंबकीय अनुनाद इमेजिंग स्कैनर का उपयोग वोक्सल-आधारित मॉडल नामक आंतरिक शरीर सुविधाओं के ठोस मॉडल बनाने के लिए किया जा सकता है, जिसमें [[मात्रा प्रतिपादन]] का उपयोग करके छवियां उत्पन्न होती हैं। ऑप्टिकल [[3डी स्कैनर]] का उपयोग पॉइंट क्लाउड या बाह्य शरीर सुविधाओं के [[बहुभुज जाल]] मॉडल बनाने के लिए किया जा सकता है। | ||
| Line 109: | Line 105: | ||
=== इंजीनियरिंग === | === इंजीनियरिंग === | ||
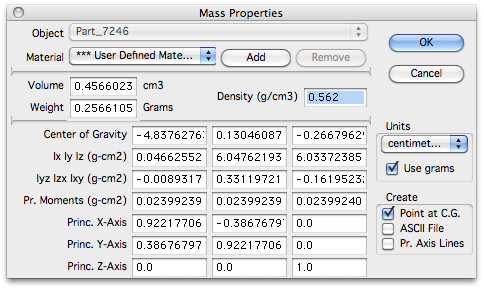
[[File:Cobalt Properties window.png|frame|right|alt=Property window outlining the mass properties of a model in [[कोबाल्ट (सीएडी कार्यक्रम)]] | कोबाल्ट (सीएडी कार्यक्रम) में एक मॉडल की मास गुण विंडो]]क्योंकि कंप्यूटर पर चल रहे सीएडी प्रोग्राम जटिल आकृतियों वाली सही ज्यामिति को समझते हैं, 3 के लिए/की कई विशेषताएँ{{nbhyph}}डी ठोस, जैसे गुरुत्वाकर्षण, मात्रा और द्रव्यमान का केंद्र, जल्दी से गणना की जा सकती है। उदाहरण के लिए, इस आलेख के शीर्ष पर दिखाए गए गोल किनारों वाले घन का माप समतल से समतल तक 8.4 मिमी है। इसके कई त्रिज्या और इसके छह चेहरों में से प्रत्येक पर उथले पिरामिड के बावजूद, इसके गुणों की आसानी से डिजाइनर के लिए गणना की जाती है, जैसा कि दाईं ओर स्क्रीनशॉट में दिखाया गया है। | |||
[[File:Cobalt Properties window.png|frame|right|alt=Property window outlining the mass properties of a model in [[कोबाल्ट (सीएडी कार्यक्रम)]] | कोबाल्ट (सीएडी कार्यक्रम) में एक मॉडल की मास गुण विंडो]]क्योंकि कंप्यूटर पर चल रहे | |||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 18:11, 20 February 2023
3 डी मॉडलिंग (या सॉलिड मॉडलिंग) त्रि-आयामी आकार solid (mathematics)|(solid) के गणितीय और कंप्यूटर मॉडलिंग के लिए सिद्धांतों का सुसंगत सेट है। ठोस प्रतिरूपण ज्यामितीय प्रतिरूपण और कंप्यूटर चित्रलेख के संबंधित क्षेत्रों से अलग है, जैसे कि 3डी प्रतिरूपण, भौतिक निष्ठा पर जोर देने के कारण।[1] साथ में, ज्यामितीय और ठोस मॉडलिंग के सिद्धांत कंप्यूटर एडेड डिजाइन की नींव बनाते हैं और सामान्य रूप से भौतिक वस्तुओं के डिजिटल मॉडल के निर्माण, विनिमय, दृश्य, एनीमेशन, पूछताछ और एनोटेशन का समर्थन करते हैं।
सिंहावलोकन
ठोस मॉडलिंग तकनीकों का उपयोग डिजाइन प्रक्रिया के भाग के रूप में की जाने वाली कई कठिन इंजीनियरिंग गणनाओं की स्वचालन प्रक्रिया की अनुमति देता है। मशीनिंग और समनुक्रम जैसी प्रक्रियाओं का अनुकरण, योजना और सत्यापन ठोस मॉडलिंग के विकास के लिए मुख्य उत्प्रेरकों में से एक थे। हाल ही में, धातु की चादर उत्पादन, अंतः क्षेपण ढलाई, वेल्डिंग, पाइपलाइन रूटिंग आदि को शामिल करने के लिए समर्थित निर्माण अनुप्रयोगों की सीमा का विस्तार किया गया है। पारंपरिक निर्माण से परे, ठोस मॉडलिंग तकनीकें तेजी तीव्र प्रोटोटाइपिंग, डिजिटल डेटा अभिलेखीय और रिवर्स इंजीनियरिंग के लिए नींव के रूप में काम करती हैं। भौतिक वस्तुओं पर नमूना बिंदुओं से ठोस पदार्थों का पुनर्निर्माण करके, परिमित तत्व का उपयोग करके यांत्रिक विश्लेषण, गति योजना और एनसी पथ सत्यापन, तंत्र (इंजीनियरिंग) के गतिकी और गतिशीलता (भौतिकी), और इसी तरह। इन सभी अनुप्रयोगों में केंद्रीय समस्या वास्तविक कलाकृतियों के भौतिक व्यवहार के अनुरूप तीन आयामी ज्यामिति का प्रभावी ढंग से प्रतिनिधित्व और हेरफेर करने की क्षमता है। ठोस मॉडलिंग अनुसंधान और विकास ने इनमें से कई मुद्दों को प्रभावी ढंग से संबोधित किया है, और कंप्यूटर एडेड इंजीनियरिंग का केंद्रीय फोकस बना हुआ है।
गणितीय नींव
आज प्रचलित ठोस मॉडलिंग की धारणा यांत्रिक ज्यामितीय मॉडलिंग प्रणालियों में सूचनात्मक पूर्णता की विशिष्ट आवश्यकता पर निर्भर करती है, इस अर्थ में कि किसी भी कंप्यूटर मॉडल को सभी ज्यामितीय प्रश्नों का समर्थन करना चाहिए जो इसके संबंधित भौतिक वस्तु से पूछे जा सकते हैं। आवश्यकता स्पष्ट रूप से एक ही भौतिक वस्तु के कई कंप्यूटर अभ्यावेदन की संभावना को पहचानती है जब तक कि कोई भी दो अभ्यावेदन सुसंगत हैं। प्रतिनिधित्व की सूचनात्मक पूर्णता को कम्प्यूटेशनल रूप से सत्यापित करना असंभव है जब तक कि किसी भौतिक वस्तु की धारणा को गणना योग्य गणितीय गुणों और किसी विशेष प्रतिनिधित्व से स्वतंत्र के रूप में परिभाषित नहीं किया जाता है। इस तरह के तर्क ने मॉडलिंग प्रतिमान के विकास को जन्म दिया जिसने ठोस मॉडलिंग के क्षेत्र को आकार दिया है जैसा कि आज हम जानते हैं।[2] सभी निर्मित घटकों में परिमित आकार और अच्छी तरह से व्यवहार वाली सीमा (टोपोलॉजी) है, इसलिए शुरू में सजातीय समदैशिक सामग्री से बने कठोर भागों को गणितीय रूप से मॉडलिंग करने पर ध्यान केंद्रित किया गया था जिसे जोड़ा या हटाया जा सकता था। इन अभिगृहीत गुणों को क्षेत्रों के गुणों में अनुवादित किया जा सकता है, त्रि-आयामी यूक्लिडियन अंतरिक्ष के सबसेट। दृढ़ता को परिभाषित करने के लिए दो सामान्य दृष्टिकोण क्रमशः बिंदु-सेट टोपोलॉजी और बीजगणितीय टोपोलॉजी पर निर्भर करते हैं। दोनों मॉडल निर्दिष्ट करते हैं कि सरल टुकड़ों या कोशिकाओं से ठोस कैसे बनाया जा सकता है।
दृढ़ता के सातत्य बिंदु-सेट मॉडल के अनुसार, किसी भी X ⊂ ℝ के सभी बिंदु3 को उनके पड़ोस (टोपोलॉजी) के अनुसार एक्स के संबंध में आंतरिक (टोपोलॉजी), बाहरी (टोपोलॉजी), या सीमा (टोपोलॉजी) बिंदुओं के रूप में वर्गीकृत किया जा सकता है। मान लीजिए3 विशिष्ट यूक्लिडियन मीट्रिक से संपन्न है, बिंदु p ∈X का पड़ोस गेंद (गणित) का रूप ले लेता है। X को ठोस माने जाने के लिए, किसी भी p ∈X का प्रत्येक पड़ोस लगातार त्रिविमीय होना चाहिए; निम्न-आयामी पड़ोस वाले बिंदु दृढ़ता की कमी का संकेत देते हैं। पड़ोस की आयामी एकरूपता की गारंटी 'बंद नियमित सेट' के वर्ग के लिए है, जिसे उनके इंटीरियर के क्लोजर (टोपोलॉजी) के बराबर सेट के रूप में परिभाषित किया गया है। कोई एक्स ⊂ ℝ3 को बंद नियमित सेट में बदला जा सकता है या इसके इंटीरियर को बंद करके नियमित किया जा सकता है, और इस प्रकार ठोस पदार्थों के मॉडलिंग स्थान को गणितीय रूप से ℝ के बंद नियमित उपसमुच्चय के स्थान के रूप में परिभाषित किया जाता है।3 (हेइन-बोरेल प्रमेय द्वारा | हेइन-बोरेल प्रमेय यह निहित है कि सभी ठोस कॉम्पैक्ट जगह सेट हैं)। इसके अलावा, सेट यूनियन, चौराहे और अंतर के बूलियन संचालन के तहत ठोस पदार्थों को बंद करना आवश्यक है (सामग्री को जोड़ने और हटाने के बाद ठोसता की गारंटी देने के लिए)। मानक बूलियन संचालन को बंद नियमित सेट पर लागू करने से बंद नियमित सेट का उत्पादन नहीं हो सकता है, लेकिन मानक बूलियन संचालन को लागू करने के परिणाम को नियमित करके इस समस्या को हल किया जा सकता है।[3] नियमित सेट संचालन को ∪ दर्शाया जाता है∗, ∩∗, और −∗.
सेट X ⊂ ℝ का संयोजी लक्षण वर्णन3 ठोस के रूप में एक्स को ओरिएंटेबल सीडब्ल्यू कॉम्प्लेक्स के रूप में प्रस्तुत करना शामिल है ताकि कोशिकाएं अन्यथा असंख्य सातत्य में बिंदुओं के लिए परिमित स्थानिक पते प्रदान कर सकें।[1]यूक्लिडियन अंतरिक्ष के अर्ध-विश्लेषणात्मक घिरा हुआ सेट उपसमुच्चय का वर्ग बूलियन संचालन (मानक और नियमित) के तहत बंद है और अतिरिक्त संपत्ति प्रदर्शित करता है कि प्रत्येक अर्ध-विश्लेषणात्मक सेट स्तरीकरण (गणित) हो सकता है जो आयामों के असंबद्ध कोशिकाओं के संग्रह में हो सकता है 0,1 ,2,3. बिंदुओं, रेखा खंड, त्रिकोणीय चेहरे (ज्यामिति), और चतुष्फलकीय तत्वों के संग्रह में अर्ध-विश्लेषणात्मक सेट का त्रिभुज (टोपोलॉजी) स्तरीकरण का उदाहरण है जो आमतौर पर उपयोग किया जाता है। ठोसता के संयोजी मॉडल को यह कहते हुए संक्षेप में प्रस्तुत किया जाता है कि अर्ध-विश्लेषणात्मक बाध्य उपसमुच्चय होने के अलावा, ठोस त्रि-आयामी टोपोलॉजिकल पॉलीहेड्रा हैं, विशेष रूप से सीमा के साथ तीन-आयामी ओरिएंटेबल मैनिफोल्ड।[4] विशेष रूप से इसका तात्पर्य संयोजी सीमा की यूलर विशेषता से है[5] पॉलीहेड्रॉन का 2 है। सॉलिडिटी का कॉम्बिनेटरियल मैनिफोल्ड मॉडल भी जॉर्डन वक्र प्रमेय के परिणाम के रूप में ठोस अलग स्थान की सीमा को ठीक दो घटकों में गारंटी देता है। निर्माण करना असंभव है।
ठोस पदार्थों के बिंदु-सेट और संयोजी मॉडल पूरी तरह से एक-दूसरे के साथ संगत होते हैं, एक दूसरे के स्थान पर उपयोग किए जा सकते हैं, निरंतर या संयोजी गुणों पर निर्भर करते हुए आवश्यकतानुसार, और n आयामों तक बढ़ाया जा सकता है। इस स्थिरता को सुविधाजनक बनाने वाली प्रमुख संपत्ति यह है कि ℝ के बंद नियमित उपसमुच्चय का वर्गn सजातीय रूप से n-आयामी टोपोलॉजिकल पॉलीहेड्रा के साथ सटीक रूप से मेल खाता है। इसलिए, प्रत्येक एन-आयामी ठोस को इसकी सीमा द्वारा स्पष्ट रूप से दर्शाया जा सकता है और सीमा में एन-1-आयामी पॉलीहेड्रॉन की मिश्रित संरचना होती है जिसमें सजातीय रूप से एन-1-आयामी पड़ोस होते हैं।
ठोस प्रतिनिधित्व योजनाएँ
अनुमानित गणितीय गुणों के आधार पर, ठोस पदार्थों का प्रतिनिधित्व करने की कोई भी योजना यूक्लिडियन अंतरिक्ष के अर्ध-विश्लेषणात्मक उपसमुच्चय के वर्ग के बारे में जानकारी प्राप्त करने की विधि है। इसका मतलब है कि सभी प्रतिनिधित्व एक ही ज्यामितीय और सामयिक डेटा को डेटा संरचना के रूप में व्यवस्थित करने के विभिन्न तरीके हैं। सभी प्रतिनिधित्व योजनाओं को प्रिमिटिव के सेट पर परिमित संख्या में संचालन के संदर्भ में व्यवस्थित किया जाता है। इसलिए, किसी विशेष प्रतिनिधित्व का मॉडलिंग स्थान परिमित है, और कोई एकल प्रतिनिधित्व योजना सभी प्रकार के ठोस पदार्थों का प्रतिनिधित्व करने के लिए पूरी तरह से पर्याप्त नहीं हो सकती है। उदाहरण के लिए, रचनात्मक ठोस ज्यामिति के माध्यम से परिभाषित ठोस को बहुत ही सरल मामलों को छोड़कर, अंतरिक्ष प्रक्षेपवक्र के अनुसार आदिम गति के ठोस झाडू के रूप में प्रस्तुत नहीं किया जा सकता है। यह आधुनिक ज्यामितीय मॉडलिंग प्रणालियों को ठोस पदार्थों की कई प्रतिनिधित्व योजनाओं को बनाए रखने और प्रतिनिधित्व योजनाओं के बीच कुशल रूपांतरण की सुविधा प्रदान करने के लिए मजबूर करता है।
नीचे ठोस मॉडल बनाने या प्रस्तुत करने के लिए उपयोग की जाने वाली सामान्य तकनीकों की सूची दी गई है।[4]आधुनिक मॉडलिंग सॉफ़्टवेयर ठोस का प्रतिनिधित्व करने के लिए इन योजनाओं के संयोजन का उपयोग कर सकता है।
आदिम उदाहरण
यह योजना वस्तु के परिवारों की धारणा पर आधारित है, परिवार के प्रत्येक सदस्य को कुछ मापदंडों द्वारा दूसरे से अलग किया जाता है। प्रत्येक वस्तु परिवार को सामान्य आदिम कहा जाता है, और परिवार के भीतर अलग-अलग वस्तुओं को आदिम उदाहरण कहा जाता है। उदाहरण के लिए, बोल्ट का परिवार सामान्य आदिम है, और मापदंडों के विशेष सेट द्वारा निर्दिष्ट एकल बोल्ट आदिम उदाहरण है। शुद्ध पैरामीटरयुक्त इंस्टेंसिंग योजनाओं की विशिष्ट विशेषता नई संरचनाओं को बनाने के लिए उदाहरणों के संयोजन के साधनों की कमी है जो नई और अधिक जटिल वस्तुओं का प्रतिनिधित्व करती हैं। इस योजना का अन्य मुख्य दोष प्रस्तुत ठोस पदार्थों के कंप्यूटिंग गुणों के लिए कलन विधि लिखने में कठिनाई है। एल्गोरिदम में काफी मात्रा में परिवार-विशिष्ट जानकारी का निर्माण किया जाना चाहिए और इसलिए प्रत्येक सामान्य आदिम को विशेष मामले के रूप में माना जाना चाहिए, जिससे कोई समान समग्र उपचार नहीं हो सके।
स्थानिक अधिभोग गणना
यह योजना अनिवार्य रूप से ठोस द्वारा व्याप्त स्थानिक कोशिकाओं की सूची है। कोशिकाएँ, जिन्हें स्वर भी कहा जाता है, निश्चित आकार के घन होते हैं और निश्चित स्थानिक ग्रिड में व्यवस्थित होते हैं (अन्य बहुफलकीय व्यवस्थाएँ भी संभव हैं लेकिन घन सबसे सरल हैं)। प्रत्येक सेल को बिंदु के निर्देशांक द्वारा दर्शाया जा सकता है, जैसे कि सेल का केन्द्रक। आम तौर पर विशिष्ट स्कैनिंग ऑर्डर लगाया जाता है और निर्देशांक के संबंधित ऑर्डर किए गए सेट को स्थानिक सरणी कहा जाता है। स्थानिक सरणियाँ असंदिग्ध और अद्वितीय ठोस निरूपण हैं लेकिन 'मास्टर' या निश्चित अभ्यावेदन के रूप में उपयोग के लिए बहुत अधिक वर्बोज़ हैं। हालांकि, वे भागों के मोटे अनुमानों का प्रतिनिधित्व कर सकते हैं और ज्यामितीय एल्गोरिदम के प्रदर्शन को बेहतर बनाने के लिए इस्तेमाल किया जा सकता है, खासकर जब रचनात्मक ठोस ज्यामिति जैसे अन्य अभ्यावेदन के साथ प्रयोग किया जाता है।
सेल अपघटन
यह योजना ऊपर वर्णित ठोस पदार्थों के संयोजी (बीजीय सांस्थितिकीय) विवरणों से अनुसरण करती है। ठोस को उसके अपघटन द्वारा कई कोशिकाओं में दर्शाया जा सकता है। स्थानिक अधिभोग गणना योजनाएँ कोशिका अपघटन का विशेष मामला है जहाँ सभी कोशिकाएँ घनाकार होती हैं और नियमित ग्रिड में स्थित होती हैं। सेल अपघटन ठोस के कुछ टोपोलॉजिकल गुण की गणना के लिए सुविधाजनक तरीके प्रदान करते हैं जैसे कि इसके जुड़ा हुआ स्थान (टुकड़ों की संख्या) और जीनस (गणित) (छिद्रों की संख्या)। त्रिकोणीय के रूप में सेल अपघटन आंशिक अंतर समीकरणों के संख्यात्मक समाधान के लिए 3डी परिमित तत्वों में उपयोग किए जाने वाले प्रतिनिधित्व हैं। रोबोट मोशन प्लानिंग में अनुप्रयोगों के लिए अन्य सेल अपघटन जैसे व्हिटनी नियमित रूप से स्तरीकृत स्थान या मोर्स अपघटन का उपयोग किया जा सकता है।Cite error: Closing </ref> missing for <ref> tag सीएसजी की लोकप्रियता में और योगदान दिया है।
स्वीपिंग
व्यापक योजनाओं में सन्निहित मूल धारणा सरल है। अंतरिक्ष के माध्यम से चलने वाला सेट वॉल्यूम (ठोस) का पता लगा सकता है या स्वीप कर सकता है जिसे मूविंग सेट और उसके प्रक्षेपवक्र द्वारा दर्शाया जा सकता है। इस तरह का प्रतिनिधित्व अनुप्रयोगों के संदर्भ में महत्वपूर्ण है जैसे कटर से निकाली गई सामग्री का पता लगाने के रूप में यह निर्दिष्ट प्रक्षेपवक्र के साथ चलता है, सापेक्ष गति से गुजरने वाले दो ठोस पदार्थों के गतिशील हस्तक्षेप की गणना, गति योजना, और यहां तक कि कंप्यूटर ग्राफिक्स अनुप्रयोगों जैसे अनुरेखण में भी ब्रश की गति कैनवास पर चलती है। अधिकांश वाणिज्यिक सीएडी प्रणालियां स्वेप्ट सॉलिड्स के निर्माण के लिए (सीमित) कार्यक्षमता प्रदान करती हैं, जो ज्यादातर दो आयामी क्रॉस सेक्शन के रूप में होती हैं, जो स्पेस ट्रैजेक्टरी ट्रांसवर्सल पर सेक्शन में चलती हैं। हालाँकि, वर्तमान शोध ने तीन आयामी आकृतियों के पैरामीटर और यहां तक कि बहु-पैरामीटर गतियों के कई अनुमानों को दिखाया है।
अंतर्निहित प्रतिनिधित्व
अंक X के सेट को परिभाषित करने का बहुत ही सामान्य तरीका विधेय (गणितीय तर्क) निर्दिष्ट करना है जिसका मूल्यांकन अंतरिक्ष में किसी भी बिंदु पर किया जा सकता है। दूसरे शब्दों में, एक्स को निहित रूप से परिभाषित किया गया है जिसमें वे सभी बिंदु शामिल हैं जो विधेय द्वारा निर्दिष्ट शर्तों को पूरा करते हैं। विधेय का सबसे सरल रूप वास्तविक मूल्यवान फ़ंक्शन के संकेत पर स्थिति है जिसके परिणामस्वरूप समानता और असमानताओं द्वारा सेट का परिचित प्रतिनिधित्व होता है। उदाहरण के लिए, अगर शर्तें , , और प्रतिनिधित्व करते हैं, क्रमशः, एक विमान और दो खुले रैखिक अर्ध-स्थान (ज्यामिति)। सरल विधेय के बूलियन संयोजनों द्वारा अधिक जटिल कार्यात्मक आदिम परिभाषित किए जा सकते हैं। इसके अलावा, रवाचेव समारोह का सिद्धांत | आर-फ़ंक्शंस ऐसे प्रतिनिधित्वों के रूपांतरण को किसी भी बंद अर्ध विश्लेषणात्मक सेट के लिए एकल फ़ंक्शन असमानता में बदलने की अनुमति देते हैं। इस तरह के प्रतिनिधित्व को बहुभुजीकरण एल्गोरिदम का उपयोग करके सीमा प्रतिनिधित्व में परिवर्तित किया जा सकता है, उदाहरण के लिए, मार्चिंग क्यूब्स एल्गोरिदम।
पैरामीट्रिक और फीचर-आधारित मॉडलिंग
सुविधाओं को आंतरिक ज्यामितीय मापदंडों (लंबाई, चौड़ाई, गहराई आदि), स्थिति और अभिविन्यास, ज्यामितीय सहिष्णुता, भौतिक गुणों और अन्य विशेषताओं के संदर्भ जैसी विशेषताओं से जुड़े पैरामीट्रिक आकार के रूप में परिभाषित किया गया है।[6] सुविधाएँ संबंधित उत्पादन प्रक्रियाओं और संसाधन मॉडल तक पहुँच भी प्रदान करती हैं। इस प्रकार, आदिम बंद नियमित सेटों की तुलना में सुविधाओं का शब्दार्थ उच्च स्तर है। सुविधाओं से आम तौर पर सीएडी को डाउनस्ट्रीम मैन्युफैक्चरिंग एप्लिकेशन के साथ जोड़ने और डिजाइन डेटा के पुन: उपयोग के लिए डेटाबेस को व्यवस्थित करने के लिए आधार बनाने की उम्मीद की जाती है। इंजीनियरिंग में जटिल वस्तुओं की प्रणालियों का पूरी तरह से वर्णन करने के लिए पैरामीट्रिक फीचर आधारित मॉडलिंग को अक्सर रचनात्मक बाइनरी सॉलिड ज्योमेट्री (CSG) के साथ जोड़ा जाता है।
ठोस मॉडलर्स का इतिहास
सॉलिड मॉडलर्स के ऐतिहासिक विकास को पूरे कंप्यूटर-एडेड डिज़ाइन के संदर्भ में देखा जाना चाहिए, प्रमुख मील के पत्थर अनुसंधान प्रणाली BUILD के विकास के बाद इसके वाणिज्यिक स्पिन-ऑफ रोमुलस (बी-रेप सॉलिड मॉडलर) के रूप में आगे बढ़े। पैरासॉलिड, एसीआईएस और ठोस मॉडलिंग समाधान के विकास को प्रभावित करते हैं। स्वतंत्र राष्ट्रों का राष्ट्रमंडल (CIS) में पहले सीएडी डेवलपर्स में से एक, ASCON ने 1990 के दशक में अपने स्वयं के ठोस मॉडलर का आंतरिक विकास शुरू किया।[7] नवंबर 2012 में, ASCON का गणितीय प्रभाग अलग कंपनी बन गया, और इसका नाम C3D रखा गया। इसे C3D ज्यामितीय मॉडलिंग कर्नेल को स्टैंडअलोन उत्पाद के रूप में विकसित करने का कार्य सौंपा गया था - रूस से एकमात्र वाणिज्यिक 3D मॉडलिंग कर्नेल।[8] अन्य योगदान उनके GWB और GPM प्रोजेक्ट के साथ Mäntylä से आया, जिसने 1980 के दशक की शुरुआत में, अन्य बातों के अलावा, हाइब्रिड मॉडलिंग तकनीकों में योगदान दिया। यह तब भी है जब रोम विश्वविद्यालय में सॉलिड मॉडलिंग पीएलएसएम की प्रोग्रामिंग भाषा की कल्पना की गई थी।
कंप्यूटर एडेड डिजाइन
ठोस पदार्थों की मॉडलिंग कंप्यूटर-एडेड डिजाइन#क्षमताओं|सीएडी प्रणाली की क्षमताओं की केवल न्यूनतम आवश्यकता है। पिछले दस वर्षों में इंजीनियरिंग विभागों में ठोस मॉडलर आम हो गए हैं[when?] तेज कंप्यूटर और प्रतिस्पर्धी सॉफ्टवेयर मूल्य निर्धारण के कारण। ठोस मॉडलिंग सॉफ्टवेयर मशीन डिजाइन और विश्लेषण के लिए घटकों का आभासी 3डी प्रतिनिधित्व बनाता है।[9] विशिष्ट जीयूआई में प्रोग्रामेबल मैक्रोज़, कीबोर्ड शॉर्टकट और डायनेमिक मॉडल हेरफेर शामिल हैं। रीयल-टाइम छायांकित 3-डी में मॉडल को गतिशील रूप से पुन: उन्मुख करने की क्षमता पर जोर दिया जाता है और डिजाइनर को मानसिक 3-डी छवि बनाए रखने में मदद मिलती है।
ठोस भाग मॉडल में आमतौर पर सुविधाओं का समूह होता है, जब तक कि मॉडल पूरा नहीं हो जाता, तब तक एक-एक करके जोड़ा जाता है। इंजीनियरिंग ठोस मॉडल ज्यादातर स्केचर-आधारित सुविधाओं के साथ बनाए जाते हैं; 2-डी रेखाचित्र जो 3-डी बनने के मार्ग के साथ बह गए हैं। उदाहरण के लिए ये कट या एक्सट्रूज़न हो सकते हैं। घटकों पर डिजाइन का काम आमतौर पर पूरे उत्पाद के संदर्भ में असेंबली मॉडलिंग विधियों का उपयोग करके किया जाता है। असेंबली मॉडल में अलग-अलग भाग मॉडल के संदर्भ शामिल होते हैं जिनमें उत्पाद शामिल होता है।[10]
अन्य प्रकार की मॉडलिंग तकनीक 'सरफेसिंग' (फ्रीफॉर्म सतह मॉडलिंग) है। यहाँ, सतहों को परिभाषित, छंटनी और विलय किया जाता है, और ठोस बनाने के लिए भरा जाता है। सतहों को आमतौर पर अंतरिक्ष में डेटम कर्व्स और कई तरह के जटिल कमांड के साथ परिभाषित किया जाता है। सरफेसिंग अधिक कठिन है, लेकिन इंजेक्शन मोल्डिंग जैसी कुछ निर्माण तकनीकों के लिए बेहतर है। इंजेक्शन ढाले भागों के लिए ठोस मॉडल में आमतौर पर सरफेसिंग और स्केचर आधारित विशेषताएं होती हैं।
इंजीनियरिंग चित्र अर्ध-स्वचालित रूप से बनाए जा सकते हैं और ठोस मॉडल को संदर्भित कर सकते हैं।
पैरामीट्रिक मॉडलिंग
पैरामीट्रिक मॉडलिंग मॉडल को परिभाषित करने के लिए पैरामीटर का उपयोग करता है (उदाहरण के लिए आयाम)। मापदंडों के उदाहरण हैं: मॉडल सुविधाओं को बनाने के लिए उपयोग किए जाने वाले आयाम, सामग्री घनत्व, स्वेप्ट सुविधाओं का वर्णन करने के लिए सूत्र, आयातित डेटा (उदाहरण के लिए, संदर्भ सतह का वर्णन)। पैरामीटर को बाद में संशोधित किया जा सकता है, और संशोधन को दर्शाने के लिए मॉडल अपडेट होगा। आमतौर पर, भागों, विधानसभाओं और रेखाचित्रों के बीच संबंध होता है। एक भाग में कई विशेषताएं होती हैं, और असेंबली में कई भाग होते हैं। चित्र या तो भागों या विधानसभाओं से बनाए जा सकते हैं।
उदाहरण: 100 मिमी के वृत्त को एक्सट्रूड करके शाफ़्ट बनाया जाता है। शाफ्ट के अंत में हब इकट्ठा किया जाता है। बाद में, शाफ्ट को 200 मिमी लंबा करने के लिए संशोधित किया गया है (शाफ्ट पर क्लिक करें, लंबाई आयाम का चयन करें, 200 में संशोधित करें)। जब मॉडल को अपडेट किया जाता है तो शाफ्ट 200 मिमी लंबा हो जाएगा, हब उस शाफ्ट के अंत में स्थानांतरित हो जाएगा जहां इसे इकट्ठा किया गया था, और इंजीनियरिंग चित्र और द्रव्यमान गुण स्वचालित रूप से सभी परिवर्तनों को दर्शाएंगे।
मापदंडों से संबंधित, लेकिन थोड़ा अलग, बाधा (कंप्यूटर एडेड डिजाइन) हैं। प्रतिबन्ध संस्थाओं के बीच संबंध हैं जो विशेष आकार बनाते हैं। खिड़की के लिए, पक्षों को समानांतर और समान लंबाई के रूप में परिभाषित किया जा सकता है। पैरामीट्रिक मॉडलिंग स्पष्ट और सहज है। लेकिन सीएडी के पहले तीन दशकों में ऐसा नहीं था। संशोधन का अर्थ है फिर से खींचना, या पुराने के ऊपर नया कट या फलाव जोड़ना। दिखाए जाने के बजाय इंजीनियरिंग ड्रॉइंग पर आयाम बनाए गए। पैरामीट्रिक मॉडलिंग बहुत शक्तिशाली है, लेकिन मॉडल निर्माण में अधिक कौशल की आवश्यकता होती है। इंजेक्शन मोल्डिंग भाग के लिए जटिल मॉडल में एक हजार विशेषताएं हो सकती हैं, और शुरुआती विशेषता को संशोधित करने से बाद की विशेषताएं विफल हो सकती हैं। कुशलता से बनाए गए पैरामीट्रिक मॉडल को बनाए रखना और संशोधित करना आसान है। पैरामीट्रिक मॉडलिंग भी खुद को डेटा के पुन: उपयोग के लिए उधार देती है। उदाहरण के लिए, पेंच का पूरा परिवार मॉडल में समाहित हो सकता है।
मेडिकल ठोस मॉडलिंग
आधुनिक गणना अक्षीय टोमोग्राफी और चुंबकीय अनुनाद इमेजिंग स्कैनर का उपयोग वोक्सल-आधारित मॉडल नामक आंतरिक शरीर सुविधाओं के ठोस मॉडल बनाने के लिए किया जा सकता है, जिसमें मात्रा प्रतिपादन का उपयोग करके छवियां उत्पन्न होती हैं। ऑप्टिकल 3डी स्कैनर का उपयोग पॉइंट क्लाउड या बाह्य शरीर सुविधाओं के बहुभुज जाल मॉडल बनाने के लिए किया जा सकता है।
चिकित्सा ठोस मॉडलिंग का उपयोग;
- विज़ुअलाइज़ेशन
- विशिष्ट शरीर के ऊतकों का दृश्य (उदाहरण के लिए केवल रक्त वाहिकाओं और ट्यूमर)
- कृत्रिम अंग, orthotics और अन्य चिकित्सा और दंत चिकित्सा उपकरणों को डिजाइन करना (इसे कभी-कभी बड़े पैमाने पर अनुकूलन कहा जाता है)
- तेजी से प्रोटोटाइप के लिए बहुभुज जाल मॉडल बनाना (उदाहरण के लिए कठिन सर्जरी की तैयारी करने वाले सर्जनों की सहायता के लिए)
- कंप्यूटर-एडेड डिज़ाइन सॉलिड मॉडलिंग (उदाहरण के लिए हिप रिप्लेसमेंट पार्ट्स का डिज़ाइन) के साथ पॉलीगॉन मेश मॉडल का संयोजन
- जटिल जैविक प्रक्रियाओं का कम्प्यूटेशनल विश्लेषण, उदा। वायु प्रवाह, रक्त प्रवाह
- विवो में नए चिकित्सा उपकरणों और प्रत्यारोपण का कम्प्यूटेशनल सिमुलेशन
यदि उपयोग स्कैन डेटा के विज़ुअलाइज़ेशन से परे जाता है, तो स्कैन डेटा का सटीक और यथार्थवादी ज्यामितीय विवरण उत्पन्न करने के लिए छवि विभाजन और इमेज-आधारित मेशिंग जैसी प्रक्रियाएँ आवश्यक होंगी।
इंजीनियरिंग
क्योंकि कंप्यूटर पर चल रहे सीएडी प्रोग्राम जटिल आकृतियों वाली सही ज्यामिति को समझते हैं, 3 के लिए/की कई विशेषताएँ‑डी ठोस, जैसे गुरुत्वाकर्षण, मात्रा और द्रव्यमान का केंद्र, जल्दी से गणना की जा सकती है। उदाहरण के लिए, इस आलेख के शीर्ष पर दिखाए गए गोल किनारों वाले घन का माप समतल से समतल तक 8.4 मिमी है। इसके कई त्रिज्या और इसके छह चेहरों में से प्रत्येक पर उथले पिरामिड के बावजूद, इसके गुणों की आसानी से डिजाइनर के लिए गणना की जाती है, जैसा कि दाईं ओर स्क्रीनशॉट में दिखाया गया है।
यह भी देखें
- कम्प्यूटेशनल ज्यामिति
- कंप्यूटर चित्रलेख
- इंजीनियरिंग ड्राइंग
- यूलर सीमा प्रतिनिधित्व
- CAx कंपनियों की सूची
- PLaSM - सॉलिड मॉडलिंग की प्रोग्रामिंग लैंग्वेज।
- टेक्निकल ड्राइंग
संदर्भ
- ↑ 1.0 1.1 Shapiro, Vadim (2001). Solid Modeling. Elsevier. Retrieved 20 April 2010.
- ↑ Requicha, A.A.G & Voelcker, H. (1983). "Solid Modeling: Current Status and Research Directions". IEEE Computer Graphics and Applications. IEEE Computer Graphics. 3 (7): 25–37. doi:10.1109/MCG.1983.263271. S2CID 14462567.
- ↑ Tilove, R.B.; Requicha, A.A.G. (1980), "Closure of Boolean operations on geometric entities", Computer-Aided Design, 12 (5): 219–220, doi:10.1016/0010-4485(80)90025-1
- ↑ 4.0 4.1 Requicha, A.A.G. (1980). "Representations for Rigid Solids: Theory, Methods, and Systems". ACM Computing Surveys. 12 (4): 437–464. doi:10.1145/356827.356833. S2CID 207568300.
- ↑ Hatcher, A. (2002). Algebraic Topology. Cambridge University Press. Retrieved 20 April 2010.
- ↑ Mantyla, M., Nau, D. , and Shah, J. (1996). "Challenges in feature based manufacturing research". Communications of the ACM. 39 (2): 77–85. doi:10.1145/230798.230808. S2CID 3340804.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Yares, Evan (April 2013). "Russian CAD". Design World. WTWH Media, LLC. 8 (4). ISSN 1941-7217. Archived from the original on 30 January 2015.
- ↑ Golovanov, Nikolay (2014). Geometric Modeling: The mathematics of shapes. CreateSpace Independent Publishing Platform (24 December 2014). p. Back cover. ISBN 978-1497473195.
- ↑ LaCourse, Donald (1995). "2". Handbook of Solid Modeling. McGraw Hill. p. 2.5. ISBN 978-0-07-035788-4.
- ↑ LaCourse, Donald (1995). "11". Handbook of Solid Modeling. McGraw Hill. p. 111.2. ISBN 978-0-07-035788-4.