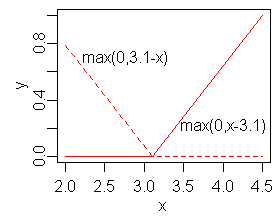रैंप फंक्शन: Difference between revisions
m (Deepak moved page रैंप समारोह to रैंप फंक्शन without leaving a redirect) |
No edit summary |
||
| Line 1: | Line 1: | ||
[[File:Ramp function.svg|thumb|325px|रैम्प फ़ंक्शन के एक फ़ंक्शन का ग्राफ़]]रैम्प फलन एक [[एकात्मक समारोह|एकात्मक फलन]] वास्तविक फलन है, जिसका का ग्राफ़ रैम्प के आकार का होता है। इसे कई परिभाषाओं द्वारा व्यक्त किया जा सकता है, उदाहरण के लिए ऋणात्मक इनपुट के लिए 0, आउटपुट गैर-ऋणात्मकइ नपुट के लिए इनपुट के बराबर है। रैम्प शब्द का उपयोग [[स्केलिंग और स्थानांतरण]] द्वारा प्राप्त अन्य कार्यों के लिए भी किया जा सकता है, और इस लेख में फलन ''यूनिट'' रैम्प फलन (ढलान 1, 0 से प्रारम्भ) है। | |||
[[File:Ramp function.svg|thumb|325px| | |||
गणित में, रैम्प फलन को धनात्मक भाग के रूप में भी जाना जाता है। | गणित में, रैम्प फलन को धनात्मक भाग के रूप में भी जाना जाता है। | ||
[[ यंत्र अधिगम ]] में, इसे आमतौर पर रेक्टिफायर_(न्यूरल_नेटवर्क्स) [[ सक्रियण समारोह ]] के रूप में जाना जाता है<ref name='brownlee'>{{cite web |last1=Brownlee |first1=Jason |title=परिशोधित रेखीय इकाई (ReLU) का एक सौम्य परिचय|url=https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/ |website=Machine Learning Mastery |access-date=8 April 2021 |date=8 January 2019}}</ref><ref name="medium-relu">{{cite web |last1=Liu |first1=Danqing |title=ReLU के लिए एक प्रैक्टिकल गाइड|url=https://medium.com/@danqing/a-practical-guide-to-relu-b83ca804f1f7 |website=Medium |access-date=8 April 2021 |language=en |date=30 November 2017}}</ref> या [[ विद्युत अभियन्त्रण ]] में [[आधा लहर सुधार]] के अनुरूप एक रेक्टिफायर (तंत्रिका नेटवर्क)। आँकड़ों में (जब संभावना कार्य के रूप में उपयोग किया जाता है) इसे [[टोबिट मॉडल]] के रूप में जाना जाता है। | [[ यंत्र अधिगम |यंत्र अधिगम]] में, इसे आमतौर पर रेक्टिफायर_(न्यूरल_नेटवर्क्स) [[ सक्रियण समारोह ]] के रूप में जाना जाता है<ref name='brownlee'>{{cite web |last1=Brownlee |first1=Jason |title=परिशोधित रेखीय इकाई (ReLU) का एक सौम्य परिचय|url=https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/ |website=Machine Learning Mastery |access-date=8 April 2021 |date=8 January 2019}}</ref><ref name="medium-relu">{{cite web |last1=Liu |first1=Danqing |title=ReLU के लिए एक प्रैक्टिकल गाइड|url=https://medium.com/@danqing/a-practical-guide-to-relu-b83ca804f1f7 |website=Medium |access-date=8 April 2021 |language=en |date=30 November 2017}}</ref> या [[ विद्युत अभियन्त्रण ]] में [[आधा लहर सुधार]] के अनुरूप एक रेक्टिफायर (तंत्रिका नेटवर्क)। आँकड़ों में (जब संभावना कार्य के रूप में उपयोग किया जाता है) इसे [[टोबिट मॉडल]] के रूप में जाना जाता है। | ||
इस फ़ंक्शन में गणित और इंजीनियरिंग में कई #अनुप्रयोग हैं, और संदर्भ के आधार पर विभिन्न नामों से जाना जाता है। | इस फ़ंक्शन में गणित और इंजीनियरिंग में कई #अनुप्रयोग हैं, और संदर्भ के आधार पर विभिन्न नामों से जाना जाता है। रैम्प फ़ंक्शन के रेक्टीफायर_ (तंत्रिका_नेटवर्क) # अन्य_गैर-रैखिक_वेरिएंट हैं। | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
रैम्प समारोह ({{math|''R''(''x'') : '''R''' → '''R'''<sub>0</sub><sup>+</sup>}}) विश्लेषणात्मक रूप से कई तरीकों से परिभाषित किया जा सकता है। संभावित परिभाषाएँ हैं: | |||
* एक टुकड़े का कार्य: <math display="block">R(x) := \begin{cases} | * एक टुकड़े का कार्य: <math display="block">R(x) := \begin{cases} | ||
x, & x \ge 0; \\ | x, & x \ge 0; \\ | ||
| Line 20: | Line 19: | ||
* हैविसाइड स्टेप फंक्शन का [[अभिन्न]] अंग:<ref>{{MathWorld|title=Ramp Function|id=RampFunction}}</ref> <math display="block">R(x) := \int_{-\infty}^{x} H(\xi)\,d\xi</math> | * हैविसाइड स्टेप फंक्शन का [[अभिन्न]] अंग:<ref>{{MathWorld|title=Ramp Function|id=RampFunction}}</ref> <math display="block">R(x) := \int_{-\infty}^{x} H(\xi)\,d\xi</math> | ||
* [[मैकाले कोष्ठक]]: <math display="block">R(x) := \langle x\rangle</math> | * [[मैकाले कोष्ठक]]: <math display="block">R(x) := \langle x\rangle</math> | ||
* पहचान कार्य के [[सकारात्मक और नकारात्मक भाग]]: <math display="block">R := \operatorname{id}^+</math> | * पहचान कार्य के [[सकारात्मक और नकारात्मक भाग|सकारात्मक और ऋणात्मकभाग]]: <math display="block">R := \operatorname{id}^+</math> | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
रैम्प फ़ंक्शन में इंजीनियरिंग में कई अनुप्रयोग हैं, जैसे कि [[ अंकीय संकेत प्रक्रिया ]] के सिद्धांत में। | |||
[[File:Long call option.svg|thumb|अदायगी और कॉल विकल्प खरीदने से मुनाफा।]][[वित्त]] में, कॉल विकल्प का भुगतान एक | [[File:Long call option.svg|thumb|अदायगी और कॉल विकल्प खरीदने से मुनाफा।]][[वित्त]] में, कॉल विकल्प का भुगतान एक रैम्प (स्ट्राइक प्राइस द्वारा स्थानांतरित) है। रैम्प को क्षैतिज रूप से फ़्लिप करने से एक पुट विकल्प प्राप्त होता है, जबकि लंबवत रूप से फ़्लिप करना (ऋणात्मकलेना) एक विकल्प को बेचने या छोटा करने से मेल खाता है। वित्त में, आकार को [[आइस [[ हाँकी स्टिक ]]]] के समान होने के कारण व्यापक रूप से हॉकी स्टिक कहा जाता है। | ||
[[File:Friedmans mars hinge functions.png|thumb|x=3.1 पर एक गांठ के साथ बहुभिन्नरूपी अनुकूली प्रतिगमन स्प्लाइन#हिंज फ़ंक्शंस की एक मिरर की गई जोड़ी]]आँकड़ों में, बहुभिन्नरूपी अनुकूली प्रतिगमन splines # बहुभिन्नरूपी अनुकूली प्रतिगमन splines (MARS) के काज कार्य | [[File:Friedmans mars hinge functions.png|thumb|x=3.1 पर एक गांठ के साथ बहुभिन्नरूपी अनुकूली प्रतिगमन स्प्लाइन#हिंज फ़ंक्शंस की एक मिरर की गई जोड़ी]]आँकड़ों में, बहुभिन्नरूपी अनुकूली प्रतिगमन splines # बहुभिन्नरूपी अनुकूली प्रतिगमन splines (MARS) के काज कार्य रैम्प हैं, और [[प्रतिगमन मॉडल]] बनाने के लिए उपयोग किए जाते हैं। | ||
== विश्लेषणात्मक गुण == | == विश्लेषणात्मक गुण == | ||
| Line 46: | Line 45: | ||
=== दूसरा व्युत्पन्न === | === दूसरा व्युत्पन्न === | ||
रैम्प फ़ंक्शन अंतर समीकरण को संतुष्ट करता है: | |||
<math display="block"> \frac{d^2}{dx^2} R(x - x_0) = \delta(x - x_0), </math> | <math display="block"> \frac{d^2}{dx^2} R(x - x_0) = \delta(x - x_0), </math> | ||
कहाँ {{math|''δ''(''x'')}} [[डिराक डेल्टा]] है। इस का मतलब है कि {{math|''R''(''x'')}} दूसरे डेरिवेटिव ऑपरेटर के लिए ग्रीन का कार्य है। इस प्रकार, कोई भी कार्य, {{math|''f''(''x'')}}, एक पूर्णांक द्वितीय व्युत्पन्न के साथ, {{math|''f''″(''x'')}}, समीकरण को संतुष्ट करेगा: | कहाँ {{math|''δ''(''x'')}} [[डिराक डेल्टा]] है। इस का मतलब है कि {{math|''R''(''x'')}} दूसरे डेरिवेटिव ऑपरेटर के लिए ग्रीन का कार्य है। इस प्रकार, कोई भी कार्य, {{math|''f''(''x'')}}, एक पूर्णांक द्वितीय व्युत्पन्न के साथ, {{math|''f''″(''x'')}}, समीकरण को संतुष्ट करेगा: | ||
| Line 64: | Line 63: | ||
=== पुनरावृत्ति आक्रमण === | === पुनरावृत्ति आक्रमण === | ||
रैम्प मैपिंग का प्रत्येक पुनरावृत्त कार्य स्वयं ही है | |||
<math display="block"> R \big( R(x) \big) = R(x) .</math> | <math display="block"> R \big( R(x) \big) = R(x) .</math> | ||
{{math proof | proof = | {{math proof | proof = | ||
Revision as of 15:06, 29 June 2023
रैम्प फलन एक एकात्मक फलन वास्तविक फलन है, जिसका का ग्राफ़ रैम्प के आकार का होता है। इसे कई परिभाषाओं द्वारा व्यक्त किया जा सकता है, उदाहरण के लिए ऋणात्मक इनपुट के लिए 0, आउटपुट गैर-ऋणात्मकइ नपुट के लिए इनपुट के बराबर है। रैम्प शब्द का उपयोग स्केलिंग और स्थानांतरण द्वारा प्राप्त अन्य कार्यों के लिए भी किया जा सकता है, और इस लेख में फलन यूनिट रैम्प फलन (ढलान 1, 0 से प्रारम्भ) है।
गणित में, रैम्प फलन को धनात्मक भाग के रूप में भी जाना जाता है।
यंत्र अधिगम में, इसे आमतौर पर रेक्टिफायर_(न्यूरल_नेटवर्क्स) सक्रियण समारोह के रूप में जाना जाता है[1][2] या विद्युत अभियन्त्रण में आधा लहर सुधार के अनुरूप एक रेक्टिफायर (तंत्रिका नेटवर्क)। आँकड़ों में (जब संभावना कार्य के रूप में उपयोग किया जाता है) इसे टोबिट मॉडल के रूप में जाना जाता है।
इस फ़ंक्शन में गणित और इंजीनियरिंग में कई #अनुप्रयोग हैं, और संदर्भ के आधार पर विभिन्न नामों से जाना जाता है। रैम्प फ़ंक्शन के रेक्टीफायर_ (तंत्रिका_नेटवर्क) # अन्य_गैर-रैखिक_वेरिएंट हैं।
परिभाषाएँ
रैम्प समारोह (R(x) : R → R0+) विश्लेषणात्मक रूप से कई तरीकों से परिभाषित किया जा सकता है। संभावित परिभाषाएँ हैं:
- एक टुकड़े का कार्य:
- मैक्सिमा और मिनिमा:
- एक स्वतंत्र चर और उसके निरपेक्ष मूल्य का अंकगणितीय माध्य (एकता ढाल और उसके मापांक के साथ एक सीधी रेखा): यह निम्नलिखित परिभाषा को ध्यान में रखते हुए प्राप्त किया जा सकता है max(a, b),जिसके लिए a = x और b = 0
- हैवीसाइड स्टेप फंक्शन को एकता ग्रेडिएंट के साथ एक सीधी रेखा से गुणा किया जाता है:
- खुद के साथ हीविसाइड स्टेप फंक्शन का कनवल्शन:
- हैविसाइड स्टेप फंक्शन का अभिन्न अंग:[3]
- मैकाले कोष्ठक:
- पहचान कार्य के सकारात्मक और ऋणात्मकभाग:
अनुप्रयोग
रैम्प फ़ंक्शन में इंजीनियरिंग में कई अनुप्रयोग हैं, जैसे कि अंकीय संकेत प्रक्रिया के सिद्धांत में।
वित्त में, कॉल विकल्प का भुगतान एक रैम्प (स्ट्राइक प्राइस द्वारा स्थानांतरित) है। रैम्प को क्षैतिज रूप से फ़्लिप करने से एक पुट विकल्प प्राप्त होता है, जबकि लंबवत रूप से फ़्लिप करना (ऋणात्मकलेना) एक विकल्प को बेचने या छोटा करने से मेल खाता है। वित्त में, आकार को [[आइस हाँकी स्टिक ]] के समान होने के कारण व्यापक रूप से हॉकी स्टिक कहा जाता है।
आँकड़ों में, बहुभिन्नरूपी अनुकूली प्रतिगमन splines # बहुभिन्नरूपी अनुकूली प्रतिगमन splines (MARS) के काज कार्य रैम्प हैं, और प्रतिगमन मॉडल बनाने के लिए उपयोग किए जाते हैं।
विश्लेषणात्मक गुण
गैर-नकारात्मकता
किसी फलन के पूरे क्षेत्र में फलन गैर-ऋणात्मक होता है, इसलिए इसका निरपेक्ष मान स्वयं ही होता है, अर्थात
by the mean of definition 2, it is non-negative in the first quarter, and zero in the second; so everywhere it is non-negative.
व्युत्पन्न
इसका व्युत्पन्न हीविसाइड स्टेप फंक्शन है:
दूसरा व्युत्पन्न
रैम्प फ़ंक्शन अंतर समीकरण को संतुष्ट करता है:
फूरियर रूपांतरण
लाप्लास रूपांतरण
एक तरफा लाप्लास का रूपांतरण R(x) इस प्रकार दिया गया है,[4]
बीजगणितीय गुण
पुनरावृत्ति आक्रमण
रैम्प मैपिंग का प्रत्येक पुनरावृत्त कार्य स्वयं ही है
यह भी देखें
- टोबिट मॉडल
संदर्भ
- ↑ Brownlee, Jason (8 January 2019). "परिशोधित रेखीय इकाई (ReLU) का एक सौम्य परिचय". Machine Learning Mastery. Retrieved 8 April 2021.
- ↑ Liu, Danqing (30 November 2017). "ReLU के लिए एक प्रैक्टिकल गाइड". Medium (in English). Retrieved 8 April 2021.
- ↑ Weisstein, Eric W. "Ramp Function". MathWorld.
- ↑ "कार्यों का लाप्लास रूपांतरण". lpsa.swarthmore.edu. Retrieved 2019-04-05.