समपूरक जाली

Error creating thumbnail:

l}फैनो विमान के } पूरक हैं अगर और केवल अगर p झूठ नहीं बोलता l.

आदेश सिद्धांत के गणित अनुशासन में, एक पूरक जाली एक बंधी हुई जाली (क्रम) है (कम से कम तत्व 0 और सबसे बड़ा तत्व 1), जिसमें प्रत्येक तत्व ए का एक पूरक है, यानी एक तत्व बी संतोषजनक a ∨ b = 1 और a ∧ b = 0।

पूरक अद्वितीय नहीं होना चाहिए।

एक अपेक्षाकृत पूरक जाली एक जाली है जैसे कि प्रत्येक अंतराल (आंशिक क्रम) [c, d], जिसे अपने आप में एक बंधी हुई जाली के रूप में देखा जाता है, एक पूरक जाली है।

एक पूरक जाली पर एक ऑर्थोकोम्प्लीमेंटेशन एक इनवोल्यूशन (गणित) है जो क्रम उलटना है और प्रत्येक तत्व को एक पूरक के रूप में मैप करता है। मॉड्यूलर जाली के कमजोर रूप को संतुष्ट करने वाली एक ऑर्थोकोम्प्लीमेंटेड जाली को ऑर्थोमॉड्यूलर जाली कहा जाता है।

परिबद्ध वितरण जालक में, पूरक अद्वितीय होते हैं। प्रत्येक पूरक वितरण जाली में एक अद्वितीय ऑर्थोकोम्प्लिमेंटेशन होता है और वास्तव में एक बूलियन बीजगणित (संरचना) है।

परिभाषा और बुनियादी गुण

एक पूरक जाली एक बंधी हुई जाली है (कम से कम तत्व 0 और सबसे बड़ा तत्व 1 के साथ), जिसमें प्रत्येक तत्व a का एक पूरक है, अर्थात एक तत्व b ऐसा है कि

a ∨ b = 1     and   a ∧ b = 0।

सामान्य तौर पर एक तत्व में एक से अधिक पूरक हो सकते हैं। हालांकि, एक (बाध्य) वितरण जाली में प्रत्येक तत्व में अधिकतम एक पूरक होगा। एक जाली जिसमें प्रत्येक तत्व का ठीक एक पूरक होता है, एक विशिष्ट पूरक जाली कहलाता है संपत्ति के साथ एक जाली जिसे हर अंतराल (एक उप-जाल के रूप में देखा जाता है) को पूरक किया जाता है, उसे अपेक्षाकृत पूरक जाली कहा जाता है। दूसरे शब्दों में, एक अपेक्षाकृत पूरक जाली की संपत्ति की विशेषता होती है कि अंतराल में प्रत्येक तत्व ए के लिए [ सी , डी ] एक तत्व बी होता है

a ∨ b = d     and   a ∧ b = c।

ऐसे तत्व बी को अंतराल के सापेक्ष ए का पूरक कहा जाता है।

एक वितरण जाली को पूरक किया जाता है अगर और केवल अगर यह बाध्य और अपेक्षाकृत पूरक हो। एक सदिश स्थान के सदिश उपस्थानों की जाली एक पूरक जाली का एक उदाहरण प्रदान करती है जो सामान्य रूप से वितरण नहीं है।

ऑर्थोकंप्लीमेंटेशन

See also: De Morgan algebra

एक बंधे हुए जाली पर एक ऑर्थोकोम्प्लिमेंटेशन एक ऐसा कार्य है जो प्रत्येक तत्व ए को ऑर्थोकोम्प्लीमेंट ए से मैप करता है।^⊥ इस तरह से कि निम्नलिखित स्वयंसिद्ध संतुष्ट हों: पूरक कानून: ए^⊥ ∨ ए = 1 और ए^⊥ ∧ ए = 0। इन्वोल्यूशन लॉ: ए^⊥⊥ = ए। ऑर्डर-रिवर्सिंग: अगर ए ≤ बी तो बी^⊥ ≤ ए^{⊥</सुप>। एक ऑर्थोकम्प्लिमेंटेड लैटिस या ऑर्थोलैटिस एक बाउंडेड लैटिस है जो ऑर्थोकोम्प्लिमेंटेशन से लैस है। एक आंतरिक उत्पाद स्थान के उप-स्थानों की जाली, और ऑर्थोगोनल पूरक ऑपरेशन, ऑर्थोकोम्प्लीमेंटेड जाली का एक उदाहरण प्रदान करता है जो सामान्य रूप से वितरण नहीं है।}

• Some complemented lattices
• 

  पेंटागन जाली में N₅, दाईं ओर के नोड में दो पूरक हैं।

• हीरा जाली एम₃ कोई orthocomplementation स्वीकार नहीं करता है।

• जाली एम₄ 3 orthocomplementations को स्वीकार करता है।

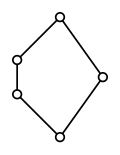
• Hexagon lattice.svg

  हेक्सागोन जाली एक अद्वितीय ऑर्थोकोम्प्लीमेंटेशन स्वीकार करती है, लेकिन यह विशिष्ट रूप से पूरक नहीं है।

बूलियन बीजगणित (संरचना) orthocomplemented lattices का एक विशेष मामला है, जो बदले में पूरक lattices (अतिरिक्त संरचना के साथ) का एक विशेष मामला है। ऑर्थोलैटिस का उपयोग अक्सर क्वांटम तर्क में किया जाता है, जहां एक पृथक स्थान हिल्बर्ट अंतरिक्ष के बंद सेट रेखीय उप-स्थान क्वांटम प्रस्तावों का प्रतिनिधित्व करते हैं और एक ऑर्थोकोम्प्लीमेंटेड जाली के रूप में व्यवहार करते हैं।

ऑर्थोकम्प्लीमेंटेड लैटिस, जैसे बूलियन बीजगणित, मॉर्गन के नियमों को पूरा करते हैं:

• (ए ∨ बी)^⊥ = ए^⊥ ∧ बी^{⊥</सुप>}
• (ए ∧ बी)^⊥ = ए^⊥ ∨ ख^{⊥</सुप>।}

ऑर्थोमॉड्यूलर लैटिस

एक जाली को मॉड्यूलर जाली कहा जाता है यदि सभी तत्वों के लिए ए, बी और सी निहितार्थ हैं

अगर a ≤ c, तो a ∨ (b ∧ c) = (a ∨ b) ∧ c

रखती है। यह वितरणात्मक जाली से कमजोर है; उदा. ऊपर दिखाया गया जाली एम₃ मॉड्यूलर है, लेकिन वितरण नहीं है।

क्वांटम लॉजिक में अनुप्रयोगों के लिए आवश्यक ऑर्थोकोम्प्लीमेंटेड लैटिस के लिए इस स्थिति का एक और कमजोर होना, केवल विशेष मामले b = a में इसकी आवश्यकता है^{⊥</सुप>। एक ऑर्थोमॉड्यूलर जाली को एक ऑर्थोकोम्प्लीमेंटेड जाली के रूप में परिभाषित किया गया है जैसे कि किसी भी दो तत्वों के लिए निहितार्थ}

अगर ए ≤ सी, तो ए ∨ (ए^⊥ ∧ सी) = सी

रखती है।

क्वांटम लॉजिक के अध्ययन के लिए इस रूप के लैटिस महत्वपूर्ण हैं, क्योंकि वे क्वांटम यांत्रिकी के क्वांटम यांत्रिकी के हिल्बर्ट अंतरिक्ष गणितीय सूत्रीकरण के स्वयंसिद्ध का हिस्सा हैं। गैरेट बिरखॉफ और जॉन वॉन न्यूमैन ने देखा कि क्वांटम तर्क में प्रस्तावन तर्क तार्किक कलन औपचारिक रूप से चौराहे, रैखिक_सबस्पेस # सम्स और ऑर्थोगोनल पूरक के संबंध में रैखिक उप-स्थानों [एक हिल्बर्ट अंतरिक्ष के] की गणना से अप्रभेद्य है और, या की भूमिकाओं के अनुरूप है। और बूलियन लैटिस में नहीं। इस टिप्पणी ने हिल्बर्ट अंतरिक्ष के बंद उप-स्थानों में रुचि पैदा की है, जो एक ऑर्थोमॉड्यूलर जाली बनाते हैं।

यह भी देखें

• छद्म पूरक जाली

संदर्भ

• Birkhoff, Garrett (1961). Lattice Theory. American Mathematical Society.
• Grätzer, George (1971). Lattice Theory: First Concepts and Distributive Lattices. W. H. Freeman and Company. ISBN 978-0-7167-0442-3.
• Grätzer, George (1978). General Lattice Theory. Basel, Switzerland: Birkhäuser. ISBN 978-0-12-295750-5.
• Rutherford, Daniel Edwin (1965). Introduction to Lattice Theory. Oliver and Boyd.

बाहरी संबंध

• "Complemented lattice". PlanetMath.
• "Relative complement". PlanetMath.
• "Uniquely complemented lattice". PlanetMath.
• "Orthocomplemented lattice". PlanetMath.