संबंधों की श्रेणी: Difference between revisions
m (5 revisions imported from alpha:संबंधों_की_श्रेणी) |
No edit summary |
||
| Line 59: | Line 59: | ||
* {{cite book |first=Francis |last=Borceux |series=Handbook of Categorical Algebra |volume=2 |title=Categories and Structures|url=https://books.google.com/books?id=5i2v9q0m5XAC&pg=PA115|year=1994|publisher=[[Cambridge University Press]]|isbn=978-0-521-44179-7|page=115}} | * {{cite book |first=Francis |last=Borceux |series=Handbook of Categorical Algebra |volume=2 |title=Categories and Structures|url=https://books.google.com/books?id=5i2v9q0m5XAC&pg=PA115|year=1994|publisher=[[Cambridge University Press]]|isbn=978-0-521-44179-7|page=115}} | ||
{{refend}} | {{refend}} | ||
[[Category:Created On 01/05/2023]] | [[Category:Created On 01/05/2023]] | ||
[[Category:Vigyan Ready]] | [[Category:Machine Translated Page]] | ||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:द्विआधारी संबंध]] | |||
[[Category:मोनोइडल श्रेणियां]] | |||
Latest revision as of 12:06, 18 May 2023
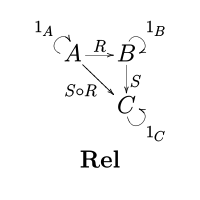
गणित में, श्रेणी (गणित) Rel (रिले) में ऑब्जेक्ट (श्रेणी सिद्धांत) के रूप में समुच्चय (गणित) का वर्ग और आकृतिवाद (श्रेणी सिद्धांत) के रूप में द्विआधारी संबंध हैं।
एक आकारिकी (या एरो) R : A → B इस श्रेणी में समुच्चय A और B के बीच एक संबंध है, इसलिए R ⊆ A × B.
संबंधों की संरचना आर: A → B और S: B → C द्वारा दी गई है
- (a, c) ∈ S o R ⇔ किसी b ∈ B, (a, b) ∈ R और (b, c) ∈ S के लिए।[1]
Rel को समुच्चयों के पत्राचार की श्रेणी भी कहा गया है।[2]
गुण
श्रेणी Rel में समुच्चय की श्रेणी होती है जिसे एक (विस्तृत) उपश्रेणी के रूप में समुच्चय किया जाता है, जहाँ एरो f : X → Y समुच्चय में संबंध से मेल खाता है F ⊆ X × Y द्वारा परिभाषित (x, y) ∈ F ⇔ f(x) = y.[note 1][3]
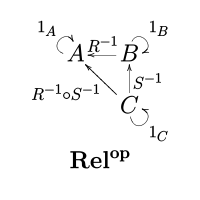
Rel में एक रूपवाद एक संबंध है, और Rel के विपरीत श्रेणी में संबंधित आकारिकी में एरो उलटे हैं, इसलिए यह विलोम संबंध है। इस प्रकार Rel में इसका विपरीत है और यह द्वैत (श्रेणी सिद्धांत) है | स्व-द्वैत है।[4]
उलटा संबंध लेकर प्रतिनिधित्व किया गया समावेशन (गणित) Rel को डैगर श्रेणी बनाने के लिए डैगर प्रदान करता है।
मैं काम कर रहा हूं द्वारा दी गई श्रेणी में दो ऑपरेटर हैं: एक बाइनरी रिलेशन R ⊆ A × B और इसका ट्रांसपोज़ RT ⊆ B × A की रचना या तो R RT के रूप में की जा सकती है या R के रूप में RT R. पहली रचना A पर बाइनरी_रिलेशन # परिभाषा में परिणत होती है और दूसरी B पर होती है। चूंकि इन होम फंक्शनलर्स की छवियां 'Rel' में ही हैं, इस मामले में होम एक आंतरिक होम फंक्शनल है। अपने आंतरिक होम फ़ंक्शन के साथ, 'Rel' एक बंद श्रेणी है, और इसके अलावा एक डैगर कॉम्पैक्ट श्रेणी भी है।
श्रेणी 'Rel' श्रेणी 'समुच्चय' से प्राप्त की जा सकती है, जो मोनाड (श्रेणी सिद्धांत) के लिए क्लेस्ली श्रेणी के रूप में प्राप्त की जा सकती है, जिसका फ़ैक्टर सत्ता स्थापित से मेल खाता है, जिसे सहसंयोजक फ़ंक्टर के रूप में व्याख्या किया गया है।
शायद पहली नजर में थोड़ा आश्चर्य की बात यह है कि उत्पाद (श्रेणी सिद्धांत) 'Rel' में असम्बद्ध संघ द्वारा दिया गया है[4]: 181 (कार्तीय उत्पाद के बजाय जैसा कि यह समुच्चय में है), और इसलिए प्रतिउत्पाद है।
Rel बंद मोनोइडल (monoidal) श्रेणी है, दोनों मोनोइडल उत्पाद A ⊗ B और समुच्चय के कार्टेशियन उत्पाद द्वारा दिए गए आंतरिक होम A ⇒ B दोनों के साथ।
Rel श्रेणी 1990 में पीटर जे. फ्रीड और आंद्रे स्केड्रोव द्वारा एक रूपक (श्रेणी सिद्धांत) नामक बीजगणितीय संरचना के लिए प्रोटोटाइप थी।[5] एक नियमित श्रेणी और एक फ़ैक्टर F: A → B से प्रारम्भ होने पर, वे प्रेरित फ़ैक्टर Rel (A, B) → Rel (FA, FB) के गुणों को नोट करते हैं। उदाहरण के लिए, यह रचना, रूपांतरण और प्रतिच्छेदन को संरक्षित करता है। इस तरह के गुण एक रूपक के लिए अभिगृहीत प्रदान करने के लिए उपयोग किए जाते हैं।
वस्तुओं के रूप में संबंध
डेविड राइडहेर्ड और रॉड बर्स्टाल ने Rel को उन वस्तुओं के रूप में माना है जो सजातीय संबंध हैं। उदाहरण के लिए, A एक समुच्चय है और R⊆ A × A A पर एक द्विआधारी संबंध है। इस श्रेणी के morphisms समुच्चय के बीच कार्य हैं जो एक संबंध को संरक्षित करते हैं: S ⊆ B × B एक दूसरा संबंध है और f: A → ' 'B' एक ऐसा कार्य है जो तो f एक आकारिकी है।[6]
यही विचार एडमेक, हेरलिच और स्ट्रेकर द्वारा आगे बढ़ाया गया है, जहां वे वस्तुओं (A, R) और (B, S), समुच्चय और संबंध को निर्दिष्ट करते हैं।[7]
टिप्पणियाँ
- ↑ This category is called SetRel by Rydeheard and Burstall.
संदर्भ
- ↑ Mac Lane, S. (1988). कामकाजी गणितज्ञ के लिए श्रेणियाँ (1st ed.). Springer. p. 26. ISBN 0-387-90035-7.
- ↑ Pareigis, Bodo (1970). श्रेणियां और कारक. Pure and Applied Mathematics. Vol. 39. Academic Press. p. 6. ISBN 978-0-12-545150-5.
- ↑ Bergman, George (1998). "§7.2 RelSet". सामान्य बीजगणित और सार्वभौमिक निर्माण के लिए एक आमंत्रण. Henry Helson. ISBN 0-9655211-4-1.
- ↑ 4.0 4.1 Barr, Michael; Wells, Charles (1990). कम्प्यूटिंग विज्ञान के लिए श्रेणी सिद्धांत (PDF). Prentice Hall. p. 181. ISBN 978-0131204867.
- ↑ Freyd, Peter J.; Scedrov, Andre (1990). श्रेणियाँ, रूपक. North Holland. pp. 79, 196. ISBN 0-444-70368-3.
- ↑ Rydeheard, David; Burstall, Rod (1988). कम्प्यूटेशनल श्रेणी सिद्धांत. Prentice-Hall. p. 41. ISBN 978-0131627369.
- ↑ Adamek, Juri; Herrlich, Horst; Strecker, George E. (2004) [1990]. "§3.3, example 2(d)". सार और ठोस श्रेणियाँ (PDF). KatMAT Research group, University of Bremen. p. 22.
- Borceux, Francis (1994). Categories and Structures. Handbook of Categorical Algebra. Vol. 2. Cambridge University Press. p. 115. ISBN 978-0-521-44179-7.