फ्लक्स सीमक: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
[[फ्लक्स]] लिमिटर्स का उपयोग उच्च रिज़ॉल्यूशन योजनाओं में किया जाता है - [[आंशिक अंतर समीकरण]] (पीडीई) द्वारा वर्णित विज्ञान और इंजीनियरिंग, विशेष रूप से द्रव गतिशीलता में समस्याओं को हल करने के लिए उपयोग की जाने वाली संख्यात्मक योजनाएं। इनका उपयोग उच्च रिज़ॉल्यूशन योजनाओं में किया जाता है, जैसे कि [[MUSCL योजना]], नकली दोलनों (विगल्स) से बचने के लिए जो अन्यथा समाधान डोमेन में झटके, असंतोष या तेज बदलाव के कारण उच्च क्रम स्थानिक विवेकीकरण योजनाओं के साथ घटित होंगे। फ्लक्स लिमिटर्स का उपयोग, उपयुक्त उच्च रिज़ॉल्यूशन योजना के साथ, समाधान को कुल भिन्नता कम करने वाला (टीवीडी) बनाता है। | |||
[[फ्लक्स]] लिमिटर्स का उपयोग उच्च रिज़ॉल्यूशन योजनाओं में किया जाता है - [[आंशिक अंतर समीकरण]] | |||
ध्यान दें कि फ्लक्स लिमिटर्स को ढलान लिमिटर्स के रूप में भी जाना जाता है क्योंकि उन दोनों का गणितीय रूप समान है, और दोनों में झटके या असंतोष के पास समाधान ढाल को सीमित करने का प्रभाव होता है। सामान्य तौर पर, फ्लक्स लिमिटर शब्द का उपयोग तब किया जाता है जब लिमिटर सिस्टम ''फ्लक्स'' पर कार्य करता है, और ढलान लिमिटर का उपयोग तब किया जाता है जब लिमिटर सिस्टम ''स्टेट्स'' (जैसे दबाव, वेग आदि) पर कार्य करता है। | ध्यान दें कि फ्लक्स लिमिटर्स को ढलान लिमिटर्स के रूप में भी जाना जाता है क्योंकि उन दोनों का गणितीय रूप समान है, और दोनों में झटके या असंतोष के पास समाधान ढाल को सीमित करने का प्रभाव होता है। सामान्य तौर पर, फ्लक्स लिमिटर शब्द का उपयोग तब किया जाता है जब लिमिटर सिस्टम ''फ्लक्स'' पर कार्य करता है, और ढलान लिमिटर का उपयोग तब किया जाता है जब लिमिटर सिस्टम ''स्टेट्स'' (जैसे दबाव, वेग आदि) पर कार्य करता है। | ||
| Line 9: | Line 8: | ||
:<math>\frac{d u_i}{d t} + \frac{1}{\Delta x_i} \left[ | :<math>\frac{d u_i}{d t} + \frac{1}{\Delta x_i} \left[ | ||
F \left( u_{i + {1}/{2}} \right) - F \left( u_{i - {1}/{2}} \right) \right] = 0, </math> | F \left( u_{i + {1}/{2}} \right) - F \left( u_{i - {1}/{2}} \right) \right] = 0, </math> | ||
कहाँ, <math> F \left( u_{i + {1}/{2}} \right) </math> और <math> F \left( u_{i - 1/2} \right) </math> आई-वें सेल के लिए एज फ्लक्स का प्रतिनिधित्व करें। यदि इन किनारे के फ्लक्स को निम्न और उच्च रिज़ॉल्यूशन योजनाओं द्वारा दर्शाया जा सकता है, तो | कहाँ, <math> F \left( u_{i + {1}/{2}} \right) </math> और <math> F \left( u_{i - 1/2} \right) </math> आई-वें सेल के लिए एज फ्लक्स का प्रतिनिधित्व करें। यदि इन किनारे के फ्लक्स को निम्न और उच्च रिज़ॉल्यूशन योजनाओं द्वारा दर्शाया जा सकता है, तो फ्लक्स लिमिटर विशेष सेल के करीब ग्रेडिएंट के आधार पर इन योजनाओं के बीच स्विच कर सकता है, निम्नानुसार: | ||
<math display="block">F \left( u_{i + 1/2} \right) = f^\text{low}_{i + 1/2} - \phi\left( r_i \right) \left( f^\text{low}_{i + 1/2} - f^\text{high}_{i + 1/2} \right) ,</math> | <math display="block">F \left( u_{i + 1/2} \right) = f^\text{low}_{i + 1/2} - \phi\left( r_i \right) \left( f^\text{low}_{i + 1/2} - f^\text{high}_{i + 1/2} \right) ,</math><math display="block">F \left( u_{i - 1/2} \right) = f^\text{low}_{i - 1/2} - \phi\left( r_{i-1} \right) \left( f^\text{low}_{i - 1/2} - f^\text{high}_{i - 1/2} \right) ,</math> | ||
<math display="block">F \left( u_{i - 1/2} \right) = f^\text{low}_{i - 1/2} - \phi\left( r_{i-1} \right) \left( f^\text{low}_{i - 1/2} - f^\text{high}_{i - 1/2} \right) ,</math> | |||
कहाँ | कहाँ | ||
*<math>f^\text{low} </math> निम्न विभेदन प्रवाह है, | *<math>f^\text{low} </math> निम्न विभेदन प्रवाह है, | ||
| Line 18: | Line 16: | ||
*<math>\phi\ (r) </math> फ्लक्स सीमक फ़ंक्शन है, और | *<math>\phi\ (r) </math> फ्लक्स सीमक फ़ंक्शन है, और | ||
*<math> r </math> समाधान जाल पर क्रमिक ग्रेडिएंट के अनुपात का प्रतिनिधित्व करता है, अर्थात, <math display="block"> r_{i} = \frac{u_{i} - u_{i-1}}{u_{i+1} - u_{i}} .</math> | *<math> r </math> समाधान जाल पर क्रमिक ग्रेडिएंट के अनुपात का प्रतिनिधित्व करता है, अर्थात, <math display="block"> r_{i} = \frac{u_{i} - u_{i-1}}{u_{i+1} - u_{i}} .</math> | ||
सीमक फ़ंक्शन शून्य से अधिक या उसके बराबर होने के लिए बाध्य है, अर्थात, <math>\phi\ (r) \ge 0 </math>. इसलिए, जब सीमक शून्य (तीव्र ढाल, विपरीत ढलान या शून्य ढाल) के बराबर होता है, तो फ्लक्स को कम रिज़ॉल्यूशन योजना द्वारा दर्शाया जाता है। इसी प्रकार, जब लिमिटर 1 (सुचारू समाधान) के बराबर होता है, तो इसे उच्च रिज़ॉल्यूशन योजना द्वारा दर्शाया जाता है। विभिन्न सीमाओं में अलग-अलग स्विचिंग विशेषताएँ होती हैं और उन्हें विशेष समस्या और समाधान योजना के अनुसार चुना जाता है। सभी समस्याओं के लिए अच्छा काम करने वाला कोई विशेष अवरोधक नहीं पाया गया है, और | सीमक फ़ंक्शन शून्य से अधिक या उसके बराबर होने के लिए बाध्य है, अर्थात, <math>\phi\ (r) \ge 0 </math>. इसलिए, जब सीमक शून्य (तीव्र ढाल, विपरीत ढलान या शून्य ढाल) के बराबर होता है, तो फ्लक्स को कम रिज़ॉल्यूशन योजना द्वारा दर्शाया जाता है। इसी प्रकार, जब लिमिटर 1 (सुचारू समाधान) के बराबर होता है, तो इसे उच्च रिज़ॉल्यूशन योजना द्वारा दर्शाया जाता है। विभिन्न सीमाओं में अलग-अलग स्विचिंग विशेषताएँ होती हैं और उन्हें विशेष समस्या और समाधान योजना के अनुसार चुना जाता है। सभी समस्याओं के लिए अच्छा काम करने वाला कोई विशेष अवरोधक नहीं पाया गया है, और विशेष विकल्प आमतौर पर परीक्षण और त्रुटि के आधार पर बनाया जाता है। | ||
== सीमक कार्य == | == सीमक कार्य == | ||
| Line 32: | Line 30: | ||
* एचसीयूएस [दूसरा क्रम टीवीडी नहीं] <ref name="WatersonDeconinck">{{citation |last1=Waterson |first1=N.P. |first2=H. |last2=Deconinck |year=1995 |title=A unified approach to the design and application of bounded higher-order convection schemes |type=[[Von Karman Institute|VKI]] Preprint 1995-21 }}</ref> <math display="block"> \phi_{hc}(r) = \frac{ 1.5 \left(r+\left| r \right| \right)}{ \left(r+2 \right)} ; \quad \lim_{r \to \infty}\phi_{hc}(r) = 3.</math> | * एचसीयूएस [दूसरा क्रम टीवीडी नहीं] <ref name="WatersonDeconinck">{{citation |last1=Waterson |first1=N.P. |first2=H. |last2=Deconinck |year=1995 |title=A unified approach to the design and application of bounded higher-order convection schemes |type=[[Von Karman Institute|VKI]] Preprint 1995-21 }}</ref> <math display="block"> \phi_{hc}(r) = \frac{ 1.5 \left(r+\left| r \right| \right)}{ \left(r+2 \right)} ; \quad \lim_{r \to \infty}\phi_{hc}(r) = 3.</math> | ||
* त्वरित [दूसरे क्रम के टीवीडी नोट्स] <ref name="WatersonDeconinck"/> <math display="block"> \phi_{hq}(r) = \frac{2 \left(r + \left|r \right| \right)}{ \left(r+3 \right)} ; \quad \lim_{r \to \infty}\phi_{hq}(r) = 4.</math> | * त्वरित [दूसरे क्रम के टीवीडी नोट्स] <ref name="WatersonDeconinck"/> <math display="block"> \phi_{hq}(r) = \frac{2 \left(r + \left|r \right| \right)}{ \left(r+3 \right)} ; \quad \lim_{r \to \infty}\phi_{hq}(r) = 4.</math> | ||
*कोरेन<ref>{{citation |last=Koren |first=B. |year=1993 |contribution=A robust upwind discretisation method for advection, diffusion and source terms |title=Numerical Methods for Advection–Diffusion Problems |editor1-first=C.B. |editor1-last=Vreugdenhil |editor2-first=B. |editor2-last=Koren |publisher=Vieweg |location=Braunschweig |page=117 |isbn=3-528-07645-3 }}</ref> - पर्याप्त रूप से सुचारू डेटा के लिए तीसरे क्रम का सटीक<ref>{{Citation | first=D. |last=Kuzmin |title=On the design of general-purpose flux limiters for implicit FEM with a consistent mass matrix. I. Scalar convection |journal=Journal of Computational Physics |volume=219 |issue=2 |year=2006 |pages=513–531 |doi=10.1016/j.jcp.2006.03.034 |bibcode = 2006JCoPh.219..513K }}</ref> | *कोरेन<ref>{{citation |last=Koren |first=B. |year=1993 |contribution=A robust upwind discretisation method for advection, diffusion and source terms |title=Numerical Methods for Advection–Diffusion Problems |editor1-first=C.B. |editor1-last=Vreugdenhil |editor2-first=B. |editor2-last=Koren |publisher=Vieweg |location=Braunschweig |page=117 |isbn=3-528-07645-3 }}</ref> - पर्याप्त रूप से सुचारू डेटा के लिए तीसरे क्रम का सटीक<ref>{{Citation | first=D. |last=Kuzmin |title=On the design of general-purpose flux limiters for implicit FEM with a consistent mass matrix. I. Scalar convection |journal=Journal of Computational Physics |volume=219 |issue=2 |year=2006 |pages=513–531 |doi=10.1016/j.jcp.2006.03.034 |bibcode = 2006JCoPh.219..513K }}</ref> <math display="block"> \phi_{kn}(r) = \max \left[ 0, \min \left(2 r, \min \left( \dfrac{(1 + 2 r)}{3}, 2 \right) \right) \right]; \quad \lim_{r \to \infty}\phi_{kn}(r) = 2.</math> | ||
* मिनमोड - सममित <ref name="Roe">{{citation |last=Roe |first=P.L. | author1-link = Philip L. Roe | year=1986 |title=Characteristic-based schemes for the Euler equations |journal=Annu. Rev. Fluid Mech. |volume=18 |pages=337–365 | doi = 10.1146/annurev.fl.18.010186.002005 |bibcode = 1986AnRFM..18..337R }}</ref> <math display="block"> \phi_{mm} (r) = \max \left[ 0 , \min \left( 1 , r \right) \right] ; \quad \lim_{r \to \infty} \phi_{mm}(r) = 1.</math> | * मिनमोड - सममित <ref name="Roe">{{citation |last=Roe |first=P.L. | author1-link = Philip L. Roe | year=1986 |title=Characteristic-based schemes for the Euler equations |journal=Annu. Rev. Fluid Mech. |volume=18 |pages=337–365 | doi = 10.1146/annurev.fl.18.010186.002005 |bibcode = 1986AnRFM..18..337R }}</ref> <math display="block"> \phi_{mm} (r) = \max \left[ 0 , \min \left( 1 , r \right) \right] ; \quad \lim_{r \to \infty} \phi_{mm}(r) = 1.</math> | ||
* मोनोटोनाइज्ड सेंट्रल (एमसी) - सममित <ref>{{citation |last=van Leer |first=B. | author-link = Bram van Leer |year=1977 |title=Towards the ultimate conservative difference scheme III. Upstream-centered finite-difference schemes for ideal compressible flow |journal=J. Comput. Phys. |volume=23 |pages=263–275 |doi=10.1016/0021-9991(77)90094-8 |issue=3 |bibcode = 1977JCoPh..23..263V }}</ref> <math display="block"> \phi_{mc} (r) = \max \left[ 0 , \min \left( 2 r, 0.5 (1+r), 2 \right) \right] ; \quad \lim_{r \to \infty}\phi_{mc}(r) = 2.</math> | * मोनोटोनाइज्ड सेंट्रल (एमसी) - सममित <ref>{{citation |last=van Leer |first=B. | author-link = Bram van Leer |year=1977 |title=Towards the ultimate conservative difference scheme III. Upstream-centered finite-difference schemes for ideal compressible flow |journal=J. Comput. Phys. |volume=23 |pages=263–275 |doi=10.1016/0021-9991(77)90094-8 |issue=3 |bibcode = 1977JCoPh..23..263V }}</ref> <math display="block"> \phi_{mc} (r) = \max \left[ 0 , \min \left( 2 r, 0.5 (1+r), 2 \right) \right] ; \quad \lim_{r \to \infty}\phi_{mc}(r) = 2.</math> | ||
| Line 45: | Line 43: | ||
* लीयर से - सममित <ref>{{citation |last=van Leer |first=B. | author-link = Bram van Leer |year=1974 |title=Towards the ultimate conservative difference scheme II. Monotonicity and conservation combined in a second order scheme |journal=J. Comput. Phys. |volume=14 |pages=361–370 |doi=10.1016/0021-9991(74)90019-9 |issue=4 |bibcode = 1974JCoPh..14..361V }}</ref> <math display="block"> \phi_{vl} (r) = \frac{r + \left| r \right| }{1 + \left| r \right| } ; \quad \lim_{r \to \infty}\phi_{vl} (r) = 2.</math> | * लीयर से - सममित <ref>{{citation |last=van Leer |first=B. | author-link = Bram van Leer |year=1974 |title=Towards the ultimate conservative difference scheme II. Monotonicity and conservation combined in a second order scheme |journal=J. Comput. Phys. |volume=14 |pages=361–370 |doi=10.1016/0021-9991(74)90019-9 |issue=4 |bibcode = 1974JCoPh..14..361V }}</ref> <math display="block"> \phi_{vl} (r) = \frac{r + \left| r \right| }{1 + \left| r \right| } ; \quad \lim_{r \to \infty}\phi_{vl} (r) = 2.</math> | ||
* उपरोक्त सभी सीमाएं सममित होने के रूप में इंगित की गई हैं, निम्नलिखित समरूपता गुण प्रदर्शित करती हैं, <math display="block">\frac{ \phi \left( r \right)}{r} = \phi \left( \frac{1}{r} \right) .</math> | * उपरोक्त सभी सीमाएं सममित होने के रूप में इंगित की गई हैं, निम्नलिखित समरूपता गुण प्रदर्शित करती हैं, <math display="block">\frac{ \phi \left( r \right)}{r} = \phi \left( \frac{1}{r} \right) .</math> | ||
यह | यह वांछनीय गुण है क्योंकि यह सुनिश्चित करता है कि आगे और पीछे के ग्रेडिएंट के लिए सीमित क्रियाएं समान तरीके से संचालित होती हैं। | ||
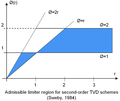
[[File:LimiterRegion.png|thumb|102x102px|right|दूसरे क्रम की टीवीडी योजनाओं के लिए स्वीकार्य सीमक क्षेत्र।]]जब तक इसके विपरीत संकेत न दिया जाए, उपरोक्त सीमक कार्य दूसरे क्रम की कुल भिन्नता को कम करने वाले हैं। इसका मतलब यह है कि उन्हें इस तरह से डिज़ाइन किया गया है कि वे योजना की स्थिरता की गारंटी के लिए समाधान के | [[File:LimiterRegion.png|thumb|102x102px|right|दूसरे क्रम की टीवीडी योजनाओं के लिए स्वीकार्य सीमक क्षेत्र।]]जब तक इसके विपरीत संकेत न दिया जाए, उपरोक्त सीमक कार्य दूसरे क्रम की कुल भिन्नता को कम करने वाले हैं। इसका मतलब यह है कि उन्हें इस तरह से डिज़ाइन किया गया है कि वे योजना की स्थिरता की गारंटी के लिए समाधान के निश्चित क्षेत्र से गुजरते हैं, जिसे टीवीडी क्षेत्र के रूप में जाना जाता है। दूसरे क्रम के, टीवीडी लिमिटर्स कम से कम निम्नलिखित मानदंडों को पूरा करते हैं: | ||
*<math> r \le \phi(r) \le 2r, \left( 0 \le r \le 1 \right) \ </math>, | *<math> r \le \phi(r) \le 2r, \left( 0 \le r \le 1 \right) \ </math>, | ||
| Line 54: | Line 52: | ||
*<math> \phi(1) = 1 \ </math>, | *<math> \phi(1) = 1 \ </math>, | ||
दूसरे क्रम की टीवीडी योजनाओं के लिए स्वीकार्य सीमक क्षेत्र स्वेबी आरेख में विपरीत दिखाया गया है,<ref name="Sweby"/>और टीवीडी क्षेत्र पर लिमिटर फ़ंक्शंस को दिखाने वाले प्लॉट नीचे दिखाए गए हैं। इस छवि में, ओशर और स्वेबी लिमिटर्स का उपयोग करके प्लॉट तैयार किए गए हैं <math> \beta = 1.5 </math>. | दूसरे क्रम की टीवीडी योजनाओं के लिए स्वीकार्य सीमक क्षेत्र स्वेबी आरेख में विपरीत दिखाया गया है,<ref name="Sweby"/> और टीवीडी क्षेत्र पर लिमिटर फ़ंक्शंस को दिखाने वाले प्लॉट नीचे दिखाए गए हैं। इस छवि में, ओशर और स्वेबी लिमिटर्स का उपयोग करके प्लॉट तैयार किए गए हैं <math> \beta = 1.5 </math>. | ||
[[File:LimiterPlots1.png|center|266x266px|thumb|{{center|Limiter functions overlaid onto second-order TVD region.}}]] | [[File:LimiterPlots1.png|center|266x266px|thumb|{{center|Limiter functions overlaid onto second-order TVD region.}}]] | ||
| Line 60: | Line 58: | ||
=== सामान्यीकृत मिनमॉड सीमक === | === सामान्यीकृत मिनमॉड सीमक === | ||
एक अतिरिक्त लिमिटर जिसका | एक अतिरिक्त लिमिटर जिसका दिलचस्प रूप है, वैन-लीयर का मिनमॉड लिमिटर्स का एक-पैरामीटर परिवार है।<ref>{{citation |last=Van Leer |first=B. | author-link = Bram van Leer |year=1979 |title=Towards the ultimate conservative difference scheme V. A second order sequel to Godunov's method |journal=J. Comput. Phys. |volume=32 |issue=1 |pages=101–136 |doi=10.1016/0021-9991(79)90145-1 |bibcode = 1979JCoPh..32..101V }}</ref><ref>{{citation |last1=Harten |first1=A. |first2=S. |last2=Osher |year=1987 |title=Uniformly high-order accurate nonoscillatory schemes. I |journal=SIAM J. Numer. Anal. |volume=24 |pages=279–309 |doi=10.1137/0724022 |issue=2 |bibcode = 1987SJNA...24..279H |s2cid=15957238 |url=http://www.dtic.mil/get-tr-doc/pdf?AD=ADA158177 |archive-url=https://web.archive.org/web/20170923124820/http://www.dtic.mil/get-tr-doc/pdf?AD=ADA158177 |url-status=dead |archive-date=September 23, 2017 }}</ref><ref>{{citation |last1=Kurganov |first1=A. |first2=E. |last2=Tadmor|author2-link=Eitan Tadmor |year=2000 |title=Solution of Two-Dimensional Riemann problems for Gas Dynamics without Riemann Problem Solvers |publisher=Report by Dept. of Mathematics, Univ. Michigan }}. Available on-line at: [http://citeseer.ist.psu.edu/410715.html CiteSeer].</ref> इसे इस प्रकार परिभाषित किया गया है | ||
<math display="block"> \phi_{mg}(u,\theta) = \max\left(0,\min\left(\theta r,\frac{1+r}{2},\theta\right)\right),\quad\theta\in\left[1,2\right]. </math> | <math display="block"> \phi_{mg}(u,\theta) = \max\left(0,\min\left(\theta r,\frac{1+r}{2},\theta\right)\right),\quad\theta\in\left[1,2\right]. </math> | ||
टिप्पणी: <math> \phi_{mg} </math> के लिए सर्वाधिक अपव्ययकारी है <math> \theta=1, </math> जब यह कम हो जाता है <math> \phi_{mm}, </math> और यह सबसे कम अपव्ययकारी है <math> \theta = 2 </math>. | टिप्पणी: <math> \phi_{mg} </math> के लिए सर्वाधिक अपव्ययकारी है <math> \theta=1, </math> जब यह कम हो जाता है <math> \phi_{mm}, </math> और यह सबसे कम अपव्ययकारी है <math> \theta = 2 </math>. | ||
Revision as of 09:05, 12 August 2023
फ्लक्स लिमिटर्स का उपयोग उच्च रिज़ॉल्यूशन योजनाओं में किया जाता है - आंशिक अंतर समीकरण (पीडीई) द्वारा वर्णित विज्ञान और इंजीनियरिंग, विशेष रूप से द्रव गतिशीलता में समस्याओं को हल करने के लिए उपयोग की जाने वाली संख्यात्मक योजनाएं। इनका उपयोग उच्च रिज़ॉल्यूशन योजनाओं में किया जाता है, जैसे कि MUSCL योजना, नकली दोलनों (विगल्स) से बचने के लिए जो अन्यथा समाधान डोमेन में झटके, असंतोष या तेज बदलाव के कारण उच्च क्रम स्थानिक विवेकीकरण योजनाओं के साथ घटित होंगे। फ्लक्स लिमिटर्स का उपयोग, उपयुक्त उच्च रिज़ॉल्यूशन योजना के साथ, समाधान को कुल भिन्नता कम करने वाला (टीवीडी) बनाता है।
ध्यान दें कि फ्लक्स लिमिटर्स को ढलान लिमिटर्स के रूप में भी जाना जाता है क्योंकि उन दोनों का गणितीय रूप समान है, और दोनों में झटके या असंतोष के पास समाधान ढाल को सीमित करने का प्रभाव होता है। सामान्य तौर पर, फ्लक्स लिमिटर शब्द का उपयोग तब किया जाता है जब लिमिटर सिस्टम फ्लक्स पर कार्य करता है, और ढलान लिमिटर का उपयोग तब किया जाता है जब लिमिटर सिस्टम स्टेट्स (जैसे दबाव, वेग आदि) पर कार्य करता है।
वे कैसे काम करते हैं
फ्लक्स लिमिटर योजनाओं के निर्माण के पीछे मुख्य विचार स्थानिक व्युत्पन्नों को यथार्थवादी मूल्यों तक सीमित करना है - वैज्ञानिक और इंजीनियरिंग समस्याओं के लिए इसका मतलब आमतौर पर भौतिक रूप से प्राप्य और सार्थक मूल्य हैं। इनका उपयोग पीडीई द्वारा वर्णित समस्याओं को हल करने के लिए उच्च रिज़ॉल्यूशन योजनाओं में किया जाता है और केवल तभी परिचालन में आते हैं जब तेज तरंग मोर्चे मौजूद होते हैं। सुचारू रूप से बदलती तरंगों के लिए, फ्लक्स लिमिटर्स संचालित नहीं होते हैं और स्थानिक व्युत्पन्नों को नकली दोलनों को प्रस्तुत किए बिना उच्च क्रम सन्निकटन द्वारा दर्शाया जा सकता है। नीचे दी गई 1डी अर्ध-असतत योजना पर विचार करें,
कहाँ, और आई-वें सेल के लिए एज फ्लक्स का प्रतिनिधित्व करें। यदि इन किनारे के फ्लक्स को निम्न और उच्च रिज़ॉल्यूशन योजनाओं द्वारा दर्शाया जा सकता है, तो फ्लक्स लिमिटर विशेष सेल के करीब ग्रेडिएंट के आधार पर इन योजनाओं के बीच स्विच कर सकता है, निम्नानुसार:
- निम्न विभेदन प्रवाह है,
- उच्च विभेदन प्रवाह है,
- फ्लक्स सीमक फ़ंक्शन है, और
- समाधान जाल पर क्रमिक ग्रेडिएंट के अनुपात का प्रतिनिधित्व करता है, अर्थात,
सीमक फ़ंक्शन शून्य से अधिक या उसके बराबर होने के लिए बाध्य है, अर्थात, . इसलिए, जब सीमक शून्य (तीव्र ढाल, विपरीत ढलान या शून्य ढाल) के बराबर होता है, तो फ्लक्स को कम रिज़ॉल्यूशन योजना द्वारा दर्शाया जाता है। इसी प्रकार, जब लिमिटर 1 (सुचारू समाधान) के बराबर होता है, तो इसे उच्च रिज़ॉल्यूशन योजना द्वारा दर्शाया जाता है। विभिन्न सीमाओं में अलग-अलग स्विचिंग विशेषताएँ होती हैं और उन्हें विशेष समस्या और समाधान योजना के अनुसार चुना जाता है। सभी समस्याओं के लिए अच्छा काम करने वाला कोई विशेष अवरोधक नहीं पाया गया है, और विशेष विकल्प आमतौर पर परीक्षण और त्रुटि के आधार पर बनाया जाता है।
सीमक कार्य
फ़्लक्स/ढलान सीमक फ़ंक्शन के सामान्य रूप निम्नलिखित हैं, :
- आकर्षण [दूसरे क्रम का टीवीडी नहीं] [1]
- एचसीयूएस [दूसरा क्रम टीवीडी नहीं] [2]
- त्वरित [दूसरे क्रम के टीवीडी नोट्स] [2]
- कोरेन[3] - पर्याप्त रूप से सुचारू डेटा के लिए तीसरे क्रम का सटीक[4]
- मिनमोड - सममित [5]
- मोनोटोनाइज्ड सेंट्रल (एमसी) - सममित [6]
- ओशर [7]
- ओस्प्रे - सममित [2]
- स्मार्ट [दूसरे क्रम का टीवीडी नहीं] [8]
- सुपरबी - सममित [5]
- स्वेबी - सममित [9]
- UMIST - सममित [10]
- वैन अल्बाडा 1 - सममित [11]
- वैन अल्बाडा 2 - वैकल्पिक रूप [2रे क्रम का टीवीडी नहीं] उच्च स्थानिक क्रम योजनाओं पर उपयोग किया जाता है [12]
- लीयर से - सममित [13]
- उपरोक्त सभी सीमाएं सममित होने के रूप में इंगित की गई हैं, निम्नलिखित समरूपता गुण प्रदर्शित करती हैं,
यह वांछनीय गुण है क्योंकि यह सुनिश्चित करता है कि आगे और पीछे के ग्रेडिएंट के लिए सीमित क्रियाएं समान तरीके से संचालित होती हैं।
जब तक इसके विपरीत संकेत न दिया जाए, उपरोक्त सीमक कार्य दूसरे क्रम की कुल भिन्नता को कम करने वाले हैं। इसका मतलब यह है कि उन्हें इस तरह से डिज़ाइन किया गया है कि वे योजना की स्थिरता की गारंटी के लिए समाधान के निश्चित क्षेत्र से गुजरते हैं, जिसे टीवीडी क्षेत्र के रूप में जाना जाता है। दूसरे क्रम के, टीवीडी लिमिटर्स कम से कम निम्नलिखित मानदंडों को पूरा करते हैं:
- ,
- ,
- ,
- ,
दूसरे क्रम की टीवीडी योजनाओं के लिए स्वीकार्य सीमक क्षेत्र स्वेबी आरेख में विपरीत दिखाया गया है,[9] और टीवीडी क्षेत्र पर लिमिटर फ़ंक्शंस को दिखाने वाले प्लॉट नीचे दिखाए गए हैं। इस छवि में, ओशर और स्वेबी लिमिटर्स का उपयोग करके प्लॉट तैयार किए गए हैं .
सामान्यीकृत मिनमॉड सीमक
एक अतिरिक्त लिमिटर जिसका दिलचस्प रूप है, वैन-लीयर का मिनमॉड लिमिटर्स का एक-पैरामीटर परिवार है।[14][15][16] इसे इस प्रकार परिभाषित किया गया है
यह भी देखें
- गोडुनोव का प्रमेय
- उच्च संकल्प योजना
- MUSCL योजना
- सर्गेई के. गोडुनोव
- कुल भिन्नता कम हो रही है
टिप्पणियाँ
- ↑ Zhou, G. (1995), Numerical simulations of physical discontinuities in single and multi-fluid flows for arbitrary Mach numbers (PhD Thesis), Goteborg, Sweden: Chalmers Univ. of Tech.
- ↑ 2.0 2.1 2.2 Waterson, N.P.; Deconinck, H. (1995), A unified approach to the design and application of bounded higher-order convection schemes (VKI Preprint 1995-21)
- ↑ Koren, B. (1993), "A robust upwind discretisation method for advection, diffusion and source terms", in Vreugdenhil, C.B.; Koren, B. (eds.), Numerical Methods for Advection–Diffusion Problems, Braunschweig: Vieweg, p. 117, ISBN 3-528-07645-3
- ↑ Kuzmin, D. (2006), "On the design of general-purpose flux limiters for implicit FEM with a consistent mass matrix. I. Scalar convection", Journal of Computational Physics, 219 (2): 513–531, Bibcode:2006JCoPh.219..513K, doi:10.1016/j.jcp.2006.03.034
- ↑ 5.0 5.1 Roe, P.L. (1986), "Characteristic-based schemes for the Euler equations", Annu. Rev. Fluid Mech., 18: 337–365, Bibcode:1986AnRFM..18..337R, doi:10.1146/annurev.fl.18.010186.002005
- ↑ van Leer, B. (1977), "Towards the ultimate conservative difference scheme III. Upstream-centered finite-difference schemes for ideal compressible flow", J. Comput. Phys., 23 (3): 263–275, Bibcode:1977JCoPh..23..263V, doi:10.1016/0021-9991(77)90094-8
- ↑ Chakravarthy, S.R.; Osher, S. (1983), "High resolution applications of the Osher upwind scheme for the Euler equations", Proc. AIAA 6th Computational Fluid Dynamics Conference, pp. 363–373, AIAA Paper 83-1943, archived from the original on 2011-05-17, retrieved 2008-03-31
- ↑ Gaskell, P.H.; Lau, A.K.C. (1988), "Curvature-compensated convective transport: SMART, a new boundedness-preserving transport algorithm", Int. J. Num. Meth. Fluids, 8 (6): 617–641, Bibcode:1988IJNMF...8..617G, doi:10.1002/fld.1650080602
- ↑ 9.0 9.1 Sweby, P.K. (1984), "High resolution schemes using flux-limiters for hyperbolic conservation laws", SIAM J. Numer. Anal., 21 (5): 995–1011, Bibcode:1984SJNA...21..995S, doi:10.1137/0721062
- ↑ Lien, F.S.; Leschziner, M.A. (1994), "Upstream monotonic interpolation for scalar transport with application to complex turbulent flows", Int. J. Num. Meth. Fluids, 19 (6): 527–548, Bibcode:1994IJNMF..19..527L, doi:10.1002/fld.1650190606
- ↑ Van Albada, G.D.; Van Leer, B.; Roberts, W.W. (1982), "A comparative study of computational methods in cosmic gas dynamics", Astronomy and Astrophysics, 108 (1): 76–84, Bibcode:1982A&A...108...76V
- ↑ Kermani, M.J.; Gerber, A.G.; Stockie, J.M. (2003), "Thermodynamically Based Moisture Prediction Using Roe's Scheme", 4th Conference of Iranian AeroSpace Society, Amir Kabir University of Technology, Tehran, Iran, January 27–29
{{citation}}: CS1 maint: location (link) CS1 maint: location missing publisher (link) - ↑ van Leer, B. (1974), "Towards the ultimate conservative difference scheme II. Monotonicity and conservation combined in a second order scheme", J. Comput. Phys., 14 (4): 361–370, Bibcode:1974JCoPh..14..361V, doi:10.1016/0021-9991(74)90019-9
- ↑ Van Leer, B. (1979), "Towards the ultimate conservative difference scheme V. A second order sequel to Godunov's method", J. Comput. Phys., 32 (1): 101–136, Bibcode:1979JCoPh..32..101V, doi:10.1016/0021-9991(79)90145-1
- ↑ Harten, A.; Osher, S. (1987), "Uniformly high-order accurate nonoscillatory schemes. I", SIAM J. Numer. Anal., 24 (2): 279–309, Bibcode:1987SJNA...24..279H, doi:10.1137/0724022, S2CID 15957238, archived from the original on September 23, 2017
- ↑ Kurganov, A.; Tadmor, E. (2000), Solution of Two-Dimensional Riemann problems for Gas Dynamics without Riemann Problem Solvers, Report by Dept. of Mathematics, Univ. Michigan. Available on-line at: CiteSeer.
संदर्भ
- Hirsch, C. (1990), Numerical Computation of Internal and External Flows, Volume 2: Computational Methods for Inviscid and Viscous Flows, Wiley, ISBN 978-0-471-92452-4
- Leonard, B.P.; Leschziner, M.A.; McGuirk, J. (1978), "The QUICK algorithm: a uniformly 3rd-order finite-difference method for highly convective flows", Proc. 1st Conf. on Numerical Methods in Laminar & Turbulent Flow, Swansea, p. 807
{{citation}}: CS1 maint: location missing publisher (link)
अग्रिम पठन
- Laney, Culbert B. (1998), Computational Gasdynamics, Cambridge University Press, ISBN 978-0-521-57069-5
- LeVeque, Randall (1990), Numerical Methods for Conservation Laws, ETH Lectures in Mathematics Series, Birkhauser-Verlag, ISBN 3-7643-2464-3
- LeVeque, Randall (2002), Finite Volume Methods for Hyperbolic Problems, Cambridge University Press, ISBN 0-521-00924-3
- Toro, E.F. (1999), Riemann Solvers and Numerical Methods for Fluid Dynamics (2nd ed.), Springer-Verlag, ISBN 3-540-65966-8
- Tannehill, John C.; Anderson, Dale Arden; Pletcher, Richard H. (1997), Computational Fluid Mechanics and Heat Transfer (2nd ed.), Taylor and Francis, ISBN 1-56032-046-X
- Wesseling, Pieter (2001), Principles of Computational Fluid Dynamics, Springer-Verlag, ISBN 3-540-67853-0